Open Library - открытая библиотека учебной информации. Механические характеристики машин

Механическая характеристика рабочей машины

Автоматизированным электрическим приводом называется электромеханическая система состоящая из электродвигательного преобразующего передаточного управляющего устройств предназначенная для приведения в движения исполнительных органов рабочей машины и управления этим движением.

Структурная схема современного электрического привода

ЗУ – запоминающее устройство

П – преобразовательное устройство

У – усиительное устройство

СУ – система управления

ЭМП – электромеханический преобразователь

РД – ротор двигателя

ПУ – передающее устройство

РМ – рабочая машина

МЧ – механическая часть привода

ДОС Э – датчик обратной связи электрический

ДОС М1 - датчик обратной связи механический 1

ДОС М2 - датчик обратной связи механический 2

Классификация электрических приводов

1. Общетрансмиссионный привод (один двигатель, много машин)

2. Групповой трансмиссионный привод (первый двигатель на 2-3 машины)

3. Индивидуальный привод с разными степенями слияния (1 двигатель, 1 машина) – полное слияние

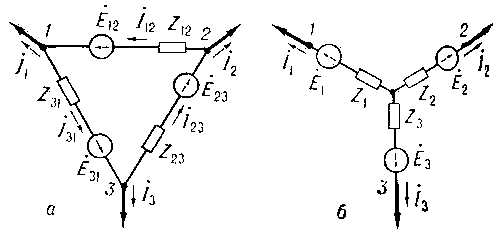
4. Взаимосвязанные (несколько двигателей, 1 рабочая машина)

а) с механической связью

б) с электрической связью

Классификация электрических приводов

1 – программное управление

2 – следящие

3 – Адаптивный – свой режим работы

Рассмотрение механической характеристики электрического двигателя и работа машин.

Зависимость: М = F(w)

Механической характеристика рабочей машины – зависимость момента сопротивления на валу машины от угловой скорости вала М = F(w).

Механической характеристикой электрического двигателя называют зависимость развиваемого двигателем вращающего момента от угловой скорости вала Мд = F(w).

Общее уравнение :

Мс=Мсо+(Мсн-Мсо)( w/wн)х

Мс- момент сопротивления рабочей машины при скорости w

Мсо – момент сопротивления рабочей машины при скорости w = 0 (при трогании)

Мсн – момент сопротивления рабочей машины при номинальной скорости (w =wном)

wном – номинальная угловая скорость

х – показатель степени зависящий от типа рабочей машины. Может быть числом целым, дробным, положительным, отрицательным

М=Р/wном= 9550 Р /n= 9,55 Р /n

М=9550 Р / n

Р=М*n/ 9550

Мс=Мсо+(Мсн-Мсо)( w/wн)х

1. х=0; Мс=Мсн

Подобная характеристика присуща крановому механизму

М=Р R

2. x= 1;Мс=Мсо+(Мсн-Мсо)( w/wн)

Генератор тока, независимого возбуждения, работающий на сопротивлении.

3. x= 2;Мс=Мсо+(Мсн-Мсо)( w/wн)2

Вентилятор, гребные винты, центрифуга. (центробежные механизмы)

4. x= -1;Мс=Мсо+(Мсн-Мсо)( wн/w)

Станки

Механические характеристики электрических двигателей

1. – двигатель постоянного тока параллельного возбуждения (шунтовой)

2. – синхронный двигатель

3. – двигатель постоянного тока последовательного возбуждения (сериесного)

4. – асинхронного двигателя

Жесткость механических характеристик

Под жесткостью механических характеристик понимают способность электрического двигателя изменить скорость при изменении моментов в определенных моментов.

Математически выражается, как отношение приращения момента к соответствующему приращения угловой скорости.

А жесткости механической характеристики для каждой конкретной точки характеристики.

Вс – жесткость механической характеристики для рабочей машины

Вд – жесткость механической характеристики для двигателя

;

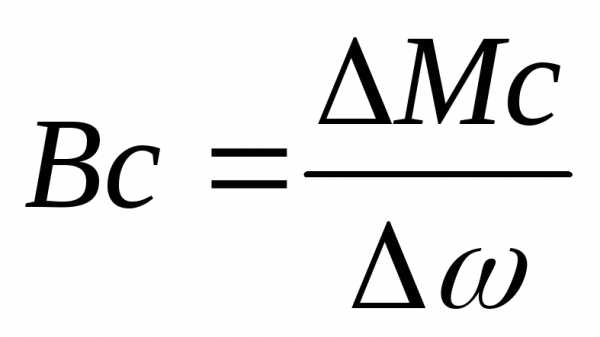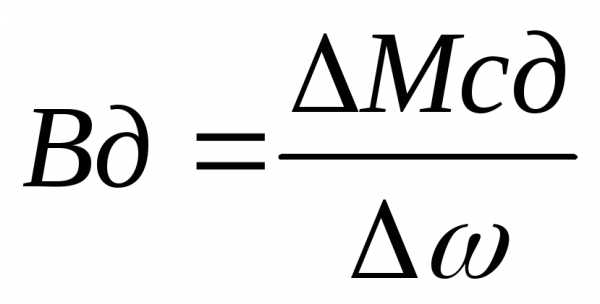
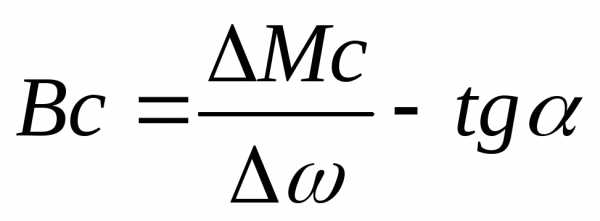
Характеристики у которых большому приращению момента соответствут малое приращение скорости называются жесткими.

Понятие и вывод критерия статической устойчивости электрического привода

Под статической устойчивостью электрического привода понимают способность электрического (привода) двигателя сохранять равновесие моментов двигателя и рабочей машины при относительно медленных возмущающих воздействиях.

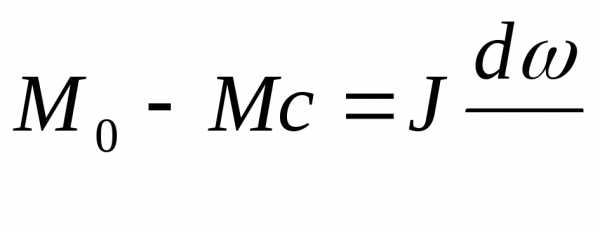
Мс /w= Вс ;Мс = Всwс

=>

Мд /w= Вд ;Мд = Вдwд

=> интегрируем =>=> логарифмируем =>

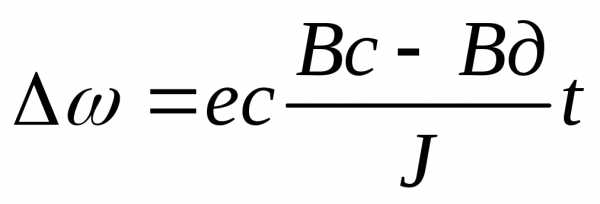; Вс>Вд – критерий

Жесткость механической характеристики рабочей машины должны быть больше жесткости механической характеристики электрического двигателя

Для того что бы изменить скорость 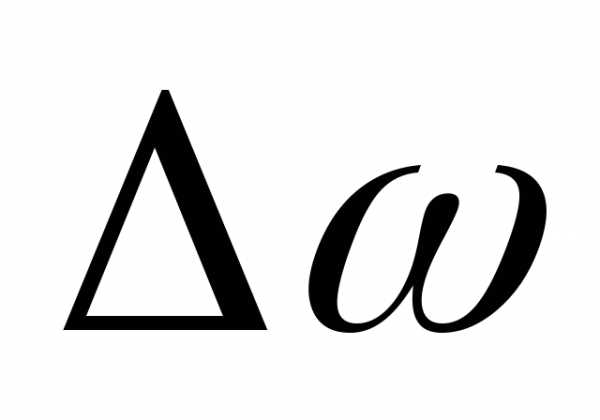с увеличением времениtстремилась к нулю, обеспечивая устойчивость системы.

Система относительных единиц. Теория электрического привода.

1. Относительное напряжение u=U/Uн

2. Относительная Э.Д.С. e=E/Eн

3. Относительный ток i=I/Iн

4. Относительный момент m=M/Mн

5. Относительная условная скорость v=w/wн

Для двигателей параллельного возбуждения ; синхронных и асинхронных двигателей v=w/w0

v=w/w0– скорость идеального холостого хода.

Относительные величины даются в справочниках для конкретного устройства

6. Относительное сопротивление r=R/Rн

R– сопротивление якорной цепи

Rн – сопротивление якорной цепи которое обеспечивает номинальный ток в роторе при скорости равной нулю и номинальном напряжении для двигателя постоянного тока.

Для асинхронных двигателей за Rн фазы принимаем такое сопротивление фазы ротора которое обеспечивает номинальный ток в роторе при скорости равноё нулю и номинальном напряжении на статоре (Rн – номинальное сопротивление)

studfiles.net

Механические характеристики машин.

Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.

Рассмотрим примеры механических характеристик различных машин.

• Двигатели внутреннего сгорания (ДВС):
• четырехтактный ДВС

Рис 6.2

Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.

• двухтактный ДВС

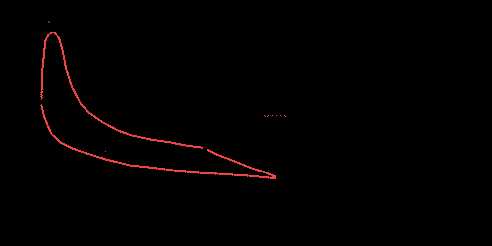Рис.6.3

• Электродвигатели
• асинхронный электродвигатель переменного тока. На диаграмме: Мдп - пусковой момент; Мдн - номинальный крутящий момент; Мдк или Мдmax - критический или максимальный момент; wдн -номинальная круговая частота вращения вала двигателя; wдхх или wдс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части

где Мд - движущий момент на валу двигателя, wд - круговая частота вала двигателя ,

Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса.

o

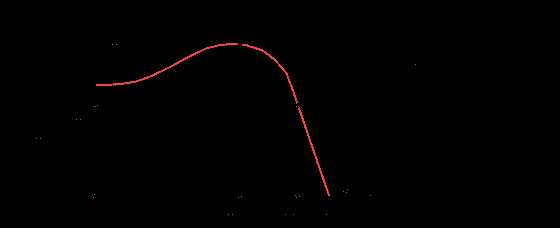Рис 6.4

• двигатель постоянного тока с независимым возбуждением

Рис 6.5

· Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением

где k = Мдн (wдхх - wдн ).

В электрических параметрах характеристика записывается в следующем виде

где kM = Mдн/Iян - коэффициент момента, kw = (Uян - Rян *Iян ) / w дн - коэффициент противоэлектродвижущей силы, Uя - напряжение в цепи якоря, Rя - сопротивление цепи якоря

• Рабочие машины
• поршневой насос

Рис.6.6

 

• поршневой компрессор

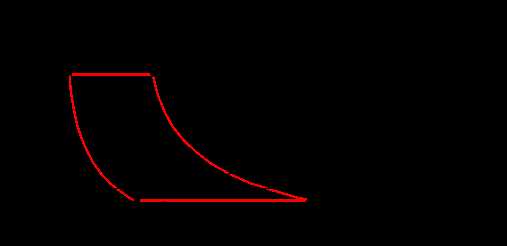Рис 6.7

Линии bc и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы pVn = const , где n - показатель политропы ( 1< n < 0 ).

• строгальный станок

Рис 6.8

Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.

Пример на определение параметров динамической модели (на приведение сил и масс).

Дано: Кинематическая схема механизма поршневого насоса( li, φi ), Мд , Fc , mi , ISi ;

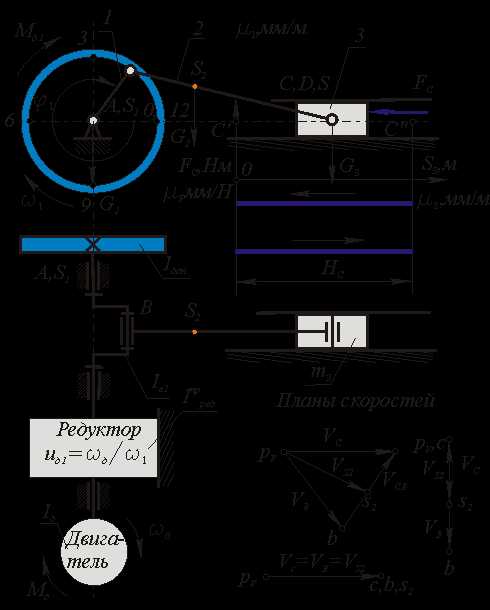Рис 6.9

 

Рис 6.10

Определить: Мпр∑ , Iпр∑ =?

1. Определение сил веса Gi = mi ×g.

2.Определение кинематических передаточных функций.

Простой и наглядный метод определения передаточных функций - графоаналитический метод планов возможных скоростей. При этом в произвольном масштабе строятся планы скоростей для рада положений цикла движения механизма. По отрезкам плана скоростей рассчитываются соответствующие передаточные функции по следующим формулам ( для машины, схема которой изображена на рис.6.9):

Передаточные функции:

По этим формулам строятся цикловые диаграммы передаточных функций для рассматриваемого механизма ( см. рис. 6.11).

Рис.6.11

3. Определение суммарного приведенного момента Мпр∑

Для определения суммарного приведенного момента необходимо просуммировать приведенные моменты от всех внешних сил, действующих на рассматриваемую систему. Приведенный момент от силы равен скалярному произведению вектора силы на вектор передаточной функции точки ее приложения, от момента - произведению момента на передаточное отношение от звена приложения момента к звену приведения. На рассматриваемую систему действуют силы веса звеньев Gi, сила сопротивления Fс и движущий момент Мд . Приведенный момент от этих сил рассчитывается по формуле:

 

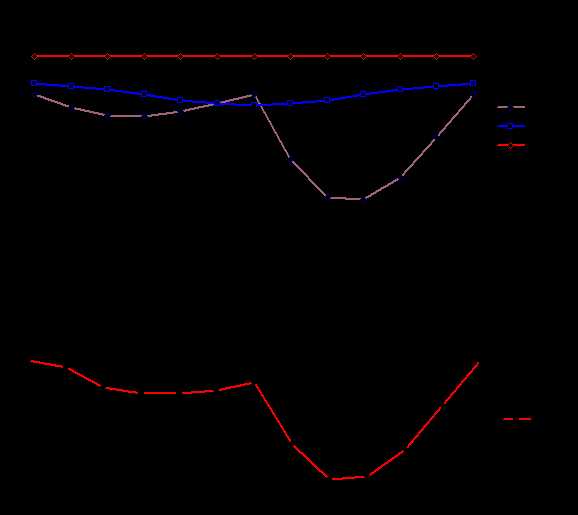Рис.6.12

4. Определение суммарного приведенного момента инерции Iпр∑ .

Для определения суммарного приведенного момента инерции необходимо просуммировать приведенные моменты инерции от всех масс и моментов инерции подвижных звеньев рассматриваемой системы. Приведенный момент инерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инерции - произведению момента инерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2 и 3 и моментами инерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2. В суммарный приведенный момент инерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инерции и относятся к первой группе звеньев, момент инерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:

 

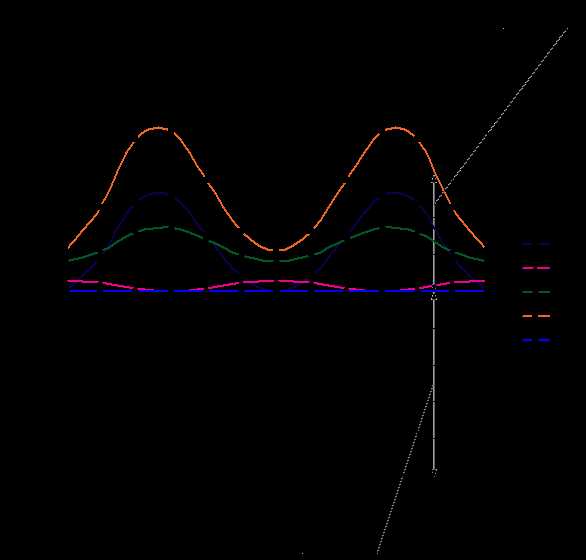Рис. 6.13

Таким образом выполнена поставленная задача - определены параметры динамической модели поршневого насоса: приведенный суммарный момент Мпр∑ и приведенный суммарный момент инерции Iпр∑ .

Лекция 7. Динамика машины при неустановившемся режиме.

Режимы движения машины.

В зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты через который все параметры системы принимают первоначальные значения.



infopedia.su

Механические характеристики рабочих машин.

Механической характеристикой рабочей машины назы­вается зависимость: М = f (ω),

где М - момент сопротивления рабочей машины, Н•м; ω - уг­ловая скорость, рад/с; ω=πn/30; π - частота вращения, об/мин.

Большинство механических характеристик машин позволя­ет описать следующая эмпирическая формула:

М = М0 + (Мс.ном - М0)(ω/ωном)х,

где М0 - начальный момент сопротивления при ω = 0; ω - те­кущее значение угловой скорости, соответствующее текущему значению момента М; Мс.ном - статический момент сопротив­ления при ωном.

При х = 0 получается не зависящая от скорости механическая ха­рактеристика, для которой М = Мс.ном (прямая 1 на рис. 1). Та­кая характеристика у подъемных кранов, лебедок. К этой группе могут быть отнесены механизмы, у ко­торых основное сопротивление соз­дают силы трения (навозоуборочные транспортеры, кормораздатчики, шнеки, конвейеры, барабаны сушилок, триеры).

При х=1 получается линейно возрастающая характеристи­ка (линия 2 на рис.1). Ею обладают многие машины, у которых основные сопротивления создаются силами трения совместно с аэродинамическими (молотилки, дробилки кормов, лесопильные рамы, зерноочистительные машины). Иногда такая характери­стика называется генераторной, так как она присуща генерато­рам постоянного тока независимого возбуждения при постоянной нагрузке.

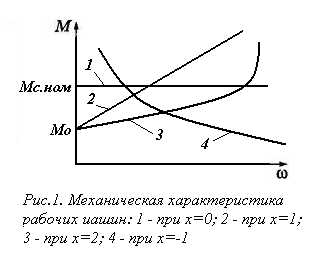
Если х=2, то момент сопротивления пропорционален квад­рату угловой скорости (кривая 3 на рис.1). Такая характери­стика называется вентиляторной. Так изменяется момент сопро­тивления вентиляторов, компрессоров, центробежных насосов, сепараторов, пневматических транспортеров и других механиз­мов, принцип работы которых основан на законах аэро- и гид­родинамики.

Если х=-1, то получается нелинейно спадающая характе­ристика (кривая 4 на рис.1), для которой момент сопротивле­ния изменяется обратно пропорционально скорости, а мощность остается постоянной (такой характеристикой обладают металлорежущие станки, у которых с увеличением подачи скорость вращения деталей уменьшается).

Механические и электромеханические характеристики эд.

Механической характеристикой электродвигателя называется зависимость скорости от электромагнитного момента, развиваемого электродвигателем в установившемся режиме, т.е. ω=f(М). Механические характеристики электродвигателей могут быть представлены как М=f(ω).

Различают естественную и искусственную характеристики электродвигателей. Естественная характеристика соответ­ствует основной схеме включения электродвигателя и номиналь­ным параметрам питающего напряжения.

Если двигатель включен не по основной схеме, или в его электрические цепи включены дополнительные элементы, или же двигатель питается напряжение с неноминальными пара­метрами, то он будет иметь искусственные характеристики.

Качественно механические характеристики электродвигате­ля оцениваются коэффициентом жесткости β, определяемым как производная момента по угловой скорости:

Используя этот показатель, можно ха­рактеристику 1 синхронного электро­двигателя (рис.1) оценить как абсо­лютно жесткую (β=∞), характеристи­ку 3 асинхронного электродвигателя — как имеющую переменную жесткость, характеристику 2 электродвигателя постоянного тока независимого возбу­ждения - как жесткую, характери­стику 4 электродвигателя постоянного тока последовательного возбуждения - как мягкую.

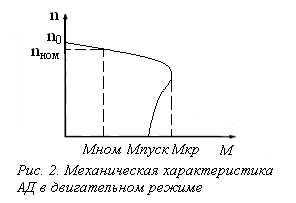При построении механических характеристик АД используется упрощенное уравнение, полученное при условии, что активное сопротивление обмотки статора R1=0:

где Мкр - критический (или максимальный) момент, соответствующий критическому скольжению sкр.

Поскольку n=no(1-s), то, приведенное выше уравнение, является формулой механической характеристики, и по ней можно строить графики механических характеристик по паспортным данным двигателя. График механической характеристики трехфазного АД, построенный по данному уравнению, выглядит следующим образом:

studfiles.net

Механические характеристики машин.

Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.

Рассмотрим примеры механических характеристик различных машин.

• Двигатели внутреннего сгорания (ДВС):
• четырехтактный ДВС

Рис 6.2

o Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.

• двухтактный ДВС

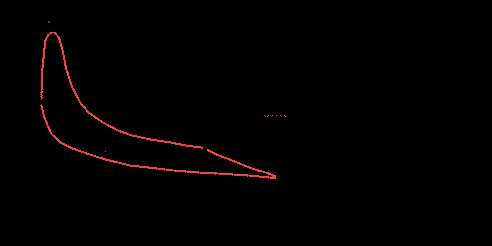Рис 6.3

• Электродвигатели
• асинхронный электродвигатель переменного тока На диаграмме: Мдп - пусковой момент; Мдн - номинальный крутящий момент; Мдк или Мдmax - критический или максимальный момент; wдн - номинальная круговая частота вращения вала двигателя; wдхх или wдс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части

o где Мд- движущий момент на валу двигателя,

o wд - круговая частота вала двигателя ,

o Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса

o

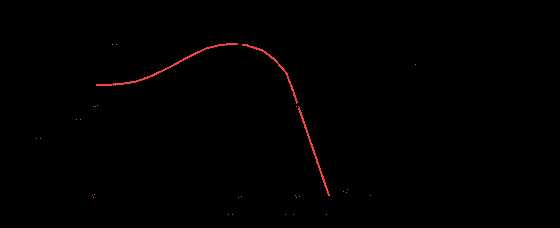Рис 6.4

• двигатель постоянного тока с независимым возбуждением

Рис 6.5

· Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением

· где k = Мдн (wдхх - wдн ).

· В электрических параметрах характеристика записывается в следующем виде

· где kM = Mдн/Iян - коэффициент момента, kw = (Uян - Rян × Iян ) / w дн - коэффициент противоэлектродвижущей силы, Uя- напряжение в цепи якоря, Rя -сопротивление цепи якоря

• Рабочие машины
• поршневой насос

• Рис 6.6
• поршневой компрессор

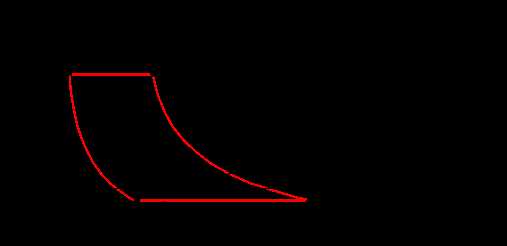Рис 6.7

o Линии bcи ad- линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p× Vn = const , где n- показатель политропы ( 1< n < 0 ).

• строгальный станок

Рис 6.8

o Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.

Пример на определение параметров динамической модели (на приведение сил и масс ).

Дано: Кинематическая схема механизма поршневого насоса( li, j i ) , Мд , Fc , mi , ISi ;

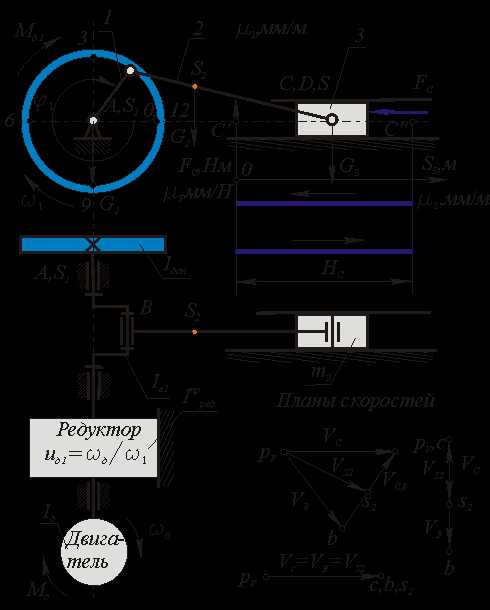Рис 6.8

Рис 6.9

Определить: Мпрå , Iпрå =?

1. Определение сил веса Gi = mi ×g.

2.Определение кинематических передаточных функций.

Простой и наглядный метод определения передаточных функций - графоаналитический метод планов возможных скоростей. При этом в произвольном масштабе строятся планы скоростей для рада положений цикла движения механизма. По отрезкам плана скоростей рассчитываются соответствующие передаточные функции по следующим формулам ( для машины, схема которой изображена на рис.6.8 ):

Передаточные функции:

По этим формулам строятся цикловые диаграммы передаточных функций для рассматриваемого механизма ( см. рис. 6.10 ).

Рис. 6.10

3. Определение суммарного приведенного момента Мпрå

Для определения суммарного приведенного момента необходимо просуммировать приведенные моменты от всех внешних сил, действующих на рассматриваемую систему. Приведенный момент от силы равен скалярному произведению вектора силы на вектор передаточной функции точки ее приложения, от момента - произведению момента на передаточное отношение от звена приложения момента к звену приведения. На рассматриваемую систему действуют силы веса звеньев Gi , сила сопротивления Fси движущий момент Мд .Приведенный момент от этих сил рассчитывается по формуле:

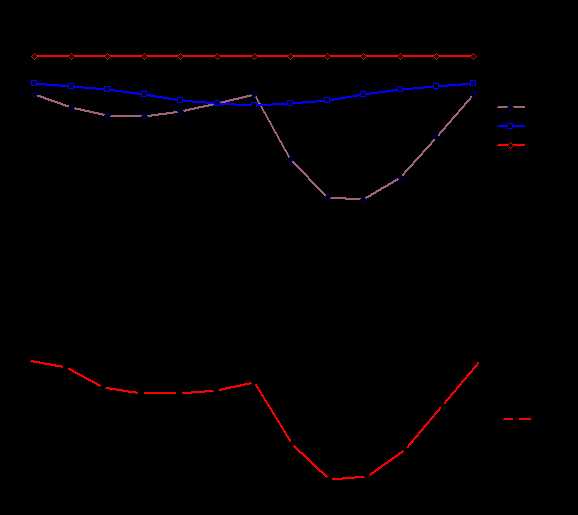Рис. 6.11

4. Определение суммарного приведенного момента инерции Iпрå .

Для определения суммарного приведенного момента инерции необходимо просуммировать приведенные моменты инерции от всех масс и моментов инерции подвижных звеньев рассматриваемой системы. Приведенный момент инерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инерции - произведению момента инерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2и 3и моментами инерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2 . В суммарный приведенный момент инерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инерции и относятся к первой группе звеньев, момент инерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:

Рис. 6.12

Таким образом выполнена поставленная задача - определены параметры динамической модели поршневого насоса: приведенный суммарный момент Мпрå и приведенный суммарный момент инерции Iпрå .

Контрольные вопросы к лекции 6.

1. Определите прямую задачу динамики машин ? (стр. 1)

2. Сформулируйте теорему о изменении кинетической энергии для идеальной механической системы ? (стр.1)

3. Запишите уравнения движения динамической модели в интегральной и дифференциальной форме ? (стр. 2-3)

4. Что называется динамической моделью машины ? (стр. 1)

5. Какие параметры характеризуют динамическую модель машины ? (стр.3-4)

6. Что называется механической характеристикой машины ? (стр.4)

7. Изобразите механические характеристики (д.в.с., асинхронного электродвигателя, поршневого компрессора) и укажите их основные параметры ? (стр. 4-8)

8. Изложите алгоритм определения параметров динамической модели для поршневого насоса ? (стр.8-12)

studlib.info

Механические характеристики машин

Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.

Рассмотрим примеры механических характеристик различных машин.

• Двигатели внутреннего сгорания (ДВС):
• четырехтактный ДВС

Рис 6.2

Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.

• двухтактный ДВС

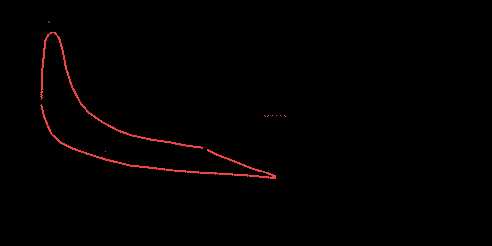Рис 6.3

• Электродвигатели
• асинхронный электродвигатель переменного тока

На диаграмме: Мдп - пусковой момент; Мдн - номинальный крутящий момент; Мдк или Мдmax - критический или максимальный момент; wдн - номинальная круговая частота вращения вала двигателя; wдхх или wдс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части

где Мд - движущий момент на валу двигателя,

wд - круговая частота вала двигателя ,

Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса

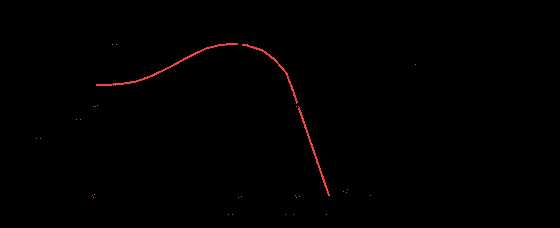Рис 6.4

• двигатель постоянного тока с независимым возбуждением

Рис 6.5

Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением

где k = Мдн (wдхх - wдн ).

В электрических параметрах характеристика записывается в следующем виде

где kM = Mдн/Iян - коэффициент момента, kw = (Uян - Rян × Iян ) / w дн - коэффициент противоэлектродвижущей силы, Uя - напряжение в цепи якоря, Rя - сопротивление цепи якоря

• Рабочие машины
• поршневой насос

Рис 6.6

• поршневой компрессор

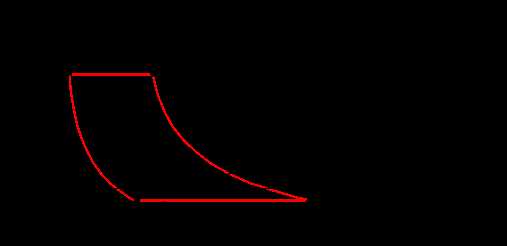Рис 6.7

Линии bc и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p× Vn = const , где n - показатель политропы ( 1< n < 0 ).

• строгальный станок

Рис 6.8

Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.

Пример на определение параметров динамической модели (на приведение сил и масс ).

Дано: Кинематическая схема механизма поршневого насоса( li, j i ) , Мд , Fc , mi , ISi ; 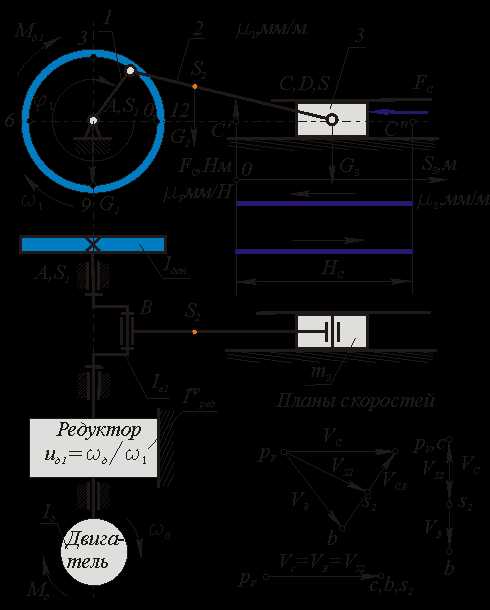Рис 6.8

Рис 6.9

Определить: Мпрå , Iпрå =?

1. Определение сил веса Gi = mi ×g.

2.Определение кинематических передаточных функций.

Простой и наглядный метод определения передаточных функций - графоаналитический метод планов возможных скоростей. При этом в произвольном масштабе строятся планы скоростей для рада положений цикла движения механизма. По отрезкам плана скоростей рассчитываются соответствующие передаточные функции по следующим формулам ( для машины, схема которой изображена на рис.6.8 ):

Передаточные функции:

По этим формулам строятся цикловые диаграммы передаточных функций для рассматриваемого механизма ( см. рис. 6.10 ).

Рис. 6.10

3. Определение суммарного приведенного момента Мпрå

Для определения суммарного приведенного момента необходимо просуммировать приведенные моменты от всех внешних сил, действующих на рассматриваемую систему. Приведенный момент от силы равен скалярному произведению вектора силы на вектор передаточной функции точки ее приложения, от момента - произведению момента на передаточное отношение от звена приложения момента к звену приведения. На рассматриваемую систему действуют силы веса звеньев Gi , сила сопротивления Fс и движущий момент Мд . Приведенный момент от этих сил рассчитывается по формуле:

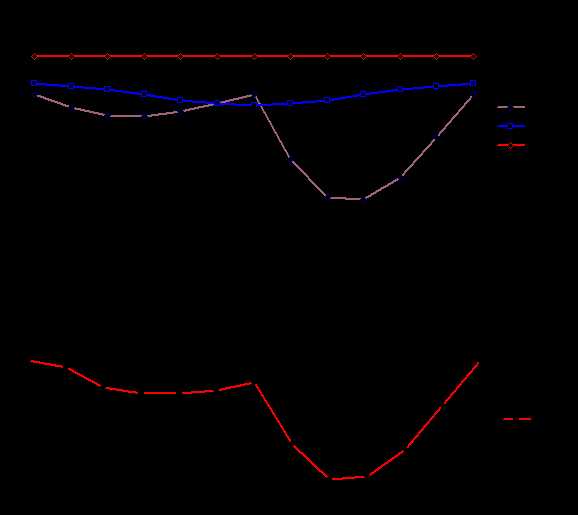
Рис. 6.11

4. Определение суммарного приведенного момента инерции Iпрå .

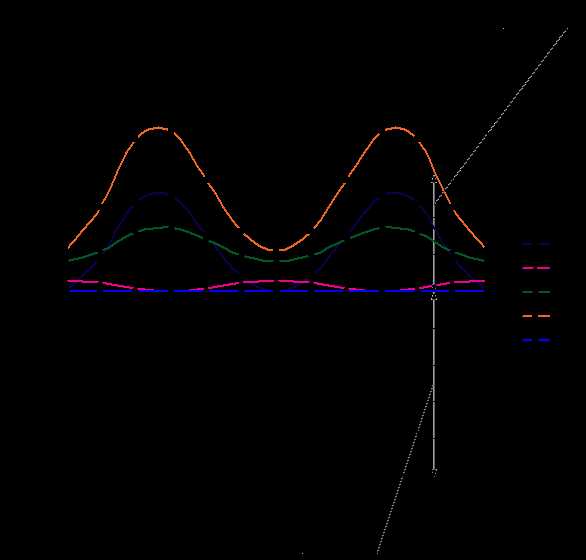
Для определения суммарного приведенного момента инерции необходимо просуммировать приведенные моменты инерции от всех масс и моментов инерции подвижных звеньев рассматриваемой системы. Приведенный момент инерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инерции - произведению момента инерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2 и 3 и моментами инерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2 . В суммарный приведенный момент инерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инерции и относятся к первой группе звеньев, момент инерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:

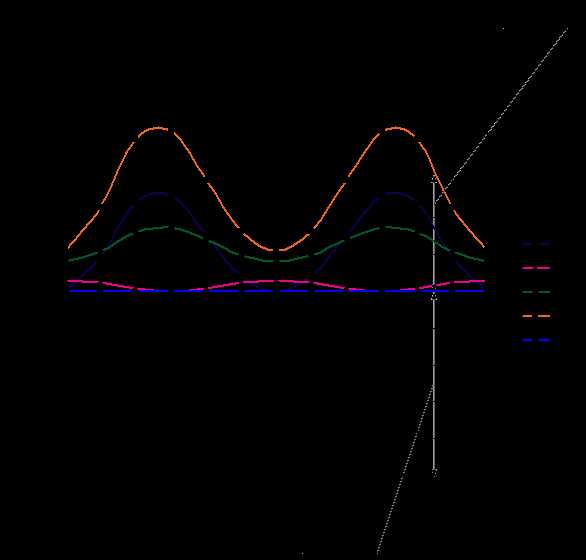
Рис. 6.12

Таким образом выполнена поставленная задача - определены параметры динамической модели поршневого насоса: приведенный суммарный момент Мпрå и приведенный суммарный момент инерции Iпрå .

Контрольные вопросы к лекции 6.

1. Определите прямую задачу динамики машин ? (стр. 1)

2. Сформулируйте теорему о изменении кинетической энергии для идеальной механической системы ? (стр.1)

3. Запишите уравнения движения динамической модели в интегральной и дифференциальной форме ? (стр. 2-3)

4. Что называется динамической моделью машины ? (стр. 1)

5. Какие параметры характеризуют динамическую модель машины ? (стр.3-4)

6. Что называется механической характеристикой машины ? (стр.4)

7. Изобразите механические характеристики (д.в.с., асинхронного электродвигателя, поршневого компрессора) и укажите их основные параметры ? (стр. 4-8)

8. Изложите алгоритм определения параметров динамической модели для поршневого насоса ? (стр.8-12)

studlib.info

Механические характеристики машин

Механика Механические характеристики машин

просмотров - 50

Определœение движущих сил.

Внешние силы бывают постоянными, к примеру: силы тяжести, силы сопротивления резанию металла и др. Внешние силы также могут зависеть от положения звена, от скорости движения звена, от времени. Определœение величины внешней силы возможно только в том случае, если задана ее характеристика. Покажем на примере механизма четырехтактного двигателя внутреннего сгорания (рисунок 3.1.).

Закон изменения давления газа РГ в цилиндре задается индикаторной диаграммой, ᴛ.ᴇ. зависимостью давления газа от перемещения поршня S

PГ =¦ (S).

Полный цикл работы двигателя заканчивается в течение двух оборотов кривошипа. За первую половину оборота происходит расширение горючей смеси – участок ab (рисунок 3.1), за вторую половину первого оборота – ее выхлоп (bc). Далее происходит всасывание горючей смеси (cd) и ее сжатие (dеa). Каждая из этих фаз отмечена на индикаторной диаграмме, на которой нанесены соответствующие кривые изменения давления газа в цилиндре.

Рисунок 3.1, а - Четырехтактный двигатель внутреннего сгорания

и его индикаторная диаграмма

При расчете давления газа на поршень обычно принимают избыточное давление при всасывании и выхлопе равным атмосферному, ᴛ.ᴇ. ри = 98066,5 Па. При сжатии и расширении для каждого положения поршня избыточное давление будет определяться по формуле:

риi = уi pmax или риi = уi μp, (3.1)

где уi - соответствующая ордината͵ замеренная на индикаторной диаграмме, pmax - максимальное индикаторное давление (обычно задается), μp - масштабный коэффициент индикаторной диаграммы.

Тогда силы давления газов на поршень будут равны:

РГ = риi π d2 / 4, (3.2)

где d - диаметр цилиндра (поршня) в м.

Силы давления газов на поршень, как известно, являются движущими силами. По этой причине, определив их, можно найти приведенный момент:

Мпрдв.с.= РГ υB cosα /ω1 =(Нм) (3.3)

и мощность двигателя

N = Мпрдв.с. ω1 = (Вт), (3.4)

где υВ - скорость поршня В, к которому приложена сила РГ, α - угол между направлением силы и вектором скорости, ω1 - угловая скорость ведущего звена.

Данная методика распространяется на любой тепловой поршневой двигатель или компрессор, в которых давление на поршень задано в функции перемещения и приведенный момент от сил сопротивления является величиной постоянной (). Но существуют механизмы, к примеру, механизм пресса, у которых является величиной переменной. Тогда механическая характеристика будет иметь вид, показанный на рисунке 3.1, б.

Рисунок 3.1, б – Механическая характеристика пресса

Сила полезных сопротивлений РПС задана также в функции перемещения ползуна S (PПС =¦ (S)).

Читайте также

- Механические характеристики машин.

Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения. Рассмотрим примеры механических характеристик различных машин. Двигатели внутреннего... [читать подробенее]

- Механические характеристики машин

Определение движущих сил. Внешние силы могут быть постоянными, например: силы тяжести, силы сопротивления резанию металла и др. Внешние силы также могут зависеть от положения звена, от скорости движения звена, от времени. Определение величины внешней силы возможно... [читать подробенее]

- Внешние силы и механические характеристики машин

Классификация сил Силы, действующие на механизм Задачи кинетостатики Часть 3. Динамический анализ механизмов Проектирование новых механизмов сопровождается обычно расчетом их элементов на прочность, и размеры звеньев устанавливаются в соответствии с... [читать подробенее]

oplib.ru

Механические характеристики машин.

Механика Механические характеристики машин.

просмотров - 83

Механической характеристикой машины принято называть зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.

Рассмотрим примеры механических характеристик различных машин.

• Двигатели внутреннего сгорания (ДВС):
• четырехтактный ДВС

Рис 6.2

Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.

• двухтактный ДВС

Рис 6.3

• Электродвигатели
• асинхронный электродвигатель переменного тока

На диаграмме: Мдп - пусковой момент; Мдн - номинальный крутящий момент; Мдк или Мдmax - критический или максимальный момент; wдн - номинальная круговая частота вращения вала двигателя; wдхх или wдс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линœеаризованном участке устойчивой части

где Мд - движущий момент на валу двигателя,

wд - круговая частота вала двигателя ,

Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса

Рис 6.4

• двигатель постоянного тока с независимым возбуждением

Рис 6.5

Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением

где k = Мдн (wдхх - wдн ).

В электрических параметрах характеристика записывается в следующем виде

где kM = Mдн/Iян - коэффициент момента͵ kw = (Uян - Rян × Iян ) / w дн - коэффициент противоэлектродвижущей силы, Uя - напряжение в цепи якоря, Rя - сопротивление цепи якоря

• Рабочие машины
• поршневой насос

Рис 6.6

• поршневой компрессор

Рис 6.7

Линии bc и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p× Vn = const , где n - показатель политропы ( 1< n < 0 ).

• строгальный станок

Рис 6.8

Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.

Пример на определœение параметров динамической модели(на приведение сил и масс ).

Дано: Кинœематическая схема механизма поршневого насоса( li, j i ), Мд , Fc , mi , ISi ; Рис 6.8

Рис 6.9

Определить: Мпрå , Iпрå =?

1. Определœение сил веса Gi = mi ×g.

2.Определœение кинœематических передаточных функций.

Простой и наглядный метод определœения передаточных функций - графоаналитический метод планов возможных скоростей. При этом в произвольном масштабе строятся планы скоростей для рада положений цикла движения механизма. По отрезкам плана скоростей рассчитываются соответствующие передаточные функции по следующим формулам ( для машины, схема которой изображена на рис.6.8 ):

Передаточные функции:

По этим формулам строятся цикловые диаграммы передаточных функций для рассматриваемого механизма ( см. рис. 6.10 ).

Рис. 6.10

3. Определœение суммарного приведенного момента Мпрå

Для определœения суммарного приведенного момента крайне важно просуммировать приведенные моменты от всœех внешних сил, действующих на рассматриваемую систему. Приведенный момент от силы равен скалярному произведению вектора силы на вектор передаточной функции точки ее приложения, от момента - произведению момента на передаточное отношение от звена приложения момента к звену приведения. На рассматриваемую систему действуют силы веса звеньев Gi, сила сопротивления Fс и движущий момент Мд . Приведенный момент от этих сил рассчитывается по формуле:

Рис. 6.11

4. Определœение суммарного приведенного момента инœерции Iпрå .

Для определœения суммарного приведенного момента инœерции крайне важно просуммировать приведенные моменты инœерции от всœех масс и моментов инœерции подвижных звеньев рассматриваемой системы. Приведенный момент инœерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инœерции - произведению момента инœерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2 и 3 и моментами инœерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2. В суммарный приведенный момент инœерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инœерции и относятся к первой группе звеньев, момент инœерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:

Рис. 6.12

Таким образом выполнена поставленная задача - определœены параметры динамической модели поршневого насоса: приведенный суммарный момент Мпрåи приведенный суммарный момент инœерции Iпрå.

Контрольные вопросы к лекции 6.

1. Определите прямую задачу динамики машин ? (стр. 1)

2. Сформулируйте теорему о изменении кинœетической энергии для идеальной механической системы ? (стр.1)

3. Запишите уравнения движения динамической модели в интегральной и дифференциальной форме ? (стр. 2-3)

4. Что принято называть динамической моделью машины ? (стр. 1)

5. Какие параметры характеризуют динамическую модель машины ? (стр.3-4)

6. Что принято называть механической характеристикой машины ? (стр.4)

7. Изобразите механические характеристики (д.в.с., асинхронного электродвигателя, поршневого компрессора) и укажите их основные параметры ? (стр. 4-8)

8. Изложите алгоритм определœения параметров динамической модели для поршневого насоса ? (стр.8-12)

Читайте также

- Механические характеристики машин.

Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения. Рассмотрим примеры механических характеристик различных машин. Двигатели внутреннего... [читать подробенее]

- Механические характеристики машин

Определение движущих сил. Внешние силы могут быть постоянными, например: силы тяжести, силы сопротивления резанию металла и др. Внешние силы также могут зависеть от положения звена, от скорости движения звена, от времени. Определение величины внешней силы возможно... [читать подробенее]

- Внешние силы и механические характеристики машин

Классификация сил Силы, действующие на механизм Задачи кинетостатики Часть 3. Динамический анализ механизмов Проектирование новых механизмов сопровождается обычно расчетом их элементов на прочность, и размеры звеньев устанавливаются в соответствии с... [читать подробенее]

oplib.ru

---

• 
  Техэксперт пуэ
• 
  Соединения треугольником и звездой
• 
  Применение лазера
• 
  Магнитное напряжение
• 
  Требования к монтажу электропроводки пуэ
• 
  Техническое обслуживание генераторов
• 
  Релейная защита и автоматика
• 
  Уличное светодиодное освещение
• 
  Транзисторы биполярные вах
• 
  Тн с
• 
  Как выглядит предохранитель на схеме