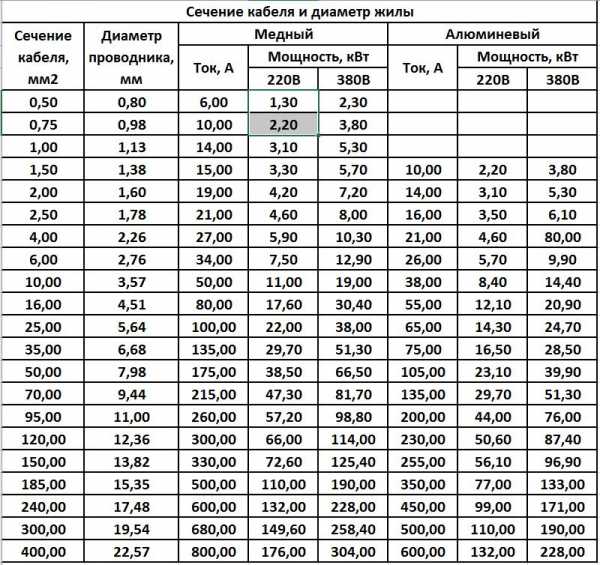
Методика расчета цепи методом контурных токов. Методом контурных токов определить токи в ветвях

Расчёт электрической цепи методом контурных токов

⇐ ПредыдущаяСтр 4 из 8Следующая ⇒

Прежде, чем приступить к рассмотрению примера расчёта схемы методом контурных токов, рассмотрим основные положения этого метода и последовательность расчёта в соответствии с .

Сложные схемы характеризуются наличием значительного числа ветвей. В случае применения предыдущего метода это приводит к необходимости решать систему из значительного числа уравнений. Метод контурных токов позволяет уменьшить число исходных уравнений, а значит несколько облегчить расчёт.

При расчёте методом контурных токов используются понятия не зависимого контура и зависимого контура, которые использовались в предыдущем методе. Кроме них в этом методе используются ещё следующие понятия:

- собственный элемент контура - элемент, относящийся только к одному контуру;

- общий элемент контура - элемент, относящийся к двум и более контурам цепи.

Обозначаем, как и раньше, через К число узлов, а через n число ветвей цепи. Тогда число независимых контуров цепи определяется по уже известной формуле [n-(К-1)].

Метод основывается на предположении, что в каждом не зависимом контуре течёт собственный контурный ток, и вначале находят контурные токи в не зависимых контурах. Токи в ветвях цепи определяют через контурные токи. При этом исходят из того, что в собственных элементах контура токи совпадают с контурным током данного контура, а в общих элементах ток равен алгебраической сумме контурных токов тех контуров, к которым принадлежит данный элемент.

Последовательность расчёта:

1. Определяется число ветвей (n) и число узлов (К) цепи. Находится число независимых контуров [n-(К-1)].

2. Выбирается [n-(К-1)] не зависимых контура.

3. Выбирается условно-положительное направление контурных токов в каждом из независимых контуров (обычно показывается стрелкой).

4. Для каждого из независимых контуров составляется уравнение по второму закону Кирхгофа. При этом падение напряжения на собственных элементах определяется как произведение контурного тока на величину сопротивления, а на общих элементах - как произведение алгебраической суммы всех контурных токов, протекающих через данный элемент, на величину его сопротивле-

 

 

ния. Обход контура производится, как правило, в направлении собственного контурного тока.

5. Решается система из [n-(К-1)] уравнений и находятся контурные токи.

6. Токи в ветвях схемы находятся следующим образом:

- в собственных элементах контура ток равен контурному току;

- в общих элементах контура ток равен алгебраической сумме токов, протекающих через данный элемент.

Пример применения метода контурных токов при расчёте электрических цепей рассмотрим на той же схеме (рис.6) и представим её на рис.11. Как рассматривалось выше, в этой схеме три независимых контура. Тогда в каждом независимом контуре выбираем направления контурных токов и показываем эти контурные токи.

 

 

 

 

 

Для дальнейшего удобства расчёта расставим в схеме условно-положительные направления токов и напряжений. Далее, в соответствии с п.4 «последовательности расчёта», для каждого независимого контура составляем уравнения по второму закону Кирхгофа. В результате этих действий получаем систему (18) из трёх уравнений:

(18)

В полученных уравнениях раскрываем скобки и приводим подобные:

(19)

Из третьего уравнения системы (19) находим ток :

 

(20)

 

Подставляем выражение тока (20) во второе уравнение системы (19), в результате чего, после приведения подобных членов, эта система принимает вид:

(21)

 

Во втором уравнении системы (21) коэффициент при токе имеет довольно громоздкий вид. Для дальнейшего анализа будет удобно обозначить его какой-нибудь буквой, например , т.к. этот коэффициент имеет размерность сопротивления:

. (22)

Подставим численные значения в формулу (22) и найдём значение в алгебраической и показательной форме:

(23)

С учётом (22) система уравнений (21) принимает вид:

(24)

 

Из второго уравнения системы (24) найдём ток :

. (25)

Подставим выражение для тока (25) в первое уравнение системы (24) и после приведения к общему знаменателю, получим:

 

. (26)

Из уравнения (26) находим ток :

.

В полученное выражение для тока подставляем численные значения и находим значение тока в алгебраической и показательной форме:

.

 

Для определения тока воспользуемся формулой (25), подставляем в неё численные значения и находим значение тока в алгебраической и показательной форме:

.

Теперь определяем ток , для чего используем формулу (20). Здесь удобнее будет использовать ток в показательной форме. Подставляем численные значения в (20) и в результате очевидных преобразований получим значение в показательной и алгебраической форме:

.

После определения контурных токов переходим к определению токов в ветвях. В соответствии с методом расчёта токи в собственных ветвях контуров равны контурным токам этих контуров. В соответствии с этим находим токи и :

Токи в общих ветвях определяются как алгебраическая сумма контурных токов, протекающих через эти ветви. Ток равен разности контурных токов и , так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов и в алгебраической форме и находим значение тока в алгебраической и показательной форме:

Ток равен разности контурных токов и , так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов и в алгебраической форме и находим значение тока в алгебраической и показательной форме:

Находим напряжения на элементах:

В.

В.

В.

В.

В.

 

Читайте также:

lektsia.com

Метод контурных токов

Метод контурных токов применяется для расчета сложных электрических цепей, имеющих больше двух узловых точек. На рисунке 1, а изображена такая электрическая цепь. В ней три контура, причем средний контур имеет участки, входящие в состав двух соседних контуров, которые входят в состав одного контура.

Рисунок 1. Метод контурных токов пример

Сущность метода контурных токов заключается в предположении, что в каждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров.

Выберем положительные направления трех контурных токов так, как указано на чертеже стрелками. Затем составим уравнения по второму закону Кирхгофа, обходя все три контура в одном направлении, например в направлении движения часовой стрелки.

Для контура I:

E1 = I1 × r1 + (I1 – I2) × r2 .

(а)

Для контура II:

0 = I2 × r3 + (I2 – I1) × r2 + (I2 – I3) × r4 .

(б)

Для контура III:

E2 = I3 × r5 + (I3 – I2) × r4 .

(в)

Как мы видим, число уравнений равно числу контуров, то есть число уравнений меньше, чем при решении задачи по законам Кирхгофа. Решая систему уравнений, находим контурные токи, по которым определяются токи в ветвях. Пример решения задач методом контурных токов показан ниже.

Пример 1. Определить, как распределяются токи в цепи, представленной на рисунке 1, а, если E1 = 14 В, E2 = 20 В, r1 = 2 Ом, r2 = 3 Ом, r3 = 4 Ом, r4 = 2 Ом, r5 = 6 Ом. Произведем расчет методом контурных токов.

Решение.

Уравнение для контура I по формуле (а):

14 = I1 × 2 + (I1 – I2) × 3 ,

14 = 2I1 + 3I1 – 3I2 ,

14 = 5I1 – 3I2 .

(а')

Уравнение для контура II по формуле (б):

0 = I2 × 4 + (I2 – I1) × 3 + (I2 – I3) × 2 ,

0 = 4I2 + 3I2 – 3I1 + 2I2 – 2I3 ,

0 = 9I2 – 3I1 – 2I3 .

(б')

Уравнение для контура III, по формуле (в):

20 = I3 × 6 + (I3 – I2) × 2 ,

20 = 6I3 + 2I3 – 2I2 ,

20 = 8I3 – 2I2 ,

10 = 4I3 – I2 .

(в')

Складывая выражения (а’) и (б’), получим:

или

Складывая выражения (в’) и (г), получим:

или

Подставляя значение тока I2 в уравнение (в’), получим:

10 = 4I3 – 2 ,

10 + 2 = 4I3 ,

откуда

Подставляя значение тока I2 в уравнение (а’), получим:

14 – 5I1 – 6 ,

20 = 5I1 ,

откуда

Таким образом, все контурные токи найдены.

Определяем на отдельных участках цепи алгебраически, складывая протекающие по ним токи. Токораспределение на отдельных участках цепи показано на рисунке 1, б.

Источник: Кузнецов М. И., "Основы электротехники" - 9-е издание, исправленное - Москва: Высшая школа, 1964 - 560с.

www.electromechanics.ru

Методика расчета цепи методом контурных токов

Поиск Лекций

В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.

Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:

1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.

2 Определяем все независимые контуры.

3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.

4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5 Решаем любым методом полученную систему относительно контурных токов и определяем их.

6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на мин

Метод контурных токов можно применить для расчета сложных электриче­ских цепей, имеющих больше двух узловых точек. Сущность метода контурных токов заключается в предположении, что в ка­ждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе двух соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров.

 

Метод узловых потенциалов (напряжений). Методом узловых потенциалов составляются и решаются уравнения только первого закона Кирхгофа. Все источники ЭДС преобразуются в эквивалентные источники тока. Метод эффективно используется тогда, когда мало узлов, но много ветвей. Если число уравнений первого закона Кирхгофа меньше числа уравнений второго закона Кирхгофа, то этот метод эффективен.

Найдем токи ветвей (рис. 1.14), считая известными потенциалы узлов и проводимости ветвей:

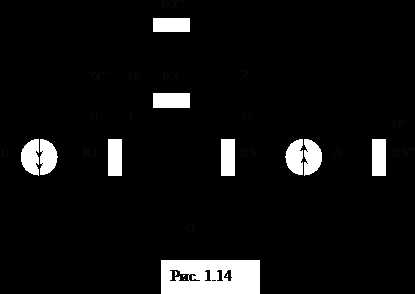
Составим уравнения первого закона Кирхгофа:

В полученные уравнения подставим заранее найденные токи:

(1.11)

Из уравнений (1.11) сформируем уравнения узловых потенциалов:

(1.12)

Обозначим коэффициент при потенциале первого уравнения системы (1.12), а коэффициент при второго уравнения - и назовем их узловыми проводимостями.

Из уравнений (1.12) видно, что узловые проводимости состоят из суммы проводимостей всех ветвей, принадлежащих узлу.

Остальные коэффициенты уравнений (1.12) называют межузловыми проводимостями и обозначают: и .

Узловые токи источников тока , равны соответственно правым частям уравнений (1.12).

С учетом введенных обозначений уравнения (1.12) примут вид:

(1.13)

Метод узловых потенциалов, как и метод контурных токов, требует совместного решения меньшего числа независимых уравнений по сравнению с методом узловых и контурных уравнений (применением двух законов Кирхгофа), что сокращает расчеты. Он основан на применении первого закона Кирхгофа.

Для расчета токов методом узловых потенциалов, кроме первого закона Кирхгофа, применяется обобщенный закон Ома.

8. Метод суперпозиции. Воздействие нескольких источников, на какой либо элемент цепи можно рассматривать как результат воздействия на этот элемент каждого из источников в отдельности независимо от других: то есть ток в любой ветви рассматривают как результат наложения токов, получающихся от отдельных источников, действующих независимо друг от друга.

Метод суперпозиции.Источник ЭДС Е2 заменяется его внутренним сопротивлением (в рассматриваемой задаче приняты идеальные источники ЭДС, то есть их внутренние сопротивления равны 0)

Принцип наложения формулируется следующим образом: ток в k-ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных электрических цепей.

Принцип наложения положен в основу метода расчета, получившего название метода наложения.

При расчете цепей данным методом поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов. Заметим, что методом наложения нельзя пользоваться для подсчета выделяемых всопротивлениях мощностей как суммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока (Р = RI2).

9. Метод эквивалентного генератора. Если в электрической цепи необходимо определить ток только в одной из ветвей, то используют метод эквивалентного генератора. Метод основан на теореме о двухполюснике, в соответствии с которой любой активный двухполюсник можно представить реальным источником ЭДС.

Если в любой электрической цепи выделить черный ящик А (рис. 1.15) и назвать его активным двухполюсником (рис. 1.16), для которого , то найти этот ток не представляет труда.

Докажем теорему об активном двухполюснике. Для этого в выделенную ветвь введем два последовательно включенных источника Е (рис. 1.17). При этом в схеме ничего не изменится, так как эти одинаковые источники включены встречно.

Далее применим метод наложения и представим схему (рис. 1.17) двумя схемами (рис. 1.18). В цепи (рис 1.17) выбрано значение ЭДС Е таким, что а это возможно только в том случае, если Е = ЕГ, тогда в соответствии с принципом наложения , т.е. истинный ток будет равен:, или после вычислений:

.

Таким образом, любой активный двухполюсник можно заменить последовательно соединенными и ЕГ. Для того чтобы определить и достаточно проделать опыт холостого хода и короткого замыкания.

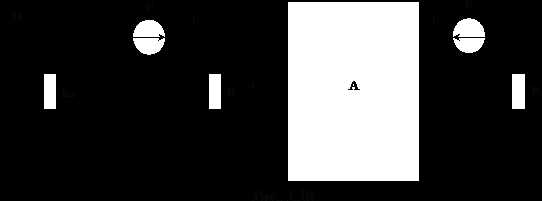
Холостой ход: .

Режим короткого замыкания: .

10. Энергетический баланс в электрических цепях. При протекании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, вы-деляющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени (мощность), равную EI, и произведение EI входит в уравнение энергетического баланса с положительным знаком.Если же направление тока I встречно направлению ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение EI войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид

Когда схема питается не только от источников ЭДС, но и от источников тока, т. е. к отдельным узлам схемы подтекают и от них утекают токи источников тока, при составлении уравнения энерге-тического баланса необходимо учесть и энергию, доставляемую источниками тока. Допустим, что к узлу а схемы подтекает токI от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UabJ. Напряжение Uab и токи в ветвях схемы должны быть подсчитаны с учетом тока, подтекающего от источника тока. Последнее проще всего сделать по методу узловых потенциалов (см. § 2.22). Общий вид уравнения энергетического баланса:

Для практических расчетов электрических цепей разработаны методы, более экономичные в смысле затраты времени и труда, чем метод расчета цепей по законам Кирхгофа. Рассмотрим эти методы.

11.Режимы работы электрической цепи Известно, что электрическая цепь – это совокупность определённых устройств, которые обеспечивают постоянное, непрерывное прохождение электрического тока. Работа цепи невозможна, если в ней отсутствуют какие-либо элементы; в обязательном порядке должны присутствовать как источники энергии, так и её проводники, а приёмники, как правило, - это основные устройства, образующие данную цепь. Выделяют три основных режима работы: нагрузочный (или согласованный), режим короткого замыкания, а также режим холостого хода. Они отличаются друг от друга нагрузкой на электрическую цепь. Нагрузочный, или согласованный режим работы. Если к источнику энергии в электрической цепи подключается какой-либо приёмник, то он обладает неким сопротивлением. Таким приёмником может быть любое устройство, например электрическая лампочка. Если есть напряжение, то действует закон Ома, таким образом, ЭДС источника получается из суммы напряжений внешнего участка цепи и на внутреннем сопротивлении источника. Падение напряжение во внешней цепи будет равным напряжению на зажимах источника. Оно зависит от нагрузочного тока: чем меньше сопротивление нагрузки, тем больше ток и, соответственно, меньше напряжение на зажимах источника питания цепи. Другими словами можно сказать, что нагрузочный или согласованный режим работы представляет собой режим, при котором происходит передача нагрузки повышенной мощности от источника. В этом режиме сопротивление нагрузки равно внутреннему сопротивлению источника, при этом расходуется максимальная мощность. Однако, такой режим не рекомендуется использовать, так как при длительном превышении номинальных значений устройства могут выйти из строя. Режим работы холостого хода. Этот режим работы электрической цепи характеризует разомкнутое её состояние – ток отсутствует, и все элементы отключены от источника питания. В таком состоянии цепи внутреннее падение напряжение равно нулю, а напряжение на зажимах источника питание совпадает с ЭДС источника. Т. е., можно сказать, что режим холостого хода характеризует электрическую цепь, когда она находится в разомкнутом состоянии, а сопротивление нагрузки отсутствует полностью или отключено. Такое состояние цепи можно использовать для измерения ЭДС источника питания. Режим короткого замыкания. Этот режим работы считается аварийным, электрическая цепь не может работать нормально. Короткое замыкание возникает при соединении двух различных точек цепи, разница потенциалов которых отличается. Такое состояние не предусмотрено изготовителем устройства и нарушает его нормальную работу.

 

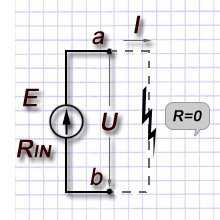В этом режиме работы зажимы источника энергии замкнуты проводником («закорочены»), при этом его сопротивление близко к нулю. Часто, короткое замыкание происходит в тех случаях, когда соединяются два провода, которые связывают между собой источник и приёмник в цепи, как правило, их сопротивление незначительно, так что его можно назвать нулевым. При возникновении режима короткого замыкания, ток в цепи значительно превышает номинальные значения (из-за отсутствия сопротивления). Это может привести в непригодное состояние источник энергии и приёмники в электрической цепи. В некоторых случаях это является результатом неправильных действий со стороны персонала, работающего с электротехническим оборудованием.

12. Синусоидальный ток и основные характеризующие его величины.Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону (рис. 2.1):

Ток i(t) называют мгновенным. Максимальное значение тока называют амплитудой и обозначают . Период – это время, за которое совершается одно полное колебание. Частота равна числу колебаний в секунду , единица частоты - герц (Гц).

Угловая частота , единица угловой частоты рад/с или . Аргумент синуса, т.е. , называют фазой. Фаза характеризует состояние колебания в данный момент времени .

Начальная фаза тока - .

poisk-ru.ru

Расчет цепи методом контурных токов.

Метод контурных токов.

Метод контурных токов используется для расчета как резистивных линейных

цепей с постоянными токами, так и комплексных схем замещения линейных

цепей с гармоническими токами.

В расчет вводятся так называемые контурные или фиктивные токи, которые замыкаются в независимых замкнутых контурах. Независимые контуры отличаются друг от друга наличием хотя бы одной новой ветви. Контурные токи принимают за неизвестные, находят сначала их, и уже затем через контурные токи определяют неизвестные токи в ветвях.

Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, число неизвестных можно существенно сократить, включая источники в разные контуры. В таких схемах применение этого метода наиболее рационально.

Число неизвестных в данном методе равно количеству уравнений, которые необходимо составить по второму правилу Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока.

Основой для расчёта режима работы любой электрической цепи являются законы Ома и правила Кирхгофа. С их помощью, зная параметры элементов электрической цепи можно определить протекающие в ней токи и действующие напряжения. Можно решить обратную задачу по определению параметров цепи, которые обеспечивают требуемые токи и напряжения.

Расчет цепи методом контурных токов.

Найти токи в ветвях схемы I1, I2, I3, I4

Дано: R1=5 Ом; R2=10 Ом; R3=10 Ом;R4=3 Ом; R5 =40 Ом; R6=7 Ом;

E1 = 40 В; E2 = 10 В; J = 1 А

=

 

 

1. Топология.

Определяем общее число ветвей: p*=5.

Определяем число ветвей с источниками тока: pит=1.

Определяем число ветвей с неизвестными токами: p*- pит=4.

Количество узлов q=3.

Определяем необходимое и достаточное число контуров:

M = p*-(q-1) = 5 – (3-1)= 3.

 

Алгоритм расчета

 

2. Произвольно наносим на схему номера и направления 4-х неизвестных токов I1, I2 , I3, I4..

3. Обозначаем на схеме контура I, II, III и произвольно выбираем направления их обхода и контурные токи в них I11, I22, I33.

4. Записываем выражения для токов в ветвях через контурные токи:

 

I1=I11+I33, I2=I11- I22, I3= I22+ I33, I4= I22, I5= J

5. Составляем уравнения по второму правилу Кирхгофа для тех контуров, токи в которых неизвестны (для контуров без источника тока):

I1R1 + I2R2 = E1, I3R1 – I2R2 +I4(R4+R6) = E2

6. В этой системе заменяем токи в ветвях выражениями, полученными в пункте 4:

 

R3(I11 + I33) + R2(I11 – I22) = E1

R1(I22+I33) – R2(I11- I22) + I22(R4+R6) = E2

7. Подставим заданные числовые значения сопротивлений и ЭДС и после приведения подобных получим простую систему уравнений:

 

2I11 – I22 = 3А, 5I22 - 2I11= 1Аоткуда I11 = 2A, I22 = 1A

8. Подставим эти значения контурных токов в уравнений в п. 4 и окончательно получаем:

I1 = 3A, I2 = 1A, I3 = 2A, I4 = 1A

Похожие статьи:

poznayka.org

Метод контурных токов - ТОЭ, РЗА

Если цепь имеет N узлов и К независимых контуров, то для расчета токов на всех участках такой цепи правила Кирхгофа дают (N−1)+К  уравнений. Метод узловых потенциалов позволяет обойтись системой лишь (N−1) уравнений, т. е. сколько дает первое правило Кирхгофа. Метод контурных токов приводит к К уравнениям, т. е. сколько дает лишь второе правило Кирхгофа. Этот метод состоит в следующем.

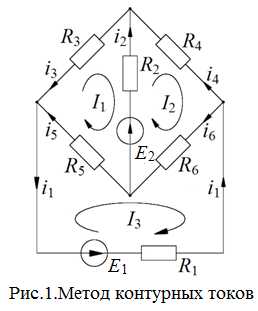 Пусть цепь имеет К независимых контуров. Каждому из них ставится в соответствие некоторый ток In (n= 1, 2, …, К), постоянный вдоль всего контура. Такие токи называются контурными. Удобно все контурные токи направлять одинаково, скажем, по часовой стрелке. Рассмотрим, для определенности, мостовую схему, что на рис. 1. Она имеет три независимых контура (выберем их простыми), следовательно, в ней задаются три контурных тока: I1, I2, I3 (рис.5). При одинаковом направлении контурных токов, истинные токи в смежных ветвях (i2, i5 и i6) будут равны разностям двух соседних контурных токов, а в ветвях, не являющихся смежными, истинные токи (i1, i3 и i4) будут совпадать с контурными.

Для изображенной на рис. 1 схемы второе правило Кирхгофа для контурных токов дает:

или:

Решая эту систему уравнений, получим три неизвестных контурных тока : I1, I2 и I3. Затем определяем истинные токи в ветвях с их знаками относительно выбранных стрелок:

i1 = − I3,     i2 = I2 − I1,

i3 = −I1,     i4 = −I2,

i5 = I1 − I3,  i6 = I2 − I3.

Следует отметить, что в методе контурных токов первое правило Кирхгофа выполняется автоматически, в силу самой идеи метода. Действительно, например, для представленной на рис. 1 схемы:

Выбор того или иного метода расчета зависит от конкретного графа (сетки) электрической цепи: если граф таков, что в нем много контуров, но мало узлов, то удобно пользоваться методом узловых потенциалов, в противном случае – методом контурных токов. 

 

Возможно Вам будет полезна следующая статья по теме:

elekt.com.ua

---

• 
  Создание тсн пошаговая инструкция 2018 год с документами
• 
  Как переделать автомобильный генератор на 220 вольт
• 
  Разбилась энергосберегающая лампочка что делать
• 
  Газ природный где используется
• 
  Типы двигателей асинхронных
• 
  Применение магнитных полей
• 
  Сечение диаметр таблица
• 
  Высоковольтный конденсатор как проверить
• 
  Аэс мощность
• 
  Тор трансформатор
• 
  Гарантирующий поставщик водоснабжения это