11. Последовательное, параллельное и смешанное соединения резисторов. Мощность резисторов при параллельном и последовательном соединении. Мощность резисторов при последовательном соединении
Содержание:
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов. Свойства и технические характеристики резисторовКак уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств. Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное. На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления. Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%. Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления. Для соединения резисторов в схемах используются три разных способа подключения - параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях. Мощность при последовательном соединениеПри соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом. Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I2 x R = 0,2562 x 390 = 25,55 Вт. Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт. Мощность при параллельном соединениеПри параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же. Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P1 = U2/R1 = 1002/200 = 50 Вт; P2 = U2/R2 = 1002/100 = 100 Вт; P3 = U2/R3 = 1002/51 = 195,9 Вт; P4 = U2/R4 = 1002/39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт. Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты. |
xn--90adflmiialse2m.xn--p1ai
§ 11. Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Рис. 25. Схемы последовательного соединения приемников
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходитодин и тот же ток I.Последовательное соединение приемников поясняет рис. 25, а..Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк (19)
где Rэк = R1 + R2 + R3.Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то длярассматриваемой цепи
U = U1 + U2 +U3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U1 : U2 : U3 = R1 : R2 : R3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
U1 = U/n. (22)
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Рис. 27. Схемы смешанного соединения приемников
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
electrono.ru
Как определить мощность резисторов. Мощность резисторов при параллельном соединении
Все электронные устройства содержат резисторы, являющиеся их основным элементом. С его помощью изменяют величину тока в электрической цепи. В статье приведены свойства резисторов и методы расчёта их мощности.
Назначение резистора
Для регулировки тока в электрических цепях применяются резисторы. Это свойство определено законом Ома:
I=U/R (1)
Из формулы (1) хорошо видно, что чем меньше сопротивление, тем сильнее возрастает ток, и наоборот, чем меньше величина R, тем больше ток. Именно это свойство электрического сопротивления используется в электротехнике. На основании этой формулы создаются схемы делителей тока, широко применяющиеся в электротехнических устройствах.
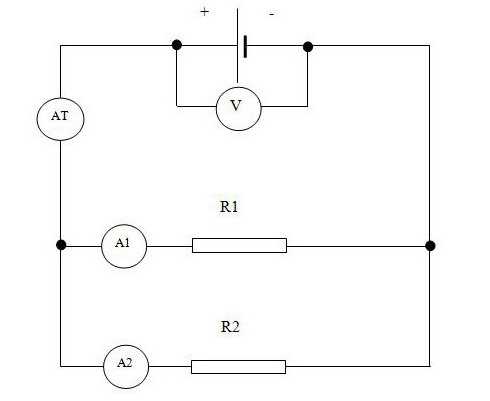
В этой схеме ток от источника делится на два, обратно пропорциональных сопротивлениям резисторов.
Кроме регулировки тока, резисторы используются в делителях напряжения. В этом случае опять используется закон Ома, но немного в другой форме:
U=I∙R (2)
Из формулы (2) следует, что при увеличении сопротивления увеличивается напряжение. Это свойство используется для построения схем делителей напряжения.

Из схемы и формулы (2) ясно, что напряжения на резисторах распределяются пропорционально сопротивлениям.
Изображение резисторов на схемах
По стандарту резисторы изображаются прямоугольником с размерами 10 х 4 мм и обозначаются буквой R. Часто указывается мощность резисторов на схеме. Изображение этого показателя выполняется косыми или прямыми чёрточками. Если мощность более 2 Ватт, то обозначение производится римскими цифрами. Обычно это делается для проволочных резисторов. В некоторых государствах, например в США, применяются другие условные обозначения. Для облегчения ремонта и анализа схемы часто приводится мощность резисторов, обозначение которых выполняется по ГОСТ 2.728-74.
Технические характеристики устройств
Основная характеристика резистора – номинальное сопротивление Rн, которое указывается на схеме возле резистора и на его корпусе. Единица измерения сопротивления – ом, килоом и мегаом. Изготавливаются резисторы с сопротивлением от долей ома и до сотен мегаомов. Существует немало технологий производства резисторов, все они имеют и преимущества, и недостатки. В принципе, не существует технологии, которая позволила бы абсолютно точно изготавливать резистор с заданным значением сопротивления.
Второй важной характеристикой является отклонение сопротивления. Оно измеряется в % от номинального R. Существует стандартный ряд отклонения сопротивления: ±20, ±10, ±5, ±2, ±1% и далее вплоть до значения ±0,001%.
Следующей важной характеристикой является мощность резисторов. При работе они нагреваются от проходящего по ним тока. Если рассеиваемая мощность будет превышать допустимое значение, то устройство выйдет из строя.
Резисторы при нагревании изменяют своё сопротивление, поэтому для устройств, работающих в широком диапазоне температур, вводится ещё одна характеристика – температурный коэффициент сопротивления. Он измеряется в ppm/°C, то есть 10-6 Rн/°C (миллионная часть от Rн на 1°C).
Последовательное соединение резисторов
Резисторы могут соединяться тремя разными способами: последовательным, параллельным и смешанным. При последовательном соединении ток поочерёдно проходит через все сопротивления.
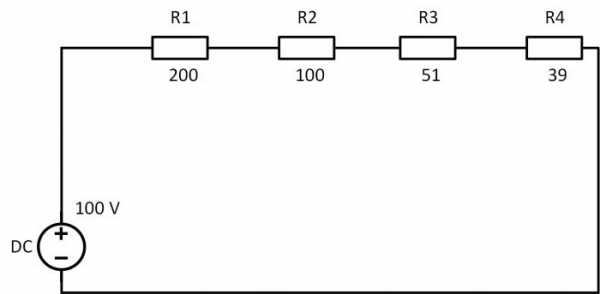
При таком соединении ток в любой точке цепи один и тот же, его можно определить по закону Ома. Полное сопротивление цепи в этом случае равно сумме сопротивлений:
R=200+100+51+39=390 Ом;
I=U/R=100/390=0,256 А.
Теперь можно определить мощность при последовательном соединении резисторов, она рассчитывается по формуле:
P=I2∙R= 0,2562∙390=25,55 Вт.
Аналогично определяется мощность остальных резисторов:
P1= I2∙R1=0,2562∙200=13,11 Вт;
P2= I2∙R2=0,2562∙100=6,55 Вт;
P3= I2∙R3=0,2562∙51=3,34 Вт;
P4= I2∙R4=0,2562∙39=2,55 Вт.
Если сложить мощность резисторов, то получится полная P:
P=13,11+6,55+3,34+2,55=25,55 Вт.
Параллельное соединение резисторов
При параллельном соединении все начала резисторов подключаются к одному узлу схемы, а концы – к другому. При таком соединении ток разветвляется и течёт по каждому устройству. Величина тока, согласно закону Ома, обратно пропорциональна сопротивлениям, а напряжение на всех резисторах одинаково.

Прежде чем найти ток, нужно рассчитать полную проводимость всех резисторов по общеизвестной формуле:
1/R=1/R1+1/R2+1/R3+1/R4=1/200+1/100+1/51+1/39=0,005+0,01+0,0196+0,0256= 0,06024 1/Ом.
Сопротивление – величина, обратная проводимости:
R=1/0,06024= 16,6 Ом.
Воспользовавшись законом Ома, находят ток через источник:
I= U/R=100∙0,06024=6,024 A.
Зная ток через источник, находят мощность параллельно соединённых резисторов по формуле:
P=I2∙R=6,0242∙16,6=602,3 Вт.
По закону Ома рассчитывается ток через резисторы:
I1=U/R1=100/200=0,5 А;
I2=U/R2=100/100=1 А;
I3=U/R1=100/51=1,96 А;
I1=U/R1=100/39=2,56 А.
Немного по другой формуле можно рассчитать мощность резисторов при параллельном соединении:
P1= U2/R1=1002/200=50 Вт;
P2= U2/R2=1002/100=100 Вт;
P3= U2/R3=1002/51=195,9 Вт;
P4= U2/R4=1002/39=256,4 Вт.
Если всё это сложить, то получится мощность всех резисторов:
P= P1+ P2+ P3+ P4=50+100+195,9+256,4=602,3 Вт.
Смешанное соединение
Схемы со смешанным соединением резисторов содержат последовательное и одновременно параллельное соединение. Эту схему несложно преобразовать, заменив параллельное соединение резисторов последовательным. Для этого заменяют сначала сопротивления R2 и R6 на их общее R2,6, используя формулу, приведённую ниже:
R2,6=R2∙R6/R2+R6.
Точно так же заменяются два параллельных резистора R4, R5 одним R4,5:
R4,5=R4∙R5/R4+R5.
В результате получается новая, более простая схема. Обе схемы приведены ниже.
Мощность резисторов на схеме со смешанным соединением определяется по формуле:
P=U∙I.
Для расчёта по этой формуле сначала находят напряжение на каждом сопротивлении и величину тока через него. Можно использовать другой метод, чтобы определить мощность резисторов. Для этого используется формула:
P=U∙I=(I∙R)∙I=I2∙R.
Если известно только напряжение на резисторах, то применяют другую формулу:
P=U∙I=U∙(U/R)=U2/R.
Все три формулы часто используются на практике.
Расчёт параметров схемы
Расчёт параметров схемы заключается в нахождении неизвестных токов и напряжений всех ветвей на участках электрической цепи. Имея эти данные, можно рассчитать мощность каждого резистора, входящего в схему. Простые методы расчёта были показаны выше, на практике же дело обстоит сложнее.
В реальных схемах часто встречается соединение резисторов звездой и треугольником, что создаёт значительные трудности при расчётах. Для упрощения таких схем были разработаны методы преобразования звезды в треугольник, и наоборот. Этот метод проиллюстрирован на схеме, представленной ниже:
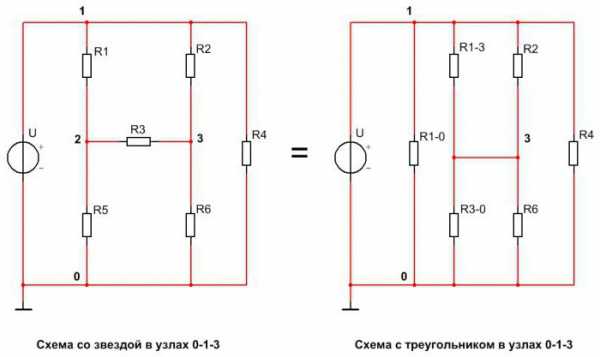
Первая схема имеет в своём составе звезду, подключенную к узлам 0-1-3. К узлу 1 подсоединён резистор R1, к узлу 3 – R3, а к узлу 0 – R5. На второй схеме к узлам 1-3-0 подключены резисторы треугольника. К узлу 1 подключены резисторы R1-0 и R1-3, к узлу 3 – R1-3 и R3-0, а к узлу 0 – R3-0 и R1-0. Эти две схемы полностью эквивалентны.
Для перехода от первой схемы ко второй рассчитываются сопротивления резисторов треугольника:
R1-0=R1+R5+R1∙R5/R3;
R1-3=R1+R3+R1∙R3/R5;
R3-0=R3+R5+R3∙R5/R1.
Дальнейшие преобразования сводятся к вычислению параллельно и последовательно соединённых сопротивлений. Когда будет найдено полное сопротивление цепи, находят по закону Ома ток через источник. Используя этот закон, несложно найти токи во всех ветвях.
Как определить мощность резисторов после нахождения всех токов? Для этого используют общеизвестную формулу: P=I2∙R, применяя её для каждого сопротивления, найдём их мощности.
Экспериментальное определение характеристик элементов схемы
Для экспериментального определения нужных характеристик элементов требуется собрать заданную схему из реальных компонентов. После этого с помощью электроизмерительных приборов выполняют все необходимые измерения. Этот метод трудоёмкий и дорогостоящий. Разработчики электрических и электронных устройств для этой цели используют моделирующие программы. С помощью них производятся все необходимые вычисления, и моделируется поведение элементов схемы в различных ситуациях. Только после этого собирается опытный образец технического устройства. Одной из таких распространённых программ является мощная система моделирования Multisim 14.0 фирмы National Instruments.
Как определить мощность резисторов с помощью этой программы? Это можно сделать двумя методами. Первый метод – это измерить ток и напряжение с помощью амперметра и вольтметра. Перемножив результаты измерений, получают искомую мощность.

Из этой схемы определяем мощность сопротивления R3:
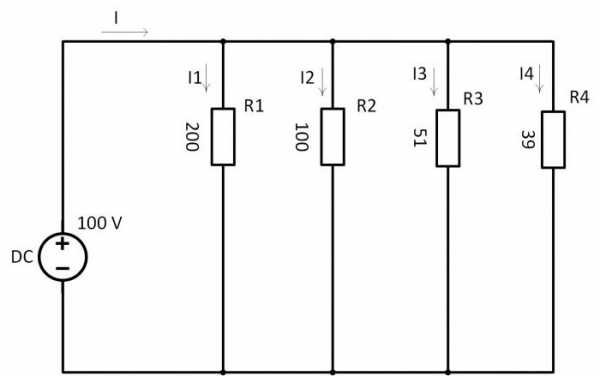
P3=U∙I=1,032∙0,02=0,02064 Вт=20,6 мВт.
Второй метод – это непосредственное измерение мощности при помощи ваттметра.
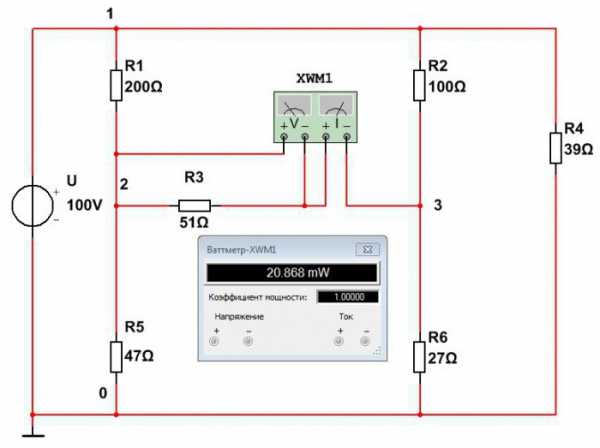
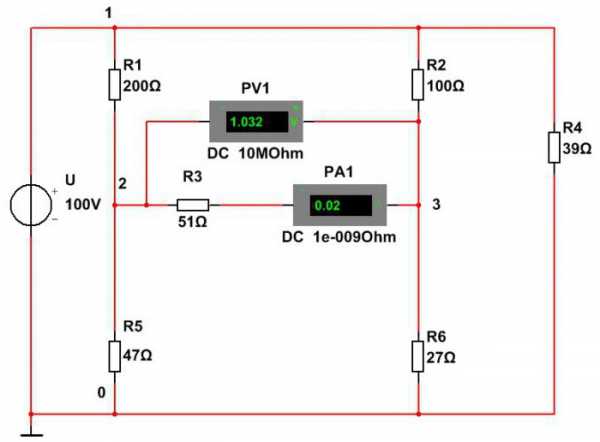
Из этой схемы видно, что мощность сопротивления R3 равна P3=20,8 мВт. Расхождение из-за погрешности в первом методе больше. Точно так же определяются мощности остальных элементов.
загрузка...
worldfb.ru
Последовательное соединение сопротивлений (резисторов) | Электрикам
Если несколько резисторов (или приемников энергии) соединены один за другим без разветвлений (рис. 1) и по ним проходит один и тот же ток, то они образуют одну ветвь, такое соединение резисторов называется последовательным.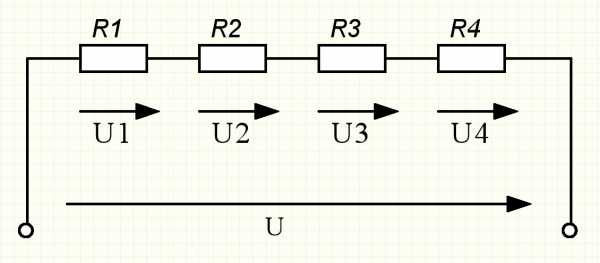
R = R1+R2+R3…+Rn; (1)
U = U1+U2+U3…+Un; (2)
I = I1 = I2 = I3 = In; (3)
P = P1 + P2 +P3…+Pn; (4)
Доказательство
Согласно закону Ома напряжения на резисторах или падения напряжения определяются выражениями
U1 = I*R1; U2 = I*R2; U3 = I*R3; U4 = I*R4;
Таким образом, падения напряжения на последовательно соединенных резисторах пропорциональны значениям их сопротивлений.
Так же мы знаем что при последовательном соединении напряжение на всём участке цепи равно сумме падения напряжения на каждом элементе последовательной цепи.
U = U1+U2+U3…+Un; (2)
Ряд последовательно соединенных резисторов можно заменить эквивалентным (общим) сопротивлением R, причем так, чтобы эта замена при неизменном напряжении на выводах соединения не вызвала изменения тока в цепи. Разделив на ток правую и левую части уравнения (2), получим
откуда следует, что эквивалентное сопротивление ряда последовательно соединенных резисторов равно сумме их сопротивлений.
Из предыдущего выражения, умножая его на I², находим, что
R1*I² + R2*I² +R3*I² +Rn*I² = R*I²;
P1 + P2 + P3 + Pn = P ;
т. е мощность, развиваемая в эквивалентном резисторе, равна сумме мощностей всех резисторов. При последовательном соединении резисторов ток в них один и тот же, поэтому мощности, развиваемые в отдельных участках (P = R*I²), пропорциональны их сопротивлениям.
electrikam.com
11. Последовательное, параллельное и смешанное соединения резисторов. Мощность резисторов при параллельном и последовательном соединении
ГлавнаяМощностьМощность резисторов при параллельном и последовательном соединении11. Последовательное, параллельное и смешанное соединения резисторов.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго - с
началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.
Последовательное соединение приемников поясняет рис. 19,а. Заменяя лампы резисторами с сопротивлениямиR1, R2 и R3 получим схему, показанную на рис. 19,б.Если принять, что в источнике R0 = 0, то для трех последова-тельно соединенных резисторов согласно второму Кирхгофа можно написать:
E = IR1 +IR2 +IR3 = I( R1+ R2+ R3 ) = IRобщ ;
где: Rобщ = R1+ R2+ R3
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.
Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Соединять последовательно целесообразно только приемники с одинаковыми сопротивлениями. В противном случае приложенное напряжение источника электрической энергии распределяется между ними неравномерно и отдельные приемники могут оказаться под недопустимо высоким для них напряжением.
При последовательном соединении приемников изменение сопротивления одного из них влечет за собой изменение напряжения на других связанных с ним приемниках. При обрыве электрической цепи в одном из приемников в остальных прекращается ток.
При параллельном соединении приемники включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 20,а). Заменяя лампы резисторами с сопро-тивлениями R1, R2 и R3, получим схему, показанную на рис. 20,б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжениеU. Поэтому согласно закону Ома:
I1 = U/R1, I2 =U/R2 , I3 = U/R3
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I=I1+I2 +I3 или
I= U/R1 + U/R2 + U/R3 = U (1/ R1 + 1/ R2+ 1/ R3) = U/Rэкв
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/ Rэкв= 1/ R1 + 1/ R2+ 1/ R3
При увеличении числа параллельно включаемых резисторов результирующее сопротивление уменьшается.
При параллельном соединении приемников все они находятся под одним и тем же напряжением и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.
Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом
преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую.
studfiles.net
Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская? - Ну, Света наверное. - Вот! А мне, как кладовщику, видится немного другое: "поблядушка обыкновенная" - 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме? - С Божьей помощью, батюшка! С Божьей помощью...»
Ну да ладно, достаточно! Шутки - штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю - где надо...», а заодно набросаю пару-тройку калькуляторов на заданную тему.
Итак. При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках. Поясним рисунком с распределением напряжений, токов и формулами.
 Рис.1
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными. Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить... Короче, все вводные, помеченные * - к заполнению не обязательны.
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ проводников
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности. Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными. Почему переменными? А потому, что для постоянных значений этих величин - сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек - ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи - подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук. Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2+....+ Сn и 1/L = 1/L1+ 1/L2 +...+ 1/Ln для параллельных цепей и L = L1 + L2 +....+ Ln и 1/С = 1/С1+ 1/С2+...+ 1/Сn для последовательных.
Как и в предыдущей таблице вводные, помеченные * - к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ конденсаторов
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ катушек
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.
vpayaem.ru
Последовательное и параллельное соединение резисторов
Последовательное и параллельное соединение резисторов
П
xn----7sbeb3bupph.xn--p1ai
Как определить мощность резисторов. Мощность резисторов при параллельном соединении
Технологии 6 марта 2016Все электронные устройства содержат резисторы, являющиеся их основным элементом. С его помощью изменяют величину тока в электрической цепи. В статье приведены свойства резисторов и методы расчёта их мощности.
Назначение резистора
Для регулировки тока в электрических цепях применяются резисторы. Это свойство определено законом Ома:
I=U/R (1)
Из формулы (1) хорошо видно, что чем меньше сопротивление, тем сильнее возрастает ток, и наоборот, чем меньше величина R, тем больше ток. Именно это свойство электрического сопротивления используется в электротехнике. На основании этой формулы создаются схемы делителей тока, широко применяющиеся в электротехнических устройствах.

В этой схеме ток от источника делится на два, обратно пропорциональных сопротивлениям резисторов.
Кроме регулировки тока, резисторы используются в делителях напряжения. В этом случае опять используется закон Ома, но немного в другой форме:
U=I∙R (2)
Из формулы (2) следует, что при увеличении сопротивления увеличивается напряжение. Это свойство используется для построения схем делителей напряжения.
Из схемы и формулы (2) ясно, что напряжения на резисторах распределяются пропорционально сопротивлениям.
Изображение резисторов на схемах
По стандарту резисторы изображаются прямоугольником с размерами 10 х 4 мм и обозначаются буквой R. Часто указывается мощность резисторов на схеме. Изображение этого показателя выполняется косыми или прямыми чёрточками. Если мощность более 2 Ватт, то обозначение производится римскими цифрами. Обычно это делается для проволочных резисторов. В некоторых государствах, например в США, применяются другие условные обозначения. Для облегчения ремонта и анализа схемы часто приводится мощность резисторов, обозначение которых выполняется по ГОСТ 2.728-74.
Видео по теме
Технические характеристики устройств
Основная характеристика резистора – номинальное сопротивление Rн, которое указывается на схеме возле резистора и на его корпусе. Единица измерения сопротивления – ом, килоом и мегаом. Изготавливаются резисторы с сопротивлением от долей ома и до сотен мегаомов. Существует немало технологий производства резисторов, все они имеют и преимущества, и недостатки. В принципе, не существует технологии, которая позволила бы абсолютно точно изготавливать резистор с заданным значением сопротивления.
Второй важной характеристикой является отклонение сопротивления. Оно измеряется в % от номинального R. Существует стандартный ряд отклонения сопротивления: ±20, ±10, ±5, ±2, ±1% и далее вплоть до значения ±0,001%.
Следующей важной характеристикой является мощность резисторов. При работе они нагреваются от проходящего по ним тока. Если рассеиваемая мощность будет превышать допустимое значение, то устройство выйдет из строя.
Резисторы при нагревании изменяют своё сопротивление, поэтому для устройств, работающих в широком диапазоне температур, вводится ещё одна характеристика – температурный коэффициент сопротивления. Он измеряется в ppm/°C, то есть 10-6 Rн/°C (миллионная часть от Rн на 1°C).
Последовательное соединение резисторов
Резисторы могут соединяться тремя разными способами: последовательным, параллельным и смешанным. При последовательном соединении ток поочерёдно проходит через все сопротивления.

При таком соединении ток в любой точке цепи один и тот же, его можно определить по закону Ома. Полное сопротивление цепи в этом случае равно сумме сопротивлений:
R=200+100+51+39=390 Ом;
I=U/R=100/390=0,256 А.
Теперь можно определить мощность при последовательном соединении резисторов, она рассчитывается по формуле:
P=I2∙R= 0,2562∙390=25,55 Вт.
Аналогично определяется мощность остальных резисторов:
P1= I2∙R1=0,2562∙200=13,11 Вт;
P2= I2∙R2=0,2562∙100=6,55 Вт;
P3= I2∙R3=0,2562∙51=3,34 Вт;
P4= I2∙R4=0,2562∙39=2,55 Вт.
Если сложить мощность резисторов, то получится полная P:
P=13,11+6,55+3,34+2,55=25,55 Вт.
Параллельное соединение резисторов
При параллельном соединении все начала резисторов подключаются к одному узлу схемы, а концы – к другому. При таком соединении ток разветвляется и течёт по каждому устройству. Величина тока, согласно закону Ома, обратно пропорциональна сопротивлениям, а напряжение на всех резисторах одинаково.
Прежде чем найти ток, нужно рассчитать полную проводимость всех резисторов по общеизвестной формуле:
1/R=1/R1+1/R2+1/R3+1/R4=1/200+1/100+1/51+1/39=0,005+0,01+0,0196+0,0256= 0,06024 1/Ом.
Сопротивление – величина, обратная проводимости:
R=1/0,06024= 16,6 Ом.
Воспользовавшись законом Ома, находят ток через источник:
I= U/R=100∙0,06024=6,024 A.
Зная ток через источник, находят мощность параллельно соединённых резисторов по формуле:
P=I2∙R=6,0242∙16,6=602,3 Вт.
По закону Ома рассчитывается ток через резисторы:
I1=U/R1=100/200=0,5 А;
I2=U/R2=100/100=1 А;
I3=U/R1=100/51=1,96 А;
I1=U/R1=100/39=2,56 А.
Немного по другой формуле можно рассчитать мощность резисторов при параллельном соединении:
P1= U2/R1=1002/200=50 Вт;
P2= U2/R2=1002/100=100 Вт;
P3= U2/R3=1002/51=195,9 Вт;
P4= U2/R4=1002/39=256,4 Вт.
Если всё это сложить, то получится мощность всех резисторов:
P= P1+ P2+ P3+ P4=50+100+195,9+256,4=602,3 Вт.
Смешанное соединение
Схемы со смешанным соединением резисторов содержат последовательное и одновременно параллельное соединение. Эту схему несложно преобразовать, заменив параллельное соединение резисторов последовательным. Для этого заменяют сначала сопротивления R2 и R6 на их общее R2,6, используя формулу, приведённую ниже:
R2,6=R2∙R6/R2+R6.
Точно так же заменяются два параллельных резистора R4, R5 одним R4,5:
R4,5=R4∙R5/R4+R5.
В результате получается новая, более простая схема. Обе схемы приведены ниже.
Мощность резисторов на схеме со смешанным соединением определяется по формуле:
P=U∙I.
Для расчёта по этой формуле сначала находят напряжение на каждом сопротивлении и величину тока через него. Можно использовать другой метод, чтобы определить мощность резисторов. Для этого используется формула:
P=U∙I=(I∙R)∙I=I2∙R.
Если известно только напряжение на резисторах, то применяют другую формулу:
P=U∙I=U∙(U/R)=U2/R.
Все три формулы часто используются на практике.
Расчёт параметров схемы
Расчёт параметров схемы заключается в нахождении неизвестных токов и напряжений всех ветвей на участках электрической цепи. Имея эти данные, можно рассчитать мощность каждого резистора, входящего в схему. Простые методы расчёта были показаны выше, на практике же дело обстоит сложнее.
В реальных схемах часто встречается соединение резисторов звездой и треугольником, что создаёт значительные трудности при расчётах. Для упрощения таких схем были разработаны методы преобразования звезды в треугольник, и наоборот. Этот метод проиллюстрирован на схеме, представленной ниже:

Первая схема имеет в своём составе звезду, подключенную к узлам 0-1-3. К узлу 1 подсоединён резистор R1, к узлу 3 – R3, а к узлу 0 – R5. На второй схеме к узлам 1-3-0 подключены резисторы треугольника. К узлу 1 подключены резисторы R1-0 и R1-3, к узлу 3 – R1-3 и R3-0, а к узлу 0 – R3-0 и R1-0. Эти две схемы полностью эквивалентны.
Для перехода от первой схемы ко второй рассчитываются сопротивления резисторов треугольника:
R1-0=R1+R5+R1∙R5/R3;
R1-3=R1+R3+R1∙R3/R5;
R3-0=R3+R5+R3∙R5/R1.
Дальнейшие преобразования сводятся к вычислению параллельно и последовательно соединённых сопротивлений. Когда будет найдено полное сопротивление цепи, находят по закону Ома ток через источник. Используя этот закон, несложно найти токи во всех ветвях.
Как определить мощность резисторов после нахождения всех токов? Для этого используют общеизвестную формулу: P=I2∙R, применяя её для каждого сопротивления, найдём их мощности.
Экспериментальное определение характеристик элементов схемы
Для экспериментального определения нужных характеристик элементов требуется собрать заданную схему из реальных компонентов. После этого с помощью электроизмерительных приборов выполняют все необходимые измерения. Этот метод трудоёмкий и дорогостоящий. Разработчики электрических и электронных устройств для этой цели используют моделирующие программы. С помощью них производятся все необходимые вычисления, и моделируется поведение элементов схемы в различных ситуациях. Только после этого собирается опытный образец технического устройства. Одной из таких распространённых программ является мощная система моделирования Multisim 14.0 фирмы National Instruments.
Как определить мощность резисторов с помощью этой программы? Это можно сделать двумя методами. Первый метод – это измерить ток и напряжение с помощью амперметра и вольтметра. Перемножив результаты измерений, получают искомую мощность.
Из этой схемы определяем мощность сопротивления R3:
P3=U∙I=1,032∙0,02=0,02064 Вт=20,6 мВт.
Второй метод – это непосредственное измерение мощности при помощи ваттметра.
Из этой схемы видно, что мощность сопротивления R3 равна P3=20,8 мВт. Расхождение из-за погрешности в первом методе больше. Точно так же определяются мощности остальных элементов.
Источник: fb.rumonateka.com
Последовательное соединение резисторов
Господа, наш сегодняшний материал посвящен рассмотрению последовательного соединения резисторов. На практике сплошь и рядом соединяют резисторы друг с другом тем или иным способом для достижения той или иной цели, поэтому весьма важно хорошо разбираться в этом вопросе.
Начинаем сразу с определений. Всего есть два вида соединения сопротивлений: последовательное и параллельное. Взгляните на рисунок 1, там наглядно представлены эти виды соединений.
А) – Последовательное соединение
В) – Параллельное соединение
Рисунок 1 – Последовательное и параллельное соединение
Что мы видим на рисунке 1?
А то, что последовательное соединение – это такое соединение, при котором конец первого резистора совпадает с началом второго, конец второго с началом третьего и т.д.
Параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.
В этой статье мы попробуем подробнее проанализировать на основе уже имеющихся знаний последовательное сопротивление. Параллельное же будет в другой статье. Взглянем на рисунок 2. Там подробно разрисовано положение дел для последовательного соединения резисторов.

Рисунок 2 – Последовательное соединение резисторов
Господа, как вы видите из рисунка 2, при последовательном соединении резисторов у нас нет никаких узлов в схеме. То есть ток нигде никуда не ответвляется. Из этого можно сделать вывод, что при последовательном соединении резисторов через все резисторы течет один и тот же ток I. То есть этот ток величиной I втекает в первый резистор R1, проходит через всю цепочку, вытекает из резистора R3 и течет дальше. При этом его величина неизменна для всех резисторов.
С напряжением все не так просто. Сейчас нам понадобиться вспомнить статью про потенциалы. Положим, что на входе резистора R1 у нас потенциал φ1, точка соединения резисторов R1 и R2 имеет потенциал φ2, точка соединения резисторов R2 и R3 имеет потенциал φ3, а конец резистора R3 имеет потенциал φ4. Короче, лучше смотрите рисунок 2, там все эти потенциалы нарисованы . Дальше вспомним утверждение, что напряжение – это разность потенциалов. То есть разность потенциалов между концами резистора R1 – это напряжение на резисторе R1, ну и так для всех. Запишем это
Сложим левые и правые части этих трех уравнений. Получим
Ну и общее напряжение на всех трех резисторах тоже запишем через разность потенциалов
Сравнивая это выражение и предыдущее, приходим к выводу, что
Да, приложенное к цепочке последовательно соединенных резисторов напряжение равно сумме напряжений на всех резисторах этой цепочки. Напряжение делится между всеми резисторами: на каком-то оно будет побольше, на каком-то поменьше. А в сумме оно будет равно приложенному к цепочке напряжению.
Рассмотрим пример. Допустим, что к нашей цепочке из трех резисторов проложено напряжение U=100 В. Значит, возможна ситуация, когда на резисторах R1, R2 и R3 падает 20 В, 37 В и 43 В (в сумме тоже 100 В). А ситуация, когда на резисторах R1, R2 и R3 падает 50 В, 44 В и 78 В (в сумме 172 В) невозможна. Точно также невозможна ситуация, когда на них падает 10 В, 13 В и 32 В (в сумме 55 В). То есть, если к цепочке последовательно соединенных резисторов приложено 100 В, то суммарное напряжение на всех резисторах тоже должно быть 100 В – не больше и не меньше! Как же именно распределено напряжение между резисторами? Ответ на этот вопрос даст все тот же закон Ома, который не раз нас уже выручал! Согласно закону Ома напряжение на резисторе равно произведению силы тока через него на сопротивление этого резистора. Мы знаем сопротивление данного резистора и ток через него. Поэтому легко находим напряжения на всех резисторах
Едем дальше. Воспользуемся этими соотношениями соотношением и с помощью них преобразуем нашу формулку с суммами напряжений. При этом помним, что через все резисторы у нас течет один и тот же ток I.
Разделим левую и правую часть уравнения на I:
Все та же статья про закон Ома говорит нам, что сопротивление равно напряжение разделить на ток. Поэтому мы можем записать
где R – общее сопротивление нашей цепи из трех резисторов.
Итак, господа, мы получили важное соотношение: при последовательном соединении резисторов общее сопротивление схемы равно сумме отдельных сопротивлений. Запомните это соотношение, оно весьма важное! В чем же его практический смысл? Взгляните на рисунок 3
Рисунок 3 – Последовательное соединение
На нем показано, что цепочку из нескольких (в данном случае из 3-х) последовательно соединенных резисторов для упрощения расчетов вполне можно заменить одним резистором с сопротивлением, равным сумме отдельных резисторов. В связи с этим выводом возможно возникновение вопроса: а зачем вообще на практике соединяют резисторы последовательно, если в конечном счете все можно свести к одному резистору? Господа, причин несколько и основные мы сейчас рассмотрим.
1) Резисторы соединяются последовательно в схемах так называемых делителей напряжения. Кто знает, что это такое – отлично, кто нет – чуть позже разберемся в этом вопросе .
2) Последовательное сопротивление резисторов сплошь и рядом применяется в высоковольтной технике. Господа, к резистору можно прикладывать безболезненно для него отнюдь не бесконечно большое напряжение. Максимально допустимое напряжение, которое можно приложить к резистору, всегда прописывается в документации на данный конкретный резистор и его обязательно надо принимать в расчет при выборе резистора в своей схеме. В большинстве своем предельное напряжение ограничено несколькими десятками-сотнями вольт. А как быть, если мы имеем дело с напряжением в тысячи или десятки тысяч вольт? Правильно, резисторы можно соединить последовательно. Как мы помним, при таком соединении общее приложенное напряжение распределяется между резисторами и на каждый из них придется только часть общего.
Рассмотрим конкретный пример. Скажем, у нас есть высоковольтный источник, который формирует напряжение 5 кВ. И нам надо подобрать под него такую нагрузку, чтобы обеспечить ток в 1 мА.
Будем применять резисторы Р1-12-0,25. Это резисторы, рассчитанные на поверхностный монтаж, и они выдерживают напряжение 200 В. Рассчитаем требуемое количество резисторов как отношение напряжения 5 кВ к максимальному напряжению на один резистор 200 В. При расчете обязательно будем использовать коэффициент запаса равный, скажем, 1,25. Это очень примерная и часто компромиссная величина, но какой-то он обязательно должен быть, никогда нельзя работать на пределе. Итак, нам надо использовать
По закону Ома (зная напряжение источника и ток, который необходимо обеспечить) рассчитываем, какое суммарное сопротивление должно быть у этой цепочки резисторов.
Теперь остается только лишь найти сопротивление каждого резистора в этой цепочке
В принципе, этот номинал резистора доступен в номинальном ряду Е192 и его можно купить. Если же именно такого номинала нет в наличии, то берется ближайший доступный и после этого пересчитывается общее сопротивление и при необходимости уточняется количество резисторов.
В заключении надо обязательно проверить, какая мощность будет выделяться на каждом из резисторов в такой схеме. Как мы помним из статьи про мощность ее можно посчитать, например, так:
Один резистор Р1-12-0,25 без проблем рассеивает 0,25 Вт, то есть нашим резисторам перегрев не угрожает.
Итак, для обеспечения тока в 1 мА у источника с напряжением 5 кВ требуется использовать 32 резистора Р1-12-0,25-156 кОм.
Мда, что-то я увлекся рассказом про высоковольтные нагрузки . Это можно объяснить тем, что одно время я плотно работал в отделе разработки высоковольтной техники. Это были очень крутые годы . Есть что вспомнить, есть что рассказать. Немного жаль, что обстоятельства вынудили сменить место работы, но и попробовать себя в новой области тоже интересно…ладно, едем дальше!
3) Последовательное соединение резисторов можно использовать для распределения мощности источника. Иными словами, мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на последовательно соединенных резисторах. В этом легко убедиться. Надеюсь, вы еще не забыли вот это выражение?
Умножим левую и правую части на ток I
Или, другими словами
где Р – мощность, выдаваемая источником;
P1 – мощность, рассеиваемая на резисторе R1;
P2 – мощность, рассеиваемая на резисторе R2;
P3 – мощность, рассеиваемая на резисторе R3;
Как это можно применить? Допустим вот так. Нам, скажем, нужно 1 Вт мощности для обогрева домика нашему хомячку в зимние холода, или еще для чего-то, не важно. У нас на руках есть только резисторы Р1-12-0,25, которые, как мы помним, выдерживают только 0,25 Вт. Как же снять с источника питания 1 Вт без вреда для резисторов? Как вариант, соединив последовательно 4 резистора, подобрав их так, что бы на каждом было 0,25 Вт. В сумме на них будет выделяться как раз-таки 1 Вт. Конечно, помня про коэффициент запаса, лучше брать не 4, а хотя бы 5 резисторов, рассеивая на каждом не 0,25, а 0,2 Вт. Не надо работать на пределе, пусть будет какой-то запас всегда.
Наверняка, можно придумать еще варианты применений последовательного соединения резисторов, но, основные мы рассмотрели. Спасибо что прочитали, огромной вам всем удачи и – пока!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
myelectronix.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.