Мощности в цепях переменного тока
Расчетные формулы для цепей однофазного тока
1. Мгновенное значение мощности в цепи с активным сопротивлением r, Вт:
Среднее значение активной мощности в цепи с активным сопротивлением г, Вт:
2. Цепи с чисто индуктивным сопротивлением: ток в цепи i=Im sinωt, тогда ЭДС самоиндукции
т.е. ЭДС отстает от тока, ее вызвавшего, на угол |
Падение напряжения на катушке |
Мгновенная мощность катушки |
Средняя за период мощность идеальной катушки:
Это означает, что в течение периода идеальная катушка дважды получает от источника энергию, преобразуя ее в магнитное поле, и дважды возвращает ее. .
.
Емкостное сопротивление, Ом, |
ействующее значение тока, А,
Мгновенная мощность
Средняя мощность
В течение периода конденсатор дважды получает от источника энергию для заряда (создания электрического поля в диэлектрике) и дважды возвращает ее источнику (разряжается).
Реактивная мощность конденсатора, вар,
Из изложенного следует важный для практики вывод: токи индуктивности и емкости в цепи переменного тока в каждый момент времени направлены в противоположные стороны. Другими словами, в каждый момент времени, когда катушка получает от источника электромагнитную энергию, конденсатор возвращает ее источнику и наоборот.
4. Цепь, содержащая последовательно включенные активное, индуктивное и емкостное сопротивления (рис. 1.9).
Реактивное сопротивление цепи, Ом,
Полное сопротивление цепи, Ом,
Угол сдвига фаз между векторами напряжения и тока
Коэффициент мощности цепи
Мгновенное значение приложенного напряжения равно сумме мгновенных значений падений напряжений на участках цепи:
Мгновенное значение мощности для этой цепи, Вт,
Среднее значение мощности равно активной мощности, Вт:
Реактивная мощность, вар,
Полная мощность, В-А,
При xL = xc имеет место резонанс напряжения, цепь ведет себя как чисто активная, а ток имеет наибольшее (при U = const) значение.
5. Цепь, содержащая параллельно включенные активное, индуктивное и емкостное сопротивления (рис. 1.10).
В такой цепи все элементы находятся под одинаковым напряжением источника
Проводимости элементов цепи:
активная, См,
емкостная,См,
индуктивная, См,
Угол сдвига фаз тока и напряжения |
Полная проводимость цепи, содержащей элементы R, L, С, См:
Значения мощностей рассчитываются по приведенным выше формулам.
При вс= Bl имеет место резонанс токов. Общий ток в цепи имеет минимальное значение и активный характер.
Общий ток в цепи имеет минимальное значение и активный характер.
На практике параллельное включение конденсаторов в однофазной и трехфазной цепях широко используется для разгрузки питающих линий (проводов, кабелей, шин) от реактивной (индуктивной) составляющей тока. Это позволяет уменьшить потери электроэнергии в передающих линиях, и тем самым экономить ее, выбирать меньшие сечения проводов и кабелей для питания тех же самых электроприемников.
Открытая Физика. Закон Ома для цепи переменного тока. Мощность
В § 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности:
RIR=UR; 1ωCIC=UC; ωLIL=UL.
Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.
Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C. Физические величины R, 1ωC и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
Физические величины R, 1ωC и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J ċ u. Практический интерес представляет среднее за период переменного тока значение мощности
P=Pср=I0 U0cosωtcos(ωt+φ)¯.
Здесь I0 и U0 – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0:
PR=IRURcos2ωt¯=IRUR2=IR2R2.
Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения:
Iд=I02; Uд=U02.
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна
PR=IдUд.
Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением φ=π2. Поэтому
PC=ICUCcosωtcos(ωt+π2)¯=ICUCcosωt( -sin ωt)¯=0.
Аналогично можно показать, что PL = 0.
Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.
Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать
J (t) = I0 cos ωt; e (t) = ℰ0 cos (ωt + φ).
Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна
P=I0ℰ0cosωtcos(ωt+φ)¯=I0ℰ02cosφ=Iдℰдcosφ.
Как видно из векторной диаграммы, UR = ℰ0 · cos φ, поэтому P=I0UR2. Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.
В § 2.3 было выведено соотношение между амплитудами тока I0 и напряжения ℰ0 для последовательной RLC-цепи:
I0=ℰ0R2+(ωL-1ωC)2.
Величину
Z=R2+(ωL-1ωC)2
называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде
ZI0 = ℰ0.
Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).
Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1).
При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.
2.4.2.
Из диаграммы следует:
I0=ℰ0(1R)2+(ωL-1ωC)2.
Поэтому полное сопротивление параллельного RLC-контура выражается соотношением
Z=1(1R)2+(ωL-1ωC)2.
При параллельном резонансе (ω2 = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора:
Z = Zmax = R.
Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.
Формула расчета мощности электрического тока
При проектировании любых электрических цепей выполняется расчет мощности. На его основе производится выбор основных элементов и вычисляется допустимая нагрузка. Если расчет для цепи постоянного тока не представляет сложности (в соответствии с законом Ома, необходимо умножить силу тока на напряжение – Р=U*I), то с вычислением мощности переменного тока – не все так просто. Для объяснения потребуется обратиться к основам электротехники, не вдаваясь в подробности, приведем краткое изложение основных тезисов.
Для объяснения потребуется обратиться к основам электротехники, не вдаваясь в подробности, приведем краткое изложение основных тезисов.
Полная мощность и ее составляющие
В цепях переменного тока расчет мощности ведется с учетом законов синусоидальных изменений напряжения и тока. В связи с этим введено понятие полной мощности (S), которая включает в себя две составляющие: реактивную (Q) и активную (P). Графическое описание этих величин можно сделать через треугольник мощностей (см. рис.1).
Под активной составляющей (Р) подразумевается мощность полезной нагрузки (безвозвратное преобразование электроэнергии в тепло, свет и т.д.). Измеряется данная величина в ваттах (Вт), на бытовом уровне принято вести расчет в киловаттах (кВт), в производственной сфере – мегаваттах (мВт).
Реактивная составляющая (Q) описывает емкостную и индуктивную электронагрузку в цепи переменного тока, единица измерения этой величины Вар.
Рис. 1. Треугольник мощностей (А) и напряжений (В)
В соответствии с графическим представлением, соотношения в треугольнике мощностей можно описать с применением элементарных тригонометрических тождеств, что дает возможность использовать следующие формулы:
- S = √ P 2 +Q 2 , – для полной мощности;
- и Q = U*I*cos φ , и P = U*I*sin φ – для реактивной и активной составляющих.

Эти расчеты применимы для однофазной сети (например, бытовой 220 В), для вычисления мощности трехфазной сети (380 В) в формулы необходимо добавить множитель – √ 3 (при симметричной нагрузке) или суммировать мощности всех фаз (если нагрузка несимметрична).
Для лучшего понимания процесса воздействия составляющих полной мощности давайте рассмотрим «чистое» проявление нагрузки в активном, индуктивном и емкостном виде.
Активная нагрузка
Возьмем гипотетическую схему, в которой используется «чистое» активное сопротивление и соответствующий источник переменного напряжения. Графическое описание работы такой цепи продемонстрировано на рисунке 2, где отображаются основные параметры для определенного временного диапазона (t).
Емкостная нагрузка
Как видно на рисунке 3, график характеристик емкостной нагрузки несколько отличается от активной.
Индуктивная нагрузка
Представленный ниже график демонстрирует характер «чистой» индуктивной нагрузки. Как видим, изменилось только направление мощности, что касается наращения, оно равно нулю.
Как видим, изменилось только направление мощности, что касается наращения, оно равно нулю.
Негативное воздействие реактивной нагрузки
В приведенных выше примерах рассматривались варианты, где присутствует «чистая» реактивная нагрузка. Фактор воздействия активного сопротивления в расчет не принимался. В таких условиях реактивное воздействие равно нулю, а значит, можно не принимать его во внимание. Как вы понимаете, в реальных условиях такое невозможно. Даже, если гипотетически такая нагрузка бы существовала, нельзя исключать сопротивление медных или алюминиевых жил кабеля, необходимого для ее подключения к источнику питания.
Реактивная составляющая может проявляться в виде нагрева активных компонентов цепи, например, двигателя, трансформатора, соединительных проводов, питающего кабеля и т.д. На это тратится определенное количество энергии, что приводит к снижению основных характеристик.
Реактивная мощность воздействует на цепь следующим образом:
- не производит ни какой полезной работы;
- вызывает серьезные потери и нештатные нагрузки на электроприборы;
- может спровоцировать возникновение серьезной аварии.

Именно по этому, производя соответствующие вычисления для электроцепи, нельзя исключать фактор влияния индуктивной и емкостной нагрузки и, если необходимо, предусматривать использование технических систем для ее компенсации.
Расчет потребляемой мощности
В быту часто приходится сталкиваться с вычислением потребляемой мощности, например, для проверки допустимой нагрузки на проводку перед подключением ресурсоемкого электропотребителя (кондиционера, бойлера, электрической плиты и т.д.). Также в таком расчете есть необходимость при выборе защитных автоматов для распределительного щита, через который выполняется подключение квартиры к электроснабжению.
В таких случаях расчет мощности по току и напряжению делать не обязательно, достаточно просуммировать потребляемую энергию всех приборов, которые могут быть включены одновременно. Не связываясь с расчетами, узнать эту величину для каждого устройства можно тремя способами:
- обратившись к технической документации устройства;
- посмотрев это значение на наклейке задней панели; Потребляемая мощность прибора часто указывается на тыльной стороне
- воспользовавшись таблицей, где указано среднее значение потребляемой мощности для бытовых приборов.

Таблица значений средней потребляемой мощности
При расчетах следует учитывать, что пусковая мощность некоторых электроприборов может существенно отличаться от номинальной. Для бытовых устройств этот параметр практически никогда не указывается в технической документации, поэтому необходимо обратиться к соответствующей таблице, где содержатся средние значения параметров стартовой мощности для различных приборов (желательно выбирать максимальную величину).
Пожаловалась бабушка соседка снизу: подарили мне дети моющий пылесос. Он прекрасно работает, но откуда-то идет запах гари.
Пошел смотреть. Проводка у нас старая: лапша из алюминия 2,5 квадрата. А пылесос потребляет 2,5 kW. Прикинул, как работает формула расчета мощности по току и напряжению для этого случая.
Разделил 2500 ватт на 220 вольт. Получил чуть больше 11 ампер. Наши провода держат нагрузку 22 А. Имеем практически двойной резерв потоку. Другие потребители при уборке отключены.
Стали проверять и нюхать: запах около квартирного щитка. Открыл, осмотрел: шина сборки ноля в саже, на одной перемычке горелая изоляция. Винт крепления ослаблен. Вот и причина начала возгорания. Исправил.
Открыл, осмотрел: шина сборки ноля в саже, на одной перемычке горелая изоляция. Винт крепления ослаблен. Вот и причина начала возгорания. Исправил.
На этом примере я показываю, что всегда надо оценивать мощность потребления электроприборов и возможности проводки с защитными устройствами. Об этом рассказываю ниже.
Что такое мощность в электричестве: просто о сложном
Вспомнилась былина об Илье Муромце, когда он приложил всю свою мощь к соловью разбойнику. У бедолаги сразу посыпались искры из глаз, как пламя с верхней картинки на проводке с неправильным монтажом.
Простыми словами: мощность в электричестве — это силовая характеристика энергии, которой оценивают, как способности генераторных установок ее вырабатывать, так возможности потребителей и транспортных магистралей.
Все эти участки должны быть точно смонтированы и налажены для обеспечения безопасной работы. Как только в любом месте возникает неисправность, так сразу развивается авария во всей схеме.
Если говорить о домашнем электрическом оборудовании, то приходится постоянно соблюдать баланс между:
- включенными в сеть приборами;
- конструкцией проводов и кабелей;
- настройкой защитных устройств.

Только комплексное решение этих трех вопросов может обеспечить безопасность проводки и жильцов.
Как рассчитать электрическую мощность в быту
Формулы расчета мощности в электричестве позволяют выполнить качественную оценку безопасности каждого из перечисленных выше пунктов.
Пользоваться ими не сложно. Я уже приводил в предыдущих статьях шпаргалку электрика, где они помещены в наглядной форме для цепей постоянного тока.
Они полностью справедливы для активной составляющей мощности переменного тока, совершающей полезную работу. Кстати, кроме нее есть еще и бесполезная — реактивная, связанная с потерями энергии. Ее описанию посвящен второй раздел.
Такие вычисления удобно делать с помощью онлайн калькулятора. Он избавляет от рутинных математических вычислений и арифметических ошибок.
При любом из способов для расчета активной мощности требуется знать две из трех электрических величин:
Как измерить электрическую мощность дома
Существует еще одна возможность оценки активной мощности: ее измерение в действующей схеме специальными приборами: ваттметрами.
Точные замеры может обеспечить промышленный лабораторный ваттметер. Он изготавливается как прибор, работающий на аналоговых сигналах,так и с помощью цифровых технологий.
В бытовой проводке точные вычисления не нужны. Для нее выпускаются различные виды более простых ваттметров.
Популярностью пользуются приборы, которые можно вставить в розетку и подключить к ним шнур питания от потребителя, включить их в работу и сразу снять показания на дисплее в ваттах.
Их так и называют: ваттметр розетка. Они измеряют чисто активную мощность переменного тока.
Такие приборы избавляют электрика от выполнения сложных операций под напряжением, когда требуется замерять:
- действующее напряжение;
- силу тока;
- угол сдвига фаз между векторами тока и напряжения.
Потом все данные дополнительно требуется вводить в формулу расчета мощности по току и напряжению, делать по ней вычисления.
Этот метод можно упростить, если внимательно наблюдать за показаниями электрического счетчика индукционной системы с вращающимся диском. Он считает совершенную работу: потребленную мощность за определенную время.
Он считает совершенную работу: потребленную мощность за определенную время.
Однако скорость вращения диска как раз и характеризует величину потребления. Надо просто посчитать сколько раз он обернется за минуту и перевести в ватты по табличке, расположенной на корпусе.
Почему реактивное сопротивление схемы влияет на мощность переменного тока
Синусоидальная гармоника напряжения, поступая на резистивное сопротивление, изменяет величину тока без его отклонения на комплексной плоскости.
Такой ток совершает полезную работу с минимальными потерями энергии, вырабатывая активную мощность. Частота колебания сигнала не оказывает на нее никакого влияния.
Сопротивление конденсатора и индуктивности зависит от частоты гармоники. Его противодействие отклоняет направление тока на каждом из этих элементов в разные стороны.
Такие процессы связаны с потерей части энергии на бесполезные преобразования. На них расходуется мощность Q, которую называют реактивной. Ее влияние на полную мощность S и связь с активной P удобно представлять графически прямоугольным треугольником.
Ее влияние на полную мощность S и связь с активной P удобно представлять графически прямоугольным треугольником.
Захотелось его нарисовать на фоне оборудования из нагромождений фарфора и металла, где пришлось поработать довольно долго.Отвлекся. Не судите за это строго.
Сравните его с опубликованным мною ранее треугольником сопротивлений. Находите общие черты?
Ими являются геометрические пропорции фигуры, описывающие их формулы и угол φ, определяющий потери полной мощности. Перехожу к их более подробному рассмотрению.
Формулы расчета мощности для однофазной и трехфазной схемы питания
В идеальном теоретическом случае трехфазная схема состоит из трех одинаковых однофазных цепей. На практике всегда есть какие-то отклонения. Но, в большинстве случаев при анализах ими пренебрегают.
Поэтому рассматриваем вначале наиболее простой вопрос.
Графики и формулы под однофазное напряжение
Как работает резистор
На чисто резистивном сопротивлении синусоиды тока и напряжения совпадают по углу, направлены на каждом полупериоде одинаково.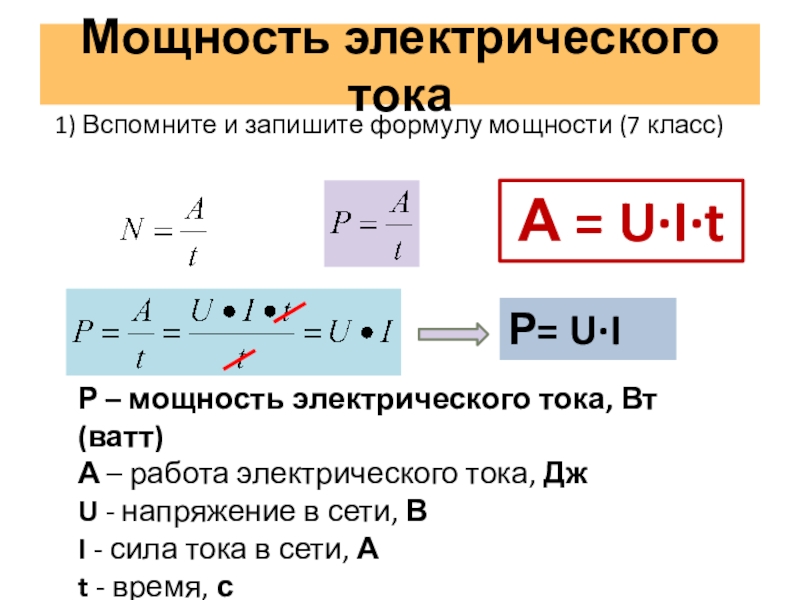 Поэтому их произведение, выражающее мощность, всегда положительно.
Поэтому их произведение, выражающее мощность, всегда положительно.
Его значение в произвольный момент времени t называют мгновенным, обозначая строчной буквой p.
Среднее значение мощности в течение одного периода называют активной составляющей. Ее график для переменного тока имеет фигуру симметричного всплеска с максимальным значением Pm в середине каждого полупериода Т/2.
Если взять половину его величины Pm/2 и провести прямую линию в течении одного периода Т, то получим прямоугольник с ординатой P.
Его площадь равна двум площадям графиков активной составляющих одного любого полупериода. Если посмотреть на картинку внимательнее, то можно представить, что верхняя часть всплеска отрезана,перевернута и заполнила свободное пространство внизу.
Представление этого графика помогает запомнить, что на активном сопротивлении мощность постоянного и переменного тока вычисляется по одной формуле, не меняет своего знака.
На резисторе не создается реактивных потерь.
Как работает индуктивность
Катушка с обмоткой своими витками запасает энергию магнитного поля. Благодаря процессу ее накопления индуктивное сопротивление отодвигает вперед на 90 градусов вектор тока относительно приложенного напряжения на комплексной плоскости.
Перемножая их мгновенные величины получаем значения мощности, которое за один период меняет знаки (направление) в каждом полупериоде.
Частота изменения мощности на индуктивности в два раза выше,чем у ее составляющих: синусоид тока и напряжения. Она состоит из двух частей:
- активной, обозначаемой индексом PL;
- реактивной QL.
Реактивная часть на индуктивности создается за счет постоянного обмена энергией между катушкой и приложенным источником. На ее величину влияет значение индуктивного сопротивления XL.
Как работает конденсатор
Емкость конденсатора постоянно накапливает заряд между своими обкладками. За счет этого происходит сдвиг вектора тока вперед на 90 градусов относительно приложенного напряжения.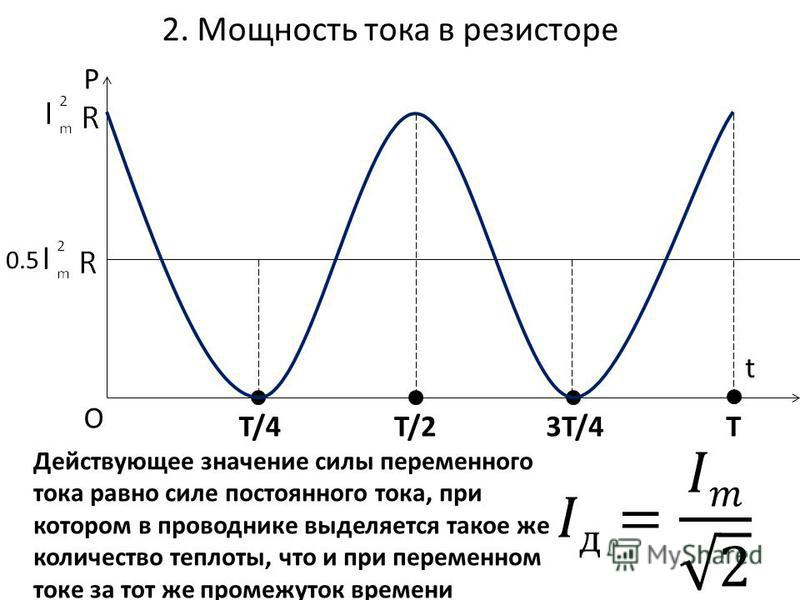
График мгновенной мощности напоминает вид предыдущего, но начинается с отрицательной полуволны.
Реактивная составляющая, выделяемая на конденсаторе, зависит от величины емкостного сопротивления XC.
Как работает реальная схема со всеми видами сопротивлений
В чистом виде приведенные выше графики и выражения встречаются не так часто. На самом деле передача электроэнергии и ее работа на переменном токе связаны с комплексным преодолением сил электрического сопротивления резисторов, конденсаторов и индуктивностей.
Причем, какая-то из этих составляющих будет преобладать. Для таких случаев преобразования электрической энергии в мгновенную мощность могут иметь один из следующих видов.
На верхней картинке показан случай, когда вектор тока отстает от приложенного напряжения, а на нижней — опережает.
В обоих случаях величина активной составляющей уменьшается от значения полной на значение, выражаемое как cosφ. Поэтому его принято называть коэффициентом мощности.
Как работает схема трехфазного электроснабжения
На ввод распределительного щита многоэтажного здания поступает трехфазное напряжение от электроснабжающей организации, вырабатываемое промышленными генераторами.
Его же, за отдельную плату, при желании может подключить владелец частного дома, что многие и делают. При этом рабочая схема и диаграмма напряжений выглядит следующим образом.
В старой системе заземления TN-C она выполняется четырехпроводным подключением, а у новой TN-S — пятипроводным с добавлением защитного РЕ проводника. Его на этой схеме я не показываю для упрощения.
Каждую из фаз при работе необходимо стараться нагружать одинаково равными по величине токами. Тогда в домашней проводке будет создаваться наиболее благоприятный оптимальный режим без опасных перекосов энергии.
В этом случае формула расчета мощности по току и напряжению для трехфазной схемы может быть представлена простой суммой аналогичных формул для составляющих однофазных цепей.
А поскольку они все идентичные, то их просто утраивают.
Например, когда активная мощность фазы В имеет выражением Рв=Uв×Iв×cosφ, то для всей трехфазной схемы она будет выражена следующей формулой:
Если пометить фазное выражение буквой ф. например Pф, томожно записать:
Аналогично будет вычисляться реактивная составляющая
Поскольку P и Q представляют величины катетов прямоугольного треугольника, то гипотенузу или полную составляющую можно вычислить как квадратный корень из суммы их квадратов.
Как учитывается трехфазная полная мощность
В энергосистеме, да и в частном доме, требуется анализировать подключенные нагрузки, равномерно распределять их по источникам напряжений.
С этой целью работают многочисленные конструкции измерительных приборов. На щитах управления подстанций расположены щитовые ваттметры и варметры, предназначенные для работы в разных долях кратности.
Старые аналоговые приборы показаны на этой картинке.
Для того, чтобы не путаться в записях вычислений введены разные наименования единиц. Они обозначаются:
Они обозначаются:
- ВА — (русское), VA (международное) вольтампер для полной величины мощности;
- Вт —(русское), var (международное) ватт —активной;
- вар (русское), var (международное) — реактивной.
Аналоговые приборы измеряют только активную или реактивную составляющую, а полную величину необходимо вычислять по формулам.
Многие современные цифровые приборы способны осуществлять эту функцию автоматически.
Видеоурок Павла Виктор дополняет мой материал. Рекомендую посмотреть.
Калькулятор мощности для своих
Здесь вы можете выполнить вычисления онлайн без использования формул и арифметических действий. Просто введите ваши исходные данные в таблицу и жмите кнопку “Рассчитать ток”.
А в заключение напоминаю, что для ваших вопросов создан раздел комментариев. Задавайте их, я отвечу.
Иногда можно услышать такой простой вопрос: «какая мощность в розетке?».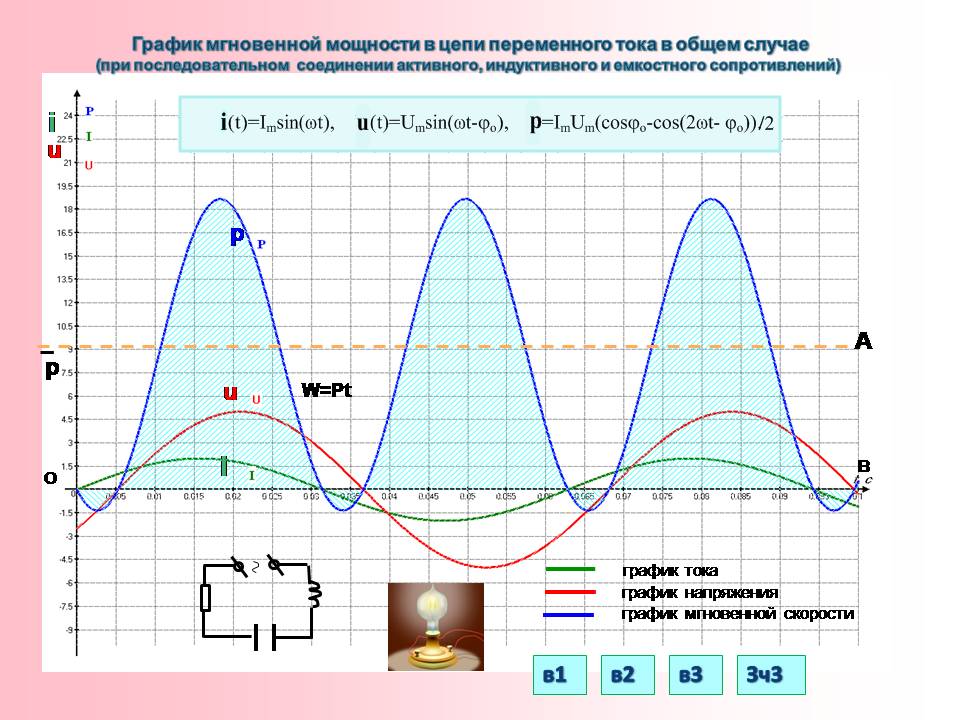 Ответ, как ни странно, чаще всего такой: 10 ампер. Или – 220 вольт. Понятно, что вопрос – дурацкий. Но и объяснение не лучше – «А на розетке так написано».
Ответ, как ни странно, чаще всего такой: 10 ампер. Или – 220 вольт. Понятно, что вопрос – дурацкий. Но и объяснение не лучше – «А на розетке так написано».
Мощность и ток
Если правильно отвечать на поставленный вопрос, то для читателей, прогуливающих в детстве уроки физики, можно сказать, что мощность электричества зависит от двух величин:
- величины напряжения;
- силы тока.
В общем, эти две величины определяют величину мощности как переменного, так и постоянного тока. Память может подсказать что-то типа: для участка цепи, для полной цепи. Это отголоски того же школьного учебника физики, где говорится о законе Ома.
Да, этот знаменитый закон и позволяет рассчитать мощность электрического тока. Конечно, школьная программа представляла этот закон для цепей постоянного тока, но суть от этого не меняется. Формула вечная и неизменная: P = U х I.
Перефразируя закон ома в простой язык, получаем простой ответ на вопрос о мощности в розетке: сила тока зависит от нагрузки.
Сила тока и приложенная нагрузка
Тривиальное понятие этого тезиса позволит не производить элементарных действий, постоянно совершаемых нами, или окружающими нас людьми:
- включать один электрический удлинитель в другой, втыкая в оба все доступные вилки от разных, иногда достаточно мощных, потребителей электроэнергии;
- подключать к севшему аккумулятору автомобиля другой, соединяя их проводами от старой электропроводки;
- наращивать провода от электрического чайника кабелем с витой парой;
- устанавливать в гараже нагреватель, мощностью 5 квт, подключая его к обыкновенной розетке.
Аналогичные примеры неграмотных действий можно приводить до бесконечности. Человеческая беспечность не знает границ. Чтобы больше не допускать подобных ошибок, давайте разберем как правильно производить расчет электрической мощности.
Чайник и электрическая мощность
Не забивая головы простейшими формулами (есть дела и поважнее этого), запомним простое соотношение, достаточное для применения его в быту. Точность его не соответствует формуле расчета, но позволяет помнить, что: 1 квт электроэнергии – это приблизительно 5 ампер тока в сети 220 вольт.
Точность его не соответствует формуле расчета, но позволяет помнить, что: 1 квт электроэнергии – это приблизительно 5 ампер тока в сети 220 вольт.
Таким образом, становится понятно, что электрический чайник, включенный в кухонную розетку, потребляет около 5 ампер тока. А лампа накаливания, мощностью 100 Вт – в десять раз меньше: 0,5 ампера. Конечно, такие примитивные знания нужны для домохозяек, расчет мощности электрического тока производится по формулам.
Необходимость расчетов мощности
Человек мало сталкивается с необходимостью проведения расчетов (мощностей постоянного электрического тока) в быту. Чаще всего такая необходимость возникает при ремонте автомобиля, где источником тока служит аккумулятор. Или какой-то продвинутый пользователь начинает подбирать новый кулер для своего процессора в компьютере.
Чаще возникает необходимость провести элементарные расчеты при ремонтных работах в квартире, при подборе сгоревшего блока питания и пр.
Расчет мощности электрического тока по формулам
Существует формула расчета электрического тока для однофазной и трехфазной сети. Вряд ли кто-то захочет и сможет ими воспользоваться – разбираться что такое cosφ при замене электрической проводки в доме или квартире нецелесообразно.
Реально можно произвести все необходимые расчеты в режиме онлайн. Интернет набит разными таблицами, соответствующими графиками и калькуляторами. Для очень нуждающихся читателей можно добавить, что сечение кабеля для осветительной сети — 1,5 кв. мм. А для электропитания розеток применяется кабель сечением 2,5 кв. мм.
Остальные расчеты, требующиеся при производстве электромонтажных работ в различных областях деятельности – лучше доверить специалистам, которые в своей работе используют различные приборы: амперметры, вольтметры, индикаторы фазы, измерители сопротивления изоляции, измерители сопротивления заземления и пр.
Ремонт и строительство домов и квартир, особенности расчетов
Чтобы произвести расчет электропроводки в квартире недостаточно произвести подбор сечения электрических проводов. В электрическом щите устанавливаются и электрические автоматы, и защитные устройства и электрический счетчик. Эти установочные изделия также подбираются и рассчитываются при разработке проекта электропитания, в котором производится также расчет количества и параметров устройств защитного заземления.
В электрическом щите устанавливаются и электрические автоматы, и защитные устройства и электрический счетчик. Эти установочные изделия также подбираются и рассчитываются при разработке проекта электропитания, в котором производится также расчет количества и параметров устройств защитного заземления.
Для расчетов и подбора видов электропроводки, использующейся при изготовлении удлинителей, организации временных схем электропитания, необходимо понимать, что силовые кабели для однофазной и трехфазной цепи различны по количеству жил, условиям прокладки, токовым нагрузкам и прочим параметрам.
При использовании кабелей и проводов необходимо учитывать и материал изготовления токопроводящих жил.
Наличие в загородном доме, даче трехфазных потребителей электроэнергии, таких как скважинный насос, электродвигатели, сварочное оборудование, требует при подборе кабелей электропроводки учитывать их пусковые токи. А при выборе электрического счетчика электроэнергии – активную и реактивную составляющую в потребляемой мощности, если предполагается постоянная работа трехфазного оборудования.
А при выборе электрического счетчика электроэнергии – активную и реактивную составляющую в потребляемой мощности, если предполагается постоянная работа трехфазного оборудования.
“>
Активное сопротивление в цепи переменного тока
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
u = Umsinωt
Найдём ток и мощность в цепи.
Ток в цепи переменного тока с активным сопротивлением.
По закону Ома найдем выражение для мгновенного тока:
где Im = Um/R — амплитуда тока
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
Действующий ток найдем, разделив амплитуду на √ 2:
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R = U2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Электрическая мощность. Краткие определения. Расчет и формула мощности.
Электрическая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).
Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).
Обозначается литерой — P.
Формулы расчета электрической мощности:
P = U * I P — мощность в ваттах, U — напряжение в вольтах, I — Ток в амперах. | P = I2 * R P — мощность в ваттах, I — ток в амперах, R — сопротивление нагрузки в омах | P = U2 / R P — мощность в ваттах, U — напряжение в вольтах, R — сопротивление нагрузки в омах |
Пример расчета.
Мы имеем в однофазной сети 220 вольт кабельную линию защищенную автоматом с номинальным током 16 ампер. Соответственно, максимальный электропотребитель, который мы можем запитать через эту кабельную линию — 3520 Ватт ( 220 вольт умноженны на 16 Ампер).
Либо у нас есть электрический обогреватель на 2 кВт (2000 ватт) при включении его в розетку его потребляемый ток (ток в цепи) будет 9,1 Ампер.
Мощность установленная и расчетная в чем разница.
Часто на схемах энергоснабжения и в пояснениях встречаются понятия установленной и расчетной мощности.
Установленная мощность — Pу — максимальная потребляемая мощность электроприбора.
Расчетная мощность (расчетная нагрузка) Рр — это установленная мощность с определенным коэффициентом спроса К, которые можно посмотреть в СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
Расчетная мощность относится не конкретно к какому-либо электропотребителю, а к группе потребителей.
Примеры для понимания:
1. У нас есть три потребителя — 4х комфорочная электроплита, телевизор, люстра, бра.
Установленная мощность — это сумма максимальной потребляемой мощности всех этих электроприборов. То есть мощность включенной со всеми комфорками электроплиты + люстра + телевизор + бра.
Но поскольку, мы редко включаем все потребители полностью, для расчетов используется расчетная мощность групп потребителей, которая всегда меньше установленной мощности, за исключением уличного освещения.
2. В многоквартирном доме 100 квартир-студий, в каждой из которых по одному светильнику на 20 Вт. В данном случае Ру = 2000 Вт.
Но в связи с тем, что вероятность включения светильников во всех квартирах одновременно низка, для расчетов используются определенные коэффициенты и Рр = Ру * К
Мощность постоянного и переменного электрического тока.
Мощность
постоянного тока
Так
как значения силы тока и напряжения
постоянны и равны мгновенным значениям
в любой момент времени, то мощность
можно вычислить по формуле:
.
Для
пассивной линейной цепи, в которой
соблюдается закон
Ома,
можно записать:
,
где — электрическое
сопротивление.
Если
цепь содержит источник ЭДС,
то отдаваемая им или поглощаемая на нём
электрическая мощность равна:
,
где —
ЭДС.
Если
ток внутри ЭДС противонаправлен градиенту
потенциала (течёт внутри ЭДС от плюса
к минусу), то мощность поглощается
источником ЭДС из сети (например, при
работе электродвигателя или
заряде аккумулятора),
если сонаправлен (течёт внутри ЭДС от
минуса к плюсу), то отдаётся источником
в сеть (скажем, при работегальванической
батареи или генератора).
При учёте внутреннего
сопротивления источника
ЭДС выделяемая на нём мощность прибавляется
к поглощаемой или вычитается из
отдаваемой.
Мощность
переменного тока[править | править
вики-текст]
В
цепях переменного тока формула для
мощности постоянного тока может быть
применена лишь для расчёта мгновенной
мощности, которая сильно изменяется во
времени и для практических расчётов
бесполезна. Прямой расчёт среднего
значения мощности требует интегрирования
по времени. Для вычисления мощности в
цепях, где напряжение и ток изменяются
периодически, среднюю мощность можно
вычислить, интегрируя мгновенную
мощность в течение периода. На практике
На практике
наибольшее значение имеет расчёт
мощности в цепях переменного синусоидального
напряжения и тока.
Для
того, чтобы связать понятия полной,
активной, реактивной мощностей
и коэффициента
мощности,
удобно обратиться к теории комплексных
чисел.
Можно считать, что мощность в цепи
переменного тока выражается комплексным
числом таким, что активная мощность
является его действительной частью,
реактивная мощность — мнимой частью,
полная мощность — модулем, а
угол (сдвиг
фаз) — аргументом. Для такой модели
оказываются справедливыми все выписанные
ниже соотношения.
Активная
мощность[править | править
вики-текст]
Единица
измерения — ватт (W, Вт).
Среднее
за период значение
мгновенной мощности называется активной
мощностью: .
В цепях однофазного синусоидального
тока ,
где и — среднеквадратичные
значения напряжения и тока, — угол
сдвига фаз между
ними. Для цепей несинусоидального тока
электрическая мощность равна сумме
соответствующих средних мощностей
отдельных гармоник. Активная мощность
Активная мощность
характеризует скорость необратимого
превращения электрической энергии в
другие виды энергии (тепловую и
электромагнитную). Активная мощность
может быть также выражена через силу
тока, напряжение и активную составляющую
сопротивления цепи или
её проводимость по
формуле .
В любой электрической цепи как
синусоидального, так и несинусоидального
тока активная мощность всей цепи равна
сумме активных мощностей отдельных
частей цепи, для трёхфазных
цепейэлектрическая
мощность определяется как сумма мощностей
отдельных фаз. С полной мощностью активная
связана соотношением .
В
теории длинных
линий (анализ
электромагнитных процессов в линии
передачи, длина которой сравнима с
длиной электромагнитной волны) полным
аналогом активной мощности является
проходящая мощность, которая определяется
как разность между падающей мощностью
и отраженной мощностью.
Реактивная
мощность[править | править
вики-текст]
Единица
измерения — вольт-ампер реактивный
(var, вар)
Реактивная
мощность — величина, характеризующая
нагрузки, создаваемые в электротехнических
устройствах колебаниями энергии
электромагнитного поля в цепи
синусоидального переменного тока, равна
произведению среднеквадратичных
значений напряжения и
тока ,
умноженному на синус угла сдвига
фаз между
ними: (если
ток отстаёт от напряжения, сдвиг фаз
считается положительным, если опережает —
отрицательным). Реактивная мощность
Реактивная мощность
связана с полной мощностью и
активной мощностью соотношением: .
Физический
смысл реактивной мощности — это
энергия, перекачиваемая от источника
на реактивные элементы приёмника
(индуктивности, конденсаторы, обмотки
двигателей), а затем возвращаемая этими
элементами обратно в источник в течение
одного периода колебаний, отнесённая
к этому периоду.
Необходимо
отметить, что величина для
значений от
0 до плюс 90° является положительной
величиной. Величина для
значений от
0 до −90° является отрицательной величиной.
В соответствии с формулой ,
реактивная мощность может быть как
положительной величиной (если нагрузка
имеет активно-индуктивный характер),
так и отрицательной (если нагрузка имеет
активно-ёмкостный характер). Данное
обстоятельство подчёркивает тот факт,
что реактивная мощность не участвует
в работе электрического тока. Когда
устройство имеет положительную реактивную
мощность, то принято говорить, что оно
её потребляет, а когда отрицательную —
то производит, но это чистая условность,
связанная с тем, что большинство
электропотребляющих устройств
(например, асинхронные
двигатели),
а также чисто активная нагрузка,
подключаемая через трансформатор,
являются активно-индуктивными.
Синхронные
генераторы, установленные на электрических
станциях, могут как производить, так и
потреблять реактивную мощность в
зависимости от величины тока возбуждения,
протекающего в обмотке ротора генератора.
За счёт этой особенности синхронных
электрических машин осуществляется
регулирование заданного уровня напряжения
сети. Для устранения перегрузок и
повышения коэффициента
мощности электрических
установок осуществляется компенсация
реактивной мощности.
Применение
современных электрических измерительных
преобразователей на микропроцессорной
технике позволяет производить более
точную оценку величины энергии
возвращаемой от индуктивной и емкостной
нагрузки в источник переменного
напряжения.
Полная
мощность
Единица
полной электрической
мощности — вольт-ампер (V·A, В·А)
Полная
мощность — величина, равная произведению
действующих значений периодического
электрического тока в
цепи и напряжения на
её зажимах: ;
связана с активной и реактивной мощностями
соотношением: где —
активная мощность, —
реактивная мощность (при индуктивной
нагрузке ,
а при ёмкостной ).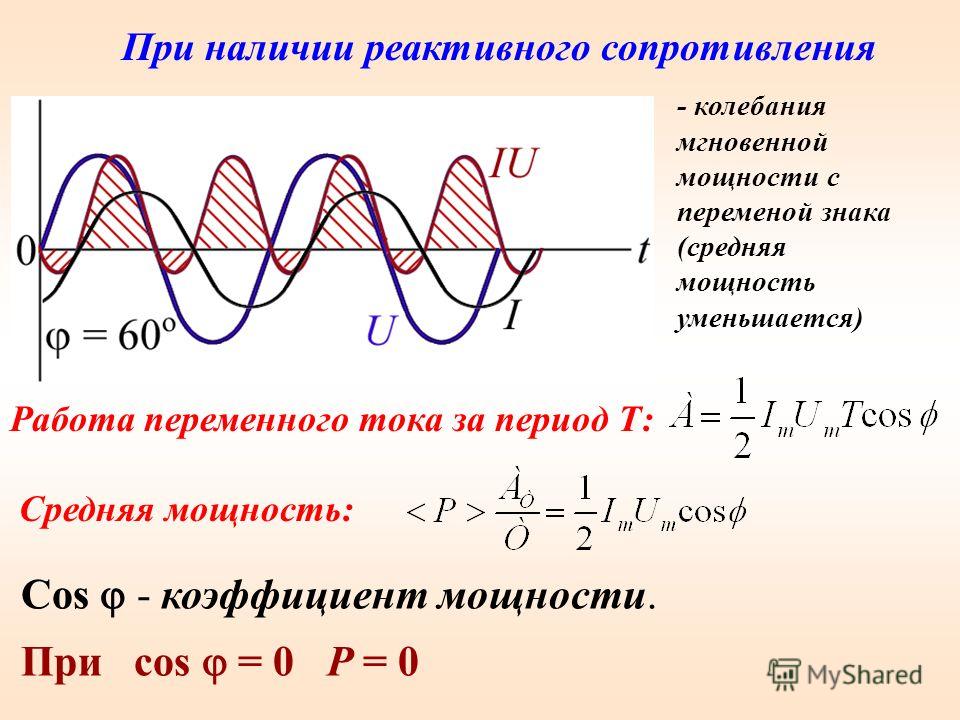
Векторная
зависимость между полной, активной и
реактивной мощностью выражается
формулой:
Полная
мощность имеет практическое значение,
как величина, описывающая нагрузки,
фактически налагаемые потребителем на
элементы подводящей электросети
(провода, кабели, распределительные
щиты, трансформаторы, линии
электропередачи),
так как эти нагрузки зависят от
потребляемого тока, а не от фактически
использованной потребителем энергии.
Именно поэтому полная мощность
трансформаторов и распределительных
щитов измеряется в вольт-амперах, а не
в ваттах.
Комплексная
мощность[править | править
вики-текст]
Мощность,
аналогично импедансу,
можно записать в комплексном виде:
где —
комплексное напряжение, —
комплексный ток, —
импеданс, * — оператор комплексного
сопряжения.
Модуль
комплексной мощности равен
полной мощности .
Действительная часть равна
активной мощности ,
а мнимая —
реактивной мощности с
корректным знаком в зависимости от
характера нагрузки.
Закон Ома для цепи переменного тока. Мощность
RIR=UR; 1ωCIC=UC; ωLIL=UL.
Указанные выше формулы внешне могут напоминать закон Ома на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.
Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.
Определение 1
R – активное сопротивление резистора.
1ωС – емкостное сопротивление конденсатора.
ωL – индуктивное сопротивление катушки в цепи переменного тока.
Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.
Определение 2
Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.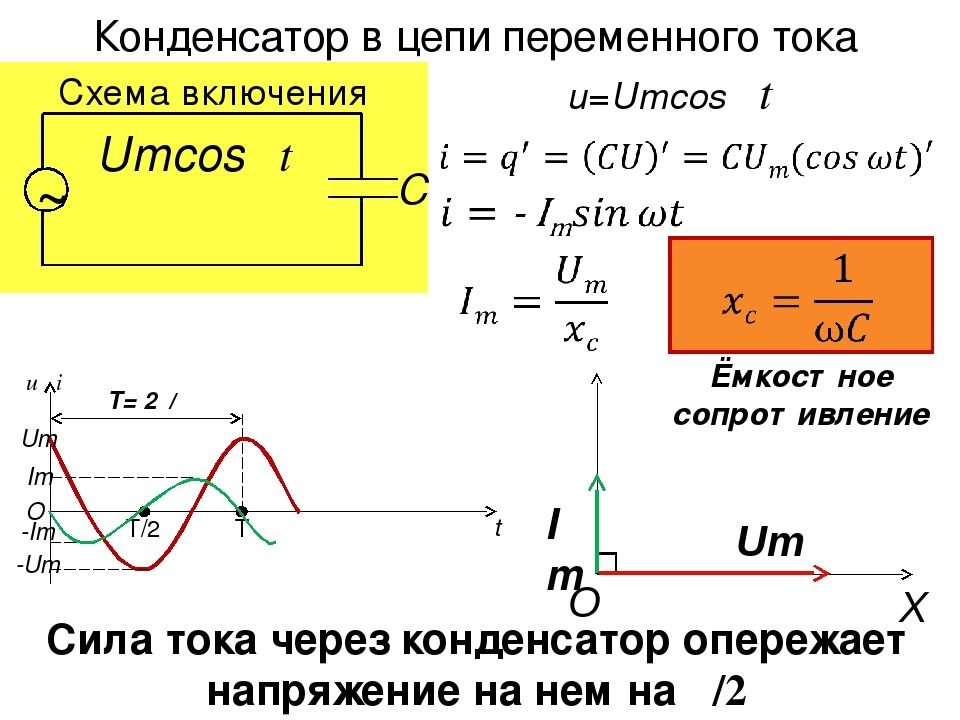
Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:
P=Pcα=I0U0cos ωt cos ωt+φ.
В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю:
PR=IRURcos2ωt=IRUR2=IR2R2.
Действующие значения силы тока и напряжения
Определение 3
По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения:
IД=l02; UД=U02.
Мощность переменного тока на участке цепи
Определение 4
Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется:
PR=IДUД.
Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:
Отсюда, справедливо следующее выражение:
PC=ICUCcos ωt cosωt+π2=ICUCcos ωt-sin ωt=0.
Таким же способом можно проиллюстрировать, что PL=0.
Исходя из описанного выше получим следующие определение.
Определение 5
Мощность в цепи переменного тока выделяется только на активном сопротивлении, а среднее значение мощности переменного тока на конденсаторе и катушке индуктивности равняется нулю.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание
Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты ω. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) проявляется фазовый сдвиг на определенный угол φ.
Исходя из приведенных выше фактов, мы можем записать:
J(t)=I0cos ωt; e(t)=δ0cos ωt+φ.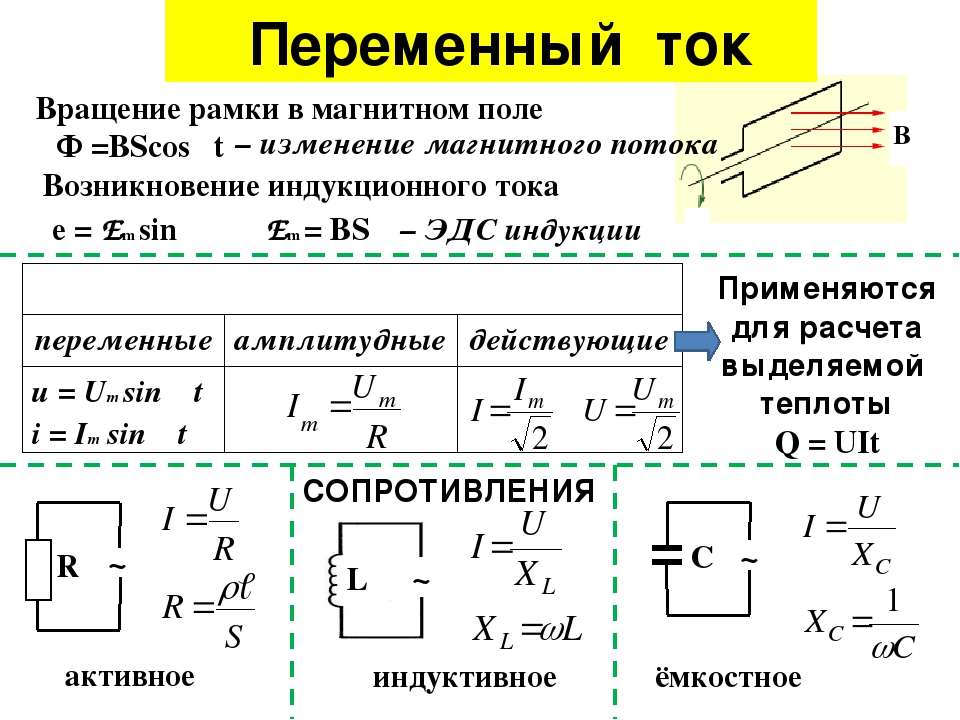
Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. 2.3.2).
Рисунок 2.3.2. Гармонические колебания A cos (ωt+φ1), B cos (ωt+φ2) и их суммы C cos (ωt+φ) на векторной диаграмме.
Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:
P=I0δ0cos ωt cos ωt+φ=I0δ02cos φ=IДδД cos φ.
Исходя из данных векторной диаграммы можно заявить, что UR=δ0·cos φ, следовательно,
P=I0UR2, а вся мощность, которую развивает источник питания, теряется в виде джоулева тепла на резисторе.
В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока I0 и напряжений δ0 в условиях последовательной RLC-цепи:
I0=δ0R2+ωL-1ωC2
Определение 6
Z=R2+ωL-1ωC2– это величина, имеющая название полное сопротивление цепи переменного тока.
Определение 7
Связь между амплитудными значениями тока и напряжения в цепи имеет вид:
ZI0=δ0.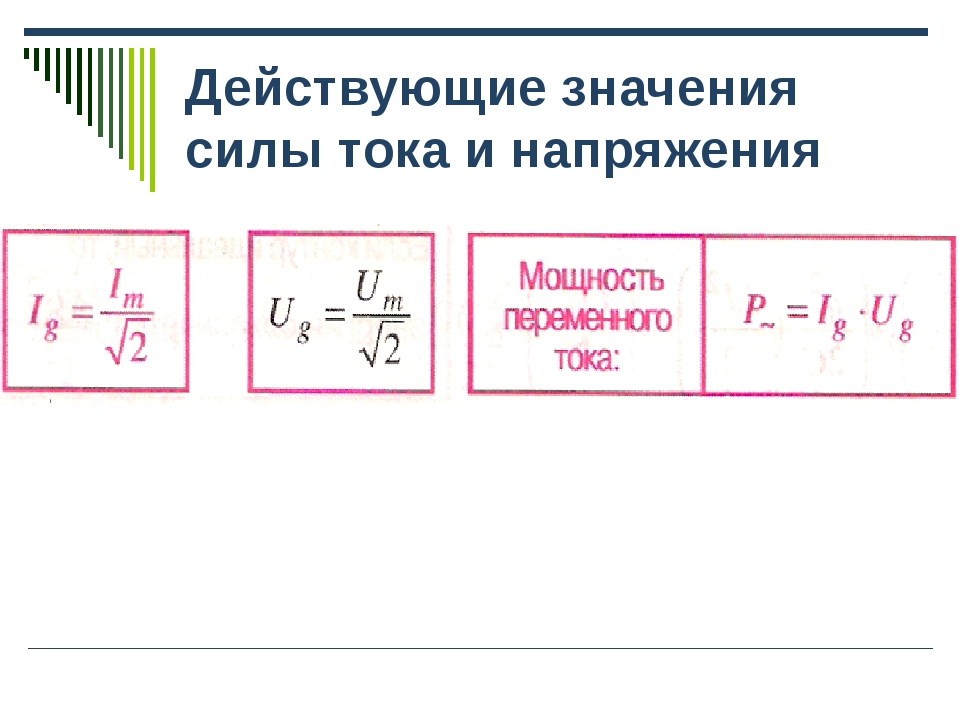
Данное выражение представляет собой закон Ома для цепи переменного тока.
Закон Ома в условиях параллельной RLC-цепи
В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. 2.4.1) RLC-контур:
Рисунок 2.4.1. Параллельный RLC-контур.
При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах R, C и L идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока. Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контур.
Исходя из вида диаграммы, следует:
I0=δ01R2+ωL-1ωC2.
Определение 8
Соответственно, полное сопротивление параллельного RLC-контура выражается в виде следующего соотношения:
Z=11R2+ωL-1ωC2.
Определение 9
При параллельном резонансе (ω2=1LC) полное сопротивление цепи принимает свое максимальное значение, которое эквивалентно активному сопротивлению резистора:
Z=Zmax=R.
А значение фазового сдвига φ между током и напряжением при параллельном резонансе равняется нулю.
Мощность в цепи переменного тока — Circuit Globe
Мощность трехфазной цепи переменного тока используется в крупных отраслях промышленности для работы тяжелых машин. Питание от однофазной сети переменного тока используется для работы небольших бытовых приборов. Величина мощности трехфазной цепи переменного тока в три раза больше, чем мощность однофазной цепи.
Величина мощности трехфазной цепи переменного тока в три раза больше, чем мощность однофазной цепи.
Рассмотрим, если P — это мощность однофазной цепи, то 3P — это мощность трехфазной симметричной цепи переменного тока. Мощность несимметричной трехфазной цепи определяется сложением мощности отдельной фазы.
Как рассчитать мощность цепи переменного тока?
В цепи постоянного тока значение напряжения и тока становится постоянным. Но в цепи переменного тока мгновенные значения тока и напряжения и, следовательно, мощность источника питания постоянно меняются со временем. Поэтому для измерения мощности цепей переменного и постоянного тока используются разные методы.
Мгновенная мощность цепи переменного тока непрерывно изменяется при изменении их напряжения и тока. Мгновенная мощность — это мощность цепи в определенный момент времени.Пусть p — мощность в любой момент, v — напряжение, а «i» — ток цепи.
Если синусоидальный ток и напряжение протекают через цепь переменного тока, а ток отстает от напряжения на угол Φ, в этом случае значение мгновенной мощности определяется выражением
Если напряжение и ток не совпадают по фазе друг с другом, то значение тока и напряжения становится равным
.
Мгновенная мощность цепи выражается как
.
Пусть, Θ = ωt
Средняя мощность схемы
Член cosΦ в данном выражении показывает, что ваттметр необходим для измерения мощности цепи переменного тока.
Как мощность цепи переменного тока зависит от коэффициента мощности?
Коэффициент мощности определяет общие потоки полезной мощности в цепи. Для понимания роли коэффициента мощности в цепи переменного тока рассмотрим три условия.
Питание переменного тока в чисто резистивной цепи
Резистор — это электрический компонент, потребляющий электрическую мощность цепи переменного тока.
В чисто резистивной схеме ток, протекающий через резистор, находится в фазе с напряжением питания, т.е.е., формы волн напряжения и тока синфазны друг с другом. Разность фаз нулевого градуса возникает между формой волны напряжения и тока.
Питание переменного тока в чисто индуктивной цепи
В чисто индуктивной цепи значения напряжения и тока не совпадают по фазе друг с другом. Напряжение и ток растут и падают вместе при фазовом сдвиге 90º. Выражение дает мощность чисто индуктивной цепи. Вышеприведенное уравнение показывает, что индуктор не потребляет и не рассеивает электрическую мощность.
Напряжение и ток растут и падают вместе при фазовом сдвиге 90º. Выражение дает мощность чисто индуктивной цепи. Вышеприведенное уравнение показывает, что индуктор не потребляет и не рассеивает электрическую мощность.
Питание переменного тока в чисто емкостной цепи
В чисто емкостной цепи переменного тока формы сигналов напряжения и тока не совпадают по фазе друг с другом. Ток в цепи опережает их напряжение под углом 90º. Несмотря на рассеивание мощности, конденсатор сохраняет электрическую энергию.
Эта страница дает ответы на эти вопросы. Значения мощности и RMS
В последней строке мы использовали стандартное тригонометрическое тождество, которое cos (2A) Этот последний набор уравнений полезен, потому что они в точности те, что обычно Когда говорят о переменном токе, значения RMS используются настолько часто, что, если не указано иное * Исключение: производители и продавцы HiFi оборудования иногда используют Мощность в резисторе. В резисторе R пиковая мощность (достигается мгновенно Мощность в индукторах и конденсаторах. В идеальных катушках индуктивности и конденсаторах, Трехфазный переменный ток
и дифференциаторы или чтобы  |
Мгновенная, средняя, активная и реактивная мощность
Нападающий
В нескольких последних статьях мы обсудили и разработали некоторые важные концепции линий электропередачи.В прошлый раз мы говорили о протяженных линиях электропередачи. Здесь мы обсуждаем простую, но важную базовую концепцию «Электроэнергия». Это освежит наши знания, прежде чем мы двинемся дальше.
Электрическая энергия имеет то же значение, что и механическая энергия, но здесь энергия или энергия, которые нас интересуют, находятся в электрической форме. Мы часто сталкиваемся с такими терминами, как мгновенная, средняя, полная, действительная, реактивная, полная и комплексная мощность или просто мощность. Что они имеют в виду? как они связаны? Об этом мы поговорим здесь и в следующей статье.
Что они имеют в виду? как они связаны? Об этом мы поговорим здесь и в следующей статье.
Цепь постоянного тока
Пока наш анализ ограничивается цепью постоянного тока (DC), мощность, потребляемая резистивной нагрузкой, является произведением напряжения на сопротивлении и тока, протекающего через сопротивление.Это действительно просто.
P = V. я
Мощность, потребляемая нагрузкой, является произведением напряжения на нагрузке и тока, потребляемого нагрузкой (рис. A).Или мощность, подаваемая источником постоянного тока (батарея / элемент), является произведением напряжения на элементе и тока, подаваемого элементом. Оба они равны в нашем примере (с учетом идеальной батареи с нулевым внутренним сопротивлением). Закон сохранения энергии подразумевает, что мощность, подаваемая источником, должна быть такой же, как мощность, потребляемая цепью. В случае цепи постоянного тока мгновенная мощность равна средней мощности.
A).Или мощность, подаваемая источником постоянного тока (батарея / элемент), является произведением напряжения на элементе и тока, подаваемого элементом. Оба они равны в нашем примере (с учетом идеальной батареи с нулевым внутренним сопротивлением). Закон сохранения энергии подразумевает, что мощность, подаваемая источником, должна быть такой же, как мощность, потребляемая цепью. В случае цепи постоянного тока мгновенная мощность равна средней мощности.
Цепь переменного тока
Что это за мощность, о которой мы говорим при анализе цепей переменного тока.Основная проблема заключается в том, что переменное напряжение и ток синусоидально изменяются со временем. Кроме того, наличие в цепи реактивных элементов, таких как индуктор и конденсатор, сдвигает волну тока относительно волны напряжения (угла сдвига фаз).
Мощность — это скорость, с которой энергия потребляется нагрузкой или производится генератором. Будь то цепь постоянного или переменного тока, значение мгновенной мощности получается путем умножения мгновенного напряжения на мгновенный ток.Если в любой момент времени t значения напряжения и тока представлены синусоидальными функциями как
v = V m sin ωt
i = I м sin (ωt-φ)
V m и I m — максимальные значения синусоидального напряжения и тока.Здесь ω = 2 π f
f — частота, а ω — угловая частота вращающихся векторов напряжения или тока. Должно быть понятно, что для энергосистемы f обычно составляет 50 или 60 Гц
φ — разность фаз между напряжением и током.
Как мы уже говорили, мгновенная мощность — это произведение мгновенного напряжения и тока, если мы назовем мгновенную мощность как p, то
p = v.i = V м sin ωt . I m sin (ωt-φ)
или p = V m I m sin ωt sin (ωt-φ)
Применяя тригонометрическую формулу 2.sin A.sin B = cos (AB) — cos (A + B) получаем
Его можно записать как
Это уравнение мгновенной мощности
. На фиг.8-C нарисованы все три волны, соответствующие v, i и p. Графически мы также можем получить значение мгновенной мощности (p) в любой момент времени t, просто умножив значение тока i и напряжения v в этот конкретный момент t.(Вы можете проверить, что на диаграмме p отрицательно, когда либо v, либо i отрицательно, в противном случае p положительно. См. Точки, где p равно нулю). На графике мы показали горизонтальную ось как угол φ вместо времени t для упрощения визуализации. Должно быть ясно, что оба варианта верны.
На графике мы показали горизонтальную ось как угол φ вместо времени t для упрощения визуализации. Должно быть ясно, что оба варианта верны.
Ясно, что мгновенная мощность p состоит из двух членов. Первый член постоянен, потому что для данной нагрузки фазовый угол φ фиксирован.Он не изменится, если не изменится нагрузка. Второй член изменяется во времени синусоидально из-за наличия члена cos (2ωt-φ). Обратите внимание, что мгновенная частота сети в два раза превышает частоту напряжения или тока, поэтому мгновенная мощность в однофазной цепи изменяется синусоидально.
Мгновенная мощность, p = постоянный член + синусоидальный колебательный член.
За один полный период среднее значение колеблющегося члена равно нулю.
Тогда какова средняя мощность в заданное время, скажем, за один период времени волны?
Это постоянный член.
Вот еще один способ думать о средней мощности.
Просто обратите внимание, что мгновенная мощность на короткое время отрицательна.Для любого временного интервала вы просто найдете общую + ve площадь A + (над горизонтальной осью (синяя линия) и под кривой p) и общую площадь -ve A- (под горизонтальной осью и над кривой p). Чистая площадь получается вычитанием A- из A +. Разделив эту чистую площадь (на интервал времени T и , мы получим среднюю мощность (P). Вы можете сделать это с помощью расчетов. В конечном итоге вы получите только первый член в приведенной выше формуле для мгновенной мощности p.
Еще одним способом легче понять, что формула для мгновенной мощности p имеет постоянный член (V m .I m /2) cos φ и другой синусоидальный член (V m . I m /2) cos (2 wt — φ). Фактически p — это колебательная мощность, которая колеблется около среднего постоянного члена (V m .I m /2) cos φ.
I m /2) cos (2 wt — φ). Фактически p — это колебательная мощность, которая колеблется около среднего постоянного члена (V m .I m /2) cos φ.
Так что средняя мощность
Вышеуказанная формула может быть записана как
здесь,
V и I являются векторным представлением среднеквадратичных значений * синусоид напряжения и тока.Символы | V | и | I | — величины векторов V и I. (См. на нижней панели определение среднеквадратичного значения).
Эта формула выше — ваша любимая формула полезной мощности, которая нас больше всего беспокоит. Эта формула средней мощности используется для определения мощности, потребляемой нагрузкой. Ежемесячный счет за электроэнергию дома основан на этой мощности.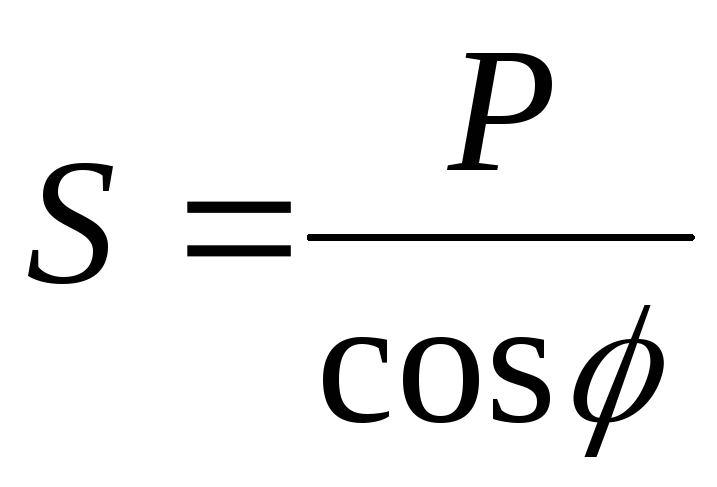 Инженеры и техники в энергетике или электротехнике просто используют термин мощность вместо средней мощности. Поэтому всякий раз, когда мы просто называем мощность, это означает среднюю мощность.
Инженеры и техники в энергетике или электротехнике просто используют термин мощность вместо средней мощности. Поэтому всякий раз, когда мы просто называем мощность, это означает среднюю мощность.
Конечно, мгновенная мощность колеблется по своей природе. Как мы уже говорили, он колеблется не вокруг горизонтальной оси, а вокруг средней мощности P (голубая горизонтальная линия).
P будет равно нулю, когда cos φ = 0 или φ = 90 градусов, то есть когда фазовый угол между волнами напряжения и тока составляет 90 градусов.Это только тогда, когда нагрузка чисто индуктивная или емкостная. В этом случае второй член остается только в формуле мгновенной мощности.
Из приведенного выше рисунка на некоторое время мощность станет отрицательной, что означает, что нагрузка подает энергию к источнику за этот период. Это связано с наличием в нагрузке реактивного элемента.
Это связано с наличием в нагрузке реактивного элемента.
Приведенную выше формулу для мгновенной мощности можно записать в другой форме. Эта форма на самом деле является попыткой отличить колеблющуюся реактивную мощность от формулы мгновенной мощности.Переставляя члены в уравнении для мгновенной мощности выше, мы получаем
p = | V | | Я | cos φ (1-cow2ωt) — | V | | Я | sin φ sin2ωt
В этом уравнении первый член | V | | Я | cos φ (1-cow2ωt) колеблется, среднее значение которого | V | | Я | cos φ. Об этой средней мощности мы уже говорили.
Второй член | V | | Я | sin φ sin2ωt, который также является колебательным, но с нулевым средним значением. Максимальное значение этого члена составляет | V | | Я | грех φ. Это так называемая реактивная мощность.Таким образом, реактивная мощность — это максимальное значение колебательной мощности, которая многократно отбирается от источника и снова возвращается к источнику в течение каждого цикла. Таким образом, среднее значение этой реактивной мощности равно нулю.
Средняя мощность P называется реальной мощностью. Иногда ее еще называют активной мощностью.
Активная мощность = P = | V | | Я | cos φ
Обычно записывается как P = VI cos φ. Но следует помнить, что V и I — среднеквадратичные значения напряжения и тока. Например, когда мы говорим однофазный 220 вольт переменного тока, это означает, что действующее значение напряжения составляет 220 вольт (это не максимальное значение синусоиды напряжения)
Реактивная мощность = Q = | V | | Я | sin φ
Реальная мощность измеряется в ваттах, а реактивная мощность — в вар (вольт-ампер-реактивность).В энергетическом секторе эти блоки слишком малы, поэтому реальная мощность измеряется в мегаваттах (МВт), а реактивная мощность — в мегаварах (МВАр). Буква R в конце обозначает реактивную мощность.
Часто студенты и практикующие инженеры не понимают средней мощности (часто называемой просто мощностью). Они думают, что умножая действующее значение напряжения на среднеквадратичный ток, они получают среднеквадратичную мощность. Нет, это неправильно. Нет мощности RMS. RMS мощность не имеет значения или не определена. (Также см. Определение RMS-значения ниже в конце).Это средняя мощность, или реальная мощность, или истинная мощность.
Нет, это неправильно. Нет мощности RMS. RMS мощность не имеет значения или не определена. (Также см. Определение RMS-значения ниже в конце).Это средняя мощность, или реальная мощность, или истинная мощность.
Трехфазная сбалансированная система с питанием
Рассмотрим трехфазную сбалансированную систему. Трехфазная сбалансированная система анализируется с учетом только одной фазы и нейтрали. Это называется поэтапным анализом. Таким образом, приведенный выше анализ для одной фазы верен для сбалансированного трехфазного случая. Пусть здесь полная мощность P t . Тогда мы получаем общую трехфазную мощность как трижды по сравнению с однофазным случаем.
P t = 3 | V | | Я | cos φ
Следует помнить, что | V | и | Я | — значения для каждой фазы.и φ — фазовый угол нагрузки в пофазном анализе.
Вышеупомянутая формула для сбалансированной трехфазной системы может быть записана как
P t = √3 | V l | | I l | cos φ
В приведенной выше формуле V l и I l являются линейным напряжением и током (фиг.-D).Это уравнение не зависит от типа подключения трехфазной нагрузки, то есть нагрузки, подключенной по схеме треугольник или звезда. Вы должны знать линейное напряжение, линейный ток и фазовый угол φ, как указано выше. Эта форма очень удобна и часто используется при расчете мощности.
Есть одно основное различие между однофазным и трехфазным питанием. Мгновенная однофазная мощность пульсирует.В сбалансированном трехфазном случае мгновенная мощность каждой фазы пульсирует, но три пульсирующих волны мощности смещены друг от друга на 120 градусов. В любой момент времени сумма этих трех мгновенных волн мощности является постоянной величиной 3 | V | | Я | cos φ. Таким образом, общая мощность, потребляемая в трехфазной сбалансированной системе, не является пульсирующей. Непульсирующая мощность также подразумевает желаемый непульсирующий крутящий момент в случае трехфазных вращающихся машин. В больших трехфазных двигателях это действительно необходимо.
Мгновенная однофазная мощность пульсирует.В сбалансированном трехфазном случае мгновенная мощность каждой фазы пульсирует, но три пульсирующих волны мощности смещены друг от друга на 120 градусов. В любой момент времени сумма этих трех мгновенных волн мощности является постоянной величиной 3 | V | | Я | cos φ. Таким образом, общая мощность, потребляемая в трехфазной сбалансированной системе, не является пульсирующей. Непульсирующая мощность также подразумевает желаемый непульсирующий крутящий момент в случае трехфазных вращающихся машин. В больших трехфазных двигателях это действительно необходимо.
* Действующее значение синусоид переменного тока
Значение переменного напряжения или тока, которое вызывает такой же нагрев (или такую же энергию), который вырабатывается, если вместо переменного тока применяется постоянное напряжение или ток, численно равные действующему значению переменного тока. Эта концепция помогает сделать формулы мощности похожими для цепей постоянного и переменного тока.
Эта концепция помогает сделать формулы мощности похожими для цепей постоянного и переменного тока.
Вам следует прочитать следующую статью о Треугольнике степеней и Комплексной мощности.
Мощность
RMS vs.Средняя мощность
ВОПРОС:
Следует ли мне использовать единицы среднеквадратичного значения мощности (СКЗ) для определения или описания мощности переменного тока, связанной с моим сигналом, системой или устройством?
Ответ:
Это зависит от того, как вы определяете среднеквадратичную мощность.
Вы не хотите рассчитывать среднеквадратичное значение сигнала мощности переменного тока. Это дает результат, который не имеет физического смысла.
Вы действительно используете среднеквадратичные значения напряжения и / или тока для расчета средней мощности, что дает значимые результаты.
Обсуждение:
Сколько мощности рассеивается, когда на резистор 1 Ом подается синусоидальное напряжение 1 В (среднеквадратичное значение)?
Это хорошо понятно 1 , и здесь нет никаких противоречий.
Теперь давайте посмотрим, как это соотносится со значением из расчета среднеквадратичной мощности.
На рисунке 1 показан график синусоиды 1 В.Размах размаха составляет 1 В среднеквадр. × 2 √2 = 2,828 В с изменением от +1,414 В до –1,414 В. 2
Рис. 1. График синусоиды 1 В.
На рисунке 2 представлен график мощности, рассеиваемой этой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом (P = V 2 / R), который показывает:
Рис. 2. График мощности, рассеиваемой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом.
- Кривая мгновенной мощности имеет смещение на 1 Вт и колеблется от 0 Вт до 2 Вт.
- Среднеквадратичное значение этого сигнала мощности равно 1.
 225 Вт.
225 Вт.- Одним из методов вычисления этого числа является уравнение 2 3 :
- Это можно проверить, используя более подробную формулу 4 в MATLAB ® или Excel.
- Среднее значение этого сигнала мощности составляет 1 Вт. Это очевидно при осмотре; форма сигнала колеблется симметрично выше и ниже 1 Вт. Это же значение получается при вычислении среднего числового значения точек данных формы сигнала.
- Среднее значение мощности соответствует мощности, рассчитанной с использованием среднеквадратичного значения напряжения.
Мощность, рассеиваемая синусоидальным среднеквадратичным напряжением 1 В на резисторе 1 Ом, составляет 1 Вт, а не 1,225 Вт. Таким образом, именно средняя мощность дает правильное значение, и, следовательно, именно средняя мощность имеет физическое значение. Среднеквадратичная мощность (как определено здесь) не имеет очевидного полезного значения (не имеет очевидного физического / электрического значения), кроме как величина, которую можно рассчитать как упражнение.
Выполнить такой же анализ с использованием синусоидального тока 1 А среднеквадратичного значения через резистор 1 Ом — тривиальное упражнение.Результат тот же.
Источники питания для интегральных схем (ИС) обычно являются источниками постоянного тока, поэтому среднеквадратичная мощность не является проблемой для питания ИС. Для постоянного тока среднее и среднеквадратичное значение такие же, как и для постоянного тока. Важность использования средней мощности в отличие от среднеквадратичной мощности, как определено в этом документе, относится к мощности, связанной с изменяющимися во времени напряжением и током, то есть шумом, радиочастотными сигналами и генераторами.
Используйте среднеквадратичное значение напряжения и / или среднеквадратичного значения тока для расчета средней мощности, что дает значимые значения мощности.
1 Мощность, рассеиваемая напряжением на резисторе, является фундаментальным соотношением, которое легко выводится из закона Ома (V = IR) и основных определений напряжения (энергия / единица заряда) и тока (единица заряда / времени). Напряжение × ток = энергия / время = мощность
Напряжение × ток = энергия / время = мощность
2 Размах амплитуды синусоиды — это среднеквадратичное значение, умноженное на 2√2. Для синусоидального напряжения V p-p = V rms × 2√2, где V p-p — размах напряжения, а V rms — среднеквадратичное напряжение.Это хорошо известная связь, которая описана в бесчисленных учебниках, а также здесь: en.wikipedia.org/wiki/Root_mean_square.
3 Это адаптировано из среднеквадратичного значения, рассчитанного из постоянного значения смещения постоянного тока плюс отдельное среднеквадратичное значение переменного тока, и из примечания по применению «Улучшите измерения среднеквадратичного значения переменного тока с помощью цифрового мультиметра» от Keysight.
4 Стандартное определение из учебника является одним из примеров более подробной формулы.
Как рассчитать трехфазную мощность
Обновлено 12 ноября 2018 г.
Ли Джонсон
Трехфазная мощность — широко используемый метод для выработки и передачи электроэнергии, но вычисления, которые вам нужно выполнить, немного сложнее чем для однофазных систем. Тем не менее, при работе с уравнениями трехфазной мощности вам не нужно ничего делать, поэтому вы сможете легко решить любую поставленную вам задачу трехфазного питания. Главное, что вам нужно сделать, это найти ток с учетом мощности в цепи или наоборот.
Тем не менее, при работе с уравнениями трехфазной мощности вам не нужно ничего делать, поэтому вы сможете легко решить любую поставленную вам задачу трехфазного питания. Главное, что вам нужно сделать, это найти ток с учетом мощности в цепи или наоборот.
TL; DR (слишком долго; не читалось)
Выполните расчет трехфазной мощности по формуле:
P = √3 × pf × I × V
Где pf — коэффициент мощности, I — ток, В, — напряжение, а P — мощность.
Однофазное и трехфазное питание
Однофазное и трехфазное питание — это термины, описывающие электричество переменного тока (AC). Ток в системах переменного тока постоянно изменяется по амплитуде (то есть по размеру) и направлению, и это изменение обычно принимает форму синусоидальной волны. Это означает, что он плавно изменяется с серией пиков и спадов, описываемых синусоидальной функцией. В однофазных системах такая волна всего одна.
В однофазных системах такая волна всего одна.
Двухфазные системы разделяют его на две части.Каждая секция тока сдвинута по фазе с другой на половину цикла. Поэтому, когда одна из волн, описывающих первую часть переменного тока, находится на пике, другая — на минимальном значении.
Однако двухфазное питание встречается нечасто. Трехфазные системы используют тот же принцип разделения тока на противофазные составляющие, но с тремя вместо двух. Три части тока сдвинуты по фазе на треть цикла каждая. Это создает более сложную схему, чем двухфазное питание, но они одинаково компенсируют друг друга.Каждая часть тока одинакова по размеру, но противоположна направлению двух других частей, вместе взятых.
Формула трехфазной мощности
Наиболее важные уравнения трехфазной мощности связывают мощность ( P , в ваттах) с током ( I , в амперах) и зависят от напряжения ( V ). В уравнении также присутствует «коэффициент мощности» ( pf ), который учитывает разницу между реальной мощностью (которая выполняет полезную работу) и полной мощностью (которая подается в схему).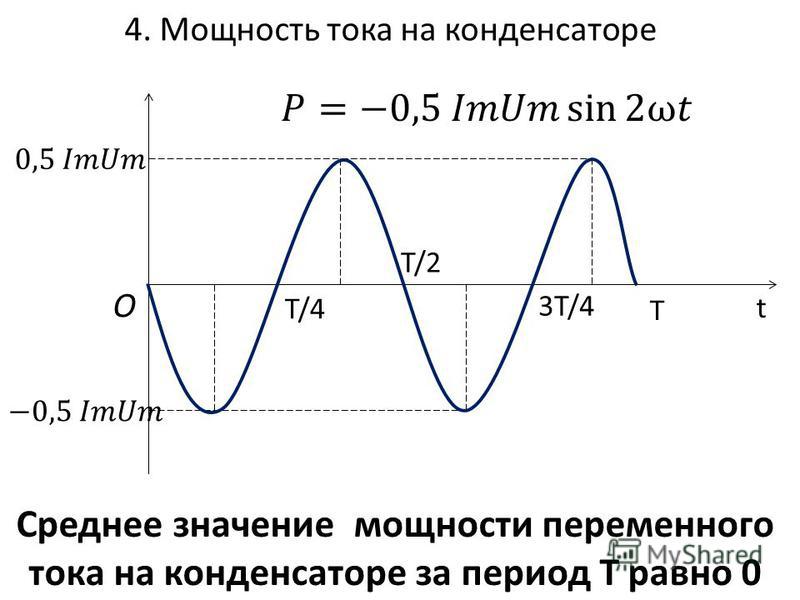 Большинство типов расчетов трехфазной мощности выполняется с использованием этого уравнения:
Большинство типов расчетов трехфазной мощности выполняется с использованием этого уравнения:
P = √3 × pf × I × V
Здесь просто указано, что мощность является квадратным корнем из трех (около 1,732), умноженным на коэффициент мощности (обычно от 0,85 до 1, см. Ресурсы), ток и напряжение. Не позволяйте символам пугать вас, используя это уравнение; Как только вы включите все необходимые составляющие в уравнение, им будет легко пользоваться.
Преобразование кВт в А
Допустим, у вас есть напряжение, общая мощность в киловаттах (кВт) и коэффициент мощности, и вы хотите узнать ток (в амперах) в цепи.Изменив приведенную выше формулу расчета мощности, получим:
I = P / (√3 × pf × V)
Если ваша мощность выражена в киловаттах (т. Е. Тысячах ватт), лучше либо преобразовать ее в ватт (умножив на 1000) или оставьте его в киловаттах. Убедитесь, что ваше напряжение указано в киловольтах (кВ = вольт ÷ 1000). Например, если у вас коэффициент мощности 0,85, мощность 1,5 кВт и напряжение 230 В, просто укажите мощность как 1500 Вт и вычислите:
Например, если у вас коэффициент мощности 0,85, мощность 1,5 кВт и напряжение 230 В, просто укажите мощность как 1500 Вт и вычислите:
I = P / (√3 × pf × V)
= 1500 Вт / √3 × 0.85 × 230 В
Аналогично, мы могли бы работать с кВ (учитывая, что 230 В = 0,23 кВ), и нашли бы то же самое:
I = P / (√3 × pf × V)
= 1,5 кВт / √3 × 0,85 × 0,23 кВ
Преобразование ампер в кВт
Для обратного процесса используйте форму приведенного выше уравнения:
P = √3 × pf × I × V
Просто умножьте свои известные значения, чтобы найти ответ. Например, при I = 50 A, V = 250 V и pf = 0.9, это дает:
P = √3 × pf × I × V
= √3 × 0,9 × 50 A × 250 В
Поскольку это большое число, преобразуйте его в кВт, используя (значение в Вт) / 1000 = (значение в киловаттах).
19 486 Вт / 1000 = 19 486 кВт
Треугольник мощности и коэффициента мощности | Глава 3 — Питание в системах переменного тока
В чисто резистивной цепи переменного тока мощность — это просто мощность. Если мы добавим к цепи индуктивность или емкость, ситуация изменится.Как вы теперь знаете, емкость и индуктивность влияют на соотношение фаз между напряжением и током, и нам нужно понять некоторые специальные методы, прежде чем мы сможем анализировать мощность, когда напряжение и ток не совпадают по фазе.
Активная и реактивная мощность
Мощность — это напряжение, умноженное на ток. Это определение не требует дополнительных объяснений, когда мы работаем с резистивной цепью переменного тока: ток и напряжение имеют идеальное выравнивание фаз, и, следовательно, мы всегда будем умножать два положительных числа или два отрицательных числа.
Рис. 1. В этом случае вычисления мощности всегда будут давать положительное число, поскольку выравнивание фаз гарантирует, что мы умножим положительное напряжение на положительный ток или отрицательное напряжение на отрицательный ток.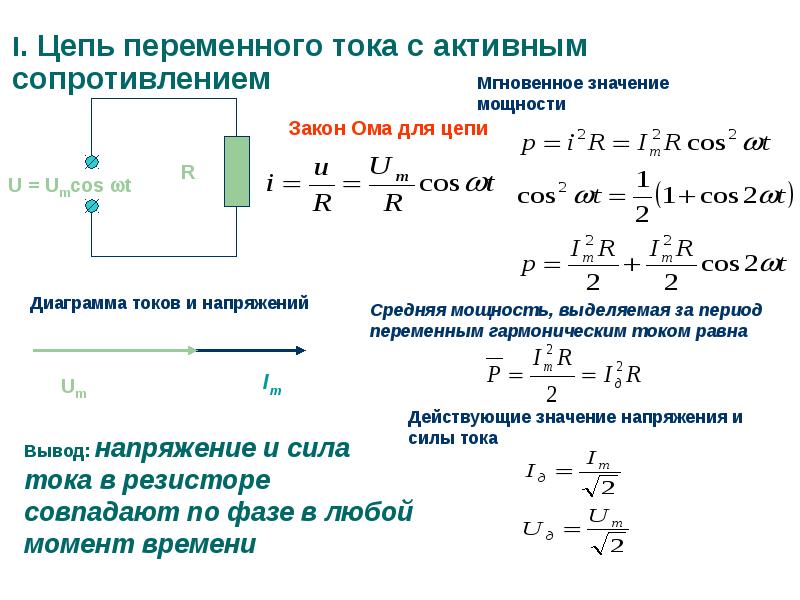
Однако даже небольшая разность фаз между током и напряжением создаст две части цикла переменного тока, в которых одна из величин положительна, а другая — отрицательна.Расчетная мощность на этом участке сигнала будет отрицательным числом.
Рис. 2. Несовпадение фаз между током и напряжением приводит к отрицательному значению мощности от 0 ° до приблизительно 30 ° и от 180 ° до приблизительно 210 °.
Теперь – нуждаются в дополнительных пояснениях. Что такое отрицательная сила? Может ли компонент выделять отрицательное количество энергии в окружающую среду? Поначалу отрицательная мощность может немного сбивать с толку.Отрицательное значение мощности указывает на то, что питание не работает. Чтобы быть более конкретным, части цикла переменного тока с отрицательной мощностью указывают, что мощность подается в систему, но не передает энергию в систему; скорее энергия возвращается к источнику.
Этот вид электроэнергии называется , реактивная мощность . Это имя будет легко запомнить, если вы уже знаете, что катушки индуктивности и конденсаторы, которые создают фазовый сдвиг, который, в свою очередь, приводит к реактивной мощности, считаются реактивными компонентами .Реактивная мощность не передает энергию от источника к нагрузке, но она не «тратится впустую», потому что реактивные нагрузки не могут работать без нее.
Мощность, которая работает где-то в цепи нагрузки, называется активной мощностью (также используются «реальная мощность» и «истинная мощность»). Активная мощность активна в нагрузке, то есть она действительно что-то делает, например, нагревает паяльник или освещает лабораторию. Реактивная мощность отличается от активной за счет использования другого устройства. Вольт-ампер реактивная (вар) — это единица измерения реактивной мощности, а для активной мощности используется уже известная нам единица, а именно ватты.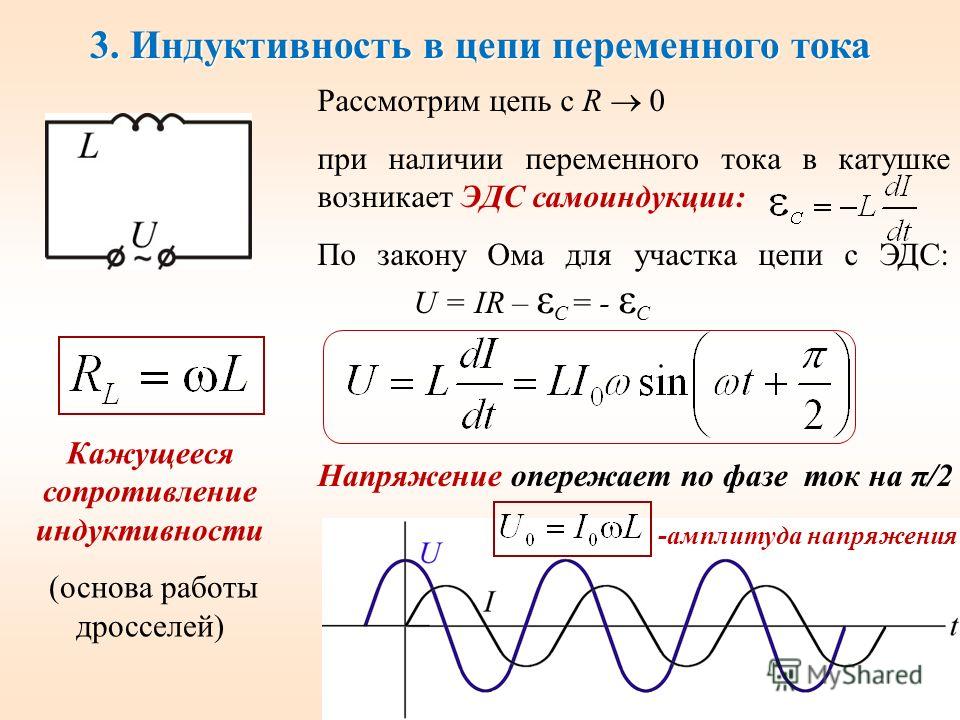
Понимание треугольника силы
Активная мощность обозначается P, а реактивная мощность обозначается Q. Давайте введем три дополнительные величины, которые участвуют в анализе потребляемой мощности в реактивных цепях:
- Комплексная мощность , обозначенная S, представляет собой векторную сумму активной и реактивной мощности.
- Полная мощность , обозначаемая | S |, представляет собой величину комплексной мощности. В нем используется единица измерения вольт-ампер (ВА), а не ватт.
- Коэффициент мощности , сокращенно PF, будет рассмотрен в ближайшее время.
Следующая диаграмма называется треугольником мощности.
Рис. 3. Треугольник мощности дает визуальное (и математическое) представление активной мощности, реактивной мощности и полной мощности системы.
Полная мощность
Если вы измеряете среднеквадратичное напряжение нагрузки и среднеквадратичный ток, а затем умножаете эти два значения, результатом будет полная мощность. Вот почему он называется «кажущимся»: он соответствует рассеиваемой мощности, которую мы ожидаем , основываясь только на среднеквадратичных значениях напряжения и тока. Однако теперь мы знаем, что кажущаяся мощность может быть выше, чем реальная рассеиваемая мощность, потому что разность фаз между напряжением и током создает реактивную мощность, которая способствует полной мощности.
Вот почему он называется «кажущимся»: он соответствует рассеиваемой мощности, которую мы ожидаем , основываясь только на среднеквадратичных значениях напряжения и тока. Однако теперь мы знаем, что кажущаяся мощность может быть выше, чем реальная рассеиваемая мощность, потому что разность фаз между напряжением и током создает реактивную мощность, которая способствует полной мощности.
Рассмотрим, однако, что происходит в чисто резистивной цепи. Нет реактивной мощности; следовательно, угол между активной мощностью и комплексной мощностью будет равен нулю. Таким образом, в этом случае полная мощность (то есть длина комплексного вектора мощности) будет равна активной мощности.
Полная мощность также может быть описана как количество мощности, подаваемой в систему источником. Опять же, это не то же самое, что фактическое рассеивание мощности, потому что часть этой поставленной мощности возвращается к источнику, а не рассеивается на нагрузке.
Коэффициент мощности
Отношение активной мощности к полной мощности называется коэффициентом мощности.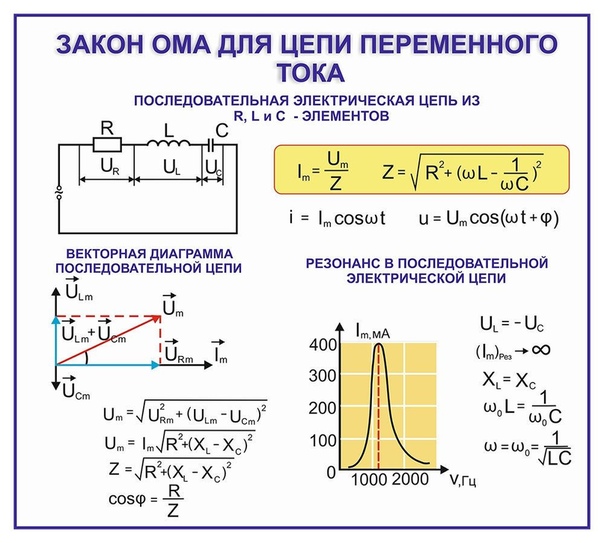 Другими словами, коэффициент мощности — это мощность, эффективно используемая устройством, P, деленная на то, что передается этому устройству через электросеть, | S |. Коэффициент мощности также можно рассчитать как косинус угла полного сопротивления нагрузки (т. Е. Угла между активной мощностью и комплексной мощностью, обозначенный θ на рисунке 3).
Другими словами, коэффициент мощности — это мощность, эффективно используемая устройством, P, деленная на то, что передается этому устройству через электросеть, | S |. Коэффициент мощности также можно рассчитать как косинус угла полного сопротивления нагрузки (т. Е. Угла между активной мощностью и комплексной мощностью, обозначенный θ на рисунке 3).
В чисто резистивной цепи реактивной мощности нет, и, следовательно, активная мощность равна полной мощности, а коэффициент мощности равен единице.Треугольник власти сведен к линии. В общем, мы хотим, чтобы коэффициент мощности был как можно ближе к единице, потому что это указывает на то, что электрическая энергия сети используется более эффективно.
Допустим, сеть должна обеспечивать питание двигателя мощностью 240 Вт. Если этот двигатель (вместе со схемой управления) рассчитан на коэффициент мощности, равный единице, он потребляет 2 А тока из сети. Если коэффициент мощности ниже единицы, он будет потреблять ток более 2 А, но реальная рассеиваемая мощность все равно будет 240 Вт. Таким образом, энергосеть должна подавать дополнительный ток для выполнения того же объема работы, а это приводит к большим потерям резистивной мощности в распределительных проводах и более высокой стоимости оборудования.
Таким образом, энергосеть должна подавать дополнительный ток для выполнения того же объема работы, а это приводит к большим потерям резистивной мощности в распределительных проводах и более высокой стоимости оборудования.
И конденсаторы, и катушки индуктивности создают разность фаз, которая приводит к реактивной мощности, но их специфическое влияние на фазу прямо противоположно и может уравновешивать друг друга. Коррекция коэффициента мощности относится к процессу улучшения коэффициента мощности путем преднамеренного добавления реактивного сопротивления (например, конденсатора) в цепь таким образом, чтобы уменьшить влияние другого реактивного сопротивления (например, индуктивности катушки двигателя).Вы часто можете встретить батареи очень больших конденсаторов на промышленных объектах. Их цель — противодействовать влиянию катушек индуктивности и тем самым улучшить коэффициент мощности.
Треугольник импеданса
Пока мы говорим о коэффициенте мощности, давайте кратко обсудим другой тип треугольника, который полезен при анализе мощности переменного тока.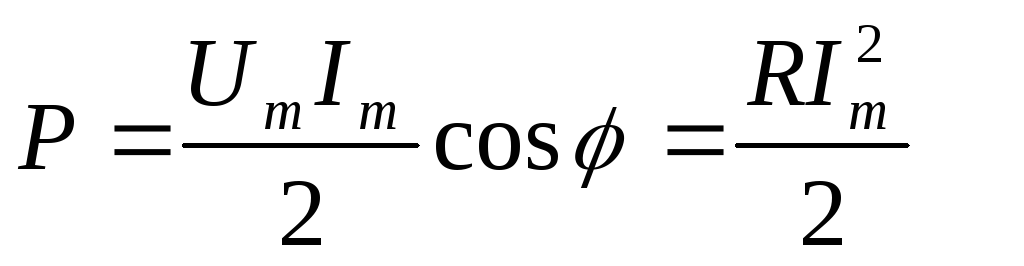 Треугольник импеданса передает характеристики импеданса цепи; горизонтальная и вертикальная стороны соответствуют сопротивлению и реактивному сопротивлению соответственно, а гипотенуза — комплексному сопротивлению.
Треугольник импеданса передает характеристики импеданса цепи; горизонтальная и вертикальная стороны соответствуют сопротивлению и реактивному сопротивлению соответственно, а гипотенуза — комплексному сопротивлению.
Рис. 4. Треугольник импеданса. Вы также можете думать об этом как о графическом представлении, в котором используется комплексная плоскость. Общий импеданс — это вектор, который состоит из действительной части (по горизонтальной оси) и мнимой части (по вертикальной оси).
Угол между сопротивлением и импедансом такой же, как угол между активной мощностью и комплексной мощностью в треугольнике мощности. Это дает нам еще один способ расчета коэффициента мощности:
Далее: Пассивные компоненты в цепях переменного тока
Мы рассмотрели некоторые важные темы, связанные с рассеиванием мощности переменного тока, и представили треугольник мощности, который является полезным инструментом, который может помочь вам проанализировать цепи переменного тока, содержащие реактивные компоненты.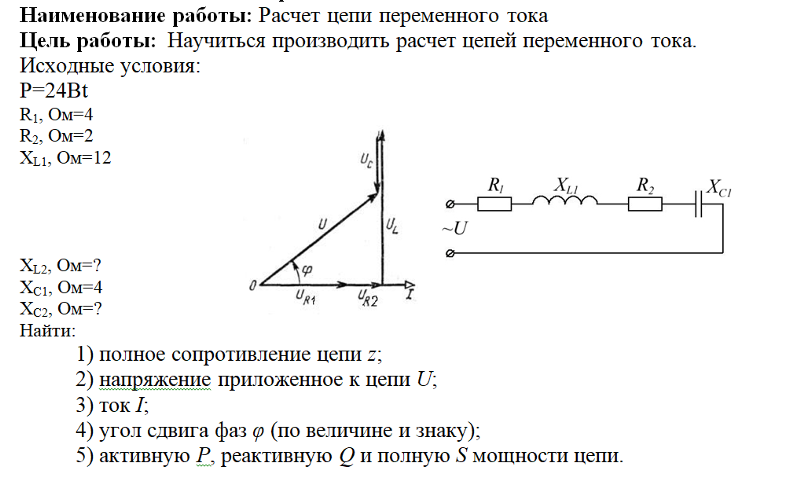 На следующей странице мы продолжим изучение пассивных компонентов в контексте анализа цепей переменного тока.
На следующей странице мы продолжим изучение пассивных компонентов в контексте анализа цепей переменного тока.
Цепи переменного тока серии
RLC | Физика
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Когда один в цепи переменного тока, индукторы, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку индукторы и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом данного раздела. Суть анализа цепи RLC — это частотная зависимость X L и X C , а также их влияние на фазу напряжения в зависимости от тока (установлено в предыдущий раздел).Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.
Суть анализа цепи RLC — это частотная зависимость X L и X C , а также их влияние на фазу напряжения в зависимости от тока (установлено в предыдущий раздел).Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.
Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.
Комбинированный эффект сопротивления R , индуктивного реактивного сопротивления X L и емкостного реактивного сопротивления X C определяется как полное сопротивление , аналог сопротивления переменного тока в цепи постоянного тока.Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].
Здесь I 0 — пиковый ток, В 0 — пиковое напряжение источника, а Z — полное сопротивление цепи. Единицы измерения сопротивления — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток.Чтобы получить выражение для Z через R , X L и X C , мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение. Эти напряжения обозначены как В R , В L и В C на рисунке 1. Для сохранения заряда ток должен быть одинаковым в каждой части цепи. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны.Но мы знаем из предыдущего раздела, что напряжение на катушке индуктивности В L опережает ток на одну четверть цикла, напряжение на конденсаторе В C следует за током на единицу.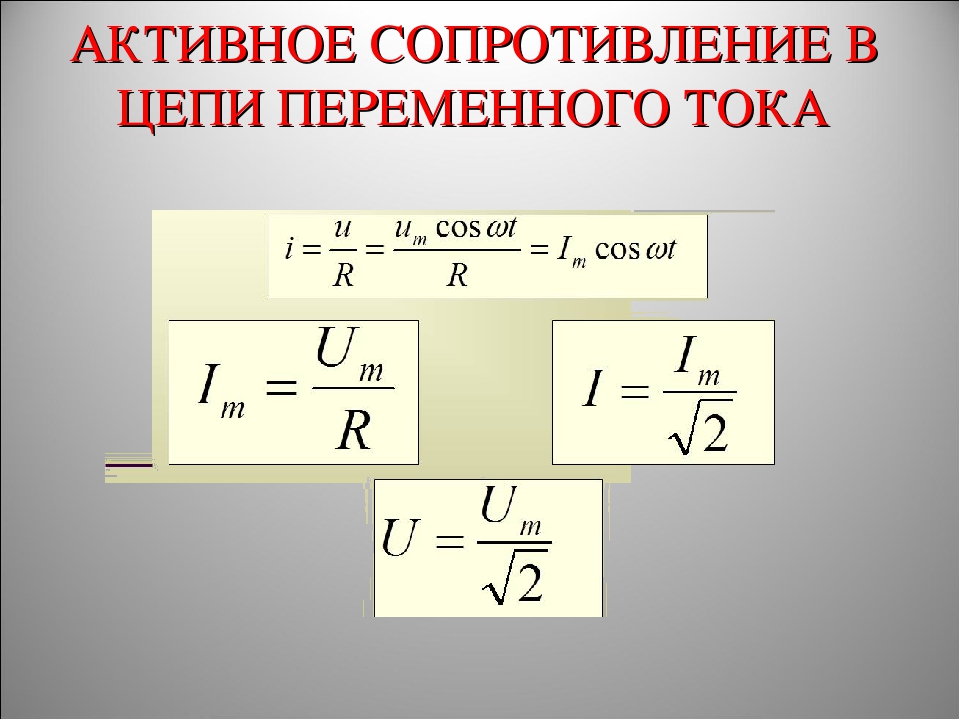 -четвертая часть цикла, и напряжение на резисторе В, , , R , точно совпадает по фазе с током. На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи В = В R + В L + V C , где все четыре напряжения — мгновенные значения.Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. Из рисунка 2 видно, что в то время как V R находится в фазе с током, V L опережает 90º, а V C следует на 90º. Таким образом, V L и V C сдвинуты по фазе на 180 ° (от пика до впадины) и имеют тенденцию отменяться, хотя и не полностью, если они не имеют одинаковой величины.{2}}} \\ [/ latex],
-четвертая часть цикла, и напряжение на резисторе В, , , R , точно совпадает по фазе с током. На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи В = В R + В L + V C , где все четыре напряжения — мгновенные значения.Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. Из рисунка 2 видно, что в то время как V R находится в фазе с током, V L опережает 90º, а V C следует на 90º. Таким образом, V L и V C сдвинуты по фазе на 180 ° (от пика до впадины) и имеют тенденцию отменяться, хотя и не полностью, если они не имеют одинаковой величины.{2}}} \\ [/ latex],
, где V 0 R , V 0 L и V 0 C — пиковые напряжения на R , L , и соответственно. {2}} \\ [/ latex],
{2}} \\ [/ latex],
, который представляет собой полное сопротивление цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора, возьмите X L = 0; а для тех, у кого нет конденсатора, возьмите X C = 0.
Рис. 2. На этом графике показано соотношение напряжений в цепи RLC и тока. Напряжения на элементах схемы складываются, чтобы равняться напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1.Расчет импеданса и тока
Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела Реактивное, индуктивное и емкостное. (b) Если источник напряжения имеет В среднеквадратичное значение = 120 В, что будет I среднеквадратичное значение на каждой частоте?
Стратегия
Для каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} — {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {kHz} \ end {array} \\ [/ latex]
{ 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {kHz} \ end {array} \\ [/ latex]
Обсуждение для (а)
В обоих случаях результат почти такой же, как и наибольшее значение, и импеданс определенно не является суммой отдельных значений. Ясно, что X L доминирует на высокой частоте, а X C доминирует на низкой частоте.
Решение для (b)
Текущее значение I среднеквадратичное значение можно найти, используя версию закона Ома по переменному току в уравнении I среднеквадратичное значение = В действующее значение / Z :
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц
Наконец, на частоте 10,0 кГц находим
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц
Обсуждение для (а)
Ток при 60,0 Гц такой же (до трех цифр), что и для одного конденсатора в Примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь незначительно отличается от того, который был обнаружен для одной катушки индуктивности в Примере 1 из раздела «Реактивное сопротивление, индуктивный и емкостной».{2}}} \\ [/ latex]
Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь незначительно отличается от того, который был обнаружен для одной катушки индуктивности в Примере 1 из раздела «Реактивное сопротивление, индуктивный и емкостной».{2}}} \\ [/ latex]
Реактивные сопротивления меняются в зависимости от частоты: X L большое на высоких частотах и X C большое на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f 0 реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса, и максимальное значение для I среднеквадратичное значение результаты .Мы можем получить выражение для f 0 , взяв
X L = X C .
Замена определений X L и X C ,
[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].
Решение этого выражения для f 0 дает
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],
, где f 0 — резонансная частота последовательной цепи RLC .Это также собственная частота , на которой цепь будет колебаться, если не будет управляться источником напряжения. При f 0 влияние катушки индуктивности и конденсатора компенсируется, так что Z = R и I среднеквадратичное значение является максимальным.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызываемое источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой цепь RLC , которая лучше всего колеблется на ее f 0 . Переменный конденсатор часто используется для настройки f 0 , чтобы получить желаемую частоту и отклонить другие. Фиг.3 представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I среднеквадратичное значение при f 0 . Две кривые относятся к двум разным цепям, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.
Фиг.3 представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I среднеквадратичное значение при f 0 . Две кривые относятся к двум разным цепям, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.
Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f 0 , но для более высокого сопротивления резонанс ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В 0 .
Пример 2. Расчет резонансной частоты и тока
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктор 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I среднеквадратичное значение при резонансе, если В среднеквадратичное значение равно 120 В.
(b) Рассчитайте I среднеквадратичное значение при резонансе, если В среднеквадратичное значение равно 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]
Обсуждение для (а)
Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.
Решение для (b)
Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40. 0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].
0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].
Обсуждение для (б)
В резонансе ток больше, чем на более высоких и низких частотах, рассмотренных для той же цепи в предыдущем примере.
Питание в цепях переменного тока серии
RLC
Если ток изменяется в зависимости от частоты в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]
Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I действующее значение ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность составляет
На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I действующее значение ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность составляет
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.
Пример 3. Расчет коэффициента мощности и мощности
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В среднеквадратичное значение 120 В: угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.
(б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.
Стратегия и решение для (a)
Коэффициент мощности при 60,0 Гц находится из
.
[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].
Нам известно Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что
[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].
Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].
Обсуждение для (а)
Фазовый угол близок к 90 °, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90 °).
Стратегия и решение для (b)
Средняя мощность при 60,0 Гц —
P ср. = I среднеквадратичное значение V среднеквадратичное значение cos ϕ .
= I среднеквадратичное значение V среднеквадратичное значение cos ϕ .
I среднеквадратичное значение оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает
P средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.
Стратегия и решение для (c)
На резонансной частоте мы знаем, что cos ϕ = 1, и I среднеквадратичное значение оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P пр. = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)
Обсуждение
Как ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на высоких и низких частотах.
Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора).
Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора).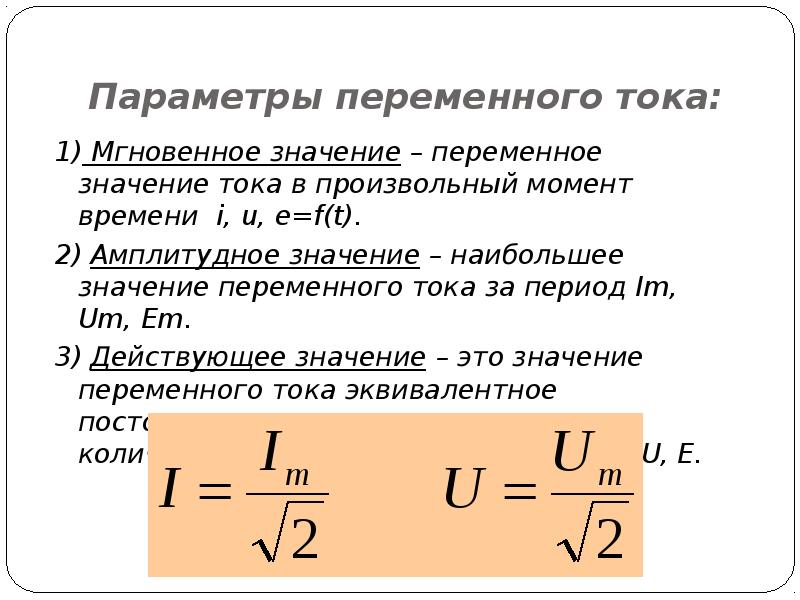 Амплитуда движения колес максимальна, если неровности дороги достигаются с резонансной частотой.
Амплитуда движения колес максимальна, если неровности дороги достигаются с резонансной частотой.
Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.
Чистая цепь LC с пренебрежимо малым сопротивлением колеблется на частоте f 0 , той же резонансной частоте, что и цепь RLC . Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.
Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
5. LC-контур аналогичен массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
Исследования PhET: комплект для конструирования цепей (AC + DC), виртуальная лаборатория
Создавайте схемы с конденсаторами, индукторами, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Аналогом сопротивления переменному току является импеданс Z , комбинированный эффект резисторов, катушек индуктивности и конденсаторов, определяемый версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],
, где I o — пиковый ток, а В o — пиковое напряжение источника.
 {2}} \\ [/ латекс].
{2}} \\ [/ латекс]. - Резонансная частота f 0 , при которой X L = X C , составляет
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]
- В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],
- ϕ = 0º для чисто резистивной цепи или цепи RLC в резонансе.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.
Концептуальные вопросы
1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.
2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.
Задачи и упражнения
1. Цепь RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.
2. Схема RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.
3. Цепь LC состоит из индуктора 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
(b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?
5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?
6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?
7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8. Какая индуктивность необходима для создания резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?
9. Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?
Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?
10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В среднеквадратичное значение = 5,60 В, что будет I среднеквадратичное значение на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I RMS в резонансе?
11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В среднеквадратичное значение = 408 В, что будет I среднеквадратичное значение на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I RMS в резонансе?
(c) Если источник напряжения имеет В среднеквадратичное значение = 408 В, что будет I среднеквадратичное значение на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I RMS в резонансе?
12. Последовательная цепь RLC имеет 2.Резистор 50 Ом, индуктор 100 мкГн и конденсатор 80,0 мкФ. (a) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.
13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.
14. Последовательная цепь RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. {2}} \\ [/ latex]
{2}} \\ [/ latex]
- резонансная частота:
- — частота, при которой полное сопротивление в цепи является минимальным, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]
- фазовый угол:
- обозначается ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
- Коэффициент мощности:
- — величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ
Избранные решения проблем и упражнения
1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц. (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора.






 Это страница ресурса Physclips. Это вспомогательная страница для
Это страница ресурса Physclips. Это вспомогательная страница для Теперь синусоидальный член усредняет
Теперь синусоидальный член усредняет



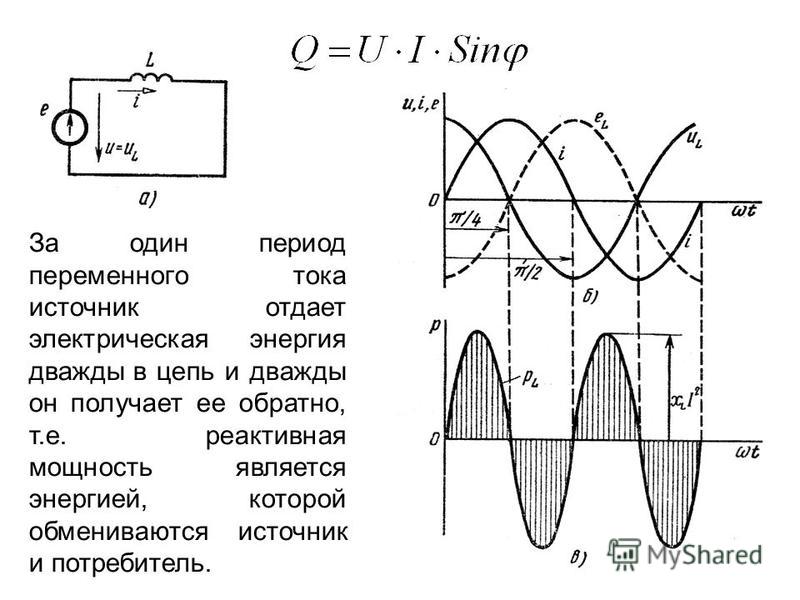 225 Вт.
225 Вт. {2}} \\ [/ латекс].
{2}} \\ [/ латекс].