схема, принцип действия и т.д.
Мост Уитстона — это одна из наиболее часто используемых мостовых схем в контрольно-измерительных приборах.
Схема моста Уитстона часто используется в системах измерения температуры. В этих системах устройство, называемое термометр сопротивления или терморезистор, обычно помещается в одной из ветвей схемы мостика.
 Принципиальная схема мостика Уитстона
Принципиальная схема мостика Уитстона
Обратите внимание на основы электричества и на приборы электроники.
Величина тока в мосте Уитстона определяется величиной разности сопротивлений: чем больше разность, тем больше будет течь ток; а если разность сопротивлений меняется, количество протекающего тока будет тоже меняться. Именно это свойство делает схему мосте Уитстона очень полезной в контрольно-измерительных устройствах и системах управления. Точные измерения переменных величин процессов достигаются тем, что переменные параметры процессов изменяют сопротивление в схеме мостика. Даже очень малые изменения величины сопротивления могут быть обнаружены при измерении тока, протекающего через мостик.
Принцип работы моста Уитстона
Схема моста Уитстона имеет два плеча сопротивления, каждое из которых содержит два резистора. Третья ветвь схемы — это соединение между двумя параллельными ветвями. Эта третья ветвь называется мостиком. Ток течет от отрицательной клеммы батарейки к верхней точке мостовой схемы. Затем, ток делится между двумя параллельными ветвями, причем количество тока, протекающее по каждой из ветвей, зависит от величины сопротивления в ветви. Наконец, ток возвращается к положительной клемме батарейки.
При равных величинах сопротивлений равное количество тока течет в каждой из ветвей. По мостику ток не течет, на что указывает нулевое положение измерителя. При этом условии о мостике говорят, что он уравновешен.
 Уравновешенная схема мостика Уитстона
Уравновешенная схема мостика Уитстона
При неравных величинах сопротивления в ветвях, ток течет в схеме от ветви с большим сопротивлением к ветви с меньшим сопротивлением. Это будет верно, пока два верхних резистора фиксированы и равны по величине, как это имеет место в схемах мостика Уитстона, используемых в контрольно-измерительных системах. Измеритель на рисунке показывает, что ток в мостике течет слева направо.
 Неуравновешенная схема мостика Уитстона
Неуравновешенная схема мостика Уитстона
Радио для всех — Мост Уитстона
Мост Уитстона был первоначально разработан Чарльзом Уитстоном, чтобы измерить неизвестные значения сопротивления и как средство калибровки измерительных приборов, вольтметров, амперметров и т. Д., Используя длинный резистивный провод скольжения. Хотя сегодня цифровые мультиметры обеспечивают самый простой способ измерения сопротивления. Мост Уитстона все еще можно использовать для измерения очень низких значений сопротивлений в диапазоне милли-Ом. Мост моста Уитстона (или мост сопротивления) может использоваться в ряде приложений, и сегодня, с современными операционными усилителями, мы можем использовать мост моста Уитстона для подключения различных преобразователей и датчиков к этим схемам усилителя. Контур моста Уитстона представляет собой не что иное, как два простых последовательно-параллельных устройства сопротивлений, соединенных между клеммой источника питания и землей, создающей разность нулевого напряжения между двумя параллельными ветвями при балансировке. Мостовая схема Уитстона имеет две входные клеммы и две выходные клеммы, состоящие из четырех резисторов, сконфигурированных в алмазоподобном устройстве, как показано. Это типично для того, как нарисован мост Уитстона.
Мост Уитстона
При балансировке мост Уитстона можно анализировать просто как две серии последовательностей. В нашем учебнике о резисторах в сериях мы видели, что каждый резистор в цепочке серий производит инфракрасное падение или падение напряжения на себя как следствие протекания тока через него, как это определено законом Ом. Рассмотрим последовательную схему ниже.
Поскольку два резистора последовательно, один и тот же ток ( i ) проходит через оба из них. Поэтому ток, протекающий через эти два резистора последовательно, задается как: V / R T.
I = V ÷ R = 12 В ÷ (10 Ом + 20 Ом) = 0,4 А
Напряжение в точке C , которое также является падением напряжения на нижнем резисторе, R 2 рассчитывается как:
V R2 = I × R 2 = 0,4A × 20Ω = 8 вольт
Затем мы видим, что напряжение источника V S делится между резисторами двух рядов прямо пропорционально их сопротивлениям как V R1 = 4V и V R2 = 8V . Это принцип деления напряжения, создающий то, что обычно называют цепью делителя напряжения или сетью делителя напряжения. Теперь, если мы добавим еще одну последовательную резисторную схему, используя те же самые значения резисторов параллельно с первой, у нас будет следующая схема.
Поскольку схема второй серии имеет одинаковую резистивную величину первой, напряжение в точке D , которое также является падением напряжения на резисторе, R 4 будет одинаковым при 8 вольтах относительно нуля (отрицательный аккумулятор), поскольку Напряжение является общим, и две резистивные сети одинаковы. Но что-то еще в равной степени важно, так это то, что разность напряжений между точкой C и точкой D будет равна нулю, так как обе точки имеют одинаковое значение 8 вольт, так как: C = D = 8 вольт , тогда разность напряжений равна 0 вольтам. Когда это происходит, обе стороны параллельной сети моста считаются сбалансированными, потому что напряжение в точке C является тем же значением, что и напряжение в точке D, причем их разность равна нулю. Теперь давайте рассмотрим, что произойдет, если мы изменим положение двух резисторов R 3 и R 4 во второй параллельной ветви по отношению к R 1 и R 2 .
С резисторами R 3 и R 4 меняются назад, тот же ток протекает через последовательную комбинацию и напряжение в точке D , которое также является падением напряжения на резисторе, R 4 будет:
V R4 = 0,4 А × 10 Ом = 4 вольта
Теперь, когда V R4, имеющий 4 вольта, упал на него, разность напряжений между точками C и D будет составлять 4 вольта, так как: C = 8 вольт и D = 4 вольта . Тогда разница на этот раз: 8 — 4 = 4 вольта
Результатом замены двух резисторов является то, что обе стороны или «плечи» параллельной сети отличаются друг от друга, поскольку они создают различные падения напряжения. Когда это происходит , параллельная сеть считается несимметричной , поскольку напряжение в точке C находится под другим значением напряжения в точке D. Затем мы видим, что отношение сопротивления этих двух параллельных рычагов, ACB и ADB приводит к разности напряжений между 0 вольтами (сбалансированным) и максимальным напряжением питания (неуравновешенным), и это основной принцип схемы моста Уитстона . Таким образом, мы видим, что схема моста Уитстона может использоваться для сравнения неизвестного сопротивления R X с другими известными значениями, например R 1 и R 2 , с фиксированными значениями, а R 3 может быть переменным. Если бы мы подключили вольтметр, амперметр или классически гальванометр между точками C и D , а затем меняли резистор, R 3 до тех пор, пока счетчики не начнут отсчитывать ноль, это приведет к балансу двух рычагов и значению R X (заменяя R 4 ) Как показано.
Цепь моста Уитстона
Путем замены R 4 выше на сопротивление известного или неизвестного значения в чувствительном плече моста Уитстона, соответствующего R X, и настройке противоположного резистора, R 3 для «балансировки» сети моста приведет к выводу нулевого напряжения. Затем мы видим, что баланс происходит, когда:
Уравнение Моста Уитстона, необходимое для определения значения неизвестного сопротивления, R X при балансе задается как:
Где резисторы, R 1 и R 2 являются известными или заданными значениями.
Мост Уитстона Пример №1
Построен следующий несбалансированный мост Уитстона. Рассчитайте выходное напряжение в точках C и D и значение резистора R 4, необходимое для баланса мостовой схемы.
Для первого ряда arm, ACB
Для группы второго ряда, АБР
Напряжение в точках CD определяется как:
Значение резистора R 4, необходимое для уравновешивания моста, определяется как:
Мы видели выше, что мост Уитстона имеет два входных терминала ( AB ) и два выходных терминала ( CD ). Когда мост сбалансирован, напряжение на выходных клеммах составляет 0 вольт. Однако, когда мост не сбалансирован, выходное напряжение может быть как положительным, так и отрицательным в зависимости от направления дисбаланса.
Светодиодный детектор на мосте Уитстона
Сбалансированные мостовые схемы находят много полезных электронных приложений, например, для измерения изменений интенсивности света, давления или деформации. Типы резистивных датчиков, которые могут использоваться в мостовой схеме пшеничного мостика, включают: фоторезистивные датчики (LDR), позиционные датчики (потенциометры), пьезорезистивные датчики (тензодатчики) и температурные датчики (термисторы) и т. Д. Существует множество применений мостовых мостовых косточек для измерения целого ряда механических и электрических величин, но одно очень простое применение мостового мостового слоя заключается в измерении света с помощью фоторезистивного устройства. Один из резисторов в сети моста заменяется резистором, зависящим от света, или LDR. LDR, также известный как кадмий-сульфидный (Cds) фотоэлемент, представляет собой пассивный резистивный датчик, который преобразует изменения уровня видимого света в изменение сопротивления и, следовательно, напряжения. Светоизлучающие резисторы могут использоваться для мониторинга и измерения уровня интенсивности света, или источник света включен или выключен. Типичная кадмиевая сульфидная (CdS) ячейка, такая как резистор, зависящий от света ORP12, обычно имеет сопротивление около одного Megaohm (MΩ) в темном или тусклом свете, около 900 Ом при интенсивности света 100 люкс (типичный для хорошо освещенной комнаты), До 30 Ом при ярком солнечном свете. Затем при увеличении интенсивности света сопротивление уменьшается. Подключив резистор, зависящий от света, к схеме моста Уитстона выше, мы можем отслеживать и измерять любые изменения уровней освещенности, как показано на рисунке.
Фотоэлемент LDR подключается к схеме моста Уитстона, как показано на рисунке, для создания светочувствительного переключателя, который активируется, когда измеряемый уровень света выходит выше или ниже заданного значения, определенного V R1 . В этом примере V R1 используется потенциометр 22k или 47k. ОУ-усилитель подключается как компаратор напряжения с опорным напряжением V D , применяемым к инвертирующему выводу. В этом примере, поскольку оба R 3 и R 4 имеют одинаковое значение 10 кОм , опорное напряжение, установленное в точке D, будет поэтому равно половине Vcc. Это Vcc / 2 . Потенциометр V R1 устанавливает напряжение отключения V C , которое подается на неинвертирующий вход и устанавливается на требуемый номинальный уровень освещенности. Реле включается «ON», когда напряжение в точке C меньше напряжения в точке D. Регулировка V R1 устанавливает напряжение в точке C для балансировки мостовой схемы на требуемом уровне освещенности или интенсивности. LDR может представлять собой любое сульфидное устройство кадмия, которое имеет высокий импеданс при низких уровнях освещенности и низкий импеданс при высоких уровнях освещенности. Обратите внимание, что схема может использоваться как «световая активированная» коммутационная схема или «темная активированная» коммутационная схема просто путем переноса положений LDR и R 3 в рамках конструкции. Мост Уитстона имеет много применений в электронных схемах, кроме сравнения неизвестного сопротивления с известным сопротивлением. При использовании с операционными усилителями мостовую схему Уитстона можно использовать для измерения и усиления небольших изменений сопротивления, например RX, к изменениям интенсивности света, как мы видели выше. Но мостовая схема также подходит для измерения изменения сопротивления других изменяющихся величин, поэтому, заменив вышеуказанный фоторезистивный датчик LDR для термистора, датчика давления, тензодатчика и других таких преобразователей, а также заменив положения LDR и V R1 , мы можем использовать их в различных других приложениях моста Уитстона. Кроме того, в четырех плечах (или ветвях) моста, образованного резисторами R 1 -R 4, может использоваться более одного резистивного датчика для создания «полномостового», «полумостового» или «четвертьмостового» схем, обеспечивающего Тепловая компенсация или автоматическая балансировка моста Уитстона.
Измерительные мосты постоянного и переменного тока. Принципы измерений: мост Уитстона
При обслуживании металлических кабельных линий наиболее часто пользуются измерительными мостами, хотя для поиска мест повреждения кабеля существуют и другие приборы. Во-первых, они обеспечивают высокую точность в широком диапазоне измеряемых величин. Во-вторых, их применение позволяет организовать измерения таким образом, чтобы компенсировать посторонние влияния, что незаменимо для локализации неисправности. В-третьих, они недороги.
Учитывая сказанное, полезно ознакомиться не только с устройством измерительных мостов, но и с принципами их применения для локализации неисправностей. Впрочем, говоря языком математики, для построения оптимальных схем измерения такие знания необходимы, но недостаточны. Диагностика — это всегда и опыт, и искусство.

Принцип работы мостовой схемы измерения продемонстрировано на Рисунке 1 (RM1a), а способ ее применения на практике — на Рисунке 2 (RM2a). Сопротивление R1 вычисляется исходя из полученного при балансировке моста соотношения R4/R3, в качестве R2 используется резистор с известным значением. Конечно, сказанное дает только самое общее представление об измерительной схеме моста. На самом деле он устроен гораздо сложнее — современные мосты создаются на основе цифровых процессоров. Микропроцессорное ядро позволяет автоматизировать процедуру измерения (в первых моделях оператор должен был пользоваться калькулятором, сегодня же все расчеты выполняются аппаратурой), обеспечить многофункциональность устройства (многие мосты интегрированы с другими измерительными приборами — мультиметрами, рефлектометрами и т. п.), устранить помехи (посторонние постоянные и переменные напряжения почти всегда присутствуют на жилах кабелей), организовать дальнейшую обработку накопленных результатов измерений (хранение, обмен с компьютером, печать протоколов) и др.

Рассмотренный выше мост, используемый для измерения сопротивления, носит имя Уитстона (Wheatstone). Для подключения измеряемых цепей в нем применяются всего две клеммы (B и C). Более сложные схемы реализованы в двух других мостах — Муррея (Murray) и Купфмюллера (Kupfmuller) (RM2в). Здесь измеряемые цепи подключаются с помощью трех клемм (A, B и C). В более сложных схемах Хиборна/Графа (Hilborn/Graf) задействуются четыре клеммы (A, B, B’ и C) (RM3). Смысл увеличения числа точек подключения станет понятен при рассмотрении схем измерения с применением мостов.

Еще один момент. Все упомянутые мостовые схемы используются для измерений при постоянном токе (определяются величины активных сопротивлений, подключенных к клеммам). Кроме того, мостовые схемы Уитстона и Муррея используются для измерений при переменном токе (определяются величины емкостей, подключенных к клеммам). В таких мостах источником напряжения служит генератор синусоидального напряжения.
Теперь остановимся на схемах измерений. С помощью моста Уитстона при постоянном токе измеряют сопротивление витой пары (шлейфа), сопротивление изоляции жил пары, сопротивление изоляции между жилами и экраном (RM3, RM4, RM5).

Значения упомянутых параметров используются для диагностики кабельных линий. Локализация же неисправностей требует определения места повреждения на кабельной линии. При помощи моста постоянного тока несложно вычислить расстояние до места повреждения. Зная сопротивление шлейфа Rшл и погонное сопротивление жил кабеля Rпог, можно воспользоваться формулой: Lпары = Rшл / 2Rпог, и рассчитать длину витой пары.

Погонное сопротивление медных жил определяется табличным способом по их сечению. Оно зависит не только от сечения жил, но и от их температуры. Чтобы избежать ошибки, нужно использовать значение погонного сопротивления для соответствующей температуры (особенно важно это для воздушных кабельных линий, где температура меняется в широких пределах). В простых мостах значения вводятся оператором вручную из таблиц. В более сложных приборах при помощи автоматической или полуавтоматической калибровочной процедуры определяется поправочный коэффициент по измеренному значению температуры (для чего в комплекте прибора присутствует щуп-датчик).

Длина витой пары может быть установлена также мостовым методом при переменном токе. В таком случае измеряемым параметром является емкость витой пары. Разделив емкость витой пары на ее погонную емкость, получим длину витой пары.

Аналогично рассмотренным выше измерениям при постоянном токе, с помощью моста Уитстона при переменном токе определяются емкость витой пары (шлейфа) и емкость каждой из жил пары относительно экрана. Длина жил может быть вычислена по их погонной емкости. Погонная емкость (нФ/км) витой пары зависит от сечения жил, типа скрутки, вида и материала изоляции и определяется табличным способом по типу кабеля.
Резкое увеличение емкости витой пары по сравнению с ее паспортным значением, как правило, свидетельствует о наличии воды в сердечнике кабеля. Для локализации повреждений этого типа применяются другие методы, прежде всего зондирование поврежденной пары с помощью рефлектометра.

Отметим, что, в отличие от сопротивления, погонная емкость слабо зависит от температуры, что существенно упрощает измерения.
Мост Уитстона (мост постоянного тока) — Студопедия
Компенсационный способ измерения сопротивлений является наиболее точным. Принципиальная схема метода (мост Уитстона) дана на рис. 5. Мостовая схема представляет собой замкнутый четырехугольник abcd, составленный из сопротивлений R1, R2, R3, R4, называемых плечами моста. Противоположные вершины ас и bd соединены диагоналями моста. В одну диагональ включен источник тока, в другую – нулевой гальванометр Г. При некотором соотношении между сопротивлениями плеч ток, протекающий через гальванометр, обращается в ноль (ig = 0). В этом случае говорят, что мост уравновешен.
Условие равновесия моста. Обозначим токи в плечах соответственно через i1 , i2 , i3 , i4 . Так как ig = 0, то, во-первых, i1 = i2 , а i3 = i4 и, во-вторых, φb = φd. По закону Ома разности потенциалов для плеч равны:
1. φa– φb= i1R1 ;3. φb– φc= i2R2 = i1R2 ;
2. φa – φd= i3R3 ; 4. φd– φc= i4R4 = i3R4 .
Так как φb= φd,то i1R1= i3R3и i1R2= i3R4 , откуда
R1 / R2= R3 / R4 (6)
Это и есть условие равновесия моста. Его используют для расчета одного из 4-х сопротивлений. Пусть вместо R1 в цепь включен резистор с неизвестным сопротивлением RX . При трех остальных известных сопротивлениях
RХ = R2·R3 / R4. (7)
Таким образом, измерение неизвестного сопротивления сводится к уравновешиванию моста с тремя известными и одним неизвестным сопротивлением и расчета последнего по формуле (7).
Уравновесить мост, т.е. добиться отсутствия тока через гальванометр, можно двумя способами. Во-первых, установив постоянное отношение R3 / R4, подбирать соответствующее сопротивление R2и, во-вторых, установив постоянное сопротивление R2, изменять отношение плеч R3 / R4. Первый способ используется в декадных мостах. Второй способ реализуется в линейных мостах (рис. 6). Здесь RХ – неизвестное сопротивление, R2 – магазин сопротивлений. Сопротивления R3 и R4 заменены отрезками l3 и l4 калиброванной проволоки (реохорда). Перемещая движок D вдоль реохорда, можно плавно изменять отношения плеч R3 / R4 . Так как сопротивление проволоки пропорционально длине, то отношение сопротивлений R3 / R4 можно заменить отношением соответствующих отрезков реохорда l3/l4 . Таким образом, измерение неизвестного сопротивления сводится к следующему:
1. Замыкая на короткое время кнопку К и перемещая движок D вдоль реохорда, следует добиться равновесия моста (при замкнутом ключе К ток через гальванометр не течет ig = 0).
2. Определить по линейке реохорда длины отрезков l3 и l4 = l – l3 , где l – длина всего реохорда.
3. Рассчитать неизвестное сопротивление по формуле:
RХ = R2·l3 / l4 . (8)
Для повышения точности измерений следует стремиться к тому, чтобы мост был уравновешен при отношении плеч l3/l4 близком к 1, т.е. чтобы движок D находился примерно в средней трети длины реохорда. Для этого сопротивление R2 должно быть приблизительно равно RХ . Если сопротивление RХ неизвестно даже приблизительно, то, выбрав R2 произвольно, уравновешивают мост и рассчитывают RХсначала приближенно, а затем, установив на магазине сопротивлений R2 » RХ, повторяют измерения и рассчитывают RХ более точно.
Поскольку сопротивление реохорда мало, мост Уитстона описанного типа применяется, как правило, для измерения небольших сопротивлений (от 1 до 1000 Ом).
Мост Уинстона — это… Что такое Мост Уинстона?
Измерительный мост — устройство для измерения электрического сопротивления, предложенное в 1833 Самуэлем Хантером Кристи, и в 1843 году усовершенствованное Чарльзом Витстоном. Принцип измерения основан на взаимной компенсации сопротивлений двух звеньев, одно из которых включает измеряемое сопротивление. В качестве индикатора обычно используется чувствительный гальванометр, показания которого должны быть равны нулю в момент равновесия моста.

Измерительный мост с вольтметром
На схеме R1, R2, R3, R4 – плечи моста, AD — диагональ питания, CB — измерительная диагональ. Rx представляет собой неизвестное сопротивление; R1, R2 и R3 — известные сопротивления, причём значение R2 может регулироваться. Если отношение сопротивлений (R1 / R2) равно отношению сопротивлений другого (Rx / R3), то разность потенциалов между двумя средними точками будет равна нулю, и ток между ними не будет протекать. Сопротивление R2 регулируется до получения равновесия, а направление протекания тока показывает, в какую сторону нужно регулировать R2.
С помощью гальванометра момент равновесия можно установить с большой точностью, и если сопротивления R1, R2 и R3 имеют маленькую погрешность, то Rx может быть измерено очень точно, ведь даже небольшие изменения Rx вызывают заметное нарушение баланса всего моста.
Таким образом, если мост сбалансирован (ток через гальванометр, сопротивление которого можно обозначить как Rg, равен нулю), эквивалентное сопротивление цепи будет:
R1 + R2 в параллели с R3 + Rx, то есть
С другой стороны, если R1, R2 и R3 известны, но R2 не регулируется, то значение напряжения или тока через гальванометр также можно использовать для расчёта Rx, используя законы Кирхгофа. Такой метод применяется в тензометрических измерителях для расчёта величины механических деформаций, а также в электронных термометрах.
Запишем первый закон Кирхгофа для точек B и C (Ig — ток, протекающий через гальванометр):
- B:

- C:

Теперь рассчитаем потенциал в цепях ABC и BCD, используя второй закон Кирхгофа:
- ABC:

- BCD:

Учитывая, что мост сбалансирован и Ig = 0, запишем систему уравнений:
Решая систему уравнений, получим:
Если известны значения всех четырёх сопротивлений, а также напряжение (Vs), то напряжение на плечах моста можно найти, используя формулы делителя напряжения, а затем вычесть их друг из друга, чтобы найти V:
Если упростить выражение:
Измерительный мост показывает пример так называемых дифференциальных измерений, которые могут обладать очень высокой точностью. Варианты измерительного моста могут использоваться также для измерения электрической ёмкости, индуктивности, импеданса и даже количества взрывчатых газов в пробе при помощи эксплозиметра.
Идея измерительного моста была применена лордом Кельвином в 1861 для измерения малых сопротивлений, Максвеллом в 1865 для измерения в области переменных токов, а также Аланом Блюмлейном в 1926, который за усовершенствованный вариант получил патент, а устройство было названо его именем.
См. также
Wikimedia Foundation.
2010.
Мостовые схемы измерителей параметров элементов — Студопедия
Для измерения параметров элементов цепей методом сравнения применяют мосты. В сравнении измеряемой величины (сопротивление, индуктивность, емкость) с образцовой меры при помощи моста измеряют автоматически или вручную на переменном или постоянном токе. Мостовые схемы обладают высокой точностью, широким диапазоном измеряемых значений параметров элементов. На основе мостовых методов строят приборы, предназначенные для измерения какой-либо одной величины, так и универсальные. Существует несколько элементов мостовых схем RLC: четырехплечие, уравновешенные, неуравновешенные и процентные. В зависимости от вида мостовых схем количество входящих в ее состав ветвей (плеч) мосты можно разделить на: четырехплечие, многоплечие, Т-образные и т.д. наиболее распространенные четырехплечие (одинарные) мосты. Т-образные мосты обычно применят для измерения параметров электрических цепей на высоких и сверхвысоких частотах. В состав каждой мостовой схемы входят измеряемые параметры и переменные образцовые меры. В зависимости от соотношения между параметрами мостовой схемы может быть, а может и отсутствовать напряжение (ток), в результате чего мосты делятся на неуравновешенные (есть ток) и уравновешенные (нет тока).
Принцип действия четырехплечего (одинарного) моста.
Одинарный мост имеет 4 плеча (Z1,Z2,Z3,Z4), источник питания (U), ноль-индикатор. Если сопротивления таковы что точки А и В имеют равные потенциалы, то через ноль-индикатор отсутствует; в этом случае говорят что достигается равновесие моста. Z1*Z4=Z2*Z3 (1). Если Z4 неизвестное сопротивление, то его значение можно определить из условия равновесия Z4=Z2*Z3/Z1 (2). Отсюда следует, что равновесие не зависит от сопротивления ноль-индикатора, т.к. ток не течет через него, а также от напряжения и сопротивления источника питания. Таким образом, высокостабильный источник питания не требуется. Z3 – плечо сравнения, а отношение Z1/Z2 определяет диапазон изменения измеряемой величины. Чтобы охватить широкий диапазон известных импедансов мосты снабжают переключателем, которые изменяют сопротивление Z1 и Z2 в 10 раз. Сопротивление моста в общем случае имеет комплексный характер: Z1=Z1*ejf1, Z2=Z2*ejf2, Z3=Z3*ejf3, Z4=Z4*ejf4.
Zj – модули комплексных сопротивлений
fi – соответствующая фаза
φ1+φ4=φ2+φ3 (3)
Когда равновесие моста определяется выражениями 1 и 3 тогда мост переменного тока нуждается в регулировке двух независимых параметров, чтобы обеспечить равновесие модулей и фазовых углов.
Чувствительность моста очень важный параметр и определяется, как способность менять на малые отклонения. Оно выражается как изменение тока через ноль-индикатор при единичном отклонении моста регулируемого в положении равновесия. При максимальной чувствительности моста если Z2=Z4, то и Z1=Z3. на практике это условие выполняется редко, т.к. Z3 должно быть достаточно большим чтобы обеспечить требуемую точность. Наибольшая чувствительность достигается, когда ноль-индикатор включен между контактами двух плеч с максимальным и минимальным импедансом. Чувствительность моста также пропорциональна напряжению источника питания. В качестве ноль-индикатора в мосте постоянного тока можно использовать магнитно-электрический прибор. Простейшим индикатором для моста переменного тока является головной телефон; на частотах, на которых чувствительность уха низка применяют радиоприемник или измерительные усилители. Для достижения высокой чувствительности и избирательности требуется генератор непрерывного сигнала и гетеродинный индикатор. Для уравновешивания моста используют также подключенный к осциллографу усилитель. Напряжение источника питания не должно превышать максимально допустимого напряжения и не выделять избыточного тепла. Чем ниже напряжение, тем ниже чувствительность моста и система более восприимчива к высокочастотным помехам. Для мостов переменного тока на низкой частоте можно использовать сетевое напряжение 50 Гц. Выпускаемые промышленные мосты обычно содержат источники питания с различными частотами, т.к. чувствительность мостов с реактивными сопротивлениями пропорционально частоте и эта зависимость может быть крутой на одном конце сопротивления и пологой на другом. Максимальная частота источника питания должна быть ниже собственной резонансной частоты измеряемых элементов, чтобы уменьшить ошибки измерений. Если точка равновесия моста чувствительна к частоте, то источник питания должен иметь стабильную частоту и не генерировать гармоники, т.к. уравновешенные на одной частоте не остаются в равновесии на гармонике.
Резистивные мосты.
Мост Уитстона.
Наибольшее распространение получил резистивный мост называемый мостом Уитстона.
Rx – неизвестное сопротивление
R1, R2, R3 – регулируются до тех пор пока ток через ноль-индикатор не станет равным нулю. В таком положении Rх определяется: Rх=R3R2/R1 (4)
R1 и R2 – неизвестные фиксированные сопротивления в диапазоне от 1Ом до 1кОм, при этом R2/R1 составляет от 10-3 до 103.
R3 регулируется шагом 1 или 1.1Ом вплоть до 10кОм, чтобы уравновесить мост. При измерении, R1 и R2 выбираются такими, чтобы чувствительность моста была максимальной. R4 сначала включают в цепь для защиты ноль-индикатора, но может быть и закорочено для повышения чувствительности, когда равновесие достигнуто.
Мост Уитстона используют для измерения сопротивлений резистора с двумя зажимами от 1Ом до 100 МОм. Нижний предел измерения сопротивлений зависит от импеданса соединений проводов и контактов. Для измерения сопротивлений ниже 1ом используют второй мост Уитстона. При измерении до 100 Ом мост дает ошибку (5-100)10-6. В мосте используются резисторы из манганина, который имеет низкий температурный коэффициент сопротивления, высокую стабильность, и низкий термоЭДС. При проведении измерений с мотом Уитстона обычно берут 2 отсчета при разных полярностях батареи, а затем усредняют результат, исключая эффект термоЭДС. Пиковый ток через резисторы должен поддерживаться на низком уровне, чтобы избежать изменения сопротивления из-за их нагрева током. Чтобы использовать мост Уитстона для измерений выше 100 МОм требуется высокое напряжение, тогда токи утечки на землю могут приводить к заметным погрешностям. Их можно уменьшить и расширить рабочий диапазон моста до 1012 Ом, если использовать высокочувствительный индикатор и методы защиты (экранирование, заземление экрана и другое).
Мосты для измерения индуктивности.
Для измерения индуктивности в этих мостах используется метод сравнения с известной индуктивностью. Для питания используется переменный ток, при этом две составляющие моста должны быть регулируемые, чтобы обеспечить уравновешивание, как по модулю, так и по фазе. Предполагается, что неизвестная катушка имеет собственную индуктивность Lx, взаимную Nx и сопротивление Rx.
Мост для измерения индуктивности методом сравнения с мерой.
Наиболее прямой метод измерения индуктивности состоит в сравнении с известной с помощью моста.
R1 – регулируемое сопротивление, которое включает сопротивление катушки L1
r – резистор (необязателен)
При равновесии моста Rx и Lx определяется:
Rx=(R1*R3/R2)-r (5)
Lx=L1R3/R2 (6)
Регулируя L1 и R1, уравновешивающийся мост достигает равновесия с Rx и Lx. Поскольку индуктивности имеют относительно большие собственные сопротивления, можно включит в схему r и изменить его сопротивление в процессе уравновешивания, чтобы расширить диапазон измеряемых индуктивностей. Если использовать меры индуктивности, то уравновешивание моста можно обеспечит регулировкой R1 и R3/R2, но при регулировке они будут влиять друг на друга, в результате время уравновешивания увеличивается и зависит от добротности Q неизвестной индуктивности. Такой измеритель индуктивности используется редко из-за трудности получения стабильных и точных индуктивностей.
Мост Максвелла-Вина.
В модификации моста Максвелла предложенной Вином для измерения неизвестной индуктивности используется параллельное соединение сопротивлений и емкостей.
Поскольку ток через конденсатор опережает ток через индуктивность, необходима фазовая компенсация. Следовательно, емкостные и индуктивные компоненты следует размещать в противоположных плечах моста. Условие равновесия моста:
Rx=R1R3/R2 (7)
Lx=R1R3/C (8)
Qx=ωLx/Rx=ωR2C (9)
Индуктивность измеряется с помощью емкостей высокого качества, которые значительно точнее и легче в изготовлении, чем образцовые, и создают незначительное поле. Равновесие обычно достигается регулировкой R2 и С, т.к. этим обеспечивается независимое уравновешивание Rx и Lx. Однако можно использовать фиксированную С и регулировать R2, R1 или R3, хотя при этом время уравновешивания возрастает. Мост широко используется для измерения индуктивности катушек с добротностью Q ниже 10. Этот верхний предел Q обусловлен тем, что как следует из (3) сумма фазовых углов противоположных плеч моста должны быть равны при равновесии. Т.к. R1 и R3 активные сопротивления, то их фазовые углы равны нулю. Ток через индуктивность с большой Q будет отставать по фазе почти на 900. это означает, что резистор R2 должен иметь слишком большое сопротивление. Эта трудность преодолена в мосте Хея.
Мост Хея.
Rx=R1R3/R2(1+Q2x) (10)
Lx=R1R3C/(1+1/Q2x) (11)
Qx=ωLx/Rx=1/ωR2c (12)
(10) и (12) – условие равновесия
R2 соединен последовательно с емкостью С. При высокой добротности Lx R2 можно выбрать очень маленьким. Недостаток: равновесие зависит так, что шкалу прибора невозможно проградуировать в значениях индуктивности. Мост Хея обычно используют только для измерения катушек с добротностью Q меньше 10. если пренебречь в (11) членом Q2x, то значение индуктивности не зависет от частоты, и погрешность составит менее1%.
Мост Оуэна.
Rx=(R1C1/C2)-r (13)
Lx=R1R2C1 (14)
(13) и (14) условие равновесия моста. Если R2 и С2 регулируемые элементы схемы, то можно обеспечить независимое равновесие для Rx и Lx. Хотя это возможно для регулировки R1 и R2. r подключать необязательно, нужно для расширения диапазона возможного баланса сопротивлений. Данный мост полезен для определения дифференциальной индуктивности.
Мост Кемпбелла.
Mx=M1R3/R2 (15)
Rx=R1R3/R2 (16)
Lx=L1R3/R2 (17)
Используют для измерений взаимной индуктивности со сравнением с образцовой. (15) и (17) — условие равновесия. Положение 2: калибровка регулированием L1 и R1. Положение 1: измерение. М1 регулируют до установления с Мх.
Измерение индуктивности, добротности, емкости, тангенс дельта мостами переменного тока
Мостовые схемы измерения индуктивности и добротности с образцовыми элементами: а) — с катушками, б) с конденсатором. В них используется источник гармонического тока с напряжением U и угловой частотой ω. Эти мосты обеспечивают наилучшее уравновешивание. Эквивалентная схема замещения для катушек индуктивности с потерями могут быть последовательными или параллельными в зависимости от потерь отраженных активным сопротивлением. Условие равновесия моста для схемы а): R1(Rx+jωLx)=R2(Ro+jωLo) (1).
Где Lх и Rх измеряемое индуктивность и сопротивление омических потерь в катушке, Lo и R0 — образцовая индуктивности и сопротивление. Приравняв, действительные и мнимые части в выражении (1) находим: Rx=RoR2/R1, Lx=LoR2/R1 (2).
Поскольку изготовление высокодобротных образцов катушек вызывает определенные трудности, часто в качестве образцовой меры в мостах переменного тока применяют конденсатор (рис б). Для этой схемы справедливо: Rx+jωLx=R2R3(1/Ro+jωCo) (3).
Если в данном уравнении приравнять действительную и мнимую части, то получим следующее выражение: Rx=R2R3/Ro Lx=CoR2R3 (4).
Добротность катушки определяется: Q=ωLx/Rx=RoωCo (5)
Мосты для измерения емкостей.
Для измерения емкости и тангенса угла потерь конденсаторов с достаточно малыми потерями применяют мостовые схемы с последовательным соединением Сх и Rх, а для конденсаторов с большими потерями — схемы с параллельным соединением Сх и Rх. Для измерения емкости используются три вида моста: мост для измерения методом сравнения с мерой, мост Шеринга и мост Вина. Рассмотрим мост для измерения емкости методом сравнения с мерой.
Принципиальные схемы мостов для измерения емкости методом сравнения с мерой: а) — последовательное включение, б) – параллельное, где С1 образцовая емкость с внутренним сопротивлением R1
Условие равновесия моста имеет вид:
Rx=R1R3/R2 (6)
Cx=C1R2/R3 (7)
tgδ=ωC1R1 (8)
Сопротивление R1 и R2 регулируется до уравновешивания моста, и поскольку они связаны, нужно выполнить несколько попыток. Емкость С1 — обычно образцовый конденсатор высок точности, который не регулируется. Для измерения емкости с высоким тангенсом угла диэлектрических потерь предпочтительно использовать схему с параллельным включением, т.к. при последовательном включении R1 должно быть большим. Равновесие моста определяется выражениями 6,7 и 8, а тангенс угла диэлектрических потерь: tgδ=1/ωC1R1.
Метод сравнения с мерой не очень точен для измерения емкостей с малым tgδ, в этих случаях лучше использовать мост Шеринга.
Мост Шеринга.
Этот мост широко используется для измерения емкости, для точного определения tgδ. Он также используется в мостах высокого напряжения методом сравнения с образцовыми емкостями высокого напряжения и применением экранирования.
Условие равновесия:
Rx=C2R3/C1 (10)
Cx=C1R2/R3 (11)
tgδ=ωC2R2 (12)
С1 – образцовая емкость с малыми потерями tgδ, С2 и R2 регулируются до достижения равновесия. Уравновешивание схем обеспечивается поочередным регулированием образцовых сопротивлений или емкостей. Эту процедуру называют шагами, а количество шагов определяется сходимостью моста. Мост с хорошей сходимостью имеет не больше 5 шагов. Мост переменного тока используется на низких частотах 500-5000 Гц, поскольку при работе на повышенных частотах погрешности резко возрастают. Погрешность измерения моста переменного тока определяет погрешность элементов образующих мост, переходных сопротивлений контактов и чувствительность схемы. Мосты переменного тока больше, чем мосты постоянного, подвержены влиянию помех, и паразитных связей между плечами, плечами и землей и т.д. Поэтому даже при тщательном экранировании моста и принятии других мер защиты погрешности у мостов переменного тока больше, чем у моста постоянного тока.
Измерение частоты.
С помощью моста Вина можно измерить неизвестную емкость Сх, но чаще он применяется для измерения неизвестной частоты. При этом вместо Сх включается образцовая емкость.
Условие равновесия: Cx/C1=R2/R3-R1/Rx (13), C1Cx=1/ω2R1Rx (14).
Решая, уравнения 13 и14 можем, найти частоту: f=1/2П(C1CxR1Rx)1/2 (15).
Применяемых на практике мостах емкости С1 и Сх фиксированы, а R1 и Rх — известные переменные сопротивления, которые регулируются общей ручкой, так что R1=Rх. Значение R2 принимают равным 2R3, так что выражение 15 принимает вид: f=1/2ПC1R1 (16).
Следовательно, мост уравновешивается изменением одного лишь сопротивления R1, калибровка осуществляется непосредственно в значениях частоты. Поскольку мост Вина чувствителен к изменениям частоты — его трудно уравновесить, если входной сигнал содержит гармоники, поэтому такой сигнал необходимо, сначала отфильтровать.
Уитстонов мост – Уикипедия

Уитстонов мост или електроизмервателен мост на Уитстън е електрическа схема, която се използва за измерване по сравнителен метод на съпротивления (или други неелектрически величини, свързани със съпротивленията с известна зависимост). Предложен е през 1833 г. от Самуел Хънтър Кристи (англ. Samuel Hunter Christie), а през 1843 г. е усъвършенстван от Чарлз Уитстън[1]
Принципът за измерване на съпротивлението е основан на изравняване на потенциалите на средните изводи на двата клона ABC и ADC.
- В единия клон е включен двуполюсникът (резисторът), съпротивлението на който трябва да се измери (Rx{\displaystyle R_{x}}).
Другият клон съдържа елемент, съпротивлението на който може да се регулира (R2{\displaystyle R_{2}}; например, потенциометър).
Между клоновете, в точките B и D се включва индикатор VG. Като индикатор може да се използва:
Обикновено за индикатор се използва галванометър.
- Съпротивлението R2{\displaystyle R_{2}} във втория клон се изменя, докато показанията на галванометъра не станат равни на нула, т.е. потенциалите на точките D и B не станат равни.
Когато галванометърът показва нула, се казва, че е настъпило „равновесие на моста“. При това:
- отношението R2/R1{\displaystyle R_{2}/R_{1}} е равно на отношението Rx/R3{\displaystyle R_{x}/R_{3}}:
- R2R1=RxR3{\displaystyle {\frac {R_{2}}{R_{1}}}={\frac {R_{x}}{R_{3}}}}
откъдето
- Rx=R2R3R1;{\displaystyle R_{x}={\frac {R_{2}R_{3}}{R_{1}}};}
- ↑ Марио Лоци „История физики“ – Москва, изд. Мир, 1970 – с. 261.
Цепь моста Уитстона
: принцип и применение
Объедините творчество и создайте схему, как в реальной жизни. Расширьте свои навыки проектирования схем с помощью виртуальной лаборатории уже сегодня!
Сэмюэл Хантер Кристи изобрел мост Уитстона в 1833 году, который стал популярным благодаря работам сэра Чарльза Уитстона в 1843 году.
Электрическая цепь, настроенная для измерения неизвестного значения резистора и создающая баланс между двумя ножками мостовой схемы, называется мостом Уитстона.Как показано на рисунке ниже, известны три сопротивления (одно регулируемое / регулируемое), а четвертое необходимо определить. Мы будем делать это с помощью закона Ома.
По сравнению с другими измерительными приборами, такими как делитель напряжения, концепция моста Уитстона широко используется из-за точности измерения сопротивления.
Компоненты эксперимента с мостом Уитстона
- Резистор с неизвестным значением сопротивления.
- Два резистора (с известным значением сопротивления)
- Переменный резистор (может работать такое устройство, как Rheostat или Preset)
- Источник напряжения / постоянного тока
- Гальванометр (или любое устройство, показывающее разницу напряжений или протекание тока)
- Соединительные провода
Строительство схемы

Мост Уитстона — это структура мостового типа, имеющая четыре резистора, три резистора известного и один неизвестного номинала.
Здесь R1, R2 и R3 имеют известные значения, среди которых R2 регулируется и, наконец, Rx — это значение, которое необходимо измерить.Наряду с этими сопротивлениями между B и D есть гальванометр (Vg), а между A и C — источник постоянного тока.
Принцип работы моста Уитстона
Теперь, согласно принципу моста Уитстона, если соотношение двух сопротивлений (R1 / R2) на одном ребре равно отношению двух сопротивлений (R3 / Rx) на другом ребре, тогда не будет протекания тока между ними. середины двух краев сопротивления. Это состояние моста известно как состояние сбалансированного моста .
В состоянии сбалансированного моста ток через гальванометр равен нулю, а также разность напряжений между точками B и D становится равной нулю, т.е. в обеих точках уровень напряжения будет одинаковым.
Запись уравнений для состояния сбалансированного моста будет выглядеть так:
R1 / R2 = R3 / Rx (или) R1 * Rx = R2 * R3
Таким образом, Rx = R3 * (R2 / R1)
Это обнаружение нулевого тока в гальванометре отличается высокой точностью, поэтому в зависимости от уровня точности известных значений неизвестное сопротивление может быть обнаружено с наивысшей точностью и точностью.
В эксперименте с мостом Уитстона один резистор всегда должен быть переменным, чтобы получить сбалансированное состояние. Схема работает наилучшим образом, когда используется регулируемый источник напряжения, а не ток с характеристиками отталкивания.
Пример схемы:
Давайте рассмотрим приведенную ниже схему, где мост находится в несбалансированном состоянии, и нам нужно вычислить разность напряжений между Q1 и Q2, то есть Vout и, следовательно, значение R4, необходимое для балансировки моста.

Согласно закону разделения напряжения,
Vq1 = (R3 / (R3 + R1)) * Vs, где Vs = 100 вольт (источник напряжения)
положив значения R3 = 40 Ом, R1 = 50 Ом и Vs = 100 вольт, получаем
Vq1 = 44,4 В
Аналогично Vq2 = (R4 / (R4 + R2)) * Vs
выставив значения, R4 = 50 Ом, R2 = 100 Ом и Vs = 100 вольт, получаем
В q2 = 33,3 В
Таким образом, Vout можно найти как,
Vout = Vq1 — Vq2
Итак, Vout = 44.4 — 33,3 = 11,1 вольт
Теперь, чтобы сбалансировать мост, мы можем найти подходящее значение для R4, как показано ниже:
R4 = R2 * (R3 / R1)
, подставив значения R1, R2 и R3, получим
R4 = 100 * (40/50)
= 80 вольт
Следовательно, R4 = 80 вольт. — это номинал резистора, который следует использовать для приведения моста в сбалансированное состояние.
Применение моста Уитстона
Схема имеет множество применений, которые можно легко найти в нашей повседневной жизни.Некоторые из них обсуждаются ниже.
Применение для измерения деформации
.
Что такое мост Уитстона? Схема, теория, принцип и применение
«Сердце науки — измерение», , а для измерения используются мостовые схемы для определения всех видов электрических и электронных параметров. Мы изучили несколько мостов в Electrical и Electronics Measurement and Instrumentation . В таблице ниже показаны различные мосты с их использованием:
| S. No. | Название моста | Определяемый параметр |
| 1. | Уитстон | измерить неизвестное сопротивление |
| 2. | Андерсон | измерить самоиндукцию катушки |
| 3. | De-sauty | измерение очень малого значения емкости |
| 4. | Максвелл | измерить неизвестную индуктивность |
| 5. | Кельвин | используется для измерения неизвестных электрических резисторов ниже 1 Ом. |
| 6. | Вейн | Измерение емкости по сопротивлению и частоте |
| 7. | Сено | измерение неизвестного индуктора высокого значения |
Здесь мы поговорим о мосте Уитстона , который используется для измерения неизвестного сопротивления. Современный цифровой мультиметр помогает легко измерить сопротивление.Но преимущество моста Уитстона перед этим состоит в том, что он обеспечивает измерение очень низких значений сопротивления в диапазоне миллиОм.
Мост Уитстона
Сэмюэл Хантер Кристи изобрел мост Уитстона в 1833 году, и этот мост был улучшен и популяризирован сэром Чарльзом Уитстоном в 1843 году. Мост Уитстона представляет собой соединение четырех сопротивлений , образующих мост. Четыре сопротивления в цепи называются плечами моста.Мост используется для нахождения значения неизвестного сопротивления, соединенного с двумя известными резисторами, одним переменным резистором и гальванометром. Чтобы найти значение неизвестного сопротивления, отклонение гальванометра доводят до нуля, регулируя переменный резистор. Эта точка известна как точка баланса моста Уитстона.

Вывод
Как видно на рисунке, R1 и R2 — известные резисторы. R3 — переменный резистор, а Rx — неизвестное сопротивление.Мост подключен к источнику постоянного тока (аккумулятор).
Теперь, если мост находится в сбалансированном состоянии , то не должно быть тока, протекающего через гальванометр, и тот же ток I1 будет течь через R1 и R2. То же самое для R3 и Rx, означает, что ток (I2) через R3 и Rx останется прежним. Итак, ниже приведены расчеты для определения неизвестного значения сопротивления , когда мост находится в сбалансированном состоянии (отсутствие тока между точками C и D).
V = IR (по закону Ома) VR1 = I1 * R1... уравнение (1) VR2 = I1 * R2 ... уравнение (2) VR3 = I2 * R3 ... уравнение (3) VRx = I2 * Rx ... уравнение (4)
Падение напряжения на R1 и R3 одинаково, а падение напряжения на R2 и R4 также одинаково в состоянии сбалансированного моста .
I1 * R1 = I2 * R3 ... уравнение (5) I1 * R2 = I2 * Rx ... уравнение (6)
При делении уравнения (5) и уравнения (6)
R1 / R2 = R3 / Rx Rx = (R2 * R3) / R1
Итак, отсюда мы получаем значение Rx, которое является нашим неизвестным сопротивлением, и, следовательно, именно так мост Уитстона помогает в измерении неизвестного сопротивления.
Эксплуатация
Фактически, переменное сопротивление регулируется до тех пор, пока значение тока через гальванометр не станет равным нулю. В этом случае мост называется сбалансированным мостом Уитстона . Получение нулевого тока через гальванометр дает высокую точность, так как незначительное изменение переменного сопротивления может нарушить состояние баланса.
Как показано на рисунке, в мосте R1, R2, R3 и Rx четыре сопротивления. Где R1 и R2 — неизвестный резистор, R3 — переменное сопротивление, а Rx — неизвестное сопротивление.Если соотношение известных резисторов равно отношению настроенного переменного сопротивления и неизвестного сопротивления, в этом состоянии ток не будет течь через гальванометр.
В уравновешенном состоянии,
R1 / R2 = R3 / Rx
Теперь, в этот момент мы имеем значение R1 , R2 и R3, поэтому легко найти значение Rx из приведенной выше формулы.
Из вышеуказанного условия
Rx = R2 * R3 / R1
Следовательно, значение неизвестного сопротивления рассчитывается по этой формуле, учитывая, что ток через гальванометр равен нулю.
Таким образом, нам нужно настроить потенциометр до точки, когда напряжение на C и D будет равным, в этом состоянии ток через точки C и D будет равен нулю, а показания гальванометра будут равны нулю, в этом конкретном положении называется в сбалансированном состоянии . Эта полная операция объясняется в Видео , приведенном ниже:
Пример
Давайте возьмем пример для , понимающий концепцию моста Уитстона , поскольку мы берем неуравновешенный мост, чтобы вычислить соответствующее значение Rx (неизвестное сопротивление) для балансировки моста.Как мы знаем, если разница падений напряжения в точках C и D равна нулю, то мост находится в состоянии баланса.

Согласно принципиальной схеме,
Для первого плеча ADB,
Vc = {R2 / (R1 + R2)} * Vs При вводе значений в формулу выше
Vc = {80 / (40 + 80)} * 12 = 8 вольт Для ACB второго плеча,
Vd = {R4 / (R3 + R4)} * Vs
Vd = {120 / (360+ 120)} * 12 = 3 вольта Итак, разница напряжений между точками C и D составляет:
Vout = Vc - Vd = 8 - 3 = 5 вольт
Если разница в падении напряжения на C и D положительная или отрицательная (положительная или отрицательная показывает направление дисбаланса), это означает, что мост неуравновешен, и для его устранения баланс нам нужно другое значение сопротивления взамен R4.
Номинал резистора R4, необходимого для балансировки цепи, составляет:
R4 = (R2 * R3) / R1 (состояние балансировочного моста) R4 = 80 * 360/40 R4 = 720 Ом
Следовательно, значение R4, необходимое для балансировки моста, составляет 720 Ом, потому что, если мост сбалансирован, разница в падении напряжения на C и D равна нулю, и если вы можете использовать резистор 720 Ом разница напряжений будет равна нулю.
Приложения
- В основном используется для измерения очень низкого значения неизвестного сопротивления в диапазоне миллиом.
- При использовании варистора с мостом Уитстона мы также можем определить значение некоторых параметров, таких как емкость, индуктивность и импеданс.
- Использование моста Уитстона с операционным усилителем помогает измерять различные параметры, такие как температура, деформация, свет и т. Д.
.
Мост Уитстона: ПРИНЦИП РАБОТЫ И ПРИМЕНЕНИЕ
Мост Уитстона был изобретен Сэмюэлем Хантером Кристи в 1833 году, а затем импровизирован
сэром Чарльзом Уитстоном в 1843 году, после чего он стал популярным.
Мост Уитстона — это электрическая цепь, используемая для измерения неизвестного значения сопротивления путем поддержания баланса между двумя ветвями мостовой схемы. Основным преимуществом использования моста Уитстона является его точность определения неизвестного значения (электрического сопротивления) по сравнению с такими приборами, как простой делитель напряжения.
Строительство моста Уитстона
Мост
Уитстона спроектирован в виде конструкции мостового типа, имеющей четыре сопротивления, три известных и одно неизвестное.
Здесь R1, R2 — известные сопротивления, R3 — переменное (регулируемое), а R2 — это сопротивление, которое необходимо измерить. Помимо сопротивления, между точками C и B подключен вольтметр, а между A и D — источник постоянного тока.
Принцип работы моста Уитстона
Как объяснялось выше, в мосте Уитстона R1, R2 и R3 — это сопротивления известного значения, а сопротивление R2 — это сопротивление, которое необходимо регулировать до тех пор, пока через гальванометр V не перестанет течь ток.
Это состояние, при котором ток через гальванометр равен нулю и, следовательно, напряжение между двумя средними точками B и C также становится равным нулю, называется сбалансированным состоянием невесты моста Уитстона.
Следовательно, отношение двух сопротивлений в одной ветви (R1 / R2) равно отношению двух других сопротивлений в другой ветви (Rx / R3). Если каким-то образом мост неуравновешен, направление тока указывает, слишком ли высокий или слишком низкий R2.
В состоянии балансировки моста,
R 2 / R 1 = R x / R 3
и, следовательно, Rx = R 3 * (R 2 / R 1) можно легко измерить.
Это обнаружение нулевого тока в гальванометре может быть выполнено с высокой точностью, таким образом, если R1, R2 и R3 известны с высокой точностью, то измерение Rx также будет иметь высокую точность. Кроме того, даже небольшое изменение значения Rx нарушит баланс и может быть легко обнаружено. В качестве альтернативы, если R2 не изменяется, для расчета Rx можно использовать разность напряжений или ток, протекающий через счетчик. Этот метод более быстрый для измерения неизвестного сопротивления моста Уитстона.
Пример моста Уитстона
Рассмотрим схему, показанную выше, где мост Уитстона находится в несбалансированном состоянии и выводит напряжение на C & amp; D и значение R 4 должны быть измерены для состояния сбалансированного моста.
Теперь по закону деления напряжения,
Vc = (R2 / (R1 + R2)) * против
Положим R2 = 12 Ом, R2 = 8 Ом, Vs = 10 В
В = (12 / (8 + 12)) * 10
= 6 В
Во втором плече, применяя закон деления напряжения,
Vd = (R4 / (R3 + R4)) * против
V2 = (16 / (48 + 16)) * 10
= 2.5 вольт
Напряжение между точками C & amp; D можно рассчитать как
Vcd = Vc — Vd
Vout = 6 — 2,5 = 3,5 вольт.
Теперь, чтобы рассчитать R 4, состояние сбалансированного моста можно измерить как R4 = (R3 / R1) * R2 = 72 Ом.
Итак, здесь мы можем заключить, что мост Уитстона действует как сеть с 2 портами, имеющая 2 входа (A и B) и 2 выхода (C и D). Также, если напряжение на выходной клемме равно 0 вольт, тогда мост называется сбалансированным, а в несбалансированном состоянии напряжение может иметь любое значение (положительное или отрицательное) в зависимости от параметров схемы.
Применение моста Уитстона
Измерение деформации
Обычно для измерения деформации используются тензодатчики, сопротивление которых изменяется пропорционально деформации, присутствующей в устройстве. Практически сопротивление тензодатчика составляет от 30 Ом до 300 Ом. Поскольку изменение сопротивления может составлять лишь часть полной шкалы, требуется высокоточный и точный измерительный прибор
, и мост Уитстона идеально подходит для этого.
В этом приложении неизвестное сопротивление заменяется тензодатчиком. Здесь R1 и R3 имеют одинаковое значение, а R2 — переменное. Теперь, не прилагая усилия к тензодатчику, реостат изменяют до тех пор, пока вольтметр не покажет нулевое отклонение. Это указывало на то, что мост уравновешен и, следовательно, не натягивается датчик.
Схема светового извещателя
Это одно из самых простых применений моста Уитстона с использованием фоторезистивного устройства.Светозависимый резистор помещается на место неизвестного резистора в мосте Уитстона. LDR, который представляет собой пассивный резистивный датчик, используется для преобразования уровней видимого света в изменение сопротивления, а затем в напряжение. LDR имеет сопротивление около 900 Ом в темном свете (при интенсивности света 100 люкс) и менее 30 Ом при ярком свете.
Таким образом, подключение резистора, зависящего от света, в мосте Уитстона поможет в измерении и мониторинге изменений уровня освещенности.
Мост Уитстона основан на концепции разностного измерения, которое может быть очень точным.
Некоторые варианты моста Уитстона могут использоваться для измерения емкости, индуктивности, импеданса и т. Д. Некоторые другие приложения могут быть следующими:
- Детектор света с мостом Уитстона
- Измерение освещенности с помощью фоторезистивного устройства (резистор, зависимый от света, заменяет один из резисторов)
- Измерение деформации с помощью моста (тензодатчик используется вместо переменного резистора)
- Он также используется для измерения механических и электрических величин.
- Контур используется для измерения изменений давления.
- Используется в термометрах для измерения температуры с высокой точностью.
Ограничения моста Уитстона
- Восприимчивости к сильному постоянному току нет.
- В несбалансированном состоянии показания могут быть неточными.
- Сопротивление, измеренное мостом Уитстона, находится в диапазоне от «нескольких» Ом до «мегам»
- С помощью приложенного напряжения (ЭДС) можно увеличить верхний диапазон моста, в то время как нижний диапазон можно ограничить, подключив провод к зажиму.
Теперь, если мы суммируем все, что мы изучили до сих пор, мы можем сказать, что мост Уитстона является наиболее распространенной и простой мостовой сетью для определения сопротивления. Благодаря способности измерять точные изменения, они в основном используются для датчиков, где изменение сопротивления преобразуется в изменение напряжения (для преобразователя).
Комбинация операционного усилителя и моста Уитстона широко используется в промышленности для различных датчиков и преобразователей.Также, как было сказано ранее, любые изменения в таких величинах, как температура, интенсивность света, деформация, электрические и механические измерения, давление и т. Д., Могут быть измерены наиболее точным и точным образом.
Единственное изменение, необходимое для расчета этих значений, — это замена неизвестного сопротивления в мостовой схеме на требуемое значение (упомянутое выше). Это причина того, что мост Уитстона является самой простой схемой и является одной из наиболее часто используемых мостовых схем.
Аджай Дирадж
Разработчик технического контента
Нравится:
Нравится Загрузка…
Вам также может понравиться
.
Что такое мост Уитстона? — Определение, конструкция, работа, ограничения и чувствительность
Определение : Устройство использует для измерения из минимального сопротивления с помощью метода сравнения — , известный как как мост Уитстона . Значение неизвестного сопротивления определяется путем сравнения с известного сопротивления . Мост Уитстона работает по принципу нулевого отклонения , т.е.е. соотношение их сопротивлений одинаково, и ток через гальванометр не течет. Мост очень надежный и дает точный результат .
В нормальном состоянии мост остается в неуравновешенном состоянии, т. Е. Через гальванометр протекает ток. Когда через гальванометр проходит нулевой ток, мост считается сбалансированным. Это можно сделать, настроив известное сопротивление P, Q и переменное сопротивление S.
Работа моста аналогична работе потенциометра.Мост Уитстона используется только для определения среднего сопротивления. Для измерения высокого сопротивления в цепи используется чувствительный амперметр.
Строительство моста Уитстона
Базовая схема моста Уитстона показана на рисунке ниже. Мост имеет четыре плеча, которые состоят из двух неизвестных сопротивлений, одного переменного сопротивления и одного неизвестного сопротивления, а также источника ЭДС и гальванометра.
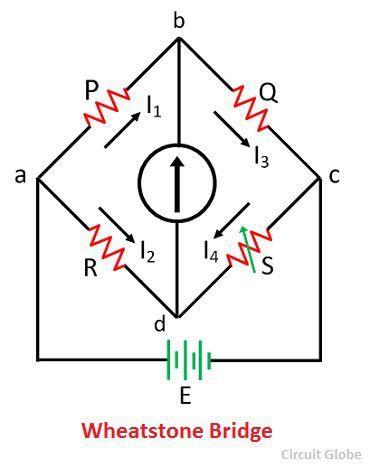
Источник ЭДС подключается между точками a и b, а гальванометр подключается между точками c и d.Ток через гальванометр зависит от разности потенциалов на нем.
Работа гальванометра
Мост находится в состоянии баланса, когда через катушку не течет ток или разность потенциалов на гальванометре равна нулю. Это состояние возникает, когда разность потенциалов на линиях от a до b и от a до d равны, а разность потенциалов на линиях от b до c и от c до d остается неизменной.
Ток, поступающий в гальванометр, делится на I 1 и I 2 , и их величина остается неизменной.Следующее условие существует, когда ток через гальванометр равен нулю.
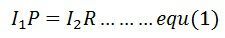
Мост в уравновешенном состоянии выражается как 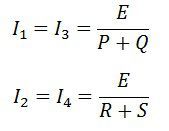
Где E — ЭДС батареи.
Подставляя значения I 1 и 1 2 в уравнение (1), получаем.
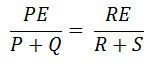
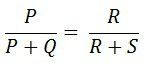
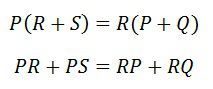
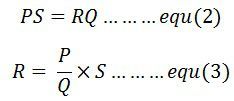
Уравнение (2) показывает состояние баланса моста Уитстона.
Величина неизвестного сопротивления определяется с помощью уравнения (3).R — это неизвестное сопротивление, S — стандартное плечо моста, а P и Q — плечо передаточного числа моста.
Ошибки в мосте Уитстона
Ниже приведены ошибки моста Уитстона.
- Разница между истинным и номинальным значениями трех сопротивлений может вызвать ошибку измерения.
- Гальванометр менее чувствителен. Таким образом, возникает неточность в точке баланса.
- Сопротивление моста изменяется из-за самонагрева, что вызывает ошибку.
- Термическая ЭДС вызывает серьезные затруднения при измерении малых сопротивлений.
- Персональная ошибка возникает в гальванометре при снятии показаний или при нахождении нулевой точки.
Вышеупомянутую ошибку можно уменьшить, используя резистор и гальванометр лучшего качества. Погрешность из-за самонагрева сопротивления можно минимизировать, измерив сопротивление за короткое время. Тепловой эффект также можно уменьшить, подключив реверсивный переключатель между аккумулятором и мостом.
Ограничение моста из пшеничного камня
Мост Уитстона дает неточные показания, если он не сбалансирован. Мост Уитстона измеряет сопротивление от нескольких Ом до МОм. Верхний диапазон моста можно увеличить с помощью приложенной ЭДС, а нижний диапазон ограничить, подключив провод к b
.









