физика леч / методичка / цикл 2 / реография4. Написать уравнения выражающие зависимость напряжения и силы тока от времени

Задачи на тему Переменный ток

Нашли ошибку? Сообщите в комментариях (внизу страницы)

Частоту вращения проволочной рамки в однородном магнитном поле увеличили в 3 раза. Во сколько раз изменится частота переменного тока в рамке и ЭДС индукцииРЕШЕНИЕ

Рамка площадью 200 см2 вращается с частотой 8 с-1 в магнитном поле индукцией 0,4 Тл. Написать уравнения Ф = Ф(t) и е = e(t), если при t = 0 нормаль к плоскости рамки перпендикулярна линиям индукции поля. Найти амплитуду ЭДС индукцииРЕШЕНИЕ

При вращении проволочной рамки в однородном магнитном поле пронизывающий рамку магнитный поток изменяется в зависимости от времени по закону Ф = 0,01 sin 10πt. Вычислив производную Ф , написать формулу зависимости ЭДС от времени e= e(t). В каком положении была рамка в начале отсчета времени? Какова частота вращения рамки? Чему равны максимальные значения магнитного потока и ЭДСРЕШЕНИЕ

Сколько витков имеет рамка площадью 500 см2, если при вращении ее с частотой 20 с 1 в однородном магнитном поле индукцией 0,1 Тл амплитудное значение ЭДС равно 63 ВРЕШЕНИЕ

Какую траекторию опишет электрон, пролетая между пластинами плоского конденсатора, на которые подано: а) постоянное напряжение; б) переменное напряжение достаточно высокой частотыРЕШЕНИЕ

Будет ли проходить ток через электролитическую ванну с раствором медного купороса, если ее подключить к источнику переменного напряжения? Будет ли выделяться на электродах медьРЕШЕНИЕ

По графику (рис. 106) найти амплитудное значение переменной ЭДС, ее период и частоту. Записать формулу изменения ЭДС со временемРЕШЕНИЕ

Какое значение принимает напряжение через 10, 15 и 30 мс, если амплитуда напряжения 200 В и период 60 мсРЕШЕНИЕ

Ток В цепи меняется по гармоническому закону. Мгновенное значение силы тока для фазы Π/6 равно 6 А. Определить амплитудное и действующее значения силы токаРЕШЕНИЕ

На какое напряжение надо рассчитывать изоляторы линии передачи, если действующее напряжение 430 кВРЕШЕНИЕ

Написать уравнения зависимости напряжения и силы тока от времени для электроплитки сопротивлением 50 Ом, включенной в сеть переменного тока с частотой 50 Гц и напряжением 220 ВРЕШЕНИЕ

При каких фазах в пределах одного периода мгновенное значение напряжения равно по модулю половине амплитудногоРЕШЕНИЕ

Неоновая лампа начинает светить, когда напряжение на ее электродах достигает строго определенного значения. Какую часть периода будет светить лампа, если ее включить в сеть, действующее значение напряжения в которой равно этому напряжению? Считать, что напряжение, при котором лампа гаснет, равно напряжению зажиганияРЕШЕНИЕ

Конденсатор переменной емкости включен в цепь последовательно с лампочкой от карманного фонаря. Схема питается от генератора звуковой частоты ЗГ1. Как изменяется накал лампочки, если: а) не меняя емкости конденсатора, увеличивать частоту переменного тока; б) не меняя частоту, увеличивать емкость конденсатораРЕШЕНИЕ

Каково сопротивление конденсатора емкостью 4 мкФ в цепях с частотой переменного тока 50 и 400 ГцРЕШЕНИЕ

Конденсатор включен в цепь переменного тока стандартной частоты. Напряжение в сети 220 В. Сила тока в цепи этого конденсатора 2,5 А. Какова емкость конденсатораРЕШЕНИЕ

Последовательно с лампочкой карманного фонаря к ЗГ подключена катушка. Как изменится накал лампочки, если: а) не меняя частоту, поместить в катушку железный сердечник; б) уменьшить частотуРЕШЕНИЕ

Каково индуктивное сопротивление катушки индуктивностью 0,2 Гн при частоте тока 50 Гц? 400 ГцРЕШЕНИЕ

Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 2,5 А. Какова индуктивность катушкиРЕШЕНИЕ

Лампы (рис. 107) питаются от ЗГ. При некоторой частоте накал ламп одинаков. Как изменится их накал, если частоту: а) увеличить; б) уменьшитьРЕШЕНИЕ

Цепи, изображенные на рисунке 108, питаются сначала от источника постоянного тока, а затем от источника переменного тока, причем действующее значение переменного напряжения равно напряжению на полюсах источника постоянного тока. Как при этом изменялись показания амперметраРЕШЕНИЕ

В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Конденсатор какой емкости надо включить в эту цепь, чтобы осуществился резонансРЕШЕНИЕ

В цепь включены конденсатор емкостью 2 мкФ и катушка индуктивностью 0,005 Гн. При какой частоте тока в этой цепи будет резонансРЕШЕНИЕ

Почему турбогенераторы, вырабатывающие ток стандартной частоты (50 Гц), имеют, как правило, одну пару полюсов, а гидрогенераторы — во много раз большеРЕШЕНИЕ

Допустимо ли, сняв катушку школьного трансформатора с сердечника, подавать на нее переменное напряжение, указанное на катушкеРЕШЕНИЕ

Трансформатор, содержащий в первичной обмотке 840 витков, повышает напряжение с 220 до 660 В. Каков коэффициент трансформации? Сколько витков во вторичной обмотке? В какой обмотке провод имеет большую площадь поперечного сеченияРЕШЕНИЕ

Чтобы узнать, сколько витков содержится в первичной и вторичной обмотках трансформатора, на вторичную катушку намотали 11 витков провода. При включении первичной обмотки в сеть напряжением 220 В вольтметр показал, что на обмотке с 11 витками напряжение равно 4,4 В, а на вторичной обмотке — 12 В. Сколько витков в первичной и вторичной обмоткахРЕШЕНИЕ

Понижающий трансформатор с коэффициентом трансформации, равным 10, включен в сеть напряжением 220 В. Каково напряжение на выходе трансформатора, если сопротивление вторичной обмотки 0,2 Ом, а сопротивление полезной нагрузки 2 ОмРЕШЕНИЕ

Трансформатор включен в сеть (рис. 109). Как изменятся показания приборов при увеличении полезной нагрузки (уменьшении сопротивления R резистора)РЕШЕНИЕ

Вторичная обмотка трансформатора, имеющая 99 витков, пронизывается магнитным потоком, изменяющимся со временем по закону Ф = 0,01 sin 100πt. Написать формулу зависимости ЭДС во вторичной обмотке от времени и найти действующее значение этой ЭДСРЕШЕНИЕ

Трансформатор включен в сеть с переменным напряжением U1 = 220 В. Напряжение на зажимах вторичной обмотки U2 = 20 В, ее сопротивление r = 1 Ом, сила тока во вторичной обмотке I2 = 2 А. Найти коэффициент трансформации и КПД трансформатора, пренебрегая потерями в первичной обмотке и сердечникеРЕШЕНИЕ

bambookes.ru

Вынужденные электромагнитные колебания. Переменный ток. Индуктивность и емкость в цепи переменного тока. Мощность переменного тока. Трансформатор

1. Определить амплитудное и действующее значения переменной э.д.с., возникающей в рамке при ее вращении с постоянной скоростью в однородном магнитном поле, если при угле поворота рамки на 45 град. мгновенное значение э.д.с. равно 156 В.

Дано:

a = 45 град;

e = 156 В

Найти:

e0 - ? eд - ?

Мгновенное значение э.д.с., возникающей в рамке при равномерном вращении в однородном магнитном поле, прямо пропорционально минусу угла поворота плоскости рамки относительно направления линий индукции магнитного поля, т.е., согласно формуле имеем:

.

Отсюда: ; .

Учитывая связь между амплитудными и действующими значениями физических величин, получим:

.

2. Магнитный поток в рамке, состоящей из 1000 витков и равномерно вращающейся в однородном магнитном поле, изменяется по закону . Найти зависимость мгновенной э.д.с. индукции, возникающей в рамке, от времени. Определить амплитудное и действующее значения э.д.с., период и частоту тока.

N = 1000

Найти:

e(t),e0,eд,T,n- ?

Мгновенное значение э.д.с., возникающей в каждом витке e1 равно первой производной от магнитного потока по времени, взятой со знаком минус. Следовательно: ; .

Учитывая тот факт, что имеется не один виток, а N витком получим:

; .

Анализируя полученное выражение и сравнивая его с формулой, получим: .

Соответственно, действующее значение э.д.с.:

Для нахождения периода Т и частоты n надо учесть связь между круговой частотой w и периодом Т: и связь круговой частоты w с линейной частотой n: .

Окончательно получим:

; ; ; .

 

3. В сеть переменного тока с действующим напряжением 220 В и частотой 50 Гц включен контур, состоящий из резистора сопротивлением 100 Ом, конденсатора емкостью 35,4 мкФ и катушки с индуктивностью 0,7 Гн. Написать уравнения U(t) и i(t) зависимости напряжения и силы тока от времени.

Дано:

Uд = 220 В

n = 50 Гц

Ra = 100 Ом

С = 35,4 мкФ

L = 0,7 Гн

Найти:

i(t) - u(t) -

Чтобы успешно справиться с этой задачей, надо помнить, что в цепи переменного тока колебания силы тока и напряжения происходят по синусоидальному закону с одинаковой круговой частотой w, но со сдвигом по фазе j:

; .

Амплитудное значение напряжения U0 и круговая частота w легко находятся из данных условия задачи. Действительно: ; ; ; .

Для определения амплитудного значения силы тока J0 надо воспользоваться законом Ома с учетом формул:

; .

Сдвиг фаз между колебаниями силы тока и внешнего напряжения определяется соотношением:

; ; .

С учетом полученных числовых значений J0, U0, w, j уравнения зависимости силы тока i и напряжения U от времени t получим:

; .

Следовательно, в данной цепи напряжение опережает по фазе силу тока на 0,3 p рад, или на 54 град.

 

4. Найти падение напряжения на резисторе, конденсаторе и катушке, а также определить частоту переменного тока, при которой в цепи наступит резонанс, воспользовавшись данными предыдущей задачи.

Дано:

Uд = 220 В

Ra = 100 Ом

С = 35,4 мкФ

L = 0,7 Гн

Найти:

UR,UC,UL, n0-

Расчет падения напряжения на различных элементах цепи переменного тока принципиально ничем не отличается от подобного расчета в цепи постоянного тока. Так как элементы цепи соединены последовательно, то:

; ; ; ,

где: .

Окончательно получим:

; ; ; ; ; .

Для нахождения резонансной частоты воспользуемся формулой :

; .

Откуда: ; .

 

5. Конденсатор емкостью 0,5 мкФ включен в сеть переменного тока. Определить период колебаний переменного тока, если емкостное сопротивление конденсатора равно 20 Ом.

Дано:

С = 510-5 Ф

ХС = 20 Ом

Найти:

Т -

Из формулы емкостного сопротивления с учетом выразим Т: .

Откуда: ; .

 

6. Катушка индуктивностью 15 мГн включена в сеть промышленного переменного тока. Определить ее индуктивное сопротивление.

Дано:

L=1,510-2Гн

n = 50 Гц

Найти:

ХL - ?

В данной задаче надо помнить о том, что частота промышленного тока 50 Гц.

Далее по формуле с учетом - находим:

; ;

 

7. При включении конденсатора сила тока в цепи переменного тока с частотой 50 Гц и напряжением 220 В равна 0,14 А. Определите емкость конденсатора. Активным сопротивлением цепи можно пренебречь.

Дано:

n = 50 Гц

Uд = 220 В

Jд = 0,14 А

Найти:

С –

Воспользуемся законом Ома для цепи переменного тока: .

Так как: и индуктивное сопротивление , то закон Ома для цепи с емкостной нагрузкой будет в виде:

.

Отсюда: ; . С учетом соотношения - перепишем емкостное сопротивление ХС в виде:

. Откуда: ; .

 

8. В сеть переменного тока с частотой 50 Гц и напряжением 220 В включена катушка с индуктивностью 60 мГн и ничтожно малым активным сопротивлением. Найдите действующее и амплитудное значение силы тока в цепи катушки.

Дано:

n = 50 Гц

Uд = 220 В

L = 6010-3 = = 0,06 Гн

Найти:

Jд, J0 - ?

Индуктивное сопротивление катушки найдем по формуле:

; .

Закон Ома для цепи с индуктивной нагрузкой при и имеет вид: .

Отсюда: .

Амплитудное значение силы тока вычислим по формуле:

; .

 

9. Конденсатор емкостью 24 мкФ и катушка индуктивностью 0,05 Гн с активным сопротивлением 100 Ом подключены последовательно к источнику переменного тока, в котором напряжение на зажимах равно 120 В при частоте 50 Гц. Определить действующие значения силы тока в цепи напряжения на конденсаторе и катушке.

Дано:

С = 210-5 Ф

R = 100 Ом

L = 0,05 Гн

n = 50 Гц

Uд = 120 В

Найти:

Jд, UC, UL - ?

В данной задаче имеются все элементы цепи переменного тока, поэтому для нахождения силы тока надо воспользоваться законом Ома в общем виде с учетом формулы:

.

Учитывая связь - , окончательно получаем:

.

Для вычисления действующего напряжения на конденсаторе необходимо силу тока в цепи умножить на емкостное сопротивление конденсатора:

; .

Действующее значение напряжения на катушке равно силе тока, умноженной на полное сопротивление катушки с учетом того, что катушка индуктивности имеет как индуктивное сопротивление, так и активное сопротивление:

; .

 

10. В сеть переменного тока с действующим напряжением 110 В включены последовательно конденсатор с емкостью 510-5 Ф, катушки индуктивностью 200 мГн и активным сопротивлением 4 Ом. Определить амплитудное значение силы тока в цепи, если частота переменного тока 100 Гц, а также частоту переменного тока, при которой в данном контуре наступит резонанс напряжений.

Дано:

Uд = 110 В

С = 510-5 Ф

L = 0,2 Гн

R = 4 Ом

n = 100 Гц

Найти:

J0, n рез - ?

По закону Ома амплитудное значение силы тока: .

С учетом: и окончательно получаем:

; .

При резонансе частота вынужденных колебаний переменного тока совпадает с частотой собственных колебаний контура. Отсюда:

; .

 

11. Электропечь, сопротивление которой 22 Ом, питается от генератора переменного тока. Определить количество теплоты, выделяемое печью за 1 час, если амплитудное значение силы тока 10 А.

Дано:

R = 22 Ом

t = 3,6104 с

J0 = 10 А

Найти:

Q - ?

Количество теплоты, выделяемое в цепи переменного тока на активном сопротивлении, можно вычислять по закону Джоуля-Ленца, используя действующие значения силы тока или напряжения. В данном случае: .

Учитывая связь - , окончательно получаем: ; ; .

 

12. На входе линии электропередачи, потребляющей мощности 100 кВт, подается напряжение 220 В. Определить потери мощности в проводах, сопротивление которых 0,01 Ом при сдвиге фазы 37 град. между колебаниями силы тока и напряжения.

Дано:

P = 105 B

Uд = 220 В

R = 0,01 Ом

j = 37 град

Найти:

Р1 - ?

Мощность, потребляемая активным сопротивлением, как и в случае постоянного тока, вычисляется по формуле:

.

Действующее значение силы тока может быть вычислено по формуле: , откуда: .

Окончательно получаем: ; .

 

13. Трансформатор имеет коэффициент трансформации 18. Напряжение на первичной обмотке, содержащей 450 витков, равно 220 В. Определите напряжение на вторичной обмотке и число витков в ней.

Дано:

k = 18

N1 = 450

U1 = 220 B

Найти:

U2, N2 - ?

Решение:

Воспользуемся формулой для коэффициента трансформации:

.

Откуда:

; ; ; .

 

14. Сила тока в первичной обмотке трансформатора J1 = 15000 А и напряжение на ее зажимах U1 = 11000 В. Сила тока во вторичной обмотке J2 = 1500 А. Определить напряжение на зажимах вторичной обмотки трансформатора, если к.п.д. равен 96 %.

Дано:

J1 = 15000 A

U1 = 11000 B

J2 = 1500 A

к.п.д. = 0,96

Найти:

U2 - ?

Коэффициент полезного действия трансформатора по определению вычисляется по формуле:

К.п.д. = ,

где: ; .

Отсюда к.п.д. = .

Окончательно получаем:

; .

 

15. Первичная обмотка трансформатора имеет 500 витков, вторичная - 50 витков. В первичной обмотке сила тока изменяется по закону: . По какому закону изменяется сила тока во вторичной обмотке в рабочем режиме трансформатора Считать, что токи в первичной и вторичной обмотках совершают колебания в одинаковых фазах.

Дано:

N1 = 500

N2 = 50

Найти:

i2(t) - ?

Так как колебания тока в обмотках совершаются в одинаковых фазах, то законы изменения силы тока будут отличаться только амплитудными значениями силы тока.

Для того, чтобы найти амплитудное значение тока во вторичной обмотке трансформатора, надо воспользоваться выражениями для коэффициента трансформации:

.

Отсюда получим: ; .

Теперь можно записать закон изменения силы тока во вторичной обмотке: .

 

studopedya.ru

Слободянюк А.И. Физика 10/18.4 — PhysBook

Содержание книги

Предыдующая страница

§18. Переменный электрический ток

18.4 Емкость в цепи переменного тока. Емкостное сопротивление.

Рассмотрим электрическую цепь, содержащую резистор с активным сопротивлением R и конденсатор емкости C, подключенную к источнику переменной ЭДС (Рис. 248).

Конденсатор, подключенный к источнику постоянной ЭДС полностью препятствует прохождения тока – за некоторый промежуток времени конденсатор заряжается, напряжение между его обкладками становится равным ЭДС источника, после чего ток в цепи прекращается. Если же конденсатор включен в цепь переменного тока, то ток в цепи не прекращается – фактически конденсатор периодически перезаряжается, заряды на его обкладках периодически изменяются как по величине, так и по знаку. Конечно, никакие заряды не протекают между обкладками, электрического тока в строгом определении между ними нет. Но, часто не вдаваясь в детали и не слишком корректно, говорят о токе через конденсатор, подразумевая под этим ток в цепи, к которой подключен конденсатор. Такой же терминологией будем пользоваться и мы.

По-прежнему, для мгновенных значений справедлив закон Ома для полной цепи: ЭДС источника равна сумме напряжений на всех участках цепи. Применение этого закона к рассматриваемой цепи приводит к уравнению

\(~\varepsilon = U_R + U_C = IR + \frac{q}{C}\) , (1)

здесь \(U_R = IR\) - напряжение на резисторе, \(U_C = \frac{q}{C}\) - напряжение на конденсаторе, q - электрический заряд на его обкладках. Уравнение (1) содержит три изменяющихся во времени величины (известную ЭДС, и пока неизвестные силу тока и заряд конденсатора), учитывая, что сила тока равна производной по времени от заряда конденсатора \(I = q′\), это уравнение может быть точно решено. Так как ЭДС источника изменяется по гармоническому закону, то и напряжение на конденсаторе и сила тока в цепи также будут изменяться по гармоническим законам с той же частотой – это утверждение непосредственно следует и уравнения (1).

Сначала установим связь между силой тока в цепи напряжением на конденсаторе. Зависимость напряжения от времени представим в виде

\(~U_C(t) = U_0 \cos \omega t\) . (2)

Подчеркнем, что в данном случае напряжение на конденсаторе отличается от ЭДС источника, как будет видно из дальнейшего изложения, между этими функциями существует также и разность фаз. Поэтому при записи выражения (2), мы выбираем произвольную начальную фазу нулевой, при таком определении фазы ЭДС, напряжения на резисторе и силы тока отсчитываются относительно фазы колебаний напряжения на резисторе.

Используя связь между напряжением и зарядом конденсатора, запишем выражение для зависимости последнего от времени

\(~q = U_0 C \cos \omega t\) , (3)

которое позволяет найти временную зависимость силы тока

\(~I_C = q' = -U_0 C \omega \sin \omega t = U_0 C \omega \cos \left( \omega t + \frac{\pi}{2} \right)\) , (4)

на последнем шаге использована тригонометрическая формула приведения, для того, чтобы в явном виде выделить сдвиг фаз между током и напряжением.

Итак, мы получили, что амплитудное значение силы тока через конденсатор связано с напряжением на нем соотношением

\(~I_{C0} = U_{C0} C \omega\) , (5)

а также между колебаниями силы тока и напряжения существует разность фаз, равна \(~\Delta \varphi = \frac{\pi}{2}\). Эти результаты суммированы на рис. 249, где также представлена векторная диаграмма колебаний силы тока и напряжения.

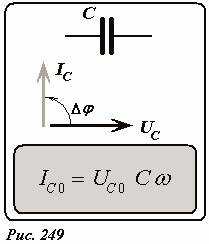
Для того, чтобы сохранить форму закона Ома для участка цепи, вводят понятие емкостного сопротивления, которое определяется по формуле

\(~Z_C = \frac{1}{C \omega}\) . (6)

В этом случае соотношение (5) становится традиционным для закона Ома

\(~I_{C0} = \frac{U_{C0}}{Z_C}\) . (7)

При изучении закона Ома для цепей постоянного тока, мы указывали, что электрическое поле заставляет упорядоченно двигаться заряженные частицы внутри проводника, то есть создает электрический ток. Иными словами, «напряжение является причиной возникновения тока». В данном случае ситуация обратная – благодаря электрическому току на обкладках возникают электрические заряды, создающие электрическое поле, поэтому можно сказать, что в данном случае «сила тока является причиной возникновения напряжения». Хотя, к данным рассуждениям следует относиться несколько скептически, так движение зарядов (электрический ток) и электрическое поле «подстраиваются» друг к другу, пока между ними не устанавливается определенное соотношение, соответствующее установившемуся режиму. Так при постоянном токе условием стационарности является условие постоянства тока. В цепи переменного тока в установившемся режиме согласуются не только амплитудные значения токов и напряжений, но разность фаз между ними. Иными словами, обсуждаемый здесь причинно-следственный вопрос подобен вопросу о том, «что появилось раньше, курица или яйцо?»

Так как между током и напряжением существует сдвиг фаз равный \(~\Delta \varphi = \frac{\pi}{2}\), то средняя мощность тока через конденсатор равна нулю. Действительно,

\(~

= <U_C(t) \cdot I_C(t)> = U_{C0} \cdot I_{C0} <\cos \omega t \cdot \cos \left( \omega t + \frac{\pi}{2} \right)> = 0\) .</center>

Иными словами, потерь энергии при протекании тока через конденсатор в среднем не происходит. Конечно, конденсатор влияет на протекание тока в цепи. В ходе зарядки конденсатора энергия электрического тока превращается в энергию электростатического поля между обкладками конденсатора, а при разрядке конденсатор отдает в цепь накопленную энергию, при этом, средняя энергия, потребляемая конденсатором, остается равной нулю. Поэтому емкостное сопротивление называют реактивным.

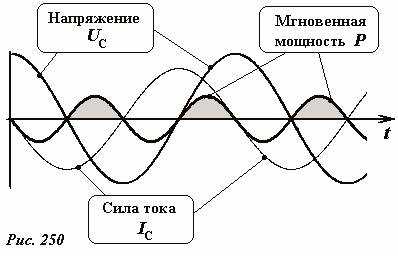
Графики зависимости силы тока, напряжения и мгновенной мощности тока в рассматриваемой цепи показаны на рис. 250.

Заливкой выделены промежутки времени, в течении которых конденсатор накапливает энергия – в этих промежутках сила тока и напряжение имеют один знак.

Уменьшение емкостного сопротивления при возрастании частоты очевидна – чем выше частота тока, тем меньший заряд на конденсаторе успевает накопиться на обкладках конденсатора за половину периода (пока ток идет в одном направлении), тем меньше напряжение на нем, тем меньше он препятствует прохождению тока в цепи. Аналогичные рассуждения справедливы и для объяснения зависимости этого сопротивления от емкости конденсатора.

Вернемся к рассмотрению цепи, показанной на рис. 248, которая описывается уравнением (1). Пренебрегая внутренним сопротивлением источника, запишем явное выражение для напряжения, создаваемого источником

<center>\(~U_0 \cos \omega t = IR + \frac{q}{C}\) . (8)</center>

Здесь U0 - амплитудное значение напряжения, равное амплитудному значению ЭДС источника. Кроме того, теперь мы считаем начальную фазу ЭДС источника равной нулю (ранее за нуль мы принимали фазу колебаний напряжения на резисторе).

Используя это уравнение и связь между силой тока и зарядом конденсатора, найдем явное выражение для зависимости силы тока в цепи от времени. Представим эту зависимость в виде

<center>\(~I = I_0 \cos (\omega t + \varphi)\) , (9)</center>

где I0 и φ - подлежащие определению амплитудное значение силы тока и разности фаз между колебаниями тока и напряжения источника. Легко заметить, что в этом случае заряд конденсатора изменяется по закону

<center>\(~q(t) = q_0 \sin (\omega t + \varphi) = \frac{I_0}{\omega} \sin (\omega t + \varphi)\) . (10)</center>

Для проверки этого соотношения достаточно вычислить производную от приведенной функции и убедится, что она совпадает с функцией (9).

Подставим эти выражения в уравнение (8)

<center>\(~U_0 \cos \omega t = I_0 R \cos (\omega t + \varphi) + \frac{I_0}{C \omega} \sin (\omega t + \varphi)\)</center>

и преобразуем тригонометрическую сумму

<center>\(~\begin{matrix} R \cos (\omega t + \varphi) + \frac{1}{C \omega} \sin (\omega t + \varphi) = \\ = \sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2} \left( \frac{R}{\sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2}} \cos (\omega t + \varphi) + \frac{\frac{1}{C \omega}}{\sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2}} \sin (\omega t + \varphi) \right) = \\ = \sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2} \cos (\omega t + \varphi + \varphi_1) \end{matrix}\) ,</center>

где через φ1 обозначена величина, удовлетворяющая условию

<center>\(~\operatorname{tg} \varphi_1 = - \frac{\frac{1}{C \omega}}{R}\) .</center>

Теперь видно, что для того, чтобы функция (9) являлась решение уравнения (8), необходимо, чтобы ее параметры принимали значения:

амплитуда <center>\(~I_0 = \frac{U_0}{\sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2}}\) ; (11)</center> искомая разность фаз связана с появившимся параметром φ1 соотношением \(\varphi + \varphi_1 = 0\), то есть <center>\(~\operatorname{tg} \varphi = \frac{\frac{1}{C \omega}}{R}\) . (12)</center>

Таким образом, найдена явная зависимость силы тока от времени.

В принципе таким методом, можно рассчитать любую цепь переменного тока. Но такой подход требует громоздких тригонометрических и алгебраических преобразований. К тем же результатам можно прийти гораздо проще, используя формализм векторных диаграмм. Покажем, как метод векторных диаграмм применяется к рассматриваемой цепи. Самое важное при использовании этого метода – построение векторной диаграммы, изображающей колебания токов и напряжений на различных участках цепи.

Так как конденсатор и резистор соединены последовательно, то силы токов через них одинаковы в любой момент времени. Изобразим силу тока в идее произвольно направленного вектора (например, горизонтально[1], как на рис. 251). Далее изобразим векторы колебаний напряжения на резисторе UR, который параллелен вектору колебаний тока (так как сдвиг фаз между этими колебаниями равен нулю) и напряжения на конденсаторе UC, который перпендикулярен вектору колебаний тока (так как сдвиг фаз меду ними равен \(~\frac{\pi}{2}\) - см. Рис. 249). Сумма этих напряжений равна напряжению источника, поэтому вектор суммы векторов, изображающих колебания UR и UC, изображает колебания напряжения источника U(t). Из построенной диаграммы следует, что амплитудные значения рассматриваемых напряжений связаны соотношением (следующим из теоремы Пифагора)

<center>\(~U^2_0 = U^2_{R0} + U^2_{C0}\) .</center>

Выражая амплитуды напряжений через амплитуду силы тока с помощью известных соотношений \(~U_{R0} = I_{R0} R\) и \(~U_{C0} = \frac{I_{C0}}{C \omega}\), получаем элементарное уравнение для определения амплитуды силы тока

<center>\(~U^2_0 = (I_0 R)^2 + \left( \frac{I_0}{C \omega} \right)^2\) , (13)</center>

из которого находим амплитуду силы тока в цепи

<center>\(~I_0 = \frac{U_0}{\sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2}}\) ; (14)</center>

что, естественно, совпадает с выражением (11), полученным ранее громоздким алгебраическим методом. Векторная диаграмма также позволяет легко определить сдвиг фаз между колебаниями силы тока и напряжения источника

<center>\(~\operatorname{tg} \varphi = \frac{U_C}{U_R} = \frac{\frac{1}{C \omega}}{R}\) , (15)</center>

что также совпадает с полученным ранее.

Как видно, метод векторных диаграмм позволяет полностью рассчитать характеристики цепей переменного тока, гораздо проще, чем рассмотренным выше методом аналитического решения соответствующего уравнения.

Следует подчеркнуть, что физическая сущность обоих методов одна и та же, она выражается уравнением (10), различие только в математическом языке, на котором решается это уравнение.

Рассчитаем, среднюю мощность, развиваемую источником. Мгновенное значение этой мощности равно произведению ЭДС на силу тока \(P = \varepsilon I\). Подставляя явные значения для этих величин и проводя усреднение, получим

<center>\(~<P> = <\varepsilon I> = <U_0 \cos \omega t \cdot I_0 \cos (\omega t + \varphi)> = U_0 I_0 <\cos \omega t \cdot \cos (\omega t + \varphi)> = \frac{U_0 I_0}{2} \cos \varphi\) . (16)</center>

Обратите внимание, что полученное выражение для средней мощности является общим для переменного тока: средняя мощность переменного тока равна половине произведения амплитуд силы тока, напряжения и косинуса разности фаз между ними. Если использовать не амплитудные, а действующие значения силы тока и напряжения, то формула (16) приобретает вид

<center>\(~<P> = U_D I_D \cos \varphi\) , (17)</center>

средняя мощность переменного электрического тока равна произведению действующих значений силы тока, напряжения и косинуса разности фаз между ними. Часто косинус сдвига фаз между силой тока и напряжением называют коэффициентом мощности.

В тех случаях, когда по электрической линии требуется передать максимальную мощность, необходимо стремиться, чтобы сдвиг фаз между током и напряжением был минимальным (оптимально – нулевым), так как в этом случае передаваемая мощность будет максимальна.

Применим полученную формулу для расчета мощности тока в рассматриваемой цепи, для чего выразим косинус сдвига фаз из выражения (12) и подставим в формулу (17), в результате чего получим

<center>\(~<P> = \frac{U_0 I_0}{2} \frac{R}{\sqrt{R^2 + \left( \frac{1}{C \omega} \right)^2}} = \frac{1}{2} I^2_0 R = I^2_D R\) , (18)</center>

При выводе этого соотношения использована формула (14) для амплитуды силы тока в цепи. Полученный результат очевиден – средняя мощность, развиваемая источником, равна средней мощности теплоты, выделяющейся на резисторе. Этот вывод еще раз подтверждает, что на конденсаторе не происходит потерь энергии электрического тока. Расчет мощности тока также можно проводить с помощью построенной векторной диаграммы, из которой следует, что произведение амплитуды напряжения источника на косинус сдвига фаз равно амплитуде напряжения на резисторе \(U_0 \cos \varphi = U_{R0}\), откуда сразу следует формула (18).

Так как амплитудные и действующие значения сил токов и напряжений пропорциональны друг другу, то длины векторов векторных диаграмм можно считать пропорциональными действующим (а не амплитудным) значениям. При таком определении среднее произведение двух гармонических функций равно скалярному произведению векторов, изображающих эти функции.

Примечания

1. ↑ Мы постоянно подчеркиваем, что начальная фаза отдельного колебания, ни в каких процессах не существенна, она может быть изменена простым переносом начала отсчета времени. Физический смысл имеют разности фаз между различными величинами, изменяющимися по гармоническим законам. Здесь мы как бы, очередной раз изменяем «точку отчета» фазы – при горизонтальном расположении вектора колебаний тока мы неявно принимаем начальную фазу колебаний силы тока равной нулю.

<p> Следующая страница

www.physbook.ru

реография4

ЛАБОРАТОРНАЯ РАБОТА № 4

Тема: «ИССЛЕДОВАНИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА. ПРИНЦИП РЕОГРАФИИ»

ЦЕЛЬ. Изучить теоретические основы реографии, исследовать цепь переменного тока и научиться рассчитывать импеданс данной цепи.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ. Катушка индуктивности,

конденсатор, реостат, амперметр, вольтметр, переключатель.

ПЛАН ИЗУЧЕНИЯ ТЕМЫ

1.Понятие переменного электрического тока.

2.Понятие мгновенного, амплитудного, действующего значения напряжения.

3.Получение переменного тока.

4.Цепь переменного тока с активным сопротивлением.

5.Цепь переменного тока с индуктивным сопротивлением.

6.Цепь переменного тока с емкостным сопротивлением.

7.Полное сопротивление цепи переменного тока. Импеданс тканей организма. Резонанс в электрических цепях.

8.Использование переменного тока в медицине. Реография.

КРАТКАЯ ТЕОРИЯ

Ток, изменяющийся по величине и направлению с течением времени, называют переменным током.

Наиболее распространенным является ток, изменяющийся по времени по гармоническому закону (закону синуса или косинуса)

i I m cos( 0 t0 )					(1)
или для напряжения
u U	m	cos(	0	t )	(2)
				0

где i, u – мгновенные значения силы тока (1) и напряжения (2),Im , Um – максимальные значения,

0 – начальная фаза колебаний,0 – круговая или циклическая частота – характеризует число

колебаний за 2 секунд,

0	=2 , где		- собственная частота переменного тока – число
колебаний переменного тока за секунду.
Для промышленного переменного тока =50 Гц.
	1	, где	T – период переменного тока – промежуток времени, в
	T

течение которого напряжение и сила тока совершают одно полное колебание.

T 2 0

Переменный ток можно рассматривать как вынужденные электромагнитные колебания.

В цепи переменного напряжения u U m cos 0 t могут быть включены

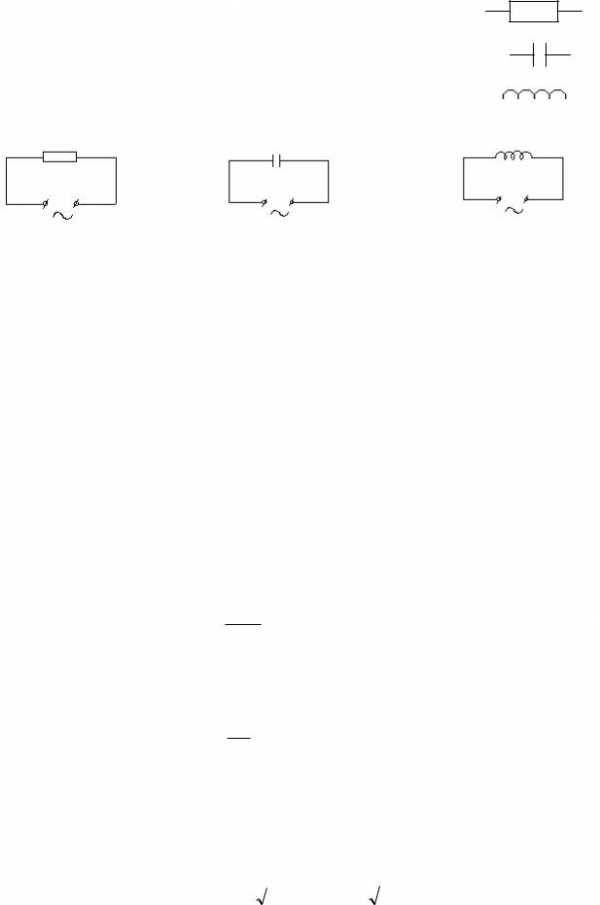
а) резистор (R)

б) конденсатор (С)

в) катушка индуктивности (L)

Рис. 1.

Отметим, что сила тока в цепи с резистором (а) будет изменяться в фазе с приложенным напряжением:

i I m cos 0 t,

сила тока в цепи с конденсатором (б) будет опережать по фазе напряжение на 2 :

iI m cos(0 t 2 ),

ав цепи С катушкой индуктивности (в) будет отставать по фазе от приложенного напряжения на 2 :

i I m cos( 0 t2 )

Для цепи с резистором имеем омическое сопротивление:

R U m ax

I m ax

Для цепи с катушкой индуктивности – индуктивное сопротивление:

X L L , гдеL – индуктивность катушки. Для цепи с конденсатором – емкостное сопротивление:

X c 1 , где С – емкость конденсатора.

C

Амперметры или вольтметры показывают действующее (или эффективное) значение силы тока или напряжения.

Действующей, или эффективной, силой переменного тока Iэф называют такой постоянный ток, который выделяет в цепи с сопротивлениемR количество теплоты, одинаковое с переменным током:

I эф	I	м		,	U эф		U	м
		2						2

Так, если говорят, что напряжение в цепи переменного тока 220 В, это означает действующее значение. Амплитуда напряжения при этом

Uм Uэф 2 220 1,4 308 В . Это обстоятельство необходимо учитывать, в

частности, при расчете изоляции сети.

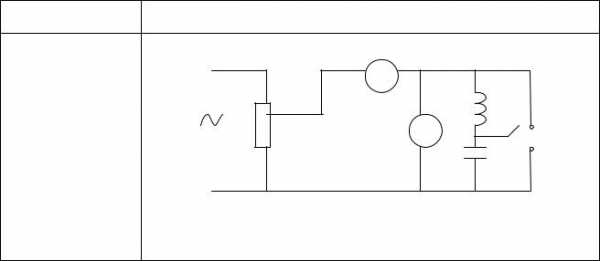
Представим цепь, в которой последовательно соединены резистор, катушка и конденсатор (см. рис.2)

Рис. 2.

Напряжение в цепи выражается зависимостью u U m cos t , а сила тока, вследствие сдвига фаз между током и напряжением на катушке и конденсаторе, в общем случае изменяется по законуi Im cos( t ) , где -

разность фаз напряжения и силы тока.

Используя сложные тригонометрические преобразования (что выходит за рамки изложения) или с помощью векторных диаграмм, можно получить выражение для расчета общего (полного) сопротивления Z цепи переменного тока (импеданс), содержащей последовательно соединенные R, L и C:

										1 2
		2		2			2
Z	R		(XL XC )			R			L
										C

Омическое сопротивление R цепи называют активным, т.к. оно обусловливает превращение электрической энергии в тепловую.

Полное сопротивление в цепи переменного тока называют импедансом. СопротивленияXL, XC и их разностьXL-XC - реактивными сопротивлениями, они не вызывают нагревания элементов электрической

цепи.

Закон Ома для цепи переменного тока имеет вид:

I	U					U
	Z			R	2	X L XC	2

Если XL =XC , то Z=R. Этот случай вынужденных электрических колебаний называютрезонансом напряжения.

Ткани организма проводят не только постоянный, но и переменный

ток.

В организме нет таких систем, которые были бы подобны катушкам индуктивности, поэтому индуктивность тканей организма близка к нулю

(XL=0).

Биологические мембраны и весь организм в целом обладают емкостными свойствами, в связи с этим полное сопротивление тканей организма (импеданс) определяется только омическим и емкостным сопротивлениями:

								1 2
		2	2			2
Z	R		X C		R
								C

Зависимость импеданса от частоты характеризует жизнеспособность тканей организма. Импеданс тканей и органов зависит также и от их физиологического состояния. Так, при кровенаполнении сосудов импеданс изменяется в зависимости от состояния сердечно-сосудистойсистемы.

Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называют реографией (импеданс-плетизмография).С помощью этого метода получают реограммы головного мозга, сердца, магистральных сосудов, конечностей и др.

Измерения обычно проводят на частоте 30 кГц, ток подается на электроды, накладываемые на границы исследуемого участка ткани.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Какой ток называется переменным?

2.Как выражается зависимость силы переменного тока (напряжения) от времени?

3.Что такое мгновенное, амплитудное и действующее значение переменного тока, напряжения, ЭДС? Какое значение силы тока и напряжения показывают амперметр и вольтметр в цепи переменного тока?

4.Напишите формулу, связывающую эффективные и максимальные значения переменного синусоидального тока и напряжения.

5.Что такое круговая частота?

6.Что такое активное и реактивное сопротивление?

7.Что называется емкостью конденсатора? В каких единицах измеряется?

8.Чему равно емкостное сопротивление в цепи постоянного тока?

9.Что такое импеданс? Запишите формулу.

10.Как влияет величина емкости (индуктивности) цепи на полное сопротивление?

11.Что такое электрический резонанс?

12.Каковы физические основы реографии? Ее применение в

медицине.

	ПЛАН ВЫПОЛНЕНИЯ РАБОТЫ
Последовательност		Способ выполнения задания
ь действий
1. Определение	1. Проверьте соответствие измерительной схемы рис. 3.
емкостного
сопротивления и		A		L
емкости
конденсатора.
	220	Rp	V	K

C

Рис. 3.

2. Включите в цепь конденсатор, поставив ключ в положение (С) по схеме на панели.

		3.	Измерьте	силу тока в цепи конденсатора не менее 3-храз при
			напряжениях 90 - 150 В.
			Результаты измерений занесите в таблицу.
№ п/п	Uэф,		Iэф, А	хс, Ом	С, Ф
	В

1

2

3

4.Используя закон Ома I = U/Xс (R = 0; L = 0), рассчитайте емкостное сопротивление конденсатора по формуле: Xc=Uэф/Iэф.

5.Используя значение емкостного сопротивления Хс и формулу емкостного сопротивления, рассчитайте емкость конденсатора.

			x c c;	f 50Гц	2 f ;		C		1
								x c	2 f
2. Определение		1.	Включите в цепь только катушку индуктивности, поставив ключ
индуктивного			К1 в положение L.
сопротивления и		2.	Измерьте	не менее 3-храз силу тока в цепи при напряжениях
индуктивности			90 - 150 В.
катушки.		3.	Результаты измерений занести в таблицу.
№ п/п		Uэф, В		Iэф, А		xL, Ом					L ,Гн
1.
2
3

4.Рассчитайте индуктивное сопротивление катушки; т.к. при подаче на зажимы цепи переменного напряжения вольтметр покажет значения падения напряжения на полном сопротивлении катушки, то по закону Ома:

I

U

; (x

0) и

X

U эф2

R2

L

R2

x

c

Iэф2

L

5.Активное сопротивление катушки см. на установке. Используя значение индуктивного сопротивления, рассчитайте индуктивность катушки.

	xL L			L	xL
	2f				2f
3. Определение	1. Поставив контакт ключа К1 в положение Z включите в цепь
полного	источника катушку и конденсатор.								В этом случае цепь будет
сопротивления	состоять из активного, индуктивного и емкостного сопротивления.
цепи.	Измерьте силу тока в цепи не менее 3-храз при напряжениях
	90 - 150 В. Результаты измерений занесите в таблицу.
№ п/п	Uэф, В		Iэф, А				Z, Ом		Z', Ом
1
2
3
	3. Используя закон Ома I = U/Z, рассчитайте полное сопротивление

по формуле: Z Uэф

Iэф

4. Используя полученные в заданиях 1 и 2 значения индуктивности катушки L и емкости конденсатора C, а также значения активного сопротивления R, рассчитайте полное сопротивление цепи по формуле:

Z R2 (2 fL 1/ 2 fC)2

5. Сравните полученные значения с определенным из опыта полным сопротивлением Zср и сделайте вывод.

studfiles.net

---

• 
  Регулировка по току
• 
  Настроить антенну мтс
• 
  Гатчинские сети
• 
  Новости энергетики россии
• 
  Льготы по оплате электроэнергии пенсионерам
• 
  Схема поршневой компрессор
• 
  Заземление защитное и рабочее
• 
  Полярность светодиодов smd
• 
  Цепи последовательные и параллельные
• 
  Автомат и узо в чем разница
• 
  Управление что такое связь