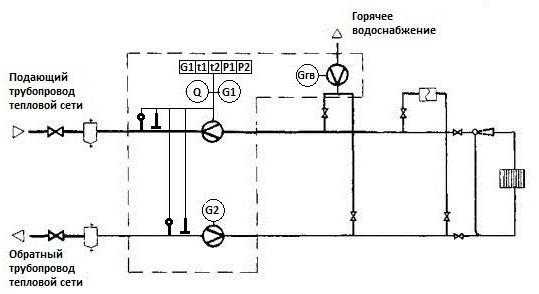
Последовательное, параллельное и смешанное соединение элементов эл. Ц. Цепи последовательные и параллельные

Вопрос7.Последовательные,параллельные и смешанные цепи однофазного переменного тока с активными и реактивными сопротивлениями.

Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно.

Если проводники соединены таким образом, что по ним прохо­дит один и тот же ток, то такое соединение проводников называется последовательным (рис. 26).

Следовательно, ток на отдельных участках последовательной цепи имеет одинаковую величину:

Сумма падений напряжений на отдельных участках равна на­пряжениювсей цепи:

Напряжение цепи мож­но представить как

где r — общее сопротивле­ние всей цепи. Следовательно,

Сокращая обе части равенства на I получим

Общее сопротивление цепи, состоящей из нескольких последо­вательно соединенных сопротивлений, равно сумме этих сопротив­лений.

Если два или большее число проводников присоединены к двум узловым точкам, то такое соединение проводников называется параллельным (рис. 28). Напряжение на каждом из про­водников равно напряжению U, приложенному к узловым точкам цепи А и В.

На рисунке видно, что при параллельном соединении провод­ников для прохождения тока имеется несколько путей. Ток, при­текая к точке разветвления А, растекается далее по трем сопро­тивлениям и равен сумме токов, уходящих от этой точки:

Если токи, приходящие к точке разветвления, считать по­ложительными,   а   уходящие — отрицательными,  то для  точки разветвления можно напи­сать:

т. е. алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение на­зывается первым за­коном   Кирхгофа.

Обычно при расчете  электрических цепей на­правления токов в ветвях, присоединенных к какой-либо точке разветвления, неизвестны. Поэтому для возможности самой запи­си уравнения первого закона Кирхгофа нужно перед началом рас­чета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме. Действительные направления токов определятся в ре­зультате расчета.

Пользуясь законом Ома,  можно вывести  формулу для подсчета общего сопротивления  при  параллельном соединении потребителей. Общий ток, приходящий к точке А, равен

Токи в каждой из ветвей имеют значения:

По первому закону  Кирхгофа

или

Вынося U в правой части равенства за скобки, получим

Сокращая обе части равенства на U, получим формулу подсчета общей проводимости 

или

Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.

Если в электрической цепи имеются как последовательные, так и параллельные соединения отдельных проводников, то мы имеем дело со смешанным    соединением.

Вопрос 8.Резонансный режим работы двухполюсника.Резонанс тока.Резонанс напряжений.

Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.Методика расчёта линейных электрических цепей переменного тока Электротехника курсовая работаДля определения условий возникновения режима резонанса в электрической цепи нужно:

Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.Уравнение Im[Z]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.В электрических цепях резонанс может рассматриваться в задачах:

Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром. Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор).

studfiles.net

Последовательное, параллельное и смешанное соединение элементов эл. Ц.

Последовательное, параллельное и смешанное соединения резисторов.Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенноесопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способысоединения резисторов(приемников электрической энергии): последовательное, параллельное и смешанное.Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходитодин и тот же ток I.Последовательное соединение приемников поясняет рис. 25, а..Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:E = IR1+ IR2+ IR3= I(R1+ R2+ R3) = IRэк(19) где Rэк = R1 + R2 + R3.Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то длярассматриваемой цепиU = U1+ U2+U3(20) Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям: U1: U2: U3= R1: R2: R3 (21) т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение. В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U: U1 = U/n. (22) При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяялампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:I1=U/R1; I2=U/R2; I3=U/R3.Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, илиI = U / R1+ U / R2+ U / R3= U (1/R1+ 1/R2+ 1/R3) = U / Rэк (23)Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой1/Rэк = 1/R1+ 1/R2+ 1/R3 (24)Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим:эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:Gэк= G1+ G2+G3 (25)

5.Топология электрической цепи. Основные определения.Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Ветвью называется участок цепи, обтекаемый одним и тем же током.Узел – место соединения трех и более ветвей. Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны. Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3. Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом. Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным. Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе. В теории электрических цепей важное значение имеют следующие подграфы: 1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно. 2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным. 3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. 4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа. Если граф содержит m узлов и n ветвей, то число ветвей любого дерева , а числа ветвей связи графа . 5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 иS2 . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.

6.Топологические матрицы. Топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений. 1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы. Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу АН , принимая, что элемент матрицы (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим .Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа. 2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы Всоответствуют контурам, а столбцы – ветвям схемы.Элемент bijматрицы В равен 1, если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1, если не совпадает с направлением обхода контура, и 0, если ветвьj не входит в контурi.Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.Перейдем теперь ко второму закону Кирхгофа.Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е. 3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа. Матрица Q, составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Qравно числу независимых сечений. Элемент qijматрицы Q равен 1, если ветвьвходит в i-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1, если ориентирована противоположно направлению сечения, и 0, если ветвьj не входит в i-е сечение.В качестве примера составим матрицу Qглавных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеемВ заключение отметим, что для топологических матриц А, В и Q, составленных для одного и того же графа, выполняются соотношения

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

megalektsii.ru

Преобразование последовательной цепи в параллельную и обратно

Условием эквивалентных пассивных линейных двухполюсников является равенство их комплексных сопротивлений и проводимостей.

Пусть заданы параметры , последовательной RL-цепи (рис. 7.3, а) и требуется найти параметры и эквивалентной ей параллельной RL-цепи (рис. 7.3, б).

а) б) а) б)

Рис. 7.3 Рис. 7.4

Определим комплексную проводимость последовательной RL-цепи

и комплексную проводимость параллельной цепи

.

Приравнивая вещественные и мнимые составляющие комплексных проводимостей последовательной и параллельной цепей, находим

; .

Если заданы параметры и параллельной RС-цепи (рис. 7.4, а),. то она может быть аналогичным образом преобразована в эквивалентную ей последовательную RС-цепь (рис. 7.4, б), параметры которой определяются по формулам:

; .

Таким же путём можно найти формулы для пересчёта параметров параллельной RL-цепи в последовательную, последовательной RC-цепи в параллельную и т.п.

Однако следует иметь в виду, что вышеприведенные эквивалентные преобразования применимы только для фиксированной частоты внешнего воздействия. Изменение частоты внешнего воздействия вызовет изменение значений параметров элементов эквивалентной цепи, поскольку частота входит в расчётные формулы.

Похожие статьи:

poznayka.org

1. Что такое последовательно-параллельная цепь? | 6. Последовательно-параллельные цепи | Часть1

1. Что такое последовательно-параллельная цепь?

Что такое последовательно-параллельная цепь?

В простой последовательной цепи все компоненты связаны между собой таким образом, что они образуют только один путь для потока электронов:

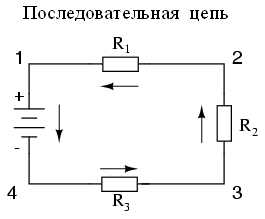
В простой параллельной цепи все компоненты связаны между собой двумя наборами электрически общих точек, создавая тем самым несколько путей для потока электронов:

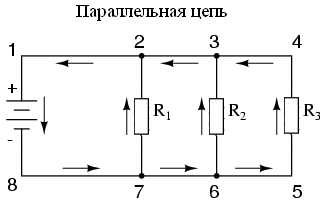
Для каждой из этих цепей существуют определенные наборы правил, описывающие поведение тока, напряжения и сопротивления:

Последовательная цепь:

• Общее напряжение цепи равно сумме напряжений на отдельных ее компонентах.

• Сила тока одинакова на любом компоненте цепи.

• Общее сопротивление цепи равно сумме ее отдельных сопротивлений.

Параллельная цепь:

• Напряжение на всех компонентах цепи одинаково.

• Общая сила тока цепи равна сумме отдельных ее токов.

• Общее сопротивление цепи меньше любого из ее отдельных сопротивлений.

Однако, если компоненты схемы соединены последовательно в одних ее частях и параллельно в других, то мы не сможем применить один из этих наборов правил ко всем частям схемы. Вместо этого мы должны будем определить, какие части схемы представляют собой последовательные цепи, а какие параллельные, и только после этого можно будет применить соответствующие правила для анализа соответствующих частей схемы. В качестве примера можно рассмотреть следующую схему:

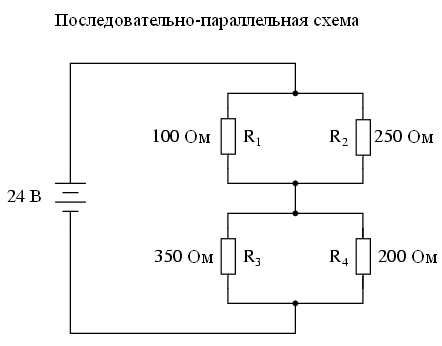
Эта схема не является ни простой последовательной, ни простой параллельной цепью. Она содержит в себе элементы обеих этих цепей. Поток электронов в данной схеме выходит из основания батареи, по ходу своего движения он распадается на резисторах R3 и R4, на их выходах он снова воссоединяется, далее он распадается на резисторах R1 и R2, затем опять воссоединяется и возвращается к верхней части батареи. Исходя из этого можно прийти к выводу, что здесь у нас существует более одного пути для потока электронов (схема не является последовательной), и более двух наборов электрически общих точек (схема не является параллельной).

Поскольку данная схема является комбинацией последовательных и параллельных цепей, мы не можем применить наборы правил для заполнения вышеприведенной таблицы, как делали это с простыми цепями по отдельности. К примеру, в случае с простой последовательной цепью, мы могли сложить значения всех сопротивлений, чтобы получить общее, затем мы рассчитывали общую силу тока, а потом вычисляли напряжения на всех резисторах. Аналогично мы поступали с простой параллельной цепью: сначала мы рассчитывали токи на отдельных ее ветвях, потом их суммировали и получали общую силу тока, затем, отталкиваясь от общего напряжения и общей силы тока мы вычисляли общее сопротивление этой цепи. Но все это было анализом простых схем. Проанализировать нашу схему будет несколько сложнее.

Таблица по-прежнему будет помогать нам в расчетах значений последовательно-параллельной схемы, но мы должны четко знать как и где можно применить различные правила для последовательных и параллельных цепей. В вертикальных столбцах нашей таблицы без каких-либо ограничений будет работать Закон Ома.

Если мы в состоянии определить, какие части схемы являются последовательными, а какие параллельными, то мы мы можем проанализировать ее поэтапно, применяя на каждом этапе соответствующие правила для расчета напряжения, тока и сопротивления. В следующих статьях данного раздела мы с вами подробно рассмотрим методы анализа комбинированных схем. 

www.radiomexanik.spb.ru

• 
  Автомат и узо в чем разница
• 
  Управление что такое связь
• 
  Три провода в розетке
• 
  Обозначения на тепловых схемах
• 
  Гост электрические схемы размеры элементов
• 
  Восьмеричная система счисления имеет основание
• 
  Подать сведения за воду
• 
  Клещи эл измерительные
• 
  При нагреве сопротивление увеличивается или уменьшается
• 
  Трехфазные сети
• 
  Трубы в обмен на газ