Вектор индукции магнитного поля. Направление вектора индукции магнитного поля в данной точке

46.4 Вектор индукции магнитного поля.

46.4 Вектор индукции магнитного поля.

 Вспомним, электрическое поле действует с некоторой силой F на неподвижный электрический заряд, величина этой силы пропорциональна величине заряда q, поэтому отношение силы, действующей на электрический заряд к его величине, не зависит от свойств заряда, следовательно, является характеристикой, электрического поля − его напряженностью E = F/q. В этом случае пробный заряд фактически выступает в роли прибора для обнаружения поля и измерения его характеристик. Магнитное поле действует на движущиеся заряды, следовательно, и характеристика этого поля должна быть связана с этой силой. Но движущийся заряд описывается не только величиной заряда, но и вектором скорости, следовательно, и сила, действующая на этот заряд, зависит также от вектора его скорости. Поэтому движущийся пробный заряд, как прибор для обнаружения магнитного поля не обладает сферической симметрией (как неподвижный точечный заряд), следовательно, характеристика магнитного поля не может быть определена так же просто как напряженность электрического поля1. Практически более удобно в качестве «пробного» прибора для изучения магнитного поля использовать малый проводящий контур с электрическим током2, поведение которого в магнитном поле аналогично поведению намагниченной стрелки. Вспомним, что для создания постоянного тока в замкнутом контуре необходим источник ЭДС, тем не менее, можно реально создать малый контур с постоянным током. Для этого достаточно подвесить проводящую рамку на двух тонких проводах, подключенных к источнику (рис. 413).

рис. 413  Так как в подводящих проводах токи текут в противоположных направлениях, то суммарный ток равен нулю.  Как было установлено Эрстедом и подтверждено А. Ампером в магнитном поле контур с током стремится занять определенную ориентацию в пространстве, стремится повернуться, следовательно, со стороны магнитного поля на контур (как и на стрелку) действует вращающий момент сил. Момент сил (а не сила, как в случае электрического поля), действующих на контур, служит для определения характеристики магнитного поля.  Опыт показывает, что момент сил, действующих на контур, зависит от его ориентации в пространстве, следовательно, физическая величина, описывающее магнитное поле, должна быть векторной. В общем случае этот вектор может изменяться от точки к точке, поэтому магнитное поле должно описываться математически как уже знакомое нам векторной поле.  Так как мы хотим определить «точечную» характеристику магнитного поля, то такой контур (или магнитную стрелку) следует считать бесконечно малым.  В очередной раз мы должны сделать традиционную оговорку − бесконечно малый контур физически нереализуем − даже провода имеют конечную толщину, поэтому переход к бесконечно малому контуру следует понимать в физическом смысле − мал, настолько, что с математической точки можно считать бесконечно малым, но реально реализуемым.  Чтобы избавиться от неоднозначности измеряемого момента сил, связанной с ориентацией контура, выберем такое положение контура, при котором модель момента сил максимален Mmax. Наконец, учтем еще один экспериментальный факт − момент сил, действующих на контур, пропорционален силе тока в контуре I и площади контура S.  Следовательно, отношение момента сил к произведению силы тока в контуре на его площадь является величиной, не зависящей от свойств контура, поэтому является характеристикой поля, которая называется индукцией магнитного поля  Теперь необходимо определиться с направлением вектора индукции магнитного поля. Наиболее наглядно направление этого вектора в данной точке указывает северный полюс магнитной стрелки в состоянии устойчивого равновесия. Свяжем теперь это направление с ориентацией контура с током, который мы выбрали в качестве индикатора поля. Для этого введем еще одну характеристику контура − его магнитный момент3.  Магнитными моментом контура (рис. 414) называется вектор направленный перпендикулярно плоскости контура, модуль которого равен произведению силы тока в контуре на его площадь pm = IS.рис. 414  Направление этого вектора определяется по правилу правого винта − если направление тока совпадает с направлением вращения винта, то направление движения последнего совпадает с направлением вектора магнитного момента. Если смотреть с конца вектора момента, то направление обхода контура по направлению тока положительной, то есть против часовой стрелки.  Таким образом, направление вектора индукции магнитного поля совпадает с направлением вектора магнитного момента контура, помещенного в данную точку поля и находящегося в положении устойчивого равновесия.  Еще раз рассмотрим ориентации векторов, которые задействованы в определении вектора индукции магнитного поля. Пусть в некоторой области пространства магнитное поле можно считать однородным (то есть вектор индукции во всех точках постоянен, как по величине, так и по направлению). Будем также считать, что ось вращения контура перпендикулярна направлению вектора индукции магнитного поля (рис. 415 − показан вид сверху на рамку с током в магнитном поле).рис. 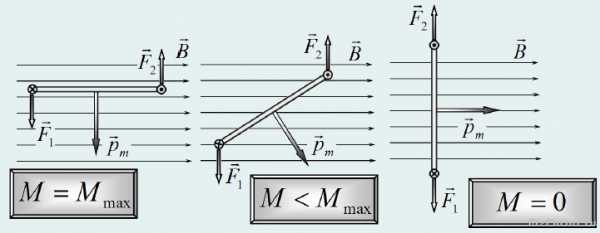415  Вектор момента сил M перпендикулярен вектору магнитной индукции B и вектору магнитного момента контура pm. На контур будет действовать со стороны магнитного поля максимальный момент сил в том случае, когда эти векторы перпендикулярны (то есть вектор индукции поля лежит в плоскости контура), а в положении равновесия вектор индукции перпендикулярен плоскости контура.  Наконец, запишем общее выражение для момента силы, действующего на контур с током со стороны магнитного поля, воспользовавшись операцией векторного произведения  Простота этой формулы оправдывает все наши долгие рассуждения по определению характеристики магнитного поля. Фактически эта формула может рассматриваться как определение вектора индукции магнитного поля.  Сравните с выражением для силы, действующей со стороны электрического поля на точечный заряд F = qE. Похоже: q − характеристика индикатора электрического поля, pm − характеристика индикатора магнитного поля; E − основная характеристика электрического поля, B − основная характеристика магнитного поля; F − результат воздействия электрического поля на точечный заряд, M − результат воздействия магнитного поля на контур.  Индукция магнитного поля является размерной физической величиной. В системе СИ единицей измерения индукции является Тесла (сокращенно Тл), названная в честь американского (югославского происхождения) физика и инженера Николы Тесла. Эта единица является производной, она может быть выражена через другие единицы с помощью формулы (9): 1Хотя бы потому, что операция деления вектора на вектор не определена.2Может быть, магнитная стрелка в качестве пробного прибора и более наглядна, но физические характеристики контура с током легче задать и определить.3В некотором смысле она аналогична дипольному моменту в электростатике. Магнитная стрелка компаса, некоторые атомы и молекулы, такие элементарные частицы как электрон, протон, нейтрон обладают собственными магнитными моментами, хотя говорить об их площади, или силе тока говорить не приходится.

fizportal.ru

Магнетизм. Магнитное поле. ОСНОВНЫЕ ПОЛОЖЕНИЯ

Электрический ток оказывает магнитное действие Таким образом, магнитное поле порождается движущимися зарядами.

Вектор магнитной индукции — векторная физическая величина, направление которой в данной точке совпадает с направлением, указываемым в этой точке северным полюсом свободной магнитной стрелки.

Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины отрезка проводника:

Электрический ток оказывает магнитное действие Таким образом, магнитное поле порождается движущимися зарядами.

Вектор магнитной индукции — векторная физическая величина, направление которой в данной точке совпадает с направлением, указываемым в этой точке северным полюсом свободной магнитной стрелки.

Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины отрезка проводника:

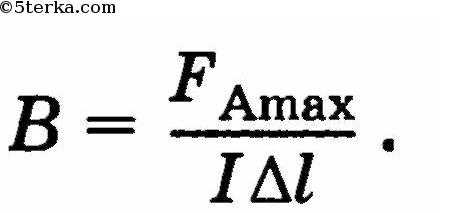Единица магнитной индукции — тесла (1 Тл).

Правило буравчика для прямого тока: если ввинчивать буравчик по направлению тока в проводнике, то направление скорости движения конца его рукоятки совпадает с направлением вектора магнитной индукции в этой точке.

Правило правой руки для прямого тока: если охватить проводник правой рукой, направив отогнутый большой палец вдоль тока, то кончики остальных пальцев в данной точке покажут направление вектора индукции в этой точке.

Принцип суперпозиции магнитных полей: результирующая магнитная индукция в данной точке складывается из векторов магнитной индукции, созданной различными токами в этой точке:

Правило буравчика для витка с током (контурного тока): если вращать рукоятку буравчика по направлению тока в витке, то поступательное перемещение буравчика совпадает с направлением вектора магнитной индукции, созданной током в витке на своей оси.

Линии магнитной индукции — линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции. Линии магнитной индукции всегда замкнуты: они не имеют начала и конца. Магнитное поле — вихревое поле, т.е поле с замкнутыми линиями магнитной индукции

Магнитный поток (поток магнитной индукции) через поверхность определенной площади — физическая величина, равная скалярному произведению вектора магнитной индукции на вектор площади:

Единица магнитного потока — вебер (1 Вб) 1 Вб= 1 Тл•м2.

Закон Ампера: сила, с которой магнитное поле действует на помещенный в него отрезок проводника с током, равна произведению силы тока, магнитной индукции, длины отрезка проводника и синуса угла между направлениями тока и вектором магнитной индукции:

В однородном магнитном поле замкнутый контур стремится установиться так, чтобы направление его собственной индукции совпало с направлением внешней индукции.

Сила Лоренца — сила, действующая на движущуюся со скоростью v заряженную частицу со стороны магнитного поля В:

где q — заряд частицы, а — угол между скоростью частицы и индукцией магнитного поля.

Направление силы Лоренца определяет правило левой руки: если кисть левой руки расположить так, чтобы четыре вытянутых пальца указывали направление скорости положительного заряда (или противоположное скорости отрицательного заряда), а вектор магнитной индукции входил в ладонь, то отогнутый (в плоскости ладони) на 90° большой палец покажет направление силы, действующей на данный заряд.

Заряженная частица, влетающая в однородное магнитное поле параллельно линиям магнитной индукции, движется равномерно вдоль этих линий. Заряженная частица, влетающая в однородное магнитное поле в плоскости, перпендикулярной линиям магнитной индукции, движется в этой плоскости по окружности. Параллельно расположенные проводники, по которым протекают токи в одном направлении, притягиваются, а в противоположных — отталкиваются. Магнитные поля, создаваемые токами I1,I2, протекающими по бесконечно длинным параллельным проводникам, находящимся на расстоянии r друг от друга, приводят к возникновению на каждом отрезке проводников длиной Δl силы взаимодействия

где km — коэффициент пропорциональности, km = 2 • 10-7 Н/А2

Единица силы тока — ампер (1 А) Сила постоянного тока равна 1 А, если ток, протекая по двум параллельным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызывает на отрезке проводника длиной 1 м силу взаимодействия, равную 2 • 10-7Н

Индукция магнитного поля убывает при увеличении расстояния до проводника с током Взаимодействие проводников с током является следствием магнитного взаимодействия движущихся зарядов в проводниках Под действием магнитной силы движущиеся параллельно в противоположных направлениях разноименные заряды притягиваются, а одноименные — отталкиваются

Индуктивность контура (или коэффициент самоиндукции) — физическая величина, равная коэффициенту пропорциональности между магнитным потоком через площадь, ограниченную контуром проводника, и силой тока в контуре. Единица индуктивности — генри (1 Гн)

Энергия магнитного поля, созданного при протекании силы тока I по проводнику с индуктивностью L, равна

Магнитная проницаемость среды — физическая величина, показывающая во сколько раз индукция магнитного поля в однородной среде отличается от магнитной индукции внешнего (намагничивающего) поля в вакууме.

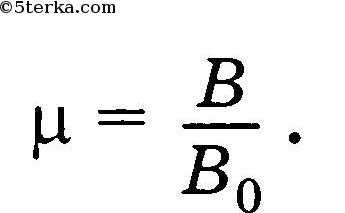Диамагнетики, парамагнетики, ферромагнетики — основные классы веществ с резко отличающимися магнитными свойствами

Диамагнетик— вещество, в котором внешнее магнитное поле незначительно ослабляется( μ <= 1)

Парамагнетик— вещество, в котором внешнее магнитное поле незначительно усиливается(μ >= 1)

Ферромагнетик — вещество, в котором внешнее магнитное поле значительно усиливается (μ >> 1)

Кривая намагничивания — зависимость собственной магнитной индукции от индукции внешнего магнитного поля

Коэрцитивная сила — магнитная индукция внешнего поля, необходимая для размагничивания образца

Магнито-жесткие ферромагнетики — ферромагнетики с большой остаточной намагниченностью Магнито-мягкие ферромагнетики — ферромагнетики с малой остаточной намагниченностью Петля гистерезиса — замкнутая кривая намагничивания и размагничивания ферромагнетика Температура Кюри — критическая температура, выше которой происходит переход вещества из ферромагнитного состояния в парамагнитное

5terka.com

Вектор индукции магнитного поля

Определение

Силовой характеристикой магнитного поля является вектор магнитной индукции $\overrightarrow{B}$. Вектор магнитной индукции является основной характеристикой магнитного поля. Он равен пределу отношения силы, с которой магнитное поле действует на элементарный ток ($Idl$) к произведению тока $(I)$ и величины элемента проводника ($dl$):

Вектор индукции направлен перпендикулярно направлению элементарного тока (или чаще говорят элементу проводника ($\overrightarrow{dl}$)) из (1) и перпендикулярен направлению силы, которая действует со стороны магнитного поля.

Если $\overrightarrow{B}$=const, то магнитное поле называют однородным. Если магнитное поле неизменно во времени, то его называют постоянным.

Иногда модуль вектора индукции однородного магнитного поля определяют как:

где $M_{max}$ -- максимальный вращающий момент, действующий на контур с током, который помещен в магнитное поле, $p_m=IS$ -- магнитный момент контура ($S$- площадь контура). За направление вектора $\overrightarrow{B}$ принимают направление, в котором устанавливается под действием поля положительная нормаль к контуру с током. Или иначе, говорят, что вектор магнитной индукции направлен в сторону поступательного перемещения правого винта, если его вращать по направлению течения тока в контуре.

Очень часто, определение для вектора магнитной индукции записывают в виде:

где $\overrightarrow{dF}$ -- сила, действующая на элемент с током. В том случае, если проводник прямолинейный и магнитная индукция во всех точках постоянна, то формулу (2) можно преобразовать в выражение:

Рис. 1

Модуль вектора индукции можно определить, так же исходя из силы Лоренца ($\overrightarrow{F}$), которая действует на движущуюся, со скоростью $\overrightarrow{v}$ заряженную частицу (заряд q) в магнитном поле:

Основной единицей измерения магнитной индукции в системе СИ является тесла (Тл).

Принцип суперпозиции вектора индукции магнитного поля

Эмпирический доказано, что для магнитного поля выполняется принцип суперпозиции:

Если магнитное поле порождается несколькими токами (движущимися зарядами), то оно равно векторной сумме отдельных полей:

Пример 1

Задание: Проводник имеет форму квадрата, сторона которого равна d, по нему течет ток силы I. Найдите магнитную индукцию поля в точке пересечения диагоналей квадрата.

Решение:

Допустим, что плоскость проводника совпадает с плоскостью рис.2. Зададим направление токов.

Рис. 2

В точке О магнитное поле создают четыре прямолинейные проводника с током. Напряженности всех четырех полей направлены в соответствии с правилом правого винта от нас, перпендикулярно плоскости рисунка. Следовательно, векторную сумму полей в принципе суперпозиции заменим на алгебраическую, запишем:

\[B=B_1+B_2+B_3+B_4\left(1.1\right).\]

Причем из симметрии, очевидно, что модули всех индукций равны, значит, запишем, что:

\[B=4B_1\left(1.2\right).\]

В разделе «Электромагнетизм» мы нашли, формулу для расчета модуля вектора магнитной индукции прямолинейного проводника с током. В применении к нашему случаю модуль $\overrightarrow{B}$ будет иметь вид:

\[B_1=\frac{{\mu }_0I}{4\pi b}\left(cos\alpha -cos\beta \right)\left(1.3\right),\]

углы $\alpha $ и $\beta $ указаны на рис.1. В (1.3) $\beta =\pi -\alpha \to cos\beta ={cos \left(\pi -\alpha \right)\ }=-cos\alpha .$ Перепишем (1.3):

\[B_1=\frac{{\mu }_0I}{2\pi b}cos\alpha \left(1.4\right).\]

Так как мы имеем дело с квадратом, то заметим, что: $b=\frac{d}{2},\alpha =\frac{\pi }{4}\to cos\alpha =\frac{\sqrt{2}}{2}.$ Подставим в (1.4), то что мы получили и (1.4) подставим в (1.2), имеем:

\[B=4\cdot \frac{{\mu }_0I}{\pi d}\cdot \frac{\sqrt{2}}{2}=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.\]

Ответ: $B=\frac{2\sqrt{2}}{\pi d}{\mu }_0I.$

Пример 2

Задание: Бесконечно длинный проводник с током (I) согнут под прямым углом (рис.2). Найдите магнитную индукцию поля в точке А, которая указана на рис. 3.

Рис. 3

Решение:

В точке А поле создается двумя частями проводника:

\[\overrightarrow{B}=\overrightarrow{B_{II}}+\overrightarrow{B_{\bot }}\left(2.1\right).\]

Рассмотрим горизонтальный участок, на продолжении которого лежит точка А. Этот участок проводника с током создает поле в точке А индукция $(\overrightarrow{B_{II}})$которого, равна нулю, так как в точке А углы между всеми элементами с током и радиус-векторами будут равны $\pi .\ $Следовательно, векторное произведение ($\left[d\overrightarrow{l}\overrightarrow{r}\right]$), в законе Био -- Савара -- Лапласа равно нулю:

\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\oint{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\left(2.2\right),\]

где $\overrightarrow{r}$ -- радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$).

Индукция магнитного поля бесконечного прямолинейного проводника с током (I) в точке А была бы равна:

\[B'=\frac{{\mu }_0}{2\pi }\frac{I}{b}\left(2.3\right).\]

У нас полу бесконечный проводник, следовательно, из принципа суперпозиции получим, что для нашего проводника индукция равна:

\[{B=B}_{\bot }=\frac{1}{2}B'=\frac{{\mu }_0}{\pi }\frac{I}{b}.\]

Ответ: $B=\frac{{\mu }_0}{\pi }\frac{I}{b}.$

spravochnick.ru

Вектор индукции магнитного поля

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E  электрического поля. Такой характеристикой является вектор магнитной индукции B. Вектор магнитной индукции B определяет силы, действующие на токи или движущиеся заряды в магнитном поле. За положительное направление вектора B принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора B. Такое исследование позволяет представить пространственную структуру магнитного поля.

• Закон Био-Савара-Лапласа

физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Пусть постоянный ток течёт по контуру (проводнику), находящемуся в вакууме,— точка, в которой ищется (наблюдается) поле, тогдаиндукция магнитного поля в этой точке выражается так:

• Принцип суперпоз. Маг. Полей

магнитное поле любого тока может быть вычислено как результат векторного сложения (суперпозиции) магнитных полей, создаваемых отдельными элементами тока. Это правило получило название принципа суперпозиции магнитных полей.

№15

Теорема о циркуляции вектора индукции магнитного поля в дифференциальной и интегральной форме.

rotB=rotrotA=graddivA-∆A=μ0I;

rotB=μ0I. – дифференциальная форма теоремы о циркуляции вектора магнитной индукции.

По формуле Стокса

∫rotBdS=μ0∫IdS=μ0∑I; μ0∫IdS=∫BdL – интегральная форма теоремы о циркуляции вектора магнитной индукции.

№16

• Расчет маг. Поля соленоида и тороида.

1) Соленоид: Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора B по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции,

откуда B = μ0 I n.

2) Тороид: — кольцевая катушка, у которой витки намотаны на сердечник, который имеет форму тора. Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю. В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, B•2πr=μ0NI, откуда следует, что магнитная индукция внутри тороида (в вакууме) ,где N — число витков тороида. Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует

• Намагниченность вещества

Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества: Здесь,M — вектор намагниченности; m - вектор магнитного момента; V — объём. В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как и является функцией координат.

№18

studfiles.net

александр леготкин                                                                                                  -магнитное поле-

Тип урока: урок изучения нового материала.

Вид урока: лекция с элементами эвристической беседы и демонстрационным экспериментом.

Цели: 

•  Сформулировать  определение магнитного поля.

• Рассмотреть магнитное поле электрического тока и сопоставить его с магнитным полем постоянных магнитов.

• Ввести понятие силовой характеристики магнитного поля.

• Продолжить развитие умения наблюдать явления, анализировать увиденное и проводить сопоставление эксперимента с теорией.

Всякий электрический ток создает вокруг себя магнитное поле. Магнитное поле, окружающее длинную катушку из проволоки, которую часто называют соленоидом, очень похоже на поле намагниченного стержня.

Катушка с током во всем подобна магниту. Если ее подвесить, она будет поворачиваться, пока ее ось не укажет в направлении N—S. Она ведет себя так, как будто имеет на концах «полюсы», которые притягивают или отталкивают полюсы других магнитов. Небольшая катушка с током, помещенная               в магнитное поле Земли, магнита или другой катушки, будет поворачиваться наподобие стрелки компаса, пока ее магнитная ось не станет параллельной внешнему полю.

Внутри полой катушки, как и внутри полосового магнита, магнитные силовые линии идут плотным параллельным пучком, образуя сильное однородное магнитное поле.

Сила, с которой поле действует на помещенную в это поле магнитную стрелку, одинакова как по модулю, так и по направлению во всех точках. Поэтому такое поле называется однородным. Линии неоднородного магнитного поля искривлены, их густота меняется от точки к точке.

Загрузит модель

Наряду с постоянными магнитами существуют и электромагниты, нашедшие в настоящее время колоссальное применение в науке и технике.

Современные электромагниты способны поднимать десятки тонн металла, заменяя тем самым огромное число рабочих и повышая производительность труда.

Вопрос: каким образом можно изготовить электромагнит?

 

 

 

 

 

 

Вектор магнитной индукции B – физическая величина, характеризующая магнитное поле.

Направление вектора магнитной индукции совпадает с направлением северного полюса свободной магнитной стрелки в данной точке.

Правило буравчика для прямого тока :

Если ввинчивать буравчик по направлению тока в проводнике, то направление вращения ручки буравчика в данной точке укажет направление вектора магнитной индукции B в этой точке.

Правило правой руки для прямого тока:

Если охватить проводник правой рукой, направив отогнутый большой палец по направлению тока, то кончики остальных пальцев покажут направление вектора магнитной индукции в данной точке.

Принцип суперпозиции:

Результирующий вектор магнитной индукции в данной точке складывается  из векторов магнитной индукции, созданной различными токами в этой точке: B = B1 + B2 +…+ Bn

Правило буравчика для витка с током (контура) :

Если вращать ручку буравчика по направлению тока в витке, то поступательное перемещение буравчика совпадает с направлением вектора магнитной индукции созданной током в витке на своей оси.

Магнитное поле сильнее вблизи провода и ослабевает вдали от него. Этот первый эффект магнитного действия электрического тока был открыт следующим образом. В конце своей лекции о свойствах электрического тока датский ученый Эрстед поместил токонесущий провод около компасной стрелки и был до глубины души изумлен, увидев, что стрелка повернулась. «Опыты, которые он начал проводить в апреле 1820 г., являются одними из самых памятных во всей истории науки».  Компасная стрелка, расположенная параллельно проводнику, при включении тока поворачивалась на 90°. Таким образом, силы действовали на компасную стрелку не в направлении прямой, соединяющей ее полюс с проводником, а в перпендикулярном направлении.

Последующие опыты подтвердили это заключение и показали, что сила, действующая со стороны магнита на ток, перпендикулярна как направлению магнитного поля, так и направлению тока — проводник с током, помещенный в магнитное поле, испытывает боковое усилие. Эти новые силы полностью отличались от уже известных обычных сил. До открытия Эрстеда были известны только такие силы, которые действуют вдоль прямой, соединяющей взаимодействующие тела.

-          вид материи посредством которого осуществляется взаимодействие токов, находящихся на расстоянии;

-          вихревое;

-          обладает энергией;

-          распространяется со скоростью света;

-          убывает с расстоянием;

-          характеризуется вектором магнитной индукции;

-          не имеет источников;

-          работа при перемещении проводника с током по замкнутому контуру в магнитном поле НЕ равна 0 ;

§ 18, 19. Вопросы.

 

 

 

 

 

 

mpf-pro.narod.ru

1)Какие источники у магнитного поля? 2)Направление вектора индукции

Источники магнитного поля Источниками магнитного поля являются движущиеся электрические заряды (токи) Магнитное поле существует вокруг: Токов Постоянных магнитов Земли За положительное направление вектора В принимается направление от южного полюса S к северному полюсу N внутри магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое постоянным магнитом или током, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора магнитной индукции

Источниками магнитного поля являются движущиеся электрические заряды (токи).

Источниками магнитного поля являются движущиеся электрические заряды (токи) магнитное поле сущ-ет например вокруг металлического проводника с током (если у тя книга Перышкин 9 класс то страница 140) линиями магн индукции наз-ся линии, касательные к которым в каждой точке поля совпадают с направлением вектора магн. индукции ( с книги) хватит? =)

<img src="//otvet.imgsmail.ru/download/44281345_98139bfe2218c7210b1000a82a3ebc10_800.jpg" alt="" data-lsrc="//otvet.imgsmail.ru/download/44281345_98139bfe2218c7210b1000a82a3ebc10_120x120.jpg" data-big="1">

touch.otvet.mail.ru

Вектор магнитной индукции, теория и примеры

Определение и общие понятия вектора магнитной индукции

Результаты экспериментов Ампера с проводниками в магнитном поле показали, что способность магнитного поля вызывать появление механической силы, которая оказывает действие на элемент с током, можно количественно описать, если задать в каждой точке поля некоторый вектор (), который назвали вектором магнитной индукции. Сила, которая действует на элемент тока () равна:

   

где – сила Ампера. Выражение (1) можно считать определением магнитной индукции. Величина B равна пределу отношения силы (dF), с которой действует магнитное поле на элементарный проводник с током, к силе тока (I) умноженной на длину этого проводника (dl), при длине проводника стремящейся к нулю. При этом проводник имеет такое расположение в магнитном поле, что данный предел имеет максимальное значение:

   

Эмпирически легко показать, что магнитное поле, воздействуя на рамку с током, оказывает на нее ориентирующее действие, разворачивая ее определенным образом. Это связано с тем, что магнитное поле имеет направление. За направление магнитного поля в точке принимают направление положительной нормали к рассматриваемой рамке. В качестве направления магнитного поля, так же можно принимать направление силы, которая оказывает воздействие на северный полюс магнитной стрелки, если его размещают в точку поля.

Принцип суперпозиции для вектора магнитной индукции

Для магнитного поля выполняется принцип наложения (суперпозиции), который означает, что если присутствует несколько контуров с током и каждый из них создает поле с какой – то магнитной индукцией, то индукция результирующего поля равна векторной сумме отдельных индукций:

   

В частности магнитную индукцию поля, которое создано контуром с током находят как сумму индукций отдельных элементов тока, на которые разбивают рассматриваемый контур.

Закон Био-Савара-Лапласа

Этот закон дает возможность определить вектор магнитной индукции () в любой точке магнитного поля, которое создает в вакууме элемент проводника с током:

   

где I – сила тока; – вектор элемента проводника, который по модулю равен длине проводника, а направление его совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой ищут поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).

В однородном изотропном магнетике, заполняющем пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связаны соотношением:

   

где – относительная магнитная проницаемость вещества.

Примеры решения задач

ru.solverbook.com

---

• 
  Длительно допустимый ток шин
• 
  Арматура и изоляторы для воздушных линий электропередачи
• 
  Уровень жесткости воды в москве
• 
  Ртм 03а
• 
  Высота троллейбусных линий от земли
• 
  Формула относительной
• 
  Генератор электрического тока дизельный
• 
  Мосэнергосбыт телефон оператора
• 
  Красэнерго передать показания
• 
  Фото токи
• 
  Ii группа электробезопасности