Определение и классификация конденсаторов. Определение конденсатор

Конденсатор – ldsound.ru

Конденсатор — это двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.

Список конденсаторов

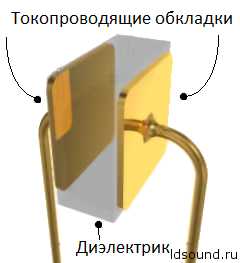
Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).

Изобрел первую конструкцию-прототип электрического конденсатора «лейденскую банку» в 1745 году, в Лейдене, немецкий каноник Эвальд Юрген фон Клейст и независимо от него голландский физик Питер ван Мушенбрук.

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.

При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью, собственной индуктивностью и сопротивлением потерь.

Резонансная частота конденсатора равна: fр = 1/ (2∏ ∙ √Lс ∙ C).

При f > fp конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f < fp, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.

Отечественные неполярные конденсаторы:

На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1·106 пФ = 1·10−6 Ф) и пикофарадах, но нередко и в нанофарадах (1 нФ = 1·10−9 Ф). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 — 180».

Основные параметры конденсаторов:

1. Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками. Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.
2. Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
3. Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита.
4. Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается, что связано с увеличением тепловой скорости движения носителей заряда и, соответственно, снижению требований для образования электрического пробоя.
5. Полярность. Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.

Обозначение на схемах:

Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др.

По виду диэлектрика различают:

1. Конденсаторы вакуумные (между обкладками находится вакуум).
2. Конденсаторы с газообразным диэлектриком.
3. Конденсаторы с жидким диэлектриком.
4. Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические, стеклоплёночные), слюдяные, керамические, тонкослойные из неорганических плёнок.
5. Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные, комбинированные — бумажноплёночные, тонкослойные из органических синтетических плёнок.
6. Электролитические и оксидно-полупроводниковые конденсаторы. Такие конденсаторы отличаются от всех прочих типов прежде всего большой удельной ёмкостью. В качестве диэлектрика используется оксидный слой на металлическом аноде. Вторая обкладка (катод) — это или электролит (в электролитических конденсаторах), или слой полупроводника (в оксидно-полупроводниковых), нанесённый непосредственно на оксидный слой. Анод изготовляется, в зависимости от типа конденсатора, из алюминиевой, ниобиевой или танталовой фольги или спечённого порошка. Время наработки на отказ типичнного электролитического конденсатора 3000-5000 часов при максимально допустимой температуре, качественные конденсаторы имеют время наработки на отказ не менее 8000 часов при температуре 105°С. Рабочая температура — основной фактор, влияющий на продолжительность срока службы конденсатора. Если нагрев конденсатора незначителен из-за потерь в диэлектрике, обкладках и выводах, (например, при использовании его во времязадающих цепях при небольших токах или в качестве разделительных), можно принять, что интенсивность отказов снижается вдвое при снижении рабочей температуры на каждые 10 °C вплоть до +25 °C. Твердотельные конденсаторы — вместо традиционного жидкого электролита используется специальный токопроводящий органический полимер или полимеризованный органический полупроводник. Время наработки на отказ ~50000 часов при температуре 85°С. ЭПС меньше чем у жидко-электролитических и слабо зависит от температуры. Не взрываются.

Вакуумный конденсатор:

Кроме того, конденсаторы различаются по возможности изменения своей ёмкости:

1. Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости (кроме как в течение срока службы).
2. Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости в процессе функционирования аппаратуры. Управление ёмкостью может осуществляться механически, электрическим напряжением (вариконды, варикапы) и температурой (термоконденсаторы). Применяются, например, в радиоприёмниках для перестройки частоты резонансного контура.
3. Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры. Их используют для подстройки и выравнивания начальных ёмкостей сопрягаемых контуров, для периодической подстройки и регулировки цепей схем, где требуется незначительное изменение ёмкости.

Два бумажных электролитических конденсатора 1930 года:

В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и другие конденсаторы.

Серебрянный конденсатор для аудио.

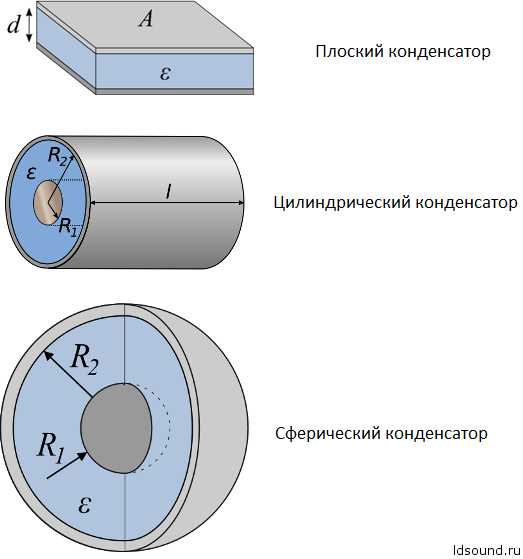
Также различают конденсаторы по форме обкладок:

ldsound.ru

Определение и классификация конденсаторов

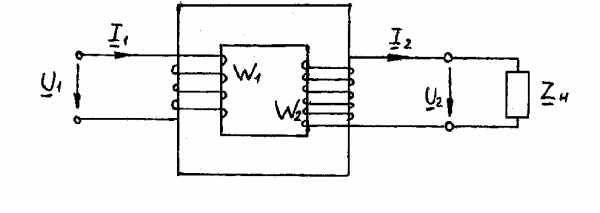
Электрический конденсатор — это элемент электрической цепи, предназначенный для использования его емкости. Конденсатор представляет собой систему из двух электродов (обкладок), разделенных диэлектриком, и обладает способностью накапливать электрическую энергию.

Емкость конденсатора — электрическая емкость между электродами конденсатора, определяемая отношением накапливаемого в нем электрического заряда к приложенному напряжению. Емкость конденсатора зависит от материала диэлектрика, формы и взаимного расположения электродов C=q/U, где C—емкость, Ф; q— заряд, Кл; U — разность потенциалов на обкладках конденсатора, В.

За единицу емкости в Международной системе СИ принимают емкость такого конденсатора, у которого потенциал возрастает на один вольт при сообщении ему заряда один кулон (Кл). Эту единицу называют Фарадой (Ф). Для практических целей она слишком велика, поэтому на практике используют более мелкие единицы емкости: микрофараду (мкФ), нанофараду (нФ), пикофараду (пФ). 1 Ф= 106 мкФ = 109 нФ = 1012 пФ.

В основу классификации конденсаторов положено деление их на группы по виду применяемого диэлектрика и по конструктивным особенностям, определяющим использование их в конкретных цепях аппаратуры.

Вид диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность емкости, величину потерь и др. Конструктивные особенности определяют характерные области применения: помехоподавляющие, подстроечные, дозиметрические, импульсные и др.

Дальнейшее деление групп конденсаторов по виду диэлектрика связано с использованием их в конкретных цепях аппаратуры, назначением и выполняемой функцией, например, низковольтные и высоковольтные, низкочастотные и высокочастотные, импульсные и др.

В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространенные низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся: высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и др.

По характеру изменения емкости различают конденсаторы постоянной емкости, переменной емкости и подстроечные.

Из названия конденсаторов постоянной емкости вытекает, что их емкость является фиксированной и в процессе эксплуатации не регулируется.

Конденсаторы переменной емкости допускают изменение емкости в процессе функционирования аппаратуры. Управление емкостью может осуществляться механически, электрическим напряжением (вариконды) и температурой (термоконденсаторы). Их применяют для плавной настройки колебательных контуров, в цепях автоматики и т. п.

Емкость подстроечных конденсаторов изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры. Их используют для подстройки и выравнивания начальных емкостей сопрягаемых контуров, для периодической подстройки и регулировки цепей схем, где требуется незначительное изменение емкости.

В зависимости от способа монтажа конденсаторы могут выполняться для печатного и для навесного монтажа, а также для сопряжения с ними. Выводы конденсаторов для навесного монтажа могут быть жесткие или мягкие, аксиальные или радиальные, из проволоки круглого сечения или ленты, в виде лепестков, с кабельным вводом, в виде проходных шпилек, опорных винтов. У конденсаторов для микросхем и микромодулей, а также СВЧ-конденсаторов в качестве выводов могут использоваться части их поверхности (безвыводные конденсаторы). У большинства типов оксидных, а также проходных и опорных конденсаторов одна из обкладок соединяется с корпусом, который служит вторым выводом.

По характеру защиты от внешних воздействий конденсаторы выполняются: незащищенными, защищенными, неизолированными, изолированными, уплотненными и герметизированными.

Незащищенные конденсаторы допускают эксплуатацию в условиях повышенной влажности только в составе герметизированной аппаратуры. Защищенные конденсаторы допускают эксплуатацию в аппаратуре любого конструктивного исполнения.

Неизолированныеконденсаторы (с покрытием или без покрытия) не допускают касания своим корпусом шасси аппаратуры. Напротив, изолированные конденсаторы имеют достаточно хорошее изоляционное покрытие (компаунды, пластмассы) и допускают касания корпусом шасси или токоведущих частей аппаратуры.

Уплотненные конденсаторы имеют уплотненную органическими материалами конструкцию корпуса.

Герметизированные конденсаторы имеют герметичную конструкцию корпуса, который исключает возможность сообщения окружающей среды с его внутренним пространством. Герметизация осуществляется с помощью керамических и металлических корпусов или стеклянных колб.

По виду диэлектрика также можно разделить конденсаторы с органическим, неорганическим, газообразным и оксидным диэлектриком, который является также неорганическим, но в силу особой специфики характеристик выделен в отдельную группу.

На рис. 1.5 показано условное обозначение конденсаторов.

Рис. 1.5 Условные обозначения конденсаторов.

а – конденсатор постоянной емкости; б – конденсатор переменной емкости; в – подстроечный конденсатор

 

Читайте также:

lektsia.com

Определение емкости конденсатора.

Собрать схему (Рис. 3), выставить напряжение источника переменного тока ВС-24 U = 10 В и рассчитать емкость конденсатора, зная, что частота промышленного тока n = 50 Гц:

.

Определение активного сопротивления и индуктивности катушки.

Собрать схему (Рис. 4), выставить напряжение источника переменного тока U0 @ 10 В. Используя показания амперметра и ваттметра рассчитать активное сопротивление:

,

а по закону Ома – полное сопротивление катушки, включающее в себя и активную, и реактивную составляющие:

.

Исходя из получаем формулу для расчета индуктивности катушки:

.

Проверка закона Ома для переменного тока.

По полученным значениям индуктивности и емкости и выбранном значении активного сопротивления R порядка 500 Ом рассчитать величину тока, который должен протекать в цепи при напряжении источника переменного тока U = 10 В:

,

где R0 включает в себя активные сопротивления магазина сопротивлений, катушки и амперметра .

Собрать схему, приведенную на (Рис. 5), и убедиться, что экспериментально измеренный ток соответствует расчетному. Тем самым будет подтверждена выполнимость закона Ома для переменного тока.

Изучение резонанса напряжений в цепи переменного тока.

Зная индуктивность катушки и емкость конденсатора, входящих в последовательный контур, рассчитать резонансную частоту:

.

Для экспериментального наблюдения резонанса напряжений можно воспользоваться схемой из предыдущего задания, заменив ВС-24 на звуковой генератор ГЗМ и добавив цифровой вольтметр Щ-4313 для последовательных измерений напряжения на магазине сопротивлений, конденсаторе и катушке (Рис. 6). Резонанс будет тем заметнее, чем меньше активное сопротивление цепи, поэтому необходимо установить на магазине сопротивлений R = 100 Ом. Изменяя частоту в диапазоне от n = 0 до удвоенной резонансной частоты n = 2nрез при неизменном напряжении U0, снять зависимости падений напряжения на активном сопротивлении, емкости и индуктивности от частоты.

Построить и проанализировать зависимости , , , и .

Вопросы к зачету по работе.

– Что такое переменный ток, и какие параметры характеризуют переменный ток?

– Как определяется напряжение переменного тока в цепи, содержащей резистор, конденсатор и катушку индуктивности?

– Объяснить вид векторной диаграммы, характеризующей соотношение фаз напряжений на активных и реактивных элементах цепи.

– Как рассчитывается полное сопротивление электрической цепи переменного тока, содержащей резистор, конденсатор и катушку индуктивности?

– Что такое резонанс напряжений, и при каком условии он возникает в последовательной цепи переменного тока?

– От чего зависит соотношение напряжений на активном и реактивных элементах цепи?

 

Лабораторная работа № 11

Изучение явления термоэлектронной эмиссии

Цель работы.

Изучение условий и закономерностей протекания тока в вакууме на примере явления термоэлектронной эмиссии.

Знания, необходимые для допуска к работе.

– Понятие "электронного газа" в металлах;

– Условия протекания тока в вакууме;

– Закон Богуславского-Ленгмюра.

Краткие сведения из теории.

Протекание тока в вакууме можно рассмотреть на примере вакуумной двухэлектродной лампы (вакуумного диода). Она представляет собой герметично запаянную стеклянную колбу, из которой откачан воздух, с двумя электродами (Рис. 1). Для того, чтобы через вакуум протекал электрический ток, необходимо электрическое поле и наличие свободных носителей заряда в промежутке между электродами. Понятно, что в вакууме практически нет носителей, поэтому нужно каким-либо способом внести некоторое количество заряженных частиц в вакуумный промежуток.

Познакомимся с поведением электронов проводимости внутри металла. При объединении отдельных атомов металла в кристалл внешние валентные электроны обобществляются, т.е. становятся принадлежащими не "своему" атому, а кристаллу в целом. Они представляют собой "электронный газ", заключенный внутри металла, и в отсутствии внешнего электрического поля хаотически движутся в периодическом поле, создаваемом положительными ионами кристаллической решетки. Отдельные электроны, находящиеся вблизи края металла, могут вылететь за его пределы, но там на них действуют силы притяжения со стороны положительных ионов решетки,

возвращающие электроны в металл. Металл окружен "облаком", состоящим из электронов.

Потенциальные энергии электронов иллюстрирует энергетическая диаграмма (Рис. 2). Уровень W0 соответствует энергии покоящегося электрона вне металла, Eс – наименьшая энергия электронов проводимости (дно зоны проводимости). Распределение потенциальной энергии имеет вид потенциальной ямы, глубина которой называется электронным сродством и является важной характеристикой вещества. Понятно, что если электрон имеет полную энергию W меньше W0, то он не может покинуть металл. Для этого ему нужно сообщить дополнительную энергию, и в зависимости от способа сообщения этой энергии явление выхода электронов из металла называется термоэлектронной (при нагревании), фотоэлектронной (под воздействием света), вторичной электронной (в результате бомбардировки другими частицами) эмиссией.

Рассмотрим один из способов – термоэлектронную эмиссию. Это явление испускания электронов металлом при нагревании. Если собрать цепь, содержащую вакуумный диод, источник напряжения и амперметр (Рис. 3), то при холодном отрицательном электроде (катоде) амперметр показывает нуль при подаче напряжения на положительный электрод (анод). Если нагреть катод, подключив к нему дополнительный источник напряжения, амперметр обнаружит появление тока. Зависимость анодного тока от напряжения между анодом и катодом нелинейная, т.е. при протекании тока в вакууме закон Ома не выполняется. Даже при отсутствии разности потенциалов амперметр регистрирует ток, так как часть электронов, покинувших катод, движется в сторону анода и может его достичь. При увеличении напряжения таких электронов становится все больше, и при некотором напряжении наступает насыщение (сколько электронов в единицу времени покидает катод, столько же достигает анода). Ясно, что чем больше температура катода, тем больше электронов вылетает из него, и, соответственно, тем выше ток насыщения. Зависимость тока от напряжения в области нарастания тока имеет вид:

,

где C – постоянная, зависящая от формы и размеров электродов. Например для плоских электродов с площадью S и расстоянием между ними d

.

Формула зависимости тока от напряжения носит название закона Богуславского-Ленгмюра или "закона ".

Характер зависимости можно объясняеть следующим образом. При эмиссии электронов из катода между электродами находится созданный этими электронами объемный отрицательный заряд, плотность которого плавно уменьшается по мере приближения к аноду (Рис. 4). Этот заряд оказывает тормозящее действие на движущиеся к аноду электроны. Увеличение анодного напряжения приводит к быстрому уходу электронов от катода и, следовательно, уменьшению плотности объемного заряда, вследствие чего анодный ток увеличивается.

Зависимость анодного тока насыщения от температуры катода выражается формулой Ричардсона-Дешмана:

,

где – плотность тока насыщения, К – постоянная, которая для всех металлов с совершенно чистой поверхностью имеет примерно одинаковые значения, А – величина, имеющая размерность энергии, называемая термоэлектронной работой выхода и равная разности между энергией покоящегося электрона в вакууме W0 и наибольшей кинетической энергией электрона в металле (уровнем Ферми) ЕF:

.

Работа выхода электронов из металла также является одной из важнейших характеристик эмиссионных свойств металлов.

Практические задания



infopedia.su

Определение - емкость - конденсатор

Определение - емкость - конденсатор

Cтраница 1

Определение емкости конденсатора С осуществляется следующим образом.  [2]

Определение емкостей конденсаторов звеньев фильтра связано со стремлением получить наименьшее емкостное сопротивление конденсаторов фильтра.  [3]

Для определения емкости конденсатора определим разность потенциалов между его обкладками.  [4]

Метод определения емкости конденсатора, рассмотренный в данной задаче, является наиболее грубым по точности, но он прост и не требует сложных расчетов и больших средств для применения на практике.  [5]

При определении емкости конденсатора Ск необходимо найти законы изменения напряжений иа к на участке анод - катод горящего и пога - сающего тиратронов.  [6]

Поэтому задача определения емкости конденсатора сводится к установлению формулы, дающей в каждом, конкретном случае эту зависимость.  [7]

Нам необходимо дать определение емкости конденсатора.  [9]

Существует несколько методов определения емкостей конденсаторов; наиболее распространенным из них является метод биений.  [10]

Существует несколько методов определения емкостей конденсаторов; наиболее распространенным из них является метод биений.  [11]

Существует несколько методов определения емкостей конденсаторов, наиболее распространенным из них является метод биений.  [12]

Аналогично если при определении емкости конденсатора контура, составленного из катушки 5 мкгн и неизвестной емкости, резонансная частота получилась равной, например, 8 Мгц, то эта емкость равна 80 пф.  [13]

Из практики установлены следующие формулы определения емкости конденсаторов для различных схем включения трехфазных асинхронных двигателей в однофазную сеть.  [14]

Измерение диэлектрической проницаемости растворов сводится к определению емкости конденсатора, заполненного воздухом или другим веществом с известной диэлектрической проницаемостью и исследуемым веществом.  [15]

Страницы:      1    2

www.ngpedia.ru

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

БАЛЛИСТИЧЕСКИМ МЕТОДОМ

ЦЕЛЬ РАБОТЫ: Ознакомление с методом измерения емкости конденсатора баллистическим методом.

КРАТКАЯ ТЕОРИЯ. Электрическая емкость конденсатора (далее просто емкость) связана с зарядом, находящимся на его обкладках, соотношением:

(1)

Напряжение на конденсаторе легко определить по напряжению источника тока, заряжающего конденсатор.

Для получения необходимой емкости на практике (в электротехнике) конденсаторы соединяют в батареи, соединяя их параллельно и последовательно. При параллельном соединении общая емкость:

. (2)

При последовательном:

. (3)

Существует несколько способов измерения емкости: метод электростатического вольтметра, метод моста переменного тока, метод баллистического гальванометра. Заряд конденсатора для определения С, согласно (1), можно измерить с помощью гальванометра, работающего в баллистическом режиме, а напряжение - на источнике тока перед разрядом.

Гальванометрами называются приборы для измерения малых токов (или напряжений) порядка 10-6 ¸ 10-12А (10-6 ¸ 10-10В). Главной частью гальванометра магнитоэлектрической системы является подвешенная на вертикальной нити рамка, помещенная в поле постоянного магнита со специальными полюсными наконечниками. При протекании по рамке тока взаимодействие магнитных полей тока и постоянного магнита приводит рамку в движение. Скрепленная с рамкой стрелка (зеркальце для отражения луча) позволяет измерять угол поворота рамки. В баллистическом гальванометре к рамке подвешивается полый цилиндр из мягкого железа, увеличивающий её момент инерции. Кроме того, поле вблизи витков становится радиально симметричным.

При протекании тока на рамку будут действовать:

а) вращающий момент М1, возникающий в результате действия магнитного поля магнита на ток;

б) момент М2, обусловленный закручиванием нити подвеса;

в) тормозящий момент М3, определяющий действие магнита на индукционный ток в катушке при её вращении.

Моментом трения, ввиду его малости (Мтр << М1; М2; М3), пренебрегают.

Если В – индукция магнитного поля в зазоре, N – число витков в катушке, S – площадь витка, D – момент сил закручивания подвеса при повороте рамки на единицу угла, R – сопротивление в цепи гальванометра, i – ток, протекающий по катушке, ii – индукционный ток; , – угол поворота и угловая скорость, то указанные выше моменты будут равны:

Уравнение движение рамки гальванометра с моментом инерции I :

.

(5)

Если время прохождения тока разряда конденсатора через рамку значительно меньше периода ее собственных колебаний (t << Т), то с достаточной степенью точности можно считать, что за это время t рамка практически не успевает выйти из положения равновесия. При этом из уравнения движения приближенно получим:

I = BSNit = BSNq (5)

Откуда

, (6)

где q – прошедший через рамку заряд, – угловая скорость рамки,

– постоянный коэффициент, определяемый конструкцией прибора.

Кинетическая энергия, приобретенная рамкой вследствие прохождения тока (без учета потерь) при ее максимальном отклонении, превращается в потенциальную энергию закрученного подвеса:

= , (7)

где am - максимальный угол первого отклонения.

Из уравнений (6) и (7) находим:

am (8)

Из соотношения (8) следует, что заряд, прошедший через рамку, пропорционален ее первому отклонению.

Отклонение рамки в баллистическом гальванометре пропорционально отклонению стрелки гальванометра, поэтому можно записать соотношение:

q = A×n , (9)

где n – число делений шкалы, на которое отклоняется стрелка гальванометра,

А - баллистическая постоянная гальванометра (Кулон/деление шкалы).

Значение постоянной А определяется экспериментально. Конденсатор известной емкости Сэт, заряженный до разности потенциалов U, разряжают через баллистический гальванометр. По значению n в соответствии с (9) и (1) вычисляют баллистическую постоянную:

(10)

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ:Экспериментальная установкасобирается по схеме, приведенной на рисунке. Пунктиром выделена монтажная панель. На ней закреплены кнопочные переключатели П, К и клеммы для подключения приборов. Исследуемый конденсатор С заряжается источником регулируемого напряжения (ИРН). Напряжение на конденсаторе измеряется вольтметром V. При нажатии на кнопку П происходит разряд конденсатора через гальванометр G. Фиксируется число делений при первом отклонении стрелки. После этого указатель совершает колебания. Для остановки необходимо замкнуть цепь гальванометра при прохождении указателя через нулевое положение шкалы кнопкой К. По измеренным значениям вычисляется емкость конденсатора:

C = (11)

ЗАДАНИЕ.

1. Ознакомиться со схемой подключения кнопок и клемм на монтажной панели, элементами управления источника напряжения.

2. Определить баллистическую постоянную гальванометра А. Для этого провести измерения с эталонным конденсатором известной емкости Сэ. Измерения отклонений стрелки гальванометра n произвести не менее 10 раз при различных напряжениях U. Результаты измерений занести в Таблицу 1. Рассчитать значения баллистической постоянной по формуле для каждого измерения и найти среднее значение Аср. Рассчитать погрешность измерения баллистической постоянной А.

3. Определить емкости двух различных конденсаторов, поочередно включая их в схему. Для этого измерить отклонения n при различных значениях U (не менее чем по пяти отсчетам). Результаты измерений занести в Таблицы 2 и 3.

4. Измерить емкость батареи из этих двух конденсаторов при их параллельном и последовательном соединениях. Результаты измерений занести в Таблицы 4 и 5.

5. Рассчитать средние значения емкостей С1, С2, Спосл. и Спар и случайные погрешности их измерений.

6. Оценить приборные погрешности измерения емкостей С1, С2, Спосл. и Спар, сравнить их со случайными погрешностями и записать окончательные результаты измерений.

7. Рассчитать значения емкостей батарей при параллельном Спар и последовательном Спосл соединении конденсаторов по соответствующим формулам (2,3).

8. Расчетные и экспериментальные значения емкостей занести для сравнения в Таблицу 6.

9. Сделать выводы.

Примечание: С целью уменьшения погрешности определения С напряжение подбирается таким, чтобы первое отклонение стрелки гальванометра составляло не менее 7-10 делений.

 

Значения баллистической постоянной гальванометра А. Таблица 1

U, В
n, дел
А, …

 

Емкость первого конденсатора. Таблица 2

№ /п	А, …	U, …	n,	Ci , …	DCi , …	C1 = < C> ± DC
Средн	XXXXX	XXXXX

 

Емкость второго конденсатора. Таблица 3

№п/п	А, …	U, …	n	Ci , …	DCi , …	C2 = < C> ± DC
Средн	XXXXX	XXXXX

 

Параллельное соединение конденсаторов. Таблица 4

№п/п	А, …	U, …	n	Ci , …	DCi ,..	Cпар = < C> ± DC
Средн	XXXXX	XXXXX

 

Последовательное соединение конденсаторов. Таблица 5

№п/п	А, …	U, …	n	Ci , …	DCi , …	Cпосл = < C> ± DC
Средн	XXXXX	XXXXX

 

Таблица 6

Теоретические значения	Экспериментальные значения
Спар = <C> ±DC = ………………………	Спар = <C>±DC = …………………….
Спосл = <C>±DC = …………………..	Спосл = <C>±DC = ………………………

 

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Что понимают под электрической емкостью? Что такое конденсатор?

2. В чем заключается принцип измерения емкостей баллистическим методом.

3. Покажите, из каких уравнений выводится выражение для баллистической постоянной гальванометра.

4. Опишите, как определяется баллистическая постоянная гальванометра в выполняемой Вами лабораторной работе.

5. Докажите формулу для расчета емкости последовательно соединенных конденсаторов.

6. Докажите формулу для расчета емкости параллельно соединенных конденсаторов.

 

ЛИТЕРАТУРА.

1. Трофимова Т.И. Курс физики. М.: Высш.шк., 1985., Гл.11, §§ 91-93.

2. Савельев И.В. Курс общей физики. Кн.2. Электричество и магнетизм. Волны. Оптика, М.:”Наука”, 1998, Гл.3, §§ 26, 27.

3. Практикум по общей физике. Под ред. проф. В.Ф.Ноздрева. М., «Просвещение», 1971, Гл.III, С.180.

ЛАБОРАТОРНАЯ РАБОТА № 6

 

Читайте также:

lektsia.com

Определение электроёмкости конденсатора

1. Цель работы: определение ёмкостей конденсаторов с помощью баллистического гальванометра.

 

Краткая теория

Взаимодействие зарядов, находящихся на расстоянии друг от друга, осуществляется через электрическое поле. Если в некоторой точке поля заряда q внесён малый положительный заряд , называемый «пробный», то на него, по закону Кулона, будет, действовать сила

. (1)

В этой формуле величина — электрическая постоянная (в «СИ» единицей измерения является фарада на метр — Ф/м), величина ε — относительная диэлектрическая проницаемость, характеризует электрические свойства среды, в которой взаимодействуют заряды, r — расстояние между зарядами. Отношение не зависит от величины пробного заряда и поэтому может служить характеристикой электростатического поля (т. е. поля, создаваемого неподвижными зарядами). Векторная величина, численно равная силе, действующей на единичный положительный заряд, называется напряженностью электрического поля.

. (2)

Из формулы (2), учтя выражение кулоновской силы, получим

. (3)

Как следует из формулы (2), в системе СИ единицей напряженности будет Н/Кл.

Электрическое поле весьма наглядно можно изобразить с помощью силовых линий (линии напряженности).

Силовой линией, электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля .

На рис. 18 изображены электрические поля положительного и отрицательного точечного заряда.

Условились силовые линии изображать с такой густотой, чтобы их число, приходящееся па перпендикулярную к ним единицу поверхности, было численно равно напряженности поля.

Число силовых линий, пронизывающих некоторую поверхность S, расположенную перпендикулярно к ним, называется потоком напряженности поля . Для количества силовых линий, пронизывающих произвольную поверхность

, (4)

где —проекция вектора на нормаль n к поверхности (рис. 19).

, (4*)

где — угол между вектором и нормалью к поверхности S. Если поле однородное и поверхность плоская, то

. (5)

Напряжённость электрического поля и характеризующая её густота силовых линий изменяются скачком при переходе через границу двух сред с различной диэлектрической проницаемостью (рис. 20). Это создает определённые затруднения при расчёте электрических полей, различных приборов и аппаратов (конденсаторы, кабели и др.). Поэтому вводят вспомогательный вектор

. (6)

Вектор носит название вектора электрического смещения (вектора индукции). Если подставить в формулу (6) выражение (3), то получим для поля точечного заряда

. (7)

Легко видеть, что электрическое смещение, в отличие от напряженности, не зависит от свойств среды (рис. 21). В системе СИ электрическое смещение измеряется в .

 

Большой практический интерес представляет теорема Остроградского-Гаусса. С её помощью можно очень просто определить напряженность полей, создаваемых заряженными телами различной формы. Теорема Остроградского-Гаусса формулируется следующим образом: поток вектора напряжённости электрического поля через замкнутую поверхность равен алгебраической сумме заключённых внутри неё зарядов, делённой на абсолютную диэлектрическую проницаемость, то есть

, (8)

где — заряды, заключённые внутри поверхности.

Рассмотрим два частных случая применения теоремы Остроградского-Гаусса.

1. Определим напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью.

Допустим, поверхностная плотность зарядов плоскости (т. е. заряд, приходящийся на единицу площади) равна . Силовые линии поля бесконечно заряженной плоскости перпендикулярны этой плоскости (рис. 22). Построим воображаемую цилиндрическую поверхность (гауссова поверхность), ось которой перпендикулярна плоскости. Плоскость делит цилиндр пополам. Поток вектора напряжённости проходит только через основания цилиндра, так как линии напряжённости параллельны боковой поверхности цилиндра. Поэтому суммарный поток вектора напряженности будет равен (S — площадь основания цилиндра).

По теореме Остроградского-Гаусса имеем:

(9)

или

. (10)

Учитывая, что , получим выражение для напряженности поля бесконечной равномерно заряженной плоскости в системе СИ:

. (11)

Таким образом, на любых расстояниях от плоскости напряжённость поля одинаковая по величине. Следовательно, электрическое поле плоскости является однородным.

2.Определим напряженность поля между двумя бесконечными параллельными разноимённо заряженными плоскостями. На рис. 23 поле положительно заряженной плоскости изображено сплошными линиями, отрицательно заряженной плоскости — прерывистыми. Напряжённость поля между двумя бесконечными параллельными плоскостями равна сумме напряжённостей полей, ими создаваемых:

. (12)

Слева и справа от плоскостей силовые линии направлены в противоположные стороны и поэтому в пространстве за плоскостями напряженность поля . Такой же вид имеет поле между параллельными плоскостями конечных размеров. Заметное отклонение поля от однородности имеется только вблизи краев пластин. Система из двух близко расположенных параллельных металлических пластин, разделенных диэлектриком, представляет собой простейший конденсатор. С помощью формулы (12) можно рассчитать напряженность поля внутри плоского конденсатора. Энергетической характеристикой электрического поля является потенциал. Потенциал численно равен работе, которую совершают силы электрического поля над единичным положительным зарядом при удалении его из данной точки поля в другую, где поле отсутствует (например, в бесконечность)

. (13)

Работа сил поля по перемещению заряда q из точки (1) в точку (2) поля может быть выражена через разность потенциалов:

. (14)

Согласно формуле (13), потенциал (электрическое напряжение U) в системе СИ измеряется в вольтах

.

Напряжение связано с напряженностью поля Е и расстоянием между пластинами соотношением

. (15)

Напряженность поля между пластинами в соответствии с (12) равна:

.

Учитывая, что поверхностная плотность зарядов пластины , можно записать:

, (16)

или

. (17)

Из этой формулы следует, что напряжение U, приложенное к пластинам, пропорционально заряду

. (18)

Коэффициент пропорциональности называется электроёмкостью (сокращённо — ёмкостью) пластин. Электроёмкость любого проводника (или системы проводников) численно равна отношению заряда, сообщённого проводнику, к потенциалу, до которого зарядился проводник:

. (19)

Из формулы (17) следует, что ёмкость плоского конденсатора в системе СИ

, (20)

где — площадь пластины (обкладки) конденсатора, — величина зазора между обкладками, — относительная диэлектрическая проницаемость вещества, заполняющего зазор.

Величина ёмкости плоского конденсатора, как следует, из формулы 20, определяется геометрией конденсатора (формой и размерами пластин и величиной зазора между ними), а также свойствами диэлектрика, находящегося между пластинами. Для получения больших ёмкостей применяют так называемые сложные конденсаторы, в которых пластины сделаны из алюминия, а диэлектриком являются листы провощенной бумаги.

Единицей измерения ёмкости в СИ является фарада (Ф)

.

На практике применяются более мелкие единицы: микрофарада (мкФ) и пикофарада (пФ)

.

Помимо ёмкости конденсатор характеризуется предельным напряжением . Подключение к пластинам конденсатора напряжения выше может вызвать его пробой, в результате чего диэлектрик разрушится и конденсатор выйдет из строя.

При включении в электрическую цепь нескольких конденсаторов применяют параллельное, последовательное и смешанное их соединения. При параллельном соединении (рис. 24) общая (эквивалентная) ёмкость равна сумме ёмкостей отдельных конденсаторов:

. (21)

При последовательном соединении (рис. 25) конденсаторов обратная величина общей ёмкости равна сумме обратных величин ёмкостей отдельных конденсаторов:

. (22)

В настоящее время изготавливаются конденсаторы с самыми различными диэлектриками различной формы. Кроме плоской, конденсаторы могут иметь цилиндрическую или сферическую формы. Кроме того, конденсаторы изготавливаются постоянной, переменной и полупеременной ёмкости (триммеры). Ёмкость переменных и полупеременных конденсаторов изменяется путём поворота одних пластин по отношению к другим. При этом изменяется площадь пластин, находящаяся в электрическом поле. В конденсаторах переменной и полупеременной ёмкости применяются обычно газообразные и жидкие диэлектрики.

Конденсаторы широко применяются в электрорадиотехнических устройствах. Конденсаторы переменной ёмкости используются для настройки контуров радиосхем передатчиков и приёмников.

Существуют различные методы измерения ёмкости конденсатора. Одним из них является определение ёмкости конденсатора баллистическим методом.

Ёмкость конденсатора связана с зарядом соотношения . Напряжение на конденсаторе определяется по вольтметру, подключенному к источнику, заряжающему конденсатор. Таким образом, для определения ёмкости конденсатора нужно измерить заряд, находящийся на пластинках конденсатора. Заряд конденсатора можно измерить с помощью зеркального баллистического гальванометра, работающего в баллистическом режиме.

Гальванометр — это прибор высокой чувствительности, который используется для измерения малых значений тока, напряжений и количества электричества. Наибольшее распространение получили гальванометры магнитоэлектрической системы.

Баллистический гальванометр представляет собой разновидность зеркального гальванометра (рис. 26). Измерительный механизм гальванометра состоит из подвешенной на вертикальной нити рамки 3, помещённой в поле постоянного магнита 1. К рамке прикреплён полый цилиндр 2 из мягкого железа, благодаря которому магнитное поле вблизи рамки делается радиально симметричным. Прямоугольная рамка 3 намотана из медной изолированной проволоки диаметром в несколько сотых миллиметра. По рамке пропускается измеряемый ток, который подводится через нить подвеса 4 из платиновой проволоки (диаметром в несколько микрон) и серебряный или золотой волосок 5 (толщиной в несколько микрон).

Рамка вместе с цилиндром может свободно поворачиваться в магнитном поле.

Прикрепленный к рамке цилиндр сильно увеличивает момент инерции и, следовательно, период колебания подвижной системы.

Если пропустить через рамку короткий импульс тока, то можно считать, что весь ток успевает пройти при неотклонённом положении. Рамка, однако, при этом получает толчок, в результате которого возникает её колебательное затухающее движение. Можно показать, что угол отброса рамки пропорционален количеству электричества, протекающему через баллистический гальванометр, если длительность импульса тока меньше одной десятой периода колебания подвижной системы. При этом можно принять

, (13)

где — баллистическая постоянная гальванометра.

Величина , обратная ,

(14)

называется баллистической чувствительностью гальванометра; она зависит от его конструкции и сопротивления внешней цепи гальванометра.

Из изложенного следует, что для получения достаточно точного измерения заряда конденсатора необходимо, чтобы гальванометр имел большой период колебаний (в десятки раз превышающий длительность импульса тока).

Гальванометр должен иметь настолько большой период колебаний, чтобы можно было успеть произвести отсчёт величины наибольшего отброса . С этой целью в баллистическом гальванометре подвижную часть делают с относительно большим моментом инерции. Увеличение момента инерции достигается увеличением массы подвижной части гальванометра, например, за счёт применения двух или четырёх грузиков 6.

Угол поворота рамки измеряется с помощью светового указателя с двукратным отражением луча. От лампы 7, имеющей оптическую систему и диафрагму, луч после отражения от зеркала 9 подвижной части попадает на шкалу 10 и даёт изображение светового пятна. Поворот подвижной части вызовет перемещение по шкале светового пятна («зайчика»). Таким образом, представляет собой угол поворота подвижной части (при первом её отклонении), измеряемый в делениях шкалы .

Значение баллистической постоянной можно определить, разряжая через баллистический гальванометр конденсатор известной ёмкости , заряженный до разности потенциалов U.

 

Описание установки

Для определения ёмкости конденсатора баллистическим методом, используется схема, изображенная на рис. 27.

На рисунке схемы G — баллистический гальванометр, С — исследуемый конденсатор. Когда переключатель П установлен в положение I, происходит зарядка конденсатора от батареи Е. Когда переключатель установлен в положение II, конденсатор разряжается через гальванометр G. Ключ К служит для резкого торможения подвижной части гальванометра, после прекращения импульса тока в рамке. Этот ключ замыкается только на короткое время в момент прохождения светового луча через среднее положение.

 

Порядок выполнения работы

 

Задание 1. Определение баллистической постоянной гальванометра

1. Включить в схему эталонный конденсатор , для чего присоединить его к клеммам переключателя П.

2. Пользуясь потенциометром Р, вольтметром и переключателем П, устанавливаемым в положение I, зарядить конденсатор до ЗВ.

3. Произвести разряд конденсатора на гальванометр, переключая ключ П из положения I в положение II.

4. Замер повторить пять раз при напряжениях: 2, 4, 5, 6, 7В. Результаты занести в табл. 1.

5. Найти баллистическую постоянную по формуле:

.

Таблица 1

 

6.Вычислите доверительный интервал по заданной доверительной вероятности :

.

7.Оценить границу абсолютной допустимой ошибки вольтметра и гальванометра .

8.Вычислить относительную приборную ошибку, допущенную при определении баллистической постоянной по формуле:

,

где берутся из табл. 1 и соответствуют случаю, когда , .

9.Вычислить абсолютную приборную погрешность баллистической постоянной:

.

10.Сравнить абсолютную приборную погрешность и доверительный интервал . Если они одного порядка, то ошибка измерения вычисляется по формуле:

.

Если они отличаются хотя бы на порядок, то берется наибольшая ошибка.

 

Задание 2. Определение ёмкости конденсатора

1.Включить в схему вместо эталонного конденсатора конденсатор неизвестной ёмкости . Измерения провести при 3-х напряжениях (3, 6 и 8 В).

2.То же самое проделать применительно ко второму конденсатору неизвестной ёмкости.

3.Воспользовавшись результатами расчёта баллистической постоянной из предыдущего эксперимента, вычислить ёмкости конденсаторов и по формуле для трёх напряжений. Определить среднее значение и .

4.Результаты эксперимента и расчёта занести в табл. 2.

Таблица 2

Задание 3. Определение ёмкости батареи из двух конденсаторов при параллельном и последовательном соединениях

1.Присоединить к клеммам переключателя П конденсаторы и сначала параллельно, а потом последовательно и произвести измерения. Если при параллельном соединении «зайчик» уходит за пределы шкалы, то надо уменьшить напряжение заряда конденсатора.

2.Результаты эксперимента по определению общей ёмкости батарей конденсаторов и занести в табл. 3.

3.Сравнить результаты опыта с результатами вычислений ёмкости батарей по формулам (21) и (22), при этом вместо и подставить их средние значения из табл. 2. Результаты вычислений сравнить с результатами эксперимента.

Таблица 3

Вид соединения в батарею	Номер опыта	U			Общая ёмкость батареи
из опыта	Из вычислений
Параллельно
Последовательно

 

Контрольные вопросы

1. Что называется напряжённостью электрического поля? В чём она измеряется и каков физический смысл этой величины?

2. Что такое потенциал поля? В чём он измеряется и каков его физический смысл?

3. Нарисуйте силовые линии точечных положительного и отрицательного зарядов.

4. Что называется поверхностной плотностью зарядов?

5. Что такое электроёмкость проводника? В чём она измеряется?

6. Что такое конденсатор? Каково его устройство? Какие бывают виды конденсаторов? Запишите формулы для ёмкостей известных вам конденсаторов.

7. Какое устройство имеют конденсаторы переменной ёмкости и где они применяются?

8. Изобразите схемы параллельного, последовательного и смешанного соединений проводников.

9. Как изменится ёмкость батареи конденсаторов, если один из них выйдет из строя в случае, когда конденсаторы соединены:

а) параллельно?

б) последовательно?

 

 

ЛАБОРАТОРНАЯ РАБОТА № 11

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Определение электрической емкости конденсатора — КиберПедия

Цель работы: изучить понятия о электрической емкости и емкостном сопротивле-

нии конденсатора, определить емкости отдельных конденсаторов и

емкость батареи последовательно и параллельно соединенных кон-

денсаторов.

Приборы и принадлежности: два конденсатора, амперметр, вольтметр, реостат, со-

единительные провода.

Теория работы

 

Конденсатором называется устройство, обладающее способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать и отдавать значительные по величине электрические заряды. Конденсаторы применяются в электрических цепях (сосредоточенные емкости), в импульсных генераторах напряжения, в электроэнергетике (компенсаторы реактивной мощности), в измерительных целях (измерительные конденсаторы и емкостные датчики).

Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком или вакуумом, толщина которого намного меньше линейных размеров проводников.

Основной характеристикой конденсатора является его емкость, под которой понимается электрическая емкость между обкладками конденсатора. Емкость конденсатора численно равна заряду q, приходящемуся на единицу разности потенциалов j1-j2 между обкладками:

. (1)

 

Единицей измерения емкости в системе СИ является фарад (Ф). Это емкость такого проводника, потенциал которого изменяется на один вольт при изменении заряда на нем в один кулон:

 

.

 

1 фарад – очень большая величина, поэтому в практике для измерения емкости применяются дольные единицы: микрофарад (1 мкФ = 10-6 Ф) и пикофарад(1 пФ =

= 10-12 Ф). На электрических схемах конденсатор условно обозначается буквой С.

Емкость конденсатора определяется его геометрией (формой и размерами обкладок, величиной зазора между ними), а также диэлектрическими свойствами среды, заполняющей пространство между обкладками. В зависимости от формы обкладок конденсаторы делятся на плоские (проводники в виде двух плоских параллельных пластин), цилиндрические (два коаксиальных цилиндра) и сферические (две концентрические сферы).

Емкость плоского конденсатора равна

 

, (2)

 

где e0 =8,85×10-12 - электрическая постоянная; e - относительная диэлектрическая проницаемость диэлектрика; S – площадь обкладок; d - расстояние между обкладками.

а)

При последовательном соединении n конденсаторов (рис. 1 а) их общая емкость определяется из выражения   . (3)

б) Рис. 1

При параллельном соединении n конденсаторов (рис. 1 б) их общая емкость равна   С= С1+ С2+…+ Сn. (4)   В формулах (3), (4) С1, С2,…, Сn - емкости отдельных конденсаторов. Если конденсатор включен в цепь постоянного тока, то в стационарном (установившемся) режиме ток в ветви с конденсатором отсутствует, поскольку диэлектрик между пластинами конденсатора не имеет свободных носителей заряда; конденсатор представляет собой разрыв цепи. При включении конденсатора в цепь переменного тока изменяется во времени заряд и потенциал обкладок конденсатора. Мгновенное значение тока в конден-

саторе равно скорости изменения заряда q на обкладках конденсатора:

 

(5)

 

При увеличении тока конденсатор заряжается, при уменьшении - разряжается. Цепь переменного тока конденсатор не разрывает: попеременно заряжаясь и разряжаясь, он обеспечивает движение носителей заряда (электрический ток) во внешней электрической цепи.

При увеличении тока растет заряд конденсатора, и в нем накапливается энергия Wэ, локализованная в электрическом поле Е,занимающем объем V между обкладками конденсатора:

, (6)

 

где U = j1-j2 – напряжение или разность потенциалов между обкладками конденсатора.

При уменьшении тока уменьшается заряд конденсатора, и накопленная энергия Wэ возвращается к источнику переменного тока.

Таким образом, в цепи переменного синусоидального тока конденсатор без потерь то потребляет энергию от источника, то отдает ее обратно источнику, т.е. за период не потребляет энергии тока, но определяет величину этого тока, оказывая сопротивление его протеканию. Такое сопротивление переменному току, при котором не потребляется энергия этого тока, называется реактивным. Для цепи с конденсатором, обладающей только емкостью (рис. 2 а), реактивное сопротивление является емкостным сопротивлением и равно

 

, (7)

 

где w = 2pf - круговая (циклическая) частота переменного синусоидального тока; f- частота переменного тока.

 

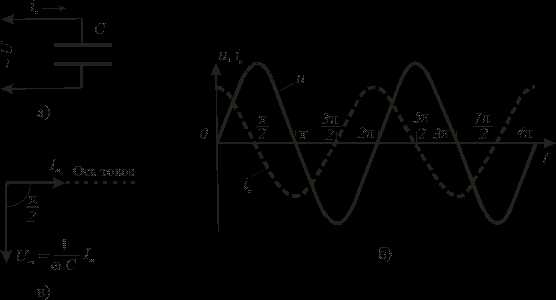
Рис. 2

 

Подключим конденсатор к источнику переменного напряжения, изменяющегося по синусоидальному закону

 

u=Umsin wt, (8)

 

где u - мгновенное значение напряжения в момент времени t; Um – максимальное (амплитудное) значение напряжения; wt - фаза.Через конденсатор потечет переменный ток этой же частоты w:

 

(9)

 

где амплитуда тока Im =CwUm. Таким образом, ток будет опережать напряжение на четверть периода (начальная фаза ).

На рис. 2 б показана волновая диаграмма, а на рис. 2 в - векторная диаграмма, иллюстрирующие опережение током напряжения по фазе на величину φ0= 900, вызываемое наличием в цепи переменного тока емкости С.

Под векторной диаграммой понимается диаграмма, изображающая совокупность векторов, построенная с соблюдением их взаимной ориентации по фазе. Длина каждого вектора равна амплитуде колебания, а направление вектора образует с некоторой осью (в нашем случае это горизонтальная ось – ось токов) угол, равный начальной фазе колебания.

В формулы (8), (9) входят максимальные значения тока Im и напряжения Um. Измерительные приборы, работающие в цепи переменного синусоидального тока, показывают действующие значения тока I и напряжения U, которые связаны с максимальными значениями Im и Um посредством формул

 

. (10)

 

Действующее значение переменного тока через конденсатор может быть определено с помощью закона Ома:

. (11)

С учетом (7) и (11) выражение для емкостного сопротивления конденсатора равно , откуда емкость конденсатора

. (12)

 

В Российской Федерации стандартная частота переменного синусоидального тока f = 50 Гц.

Порядок выполнения работы

 

I. Собрать электрическую цепь в соответствии со схемой, представленной на рис. 3, подключив конденсатор С1. Обозначения на рис. 3: SА - выключатель, RР - потенциометр, PA - амперметр, PV- вольтметр, C1, C2 - конденсаторы.

 

cyberpedia.su

---

• 
  Способы оказания первой помощи при поражении электрическим током
• 
  Как научиться варить полуавтоматом с нуля
• 
  Куда вносить показания счетчиков воды
• 
  Нет отопления в квартире
• 
  Легкая промышленность включает в себя
• 
  Выключатель трехклавишный подключить
• 
  Однофазный трансформатор устройство и принцип действия
• 
  Что нужно чтобы провести свет в гараж
• 
  Индукции магнитного поля формулы
• 
  Люстра с пультом управления светодиодная инструкция
• 
  2 группа по электробезопасности кому присваивается