Реферат на тему "Определение индукции магнитного поля и проверка формулы Ампера". Индукции магнитного поля формулы

Реферат на тему "Определение индукции магнитного поля и проверка формулы Ампера". Индукции магнитного поля формулы

Формула напряжённости магнитного поля

связь магнитного потока и ВМИ

Определение индукции магнитного поля и проверка формулы Ампера

Определение индукции магнитного поля земли

Определение индукции магнитного поля и проверка формулы Ампера

Индукция и напряженность магнитного поля. — КиберПедия

РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА Основные С ТОКОМ В МАГНИТНОМ ПОЛЕ. ФОРМУЛЫ ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ИНДУКТИВНОСТЬ

Формула напряжённости магнитного поля

связь магнитного потока и ВМИ

Определение индукции магнитного поля и проверка формулы Ампера

Определение индукции магнитного поля земли

Определение индукции магнитного поля и проверка формулы Ампера

Индукция и напряженность магнитного поля. — КиберПедия

РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА Основные С ТОКОМ В МАГНИТНОМ ПОЛЕ. ФОРМУЛЫ ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ИНДУКТИВНОСТЬ

Примеры решения задач по теме «Напряжённость магнитного поля»

Магнитное поле

Вектор магнитной индукции

Магнитный поток

Видео

Теоретическое введение

Примеры решения задач по теме «Напряжённость магнитного поля»

Магнитное поле

Вектор магнитной индукции

Магнитный поток

Видео

Теоретическое введение

Видеоматериалы

Актуальные темы

Рубрикатор

Пользователю

Доп.информация

Наглядное отображение линий магнитной индукции

Направление магнитной индукции

Модуль вектора

Наглядное отображение линий магнитной индукции

Направление магнитной индукции

Модуль вектора

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

ОПРЕДЕЛЕНИЕ

Напряжённость магнитного поля равна разности вектора магнитной индукции и вектора намагниченности.

Здесь – напряжённость магнитного поля, – магнитная индукция, – магнитная постоянная, — намагниченность.

Единица измерения напряжённости магнитного поля – А/м (ампер на метр).

Напряжённость – векторная величина, характеризующая интенсивность воздействия магнитного поля на намагниченную заряжённую частицу (пробный магнит) в конкретной точке. В векторной форме уравнение выглядит так:

ПРИМЕР 1

Задание	Найти напряжённость магнитного поля в точке, в которой магнитная индукция равна 9 Тл, а намагниченность 7 мА/м.
Решение	Переведём кА в А : мА = А. Подставим значения в формулу:
Ответ	Напряжённость магнитного поля равна ампер на метр.

ПРИМЕР 2

Задание

Катушка создаёт внутри себя однородное магнитное поле напряжённостью H. Вектор отличается от на угол в плоскости и в плоскости . Вектор отличается от на углы и соответственно. Найти значения Hв проекции на указанные плоскости. В данной системе координат вектор Hсовпадает с осью .

Решение

В векторном виде формула напряжённости поля выглядит так:

Если рассмотреть плоскость , то вектор Hбудет катетом прямоугольного треугольника, а вектор – гипотенузой. Угол вежду ними известен: . В плоскости тоже будет катетом, а – гипотенузой. Значит в обоих случаях:

Аналогичные рассуждения верны и для . Значит:

Ответ

Во всех областях электротехники, кроме электростатики, используется понятие о магнитном поле. Вектор магнитной индукции описывает силу и направление этого поля в определённом месте рядом с источником поля. Как и для всего в электротехнике, для расчета этого параметра используются соответствующие формулы. В этой статье рассказывается, как найти вектор магнитной индукции, как находить его направление и как найти модуль вектора магнитной индукции.

Силовые линии магнитного поля

Магниты известны людям много сотен лет. Ещё в Древней Греции использовали в качестве компаса намагниченную иголку. В 1820 году Ганс Эрстед обнаружил связь между магнетизмом и электромагнетизмом. Его опыты показали, что стрелка компаса, находящаяся возле проводника, поворачивается при прохождении по нему электрического тока так же, как и при приближении постоянного магнита. Это происходит потому, что при движении электрических зарядов всегда появляются электрический ток и магнитное поле. Параметры вектора магнитной индукции характеризуют магнитное поле в определённой точке, находящейся возле магнита.

Справка. Поле, все силовые линии которого являются замкнутыми, называется вихревым. Магнитное поле – это вихревое поле.

Для того чтобы наглядно увидеть линии индукции магнитного поля, есть два способа:

Использовать компас. При этом поле стрелки взаимодействует с магнитом или проводником с током. В точке, в которой измеряется это направление, она располагается по направлению вектора индукции. Северным считается то, в которое будет направлен конец стрелки, обозначенный «N». При движении компаса вокруг прибора её направление будет меняться вместе с изменением направления силовых линий;
Поместить провод или катушку под лист бумаги или стекло, а сверху насыпать железные опилки. Проводники можно также пропустить сквозь бумагу. При этом опилки расположатся вдоль силовых линий поля. Этот опыт демонстрирует также взаимодействие двух магнитов.

Все физические параметры делятся на две группы:

Скалярные. Это такие величины, которые не имеют направления: вес, объём, электрическое напряжение или ток;
Векторные. Это параметры, имеющие направление: скорость, ускорение или инерция.

Магнитная индукция – это векторная величина. Её направленность совпадает с касательной к линиям поля. Форма и направление линий индукции зависят от проводника.

В прямом проводнике поле имеет форму кругов, перпендикулярно которых проходит этот проводник, а его центр совпадает с ними. Чем ближе к центру, тем больше силовых линий проходит через точку пространства и сильнее поле. Его направление определяется по правилу правой руки.

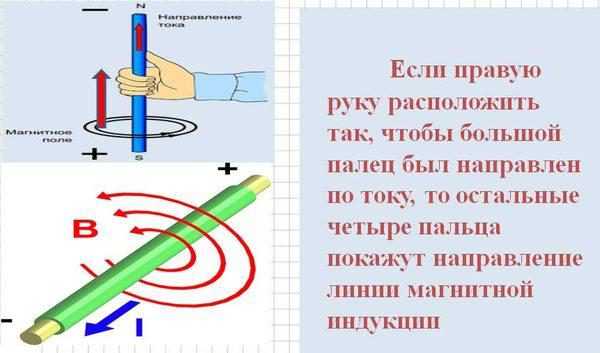
Правило правой руки

Если провод свернуть в кольцо, то поле приобретает форму тора (бублика). Если витков много, и длина превышает диаметр катушки, то внутри неё силовые линии идут равномерно и параллельно. Магнитные свойства этого прибора аналогичны постоянному магниту. Если обмотку намотать на сердечник, изготовленный из материала с высокой магнитопроницаемостью, то получится электромагнит, форма которого зависит от сердечника: плоский, квадратный или подковообразный. Направление магнитного поля, идущего через такие устройства, можно найти по правилу буравчика.

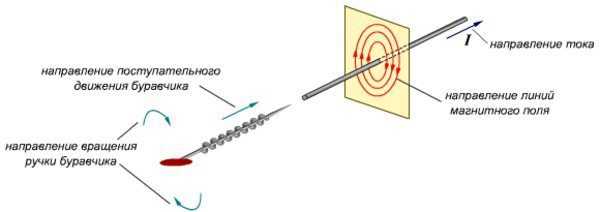
Правило буравчика

Вектор, кроме величины, имеет модуль, или размер, – это показатель, характеризующий численное значение параметра. Если сама магнитная индукция обозначается В, направленность – B→, то модуль обозначается |B|. Этот параметр зависит от тока и расстояния до проводника. Для определения модуля выражение имеет вид |В|=k*(I/r), где:

k – коэффициент. Он зависит от конкретных условий. В катушке с магнитопроницаемым сердечником и большим количеством витков коэффициент больше, чем в прямом отрезке провода;
I – сила тока. Чем она больше, тем сильнее создаваемое им поле и больше величина вектора;
r – расстояние от места измерения до катушки или проводника. Чем ближе к магниту, тем плотнее расположены силовые линии, и больше модуль.

Рядом расположенные провода или катушки с электротоком влияют друг на друга. Сила этого взаимодействия находится по формуле:

F=|B|*I*l, где l – длина проводов.

Если эту формулу преобразовать по законам алгебры, чтобы определить вектор магнитной индукции, она примет следующий вид:

|B|=(F/(I*l).

С её помощью можно рассчитать величину вектора, зная силу взаимного влияния, силу тока и длину проводов.

Интересно. Это взаимодействие можно увидеть при изменении силы сварочного тока в проходящих рядом кабелях.

Параметр, количественно характеризующий уровень магнитного поля, проходящего через контур с протекающим по нему электрическим током или другую площадь, называется магнитный поток. Это скалярный параметр. Он зависит от индукции «В», площади поверхности «S» и «cos α» – косинуса угла, с которым линии магнитной индукции пересекают поверхность. Магнитный поток и вектор магнитной индукции связаны формулой:

Ф=|B|*S*cos α,

или, если преобразовать это выражение, получается:

|B|=Ф/(S*cos α), где S – площадь, через которую проходит поток в сантиметрах.

Следовательно, величина магнитного потока, проходящего перпендикулярно через 1 см2, количественно равна модулю магнитной индукции.

Интересно. Таким образом, в электродвигателе постоянного тока максимальное влияние обмотка возбуждения оказывает в положении якоря, при котором его обмотки параллельны.

Знание того, как рассчитывается направление магнитного поля, и как определяется модуль вектора магнитной индукции, а также формул, используемых при расчетах, необходимо при проектировании электродвигателей, а также во многих других областях электротехники.

Оцените статью:

elquanta.ru

Определение индукции магнитного поля и исследование формулы Ампера Введение В последнее время физики вновь обратились к необходимости использования различных экспериментальных работ для более углубленного и осмысленного изучения физики. Данная экспериментальная работа не представлена в учебниках, как лабораторная, поэтому мы предлагаем ее учителям для использования в лабораторном практикуме и для более углубленного изучения теории по теме «Действие магнитного поля на проводник с током. Сила Ампера». Целью данной работы является определение индукции магнитного поля подковообразного магнита, действие данного поля на проводник с током, а также исследование прямой пропорциональной зависимости силы Ампера от длины проводника, силы тока в цепи и индукции магнитного поля. Главной задачей данной исследовательской работы является изготовление установки для проведения всех измерений по данной теме, а также разработка методического пособия в помощь для учителей и учащихся, которые заинтересуются углубленным изучением данной темы. Теория по данной теме основывается на изучении учебников под редакцией Г.С. Ландсберга «Элементарный учебник физики. т. 2», Б.И. Спасского «Хрестоматия по физике 8–10», учебника «Физика 10» авторов Г.Я. Мякишева, Б.Б. Буховцева, учебник по физике Л. Эллиота, У. Уилкокса, а также статьи автора И.И. Гейнбихнера в журнале «Физика в школе». Так как важнейшим применением силы Ампера является ее использование в электрических двигателях, то данная работа позволяет учащимся познать их принцип действия, а в будущем, возможно, подтолкнет на создание более мощных электрических приборов.

1. Магнитное поле Движущиеся заряды образуют электрический ток. Следовательно, магнитное поле – это поле, создаваемое электрическим током. Оно осуществляет взаимодействие электрических токов. Между неподвижными электрическими зарядами действуют силы, определяемые законом Кулона. Согласно теории близкодействия это взаимодействие осуществляется так: каждый из зарядов создает электрическое поле, которое действует на другой заряд, и наоборот. Однако между электрическими зарядами могут существовать силы и иной природы. Их можно обнаружить с помощью следующего опыта. Возьмем два гибких проводника, укрепим их вертикально, а затем присоединим нижними концами к полюсам источника тока. Притяжения или отталкивания проводников при этом не обнаружится. Но если другие концы проводников замкнуть проволокой так, чтобы в проводниках возникли токи противоположного направления, то проводники начнут отталкиваться друг от друга. В случае токов одного направления проводники притягиваются Взаимодействия между проводниками с током, т.е. взаимодействия между движущимися электрическими зарядами, называют магнитными. Силы, с которыми проводники с током действуют друг на друга, называют магнитными силами. Согласно теории близкодействия ток в одном из проводников не может непосредственно действовать на ток в другом проводнике. Подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле, в пространстве, окружающем токи, возникает поле, называемое магнитным. Электрический ток в одном из проводников создает вокруг себя магнитное поле, которое действует на ток во втором проводнике. А поле, созданное электрическим током второго проводника, действует на первый. Магнитное поле представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами. Перечислим основные свойства магнитного поля, устанавливаемые экспериментально: 1. Магнитное поле порождается электрическим током. 2. Магнитное поле обнаруживается по действию на электрический ток. Экспериментальным доказательством реальности магнитного поля, как и реальности электрического поля, является факт существования электромагнитных волн 1.1 Замкнутый контур с током в магнитном поле Для изучения магнитного поля можно взять замкнутый контур малых размеров. Например, можно взять маленькую плоскую проволочную рамку произвольной формы. Подводящие ток проводники нужно расположить близко друг к другу или сплести вместе. Тогда результирующая сила, действующая со стороны магнитного поля на эти проводники, будет равна нулю. Выяснить характер действия магнитного поля на контур с током можно с помощью следующего опыта. Подвесим на тонких гибких проводниках, сплетенных вместе, маленькую плоскую рамку, состоящую из нескольких витков проволоки. На расстоянии, значительно большем размеров рамки, вертикально расположим провод. При пропускании электрического тока через провод и рамку рамка поворачивается и располагается так, что провод оказывается в плоскости рамки. При изменении направления тока в проводе рамка повернется на 180°. Магнитное поле создается не только электрическим токе но и постоянными магнитами. Если мы подвесим на гибких проводах рамку с током между полюсами магнита, то рамка будет поворачиваться до тех пор, пока плоскость ее не установится перпендикулярно к линии, соединяющей полюсы магнита. Таким образом, магнитное поле оказывает на рамку с ток ориентирующее действие. 1.2 Вектор магнитной индукции Величина, характеризующая магнитное поле количественно называется вектором магнитной индукции и обозначают Ориентирующее действие магнитного поля на магнитную стрелку или рамку с током можно использовать для определения направления вектора магнитной индукции. За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле. Это направление совпадает с направлением положительной нормали к замкнутому контуру с током. рис. 4 Положительная нормаль направлена в ту сторону, куда перемещается буравчик, если вращать его по направлению тока в рамке. Располагая рамкой с током или магнитной стрелкой, можно определить направление вектора магнитной индукции в любой точке поля. В магнитном поле прямолинейного проводника с током магнитная стрелка в каждой точке устанавливается по касательной к окружности. Плоскость окружности перпендикулярна проводу, а центр ее лежит на оси провода. Направление вектора магнитной индукции устанавливают с помощью правила буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции. 1.3 Линии магнитной индукции Наглядную картину магнитного поля можно получить, если построить линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор в данной точке поля. Для прямолинейного проводника с током линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной этому проводнику с током. Центр окружностей находится на оси проводника. Стрелки на линиях указывают, в какую сторону направлен вектор магнитной индукции, касательный к данной линии. Для катушки с током картина линий магнитной индукции, построенная с помощью магнитных стрелок или малых контуров с током, показана на рис. 6. Если длина соленоида много больше его диаметра, то магнитное поле внутри! соленоида можно считать однородным. Линии магнитной индукции такого поля параллельны. Картину линий магнитной индукции можно сделать видимой, воспользовавшись мелкими железными опилками. В магнитном поле каждый кусочек железа, насыпанный на лист картона, намагничивается и ведет себя как маленькая магнитная стрелка. Наличие большого количестве таких стрелок позволяет в большее числе точек определить направление магнитного поля и, следовательно более точно выяснить расположение линий магнитной индукции. Важная особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Магнитное поле – вихревое поле. Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобных электрическим в природе нет. 2. Сила Ампера Магнитное поле действует на все участки проводника с током. Зная силу, действующую на каждый малый участок проводника, можно вычислить силу, действующую на весь замкнутый проводник в целом. Закон, определяющий силу, действующую на отдельный участок проводника, был установлен в 1820 г. А. Ампером. Так как создать обособленный элемент тока нельзя, то Ампер проводил опыты с замкнутыми проводниками. Меняя форму проводников и их расположение, Ампер сумел установить выражение для силы, действующей на отдельный элемент тока. 2.1 Биография и научная деятельность Андре Мари Ампера Андре Мари Ампер – французский физик и математик. Ампер родился в г. Лионе. Его отец, хорошо образованный человек, был коммерсантом и впоследствии Королевским прокуром г. Лиона. В раннем возрасте у Ампера проявились любовь к чтению, математические способности, стремление к разносторонним знаниям. Под руководством отца он получил так называемое домашнее образование. Юный Ампер самостоятельно изучал книги по математике, сочинения, по ботанике, занимался физикой. Он рано проникся любовью к естественным наукам и философии. Важнейшим источником знаний для него была «Энциклопедия», издававшаяся под редакцией знаменитых французских просветителей Д. Дидро и Ж. Даламбера. Амперу было 14 лет, когда он уже прочитал все 20 томов «Энциклопедии». Трудовую деятельность Ампер начал в качестве домашнего учителя: он стал давать частные уроки математики, физики, химии. Уроки Ампера имели успех. В 1801 г. он был принят на должность учителя физики и химии в Центральную школу в Бурк-ан-Брес. Первые труды Ампера по математике получают высокую оценку Даламбера и Лапласа – известных французских ученых того времени. В 1805 г. Ампер занимает место преподавателя математики в одном из лучших учебных заведений Франции – Политехнической школе в Париже. В 1814 г. Ампера избирают членом Парижской академии наук. В 1824 г. после 20 лет работы в Политехнической школе Ампер занимает должность профессора физики Нормальной школы в Париже. Научные работы Ампера до 1820 г. относятся преимущественно к математике и химии. Известие об опытах Эрстеда чрезвычайно заинтересовало Ампера. Оно натолкнуло его на мысль о том, что магнитные взаимодействия сводятся к взаимодействию электрических токов. 18 сентября 1820 г. он выступил на заседании Парижской академии наук с первым и 25 сентября – со вторым докладами о результатах проведенных им исследований электромагнитных явлений. В протоколе Академии наук о заседании 25 сентября записано: «Я придал большое развитие этой теории и известил о новом факте притяжения и отталкивания двух электрических токов без участия какого-либо магнита, а также о факте, который я наблюдал со спиралеобразными проводниками. Я повторил эти опыты во время этого заседания». Таким образом, Ампер открыл механическое взаимодействие токов. Далее он ставит перед собой задачу – установить закон, которому подчиняется это явление. Эта нелегкая задача была им решена. На основании гипотезы о существовании молекулярных токов Ампер построил первую теорию магнетизма. Преподавательская работа требовала от Ампера большой затраты времени. Ампер в одном из своих писем сообщал: «Я принужден бодрствовать глубокой ночью… Будучи нагружен чтением двух курсов лекций, я тем не менее не хочу полностью забросить мои работы о вольтаических проводниках и магнитах. Я располагаю считанными минутами». Несмотря на такую загруженность, Ампер подготовил и издал в 1826 г. свой основной труд – «Теория электродинамических явлений, выведенная исключительно из опыта». 2.2 Модуль вектора магнитной индукции Свободно подвешенный горизонтально проводник находится в поле постоянного подковообразного магнита. Поле магнита сосредоточено в основном между его полюсами, поэтому магнитная сила действует практически только на часть проводника длиной , расположенную непосредственно между полюсами. Сила измеряется с помощью специальных весов, связанных с проводником двумя стерженьками. Она направлена горизонтально перпендикулярно проводнику и линиям магнитной индукции. Увеличивая силу тока в 2 раза, можно заметить, что и действующая на проводник сила также увеличивается в 2 раза. Прибавив еще один магнит, в 2 раза увеличив размеры области, где существует магнитное поле, и тем самым в 2 раза увеличив длину части проводника, на которую действует магнитное поле. Сила при этом также увеличивается в 2 раза. И наконец, сила Ампера зависит от угла, образованного вектором В с проводником. В этом можно убедиться, меняя наклон подставки, на которой находятся магниты, так, чтобы изменялся угол между проводником и линиями магнитной индукции. Сила достигает максимального значения Fт, когда магнитная индукция перпендикулярна проводнику. Следовательно, максимальная сила, действующая на участок проводника длиной , по которому идет ток, прямо пропорциональна произведению силы тока I на длину участка : .

Увеличивая силу тока в 2 раза, можно заметить, что и действующая на проводник сила также увеличивается в 2 раза. Прибавив еще один магнит, мы в 2 раза увеличим размеры области, где существует магнитное поле, и тем самым в 2 раза увеличим длину части проводника, на которую действует магнитное поле. Сила при этом также увеличивается в 2 раза. И наконец, сила Ампера зависит о^ угла, образованного вектором В с проводником. В этом можно убедиться, меняя наклон подставки, на которой находятся магниты, так, чтобы изменялся угол между проводником и линиями магнитной индукции. Сила достигает максимального значения Рт, когда магнитная индукция перпендикулярна проводнику. Итак, максимальная сила, действующая на участок проводника длиной А/, по которому идет ток, прямо пропорциональна произведению силы тока / на длину участка Д/: /7т/Л/.

Модулем вектора магнитной индукции назовем отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка: Магнитное поле полностью характеризуется вектором магнитной индукции В. В каждой точке магнитного поля могут быть определены направление вектора магнитной индукции и его модуль с помощью измерения силы, действующей на участок проводника с током. 2.3 Модуль силы Ампера Пусть вектор магнитной индукции В составляет угол с направлением отрезка проводника с током. Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает никакого действия на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора В, перпендикулярной проводнику, т.е. от , и не зависит от параллельной составляющей вектора В, направленной вдоль проводника. Максимальная сила Ампера равна: ей соответствует . При произвольном значении угла сила пропорциональна не , а составляющей. Поэтому выражение для модуля силы F, действующей на малый отрезок проводника , по которому течет ток I, со стороны магнитного поля с индукцией , составляющей с элементом тока угол , имеет вид: Это выражение называют законом Ампера. Сила Ампера равна произведению вектора магнитной индукции на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника. 2.4 Направление силы Ампера В рассмотренном выше опыте вектор перпендикулярен элементу тока и вектору . Его направление определяется правилом левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции В входила в ладонь а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на отрезок проводника За единицу магнитной индукции можно принять магнитную индукцию однородного поля, в котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила Fm=1 Н. Единица магнитной индукции получила название тесла в честь югославского ученого-электротехника Н. Тесла. Опираясь на измерение силы, действующей со стороны магнитного поля на участок проводника с током, можно определить модуль вектора магнитной индукции.

3. Экспериментальное определение индукции магнитного поля и исследование силы Ампера Опытный закон Ампера устанавливает зависимость величины силы, действующей на прямолинейный участок проводника с током, помещенный в магнитное поле, от основной характеристики магнитного поля – вектора индукции магнитного поля: где l – длина активной части прямолинейного участка проводника, по которому протекает ток силой I, В-численное значение вектора индукции магнитного поля в месте расположения проводника, – угол между направлением оси проводника и направлением вектора, Если проводник расположить так, чтобы = 90°, то Таким образом, измерив действующую силу в ньютонах, величину тока в амперах и длину активной части проводника в метрах, легко определить величину индукции магнитного поля. В данной экспериментальной работе необходимо определить индукцию магнитного поля В между полюсами различных подковообразных магнитов, а также экспериментально проверить прямую пропорциональную зависимость силы F от величины тока, длины активной части проводника и индукции магнитного поля: Оставляя поочередно две величины, входящие в формулу, постоянными, можно установить зависимость силы, с которой магнитное поле действует на проводник с током, от третьей величины. Поскольку в формулу входят три величины, от которых зависит величина силы, то и нужно провести три серии измерений. 3.1. Описание и принцип действия установки Для работ используется следующее оборудование: электродинамическая рамка, штатив с принадлежностями, лабораторные весы с разновесками, лабораторные амперметр и реостат, источник постоянного напряжения на 4–6 В, два или три подковообразных магнита. Собирают установку как показано на рисунке 13, а также на фотографиях в приложении №1 и уравновешивают весы. Самодельную рамку с отводами включают в цепь по схеме рисунка 14. Магнит для устойчивости устанавливают либо на немагнитной коробке, соответствующего размера, либо на специальной подставке из дерева. Все применяемые в работах магниты целесообразно предварительно перенумеровать несмываемой краской. На проводник с током, помещенный в магнитное постоянного подковообразного магнита поле действует сила Ампера. Следовательно, замыкая электрическую цепь, равновесие весов нарушается за счет действия силы Ампера со стороны магнитного поля. Уравновешивая весы с помощью разновесов, можно определить значение силы тяжести, а следовательно и силы Ампера. Зная длину активной части проводника, силу тока в цепи, можно вычислить индукцию магнитного поля данного подковообразного магнита.

При изменении силы тока, а также длины проводника, сила Ампера также будет изменяться. Эти свойства и использовались в ходе данной исследовательской работы. 3.2 Этапы и результаты проведения работы Для измерений были взяты 3 магнита: два одинаковой длины в поперечнике и один в два раза уже. Выполняют серии измерений с магнитом №1 при включении рамки на 15 витков. Указанные измерения проводят для различных токов: 0,18А, 0,2 А, 0,3 А, 0,4 А и 0,5 А. Такие же измерения выполняют с магнитом №2 и №3. Затем измерения проводят с двумя магнитами №2 и №3, а также с магнитами №1 и №2, скрепленными между собой одинаковыми полюсами. Все результаты заносим в таблицу. Для каждого случая измерений вычисляем значение силы Ампера, а также индукции магнитного поля каждого подковообразного магнита с вычислением значений абсолютной и относительной погрешности. По данным результатам строим графики зависимости силы Ампера от силы приложенного тока и от длины проводника. По полученным графикам убеждаемся в прямой зависимости данных величин и в выполнении закона Ампера. В приложении №6 представлена разработка лабораторной работы по данной теме.

Заключение В результате изучения и исследования данной темы можно сделать вывод о том, что цели и задачи, поставленные в начале данной работы выполнены. Главной задачей данной исследовательской работы явилось изготовление установки для проведения всех измерений по данной теме. Особых трудностей это не представляет, так как оборудование для изготовления описанной установки есть в любом кабинете физики. Целью данной работы являлось определение индукции магнитного поля подковообразного магнита, действие данного поля на проводник с током, а также исследование прямой пропорциональной зависимости силы Ампера от длины проводника, силы тока в цепи и индукции магнитного поля. Для всех трех магнитов, а также для их комбинаций была определена индукция магнитного поля. В результате проведенных вычислений оказалось, что все магниты имеют одинаковую магнитную индукцию, поэтому исследовать зависимость силы Ампера от индукции магнитного тока не удалось. Однако прямая зависимость силы Ампера от длины проводника и силы тока четко просматривается и представляется на графиках. Также была разработана лабораторная работа по данной теме, которую учителя могут предложить учащимся на лабораторном практикуме для более углубленного изучения темы «Действие магнитного поля на проводник с током. Сила Ампера»

Список литературы 1. Г.Я. Мякишев, Б.Б. Буховцев. Физика 10. М.: Просвещение, 1998. 2. Л. Эллиот, У. Уилкокс. Физика. М.: Наука, 1975. 3. Хрестоматия по физике 8–10. под редакцией Б.И. Спасского. М.: Просвещение, 1987. 4. Элементарный учебник физики. т. 2. под редакцией Г.С. Ландсберга. М.: Наука, 1972. 5. И.И. Гейнбихнер.: Определение индукции магнитного поля. – «Физика в школе», 1972, №1.

www.coolreferat.com

Цель работы: определить горизонтальную составляющую индукции магнитного поля Земли.

Оборудование: тангенс–гальванометр, источник тока, переключатель, амперметр.

Магнитное поле – это форма материи, которая обнаруживает себя действием на магниты, на проводники с током, на движущиеся электрические заряды, на элементарные частицы, обладающие магнитным моментом. И наоборот, источником магнитного поля могут быть постоянные магниты, проводники с электрическим током, движущиеся заряды.

Силовой характеристикой магнитного поля является вектор магнитной индукции В. По определению, индукция магнитного поля равна отношению вращающего момента сил, действующего на магнитную стрелку или рамку с током, к их магнитному моменту: 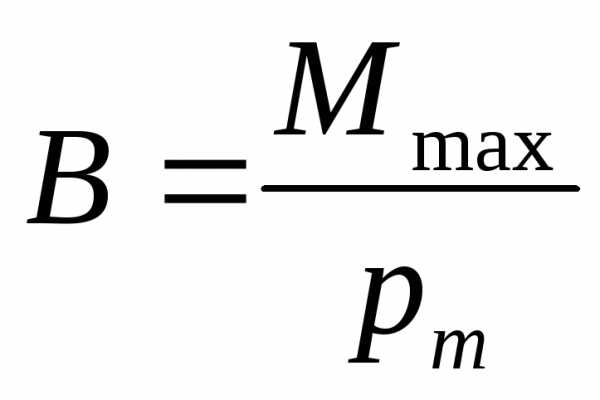; либо, согласно закону Ампера, как отношение максимальной силы, действующая на проводник, к силе тока и длине проводника:.

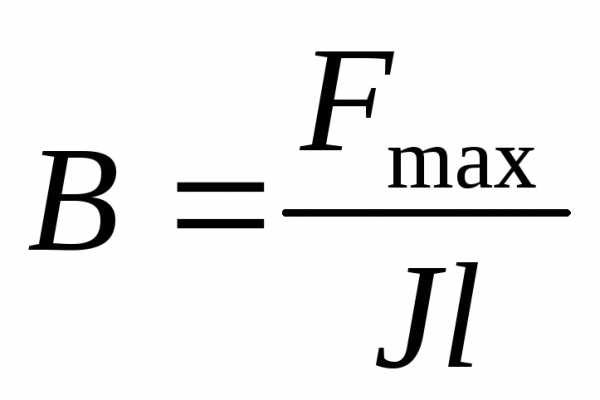Магнитное поле изображают с помощью силовых линий. Это линия, касательная к которой совпадает с вектором индукции. Силовые линии всегда замкнутые, что обусловлено тем, что в природе в отличие от электрических, магнитные заряды отсутствуют.

Теоретический расчёт индукции магнитного поля проводников любой формы основан на применении принципа суперпозиции и закона Био – Савара – Лапласа для элемента проводника длиной dl, по которому течёт ток силой J:

. (2)

Здесь  – относительная магнитная проницаемость среды, – магнитная постоянная,r – радиус-вектор, проведенный из элемента dl проводника в точку наблюдения,  – угол между элементом dl и радиус-вектором r (рис.1).

Направление вектораdB можно определить правилом буравчика. Если вкручивать буравчик в направлении тока в проводнике, то направление движения конца ручки буравчика в точке наблюдения покажет направление вектора индукции магнитного поля (рис. 1).

Определим, используя закон Био – Савара – Лапласа, индукцию магнитного поля в центре витка радиуса R, с током J (рис. 2). Выберем элемент витка малой длины dl. Вектор dl направлен по касательной к витку в направлении тока, sin α = 1. Вектор индукции элемента витка dВ, по правилу буравчика, направлен по оси витка вверх. Так же будут направлены векторы индукции других элементов. То есть индукция витка равна сумме индукций элементов, то есть интегралу:

. (3)

Магнитное поле Земли, по одной из гипотез, обусловлено электрическими токами при конвективном течении магмы, которая приобретает заряд вследствие трения. Силовые линии магнитного поля выходят из северного магнитного полюса, расположенного в Антарктиде, и входят в южный магнитный полюс в Арктике. Вблизи поверхности Земли в северном полушарии силовые линии идут наклонно. Вектор индукции магнитного поля можно разложить на две составляющие: вертикальную и горизонтальную. Магнитная стрелка, которая может вращаться только в горизонтальной плоскости, устанавливается вдоль горизонтальной составляющей индукции поля, северным концом на Север.

Одним из методов экспериментального измерения индукции магнитного поля Земли является метод сравнения его с известной индукцией магнитного поля катушки с током. Катушка представляет собой несколько витков проволоки, в центре которых расположен компас. Такой прибор называетсятангенс–гальванометром (рис. 3). Если плоскость витков совпадает с плоскостью магнитного меридиана Земли, то магнитная стрелка будет расположена в плоскости катушки. Если включить электрический ток в катушке, то появится еще магнитное поле катушки. Индукция магнитного поля катушки Вкат перпендикулярна плоскости витков, значит, перпендикулярна горизонтальной составляющей индукции магнитного поля Земли. Магнитная стрелка повернется к направлению результирующей индукции обоих полей на некоторый угол . Тангенс угла поворота равен отношению катетов треугольника векторов:

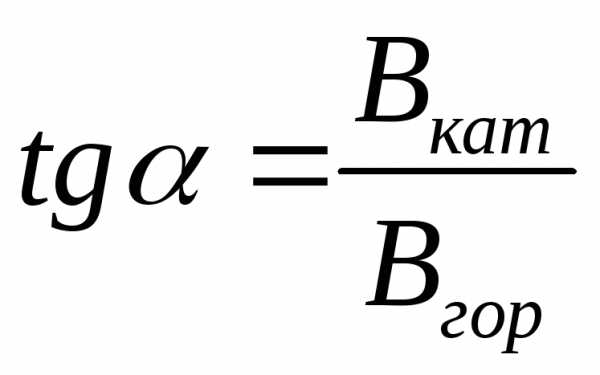. (4)

Так как индукцию магнитного поля катушки можно рассчитать по формуле (3), умножив ее на число витков, то горизонтальную составляющую магнитного поля Земли можно определить по формуле

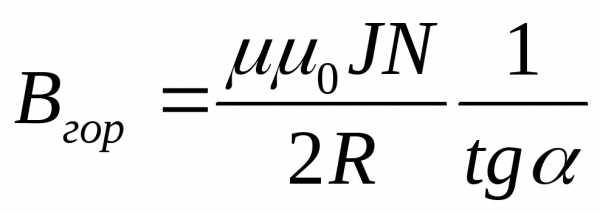. (5)

В лабораторной установке катушка подключаются к источнику постоянного напряжения БП. Сила тока регулируется реостатом R и измеряется амперметром. Направление тока изменяется ключом. В центре катушки установлен компас. Угол отклонения стрелки измеряется по шкале компаса.

ВЫПОЛНЕНИЕ РАБОТЫ

1. Установить катушку тангенс-гальванометра в плоскости магнитного меридиана, то есть плоскость витков должна быть вертикальной и совпадать с направлением на Север. При этом северный конец стрелки компаса должен показывать 0о и 360о по шкале.

2. Сосчитать число витков. Измерить радиус витков. Результаты записать в табл. 1.

Таблица 1

Число витков N
Радиус витков R, м

3. Включить блок питания в сеть 220 В. С помощью реостата установить силу тока 0,2 А.

Измерить угол отклонения 1 магнитной стрелки по шкале компаса. Изменить с помощью ключа направление тока и измерить угол отклонения 2. Если стрелка отклоняется по часовой стрелки, то угол поворота определять как разность между 3600 и показанием. Результаты записать в табл. 2.

4. Повторить измерения не менее 5 раз, изменяя силу тока в интервале 0,2…1,0 А. Результаты записать в табл. 2.

Выключить установку.

5. Произвести расчеты. Определить в каждом опыте среднее значение угла отклонения стрелки  = (1+2)/2 и тангенсы средних углов. Записать в табл. 2.

6. Определить в каждом опыте горизонтальную составляющую индукции магнитного поля по формуле (5). Результаты записать в табл. 2. Определить их среднее значение Вгор.

Таблица 2

7. Оценить случайную погрешность измерения индукции по формуле

. (6)

8. Записать результат: Вгор = Вгор  ВгорР = … Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение магнитного поля, индукции магнитного поля. Как изображают магнитное поле с помощью силовых линий?

2. Запишите закон Био – Савара – Лапласа. Объясните смысл закона. Объясните применение правила буравчика.

3. Выведите формулу для индукции магнитного поля в центре витка, применяя закон Био – Савара – Лапласа.

4. Объясните природу и распределение магнитного поля Земли.

5. Выведите расчетную формулу для определения горизонтальной составляющей индукции магнитного поля Земли с помощью тангенс–гальванометра.

6. Объясните назначение элементов электрической схемы лабораторной установки.

Работа 27

studfiles.net

www.referatnatemu.com

Магнитная индукция-векторная физическая величина, характеризующая магнитное поле.Вектор магнитной индукции всегда направлен по касательной к магнитной линии

Расчетная формула:

Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током

B - магнитная индукцияμ - относительная магнитная проницаемостьμ0 - магнитная постояннаяI - сила тока r - расстояние до проводника

Магнитная индукция поля в центре кругового тока (витка)

B - магнитная индукцияμ - относительная магнитная проницаемостьμ0 - магнитная постояннаяI - сила тока R - радиус

Напряженностью магнитного поля называют векторную величину , характеризующую магнитное поле и определяемую следующим образом:,

Напряжённость магнитного поля: бесконечной прямой провод

H - напряжённость магнитного поля I - сила тока r - расстояние до проводника

Напряжённость магнитного поля в центре витка

H - напряжённость магнитного поляI - сила тока R - радиус

Закон Био-Савара-Лапласа.

Закон БиоСавара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.

Формулировка

Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме, —точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)

Направление перпендикулярно и , то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление , еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора определяется выражением (в системе СИ)

Векторный потенциал даётся интегралом (в системе СИ)

2.9.

Поток индукции магнитного поля.

Магнитный поток (поток линий магнитной индукции) через контур численно равен произведению модуля вектора магнитной индукции на площадь, ограниченную контуром, и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной этим контуром.

Формула работы силы Ампера при движении прямого проводника с постоянным током в однородном магнитном поле.

Таким образом, работа силы Ампера может быть выражена через силу тока в перемещаемом проводнике и изменение магнитного потока через контур, в который включен этот проводник:

Индуктивность контура.

Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.Также индуктивность можно рассчитать по формуле:

где Ф - магнитный поток через контур, I - сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Энергия магнитного поля.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.

2.10.

Электромагнитная индукция.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменениимагнитного потока, проходящего через него.

cyberpedia.su

1. Работа перемещения замкнутого контура с током в магнитном поле А= I∆Ф,

где ∆Ф – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре.

2. Основной закон электромагнитной индукции (закон Фарадея–Максвелла)

еi= −N dt= − dt,

где ei– электродвижущая сила индукции; N – число витков контура; y – потокосцепление. Частные случаи применения основного закона электромагнитной индукции:

разность потенциалов U на концах проводника длиной l, движущегося со скоростью v в однородном магнитном поле,

U = Blv×sin a,

где a – угол между направлениями векторов скорости v и магнитной индукции В; электродвижущая сила

индукции i, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью w в однородном магнитном поле с индукцией В

ei= BNSw×sinwt,

где wt – мгновенное значение угла между вектором rи вектором нормали rк плоскости рамки. 3. Количество электричества Q, протекающего в контуре,

Q = ∆y,

где R – сопротивление контура; ∆y – изменение потокосцепления.

4. Электродвижущая сила самоиндукции i, возникающая в замкнутом контуре при изменении силы тока в нем,

ei= −L dI, или еi = −L ∆t,

где L – индуктивность контура.

5. Потокосцепление контура

y = L×I,

где L – индуктивность контура.

6. Индуктивность соленоида (тороида):

где V – объем соленоида.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

L =µ0µn2V,

Основные

ФОРМУЛЫ

1. Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L , опреде-ляется формулой

W = 1LI2,

где I – сила тока в контуре.

2. Объемная (пространственная) плотность энергии однородного магнитного поля длинного соленои-да

w = µ02 2= 2В0µ= B×H.

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ Основные И ВОЛНЫ ФОРМУЛЫ

1. Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

T = 2p LC,

где L – индуктивность контура; С – его электроемкость.

2. Связь длины электромагнитной волны с периодом Т и частотой n колебаний

l = сТ или l = с,

где с – скорость электромагнитных волн в вакууме (с = 3×108м/с). 3. Скорость электромагнитных волн в среде

V =

eµ

где e – диэлектрическая проницаемость; µ – магнитная проницаемость среды.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ЗАДАЧА 1. Определить индукцию магнитного поля в центре проволочной квадратной рамки со сто-роной а, если в рамке течет ток I.

Дано: Решение

а,I a2 =180o− a1

В = ? a2

В = 4В1

1 = µ0 ×I× cosa1 −cosa2 ) 4pç2ø

B= 4× æ Iö ×2cosa1

è 2ø

ЗАДАЧА 2. По двум бесконечно длинным прямым параллельным проводникам, расстояние между ко-торыми d, текут токи I1 и I2 в противоположных направлениях. Определите магнитную индукцию В в точке А, удаленной на расстоянии r1от первого и r2от второго проводника.

Дано: Решение

I1, I2, d,

в b = 180º – a B

a r2

I1 d r1, r2

B = ?

µ0I11 2pr

B2=µ0I2. B=B+B2.2

Результирующую магнитную индукцию найдем по теореме косинусов: В= 12 22+2В2 cosb, cosa = 12+r2−d2,

1 2

B=µ0× I12+I22−I1I2×r2+r2−d2.

r r r r

ЗАДАЧА 3. Напряженность Н магнитного поля в центре кругового витка с магнитным моментом pm=1,5A×м2равна 150 А/м. Определите: 1) радиус витка; 2) силу тока в витке.

Дано: Решение

Н = 150 А/м pm=1,5 А·м2

H = I; pm= I ×S = IpR2= H ×Ip2R3,

R = ?

I = ?

откуда R = 3H×I×2p=11,7×10−2м,

I = H ×2R =35,1 А.

ЗАДАЧА 4. Бесконечно длинный провод образует круговую петлю, касательную к проводу. По прово-ду идет ток силой I. Найти радиус петли, если известно, что напряженность магнитного поля в центре пет-ли равна Н.

Дано: Решение

H, I I

R = ?

По принципу суперпозиции полей:

H = h2+ h3= I+ 2I = Iæ1+ 1ö= I×0,66 A/м ,

откуда R = I×0,66.

ЗАДАЧА 5. Между полюсами магнита на двух тонких нитях подвешен горизонтально линейный про-водник весом Р = 0,1 Н и длиной l = 0,2 м. Напряженность однородного магнитного поля Н = 2×105А/м и направлена вертикально. Весь проводник находится в магнитном поле. На какой угол a от вертикали от-клонятся нити, поддерживающие проводник, если по нему пропустить ток I = 2 A? Весом нитей пренеб-речь.

Дано: Решение

Р = 0,1 Н l = 0,2 м

Н = 2×105А/м

I= 2 A FA

a = ?

T a a

Сила Ампера FA= B× I ×l

B p

Условие равновесия проводника:

r+FA+P=0,т. е.

T sina = F , T cosa = Р,

или

tg×a = Р= BI ×l = µ0HI ×l »1, тогда

a = 45o.

ЗАДАЧА 6. a-частица, момент импульса которой L =1,33×10−22кг ×м2/с, влетает в однородное маг-

нитное поле, перпендикулярное скорости ее движения. Индукция магнитного поля равна 2,5×10−2Тл. Най-ти кинетическую энергию a-частицы.

Дано: Решение

L =1,33×10−22кг×м2/с B = 2,5×10−2Тл

B ^ v

q v

Fл

q =3,2×10−19Кл rm = 6,64×10−27кг

ЕК= ?

На заряд, движущийся в магнитном поле, действует сила Лоренца, которая выполняет роль центрост-ремительной силы:

Bqv = m×v2,

откуда

R= m×v.

L = mvR = mv× Bq= Bq×mv2,

mv2 = L×B×q,

следовательно,

mv2 L×B×q 1,33×10−22×2,5×10−2×3,2×10−19k 2 m×2 6,64×10−27×2

=0,8×10−16Дж =500эВ.

ЗАДАЧА 7. Тонкий медный провод массой m = 1 г согнут в виде квадрата, и концы его замкнуты. Квад-рат помещен в однородное магнитное поле (В = 0,1 Тл) так, что плоскость его перпендикулярна линиям ин-дукции поля. Определить количество электричества, если квадрат, потянув за противоположные вершины, вытянуть в линию.

Дано:

m =10−3 кг В = 0,1Тл,

r =8600кг/м3

r =1,7×10−8 Ом×м

q = ?

Решение

Согласно закону Фарадея для электро-магнитной индукции:

ei= − dФ.

По закону Ома для полной цепи I = R, где I = dq,

dtR = − dt, dq = − R× dt. (1)

Выражение (1) проинтегрируем:

q = − 1 ×( 2 −Ф1)

где Ф2=0, Ф = В×S.

q = B×S, m = r ×V = r ×4a×S ,

где S1 – площадь поперечного сечения проводника; а – сторона квадрата; r1 – плотность меди; V – объем проводника.

a = r×41. Сопротивление

R = r×l= r×4a,

1 1

где r – удельное сопротивление.

q = B×a4×S= B×a×S= r×4×r1×4× 1= 16×r×r = 42,7×10−3Кл.

ЗАДАЧА 8. В однородное магнитное поле напряженностью Н помещена квадратная рамка со стороной а. Плоскость рамки составляет с направлением магнитного поля угол a. Определить магнитный поток, пронизывающий рамку.

Дано: Решение

Н, а, a r– нормаль к рамке. H Магнитный поток

megaobuchalka.ru

Сила тока J, A

Угол отклонения 1,град.

Угол отклонения 2, град.

Среднее отклонение , град.

Тангенс отклонения tg

Индукция В, мкТл

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30