Что такое удельное сопротивление проводника. Удельное сопротивление проводников
Удельное сопротивление - проводник - Большая Энциклопедия Нефти и Газа, статья, страница 1
Удельное сопротивление - проводник
Cтраница 1
Удельное сопротивление проводника зависит от температуры, давления, материала и др., вследствие чего от этих же факторов зависит и сопротивление проводника. Наибольшее практическое значение имеет зависимость удельного сопротивления, а следовательно, и сопротивления проводника, от температуры. В общем случае эта зависимость достаточно сложна. [1]
Удельное сопротивление проводников является величиной не постоянной, а зависящей от температуры. Для всех металлов сопротивление увеличивается с увеличением температуры. При небольших колебаниях температуры зависимость удельного сопротивления от температуры следует линейному закону. Для каждого металла существует определенный температурный коэффициент сопротивления а, который определяет собой изменение удельного сопротивления проводника, отнесенное к одному ому при повышении температуры на ГС. [2]
Удельное сопротивление проводников лежит в пределах от 10 - 6 до 10 - 2 ом-см, а технических диэлектриков от 109 до 1020 ом-см. Эти пределы в известной мере условны, но приближенно отражают установившиеся в технике представления. [3]
Удельное сопротивление проводника представляет собой сопротивление провода длиной I м и площадью поперечного сечения 1 мм2 при температуре 20 С. [4]
Удельное сопротивление проводников и непроводников зависит от температуры. [5]
Удельное сопротивление проводников первого рода зависит от температуры. Как правило, с ростом температуры оно повышается. Исключение составляют графит и уголь. [6]
Чем меньше удельное сопротивление проводника, тем меньшее количество тепла ( при том же токе) в нем выделяется. При состоянии сверхпроводимости, когда удельное сопротивление становится неизмерим э малым, в проводнике при прохождении тока не выделяется сколько-нибудь заметного количества тепла. Так как при этом энергия тока никуда не тратится, то раз возбужденный в замкнутом сверхпроводнике то; поддерживается в нем неопределенно долго без затраты энергии извне. [7]
Изменение удельного сопротивления проводника под действием растягивающих или сжимающих усилий называют тензорезистивным эффектом. Он характеризуется тензочувст-вительностью, устанавливающей связь между относительным изменением сопротивления и относительной деформацией. [8]
Здесь р - удельное сопротивление проводника, остальные обозначения расшифрованы в предыдущей задаче. [9]
От чего зависит удельное сопротивление проводника. [10]
Если бы величина удельного сопротивления проводника р не зависела от его температуры, соотношение между допустимой плотностью тока / 1ДОп и допустимым превышением температуры проводника при коротком замыкании было бы относительно простым. В действительности удельное сопротивление р изменяется с нагревом проводника, и соотношение между плотностью тока и превышением температуры получается более сложным. [11]
Чтобы повысить величину удельного сопротивления проводников, применяют сплавы нескольких металлов. Установлено, что только сплавы с неупорядоченной структурой обладают повышенными значениями удельного сопротивления и малыми значениями температурного коэффициента сопротивления. Сплавами с неупорядоченной структурой называются такие, в кристаллической решетке которых нет правильного чередования атомов металлов, составляющих сплав. Эти сплавы составляют группу проводниковых материалов с большим удельным сопротивлением и малыми значениями температурного коэффициента удельного сопротивления. Все перечисленные группы проводников обладают высокой пластичностью, позволяющей получать провода диаметром до 0 01 мм и ленты толщиной 0 05 - 0 1 мм. [12]
Величина р называется удельным сопротивлением проводника. [13]
Ом; Р - удельное сопротивление проводника. [14]
При этом учитывается возрастание удельного сопротивления проводника при его нагреве. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
М5 удельное сопротивление проводника
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Физика»
ФИЗИКА
Электричество и магнетизм
УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ПРОВОДНИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНОЙ РАБОТЕ
по дисциплине «Физика»
Работа М5
МОСКВА 2013
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Физика»
ФИЗИКА
Электричество и магнетизм
Под редакцией профессора И.А. Паньшина
Рекомендовано редакционно-издательским советом
университета в качестве методических указаний для студентов
ИУИТ, ИТТСУ, ИЭФ, ИПСС
МОСКВА 2013
УДК 534
Л 97
Васильев Е.В. Физика. Удельное сопротивление проводника. Методическое указание к лабораторной работе М5 по физике./ Под редакцией профессора И.А. Паньшина. – М.: МИИТ, 2013. – 11 с.
Методические указания к лабораторной работе по физике М5 соответствуют программе и учебным планам по курсу общей физики (раздел «Электричество и магнетизм») и предназначены для студентов всех специальностей.
МИИТ, 2013
Работа М5
УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ПРОВОДНИКА
Цель работы: Измерить удельное сопротивление металлической проволоки (проводника), определить по справочным данным материал, из которого изготовлена проволока, уяснить понятие приборной и систематической погрешности, метод их определения и расчёт результирующей погрешности.
ВВЕДЕНИЕ
Удельное сопротивление проводника это физическая величина ρ равная электрическому сопротивлению цилиндра проводника единичной длины и единичной площади его поперечного сечения. Электрическое сопротивление – величина характеризующая противодействие постоянному току, поэтому его называют активным или омическим. Величина электрического сопротивления зависит от химического состава материала, его размеров, формы и температуры. Поэтому оно служит основной технической характеристикой при разработке резисторов (активных сопротивлений) и проводящих материалов для электрических цепей, а также для расчётов электрических потерь. Если известен материал, из которого изготовлен проводник, его длина l и площадь поперечного сечения S, то сопротивление рассчитывается по известной формуле:
 . (1)
. (1)
Пользуясь этой формулой, мы предполагаем, что площадь поперечного сечения и электрические свойства проводника постоянны по всей длине. На практике довольно хорошо выполняется предположение об одинаковости свойств, т. е, ρ по всему объёму проводника.
В отношении площади поперечного сечения и длины проводника приходится учитывать, что эти величины определяются экспериментально, т. е. имеют ошибки, обусловленные погрешностями измерений. Для экспериментального определения удельного сопротивления достаточно определить сопротивление проводника и, измерив, его геометрические размеры, рассчитать, исходя из (1), удельное сопротивление:
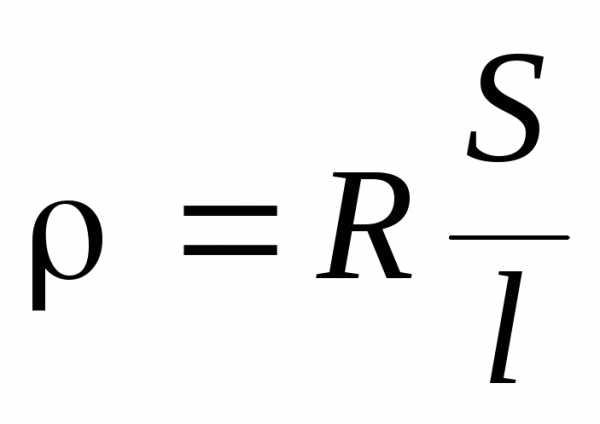 . (2)
. (2)
Определить сопротивление R проводника можно, пользуясь законом Ома для однородного участка цепи, если известны ток I, протекающий по проводнику и падение напряжения U на этом проводнике:
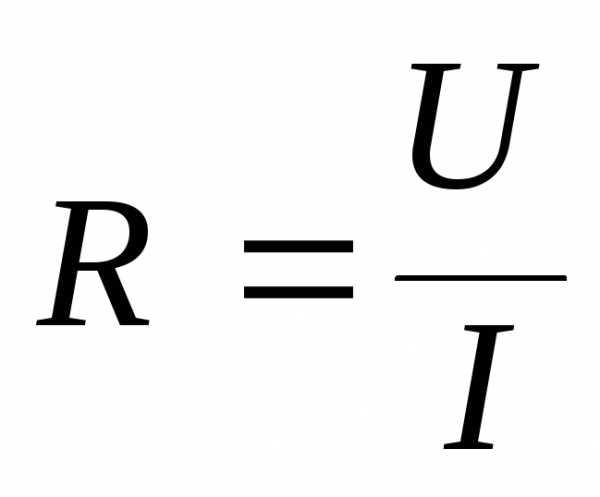 . (3)
. (3)
Т. к. на практике ток I и напряжение U определяются экспериментально, с помощью амперметра и вольтметра, то рассчитанное по этим измерениям значение R будет иметь ошибки, обусловленные конечной точностью амперметра и вольтметра, которые характеризуются так называемым классом прибора. Классом прибора называют отношение предельного (максимального) значения абсолютной погрешности измерения (например, ΔU, ΔI и т.д.) к пределу измерений прибора (Uм, Iм и т. д.), т. е. тому максимальному значению измеряемой величины, при котором стрелка прибора отклоняется до конца шкалы. Класс прибора выражается в процентах, поэтому, например, класс вольтметра KU:
KU = ΔU / Uм ·100%. (4)
Аналогично для амперметра:
KI = ΔI / Iм ·100%. (5)
Относительная погрешность измерения:
, (6)
. (7)
Из (6) видно, что относительная погрешность измерения тем больше, чем меньше измеряемое значение по сравнению с пределом измерений. Поэтому рекомендуется пользоваться прибором с таким пределом измерений, чтобы его стрелка при измерениях находилась в последней трети шкалы.
Сопротивление может измеряться различными методами, имеющими свои погрешности. Здесь мы остановимся на схеме измерения сопротивления методом амперметра — вольтметра и рассмотрим погрешности этого метода.
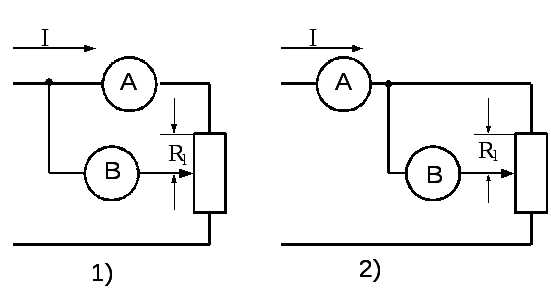
Рис 1.
Схемы измерения неизвестного сопротивления методом амперметра — вольтметра приведены на рис. 1, где А — измеритель тока (амперметр), В — измеритель напряжения (вольтметр). Установка имеет две схемы измерения. Каждая из этих схем имеет свою систематическую ошибку.
Так, в схеме рис. 1-1 вольтметр измеряет падение напряжения не только на неизвестном сопротивлении (участке проводника Rl), но и на измерителе тока (амперметре). Сопротивление, включенное между зажимами вольтметра, найденное как:
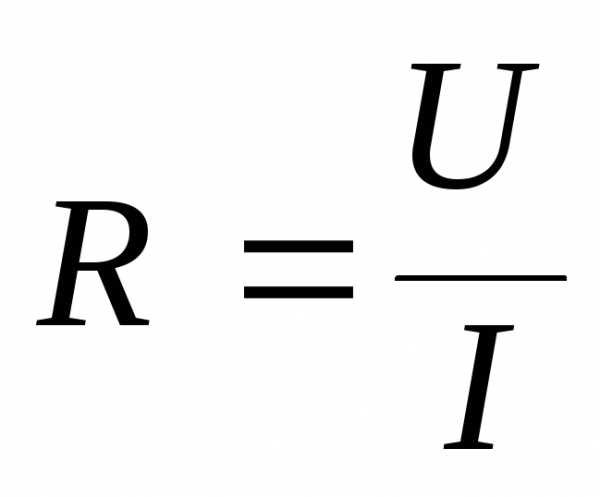 , (3)
, (3)
будет представлять собой сумму: R = RА + Rl, где RA — внутреннее сопротивление амперметра, Rl — сопротивление участка проводника.
R = U/I = RA + Rl = Rl (1 + (RА/ Rl)) = Rl (1 + δR), (8)
где δR—RA/ Rl — систематическая относительная погрешность при измерении по схеме рис. 1-1.
Из (7) видно, что эта погрешность будет тем меньше, чем больше отношение Rl/RА. Поэтому эту схему измерения целесообразно применять, когда, ток, протекающий по измеряемому сопротивлению, мал, а сопротивление проводника велико по сравнению с RA, погрешность измерений за счёт падения напряжения на амперметре становится пренебрежимо малой и погрешности определения R определяются только точностью измерений U и I. При использовании схемы рис. 1-1 для измерения сопротивлений, незначительно отличающихся от сопротивления Rl, последнее будет представлять собой систематическую погрешность, которую необходимо исключить (как это делается, указано в порядке выполнения работы).
При использовании схемы рис. 1-2 амперметр будет намерять полный ток, прошедший через амперметр и вольтметр:
I = IВ + Il,
т.к. вольтметр и проводник включены параллельно, то падение напряжения на них одинаково:
IВRВ = IlRl ; IВ/ Il = Rl / RВ.
I = IВ + Il = Il (1 + IВ/ Il) = Il (1 + (Rl / RВ)).
Видно, что во втором случае погрешность будет тем меньше, чем меньше отношение Rl/RВ. Таким образом, с целью уменьшения систематической погрешности схему 1-2 целесообразно применять для измерения малых сопротивлений, когда IВ << Il и RВ >> Rl, и можно пренебречь частью тока, прошедшего через вольтметр в обход Rl.
Помимо погрешностей намерения U и I существуют погрешности определения диаметра проводника d и его длины l, которые так же будут сказываться на погрешности определения .
Рассмотрим погрешность определения по схеме рис. 1-1. Перемещая подвижный контакт, определяется экспериментальная зависимость U(l; I), .где l — длина проводника между подвижным контактом и амперметром, I — ток, измеренный амперметром для каждой длины проводника. Суммарное сопротивление, рассчитанное по формуле (3) будет представлять собой сумму (RА + Rl):
R = U/I = RА + Rl, (9)
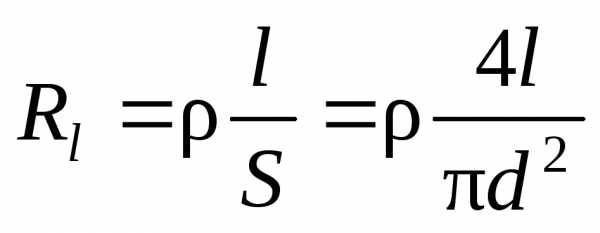 , (10)
, (10)
где — удельное электрическое сопротивление материала проводника, l и d — его длина и диаметр.
R = RA + (4/d2)l. (11)
Видно, что в этом случае зависимость R(l) будет представлять собой прямую линию, которая при экстраполяции до значения l = 0 даёт значение R = RA. Таким образом, можно исключить систематическую погрешность, обусловленную конечным значением RA. Значение можно в этом случае рассчитать по формуле:
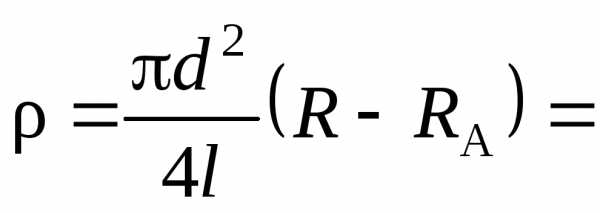
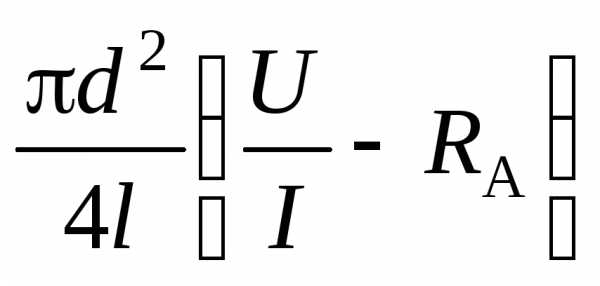 , (12)
, (12)
где I и U — ток и измеренное падение напряжения на проводнике длиной l. Погрешность определяется точностью измерений d, l, U, I и точностью определения RА графика.
При расчёте погрешностей U и I надо сравнить их с погрешностями считывания показаний. Её обычно принимают равной половине минимальной цены деления шкалы. Эту величину рассчитывают как отношение максимальной измеряемой величины (предел измерений на данной шкале, диапазоне) к числу делений шкалы:
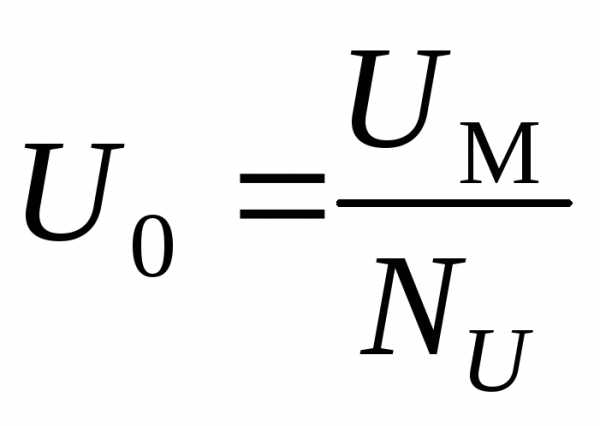 ;
; 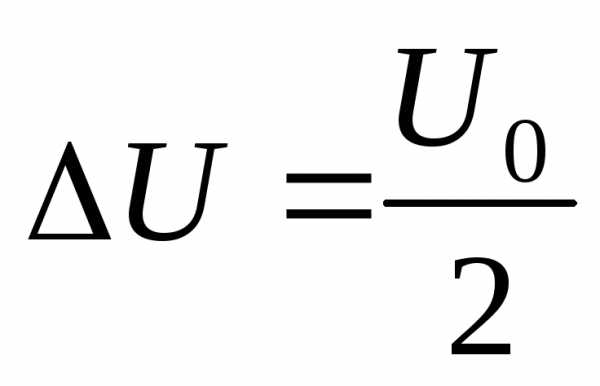 . (13)
. (13)
Рассматривая схему рис. 1-2, найдём, что сопротивление равно:
.
Для всего возможного диапазона изменений Rl эта зависимость является нелинейной и только при Rl << RВ т. е. в нашем случае при малых значениях l будет близкой к Rl. Казалось бы, что использование схемы рис. 1-2 при малых длинах проводника полностью решает задачу определения без систематической погрешности, присущей схеме рис. 1-1. Но здесь надо учитывать, что при малых l падение напряжения U на проводнике будет мало и это приведет к сильному возрастанию относительной погрешности δU. Используя R, рассчитанное по формуле (9) для малых l (<0,3 ... 0,4 lмакс ), определяем согласно (11):
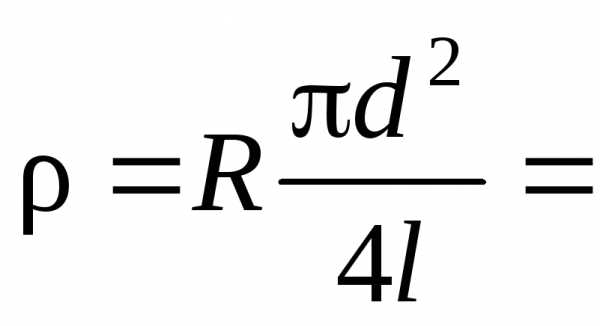
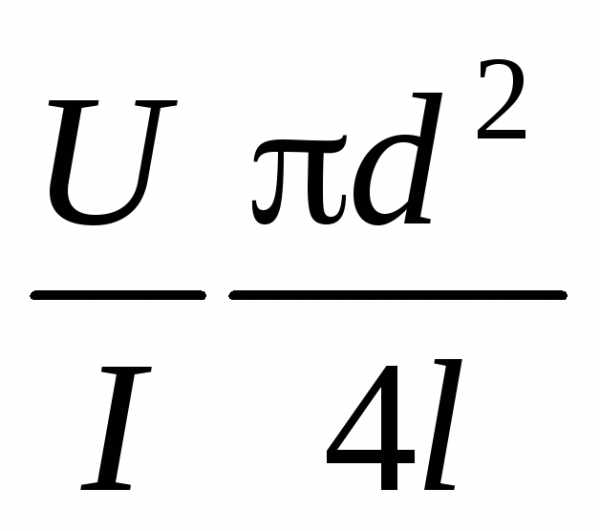 . (14)
. (14)
Вид установки для измерения удельного сопротивления проводника приведён на рисунке 2.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
1. Определите с помощью штангенциркули или микрометра диаметр проволоки по всей длине в 12 точках. Результаты измерений занесите в таблицу 1.
Таблица 1
| d1 | d2 | d3 | d4 | d5 | d6 | d7 | d8 | d9 | d10 | d11 | d12 | | |
По результатам измерений определите средний диаметр проволоки:
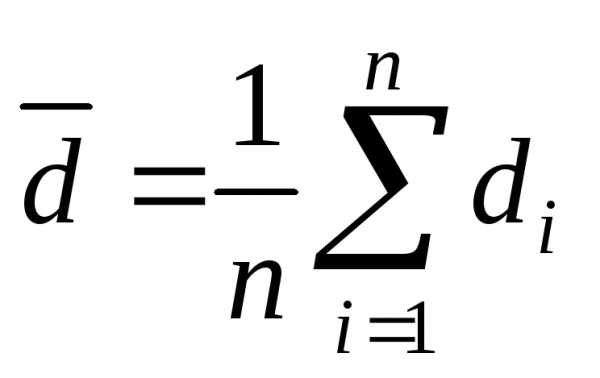 . (15)
. (15)

Рис. 2.
По методу Стьюдента определите величину погрешности измерения диаметра проволоки 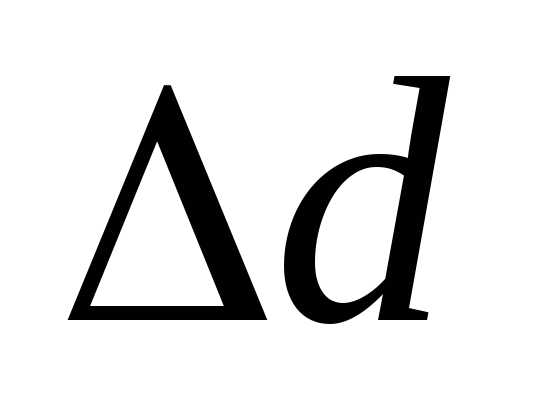 :
:
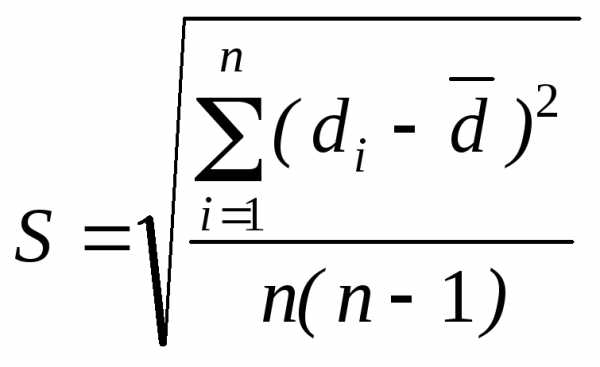 ; (16)
; (16)
, (17)
где - коэффициент Стьюдента. Для 12 измерений его величина равна 2,2 при доверительной вероятности равной 0,95.
2. Для схем рис.1-1 и рис. 1-2 (для переключения схем используется кнопка на передней панели установки) определите экспериментальную зависимость сопротивления проводника Rl от его длины l. Измерения проведите для 12 значений длины проводника, начиная с l = 0,1 м через 0,03 м. Результаты измерений занесите в таблицу 2.
Таблица 2
| № п/п | l, м | I, А | схема 1 | схема 2 | схема 1 Rl = U1/I - RА, Ом | схема 2 R2 = Rl = = U2/I, Ом | схема 1 , Ом·м | схема 2 , Ом·м | |
| U1, В | U2, В | R1 = =U1/I | Rl | ||||||
| 1. | 0,1 | ||||||||
| 2. | |||||||||
| ….. | |||||||||
| 12 | |||||||||
Для каждой длины рассчитайте сопротивление по формуле (3). По этим данным постройте экспериментальные зависимости R(l).
Для схемы рис. 1-1 экстраполируйте полученную зависимость до пересечения с осью ординат, проведя её через l1 = lмин и l2 = lмакс. Полученное значение представляет значение внутреннего сопротивления амперметра RA. Используя найденное значение внутреннего сопротивления амперметра RА, рассчитайте сопротивление Rl проводника, длиной l:
Rl= R - RA = (U/I) - RA, (18)
и соответствующее значение по формуле (11). Из полученных значений рассчитайте среднее значение
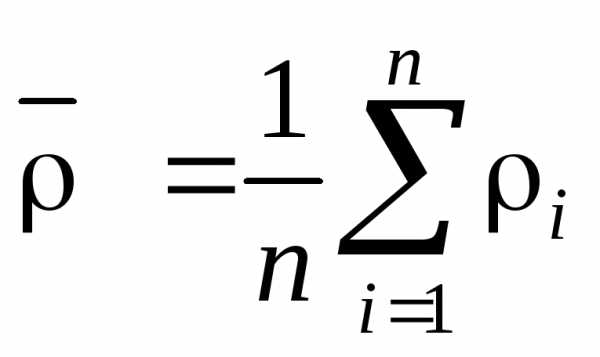 . (19)
. (19)
Относительная погрешность можно оценить по формуле:
. (20)
Для погрешностей U, I, d справедливо все написанное выше. Погрешность l рассчитывается как половина цены деления прибора [4]. Значение величины π известно с большой точностью, значит относительная ошибка, Δπ/π может быть сделана практически как угодно малой.
Рассчитайте по формуле (20), определите величину = 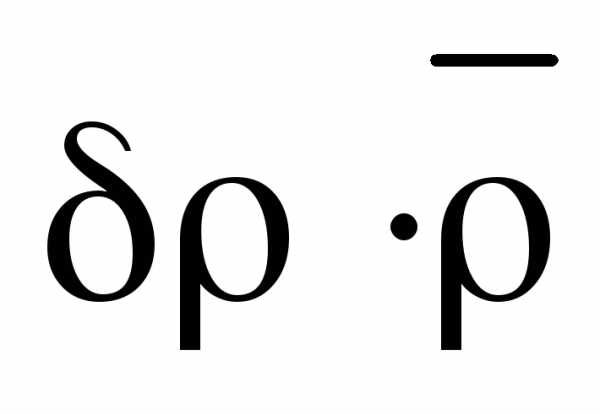 и запишите в окончательном виде:
и запишите в окончательном виде:
1 =  ±. (21)
±. (21)
Аналогично для таблицы 2 рассчитайте для схемы рис. 1-2 по формуле (13), рассчитайте среднее значение по формуле (19). Рассчитайте по формуле (20), определите величину = 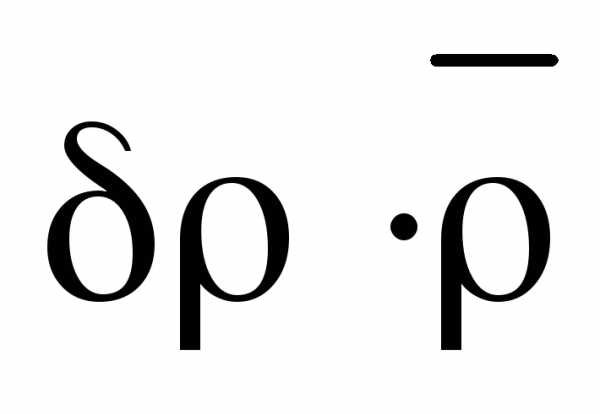 и запишите в окончательном виде:
и запишите в окончательном виде:
2 =  ±. (22)
±. (22)
По полученным результатам определите материал, из которого изготовлена проволока.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Что такое удельное сопротивление проводника? Какова размерность этой величины?
Как изменяется сопротивление проводника а) при изменении его длины при постоянном сечении? б) при изменении его диаметра при постоянной длине?
Как должно изменяться отношение длины проводника к его диаметру для сохранения постоянного сопротивления?
Какой из измерительных приборов лучше использовать в данной работе: класса 1,5 или класса 0,1?
Как изменяется абсолютная и относительная погрешности определения напряжения (тока) при уменьшении её значения от Uм (Iм) до нуля?
Постройте зависимость U/I для схем рис. 1-1 и 1-2 при изменении длины проводника от l = 0 до l = ∞.
Оцените, какая величина наиболее сильно влияет на погрешность определения для схем рис. 1-1 и 1-2.
Список литературы
Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высш. шк. – 2000.
Савельев И.В. Курс физики. – Т. 2. – М.: Наука – 1998 и далее.
Трофимова Т.И. Курс физики. – М., 2000 и далее.
Селезнёв В.А., Тимофеев Ю. П. Вводное занятие в лабораториях кафедры физики. – М.: МИИТ. – 2011. – 38 с.
Учебно-методическое издание
Васильев Евгений Васильевич
ФИЗИКА
Под общей редакцией профессора И.А. Паньшина
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
по дисциплине «ФИЗИКА»
Работа М5 «Удельное сопротивление проводника»
| Подписано в печать Усл.-печ. л. – | Формат 60х84/16. Заказ – | Изд. № 174-12 Тираж 500 экз. |
12
studfiles.net
Таблица удельных сопротивлений проводников — Zygar
Электрическое сопротивление 1 метра провода (в Ом), сечением 1 мм², при температуре 20 С°. Формула: ρ = Ом · мм²/м.
| Серебро | 0.015 |
| Медь | 0.0175 |
| Золото | 0.023 |
| Латунь | 0,025... 0,108 |
| Хром | 0,027 |
| Алюминий | 0.028 |
| Натрий | 0.047 |
| Иридий | 0.0474 |
| Вольфрам | 0.05 |
| Цинк | 0.054 |
| Молибден | 0.059 |
| Никель | 0.087 |
| Бронза | 0,095... 0,1 |
| Железо | 0.1 |
| Сталь | 0,103... 0,137 |
| Олово | 0.12 |
| Свинец | 0.22 |
| Никелин (сплав меди, никеля и цинка) | 0.42 |
| Манганин (сплав меди, никеля и марганца) | 0,43... 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,44-0,52 |
| Копель ( медно-никелевый сплав с 43% никеля и 0,5% марганца) | 0.5 |
| Титан | 0.6 |
| Ртуть | 0.94 |
| Хромель (хром 8,7—10 %; никель 89—91 %; кремний, медь, марганец, кобальт — примеси) | 1.01 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05... 1,4 |
| Фехраль | 1,15... 1,35 |
| Висмут | 1.2 |
| Хромаль (Сплав 4.5 – 6% алюминия, 17%-30% хрома, остальное железо) | 1,3... 1,5 |
Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм².
zygar.ru
мир электроники - Удельное сопротивление проводников
Основы электротехники
материалы в категории
Удельное сопротивление это параметр характеризующий свойства вещества препятствовать прохождению электрического тока. За единицу измерения принято считать сопротивление отдельно взятого участка (скажем длиною 1 метр и сечением 1 мм) однородного вещества.
Величина удельного сопротивления обозначается греческой буквой
Сопротивление проводника с удельным сопротивлением , длиной и площадью сечения может быть рассчитано по формуле
Как нетрудно заметить сопротивление любого провода напрямую зависит от материала из которого он изготовлен, от его длины и площади сечения: чем больше длина и меньше диаметр тем сопротивление будет выше. И при одинаковой длине и диаметре проводники из разных материалов будут иметь разные сопротивления.
Ниже приводится таблица удельного сопротивления различных проводников:
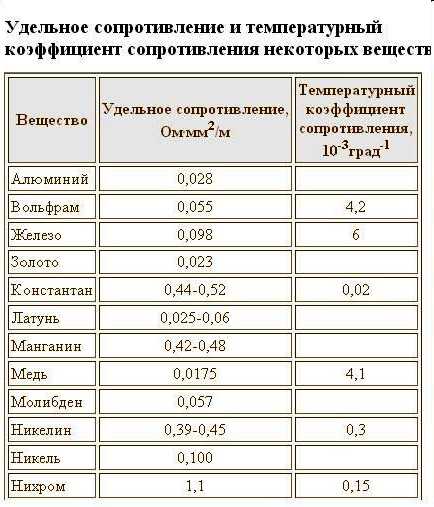
Как мы видим самым наименьшим сопротивлением обладают медь и алюминий поэтому они и получили наибольшее распространение на практике.
Пример когда требуется знать удельное сопротивление проводников: статья Как рассчитать сечение провода
Есть вопросы: заходите на ФОРУМ!!
radio-uchebnik.ru
Содержание
Если замкнуть электрическую цепь, создав на ее концах разность потенциалов, то по ней побежит электрический ток, силу которого можно измерить Амперметром. Но сила эта будет варьироваться, если в цепи заменить один проводник другим. Это говорит о том, что не только напряжение влияет на силу тока, но и материал, из которого сделан проводник. Вот это свойство проводника препятствовать прохождению электрического тока и называется сопротивлением.Каждое тело по отношению к электрическому току характеризуется своим сопротивлением. Если вспомнить электронную теорию, то согласно ей, все вещества состоят из атомов и молекул. Эти атомы и молекулы в разных веществах имеют разную структуру. И именно они встречаются на пути движения свободных электронов в проводнике, когда по электрической цепи идет ток. То есть, когда свободный электрон сталкивается с ионом кристаллической решетки материала проводника, он неизбежно теряет часть своей кинетической энергии и испытывает как бы сопротивление своему движению.Чем больше сопротивление проводника, тем он хуже пропускает электрический ток. Обозначается электрическое сопротивление латинской буквой R, а за единицу измерения принят 1 Ом.Обратной характеристикой сопротивления вещества является его проводимость. Чем выше электрическая проводимость материала, тем лучше он проводит ток. Изоляторы отличаются от проводников по проводимости в огромное число раз, измеряемое единицей с двадцатью двумя нулями! Удельное сопротивление. Определение и расчетИтак, электрическое сопротивление зависит от материала, из которого изготовлен проводник. Но есть еще два важных параметра – это длина проводника и площадь его поперечного сечения. Очевидно, что чем длиннее проводник, тем дольше ионы его вещества будут мешать движению свободных электронов. А вот чтобы лучше понять, почему сопротивление зависит от площади поперечного сечения, нужно провести аналогию с водой. Представьте два одинаковых сосуда, соединенных в одном случае тонкой трубкой, а в другом – толстой. По тонкой или по толстой трубке вода быстрее перельется из одного сосуда в другой? Ясно, что по толстой. Удельное сопротивление – это сопротивление проводника, длиной 1 метр и площадью поперечного сечения 1 мм2. Наименьшим удельным сопротивлением обладают серебро и медь.Таким образом, чтобы вычислить электрическое сопротивление проводника, надо воспользоваться формулой: R = pl/S, где p – удельное сопротивление, l – длина проводника, S – площадь поперечного сечения проводника.Интересные фактыПри повышении температуры металлического проводника, его сопротивление увеличивается. Объяснить это явление можно тем, что при передаче тепловой энергии телу повышается интенсивность движения атомов его вещества, и это в большей степени препятствует свободному току электронов. С понижением же температуры в металлах создаются лучшие условия для проведения электрического тока. Существует даже такое понятие, как сверхпроводимость, то есть такое состояние металлического проводника, когда его сопротивление равно нулю. При этом атомы металла практически застывают на месте, абсолютно не препятствуя движению свободных электронов. Происходит это при температуре -273оС. |
completerepair.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.