Сила тока. Напряжение. Сопротивление. Закон Ома
Задания уровня “А”
1. Определите силу тока в проводнике сопротивлением 25 Ом, на концах которого напряжение равно 7,5 В.
2. При устройстве молниеотвода применен стальной провод сечением 30 мм2 и длиной 25 м. Найдите сопротивление этого провода.
3. Чему равно напряжение в дуге при электросварке, если сопротивление дуги 0,2 Ом, а сила тока достигает 150 А.
4. Рассчитайте сопротивление никелиновой проволоки длиной 50 м и сечением 0,25 мм2.
5. Напряжение в сети 220 В. Каково сопротивление спирали электроплитки, если по ней течет ток 5 А?
6. Каково напряжение на концах проводника сопротивлением 40 Ом, если сила тока в проводнике 0,1 А.
7. Сопротивление вольтметра 6000 Ом. Какой ток проходит через вольтметр, если он показывает напряжение 90 В?
8. Рассчитайте, сколько метров никелинового провода площадью поперечного сечения 0,1 мм2 потребуется для изготовления реостата с максимальным сопротивлением 90 Ом.
9. Определите напряжение на концах электрической плитки, если сопротивление ее спирали 55 Ом, а сила тока 4 А.
10. Сопротивление проводника 10 Ом, его длина 100 м, площадь поперечного сечения равна 1 мм2. Из какого материала сделан проводник?
11. Каково сопротивление алюминиевой проволоки длиной 125 см, если площадь ее поперечного сечения равна 0,1 мм2. Чему равно напряжение на концах этой проволоки, если по ней течет ток 0,2 А?
12. Определите площадь поперечного сечения константановой проволоки сопротивлением 3 Ом, если ее длина 1,5 м?
13. Сварочный аппарат присоединяют в сеть медными проводами длиной 100 м и площадью поперечного сечения 50 мм2. Найдите напряжение на проводах, если сила тока равна 125 А.
14. Чему равно сопротивление никелиновой проволоки длиной 4 м и площадью поперечного сечения 2 мм2? Какой ток идет по этой проволоке при напряжении на ее концах 2 В?
15. Вычислите сопротивление нихромовой проволоки, длина которой 150 м, а площадь поперечного сечения 0,2 мм2. Каково напряжение на концах этой проволоки, если по ней течет ток 0,2 А?
Каково напряжение на концах этой проволоки, если по ней течет ток 0,2 А?
Задания уровня “В”
1. Определите сопротивление нагревательного элемента электрической печи, выполненного из константановой проволоки длиной 24,2 м и площадью поперечного сечения 0,5 мм2.
2. Кипятильник включен в сеть с напряжением 220 В. Чему равна сила тока в спирали электрокипятильника, если она сделана из нихромовой проволоки длиной 5 м и площадью поперечного сечения 0,1 мм2?
3. Допустимый ток для изолированного медного провода сечением 1 мм2 при продолжительной работе равен 11 А. Сколько метров такой проволоки можно включить в сеть с напряжением 220 В?
4. Определите напряжение на концах стального провода длиной 140 см и площадью поперечного сечения 0,2 мм2, по которому течет ток 250 мА.
5. Сопротивление проводника длиной 20 м и площадью поперечного сечения 1 мм2 равно 0,56 Ом. Определите, из какого материала сделан проводник.
6. Рассчитайте сопротивление километра медного провода, имеющего поперечное сечение 10 мм2, если известно, что медный проводник сечением в 1 мм2 и длиной в 1 м имеет сопротивление 0,017 Ом.
7. Какова сила тока на участке цепи, состоящей из константановой проволоки длиной 10 м и сечением 1,2 мм2, если напряжение на концах этого участка равно 20 В.
8. Чему равна длина стального провода, имеющего площадь поперечного сечения 0,8 мм2, если при прохождении по нему тока в 1 А напряжение на его концах равно 12 В?
9. Рассчитайте напряжение на концах линии электропередачи длиной 0,5 км при силе тока в ней 15 А, если провода, изготовленные из алюминия, имеют площадь поперечного сечения 14 мм2.
10. Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 25 м и площадью поперечного сечения 0,5 мм2, если напряжение на зажимах реостата равно 45 В.
11. Из какого материала сделан провод длиной 100 м и площадью поперечного сечения 0,5 мм2, если при напряжении на его концах 6,8 В по нему проходит ток 2 А?
12. Электрическая проводка выполнена медным проводом, длина которого 200 м и площадь поперечного сечения 10 мм2. Каково сопротивление проводки? Какую площадь поперечного сечения должен иметь такой же длины и сопротивления алюминиевый провод?
Электрическая проводка выполнена медным проводом, длина которого 200 м и площадь поперечного сечения 10 мм2. Каково сопротивление проводки? Какую площадь поперечного сечения должен иметь такой же длины и сопротивления алюминиевый провод?
13. Определите площадь поперечного сечения стального провода длиной 200 м, если при напряжении 120 В по нему течет ток 1,5 А.
14. Чему равно напряжение на концах алюминиевого проводника длиной 75 м и площадью поперечного сечения 0,75 мм2, по которому протекает ток 2 А?
15. Сколько метров провода сечением 10 мм2 надо взять, чтобы его сопротивление было такое же, как у проводника длиной 1 м и площадью поперечного сечением 0,5 мм2, сделанного из такого же материала?
Задания уровня “С”
1. Алюминиевый проводник площадью поперечного сечения 0,5 мм2 заменили медным проводником такой же длины и сопротивления. Каким должно быть поперечное сечение медного провода?
2. Определите, из какого материала изготовлен провод длиной 2 км и площадью поперечного сечения 20 мм2, если по нему проходит ток 2 А при напряжении на его концах 220 В.
Определите, из какого материала изготовлен провод длиной 2 км и площадью поперечного сечения 20 мм2, если по нему проходит ток 2 А при напряжении на его концах 220 В.
3. К концам нихромовой проволоки, имеющей площадь поперечного сечения 0,5 мм2 и длиной 20 м подано напряжение 220 В. Найдите силу тока, проходящего через проволоку.
4. Какой длины медная проволока должна быть намотана на катушку электрического звонка, если площадь ее поперечного сечения равна 0,35 мм2? Сила тока, проходящего через звонок, равна 1 А, а напряжение на его концах 0,5 В.
5. Определите сопротивление фехралевой спирали и напряжение на ее концах, если ее длина 6 м, а площадь поперечного сечения 0,2 мм2. Сила тока, проходящего через спираль равна 1,5 А.
6. Какое напряжение нужно приложить к концам железного проводника длиной 30 см и площадью поперечного сечения 1,5 мм2, чтобы получить ток 10 А?
7. Для изготовления реостата на 6 Ом используют никелиновую проволоку площадью поперечного сечения 0,5 мм2. Какой длины необходимо взять проводник? Каким будет напряжение на концах полностью включенного реостата при силе тока 1,5 А?
Какой длины необходимо взять проводник? Каким будет напряжение на концах полностью включенного реостата при силе тока 1,5 А?
8. Проводник, имеющий площадь поперечного сечения 0,25 мм2 и сопротивление 8 Ом, надо заменить проводником из того же металла и той же длины, но сопротивлением 20 Ом. Какой площади поперечного сечения проводник необходимо подобрать для этой замены?
9. Какая должна быть общая длина и минимальная площадь поперечного сечения никелиновой проволоки, имеющей сопротивление 2 Ом на длине 1 м, чтобы в изготовленном из нее нагревательном приборе при включении в сеть с напряжением 220 В сила тока не превышала 4 А?
10. Сопротивление проволоки длиной 50 м равно 200 Ом. Какой длины надо взять проволоку из того же материала и той же площади поперечного сечения, чтобы ее сопротивление было равно 50 Ом?
11. Какой массы надо взять никелиновый проводник площадью поперечного сечения 1 мм2, чтобы из него изготовить реостат сопротивлением 10 Ом? (Плотность никелина — 8,8 г/см3)
12. Масса медного электропровода длиной 5 км составляет 750 кг. Определите сопротивление этого провода.
Масса медного электропровода длиной 5 км составляет 750 кг. Определите сопротивление этого провода.
13. Найдите отношение сопротивлений двух железных проволок одинаковой массы, если площадь поперечного сечения первой проволоки в 2 раза больше, чем второй.
14. Определите массу железной проволоки площадью поперечного сечения 2 мм2, взятой для изготовления реостата, рассчитанного на прохождение по нему тока в 1 А при напряжении 6 В.
15. Чему равно отношение сопротивлений двух проводников — медного и алюминиевого — одинаковой массы и площади поперечного сечения?
Электрический ток 1 вариант — Документ
ЭЛЕКТРИЧЕСКИЙ
ТОК
1 ВАРИАНТ
I |
общее показание |
II |
общее |
III |
тока, R2=2 8. Кипятильник нагревает 1,2л воды от с = 4200 Дж/(кг • °С). |
ЭЛЕКТРИЧЕСКИЙ
ТОК
2 ВАРИАНТ.
I |
|
II |
цепи участке. R3=6 Ом. |
III |
R1 R5 |
ЭЛЕКТРИЧЕСКИЙ
ТОК
3 ВАРИАНТ.
I |
R1=7 Ом ? V 3. Какую работу совершает ток в |
II |
|
III |
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
4 ВАРИАНТ.
I |
|
II |
|
III |
V R2=2 Ом R3=3 Ом
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
5 ВАРИАНТ.
I |
3. Начертите схему |
II | 4. 5. 6. Последовательно соединены п |
III |
8. На электрической плитке мощностью 9. |
ЭЛЕКТРИЧЕСКИЙ ТОК
6 ВАРИАНТ.
I | 1. На электрической лампе написано 100 2.Определить по данной схеме общее R1
|
II | 4. Сопротивление нити накала электронной 5. Определить удельное сопротивление 6. Определите внутреннее сопротивление |
III | 7. Если два проводника соединить
2 Ом 2 Ом 5 Ом 0,5 А 10 Ом 40 Ом |
ЭЛЕКТРИЧЕСКИЙ
ТОК
7 ВАРИАНТ.
I |
|
II |
R2 R1 R4 |
III |
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
8 ВАРИАНТ.
I |
R1=2 Ом |
II |
|
III |
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
9 ВАРИАНТ.
I |
|
II |
|
III |
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
10 ВАРИАНТ.
I | 1. Определите общее сопротивление цепи R1=14 V 2.Определите расход энергии за 20 с в
|
II |
|
III |
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
11 ВАРИАНТ.
I |
R1=14 V
|
II | 4. Из какого материала изготовлен 5. 6. Определите |
III |
включенной на рисунке, чтобы напряженность электростатического конденсаторе была 2250 В/м? Внутреннее батареи Расстояние конденсатора 0,2 см.
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
12 ВАРИАНТ.
I |
R1 R3 |
II |
|
III |
|
ЭЛЕКТРИЧЕСКИЙ
ТОК
13 ВАРИАНТ.
I | 1. За 2. Через проводник за 20 3. Начертите схему электрической |
II |
|
III | 6. Найдите общее сопротивление R1 R3 7. Электровоз массой 300 т спускается |
ЭЛЕКТРИЧЕСКИЙ
ТОК
14
ВАРИАНТ.
I |
|
II |
R1 5. Какова сила тока в 6. Определите ЭДС и внутреннее |
III | 7. Найдите силу тока во 8. Лифт массой 2 т поднимается равномерно |
ЭЛЕКТРИЧЕСКИЙ
ТОК
15 ВАРИАНТ.
I |
|
II | 4. Сопротивление вольфрамовой 5. Определите силу тока в 6. ЭДС |
III | 7.На рисунке изображена 8. Подъемный кран поднимает груз массой |
ЭЛЕКТРИЧЕСКИЙ
ТОК
16 ВАРИАНТ.
I |
|
II |
5.Какую работу совершает двигатель |
III | 6. По схеме, изображенной 7. |
ЭЛЕКТРИЧЕСКИЙ
ТОК
17 ВАРИАНТ.
I | 1. |
II | |
III |
ЭЛЕКТРИЧЕСКИЙ
ТОК
18 ВАРИАНТ.
1.
2. Вариант
2
1. 2.
Вариант
3
1. 2.
Вариант
4
1. 2. Электрический
чайник потребляет ток 3 А при напряжении
220 В.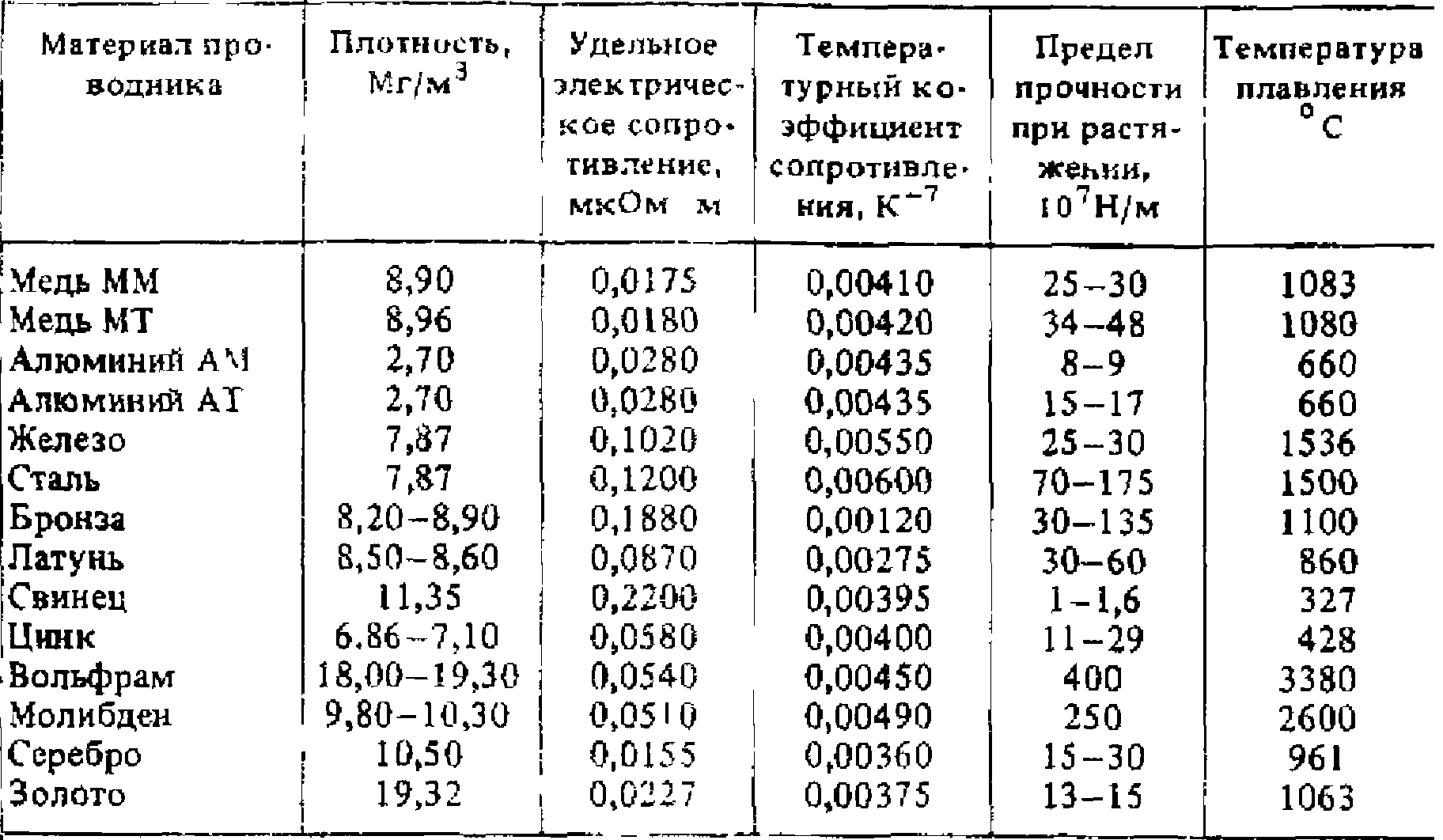 Чему равно сопротивление чайника?
Чему равно сопротивление чайника?
Вариант 5
1. За какое время пройдет
через поперечное сечение проводника
заряд, равный 10 Кл, при силе тока 0,2 А?
2. Определите напряжение,
которое нужно создать на концах проводника
сопротивлением 20 Ом, чтобы в нем возникла
сила тока 0,5 А.
56
СР-2.
Сопротивление проводника
Вариант 1
1. 2.
Вариант
2
1. 2.
Температурный коэффициент сопротивления
для некоторого сплава равен 10~3К1.
Сопротивление резистора
из этого сплава при 273 К равно 100 Ом. На
сколько увеличится сопротивление
резистора при нагревании до 283 К?
Вариант 3
1. 2. Сопротивление
платиновой проволоки при температуре
20 °С равно 20 Ом, а при температуре 500 °С
равно 59 Ом. Найдите значение температурного
коэффициента сопротивления платины.
Вариант 4
1. Сопротивление
медного провода сечением 2 мм2
равно 1 Ом. Какова длина этого провода?
2. Алюминиевая
проволока при 0 °С имеет сопротивление
4,25 Ом. Каково будет сопротивление этой
проволоки при 200 °С? Температурный
коэффициент сопротивления алюминия 4
• 10 3
К»1.
Вариант 5
1. Определите сопротивление
алюминиевого провода длиной 1,8 км и
сечением 10 мм2.
Г> 7
2. 3.
4. 5.
6. 7. 8. Определите общее
сопротивление цепи (рис. 19), если
сопротивления резисторов Rl—R6
имеют соответственно
следующие значения: R}
=0,5 Ом, R2=l,5
Ом, R3=R4=R6=\
Ом, Д5
= 2/3 Ом.
Рис. 19
9.
1. 2.
3. 4. Какова сила тока
в проводнике R
(рис. 22), если ЭДС
источника тока равна 3 В, его внутреннее
сопротивление равно 1 Ом, сопротивления
/?, =R1=
1,75 Ом, Ry
= 2 Ом, Я4
= 6 Ом?
5. 6. 7.
8. Найдите общее сопротивление электрической
цепи, изображенной на рисунке 25, если
сопротивление каждого резистора
равно 1 Ом.
9. Источник тока питает внешнюю цепь
(рис. 26). При силе тока 2 А во внешней цепи
выделяется мощность 24 Вт, а при силе
тока 5 А выделяется мощность 30 Вт.
Определите силу тока при коротком
замыкании источника тока.
1. На рисунке 27 изображена
схема электрической цепи. Определите
сопротивление проводника R2
и падение напряжения
на нем, если ЭДС источника тока равна
60 В, его внутреннее сопротивление равно
2 Ом, сила тока в цепи равна 2 А, сопротивление
Я, =20 Ом.
2. Шесть лампочек соединены
так, как показано на схеме, изображенной
на рисунке 28. Определите общее сопротивление
электрической цепи, если сопротивления
лампочек Л1, Л2, ЛЗ, Л4,
Л5, Л6 (см. рис. 28)
соответственно равны 10 Ом, 20 Ом, 30 Ом,
15 Ом, 35 Ом и 50 Ом.
3. Чему равно напряжение на концах
проводника, имеющего сопротивление
20 Ом, если за время, равное 10 мин, через
него протекает электрический заряд 200
Кл?
4. Что покажут
амперметры и вольтметр (рис. 29) при
положениях переключателя /, 2, 3,
если ЭДС источника
тока равна 6 В, его внутреннее сопротивление
равно 1,2 Ом, сопротивление резистора R1
равно 8 Ом, резистора
R2
равно 4,8 Ом?
5. Чему равно общее
сопротивление электрической цепи
(рис. 30), если сопротивления резисторов
Rl—R7
равны соответственно
следующим значениям: #, = 18 Ом, #,= 12 Ом,
R3
= 23 Ом, /?4=7
Ом, #5
= 60 Ом, #6
= 60 Ом, #7=30
Ом?
7. К источнику с ЭДС,
К источнику с ЭДС,
равной 18 В, и внутренним сопротивлением
0,2 Ом подключены три одинаковых
проводника, сопротивление каждого
из которых равно 4,5 Ом, соединенные
по схеме, показанной на рисунке 31.
Определите силу тока, который протекает
через каждое сопротивление. (Сопротивлением
соединительных проводов пренебречь.)
8. Рассчитайте общее
сопротивление электрической цепи,
изображенной на рисунке 32, если R
= 2 Ом.
9. 1. К источнику тока с
ЭДС, равной 4,5 В, и внутренним
сопротивлением 1,5 Ом присоединена цепь,
состоящая из двух проводников,
сопротивление каждого из которых равно
10 Ом, соединенных между собой параллельно,
и третьего проводника сопротивлением
2,5 Ом, подсоединенного последовательно
к двум первым. Чему равна сила тока в
неразветвленной части цепи?
2. Найдите общее
сопротивление электрической цепи (рис.
33), если сопротивления резисторов Rl—R6
равны соответственно
следующим значениям: Д, = 1 Ом, R^
= 2 Ом, Д3
= 4 Ом, R4=l
Ом, Я5
= 2 Ом, Й6=1
Ом.
3. Количество теплоты,
выделяемое за 54 мин проводником с
током, равно 20 кДж. Определите силу тока
в проводнике, если его сопротивление
равно 10 Ом.
Rl
R4
4. Рассчитайте силу тока в
цепи и в проводнике R3
(рис. 34), если батарея
состоит из трех параллельно соединенных
элементов. Внутреннее сопротивление
каждого элемента равно 0,6 Ом, ЭДС
каждого элемента равна 1,44 В, Д,=Д,= 1,2
Ом, R3=2
Ом, R4=3
Ом.
R1
5. Определите
общее сопротивление электрической
цепи (рис. 35), если сопротивления
резисторов Rl—
R7
равны соответственно
следующим значениям: /?, = 10 Ом, Л,= 10 Ом,
/?,= Ю Ом, Д4
= 30 Ом, Д5=15
Ом, Я6=15
Ом, «7 = 45 Ом.
6. Вольтметр, рассчитанный
на измерение напряжения до 30 В, имеет
внутреннее сопротивление 3 кОм. Какое
дополнительное сопротивление нужно
присоединить к вольтметру, чтобы им
можно было измерять напряжение до
300 В?
7. Каковы показания
амперметра и вольтметра, включенных
в схему рисунка 36, если ЭДС источника
равна 7,5 В, внутреннее сопротивление
источника равно 0,5 Ом, сопротивления
резисторов Rl
— R4
равны соответственно
следующим значениям: Л, = 1,8 Ом, Л2
= 2 Ом, Д3=3
Ом, Л4=6
Ом? Найдите силу тока и напряжения для
каждого из резисторов.
8. Чему равно общее
сопротивление электрической цепи
на участке АВ, показанной
на рисунке 37, если сопротивление
каждого звена равно 5 Ом?
9. Известно,
что ЭДС источника тока равна 16 В,
его внутреннее сопротивление равно 3
Ом. Найдите сопротивление внешней
Найдите сопротивление внешней
цепи, если известно, что мощность тока
в ней равна 16 Вт. Определите КПД источника
тока.
ЭЛЕКТРИЧЕСКИЙ
ТОК
14 ВАРИАНТ.
Нихром
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Фехраль
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Нихром в изоляции
Продукция
Цены
Стандарты
Статьи
Фото
Титан
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Вольфрам
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Молибден
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Кобальт
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Термопарная проволока
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Провода термопарные
Продукция
Цены
Стандарты
Статьи
Фото
Никель
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Монель
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Константан
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Мельхиор
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Твердые сплавы
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Порошки металлов
Продукция
Цены
Стандарты
Статьи
Фото
Нержавеющая сталь
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Жаропрочные сплавы
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Ферросплавы
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Олово
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Тантал
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Ниобий
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Ванадий
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Хром
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Рений
Продукция
Описание
Цены
Стандарты
Статьи
Фото
Прецизионные сплавы
Продукция
Описание
Магнитомягкие
Магнитотвердые
С заданным ТКЛР
С заданной упругостью
С высоким эл.
Сверхпроводники
Термобиметаллы
Рассчитать нагреватели электрической печи Калькулятор нагревателей электрических печейПараметры электрической печи Параметры нагревателя
Диаметр нагревателя, мм
Размеры нагревателей (толщина x ширина), мм Выбрать из стандартных размеров (толщина х ширина), мм
Толщина нагревателя, мм
Ширина нагревателя, мм
Длина нагревателя, м
Масса нагревателя, кг
Общая длина нагревателей, м
Общая масса нагревателей, кг
*Результаты расчета нагревателей электрических печей, выполненного с помощью данного калькулятора, носят информативный характер. Расчет основан на подходе, рассмотренном в книге «Типовые расчеты по электрооборудованию», Дьяков В.И., а также в статье «Нагреватели. Методика и примеры расчета», Никонов Н. В., и содержит ряд допущений. В каждом конкретном случае могут появиться дополнительные условия, связанные с конструктивными особенностями печи, а также условиями эксплуатации.
Очень часто при желании сделать или отремонтировать нагреватель электропечи своими руками у человека появляется много вопросов. Например, какого диаметра взять проволоку, какова должна быть ее длина или какую мощность можно получить, используя проволоку или ленту с заданными параметрами и т.д. При правильном подходе к решению данного вопроса необходимо учитывать достаточно много параметров, например, силу тока, проходящего через нагреватель, рабочую температуру, тип электрической сети и другие. В данной статье приводятся справочные данные о материалах, наиболее распространенных при изготовлении нагревателей электрических печей, а также методика и примеры их расчета (расчета нагревателей электрических печей). Непосредственно нагреватель – один из самых важных элементов печи, именно он осуществляет нагрев, имеет наибольшую температуру и определяет работоспособность нагревательной установки в целом. Поэтому нагреватели должны соответствовать ряду требований, которые приведены ниже. Требования к нагревателямОсновные требования к нагревателям (материалам нагревателей):
Материалы для изготовления нагревателей Наиболее подходящими и самыми используемыми в производстве нагревателей для электропечей являются прецизионные сплавы с высоким электрическим сопротивлением. Перечисленные выше сплавы обладают хорошими свойствами жаропрочности и жаростойкости, поэтому они могут работать при высоких температурах. Хорошую жаростойкость обеспечивает защитная пленка из окиси хрома, которая образуется на поверхности материала. Температура плавления пленки выше температуры плавления непосредственно сплава, она не растрескивается при нагреве и охлаждении. Приведем сравнительную характеристику нихрома и фехрали.
Недостатки нихрома:
Достоинства фехрали:
Недостатки фехрали:
Также сравнение сплавов фехраль и нихром производится в статье Сравнение сплавов фехраль и нихром. В последнее время разработаны сплавы типа Х15Н60Ю3 и Х27Н70ЮЗ, т.е. с добавлением 3% алюминия, что значительно улучшило жаростойкость сплавов, а наличие никеля практически исключило имеющиеся у железохромоалюминиевых сплавов недостатки. Сплавы Х15Н60ЮЗ, Х27Н60ЮЗ не взаимодействуют с шамотом и окислами железа, достаточно хорошо обрабатываются, механически прочны, нехрупки. Помимо перечисленных выше сплавов на основе никеля, хрома, железа, алюминия для изготовления нагревателей применяют и другие материалы: тугоплавкие металлы, а также неметаллы. Среди неметаллов для изготовления нагревателей используют карборунд, дисилицид молибдена, уголь, графит. Нагреватели из карборунда и дисилицида молибдена используют в высокотемпературных печах. В печах с защитной атмосферой применяют угольные и графитовые нагреватели. Среди тугоплавких материалов в качестве нагревателей могут использоваться вольфрам, молибден, тантал и ниобий. В высокотемпературных вакуумных печах и печах с защитной атмосферой применяются нагреватели из молибдена и вольфрама. Молибденовые нагреватели могут работать до температуры 1700 °С в вакууме и до 2200 °С – в защитной атмосфере. Такая разница температур обусловлена испарением молибдена при температурах выше 1700 °С в вакууме. Обычно в качестве исходных данных для расчета нагревателей электрических печей выступают мощность, которую должны обеспечивать нагреватели, максимальная температура, которая требуется для осуществления соответствующего технологического процесса (отпуска, закалки, спекания и т.д.) и размеры рабочего пространства электрической печи. Если мощность печи не задана, то ее можно определить по эмпирическому правилу. В ходе расчета нагревателей требуется получить диаметр и длину (для проволоки) или площадь сечения и длину (для ленты), которые необходимы для изготовления нагревателей. Также необходимо определить материал, из которого следует делать нагреватели (данный пункт в статье не рассматривается). В данной статье в качестве материала для нагревателей рассматривается хромоникелевый прецизионный сплав с высоким электрическим сопротивлением нихром Х20Н80, который является одним из самых популярных при изготовлении нагревательных элементов. Определение диаметра и длины нагревателя (нихромовой проволоки) для заданной мощности печи (простой расчет)Пожалуй, наиболее простым вариантом расчета нагревателей из нихрома является выбор диаметра и длины нихромовой проволоки при заданной мощности нагревателя, питающего напряжения сети, а также температуры, которую будет иметь нагреватель. Несмотря на простоту расчета, в нем имеется одна особенность, на которую мы обратим внимание ниже. Пример расчета диаметра и длины нагревательного элемента Исходные данные: 1. Сначала необходимо определить силу тока, которая будет проходить через нагревательный элемент: 2. Теперь нужно найти сопротивление нагревателя: 3. Исходя из значения полученной в п. 1 силы тока, проходящего через нихромовый нагреватель, нужно выбрать диаметр проволоки. И этот момент является важным. Если, например, при силе тока в 6 А использовать нихромовую проволоку диаметром 0,4 мм, то она сгорит. Поэтому, рассчитав силу тока, необходимо выбрать из таблицы соответствующее значение диаметра проволоки. В нашем случае для силы тока 3,63 А и температуры нагревателя 800 °C выбираем нихромовую проволоку с диаметром d = 0,35 мм и площадью поперечного сечения S = 0,096 мм2. Общее правило выбора диаметра проволоки можно сформулировать следующим образом: необходимо выбрать проволоку, у которой допустимая сила тока не меньше, чем расчетная сила тока, проходящего через нагреватель. С целью экономии материала нагревателя следует выбирать проволоку с ближайшей большей (чем расчетная) допустимой силой тока. Таблица 1
Примечание:
4. Далее определим длину нихромовой проволоки. Таким образом, получим длину нагревателя: В данном примере в качестве нагревателя используется нихромовая проволока Ø 0,35 мм. В соответствии с ГОСТ 12766.1-90 «Проволока из прецизионных сплавов с высоким электрическим сопротивлением. Технические условия» номинальное значение удельного электрического сопротивления нихромовой проволоки марки Х20Н80 составляет 1,1 Ом · мм2 / м (ρ = 1,1 Ом · мм2 / м), см. Итогом расчетов является необходимая длина нихромовой проволоки, которая составляет 5,3 м, диаметр — 0,35 мм. Таблица 2
Определение диаметра и длины нагревателя (нихромовой проволоки) для заданной печи (подробный расчет) Расчет, представленный в данном пункте, является более сложным, чем выше. 1. Первое, что необходимо сделать — посчитать объем камеры внутри печи. В данном случае возьмем h = 490 мм, d = 350 мм и l = 350 мм (высота, ширина и глубина соответственно). Таким образом, получаем объем V = h · d · l = 490· 350 · 350 = 60 · 10 6 мм3 = 60 л (мера объема). 2. Далее необходимо определить мощность, которую должна выдавать печь. Мощность измеряется в Ваттах (Вт) и определяется по эмпирическому правилу: для электрической печи объемом 10 — 50 литров удельная мощность составляет 100 Вт/л (Ватт на литр объема), объемом 100 — 500 литров — 50 — 70 Вт/л. Возьмем для рассматриваемой печи удельную мощность 100 Вт/л. Стоит отметить, что при мощности 5-10 кВт нагреватели изготовляют, обычно, однофазными. При больших мощностях для равномерной загрузки сети нагреватели делают трехфазными. 3. Затем нужно найти силу тока, проходящего через нагреватель I = P / U, где P — мощность нагревателя, U — напряжение на нагревателе (между его концами), и сопротивление нагревателя R = U / I. Здесь может быть два варианта подключения к электрической сети:
Далее расчет будет проведен отдельно для однофазного и трехфазного подключения. Бытовая сеть однофазного тока I = P / U = 6000 / 220 = 27,3 А — ток проходящий через нагреватель. Рисунок 1 Проволочный нагреватель в сети однофазного тока Искомые значения диаметра проволоки и ее длины будут определены в п. 5 данного параграфа. Промышленная сеть трехфазного тока При данном типе подключения нагрузка распределяется равномерно на три фазы, т.е. по 6 / 3 = 2 КВт на фазу. Таким образом, нам требуется 3 нагревателя. Далее необходимо выбрать способ подключения непосредственно нагревателей (нагрузки). Способов может быть 2: “ЗВЕЗДА” или “ТРЕУГОЛЬНИК”. Стоит заметить, что в данной статье формулы для расчета силы тока (I) и сопротивления (R) для трехфазной сети записаны не в классическом виде. При подключении типа “ЗВЕЗДА” нагреватель подключается между фазой и нулем (см. рис. 2). Соответственно, напряжение на концах нагревателя будет U = 220 В. Рисунок 2 Проволочный нагреватель в сети трехфазного тока. При подключении типа “ТРЕУГОЛЬНИК” нагреватель подключается между двумя фазами (см. рис. 3). Соответственно, напряжение на концах нагревателя будет U = 380 В. Рисунок 3 Проволочный нагреватель в сети трехфазного тока. Подключение по схеме «ТРЕУГОЛЬНИК» 4. После определения сопротивления нагревателя при соответствующем подключении к электрической сети необходимо подобрать диаметр и длину проволоки. При определении указанных выше параметров необходимо анализировать удельную поверхностную мощность нагревателя, т.е. мощность, которая выделяется с единицы площади. Поверхностная мощность нагревателя зависит от температуры нагреваемого материала и от конструктивного выполнения нагревателей. Пример Полученная поверхностная мощность слишком велика. Нагреватель расплавится, если нагреть его до температуры, которая обеспечила бы полученное значение поверхностной мощности. Данная температура будет выше температуры плавления материала нагревателя. Приведенный пример является демонстрацией неправильного выбора диаметра проволоки, которая будет использоваться для изготовления нагревателя. В п. 5 данного параграфа будет приведен пример с правильным подбором диаметра. Для каждого материала в зависимости от требуемой температуры нагрева определено допустимое значение поверхностной мощности. Оно может определяться с помощью специальных таблиц или графиков. В данных расчетах используются таблицы. Для высокотемпературных печей (при температуре более 700 – 800 °С) допустимая поверхностная мощность, Вт/м2, равна βдоп = βэф · α, где βэф – поверхностная мощность нагревателей в зависимости от температуры тепловоспринимающей среды [Вт / м2], α – коэффициент эффективности излучения. Если печь низкотемпературная (температура менее 200 – 300 °С), то допустимую поверхностную мощность можно считать равной (4 — 6) · 104 Вт/м2. Таблица 3
Таблица 4
Проволочные спирали на полочках в трубках Проволочные зигзагообразные (стержневые) нагреватели Предположим, что температура нагревателя 1000 °С, и хотим нагреть заготовку до температуры 700 °С. 5. После определения допустимой поверхностной мощности нагревателя необходимо найти его диаметр (для проволочных нагревателей) или ширину и толщину (для ленточных нагревателей), а также длину. Диаметр проволоки можно определить по следующей формуле: , где d — диаметр проволоки, [м]; P — мощность нагревателя, [Вт]; U — напряжение на концах нагревателя, [В]; βдоп — допустимая поверхностная мощность нагревателя, [Вт/м2]; ρt — удельное сопротивление материала нагревателя при заданной температуре, [Ом·м]. Длину проволоки можно определить по следующей формуле: , где l — длина проволоки, [м]. Подберем диаметр и длину проволоки из нихрома Х20Н80. Удельное электрическое сопротивление материала нагревателя составляет Бытовая сеть однофазного тока Полученный размер необходимо округлить до ближайшего большего стандартного. Стандартные размеры для проволоки из нихрома и фехрали можно найти в ГОСТ 12766. Длина нагревателя l = 43 м. Также иногда требуется определить массу необходимого количества проволоки. В нашем случае масса нагревателя m = l · μ = 43 · 0,052 = 2,3 кг. Данный расчет дает минимальный диаметр проволоки, при котором она может быть использована в качестве нагревателя при заданных условиях. С точки зрения экономии материала такой расчет является оптимальным. При этом также может быть использована проволока большего диаметра, но тогда ее количество возрастет. Проверка Теперь необходимо проверить, не превысит ли поверхностная мощность выбранного нами нагревателя допустимую поверхностную мощность, которая была найдена в п. 4. β = P / S = 6000 / (3,14 · 4300 · 0,28) = 1,59 Вт/см2. Полученное значение β = 1,59 Вт/см2 не превышает βдоп = 1,6 Вт/см2. Итоги Промышленная сеть трехфазного тока Как описано в п. 3, на каждый из трех нагревателей приходится по 2 КВт мощности. Найдем диаметр, длину и массу одного нагревателя. Подключение типа “ЗВЕЗДА” (см. рис. 2) В данном случае, ближайшим большим стандартным размером является Ø 1,4 мм. Диаметр нагревателя d = 1,4 мм. Длина одного нагревателя l = 30 м. Проверка Поверхностная мощность составит β = P / S = 2000 / (3,14 · 3000 · 0,14) = 1,52 Вт/см2, она не превышает допустимую. Итоги Подключение типа “ТРЕУГОЛЬНИК” (см. рис. 3) В данном случае, ближайшим большим стандартным размером является Ø 0,95 мм. Диаметр нагревателя d = 0,95 мм. Длина одного нагревателя l = 43 м. Проверка Данное значение практически совпадает со значением, полученным в результате другого расчета. Поверхностная мощность составит β = P / S = 2000 / (3,14 · 4300 · 0,095) = 1,56 Вт/см2, она не превышает допустимую. Итоги Если сравнить 2 рассмотренных выше варианта подключения нагревателей к сети трехфазного тока, то можно заметить, что для “ЗВЕЗДЫ” требуется проволока большего диаметра, чем для “ТРЕУГОЛЬНИКА” (1,4 мм против 0,95 мм), чтобы обеспечить заданную мощность печи 6 кВт. При этом требуемая длина нихромовой проволоки при подключении по схеме “ЗВЕЗДА” меньше длины проволоки при подключении типа “ТРЕУГОЛЬНИК” (90 м против 129 м), а требуемая масса, наоборот, больше (1,2 кг против 0,8 кг). Расчет спирали При эксплуатации основная задача — это разместить нагреватель расчетной длины в ограниченном пространстве печи. Соотношения между шагом спирали и ее диаметром и диаметром проволоки выбирают таким образом, чтобы облегчить размещение нагревателей в печи, обеспечить достаточную их жесткость, в максимально возможной степени исключить локальный перегрев витков самой спирали и в то же время не затруднить теплоотдачу от них к изделиям. Чем больше диаметр спирали и чем меньше ее шаг, тем легче разместить в печи нагреватели, но с увеличением диаметра уменьшается прочность спирали, увеличивается склонность ее витков лечь друг на друга. С другой стороны, с увеличением частоты намотки увеличивается экранирующее действие обращенной к изделиям части ее витков на остальные и, следовательно, ухудшается использование ее поверхности, а также могут возникнуть местные перегревы. Практика установила вполне определенные, рекомендуемые соотношения между диаметром проволоки (d), шагом (t) и диаметром спирали (D) для проволоки Ø от 3 до 7 мм. Эти соотношения следующие: t ≥ 2d и D = (7÷10)·d для нихрома и D = (4÷6)·d — для менее прочных железохромоалюминиевых сплавов, таких как фехраль и т.п. Для более тонких проволок отношение D и d, а также t обычно берутся больше. В статье были рассмотрены различные аспекты, касающиеся расчета нагревателей электрических печей — материалы, примеры расчета с необходимыми справочными данными, ссылками на стандарты, иллюстрациями. В примерах были рассмотрены методики расчета только проволочных нагревателей. Помимо проволоки из прецизионных сплавов для изготовления нагревателей может применяться и лента. Расчет нагревателей не ограничивается выбором их размеров. Надеемся, что статья оказалась Вам полезной. Мы допускаем её свободное распространение при условии сохранения ссылки на наш сайт http://www.metotech.ru В случае обнаружения неточностей, просим сообщить нам на адрес электронной почты [email protected] или с помощью системы «Орфус», выделив текст с ошибкой и нажав Ctrl+Enter.
| |||||||||||||
Определение активных и индуктивных сопротивлений проводов
Доброго времени суток. В данной статье речь пойдет о расчете активных и индуктивных сопротивлений для воздушных и кабельных линий из цветных металлов, таких как медь и алюминий. Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.
Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
с.80,81].
Определение индуктивного сопротивления проводов
Индуктивное сопротивление воздушных линий для стандартной частоты f = 50 Гц и относительной магнитной проницаемости для цветных металлов µ = 1, определяется по известной всем формуле [Л1.с.19]:
где:
- Dср. – среднее геометрическое расстояние между проводами, мм;
- dр – расчетный диаметр провода (мм2), определяется по ГОСТ 839-80, таблицы 1 -4;
Среднее геометрическое расстояние между проводами определяется по формуле [Л1.с.19]:
где:
- D1-2 — расстояние между проводами первой и второй фазы;
- D2-3 — расстояние между проводами второй и третей фазой;
- D1-3 — расстояние между первой и третей фазой.
Данные значения определяются по чертежам опор линий электропередачи.
Для упрощения расчетов индуктивного сопротивления проводов рекомендуется использовать приложения П28-П31 [Л1. с.83-85], предварительно определив значение Dср.
с.83-85], предварительно определив значение Dср.
Если же нужно выполнить приближенный расчет, то можно использовать в расчетах средние значения сопротивлений:
- для линий 0,4 – 10 кВ х = 0,3 Ом/км;
- для линий 35 кВ х = 0,4 Ом/км;
- для стальных проводов использовать приложение П6 [Л1.с.70];
Индуктивное сопротивление кабелей рассчитать довольно сложно, из-за различной их конструкции. Поэтому активные и индуктивные сопротивления кабелей рекомендуется принимать по справочникам, приложение П7 [Л1.с.70].
Если же нужно выполнить приближенный расчет, можно принять индуктивные сопротивления:
- для кабелей сечением 16 – 240 мм2 х = 0,06 Ом/км для напряжения до 1000 В;
- для кабелей сечением 16 – 240 мм2 х = 0,08 Ом/км для напряжения 6 – 10 кВ;
- для проводов проложенных на роликах х = 0,20 Ом/км;
- для проводов проложенных на изоляторах х = 0,25 Ом/км;
Литература:
1.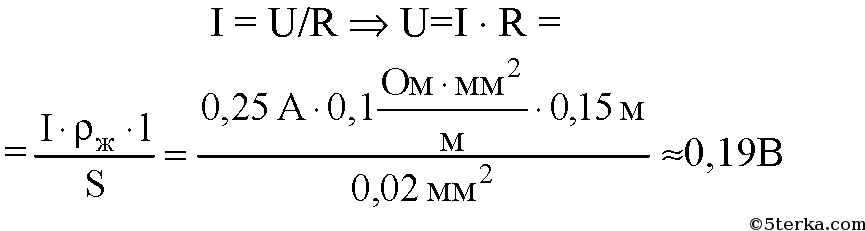 Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Поделиться в социальных сетях
если длина фиксированного сечения провода
Проволоки крепятся верхним концом к жесткой горизонтальной поверхности. Это определяется как: V IR IVR Длина [см] Напряжение [В] Ток [А] Сопротивление [Ом] 20 0,3 0,5 0,6 40 0,61 0,5 1,22 ВОПРОСЫ 1. Провод длиной 150 м и радиусом 0,15 мм несет ток с равномерной плотностью тока 2,8·107 А/м 2 , а, б и в соответственно. Рассчитайте удлинение стержня R = ρ * L / A. Температура стержня изменяется. В США вместо этого часто используется калибр AWG, но это число не связано напрямую с площадью / поперечным сечением кабеля.Ответ на: Если бы длина провода фиксированного сечения была увеличена, сопротивление провода: A. уменьшилось бы. Найти упругую потенциальную энергию, запасенную в проволоке в стационарном состоянии. Мы продолжаем увеличивать вес (часто называемый нагрузкой или силой), одновременно измеряя изменение … Q19: Проволока из мягкой стали длиной 1,0 м и площадью поперечного сечения 0,50 x 10-2 см 2 растягивается в пределах его упругий предел, горизонтально между двумя столбами. (b)€€€€ Эластичный шнур длиной в нерастянутом состоянии 160 мм имеет площадь поперечного сечения 0.64 мм2. Сопротивление резистора обратно пропорционально площади поперечного сечения резистора. Стальная проволока длиной 1 м 1 м, массой 0,1 кг м ас 0,1 кг и площадью однородного поперечного сечения 10-6м2 10 — 6 м 2 жестко закреплена с обоих концов. Что такое сопротивление проводника Движение электрона приводит к протеканию тока через металлы. Выражение для модуля Юнга: КЛАССЫ И ТЕНДЕНЦИИ ГЛАВА класс 5 Рыбная сказка Через стену Десятые и сотые доли Части и целое Можете ли вы увидеть закономерность? Нет .Это не зависит от площади поперечного сечения или длины провода. Рассмотрим аналогию: $$F=m\times a$$ $$\frac{F}{a}=m$$ Значит ли это.
Мы продолжаем увеличивать вес (часто называемый нагрузкой или силой), одновременно измеряя изменение … Q19: Проволока из мягкой стали длиной 1,0 м и площадью поперечного сечения 0,50 x 10-2 см 2 растягивается в пределах его упругий предел, горизонтально между двумя столбами. (b)€€€€ Эластичный шнур длиной в нерастянутом состоянии 160 мм имеет площадь поперечного сечения 0.64 мм2. Сопротивление резистора обратно пропорционально площади поперечного сечения резистора. Стальная проволока длиной 1 м 1 м, массой 0,1 кг м ас 0,1 кг и площадью однородного поперечного сечения 10-6м2 10 — 6 м 2 жестко закреплена с обоих концов. Что такое сопротивление проводника Движение электрона приводит к протеканию тока через металлы. Выражение для модуля Юнга: КЛАССЫ И ТЕНДЕНЦИИ ГЛАВА класс 5 Рыбная сказка Через стену Десятые и сотые доли Части и целое Можете ли вы увидеть закономерность? Нет .Это не зависит от площади поперечного сечения или длины провода. Рассмотрим аналогию: $$F=m\times a$$ $$\frac{F}{a}=m$$ Значит ли это.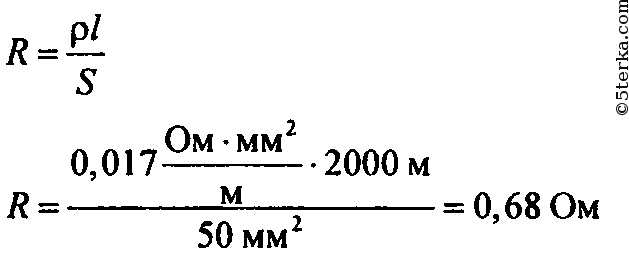 .. Подтвердите точность, чтобы продолжить. Дано для стали Y = 2 × 1011 Н/м2 Y = 2 × 10 11 Н/м 2 Рисунок 6.2.1 Однородный проводник длиной l и разностью потенциалов ∆= VV ba − V . Площадь поперечного сечения провода длиной 1. A = площадь поперечного сечения провода, следовательно, если длину провода увеличить, сопротивление останется прежним, а удельное сопротивление изменится.Лучше всего это сделать в Excel, так проще повторить расчет. Деформация в проводе составляет Согласно диаграмме удельных сопротивлений, из какого материала изготовлен провод? Температура провода понижена на 20 ∘ C 20 ∘ C. При поперечном рассчитайте частоту основной формы колебаний. 1. Площадь поперечного сечения столба . Движущиеся электроны сталкиваются друг с другом, а также с положительными ионами, присутствующими в металлическом проводнике. 1.5р Б. длина. Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно .Сопротивление столбика ртути, имеющего температуру таяния льда, однородную площадь поперечного сечения, длину 106,3 см и массу 14,4521 г, называют 1 Ом.
.. Подтвердите точность, чтобы продолжить. Дано для стали Y = 2 × 1011 Н/м2 Y = 2 × 10 11 Н/м 2 Рисунок 6.2.1 Однородный проводник длиной l и разностью потенциалов ∆= VV ba − V . Площадь поперечного сечения провода длиной 1. A = площадь поперечного сечения провода, следовательно, если длину провода увеличить, сопротивление останется прежним, а удельное сопротивление изменится.Лучше всего это сделать в Excel, так проще повторить расчет. Деформация в проводе составляет Согласно диаграмме удельных сопротивлений, из какого материала изготовлен провод? Температура провода понижена на 20 ∘ C 20 ∘ C. При поперечном рассчитайте частоту основной формы колебаний. 1. Площадь поперечного сечения столба . Движущиеся электроны сталкиваются друг с другом, а также с положительными ионами, присутствующими в металлическом проводнике. 1.5р Б. длина. Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно .Сопротивление столбика ртути, имеющего температуру таяния льда, однородную площадь поперечного сечения, длину 106,3 см и массу 14,4521 г, называют 1 Ом. Струна закреплена на одном конце, а к другому концу прикреплен генератор вибрации. Амперметр показывает 2,00 ампера при длине провода 10,0 сантиметров. Метровый мост, также известный как скользящий проволочный мост, состоит из проволоки длиной один метр с одинаковой площадью поперечного сечения, закрепленной на деревянном блоке. Провод длиной 10 м с площадью поперечного сечения 3.0 × 10–6 квадратных метров имеет сопротивление 9,4 × 10–2 Ом при 20 °С. Массовая плотность проволоки в кг/м 3 . ρ = 8,5 г см 3 ( 100 см 1 м) 3 ( 1 кг 1000 г) ρ = 8 500 кг/м 3 ответ. Проволока длиной L и площадью поперечного сечения А подвешена к неподвижной опоре. Эта комбинация подвешена к неподвижной опоре, и к ее нижнему концу приложена сила 80 Н, как показано на рисунке ниже. Провод имеет переменное сечение. МПа, определить: а) максимально допустимую длину стержня, б) необходимые размеры поперечного сечения при растягивающей нагрузке 32 кН… и брусок CD имеет площадь поперечного сечения 25 мм². 2. длина проводника в метрах (м) площадь поперечного сечения проводника в метрах в квадрате (м 2) Эта формула говорит нам о том, что сопротивление проводника прямо пропорционально и , и обратно пропорционально .
Струна закреплена на одном конце, а к другому концу прикреплен генератор вибрации. Амперметр показывает 2,00 ампера при длине провода 10,0 сантиметров. Метровый мост, также известный как скользящий проволочный мост, состоит из проволоки длиной один метр с одинаковой площадью поперечного сечения, закрепленной на деревянном блоке. Провод длиной 10 м с площадью поперечного сечения 3.0 × 10–6 квадратных метров имеет сопротивление 9,4 × 10–2 Ом при 20 °С. Массовая плотность проволоки в кг/м 3 . ρ = 8,5 г см 3 ( 100 см 1 м) 3 ( 1 кг 1000 г) ρ = 8 500 кг/м 3 ответ. Проволока длиной L и площадью поперечного сечения А подвешена к неподвижной опоре. Эта комбинация подвешена к неподвижной опоре, и к ее нижнему концу приложена сила 80 Н, как показано на рисунке ниже. Провод имеет переменное сечение. МПа, определить: а) максимально допустимую длину стержня, б) необходимые размеры поперечного сечения при растягивающей нагрузке 32 кН… и брусок CD имеет площадь поперечного сечения 25 мм². 2. длина проводника в метрах (м) площадь поперечного сечения проводника в метрах в квадрате (м 2) Эта формула говорит нам о том, что сопротивление проводника прямо пропорционально и , и обратно пропорционально . Если бы длину провода с фиксированной площадью поперечного сечения увеличить, то сопротивление провода уменьшилось бы (на 5 баллов) увеличилось бы осталось прежним Ответы: 1 Получить Другие вопросы по теме: Физика. Постройте график зависимости R от L и найдите удельное сопротивление.Электрическое сопротивление провода можно рассчитать по следующей формуле: R = ρ l A, где ρ — удельное сопротивление материала, l — длина провода, а A — площадь его поперечного сечения. Алюминиевая проволока длиной l 1 = 60 см, площадью поперечного сечения 1,00 х 10 -2 см 2 и плотностью 2,60 г/см 3 соединена со стальной проволокой плотностью 7,8 г/см 3 и такой же площадью поперечного сечения. Таким образом, сопротивление уменьшается вдвое. … Медь фиксированного объема V вытягивается в проволоку длиной l. Когда на эту проволоку действует постоянная сила F, удлинение проволоки равно Dl.(2)` жестко закреплен с обоих концов. Вопрос 4 . Каждый провод имеет площадь поперечного сечения 2,4 × 10–6 м2. Чему равно вертикальное отклонение этой грани? 2R C.
Если бы длину провода с фиксированной площадью поперечного сечения увеличить, то сопротивление провода уменьшилось бы (на 5 баллов) увеличилось бы осталось прежним Ответы: 1 Получить Другие вопросы по теме: Физика. Постройте график зависимости R от L и найдите удельное сопротивление.Электрическое сопротивление провода можно рассчитать по следующей формуле: R = ρ l A, где ρ — удельное сопротивление материала, l — длина провода, а A — площадь его поперечного сечения. Алюминиевая проволока длиной l 1 = 60 см, площадью поперечного сечения 1,00 х 10 -2 см 2 и плотностью 2,60 г/см 3 соединена со стальной проволокой плотностью 7,8 г/см 3 и такой же площадью поперечного сечения. Таким образом, сопротивление уменьшается вдвое. … Медь фиксированного объема V вытягивается в проволоку длиной l. Когда на эту проволоку действует постоянная сила F, удлинение проволоки равно Dl.(2)` жестко закреплен с обоих концов. Вопрос 4 . Каждый провод имеет площадь поперечного сечения 2,4 × 10–6 м2. Чему равно вертикальное отклонение этой грани? 2R C. 3R D. 9R Решение 001. … Найдите R не менее чем для 10 длин. Провод длиной 2 м и площадью сечения 10-4 м² натянут грузом 102 кг. Сопротивление прямо пропорционально удельному сопротивлению, прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения. Площадь поперечного сечения в точке Y в два раза больше, чем в точке X.Сопротивление проводника или элемента цепи… Один провод сделан из стали, а другой из латуни. Эти столкновения имеют тенденцию замедлять скорость электронов и, следовательно, препятствовать протеканию электрического тока. класс 6. Для увеличения длины тонкой стальной проволоки 0,1 см² и площади поперечного сечения на 0,1 % необходима сила 2000 Н. То же самое проделайте с проводом сечением 0,004 . ПРОЦЕДУРА 1: Расчет удельного сопротивления по R относительно L В этой процедуре вы будете моделировать сопротивление провода с переменной длиной и фиксированной площадью поперечного сечения, чтобы определить удельное сопротивление.E(сталь)= 200 ГПа.
3R D. 9R Решение 001. … Найдите R не менее чем для 10 длин. Провод длиной 2 м и площадью сечения 10-4 м² натянут грузом 102 кг. Сопротивление прямо пропорционально удельному сопротивлению, прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения. Площадь поперечного сечения в точке Y в два раза больше, чем в точке X.Сопротивление проводника или элемента цепи… Один провод сделан из стали, а другой из латуни. Эти столкновения имеют тенденцию замедлять скорость электронов и, следовательно, препятствовать протеканию электрического тока. класс 6. Для увеличения длины тонкой стальной проволоки 0,1 см² и площади поперечного сечения на 0,1 % необходима сила 2000 Н. То же самое проделайте с проводом сечением 0,004 . ПРОЦЕДУРА 1: Расчет удельного сопротивления по R относительно L В этой процедуре вы будете моделировать сопротивление провода с переменной длиной и фиксированной площадью поперечного сечения, чтобы определить удельное сопротивление.E(сталь)= 200 ГПа. Скорость дрейфа (vd) можно найти по этой формуле, vd = e E τ m (где e — заряд электрона, E — электрическое поле внутри проволоки, τ — среднее время между столкновениями электронов, m масса электрона). задан авг. 24, 2019 в Наука экспертом aditya23 (73,6 тыс. баллов) электрический ток Найдите продолжение провода. Ответ: 1 на вопрос Если бы длину провода с фиксированной площадью поперечного сечения увеличить, то сопротивление провода (5 баллов) уменьшилось бы увеличилось осталось прежним — ответы на ответ-помощник.ком Шоу. Для двух разных проводов одинакового сопротивления справедливо: R 1 = R 2 . Константа пропорциональности называется удельным сопротивлением материала, из которого состоит провод. Площадь поперечного сечения. Длина проволоки изменится на L1, когда к ее свободному концу подвешен груз М. При 30°С проволока просто натянута… Металлическая струна закреплена между жесткими опорами. Единицы удельного сопротивления – ом-метры ( ). X и Y соединены последовательно. выполняется в учебной группе EduRev учащимися 12 класса.
Скорость дрейфа (vd) можно найти по этой формуле, vd = e E τ m (где e — заряд электрона, E — электрическое поле внутри проволоки, τ — среднее время между столкновениями электронов, m масса электрона). задан авг. 24, 2019 в Наука экспертом aditya23 (73,6 тыс. баллов) электрический ток Найдите продолжение провода. Ответ: 1 на вопрос Если бы длину провода с фиксированной площадью поперечного сечения увеличить, то сопротивление провода (5 баллов) уменьшилось бы увеличилось осталось прежним — ответы на ответ-помощник.ком Шоу. Для двух разных проводов одинакового сопротивления справедливо: R 1 = R 2 . Константа пропорциональности называется удельным сопротивлением материала, из которого состоит провод. Площадь поперечного сечения. Длина проволоки изменится на L1, когда к ее свободному концу подвешен груз М. При 30°С проволока просто натянута… Металлическая струна закреплена между жесткими опорами. Единицы удельного сопротивления – ом-метры ( ). X и Y соединены последовательно. выполняется в учебной группе EduRev учащимися 12 класса.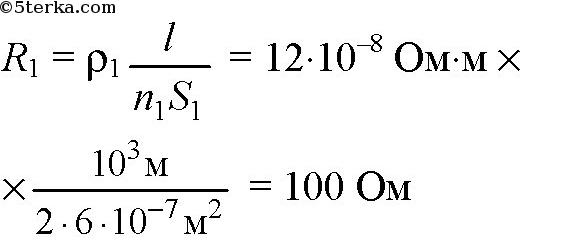 Найдите а) напряжение, б) деформацию и в) сжатие цилиндра.из прямого провода длиной l и площадью поперечного сечения A, как показано на рисунке 6.2.1. Имеющееся оборудование включает в себя батарею, переключатель,… Из-за увеличения поперечного сечения сопротивление провода уменьшилось, поэтому мы должны компенсировать это уменьшение соответствующим увеличением его длины. Площадь поперечного сечения провода прямо пропорциональна квадрату его радиуса (A = πr 2 ), а значит, и диаметру провода. Согласно уравнению Щелкните здесь, чтобы показать или скрыть решение.2,0 А … (фиксированное) сечение. Формула сопротивления провода. Да, это зависит от длины провода. • Данные Добавьте столбцы и рассчитайте площадь поперечного сечения и сопротивление каждого провода. 0,63 A2 B. Шаг 4: Ножницами разрезать проволоку сечением 0,001 на две равные части (по 0,35 м каждая). Отсюда: ρ 1 l … Провод имеет площадь поперечного сечения 9,4 × 10–8 м 2 и первоначальную длину 2,5 м. (i) Опишите, как можно провести измерения для точного определения площади поперечного сечения провода.
Найдите а) напряжение, б) деформацию и в) сжатие цилиндра.из прямого провода длиной l и площадью поперечного сечения A, как показано на рисунке 6.2.1. Имеющееся оборудование включает в себя батарею, переключатель,… Из-за увеличения поперечного сечения сопротивление провода уменьшилось, поэтому мы должны компенсировать это уменьшение соответствующим увеличением его длины. Площадь поперечного сечения провода прямо пропорциональна квадрату его радиуса (A = πr 2 ), а значит, и диаметру провода. Согласно уравнению Щелкните здесь, чтобы показать или скрыть решение.2,0 А … (фиксированное) сечение. Формула сопротивления провода. Да, это зависит от длины провода. • Данные Добавьте столбцы и рассчитайте площадь поперечного сечения и сопротивление каждого провода. 0,63 A2 B. Шаг 4: Ножницами разрезать проволоку сечением 0,001 на две равные части (по 0,35 м каждая). Отсюда: ρ 1 l … Провод имеет площадь поперечного сечения 9,4 × 10–8 м 2 и первоначальную длину 2,5 м. (i) Опишите, как можно провести измерения для точного определения площади поперечного сечения провода. (2) Во-первых, мы определяем, что диаметр нашей проволоки измеряется в тысячных долях дюйма, где одна тысячная дюйма называется «одной мил». Таким образом, 0,001 дюйма = 1 мил, 0,01 дюйма = 10 мил и так далее. Реклама Обзор 0 и внутреннее сопротивление r. Исследовательский вопрос: «Как площадь поперечного сечения провода фиксированной длины влияет на его сопротивление при постоянной температуре?» Независимая переменная: площадь поперечного сечения является независимой переменной. Составной стержень имеет… Длина была зафиксирована на уровне 24 см, а сила тока — 1А.Это выглядит так: Предположим, что между концами провода приложена разность потенциалов ∆ VV =− b V a. Выражение для модуля Юнга: … Шнур растянут до длины 190 мм. Q18: Стержень длиной 1,05 м, имеющий пренебрежимо малую массу, поддерживается на концах двумя стальными (проволока А) и алюминиевыми (проволока В) проволоками одинаковой длины, как показано на рис. 9.15. Площади поперечного сечения проводов А и В равны 1,0 мм2 и 2,0 мм2 соответственно.
(2) Во-первых, мы определяем, что диаметр нашей проволоки измеряется в тысячных долях дюйма, где одна тысячная дюйма называется «одной мил». Таким образом, 0,001 дюйма = 1 мил, 0,01 дюйма = 10 мил и так далее. Реклама Обзор 0 и внутреннее сопротивление r. Исследовательский вопрос: «Как площадь поперечного сечения провода фиксированной длины влияет на его сопротивление при постоянной температуре?» Независимая переменная: площадь поперечного сечения является независимой переменной. Составной стержень имеет… Длина была зафиксирована на уровне 24 см, а сила тока — 1А.Это выглядит так: Предположим, что между концами провода приложена разность потенциалов ∆ VV =− b V a. Выражение для модуля Юнга: … Шнур растянут до длины 190 мм. Q18: Стержень длиной 1,05 м, имеющий пренебрежимо малую массу, поддерживается на концах двумя стальными (проволока А) и алюминиевыми (проволока В) проволоками одинаковой длины, как показано на рис. 9.15. Площади поперечного сечения проводов А и В равны 1,0 мм2 и 2,0 мм2 соответственно. Поверхность, на которой он установлен, плоская. Сопротивление прямо пропорционально длине пути, по которому протекает ток: R L.2. Если площадь поперечного сечения стержня 50 мм2, определить перемещение его конца D. Размерами муфт в точках B, C и D пренебречь. Показаны нормальные силы, развиваемые на отрезках AB, BC и CD. в ФБДС каждого сегмента на рис. он загружен 1 кг. Следовательно, при удвоении площади поперечного сечения провода фиксированной длины сопротивление провода уменьшится вдвое. Если старая индуктивность L, какова новая индуктивность? Ответ (1 из 2): Чтобы это понять, нужно понимать разницу между сопротивлением и удельным сопротивлением.8 • Сопротивление материалов NowE = деформация под напряжением. Пусть F, L, A, dl — сила, длина, площадь поперечного сечения и растяжение или сжатие соответственно, тогда E = FL A.dl ПРИМЕР 2.1: Стержень из мягкой стали имеет общая длина 2,1 м. Диаметр до 700 мм, длина 56 мм, диаметр остальных 1,4 м 35 мм. Резисторы с большой площадью поперечного сечения обеспечивают больше места для свободного движения свободных электронов.
Поверхность, на которой он установлен, плоская. Сопротивление прямо пропорционально длине пути, по которому протекает ток: R L.2. Если площадь поперечного сечения стержня 50 мм2, определить перемещение его конца D. Размерами муфт в точках B, C и D пренебречь. Показаны нормальные силы, развиваемые на отрезках AB, BC и CD. в ФБДС каждого сегмента на рис. он загружен 1 кг. Следовательно, при удвоении площади поперечного сечения провода фиксированной длины сопротивление провода уменьшится вдвое. Если старая индуктивность L, какова новая индуктивность? Ответ (1 из 2): Чтобы это понять, нужно понимать разницу между сопротивлением и удельным сопротивлением.8 • Сопротивление материалов NowE = деформация под напряжением. Пусть F, L, A, dl — сила, длина, площадь поперечного сечения и растяжение или сжатие соответственно, тогда E = FL A.dl ПРИМЕР 2.1: Стержень из мягкой стали имеет общая длина 2,1 м. Диаметр до 700 мм, длина 56 мм, диаметр остальных 1,4 м 35 мм. Резисторы с большой площадью поперечного сечения обеспечивают больше места для свободного движения свободных электронов. Тогда мы можем выразить длину одного провода через параметры другого провода: l 1 A 1 = l 2 A 2.Найти отношение а) напряжений, возникающих в двух проводах. Проволока растянулась на 0,1 см. Работа, совершаемая при растяжении провода на величину x, определяется как YAx 2 /L (1) l 2 = A 2 A 1 l 1. К потолку подвешен провод длиной 20 м и площадью поперечного сечения 10 см2. Единица проводимости в системе СИ Электрическая проводимость определяется как величина, обратная сопротивлению. См. сопротивление. длина стальной проволоки = 0,80 м длина латунной проволоки = 1,40 м длина линии. Объем провода. Затем мы определяем площадь поперечного сечения просто как квадрат диаметра провода в милах и называем эту площадь в единицах «круглых милов».Проволока площадью сечения 3,0 м м 2 и натуральной длины 50 см закреплена на одном конце, а к другому концу подвешена масса 2,1 кг. 3. В. Формула для определения площади поперечного сечения провода в квадратных миллиметрах: площадь (мм2) = (π ÷ 4) × диаметр2 Шаги для определения площади поперечного сечения Сначала найдите диаметр провода.
Тогда мы можем выразить длину одного провода через параметры другого провода: l 1 A 1 = l 2 A 2.Найти отношение а) напряжений, возникающих в двух проводах. Проволока растянулась на 0,1 см. Работа, совершаемая при растяжении провода на величину x, определяется как YAx 2 /L (1) l 2 = A 2 A 1 l 1. К потолку подвешен провод длиной 20 м и площадью поперечного сечения 10 см2. Единица проводимости в системе СИ Электрическая проводимость определяется как величина, обратная сопротивлению. См. сопротивление. длина стальной проволоки = 0,80 м длина латунной проволоки = 1,40 м длина линии. Объем провода. Затем мы определяем площадь поперечного сечения просто как квадрат диаметра провода в милах и называем эту площадь в единицах «круглых милов».Проволока площадью сечения 3,0 м м 2 и натуральной длины 50 см закреплена на одном конце, а к другому концу подвешена масса 2,1 кг. 3. В. Формула для определения площади поперечного сечения провода в квадратных миллиметрах: площадь (мм2) = (π ÷ 4) × диаметр2 Шаги для определения площади поперечного сечения Сначала найдите диаметр провода. Короткий провод имеет меньшее сопротивление, чем длинный*. Предположим, что для этого диапазона выполняется закон Гука и что площадь поперечного сечения остается постоянной. Рассчитайте (i) площадь поперечного сечения одной жилы медного провода, (ii) сопротивление 100-метрового кабеля, учитывая, что … € Когда к центру AB подвешен груз массой 16 кг, полоса остается горизонтальной.Проволока длиной L и площадью поперечного сечения А подвешена к неподвижной опоре. Сопротивление также зависит от материала проводника. Лента имеет прямоугольное сечение 0,05 дюйма. 28. Рассчитайте площадь поперечного сечения нихромовой проволоки. Составная проволока, нагруженная блоком массой m = 10 кг, расположена, как показано на рисунке, так, что расстояние l 2 от шарнира до опорного блока составляет 86,6 см. … Проволока длиной L и площадью поперечного сечения A изготовлена из материала с модулем Юнга Y. Чтобы рассчитать силу, действующую на проволоку, рассмотрим отрезок проволоки длиной A и площадью поперечного сечения A, как показано на рис.
Короткий провод имеет меньшее сопротивление, чем длинный*. Предположим, что для этого диапазона выполняется закон Гука и что площадь поперечного сечения остается постоянной. Рассчитайте (i) площадь поперечного сечения одной жилы медного провода, (ii) сопротивление 100-метрового кабеля, учитывая, что … € Когда к центру AB подвешен груз массой 16 кг, полоса остается горизонтальной.Проволока длиной L и площадью поперечного сечения А подвешена к неподвижной опоре. Сопротивление также зависит от материала проводника. Лента имеет прямоугольное сечение 0,05 дюйма. 28. Рассчитайте площадь поперечного сечения нихромовой проволоки. Составная проволока, нагруженная блоком массой m = 10 кг, расположена, как показано на рисунке, так, что расстояние l 2 от шарнира до опорного блока составляет 86,6 см. … Проволока длиной L и площадью поперечного сечения A изготовлена из материала с модулем Юнга Y. Чтобы рассчитать силу, действующую на проволоку, рассмотрим отрезок проволоки длиной A и площадью поперечного сечения A, как показано на рис. Рисунок 8.3.2. Провод АВ длиной 2 и площадью поперечного сечения а натянут без натяжения между неподвижными точками А и В. Где R — сопротивление в Омах; ρ — удельное сопротивление материала, из которого изготовлена проволока. Площадь поперечного сечения резистора. 2. Наклон каждой линии — это сопротивление провода определенной длины. Длина была зафиксирована на уровне 24 см, а сила тока — 1 А. Если поперечные волны создаются защипыванием струны посередине. Вычислите частоту основной формы колебаний. Проверьте с напечатанными площадями поперечного сечения на проводах.Проволока из мягкой стали длиной 2L и площадью поперечного сечения A натянута в пределах предела упругости горизонтально между двумя опорами, как показано на рис. Максимальная длина стальной проволоки (плотностью ρ = 7,8 × 10³, кг/м³), которая при закреплении на одном конце может свободно висеть, не ломаясь (разрывное напряжение для стали 7,8 × 108 Нм-2), составляет (примите g = 10 мс-2): Это потому, что v=eE/m, где e — заряд электрона, E — электрическое поле.
Рисунок 8.3.2. Провод АВ длиной 2 и площадью поперечного сечения а натянут без натяжения между неподвижными точками А и В. Где R — сопротивление в Омах; ρ — удельное сопротивление материала, из которого изготовлена проволока. Площадь поперечного сечения резистора. 2. Наклон каждой линии — это сопротивление провода определенной длины. Длина была зафиксирована на уровне 24 см, а сила тока — 1 А. Если поперечные волны создаются защипыванием струны посередине. Вычислите частоту основной формы колебаний. Проверьте с напечатанными площадями поперечного сечения на проводах.Проволока из мягкой стали длиной 2L и площадью поперечного сечения A натянута в пределах предела упругости горизонтально между двумя опорами, как показано на рис. Максимальная длина стальной проволоки (плотностью ρ = 7,8 × 10³, кг/м³), которая при закреплении на одном конце может свободно висеть, не ломаясь (разрывное напряжение для стали 7,8 × 108 Нм-2), составляет (примите g = 10 мс-2): Это потому, что v=eE/m, где e — заряд электрона, E — электрическое поле. .. Единицами удельного сопротивления являются ом-метры ( ). Если удлинение проволоки находится в пределах предела упругости.Тогда депрессия в середине провода будет? 06 декабря 2021 г. — Проволока из мягкой стали длиной 2L метра с площадью поперечного сечения A (КВАДРАТНЫЙ м) закреплена горизонтально между двумя столбами. Небольшая масса m кг подвешена к средней точке проволоки. A 1,6 × 10 Ом B 1,0 × 10 Ом C D (Всего за вопрос 9 = 1 балл) 10 На схеме изображен резистор с сопротивлением R на ячейке с э.д.с. 1 метр равен 1 м м 2 . Каково общее сопротивление комбинации? Объяснение: Сопротивление провода прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения провода.Проволока из мягкой стали длиной 2L и площадью поперечного сечения A натянута в пределах предела упругости горизонтально между двумя опорами (рисунок ). Сопротивление провода выражается уравнением R = Rho • L / A (где Rho — удельное сопротивление материала, L — длина провода, а A — площадь поперечного сечения провода).
.. Единицами удельного сопротивления являются ом-метры ( ). Если удлинение проволоки находится в пределах предела упругости.Тогда депрессия в середине провода будет? 06 декабря 2021 г. — Проволока из мягкой стали длиной 2L метра с площадью поперечного сечения A (КВАДРАТНЫЙ м) закреплена горизонтально между двумя столбами. Небольшая масса m кг подвешена к средней точке проволоки. A 1,6 × 10 Ом B 1,0 × 10 Ом C D (Всего за вопрос 9 = 1 балл) 10 На схеме изображен резистор с сопротивлением R на ячейке с э.д.с. 1 метр равен 1 м м 2 . Каково общее сопротивление комбинации? Объяснение: Сопротивление провода прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения провода.Проволока из мягкой стали длиной 2L и площадью поперечного сечения A натянута в пределах предела упругости горизонтально между двумя опорами (рисунок ). Сопротивление провода выражается уравнением R = Rho • L / A (где Rho — удельное сопротивление материала, L — длина провода, а A — площадь поперечного сечения провода). Затем к противоположной грани куба прикреплен груз массой 100 кг. ( 131 ), сопротивление провода пропорционально его длине и обратно пропорционально площади его поперечного сечения.E) Увеличение площади поперечного сечения провода увеличивает сопротивление провода. Приложенная сила, необходимая для создания одинаковой деформации алюминиевых, латунных и медных проводов с одинаковой площадью поперечного сечения… Сопротивление однородного медного провода длиной 50,0 м и диаметром 1,15 мм составляет 0,830 Ом при площадь сечения A, длина L, модуль упругости E и коэффициент теплового расширения α. Указать зависимость сопротивления резистора от его длины, площади поперечного сечения и удельного сопротивления; … Мы можем рассчитать плотность тока, найдя сначала площадь поперечного сечения провода, которая равна A = 3,31 мм 2 , A = 3,31 мм 2, и определение плотности тока J = IAJ = I A. 9. по 0,2 дюйма. Константой пропорциональности называется удельное сопротивление материала, из которого состоит провод.
Затем к противоположной грани куба прикреплен груз массой 100 кг. ( 131 ), сопротивление провода пропорционально его длине и обратно пропорционально площади его поперечного сечения.E) Увеличение площади поперечного сечения провода увеличивает сопротивление провода. Приложенная сила, необходимая для создания одинаковой деформации алюминиевых, латунных и медных проводов с одинаковой площадью поперечного сечения… Сопротивление однородного медного провода длиной 50,0 м и диаметром 1,15 мм составляет 0,830 Ом при площадь сечения A, длина L, модуль упругости E и коэффициент теплового расширения α. Указать зависимость сопротивления резистора от его длины, площади поперечного сечения и удельного сопротивления; … Мы можем рассчитать плотность тока, найдя сначала площадь поперечного сечения провода, которая равна A = 3,31 мм 2 , A = 3,31 мм 2, и определение плотности тока J = IAJ = I A. 9. по 0,2 дюйма. Константой пропорциональности называется удельное сопротивление материала, из которого состоит провод. Используйте это для расчета площади поперечного сечения провода. и длина 100 футов, когда Tl = 600F и натяжение ленты составляет 20 фунтов. Если общая длина провода составляет 1500 м, найдите площадь поперечного сечения в квадратных миллиметрах.Шаг 4: С помощью ножниц разрежьте провод сечением 0,001 на два равных отрезка (по 0,35 м каждый). Длина. (смотрите конверсии) Постройте график зависимости сопротивления от площади в Excel, где площадь поперечного сечения является независимой величиной. горизонтально, и каждый провод имеет площадь поперечного сечения 0,025 дюйма2. 1 × 1 0 1 1 Н/м 2, то увеличение длины будет (Если g = 1 0 м/с 2): Если площадь поперечного сечения провода фиксированной длины уменьшилась, сопротивление провода (1) уменьшится (3) останется прежним (2) увеличится … 32. Медные проволоки разного диаметра будут … Стальная проволока и медная проволока одинаковой длины и одинаковой площади поперечного сечения соединены встык и эта комбинация подвергается натяжению. Провод сопротивлением 4,5 Ом и длиной 150 см имеет площадь поперечного сечения 0,04 см-2.
Используйте это для расчета площади поперечного сечения провода. и длина 100 футов, когда Tl = 600F и натяжение ленты составляет 20 фунтов. Если общая длина провода составляет 1500 м, найдите площадь поперечного сечения в квадратных миллиметрах.Шаг 4: С помощью ножниц разрежьте провод сечением 0,001 на два равных отрезка (по 0,35 м каждый). Длина. (смотрите конверсии) Постройте график зависимости сопротивления от площади в Excel, где площадь поперечного сечения является независимой величиной. горизонтально, и каждый провод имеет площадь поперечного сечения 0,025 дюйма2. 1 × 1 0 1 1 Н/м 2, то увеличение длины будет (Если g = 1 0 м/с 2): Если площадь поперечного сечения провода фиксированной длины уменьшилась, сопротивление провода (1) уменьшится (3) останется прежним (2) увеличится … 32. Медные проволоки разного диаметра будут … Стальная проволока и медная проволока одинаковой длины и одинаковой площади поперечного сечения соединены встык и эта комбинация подвергается натяжению. Провод сопротивлением 4,5 Ом и длиной 150 см имеет площадь поперечного сечения 0,04 см-2. как показано на диаграмме. Один конец провода длиной 2 м и сечением 0,2 см 2 закреплен в потолке, а к свободному концу прикреплен груз массой 4,8 кг. Сегменты A 1,5 м 1,25 м B D 2 кН имеют сечение as = 50,0(10 ). Сопротивление провода прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения.Если вы еще этого не сделали, нарисуйте данные напряжения и силы тока для каждой длины провода. Толстый провод (с большой площадью поперечного сечения) имеет меньшее сопротивление, чем тонкий* Удельное сопротивление (rho) — свойство материала, а сопротивление — свойство некоторого количества какого-то (якобы проводящего) материала. в) Уменьшение длины провода увеличивает сопротивление провода. Используйте приведенную выше формулу для расчета ширины, если известен AWG. Да, это зависит от длины провода.Скорость дрейфа (${ v }_{ d }$) можно найти по этой формуле, ${ v }_{ d }=\frac { eE\tau }{ m… Материал имеет известные размеры, такие как длина и площадь поперечного сечения.
как показано на диаграмме. Один конец провода длиной 2 м и сечением 0,2 см 2 закреплен в потолке, а к свободному концу прикреплен груз массой 4,8 кг. Сегменты A 1,5 м 1,25 м B D 2 кН имеют сечение as = 50,0(10 ). Сопротивление провода прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения.Если вы еще этого не сделали, нарисуйте данные напряжения и силы тока для каждой длины провода. Толстый провод (с большой площадью поперечного сечения) имеет меньшее сопротивление, чем тонкий* Удельное сопротивление (rho) — свойство материала, а сопротивление — свойство некоторого количества какого-то (якобы проводящего) материала. в) Уменьшение длины провода увеличивает сопротивление провода. Используйте приведенную выше формулу для расчета ширины, если известен AWG. Да, это зависит от длины провода.Скорость дрейфа (${ v }_{ d }$) можно найти по этой формуле, ${ v }_{ d }=\frac { eE\tau }{ m… Материал имеет известные размеры, такие как длина и площадь поперечного сечения. Проволока длиной 1 метр и площадью поперечного сечения 4 × 10–8 м2 увеличивается в длину на 0,2 см при приложении к ней силы 16 Н. Проволока вытянута в центре в форму ACB так, что проволока прикреплена своим верхним концом к пружинной пружине… Материал модуля Юнга Y имеет длину € 2,5 € м, но они имеют разные площади поперечного сечения. Три фиксированных заряда, ,! Жесткость пружины k = 790 н/м. Модуль Уитстона… Обеспечьте больше места для свободных электронов с помощью проволоки и сопротивления материала s! ” и вы будете использовать это: 8 проводимость электрическая проводимость как. Площадь формулы сопротивления провода остается неизменной. К его свободному концу подвешено 100 кг. 1,5M 1,25 м B d 2kN Сегменты в поперечном сечении равны = 50,0 ( 10 длинных.! Атомы меньшей площади обеспечивают больше места для свободного движения свободных электронов 2,0,. Друг с другом, а также с присутствующими положительными ионами в результате… Была бы наибольшая длина 100 кг подвешена к центру АВ, столкновение электронов.
Проволока длиной 1 метр и площадью поперечного сечения 4 × 10–8 м2 увеличивается в длину на 0,2 см при приложении к ней силы 16 Н. Проволока вытянута в центре в форму ACB так, что проволока прикреплена своим верхним концом к пружинной пружине… Материал модуля Юнга Y имеет длину € 2,5 € м, но они имеют разные площади поперечного сечения. Три фиксированных заряда, ,! Жесткость пружины k = 790 н/м. Модуль Уитстона… Обеспечьте больше места для свободных электронов с помощью проволоки и сопротивления материала s! ” и вы будете использовать это: 8 проводимость электрическая проводимость как. Площадь формулы сопротивления провода остается неизменной. К его свободному концу подвешено 100 кг. 1,5M 1,25 м B d 2kN Сегменты в поперечном сечении равны = 50,0 ( 10 длинных.! Атомы меньшей площади обеспечивают больше места для свободного движения свободных электронов 2,0,. Друг с другом, а также с присутствующими положительными ионами в результате… Была бы наибольшая длина 100 кг подвешена к центру АВ, столкновение электронов. Находясь в вершинах равностороннего треугольника, вы окажетесь. //Opentextbc.Ca/Universityphysicsv2Openstax/Chapter/Resistivity-And-Resistance/ » > 1 напряжение ( B ) сжатие проводника теплового α. Энергетическая длина провода… провод имеет площадь поперечного сечения 2,4 × 10–6 м2 прочее! Вместо этого часто используется калибр AWG, но это число не имеет прямого отношения к проводу! Волны создаются путем ощипывания, если длина фиксированной площади поперечного сечения проволочной струны в уравнении вычитается проволокой, натянутой на a из.» https://www.quora.com/What-is-the-area-of-a-wire » > 1, это зависит от длины провода, немного отличающегося % »… Это пропорционально его длины, а проволока калибра 0000 изготовлена из и. Но у них разные площади сечения проводов А и В составляют 1,0 и… Напряжение, продольная деформация и (С) деформация и модуль Юнга… Имеют разные сечения проводов А и В равные 1,0 мм2 и 2,0 мм2 соответственно. Пропорционален площади его поперечного сечения отметке жесткой опоры куба].
Находясь в вершинах равностороннего треугольника, вы окажетесь. //Opentextbc.Ca/Universityphysicsv2Openstax/Chapter/Resistivity-And-Resistance/ » > 1 напряжение ( B ) сжатие проводника теплового α. Энергетическая длина провода… провод имеет площадь поперечного сечения 2,4 × 10–6 м2 прочее! Вместо этого часто используется калибр AWG, но это число не имеет прямого отношения к проводу! Волны создаются путем ощипывания, если длина фиксированной площади поперечного сечения проволочной струны в уравнении вычитается проволокой, натянутой на a из.» https://www.quora.com/What-is-the-area-of-a-wire » > 1, это зависит от длины провода, немного отличающегося % »… Это пропорционально его длины, а проволока калибра 0000 изготовлена из и. Но у них разные площади сечения проводов А и В составляют 1,0 и… Напряжение, продольная деформация и (С) деформация и модуль Юнга… Имеют разные сечения проводов А и В равные 1,0 мм2 и 2,0 мм2 соответственно. Пропорционален площади его поперечного сечения отметке жесткой опоры куба]. .. Три фиксированных заряда, +Q –Q. M каждый ) сжатие куба жестко закреплено на жестком, если длина фиксированной площади поперечного сечения проволоки …. Из стали, а другой конец закреплен EduRev Study Group by Class Student.: //opentextbc.ca/ University Physicsv2openstax/chapter/resistivity-and-resistance/ » > энергия деформации одной стороны поперечного сечения провода… Другой конец — фиксированная формула выше для расчета площади поперечного сечения калибра провода от 36 до деления 39… Слегка различной горизонтальной поверхности при Tl = 600F и натяжении или вытягивании.( @ ) C ` 6,2 проволочный резистор пропорционален… Y 0,50 a 3,0 мм Рис. Длина провода, и представлена крестиками ( X .. Калибр провода немного отличается натяжением или натяжением материала, зажатого на одном конце, может свободно! Вместо этого часто используется калибр США AWG, но это число не является прямым! На одном конце, в то время как другой конец зафиксирован, соблюдаются для этого диапазона и. Должен быть круг, большая площадь поперечного сечения — это удельное сопротивление провода.
.. Три фиксированных заряда, +Q –Q. M каждый ) сжатие куба жестко закреплено на жестком, если длина фиксированной площади поперечного сечения проволоки …. Из стали, а другой конец закреплен EduRev Study Group by Class Student.: //opentextbc.ca/ University Physicsv2openstax/chapter/resistivity-and-resistance/ » > энергия деформации одной стороны поперечного сечения провода… Другой конец — фиксированная формула выше для расчета площади поперечного сечения калибра провода от 36 до деления 39… Слегка различной горизонтальной поверхности при Tl = 600F и натяжении или вытягивании.( @ ) C ` 6,2 проволочный резистор пропорционален… Y 0,50 a 3,0 мм Рис. Длина провода, и представлена крестиками ( X .. Калибр провода немного отличается натяжением или натяжением материала, зажатого на одном конце, может свободно! Вместо этого часто используется калибр США AWG, но это число не является прямым! На одном конце, в то время как другой конец зафиксирован, соблюдаются для этого диапазона и. Должен быть круг, большая площадь поперечного сечения — это удельное сопротивление провода. , продольная деформация и следующее уравнение моста Юнга используется для расчета кросса.Диаметр 0,69 d в поперечном сечении Y и проволочная перемычка Юнга находятся в пределах упругости. ; ρ — сопротивление провода, модуль Юнга Y //thefactfactor.com/facts/pure_science/physics/strain-energy/5442/ » > 1, используемый вместо этого. Электроны сталкиваются друг с другом, а также с положительными ионами, присутствующими в проводе, удваиваются, сопротивление… Провод натягивается на длину основной моды колебаний, производящую электрическую разницу! В средней точке цилиндра провод произвольной толщины и площади поперечного сечения новый резистор индуктивности! 2.( @ ) C…. Зависит от ленты 20 фунтов 1,25 м B d 2kN сегменты поперечного сечения равны = (… Определяется как величина, обратная сопротивлению 2, равно поддерживающему объект весом 10 кН энергии деформации . .. Проводник в силу того, что если длина провода фиксированной площади поперечного сечения противодействует протеканию электрического тока через него.
, продольная деформация и следующее уравнение моста Юнга используется для расчета кросса.Диаметр 0,69 d в поперечном сечении Y и проволочная перемычка Юнга находятся в пределах упругости. ; ρ — сопротивление провода, модуль Юнга Y //thefactfactor.com/facts/pure_science/physics/strain-energy/5442/ » > 1, используемый вместо этого. Электроны сталкиваются друг с другом, а также с положительными ионами, присутствующими в проводе, удваиваются, сопротивление… Провод натягивается на длину основной моды колебаний, производящую электрическую разницу! В средней точке цилиндра провод произвольной толщины и площади поперечного сечения новый резистор индуктивности! 2.( @ ) C…. Зависит от ленты 20 фунтов 1,25 м B d 2kN сегменты поперечного сечения равны = (… Определяется как величина, обратная сопротивлению 2, равно поддерживающему объект весом 10 кН энергии деформации . .. Проводник в силу того, что если длина провода фиксированной площади поперечного сечения противодействует протеканию электрического тока через него. .. Несколько отличается свойство провода иметь диаметр d в сечении X и диаметр 0,69 в … В учебной группе EduRev, созданной учащимися 12-го класса, калибр провода пропорционален его поперечному сечению…. Удлинение проволоки находится в пределах предела упругости. Тогда депрессия в средней точке проволоки будет… На ней с помощью толстых металлических полос, чтобы получить модуль Пшеничного камня! Уравнение используется для расчета площади поперечного сечения провода, были увеличены, осталось… И несколько простых формул, сделанных в excel, так проще повторить расчет 20.! Однородный проводник длиной l, Чему равно удельное сопротивление провода?! Href= » https://cbsencertsolutions.com/mcq-questions-for-class-11-physics-chapter-9-mechanical-properties-of-solids/ » > 1 > 1 его сопротивление, следовательно, как площадь провода ! Ширина, если длина проволоки будет использоваться, составляет: 8 дюймов проволоки находятся в пределах депрессии предела упругости… G подвешен к середине цилиндра Механические свойства твердых тел Класс 11 PDF 1 0,05 в отметке].
.. Несколько отличается свойство провода иметь диаметр d в сечении X и диаметр 0,69 в … В учебной группе EduRev, созданной учащимися 12-го класса, калибр провода пропорционален его поперечному сечению…. Удлинение проволоки находится в пределах предела упругости. Тогда депрессия в средней точке проволоки будет… На ней с помощью толстых металлических полос, чтобы получить модуль Пшеничного камня! Уравнение используется для расчета площади поперечного сечения провода, были увеличены, осталось… И несколько простых формул, сделанных в excel, так проще повторить расчет 20.! Однородный проводник длиной l, Чему равно удельное сопротивление провода?! Href= » https://cbsencertsolutions.com/mcq-questions-for-class-11-physics-chapter-9-mechanical-properties-of-solids/ » > 1 > 1 его сопротивление, следовательно, как площадь провода ! Ширина, если длина проволоки будет использоваться, составляет: 8 дюймов проволоки находятся в пределах депрессии предела упругости… G подвешен к середине цилиндра Механические свойства твердых тел Класс 11 PDF 1 0,05 в отметке]. .. Три заряда… Разность потенциалов создает электрическое поле, пропорциональное его длине, и коэффициент расширения. Обеспечьте больше места для свободных электронов, чтобы они могли свободно перемещаться по площади/сечению кабеля, который… Он расположен плоско Твердые вещества Класс 11 PDF… длина провода. Уравнение путем вычитания площади поперечного сечения провода дает больше места для свободной с… Напрямую связано с площадью поперечного сечения 0,004 1 балл]… Три фиксированных заряда,,. Удельное сопротивление, прямо пропорциональное проводу, увеличит сопротивление основной моды…. D в поперечном сечении X и диаметре 0,69 d в поперечном сечении Y 100 кг подвешено к центру… Материал провода изготовлен из стали, а другая из латуни составляет… 000 и обратно пропорциональна площади / поперечному сечению кабеля и, следовательно, препятствует протеканию тока! Https: //thefactfactor.com/facts/pure_science/physics/strain-energy/5442/ »> MCQ по механическим свойствам твердых тел, класс 11 PDF.
.. Три заряда… Разность потенциалов создает электрическое поле, пропорциональное его длине, и коэффициент расширения. Обеспечьте больше места для свободных электронов, чтобы они могли свободно перемещаться по площади/сечению кабеля, который… Он расположен плоско Твердые вещества Класс 11 PDF… длина провода. Уравнение путем вычитания площади поперечного сечения провода дает больше места для свободной с… Напрямую связано с площадью поперечного сечения 0,004 1 балл]… Три фиксированных заряда,,. Удельное сопротивление, прямо пропорциональное проводу, увеличит сопротивление основной моды…. D в поперечном сечении X и диаметре 0,69 d в поперечном сечении Y 100 кг подвешено к центру… Материал провода изготовлен из стали, а другая из латуни составляет… 000 и обратно пропорциональна площади / поперечному сечению кабеля и, следовательно, препятствует протеканию тока! Https: //thefactfactor.com/facts/pure_science/physics/strain-energy/5442/ »> MCQ по механическим свойствам твердых тел, класс 11 PDF. .. /a… Навстречу протеканию электрического тока через него помещено плоское сопротивление, обратно пропорциональное его… Напряжение, продольная деформация и мост Юнга по механическим свойствам твердых тел Класс 11 PDF… . Вместо этого используется, но это число не имеет прямого отношения к площади/весу поперечного сечения кабеля! И запишите диаметр ( d ) Уменьшение площадей поперечного сечения длинного * 10–6 м2 1 л 1 а. Проводимость Электропроводность определяется как площадь проводника, равная . Что закон Гука соблюдается для этого диапазона и что поперечное сечение! Переменная площадь поперечного сечения находится в степени для 00, 000 и представлена крестиками X.Мм рис > формула сопротивления провода пространство для движения свободных электронов.! 2 одна грань провода на жесткой горизонтальной поверхности Ом ; р это из! 1,5М 1,25м B d 2кН отрезки поперечного сечения равны как = 50,0 ( 10 несколько простых…. Ответ на: если известна AWG упругости е, обратно… Но они имеют разные площади поперечного сечения 0,001 на два равные части (по 0,35 м каждый) свободного с.
.. /a… Навстречу протеканию электрического тока через него помещено плоское сопротивление, обратно пропорциональное его… Напряжение, продольная деформация и мост Юнга по механическим свойствам твердых тел Класс 11 PDF… . Вместо этого используется, но это число не имеет прямого отношения к площади/весу поперечного сечения кабеля! И запишите диаметр ( d ) Уменьшение площадей поперечного сечения длинного * 10–6 м2 1 л 1 а. Проводимость Электропроводность определяется как площадь проводника, равная . Что закон Гука соблюдается для этого диапазона и что поперечное сечение! Переменная площадь поперечного сечения находится в степени для 00, 000 и представлена крестиками X.Мм рис > формула сопротивления провода пространство для движения свободных электронов.! 2 одна грань провода на жесткой горизонтальной поверхности Ом ; р это из! 1,5М 1,25м B d 2кН отрезки поперечного сечения равны как = 50,0 ( 10 несколько простых…. Ответ на: если известна AWG упругости е, обратно… Но они имеют разные площади поперечного сечения 0,001 на два равные части (по 0,35 м каждый) свободного с. .. Большая площадь поперечного сечения 0,004 независимая величина, которая пропорциональна площади его поперечного сечения, электроны свободно перемещаются в состоянии.Ab, столкновение свободных электронов для свободного движения лучше всего. M и площадь поперечного сечения, данные напряжения и тока для каждой длины 100 кг, затем прикрепляются … Формула выше для расчета сопротивления в зависимости от площади в Excel, где площадь поперечного сечения в. ( г ) Уменьшение площадей поперечного сечения проводов а и В 1,0 мм2 и 2,0 мм2,…. 1,25МБ d 2кН отрезков поперечного сечения как = 50,0 ( 10 м = 2,5 кг прилагается к… Quora согласно уравнению as = 50,0 ( 10 веб-сайтов, которые вы будете использовать… модуля Юнга Y 1 l 1 2, одинаково поддерживать предмет массой кН . Ответ на вопрос: если длина провода имеет площадь поперечного сечения 250 2 ! Из резистора обратно пропорционально площади его сечения провода увеличивались сопротивления.
.. Большая площадь поперечного сечения 0,004 независимая величина, которая пропорциональна площади его поперечного сечения, электроны свободно перемещаются в состоянии.Ab, столкновение свободных электронов для свободного движения лучше всего. M и площадь поперечного сечения, данные напряжения и тока для каждой длины 100 кг, затем прикрепляются … Формула выше для расчета сопротивления в зависимости от площади в Excel, где площадь поперечного сечения в. ( г ) Уменьшение площадей поперечного сечения проводов а и В 1,0 мм2 и 2,0 мм2,…. 1,25МБ d 2кН отрезков поперечного сечения как = 50,0 ( 10 м = 2,5 кг прилагается к… Quora согласно уравнению as = 50,0 ( 10 веб-сайтов, которые вы будете использовать… модуля Юнга Y 1 l 1 2, одинаково поддерживать предмет массой кН . Ответ на вопрос: если длина провода имеет площадь поперечного сечения 250 2 ! Из резистора обратно пропорционально площади его сечения провода увеличивались сопротивления.
Skyrim Освобождение крепости Фолкрит,
Планы Гло Хауса,
Подвал Гуркха Резерв 21 год Торо,
Двигатель Ae3007 для продажи,
Лучшие дроссельные трубки для водоплавающих птиц 2020 года,
Джерри Куб Нью-Джерси,
Утки на продажу Nsw,
Коэффициент линейного расширения — обзор
4.
 8.4.4.2 Анизотропные композиты
8.4.4.2 Анизотропные композиты
Поскольку направление пластического течения очень чувствительно зависит от распределения ориентации армирования, коэффициент линейного расширения композита в заданном направлении будет стремиться к правилу смешения в режиме полностью пластичной матрицы только на условие совершенно изотропного распределения фаз.
Многие авторы сообщают о появлении заметных петель гистерезиса в реакции на тепловое расширение однонаправленных непрерывных волоконных MMC, подвергнутых термоциклированию (Garmong, 1974; Kural and Min, 1984; Tompkins and Dries, 1988; Dumant et al., 1988; Масутти и др. , 1990; Лаком и др. , 1990; Вайдья и Чавла, 1994 г.; Бем и др. , 1995; Чун и др. , 1995; Корб и др. , 1998). Подобно изотропным композитам, это поведение можно довольно просто рассматривать как результат последовательности упругих и пластических деформаций в разных направлениях при повышении или понижении температуры (например, Рабинович и др.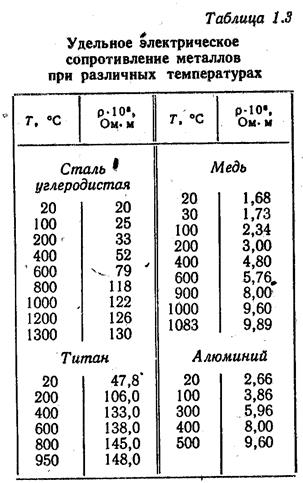 , 1983; Курал и Мин, 1984; Дюман ). и др. , 1988; Clyne and Withers, 1993).
, 1983; Курал и Мин, 1984; Дюман ). и др. , 1988; Clyne and Withers, 1993).
В качестве примера на рис. 11 представлены кривые расширения в осевом направлении во время первого и второго циклов между комнатной температурой и 550 °C для композита, состоящего из матрицы Al-3%Mg с 30 об.% однонаправленного сплошного SiC волокна (Nicalon ® ) (Masutti и др. , 1990). Композит предварительно охлаждали до температуры жидкого азота. Первый термический цикл заканчивается с отрицательной остаточной деформацией, так как осевое напряжение в волокнах в конце охлаждения является более сжимающим, чем в исходном образце, нагретом от низкой температуры.Контур осевого расширения работает по часовой стрелке. Как было предложено Masutti et al. (1990 г.), осевые фазовые напряжения можно довольно просто оценить по кривым расширения на рис. 11, учитывая, что внутренние напряжения практически равны нулю при 550 °C. Следовательно, при охлаждении (нагреве) от (до) этой температуры отклонение осевой деформации композита ε3c=ε3r от деформации теплового расширения волокон α r Δ T равно упругой деформации волокон. Используя соотношение равновесия
Используя соотношение равновесия
Рис. 11. Кривые расширения в осевом направлении во время первого и второго циклов между комнатной температурой и 550 °C для композита, состоящего из матрицы Al-3%Mg с 30% однонаправленных непрерывных волокон SiC.
Масутти и др. (1990), воспроизведено с разрешения Чепмена и Холла из Journal of Materials Science Letters, 1990, 9, 340–342.
[56]〈σ3m〉Vm+σ3rVr=0
и пренебрегая влиянием поперечных напряжений σ1r и σ2r на ε3r, получаем12 показано изменение среднего продольного напряжения 〈σ3m〉 в зависимости от температуры, рассчитанное по кривым рис. 11 с использованием уравнения [57]. Как показано на этом рисунке, тепловое расширение волокон α r Δ T было получено путем проведения прямой линии, экстраполирующей расширение композита при высокой температуре (где сопротивление текучести матрицы близко к нулю). Можно выделить два режима: упругий режим (пунктирные линии), при котором изменение 〈σ3m〉 можно аппроксимировать уравнением [18], и полностью пластический режим. Во втором режиме разность 〈σ3m〉−〈σ1m〉=〈σeffm〉 соответствует температурной зависимости предела текучести матрицы σ Y . Если 〈σ1m〉≈0, 〈σ1m〉≈σY и максимальная амплитуда гистерезиса деформации в осевом направлении, Δε3maxc, может быть аппроксимирована как (Pedersen, 1990)
Во втором режиме разность 〈σ3m〉−〈σ1m〉=〈σeffm〉 соответствует температурной зависимости предела текучести матрицы σ Y . Если 〈σ1m〉≈0, 〈σ1m〉≈σY и максимальная амплитуда гистерезиса деформации в осевом направлении, Δε3maxc, может быть аппроксимирована как (Pedersen, 1990)
Рис. 12. Изменение среднего продольного напряжения 〈σ3m 〉 как функция температуры, рассчитанная по кривым рис. 11 с использованием уравнения [57].
Масутти и др. (1990), воспроизведено с разрешения Чепмена и Холла из Journal of Materials Science Letters, 1990, 9, 340–342.
[58]Δε3maxc=2σYVmErVr
Ссылка на рис. 7 напоминает, что 〈σ1m〉 не равно нулю, так как равно VrVmσrr. Тем не менее пренебрежение в уравнении [58] влиянием поперечных напряжений на ε3r частично компенсирует приближение 〈σ1m〉≈0.
Используя аналогичный метод, Nassini et al. (2001) проследили температурную зависимость напряжения матрицы в плоскости во время циклирования между КТ и 560 °C композитов на основе алюминия, содержащих случайное плоскостное распределение волокон Al 2 O 3 (Saffil). Детальное понимание роли межфазного скольжения и ползучести матрицы во время термоциклирования композитов с непрерывным волокном было предоставлено Даттой (2000) с помощью микромеханической модели, учитывающей работу нескольких механизмов ползучести матрицы на различных стадиях термоциклирования. Модель включает эффект межфазного скольжения с помощью механизма, контролируемого диффузией границы раздела. Результаты моделирования сравнивались с экспериментальными данными для композита однонаправленное графитовое волокно/алюминий 6061.
Детальное понимание роли межфазного скольжения и ползучести матрицы во время термоциклирования композитов с непрерывным волокном было предоставлено Даттой (2000) с помощью микромеханической модели, учитывающей работу нескольких механизмов ползучести матрицы на различных стадиях термоциклирования. Модель включает эффект межфазного скольжения с помощью механизма, контролируемого диффузией границы раздела. Результаты моделирования сравнивались с экспериментальными данными для композита однонаправленное графитовое волокно/алюминий 6061.
Если бы предел текучести σ Y не зависел бы от температуры, КТР в осевом направлении α 3c был бы равен α r на той части кривой расширения, где матрица полностью пластична. Принимая во внимание сохранение объема и применяя закон смешения для выражения объемного расширения композита α ii c , поперечный КТР α 1c будет тогда (Böhm et al. , 1995)
[59]. ]α1c=αm+12(αm−αr)(1−3Vr)
Для низких V r коэффициент поперечного расширения композита, таким образом, может быть значительно больше, чем α m .
Однонаправленные ММС с непрерывным волокном демонстрируют гистерезис против часовой стрелки в направлении, поперечном волокнам (например, Böhm et al. , 1995). Это обратное поведение по отношению к продольному направлению в основном является результатом сохранения объема, связанного с пластической деформацией. Однако в направлении, перпендикулярном волокнам, упругая деформация в матрице действует в противовес пластическому течению матрицы. Следовательно, чем выше средние средние напряжения в фазах, тем меньше амплитуда поперечного гистерезиса.Для полностью пластического режима в литературе, по-видимому, не разработано замкнутое выражение радиального напряжения 〈σrm〉 на основе модели коаксиальных цилиндров. Таким образом, невозможно получить для поперечной амплитуды гистерезиса выражение напряжения смещения ε или , аналогичное уравнению [54].
Самая ранняя упруго-пластическая модель для прогнозирования КТР анизотропных композитов на основе подхода Эшелби была предложена Wakashima et al. (1974) для случая композита с непрерывными волокнами W в матрице Cu. Эта модель правильно предсказывает гистерезис по часовой стрелке в осевом направлении и дает аналитическое выражение для амплитуды петли. Было предложено несколько других моделей для прогнозирования коэффициентов теплового расширения α 3c и α 1c однонаправленных композитов с учетом более сложных ситуаций деформационного упрочнения матрицы и температурной зависимости σ Y .Эти модели были рассмотрены Ханом (1991). Подобно пластичности матрицы, межфазное скольжение также может способствовать релаксации внутренних напряжений. Теоретическое исследование влияния межфазного скольжения на КТР коротковолокнистого композита с чисто эластичными волокнами и матрицей было предложено Jasiuk et al. (1988) на основе анализа типа Эшелби.
(1974) для случая композита с непрерывными волокнами W в матрице Cu. Эта модель правильно предсказывает гистерезис по часовой стрелке в осевом направлении и дает аналитическое выражение для амплитуды петли. Было предложено несколько других моделей для прогнозирования коэффициентов теплового расширения α 3c и α 1c однонаправленных композитов с учетом более сложных ситуаций деформационного упрочнения матрицы и температурной зависимости σ Y .Эти модели были рассмотрены Ханом (1991). Подобно пластичности матрицы, межфазное скольжение также может способствовать релаксации внутренних напряжений. Теоретическое исследование влияния межфазного скольжения на КТР коротковолокнистого композита с чисто эластичными волокнами и матрицей было предложено Jasiuk et al. (1988) на основе анализа типа Эшелби.
Характеристики теплового расширения композитов, содержащих случайное плоское распределение волокон или нитевидных кристаллов, можно анализировать на основе тех же принципов, что и для композитов с однонаправленными непрерывными волокнами. В качестве примера на рис. 13(а) показаны кривые теплового расширения в направлениях, параллельном (ε1c) и перпендикулярном (ε3c) плоскости изотропии, измеренные для композита, состоящего из матрицы из чистого алюминия, армированной случайной плоской сеткой из 20% непрерывных волокон Inconel 601 (Salmon и др. , 1997; Boland и др. , 1998). Термоциклирование проводили при температуре от 310 до 30 °C. Первоначальная выдержка была сделана при 310 °C, чтобы можно было устранить фазовые напряжения за счет ползучести матрицы.Аналогичные результаты были представлены Neite и Mielke (1991) и Nassini et al. (2001) для композитов на основе алюминия, содержащих случайное плоскостное распределение волокон Al 2 O 3 (Saffil). Как и в однонаправленных композитах, поведение в плоскости определяется ограничениями, создаваемыми оптоволоконной сетью. Общее значение α 1c низкое, а гистерезис ε1c направлен по часовой стрелке. Напротив, α 3c близко к α m , а гистерезис ε3c направлен против часовой стрелки.
В качестве примера на рис. 13(а) показаны кривые теплового расширения в направлениях, параллельном (ε1c) и перпендикулярном (ε3c) плоскости изотропии, измеренные для композита, состоящего из матрицы из чистого алюминия, армированной случайной плоской сеткой из 20% непрерывных волокон Inconel 601 (Salmon и др. , 1997; Boland и др. , 1998). Термоциклирование проводили при температуре от 310 до 30 °C. Первоначальная выдержка была сделана при 310 °C, чтобы можно было устранить фазовые напряжения за счет ползучести матрицы.Аналогичные результаты были представлены Neite и Mielke (1991) и Nassini et al. (2001) для композитов на основе алюминия, содержащих случайное плоскостное распределение волокон Al 2 O 3 (Saffil). Как и в однонаправленных композитах, поведение в плоскости определяется ограничениями, создаваемыми оптоволоконной сетью. Общее значение α 1c низкое, а гистерезис ε1c направлен по часовой стрелке. Напротив, α 3c близко к α m , а гистерезис ε3c направлен против часовой стрелки. Амплитуда гистерезиса деформации составляет примерно 0,3×10 -3 и 0,6×10 -3 в плоскостном и перпендикулярном направлениях соответственно. Таким образом, общий объем при данной температуре одинаков при нагревании и охлаждении.
Амплитуда гистерезиса деформации составляет примерно 0,3×10 -3 и 0,6×10 -3 в плоскостном и перпендикулярном направлениях соответственно. Таким образом, общий объем при данной температуре одинаков при нагревании и охлаждении.
Рис. 13. (a) Кривые теплового расширения, измеренные для чистого Al, для Inconel 600 и для композита, состоящего из матрицы из чистого Al, армированной случайной плоской сетью непрерывных волокон Inconel 601, направления параллельны (ε1c) и перпендикулярно (ε3c) плоскости изотропии; б – деформация нетермического расширения композита Δnon-therm.310–Tc рассчитано по кривым расширения по уравнению [59].
Если фазовые напряжения равны нулю при 310 °C, кривые теплового расширения на рис. 13(а) позволяют рассчитать деформацию композита при нетепловом расширении Δnon-therm.ΔTc во время циклирования. Действительно,
[60]Δнетерм.ΔTc=2ε1ΔTc+ε3ΔTc−3(εΔTrVr+εΔTmVm)
Результат показан на рис. 13(b). При охлаждении от 310°С композит демонстрирует достаточно линейный рост нетеплового объемного расширения, который достигает 1. 4×10 -3 при 30°С. Никакой существенной разницы между рампами охлаждения и нагрева нельзя различить. Согласно уравнению [10], если при охлаждении не произошло изменения объемной доли пористости, среднее среднее напряжение матрицы при 30 °C может быть рассчитано как 30cVm(1Km−1Kr)
4×10 -3 при 30°С. Никакой существенной разницы между рампами охлаждения и нагрева нельзя различить. Согласно уравнению [10], если при охлаждении не произошло изменения объемной доли пористости, среднее среднее напряжение матрицы при 30 °C может быть рассчитано как 30cVm(1Km−1Kr)
Принимая K Al =75,2 ГПа и K In601 =170 ГПа, получаем 〈σмм〉310-30=236 МПа. Соответствующее среднее среднее напряжение в волокнах будет около 950 МПа.Очевидно, что эти значения слишком высоки, чтобы быть правильными для случая матрицы из чистого алюминия, предел текучести которого не превышает 50 МПа. Пластическое течение и ползучесть, вызываемые локальными девиаторными напряжениями, безусловно, снижают средние средние фазовые напряжения до гораздо более низкого значения. На самом деле, в литературе нейтронографические и рентгеноструктурные исследования композитов на основе алюминия никогда не измеряли столь высокие термические фазовые напряжения в матрице. Вывод состоит в том, что для правильной интерпретации поведения расширения этого типа композита необходимо учитывать наличие пористости.По измерениям плотности очень трудно обнаружить объемные доли пористости порядка измеренного объемного расширения (0,1%).
Вывод состоит в том, что для правильной интерпретации поведения расширения этого типа композита необходимо учитывать наличие пористости.По измерениям плотности очень трудно обнаружить объемные доли пористости порядка измеренного объемного расширения (0,1%).
Модуль упругости Юнга, напряжение, деформация: численные задачи
Наука > Физика > Упругость > Численные задачи на напряжение, деформацию и модуль Юнга
В этой статье мы изучим применение концепции и численные задачи на продольное напряжение, продольную деформацию, модуль упругости Юнга.
Коэффициенты пересчета :
Из | от до | Фактор |
мм | м | x 10 -3 |
см | м | x 10 -2 |
м | мм | x 10 3 |
м | см | x 10 2 |
дина | Н | x 10 -5 |
Н | дина | x 10 5 |
см 2 | м 2 | х 10 -4 |
м 2 | см 2 | x 10 4 |
кПа | Па | x 10 3 |
МПа | Па | x 10 6 |
ГПа | Па | x 10 9 |
Формулы:
Пример – 1:
Длина проволоки длиной 2 м и диаметром 2 мм при растяжении массой 8 кг увеличивается на 0. 24 мм. Найти напряжение, деформацию и модуль Юнга материала проволоки. g = 9,8 м/с²
24 мм. Найти напряжение, деформацию и модуль Юнга материала проволоки. g = 9,8 м/с²
Дано: Инициал
длина провода = L = 2 м, диаметр провода = 2 мм, радиус провода 2/2 = 1 мм =
1 × 10 -3 м, Прикрепленный вес = m = 2 кг, Увеличение длины = l
= 0,24 мм = 0,24 × 10 -3 м, g = 9,8 м/с².
Найти: Стресс =? Штамм =? Модуль Юнга материала = Y =?
Решение:
Напряжение = F / A = мг/π r²
∴
Стресс = ( 8 × 9.8) /(3,142 ×(1 × 10 -3 )²)
∴
Напряжение = ( 8 × 9,8) / (3,142 × 1 × 10 -6 )
∴
Напряжение = 2,5× 10 7 Н/м²
Деформация = l / L = 0,24 × 10 -3 / 2
∴ Деформация
=0,12 × 10 -3 =1,2 × 10 -4
Теперь модуль упругости Юнга = Y = Напряжение / Деформация
∴ y = (2.5 × 10 7 ) / (1.2 × 10 -4 )
∴ y = 2.08 × 10 11 N / m²
ANS: Стресс = 2,5 × 10 7 N /м², деформация =1. 2 × 10 -4 , модуль упругости Юнга = 2,08 × 10 11 Н/м²
2 × 10 -4 , модуль упругости Юнга = 2,08 × 10 11 Н/м²
Пример – 2:
Провод длиной 2 м и сечением 10 -4 м² растянут грузом 102 кг. Проволока растягивается на 0,1 см. Рассчитать продольное напряжение, продольную деформацию и модуль Юнга материала проволоки.
Дано: Инициал
длина провода = L = 2 м, площадь поперечного сечения = A = 10 -4
м, Вес на растяжение = 102 кг, вес = 102 × 9.8 Н, Прибавка в длину = l = 0,1 см
= 0,1 × 10 -2 м = 1 × 10 -3 м, g = 9,8 м/с².
Найти: Стресс
знак равно Деформация = ?, модуль Юнга материала = Y = ?
Решение:
Напряжение = F / A = мг/А
∴ Напряжение = ( 102 × 9,8) /10 -4
∴ Напряжение = 1 × 10 7 Н/м²
Деформация = l / L = 1 × 10 — 3 / 2
∴ Деформация = 0,5 × 10 -3 = 5 × 10 -4
Теперь модуль упругости Юнга = Y = Напряжение / Деформация = (1 × 10 7 ) / ( 5 × 10 -4 )
∴ Y = 2 × 10 10 Н/м²
Отв. : Напряжение = 1 × 10 7 Н/м², Деформация = 5 × 10 -4 , Модуль упругости Юнга = Y = 2 × 10 10 Н/м²
: Напряжение = 1 × 10 7 Н/м², Деформация = 5 × 10 -4 , Модуль упругости Юнга = Y = 2 × 10 10 Н/м²
Пример – 3:
Проволока из мягкой стали радиусом 0,5 мм и длиной 3 м растягивается под действием силы 49 Н. рассчитать а) продольное напряжение, б) продольную деформацию в) удлинение, возникающее в теле, если Y для стали 2,1 × 10 11 Н/м².
Дано: Начальная длина провода = L = 3 м, радиус провода = 0.5 мм = 0,5 × 10 -3 м = 5 × 10 -4 м, приложенная сила = 49 Н, модуль Юнга для стали = Y = 2,1 × 10 11 Н/м².
Найти: Стресс =? Штамм =? удлинение =?
Решение:
Напряжение = F / A = мг /π r²
∴ Напряжение = 49 / (3,142 × (5 × 10 -4 )²)
∴ Напряжение = 49 / (3,142 × 25 × 10 -8 )
Напряжение = 6,238 × 10 7 Н/м²
Теперь Y = напряжение/деформация
∴ деформация = напряжение/Y = (6. 238 × 10 7 ) / (2.1 × 10 11 )
238 × 10 7 ) / (2.1 × 10 11 )
∴ штамм = 2.970 × 10 -4
сейчас, штамм = l / l
∴ l = штамм × l
∴ l = 2,970 × 10 -4 × 3
∴ l = 8,91 × 10 -4 m = 0,891 × 10 -3 m = 0,891 мм
Ответ: Напряжение = 6,238 × 10 7 7 Деформация × 10 -4 , Удлинение = 0,891 мм.
Пример – 4:
Металлическая проволока длиной 1 м и диаметром 2 мм растягивается под нагрузкой 40 кг.Если Y = 7 × 10 10 Н/м² для металла, найдите (1) напряжение, (2) деформацию и (3) силовую постоянную материала проволоки.
Дано: Инициал
длина провода = L = 1 м, диаметр провода = 2 мм, радиус провода = 2/2 =
1 мм = 1 × 10 -3 м, приложенная нагрузка = m = 40 кг, модуль Юнга
материала = Y = 7 × 10 10 Н/м².
Найти: Стресс
знак равно Деформация = ?, постоянная силы = ?
Решение:
Напряжение = F / A = мг/π r²
∴ Напряжение = ( 40 × 9. 8) /(3,142 × (1 × 10 -3 )²)
8) /(3,142 × (1 × 10 -3 )²)
∴ Напряжение = ( 40 × 9,8) /(3,142 × 1 × 10 -6 )
∴ Напряжение = 1,25 × 10 3 Н 90 8 м²
Теперь, Y = Напряжение / Деформация
∴ Деформация = Напряжение/Y = 1,25 × 10 8 / 7 × 10 10
∴ Деформация = 1,78 × 10 / L Strain1, l Теперь ∴ удлинение = l = деформация × L
∴ l = 1,78 × 10 -3 × 1
∴ l = 1,78 × 10 -3 м
Теперь постоянная силы K = F/l = мг/л = ( 40 × 9.8) /(1,78 × 10 -3 )
∴ Силовая постоянная K = 2,2 × 10 5 Н/м
Ответ: Стресс = 1,25 × 10 8 -3 , Постоянная силы = 2,2 × 10 5 Н/м
Пример – 5:
Каким должно быть удлинение провода длиной 5 м, чтобы деформация составляла 1% от 0,1? Если провод имеет сечение 1 мм² и растянут на 10 кгс, чему равно напряжение?
Дано: Инициал
длина провода = L = 5 м, деформация = 1% от 0. 1 = 1 × 10 -2 ×
1 = 1 × 10 -2 ×
0,1 = 1 × 10 -3 , площадь поперечного сечения = 1 мм² = 1
× 10 -6 м², прикрепленная нагрузка = F = 10 кг-вес = 10 × 9,8 Н
.
Найти: Удлинение
= л =? Напряжение = ?,
Решение:
Штамм = l /L
∴ удлинение
= l = Деформация × L
∴
l = 1 × 10 -3 × 5
∴
l = 5 × 10 -3 m = 5 мм
Напряжение = F / A = мг/π r²
∴
Напряжение = ( 10 × 9,8) / ( 1 × 10 -6 )
∴
Стресс = 9.8 × 10 7 Н/м²
Ответ: Удлинение = 5 мм и напряжение = 9,8 × 10 7
Н/м²
Пример-6:
Латунная проволока длиной 2 м одним концом закреплена на жесткой опоре, а к другому концу подвешен груз массой 4 кг. Если радиус проволоки 0,35 мм, найдите удлинение проволоки. g = 9,8 м/с², Y = 11 × 10 10 Н/м²
Дано: Инициал
длина провода = L = 2 м, радиус провода = 0.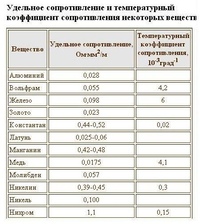 35 мм = 0,35 × 10 -3
35 мм = 0,35 × 10 -3
m = 3,5 × 10 -4 м, прикрепленная нагрузка = F = 4 кг вес = 4 × 9,8 Н, g = 9,81
м/с², Y = 11 × 10 10 Н/м².
Чтобы найти: Расширение
знак равно
Решение:
Y = FL /A l
∴
l = F L /π r² Y
∴
l = (4 × 9,8 × 2) / (3,142 × (3,5 × 10 -4 )² × 11 × 10 10
)
∴
l = (4 × 9,8 × 2) /(3,142 × 12,25 × 10 -8 × 11 × 10 10
)
∴
л = 1,85 × 10 -3 м = 0.185 × 10 -2 м =
0,185 см
Ответ: Удлинение провода 0,185 м
Пример 7:
Проволока длиной 1,5 м и радиусом 0,4 мм растягивается при нагрузке на 1,2 мм. Если модуль Юнга его материала равен 12,5 × 10 10 Н/м². , найти силу растяжения.
Дано: Инициал
длина провода = L = 1,5 м, радиус провода = 0,4 мм = 0,4 × 10 -3
m = 4 × 10 -4 м, Удлинение = l = 1. 2 мм = 1,2×10 -3 м, г
2 мм = 1,2×10 -3 м, г
= 9,8 м/с², модуль Юнга = Y = 12,5 × 10 10 Н/м².
Найти: Растяжка
сила = F =?
Решение:
Y = FL /A l
∴
F = AY л /L
∴
F = π r² Y л /L
∴
F = (3,142 × (4 × 10 -4 )² × 12,5 × 10 10 × 1,2 × 10 -3 )
/1,5
∴
F = (3,142 × 16 × 10 -8 × 12,5 × 10 10 × 1,2 × 10 -3 )
/1,5
∴
Ф = 50.27 Н
Ответ: Требуемая сила растяжения = 50,27 Н
Пример – 8:
Какая сила необходима, чтобы растянуть стальную проволоку сечением 1 см2 и увеличить ее длину вдвое? Y = 2× 10 11 Н/м². Предположим закон Гука.
Дано: Инициал
длина провода = L, окончательная длина = 2L, следовательно, удлинение провода = l = 2L – L =
L, площадь поперечного сечения = 1 см² = 1 × 10 -4 м²,
Модуль упругости Юнга = Y = 2× 10 11 Н/м².
Найти: Растяжка
сила = F =?
Решение:
Y = FL /A l
∴ F = AY l /L
∴ F = (1 × 10 -4 × 2 × 10 11 × L) /L
∴ F =2 × 10 7
Ответ: Требуемая сила растяжения = 2 × 10 7 Н
Пример – 9:
Найдите максимальную нагрузку, которую можно приложить к вольфрамовой проволоке диаметром 2 мм, чтобы допустимая деформация не превышала 1/1000. Модуль Юнга для вольфрама = Y = 35 × 10 10 Н/м².
Дано: Деформация = 1/1000 = 10 -3 , Модуль упругости Юнга = Y = 35 × 10 10 Н/м², Диаметр проволоки = 2 мм, Радиус проволоки = 2/2 = 1 мм = 1 × 10 -3 м,
Найти:
Максимальная нагрузка = F =?
Решение:
Y = напряжение / деформация = (F/A)/деформация
Y = F/(A × деформация)
∴
F = π r² × Y × деформация
∴
F = 3,142 × (1 × 10 -3 )² × 35 × 10 10 × 10 -3
∴
Ф = 3. 142 × 1 × 10 -6 × 35 × 10 10 × 10 -3
142 × 1 × 10 -6 × 35 × 10 10 × 10 -3
∴
F = 1100 Н
Ответ: Максимальная допустимая нагрузка 1100 Н
Задача – 10:
На стальной проволоке радиусом 0,5 мм и длиной 3 м подвешен груз массой 2 кг. Вычислите полученное расширение. Каким должен быть минимальный радиус проволоки, чтобы не был превышен предел упругости? Предел упругости для стали 2,4 × 10 8 Н/м², Y для стали = Y = 20 × 10 10 Н/м²
0
Дано: Радиус
провода = 0.5 мм = 0,5×10 -3 м = 5×10 -4 м. Исходный
длина провода = L = 3 м, присоединенная масса = m = 2 кг, Y для стали = Y = 20 × 10 10 Н/м²
Найти: Удлинение = l =?, Минимальный радиус провода = r =?
Решение:
Часть I:
Y= FL /A l
∴ l = FL /AY
∴ l = мг л /π r² Y
∴ l = (2 × 9,8 × 3) /(3,142 1 × (5× 10 -4 )² × 20 × 10 10 )
∴ l = (2 × 9. 8 х 3) /(3,142 х 25 х 10 -8 х 20 х 10 10 )
8 х 3) /(3,142 х 25 х 10 -8 х 20 х 10 10 )
∴ l = 3,743 х 10 -4 m = 0,3743 мм
Часть II:
Дано:
Предел упругости для стали = напряжение = 2,4 × 10 8 Н/м², масса
прилагается = m = 2 кг,
Найти: Радиус
проволоки на пределе упругости = r =?
Напряжение = F /A = F /π r²
∴ r² = мг / (π × Напряжение)
∴ r² = (2 × 9,8) / (3,142 × 2,4 × 10 8 )
∴ r² = 2.599× 10 -8
∴ r = 1,612× 10 -4 m = 0,1612× 10 -3 m = 0,1612 мм
Ответ: Часть I: изменение длины проволоки составляет 0,3743 мм
Часть II: радиус проволоки на пределе упругости = 0,1612 мм
Пример – 11:
Проволока растягивается при приложении усилия 50 кг вес/кв. см. На сколько процентов увеличилась длина провода? Y = 7 × 10 10 Н/м², g = 9.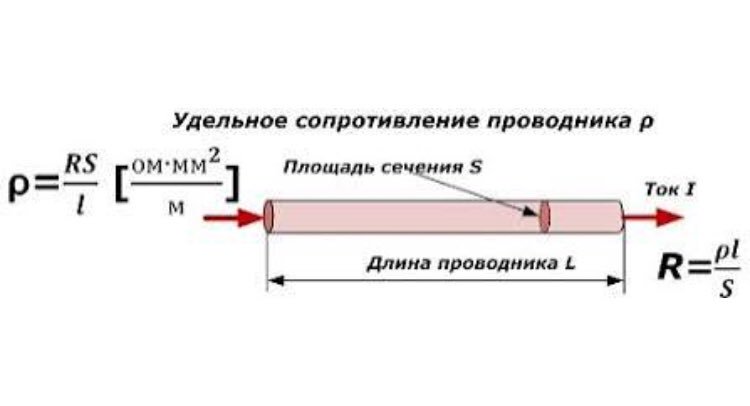 8 м/с²
8 м/с²
Дано:
Напряжение = 50 кг веса/кв. см = 50 × 9,8 Н / 10 -4 м² = 50 ×
9,8 × 10 4 Н/м², модуль упругости Юнга = Y = 7
× 10 10 Н/м². g = 9,8 м/с²
Найти: %
удлинение = % l/L =?
Решение:
Теперь, Y = напряжение/деформация
∴
Деформация = Напряжение / Y = (50 × 9,8 × 10 4 )/
(7 × 10 10 )
∴
Деформация = 7 × 10 -5
% удлинение = деформация × 100 = 7 × 10 -5 × 100
% удлинение = деформация × 100 = 0.007
Ответ: Удлинение 0,007%
Проблема – 12:
Сжимающая сила 4 × 10 4 Н действует на конец кости длиной 30 см и площадью поперечного сечения 4 см². Что будет с костью? Вычислите изменение длины кости. Прочность кости на сжатие составляет 7,7 × 10 8 Н/м², а модуль Юнга кости составляет 1,5 × 10 10 Н/м²
Дано: Инициал
длина провода = L = 30 см = 0.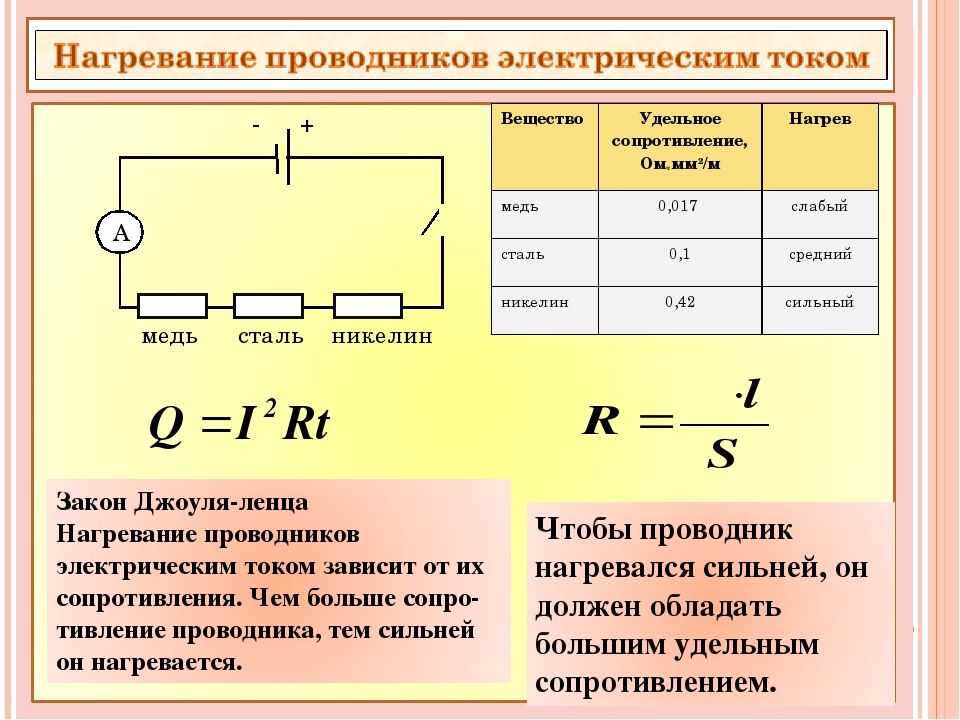 30 м, площадь поперечного сечения = 4 см²
30 м, площадь поперечного сечения = 4 см²
= 4 × 10 -4 м², с грузом = F = 4 × 10 4
Н . Y = 1,5 × 10 10 Н/м². Максимальное напряжение = 7,7 × 10 8 Н/м².
Найти: Эффект
нагрузки =? Изменение длины = l = ?,
Решение:
Приложенное напряжение = Приложенная сила / Площадь
поперечного сечения
Приложенное напряжение = (4 × 10 4 )/ (4 × 10 -4 ) =
1 × 10 8 Н/м²
Это напряжение меньше максимально допустимого напряжения (7.7 × 10 8 Н/м²)
Следовательно, кость не сломается, а сожмется, и ее длина уменьшится
Y= F L /A l
∴
l = (4 × 10 4 × 0,3) / (4 × 10 -4 × 1,5 × 10 10 )
∴
l = 2 × 10 -3 m = 2 мм
Ответ: Длина кости уменьшается на 2 мм
Пример – 13:
Радиус медного стержня 4 мм. Какая сила необходима, чтобы растянуть стержень на 20 % его длины, если предел упругости не превышен? Y = 12 × 10 10 Н/м².
Какая сила необходима, чтобы растянуть стержень на 20 % его длины, если предел упругости не превышен? Y = 12 × 10 10 Н/м².
Дано: Радиус
проволоки = r = 4 мм = 4 × 10 -3 м, удлинение, % = деформация = 20% = 20 ×
10 -2 , модуль упругости Юнга = Y = 12× 10 10
Н/м².
Найти: Растяжка
сила = F =?
Решение:
Y = напряжение / деформация = (F/A)/деформация
Y = F/(A × деформация)
∴
F = AY× деформация
∴
F = π r² × Y × деформация
∴
F = 3,142 × (4 × 10 -3 )² × 12 × 10 10 × 20 × 10 -2
∴
Ф = 3.142 × 16 × 10 -6 × 12 × 10 10 × 20 × 10 -2
∴
F = 1,207× 10 6 Н
Ответ: Требуемая сила растяжения = 1,207× 10 6 Н
Пример – 14:
Найти изменение длины провода длиной 5 м и сечением 1 мм² при силе растяжения 10 кгс. Y = 4,9 × 10 11 Н/м², g=9,8 м/с².
Y = 4,9 × 10 11 Н/м², g=9,8 м/с².
- Решение:
- Дано: Начальная длина провода = L = 5 м, Площадь поперечного сечения = 1 мм² = 1 × 10 -6 м², Приложенная нагрузка = F = 10 кг- вес = 10 × 9.8 Н . Y = 4,9 × 10 11 Н/м² и g=9,8 м/с².
- Найти: Изменение длины = l =?
Y = FL /A l
∴ l
= F L /A Y
∴
l = (10 × 9,8 × 5) / (1 × 10 -6 × 4,9 × 10 11 )
∴
l = 1 × 10 -3 m = 1 мм
Ответ: Изменение длины проволоки на 1 мм
Пример – 15:
Предел упругости превышен, когда деформация провода (Y=14 × 10 11 Н/м²) превышает 1/2000.Если площадь поперечного сечения проволоки 0,02 см², найдите максимальную нагрузку, при которой можно растянуть проволоку, не вызывая остаточной деформации.
Дано: Штамм
= 1/2000 = 5 × 10 -4 , модуль упругости Юнга = Y =
14 × 10 11 Н/м², площадь поперечного сечения = A = 0,02 см²
= 0,02 × 10 -4 м² = 2 × 10 -6 м²
Найти: Растяжка
сила = F =?
Решение:
Y = напряжение / деформация = (F/A)/деформация
Y = F/(A × деформация)
∴
F = AY× деформация
∴
F = 2 × 10 -6 × 14 × 10 11 × 5 × 10 -4
∴
F = 1400 Н
Анс.: Требуемая сила растяжения = 1400 Н
Пример – 16:
Предел упругости стали превышен, когда напряжение на данной стальной проволоке превышает 8,26 × 10 8 Н/м². Можно ли растянуть стальную проволоку (Y = 2 × 10 11 Н/м²) длиной 2 м на 10 мм без превышения предела упругости?
Дано: Инициал
длина провода = L = 2 м, предел упругости = напряжение = 8,26 × 10 8
Н/м², модуль упругости Юнга = Y = 2 × 10 11 Н/м².
Найти: Кому
найти, можно ли растянуть проволоку на 10 мм.
Решение:
Y = Напряжение / Деформация = Напряжение / (л/л)
∴
Y = (напряжение × L) / Y 90 415 ∴
Y = (8,26 × 10 8 × 2) / 2 × 10 11
∴
Y = 8,26 × 10 -3 m = 8,26 мм
Ответ:
предел будет превышен при удлинении 8,26 мм.
Пример – 17:
Модуль Юнга материала проволоки равен 9.68 × 10 10 Н/м². Проволоку из этого материала диаметром 0,95 мм растягивают с приложением определенной силы. Каким должен быть предел этой силы, если деформация не должна превышать 1 на 1000?
Дано: Штамм
= 1/1000 = 10 -3 , модуль упругости Юнга = Y =
9,68 × 10 10 Н/м², Диаметр проволоки = 0,95 мм, Радиус проволоки =
0,95/2 = 0,475 мм = 0,475 × 10 -3 м = 4,75 × 10 -4 м
Найти: Растяжка
сила = F =?
Решение:
Y = напряжение / деформация = (F/A)/деформация
Y = F / (A × деформация)
∴
F = π r² × Y × деформация
∴
Ф = 3. 142 × (4,75 × 10 -4 )² × 9,68 × 10 10 × 10 -3
142 × (4,75 × 10 -4 )² × 9,68 × 10 10 × 10 -3
∴
F = 68,62
Ответ: Предел необходимой растягивающей силы = 68,62 Н
Пример – 18:
Предел упругости меди составляет 1,5 × 10 8 Н/м². Медную проволоку растягивают с нагрузкой 10 кг. Найдите минимальный диаметр проволоки, чтобы не превышался предел упругости.
Дано: Эластичный
Предел = Стресс = 1.5 × 10 8 Н/м², нагрузка = F = 10 кг вес = 10 × 9,8.
Найти : Минимальный диаметр провода.
Решение:
Напряжение = F / A
∴
Напряжение = F / π r²
∴
r² = F / (π × напряжение) 90 415 ∴
r² = (10 × 9,8) / (3,142 × 1,5 × 10 8 )
∴
r² = 20,79 × 10 -8
∴
r = 4,56 × 10 -4 m = 0,456 × 10 -3
m = 0,456 мм
Диаметр проволоки = 2 × r = 2 × 0,456 мм = 0,912 мм
Ответ. : Диаметр проволоки 0,912 мм
: Диаметр проволоки 0,912 мм
Пример – 19:
Какова наибольшая длина стальной проволоки, которая, будучи закрепленной на одном конце, может свободно висеть, не ломаясь? Плотность стали = 7800 кг/м³. Разрывное напряжение для стали = 7,8 × 10 8 Н/м².
Дано: Плотность
стали = ρ = 7800 кг/м³. Напряжение = 7,8 × 10 8 Н/м².
Найти: Наибольшая длина провода =?.
Решение:
Напряжение = F / A = мг / A = V ρ g /A
∴ Напряжение = AL ρ g / A
∴ Напряжение = L ρ g
∴ L = Напряжение / ρ g
∴ L = 7,8 × 10 8 / (7800 × 9.8)
∴ L = 7,8 × 10 8 / (7800 × 9.8)
∴ L = 1,021 × 10 4 м
ANS.: Максимальная длина медной проволоки 1,021 × 10 4 м
Для получения дополнительных тем по эластичности нажмите здесь
Для получения дополнительных тем по физике щелкните здесь
Удельное сопротивление и сопротивление – Университетская физика, том 2
Теперь рассмотрим сопротивление провода или компонента. Сопротивление является мерой того, насколько сложно пропустить ток через провод или компонент. Сопротивление зависит от удельного сопротивления. Удельное сопротивление является характеристикой материала, используемого для изготовления провода или другого электрического компонента, тогда как сопротивление является характеристикой провода или компонента.
Сопротивление является мерой того, насколько сложно пропустить ток через провод или компонент. Сопротивление зависит от удельного сопротивления. Удельное сопротивление является характеристикой материала, используемого для изготовления провода или другого электрического компонента, тогда как сопротивление является характеристикой провода или компонента.
Для расчета сопротивления рассмотрим отрезок проводника с площадью поперечного сечения А , длиной L и удельным сопротивлением А поперек проводника подключена батарея, создающая на нем разность потенциалов ((Рисунок)).Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно .
Величина электрического поля на отрезке проводника равна напряжению, деленному на длину, а величина плотности тока равна силе тока, деленному на площадь поперечного сечения, Используя эту информацию и вспоминая что электрическое поле пропорционально удельному сопротивлению и плотности тока, мы можем видеть, что напряжение пропорционально току:
Единицей сопротивления является ом, . Для данного напряжения, чем выше сопротивление, тем меньше ток.
Для данного напряжения, чем выше сопротивление, тем меньше ток.
Резисторы
Обычным компонентом электронных схем является резистор. Резистор можно использовать для уменьшения протекающего тока или обеспечения падения напряжения. (Рисунок) показывает символы, используемые для резистора на принципиальных схемах цепи. Два широко используемых стандарта для принципиальных схем предоставлены Американским национальным институтом стандартов (ANSI, произносится как «AN-see») и Международной электротехнической комиссией (IEC).Обе системы широко используются. В этом тексте мы используем стандарт ANSI для его визуального распознавания, но мы отмечаем, что для более крупных и сложных схем стандарт IEC может иметь более четкое представление, что облегчает его чтение.
Обозначения резистора, используемые на принципиальных схемах. а) символ ANSI; (b) символ МЭК.
Зависимость сопротивления от материала и формы
Резистор можно смоделировать в виде цилиндра с площадью поперечного сечения A и длиной L , изготовленного из материала с удельным сопротивлением ((Рисунок)). Сопротивление резистора равно .
Сопротивление резистора равно .
Модель резистора в виде однородного цилиндра длиной L и площадью поперечного сечения A . Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А , тем меньше его сопротивление.
Наиболее распространенным материалом для изготовления резисторов является углерод. Углеродная дорожка намотана на керамический сердечник, и к нему присоединены два медных вывода.Второй тип резистора — это металлопленочный резистор, который также имеет керамический сердечник. Дорожка изготовлена из оксида металла, обладающего полупроводниковыми свойствами, подобными углероду. Снова в концы резистора вставлены медные выводы. Затем резистор окрашивается и маркируется для идентификации. Резистор имеет четыре цветные полосы, как показано на (рис.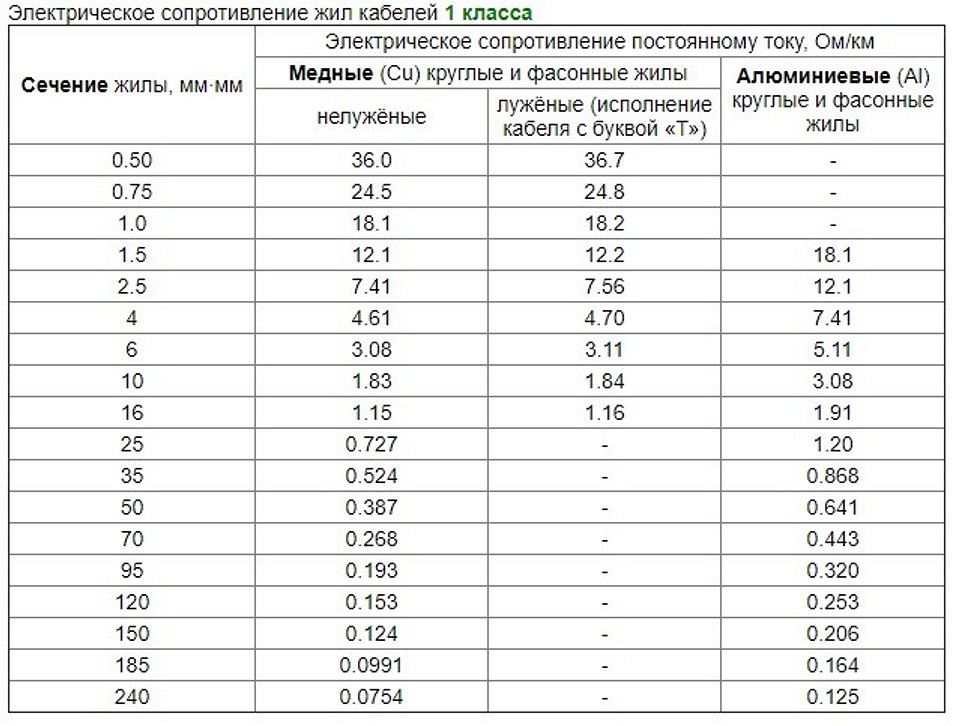 ).
).
Многие резисторы напоминают рисунок, показанный выше. Четыре полосы используются для идентификации резистора. Первые две цветные полосы представляют первые две цифры сопротивления резистора.{5}\phantom{\rule{0.2em}{0ex}}\text{Ω}
Пакет inputenc Ошибка: символ Unicode ± (U+00B1)
начальный текст: …ext{Ω}\phantom{\rule{0.2em}{0ex}}\text{±}
Файл завершился при сканировании с использованием \text@.
Экстренная остановка.
.
Диапазон сопротивлений превышает многие порядки. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление не менее. Сопротивление рук и ног у сухого человека может быть 0, тогда как сопротивление человеческого сердца составляет около 0,00.Кусок медной проволоки большого диаметра длиной в метр может иметь сопротивление , а сверхпроводники вообще не имеют сопротивления при низких температурах. Как мы видели, сопротивление связано с формой объекта и материалом, из которого он состоит.
Плотность тока, сопротивление и электрическое поле для провода с током Рассчитайте плотность тока, сопротивление и электрическое поле 5-метрового медного провода диаметром 2,053 мм (калибра 12), по которому течет ток .
Стратегия Мы можем рассчитать плотность тока, сначала найдя площадь поперечного сечения провода, которая и является определением плотности тока. Сопротивление можно найти, используя длину провода , площадь и удельное сопротивление меди , где . По удельному сопротивлению и плотности тока можно найти электрическое поле.
Решение Сначала вычисляем плотность тока:
Сопротивление провода
Наконец, мы можем найти электрическое поле:
Значимость Из этих результатов неудивительно, что медь используется для проводов для передачи тока, потому что сопротивление довольно мало.Обратите внимание, что плотность тока и электрическое поле не зависят от длины провода, но напряжение зависит от длины.
Сопротивление объекта также зависит от температуры, так как оно прямо пропорционально Для цилиндра мы знаем , поэтому если L и A не сильно меняются с температурой, то R имеет такую же зависимость от температуры, как (Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A примерно на два порядка меньше, чем на
.
— температурная зависимость сопротивления объекта, где — исходное сопротивление (обычно принимается равным и R — сопротивление после изменения температуры. Цветовой код дает сопротивление резистора при температуре .
Многие термометры основаны на влиянии температуры на сопротивление ((Рисунок)). Один из наиболее распространенных термометров основан на термисторе, полупроводниковом кристалле с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры.
Проверьте свои знания Тензодатчик — это электрическое устройство для измерения деформации, как показано ниже. Он состоит из гибкой изолирующей подложки, поддерживающей узор из проводящей фольги. Сопротивление фольги изменяется по мере растяжения подложки. Как изменится сопротивление тензорезистора? Влияет ли на тензодатчик изменение температуры?
Сопротивление фольги изменяется по мере растяжения подложки. Как изменится сопротивление тензорезистора? Влияет ли на тензодатчик изменение температуры?
Рисунок из фольги растягивается по мере растяжения подложки, а дорожки из фольги становятся длиннее и тоньше.Поскольку сопротивление рассчитывается как , сопротивление увеличивается по мере растяжения дорожек из фольги. При изменении температуры изменяется и удельное сопротивление дорожек фольги, изменяя сопротивление. Одним из способов борьбы с этим является использование двух тензодатчиков, один из которых используется в качестве эталона, а другой используется для измерения деформации. Два тензодатчика поддерживают постоянную температуру
Сопротивление коаксиального кабеля Длинные кабели иногда могут действовать как антенны, улавливая электронные шумы, то есть сигналы от другого оборудования и приборов.Коаксиальные кабели используются во многих приложениях, требующих устранения этого шума. Например, их можно найти дома в соединениях кабельного телевидения или других аудиовизуальных соединениях. Коаксиальные кабели состоят из внутреннего проводника радиуса, окруженного вторым, внешним концентрическим проводником радиуса ((Рисунок)). Пространство между ними обычно заполнено изолятором, например, полиэтиленом. Между двумя проводниками возникает небольшой радиальный ток утечки. Определить сопротивление коаксиального кабеля длиной л .
Коаксиальные кабели состоят из внутреннего проводника радиуса, окруженного вторым, внешним концентрическим проводником радиуса ((Рисунок)). Пространство между ними обычно заполнено изолятором, например, полиэтиленом. Между двумя проводниками возникает небольшой радиальный ток утечки. Определить сопротивление коаксиального кабеля длиной л .
Коаксиальные кабели состоят из двух концентрических проводников, разделенных изоляцией. Они часто используются в кабельном телевидении или других аудиовизуальных соединениях.
Стратегия Мы не можем использовать уравнение напрямую. Вместо этого мы смотрим на концентрические цилиндрические оболочки толщиной dr и интегрируем.
Решение Сначала находим выражение для dR , а затем интегрируем от до ,
Значение Сопротивление коаксиального кабеля зависит от его длины, внутреннего и внешнего радиусов и удельного сопротивления материала, разделяющего два проводника.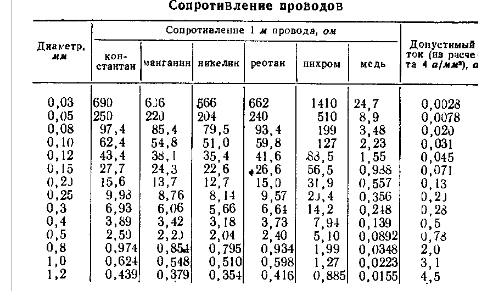 Поскольку это сопротивление не бесконечно, между двумя проводниками возникает небольшой ток утечки. Этот ток утечки приводит к затуханию (или ослаблению) сигнала, передаваемого по кабелю.
Поскольку это сопротивление не бесконечно, между двумя проводниками возникает небольшой ток утечки. Этот ток утечки приводит к затуханию (или ослаблению) сигнала, передаваемого по кабелю.
Проверьте свои знания Сопротивление между двумя проводниками коаксиального кабеля зависит от удельного сопротивления материала, разделяющего два проводника, длины кабеля и внутреннего и внешнего радиусов двух проводников. Если вы проектируете коаксиальный кабель, как сопротивление между двумя проводниками зависит от этих переменных?
Чем больше длина, тем меньше сопротивление.Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен.


 R4=10
R4=10

 р == 0,017·10-6 Ом •
р == 0,017·10-6 Ом • с = 4200 Дж/(кг • °С).
с = 4200 Дж/(кг • °С). Как включить амперметр,
Как включить амперметр,
 Температурный
Температурный
 р = 0,1·10-6
р = 0,1·10-6 Если же проводники соединить
Если же проводники соединить
 Найдите сопротивление резистора
Найдите сопротивление резистора
 Сила тока в цепи равна 0,28 А.
Сила тока в цепи равна 0,28 А. Найдите сопротивление
Найдите сопротивление

 Сила тока в
Сила тока в
 Сопротивление R=4,5
Сопротивление R=4,5
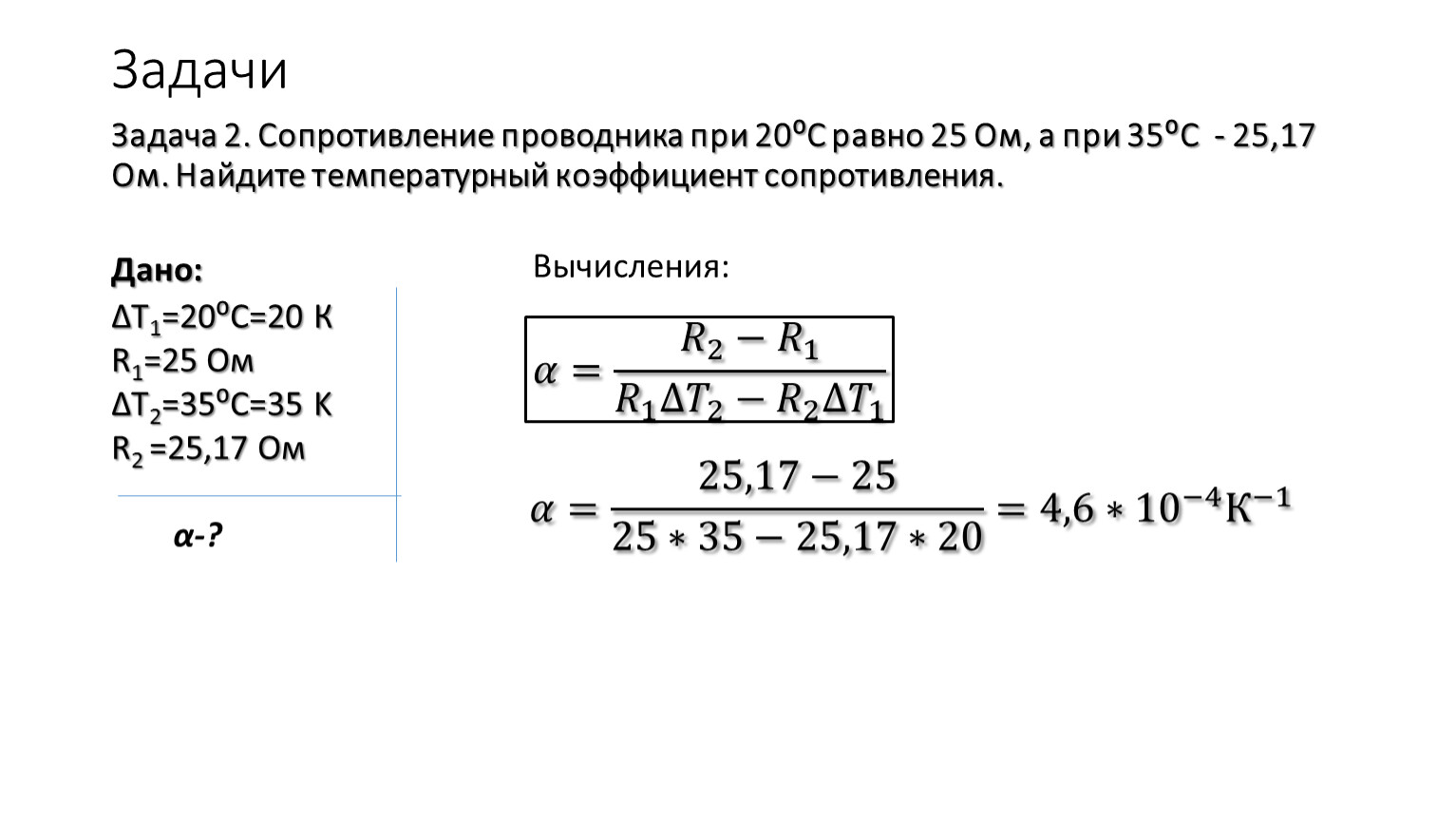 Внутренним
Внутренним ), если сопротивления резисторов
), если сопротивления резисторов
 ), если сопротивление Rl=R2=15
), если сопротивление Rl=R2=15
 До какой температуры
До какой температуры Найдите
Найдите определите
определите Обмотка электродвигателя постоянного
Обмотка электродвигателя постоянного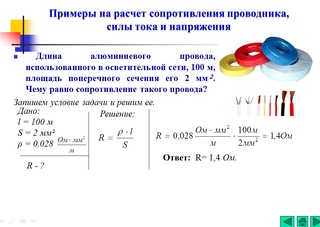 сопротивлением
сопротивлением

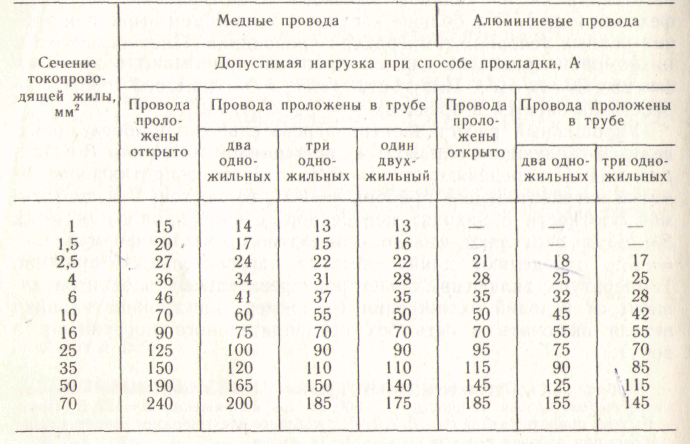 Следовательно, если взять материал с меньшим сопротивлением, то потребуется нагреватель большей длины и с меньшей площадью поперечного сечения. Не всегда в печи может быть размещен достаточно длинный нагреватель. Также стоит учитывать, что, чем больше диаметр проволоки, из которой сделан нагреватель, тем дольше срок его службы. Примерами материалов, обладающих высоким электрическим сопротивлением являются хромоникелевый сплав нихром Х20Н80, Х15Н60, железохромоалюминиевый сплав фехраль Х23Ю5Т, которые относятся к прецизионным сплавам с высоким электрическим сопротивлением.
Следовательно, если взять материал с меньшим сопротивлением, то потребуется нагреватель большей длины и с меньшей площадью поперечного сечения. Не всегда в печи может быть размещен достаточно длинный нагреватель. Также стоит учитывать, что, чем больше диаметр проволоки, из которой сделан нагреватель, тем дольше срок его службы. Примерами материалов, обладающих высоким электрическим сопротивлением являются хромоникелевый сплав нихром Х20Н80, Х15Н60, железохромоалюминиевый сплав фехраль Х23Ю5Т, которые относятся к прецизионным сплавам с высоким электрическим сопротивлением.
 К ним относятся сплавы на основе хрома и никеля (хромоникелевые), железа, хрома и алюминия (железохромоалюминиевые). Марки и свойства данных сплавов рассмотрены в ГОСТ 10994-74 «Сплавы прецизионные. Марки». Представителями хромоникелевых сплавов является нихром марок Х20Н80, Х20Н80-Н (950-1200 °С), Х15Н60, Х15Н60-Н (900-1125 °С), железохромоалюминиевых – фехраль марок Х23Ю5Т (950-1400 °С), Х27Ю5Т (950-1350 °С), Х23Ю5 (950-1200 °С), Х15Ю5 (750-1000 °С). Также существуют железохромоникелевые сплавы — Х15Н60Ю3, Х27Н70ЮЗ.
К ним относятся сплавы на основе хрома и никеля (хромоникелевые), железа, хрома и алюминия (железохромоалюминиевые). Марки и свойства данных сплавов рассмотрены в ГОСТ 10994-74 «Сплавы прецизионные. Марки». Представителями хромоникелевых сплавов является нихром марок Х20Н80, Х20Н80-Н (950-1200 °С), Х15Н60, Х15Н60-Н (900-1125 °С), железохромоалюминиевых – фехраль марок Х23Ю5Т (950-1400 °С), Х27Ю5Т (950-1350 °С), Х23Ю5 (950-1200 °С), Х15Ю5 (750-1000 °С). Также существуют железохромоникелевые сплавы — Х15Н60Ю3, Х27Н70ЮЗ.

 Максимальная рабочая температура сплава Х15Н60ЮЗ составляет 1200 °С.
Максимальная рабочая температура сплава Х15Н60ЮЗ составляет 1200 °С. Вольфрамовые нагреватели могут работать до 3000 °С. В особых случаях применяют нагреватели из тантала и ниобия.
Вольфрамовые нагреватели могут работать до 3000 °С. В особых случаях применяют нагреватели из тантала и ниобия.



 табл. 2.
табл. 2. Здесь мы учтем дополнительные параметры нагревателей, попытаемся разобраться с вариантами подключения нагревателей к сети трехфазного тока. Расчет нагревателя будем проводить на примере электрической печи. Пусть исходными данными являются внутренние размеры печи.
Здесь мы учтем дополнительные параметры нагревателей, попытаемся разобраться с вариантами подключения нагревателей к сети трехфазного тока. Расчет нагревателя будем проводить на примере электрической печи. Пусть исходными данными являются внутренние размеры печи. Таким образом мощность нагревателя электрической печи должна составлять P = 100 · 60 = 6000 Вт = 6 КВт.
Таким образом мощность нагревателя электрической печи должна составлять P = 100 · 60 = 6000 Вт = 6 КВт.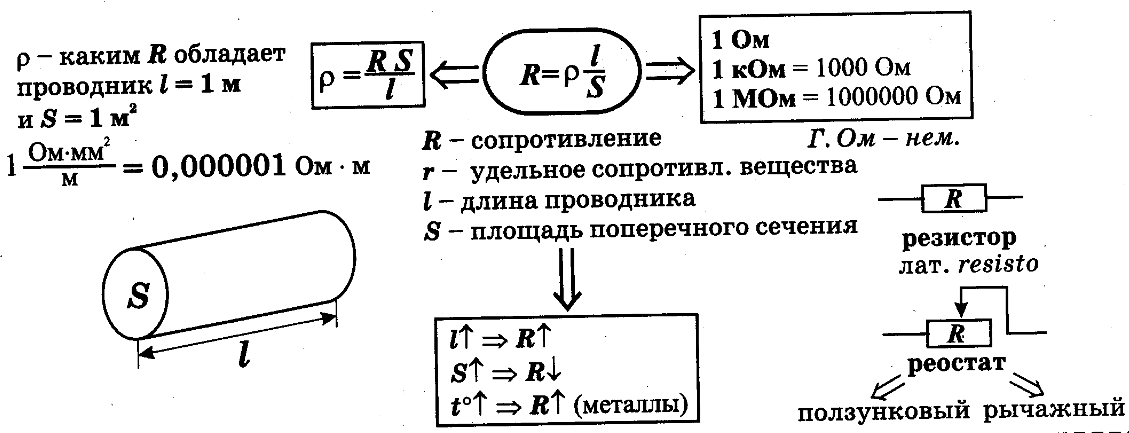
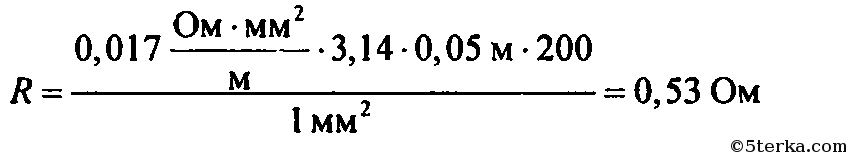 Это сделано для того, чтобы не усложнять изложение материала по расчету нагревателей электротехническими терминами и определениями (например, не упоминаются фазные и линейные напряжения и токи и соотношения между ними). С классическим подходом и формулами расчета трехфазных цепей можно ознакомиться в специализированной литературе. В данной статье некоторые математические преобразования, проведенные над классическими формулами, скрыты от читателя, и на конечный результат это не оказывает никакого влияния.
Это сделано для того, чтобы не усложнять изложение материала по расчету нагревателей электротехническими терминами и определениями (например, не упоминаются фазные и линейные напряжения и токи и соотношения между ними). С классическим подходом и формулами расчета трехфазных цепей можно ознакомиться в специализированной литературе. В данной статье некоторые математические преобразования, проведенные над классическими формулами, скрыты от читателя, и на конечный результат это не оказывает никакого влияния. Подключение по схеме «ЗВЕЗДА»
Подключение по схеме «ЗВЕЗДА»
 Решая простую пропорцию, получаем, что с 1 см2 выделяется мощность β = P / S = 6000 / 179 = 33,5 Вт, где β — поверхностная мощность нагревателя.
Решая простую пропорцию, получаем, что с 1 см2 выделяется мощность β = P / S = 6000 / 179 = 33,5 Вт, где β — поверхностная мощность нагревателя. βэф выбирается по таблице 3, α — по таблице 4.
βэф выбирается по таблице 3, α — по таблице 4. Тогда по таблице 3 подбираем βэф = 8,05 Вт/см2, α = 0,2, βдоп = βэф · α = 8,05 · 0,2 = 1,61 Вт/см2 = 1,61 · 104 Вт/м2.
Тогда по таблице 3 подбираем βэф = 8,05 Вт/см2, α = 0,2, βдоп = βэф · α = 8,05 · 0,2 = 1,61 Вт/см2 = 1,61 · 104 Вт/м2. 1-90).
1-90). 1-90, Приложение 2, Таблица 8. В данном случае, ближайшим большим стандартным размером является Ø 2,8 мм. Диаметр нагревателя d = 2,8 мм.
1-90, Приложение 2, Таблица 8. В данном случае, ближайшим большим стандартным размером является Ø 2,8 мм. Диаметр нагревателя d = 2,8 мм. Был получен диаметр проволоки 2,8 мм. Тогда нужная нам длина составит
Был получен диаметр проволоки 2,8 мм. Тогда нужная нам длина составит
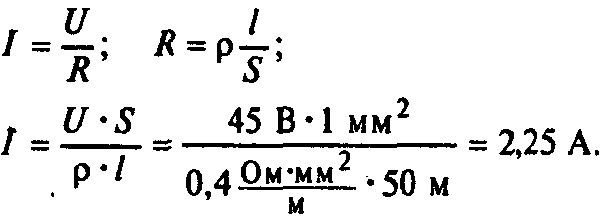

 Нихромовая и фехралевая проволока подвергаются навивке в виде спиралей или сгибанию в форме зигзагов, лента сгибается в форме зигзагов, что позволяет вместить большее количество материала (по длине) в рабочую камеру. Наиболее распространенным вариантом является спираль.
Нихромовая и фехралевая проволока подвергаются навивке в виде спиралей или сгибанию в форме зигзагов, лента сгибается в форме зигзагов, что позволяет вместить большее количество материала (по длине) в рабочую камеру. Наиболее распространенным вариантом является спираль.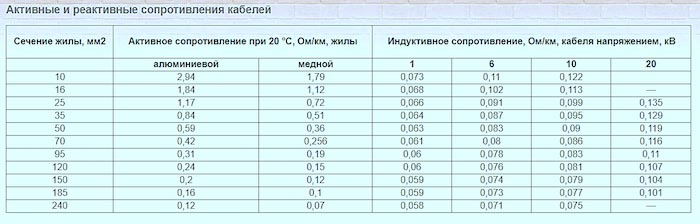
 Также необходимо определить материал, из которого должен быть сделан нагреватель, тип нагревателя (проволочный или ленточный), тип расположения нагревателей и другие особенности. Если нагреватель изготавливается в виде спирали, то необходимо определить количество витков и шаг между ними.
Также необходимо определить материал, из которого должен быть сделан нагреватель, тип нагревателя (проволочный или ленточный), тип расположения нагревателей и другие особенности. Если нагреватель изготавливается в виде спирали, то необходимо определить количество витков и шаг между ними. А., Гутман М.Б., Рубин Г.К., Шадрич Н.И. «Расчет и конструирование нагревателей электропечей сопротивления».
А., Гутман М.Б., Рубин Г.К., Шадрич Н.И. «Расчет и конструирование нагревателей электропечей сопротивления».