При последовательном соединении сопротивления складываются. Параллельное соединение проводников
Содержание:
В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом. То есть, начало одного резистора соединяется с концом второго, а начало второго — с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.
Последовательное и параллельное соединение сопротивлений
Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.
Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.
В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии — нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3. Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь. То есть начало R1 соединяется с концом R2, а начало R2 — с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах .
На всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.
Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.
При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.
Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.
Для того чтобы отобразить эти свойства, вновь понадобится закон Ома.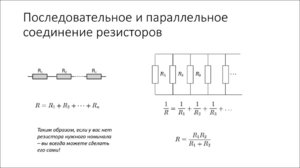 В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока — I = I1 + I2 + I3, напряжение — U = U1 = U2 = U3, сопротивление — 1/R = 1/R1 + 1/R2 + 1/R3.
В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока — I = I1 + I2 + I3, напряжение — U = U1 = U2 = U3, сопротивление — 1/R = 1/R1 + 1/R2 + 1/R3.
При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.
В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как . Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.
Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.
Законы последовательного и параллельного соединения проводников
Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке. В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.
Более сложные вычисления с участием других величин требуют применения . Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.
Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.
В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом.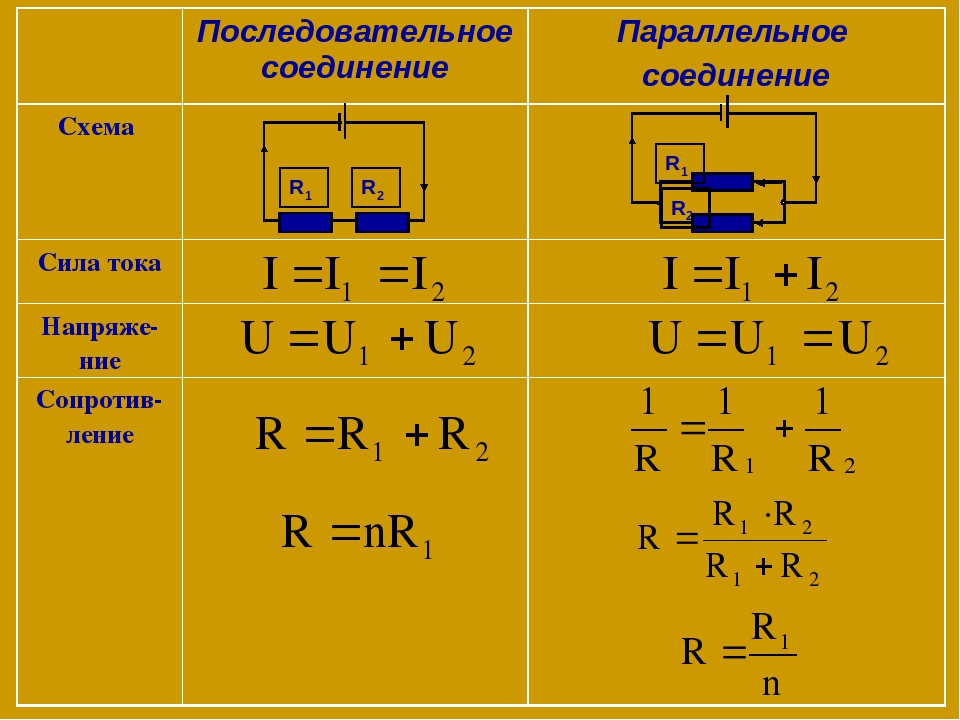 Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Основные электрические величины цепи
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
Взаимная зависимость электрических величин
Теперь необходимо определиться
, как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки.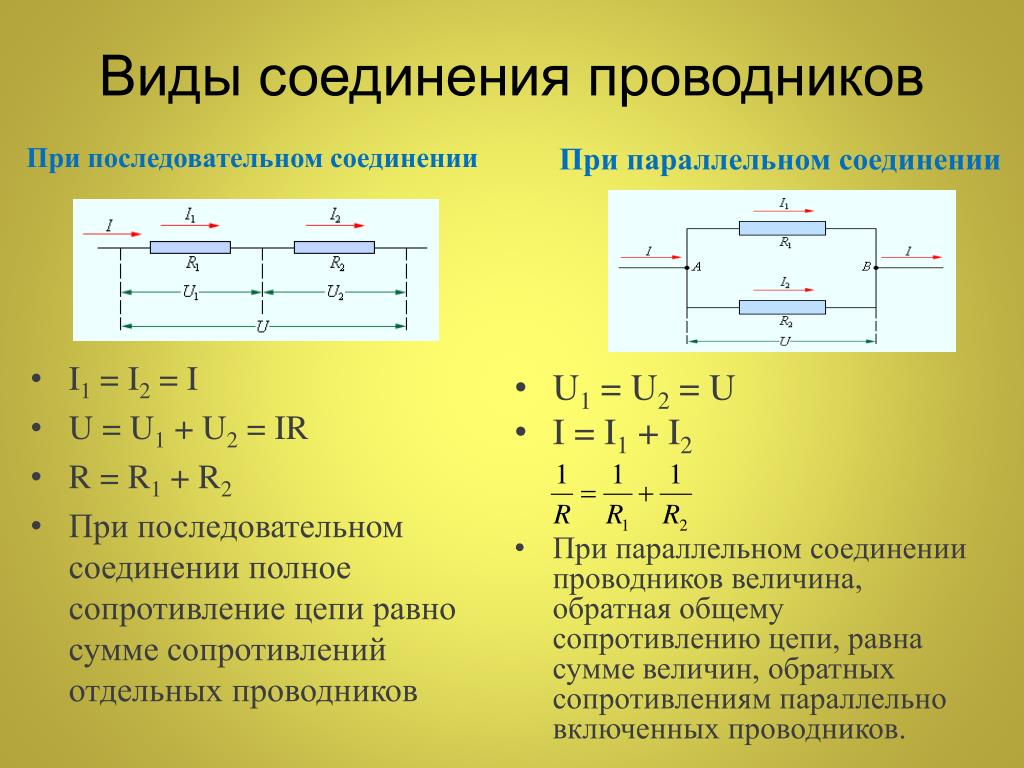 Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника
? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.

- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
= 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ
. – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет.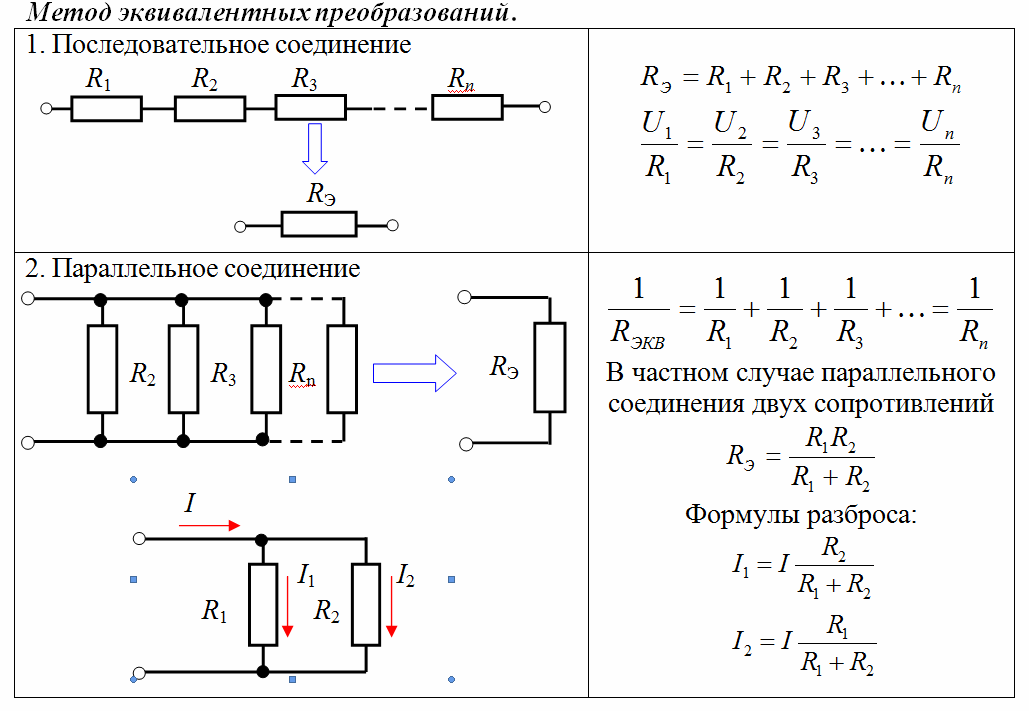 Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3. То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше. Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.

- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания
? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ. 23, соединенных последовательно:
23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ.245).
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.
Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.
Рисунок 1 — последовательное соединение проводников
Падение напряжения на сопротивлениях можно определить исходя из закона Ома.
Формула 1 — Падение напряжения на сопротивлении
Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.
То есть можно записать.
Формула 2 — соотношение между сопротивлением и напряжением
Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.
Формула 3 — вычисление суммарного сопротивления при параллельном включении
Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.
Рисунок 2 — Параллельное соединение проводников
Формула 4 — соотношение между токами в параллельных ветвях
Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.
Формула 5 — Распределение токов в параллельных ветвях
Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.
Формула 6 — Сопротивление параллельно включённых проводников
Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.
Последовательное соединение сопротивлений
Возьмем три неизменных сопротивления R1, R2 и R3
и включим их в цепь так, чтоб конец первого сопротивления R1
был соединен с началом второго сопротивления R
2, конец второго — с началом третьего R
3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1
).
Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.
Рис 1
. Последовательное соединение сопротивлений
Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2
и U3 = IR3
либо
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I
за скобки, получим IR = I(R1 + R2 + R3)
.
Поделив сейчас обе части равенства на I
, будем совсем иметь R = R1 + R2 + R3
Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1
== 10 Ом, R
2 = 20 Ом и R
3 = 50 Ом). Соединим их поочередно (рис. 2
) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример поочередного соединения 3-х сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R
= 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80
= 0
,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U
1 = 0,75х 10 = 7,5 В, U
2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U
= 7,5+15 + 37,5 = 60 В.
Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.
Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а.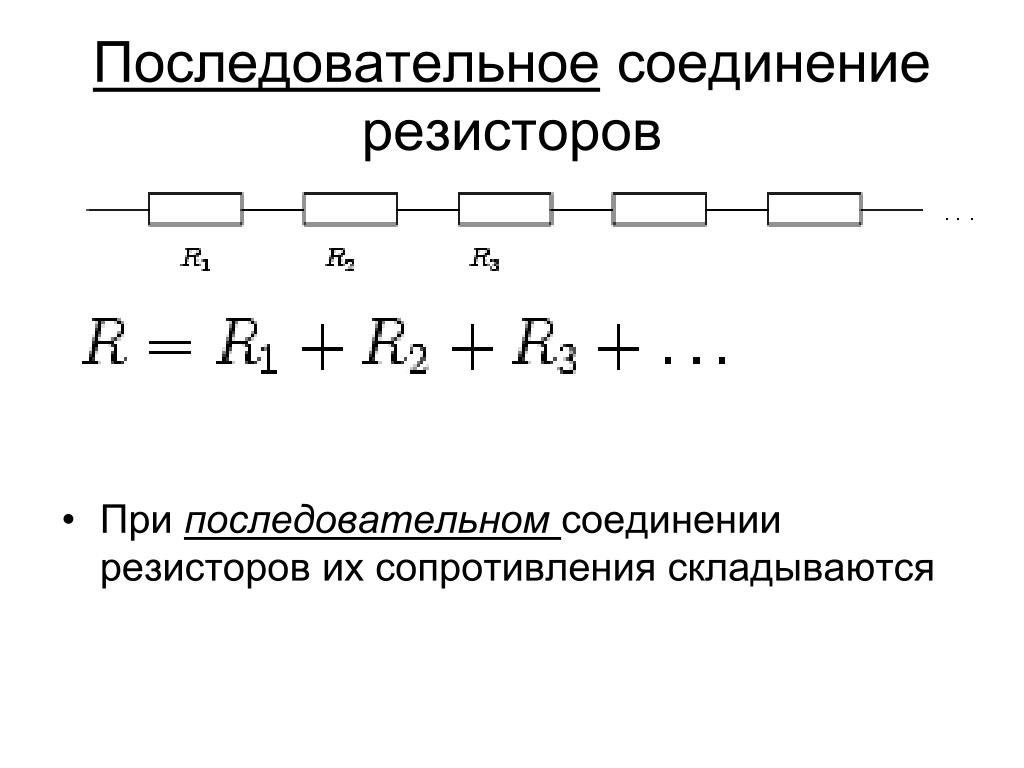 В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1
В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1
и I
2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.
Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Означает, сила тока в цепи до ее разветвления
(до точки а) равна силе тока после разветвления цепи
(после точки б).
Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветки амперметр покажет силу тока I1
Пусть в первой ветки амперметр покажет силу тока I1
, а во 2-ой — I
2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I
до разветвления (до точки а).
Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки.
I = I1 + I2
Выражая это формулой, получим
Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи
.
Разглядим сейчас, каково будет соотношение меж токами в ветвях.
Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3
, конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1
и U2 на сопротивлениях R1
и R2, потому что он соединен с началом и концом каждого сопротивления.
Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.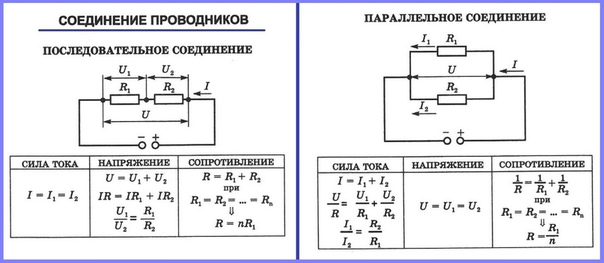
Это дает нам право написать, что U = U1 = U2
,
где U — напряжение на зажимах источника тока; U1
— падение напряжения на сопротивлении R1
, U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR
.
Потому для каждой ветки можно написать: U1 = I1R1
и U2 = I2R2
, но потому что U1
= U2, то и I1R1 = I2R2
.
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.
Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток.
По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.
Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1
и R
2, присоединенных к источнику тока. Пусть R1
= 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:
I1 =
U / R1 = 3 / 10 = 0
,3 А = 300 мА
I
2 =
U / R
2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1
+I2
= 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.
Вправду, R1
== 10 Ом в два раза меньше R
2 = 20 Ом, при всем этом I1
= 300 мА в два раза больше I2
= 150 мА. Общий ток в цепи I
= 450 мА разветвился на две части так, что большая его часть (I1
= 300 мА) пошла через наименьшее сопротивление (R1
= 10 Ом), а наименьшая часть (R2
= 150 мА) -через большее сопротивление (R
2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Рис. 4
Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.
Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления.
Такое сопротивление именуется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R
, где I
— ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т. е. эквивалентное сопротивление.
е. эквивалентное сопротивление.
Точно так же для каждой ветки I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления веток.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Потому что при параллельном соединении U = U1 = U2
, то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U
(1 / R1 +
1 / R2
)
Разделив сейчас обе части равенства на U
, будем совсем иметь 1 / R
=
1 / R1 +
1 / R2
Помня, что проводимостью именуется величина, оборотная сопротивлению
, мы можем сказать, что в приобретенной формуле 1 / R —
проводимость наружной цепи; 1 / R1
проводимость первой ветки; 1 / R2-
проводимость 2-ой ветки.
На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.
Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?
Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.
Чтоб убедиться в этом, разглядим последующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
R = 1 / 6
Как следует, эквивалентное сопротивление
R = 6 Ом.
Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений
, т. е. меньше сопротивления R1.
е. меньше сопротивления R1.
Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.
Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3
равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1
,2 А I
2 = U/R
2 = 12 /
20 = 1
,6 А I
3 = U/R1 = 12 /
60 =
0,2
А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3
=1,2 + 0,6 + 0,2 =
2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U
/
R
= 12 / 6 = 2
А
Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток.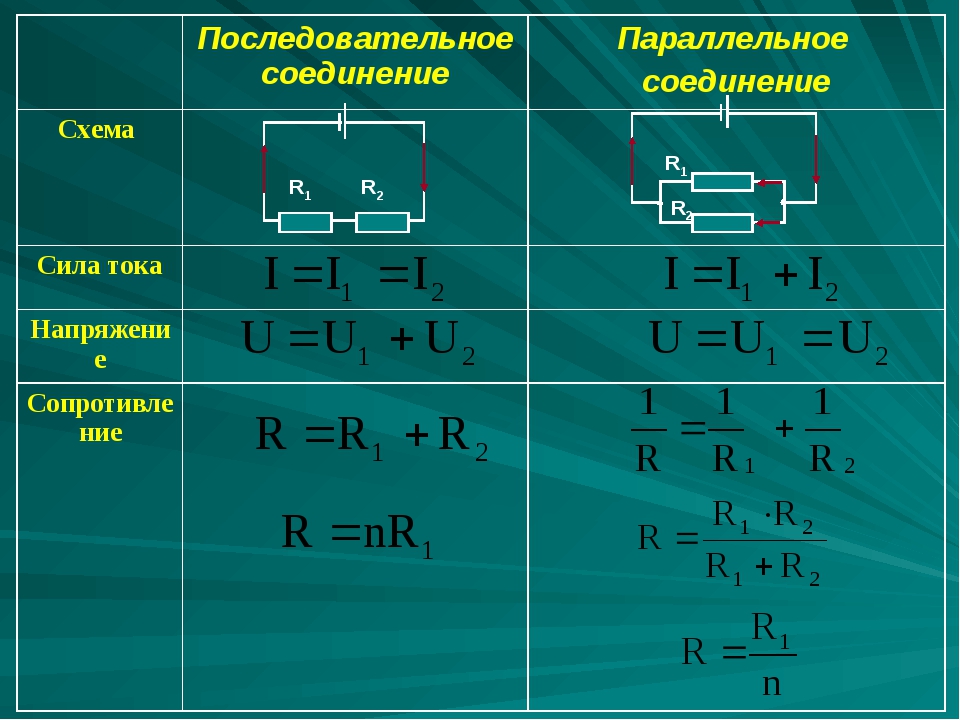 Показания амперметра и в том и в другом случае будут приблизительно схожими.
Показания амперметра и в том и в другом случае будут приблизительно схожими.
На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.
К примеру, если соединены параллельно два сопротивления R1
и R2
, то формулу 1 / R
=
1 / R1 +
1 / R2
можно конвертировать так: 1/R = (R2 + R1) / R1 R2
и, решая равенство относительно R, получить R = R1
х R2 /
(R1 + R2
), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R
= 1/U
, где
R
= 1
Ом
А мощность будет выделяться P
=
I
*
U
,
то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же.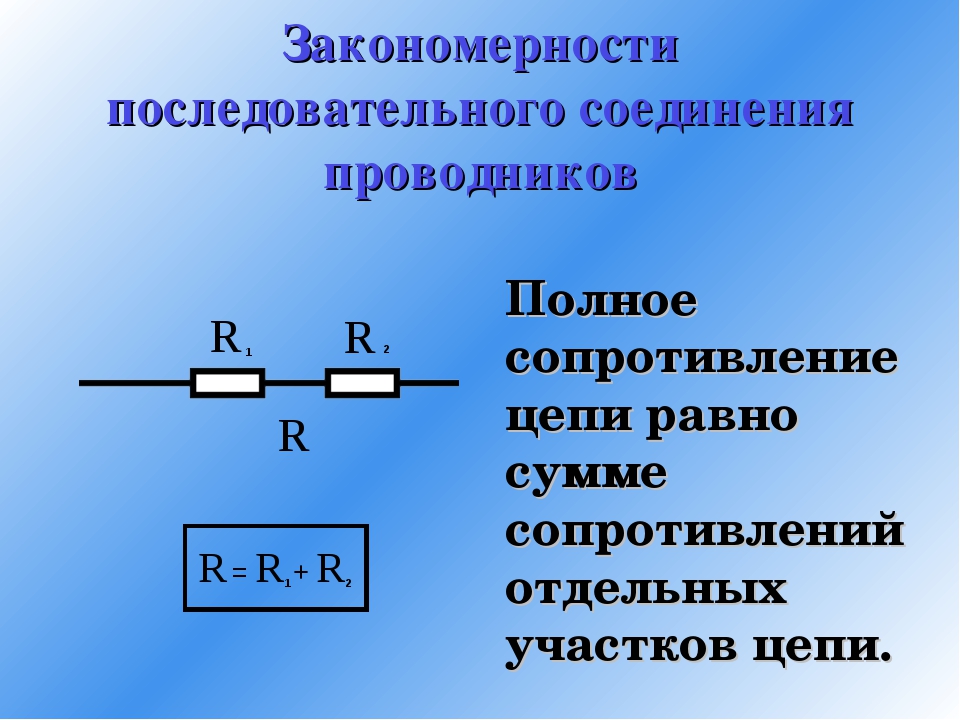 А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В.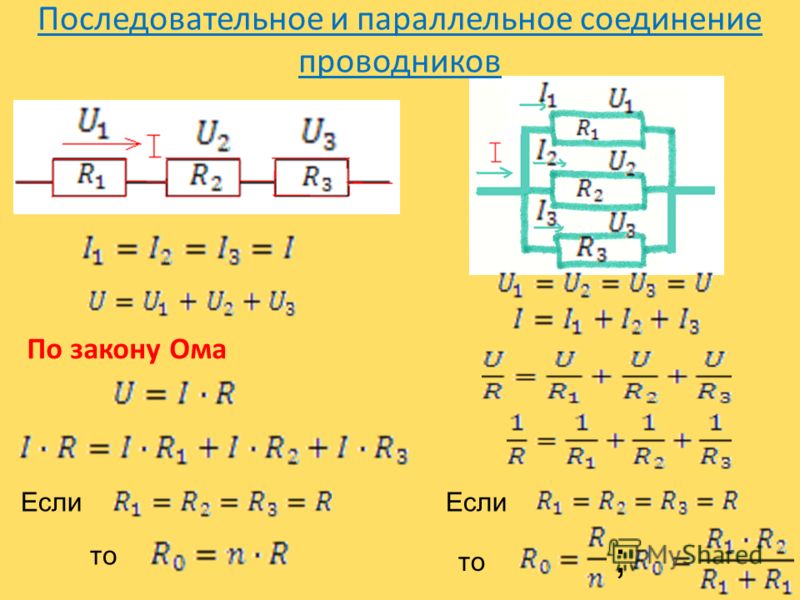 И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G
, по аналогии с сопротивлением R
и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I
=
U
*
G
&
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих.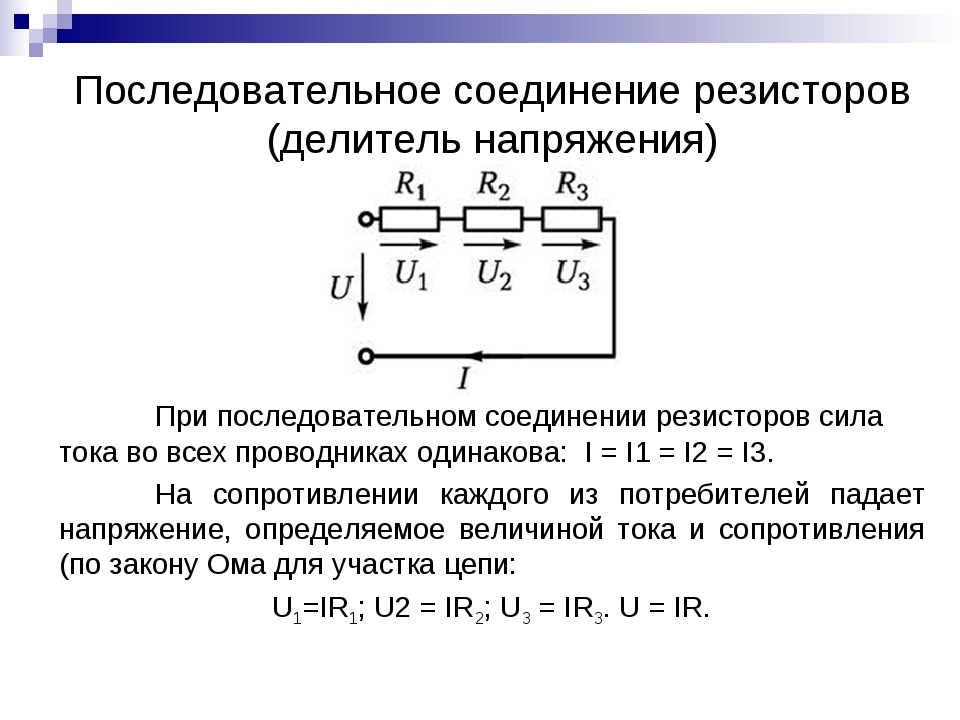 Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Параллельное соединение трех проводников. Теперь используем формулу расчета сопротивления. Последовательное соединение проводников
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение
– это такое соединение, при котором сила тока на всем участке цепи одинакова.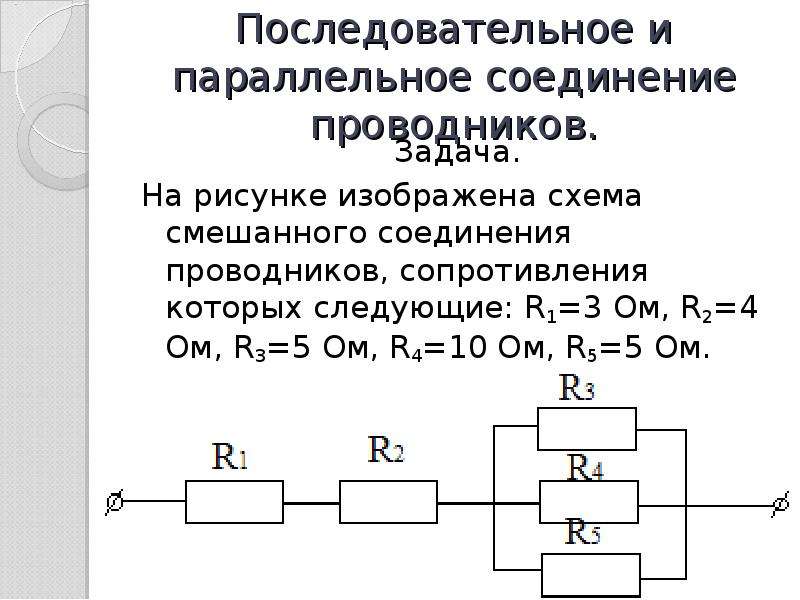 Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение
– это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение
– соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Содержание:
Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении.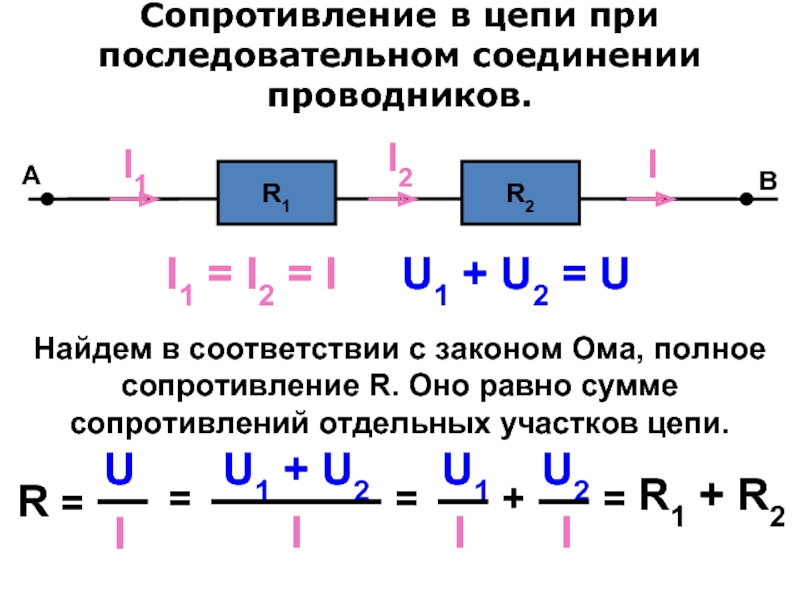 Данное свойство отражается формулой: R общ = R 1 + R 2 .
Данное свойство отражается формулой: R общ = R 1 + R 2 .
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Нужно вычислить сопротивление последовательной, параллельной или комбинированной цепей? Нужно, если вы не хотите сжечь плату! Эта статья расскажет вам, как это сделать. Перед чтением, пожалуйста, уясните, что у резисторов нет «начала» и нет «конца». Эти слова вводятся для облегчения понимания изложенного материала.
Шаги
Сопротивление последовательной цепи
Сопротивление параллельной цепи
Сопротивление комбинированной цепи
Некоторые факты
- Каждый электропроводный материал имеет некоторое сопротивление, являющееся сопротивляемостью материала электрическому току.

- Сопротивление измеряется в Омах. Символ единицы измерения Ом — Ω.
- Разные материалы имеют разные значения сопротивления.
- Например, сопротивление меди 0.0000017 Ом/см 3
- Сопротивление керамики около 10 14 Ом/см 3
- Чем больше значение сопротивления, тем выше сопротивляемость электрическому току. Медь, которая часто используется в электрических проводах, имеет очень малое сопротивление. С другой стороны, сопротивление керамики очень велико, что делает ее прекрасным изолятором.
- Работа всей цепи зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
- U=IR. Это закон Ома, установленный Георгом Омом в начале 1800х. Если вам даны любые две из этих переменных, вы легко найдете третью.
- U=IR: Напряжение (U) есть результат умножения силы тока (I) * на сопротивление (R).
- I=U/R: Сила тока есть частное от напряжение (U) ÷ сопротивление (R).
- R=U/I: Сопротивление есть частное от напряжение (U) ÷ сила тока (I).

- Запомните: при параллельном соединении существует несколько путей прохождения тока по цепи, поэтому в такой цепи общее сопротивление будет меньше сопротивления каждого отдельного резистора. При последовательном соединении ток проходит через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
- Общее сопротивление в параллельной цепи всегда меньше сопротивления одного резистора с самым низким сопротивлением в этой цепи. Общее сопротивление в последовательной цепи всегда больше сопротивления одного резистора с самым высоким сопротивлением в этой цепи.
Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье.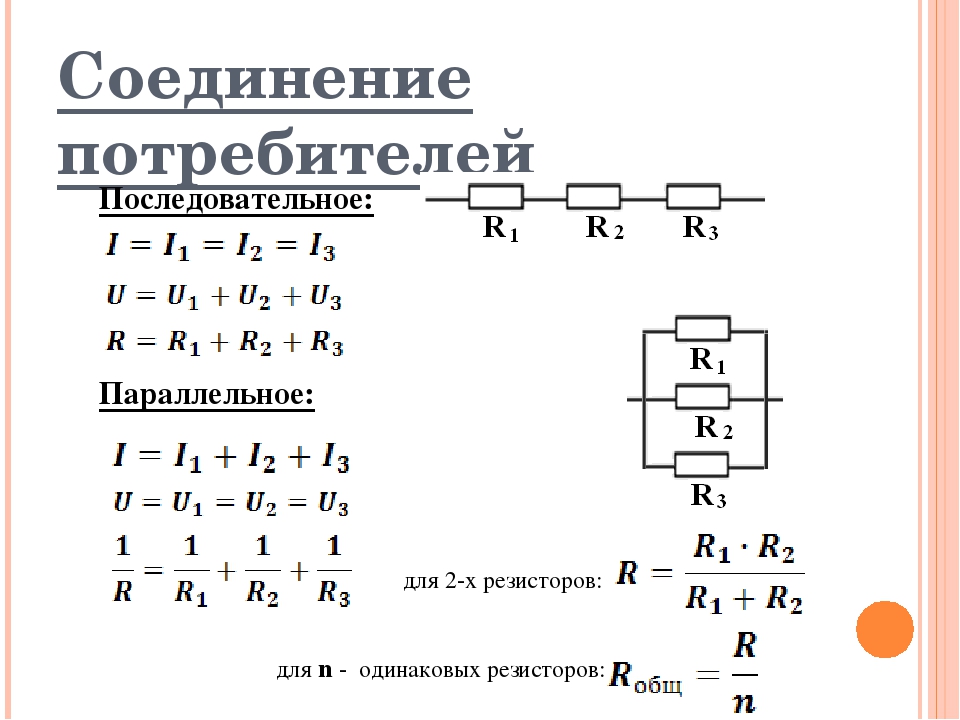 Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.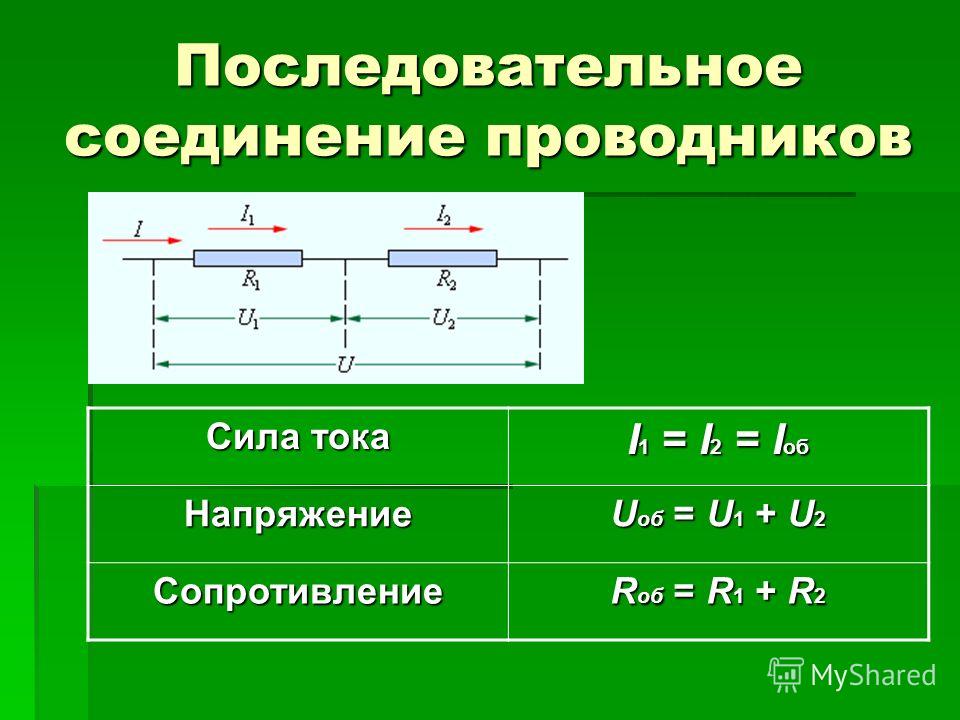
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии.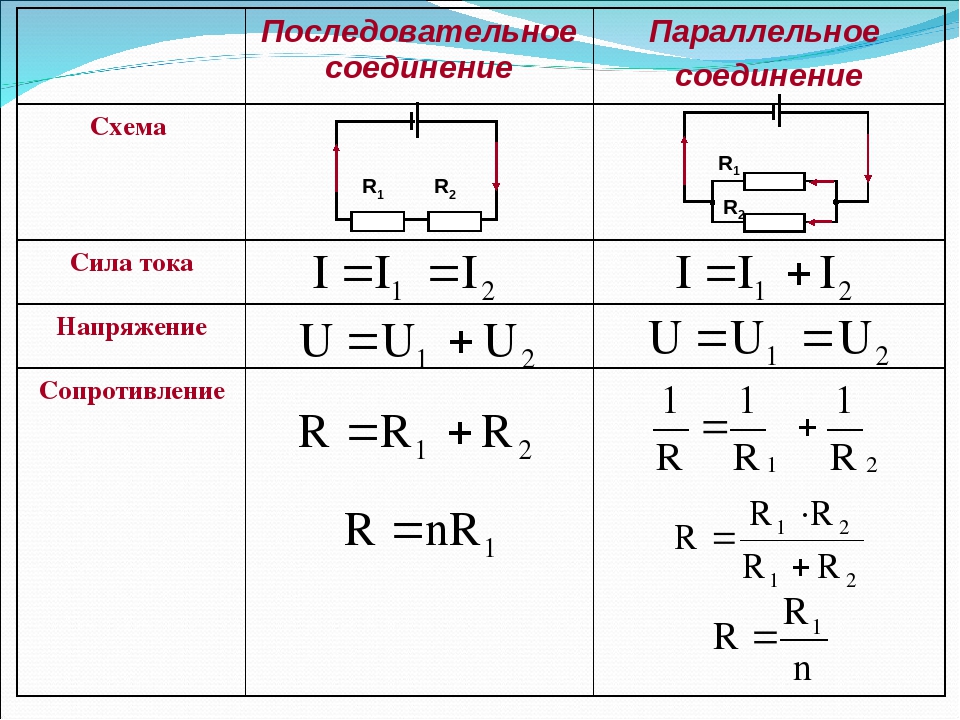 Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
Схема, иллюстрирующая второй закон Кирхгофа.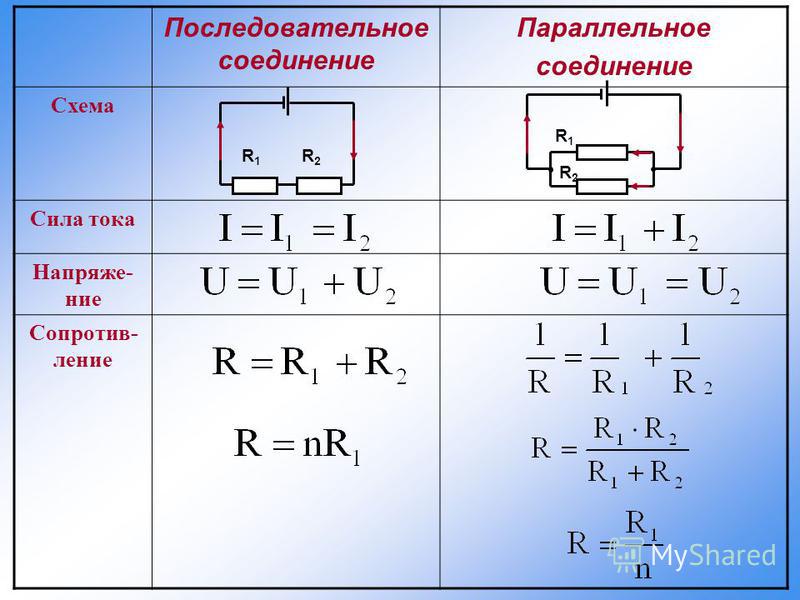
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным.
 Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник. - Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.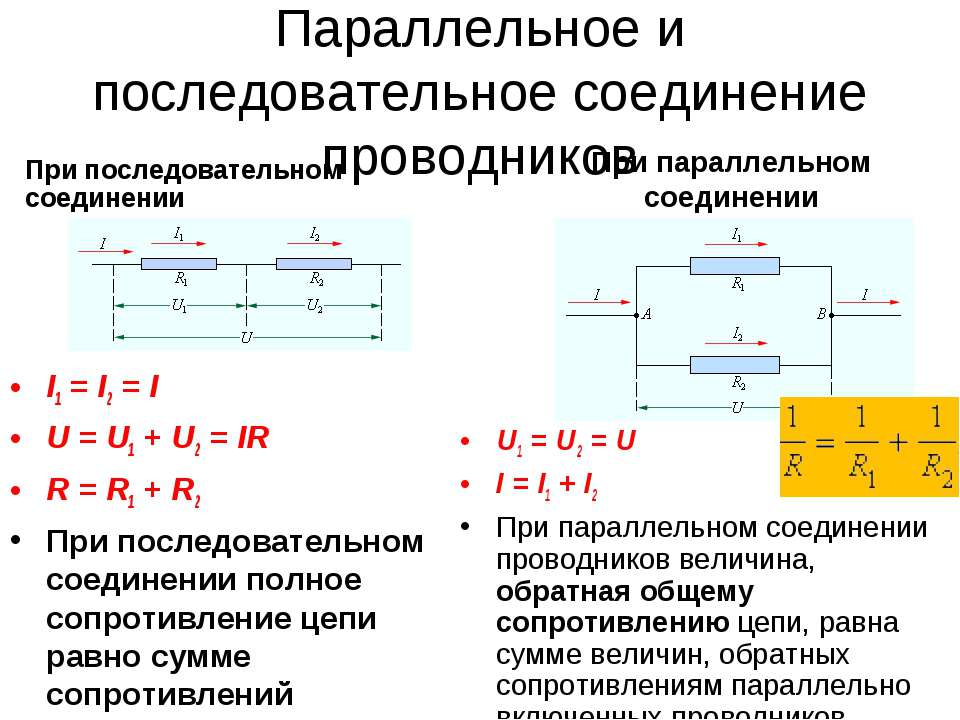
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор.
 В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины. - Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Ток в цепи из последовательно соединенных сопротивлений. Ток проводников в параллельном и последовательном соединении
Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.
Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.
Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.
Рисунок 1 — последовательное соединение проводников
Падение напряжения на сопротивлениях можно определить исходя из закона Ома.
Формула 1 — Падение напряжения на сопротивлении
Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.
Формула 2 — соотношение между сопротивлением и напряжением
Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.
Формула 3 — вычисление суммарного сопротивления при параллельном включении
Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.
Рисунок 2 — Параллельное соединение проводников
Формула 4 — соотношение между токами в параллельных ветвях
Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.
Формула 5 — Распределение токов в параллельных ветвях
Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.
Формула 6 — Сопротивление параллельно включённых проводников
Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.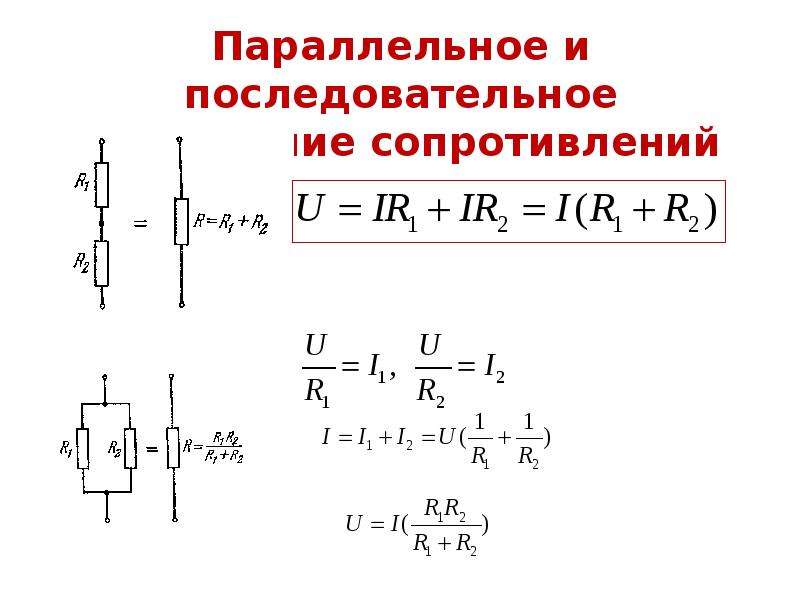
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Если нам надо, чтобы электроприбор работал, мы должны подключить его к . При этом ток должен проходить через прибор и возвращаться вновь к источнику, то есть цепь должна быть замкнутой.
Но подключение каждого прибора к отдельному источнику осуществимо, в основном, в лабораторных условиях. В жизни же приходится иметь дело с ограниченным количеством источников и довольно большим количеством потребителей тока. Поэтому создают системы соединений, позволяющие нагрузить один источник большим количеством потребителей. Системы при этом могут быть сколь угодно сложными и разветвленными, но в их основе лежит всего два вида соединения: последовательное и параллельное соединение проводников. Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.
Последовательное соединение проводников
Последовательное соединение проводников – это включение в электрическую цепь нескольких приборов последовательно, друг за другом. Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.
Напряжение всей цепи при последовательном соединении будет равно сумме напряжений на каждом включенном в цепь элементе. Сила тока в цепи будет одинакова в любой точке. А сумма сопротивлений всех элементов составит общее сопротивление всей цепи. Поэтому последовательное сопротивление можно выразить на бумаге следующим образом:
I=I_1=I_2=⋯=I_n ; U=U_1+U_2+⋯+U_n ; R=R_1+R_2+⋯+R_n ,
Плюсом последовательного соединения является простота сборки, а минусом – то, что если один элемент выйдет из строя, то ток пропадет во всей цепи. В такой ситуации неработающий элемент будет подобен ключу в выключенном положении.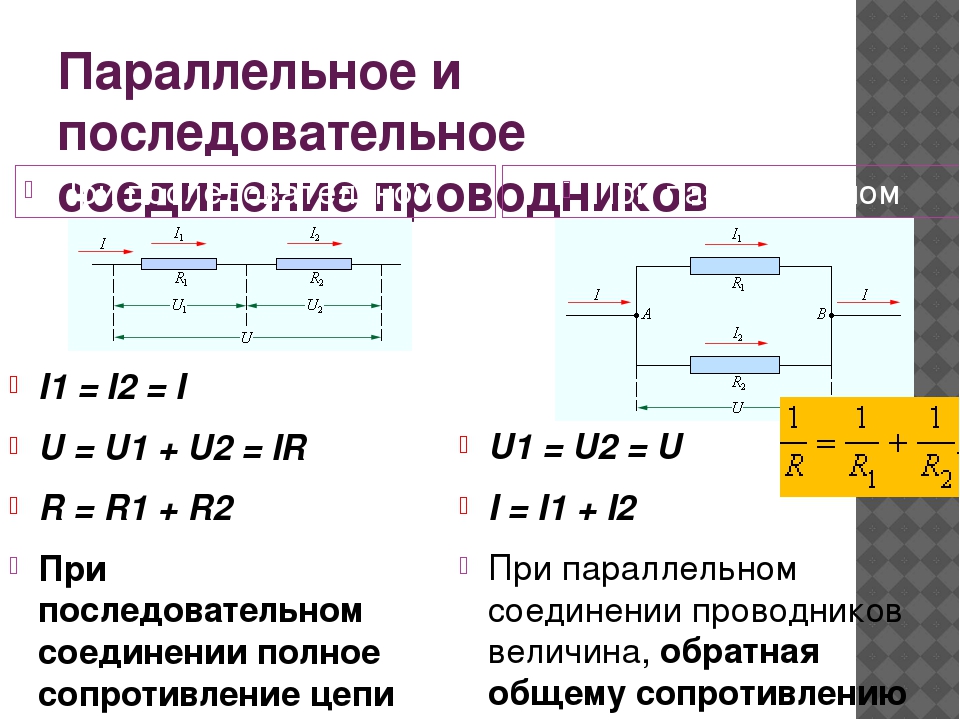 Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
Если в такой гирлянде выходила из строя хотя бы одна лампочка, приходилось перебирать их все, пока не найдешь ту самую, перегоревшую. В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.
Параллельное соединение проводников
При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.
Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается. Параллельное соединение описывается следующими соотношениями:
U=U_1=U_2=⋯=U_n ; I=I_1+I_2+⋯+I_n ; 1/R=1/R_1 +1/R_2 +⋯+1/R_n ,
где I — сила тока, U- напряжение, R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.
Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Нужна помощь в учебе?
Предыдущая тема: Расчёт сопротивления проводников и реостаты: формулы
Следующая тема:   Работа и мощность тока
Последовательное, параллельное и смешанное соединения резисторов.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление.
Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями.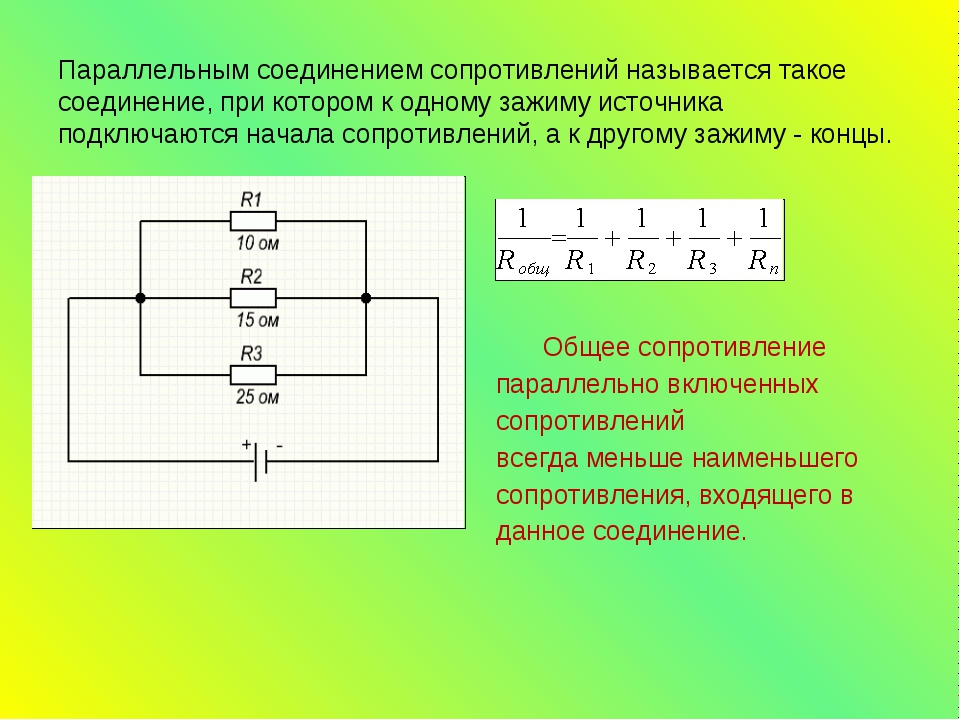 Различают следующие способы соединения резисторов
Различают следующие способы соединения резисторов
(приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк
(19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.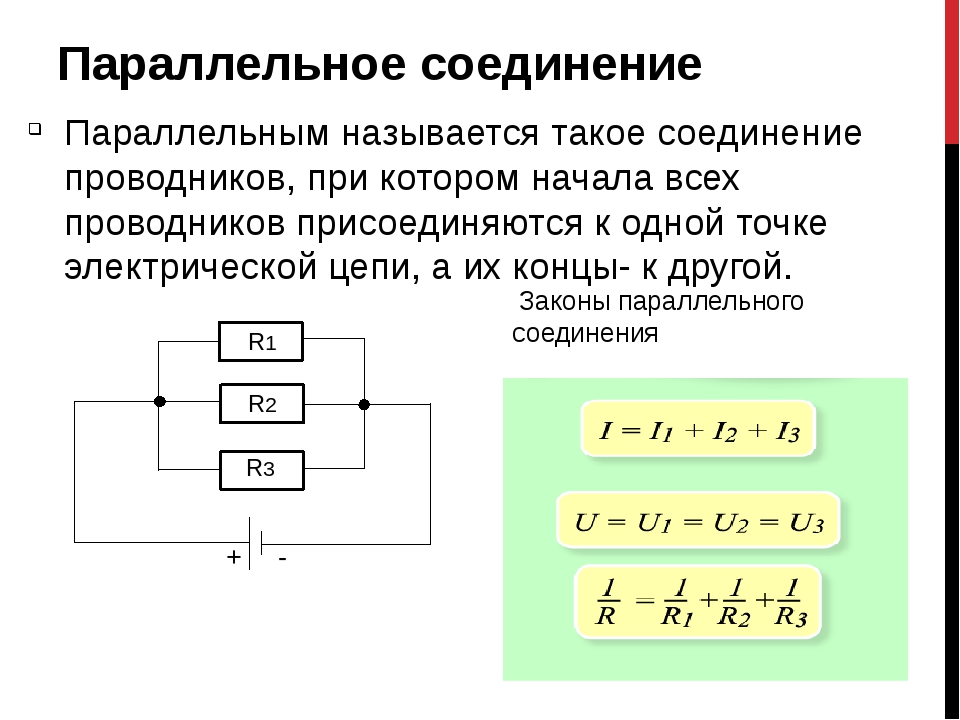 Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3
(20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3
(21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк
(23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк
=
1/R 1 + 1/R 2 + 1/R 3
(24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов
:
G эк = G 1 + G 2 +G 3
(25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3
(26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n
(27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n
(28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
п. с. постоянного тока.
Последовательное соединение сопротивлений
Возьмем три неизменных сопротивления R1, R2 и R3
и включим их в цепь так, чтоб конец первого сопротивления R1
был соединен с началом второго сопротивления R
2, конец второго — с началом третьего R
3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1
).
Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.
Рис 1
. Последовательное соединение сопротивлений
Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2
и U3 = IR3
либо
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I
за скобки, получим IR = I(R1 + R2 + R3)
.
Поделив сейчас обе части равенства на I
, будем совсем иметь R = R1 + R2 + R3
Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1
== 10 Ом, R
2 = 20 Ом и R
3 = 50 Ом). Соединим их поочередно (рис. 2
) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример поочередного соединения 3-х сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R
= 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80
= 0
,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U
1 = 0,75х 10 = 7,5 В, U
2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.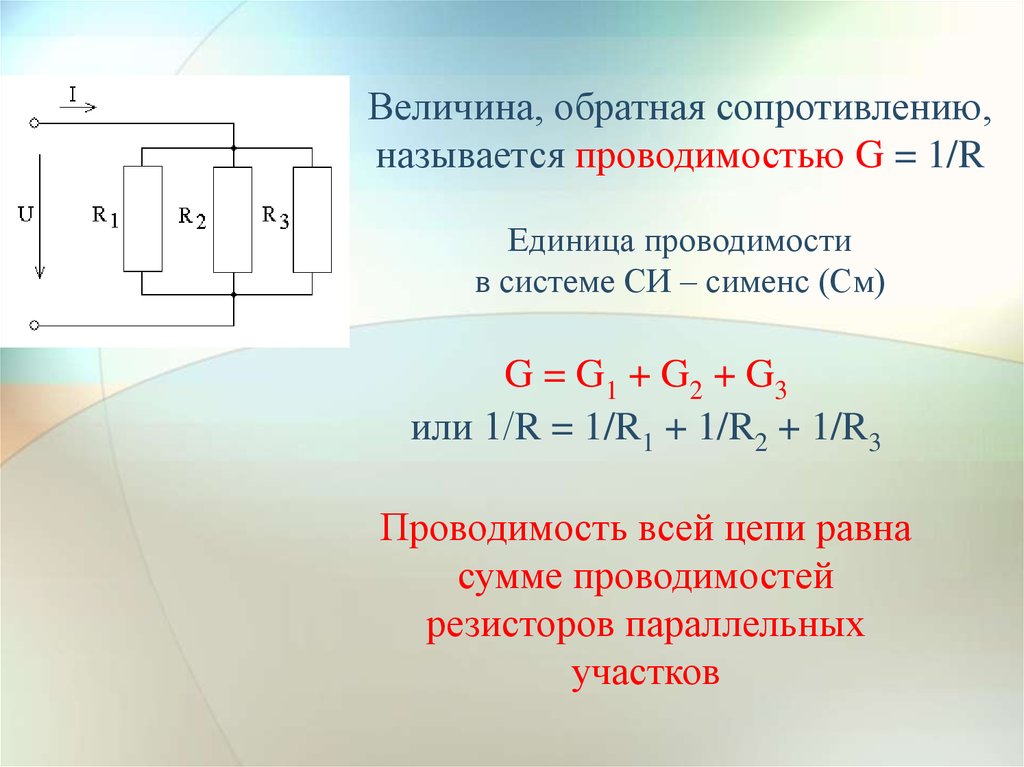
Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U
= 7,5+15 + 37,5 = 60 В.
Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.
Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1
В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1
и I
2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.
Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Означает, сила тока в цепи до ее разветвления
(до точки а) равна силе тока после разветвления цепи
(после точки б).
Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора.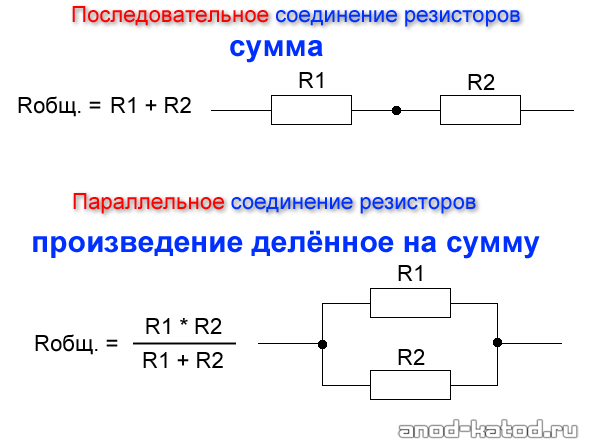 Пусть в первой ветки амперметр покажет силу тока I1
Пусть в первой ветки амперметр покажет силу тока I1
, а во 2-ой — I
2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I
до разветвления (до точки а).
Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки.
I = I1 + I2
Выражая это формулой, получим
Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи
.
Разглядим сейчас, каково будет соотношение меж токами в ветвях.
Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3
, конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1
и U2 на сопротивлениях R1
и R2, потому что он соединен с началом и концом каждого сопротивления.
Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2
,
где U — напряжение на зажимах источника тока; U1
— падение напряжения на сопротивлении R1
, U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR
.
Потому для каждой ветки можно написать: U1 = I1R1
и U2 = I2R2
, но потому что U1
= U2, то и I1R1 = I2R2
.
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.
Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток.
По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.
Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1
и R
2, присоединенных к источнику тока. Пусть R1
= 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:
I1 =
U / R1 = 3 / 10 = 0
,3 А = 300 мА
I
2 =
U / R
2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1
+I2
= 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.
Вправду, R1
== 10 Ом в два раза меньше R
2 = 20 Ом, при всем этом I1
= 300 мА в два раза больше I2
= 150 мА. Общий ток в цепи I
= 450 мА разветвился на две части так, что большая его часть (I1
= 300 мА) пошла через наименьшее сопротивление (R1
= 10 Ом), а наименьшая часть (R2
= 150 мА) -через большее сопротивление (R
2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.
Рис. 4
Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.
Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления.
Такое сопротивление именуется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R
, где I
— ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т.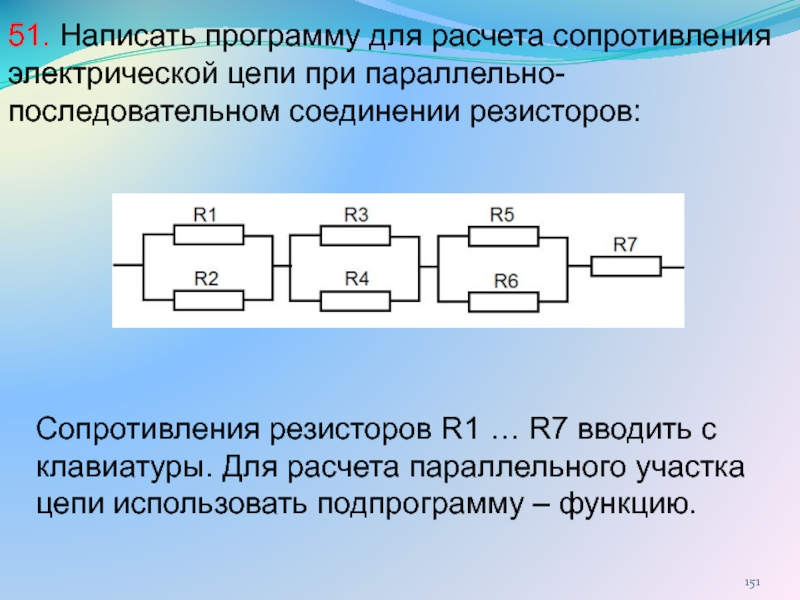 е. эквивалентное сопротивление.
е. эквивалентное сопротивление.
Точно так же для каждой ветки I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления веток.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Потому что при параллельном соединении U = U1 = U2
, то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U
(1 / R1 +
1 / R2
)
Разделив сейчас обе части равенства на U
, будем совсем иметь 1 / R
=
1 / R1 +
1 / R2
Помня, что проводимостью именуется величина, оборотная сопротивлению
, мы можем сказать, что в приобретенной формуле 1 / R —
проводимость наружной цепи; 1 / R1
проводимость первой ветки; 1 / R2-
проводимость 2-ой ветки.
На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.
Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?
Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.
Чтоб убедиться в этом, разглядим последующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
R = 1 / 6
Как следует, эквивалентное сопротивление
R = 6 Ом.
Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений
, т.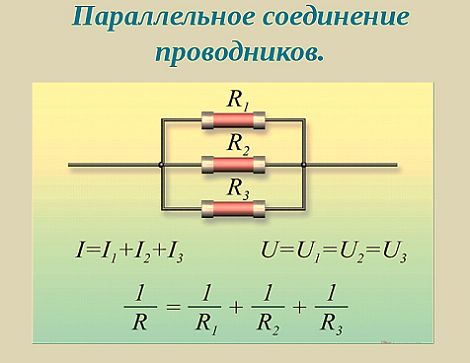 е. меньше сопротивления R1.
е. меньше сопротивления R1.
Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.
Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3
равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1
,2 А I
2 = U/R
2 = 12 /
20 = 1
,6 А I
3 = U/R1 = 12 /
60 =
0,2
А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3
=1,2 + 0,6 + 0,2 =
2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U
/
R
= 12 / 6 = 2
А
Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток.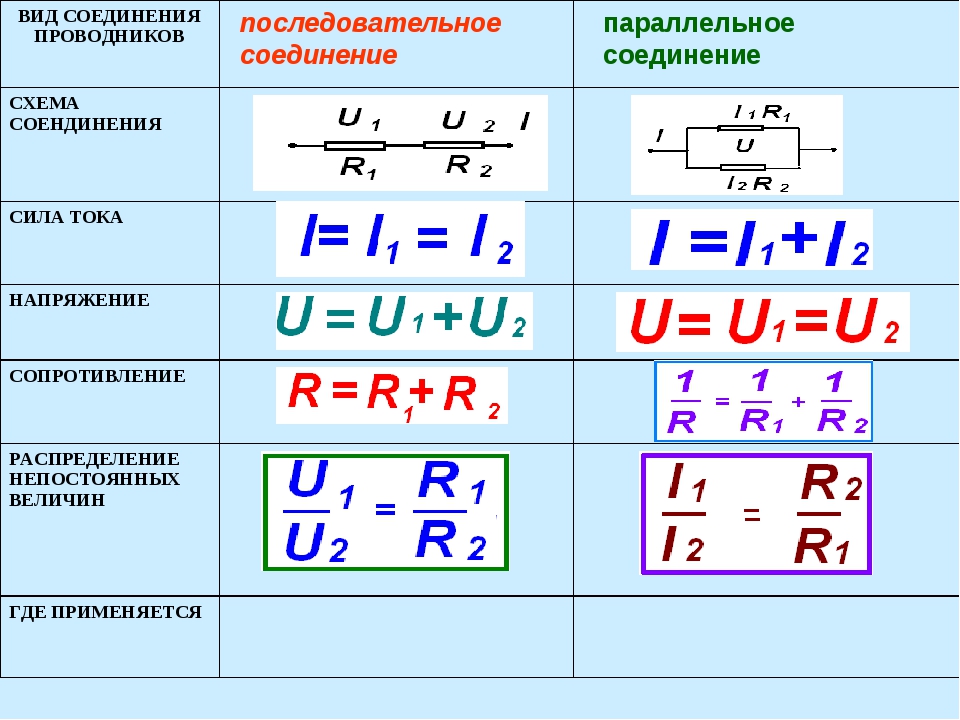 Показания амперметра и в том и в другом случае будут приблизительно схожими.
Показания амперметра и в том и в другом случае будут приблизительно схожими.
На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.
К примеру, если соединены параллельно два сопротивления R1
и R2
, то формулу 1 / R
=
1 / R1 +
1 / R2
можно конвертировать так: 1/R = (R2 + R1) / R1 R2
и, решая равенство относительно R, получить R = R1
х R2 /
(R1 + R2
), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Последовательное, параллельное и смешанное соединения резисторов
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Рис. 25. Схемы последовательного соединения приемников
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а. Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк (19)
где Rэк = R1 + R2 + R3.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то для рассматриваемой цепи
U = U1 + U2 +U3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U1 : U2 : U3 = R1 : R2 : R3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
U1 = U/n. (22)
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
26, а). Заменяя лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
Рис. 26. Схемы параллельного соединения приемников
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.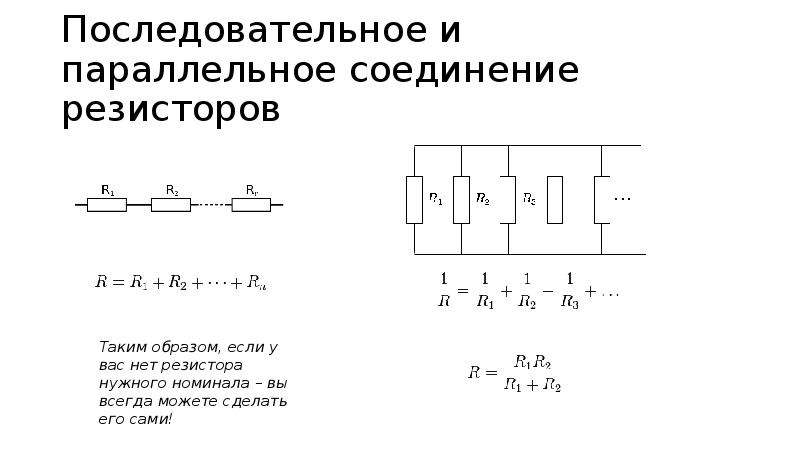
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т. е.
е.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.
Рис. 27. Схемы смешанного соединения приемников
Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).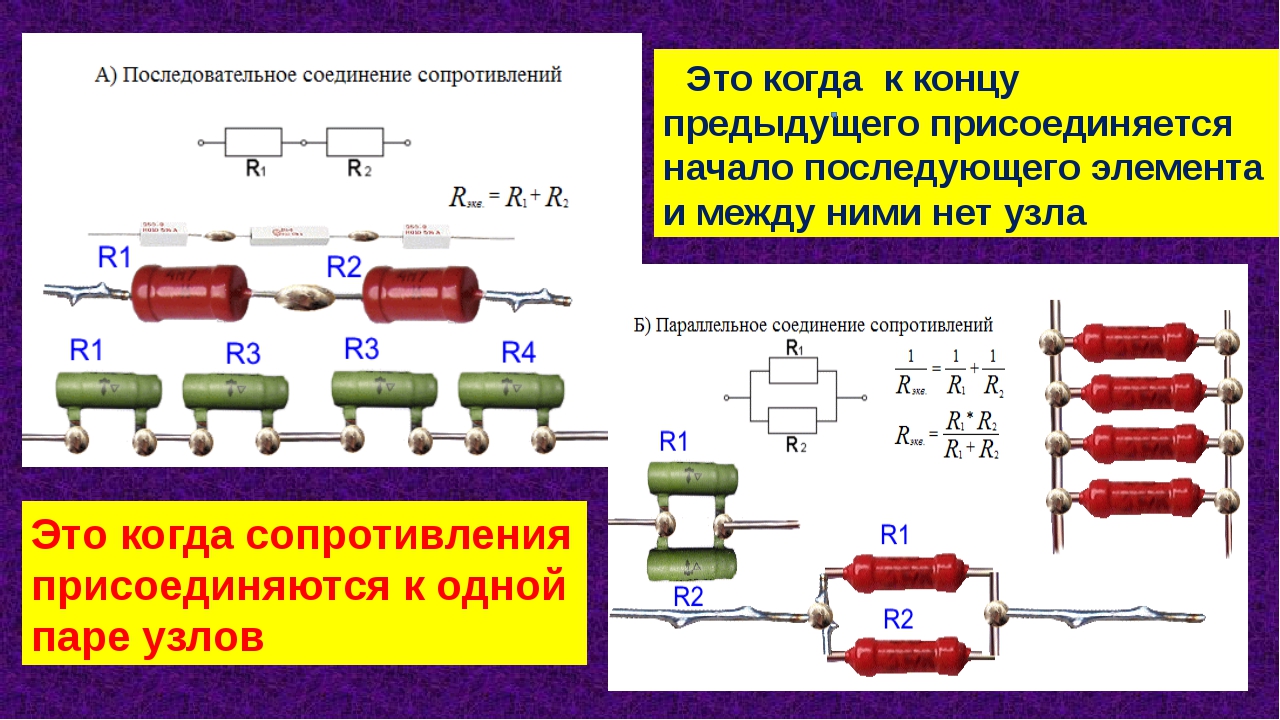
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Последовательное и параллельное соединение сопротивлений
Чтобы убедиться в том, что с увеличением ток в цепи уменьшается, можно проделать простой опыт: в карманном фонаре включить вместо одной лампочки Л1 две — Л1 и Л2, соединенные последовательно, то есть соединенные так, что электроны, двигаясь по цепи, проходят последовательно сначала одну, а затем и вторую лампочку (рис. 11).
Общее сопротивление при последовательном соединении равно сумме отдельных сопротивлений (листы 28, 30).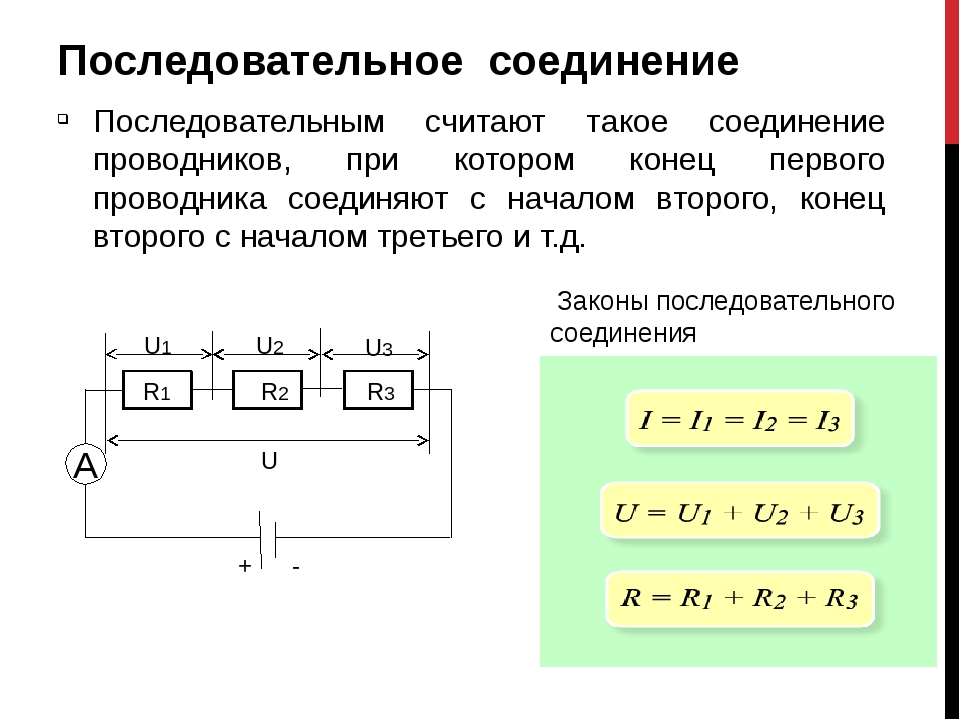
где R1 — сопротивление первой лампочки, R2 — сопротивление второй, а Rобщ — их общее сопротивление. Формула эта не требует особых пояснений: включить две лампочки последовательно равносильно тому, что включить одну, у которой нить вдвое длиннее. Если каждая из двух лампочек имеет нить с сопротивлением 75 ом, то их общее сопротивление равно 150 ом.
Подключив обе лампочки к батарейке, вы убедитесь, что ни одна из них не светится полным светом. Объясняется это тем, что с увеличением сопротивления цепи ток в ней уменьшился и энергии электронов уже не хватает, чтобы полностью накалить нить. Однако мы соединяли две лампочки не для того, чтобы доказывать эту и без того очевидную истину. Собранная цепь должна помочь нам познакомиться с таким важным понятием, как напряжение. Прежде чем начинать это знакомство, нам нужно рассмотреть еще один вопрос — о направлении тока в цепи.
Разбирая процессы в сложных электротехнических и радиоаппаратах, очень удобно следить за прохождением тока, пользуясь принципиальной схемой.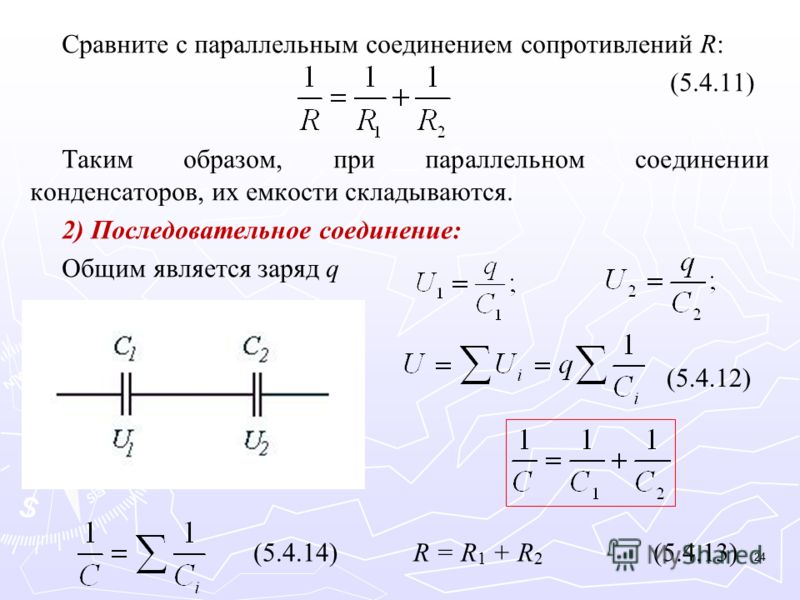 При этом часто бывает необходимо знать, какой конец того или иного элемента (например, лампочки или мотора) соединен с «плюсом» источника тока, а какой — с «минусом». В случае простых цепей для решения этого вопроса достаточно взглянуть на схему — и сразу видно, где «плюс», где «минус». В сложных цепях очень часто подобный вопрос приходится решать косвенным путем, исходя из того, в какую сторону двигаются заряды.
При этом часто бывает необходимо знать, какой конец того или иного элемента (например, лампочки или мотора) соединен с «плюсом» источника тока, а какой — с «минусом». В случае простых цепей для решения этого вопроса достаточно взглянуть на схему — и сразу видно, где «плюс», где «минус». В сложных цепях очень часто подобный вопрос приходится решать косвенным путем, исходя из того, в какую сторону двигаются заряды.
Так, например, если известно, что через лампочку электроны двигаются сверху вниз (по схеме), то можно сразу же сделать вывод, что нижний (по схеме) провод, идущий от лампочки, подключен к «плюсу», а верхний — к «минусу». Вывод этот основан на том, что электроны всегда двигаются от «минуса» к «плюсу». К такому же выводу мы пришли бы, если было бы известно, что по лампочке снизу вверх двигаются положительные заряды, так как направление их движения — от «плюса» к «минусу».
Для того чтобы не создавать лишнюю путаницу, особенно при рассмотрении больших схем, оказывается удобным ввести понятие об условном направлении тока и учитывать при этом движение одних каких-нибудь зарядов. Исторически получилось так, что за основное направление принято направление движения положительных зарядов. Потому при рассмотрении схем мы условно считаем, что ток во всех цепях представляет собой упорядоченное движение только положительных зарядов, направляющихся от «плюса» к «минусу», то есть от места, где их слишком много, к месту, где положительных зарядов не хватает (рис. 12, 13).
Исторически получилось так, что за основное направление принято направление движения положительных зарядов. Потому при рассмотрении схем мы условно считаем, что ток во всех цепях представляет собой упорядоченное движение только положительных зарядов, направляющихся от «плюса» к «минусу», то есть от места, где их слишком много, к месту, где положительных зарядов не хватает (рис. 12, 13).
Такая условность немного несправедлива, так как в большинстве случаев ток образуется электронами. Но от этой несправедливости никто не пострадает. Электроны будут по-прежнему двигаться своим путем, а все вопросы будут решаться с помощью условного тока, точно так же как они решались бы с учетом истинного направления движения электронов. Не все ли равно, как считать: что электроны в какой-нибудь цепи двигаются справа налево или что условный ток (то есть положительные заряды) двигается в этой цепи слева направо? Ведь и в том и в другом случае справа будет «минус», а слева «плюс»! А если при разборе какой-нибудь схемы в соответствии с правилом: ток течет от «плюса» к «минусу», вас начнут смущать двигающиеся в обратном направлении электроны, то условно замените их положительными зарядами — и все ваши сомнения моментально рассеются.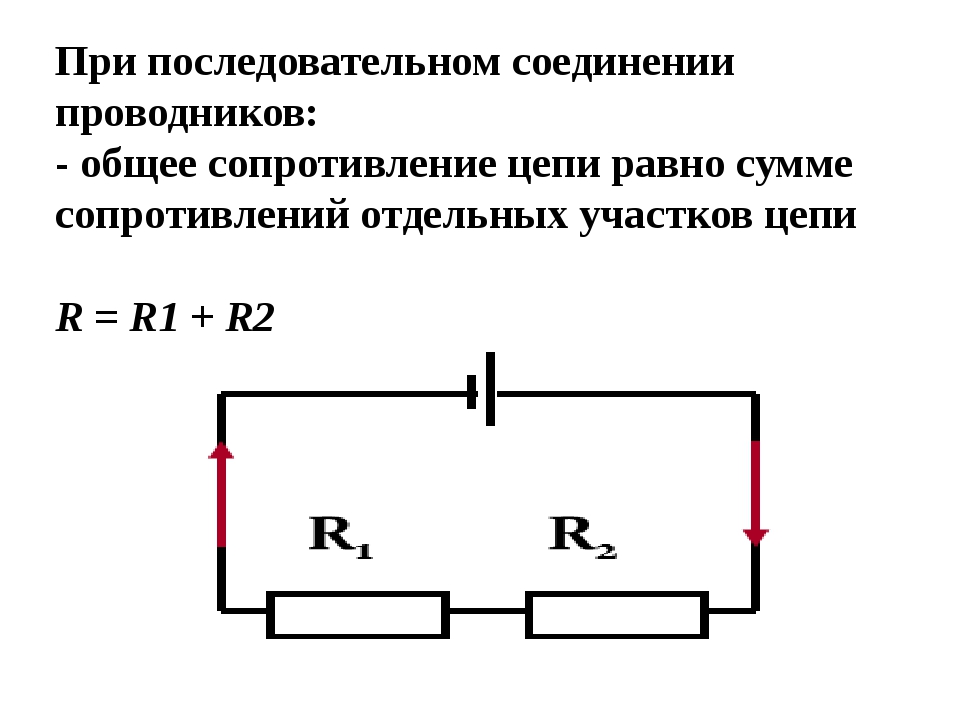
Какие есть способы соединения приемников электрической энергии
Какие есть способы соединения приемников электрической энергии
Приемник электрической энергии — устройство, в котором происходит преобразование электрической энергии в другой вид энергии для ее использования.
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т.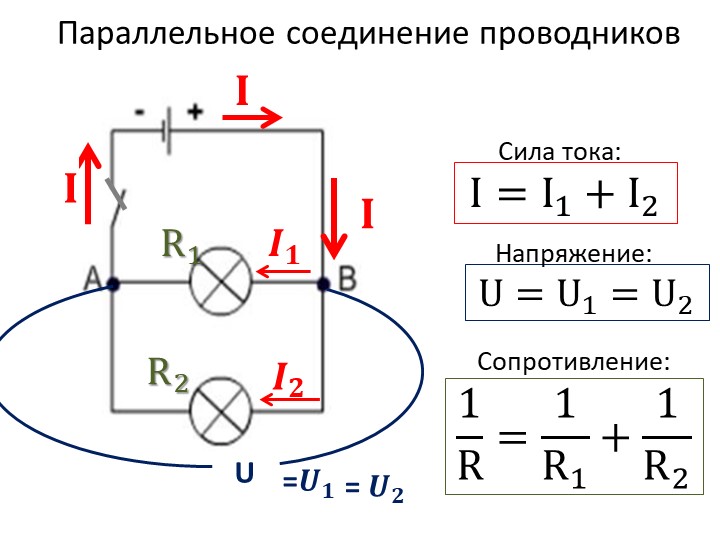 д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.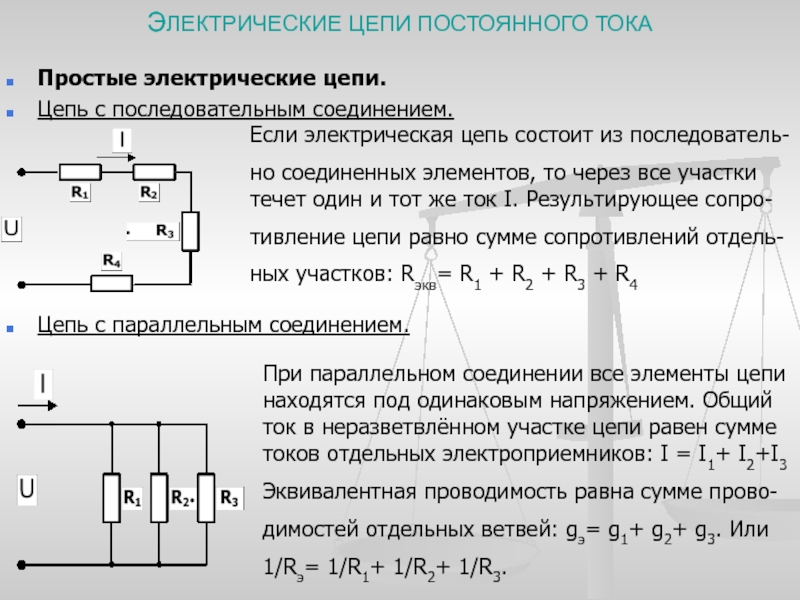
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I – ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях.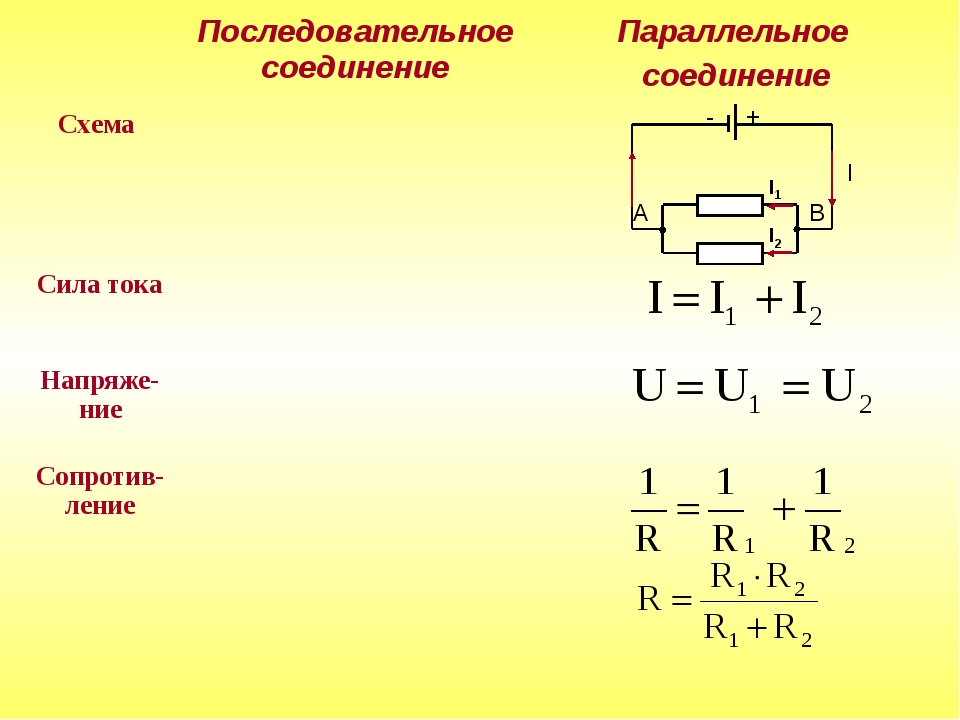 Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Смешанное соединение
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.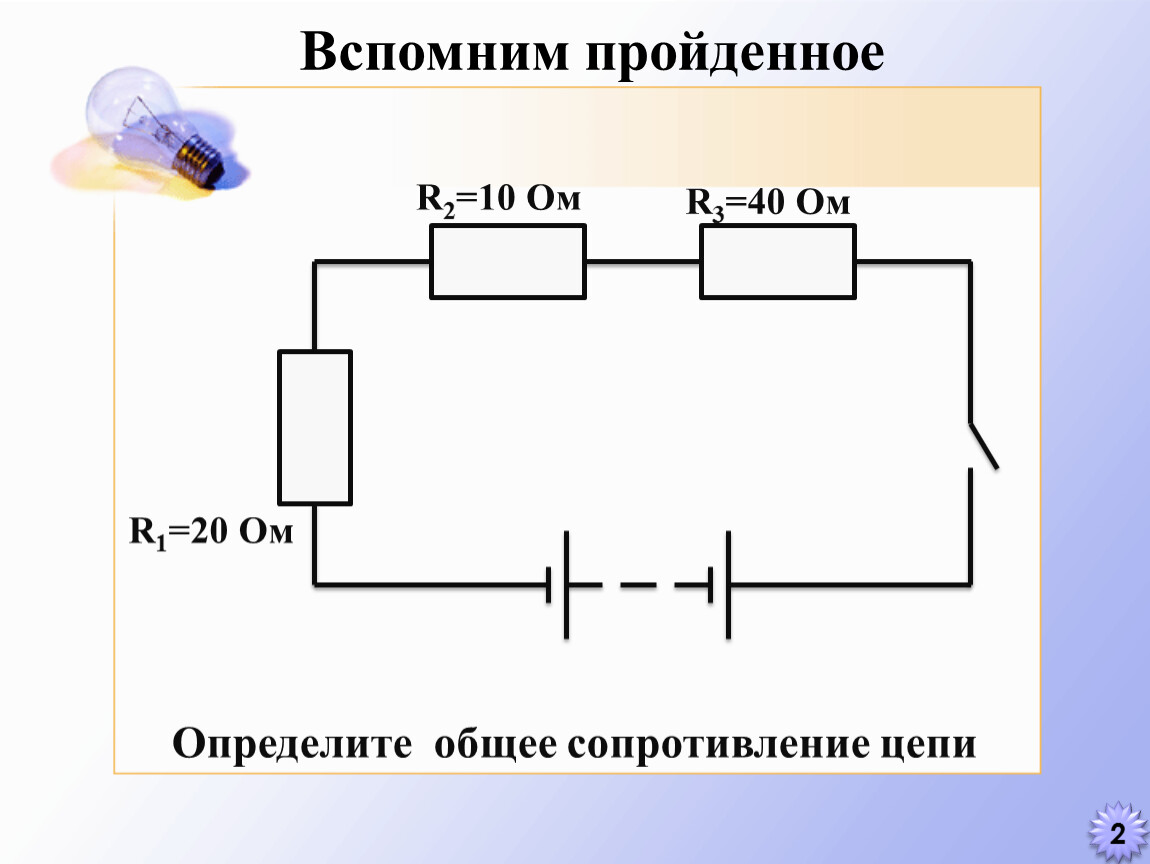
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда электролитических конденсаторов в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.
Ранее ЭлектроВести писали, что львовянка Оксана Денис подключила свою квартиру к солнечным панелям и ветроэнергетическим установкам.
По материалам: electrik.info.
При последовательном соединении сопротивление равно.
 Параллельное соединение сопротивлениий (резисторов)
Параллельное соединение сопротивлениий (резисторов)
Последовательное, параллельное и смешанное соединения резисторов.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление.
Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов
(приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис.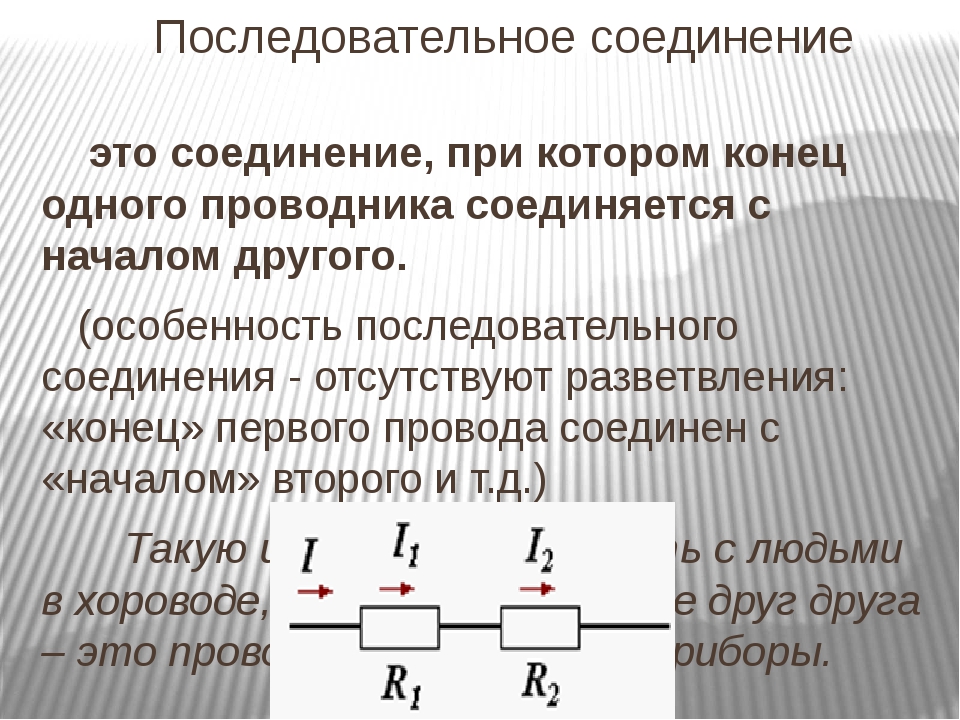 25, а.
25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк
(19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3
(20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3
(21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк
(23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк
=
1/R 1 + 1/R 2 + 1/R 3
(24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов
:
G эк = G 1 + G 2 +G 3
(25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3
(26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n
(27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n
(28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
п. с. постоянного тока.
1. При последовательном соединении
проводников
1.
Сила тока во всех проводниках одинакова
:
I
1 = I
2 = I
2.
Общее напряжение
U
на обоих проводниках равно сумме напряжений
U
1 и U
2 на каждом проводнике
:
U
= U
1 + U
2
3.
По закону Ома, напряжения U
1 и U
2 на проводниках равны U
1 = IR
1 , U
2 = IR
2 а общее напряжение U
= IR
где R
– электрическое сопротивление всей цепи, тогда
IR
= IR
1 + I
R
2. Отсюда следует
R
=
R
1
+
R
2
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
2. При параллельном соединении
проводников
1.
Напряжения
U
1 и U
2 на обоих проводниках одинаковы
U
1 = U
2 = U
2.
Сумма токов
I
1 + I
2 , протекающих по обоим проводникам, равна току в неразветвленной цепи
:
I
= I
1 + I
2
Этот результат следует из того, что в точках разветвления токов (узлы A
и B
) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A
за время Δt
подтекает заряд I
Δt
, а утекает от узла за то же время заряд I
1 Δt
+ I
2 Δt
. Следовательно, I
= I
1 + I
2 .
3.
Записывая на основании закона Ома
где R
– электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.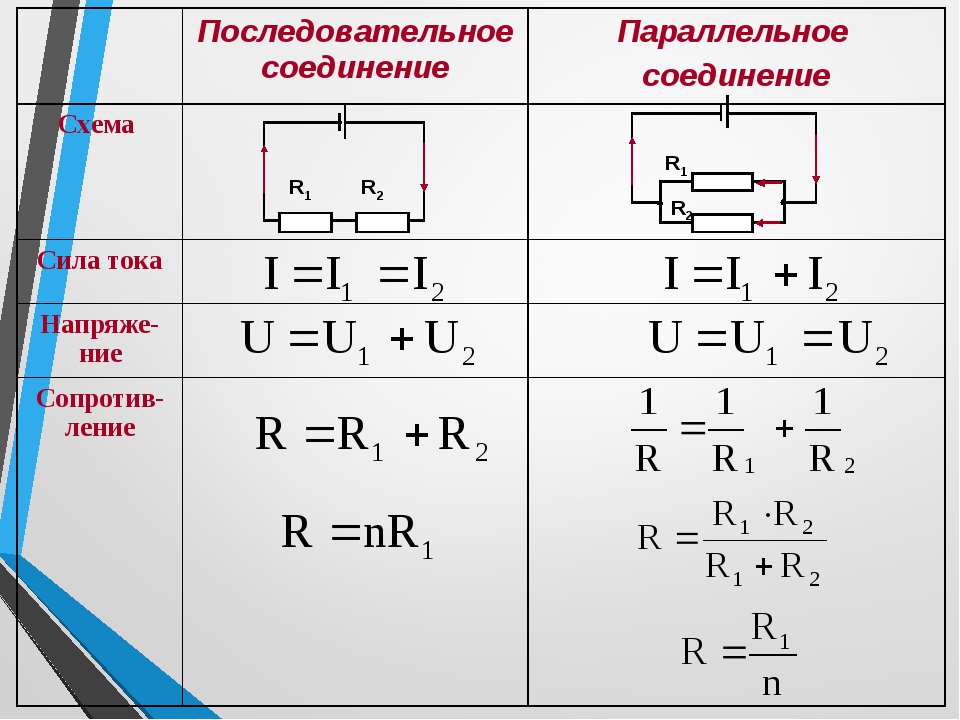
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).
На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.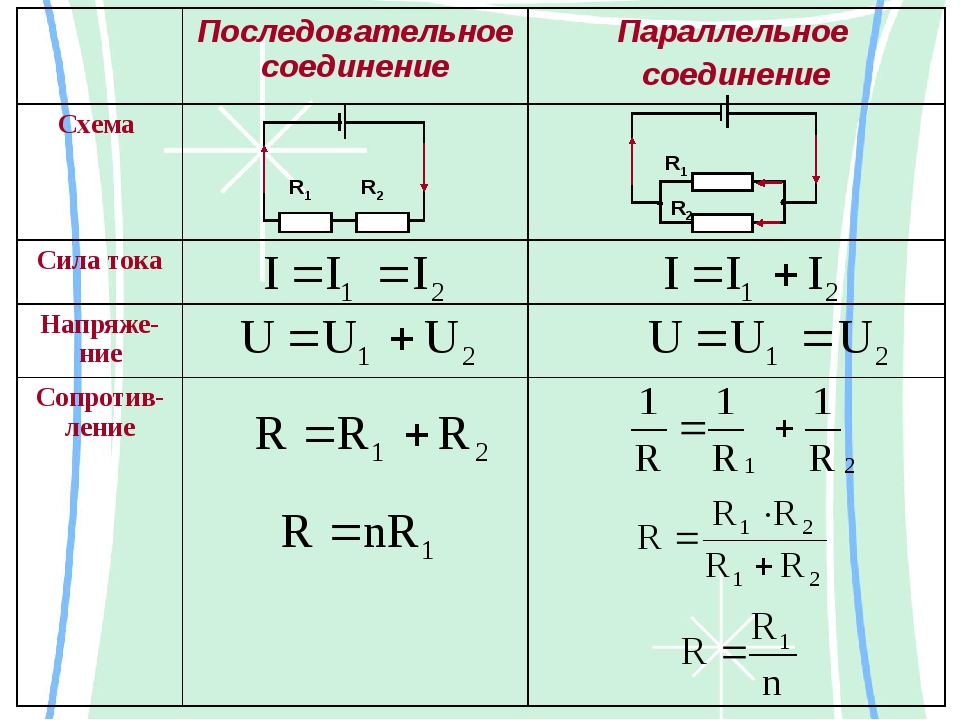
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
1.
ЭДС батареи равна сумме ЭДС отдельных источников
ε= ε 1 + ε 2 + ε 3
2
.
Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников
r батареи = r 1 + r 2 + r 3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1
3.
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или
n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники
с одинаковой ЭДС
. Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
1.
ЭДС батареи одинаковых источников равна ЭДС одного источника.
ε= ε 1 = ε 2 = ε 3
2.
Сопротивление батареи меньше, чем сопротивление одного источника
r батареи = r 1 /n
3.
Сила тока в такой цепи по закону Ома
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.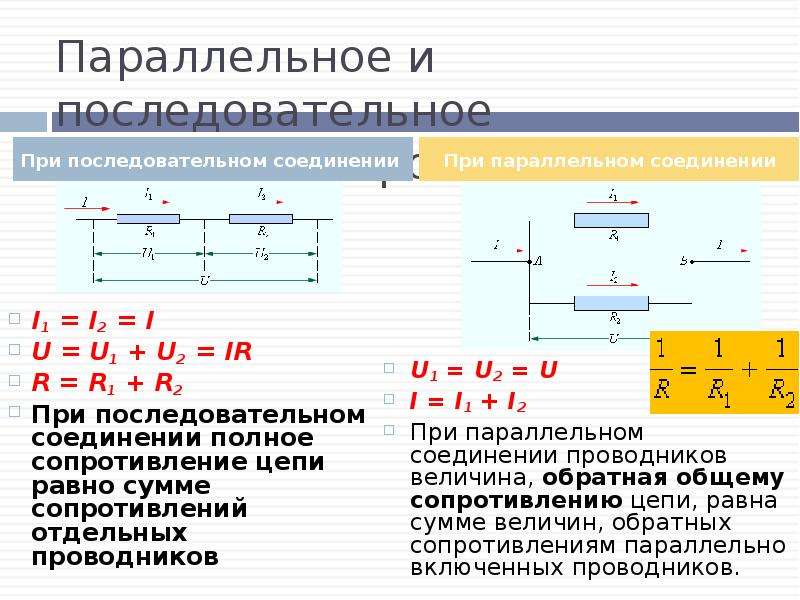
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U
1
= U
2
=U
3
=U
;
Проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R
1
+ 1/R
2
+ 1/R
3
= R
1
R
2
+ R
1
R
3
+ R
2
R
3
/R
1
R
2
R
3
,
где
R —
эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае
R
1
, R
2
и
R
3
)
.
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости.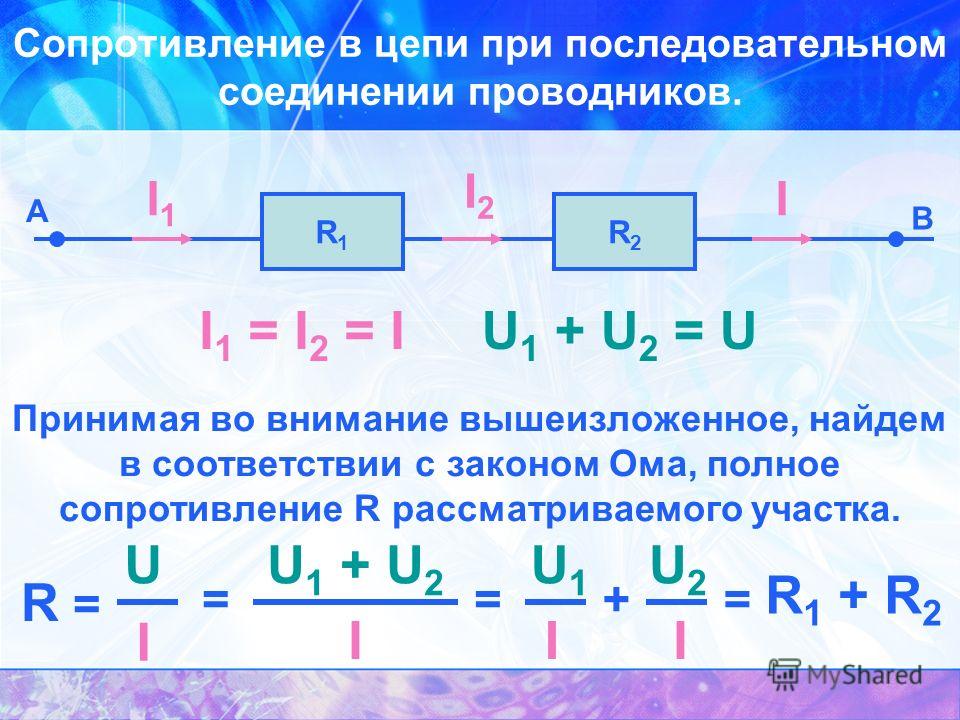 Следовательно, сопротивление параллельного разветвления из трёх резисторов:
Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R
1
R
2
R
3
/R
1
R
2
+ R
2
R
3
+ R
1
R
3
.
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.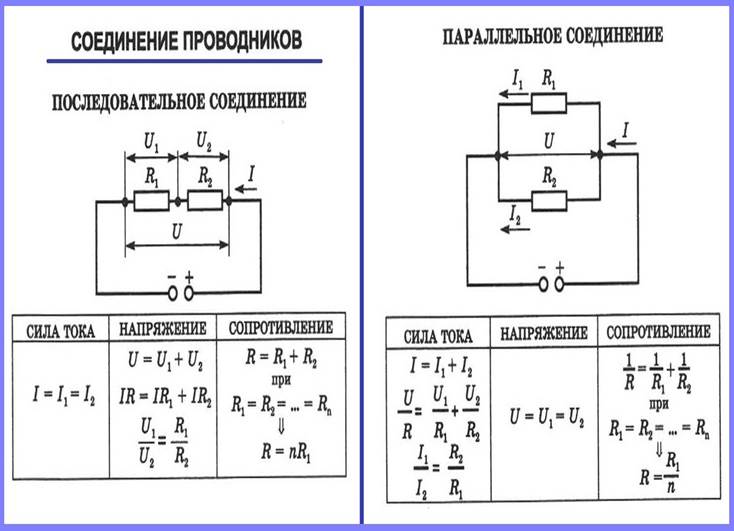
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений
R
1
и
R
2
(см. рис.). Проводимость первой ветви равна
1/R
1
, проводимость второй ветви —
1/R
2
. Общая проводимость:
1/R = 1/R
1
+ 1/R
2
.
Приведём к общему знаменателю:
1/R = R
2
+ R
1
/R
1
R
2
,
отсюда эквивалентное сопротивление
R = R
1
R
2
/R
1
+ R
2
.
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении
n
равных сопротивлений
R
1
эквивалентное сопротивление их будет в
n
раз меньше, т.е.
R = R
1
/n
.
На схеме, изображённой на последнем рисунке, включено пять сопротивлений
R
1
по 30 Ом каждое. Следовательно, общее сопротивление
R
будет
R = R
1
/5 = 30/5 = 6
Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I
1
+ I
2
+ I
3
.
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями
R
1
и
R
2
(второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I
1
R
1
и
U = I
2
R
2
.
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I
1
R
1
= I
2
R
2
,
или
I
1
/I
2
= R
2
/R
1
,
Т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление
R
1
=
25 Ом, а
R
2
=
50 Ом. Определить общее сопротивление цепи
R
общ
.
Решение.
R
общ =
R
1
R
2
/R
1
+ R
2
= 25
.
50 / 25 + 50
≈
16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы
I
1
=
1 ампер, второй
I
2
=
1, 5 ампера и третьей
I
3
=
2, 5 ампера. Определить общий ток цепи накала ламп усилителя
I
общ
.
Решение.
I
общ
=
I
1
+ I
2
+ I
3
=
1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Резисторы, соединенные последовательно и параллельно — Электрические цепи — WJEC — GCSE Physics (Single Science) Revision — WJEC
Резисторы, соединенные последовательно
Когда резисторы соединены последовательно, ток через каждый резистор одинаков. Другими словами, ток одинаков во всех точках последовательной цепи.
При последовательном соединении резисторов общее напряжение (или разность потенциалов) на всех резисторах равно сумме напряжений на каждом резисторе.
Другими словами, напряжения вокруг цепи складываются с напряжением источника питания.
Общее сопротивление ряда резисторов, соединенных последовательно, равно сумме всех сопротивлений по отдельности.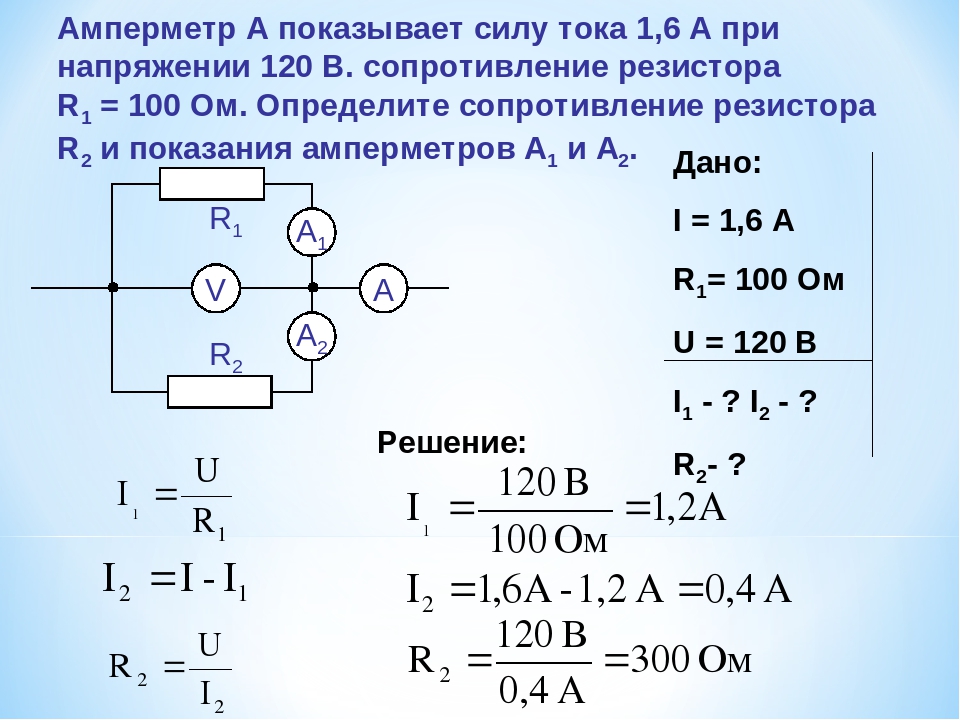
В этой схеме применяется следующее.
I 1
= I 2 = I 2 = I 3
V T = V 1 + V 2 + V 3
и R T = R 14yzwhvkluc.0.0.0.1:0.1.0.$0.$1.$9.$3″> 1 + R 2 + R 3
Последовательное добавление компонентов увеличивает общее сопротивление цепи.
Резисторы, соединенные параллельно
Когда резисторы соединены параллельно, ток питания равен сумме токов через каждый резистор. Токи в ветвях параллельной цепи складываются с током питания.
Когда резисторы соединены параллельно, они имеют одинаковую разность потенциалов. Любые компоненты, соединенные параллельно, имеют одинаковую разность потенциалов.
Для расчета общего сопротивления двух параллельно соединенных резисторов используется это уравнение.
14yzwhvkluc.0.0.0.1:0.1.0.$0.$1.$15″> \[\frac{1}{R}=\frac{1}{R}_{1}+\frac{1}{R}_{2}\]Для расчета общего сопротивления трех резисторов соединенных параллельно, добавляем в уравнение третий резистор (и так далее).
\[\frac{1}{R}=\frac{1}{R}_{1}+\frac{1}{R}_{2}+\frac{1}{R}_{3 }\]
Параллельное добавление компонентов уменьшает общее сопротивление в цепи.
- Вопрос
Рассчитайте сопротивление этой параллельной комбинации.
- Показать ответ
\[\frac{1}{R}=\frac{1}{R}_{1}+\frac{1}{R}_{2}+\frac{1} {R}_{3}\]
14yzwhvkluc.0.0.0.1:0.1.0.$0.$1.$19.3.$1″> \[\frac{1}{R}=\frac{1}{3}+\frac{1}{6}+\frac{1}{9}\]Р = 1.64 Ом
Общее сопротивление меньше наименьшего сопротивления.
Сопротивления последовательно и параллельно
Более одного электрического сопротивления могут быть соединены последовательно или параллельно, кроме того, более двух сопротивлений также могут быть соединены последовательно и параллельно. Здесь мы обсудим в основном последовательное и параллельное комбинирование.
Сопротивления в серии
Предположим, у вас есть резисторы трех разных типов — R 1 , R 2 и R 3 — и вы соединяете их встык, как показано на рисунке ниже, тогда это будет называться как сопротивления в серии .В случае последовательного соединения эквивалентное сопротивление комбинации представляет собой сумму этих трех электрических сопротивлений.
Это означает, что сопротивление между точками A и D на рисунке ниже равно сумме трех отдельных сопротивлений. Ток входит в точку A комбинации, а также выходит из точки D, так как в цепи не предусмотрен другой параллельный путь.
Теперь скажем, что этот ток равен I. Таким образом, этот ток I будет проходить через сопротивления R 1 , R 2 и R 3 .Применяя закон Ома, можно найти, что падения напряжения на сопротивлениях будут В 1 = IR 1 , В 2 = IR 2 и В 3 = IR 3 . Теперь, если общее напряжение, приложенное к комбинации сопротивлений в серии , равно В.
Тогда, очевидно,
Поскольку сумма падений напряжения на отдельном сопротивлении есть не что иное, как равная приложенному напряжению на комбинации.
Теперь, если рассматривать общую комбинацию сопротивлений как один резистор с величиной электрического сопротивления R, то по закону Ома
В = IR …………. (2)
(2)
Теперь, сравнивая уравнения (1) и (2), мы получаем
Итак, приведенное выше доказательство показывает, что эквивалентное сопротивление комбинации последовательно соединенных сопротивлений равно сумме индивидуальных сопротивлений. Если бы было n сопротивлений вместо трех сопротивлений, эквивалентное сопротивление было бы
. Эти резисторы соединены таким образом, что правая и левая клеммы каждого резистора соединены вместе, как показано на рисунке ниже.
Эта комбинация называется сопротивления параллельно . Если к этой комбинации приложить разность электрических потенциалов, то она будет потреблять ток I (скажем).
Поскольку этот ток будет проходить по трем параллельным путям через эти три электрических сопротивления, ток будет разделен на три части. Скажем, токи I 1 , I 1 и I 1 проходят через резисторы R 1 , R 2 и R 3 соответственно.
Где общий ток источника
Теперь, как видно из рисунка, каждое из сопротивлений параллельно подключено к одному и тому же источнику напряжения, падение напряжения на каждом резисторе одинаково, и оно такое же, как напряжение питания V (скажем).
Отсюда по закону Ома
Теперь, если считать, что эквивалентное сопротивление комбинации равно R.
Тогда,
Теперь подставляя значения I, I 1 , I 2 и I 3 в уравнении (1) мы получаем,
Приведенное выше выражение представляет собой эквивалентное сопротивление резистора, включенного параллельно. Если бы было n сопротивлений, соединенных параллельно, вместо трех сопротивлений, выражение эквивалентного сопротивления было бы
Пример: Батареи, соединенные последовательно и параллельно
Понимание ситуации
В наших предыдущих двух примерах использования принципов Кирхгофа для анализа электрических цепей, последовательного и параллельного резисторов анализ был довольно простым.
В последовательном случае два резистора действовали как один эффективный резистор с сопротивлением, равным сумме сопротивлений отдельных резисторов. В параллельном случае два резистора действовали как один эффективный резистор, равный сумме взаимных сопротивлений, дающих эффективное взаимное сопротивление.
Это связано с тем, что через резисторы, соединенные последовательно, труднее пропустить ток — ток должен проходить через оба резистора — а через резисторы, соединенные параллельно, ток легче пропустить — ток может разделиться между двумя резисторами.Таким образом, как последовательные, так и параллельные резисторы в некотором смысле эквивалентны простейшему случаю, когда один резистор подключен к одной батарее.
Но многие важные электрические ситуации в биологии не могут быть смоделированы такими простыми системами. Например, то, что происходит в клеточной мембране (особенно в нервной клетке), представляет собой сильно электрическое явление, зависящее от зарядов, протекающих через мембрану. Ионные насосы действуют как батареи для создания разности потенциалов, а поскольку существует несколько ионных насосов, которые могут перекачивать ионы в клетки или из них, модели с одной батареей недостаточно.Кроме того, рассмотрение моделей с более чем одной батареей дает нам лучшее представление о том, как на самом деле работают принципы Кирхгофа в более реалистичных схемах, и показывает их ценность при интерпретации более сложных ситуаций.
Чтобы увидеть, как это работает, давайте решим задачу с игрушечной моделью с двумя идеальными батареями, соединенными последовательно, и двумя идеальными батареями, соединенными параллельно.
Демонстрация примера задачи
Рассмотрим три электрические сети, показанные справа. К одной и той же лампочке по-разному подключены одинаковые батареи.Предположим, что батареи имеют незначительное внутреннее сопротивление. Положительная клемма каждой батареи помечена плюсом. Проранжируйте эти схемы по яркости лампы от самой высокой до самой низкой.
Решение этой проблемы
Яркость лампы пропорциональна мощности, которую она рассеивает (мощность). Если мы перемещаем небольшой заряд $dq$ через резистор так, чтобы он испытывал разность потенциалов $ΔV$, мы совершаем работу $dq ΔV$. Если мы сделаем это за время $dt$, скорость использования энергии составит $dq/dt ΔV$ или 90 005
$$P = I ΔV$$
произведение тока через резистор на падение напряжения на нем.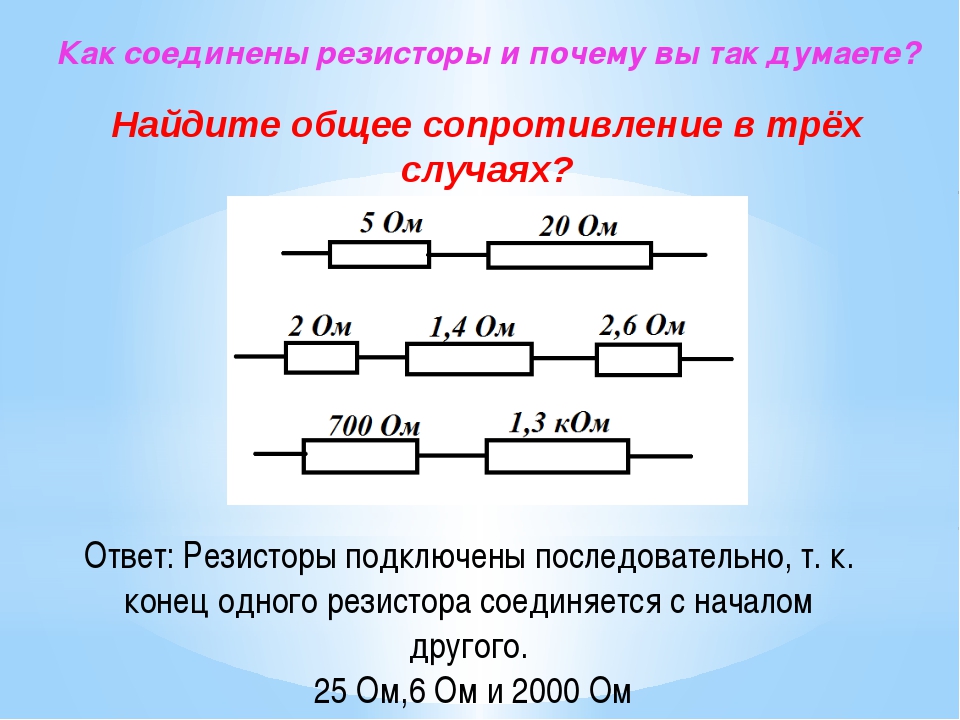 2 р $.
2 р $.
Это говорит нам о том, что если лампочка преобразует всю электрическую энергию, которую она рассеивает на своем сопротивлении, в свет (не совсем верно для лампы накаливания, которая нагревается, но лучше для светодиода), яркость лампочки будет пропорциональна квадрату ток через него. Итак, давайте найдем ток в каждой из лампочек для трех случаев.
Давайте рассмотрим дела по одному.
Вариант A: одна батарея
Случай A прост: всего одна батарея, подключенная к одному резистору.Текущее правило Кирхгофа говорит нам, что один и тот же ток должен проходить через все. Назовем его $I$. Выберите нижний конец батареи в качестве нашего 0. Затем верхний конец батареи находится в $V_0$, и наша эвристика безрезистивного проводника позволяет нам отображать потенциал везде, как показано. Мы видим, что падение напряжения на резисторе равно $V_0$, а ток через него равен $I$. Закон Ома связывает падение напряжения на резисторе с током через него. В этом случае мы можем предположить, что нам задано повышение напряжения для батареи, $V_0$, и сопротивление лампы, $R$.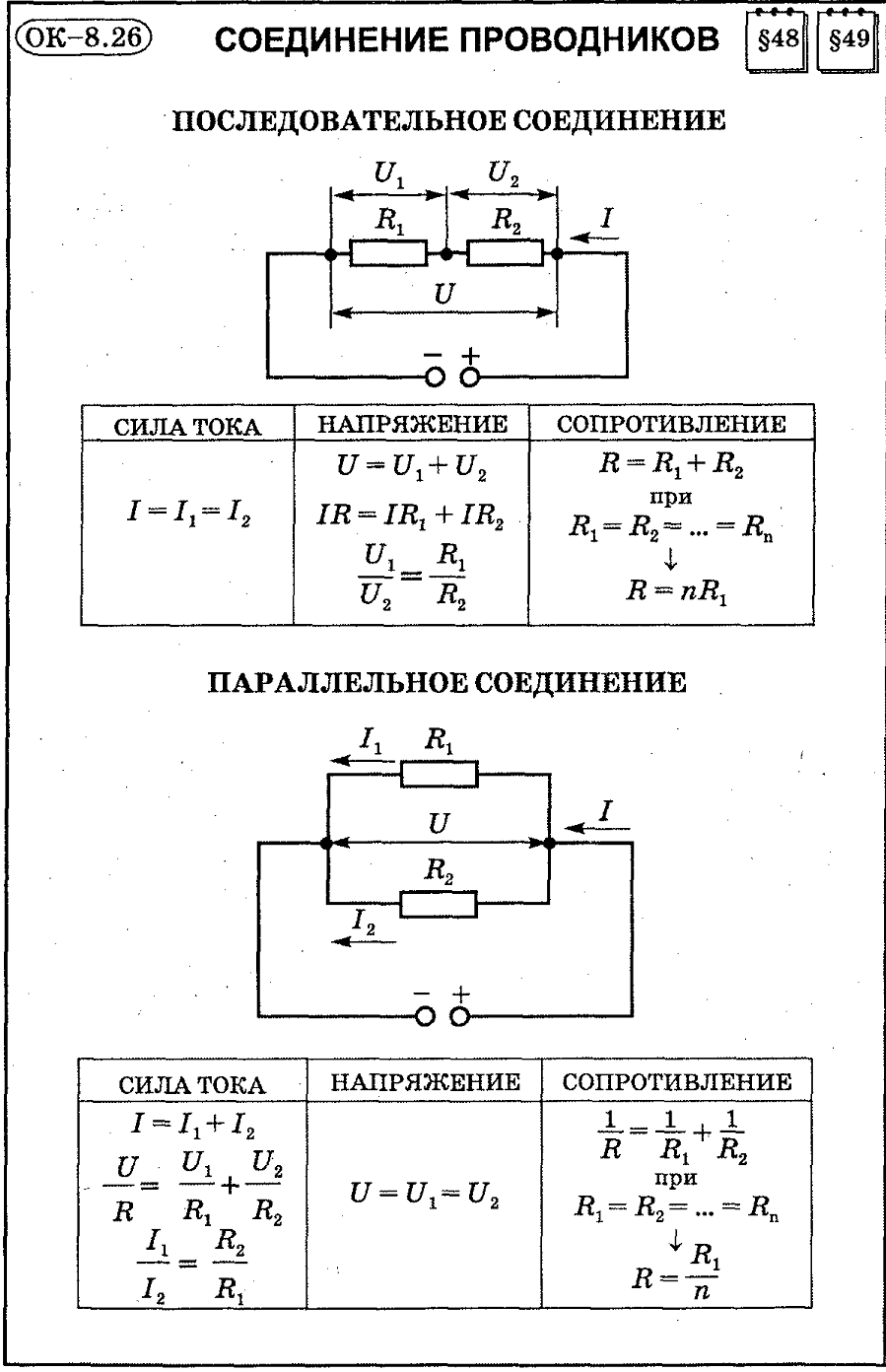 2}{R}$$
2}{R}$$
Случай B: Батареи в серии
Теперь давайте рассмотрим случай B. У нас все еще есть только одна петля, поэтому все, что проходит через один элемент, должно пройти через них все по правилу циклов Кирхгофа.
Теперь давайте нанесем на карту потенциал. Мы можем выбрать один 0 для потенциала, поэтому давайте выберем его как нижний предел правой батареи. Мы можем продолжить эти 0 вниз по правой стороне, как мы делали раньше, но когда мы идем налево, происходит что-то другое. Верхняя сторона левой батареи соединена с низкой стороной правой батареи! Таким образом, мы не можем принять низкую сторону левой батареи за 0: она должна иметь потенциал В 0 .Но мы знаем, что батарея повышает потенциал от низкого вывода до высокого на фиксированную величину, каким бы ни было значение нижнего вывода. Таким образом, если мы поднимемся на В 0 , проходя через левую батарею, мы должны получить потенциал 2 В 0 ! Согласно нашей эвристике проводника без сопротивления, мы должны иметь одно и то же значение на всем протяжении провода, пока не доберемся до резистора.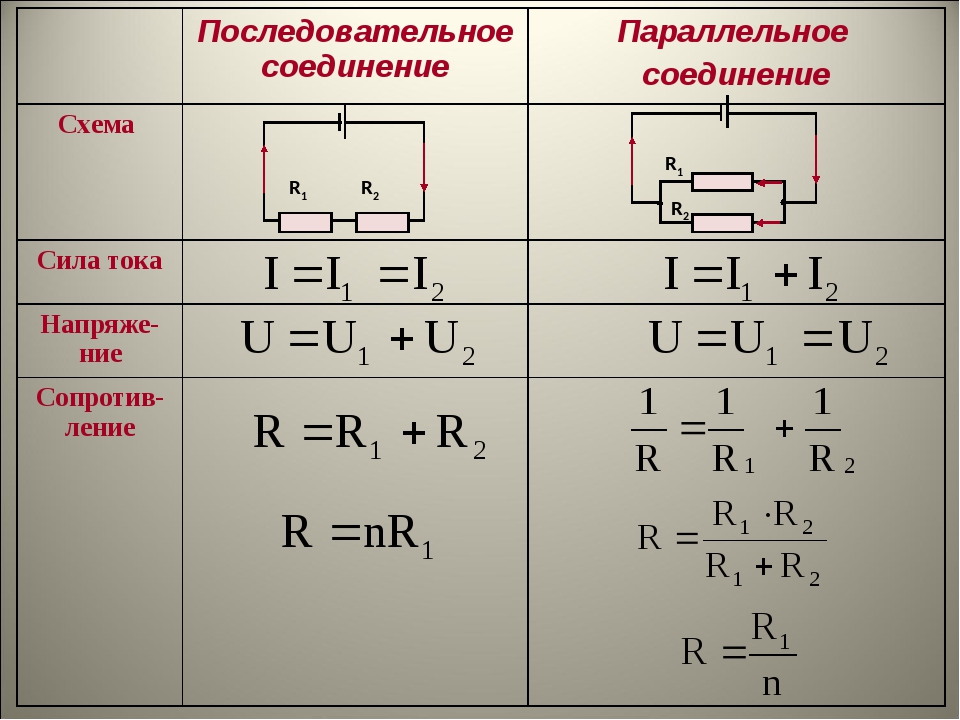 2}{R}$$
2}{R}$$
Две последовательно соединенные батареи позволяют лампочке потреблять в четыре раза больше энергии, чем одна! Удвоение напряжения в этой схеме удваивает падение напряжения на резисторе и ток через него.Лампочка будет намного ярче.
Случай C: Батареи в параллельном соединении
Теперь давайте рассмотрим случай C. Это немного сложнее, так как есть два цикла. Нас интересует только ток через лампочку (резистор), поэтому давайте назовем ток через этот контур $I$. После прохождения через резистор, когда он достигает первого разделения, сумма токов, выходящих из двух возможных путей, должна составлять I по правилу тока Кирхгофа. Поскольку два пути, по которым он может идти, идентичны, мы предполагаем, что он разделяется пополам, как показано на рисунке.(Примечание: метки тока в верхнем контуре означают «ток, деленный на 2», а не «половину».)
Теперь займемся картой потенциала. Мы можем выбрать одну точку в сети как 0 нашего потенциала. Возьмем его как нижний предел нижней батареи.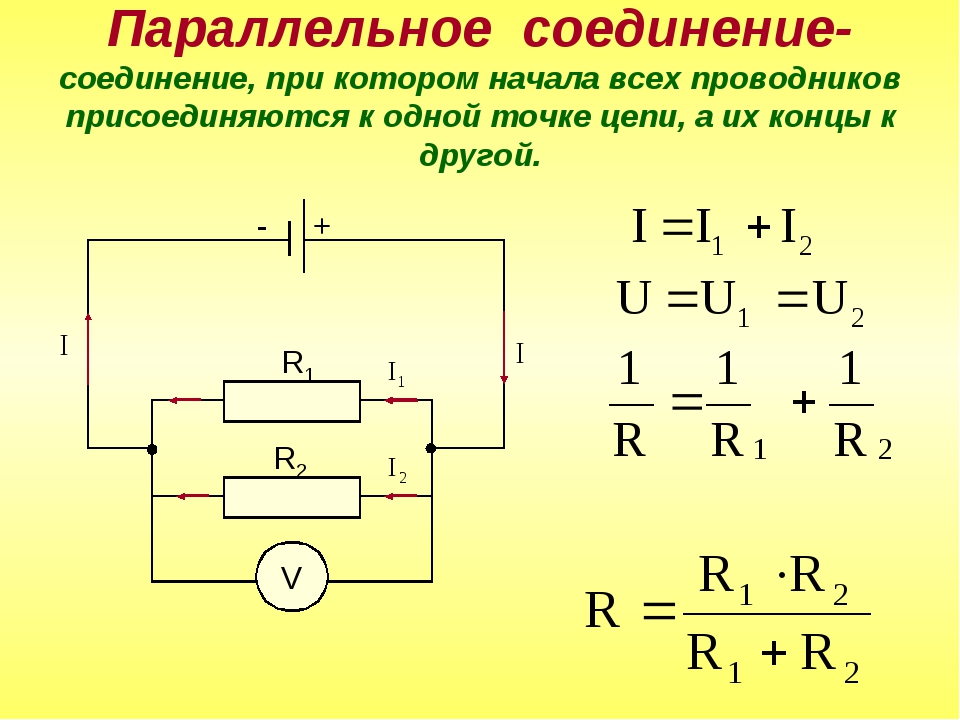 По принципу проводника без сопротивления любая часть провода, подключенная к этой точке без сопротивления между ними, также должна быть на 0. Это означает нижний конец второй батареи и правую сторону резистора. (Следуйте за проводами от нижнего конца батареи и увидите все места, которые мы пометили как 0.)
По принципу проводника без сопротивления любая часть провода, подключенная к этой точке без сопротивления между ними, также должна быть на 0. Это означает нижний конец второй батареи и правую сторону резистора. (Следуйте за проводами от нижнего конца батареи и увидите все места, которые мы пометили как 0.)
Принцип, согласно которому батарея создает повышение потенциала на фиксированное значение на своих клеммах, означает, что верхняя сторона обеих батарей должна быть $V_0$. Используя принцип проводника без сопротивления, мы можем найти значения потенциала повсюду в цепи, в том числе на другом конце резистора. Это говорит нам о том, что падение потенциала на резисторе равно $V_0$. По закону Ома (принцип сопротивления Кирхгофа) мы можем связать ток с падением на резисторе:
$$I= \frac{ΔV}{R} = \frac{V_0}{R}.$$
Это тот же результат, что и в случае A, поэтому порядок яркости для трех случаев равен
.
В > А = С.
Интерпретация результатов.
Две последовательно соединенные батареи обеспечивают в два раза больший «толчок» (электрическое напряжение), чем одна, поэтому мы получаем больший ток и больше мощности, рассеиваемой в лампе.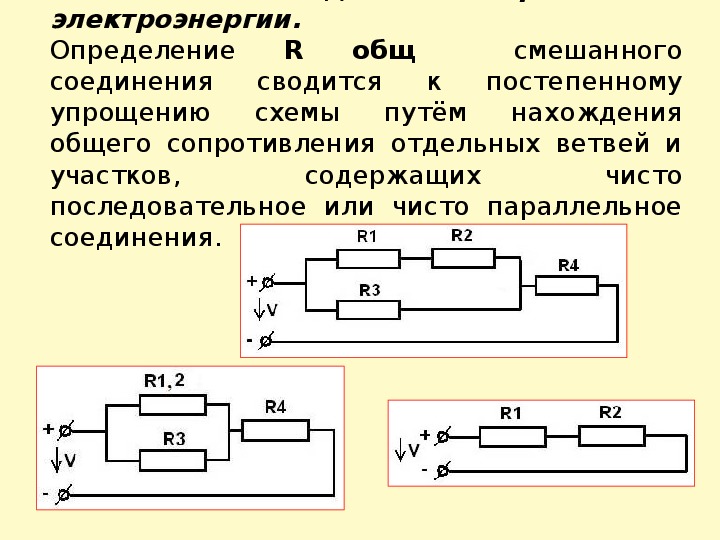 Две батареи, включенные параллельно, обеспечивают одинаковое падение напряжения, поэтому наша лампочка не будет ярче, но, поскольку ток через каждую батарею уменьшается вдвое, батареи будут работать дольше.
Две батареи, включенные параллельно, обеспечивают одинаковое падение напряжения, поэтому наша лампочка не будет ярче, но, поскольку ток через каждую батарею уменьшается вдвое, батареи будут работать дольше.
Хотя это и решает нашу проблему, стоит еще немного рассмотреть случай C. Мы предположили, что батареи идентичны, но предположим, что это не так? Мы бы попали в беду! Мы бы прогнали наши нулевые значения $V$ вверх по правой стороне, а затем перепрыгнули бы через каждую батарею с их соответствующими повышениями и получили бы разные значения того, какой потенциал должен быть вниз по левой стороне сети. Противоречие! Причина этого в том, что мы изначально исходили из того, что наши батареи идеальны: они всегда поддерживают фиксированную разницу напряжений на своих клеммах и не имеют внутреннего сопротивления.Мы также предположили, что наши провода были идеальными: имели 0 сопротивление.
Эти предположения верны, если в цепях всегда есть резисторы, которые значительно больше, чем (обычно небольшие) сопротивления батарей и проводов.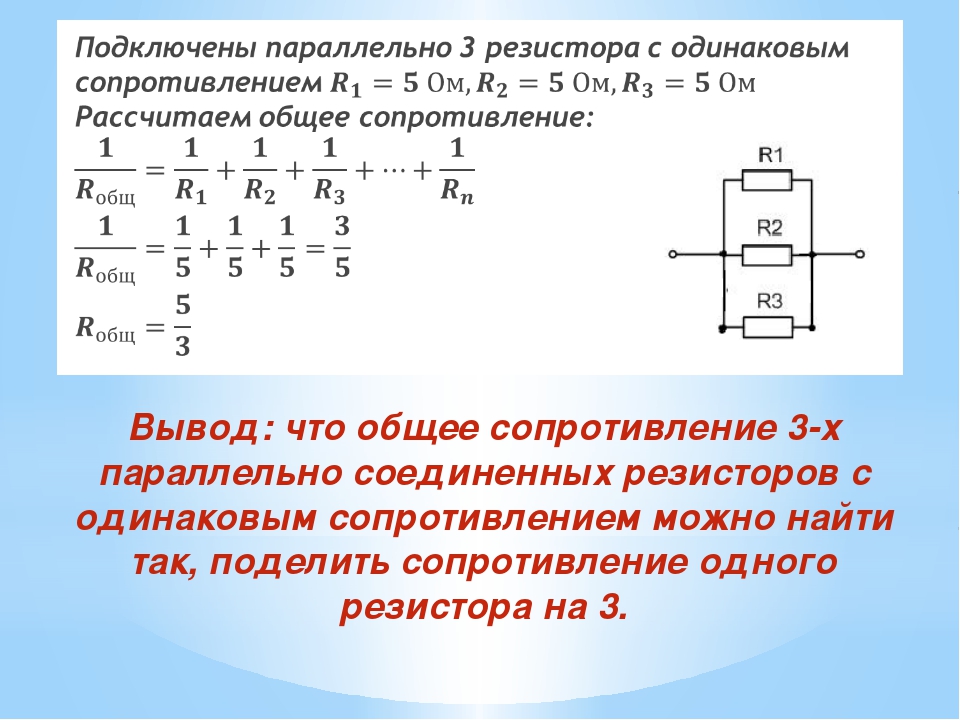 Но в верхней петле случая С мы соединили две батареи вместе в петлю без каких-либо резисторов. Это все равно, что соединить обе клеммы аккумулятора друг с другом одним проводом — короткое замыкание. Поскольку $ΔV$ фиксировано, а $R ~ 0$, мы получаем, что $I = ΔV/R$ очень велико.Большой ток означает, что большая мощность рассеивается при очень малом сопротивлении провода. Он сильно нагревается и очень быстро разряжает батарею. Не пытайтесь повторить это дома! (Или в вашей лаборатории!) Вы не можете разжечь огонь, но вы почти наверняка разрядите свои батареи.
Но в верхней петле случая С мы соединили две батареи вместе в петлю без каких-либо резисторов. Это все равно, что соединить обе клеммы аккумулятора друг с другом одним проводом — короткое замыкание. Поскольку $ΔV$ фиксировано, а $R ~ 0$, мы получаем, что $I = ΔV/R$ очень велико.Большой ток означает, что большая мощность рассеивается при очень малом сопротивлении провода. Он сильно нагревается и очень быстро разряжает батарею. Не пытайтесь повторить это дома! (Или в вашей лаборатории!) Вы не можете разжечь огонь, но вы почти наверняка разрядите свои батареи.
Джо Редиш 15.03.16
Физика для науки и техники II
6.11 Соединение сопротивлений: последовательно и параллельно из Office of Academic Technologies на Vimeo.
- Пример: соединение сопротивлений: последовательное и параллельное
6. 11 Соединение сопротивлений – последовательное и параллельное
11 Соединение сопротивлений – последовательное и параллельное
Хорошо, теперь рассмотрим соединения сопротивлений. Соединения резисторов.
Итак, как мы видели в случае соединения конденсаторов, резисторы также могут быть соединены двумя различными способами в электрических цепях. А именно, параллельные и последовательные соединения. Если рассмотреть сначала последовательное соединение резисторов, то в этом случае, опять же, как и в случае с конденсаторами, резисторы соединены один за другим, как запонки вагонов поезда на одном и том же железнодорожном полотне.Если рассмотреть три резистора с сопротивлениями R 1 , R 2 и R 3 , соединим их последовательно таким образом и, скажем, тогда, приложим разность потенциалов к комбинация путем подключения концов комбинации к клеммам источника питания или электродвижущей силы, создающей ε вольт разности потенциалов.
Как только мы включим выключатель, ток i выйдет из положительной клеммы и потечет через комбинацию к отрицательной клемме источника питания. Мы легко можем видеть, что, поскольку у нас есть только один доступный путь для движения зарядов, величина тока, проходящего через каждый резистор в последовательной комбинации, будет одинаковой. Следовательно, первое свойство этой связи состоит в том, что i 1 будет равно i 2 , что будет равно i 3 , и все они будут равны я .
Мы легко можем видеть, что, поскольку у нас есть только один доступный путь для движения зарядов, величина тока, проходящего через каждый резистор в последовательной комбинации, будет одинаковой. Следовательно, первое свойство этой связи состоит в том, что i 1 будет равно i 2 , что будет равно i 3 , и все они будут равны я .
Теперь вот один момент, распространенная ошибка или заблуждение, иногда люди думают, что когда ток входит в резистор и когда он выходит из резистора, то он как-то становится меньше по сравнению с моментом, когда он входил в резистор.Опять же, это не может быть правдой, потому что если бы это было правдой, это нарушило бы принцип сохранения заряда. Другими словами, если у вас есть 5 зарядов, допустим, входящих в это сопротивление R 1 , то у нас должно выйти 5 зарядов. У нас не может быть случая, чтобы выходили только 3 заряда, а остальные просто пропадали.
Итак, да, что-то становится меньше по мере того, как заряды выходят из сопротивляющейся среды, и это что-то не количество заряда, а энергия, связанная с каждым из этих зарядов. Другими словами, входящие заряды, прежде чем попасть в сопротивляющуюся среду, обладают большей потенциальной энергией. И когда они проходят через эту резистивную среду, из-за столкновений, которые они совершают с атомами среды, они теряют часть своей потенциальной энергии в виде тепла. Вот почему, когда они выходят из резистивной среды, они не будут иметь той же электрической потенциальной энергии, которой они обладали до входа в эту резистивную среду. Так что вы должны прояснить этот момент в своем уме.
Другими словами, входящие заряды, прежде чем попасть в сопротивляющуюся среду, обладают большей потенциальной энергией. И когда они проходят через эту резистивную среду, из-за столкновений, которые они совершают с атомами среды, они теряют часть своей потенциальной энергии в виде тепла. Вот почему, когда они выходят из резистивной среды, они не будут иметь той же электрической потенциальной энергии, которой они обладали до входа в эту резистивную среду. Так что вы должны прояснить этот момент в своем уме.
Ну, опять же, как мы помним из последовательного соединения конденсаторов, это свойство, общее свойство последовательного соединения состоит в том, что разность потенциалов по всей комбинации. И в этом случае эта разность потенциалов будет равна разности потенциалов, генерируемой источником питания, которая составляет ε вольт. Таким образом, в комбинации мы будем иметь разность потенциалов ε вольт, и она будет равна некоторой разности потенциалов на каждом резисторе.
Другими словами, если мы просто возьмем вольтметр, который представляет собой устройство, измеряющее разность потенциалов между двумя точками, и соединим точки через резистор R 1 , мы будем читать В 1 из вольт. Затем, если мы проделаем то же самое с R 2 , получится В 2 вольт. И делая это через R 3 , мы будем читать V 3 вольт. Мы видим, что ε , представляющее собой разность потенциалов для всей комбинации, будет равно В 1 плюс В 2 плюс В 3 .Итак, это второе свойство последовательного соединения резисторов.
Теперь, как и в случае с подключением конденсаторов, мы снова упростим эту схему, просто заменив эти три резистора, которые включены последовательно с одним сопротивлением, чтобы она выполняла ту же работу, что и эти три резистора. делать последовательное соединение в этой цепи. Что ж, чтобы иметь возможность выполнять ту же работу, резистор, который заменит эти три, всякий раз, когда он подключен к цепи, должен потреблять такое же количество тока от одной и той же батареи.
Поэтому, если мы перерисуем вот эту схему в упрощенной версии, мы получим вот такую простую схему. И это сопротивление называется «эквивалентом R» ( R eq ). И мы хотим, чтобы этот R eq выполнял ту же работу, что и эти три, R 1 , R 2 и R 3 . Означает, что мы хотели получить ток и от той же батареи, или той же ЭДС, или того же источника питания.
Ну, если вспомнить здесь закон Ома, то R экв будет равно отношению разности потенциалов между концом этого резистора, которая будет ε вольт — то есть напряжение, создаваемое электродвижущей силой, — к сумме токов, проходящих через эти точки. Следовательно, у нас будет ε на i . Используя закон Ома, мы можем выразить R 1 , R 2 и R 3 аналогичным образом.И решив это уравнение для ε , мы получим i умножить на R eq .
Следовательно, мы можем сказать, что V 1 будет равно i 1 , умноженному на R 1 . Но из свойства 1, i 1 равно i , поэтому это будет равно i , умноженному на R 1 . Аналогично, V 2 будет равно i 2 , умноженному на R 2 .Опять же, i 2 равно i . Таким образом, мы можем записать это как i раз R 2 . И, наконец, мы можем выразить V 3 как i 3 , умноженное на R 3 . И это тоже будет равно i умножить на R 3 , потому что такой же ток будет течь через сопротивление R 3 и при последовательном соединении.
Теперь из свойства 2 ε равно В 1 плюс В 2 плюс В 3 .А за ε , мы можем записать его как, из закона Ом, I Time R EQ , который будет равен I Times R 1 для V 1 .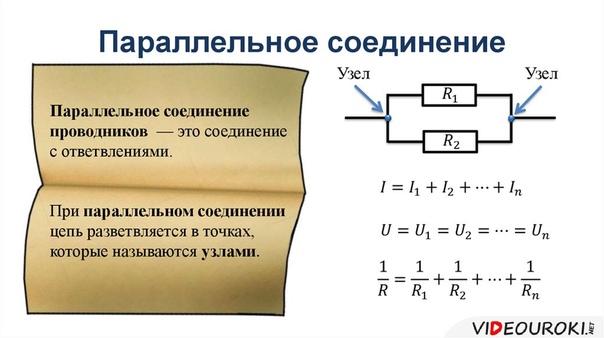 i раз R 2 для V 2 , плюс i раз R 3 для 3 3 Поскольку ток i является общим в каждом члене, разделив обе части на i , мы можем исключить ток и, следовательно, эквивалентное сопротивление этих трех сопротивлений, R 1 , R 2 и R 3 при последовательном соединении становится равным R 1 плюс R 2 плюс R 3 .
i раз R 2 для V 2 , плюс i раз R 3 для 3 3 Поскольку ток i является общим в каждом члене, разделив обе части на i , мы можем исключить ток и, следовательно, эквивалентное сопротивление этих трех сопротивлений, R 1 , R 2 и R 3 при последовательном соединении становится равным R 1 плюс R 2 плюс R 3 .
Конечно, мы можем легко обобщить это, сказав, что для N числа сопротивлений при последовательном соединении эквивалентное сопротивление становится равным сумме, i от 1 до N из R i . Другими словами, эквивалентное сопротивление становится суммой сопротивлений всех резисторов, соединенных последовательно. Итак, когда мы соединяем сопротивления последовательно, то общее сопротивление цепи увеличивается и становится больше, чем наибольшее сопротивление в сочетании.
Двигаясь дальше, для второго типа соединения, которое представляет собой параллельное соединение сопротивлений или резисторов, и снова, как и в случае с конденсаторами, мы соединяем сопротивления так, чтобы разность потенциалов на каждом резисторе или сопротивлении становилась равной другой. . Для этого мы подключаем их вот так и применяем разность потенциалов к комбинации, подключая их к клеммам источника питания. Нравится.
Итак, ЭДС, электродвижущая сила, генерирует ε вольт разности потенциалов.Допустим, это наше сопротивление R 1 , R 2 и R 3 . Если мы возьмем наш вольтметр и подключим его к каждому резистору, мы получим одинаковую разность потенциалов в комбинации между этими двумя концами, у нас будет ε вольт разности потенциалов, что будет равно ε . R 3 , ε вольт R 2 и ε вольт R 1
Таким образом, первым свойством параллельного соединения будет то, что разность потенциалов на каждом из сопротивлений будет равна друг другу, и все они будут равны результирующей разности потенциалов по всей комбинации.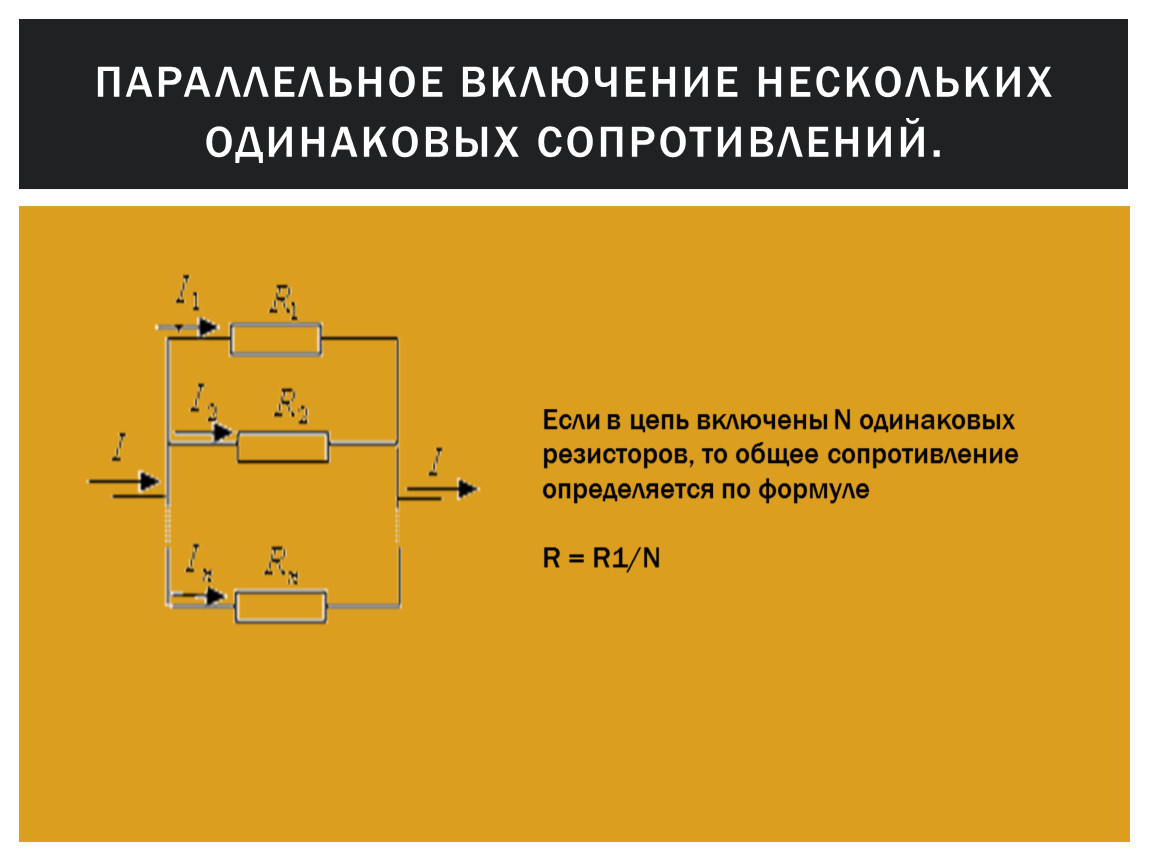 В этом случае это будет равно ε вольт.
В этом случае это будет равно ε вольт.
Конечно, это связано с принципом сохранения энергии, а второе свойство связано с сохранением заряда. Как только мы включим переключатель, ток и выйдет из положительной клеммы источника питания и будет течь по этому пути.Всякий раз, когда дело доходит до этой точки, заряд будет видеть три доступных пути, которые мы называем этой точкой как точка соединения. Некоторая часть тока пройдет через этот первый путь по этой ветви как ток i 1 . Некоторая часть пройдет через резистор R 2 как i 2 . А оставшаяся дробь пройдет по этой ветке как i 3 через R 3 .
Все эти токи вернутся и снова соединятся в этой точке соединения, и они соединятся вместе, и они снова создадут ток i .Следовательно, второе свойство будет состоять в том, что величина тока, входящего в любой из этих переходов, будет равна сумме токов, выходящих из этого перехода: 3 .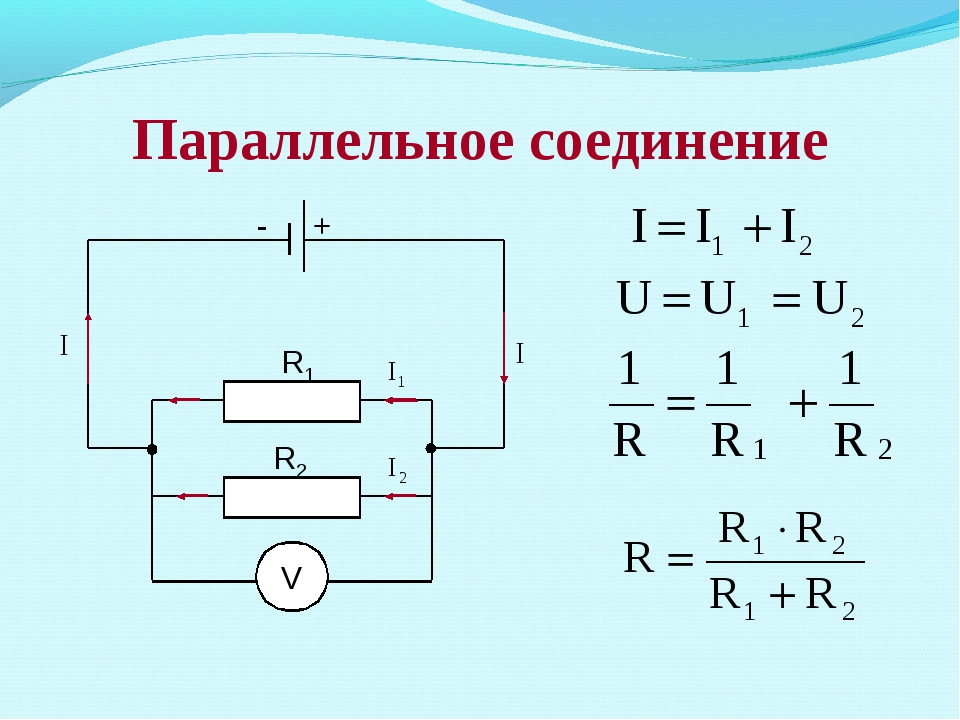 Поэтому мы можем записать это здесь в компактной форме, сказав, что сумма токов в точку соединения равна сумме токов из этого соединения, и это напрямую связано с принципом сохранения заряда.
Поэтому мы можем записать это здесь в компактной форме, сказав, что сумма токов в точку соединения равна сумме токов из этого соединения, и это напрямую связано с принципом сохранения заряда.
Хорошо, снова давайте проделаем тот же процесс, упростим эту схему, чтобы мы могли заменить все эти три сопротивления в параллельном соединении одним сопротивлением, чтобы оно выполняло ту же работу, что и эти три сопротивления в параллельном соединении в этой цепи. . Поэтому мы просто берем этот блок, эти три резистора, и заменяем их одним, и мы снова назовем этот единственный R eq . И соедините концы этого резистора с выводами той же ЭДС, которая генерирует ε вольт.
Здесь снова, как только мы включим переключатель, мы хотим, чтобы этот R eq выполнял ту же работу, что и эти три, поэтому он будет потреблять тот же ток от той же электродвижущей силы, ток i , который будет течь через это сопротивление. Применяя закон Ома, R экв.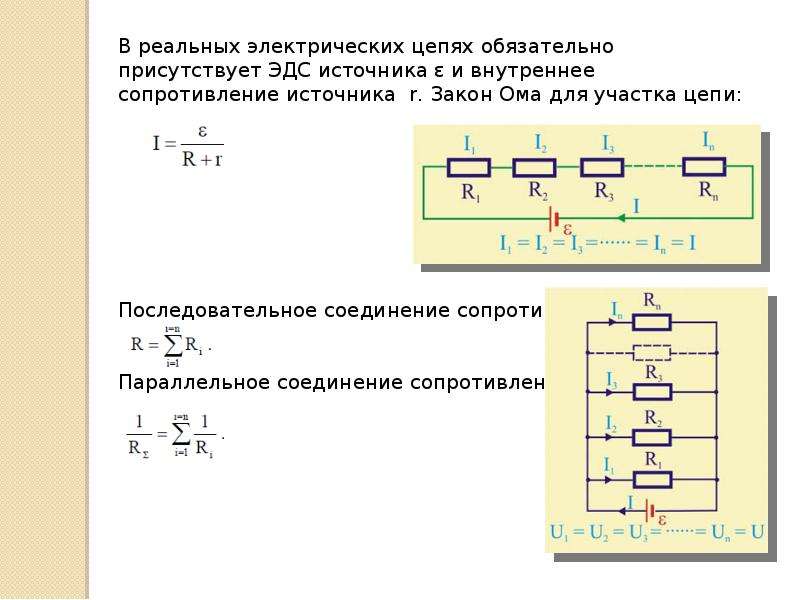 будет равно потенциалу напротив резистора, а в данном случае это ε вольт, деленное на величину тока, проходящего через резистор, и это я .
будет равно потенциалу напротив резистора, а в данном случае это ε вольт, деленное на величину тока, проходящего через резистор, и это я .
Ну, здесь мы можем записать i как ε сверх R eq . Используя аналогичную зависимость, мы можем выразить ток, протекающий через сопротивление R 1 , как разность потенциалов между R 1 , деленную на сопротивление R 1 . Но поскольку В 1 равно ε вольт, то мы можем выразить это как ε на R 1 .Точно так же, I 2 2 будет равным V 2 более г 2 , и это тоже будет равно ε более г 2 , потому что, опять же, V 2 при параллельном соединении будет равно разности потенциалов всей комбинации, которая составляет ε вольт. И, наконец, i 3 будет V 3 больше R 3 , и это также будет равно ε больше R
Если вы вернетесь к общим свойствам и посмотрите на свойство 2, из свойства 2 текущее i равно i 1 плюс i 2 плюс i 3 3 Мы можем записать ε более r уравнение для I , ε , R 1 для I 1 , плюс ε более R 2 для i 2 и плюс ε к R 3 вместо i 3 . Поскольку ε вольт приходятся на каждый член, если вы разделите обе части на ε , мы исключим ε из обеих частей уравнения, и мы получим 1 больше R экв. равно 1 больше R 1 плюс 1 к R 2 плюс 1 к R 3 .
Поскольку ε вольт приходятся на каждый член, если вы разделите обе части на ε , мы исключим ε из обеих частей уравнения, и мы получим 1 больше R экв. равно 1 больше R 1 плюс 1 к R 2 плюс 1 к R 3 .
Опять же, если мы обобщим это для N количества сопротивлений, 1 на R eq будет равно сумме i от 1 до N из 1 на R i 9Другими словами, инверсия эквивалентного сопротивления будет равна сумме инверсий каждого сопротивления при параллельном соединении. В результате этого эквивалентное сопротивление будет меньше наименьшего сопротивления в комбинации. Итак, как только мы соединим сопротивления параллельно, общее сопротивление цепи уменьшится.
Теперь снова, если мы вернемся к нашей принципиальной схеме и увидим разницу между параллельным соединением и последовательным соединением, и, как вы можете видеть в последовательном соединении, все компоненты, все сопротивления будут иметь одинаковый ток. Итак, если вы думаете об этой схеме с точки зрения светового короба, и если мы заменим R 1 , R 2 и R 3 на световой короб здесь, и если один из лампочки перегорают, то у нас будет обрыв цепи. Другими словами, у нас не будет полного пути движения зарядов. Следовательно, ток упадет до 0 через каждую из этих лампочек. Следовательно, ни одна из лампочек не будет излучать свет.
Итак, если вы думаете об этой схеме с точки зрения светового короба, и если мы заменим R 1 , R 2 и R 3 на световой короб здесь, и если один из лампочки перегорают, то у нас будет обрыв цепи. Другими словами, у нас не будет полного пути движения зарядов. Следовательно, ток упадет до 0 через каждую из этих лампочек. Следовательно, ни одна из лампочек не будет излучать свет.
Позвольте мне включить этот переключатель.Так обстоит дело, например, с гирляндой на рождественской елке, для некоторых из них, что если одна из лампочек перегорела, то нужно действительно искать и находить эту лампочку, потому что ни одна из лампочек не сможет сгореть. быть включен.
Но при параллельном соединении каждое сопротивление будет иметь свой уникальный ток. Опять же, если вы замените эти сопротивления лампочками, то даже если одно из них перегорит, только оно не будет излучать свет, а остальные продолжат гореть — позвольте мне включить выключатель — потому что их ток не будет зависеть от ток, который в основном имеет сгоревший.
В связи с этим бытовые цепи всегда соединяются параллельно, так что если один из приборов, работающих с электричеством, выйдет из строя, это не повлияет на остальные. Другими словами, например, всякий раз, когда ваш холодильник выходит из строя, ваш телевизор будет продолжать работать в результате этого параллельного соединения. Таким образом, вы можете запомнить эти соединения, думая, что независимые пути для тока в случае параллельного соединения и те же пути для компонентов в случае последовательного соединения.
Еще одна вещь, на которую следует всегда обращать внимание при расчете эквивалентного сопротивления при параллельном соединении: опять же, у нас был аналогичный тип корпуса и для конденсаторов, но он был для последовательного соединения. Вы получите обратное значение эквивалентного сопротивления, применяя это выражение. Поэтому, как только вы вычислите правую часть, вы должны просто продолжить и взять обратное значение, чтобы иметь возможность получить эквивалентное сопротивление параллельного соединения.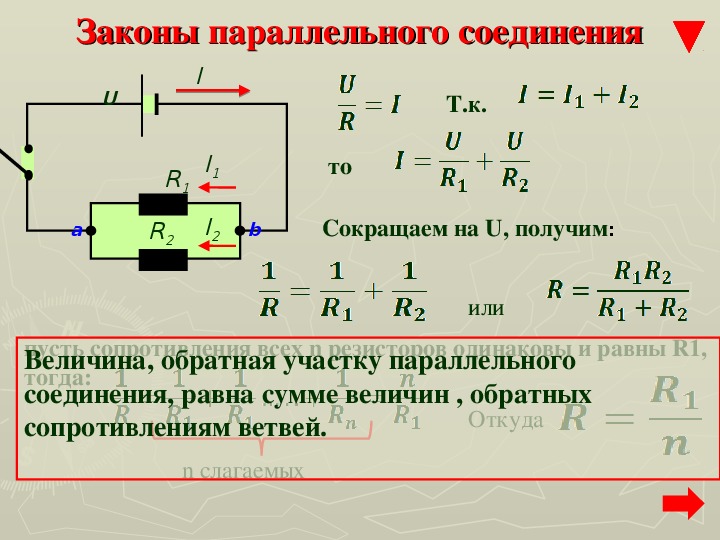
Еще один интересный момент: математическая форма этих уравнений прямо противоположна для соединений по сравнению с соединениями конденсаторов. Другими словами, в случае с конденсаторами, когда мы соединили их параллельно, общая емкость была суммой емкостей каждого конденсатора. В то время как в случае резисторов мы получаем инверсию эквивалентного сопротивления как сумму инверсий каждого сопротивления в комбинации.
10.2 резистора последовательно и параллельно — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Определение термина эквивалентное сопротивление
- Рассчитать эквивалентное сопротивление резисторов, соединенных последовательно
- Рассчитать эквивалентное сопротивление резисторов, соединенных параллельно
В разделе «Ток и сопротивление» мы описали термин «сопротивление» и объяснили базовую конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где V=IR. V=IR. Большинство схем имеют более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, отдаваемый батареей, зависит от эквивалентного сопротивления цепи.
V=IR. Большинство схем имеют более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, отдаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены. Простейшими сочетаниями резисторов являются последовательное и параллельное соединения (рис. 10.11). В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему в параллельных соединениях.
Фигура
10.11
а) При последовательном соединении резисторов ток в каждом резисторе одинаков.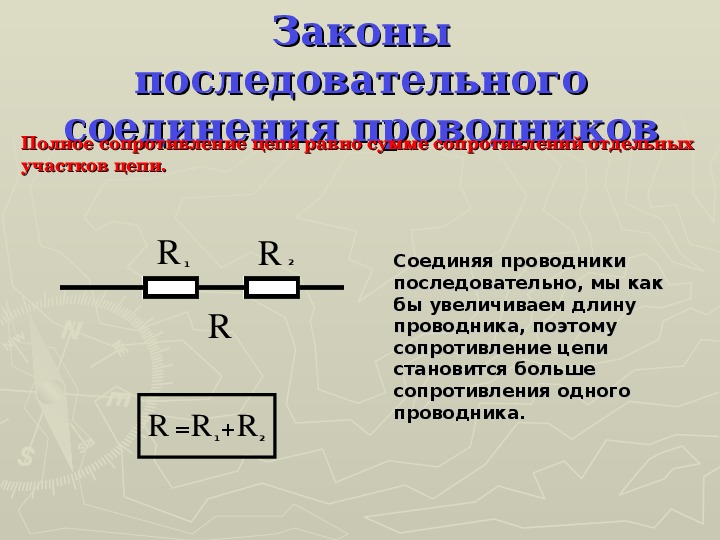 б) при параллельном соединении резисторов напряжение на каждом резисторе одинаково.
б) при параллельном соединении резисторов напряжение на каждом резисторе одинаково.
Резисторы серии
Резисторы называются последовательными, если ток течет через резисторы последовательно. Рассмотрим рис. 10.12, на котором показаны три последовательно соединенных резистора с приложенным напряжением, равным Vab.Ваб. Поскольку существует только один путь для протекания зарядов, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме сопротивлений отдельных элементов.
Фигура
10.12
а) Три резистора, соединенные последовательно к источнику напряжения. (b) Исходная схема сводится к эквивалентному сопротивлению и источнику напряжения.
На рис. 10.12 ток, поступающий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при протекании тока через каждый резистор. Согласно закону Ома, падение потенциала В на резисторе при протекании через него тока рассчитывается по уравнению V=IR,V=IR, где I — ток в амперах (А), а R — сопротивление в омах (Ом).(Ом). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на один заряд, сумма напряжения, приложенного к цепи источником, и падений потенциала на отдельных резисторах вокруг петли должна быть равна нулю:
Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при протекании тока через каждый резистор. Согласно закону Ома, падение потенциала В на резисторе при протекании через него тока рассчитывается по уравнению V=IR,V=IR, где I — ток в амперах (А), а R — сопротивление в омах (Ом).(Ом). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на один заряд, сумма напряжения, приложенного к цепи источником, и падений потенциала на отдельных резисторах вокруг петли должна быть равна нулю:
Это уравнение часто называют петлевым законом Кирхгофа, который мы рассмотрим более подробно далее в этой главе. Для рисунка 10.12 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
V-V1-V2-V3=0,V=V1+V2+V3,=IR1+IR2+IR3, I=VR1+R2+R3=VRS.V-V1-V2-V3=0,V=V1+V2+V3,=IR1+IR2+IR3, I=VR1+R2+R3=VRS.
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.
Последовательно можно соединить любое количество резисторов. Если резисторы N соединены последовательно, то эквивалентное сопротивление составит
Ом.
RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi.RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi.
10.2
Одним из результатов последовательного соединения компонентов является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты.Например, если несколько ламп соединены последовательно и одна лампочка перегорает, все остальные лампы гаснут.
Пример
10.2
Эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В включена в цепь, состоящую из четырех последовательно соединенных резисторов сопротивлением 20 Ом 20 Ом и одного 10 Ом 10 Ом (рис.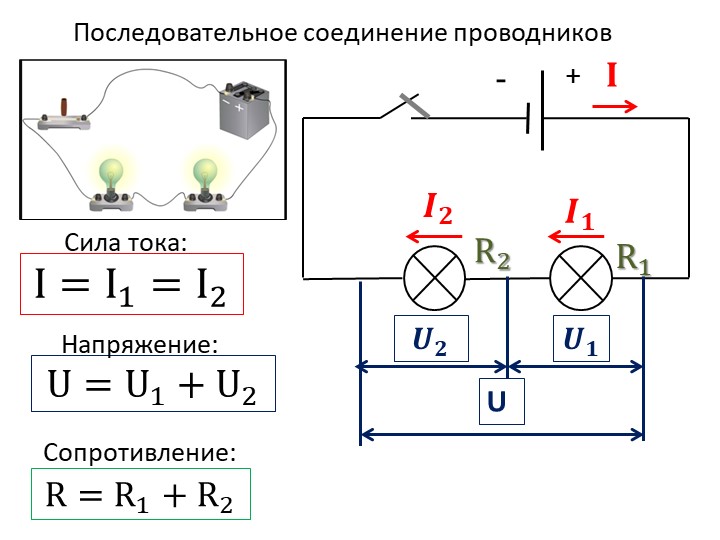 10.13). Предположим, что батарея имеет незначительное внутреннее сопротивление. а) Рассчитайте эквивалентное сопротивление цепи. б) Рассчитайте ток через каждый резистор.в) Рассчитайте падение потенциала на каждом резисторе. г) Определите общую мощность, рассеиваемую резисторами, и мощность, отдаваемую батареей.
10.13). Предположим, что батарея имеет незначительное внутреннее сопротивление. а) Рассчитайте эквивалентное сопротивление цепи. б) Рассчитайте ток через каждый резистор.в) Рассчитайте падение потенциала на каждом резисторе. г) Определите общую мощность, рассеиваемую резисторами, и мощность, отдаваемую батареей.
Фигура
10.13
Простая последовательная цепь с пятью резисторами.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений. Сила тока в цепи определяется по закону Ома и равна напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти по закону Ома.Мощность, рассеиваемая каждым резистором, может быть найдена с помощью P=I2RP=I2R, а общая мощность, рассеиваемая резисторами, равна сумме мощностей, рассеиваемых каждым резистором. Мощность, выдаваемая батареей, может быть найдена с помощью P=IεP=Iε.
Решение
- Эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений:
RS=R1+R2+R3+R4+R5=20Ом+20Ом+20Ом+20Ом+10Ом=90Ом. RS=R1+R2+R3+R4+R5=20Ом+20Ом+20Ом+20Ом+10Ом=90Ом.
RS=R1+R2+R3+R4+R5=20Ом+20Ом+20Ом+20Ом+10Ом=90Ом. - Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление:
I=VRS=9V90Ω=0.1A.I=VRS=9V90Ω=0,1A. - Падение потенциала на каждом резисторе можно найти по закону Ома:
V1=V2=V3=V4=(0,1А)20Ом=2В,V5=(0,1А)10Ом=1В,V1+V2+V3+V4+V5=9В.V1=V2=V3=V4=(0,1А) 20 Ом = 2 В, V5 = (0,1 А) 10 Ом = 1 В, V1 + V2 + V3 + V4 + V5 = 9 В.
Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, выдаваемому батареей. - Мощность, рассеиваемая резистором, равна P=I2RP=I2R, а мощность, отдаваемая батареей, равна P=IεP=Iε:
P1 = P2 = P3 = P4 = (0,1 А) 2 (20 Ом) = 0,2 Вт, P5 = (0.1A)2(10 Ом)=0,1 Вт,Pрассеиваемая=0,2 Вт+0,2 Вт+0,2 Вт+0,2 Вт+0,1 Вт=0,9 Вт,Pисточник=Iε=(0,1 А)(9 В)=0,9 Вт.P1=P2=P3 =P4=(0,1A)2(20Ом)=0,2Вт,P5=(0,1А)2(10Ом)=0,1Вт,Pрассеиваемая=0,2Вт+0,2Вт+0,2Вт+0,2Вт+0,1Вт=0,9Вт,Pисточник =Iε=(0,1А)(9В)=0,9Вт.
Значение
Есть несколько причин, по которым мы будем использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора нужного размера нет в наличии, или нам нужно отводить выделяющееся тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть заметной.
Возможно, резистора нужного размера нет в наличии, или нам нужно отводить выделяющееся тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть заметной.
Проверьте свое понимание
10.2
Проверьте свое понимание Некоторые цепочки миниатюрных праздничных огней закорачивают, когда перегорает лампочка. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на наложение куска провода на компонент. Луковицы обычно сгруппированы в серии из девяти луковиц.Если перегорает слишком много лампочек, шунты со временем открываются. Что вызывает это?
Кратко опишем основные характеристики последовательно соединенных резисторов:
Сопротивления серии
- суммируются, чтобы получить эквивалентное сопротивление:
RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi. RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi.
RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi. - Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его. Общее падение потенциала на последовательных резисторах равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рис. 10.14 показаны резисторы, подключенные параллельно к источнику напряжения. Резисторы параллельны, когда один конец всех резисторов соединен непрерывным проводом с пренебрежимо малым сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с пренебрежимо малым сопротивлением. Падение потенциала на каждом резисторе одинаково. Ток через каждый резистор можно найти, используя закон Ома I=V/R, I=V/R, где напряжение постоянно на каждом резисторе.Например, автомобильные фары, радио и другие системы соединены параллельно, так что каждая подсистема использует полное напряжение источника и может работать совершенно независимо. То же самое относится и к проводке в вашем доме или любом здании.
То же самое относится и к проводке в вашем доме или любом здании.
Фигура
10.14
а) Два резистора, подключенные параллельно к источнику напряжения. (b) Исходная схема сводится к эквивалентному сопротивлению и источнику напряжения.
Ток, протекающий от источника напряжения на рисунке 10.14 зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и поступает в переход или узел, где цепь разделяется, протекая через резисторы R1R1 и R2R2. Поскольку заряды текут от батареи, некоторые из них проходят через резистор R1R1, а некоторые — через резистор R2.R2. Сумма токов, втекающих в соединение, должна быть равна сумме токов, вытекающих из соединения:
∑Iвх=∑Iвых.∑Iвх=∑Iвых.
Это уравнение называется правилом пересечения Кирхгофа и будет подробно обсуждаться в следующем разделе. На рис. 10.14 правило соединения дает I=I1+I2I=I1+I2. В этой схеме есть два контура, что приводит к уравнениям V=I1R1V=I1R1 и I1R1=I2R2I1R1=I2R2. Обратите внимание, что напряжения на параллельных резисторах одинаковы (V=V1=V2)(V=V1=V2), а ток суммируется:
Обратите внимание, что напряжения на параллельных резисторах одинаковы (V=V1=V2)(V=V1=V2), а ток суммируется:
I=I1+I2=V1R1+V2R2=VR1+VR2=V(1R1+1R2)=VRPRP=(1R1+1R2)−1.I=I1+I2=V1R1+V2R2=VR1+VR2=V(1R1+1R2 )=ВРПРП=(1R1+1R2)−1.
Обобщая любое количество резисторов N , эквивалентное сопротивление RPRP параллельного соединения связано с отдельными сопротивлениями как
RP=(1R1+1R2+1R3+⋯+1RN−1+1RN)−1=(∑i= 1N1Ri)−1.RP=(1R1+1R2+1R3+⋯+1RN−1+1RN)−1=(∑i=1N1Ri)−1.
10.3
Это соотношение приводит к эквивалентному сопротивлению RPRP, которое меньше, чем наименьшее из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника протекает больший ток, чем по каждому из них по отдельности, поэтому общее сопротивление меньше.
Пример
10.3
Анализ параллельной цепи
Три резистора R1=1,00 Ом, R2=2,00 Ом, R1=1,00 Ом, R2=2,00 Ом и R3=2,00 Ом, R3=2,00 Ом соединены параллельно. Параллельное соединение подключено к источнику напряжения V=3. 00VV=3.00V. а) чему равно сопротивление? б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором.(e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
00VV=3.00V. а) чему равно сопротивление? б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором.(e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов находится по формуле RP=(∑i1Ri)−1RP=(∑i1Ri)−1.
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, подставив RPRP вместо полного сопротивления I=VRP.I=VRP.
(c) Индивидуальные токи легко рассчитать по закону Ома (Ii=ViRi)(Ii=ViRi), поскольку на каждый резистор подается полное напряжение.Общий ток представляет собой сумму отдельных токов: I=∑iIi.I=∑iIi.
(d) Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Возьмем Pi=V2/Ri,Pi=V2/Ri, так как на каждый резистор подается полное напряжение.
Возьмем Pi=V2/Ri,Pi=V2/Ri, так как на каждый резистор подается полное напряжение.
(e) Суммарная мощность также может быть рассчитана несколькими способами, используйте P=IVP=IV.
Решение
- Общее сопротивление для параллельной комбинации резисторов находится по уравнению 10.3. Ввод известных значений дает
RP=(1R1+1R2+1R3)−1=(11.00Ω+12.00Ω+12.00Ω)−1=0.50Ω.RP=(1R1+1R2+1R3)−1=(11.00Ω+12.00Ω+12.00Ω) −1=0,50 Ом.
Общее сопротивление с правильным количеством значащих цифр равно RP=0,50 Ом. RP=0,50 Ом. Как и предполагалось, RPRP меньше наименьшего индивидуального сопротивления. - Полный ток можно найти из закона Ома, подставив RPRP вместо полного сопротивления. Это дает
I=VRP=3.00V0.50Ω=6.00A.I=VRP=3.00V0.50Ω=6.00A.
Ток I для каждого устройства значительно больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример).Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
- Индивидуальные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
I1=VR1=3,00В1,00Ом=3,00А.I1=VR1=3,00В1,00Ом=3,00А.
Так же,
I2=VR2=3,00В2,00Ом=1,50AI2=VR2=3,00В2,00Ом=1,50А
и
I3=VR3=3,00В2,00Ом=1,50А.I3=VR3=3,00В2,00Ом=1,50А.
Общий ток представляет собой сумму отдельных токов:
I1+I2+I3=6,00 А. I1+I2+I3=6,00 А. - Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Будем использовать P=V2/R,P=V2/R, так как на каждый резистор подается полное напряжение. Таким образом,
P1=V2R1=(3,00 В)21,00 Ом=9,00 Вт.P1=V2R1=(3,00 В)21,00 Ом=9,00 Вт.
Так же,
P2=V2R2=(3,00 В)22,00 Ом=4,50 WP2=V2R2=(3,00 В)22,00 Ом=4,50 Вт
и
P3=V2R3=(3,00 В)22,00 Ом=4,50 Вт. P3=V2R3=(3,00 В)22,00 Ом=4,50 Вт. - Общая мощность также может быть рассчитана несколькими способами. Выбор P=IVP=IV и ввод общей текущей доходности
P=IV=(6,00 А)(3,00 В)=18,00 Вт. P=IV=(6,00 А)(3,00 В)=18,00 Вт.
P=IV=(6,00 А)(3,00 В)=18,00 Вт.
Значение
Суммарная мощность, рассеиваемая резисторами, также равна 18.00 Вт:
P1+P2+P3=9,00 Вт+4,50 Вт+4,50 Вт=18,00 Вт.P1+P2+P3=9,00 Вт+4,50 Вт+4,50 Вт=18,00 Вт.
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Проверьте свое понимание
10.3
Проверьте свои знания Рассмотрим ту же разность потенциалов (V=3,00 В)(V=3,00 В), приложенную к тем же трем резисторам, соединенным последовательно. Будет ли эквивалентное сопротивление последовательной цепи выше, ниже или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи больше, меньше или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая резистором, включенным последовательно, будет отличаться от мощности, рассеиваемой резисторами, включенными параллельно?
Проверьте свое понимание
10.
 4
4
Проверьте свое понимание Как бы вы использовали реку и два водопада для моделирования параллельной конфигурации двух резисторов? Как разрушается эта аналогия?
Подытожим основные характеристики резисторов при параллельном включении:
- Эквивалентное сопротивление находится из
RP=(1R1+1R2+1R3+⋯+1RN−1+1RN)−1=(∑i=1N1Ri)−1,RP=(1R1+1R2+1R3+⋯+1RN−1+1RN)−1=(∑i =1N1Ri)−1,
и меньше, чем любое индивидуальное сопротивление в комбинации. - Падение потенциала на каждом параллельном резисторе одинаково.
- Параллельные резисторы не получают суммарный ток каждый; они его делят. Ток, входящий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый параллельный резистор.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Возможно, вы помните, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Схемы часто содержат как конденсаторы, так и резисторы.В таблице 10.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательного и параллельного соединений.
Схемы часто содержат как конденсаторы, так и резисторы.В таблице 10.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательного и параллельного соединений.
| Параллельная комбинация | ||
|---|---|---|
| Эквивалентная емкость | 1CS=1C1+1C2+1C3+⋯1CS=1C1+1C2+1C3+⋯ | CP=C1+C2+C3+⋯CP=C1+C2+C3+⋯ |
| Эквивалентное сопротивление | RS=R1+R2+R3+⋯=∑i=1NRiRS=R1+R2+R3+⋯=∑i=1NRi | 1RP=1R1+1R2+1R3+⋯1RP=1R1+1R2+1R3+⋯ |
Таблица
10. 1
1
Сводка по эквивалентному сопротивлению и емкости в последовательном и параллельном соединении
Комбинации серий и параллелей
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединений. Такие комбинации распространены, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно привести к одному эквивалентному сопротивлению с помощью метода, показанного на рисунке 10.15. Различные части могут быть идентифицированы как последовательные или параллельные соединения, приведены к их эквивалентным сопротивлениям, а затем уменьшены до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс скорее трудоемкий, чем сложный. Здесь мы отмечаем эквивалентное сопротивление как Req.Req.
Фигура
10. 15
15
(а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы R3R3 и R4R4 соединены последовательно, и их эквивалентное сопротивление равно R34=10 Ом. R34=10 Ом. (c) Шаг 2: На уменьшенной схеме показаны резисторы R2R2 и R34R34, соединенные параллельно, с эквивалентным сопротивлением R234 = 5 Ом.R234=5 Ом. (d) Шаг 3: Уменьшенная схема показывает, что R1R1 и R234R234 соединены последовательно с эквивалентным сопротивлением R1234=12 Ом, R1234=12 Ом, что соответствует эквивалентному сопротивлению Req.Req. (e) Уменьшенная схема с источником напряжения V=24VV=24V с эквивалентным сопротивлением Req=12Ω.Req=12Ω. Это приводит к току I=2AI=2A от источника напряжения.
Обратите внимание, что резисторы R3R3 и R4R4 включены последовательно. Их можно объединить в одно эквивалентное сопротивление. Одним из методов отслеживания процесса является включение резисторов в качестве индексов.Здесь эквивалентное сопротивление R3R3 и R4R4 равно
Ом.
R34=R3+R4=6Ом+4Ом=10Ом.R34=R3+R4=6Ом+4Ом=10Ом.

Теперь схема сокращается до трех резисторов, как показано на рис. 10.15(c). Перерисовав, мы теперь видим, что резисторы R2R2 и R34R34 составляют параллельную цепь. Эти два резистора можно уменьшить до эквивалентного сопротивления:
.
R234=(1R2+1R34)-1=(110 Ом+110 Ом)-1=5 Ом. R234=(1R2+1R34)-1=(110 Ом+110 Ом)-1=5 Ом.
На этом этапе процесса схема сокращается до двух резисторов, как показано на рис. 10.15(d).Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно привести к эквивалентному сопротивлению, которое является эквивалентным сопротивлением цепи:
Треб.=R1234=R1+R234=7Ом+5Ом=12Ом. Треб.=R1234=R1+R234=7Ом+5Ом=12Ом.
Основная цель этого анализа цепи достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен I=VReq=24V12Ω=2A.I=VReq=24V12Ω=2A. Этот ток протекает через резистор R1R1 и обозначается как I1. I1. Падение потенциала на R1R1 можно найти по закону Ома:
I1. Падение потенциала на R1R1 можно найти по закону Ома:
V1=I1R1=(2А)(7Ом)=14В. V1=I1R1=(2А)(7Ом)=14В.
Глядя на рисунок 10.15(c), это оставляет 24V-14V=10V24V-14V=10V на параллельную комбинацию R2R2 и R34.R34. Ток через R2R2 можно найти по закону Ома:
I2=V2R2=10В10Ом=1А.I2=V2R2=10В10Ом=1А.
Резисторы R3R3 и R4R4 включены последовательно, поэтому токи I3I3 и I4I4 равны
.
I3=I4=I-I2=2А-1А=1А.I3=I4=I-I2=2А-1А=1А.
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Падение потенциала: V3=I3R3=6VV3=I3R3=6В и V4=I4R4=4В.V4=I4R4=4В. Окончательный анализ заключается в рассмотрении мощности, подаваемой источником напряжения, и мощности, рассеиваемой резисторами. Мощность, рассеиваемая резисторами
P1=I12R1=(2A)2(7Ом)=28Вт,P2=I22R2=(1А)2(10Ом)=10Вт,P3=I32R3=(1А)2(6Ом)=6Вт,P4=I42R4=(1А)2 (4 Ом) = 4 Вт, Pрассеиваемая = P1 + P2 + P3 + P4 = 48 Вт. P1 = I12R1 = (2A) 2 (7 Ом) = 28 Вт, P2 = I22R2 = (1 A) 2 (10 Ом) = 10 Вт, P3 = I32R3 = (1А)2(6Ом)=6Вт,P4=I42R4=(1А)2(4Ом)=4Вт,Pрассеиваемая=P1+P2+P3+P4=48Вт.
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, равна Ps=IV=(2A)(24В)=48Вт. Ps=IV=(2А)(24В)=48Вт. Анализ мощности, подаваемой в цепь, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример
10.4
Объединение последовательных и параллельных цепей
На рис. 10.16 показано последовательное и параллельное соединение резисторов. Мы можем рассматривать R1R1 как сопротивление проводов, ведущих к R2R2 и R3.Р3. а) Найдите эквивалентное сопротивление цепи. б) Чему равно падение потенциала V1V1 на резисторе R1R1? в) Найдите ток I2I2 через резистор R2R2. г) Какую мощность рассеивает R2R2?
Фигура
10.16
Эти три резистора подключены к источнику напряжения так, что R2R2 и R3R3 параллельны друг другу, а эта комбинация последовательно с R1.R1.
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения R2R2 и R3.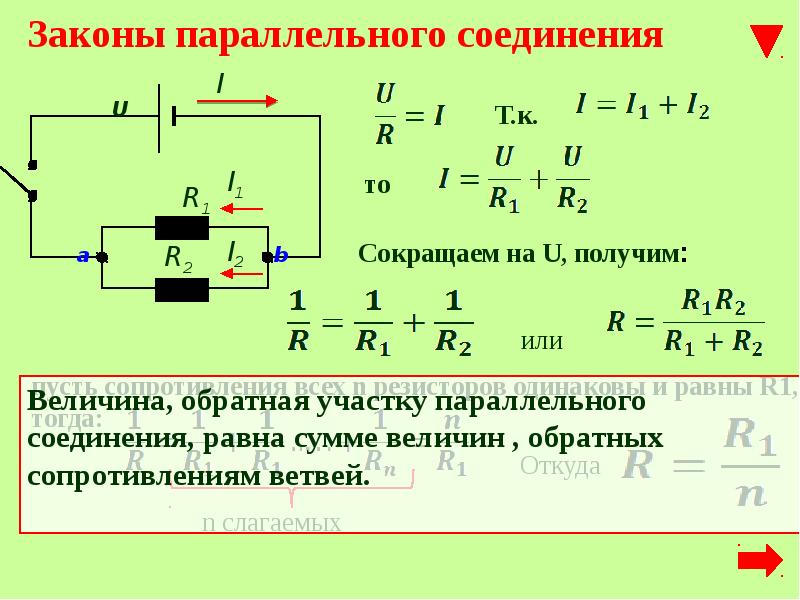 Р3. Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с R1.R1.
Р3. Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с R1.R1.
(b) Ток через R1R1 можно найти, используя закон Ома и приложенное напряжение. Ток через R1R1 равен току от батареи. Падение потенциала V1V1 на резисторе R1R1 (которое представляет собой сопротивление соединительных проводов) можно найти с помощью закона Ома.
(c) Ток через R2R2 можно найти по закону Ома I2=V2R2.I2=V2R2. Напряжение на R2R2 можно найти, используя V2=V−V1.В2=В-В1.
(d) Используя закон Ома (V2=I2R2)(V2=I2R2), мощность, рассеиваемую резистором, также можно найти, используя P2=I22R2=V22R2P2=I22R2=V22R2.
Решение
- Чтобы найти эквивалентное сопротивление цепи, обратите внимание, что параллельное соединение R2R2 и R3R3 последовательно с R1R1, поэтому эквивалентное сопротивление равно
Req=R1+(1R2+1R3)−1=1,00 Ом+(16,00Ω+113,00Ω)−1=5,10Ω.Req=R1+(1R2+1R3)−1=1,00Ω+(16,00Ω+113,00Ω)−1 =5,10 Ом.
Общее сопротивление этой комбинации является промежуточным между чисто последовательными и чисто параллельными значениями (20. 0 Ом 20,0 Ом и 0,804 Ом 0,804 Ом соответственно).
0 Ом 20,0 Ом и 0,804 Ом 0,804 Ом соответственно). - Ток через R1R1 равен току, отдаваемому батареей:
I1=I=VReq=12,0 В5,10 Ом=2,35 А. I1=I=VReq=12,0 В 5,10 Ом=2,35 А.
Напряжение на R1R1 равно
V1=I1R1=(2,35 А)(1 Ом)=2,35 В. V1=I1R1=(2,35 А)(1 Ом)=2,35 В.
Напряжение, подаваемое на R2R2 и R3R3, меньше напряжения, подаваемого батареей, на величину V1.V1. Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R2R2 и R3R3. - Чтобы найти ток через R2R2, мы должны сначала найти приложенное к нему напряжение.Напряжение на двух резисторах, включенных параллельно, одинаково:
V2=V3=V-V1=12,0В-2,35В=9,65В.V2=V3=V-V1=12,0В-2,35В=9,65В.
Теперь мы можем найти ток I2I2 через сопротивление R2R2 по закону Ома:
I2=V2R2=9,65 В6,00 Ом=1,61 А. I2=V2R2=9,65 В6,00 Ом=1,61 А.
Ток меньше, чем 2,00 А, которые протекали через R2R2, когда он был подключен параллельно батарее в предыдущем примере с параллельной схемой. - Мощность, рассеиваемая резистором R2R2, определяется выражением
P2=I22R2=(1,61 А)2(6,00 Ом)=15,5 Вт. P2=I22R2=(1,61 А)2(6.00 Ом) = 15,5 Вт.
P2=I22R2=(1,61 А)2(6.00 Ом) = 15,5 Вт.
Значение
Анализ сложных цепей часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если всю схему нельзя свести к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы можно уменьшить, что значительно упростит анализ.
Проверьте свое понимание
10,5
Проверьте свое понимание Рассмотрите электрические цепи в вашем доме.Приведите не менее двух примеров схем, которые должны использовать комбинацию последовательных и параллельных цепей для эффективной работы.
Практические выводы
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение напряжения в проводах IR также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Если потребляется большой ток, падение напряжения в проводах IR также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рис. 10.17. Устройство, представленное R3R3, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение напряжения в проводах, представленных R1R1, уменьшая напряжение на лампочке (которой является R2R2), которая затем заметно тускнеет.
Фигура
10.17
Почему гаснет свет при включении большого электроприбора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на светильнике.
Стратегия решения проблем
Последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения.Этот шаг включает в себя список известных значений для проблемы, поскольку они помечены на вашей принципиальной схеме.
- Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные.Есть один список для серий и другой для параллельных.
- Проверьте, разумны ли и последовательны ли ответы.

Пример
10,5
Объединение последовательных и параллельных цепей
Два последовательно соединенных резистора (R1,R2)(R1,R2) соединены с двумя резисторами, соединенными параллельно (R3,R4)(R3,R4). Последовательно-параллельная комбинация подключается к аккумулятору. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и батарею, имеют незначительное сопротивление.Через резистор R1.R1 протекает ток 2,00 А. Какое напряжение выдает источник напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
- Нарисуйте четкую принципиальную схему (рис. 10.18).
Фигура
10.18Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
- Неизвестно — напряжение батареи.Чтобы найти напряжение, выдаваемое батареей, необходимо найти эквивалентное сопротивление.

- В этой схеме мы уже знаем, что резисторы R1R1 и R2R2 включены последовательно, а резисторы R3R3 и R4R4 — параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов R3R3 и R4R4 последовательно с последовательной конфигурацией резисторов R1R1 и R2R2.
- Напряжение, подаваемое аккумулятором, можно найти, умножив ток от аккумулятора на эквивалентное сопротивление цепи.Ток от аккумулятора равен току через R1R1 и равен 2,00 А. Нам нужно найти эквивалентное сопротивление путем сокращения цепи. Чтобы уменьшить схему, сначала рассмотрим два резистора параллельно. Эквивалентное сопротивление: R34=(110,00 Ом+110,00 Ом)-1=5,00 Ом. R34=(110,00 Ом+110,00 Ом)-1=5,00 Ом. Эта параллельная комбинация соединена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление цепи Req=R1+R2+R34=25,00 Ом. Req=R1+R2+R34=25,00 Ом. Таким образом, напряжение, подаваемое батареей, равно V=IReq=2.00А(25,00Ом)=50,00В.V=IReq=2,00А(25,00Ом)=50,00В.
- Один из способов проверить согласованность результатов — рассчитать мощность, отдаваемую батареей, и мощность, рассеиваемую резисторами.
 Мощность, подаваемая аккумулятором, составляет Pbatt=IV=100,00 Вт. Pbatt=IV=100,00 Вт.
Мощность, подаваемая аккумулятором, составляет Pbatt=IV=100,00 Вт. Pbatt=IV=100,00 Вт.
Поскольку они включены последовательно, ток через R2R2 равен току через R1.R1. Поскольку R3=R4R3=R4, ток через каждый будет 1,00 Ампер. Мощность, рассеиваемая резисторами, равна сумме мощностей, рассеиваемых каждым резистором:
P=I12R1+I22R2+I32R3+I42R4=40.00Вт+40.00Вт+10.00Вт+10.00Вт=100.00Вт.P=I12R1+I22R2+I32R3+I42R4=40.00Вт+40.00Вт+10.00Вт+10.00Вт=100.00Вт.
Поскольку мощность, рассеиваемая резисторами, равна мощности, выдаваемой батареей, наше решение выглядит последовательным.
Значение
Если в задаче есть сочетание последовательного и параллельного, как в этом примере, ее можно уменьшить пошагово, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений. При нахождении ReqReq для параллельного соединения следует внимательно относиться к обратному.Кроме того, единицы измерения и численные результаты должны быть разумными. Например, эквивалентное последовательное сопротивление должно быть больше, тогда как эквивалентное параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
Например, эквивалентное последовательное сопротивление должно быть больше, тогда как эквивалентное параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
Цепи серии
Представьте себе
электрический ток, выходящий из батареи. Если резисторы соединены таким
таким образом, чтобы часть тока могла проходить через один резистор, а остальные
ток может идти через другой резистор, тогда схема параллельна
цепь .
И Т
— полный ток параллельной цепи. Вы бы измерили этот ток
в любом месте до или после трехстороннего разделения, ведущего к трем резисторам. В
между перекрестком и R 1 вы измерите I 1 . Между переходом и R 2 ,
вы бы измерили I 2 и т.д.
С момента
общий ток, I T , делится на три разные группы
электронов, каждый из которых путешествует по своему маршруту,
И Т
= I 1 + I 2 + I 3 +.
В параллельных цепях все
резисторы, независимо от их сопротивлений, испытывают одинаковое падение напряжения или
потенциальная разница, потому что все они имеют одинаковые точки входа и выхода
(соединения).
В Т = В 1 = В 2 = В 3 = В n
Если мы разделим
формулу тока по зависимости напряжения получаем:
или R T =
[Р 1 -1 + Р 2 -1 + Р 3 -1
+ ] -1
Пример 1
а.
Чему равно полное сопротивление цепи?
Р Т =
[R 1 -1 + R 2 -1 + R 3 -1 ] -1
Р Т =
[12 -1 + 12 -1 +12 -1 ] -1 = 4 Вт
б.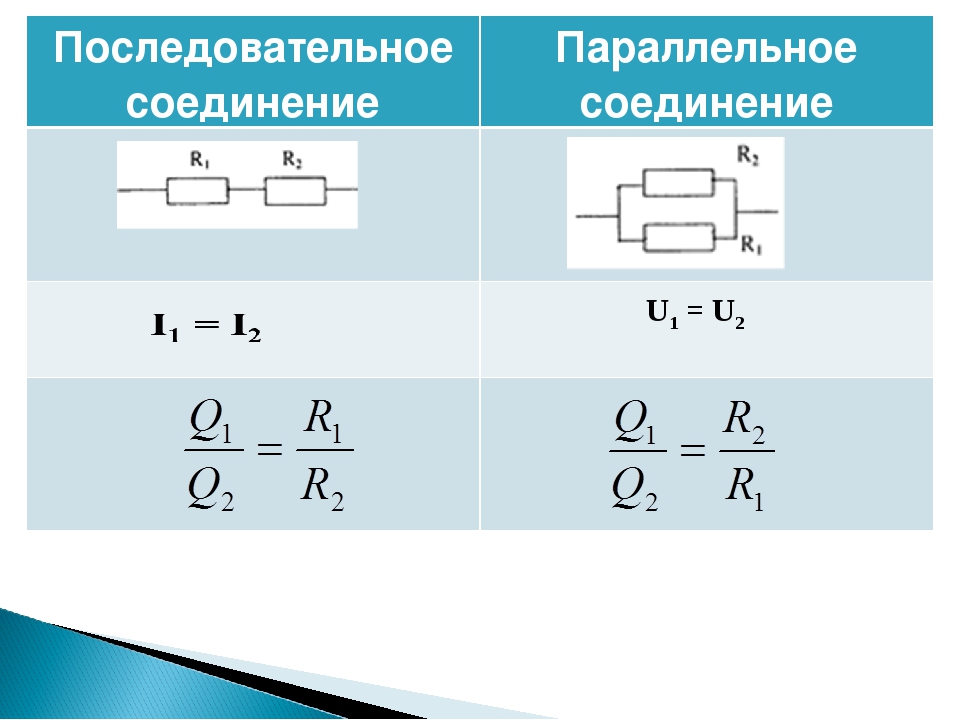
Каков общий ток?
I T = V/R T = 12/4 = 3 А
с.Какое напряжение (V 1 ) будет
измеряется на каждом отдельном резисторе?
12
В (Напряжение постоянное при параллельном подключении.)
с.
Какой ток потребляет
каждый резистор?
I 1 = V/R 1 = 12/12 = 1А. Остальные также
по 1 А каждый, всего 3А.
Пример 2
рисунок кажется запутанным, но обратите внимание, что это параллельная цепь, потому что
у электрона есть выбор.На стыке (показан красной точкой) электроны
либо следуйте по зеленому маршруту, либо по оранжевому маршруту.
Применение I
1 = 1А; I 2 = 0,5 А; Р 1
= 10 Вт.
- Найти V 2 .
Помните, что параллельное напряжение постоянно. Итак, если мы найдем V 1 ,
Итак, если мы найдем V 1 ,
мы будем знать V 2 .
В 1 = I 1 R 1 = 1(10) = 10 В.
В 2 = В 1 = 10 В
- Найти R 2 .
R 2 = V/I 2 = 10/0,5 = 20 Вт.
- Используйте два метода, чтобы получить R T .
(1)
Р Т = [Р 1 -1
+ R 2 -1 ] -1 = [20 -1 + 10 -1
] -1 = 6.7 Ш.
(2) I T
= I 3 = I 1 + I 2 = 1 + 0,5 = 1,5 А.
R T = V/ I T = 10/1,5 = 6,7 W.
Пример 3
В параллельной цепи, какой эффект дает добавление дополнительных резисторов
есть на общий ток?
Ток увеличивается !
В цепи серии добавление дополнительных резисторов увеличивает
полное сопротивление и, таким образом, снижает ток. Но обратное верно в
Но обратное верно в
параллельная схема, потому что добавление большего количества резисторов параллельно создает больше вариантов
и снижает общее сопротивление. Если тот же аккумулятор подключен к
резисторы, ток увеличится. Не убежден? Попробуйте:
[10 -1 + 10 -1 ] -1 = 5 Вт, но добавить
резистор параллельно, и вы получите [10 -1 + 10 -1 + 10 -1 ] -1 = всего 3,3 Вт.
меньшее сопротивление, вы столкнулись с более высоким общим током.
Еще одна интересная особенность параллельных цепей заключается в том, что если
один компонент выключен, другие пути остаются жизнеспособными, так что
электроны могут продолжать течь по цепи. Это причина того, что
большинство ламп и розеток в доме подключены параллельно.
Распределение тока и напряжения параллельно и последовательно
Вот краткое объяснение распределения тока и напряжения при последовательном и параллельном соединении.
Распределение тока при параллельном соединении: Когда все устройства соединены с помощью параллельных соединений, цепь называется параллельной. В параллельной схеме каждое устройство размещено в своей отдельной ветке . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить по внешней цепи.
Когда резисторы соединены параллельно, разность потенциалов на них одинакова и ток делится обратно пропорционально их сопротивлению.Поскольку i = V/R, где i – ток, V – напряжение, а R – сопротивление. А для параллельной цепи V остается прежним, поэтому i α V/R
Например: i₁ : i₂ : i₃ = ½ : ⅓ : ¼ = 6 : 4 : 3
, поэтому \({{i}_{1}}=\frac{6i}{6+4+3}=\frac{6i}{13};\,{{i}_{2}}=\frac {4i}{6+4+3}=\frac{4i}{13};\,{{i}_{3}}=\frac{3i}{6+4+3}=\frac{3i} {13}\).
Распределение потенциала в последовательной цепи: когда резисторы соединены последовательно, ток через них одинаков, а потенциал распределяется пропорционально их сопротивлениям, поскольку V = iRAnd для одного и того же i, i α V/R
Например, V₁ : V₂ : V₃ = 2 : 3 : 4
Итак, \({{V}_{1}}=\left( \frac{2}{2+3+4} \right)V=\frac{2V}{9}\).
\({{V}_{2}}=\left( \frac{3}{2+3+4} \right)V=\frac{3V}{9};\,{{V}_{ 3}}=\left( \frac{4}{2+3+4} \right)V=\frac{4V}{9}\).
Определение эквивалентной ЭДС более чем одной разнородной ячейки, соединенной параллельно показано. Вся сеть может быть заменена одним источником ЭДС E eq и внутреннего сопротивления r eq .{-1}}\).
Для двух параллельных ячеек \({{E}_{eq}}=\frac{{{E}_{1}}{{r}_{2}}+{{E}_{2}}{ {r}_{1}}}{{{r}_{1}}+{{r}_{2}}}\).
или \({{r}_{eq}}=\frac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r }_{2}}}\).
Обратите внимание, что положительные клеммы всех ячеек находятся в одной точке, а отрицательные — в другой общей точке. Если некоторые из ячеек соединены противоположно, то \({{E}_{eq}}=\frac{\frac{{{E}_{1}}}{{{r}_{1}}}- \frac{{{E}_{2}}}{{{r}_{2}}}+…+\frac{{{E}_{n}}}{{{r}_{n}} }}{\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+…+\frac{1}{{{r}_ {н}}}}\).
\(\frac{1}{{{r}_{eq}}}=\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2 }}}+…\frac{1}{{{r}_{n}}}\).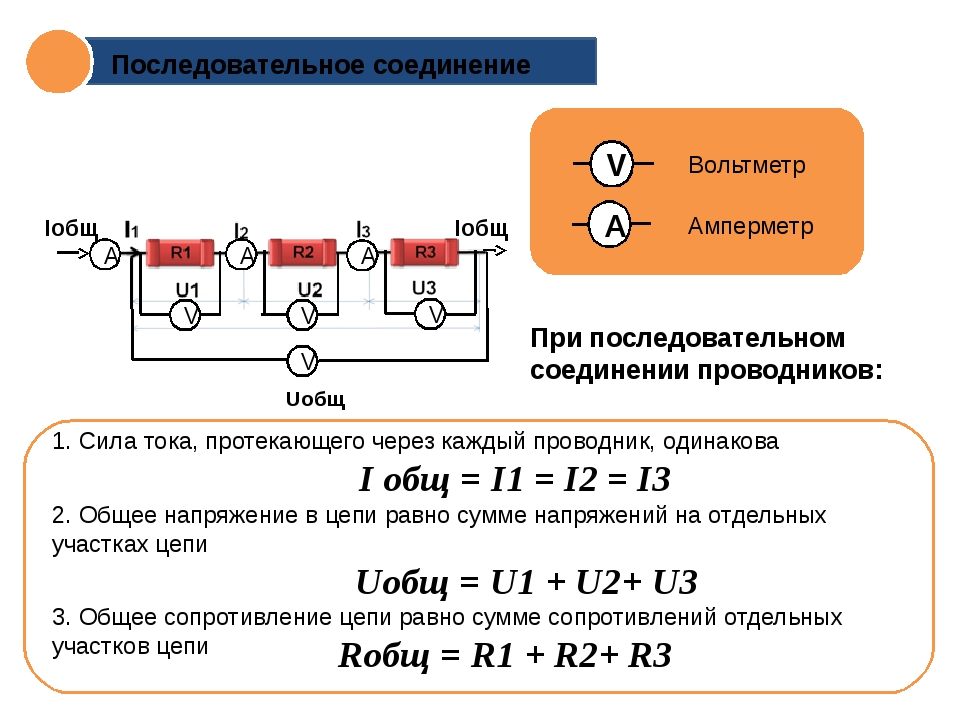


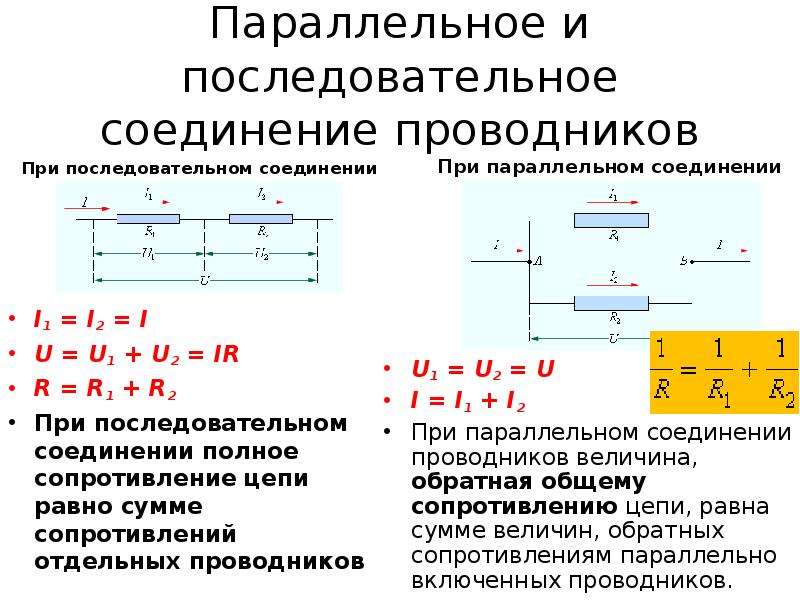
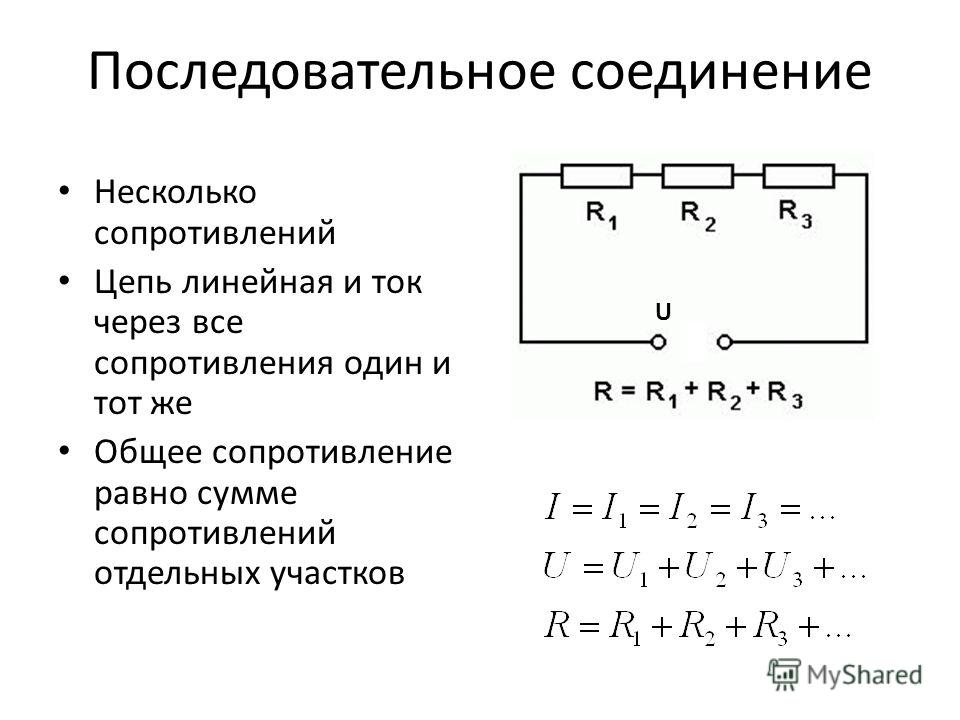
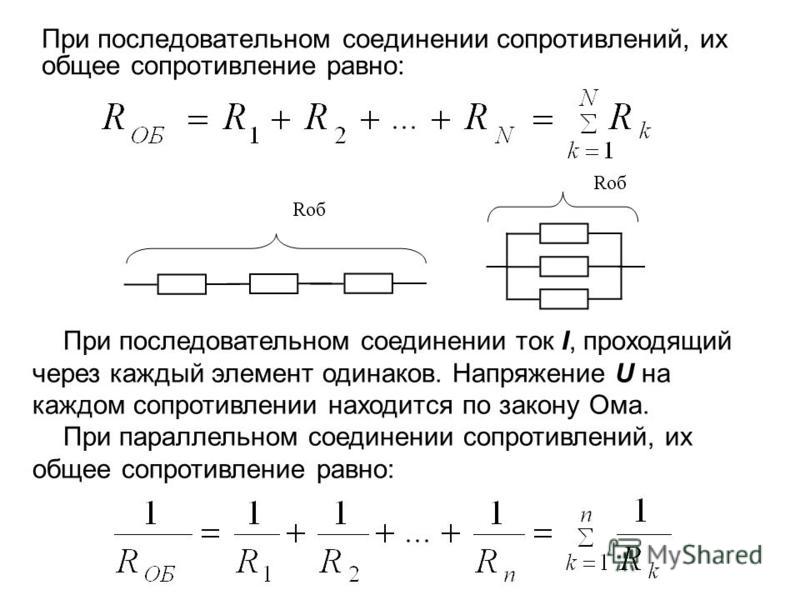 Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.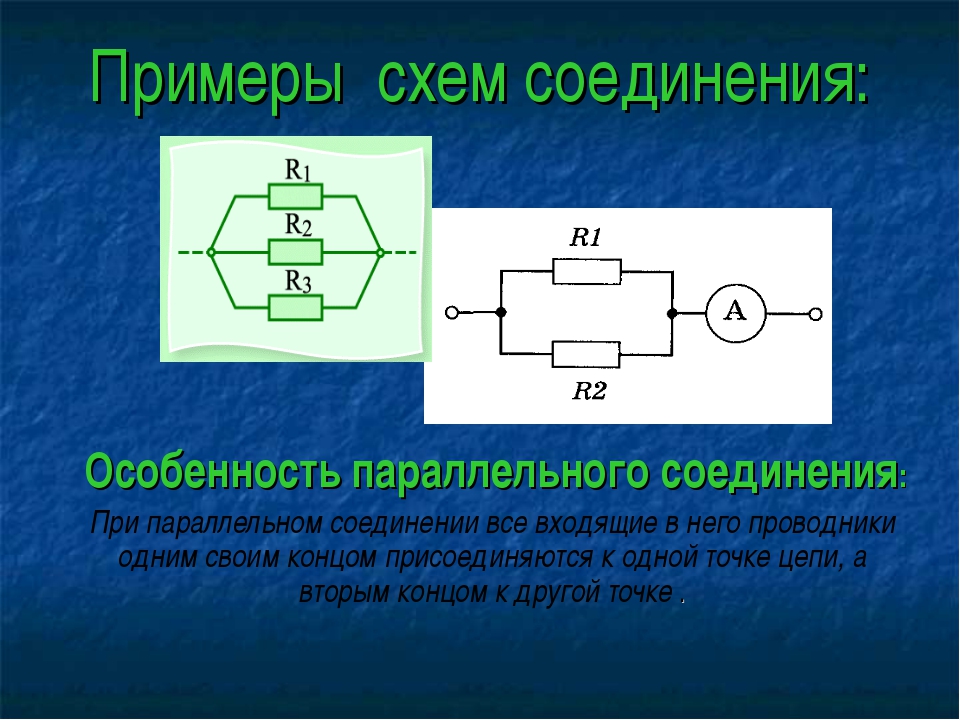 RS=R1+R2+R3+R4+R5=20Ом+20Ом+20Ом+20Ом+10Ом=90Ом.
RS=R1+R2+R3+R4+R5=20Ом+20Ом+20Ом+20Ом+10Ом=90Ом. RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi.
RS=R1+R2+R3+⋯+RN-1+RN=∑i=1NRi.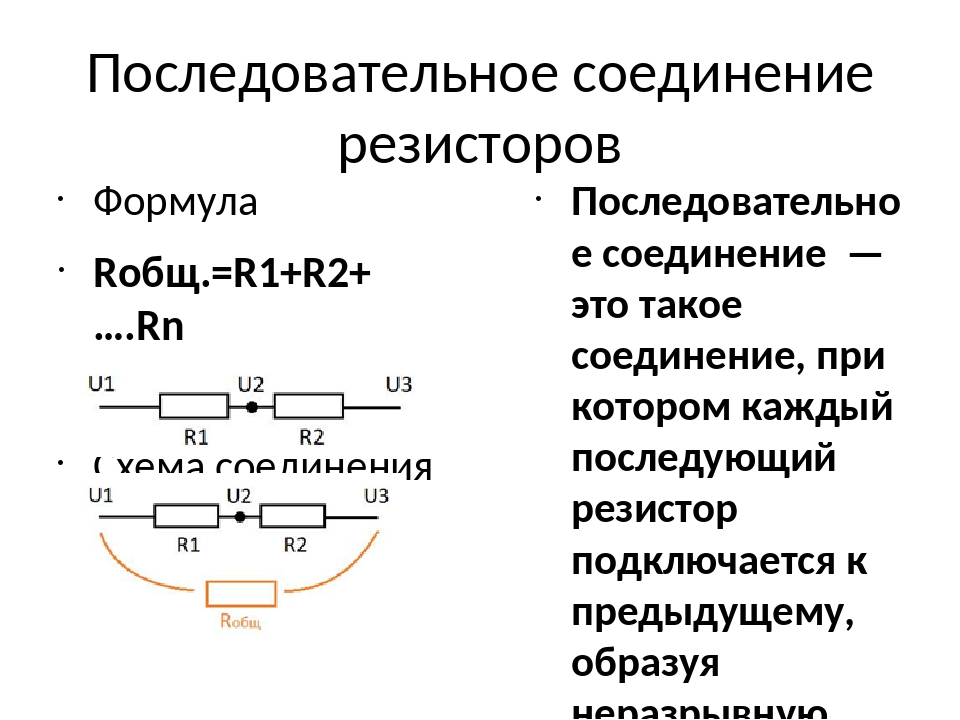
 P=IV=(6,00 А)(3,00 В)=18,00 Вт.
P=IV=(6,00 А)(3,00 В)=18,00 Вт.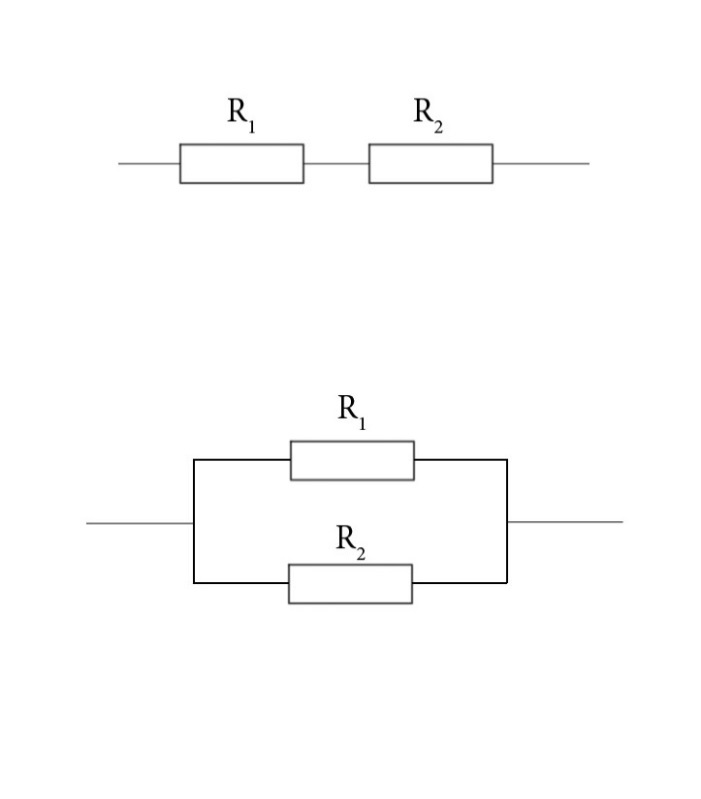 0 Ом 20,0 Ом и 0,804 Ом 0,804 Ом соответственно).
0 Ом 20,0 Ом и 0,804 Ом 0,804 Ом соответственно). P2=I22R2=(1,61 А)2(6.00 Ом) = 15,5 Вт.
P2=I22R2=(1,61 А)2(6.00 Ом) = 15,5 Вт.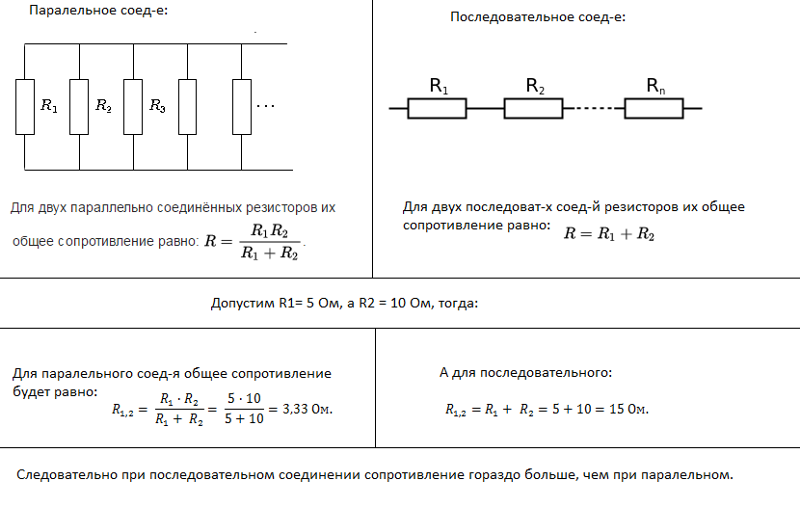

 Мощность, подаваемая аккумулятором, составляет Pbatt=IV=100,00 Вт. Pbatt=IV=100,00 Вт.
Мощность, подаваемая аккумулятором, составляет Pbatt=IV=100,00 Вт. Pbatt=IV=100,00 Вт.