Переходные процессы в электрических цепях. Переходные процессы в электрических цепях

Переходные процессы в электрических цепях

Всякий режим, длительно существующий в электрической цепи и характеризующийся неизменными значениями токов и напряжений, называется стационарным (установившимся) режимом. Такому режиму соответствует определённый запас энергии, сосредоточивающийся в реактивных элементах цепи – индуктивностях и ёмкостях.

Любые изменения нагрузки или напряжения источника питания (включение или выключение его) приводят в итоге к новому установившемуся режиму с другими значениями токов, напряжений и, следовательно, запасом энергии в реактивных элементах.

Переход от одного стационарного состояния к другому называется переходным (нестационарным) процессом, который связан с изменением запаса энергии.

Всякое изменение запаса электрической или магнитной энергии не может происходить мгновенно, а сопровождается процессом установления нового энергетического режима в цепи. При воздействии на вход электрической цепи импульсов с крутым фронтом без особых погрешностей можно полагать, что воздействие этого импульса на электрическую цепь происходит скачкообразно, подобно мгновенному включению или выключению напряжения (тока).

Теоретически можно считать, что коммутация цепи (т.е. изменение параметров цепи или схемы самой цепи) происходит мгновенно, т.е. на включение и выключение цепи время не расходуется. Тем не менее, переход от одного режим работы цепи к другому происходит не мгновенно, а в течение некоторого промежутка времени. Объясняется это тем, что каждому состоянию цепи соответствует определённый запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия магнитного поля

………………………(1.1)

и электрического поля

…………………….. (1.2)

не может мгновенно изменяться, энергия может изменяться только плавно.

Если попытаться предположить обратное, то на индуктивности появилось бы бесконечно большое напряжение:

,

(где – поток магнитной индукции), что лишено физического смысла так как

при dt → 0.

Аналогично невозможно себе представить скачкообразное изменение электрического поля ёмкости, так как в противном случае через ёмкость должен был бы протекать бесконечно большой ток

при dt → 0,

что также лишено физического смысла.

Наконец, известно, что мощность . Если предположить, что запасённая в реактивном элементе энергия может изменяться скачком, то при условии dt → 0 мощность должна достигать бесконечно больших значений, а это возможно было бы при внутреннем сопротивлении источника Ri = 0.

Ясно, что этого быть не может.

Свойство реактивных элементов цепи (L и C) запасать или расходовать определённую энергию в конечный промежуток времени характеризует их электрическую инерционность. Именно это свойство реактивных элементов цепи и лежит в основе переходных процессов. В линейных цепях, не содержащих реактивных элементов, переходные процессы отсутствуют.

Для количественной характеристики длительности переходных процессов в простых электрических цепях, содержащих комбинации R, L и C вводится понятие постоянной времени (τ). Этот параметр имеет размерность

времени (с).

Сущность параметра τ можно показать на примере цепей, в которых переходные процессы имеют ярко выраженный экспоненциальный характер (рис.1.1).

Рис.1.1. Цепь RС с экспоненциальным зарядом конденсатора

 

Такие электрические цепи обязательно содержат реактивные элементы

L или C, а также активное сопротивление R. Так, для цепи заряда ёмкости C от мгновенного включения источника постоянного напряжения Uвх = Е (рис.1.1)закон изменения тока заряда ёмкости имеет вид:

……………………………(1.3).

Напряжение на выходе цепи

…………………. (1.4).

(Это выражение получается при математическом анализе переходного процесса в данной цепи; мы даём его без вывода).

Выражение (1.4) называется экспоненциальной функцией. Другая её запись:

……………………… (1.5).

Произведение

……………………………………… (1.6)

называется постоянной времени цепи.

Особенностью этой функции является то, что при t ≥ 0 она монотонно убывает. Все значения этой функции положительны. Максимальное значение функции соответствует моменту времени . Минимальное значение функции равно нулю при и является предельным её значением. Стремление функции к этому значению происходит асимптотически. Для достижения предельного значения требуется бесконечно большое время.

Постоянная времени характеризует скорость установления стационарного режима в цепи, т.е. скорость переходного процесса. Численно постоянная времени равна времени, в течение которого амплитуда напряжения (тока) в цепи изменяется в е раз (е ≈ 2,72). Если напряжение (ток) возрастает от какого-либо уровня (в том числе и от нулевого), то постоянная времени численно равна интервалу времени, в течение которого экспоненциально возрастающий сигнал достигает примерно63%своей максимальной величины (рис.1.2).

Рис.1.2. Закон изменения напряжения на ёмкости цепи,

изображённой на рис.1.1.

 

Напряжение на ёмкости изменяется по экспоненциальному закону

………………………… (1.7).

Если же напряжение (ток) уменьшается от какого-либо уровня (в том числе и от максимального), то постоянная времени численно равна времени, в течение которого сигнал экспоненциально убывает примерно до 37% от своего максимума (рис.1.3).

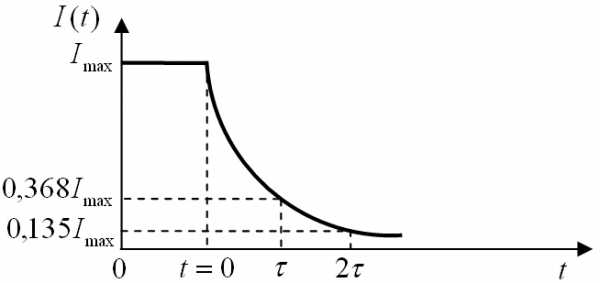
Рис.1.3. Закон изменения тока, протекающего через ёмкость цепи,

изображённой на рис.1.1.

 

Ток, протекающий через ёмкость, изменяется по экспоненциальному

закону:

……………………………. (1.8).

В справедливости выражений (1.7) и (1.8) легко убедиться, подставляя в них последовательно значения t = τ; t = 2τ; t = 3τ и т.д. (табл.1.1):

Табл.1.1.

	Закон спадания напряжения (тока)	Закон нарастания напряжения (тока)
	0,367 Е	0,633 Е
	0,135 Е	0,865 Е
	0,050 Е	0,950 Е
	0,018 Е	0,982 Е
	0,007 Е	0,993 Е

Отсюда следует вывод, что для окончания переходного процесса требуется время

t = (3…5)τ ………………………………... (1.9).

За это время любой переходный процесс прекращается на (95…99)%.

Таким образом, мы убедились в том, что для переходного процесса требуется вполне конкретное время, определяемое длительностью импульса, действующего на входе цепи, и параметрами этой цепи.

Тем не менее, в импульсной технике принимают следующие допущения, позволяющие упростить анализ электрических цепей с сосредоточенными параметрами. Эти допущения носят название законов коммутации:

1. Токи, протекающие через конденсаторы и резисторы, могут изменяться скачкообразно.

2. Напряжения на индуктивностях и резисторах могут изменяться скачкообразно.

Первый закон коммутации можно объяснить следующим образом. Известно, что ток, протекающий через ёмкость, и напряжение на этой ёмкости связаны следующими соотношениями:

…………………………...... (1.10)

и ……………………(1.11).

Из выражения (1.11) следует, что при любом конечном изменении тока

ic(t), заряжающего конденсатор, напряжение на нём скачком изменяться не может.

Аналогично можно объяснить второй закон коммутации.

Известно, что напряжение, приложенное к индуктивности, и протекающий через неё ток связаны следующими соотношениями:

 

………………………….... (1.12)

и ……………….... (1.13).

Из выражения (1.13) следует, что при любом конечном изменении напряжения на индуктивности ток через неё скачком изменяться не может.

Наличие переходных процессов является причиной искажения формы импульсов, действующих в линейной цепи. Если бы все процессы в цепи устанавливались мгновенно, то никаких искажений импульсов в линейной цепи не было бы.

 



infopedia.su

Переходные процессы в электрических цепях

Перехо́дные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Переходный процесс в цепи описывается дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Длительность протекания

Переходные процессы обычно являются быстро протекающими: от миллиардных долей секунды до секунды. Редко они достигают десятков секунд.

Законы (правила) коммутации

Первый закон коммутации

Ток через индуктивный элемент L непосредственно до коммутации равен току во время коммутации и току через этот же индуктивный элемент непосредственно после коммутации , так как ток в катушке мгновенно измениться не может:

Второй закон коммутации

Напряжение на конденсаторе С непосредственно до коммутации равно напряжению во время коммутации и напряжению на конденсаторе непосредственно после коммутации , так как невозможен скачок напряжения на конденсаторе:

Примечание

1.  — время непосредственно до коммутации
2. — непосредственно во время коммутации
3.  — время непосредственно после коммутации

Начальные значения величин

Начальные значения (условия) — значения токов и напряжений в схеме при t=0.

Напряжения на индуктивных элементах и резисторах, а также токи через конденсаторы и резисторы могут изменяться скачком, то есть их значения после коммутации чаще всего оказываются не равными их значениям до коммутации .

Независимые начальные значения — это значения токов через индуктивные элементы и напряжений на конденсаторах, известные из докоммутационного режима

Зависимые начальные значения — это значения остальных токов и напряжений при в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа.

Методы расчёта переходных процессов

• Классический метод — использует решение дифференциальных уравнений с постоянными параметрами методами классической математики.
• Операторный метод — перенос расчёта переходного процесса из области функций действительной переменной (времени ) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические.
• Метод переменных состояния. — основывается на составлении и решении системы дифференциальных уравнений первого порядка, разрешенной относительно производных. Число переменных состояний равно числу независимых накопителей энергии.

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

• Бессонов Л.А. Гл. 8. Переходные процессы в линейных электрических цепях // Теоретические основы электротехники. Электрические цепи: учебник. — 11-е изд., перераб. и доп.. — М.: "Гардарики", 2007. — С. 231, 235-236. — 701 с. — 5000 экз. — ISBN 5-8297-0046-8, ББК 31.21, УДК 621.3.013(078.5)

Ссылки

dic.academic.ru

Переходные процессы в электрических цепях

Рассматривая переходные процессы в электрических цепях, нельзя не отметить тот факт, что подобные явления вполне закономерны и в какой-то степени предсказуемы. Мало того, каждый человек сталкивается с их проявлением в своей повседневной жизни. Например, у включенного в сеть нагревательного элемента (ТЭН электроплитки, масляный обогреватель) температура повышается не бесконечно, а до определенного значения, зависящего от ряда факторов: таких, как температура окружающего воздуха, уровень влажности, характеристика проволоки и пр. Соответственно, и остывание происходит до некого установившегося значения, а не до абсолютного нуля. Другими словами, все физические явления условно могут быть разделены на переходные и установившиеся. Первые представляют собой изменение между начальным и конечным установившимися.

Что такое переходные процессы в электрических цепях? При анализе любого контура необходимо учитывать два возможных режима работы: установившийся и переходный. Первый характеризуется повторяющимися за единицу времени мгновенными значениями переменного тока и напряжения на всех участках цепи. Переходные процессы в электрических цепях более просты для понимания: когда такие изменения прекращаются, то можно говорить о наступлении установившегося режима. Следствие следующее: состояние, при котором отсутствуют изменения, теоретически, может продолжаться неограниченное время.

Переходные процессы в линейных электрических цепях знакомы всем. Наверняка, у каждого случалось, что после щелчка домашним выключателем лампа перегорала или даже разлеталась на осколки сама стеклянная колба. Причем, это может случиться как с бюджетными лампами, так и с дорогими фирменными. В этом «виновны» переходные процессы в электрических цепях. В данном случае тот щелчок выключателем послужил причиной изменений, инициировал переходный процесс, называемый коммутацией (т.е. переключением). На самом деле причины могут быть различны: изменение параметров источника питания, в частности короткое замыкание, внешние воздействия (магнитное поле, температура) и пр. Прямой расчет изменяющихся за единицу времени напряжения и тока возможен посредством составления дифференциальных уравнений и вычисления интеграла. В формулах количество производных непосредственно зависит от элементов самой цепи.

Так как обычно длительность переходного процесса исчисляется даже не секундами, а сотыми и тысячными долями секунды, то иногда возникает вопрос о целесообразности расчетов. Действительно, что может случиться за столь малое время? Увы, это так лишь отчасти, и практика показывает, что довольно многое. Например, силовые контакты пускателей всегда рассчитаны на гораздо больший ток, чем номинальный. Кроме того, контакты часто закрываются дугогасительными камерами (решетками). Это объясняется тем, что в момент коммутации (включения/разрыва цепи) ток возрастает в десятки раз, и для устранения возможных последствий применяются данные решения.

Рассмотрим переходные процессы в rc цепях. Для примера возьмем контур, состоящий из источника питания, пары резисторов (R1 и R2), конденсатора (С) и вольтметра (V), включенного параллельно. Если используемый конденсатор обладает емкостью в десятки микрофарад, а сопротивление R1 и R2 – по паре сотен килоом соответственно, то при включении источника стрелка вольтметра не сразу укажет на действующее значение напряжения, а постепенно отклонится от нуля. Данный переходный процесс обусловлен накоплением заряда в емкости. Соответственно, установившийся режим наступает в тот момент, когда прекращается потребление реактивной составляющей.

fb.ru

Переходные процессы в электрических цепях

Перехо́дные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Переходный процесс в цепи описывается дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Длительность протекания

Переходные процессы обычно являются быстро протекающими: от миллиардных долей секунды до секунды. Редко они достигают десятков секунд.

Законы (правила) коммутации

Первый закон коммутации

Ток через индуктивный элемент L непосредственно до коммутации равен току во время коммутации и току через этот же индуктивный элемент непосредственно после коммутации , так как ток в катушке мгновенно измениться не может:

Второй закон коммутации

Напряжение на конденсаторе С непосредственно до коммутации равно напряжению во время коммутации и напряжению на конденсаторе непосредственно после коммутации , так как невозможен скачок напряжения на конденсаторе:

Примечание

1.  — время непосредственно до коммутации
2. — непосредственно во время коммутации
3.  — время непосредственно после коммутации

Начальные значения величин

Начальные значения (условия) — значения токов и напряжений в схеме при t=0.

Напряжения на индуктивных элементах и резисторах, а также токи через конденсаторы и резисторы могут изменяться скачком, то есть их значения после коммутации чаще всего оказываются не равными их значениям до коммутации .

Независимые начальные значения — это значения токов через индуктивные элементы и напряжений на конденсаторах, известные из докоммутационного режима

Зависимые начальные значения — это значения остальных токов и напряжений при в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа.

Методы расчёта переходных процессов

• Классический метод — использует решение дифференциальных уравнений с постоянными параметрами методами классической математики.
• Операторный метод — перенос расчёта переходного процесса из области функций действительной переменной (времени ) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические.
• Метод переменных состояния. — основывается на составлении и решении системы дифференциальных уравнений первого порядка, разрешенной относительно производных. Число переменных состояний равно числу независимых накопителей энергии.

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

• Бессонов Л.А. Гл. 8. Переходные процессы в линейных электрических цепях // Теоретические основы электротехники. Электрические цепи: учебник. — 11-е изд., перераб. и доп.. — М.: "Гардарики", 2007. — С. 231, 235-236. — 701 с. — 5000 экз. — ISBN 5-8297-0046-8, ББК 31.21, УДК 621.3.013(078.5)

Ссылки

biograf.academic.ru

Переходные процессы в электрических цепях

Перехо́дные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Переходный процесс в цепи описывается дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Длительность протекания

Переходные процессы обычно являются быстро протекающими: от миллиардных долей секунды до секунды. Редко они достигают десятков секунд.

Законы (правила) коммутации

Первый закон коммутации

Ток через индуктивный элемент L непосредственно до коммутации равен току во время коммутации и току через этот же индуктивный элемент непосредственно после коммутации , так как ток в катушке мгновенно измениться не может:

Второй закон коммутации

Напряжение на конденсаторе С непосредственно до коммутации равно напряжению во время коммутации и напряжению на конденсаторе непосредственно после коммутации , так как невозможен скачок напряжения на конденсаторе:

Примечание

1.  — время непосредственно до коммутации
2. — непосредственно во время коммутации
3.  — время непосредственно после коммутации

Начальные значения величин

Начальные значения (условия) — значения токов и напряжений в схеме при t=0.

Напряжения на индуктивных элементах и резисторах, а также токи через конденсаторы и резисторы могут изменяться скачком, то есть их значения после коммутации чаще всего оказываются не равными их значениям до коммутации .

Независимые начальные значения — это значения токов через индуктивные элементы и напряжений на конденсаторах, известные из докоммутационного режима

Зависимые начальные значения — это значения остальных токов и напряжений при в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа.

Методы расчёта переходных процессов

• Классический метод — использует решение дифференциальных уравнений с постоянными параметрами методами классической математики.
• Операторный метод — перенос расчёта переходного процесса из области функций действительной переменной (времени ) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические.
• Метод переменных состояния. — основывается на составлении и решении системы дифференциальных уравнений первого порядка, разрешенной относительно производных. Число переменных состояний равно числу независимых накопителей энергии.

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

• Бессонов Л.А. Гл. 8. Переходные процессы в линейных электрических цепях // Теоретические основы электротехники. Электрические цепи: учебник. — 11-е изд., перераб. и доп.. — М.: "Гардарики", 2007. — С. 231, 235-236. — 701 с. — 5000 экз. — ISBN 5-8297-0046-8, ББК 31.21, УДК 621.3.013(078.5)

Ссылки

dal.academic.ru

Переходные процессы в электрических цепях

Перехо́дные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Переходный процесс в цепи описывается дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Длительность протекания

Переходные процессы обычно являются быстро протекающими: от миллиардных долей секунды до секунды. Редко они достигают десятков секунд.

Законы (правила) коммутации

Первый закон коммутации

Ток через индуктивный элемент L непосредственно до коммутации равен току во время коммутации и току через этот же индуктивный элемент непосредственно после коммутации , так как ток в катушке мгновенно измениться не может:

Второй закон коммутации

Напряжение на конденсаторе С непосредственно до коммутации равно напряжению во время коммутации и напряжению на конденсаторе непосредственно после коммутации , так как невозможен скачок напряжения на конденсаторе:

Примечание

1.  — время непосредственно до коммутации
2. — непосредственно во время коммутации
3.  — время непосредственно после коммутации

Начальные значения величин

Начальные значения (условия) — значения токов и напряжений в схеме при t=0.

Напряжения на индуктивных элементах и резисторах, а также токи через конденсаторы и резисторы могут изменяться скачком, то есть их значения после коммутации чаще всего оказываются не равными их значениям до коммутации .

Независимые начальные значения — это значения токов через индуктивные элементы и напряжений на конденсаторах, известные из докоммутационного режима

Зависимые начальные значения — это значения остальных токов и напряжений при в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа.

Методы расчёта переходных процессов

• Классический метод — использует решение дифференциальных уравнений с постоянными параметрами методами классической математики.
• Операторный метод — перенос расчёта переходного процесса из области функций действительной переменной (времени ) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические.
• Метод переменных состояния. — основывается на составлении и решении системы дифференциальных уравнений первого порядка, разрешенной относительно производных. Число переменных состояний равно числу независимых накопителей энергии.

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

• Бессонов Л.А. Гл. 8. Переходные процессы в линейных электрических цепях // Теоретические основы электротехники. Электрические цепи: учебник. — 11-е изд., перераб. и доп.. — М.: "Гардарики", 2007. — С. 231, 235-236. — 701 с. — 5000 экз. — ISBN 5-8297-0046-8, ББК 31.21, УДК 621.3.013(078.5)

Ссылки

veter.academic.ru

Переходные процессы в электрических цепях

Перехо́дные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Переходный процесс в цепи описывается дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Длительность протекания

Переходные процессы обычно являются быстро протекающими: от миллиардных долей секунды до секунды. Редко они достигают десятков секунд.

Законы (правила) коммутации

Первый закон коммутации

Ток через индуктивный элемент L непосредственно до коммутации равен току во время коммутации и току через этот же индуктивный элемент непосредственно после коммутации , так как ток в катушке мгновенно измениться не может:

Второй закон коммутации

Напряжение на конденсаторе С непосредственно до коммутации равно напряжению во время коммутации и напряжению на конденсаторе непосредственно после коммутации , так как невозможен скачок напряжения на конденсаторе:

Примечание

1.  — время непосредственно до коммутации
2. — непосредственно во время коммутации
3.  — время непосредственно после коммутации

Начальные значения величин

Начальные значения (условия) — значения токов и напряжений в схеме при t=0.

Напряжения на индуктивных элементах и резисторах, а также токи через конденсаторы и резисторы могут изменяться скачком, то есть их значения после коммутации чаще всего оказываются не равными их значениям до коммутации .

Независимые начальные значения — это значения токов через индуктивные элементы и напряжений на конденсаторах, известные из докоммутационного режима

Зависимые начальные значения — это значения остальных токов и напряжений при в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа.

Методы расчёта переходных процессов

• Классический метод — использует решение дифференциальных уравнений с постоянными параметрами методами классической математики.
• Операторный метод — перенос расчёта переходного процесса из области функций действительной переменной (времени ) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические.
• Метод переменных состояния. — основывается на составлении и решении системы дифференциальных уравнений первого порядка, разрешенной относительно производных. Число переменных состояний равно числу независимых накопителей энергии.

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

• Бессонов Л.А. Гл. 8. Переходные процессы в линейных электрических цепях // Теоретические основы электротехники. Электрические цепи: учебник. — 11-е изд., перераб. и доп.. — М.: "Гардарики", 2007. — С. 231, 235-236. — 701 с. — 5000 экз. — ISBN 5-8297-0046-8, ББК 31.21, УДК 621.3.013(078.5)

Ссылки

dikc.academic.ru

---

• 
  Регулятор частоты
• 
  Разрядность счетчика электроэнергии
• 
  Что называют излучением
• 
  Атмосферное давление единицы измерения
• 
  Какие бывают припои
• 
  Индукция трансформатора
• 
  Какая часть вольт амперной характеристики германиевого диода отражает
• 
  Электро выставка в москве 2018
• 
  Токоограничивающий реактор 10 кв
• 
  Устройство магнитной плиты
• 
  Вру это что