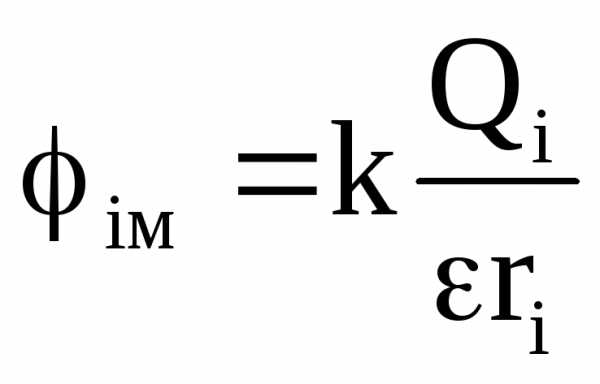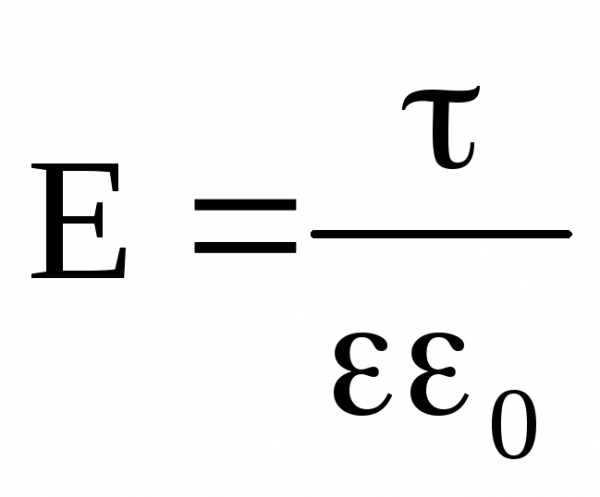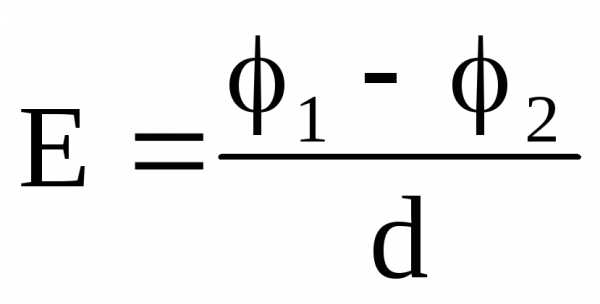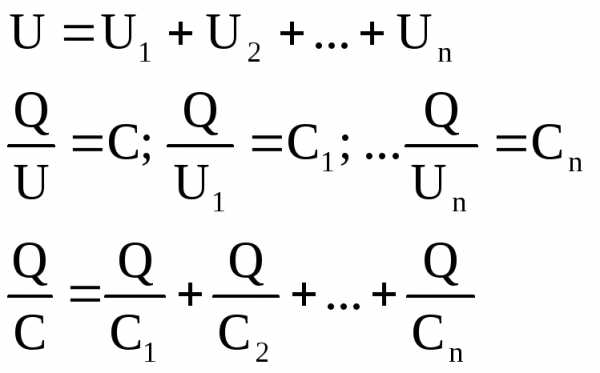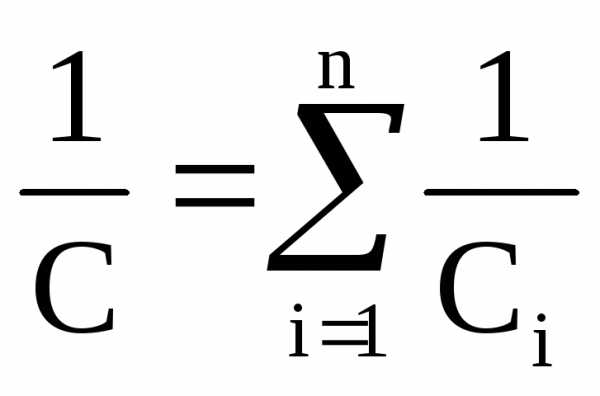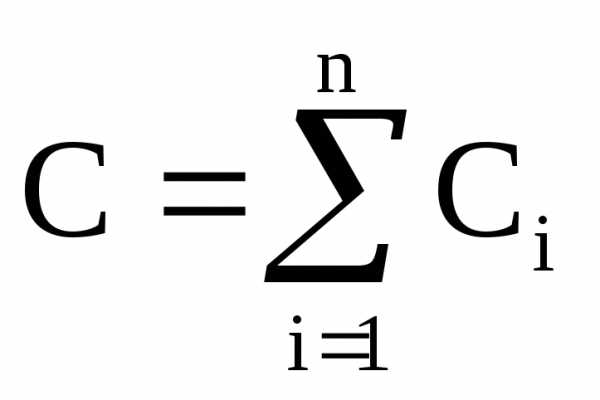fizika / Коденсаторы. Емкость плоского конденсатора. По какой формуле вычисляется емкость плоского конденсатора
6. Электроемкость. Конденсаторы. Емкость плоского конденсатора
Потенциал уединенного проводника пропорционален сообщенному ему заряду, поэтому отношение заряда проводника к его потенциалу не зависит от заряда и является характеристикой данного проводника.
Электроемкостью уединенного проводника называют величину, равную отношению заряда проводника к потенциалу этого проводника.
.
На практике применяются
Электроемкость проводника не зависит от вещества, из которого он изготовлен, а зависит от его формы, размеров и диэлектрической проницаемости среды, в которой находится этот проводник.
Используя формулу потенциала электрического поля, созданного равномерно заряженным шаром
, для емкости шара получим .
КОНДЕНСАТОРЫ
Уединенные проводники обладают малой емкостью. На практике возникает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе значительные заряды.
Конденсатором называют систему, состоящую из двух разделенных диэлектриком проводников, на которых могут накапливаться заряды противоположных знаков.
Проводники, образующие конденсатор, называют обкладками.
Чтобы внешние тела не влияли на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две близко расположенные пластины, два коаксиальных цилиндра и две концентрические сферы.
Емкостью конденсатора называют величину, равную отношению заряда конденсатора к разности потенциалов (напряжению) между его обкладками
=.
ЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
Напряженность поля между обкладками плоского конденсатора
.
Для однородного поля справедливо соотношение
.
Следовательно, емкость плоского конденсатора
(S – площадь обкладок, d – расстояние между обкладками).
7. Соединение конденсаторов. Энергия заряженного конденсатора
При параллельном соединении конденсаторов напряжения на каждом конденсаторе одинаковы и равны напряжению на клеммах батареи
.
Заряд батареи
.
Исходя из того, что , имеем
,
поэтому
.
При последовательном соединении конденсаторов
, .
Учитывая, что , имеем
,
поэтому при последовательном соединении конденсаторов
.
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
При зарядке конденсатора совершается работа по перемещению электрических зарядов против сил электрического поля. При перемещении заряда совершается работа. Учитывая, что, получим. Следовательно,
.
По закону сохранения энергии эта работа равна энергии заряженного конденсатора, т.е.
.
Используя формулы и, получим
и .
8. Закон Ома для однородного участка цепи. Сопротивление проводников
Участок цепи, на котором не действуют сторонние силы, приводящие к возникновению ЭДС, называется однородным.
Согласно закону Ома для однородного участка цепи постоянного тока: сила тока в однородном проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению данного проводника.
.
Опыты показывают, что сопротивление R проводника пропорционально его длине, обратно пропорционально площади его поперечного сечения и зависит от вещества, из которого изготовлен проводник. Для однородного проводника длиной l и неизменной площадью поперечного сечения S эту зависимость выражают формулой
,
где - коэффициент пропорциональности, называемый удельным электрическим сопротивлением. Удельное сопротивление равно сопротивлению проводника, изготовленного из данного вещества и имеющего единичную длину и единичную площадь поперечного сечения. Удельное сопротивление есть свойство проводника и зависит от его состояния.
Сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений этих проводников.
.
Сопротивление цепи, состоящей из параллельно соединенных проводников можно определить из формулы
studfiles.net
Ёмкость плоского конденсатора.
Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.
Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:
.
Используя определение емкости конденсатора, получаем:
Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет собой систему двух концентрических сфер с радиусами и. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно:
.
Для ёмкости сферического конденсатора получаем:
.
Это формула точная.
Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
..
Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.
Соединение конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:
или .
Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении).
Для последовательно соединенных конденсаторов емкость вычисляется по формуле:
.
В случае одинаковых конденсаторов: .
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
,
а напряжение . По определению емкости получаем:
.
Для параллельно соединенных конденсаторов:.
В случае одинаковых конденсаторов: .
Пример.
Оценить емкость батареи (см. рисунок) .
.
Ответ:.
Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).
Для расчета ёмкости батареи получаем:
,
.
Откуда: , так как, то.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярнымиинеполярными.Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных» зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.
Под действием электрического поля диполи ориентируются преимущественно в направлении поля. Рассмотрим подробнее этот механизм (см. рисунок). Пара сил исоздает вращательный момент равный, где- дипольный момент молекулы. Этот момент стремится ориентировать диполь вдоль поля. В ионных кристаллах под действием электрического поля все положительные ионы смещаются по полю, отрицательные – против поля. Отметим, что смещение зарядов очень малы даже по сравнению с размерами молекул. Это связано с тем, что напряженность внешнего электрического поля обычно много меньше напряженности внутренних электрических полей в молекулах.
Отметим, что существуют диэлектрики, поляризованные даже при отсутствии внешнего поля (электреты, сегнетоэлектрики). Мы остановимся на рассмотрении только однородных диэлектриков, в которых отсутствует остаточная поляризация, а объемный и «связанный» заряд всегда равен нулю .
studfiles.net
По какой формуле находится емкость конденсатора?
<img src="//otvet.imgsmail.ru/download/4984b835d9394e905dcc3234b1ec41e5_i-546.jpg" > "плоский конденсатор состоит из двух круглых пластин диаметром 8 см, между пластинами зажата стеклянная пластина толщиной 5 мм" формула самая первая на рисунке А=пи*рквадрат d=5мм диэлектрическую проницаемость стекла возьмёшь <a rel="nofollow" href="http://ru.wikipedia.org/wiki/Относительная_диэлектрическая_проницаемость" target="_blank" >здесь</a>.
Ну уж это-то хоть посмотри сама в учебнике!
? а какие исходные
Есть онлайн калькулятор емкости, набери в поисковике "Расчет емкости конденсатора Онлайн"
touch.otvet.mail.ru
III.Электроемкость проводников.
Имеется уединенный проводник. Ему сообщен заряд Q. Вычислим электрический потенциал в точке М.
|
| Для заряда единичного: Для заряда Q: |
Если на проводник поместить заряд Q·b, то
Потенциал в каждой точке поля возрастает прямо пропорционально заряду проводника, т.е. φ ~ Q.
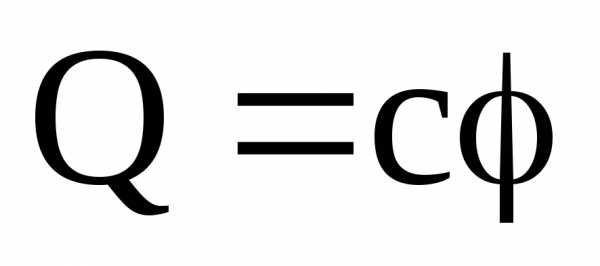 , (2)
, (2)
где с – электрическая ёмкость (ёмкость)
Или можно показать: ΔQ=cΔφ
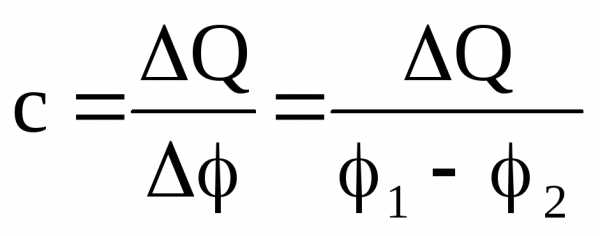 (3)
(3)
Физический смысл емкости.
| Электрическая емкостьпроводника численно равна величине заряда, который нужно сообщить проводнику для увеличения его потенциала на единицу. |
Отметим, что все предыдущее справедливо, если при этом не меняются формы и размеры проводника, а также внешние условия (среда, расположение окружающих предметов).
СИ: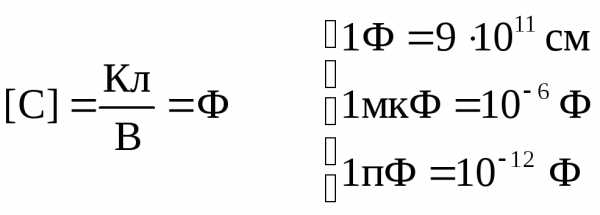
IV.Конденсаторы.Вычисление емкости конденсаторов.
Конденсаторомназывается система двух (или более) проводников, имеющих такую форму и расположение относительно друг друга, что поле, создаваемое такой системой, локализовано в ограниченной области пространства.
Примеры конденсаторов:
| а) плоский;
| б) шаровой: | в) цилиндрический |
Проводники, образующие конденсатор, называются обкладками.
Чтобы зарядить конденсатор, нужно присоединить его обкладки к источнику напряжения или одну обкладку соединить с Землей, а другую («+») с клеммой источника.
| Рассмотрим плоский конденсатор (или любой другой). На пластине А заряд (+Q), на пластине В по индукции заряд (–Q). Причем +Q=–Q. Поле сосредоточено между пластинами, потенциалы которых φAиφB. |
Емкостью конденсатора Сназывается величина, измеряемая отношением зарядаQна одной пластине к разности потенциалов между пластинами:
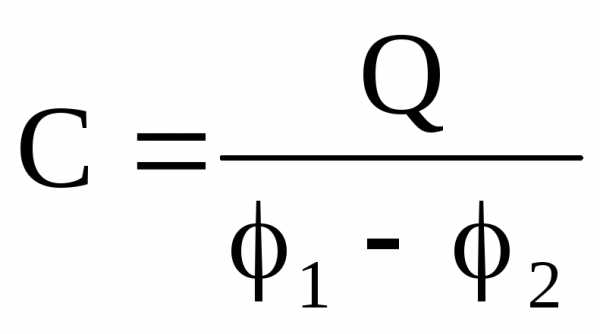 (4)
(4)
Примеры вычисления емкости конденсаторов.
1. Плоский конденсатор.
| d<<S, тогда, согласно теоремы Остроградского-Гаусса, поле между пластинами: С другой стороны: |
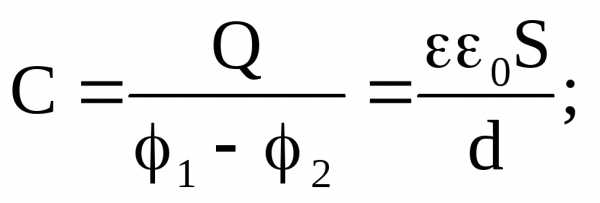
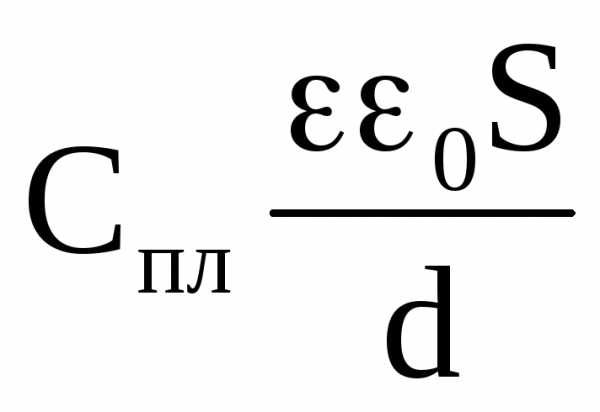 (5)
(5)
2. Сферический конденсатор.
Положим: r1–r2=d;d<<r1, тогдаr1≈r2≈r
Следствие: если зазор мал, то Спл= Ссф
если r1>>r2, то Ссф= 4πεε0r→Cсф= Сшара
3. Цилиндрический конденсатор.
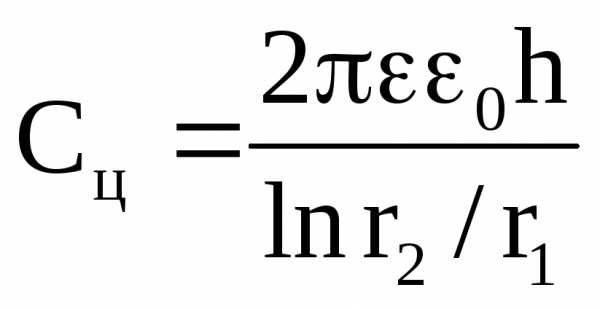 (7)
(7)
Если напряжение Uна конденсаторе сделать слишком большим, то происходит разряд через слой диэлектрика – пробой. Поэтому каждый конденсатор характеризуется не только своей емкостью С, но и максимальным рабочим напряжениемUmax=Uпр.
Располагая разными по ёмкости конденсаторами, можно получить желаемую емкость, путем соединения конденсаторов:
| а) последовательное: | б) параллельное: | в) смешенное | |
|
| Q = Q1 + Q2 + … + Qn UC = Q CU = C1U + C2U + … +CnU C = C1 + C2 + … +Cn
| ||
V.Энергия заряженного конденсатора.Энергия электрического поля.
Для многих вопросов теории и практики необходимо определять электрическую энергию заряженного проводника. (Определяем через работу разряда проводника).
Пусть имеется проводник с зарядом Qи начальным потенциалом φ0. Тогда элементарная работа при переходе элементарного зарядаdQс проводника на землю равна:
dA=φ·dQ, где
– мгновенное значение потенциала, но
dQ= –Cdφ(“–“ – означает уменьшение потенциала).
dA = –Cφ·dφ
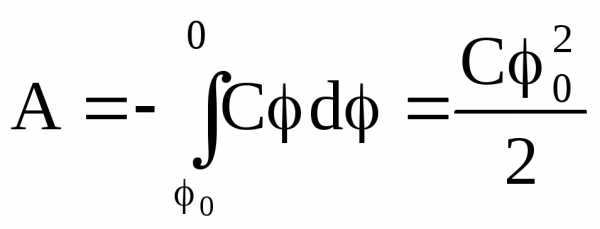
Найденная работа совершилась за счет убыли потенциальной энергии и численно равна энергии заряженного проводника W:
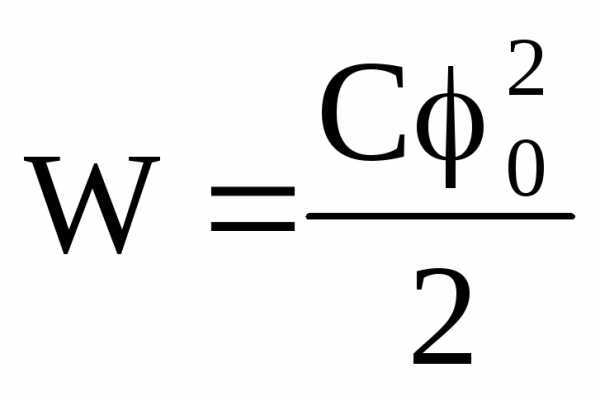
| Энергия заряженного конденсатора: |
Формула для энергии заряженного тела по существу определяет и энергию электрического поля созданного заряженным телом:
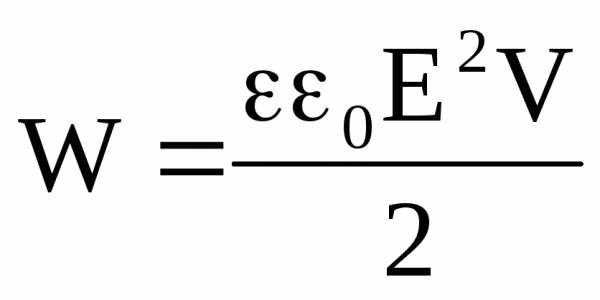 (8)
(8)
Объемная плотность энергииэлектростатического поля – физическая величина, численно равная отношению потенциальной энергии поля в единице объема.
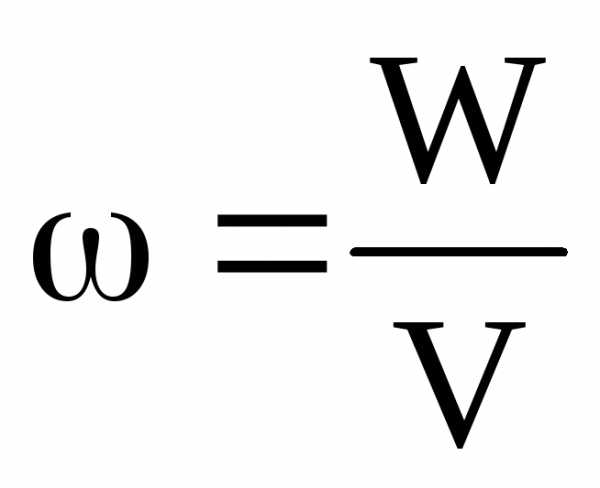
(9)
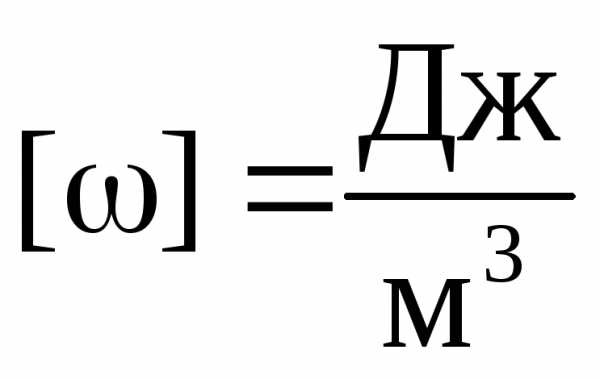
studfiles.net
Коденсаторы. Емкость плоского конденсатора
Коденсаторы. Емкость плоского конденсатора.
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкции состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).
| Содержание | Величина | Наименование |
| Конденсатор - электрический прибор, состоящий из двух проводящих пластин, разделенных слоем диэлектрика. Конденсаторы служат для накопления зарядов с целью их отдачи в нужный момент времени, а также в цепях переменного тока для деления зарядов (параллельное соединение) и для деления напряжения (последовательное соединение). - обозначение конденсатора на схеме. - емкость конденсатора (С). Если его пластины образуют параллельные плоскости, то его называют плоским. - емкость плоского конденсатора. Зависит от площади его пластин S; от расстояния между его пластинами d; от материала, заполняющего пространство между пластинами ε. При изготовлении конденсатора большой емкости стремятся сделать большое S при малом d, а также заполнить его пространство веществами с большим ε. Не зависит от напряжения U и от заряда q. Формулы, где встречается С: - энергия заряженного конденсатора -формула Томсона для периода электромагнитных колебаний в колебательном контуре LC. | С - емкость конденсатора | Ф |
| ε - относительная диэлектрическая проницаемость (см. в справочных таблицах) | - | |
| ε0 = 8,85.10-12 Ф/м - абсолютная диэлектрическая проницаемость, мировая постоянная | Ф/м | |
| U - напряжение между пластинами | В | |
| q - заряд одной из пластин | Кл | |
| S - площадь одной из пластин | м2 | |
| d - расстояние между пластинами | м | |
| Wэл - электрическая энергия | Дж | |
| Т - период колебаний | с | |
| L - индуктивность катушки контура | Гн | |
studfiles.net
Электроемкость конденсатора, теория и примеры
Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная:
называется емкостью конденсатора. Где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():
где – диэлектрическая проницаемость диэлектрика.
Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф).
Электроемкость плоского конденсатора
Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Электрическая емкость цилиндрического конденсатора
Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач
ru.solverbook.com
Идеальный конденсатор
Одна из характеристик конденсатора называется емкость.
Способность проводника и окружающей его среды накапливать электрическое поле называется электрической емкостью.
Универсальная формула для нахождения емкости конденсатора
,
где Q - величина электрического заряда в кулонах [Кл];
Δφ - разность потенциалов между обкладками конденсатора или разность потенциалов между проводником и средой в вольтах [В].
Как легко найти емкость плоского конденсатора
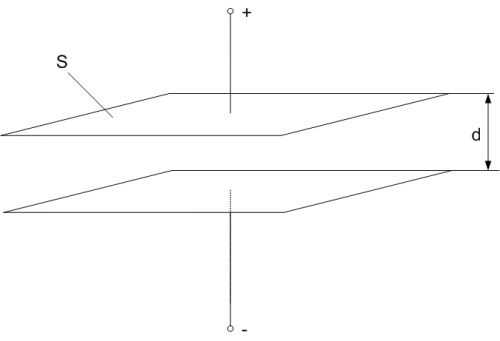
Так же емкость плоского конденсатора можно рассчитать по формуле:
,
Где ε0 = 8,85 *10-12- относительная диэлектрическая проницаемость;
Где ε - диэлектрическая проницаемость среды (диэлектрика) между обкладками;
S - площадь обкладки конденсатора;
d - расстояние между обкладками конденсатора.
Емкость провода в оплётке
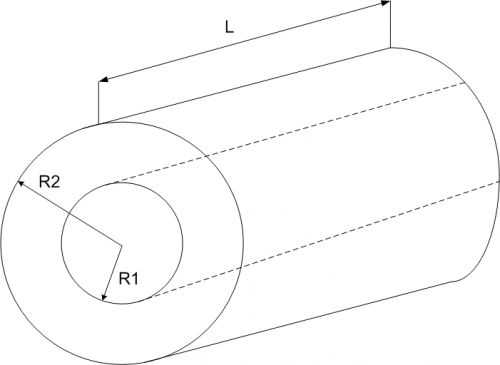
,
Где ε0 = 8,85 *10-12- относительная диэлектрическая проницаемость;
Где ε - диэлектрическая проницаемость среды (диэлектрика) между проводниками;
L - длина проводника;
R1 - внутренний радиус провода;
R2 - внешний радиус оплетки.
www.kurstoe.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.