Резонанс в цепи при параллельном соединении элементов. Почему в последовательной цепи резонансный ток максимален

Резонанс в электрических цепях. Почему в последовательной цепи резонансный ток максимален

ГлавнаяРазноеПочему в последовательной цепи резонансный ток максимален

Резонанс в электрических цепях

Резонанс в электрических цепях

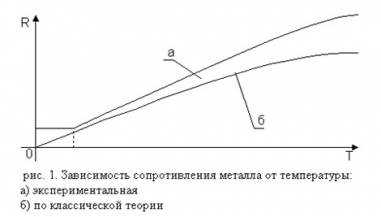
Реактивное сопротивление или проводимость двухполюсника, в состав которого входят конденсаторы и катушки индуктивности, в зависимости от частоты приложенного напряжения могут принимать как положительные, так и отрицательные значения. При определенных условиях реактивное сопротивление (проводимость) может оказаться равным нулю, а эквивалентное сопротивление (проводимость) всей цепи становится активным. В этом случае ток и напряжение на входе цепи совпадают по фазе. Такое явление называют резонансом, а соотношение 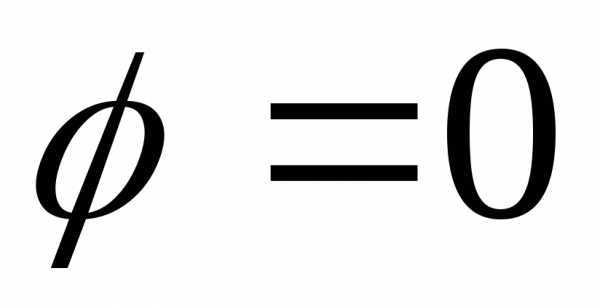−условием резонанса.

Эквивалентные параметры двухполюсника связаны соотношениями

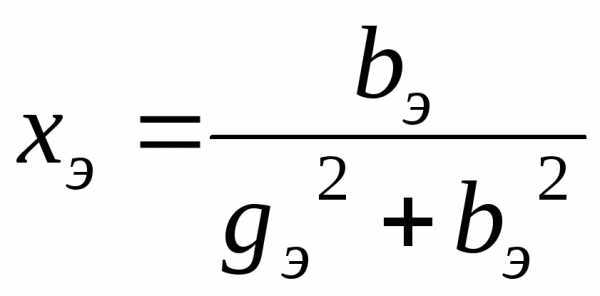и ,

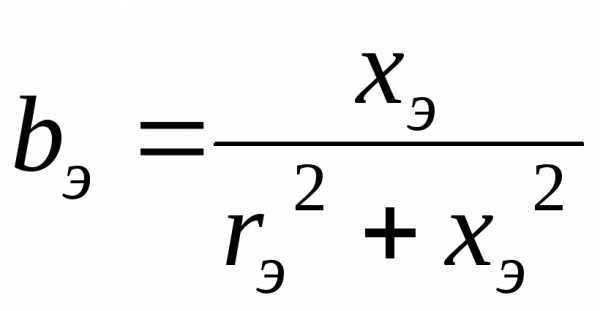поэтому условие 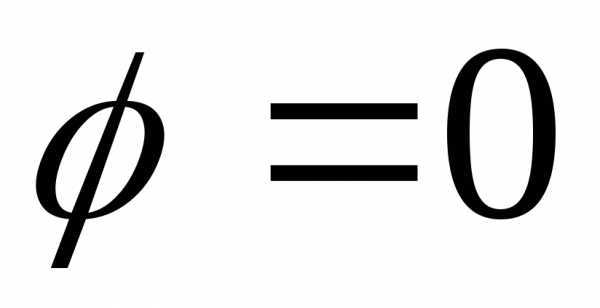эквивалентно выполнению равенств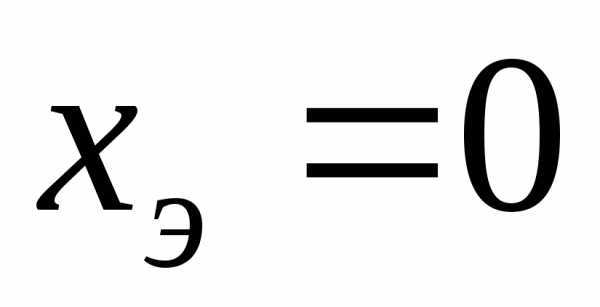или.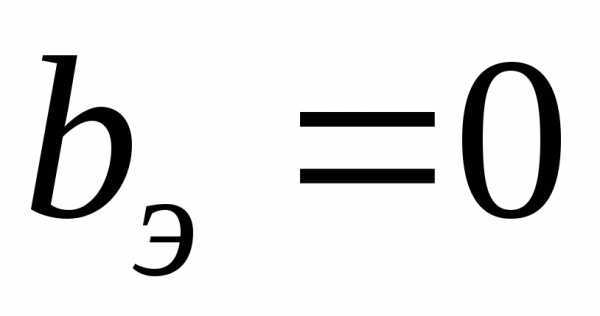

Из условий 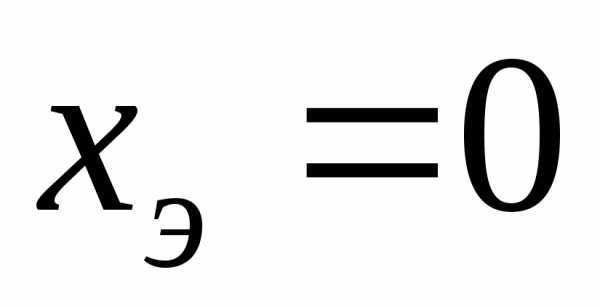,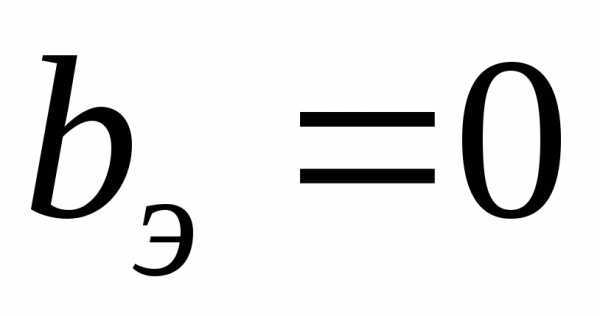могут быть определены значения параметров элементов электрической цепи, при которых наблюдается явление резонанса, а также значения частотырезонанса.

Если для двухполюсника 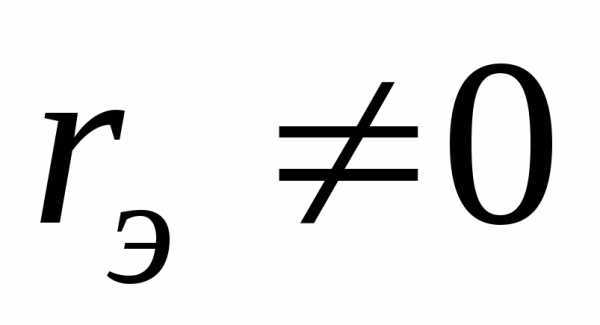и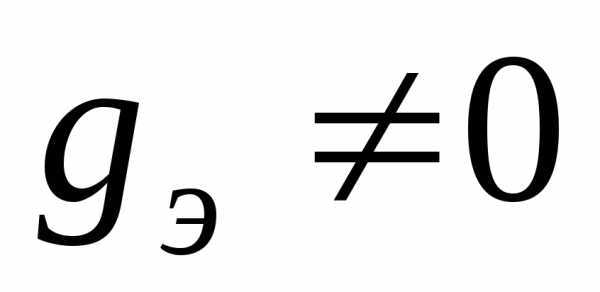, то для определения значений резонансных частот может быть использовано любое из услови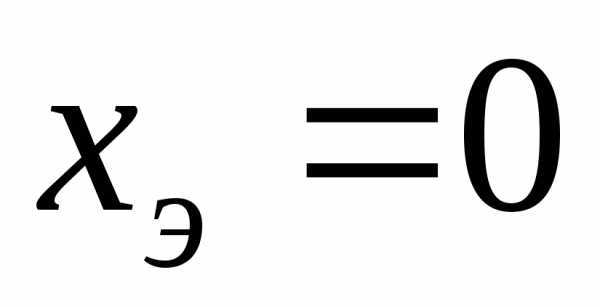йили.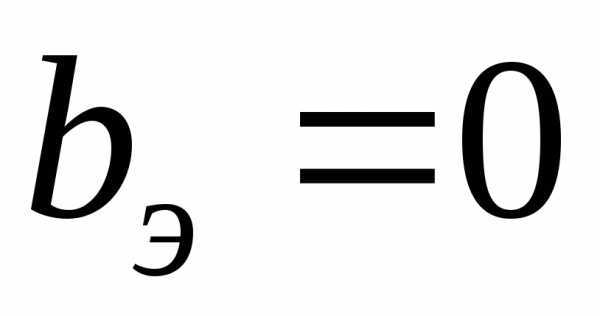

В случае, когда активное эквивалентное сопротивление или активная эквивалентная проводимость двухполюсника равны нулю, для определения значений резонансных частот следует использовать оба условия 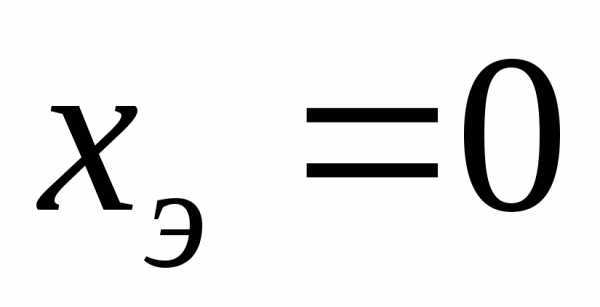и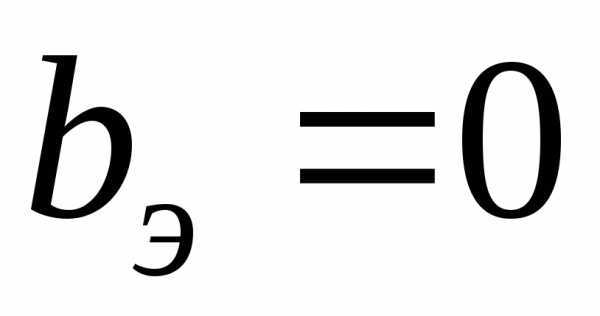, так как при этом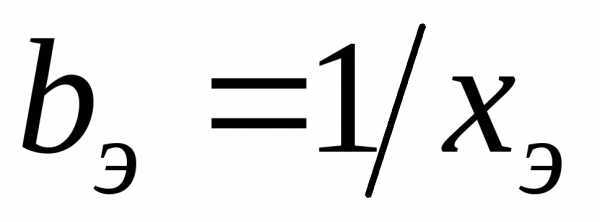. Равенства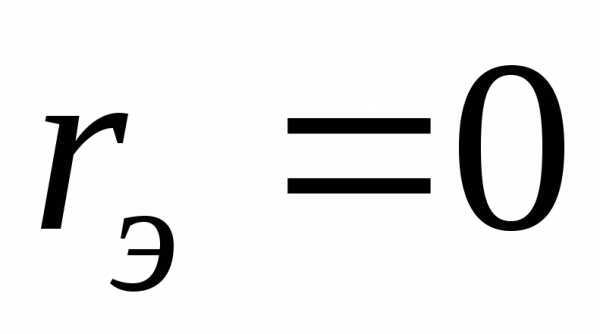и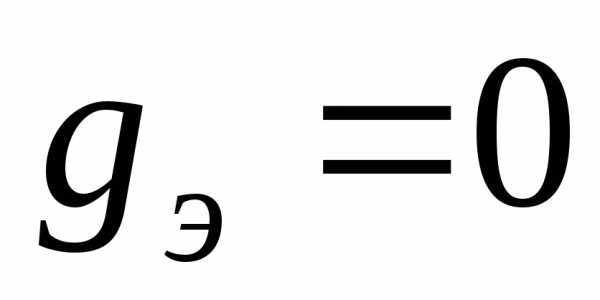выполняются, в частности, для цепей, содержащих только катушки индуктивности и конденсаторы.

Для описания частотных свойств электрических цепей широко используются частотные характеристики. Под частотными характеристиками понимают зависимости от частоты входных параметров цепи: r , x , z , g , b , y , а также величин, определяемых этими параметрами ,и т.д. Рассмотрим далее частотные свойства простейших цепей, в которых возможен резонанс.

Резонанс в цепи при последовательном соединении элементов

Рассмотрим цепь, изображенную на рис. 10.1а

Комплексное сопротивление цепи равно

Угол сдвига между входным током и напряжением обращается в нуль при равенстве нулю реактивного сопротивления цепи, то есть при выполнении условия. Таким образом, состояние резонанса в цепи наступает при частоте. Эта угловая частота называетсярезонансной. Векторная диаграмма для токов и напряжений в последовательном rLC контуре, построенная при 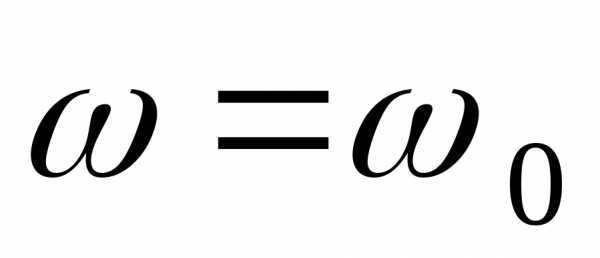, изображена на рис. 10.1б. Как видно из векторной диаграммы, вектора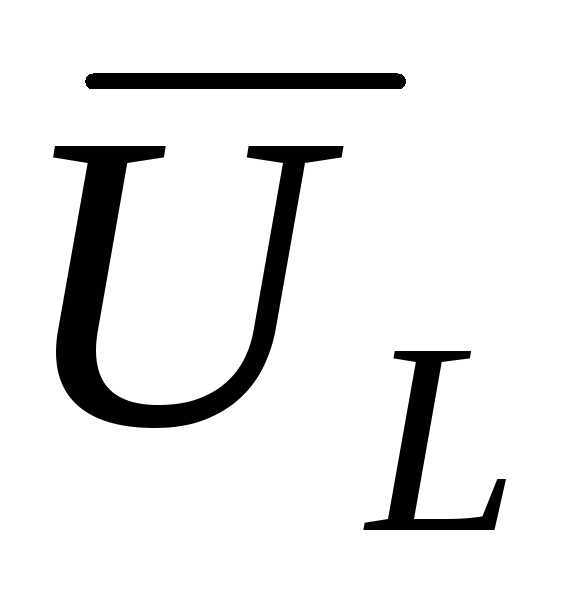и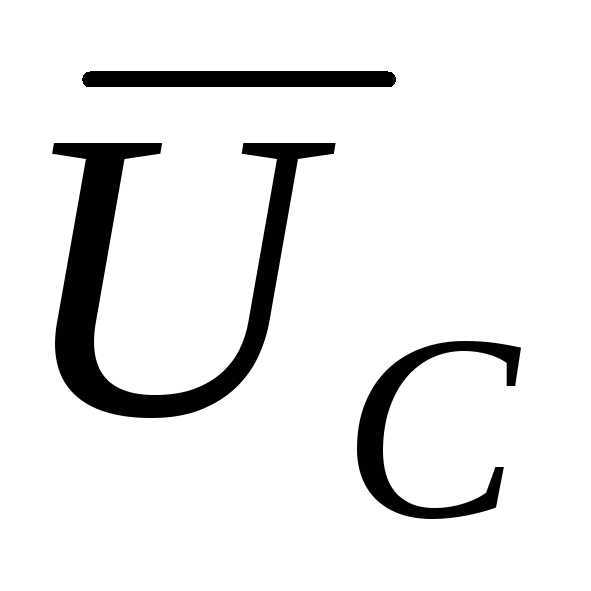равны по величине и противоположны по направлению, таким образом, напряжение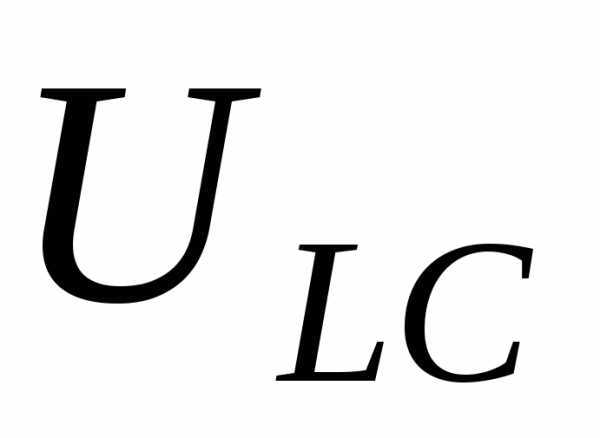при резонансной частоте равно нулю. Индуктивное и равное ему емкостное сопротивление цепи при резонансной частоте

,

обозначаемое символом , носит названиеволнового сопротивления колебательного контура и измеряется в омах.

Отношение волнового сопротивления к активному сопротивлению в последовательном колебательном контуре называется добротностью, а величина, обратная добротности − затуханием:

, .

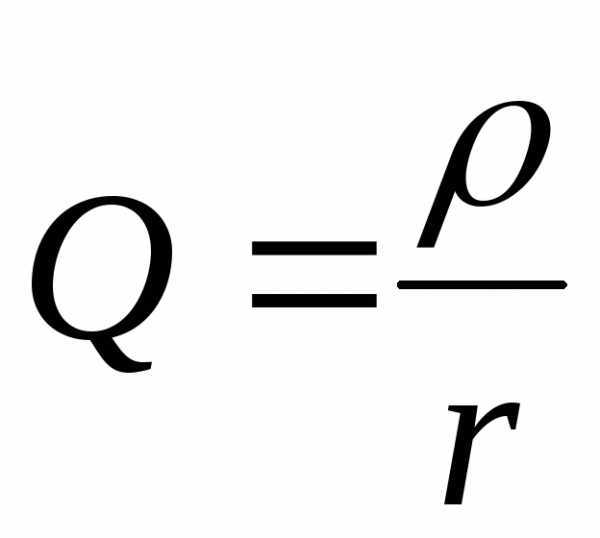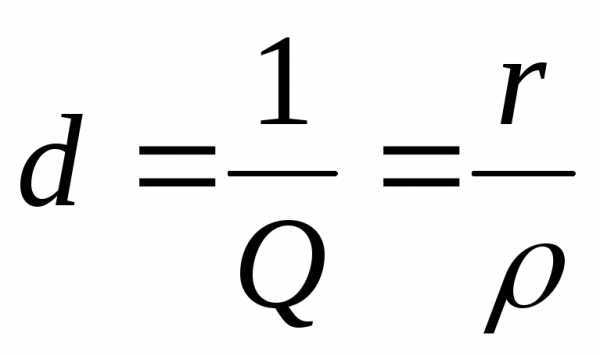Как следует из приведенных соотношений, добротность и затухание являются безразмерными величинами. Поскольку во всех элементах цепи, изображенной на рис. 10.1а протекает один и тот же ток, добротность показывает, во сколько раз напряжение на реактивных элементах при резонансе превышает входное напряжение. В реальных колебательных контурах эта величина может достигать значительного уровня. Поэтому резонанс в цепи с последовательным соединением элементов r ,L ,C иногда называютрезонансом напряжений.

При резонансной частоте полное сопротивление z

равно сопротивлению резистора r , ток и входное напряжение совпадают по фазе.

Таким образом, вся мощность, поставляемая в цепь источником, равна активной мощности, потребляемой единственным резистивным элементом, а реактивная мощность цепи равна нулю. Это означает, что в резонансе взаимный обмен энергии происходит только между конденсатором и катушкой индуктивности. Уменьшение энергии электрического поля при разряде конденсатора сопровождается увеличением энергии магнитного поля катушки и наоборот. Обмен энергией между источником и реактивными элементами отсутствует.

Рассмотрим частотные свойства цепи с последовательно соединенными элементами r ,L ,C . Будем считать, что на входе цепи действует синусоидальное напряжение с постоянной амплитудой и угловой частотой , меняющейся в пределах от 0 до ∞ . Изменение частоты приводит к изменению параметров цепиx , z , . На рисунке 10.2 приведены соответствующие частотные характеристики

,

Рис. 10.2

Активное сопротивление рассматриваемой цепи не зависит от частоты, а реактивное при определенных значениях частоты ( ) становится равным либо нулю либо бесконечности. Эти характерные значения называют соответственно нулями и полюсами частотной характеристики. Важным свойством функции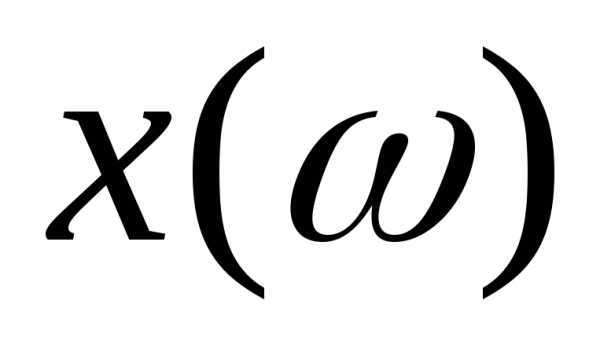является то, что она монотонно возрастает при увеличении частоты. В интервале частотреактивное сопротивление возрастает от − ∞ до 0 и имеетемкостнойхарактер, при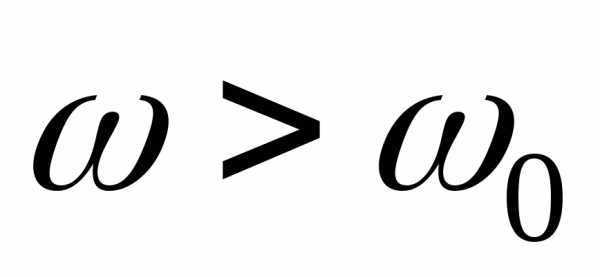реактивное сопротивление возрастает от 0 до ∞ и имеетиндуктивныйхарактер.

Рассмотрим зависимость тока в rLC контуре от частоты приложенного напряжения:

.

Анализ этого выражения показывает, что при максимального значения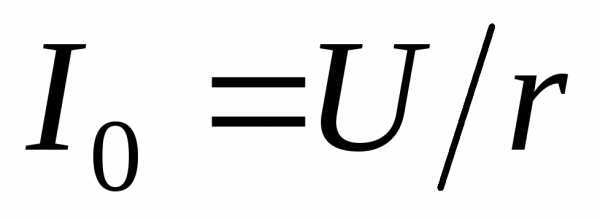ток достигает в точке, соответствующей резонансной частоте.

Важной характеристикой rLC контура является ширина резонансной кривой или полоса пропускания, которую оп

xn--90adflmiialse2m.xn--p1ai

Резонанс в цепи при параллельном соединении элементов

Рассмотрим электрическую цепь ( рис. 10.5а ), представляющую собой параллельный колебательный контур

При анализе частотных свойств цепи с параллельным соединением элементов g , L , C целесообразно рассмотреть комплексную проводимость цепи

.

Условием резонанса здесь также будет равенство нулю угла сдвига между входным током и напряжением, которое в данном случае сводится к условию равенства нулю реактивной проводимости

Из последнего равенства следует, что резонанс наступает при частоте

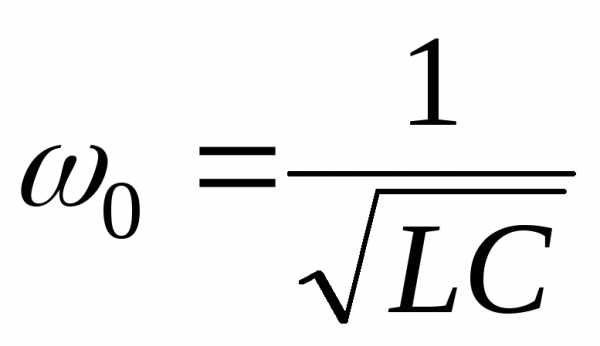
Векторная диаграмма для токов и напряжений при частоте резонанса изображена для параллельного колебательного контура на рис. 10.5б. Как следует из диаграммы, при резонансе токи катушки индуктивности и конденсатора равны по величине и противоположны по направлению, следовательно ток 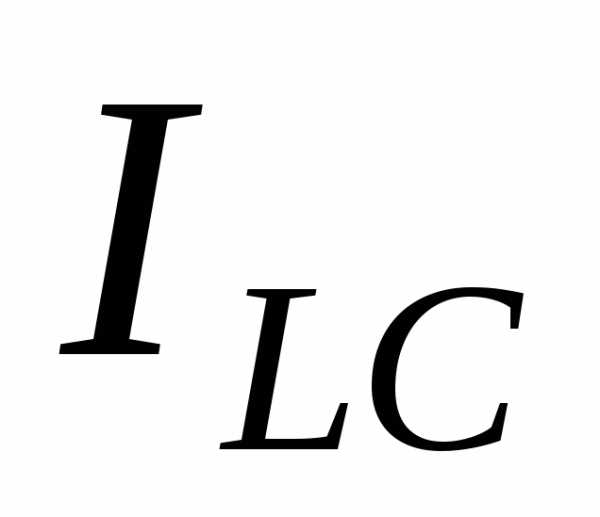равен нулю. Для рассматриваемой цепи вводятся понятия:

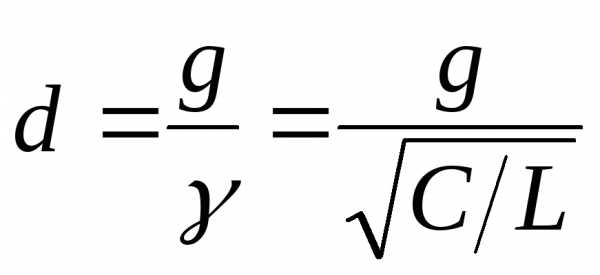
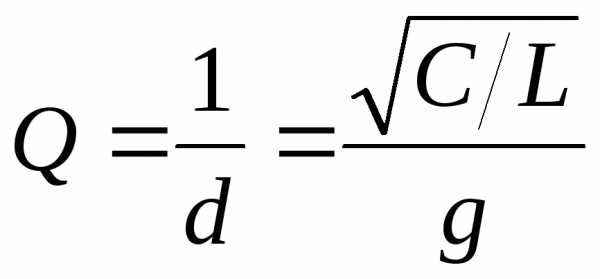
В режиме резонанса полная проводимость цепи

равна проводимости резистора и входной ток совпадает с током через этот резистор

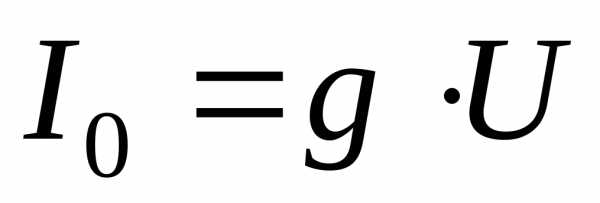
Поскольку входное напряжение одновременно приложено и к конденсатору и к катушке индуктивности, токи в этих элементах

,

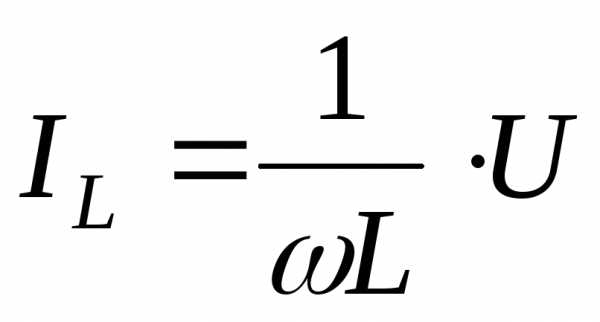при соответствующей величине их параметров могут существенно превышать входной ток. Поэтому резонанс в цепи с параллельным соединением элементов g , L , C иногда называют резонансом токов. Полная мощность, поставляемая в цепь источником, равна активной мощности, выделяемой на резисторе. Обмен энергией в резонансе происходит только между конденсатором и катушкой индуктивности, входящих в состав цепи, но не между источником и реактивными элементами.

На рисунке 10. 6а приведены зависимости активной, реактивной и полной проводимостей от частоты приложенного напряжения.

,

Рис. 10.6

Реактивная проводимость имеет три характерных значения при частотах 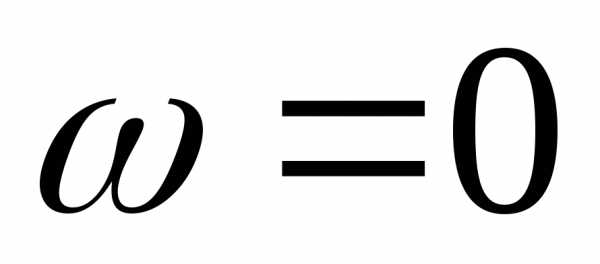и, для которых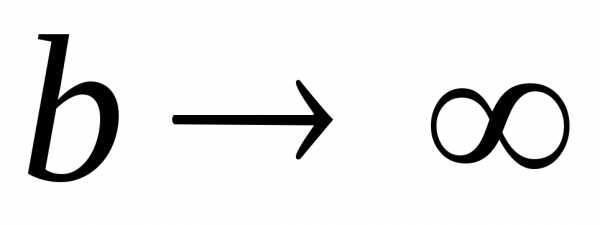( полюса функци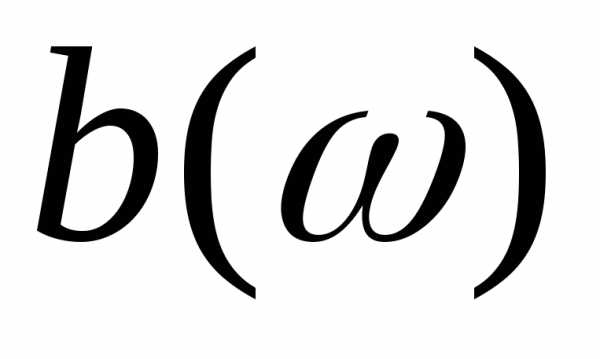и) и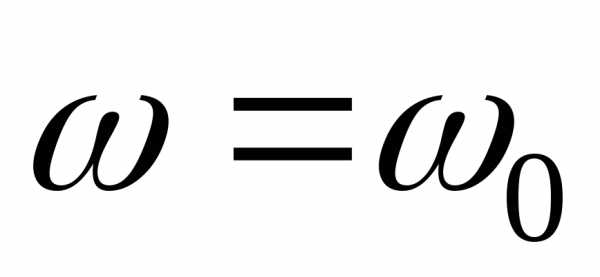− нуль функции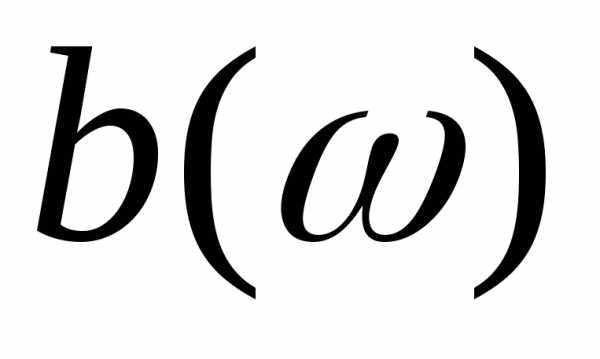. В диапазоне частотреактивная проводимость имеетиндуктивный характер, при 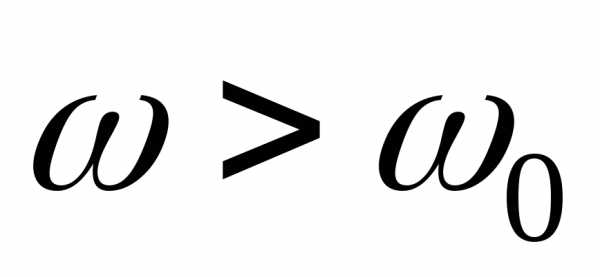− емкостной. Во всем диапазоне частот наблюдается монотонное уменьшение проводимости от + ∞ до −∞ . Соответствующая зависимость разности фаз между током и напряжением в цепи с параллельным соединением элементовg , L , C приведена на рис. 10. 6б.

Рассмотрим зависимость напряжения от частоты при постоянной амплитуде входного тока

.

Напряжение достигает максимального значения 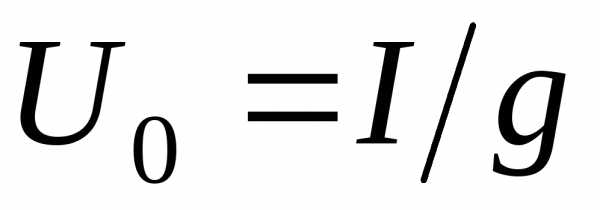при резонансной частоте. Форма кривой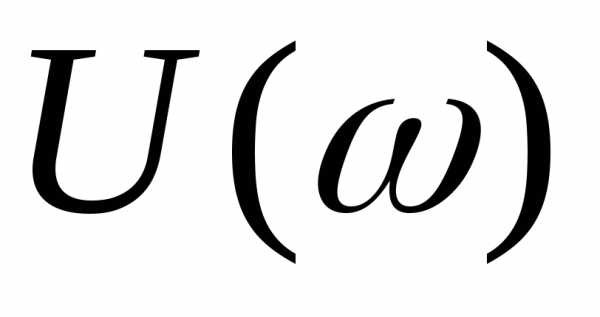зависит от затухания цепи.

Аналогично тому, как это было сделано при рассмотрении резонанса напряжений, можно показать, что ширина резонансного пика ( ширина полосы пропускания ), определенная по уровню 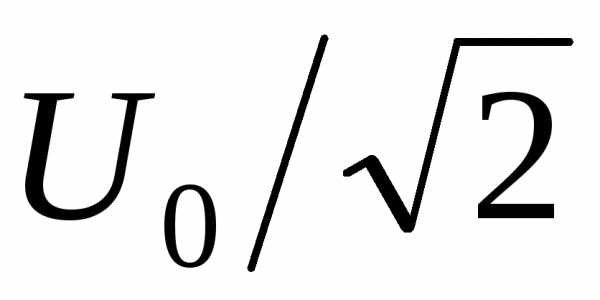, как и в случае резонанса в последовательном контуре, равна. На рисунке 10. 7 приведены зависимости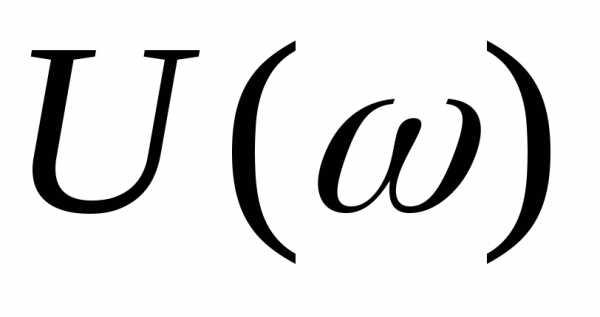при различных значениях затухания в системе относительных координат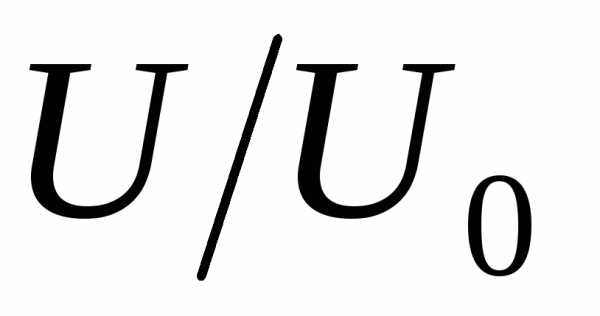и.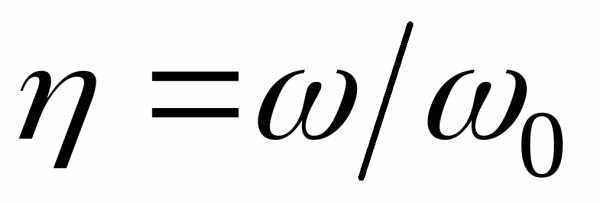

Зависимость тока в ветви с конденсатором от частоты определяется соотношением

При нулевой частоте ток , приток в конденсаторе стремится к постоянному значению.

Можно показать, что эта зависимость при имеет монотонный характер, при она имеет максимум (рис. 10.8). Ток в катушке индуктивности при нулевой частоте равен входному току и при. В зависимости от затухания цепи соответствующая резонансная кривая может иметь максимум (при) или быть монотонной (при).

studfiles.net

с помощью каких приборов и по каким признакам можно судить о наступлении режимов резонанса токов и резонанса напряжений?

РЕЗОНАНС НАПРЯЖЕНИЙ: Соединяешь ПОСЛЕДОВАТЕЛЬНО резистор (обычное сопротивление) , конденсатор переменной емкости, катушку индуктивности, амперметр и всю цепь подсоединяешь к источнику переменного напряжения (220 В, например) . Меняешь емкость конденсатора и одновременно наблюдаешь за показаниями амперметра. В тот момент, когда они будут МАКСИМАЛЬНЫ, в цепи получится резонанс напряжений. РЕЗОНАНС ТОКОВ: Соединяешь ПАРАЛЛЕЛЬНО резистор, конденсатор переменной емкости, катушку индуктивности, а к ним последовательно амперметр и всю цепь подсоединяешь к источнику переменного напряжения. Меняешь емкость конденсатора и одновременно наблюдаешь за показаниями амперметра, который меряет общий ток, текущий через параллельно соединенные конденсатор, катушку и резистор. В тот момент, когда показания амперметра будут МИНИМАЛЬНЫ, в цепи получится резонанс токов. Т. е. момент наступления ОБОИХ резонансов можно определить с помощью ОДНОГО-ЕДИНСТВЕННОГО АМПЕРМЕТРА! Главное - это правильно собрать цепь. Далее можно куда-нибудь еще каких-нибудь дополнительных амперметров-вольтметров-осциллографов поподключать, но это будет уже более сложный вариант с НЕСКОЛЬКИМИ ИЗМЕРИТЕЛЬНЫМИ ПРИБОРАМИ.

при резонансе напряжение на контуре резко возрастает, и может превышать подводимое

Ток меряют Амперметром, Напряжение — Вольтметром. Форму напряжения наблюдают на Осциллографе...

touch.otvet.mail.ru

---

• 
  Зависимость сопротивления проводника от длины
• 
  Трансформатор тока трехфазный
• 
  Районы размещения крупнейших гэс
• 
  Генераторы электрические
• 
  Масло для поршневого компрессора воздушного
• 
  Кто звонил 4959819819
• 
  Момент номинальный
• 
  Кремниевый диод на 10 ампер
• 
  Момент номинальный
• 
  Аккумулятор автомобильный из чего состоит
• 
  Коммунальные услуги по газу