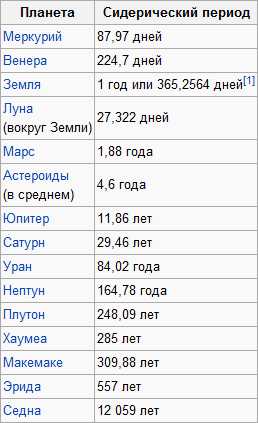
Последовательное, параллельное и смешанное соединение резисторов. Последовательно и параллельно соединенные резисторы

Последовательное и параллельное соединение РЕЗИСТОРОВ и КОНДЕНСАТОРОВ

Последовательное и параллельное соединение Январь 23, 2014

В статье про последовательное и параллельное соединение резисторов и конденсаторов — просто, понятно и доходчиво: как вычислять получающееся сопротивление и емкость при таких подключениях. Простые схемы, простые формулы, наглядные рисунки для последовательного и параллельного соединения.

Главное, объяснить так, чтобы поняли и запомнили на всю жизнь даже блондинка, даже ребенок. 🙂

Лучше всего запоминается и усваивается то, что дошло до сознания, до самой сути его, стало выглядеть простым и даже банальным. И чаще всего люди путаются в самых простых вещах, а всё потому, что в свое время не нашелся кто-то, кто бы подал материал в простой, доступной и удобной форме.

Наверное так происходит и с понятиями о последовательных и параллельных соединениях, особенно, когда дело касается соединения таком образом резисторов и конденсаторов. Видимо, происходит частая путаница в вычислениях сопротивлений и ёмкостей в подобных случаях. Об этом можно судить по большой частотности запросов в поисковых системах насчет параллельных и последовательных подключениях.

Последовательное и параллельное соединение РЕЗИСТОРОВ

Для понимания сути сего момента нужно понять и представить, что резистор = сопротивление. То есть, включая его в цепь, мы таким образом, увеличиваем как бы трудность прохождения пути. И, если представить резистор как некий отрезок пути с трудностями, потерями, то сразу станет ясным, что сложив два отрезка пути последовательно друг за другом, мы получим сумму этих трудностей. А расположив эти два отрезка параллельно и, пустив по ним нечто, мы уменьшим общие препятствия и потери, получив на выходе бОльшую скорость выхода этого нечто.

Расчет при соединении РЕЗИСТОРОВ

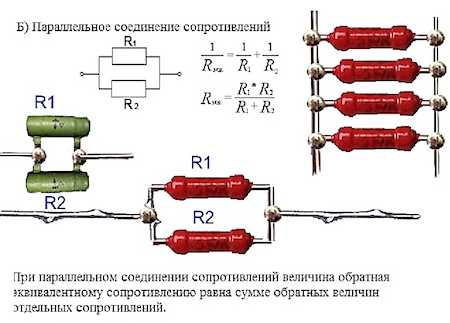
1. Последовательно = сумма2. Параллельно = произведение делить на сумму

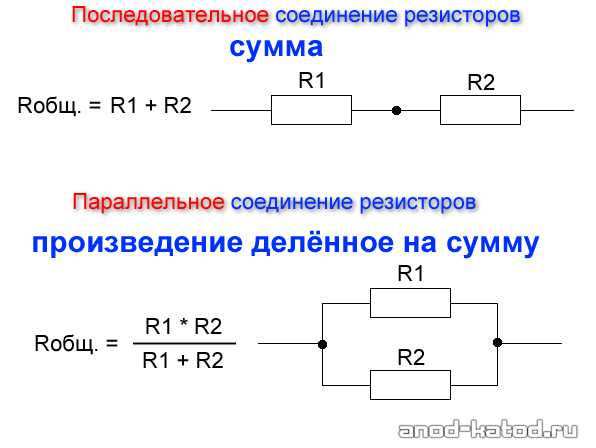
Последовательное и параллельное соединение КОНДЕНСАТОРОВ

Для понятия и усвоения расчета при соединении конденсаторов можно представить еще более близким к реальности такое: конденсатор это две близко расположенные пластины, либо много пластин, разделенных на две группы. То есть, чтобы увеличить (суммировать) ёмкость всех пластин, нужно их запараллелить. То есть в случае последовательного и параллельного соединения с конденсаторами, всё точно так же как с резисторами, но с точностью до наоборот:

Расчет при соединении КОНДЕНСАТОРОВ

1. Параллельно = сумма2. Последовательно = произведение делить на сумму

Вот такие простые расчеты для последовательных и параллельных соединений конденсаторов и резисторов для вычислений общих ёмкостей и сопротивлений. Картинки можете эти сохранить, на первое время может понадобится, чтобы освежить. Но я лично один раз усвоил суть и после этого запомнил на всю жизнь, хоть во сне разбуди — отчеканю без запинки.

Кому нужно, может воспользоваться калькулятором прямо здесь.

Расчет общего сопротивления или ёмкости по двум номиналам

По формуле произведение делить на сумму

Как сделать простой электродвигатель

Похожие статьи:

anod7.ru

Параллельное соединение резисторов: расчет и формулы

Содержание: Схемы последовательного и параллельного соединения Отличие параллельного и последовательного соединения Формула расчета параллельного соединения резисторов Онлайн калькулятор Видео В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы. Схемы последовательного и параллельного соединения Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами. При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений. При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них. Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства. Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов. Отличие параллельного и последовательного соединения Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении. В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение. Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты. Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники. Формула расчета параллельного соединения резисторов Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2. Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения. Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2. Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1\n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов. Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом. Онлайн калькулятор В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора. Достаточно всего лишь ввести в нужные окна исходные данные, и после нажатия кнопки получить результат.

electric-220.ru

Последовательное и параллельное соединение электрических сопротивлений

Рассмотрим пример электрической цепи, несколько более сложной, чем рассмотрен­ная ранее цепь с выключателем и лампочкой. Итак, обратимся к схеме на рис. 1. Имеется электрическая цепь, составленная из трех резисторов. Мы хотим узнать об­щее сопротивление между клеммами А и В.

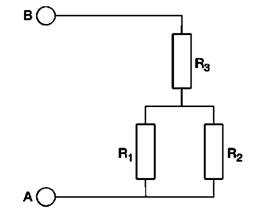
Рис. 1   цепь с последовательно параллельным соединением резисторов

 

Итак, имеются три резистора: R1 соединен (включен) параллельно R2, а эта пара соединена последовательно с R3

Разобьем цепь на простейшие части, что всегда удобно при анализе сложных це­пей и схем. Если мы знаем метод определения величины резисторов, соединенных последовательно, можно использовать его для вычисления сопротивления, образуе­мого R3, соединенного последовательно с парой R1 и R2. Но так как мы еще не знаем способа нахождения величины сопротивления параллельного соединения, то сначала требуется разобраться с этим. Вопрос о последовательности анализа цепей и схем очень важен, и мы еще не раз будем к нему обращаться.

Если два резистора (или любых другие компонентов) соединены параллельно, то они должны иметь одинаковое падение напряжения на них. Следовательно, в качест­ве отправной точки, можно воспользоваться законом Ома.

I=V/R.

Теперь, применяя закон Кирхгофа о токах, можно смело утверждать что:

Iобщий= IR1+IR2+…

Значит:       V/Rпаралельное = V/R1 + V/R2 + …

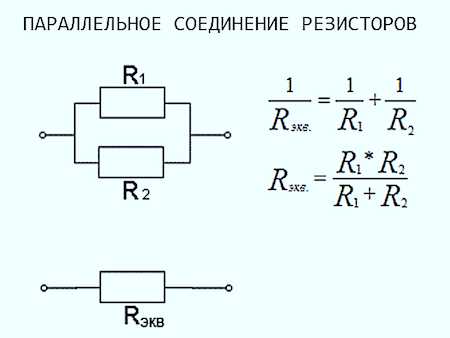
Разделив на V, получим:      1/Rпаралельное = 1/R1 + 1/R2 + …

Итак: обратная величина общего параллельного сопротивления равна сумме об­ратных величин всех резисторов.

Величину, обратную сопротивлению, в электротехнике часто называют про­водимостью, и обозначают буквой С. Тогда

Gобщ =G1+G2

Таким образом, при параллельном включении элементов, алгебраически склады­ваются их проводимости.

В частном случае, когда параллельно включены два резистора, можно вывести более удобную формулу для расчета общего сопротивления (это выражение часто называют «произведение над суммой»):

 

Rпараллельное = R1R2/R1+R2

Итак, мы решили проблему вычисления параллельного включения сопротивле­ний, а теперь необходимо разобраться с последовательным включением.

Для начала, упростим схему, поскольку мы уже умеем вычислять общее сопротив­ление параллельного соединения, которое теперь можно заменить одним сопротив­лением соответствующей величины. Таким образом, на рис. 1.5 показан упрощенный вид все той же цепи, что и на рис. 2, но параллельное включение двух сопротивле­ний заменено одним, так называемым эквивалентным.

 

 

Используя закон Кирхгофа о напряжениях, легко сделать вывод, что сумма паде­ний напряжений на резисторах должна быть равна приложенной ЭДС:

Vобщее = VR1 + V R2 +…

 

 

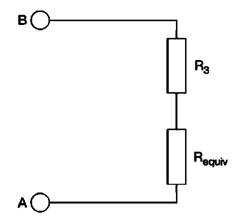
Рис. 2 Упрощение схемы на рис. 1,используя эквивалентное сопротивление

Теперь применив закон Ома, получим:

VобщееI = IR1 + IR2 +…

 

Но поскольку мы пытаемся рассчитать эквивалентное сопротивление, величина которого равна общему сопротивлению, то удобнее записать

IRобщее = IR1 + I R2 +…

Откуда:

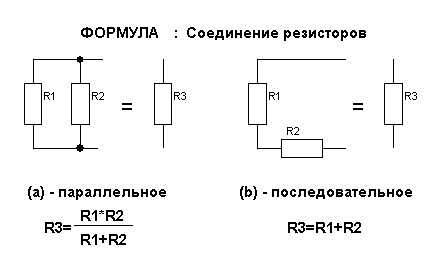
R последовательное=R1 + R2 +…

Общее сопротивление последовательно соединенных резисторов равно сумме со­противлений резисторов.

Используя формулы для параллельного и последовательного включения со­противлений, можно вычислить общее сопротивление любой сложной цепи, как бы «устрашающе» на первый взгляд она не выглядела.

Схемы могут быть очень сложными, но задача их анализа вполне разрешима, если подойти к ней логически. Здесь главное найти изначальный подход к решению, а ма­нипуляции с числами — проблема второстепенная.

Обратимся к цепи, изображенной на рис. 3. Требуется вычислить общее сопро­тивление цепи, то есть сопротивление между клеммами А и В. Поскольку цепь слож­ная, у нас нет правила для нахождения ее эквивалентного сопротивления напрямую, а значит, мы должны разбить сложную цепь на простейшую, к которой где можно применить уже известные нам правила. Таким образом, требуется выделить из слож­ной цепи группы компонентов, имеющие только последовательные или только парал­лельные соединения.

 

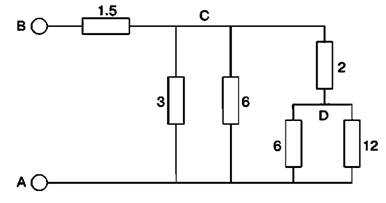
Рис. 3 Сложная развлетвленная цепь

 

В этом примере — между узлами А и D только параллельно включенные компо­ненты. Можно вычислить значение их эквивалентного сопротивления и подставить его в схему:

 

Rпараллельное = произведение / сумма = 6×12/6+12 = 4 Ом.

 

Теперь перечерчиваем схему, заменяя параллельное включение этихдвух элемен­тов их эквивалентным сопротивлением (рис. 4).

 

Рис. 4 Первое упрощение сложной цепи с рис. 3

 

Теперь имеются только последовательные и параллельные соединения между узлами А и С. Имеется выбор расчета — либо сперва рассчитать последовательное соединение 2 Ом и 4 Ом, либо параллельное соединение 3 Ом и 6 Ом. Рассчитаем сперва последовательное соединение, поскольку в результате получим эквивалент­ное сопротивление, включенное параллельно сопротивлениям 3 Ом и 6 Ом, а затем найдем сопротивление трех параллельно включенных резисторов.

 

Rпоследовательное = R1 + R2=4 + 2 = 6 Ом.

 

Снова перечерчиваем схему, заменив только что рассчитанное последовательное соединение двух резисторов, одним эквивалентным (рис. 1.8).

Рис. 5 Второе упрощение сложной цепи с рис. 3

Теперь имеются три компонента, включенные параллельно. Тогда:

1/R = 1/R1 + 1/R2 + 1/R3 = 1/3 + 1/6 + 1/6 = 2/3,

Rпаралельное=1,5 Ом

Теперь имеется совсем простая цепь, состоящая из двух последовательно вклю­ченных сопротивлений по 1,5 Ом. Применив правило для последовательного включе­ния двух резисторов, не трудно сказать, общее сопротивление всей цепи равно 3 Ом.

Итак, методами последовательного и параллельного соединения элементов, а так­же путем непосредственного применения законов Ома и Кирхгофа, можно анализиро­вать цепи любой сложности. Однако, существует ряд полезных методов, которые дают возможность несколько упростить и ускорить анализ электрических цепей и схем. Су­ществует множество различных учебников и книг по теории электрических цепей и электротехники, где разбираются различные методы анализа сложных цепей. Рассмат­ривать их все здесь вряд ли является целесообразным, поскольку цели настоящей книги несколько иные. Однако, к ряду таких методов мы будем обращаться далее, где и остано­вимся на них подробнее. Здесь же приведем некоторые самые общие рекомендации.

• выбор отправной точки (то есть той группы элементов цепи, с которой начина­ется анализ сцепи (см., например, рассуждения к рис. 2) для решения задачи анализа цепи является очень важным и зачастую критическим;
• отправную точку нужно стараться выбирать как можно дальше от внешних клемм цепи;
• в качестве отправной точки выбирают группы элементов, включенные только последовательно или только параллельно;
• анализ обычно проводится от в направлении от отправной точки к внешним клеммам;
• Процессу анализа цепи очень помогает перечерчивание схемы, постепенно упрощая ее путем замены уже рассчитанной группы элементов на один эквива­

Морган Джонс. Ламповые усилителию. Перевод с английского под общей научной редакцией к.т.н. доц. Иванюшкина Р Ю.

500 Internal Server Error

Ошибка в настройках сайта Вероятнее всего, эта ошибка возникла из-за несовместимых настроек .htaccess

hifisound.com.ua

Последовательное, параллельное и смешанное соединение резисторов.

Поиск Лекций

Контрольная работа № 1

вариант № 10

учащегося (щейся) Кот А.А.(фамилия, имя, отчество)

 

1 курса 90-хк группыспециальности технология пищевых производствШифр учащегося (щейся) 210

 

Последовательное, параллельное и смешанное соединение резисторов.

 

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

 

 

 

Рис. 1. Схемы последовательного соединения приемников

 

Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходитодин и тот же ток I.Последовательное соединение приемников поясняет рис. 1.Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк

где Rэк = R1 + R2 + R3.

 

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов. Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз

и в данном случае E = U, то для рассматриваемой цепи

U = U1 + U2 +U3

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U1 : U2 : U3 = R1 : R2 : R3

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например n, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в n раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n.

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 2).

 

Рис. 2 Схемы параллельного соединения приемников

 

При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I1=U/R1; I2=U/R2; I3=U/R3.

 

Ток в неразветвленной части цепи согласно первому закону Кирхгофа

I = I1+I2+I3, или

I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/Rэк = 1/R1 + 1/R2 + 1/R3

Вводя в формулу вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

Gэк = G1+ G2 +G3

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

Rэк=R1R2/(R1+R2)

при трех параллельно включенных резисторах

Rэк=R1R2R3/(R1R2+R2R3+R1R3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

Rэк = R1 / n

Проходящий по каждой ветви ток I1, в этом случае будет в n раз меньше общего тока:

I1 = I / n

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Рис. 3. Схемы смешанного соединения приемников

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

 

Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 3, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 3, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис.3, а заменяется эквивалентной схемой рис. 3, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).

При этом схема рис. 3, б заменяется эквивалентной схемой рис. 3, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4

 

Неразветвленная цепь переменного тока с активным сопротивлением, индуктивностью, емкостью. Полное сопротивление, активная, реактивная, полная мощность, векторная диаграмма тока и напряжений, треугольники сопротивлений и мощностей. Резонанс напряжений.

Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.4).

Рис. 4

 

В схеме протекает синусоидальный ток

Определим напряжение на входе схемы.

В соответствии со вторым законом Кирхгофа,

(1)

Подставдяем эти формулы в уравнение (1). Получаем:

Из выражения (2) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение (2) в комплексной форме:

(3)

Поделим левую и правую части уравнения (3) на √2. Получим уравнение для комплексов действующих значений токов и напряжений

, (4)

где - комплексное сопротивление цепи; - модуль комплексного сопротивления, или полное сопротивление цепи; - начальная фаза комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

1. XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис 5).

2. Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6).

3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.7).

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

Условие возникновения резонанса: , отсюда резонансная частота равна

.

Из формулы следует, что режима резонанса можно добиться следующими способами:

1. изменением частоты;

2. изменением индуктивности;

3. изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

.

Рис. 5 Рис. 6 Рис. 7

“UL” и “UС” – могут быть выше чем “UОБЩ”.

 

poisk-ru.ru

---

• 
  Скрутить счетчик электроэнергии
• 
  Куда жаловаться на энергосбыт
• 
  Проверка или замена счетчиков воды
• 
  Как телевизионный кабель выбрать
• 
  Как узнать характеристики трансформатора
• 
  Лэп влияние на здоровье
• 
  В чем измеряется частота обращения
• 
  Лампа дрл не разгорается
• 
  Что такое акт разграничения
• 
  Электросбыт санкт петербург личный кабинет
• 
  Когда в ростове на дону включат отопление