Потери в силовом трансформаторе | Дактекс
30.11.2021
Основные характеристики трансформатора – это напряжение первичной и вторичной обмотки, а также мощность трансформатора. Мощность подается от первичной обмотки на вторичную электромагнитным путем. При этом не вся мощность из электрической сети доходит до нагрузки, которая питает потребителей. Разница мощности, которая поступает на первичную обмотку и мощности, которая возникает во вторичной обмотке называется потерями трансформатора.
Виды потерь силового трансформатора
Так как силовой трансформатор, является статическим электромагнитным устройством – то он не имеет движущихся деталей. Это значит, что механические потери такому оборудованию не свойственны. Потери в нем – это потери активной мощности. Они происходят в магнитном сердечнике, обмотках и других частях оборудования. Во время разных режимов работы трансформатора величина потерь меняется.
Потери холостого хода трансформатора
На холостом ходу к вторичной обмотке трансформатора не подключена нагрузка. Поэтому весь ток, который подается на первичную обмотку, идет на намагничивание сердечника. Такие потери принято назвать магнитными и обозначать Рм. Общее значение потерь холостого хода рассчитывается при номинальной силе тока и напряжении.
Поэтому весь ток, который подается на первичную обмотку, идет на намагничивание сердечника. Такие потери принято назвать магнитными и обозначать Рм. Общее значение потерь холостого хода рассчитывается при номинальной силе тока и напряжении.
Ро = Рм+I2о * r1,
Iо – сила тока в первичной обмотке,
r1 – это сопротивление первичной обмотки.
Потери холостого хода – это постоянная цифра, которая зависит от суммы намагничивающей и активной части. А эти величины неизменны, так как на них влияют характеристики обмотки и магнитного сердечника. По значению потерь холостого хода можно судить о работе трансформатора.
Основные потери в обмотках трансформатора
В трансформаторе под нагрузкой электромагнитная мощность, которая поступает на первичную обмотку, передается вторичной. При этом во вторичной обмотке возникает электрический ток I2, а в первичной – ток I1. Первичный ток напрямую зависит от тока нагрузки I2.
Часть мощности теряется в обмотках. Эти потери называются общими потерями мощности под нагрузкой – Рнагр. Они пропорциональны квадратам первичного и вторичного тока, а также значениям сопротивления обмоток.
Рнагр = I21r1 + I22r2,
где I1 и I2 — токи в первичной и вторичной обмотках,
r1 и r2 — значения сопротивлений первичной и вторичной обмоток.
Как видите, потери под нагрузкой полностью зависят от нагрузки трансформатора. Поэтому они носят непостоянный характер.
Дополнительные потери в обмотках трансформатора
В обмотках трансформатора и ферромагнитном сердечнике возникают не только токи нагрузки. Есть токи, которые появляются и замыкаются внутри проводов или внутри пластин магнитопровода – они называются вихревыми токами. Есть токи, которые появляются между параллельными витками обмотки или между отдельными пластинами сердечника – это циркулирующие токи. Направление этих побочных потоков перпендикулярно основному току в обмотках и сердечнике. Поэтому появление вихревых и циркулирующих токов снижает эффективность работы трансформатора.
Направление этих побочных потоков перпендикулярно основному току в обмотках и сердечнике. Поэтому появление вихревых и циркулирующих токов снижает эффективность работы трансформатора.
Кроме обмоток, добавочные потери возникают в стенках самого бака, в прессующих кольцах, в ярмовых балках и других элементах конструкции трансформатора.
Конструкторы электромагнитного оборудования постоянно ищут способы уменьшения потерь и увеличения КПД трансформатора. Например, магнитный сердечник трансформатора делается не монолитным, а набирается из отдельных тонких пластин, которые тщательно изолируются. Изоляция отдельных витков обмоток также положительно сказывается на КПД оборудования. У современных силовых трансформаторов полезная мощность КПД достигает 90% и выше.
Потери мощности в трансформаторах
5.2. Потери
мощности в трансформаторах
Передача мощности через
трансформаторы также сопровождаются потерями мощности. При этом потери мощности
При этом потери мощности
в активной и реактивной проводимостях трансформатора
определяются уровнем подведенного к нему напряжения
(5.8)
(5.9)
В таком виде потери мощности
учитываются при расчете трансформаторов высоких классов напряжения.
Как видно, они не зависят
от передаваемой через трансформатор мощности и могут находиться по паспортным
данным и ().
Заметим, что определение
потерь мощности холостого хода не зависит от типа трансформатора.
Потери мощности в
сопротивлениях обмоток разных трансформаторов находятся по разному, так как они
характеризуются различными схемами замещения.
В двухобмоточном
трансформаторе, где обе обмотки представляются одним сопротивлением, потери
активной мощности в активном сопротивлении определяют по выражению
, (5. 10)
10)
а реактивной мощности в реактивном
сопротивлении
(5.11)
В эти формулы значения тока и
напряжения подставляется для той обмотки трансформатора, к которой были
приведены сопротивления и (см. формулы (4.15) и (4.16)).
Данные потери главным образом зависят от передаваемой через трансформатор
мощности от уровня подведенного к нему напряжения.
Отметим, что потери
мощности в обмотках и потери холостого хода по разному зависят от напряжения.
Суммарные активные и
реактивные потери в двухобмоточных трансформаторах с учетом потерь в
проводимостях составят
(5.12)
(5.13)
Потери мощности в трансформаторе
могут быть определены по его паспортным данным и мощности нагрузки
; (5. 14)
14)
(5.15)
Здесь отношение называется коэффициентом загрузки трансформатора. Видно, что
при потери мощности в трансформаторе
Отметим, что расчет потерь
мощности по формулам (5.14) и (5.15) возможно и более простой, но менее точный,
так как не учитывает влияния уровня напряжения на результат расчета.
Если на подстанции с
суммарной нагрузкой S
работают параллельно n
одинаковых трансформаторов, то их эквивалентные сопротивления в n раз меньше, а проводимости в n раз больше. С учетом этого формулы
(5.14) и (5.15) можно записать так:
(5.16)
(5.17)
В трансформаторах с
расщепленной обмоткой при раздельной работе обмоток низшего напряжения на свою
нагрузку (рис. 5.2) потери мощности находят по формулам
5.2) потери мощности находят по формулам
(5.18)
(5.19)
В трехобмоточном
трансформаторе в схеме замещения каждая обмотка представляется своим
сопротивлением, и по каждой из них передается разная мощность (рис.5.3).
Поэтому формулы (5.12-5.15) для них примут следующий вид
(5.20)
, (5.21)
где 1, 2, 3 — обозначения параметров
соответственно обмоток высшего, среднего и низшего напряжения.
Откуда взялись формулы расчета трансформаторов и дросселей? | Разумный мир
Ранее я описал физику работы трансформатора. Однако, глядя на формулы или номограммы для инженерного расчета трансформаторов трудно представить их связь с физическими основами. А это не способствует пониманию особенностей той, или иной, методики расчета и принятых при этом допущений и ограничений. И дает простор для мифотворчества.
А это не способствует пониманию особенностей той, или иной, методики расчета и принятых при этом допущений и ограничений. И дает простор для мифотворчества.
Я не ставлю задачу выбора лучшей методики расчета, как и подробного описания любой из них. Я просто покажу, откуда взялись все эти формулы, и что они значат.
Но сначала нужно сказать пару слов о самих трансформаторах. Трансформатор может не иметь сердечника, такой трансформатор называют воздушным. Сердечник может быть выполнен не из ферромагнитного материала, но область применения таких трансформаторов несколько ограничена. Сердечник может быть ферромагнитным, например, из электротехнической стали (трансформаторное железо), феррита, пермалоя, и т.п. Именно такие трансформаторы встречаются чаще всего. Кроме того, сердечники могут быть разной формы, что несколько влияет на расчет.
Особенностью ферромагнитных материалов является то, что связь индукции и напряженности магнитного поля в них не линейна. Я приводил в статье о трансформаторах иллюстрацию, повторю ее здесь
Я приводил в статье о трансформаторах иллюстрацию, повторю ее здесь
В отличии от вакуума, перемагничивание ферромагнетиков происходит не по прямой, а по семейству кривых, называемых петлями гистерезиса. Другими словами, магнитная проницаемость ферромагнетика не является постоянной. Я говорил ранее про дифференциальную индуктивность (формула (15) в упомянутой статье), но в инженерных расчетах, вместо аналитических, используют максимальные величины индукции. При этом работа сердечника происходит на линейных, или условно линейных, участках кривой намагничивания.
Правильно рассчитанный трансформатор в штатных режимах эксплуатации всегда работает без насыщения сердечника! Про специальные насыщающиеся трансформаторы я скажу немного позже. Работа трансформатора без насыщения сердечника обозначает пропорциональность токов, напряжений и сопротивлений между первичной и вторичной цепями. Все формулы из статьи о работе трансформатора, безусловно верны, но крайне неудобны для практических, инженерных расчетов. Давайте рассмотрим практический подход.
Давайте рассмотрим практический подход.
Мы уже знаем, что общий магнитный поток в сердечнике трансформатора, в штатном режиме и без насыщения сердечника, постоянен и равен потоку холостого хода. То есть, при отсутствии тока во вторичной обмотке. Другими словами, магнитный поток холостого хода определяется током первичной обмотки на холостом ходе. Если мы не будет рассматривать общий случай для напряжения любой формы, то решения дифференциальных уравнений дадут нам
для гармонического (синусоидального) напряжения. Здесь R сопротивление обмотки постоянному току, f частота , L индуктивность обмотки. Для напряжения прямоугольной формы формула будет отражать, по факту, переходный процесс в катушке
В реальном трансформаторе ток холостого хода будет выше, из-за паразитных индуктивностей рассеивания и потерь в магнитопроводе. Соответствующие коэффициенты, обычно, приводятся в виде таблицы к методике расчета. Обратите внимание, что для гармонического сигнала у нас формула отражает действующее значение тока, а для прямоугольного мгновенное.
Ток холостого хода стараются стараются сделать поменьше, в разумных пределах, конечно. Для маломощных трансформаторов он, обычно, не превышает 10%, а для мощных порядка 3%, от тока первичной обмотки при полной нагрузке трансформатора. Таким образом, для заданной амплитуды первичного напряжения и частоты, или длительности импульсов, и желаемого тока холостого хода получаем требуемую индуктивность первичной обмотки. Индуктивность обмотки зависит от числа витков, магнитной проницаемости сердечника и геометрии обмотки, которая зависит от формы сердечника. Таким образом, мы получили один из параметров трансформатора — число витков первичной обмотки. Число витков вторичной обмотки определяется коэффициентом трансформации.
Связанный с током холостого хода магнитный поток, в очень грубом первом приближении, можно оценить по формуле (3) из упоминаемой статьи. Магнитный поток это интеграл от вектора магнитной индукции по поверхности, в нашем случае, по поперечному сечению сердечника-магнитопровода (формула (4) статьи).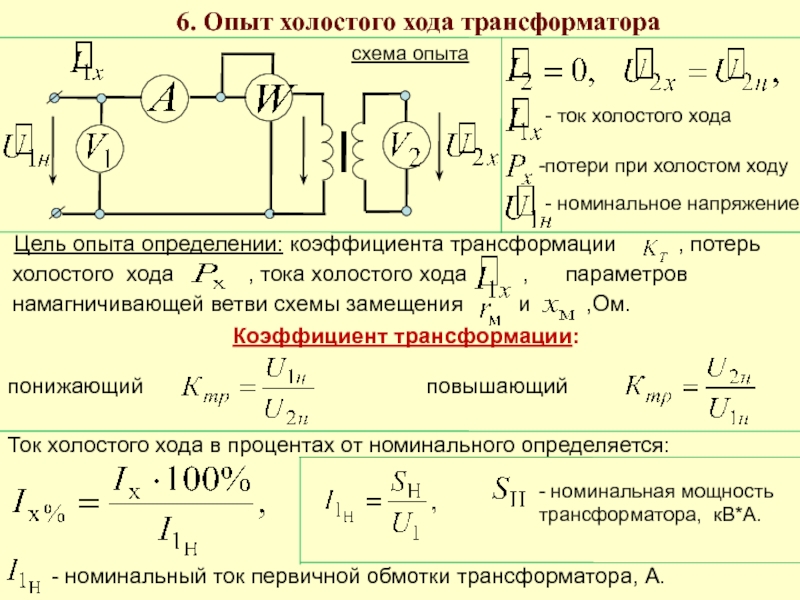
Таким образом, мы получаем значение магнитной индукции для заданной частоты питающего напряжения, или длительности прямоугольных импульсов, и заданной индуктивности обмотки. Причем нам нужны амплитудные значения индукции, а не действующие. С учетом максимально допустимой для сердечника магнитной индукции (для работы на линейном участке), мы получаем один из параметров сердечника — площадь сечения.
Обмотки трансформатора размещаются в окнах сердечника. Исключением является стержневой сердечник. Что бы обмотки можно было намотать, нужно иметь достаточный размер окна, или его площадь. Площадь требуемого окна зависит не только от количества обмоток и числа их витков, но и от диаметра провода обмоток. Диаметр провода выбирается исходя из допустимой плотности тока и температуры.
Теперь у нас есть все данные для изготовления трансформатора. У нс были сходные параметры: форма и амплитуды напряжения на первичной обмотке, ток холостого хода, требуемая амплитуда напряжения на вторичной обмотке. Мы получили промежуточные параметры: индуктивность первичной обмотки, коэффициент трансформации, магнитная индукция в сердечнике на холостом ходу. Использовали параметры сердечника: магнитную проницаемость и максимальную магнитную индукцию, форму сердечника. В результате получаем параметры для изготовления: число витков обмоток и диаметр провода, площадь сечения сердечника, которая позволяет выбрать требуемый размер сердечника. Мы достигли нужного результата!
Мы получили промежуточные параметры: индуктивность первичной обмотки, коэффициент трансформации, магнитная индукция в сердечнике на холостом ходу. Использовали параметры сердечника: магнитную проницаемость и максимальную магнитную индукцию, форму сердечника. В результате получаем параметры для изготовления: число витков обмоток и диаметр провода, площадь сечения сердечника, которая позволяет выбрать требуемый размер сердечника. Мы достигли нужного результата!
Как я уже говорил, существуют разные методики инженерного (упрощенного) расчета трансформаторов. Я не могу привести и описать их все. Формулы в этих методиках часто носят эмпирический характер, позволяя учесть основные соотношения с допустимой точностью без излишнего усложнения и углубления в физику процессов и тонкости математических преобразований. При правильном применении, в границах, установленных для конкретной методики, это позволяет значительно упростить расчет и получить приемлемый результат. При неверном выборе методики результат может быть катастрофическим.
Обычно, расчеты начинают с определения мощности трансформатора с учетом потерь. Такую мощность часто называют габаритной мощностью трансформатора. Исходя из мощности рассчитывают диаметр провода обмоток. Задав ток холостого хода первичной обмотки получают число ее витков. Причем, не редко, число витков считается не через ток холостого хода, а через «число витков на вольт», которое определяется из таблицы или по номограмме. Выбор сердечника может свестись к определению площади поперечного сечения, предоставляя выбор площади окна разработчику. А может быть использован параметр «произведение площади сечения сердечника на площадь окна», который кажется лишней степенью свободы при выборе размеров сердечника. Но он позволяет выбрать сердечник из стандартного ряда на который точно получится намотать все обмотки.
Расчет импульсных трансформаторов, не только для передачи сигнала, но и для применения, например, в двухтактных преобразователях, ведут по другим методикам, так как требования несколько иные. Но сама суть расчета точно такая же.
Но сама суть расчета точно такая же.
Я много говорил, что дроссели нельзя путать с трансформаторами, так как они, в отличии от трансформаторов, накапливают энергию в магнитном поле. Но сейчас я скажу то, что может показаться ересью и полным отрицанием моих же слов. Расчет дросселя почти не отличается от расчета трансформатора! Энергия, накопленная в магнитном поле, определяется током в катушке — обмотке дросселя. Вместо тока холостого хода мы должны использовать ток, обеспечивающий требуемую энергию. Собственно говоря, на этом различия расчета заканчиваются. Однако, для дросселей желательно иметь максимально протяженный линейный участок кривой намагничивания сердечника и, как следствие, максимально стабильная магнитная проницаемость сердечника. Для этого в сердечник вводят немагнитный зазор. Он снижает магнитную проницаемость, но линеаризует кривую намагничивания. Кажущееся радикальным различие в методиках расчета дросселя и трансформатора сводится к учету этого немагнитного зазора.
Я обещал немного рассказать о насыщающихся трансформаторах. Оставим в стороне магнитные усилители, все таки для большинства это экзотика. Рассмотрим широко известный блокинг-генератор.
В этой схеме трансформатор (дроссель) работает с насыщением сердечника. Пока ток коллектора транзистора нарастает, а сердечник не вошел в насыщение, на базовой обмотке наводится ЭДС, что создает положительную обратную связь и поддерживает транзистор открытым. Когда сердечник вошел в насыщение, ЭДС наводимая на базовой обмотке становится недостаточной для поддержания тока коллектора. А это вызывает закрывание транзистора. Накопленная в трансформаторе энергия уходит во вторичную цепь или рассеивается на демпферном диоде (на схеме не показан). Если объединить два блокинг-генератора, то получим широко известную схему двухтактного самовозбуждающегося преобразователя с насыщающимся трансформатором.
Однако, потери в трансформаторе для подобных схем слишком велики. Поэтому для относительно мощных преобразователей используют не насыщающийся силовой трансформатор, а ключевые транзисторы коммутируют внешним генератором, который может быть собран, в том числе, на основе подобной схемы.
Поэтому для относительно мощных преобразователей используют не насыщающийся силовой трансформатор, а ключевые транзисторы коммутируют внешним генератором, который может быть собран, в том числе, на основе подобной схемы.
Осталось коснуться особенностей работы трансформаторов на выпрямители с накопительной емкостью. Это работа на реактивную нагрузку, что вносит существенные коррективы в режим работы трансформатора. Тут два влияющих фактора. Первый, это собственно работа на емкостную нагрузку создающую дополнительный сдвиг фаз между напряжением и током. Возможные резонансы можно даже не учитывать. Второй, это то, что диоды выпрямителя откроются только при превышении напряжения на вторичной обмотке напряжения на конденсаторе, с учетом падения напряжения на самом диоде. Это так называемый угол открывания диодов выпрямителя. В результате, получаем ток вторичной обмотки существенно отличающимся от синусоидального. Что не может не влиять процессы в трансформаторе.
Однако, такой режим работы, обычно, уже учтен в формулах и номограммах методик расчета. Поэтому можно особо не переживать на этот счет.
Поэтому можно особо не переживать на этот счет.
Важно отметить, что упрощенные инженерные методики и формулы верны только для таких вот «стандартных» режимов использования трансформатора. Для не стационарных режимов, для переходных процессов, и в любых случаях, когда требуется точный учет влияния трансформатора, эти формулы и методики не применимы.
На этом все. Надеюсь, что теперь вам будет понятнее, откуда берутся эти упрощенные формулы и как они связаны с физикой работы трансформатора.
КПД трансформатора | ООО «НОМЭК»
При работе в трансформаторе возникают потери энергии. Коэффициентом полезного действия трансформатора (КПД) называют отношение отдаваемой мощности Р2 к мощности Р1 поступающей в первичную обмотку:
η = P2/P1 = (U2I2 cos φ2)/(U1I1 cos φ1)
или
η = (Р1 — ΔР)/Р1 = 1 — ΔР/(Р2 + ΔР), (2.49)
где ΔР — суммарные потери в трансформаторе.
Высокие значения КПД трансформаторов не позволяют определять его с достаточной степенью точности путем непосредственного измерения мощностей Р1 и Р2, поэтому его вычисляют косвенным методом по значению потерь мощности.
| Рис. 2.38. Энергетическая диаграмма трансформатора |
Процесс преобразования энергии в трансформаторе характеризует энергетическая диаграмма (рис. 2.38). При передаче энергии из первичной обмотки во вторичную возникают электрические потери мощности в активных сопротивлениях первичной и вторичной обмоток ΔРэл1 и ΔРзл2, а также магнитные потери в стали магнитопровода ΔРм (от вихревых токов и гистерезиса). Поэтому
Р2 = Р1 — ΔРэл1 — ΔРэл2 — ΔРм (2.50)
и формулу (2.49) можно представить в виде
η = |
| = 1 — |
| (2. |
Величину Рэм = Р1 — ΔРэл1 — ΔРм, поступающую во вторичную обмотку, называютвнутренней электромагнитной мощностью трансформатора. Она определяет габаритные размеры и массу трансформатора.
Определение потерь мощности. Согласно требованиям ГОСТа потери мощности в трансформаторе определяют по данным опытов холостого хода и короткого замыкания. Получаемый при этом результат имеет высокую точность, так как при указанных опытах трансформатор не отдает мощность нагрузке. Следовательно, вся мощность, поступающая в первичную обмотку, расходуется на компенсацию имеющихся в нем потерь.
При опыте холостого хода ток I0 невелик и электрическими потерями мощности в первичной обмотке можно пренебречь. В то же время магнитный поток практически равен потоку при нагрузке, так как его величина определяется приложенным к трансформатору напряжением. Магнитные потери в стали пропорциональны квадрату значения магнитного потока. Следовательно, с достаточной точностью можно считать, что магнитные потери в стали магнитопровода равны мощности, потребляемой трансформатором при холостом ходе и номинальном первичном напряжении, т. е.
е.
ΔРм ≈ Р0. (2.52)
Для определения суммарных электрических потерь согласно упрощенной схеме замещения (см. рис. 2.33,a) полагают, что 1’2 = 11. При этом
ΔPэл = ΔPэл1 + ΔPэл2 = I12R1 + I’22R2 ≈ I’22 (R1 + R’2) ≈ I’22Rк, (2.53)
или
ΔРэл ≈ β2I’22номRк ≈ β2ΔPэл.ном,(2.54)
где ΔPэл.ном — суммарные электрические потери при номинальной нагрузке.
За расчетную температуру обмоток — условную температуру, к которой должны быть отнесены потери мощности ΔРэл и напряжение ик, принимают: для масляных и сухих трансформаторов с изоляцией классов нагревостойкости А, Е, В (см. § 12.1) температуру 75°С; для трансформаторов с изоляцией классов нагревостойкости F, Н — температуру 115 °С.
Величину ΔРэл.ном ≈ I’22номRк ≈ I12номRк можно с достаточной степенью точности принять равной мощности Рк, потребляемой трансформатором при опыте короткого замыкания, который проводится при номинальном токе нагрузки. При этом магнитные потери в стали ΔРмвесьма малы по сравнению с потерями ΔPэл из-за сильного уменьшения напряжения U1, a следовательно, и магнитного потока трансформатора и ими можно пренебречь. Таким образом,
При этом магнитные потери в стали ΔРмвесьма малы по сравнению с потерями ΔPэл из-за сильного уменьшения напряжения U1, a следовательно, и магнитного потока трансформатора и ими можно пренебречь. Таким образом,
ΔРэл = β2Pк(2.55)
Полные потери
ΔP = Po + β2Pк (2.56)
Подставляя полученные значения Р в (2.51) и учитывая, что Р2 = U2I2cosφ2 ≈ βSномcosφ2, находим
η = 1 — (β2Pк + P0)/(βSномcosφ2 + β2Pк + P0). | (2.57) |
Эта формула рекомендуется ГОСТом для определения КПД трансформатора. Значения Ро и Рк для силовых трансформаторов приведены в соответствующих стандартах и каталогах.
Зависимость КПД от нагрузки. По (2.57) можно построить зависимость КПД от нагрузки (рис. 2.39, а). При β = 0 полезная мощность и КПД равны нулю. С увеличением отдаваемой мощности КПД увеличивается, так как в энергетическом балансе уменьшается удельное значение магнитных потерь в стали, имеющих постоянное значение. При некотором значении βопт кривая КПД достигает максимума, после чего начинает уменьшаться с увеличением нагрузки. Причиной этого является сильное увеличение электрических потерь в обмотках, возрастающих пропорционально квадрату тока, т. е. пропорционально β2, в то время как полезная мощность Р2возрастает только пропорционально β.
При некотором значении βопт кривая КПД достигает максимума, после чего начинает уменьшаться с увеличением нагрузки. Причиной этого является сильное увеличение электрических потерь в обмотках, возрастающих пропорционально квадрату тока, т. е. пропорционально β2, в то время как полезная мощность Р2возрастает только пропорционально β.
Максимальное значение КПД в трансформаторах большой мощности достигает весьма высоких пределов (0,98—0,99).
| Рис. 2.39. Зависимость КПД трансформаторов η от нагрузки β |
Оптимальный коэффициент нагрузки βопт, при котором КПД имеет максимальное значение, можно определить, взяв первую производную dη/dβ по формуле (2.57) и приравняв ее нулю. При этом
β2оптPк = P0 или ΔРэл = ΔРм | (2.58) |
Следовательно, КПД имеет максимум при такой нагрузке, при которой электрические потери в обмотках равны магнит ным потерям в стали. Это условие (равенство постоянных и переменных потерь) приближенно справедливо и для других типов электрических машин. Для серийных силовых трансформаторов
Это условие (равенство постоянных и переменных потерь) приближенно справедливо и для других типов электрических машин. Для серийных силовых трансформаторов
βопт = √P0/Pк ≈ √0,2 ÷ 0,25 ≈ 0,45 ÷ 0,5(2.59)
Указанные значения βопт получены при проектировании трансформаторов на минимум приведенных затрат (на их приобретение и эксплуатацию). Наиболее вероятная нагрузка трансформатора соответствует β = 0,5 ÷ 0,7.
В трансформаторах максимум КПД выражен сравнительно слабо, т. е. он сохраняет высокое значение в довольно широком диапазоне изменения нагрузки (0,4 < β < 1,5). При уменьшении cosφ2 КПД снижается (рис. 2.39,6), так как возрастают токи 12 и I1 при которых трансформатор имеет заданную мощность Р2.
В трансформаторах малой мощности в связи с относительным увеличением потерь КПД существенно меньше, чем в трансформаторах большой мощности. Его значение составляет 0,6—0,8 для трансформаторов, мощность которых менее 50 Вт; при мощности 100-500 Вт КПД равен 0,90-0,92.
Потери без нагрузки в трансформаторе
Что такое потери холостого хода (потери возбуждения)?
Потери холостого хода трансформатора возникают, когда трансформатор возбуждается при номинальном напряжении и частоте, сохраняя при этом вторичную цепь разомкнутой. Потери холостого хода трансформатора представляют собой комбинированные потери, вызванные потерями на вихревые токи, потерями на гистерезис, потерями на блуждающие вихревые токи и диэлектрическими потерями. Максимальные потери при работе трансформатора без нагрузки происходят в сердечнике. Поэтому потери трансформатора без нагрузки также называются потерями в стали или потерями возбуждения. Потери холостого хода трансформатора постоянны от холостого хода до полной нагрузки, поэтому потери холостого хода также называются постоянными потерями.
Трансформатор представляет собой статическое устройство, и в трансформаторе нет движущихся частей. Следовательно, потери на трение и аэродинамические потери в трансформаторе равны нулю. Трансформатор повышает или понижает напряжение, сохраняя частоту неизменной. Потери в трансформаторе возникают из-за протекания тока в обмотке и магнитного поля в сердечнике.
Следовательно, потери на трение и аэродинамические потери в трансформаторе равны нулю. Трансформатор повышает или понижает напряжение, сохраняя частоту неизменной. Потери в трансформаторе возникают из-за протекания тока в обмотке и магнитного поля в сердечнике.
У идеального трансформатора входная мощность равна выходной мощности, однако в действительности это не так.Выходная мощность трансформатора всегда меньше входной мощности. Энергию нельзя ни создать, ни уничтожить; тот же принцип применим и для балансировки энергии трансформатора.
Мощность, потребляемая на первичной обмотке, равна потерям в трансформаторе плюс мощность, отдаваемая на вторичной обмотке трансформатора. Потери в трансформаторе можно разделить на две категории;
1. Потери в стали или сердечнике, диэлектрические потери и потери на блуждающие вихревые токи
2.Потери в меди и паразитные потери
Потери в стали или потери в сердечнике:
Напряжение, подаваемое на первичную обмотку, создает магнитное поле в сердечнике. Поток, создаваемый первичным током, проходит через сердечник, связывается со вторичной обмоткой трансформатора и индуцирует напряжение во вторичной обмотке трансформатора.
Поток, создаваемый первичным током, проходит через сердечник, связывается со вторичной обмоткой трансформатора и индуцирует напряжение во вторичной обмотке трансформатора.
В этом индукционном процессе, когда трансформатор находится без нагрузки, трансформатор страдает от потерь в железе или сердечнике, которые можно разделить на две категории, а именно.потери на гистерезис, потери на вихревые токи, потери на блуждающие вихревые токи и диэлектрические потери. Все эти потери являются постоянными, поэтому потери холостого хода также называют постоянными потерями трансформатора.
Гистерезис потерь
Что такое гистерезисные потери в трансформаторе?
Когда напряжение подается на первичную обмотку трансформатора, переменный ток, протекающий по первичной обмотке, намагничивает сердечник. Сердечник проходит процесс намагничивания и размагничивания из-за протекания тока в прямом и обратном направлении.При изменении направления переменного тока энергия теряется в виде тепла в сердечнике. Потери тепла из-за многократного изменения направления магнитного поля в сердечнике известны как гистерезисные потери.
Потери тепла из-за многократного изменения направления магнитного поля в сердечнике известны как гистерезисные потери.
Потери на гистерезис можно рассчитать, найдя площадь кривой B-H. Чтобы свести к минимуму потери на гистерезис, сердечник трансформатора изготовлен из холоднокатаной кремниевой стали с ориентированным зерном (CRGO), поскольку площадь кривой намагничивания этого материала меньше по сравнению с другими магнитными материалами.
Гистерезисные потери в сердечнике трансформатора можно рассчитать по данной формуле гистерезисных потерь.
Формула гистерезисных потерь
Потери на вихревые токи
Что такое потери на вихревые токи в трансформаторе?
Поток, проходящий через сердечник, индуцирует напряжение различной величины в различных местах на поверхности сердечника и других токопроводящих частях трансформатора. Из-за разности потенциалов в разных местах на поверхности сердечника в сердечнике возникает ток.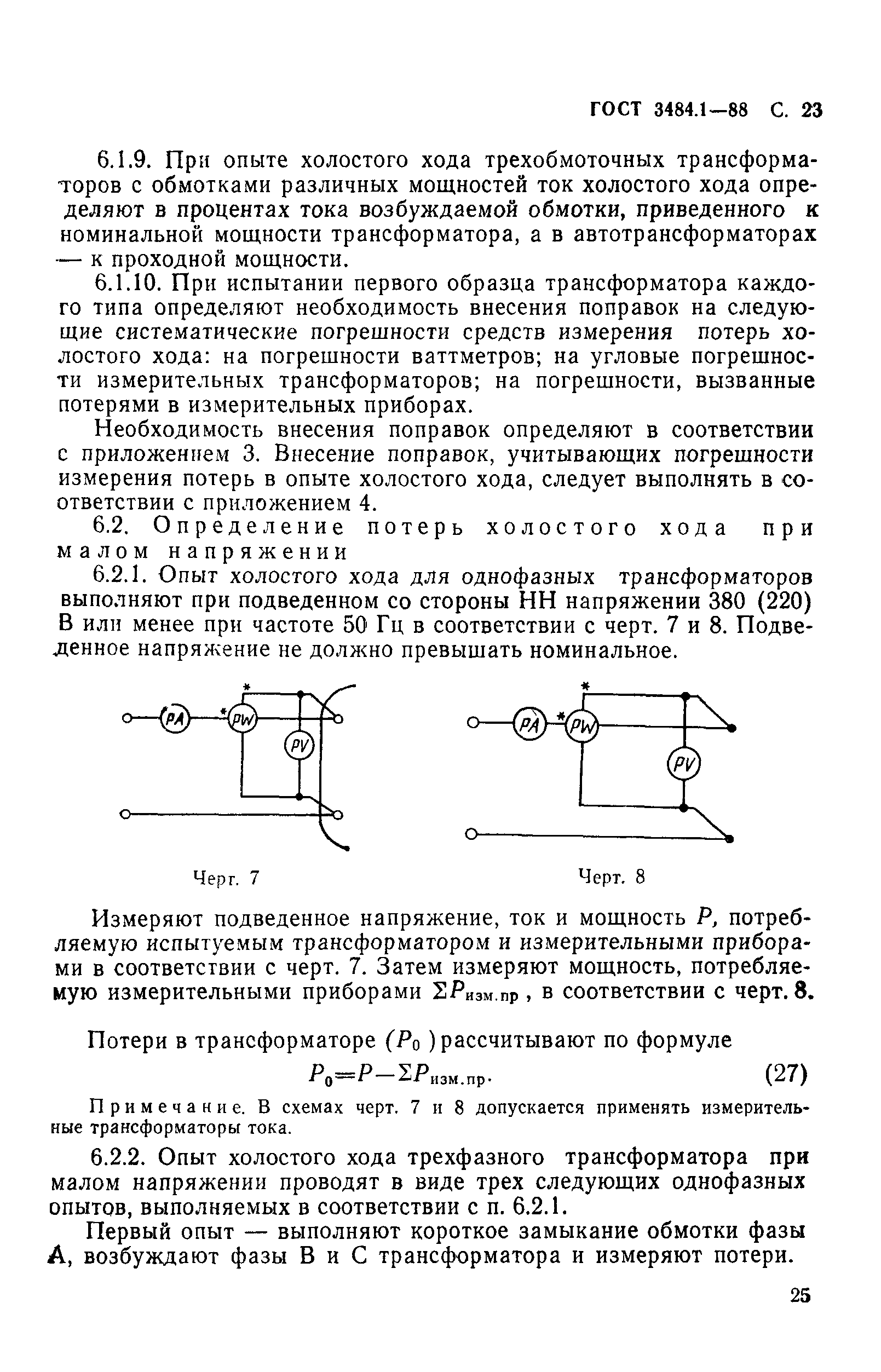 Эти текущие настройки в ядре называются видами токами.
Эти текущие настройки в ядре называются видами токами.
из-за вихревых токов, потери тепла, равные I 2 R потерь происходит в ядре.
Потеря вихревого тока зависит от квадрата тока, протекающего в верхней части сердечника и сопротивлением основного материала. Сплошной лист железного блока имеет меньшее сопротивление из-за большей площади поперечного сечения. Величина напряжения, индуцированной в твердом блоке, более и в результате потери вихревого тока больше в твердом железном блоке.
Почему железный сердечник трансформатора ламинирован?
Чтобы свести к минимуму потери на вихревые токи, железный сердечник формируется из нескольких тонких электроизолированных листов, называемых ламинированием.
Уменьшается площадь пути вихревого тока и уменьшаются потери из-за уменьшения наведенного напряжения и увеличения сопротивления. Тонкий ламинированный лист имеет более высокое сопротивление. Поток вихревых токов в ламинированных листах показан ниже.
Поток вихревых токов в ламинированных листах показан ниже.
Ток, протекающий по листу, равен;
I = разность потенциалов ЭДС, индуцированной в ламинированном сердечнике/сопротивлении листа.
Поскольку тонкий лист имеет более высокое сопротивление по сравнению с сопротивлением толстого листа, ток, протекающий через тонкий лист, очень мал по сравнению с током, протекающим через толстый лист. С уменьшением величины вихревых токов при тонкой штамповке потери на вихревые токи резко уменьшаются. Поэтому сердечник трансформатора изготовлен из тонких ламинированных листов.
Помимо зависимости вихревых токов от сопротивления штамповке, другие электрические параметры, такие как первичное напряжение и частота , также влияют на потери от вихревых токов.
Формула потерь на вихревые токи трансформатора приведена ниже.
Формула потерь на вихревые токи
Влияние колебаний напряжения и частоты на трансформатор
Трансформатор рассчитан на определенное напряжение и частоту. Изменение напряжения питания и частоты от расчетного значения в дальнейшем приведет к увеличению потерь на вихревые токи. Изготовитель трансформатора дает гарантию на потери в стали для работы трансформатора при номинальном напряжении и частоте.
Изменение напряжения питания и частоты от расчетного значения в дальнейшем приведет к увеличению потерь на вихревые токи. Изготовитель трансформатора дает гарантию на потери в стали для работы трансформатора при номинальном напряжении и частоте.
Если напряжение в системе увеличивается, максимальная плотность потока в сердечнике увеличивается, и, следовательно, увеличиваются потери на вихревые токи и потери на гистерезис. Чтобы защитить трансформатор от избыточного потока, измеряется отношение V/F, и трансформатор может быть отключен, если поток в сердечнике превысит указанный предел потока трансформатора.
Потери на вихревые токи резко увеличиваются с увеличением частоты, если напряжение также увеличивается в той же пропорции, потому что потери на вихревые токи пропорциональны квадрату частоты.
Обычно системная частота остается в пределах номинальной частоты +/- 1,5 Гц; однако, если электрическая сеть богата гармониками, это может привести к увеличению потерь на вихревые токи. С увеличением частоты потери на вихревые токи увеличиваются намного больше, чем потери на гистерезис, потому что потери на вихревые токи пропорциональны квадрату частоты, тогда как потери на вихревые токи пропорциональны частоте.
С увеличением частоты потери на вихревые токи увеличиваются намного больше, чем потери на гистерезис, потому что потери на вихревые токи пропорциональны квадрату частоты, тогда как потери на вихревые токи пропорциональны частоте.
Таким образом, потери холостого хода трансформатора равны сумме потерь на вихревые токи и потерь на гистерезис.
Потери холостого хода трансформатора постоянны для номинального напряжения и частоты. Поэтому потери холостого хода также называют постоянными потерями. Потери холостого хода изменяются, если трансформатор работает с плотностью потока выше номинальной. Более того, повышенная плотность потока приводит к искажению вторичного выходного напряжения, и трансформатор, если он работает выше номинальной плотности потока, может выйти из строя. Поэтому для защиты трансформатора используется защита от перенапряжения.
Изменение потерь холостого хода при изменении напряжения и/или частоты
Давайте разберемся, как на гистерезис и потери на вихревые токи влияют изменения частоты и напряжения. Возьмем четыре случая для исследования потерь холостого хода трансформаторов.
Возьмем четыре случая для исследования потерь холостого хода трансформаторов.
Случай 1
Влияние на потери холостого хода – при увеличении/уменьшении частоты при сохранении постоянного напряжения
Потери на гистерезис пропорциональны частоте. Гистерезисные потери должны увеличиваться с увеличением частоты, однако гистерезисные потери остаются практически неизменными. Причина в том, что плотность потока в сердечнике уменьшается в той же пропорции, что и увеличение частоты.
Аналогичным образом гистерезисные потери должны уменьшаться с уменьшением частоты, однако гистерезисные потери остаются практически неизменными из-за увеличения плотности потока в сердечнике.
Потери на вихревые токи пропорциональны квадрату плотности потока и частоты. С увеличением частоты вихревой ток остается неизменным, поскольку произведение B 2 m f 2 остается неизменным, поскольку поток пропорционален отношению V/f. С уменьшением частоты плотность потока в сердечнике увеличивается в той же пропорции, что и уменьшение частоты, и, таким образом, потери на вихревые токи остаются неизменными.
С уменьшением частоты плотность потока в сердечнике увеличивается в той же пропорции, что и уменьшение частоты, и, таким образом, потери на вихревые токи остаются неизменными.
Случай 2
Влияние на потери холостого хода — при увеличении/уменьшении напряжения при сохранении постоянной частоты
Гистерезисные потери прямо пропорциональны напряжению и плотности потока. Гистерезисные потери увеличиваются с увеличением напряжения. Плотность магнитного потока также пропорциональна напряжению.Таким образом, гистерезисные потери пропорциональны квадрату напряжения, если частота поддерживается постоянной.
Таким образом,
Гистерезисные потери, Втч ∝ В 2
Потери на вихревые токи, Вт ∝ В 3
Случай 3
Влияние на потери холостого хода – при увеличении/уменьшении частоты и увеличении/уменьшении напряжения в той же пропорции
Если увеличить частоту и напряжение в той же пропорции, то плотность потока в сердечнике останется неизменной, и в этом случае гистерезисные потери будут увеличиваться пропорционально увеличению частоты. Потери на вихревые токи будут увеличиваться в квадратная доля увеличенной частоты.
Потери на вихревые токи будут увеличиваться в квадратная доля увеличенной частоты.
Случай 4
Влияние на потери холостого хода – когда частота увеличивается/уменьшается, а также увеличивается/уменьшается напряжение в разных пропорциях
В этой ситуации потери на вихревые токи и гистерезис будут увеличиваться или уменьшаться по следующим причинам.
- Увеличение/уменьшение частоты
- Увеличение/уменьшение плотности потока
Связанный пост s
- Потери в меди в трансформаторе
- Что такое потери на вихревые токи? — Определение и выражение
Пожалуйста, подпишитесь на нас и поставьте лайк:
Расчет потерь холостого хода распределительных трансформаторов, питаемых несинусоидальным напряжением, с использованием трехмерного конечно-элементного анализа
https://doi.org/10.1016/j.energy. 2012.09.050Получить права и содержание
2012.09.050Получить права и содержание
Abstract
Трансформаторы в основном предназначены для работы при номинальном напряжении, номинальной частоте, а также при чисто синусоидальном токе нагрузки. В последнее десятилетие изменение типа нагрузки и более широкое использование силовых электронных устройств с их несинусоидальной формой волны тока также искажают форму волны напряжения в системе. Потери трансформаторов включают потери под нагрузкой и потери холостого хода. Потери холостого хода постоянно приводили к потерям энергии в трансформаторах, которые подключены к сети в течение всех 24 ч.Учитывая большое значение энергии и нежелательное влияние потерь на старение трансформаторов, потери холостого хода рассматриваются как критический фактор. В настоящее время необходимо применять подходящий метод расчета потерь холостого хода при наличии гармоник напряжения и условий перевозбуждения, особенно для распределительных трансформаторов, в результате гармонического повышения напряжения и тока в сети и отдельных Приложения. В этой статье метод конечных элементов (FEM) использовался для моделирования влияния несинусоидального напряжения на потери холостого хода трансформаторов.Такое моделирование позволяет программному обеспечению моделировать и анализировать различные электромагнитные параметры, такие как линии потока, плотность потока, потери и т. д., при различных входных источниках и с высокой точностью. Кроме того, было исследовано влияние несинусоидальных напряжений на потери холостого хода на типичном экспериментальном трансформаторе с использованием нескольких практических испытаний.
В этой статье метод конечных элементов (FEM) использовался для моделирования влияния несинусоидального напряжения на потери холостого хода трансформаторов.Такое моделирование позволяет программному обеспечению моделировать и анализировать различные электромагнитные параметры, такие как линии потока, плотность потока, потери и т. д., при различных входных источниках и с высокой точностью. Кроме того, было исследовано влияние несинусоидальных напряжений на потери холостого хода на типичном экспериментальном трансформаторе с использованием нескольких практических испытаний.
Особенности
► МКЭ использовался для расчета потерь распределительного трансформатора при искажении напряжения. ► Этот метод дает точные результаты по сравнению со стандартными или схематическими методами.► Использована новая версия 3D FEM, этот подход основан на электромагнитном поле. ► В литературе МКЭ всегда использовался для изучения потерь нагрузки трансформатора, и большинство из них основано на магнитостатическом МКЭ. ► Результаты МКЭ подтверждены экспериментально для небольшого тестового трансформатора.
► Результаты МКЭ подтверждены экспериментально для небольшого тестового трансформатора.
Ключевые слова
Распределительный трансформатор
Метод конечных элементов
Потери холостого хода
Гармоники напряжения
Рекомендованные статьиСсылки на статьи (0)
Показать полный текст
Copyright © 2012 Elsevier Ltd.Все права защищены.
Рекомендуемые статьи
Ссылки на статьи
Проектирование > Потери в массиве и системе > Потери во внешнем трансформаторе
Определение внешних трансформаторов
Во многих крупных фотоэлектрических установках (в диапазоне МВт) трансформатор не является частью инвертора, а является внешним устройством, напрямую подключенным к сети среднего или даже высокого напряжения.
У вас есть возможность определить:
— Один или несколько инверторов среднего напряжения во всей системе (они будут поровну разделены между всеми выходами инвертора)
— Один инвертор среднего напряжения в каждом подмассиве. Это может быть разным в разных подмассивах, но каждый подмассив должен определять преобразователь.
Это может быть разным в разных подмассивах, но каждый подмассив должен определять преобразователь.
— В конечном итоге трансформатор высокого напряжения (СН => ВН в точке ввода).
Определение трансформатора
Основные потери, связанные с трансформатором:
— Потери в железе (в основном из-за гистерезиса и вихревых токов в сердечнике) пропорциональны квадрату потока сердечника, т.е. квадрату напряжения. Поскольку у нас постоянное напряжение сети, это считается постоянными потерями.PVsyst предлагает значение по умолчанию 0,1 % от эталонной номинальной мощности.
NB: Потери в железе остаются активными и постоянными в течение всего времени подключения и могут представлять собой значительные потери энергии. Это проявляется как отрицательный выход системы E_Grid в ночное время. Поэтому может быть экономически выгодно предусмотреть выключатель для отключения трансформатора от сети в ночное время. Для симуляции доступна опция «Ночное отключение».
— Омические потери, часто называемые потерями в меди, как в первичной, так и во вторичной обмотках. Они могут быть представлены эквивалентным сопротивлением первичной обмотки, а потери будут вычисляться как R * I² во время моделирования. Что касается потерь в проводке, то это означает, что относительные потери пропорциональны току (или мощности).
Они могут быть представлены эквивалентным сопротивлением первичной обмотки, а потери будут вычисляться как R * I² во время моделирования. Что касается потерь в проводке, то это означает, что относительные потери пропорциональны току (или мощности).
Общее определение
Что касается потерь в проводке, PVsyst предлагает общее начальное относительное значение омических потерь для ранней стадии разработки проекта.
Определяется как потеря в процентах по отношению к эталонной номинальной мощности, т.е.е. либо PNomPV(ac), либо PNom(Inv).
Определение спецификаций
Вы также можете определить реальные параметры выбранного трансформатора (рекомендуется).
Основная необходимая информация – это номинальная мощность, потери в стали (часто называемые «потери без нагрузки») и потери в меди.
В спецификациях могут быть указаны либо общие потери при PNom, либо общий КПД, из которых PVsyst выводит потери в меди.
Определение реальных параметров из описания трансформатора исправит общие значения.
Связь между значениями Generic и Datasheets.
Определение параметров с использованием указанных параметров Transfo в PnomTrf:
Производитель трансформатора может указать мощность:
| — Глобальная потеря при этой номинальной мощности | PGLOBLOSSTRF [KW] |
| — железная потеря без нагрузки | PironLSSTRF [KW] |
| => Потеря резистивных мощностей составляет | PResLssTrf = (PGlobLossTrf — PIronLssTrf) [кВт] |
или альтернативно с точки зрения коэффициента потерь при PNom :
| — глобальный коэффициент потерь при PNom | FGlobLossTrf [%] = 100 * PGlobLossTrf / PNomTrf |
| — коэффициент потерь в железе %Trons без нагрузки | r |
| — коэффициент резистивных потерь | FResLssTrf [%] . = 100 * PResLssTrf / PNomTrf = 100 * PResLssTrf / PNomTrf |
Мы можем рассчитать сопротивление трансформатора (основной параметр при моделировании):
| — Номинальный ток при номинальной мощности | INOMTRF = PNOMTRF / (UNOM * SQRT (3)) |
| — => трансформаторное сопротивление | RESTREF = PRESLSSTRF / INOMTRF ² (для одного провода) |
Помните, что резистивная потеря мощности пропорциональна квадрату тока, т.е.е. Рабочая мощность Попер.
Переход к параметрам PVsyst со ссылкой на PnomAC:
В PVsyst потери трансформатора указываются в процентах от эталонной номинальной мощности (либо PNomPV(ac), либо PNom(Inv)).
NB: этот PNom_Ref. является определением для расчетов. Это следует рассматривать как не зависящее от ограничений инвертора или подачи энергии в сеть.
| — | |
| — | pironlss (pvsyst) = pironlsstrf [кВт] (не зависит от pnom) |
| — | Фиронлы (PVSYST) = PironLSSTRF [KW] / PNOM_REF = FIRONLSSTRF * PNOMTRF / PNOM_REF |
| — | PResLss (PVsyst) = PResLssTrf * PNom_Ref ² / PNomTrf ² |
| — | FResLss (PVsyst) = PResLss (PVsyst) / PNom_Ref = FResLssTrf * PNom_Ref / PNomTr, |
я. е. поведение, противоположное потерям в железе (чем выше PNom_Ref, тем выше коэффициент резистивных потерь).
е. поведение, противоположное потерям в железе (чем выше PNom_Ref, тем выше коэффициент резистивных потерь).
Например:
Параметры трансформатора из техпаспорта:
| — | |
| — | pironlsstrf = 1,5 кВт (т.е. 0,1% от pnomtrf) |
=> Резистовая потеря PGLOBLOSSTRF — PIronLssTrf = 15 кВт (т.е. 1,5% от РномТрф).
В PVsyst, если мы выбираем PNom_Ref = PNomPV(ac), и если у нас есть фотоэлектрическая система мощностью 1,05 МВт с эффективностью инвертора = 95% @PNom
=> PnomPV(ac) = 1 МВт (значение PNomPV(ac) отображается как «Pac» в диалоговом окне потерь в цепи переменного тока).
Применение предыдущих выражений:
| — | PIronLss(PVsyst) = 1,5 кВт |
| — | FIronLss(PVsyst) = 1,5 кВт / 1 МВт = 0.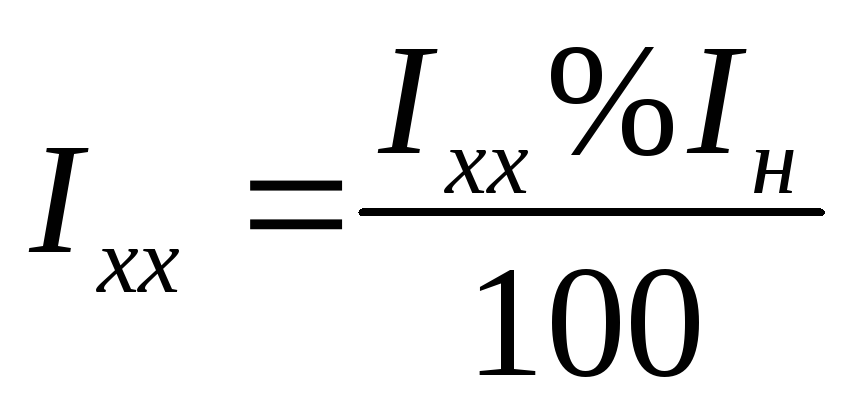 15% 15% |
| — | ||
| — | — | PRESLS (PVSYST) = 15 кВт * (1 МВт / 1,5 МВт) ² = 15 кВт * 0,444 = 6,66 кВт |
| — | Freslss (PVSYST) = 6.66 кВт / 1 МВт = 0,66 % |
Значения 0,15 % и 0,66 % должны быть введены в качестве общих значений в PVsyst.
По какой формуле рассчитать потери и КПД трансформатора. я хочу
какова схема проверки векторной группы трансформатора?
4 ответа
Зеленая сила,
как найти значение сопротивления при потреблении 1кВт на 10
минут
1 Ответ
Больница Манипала,
как сработает высокий уровень сигнала вибрационного выключателя
двигатель? Можете ли вы объяснить с некоторыми примерами и проводкой
диаграммы?
1 Ответ
Бхел, Вартсила,
Электродвижущая сила обеспечивается: (a) Сопротивлением (b) Проводящим путем (c) Электрическим током (d) Источником электропитания
2 ответа
Как идентифицировать счетчик переменного или постоянного тока без использования символа?
4 ответа
ЧТО ТАКОЕ СПЕЦИФИКАЦИИ DG OIL И ЧТО ТАКОЕ
РАЗНИЦА МЕЖДУ МАСЛОМ DG И ТРАНСФОРМАТОРНЫМ МАСЛОМ
4 ответа
1. Что будет храниться в оперативной памяти ИБП EPROM IC?
Что будет храниться в оперативной памяти ИБП EPROM IC?
0 ответов
ИБМ,
Сэр, мне нужен блок питания на 380В. Предложение, которое я получаю
три фазы рассчитаны на 415В. Общий запас, который у меня есть от
снабженческая компания 70кВт. Пожалуйста, сообщите, если это лучше
используйте для этой цели стабилизатор напряжения или трансформатор
3 ответа
в штепсельной вилке, почему размер отверстия вверху большой?
9 ответов
Бхел, ТКС,
Что такое реактивная мощность и где она используется.
0 ответов
Что означает термин Back-to-back в передаче HVDC?
1 Ответ
ССК,
Что такое RTCC в трансформаторе и укажите его функцию.
11 ответов
МКБ, Vodafone,
Динамика потерь холостого хода в силовых трансформаторах
[1]
Красовский, П. Ю. (2012), Рабочая динамика параметров и технических потерь в силовых трансформаторах, Горничная электромеханика та автоматика, т. 1, с. 89, стр. 20-23.
Ю. (2012), Рабочая динамика параметров и технических потерь в силовых трансформаторах, Горничная электромеханика та автоматика, т. 1, с. 89, стр. 20-23.
[2]
Красовский, П.Ю. (2015), Расчет технологических потерь электроэнергии в силовых трансформаторах с учетом периода эксплуатации // Электрификация транспорта. 10, стр. 74-80.
[3]
Казаков, Ю. Козлов А.Б., Коротков В.В. (2006), Учет изменения потерь холостого хода трансформаторов в период эксплуатации при расчете потерь в распределительных сетях // Электротехника. 5, стр. 11-16.
Козлов А.Б., Коротков В.В. (2006), Учет изменения потерь холостого хода трансформаторов в период эксплуатации при расчете потерь в распределительных сетях // Электротехника. 5, стр. 11-16.
[4]
Коротков, А.В., Фролов В.Я. (2014), Методика оценки работоспособности оборудования электротехнических комплексов городских распределительных сетей, Электрика, т. 2, с. 1, стр. 6-10.
[5]
Заугольников, В. Балабин Ф. А., Савинков А. А. Некоторые аспекты экономической эксплуатации силовых трансформаторов // Промышленная энергетика. 4, стр. 10-14.
Балабин Ф. А., Савинков А. А. Некоторые аспекты экономической эксплуатации силовых трансформаторов // Промышленная энергетика. 4, стр. 10-14.
[6]
Балабин, А.А., Волчков Ю. Д. (2009), Повышение точности расчета потерь мощности в трансформаторах 10(6)/0,4 кВ // Механизация и электрификация сельского хозяйства. 4, стр. 22-23.
[7]
Худяков, З. I. (1986), Ремонт трансформаторов, Высшая школа, Москва, Россия.
I. (1986), Ремонт трансформаторов, Высшая школа, Москва, Россия.
[8]
Волчков, Ю.Д., Балабин А.А. (2008), Повышение точности расчета потерь мощности в трансформаторах 35 и 110 кВ // Механизация и электрификация сельского хозяйства. 12, стр. 41-43.
Эффективность трансформатора — ваш электрический гид
КПД трансформатора определяется как отношение выходной мощности к входной мощности. Обозначается ἠ.
Обозначается ἠ.
Поскольку выходная мощность всегда меньше входной мощности из-за потерь в трансформаторе, КПД трансформатора практически всегда находится в диапазоне от 0 до 1, т. е. от 0 % до 100 %, но никогда не может быть 1 или 100 %.
КПД идеального трансформатора равен 1 или 100 %, так как потери в идеальном трансформаторе равны нулю.
График зависимости выходной мощности от КПД трансформатора показан на рисунке. Из рисунка видно, что КПД увеличивается с увеличением выходной мощности до определенного значения, а после определенного значения выходной мощности КПД трансформатора снижается.
Значение КПД трансформатора будет максимальным, когда потери в меди будут равны потерям в железе в трансформаторе. Значение максимального КПД можно найти, приняв общие потери равными 2P i . Он также зависит от коэффициента мощности нагрузки и имеет максимальное значение при коэффициенте мощности, равном единице.
Трансформатор с переменной нагрузкой (например, распределительный трансформатор ) рассчитан на максимальную эффективность примерно при 75% полной нагрузки.
И если он постоянно работает при полной нагрузке (например, силовые трансформаторы ), то он рассчитан на максимальную эффективность при полной нагрузке или вблизи нее.
Трансформатор не имеет движущихся частей, поэтому потери на трение и ветер отсутствуют, поэтому его КПД очень высок. Он может быть по крайней мере равен 90%. Его выход и вход имеют почти одинаковое значение. Следовательно, их соотношение не может быть точно найдено путем измерения входной и выходной мощности.
Чтобы решить эту проблему , лучше отдельно измерить потери трансформатора , а затем найти КПД трансформатора по формуле КПД трансформатора . Потери в железе и меди могут быть очень легко и точно определены с помощью испытаний на холостом ходу и испытаний на короткое замыкание на трансформаторе соответственно.
Эффективность трансформатора в течение всего дня
Обсуждаемый до сих пор КПД представляет собой обычный, коммерческий или энергетический КПД трансформатора.Но для распределительного трансформатора это не дает истинного представления о производительности трансформатора, поскольку нагрузка на распределительный трансформатор колеблется в течение дня. Этот трансформатор находится под напряжением в течение 24 часов, но большую часть дня он обеспечивает очень легкую нагрузку.
Таким образом, потери в железе имеют место в течение всего дня, а потери в меди — только при нагрузке трансформатора.
Следовательно, производительность такого трансформатора (например, распределительного трансформатора) не может оцениваться по энергоэффективности.Но об этом можно судить по особому типу КПД трансформатора, известному как энергоэффективность или КПД в течение всего дня. Эффективность в течение всего дня рассчитывается на основе энергии, потребленной в течение суток.
КПД трансформатора в течение всего дня определяется как отношение выходной энергии (в кВтч) к входной энергии (в кВтч) в течение суток.
Чтобы найти КПД трансформатора в течение всего дня, нам нужно знать цикл нагрузки трансформатора.
Расчет эффективности трансформатора
Пример : Трансформатор мощностью 500 кВА имеет потери в железе 2500 Вт и потери в меди 7500 Вт при полной нагрузке. Коэффициент мощности составляет 0,8 отставания. Рассчитать:
- КПД трансформатора при полной нагрузке,
- максимальный КПД трансформатора,
- выходная мощность кВА, соответствующая максимальной эффективности,
- при половинной нагрузке.
КПД трансформатора
Решение : Номинальная мощность трансформатора = 500 кВА
Выходная мощность трансформатора = 500 000 x 0.8 = 400 000 Вт
Потери в стали (P i ) = 2500 Вт
Потери в меди при полной нагрузке (P cu ) = 7500 Вт
Эффективность трансформатора при полной нагрузке
= [(выходная мощность)/(выходная мощность + P i + P cu )] x 100 Ответ)
Максимальная эффективность трансформатора
Для максимальной эффективности потери в меди (P c ) = потери в стали (P i ) = 2500 Вт x 100
Следовательно, максимальная эффективность = [(400 000)/(400 000 + 2500 + 2500)] x 100
= 98. 76% (ответ)
76% (ответ)
Выходная мощность, кВА, соответствующая максимальной эффективности
= полная нагрузка KVA X √ (P I / P C )
= 500 x √ (2500/7500)
= 500 x √0.333 = 166,5 кВА (ANS)
Эффективность трансформатора при половинной нагрузке
Доля нагрузки, при которой рассчитывается КПД (x) = половинная нагрузка = ½ = 0,5
Следовательно, x = 0,5
Следовательно, подставьте x = 0,5 в вышеприведенную формулу, чтобы получить КПД трансформатора при половинной нагрузке
= [(0.5 x 400 000)/{(0,5 x 400 000) + 2500 + (0,5) 2 x 7500)}] x 100
= [ 200 000/ { 200 000 + 2500 + 3900 } x 9,2 8 An
Расчет КПД трансформатора в течение всего дня
Пример : Трансформатор мощностью 20 кВА на бытовой нагрузке, коэффициент мощности которого можно принять равным единице, имеет КПД при полной нагрузке 95,3%, при этом потери в меди в два раза превышают потери в железе. Рассчитайте его эффективность в течение дня при следующем дневном цикле:
Рассчитайте его эффективность в течение дня при следующем дневном цикле:
- без нагрузки в течение 10 часов,
- половинная загрузка на 8 часов,
- полная загрузка на 6 часов.
Решение : Выходная мощность при полной нагрузке = 20 x 1 = 20 кВт
Потребляемая мощность при полной нагрузке = мощность/КПД = (20/95,3) x 100 = 20,986 кВт
Общие потери = P i + 4 cu = Вход – Выход = 20,986 – 20 = 0,986 кВт
Теперь P у.е. = 2P i (задано)
Следовательно, P i + 2P i = 101 4 4 900 кВт ) = 0,3287 кВт
Потери в меди при полной нагрузке (P cu ) = 2 x 0.3287 = 0,6574 кВт
кВтч мощность за 24 часа = {(1/2) x 20 x 8} + (1 x 20 x 6) = 200 кВтч
Потери в железе за 24 часа = 0,3287 x 24 = 7,89 кВт
Потери меди за 24 часа = потери меди за 8 часов при половинной нагрузке + потери меди за 6 часов при полной нагрузке
= 5,259 кВтч
Вход за 24 часа = кВтч выход за 24 часа + потери в железе и меди за 24 часа
= 200 + 7. 89 + 5,259 = 213,149 кВтч
89 + 5,259 = 213,149 кВтч
КПД трансформатора в течение всего дня = (выработка кВтч за 24 часа / потребляемая кВтч за 24 часа) x 100
= (200/213,149) = 93,83% (ответ)
1 9 Спасибо за чтение о формуле КПД трансформатора
.
Трансформатор | Все сообщения
© https://yourelectricalguide.com/ формула и расчет КПД трансформатора.
Расчет потерь трансформатора без нагрузки
Трансформаторы имеют два основных компонента, определяющих потери: сердечник и катушки.Типичный сердечник представляет собой сборку из многослойной стали, и потери в сердечнике в основном связаны с намагничиванием (возбуждением) сердечника. Потери в линии и потери в трансформаторе после PCC.
В последнее десятилетие изменение типов нагрузок и более широкое использование силовых электронных устройств с несинусоидальной формой волны тока привели к искажению . Будут описаны требования к приборам для измерения потерь холостого хода, чтобы гарантировать правильное применение поправочной формулы.
Это исследование посвящено параметрическому анализу потерь холостого хода трансформатора под действием напряжения возбуждения с несколькими субгармоническими составляющими.
В литературе по электротехнике измерение и расчет обеих потерь хорошо известны для случаев синусоидального напряжения и линейной нагрузки (синусоидальный ток).
Введение в измерение потерь. Ведущий автор этого документа: Анджело Баггини (ECD). Потери силового трансформатора можно разделить на две основные составляющие: потери холостого хода и потери нагрузки. Потери — это потери энергии в устройстве, которые влияют на общую эффективность устройства.
Таким образом, необходимо знать потери устройства, чтобы спроектировать компонент с минимальными потерями. Трансформатор — это компонент электрической изоляции, который передает мощность от первичной обмотки к вторичной без какого-либо физического контакта. Дан краткий обзор этих потерь, хотя в большинстве анализов предполагается, что потери холостого хода состоят из потерь на гистерезис и вихревых токов.
Расчет потерь в магнитных материалах для искаженных форм магнитных волн довольно сложен.Это дает вам информацию о самом энергоэффективном трансформаторе в течение всего срока службы. Оценка наиболее экономичного трансформатора будет производиться по капитализированной стоимости, сроку окупаемости и внутренней норме прибыли. Номинальная мощность, кВА, коэффициент напряжения, заводской номер (SPN). Существуют различные методы расчета убытков по приведенной стоимости, в том числе один, специально разработанный для . РАСЧЕТЫ ПОТЕРИ НАГРУЗКИ И СОПРОТИВЛЕНИЯ, Входные данные в желтых ячейках.
Метод совокупной стоимости владения (TOC) обеспечивает эффективный способ оценки первоначальных закупочных цен различных трансформаторов и стоимости потерь.Общие потери в цепи DT равны 8. Термины индекса — фидерная цепь, расчет потерь, коэффициент потерь,. Поэтому для распределительных трансформаторов нет записей об измеренных нагрузках. Потери в железе = испытание без нагрузки, потери в меди = испытание на короткое замыкание.

 51)
51)