Параллельное соединение резистора и конденсатора
Автор Aluarius На чтение 5 мин. Просмотров 926 Опубликовано
Для чего предназначены резисторы и конденсаторы
Резисторы – одни из наиболее распространённых элементов в электронике. Их главное назначение – сопротивление течению тока и преобразовывать его в тепло. Главной характеристикой данных элементов является значение R.
Чем больше величина R, тем большая часть электроэнергии сможет рассеется в тепло. В схемах, которые питаются небольшим напряжением от 5 до 12 В, чаще всего используют резисторы имеющие величину R от 100 Ом до 100 кОм.
Конденсаторы – устройства, главная задача которых накапливать электрические заряды. Стоит отметить, что эту же функцию выполняет и аккумулятор, но в отличие от батареи конденсатор сразу же отдаёт весь накопившийся заряд.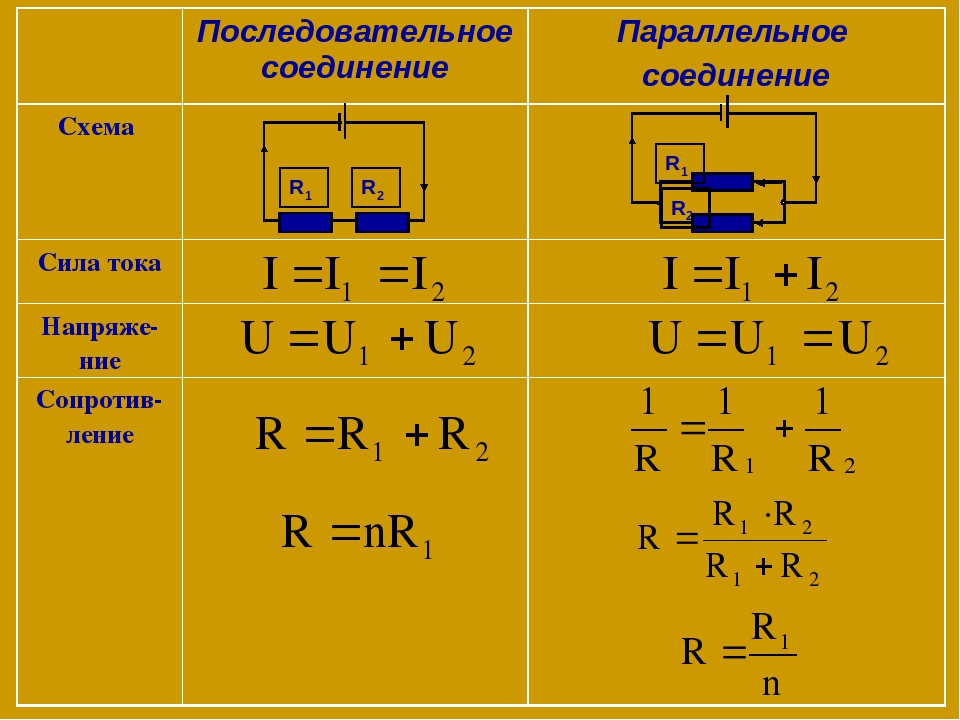 Величина, которую способно накопить устройство, называют «ёмкость».
Величина, которую способно накопить устройство, называют «ёмкость».
Когда подсоединяется цепь к источнику электроэнергии: через конденсатор течет электрический ток. Сила тока в начале прохождения через устройство имеет наивысшее значение, в это же время напряжение станет низким.
После того, как устройство начнет накопление заряда, сила тока упадёт до нуля, а напряжение наоборот станет увеличиваться.
Особенности соединения резистора и конденсатора в цепи
Существует два типа соединения резисторов и конденсаторов: параллельное и последовательное.
Параллельное соединение резистора и конденсатора
Для того, чтобы осуществить параллельное соединение резистора и конденсатора, необходимо объединить все элементы цепи двумя узлами. Они не должны иметь связи с другими элементами.
При таком соединении, величина напряжения между обоими узлами станет падать, и оно станет равным для каждого элемента. А величина, которая обратна общему R, будет равняться сумме величин, которые обратны R всех проводников.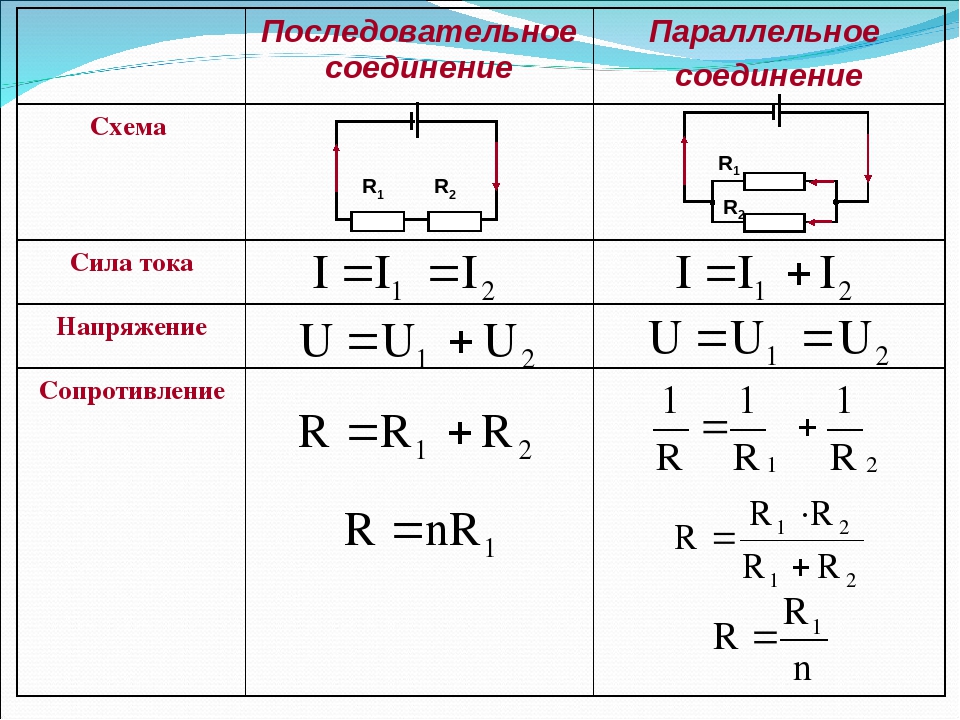
Когда осуществляется параллельное соединение резисторов, проводимость всех резисторов станет равняться проводимости цепи.
Если резистор соединить к заряженному конденсатору то вполне возможно короткое замыкание.
Последовательное соединение
Последовательное соединение – связка элементов между собой так, чтобы начальный участок цепи не имел ни одного узла. При таком соединении величина тока на проводниках станет равна между собой.
Когда осуществляется последовательное соединение всех элементов, то их общая ёмкость имеет формулу 1/Собщ = 1/С1 + 1/С2 + … + 1/Сn.
Как рассчитать импеданс в цепи
Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.
Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.
Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.
К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.
Стоит отметить! Активное R, имеет одно и тоже значение, как при последовательном, так и при параллельном соединении.
Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.
Практические расчеты импеданса чаще всего выполняются по следующей формуле:
Z = Um/Im.
Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.
Энергия будет храниться и выделяться в двух типах:
- Магнитного поля.
 Реактивная часть является индуктивной.
Реактивная часть является индуктивной. - Электрического поля.
Как рассчитать время разряда и заряда конденсатора через резистор
Чтобы осуществить заряд устройства, нужно включить устройство в цепь и присоединить к зажимам генератора. Как вы уже знаете, генератор имеет внутреннее сопротивление.
Если резистор подключить к заряженному конденсатору то ключ будет замкнут и конденсатор начнёт зарядку до напряжения между обкладками, которая станет равна э.д.с генератора и равна Uc=E. При этом, обкладка которая соединена с положительным зажимом, получит положительный заряд, вторая же получит отрицательный заряд.
Чтобы обе обкладки устройства полностью зарядились, нужно, чтобы одни из них приобрела определенное количество электронов, а вторая столько же потеряла.
Зарядный ток в цепи будет протекать сотые доли секунды, пока величина напряжения на устройстве достигнет такой же уровня, что и на генераторе. В то время, пока конденсатор будет заряжаться, по всей цепи будет проходить зарядный ток.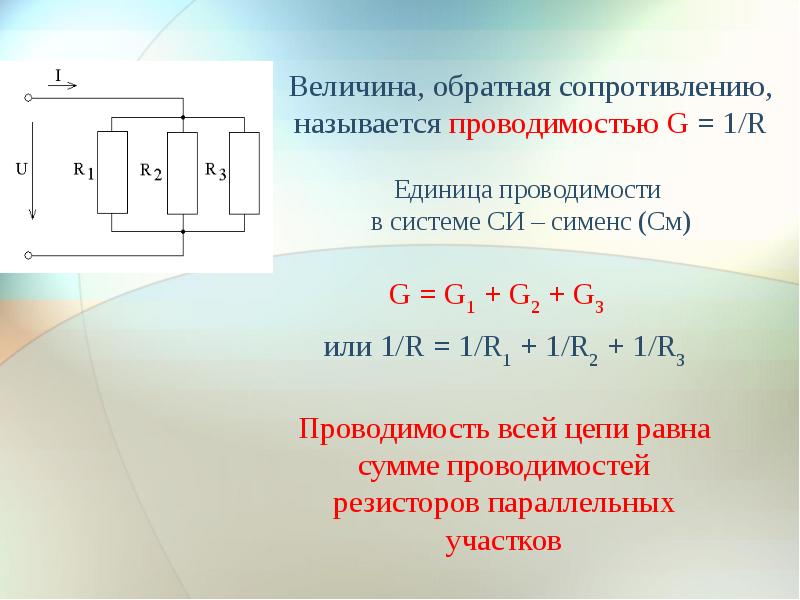 Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.
Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.
По мере того как конденсатор станет заряжаться, величина R на нём будет падать.
Время процесса зарядки будет зависеть от следующих величин:
- Внутреннее сопротивление электрического генератора.
- Способность конденсатора принять количество тока.
Для того, чтобы разрядить устройство нужно отключить его от генератора переменного тока и присоединить к его обкладкам сопротивление. Дело в том, что на обкладках уже есть разность потенциалов, поэтому в цепи потечет ток.
Он будет проходить от одной обкладки через сопротивление к другой. Процесс разряда будет проходить до тех пор, пока обе обкладки не станут равны, т.е. пока напряжение между ними станет равно 0.
В самом начале, напряжение будет максимальным, сила тока – наибольшая. Как только начнется разрядка, напряжение и сила тока будут уменьшаться.
Продолжительность разряда устройства имеет зависимость от:
- Отношению заряда к разности потенциалов;
- Удельному электрическому сопротивлению.

Чем значение сопротивления выше, тем дольше будет происходить разряд конденсатора. Это можно объяснить тем, что при максимальном сопротивлении, сила тока небольшая, а величина заряда станет медленно уменьшаться.
Важно! Заряженный конденсатор не станет пропускать постоянный ток, потому что диэлектрик между его положительной и отрицательной обкладками будет размыкать цепь.
Для того, чтобы рассчитать время заряда и разряда на устройстве, лучше всего воспользоваться онлайн калькулятором.
как подключить резистор в цепь
Резистор — это прибор, который обладает устойчивым, стабильным показателем сопротивления. Это помогает производить регулировку параметров на любом участке схемы. В этой статье говорится о том, как подключить резистор в цепь и какие методы для этого существуют. Также продемонстрированы несколько простых, но полезных схем, которые могут пригодиться при работе с электрикой.
Что такое соединение резисторов
Подключение приборов различными методами помогает получить нужное число мощности одной единицы цепи.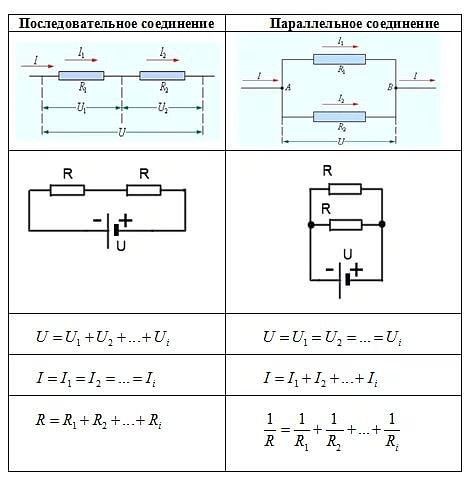 Есть три основных метода подключения прибора — последовательное, параллельное и смешанное. Ниже подробно рассказано о каждом из них.
Есть три основных метода подключения прибора — последовательное, параллельное и смешанное. Ниже подробно рассказано о каждом из них.
Как выглядят резисторы
Внимание! Для работы необходимо использовать только качественные приборы, на которые действует гарантия.
Как подключить резистор в цепь
Для сборки составного устройства необходимо соединить несколько элементов одним из основных методов и таким образом получить нужный номинальный показатель. В практике это используется очень часто. Навыки правильного подключения устройств и расчета их общего сопротивления используются мастерами для ремонта проводки или радиолюбителями при сборке устройства. В интернете можно найти много схем с различным видом подключения. Ниже описано какое соединение резисторов называется параллельным.
Параллельное соединение резисторов схема
Параллельно
Параллельное — это одно из двух типов электрических соединений, когда два вывода единственного устройства соединены с соответствующими выводами других элементов. Очень часто их могут соединять последовательно или параллельно, чтобы сделать более усложненные электрические схемы.
Очень часто их могут соединять последовательно или параллельно, чтобы сделать более усложненные электрические схемы.
При этом виде соединения напряжение на всех устройствах будет равным, а проходящий через них ток — пропорционален их сопротивлению.
Такой вариант подключения один из простых, очень часто именно его рекомендуют использовать тем, кто не имеет опыта работы с электрикой.
Последовательно
Формула расчета достаточно легкая. Общее сопротивление при параллельном соединении формула:
Rобщ. = R1+R2+R3+…+Rn.
Сопротивление двух и более параллельно соединенных резисторов указано как Rобщ.
Последовательный способ подключения
Остальные элементы указываются как R, R2, R3 и так далее.
Обратите внимание! Используя последовательное соединение, необходимо запомнить один важный нюанс. Из общего количества компонентов, соединённых последовательным методом, основную роль занимает тот, у которого самое высокое сопротивление.
Как это понять? Для примера, если необходимо соединить три устройства, номинал которых будет равняться 1, 10 и 100 Ом, то в итоге получится составной на 111 Ом.
Смешанный тип подключения
Если исключить прибор на 100 Ом, то все сопротивление схемы резко снизится до 11 Ом. А если исключить, например, на 1 Ом, то показатель получится уже 110 Ом. В итоге устройства с небольшим сопротивлениями в последовательной цепочке почти не влияют на все показатели.
Какая мощность тока при последовательном и параллельном соединении
При соединении устройств последовательным методом ток будет проходить через каждое сопротивление. Показатель тока в любом месте цепочки будет равным. Это правило определяется при помощи закона Ома. Если суммировать все показатели в цепи, получится такое выражение:
Образец цепи
R = 200+100+51+39 = 390 Ом.
Напряжение на схеме равняется 100 В, по правилу Ома сила тока будет выражаться:
I = U/R = 100/390 = 0,256 A.
Теперь с помощью этих уравнений можно посчитать мощность при последовательном подключении, используя это выражение:
P = I2 x R = 0,2562×390 = 25,55 Вт.
При параллельном соединении все основания нужно подсоединить к одному узлу цепи, а концы — к другому. В таком варианте получается разветвление тока, и он будет проходить по каждому узлу. По правилу Ома, сила тока будет обратно пропорциональна всем имеющимся устройствам, а показатель напряжения везде одинаковый.
При смешанном подключении используются свойства обоих видов соединений.
Закон Ома для участка цепи
Как правильно рассчитать сопротивление
Для выбора и установки элементов в цепь нужно заранее просчитать номинал и мощность составных частей.
Применяют для этого правило Ома для участка цепи, чтобы рассчитать сопротивление, выражение выглядит так:
R = U/I.
U — будет напряжением на выводах компонента.
I — показатель тока на участке цепи.
Это выражение используется для токов постоянного направления.
Если трудно самостоятельно рассчитать этот показатель, то существуют специальные онлайн-калькуляторы. Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Внимание! Если нет опыта в работе с электрикой, желательно не выполнять ремонт проводки самостоятельно, потому что при неправильной работе может случиться короткое замыкание, что чревато возникновением пожара. Также необходимо помнить, что при работе с проводкой нужно полностью обесточить сеть.
Подключение для светодиодов
В заключении необходимо отметить, что подключать резисторы можно тремя способами: параллельно, последовательно и смешанно. Для тех, кто не имеет особых навыков работы с электрикой, рекомендуется выбирать последовательный метод соединения.
Параллельное соединение резисторов
Параллельное соединение резисторов.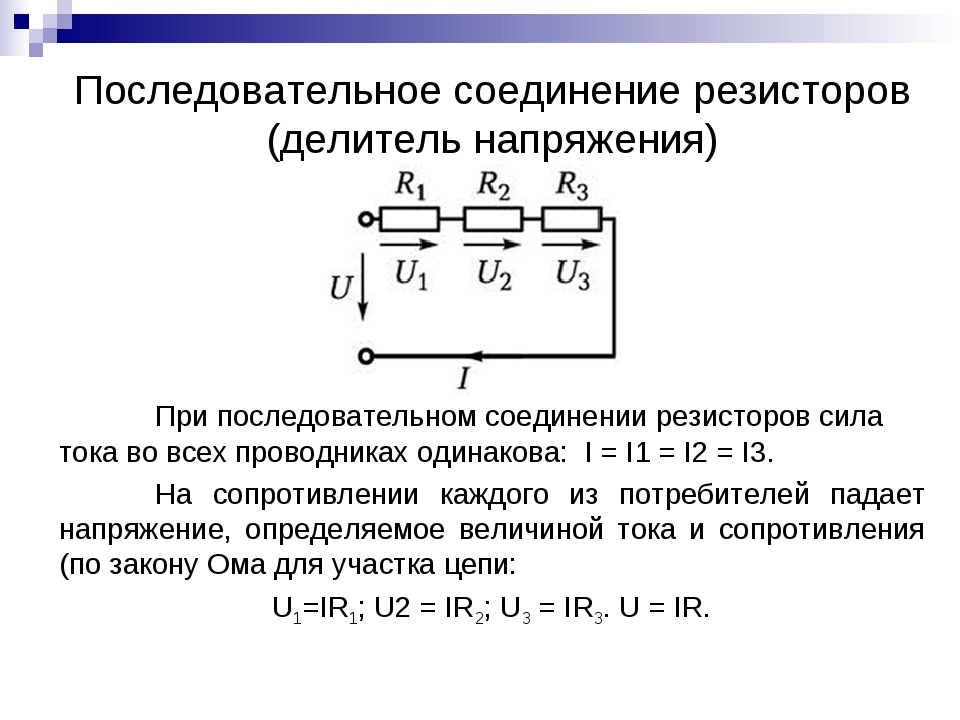 При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.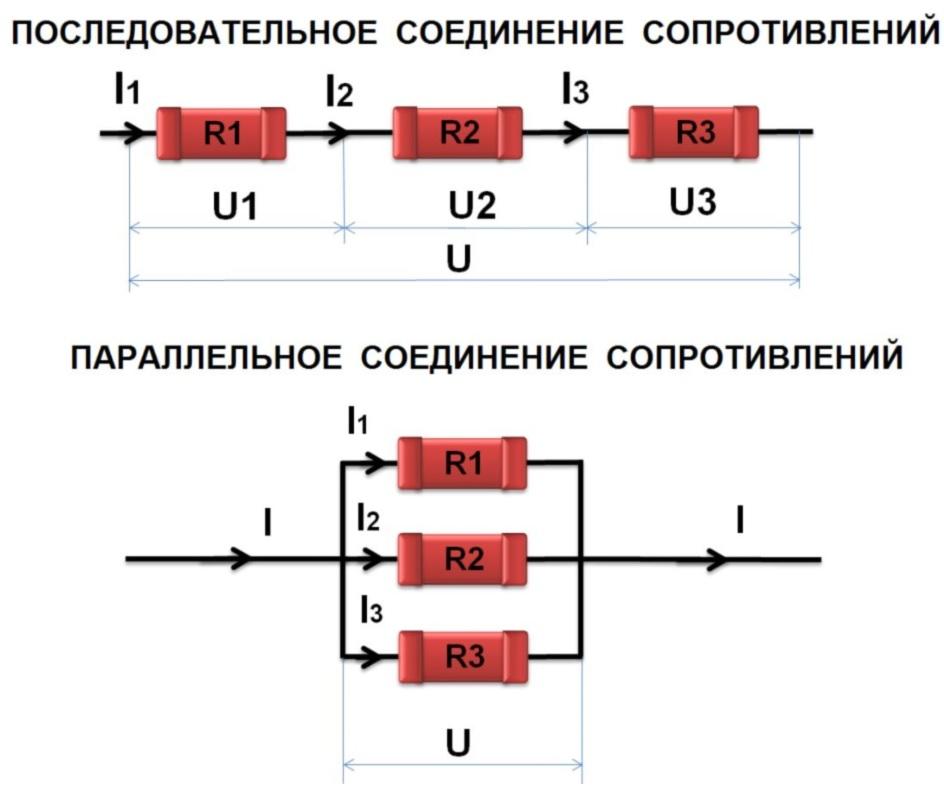
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т. е.
е.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Как распределяются токи при параллельном соединении резисторов
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму – концы.
Общее сопротивление параллельно включенных сопротивлений определяется по формуле
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение.
На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.
Первый частный случай
Если параллельно включено только два резистора то их общее сопротивление можно определить по формуле
Второй частный случай
Если параллельно включено любое количество резисторов одинаковых сопротивлений то их общее сопротивление можно определить если сопротивление одного резистора разделить на количество резисторов.
Так как начала всех сопротивлений сведены в одну общую точку, а концы – в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.
Второе свойство цепи с параллельным соединением заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит что чем больше сопротивление тем меньше по нему пойдет ток.
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:
Следовательно, третье свойство параллельного соединения может сформулирована так:
Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.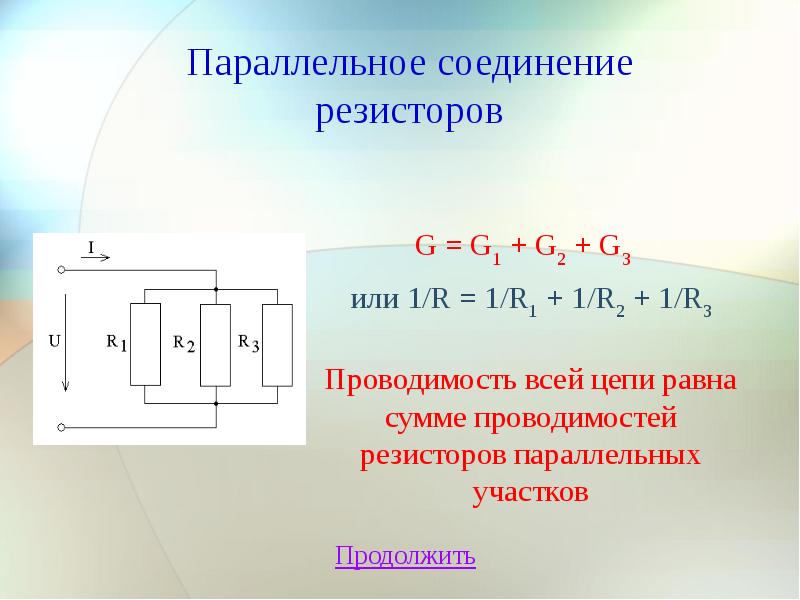
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.

- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).
Рис. 1 Изображение параллельного соединения трех резисторов
1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении
Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений
Для двух параллельно соединенных сопротивлений
Для ветвей с одинаковым сопротивлением где n количество ветвей
Ток при параллельном соединении
Мощность при параллельном соединении
Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам
Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость
и эквивалентное сопротивление
Для двух резисторов
Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой
в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
Параллельное соединение резисторов в цепи постоянного тока — КиберПедия
Общие сведения
Если резисторы или любые другие нагрузки соединены параллельно (рис. 2.3.1), все они находятся под одинаковым напряжением:
2.3.1), все они находятся под одинаковым напряжением:
U = UR1 = UR2 = UR3
Рис. 2.3.1
В каждой ветви цепи протекает свой ток. Сумма токов всех ветвей в соответствии с первым законом Кирхгофа равна полному току:
I = I1 + I2 + I3.
Величина тока ветви зависит от приложенного напряжения и сопротивления данной ветви:
Ток в неразветвленной части цепи зависит от приложенного напряжения и эквивалентного сопротивления цепи:
Для вычисления эквивалентного сопротивления цепи служит формула:
Для цепи с двумя параллельно соединенными резисторами:
Экспериментальная часть
Задание
Измеряя напряжения и токи, убедиться, что напряжение, прикладываемое к каждому резистору, одинаково и что сумма токов ветвей равна полному току цепи. Проверить результаты измерения расчётом.
Порядок выполнения эксперимента
- Соберите цепь согласно монтажной схеме (рис. 2.3.2), вставив последовательно с каждым и резисторов (330, 220 и 470 Ом) специальные миниблоки для подключения амперметра.
- Измерьте напряжение на каждом резисторе, а также напряжение на источнике. Убедитесь, что все они одинаковы и запишите значение напряжения в табл. 2.3.1.
- С помощью мультиметра, специального кабеля со штекером и миниблоков для подключения амперметра измерьте токи в каждом резисторе и на входе цепи. Результаты запишите в табл. 2.3.1.
- Рассчитайте эквивалентное сопротивление цепи, ток в каждом резисторе и на входе цепи. Результаты занесите в табл. 2.3.1 и сравните с измеренными значениями.
- Проверьте как по экспериментальным, так и по расчётным данным, выполняется ли первый закон Кирхгофа:
I = I1 + I2 + I3.
Таблица 2.3.1
|
Напряжение (U), B | Токи в ветвях, мА | Ток на входе цепи, мА | |||
| 330 Ом
(I1) | 220 Ом
(I2) | 470 Ом (I3) | Rэкв=… Ом
(I) | ||
| Измеренные значения | |||||
| Рассчитанные значения |
Рис. 2.3.2
Лабораторная работа № 3
Цепь постоянного тока при смешанном соединении резисторов
Общие сведения
На рис. 2.4.1 показан пример цепи со смешанным (т.е. последовательно-параллельным) соединением резисторов. Цепь состоит из последовательно (R1 и R2) и параллельно (R3 и R4) соединенных резисторов.
Рис. 2.4.1
Участки цепи с последовательным и параллельным соединением резисторов относительно друг друга соединены последовательно. Чтобы вычислить полное сопротивление цепи сначала определяют эквивалентное сопротивление параллельного участка:
Затем определяют эквивалентное сопротивление всей цепи, состоящей теперь из трёх последовательно соединённых сопротивлений:
Для расчёта токов в этой цепи необходимо сначала определить по закону Ома ток в эквивалентном сопротивлении, он же в сопротивлениях R1 и R2:
.
После этого опять же по закону Ома определяются напряжение на участке с параллельным соединением и токи в параллельных ветвях:
.
Экспериментальная часть
Задание
Измерить токи, напряжения и мощность в цепи при смешанном соединении резисторов. Проверить результаты измерений расчётом. Проверить выполнение первого и второго законов Кирхгофа и баланса мощностей.
Параллельное соединение резистора и конденсатора — КиберПедия
Общие сведения
Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
Рис. 6.2.1
Общий ток цепи I разветвляется на ток в конденсаторе IC(емкостная составляющая общего тока) и ток в резисторе IR(активная составляющая).
Между токами I, IC и IR существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением XC конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).
| Рис. 6.2.2 | Рис. 6.2.3 |
Фазовый сдвиг между напряжением U цепи и током в резисторе IRотсутствует, тогда как между этим напряжением и током в конденсаторе IC равен –900 (т.е. ток опережает напряжение на 900). При этом сдвиг между полным током Iи напряжением U цепи определяется соотношением междупроводимостями BC и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3).
В треугольнике проводимостей G=1/R, BC=1/XC, а Y представляет собой так называемую полную проводимость цепи в См, тогда как G – активная, а BC– реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = IR +IC.
Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи
; I = U ¤ Z = UY.
Полная проводимость цепи
; Y = I ¤U = 1/Z ,
гдеZ— полное сопротивление цепи.
Угол сдвига фаз
j = arctg (I C ¤ IR) = arctg (BC ¤ G).
Активная и реактивная проводимости
G = Y cosj; BC = Y sinj.
Экспериментальная часть
Задание
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IR и конденсаторе I C, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и емкостную реактивную проводимость BC.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.
Рис. 6.2.4
· Выполните измерения U, I, IC, IR и занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте также R, j, XC, Z.
Таблица 6.2.1
| U, B | I, мА | IС, мА | IR, мА | j, град | R, Ом | XC, Ом | Z, Ом | Примечание |
| Расчет | ||||||||
| Вирт. Изм |
· Вычислите и запишите в таблицу:
Фазовый угол
j = arctg (I C ¤ I R) =
Активные проводимость цепи и сопротивление цепи
G = IR ¤ U ; R = U ¤ IR.
Емкостные реактивные проводимость и сопротивление цепи
BC = IC ¤ U ; XC = U ¤ IC.
Полные проводимость и сопротивление цепи
; Z = 1 ¤ ÖY.
· Сравните результаты вычислений с результатами виртуальных измерений (если они есть).
· Постройте векторную диаграмму токов (рис. 6.2.5) и треугольник проводимостей (рис. 6.2.6).
Рис. 6.2.5 Рис. 6.2.6
Комбинация резисторов — последовательно и параллельно — Учебный материал для IIT JEE
- Полный курс физики — 11 класс
ПРЕДЛАГАЕМАЯ ЦЕНА: рупий.2 968
- Просмотр подробностей
Введение в сочетание резисторов — последовательных и параллельных
Электрический ток — это поток заряженных частиц.Поток зарядов будет постоянным в текущей электроэнергии. Электрический ток течет от более высокого электрического потенциала к более низкому электрическому потенциалу. Для протекания тока требуется замкнутый контур из проводящего материала. Схема состоит из проводов, соединенных встык, и электроны текут в одном направлении.
Схема имеет жилы (провод), переключатель, нагрузку и источник питания. Схема начинается и останавливается в одной и той же точке. Обычно медные провода используются как жилы без изоляции.Именно через проводник течет ток. Переключатель используется для размыкания или замыкания цепи. Когда переключатель замкнут, ток течет по цепи, а когда переключатель разомкнут, он размыкает цепь, и ток через нее не течет. Клетка может быть источником энергии. Если мы поместим более одной ячейки, она станет батареей.
Нагрузка, также известная как резистор , , использует электрическую энергию и преобразует ее в другую форму энергии. Это может быть лампочка или что-нибудь еще.Если в цепи нет нагрузки, это будет короткое замыкание.
Схема А
Параметры цепи
Электрический ток измеряется в амперах (амперах) амперметром, который подключается последовательно с другими компонентами в цепи. Ток, I = Q / t, где Q — заряд в кулонах, а t — время в секундах. Андре Мари Ампер обнаружил, что два параллельных провода притягиваются друг к другу, когда электрический ток течет в одном направлении.Кроме того, два параллельных провода отталкиваются друг от друга, когда электрический ток течет в противоположных направлениях. В результате его открытий в этой области, единица измерения тока была получена из его имени, которое называется « amp ». Один ампер равен одному кулону заряда в секунду времени.
Напряжение определяется как разность электрических потенциалов между двумя точками в цепи. Единица измерения напряжения — вольт. Устройство происходит от имени Алессандро Вольта. Элементы или батареи обеспечивают необходимое напряжение или разность потенциалов.
Сопротивление препятствует прохождению тока. Это мера способности объекта удерживать поток электронов. Сопротивление будет низким в проводнике и высоким в изоляторе. Измеряется в омах. Единица ома названа в честь ученого Георга Симона Ома, сформулировавшего закон Ома.
Резисторы используются для управления прохождением электрического тока в цепи. Он преобразует электрическую энергию в тепло и свет. Резистор является пассивным компонентом, поскольку он потребляет мощность, но не генерирует ее.Обычно они состоят из металла, углерода или пленки оксида металла. Резисторы используются для ограничения тока и защиты полупроводниковых устройств, таких как светодиоды. Он также используется для ограничения частотной характеристики в цепи фильтра.
Закон Ома
Георг Симон Ом показал взаимосвязь между напряжением, током и сопротивлением и сформулировал закон Ома. Этот закон лежит в основе электричества.
Закон гласит, что V = I R, где напряжение V выражено в вольтах, ток I — в амперах, а сопротивление R — в омах.
Таким образом, I = V / R и R = V / I.
Для большей наглядности электричество можно отнести к воде. Таким образом, напряжение в цепи, единицей измерения которой являются вольты, идентично давлению воды, текущей в трубе. Ток в цепи, где единица измерения равен амперам, эквивалентен воде, протекающей по трубе. Сопротивление в контуре, измеряемое в омах, такое же, как сопротивление трения и размер трубы, которая ограничивает поток воды.
Закон Ома
Серия и параллельное соединение
В основном есть два типа цепей: последовательные и параллельные.И последовательная, и параллельная цепи состоят из более чем одной нагрузки. Резисторы могут быть подключены последовательно, параллельно или их комбинация.
В последовательной цепи электронов движутся только по одному пути. Здесь будет тот же ток, который проходит через каждый резистор. Напряжение на резисторе при последовательном включении будет другим. При последовательном соединении, если один резистор сломан или возникает какая-либо неисправность, вся цепь выключается. Последовательные цепи нелегко перегреть.Конструкция последовательной схемы проста по сравнению с параллельной схемой.
Некоторые огни рождественской елки могут быть включены в последовательные цепи. Если погаснет одна лампочка, погаснет вся струна. Предохранитель или автоматические выключатели будут подключены последовательно, чтобы защитить всю проводку от перегрузки по току. Его можно использовать как делитель напряжения. Батарейки в пульте подключены последовательно.
Последовательная цепь
В параллельной цепи электронов проходят через множество ее ветвей.В этом случае напряжение на каждом резисторе в цепи остается неизменным. Здесь ток в цепи делится между каждой ветвью и, наконец, рекомбинирует, когда ветви встречаются в общей точке. Параллельная цепь может быть сформирована разными способами, что означает, что резисторы могут быть расположены в различных формах. Его можно использовать как делитель тока.
В большинстве случаев цепи подключаются параллельно. Это потому, что если один резистор сломан или поврежден, он не отключит всю систему.Но из-за этого эффекта трудно обнаружить отказ, если в цепи что-то пойдет не так, и поэтому в определенные моменты это может быть опасно. Легко подключить или отключить новый резистор или другой компонент, не затрагивая другие элементы в параллельной цепи. Но он использует много проводов и, следовательно, становится сложным. В основном в зданиях и домах мы используем параллельное подключение.
Параллельная цепь
Комбинация резисторов при последовательном включении
Рассмотрим три резистора R 1 , R 2 , R 3 , которые соединены последовательно.Здесь заряд сначала проходит через R 1 , входит в R 2 и, наконец, достигает R 3 .
Комбинация из трех последовательно соединенных резисторов
По закону Ома разность потенциалов на R 1 = V 1 = I R 1
Разность потенциалов на R 2 = V 2 = I R 2 .
Разность потенциалов на R 3 = V 3 = I R 3 .
Таким образом, разность потенциалов V на этом последовательном соединении резисторов
В = В 1 + В 2 + В 3
= I R 1 + I R 2 + I R 3
= Я ( 1 + 2 + 3 )
Таким образом, в случае последовательного соединения эквивалентное сопротивление R eq = V / I = (R 1 + R 2 + R 3 ).
Для n числа резисторов, соединенных последовательно, эквивалентное сопротивление R eq = R 1 + R 2 + R 3 ………………… R n .
Эквивалентное сопротивление — это полное сопротивление цепи. Это единственное значение сопротивления, которое может заменить количество резисторов в цепи без изменения тока и напряжения в сети. Таким образом, при последовательном соединении общее сопротивление цепи определяется путем сложения сопротивлений каждого отдельного резистора.
Для примера рассмотрим последовательную цепь, состоящую из трех резисторов с сопротивлением 5 Ом, 10 Ом, 5 Ом соответственно с батареей 15 В.
Итак, полное сопротивление R = R 1 + R 2 + R 3 = 5 + 10 + 5 = 20 Ом
Мы знаем, что V = I R.
Ток I = V / R = 15/20 = 0,75 А. Хотя ток в последовательной сети одинаков, падение напряжения на каждом резисторе разное. Каждый резистор с разным сопротивлением обеспечивает разное падение напряжения, и мы можем найти полное напряжение по закону Ома, V = I R. Давайте возьмем предыдущий пример. Упомянутое здесь напряжение составляет 15 В.Мы можем проверить это, вычислив таким образом. V = I R 1 + I R 2 + I R 3 = 0,75 (5 +10 + 5) = 15 В. Это точное измерение напряжения, которое мы предоставили в этом примере. Обнаружено, что резистор с большим сопротивлением имеет большее падение напряжения.
Комбинация резисторов при параллельном подключении
Рассмотрим три резистора R 1 , R 2 , R 3 , которые соединены параллельно. Заряд делится на три и проходит через 1 рандов, 2 рандов и рандов 3.
Комбинация из трех параллельно включенных резисторов
Ток I = I 1 + I 2 + I 3.
Разность потенциалов, приложенная к R1 = V = I 1 R 1
Разность потенциалов на R 2 = V = I 2 R 2
Разность потенциалов на R 3 = V = I 3 R 3
Таким образом, I = I 1 + I 2 + I 3
= V / R 1 + V / R 2 + V / R 3
= V (1 / R 1 + 1 / R 2 + 1 / R 3 )
Если эту параллельную комбинацию заменить эквивалентным сопротивлением, R eq
Тогда I = V / R экв
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3
Таким образом, для количества резисторов, включенных параллельно, 1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3 ………………………. 1 / Р № .
Таким образом, при параллельном соединении полное сопротивление цепи определяется путем сложения обратной величины сопротивления каждого отдельного резистора.
Для примера рассмотрим параллельную схему, состоящую из трех резисторов с сопротивлением 5 Ом, 10 Ом, 5 Ом соответственно с батареей 15 В.
Таким образом, общее сопротивление, 1 / R = 1 / R 1 + 1 / R 2 + 1 / R 3 = 1/5 + 1/10 + 1/5 = 5/10. Итак, R = 2Ω.
При параллельном подключении общее сопротивление или эквивалентное сопротивление всегда будет меньше наименьшего резистора, присутствующего в цепи. Значение эквивалентного сопротивления будет находиться между наименьшим сопротивлением в цепи и наименьшим сопротивлением, разделенным на количество резисторов, присутствующих в цепи. В этом примере наименьший резистор имеет сопротивление 5 Ом, а значение общего сопротивления составляет 2 Ом, что явно подтверждает вышеупомянутый факт.
Напряжение на каждом резисторе составляет 15 В.Теперь, чтобы найти ток через каждую ветвь, формула: I = V / R.
I 1 = 15/5 = 3A
I 2 = 15/10 = 1,5A
I 3 = 15/5 = 3A
Общий ток I = 3 + 1,5 + 3 = 7,5 A
Комбинация последовательных и параллельных резисторов
Рассмотрим схему, в которой R 2 и R 3 подключены параллельно, а R 1 включены последовательно с R 2 и R 3.
Комбинация последовательных и параллельных резисторов
Сначала рассмотрим R 2 и R 3 и, следовательно, 1 / R 23eq = 1 / R 2 + 1 / R 3
R 23eq = R 2 R 3 / R 2 + R 3
R 123eq = R 23eq + R 1
Таким образом, ток I = V / R 123eq = V / [R 1 + (R 2 R 3 / R 2 + R 3 )]
= V (R 2 + R 3 ) / R 1 R 2 + R 1 R 3 + R 2 R 3.
Сводка
Электрический ток — это поток заряженных частиц в цепи. Схема состоит из проводника, резистора, переключателя и источника питания.
Ток, I = Q / t, где Q — заряд в кулонах, а t — время в секундах. Напряжение — это разность электрических потенциалов между двумя точками в цепи. Вольт — это единица измерения напряжения.
Сопротивление — это способность управлять потоком электронов в цепи, а единицей измерения сопротивления является ом.
Закон Ома гласит, что V = I R. Таким образом, I = V / R и R = V / I.
Существует два типа цепей: последовательные и параллельные.
При последовательном соединении ток, протекающий только по одному пути, будет одинаковым при прохождении через каждый резистор.
При параллельном подключении напряжение на каждом резисторе в цепи остается неизменным, а ток распределяется между ветвями.
Посмотрите это видео, чтобы узнать больше
Другие показания
Комбинация резисторов — Series и Paralle
Особенности курса
- 101 Видеолекция
- Примечания к редакции
- Документы за предыдущий год
- Ментальная карта
- Планировщик обучения
- Решения NCERT
- Обсуждение Форум
- Тестовая бумага с видео-решением
4.1 Последовательные и параллельные резисторы
Последовательные резисторы
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно. Например, если ток протекает через человека, держащего отвертку, в землю, тогда R1.R1. размер 12 {R rSub {размер 8 {1}}} {} на рис. 4.2 (a) может быть сопротивлением вала отвертки, R2R2 размер 12 {R rSub {размер 8 {2}}} {} сопротивлением его ручка, R3R3 размер 12 {R rSub {размер 8 {3}}} {} сопротивление тела человека и R4R4 размер 12 {R rSub {размер 8 {4}}} {} сопротивление ее обуви.
На рисунке 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением к прибору, который уменьшал бы рабочий ток.
Рис. 4.3 Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе на рисунке 4.3.
Согласно закону Ома падение напряжения, V, V, размер 12 {V} {} на резисторе, когда через него протекает ток, рассчитывается по формуле V = IR, V = IR, размер 12 {V = ital «IR»} {}, где размер II 12 {I} {} равен току в амперах (A), а размер RR 12 {R} {} — сопротивление в Ом Ом.Ω. размер 12 {слева (% OMEGA справа)} {} Другой способ представить это: VV размером 12 {V} {} — это напряжение, необходимое для протекания тока II размера 12 {I} {} через сопротивление RR размера 12 {R} {}
Таким образом, падение напряжения на R1R1 размером 12 {R rSub {size 8 {1}}} {} равно V1 = IR1, V1 = IR1, size 12 {V rSub {size 8 {1}} = ital «IR» rSub { размер 8 {1}}} {}, что для R2R2 размер 12 {R rSub {размер 8 {2}}} {} равен V2 = IR2, V2 = IR2, размер 12 {V rSub {size 8 {2}} = ital «IR» rSub {размер 8 {2}}} {}, а для R3R3 размера 12 {R rSub {размер 8 {3}}} {} — V3 = IR3.V3 = IR3. размер 12 {V rSub {size 8 {3}} = ital «IR» rSub {size 8 {3}}} {} Сумма этих напряжений равна выходному напряжению источника; то есть
4,1 В = V1 + V2 + V3. V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}
Это уравнение основано на сохранении энергии и сохранении плата. Электрическая потенциальная энергия может быть описана уравнением PE = qV, PE = qV, size 12 {ital «PE» = ital «qV»} {}, где qq size 12 {q} {} — электрический заряд, а размер VV 12 { V} {} — напряжение.Таким образом, энергия, подаваемая источником, равна qV, qV, размер 12 {ital «qV»} {}, а энергия, рассеиваемая резисторами, равна
.
4.2 qV1 + qV2 + qV3. QV1 + qV2 + qV3. размер 12 {ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {}
Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, qV = qV1 + qV2 + qV3.qV = qV1 + qV2 + qV3. размер 12 {ital «qV» = ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {} заряд qq размер 12 {q} {} отменяется, давая V = V1 + V2 + V3, V = V1 + V2 + V3, размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2 }} + V rSub {размер 8 {3}}} {}, как указано.(Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь замена значений отдельных напряжений дает
4,3 В = IR1 + IR2 + IR3 = I (R1 + R2 + R3). V = IR1 + IR2 + IR3 = I (R1 + R2 + R3). размер 12 {V = ital «IR» rSub {size 8 {1}} + ital «IR» rSub {size 8 {2}} + ital «IR» rSub {size 8 {3}} = I \ (R rSub { размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} \)} {}
Обратите внимание, что для эквивалентного сопротивления одиночной серии Rs, Rs, мы имеем
Это означает что полное или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs = R1 + R2 + R3.Rs = R1 + R2 + R3. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}
Эта логика действительно для любого количества последовательно подключенных резисторов; таким образом, полное сопротивление RsRs последовательного соединения составляет
4,5 Rs = R1 + R2 + R3 + …, Rs = R1 + R2 + R3 + …, размер 12 {R rSub {size 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} + «.» «.» «.» } {}
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 4.3 составляет 12,0 В 12,0 В, размер 12 {«12» «.» 0`V} {} и сопротивления: R1 = 1,00 Ом, R1 = 1,00 Ом, размер 12 {R rSub {size 8 {1}} = 1 «.» «00»% OMEGA} {} R2 = 6,00 Ом, R2 = 6,00 Ом, размер 12 {R rSub {размер 8 {2}} = 6 дюймов «. «00»% OMEGA} {} и R3 = 13,0 Ом. R3 = 13,0 Ом. размер 12 {R rSub {размер 8 {3}} = «13» «.» 0% OMEGA} {} (а) Какое полное сопротивление? (б) Найдите ток.(c) Рассчитайте падение напряжения на каждом резисторе и покажите, что в сумме они равны выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая уравнением
.
4,6 Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.
Стратегия и решение для (b)
Ток определяется по закону Ома, V = IR.V = IR. размер 12 {V = ital «IR»} {} Ввод значения приложенного напряжения и общего сопротивления дает ток в цепи.
4,7 I = VRs = 12,0 В 20,0 Ом = 0,600 AI = VRs = 12,0 В 20,0 Ом = 0,600 A, размер 12 {I = {{V} больше {R rSub {size 8 {s}}}} = {{» 12 «». » 0 «V»} больше {«20» «.» «0»% OMEGA}} = 0 «.» «600» «A»} {}
Стратегия и решение для (c)
Падение напряжения — или IRIR размер 12 {ital «IR»} {} — в резисторе определяется законом Ома.Ввод текущего значения и значения первого сопротивления дает
.
4,8 В1 = IR1 = (0,600 A) (1,0 Ом) = 0,600 В. V1 = IR1 = (0,600 A) (1,0 Ом) = 0,600 В. размер 12 {V rSub {размер 8 {1}} = ital «IR» rSub {size 8 {1}} = \ (0 «.» «600» «A» \) \ (1 «.» 0% OMEGA \) = 0 «.» «600» «V»} {}
Аналогично
4,9 В2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 ВV2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В, размер 12 {В rSub {размер 8 {2}} = ital «IR» rSub {размер 8 {2}} = \ (0 «.» «600» «A» \) \ (6 «.» 0% OMEGA \) = 3 «.» «60» «V»} {}
и
4.10 V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. размер 12 {V rSub {размер 8 {3}} = курсив «IR» rSub {size 8 {3}} = \ (0 «.» «600» «A» \) \ («13» «.» 0% OMEGA \) = 7 «.» «80» «V»} {}
Обсуждение для (c)
Три капли IRIR размера 12 {ital «IR»} {} добавляют к 12,0 В, 12,0 В, размер 12 {«12» «». 0`V} {} как и ожидалось.
4,11 V1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 VV1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 В размер 12 {V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}} = \ (0 «.»» 600 «+3». «» 60 «+7». «» 80 «\)» V «=» 12 «». «0» V «} {}
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P = IV, P = IV, размер 12 {P = курсив «IV»} {}, где PP размер 12 {P} {} — электроэнергия. В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома V = IRV = IR, размер 12 {V = ital «IR»} {} в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
4.12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}
Аналогично
4,13 P2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 WP2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт размер 12 {P rSub {размер 8 {2}} = I rSup {размер 8 {2}} R rSub {размер 8 {2}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (6 «.» «00»% OMEGA \) = 2 «.» «16» «W»} {}
и
4.14 P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. Размер 12 {P rSub {размер 8 {3}} = I rSup {size 8 {2}} R rSub {size 8 {3}} = \ (0 «.» «600» «A» \) rSup {size 8 {2}} \ («13» «.» 0% OMEGA \) = 4 «.» «68» «W»} {}
Обсуждение для (d)
Мощность также можно рассчитать, используя либо P = IVP = IV, размер 12 {P = ital «IV»} {}, либо P = V2R, P = V2R, размер 12 {P = {{V rSup {size 8 {2}} } over {R}}} {}, где величина VV 12 {V} {} — это падение напряжения на резисторе (а не полное напряжение источника).Будут получены такие же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV, P = IV, размер 12 {P = ital «IV»} {}, где VV размером 12 {V} {} — это напряжение источника. Это дает
4,15 P = (0,600 A) (12,0 В) = 7,20 WP = (0,600 A) (12,0 В) = 7,20 Вт. Размер 12 {P = \ (0 «.» «600» «A» \) \ («12 «». «0» V «\) = 7″. » «20» «W»} {}
Обсуждение для (e)
Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
4,16 P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. размер 12 {P rSub {размер 8 {1}} + P rSub {размер 8 {2}} + P rSub {размер 8 {3}} = \ (0 «.» «360» +2 «.» «» 16 «+4». «» 68 «\)» W » = 7 «.» «20» «Вт»} {}
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавляют Rs = R1 + R2 + R3 +…. Rs = R1 + R2 + R3 + …. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub { размер 8 {3}} + «.» «.» «.» «.» } {}
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не дают полного напряжения источника, а скорее делят его.
21.1 Последовательные и параллельные резисторы — College Physics
21.1 Последовательные и параллельные резисторы — College Physics | OpenStaxSkip к контенту
- Предисловие
- 1 Введение: Природа науки и физики
- Введение в науку и область физики, физических величин и единиц измерения
- 1.1 Физика: Введение
- 1.2 Физические величины и единицы
- 1.3 Точность, прецизионность и значащие числа
- 1.4 Приближение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 64
- Введение в двумерную кинематику
- 3.1 Кинематика в двух измерениях: введение
- 3.2 Сложение и вычитание векторов: графические методы
- 3.3 Сложение и вычитание векторов: аналитические методы
- 3.4 Движение снаряда
- 3.5 Сложение скоростей
- Глоссарий
- Краткое содержание раздела
- Введение в динамику: законы движения Ньютона
- 4.1 Разработка концепции силы
- 4,2 Первый закон движения Ньютона: инерция
- 4,3 Второй закон движения Ньютона: концепция системы
- 4,4 Третий закон движения Ньютона: симметрия сил
- 4,5 Нормаль, напряжение и другие примеры of Forces
- 4.6 Стратегии решения проблем
- 4.7 Дальнейшие применения законов движения Ньютона
- 4.8 Расширенная тема: Четыре основных силы — Введение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение: дополнительные применения законов Ньютона
- 5.1 Трение
- 5.2 Силы сопротивления
- 5.3 Эластичность: напряжение и деформация
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 9000
- Введение в линейный импульс и столкновения
- 8.1 Линейный импульс и сила
- 8.2 Импульс
- 8.3 Сохранение импульса
- 8.4 Упругие столкновения в одном измерении
- 8.5 Неупругие столкновения в одном измерении
- 8.6 Столкновения точечных масс в двух измерениях
- 8.7 Введение в ракетное движение
- Глоссарий
- 000 Краткое содержание раздела Концептуальные вопросы
- Задачи и упражнения
- Введение в статику и крутящий момент
- 9.1 Первое условие равновесия
- 9.2 Второе условие равновесия
- 9.3 Стабильность
- 9.4 Приложения статики, включая стратегии решения проблем
- 9.5 Простые механизмы
- 9.6 Силы и моменты в мышцах и суставах
- Глоссарий
- Резюме раздела
- Концептуальные вопросы Задачи и упражнения
- Введение в вращательное движение и угловой момент
- 10.1 Угловое ускорение
- 10.2 Кинематика вращательного движения
- 10.3 Динамика вращательного движения: вращательная инерция
- 10.4 Кинетическая энергия вращения: новый взгляд на работу и энергию
- 10,5 Угловой момент и его сохранение
- 10,6 Столкновения 9000 протяженных тел 4
- 10.7 Гироскопические эффекты: векторные аспекты углового момента
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
Два
- Введение в статику жидкостей
- 11.1 Что такое жидкость?
- 11.2 Плотность
- 11.3 Давление
- 11.4 Изменение давления в зависимости от глубины в жидкости
- 11,5 Принцип Паскаля
- 11,6 Манометрическое давление, абсолютное давление и измерение давления
- 11,7 Принцип Архимеда
- 11,8 : Поверхностное натяжение и капиллярное действие
- 11.9 Давления в теле
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в динамику жидкости Биологические и медицинские приложения
- 12.1 Расход и его связь со скоростью
- 12.2 Уравнение Бернулли
- 12.3 Наиболее общие приложения уравнения Бернулли
- 12.4 Вязкость и ламинарный поток; Закон Пуазейля
- 12.5 Начало турбулентности
- 12.6 Движение объекта в вязкой жидкости
- 12.7 Явления молекулярного переноса: диффузия, осмос и связанные процессы
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Концептуальные вопросы
- Введение в температуру, кинетическую теорию и законы газа
- 13.1 Температура
- 13.2 Тепловое расширение твердых тел и жидкостей
- 13.3 Закон идеального газа
- 13.4 Кинетическая теория: атомное и молекулярное объяснение давления и температуры
- 13,5 Фазовые изменения
- 13,6 Влажность, испарение и кипение
- Введение в методы теплопередачи
- 14.1 Тепло
- 14.2 Изменение температуры и теплоемкость
- 14.3 Фазовое изменение и скрытая теплота
- 14.4 Методы теплопередачи
- 14,5 Проводимость
- 14,6 Конвекция
- 14,7 Излучение
- Глоссарий
- Краткое содержание раздела
- Вопросы по концепции
И упражнения
- Введение в термодинамику
- 15.1 Первый закон термодинамики
- 15.2 Первый закон термодинамики и некоторые простые процессы
- 15.3 Введение во второй закон термодинамики: тепловые двигатели и их эффективность
- 15.4 Идеальный тепловой двигатель Карно: пересмотр второго закона термодинамики
- 15.5 Приложения термодинамики: тепловые насосы и холодильники
- 15.6 Энтропия и второй закон термодинамики: Беспорядок и недоступность энергии
- 15.7 Статистическая интерпретация энтропии и второй закон термодинамики: основное объяснение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
Введение в колебательное движение и волны
- Введение в физику слуха
- 17.1 Звук
- 17,2 Скорость звука, частота
- 17.3 Интенсивность звука и уровень звука
- 17.4 Эффект Доплера и звуковые удары
- 17.5 Звуковые помехи и резонанс: стоячие волны в столбе воздуха
- 17.6 Слух
- 17.7 Ультразвук
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Проблемы и упражнения
- Введение в электрический заряд и электрическое поле
33 1833.100
903 1833.100
и параллельные резисторы [Analog Devices Wiki]
Цель:
Целью этой лабораторной работы является исследование последовательно и параллельно соединенных резисторов.
Серия
и параллельные схемы
Простые схемы, состоящие всего из нескольких компонентов, как правило, просты для понимания новичками. Но все усложняется, когда в смесь входит большее количество компонентов. Куда идет ток? Что делают узловые напряжения? Можно ли упростить схему и облегчить понимание? Следующая информация должна помочь.
В этом лабораторном занятии мы сначала обсудим разницу между последовательными цепями и параллельными цепями, используя цепи, содержащие самые основные компоненты, резисторы и батареи (или источники напряжения), чтобы показать разницу между двумя конфигурациями.
Прежде чем мы углубимся в объяснение, нам необходимо определить, что такое узел схемы. Узел в цепи — это не что иное, как электрическое соединение между двумя или более компонентами. Когда схема изображена на схеме, такой как рисунок 1, узлы представлены проводами (линиями) между компонентами.
Рисунок 1, Пример схемы узла
На схеме изображена схема с 4 резисторами и источником напряжения. Также есть четыре уникальных узла.Цветные узлы (линии) Красный соединяет (+) конец источника напряжения с резистором R 1 , оранжевый соединяет R 1 и R 2 вместе, синий соединяет R 2 с R 3 и R 4 и зеленый соединяет (-) конец источника напряжения с R 3 и R 4 . Обратите внимание, что мы обычно определяем один узел как общий узел, на который ссылаются все остальные узлы, в данном случае это зеленый наземный узел.
Нам также необходимо понять, как ток течет по цепи.Обычный ток течет от более высокого или более положительного напряжения к более низкому или менее положительному напряжению в цепи. Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки наименьшего напряжения, обычно называемой землей (0 вольт). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы источника напряжения к отрицательной клемме.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток на входе такой же, как на выходе.В других узлах (в частности, трехсторонний переход между R 2 , R 3 и R 4 ) основной (красный) ток разделяется на два разных: фиолетовый ток, текущий в R 3 и оранжевый ток протекает в R 4 . Также обратите внимание, что токи I R3 и I R4 рекомбинируют как зеленый ток. Это подчеркивает ключевое различие между последовательным и параллельным подключением.
Определение цепей серии
Когда резисторы подключаются последовательно (как показано на рисунке 2), вывод одного резистора подключается непосредственно к выводу следующего резистора без других возможных путей, так что весь ток в одном резисторе должен течь в следующий и скоро.
Когда резисторы включены последовательно, они могут быть объединены или объединены в один эквивалентный резистор с сопротивлением, равным сумме последовательных сопротивлений, , то есть ,
Рисунок 2: Последовательные резисторы, R СЕРИЯ = R 1 + R 2 + R 3 +…
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.Итак, для приведенной выше последовательной схемы:
Мы знаем, что все резисторы имеют одинаковый ток I S .
Аналогично для остальных трех резисторов так:
Или вычитая I S :
Таким образом, полное эквивалентное сопротивление — это просто сумма их значений.
Определение параллельных цепей
Когда резисторы включены параллельно (как показано на рисунке 3), все их первые выводы соединены вместе, а все их вторые выводы соединены вместе.
Когда резисторы включены параллельно, они могут быть объединены или объединены в один эквивалентный одиночный резистор, значение которого определяется следующим уравнением:
Для двух параллельных резисторов это упрощает:
Рисунок 3: Параллельные резисторы
Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление. Итак, для вышеуказанной параллельной схемы:
Мы знаем, что все резисторы имеют одинаковое напряжение В S .
Ток, подаваемый источником напряжения В S , представляет собой сумму токов в резисторах.
Подставляя четыре резистора, получаем:
Или за вычетом V S :
Переставляя сопротивления, получаем полное эквивалентное сопротивление:
Эксперименты
Материалы:
Аппаратный модуль ADALM1000
Макетная плата без пайки и перемычки
Резисторы 3–100 Ом
Резисторы 3–470 Ом
Резисторы в серии:
Поместите три резистора 100 Ом последовательно на беспаечную макетную плату, как показано на рисунке 4.Подключите с помощью перемычек вход CH A к левой стороне первого резистора, а вход CH B — к правой стороне того же резистора.
Рисунок 4, последовательно соединенные резисторы
Запустите прибор ALICE M1K Ohm Meter. Здесь показан экран. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор на 50 Ом, который можно использовать для этого. Убедитесь, что выбран параметр Int. Уровень напряжения, который используется для измерения резистора, может быть установлен.Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите Run, и вы должны увидеть что-то подобное с единственным резистором 100 Ом.
Переместите перемычку CH B к правому концу второго резистора, как показано ниже.
Рисунок 5, два резистора последовательно
Омметр должен теперь показать значение для двух последовательно соединенных резисторов или около 200 Ом. Теперь переместите перемычку CH B к правому концу третьего резистора, как показано ниже.
Рисунок 6, три резистора последовательно
Омметр должен теперь показать значение трех последовательно соединенных резисторов или около 300 Ом.
Параллельные резисторы:
Теперь замените резисторы 100 Ом на резисторы 470 Ом, как показано на рисунке 7.
Измерение одного резистора 470 Ом
Омметр должен теперь показать значение одиночного резистора или около 470 Ом. Переместите средний резистор 470 Ом так, чтобы он был параллелен резистору справа, как показано ниже.
Измерение двух параллельных резисторов 470 Ом
Омметр должен теперь показать значение для двух резисторов 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?
Переместите третий резистор 470 Ом так, чтобы он был параллелен двум другим резисторам справа, как показано ниже.
Измерение трех резисторов 470 Ом параллельно
Омметр должен теперь показать значение для трех резисторов 470 Ом, включенных параллельно.Соответствует ли измеренное значение формуле для параллельных резисторов?
Поэкспериментируйте с другими комбинациями резисторов и номиналов, чтобы убедиться, что формулы верны для любого номинала резистора.
Комбинированные схемы
Более сложные соединения резисторов обычно представляют собой просто комбинации последовательного и параллельного соединения. Это часто встречается, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная схема может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на рисунке 7. На рисунке общее сопротивление можно рассчитать, связав три резистора друг с другом последовательно или параллельно.
Комбинированные последовательные и параллельные резисторы
R 2 и R 3 соединены параллельно друг другу, поэтому мы знаем, что для этих двух резисторов эквивалентное сопротивление будет:
Комбинированное сопротивление R 2 и R 3 последовательно с R1, поэтому общее эквивалентное сопротивление будет:
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
Для дальнейшего изучения:
Академия Хана — схемы резисторов
Безграничная физика
Последовательные и параллельные схемы (в области физики)
Последовательные и параллельные схемы
Вернуться к разделу «Введение в работу электротехнической лаборатории» Содержание
университет / курсы / alm1k / intro / series-parallel-2.txt · Последнее изменение: 19 июля 2020 г., 18:40, автор: dmercer
Серия
и параллельные резисторы
- Изучив этот раздел, вы сможете:
- Рассчитайте значения общего сопротивления в цепях с последовательным сопротивлением.
- Используйте соответствующие формулы для расчета сопротивления в цепях с параллельным сопротивлением.
- • Вычисление суммы обратных величин.
- • Произведение над суммой.
- Рассчитайте значения общего сопротивления в последовательной / параллельной сети.
Расчеты в последовательно- и параллельных резисторных цепях
Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:
ПОСЛЕДОВАТЕЛЬНО, так что один и тот же ток течет через все компоненты, но различная разность потенциалов (напряжение) может существовать на каждом из них.
ПАРАЛЛЕЛЬНО, так что на всех компонентах существует одинаковая разность потенциалов (напряжение), но каждый компонент может проводить разный ток.
Рис. 4.2.1 Резисторы серии
Рис. 4.2.2 Параллельные резисторы
В любом случае (для резисторов) полное сопротивление той части цепи, которая содержит резисторы, может быть рассчитано с использованием методов, описанных ниже.
Возможность рассчитать суммарное (общее) значение резисторов таким способом позволяет легко вычислить неизвестные значения сопротивления, тока и напряжения для довольно сложных схем с использованием относительно простых методов.Это очень полезно при поиске неисправностей.
ПЕРЕД ДАЛЬНЕЙШЕЙ ДАЛЬНЕЙШЕЙ ПОПРАКТИКОЙ ИСПОЛЬЗУЙТЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ОБЩИХ ЗНАЧЕНИЙ СЕРИИ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.
Для резисторов в серии:
Общее сопротивление двух или более резисторов, подключенных последовательно , определяется простым сложением индивидуальных значений резисторов, чтобы найти общую сумму (R TOT ):
Для резисторов, включенных параллельно:
Для расчета общего сопротивления цепи, в которой используются параллельные резисторы, можно использовать следующую формулу.
Обратите внимание, однако, что эта формула НЕ дает вам полного сопротивления R TOT .
Это дает вам ВЗАИМОДЕЙСТВИЕ R TOT или:
Это совсем другое значение — и НЕ является полным сопротивлением. Он делится на 1, деленный на TOT . Чтобы получить правильное значение для R TOT (которое будет обратным 1 / R TOT , т. Е. TOT /1, просто нажмите соответствующую клавишу на вашем калькуляторе (отмеченную 1 / x или x-1) .
Другой способ расчета параллельных цепей.
Суммарное сопротивление двух резисторов, включенных параллельно , не имеющее обратных величин, определяется по формуле:
Эту формулу часто называют «произведение над суммой».
Он рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее сопротивление, как если бы это был один резистор, и составьте еще одну пару с третьим резистором.Определите новую сумму и так далее, пока вы не включите все параллельные резисторы в этой конкретной сети.
О, еще одна вещь, которую следует помнить о произведении над суммой, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это ДО того, как использовать его для разделения продукта (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неправильным.
Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто встречаетесь с множеством параллельных сетей с гораздо более чем двумя резисторами.Тем не менее, какую формулу вы выберете, зависит от вас, взаимная или сумма продукта.
подсказок
Использование обратного метода
Если вы используете МЕТОД ВЗАИМОДЕЙСТВИЯ для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили обратные величины отдельных резисторов — вы должны снова найти обратную величину 1 / R1 + 1 / R2 + 1 / R3 = 1 / R TOT и чтобы найти R TOT , вы должны найти обратную величину 1 / R TOT .
Упрощающие схемы
Для комбинированных последовательных и параллельных цепей сначала разработайте участок цепи (последовательный или параллельный).Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, по которой можно найти R TOT .
Вы можете использовать формулу «произведение на сумму»:
Для цепей с более чем двумя параллельными резисторами просто определите два параллельных резистора одновременно, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резистора одним резистором, значение которого является объединенным сопротивлением двух .
Теперь вы можете использовать ваше первое комбинированное значение в качестве единственного резистора со следующим параллельным резистором и так далее. Таким образом, можно выработать большое количество параллельных резисторов с использованием произведения на сумму.
Когда все параллельные резисторы одинакового номинала.
Если несколько одинаковых параллельных резисторов подключены, общее сопротивление будет равно номиналу резистора, умноженному на обратную величину количества резисторов.
, т. Е. Два параллельных резистора 12 кОм имеют суммарное сопротивление
.
12K x 1/2 = 6K
Три параллельных резистора 12K имеют общее сопротивление
12K x 1/3 = 4K и т. Д.
Проверяю ответ
Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.
Серия
и параллельная комбинация
Попробуйте несколько вычислений, основанных на последовательной и параллельной цепях резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят вычислить полное сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать
Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».
Прежде чем начать, подумайте над этими несколькими советами. Они упростят задачу, если вы будете внимательно им следовать.
1. Разработайте ответы карандашом и бумагой; перерисуйте схему, над которой работаете.
2. Конечно, ответ будет не просто числом, это будет определенное количество Ом, не забудьте указать правильную единицу (например,грамм. Ω, KΩ или MΩ), иначе ваш ответ не имеет смысла.
3. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
Итак, вы прочитали эти инструкции и готовы приступить к работе. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.
Пример последовательной и параллельной цепи.
Хорошо, есть что вспомнить, так почему бы не попробовать несколько практических вопросов в Resistors Module 4.5 по определению полного сопротивления некоторых цепей резисторов?
Серия
и параллельные схемы — learn.sparkfun.com
Добавлено в избранное
Любимый
51
Серия
и параллельные схемы
Простые схемы (состоящие всего из нескольких компонентов) обычно довольно просты для понимания новичками.Но когда на вечеринку приходят другие компоненты, все может стать неприятным. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, бесстрашный читатель. Ценная информация следует.
В этом руководстве мы сначала обсудим разницу между последовательными цепями и параллельными цепями, используя схемы, содержащие самые основные компоненты — резисторы и батареи, чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы комбинируете компоненты разных типов, такие как конденсаторы и катушки индуктивности.
Рассмотрено в этом учебном пособии
- Как выглядят конфигурации последовательной и параллельной цепей
- Как пассивные компоненты действуют в этих конфигурациях
- Как источник напряжения будет воздействовать на пассивные компоненты в этих конфигурациях
Рекомендуемая литература
Вы можете посетить эти руководства по основным компонентам перед тем, как погрузиться в построение схем в этом руководстве.
Видео
Цепи серии
Узлы и текущий поток
Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел .Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема моделируется на схеме, эти узлы представляют собой провода между компонентами.
Пример схемы с четырьмя узлами уникального цвета.
Это полдела на пути к пониманию разницы между последовательным и параллельным. Нам также нужно понять , как ток проходит через по цепи. Ток течет от высокого напряжения к более низкому напряжению в цепи.Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки самого низкого напряжения (обычно называемой землей). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы батареи к отрицательной:
Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же схеме, что и выше. Разные токи обозначены разными цветами.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток на входе такой же, как на выходе.В других узлах (в частности, трехсторонний переход между R 2 , R 3 и R 4 ) основной (синий) ток разделяется на два разных. Это ключевое различие между последовательным и параллельным подключением!
Определение цепей серии
Два компонента соединены последовательно, если они имеют общий узел и протекает через них одинаковым током . Вот пример схемы с тремя последовательными резисторами:
В указанной выше цепи есть только один способ протекания тока.Начиная с положительной клеммы аккумулятора, ток сначала встречает R 1 . Оттуда ток будет течь прямо на R 2 , затем на R 3 и, наконец, обратно на отрицательную клемму батареи. Обратите внимание, что у текущего есть только один путь. Эти компоненты включены последовательно.
Параллельные схемы
Определение параллельных цепей
Если компоненты используют два общих узла , они работают параллельно.Вот пример схемы трех резисторов, подключенных параллельно батарее:
От положительного полюса аккумуляторной батареи ток течет к R 1 … и R 2 , и R 3 . Узел, который подключает аккумулятор к R 1 , также подключен к другим резисторам. Остальные концы этих резисторов аналогично связываются вместе, а затем снова подключаются к отрицательной клемме батареи. Существует три различных пути, по которым ток может пройти перед возвращением в батарею, а соответствующие резисторы считаются параллельными.
Если все последовательные компоненты имеют одинаковые токи, протекающие через них, все параллельные компоненты имеют одинаковое падение напряжения на них — series: current :: parallel: Voltage.
Совместная работа параллельных цепей и серии
Оттуда мы можем смешивать и сочетать. На следующем снимке мы снова видим три резистора и батарею. С положительной клеммы аккумуляторной батареи ток сначала достигает R 1 . Но на другой стороне R 1 узел разделяется, и ток может идти как на R 2 , так и на R 3 .Пути тока через R 2 и R 3 затем снова связываются вместе, и ток возвращается к отрицательному выводу батареи.
В этом примере, R 2 и R 3 параллельны друг другу, а R 1 последовательно с параллельной комбинацией R 2 и R 3 .
Расчет эквивалентных сопротивлений в последовательных цепях
Вот информация, которая может быть вам полезна.Когда мы соединяем резисторы таким образом, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть питание 10 В через 10 кОм; резистора, закон Ома гласит, что у нас протекает ток 1 мА.
Если потом поставить еще 10к & ом; резистор, включенный последовательно с первым и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление увеличилось вдвое.
Другими словами, для тока по-прежнему существует только один путь, и мы только усложнили его прохождение.Насколько сложнее? 10 кОм; + 10к & Ом; = 20 кОм ;. Вот как мы рассчитываем последовательно включенные резисторы — всего складываем их значения .
Если выразить это уравнение в более общем виде: полное сопротивление Н — некоторое произвольное количество — резисторов — это их общая сумма.
Расчет эквивалентных сопротивлений в параллельных цепях
А как насчет параллельных резисторов? Это немного сложнее, но ненамного.Рассмотрим последний пример, в котором мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавляем еще 10кОм; параллельно, а не последовательно. Теперь у тока есть два пути. Поскольку напряжение питания не изменилось, закон Ома гласит, что первый резистор по-прежнему будет потреблять 1 мА. Но то же самое и со вторым резистором, и теперь у нас есть 2 мА, исходящие от источника питания, что вдвое превышает первоначальный 1 мА. Это означает, что мы уменьшили общее сопротивление вдвое.
Пока можно сказать, что 10к & ом; || 10 кОм; = 5 кОм; («||» примерно переводится как «параллельно»), у нас не всегда будет 2 одинаковых резистора.Что тогда?
Уравнение для добавления произвольного количества резисторов параллельно:
Если обратные значения вам не подходят, мы также можем использовать метод, называемый «произведение на сумму», когда у нас есть два резистора параллельно:
Однако этот метод подходит только для двух резисторов в одном вычислении. Используя этот метод, мы можем объединить более 2 резисторов, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (снова как произведение на сумму), но обратный метод может быть меньше работы.
Время эксперимента — Часть 1
Что вам понадобится:
Давайте проведем простой эксперимент, чтобы доказать, что все работает именно так, как мы говорим.
Во-первых, мы собираемся подключить 10 кОм; последовательно подключите резисторы и наблюдайте, как они складываются самым необычным образом. Используя макетную плату, поместите один 10 кОм; резистор, как показано на рисунке, и измерить мультиметром. Да, мы уже знаем, что на нем будет указано 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Убедившись, что мир существенно не изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогично, но с проводом от каждого резистора, электрически подключенным через макетную плату, и снова произведите измерение. Измеритель теперь должен показывать что-то близкое к 20 кОм.
Вы можете заметить, что сопротивление, которое вы измеряете, может быть не совсем таким, каким должно быть резистор. Резисторы имеют определенный допуск , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10.01кОм. Пока оно близко к правильному значению, все должно работать нормально.
Читателю следует продолжать это упражнение до тех пор, пока он не убедится, что знает, что будет в результате, прежде чем делать это снова, или у него закончатся резисторы, которые можно вставить в макет, в зависимости от того, что наступит раньше.
Время эксперимента — Часть 2
Теперь давайте попробуем это с резисторами в конфигурации параллельно .Поместите один 10 кОм; резистор в макетной плате, как и раньше (мы полагаем, читатель уже считает, что один резистор 10 кОм будет измерять на мультиметре что-то близкое к 10 кОм). Теперь поместите второй 10кОм; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора находились в электрически соединенных рядах. Но перед тем, как измерить комбинацию, вычислите, используя метод «произведение над суммой» или обратный метод, каким должно быть новое значение (подсказка: оно будет 5 кОм;).Затем измерьте. Это что-то близкое к 5к & ом ;? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.
Повторите упражнение с 3, 4 и 5 резисторами. Расчетные / измеренные значения должны быть 3,33 кОм, 2,5 кОм; и 2кОм соответственно. Все ли получилось по плану? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Прежде чем продолжить, выпейте молочный коктейль. Ты заслужил это.
Практические правила для последовательных и параллельных резисторов
Есть несколько ситуаций, которые могут потребовать творческих комбинаций резисторов.Например, если мы пытаемся создать очень специфический источник опорного напряжения вы почти всегда необходимо очень специфическое соотношение резисторов, значения которых вряд ли будут «стандартные» значения. И хотя мы можем получить очень высокую степень точности значений резисторов, мы можем не захотеть ждать X дней, необходимых для доставки чего-либо, или платить цену за нестандартные значения, отсутствующие на складе. Так что в крайнем случае мы всегда можем создать собственные номиналы резисторов.
Совет №1: Равные резисторы, включенные параллельно
Добавление Н резисторов с одинаковым номиналом R , включенных параллельно, дает R / N Ом.Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм / 4 = 2,5 кОм.
Совет № 2: Допуск
Знайте, какую терпимость вы можете терпеть. Например, если вам нужен 3.2k & ohm; резистор, можно было поставить 3 10кОм; резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% отклонения от необходимого значения. Но если схема, которую вы строите, должна иметь допуск ближе, чем 4%, мы можем измерить наш запас в 10 кОм, чтобы увидеть, какие из них самые низкие, потому что они также имеют допуск.По идее, если заначка 10к & ом; все резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители запчастей, как известно, допускают именно такого рода ошибки, поэтому стоит немного покопаться.
Совет № 3: Номинальная мощность при последовательном / параллельном подключении
Такая комбинация резисторов последовательно и параллельно работает и с номинальной мощностью. Допустим, нам нужен 100 & Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это связка 1 кОм; резисторы на четверть ватта (Вт) (а сейчас 3 часа ночи, вся Mountain Dew исчезла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень красиво, но это поможет нам завершить финальный проект и даже может принести дополнительные баллы за способность думать на ногах.
Нам нужно быть немного более осторожными, когда мы объединяем резисторы разных номиналов параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Для читателя это должно быть совершенно очевидно, но …
Совет № 4: Разные резисторы параллельно
Суммарное сопротивление двух резисторов разного номинала всегда меньше, чем резистор наименьшего номинала.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм || 10 кОм; НЕ равняется чему-либо около 5 кОм ;!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет №4 10 раз.
Совет № 5: Параллельное рассеяние мощности
Мощность, рассеиваемая при параллельной комбинации резисторов разных номиналов, не распределяется между резисторами равномерно, потому что токи не равны.Используя предыдущий пример (1k & ohm; || 10k & ohm;), мы видим, что 1k & ohm; будет потреблять в 10 раз больше тока 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор рассеивает в 10 раз мощность, превышающую 10 кОм.
В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять более пристальное внимание тому, что мы делаем при параллельном соединении резисторов разных номиналов. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.
Конденсаторы серии
и параллельные
Объединение конденсаторов аналогично объединению резисторов … только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?
Конденсатор — это просто две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.И если пластины отодвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.
Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенные последовательно, и предположим, что они оба заряжены и готовы к разрядке в друга, сидящего рядом с вами.
Помните, что в последовательной цепи есть только один путь для прохождения тока. Отсюда следует, что количество электронов, выходящих из колпачка снизу, будет таким же, как и количество электронов, выходящих из колпачка наверху.Значит, емкость не увеличилась?
На самом деле все еще хуже. Разместив конденсаторы последовательно, мы эффективно раздвинули пластины друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора. И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.
Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.
Добавление конденсаторов параллельно похоже на добавление резисторов последовательно: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Просто.
Время эксперимента — Часть 3
Что вам понадобится:
Давайте посмотрим, как работают последовательно и параллельно соединенные конденсаторы. Это будет немного сложнее, чем примеры резисторов, потому что измерить емкость напрямую мультиметром труднее.
Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается с нуля вольт. Когда ток начинает идти по одному из выводов, равное количество тока выходит из другого.А если последовательно с конденсатором нет сопротивления, то может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, и медленнее будет стекать до тех пор, пока напряжения не станут равными, когда ток полностью прекратится.
Как указано выше, потребляемый ток может быть довольно большим, если нет сопротивления последовательно с конденсатором, а время зарядки может быть очень коротким (например, миллисекунды или меньше). Для этого эксперимента мы хотим иметь возможность наблюдать за зарядом конденсатора, поэтому мы собираемся использовать 10 кОм; резистор, включенный последовательно, чтобы замедлить действие до точки, где мы его легко увидим.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.
В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в фарадах. Просто? Нет? Продемонстрируем на следующей странице.
Время эксперимента — часть 3, продолжение …
Для первой части этого эксперимента мы собираемся использовать один резистор 10 кОм и один резистор 100 мкФ (что равно 0,0001 фарад). Эти две части создают постоянную времени в 1 секунду:
При зарядке конденсатора емкостью 100 мкФ через 10 кОм; резистора, мы можем ожидать, что напряжение на цоколе вырастет примерно до 63% от напряжения питания за 1 постоянную времени, которая составляет 1 секунду.Через 5 постоянных времени (в данном случае 5 секунд) конденсатор заряжается примерно на 99% до напряжения питания, и он будет следовать кривой заряда, подобной графику ниже.
Теперь, когда мы это знаем, мы собираемся подключить схему на схеме (убедитесь, что полярность на этом конденсаторе правильная!).
С помощью нашего мультиметра, установленного для измерения вольт, проверьте выходное напряжение блока при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5В (будет немного больше, если батарейки новые). Теперь подключите схему, убедившись, что переключатель на аккумуляторном блоке находится в положении «ВЫКЛ», прежде чем вставлять его в макетную плату. Также позаботьтесь о том, чтобы красный и черный провода были в нужных местах. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного раздвинуть эти ножки, чтобы упростить задачу).
Когда мы убедимся, что схема выглядит правильно, а наш счетчик включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ON».Примерно через 5 секунд показания счетчика должны быть довольно близки к напряжению аккумуляторной батареи, что демонстрирует, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще довольно хорошо держит это напряжение, не так ли? Это потому, что ток не может разрядить конденсатор; у нас разомкнутая цепь. Для разряда конденсатора можно использовать еще один резистор на 10 кОм параллельно. Примерно через 5 секунд он вернется к почти нулю.
Experiment Time — Часть 3, и даже больше…
Теперь мы переходим к интересным моментам, начиная с последовательного соединения двух конденсаторов. Помните, что мы сказали, что результат будет аналогичен параллельному соединению двух резисторов. Если это правда, мы можем ожидать (используя произведение над суммой)
Что это будет делать с нашей постоянной времени?
Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что счетчик показывает ноль вольт (или около того), и переведите переключатель в положение «ON».Зарядка до напряжения аккумуляторной батареи занимала примерно половину времени? Это потому, что емкость вдвое меньше. Электронный бензобак стал меньше, поэтому на его зарядку уходит меньше времени. Для этого эксперимента предлагается третий конденсатор, просто чтобы доказать это, но мы держим пари, что читатель сможет увидеть надпись на стене.
Теперь мы попробуем подключить конденсаторы параллельно, помня, что мы говорили ранее, что это будет похоже на добавление резисторов последовательно. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет
.
Это означает, что теперь потребуется около 10 секунд, чтобы увидеть, как параллельные конденсаторы заряжаются до напряжения питания 4.5В.
Для доказательства начнем с нашей исходной схемы из одного 10 кОм; последовательно подключены резистор и один конденсатор емкостью 100 мкФ, как показано на первой схеме этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно за 5 секунд. Теперь подключите второй конденсатор параллельно. Убедитесь, что показания измерителя близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и переведите переключатель на батарейном блоке в положение «ON». Нужно много времени, правда? Разумеется, мы увеличили размер электронного бензобака, и теперь на его заполнение уходит больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и понаблюдайте, как он заряжается в течение долгого времени.
Дроссели серии
и параллельные индукторы
Катушки индуктивности серии
и параллельные
Случаи, когда катушки индуктивности должны быть добавлены последовательно или параллельно, довольно редки, но не редкость. В любом случае, давайте рассмотрим их для полноты картины.
Вкратце, они складываются так же, как и резисторы, то есть они складываются со знаком плюс, когда включены последовательно, и с превышением произведения, когда подключены параллельно.Сложность возникает, когда они размещаются близко друг к другу, чтобы иметь взаимодействующие магнитные поля, намеренно или нет. По этой причине предпочтительнее иметь один компонент, чем два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.
В любом случае достаточно сказать, что они добавляют, как резисторы. Дополнительная информация о катушках индуктивности выходит далеко за рамки этого руководства.
Ресурсы и дальнейшее развитие
Теперь, когда вы знакомы с основами последовательных и параллельных схем, почему бы не ознакомиться с некоторыми из этих руководств?
- Делители напряжения — Одна из самых простых и повторяющихся схем — это делитель напряжения.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
- Что такое Ардуино? — Теперь, когда у вас есть основы схемотехники, вы можете перейти непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino.
- — В этом руководстве мы говорили о некоторых наиболее основных элементах схемы, но это не был один из них. Переключатели — важный компонент практически в каждом электронном проекте.Узнайте все о переключателях в этом руководстве
- Шитье токопроводящей нитью — схемы не обязательно должны состоять из макетов и проводов. Электронный текстиль использует токопроводящую нить для вшивания светильников и другой электроники в одежду или другую ткань.
Основы работы с коммутатором
.

 Реактивная часть является индуктивной.
Реактивная часть является индуктивной.
