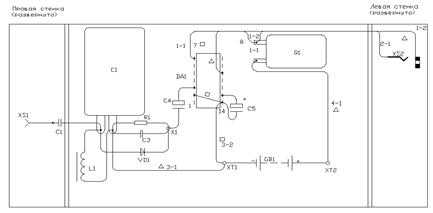
§ 102. Закон сохранения энергии. Проиллюстрируйте закон сохранения энергии на примерах

Примеры закона сохранения механической энергии

2014-05-27

а) Колебания пружинного маятника

Груз на пружине опустили вниз (см. рисунок).

После опускания груза пружина сжимается. По мере ее сжатия сила упругости пружины уменьшается, значит, уменьшается и потенциальная энергия пружины. Однако одновременно возрастает кинетическая энергия груза, так как при разгоне вверх увеличивается его скорость. Одновременно растет и потенциальная энергия груза под действием силы тяжести, так как груз поднимается выше. В этом примере энергия перешла из одного вида в другие: с потенциальной под действием силы упругости в кинетическую и потенциальную под действием силы тяжести.

б) Колебания нитяного маятника

Отклоним шарик на нитке вправо и отпустим: он движется влево, увеличивая скорость. Итак, кинетическая энергия возрастает. Одновременно шарик опускается, и в среднем положении ее потенциальная энергия становится наименьшей. Однако в этот момент скорость является наибольшей. Следовательно, за счет запаса кинетической энергии шарик продолжает двигаться влево, поднимаясь все выше. Это приводит к росту ее потенциальной энергии. Одновременно скорость уменьшается, что приводит к уменьшению кинетической энергии шарика.

В этом примере энергия переходила из одного вида в другой: из кинетической энергии в потенциальную энергию и наоборот.

в) Торможение тела силой трения

Тормозные колодки прижались к колесу. Сила трения, возникшего между колесом и колодками, замедляет вращение колеса, а следовательно, и скорость поезда. При трении они нагреваются настолько сильно, что, коснувшись рукой, можно получить ожог.

Мы наблюдаем преобразования энергии из одного ее вида в другой и одновременно переход от одного тела к другим: кинетическая энергия всего поезда превращалась во внутреннюю энергию его тормозных колодок, колес и окружающего воздуха.

Этот пример иллюстрирует превращение энергии

категория: Физика

moykonspekt.ru

Закон сохранения энергии | Проекты

Предмет: Физика

Класс: 10

Тема: «Закон сохранения энергии»

Проблемный вопрос: Как закон сохранения энергии может пригодиться нам в жизни?

Цели: Изучение закона сохранения энергии и получение сведений о  его применимости  в науке и жизни.

Задачи:

1. Создать условия для формирования умений, обеспечивающих самостоятельное успешное применение закона сохранения механической энергии в жизни.
2. Провести опыты, помогающие выяснить, значение закона сохранения энергии в нашей жизни.

 Гипотеза: Знание  закона сохранения энергии может пригодиться  школьникам при решении задач по физике и инженерам на производстве.

Этапы:

1. Изучение литературы, поиск информации в интернете
2. Проведение эксперимента
3. Результаты исследований
4. Выводы

 

I. Изучая различную литературу и информацию в интернете, мы узнали:

Мы установили, что потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия — движущиеся тела.

И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля.

При взаимодействиях тел, образующих замкнутую систему: если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:

. (1)

Вместе с тем по теореме о кинетической энергии работа тех же сил равна изменению кинетической энергии:

. (2)

Из сравнения равенств (1) и (2) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:

или

. (3)

Из равенства (3) следует, что сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упру гости, остается постоянной. Это утверждение называется законом сохранения энергии в механических процессах.

Сумма кинетической и потенциальной энергии тел называется полной механической энергией.

Для полной механической энергии закон сохранения энергии имеет следующее выражение: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.

Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергии тел в равной количественной мере при взаимодействии тел.

Закон сохранения энергии раскрывает физический смысл понятия работы.

Работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, — уменьшению потенциальной энергии тел.   Следовательно, работа равна энергии, превратившейся из одного вида в другой.

Закон сохранения полной механической энергии в процессах с участием сил упругости и гравитационных сил является одним из основных законов механики. Знание этого закона упрощает решение многих задач, имеющих большое значение в практической жизни.

II. Мы нашли простые иллюстрации закона сохранения энергии:

 

       Наиболее часто встречающаяся нам в повседневной жизни – механическая энергия. Это энергия непосредственного взаимодействия и движения физических тел и их частей. В рамках Механики (раздела Физики), механическую энергию подразделяют на потенциальную (для покоящихся тел) и кинетическую (для движущихся).

Суммарно потенциальная и кинетическая энергия системы тел составляют полную механическую энергию для этой системы тел.Механическая энергия широко известна Человеку с древнейших времен и применяется в таких устройствах, как: стрела, копье, нож, топор, праща, баллиста, повозка, маятник, журавль, ветряная мельница, водяное колесо, парус, гончарный круг, часы, и другие самые разнообразные механизмы…Приведем примеры наиболее распространенных и используемых источников механической энергии:ветер, течение рек, приливы и отливы морей и океанов, сельскохозяйственные животные, и сам человек.Зачастую механическая работа используется как промежуточный этап при выработке электроэнергии. Преобразование механической энергии в электрическую энергию осуществляется генераторами тока. В генераторе происходит превращение вращательного движения вала в электричество. Для вращения вала применяют следующие источники механической энергии: течение рек, океанские и морские приливы-отливы, ветер.Однако основное количество генераторов тока по-прежнему работает на тепловых станциях. Здесь химическая энергия ископаемого топлива преобразуется в тепловую энергию пара, которая затем превращается в электрическую энергию тока – универсальный стандарт, удобный для использования и передачи на большие расстояния.

1. Рассмотрим закон сохранения механической энергии на примере колебаний нитяного маятника :
2. III.  Провели эксперимент с известным «маятником Максвелла»

                                                                                                                                                                                                                                         

Изучили информацию из опытов программы «Галилео»:

IV. Анализ результатов и выводы:

1. Проведя эксперименты, мы изучили закон сохранения энергии и выявили возможные его применения в повседневной жизни. 
2. Энергия тела никогда не исчезает и не появляется вновь: она лишь превращается из одного вида в другой.
3. Полностью внутреннюю энергию нельзя превратить в механическую.
4. Закон сохранения энергии используется не только инженерами, но и в нашей повседневной жизни: наиболее распространенных и используемых источников  энергии можно встретить в таких явлениях,как :ветер, течение рек, приливы и отливы морей и океанов.
5. Мы выяснили, что школьники решая задачи на закон сохранения энергии, могут лучше понять, как применять его  в жизни.

Дополнительные материалы:                                                                                                                                                                                        

Закон сохранения энергии буклет

iteach.vspu.ru

Закон сохранения энергии.

Титульная Механика Литература

Силы, работа которых не зависит от формы траектории, а определяется начальным и конечным положением тела, называются потенциальными. Очевидно, что работа потенциальных сил на замкнутой траектории равна нулю. Все силы, работа которых зависит от формы траектории, называются непотенциальными. Непотенциальными силами являются силы трения, сопротивления. Для системы тел, в которой действуют потенциальные силы взаимодействия, можно ввести понятие потенциальной энергии. Потенциальная энергия - некоторая функция, описывающая взаимное расположение тел в системе, изменение которой взятое с обратным знаком, равно работе потенциальных сил, действующих между телами ситемы или же это энергия взаимного действия, взаимного расположения тел относительно друг друга: Пример.При прыжке ныряльщика в воду потенциальная сила притяжения совершает работу, которая равна изменению потенциальной энергии ныряльщика. Эта работа идет на изменение кинетической энергии прыгуна. Свойства потенциальной энергии: это энергия системы тел, между которыми действуют потенциальные силы взаимодействия; потенциальная энергия определяется с точностью до постоянного слагаемого. При этом за нулевой уровень потенциальной энергии можно принять любое состояние системы; формула для расчета потенциальной энергии может быть разной и зависит от характера взаимодействия тел; общим для всех видов потенциальной энергии является ее связь с работой потенциальных сил: A=Epсил=-(Ep1-Ep2) Кинетическая энергия - энергия движения. Работа силы, приложенной к телу при изменении его V, равна изменению кинетической энергии: Закон сохранения энергии. Приращение потенциальной энергии брошенного вверх тела происходит за счет убыли его кинетической энергии; при падении тела, приращение кинетической энергии происходит за счет убыли потенциальной энергии, так что полная механическая энергия тела не меняется. Аналогично, если на тело действует сжатая пружина, то она может сообщить телу некоторую скорость, т. е. кинетическую энергию, но при этом пружина будет распрямляться, и ее потенциальная энергия будет соответственно уменьшаться; сумма потенциальной и кинетической энергий останется постоянной. Если на тело, кроме пружины, действует еще и сила тяжести, то хотя при движении тела энергия каждого вида будет изменяться, но сумма потенциальной энергии тяготения, потенциальной энергии пружины и кинетической энергии тела опять-таки будет оставаться постоянной. Энергия может переходить из одного вида в другой, может переходить от одного тела к другому, но общий запас механической энергии остаётся неизменным. Опыты и теоретические расчеты показывают, что при отсутствии сил трения и при воздействии только сил упругости и тяготения суммарная потенциальная и кинетическая энергия тела или системы тел остается во всех случаях постоянной. В этом и заключается закон сохранения механической энергии. Докажем закон сохранения энергии в следующем опыте. Стальной шарик, упавший с некоторой высоты на стальную или стеклянную плиту и ударившийся об неё, подскакивает почти на ту же высоту, с которой упал. Во время движения шарика происходит целый ряд превращений энергии. При падении потенциальная энергия переходит в кинетическую энергию шарика. Когда шарик прикоснется к плите, и он и плита начинают деформироваться. Если рассмотреть кинетическую энергию, то можно сделать вывод, что она превращается в потенциальную энергию упругой деформации шарика и плиты, причем этот процесс продолжается до тех пор, пока шарик не остановится, т. е. пока вся его кинетическая энергия не перейдёт в потенциальную энергию упругой деформации. Затем под действием сил упругости деформированной плиты шарик приобретает скорость, направленную вверх: энергия упругой деформации плиты и шарика превращается в кинетическую энергию шарика. При дальнейшем движении вверх скорость шарика под действием силы тяжести уменьшается, и кинетическая энергия превращается в потенциальную энергию тяготения. В наивысшей точке шарик обладает снова только потенциальной энергией тяготения. Поскольку можно считать, что шарик поднялся на ту же высоту, с которой он начал падать, потенциальная энергия шарика в начале и в конце описанного процесса одна и та же. Более, того, в любой момент времени при всех превращениях энергии сумма потенциальной энергии тяготения, потенциальной энергии упругой деформации и кинетической энергии все время остается одной и той же. Для процесса превращения потенциальной энергии, обусловленной силой тяжести, в кинетическую и обратно при падении и подъеме шарика это было показано простым расчетом. Можно было бы убедиться, что и при превращении кинетической энергии в потенциальную энергию упругой деформации плиты и шарика и затем при обратном процессе превращения этой энергии в кинетическую энергию отскакивающего шарика сумма потенциальной энергии тяготения, энергии упругой деформации и кинетической энергии также остается неизменной, т. е. закон сохранения механической энергии выполнен. Теперь мы можем объяснить, почему нарушался закон сохранения работы в простой машине, которая деформировалась при передаче работы: дело в том, что работа, затраченная на одном конце машины, частично или полностью затрачивалась на деформацию самой простой машины (рычага, веревки и т.д.), создавая в ней некоторую потенциальную энергию деформации, и лишь остаток работы передавался на другой конец машины. В сумме же переданная работа вместе с энергией деформации оказывается равной затраченной работе. В случае абсолютной жесткости рычага, нерастяжимости веревки и т. д. простая машина не может накопить в себе энергию, и вся работа, произведенная на одном ее конце, полностью передается на другой конец. Силы трения и закон сохранения механической энергии. Присматриваясь к движению шарика, подпрыгивающего на плите, можно обнаружить, что после каждого удара шарик поднимается на несколько меньшую высоту, чем раньше, т. е. полная энергия не остается в точности постоянной, а понемногу убывает; это значит, что закон сохранения энергии в таком виде, как мы его сформулировали, соблюдается в этом случае только приближённо. Причина заключается в том, что в этом опыте возникают силы трения, сопротивление воздуха, в котором движется шарик, и внутреннее трение в самом материале шарика и плиты. Вообще, при наличии трения закон сохранения механической энергии всегда нарушается и полная энергия тел уменьшается. За счет этой убыли энергии и совершается работа против сил трения. Например, при падении тела с большой высоты скорость, вследствие действия возрастающих сил сопротивления среды, вскоре становится постоянной; кинетическая энергия тела перестает меняться, но его потенциальная энергия уменьшается. Работу против силы сопротивления воздуха совершает сила тяжести за счет потенциальной, энергии тела. Хотя при этом и сообщается некоторая кинетическая энергия окружающему воздуху, но она меньше, чем убыль потенциальной энергии тела, и, значит, суммарная механическая энергия убывает. Работа против сил трения может совершаться и за счет кинетической энергии. Например, при движении лодки, которую оттолкнули от берега пруда, потенциальная энергия лодки остается постоянной, но вследствие сопротивления воды уменьшается скорость движения лодки, т. е. ее кинетическая энергия, приращение кинетической энергии воды, наблюдающееся при этом, меньше, чем убыль кинетической энергии лодки. Подобно этому действуют и силы трения между твердыми телами. Например, скорость, которую приобретает груз, соскальзывающий с наклонной плоскости, а, следовательно, и его кинетическая энергия, меньше той, которую он приобрёл бы в отсутствие трения. Можно так подобрать угол наклона плоскости, что груз будет скользить равномерно. При этом его потенциальная энергия будет убывать, а кинетическая - оставаться постоянной, и работа против сил трения будет совершаться за счет потенциальной энергии. В природе все движения (за исключением движений в вакууме, например, движений небесных тел) сопровождаются трением. Поэтому при таких движениях закон сохранения механической энергии нарушается, и это нарушение происходит всегда в одну сторону - в сторону уменьшения полной энергии. Превращение механической энергии во внутреннюю энергию. Особенность сил трения состоит, как мы видели, в том, что работа, совершённая против сил трения, не переходит полностью в кинетическую или потенциальную энергию тел; вследствие этого суммарная механическая энергия тел уменьшается. Однако работа против сил трения не исчезает бесследно. Прежде всего, движение тел при наличия трения ведет к их нагреванию. Мы можем легко обнаружить это, крепко потирая руки или протягивая металлическую полоску между сжимающими ее двумя кусками дерева; полоска даже на ощупь заметно нагревается. Первобытные люди, как известно, добывали огонь быстрым трением сухих кусков дерева друг о друга. Нагревание происходит также при совершении работы против сил внутреннего трения, например, при многократном изгибании проволоки. Нагревание при движении, связанном с преодолением сил трения, часто бывает очень сильным. Например, при торможении поезда тормозные колодки сильно нагреваются. При спуске корабля со стапелей на воду для уменьшения трения стапеля обильно смазываются, и все же нагревание так велико, что смазка дымится, а иногда даже загорается. При движении тел в воздухе с небольшими скоростями, например, при движении брошенного камня, сопротивление воздуха невелико, на преодоление сил трения затрачивается небольшая работа, и камень практически не нагревается. Но быстро летящая пуля разогревается значительно сильнее. При больших скоростях реактивных самолетов приходится уже принимать специальные меры для уменьшения нагревания обшивки самолета. Мелкие метеориты, влетающие с огромными скоростями (десятки километров в секунду) в атмосферу Земли, испытывают такую большую силу сопротивления среды, что полностью сгорают в атмосфере. Нагревание в атмосфере искусственного спутника Земли, возвращающегося на Землю, так велико, что на нем приходится устанавливать специальную тепловую защиту. Кроме нагревания, трущиеся тела могут испытывать и другие изменения. Например, они могут измельчаться, растираться в пыль, может происходить плавление, т. е. переход тел из твердого в жидкое состояние: кусок льда может расплавиться в результате трения о другой кусок льда или о какое-либо иное тело. Итак, если движение тел связано с преодолением сил трения, то оно сопровождается двумя явлениями: сумма кинетической и потенциальной энергий всех участвующих в движении тел уменьшается; происходит изменение состояния тел, в частности может происходить нагревание. Это изменение состояния тел происходит всегда таким образом, что в новом состоянии тела могут производить большую работу, чем в исходном. Так, например, если налить в закрытую с одного конца металлическую трубку немного эфира и, заткнув трубку пробкой, зажать ее между двумя пластинками и привести в быстрое вращение, то эфир испарится и вытолкнет пробку. Значит, в результате работы по преодолению сил трения трубки о пластинки трубка с эфиром пришла в новое состояние, в котором она смогла совершить работу, требующуюся для выталкивания пробки, т. е. работу против сил трения, удерживающих пробку в трубке, и работу, идущую на сообщение пробке кинетической энергии. В исходном состоянии трубка с эфиром не могла совершить эту работу. Таким образом, нагревание тел, равно как и другие изменения, их состояния, сопровождается изменением "запаса" способности этих тел совершать работу. Мы видим, что "запас работоспособности" зависит, помимо положения тел относительно Земли, помимо их деформации и их скорости, еще и от состояния тел. Значит, помимо потенциальной энергии тяготения и упругости и кинетической энергии тело обладает и энергией, зависящей, от его состояния. Будем называть ее внутренней энергией. Внутренняя энергия тела зависит от его температуры, от того, является ли тело твердым, жидким или газообразным, как велика его поверхность, является ли оно сплошным или мелко раздробленным и т. д. В частности, чем температура тела выше, тем больше его внутренняя энергия. Таким образом, хотя при движениях, связанных с преодолением сил трения, механическая энергия систем движущихся тел уменьшается, но зато возрастает их внутренняя энергия. Например, при торможении поезда уменьшение его кинетической энергии сопровождается увеличением внутренней энергии тормозных колодок, бандаж колес, рельсов, окружающего воздуха и т. д. в результат нагревания этих тел. Все сказанное относится также и к тем случаям, когда силы трения возникают внутри тела, например, при разминании куска воска, при неупругом ударе свинцовых шаров, при перегибании куска проволоки. Всеобщий характер закона сохранения энергии. Силы трения занимают особое положение в вопросе о законе сохранения механической энергии. Если сил трения нет, то закон сохранения механической энергии соблюдается: полная механическая энергия системы остается постоянной. Если же действуют силы трения, то энергия уже не остается постоянной, а убывает при движении. Но при этом всегда растет внутренняя энергия. С развитием физики обнаруживались все новые виды энергии: была обнаружена световая энергия, энергия электромагнитных волн, химическая энергия, проявляющаяся при химических реакциях (в качестве примера достаточно указать хотя бы на химическую энергию, запасённую во взрывчатых веществах и превращающуюся в механическую и тепловую энергию при взрыве), наконец, была открыта ядерная энергия. Оказалось, что совершаемая над телом работа равна сумме всех видов энергии тела; работа же, совершаемая некоторым телом над другими телами, равна убыли суммарной энергии данного тела. Для всех видов энергии оказалось, что возможен переход энергии из одного вида в другой, переход энергии от одного тела к другому, но что при всех таких переходах общая энергия всех видов остаётся все время строго постоянной. В этом заключается всеобщность закона сохранения энергии. Хотя общее количество энергии остается постоянным, количество полезной для нас энергии может уменьшаться и в действительности постоянно уменьшается. Переход энергии в другую форму может означать переход ее в бесполезную для нас форму. В механике чаще всего это - нагревание окружающей среды, трущихся поверхностей и т. п. Такие потери не только невыгодны, но и вредно отзываются на самих механизмах; так, во избежание перегревания приходится специально охлаждать трущиеся части механизмов.

sch119comp2.narod.ru

Закон сохранения энергии

В примере, разобранном в предыдущем параграфе, выяснилось, что приращение потенциальной энергии брошенного вверх тела происходит за счет убыли его кинетической энергии; при падении тела приращение кинетической энергии происходит за счет убыли потенциальной энергии, так что полная механическая энергия тела не меняется. Аналогично, если на тело действует сжатая пружина, то она может сообщить телу некоторую скорость, т. е. кинетическую энергию, но при этом пружина будет распрямляться, и ее потенциальная энергия будет соответственно уменьшаться; сумма потенциальной и кинетической энергий останется постоянной. Если на тело, кроме пружины, действует еще и сила тяжести, то хотя при движении тела энергия каждого вида будет изменяться, но сумма потенциальной энергии тяготения, потенциальной энергии пружины и кинетической энергии тела опять-таки будет оставаться постоянной.

Энергия может переходить из одного вида в другой, может переходить от одного тела к другому, но общий запас механической энергии остается неизменным. Опыты и теоретические расчеты показывают, что при отсутствии сил трения и при воздействии только сил упругости и тяготения суммарная потенциальная и кинетическая энергия тела или системы тел остается во всех случаях постоянной. В этом и заключается закон сохранения механической энергии.

Рис. 168. Отразившись от стальной плиты, стальной шарик подскакивает снова на ту же высоту, с которой он был брошен.

Проиллюстрируем закон сохранения энергии на следующем опыте. Стальной шарик, упавший с некоторой высоты на стальную или стеклянную плиту и ударившийся об нее, подскакивает почти на ту же высоту, с которой упал (рис. 168). Во время движения шарика происходит целый ряд превращений энергии. При падении потенциальная энергия переходит в кинетическую энергию шарика. Когда шарик прикоснется к плите, и он и плита начинают деформироваться. Кинетическая энергия превращается в потенциальную энергию упругой деформации шарика и плиты, причем этот процесс продолжается до тех пор, пока вся его кинетическая энергия не перейдет в потенциальную энергию упругой деформации. Затем под действием сил упругости деформированной плиты шарик приобретает скорость, направленную вверх: энергия упругой деформации плиты и шарика превращается в кинетическую энергию шарика. При дальнейшем движении вверх скорость шарика под действием силы тяжести уменьшается, и кинетическая энергия превращается в потенциальную энергию тяготения. В наивысшей точке шарик обладает снова только потенциальной энергией тяготения.

Поскольку можно считать, что шарик поднялся на ту же высоту, с которой он начал падать, потенциальная энергия шарика в начале и в конце описанного процесса одна и та же. Более того, в любой момент времени при всех превращениях энергии сумма потенциальной энергии тяготения, потенциальной энергии упругой деформации и кинетической энергии все время остается одной и той же. Для процесса превращения потенциальной энергии, обусловленной силой тяжести, в кинетическую и обратно при падении и подъеме шарика это было показано простым расчетом в § 101. Можно было бы убедиться, что и при превращении кинетической энергии в потенциальную энергию упругой деформации плиты и шарика и затем при обратном процессе превращения этой энергии в кинетическую энергию отскакивающего шарика сумма потенциальной энергии тяготения, энергии упругой деформации и кинетической энергии также остается неизменной, т. е. закон сохранения механической энергии выполнен.

Теперь мы можем объяснить, почему нарушался закон сохранения работы в простой машине, которая деформировалась при передаче работы (§ 95): дело в том, что работа, затраченная на одном конце машины, частично или полностью затрачивалась на деформацию самой простой машины (рычага, веревки и т. д.), создавая в ней некоторую потенциальную энергию деформации, и лишь остаток работы передавался на другой конец машины. В сумме же переданная работа вместе с энергией деформации оказывается равной затраченной работе. В случае абсолютной жесткости рычага, нерастяжимости веревки и т. д. простая машина не может накопить в себе энергию, и вся работа, произведенная на одном ее конце, полностью передается на другой конец.

Пользуясь двумя законами сохранения: законом сохранения импульса и законом сохранения энергии, можно решить задачу о соударении идеально упругих шаров, т. е. шаров, которые после соударения отскакивают друг от друга, сохраняя суммарную кинетическую энергию.

Пусть два шара движутся по одной прямой (по линии центров). Предположим, что, кроме сил взаимодействия при их соприкосновении, на шары не действуют никакие силы со стороны каких-либо других тел. После соударения (соударение произойдет, если шары движутся навстречу друг другу или если один из них догоняет второй) они будут двигаться по той же прямой, но с измененными скоростями. Будем считать, что нам известны массы шаров  и  и их скорости  и  до соударения. Требуется найти их скорости  и  после соударения.

Из закона сохранения импульса следует, что ввиду того, что на шары не действуют никакие силы, кроме сил их взаимодействия, суммарный импульс должен сохраняться, т. е. импульс до соударения должен равняться импульсу после соударения:

(102.1)

Скорости  и  направлены вдоль линии центров (в одну и ту же либо в противоположные стороны). Из соображений симметрии следует, что скорости    также будут направлены вдоль линии центров. Примем эту линию за ось  и спроектируем векторы, входящие в уравнение (102.1), на эту ось. В результате получим уравнение

(102.2)

Далее, из условия идеальной упругости шаров следует, что сохраняется также кинетическая энергия шаров, т. е. должно выполняться равенство

(102.3)

(в данном случае  и т. д.).

Из уравнений (102.2) и (102.3) можно найти неизвестные величины  и . Для этого перепишем эти уравнения в виде

Деля почленно второе уравнение на первое, получим

. (102.4)

Умножив (102.4) на  и вычтя из (102.2), придем к соотношению

,

откуда

. (102.5)

Подобным же образом, умножив (102.4) на  и сложив с (102.2), найдем

Если, например, первый шар движется в направлении оси , а второй — ему навстречу, то  равна модулю скорости , т. е. , а  равна модулю скорости , взятому со знаком минус, т. е. . Подставив эти значения в формулы (102.5) и (102.6), получим

Знак получившихся значений  и  укажет направления соответствующих скоростей относительно оси , а абсолютные значения  и  дадут модули скоростей.

Особенно упрощается соотношение скоростей при соударении шаров одинаковой массы . В этом случае , т. е. шары обмениваются скоростями. В частности, если шар соударяется с неподвижным шаром той же массы, то он сообщает ему свою скорость, а сам останавливается.

Если масса одного шара гораздо больше массы другого, например  много больше , то в знаменателе и в числителе формулы (102.5) можно пренебречь членами, содержащими . Если, кроме того, массивный шар покоится, то получаем , т. е. шар отскакивает, как от неподвижной стенки. Действительно, как видно из (102.5), большой шар получит при этом малую скорость, равную приблизительно .

sfiz.ru

---

• 
  Периодичность пересмотра схем и инструкций
• 
  Счетчик входа и выхода
• 
  Правила оформления электрических схем гост
• 
  Класс точности 2 0
• 
  Диодный тиристор
• 
  Тип узо
• 
  Монтаж солнечных панелей
• 
  Электричество из газа
• 
  Скорость света это
• 
  Фаза электрическая это
• 
  Ток кз