3) Виды измерений (прямые, косвенные, совокупные, совместные). Прямые измерения примеры
3. Прямые и косвенные измерения
Прямыми измерениями называют такие измерения, которые получены непосредственно с помощью измерительного прибора. К прямым измерениям можно отнести измерение длины линейкой, штангенциркулем, измерение напряжения вольтметром, измерение температуры термометром и т.п. На результатах прямых измерений могут оказать влияние различные факторы. Поэтому погрешность измерений имеет различный вид, т.е. имеет место погрешность прибора, систематические и случайные погрешности, ошибки округления при снятии отсчета со шкалы прибора, промахи. В связи с этим важно выявить в каждом конкретном эксперименте, какая из ошибок измерения является наибольшей, и если окажется, что одна из них на порядок превышает все остальные, то последними погрешностями можно пренебречь.
Если же все учитываемые погрешности по порядку величины одинаковы, то необходимо оценить совместный эффект нескольких различных погрешностей. В общем случае суммарная ошибка подсчитывается по формуле:
, (7)
где – случайная погрешность, – погрешность прибора, – погрешность округления.
В большинстве экспериментальных исследований физическая величина измеряется не прямо, а через другие величины, которые в свою очередь определяются прямыми измерениями. В этих случаях измеряемая физическая величина определяется через прямо измеренные величины посредством формул. Такие измерения называются косвенными. На языке математики это означает, что искомая физическая величина f связана с другими величинами х1, х2, х3,…,.хn функциональной зависимостью, т.е
F=f(x1,x2,….,хn)
Примером таких зависимостей может служить объем шара
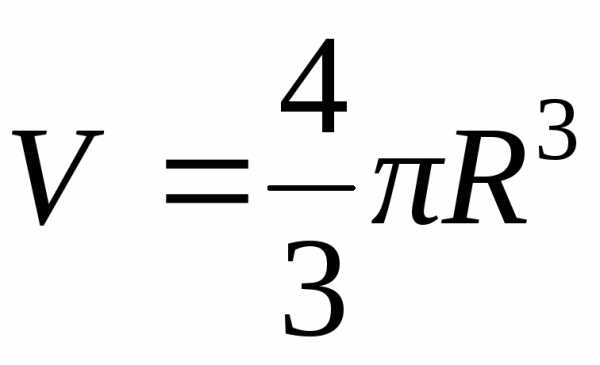 .
.
В данном случае косвенно измеряемой величиной является V - шара, которая определится при прямом измерении радиуса шара R. Данная измеряемая величина V является функцией одной переменной.
Другим примером может быть плотность твердого тела
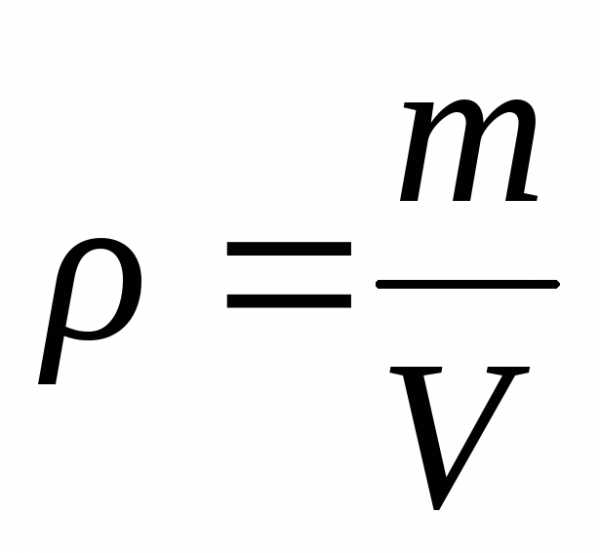 . (8)
. (8)
Здесь – является косвенно измеряемая величина, которая определяется прямым измерением массы тела m и косвенной величиной V. Данная измеряемая величина является функцией двух переменных, т.е.
= (m, V)
Теория погрешностей показывает, что погрешность функции оценивается суммой погрешностей всех аргументов. Погрешность функции будет тем меньше, чем меньше погрешностей её аргументов.
4.Построение графиков по экспериментальным измерениям.
Существенным моментом экспериментального исследования является построение графиков. При построении графиков, прежде всего необходимо выбрать систему координат. Наиболее распространенной является прямоугольная система координат с координатной сеткой, образованной равностоящими друг от друга параллельными прямыми (например, миллиметровая бумага). На осях координат через определенные промежутки наносятся деления в определенном масштабе для функции и аргумента.
В лабораторных работах при изучении физических явлений приходится учитывать изменения одних величин в зависимости от изменения других. Например: при рассмотрении движения тела устанавливается функциональная зависимость пройденного пути от времени; при изучении электросопротивления проводника от температуры. Можно привести еще множество примеров.
Переменную величину У называют функцией другой переменной величины Х (аргумент), если каждому значение У будет соответствовать вполне определенное значение величины Х, то можно записать зависимость функции в виде У = У(Х).
Из определения функции следует, что для её задания необходимо указать два множества чисел (значений аргумента Х и функции У), а так же закон взаимозависимости и соответствия между ними (Х и У). Экспериментально функция может быть задана четырьмя способами:
Таблицей; 2. Аналитически, в виде формулы; 3. Графически; 4. Словесно.
Например: 1. Табличный способ задания функции –зависимости величины постоянного тока I от величины напряжения U, т.е. I=f(U).
Таблица 2
| U(B) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| I(mA) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
2.Аналитический способ задания функции устанавливается формулой, при помощи которой по заданным (известным) значениям аргумента можно определить соответствующие значения функции. Например, функциональная зависимость, приведенная в таблице 2, может быть записана формулой:
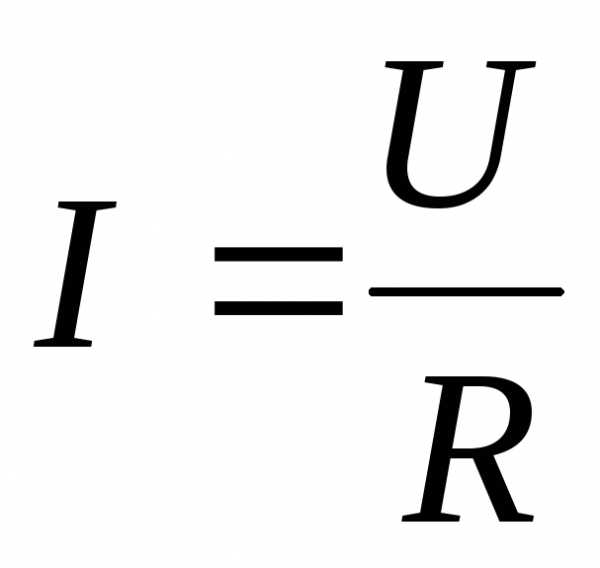 (9)
(9)
3.Графический способ задания функции.
Графиком функции I=f(U) в декартовой системе координат называется геометрическое место точек, построенное по числовым значениям координатной точки аргумента и функции.
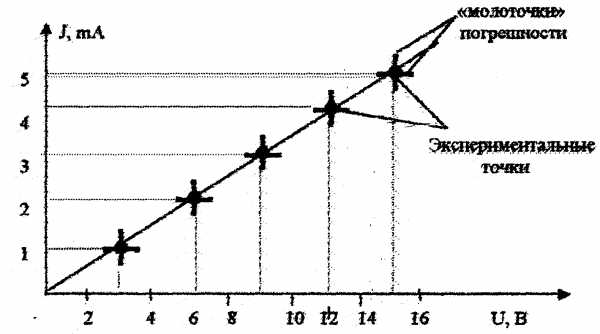
На рис. 1 построен график зависимости I=f(U), заданный таблицей.
I, ma
Рис. 1
Точки, найденные на опыте и наносимые на график, отмечаются отчетливо в виде кружочков, крестиков. На графике для каждой построенной точки необходимо указывать погрешности в виде «молоточков» (см. рис 1). Размеры этих «молоточков» должны быть равны удвоенному значению абсолютных ошибок функции и аргумента.
Масштабы графиков надо выбирать так, чтобы наименьшее расстояние, отсчитываемое по графику, было бы не меньше наибольшей абсолютной погрешности измерений. Однако такой выбор масштаба не всегда удобен. В некоторых случаях удобней взять по одной из осей несколько больший или меньший масштаб.
Если исследуемый интервал значений аргумента или функции отстоит от начала координат на величину, сравнимую с величиной самого интервала, то целесообразно перенести начало координат в точку, близкую к началу исследуемого интервала, как по оси абсцисс, так и по оси ординат.
Проведение кривой (т.е. соединение экспериментальных точек) через точки обычно осуществляется в соответствии с идеями метода наименьших квадратов. В теории вероятностей показано, что наилучшим приближением к экспериментальным точкам будет такая кривая (или прямая), для которой сумма наименьших квадратов отклонений по вертикали от точки до кривой будет минимальной.
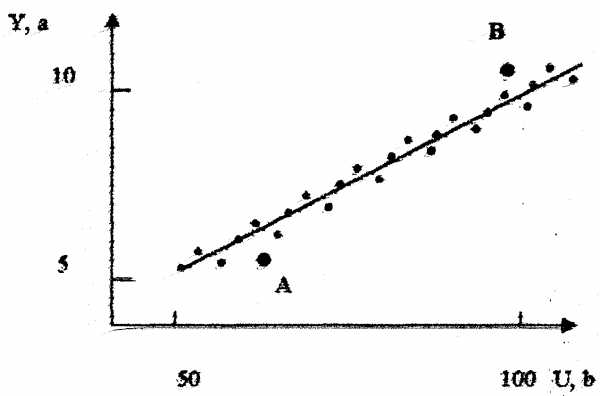
Нанесенные на координатную бумагу точки соединяют плавной кривой, причем кривая должна проходить возможно ближе ко всем экспериментальным точкам. Проводить кривую следует так, чтобы она лежала возможно ближе к точкам не превышаемые погрешности и чтобы по обе стороны кривой оказывалось приблизительно равное их количество ( см. рис. 2).
I, ma
В
Рис. 2.
Если при построении кривой одна или несколько точек выходят за пределы области допустимых значений (см. рис. 2, точки А и В), то кривую проводят по остальным точкам, а выпавшие точки А и В как промахи не берут в учет. Затем проводят повторные измерения в этой области (точки А и В) и устанавливается причина такого отклонения ( либо это промах или законное нарушение найденной зависимости).
Если исследуемая, экспериментально построенная функция обнаруживает «особые» точки, (например, точки экстремума, перегиба, разрыва и т.д.). То увеличивается число экспериментов при малых значениях шага (аргумента) в области особых точек.
studfiles.net
Метрология. Прямые и косвенные измерения.
Метрологией называется наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Измерением называется нахождение значения физической величины опытным путем с помощью специальных технических средств. Результатом измерения является количественная характеристика физической величины в виде числа единиц измеряемой величины и погрешность, с которой получено данное число.
Виды измерений. В зависимости от способа получения числового значения измеряемой величины измерения делятся на прямые, косвенные и совокупные измерения.
Прямыми называются измерения, при которых искомое значение величины получают из опытных данных. При прямых измерениях экспериментальные операции производятся над самой измеряемой величиной. Числовое значение измеряемой величины получают в экспериментальном сравнении с мерой или по показаниям приборов. Например, измерение тока амперметром, напряжения вольтметром, температуры термометром, массы на весах.
Косвенными называют такие измерения, при которых числовое значение измеряемой величины определяется по известной функциональной зависимости через другие величины, которые можно прямо измерить. При косвенных измерениях числовое значение измеряемой величины получают с участием оператора на основе прямых измерений – решением одного уравнения. К косвенным измерениям прибегают в тех случаях, когда неудобно или невозможно осуществить автоматическое вычисление известной зависимости между одной или несколькими входными величинами и измеряемой величиной. Например, мощность в цепях постоянного тока определяет оператор, умножая напряжение на ток, измеренные прямым измерением с помощью амперметра и вольтметра.
Отклонение результата измерения от истинного значения измеряемой величины называют погрешностью измерения.
Абсолютная погрешность измерения равна разности между результатом измерения и истинным значением измеряемой величины : .
Относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к истинному значению измеряемой величины. Обычно относительная погрешность выражается в процентах %.
25. Основные понятия и определения: информация, алгоритм, программа, команда, данные, технические устройства.
Информация — от латинского слова "information", что означает сведения, разъяснения, изложение.
Применительно к компьютерной обработке данных под информацией понимают некоторую последовательность символических обозначений (букв, цифр, закодированных графических образов и звуков и т.п.), несущую смысловую нагрузку и представленную в понятном компьютеру виде. Каждый новый символ в такой последовательности символов увеличивает информационный объём сообщения.
Алгоритм — последовательность чётко определенных действий, выполнение которых ведёт к решению задачи. Алгоритм, записанный на языке машины, есть программа решения задачи.
Свойства алгоритмов: дискретность, понятность, результативность, определенность, массовость.
Программа — последовательность действий, инструкций, предписаний для некоторого вычислительного устройства; файл, содержащий эту последовательность действий.
Команда — это указание компьютерной программе действовать как некий интерпретатор для решения задачи. В более общем случае, команда — это указание некоему интерфейсу командной строки.
Данные - информация, представленная в формализованном виде, что обеспечивает возможность ее хранения, обработки и передачи.
Технические устройства (средства информатизации) – это совокупность систем, машин, приборов, механизмов, устройств и прочих видов оборудования, предназначенных для автоматизации различных технологических процессов информатики, причем таких, выходным продуктом которых является именно информация (сведения, знания) или данные, используемые для удовлетворения информационных потребностей в разных областях предметной деятельности общества.
Все технические средства информатизации в зависимости от выполняемых функций можно разделить на шесть групп : устройства ввода информации, устройства вывода информации, устройства обработки информации, устройства передачи и приема информации, устройства хранения информации, многофункциональные устройства.
infopedia.su
прямые, косвенные, абсолютные и относительные.
В результате измерения определяют числовое значение измеряемой величины, равное отношению измеряемой величины к единице измерения или эталону. В зависимости от конкретных условий, применяемых измерительных средств и приемов их использования измерения могут производиться различными способами или методами. С точки зрения общих приемов получения результатов измерения различают: прямые икосвенные.
Прямые измерения
При прямых измерениях искомая величина определяется непосредственно показаниями прибора или измерительной шкалы инструмента. К прямым измерениям относятся измерения длин линейками, штангенинструментом, микрометрами, широкодиапазонными инкрементными измерительными головками с цифровым отсчетом, высотомерами, измерения углов - угломерами и др.
Косвенные измерения
При косвенных измерениях искомая величина (размер или отклонение) определяется по результатам прямых измерений одной или нескольких величин, связанных с искомой величиной определенной функциональной зависимостью, т. е. после определения косвенных величин, влияющих на искомую, определяют искомую величину, используя математические методы вычислений или преобразований. Примером косвенных измерений могут служить измерения диаметра вала по длине его окружности с помощью рулетки или обкатного ролика, измерения на координатно-измерительных машинах (КИМ), и др.
Прямые измерения более просты и сразу приводят к результату измерения, поэтому они имеют преимущественное распространение в машиностроении. Однако в ряде случаев прямые измерения не могут быть осуществлены, например, при измерении штангенциркулем расстояния между осями отверстий, при измерениях на КИМ, при измерении валов большого диаметров и др. Прямые измерения иногда уступают по точности косвенным измерениям, как это имеет место при измерении углов угломерами, погрешности которых в десятки раз превышают погрешности синусных линеек.
Косвенные измерения широко применяют при координатных измерениях, потому что результат измерения всегда получают расчетом по определенным при измерении координатам двух или нескольких точек.
Каждое измерение может производиться абсолютным илиотносительным методом.
Абсолютный метод измерения
При абсолютном методе весь измеряемый размер определяется непосредственно по показаниям прибора. В настоящее время большинство приборов и инструментов измеряют абсолютным методом – штангенинструмент, микрометры, широкодиапазонные индикаторы и преобразователи, высотомеры, КИМ, угловые энкодеры и др. Относительный метод измерения
Относительный (сравнительный) метод измерения дает только отклонение размера от установочной меры или образца, по которым прибор был установлен на ноль. Определение размера в этом случае производится алгебраическим суммированием размера установочной меры и показаний прибора при измерении.
Приборы для относительных измерений требуют дополнительной затраты времени для предварительной настройки прибора по установочной мере, что существенно снижает производительность измерений при небольших партиях проверяемых деталей. Снижение производительности становится несущественным, если после настройки прибором производят большое число измерений.
Приборы для относительных измерений в ряде случаев позволяют получить более высокую точность, а при измерении больших партий деталей и более высокую производительность контроля, благодаря удобству отсчета отклонений размера по шкале прибора.
Относительный метод измерения применяется на контрольных приспособлениях и автоматах, в приборах активного контроля.
studfiles.net
Прямые и косвенные измерения
По способу получения результата измерения делятся на прямые и косвенные. Если значение физической величины находят непосредственным отсчетом по шкале прибора, то такие измерения называются прямыми (измерения давления барометром, температуры – термометром, времени – секундомером, длины – штангенциркулем или линейкой, силы тока – амперметром и т.п.). Эти измерения могут быть однократными и многократными. Многократное измерение – повторение экспериментельной операции, в результате которой получается одно из значений измеряемой величины 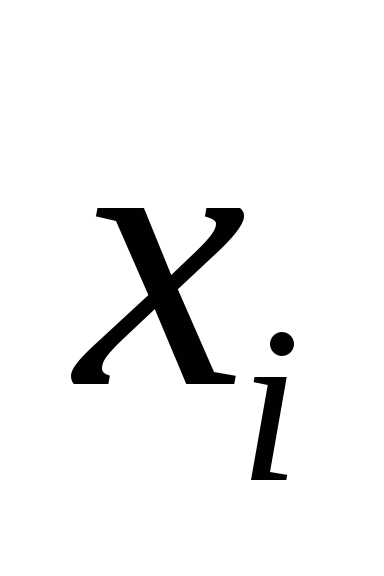 , называемыхрезультатами наблюдений. Совокупность результатов наблюдений подлежит совместной обработке для получения результата измерения.
, называемыхрезультатами наблюдений. Совокупность результатов наблюдений подлежит совместной обработке для получения результата измерения.
Часто прямое измерение физической величины оказывается невозможным или слишком трудоемким. При косвенных измерениях результат определяется по формулам на основе результатов прямых измерений других величин (например, определение электрического cопротивления образца по измеренным силе тока и напряжению). Одну и ту же величину часто можно найти путем как прямых, так и косвенных измерений. Например, скорость автомобиля может быть определена по спидометру (прямое измерение) или найдена делением пройденного пути на время движения (косвенное измерение).
При косвенных измерениях погрешность искомой физической величины накапливается из погрешностей прямых измерений величин, входящих в расчетную формулу.
Погрешности многократных прямых измерений (случайные погрешности)
Пусть изучается физическая величина 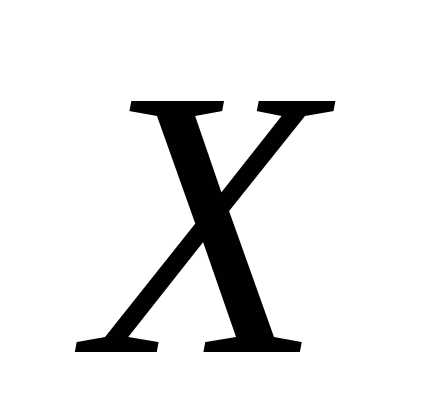 и многократными измерениями получены
и многократными измерениями получены 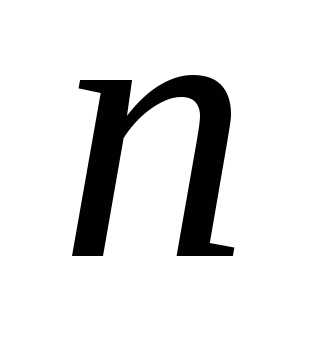 результатов наблюдений
результатов наблюдений
,
причем все измерения выполнены одним и тем же методом и с одинаковой степенью тщательности. Этот ряд значений величины называется выборкой.Предположим, что на результат измерений оказывают действие только случайные (неконтролируемые) факторы, а промахи и систематические ошибки отсутствуют.
Задача экспериментатора состоит в том, чтобы найти наилучшую оценку и доверительную погрешность результата измерений для заданного значения доверительной вероятности. (При обработке экспериментальных результатов можно поступать и по–другому: произвольно задавать значение доверительной погрешности и вычислять соответствующее ей значение вероятности). Указанная задача строго решается с помощью теории вероятностей и математической статистики.
В большинстве случаев случайные ошибки подчиняются установленному Гауссом нормальному закону распределения, вид которого может быть получен на основании следующих предположений:
1) величина случайной погрешности может иметь любое значение;
2) вероятность появления погрешности снижается с ростом ее величины – большие погрешности маловероятны;
3) погрешности, равные по величине, но разные по знаку, встречаются одинаково часто – равные по модулю погрешности равновероятны.
Выведенный на основе указанных предположений закон нормального распределения случайных величин (распределение Гаусса) выражается формулой
, (3)
где 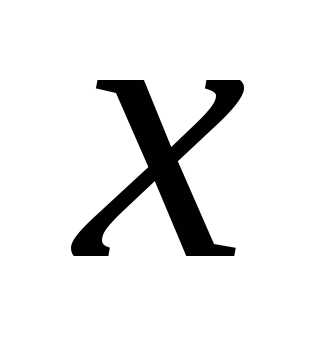 – числовое значение определяемой величины
– числовое значение определяемой величины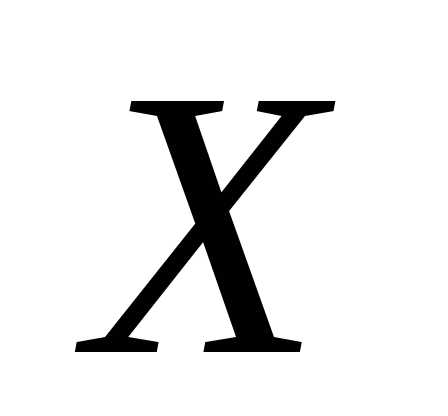 ,
, и
и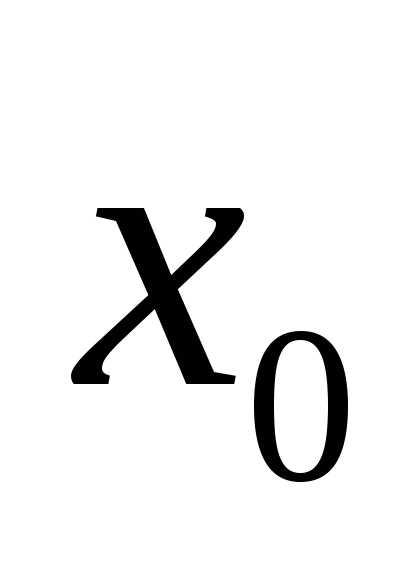 – параметры распределения;
– параметры распределения;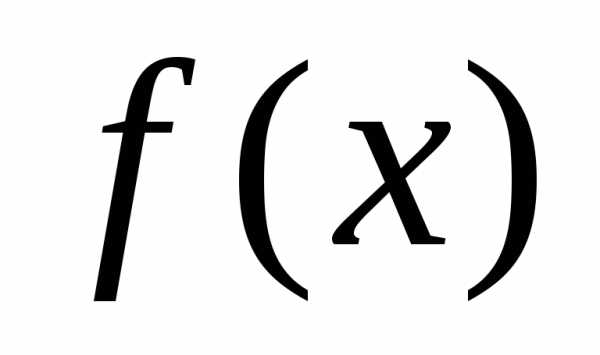 – плотность вероятности (вероятность того, что значение
– плотность вероятности (вероятность того, что значение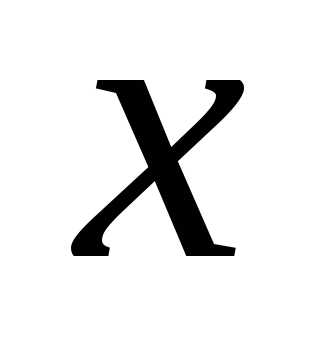 принадлежит некоторому единичному интервалу значений), так что функцияопределяет вероятность попадания значения
принадлежит некоторому единичному интервалу значений), так что функцияопределяет вероятность попадания значения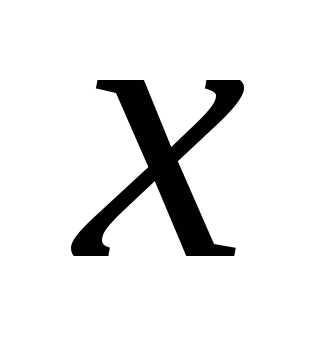 в интервал от
в интервал от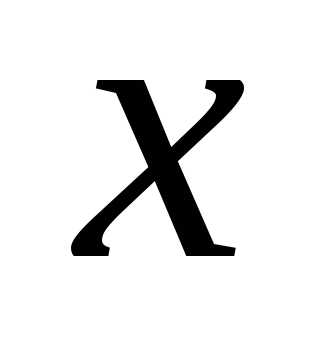 до
до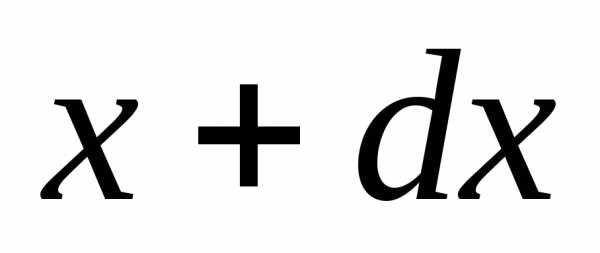 .
.
Параметр 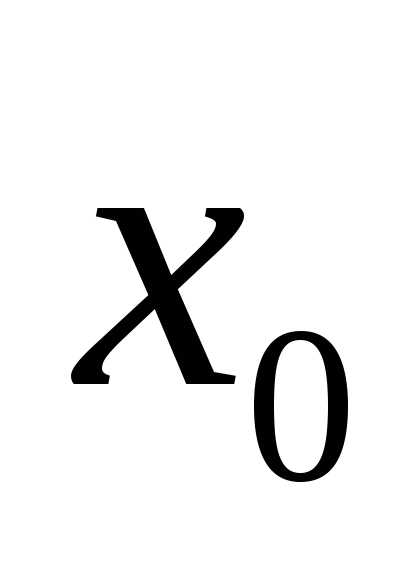 , соответствующий максимуму плотности вероятности
, соответствующий максимуму плотности вероятности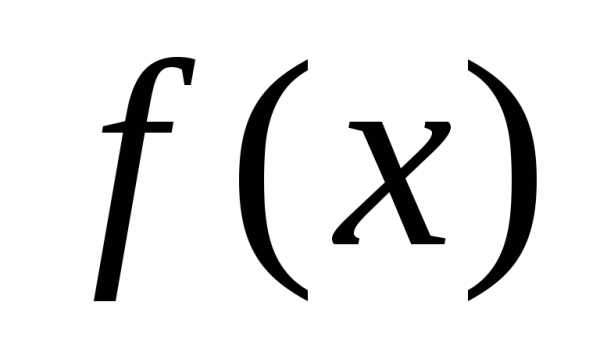 , называетсяматематическим ожиданиемслучайной величины
, называетсяматематическим ожиданиемслучайной величины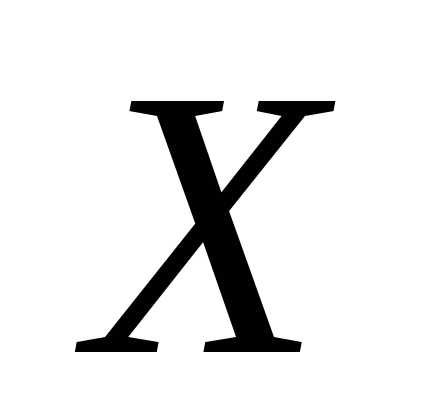 . Параметр
. Параметр называетсясредним квадратическим отклонением величины
называетсясредним квадратическим отклонением величины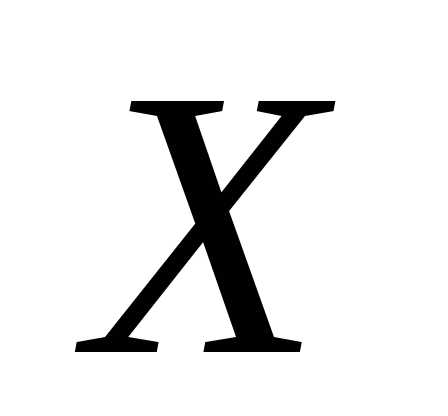 от ее математического ожидания
от ее математического ожидания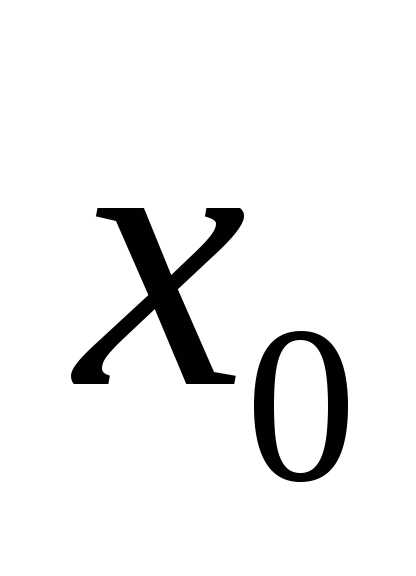 и характеризует меру ее разброса относительно
и характеризует меру ее разброса относительно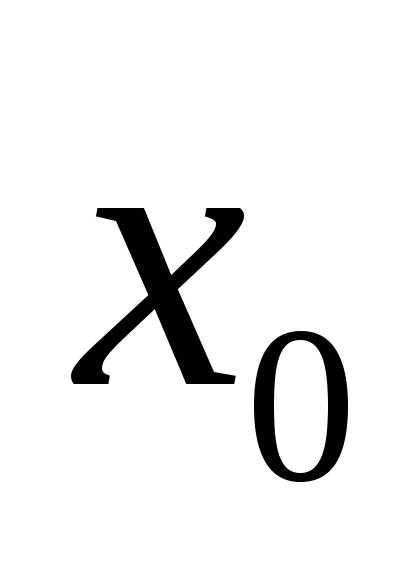 . Очевидно, что
. Очевидно, что
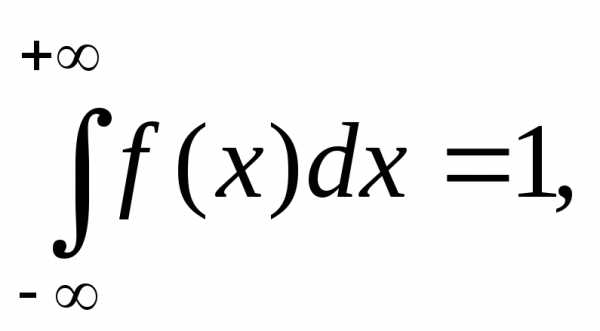
т.е. вероятность того, что случайная величина 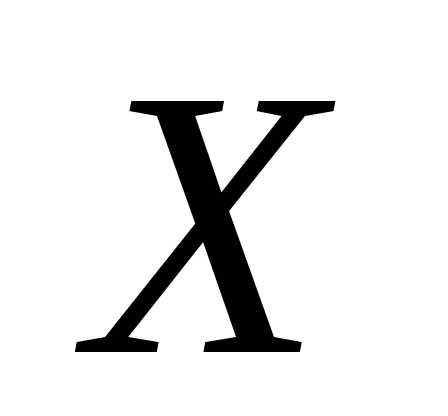 вообще имеет какое–то значение, равна единице.
вообще имеет какое–то значение, равна единице.
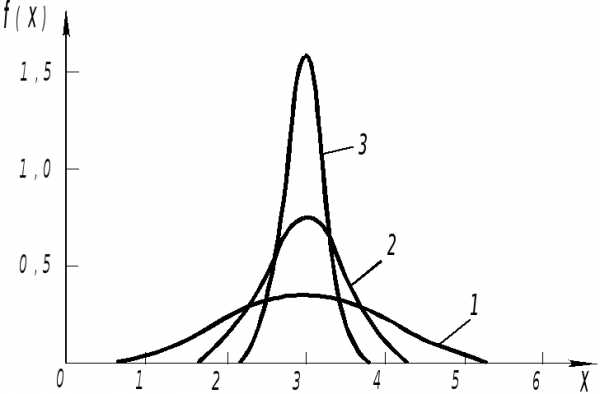 Поскольку максимальное значение плотность вероятности
Поскольку максимальное значение плотность вероятности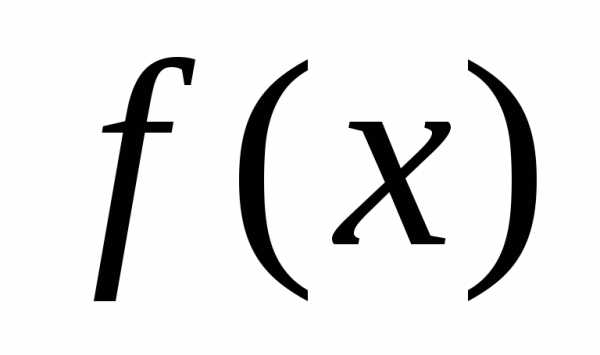 принимает при
принимает при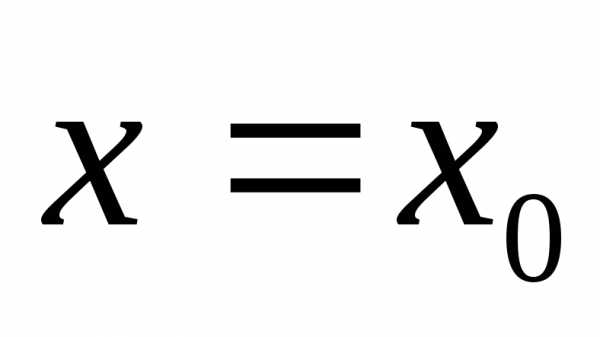 , то величину
, то величину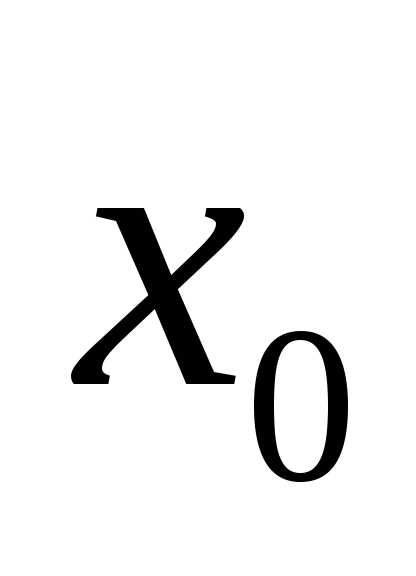 часто считают приблизительно равной истинному значению измеряемой величины. На рис.
часто считают приблизительно равной истинному значению измеряемой величины. На рис. представлен график этой функции. Из вышесказанного ясно, что площадь заштрихованной фигуры численно равна вероятности, с которой любой отсчет попадает в интервал от
представлен график этой функции. Из вышесказанного ясно, что площадь заштрихованной фигуры численно равна вероятности, с которой любой отсчет попадает в интервал от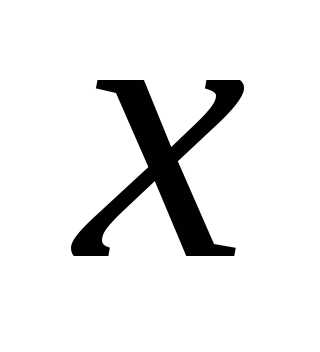 до
до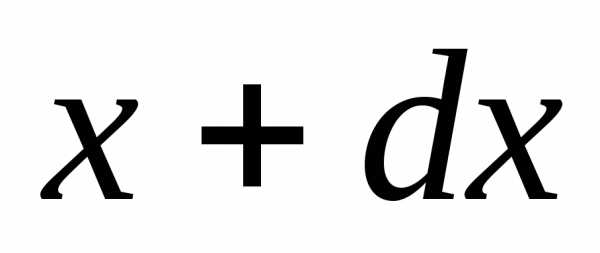 .
.
Рис.1. Нормальное (гауссово) распределение
(1–,2–/2,3–/4) .
Из теории следует, что наилучшей оценкой истинного значения 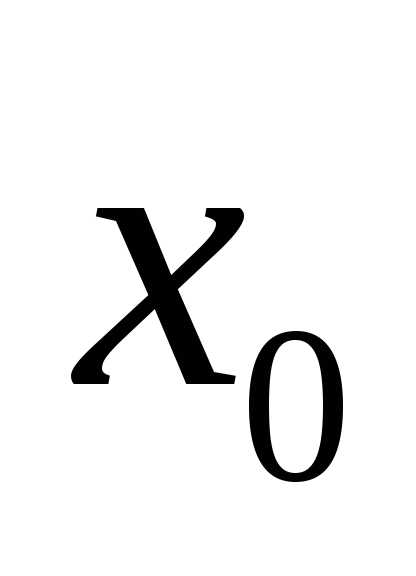 измеряемой случайной величины
измеряемой случайной величины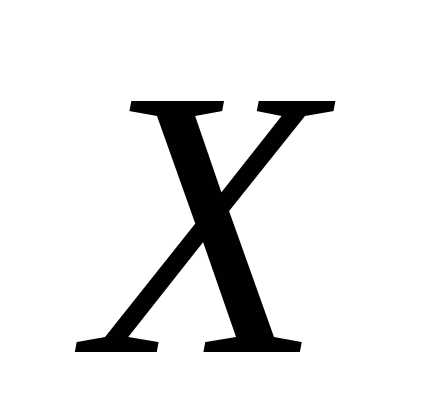 является среднее арифметическое (выборочное среднее) значение
является среднее арифметическое (выборочное среднее) значение
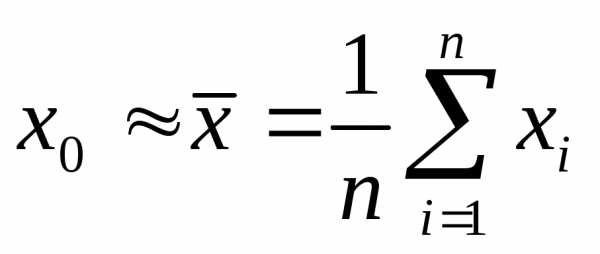 . (4)
. (4)
Заметим также, что с увеличением значения  увеличивается разброс отсчетов, т.е. точность измерений понижается. В условиях реального эксперимента точное значение
увеличивается разброс отсчетов, т.е. точность измерений понижается. В условиях реального эксперимента точное значение , как правило, неизвестно. По многократным измерениям
, как правило, неизвестно. По многократным измерениям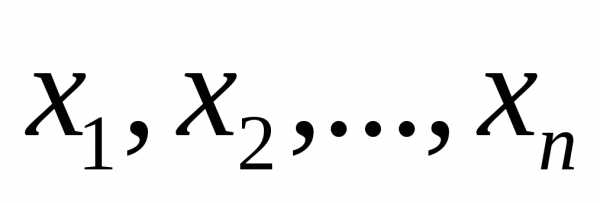 можно получить приближенную оценку этого параметра в виде среднеквадратичной погрешности
можно получить приближенную оценку этого параметра в виде среднеквадратичной погрешности 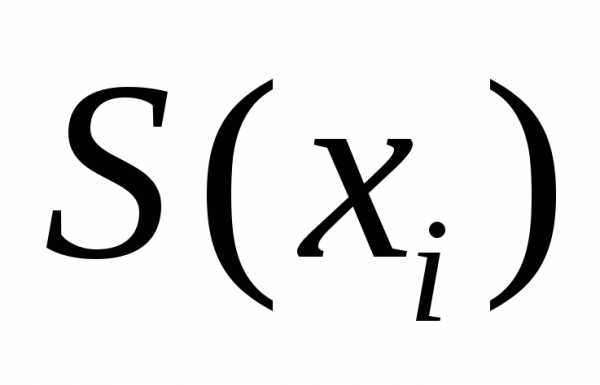 отдельного результатаизмерения
отдельного результатаизмерения
, (5)
которая характеризует ошибку каждого отдельного измерения и при неограниченном увеличении числа наблюдений () стремится к истинной среднеквадратичной ошибке .
.
Если произвести несколько серий многократных измерений, т.е. получить несколько выборок и для каждой вычислить выборочное среднее, то получим выборку для новой случайной величины 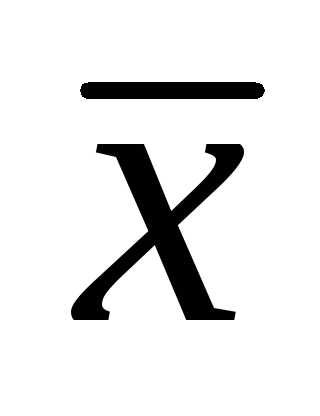 , которая также распределена нормально с математическим ожиданием
, которая также распределена нормально с математическим ожиданием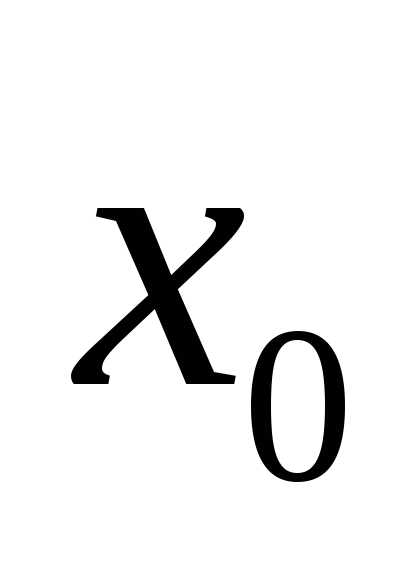 . Однако параметр
. Однако параметр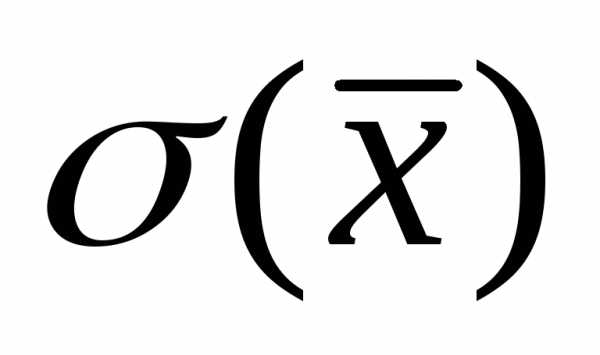 меньше, чем
меньше, чем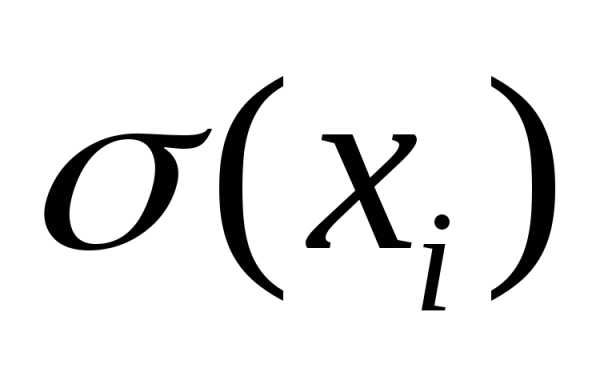 :
:
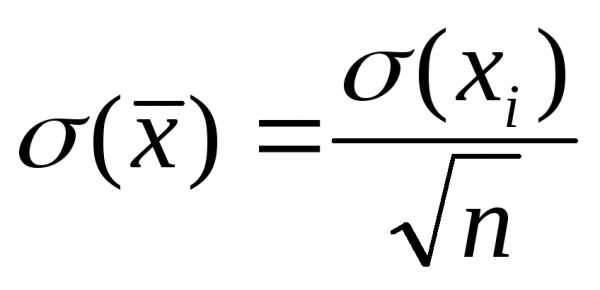 .
.
Это означает, что выборочное среднее 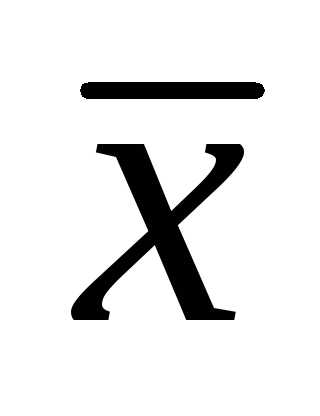 имеет приблизительно в
имеет приблизительно в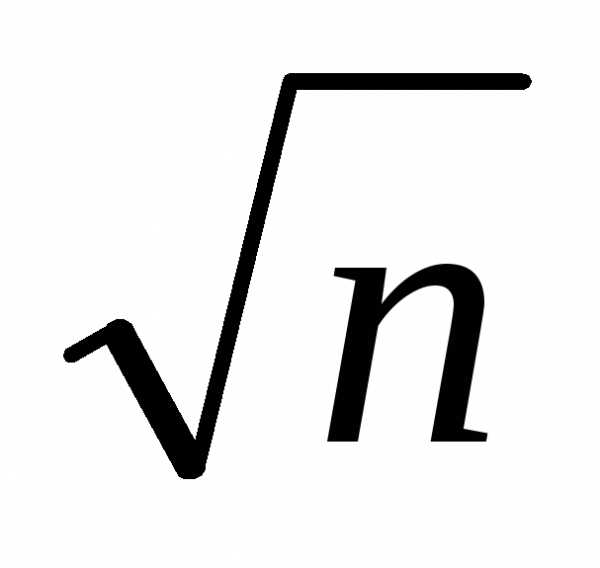 меньший разброс, чем единичное измерение
меньший разброс, чем единичное измерение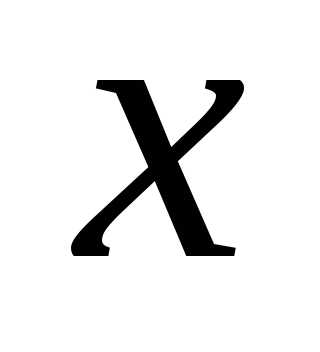 . Поэтому для оценки
. Поэтому для оценки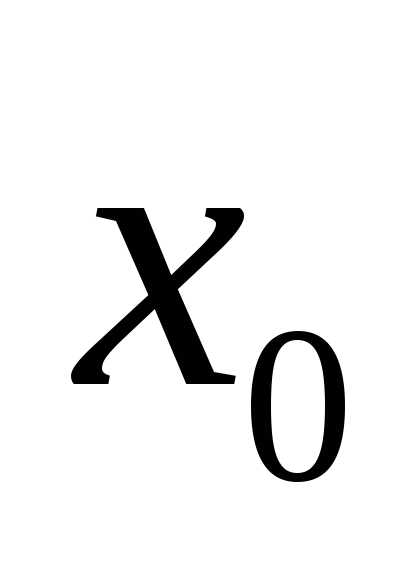 лучше использовать выборочное среднее
лучше использовать выборочное среднее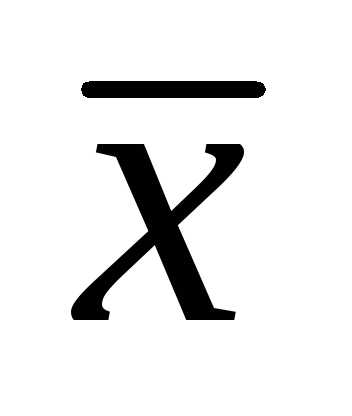 и среднеквадратичную погрешность
и среднеквадратичную погрешность 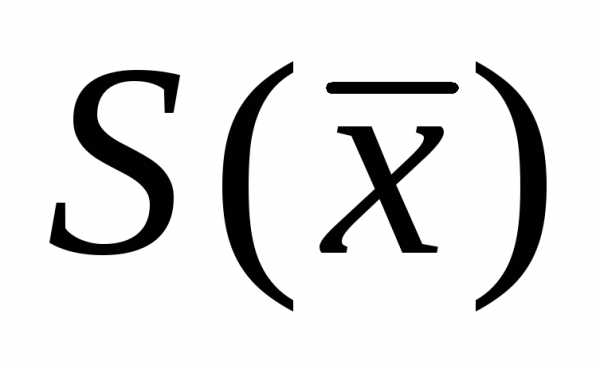 среднего арифметического результатаизмерения, которая вычисляется по формуле
среднего арифметического результатаизмерения, которая вычисляется по формуле
, (6)
В выражениях (5) и (6) обозначение среднеквадратичной ошибки  заменено на обозначение
заменено на обозначение , чтобы подчеркнуть, что величины
, чтобы подчеркнуть, что величины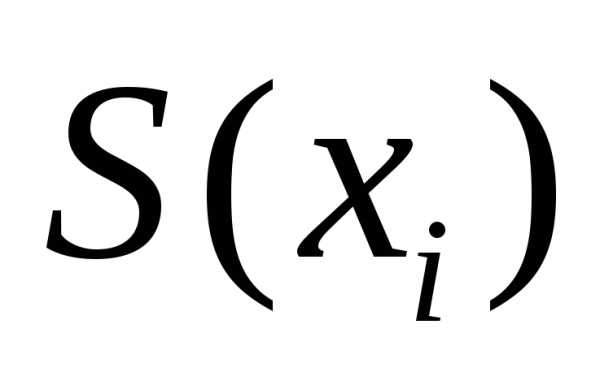 и
и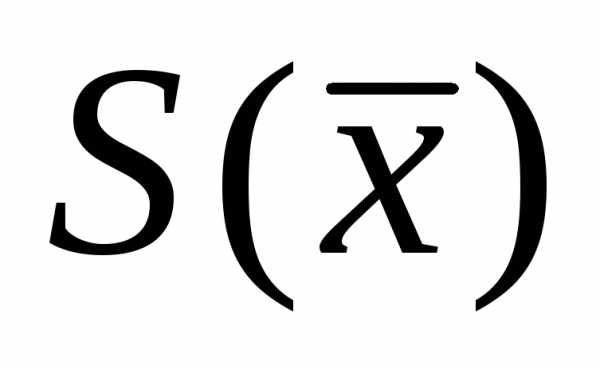 вычисляются на основе ограниченного числа наблюдений, т.е. являются эмпирическими оценками теоретических параметров
вычисляются на основе ограниченного числа наблюдений, т.е. являются эмпирическими оценками теоретических параметров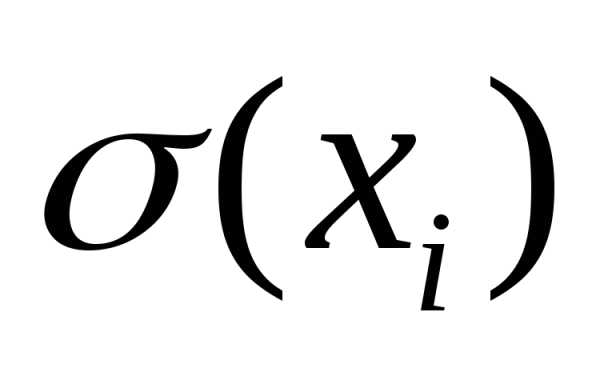 и
и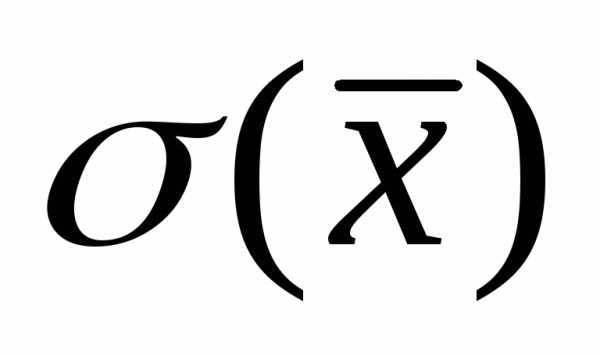 .
.
При проведении реальных технических измерений число отдельных измерений, как правило, невелико и лежит в пределах от  до
до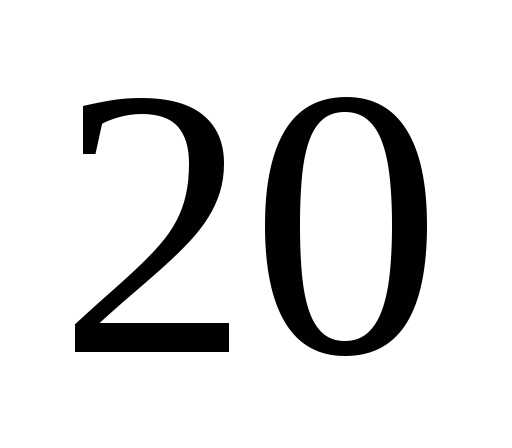 . В такой ситуации рассмотренный метод приводит к существенному искажению результатов. В теории погрешностей при малом числе измерений применяют специальный метод вычисления доверительного интервала, основанный на распределении Стьюдента. В 1908 г. английский математик У. Госсет (псевдоним ’’Стьюдент’’) доказал, что указанными соотношениями можно пользоваться и при небольшом числе наблюдений
. В такой ситуации рассмотренный метод приводит к существенному искажению результатов. В теории погрешностей при малом числе измерений применяют специальный метод вычисления доверительного интервала, основанный на распределении Стьюдента. В 1908 г. английский математик У. Госсет (псевдоним ’’Стьюдент’’) доказал, что указанными соотношениями можно пользоваться и при небольшом числе наблюдений
(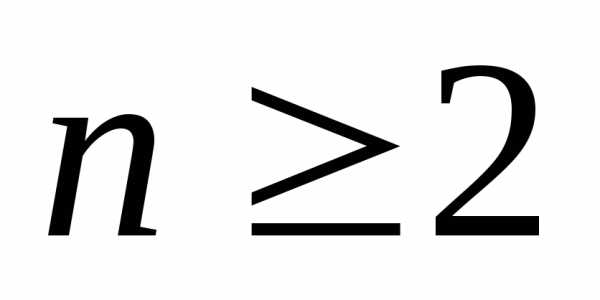 ), следует только на конечной стадии ввести в расчет специальный коэффициент, величина которого зависит от числа наблюдений
), следует только на конечной стадии ввести в расчет специальный коэффициент, величина которого зависит от числа наблюдений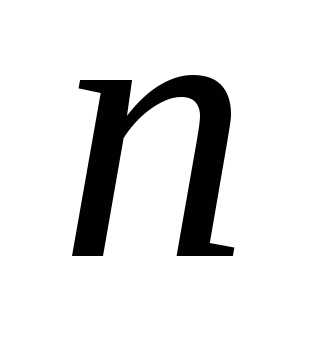 и требуемого значения доверительной вероятности
и требуемого значения доверительной вероятности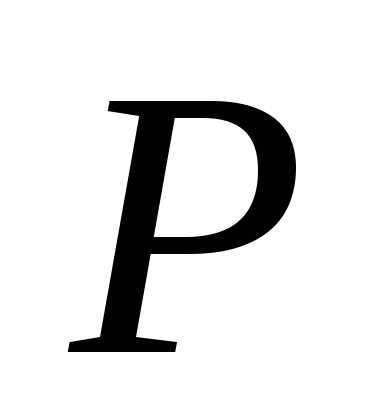 , – так называемый коэффициент Стьюдента
, – так называемый коэффициент Стьюдента .
.
Таблица 1
Коэффициенты Стьюдента  .
.
|
|
| |||||
| 0,68 | 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | |
| 2 | 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 |
| 3 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 |
| 4 | 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 |
| 5 | 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 |
| 6 | 1,2 | 1,5 | 2,0 | 2,6 | 3.4 | 4,3 |
| 7 | 1,1 | 1,4 | 1.9 | 2,4 | 3,1 | 4,0 |
| 8 | 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,7 |
| 9 | 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 |
| 10 | 1,1 | 1,4 | 1,83 | 2,26 | 2,8 | 3,35 |
| 60 | 1,0 | 1,3 | 1,7 | 2,0 | 2,4 | 2,7 |
|
| 1,0 | 1,3 | 1,64 | 1,96 | 2.3 | 2,58 |
Выполнение и обработку результатов прямых многократных измерений рекомендуется производить в следующем порядке.
1. Прямыми измерениями получить ряд значений измеряемой величины.
2. Вычислить среднеарифметическое значение результата измерений
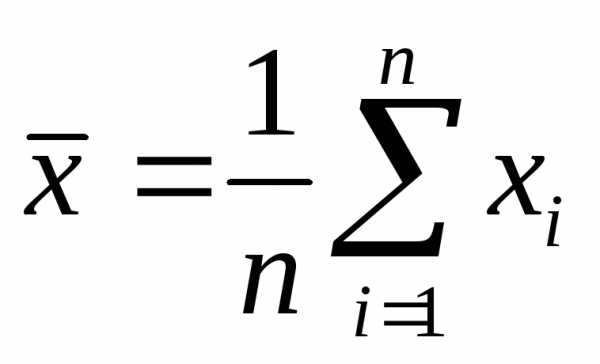 .
.
3. Вычислить отклонения отдельных результатов наблюдений от среднего
4. Вычислить значения 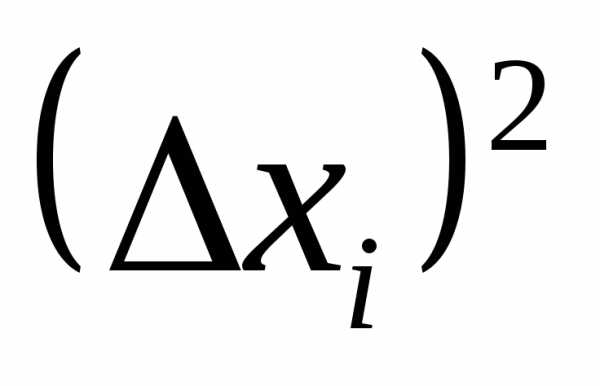 и сумму
и сумму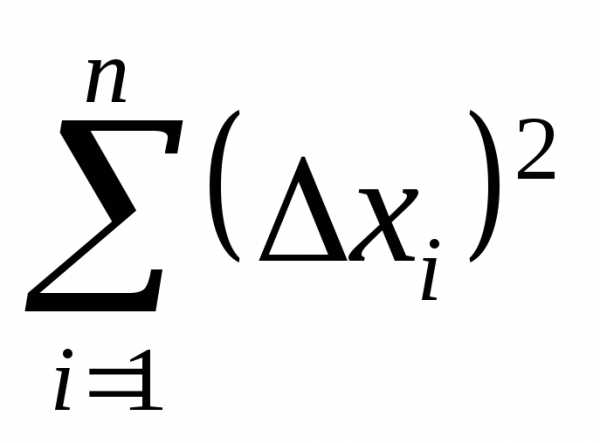 .
.
5. Для данных значений числа измерений 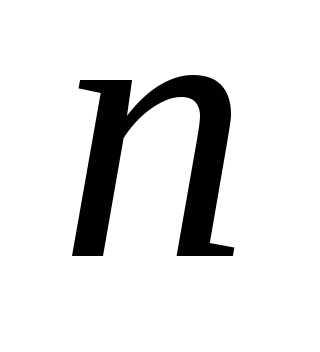 и доверительной вероятности
и доверительной вероятности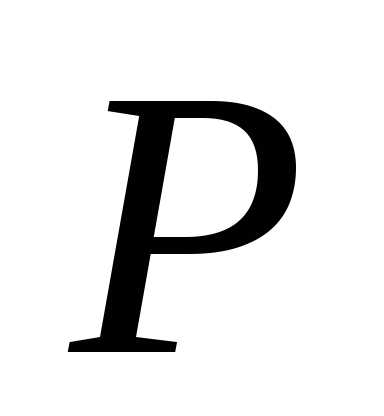 найти по таблице коэффициент Стьюдента
найти по таблице коэффициент Стьюдента и вычислить случайную погрешность
и вычислить случайную погрешность
. (7)
6. Округлив погрешность и предварительный результат, записать окончательный результат измерений в виде
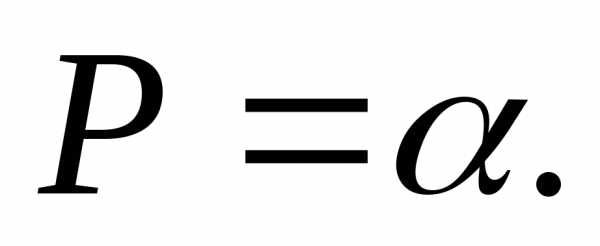
Пример. Обработка результатов прямых многократных измерений диметра  некоторого вала штангенциркулем.
некоторого вала штангенциркулем.
Получены 6 значений 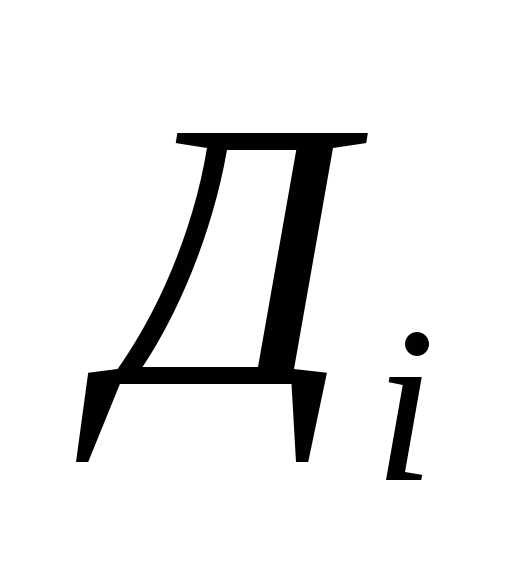 , которые внесены во 2–й столбец таблицы 2.
, которые внесены во 2–й столбец таблицы 2.
Таблица 2
studfiles.net
3) Виды измерений (прямые, косвенные, совокупные, совместные).
Вид измерения – это часть области измерения, имеющие свои особенности и отличающиеся однородностью измеряемых величин.
По способу нахождению численного значения физической величины:
Прямые измерения - это такие измерения, при которых искомое значение физической величины определяются непосредственно путем сравнения с мерой этой величины.
Косвенные измерения – значения искомой величины находят на основании известной зависимости между этой величиной и величинами подвергаемой прямым измерениям.
Совместные измерения – это измерения двух или нескольких неодноимённых величин, значения которых находятся решением системы уравнения.
Совокупные измерения – это проводимые одновременные измерения нескольких одноимённых величин, при которых искомые значения находятся решением системы уравнения.
4) Классификация измерений (по числу, по характеристике точности, по характеру изменения во времени измеряемой величины, по способу представления результатов измерений).
1. По числу измерений:
Однократное измерение — измерение, выполненное один раз.
Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений.
2. По характеристике точности измерения делятся на равноточные и неравноточные.
Равноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерений (СИ), обладающих одинаковой точностью, в идентичных исходных условиях.
Неравноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерения, обладающих разной точностью, и (или) в различных исходных условиях.
3. По характеру изменения во времени измеряемой величины:
Статические измерения – измеряемая величина остаётся постоянной во времени и в процессе неизменной.
Динамические измерения – измерение величины, изменяющиеся в процессе изменения и является непостоянной во времени.
4. По способу представления результатов измерений:
Абсолютные измерения – основанные на прямых измерениях и исполнение физической константы.
Относительные измерения – измерения относительных величин к одноимённой величине, играющий роль к единице по отношению к одноимённой величине, применяемой за исходной.
5) Погрешность измерения по способу выражения (абсолютная, относительная, приведенная)
Абсолютная погрешность Δ — это разность между измеренным X и истинным Xи значениями измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины: Δ = Х – Хи .Поскольку истинное значение измеряемой величины определить невозможно, вместо
него на практике используют действительное значение измеряемой величины Хд. Действительное значение находят экспериментально, путем применения достаточно точных методов и средств измерений. Оно мало отличается от истинного значения и для решения
поставленной задачи может использоваться вместо него. При поверке за действительное
значение обычно принимают показания образцовых средств измерений. Таким образом,
на практике абсолютную погрешность находят по формуле Δ = Х – Хд .
Абсолютная погрешность — является оценкой абсолютной ошибки измерения. Вычисляется разными способами. Способ вычисления определяется распределением случайной величины. Соответственно, величина абсолютной погрешности в зависимости от распределения случайной величиныможет быть различной. Если— измеренное значение, а— истинное значение, то неравенстводолжно выполняться с некоторой вероятностью, близкой к 1. Если случайная величинараспределена по нормальному закону, то обычно за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
Относительная погрешность Δ — это отношение абсолютной погрешности измерения
к истинному (действительному) значению измеряемой величины (она обычно выражается
в процентах.
Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или среднему значению измеряемой величины
Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле , где— нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то определяется равным верхнему пределу измерений;
если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.
studfiles.net
Прямые и косвенные измерения
По способу получения результата измерения делятся на прямые и косвенные. Если значение физической величины находят непосредственным отсчетом по шкале прибора, то такие измерения называются прямыми (измерения давления барометром, температуры – термометром, времени – секундомером, длины – штангенциркулем или линейкой, силы тока – амперметром и т.п.). Эти измерения могут быть однократными и многократными. Многократное измерение – повторение экспериментельной операции, в результате которой получается одно из значений измеряемой величины 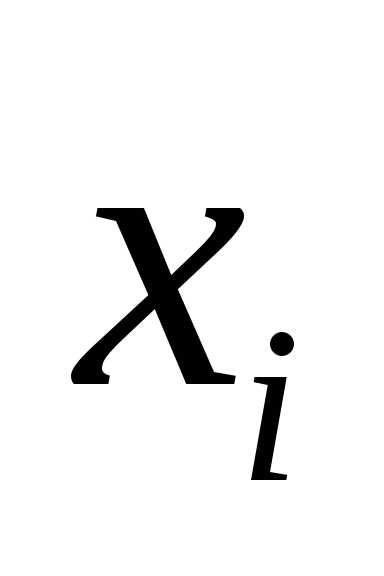 , называемыхрезультатами наблюдений. Совокупность результатов наблюдений подлежит совместной обработке для получения результата измерения.
, называемыхрезультатами наблюдений. Совокупность результатов наблюдений подлежит совместной обработке для получения результата измерения.
Часто прямое измерение физической величины оказывается невозможным или слишком трудоемким. При косвенных измерениях результат определяется по формулам на основе результатов прямых измерений других величин (например, определение электрического cопротивления образца по измеренным силе тока и напряжению). Одну и ту же величину часто можно найти путем как прямых, так и косвенных измерений. Например, скорость автомобиля может быть определена по спидометру (прямое измерение) или найдена делением пройденного пути на время движения (косвенное измерение).
При косвенных измерениях погрешность искомой физической величины накапливается из погрешностей прямых измерений величин, входящих в расчетную формулу.
Погрешности многократных прямых измерений (случайные погрешности)
Пусть изучается физическая величина 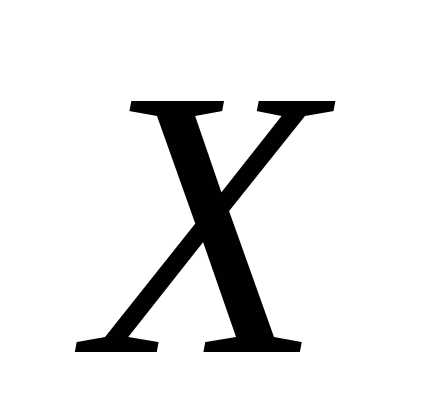 и многократными измерениями получены
и многократными измерениями получены 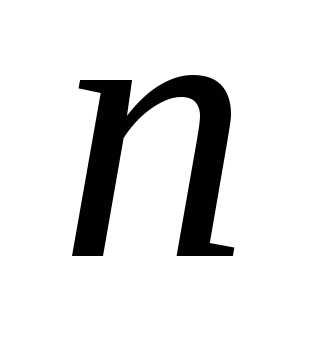 результатов наблюдений
результатов наблюдений
,
причем все измерения выполнены одним и тем же методом и с одинаковой степенью тщательности. Этот ряд значений величины называется выборкой.Предположим, что на результат измерений оказывают действие только случайные (неконтролируемые) факторы, а промахи и систематические ошибки отсутствуют.
Задача экспериментатора состоит в том, чтобы найти наилучшую оценку и доверительную погрешность результата измерений для заданного значения доверительной вероятности. (При обработке экспериментальных результатов можно поступать и по–другому: произвольно задавать значение доверительной погрешности и вычислять соответствующее ей значение вероятности). Указанная задача строго решается с помощью теории вероятностей и математической статистики.
В большинстве случаев случайные ошибки подчиняются установленному Гауссом нормальному закону распределения, вид которого может быть получен на основании следующих предположений:
1) величина случайной погрешности может иметь любое значение;
2) вероятность появления погрешности снижается с ростом ее величины – большие погрешности маловероятны;
3) погрешности, равные по величине, но разные по знаку, встречаются одинаково часто – равные по модулю погрешности равновероятны.
Выведенный на основе указанных предположений закон нормального распределения случайных величин (распределение Гаусса) выражается формулой
, (3)
где 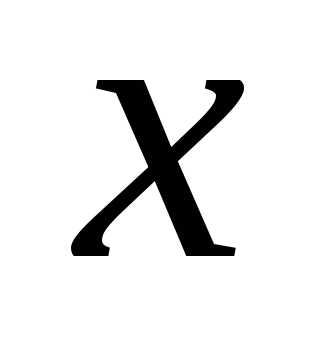 – числовое значение определяемой величины
– числовое значение определяемой величины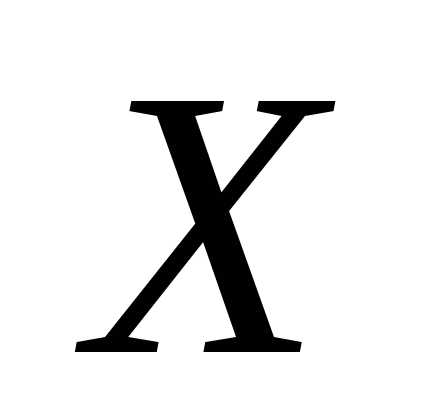 ,
, и
и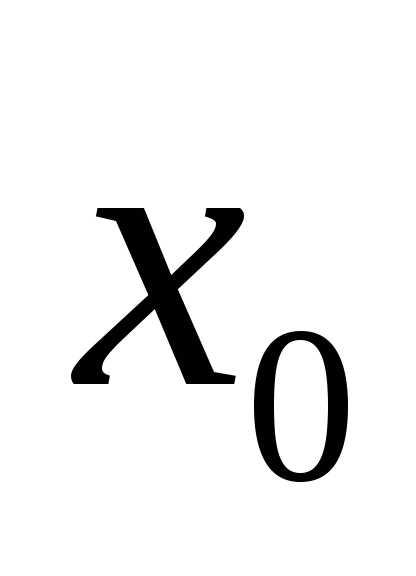 – параметры распределения;
– параметры распределения;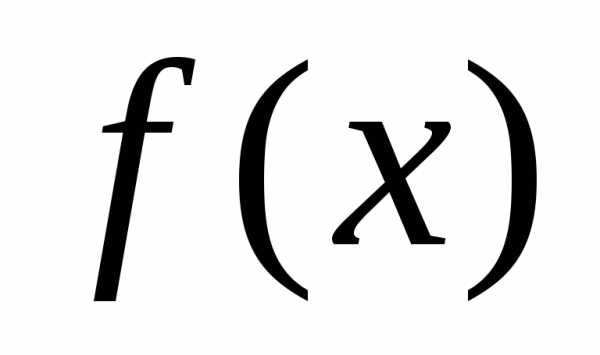 – плотность вероятности (вероятность того, что значение
– плотность вероятности (вероятность того, что значение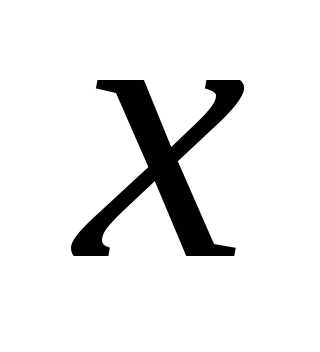 принадлежит некоторому единичному интервалу значений), так что функцияопределяет вероятность попадания значения
принадлежит некоторому единичному интервалу значений), так что функцияопределяет вероятность попадания значения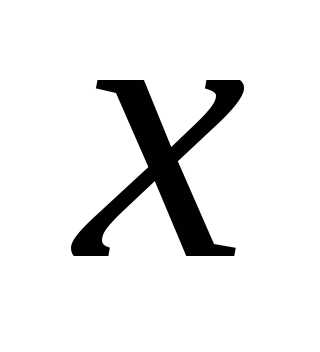 в интервал от
в интервал от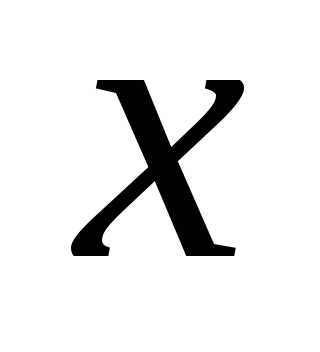 до
до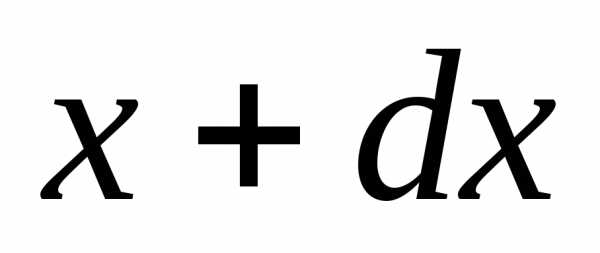 .
.
Параметр 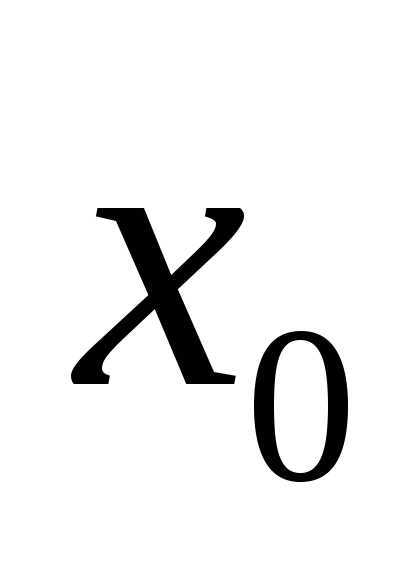 , соответствующий максимуму плотности вероятности
, соответствующий максимуму плотности вероятности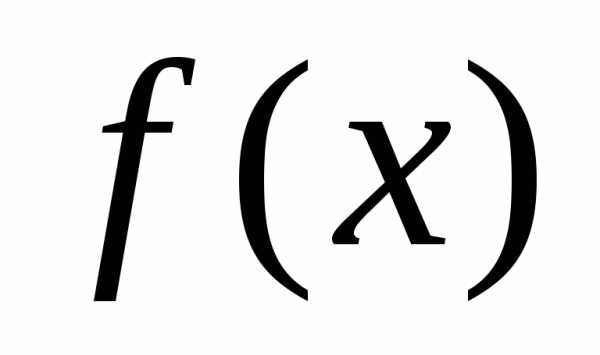 , называетсяматематическим ожиданиемслучайной величины
, называетсяматематическим ожиданиемслучайной величины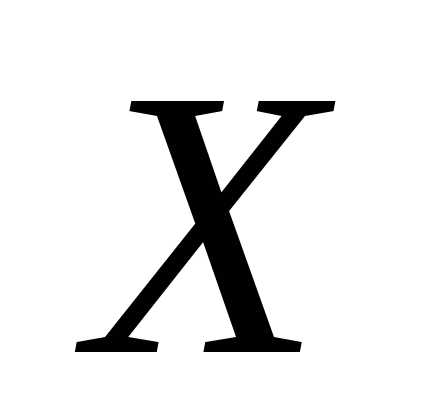 . Параметр
. Параметр называетсясредним квадратическим отклонением величины
называетсясредним квадратическим отклонением величины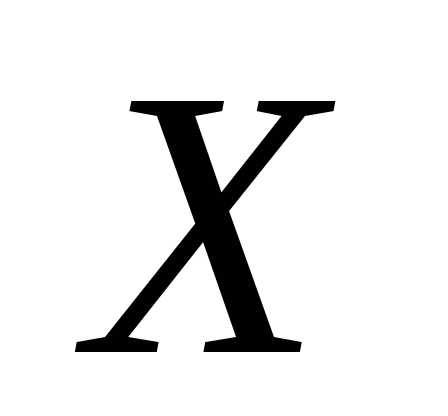 от ее математического ожидания
от ее математического ожидания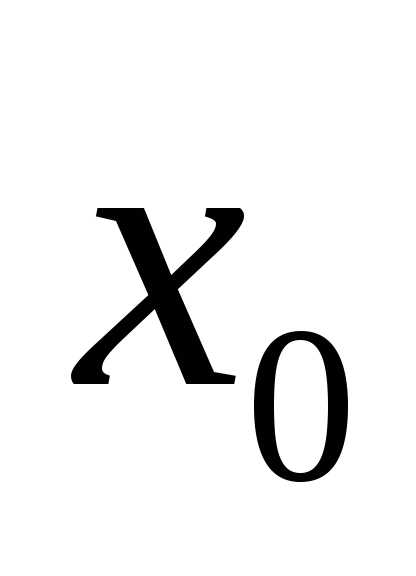 и характеризует меру ее разброса относительно
и характеризует меру ее разброса относительно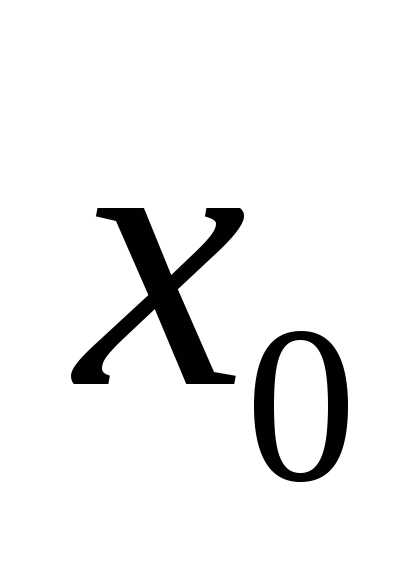 . Очевидно, что
. Очевидно, что
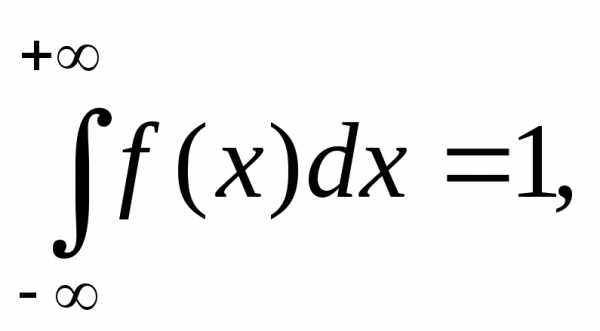
т.е. вероятность того, что случайная величина 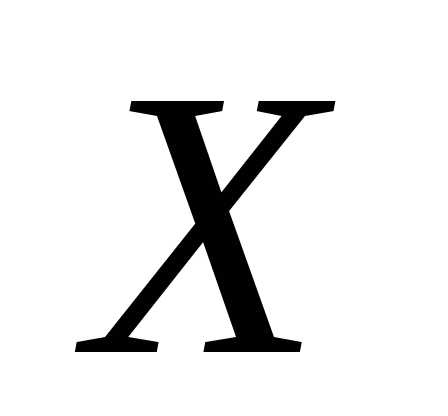 вообще имеет какое–то значение, равна единице.
вообще имеет какое–то значение, равна единице.
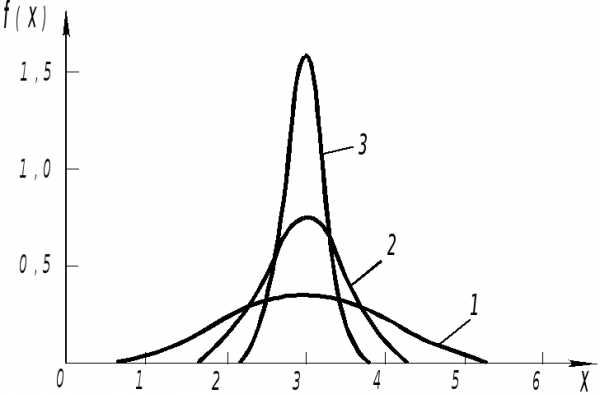 Поскольку максимальное значение плотность вероятности
Поскольку максимальное значение плотность вероятности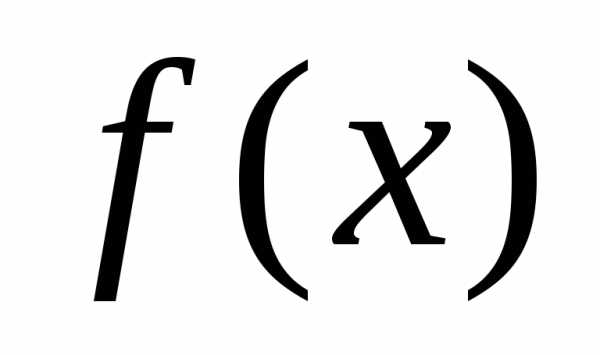 принимает при
принимает при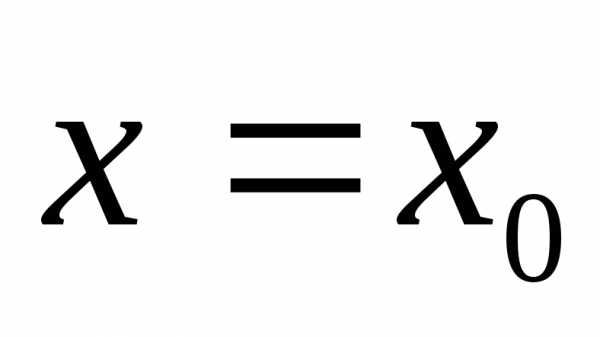 , то величину
, то величину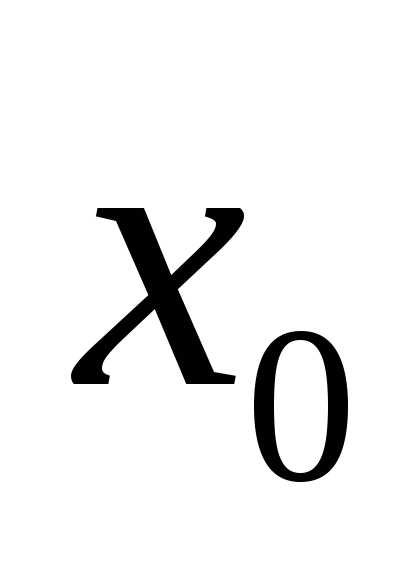 часто считают приблизительно равной истинному значению измеряемой величины. На рис.
часто считают приблизительно равной истинному значению измеряемой величины. На рис. представлен график этой функции. Из вышесказанного ясно, что площадь заштрихованной фигуры численно равна вероятности, с которой любой отсчет попадает в интервал от
представлен график этой функции. Из вышесказанного ясно, что площадь заштрихованной фигуры численно равна вероятности, с которой любой отсчет попадает в интервал от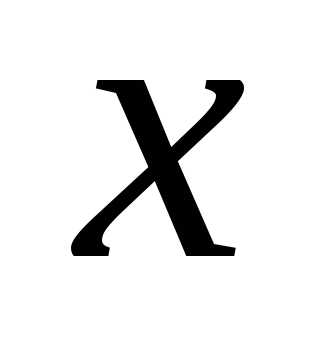 до
до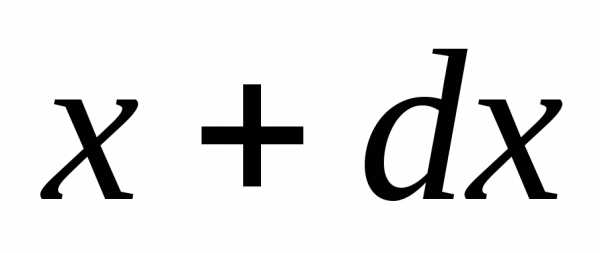 .
.
Рис.1. Нормальное (гауссово) распределение
(1–,2–/2,3–/4) .
Из теории следует, что наилучшей оценкой истинного значения 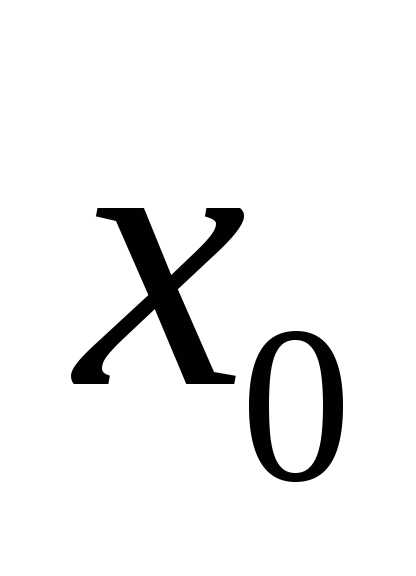 измеряемой случайной величины
измеряемой случайной величины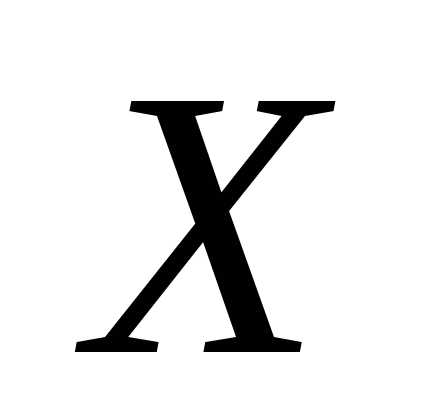 является среднее арифметическое (выборочное среднее) значение
является среднее арифметическое (выборочное среднее) значение
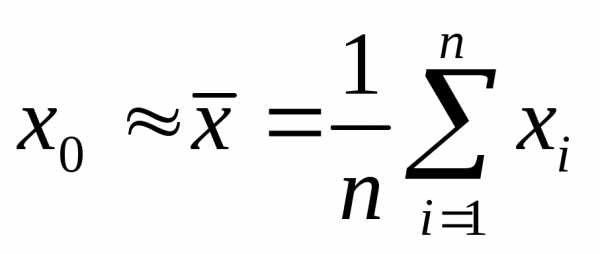 . (4)
. (4)
Заметим также, что с увеличением значения  увеличивается разброс отсчетов, т.е. точность измерений понижается. В условиях реального эксперимента точное значение
увеличивается разброс отсчетов, т.е. точность измерений понижается. В условиях реального эксперимента точное значение , как правило, неизвестно. По многократным измерениям
, как правило, неизвестно. По многократным измерениям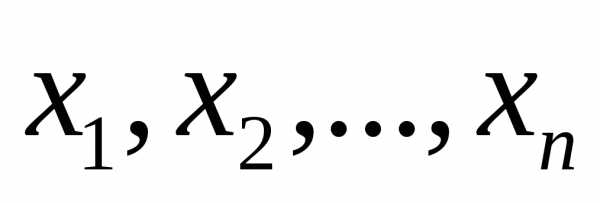 можно получить приближенную оценку этого параметра в виде среднеквадратичной погрешности
можно получить приближенную оценку этого параметра в виде среднеквадратичной погрешности 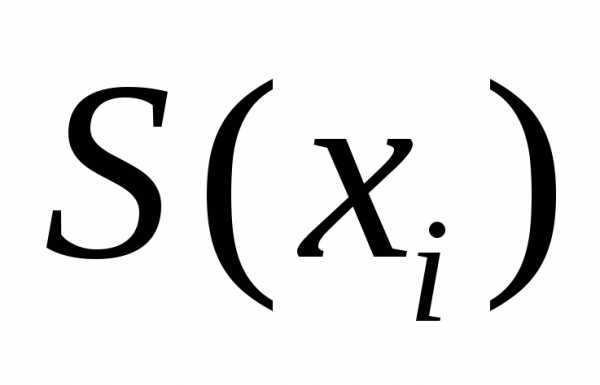 отдельного результатаизмерения
отдельного результатаизмерения
, (5)
которая характеризует ошибку каждого отдельного измерения и при неограниченном увеличении числа наблюдений () стремится к истинной среднеквадратичной ошибке .
.
Если произвести несколько серий многократных измерений, т.е. получить несколько выборок и для каждой вычислить выборочное среднее, то получим выборку для новой случайной величины 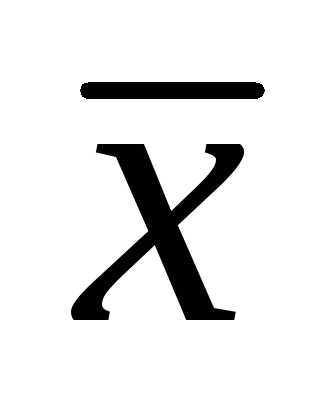 , которая также распределена нормально с математическим ожиданием
, которая также распределена нормально с математическим ожиданием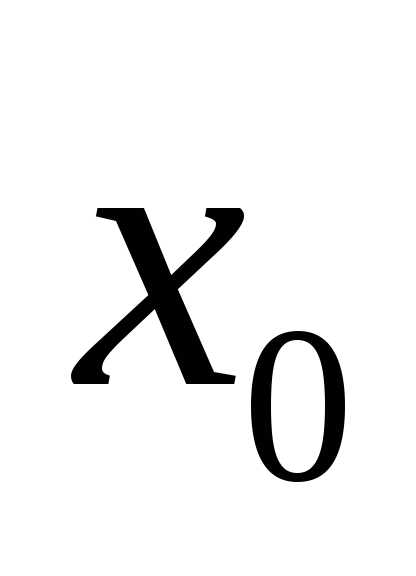 . Однако параметр
. Однако параметр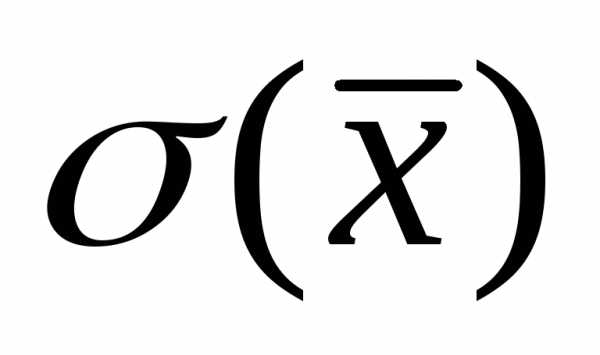 меньше, чем
меньше, чем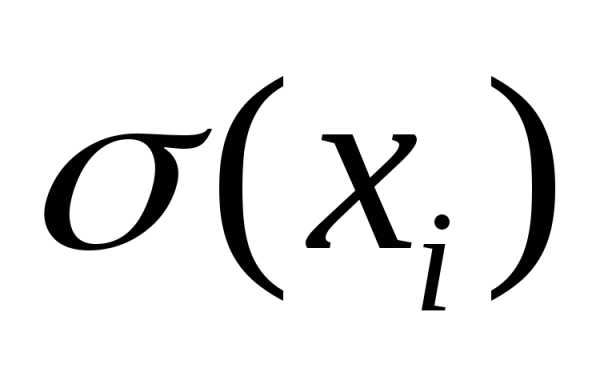 :
:
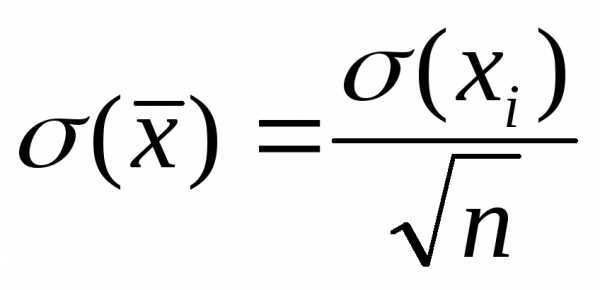 .
.
Это означает, что выборочное среднее 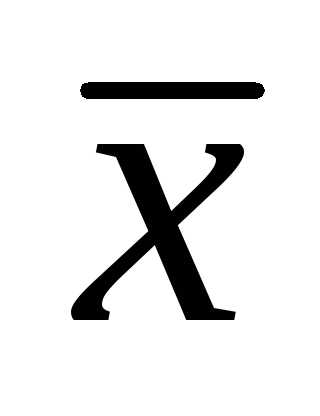 имеет приблизительно в
имеет приблизительно в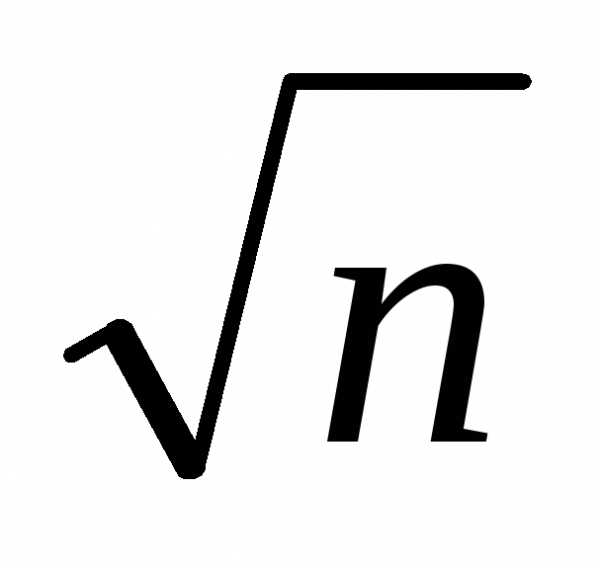 меньший разброс, чем единичное измерение
меньший разброс, чем единичное измерение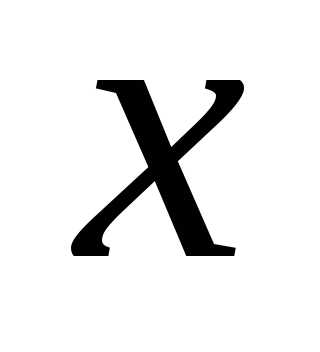 . Поэтому для оценки
. Поэтому для оценки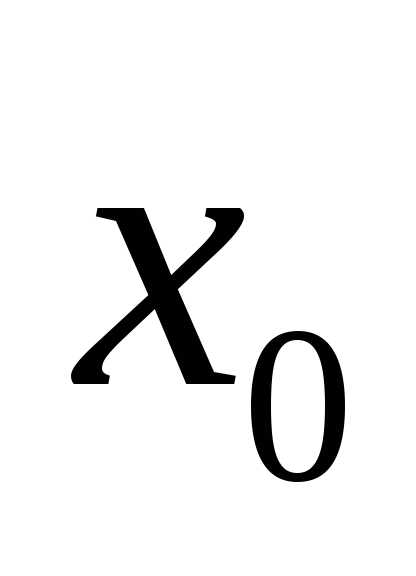 лучше использовать выборочное среднее
лучше использовать выборочное среднее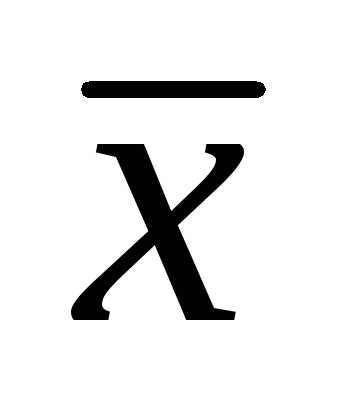 и среднеквадратичную погрешность
и среднеквадратичную погрешность 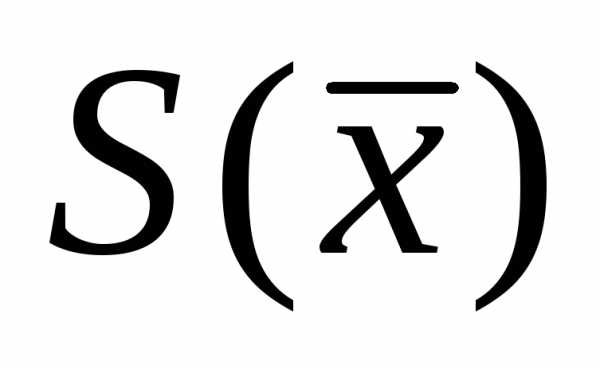 среднего арифметического результатаизмерения, которая вычисляется по формуле
среднего арифметического результатаизмерения, которая вычисляется по формуле
, (6)
В выражениях (5) и (6) обозначение среднеквадратичной ошибки  заменено на обозначение
заменено на обозначение , чтобы подчеркнуть, что величины
, чтобы подчеркнуть, что величины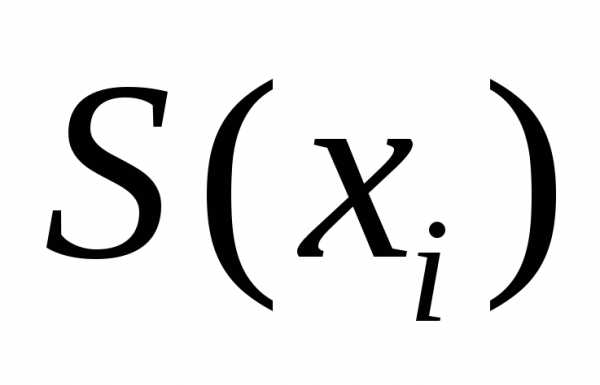 и
и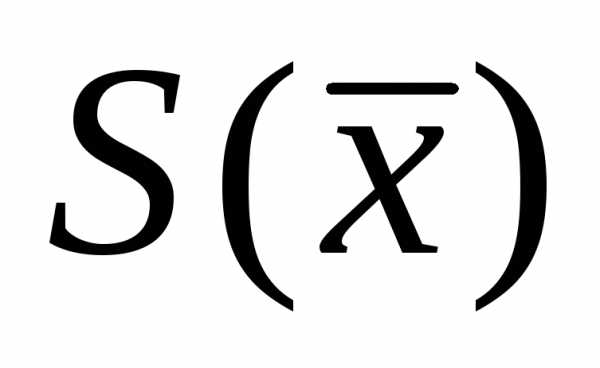 вычисляются на основе ограниченного числа наблюдений, т.е. являются эмпирическими оценками теоретических параметров
вычисляются на основе ограниченного числа наблюдений, т.е. являются эмпирическими оценками теоретических параметров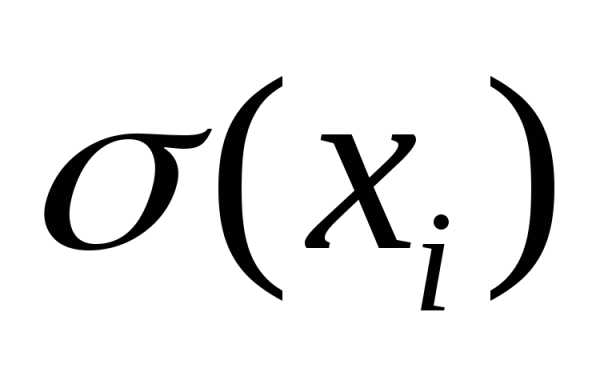 и
и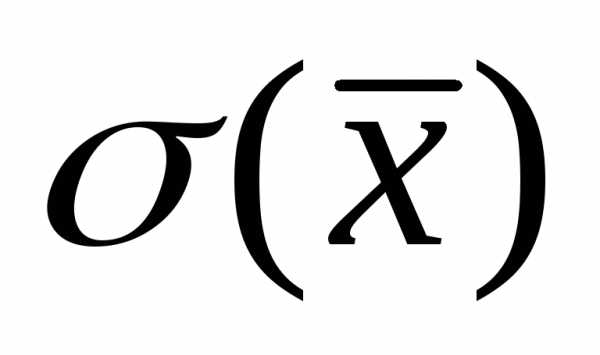 .
.
При проведении реальных технических измерений число отдельных измерений, как правило, невелико и лежит в пределах от  до
до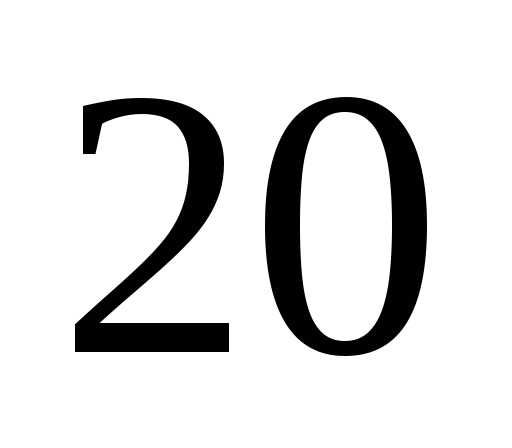 . В такой ситуации рассмотренный метод приводит к существенному искажению результатов. В теории погрешностей при малом числе измерений применяют специальный метод вычисления доверительного интервала, основанный на распределении Стьюдента. В 1908 г. английский математик У. Госсет (псевдоним ’’Стьюдент’’) доказал, что указанными соотношениями можно пользоваться и при небольшом числе наблюдений
. В такой ситуации рассмотренный метод приводит к существенному искажению результатов. В теории погрешностей при малом числе измерений применяют специальный метод вычисления доверительного интервала, основанный на распределении Стьюдента. В 1908 г. английский математик У. Госсет (псевдоним ’’Стьюдент’’) доказал, что указанными соотношениями можно пользоваться и при небольшом числе наблюдений
(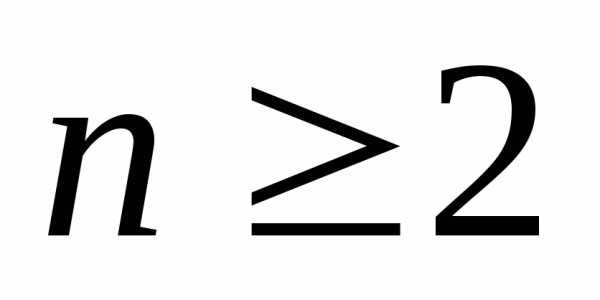 ), следует только на конечной стадии ввести в расчет специальный коэффициент, величина которого зависит от числа наблюдений
), следует только на конечной стадии ввести в расчет специальный коэффициент, величина которого зависит от числа наблюдений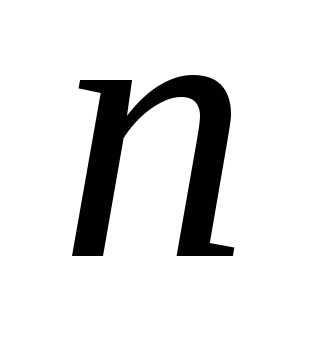 и требуемого значения доверительной вероятности
и требуемого значения доверительной вероятности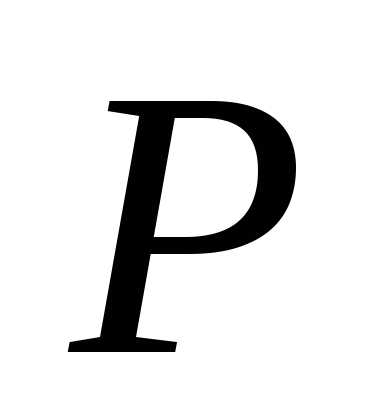 , – так называемый коэффициент Стьюдента
, – так называемый коэффициент Стьюдента .
.
Таблица 1
Коэффициенты Стьюдента  .
.
|
|
| |||||
| 0,68 | 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | |
| 2 | 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 |
| 3 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 |
| 4 | 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 |
| 5 | 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 |
| 6 | 1,2 | 1,5 | 2,0 | 2,6 | 3.4 | 4,3 |
| 7 | 1,1 | 1,4 | 1.9 | 2,4 | 3,1 | 4,0 |
| 8 | 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,7 |
| 9 | 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 |
| 10 | 1,1 | 1,4 | 1,83 | 2,26 | 2,8 | 3,35 |
| 60 | 1,0 | 1,3 | 1,7 | 2,0 | 2,4 | 2,7 |
|
| 1,0 | 1,3 | 1,64 | 1,96 | 2.3 | 2,58 |
Выполнение и обработку результатов прямых многократных измерений рекомендуется производить в следующем порядке.
1. Прямыми измерениями получить ряд значений измеряемой величины.
2. Вычислить среднеарифметическое значение результата измерений
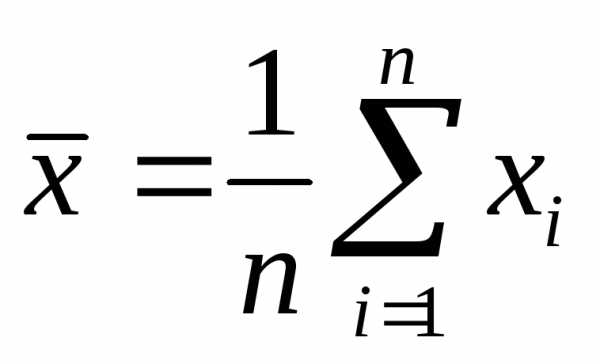 .
.
3. Вычислить отклонения отдельных результатов наблюдений от среднего
4. Вычислить значения 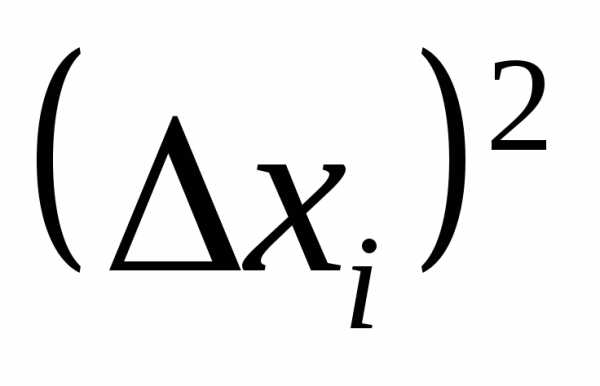 и сумму
и сумму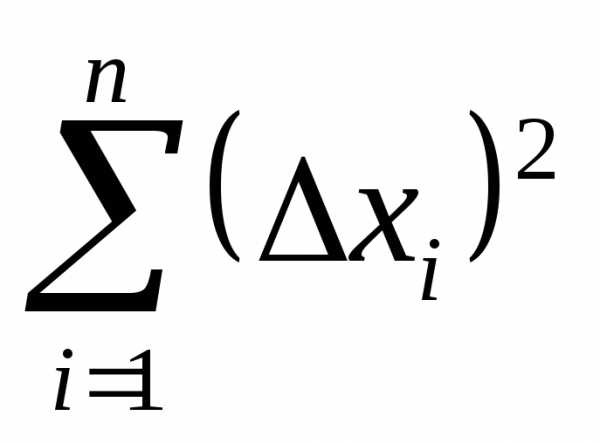 .
.
5. Для данных значений числа измерений 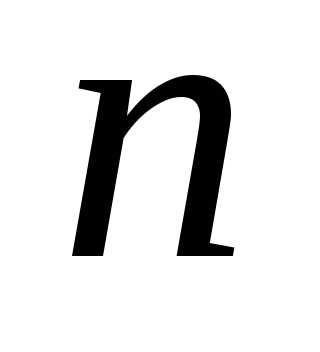 и доверительной вероятности
и доверительной вероятности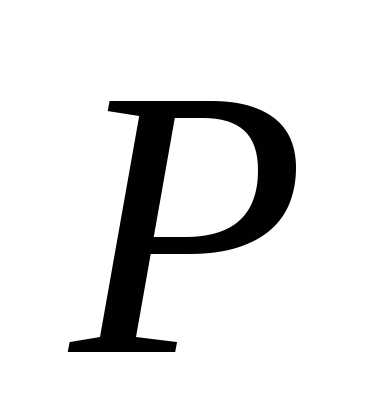 найти по таблице коэффициент Стьюдента
найти по таблице коэффициент Стьюдента и вычислить случайную погрешность
и вычислить случайную погрешность
. (7)
6. Округлив погрешность и предварительный результат, записать окончательный результат измерений в виде
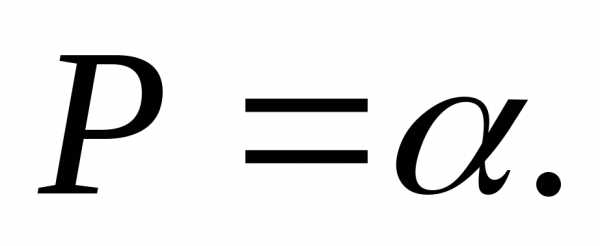
Пример. Обработка результатов прямых многократных измерений диметра  некоторого вала штангенциркулем.
некоторого вала штангенциркулем.
Получены 6 значений 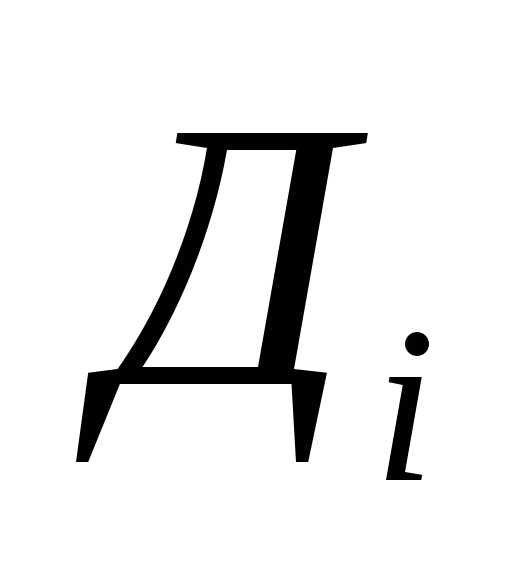 , которые внесены во 2–й столбец таблицы 2.
, которые внесены во 2–й столбец таблицы 2.
Таблица 2
studfiles.net
Пример записи результатов прямых измерений
В лаборатории при измерении любой величины результаты должны заноситься в таблицу, которую необходимо составить заранее.
Например: необходимо измерить диаметр цилиндра. Для записи результатов измерений составим таблицу:
| №№ опыта | di, мм | |
| 1 | 13,65 | 0,03 |
| 2 | 13,65 | 0,03 |
| 3 | 13,60 | 0,02 |
| 4 | 13,55 | 0,07 |
| 5 | 13,65 | 0,03 |
| Средние значения | 13,62 | 0,036 |
Далее определим среднюю квадратичную ошибку среднего арифметического
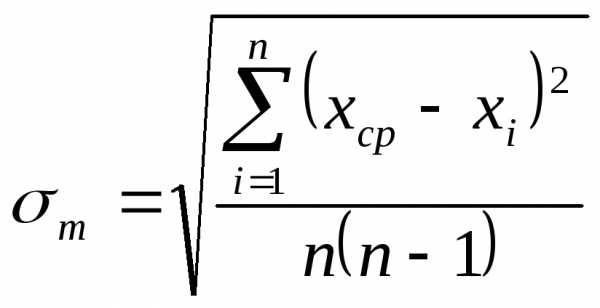
Выберем доверительную вероятность результата  = 0,95. Тогда из таблицы №1 коэффициент Стьюдента будет равен:
= 0,95. Тогда из таблицы №1 коэффициент Стьюдента будет равен: 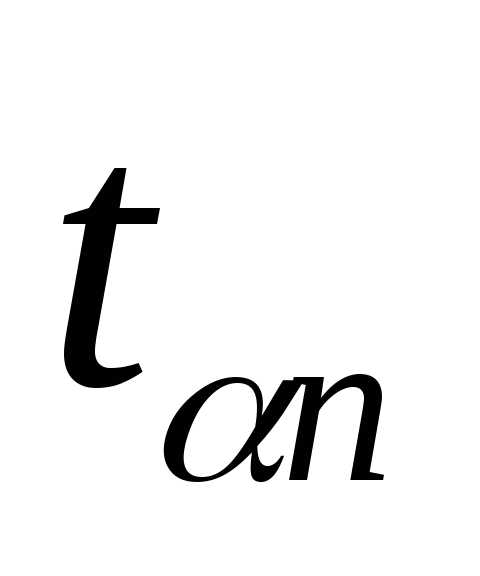 = 2,8, и абсолютная погрешность результата составит х = tn m
= 2,8, и абсолютная погрешность результата составит х = tn m
Запишем результат:
Обычно результат округляютдосомнительнойцифры. Сомнительной является цифра, разряд которой совпадает с разрядом старшей, отличной от 0, цифры ошибки. В данном результате – это «2». Причем, при округлении последняя цифра остается без изменения, если старшая отбрасываемая цифра меньше 5; увеличивается на 1, если эта цифра больше 5. Если отбрасываемая цифра 5, то последняя сохраняется, если она четная, и увеличивается на единицу, если она нечетная.
Исключение: при округлении ошибок (погрешностей) последняя сохраняемая цифра всегда увеличивается на единицу, если только старшая отбрасываемая цифра не нуль.
Ошибки обычно округляются до одной значащей цифры. В некоторых случаях, когда первая значащая цифра меньше или равна 3, оставляются две значащие цифры. Это связано с тем, что сами погрешности определяются с погрешностью, например, при 10 измерениях эта погрешность составляет величину 30%.
Таким образом, результат измерения диаметра после округления запишется:
d = .
Если проведенная серия измерений дала одинаковые результаты, то это означает, что величина случайных отклонений меньше точности прибора. В этом случае за ошибку принимают величину, обусловленную классом точности прибора или половиной цены его наименьшего деления, а в случае, если случайная ошибка и погрешность измерительного прибора сравнимы, то общая ошибка складывается из них. Правила сложения даны ниже.
Суммарная погрешность определяется согласно формуле:
,
где хсл – случайная ошибка, - погрешность измерительного прибора.
Функция случайной величины и ошибка в ее определении
В большинстве случаев искомая величина не может быть измерена непосредственно, а определяется через другие, которые можно измерить. Например, для определения объема шара мы измеряем его диаметр d и потом вычисляем объем 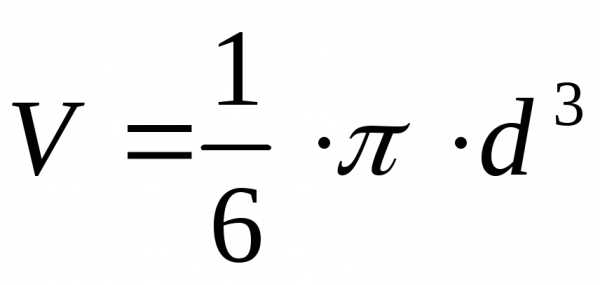 . Таким образом, объем в данном случае есть функция диаметра, а сам диаметр измерен с некоторой ошибкой и представляет собой целый ряд значений внутри интервала, ширина которого этой ошибкой обусловлена.
. Таким образом, объем в данном случае есть функция диаметра, а сам диаметр измерен с некоторой ошибкой и представляет собой целый ряд значений внутри интервала, ширина которого этой ошибкой обусловлена.
Во всех подобных случаях мы имеем дело с функцией случайной величины, т. к. истинного значения аргумента (в данном случае диаметра) мы не знаем.
Но если значение аргумента находится с определенной степенью точности, то и зависящая от него функция также определяется с ошибкой. На рис.2 представлен график зависимости V от d, из которого видно, что интервалу d значений аргумента соответствует интервал ∆V значений функции. Среднему же значению диаметра dср будет соответствовать среднее значение объема Vср.
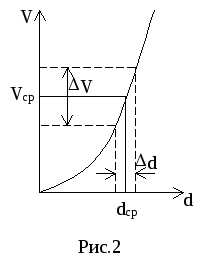
Обозначим в общем случае функцию случайной величины буквой Z, а аргумент – буквой А, тогда . Вид этой функции может быть различным. Наиболее распространенные варианты подобных функций и указания, как найти ошибку в ее определении ∆Z, если задана ошибка в определении аргумента ∆А, даны в Приложении 4. В общем случае Z = Z(A): абсолютная погрешность измерения будет равна 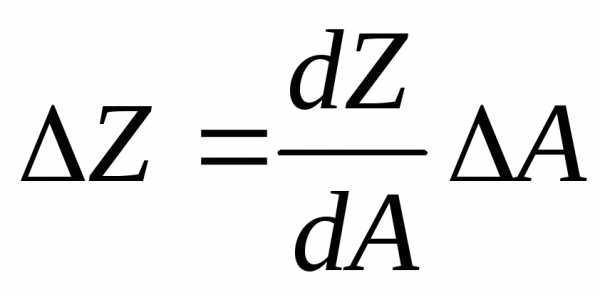 , где
, где 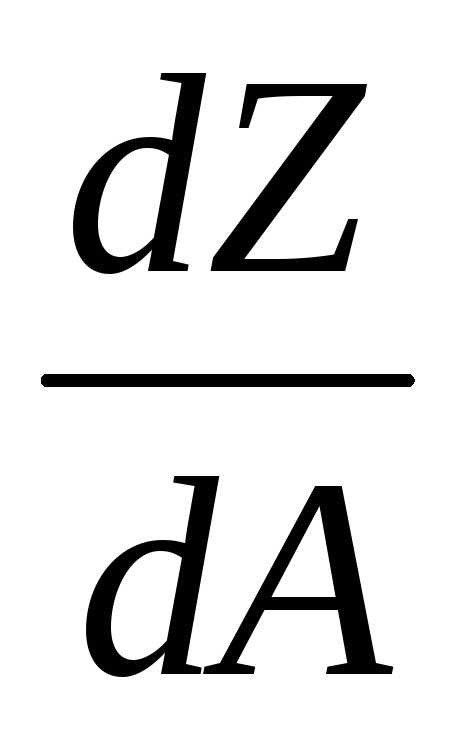 определяет степень зависимостиZ от А в интересующей нас точке.
определяет степень зависимостиZ от А в интересующей нас точке.
studfiles.net
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
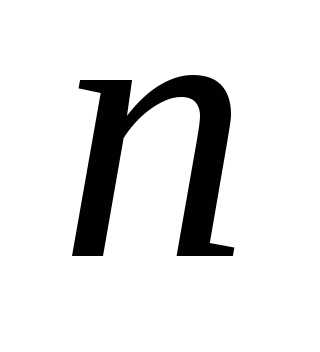
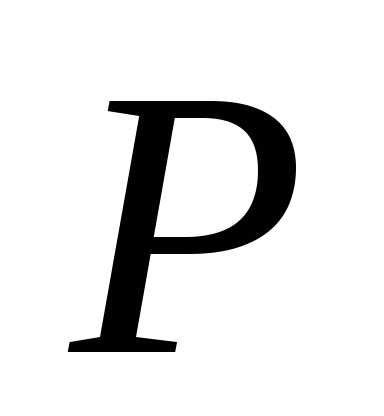

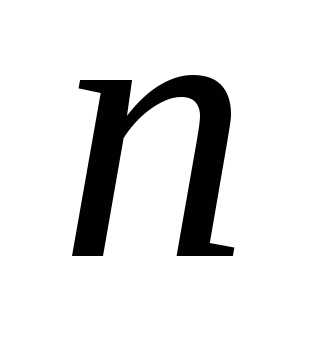
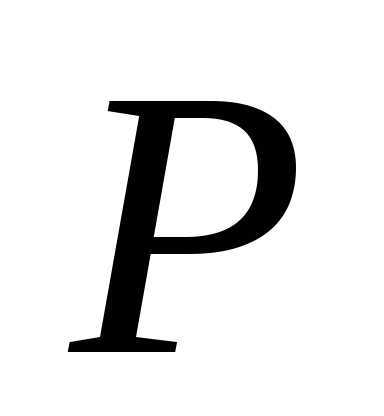

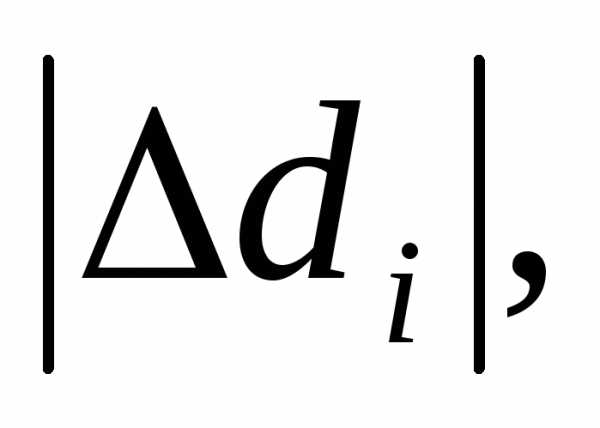 мм
мм