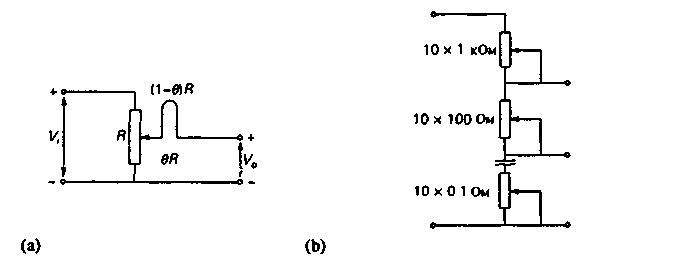Практическая работа «Расчёт резистивного делителя напряжения»
Практическая работа № 1
Расчёт резистивного делителя напряжения
Цель: Уметь рассчитывать элементы схемы; знать принципы соотношений между значениями показателей сигналов; уметь применять полученные данные для построения временной диаграммы.
1 Задание
1.1 Начертить схему резистивного делителя напряжения.
1.2 Рассчитать сопротивления резисторов для получения коэффициента передачи.
1.3 Округлить найденное сопротивление до стандартного номинала.
1.4 Определить полученный коэффициент передачи, сравнить его с заданным, оценить погрешность и сделать выводы к её допуску.
1.5 Определить амплитуду выходного напряжения.
1.6 Рассчитать мощность, которую рассеивают резисторы и обозначить на схеме номиналы мощностей резисторов.
1. 7 Показать в масштабе эпюры входного и выходного напряжений, обращая внимание на фазу сигналов (вверху входное напряжение, внизу – выходное). Внимание! Размещение эпюр в разных столбцах или на разных страницах не разрешается.
7 Показать в масштабе эпюры входного и выходного напряжений, обращая внимание на фазу сигналов (вверху входное напряжение, внизу – выходное). Внимание! Размещение эпюр в разных столбцах или на разных страницах не разрешается.
2 Исходные данные
2.1 Входное сопротивление Rвх ≥ 1 кОм.
2.2 Амплитуда входного напряжения Um вх = 10 + M, В.
Здесь и дальше: М – предпоследняя, а N – последняя цифры зачётной книжки.
3 Методические указания к решению задания
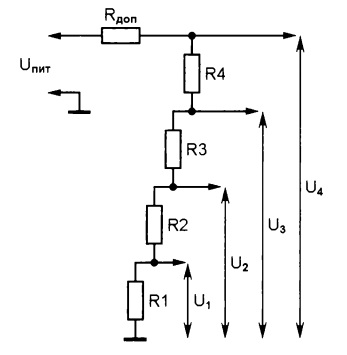
3.1 Привести схему резистивного делителя напряжения.
Рисунок 3.1 – Схема резисторного делителя напряжения
3.2 Рассчитать заданный коэффициент передачи делителя.
Согласно условию задания
Rвх ≥ 1 кОм
А так как в данном случае резисторы соединены последовательно, то входное сопротивление цепи равно:
Rвх (1. 1)
1)
Из данной формулы видно, что коэффициент передачи будет равным:
(1.2)
Как видно по рисунку 1 и формуле 1.1 входное сопротивление зависит как от сопротивления резистора R1, так и от сопротивления резистора R2. Для выполнения условия задачи можно задать сопротивление одного из этих резисторов равным 1 кОм. Если задать R2 = 1 кОм, то в таком случае Rвх > 1кОм.
Тогда значение резистора R1
R1 =((10+N)-1) . 1000, Ом
3.3 Из Приложения найти ближайшую стандартную величину R1.
3.4 Рассчитать коэффициент передачи делителя с новыми значениями.
Крас =
Определить погрешность коэффициента передачи:
∆К = Крас – К
δ% =
Так как в реальности нельзя изготовить идеальный резистор, все резисторы имеют шкалу допуска разброса параметров.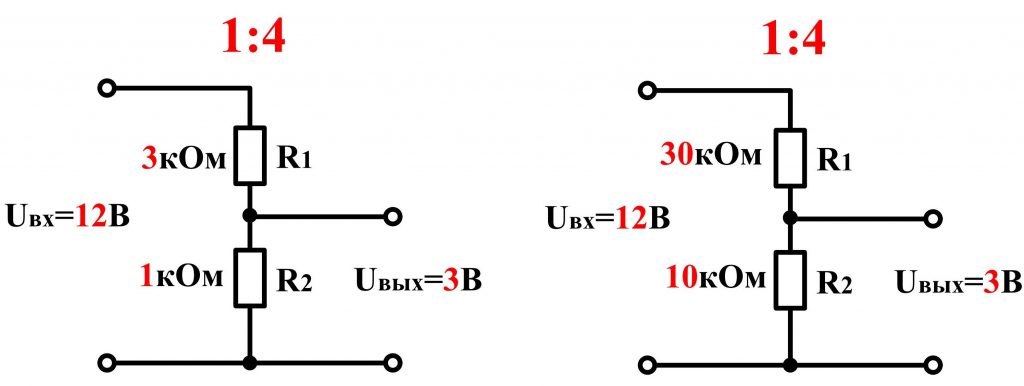 Необходимо выбрать тип резистора из Рядов номинальных значений сопротивлений с ближайшим допустимым отклонением от номинала. Соответственно погрешность δ% будет равна номинальному отклонению.
Необходимо выбрать тип резистора из Рядов номинальных значений сопротивлений с ближайшим допустимым отклонением от номинала. Соответственно погрешность δ% будет равна номинальному отклонению.
3.5 Определить амплитуду выходного напряжения
Um вых = Крас . Um вх (1.3)
3.6 Рассчитать мощности, которые рассеивают резисторы по формуле:
P = U . I = U2 / R = I2 . К (1.4)
Также используйте формулу:
Um вх = Um R1 + Um R2 = Um R1 + Um вых (1.5)
Выберите номинальные величины мощностей резисторов.
3.7 На графике покажите эпюры входного и выходного напряжений.
4 Пример расчета (для М =1, N=4)
4.1 Приведем схему резистивного делителя напряжения.
Рисунок 4.1 – Схема резистивного делителя напряжения
4.2 Рассчитаем заданный коэффициент передачи делителя.
Согласно условию задания
Rвх ≥ 1 кОм
А так как в данном случае резисторы соединены последовательно, то входное сопротивление цепи равно:
Rвх (1.1)
Из данной формулы видно, что коэффициент передачи будет равным:
(1.2)
Как видно по рисунку 3.1 и формуле 1.1 входное сопротивление зависит как от сопротивления резистора R1, так и от сопротивления резистора R2. Для выполнения условия задачи можно задать сопротивление одного из этих резисторов равным 1 кОм.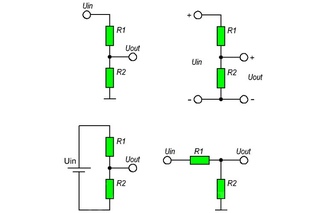 Если задать R2 = 1 кОм, то в таком случае Rвх > 1кОм.
Если задать R2 = 1 кОм, то в таком случае Rвх > 1кОм.
Тогда значение резистора R1
R1 =((10+ -1) . 1000=(14-1) . 1000=13000, Ом
4.3 Из Приложения находим ближайшую стандартную величину R1=13кОм.
4.4 Рассчитать коэффициент передачи делителя с новыми значениями.
Крас
Определить погрешность коэффициента передачи:
∆К = Крас – К=0,071 – 0,071=0
δ% = = . 100%= 0%
Но так как в реальности нельзя изготовить идеальный резистор, все резисторы имеют шкалу допуска разброса параметров. Мы выбрали тип резистора из ряда Е24, для которого допустимые отклонения от номинала составляет ± 5% . Соответственно δ% = 5% .
Полученное значение погрешности не превышает 5%, что удовлетворяет условию.
4.5 Определим амплитуду выходного напряжения
Um вых = Крас . Um вх (1.3)
Um вх (1.3)
4.6 Рассчитаем мощности, которые рассеивают резисторы по формуле:
P = U . I = U2 / R = I2 . К (1.4)
Um вх = 10 + M = 10 + 1 = 11 В
Um вых = 0,071 . 11 = 0,781 В
Так как Um вх = Um R1 + Um R2 = Um R1 + Um вых
Um R1 = Um вх — Um вых = 11 – 0,781 = 10,219, В
PR2 = U2m вых / R2 = 0,7812 / 1000 = 6,1 . 10-4, Вт
PR1 = U2m R1 / R1 = 10,2192 / 13000 = 8,03 . 10-3, Вт
10-3, Вт
Выбираем номинальные величины мощностей резисторов.
PR1 = 0,125 Вт; PR2 = 0,125 Вт.
4.7 На графике покажем эпюры входного и выходного напряжений.
Рисунок 4.2 – Эпюры входного и выходного напряжений делителя
Приложение
Ряды номинальных значений сопротивлений, емкостей и индуктивностей с допуском ±5 % и более
Е3Е6
Е12
Е24
Е3
Е6
Е12
Е24
Е3
Е6
Е12
Е24
1
1
1
1
2.
 2
2
2.2
2.2
2.2
4.7
4.7
4.7
4.7
1.1
2.4
5.1
1.2
1.2
2.7
2.7
5.6
5.6
1.
 3
3
3
6.2
1.5
1.5
1.5
3.3
3.3
3.3
6.8
6.8
6.8
1.6
3.6
7.5
1.
 8
8
1.8
3.9
3.9
8.2
8.2
2
4.3
9.1
Номиналы соответствуют числам, приведенным в таблице и числам, полученным умножением на 10n, где n — целое положительное или отрицательное число.
Ряд Е3 соответствует отклонению от номинального значения ±50%
Ряд Е6 соответствует отклонению от номинального значения ±20%
Ряд Е12 соответствует отклонению от номинального значения ±10%
Ряд Е24 соответствует отклонению от номинального значения ±5%.
Расчет сборка и изучение схемы делителя напряжения. Делитель напряжения
В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U
вых связано с входным U
вх (без учета возможного сопротивления нагрузки) следующим соотношением:
U
вых = U
вх х (R2 / R1 + R2)
Рис. 1. Делитель напряжения
Пример.
С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 1.
Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.
Следовательно, R2 / (R1 +R2) R2 = 0,2
R2 = 0
,2R1 +
0,2R2
.
R1 = 4R2
Поэтому можно выбрать R2 = 1 кОм, R1 — 4 кОм. Сопротивление R1
получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполненных на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт).
Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.
Для получения заданного значения напряжения следует применять высокоточные резисторы.
Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение (U
вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U
выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.
Важно помнить о том, что с уменьшением сопротивлений резисторов R1
и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1-10 мА.
Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2
ток I
составляет часть общего тока I
вх, определяемую сопротивлениями резисторов Rl и R2, т. е. можно записать, что I
е. можно записать, что I
вых = I
вх х (R1 / R2 + R1)
Пример.
Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА (см. рис. 3)
.
Рис. 2 Делитель тока
Рис. 3.
Коэффициент деления тока определяется соотношением:
I
вых / I
вх = 1/10 = 0,1 = R1 / R2 + R1
, R2 = 100
Ом.
Отсюда,
0,1R1 +
0,1R2 = R1
0,1R1 + 10 = R1
R1 = 10/0
,9 = 11,1 Ом
Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это .
Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.
Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.
Что такое делитель напряжения? Формулировка проста — это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.
Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно потребителей. Как известно, при последовательном способе включения равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
Как известно, при последовательном способе включения равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два — это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.
Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2.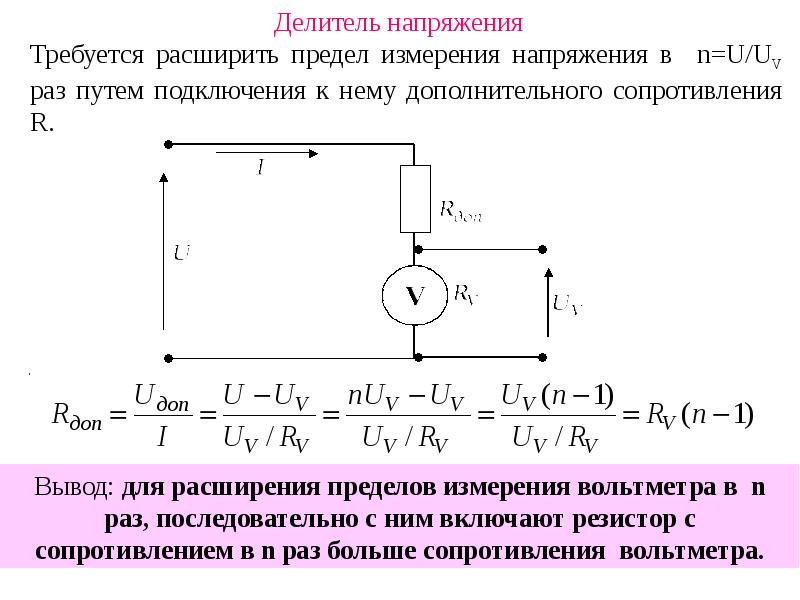 Ток при этом равен Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Ток при этом равен Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Чему же равен ток при данных условиях? Обобщая уравнения, получаем:
I = U / (R1+R2).
Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):
U exit = U * R2 / (R1+R2).
Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.
Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин — это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.
Значение сопротивления подключенной нагрузки не должно быть меньше, чем схемы самого делителя, в противном случае всю систему потребуется пересчитывать.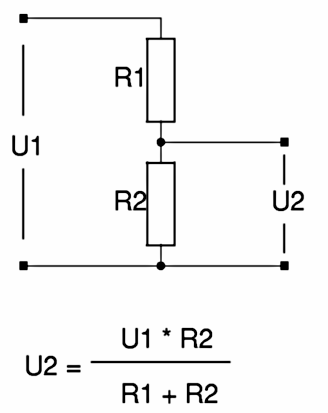 В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее а заниженные будут перегреваться, затрачивая энергию на нагрев.
В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее а заниженные будут перегреваться, затрачивая энергию на нагрев.
Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).
Делить…всем Вам знакомо это слово. Делить водку, делить бабло, делить хавку:-) А вот кто-нибудь из Вас делил когда-нибудь напряжение? Думаю, таких мало. Ну что же, давайте разберемся, как можно его поделить.
Для того, чтобы поделить напряжение, нам нужно всего-навсего два и более резисторов. Для начала рассмотрим вот такой рисуночек:
Наш схемка состоит из двух резисторов, подключенных последовательно. На эти резисторы подается напряжение, оно может быть как переменное, так и постоянное. Назовем его U. Ну вот пропускаем мы напряжение через эти резисторы и нас сразу же заработал Закон Ома . Мы знаем, если резисторы соединены последовательно, то их Сопротивление будет равняться сумме их номиналов. То есть получается, что
На эти резисторы подается напряжение, оно может быть как переменное, так и постоянное. Назовем его U. Ну вот пропускаем мы напряжение через эти резисторы и нас сразу же заработал Закон Ома . Мы знаем, если резисторы соединены последовательно, то их Сопротивление будет равняться сумме их номиналов. То есть получается, что
I=U/R общее, где R общее =R1+R2
то есть можно написать
I=U/(R1+R2)
При последовательном соединении резисторов, сила тока —
I
, проходящая через каждый резистор одинакова
— это есть закон последовательного соединения резисторов, вам его надо бы запомнить, иначе можно вообще не лезть в электронику:-). Так, разобрались. Но у нас каждый резистор обладает своим каким то сопротивлением. Отсюда напрашивается вывод из Закона Ома , что и на каждом сопротивлении у нас будет абсолютно разное напряжение, все зависит от закона Ома.
На сопротивлении R1
у нас будет напряжение U1
, а на сопротивлении R2
у нас будет напряжение U2
I=U2/R2=U1/R1=U/(R1+R2)
Давайте найдем значения U1
и U2
. Думаю, все учились в школе, и сможете без проблем решить эту уравнение. Умножаем, сокращаем, материмся и бошку ломаем, и в конце концов получаем, что
Думаю, все учились в школе, и сможете без проблем решить эту уравнение. Умножаем, сокращаем, материмся и бошку ломаем, и в конце концов получаем, что
U1=UxR1/(R1+R2)
U2=UxR2/(R1+R2)
А вы знаете, что если сложить правые части уравнения, получим U
? Не верите? Проверьте! Отсюда получаем, что U=U1+U2
. Короче говорю простым языком чайника: если резисторы включены в цепь последовательно, то на каждом резисторе падает напряжение (падает, значит на концах резистора имеется это напряжение) и сумма падений напряжений на всех резисторах будет равняться напряжению источника (батарейки, блока питания или какого-нибудь генератора напряжения).
Мы тупо разделили напряжение источника U
на два разных напряжения U1 и U2.
R1 и R2
— это условные обозначения резисторов. Если допустим у нас источник напруги 50 Вольт, и нам надо закрутить 5 вольтовый вентилятор от компа, то измеряем сопротивление обмотки вентилятора и высчитываем по формуле, какой резистор цеплять последовательно к вентилятору. Думаю, с этим все понятно. Формулы есть, оперируйте с ними.
Думаю, с этим все понятно. Формулы есть, оперируйте с ними.
Итак у нас имеются вот такие два резистора и наш любимый мультик:
Замеряем сопротивление мелкого резистора, R1=109,7 Ом.
Замеряем сопротивление толстого резистора R2=52,8 Ом.
Выставляем на блоке питания ровненько 10 Вольт, замеряем напругу с помощью мультика (не смотрите на показания блока питания, он обладает бОльшей погрешностью, чем мультик) .
Цепляемся блоком питания за эти два резистора, запаянные последовательно, напомню, что на блоке ровно 10 Вольт. Показания амперметра на блоке тоже немного неточны, силу тока мы будем замерять с помощью мультика тоже.
Замеряем напругу на толстом резисторе. На толстом резисторе падает напруга 3,21 Вольт.
Замеряем напругу на тонком резисторе. На тонком резисторе падает напруга 6,77 Вольт
Ну что, с математикой думаю у всех в порядке. Складываем эти два значения напряжения 3,21+6,77 =9,98 Вольт. А куда делись еще 0,02 Вольта? Они упали на сопротивлении щупов, они ведь тоже обладают сопротивлением, если вы помните. Вот наглядный пример того, чтобы мы смогли разделить напряжение на два разных напряжения.
А куда делись еще 0,02 Вольта? Они упали на сопротивлении щупов, они ведь тоже обладают сопротивлением, если вы помните. Вот наглядный пример того, чтобы мы смогли разделить напряжение на два разных напряжения.
Давайте же и убедимся, что сила тока при последовательном соединении резисторов везде одинакова. 0,04 А или 40 мА.
Ну, убедились? 🙂
Для того, чтобы делить напряжение плавно, человек изобрел очень удобную вещь, переменный резистор
.
Принцип такой: между двумя крайними контактами постоянное сопротивление, сопротивление относительно среднего контакта по отношению к крайним может меняться в зависимости от того, куда мы будем крутить крутилку этого переменного резистора. Этот резистор рассчитан на мощность 1Вт и сопротивление 330 Ом. Давайте же глянем, как он будет делить напряжение!
Так как мощность небольшая, всего 1 Вт, то не будем нагружать его большой напругой, формула мощности P=IхU. Ток потребления из закона Ома I=U/R.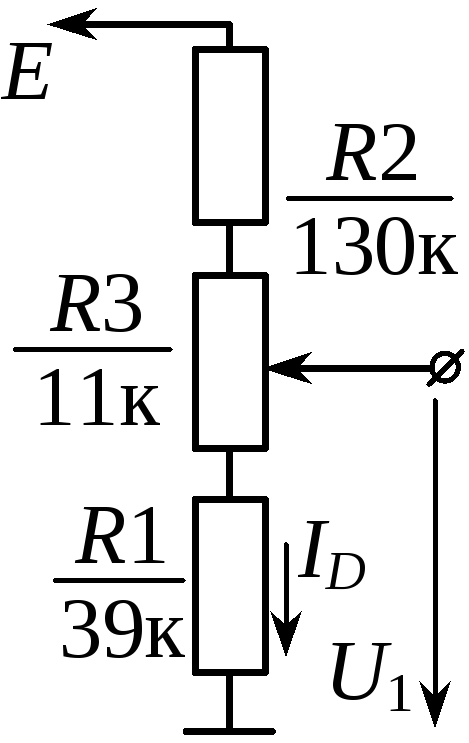 Значит, этот переменный резистор может делить только маленькое напряжение при маленьком сопротивлении нагрузки и наоборот. Главное, чтобы значение мощности этого резистора не вышло за грани. Поэтому я буду делить напряжение в 1 Вольт.
Значит, этот переменный резистор может делить только маленькое напряжение при маленьком сопротивлении нагрузки и наоборот. Главное, чтобы значение мощности этого резистора не вышло за грани. Поэтому я буду делить напряжение в 1 Вольт.
Для этого выставляем на блоке напругу в 1 Вольт и цепляемся к нашему резику по крайним контактам.
Крутим крутилку в каком-нибудь произвольном направлении и останавливаем ее. Замеряем напругу между левым и средним контактом:
Замеряем напругу между средним и правым контактом
Суммируем напругу и получаем 0,34+0,64=0,98 вольт. 0,02 Вольта опять потеряли на щупах.
Такие переменные резисторы используются для добавления громкости на ваших колонках от компа, на радиоприемниках, а также на допотопных ТВ.
В настоящее время делители напряжения создаются с помощью абсолютно других законов электроники. Это может быть полупроводниковые схемы или даже схемы с использованием микроконтроллеров. Но, если требуется быстро получить делитель напряжения и изменять малую мощность напряжения или сигнала в электронике, то делитель напряжения на резисторах вам пригодится как нельзя кстати.
Устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. Делитель можно представить, как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Чаще всего делитель напряжения строится из двух резисторов. Такой делитель называют резисторным. Каждый резистор в таком делителе называют плечом. Плечо соединённое с землёй называют нижним, то что соединено с плюсом — верхним. Точка соединения двух резисторов называется средним плечом или средней точкой. Если говорить совсем упрощённо, то можно представить среднее плечо, как бассейн. Делитель напряжения позволяет нам управлять двумя «шлюзами», «сливая» напряжение в землю (уменьшая сопротивление нижнего плеча) или «подливая» напряжения в бассейн (уменьшая сопротивление верхнего плеча). Таким образом, делитель может использоваться для того, чтобы получить из исходного напряжения лишь его часть.
Принципиальная схема делителя напряжения
В рассматриваемом примере на вход (Uвх) подаётся напряжение 9В. Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?
Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?
Расчёт делителя напряжения
Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.
Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:
Rобщ = R1 + R2 = 400 + 500 = 900 Ом
По закону Ома находим силу тока, протекающего через резисторы:
I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА
Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):
Uвых = I * R2 = 0.01А * 500 Ом = 5В
Или упрощая цепочку вычислений:
Uвых = Uвх * (R2 / (R1+R2))
Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:
R1 = (Uвх-Uвых)/Iд+Iн
R2 = Uвых / Iд
Здесь Iд
и Iн
— ток делителя и ток нагрузки соответственно.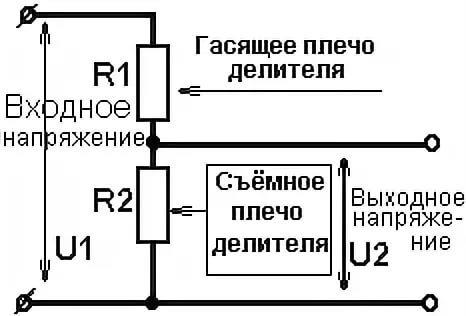 В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд
В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд
= 0.01 А (10 мА), а Iн
= 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:
R1 = (Uвх-Uвых) * 100
R2 = Uвых * 100
P.S. Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд
у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель.
Проверяем:
Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:
R1 = (9-5) * 100 = 400 Ом
R2 = 5 * 100 = 500 Ом
Всё сходится!
Применение делителя напряжений
В основном делитель напряжения используется там, где нужно измерить изменяющееся сопротивление. На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.
На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.
Радио для всех — Лаборатория
В разделе представлены on-line калькуляторы
Цветовая маркировка резисторов
Расчет индуктивности
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Расчёт резистивного и ёмкостного делителей
Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ
Компенсация реактивной мощности
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
Расчет элементов J антенны
Расчет резонансной частоты LC-контура
Расчет резистивного Пи аттенюатора
Делитель напряжения
Цветовой код конденсаторов
Стабилизация напряжения
Дроссели, намотанные на резисторах МЛТ
Реактивное сопротивление конденсатора
Реактивное сопротивление катушки индуктивности
Калькулятор определения номинала SMD-резистора
Расчет значения резистора для LM317
Онлайн калькулятор таймер 555
Расчет «Cantenna» (баночной антенны) для Wi Fi
Расчет усилителя на биполярном транзисторе
Калькулятор расчета компактных монолитных усилителей
Расчет силового трансформатора
Расчет дискоконусной антенны
Сопротивления для согласующего трансформатора
Расчет для тороидальных (ферритовых) сердечников Amidon
Расчет петлевого вибратора
Калькулятор DC-DC преобразователя MC34063A
Расчет выпрямителя для блока питания
Расчет гасящего конденсатора в блоке питания
Расчет резистора для подключения светодиода
Цветовая маркировка резисторов
Расчет индуктивности
Расчёты электронных цепей.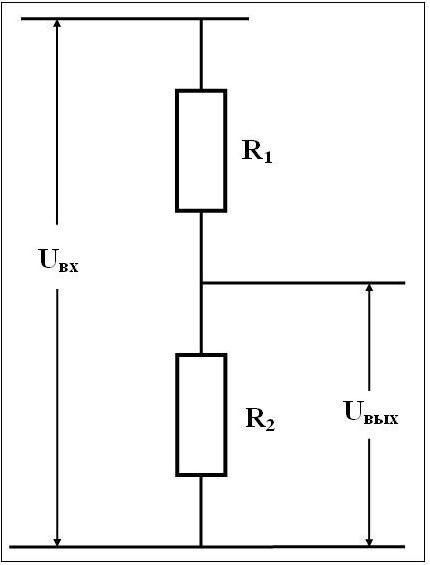
Вписываем значения и кликаем мышкой в таблице
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
Реактивное сопротивление ёмкости | Реактивное сопротивление индуктивности |
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Параллельное соединение двух сопротивлений | Последовательное соединение двух ёмкостей |
Расчёт резистивного и ёмкостного делителей
Расчёт резистивного делителя напряжения | Расчёт ёмкостного делителя напряжения |
Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ
Частота среза фильтра ФНЧ и ФВЧ
Частота резонанса колебательного контура LC | Пост. времени τ RC и частота среза RC-фильтра |
Компенсация реактивной мощности
Реактивная мощность Q = √((UI)²-P²) |
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
После сброса ввести два любых известных параметра I=U/R; U=IR; R=U/I; P=UI P=U²/R; P=I²R; R=U²/P; R=P/I² U=√(PR) I= √(P/R) |
Расчет элементов J антенны
Дополнение: Арифметические калькуляторы и конвертеры величин
Делитель напряжения
В этой статье расскажем про делитель напряжения и покажем примеры с решениями.
Для уменьшения значения входного (питающего) напряжения используют делитель напряжения на резисторах. В нём, выходное напряжение Uвых зависит от значения входного (питающего) напряжения Uвх и значения сопротивления резисторов. Делитель напряжения – наиболее часто применяемое соединение резисторов. Например, переменный резистор, используемый в качестве регулятора громкости Ваших компьютерных колонок, является делителем напряжения с изменяемыми сопротивлениями плеч, где он выполняет роль ограничителя амплитуды входного сигнала.
| Так как, сопротивление нагрузки влияет на выходное напряжение Uвых делителя, для обеспечения точности делителя напряжения, необходимо выполнять правило (2):Значение резистора R2 должно быть приблизительно на два порядка меньше (в 100 раз) сопротивления нагрузки подключаемой к выходу делителя. Если Вам не нужна высокая точность, то эту разницу можно снизить до 10 раз. |
Используя закон Ома, и пренебрегая малым током нагрузки, делитель напряжения можно описать соотношением:
(8)
Преобразовывая указанную формулу так, как нам удобно, можно определить:
1. Выходное напряжение Uвых по известным значениям входного напряжения Uвх и сопротивлений резисторов R1, R2 :
(9)
Пример: Необходимо определить выходное напряжение Uвых делителя при известных напряжении источника тока Uвх = 50 В, и значениях R1 = 10 кОм и R2 = 500 Ом.
Решение: По формуле вычисляем Uвых = 50 * 500 / (10000 + 500) = 2,38 В.
2. Входное напряжение делителя Uвх , по известным значениям выходного напряжения Uвых и сопротивлений резисторов R1, R2 :
(10)
Пример: Необходимо определить входное напряжение Uвх делителя при необходимых выходном напряжении Uвых = 4 В, и значениях R1 = 15 кОм и R2 = 3 кОм.
Решение: По формуле вычисляем Uвх = 4 * (15000 + 3000) / 3000 = 24 В.
3. Значение R1 по известным значениям входного напряжения Uвх , выходного напряжения Uвых и сопротивления резистора R2 :
(11)
Пример: С помощью делителя напряжения необходимо получить на нагрузке сопротивлением 50 кОм напряжение Uвых = 10 В от источника напряжением Uвх = 50 В.
Решение: Сопротивление резистора R2 должно быть в 100 раз меньше сопротивления нагрузки 50 кОм (см. правило 2). Выполняем это условие: R2 = 500 Ом.
По формуле вычисляем R1 = 50 * 500 / 10 – 500 = 2000 Ом = 2 кОм
Не забывайте, что сам делитель потребляет ток от источника тока, в соответствии с законом Ома (формула 1): Iдел = Uвх / (R1 + R2) = 50/(2000+500) = 0,02 А (20 мА).
Определим рассеиваемую мощность резисторов по формуле (3):
Для резистора R1 : P = 0,02 * 0,02 * 2000 = 0,8 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт;
Для резистора R2 : P = 0,02 * 0,02 * 500 = 0,2 Вт; по правилу (1) выбираем резистор мощностью P = 0,5 Вт.
4. Значение R1 и R2 по известным значениям входного напряжения Uвх , выходного напряжения Uвых и входного (общего) сопротивления делителя Rобщ , где Rобщ = R1 + R2 :
(12)
(13)
</div
Пример: Определить значения R1 и R2 делителя напряжения, если их сумма R1+R2 = 1кОм, при входном напряжении источника Uвх = 50 В и напряжении на выходе Uвых = 20 В.
Решение: По формуле (4) вычисляем R2 = 20 * 1000 / 50 = 400 Ом;
По формуле (5) вычисляем R1 = 1000 — 400 = 600 Ом;
Не забывайте, что сам делитель потребляет ток от источника тока, в соответствии с законом Ома (формула 1): Iдел = Uвх / (R1 + R2) = 50/(600+400) = 0,05 А (50 мА).
Определим рассеиваемую мощность резисторов по формуле (3):
Для резистора R1 : P = 0,05 * 0,05 * 600 = 1,5 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт;
Для резистора R2 : P = 0,05 * 0,05 * 400 = 1 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт.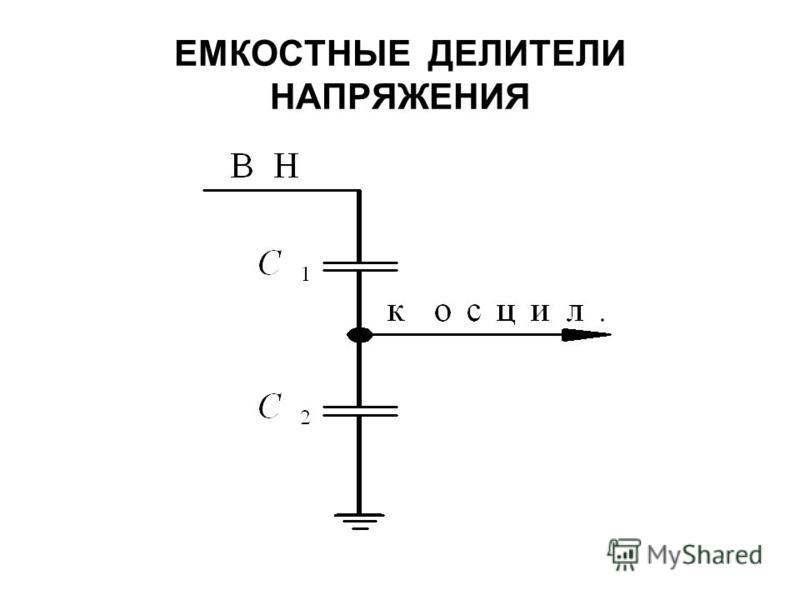
Напрашивается законный вопрос: Если есть делитель, значит должен быть и коэффициент деления? Конечно! Но он Вам пригодится лишь тогда, когда вы будете иметь дело с другими элементами, например трансформатором, а не резисторами.
В качестве R2 делителя напряжения может применяться сама нагрузка с её внутренним сопротивлением. В таком случае, R2 указанное в формуле, приравняйте к сопротивлению нагрузки Rн, и используйте те же формулы, которые применимы к двум независимым резисторам. Тогда, правило (2) не используется.
В следующей статье рассмотрим делитель тока.
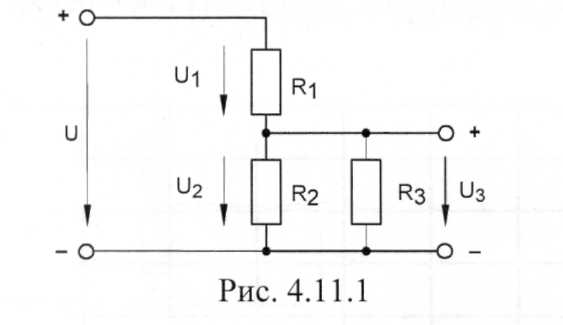
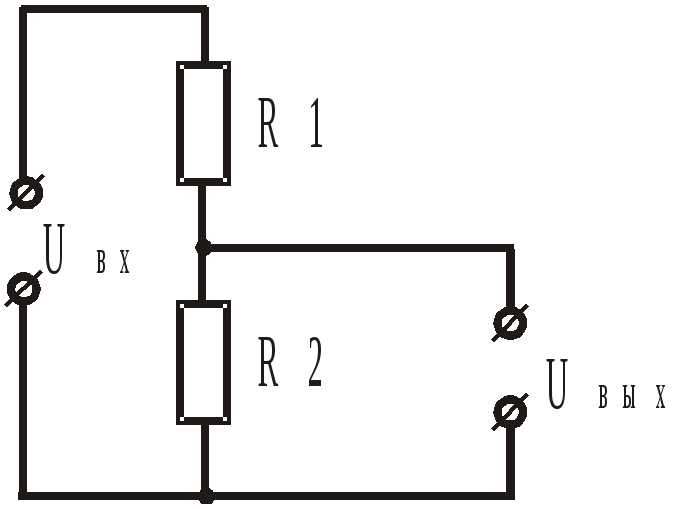
Практика 7. Расчет делителей напряжения и тока
Практическая работа №7
Расчет делителей напряжения и тока.
Теоретические сведения
Делители напряжения. Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора R1 и R2,
подключённых к источнику напряжения U. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа.
Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа.
Рис. 7.1. Схема резистивного делителя напряжения.
Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U I R
Для каждого резистора имеем:
U1 I R1
U2 I R2
Разделив выражение для U1 на выражение для U2 в итоге получаем:
U1 R1
U2 R2
Таким образом, отношение напряжений U1 и U2 в точности равно отношению сопротивлений R1 и R2.
Далее
U1 |
| R1 |
| U2 | |||
| R2 | ||||||
|
|
|
|
| |||
U1 U2 | R1 | U2 U2 | |||||
| |||||||
|
|
| R2 |
|
| ||
| R1 |
|
|
| |||
U |
|
|
| 1 U2 | |||
R2 | |||||||
|
|
|
| ||||
R1 R2 |
| |||
Т. |
|
| U2 | |
R2 | ||||
|
|
| ||
Откуда:
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя,
так, чтобы в расчетах этим сопротивлением, включенным параллельно R2 можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 и больше раз по величине), потребляемого нагрузкой, но,
однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R1+R2.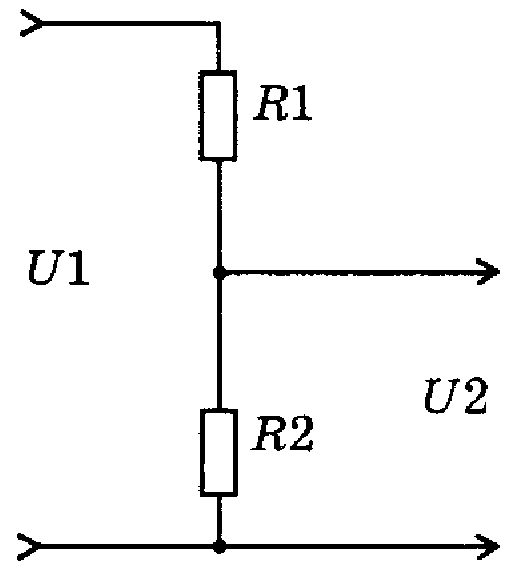 Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, сумма величин близка расчетной.
Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, сумма величин близка расчетной.
При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений,
диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов – она должна превышать выделяемую на них мощность.
Стандартный ряд сопротивлений: 1,0; 1,1; 1,2; 1,3; 1,5; 1,6; 1,8; 2,0; 2,2; 2,4; 2,7; 3,0; 3,3; 3,6; 3,9; 4,3; 4,7; 5,1; 5,6; 6,2; 6,8; 7,5; 8,2; 9,1.
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД)
Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД)
режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. На практике это невозможно, поскольку, увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов:
электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Делители тока. Простейший резистивный делитель тока — это два параллельно включённых резистора R1 и R2, подключённых к источнику напряжения U. Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.
Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.
Рис. 7.2. Схема резистивного делителя тока.
Ток через них можно определить согласно закону Ома:
I1 U
R1
I2 U
R2
Общий ток в цепи согласно первому закону Кирхгофа:
I I1 I2
Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в
10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше)
пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры,
стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок.
Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.
Примеры решения задач. Для делителя напряжения определить:
1. Выходное напряжение Uвых по известным значениям входного напряжения Uвх и сопротивлений резисторов R1, R2 :
Пример: Необходимо определить выходное напряжение Uвых делителя при известных напряжении источника тока Uвх = 50 В, и значениях R1 = 10 кОм и
R2 = 500 Ом.
Решение: По формуле вычисляем Uвых = 50 * 500 / (10000 + 500) = 2,38 В.
2. Входное напряжение делителя Uвх, по известным значениям выходного напряжения Uвых и сопротивлений резисторов R1, R2:
Пример: Необходимо определить входное напряжение Uвх делителя при необходимых выходном напряжении Uвых=4 В, и значениях R1=15 кОм и
R2=3 кОм.
Решение: По формуле вычисляем Uвх = 4 * (15000 + 3000) / 3000 = 24 В.
3. Значение R1 по известным значениям входного напряжения Uвх,
выходного напряжения Uвых и сопротивления резистора R2:
Пример: С помощью делителя напряжения необходимо получить на нагрузке сопротивлением 50 кОм напряжение Uвых = 10 В от источника напряжением
Uвх = 50 В.
Решение: Сопротивление резистора R2 должно быть в 100 раз меньше сопротивления нагрузки 50 кОм. Выполняем это условие: R2 = 500 Ом.
По формуле вычисляем R1 = 50 * 500 / 10 – 500 = 2000 Ом = 2 кОм.
Сам делитель потребляет ток от источника тока, в соответствии с законом Ома: Iдел = Uвх / (R1 + R2) = 50/(2000+500) = 0,02 А (20 мА).
Определим рассеиваемую мощность резисторов:
для резистора R1 : P = 0,02 * 0,02 * 2000 = 0,8 Вт;
для резистора R2 : P = 0,02 * 0,02 * 500 = 0,2 Вт.
4. Значение R1 и R2 по известным значениям входного напряжения Uвх,
выходного напряжения Uвых и входного (общего) сопротивления делителя Rобщ,
где Rобщ = R1 + R2:
Пример: Определить значения R1 и R2 делителя напряжения, если их сумма
R1+R2 = 1кОм, при входном напряжении источника Uвх = 50 В и напряжении на выходе Uвых = 20 В.
Решение: вычисляем R2 = 20 * 1000 / 50 = 400 Ом;
вычисляем R1 = 1000 — 400 = 600 Ом;
Сам делитель потребляет ток от источника тока, в соответствии с законом Ома: Iдел = Uвх / (R1 + R2) = 50/(600+400) = 0,05 А (50 мА).
Определим рассеиваемую мощность резисторов:
для резистора R1 : P = 0,05 * 0,05 * 600 = 1,5 Вт;
для резистора R2 : P = 0,05 * 0,05 * 400 = 1 Вт.
Для делителя тока определить:
1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2:
Пример: Определить значения I1 и I1 делителя тока, если значение общего тока Iобщ = 0,6А, сопротивление R1 =100 Ом, а R2 = 20 Ом.
Решение: вычисляем : I1 = 0,6 * 20 / (100 + 20) = 0,1 А;
вычисляем : I2 = 0,6 * 100 / (100 + 20) = 0,5 А;
резисторы поглощают мощность: P = I * I * R;
рассеиваемая мощность резисторов:
для резистора R1: P = 0,1 * 0,1 * 100 = 1 Вт;
для резистора R2: P = 0,5 * 0,5 * 20 = 5 Вт.
2. Рассчитать шунт R2 в цепи измерительного прибора, при известных:
внутреннем сопротивлении R1, максимальном токе обмотки катушки прибора I1 и
максимальном значении общего тока Iобщ цепи делителя тока, представленного на схеме:
Пример: Полное отклонение стрелки миллиамперметра при значении I1 = 1
мА, внутреннее сопротивление катушки прибора R1 = 200 Ом. Рассчитайте шунт
Рассчитайте шунт
R2, чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.
Решение: вычисляем: R2 = 0,001 * 200 / (1 – 0,001) = 0,2 Ом;
поглощаемая (рассеиваемую) мощность R2: P = I2 * I2 * R2,
где I2 = Iобщ — I1 = 999 мА, P = 0,999 * 0,999 * 0,2 = 0,199 Вт.
Для достижения точности в измерительных цепях, выбирают высокоточные резисторы, кроме того, используют их последовательное и параллельное соединение.
Деление дробей в столбик. Делитель напряжения
Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение. Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Как работает делитель напряжения на резисторах
Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой (см. картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора.
картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора.
Резистор, находящийся ближе к плюсу входного напряжения Vвх
, обозначен R1
, резистор находящийся ближе к минусу обозначен R2
. Падение напряжения Vвых
— это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения. Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов.
Расчет делителя напряжения на резисторах основан на законе Ома .
V вых = R2 х V вых / R1 + R2
Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2. На этом принципе работают потенциометры (переменные резисторы) и многие резистивные датчики, например, датчик освещенности на фоторезисторе . Смотрите калькулятор делителя напряжения на резисторах онлайн.
Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз. Например, величина входного напряжения 50 В
, а выходное напряжение нужно получить в 10 раз меньше, т. е. 5 В
(рис. 1
). Для этого используются делители напряжения.
Рис. 1 — Структурная схема делителя напряжения
Они бывают разных типов и выполняются на безе , катушек индуктивности (рис. 2
). Однако мы рассмотрим только наиболее применяемые на практике делители напряжения.
Рис. 2 — Элементы, применяемые в качестве делителей напряжения
Наиболее простым делителем напряжения являются два последовательно соединенных резистора R1
и R2
, которые подключены к источнику напряжения U
(рис. 3
). Если сопротивление резисторов одинаковы R1 = R2
Если сопротивление резисторов одинаковы R1 = R2
, то напряжение источника питания разделится поровну на них U1 = U2 = U/2
.
Рис. 3 — Общая схема делителя напряжения на резисторах
Расчет делителя напряжения на резисторах
Давайте разберемся как происходит деление напряжения. Для этого нам понадобится знание только закона Ома, который, если говорить очень обобщенно, звучит так: ток I
, протекающий в цепи (или на ее участке), прямопропорционален приложенному напряжению U
и обратнопропорционален сопротивлению цепи (или ее участка) R
, т. е.
откуда
Также следует знать, что в последовательной цепи, т. е. в цепи, в которой все резисторы соединены последовательно, ток I
протекает одной и той же величины через все резисторы, а общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений всех резисторов Rобщ = R1+R2
.
Теперь, на основании выше сказанного, давайте определим напряжения на резисторах в зависимости от величины их сопротивлений и напряжения источника питания.
Ток I
, протекающий в цепи, равен отношению напряжения U
к сумме сопротивлений R1+R2
, т. е.
Падение напряжения на первом резисторе равно
По аналогии находим падение напряжения на втором резисторе
Теперь в выражение (2) и (3) подставим значение тока из выражения (1), в результате получим
Делитель напряжения на резисторах. Различные номиналы резисторов
С помощью полученных формул можно определить падение напряжения на резисторе, зная только величину входного напряжения и сопротивления самих резисторов. Однако такие формулы часто применимы лишь в теоретических расчётах. На практике же гораздо проще пользоваться основным свойством любого делителя напряжения, которое заключается в том, что при соответствующем подборе сопротивлений резисторов R1
и R2
выходное напряжение составляет часто входного (рис. 4
4
).
Рис. 4 — Схемы делителей напряжения на резисторах
Следует обратить внимание на то, что величина выходного напряжения зависит от относительного
значения сопротивлений резисторов R1
и R2
, а не от абсолютного.
Рис. 5 — Схемы делителей напряжения с одинаковым коэффициентом деления при разных номиналах резисторов
Здесь возникает вопрос: какие же номиналы резисторов R1
и R2
применять, 3 кОм
и 1 кОм
или 30 кОм
и 10 кОм
? Все зависит от конкретного случая. Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1
и R2
, тем больший ток будет протекать в цепи и тем большую мощность можно получить с выхода делителя напряжения, но нужно помнить, что эта мощность ограничивается мощностью источник питания и не может ее превысить.
Также делитель напряжения можно выполнять из нескольких последовательно соединенных резисторов (рис. 6
).
Рис. 6 — Схема делителя напряжения с несколькими резисторами
И так, мы рассмотрели резисторный делитель напряжения с фиксированным значением выходного напряжения. Однако часто возникает необходимость в плавном изменении выходного напряжения. Например, при регулировании громкости звука мы плавно изменяем напряжение на усилителе.
Для плавного регулирования величины выходного напряжения применяются переменные и подстроечные резисторы (рис. 7
).
Рис. 7 — Переменные и подстроечные резисторы
Переменный резистор еще называют потенциометром. Конструктивно он состоит из корпуса, имеющего три вывода, и рукоятки. При вращении ручки осуществляется скользящих контакт подвижной металлической пластины, которая замыкает две токопроводящие графитные дорожки, имеющие разную проводимость в зависимости от длины. Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Схема подключения переменного резистора или же потенциометра приведена ниже (рис. 8
). Два крайних вывода подключаются к источнику питания, а между средним и одним из крайних выводов снимается выходное напряжение, величину которого можно изменять от нуля до значения входного напряжения Uвых = 0…Uвх
.
Рис. 8 — Схема включения переменного резистора для деления напряжения
Если, проворачивая ручку резистора, мы введем все сопротивление (как показано на схеме (рис. 9
)), то выходное напряжение будет равно входному Uвых = Uвх
, так как подводимое напряжение будет полностью падать на сопротивлении резистора.
Если же вывести все сопротивление, то выходное напряжение будет равно нулю Uвых = 0
.
Рис. 9 — Схема плавного изменения напряжения
9 — Схема плавного изменения напряжения
Некоторые виды переменных резисторов
В зависимости от степени относительного изменения сопротивления при вращении рукоятки переменного резистора их разделяют на три типа (рис. 10
):
1) с линейной зависимостью;
2) с логарифмической зависимостью;
3) с экспоненциальной зависимостью.
Рис. 10 — Зависимости переменных резисторов
Переменные резисторы с логарифмической зависимостью часто используются для регулировки уровня звука, поскольку ухо человека воспринимает звук именно по такой зависимости.
Кроме того переменные резисторы бывают как одинарные, так и сдвоенные. Последние находят широкое применение в звуковой технике.
Делители напряжения на резисторах одинаково работают и рассчитываются как для постоянного, так и для переменного напряжения. Однако, в качестве делителей переменного напряжения также часто используются конденсаторы и реже – катушки индуктивности.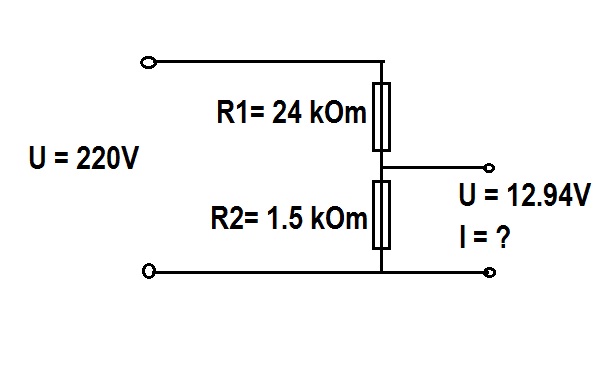
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель
напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов .
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе
V out
? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1
и R2
одинаков пока
к выходу V out
ничего не подключено. А суммарное сопротивление
пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2
, расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В.
Это простой способ получить несколько различных напряжений в одной схеме, оставив при
этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество
Существует множество
компонентов, которые меняют своё сопротивление в зависимости от внешних условий.
Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.д.
Если в приведённой выше схеме заменить R1
или R2
на один из таких
компонентов, V out
будет меняться в зависимости от внешних условий, влияющих
на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино,
можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию
на переменный компонент и общую формулу расчёта V out
.
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо
потребитель тока, который ещё называют нагрузкой
(load):
В этом случае V out
уже не может быть расчитано лишь на основе значений V in
,
R1
и R2
: сама нагрузка провоцирует дополнительное падение напряжения
(voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых
параллельно:
Подставив значение в общую формулу расчёта V out
, получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки.
И тем ощутимее будут потери,
чем больше номинал R2
по отношению к сопротивлению L
. Чтобы нивелировать этот эффект мы могли
бы использовать в качестве R1
и R2
резисторы, например, в 10 раз меньших
номиналов.
Пропорция сохраняется, V out
не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от
источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если
устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка
на R1
равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной
схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень
вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит
для получения необходимого заниженного напряжения в случаях, когда подключенная
нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является
считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .
Делитель не подходит
для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка
на сами резисторы.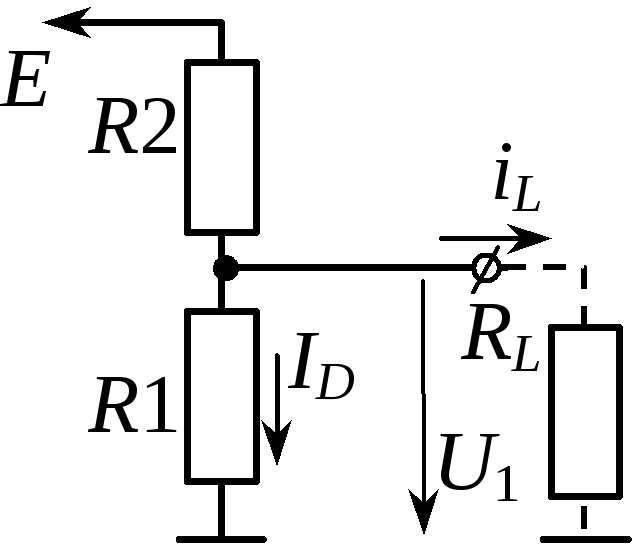 Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, V out
также будет неравномерным.
Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья. Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения.
Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.
Вашему вниманию подборка материалов: Схема традиционного резисторного делителя напряженияДля применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. Расчет резистивного делителя напряжения[Напряжение на выходе, В Из этой формулы, в частности, видно, что резисторные (резистивные) делители выдают стабильное выходное напряжение, если напряжение питания фиксировано. = [Сопротивление резистора R1, Ом Эта формула верна для ненагруженного делителя. Если делитель работает на нагрузку, то [Входное сопротивление делителя, Ом [Эквивалентное выходное сопротивление делителя, Ом = [Сопротивление резистора R2, Ом [Действующее / мгновенное / амплитудное напряжение на выходе делителя, В Эта формула верна, если ток нагрузки делителя равен нулю. Пример — делитель для осциллографаЕсли мы хотим получить осциллограмму высокого напряжения, то сразу приходит в голову делитель напряжения. Изготавливаем делитель, подключаем его вход к источнику высоковольтного сигнала, а выход к входу осциллографа. Должны получить на входе осциллографа уменьшенную копию входного сигнала. Если наш сигнал имеет достаточно большую частоту или просто резкие фронты (например, меандр), то ничего не получится. Осциллограмма не будет похожа на изначальный сигнал. Причина в том, что осциллограф имеет некоторую входную емкость, которая образует с эквивалентным выходным сопротивлением делителя фильтр нижних частот. Все высшие гармоники сигнала подавляются. Кроме того этот фильтр формирует фазовый сдвиг. Это бывает существенным для многолучевых осциллографов, когда мы анализируем соотношения сигналов. Чтобы этого избежать, резистор R1 нужно зашунтировать конденсатором. Качество усилителей звуковой частоты. Обзор, схемы…. Как не спутать плюс и минус? Защита от переполярности. Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис… Соединение светодиодов. Последовательное, параллельное включение оптоэ… Параллельное, последовательное соединение резисторов. Расчет сопротивл… |
Как решить в столбик деление 3535 14. Делитель напряжения
Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение. Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Как работает делитель напряжения на резисторах
Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой (см. картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора.
Резистор, находящийся ближе к плюсу входного напряжения Vвх
, обозначен R1
, резистор находящийся ближе к минусу обозначен R2
. Падение напряжения Vвых
— это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения. Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов.
Расчет делителя напряжения на резисторах основан на законе Ома .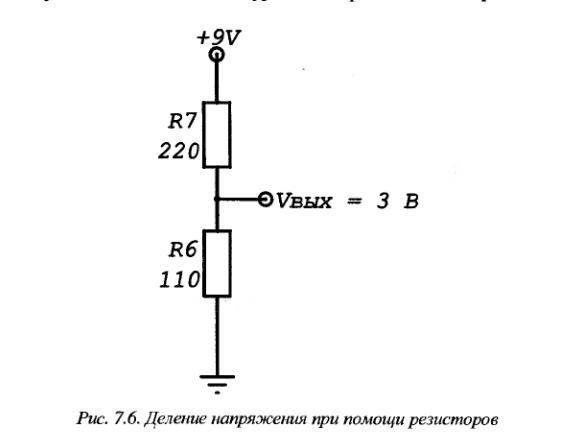
V вых = R2 х V вых / R1 + R2
Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2. На этом принципе работают потенциометры (переменные резисторы) и многие резистивные датчики, например, датчик освещенности на фоторезисторе . Смотрите калькулятор делителя напряжения на резисторах онлайн.
Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз. Например, величина входного напряжения 50 В
, а выходное напряжение нужно получить в 10 раз меньше, т. е. 5 В
(рис. 1
). Для этого используются делители напряжения.
Рис. 1 — Структурная схема делителя напряжения
Они бывают разных типов и выполняются на безе , катушек индуктивности (рис. 2
). Однако мы рассмотрим только наиболее применяемые на практике делители напряжения.
Однако мы рассмотрим только наиболее применяемые на практике делители напряжения.
Рис. 2 — Элементы, применяемые в качестве делителей напряжения
Наиболее простым делителем напряжения являются два последовательно соединенных резистора R1
и R2
, которые подключены к источнику напряжения U
(рис. 3
). Если сопротивление резисторов одинаковы R1 = R2
, то напряжение источника питания разделится поровну на них U1 = U2 = U/2
.
Рис. 3 — Общая схема делителя напряжения на резисторах
Расчет делителя напряжения на резисторах
Давайте разберемся как происходит деление напряжения. Для этого нам понадобится знание только закона Ома, который, если говорить очень обобщенно, звучит так: ток I
, протекающий в цепи (или на ее участке), прямопропорционален приложенному напряжению U
и обратнопропорционален сопротивлению цепи (или ее участка) R
, т.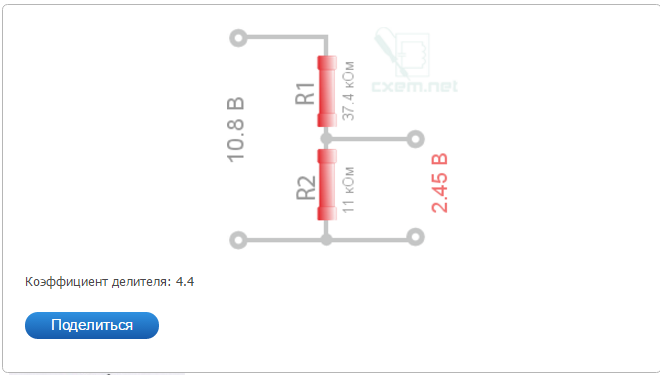 е.
е.
откуда
Также следует знать, что в последовательной цепи, т. е. в цепи, в которой все резисторы соединены последовательно, ток I
протекает одной и той же величины через все резисторы, а общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений всех резисторов Rобщ = R1+R2
.
Теперь, на основании выше сказанного, давайте определим напряжения на резисторах в зависимости от величины их сопротивлений и напряжения источника питания.
Ток I
, протекающий в цепи, равен отношению напряжения U
к сумме сопротивлений R1+R2
, т. е.
Падение напряжения на первом резисторе равно
По аналогии находим падение напряжения на втором резисторе
Теперь в выражение (2) и (3) подставим значение тока из выражения (1), в результате получим
Делитель напряжения на резисторах. Различные номиналы резисторов
С помощью полученных формул можно определить падение напряжения на резисторе, зная только величину входного напряжения и сопротивления самих резисторов. Однако такие формулы часто применимы лишь в теоретических расчётах. На практике же гораздо проще пользоваться основным свойством любого делителя напряжения, которое заключается в том, что при соответствующем подборе сопротивлений резисторов R1
Однако такие формулы часто применимы лишь в теоретических расчётах. На практике же гораздо проще пользоваться основным свойством любого делителя напряжения, которое заключается в том, что при соответствующем подборе сопротивлений резисторов R1
и R2
выходное напряжение составляет часто входного (рис. 4
).
Рис. 4 — Схемы делителей напряжения на резисторах
Следует обратить внимание на то, что величина выходного напряжения зависит от относительного
значения сопротивлений резисторов R1
и R2
, а не от абсолютного.
Рис. 5 — Схемы делителей напряжения с одинаковым коэффициентом деления при разных номиналах резисторов
Здесь возникает вопрос: какие же номиналы резисторов R1
и R2
применять, 3 кОм
и 1 кОм
или 30 кОм
и 10 кОм
? Все зависит от конкретного случая. Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1
Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1
и R2
, тем больший ток будет протекать в цепи и тем большую мощность можно получить с выхода делителя напряжения, но нужно помнить, что эта мощность ограничивается мощностью источник питания и не может ее превысить.
Также делитель напряжения можно выполнять из нескольких последовательно соединенных резисторов (рис. 6
).
Рис. 6 — Схема делителя напряжения с несколькими резисторами
И так, мы рассмотрели резисторный делитель напряжения с фиксированным значением выходного напряжения. Однако часто возникает необходимость в плавном изменении выходного напряжения. Например, при регулировании громкости звука мы плавно изменяем напряжение на усилителе.
Для плавного регулирования величины выходного напряжения применяются переменные и подстроечные резисторы (рис. 7
).
Рис. 7 — Переменные и подстроечные резисторы
Переменный резистор еще называют потенциометром. Конструктивно он состоит из корпуса, имеющего три вывода, и рукоятки. При вращении ручки осуществляется скользящих контакт подвижной металлической пластины, которая замыкает две токопроводящие графитные дорожки, имеющие разную проводимость в зависимости от длины. Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Схема подключения переменного резистора или же потенциометра приведена ниже (рис. 8
). Два крайних вывода подключаются к источнику питания, а между средним и одним из крайних выводов снимается выходное напряжение, величину которого можно изменять от нуля до значения входного напряжения Uвых = 0…Uвх
.
Рис. 8 — Схема включения переменного резистора для деления напряжения
Если, проворачивая ручку резистора, мы введем все сопротивление (как показано на схеме (рис. 9
9
)), то выходное напряжение будет равно входному Uвых = Uвх
, так как подводимое напряжение будет полностью падать на сопротивлении резистора.
Если же вывести все сопротивление, то выходное напряжение будет равно нулю Uвых = 0
.
Рис. 9 — Схема плавного изменения напряжения
Некоторые виды переменных резисторов
В зависимости от степени относительного изменения сопротивления при вращении рукоятки переменного резистора их разделяют на три типа (рис. 10
):
1) с линейной зависимостью;
2) с логарифмической зависимостью;
3) с экспоненциальной зависимостью.
Рис. 10 — Зависимости переменных резисторов
Переменные резисторы с логарифмической зависимостью часто используются для регулировки уровня звука, поскольку ухо человека воспринимает звук именно по такой зависимости.
Кроме того переменные резисторы бывают как одинарные, так и сдвоенные. Последние находят широкое применение в звуковой технике.
Последние находят широкое применение в звуковой технике.
Делители напряжения на резисторах одинаково работают и рассчитываются как для постоянного, так и для переменного напряжения. Однако, в качестве делителей переменного напряжения также часто используются конденсаторы и реже – катушки индуктивности.
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель
напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов .
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе
V out
? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1
и R2
одинаков пока
к выходу V out
ничего не подключено. А суммарное сопротивление
пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2
, расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В.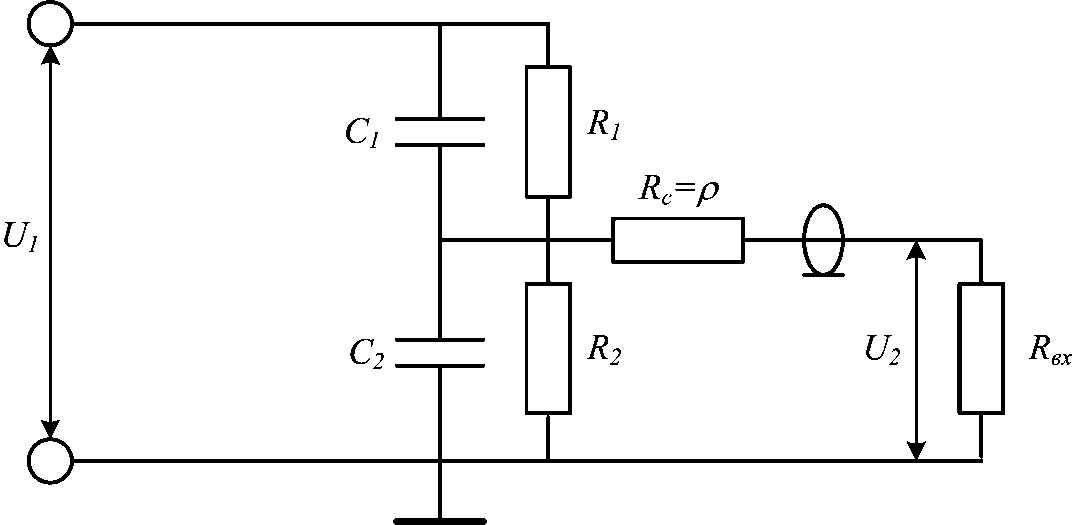
Это простой способ получить несколько различных напряжений в одной схеме, оставив при
этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество
компонентов, которые меняют своё сопротивление в зависимости от внешних условий.
Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.д.
Если в приведённой выше схеме заменить R1
или R2
на один из таких
компонентов, V out
будет меняться в зависимости от внешних условий, влияющих
на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино,
можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию
на переменный компонент и общую формулу расчёта V out
.
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо
потребитель тока, который ещё называют нагрузкой
(load):
В этом случае V out
уже не может быть расчитано лишь на основе значений V in
,
R1
и R2
: сама нагрузка провоцирует дополнительное падение напряжения
(voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых
параллельно:
Подставив значение в общую формулу расчёта V out
, получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки.
И тем ощутимее будут потери,
чем больше номинал R2
по отношению к сопротивлению L
. Чтобы нивелировать этот эффект мы могли
бы использовать в качестве R1
и R2
резисторы, например, в 10 раз меньших
номиналов.
Пропорция сохраняется, V out
не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от
источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если
устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка
на R1
равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной
схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень
вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит
для получения необходимого заниженного напряжения в случаях, когда подключенная
нагрузка потребляет небольшой ток (доли или единицы миллиампер).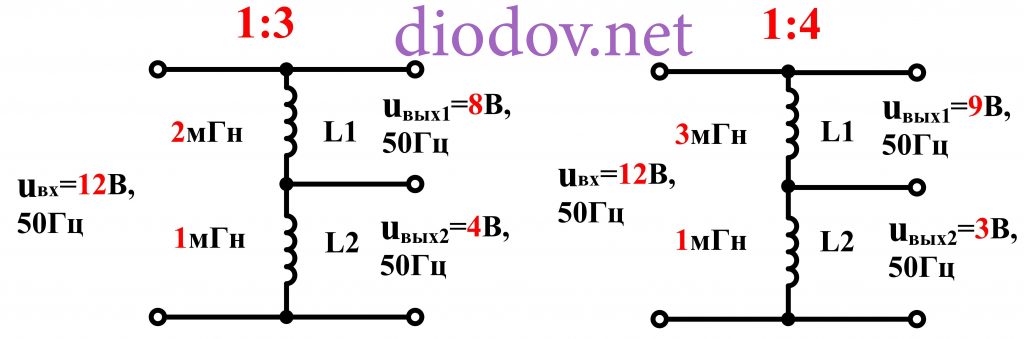 Примером подходящего использования является
Примером подходящего использования является
считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .
Делитель не подходит
для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка
на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, V out
также будет неравномерным.
Расчет делителя напряжения
Посмотрите схему делителя напряжения, представленную здесь, и рассчитайте выходное напряжение с помощью калькулятора делителя напряжения по следующей формуле делителя напряжения:
V выход = (V дюйм x R 2 ) / ( R 1 + R 2 )
Здесь:
- В в входное напряжение
- R1 — сопротивление 1-го резистора,
- R2 — сопротивление 2-го резистора,
- V out — выходное напряжение.

В качестве альтернативы вы также можете использовать этот калькулятор делителя напряжения, чтобы получить 3 любых известных значения в цепи и вычислить 4-е.
Схема делителя потенциала — очень распространенная схема, используемая в электронике, где входное напряжение должно быть преобразовано в другое напряжение, меньшее, чем оно. Эта схема очень полезна для всех аналоговых схем, где требуются переменные напряжения, поэтому важно понимать, как эта схема работает и как рассчитывать значения резисторов.
Схема делителя напряжения — это очень простая схема, состоящая всего из двух резисторов (R1 и R2), как показано выше. Требуемое выходное напряжение (Vout) можно получить на резисторе R2. Используя эти два резистора, мы можем преобразовать входное напряжение в любое требуемое выходное напряжение, это выходное напряжение определяется значением сопротивления R1 и R2. Формулы для расчета Vout показаны ниже.
V выход = (V дюйм x R 2 ) / (R 1 + R 2 9000
Где, Vout = выходное напряжение Vin = входное напряжение и R1 = верхний резистор R2 = нижний резистор
Мы можем использовать вышеупомянутый калькулятор делителя напряжения для вычисления любого из значений, упомянутых в формулах делителя напряжения , но теперь давайте узнаем, как были получены эти формулы.Рассмотрим схему ниже, которую можно использовать для преобразования входного сигнала 5 В в выходное напряжение 3,3 В для анализа
Чтобы понять, как выводятся формулы потенциального дайвера, нам нужен калькулятор закона Ома, согласно закону Ома падение напряжения в любом месте является произведением тока, протекающего по цепи, и сопротивления в ней.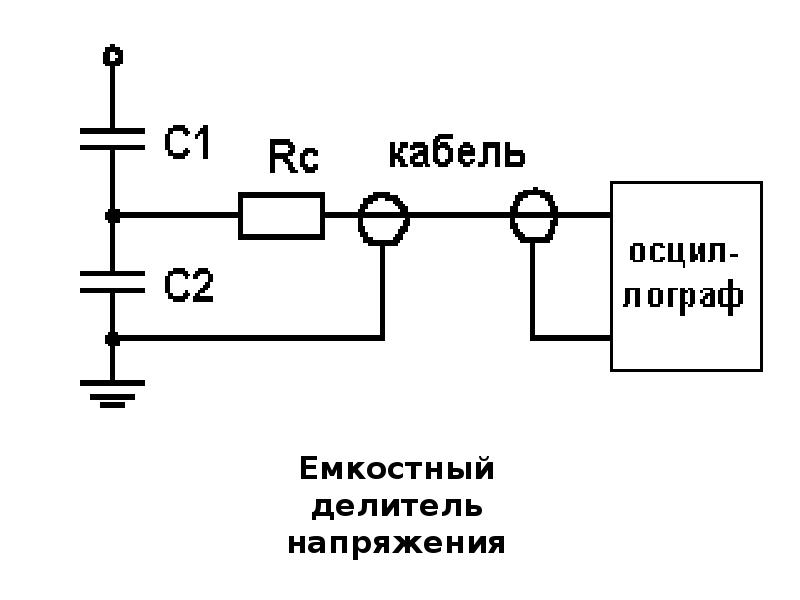
Напряжение = Ток, протекающий через × Сопротивление на напряжении
Давайте воспользуемся этим, чтобы вычислить входное напряжение (Vin) для вышеуказанной схемы.Здесь есть два резистора на входном напряжении Vin, следовательно,
Входное напряжение = ток × (сопротивление 1 + сопротивление 2)
Vin = I × (R1 + R2) ( 1)
Аналогичным образом рассчитаем выходное напряжение (Vout), здесь есть только один резистор (R2), следовательно,
Выходное напряжение = ток × сопротивление R2
Vout = I × R2 ( 2)
Если мы посмотрим на уравнения 1 и 2, мы можем заметить, что значение тока одинаковое, поэтому давайте перепишем
Уравнение 1 как, I = Vin / (R1 + R2)
Уравнение 2 как, I = Vout / R2
Поскольку ток, протекающий по цепи, постоянен, ток I останется одинаковым для обоих уравнений, поэтому мы можем приравнять их к
Вин / (R1 + R2) = Vout / R2
V выход = (V дюйм x R 2 ) / (R 1 + R 2 9000
Давайте проверим эту формулу делителя напряжения для указанной выше схемы, где Vin = 5 В, R1 = 1000 Ом и R2 = 2000 Ом.
Выход = (5 × 2000) / (1000/2000)
Выход = (10000) / (3000)
Выход = 3,3333 В
Еще одним важным фактором, который следует учитывать при выборе номиналов резистора, является его номинальная мощность (P) . Как только вы узнаете значения I (в зависимости от нагрузки), Vin, R1 и R2, сложите R1 и R2 вместе, чтобы получить R ИТОГО , и используйте калькулятор закона Ома, чтобы узнать номинальную мощность (в ваттах), необходимую для резисторов. Или просто используйте формулы P = VI, чтобы определить номинальную мощность вашего резистора.Если не выбрана правильная номинальная мощность, резистор будет перегреваться и также может сгореть.
Делители напряжения — схемы, уравнения и приложения
Делитель напряжения, также известный как делитель потенциала, представляет собой очень распространенную простую схему, которая используется для преобразования большого напряжения в небольшое. Из этой статьи вы узнаете о:
Из этой статьи вы узнаете о:
- Что такое делитель напряжения?
- Цепи делителя напряжения
- Уравнение / формула делителя напряжения
- Применение делителей напряжения
Что такое делитель напряжения?
- Пассивная линейная схема, вырабатывающая выходное напряжение, составляющее часть входного напряжения.
- Он уменьшает входное напряжение до меньшего напряжения в зависимости от соотношения двух резисторов за счет распределения входного напряжения между компонентами делителя.
- Часто используется для подачи напряжения, отличного от имеющегося в наличии аккумулятора или источника питания.
- Выходное напряжение делителя напряжения зависит от сопротивления входящей нагрузки.
Схема делителя напряжения
Схема делителя напряжения обычно выглядит так в цепи из 2-х резисторов.
- R1 = резистор, ближайший к входному напряжению (Vin)
- R2 = резистор, ближайший к земле
- В вход = входное напряжение
- В выход = выходное напряжение на R2, которое является разделенным напряжением (1/4 от входное напряжение)
Формула / уравнение делителя напряжения
Уравнение для определения выходного напряжения цепи делителя:
R2 / R1 + R2 = Ratio определяет масштабный коэффициент уменьшенного напряжения.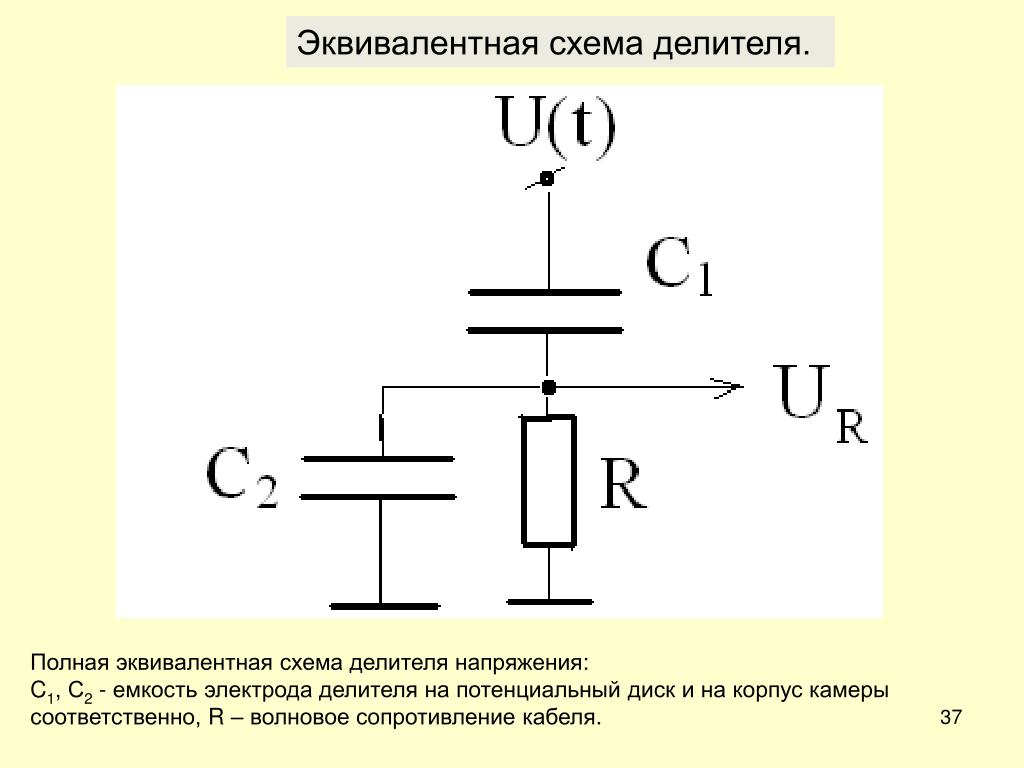
Например,
В в = 100, 1 = 20, 2 = 10
С помощью калькулятора получите:
Правило делителя напряжения
- Правило деления напряжения гласит: Напряжение, разделенное между двумя последовательными резисторами, прямо пропорционально их сопротивлению
- Это означает, что ваша схема может иметь более 2 резисторов!
- Формула правила делителя напряжения:
Пример уравнения правила делителя напряжения:
Закон Ома
Теперь мы можем использовать закон Ома для расчета напряжения, протекающего через каждый резистор:
- Уравнение для закона Ома = E = IR
- E = ток на каждом резисторе
- I = ток цепи
- R = сопротивление
| R1 | R2 | R3 | Всего | ||||
| E (Вольт) | 5 | 10 | 15294 30 I | 2. 5 м 5 м | 2,5 | 2,5 м | 2,5 м |
| R (Ом) | 2K | 4K | 6K | 12K |
Таким образом, ток на каждом резисторе составляет 5 В и 10 В соответственно!
Упрощенные уравнения
- Если вы решаете для R1,
- Если вы решаете R2,
Применение делителей напряжения
Цепи делителей напряжения
очень распространены и используются во многих приложениях.Вот несколько примеров того, где находится схема делителя напряжения:
Потенциометр
- Потенциометр — это пассивный электронный компонент с функцией скольжения или вращения, который действует как регулируемый делитель напряжения.
- Входное напряжение подается по всей длине потенциометра, а выходное напряжение (падение напряжения) регулируется с помощью фиксированного и скользящего контакта потенциометра.
- Существует два типа потенциометров
- Поворотные потенциометры (поворотная ручка)
- Линейный потенциометр (ползунок)
- Компания Seeed предлагает оба типа!
Grove — Потенциометр скольжения
- Как это работает?
- Ручной стеклоочиститель, который перемещается, касается резистивной полосы материала.
 Когда он перемещается ближе к клемме 1 и дальше от клеммы 2, сопротивление уменьшается до клеммы 1, в то время как сопротивление увеличивается на клемме 2, и наоборот.
Когда он перемещается ближе к клемме 1 и дальше от клеммы 2, сопротивление уменьшается до клеммы 1, в то время как сопротивление увеличивается на клемме 2, и наоборот.
- Ручной стеклоочиститель, который перемещается, касается резистивной полосы материала.
- Потенциометр полезен для получения переменного напряжения от источника постоянного напряжения. Он может подключать внешние клеммы потенциометра к источнику напряжения и контролировать необходимое напряжение между потенциометром и одной из внешних клемм вашей цепи.
- Потенциометр Grove — Slide включает линейный переменный резистор с максимальным сопротивлением 10 кОм.По мере перемещения ползунка выходное напряжение будет варьироваться от 0 В до применяемого вами Vcc.
- Он подключается к другим модулям Grove через стандартный 4-контактный кабель Grove.
- Ниже приведено изображение принципиальной схемы потенциометра:
- Он имеет множество целей, например, как регулируемый резистор, автономный делитель напряжения с Arduino или даже как устройство интерфейса человека (HID), что означает, что его можно использовать для управления автомобилем!
- Некоторые проекты, которые вы можете выполнять с помощью потенциометра Grove — Slide, похожи на создание собственного битбокса или бумбокс на Arduino!
Grove — Датчик угла поворота (P)
- Датчик угла поворота Grove-Rotary (P) способен выдавать аналоговый выходной сигнал от 0 до Vcc (5 В постоянного тока с Seeeduino) на разъеме D1.

- При значении сопротивления 10 кОм он идеально подходит для использования с Arduino.
- Он поддерживается на всех платформах MCU, таких как Arduino, Raspberry Pi, BeagleBone, Wio, а также LinkIt ONE.
- Один из проектов, который вы можете сделать с этим потенциометром, — это использовать его для управления яркостью светодиодов.
Использование Arduino для управления яркостью светодиода с помощью датчика угла поворота Grove (P)
Grove — Делитель напряжения
- Grove — Делитель напряжения предоставляет интерфейс для измерения внешнего напряжения, который устраняет необходимость подключения сопротивления к входному интерфейсу.
- С помощью дискового переключателя вы можете легко выбрать коэффициент усиления напряжения, что упрощает его использование.
Чтение резистивных датчиков
- Большинство датчиков представляют собой простые резистивные устройства, такие как наш Grove — инфракрасный датчик отражения.
 Однако большинство из них могут считывать только напряжение, но не сопротивление.
Однако большинство из них могут считывать только напряжение, но не сопротивление. - Добавив в схему еще один резистор, мы можем создать делитель напряжения вместе с датчиком.
- Так как мы можем проверить выход делителя напряжения, теперь мы можем рассчитать величину сопротивления датчика.
- Пример схемы показан ниже, где R2 — резистивный датчик:
- Например, резистивный датчик представляет собой датчик температуры Grove, который представляет собой термистор с сопротивлением комнатной температуры 350 Ом, где сопротивление R1 фиксировано на 350 Ом.
- Использование уравнения делителя напряжения:
| Температура | Vin (фиксированная) | R2 | R1 | R2 / (R1 + R2) | Vout |
|---|---|---|---|---|---|
| Холодная | 5V | 300 Ω .46 | 2,3 В | ||
| Комнатная температура | 5 В | 350 Ом | 350 Ом | 0,5 | 2,5 В |
| Горячий | 5V | 400 Ом | 0,5 2,65 В |
Переключатели уровня
- Что происходит, когда датчик и микроконтроллер встречаются с двумя разными напряжениями? Без выравнивания напряжения, например, напрямую связав микроконтроллер с логическим выходом 5 В с микроконтроллером 3.
 Входной датчик 3 В может вызвать повреждение цепи 3,3 В.
Входной датчик 3 В может вызвать повреждение цепи 3,3 В. - Вот где главный герой: делитель напряжения спасает положение, действуя как переключатель уровня, соединяющий две схемы, использующие разные рабочие напряжения.
- Делитель напряжения может помочь выровнять напряжение с микроконтроллера (например, с 5 В до 3,3 В), чтобы избежать повреждения датчика, что делает его безопасным для обращения с датчиком.
- Обратите внимание, что делитель напряжения может работать только в одном направлении: понижать напряжение, но не повышать.
- Вот таблица комбинаций резисторов для понижения часто встречающихся напряжений:
| Комбинация резисторов | Напряжения для выравнивания |
|---|---|
| 4,7 кОм и 3,9 кОм | 9В до 5В |
| от 12 В до 3,3 В | |
| от 3,3 кОм и 5,7 кОм | от 9 В до 3,3 В |
- Обратите внимание, что не рекомендуется использовать делитель напряжения для понижения уровня большой нагрузки, например 12 В.
 до 5 В, поскольку они не предназначены для подачи такого питания на нагрузку, как с такой нагрузкой, это может расплавить резистор.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А)
до 5 В, поскольку они не предназначены для подачи такого питания на нагрузку, как с такой нагрузкой, это может расплавить резистор.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А)
Резюме
Обладая всеми знаниями о делителях напряжения в ваших руках, вы можете превратить любое напряжение в меньшее, как фокусник! Хотите проверить свои навыки, создав свой собственный проект делителя напряжения? Вот несколько идей проекта, которые помогут вам начать использовать потенциометр и Arduino для создания битбокса или бумбокса на нашей вики-странице: Grove — Slide Potentiometer Wiki
Следите за нами и ставьте лайки:
Продолжить чтение
Расчет
, примеры и его применение
В электронике правило делителя напряжения — это простая и наиболее важная электронная схема, которая используется для преобразования большого напряжения в малое. Используя только напряжение i / p и два последовательных резистора, мы можем получить напряжение o / p. Здесь выходное напряжение является частью напряжения i / p. Лучший пример делителя напряжения — два последовательно соединенных резистора. Когда напряжение i / p приложено к паре резисторов, напряжение o / p появится из соединения между ними. Как правило, эти разделители используются для уменьшения величины напряжения или для создания опорного напряжения, а также используются на низких частотах в качестве сигнала аттенюатора.Для постоянного тока и относительно низких частот делитель напряжения может быть подходящим вариантом, если он состоит только из резисторов; где частотная характеристика требуется в широком диапазоне.
Используя только напряжение i / p и два последовательных резистора, мы можем получить напряжение o / p. Здесь выходное напряжение является частью напряжения i / p. Лучший пример делителя напряжения — два последовательно соединенных резистора. Когда напряжение i / p приложено к паре резисторов, напряжение o / p появится из соединения между ними. Как правило, эти разделители используются для уменьшения величины напряжения или для создания опорного напряжения, а также используются на низких частотах в качестве сигнала аттенюатора.Для постоянного тока и относительно низких частот делитель напряжения может быть подходящим вариантом, если он состоит только из резисторов; где частотная характеристика требуется в широком диапазоне.
Что такое правило делителя напряжения?
Определение: В области электроники делитель напряжения представляет собой базовую схему, используемую для генерации части входного напряжения, например выходного. Эта схема может быть сконструирована с двумя резисторами или любыми пассивными компонентами вместе с источником напряжения.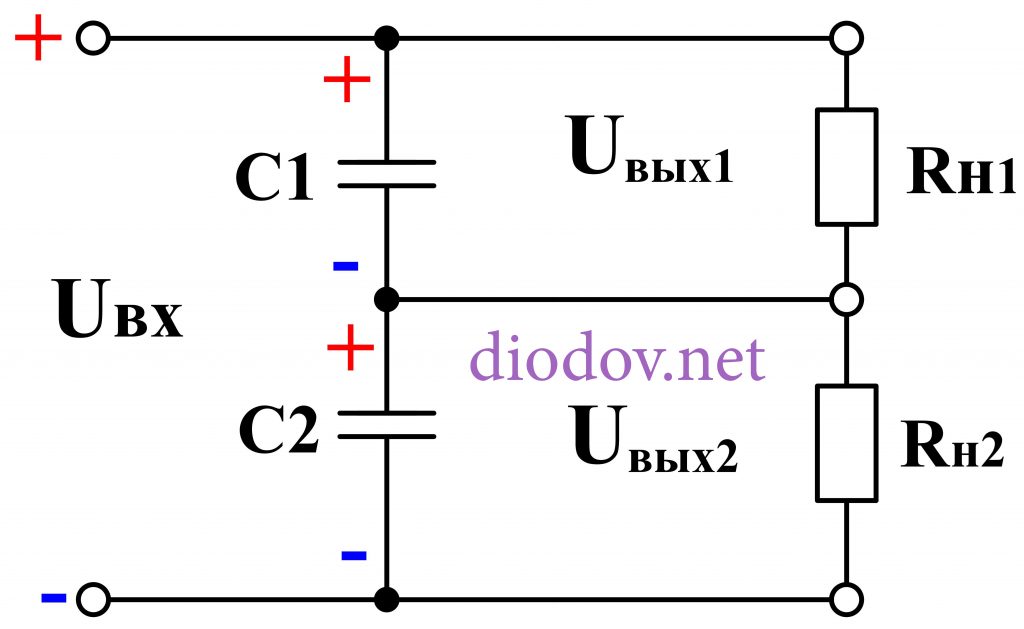 Резисторы в цепи могут быть подключены последовательно, в то время как источник напряжения подключен к этим резисторам.Эту схему еще называют делителем потенциала. Входное напряжение может передаваться между двумя резисторами в цепи, так что происходит разделение напряжения.
Резисторы в цепи могут быть подключены последовательно, в то время как источник напряжения подключен к этим резисторам.Эту схему еще называют делителем потенциала. Входное напряжение может передаваться между двумя резисторами в цепи, так что происходит разделение напряжения.
Когда использовать правило делителя напряжения?
Правило делителя напряжения используется для решения схем для упрощения решения. Применение этого правила также может полностью решить простые схемы. Основная идея этого правила делителя напряжения заключается в том, что «напряжение делится между двумя резисторами, которые соединены последовательно, прямо пропорционально их сопротивлению.Делитель напряжения состоит из двух важных частей: схемы и уравнения.
Схема другого делителя напряжения
Делитель напряжения включает в себя источник напряжения, подключенный к серии из двух резисторов. Вы можете увидеть различные схемы напряжения, нарисованные по-разному, как показано ниже. Но эти разные схемы всегда должны быть одинаковыми. Схема делителя напряжения
Но эти разные схемы всегда должны быть одинаковыми. Схема делителя напряжения
В приведенных выше схемах делителя напряжения резистор R1 находится ближе всего к входному напряжению Vin, а резистор R2 находится ближе всего к клемме заземления.Падение напряжения на резисторе R2 называется Vout, которое представляет собой разделенное напряжение цепи.
Расчет делителя напряжения
Рассмотрим следующую схему, подключенную с помощью двух резисторов R1 и R2. Где переменный резистор включен между источником напряжения. В приведенной ниже схеме R1 — это сопротивление между скользящим контактом переменной и отрицательной клеммой. R2 — сопротивление между положительной клеммой и скользящим контактом. Это означает, что два резистора R1 и R2 включены последовательно.
Правило делителя напряжения с использованием двух резисторов
Закон Ома гласит, что V = IR
Из приведенного выше уравнения мы можем получить следующие уравнения
V1 (t) = R1i (t) …………… (I)
V2 (t) = R2i (t) …………… (II)
Применение закона Кирхгофа
KVL утверждает, что когда алгебраическая сумма напряжений вокруг замкнутого контура в цепи равна нулю.
-V (t) + v1 (t) + v2 (t) = 0
V (t) = V1 (t) + v2 (t)
Следовательно,
V (t) = R1i (t) + R2i (t) = i (t) (R1 + R2)
Следовательно,
i (t) = v (t) / R1 + R2 …………….(III)
Подставляя III в уравнения I и II
V1 (t) = R1 (v (t) / R1 + R2)
V (t) (R1 / R1 + R2)
V2 (t) = R2 (v (t) / R1 + R2)
V (t) (R2 / R1 + R2)
На приведенной выше схеме показан делитель напряжения между двумя резисторами, который прямо пропорционален их сопротивлению. Это правило делителя напряжения можно распространить на схемы, в которых используется более двух резисторов.
Правило делителя напряжения с использованием трех резисторов
Правило деления напряжения для цепи с двумя резисторами
V1 (t) = V (t) R1 / R1 + R2 + R3 + R4
V2 (t) = V (t) R2 / R1 + R2 + R3 + R4
V3 (t) = V (t) R3 / R1 + R2 + R3 + R4
V4 (t) = V (t) R4 / R1 + R2 + R3 + R4
Делитель напряжения Уравнение
Уравнение правила делителя напряжения принимает, когда вы знаете, что три значения в приведенной выше схеме — это входное напряжение и два значения резистора. Используя следующее уравнение, мы можем найти выходное напряжение.
Используя следующее уравнение, мы можем найти выходное напряжение.
Vout = Vin. R2 / R1 + R2
В приведенном выше уравнении указано, что Vout (напряжение o / p) прямо пропорционально Vin (входное напряжение) и соотношению двух резисторов R1 и R2.
Резистивный делитель напряжения
Это очень легкая и простая схема для разработки и понимания. Основной тип схемы пассивного делителя напряжения может состоять из двух последовательно соединенных резисторов.Эта схема использует правило делителя напряжения для измерения падения напряжения на каждом последовательном резисторе. Схема резистивного делителя напряжения показана ниже.
В схеме резистивного делителя два резистора, такие как R1 и R2, соединены последовательно. Таким образом, ток в этих резисторах будет одинаковым. Следовательно, он обеспечивает падение напряжения (I * R) на каждом резисторе.
Резистивный тип
С помощью источника напряжения на эту цепь подается напряжение.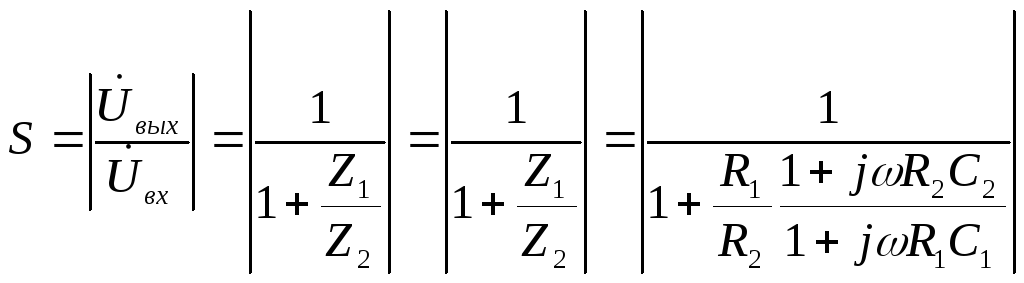 Применяя к этой схеме закон КВЛ и Ома, мы можем измерить падение напряжения на резисторе.Таким образом, поток тока в цепи может быть задан как
Применяя к этой схеме закон КВЛ и Ома, мы можем измерить падение напряжения на резисторе.Таким образом, поток тока в цепи может быть задан как
Применяя KVL
VS = VR1 + VR2
Согласно закону Ома
VR1 = I x R1
VR2 = I x R2
VS = I x R1 + I x R2 = I (R1 + R2)
I = VS / R1 + R2
Протекание тока через последовательную цепь I = V / R в соответствии с Омами Закон. Таким образом, ток в обоих резисторах одинаков. Теперь можно рассчитать падение напряжения на резисторе R2 в цепи
IR2 = VR2 / R2
Vs / (R1 + R2)
VR2 = Vs (R2 / R1 + R2)
Точно так же падение напряжения на резисторе R1 можно рассчитать как
IR1 = VR1 / R1
Вс / (R1 + R2)
VR1 = Вс (R1 / R1 + R2)
Емкостный Делители напряжения
Схема емкостного делителя напряжения генерирует падение напряжения на конденсаторах, которые подключены последовательно к источнику переменного тока.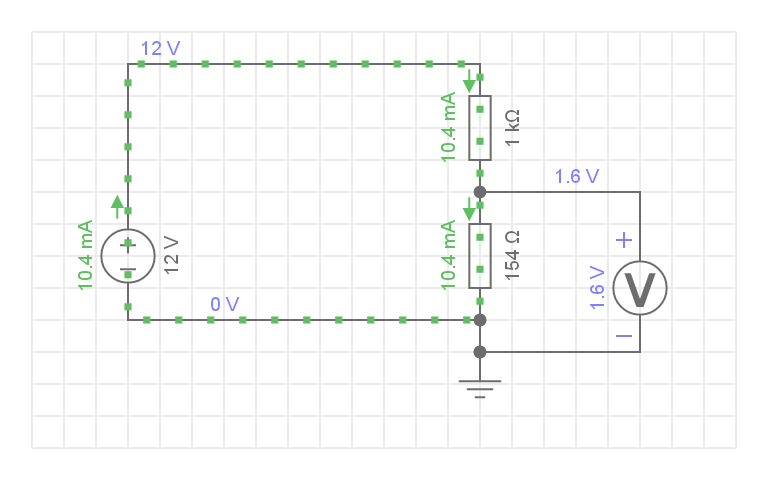 Обычно они используются для снижения чрезвычайно высокого напряжения для обеспечения сигнала низкого выходного напряжения. В настоящее время эти разделители применимы в планшетах с сенсорным экраном, мобильных телефонах и устройствах отображения.
Обычно они используются для снижения чрезвычайно высокого напряжения для обеспечения сигнала низкого выходного напряжения. В настоящее время эти разделители применимы в планшетах с сенсорным экраном, мобильных телефонах и устройствах отображения.
В отличие от схем резистивного делителя напряжения, емкостные делители напряжения работают с синусоидальным источником переменного тока, поскольку деление напряжения между конденсаторами можно рассчитать с помощью реактивного сопротивления конденсаторов (X C ), которое зависит от частоты источника переменного тока.
емкостного типа
Формула емкостного реактивного сопротивления может быть получена как
Xc = 1 / 2πfc
Где:
Xc = емкостное реактивное сопротивление (Ом)
π = 3.142 (числовая константа)
ƒ = Частота, измеренная в Герцах (Гц)
C = Емкость, измеренная в Фарадах (Ф)
Реактивное сопротивление каждого конденсатора можно измерить по напряжению, а также по частоте источника переменного тока и заменителя их в приведенном выше уравнении, чтобы получить эквивалентное падение напряжения на каждом конденсаторе. Схема емкостного делителя напряжения показана ниже.
Схема емкостного делителя напряжения показана ниже.
Используя эти конденсаторы, которые соединены последовательно, мы можем определить среднеквадратичное падение напряжения на каждом конденсаторе с точки зрения их реактивного сопротивления после их подключения к источнику напряжения.
Xc1 = 1 / 2πfc1 и Xc2 = 1 / 2πfc2
X CT = X C1 + X C2
V C1 = Vs (X CT )
V C2 = Vs (X C2 / X CT )
Емкостные делители не допускают вход постоянного тока.
Простое емкостное уравнение для входа переменного тока:
Vout = (C1 / C1 + C2) .Vin
Индуктивные делители напряжения
Индуктивные делители напряжения создают перепады напряжения на катушках, в противном случае индукторы соединяются последовательно через Питание переменного тока. Он состоит из катушки, иначе одиночной обмотки, которая разделена на две части, где бы ни поступало напряжение o / p с одной из частей.
Он состоит из катушки, иначе одиночной обмотки, которая разделена на две части, где бы ни поступало напряжение o / p с одной из частей.
Лучшим примером этого индуктивного делителя напряжения является автотрансформатор, имеющий несколько точек отвода с вторичной обмоткой. Индуктивный делитель напряжения между двумя катушками индуктивности можно измерить с помощью реактивного сопротивления катушки индуктивности, обозначенной XL.
Индуктивный тип
Формула индуктивного реактивного сопротивления может быть получена как
XL = 1 / 2πfL
«XL» — это индуктивное реактивное сопротивление, измеренное в Ом (Ом)
π = 3.142 (числовая константа)
» — частота, измеренная в герцах (Гц)
‘L’ — индуктивность, измеренная в Генри (Г)
Реактивное сопротивление двух катушек индуктивности может быть вычислено, если мы знаем частоту и напряжение источника переменного тока и использовать их с помощью закона делителя напряжения, чтобы получить падение напряжения на каждой катушке индуктивности, как показано ниже. Схема индуктивного делителя напряжения показана ниже.
Схема индуктивного делителя напряжения показана ниже.
Используя две катушки индуктивности, которые соединены последовательно в цепи, мы можем измерить среднеквадратичные падения напряжения на каждом конденсаторе с точки зрения их реактивного сопротивления после их подключения к источнику напряжения.
X L1 = 2πfL1 & X L2 = 2πfL2
X LT = X L1 + X L2
V L1 / X LT )
V L2 = Vs ( X L2 / X LT )
Вход переменного тока может быть разделен индуктивными делителями в зависимости от индуктивности:
9000 Vout = (L2 / L1 + L2) * Vin
Это уравнение предназначено для невзаимодействующих катушек индуктивности, и взаимная индуктивность в автотрансформаторе изменит результаты.Вход постоянного тока может быть разделен на основе сопротивления элементов в соответствии с правилом резистивного делителя.
Примеры проблем с делителем напряжения
Проблемы с примером делителя напряжения могут быть решены с помощью вышеуказанных резистивных, емкостных и индуктивных цепей.
1). Предположим, общее сопротивление переменного резистора составляет 12 Ом. Скользящий контакт расположен в точке, где сопротивление делится на 4 Ом и 8 Ом. Переменный резистор подключен к батарее 2,5 В.Давайте посмотрим, какое напряжение появляется на вольтметре, подключенном к 4-омному участку переменного резистора.
Согласно правилу делителя напряжения, падение напряжения будет,
Ввых. = 2,5 В x 4 Ом / 12 Ом = 0,83 В
2). Когда два конденсатора C1-8uF и C2-20uF соединены последовательно в цепи, среднеквадратичные падения напряжения могут быть рассчитаны на каждом конденсаторе, когда они подключены к источнику питания 80 Гц RMS и напряжению 80 В.
Xc1 = 1 / 2πfc1
1/2 × 3.14x80x8x10-6 = 1 / 4019,2 × 10-6
= 248,8 Ом
Xc2 = 1 / 2πfc2
1/2 × 3,14x80x20x10-6 = 1/10048 x10-6
= 99,52 Ом
XCT = XC1 + XC2
= 248,8 + 99,52 = 348,32
VC1 = Vs (XC1 / XCT)
80 (248,8 / 348,32) = 57,142
VC2 = Vs (XC2 / XCT)
80 (99,52 / 348,32)
3). Когда две катушки индуктивности L1-8 мГн и L2-15 мГн соединены последовательно, мы можем рассчитать среднеквадратичное падение напряжения на каждом конденсаторе, которое можно рассчитать, когда они подключены к источнику питания 40 В, 100 Гц.
Когда две катушки индуктивности L1-8 мГн и L2-15 мГн соединены последовательно, мы можем рассчитать среднеквадратичное падение напряжения на каждом конденсаторе, которое можно рассчитать, когда они подключены к источнику питания 40 В, 100 Гц.
XL1 = 2πfL1
= 2 × 3,14x100x8x10-3 = 5,024 Ом
XL2 = 2πfL2
= 2 × 3,14x100x15x10-3
9,42 Ом
XLT = XL1 + XL2
XLT = XL1 + XL2
Vs (XL1 / XLT)
= 40 (5,024 / 14,444) = 13,91 В
VL2 = Vs (XL2 / XLT)
= 40 (9,42 / 14,444) = 26,08 вольт
Точки отвода напряжения в сети делителя
Когда количество резисторов подключено последовательно к источнику напряжения Vs в цепи, то различные точки отвода напряжения можно рассматривать как A, B, C, D и E
Общее сопротивление в цепи можно рассчитать, добавив все значения сопротивления вроде 8 + 6 + 3 + 2 = 19 кОм.Это значение сопротивления ограничит ток, протекающий по цепи, которая генерирует напряжение питания (VS).
Для расчета падения напряжения на резисторах используются следующие уравнения: VR1 = VAB,
VR2 = VBC, VR3 = VCD и VR4 = VDE.
Уровни напряжения в каждой точке ответвления рассчитываются относительно клеммы GND (0 В). Следовательно, уровень напряжения в точке «D» будет эквивалентен VDE, тогда как уровень напряжения в точке «C» будет эквивалентен VCD + VDE.Здесь уровень напряжения в точке «C» — это величина двух падений напряжения на двух резисторах R3 и R4.
Итак, выбрав соответствующий набор номиналов резистора, мы можем сделать серию падений напряжения. Эти падения напряжения будут иметь относительное значение напряжения, которое достигается только за счет напряжения. В приведенном выше примере каждое значение напряжения o / p является положительным, поскольку отрицательная клемма источника напряжения (VS) подключена к клемме заземления.
Применения делителя напряжения
Применения делителя напряжения включают следующее.
- Делитель напряжения используется только там, где напряжение регулируется путем снижения определенного напряжения в цепи. Он в основном используется в таких системах, где энергоэффективность не обязательно должна рассматриваться серьезно.
- В нашей повседневной жизни делитель напряжения чаще всего используется в потенциометрах. Лучшими примерами потенциометров являются ручки регулировки громкости, прикрепленные к нашим музыкальным системам, радиотранзисторам и т. Д. Базовая конструкция потенциометра включает три контакта, которые показаны выше.При этом два контакта подключены к резистору, который находится внутри потенциометра, а оставшийся контакт подключен к очищающему контакту, который скользит по резистору. Когда кто-то меняет ручку на потенциометре, то напряжение будет появляться на стабильных контактах и очищающем контакте в соответствии с правилом делителя напряжения.
- Делители напряжения используются для регулировки уровня сигнала, измерения напряжения и смещения активных устройств в усилителях.
 Мультиметр и мост Уитстона включают делители напряжения.
Мультиметр и мост Уитстона включают делители напряжения. - Делители напряжения можно использовать для измерения сопротивления датчика. Чтобы сформировать делитель напряжения, датчик подключается последовательно с известным сопротивлением, и известное напряжение подается на делитель. Аналого-цифровой преобразователь микроконтроллера подключен к центральному отводу делителя, чтобы можно было измерить напряжение отвода. Используя известное сопротивление, можно рассчитать измеренное сопротивление датчика напряжения.
- Делители напряжения используются для измерения датчика, напряжения, сдвига логического уровня и регулировки уровня сигнала.
- Как правило, правило резисторного делителя в основном используется для создания опорных напряжений, иначе величина напряжения уменьшается, так что измерение становится очень простым. Кроме того; они работают как аттенюаторы сигнала на низкой частоте.
- Он используется в случае чрезвычайно меньшего количества частот и DC
- Емкостный делитель напряжения, используемый при передаче энергии для компенсации емкости нагрузки и измерения высокого напряжения.

Это все о правиле деления напряжения для цепей, это правило применимо как для источников переменного, так и для постоянного тока.Кроме того, любые сомнения относительно этой концепции или проектов электроники и электротехники, пожалуйста, дайте свой отзыв, комментируя в разделе комментариев ниже. Вот вам вопрос, какова основная функция правила делителя напряжения?
Основное руководство по делителям напряжения
В этом руководстве мы исследуем очень важный и фундаментальный элемент электронных схем, а именно делители напряжения.
Делитель напряжения — это довольно простая пассивная схема, которая играет очень важную роль.Проще говоря, делитель напряжения преобразует большое напряжение в меньшее.
Базовая схема делителя напряжения состоит из двух последовательно соединенных резисторов, которые создают выходное напряжение, составляющее лишь часть входного напряжения.
Входное напряжение подается на два резистора, а желаемое выходное напряжение поступает от соединения между двумя резисторами. Второй резистор обычно подключается к земле.
Второй резистор обычно подключается к земле.
Базовая схема делителя напряжения
Ниже приведены несколько примеров того, как вы можете увидеть схему или нарисовать схему делителя напряжения.
Все схемы делителей напряжения должны выглядеть примерно одинаково. Цепи должны состоять из двух резисторов. Один резистор должен быть подключен к земле, другой к источнику напряжения и проводу, идущему между парой с выходным напряжением.
Как вы можете видеть в базовой настройке схемы делителя напряжения, резистор, ближайший к входному напряжению ( Vin, ), обычно обозначается как R1. Резистор, ближайший к заземлению, обычно обозначается как R2 .
Падение напряжения, вызванное входным напряжением, проходящим через пару резисторов ( R1 и R2 ), обозначается как Vout .
Результирующее падение напряжения — это то, что мы будем называть нашим разделенным напряжением.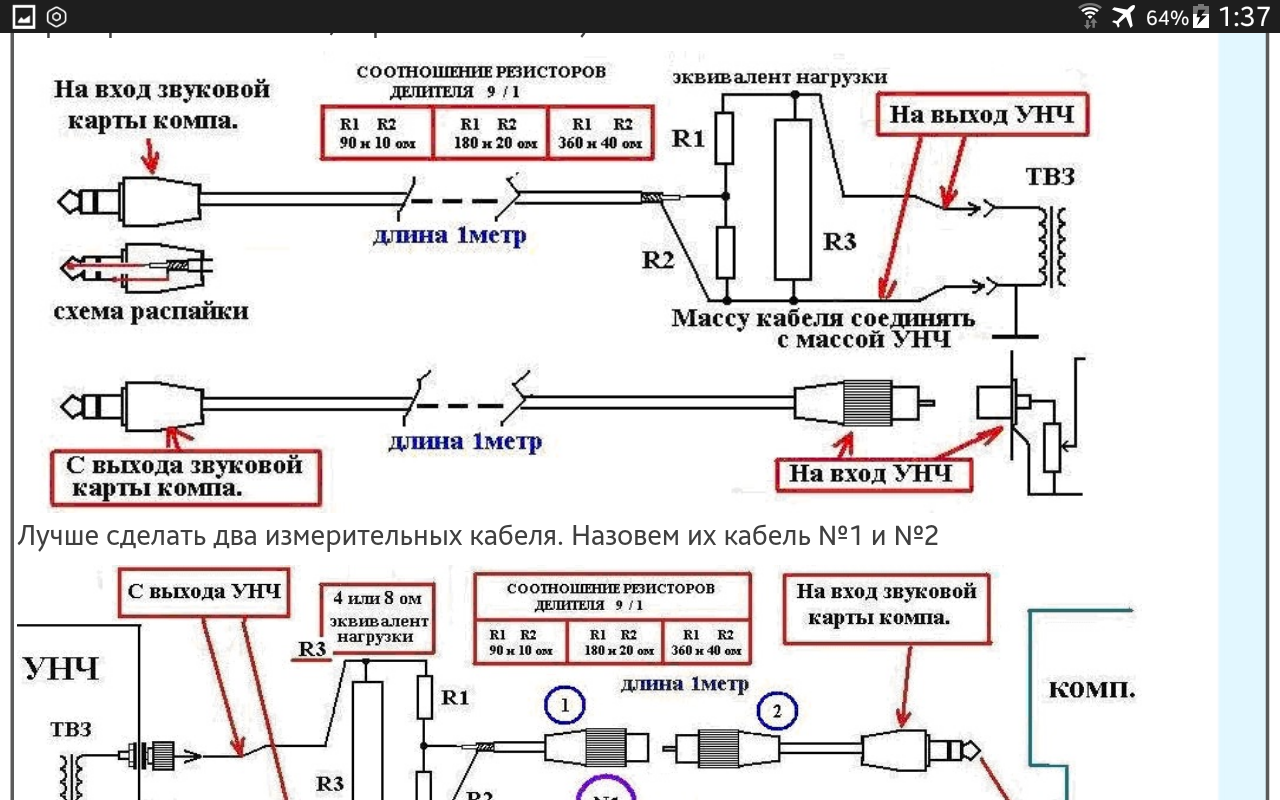 Это разделенное напряжение является частью исходного входного напряжения ( Vin ).
Это разделенное напряжение является частью исходного входного напряжения ( Vin ).
Мы используем R1 , R2 , Vin и Vout для именования элементов схемы, поскольку они имеют решающее значение для понимания значений, которые вам понадобятся для уравнения делителя напряжения.
Формула делителя напряжения
Уравнение делителя напряжения предполагает, что вам известны три значения, используемые в цепи.
Значения, которые вам нужно знать, чтобы использовать уравнение, следующие три.
Вам необходимо знать как номиналы резистора ( R1 и R2 ), так и входное напряжение ( Vin ).
Использование этих трех значений в приведенном ниже уравнении позволит нам рассчитать выходное напряжение схемы делителя напряжения.
Теперь мы в последний раз рассмотрим переменные, используемые в уравнении делителя напряжения, чтобы вы имели твердое представление о каждой переменной.
- Vin — входное напряжение, измеренное в вольтах ( В )
- R1 — сопротивление первого резистора в делителе напряжения, измеренное в Ом Ω
- R2 — сопротивление 2-й резистор в делителе напряжения, измеренный в Ом Ом
- Vout — это выходное напряжение, измеренное в вольтах ( В )
Калькулятор делителя напряжения
Если вы хотите быстро вычислить выходное напряжение генерируется вашей схемой делителя напряжения, тогда вы можете использовать наш удобный калькулятор.
Все, что вам нужно сделать, это ввести значения для ваших двух резисторов и входного напряжения, калькулятор автоматически рассчитает соответствующее выходное напряжение.
Примеры формул делителя напряжения
Для нашего первого примера использования формулы делителя напряжения мы собираемся использовать следующие значения:
- Vin как 5 v,
- R1 как 220 Ω резистор,
- и R2 как резистор 680 Ом.

Теперь, если мы подставим эти значения в уравнение делителя напряжения, мы должны получить что-то вроде того, что показано ниже.
Для начала мы сложим значения резисторов R1 и R2 вместе. Итак, в нашем примере выше это будет 220 + 680 , что равно 900 .
Мы заменим 220 + 680 в нашей формуле на наш результат, так что мы получим следующее уравнение.
Теперь, когда мы выполнили простое сложение, мы можем наконец вычислить часть деления уравнения делителя напряжения.
Просто разделите полученное значение R2 на вычисленное значение R1 + R2 . В нашем примере это будет 680 , разделенное на 900 .
Используя калькулятор, мы получим 0,7555555555555556 , но для простоты мы округлим это число до 2 десятичных знаков, то есть число станет 0.76 .
Замените часть деления в вашей формуле полученным значением. Теперь ваше уравнение должно выглядеть так, как показано ниже.
Теперь ваше уравнение должно выглядеть так, как показано ниже.
Наконец, мы можем просто умножить Vin на нашу рассчитанную величину деления резистора. В нашем случае просто умножьте 5 на 0,76 .
Результат этого умножения даст вам сумму Vout . В нашем случае это результат 3.8 Вольт.
Формула упрощения
Есть несколько упрощений, которые мы можем сделать для уравнения делителя напряжения.Однако в этом руководстве мы проведем вас только по следующему.
Используя упрощения, вы можете упростить быструю оценку схемы делителя напряжения.
Это упрощение говорит о том, что если номиналы резистора R1 и резистора R2 одинаковы, то выходное напряжение равно половине входного напряжения.
Применение делителей напряжения
Делители напряжения находят множество применений в электронных схемах и являются основным компонентом многих электронных схем.
Ниже мы покажем вам некоторые из немногих применений схемы делителя напряжения.
Потенциометры
Потенциометр является одним из наиболее часто используемых элементов электронных схем и используется в качестве основного компонента в большом количестве различных продуктов.
Некоторые примеры рода устройств, потенциометр используется в являются следующие:
- Измерение положения на джойстике
- Создание опорного напряжения
- Контролирование уровня звука в акустических систем
- Среди многих других вещей
Потенциометр — это переменный резистор, который действует как регулируемые делители напряжения.
Внутри потенциометра находится единственный резистор, отделенный стеклоочистителем. Этот дворник — это то, что вы перемещаете, что регулирует соотношение между двумя половинами резистора.
Снаружи горшка вы найдете три контакта, контакты с обеих сторон представляют собой соединение между каждым концом резистора, вы можете рассматривать их как R1 и R2 .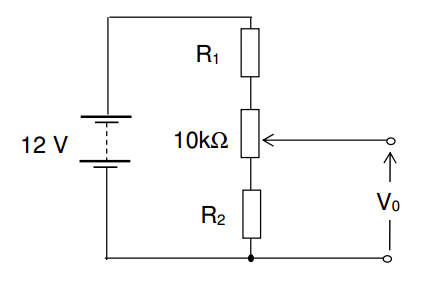
Штифт посередине — это то, что подсоединено к дворнику. Теоретически это похоже на Vout в схеме делителя напряжения.
Чтобы подключить потенциометр так, чтобы он действовал как регулируемый делитель напряжения, вам необходимо подключить одну сторону к входному напряжению ( Vin ), а другую сторону — к земле.
Если оба внешних контакта подключены правильно, средний контакт будет действовать как выход вашего делителя напряжения ( Vout ).
При повороте потенциометра в одном направлении напряжение приближается к нулю, при установке в другую сторону напряжение приближается к входному.
Вращение потенциометра в среднее положение фактически означает, что выходное напряжение будет вдвое меньше входного.
Level Shifter
Level Shifter — важная концепция, которую необходимо понимать при работе с цифровой электроникой. Их также можно назвать схемами «переключателя логического уровня» или «схемой преобразования уровня напряжения».
Уровнемеры используются для переключения напряжения с одного уровня на другой. Это часто используется для обеспечения совместимости между ИС, которые имеют разные требования к напряжению.
Некоторые из более сложных датчиков, которые используют интерфейсы, такие как UART, SPI или I2C для передачи своих показаний, часто имеют дело с разными уровнями напряжения.
Одним из примеров возможного использования этого является работа с платой микроконтроллера, такой как Raspberry Pi.
Raspberry Pi — интересный пример того, где может пригодиться переключатель уровня. Несмотря на то, что Raspberry Pi обеспечивает выходы питания как 5 В, так и 3,3 В, его контакты GPIO предназначены только для обработки входа 3,3 В.
Использование делителя напряжения в цепи позволит нам понизить напряжение с 5 В до 3,3 В для входного контакта.
Ниже мы рассмотрим пример использования схемы делителя напряжения с Raspberry Pi для сдвига уровня выходного сигнала датчика с 5 В до 3,3 В.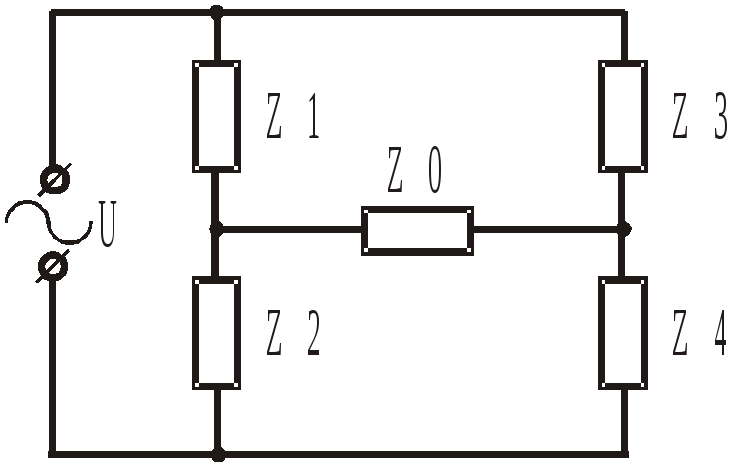
Пример смещения уровня
Например, в нашем руководстве по датчику расстояния мы используем ультразвуковой датчик HC-SR04.
Этот датчик использует входное питание 5 В, что означает, что нам нужно понизить выходной сигнал на выводе Echo с 5 В до 3.3 В до того, как он достигнет контактов GPIO.
Мы можем рассчитать резисторы, которые нам нужны, выбрав начальное значение резистора. Резисторы между 1 кОм — 10 кОм лучше всего подходят для понижения напряжения с 5 В до 3,3 В .
В нашем примере мы будем использовать резистор 1 кОм . Чтобы найти второй резистор, который нам нужно использовать, мы будем использовать еще одну перестроенную версию уравнения делителя напряжения.
Чтобы вычислить значение R2 , нам нужно знать Vin , Vout и значение нашего резистора R1, который мы планируем использовать.
Имея под рукой эти 3 значения, мы можем использовать следующее уравнение.
Заполнив это уравнение нашими известными значениями, мы можем использовать его для расчета номинала резистора, который нам нужен, чтобы понизить напряжение с 5 В до 3,3 В.
С нашими входными и выходными значениями и нашим резистором R1 1 кОм вы должны получить следующее уравнение.
Сначала вы должны вычислить обе половины деления, если вы умножите на Vout ( 3.3 ) на значение R1 ( 1000 ) должно получиться 3300 .
Теперь нам также нужно сделать нижнюю половину, вычитая , Vout из Vin , в этом примере это 5 — 3,3 , что равно 1,7 .
Наконец, разделите оба значения, чтобы получить значение сопротивления, в нашем примере это 3300 , разделенное на 1,7 .
Помещая это в калькулятор, мы получаем большое длинное число, но мы упростим его до ближайших 2 десятичных знаков.
Используя это значение, мы можем сделать вывод, что резистора 2 кОм должно быть более чем достаточно для понижения напряжения 5 В до 3,3 В .
Чтение резистивных датчиков
Вы можете заметить одну вещь: многие датчики в реальном мире представляют собой простые резистивные устройства, предназначенные для реакции на определенные элементы.
Например, датчик LDR (светозависимый резистор), подобный тому, который мы используем в нашем учебнике по датчику освещенности, работает, создавая сопротивление, пропорциональное количеству подобных, которые его касаются.
Есть также много других датчиков, которые фактически представляют собой просто модные резисторы, такие как термисторы, датчики изгиба и чувствительные к силе резисторы.
К сожалению, в отличие от напряжения (в сочетании с аналого-цифровым преобразователем) сопротивление не так просто измерить для компьютеров, таких как Raspberry Pi.
Тем не менее, мы можем упростить задачу, переделав схему в делитель напряжения. Это просто, как добавить резистор, поэтому схема будет больше похожа на схемы, которые мы показали ранее в этом руководстве.
Таким образом, мы можем использовать напряжение, подаваемое нам от делителя напряжения, для расчета текущего уровня освещенности.
Добавив резистор известного вам значения, например резистор 1 кОм, вы затем сможете вычислить сопротивление LDR при разных уровнях освещенности, изменив формулу, использованную ранее.
Все, что нам нужно знать, это номинал резистора Vin , Vout и R1 .
Используя приведенное выше уравнение, вы можете быстро рассчитать сопротивление LDR при самом темном и самом ярком уровнях света.
Это даст нам представление о самом высоком и самом низком сопротивлении.
Когда у вас есть оба этих значения сопротивления, вы можете рассчитать значение резистора, которое находится между ними, это даст вам наибольшее разрешение для расчета текущего света через аналого-цифровой преобразователь.
Например, сопротивление фотоэлемента может варьироваться от 1 кОм, на свету и приблизительно 10 кОм, в темноте.
Таким образом, используя резистор, значение которого находится где-то посередине, например, 5.Резистор 1 кОм , мы можем получить самый широкий диапазон от нашего LDR.
Я надеюсь, что это руководство помогло вам понять, что такое делитель напряжения и как его можно использовать в схемах, а также рассчитать его результирующее напряжение.
Если вы думаете, что мы что-то упустили или что-то сделали не так, обязательно сообщите нам об этом в разделе комментариев ниже. Мы также открыты для любых других отзывов, которые могут у вас возникнуть.
Калькулятор делителя напряжения
Плюсы и минусы делителей напряжения
Некоторым из вас может быть интересно, почему люди измеряют неизвестное сопротивление с помощью делителя напряжения, когда они могут просто прочитать значение силы тока, протекающей через резистор при приложении внешнего напряжения — просто закон Ома. Что ж, в общем, для этих методов не должно быть значительной разницы, но мы должны знать, что сопротивление подавляющего большинства материалов зависит от температуры. Хуже того, эти зависимости различны для металлов, полупроводников или изоляторов.
Что ж, в общем, для этих методов не должно быть значительной разницы, но мы должны знать, что сопротивление подавляющего большинства материалов зависит от температуры. Хуже того, эти зависимости различны для металлов, полупроводников или изоляторов.
Принимая во внимание металлы, их сопротивление увеличивается с повышением температуры, поэтому для определения сопротивления при некоторой стандартной температуре, например T = 25 ° C , мы должны найти тепловой коэффициент (TCR) материала.Это требует точного измерения температуры окружающей среды и выполнения некоторых расчетов, при этом надеясь, что за это время не было допущено никаких ошибок. Однако мы можем сделать это гораздо проще! Как вы уже догадались, можно использовать простой делитель напряжения!
В базовой версии у нас есть два резистора, и если они сделаны из одного материала, это означает, что их температурные зависимости сопротивления примерно такие же, как у . Независимо от того, насколько велика разница температур, эти сопротивления изменяются примерно на один и тот же процент, скажем, на 5% на каждые 20 ° C.Но, , поскольку в общем случае формула делителя напряжения имеет отношение импедансов, любое относительное изменение будет отменено, и выходное напряжение должно быть независимым от температуры (или, по крайней мере, его влияние должно быть значительно уменьшено). Более того, если мы посмотрим на уравнение из предыдущего раздела, мы получим значение сопротивления, такое же, как первое при заданной температуре — никаких дополнительных расчетов не требуется!
Независимо от того, насколько велика разница температур, эти сопротивления изменяются примерно на один и тот же процент, скажем, на 5% на каждые 20 ° C.Но, , поскольку в общем случае формула делителя напряжения имеет отношение импедансов, любое относительное изменение будет отменено, и выходное напряжение должно быть независимым от температуры (или, по крайней мере, его влияние должно быть значительно уменьшено). Более того, если мы посмотрим на уравнение из предыдущего раздела, мы получим значение сопротивления, такое же, как первое при заданной температуре — никаких дополнительных расчетов не требуется!
Во-вторых, делители напряжения удобно использовать при проектировании сложных электрических схем.Вместо использования нескольких отдельных источников напряжения, каждый из которых создает разный потенциал в системе, мы можем реализовать один источник и применить столько делителей напряжения, сколько нам нужно.
С другой стороны, мы должны помнить о том, что чем длиннее провода в нашей цепи, тем больше вероятность падения напряжения. Что ж, это далеко не так для длинных промышленных кабелей, но все же, если нам нужно провести действительно точные измерения, этот фактор следует принять во внимание и в идеале уменьшить как можно больше.
Как выбрать номинал резистора в делителе напряжения?
Главное актуально.
Взгляните на эту схему. Наведите указатель мыши на символ заземления, и вы увидите, что ток равен 25 мА. Теперь взгляните на эту схему, и вы увидите, что выходной ток равен \ $ 2.5 \ mbox {} \ mu A \ $.
Теперь посмотрим, как схемы ведут себя под нагрузкой. Вот первая схема с нагрузкой. Как видите, через нагрузочный резистор справа проходит ток 2,38 мА, и напряжение на нем больше не соответствует ожидаемому 2.5 В, но вместо 2,38 В (поскольку два нижних резистора включены параллельно). Если мы посмотрим на вторую схему здесь, мы увидим, что теперь верхний резистор падает примерно на 5 В, в то время как два нижних резистора имеют напряжение 4,99 мВ. Это потому, что здесь изменилось соотношение резисторов. Поскольку два нижних резистора теперь включены параллельно, и у нас есть один резистор со значительно большим сопротивлением, чем другой, их общее сопротивление незначительно по сравнению с сопротивлением только нижнего правого резистора (вы можете проверить это, используя формулы параллельного резистора).Таким образом, теперь выходное напряжение значительно отличается от 2,5 В, которые мы получаем в случае отсутствия нагрузки.
Теперь посмотрим на противоположную ситуацию: здесь два небольших резистора в делителе напряжения и один большой в качестве нагрузки. Опять же, суммарное сопротивление двух нижних резисторов меньше, чем сопротивление меньшего из двух резисторов. Однако в этом случае это не оказывает большого влияния на напряжение, воспринимаемое нагрузкой. Напряжение на нем еще 2,5 В и пока все нормально.
Итак, при определении сопротивления резисторов необходимо учитывать входное сопротивление нагрузки, а два резистора делителя напряжения должны быть как можно меньше.
С другой стороны, давайте сравним ток, протекающий через делитель в цепи с большими резисторами на делителе и в цепи с маленькими резисторами на делителе. Как видите, большие резисторы имеют ток всего \ $ 2,5 \ mbox {} \ mu A \ $, проходящий через них, а маленькие резисторы имеют ток 25 мА.Дело в том, что ток тратится впустую делителем напряжения, и если бы он был, например, частью устройства с батарейным питанием, это оказало бы негативное влияние на срок службы батареи. Поэтому резисторы должны быть как можно большего размера, чтобы снизить потери тока.
Это дает нам два противоположных требования: иметь как можно меньше резисторов, чтобы лучше регулировать напряжение на выходе, и как можно больше резисторов, чтобы получить как можно меньшие потери тока. Таким образом, чтобы получить правильное значение, мы должны увидеть, какое напряжение нам нужно на нагрузке, насколько оно должно быть точным, получить входное сопротивление нагрузки и на основе этого рассчитать размер резисторов, которые нам нужны, чтобы получить нагрузку с приемлемым Напряжение.Затем нам нужно поэкспериментировать с более высокими значениями резисторов делителя напряжения и посмотреть, как они повлияют на напряжение, и найти точку, в которой мы не можем иметь большее изменение напряжения в зависимости от входного сопротивления. На данный момент у нас (в целом) есть хороший выбор резисторов делителя напряжения.
Еще один момент, который необходимо учитывать, — это номинальная мощность резисторов. Это идет в пользу резисторов с большим сопротивлением, потому что резисторы с меньшим сопротивлением будут рассеивать больше мощности и больше нагреваться.Это означает, что они должны быть больше (и обычно дороже), чем резисторы с большим сопротивлением.
На практике, сделав несколько делителей напряжения, вы увидите несколько популярных значений резисторов делителя напряжения. Многие люди просто выбирают один из них и не особо утруждают себя расчетами, если с выбором нет проблем. Например, для небольших нагрузок вы можете выбрать резисторы из диапазона \ $ 100 \ mbox {} k \ Omega \ $, а для больших нагрузок вы можете использовать \ $ 10 \ mbox {} k \ Omega \ $ или даже \ $ 1 \ mbox {}. резисторов k \ Omega \ $, если у вас есть запасной ток.
Калькулятор делителя напряжения
— Хорошие калькуляторы
Вы можете использовать этот калькулятор делителя напряжения для определения любой из четырех переменных, связанных с простым двухрезисторным делителем напряжения, когда доступны значения трех других переменных.
В двухрезисторном делителе напряжения используются четыре переменных: входное напряжение ( В на ), выходное напряжение ( В на выходе ), сопротивление 1 (R1) и сопротивление 2 (R2).
Калькулятор также строит принципиальную схему и генерирует значения компонентов.
Как пользоваться калькулятором делителя напряжения:
- Введите три известные переменные
- Нажмите кнопку «Рассчитать»
- Калькулятор отобразит оставшееся значение и принципиальную схему.
Дополнительная информация
Инженеры очень часто используют схему делителя напряжения с двумя резисторами. Делитель напряжения, который также часто называют делителем потенциала, предлагает явное преимущество, заключающееся в том, что он может поляризовать другие элементы в цепи, включая интегральные схемы и транзисторы, с напряжением, отличным от напряжения основного источника напряжения.
Основная причина, по которой используется эта схема, — это масштабирование входного напряжения до более низкого значения в соответствии с соотношением двух резисторов.
Это достигается следующим образом:
- Соотношение резисторов (R1 и R2) снижает входное напряжение до более низкого выходного напряжения.
- Выходное напряжение представляет собой часть входного напряжения. Эта дробь принимает форму R2, деленного на сумму R1 + R2.
- Основная формула, которая используется для определения выходного напряжения, основана на законе Ома и выглядит следующим образом:
В выход = В вход * R2 / (R1 + R2)
Например, предположим, что мы работаем со схемой, которая имеет вход 12 В.Однако одной из микросхем в схеме нужно 9 вольт, а другой — всего 3 вольта. Делитель напряжения может использоваться для распределения напряжения между различными микросхемами в соответствии с их требованиями.
Если один резистор имеет значение 2 кОм, а другой — 6 кОм, вход 12 В будет разделен на 3 В и 9 В.
Обратите внимание: Никогда не используйте делитель напряжения для высоких напряжений, потому что полный ток должен пройти через резисторы, и это может привести к повреждению.В этом случае лучшим вариантом будет стабилизатор напряжения.
Пример:
Допустим, мы хотим определить выходное напряжение, если сопротивление резистора R1 составляет 5 кОм, сопротивление резистора R2 равно 10 кОм, а входное напряжение равно 9 В.
Решение:
В выход = В на входе * R2 / (R1 + R2) = (9 В) (10 кОм) / (5 кОм + 10 кОм) = 6 В
В выход = 6 В.
Формулы
В этом калькуляторе делителя напряжения используются следующие формулы:
В выход = В дюйм * R2 / (R1 + R2)
В вход = В выход * (R1 + R2) / R2
R1 = R2 * (V на входе — V на выходе ) / V на выходе
R2 = R1 * V выход / (V вход — V выход )
Где, В на выходе = выходное напряжение (вольты), В на входе = входное напряжение (вольты), R1 и R2 = значения резистора (Ом).

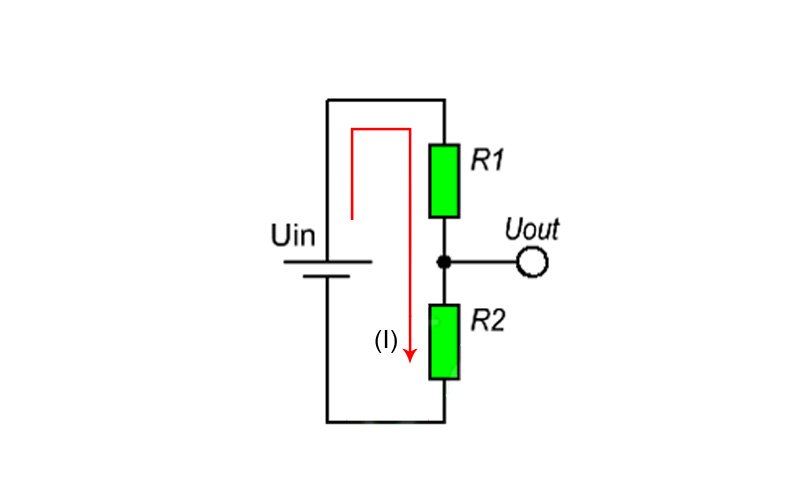
 е. U
е. U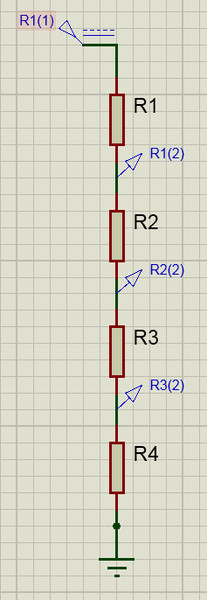 С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.
С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.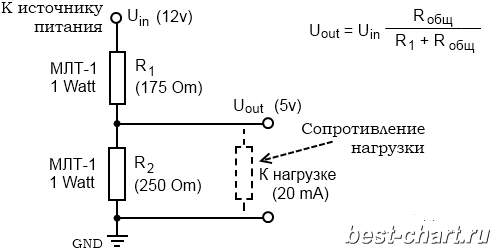
 Описание…
Описание… 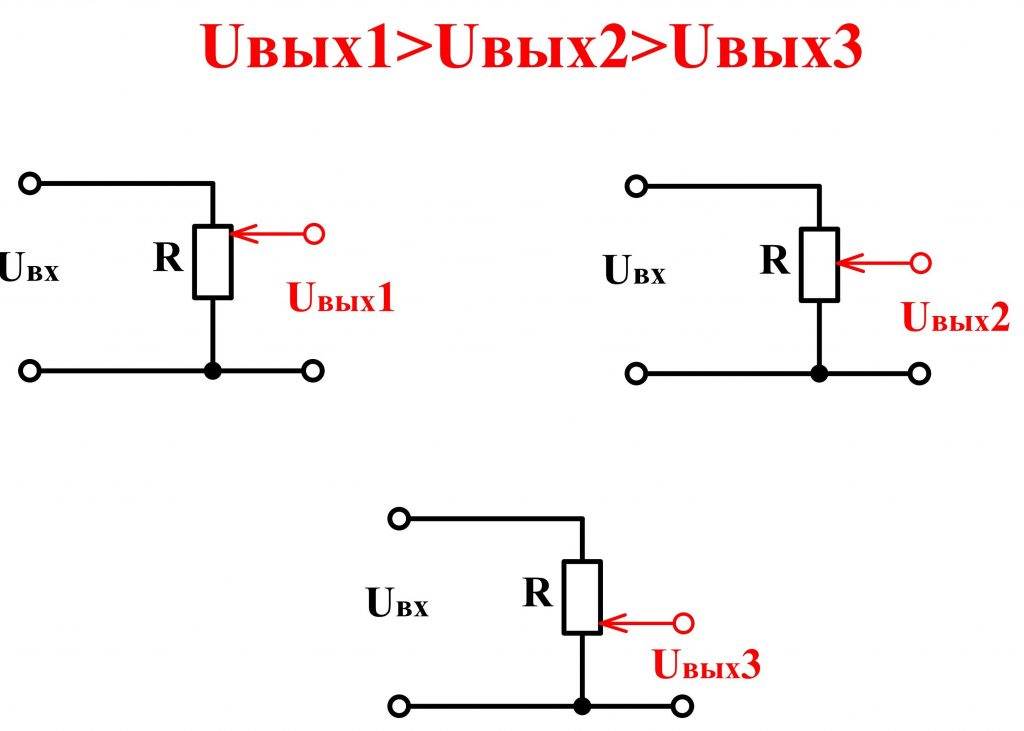
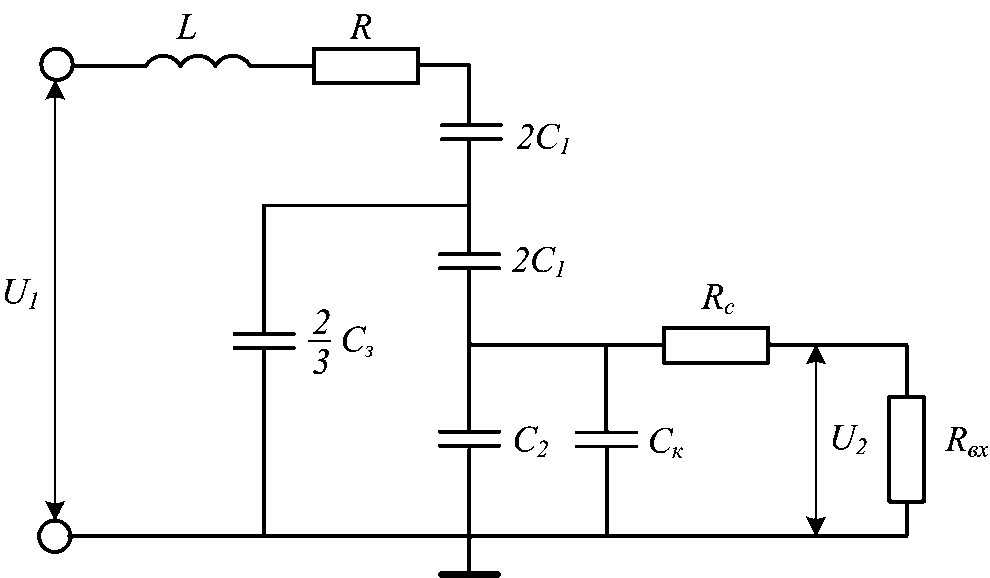 Когда он перемещается ближе к клемме 1 и дальше от клеммы 2, сопротивление уменьшается до клеммы 1, в то время как сопротивление увеличивается на клемме 2, и наоборот.
Когда он перемещается ближе к клемме 1 и дальше от клеммы 2, сопротивление уменьшается до клеммы 1, в то время как сопротивление увеличивается на клемме 2, и наоборот.
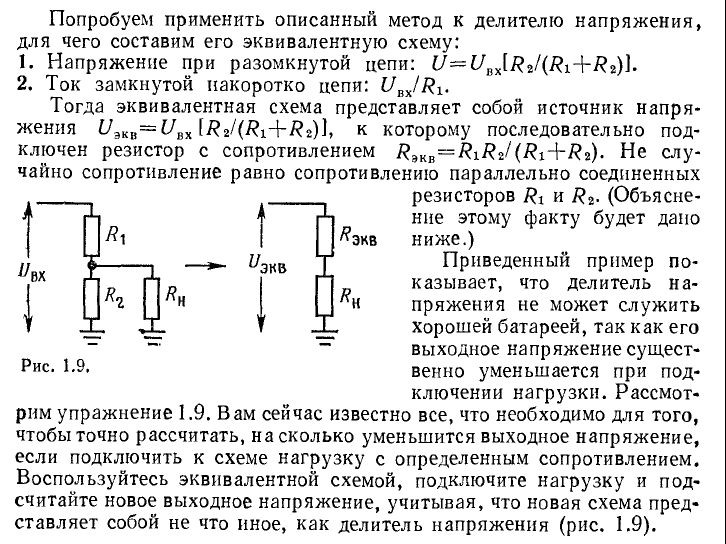 Однако большинство из них могут считывать только напряжение, но не сопротивление.
Однако большинство из них могут считывать только напряжение, но не сопротивление. Входной датчик 3 В может вызвать повреждение цепи 3,3 В.
Входной датчик 3 В может вызвать повреждение цепи 3,3 В.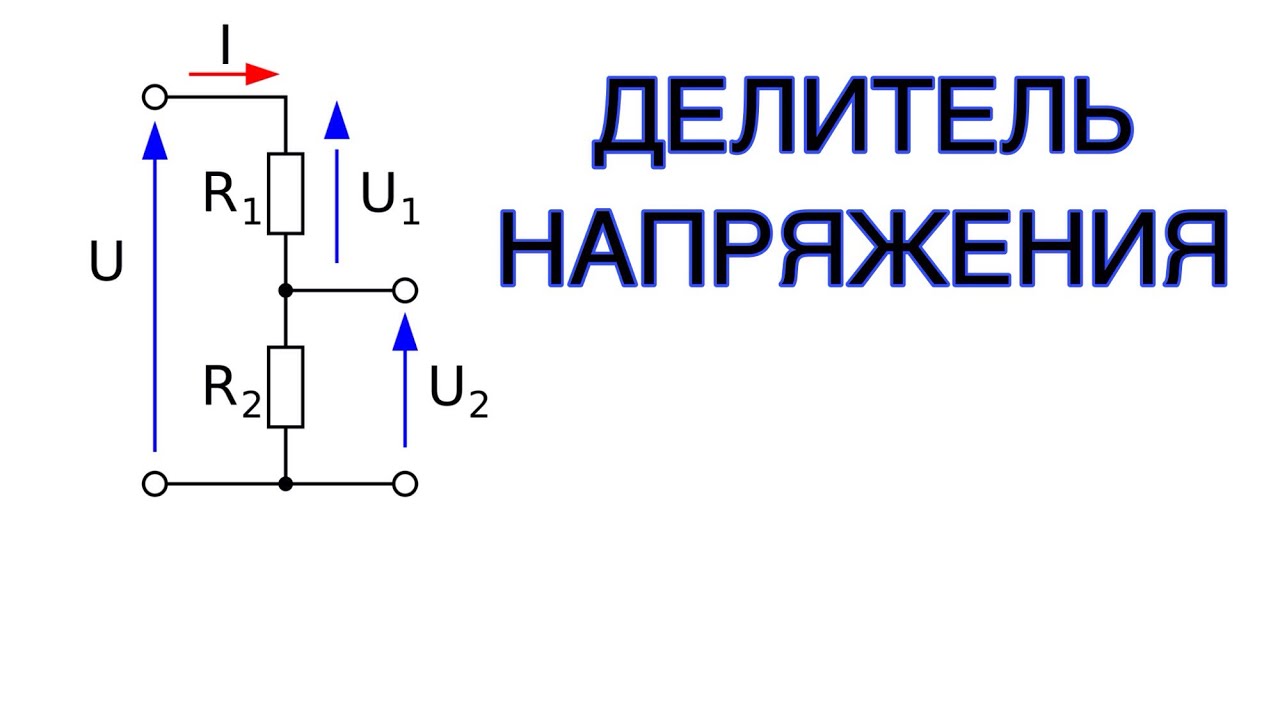 до 5 В, поскольку они не предназначены для подачи такого питания на нагрузку, как с такой нагрузкой, это может расплавить резистор.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А)
до 5 В, поскольку они не предназначены для подачи такого питания на нагрузку, как с такой нагрузкой, это может расплавить резистор.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А) Мультиметр и мост Уитстона включают делители напряжения.
Мультиметр и мост Уитстона включают делители напряжения.