Напряжения Размерность — Энциклопедия по машиностроению XXL
Величина К, зависящая от вида нагружения, величины нагрузки и формы трещины, называется коэффициентом интенсивности напряжений (размерность К — сила/длина В зависимости от вида нагрузки (см. схемы рис. 628) коэффициенты интенсивности напряжений отмечают соответственно индексами I, II или III, т. е. К, Ки, Л» , г и 9 — полярные координаты с полюсом в вершине трещины (рис. 632) [ij— некоторая функция угла 0.
[c.732]
Пусть, как и ранее, К, — статический коэффициент интенсивности напряжений, соответствующий — коэффициенты интенсивности, соответствующие (х . Kit) — динамический коэффициент интенсивности напряжений. Размерность определяется с учетом нормировки (57.4). Так как вектор перемещений с помощью линейного функционала однозначно представляет коэффициенты интенсивности напряжений, то
[c. 471]
471]
Напряжение — размерная величина. Размерность напряжения определяется на основе формулы (1.4) [c.6]
П р и м е р 8.5. Применительно к тензору напряжений (размерность МПа остальные напряжения равны нулю) [c.325]
Коэффициенты интенсивности напряжений Ki, Ки, Кш являются функциями внешней нагрузки, геометрических параметров, размеров дефекта. В отличие от коэффициента концентрации напряжений коэффициент интенсивности напряжений — размерная величина (в технике—кг/мм / ). [c.43]
Третьим требованием инвариантности является, конечно, инвариантность размерности. Это требование не накладывает каких-либо ограничений на форму уравнения состояния, а лишь означает, что последнее должно содержать определенное минимальное число размерных параметров. Можно показать, что в наиболее общем случае необходимы три параметра, имеющие размерность напряжения, времени и длины соответственно. [c.59]
Физическая размерность тензора определяется при помощи интерпретации операторного определения тензора как операции умножения. Иными словами, равенство Ь = А-а правильно в смысле размерности, если произведение размерностей а и А дает размерность Ь. Например, из равенства dt = T-ds, определяющего тензор напряжений, мы заключаем, что размерностью Т будет размерность силы, приходящейся на единицу площади.
[c.80]
Иными словами, равенство Ь = А-а правильно в смысле размерности, если произведение размерностей а и А дает размерность Ь. Например, из равенства dt = T-ds, определяющего тензор напряжений, мы заключаем, что размерностью Т будет размерность силы, приходящейся на единицу площади.
[c.80]
Размерность Snt — размерность коэффициента динамической вязкости ньютоновской жидкости т). Обозначим 5пТ = т п, под которым будем понимать общий коэффициент касательных напряжений дисперсной системы в целом. Тогда взамен (1-5) получим [c.17]
Коэффициент пропорциональности Е называется модулем продольной упругости или модулем упругости первого рода, он имеет размерность напряжений (даН/см или даН/мм ) и характеризует способность материала сопротивляться упругой деформации при растяжении и сжатии. Величину модуля продольной упругости для различных материалов определяют экспериментально. Для стали = (2,0- 2,15) 10 даН/см , для алюминия = (0,7н-0,8) 10 даН/см , для бронзы = 1,15-10 даН/см , для дерева вдоль волокон = 1-10 даН/см , для стеклопластиков = (0,18-ь н-0,4) 10 даН/см
[c. 130]
130]
Модуль упругости второго рода имеет размерность напряжения, так как относительный сдвиг является величиной безразмерной. Величины модулей упругости первого и второго рода связаны следующей формулой, вывод которой здесь не приводится
[c.186]
Как видно из формул (1.1) и (1.2), размерность напряжения [сила) / [площад > . [c.19]
Векторная величина р представляет собой полное напряжение в точке /С в сечении А. Напряжение имеет размерность силы, деленной [c.20]
Высоковольтные системы с ускоряющим напряжением 100 ООО…200 ООО В наиболее сложны в изготовлении и эксплуатации и применяются в тех случаях, когда необходимо проведение прецизионной размерной обработки и микросварки. [c.110]
Проектные данные весьма разнообразны по содержанию, размерности и функциональным свойствам. Так, например, конструктивные данные можно считать неизменными во времени, однако напряжения и токи являются в общем случае периодическими функциями времени. Одни данные (частота вращения, длина и др.)
[c.67]
Одни данные (частота вращения, длина и др.)
[c.67]
При построении вычислительных алгоритмов ЭМП для оптимального выбора варьируемых конструктивных параметров целесообразно использовать функции ограничений в виде равенств с целью сокращения размерности задач оптимизации. Отдельные параметры оптимизации могут быть однозначно определены через явные или неявные решения ограничений-равенств. Неявные решения при расчетах на ЭВМ находятся приближенно с помощью обратных итерационных связей. Для этого заранее устанавливается погрешность выполнения равенств, которая позволяет преобразовать равенства к двусторонним неравенствам. Например, для синхронного генератора ограничения-равенства по предельным значениям перегрузочной способности, механического напряжения ротора и МДС возбуждения можно представить в виде [8] [c.142]
Напряжение имеет размерность давления и выражается в Па или чаще в кратных единицах — МПа. [c.118]
Что называется напряжением в точке и какова его размерность
[c. 32]
32]
Физическая величина, характеризующая интенсивность распределения внутренних сил в окрестности точки в пределах данного сечения Напряжение имеет размерность силы, деленной на площадь. В Международной системе единиц (СИ) в качестве единицы напряжения принят паскаль (Н/м ), но эта единица очень мала, поэтому в практических расчетах используется кратная ей единица — мегапаскаль (МПа) [c.32]
Размерность единицы Е — это сила, приходящаяся на единичный заряд. Сила измеряется в динах, а заряд — в единицах СГСЭ,, так что размерность электростатической единицы напряженности электрического поля — дина на единицу СГСЭ,. Обычно размерность единицы напряженности электрического поля выражают иначе. Мы определяем единицу напряженности электрического поля как такую величину [c.114]
Здесь введена размерность единицы напряженности, равная единице потенциала СГСЭ на сантиметр, потому что (как мы подробно узнаем в гл. 5) целесообразно дать специальное название (единица потенциала СГСЭ) единице произведения электрической напряженности на длину. Если единица этого про-
[c.114]
Если единица этого про-
[c.114]
С точки зрения размерностей ясно, что любая численная мера напряжения имеет размерность силы, деленной на площадь. [c.17]
Искомыми неизвестными являются 12 перемещений вершин тетраэдра, векторы деформаций и напряжений имеют размерность, равную шести. [c.145]
Такая модификация приводит к повышению твердости материала и некоторых других физико-механических характеристик (предела прочности при разрыве, удельного объемного электросопротивления). Установлено также, что термохимическая обработка полиамидов способствует снятию внутренних напряжений, размерной и прочностной стабилизации изделий. Так, усадка образцов типа втулок (см. рис. И. 62), отлитых под давлением из гранул поликапролактама Б и не подвергавшихся термохимической обработке составила 1,8—2,2%, а для образцов, отлитых из гидрофобизированного сырья — всего 1,1—1,2%. [c.279]
Практика взрывного дела основана на эмпирическом законе подобия, согласно которому объем разрушенной породы (а также объем полости, образующейся после взрыва) прямо пропорционален объему заряда ВВ. Сейчас трудно установить, кто впервые сформулировал этот закон (одно из первых упоминаний о нем относится к 1628 г. и принадлежит французу Девилю). Коэффициент пропорциональности в нем зависит от прочности пород, характеристик ВВ, формы и расположения зарядов и т. д. Указанный закон подобия нарушается для весьма мощных взрывов из-за сравнительно большого влияния силы тяжести и, по-видимому, для весьма прочных хрупких пород, вследствие появления прочностной константы материала (критический коэффициент интенсивности напряжений), размерность которой отлична от размерности напряжения.
[c.450]
Сейчас трудно установить, кто впервые сформулировал этот закон (одно из первых упоминаний о нем относится к 1628 г. и принадлежит французу Девилю). Коэффициент пропорциональности в нем зависит от прочности пород, характеристик ВВ, формы и расположения зарядов и т. д. Указанный закон подобия нарушается для весьма мощных взрывов из-за сравнительно большого влияния силы тяжести и, по-видимому, для весьма прочных хрупких пород, вследствие появления прочностной константы материала (критический коэффициент интенсивности напряжений), размерность которой отлична от размерности напряжения.
[c.450]
Так как нри методе Брпнелля, значение твердости определяют отношение нагрузки Р (кгс) на поверхность отпечатка (мм ), то твердости может быть приписана размерность (ка,к и прочности) кгс/мм . Однако при деформации вдавливанием напряжение крайне неравномерно распределялось по поверхности во время испытания, поэтому такое деление (нагрузка на поверхность отпечатка) не имеет четкого физического смысла. Поэтому лучше не давать твердости указанной размерности, а само измерение твердости считать как технологическую пробу, косвенно характеризующую прочность.
[c.80]
Поэтому лучше не давать твердости указанной размерности, а само измерение твердости считать как технологическую пробу, косвенно характеризующую прочность.
[c.80]
Ф Примеры универсальных программных комплексов. 1. Программный комплекс Прочность-75 разработан в проблемной лаборатории тонкостенных пространственных конструкций Киевского инженерно-строительного института и ориентирован на ЭВМ БЭСМ-6. Наличие монитора и языкового процессора позволяет с полным основанием отнести Прочность-75 к программным системам. Система предназначена для исследования напряженного состояния и собственных колебаний элементов несущих конструкций. Входной информацией системы являются сведения о топологии, геометрии и физической структуре исследуемого объекта. На выходе пользователь может получить картину распределения сил и деформаций во времени. Система Прочность-75 разделена на отдельные подсистемы, предназначенные для анализа объектов определенной размерности. [c.56]
По взаимному расположению звеньев размерные цепи делят на плоские и иростраиственные. Размерную цепь называют плоской, если ее звенья расположены в одной или нескольких параллельных плоскостях. Пространственной называют размерную цепь, звенья которой непараллельны одно другому и лежат в непараллельных плоскостях. Размерные цепи, звеньями которых являются линейные размеры , называют линейными. Размерные цепи, звеньями которых являются угловые размеры, называют угловыми. При анализе точности электрических и электроин1>1х элементов машин и приборов используют цепи, звеньями которых являются значения сопротивлений, емкости, индуктивности, силы тока, напряжений и других физических параметров,
[c.249]
Размерную цепь называют плоской, если ее звенья расположены в одной или нескольких параллельных плоскостях. Пространственной называют размерную цепь, звенья которой непараллельны одно другому и лежат в непараллельных плоскостях. Размерные цепи, звеньями которых являются линейные размеры , называют линейными. Размерные цепи, звеньями которых являются угловые размеры, называют угловыми. При анализе точности электрических и электроин1>1х элементов машин и приборов используют цепи, звеньями которых являются значения сопротивлений, емкости, индуктивности, силы тока, напряжений и других физических параметров,
[c.249]
В ]очке бифуркации Уэфф О Тогда ио-уст=0. Это равенство является условием автомодельности разрушения и самоорганизации диссипативных структур. При таком подходе удается выделить пороговые напряжения, соответствующие фрактальные объекты и интервал изменения их фрактальной размерности. [c.315]
Из приведенного расчета видно, что индукция магнитного поля имеет размерность [сила] / [заряд], как и напряженность электрического поля. Однако удобно иметь отдельное название для единицы индукции магнитного поляи вот почему мы го-
[c.116]
Однако удобно иметь отдельное название для единицы индукции магнитного поляи вот почему мы го-
[c.116]
Единицей электростатического потенциала (или разности потенциалов) в гауссовой системе единиц С ГС является единица потенциала СГСЭ ( r Sv ). В гл. 4 мы видели, что единицей напряженности электрического поля является СГСЭ /см, но так как разм ерность ф отличается от Е, то ф измеряется в единицах СГСЭ . Так как размерность ф равна [заряд/длина], то единица потенциала равна СГСЭ,/см. [c.168]
С другой стороны, наступление момента конкуренции процессов ОЬА/ССА-сборт можно интерпретировать как приближение в системе к порогу перколяции в отнощении напряженности и взаимодействия локальных силовых полей от сформированных фрактальных кластеров. Достижение же критического значения концентрации фрактальных кластеров конденсированной фазы обусловливает перколяционную структуру электрических взаимодействий между ними. Для систем, погруженных в пространство с евклидовой размерностью =3, фрактальная размерность частиц, соответствующая порогу перколяции, Эг-2,5 [6]. В условиях стационарного воздействия на систему отрицательного температурного градиента (охлаждения системы внешней средой) описанное состояние системы катализирует таким образом дальнейший процесс агрегации по ССД-механизму, Подобным образом развивается волнообразный цикличный характер дальнейшей цепочки фазовых переходов второго рода (рис. 63), обусловливающий наиболее эффективный путь диссипации энергии посредством структурообразования по иерархическому принципу в открытой неравновесной системе охлаждаемого расплава.
[c.91]
В условиях стационарного воздействия на систему отрицательного температурного градиента (охлаждения системы внешней средой) описанное состояние системы катализирует таким образом дальнейший процесс агрегации по ССД-механизму, Подобным образом развивается волнообразный цикличный характер дальнейшей цепочки фазовых переходов второго рода (рис. 63), обусловливающий наиболее эффективный путь диссипации энергии посредством структурообразования по иерархическому принципу в открытой неравновесной системе охлаждаемого расплава.
[c.91]
Примеры определения нормальных и касательных напряжений. Напряжения в точке Касательным напряжением в точке сечения
Напряжение
– численная мера распределения внутренних
сил по плоскости поперечного сечения.
Его используют при исследовании и
определении внутренних сил любой
конструкции.
Выделим
на плоскости сечения площадку
A
;
по этой площадке будет действовать
внутренняя сила
R
.
Величина
отношения
R
/
A
=
p
ср
называется
средним напряжением на площадке
A
.
Истинное напряжение в точке А
получим устремив
A
к нулю:
Нормальные
напряжения возникают, когда частицы
материала стремятся отдалиться друг
от друга или, наоборот, сблизиться.
Касательные напряжения связаны со
сдвигом частиц по плоскости рассматриваемого
сечения.
Очевидно,
что
.
Касательное напряжение в свою очередь
может быть разложено по направлениям
осейx
и y
(τ
z
х
,
τ
z
у
).
Размерность напряжений – Н/м 2
(Па).
При
действии внешних сил наряду с возникновением
напряжений происходит изменение объема
тела и его формы, т. е. тело деформируется.
При этом различают начальное
(недеформированное) и конечное
(деформированное) состояния тела.
16.Закон парности касательных напряжений
Касат.
напряжение на 2-ух взаимно перпендик.
площ. направлены к ребру или от ребра и
равны по величине
17.Понятие о деформациях. Мера линейной, поперечной и угловой деформации
Деформац
– наз. взаимное перемещение точек или
сечений тела по сравн с полож-ями тела
которые они занимали до приложения внеш
сил
бывают:
упругие и пластические
а)
линейная деформация
мерой
явл относительное удлинение эпсила
=l1-l/l
б)
поперечная деф
мерой
явл. относительное сужение эпсила
штрих=|b1-b|/b
18.Гипотеза плоских сечений
Основные
гипотезы
(допущения): гипотеза о не надавливании
продольных волокон: волокна, параллельные
оси балки, испытывают деформацию
растяжения – сжатия и не оказывают
давления друг на друга в поперечном
направлении; гипотеза
плоских сечений
:
сечение балки, плоское до деформации,
остается плоским и нормальным к
искривленной оси балки после деформации.
При плоском изгибе в общем случае
возникают внутренние
силовые факторы
:
продольная сила N,
поперечная сила Q
и изгибающий момент М. N>0,
N>0,
если продольная сила растягивающая;
при М>0 волокна сверху балки сжимаются,
снизу растягиваются.
.
Слой,
в котором отсутствуют удлинения,
называется нейтральным
слоем
(осью, линией). При N=0
и Q=0,
имеем случай чистого
изгиба.
Нормальные напряжения:
,
— радиус кривизны нейтрального слоя,
y
— расстояние от некоторого волокна до
нейтрального слоя.
19.Закон Гука (1670). Физический смысл входящих в него величин
Он
установил связь между напряжением,
растяжением и продольной деформацией.
где Е
– коэффициент пропорциональности
(модуль упругости материала).
Модуль
упругости характеризует жёсткость
материала, т.е. способность сопротивляться
деформациям. (чем больше Е, тем менее
растяжимый материал)
Потенциальная
энергия деформации:
Внешние
силы, приложенные к упругому телу,
совершают работу. Обозначим её через
А. В результате этой работы накапливается
потенциальная энергия деформированного
тела U.
Кроме того, работа идёт на сообщение
скорости массе тела, т. е. преобразуется
е. преобразуется
в кинетическую энергию К. Баланс энергии
имеет вид А = U
+ К.
Если мысленно
вырезать вокруг какой-нибудь точки тела
элемент в виде бесконечного малого
кубика, то по его граням в общем случае
будут действовать напряжения,
представленные на рис. 3.1.
Совокупность
нормальных и касательных напряжений,
действующих по всем площадкам (сечениям),
содержащим какую-либо точку называют
напряженным
состоянием тела в данной точке
Рис.
3
.
1
Таким образом, на
гранях элементарного параллелепипеда,
выделенного в окрестности точки
нагруженного тела, действуют девять
компонентов напряжения. Запишем их в
виде следующей квадратной матрицы:
где в первой, второй
и третьей строках расположены составляющие
напряжений соответственно на площадках,
перпендикулярных к осям
,
,
.
Эта совокупность напряжений называется
тензором
напряжений
.
Закон парности касательных напряжений. Главные площадки и главные напряжения.
Составим уравнение
моментов всех сил, приложенных к
элементарному параллелепипеду
относительно оси
.
(рис. 3.1.).
Силы, параллельные
этой оси и пересекающие ее, в уравнение
не войдут. Моменты сил
на двух гранях, перпендикулярных оси
,
уравновешиваются, равно как и моменты
сил
на верхней и нижней гранях элемента.
Таким образом, получаем:
Отсюда следует,
что
.
Аналогично из двух
других уравнений находим:
Итак, имеем равенства
называемые законом
парности касательных напряжений
Закон парности
касательных напряжений
– касательные напряжения на двух любых,
но взаимно перпендикулярных площадках,
направленные перпендикулярно к линии
пересечения площадок, равны по величине.
При этом они стремятся повернуть элемент
в разные стороны.
При изменении
ориентации граней выделенного элемента
меняются также действующие на его гранях
напряжения. Можно провести такие
площадки, на которых касательные
напряжения равны нулю. Площадки, на
которых касательные напряжения равны
нулю, называются главными
площадками
,
а нормальные напряжения на этих площадках
– главными
напряжениями
.
Можно доказать,
что в каждой точке напряженного тела
существует три главные взаимно
перпендикулярные площадки.
Главные напряжения
обозначают
,
,
.
При этом индексы следует расставлять
так, чтобы выполнялось неравенство
Если отличны от
нуля все три главных
напряжения, то напряженное состояние
называется трехосным
или объемным
(рис.3.2,
а).
Если равно нулю
одно из
главных
напряжения, то напряженное состояние
называется двухосным
или плоским
(рис.3.2,
б).
Если равно нулю
два
главных
напряжения, то напряженное состояние
называется одноосным
или линейны
м
(рис.3.2, в).
Рис.
3
.
2
Плоское
напряженное состояние.
При
исследовании напряженного состояния
элементов конструкций наиболее часто
приходится иметь дело с плоским
напряженным состоянием. Оно встречается
при кручении, изгибе и сложном
сопротивлении. Поэтому на нем мы
остановимся несколько подробнее.
Рассмотрим
элемент, грани которого являются главными
площадками.
Рис.
3
.
3
По
ним действуют положительные напряжения
и
,
а третье главное напряжение
(направление
перпендикулярно к плоскости чертежа).
Проведем
сечение I
– I,
которое определит площадку (),
характеризуемую положительным углом
.
Напряжения
и
по этой площадке будут определяться по
формулам:
(3.3)
Сжимающие
главные напряжения подставляют в эти
формулы со знаком «минус», а угол
отсчитывают от алгебраически большего
главного напряжения.
Проведем
сечение II
– II,
которое определит площадку
,
перпендикулярную площадке
.
Нормаль
к ней образует с направлением
угол
Подставив
в формулы (3.2) и (3.3) значения угла
,
будем иметь
. (3.5)
Совокупность
формул (3.2) — (3.5) дает возможность находить
напряжения по любым взаимно перпендикулярным
наклонным площадкам, если известны
главные напряжения.
Складывая
равенства (3.2) и (3.4), обнаруживаем, что
, (3. 6)
6)
т.
е. сумма нормальных напряжений по двум
взаимно перпендикулярным площадкам не
зависит от угла наклона этих площадок
и равна сумме главных напряжений.
Из
формул (3.3) и (3.5) видим, что касательные
напряжения достигают наибольшей величины
при
,
т. е. по площадкам, наклоненным к главным
площадкам под углом
,
причем
. (3.7)
Сравнивая
формулы (3.3) и (3.5), находим, что
Это
равенство выражает закон парности
касательных напряжений.
Проведем
теперь еще два сечения (рис. 3.3): Сечение
ІІІ – ІІІ, параллельное І – І,
и сечение ІV
– ІV,
параллельное ІІ – ІІ. Элемент
,
выделенный четырьмя сечениями из
элемента
(рис. 3.4, а), будет иметь вид, показанный
на рис 3.4, б. Оба элемента определяют
одно и то же напряженное состояние, но
элемент
представляет его главными напряжениями,
а элемент
— напряжениями на наклонных площадках.
Рис.
3
.
4
В
теории напряженного состояния можно
разграничить две основные задачи.
Прямая
задача
.
В точке известны положения главных
площадок и соответствующие им главные
напряжения; требуется найти нормальные
и касательные напряжения по площадкам,
наклоненным под заданным углом
к главным.
Обратная
задача
.
В точке известны нормальные и касательные
напряжения, действующие в двух взаимно
перпендикулярных площадках; требуется
найти главные направления и главные
напряжения. Обе задачи можно решать как
аналитически, так и графически.
Прямая
задача в плоском напряженном состоянии.
Круг напряжений (круг Мора).
Аналитическое
решение прямой задачи дается формулами
(3.2) – (3.5).
Проанализируем
напряженное состояние, воспользовавшись
простым графическим построением. Для
этого введем в рассмотрение геометрическую
плоскость и отнесем ее к прямоугольным
координатным осям
и
.
Порядок расчета опишем на примере
напряженного состояния, изображенного
на рис. 3.5, а.
Выбрав
для напряжений некоторый масштаб,
откладываем на оси абсцисс (рис 3.5, б)
отрезки
На
как на диаметре строим окружность с
центром в точке
.
Построенный круг носит название круга
напряжений
или круга
Мора
.
Рис.
3
.
5
Координаты
точек круга соответствуют нормальным
и касательным напряжениям на различных
площадках. Так, для определения напряжения
на площадке, проведенной под углом
(рис. 3.5, а) из центра круга
(рис 3.5, б)
проводим
луч под углом
до пересечения с окружностью в точке
(положительные углы откладываем против
часовой стрелки). Абсцисса точки (отрезок
)
равна нормальному напряжению
,
а ордината ее (отрезок
)
– касательному напряжению
.
Напряжение
на площадке, перпендикулярной к
рассмотренной, найдем, проведя луч под
углом
и получив в пересечении с окружностью
точку
.
Очевидно, ордината точки
соответствует касательному напряжению
,
а абсцисса точки
— нормальному напряжению
.
Проведя
из точки
линию, параллельную
(в нашем случае горизонталь), до пересечения
с кругом, найдем полюс – точку
.
Линия, соединяющая полюс с любой точкой
круга, параллельна направлению нормального
напряжения на площадке, которой эта
точка соответствует. Так, например,
Так, например,
линия
параллельна главному напряжению
.
Очевидно, что линия
параллельна направлению главного
напряжения
.
Обратная
задача в плоском напряженном состоянии.
При
практических расчетах обычно определяют
нормальные и касательные напряжения
на некоторых двух взаимно перпендикулярных
площадках. Пусть, например, известны
напряжения
,
,
,
(рис. 3.6, а). По этим данным требуется
определить величины главных напряжений
и положение главных площадок.
Сначала
решим эту задачу графически. Примем,
что
>,
а
>.
В
геометрической плоскости в системе
координат
нанесем точку
,
с координатами
,
и точку
с координатами
,(рис.
3.6, б). Соединив точки
и
,
находим центр круга – точку
— и радиусом
проводим окружность. Абсциссы точек ее
пересечения с осью
— отрезки
и
— дадут соответственно величины главных
напряжений
и
.
Для
определения положения главных площадок
найдем полюс и воспользуемся его
свойством. Проведем из точки
линию параллельно линии действия
напряжения
,
т. е. горизонталь. Точка
е. горизонталь. Точка
пересечения этой линии с окружностью
и является полюсом. Соединяя полюс
с точками
и
,
получим направления главных напряжений.
Главные площадки перпендикулярны к
найденным направлениям главных
напряжений.
Рис.
3
.
6
Используем
построенный круг для получения
аналитических выражений главных
напряжений
и
:
(3.9)
(3.10)
Формула
(3.10) определяет единственное значение
угла
,
на который нужно повернуть нормаль
,
чтобы получить направление алгебраически
большего главного напряжения.
Отрицательному значению
соответствует поворот по часовой
стрелке.
Если
одно из главных напряжений окажется
отрицательным, а другое положительным,
то их следует обозначать
и
.
Если оба главных напряжения окажутся
отрицательными, то их следует обозначать
и
.
Лекция 4
.
Теории
прочности
.
Чистый
сдвиг{jcomments on}
Теории
прочности.
Важнейшей задачей
инженерного расчета является оценка
прочности элемента конструкции по
известному напряженному состоянию. Для
Для
простых видов деформаций, в частности
для одноосных напряженных состояний,
определение значений опасных напряжений
не представляет особых трудностей.
Вспомним, что под опасными напряжениями
понимают напряжения, соответствующие
началу разрушения (при хрупком состоянии
материала) или появлению остаточных
деформаций (в случае пластического
состояния материала):
По опасным
напряжениям устанавливают допускаемые
напряжения, обеспечивающие определенный
запас против наступления предельного
состояния.
При сложном
напряженном состоянии, как показывают
опыты, опасное состояние может иметь
место при различных значениях главных
напряжений
,
,
в зависимости от соотношений между
ними. В этом случае вводят гипотезу о
преимущественном влиянии на прочность
материала того или иного фактора.
Предельное значение фактора, определяющего
прочность, находят на основании простых
опытов (на растяжение, сжатие, кручение).
Выбранная указанным
образом гипотеза называется механической
теорией прочности
.
Рассмотрим
классические теории прочности.
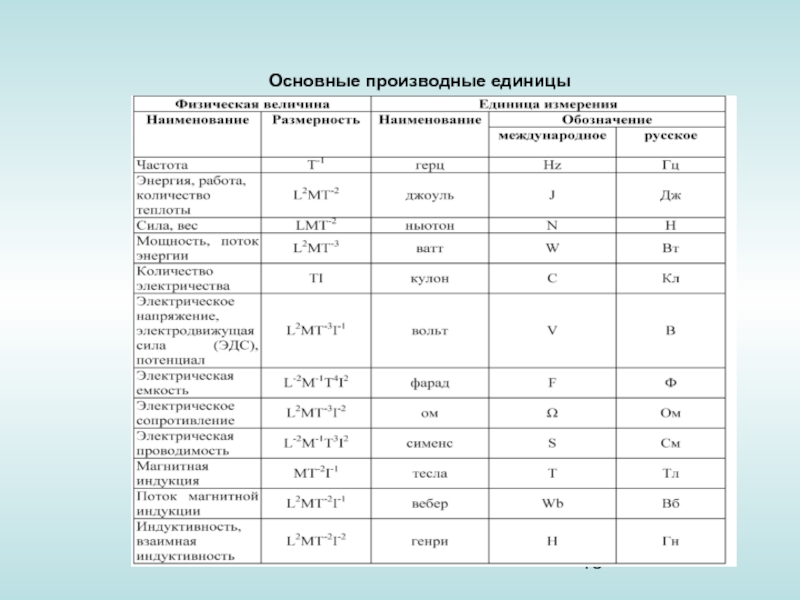 Главные моменты инерции. Главные центральные оси плоской фигуры. Моменты инерции плоских симметричных фигур.
Главные моменты инерции. Главные центральные оси плоской фигуры. Моменты инерции плоских симметричных фигур.Напряжение – мера распределения
внутренних сил по сечению.
Где
— внутренняя сила, выявленная на площадке
.
Полное напряжение
.
Нормальное напряжение – проекция
вектора полного напряжения на нормаль
обозначается через σ.
,
где Е – модуль упругости I рода, ε –
линейная деформация. Нормальное
напряжения вызывается только изменением
длин волокон, направлением их действий,
а угол поперечных и продольных волокон
не искажается.
Касательное напряжение – составляющие
напряжения в плоскости сечения.
,
где
(для изотропного материала) – модуль
сдвига (модуль упругости II рода), μ –
коэффициент Пуассона (=0,3), γ – угол
сдвига.
7. Закон Гука для одноосного напряжённого
состояния в точке и закон Гука для
чистого сдвига. Модули упругости первого
и второго рода, их физический смысл,
математический смысл и графическая
интерпретация. Коэффициент Пуассона.
— закон Гука для одноосного напряжённого
состояния в точке.
Е – коэффициент пропорциональности
(модуль упругости I рода). Модуль упругости
является физической константой материала
и определяется экспериментально.
Величина Е измеряется в тех же единицах,
что и σ, т.е. в кГ/см 2 .
— закон Гука для сдвига.
G– модуль сдвига (модуль
упругости II рода). Размерность модуляGтакая же, как и у модуля
Е, т.е. кГ/см 2 .
.
μ – коэффициент Пуассона (коэффициент
пропорциональности).
.
Безразмерная величина, характеризующая
свойства материала и определяющаяся
экспериментально и лежит в интервале
от 0,25 до 0,35 и не могут превышают 0,5 (для
изотропного материала).
8. Центральное растяжение (сжатие)
прямого бруса. Определение внутренних
продольных сил методом сечений. Правило
знаков для внутренних продольных сил.
Привести примеры расчёта внутренних
продольных сил.
Брус испытывает состояние центрального
растяжения (сжатия) в том случае, если
в его поперечных сечениях возникают
центральные продольные силы N z (т.е. внутренняя сила, линия действия
которой направлена по осиz),
а остальные 5 силовых факторов равны
нулю (Q x =Q y =M x =M y =M z =0).
Правило знаков для N z:
истинная растягивающая сила – «+»,
истинная сжимающая сила – «-».
9. Центральное растяжение (сжатие)
прямого бруса. Постановка и решение
задачи об определении напряжений в
поперечных сечениях бруса. Три стороны
задачи.
Постановка: Прямой брус из однородного
материала, растянутый (сжатый) центральными
продольными силами N.
Определить напряжение, возникающее в
поперечных сечениях бруса, деформации
и перемещения поперечных сечений бруса
в зависимости от координатzэтих сечений.
10. Центральное растяжение (сжатие)
прямого бруса. Определение деформаций
и перемещений. Жёсткость бруса при
растяжении (сжатии). Привести примеры
соответствующих расчётов.
Центральное напряжение (сж.) прямого
бруса см. в вопросе 8.
.
При центральном растяжении (сж.) бруса
в поперечном направлении в сечении
возникает только нормальное напряжение
σ z , постоянное во
всех точках поперечного сечения и равноеN z /F.
,
гдеEF– жёсткость бруса
при растяжении (сжатии). Чем больше
жёсткость бруса, тем меньше деформируется
бус при одной и той же силе. 1/(EF)
1/(EF)
– податливость бруса при растяжении
(сжатии).
11. Центральное растяжение (сжатие)
прямого бруса. Статически неопределимые
системы. Раскрытие статической
неопределимости. Влияние температурного
и монтажного факторов. Привести примеры
соответствующих расчётов.
Центральное напряжение (сж.) прямого
бруса см. в вопросе 8.
Если число линейно-независимых уравнений
статики меньше числа неизвестных,
входящих в систему этих уравнений, то
задача по определению этих неизвестных
становится статически неопределимой.
(На сколько удлинится одна часть, на
столько сожмётся вторая).
Нормальные условия — 20º С.
.f(σ,ε,tº,t)=0
– функциональная зависимость между 4
параметрами.
12. Опытное изучение механических
свойств материалов при растяжении
(сжатии). Принцип Сен-Венана. Диаграмма
растяжения образца. Разгрузка и повторное
нагружение. Наклёп. Основные механические,
прочностные и деформационные характеристики
материала.
Механические свойства материалов
вычисляют с помощью испытательных
машин, которые бывают рычажными и
гидравлическими. В рычажной машине
В рычажной машине
усилие создаётся при помощи груза,
действующего на образец через систему
рычагов, а в гидравлической – с помощью
гидравлического давления.
Принцип Сен-Венана: Характер распределения
напряжения в поперечных сечениях
достаточно удалённых (практически на
расстояния, равные характерному
поперечному размеру стержня) от места
приложения нагрузок, продольных сил не
зависит от способа приложения этих сил,
если они имеют один и тот же статический
эквивалент. Однако в зоне приложения
нагрузок закон распределения напряжения
может заметно отличаться от закона
распределения в достаточно удалённых
сечениях.
Если испытуемый образец, не доводя до
разрушения, разгрузить, то в процессе
разгрузки зависимость между силой Р и
удлинением Δlобразец
получит остаточное удлинение.
Если образец был нагружен на участке,
на котором соблюдается закон Гука, а
затем разгружен, то удлинение будет
чисто упругим. При повторном нагружении
пропадёт промежуточная разгрузка.
Наклёп (нагартовка) – явление повышения
упругих свойств материала в результате
предварительного пластического
деформирования.
Предел пропорциональности – наибольшее
напряжение, до которого материал следует
закону Гука.
Предел упругости – наибольшее напряжение,
до которого материал не получает
остаточных деформаций.
Предел текучести – напряжение, при
котором происходит рост деформации без
заметного увеличения нагрузки.
Предел прочности – максимальное
напряжение, которое может выдержать
образец, не разрушаясь.
13. Физический и условный пределы
текучести материалов при испытании
образцов на растяжение, предел прочности.
Допускаемые напряжения при расчёте на
прочность центрально растянутого
(сжатого) бруса. Нормативный и фактический
коэффициенты запаса прочности. Привести
числовые примеры.
В тех случаях, когда на диаграмме
отсутствует явно выраженная площадка
текучести, за предел текучести принимается
условно величина напряжения, при котором
остаточная деформация ε ост =0,002
или 0,2%. В некоторых случаях устанавливается
предел ε ост =0,5%.
max|σ z |=[σ].
,n>1(!) – нормативный
коэффициент запаса прочности.
— фактический коэффициент запаса
прочности.n>1(!).
14. Центральное растяжение (сжатие)
прямого бруса. Расчёты на прочность и
жёсткость. Условие прочности. Условие
жёсткости. Три типа задач при расчёте
на прочность.
Центральное напряжение (сж.) прямого
бруса см. в вопросе 8.
max|σ z | растяж ≤[σ] растяж;max|σ z | сжатия ≤[σ] сжатия.
15.Обобщённый закон Гука для трёхосного
напряжённого состояния в точке.
Относительная объёмная деформация.
Коэффициент Пуассона и его предельные
значения для однородного изотропного
материала.
,
,
.
Сложив эти уравнения, получим выражение
объёмной деформации:
.
Это выражение позволяет определить
предельное значение коэффициента
Пуассона для любого изотропного
материала. Рассмотрим случай, когда
σ x =σ y =σ z =р.
В этом случае:
.
При положительном р величина θ должна
быть также положительной, при отрицательном
р изменение объёма будет отрицательным.
Это возможно только в том случае, когда
μ≤1/2. Следовательно, значение коэффициента
Пуассона для изотропного материала не
может превышать 0,5.
16. Соотношение между тремя упругими
постоянными для изотропного материала
(без вывода формулы).
,
,
.
17. Исследование напряжённо-деформированного
состояния в точках центрально-растянутого
(сжатого) прямого бруса. Закон парности
касательных напряжений.
,
.
— закон парности касательных напряжений.
18. Центральное растяжение (сжатие)
бруса из линейно-упругого материала.
Потенциальная энергия упругой деформации
бруса и её связь с работой внешних
продольных сил, приложенных к брусу.
А=U+K. (В
результате работы накапливается
потенциальная энергия деформированного
телаU, кроме того, работа
идёт на совершение скорости массе тела,
т.е. преобразуется в кинетическую
энергию).
Если центральное растяжение (сжатие)
бруса из линейно-упругого материала
производится очень медленно, то скорость
перемещения центра масс тела будет
весьма малой. Такой процесс нагружения
называется статическим. Тело в любой
момент находится в состоянии равновесия.
В этом случае А=U, и работа
внешних сил целиком преобразуется в
потенциальную энергию деформации.
,
,
.
Напряженное и деформированное состояния упругого тела. Связь между напряжениями и деформациями
Понятие о напряжении тела в данной точке. Нормальные и касательные напряжения
Внутренние силовые факторы, возникающие при нагружении упругого тела, характеризуют состояние того или иного сечения тела, но не дают ответа на вопрос о том, какая именно точка поперечного сечения является наиболее нагруженной, или, как говорят, опасной точкой
. Поэтому необходимо ввести в рассмотрение какую-то дополнительную величину, характеризующую состояние тела в данной точке.
Если тело, к которому приложены внешние силы, находится в равновесии, то в любом его сечении возникают внутренние силы сопротивления. Обозначим через внутреннее усилие, действующее на элементарную площадку , а нормаль к этой площадке через тогда величина
(3. 1) 1) |
называется полным напряжением.
В общем случае полное напряжение не совпадает по направлению с нормалью к элементарной площадке, поэтому удобнее оперировать его составляющими вдоль координатных осей —
Если внешняя нормаль совпадает с какой-либо координатной осью, например, с осью Х
, то составляющие напряжения примут вид при этом составляющая оказывается перпендикулярной сечению и называется нормальным напряжением
, а составляющие будут лежать в плоскости сечения и называются касательными напряжениями
.
Чтобы легко различать нормальные и касательные напряжения обычно применяют другие обозначения: — нормальное напряжение, — касательное.
Выделим из тела, находящегося под действием внешних сил, бесконечно малый параллелепипед, грани которого параллельны координатным плоскостям, а ребра имеют длину . На каждой грани такого элементарного параллелепипеда действуют по три составляющие напряжения, параллельные координатным осям. Всего на шести гранях получим 18 составляющих напряжений.
Всего на шести гранях получим 18 составляющих напряжений.
Нормальные напряжения обозначаются в виде , где индекс обозначает нормаль к соответствующей грани (т.е. может принимать значения ). Касательные напряжения имеют вид ; здесь первый индекс соответствует нормали к той площадке, на которой действует данное касательное напряжение, а второй указывает ось, параллельно которой это напряжение направлено (рис.3.1).
Рис.3.1. Нормальные и касательные напряжения
Для этих напряжений принято следующее правило знаков
. Нормальное напряжение
считается положительным при растяжении, или, что то же самое, когда оно совпадает с направлением внешней нормали к площадке, на которой действует. Касательное напряжение
считается положительным, если на площадке, нормаль к которой совпадает с направлением параллельной ей координатной оси, оно направлено в сторону соответствующей этому напряжению положительной координатной оси.
Составляющие напряжений являются функциями трех координат. Например, нормальное напряжение в точке с координатами можно обозначать
Например, нормальное напряжение в точке с координатами можно обозначать
В точке, которая отстоит от рассматриваемой на бесконечно малом расстоянии, напряжение с точностью до бесконечно малых первого порядка можно разложить в ряд Тейлора:
Для площадок, которые параллельны плоскости изменяется только координата х
, а приращения Поэтому на грани параллелепипеда, совпадающей с плоскостью нормальное напряжение будет , а на параллельной грани, отстоящей на бесконечно малом расстоянии , — Напряжения на остальных параллельных гранях параллелепипеда связаны аналогичным образом. Следовательно, из 18 составляющих напряжения неизвестными являются только девять.
В теории упругости доказывается закон парности касательных напряжений
, согласно которому по двум взаимно перпендикулярным площадкам составляющие касательных напряжений, перпендикулярные линии пересечения этих площадок, равны друг другу:
Можно показать, что напряжения (3.3) не просто характеризуют напряженное состояние тела в данной точке, но определяют его однозначно. Совокупность этих напряжений образует симметричную матрицу, которая называется тензором напряжений
Совокупность этих напряжений образует симметричную матрицу, которая называется тензором напряжений
:
| (3.4) |
Так как в каждой точке будет свой тензор напряжений, то в теле имеется поле
тензоров напряжений.
При умножении тензора на скалярную величину получится новый тензор, все компоненты которого в раз больше компонентов исходного тензора.
Напряжение есть вектор и как всякий вектор может быть представлен нормальной (по отношению к площадке) и касательной составляющими (рис. 2.3). Нормальную составляющую вектора напряжений будем обозначать касательную . Экспериментальными исследованиями установлено, что влияние нормальных и касательных напряжений на прочность материала различно, и потому в дальнейшем окажется необходимым всегда раздельно рассматривать составляющие вектора напряжений.
Рис. 2.3. Нормальное и касательное напряжения в площадке
Рис. 2.4. Касательное напряжение при срезе болта
При растяжении болта (см.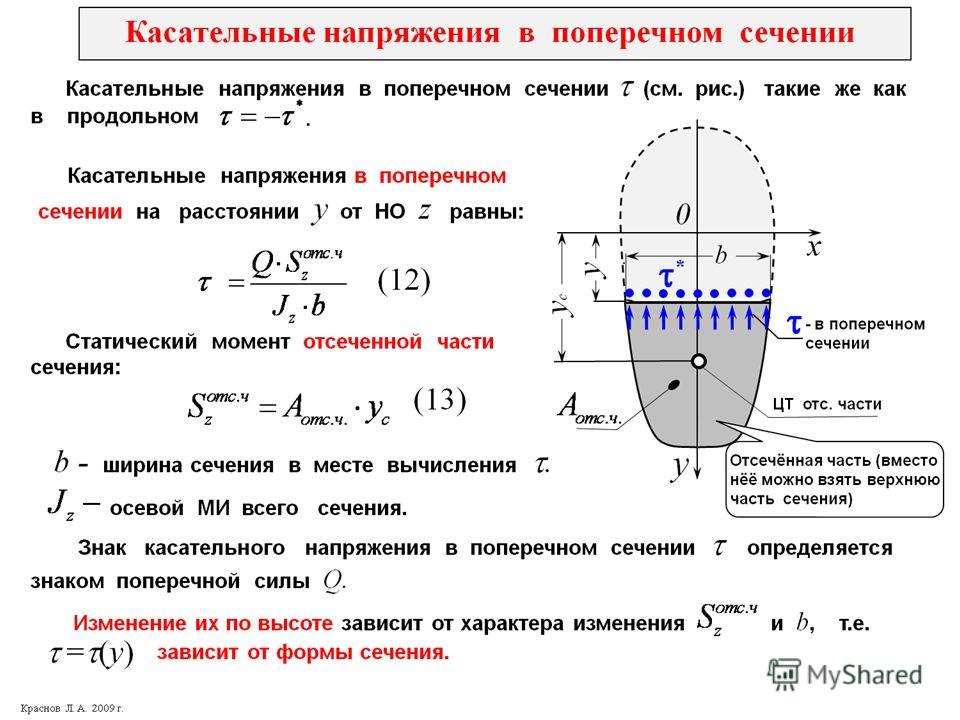 рис. 2.2) в поперечном сечении действует нормальное напряжение
рис. 2.2) в поперечном сечении действует нормальное напряжение
При работе болта на срез (рис. 2.4) в сеченйи П должно возникать усилие, уравновешивающее усилие .
Из условий равновесия следует, что
В действительности последнее соотношение определяет некоторое среднее напряжение по сечению, которым иногда пользуются для приближенных оценок прочности. На рис. 2.4 показан вид болта после воздействия значительных усилий. Началось разрушение болта, и одна его половина сместилась относительно другой: произошла деформация сдвига или среза.
Примеры определения напряжений в элементах конструкций.
Разберем простейшие примеры, в которых предположение о равномерном распределении напряжений, можно считать практически приемлемым. В таких случаях величины напряжений определяются с помощью метода сечений из уравнений статики (уравнений равновесия).
Кручение тонкостенного круглого вала.
Тонкостенный круглый вал (труба) передает крутящий момент (например, от авиационного двигателя на воздушный винт). Требуется определить напряжения в поперечном сечении вала (рис. 2.5, а). Проведем плоскость сечения П перпендикулярно оси вала и рассмотрим равновесие отсеченной части (рис. 2.5, б).
Требуется определить напряжения в поперечном сечении вала (рис. 2.5, а). Проведем плоскость сечения П перпендикулярно оси вала и рассмотрим равновесие отсеченной части (рис. 2.5, б).
Рис. 2.5. Кручение тонкостенного круглого вала
Из условия осевой симметрии, учитывая малую толщину стенки можно принять, что напряжения во всех точках поперечного сечения одинаковы.
Строго говоря, такое предположение справедливо только при очень малой толщине стенки, но в практических расчетах его используют, если толщина стенки
где — средний радиус сечения.
Внешние силы, приложенные к отсеченной части вала, сводятся только к крутящему моменту, и потому нормальные напряжения в поперечном сечении должны отсутствовать. Крутящий момент уравновешивается касательными напряжениями, момент которых равен
Из последнего соотношения находим касательное напряжение в сечении вала:
Напряжения в тонкостенном цилиндрическом сосуде (трубе).
В тонкостенном цилиндрическом сосуде действует давление (рис. 2.6, а).
2.6, а).
Проведем сечение плоскостью П, перпендикулярной оси цилиндрической оболочки, и рассмотрим равновесие отсеченной части. Давление, действующее на крышку сосуда, создает усилив
Это усилие уравновешивается силами, возникающими в поперечном сечении оболочки, и интенсивность — указанных сил — напряжение — будет равна
Толщина оболочки 5 предполагается малой по сравнению со средним радиусом , напряжения считаются равномерно распределенными во всех точках поперечного сечения (рис. 2.6, б).
Однако на материал трубы действуют не только напряжения в продольном направлении, но и окружные (или кольцевые) напряжения в перпендикулярном направлении. Для их выявления выделим двумя сечениями кольцо длиной I (рис. 2.7), а затем проведем диаметральное сечение, отделяющее половину кольца.
На рис. 2.7, а показаны напряжения на поверхностях сечения. На внутреннюю поверхность трубы радиусом действует давление
Рис. 2.8. Трещина в цилиндрической оболочке при действии разрушающего внутреннего давления
| |||||
| ✎ New thread | Private message | Name | Date | |||
| 12.2021 18:44:53″>4 | 41 | полуОФФ: это русский язык или куда? | Erdferkel | 27.12.2021 | 17:51 |
| 3 | 122 | Power of Attorney Israel | VladZaz | 25.12.2021 | 18:34 |
| 36 | 942 | About little snowflake | 1 2 3 all | Маруся-мари | 2.12.2016 | 21:58 |
| 18 | 1135 | OFF: Language Сепира в переводе на русский 1934 г. | qp | 2. 05.2012 05.2012 | 16:30 |
| 4 | 44 | Marketing Personal Proactive Products AND response products | Robot16504 | 27.12.2021 | 14:18 |
| 8 | 239 | OFF: Shotgun Parts | mahavishnu | 25.12.2021 | 14:53 |
| 2 | 106 | stand-up dude | temperevelas | 26.12.2021 | 22:21 |
| 13 | 764 | Практика перевода | Valentina1992 | 13. 12.2021 12.2021 | 15:51 |
| 6 | 88 | cribing loss and debris | amateur-1 | 26.12.2021 | 18:09 |
| 10 | 185 | На войне как на войне | nataliagrina | 26.12.2021 | 17:09 |
| 2 | 64 | A recess or excess in weld cap — тема УЗК | FHGI | 26.12.2021 | 8:16 |
| 35 | 2021 15:16:36″>1217 | Мультитран снова заработал??? | maricom | 23.12.2021 | 21:45 |
| 2 | 105 | Название онкологического заболевания | ochernen | 25.12.2021 | 18:43 |
| 772 | 14002 | Ошибки в словаре | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 all | 4uzhoj | 23.02.2021 | 13:36 |
| 9 | 111 | legal scan | maricom | 25.12.2021 | 16:23 |
| 12.2021 10:28:09″>614 | 19769 | Проблемы в работе нового сайта | 1 2 3 4 5 6 7 8 9 10 11 12 13 all | 4uzhoj | 15.05.2019 | 11:05 |
| 5 | 114 | encoded technique — тема УЗК | FHGI | 24.12.2021 | 5:47 |
| 7 | 643 | ОФФ вирусные ветки? | leka11 | 8.12.2021 | 11:10 |
| 68 | 10594 | OFF:клише для учителя английского | 1 2 all | think_over | 3. 12.2006 12.2006 | 21:30 |
| 7 | 136 | formal studies | athlonusm | 24.12.2021 | 16:56 |
| 82 | 1840 | Транскрипция | 1 2 3 all | aksa | 12.11.2021 | 23:21 |
| 24 | 917 | Спасибо,что живой | andreon | 23.12.2021 | 21:58 |
| 298 | 10514 | Предложения и вопросы по работе нового сайта | 1 2 3 4 5 6 7 8 all | 4uzhoj | 15. 05.2019 05.2019 | 11:02 |
| 6 | 146 | Габитоскопия | Dimking | 20.12.2021 | 21:02 |
| 53 | 7032 | OFF: системы автоматического перевода | 1 2 all | ttimakina | 20.11.2012 | 18:25 |
| 2 | 244 | Average и Mean — как еще перевести, кроме как «среднее»? | Lidia P. | 18.12.2021 | 23:40 |
| 4 | 153 | maximum velocity spectrum wave | adelaida | 14. 12.2021 12.2021 | 23:51 |
| 5 | 96 | Деталь криогенного насоса | Chuk | 20.12.2021 | 20:57 |
В чем разница между кВт и кВа?
В разделе «Справочная информация» содержатся пояснения о различных терминах, используемых при описании технических характеристик оборудования, которые неподготовленному человеку бывает нелегко понять.
Различия «кВА» и «кВт»
Зачастую, в прайсах различных производителей электрическая мощность оборудования указывается не в привычных киловаттах (кВт), а в «загадочных» кВА (киловольт-амперах). Как же понять потребителю сколько «кВА» ему нужно?
Существует понятие активной (измеряется в кВт) и полной мощности (измеряется в кВА).
Полная мощность переменного тока есть произведение действующего значения силы тока в цепи и действующего значения напряжения на её концах. Полную мощность есть смысл назвать «кажущейся»,так как эта мощность может не вся участвовать в совершении работы. Полная мощность — это мощность передаваемая источником, при этом часть её преобразуется в тепло или совершает работу (активная мощность), другая часть передаётся электромагнитным полям цепи — эта составляющая учитывается введением т.н. реактивной мощности.
Полную мощность есть смысл назвать «кажущейся»,так как эта мощность может не вся участвовать в совершении работы. Полная мощность — это мощность передаваемая источником, при этом часть её преобразуется в тепло или совершает работу (активная мощность), другая часть передаётся электромагнитным полям цепи — эта составляющая учитывается введением т.н. реактивной мощности.
Полная и активная мощность — разные физические величины, имеющие размерность мощности. Для того, чтобы на маркировках различных электроприборов или в технической документации не требовалось лишний раз указывать, о какой мощности идёт речь, и при этом не спутать эти физические величины, в качестве единицы измерения полной мощности используют вольт-ампер вместо ватта.
Если рассматривать практическое значение полной мощности, то это величина, описывающая нагрузки, реально налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи, генераторные установки…), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Отношение активной мощности к полной мощности цепи называется коэффициентом мощности.
Коэффициент мощности (cos фи) есть безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Численно коэффициент мощности равен косинусу этого фазового сдвига.
Значения коэффициента мощности:
|
1.00
|
идеальный показатель
|
|
0.95
|
хорошее значение
|
|
0.90
|
удовлетворительное значение
|
|
0.
|
плохое значение
|
Большинство производителей определяют потребляемую мощность своего оборудования в Ваттах.
В случае, если потребитель не имеет реактивной мощности (нагревательные приборы – такие как чайник, кипятильник, лампа накаливания, ТЭН), информация о коэффициенте мощности неактуальна, в виду того, что он равен единице. То есть в таком случае полная мощность, потребляемая прибором и необходимая для его эксплуатации, равна активной мощности в Ваттах.
P = I*U*Сos (fi) →
P = I*U*1 →
P=I*U
Пример: В паспорте электрического чайника указана потребляемая мощность – 2 кВт. Это значит, что и полная мощность, необходимая для успешного функционирования прибора, составит 2 кВА.
Если же потребителем является прибор, имеющий в своем составе реактивное сопротивление (емкость, индуктивность), в технических данных всегда указывается мощность в Ваттах и значение коэффициента мощности для данного прибора. Это значение определяется параметрами самого прибора, а конкретно – соотношением его активных и реактивных сопротивлений.
Это значение определяется параметрами самого прибора, а конкретно – соотношением его активных и реактивных сопротивлений.
Пример: В техническом паспорте перфоратора указана потребляемая мощность – 5 кВт и коэффициент мощности (Сos(fi)) – 0.85. Это значит, что полная мощность, необходимая для его работы, составит
Pполн.= Pакт./Cos(fi)
Pполн.= 5/0.85= 5,89 кВА
При выборе генераторной установки часто возникает резонный вопрос – «Сколько же мощности она все-таки сможет выдать?». Это обусловлено тем, что в характеристиках генераторных установок указывается полная мощность в кВА. Ответом на этот вопрос и служит данная статья.
Пример: Генераторная установка мощностью 100 кВА. Если потребители будут иметь только активное сопротивление, то кВА=кВт. Если также будет присутствовать и реактивная составляющая, то надо учитывать коэффициент мощности нагрузки.
Именно поэтому в характеристиках генераторных установок указывается полная мощность в кВА. А уж как Вы ее будете использовать – решать только Вам.
А уж как Вы ее будете использовать – решать только Вам.
Что такое Вольт. Определение Вольта. Формула Вольта
Вольт (обозначение: В, V) — единица измерения электрического напряжения в системе СИ.
1 Вольт равен электрическому напряжению, вызывающему в электрической цепи постоянный ток силой 1 ампер при мощности 1 ватт.
Вольт (В, V) может быть определён либо как электрическое напряжение на концах проводника, необходимое для выделения в нём тепла мощностью в один ватт (Вт, W) при силе протекающего через этот проводник постоянного тока в один ампер (A), либо как разность потенциалов между двумя точками электростатического поля, при прохождении которой над зарядом величиной 1 кулон (Кл, C) совершается работа величиной 1 джоуль (Дж, J). Выраженный через основные единицы системы СИ, один вольт равен м2 · кг · с−3 · A−1.
\[ \mbox{V} = \dfrac{\mbox{W}}{\mbox{A}} = \dfrac{\mbox{J}}{\mbox{C}} = \dfrac{\mbox{m}^2 \cdot \mbox{kg}}{\mbox{s}^{3} \cdot \mbox{A}} \]
Единица названа в честь итальянского физика и физиолога Алессандро Вольта.
Этим методом величина вольта однозначно связывается с эталоном частоты, задаваемым цезиевыми часами: при облучении матрицы, состоящей из нескольких тысяч джозефсоновских переходов, микроволновым излучением на частотах от 10 до 80 ГГц, возникает вполне определённое электрическое напряжение, с помощью которого калибруются вольтметры. Эксперименты показали, что этот метод нечувствителен к конкретной реализации установки и не требует введения поправочных коэффициентов.
1 В = 1/300 ед. потенциала СГСЭ.
Что такое Вольт. Определение
Вольт определён как разница потенциалов на концах проводника, рассеивающего мощность в один ватт при силе тока через этот проводник в один ампер.
Отсюда, базируясь на единицах СИ, получим м² · кг · с-3 · A-1, что эквивалентно джоулю энергии на кулон заряда, J/C.
Определение на основе эффекта Джозефсона
Напряжение электрического тока – это величина, характеризующая разность зарядов (потенциалов) между полюсами либо участками цепи, по которой идет ток.
С 1990 года вольт стандартизирован посредством измерения с использованием нестационарного эффекта Джозефсона, при котором используется в качестве привязки к эталону константа Джозефсона, зафиксированная 18-ой Генеральной конференцией по весам и измерениям как:
K{J-90} = 0,4835979 ГГц/мкВ.
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы вольт пишется со строчной буквы, а её обозначение — с прописной. Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием вольта. Например, обозначение единицы измерения напряжённости электрического поля «вольт на метр» записывается как В/м.
Шкала напряжений
- Разность потенциалов на мембране нейрона — 70 мВ.
- NiCd аккумулятор — 1.
 2 В.
2 В. - Щелочной элемент — 1.5 В.
- Литий-железо-фосфатный аккумулятор (LiFePO4) — 3.3 В.
- Батарейка «Крона» — 9 В.
- Автомобильный аккумулятор — 12 В (для тяжёлых грузовиков — 24 В).
- Напряжение бытовой сети — 220 В (среднеквадратичное).
- Напряжение в контактной сети трамвая, троллейбуса — 600 В.
- Электрифицированные железные дороги — 3 кВ (постоянный ток), 25 кВ (переменный ток).
- Магистральные ЛЭП — 110 кВ, 220 кВ.
- Максимальное напряжение на ЛЭП (Экибастуз-Кокчетав) — 1.15 МВ.
- Самое высокое постоянное напряжение, полученное в лаборатории на пеллетроне — 25 МВ.
- Молния — от 100 МВ и выше.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Напряжение: что это такое? (Определение, формула и способ измерения разницы потенциалов)
Что такое напряжение?
Напряжение (также известное как разность электрических потенциалов, ЭДС электродвижущей силы, электрическое давление или электрическое напряжение) определяется как разность электрических потенциалов на единицу заряда между двумя точками в электрическом поле. Напряжение выражается математически (например, в формулах) с помощью символа «V» или «E».
Напряжение выражается математически (например, в формулах) с помощью символа «V» или «E».
Если вы ищете более интуитивное объяснение, помогающее объяснить, что такое напряжение, перейдите к этому разделу статьи.
В противном случае мы продолжим ниже с более формальным определением напряжения.
В статическом электрическом поле работа, необходимая для перемещения единицы заряда между двумя точками, известна как напряжение. Математически напряжение может быть выражено как
, где проделанная работа выражается в джоулях, а заряд — в кулонах.
Мы можем определить напряжение как количество потенциальной энергии между двумя точками в цепи.
Одна точка имеет более высокий потенциал, а другая точка имеет более низкий потенциал.Разница в заряде между более высоким и более низким потенциалами называется разностью напряжений или потенциалов.
Напряжение или разность потенциалов заставляют электроны проходить через цепь.
Чем выше напряжение, тем больше сила и, следовательно, тем больше электронов проходит через цепь. Без напряжения или разности потенциалов электроны беспорядочно перемещались бы в свободном пространстве.
Без напряжения или разности потенциалов электроны беспорядочно перемещались бы в свободном пространстве.
Напряжение также известно как электрическое напряжение. Например, допустимая нагрузка на напряжение таких кабелей, как 1 кВ, 11 кВ, 33 кВ, называется кабелями низкого, высокого и сверхвысокого напряжения соответственно.
Определение разности потенциалов как потенциала электрического поля
Как уже упоминалось, напряжение определяется как разность электрических потенциалов на единицу заряда между двумя точками в электрическом поле. Опишем это с помощью уравнений.
Рассмотрим две точки A и B.
Потенциал точки A относительно точки B определяется как работа, совершаемая при перемещении a на единицу заряда из точки A в B в присутствии электрического поля E.
Математически, это может быть выражено как,
Это также разность потенциалов между точками A и B с точкой B в качестве контрольной точки.Его также можно выразить как:
. Понятие напряжения может быть довольно сложным для концептуального понимания.
Понятие напряжения может быть довольно сложным для концептуального понимания.
Итак, мы будем использовать аналогию с чем-то осязаемым — чем-то из реального мира — чтобы облегчить понимание напряжения.
Понятие напряжения по аналогии
«Гидравлическая аналогия» — распространенная аналогия, используемая для объяснения напряжения.
В гидравлической аналогии:
- Напряжение или электрический потенциал эквивалентны гидравлическому давлению воды
- Электрический ток эквивалентен расходу гидравлической воды
- Электрический заряд эквивалентен количеству воды
- Электрический проводник эквивалентен к трубе
Аналогия 1
Рассмотрим резервуар для воды, показанный на рисунке ниже.На рисунке (а) показаны два резервуара, наполненные одинаковым уровнем воды. Таким образом, вода не может перетекать из одного резервуара в другой из-за отсутствия разницы давлений. Гидравлическая аналогия 1
На рисунке (b) показаны два резервуара, заполненные разными уровнями воды. Следовательно, между этими двумя резервуарами существует некоторая разница давлений. Таким образом, вода будет перетекать из одного резервуара в другой до тех пор, пока уровень воды в обоих резервуарах не станет одинаковым.
Следовательно, между этими двумя резервуарами существует некоторая разница давлений. Таким образом, вода будет перетекать из одного резервуара в другой до тех пор, пока уровень воды в обоих резервуарах не станет одинаковым.
Точно так же, если мы соединим две батареи проводом с разными уровнями напряжения, тогда заряды могут перетекать от батареи с более высоким потенциалом к батарее с более низким потенциалом.Следовательно, батарея с более низким потенциалом заряжается до тех пор, пока потенциал обеих батарей не станет одинаковым.
Аналогия 2
Рассмотрим резервуар для воды, расположенный на определенной высоте над землей. На дне резервуара находится шланг, как показано на рисунке ниже.
Гидравлическая аналогия 2
Давление воды на конце шланга эквивалентно напряжению или разности потенциалов в электрической цепи. Вода в баке эквивалентна электрическому заряду. Теперь, если мы увеличим количество воды в баке, на конце шланга будет создаваться большее давление.
И наоборот, если мы сливаем определенное количество воды из бака, то давление, создаваемое на конце шланга, уменьшится. Можно принять этот резервуар для воды как аккумуляторную батарею. Когда напряжение батареи уменьшается, лампы тускнеют.
Аналогия 3
Давайте разберемся, как можно выполнять работу с помощью напряжения или разности потенциалов в электрической цепи. Простая аналогия между гидравлическим водяным контуром и электрической цепью показана на рисунке ниже.
Рабочая аналогия гидравлического и электрического контура
Как показано в гидравлическом водяном контуре, вода течет по трубе, приводимой в действие механическим насосом. Труба эквивалентна проводящему проводу в электрической цепи.
Теперь, если механический насос создает разницу давлений между двумя точками, то вода под давлением сможет выполнять работу, например приводить в движение турбину.
Точно так же в электрической цепи разность потенциалов батареи может вызывать прохождение тока через проводник, следовательно, работа может выполняться посредством протекания электрического тока, например, зажигания лампы.
В чем измеряется напряжение (единицы напряжения)?
Единица измерения напряжения в системе СИ
Единица измерения напряжения в системе СИ — вольты. Это представлено в В. Вольт — производная единица измерения напряжения в системе СИ. Итальянский физик Алессандро Вольта (1745-1827) изобрел гальваническую батарею, которая была первой электрической батареей, поэтому в честь них названа единица вольт.
Вольт в базовых единицах СИ
Вольт можно определить как разность электрических потенциалов между двумя точками в электрической цепи, которая рассеивает один джоуль энергии на кулон заряда, проходящего через электрическую цепь.Математически это может быть выражено как,
Следовательно, вольт может быть выражен в основных единицах СИ как или.
Его также можно измерить в ваттах на ампер или в ампер-единицах в омах.
Формула напряжения
Основная формула напряжения показана на изображении ниже.
Треугольник формулы напряжения
Формула напряжения 1 (закон Ома)
В соответствии с законом Ома напряжение можно выразить как:
Пример 1
Как показано на схеме ниже, через сопротивление 15 Ом. Определите падение напряжения в цепи.
Определите падение напряжения в цепи.
Решение:
Заданные данные: ,
Согласно закону Ома,
Таким образом, используя уравнение, мы получаем падение напряжения в цепи 60 Вольт.
Формула напряжения 2 (мощность и ток)
Передаваемая мощность является произведением напряжения питания и электрического тока.
Теперь, подставив приведенное выше уравнение, мы получим
(1)
Таким образом, мы получаем, что напряжение равно мощности, деленной на ток.Математически
Пример 2
Как показано на схеме ниже, через лампу мощностью 48 Вт протекает ток 2 А. Определите напряжение питания.
Решение:
Данные данные: ,
Согласно формуле,
Таким образом, используя уравнение, мы получаем напряжение питания 24 Вольт.
Формула напряжения 3 (мощность и сопротивление)
Согласно уравнению (1), напряжение является квадратным корнем из произведения мощности и сопротивления.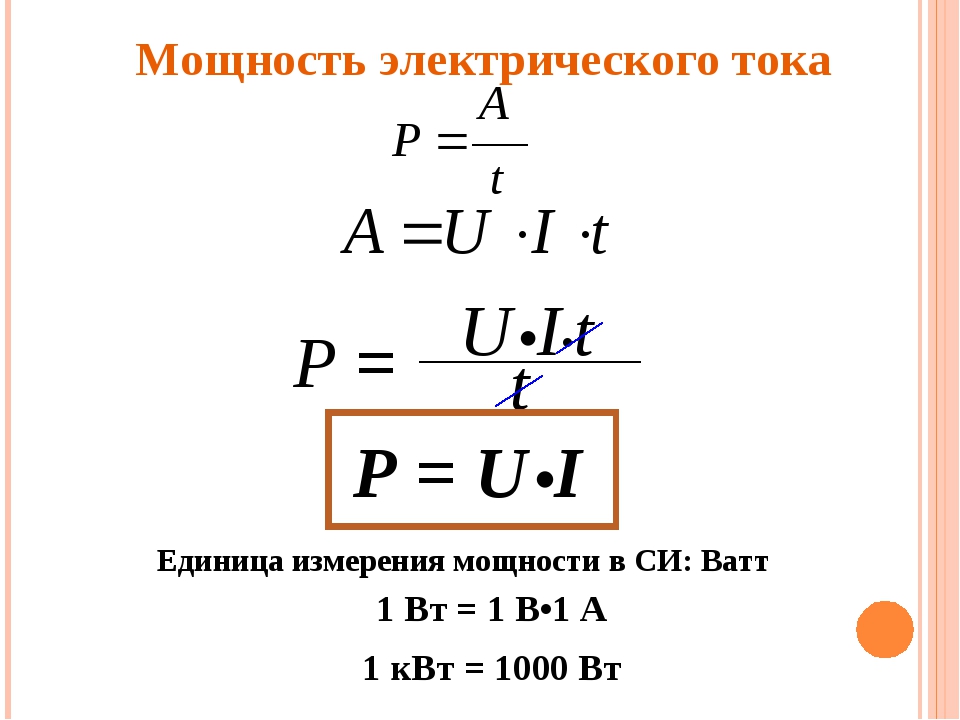 Математически
Математически
Пример 3
Как показано на схеме ниже, определите необходимое напряжение для зажигания лампы мощностью 5 Вт с сопротивлением току 2 Ом.
Решение:
Данные данные:,
По формуле,
Таким образом, используя уравнение, мы получаем необходимое напряжение для накаливания лампы 3,16 Вольт.
Символ цепи напряжения (переменного и постоянного тока)
Символ постоянного и переменного напряжения показан на изображении ниже.
Символ напряжения переменного тока
Символ напряжения переменного тока
Символ напряжения постоянного тока
Символ напряжения постоянного тока
Размеры напряжения
Напряжение (В) — это представление электрической потенциальной энергии на единицу заряда. ]
Параметры напряжения могут быть выражены через массу (M), длину (L), время (T) и ампер (A), как.
Обратите внимание, что некоторые также используют I вместо A для представления тока. В этом случае измерение напряжения может быть представлено как.
В этом случае измерение напряжения может быть представлено как.
Как измерить напряжение
В электрических и электронных схемах измерение напряжения является важным параметром, который необходимо измерять. Мы можем измерить напряжение между определенной точкой и землей или нулевой линией в цепи.
В трехфазной цепи, если мы измеряем напряжение между любой из одной фазы от трехфазной до нейтральной точки, то это называется напряжением между фазой и землей.
Точно так же, если мы измеряем напряжение между любыми двумя фазами из 3-х фазного, то оно называется линейным напряжением.
Для измерения напряжения используются различные инструменты. Давайте обсудим это по очереди.
Метод вольтметра
Напряжение между двумя точками в системе можно измерить с помощью вольтметра. Для измерения напряжения вольтметр должен быть подключен параллельно к компоненту, напряжение которого необходимо измерить.
Один вывод вольтметра должен быть подключен к первой точке, а другой — ко второй. Учтите, что вольтметр никогда не следует подключать последовательно.
Учтите, что вольтметр никогда не следует подключать последовательно.
Вольтметр
также можно использовать для измерения падения напряжения на любом компоненте или суммы падений напряжения на двух или более компонентах в цепи. На изображении ниже показано подключение вольтметра для измерения напряжения на резисторе.
Подключение напряжения для измерения напряжения на резисторе
Аналоговый вольтметр работает путем измерения тока через постоянный резистор. Теперь, согласно закону Ома, ток через резистор прямо пропорционален напряжению или разности потенциалов на фиксированном резисторе.Таким образом, мы можем определить неизвестное напряжение.
Другой пример подключения вольтметра для измерения напряжения на батарее 9 В показан на рисунке ниже.
Подключение вольтметра для измерения напряжения батареи
Метод мультиметра
В настоящее время одним из наиболее распространенных методов измерения напряжения является использование мультиметра. Мультиметр может быть аналоговым или цифровым, но чаще всего используются цифровые мультиметры из-за более высокой точности и низкой стоимости.
Напряжение или разность потенциалов на любом оборудовании можно просто измерить, подключив щупы мультиметра к двум точкам измерения напряжения. Измерение напряжения батареи с помощью мультиметра показано на изображении ниже.
Мультиметр для измерения напряжения батареи
Метод потенциометра
Потенциометр работает по принципу метода нулевого баланса. Он измеряет напряжение путем сравнения неизвестного напряжения с известным опорным напряжением.Схема потенциометра для измерения напряжения показана на рисунке ниже.
Схема потенциометра для измерения неизвестного напряжения
Другие инструменты, такие как осциллограф, электростатический вольтметр, также могут использоваться для измерения напряжения.
Разница между напряжением и током (напряжение по отношению к току)
Основное различие между напряжением и током состоит в том, что напряжение — это разность потенциалов электрических зарядов между двумя точками в электрическом поле, тогда как ток — это поток электрических зарядов от одна точка в другую точку в электрическом поле.
Мы можем просто сказать, что напряжение является причиной протекания тока, тогда как ток — это эффект напряжения.
Чем выше напряжение, тем больше ток проходит между двумя точками. Обратите внимание: если две точки в цепи имеют одинаковый потенциал, ток не может течь. Величины напряжения и тока зависят друг от друга.
Другие различия между напряжением и током обсуждаются в таблице ниже. Разница между напряжением и током
Разница между напряжением и разностью потенциалов (напряжение и разность потенциалов)
Между напряжением и разностью потенциалов нет большой разницы.Но мы можем описать разницу между ними следующим образом.
Напряжение — это количество энергии, необходимое для перемещения единичного заряда между двумя точками, тогда как разность потенциалов — это разница между более высоким потенциалом одной точки и более низким потенциалом другой точки.
Из-за точечного заряда:
Напряжение — это потенциал, полученный в некоторой точке с учетом другой опорной точки, находящейся на бесконечности. В то время как разность потенциалов — это разница потенциалов между двумя точками на конечных расстояниях от заряда.Математически они могут быть выражены как:
В то время как разность потенциалов — это разница потенциалов между двумя точками на конечных расстояниях от заряда.Математически они могут быть выражены как:
Если вы предпочитаете видео с объяснением напряжения, посмотрите видео ниже:
Что такое общее напряжение?
Общее напряжение определяется как типичный уровень напряжения или номинальные значения электрического устройства или оборудования.
Список общих напряжений для различных электрических устройств или оборудования приведен ниже.
- Свинцово-кислотные батареи, используемые в электромобилях: 12 В постоянного тока.Батарея 12 В состоит из 6 ячеек с общим напряжением каждой ячейки 2,1 В.
 Обратите внимание, что элементы соединены последовательно для увеличения номинального напряжения.
Обратите внимание, что элементы соединены последовательно для увеличения номинального напряжения. - USB: 5 В постоянного тока.
- ЛЭП высокого напряжения: от 110 кВ до 1200 кВ переменного тока.
- Высокоскоростные поезда (тяговые) ЛЭП: 12 кВ и 50 кВ переменного тока или 0,75 кВ и 3 кВ постоянного тока.
- Источник питания TTL / CMOS: 5 Вольт.
- Одноэлементная перезаряжаемая никель-кадмиевая батарея: 1,2 В.
- Батарейки фонарика: 1.5 Вольт постоянного тока.
Обычное напряжение, поставляемое распределительной компанией бытовым потребителям, составляет
- 100 В, однофазный переменный ток в Японии
- 120 В, однофазный переменный ток в Америке
- 230 В, однофазный переменный ток в Индии, Австралия
Обычное напряжение, поставляемое распределительной компанией промышленным потребителям:
- 200 В, трехфазный переменный ток в Японии
- 480 В, трехфазный переменный ток в Америке
- 415 В, трехфазный переменный ток в Индии
Приложения напряжения
Некоторые из приложений напряжения включают:
- Одним из наиболее распространенных приложений напряжения является определение падения напряжения на электрическом устройстве или оборудовании, таком как резистор.

- Для увеличения номинального напряжения требуется добавление напряжения. Следовательно, ячейки подключаются последовательно для увеличения номинального напряжения.
- Напряжение является основным источником энергии любого электрического и электронного оборудования. От малого напряжения, например, 5 В до высокого напряжения 415 В. используются в различных приложениях.
- Низкое напряжение обычно используется для многих электронных устройств и приложений управления.
- Высокое напряжение используется для
- Электростатическая печать, Электростатическая окраска, Электростатическое покрытие материала
- Космологическое исследование космоса
- Электростатический осадитель (контроль загрязнения воздуха)
- Лаборатория реактивного движения
- Рентгеновские трубки
- Усилитель высокой мощности вакуумные трубки
- Масс-спектроскопия
- Тестирование диэлектрика
- Тестирование продуктов питания и напитков
- Электрораспыление и прядение, электрофотография
- Применение на основе плазмы
- Датчик уровня
- Индукционный нагрев
- Фотовспышки
- SONAR и т.
 д.…
д.…
Каковы размеры напряжения с точки зрения массового класса 11, физика CBSE
Подсказка: В этом вопросе напишите формулу напряжения в терминах силы, смещения и заряда, чтобы вычислить размеры напряжения, а затем используйте размерная формула силы, смещения и заряда для расчета размеров напряжения.
Напряжение в электрическом поле определяется как изменение потенциальной энергии единичного положительного заряда при перемещении из одной точки в другую.
Используемая формула:
$ \ Delta V \ text {=} \ dfrac {W} {q} $, $ W = \ overrightarrow {F}. \ Text {} \ overrightarrow {d} $ и $ V = \ dfrac {\ overrightarrow {F.} \ text {} \ overrightarrow {d}} {q} $
Полный пошаговый ответ:
Мы уже знаем, что разность потенциалов или напряжение в электрическом поле — это работа, которую необходимо проделать над положительным зарядом единицы, чтобы переместить ее из одной точки в другую. Математически это можно записать так:
$ \ Delta V \ text {=} \ dfrac {W} {q} $
Где
$ \ Delta V = Voltage $
$ W = \ text {Работа выполнена} $
$ q = \ text {charge} $
Мы также знаем, что работа считается выполненной, когда сила, приложенная к объекту, перемещает его. {- 2}} $].{\ text {-1}}} \ text {} \! \!] \! \! \ text {} $
{- 2}} $].{\ text {-1}}} \ text {} \! \!] \! \! \ text {} $
Итак, правильный ответ — «Вариант D».
Примечание: Измерения любой физической величины — это выражения, показывающие степени, до которых должны быть увеличены основные единицы, чтобы получить производную единицу величины. Размеры очень полезны при преобразовании единиц измерения. Есть семь фундаментальных физических величин. Студенты должны постараться запомнить основные фундаментальные величины и их размерные формулы.
Какая величина напряжения? — AnswersToAll
Какая величина напряжения?
Напряжение определяется как работа, выполненная на единицу заряда.V = Wq. Теперь W = f × d. Размерность силы = [M1L1T − 2]
Как найти размерную формулу потенциала V?
Подсказка: Формулу размерности электрического потенциала можно найти, используя измерения энергии и заряда, поскольку электрический потенциал — это работа, совершаемая на единицу заряда. Математически $ V = \ dfrac {W} {q} $, где V — электрический потенциал, W — работа, совершаемая электрическим полем над зарядом, а q — заряд.
Математически $ V = \ dfrac {W} {q} $, где V — электрический потенциал, W — работа, совершаемая электрическим полем над зарядом, а q — заряд.
Какова размерная формула заряда?
Размерная формула заряда [q] = [IT].
Что такое размерная формула?
Подсказка — Формула измерения — это выражение единицы физической величины через фундаментальные величины. Основными величинами являются масса (M), длина (L) и время (T). Формула размеров выражается в единицах мощности M, L и T.
Какова размерная формула ампера?
Что такое размерная формула всех фундаментальных физических величин (основных величин)?
| Фундаментальные физические величины | Блок СИ | Размерная формула |
|---|---|---|
| Температура | кельвин | M0L0T0θ или M0L0T0K1 |
| Электрический ток | ампер | M0L0T0A1 |
| Сила света | кандел | M0L0T0Cd1 |
| Количество вещества | моль | M0L0T0mol1 |
Что такое размерная формула разности потенциалов?
Следовательно, разность потенциалов размерно представлена как [M1 L2 T-3 I-1].
Какая размерная формула потенциала?
Следовательно, потенциальная энергия размерно представлена как [M1 L2 T-2].
Что такое размерная формула частоты?
Следовательно, частота размерно представлена как [M0 L0 T-1].
Как рассчитать напряжение?
Закон и мощность Ом
- Чтобы найти напряжение, (В) [V = I x R] V (вольты) = I (амперы) x R (Ω)
- Чтобы найти ток, (I) [I = V ÷ R] I (амперы) = V (вольты) ÷ R (Ω)
- Чтобы найти сопротивление, (R) [R = V ÷ I] R (Ω) = V (вольты) ÷ I (амперы)
- Чтобы найти мощность (P) [P = V x I] P (Вт) = V (вольты) x I (амперы)
Что такое размерная формула сопротивления?
Следовательно, сопротивление размерно представлено как M L2 T-3 I-2.
Какова размерная формула угла?
Угол определяется как отношение длины дуги к радиусу. Подставляя в приведенную выше формулу, получаем Формулу размерности угла = M0L0T0. Мы также можем сказать, что угол — это безразмерная величина.
Измерения напряжения
: практическое руководство — NI
Несмотря на то, что многие датчики выдают напряжение постоянного тока, которое можно измерить с помощью мультиметра или устройства сбора данных, основная задача этого технического документа — изучить общие измерения постоянного тока, не требующие установки промежуточного датчика.
Основы измерения напряжения
Чтобы понять, как измерять напряжения, важно понимать основы того, как вы проводите измерения. По сути, напряжение — это разность электрических потенциалов между двумя интересующими вас точками в электрической цепи. Однако общая путаница заключается в том, как определяется контрольная точка измерения. Контрольная точка измерения — это уровень напряжения, при котором выполняется измерение.
Методы опорных точек
Существует два основных метода измерения напряжений: опорное заземление и дифференциальное.
Измерение опорного напряжения на землю
Один из методов — измерить напряжение относительно общей точки или точки «земли». Часто эти «заземления» стабильны и неизменны и чаще всего составляют около 0 В. Исторически термин «земля» возник из обычного применения, когда потенциал напряжения равен 0 В путем подключения сигнала непосредственно к земле. особенно хороши для канала, который соответствует следующим условиям:
Часто эти «заземления» стабильны и неизменны и чаще всего составляют около 0 В. Исторически термин «земля» возник из обычного применения, когда потенциал напряжения равен 0 В путем подключения сигнала непосредственно к земле. особенно хороши для канала, который соответствует следующим условиям:
- Входной сигнал высокого уровня (более 1 В)
- Длина проводов, соединяющих сигнал с устройством, составляет менее 10 футов (3 м)
- Входной сигнал может иметь общую опорную точку с другими сигналами
Заземление обеспечивается либо устройством, выполняющим измерения, либо измеряемым внешним сигналом.Когда заземление обеспечивается устройством, такая установка называется несимметричным режимом с привязкой к земле (RSE), а когда земля обеспечивается сигналом, такая установка называется несимметричным режимом без привязки (NRSE).
Большинство приборов предлагают аналогичные конфигурации контактов для измерений аналогового входа. Следующий пример демонстрирует этот тип измерения с использованием шасси CompactDAQ и модуля аналогового ввода NI 9205 (см. Рисунок 1).
Рисунок 1).
Рисунок 1.Шасси CompactDAQ с модулем аналогового ввода NI 9205
На рисунке 2 показана схема подключения для измерения напряжения RSE с использованием шасси NI cDAQ-9178 с NI 9205, а также распиновка для модуля. На рисунке 2 контакт 1 соответствует каналу «Аналоговый вход 0», а контакт 17 соответствует общему заземлению.
Рис. 2. Односторонний режим с заземлением
На рисунке 3 показана схема подключения для измерения напряжения NRSE с использованием cDAQ-9178 с NI 9205.На рисунке контакт 1 соответствует каналу «Аналоговый вход 0», а контакт 35 соответствует каналу «Контроль аналогового входа». Этот канал, особенно для измерений NRSE, может обнаруживать напряжение земли, создаваемое сигналом.
Рис. 3. Односторонний режим без ссылки
Измерение дифференциального напряжения
Другой способ измерения напряжения — определение «разности» напряжения между двумя отдельными точками в электрической цепи. Например, чтобы измерить напряжение на одном резисторе, вы измеряете напряжение на обоих концах резистора. Разница между напряжениями — это напряжение на резисторе. Обычно измерения дифференциального напряжения полезны для определения напряжения, которое существует на отдельных элементах схемы, или если источники сигнала зашумлены.
Например, чтобы измерить напряжение на одном резисторе, вы измеряете напряжение на обоих концах резистора. Разница между напряжениями — это напряжение на резисторе. Обычно измерения дифференциального напряжения полезны для определения напряжения, которое существует на отдельных элементах схемы, или если источники сигнала зашумлены.
Дифференциальные входные соединения особенно хорошо подходят для канала, который соответствует любому из следующих условий:
- Входной сигнал низкого уровня (менее 1 В)
- Длина проводов, соединяющих сигнал с устройством, превышает 3 м (10 футов)
- Входной сигнал требует отдельной опорной точки заземления или обратного сигнала
- Сигнальные провода проходят через шумную среду
На рисунке 4 показана схема подключения для измерения дифференциального напряжения с использованием cDAQ-9178 с NI 9205.На рисунке контакт 1 соответствует каналу «Аналоговый вход 0», а контакт 19 соответствует каналу «Аналоговый вход 8».
В дифференциальном режиме отрицательный сигнал подключается к аналоговому выводу, обращенному непосредственно к аналоговому каналу, который подключен к положительному сигналу. Например, «Аналоговый вход 0» будет подключен к положительному сигналу, «Аналоговый вход 8» будет подключен к отрицательным сигналам, «Аналоговый вход 1» — к положительному, «Аналоговый вход 9» — к отрицательному и так далее. Недостатком дифференциального режима является то, что он эффективно уменьшает вдвое количество аналоговых входных измерительных каналов.
Рисунок 4. Дифференциальный режим
Типы источников сигналов
Перед настройкой входных каналов и подключением сигналов необходимо определить, являются ли источники сигналов плавающими или заземленными.
Плавающие источники сигналов
Беспотенциальный источник сигнала не подключен к системе заземления здания, но имеет изолированную контрольную точку заземления. Некоторыми примерами плавающих источников сигналов являются выходы трансформаторов, термопар, устройств с батарейным питанием, оптических изоляторов и развязывающих усилителей. Инструмент или устройство с изолированным выходом является источником плавающего сигнала. Заземление плавающего сигнала должно быть подключено к заземлению устройства, чтобы установить местный или бортовой опорный сигнал для сигнала. В противном случае измеренный входной сигнал изменяется, поскольку источник выходит за пределы синфазного входного диапазона.
Инструмент или устройство с изолированным выходом является источником плавающего сигнала. Заземление плавающего сигнала должно быть подключено к заземлению устройства, чтобы установить местный или бортовой опорный сигнал для сигнала. В противном случае измеренный входной сигнал изменяется, поскольку источник выходит за пределы синфазного входного диапазона.
Наземные источники сигналов
Источник сигнала с привязкой к земле подключен к заземлению системы здания, поэтому он уже подключен к общей точке заземления по отношению к устройству, предполагая, что измерительное устройство подключено к той же системе питания, что и источник.К этой категории относятся неизолированные выходы приборов и устройств, которые подключаются к системе электроснабжения здания. Разница в потенциале земли между двумя приборами, подключенными к одной и той же энергосистеме здания, обычно составляет от 1 до 100 мВ, но разница может быть намного выше, если цепи распределения питания подключены неправильно. Если заземленный источник сигнала измерен неправильно, эта разница может проявиться как ошибка измерения. Следуя инструкциям по подключению заземленных источников сигнала, можно устранить разность потенциалов земли из измеряемого сигнала.
Если заземленный источник сигнала измерен неправильно, эта разница может проявиться как ошибка измерения. Следуя инструкциям по подключению заземленных источников сигнала, можно устранить разность потенциалов земли из измеряемого сигнала.
На рис. 5 показаны различные типы источников сигнала, а также оптимальные схемы подключения, основанные на отдельном методе измерения. Обратите внимание, что в зависимости от типа сигнала конкретный метод измерения напряжения может дать лучшие результаты, чем другие.
Рис. 5. Типы обычных источников сигнала и рекомендуемые конфигурации входов
Узнайте больше о полевой проводке и шумах для аналоговых сигналов.
Высоковольтные измерения и изоляция
При измерении более высоких напряжений необходимо учитывать множество факторов.При выборе системы сбора данных первый вопрос, который вы должны задать, — будет ли эта система безопасной. Выполнение измерений высокого напряжения может быть опасным для вашего оборудования, тестируемого устройства и даже для вас и ваших коллег. Чтобы обеспечить безопасность вашей системы, вы должны обеспечить изоляционный барьер между пользователем и опасными напряжениями с изолированными измерительными устройствами.
Чтобы обеспечить безопасность вашей системы, вы должны обеспечить изоляционный барьер между пользователем и опасными напряжениями с изолированными измерительными устройствами.
Изоляция
, средство физического и электрического разделения двух частей измерительного устройства, можно разделить на электрическую и безопасную изоляцию.Электрическая изоляция предназначена для исключения путей заземления между двумя электрическими системами. Обеспечивая электрическую изоляцию, вы можете разорвать контуры заземления, увеличить синфазный диапазон системы сбора данных и сдвинуть опорный сигнал заземления по уровню на единицу заземления системы. Изоляция безопасности ссылается на стандарты, в которых есть особые требования к изоляции людей от контакта с опасным напряжением. Он также характеризует способность электрической системы предотвращать передачу высокого напряжения и переходных напряжений через ее границу в другие электрические системы, с которыми пользователь может контактировать.
Включение изоляции в систему сбора данных выполняет три основные функции: предотвращение контуров заземления, отклонение синфазного напряжения и обеспечение безопасности.
Узнайте больше об измерениях и изоляции высокого напряжения.
Контуры заземления
Контуры заземления являются наиболее частым источником шума в приложениях для сбора данных. Они возникают, когда две подключенные клеммы в цепи имеют разные потенциалы заземления, вызывая протекание тока между двумя точками.Локальное заземление вашей системы может быть на несколько вольт выше или ниже земли ближайшего здания, а удары молнии поблизости могут вызвать разницу в несколько сотен или тысяч вольт. Это дополнительное напряжение само по себе может вызвать значительную ошибку в измерениях, но вызывающий его ток может также связывать напряжения в соседних проводах. Эти ошибки могут проявляться в виде переходных процессов или периодических сигналов. Например, если контур заземления сформирован из линий электропередачи переменного тока 60 Гц, нежелательный сигнал переменного тока проявляется как периодическая ошибка напряжения при измерении.
При наличии контура заземления измеренное напряжение Vm представляет собой сумму напряжения сигнала Vs и разности потенциалов Vg, которая существует между землей источника сигнала и землей измерительной системы (см. Рисунок 6). Этот потенциал обычно не является уровнем постоянного тока; таким образом, результатом является зашумленная система измерения, часто показывающая в показаниях компоненты частоты сети (60 Гц).
Рисунок 6). Этот потенциал обычно не является уровнем постоянного тока; таким образом, результатом является зашумленная система измерения, часто показывающая в показаниях компоненты частоты сети (60 Гц).
Рис. 6. Заземленный источник сигнала, измеренный с помощью системы с заземлением
, имеет контуры заземления
Во избежание образования контуров заземления убедитесь, что в измерительной системе имеется только один эталон заземления, или используйте изолированное измерительное оборудование.Использование изолированного оборудования устраняет путь между землей источника сигнала и измерительным устройством, тем самым предотвращая протекание тока между несколькими точками заземления.
В ранее упомянутой настройке CompactDAQ модуль аналогового ввода NI 9229 обеспечивает межканальную изоляцию 250 В.
Рис. 7. Модуль межканального изолированного аналогового ввода NI 9229
Синфазное напряжение
Идеальная дифференциальная измерительная система реагирует только на разность потенциалов между двумя своими клеммами, входом (+) и (-). Дифференциальное напряжение на паре схем является полезным сигналом, однако может существовать нежелательный сигнал, который является общим для обеих сторон пары дифференциальных схем. Это напряжение известно как синфазное напряжение. Идеальная система дифференциального измерения полностью отклоняет, а не измеряет синфазное напряжение. Однако практические устройства имеют несколько ограничений, описываемых такими параметрами, как диапазон синфазного напряжения и коэффициент отклонения синфазного сигнала (CMRR), которые ограничивают эту способность отклонять синфазное напряжение.
Дифференциальное напряжение на паре схем является полезным сигналом, однако может существовать нежелательный сигнал, который является общим для обеих сторон пары дифференциальных схем. Это напряжение известно как синфазное напряжение. Идеальная система дифференциального измерения полностью отклоняет, а не измеряет синфазное напряжение. Однако практические устройства имеют несколько ограничений, описываемых такими параметрами, как диапазон синфазного напряжения и коэффициент отклонения синфазного сигнала (CMRR), которые ограничивают эту способность отклонять синфазное напряжение.
Диапазон синфазного напряжения определяется как максимально допустимое колебание напряжения на каждом входе относительно земли измерительной системы. Нарушение этого ограничения приводит не только к ошибке измерения, но и к возможному повреждению компонентов на плате.
Коэффициент подавления синфазного сигнала описывает способность измерительной системы отклонять синфазное напряжение. Усилители с более высокими коэффициентами подавления синфазных напряжений более эффективны при подавлении синфазных напряжений.
В неизолированной дифференциальной измерительной системе электрический путь все еще существует в цепи между входом и выходом.Следовательно, электрические характеристики усилителя ограничивают уровень синфазного сигнала, который можно подать на вход. Использование развязывающих усилителей устраняет токопроводящий электрический путь и резко увеличивает коэффициент подавления синфазного сигнала.
Топологии изоляции
При настройке системы измерения важно понимать топологию изоляции устройства. Различные топологии имеют несколько связанных соображений стоимости и скорости.
Межканальный
Самая надежная топология изоляции — это изоляция каналов. В этой топологии каждый канал отдельно изолирован друг от друга и от других неизолированных компонентов системы. Кроме того, каждый канал имеет собственный изолированный источник питания.
Что касается скорости, есть несколько архитектур на выбор. Использование развязывающего усилителя с аналого-цифровым преобразователем (АЦП) на канал обычно быстрее, поскольку вы можете получить доступ ко всем каналам параллельно. Модули аналогового ввода NI 9229 и NI 9239 обеспечивают межканальную изоляцию для обеспечения высочайшей точности измерений.
Модули аналогового ввода NI 9229 и NI 9239 обеспечивают межканальную изоляцию для обеспечения высочайшей точности измерений.
Более экономичная, но более медленная архитектура предполагает мультиплексирование каждого изолированного входного канала в один АЦП.
Другой метод обеспечения межканальной развязки — использование общего изолированного источника питания для всех каналов. В этом случае синфазный диапазон усилителей ограничен шинами питания этого источника питания, если вы не используете входные аттенюаторы.
Банк
Другая топология развязки включает объединение или группирование нескольких каналов вместе для совместного использования одного развязывающего усилителя. В этой топологии разница синфазного напряжения между каналами ограничена, но синфазное напряжение между группой каналов и неизолированной частью измерительной системы может быть большим. Отдельные каналы не изолированы, но берега каналов изолированы от других берегов и от земли. Эта топология представляет собой более дешевое решение для изоляции, поскольку в этой конструкции используются один изолирующий усилитель и источник питания.
Эта топология представляет собой более дешевое решение для изоляции, поскольку в этой конструкции используются один изолирующий усилитель и источник питания.
Большинство модулей аналогового ввода NI C Series, таких как NI 9201 и NI 9221, изолированы от банка и могут обеспечивать точные аналоговые измерения напряжения при меньших затратах.
Как увидеть свои измерения: NI LabVIEW
После подключения датчика к измерительному прибору вы можете использовать программное обеспечение для графического программирования LabVIEW для визуализации и анализа данных по мере необходимости (см. Рисунок 8).
Рис. 8. Измерение напряжения LabVIEW
DC-DC преобразователь
Negatron — источник отрицательного напряжения для вашей схемы
Преобразователь постоянного тока в постоянный Negatron
Negatron — это повышающий понижающий преобразователь, который принимает положительный
напряжение и превращает его в отрицательное напряжение, которое можно использовать с
схемы усилителя и многое другое. Выход регулируется от -1,3 В до
Выход регулируется от -1,3 В до
-12В. Негатрон также может увеличивать / уменьшать величину
Напряжение. Например, вы можете накормить Negatron + 9V, и это может дать вам
-5В или -12В.
Negatron — идеальный выбор для инженеров, разочарованных попытками
создают источник отрицательного напряжения в своей цепи малой мощности.
Negatron будет работать от входных напряжений 4–14 В, а выходных
напряжение устанавливается с помощью небольшого винтового потенциометра наверху.
Negatron совместим по выводам с общей серией 78XX
линейных регуляторов напряжения, поэтому он будет работать с макетами и
другие популярные методы прототипирования.
Negatron сильно отличается от любого другого преобразователя постоянного тока в постоянный.
на рынке, поэтому, пожалуйста, внимательно прочтите всю таблицу, прежде чем
покупка или использование одного.
| Модель: | Негатрон |
| Производительность: | -1. Диапазон выходного напряжения от 3 В до -12 В Диапазон выходного напряжения от 3 В до -12 В Диапазон входного напряжения от 4 до 14 В Максимальный выходной ток 0,5 А при -5 В при питании от +9 В Максимальный выходной ток 0,25 А при -12 В при питании от +12 В (пожалуйста, смотрите технические характеристики для получения информации о номинальных токах на других входах / выходах. напряжения) Типичная пульсация ~ 100 мВ Внешние компоненты обычно не нужны |
| Защитные элементы: | Максимальная токовая защита Тепловая защита |
| Приложения: | Лабораторные работы и прототипирование Отрицательная шина питания операционного усилителя Питание небольших усилителей звука Датчики питания Приложения на солнечной энергии Зарядка аккумулятора Применение возобновляемых источников энергии |
| Лист данных: | Негатрон. doc (167kb) doc (167kb) Negatron.pdf (181kb) |
| Топология: | Бак-буст |
Одновременная визуализация потоков электронов по напряжению и плотности тока в двух измерениях
Бинаккер, К. У. Дж. И ван Хаутен, Х. Квантовый транспорт в полупроводниковых наноструктурах. Физика твердого тела. Adv. Res. Прил. 44 , 1–228 (1991).
Google Scholar
Хасан, М. З. и Кейн, К. Л. Коллоквиум: топологические изоляторы. Ред. Мод. Phys. 82 , 3045–3067 (2010).
CAS
Статья
Google Scholar
Qi, X.-L. И Чжан, С.-К. Топологические изоляторы и сверхпроводники. Ред. Мод. Phys. 83 , 1057–1110 (2011).
CAS
Статья
Google Scholar

Лукас А. и Фонг К. Гидродинамика электронов в графене. J. Phys. Конденс. Дело 30 , 053001 (2018).
Артикул
Google Scholar
Ландауэр Р. Электропроводность, определяемая по пропусканию: датчики и квантованное сопротивление сужению. J. Phys. Конденс. Matter 1 , 8099–8110 (1989).
Артикул
Google Scholar
МакЛеннан, М. Дж., Ли, Ю. и Датта, С. Падение напряжения в мезоскопических системах: численное исследование с использованием квантового кинетического уравнения. Phys. Ред. B 43 , 13846–13884 (1991).
CAS
Статья
Google Scholar
Datta, S. Electron Transp
ort Mesoscopic System (Cambridge Univ. Press, 1997).
Muralt, P. & Pohl, D.W. Сканирующая туннельная потенциометрия. Заявл. Phys. Lett. 48 , 514–516 (1986).
Заявл. Phys. Lett. 48 , 514–516 (1986).
CAS
Статья
Google Scholar
McCormick, K. L. et al. Сканирующая потенциальная микроскопия краевых и объемных токов в квантовом холловском режиме. Phys. Ред. B 59 , 4654–4657 (1999).
CAS
Статья
Google Scholar
Bachtold, A. et al. Сканирующая зондовая микроскопия электронного транспорта в углеродных нанотрубках. Phys. Rev. Lett. 84 , 6082–6085 (2000).
CAS
Статья
Google Scholar
Weitz, P., Ahlswede, E., Weis, J., Klitzing, K. V. & Eberl, K. Исследования потенциала Холла в квантовых условиях Холла с использованием сканирующей силовой микроскопии. Phys. E 6 , 247–250 (2000).
CAS
Статья
Google Scholar
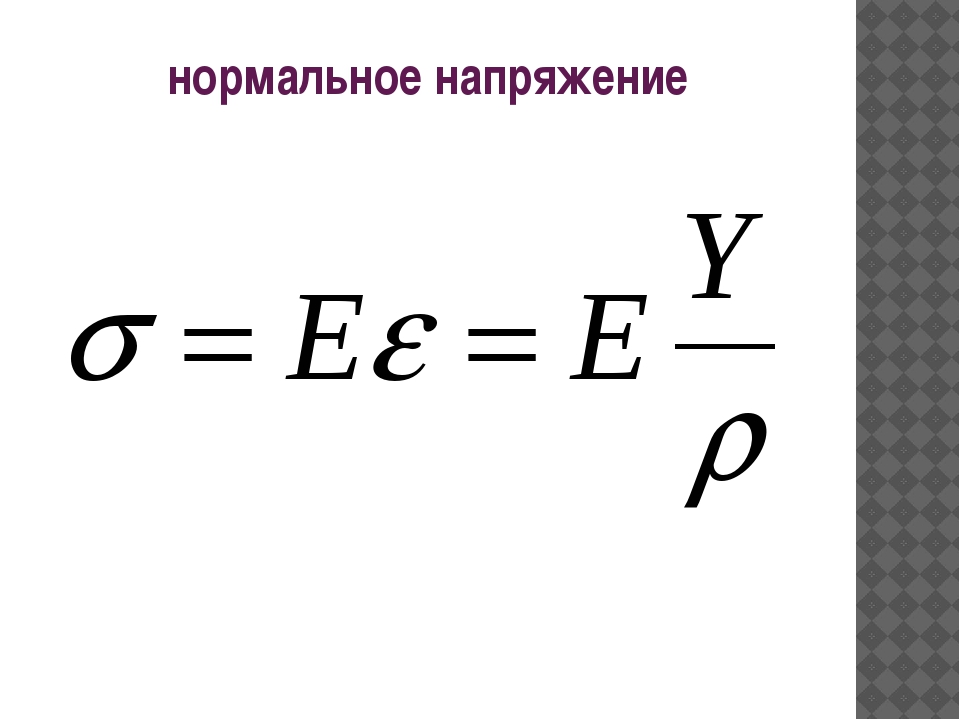
Мелиц, В., Шен, Дж., Куммель, А. С. и Ли, С. Зондовая силовая микроскопия Кельвина и ее применение. Surf. Sci. Отчет 66 , 1–27 (2011).
CAS
Статья
Google Scholar
Рот, Б. Дж., Сепульведа, Н. Г. и Виксво, Дж. П. Использование магнитометра для изображения двумерного распределения тока. J. Appl. Phys. 65 , 361–372 (1989).
Артикул
Google Scholar
Токура Ю., Хонда Т., Цубаки К. и Таруча С. Неинвазивное определение распределения тока баллистических электронов. Phys. Ред. B 54 , 1947–1952 (1996).
CAS
Статья
Google Scholar
Huber, M. E. et al. Градиометрический микро-СКВИД-сусцептометр для сканирующих измерений мезоскопических образцов. Rev. Sci. Instrum. 79 , 053704 (2008).
Артикул
Google Scholar

Rondin, L. et al. Магнитометрия с азотно-вакансионными дефектами в алмазе. Rep. Prog. Phys. 77 , 056503 (2014).
CAS
Статья
Google Scholar
Tetienne, J.-P. и другие. Квантовая визуализация течения тока в графене. Sci. Adv. 3 , e1602429 (2017).
Артикул
Google Scholar
Чанг, К., Эйхлер, А., Ренсиус, Дж., Лоренцелли, Л. и Деген, К. Л. Наноразмерное построение изображения плотности тока с помощью односпинового магнитометра. Nano Lett. 17 , 2367–2373 (2017).
CAS
Статья
Google Scholar
Васюков Д. и др. Сканирующее сверхпроводящее устройство квантовой интерференции с одноэлектронной спиновой чувствительностью. Нат. Nanotechnol. 8 , 639–644 (2013).
CAS
Статья
Google Scholar

Эрикссон, М.А. и др. Криогенное сканирование зондового исследования полупроводниковых наноструктур. Заявл. Phys. Lett. 69 , 671–673 (1996).
CAS
Статья
Google Scholar
Bhandari, S. et al. Отображение циклотронных орбит электронов в графене. Nano Lett. 16 , 1690–1694 (2016).
CAS
Статья
Google Scholar
Fei, Z. et al. Настройка затвора графеновых плазмонов, обнаруженная с помощью инфракрасного наноизображения. Nature 487 , 82–85 (2012).
CAS
Статья
Google Scholar
Chen, J. et al. Оптическое наноизображение перестраиваемых затвором графеновых плазмонов. Nature 487 , 77–81 (2012).
CAS
Статья
Google Scholar
Мюллер Т., Ся Ф. , Фрейтаг М., Цанг Дж. И Авурис П. Роль контактов в графеновых транзисторах: исследование сканирующего фототока. Phys. Ред. B 79 , 245430 (2009).
, Фрейтаг М., Цанг Дж. И Авурис П. Роль контактов в графеновых транзисторах: исследование сканирующего фототока. Phys. Ред. B 79 , 245430 (2009).
Артикул
Google Scholar
Fontein, P. F. et al. Пространственное распределение потенциала в GaAs / Al x Ga 1- x As гетероструктуры в квантовых условиях Холла исследованы с помощью линейного электрооптического эффекта. Phys. Ред. B 43 , 12090–12093 (1991).
CAS
Статья
Google Scholar
Knott, R., Dietsche, W., v. Klitzing, K., Eberl, K. & Ploog, K. Внутри двумерной электронной системы: изображения потенциала и диссипации. Твердый. Состояние. Электрон. 37 , 689–692 (1994).
CAS
Статья
Google Scholar
Gao, C., Wei, T., Duewer, F., Lu, Y. & Xiang, X. D. Количественная микроволновая импедансная микроскопия с высоким пространственным разрешением с помощью сканирующего микроволнового микроскопа ближнего поля. Заявл. Phys. Lett. 71 , 1872–1874 (1997).
& Xiang, X. D. Количественная микроволновая импедансная микроскопия с высоким пространственным разрешением с помощью сканирующего микроволнового микроскопа ближнего поля. Заявл. Phys. Lett. 71 , 1872–1874 (1997).
CAS
Статья
Google Scholar
Wang, Z. et al. Количественное измерение сопротивления листа с помощью затухающего микроволнового зонда. Заявл. Phys. Lett. 86 , 153118 (2005).
Артикул
Google Scholar
Yoo, M. J. et al. Сканирующая одноэлектронная транзисторная микроскопия: отображение отдельных зарядов. Science 276 , 579–582 (1997).
CAS
Статья
Google Scholar
Ilani, S. et al. Микроскопическая природа локализации в квантовом эффекте Холла. Nature 427 , 328–332 (2004).
CAS
Статья
Google Scholar

Honig, M. et al. Локальное электростатическое изображение порядка полосатых доменов в LaAlO 3 / SrTiO 3 . Нат. Матер. 12 , 1112–1118 (2013).
CAS
Статья
Google Scholar
Якоби, А., Гесс, Х. Ф., Фултон, Т. А., Пфайффер, Л. Н. и Уэст, К. В. Электрическая визуализация квантового состояния Холла. Solid State Commun. 111 , 1–13 (1999).
CAS
Статья
Google Scholar
Waissman, J. et al. Реализация первичных и локально настраиваемых одномерных электронных систем в углеродных нанотрубках. Нат. Nanotechnol. 8 , 569–574 (2013).
CAS
Статья
Google Scholar
Бен Шалом, М.и другие. Квантовые осцилляции критического тока и близость сильнополевой сверхпроводимости в баллистическом графене. Нат. Phys. 12 , 318–322 (2016).
12 , 318–322 (2016).
Артикул
Google Scholar
Левинсон И. Б. Распределение потенциала в квантовом точечном контакте. Сов. Phys. ЖЭТФ 68 , 1257–1265 (1989).
Google Scholar
Ся Ф., Перебейнос В., Линь Ю. М., Ву Ю. и Авурис П. Истоки и пределы сопротивления переходов металл-графен. Нат. Нанотехнологии . 6 , 179–184 (2011).
CAS
Статья
Google Scholar
Yu, Y.J. et al. Настройка работы выхода графена за счет эффекта электрического поля. Nano Lett. 9 , 3430–3434 (2009).
CAS
Статья
Google Scholar
Morikawa, S. et al. Визуализация траекторий баллистических носителей в графене с помощью сканирующей затворной микроскопии. Заявл. Phys. Lett. 107 , 243102 (2015).
Артикул
Google Scholar
Bhandari, S. et al. Визуализация потока электронов от коллимирующих контактов в графене. 2D Матер. 5 , 021003 (2018).
Артикул
Google Scholar
Tarucha, S., Saku, T., Tokura, Y. & Hirayama, Y. Сопротивление Шарвин и его пробой наблюдается в длинных баллистических каналах. Phys. Ред. B 47 , 4064–4067 (1993).
CAS
Статья
Google Scholar
Фалькович Г. и Левитов Л. Связывание пространственных распределений потенциала и тока в вязкой электронике. Phys. Rev. Lett. 119 , 066601 (2017).
Артикул
Google Scholar
Быстрое решение для оптимального скоординированного управления напряжением, основанное на уменьшении габаритов энергосистемы с помощью Modified Ward-PV
Артикул:
[1] Кундур, П. , Paserba, J., Ajjarapu, V. et al. «Определение и классификация устойчивости энергосистемы Совместная рабочая группа IEEE / CIGRE по терминам и определениям устойчивости», Int. J. IEEE Transactions on Power Systems., 19 (3), стр. 1387-1401 (2004).
, Paserba, J., Ajjarapu, V. et al. «Определение и классификация устойчивости энергосистемы Совместная рабочая группа IEEE / CIGRE по терминам и определениям устойчивости», Int. J. IEEE Transactions on Power Systems., 19 (3), стр. 1387-1401 (2004).
[2] Rabiee, A., Mohseni-Bonab, S.M., Parniani, M. et al. «Оптимальная стоимость контроля безопасности напряжения с использованием моделей нагрузки, зависящих от напряжения при наличии реакции на спрос», Int.J. Транзакции IEEE в интеллектуальной сети. 10 (3), стр. 2383-2395 (2018).
[3] Тейлор, К. У. и Эриксон, Д. К. «Запись и анализ каскадного отключения 2 июля [энергосистема западных США]», Int. J. Компьютерные приложения IEEE в Power . 10 (1), стр. 26-30 (1997).
[4] Ye, X., Le, J., Liu, Y. et al. «Метод контроля стабильности согласованного напряжения активной распределительной сети», Int. Журнал современных энергетических систем и чистой энергии . 6 (1), стр. 85-94 (2018).
6 (1), стр. 85-94 (2018).
[5] Esaka, T., Kataoka, Y., Ohtaka, T. et al. «Превентивный контроль стабильности напряжения и аварийный контроль с использованием чувствительности VIPIt», Int.Конф. IEEE PES Power Systems Conference and Exposition ., New York, USA, pp. 509–516 (2004).
[7] Антониаду-Плитария, К. Э., Кувелиотис-Лисикатос, И. Н., Георгилакис, П. С. и др. «Распределенное и децентрализованное управление напряжением интеллектуальных распределительных сетей: модели, методы и будущие исследования», Int.J. Транзакции IEEE в Smart Grid . 8 (6). С. 2999-3008 (2017).
[8] Вурнас К. и Каристианос М. «Устройства РПН в аварийном и превентивном контроле стабильности напряжения», Int. J. Транзакции IEEE по системам питания. 19 (1). С. 492-498 (2004).
J. Транзакции IEEE по системам питания. 19 (1). С. 492-498 (2004).
[9] Гу, М., Мегахапола, Л. Г. и Вонг, А. К. «Скоординированное управление напряжением и частотой в гибридных электрических сетях переменного / постоянного и постоянного тока для повышения стабильности», Int. J. IEEE Transactions on Power Systems . 36 (1), стр. 635-347 (2021).
[10] Корси, С., Поцци, М., Сабелли, С. и др. «Скоординированный автоматический контроль напряжения итальянской сети электропередач. Часть I: причины выбора и обзор консолидированной иерархической системы», Int.J. IEEE Transactions on Power Systems . 19 (4), стр 1723-1732 (2004).
[11] Корси, С., Поцци, М., Сфорна, М. и др. «Скоординированный автоматический контроль напряжения в сети электропередачи Италии — Часть II: устройства управления и эксплуатационные характеристики консолидированной иерархической системы. Причины выбора и обзор консолидированной иерархической системы», Int. J. IEEE Transactions on Power Systems . 19 (4), стр. 1733-1741 (2004).
J. IEEE Transactions on Power Systems . 19 (4), стр. 1733-1741 (2004).
[13] Van Hecke, J., Janssens, N., Deuse, J. et al. «Опыт скоординированного управления напряжением в Бельгии», В СОГЛАСОВАННОМ УПРАВЛЕНИИ НАПРЯЖЕНИЕМ В ТРАНСМИССОННОЙ СЕТИ, стр. CIGRE, стр.24-25, (2007).
[14] Пол, Дж., Леост, Дж. И Тессерон, Дж. «Обзор управления вторичным напряжением во Франции: современная реализация и исследования», Int. J. IEEE Transaction on Power Systems . 2 (2), стр. 505–511 (1987).
[15] Беккути, А.G., Demiray, T.H., Andersson, G. et al. «Алгоритм лагранжевой декомпозиции для оптимального управления аварийным напряжением», Int. J. IEEE Transactions on Power Systems . 25 (4), стр. 1769–1779 (2010).
[16] Wang, X., Wang, C., Xu, T. et al. «Оптимальное регулирование напряжения для распределительных сетей с несколькими микросетями», Int. J. ScienceDirect. Прикладная энергия . 210 , стр. 1027-1036 (2018).
210 , стр. 1027-1036 (2018).
[17] Granada, M., Rider, M.J., Mantovani, J. et al. «Децентрализованный подход к оптимальному распределению реактивной мощности с использованием метода лагранжевой декомпозиции», Int. J. ScienceDirect. Исследование электроэнергетических систем . 89 , стр. 148-156 (2012).
[18] Ислам, С.Р., Муттаки, К. М. и Сутанто, Д. «Многоагентное управление удаляющимся горизонтом с передачей данных между соседними объектами для предотвращения падения напряжения в многозональной энергосистеме», In. J. Генерация, передача и распределение ИЭПП. 8 (9), стр. 1604-1615 (2014).
[19] Li, P., Zhang, B., Cheng, C. et al. «Метод, основанный на прогнозировании распределенной модели для координированного управления напряжением энергосистемы», 10 th IET.Int. Конф. о разработках в области защиты энергосистем (DPSP 2010). Управление изменениями . (2010).
[20] Ван Фам, Х. и Ахмед, С.Н. «Подход на основе нескольких агентов для интеллектуального управления инжекцией реактивной мощности в системах передачи», в Динамическая оценка уязвимости и интеллектуальное управление: для устойчивой энергосистемы . P. Wiley-IEEE Press. Эд.1-е, с. 269 (2018).
и Ахмед, С.Н. «Подход на основе нескольких агентов для интеллектуального управления инжекцией реактивной мощности в системах передачи», в Динамическая оценка уязвимости и интеллектуальное управление: для устойчивой энергосистемы . P. Wiley-IEEE Press. Эд.1-е, с. 269 (2018).
[22] Валлем М. Р., Вьякаранам Б., Хольцер Дж. Т. и др. «Декомпозиция энергосистемы для практической реализации методов управления напряжением в основной сети», 19 th Int. Конф. по применению интеллектуальных систем в энергосистемах (ISAP) ., Сан-Антонио, Техас, США, , стр. 1-6 (2017).
[23] Ван, С., Лю, М., Ху, Б. и др. «Управление аварийным напряжением на основе MPC, метода коллокации по Радау и движущихся конечных элементов», Int. Конф. по технологии энергосистем ., Чжэцзян, Китай, стр. 1-7 (2010).
[24] Ларссон, М. и Карлссон, Д. «Скоординированная схема защиты системы от падения напряжения с использованием эвристического поиска и прогнозирующего контроля», Int. J. Обзор энергетики IEEE., 22 (6). С. 59 — 59 (2002).
и Карлссон, Д. «Скоординированная схема защиты системы от падения напряжения с использованием эвристического поиска и прогнозирующего контроля», Int. J. Обзор энергетики IEEE., 22 (6). С. 59 — 59 (2002).
[25] Wen, J., Wu, Q., Turner, D. et al. «Оптимальное согласованное регулирование напряжения для обеспечения стабильности напряжения энергосистемы», Int. J. IEEE Transactions on Power Systems ., 19 (2).С. 1115-1122 (2004).
[28] Джин, Ли., Кумар, Р. и Элиа, Н. «Стабилизация аварийного напряжения с ограничениями безопасности: подход, основанный на модельном управлении с прогнозированием», 47 th IEEE.Конф. on Decision and Control ., Канкун, Мексика, стр. 2469-2474 (2008).
[30] Чжан, Ф. , Чан, К. В. и Фанг, Д. З. «Оптимальное скоординированное аварийное управление напряжением против падения напряжения», Int. J. of Electrical Power & Energy Systems., 53 .С. 442-449 (2013).
, Чан, К. В. и Фанг, Д. З. «Оптимальное скоординированное аварийное управление напряжением против падения напряжения», Int. J. of Electrical Power & Energy Systems., 53 .С. 442-449 (2013).
[31] Отомега, Б., Главич, М. и Ван Катсем, Т. «Двухуровневая схема аварийного управления против нестабильности напряжения в энергосистеме», Int. J. Control Engineering Practice., 30 . С. 93-104 (2014).
[32] Негенборн, Р., Leirens, S., De Schutter, B. et al. «Наблюдательный нелинейный MPC для управления аварийным напряжением с помощью поиска по образцу», Int. J. Control Engineering Practice ., 7 . С. 841-848 (2009).
[33] Ларссон М., Хилл Д. Дж. И Олссон Г. «Управление аварийным напряжением с помощью поиска и прогнозирования», Int. J. Электроэнергетических и энергетических систем. 24 (2). С. 121-130 (2002).
[34] Amraee, T., Ranjbar, A. и Feuillet, R. «Адаптивная схема отключения нагрузки при пониженном напряжении с использованием управления с прогнозированием модели», Int. Журнал исследований электроэнергетических систем . 81 (7), стр. 1507-1513 (2011).
«Адаптивная схема отключения нагрузки при пониженном напряжении с использованием управления с прогнозированием модели», Int. Журнал исследований электроэнергетических систем . 81 (7), стр. 1507-1513 (2011).
[35] Пурджафари, Э.и Mojallali, H. «Прогнозирующее управление для предотвращения коллапса напряжения с использованием модифицированного дискретного многозначного алгоритма PSO», Int. J. ISA Транзакции . 50 (2). С. 195–200 (2011).
[36] Ма, Х., Мэн, К. и Хилл, Д.Дж. «Схема прыгающих генов для многоцелевого скоординированного контроля напряжения», 4th Int. Конф. на Industrial Informatics , Сингапур, (2006).[37] Ма, Х. М., Нг, К. Т. и Ман К. Ф. «Многоцелевой скоординированный контроль напряжения питания с использованием парадигмы прыгающих генов», Int. J. IEEE Transactions on Industrial Electronics . 55 (11). С. 4075-4084 (2008).
IEEE Transactions on Industrial Electronics . 55 (11). С. 4075-4084 (2008).
[38] Ма, Х. М., Нг, К.Т. и Ман К. Ф. «Схема принятия решений, основанная на множестве критериев, для управления напряжением питания в реальном времени», Int. J. Транзакции IEEE по телефону Industrial Informatics . 4 (1). С. 58-66 (2008).
[39] Ма, Х. и Хилл, Д. Дж. «Адаптивное скоординированное управление напряжением — Часть I: Базовая схема», Int. J. IEEE Transactions on Power Systems . 29 (4), стр. 1546-1553 (2013).
[40] Ма, Х. и Хилл, Д. Дж. «Адаптивное скоординированное управление напряжением — Часть II: Использование обучения для быстрого уныния», Int. J. IEEE Transactions on Power Systems . 29 (4), стр. 1554-1561 (2014).
J. IEEE Transactions on Power Systems . 29 (4), стр. 1554-1561 (2014).
[41] Кербалаи, Ф.и Шахбази, Х. «Быстрый метод решения задачи оптимального согласованного управления напряжением, основанный на уменьшении размеров системы», Int. J. Исследование электроэнергетических систем . 142 , стр. 310-319 (2017).
[43] Zhao, B., Xu, Z., Xu, C. et al. «Зональное управление напряжением на основе сетевых разделов для распределительных сетей с распределенными фотоэлектрическими системами» Int.J. IEEE Transactions on Smart Grid ., 9 (5). С. 4087-4098 (2018).
[44] Ислам, С. Р., Сутанто, Д. и Муттаки, К. М. «Скоординированное децентрализованное управление аварийным напряжением и реактивной мощностью для предотвращения долговременной нестабильности напряжения в энергосистеме», Int. J. IEEE Transaction on Power Systems . 30 (5), стр 2591-2603 (2014).
J. IEEE Transaction on Power Systems . 30 (5), стр 2591-2603 (2014).
[45] Шахбази Х. и Кербалаи Ф. «Децентрализованное управление напряжением энергосистем с использованием многоагентных систем», Int. J. of Modern Power Systems and Clean Energy., 8 (2), (2020).
[46] Ма, Х. и Хилл, Д.Дж. «Схема быстрого локального поиска для адаптивного координированного управления напряжением», Int.J. IEEE Transaction on Power Systems . 33 (3), стр. 2321-2330 (2018).
[47] Huang, Q., Huang, R., Hao, W. et al. «Аварийное управление адаптивной энергосистемой с использованием глубокого обучения с подкреплением», Int. J. Транзакции IEEE в Smart Grid . 11 (2), стр. 1171-1182 (2019).
[48] Лю Х., Су, Дж., Ци, Дж. И др. «Децентрализованное управление напряжением и мощностью многомашинных энергосистем с глобальной асимптотической устойчивостью» In. J. IEEE Access., 7 , стр. 14273-14282 (2019).
J. IEEE Access., 7 , стр. 14273-14282 (2019).
[49] Guzman, R., De Vicuna, L.G., Camacho, A. et al. «Управление с предсказанием модели убывающего горизонта для трехфазного VSI с LCL-фильтром», Int. J. IEEE Transactions on Industrial Electronics . 66 (9), стр. 6671-6680 (2018).
[50] Джин Т., Шен X., Су Т. и др. «Модель прогнозируемого управления напряжением на основе конечного набора управления с компенсацией задержки времени вычислений для фотоэлектрических систем», Int. J. IEEE Transactions on Energy Conversion . 34 (1), стр. 330-338 (2018).
[51] Ву, Ф.Ф. и Монтичелли А. «Критический обзор моделирования внешней сети для анализа сетевой безопасности», Int. Журнал электроэнергетики и энергетических систем . 5 (4), стр. 222-235 (1983).
Журнал электроэнергетики и энергетических систем . 5 (4), стр. 222-235 (1983).
[52] Mehrjerdi, H., Lefebvre, S., Asber, D. et al. «Графическое разбиение электросети для контроля аварийного напряжения», 9 th Int. Конф. Азиатская конференция по контролю (ASCC) ., Стамбул, Турция , стр. 23-26 (2013).
[53] Альзаарир, К., Саад, М., Мехрджерди, Х. и др. «Разработка нового метода идентификации для глобальной группы средств управления для согласованного онлайн-контроля напряжения в активных распределительных сетях», Int. J. Транзакции IEEE в Smart Grid . 11 (5), стр. 3921-3931 (2020).
[54] Хоссейннежад, В., Rafiee, M., Ahmadian, M. et al. «Оптимальное разделение на отдельные острова интеллектуальных распределительных систем для улучшения восстановления системы в аварийных условиях», Int.

 80
80 2 В.
2 В. Обратите внимание, что элементы соединены последовательно для увеличения номинального напряжения.
Обратите внимание, что элементы соединены последовательно для увеличения номинального напряжения.
 д.…
д.…