Электрическое напряжение. Размерность напряжения

Электрическое напряжение — Википедия РУ

У этого термина существуют и другие значения, см. Напряжение.

Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B[1].

При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). Напряжение в общем случае формируется из вкладов двух работ: работы электрических сил AABel{\displaystyle A_{AB}^{el}} и работы сторонних сил AABex{\displaystyle A_{AB}^{ex}}. Если на участке цепи не действуют сторонние силы (то есть, AABex=0{\displaystyle A_{AB}^{ex}=0}), работа по перемещению включает только работу потенциального электрического поля AABel{\displaystyle A_{AB}^{el}} (которая не зависит от пути, по которому перемещается заряд), и электрическое напряжение UAB{\displaystyle U_{AB}} между точками A и B совпадает с разностью потенциалов между этими точками (поскольку φA−φB=AABel/q{\displaystyle \varphi _{A}-\varphi _{B}=A_{AB}^{el}/q}). В общем случае напряжение UAB{\displaystyle U_{AB}} между точками A и B отличается от разницы потенциалов между этими точками[2] на работу сторонних сил по перемещению единичного положительного заряда. Эту работу называют электродвижущей силой EAB{\displaystyle {\mathcal {E}}_{AB}} на данном участке цепи: EAB=AABex/q.{\displaystyle {\mathcal {E}}_{AB}=A_{AB}^{ex}/q.}

UAB=φA−φB+EAB.{\displaystyle U_{AB}=\varphi _{A}-\varphi _{B}+{\mathcal {E}}_{AB}.}

Определение электрического напряжения можно записать в другой форме. Для этого нужно представить работу AABef{\displaystyle A_{AB}^{ef}} как интеграл вдоль траектории L, проложенной из точки A в точку B.

UAB=∫LE→efdl→{\displaystyle U_{AB}=\int \limits _{L}{\vec {E}}_{ef}d{\vec {l}}} — интеграл от проекции эффективной напряжённости поля E→ef{\displaystyle {\vec {E}}_{ef}} (включающего сторонние поля) на касательную к траектории L, направление которой в каждой точке траектории совпадает с направлением вектора dl→{\displaystyle d{\vec {l}}} в данной точке. В электростатическом поле, когда сторонних сил нет, значение этого интеграла не зависит от пути интегрирования и совпадает с разностью потенциалов.

Размерность электрического напряжения в Международной системе величин (англ. International System of Quantities, ISQ), на которой основана Международная система единиц (СИ), — L2MT-3I-1. Единицей измерения напряжения в СИ является вольт (русское обозначение: В; международное: V).

Понятие напряжение ввёл Георг Ом в работе 1827 года, в которой предлагалась гидродинамическая модель электрического тока для объяснения открытого им в 1826 году эмпирического закона Ома: U=IR{\displaystyle U\!=IR}.

Для описания цепей переменного тока применяются следующие напряжения:

• мгновенное напряжение;
• амплитудное значение напряжения;
• среднее значение напряжения;
• среднеквадратичное значение напряжения;
• средневыпрямленное значение напряжения.

Мгновенное напряжение есть разность потенциалов между двумя точками, измеренная в данный момент времени. Зависит от времени (является функцией времени):

u=u(t).{\displaystyle u=u(t).} 

Амплитудное значение напряжения есть максимальное по модулю значение мгновенного напряжения за весь период колебаний:

UM=max(|u(t)|).{\displaystyle U_{M}=\max(|u(t)|).} 

Для гармонических (синусоидальных) колебаний напряжения мгновенное значение напряжения выражается как:

u(t)=UMsin⁡(ωt+ϕ).{\displaystyle u(t)=U_{M}\sin(\omega t+\phi ).} 

Для сети переменного синусоидального напряжения со среднеквадратичным значением 220 В амплитудное напряжение равно приблизительно 311,127 В.

Амплитудное напряжение можно измерить с помощью осциллографа.

Среднее значение напряжения (постоянная составляющая напряжения) есть напряжение, определяемое за весь период колебаний, как:

Um=1T∫0Tu(t)dt.{\displaystyle U_{m}={\frac {1}{T}}\int _{0}^{T}u(t)dt.} 

Для синусоиды среднее значение напряжения равно нулю.

Среднеквадратичное значение напряжения (устаревшие наименования: действующее, эффективное) есть напряжение, определяемое за весь период колебаний, как:

Uq=1T∫0Tu2(t)dt.{\displaystyle U_{q}={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}.} 

Среднеквадратичное значение напряжения наиболее удобно для практических расчётов, так как на линейной активной нагрузке оно совершает ту же работу (например, лампа накаливания имеет ту же яркость свечения, нагревательный элемент выделяет столько же тепла), что и равное ему постоянное напряжение.

Для синусоидального напряжения справедливо равенство:

Uq=12UM≈0,707UM;UM=2Uq≈1,414Uq.{\displaystyle U_{q}={1 \over {\sqrt {2}}}U_{M}\approx 0,707U_{M};\qquad U_{M}={\sqrt {2}}U_{q}\approx 1,414U_{q}.} 

В технике и быту при использовании переменного тока под термином «напряжение» имеется в виду именно среднеквадратичное значение напряжения, и все вольтметры проградуированы исходя из его определения. Однако конструктивно большинство приборов фактически измеряют не среднеквадратичное, а средневыпрямленное (см. ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.

Средневыпрямленное значение напряжения есть среднее значение модуля напряжения:

Um=1T∫0T|u(t)|dt.{\displaystyle U_{m}={\frac {1}{T}}\int \limits _{0}^{T}|u(t)|dt.} 

Для синусоидального напряжения справедливо равенство:

Um=2πUM(≈0,637UM)=22πUq(≈0,9Uq).{\displaystyle U_{m}={2 \over \pi }U_{M}(\approx 0,637U_{M})={2{\sqrt {2}} \over \pi }U_{q}(\approx 0,9U_{q}).} 

На практике используется редко, однако большинство вольтметров переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала и проградуирована по среднеквадратичным значениям.

В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки относительно нейтрали, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в треугольник фазное напряжение равно линейному, а при соединении в звезду (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в 3{\displaystyle {\sqrt {3}}}  раз больше фазного.

На практике напряжение трёхфазной сети обозначают дробью, в числителе которой стоит фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли), а в знаменателе — линейное напряжение. Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.

http-wikipediya.ru

MYsopromat.ru: Напряжения

Мерой интенсивности внутренних сил, распределенных по сечениям, служат напряжения – усилия, приходящиеся на единицу площади сечения. Выделим в окрестности точки B малую площадку ΔF (рис. 3.1). Пусть ΔR - равнодействующая внутренних сил, действующих на эту площадку. Тогда среднее значение внутренних сил, приходящихся на единицу площади ΔF рассматриваемой площадки, будет равно:

.

(3.1)

Рис. 3.1. Среднее напряжение на площадке

Величина pm называется средним напряжением. Она характеризует среднюю интенсивность внутренних сил. Уменьшая размеры площади, в пределе получим

.

(3.2)

Величина p называется истинным напряжением или просто напряжением в данной точке данного сечения.

Единица напряжения – паскаль, 1 Па = 1 Н/м2. Так как реальные значения напряжений будут выражаться очень большими числами, то следует применять кратные значения единиц, например МПа (мегапаскаль) 1 МПа= 106 Н/м2.

Напряжения, как и силы, являются векторными величинами. В каждой точке сечения тела полное напряжение p можно разложить на две составляющие (рис. 3.2):

1) составляющую, нормальную к плоскости сечения. Эта составляющая называется нормальным напряжением и обозначается σ;

2) составляющую, лежащую(в плоскости сечения. Эта составляющая обозначается τ и называется касательным напряжением. Касательное напряжение в зависимости от действующих сил может иметь любое направление в плоскости сечения. Для удобства τ представляют в виде двух составляющих по направлению координатных осей. Принятые обозначения напряжений показаны ни рис. 3.2

У нормального напряжения ставится индекс, указывающий какой координатной оси параллельно данное напряжение. Растягивающее нормальное напряжение считается положительным, сжимающее – отрицательным. Обозначения касательных напряжений имеют два индекса: первый из них указывает, какой оси параллельна нормаль к площадке действия данного напряжения, а второй – какой оси параллельно само напряжение. Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл. Нормальное напряжение возникает, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц материала по плоскости сечения.

Рис. 3.2. Разложение вектора полного напряжения

Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечно малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. 3.3. Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела называется напряженным состоянием в данной точке.

Вычислим сумму моментов всех элементарных сил, действующих на элемент (рис.3.3), относительно координатных осей, так, например, для оси x с учетом равновесия элемента, имеем:

.

(3.3)

Повторяя указанные действия для других осей, получим закон парности касательных напряжений:

,

(3.4)

который формулируется следующим образом: составляющие касательных напряжений на двух взаимно перпендикулярных площадках, перпендикулярные общему ребру, равны по величине и противоположны по знаку, то есть либо обе направлены к ребру либо обе направлены от ребра.

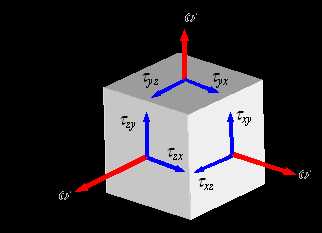
Рис. 3.3. Система напряжений в точке

  

mysopromat.ru

Список параметров напряжения и силы электрического тока — WiKi

Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является (  u(t) ,i(t){\displaystyle u(t)~,\quad i(t)}     ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение

• Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)} 

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.

U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}} 

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I{\displaystyle I}  и U{\displaystyle U}  совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt} 

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.

Средневыпрямленное значение

Средневыпрямленное значение — среднее значение модуля сигнала

U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt} 

На практике используется редко, однако большинство измерительных приборов переменного тока - магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

ru-wiki.org

---

• 
  Зарядное устройство для аккумуляторов для батареек
• 
  Резистор дополнительный
• 
  Что определяет электрический ток
• 
  Освещение в квартире коридора
• 
  Диапазон дмв
• 
  Пускатель электродвигателя
• 
  Как ваттметр включается в цепь
• 
  Схема однолинейная тп
• 
  Диапазон дмв
• 
  Параллельная работа трансформаторов пуэ
• 
  Кабель для подключения электроплиты