Электрические схемы замещения
Реальные физические системы неудобно, а чаще всего нереально использовать для анализа происходящих в них процессов. Поэтому вместо них используют их модели – схемы замещения.
Электрическая схема замещения ЭЦ – это математическая модель реальной ЭЦ. Она приблизительно отображает реальные процессы в ЭЦ. Более того, для одной ЭЦ можно представить разные схемы замещения для разных условий работы ЭЦ.
Элементы схемы замещения – это идеализированные элементы, учитывающие определенные физические процессы реальной ЭЦ. Элементы схемы можно лишь изобразить на рисунке, они не существуют физически.
Элементы схемы делятся на активные и пассивные. К активным относятся источники энергии. Они бывают независимые (неуправляемые) и управляемые.
Неуправляемый источник напряжения (э.д.с.) – это идеализированный элемент схемы замещения , напряжение на полюсах которого не зависит от проходящего через него тока. Его графическое изображение имеет вид (рис. 1.2):
Его графическое изображение имеет вид (рис. 1.2):
Рис. 1.2
Полюсное уравнение источника э.д.с. имеет вид u(t) = е(t). Вольтамперная характеристика источника э.д.с., не зависящего от времени, имеет вид (рис. 1.3):
Рис. 1.3
Единица измерения э.д.с та же, что у потенциала – Вольт (В).
Из характеристики следует, что внутреннее сопротивление RВН идеализированного источника э.д.с. равно нулю.
Если в дальнейшем нужно заменить источник э.д.с. его внутренним сопротивлением, то в месте включения источника включается коротко замкнутое соединение, то есть участок схемы будет иметь нулевое сопротивление (RВН = 0) (рис. 1.4):
Рис. 1.4
Измеряется сопротивление R в Омах (Ом).
Неуправляемый источник тока (в дальнейшем просто источник тока) – это идеализированный элемент схемы замещения, ток которого не зависит от напряжения на его полюсах. Графическое изображение источника тока имеет вид (рис. 1.5):
Рис. 1.5
Полюсное уравнение i0(t) = i(t), здесь i0(t) – ток источника тока.
Для неуправляемого источника тока, не зависящего от времени, справедливо равенство:
i(t) = i0 = const.
Внутреннее сопротивление RВН идеализированного источника тока удовлетворяет условию RВН = ∞.
Следовательно, при замене источника тока его внутренним сопротивлением в схеме появляется обрыв (рис. 1.6):
Рис. 1.6
Существует четыре типа управляемых источников.
Источник напряжения (э.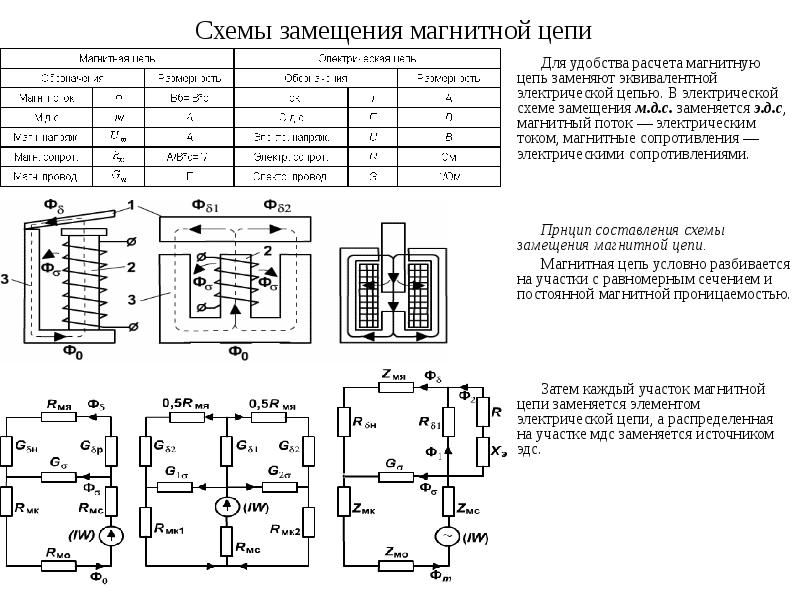 д.с.), управляемый напряжением (ИНУН)– идеализированный элемент схемы замещения, напряжение на полюсах которого не зависит от проходящего по нему тока, но зависит от управляющего им напряжения. Графическое изображение имеет вид (рис. 1.7):
д.с.), управляемый напряжением (ИНУН)– идеализированный элемент схемы замещения, напряжение на полюсах которого не зависит от проходящего по нему тока, но зависит от управляющего им напряжения. Графическое изображение имеет вид (рис. 1.7):
Рис. 1.7
Полюсное уравнение ИНУН имеет вид:
ue(t) = ℮(t) = k· uУ(t),
где uУ(t) – управляющее напряжение,
k – безразмерный коэффициент управления.
Источник напряжения (э.д.с.), управляемый током (ИНУТ)− идеализированный элемент схемы замещения , напряжение на полюсах которого не зависит от проходящего по нему тока, но зависит от управляющего им тока.
Графическое изображение имеет вид (рис. 1.8):
Рис. 1.8
1.8
Полюсное уравнение имеет вид:
ue(t) = ℮(t) = k· iУ(t),
где iУ – управляющий ток.
k – коэффициент управления, имеющий размерность В/А.
Источник тока, управляемый напряжением (ИТУН) – идеализированный элемент схемы замещения , ток которого не зависит от напряжения на полюсах, но зависит от управляющего им напряжения (рис. 1.9):
Рис. 1.9
Полюсное уравнение ИТУН имеет вид:
i0(t) = k· uУ(t),
где k – коэффициент управления, имеющий размерность А/В.
Источник тока, управляемый током (ИТУТ) – идеализированный элемент схемы замещения, ток которого не зависит от напряжения на его полюсах, но зависит от управляющего им тока (рис. 1.10):
Рис. 1.10
1.10
Полюсное уравнение ИТУТ имеет вид:
i0(t) = k· iУ(t),
где k – безразмерный коэффициент управления.
Пассивные элементы не производят, а только потребляют энергию.
Активное сопротивление– идеализированный элемент схемы замещения, учитывающий только процессы преобразования электрической энергии в другие виды энергии, кроме энергии магнитного и электрического полей.
Обозначение в схемах (рис. 1.11) и полюсное уравнение имеют вид:
Рис. 1.11
Это закон Ома во временной области. Сопротивление R – это коэффициент пропорциональности. Измеряется в Омах (Ом).
Активная проводимость g – величина, обратная активному сопротивлению:
g = R-1.
Её полюсное уравнение имеет вид:
iR(t) = g · uR(t).
Измеряется проводимость в Сименсах [См].
Индуктивность L – идеализированный элемент схемы замещения, приближенно отображающий процессы накопления энергии магнитного поля.
Обозначение в схемах (рис.1 .12) и полюсные уравнения имеют вид:
или
Рис. 1.12 .
Здесь iL(0) – постоянная интегрирования, численно равная току индуктивности в момент времени t = 0.
Измеряется индуктивность L в Генри (Гн).
Емкость С– идеализированный элемент схемы замещения, приближенно учитывающий процесс накопления энергии электрического поля.
Обозначение в схемах (рис. 1.13) и полюсные уравнения имеют вид:
или
Рис. 1.13 .
Здесь uС(0) – постоянная интегрирования, численно равная напряжению на емкости в момент времени t = 0.
Измеряется емкость С в Фарадах (Ф).
Соединение элементов схемы замещения выполняется также, как и в реальной ЭЦ. Однако в реальных устройствах соединительные провода обладают в определенной степени параметрами R, L и С, а в схемах замещения – нет. На любых частотах сопротивления проводов равны нулю.
Однако в реальных устройствах соединительные провода обладают в определенной степени параметрами R, L и С, а в схемах замещения – нет. На любых частотах сопротивления проводов равны нулю.
Следует различать элементы ЭЦ и схем замещения.
Пример 1. Определить закон изменения напряжения на активном сопротивлении
R uR(t), если ток iR(t) изменяется по закону iR(t) = 2·ехр(–ωt),
где ω – круговая частота, а R = 100 Ом.
Решение. Исходя из полюсного уравнения для активного сопротивления, полу-
чим:
uR(t) = R· iR(t) = 100·2 ехр(–ωt) = 200 ехр(–ωt) В.
Пример 2. Изобразить график функции напряжения на индуктивности uL(t), если
график функции изменения тока iL(t) имеет вид (рис. 1.14):
Рис. 1.14
1.14
При этом L = 1 Гн.
Решение. Функцию можно записать в виде
В соответствии с полюсным уравнением напряжение uL(t) определится (рис. 1.15):
Рис. 1.15
Пример 3. Определить полюсное уравнение ИНУТ ℮(t) если известно, что ем-
кость, через которую идет управляющий ток, равна 100 мкФ, а напря-
жение на емкости изменяется по закону uC(t) = 20Sin(100t). При этом
k = 10.
Решение. В общем виде полюсное уравнение ИНУТ ℮(t) = k·iУ(t), но iУ(t) – это ток емкости, определяемый полюсным уравнением емкости . Решая полюсные уравнения совместно, получим:
℮(t) = k·iУ(t) = = 10·100·10-6·20·100Cos100t = 2·Cos100t В =
= 2 Sin(100t + π/2) В.
Рассмотрим мощность и энергию, потребляемые каждым из пассивных элементов.
Мгновенная мощность активного сопротивления
рR(t) = uR(t) · (t) = = g · (t), рR(t) > 0.
Нетрудно видеть, что рR(t) – величина положительная.
Потребляемая энергия w(t) определяется формулой:
.
В любой момент времени t сопротивление может только потреблять энергию от источников и не может отдавать ее другим элементам схемы.
Мгновенная мощность емкости
рС(t) = uС(t) · (t) = .
Если uС(t) >0 и > 0, то есть uС(t) продолжает расти, то рС(t) > 0 и энергия
поступает в емкость, то есть емкость заряжается. Если же uС(t) >0, а ≤ 0, то рС(t) < 0. Емкость разряжается, то есть отдает накопленную энергию во внешнюю цепь.
Энергия электрического поля wC(t), запасенная емкостью в произвольный момент времени t, определится:
Энергия wC(t) также положительна.
Мгновенная мощность wL(t) индуктивности определится:
рL(t) = uL(t)· (t) = .
рL(t) > 0, если iL > 0 и > 0. рL(t) > 0, если индуктивность потребляет энергию от остальной части схемы, рL(t) < 0, если она отдает запасенную энергию.
Энергия wL(t), запасенная в индуктивности, определяется:
.
Энергия wL(t) также положительна.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Составление схемы замещения сети и определение её параметров
Составление схемы замещения сети и определение её параметров
Схема замещения сети составляется с использованием схем замещения её отдельных элементов. В рассматриваемой сети такими элементами являются линии электропередачи 110 и 220 кВ, трансформаторы и автотрансформаторы понижающих подстанций. Рассмотрим каждую группу элементов отдельно.
Расчет параметров схемы замещения линии электропередачи
Для линий электропередачи номинальным напряжением не более 220 кВ используем П-образную схему замещения, поперечные ветви которой представлены только неизменными значениями половины зарядной мощности (Qc/2). Потерями активной мощности на корону (∆Pкор), которые определяют значение активной проводимости линии (Gл), можно пренебречь.
Таблица 1 Расчетные данные по ветвям схемы.
| Линия | A-1 | A-2 | 1-2 | 2-3 |
| Длина линии L,км | ||||
| Марка провода | АС 300/39 | АС 400/51 | АС 240/32 | АС 95/16 |
| Диаметр провода dпр, мм | 27,5 | 21,6 | 13,5 | |
| R0 при 20 ⁰С, Ом/м | 0,096 | 0,073 | 0,118 | 0,301 |
| Uном , кВ | ||||
| Dсг, м |
Расчет линии А-1
Расчет удельных параметров схемы замещения
Для определения параметров схемы замещения линий электропередачи необходимо в начале вычислить их погонные реактивные параметры (x0 и b0) с использованием соответствующих значений среднегеометрического расстояния между фазами (Dсг) и диаметра провода (dпр). При этом можно пренебречь взаимным влиянием цепей двухцепной линии электропередачи.
Расчет эквивалентных параметров схемы замещения
Параметры схемы замещения линий электропередачи определяются с учетом числа цепей линии. Результаты расчетов параметров схем замещения линий электропередачи приведены в табл. 2.
Определим индуктивное сопротивление проводов линии (Отражает самоиндукцию провода и взаимоиндукцию проводов):
Определим емкостную проводимость линии (Отражает емкость провода относительно земли и соседних проводов):
Определим зарядную мощность (Отражает мощность, которую генерирует емкость провода относительно земли и соседних проводов):
Расчет линии А-2
Расчет удельных параметров схемы замещения
Расчет эквивалентных параметров схемы замещения
Расчет линии 1-2
Расчет удельных параметров схемы замещения
Расчет эквивалентных параметров схемы замещения
Расчет линии 2-3
Расчет удельных параметров схемы замещения
Расчет эквивалентных параметров схемы замещения
Таблица 2 Параметры схемы замещения линий электропередачи
| ЛЭП (ветвь) | Uном,
кВ | nц | L, км | Марка
провода | Погонные параметры | |||||
| , Ом/км | X0, Ом/км | B0, мкCм/км | Qc0, квар/км | |||||||
| A-1 | АС 300/39 | 0,118 | ||||||||
| A-2 | АС 400/51 | 0,118 | ||||||||
| 1-2 | АС 240/32 | 0,118 | ||||||||
| 2-3 | АС 95/16 | 0,244 |
Расчет параметров схемы замещения трансформаторов и автотрансформаторов
Для понижающих трансформаторов 220-110 кВ используется схема замещения, в которой ветвь намагничивания вводится в схему постоянным отбором мощности, равным потерям холостого хода (∆Sх). Отбор мощности осуществляется от узла, к которому подключена обмотка высшего напряжения.
Параметры схемы замещения трансформаторов и автотрансформаторов определяются по каталожным данным с учетом установки двух трансформаторов (автотрансформаторов) на каждой подстанции.
Расчет параметров схемы замещения трансформаторов
Таблица 3 Параметры схемы замещения трансформаторов.
| ПС
(узел) | Каталожные данные | Расчетные данные | |||||||||
| , | ,
кВ | ,
кВ | ,
% | ,
кВт | ,
кВт | ,
% | ,
Ом | ,
Ом | ,
МВт | ,
Мвар | |
| 11-11 | 12,0 | 0,8 | |||||||||
| 10,5 | 0,7 |
Расчет схемы замещения понижающей двухтрансформаторной подстанции ПС1
Эквивалентное активное сопротивление двух параллельно работающих трансформаторов:
Эквивалентное реактивное сопротивление двух параллельно работающих трансформаторов:
Эквивалентные потери активной мощности холостого хода в двух параллельно работающих трансформаторах:
Эквивалентные потери реактивной мощности холостого хода в двух параллельно работающих трансформаторах:
Расчет схемы замещения понижающей двухтрансформаторной подстанции ПС3
Определение приведенной и расчетной нагрузки
Первый этап.
На первом этапе определяется потери активной и реактивной мощности во всех элементах сети в предложении равенства напряжений в узлах сети соответствующему номинальному напряжению. Расчет начинается от наиболее удаленных узлов и определения в них приведенных и расчетных нагрузок.
Расчет режима линии 2-3.
Рисунок 5 Схема замещения линии 2-3.
Мощность в конце линии:
Потери мощности в линии:
Поток мощности в начале линии:
Расчет кольцевой сети
Рисунок 7 Схема кольцевой сети.
Рисунок 8 Схема кольцевой сети, разомкнутой по шинам ИП.
Проверка:
Мощность на участке кольцевой сети 1-2:
Рисунок 9 Схема замещения кольцевой линии.2-jQca1/2-jQca2/2= + -j5.4-j6.99=222.122+j77.522 МВ*А
Qcoa1=Ua*Bo=(232*1000)*2*2.68*(1/1000000)=144.24Квар/км
jQca1/2=(Qco/2)*L*n=((Qco*1000)/2)*75*1=5.4Мвар
Qcoa2=Ua*Bo=(232*1000)*2.741*(1/1000000)=147.53Квар/км
jQca2/2=(Qco/2)*L*n=((Qco*1000)/2)*95*1=6.99Мвар
Второй этап.
На втором этапе определяем модули напряжений в узлах схемы замещения по найденным потокам мощности в ветвях сети на первом этапе.
Расчет напряжения на ПС1.
Рисунок 12 Схема замещения ПС1.
Первый этап.
Мощность в конце линии 1-2:
Потери мощности на участке 1-2:
Мощность в начале участка 1-2:
Мощность в конце линии А’-2:
Потери мощности на участке А’-2:
Мощность в начале участка А’-2:
Суммарная мощность, поступающая в сеть от ИП:
Второй этап.
Расчет напряжения на ПС1.
Рисунок 14 Схема замещения ПС1.
Сторона СН.
Принимаем:
Сторона НН.
Принимаем:
Регулировочный диапазон устройства РПН достаточен для режима наибольших нагрузок.
Сторона СН.
Принимаем:
Сторона НН.
Принимаем:
Регулировочный диапазон устройства РПН достаточен для послеаварийного режима.
Сторона НН.
Регулировочный диапазон устройства РПН достаточен для режима наибольших нагрузок.
Сторона НН.
Регулировочный диапазон устройства РПН не достаточен для послеаварийного режима.
Сторона НН.
Регулировочный диапазон устройства РПН достаточен для режима наибольших нагрузок.
Сторона НН.
Регулировочный диапазон устройства РПН достаточен для послеаварийного режима.
Составление схемы замещения сети и определение её параметров
Схема замещения сети составляется с использованием схем замещения её отдельных элементов. В рассматриваемой сети такими элементами являются линии электропередачи 110 и 220 кВ, трансформаторы и автотрансформаторы понижающих подстанций. Рассмотрим каждую группу элементов отдельно.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Схема замещения электрической цепи — Студопедия
Цепи постоянного тока
СОДЕРЖАНИЕ
1 Электрическая цепь и её элементы
2 Схема замещения электрической цепи
3 Параметры и характеристики элементов электрической цепи
4 Классификация электрической цепи
5 Топологические понятия в теории цепи
6 Основные величины, характеризующие процессы в электрических цепях
7 Энергия и мощность в электрической цепи. Баланс мощности
8 Мощность потерь и КПД электрической цепи
9 Режимы работы электрической цепи
10 Основные законы электрических цепей
11 Эквивалентные преобразования пассивных участков электрической цепи
12 Расчёт электрической цепи с одним источником ЭДС
13 Анализ сложных электрических цепей с несколькими источниками ЭДС
14 Распределение потенциала в электрической цепи. Потенциальная диаграмма
15 Основные свойства и области применения мостовых цепей, потенциометров и делителей напряжений
Список использованных источников
Электрическая цепь и её элементы
Электрической цепью называют совокупность у средств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе (ЭДС), токе, напряжении и сопротивлении.
Отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определённую функцию, называется элементом электрической цепи. К основным элементам относятся источники электрической энергии и приёмники этой энергии. В источниках неэлектрические преобразуются в электрическую. К ним относятся гальванические батареи, акуммуляторы, солнечные батареи, термопары, электромагнитные генераторы.
В приёмниках происходит обратное преобразование электрической энергии в иные виды энергии. К приёмникам относятся электрические двигатели, гальванические ванны, нагревательные приборы и элементы, осветительные приборы и др.
Электрическая цепь содержит кроме того вспомогательные элементы, предназначенные для регулирования величины тока (реостаты), для регулирования напряжения (делители и потенциометры), для защиты цепи от перегрузок (предохранители), для коммутации (выключатели), для контроля режимов работы цепи (измерительные приборы) и др.
На схеме электрической цепи её элементы изображаются с помощью условных графических изображений (рис. 2.1.9)
Схема замещения электрической цепи
Электрические цепи принято изображать в виде различного рода схем. Чаще всего пользуются тремя видами схем: монтажными, принципиальными и замещения.
Монтажными цепями пользуются при изготовлении, монтаже и ремонте электрических устройств и цепей.
Принципиальными схемами пользуются при изучении принципа работы устройства, а также при монтаже и ремонте устройств и цепей.
Схемами замещения пользуются при расчёте режима работы электрической цепи. Схема замещения – графическое изображение электрической цепи, содержащее условные обозначения её основных элементов и способы их соединения. На этой схеме реальные элементы замещаются расчётными моделями (идеализированными элементами). При этом все вспомогательные элементы, не влияющие на результаты расчёта на схеме замещения, отсутствуют. На (рис. 1.1) приведена схема замещения разветвлённой электрической цепи с двумя источниками электрической энергии (источниками ЭДС) и пятью приёмниками (резисторами).
U3
1 I3 2
I1 I2 R3
R03 R02 U4 R4 U5 R5
Uab
a b I4 I5
E1+ U1 E2+ U2
_ _
3 3‘
Рис. 1.1
Расчет электрических сетей | Режимщик
Расчет установившихся режимов электрических сетей
Под установившимся режимом электрической сети понимается такой нормальный или послеаварийный режим, в котором токи, напряжения и мощности в ее элементах принимаются неизменными.
Расчет установившегося режима подразумевает определение этих токов, напряжений и мощностей, которые характеризуют режим электрической сети называются параметрами режима.
Целями и задачами расчета установившегося режима электрической сети являются:
• проверка допустимости параметров режима для элементов сети, в частности проверка допустимости величин напряжений по условиям работы изоляции, величин токов − по условиям нагрева проводов, величин мощностей − по условиям работы источников активной и реактивной мощности;
• оценка качества электроэнергии путем сравнения отклонений напряжений в сети с допустимыми отклонениями напряжений от номинальных значений;
• определение экономичности режима по величинам потерь мощности и электроэнергии в электрической сети.
Исходными данными для расчета установившегося режима электрической сети являются:
• принципиальная схема электрической сети, характеризующая взаимную связь между отдельными ее элементами;
• расчетная схема замещения электрической сети, состоящая из схем замещения отдельных элементов, т.е. из сопротивлений, проводимостей, коэффициентов трансформации, называемых параметрами схемы замещения электрической сети;
• значения активных и реактивных мощностей в узлах нагрузки;
• значения активных и реактивных мощностей источников питания, кроме одного, называемого балансирующим по мощности и покрывающим небаланс между вырабатываемой и потребляемой в ЭЭС мощностями;
• значение напряжения в одном из узлов электрической сети, называемом базисным узлом по напряжению.
Электрическая сеть с позиций теоретической электротехники является электрической цепью и для ее расчета справедливы законы Ома и Кирхгофа и все методы расчета электрических цепей, известные из теоретической электротехники.
Электрическая сеть (электрическая цепь) состоит из ветвей, узлов и контуров.
Ветвью называется участок сети, состоящий из последовательно соединенных элементов, по которым протекает один и тот же ток.
Узлом называют место соединения двух или более ветвей.
Контуром называют замкнутый участок сети, состоящий из нескольких ветвей.
Электрическая сеть, не содержащая контуров, называется разомкнутой (рисунок 1 а) ,б).
Рисунок 1. Основные типы схем районных электрических сетей
В такой сети каждый узел нагрузки получает питание с одной стороны (от одного источника).
Замкнутая сеть содержит контуры. Простейшая замкнутая сеть — это кольцевая сеть (рисунок 1, в), в которой каждый узел нагрузки получает питание с двух сторон.
В сети с двухсторонним питанием (рисунок 1, г) каждый узел нагрузки получает питание с двух сторон от разных источников питания.
Сложнозамкнутая сеть (рисунок 1, д) содержит не менее двух контуров с общими ветвями. Нагрузки в такой сети могут получать питание с двух и более сторон.
Наибольшее распространение для расчета любых электрических сетей получил итерационный метод или метод последовательных приближений. В этом методе искомые величины определяются в результате повторяющейся вычислительной процедуры (итерации). На первой итерации осуществляется переход от начальных приближений к более точным значениям искомых величин. На последующих итерациях эти значения последовательно уточняются. Вычислительная процедура заканчивается при достижении заданной точности вычислений. Начальные приближения могут задаваться на основании тех или иных представлений о возможных значениях искомых величин. Так, в частности, начальные значения искомых напряжений в узлах электрической сети могут быть заданы равными номинальному напряжению этой сети.
Операторный метод расчета переходных процессов (Лекция №27)
Сущность операторного метода заключается в том, что функции вещественной переменной t, которую
называют оригиналом, ставится в соответствие функция комплексной переменной , которую называют изображением.
В результате этого производные и интегралы от оригиналов заменяются алгебраическими
функциями от соответствующих изображений (дифференцирование заменяется умножением
на оператор р, а интегрирование – делением на него), что в свою очередь определяет
переход от системы интегро-дифференциальных уравнений к системе алгебраических
уравнений относительно изображений искомых переменных. При решении этих уравнений
находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим
моментом при этом в практическом плане является необходимость определения только
независимых начальных условий, что существенно облегчает расчет переходных процессов
в цепях высокого порядка по сравнению с классическим методом.
Изображение заданной функции определяется в соответствии с
прямым преобразованием Лапласа:
| . | (1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается,
как:
или
Следует отметить, что если оригинал увеличивается с ростом t,
то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются
на практике при расчете переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций,
часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:
- При умножении оригинала на коэффициент на тот же коэффициент умножается
изображение:
.
.
С использованием этих свойств и данных табл. 1, можно показать, например,
что
.
Изображения производной и интеграла
В курсе математики доказывается, что если , то , где — начальное значение функции
.
Таким образом, для напряжения на индуктивном элементе можно записать
или при нулевых начальных условиях
.
Отсюда операторное сопротивление катушки индуктивности
.
Аналогично для интеграла: если , то .
С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:
.
Тогда
или при нулевых начальных условиях
,
откуда операторное сопротивление конденсатора
.
Закон Ома в операторной форме
Пусть имеем некоторую ветвь (см. рис. 1), выделенную
из некоторой
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу,
при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем
случае ненулевые.
Для мгновенных значений переменных можно записать:
.
Тогда на основании приведенных выше соотношений получим:
.
Отсюда
| , | (2) |
где — операторное сопротивление рассматриваемого
участка цепи.
Следует обратить внимание, что операторное сопротивление соответствует комплексному сопротивлению
ветви в цепи синусоидального
тока при замене оператора р на .
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником
ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать
операторную схему замещения, представленную на рис. 2.
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов,
сходящихся в узле, равна нулю
.
Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости
учета ненулевых начальных условий (если они имеют место). С их учетом последнее
соотношение может быть переписано в развернутом виде
.
В качестве примера запишем
выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 —
; 2 — .
В первом случае в соответствии с законом Ома .
Тогда
и
Во втором случае, т.е. при
, для цепи на рис. 3 следует составить
операторную схему замещения, которая приведена на рис. 4. Изображения токов
в ней могут быть определены любым методом расчета линейных цепей, например,
методом контурных токов:
откуда ; и .
Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен
следующими способами:
1. Посредством обратного преобразования Лапласа
,
которое представляет собой решение интегрального уравнения (1) и сокращенно
записывается, как:
.
На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия,
охватывающих практически все задачи электротехники. Согласно данному способу
необходимо получить изображение искомой величины в виде, соответствующем табличному,
после чего выписать из таблицы выражение оригинала.
Например,
для изображения тока в цепи на рис. 5 можно записать
.
Тогда в соответствии с данными табл. 1
,
что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение искомой переменной определяется
отношением двух полиномов
,
где .
Это выражение может быть представлено в виде суммы простых дробей
| , | (3) |
где — к-й корень уравнения .
Для определения коэффициентов умножим левую и правую части
соотношения (3) на ( ):
.
При
.
Рассматривая полученную неопределенность типа по правилу Лопиталя, запишем
.
Таким образом,
.
Поскольку отношение есть постоянный коэффициент,
то учитывая, что , окончательно получаем
| . | (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней
уравнения равен нулю, т.е. , то уравнение (4) сводится к
виду
.
В заключение раздела отметим, что для нахождения начального и конечного значений оригинала можно использовать
предельные соотношения
которые также могут служить для оценки правильности полученного изображения.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные
условия? - Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты
ее написания? С использованием теоремы об
активном двухполюснике записать операторное изображение для тока через катушку
индуктивности в цепи на рис. 6.- С использованием предельных соотношений и решения предыдущей задачи найти
начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: .
Ответ: .
Эквивалентная цепь трансформатора
, относящаяся к первичной и вторичной стороне
Все трансформаторы имеют сопротивление обмотки, сердечник с конечной магнитной проницаемостью, потоком утечки, гистерезисом и потерями на вихревые токи и, следовательно, не идеальны. Их можно представить в виде эквивалентной схемы, которая позволяет нам анализировать трансформатор.
Характеристики неидеального трансформатора
Неидеальный трансформатор показан на рисунке 1. Его можно описать следующими характеристиками:
1.Существует утечка магнитного потока, что означает, что не весь магнитный поток, создаваемый одной обмоткой, будет связывать другую обмотку.
2. Первичная и вторичная обмотки имеют сопротивления, что означает, что приложенное напряжение (напряжение источника) v 1 НЕ совпадает с наведенным первичным напряжением e 1 ; то есть v 1 ≠ e 1 . Аналогично v 2 ≠ e 2 .
3. Магнитный сердечник НЕ обладает идеальной проницаемостью, что означает, что для его намагничивания требуется конечная ммс.
4. Поскольку поток в магнитопроводе переменный, существуют гистерезисные, а также потери на вихревые токи, которые в совокупности называются потерями в сердечнике или железе.
Эквивалентная схема трансформатора
При выводе эквивалентной схемы для двухобмоточного трансформатора, показанного на рисунке 1, необходимо моделировать характеристики реального трансформатора, описанные ранее.
Рассмотрим первичный контур. Уравнение напряжения вокруг контура может быть записано как
\ [\ begin {matrix} {{\ nu} _ {1}} = {{R} _ {1}} {{i} _ {1}} + { {N} _ {1}} \ frac {d {{\ lambda} _ {1}}} {dt} = {{R} _ {1}} {{i} _ {1}} + {{N} _ {1}} \ frac {d {{\ phi} _ {1}}} {dt} & {} & (1) \\\ end {matrix} \]
Были
R 1 = Сопротивление первичной обмотки
N 1 = количество витков первичной обмотки
Поток первичной обмотки ϕ 1 может быть выражен как сумма взаимного потока ϕ м и потока утечки первичной обмотки ϕ 11 :
$ \ begin {matrix} {{\ phi} _ {1}} = {{\ phi} _ {m}} + {{\ phi} _ {11}} & {} & (2) \\\ конец {матрица} $
Рис.1: Фактический трансформатор
Таким образом, уравнение (1) сводится к
\ [\ begin {matrix} {{\ nu} _ {1}} = {{R} _ {1}} {{i} _ { 1}} + {{N} _ {1}} \ frac {d {{\ phi} _ {11}}} {dt} + {{N} _ {1}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & (3) \\\ end {matrix} \]
Поскольку поток утечки является линейной функцией первичного тока i 1 , второй член справа -сторонняя часть уравнения (3) может быть выражена через индуктивность первичной обмотки. Таким образом,
\ [\ begin {matrix} {{\ nu} _ {1}} = {{R} _ {1}} {{i} _ {1}} + {{L} _ {1}} \ frac {d {{i} _ {1}}} {dt} + {{N} _ {1}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & ( 4) \\\ end {matrix} \]
Далее рассматривается вторичная цепь.Из рис. 1 уравнение напряжения во вторичной обмотке можно записать следующим образом:
\ [\ begin {matrix} {{\ nu} _ {2}} = — {{R} _ {2}} {{i } _ {2}} + {{N} _ {2}} \ frac {d {{\ lambda} _ {2}}} {dt} = — {{R} _ {2}} {{i} _ {2}} + {{N} _ {2}} \ frac {d {{\ phi} _ {2}}} {dt} & {} & (5) \\\ end {matrix} \]
С точки зрения направления потока вторичный поток может быть представлен разницей между взаимным потоком и вторичным потоком утечки:
\ [\ begin {matrix} {{\ phi} _ {2}} = {{\ phi} _ {m}} — {{\ phi} _ {12}} & {} & (6) \\\ end {matrix} \]
Подставляя уравнение (6) в (5), получаем
\ [\ begin { матрица} {{\ nu} _ {2}} = — {{R} _ {2}} {{i} _ {2}} — {{N} _ {2}} \ frac {d {{\ phi } _ {12}}} {dt} + {{N} _ {2}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & (7) \\\ end { matrix} \]
Аналогично, поток утечки является линейной функцией вторичного тока i 2 .Таким образом, уравнение (7) может быть записано с использованием индуктивности вторичной обмотки как:
\ [\ begin {matrix} {{\ nu} _ {2}} = — {{R} _ {2}} {{{ i} _ {2}} — {{L} _ {2}} \ frac {d {{i} _ {2}}} {dt} + {{N} _ {2}} \ frac {d {{ \ phi} _ {m}}} {dt} & {} & \ left (8 \ right) \\\ end {matrix} \]
В уравнениях (4) и (8) последние члены представляют индуцированные напряжения на первичной и вторичной обмотках соответственно; то есть
\ [\ begin {matrix} {{e} _ {1}} = {{N} _ {1}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & \ left (9 \ right) \\\ end {matrix} \]
\ [\ begin {matrix} {{e} _ {2}} = {{N} _ {2}} \ frac { d {{\ phi} _ {m}}} {dt} & {} & \ left (10 \ right) \\\ end {matrix} \]
Деление уравнения (9) на (10) дает отношение напряжений :
\ [\ begin {matrix} \ frac {{{e} _ {1}}} {{{e} _ {2}}} = \ frac {{{N} _ {1}}} {{ {N} _ {2}}} = a & {} & \ left (11 \ right) \\\ end {matrix} \]
На рис. 2 показана эквивалентная схема двухобмоточного трансформатора на рис.1. Элементы схемы, которые используются для моделирования намагниченности сердечника и потерь в сердечнике, могут быть добавлены либо к первичной, либо к вторичной стороне. На рисунке 2 катушка индуктивности L m1 , представляющая намагниченность сердечника, и резистор R c1 , представляющий потери в сердечнике (гистерезис и потери на вихревые токи), подключены параллельно и расположены на первичной стороне эквивалентной схемы трансформатора.
Связанные с сердечником элементы схемы R c1 и L m1 обычно определяются при номинальном напряжении и относятся к первичной стороне на рис.2. Предполагается, что они остаются практически постоянными, когда трансформатор работает в номинальных или близких к ним условиях.
Эквивалентная схема трансформатора в векторной форме
В векторной форме эквивалентная схема трансформатора принимает форму, показанную на рисунке 3. Реактивные сопротивления вычисляются путем умножения индуктивностей на радианную частоту $ \ omega = 2 \ pi f $, где f — частота. Соотношение витков a = N 1 / N 2 приблизительно равно соотношению напряжений V 1 / V 2 , отношению номинального первичного напряжения к номинальному вторичному напряжению, предоставленному производителем.
Рис. 2: Эквивалентная схема трансформатора
Рис. 3: Эквивалентная схема трансформатора в векторной форме
Векторная диаграмма для нагрузки с отстающим коэффициентом мощности (индуктивной), подключенной ко вторичной обмотке трансформатора, показанного на Рис. показан на рис.4.
Используется следующее обозначение:
\ [\ begin {array} {* {35} {l}} {{\ text {E}} _ {\ text {1}}} = \ text {} primary \ text {} индуцированное \ text {} напряжение \\ {{\ text {E}} _ {\ text {2}}} = \ text {} вторичное \ text {} индуцированное \ text {} напряжение \\ {{\ text {V}} _ {\ text {1}}} = \ text {} первичный \ text {} терминал \ text {} напряжение ~~~~~~~~~~~~~~~~~~ \\ { {\ text {V}} _ {\ text {2}}} = \ text {} вторичный \ text {} терминал, \ text {} напряжение \\ \ begin {align} & {{\ text {I}} _ {\ text {1}}} = ~ основной \ text {} текущий \\ & {{\ text {I}} _ {\ text {1}}} = ~ Дополнительный \ text {} текущий \\\ end {align } \\ {{\ text {I}} _ {\ text {e}}} = \ text {} возбуждение \ text {} текущее \\ {{\ text {I}} _ {\ text {m}}} , \ text {} {{X} _ {m}} = \ text {} намагничивание \ text {} текущее \ text {} и \ text {} реактивное сопротивление \\ {{\ text {I}} _ {\ text { c}}}, \ text {} {{R} _ {c}} = \ text {} current \ text {} и \ text {} сопротивление \ text {}, представляющее \ text {} core \ text {} loss \ \ ~~~ {{R} _ {1}} = \ text {} сопротивление \ text {} из \ text {} \ text {} первичной \ text {} обмотки \\ ~~~~ {{R} _ {2}} = \ text {} сопротивление \ text {} из \ t ext {} \ text {} вторичная \ text {} обмотка \\ ~~~~ {{X} _ {1}} = \ text {} первичная \ text {} утечка \ text {} реактивное сопротивление \\ ~~~ ~ {{X} _ {2}} = \ text {} secondary \ text {} Leakage \ text {} Реактивное сопротивление \\\ end {array} \]
Эквивалентная цепь трансформатора, относящаяся к первичной и вторичной сторонам
В схеме замещения трансформатора на рис.3, идеальный трансформатор можно переместить вправо или влево от эквивалентной схемы, если отнести все величины к первичной или вторичной обмотке соответственно, как показано на рисунке 5. Это почти всегда делается из-за большой простоты, которую он привносит в анализ трансформатора.
Рис.4: Фазорная схема эквивалентной цепи трансформатора
Рис.5 (a): Эквивалентная схема трансформатора относительно первичной стороны
Рис.5 (b): Эквивалентная схема трансформатора относительно вторичной стороны
Примерная эквивалентная схема трансформатора, относящаяся к первичной и вторичной стороне
Выведение примерных эквивалентных схем начинается со схем, показанных на рис.5. Все величины относятся к одной и той же стороне трансформатора, и идеальный трансформатор может не включаться в эквивалентную схему.
- Первым шагом в процессе упрощения является перемещение ветви намагничивания шунта из середины Т-цепи либо к первичной, либо к вторичной клемме, как показано на рис. 6 (a) и (b). На этом этапе не учитывается падение напряжения на первичной или вторичной обмотке, вызванное током возбуждения. Падение напряжения, вызванное нагрузочной составляющей тока, конечно же, все еще учитывается.{2}}} + {{X} _ {2}} $.
4. Следующим шагом в построении примерной эквивалентной схемы является полное удаление шунтирующей намагничивающей ветви. Таким образом, эквивалентная схема трансформатора сводится к простому эквивалентному последовательному сопротивлению, относящемуся к первичной или вторичной обмотке, как показано на рис. 6 c и d.
Эквивалентная схема трансформатора? Ссылка на первичную и вторичную стороны
Эквивалентная принципиальная схема любого устройства может быть весьма полезна при предварительном определении поведения устройства в различных условиях работы.Это просто схематическое представление уравнения, описывающего производительность устройства.
Нарисована упрощенная эквивалентная схема трансформатора, представляющая все параметры трансформатора либо на вторичной стороне, либо на первичной стороне. Эквивалентная принципиальная схема трансформатора приведена ниже:
ЭКВИВАЛЕНТНАЯ СХЕМА ТРАНСФОРМАТОРА
В комплекте:
Пусть эквивалентная схема трансформатора с коэффициентом трансформации K = E 2 / E 1
Индуцированная ЭДС E 1 равна приложенному первичному напряжению V 1 за вычетом падения первичного напряжения.Это напряжение вызывает ток I 0 холостого хода в первичной обмотке трансформатора. Значение тока холостого хода очень мало, поэтому им пренебрегают.
Следовательно, I 1 = I 1 ’. Ток холостого хода далее делится на две составляющие, называемые током намагничивания (I m ) и рабочим током (I w ).
Эти две составляющие тока холостого хода обусловлены током, потребляемым неиндуктивным сопротивлением R 0 и чистым реактивным сопротивлением X 0 , имеющим напряжение E 1 или (V 1 — падение первичного напряжения).
Вторичный ток I 2 —
Напряжение на зажимах V 2 на нагрузке равно наведенной ЭДС E 2 во вторичной обмотке за вычетом падения напряжения во вторичной обмотке.
Эквивалентный контур, когда все количества относятся к первичной стороне
В этом случае, чтобы нарисовать эквивалентную схему трансформатора, все величины должны относиться к первичной обмотке, как показано на рисунке ниже:
Принципиальная схема трансформатора, когда все вторичные величины относятся к первичной стороне
Ниже приведены значения сопротивления и реактивного сопротивления, указанные ниже
.
Сопротивление вторичной обмотки относительно первичной обмотки равно:
Эквивалентное сопротивление первичной обмотки:
Вторичное реактивное сопротивление по отношению к первичной стороне определяется как:
Эквивалентное реактивное сопротивление первичной обмотки определяется следующим образом:
Эквивалентная цепь, когда все количества относятся к вторичной стороне
Эквивалентная принципиальная схема трансформатора показана ниже, когда все величины относятся к вторичной стороне.
Принципиальная схема трансформатора, когда все первичные величины относятся к вторичной стороне
Ниже приведены значения сопротивления и реактивного сопротивления, указанные ниже
.
Сопротивление первичной обмотки относительно вторичной стороны равно
Эквивалентное сопротивление, относящееся к вторичной стороне, равно
Первичное реактивное сопротивление относительно вторичной стороны равно
.
Эквивалентное реактивное сопротивление вторичной обмотки равно
Ток холостого хода I 0 вряд ли от 3 до 5% номинального тока при полной нагрузке, параллельная ветвь, состоящая из сопротивления R 0 и реактивного сопротивления X 0 , может быть опущена без внесения каких-либо заметных ошибок в поведение трансформатора в нагруженном состоянии.
Дальнейшее упрощение эквивалентной схемы трансформатора можно сделать, пренебрегая параллельной ветвью, состоящей из R 0 и X 0 .
Упрощенная принципиальная схема трансформатора представлена ниже:
Упрощенная эквивалентная принципиальная схема трансформатора
Это все об эквивалентной схеме трансформатора.
Модель эквивалентной схемы для литиевой батареи электромобиля с учетом характеристики самовосстановления
Принимая во внимание явление самовосстановления литиевых батарей во время периодической разрядки, предлагается модель эквивалентной схемы литиевых батарей на основе характеристики самовосстановления.Математическое описание литиевой батареи в процессе самовосстановления получено путем анализа модели эквивалентной схемы. На экспериментальной платформе был проведен эксперимент с учетом характеристики самовосстановления. Результат показывает, что модель эквивалентной схемы литиевой батареи на основе характеристик самовосстановления может точно описывать напряжение литиевой батареи во время процесса самовосстановления.
1. Введение
Энергия является основой прогресса и развития общества, и жизненно важно разработать новый энергоаккумулятор, который был бы эффективным и экологически безопасным и, более того, обязательно приводил его в действие [1].Электромобили привлекли большое внимание из-за их таких характеристик, как чистота и высокая эффективность [2, 3]. Литий-ионный аккумулятор — один из лучших вариантов для аккумулятора электромобиля из-за его небольшого объема, легкого веса и низкой скорости саморазряда [4]. Однако аккумуляторные батареи стали важным фактором, влияющим на производительность и стабильность электромобилей [5]. Поэтому исследования безопасности и надежности литий-ионных аккумуляторов оказались в центре внимания [6–8].Хуанг и др. [9] предложили новый метод оценки состояния заряда (SOC) и состояния здоровья (SOH) батареи, используя величину изменения напряжения в единицу времени во время процесса разряда батареи. На основании данных теста на срок службы батареи установлено, что состояние здоровья имеет линейную зависимость от величины, обратной падению напряжения за единицу времени, которое является функцией состояния заряда. Этот метод реализует онлайн-оценку SOC и SOH, и доказано, что модель имеет надежность.Zou et al. [10] предложил комбинированный метод оценки SOC и SOH на основе срока службы литий-ионной батареи. Два расширенных фильтра Калмана с двумя временными шкалами используются для оценки SOC в реальном времени и обновления SOH в автономном режиме, что обеспечивает точные оценки SOC и SOH. Xiong et al. [11] использовали расширенный адаптивный фильтр Калмана (AEKF) для оценки степени заряда литиевых батарей. Алгоритм AEKF улучшает традиционный KF и устраняет неточность нелинейных задач. Кроме того, алгоритм AEKF может повысить точность прогнозирования за счет адаптивного обновления ковариации шума процесса и измерения.Однако вышеупомянутые исследования сосредоточены на идеальных рабочих условиях и не принимают во внимание периодический разряд литиевой батареи в реальной эксплуатации. Фактически, явление самовосстановления можно было обнаружить во время периодической разрядки литиевых батарей [12]. Другими словами, при стоянии емкость аккумулятора будет возрастать. Нет сомнений в том, что явление самовосстановления может способствовать продлению срока службы литиевых батарей [6]. Следовательно, при этом условии необходимы дальнейшие исследования.
В настоящее время модели аккумуляторов можно разделить на две категории: электрохимические модели и модели эквивалентных схем [13]. Основанная на электрохимической теории, в электрохимической модели используются математические методы для описания процесса реакции внутри батареи. Используя эту модель, можно установить взаимосвязь между производительностью клеток и микроскопическими количествами. Однако этот метод сложен в вычислительном отношении и затрудняет определение значений параметров [14, 15].Модель эквивалентной схемы, основанная на внешних характеристиках батареи, позволяет избежать анализа внутренних реакций и сложных расчетов параметров. Всесторонне учитывая точность и практичность модели батареи, модель эквивалентной схемы широко используется при оценке характеристик батареи в системах управления батареями [16, 17]. He et al. [18] предложили основанный на модели метод онлайн-оценки для батареи LiFePO 4 , который использует модель эквивалентной схемы Тевенина для моделирования батареи LiFePO 4 и дает соответствующее математическое уравнение.Feng et al. [19] предложили новую модель эквивалентной схемы литиевой батареи, добавив шум скользящего среднего к модели цепи резистор-конденсатор первого порядка. Эта новая модель значительно упрощает вычислительную сложность параметров модели. Sun et al. [20] предложили основанный на модели динамический многопараметрический метод оценки пиковой мощности литий-ионных батарей. Этот метод уточняет омическое сопротивление модели Тевенина для литий-ионной батареи, что повышает точность модели.Указывается, что динамический многопараметрический метод, основанный на моделях, может использоваться для более точного расчета доступной мощности, тогда как вышеупомянутые модели не могут описать изменение явления самовосстановления литиевых батарей. Поэтому, чтобы лучше описать состояние литиевой батареи в процессе самовосстановления, предлагается модель эквивалентной схемы литиевой батареи, основанная на характеристиках самовосстановления.
Остальная часть статьи организована следующим образом. Раздел 2 знакомит с феноменом самовосстановления, который очень часто встречается при реальном использовании электромобилей.В разделе 3 предлагается модель эквивалентной схемы, основанная на характеристике самовосстановления, и дается анализ модели. Раздел 4 описывает экспериментальную платформу и график экспериментов на основе LabView. В разделе 5 идентифицируются параметры модели и результаты моделирования сравниваются с экспериментом. Кроме того, анализируется ошибка между моделированием и экспериментом. В заключительном разделе даются некоторые выводы.
2. Процесс самовосстановления
На практике в литиевой батарее часто используются три состояния.Это состояние зарядки, состояние разряда и состояние ожидания. Как показано на рисунке 1, когда батарея заряжена, положительный электрод батареи будет генерировать ионы лития, и в то же время ионы лития будут проходить через электролит. Наконец, ионы лития, генерируемые на положительном электроде батареи, попадают на отрицательный катод батареи и соединяются с графитом. А емкость батареи связана с количеством ионов лития, поступающих на катод батареи.Когда батарея разряжена, ионы лития в отрицательном электроде батареи отделяются от графита и возвращаются на положительный электрод батареи. Емкость аккумулятора уменьшилась.
При фактическом использовании после завершения каждой зарядки литиевая батарея постоянно переключается между состоянием разрядки и состоянием ожидания, то есть периодической разрядкой, как показано на рис. 2. В стоячем состоянии аккумулятор самовосстанавливается. Это явление является обратным процессом разряда батареи, который похож на процесс зарядки батареи, и степень заряда батареи будет увеличиваться [21].И, в долгосрочной перспективе, это явление окончательно повлияет на состояние литиевой батареи [22]. В основном электромобиль находится в работающем и неподвижном состоянии, а литиевая батарея находится в разряженном и стоящем состоянии, поэтому явление самовосстановления очень распространено. Сила самовосстановления зависит от времени, в течение которого батарея находится в стоячем состоянии, и она будет меняться по мере увеличения времени цикла батареи. Кроме того, явление самовосстановления повлияет на оставшийся срок службы батареи.Следовательно, важно создать модель батареи, которая могла бы использоваться для описания явления самовосстановления литий-ионных батарей. В этой статье будет представлена модель эквивалентной схемы литиевой батареи, основанная на характеристиках самовосстановления.
3. Модель аккумулятора
3.1. Предложение модели
Чтобы лучше описать изменение напряжения литиевой батареи в стоячем состоянии, предлагается эквивалентная модель литиевой батареи, основанная на характеристиках самовосстановления.Как показано на рисунке 3, модель на основе характеристик самовосстановления включает в себя напряжение холостого хода
EU / Competition / Article 81 of the EC Treaty (ex Article 85)
- Следующее должно быть запрещено как несовместимое с общим рынком: все соглашения между предприятиями, решения ассоциаций предприятий и согласованные действия, которые могут повлиять на торговлю между государствами-членами и которые имеют своей целью или результатом предотвращение, ограничение или искажение конкуренция на общем рынке, и в частности те, которые:
(a) прямо или косвенно фиксировать цены покупки или продажи или любые другие торговые условия;
(b) ограничивать или контролировать производство, рынки, техническое развитие или инвестиции;
(c) фондовые рынки или источники поставок;
(d) применяет несходные условия к эквивалентным сделкам с другими торговыми сторонами, тем самым ставя их в невыгодное положение с точки зрения конкуренции;
(e) обусловливает заключение контрактов принятием другими сторонами дополнительных обязательств, которые по своему характеру или коммерческому обычаю не имеют отношения к предмету таких контрактов.
- Любые соглашения или решения, запрещенные в соответствии с настоящей статьей, автоматически теряют силу.
- Однако положения пункта 1 могут быть признаны неприменимыми в случае:
— любое соглашение или категория соглашений между предприятиями;
— любое решение или категория решений ассоциаций предприятий;
— любая согласованная практика или категория согласованных действий,
, который способствует улучшению производства или распределения товаров или содействию техническому или экономическому прогрессу, позволяя потребителям справедливую долю получаемой выгоды, и который не:
(a) налагает на заинтересованные предприятия ограничения, которые не являются необходимыми для достижения этих целей;
(b) предоставляет таким предприятиям возможность устранения конкуренции в отношении значительной части рассматриваемых продуктов.
Электрическая связь — эквивалентность T- и Pi-секций
Предположим, что желательно построить сеть, такую как рис. 5 (а). Поскольку два последовательных импеданса 1 / 2Z 1 складываются, чтобы получить полное сопротивление Z 1 , схема на фиг. 5 (а) может быть сформирована из двух Т-секций на фиг. 6 (а). Кроме того, сеть, такая как фиг. 5 (b), может быть сформирована из двух секций π фиг.6 (б).
В цепях связи иногда требуется найти участок π , который эквивалентен Т-образному участку, или наоборот. Две сети имеют общую эквивалентность : 1 , «если одна сеть может заменить другую сеть в любой системе, не изменяя каким-либо образом электрическую работу той части системы, которая является внешней по отношению к сети». Две сети имеют ограниченную эквивалентность 1 «, если одна сеть может заменить другую сеть только в какой-то конкретной системе, не изменяя каким-либо образом электрическую работу той части системы, которая является внешней по отношению к сетям.»В следующем обсуждении будет исследована ограниченная эквивалентность. Очень важно отметить, что сети часто построены с импедансами, которые меняются с частотой; обычно сети эквивалентны только на заданной частоте.
Рис. 5. Схема (a) получается путем выбора части A-B на фиг.4. Схема (6) получается путем выбора части C-D на фиг.4. На рис.7 показаны сети T и π . Чтобы вывести уравнения преобразования , , из которых может быть спроектировано эквивалентное сечение π , если
Рисунок 6. Сечения T и π . известно T-сечение (или наоборот) будут записаны три уравнения. Для Т-образного сечения полное сопротивление Z 12 , измеренное между клеммами
Рисунок 7.Схемы для вывода уравнений преобразования сети. 1-2 составляет Z 12 = Z 1 + Z 3 , а для участка π импеданс Z 12 = Z A (Z B + Z C ) / ( Z A + Z B + Z C ). Когда они приравниваются,
Соответствующие уравнения для импедансов, измеренных между клеммами 3-4:
Соответствующие уравнения для импедансов, измеренных между клеммами 1-3:
Эти три уравнения могут быть решены одновременно для Z 1 , Z 2 и Z 3 в терминах Z A , Z B и Z C .Складывая уравнения 1 и 3 и вычитая уравнение 2, можно найти, что
Точно так же сложение уравнений 2 и 3 и вычитание уравнения 1 дает
и сложение уравнений 1 и 2, а вычитание уравнения 3 дает
Эти уравнения предназначены для преобразования от π к Т-сети. Чтобы преобразовать T в сеть π , уравнения оказываются равными 2,3
а также
Теперь желательно показать, что если две сети связаны согласно этим уравнениям, они эквивалентны и могут заменять друг друга без изменения работы схемы.Для этого будет использоваться рис. 8, на котором две цепи, связанные в соответствии с только что приведенными уравнениями, подключены между одинаковыми источниками напряжения E g и одинаковыми импедансами нагрузки Z L . Если можно показать, что в каждой цепи идентичные генераторы подают токи I 1 , которые в точности совпадают, и что идентичные импедансы нагрузки Z L принимают токи I 2 , которые совершенно одинаковы, тогда T и Секции π эквивалентны клеммам 1-2 и 3-4.
Для Т-образного сечения рис. 8
Поскольку падение напряжения на двух параллельных ветвях должно быть одинаковым,
а также
Рисунок 8. Сети для изучения условий ограниченной эквивалентности. Следующий шаг — подставить в эти два уравнения значения Z 1 , Z 2 и Z 3 , указанные в уравнениях 4, 5 и 6.Выполнение этих замен в уравнении 10 и упрощение выражения дает
Выполнение этих замен в уравнении 11 дает
Теперь остается вывести выражения для I 1 и I 2 для сечения π на рис. 8 в терминах Z A , Z B и Z c и выяснить, выражения согласуются с уравнениями 12 и 13. Таким образом, для сечения π на рис.8,
и упрощая,
Чтобы найти ток I 2 в сечении π на рис.8, сначала необходимо найти ток в импедансе Z B , который может быть определен из соотношения
а также
По аналогии,
Подстановка значения I ZB в это выражение дает
Было показано, что уравнения 12 и 13, выведенные для Т-образного сечения, идентичны уравнениям 14 и 15, выведенным для π-сечения.Это доказывает, что секции будут работать точно так же, когда они вставлены между источником напряжения и импедансом нагрузки, и что, поскольку клеммы 1-2 и 3-4 относятся к цепям T и π, связанным уравнениями 4, 5 и 6, или 7, 8 и 9 эквивалентны.
Эквивалентная схема динамика / электрическая модель
Что такое аналоговая схема динамика?
Эквивалентная схема динамика — это реальное ядро теорий, разработанных Тилем и Смоллом.Каждый компонент динамика может быть «преобразован» в электрический компонент, чтобы сформировать цепь, которая действует точно так же, как динамик (электрически). Позвольте мне сказать по-другому. Вы можете измерить сопротивление динамика. А теперь представьте, что вы берете разные резисторы, катушки индуктивности и конденсаторы и располагаете их таким образом, чтобы при измерении импеданса этой вновь сформированной цепи оно было точно таким же, как импеданс динамика. То же самое происходит, когда вы помещаете динамик в коробку.В схему добавляются дополнительные компоненты. Так Тиле и Смоллу удается прогнозировать поведение вольеров.
Краткое описание колонок
Прежде чем мы перейдем к эквивалентной схеме динамика, нам нужно понять, как динамик работает в первую очередь. Начнем с правильной терминологии. Технический термин для динамика — преобразователь. Это потому, что он преобразует электрическую энергию в акустическую. Но это происходит в два этапа. Во-первых, электрический сигнал (полученный от усилителя) преобразуется в механическое движение, приводя в движение звуковую катушку.Во-вторых, конус начинает двигаться вместе со змеевиком и создает перепады давления воздуха. Таким образом, механическое движение преобразуется в акустический выход. Когда мы начнем моделировать электрическую схему, эти изменения от электрического к механическому и от механического к акустическому, проявятся как трансформаторы.
Упрощенная эквивалентная схема динамика
Давайте начнем с упрощенной версии электрической эквивалентной схемы, а затем мы расширим ее, добавив больше деталей, чтобы она была более ясной.Прежде чем мы перейдем к этому, я предлагаю вам прочитать несколько статей по этому поводу, чтобы я не застал вас врасплох какой-то инопланетной терминологией. Продолжайте читать это, это и это.
Как вы можете видеть выше, это наиболее элементарное электрическое представление динамика. Обычно у вас есть катушка индуктивности, соединенная последовательно с резистором R e , чтобы имитировать индуктивность звуковой катушки, но мы оставляем это для упрощения. Таким образом, у вас будет просто сопротивление звуковой катушки (R e ), соединенное последовательно с катушкой индуктивности, резистором и конденсатором (которые подключены параллельно между ними), которые имитируют сопротивление движению динамика.Эта эквивалентная схема динамика создаст кривую, которая будет выглядеть как диаграмма импеданса динамика.
Определим термины:
- R e — Сопротивление звуковой катушки постоянному току. На диаграмме импеданса это будет соответствовать точке минимального импеданса. Когда вы смотрите на график, вы увидите всплеск на резонансной частоте. Затем импеданс снизится, а затем снова начнет расти из-за индуктивности звуковой катушки. В точке, где он начинает расти, фазовый угол равен 0 градусов, а полное сопротивление минимально (то есть R e ).
- f s — Резонансная частота.
- T с — Соответствующая постоянная времени. T с = 1 / ω с = 1 / 2πf с .
- Q M — Механическая добротность. Это отношение параллельной резистивной составляющей импеданса движения (R M ) к его реактивному сопротивлению при резонансе.
- Q M = R M / X M .
- X M представляют собой объединенное реактивное сопротивление L M и C M из схемы.
- Q E — Коэффициент качества электрической части. Это отношение последовательного сопротивления постоянному току (Re) к его реактивному сопротивлению при резонансе.
- Q T — Общий коэффициент качества. Это выводится из электрических и механических факторов качества, и они суммируются, как параллельные сопротивления.
Это упрощенная версия. Теперь давайте углубимся в детали и посмотрим, что происходит на самом деле.
Электромеханический процесс
В первой части процесса преобразования динамик преобразует электрический сигнал в механическое движение.Это означает, что динамик является трансформатором, а это также означает, что динамик является преобразователем импеданса. Громкоговоритель будет иметь определенный входной электрический импеданс и определенный выходной механический импеданс. Коэффициент трансформации трансформатора напрямую влияет на выходное сопротивление.
Как спроектировать громкоговорители — видеокурсы
Как превратить все эти механические элементы в электрические? Что ж, к счастью, механические и электрические блоки взаимозаменяемы без использования констант.Это означает, что данная мощность (в ваттах) может быть результатом произведения тока и напряжения или произведения силы и скорости. По этой причине каждая механическая часть динамика имеет электрический эквивалент и может быть смоделирована электрически в эквивалентную схему динамика.
Итак, как вы можете видеть выше, электрический импеданс (e / i или напряжение / ток) преобразуется в механический импеданс (сила / скорость). Теперь давайте внесем этот новый элемент в эквивалентную схему нашего динамика.
Трансформатор в нашей схеме имеет соотношение Bl: 1. Произведение B * l является фактором, определяющим выходное механическое сопротивление. Сила звуковой катушки (в Ньютонах) определяется как произведение плотности потока в зазоре, B (в теслах), длины провода катушки, фактически находящейся в зазоре, l (в метрах), и измеренного тока. в амперах. Обратная ЭДС (вольт) — это произведение B (тесла), l (метры) и скорости (метры в секунду).
Это означает, что аналогия следующая:
- Скорость аналога напряжению.
- Аналог силы по току.
Наконец, мы можем убрать трансформатор с картинки и создать эквивалентную схему.
Механоакустический процесс
Поприветствуйте второй трансформатор, который преобразует механическое сопротивление в акустическое.
Передаточное отношение этого 2-го трансформатора определяется площадью поверхности диафрагмы (S). Итак, впервые мы преобразовали ток и напряжение в силу и скорость. Теперь мы преобразуем силу и скорость в давление и объемную скорость.После того, как мы удалим трансформаторы с картинки, мы получим эквивалентную схему снизу.
Эквивалентная схема конечного динамика
После всех этих преобразований покажем окончательную аналогичную электрическую схему. Чтобы завершить схему, индуктивность звуковой катушки была добавлена последовательно с R e .
Это полная электрическая эквивалентная схема. Формулы для расчета каждого компонента выглядят иначе, чем те, что указаны в нашем первом упрощенном примере.Но это только потому, что он использует разные переменные, результаты будут одинаковыми.
Динамик в закрытом ящике
Что происходит, когда вы помещаете динамик в закрытый ящик? Очевидно, схема изменится. Переменная, вводимая закрытым прямоугольником, — это его соответствие. В результате соответствие коробки будет отображаться на принципиальной схеме как дополнительный индуктор.
Интересно то, что он действует точно так же, как фильтр верхних частот 2-го порядка. Если вы помните из статьи о пассивном кроссовере, разница между фильтром высоких частот 1-го и 2-го порядка заключается в том, что вы добавляете индуктивность параллельно.По этой причине крутизна спада герметичного корпуса составляет 12 дБ / октаву.
Разъяснение новых терминов:
- C AB — Соответствие коробки.
- C AS — Соответствие динамика.
Заключение
Знакомство с основами эквивалентной схемы громкоговорителя действительно может подтолкнуть вас к пониманию того, как работает громкоговоритель и как он будет работать в данном корпусе.
- Следующее должно быть запрещено как несовместимое с общим рынком: все соглашения между предприятиями, решения ассоциаций предприятий и согласованные действия, которые могут повлиять на торговлю между государствами-членами и которые имеют своей целью или результатом предотвращение, ограничение или искажение конкуренция на общем рынке, и в частности те, которые:
