Измерение и шкалы | Современное прогнозирование
Любая система содержит очень много различной информации. Конечно же, не вся она нам нужна, но ту, которая нам нужна, надо как-то измерить и преобразовать. Для этого информации нужно предать какую-нибудь форму, то есть перевести её в данные. Например, общую информацию о том, что потребителям нравится наша продукция, и они согласны покупать её в большем количестве, можно формализовать, проведя исследования и дав оценку удовлетворённости покупателей. В результате этого мы получим данные, с которыми можно уже работать и на основе которых можно принимать решение.
Во время такого преобразования исследователь явно или неявно выбирает шкалу, в которой он будет измерять данные. Существует много различных классификаций шкал, и даже есть специальный раздел математики, изучающий шкалы и операции с ними — теория измерений. Не вдаваясь в детали это дисциплины, рассмотрим то, что может нам пригодиться в прогнозировании.
Принято считать, что любая шкала может обладать следующими характеристиками:
- описание,
- порядок,
- расстояние,
- естественная точка отсчёта,
- естественная единица измерения.

Последняя характеристика обычно опускается, так как для целей исследования особо полезной информации не несёт. С точки зрения прогнозирования выделение следующих четырёх видов шкал (упорядоченных по уровню) на основе первых четырёх характеристик вполне достаточно для использования по максимуму различных математических и не математических методов:
1. Номинальная шкала
Шкала, в которой есть только характеристика «описание». В ней нет естественного упорядочения, нет расстояния между элементами и тем более нет естественной точки отсчёта. С данными, измеренными в номинальной шкале возможна только одна операция — сравнение в форме «равно» или «неравно». То есть обладает ли объект указанным свойством или нет.
Пример (шутливый). Туристы бывают:
- белые,
- китайцы,
- русские,
- женщины,
- другие.
Из-за ограниченности номинальной шкалы, практически всё, что можно сделать с данными, измеренными в ней — это посмотреть на количество объектов, имеющих указанные признаки. Например, мы можем понять, сколько в нашем распоряжении оказалось китайских туристов, какой процент от всех туристов они составляют. Если в нашем распоряжении несколько величин, измеренных в номинальной шкале, мы можем, например, использовать коэффициент сопряжённости, для того, чтобы оценить, есть ли связь в выборе признака в одной шкале с выбором признака в другой.
Например, мы можем понять, сколько в нашем распоряжении оказалось китайских туристов, какой процент от всех туристов они составляют. Если в нашем распоряжении несколько величин, измеренных в номинальной шкале, мы можем, например, использовать коэффициент сопряжённости, для того, чтобы оценить, есть ли связь в выборе признака в одной шкале с выбором признака в другой.
Для целей анализа номинальную шкалу бывает удобно трансформировать в бинарную, в которой «1» соответствует наличию, а «0» — отсутствию свойства. В случае с нашими туристами мы получим соответственно 5 новых переменных, измеренных в такой бинарной шкале.
2. Порядковая (ранговая) шкала
Это уже более сложная шкала, в ней появляется вторая характеристика — «порядок». Данные, измеренные в этой шкале можно сравнить и упорядочить, однако сказать насколько (и уж тем более во сколько раз) одна величина больше другой нельзя. То есть к операциям с данными, в этой шкале добавляется «больше» и «меньше».
Пример. Туристы бывают:
Туристы бывают:
- грустные,
- нейтральные,
- весёлые.
В этом примере, как видим, туристы упорядочены по настроению, но при этом нет возможности сказать, насколько один может быть веселее другого. К порядковой шкале будет относиться даже шкала, которая на первый взгляд не выглядит как порядковая.
Пример. Туристы бывают:
- от 10 до 15 килограмм,
- от 15 до 20 килограмм,
- от 20 до 100 килограмм,
- больше 100 килограмм.
Измерить расстояние между элементами в такой шкале не представляется возможным, поэтому она порядковая.
Точно так же оценки за экзамен измеряются в порядковой шкале: разница между 5 и 3 формально равна двум, но при этом не имеет смысла, так как в этой шкале двойка — это просто ещё одна оценка. Если по курсу вначале получить 3,а потом — 2, то пятёрки не получится.
В порядковой шкале можно уже использовать некоторые базовые статистические инструменты. Например, можно оценить моду, для того, чтобы понять, туристы какого веса чаще встречаются в выборке. Можно так же рассчитать ранговый коэффициент корреляции (Спирмена либо Кендалла), который может показать, есть ли статистическая линейная связь между весом туристов и их настроением. Расчёт средней величины (а так же медианы и стандартного отклонения) в порядковой шкале возможен, но в этом случае получаемое значение будет просто добавлять в нашу шкалу новые значения, но не более того. Например, если в шкале оценок за экзамены появилась «4.5» (как средняя между «4» и «5»), то это значение просто расширяет нашу шкалу, которая теперь будет содержать: «2», «3», «4», «4.5» и «5». Расстояние между «4» и «4.5», а так же «4.5» и «5» всё так же невозможно адекватно измерить.
Можно так же рассчитать ранговый коэффициент корреляции (Спирмена либо Кендалла), который может показать, есть ли статистическая линейная связь между весом туристов и их настроением. Расчёт средней величины (а так же медианы и стандартного отклонения) в порядковой шкале возможен, но в этом случае получаемое значение будет просто добавлять в нашу шкалу новые значения, но не более того. Например, если в шкале оценок за экзамены появилась «4.5» (как средняя между «4» и «5»), то это значение просто расширяет нашу шкалу, которая теперь будет содержать: «2», «3», «4», «4.5» и «5». Расстояние между «4» и «4.5», а так же «4.5» и «5» всё так же невозможно адекватно измерить.
3. Интервальная шкала
В интервальной шкале добавляется ещё одна характеристика — расстояние, но в ней всё так же отсутствует естественная точка отсчёта. Приемлемые операции в этой шкале (плюс к тем, которые уже были) — сложение и вычитание. Однако операции деления и умножения в этой шкале бессмысленны.
Пример. Температура туриста.
Температура туриста.
Если температура одного туриста — 36.6ºC, а другого — 18.3ºC, то мы можем сказать, что второй турист холоднее первого на 18.3ºC, но сказать, что первый турист горячее второго в два раза нельзя — это не имеет смысла. А всё потому что 0ºC — это не естественная точка отсчёта, а искусственная, привязанная к температуре замерзания воды. Если в качестве точки отсчёта в этой шкале взять, например, абсолютный ноль, то этот бессмысленный эффект «первый в два раза горячее второго» пропадёт.
В интервальной шкале имеют смысл и средняя величина, и медиана, и стандартное отклонение, и квантили распределения. Если очень хочется, то можно рассчитать и коэффициент корреляции Пирсона, который покажет, есть ли линейная связь между показателями.
4. Абсолютная шкала.
Это последний тип шкалы, и он имеет все рассмотренные нами характеристики. Наличие естественной точки отсчёта означает, что когда показатель принимает значение «0», то это говорит о том, что исследуемое свойство у объекта просто отсутствует. В этой шкале возможны все математические операции.
В этой шкале возможны все математические операции.
Пример. Количество туристов в комнате.
Думаю, комментарии к этому примеру излишни.
У шкал есть одно удобное свойство: любые данные, измеренные в шкале более высокого уровня, можно легко преобразовать в данные, измеренные в шкале более низкого уровня.
Например, количество туристов в комнате можно перевести в интервальную шкалу, если это количество центрировать относительно какой-нибудь величины (то есть фактически избавиться от естественной точки отсчёта). В таком случае положительное число будет означать превышение установленного лимита, а отрицательные — занижение. Ноль в таком случае будет соответствовать искусственной точке, в которой количество соответствует выбранному нами эталону.
Если провести ещё одну свёртку данных и избавиться от расстояний между значениями, то можно получить порядковую шкалу, например, следующего вида:
- менее 5 туристов,
- от 5 до 10 туристов,
- более 10 туристов.

Продолжая упрощения, избавляясь от порядка, можно предложить простейшую номинальную шкалу:
- 5 туристов,
- не 5 туристов.
Очевидно, что обратное преобразование невозможно. Если мы изначально собирали данные в номинальной шкале, то получить из них данные, измеренные в шкале более высокого уровня, в принципе невозможно.
И последнее. В случае, если оказывается нужно оценить связь между показателями, измеренными в разных шкалах, нужно использовать коэффициенты, предназначенные для шкал более низкого уровня. Например, для определения связи настроения туриста с его температурой стоит обратиться к ранговому коэффициенту корреляции.
Виды шкал средств измерений — МегаЛекции
Односторонняя шкала — шкала с нулевой отметкой, расположенной в начале или в конце шкалы
Двусторонняя шкала — шкала с нулевой отметкой, расположенной между начальной и конечной отметками.
Различают симметричные (начальная и конечная отметки соответствуют одинаковым значениям измеряемой величины) и несимметричные двусторонние шкалы (начальной и конечной отметкам соответствуют разные значения).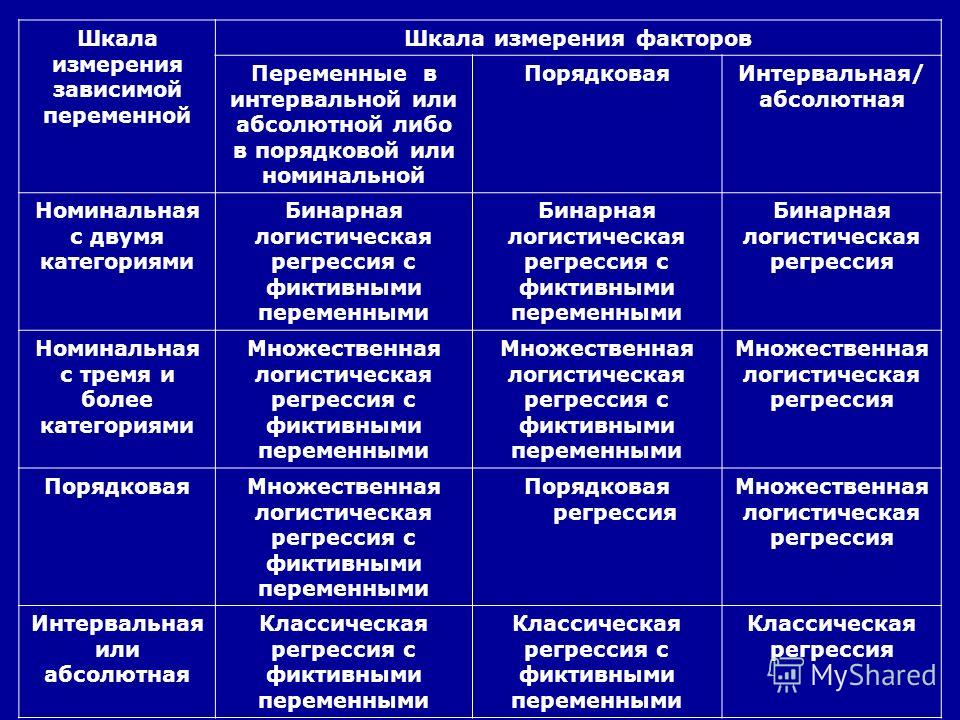
Рис. 8 Неравномерная шкала омметра
Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.
Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:
Равномерная шкала — шкала, отметки на которой нанесены равномерно.
Неравномерная шкала — шкала, отметки на которой нанесены неравномерно.
Рис.9 Амперметр
Стрелочные измерительные приборы: вольтметры, амперметры, омметры и т. д., обладают шкалами. Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка.
д., обладают шкалами. Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка.
Отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.
Рис. 10 Многофункциональный прибор, Тестер
Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет, как правило, условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.
Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.
Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.
Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.
Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.
Рис. 11 Вольтметр
У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.
Рис. 12 Миллиамперметр
Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.
На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.
В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.
Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.
Рис. 13 Многофункциональный прибор, Тестер
На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.
Цена деления шкалы микроамперметра А1.
Микроамперметр А1 измеряет силу тока до 50 мкА. Шкала прибора содержит 5 больших делений, каждое из которых разделено еще на 10 делений.
Таким образом, цена большого деления шкалы микроамперметра равна 50мкА/5 = 10мкА, цена наименьшего деления микроамперметра равна 50мкА/50 = 1мкА .
Для того чтобы определить показание микроамперметра необходимо умножить цену деления на количество делений шкалы, соответствующих отклонению стрелки прибора.
Пример 1.Отклонение стрелки соответствует 2 большим или 20 маленьким делениям. Показание микроамперметра равно 10мкА * 2 = 20 мкА или 1мкА * 20 = 20 мкА.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Измерение в психологии. Шкалы измерения. — Методы математической статистики — — Каталог статей
Автор статьи: Попов Олег Александрович.
При копировании или цитировании ссылка на сайт и автора обязательна!
В психологии
довольно часто приходится иметь дело с измерением. По сути дела любой
психологический тест является инструментом измерения, результатом которого,
чаще всего, являются числовые данные.
Измерение – операция для определения
отношения одного объекта к другому. Измерение реализуется за счет приписывания
объектам значений так, чтобы отношения между значениями отражали отношения
между объектами. К примеру, мы измеряем
рост двух людей (объект измерения — рост). Получив значения 170 и 185 см. мы
можем точно сказать, что один человек выше другого. Данный вывод был получен
благодаря измерению роста. Таким образом, отношение между объектами было
передано с помощью чисел.
В психологии
можем видеть аналогичные предыдущему примеру явления. Мы используем тесты
интеллекта, чтобы получить числовое значение IQ и иметь возможность сравнить
его с нормативным значением, используем тесты личности, чтобы на основе
полученных чисел описать психологические особенности человека, используем тесты
достижений, чтобы выяснить насколько хорошо был усвоен учебный материал.
Измерением так же является подсчет количества определённых актов поведения в
ходе наблюдения за испытуемыми, подсчет площади штриховки в проективных
рисунках, подсчет количества ошибок в корректурной пробе.
В случае с
ростом объектом измерения был не человек, а его рост. Изучая психику человека
мы так же измеряем не его самого, а определённые психологические особенности:
черты личности, интеллект, отдельные характеристики познавательной сферы и т.д.
Всё, что мы измеряем называется переменными.
Переменная – свойство, которое может
менять своё значение. Рост является свойством всех людей, но у каждого он
разный, а значит является переменной. Пол так же является переменной, но может
принимать всего 2 значения. Все показатели тестов в психологии являются
переменными.
Результаты
некоторых психологических тестов, на первый взгляд, очень трудно представить
как результат измерения и трудно понять, какие свойства (переменные) измеряются
этими тестами. Яркий пример тому – проективные тесты, особенно рисуночные и
вербальные. За каждым элементом рисунка скрывается какая-либо психологическая
За каждым элементом рисунка скрывается какая-либо психологическая
особенность (переменная) и говоря о выраженности либо невыраженности этой
переменной на основе элемента рисунка мы
производим акт измерения. Таким образом, несмотря на огромное количество
переменных, измеряемых с помощью проективных рисунков измерение чаще всего
сводится к простой констатации факта «переменная выражена / не выражена», реже
имеется три или больше градации. Гораздо проще обстоит дело с тестами, в
которых нужно что-либо упорядочить, т.к. их результат – число, отражающее
порядковое место. Ещё более очевидны результаты тестов-опросников, тестов
интеллекта и познавательных способностей.
Таким
образом, тест, как инструмент измерения, накладывает свои ограничения на
получаемый результат. Такое ограничение называется шкалой измерения.
Шкала измерения – ограничение типа
отношений между значениями переменных, накладываемое на результаты измерений.
Чаще всего, шкала измерения зависит от инструмента измерения.
К примеру,
если переменной является цвет глаз, то мы не можем сказать, что один человек
больше или меньше другого по этой переменной, мы так же не можем найти среднее
арифметическое цвета. Если переменной является порядок (именно порядок)
рождения детей в семье, то мы можем сказать, что первый ребенок однозначно
старше второго, но не можем сказать на сколько он старше (отношения
«больше/меньше»). Имея результаты теста интеллекта, мы можем однозначно сказать
на сколько один человек интеллектуальнее другого.
С.Стивенс
рассматривал четыре шкалы измерения.
1. Шкала наименований — простейшая из
шкал измерения. Числа (равно как буквы, слова или любые символы) используются
для различения объектов. Отображает те отношения, посредством которых объекты
группируются в отдельные непересекающиеся классы. Номер (буква, название)
класса не отражает его количественного содержания. Примером шкалы такого рода
может служить классификация испытуемых на мужчин и женщин, нумерация игроков
спортивных команд, номера телефонов, паспортов, штрих-коды товаров.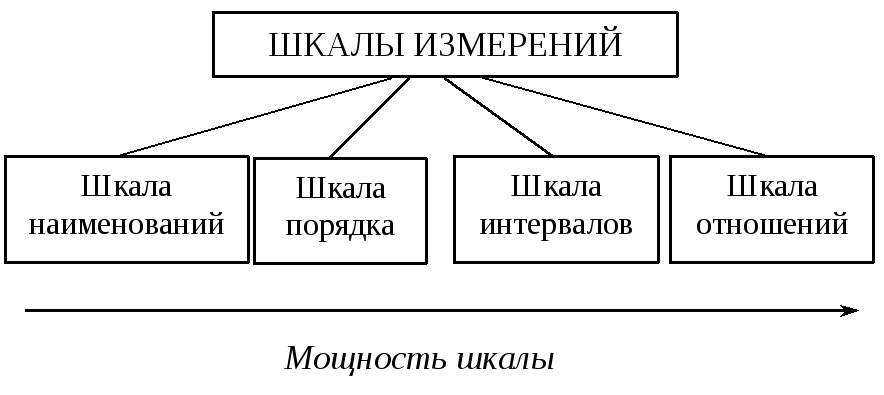 Все эти
Все эти
переменные не отражают отношений больше/меньше, а значит являются шкалой
наименований.
Особым
подвидом шкалы наименований является дихотомическая
шкала, которая кодируется двумя взаимоисключающими значениями (1/0). Пол
человека является типичной дихотомической переменной.
В шкале
наименований нельзя сказать, что один объект больше или меньше другого, на
сколько единиц они различаются и во сколько раз. Возможна лишь операция
классификации — отличается/не отличается.
В психологии
иногда невозможно избежать шкалы наименований, особенно при анализе рисунков. К
примеру, рисуя дом, дети часто рисуют солнце в верхней части листа. Можно
предположить, что расположение солнца слева, посередине, справа или отсутствие
солнца вообще может говорить о некоторых психологических качествах ребенка.
Перечисленные варианты расположения солнца являются значениями переменной шкалы
наименований. Причем, мы можем обозначить варианты расположения номерами,
буквами или оставить их в виде слов, но как бы мы их не называли, мы не можем
сказать, что один ребенок «больше» другого, если нарисовал солнце не
посередине, а слева. Но мы можем точно сказать, что ребенок, нарисовавший
Но мы можем точно сказать, что ребенок, нарисовавший
солнце справа однозначно не является тем, кто нарисовал солнце слева (или не входит в группу).
Таким
образом, шкала наименований отражает отношения типа: похож/не похож, тот/не
тот, относится к группе/не относится к группе.
2. Порядковая (ранговая) шкала —
отображение отношений порядка. Единственно возможные отношения между объектами
измерения в данной шкале – это больше/меньше, лучше/хуже.
Самой типичной
переменной этой шкалы является место, занятое спортсменом на соревнованиях.
Известно, что победители соревнований получают первое, второе и третье место и
мы точно знаем, что спортсмен с первым местом имеет лучшие результаты, чем
спортсмен со вторым местом. Кроме места, имеем возможность узнать и конкретные
результаты спортсмена.
В психологии
возникают менее определенные ситуации. К примеру, когда человека просят
проранжировать цвета по предпочтению, от самого приятного, до самого
неприятного. В этом случае, мы точно можем сказать, что один цвет приятнее
В этом случае, мы точно можем сказать, что один цвет приятнее
другого, но о единицах измерения мы не можем даже предположить, т.к. человек
ранжировал цвета не на основе каких-либо единиц измерения, а основываясь на
собственных чувствах. То же самое происходит в тесте Рокича, по результатам
которого мы так же не знаем на сколько единиц одна ценность выше (больше)
другой. Т.е., в отличие от соревнований, мы даже не имеем возможности узнать
точные баллы различий.
Проведя
измерение в порядковой шкале нельзя узнать на сколько единиц отличаются
объекты, тем более во сколько раз они отличаются.
3. Интервальная шкала — помимо
отношений указанных для шкал наименования и порядка, отображает отношение
расстояния (разности) между объектами. Разности между соседними точками в этой
шкале равны. Большинство психологических тестов содержат нормы, которые и
являются образцом интервальной шкалы. Коэфициент интеллекта, результаты теста
FPI, шкала градусов цельсия – всё это интервальные шкалы. Ноль в них условный:
Ноль в них условный:
для IQ и FPI ноль – это минимально возможный балл теста (очевидно, что даже
проставленные наугад ответы в тесте интеллекта, позволят получить какой-либо
балл отличный от нуля). Если бы мы не создавали условный ноль в шкале, а
использовали реальный ноль как начало отсчета, то получили бы шкалу отношений,
но мы знаем, что интеллект не может быть нулевым.
Не
психологический пример шкалы интервалов — шкала градусов Цельсия. Ноль здесь
условный — температура замерзания воды и существует единица измерения — градус
Цельсия. Хотя мы знаем, что существует абсолютный температурный ноль — это
минимальный предел температуры, которую может иметь физическое тело, который в
шкале Цельсия равен -273,15 градуса. Таким образом, условный ноль и наличие
равных интервалов между единицами измерения являются главными признаками шкалы
интервалов.
Измерив
явление в интервальной шкале, мы можем сказать, что один объект на определенное
количество единиц больше или меньше другого.
4. Шкала отношений. В отличие от шкалы
интервалов может отражать то, во сколько один показатель больше другого. Шкала
отношений имеет нулевую точку, которая характеризует полное отсутствие
измеряемого качества. Данная шкала допускает преобразование подобия (умножение
на константу). Определение нулевой точки — сложная задача для психологических
исследований, накладывающая ограничение на использование данной шкалы. С
помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена), т.е. всё, что имеет гипотетический абсолютный ноль.
Вывод
Любое
измерение производится с помощью инструмента измерения. То, что измеряется
называется переменной, то чем измеряют – инструмент измерения. Результаты
измерения называются данными либо результатами (говорят «были получены данные
измерения»). Полученные данные могут быть разного качества – относиться к одной
из четырех шкал измерения. Каждая шкала ограничивает использование определённых
математических операций, и соответственно ограничивает применение определённых
методов математической статистики.
Вам нужны качественные расчеты с аналитическими выводами? Обращайтесь!
Шкала средства измерений — Карта знаний
- Шкала́ (лат. scala — лестница) — часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией или техническая отметка на шкале измерительного прибора. Шкалы могут располагаться по окружности, дуге или прямой линии. Показания отсчитываются невооружённым глазом при расстояниях между делениями до 0,7 мм, при меньших — при помощи лупы или микроскопа, для долевой оценки делений применяют дополнительные шкалы — нониусы.
Следует заметить, что термин «шкала» в метрологической практике имеет, по крайней мере, два различных значения.
 Во-первых, шкалой или, точнее, шкалой измерений (шкалой физической величины) называют принятый по соглашению порядок определения и обозначения всевозможных проявлений (значений) конкретного свойства (величины). Во-вторых, шкалой называют отсчётные устройства аналоговых средств измерений, это значение используется в данной статье.
Во-первых, шкалой или, точнее, шкалой измерений (шкалой физической величины) называют принятый по соглашению порядок определения и обозначения всевозможных проявлений (значений) конкретного свойства (величины). Во-вторых, шкалой называют отсчётные устройства аналоговых средств измерений, это значение используется в данной статье.Круговую шкалу часов, курвиметров и некоторых других приборов называют циферблатом.
Источник: Википедия
Связанные понятия
Но́ниус (шкала́-но́ниус, шкала́ Но́ниуса, вернье́р) — вспомогательная шкала, устанавливаемая на различных измерительных приборах и инструментах, служащая для более точного определения количества долей делений основной шкалы.
Класс точности — обобщённая характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений.
Номогра́мма (от др.-греч. νόμος — закон и γράμμα — письмо) — графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывания линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.
Градуиро́вка (нем. graduiren «градуировать» от лат. gradus «шаг, ступень, степень») средств измерений, иногда тари́рование — метрологическая операция, при помощи которой средство измерений (меру или измерительный прибор) снабжают шкалой или градуировочной таблицей (кривой). Отметки шкалы должны с требуемой точностью соответствовать значениям измеряемой величины, а таблица (кривая) с требуемой точностью отражать связь эффекта на выходе прибора с величиной, подводимой ко входу (например, зависимость…
Измерение — совокупность действий для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений)..gif)
Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Полигонометрия (от греч. polýgonos — многоугольный и …метрия) — один из методов определения взаимного положения точек земной поверхности для построения геодезических сетей, служащей основой топографических съёмок, планировки и строительства городов, перенесения проектов инженерных сооружений в натуру и т. п. Положения пунктов в принятой системе координат определяют путём измерения на местности длин линий, последовательно соединяющих эти пункты и образующих полигонометрический ход, и горизонтальных…
С 1984 года шкала эфемеридного времени ЕТ заменена двумя шкалами динами́ческого вре́мени DT. ..
..
Подробнее: Динамическое время
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Дискрéтный шкáльный индикáтор — вид знакосинтезирующего индикатора. Предназначен для отображения информации в виде уровней или значений величин.
Подробнее: Дискретный шкальный индикатор
Твёрдость по Шору обозначается в виде числового значения шкалы, к которому приписывается буква, указывающая тип шкалы с явным указанием названия метода измерения твердости или прибора. Например…
Измеритель уровня звука — измерительный прибор, применяемый в звукотехнике для определения уровня звукового сигнала. Звук измеряется в децибелах (дБ). Это логарифмические единицы, которые хорошо отражают характеристику слуха, поскольку слух человека ощущает только относительные изменения акустического давления.
Экспозиционное число, экспозиционный канал (англ. Exposure Value, EV) — условное целое число, однозначно характеризующее экспозицию при фото- и киносъёмке. Одному и тому же экспозиционному числу могут соответствовать различные комбинации выдержки и диафрагмы (экспопары), но одно и то же количество света. В соответствии с законом взаимозаместимости эти сочетания по действию на светочувствительный материал равнозначны и соответствуют одному и тому же экспозиционному числу. При этом, экспозиционное…
Логарифми́ческая лине́йка, счётная линейка — аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб), вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую…
Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую…
Измери́тельный прибо́р — средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне. Часто измерительным прибором называют средство измерений для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия оператора.
Нивели́рование (от фр. nivellement или фр. nivèlement — «выравнивание», от фр. niveau — «уровень», «ровень») — определение разности высот двух и более точек земной поверхности, то есть определение превышения.
Базисный прибор — служит для измерения базиса при геодезических работах. Согласно современным стандартам базисный прибор должен обеспечивать измерения с относительной погрешностью не более 1 : 1 000 000.
Твёрдость — свойство материала сопротивляться внедрению более твёрдого тела — индентора.
Тахеометр (от др.-греч. ταχύς, род. пад. ταχέος — «быстрый») — геодезический инструмент для измерения расстояний, горизонтальных и вертикальных углов. Близок к классу неповторительных теодолитов, используется для определения координат и высот точек местности при топографической съёмке местности, при разбивочных работах, выносе на местность высот и координат проектных точек, прямых и обратных засечек, тригонометрического нивелирования и так далее.
Диагра́мма (греч. Διάγραμμα (diagramma) — изображение, рисунок, чертёж) — графическое представление данных линейными отрезками или геометрическими фигурами, позволяющее быстро оценить соотношение нескольких величин. Представляет собой геометрическое символьное изображение информации с применением различных приёмов техники визуализации.
Штрихова́я ме́ра длины́ — мера, представляющая одно или несколько значений длины, определённых кратчайшим расстоянием между центрами двух штрихов шкалы меры. Штриховые меры длины применяются как эталонные меры для передачи размера единицы длины мерам меньшей точности, для калибровки средств измерений длины и линейных измерительных преобразователей, как рабочие меры для регулировки средств измерений длины и станков, для прямых измерений длины и линейных перемещений в станках и приборах.
Число Штреля (англ. Strehl ratio) — величина, характеризующая качество оптического изображения, впервые предложенная Карлом Штрелем и названная в честь него. Используется в ситуациях, когда оптическое разрешение ухудшается из-за аберраций в линзе или из-за искажений при прохождении через турбулентную атмосферу. Имеет значение от 0 до 1, при этом в гипотетической идеальной оптической системе число Штреля равно 1.
Наземный лазерный сканер (НЛС) — это съёмочная система, измеряющая с высокой скоростью (от нескольких тысяч до миллиона точек в секунду) расстояния от сканера до поверхности объекта и регистрирующая соответствующие направления (вертикальные и горизонтальные углы) с последующим формированием трёхмерного изображения (скана) в виде облака точек.
Подробнее: Наземное лазерное сканирование
Компара́тор — это техническое средство, естественные или специально создаваемые среды, позволяющие сличать друг с другом меры однородных величин или показания измерительных приборов, а также сравнивать участки (точки) шкал измерений.
Виды измерений — области измерений, выделяемые по одному из классифицирующих признаков. Рассматриваются в метрологии.
Гравиметр (от лат. gravis «тяжёлый» + греч. μετρεω «измеряю») — прибор для высокоточного измерения силы тяжести; чаще всего применяется при поисках полезных ископаемых.
Твёрдость по Шору — метод определения твёрдости очень твёрдых материалов, преимущественно металлов, по высоте, на которую после удара отскакивает специальный боёк (основная часть склероскопа Шора), свободно и вертикально падающий с определённой высоты. Твердость по этому методу Шора оценивается в условных единицах, пропорциональных высоте отскакивания бойка.
Шкала Хаунсфилда — количественная шкала рентгеновской плотности (радиоденсивности).
Параметр — это обобщенное название определенного физического, геометрического или иного свойства устройства (процесса). Это могут быть, например, размер, скорость, напряжение и т. д.
Модель сейсмического воздействия «СА-482» — совокупность универсальных характеристик, предназначенных для расчётов сейсмостойкости наземных объектов, состоящая из обобщённых спектров коэффициента динамичности (СКД) и синтезированной акселерограммы (СА-482).
Спектрогра́мма (соногра́мма) — изображение, показывающее зависимость спектральной плотности мощности сигнала от времени. Спектрограммы применяются для идентификации речи, анализа звуков животных, в различных областях музыки, радио- и гидролокации, обработке речи, сейсмологии и в других областях.
Метод парных точек — метод обработки экспериментальных данных, созданный для оценивания значения углового коэффициента зависимости и определения его погрешности. Из экспериментальных точек на графике берутся те, которые находятся друг от друга примерно на одинаковом расстоянии (это расстояние должно быть максимально возможным).
Отклонение от круглости — геометрическая величина, численно равная наибольшему расстоянию от точек реального профиля до прилегающей окружности. Ранее использовался термин некруглость.
Измери́тельный мост (мост Уи́тстона, мо́стик Ви́тстона, англ. Wheatstone bridge) — электрическая схема или устройство для измерения электрического сопротивления. Предложен в 1833 году Самуэлем Хантером Кристи (англ. Samuel Hunter Christie) и в 1843 году усовершенствован Чарльзом Уитстоном (англ. Charles Wheatstone). Мост Уитстона относится к одинарным мостам в отличие от двойных мостов Томсона. Мост Уитстона — электрическое устройство, механическим аналогом которого являются аптекарские рычажные…
Корреляция цифровых изображений (англ. digital image correlation and tracking, (DIC/DDIT)) — оптический метод, используемый в техниках отслеживания и идентификации изображения для точных плоских и объемных измерений изменений на изображении. Этот метод часто используется не только для измерения деформаций, полей перемещений и оптических потоков, но и широко используется во многих областях науки и инженерного ремесла. Одно из наиболее широкоизвестных применений данного метода — идентификация перемещений…
Физи́ческая величина́ — измеряемое качество, признак или свойство материального объекта или явления, общее в качественном отношении для класса материальных объектов или процессов, явлений, но в количественном отношении индивидуальное для каждого из них. Физические величины имеют род, размер, единицу(измерения) и значение.
Метод балльных оценок — один из методов одномерного шкалирования, используемых в психологии, процедура которого заключается в построении шкал на основе балльных оценок, получаемых из суждений испытуемых. Из всех методов психологических измерений, использующих оценочные суждения человека, шкалирование, основанное на балльных оценках, является наиболее популярным в виду своей простоты. Метод распространен как в прикладных, так и в академических разделах психологии, например, при психологической оценке…
Светочувствительность цифровой фотокамеры — характеристика цифрового фотоаппарата, определяющая зависимость числовых параметров созданного им цифрового изображения от экспозиции, полученной светочувствительной матрицей. Светочувствительность цифровых фотоаппаратов принято выражать в единицах, эквивалентных светочувствительности ISO желатиносеребряных фотоэмульсий. Это позволяет пользоваться методами измерения экспозиции, свойственными классической плёночной фотографии.
Крива́я титрова́ния — графическое изображение зависимости определяемой в ходе титрования величины от объёма добавленного стандартного раствора титранта. Построение кривых проводится в инструментальных методах аналитической химии, где отсутствует возможность визуального определения точки эквивалентности (например, по индикатору).
Преобразова́ние едини́ц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта.
Дендро́метр — устройство для измерения дерева в толщину и высоту. Используется в дендрометрии.
Шкала интенсивности землетрясений Меркалли применяется для определения интенсивности землетрясения по внешним признакам, на основе данных о разрушениях. Может быть применена в том случае, когда отсутствуют прямые данные об интенсивности подземных толчков, например, из-за отсутствия соответствующего оборудования. В шкале Меркалли для определения степени интенсивности землетрясения используются римские цифры.
Разреше́ние — способность оптического прибора воспроизводить изображение близко расположенных объектов.
Признаки Хаара — признаки цифрового изображения, используемые в распознавании образов. Своим названием они обязаны интуитивным сходством с вейвлетами Хаара. Признаки Хаара использовались в первом детекторе лиц, работающем в реальном времени.
Угломер (синонимы — уклономер, угломерка, угломера, угло́метр) — угломерный прибор (инструмент, снаряд), предназначенный для измерения геометрических углов в различных конструкциях, в деталях и между поверхностями (в основном контактным методом) и между удалёнными объектами (оптическим методом). Измерение производится в градусах, на основе линейчатой шкалы, линейчато-круговой шкалы (с механическим указателем или стрелкой), нониуса или в электронном виде, в зависимости от типа прибора.
Логарифмический масштаб (шкала) — шкала, длина отрезка которой пропорциональна логарифму отношения величин, отмеченных на концах этого отрезка, в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах.
Курсовертикаль — прибор, поставляющий данные об углах между географической системой координат (ГСК) и связанной системой координат (ССК), начальная точка которой совпадает с начальной точкой ГСК, а оси соответствуют, как правило — Y — продольной оси, Z — вертикальной, X — перпендикулярной им боковой оси транспортного средства, на котором установлена курсовертикаль.
Балл — единица выражения значения величины на шкале порядка. Слово «балл» переводится как «шар», предмет, традиционно применяемый при голосовании, причём чёрный шар означал голос против обсуждаемого решения, а белый — за него. Балльные оценки популярны в гуманитарных науках, особенно в психологии, социологии и медицине, где трудно или невозможно ввести постоянные абсолютные единицы.
Шкала в психологии. Виды шкал и их характеристика
Измерительная шкала — основное понятие, также введенное в психологию С.С. Стивенсом в 1950 г.; его трактовка шкалы и сегодня используется в научной литературе. Итак, приписывание чисел объектам создает шкалу. Шкала (лат. scala — лестница) в буквальном значении есть измерительный инструмент.
Числовое значение, приписанное объекту, должно представлять (репрезентировать) ту характеристику объекта, которая интересует исследователя. Репрезентировать в данном случае означает, что по приписанному значению исследователь будет вправе сделать вывод об изучаемом свойстве.
Существует четыре группы правил, по которым свойства объекта в разной степени передаются его числовому значению (номеру). Каждому из четырех наборов правил соответствует свой вид измерения или шкала: номинативная (номинальная или шкала наименований), порядковая, интервальная и шкала отношений. Несколько упрощая, различия между шкалами примерно следующие:
- если все, что мы можем сказать об объекте, — это то, что он отличается от другого, то мы имеем номинативную шкалу;
- если мы можем сказать, что один объект больше или лучше, или в чем-то превосходит другой, мы имеем порядковую шкалу;
- если мы можем сказать, что один объект на сколько-то единиц (градусов, сантиметров) больше, чем другой, мы имеем интервальную шкалу;
- если мы можем сказать, что один объект в какое-то количество раз больше, чем другой, мы имеем шкалу отношений.
Четыре типа шкал образуют иерархию, в которой каждая последующая шкала включает в себя свойства нижележащих шкал (табл. 3).
С каждой из шкал связан определенный диапазон допустимых математико-статистических преобразований. Выход за пределы этого диапазона приводит к тому, что получаемые результаты оказываются лишенными смысла. Об этом необходимо помнить на этапе планирования работы по сбору данных. Именно от типа шкалы зависят все дальнейшие процедуры подсчета.
Рассмотрим свойства каждой шкалы более подробно.
Номинативная шкала
Номинативная шкала (лат. потеп — имя, название) — это шкала, классифицирующая по названию. Название не измеряется количественно, оно лишь позволяет отличить один объект от другого или одного субъекта от другого. Простейший случай номинативной шкалы -дихотомическая шкала, состоящая из двух наименований, например «имеет братьев и сестер — единственный ребенок в семье»; «иностранец — соотечественник»; «проголосовал «за» — проголосовал «против»» и т.п.
Телефонные и автомобильные номера, цветные фигурки на шкафчиках в детском саду — это примеры имен, которыми мы наделяем различные объекты. При этом неважно, что будет использоваться в качестве имени — цифры, буквенные сочетания, условные обозначения или другое. Основное правило — не присваивать одно и то же имя двум разным объектам. Однако если мы имеем дело с одинаковыми объектами, обладающими одинаковыми свойствами, то они должны в шкале наименований получать одинаковые имена. Количество используемых имен должно быть не меньше числа типов объектов или их свойств. Например, три имени для обозначения семейного положения (холост, женат/замужем, разведен) может оказаться недостаточно в случае наличия в выборке вдов/вдовцов.
Если для обозначения классов (типов) объектов выбраны числа, то формальные правила арифметики в этом случае не используются. Возьмем, к примеру, опросник, где мы приписываем 1 балл ответу «да», 2 — ответу «нет», 3 — «не знаю». Предположим также, что все три ответа выбираются одинаково часто. Допустим, теперь мы хотим найти, что является средним ответом. Среднее этих чисел дает нам «2» — как средний ответ. Можем мы теперь заключить, что средний ответ — «нет»? Такой вывод будет бессмысленным. Числа могут суммироваться и вычитаться, названия классов объектов не могут быть сложены или вычтены.
Статистическая обработка данных, представленных в шкале наименований, чаще всего начинается с построения таблицы сопряженности, показывающей распределение имен в соответствии с числом объектов и/или их свойств. Расклассифицировав все объекты, реакции или всех испытуемых по ячейкам классификации мы получаем возможность от наименований перейти к числам, подсчитав количество наблюдений в каждой из ячеек.
Таким образом, номинативная шкала позволяет нам подсчитывать частоты встречаемости разных наименований, или значений признака, и затем работать с этими частотами с помощью математических методов (метода %2, биноминального критерия m и углового преобразования Фишера ф).
Шкала порядка
В том случае, когда между объектами возможно установление отношений типа «быстрее», «успешнее», «вкуснее», «ярче», «громче», «тверже» и др., появляется возможность расположить объекты в порядке возрастания или убывания определенного признака. После этого остается наделить упорядоченную последовательность числами таким образом, чтобы, например, большее число соответствовало большей степени выраженности признака. В результате получим шкалу порядка, в которой отношения между числами будут соответствовать отношениям между объектами.
Порядковая шкала — это шкала, которая допускает возможность расположить пункты (или объекты) в порядке отношений между ними.
В порядковой шкале должно быть не менее трех объектов, например «положительная реакция — нейтральная реакция — отрицательная реакция».
Если расположить объекты по порядку возрастания интересующего нас признака, то можно обозначить эти объекты или А, В, С, или 1, 2, 3, или 50, 60, 70. Однако им нельзя приписать, например, такую последовательность цифр: 7, 90, 4, потому что эти цифры не соответствовали бы тому порядку, в котором данное свойство изменяет свое значение от объекта к объекту.
Примерами порядковых шкал могут являться школьные оценки (отлично, хорошо, удовлетворительно), призовые места по итогам соревнований (1 -е, 2-е и 3-е), градация званий в спорте (перворазрядник, кандидат в мастера спорта, мастер спорта). Из психологического инструментария самым ярким примером порядковой шкалы являются опросники установок и отношений, когда нужно выразить свое отношение в терминах больше — меньше, чаще — реже, и многие другие виды рейтинговых шкал.
В то же время расположение объектов в порядке возрастания определенного свойства еще не дает ответа на вопрос: насколько больше? Шкала порядка не позволяет определить «расстояние» между объектами. Об этом особенно необходимо помнить в тех случаях, когда из соображений удобства шкальные значения отделяют друг от друга равные интервалы. Например, четыре студента получили на экзамене оценки 75, 85, 90 и 100 баллов. Оценка второго студента отличается от оценки первого так же, как оценка четвертого студента отличается от оценки третьего, — на 10 баллов. Но из этого не следует, что знания второго студента больше знаний первого настолько же, насколько знания четвертого больше знаний третьего.
Рассмотрим еще один пример. Предположим, есть четыре игрока в теннис. Первый — профессиональный спортсмен, обладатель кубка Дэвиса. Второй игрок — любитель, но все свое свободное время он отдает теннису и в результате играет очень хорошо. Третий играет изредка, а четвертый взял в руки ракетку второй раз в жизни. Расположив игроков по степени мастерства, получаем порядковую шкалу, где под № 4 будет стоять первый игрок, а под № 1 — четвертый игрок, с трудом попадающий ракеткой по мячу. Теперь игрокам приписаны номера 4, 3, 2, 1. Если мы организуем игру парами и расставим игроков так: № 1 и № 4 — на одной стороне корта, № 2 и № 3 — на другой, то можем ли мы быть уверенными, что игра пройдет вничью? Ведь равенство 1 + 4 = 2 + 3 истинно. В этом примере мы имеем дело с порядковыми номерами, а не с числами, поэтому игра вничью не гарантируется такой расстановкой игроков. Разница в умении играть между № 1 и № 2 не равна разнице между № 2 и № 3.
Таким образом, выбор чисел используемых в шкале порядка в известных пределах произволен. Числа могут быть любыми, но они должны подчиняться основному требованию: объекту с большей выраженностью признака должно быть приписано большее число. Абсолютное значение числа не имеет смысла в порядковой шкале; смысл имеет только порядок чисел.
Со шкалами порядка связана одна из наиболее популярных в непараметрической статистике процедур — процедура ранжирования. Ранжирование — это процедура определения места, которое должен занять данный результат в упорядоченной последовательности всех результатов.
Особенности шкалы порядка позволяют определить для нее группу допустимых математико-статистических преобразований. Результаты, представленные в шкале порядка, нельзя использовать для пропорций (знания, оцененные на 100, не являются вдвое больше знаний, оцененных на 50). Эти результаты нельзя складывать (знания получившего на экзамене 100 баллов не равны сумме знаний получивших 40 и 60 баллов). Если говорить о мерах центральной тенденции, то из них можно применять только моду и медиану. Вычисление среднего является недопустимой операцией для шкалы порядка.
Интервальная шкала
Интервальная шкала — это шкала, классифицирующая объекты по принципу «больше на определенное количество единиц — меньше на определенное количество единиц». Каждое из возможных значений признака отстоит от другого на равном расстоянии. Это расстояние и называется интервалом. Размер интервала — величина, фиксированная и равная для всех сравниваемых объектов.
Особенность этой шкалы в том, что она не предполагает абсолютного нуля (нуль здесь условен и не указывает на отсутствие свойства). Например, когда говорят, что на улице температура 00С, то не имеют в виду, что температуры нет вообще. Этим хотят сказать, что на улице достаточно холодно, может лежать мокрый снег и могут быть лужи.
Другая популярная шкала интервалов — календарное летоисчисление. Как известно, христианское (европейское) летоисчисление берет начало от произвольно выбранной точки отсчета («рождение Христа»). Величина интервалов (день, месяц, год) привязана к видимому движению Солнца, а выражение «до нашей эры» означает, по сути, что в этой точке летоисчисление меняет свой знак.
В случае психологических измерений главная трудность — в обосновании равности интервалов. Психологические характеристики, выраженные в тестовых показателях, — это непрерывные величины, выраженные через дискретные. Допустим, первый испытуемый по тесту тревожности получил показатель со значением 20, второй получил по тому же тесту 25, третий — 30. Первый испытуемый отличается от второго настолько же, насколько второй отличается от третьего. Но означает ли это, что первый тревожен меньше, чем второй, ровно настолько же, насколько второй — по сравнению с первым? Можно ли поставить знак равенства между разностью в показателях и разностью в степени тревожности? Эти вопросы встают всякий раз, когда психолог начинает интерпретировать индивидуальные различия по тестовым показателям.
Поскольку множество психологических конструктов не может наблюдаться непосредственно, большинство измерений в психологии — скорее порядковые. Установки, потребности, мнения, личностные характеристики, психологическое благополучие — все это конструкты, имеющие различную степень выраженности у разных людей. Но все они допускают только непрямое порядковое измерение.
В психологической науке существует определенная конвенция о том, что в случае применения стандартизованных тестов исследователи могут трактовать показатели, полученные в порядковой шкале, так, как если бы они были получены в шкале интервалов. Эта договоренность распространяется только на действительно стандартизованные тесты и связана с необходимостью использовать статистические вычисления с полученными данными. Хорошо известный пример трактовки порядковых данных как данных интервальной шкалы — использование тестов IQ.
Шкала интервалов позволяет применять большинство математико-статистических методов для обработки и анализа данных, полученных с ее помощью. Можно использовать все меры центральной тенденции и рассеяния, коэффициент корреляции Пирсона и др. Имеющиеся здесь ограничения в первую очередь связаны с исключением пропорций. Отвечая на вопрос «Насколько больше?», шкала интервалов не дает ответа на вопрос «Во сколько больше?». Например, нельзя утверждать, что человек с IQ = 140 в два раза более интеллектуально развит, чем тот, у кого IQ = 70.
Шкала отношений
Шкала равных отношений — это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности измеряемого свойства. В шкалах отношений классы обозначаются числами, которые пропорциональны друг другу: 2 так относится к 4, как 4 к 8. Это предполагает наличие абсолютной нулевой точки отсчета. В физике абсолютная нулевая точка отсчета встречается при измерении длин отрезков или физических объектов и при измерении температуры по шкале Кельвина с абсолютным нулем температур. Считается, что в психологии примерами шкал равных отношений являются шкалы порогов абсолютной чувствительности (С. Стивенс, 1960; В.К. Гайда, В.П. Захаров, 1982).
Примерами измерений в шкале отношений могут быть измерения массы и роста, скорости и ускорения, времени реакции, и вообще любые измерения, предполагающие в качестве точки отсчета абсолютный нуль и имеющие равные интервалы — единицы измерения.
Следует иметь в виду, что одно и то же исследование может давать данные по разным шкалам. Если сравнивать количество решенных задач в тесте, то работа ведется в шкале отношений. Но если речь идет о сравнении участников по этому тесту, — то в шкале порядка, ведь нулевой показатель не может отражать абсолютно «нулевую» математическую способность человека. Шкалы отношений наиболее широко используются при проведении физических измерений. Их применение в психологии ограничено двумя существенными обстоятельствами. Во-первых, в психологии объект и их свойства нельзя объединить. Можно объединить два тела и сложить их массы, но объединить двух людей со средним IQ с целью получения IQ гения нельзя. Во-вторых, для объектов измерений в психологии практически невозможно указать «естественное» начало отсчета, абсолютный нуль.
Математико-статистические методы, используемые для обработки и анализа данных в шкале отношении, можно применять без каких-либо ограничений.
Типы и виды данных. Шкалы измерения
При статистическом исследованиисоциально-экономических процессов мы встречаемся с двумя типами данных: пространственные данные (cross-sectional data) и временные ряды (time-series data).
Примером пространственных данных является, например, набор сведений (объем производства, количество работников, доход и др.) по разным фирмам в один и тот же момент времени (пространственный срез). Пространственные данные часто используются для построения моделей классификации, регрессионных моделей.
Примерами временных данных могут служить ежеквартальные данные по инфляции, средней заработной плате, национальному доходу за последние годы, ежедневный курс доллара США на ММВБ и т.п. Отличительной чертой временных данных является то, что они естественным образом упорядочены во времени. Часто наблюдения в близкие моменты времени бывают зависимыми.
Наиболее информативными видами представления данных являются временные ряды, многоугольники и гистограммы распределения (частотные и кумулятивные), диаграммы (подробный анализ видов представления данных будет представлен в выпуске 2 данного тома).
Вид представления данных определяется типом шкалы измерения. Различают четыре основные вида данных, отличающихся по тому, как наблюдаемый объект измеряется или описывается (табл. 2.1).
Таблица 2.1
Основные виды данных
| Вид данных | Примеры |
| 1. Данные классификации (номинальные) | Лица, классифицированные по полу, национальности. Регионы РФ, классифицированные по принадлежности к центральным федеральным округам. |
| 2. Ранжированные (ординарные, порядковые) | Ранжирование регионов по инвестиционной привлекательности и т.д. |
| 3. Данные измерения на интервальной шкале | Температура объекта (шкала с произвольной нулевой точкой и масштабом) |
| 4. Данные измерений на относительной шкале | Измерения веса, высоты, объема и т.п. (шкалы с произвольным масштабом, но фиксированной нулевой точкой) |
Номинальная шкала (шкала наименований, классификационная шкала) является наиболее «слабой» качественной шкалой, по которой объектам дается некоторый признак. Этот тип шкал соответствует простейшему виду измерения, при котором шкальные значения используются лишь как имена объектов. Единственная цель таких измерений — выявление различий между объектами разных классов. Однако не следует пренебрегать значением этих имен; так, одной из задач кластерного анализа является назначение удачных названий выявленных групп близких по совокупности свойств объектов.
Шкала называется ранговой (шкала порядка), если множеству измеряемых объектов можно присвоить монотонно возрастающие шкальные значения. Тем самым допускается не только номинальное различение объектов, но и их упорядочение по измеряемым свойствам. Таковы балльные, рейтинговые оценки.
Измерение в шкале порядка может применяться в различных ситуациях:
— необходимо упорядочить объекты во времени или пространстве, когда интересуются не сравнением степени выраженности какого-либо свойства объектов, а лишь их взаимным пространственным или временным расположением;
— необходимо упорядочить объекты по степени выраженности какого-либо их свойства, при этом не требуется производить его точное измерение;
— какое-либо свойство в принципе измеримо, но измерение невозможно по причинам практического или теоретического характера.
Шкалы интервалов являются одним из наиболее важных типов шкал. Их отличительная особенность — возможность положительного линейного преобразования, когда меняется масштаб и начало отсчета, но сохраняется направленность измеряемого свойства. Классическим примером служат температурные шкалы Цельсия t°C и Фаренгейта t°F, связанные линейным преобразованием шкальных значений
t °F = 1,8 t °C + 32. (2.1)
Шкалы интервалов сохраняют не только различие и упорядочение объектов, но и отношение «расстояний» между парами. Однако отношение самих шкальных значений при этом не сохраняется. Например, в случае температурных шкал Цельсия и Фаренгейта нельзя сказать, что вода, нагретая до 80 °C вдвое горячее, чем вода при 40 °C, поскольку в шкале Фаренгейта соотношение температур воды будет уже другим: 176 °F и 104°F соответственно. В то же время отношение разностей этих температур в обеих шкалах сохраняется. Так, если отсчитывать разность температур двух упомянутых объектов в обеих шкалах относительно третьего объекта, охлажденного до 0 °C (32 °F), то отношение разностей в обеих температурных шкалах составляет одну и ту же величину 2:
(80 °C — 0 °C)/(40 °C — 0 °C) = (176 °F — 32 °F)/( 104 °F — 32 °F) = 2.
Частным случаем шкал интервалов являются шкалы отношений, когда нулевая точка означает отсутствие измеряемого свойства. Шкалы отношений сохраняют не только отношения свойств объектов, но и отношения «расстояний» между парами объектов. Примерами измерений в шкалах отношений являются стоимостные измерения.
Иногда рассматривают также шкалы разностей и абсолютные шкалы. Первые являются частным случаем шкал интервалов; примерами служат измерения прироста продукции в абсолютных единицах, увеличение численности учреждений и т.п. Абсолютные шкалы характеризуются единственностью измерения и применяются, например, для измерения количества объектов.
Шкалы измерения следует учитывать при вычислении средних величин. В общей теории статистики различают структурные и степенные средние. К первым относятся мода и медиана, ко вторым — арифметическая, геометрическая, квадратическая и гармоническая средние.
Наименее информативная номинальная шкала допускает лишь один вид средних — моду. При переходе к более информативной порядковой шкале в моде добавляется медиана как мера центральной тенденции. Эти средние являются частными случаями средних по Коши — функции, ставящей в соответствие совокупности измерений (х1, х2, …, хn) любое число, заключенное между наибольшим и наименьшим членом вариационного ряда.
Обобщением понятия степенных средних является средние по Колмогорову Fyn, задаваемые строго монотонными функциями y:
Fyn (х1, х2, …, хn) = y -1(1/n)S y ( хi), (2.2)
где y -1 — функция, обратная y; хi — значение i-го измерения показателя Х; n — объем выборки. При y(х) = х; ln х; х–1; х2 формула (2.2) определяет соответственно среднее арифметическое, среднее геометрическое, среднее гармоническое и среднее квадратическое.
В шкале интервалов и разностей центральную тенденцию адекватно отражает среднее арифметическое, в шкале отношений — среднее геометрическое, однако среднее геометрическое не рекомендуется применять при обработке данных, измеренных в шкале интервалов и разностей. В абсолютной шкале можно пользоваться любым средним, т.е. с усложнением типа шкалы измерения число средних, адекватных в этой шкале, увеличивается.
Похожие статьи:
Глава 8.2 Шкалы измерений
Весы
Статистическая информация, включая числа и наборы чисел, обладает особыми качествами, которые интересны исследователям. Эти качества, включая величину, равные интервалы и абсолютный ноль, определяют, какая шкала измерения используется и, следовательно, какие статистические процедуры лучше всего. Величина относится к способности узнать, больше ли одна оценка, равна или меньше другой оценки.Равные интервалы означают, что возможные оценки находятся на равном расстоянии друг от друга. И, наконец, абсолютный ноль относится к точке, в которой не существует никакой шкалы или где может быть выставлен нулевой балл.
Когда мы объединяем эти три качества шкалы, мы можем определить, что существует четыре шкалы измерения. Самый низкий уровень — это номинальная шкала, которая представляет только имена и, следовательно, не имеет ни одного из трех качеств. Список студентов в алфавитном порядке, список любимых героев мультфильмов или имена на организационной диаграмме будут классифицироваться как номинальные данные.Второй уровень, называемый порядковыми данными, имеет только величину и может рассматриваться как любой набор данных, который может быть размещен в порядке от наибольшего к наименьшему, но где нет абсолютного нуля и равных интервалов. Примеры этого типа шкалы включают весы Лайкерта и технику Терстоуна.
Третий тип шкалы называется шкалой интервалов и имеет как величину, так и равные интервалы, но не имеет абсолютного нуля. Температура — классический пример шкалы интервалов, потому что мы знаем, что каждый градус находится на одинаковом расстоянии друг от друга, и мы можем легко определить, больше ли одна температура, равна или меньше другой.У температуры, однако, нет абсолютного нуля, потому что нет (теоретически) точки, где бы не было температуры.
Наконец, четвертая и самая высокая шкала измерения называется шкалой отношения. Шкала отношений содержит все три качества и часто является той шкалой, которую предпочитают статистики, поскольку данные легче анализировать. Возраст, рост, вес и результаты 100-балльного теста — все это примеры шкал отношений. Если вам 20 лет, вы не только знаете, что старше кого-то, кому 15 лет (величина), но также знаете, что вы на пять лет старше (равные интервалы).Со шкалой отношений у нас также есть точка, в которой не существует никакой шкалы; когда человек рождается, его возраст равен нулю.
Таблица 8.1: Шкалы измерений
Масштаб Уровень
Масштаб
Качество шкалы
Пример (-ов)
4
Коэффициент
Звездная величина
Равные интервалы
Абсолютный ноль
Возраст, рост, вес, процентное соотношение
3
Интервал
Звездная величина
Равные интервалы
Температура
2
Порядковый номер
Звездная величина
Шкала Лайкерта, ранг Anything заказан
1
Номинал
Нет
Имена, Списки слов
Весы
Измерительные весы
Др.Боб Кизлик
Если вы прочитали информацию на
Страница ADPRIMA по измерению, оценке и оценке в образовании,
и попали на эту страницу, вы попали в нужное место. Эта страница
был добавлен через несколько лет после включения вышеупомянутой страницы
на моем сайте. Цель этой страницы — предоставить вам
небольшое уточнение и расширение понимания я
Надеюсь, вы почерпнули из страницы об измерениях, оценке и
оценка.
Как правило, в любое время измерение
сделано мы смотрим на объект или условие, которое соответствует определенным
критерии включения или исключения из описательных наборов. Эти
наборы — это то, что я называю измерительными шкалами. Так что если ты будешь
побалуйте меня,
Я дам описание этих весов, чтобы ваше
понимание того, что они означают и как они используются в статистических
анализ может быть улучшен.
Есть четыре основных шкалы измерения.От наименее сложных к наиболее сложным, они бывают: номинальные, порядковые,
интервал и соотношение. Они имеют основополагающее значение для процесса
измерения, и без понимания их различий, на
лучшая плохая информация будет получена, а в худшем случае ошибочная
выводы будут сделаны.
Описание шкалы измерений:
Номинальная шкала измерения см.
к тем измерениям, когда единственными значимыми результатами являются
определения того, что одно отличается от другого.Например,
если у вас есть мешок яблок и ведро угля, единственный
Возможное измерение включает номинальную шкалу. Все, что ты можешь сказать, это
один набор — яблоки, а другой — уголь. Это измерение
где единственный вывод, который вы можете сделать, это то, что одна вещь
отличается от другого. Еще один способ считать номинальный
шкала измерения — рассматривать ее как базовую классификацию
система. Также стоит взглянуть на поведенческие
глагол «классифицировать.» В
номинальную шкалу, которую вы, по сути, классифицируете по названию. это
Всегда полезно быть предельно ясным при этом.
Порядковые измерительные шкалы см.
к тем измерениям, результаты которых указывают только на одно
либо больше, либо меньше другого. Это всегда означает
измерение, которое явно подразумевает, что объекты, события или
процессы и быть размещены в некотором порядке.Присвоение оценок
на основе баллов является примером этой шкалы, например,
наблюдение, что оценка «А» представляет собой не только другую
значение, чем оценка «C», но также представляет более высокую или
большее значение.
Шкалы интервальных измерений см.
к тем измерениям, где есть равные интервалы между заданными
ценности. Шкалы интервалов используются практически во всех
измерение.На линейке используется интервальная шкала. Это означает, что
расстояние между тремя и шестью дюймами такое же, как
расстояние от девяти до двенадцати дюймов. В комнате
термометр, разница в градусах между 72 по Фаренгейту и 78
По Фаренгейту это то же самое, что и между 90 градусами по Фаренгейту и
96 градусов. Интервалы такие же.
Шкала измерения соотношения есть
то же, что и порядковые шкалы, с одним важным отличием.В
Разница в том, что шкалы измерения отношения содержат ноль.
включение нуля позволяет выражать отрицательные значения
по отношению к положительному значению. Самый очевидный и простой
понятным примером шкалы измерения соотношения является наружный
термометр. Интервалы равны, но будь то по Фаренгейту или
Цельсия, значения измерения могут быть отрицательными, как в
-10 градусов по Цельсию.
Итак, вкратце, у вас есть это.Измерение всегда связано с какой-то шкалой, а наблюдения
связанных с измерениями можно отметить как простую разницу
имя и, следовательно, простая классификация. На один шаг выше по сложности
порядковая шкала, которая подразумевает, что есть порядок к объекту
или процесса, и можно сказать, что одно не просто другое, а
больше или меньше другого. Следующая по сложности шкала интервалов является самой
часто используется для измерения и основывается на уверенности в равенстве
интервалы между последовательными точками шкалы.в заключение
есть шкалы отношений, которые в точности похожи на шкалы интервалов с
добавление нулевой точки.
Это сделано для того, чтобы
взгляд на описание образовательного измерения.
Нажмите здесь , чтобы
вернуться на страницу образовательного измерения, оценивания и
оценка.
4.2 Шкалы измерения атрибутов | GEOG 160: Отображение нашего меняющегося мира
Глава 2 посвящена шкалам измерения пространственных данных, включая масштаб карты (выраженный в виде репрезентативной доли), координатные сетки и картографические проекции (методы преобразования трехмерных в двумерные шкалы измерений).Возможно, вы знаете, что метр, стандарт длины, установленный для международной метрической системы, первоначально был определен как одна десятимиллионная расстояния от экватора до Северного полюса. Практически во всех странах, кроме Соединенных Штатов, метрическая система принесла пользу науке и торговле, заменив дроби десятичными и введя земной стандарт измерения.
Стандартизированные шкалы необходимы для измерения непространственных атрибутов, а также пространственных объектов.Однако в отличие от положений и расстояний, атрибутов местоположений на поверхности Земли часто не поддаются абсолютным измерениям. В статье 1946 года в журнале « Science», психолог С.С. Стивенс обрисовал систему из четырех уровней измерения , предназначенную для того, чтобы социологи могли систематически измерять и анализировать явления, которые просто невозможно сосчитать. (В 1997 году географ Николас Крисман указал, что для учета разнообразия географических данных необходимо всего девять уровней измерения.) Уровни важны для специалистов в области географической информации, потому что они обеспечивают руководство по правильному использованию различных статистических, аналитических и картографических операций. Далее мы рассмотрим примеры исходных четырех уровней измерения Стивенса: номинальный, порядковый, интервальный и коэффициент .
4.2.1 Номинальный уровень
Термин номинальный просто означает отношение к слову «имя». Проще говоря, данные номинального уровня — это данные, обозначенные разными именами (например,g., лес, вода, возделываемые земли, водно-болотные угодья) или категории. Данные, полученные путем отнесения наблюдений к нерейтинговым категориям, представляют собой номинальных измерений уровня . Что касается терминологии, используемой в главе 1, номинальные данные представляют собой тип категориальных (качественных) данных . В частности, данные номинального уровня могут быть дифференцированы и сгруппированы по категориям по «виду», но не ранжированы от высокого к низкому. Например, можно классифицировать растительный покров в определенном месте как леса, кусты, фруктовые сады, виноградники или мангровые заросли.Однако это различие не подразумевает, что место, классифицируемое как «лес», вдвое больше покрыто растительностью, чем другое место, классифицированное как «кустарник».
Рисунок 4.3. Атрибутные данные, измеренные на номинальном уровне: выбранные категории растительности, отображаемые на топографических картах USGS.
Кредит: USGS.
Хотя данные переписи исходят от индивидуального подсчета, большая часть того, что учитывается, — это принадлежность отдельных лиц к номинальным категориям. Раса, национальность, семейное положение, способ транспортировки на работу (автомобиль, автобус, метро, железная дорога…) и тип топлива для отопления (газ, мазут, уголь, электричество …) измеряются как количество наблюдений, отнесенных к нерейтинговым категориям. Например, карта ниже, которая появляется в первом атласе переписи 2000 года Бюро переписи населения, выделяет группы меньшинств с наибольшим процентом населения в каждом штате США. Цвета были выбраны, чтобы различать группы с помощью качественной цветовой схемы, чтобы показать различия между классами, но не для обозначения какого-либо количественного порядка. Таким образом, хотя числовые данные использовались для определения категории, к которой относится каждый штат, на карте показаны итоговые номинальные категории, а не лежащие в основе числовые данные.
Рисунок 4.4. Группа меньшинства с самым высоким процентом по штату.
Кредит: Брюэр и Сучан, 2001.
4.2.2 Порядковый уровень
Как и номинальный уровень измерения, порядковое масштабирование распределяет наблюдения по дискретным категориям. Порядковые категории, однако, ранжируются или упорядочиваются, как следует из названия. В предыдущем разделе указывалось, что номинальные категории, такие как «леса» и «мангровые заросли», не имеют приоритета друг над другом, если им не наложен набор приоритетов.Этот акт приоритезации номинальных категорий преобразует измерения номинального уровня в порядковый. Поскольку категории не основаны на числовом значении (просто указание порядка или важности), порядковые данные также считаются категориальными (или качественными).
Рисунок 4.5. Атрибутные данные, измеренные на порядковом уровне: ранжированные категории границ, отображаемые на топографических картах Геологической службы США.



 Во-первых, шкалой или, точнее, шкалой измерений (шкалой физической величины) называют принятый по соглашению порядок определения и обозначения всевозможных проявлений (значений) конкретного свойства (величины). Во-вторых, шкалой называют отсчётные устройства аналоговых средств измерений, это значение используется в данной статье.
Во-первых, шкалой или, точнее, шкалой измерений (шкалой физической величины) называют принятый по соглашению порядок определения и обозначения всевозможных проявлений (значений) конкретного свойства (величины). Во-вторых, шкалой называют отсчётные устройства аналоговых средств измерений, это значение используется в данной статье.