Сложение сопротивлений при параллельном соединении: Параллельное соединение резисторов | Онлайн калькулятор

Последовательное соединение резисторов расчет — Moy-Instrument.Ru

Последовательное и параллельное соединение резисторов

Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.

В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.

В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т. д.

В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.

Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

При включении трех резисторов расчет общего сопротивления будет таким:

Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!

Последовательное соединение резисторов. Схема соединения и примеры расчета

Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.

Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.

Последовательное соединение резисторов

На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.

Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:

То есть, в нашем случае общее сопротивление цепи будет равно:

R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм

Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.

Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.

Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь.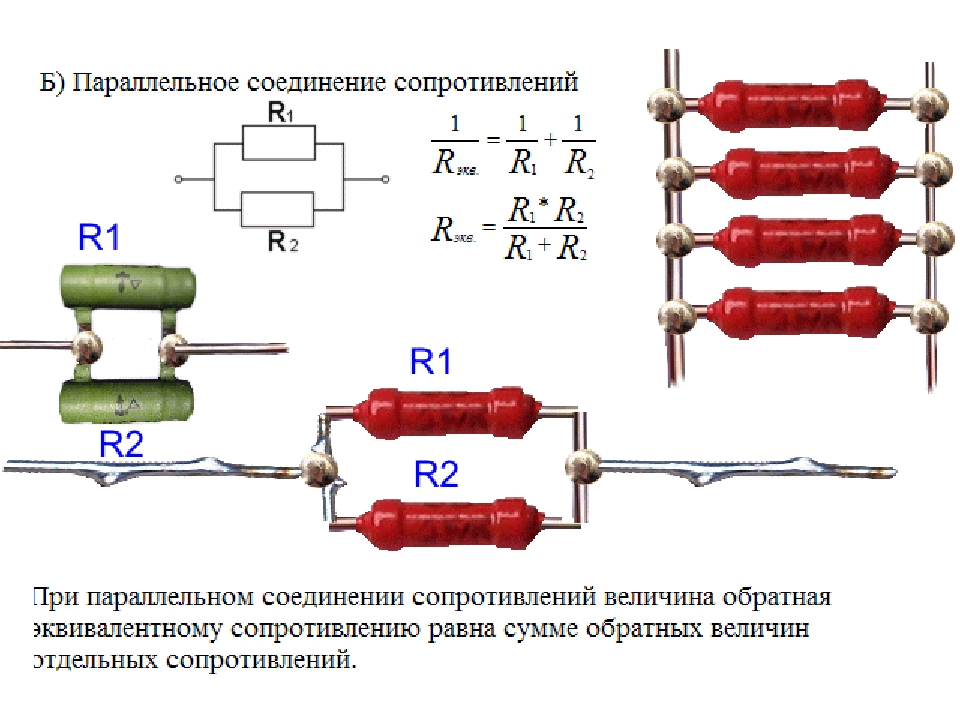 В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).

Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:

Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом:

В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.

В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:

Пример № 1

Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:

Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:

Пример № 2

Необходимо рассчитать падение напряжения на выводах «А» и «В»:

а) без подключенного резистора R3

б) с подключенным резистором R3

Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В.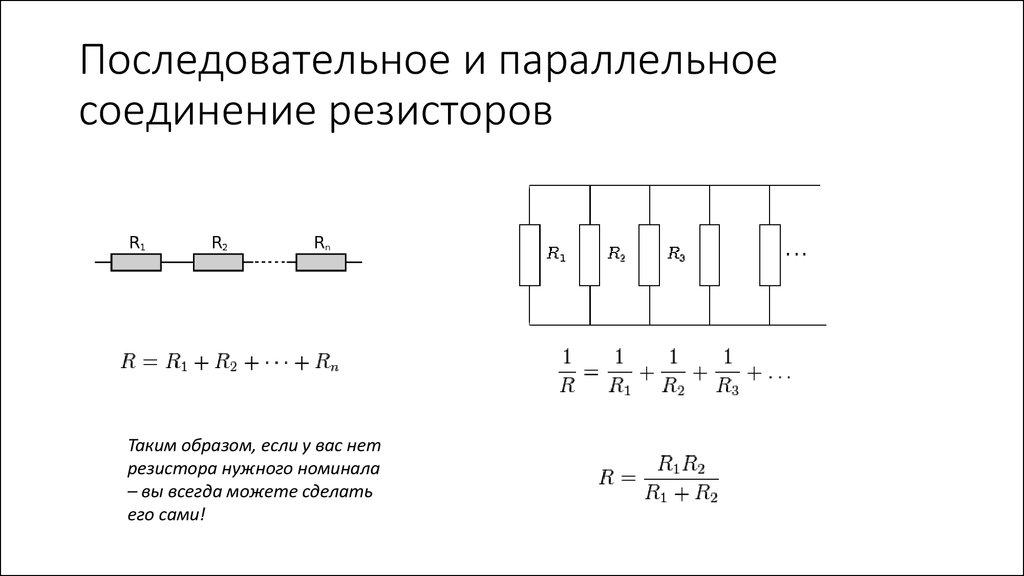 Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.

Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).

Расчет сопротивления параллельного соединения резисторов

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов.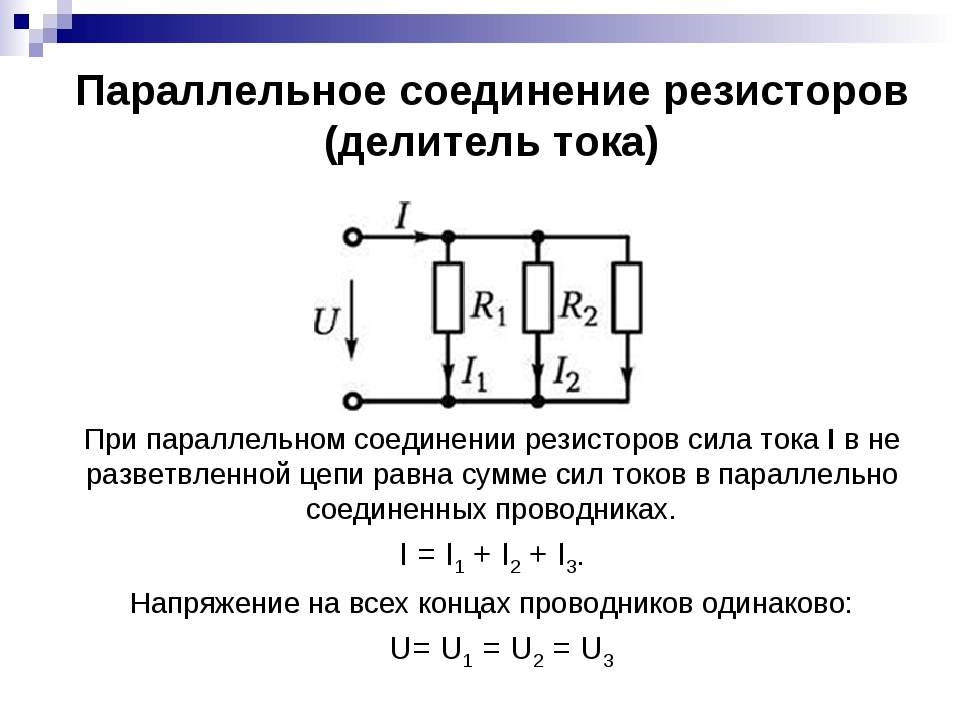 Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Соединение резисторов

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.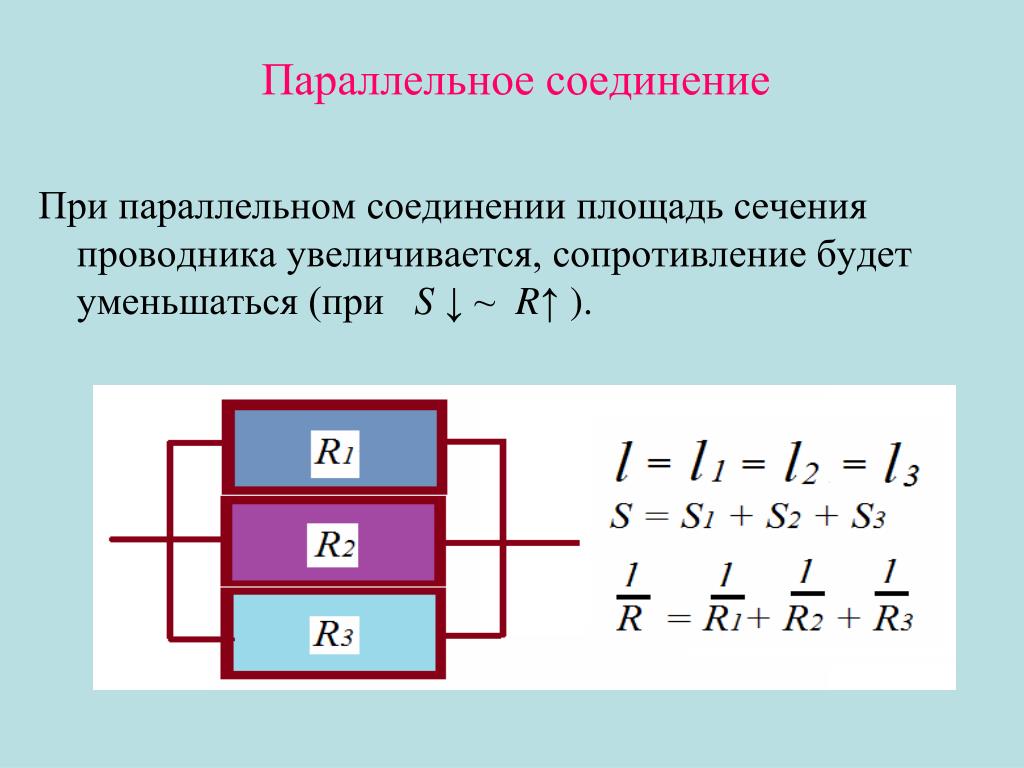

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.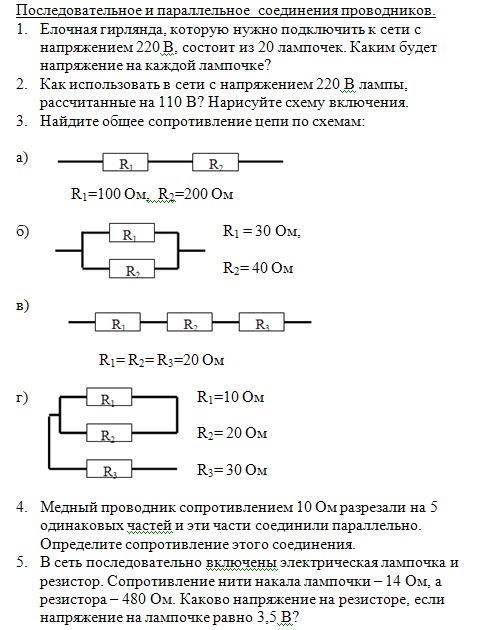

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление.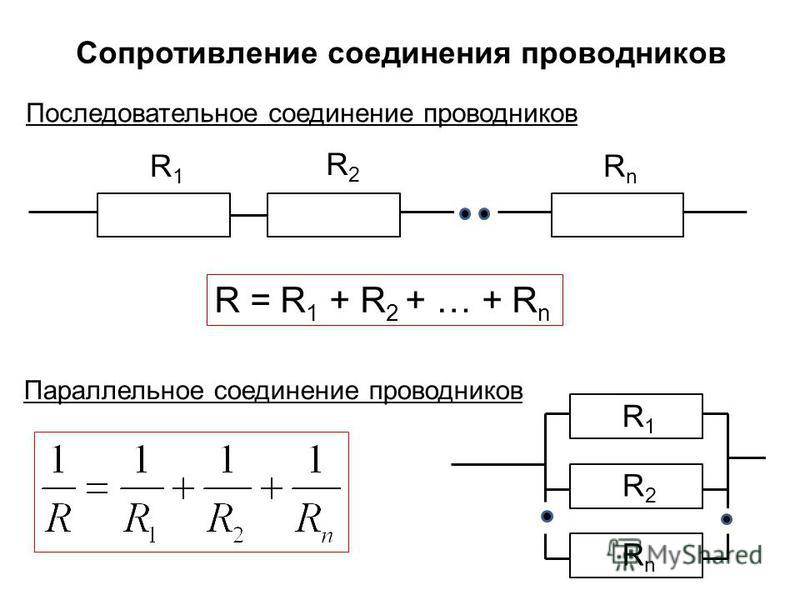 Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Соединение резисторов

Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.

Последовательное соединение резисторов

Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.

Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.

Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.

Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.

В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.

Параллельное соединение резисторов

При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.

Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G.

G = 1/R = 1/Ом = См

Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.

Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:

Если R1 = R2 = R3 = R4 = R , то

Rобщ = R/4.

Например, каждый из четырех резисторов имеет R = 10 кОм, тогда

Rобщ = 10 кОм/4 = 2,5 кОм.

Мощности рассеивания суммируются также, как и при последовательном соединении.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.

Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.

Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.

Последовательное и параллельное соединение резисторов

Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.

В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.

В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.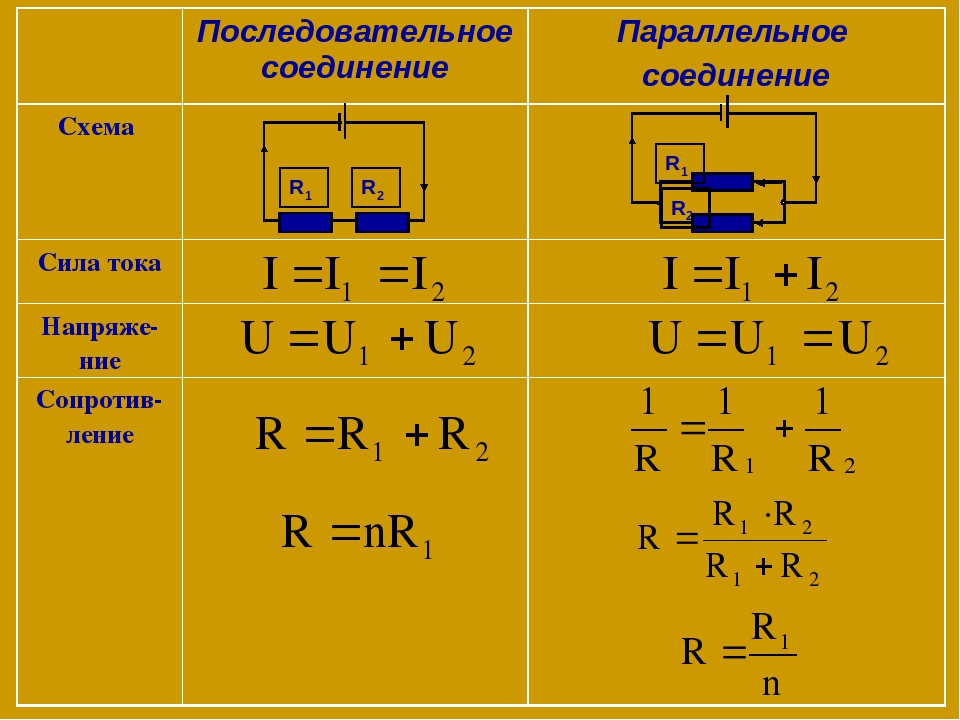

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.

В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.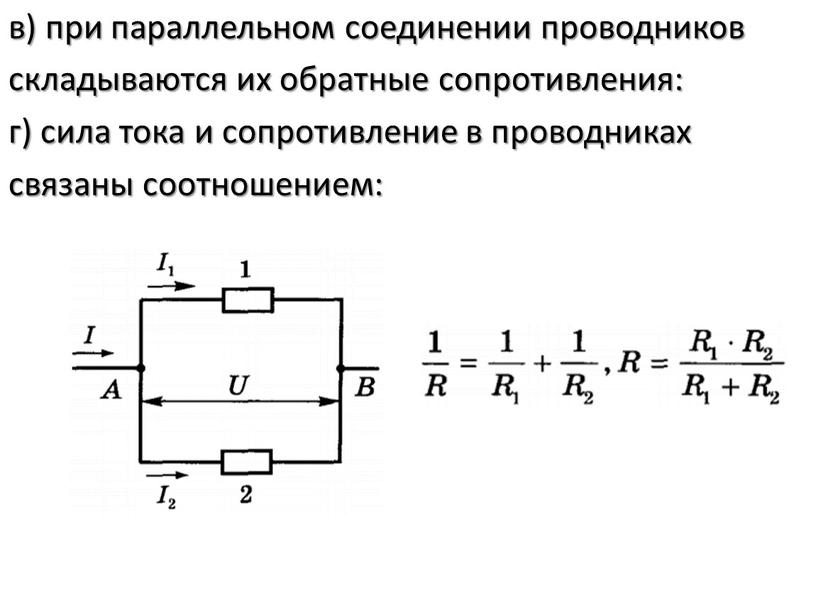

Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

При включении трех резисторов расчет общего сопротивления будет таким:

Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.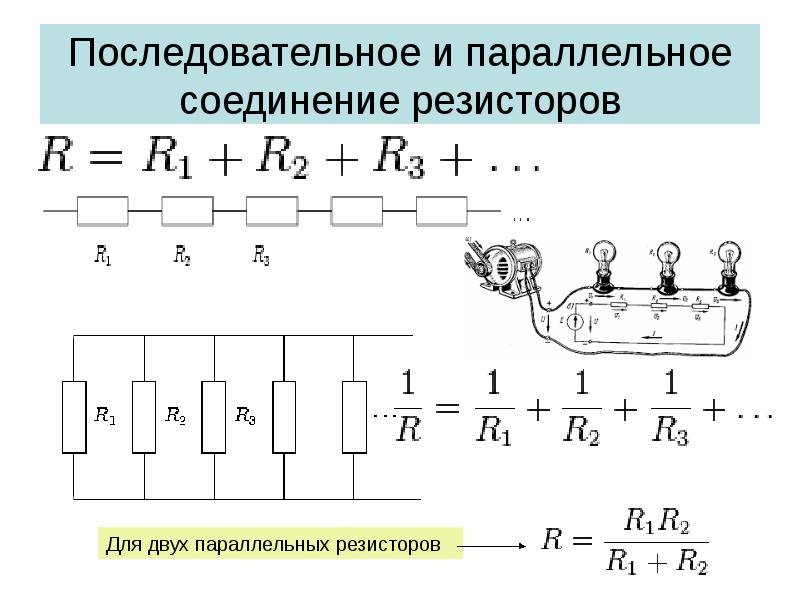

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!

1.4. Параллельное соединения сопротивлений.

При параллельном
соединении сопротивлений все они
находятся под одним и тем же напряжением,
т. е. напряжение между точками А и В, С и
D,
Е и F
равно напряжению U
на зажимах цепи (рис 1.5.)

Общий ток I
распределяется по ветвям обратно
пропорционально сопротивлениям:

I₁
=
I₂
=

I₃=

Рис. 1.5. Параллельное
соединение сопротивлений.

К цепи с параллельным
соединением сопротивлений применим
первый закон Кирхгофа: алгебраическая
сумма токов, сходящихся в любом узле
электрической цепи равна нулю, т.е. ∑I=0

Первый закон
Кирхгофа можно сформулировать так:
сумма токов, притекающих к узлу, равна
сумме токов уходящих от узла. Применительно
к рассматриваемой схеме для узла А имеем

I
= I₁
+ I₂
+ I₃

Или

(1. 7)

где R_э
– эквивалентное сопротивление цепи.

Сокращая все члены
уравнения (1.7) на U,
получим:

(1.8)

Из уравнения(1.8)
получаем выражение для расчета
эквивалентного (общего) сопротивления
параллельной цепи, состоящей из трех
ветвей

R_э=
(1.9)

Для цепи из двух
ветвей эквивалентное сопротивление
рассчитывается по выражению

R_э
=

Можно показать,
что чем больше
сопротивлений включаются параллельно
друг другу, тем
меньше будет
величина эквивалентного (общего)
сопротивления цепи. Так в случае, если
R₁
= R₂
= R₃
= R
из выражения (1.9) имеем:

R_э
=

Величина, обратная
сопротивлению, называется электрической
проводимостью и измеряется в сименсах:

g =
[См] (1.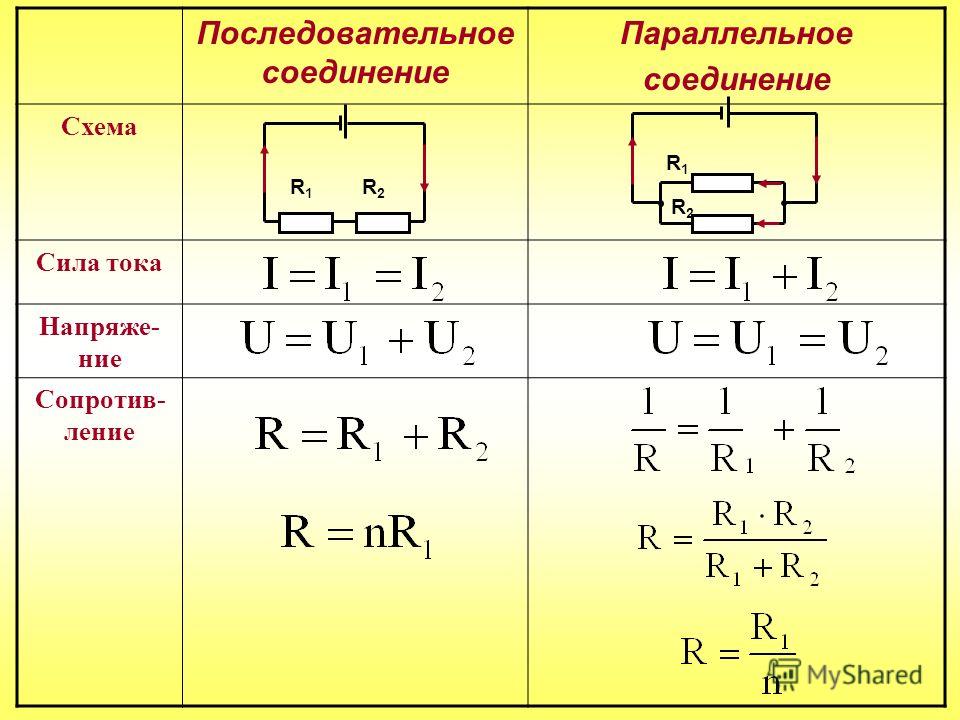 10)

Из выражения
(1.8) с учетом (1.10) получаем g_э
= g₁+
g₂+
g₃

Таким образом, при
параллельном соединении сопротивлений
общая проводимость цепи равна сумме
проводимостей всех её элементов. Закон
Ома для параллельной цепи принимает
вид: I=U
g_э

К достоинствам
параллельного соединения сопротивлений
относится возможность обеспечения
независимой и автономной работы как
генераторов, так и электроприемников.
Поэтому на практике разводка электропитания
производится таким образом, чтобы все
электроприборы подключались к сети
параллельно.

1.5. Смешанное соединение сопротивлений.

Рассмотрим
электрическую цепь со смешанным
соединением сопротивлений (рис. 1.6.)

Рис. 1.6. Смешанное
соединений сопротивлений.

Для расчета
параметров такой цепи упростим схему,
заменив группы параллельно соединенных
резисторов их эквивалентными
сопротивлениями.

Для участка ab:
R_ab=Для
участка cd:
R_cd=

В результате
получаем эквивалентную схему замещения
представленную на рис. 1.7.

Рис. 1.7. Эквивалентная
схема замещения смешанного соединения
сопротивлений.

Эквивалентное
сопротивление всей цепи равно: R_э
= R₁
+ R_ab
+ R₄+ R_cd

Ток в неразветвленных
участках цепи равен: I
=

Теперь легко найти
напряжения и токи на всех участках цепи:

U_ab=IR_ab;
U_cd
= IR_cd

I₁=I;
I₂=;
I₃
=
;
I₄=I;
I₅
=;
I₆
=

11. Последовательное, параллельное и смешанное соединения резисторов.

Значительное число
приемников, включенных в электрическую
цепь (электрические лампы,
электронагревательные приборы и др.),
можно рассматривать как некоторые
элементы, имеющие определенное
сопротивление. Это обстоятельство дает
нам возможность при составлении и
изучении электрических схем заменять
конкретные приемники резисторами с
определенными сопротивлениями. Различают
следующие способы соединения резисторов
(приемников электрической энергии):
последовательное, параллельное и
смешанное.

Последовательное
соединение.
При последовательном соединении
нескольких резисторов конец первого
резистора соединяют с началом второго,
конец второго — с

началом
третьего и т. д. При таком соединении по
всем элементам последовательной цепи
проходит один и тот же ток I.

Последовательное
соединение приемников поясняет рис.
19,а. Заменяя лампы резисторами с
сопротивлениямиR₁,
R₂ и
R₃
получим
схему, показанную на рис. 19,б.Если принять,
что в источнике
R₀
= 0, то для трех последова-тельно соединенных
резисторов согласно второму Кирхгофа
можно написать:

E
= IR₁
+IR₂
+IR₃
= I( R₁+
R₂+
R₃
) = IR_общ
;

где:
R_общ
= R₁+
R₂+
R₃

Следовательно,
эквивалентное сопротивление
последовательной цепи равно сумме
сопротивлений всех последовательно
соединенных резисторов.

Напряжение
U
на зажимах источника равно сумме
напряжений на каждом из последовательно
включенных резисторов.

Соединять
последовательно целесообразно только
приемники с одинаковыми сопротивлениями.
В противном случае приложенное напряжение
источника электрической энергии
распределяется между ними неравномерно
и отдельные приемники могут оказаться
под недопустимо высоким для них
напряжением.

При последовательном
соединении приемников изменение
сопротивления одного из них влечет за
собой изменение напряжения на других
связанных с ним приемниках. При обрыве
электрической цепи в одном из приемников
в остальных прекращается ток.

При
параллельном соединении
приемники включаются между двумя точками
электрической цепи, образуя параллельные
ветви (рис. 20,а). Заменяя лампы резисторами
с сопро-тивлениями R₁,
R₂ и
R₃,
получим схему, показанную на рис. 20,б.

При
параллельном соединении ко всем
резисторам приложено одинаковое
напряжениеU.
Поэтому согласно закону Ома:

I₁
=
U/R₁,
I₂
=U/R₂
, I₃
= U/R₃

Ток
в неразветвленной части цепи согласно
первому закону Кирхгофа I=I₁+I₂
+I₃
или

I=
U/R₁
+
U/R₂
+
U/R₃
= U (1/ R₁
+ 1/ R₂+
1/ R₃)
= U/R_экв

Следовательно,
эквивалентное сопротивление рассматриваемой
цепи при параллельном соединении трех
резисторов определяется формулой

1/
R_экв=
1/ R₁
+ 1/ R₂+
1/ R₃

При
увеличении числа параллельно включаемых
резисторов результирующее сопротивление
уменьшается.

При
параллельном соединении приемников
все они находятся под одним и тем же
напряжением и режим работы каждого из
них не зависит от остальных. Это означает,
что ток, проходящий по какому-либо из
приемников, не будет оказывать
существенного влияния на другие
приемники. При всяком выключении или
выходе из строя любого приемника
остальные приемники остаются включенными.

Смешанным
соединением
называется такое соединение, при котором
часть резисторов включается последовательно,
а часть — параллельно. Эквивалентное
сопротивление цепи при смешанном
соединении обычно определяют методом

преобразования,
при котором сложную цепь последовательными
этапами преобразовывают в простейшую.

Мощность при параллельном соединении резисторов формула

Автор На чтение 17 мин. Опубликовано 12.12.2019

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

• P₁ = I 2 x R₁ = 0,256 2 x 200 = 13,11 Вт;
• P₂ = I 2 x R₂ = 0,256 2 x 100 = 6,55 Вт;
• P₃ = I 2 x R₃ = 0,256 2 x 51 = 3,34 Вт;
• P₄ = I 2 x R₄ = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

• 1/R = 1/R₁+1/R₂+1/R₃+1/R₄ = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
• Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
• Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
• Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
• Расчет силы тока для каждого резистора выполняется по формулам: I₁ = U/R₁ = 100/200 = 0,5A; I₂ = U/R₂ = 100/100 = 1A; I₃ = U/R₃ = 100/51 = 1,96A; I₄ = U/R₄ = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P₁ = U 2 /R₁ = 100 2 /200 = 50 Вт; P₂ = U 2 /R₂ = 100 2 /100 = 100 Вт; P₃ = U 2 /R₃ = 100 2 /51 = 195,9 Вт; P₄ = U 2 /R₄ = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р₁+Р₂+Р₃+Р₄ = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторо

Последовательное и параллельное соединение сопротивлений Википедия

Резисторы разных размеров, типов, мощности с проволочными выводами
Почтовая марка Германии 1994 года

Рези́стор (англ. resistor, от лат. resisto — сопротивляюсь) — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления^[1], предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока, ограничения тока, поглощения электрической энергии и др.^[2]. Весьма широко используемый компонент практически всех электрических и электронных устройств.

Схема замещения резистора чаще всего имеет вид параллельно соединённых сопротивления и ёмкости. Иногда на высоких частотах последовательно с этой цепью включают индуктивность. В схеме замещения сопротивление — основной параметр резистора, ёмкость и индуктивность — паразитные параметры.

Линейные и нелинейные резисторы

Все резисторы делятся на линейные и нелинейные.

Сопротивления линейных резисторов не зависят от приложенного напряжения или протекающего тока.

Сопротивления нелинейных резисторов изменяются в зависимости от значения приложенного напряжения или протекающего тока. Например, сопротивление осветительной лампы накаливания при отсутствии тока в 10-15 раз меньше, чем в режиме освещения. В линейных резистивных цепях форма тока совпадает с формой напряжения, вызвавшего этот ток.

Основные характеристики и параметры резисторов

• Номинальное сопротивление — основной параметр.
• Предельная рассеиваемая мощность.
• Температурный коэффициент сопротивления.
• Допустимое отклонение сопротивления от номинального значения (технологический разброс в процессе изготовления).
• Предельное рабочее напряжение.
• Избыточный шум.
• Максимальная температура окружающей среды для номинальной мощности рассеивания.
• Влагоустойчивость и термостойкость.
• Коэффициент напряжения. Учитывает явление зависимости сопротивления некоторых видов резисторов от приложенного напряжения.

Определяется по формуле: KU=R1−R2R1∗100%{\displaystyle K_{U}={\frac {R_{1}-R_{2}}{R_{1}}}*100\%}, где R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} — сопротивления, измеренные при напряжениях, соответствующих 10%{\displaystyle 10\%}-ной и 100%{\displaystyle 100\%}-ной номинальной мощности рассеяния резистора.^[3]

Некоторые характеристики существенны при проектировании устройств, работающих на высоких и сверхвысоких частотах, это:

• Паразитная ёмкость.
• Паразитная индуктивность.

Обозначение резисторов на схемах

а) обозначение, принятое в России и в Европе
б) принятое в США

По стандартам России условные графические обозначения резисторов на схемах должны соответствовать ГОСТ 2.728-74. В соответствии с ним, постоянные резисторы обозначаются следующим образом:

Переменные, подстроечные и нелинейные резисторы обозначаются следующим образом:

Цепи, состоящие из резисторов

Последовательное соединение резисторов

При последовательном соединении резисторов их сопротивления складываются

R=R1+R2+R3+…{\displaystyle R=R_{1}+R_{2}+R_{3}+\ldots }

Доказательство

Cила тока при параллельном соединении

Параллельное соединение элементов в электрической цепи

Прежде чем приступать к формированию электропроводки в любом типе помещения, разработке электрической цепи для других топов объектов, важно изучить основные способы соединений элементов, используемые на практике.

Наибольшее распространение получили следующие варианты:

• параллельное;
• последовательное;
• смешанное соединение.

Если выбран вариант последовательного соединения, это означает, что все, используемые в цепи элементы, связываются друг с другом электрическими проводами последовательно. В результате, участок цепи, на котором устанавливается такой способ монтажа, не будет иметь в своей конструкции узлов.

Если соединение выполнено параллельно, то здесь объединение элементов в цепи будет выполнено при помощи двух узлов, при этом связь со всеми другими узлами будет отсутствовать. Важно разобраться, какая сила тока при параллельном соединении элементов будет в цепи.

Смешанный тип соединения может использоваться в сложных цепях, состоящих из множества различных элементов, многофункционального узла, выполняющего, как правило, широкий набор операций.

Сила тока в параллельном проводнике

Если в цепи использовано последовательное соединение отдельных ее элементов, то сила тока здесь на всех участках, во всех проводниках будет оставаться одинаковой. Рассчитать напряжение можно, используя простое правило – необходимо сложить все напряжения, получаемые на концах каждого из проводников и получим искомый результат.

Совсем по-другому проявляется сила тока в параллельном проводнике.

При любой нагрузке в электроцепи будет возникать определенное сопротивление. Оно, естественно, будет препятствовать прохождению электрического тока без каких-либо потерь. В целом, ток так и движется – постепенно, от источника по проложенным заранее проводникам к нагруженным элементам. Чтобы обеспечить легкое прохождение тока по проводникам, важно, чтобы этот проводник мог легко и просто отдавать электроны, т.е. – обладать хорошей проводимостью.

Большая часть современных цепей использует медные проводники, а обязательным элементом также являются приемники энергии. Каждый такой приемник создает определенную нагрузку и имеет то или иное электрическое сопротивление. От приведенных выше параметров, в конечном итоге, зависит сила тока при параллельном соединении проводников.

Особенности цепи, в которой используется параллельное соединение

Как уже отмечалось, в данном варианте монтажа электроцепи, все ее элементы, проводники, соединяются друг с другом параллельным методом. Соответственно, все начала проводников соединяются при помощи медных (преимущественно) проводников в один пучок. Аналогичным способом в одну точку также собираются и концы проводников. Как же рассчитывается сила тока в цепи при параллельном соединении? Лучше всего разобраться в данном вопросе поможет достаточно простой и понятный пример.

Нарисуем на листе бумаги такой вид соединения, который у специалистов называется «разветвленным» и обеспечим нахождение в каждой отдельной ветви по одному резистору (сопротивлению). Далее проследим, каким образом будет вести себя электрический ток, протекающий по цепи. Достигнув места разветвления, ток разделится на каждый резистор, установленный далее по определенной ветке линии. Следовательно, реальный ток в цепи будет равен величина, состоящей из суммы токов на всех сопротивлениях (с учетом количества разветвлений). Как считается сила тока разобрались, а вот напряжение при параллельном сопротивлении на всех элементах в сети будет оставаться одинаковым.

Примечательно, что все установленные на различных ветвях цепи резисторы можно заменить одним таким резистором, эквивалентным по сопротивлении сумме замещаемых элементов. Рассчитать, какова сила тока при параллельном соединении резисторов поможет важнейший закон Ома!

Область применения

А можно ли на практике использовать данные сведения? Есть ли от них реальная польза?

Люстра Arte Lamp Kenny A9514PL-5-1WG

Прежде всего, рассмотрим организацию соединения проводников и сопротивлений в домашних условиях. Как правило, такие схемы собираются доля обеспечения работы многорожковых люстр, светильников с некоторым количеством ламп освещения. Если использовать здесь последовательную схему, то все лампочки будут включаться одновременно. При использовании параллельного метода можно выводить необходимое количество светильников на один выключатель и включать одну, две и более лампочек в зависимости от ранее принятого решения, с учетом вопросов экономичности, целесообразности и, конечно же, дизайна.

Подведем итог

Наконец, все, используемые в квартире, загородном доме бытовые приборы и устройства подключены к сети напряжением 220В параллельно. Это подключение происходит с помощью распределительного щитка. Зная, чему равна сила тока при параллельном соединении, можно уверенно отметить, данный способ позволит эффективно управлять используемой электротехникой, приборами и предметами освещения в квартире.

Parallel — AWS Step Functions

Состояние Параллельно ( «Тип»: «Параллельно» ) можно использовать для создания
параллельные ветви исполнения в вашем конечном автомате.

В дополнение к общему состоянию
поля, Параллельные состояния включают эти дополнительные поля.

Филиалы (обязательно)

Массив объектов, которые указывают конечные автоматы для параллельного выполнения.Каждый
такой объект конечного автомата должен иметь поля с именами Состояния и
StartAt , значения которого точно такие же, как и на верхнем уровне состояния.
машина.

ResultPath (необязательно)

Задает место (на входе) для вывода ветвей.Вход
затем фильтруется в соответствии с полем OutputPath (если есть) перед
используется в качестве выхода состояния. Для получения дополнительной информации см. Ввод и вывод.
Обработка.

ResultSelector (Необязательно)

Передайте коллекцию пар ключ-значение, где значения являются статическими или выбираются из
то
результат.Для получения дополнительной информации см. ResultSelector.

Retry (необязательно)

Массив объектов, называемых ретриерами, которые определяют политику повтора в случае, если
state обнаруживает ошибки времени выполнения.Для получения дополнительной информации см. Примеры использования Retry и Catch.

Catch (опционально)

Массив объектов, называемых ловушками, которые определяют резервное состояние, которое
выполняется, если состояние обнаруживает ошибки времени выполнения и его политика повторных попыток исчерпана
или нет
определены.Для получения дополнительной информации см. Резервные состояния.

Состояние Parallel заставляет AWS Step Functions выполнять каждую ветвь, начиная с
состояние, указанное в поле StartAt этой ветки, как можно одновременно, и
дождитесь завершения всех ветвей (достижения конечного состояния) перед обработкой
Параллельный Поле состояния Следующее поле.

Пример параллельного состояния

  {
  "Комментарий": "Параллельный пример.",
  "StartAt": "LookupCustomerInfo",
  "Состояния": {
    "LookupCustomerInfo": {
      «Тип»: «Параллельный»,
      «Конец»: правда,
      "Ветви": [
        {
         "StartAt": "LookupAddress",
         "Состояния": {
           "LookupAddress": {
             «Тип»: «Задача»,
             "Ресурс":
               "arn: aws: lambda: us-east-1: 123456789012: function: AddressFinder",
             «Конец»: правда
           }
         }
       },
       {
         "StartAt": "LookupPhone",
         "Состояния": {
           "LookupPhone": {
             «Тип»: «Задача»,
             "Ресурс":
               "arn: aws: lambda: us-east-1: 123456789012: function: PhoneFinder",
             «Конец»: правда
           }
         }
       }
      ]
    }
  }
}  

В этом примере ветви LookupAddress и LookupPhone
выполняется параллельно.Вот как визуальный рабочий процесс выглядит в Step Functions
приставка.

Каждая ветвь должна быть автономной. Состояние в одной ветви состояния Parallel
не должно иметь поля Next , которое нацелено на поле за пределами этой ветви, а также не может
любое другое состояние вне ветви переходит в эту ветвь.

Параллельное состояние
Обработка ввода и вывода

Состояние Параллельно обеспечивает каждую ветвь копией собственных входных данных
(может быть изменено полем InputPath ).Он генерирует вывод, который является
массив с одним элементом для каждой ветви, содержащий выходные данные этой ветви. Там
нет
требование, чтобы все элементы были одного типа. Выходной массив можно вставить
в
входные данные (и все отправлено как выход состояния Parallel ) с помощью
ResultPath обычным способом (см. Ввод и вывод
Обработка).

  {
  "Комментарий": "Параллельный пример.",
  "StartAt": "FunWithMath",
  "Состояния": {
    "FunWithMath": {
    «Тип»: «Параллельный»,
    «Конец»: правда,
    "Ветви": [
      {
        "StartAt": "Добавить",
        "Состояния": {
          "Добавить": {
            «Тип»: «Задача»,
            «Ресурс»: «arn: aws: swf: us-east-1: 123456789012: задача: Добавить»,
            «Конец»: правда
          }
        }
      },
      {
        "StartAt": "Вычесть",
        "Состояния": {
          "Вычесть": {
            «Тип»: «Задача»,
            "Resource": "arn: aws: swf: us-east-1: 123456789012: task: Subtract",
            «Конец»: правда
          }
        }
      }
    ]
   }
  }
}  

Если для состояния FunWithMath был задан массив [3, 2] как
input, то оба состояния Add и Subtract получают этот массив как
ввод.Результат Добавить будет 5 , результат Вычесть
будет 1 , а выход состояния Parallel будет
массив.

  [5, 1] ​​ 

Обработка ошибок

Если какая-либо ветвь завершилась неудачно из-за необработанной ошибки или перехода к
Fail state, все состояние Parallel считается имеющим
не удалось, и все его ветви остановлены.Если ошибка не обрабатывается
Parallel само состояние, Step Functions останавливает выполнение с ошибкой.

При сбое параллельного состояния вызываемые лямбда-функции продолжают работать и
рабочие процессы, обрабатывающие токен задачи, не останавливаются.

• Чтобы остановить длительную активность, используйте сердцебиение, чтобы определить,
  ветвь была остановлена ​​Step Functions, и останавливают рабочие процессы, которые обрабатывают задачи.Вызов
  SendTaskHeartbeat , SendTaskSuccess или
  SendTaskFailure выдаст ошибку, если состояние не выполнено.
  См. Ошибки сердцебиения.

• Работающие лямбда-функции не могут быть остановлены.Если вы реализовали
  откат, используйте состояние Ожидание , чтобы выполнялась очистка
  после завершения функции лямбда.

Примеры параллельной структуры

Параллельная структура, или параллелизм, означает использование одного и того же словосочетания, чтобы показать, что два или более слова или идеи имеют одинаковую важность.Слова и фразы должны совпадать не только по структуре, но и по времени. Писатели используют параллельную структуру, чтобы сделать свой текст более ясным и понятным. Это также повышает ценность общей композиции писателя и показывает, что его письмо структурно и грамматически правильно.

Правильное использование параллельной структуры

Писатели используют параллельную структуру в словах и фразах в своих предложениях. Эта грамматическая форма может использоваться с множеством структур, включая инфинитивов, , слова, предложения и списки.

Следует использовать параллельную структуру, когда вы соединяете предложения с координирующим союзом, например: for, and, nor, or, but, so, or still. Вот некоторые примеры:

• Правильно: каждое утро мы застилаем постель, завтракаем и кормим собаку.
  Неправильно: каждое утро мы застилаем постель, завтракаем и кормим собаку.
• Правильно: я не буду петь и танцевать.
  Неправильно: я не буду петь ни песен, ни танцев.

В дополнение к координирующим соединениям, параллельная структура также используется с коррелятивными соединениями, такими как: либо…или, ни … ни, не только … но также. Вот несколько примеров такого использования:

• Правильно: спорили не только о статье, но и об обзоре.
  Неверно: Спорили не только о статье, но и о рецензии.
• Правильно: либо ей нравится его видеть, либо она не хочет его видеть.
  Неправильно: либо ей нравится его видеть, либо она не хочет его видеть.

Параллельная структура должна использоваться с инфинитивами. Некоторые примеры параллельной структуры с инфинитивами:

• Правильно: Эшли любит кататься на лыжах, плавать и прыгать через скакалку.
  Неправильно: Эшли любит кататься на лыжах, плавать и прыгать со скакалками.
• Правильно: ей нравится танцевать и петь песни.
  Неправильно: ей нравится танцевать и петь песни.

Будьте последовательны и используйте параллельную структуру со словами, заканчивающимися на -ing. Некоторые примеры параллельной структуры слов, оканчивающихся на -ing:

• Правильно: Джо любит бегать, ходить и быть активным.
  Неправильно: Джо любит бегать, ходить пешком и заниматься активным отдыхом.
• Правильно: мы любим отдыхать и сидеть на солнце.
  Неправильно: Нам нравится расслабляться и сидеть на солнышке.

При написании статей следует использовать параллельную структуру. Вот несколько примеров предложений, использующих параллельную структуру:

• Правильно: учитель сказал им, что им нужно учиться и что они должны практиковать свои слова каждую ночь.
  Неправильно: Учитель сказал им учиться и практиковать свои слова каждую ночь.
• Правильно: мои родители сказали, получи хорошее образование и не соглашайся на меньшее.
  Неправильно: Мои родители сказали, что нужно получить хорошее образование и не соглашаться на меньшее.

Еще несколько примеров параллельной структуры:

• Правильно: Мэри хотела убедиться, что она представила свою презентацию творчески, эффективно и убедительно.
  Неправильно: Мэри хотела убедиться, что она подготовила свою презентацию творчески, эффективно и убедила других.
• Правильно: Тим считался хорошим сотрудником, потому что он всегда приходил вовремя, он был очень мотивирован и был хорошим руководителем.
  Неправильно: Тим считался хорошим сотрудником, потому что он всегда приходил вовремя, он был очень мотивирован и хорошо руководил командой.

Примеры параллельной структуры в списках

Если у вас есть элементы в списке после двоеточия, все элементы должны быть в одной форме, чтобы избежать ошибки параллельной структуры.

Некоторые примеры могут проиллюстрировать этот момент:

• Верно: в торговом центре можно делать следующие действия: покупать продукты, обедать и оплачивать счета.
  Неправильно: в торговом центре можно делать следующие действия: покупать продукты, обедать и оплачивать счета.
• Правильно: в вашей спальне вы найдете следующее: кровать, шкаф и стол.
  Неправильно: в вашей спальне вы найдете следующее: кровать, шкаф и, сидя за столом.
• Правильно: собаки — отличные домашние животные по следующим причинам: они верны, они любящие и послушные.
  Неправильно: Собаки — отличные домашние животные по следующим причинам: они верны, они любящие и из-за своего послушания.
• Правильно: люди, которые продвигаются вперед, делают много разных вещей, например: учатся, много работают и поступают в институт.
  Неправильно: люди, которые продвигаются вперед, делают много разных вещей, например: учатся, много работают и учатся в колледже.

Параллельная структура в глагольном времени

Имейте в виду, что параллельная структура должна использоваться, когда речь идет о глагольном времени. Времена ваших глаголов всегда должны совпадать.

Вот несколько примеров:

• Верно: она написала письмо и отправила его в школу.
  Неправильно: она пишет письмо и отправляет его в школу.

• Правильно: вчера мы смотрели фильм, играли в видеоигры и готовили пиццу.
  Неправильно: вчера мы смотрели фильм, играли в видеоигры и готовили пиццу.

  Важность параллельной структуры

  Параллельная структура обеспечивает поток в предложении. Это сохраняет ваше письмо сбалансированным и облегчает чтение. Это также показывает, что идеи одинаково важны. Ошибки в параллельной структуре могут сделать ваше письмо странным для слушателей.Многие тесты, включая SAT, потребуют от вас выявления ошибок параллельной структуры как средства проверки ваших навыков письма.

ipyparallel — ipyparallel 6.3.0.dev документация