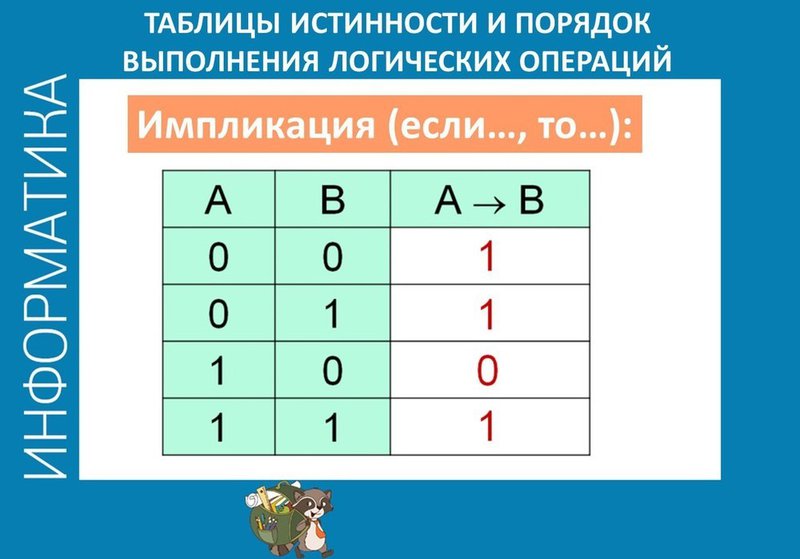
НОУ ИНТУИТ | Лекция | Более сложные логические элементы
Аннотация: В лекции рассказывается о принципах работы, характеристиках и типовых схемах включения логических элементов, выполняющих сравнительно сложные функции – элементов Исключающее ИЛИ, И-ИЛИ-НЕ, триггеров Шмитта, а также приводятся схемотехнические решения, позволяющие реализовать на их основе часто встречающиеся функции.
Элементы Исключающее ИЛИ
Элементы Исключающее ИЛИ (по-английски — Exclusive-OR) также можно было бы отнести к простейшим элементам,
но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов
Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной
сигнал в уровень единицы или нуля.
| Вход 1 | Вход 2 | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Рис.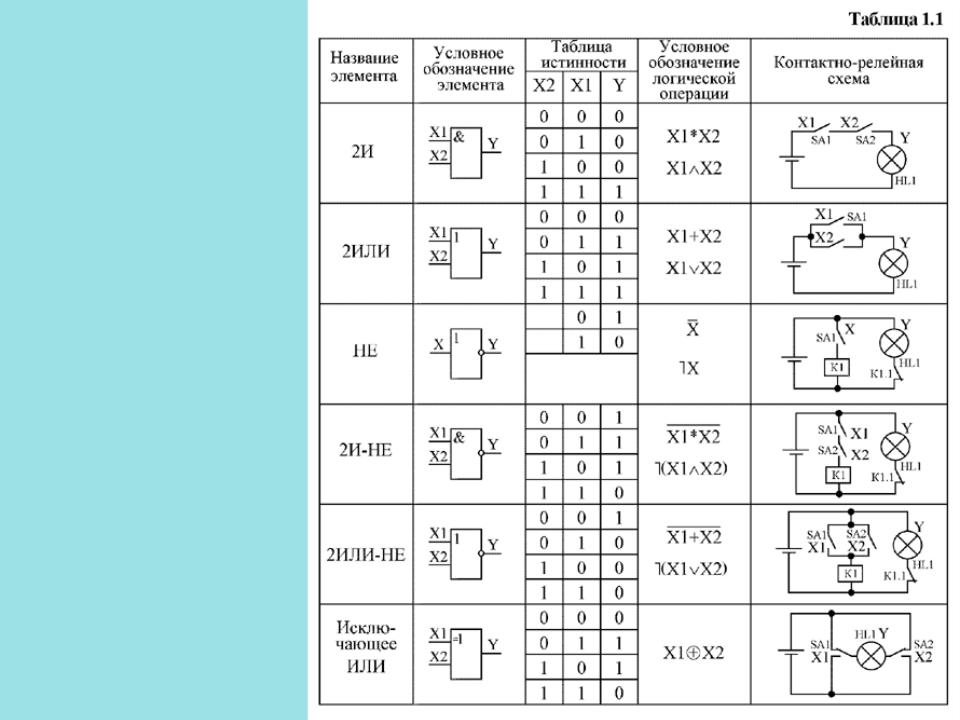
4.1.
Обозначения элементов Исключающее ИЛИ: зарубежные (слева) и отечественные (справа)
Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на
одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то
на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в
табл. 4.1.
Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1.
Надпись на отечественном
обозначении элемента Исключающее ИЛИ «=1» как раз и обозначает, что выделяется ситуация, когда на входах
одна и только одна единица.
Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5
(четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком уж
специфическая функция реализуется этими элементами.
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию так называемого суммирования
по модулю 2. Поэтому эти элементы также называются сумматорами по модулю два. Как уже отмечалось в предыдущей
лекции, обозначается суммирование по модулю 2 знаком плюса, заключенного в кружок.
Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности, состоит в
сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают),
на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента
подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий
на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы
компараторов кодов, которые будут рассмотрены в следующей лекции.
В качестве сумматора по модулю 2 элемент Исключающее ИЛИ используется также в параллельных и последовательных
делителях по модулю 2, служащих для вычисления циклических контрольных сумм.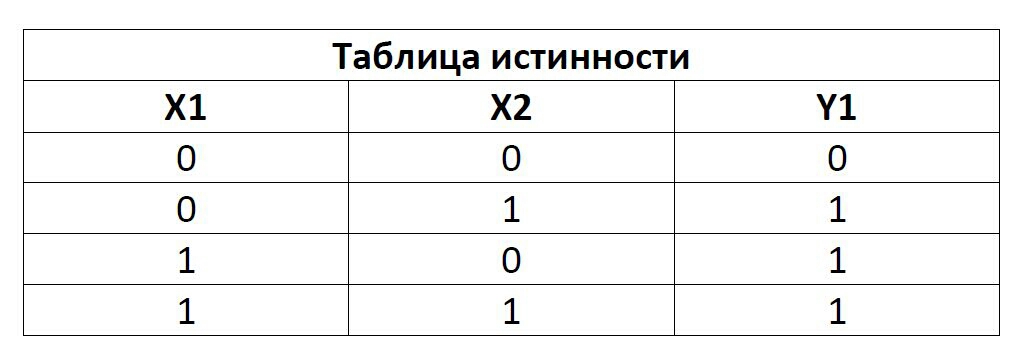 Но подробно эти схемы будут
Но подробно эти схемы будут
рассмотрены в лекциях 14,15.
Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2).
В этом случае
один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает
информационный сигнал. Если на управляющем входе единица, то входной сигнал инвертируется, если же
нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим
работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может
изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
Рис.
4.2.
Элемент Исключающее ИЛИ как управляемый инвертор
В случае, когда имеется два сигнала одинаковой полярности (положительные или отрицательные), и
при этом их одновременный приход исключается, элемент Исключающее ИЛИ может быть использован для
смешивания этих сигналов (рис. 4.3). При любой полярности входных сигналов выходные сигналы элемента
4.3). При любой полярности входных сигналов выходные сигналы элемента
будут положительными. При положительных входных сигналах элемент Исключающее ИЛИ будет работать как
элемент 2ИЛИ, а при отрицательных он будет заменять элемент 2И-НЕ. Такие замены могут быть полезны
в тех случаях, когда в схеме остаются неиспользованными некоторые элементы Исключающее ИЛИ. Правда,
при этом надо учитывать, что задержка распространения сигнала в элементе Исключающее ИЛИ обычно
несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис.
4.3.
Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов
Рис.
4.4.
Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ
Еще одно важнейшее применение элемента Исключающее ИЛИ — формирование коротких импульсов по любому
фронту входного сигнала (рис.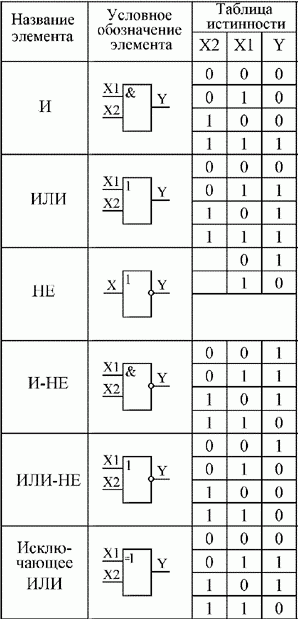 4.4). В данном случае не важно, положительный фронт входного сигнала
4.4). В данном случае не важно, положительный фронт входного сигнала
или отрицательный, на выходе все равно формируется положительный импульс. Входной сигнал задерживается
с помощью конденсатора или цепочки элементов, а затем исходный сигнал и его задержанная копия поступают
на входы элемента Исключающее ИЛИ. В обеих схемах в качестве элементов задержки используются также
двувходовые элементы Исключающее ИЛИ в неинвертирующем включении (на неиспользуемый вход подается нуль).
В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные
импульсы следуют вдвое чаще, чем входные.
Данную особенность элементов Исключающее ИЛИ надо учитывать в том случае, когда на оба входа элемента
поступают изменяющиеся одновременно сигналы. При этом на выходе элемента возможно появление коротких
паразитных импульсов по любому из фронтов входных сигналов. Исключить их влияние на дальнейшую схему можно,
например, с помощью синхронизации, подобной рассмотренной в предыдущем разделе.
что это, построение по таблице истинности
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
Определение
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
\((A\;\wedge\;\overline B\;\wedge\;C)\;\vee\;(B\;\wedge\;C)\)
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
Примечание
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
Определение
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
КНФ имеет вид:
\((A\;\vee\;\overline B\;\vee\;C)\;\wedge\;(A\;\vee\;C)\)
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.

Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная.
 В случае противного результата, в конъюнкцию включается ее отрицание.
В случае противного результата, в конъюнкцию включается ее отрицание. - Связать полученные конъюнкции операциями дизъюнкции.
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
\(F(x_1,\;x_2,\;x_3)\;=\;(\overline{x_1}\wedge\overline{x_2}\wedge\overline{x_3})\;\vee(\overline{x_1}\;\wedge\;\overline{x_2}\;\wedge\;x_3)\;\vee(x_1\;\wedge\;\overline{x_2}\;\wedge\;\overline{x_3})\;\vee\;(x_1\;\wedge\;\overline{x_2}\;\wedge\;x_3)\;\vee\;(x_1\;\wedge\;x_2\;\wedge\;x_3)\)
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.

- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
\(F(x_1,\;x_2,\;x_3)\;=\;(x_1\;\vee\;\overline{x_2}\;\vee\;x_3)\;\wedge\;(x_1\;\vee\;\overline{x_2}\;\vee\;\overline{x_3})\;\wedge\;(\overline{x_1}\;\vee\;\overline{x_2}\;\vee\;x_3)\)
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: \( \equiv , = , \Leftrightarrow .\)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций.
 В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны. - Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
\(x\;\vee\;xy\;=\;x\)
\(x(x\;\vee\;y)\;=\;x\;\)
Доказательство эквивалентности:
\(x\;\vee\;xy\;=\;x\;\cdot\;l\;\vee\;xy\;=\;x(l\;\vee\;y)\;=\;x\)
\(x(x\;\vee\;y)\;=\;xx\;\vee\;xy\;=\;x\;\vee\;xy\;=\;x\)
Склеивание
\(xy\;\vee\;x\overline y\;=\;x\)
Доказательство эквивалентности:
\(xy\;\vee\;x\overline y\;=\;x(y\;\vee\;\overline y)\;=\;x\;\cdot\;l\;=\;x\)
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
Доказательство эквивалентности
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;x\;\vee\;y\)
Доказательство эквивалентности
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Приведите к СКНФ \(((((A\rightarrow B)\rightarrow\overline A)\rightarrow\overline B)\rightarrow\overline C)\).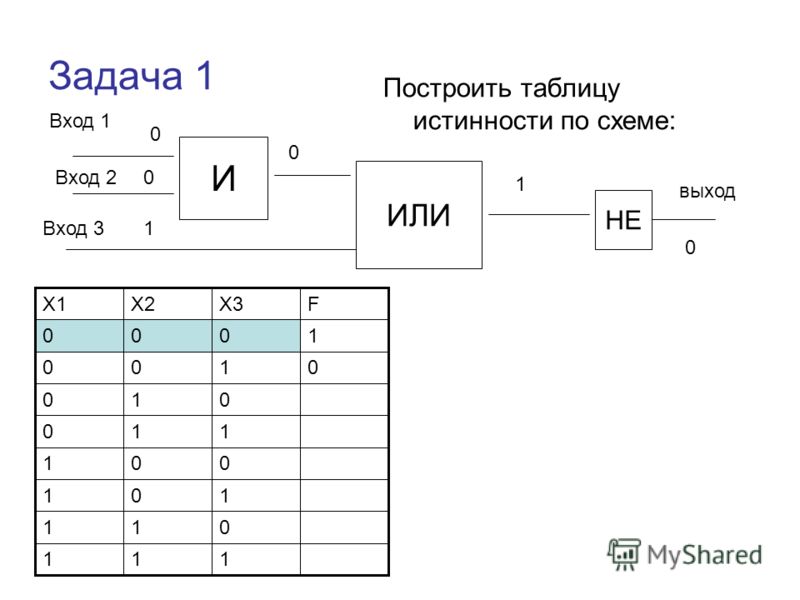
Через применение закона де Моргана и правила\( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;((\overline{((\overline A\;\vee\;B)}\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline{(\overline{(\overline A\vee B)}\;\vee\;\overline A\;)}\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;(\overline{(\overline{(\overline{(\overline A\;\vee\;B)}\;\vee\;\overline A)}\;\vee\;\overline B)}\;\vee\;\overline C)\;=\;(((A\;\vee\;B)\;\vee\;\overline A)\;\vee\;\overline B)\;\vee\;\overline C\;=\;((\overline{(\overline A\;\vee\;B)}\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline{x_1}x_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)\)
Преобразуем функцию:
\(f(\widetilde x^3) = (\overline{x_1}x_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overline{x_1}x_2\;\cdot\;\overline{x_3}\;)\;\vee\;(\overline{\overline{x_1}x_2}\;\cdot\;x_3))\;\cdot\;(\overline{x_1x_3}\;\vee\;x_2)\;=\;((\overline{x_1}x_2\overline{x_3})\;\vee\;((\overline{\overline{x_1}}\;\vee\;\overline{x_2})\;x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\)
\(=\;((\overline{x_1}x_{2\;}\overline{x_3})\;\vee\;((x_1\;\vee\;\overline{x_2})\;x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;x_1x_3\;\vee\;\overline{x_2}x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\)
\(=(\overline{x_1}x_2\overline{x_3}\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;\vee\;\overline{x_2}x_3\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2))\;=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;(x_1\;x_3\overline{x_1}\;\vee\;x_1x_3\overline{x_3}\;\vee\;x_1x_3x_2)\;\vee\;(\overline{x_2}x_3\overline{x_1}\;\vee\;\overline{x_2}x_3\overline{x_3}\;\vee\;\overline{x_2}x_3x_2)\;=\)
\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;0\;\vee\;0\;\vee\;x_1x_2x_3\;\vee\;\overline{x_1}\overline{x_2}x_3\;\vee\;0\;\vee\;0)\;=\;\overline{x_1}x_2\overline{x_3}\;\vee\;x_1x_2x_3\;\vee\;\overline{x_1}\overline{x_2}x_3\)
Таблица истинности — Truth table
Таблица истинности является математической таблицей используется в логике -specifically в связи с булевой алгеброй , булевыми функциями и исчислением высказываний -Какого из множества функциональных значений логических выражений на каждом из своих функциональных аргументов, то есть для каждой комбинации значений , принимаемая по их логическим переменным. В частности, таблицы истинности могут использоваться, чтобы показать, истинно ли пропозициональное выражение для всех допустимых входных значений, то есть логически достоверно .
В частности, таблицы истинности могут использоваться, чтобы показать, истинно ли пропозициональное выражение для всех допустимых входных значений, то есть логически достоверно .
В таблице истинности есть один столбец для каждой входной переменной (например, P и Q) и один последний столбец, в котором показаны все возможные результаты логической операции, которую представляет таблица (например, P XOR Q). Каждая строка таблицы истинности содержит одну возможную конфигурацию входных переменных (например, P = true Q = false) и результат операции для этих значений. См. Примеры ниже для дальнейшего пояснения. Людвигу Витгенштейну приписывают изобретение и популяризацию таблицы истинности в его « Логико-философском трактате» , который был завершен в 1918 году и опубликован в 1921 году. Такая система была также независимо предложена в 1921 году Эмилем Леоном Постом . Еще более ранняя итерация таблицы истинности была также обнаружена в неопубликованных рукописях Чарльза Сандерса Пирса 1893 года, предшествующих обеим публикациям почти на 30 лет.
Унарные операции
Есть 4 унарные операции:
- Всегда правда
- Никогда не правда, унарная ложь
- Унарная идентичность
- Унарное отрицание
Логическая правда
Выходное значение всегда истинно, независимо от входного значения p.
| п | Т |
|---|---|
| Т | Т |
| F | Т |
Логическая ложь
Выходное значение никогда не бывает истинным: то есть всегда ложно, независимо от входного значения p.
| п | F |
|---|---|
| Т | F |
| F | F |
Логическая идентичность
Логическая идентичность — это операция над одним логическим значением p, для которого выходным значением остается p.
Таблица истинности для оператора логической идентичности выглядит следующим образом:
| п | п |
|---|---|
| Т | Т |
| F | F |
Логическое отрицание
Логическое отрицание — это операция над одним логическим значением , обычно значением предложения , которая производит значение true, если его операнд ложный, и значение false, если его операнд истинен.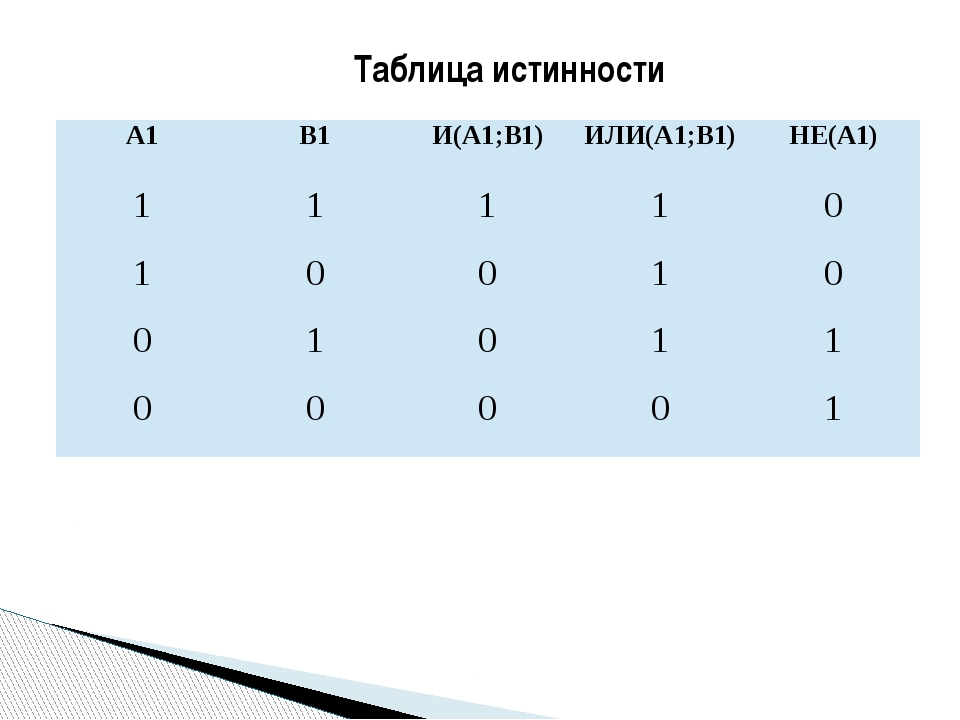
Таблица истинности для НЕ p (также записываемая как ¬p , Np , Fpq или ~ p ) выглядит следующим образом:
| п | ¬p |
|---|---|
| Т | F |
| F | Т |
Бинарные операции
Существует 16 возможных функций истинности двух двоичных переменных :
Таблица истинности для всех бинарных логических операторов
Вот расширенная таблица истинности, дающая определения всех возможных функций истинности двух булевых переменных P и Q:
| п | q | F 0 | NOR 1 | ↚ 2 | ¬p 3 | ↛ 4 | ¬q 5 | XOR 6 | NAND 7 | И 8 | XNOR 9 | q 10 | → 11 | р 12 | ← 13 | ИЛИ 14 | Т 15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Т | Т | F | F | F | F | F | F | F | F | Т | Т | Т | Т | Т | Т | Т | Т | ||
| Т | F | F | F | F | F | Т | Т | Т | Т | F | F | F | F | Т | Т | Т | Т | ||
| F | Т | F | F | Т | Т | F | F | Т | Т | F | F | Т | Т | F | F | Т | Т | ||
| F | F | F | Т | F | Т | F | Т | F | Т | F | Т | F | Т | F | Т | F | Т | ||
| Com | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| Adj | F 0 | NOR 1 | ↛ 4 | ¬q 5 | ↚ 2 | ¬p 3 | XOR 6 | NAND 7 | И 8 | XNOR 9 | р 12 | ← 13 | q 10 | → 11 | ИЛИ 14 | Т 15 | |||
| Отрицательный | Т 15 | ИЛИ 14 | ← 13 | р 12 | → 11 | q 10 | XNOR 9 | И 8 | NAND 7 | XOR 6 | ¬q 5 | ↛ 4 | ¬p 3 | ↚ 2 | NOR 1 | F 0 | |||
| Двойной | Т 15 | NAND 7 | → 11 | ¬p 3 | ← 13 | ¬q 5 | XNOR 9 | NOR 1 | ИЛИ 14 | XOR 6 | q 10 | ↚ 2 | р 12 | ↛ 4 | И 8 | F 0 | |||
| L id | F | F | Т | Т | Т, Ж | Т | F | ||||||||||||
| R id | F | F | Т | Т | Т, Ж | Т | F | ||||||||||||
где
- T = верно.

- F = ложь.
- Com строка указывает , является ли оператор, оп , является коммутативное — Р оп Q = Q оп Р .
- В строке Adj показан оператор op2 такой, что P op Q = Q op2 P
- В строке Neg показан оператор op2 такой, что P op Q = ¬ (Q op2 P)
- В Двойной ряд показывает двойной операции , полученный перестановкой Т с Р, а и с или.
- В L ID ряд показывает оператор левых тождества , если она имеет какое — либо значение — я такие , что я оп Q = Q .
- R ID строка показывает оператор правильных тождества , если он имеет какое — либо значение — я такие , что Р оп I = P .
Четыре комбинации входных значений для p, q считываются построчно из таблицы выше. Функция вывода для каждой комбинации p, q может быть прочитана построчно из таблицы.
Ключ:
Следующая таблица ориентирована по столбцам, а не по строкам.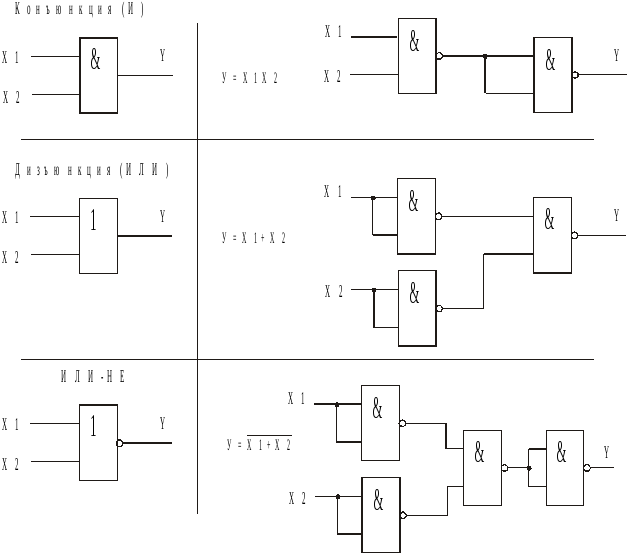 Здесь четыре столбца, а не четыре строки, для отображения четырех комбинаций p, q в качестве входных данных.
Здесь четыре столбца, а не четыре строки, для отображения четырех комбинаций p, q в качестве входных данных.
p : TTFF
q : TFTF
В этом ключе 16 строк, по одной строке для каждой двоичной функции двух двоичных переменных p, q. Например, в строке 2 этого ключа значение Converse nonimplication (‘ ‘) равно только T для столбца, обозначенного уникальной комбинацией p = F, q = T; в то время как в строке 2 значение этой операции равно F для трех оставшихся столбцов p, q. Выходная строка для , таким образом
,
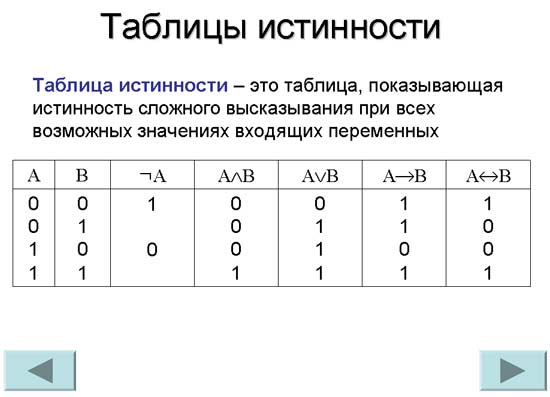
Таблицы истинности
Логические операции
удобно описывать так называемыми
таблицами истинности, в которых
отражают результаты вычислений сложных
высказываний при различных значениях
исходных простых высказываний. Простые
высказывания обозначаются переменными
(например, A и B).
Логические основы компьютера
В ЭВМ используются
различные устройства, работу которых
прекрасно описывает алгебра логики. К
К
таким устройствам относятся группы
переключателей, триггеры, сумматоры.
Кроме того, связь
между булевой алгеброй и компьютерами
лежит и в используемой в ЭВМ системе
счисления. Как известно она двоичная.
Поэтому в устройствах компьютера можно
хранить и преобразовывать как числа,
так и значения логических переменных.
Переключательные схемы
В ЭВМ применяются
электрические схемы, состоящие из
множества переключателей. Переключатель
может находиться только в двух состояниях:
замкнутом и разомкнутом. В первом случае
– ток проходит, во втором – нет. Описывать
работу таких схем очень удобно с помощью
алгебры логики. В зависимости от положения
переключателей можно получить или не
получить сигналы на выходах.
Вентили, триггеры и сумматоры
Вентиль представляет
собой логический элемент, который
принимает одни двоичные значения и
выдает другие в зависимости от своей
реализации. Так, например, есть вентили,
реализующие логическое умножение
(конъюнкцию), сложение (дизъюнкцию) и
отрицание.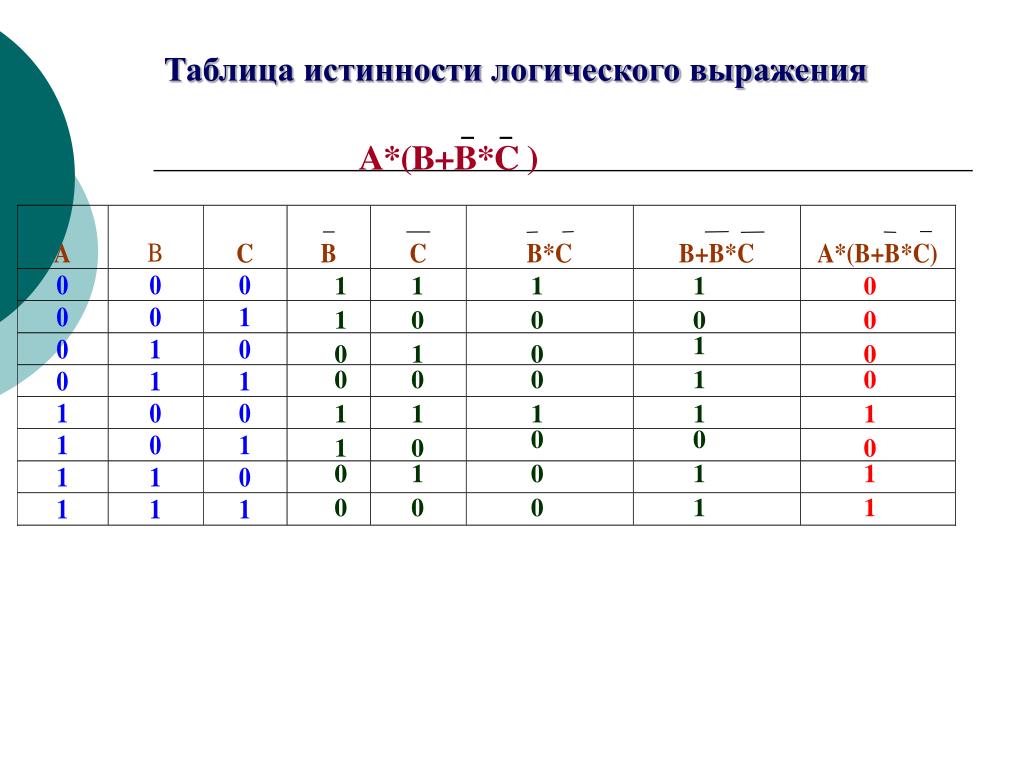
Триггеры и сумматоры
– это относительно сложные устройства,
состоящие из более простых элементов
– вентилей.
Триггер способен
хранить один двоичный разряд, за счет
того, что может находиться в двух
устойчивых состояниях. В основном
триггеры используется в регистрах
процессора.
Сумматоры широко
используются в арифметико-логических
устройствах (АЛУ) процессора и выполняют
суммирование двоичных разрядов.
Изображения, использованные в статье
Таблицы
истинности для конъюнкции, дизъюнкции
и отрицания
Законы алгебры логики
Раздел:
Логические основы компьютера
Номер темы:
2
Для логических
величин обычно используются три операции:
Конъюнкция– логическое
умножение (И) –and, &, ∧.Дизъюнкция– логическое
сложение (ИЛИ) –or, |, v.Логическое отрицание (НЕ) – not, ¬.

Логические выражения
можно преобразовывать в соответствии
с законами алгебры логики:
Законы рефлексивности
a
∨
a = a
a ∧
a = aЗаконы коммутативностиa∨b = b∨a
a∧b = b∧aЗаконы ассоциативности(a∧b)∧c = a∧(b∧c)
(a∨b)∨c = a∨(b∨c)Законы дистрибутивностиa∧(b∨c) = a∧b∨a∧c
a∨b∧c = (a∨b)∧(a∨c)Закон отрицания отрицания¬ (¬
a) = aЗаконы де
Моргана
¬ (a ∧
b) = ¬ a ∨
¬ b
¬ (a ∨
b) = ¬ a ∧
¬ bЗаконы поглощения
a
∨
a ∧
b = a
a ∧
(a ∨
b) = a
Логические элементы. Вентили
Раздел:
Логические основы компьютера
Номер темы:
3
В основе построения
компьютеров, а точнее аппаратного
обеспечения, лежат так называемые
вентили. Они представляют
собой достаточно простые элементы,
которые можно комбинировать между
собой, создавая тем самым различные
схемы.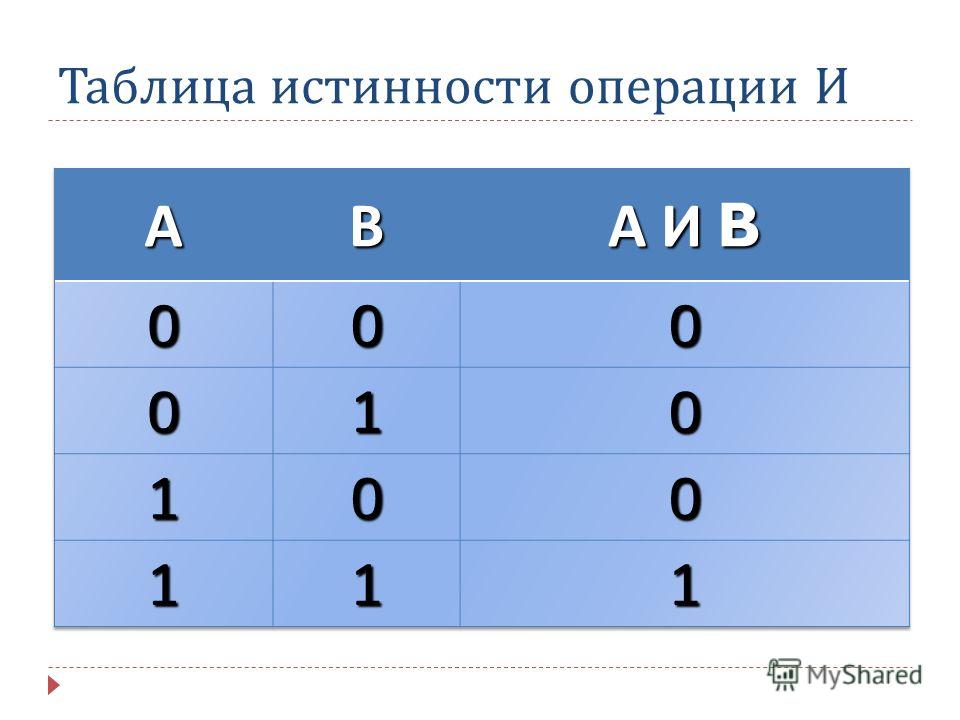 Одни схемы подходят для осуществленияарифметических операций, а на
Одни схемы подходят для осуществленияарифметических операций, а на
основе других строят различнуюпамятьЭВМ.
Простейший вентиль
представляет собой транзисторный
инвертор, который преобразует низкое
напряжение в высокое или наоборот
(высокое в низкое). Это можно представить
как преобразование логического нуля в
логическую единицу или наоборот. Т.е.
получаем вентиль НЕ.
Соединив пару
транзисторов различным способом,
получают вентили ИЛИ-НЕиИ-НЕ.
Эти вентили принимают уже не один, а два
и более входных сигнала. Выходной сигнал
всегда один и зависит (выдает высокое
или низкое напряжение) от входных
сигналов. В случае вентиля ИЛИ-НЕ получить
высокое напряжение (логическую единицу)
можно только при условии низкого
напряжении на всех входах. В случае
вентиля И-НЕ все наоборот: логическая
единица получается, если все входные
сигналы будут нулевыми. Как видно, это
обратно таким привычным логическим
операциям как И и ИЛИ.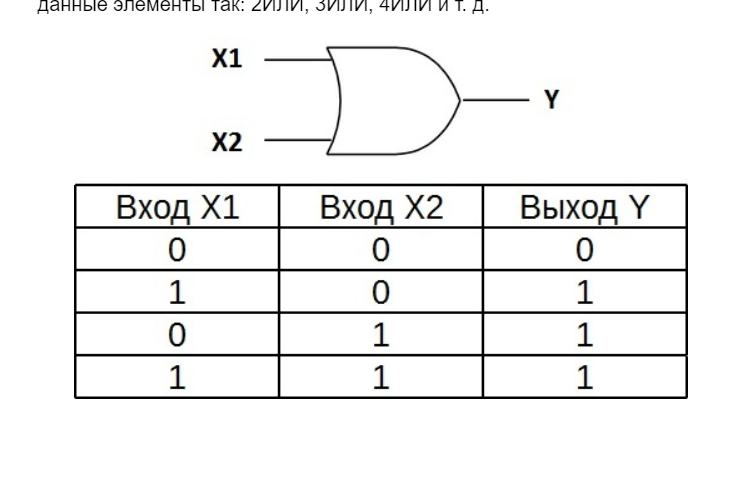 Однако обычно
Однако обычно
используются вентили И-НЕ и ИЛИ-НЕ, т.к.
их реализация проще: И-НЕ и ИЛИ-НЕ
реализуются двумя транзисторами, тогда
как логические И и ИЛИ тремя.
Выходной сигнал
вентиля можно выражать как функцию от
входных.
Транзистору требуется
очень мало времени для переключения из
одного состояния в другое (время
переключения оценивается в наносекундах).
И в этом одно из существенных преимуществ
схем, построенных на их основе.
Изображения, использованные в статье
Схемы
вентилей
§11. Логические выражения
Содержание урока
Формализация
Таблицы истинности
Составление условий
Логические схемы
Выводы
Вопросы и задания
Таблицы истинности
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
X = А • B + А • В.
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.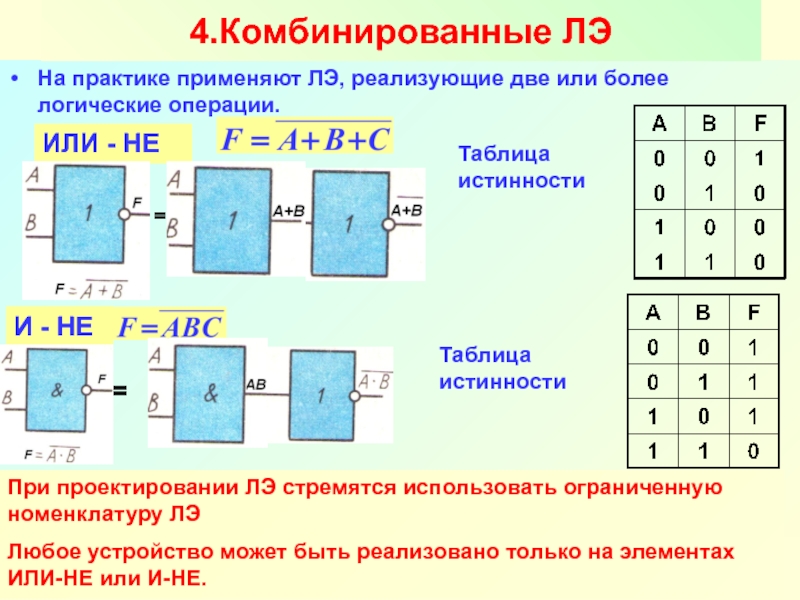
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 23 = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
а) А + В + C;
б) A • С + В;
в) А + B • С;
г) А • В • C;
д) A • B + C.
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
а) А + B + C;
б) A • С • В;
в) А • B • C;
г) A + В + С;
д) A + B + C.
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
а) A + В + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + В + C.
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
а) 1 + В + 0;
в) 0 + B + 0;
д) 0 + В + 0.
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).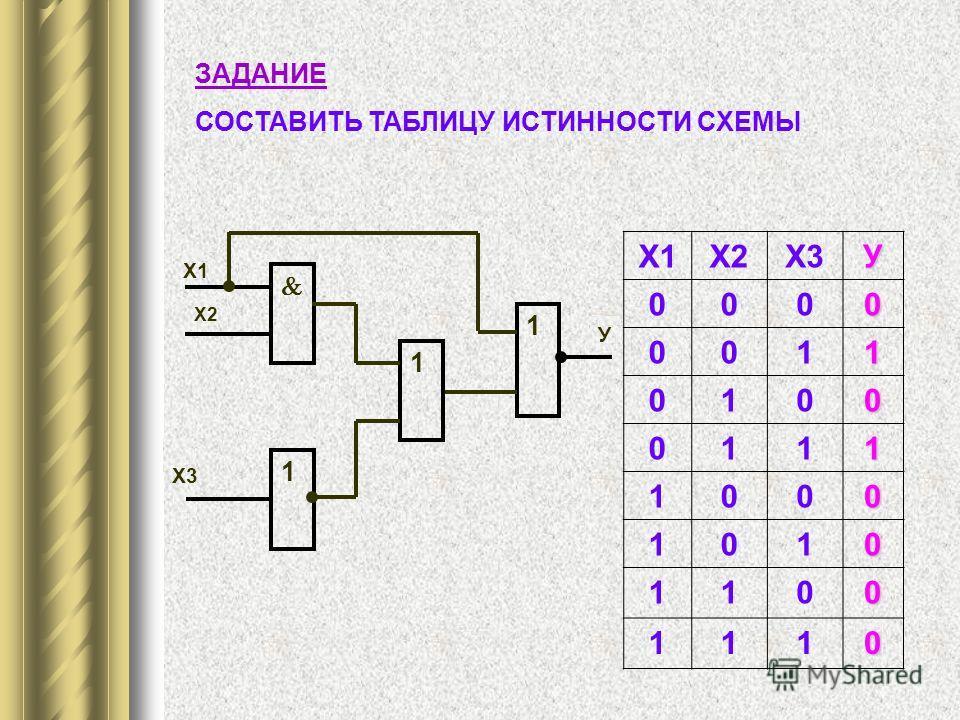
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
а) А • B + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + B + C.
Следующая страница Составление условий
Cкачать материалы урока
Практическая работа №5,6 по Информатике и ИКТ
Практическая работа №5,6
Тема: Логические величины, операции, выражения. Построение логических схем.
Цель работы: научиться составлять аналитические выражения по табличному значению функции, строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.
Студент должен
знать:
уметь:
производить синтез и анализ аналитических выражений логических функций
строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.

Теоретическое обоснование.
1. Логические элементы
Функция отрицание НЕ или инверсия
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2
Таблица истинности логического ИЛИ имеет вид:
Логический элемент ИЛИ обозначается на схемах следующим образом:
Логическое И (логическое умножение, конъюнкция): Y = X1X2 = X1&X2
Таблица истинности логического И имеет вид:
Логический элемент И обозначается на схемах следующим образом:
Функция ИЛИ-НЕ: Y = (X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:
Функция И-НЕ: Y = (X1^X2)
Таблица истинности функции И-НЕ имеет вид:
Логический элемент И-НЕ обозначается на схемах следующим образом:
2.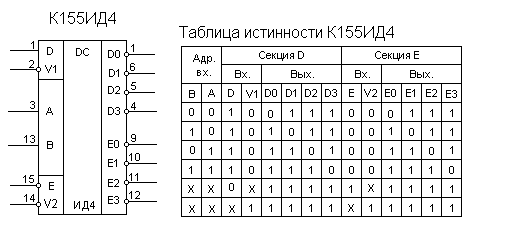 Алгоритм построение логических схем.
Алгоритм построение логических схем.
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей вентиль.
Соединить вентили в порядке выполнения логических операций.
Пример 1.
Составить логическую схему для логического выражения: F=A v B & A.
Две переменные – А и В.
Две логические операции: 1-&, 2-v.
Строим схему:
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А&Вv (ВvА). Вычислить значения выражения для А=1,В=0.
Переменных две: А и В;
Логических операций три: & и две v; А&Вv (Вv А).
Схему строим слева направо в соответствии с порядком логических операций:
3. Составление аналитического выражения функции и построение логической схемы по табличному заданию функции.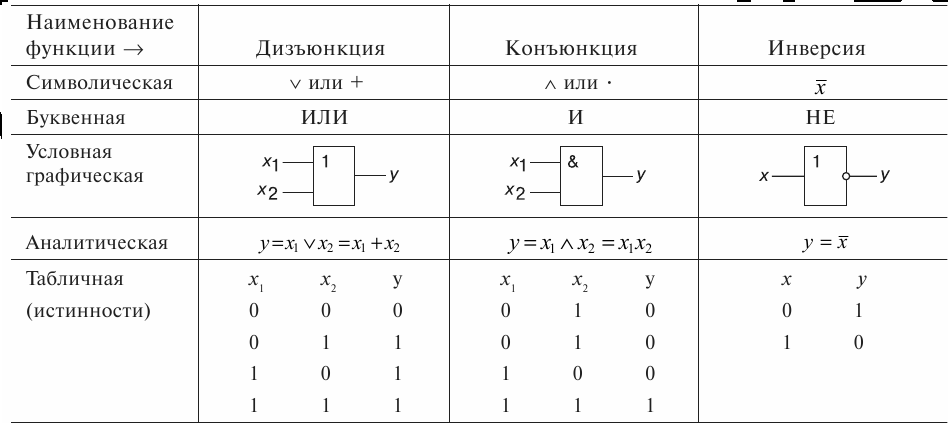
Синтез комбинационных устройств может быть произведен по табличному заданию функции по «0» и «1». Рассмотрим для примера синтез по «1». Для всех значений аргументов х1, х2, х3, где функция задана как «1» берется их конъюнкция, если аргумент равен «1», если же 0 – конъюнкция их инверсий. От полученных конъюнкций берется дизъюнкция.
Например, функция от трех аргументов задана следующей таблицей:
х1
х2
Х3
у
1
0
0
0
0
2
0
0
1
1
3
0
1
0
0
4
0
1
1
0
5
1
0
0
0
6
1
0
1
0
7
1
1
0
0
8
1
1
1
1
Это значит, что при любых наборах аргументов ч кроме второго и последнего, аргумент у будет равен 0.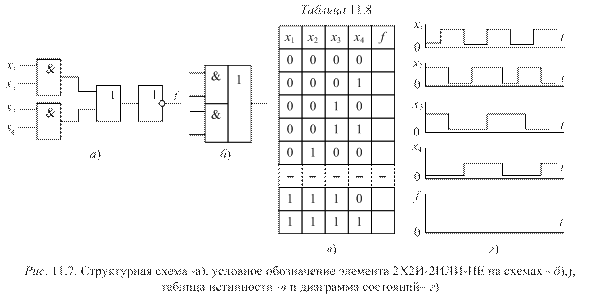 Составляем для второго набора выражение: .
Составляем для второго набора выражение: .
Для последнего набора: х1 х2 х3
Составим аналитическое выражение функции:
Схема должна содержать инверсию сигналов х1, х2, две схемы «И» и одну двухвходовую схему «ИЛИ»
х1
х2
х3
1
1
&
&
1
Ход работы:
Изучить теоретическое обоснование;
Выполнить практическое задание по вариантам;
Оформить отчет.
Ответить на контрольные вопросы по указанию преподавателя.
Практические задания:
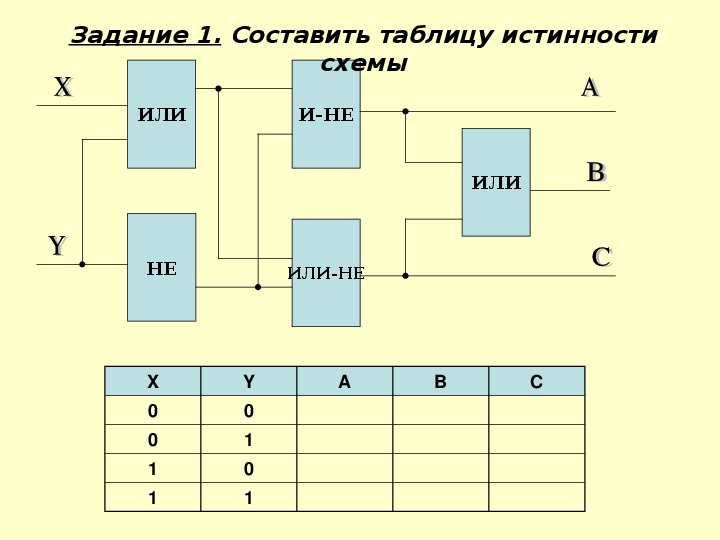
Задание 1
Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.
Вариант 1
а)
б)
A
1
&
&
1
B
Y
Вариант 2
Вариант 3
а)
б)
A
B
C
1
&
F
Вариант 4
а)
&
1
1
1
A
B
C
1
F
б)
&
1
&
1
A
B
Y
Задание 2
Построить логические схемы по формулам и составить таблицу истинности
Вариант 1
а) F= (AvB)&(Cv`B)
б) F= (A&B&C)
Вариант 2
а) F=(X&`Y)vZ.
б) F=X&Yv`Z.
В ариант 3
а)F= (XvY) & (Yv`X).
б)F= ((XvY) & (`ZvX)) & (ZvY).
Вариант 4
а) F= A&B&C&`D.
б) F= (AvB) &(`AvB).
Задание 3
По табличному заданию функции найти аналитическое выражение функции и построить логическую схему в соответствии со своим вариантом.
Вариант 1
Вариант 2
Вариант 3
Вариант 4
х1
х2
Х3
у1
у2
у3
У4
у5
у6
у7
у8
1
0
0
0
1
0
0
0
1
1
0
0
2
0
0
1
0
1
0
0
0
1
0
0
3
0
1
0
1
0
1
0
0
1
0
1
4
0
1
1
0
0
0
1
1
0
0
0
5
1
0
0
0
0
1
0
1
0
0
1
6
Таблицы истинности — отрицание, соединение, дизъюнкция («не», «и», «или»)
Таблицы истинности — это способ анализа того, как действует достоверность утверждений (называемых пропозициями), когда вы используете логическое «или» или логическое «и» для их объединения. Утверждения либо полностью верны, либо полностью ложны, поэтому любая таблица истинности захочет показать обе эти возможности для всех сделанных утверждений.
Для всех этих примеров мы будем обозначать p и q предложениями.Это могут быть высказывания типа «Мне 25 лет» или «Сейчас теплее 70 °». Любые утверждения, которые являются правдой или ложью.
реклама
Отрицание — «не р»
Отрицание — это утверждение «не p», обозначаемое \ (\ neg p \), и поэтому оно будет иметь значение истинности, противоположное p. Если p истинно, то \ (\ neg p \), если ложно. Если p ложно, то \ (\ neg p \) истинно. Обратите внимание, что таблица истинности показывает все эти возможности.
Соединение — «и»
Рассмотрим утверждение «p и q», обозначенное \ (p \ wedge q \).Чтобы проанализировать это, мы сначала должны подумать обо всех комбинациях значений истинности для обоих утверждений, а затем решить, как эти комбинации влияют на утверждение «и». Прописью:
- Строка 1 : оба утверждения могут быть верными.
В этом случае имело бы смысл, что «p и q» также являются истинным утверждением. - Строка 2 : p может быть ложным, а q — истинным.
Для того, чтобы «p и q» были истинными, нам нужны ОБЕИХ утверждения. Поскольку один из них ложен, «p и q» ложны. - Строка 3 : p может быть истинным, а q — ложным.
Если это так, то по тому же аргументу в строке 2 «p и q» ложны. - Строка 4 : оба утверждения могут быть ложными.
Если оба утверждения ложны, тогда «p и q» ложны.
Порядок строк не имеет значения — пока мы систематичны таким образом, чтобы не пропустить никаких возможных комбинаций значений истинности для двух исходных утверждений p, q.
Дизъюнкция — «или»
Вы можете этого не осознавать, но есть два типа «или».Есть включительно или , где мы допускаем тот факт, что оба утверждения могут быть правдой, и есть исключительная или , где мы строго следим за тем, чтобы истинным было только одно или другое утверждение. В математике «или», с которым мы работаем, является включающим или, обозначаемым \ (p \ vee q \). Когда мы хотим работать с эксклюзивным или, мы конкретны и используем другую нотацию (вы можете прочитать об этом здесь: эксклюзивное или). Это показано в первой строке таблицы истинности, которую мы сейчас проанализируем:
- Строка 1 : оба утверждения могут быть верными.
Поскольку мы работаем с включающим или, утверждение «p или q» в этом случае будет истинным. - Строка 2 : p может быть ложным, а q — истинным.
Это суть или. Мы говорим «одно или оба утверждения верны». Следовательно, в данном случае верно «p или q». - Строка 3 : p может быть истинным, а q — ложным.
То же, что и второй ряд. - Строка 4 : оба утверждения могут быть ложными.
Принимая во внимание значение или, если оба утверждения ложны, тогда неверно, что «p или q», поэтому мы перечисляем ложные для этого утверждения.
Сводка
Чтобы отслеживать, как работают эти идеи, запомните следующее:
- «не p» всегда имеет значение истинности, противоположное p
- «p и q» верны только тогда, когда оба утверждения верны (в противном случае — ложь)
- «p или q» неверно, только если оба утверждения ложны (в противном случае — истина)
Понимание этих таблиц истинности позволит нам позже анализировать сложные составные композиции, состоящие из и, или, не, и, возможно, даже условного оператора, поэтому убедитесь, что у вас есть эти основы!
объявление
Продолжить рассмотрение отдельных математических тем
Далее: Таблицы истинности для условных и двусмысленных (подразумевает и если и только)
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные
Таблица истинности — RationalWiki
Таблица истинности — это таблица, в которой перечислены все возможные состояния оператора. [1] Таблицы истинности обычно используются для сравнения утверждений; если два утверждения используют одну и ту же таблицу истинности, то говорят, что эти два утверждения логически эквивалентны.Таблицы истинности также могут использоваться для поиска отрицаний утверждений.
Эквивалентные ведомости [править]
Если два оператора и имеют таблицы истинности, содержащие одинаковые элементы, то эти два оператора логически эквивалентны. [2] [3] То есть два утверждения будут истинными или ложными при одних и тех же условиях. и будучи логически эквивалентным, обозначается как:. Поиск эквивалентных утверждений — это инструмент, используемый в математике, поскольку может быть сложно напрямую доказать одно утверждение, но легко доказать эквивалентное утверждение.
Пример эквивалентных утверждений [править]
Можно показать, что для двух утверждений и логически эквивалентно, показав, что они имеют одну и ту же таблицу истинности. Рассмотрим таблицу истинности для:
В приведенной выше таблице T истинно, а F ложно. Теперь рассмотрим таблицу истинности для:
Если посмотреть на две таблицы, они имеют одинаковые элементы. Таким образом, логически эквивалентно.
Отрицание утверждений [править]
Для данного утверждения другое утверждение является отрицанием того, что состояние противоположно заданным тем же условиям.То есть ложно, когда истинно, и истинно, когда ложно. Если это так, то это отрицание, записанное как (иногда как ~). [4]
| T | F |
| Ф. | т |
Отрицание,, визуализировано в приведенной выше таблице истинности.
Пример отрицания операторов [править]
Можно показать, что это отрицание с помощью таблицы истинности.
| T | Т | Т | F |
| Ф. | F | Т | F |
| т | F | F | т |
| Ф. | Т | Т | F |
См. Также [править]
Внешние ссылки [править]
Таблицы истинности, тавтологии и логические эквивалентности
Ссылки [править]
Рисунок 2.6. Таблица истинности для операций И и ИЛИ. 2.3 Таблицы истинности скачать на ppt
Презентация на тему: «Рисунок 2.6. Таблица истинности для операций И и ИЛИ. 2.3 Таблицы истинности 1.» — стенограмма презентации:
1
Рисунок 2.6. Таблица истинности для операций И и ИЛИ.2.3 Таблицы истинности 1
2
Рисунок 2.7. Трехвходовые операции И и ИЛИ. 2
3
x 1 x 2 x n x 1 x 2 x n +++ x 1 x 2 x 1 x 2 + (b) ворота OR x x (c) ворота NOT Рисунок 2.8. Основные ворота. (a) Логические вентили x 1 x 2 x n x 1 x 2 x 1 x 2 x 1 x 2 x n 2.4 Логические ворота и сети 3
4
Фигура 2.9. Функция из рисунка 2.4. x 1 x 2 x 3 fx 1 x 2 + x 3 = 4 S Источник питания S Light S X1X1 X2X2 X3X3
5
Пример логических сетей 5 x 1 x 2110 0 f 0001 1101 0011 0101 AB x 1 x 2 fx 1 x 2, () 0 1 0 1 0 0 1 1 1 1 0 1 (б) Таблица истинности AB 1 0 0 0 1
6
Пример (Продолжение): временная диаграмма 6 1 0 1 0 1 0 1 0 1 0 x 1 x 2 AB f Время (c) Временная диаграмма x 1 x 2110 0 f 0001 1101 0011 0101 AB
7
Пример (Cont ’): другая сеть с таким же логическим поведением на входе / выходе 7 1100 0011 1101 0101 g x 1 x 2
8
2.5 Булева алгебра — основа современной цифровой технологии В 1849 году впервые опубликована Джорджем Булем для алгебраического описания процессов, связанных с логическим мышлением и рассуждением. В конце 1930-х годов Клод Шеннон показал, что булева алгебра обеспечивает эффективное средство описания схем, построенных с помощью переключателей. –-> Алгебра — мощный инструмент для проектирования и анализа логических схем. 8
11
Принцип двойственности Для логического выражения его двойственность получается заменой всех операторов + на операторы ∙, и наоборот.–Путем замены всех 0 на 1 и наоборот. Двойственное любому истинному утверждению (аксиомам или теоремам) в булевой алгебре также верно. — Позже мы покажем, что двойственность подразумевает наличие по крайней мере двух разных способов выражения каждой логической функции с помощью булевой алгебры. Часто одно выражение приводит к более простой физической реализации. 11
Представление булевых функций — GeeksforGeeks
Логическая функция описывается алгебраическим выражением, состоящим из двоичных переменных, констант 0 и 1 и символов логических операций
Для данного набора значений задействованных двоичных переменных логическая функция может иметь значение 0 или 1.Например, логическая функция определяется в терминах трех двоичных переменных. Функция равна 1, если и одновременно или.
Каждая логическая функция может быть выражена алгебраическим выражением, например, упомянутым выше, или в терминах таблицы истинности. Функция может быть выражена через несколько алгебраических выражений, поскольку они логически эквивалентны, но для каждой функции существует только одна уникальная таблица истинности.
Логическая функция может быть преобразована из алгебраического выражения в принципиальную схему, состоящую из логических элементов, соединенных в определенной структуре.Принципиальная схема для —
Канонические и стандартные формы —
Любая двоичная переменная может принимать одну из двух форм, или. Логическая функция может быть выражена в виде двоичных переменных. Если все двоичные переменные объединены вместе с помощью операции И, то имеется всего комбинаций, поскольку каждая переменная может принимать две формы.
Каждая из комбинаций называется стандартным продуктом minterm или . Минтерм представлен как десятичный эквивалент двоичного числа, обозначенного минтермом.
Важное примечание — В minterm двоичная переменная не имеет штрихов, если переменная равна 1, и она загружается, если переменная равна 0, т.е. если minterm равен, то это означает и.
Например, для логической функции с двумя переменными minterms —
Аналогичным образом, если переменные объединяются вместе с помощью операции ИЛИ, полученный член называется стандартной суммой maxterm или . Параметр maxterm представлен как десятичный эквивалент двоичного числа, обозначаемого maxterm.
Важное примечание — В maxterm двоичная переменная не заполняется штрихом, если переменная равна 0, и она загружается, если переменная равна 1, т.е. если maxterm равен, то это означает и.
Например, для логической функции с двумя переменными maxterms —
Minterms и Maxterms для функции с 3 переменными —
Связь между Minterm и Maxterm — Каждый minterm является дополнением соответствующего maxterm.
Например, для логической функции от двух переменных —
В общем или
Построение логических функций — Теперь, когда мы знаем, что такое minterms и maxterms, мы можем использовать их для построения логических выражений.
«Булева функция может быть выражена алгебраически из заданной таблицы истинности путем формирования минтерма для каждой комбинации переменных, которая дает 1 в функции, а затем взятия ИЛИ всех этих терминов».
Например, рассмотрим две функции и следующие таблицы истинности —
Функция равна 1 для следующих комбинаций — 001,100,111
Соответствующие термины -,,.
Следовательно, алгебраическое выражение для is-
Аналогично алгебраическое выражение для is-
Если мы используем закон Де Морганса и все единицы становятся 0, а все 0 становятся 1. Таким образом, мы получаем-
При использовании De Morgans Снова закон —
и
Из вышеизложенного можно сделать вывод, что логические функции могут быть выражены как сумма minterms или произведение maxterms .


 В случае противного результата, в конъюнкцию включается ее отрицание.
В случае противного результата, в конъюнкцию включается ее отрицание.
 В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.