Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
остается справедливой.
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы
е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Индуктивная и емкостная нагрузка
В этой статье мы расскажем вам, что такое индуктивная и емкостная нагрузка.
Термины «емкостная нагрузка» и «индуктивная нагрузка», применительно к цепям переменного тока, подразумевают определенный характер взаимодействия потребителя с источником переменного напряжения.
Грубо это можно проиллюстрировать следующим примером: подключив к розетке полностью разряженный конденсатор, в первый момент времени мы будем наблюдать практически короткое замыкание, тогда как подключив к той же самой розетке катушку индуктивности, в первый момент времени ток через такую нагрузку окажется почти нулевым.
Так происходит потому, что катушка и конденсатор взаимодействуют с переменным током принципиально по разному, в чем и заключается ключевое различие между индуктивной и емкостной нагрузками.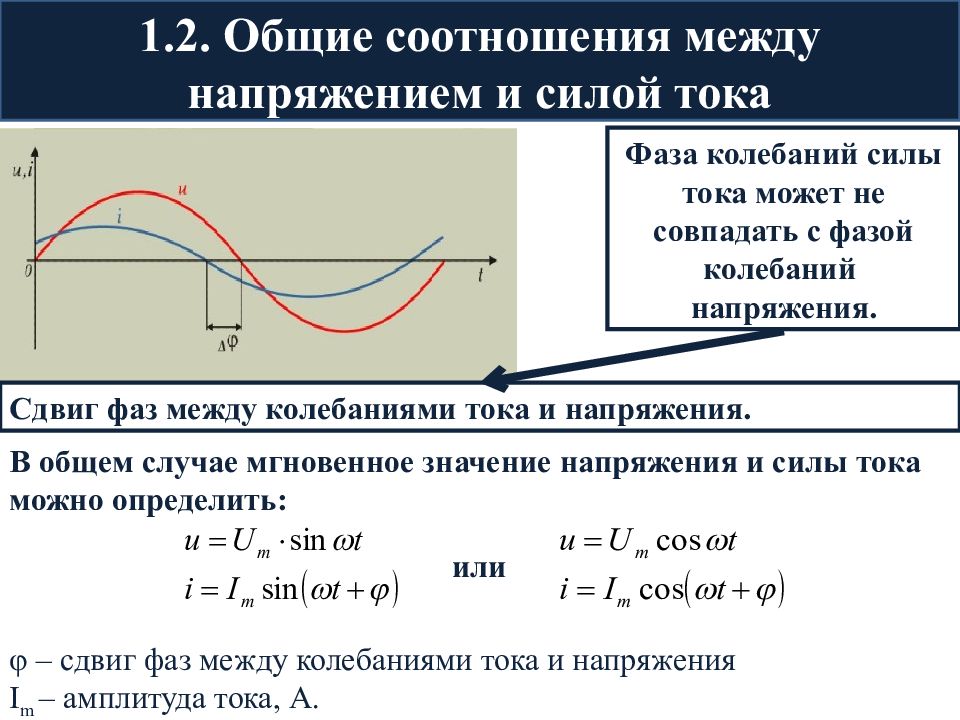
Емкостная нагрузка
Говоря о емкостной нагрузке, имеют ввиду, что она ведет себя в цепи переменного тока подобно конденсатору.
Это значит, что синусоидальный переменный ток будет периодически (с удвоенной частотой источника) перезаряжать емкость нагрузки, при этом в первую четверть периода энергия источника будет расходоваться на создание электрического поля между пластинами конденсатора. Во вторую четверть периода энергия электрического поля между пластинами конденсатора будет возвращаться к источнику.
В третью четверть периода емкость будет заряжаться от источника противоположной полярностью (по сравнению с тем что было в первую четверть периода). В четвертую четверть периода емкость снова вернет энергию электрического поля обратно в сеть. В течение следующего периода данный цикл повторится. Так ведет себя чисто емкостная нагрузка в цепи синусоидального переменного тока.
Практически получается, что при емкостной нагрузке ток опережает по фазе на четверть периода переменное напряжение, приложенное к данной нагрузке, потому что когда емкость заряжается, ток оказывается максимальным уже в первый момент, когда приложенное напряжение источника только начинает нарастать, энергия тока преобразуется в энергию увеличивающегося электрического поля накапливаемого в нагрузке заряда, как в конденсаторе.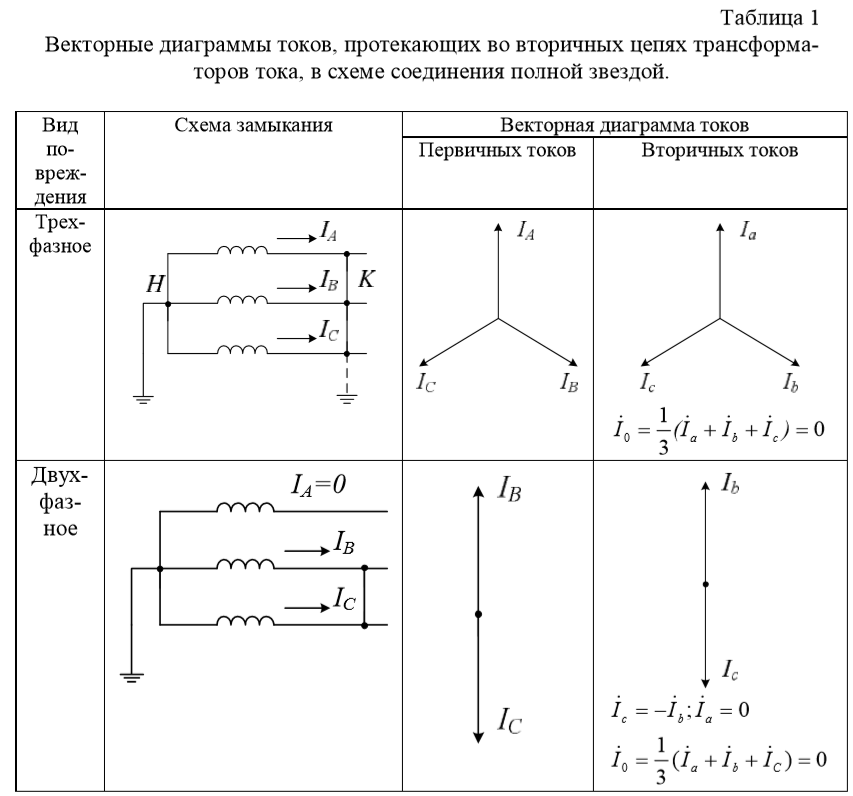
Но с ростом приложенного напряжения, емкость уже имеет достаточно много накопленного заряда, поэтому с приближением напряжения источника к своему максимуму, скорость накопления заряда в емкостной нагрузке становится меньше, и потребляемый ток при этом уменьшается вплоть до нуля.
Примеры емкостных нагрузок: конденсаторные батареи, корректоры коэффициента мощности, синхронные двигатели, ЛЭП сверхвысокого напряжения.
Индуктивная нагрузка
Если теперь обратить внимание на индуктивную нагрузку, то она ведет себя в цепи переменного тока подобно катушке индуктивности.
Это значит, что синусоидальное переменное напряжение будет периодически (с удвоенной частотой источника) порождать ток через индуктивность нагрузки, при этом в первую четверть периода энергия источника будет расходоваться на создание магнитного поля тока через катушку.
Во вторую четверть периода энергия магнитного поля катушки будет возвращаться к источнику. В третью четверть периода катушка будет намагничиваться противоположной полярностью (по сравнению с тем что было в первую четверть периода), и в четвертую четверть периода индуктивность снова вернет энергию магнитного поля обратно в сеть.
В третью четверть периода катушка будет намагничиваться противоположной полярностью (по сравнению с тем что было в первую четверть периода), и в четвертую четверть периода индуктивность снова вернет энергию магнитного поля обратно в сеть.
В течение следующего периода данный цикл повторится. Так ведет себя чисто индуктивная нагрузка в цепи синусоидального переменного тока.
На деле получается, что при индуктивной нагрузке ток отстает по фазе на четверть периода от переменного напряжения, приложенного к данной нагрузке, потому что когда индуктивность начинает намагничивается, в первый момент времени ток через нее оказывается минимальным, хотя приложенное напряжение источника и находится уже в максимальной точке.
Энергия источника преобразуется здесь в энергию увеличивающегося магнитного поля тока, протекающего через индуктивность нагрузки. При уменьшении напряжения, ток через индуктивность уже имеет достаточно большую величину, поэтому с приближением напряжения источника к своему минимуму, скорость роста тока в индуктивной нагрузке замедляется, но сам ток в индуктивности при этом максимален.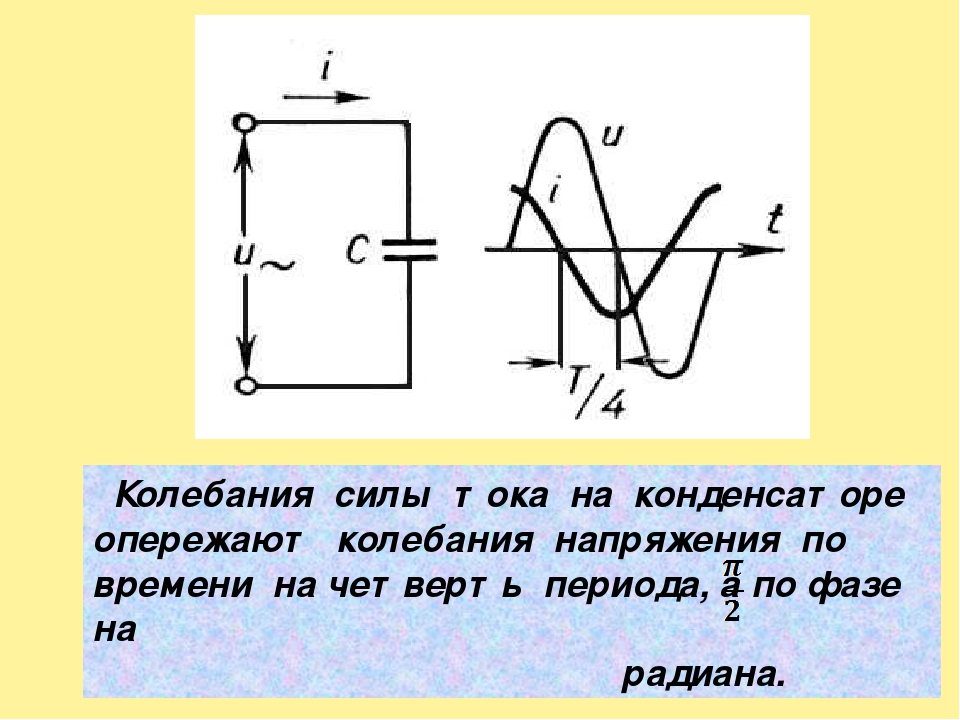
Примеры индуктивных нагрузок: асинхронные двигатели, электромагниты, дроссели, реакторы, трансформаторы, выпрямители, тиристорные преобразователи.
Ранее ЭлектроВести писали, что SMA и Infineon совместно разработали инверторы на основе карбида кремния в качестве полупроводников, что позволило не только снизить вес, но и отказаться от использования некоторых комплектующих.
По материалам: electrik.info.
Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс
Физика, 11 класс
Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока
Перечень вопросов, рассматриваемых на уроке:
Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;
Устройство и принцип действия генератора переменного тока и трансформатора;
Автоколебания;
Проблемы передачи электроэнергии и способы повышения эффективности её использования.
Глоссарий по теме
Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами.
Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.
Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:
N- число витков.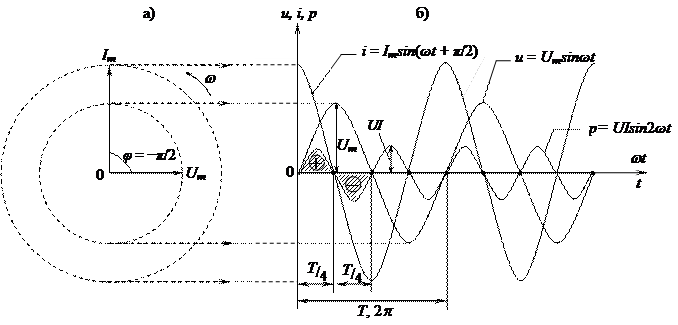
Возникает ЭДС индукции который меняется по гармоническому закону.
ЭДС индукции в рамке равна:
Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.
В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т. к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.
Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.
Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.
Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.
Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.
Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».
k– коэффициент трансформации.
U1 иU2 – напряжения на первичной и на вторичной обмотке.
N1 и N2— число витков на первичной и на вторичной обмотке.
Если k < 1 — трансформатор повышающий,
k > 1 — трансформатор понижающий.
КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:
Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.
Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция
Разбор тренировочных заданий
1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м2.
Дано:
N=50
ω=180 рад/с
B=0,4 Тл
S=0,02 м2
_________
Ԑm=?
Решение:
Ответ: 72 В.
2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.
Дано:
L=0,08 Гн
ν= 1000 Гц
U=100 В
__________
Im=?
Решение:
Напишем закон Ома для переменного тока
Т.к. ХC и R равны нулю, то
Учитывая, что , получаем:
Найдем амплитудное значение напряжения:
Подставим числовые данные в формулу для расчета амплитуды силы тока:
Ответ: Im = 0,3 А.
6.4. Сопротивление в цепи синусоидального
тока
Если напряжение
подключить к сопротивлению R, то через него протекает ток
(6.7)
Анализ выражения (6.7) показывает,
что напряжение на сопротивлении и ток, протекающий через него, совпадают
по фазе.
Формула (6.7) в комплексной форме записи
имеет вид
(6.8)
где
и — комплексные
амплитуды тока и напряжения.
Комплексному уравнению (6.8) соответствует векторная
диаграмма (рис. 6.4).
Из анализа диаграммы следует, что векторы напряжения
и тока совпадают по направлению.
Сопротивление участка цепи постоянному току называется
омическим, а сопротивление того же участка переменному току — активным
сопротивлением.
Рис.6.4
Активное сопротивление больше омического из-за явления
поверхностного эффекта. Поверхностный эффект заключается в том, что
ток вытесняется из центральных частей к периферии сечения проводника.
6.5. Индуктивная катушка
в цепи синусоидального тока
Сначала рассмотрим идеальную индуктивную
катушку, активное сопротивление которой равно нулю. Пусть по идеальной
катушке с индуктивностью L протекает синусоидальный ток .
Этот ток создает в индуктивной катушке переменное магнитное поле, изменение
которого вызывает в катушке ЭДС самоиндукции
(6.9)
Эта ЭДС уравновешивается напряжением,
подключенным к катушке: u = eL = 0.
(6.10)
Таким образом, ток в индуктивности
отстает по фазе от напряжения на 90o из-за явления самоиндукции.
Уравнение вида (6.10) для реальной катушки, имеющей
активное сопротивление R, имеет следующий вид:
(6.11)
Анализ выражения (6.11) показывает,
что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию
переменного тока, из-за чего ток в реальной индуктивной катушке отстает
по фазе от напряжения на некоторый угол φ (0oo), величина которого зависит от соотношения R и L.
Выражение (6.11) в комплексной форме записи имеет вид:
(6.12)
где ZL — полное комплексное
сопротивление индуктивной катушки ;
ZL — модуль комплексного
сопротивления;
— начальная фаза комплексного сопротивления;
—
индуктивное сопротивление (фиктивная величина, характеризующая реакцию
электрической цепи на переменное магнитное поле).
Полное сопротивление индуктивной катушки или модуль
комплексного сопротивления
.
Комплексному уравнению (6.12)
соответствует векторная диаграмма (рис.6.5).
Рис. 6.5
Из анализа диаграммы видно,
что вектор напряжения на индуктивности опережает вектор тока на 90o.
В цепи переменного тока напряжения на участках
цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений
на величину тока Im, то перейдем к подобному треугольнику
сопротивлений (рис. 6.6).
Из треугольника сопротивлений получим несколько формул:
;
;
Рис. 6.6
;
;
.
6.6. Емкость в цепи
синусоидального тока
Если к конденсатору емкостью C
подключить синусоидальное напряжение, то в цепи протекает синусоидальный
ток
;
. (6.13)
Из анализа выражений 6.13 следует,
что ток опережает напряжение по фазе на 90o.
Выражение (6.13) в комплексной
форме записи имеет вид:
, (6.14)
где
— емкостное сопротивление, фиктивная расчетная величина, имеющая размерность
сопротивления.
Если комплексное сопротивление
индуктивности положительно
, то комплексное
сопротивление емкости отрицательно
.
На рис. 6.7 изображена векторная
диаграмма цепи с емкостью.
Вектор тока опережает вектор напряжения на
90o.
Рис. 6.7
6.7. Последовательно
соединенные реальная индуктивная
катушка и конденсатор в цепи синусоидального тока
Катушка с активным сопротивлением
R и индуктивностью
L и конденсатор
емкостью С
включены последовательно (рис.6.8). В схеме протекает
синусоидальный ток
.
Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,
(6.15)
Подставим эти формулы в
уравнение (6.15). Получим:
(6.16)
Из выражения (6.16) видно: напряжение в активном
сопротивлении совпадает по фазе с током, напряжение на индуктивности
опережает по фазе ток на 90o, напряжение по емкости отстает
по фазе от тока на 90o.
Запишем уравнение (6.16) в комплексной форме:
(6.17)
Рис. 6.8
Поделим левую и правую части
уравнения (6.17) на √2.
Получим уравнение для комплексов действующих
значений токов и напряжений
,
(6.18)
где
— комплексное сопротивление цепи;
— модуль комплексного
сопротивления, или полное сопротивление цепи;
— начальная фаза комплексного сопротивления.
При построении векторных
диаграмм цепи рассмотрим три случая.
- XL > XC, цепь носит индуктивный характер.
Векторы напряжений на индуктивности и емкости направлены в противоположные
стороны, частично компенсируют друг друга. Вектор напряжения на входе
схемы опережает вектор тока (рис.6.9). - Индуктивное сопротивление меньше емкостного. Вектор напряжения на
входе схемы отстает от вектора тока. Цепь носит емкостный характер
(рис.6.10). - Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности
и емкости полностью компенсируют друг друга. Ток в цепи совпадает
по фазе с входным напряжением. В электрической цепи наступает режим
резонансного напряжения (рис.6.11).
Ток в резонансном режиме
достигает максимума, так как полное сопротивление (z)
цепи имеет минимальное значение.
Условие возникновения резонанса: ,
отсюда резонансная частота равна
.
Из формулы следует,
что режима резонанса можно добиться следующими способами:
- изменением частоты;
- изменением индуктивности;
- изменением емкости.
В резонансном режиме входное напряжение
равно падению напряжения в активном сопротивлении. На индуктивности
и емкости схемы могут возникнуть напряжения, во много раз превышающие
напряжение на входе цепи. Это объясняется тем, что каждое напряжение
равно произведению тока I0 (а он наибольший), на соответствующее
индуктивное или емкостное сопротивление (а они могут быть большими).
.
Рис. 6.9
Рис. 6.10
Рис. 6.11
6.8. Параллельно соединенные
индуктивность, емкость
и активное сопротивление в цепи синусоидального тока
К схеме на рис. 6.12 подключено
синусоидальное напряжение . Схема состоит
из параллельно включенных индуктивности, емкости и активного сопротивления.
Определим ток на входе схемы.
В соответствии с первым законом Кирхгофа:
,
(6.19)
где
— активная проводимость.
Рис. 6.12
Подставим эти формулы в
уравнение (6.19). Получим:
, (6.20)
где
— индуктивная проводимость;
— емкостная проводимость.
Из уравнения (6.20) видно, что
ток в ветви с индуктивностью отстает по фазе от напряжения на 90o,
ток в ветви с активным сопротивлением совпадает по фазе с напряжением,
ток в ветви с емкостью опережает по фазе напряжение на 90o.
Запишем уравнение (6.20) в комплексной форме.
, (6.21)
где
— комплексная проводимость;
—
полная проводимость;
—
начальная фаза комплексной проводимости.
Построим векторные диаграммы,
соответствующие комплексному уравнению (6.21).
Рис. 6.13
Рис. 6.14
Рис. 6.15
В схеме на рис. 6.12
может возникнуть режим резонанса токов. Резонанс токов возникает тогда,
когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный
и емкостный токи, направленные в противоположные стороны, полностью
компенсируют друг друга. Ток в неразветвленной части схемы совпадает
по фазе с напряжением.
Из условия возникновения резонанса тока
получим формулу для резонансной частоты тока
.
В режиме резонанса тока
полная проводимость цепи — минимальна,
а полное сопротивление — максимально.
Ток в неразветвленной части схемы в
резонансном режиме имеет минимальное значение. В идеализированном случае
R = 0,
и .
Ток в неразветвленной части цепи I = 0. Такая
схема называется фильтр — пробкой.
6.9. Резонансный режим
в цепи, состоящей
из параллельно включенных реальной индуктивной
катушки и конденсатора
Комплексная
проводимость индуктивной ветви
где
— активная проводимость индуктивной катушки;
— полное сопротивление индуктивной катушки;
— индуктивная проводимость катушки;
— емкостная проводимость второй ветви.
В режиме резонансов
токов справедливо уравнение:
или
Из этого уравнения
получим формулу для резонанса частоты
(6.22)
На рисунке
6.16 изображена векторная диаграмма цепи в резонансном режиме.
Вектор тока I2 опережает вектор напряжения на
90o. Вектор тока I1 отстает от вектора напряжения
на угол φ,
где
.
Разложим вектор тока I1 на две взаимно
перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения,
называется активной составляющей тока Iа1, другая — реактивной
составляющей тока Iр1.
Рис. 6.16
В режиме резонанса тока реактивная составляющая тока Iр1
и емкостный ток I2 , направленные в противоположные стороны,
полностью компенсируют друг друга, активная составляющая тока Iа1
совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной
части схемы совпадает по фазе с напряжением.
Рис.
6.17
Лекция 39. Тема: . Ток отстает от. напряжения по фазе на π/2 (рис. 2). Амплитуда силы тока
Тема 3.2 Переменный ток
. Вращение рамки в магнитном поле. Переменный ток 3. Трансформаторы Тема 3. Переменный ток. Вращение рамки в магнитном поле Явление электромагнитной индукции применяется для преобразования механической
Подробнее
Можно показать также, что
Индуктивно-связанные цепи «на ладони» Магнитная связь между двумя катушками появляется, если их потоки взаимно пронизывают витки (часть витков) друг друга. Потокосцеплением называется произведение потока
Подробнее
Тема 4.2. Цепи переменного тока
Тема 4.. Цепи переменного тока Вопросы темы.. Цепь переменного тока с индуктивностью.. Цепь переменного тока с индуктивностью и активным сопротивлением. 3. Цепь переменного тока с ёмкостью. 4. Цепь переменного
Подробнее
3.4. Электромагнитные колебания
3.4. Электромагнитные колебания Основные законы и формулы Собственные электромагнитные колебания возникают в электрической цепи, которая называется колебательным контуром. Закрытый колебательный контур
Подробнее
Резонанс «на ладони».
Резонанс «на ладони». Резонансом называется режим пассивного двухполюсника, содержащего индуктивные и ёмкостные элементы, при котором его реактивное сопротивление равно нулю. Условие возникновения резонанса
Подробнее
Тема 1. Линейные цепи постоянного тока.
МЕТОДИЧЕСКОЕ УКАЗАНИЕ 2 системы и технологии» Тема 1. Линейные цепи постоянного тока. 1. Основные понятия: электрическая цепь, элементы электрической цепи, участок электрической цепи. 2. Классификация
Подробнее
5. Электрические колебания
1 5 Электрические колебания 51 Колебательный контур Колебаниями в физике называют не только периодические движения тел но и всякий периодический или почти периодический процесс в котором значения той или
Подробнее
ГЛАВА 1. ЦЕПИ ПОСТОЯННОГО ТОКА
ПРЕДИСЛОВИЕ ГЛАВА 1. ЦЕПИ ПОСТОЯННОГО ТОКА 1.1.Электрическая цепь 1.2.Электрический ток 1.3.Сопротивление и проводимость 1.4.Электрическое напряжение. Закон Ома 1.5.Связь между ЭДС и напряжением источника.
Подробнее
Лекция 4 ПЕРЕМЕННЫЙ ТОК
Сегодня: среда, 18 сентября 213 г. Лекция 4 ПЕРЕМЕННЫЙ ТОК Содержание лекции: 1. Сопротивление в цепи переменного тока 2. Емкость в цепи переменного тока 3. Индуктивность в цепи переменного тока 4. Закон
Подробнее
Лекция 2.8 Переменный ток
Лекция.8 Переменный ток План:. Введение. Квазистационарные токи 3. Переменный ток через сопротивление 4. Переменный ток через индуктивность 5. Переменный ток через емкость 6. Цепь содержащая индуктивность
Подробнее
10. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
44 0 ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕКИЙ ТОК 0 Основные понятия и определения Переменным называется ток, который с течением времени изменяет свою величину Квазистационарным называется переменный ток, который во всех
Подробнее
t. (32.1.1) dt где m NBS
Лекция 3 Переменный ток В XIX веке электричества ещё не было поэтому телевизор смотрели при свечах (ответ на экзамене) Получение переменной ЭДС В настоящее время известно достаточно большое количество
Подробнее
Сборник задач для специальности ОП 251
Сборник задач для специальности ОП 251 1 Электрическое поле. Задания средней сложности 1. Два точечных тела с зарядами Q 1 =Q 2 = 6 10 11 Кл расположены в воздухе на расстоянии 12 см друг от друга. Определить
Подробнее
Тема 3.1 Электромагнитные колебания
Тема 3. Электромагнитные колебания. Колебательный контур. Уравнение колебательного контура 3. Свободные незатухающие колебания в контуре 4. Свободные затухающие колебания в контуре 5. Вынужденные колебания
Подробнее
Лабораторная работа 16 Трансформатор.
Лабораторная работа 16 Трансформатор. Цель работы: исследовать работу трансформатора в холостом режиме и под нагрузкой. Оборудование: трансформатор (собирать схему для понижающего трансформатора!), источник
Подробнее
Лабораторная работа 5 Резонанс напряжений
Лабораторная работа 5 Резонанс напряжений В механической системе онанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания
Подробнее
Проверка закона Ома для переменного тока
Лабораторная работа. Проверка закона Ома для переменного тока ЦЕЛИ РАБОТЫ. Определить омическое, индуктивное сопротивление катушки и емкостное сопротивление C конденсатора;. Проверить закон Ома для переменного
Подробнее
Тема 4.1. Переменный ток.
Тема 4.1. Переменный ток. Вопросы темы. 1. Определение, получение и характеристики переменного тока.. Действующие значения тока и напряжения. 3. Изображение переменного тока методом векторных диаграмм.
Подробнее
Тема 5. Трёхфазные электрические цепи
Тема 5. Трёхфазные электрические цепи Вопросы темы. 1. Принцип построения трехфазной системы. 2. Соединение звездой. 3. Соединение треугольником. 4. Мощность трехфазной системы. 1. Принцип построения трехфазной
Подробнее
Электрические машины
Согласно учебному плану направления 241000.62 (18.03.02) «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии», профиль «Охрана окружающей среды и рациональное использование
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА СОДЕРЖАНИЕ МАТЕРИАЛА
Учреждение образования «Могилевский государственный университет продовольствия» ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ по электротехнике для абитуриентов, на основе среднего специального образования для специальности
Подробнее
С.А. Иванская ЭЛЕКТРОТЕХНИКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКОГО КРАЯ ГОУ СПО «Минераловодский колледж железнодорожного транспорта» С.А. Иванская ЭЛЕКТРОТЕХНИКА Методические рекомендации по освоению теоретического материала и
Подробнее
http://library.bntu.by/krutov-v-teoreticheskie-osnovy-elektrotehniki ВВЕДЕНИЕ… З 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ…5 1.1. Основные сведения об электромагнитном поле…5 1.2. Электростатическое поле. Закон Кулона…
Подробнее
Лабораторная работа 2-32
Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре. Цель работы:
Подробнее
Индуктивность контура
Магнитное поле Индуктивность контура. Взаимная индукция. Трансформатор. Явление самоиндукции. Переходные процессы в моменты включения и выключения электрической цепи. Энергия магнитного поля. Колебательный
Подробнее
ЛЕКЦИЯ 11. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ЛЕКЦИЯ 11. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ Серюкова Ирина Владимировна, к.ф.-м.н., доцент кафедры «Физики» КрасГАУ Использованная литература 1. Грабовский Р.И. Курс физики.- СПб.: Издательство «Лань», 00. Трофимова
Подробнее
Разность фаз напряжения и тока
Условимся под разностью фаз φ напряжения и тока всегда понимать разность начальных фаз напряжения и тока (а не наоборот):
Поэтому на векторной диаграмме угол φ отсчитывается в направлении от вектора I к вектору U (рис. 3.10). Именно при таком определении разности фаз угол φ равен аргументу комплексного сопротивления. Угол φ положителен при отстающем токе () и отрицателен при опережающем токе ().
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При имеем и ток отстает по фазе от напряжения, . При имеем , ток совпадает по фазе с напряжением, rLC-цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при имеем , ток опережает по фазе напряжение.
Векторные диаграммы для трех возможных соотношений даны на рис. 3.11. При построении этих диаграмм начальная фаза тока ; принята равной нулю. Поэтому равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при как последовательное соединение сопротивления и индуктивности (), при как сопротивление r и при как последовательное соединение сопротивления и емкости (). При заданных L и С соотношение между зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток
и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения: . В этом случае, как следует из раздела, начальная фаза тока ; равна и противоположна по знаку разности фаз φ, т. е .
Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.
Цепь переменного тока с ёмкостью
Поскольку после того, как конденсатор зарядился полностью, он не пропускает через себя электрический ток, и поэтому идеальный конденсатор (ёмкость), установленный в цепи постоянного тока, обладает бесконечно большим сопротивлением.
Цепь переменного тока с ёмкостью
Если же произвести подключение конденсатора к источнику переменного тока, то процесс его заряда и разряда будет осуществляться непрерывно. Это означает, что через ёмкость будет проходить переменный электрический ток.
Ток i при условии включения в цепь переменного тока некоторой ёмкости будет определяется количеством электричества q, протекающего по этой цепи в единицу времени. Из этого следует, что:
где Δq – это изменение заряда q (то есть количества электричества) в течение времени Δt.
Что касается заряда q, который накоплен при изменениях напряжения u в конденсаторе, то он также подвержен непрерывному изменению, которое выражается формулой:
где Δu – это изменение напряжения u в течение промежутка времени Δt.
Та скорость, с которой изменяется напряжение (она выражается отношением Δu/Δt) будет иметь свои наибольшие значения тогда, когда угол ωt равняется 360°, 180° и 0°. Из этого следует, что значение тока i принимает свои наибольшие величины именно в эти моменты времени. Если же угол ωt равняется 270° и 90°, то i = 0, поскольку скорость изменения напряжения Δu/Δt = 0.
Ток и напряжение в цепи переменного тока с ёмкостью
Ток заряда, который принято считать положительным, в цепи течет тогда, когда происходит заряд конденсатора, то есть на протяжение первой четверти периода. По мере того, как разница потенциалов на электродах ёмкости растет вследствие накопления ею электрического заряда, значение тока i падает. Когда ωt = 90°, наступает полный заряд емкости, значение i = 0, а разность потенциалов между электродами конденсатора обретает то же самое значение, что и напряжение источника тока.
Значение тока i становится отрицательным тогда, когда он меняет свое направление. Это происходит тогда, когда ёмкость начинает разряжаться, то есть во второй четверти периода. Тогда, когда u = 0 а ωt = 180°, значение тока i становится максимальным. В этот же самый момент ток i начинает течь в обратном направлении (его принято считать отрицательным), начинается процесс перезарядки емкости, а полярность напряжения u источника также меняется на противоположную. Когда ωt = 270° значение тока i становится равным нулю, и поэтому процесс заряда прекращается. После чего начинается разряд при первоначальном (то есть положительном) направлении тока.
Получается, что ёмкость и заряжается, и разряжается два раза на протяжении одного периода изменения напряжения. Из этого следует, что переменный ток i протекает в цепи непрерывно. Когда ёмкость включается в цепь переменного тока, то ток i опережает напряжение u по фазе на угол, равный 90°. Можно также сказать, что напряжение u отстает по фазе от тока i на угол, равный 90°.
Емкостное сопротивление
Сопротивление, которое проявляет ёмкость к переменному току, носит название емкостного.
Единицей измерения этой величины является Ом, а обозначается оно Хс. Физическая природа емкостного сопротивления заключается в том, что оно обусловлено возникающей в конденсаторе ЭДС ес. Направление этой электродвижущей силы противоположно приложенному напряжению u, поскольку заряженная ёмкость рассматривается в качестве источника, у которого между пластинами действует некоторая ЭДС ес. Именно она препятствует тому, чтобы под действием напряжения u происходило изменение тока, то есть оказывает определенное сопротивление его прохождению.
Импеданс
— емкостные токоподводы, индуктивные запаздывания, но как это соотносится с напряжением на выходе?
Представьте себе конденсатор с существующим, стабильным, неизменным напряжением на нем. Это может быть источник питания постоянного тока, подключенный, например, к конденсатору, если прошло много времени, а конденсатор «зарядился». В данном случае тока нет, потому что … ну … в нем нет необходимости. Схема достигла равновесия. Он просто сидит там.
Теперь вы поворачиваете ручку, и источник постоянного тока изменяет свое напряжение.Конденсатор также должен измениться. (У вас не может быть источника питания с одним напряжением и конденсатора с другим напряжением, когда они соединены таким образом.) Но это не может измениться мгновенно, потому что конденсатор, по сути, представляет собой большой резервуар заряда, и изменив его напряжение, вы должны изменить «уровень заряда» этого резервуара. Чтобы изменить это, вы должны внести (или снять) некоторый заряд. Но для движения заряда требуется время, а вместе, движение заряда и время, у вас должен быть ток, чтобы добраться туда.
Итак, если вы измените напряжение, это должно стимулировать некоторый заряд, который потечет на конденсатор или с него. Если вы изменяете напряжение медленно, то скорость изменения заряда в резервуаре конденсатора с течением времени будет меньше. Если вы изменяете напряжение быстро, то скорость изменения заряда в резервуаре конденсатора должна быть больше. Чтобы достичь более высокой скорости изменения напряжения на конденсаторе, вы должны подавать более высокий ток, чтобы заполнить (или истощить) накопленный заряд конденсатора.
Напряжение на конденсаторе: \ $ V = \ frac {Q} {C} \ $. Таким образом, при фиксированной емкости для получения более высокого напряжения \ $ V \ $ вам потребуется больше заряда \ $ Q \ $.
Теперь, если вы посмотрите на уравнение:
$$ I = C \ cdot \ frac {\ textrm {d} \: V} {\ textrm {d} \: t} $$
Вы можете увидеть все это чудесное махание руками в пакете с красивым бантом . Ток должен быть больше, если конденсатор имеет большую емкость. Почему? Потому что это резервуар большего размера, и ему требуется больше заряда для достижения того же напряжения.Ток должен быть больше, если скорость изменения напряжения больше. По причинам, только что обсужденным выше. Это уравнение объединяет все в одном месте.
Итак, что это означает относительно запаздывающих или опережающих токов и напряжений? Что ж, взгляните на синусоидальную волну с центром на \ $ y = 0 \ $ с напряжением на оси \ $ y \ $. Затем скажите мне, при каком значении \ $ y \ $ скорость изменения синусоидальной волны наиболее высока. Это будет, когда само напряжение будет на нуле. Другими словами, ток на входе или выходе конденсатора должен быть максимальным, когда напряжение на конденсаторе само равно нулю (во всяком случае, для случая синусоидальной волны.)
Единственное, о чем нужно беспокоиться, — это отставание от опережения, и именно это в случае конденсатора. Это просто знак. \ circ \ $.
Есть много алгебраических инструментов, которые вы изучаете, чтобы упростить работу, которую вам нужно выполнить, точно так же, как умение выполнять длинное умножение — это трюк, который помогает вам умножать большие числа без необходимости выполнять много-много сложений. и более. Эти уловки основаны на хороших теоретических идеях. Но если вы просто выучите их и примените, не понимая, откуда они берутся, они все равно будут работать на вас. Точно так же, как вам не нужно понимать, почему работает длинное умножение, чтобы его использовать.
Конденсатор легче описать, потому что он работает с атрибутами, которые легче вообразить. Мы можем их посчитать. Это единицы заряда. Индуктор работает с эквивалентными единицами заряда, но в силу магнетизма. Эти единицы указаны в Webers, а не на платной основе. И трудно «представить» Вебера и посчитать их (это «вольт-секунды» или \ $ \ int V_t \: \ textrm {d} t \ $) для нас нормальных людей . У некоторых нет проблем. Другие делают. Но это симметричная единица заряда.2 \: \ textrm {d} L \\\\
\ frac {\ textrm {d} W} {I} & = L \: \ textrm {d} I + \ frac {1} {2} \: I \: \ textrm {d} L
\ end {split} $$
отметка,
$$ \ textrm {где} I = \ frac {\ textrm {d} Q} {\ textrm {d} t} \ textrm {и} V = \ frac {\ textrm {d} W} {\ textrm {d } Q} \ textrm {и d} L = 0 \ textrm {и d} C = 0 $$
получается,
$$ \ begin {split}
\ frac {\ textrm {d} W} {\ frac {\ textrm {d} W} {\ textrm {d} Q}} & = C \: \ textrm {d} V \\\\
\ frac {\ textrm {d} W} {\ textrm {d} W} \ textrm {d} Q & = C \: \ textrm {d} V \\\\
\ textrm {d} Q & = C \: \ textrm {d} V \\\\
\ int \ textrm {d} Q & = \ int C \: \ textrm {d} V \\\\
Q & = C \: V
\ end {split}
\ quad \ leftrightarrow \ quad
\ begin {split}
\ frac {\ textrm {d} W} {\ frac {\ textrm {d} Q} {\ textrm {d} t}} & = L \: \ textrm {d} I \\\\
\ frac {\ textrm {d} W} {\ textrm {d} Q} \ textrm {d} t & = L \: \ textrm {d} I \\\\
V \ textrm {d} t & = L \: \ textrm {d} I \\\\
\ int V \ textrm {d} t & = \ int L \: \ textrm {d} I \\\\
V \: t & = L \: I
\ end {split} $$
И вот вы где.Счетные вещи слева. Но странные единицы справа. Вольт-секунды (Веберы) относятся к индукторам, как кулоны заряда для конденсаторов.
Еще одна небольшая поправка из вышеперечисленного:
$$ \ begin {split}
\ textrm {d} Q & = C \: \ textrm {d} V \\\\
\ frac {\ textrm {d} Q} {\ textrm {d} t} & = C \: \ frac {\ textrm {d} V} {\ textrm {d} t} \\\\
I & = C \: \ frac {\ textrm {d} V} {\ textrm {d} t}
\ end {split}
\ quad \ leftrightarrow \ quad
\ begin {split}
V \ textrm {d} t & = L \: \ textrm {d} I \\\\
\ frac {V \ textrm {d} t} {\ textrm {d} t} & = L \: \ frac {\ textrm {d} I} {\ textrm {d} t} \\\\
V & = L \: \ frac {\ textrm {d} I} {\ textrm {d} t}
\ end {split} $$
Извините за отвлекающий маневр.Но я подумал, что это может помочь некоторым (и вам?)
Есть ли напряжение на токоподводе при разрядке в конденсаторах?
Вообще говоря, мы можем осмысленно говорить об относительной разности фаз между формами сигналов только в том случае, если две формы сигналов имеют одинаковую форму, но смещены во времени. \ circ \ $.{-t / RC} $$
Как вы можете видеть, в любом случае нет какого-либо явного параметра относительной фазы, который мы можем идентифицировать в приведенных выше осциллограммах напряжения и тока.
Для этого есть тонкая причина. В случае синусоидальной формы волны мы можем добавить к аргументу константу, которая приводит к смещению формы волны во времени; добавление этой константы изменяет фазу синусоидального сигнала:
$$ \ sin (\ omega t + \ phi) $$
— это синусоидальный сигнал, сдвинутый во времени на \ $ \ frac {\ phi} {\ omega} \ $ секунд.{-t / RC} $$
цепей переменного тока | Безграничная физика
Индуктивность
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.
Цели обучения
Опишите свойства индуктора
Основные выводы
Ключевые моменты
- В случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводе, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
- Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
- Взаимная индуктивность обозначена как. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
- Самоиндукция — это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
- Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
Ключевые термины
- взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
- самоиндукция : Отношение напряжения к изменению тока в той же цепи.
- индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.
Индуктивность
ОБЗОР
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность).Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).
ВЗАИМНАЯ ИНДУКТИВНОСТЬ
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.
Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств является фиксированной, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в форме уравнения как
[латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]
, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Единицы измерения для M : (V⋅s) / A = Ωs, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.
Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] \ text {emf} _1 = — \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]
, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью М.
Большая взаимная индуктивность M может быть, а может и не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля.(Видеть ).
Противоточная намотка : Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
САМОИНДУКЦИЯ
Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]
, где L — самоиндукция устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
.
Обозначение индуктора
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.
СОЛЕНОИДЫ
Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L, обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).
Поучительно вывести это уравнение, но мы оставляем его в качестве упражнения для читателя. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением. {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].
Ключевые термины
- характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R — сопротивление, а L — индуктивность. Когда переключатель замкнут, это время, необходимое для того, чтобы сила тока уменьшилась с коэффициентом 1 / e.
- катушка индуктивности : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.
RL Схемы
Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.
Обзор
Напомним, что индукция — это процесс, в котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность — это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция — это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности — это устройство или компонент схемы, который демонстрирует самоиндукцию.
Энергия индуктора
Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].
Катушки индуктивности в цепях
Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет течь, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.
Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещается в положение 2.
Когда переключатель сначала перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге повышается до I 0 = В / R , где R — полное сопротивление цепи, а V — напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]
— это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I 0 = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :
[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],
, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I 0 , поскольку I = I 0 (1-e -1 ) = I 0 ( 1−0,368) = 0,632I 0 . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных промежутков времени [latex] \ tau [/ latex] конечное значение почти достигнуто (см. Часть (b) на рисунке выше).
Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы добраться до него. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.
Когда переключатель в (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, создавая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI 0 2 , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I 2 R.{\ frac {- \ text {t}} {\ tau}} [/ latex]
В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от своего начального значения, поскольку I = I 0 e −1 = 0,368I 0 . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.
Цепь серии
RLC: на больших и малых частотах; Фазорная диаграмма
Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.
Цели обучения
Различать поведение цепей серии RLC на больших и малых частотах
Основные выводы
Ключевые моменты
- Цепи RLC можно описать (обобщенным) законом Ома. Что касается фазы, то при приложении синусоидального напряжения ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
- На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
- На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с конденсатор. Следовательно, среднеквадратичный ток будет представлен как В / X C, , а ток опережает напряжение почти на 90 ∘ .
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I среднеквадратичное значение = V действующее значение / Z; I среднеквадратичное значение и V среднеквадратичное значение представляют собой среднеквадратичное значение тока и напряжения) и выражения для импеданса Z из:
Цепь RLC серии : Цепь последовательного RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].
Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при подаче синусоидального напряжения ток отстает от напряжения на 90º по фазе в цепи с катушкой индуктивности, а ток опережает напряжение на 90 ∘ в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.
на больших частотах
На достаточно больших частотах [latex] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] X L намного больше, чем X C .Если частота достаточно высока, так что X L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [латекс] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним дросселем. Следовательно, среднеквадратичный ток будет составлять В / X L , а ток отстает от напряжения почти на 90 ∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление индуктора будет большим.
на малых частотах
В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостный член, предполагая, что частота достаточно высока, так что X C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичный ток будет представлен как В / X C, , а ток опережает напряжение почти на 90 ∘ .
Резисторы в цепях переменного тока
В цепи с резистором и источником питания переменного тока все еще действует закон Ома ( В, = IR ).
Цели обучения
Применение закона Ома для определения силы тока и напряжения в цепи переменного тока
Основные выводы
Ключевые моменты
- При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].
Ключевые термины
- Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.
Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая удовлетворяет многие наши потребности. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.
Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.
Мы изучили закон Ома:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]
, где I — ток, В, — напряжение, а R — сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, при напряжении переменного тока, определяемом по формуле:
[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]
, где В 0 — пиковое напряжение, а [латекс] \ nu [/ latex] — частота в герцах, ток в цепи задается как:
[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]
В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b).Ток в резисторе чередуется взад и вперед без разницы фаз, как и напряжение возбуждения.
Рассмотрим идеальный резистор, который увеличивает и уменьшает яркость 120 раз в секунду, когда ток постоянно проходит через ноль. 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]
Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ латекс]
Конденсаторы в цепях переменного тока: емкостное сопротивление и фазовые диаграммы
Напряжение на конденсаторе отстает от тока. Из-за разности фаз полезно вводить векторы для описания этих схем.
Цели обучения
Объясните преимущества использования векторного представления
Основные выводы
Ключевые моменты
- Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
- Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
- Действующее значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] — емкостное реактивное сопротивление.
Ключевые термины
- среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.
Конденсаторы в цепях переменного тока с фазорами
Фазор
Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.
Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса — это проекция вектора на действительную ось. Его амплитуда — это модуль вектора, а его аргумент — полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.
Конденсаторы в цепях переменного тока
Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.
Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ». Это показано на.
Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.
Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V max / I max полезно и называется емкостным реактивным сопротивлением (X C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].
Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I , действующее значение в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V rms — это действующее значение напряжения. Обратите внимание, что X C заменяет R в версии закона Ома для постоянного тока.
Фазовое представление
Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Рис. 4 : Фазорная диаграмма для цепи переменного тока с конденсатором
Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы
В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.
Цели обучения
Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности.
Основные выводы
Ключевые моменты
- С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90 °.
- Среднеквадратичный ток I среднеквадратичное значение через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
- Фазоры — это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- phasor : представление комплексного числа в терминах комплексной экспоненты.
Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).
Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I RMS через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V rms — среднеквадратичное напряжение на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, имеет единицы (циклов / с) (Ом · с) = Ом), что соответствует его роли в качестве эффективное сопротивление.
Представление фазора
Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора — это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.
Фазоры для индукторов в цепях переменного тока
Резонанс в цепях RLC
Резонанс — это тенденция системы к колебаниям с большей амплитудой на некоторых частотах — в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].
Цели обучения
Сравнить резонансные характеристики цепей с высоким и низким сопротивлением
Основные выводы
Ключевые моменты
- Условие резонанса последовательной цепи RLC может быть получено приравниванием X L и X C , так что два противоположных вектора компенсируют друг друга.
- В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I среднеквадратичное значение является максимальным.
- Цепи с более высоким сопротивлением не резонируют так сильно по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.
Ключевые термины
- реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.
Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],
, где I rms и V rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], при этом X L большое на высоких частотах и X C большое на низких частотах, представленных как:
[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].
На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и отменены, что даст Z = R — это минимальное значение для импеданса, а максимальное значение для I rms результатов.Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X L = X C . Подстановка определений X L и X C дает:
[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].
[латекс] \ nu_0 [/ latex] — это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I среднеквадратичное значение является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.
Приемник в радиостанции — это RLC-цепь, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.
Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.
Мощность
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и определяется как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.
Цели обучения
Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.
Основные выводы
Ключевые моменты
- Фазовый угол ϕ — это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
- На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
- Среднюю мощность, рассеиваемую в цепи RLC, можно вычислить, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.
Ключевые термины
- среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность — это не просто ток, умноженный на напряжение, как в случае чисто резистивных цепей. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный
.
[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на рисунке
Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi — фазовый угол, равный разности фаз между напряжением и током.
Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I rms ниже.
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность
[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]
(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) — ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при проектировании эффективного двигателя. На резонансной частоте cosϕ = 1.
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию назад и вперед друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).
Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке. Равномерно расположенные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.
Понимание коэффициента мощности | electricaleasy.com
Энергия нужна и используется повсюду в мире. С точки зрения удобства, эффективности и экономии, лучше всего, чтобы мы генерировали, передавали и распространяли его в электрической форме, прежде чем он будет преобразован в требуемый с помощью подходящего оборудования.По тем же причинам экономии и эффективности мы используем переменный ток, а не постоянный ток. На практике мы производим, передаем и распределяем энергию почти исключительно в форме переменного тока. Постоянный ток используется либо в приложениях постоянного тока (машины постоянного тока и электронные схемы), либо в линиях передачи постоянного тока высокого напряжения.
Везде, где используется питание переменного тока, возникает вопрос о коэффициенте мощности.
Коэффициент мощности
- Определяется как « косинус угла между напряжением и током ».
- В цепи переменного тока напряжение и ток идеально совпадают по фазе.
- Но практически между ними существует разность фаз.
- Косинус этой разности фаз называется коэффициентом мощности.
- Его можно определить и математически представить следующим образом:
Из рис. (a) выше, можно ясно отметить, что существует разность фаз угла ɸ между вектором напряжения и вектором тока.
Коэффициент мощности = cosɸ
Рис. (b) называется Power Triangle
Здесь VI sinɸ = реактивная мощность (в ВАр)
VI cosɸ = активная мощность (в ваттах)
VI = полная мощность (в ВА)
PF = cosɸ = активная мощность ( Вт) / Полная мощность (ВА)
Рис.(c) называется треугольником импеданса
Здесь R = сопротивление, X = реактивное сопротивление, Z = импеданс
Z 2 = R 2 + X 2
PF = cosɸ = R / Z
Коэффициент мощности может быть запаздывающим, опережающим или единичным.
Отстающий коэффициент мощности
- Когда ток отстает от напряжения, коэффициент мощности цепи называется «запаздывающим»
- Когда цепь индуктивная, коэффициент мощности отстает.
- Нагрузки, такие как асинхронные двигатели, катушки, лампы и т. Д., Являются индуктивными и имеют запаздывание pf.
Ведущий коэффициент мощности
- Когда ток опережает напряжение (или напряжение отстает от тока), коэффициент мощности цепи называется опережающим.
- Когда цепь емкостная, опережает pf.
- Емкостные нагрузки, такие как синхронные конденсаторы, конденсаторные батареи и т. Д., Потребляют опережающий ток. Такие схемы имеют опережающий коэффициент мощности.
Коэффициент мощности Unity
- Коэффициент мощности равен единице (т.е.е. 1) для идеальных схем.
- Когда ток и напряжение совпадают по фазе, PF = 1
- Коэффициент мощности не может быть больше единицы.
- Практически он должен быть максимально приближен к единству.
Если коэффициент мощности низкий, возникают следующие проблемы:
Влияние низкого коэффициента мощности
- Ток нагрузки
Мощность в цепи переменного тока может быть задана как: P = VI cosɸ
Следовательно, cosɸ = P / VI
I 1 / cosɸ
Аналогичное соотношение может быть получено и для трехфазной цепи.Мы видим, что ток обратно пропорционален pf.Например, предположим, что мы хотим передать мощность 10 кВА при 100 В
Если PF = 1,
I = P / (V cosɸ) = 10000 / (100 x 1) = 100 A
Если PF = 0,8 ,
I = P / (V cosɸ) = 10000 / (100 x 0,8) = 125 A
Следовательно, потребляемый ток выше при низком коэффициенте мощности. - Потери: Как указано выше, для низкого коэффициента мощности потребляемый ток будет большим. Следовательно, потери в меди (потери I 2 R) также будут высокими.Это снижает эффективность оборудования.
- Перегрев оборудования: I 2 R при потерях выделяется тепло (закон Джоуля). Следовательно, повышение температуры будет относительно большим при низком коэффициенте мощности, что приведет к дальнейшему увеличению нагрузки на изоляцию.
- Размер проводника: Низкий коэффициент мощности приводит к увеличению тока нагрузки. Если ток нагрузки увеличивается, размер необходимого проводника также увеличивается. Это еще больше увеличит стоимость кондуктора.
- кВА Номинальная мощность машины: Машины не рассчитываются в кВт при производстве, потому что коэффициент мощности источника питания неизвестен. Вместо этого они оцениваются в кВА.
Согласно определению, Cosɸ = Активная мощность (кВт) / Полная мощность (кВА).
Следовательно, номинальная мощность кВА = 1 / cos8
Следовательно, для низкого коэффициента мощности необходимо оборудование с большей номинальной мощностью кВА. Но чем выше рейтинг кВА, тем больше размер оборудования. Если размер увеличивается, увеличивается и стоимость. - Регулировка напряжения: Определяется как разница между конечным напряжением отправки и приема на единицу конечного напряжения отправки.Когда мощность передается с одного конца на другой, напряжение падает по нескольким причинам. Это падение напряжения должно быть в допустимых пределах.
P = VI cosɸ, поэтому I 1 / V
При низком коэффициенте мощности ток будет больше и, следовательно, будет увеличиваться падение напряжения. Следовательно, регулирование напряжения при низком коэффициенте мощности плохое. - Активная и реактивная мощность (передаваемая мощность): Активная и реактивная мощность передаются по линии вместе. Для питания нагрузки требуется активная мощность.Реактивная мощность необходима для поддержания напряжения в линии. Но если реактивная мощность больше, то передаваемая активная мощность уменьшается. Для низкого коэффициента мощности активная мощность мала, поскольку cosɸ = активная мощность (Вт) / полная мощность (ВА). Это приводит к неэкономичной работе.
Это результат низкого коэффициента мощности. Для оптимальной производительности коэффициент мощности должен быть как можно ближе к единице. Для этого используется оборудование для коррекции коэффициента мощности.
[Также прочтите: Сравнение различных электростанций]
Автор: Манодж Арора — студент-электрик и писатель из Гуджарата, Индия.Он пишет стихи и рассказы, когда не погружается в книгу.
Кредиты для Graphics: Kiran Daware.
Разница между опережающим и запаздывающим коэффициентами мощности (со сравнительной таблицей)
Опережающий и запаздывающий коэффициенты мощности — это два основных фактора, связанных с коэффициентом мощности электрической системы переменного тока. Решающее различие между опережающим и запаздывающим коэффициентами мощности состоит в том, что в случае опережающего коэффициента мощности ток опережает напряжение. В отличие от запаздывающего коэффициента мощности, ток отстает от подаваемого напряжения.Тенденция схемы, которая вызывает опережение или отставание тока, зависит от условий нагрузки.
Что такое коэффициент мощности?
Коэффициент мощности — важнейшее свойство электрических систем переменного тока. Он безразмерен по своей природе. Он используется как для однофазных, так и для трехфазных цепей переменного тока. Это отношение истинной или фактической мощности к полной мощности в системах переменного тока.
В цепях постоянного тока мощность цепи можно оценить, найдя произведение показаний вольтметра и амперметра.В то время как в случае цепи переменного тока это умножение этих двух дает полную мощность, но не фактическую мощность. Это так, потому что в цепях переменного тока полная подаваемая мощность, то есть полная мощность, не используется только цепью. А фактически используемая мощность схемы называется истинной мощностью.
Проще говоря, коэффициент мощности — это косинус разности фаз между V и I.
Коэффициент мощности цепей переменного тока с линейными нагрузками находится в пределах от -1 до 1.Обычно считается, что если система демонстрирует коэффициент мощности, близкий к 1, то такие системы считаются стабильными. Мы обсудим различные факторы, которые отличают ведущий коэффициент мощности от отстающего.
Содержание: опережающий коэффициент мощности по сравнению с запаздывающим
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Основа для сравнения | Опережающий коэффициент мощности | Запаздывающий коэффициент мощности |
|---|---|---|
| Basic | Ток нагрузки опережает напряжение питания на определенный фазовый угол. | Существует разность фаз между напряжением и током, при которой ток нагрузки отстает от напряжения питания. |
| Характер нагрузки в электрической цепи | Емкостной | Индуктивный |
| Корректировка низкого коэффициента мощности | Путем добавления индуктивной нагрузки. | Путем добавления емкостной нагрузки. |
| Значение | Существует от -1 до 0. | Существует от 0 до 1. |
| Реактивный компонент | Отрицательный | Положительный |
| Примеры соответствующих нагрузок | Емкостная нагрузка: Электродвигатели, конденсатор, радиосхемы и т. Д. | Индуктивная нагрузка: Электрогенератор, индуктор, реле и т. Д. |
Определение опережающего коэффициента мощности
Опережающий коэффициент мощности в электрической цепи переменного тока достигается за счет использования в цепи емкостной нагрузки. Как и при наличии чисто емкостной нагрузки или комбинации резистивно-емкостной нагрузки, на токопроводы подается напряжение. Это приводит к возникновению коэффициента мощности, который обычно считается ведущим по природе.
Как известно, коэффициент мощности — это отношение истинной мощности к полной.И, как правило, для синусоидального сигнала коэффициент мощности является косинусоидальной функцией фазового угла, существующего между напряжением и током. Рассмотрим формы волны напряжения, подаваемого в цепь переменного тока, и тока через чисто емкостную нагрузку:
Как видно из вышеприведенного рисунка, ток, я сталкиваюсь с пересечениями 0 временной оси на фазу раньше, чем напряжение V. Это называется опережающим коэффициентом мощности. На рисунке ниже показан ведущий треугольник коэффициента мощности:
Определение запаздывающего коэффициента мощности
В цепях переменного тока запаздывающий коэффициент мощности достигается, когда нагрузка является индуктивной по своей природе.Это происходит потому, что при наличии чисто емкостной или резистивной емкостной нагрузки существует разность фаз между напряжением и током, при которой ток отстает от напряжения. Таким образом, коэффициент мощности таких цепей имеет запаздывающий характер.
Рассмотрим формы сигналов напряжения, подаваемого в цепь переменного тока, и тока через чисто емкостную нагрузку как:
Здесь ток встречает пересечение 0 в некоторой фазе после напряжения. Тем самым возникает запаздывающий коэффициент мощности.Отстающий треугольник коэффициента мощности представлен ниже:
Ключевые различия между опережающим и запаздывающим коэффициентами мощности
- Ключевым фактором различия между опережающим и запаздывающим коэффициентами мощности является то, что опережающий коэффициент мощности достигается, когда ток нагрузки находится в опережающем положении по сравнению с током напряжения питания. При запаздывании коэффициента мощности видно, что ток отстает от напряжения на некоторый фазовый угол.
- Когда нагрузка линейной электрической сети является емкостной по своей природе, она создает опережающий коэффициент мощности.В отличие от индуктивной нагрузки, это приводит к запаздыванию коэффициента мощности.
- В случае опережающего коэффициента мощности фазовый угол тока положительный по отношению к напряжению. Однако в случае запаздывающего коэффициента мощности фазовый угол тока отрицателен по сравнению с фазовым углом напряжения.
- Поскольку коэффициент мощности является важным параметром электрических цепей переменного тока, корректировка весьма необходима, если коэффициент мощности достаточно низкий. Таким образом, опережающий коэффициент мощности корректируется добавлением индуктивных нагрузок.В то время как коррекция запаздывающего коэффициента мощности осуществляется путем добавления емкостных нагрузок.
- В случае емкостной нагрузки нагрузка выдает реактивную мощность. Таким образом, реактивная составляющая отрицательна, поскольку здесь на нее подается питание. Но для индуктивной нагрузки нагрузка потребляет реактивную мощность, следовательно, реактивная составляющая будет положительной.
- Значение опережающего коэффициента мощности, т.е. с емкостной нагрузкой, находится в диапазоне от -1 до 0. В то время как для отстающего коэффициента мощности, то есть с индуктивной нагрузкой, оно находится в диапазоне от 0 до 1.
Заключение
Итак, из этого обсуждения мы можем сделать вывод, что в идеале предполагается, что напряжение и ток находятся в одной фазе. Таким образом, фазовый угол между ними равен 0 °. Однако между ними существует разница по фазе, которая называется коэффициентом мощности схемы.
Фазовый сдвиг
Цепи переменного тока> Фазовый сдвиг
Как правило, цепи переменного тока могут содержать резисторы, катушки индуктивности и (или) конденсаторы. Импеданс, обозначенный буквой «Z» и измеренный в Омах, представляет собой полное сопротивление, которое цепь предлагает потоку переменного тока, это комбинация сопротивления R и реактивного сопротивления X, Z = R + jX, рисунок 1.
Рисунок 1: Диаграмма импеданса
В цепях переменного тока, поскольку наличие реактивных компонентов, напряжение и ток могут не достигать одинаковых пиков амплитуды в одно и то же время, они обычно имеют разницу во времени. Эта разница во времени называется фазовым сдвигом, f, 0 ≤ f ≤ 90, и измеряется в угловых градусах.
Цепь, содержащая только резисторы, называется резистивной цепью. Отсутствует фазовый сдвиг между напряжением и током в резистивной цепи, Φ = 0, рисунок 2a.Ток «синфазен» с напряжением.
Рисунок 2a: Связь V-I в цепи R
Конденсаторы и катушки индуктивности
называются реактивными компонентами, в которых напряжение и ток не совпадают по фазе друг с другом. В индукторе напряжение опережает ток на 90, Φ = 90, рис. 2b; в конденсаторе напряжение отстает от тока на 90, Φ = -90, рисунок 2c.
Рисунок 2b: Взаимосвязь V-I контура L
Рисунок 2c: Связь V-I контура C
Цепь, содержащая индукторы и (или) конденсаторы, называется реактивной цепью, которую можно разделить на индуктивную цепь X L > X C и емкостную цепь X C > X L .
На рис. 3а показана индуктивная цепь, состоящая из последовательно соединенных резисторов R и L. Поскольку индуктор противодействует изменению тока и накапливает энергию от источника питания в виде магнитного поля, напряжение индуктора v L опережает ток индуктора i L на 90 и опережает напряжение источника питания v на фазу. Угол Φ.
Рисунок 3a: Связь V-I цепи RL
На рисунке 3b показана емкостная цепь, состоящая из последовательно соединенных резисторов R и C.Поскольку конденсатор противодействует изменению напряжения и накапливает энергию от источника питания в виде электрического поля, напряжение конденсатора v C отстает от тока конденсатора i C на 90 и отстает от напряжения источника питания v на фазу. Угол Φ.
Рисунок 3b: Взаимосвязь V-I цепей RC
Цепи переменного тока> Фазовый сдвиг
Led Voltage — обзор
Какие наиболее важные характеристики необходимо подтвердить при установке трансформатора?
Как идентифицируются провода высокого и низкого напряжения на трансформаторе?
Нарисуйте принципиальную схему вторичной обмотки с двумя обмотками, имеющей 120 вольт на каждой обмотке для получения выходного напряжения 240 вольт.
Соответствует ли расчет в кВА первичной цепи номинальной мощности вторичной обмотки? Объяснять.
Трансформатор рассчитан на 15 кВА, 2400/600 вольт. Что такое первичный ток? Сколько вторичного тока доступно?
Трансформатор имеет двойную первичную обмотку на 600 вольт. Подключите их к источнику на 1200 вольт.
Если две 1,5-вольтовые батареи подключены положительно к положительному положению, какое напряжение будет доступно на их других клеммах?
Трансформатор рассчитан на 2400/240 вольт. h2 подключен к X1. Какое напряжение между h3 и X2?
Будет ли у 12-киловольтного трансформатора аддитивная или вычитающая полярность?
Как определить непрерывность обмотки?
Нарисуйте схему для определения полярности трансформатора с использованием источника переменного напряжения.
Если у вас есть два трансформатора, один добавочный, а другой вычитающий, которые должны быть подключены параллельно друг другу для питания нагрузки, какие клеммы на каждом трансформаторе будут подключены к одной и той же линии?
Можно ли параллельно подключать трансформаторы с разными номиналами напряжения? Объяснять.
Каков эффект параллельного соединения двух трансформаторов с разным импедансом?
Существуют ли какие-либо способы подключения, позволяющие параллельно подключать трансформаторы с разным импедансом?
Сколько градусов разделяют фазы трехфазной системы?
Количество меди в однофазной системе может быть уменьшено на ______%, если трехфазная система используется для обеспечения того же количества энергии.
В каком направлении вращается ротор генератора?
Какова алгебраическая сумма напряжений в трехфазной системе?
На рис. 2-15, если бы фазные напряжения составляли 277 вольт, какое было бы напряжение между B и C?
Как клеммы h3 трансформаторов подключаются по схеме звезды?
Перечислите преимущества использования трехфазного трансформатора вместо трех отдельных однофазных трансформаторов.
Какова взаимосвязь между линейным током и током обмотки трансформатора, соединенного звездой?
Какова взаимосвязь между линейным напряжением и напряжением обмотки трансформатора, соединенного звездой?
Какова взаимосвязь между линейным током и током обмотки трансформатора, подключенного по схеме треугольника?
Какова взаимосвязь между линейным напряжением и напряжением обмотки трансформатора, подключенного по схеме треугольника?
В какой системе, звезда или треугольник, легче сбалансировать однофазные нагрузки?
Какая система, звезда или треугольник, с большей вероятностью будет использоваться при высоком трехфазном токе с минимальной однофазной нагрузкой?
Можно ли подключить трехфазные блоки трансформаторов параллельно друг другу? Есть ли исключения?
Нарисуйте принципиальную схему простого трансформатора, соединенного треугольником.
Рассчитайте кВА трехфазного трансформатора с первичной обмоткой 2400 вольт и 15 ампер.
Какая из трехфазных систем электропроводки способна генерировать чрезмерные напряжения на третьей гармонике?
Можно ли получить три фазы для нагрузки при использовании только двух одноблочных трансформаторов? Объяснять.
При использовании двойных вторичных обмоток на 120 вольт, какое максимальное количество напряжений доступно для нагрузки? Каковы их ценности?
