как рассчитать по току и напряжению, формула
Что такое плоские конденсаторы
Определение
Конденсатор — это устройство для накопления заряда и энергии электрического поля.
Определение
Плоский конденсатор — конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые разделяет небольшой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и противоположные по знаку заряды.
Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.
Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.
Описание и технические характеристики
Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.
Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд.
Конденсатор обладает следующими техническими параметрами:
- номинальной и реальной емкостью — заявленной и фактической способностью накапливать заряд;
- удельной емкостью — отношением емкости к массе или объему диэлектрика;
- плотностью энергии;
- номинальным напряжением;
- полярностью — электролитические конденсаторы требуют корректной полярности напряжения для безопасной работы;
- электрическим сопротивлением изоляции диэлектрика;
- временем самостоятельной потери заряда;
- эквивалентным последовательным сопротивлением — внутренним электрическим сопротивлением диэлектрика, материала обкладок, выводов, контактов;
- эквивалентной последовательной индуктивностью и собственной частотой резонанса;
- температурным коэффициентом емкости — относительным изменением емкости при изменении температуры окружающей среды;
- диэлектрической абсорбцией — поглощением и сохранением части заряда при быстрой разрядке;
- пьезоэффектом — генерацией напряжения на обкладках при механических деформациях.
 {-12}\;\frac Фм\).
{-12}\;\frac Фм\).Таким образом, емкость плоского конденсатора легко изменить, погрузив его в жидкость или иную среду с нужной диэлектрической проницаемостью.
Способы расчета по току и напряжению
Конденсатор — это два проводящих тела, которые разделены диэлектриком. Они несут равные по величине и противоположные по знаку заряды \(q_1\) и \(q_2 \) имеют потенциалы \(\varphi_1\) и \(\varphi_2\).
Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника \(\varphi.\) Их зависимость выражается формулой:\(С\;=\;\frac qU\)
Где U — разность потенциалов тел, т. е. обкладок конденсатора, или напряжение на конденсаторе.
Если порции заряда малы, для простоты расчетов можно предположить, что напряжение между пластинами не меняется. Оно вычисляется по формуле:
\( U\;=\;\varphi2\;-\;\varphi_1\)
Заряд измеряется в кулонах. Заряд и сила тока связаны следующим соотношением: один кулон равен величине заряда, прошедшего через проводник за одну секунду при силе тока в один ампер.
 Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:\(q\;=\;I\;\times\;t\)
Когда конденсатор включен в колебательный контур, то, зная период электромагнитных колебаний T и индуктивность катушки контура L, можно вычислить емкость, воспользовавшись формулой Томсона:
\(T\;=\;2\mathrm\pi\sqrt{\mathrm{LC}}\)
При решении задач часто требуется вычислить емкости каждого конденсатора в цепи параллельно или последовательно соединенных, а также напряжение на каждом из них. Чтобы составить необходимые уравнения, нужно воспользоваться формулами для вычисления общей емкости цепи.
При параллельном соединении:\({\mathrm С}_{\mathrm{общ}\;}\;=\;{\mathrm С}_1\;+\;{\mathrm С}_2\;+\;{\mathrm С}_{3\;}+\;…\;+\;{\mathrm С}_{\mathrm n}\)
При последовательном:
\(\frac{1\;}{{\mathrm С}_{\mathrm{общ}\;}}=\;\frac1{{\mathrm С}_1}\;+\;\frac1{{\mathrm С}_2}\;+\;\frac1{{\mathrm С}_{3\;}}+\;.
 ..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)
..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)Примечание
Эти формулы справедливы для любого конденсатора, не только для плоского.
Ёмкость плоского конденсатора.
Плоский конденсатор состоит из двух
параллельных пластин, разделённых
небольшим зазором шириной
,
заполненным однородным диэлектриком.Нам известно, что поле между двумя
разноимённо заряженными пластинами с
одинаковой по величине поверхностной
плотностью
равно,
где,S– площадь каждой пластины.
Напряжение между обкладками:.
Используя
определение емкости конденсатора,
получаем:Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин. Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор
по сравнению с линейными размерами
пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет
собой систему двух концентрических
сфер с радиусами
и.
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно:.
Для
ёмкости сферического конденсатора
получаем:.
Это
формула точная.Если
,
полученная формула переходит в выражение
для ёмкости плоского конденсатора.Ёмкость
цилиндрического конденсатора.Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусами
и,
длиной.Рассуждая
аналогично выводу ёмкости сферического
конденсатора, получаем:..
Полученная формула является приближенной
и при малом зазоре
переходит в формулу емкости плоского
конденсатора.Соединение
конденсаторов.
В практике для получения необходимых
значений емкости используют соединения
конденсаторов: а) последовательное, б)
параллельное, в) смешанное (см. рисунок).Ёмкость
последовательного соединения
конденсаторов.Заряды последовательно соединенных
конденсаторов равны
,
а напряжение на батарее.
Из определения емкости следует:или
.Если
,
то(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).Для
последовательно соединенных конденсаторов
емкость вычисляется по формуле:.
В
случае одинаковых конденсаторов:
.Ёмкость
параллельного соединения конденсаторов.Заряд
батареи равен сумме зарядов:,
а
напряжение
.
По определению емкости получаем:.
Для
параллельно соединенных конденсаторов:.
В
случае одинаковых конденсаторов:
.Пример.
Оценить
емкость батареи (см. рисунок)
..
Ответ:.
Используя
свойство бесконечности можно представить
цепь в виде соединения (см. рисунок).Для
расчета ёмкости батареи получаем:,
.
Откуда:
,
так как,
то.Лекция 7.
Диэлектрики
в электрическом поле.Диэлектриками (изоляторами) называют
вещества, не проводящие постоянного
электрического тока. Это означает, что
в диэлектриках отсутствуют «свободные»
заряды, способные перемещаться на
значительные расстояния.Диэлектрики состоят либо из нейтральных
молекул, либо из ионов, находящихся в
узлах кристаллической решетки. Сами же
молекулы могут быть полярнымиинеполярными.Полярные молекулы
обладают дипольным моментом, у неполярных
молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных» зарядов.
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.Под действием электрического поля
диполи ориентируются преимущественно
в направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сил
исоздает
вращательный момент равный,
где-
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю
.Электроемкость проводника. Электроемкость конденсатора. — Студопедия
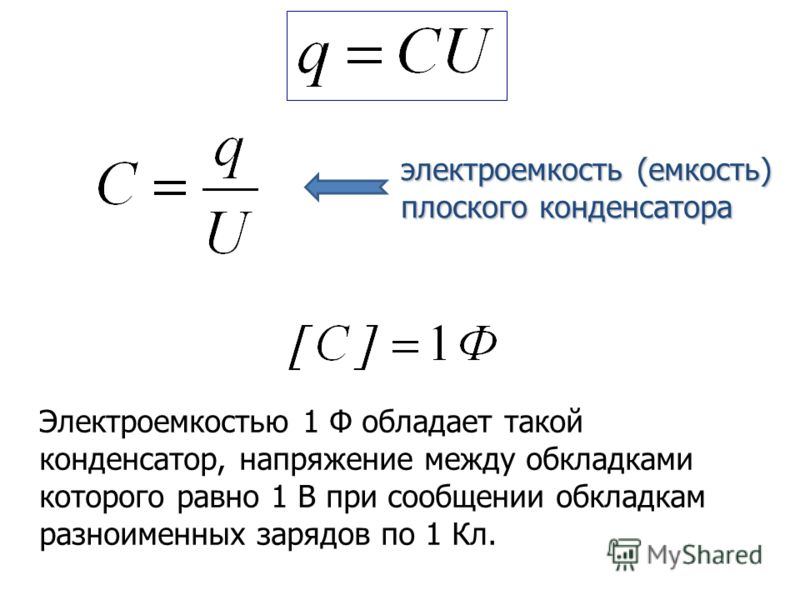
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд.
В (СИ) ёмкость измеряется в фарадах.
Электроемкость уединенного проводника есть физическая величина численно равная величине заряда, который необходимо сообщить данному проводнику для увеличения его потенциала на единицу. В математической форме данное определение имеет вид
где — заряд, — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость.
Понятие электроёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае электроёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.

Вывод формулы для плоского конденсатора (если понадобиться на всякий случай)
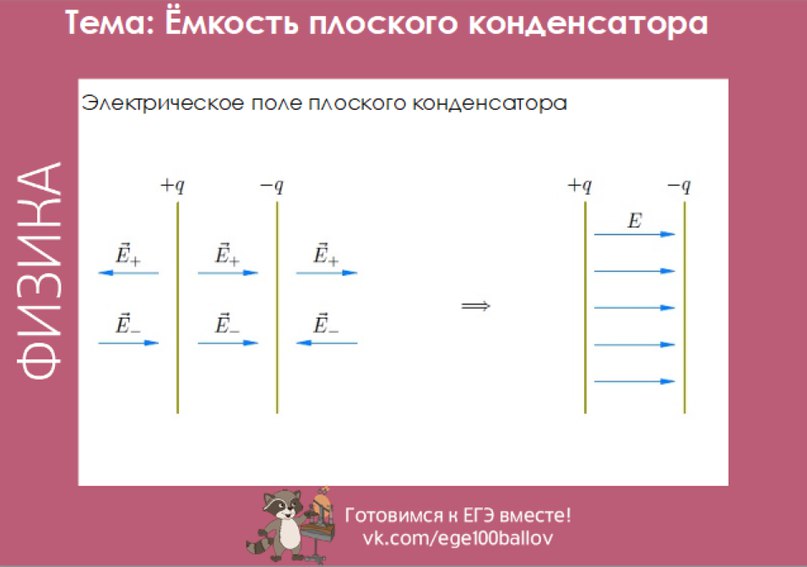
Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением
Согласно принципу суперпозиции, напряженность E поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:
Внутри конденсатора вектора и параллельны; поэтому модуль напряженности суммарного поля равен
Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними.
 Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Конденсаторы
Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы. Конденсатор — это система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные диэлектриком, образуют плоский конденсатор. Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность между пластинами будет в два раза больше, чем напряженность одной пластины. Вне пластин напряженность равна нулю.
Обозначаются конденсаторы на схемах так:При параллельном соединении конденсаторов U=U1=U2
при последовательном q=q1=q2.В зависимости от типа диэлектрика конденсаторы бывают воздушные, бумажные, слюдяные.

Конденсаторы применяются для накопления электроэнергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в выпрямителях, колебательных контурах и других радиоэлектронных устройствах.Решения
NCERT для класса 12 по естествознанию, раздел 2
Страница № 87:
Вопрос 2.1:
Два заряда 5 ×
10 −8 C и −3 × 10 −8 C
расположены на расстоянии 16 см друг от друга. В какой точке на линии, соединяющей два
зарядов электрический потенциал равен нулю? Используйте потенциал на
бесконечность равна нулю.Ответ:
Есть два заряда,
Расстояние между
два заряда, d = 16 см = 0.16 мРассмотрим точку P на
линия, соединяющая два заряда, как показано на данном рисунке.r = Расстояние
точка P от заряда q 1Пусть электрический
потенциал ( В, ) в точке P равен нулю.
Потенциал в точке P равен
сумма потенциалов, обусловленных зарядами q 1 и q 2
соответственно.Где,
=
Пределы свободного пространстваДля В = 0,
уравнение (i) сводится кТаким образом,
потенциал равен нулю на расстоянии 10 см от положительного заряда
между обвинениями.Предположим, что точка P
вне системы двух зарядов на расстоянии с от
отрицательный заряд, где потенциал равен нулю, как показано ниже
рисунок.Для этого расположения,
потенциал определяется выражением,Для В = 0,
уравнение (ii) сводится кТаким образом,
потенциал равен нулю на расстоянии 40 см от положительного заряда
вне системы начислений.Страница № 87:
Вопрос 2.2:
Правильный шестиугольник из
сторона 10 см имеет заряд 5 мкКл в каждой своей вершине. Рассчитать
Рассчитать
потенциал в центре шестиугольника.Ответ:
На данном рисунке показано
шесть одинаковых зарядов, q , в вершинах регулярного
шестиугольник.Где,
Заряд, q = 5 мкКл
= 5 × 10 −6 ССторона шестигранника, л
= AB = BC = CD = DE = EF = FA = 10 смРасстояние каждой вершины
от центра O, d = 10 смЭлектрический потенциал при
точка О,Где,
=
Пределы свободного пространстваТаким образом,
потенциал в центре шестиугольника равен 2.7 ×
10 6 В.Страница № 87:
Вопрос 2.3:
Два заряда 2 мкКл
и −2 µC размещены в точках A и B на расстоянии 6 см друг от друга.(a) Определить
эквипотенциальная поверхность системы.
(б) Что такое
направление электрического поля в каждой точке на этой поверхности?Ответ:
(a) The
ситуация представлена на данном рисунке.An
эквипотенциальная поверхность — это плоскость, на которой полный потенциал равен нулю
везде. Эта плоскость перпендикулярна прямой AB. Самолет находится по адресу
средней точки линии AB, поскольку величина зарядов равна
тем же.(b) Направление электрического поля в каждой точке этого
поверхность нормальна к плоскости в направлении AB.Страница № 87:
Вопрос 2.4:
Сферический проводник
радиусом 12 см имеет заряд 1,6 × 10 −7 Кл
равномерно распределяется по его поверхности. Что такое электрическое поле(a) Внутри
сфера(б) Просто
вне сферы(c) В точке
18 см от центра сферы?Ответ:
(a) Радиус
сферический проводник, r = 12 см = 0. 12 м
12 мЗаряд
равномерно распределена по проводнику, q = 1,6 ×
10 −7 СЭлектрический
поле внутри сферического проводника равно нулю. Это потому, что если есть
есть поле внутри проводника, то заряды переместятся, чтобы нейтрализовать
Это.(б) Электрический
поле E сразу за проводником определяется соотношениемГде,
=
Пределы свободного пространстваСледовательно,
электрическое поле вне сферы
.(c) Электрический
поле в точке 18 м от центра сферы = E 1Расстояние
точки от центра, d = 18 см = 0,18 мСледовательно,
электрическое поле в точке 18 см от центра сферы равно.
Паразитная емкость, индуктивность и ток смещения
Когда два электрических проводника находятся рядом друг с другом, несут заряд и между ними существует потенциал напряжения, они создают виртуальный конденсатор между ними, даже если проводники изолированы.
 Виртуальный конденсатор между ними известен как паразитная или паразитная емкость.
Виртуальный конденсатор между ними известен как паразитная или паразитная емкость.Это может произойти где угодно, но больше всего проблем возникает между дорожками на печатных платах, особенно когда задействованы высокочастотные сигналы. Как правило, емкость обратно пропорциональна расстоянию между проводниками. Для дорожек печатной платы рекомендуется прокладывать проводники таким образом, чтобы паразитная емкость была менее вероятной, но паразитная емкость могла образовываться между проводником и землей или плоскостью питания, между проводами и между проводом и экраном провода.Между передающей антенной и землей может образоваться паразитная емкость. Значение паразитной емкости определяется по формуле C = q / V, где C — емкость в фарадах, V — потенциал или напряжение в вольтах, а q — заряд в кулонах.
Рис. 1. Между проводящими выводами любого компонента существует паразитная емкость. Провода также будут иметь некоторую паразитную индуктивность и сопротивление, связанные с самими выводами.
 (Источник: Википедия)
(Источник: Википедия)Резисторы (или что-либо другое, имеющее сопротивление по отношению к электрическому заряду) обладают паразитной емкостью, которая ведет себя как конденсатор, подключенный параллельно резистивному элементу.Фактически, распределение электрического заряда отвечает за паразитную емкость, и то же самое распределение заряда отвечает в первую очередь за проводимость в резисторе. Если скорость изменения электрического заряда мала, влиянием паразитной емкости можно пренебречь.
Однако влияние паразитной емкости на резистор обратной связи, например, может иметь большое значение. Емкость Миллера — это паразитная емкость, которая образуется в цепи обратной связи операционного усилителя.Влияние паразитного конденсатора в петле обратной связи таково, что эффект усиливается операционным усилителем; это известно как эффект Миллера. Это правда, что интегрированные микросхемы дают больше преимуществ, чем экономия места; Опыт проектирования, который вкладывается в интегрированные микросхемы для самых заезженных проектов, также ценен.

Ток смещения
Электрические поля, которые изменяются и существуют между заряженными телами, вызывают нечто вроде протекания тока, называемого током смещения, так что изменение электрического поля на одном теле влияет на электрическое поле на соседнем теле.Идея тока смещения впервые появляется в уравнениях Максвелла и имеет те же единицы, что и электрический ток, но представляет собой изменяющееся во времени электрическое поле на больше, чем электрический ток, состоящий из движущихся зарядов. Легче понять, как конденсатор может проводить ток даже на низких частотах, если вы знаете о токе смещения. На высоких частотах картина меняется.
Паразитная емкость на высоких частотах
На более высоких частотах на протекание тока влияют паразитные конденсаторы, потому что с увеличением частоты конденсаторы становятся все лучше проводниками.Другая формула показывает взаимосвязь между током, емкостью и скоростью изменения потенциала (напряжения) во времени (также известной как частота): где i — ток, C — емкость, а dv / dt — скорость изменения напряжения за время (частота).
 Приведенная выше формула показывает, что существует взаимосвязь между током, емкостью и потенциалом напряжения во времени. Электрический сигнал, который является постоянным во времени и не изменяется, называется постоянным током (DC), и поэтому dv / dt = 0, поскольку потенциал напряжения с течением времени не изменяется.Независимо от амплитуды постоянного напряжения постоянное напряжение не дает тока ( i = 0) из приведенной выше формулы, и, таким образом, конденсатор ведет себя как разомкнутая цепь. Батарея, управляющая контуром цепи, будет видеть конденсатор в этом контуре как разомкнутую цепь, как если бы провода были перерезаны. Но если у вас есть изменение потенциала напряжения (амплитуда напряжения меняется со временем), частота изменения амплитуды влияет на ток, и dv / dt сходится к значению. Глядя на приведенную выше формулу, если dv / dt отличное от нуля значение, то ток течет.[i]
Приведенная выше формула показывает, что существует взаимосвязь между током, емкостью и потенциалом напряжения во времени. Электрический сигнал, который является постоянным во времени и не изменяется, называется постоянным током (DC), и поэтому dv / dt = 0, поскольку потенциал напряжения с течением времени не изменяется.Независимо от амплитуды постоянного напряжения постоянное напряжение не дает тока ( i = 0) из приведенной выше формулы, и, таким образом, конденсатор ведет себя как разомкнутая цепь. Батарея, управляющая контуром цепи, будет видеть конденсатор в этом контуре как разомкнутую цепь, как если бы провода были перерезаны. Но если у вас есть изменение потенциала напряжения (амплитуда напряжения меняется со временем), частота изменения амплитуды влияет на ток, и dv / dt сходится к значению. Глядя на приведенную выше формулу, если dv / dt отличное от нуля значение, то ток течет.[i]Чем выше частота, тем больше проводимость конденсатора, как у резистора, приближающегося к короткому замыканию.
 На бесконечной частоте конденсатор действует как провод. Таким образом, паразитная емкость представляет собой реальную проблему на высоких частотах, поскольку ее эффекты не сильно влияют на вещи на более низких частотах. Однако паразитная емкость, возникающая на высоких частотах, неожиданно соединяет, помимо прочего, опорную плоскость печатной платы с шасси. Обратите внимание, что паразитная емкость будет формироваться между любым проводящим телом , несущим заряд, поэтому паразитная или паразитная емкость может образоваться между антенной и грязью / землей / землей (и тем более, если земля влажная и, следовательно, более проводящая).Паразитная емкость может образоваться между металлическим столом и печатной платой, расположенной на нем (но в меньшей степени, если стол сделан из изоляционного материала). Конструкция схемы для высоких частот означает, что необходимо уделить дополнительное внимание конструкции, особенно в отношении компоновки печатной платы или размещения любого проводящего тела по отношению к другому проводящему телу.
На бесконечной частоте конденсатор действует как провод. Таким образом, паразитная емкость представляет собой реальную проблему на высоких частотах, поскольку ее эффекты не сильно влияют на вещи на более низких частотах. Однако паразитная емкость, возникающая на высоких частотах, неожиданно соединяет, помимо прочего, опорную плоскость печатной платы с шасси. Обратите внимание, что паразитная емкость будет формироваться между любым проводящим телом , несущим заряд, поэтому паразитная или паразитная емкость может образоваться между антенной и грязью / землей / землей (и тем более, если земля влажная и, следовательно, более проводящая).Паразитная емкость может образоваться между металлическим столом и печатной платой, расположенной на нем (но в меньшей степени, если стол сделан из изоляционного материала). Конструкция схемы для высоких частот означает, что необходимо уделить дополнительное внимание конструкции, особенно в отношении компоновки печатной платы или размещения любого проводящего тела по отношению к другому проводящему телу.
[i] PDF: Конденсаторы и индукторы, PI Hutchinson, 2004, MIT.edu
Лекция 14 Емкость и проводимость
1 Лекция 14 Емкость и проводимость: 6.3, 6.4, 6.5 Домашнее задание: файл домашнего задания ee
2 Определение емкости Емкость — это мера способности физической структуры накапливать свободный электрический заряд при определенном напряжении C Q V, F = C / V C N P D Eds EdL, F Закон Гаусса E Q P r E E V N Q ЛЕКЦИЯ 14 слайд
3 Емкость конденсатора с параллельными пластинами a D s n a n 0 E s a z C P s n a n a D E ds Ez A A C N Ez d d EdL 0, ФЛЕКЦИЯ 14 слайд 3
4 1.
 Конденсатор, изолятор которого имеет относительную диэлектрическую проницаемость ε r1 = 1, имеет емкость C 1 = 1 мкФ. Какой будет его емкость, если заменить изолятор другим с ε r = 30? C. Если два конденсатора (C 1 и C) смещены напряжением V = 1 кВ, каковы будут их соответствующие заряды (Q 1 и Q)? Q1 Q 3. Каков характер зарядов Q 1 и Q? (а) свободный заряд, нанесенный на поверхность электрода (б) связанный заряд, нанесенный на поверхность изолятора у электрода (в) общий заряд на поверхности электрода-изолятора ЛЕКЦИЯ 14, слайд 4
Конденсатор, изолятор которого имеет относительную диэлектрическую проницаемость ε r1 = 1, имеет емкость C 1 = 1 мкФ. Какой будет его емкость, если заменить изолятор другим с ε r = 30? C. Если два конденсатора (C 1 и C) смещены напряжением V = 1 кВ, каковы будут их соответствующие заряды (Q 1 и Q)? Q1 Q 3. Каков характер зарядов Q 1 и Q? (а) свободный заряд, нанесенный на поверхность электрода (б) связанный заряд, нанесенный на поверхность изолятора у электрода (в) общий заряд на поверхности электрода-изолятора ЛЕКЦИЯ 14, слайд 45 4.В предыдущем примере: (a) Найдите отношение свободного заряда к общему на границе раздела изолятор-электрод. (b) Найдите отношение связанного заряда к общему. (c) Сравните общие (бесплатные + связанные) значения сборов. sf sb ЛЕКЦИЯ 14 слайд 5
6 Емкость и ток энергии 1 общее выражение энергии (лекция 9) 1 We (vf V) dv v есть два электрода: один с потенциалом V 1, а другой с V заряд распределен по поверхности электродов 1 1 WV ds VQ (1) (1) e 1 sf WV ds VQ () () e sf предполагается, что конденсатор заряжается нейтральным в целом как до, так и после подачи напряжения (сохранение заряда) QQ 0 QQQ 1 1 ЛЕКЦИЯ 14 слайд 6
7 Емкость и ток Общая энергия двух электродов (1) () 1 We We We Q (V1V) We 1 QV We (CV) V CV Q 1 Q 1 Q We QCCCVW e V 1 CQW e ЛЕКЦИЯ 14 слайд 7
8 Пример емкости 1: Двухслойный пластинчатый конденсатор Напряжение между пластинами V Ed 1 1 Ed почему 1 на диэлектрической границе Dn1 Dn E E1 VV E1 s D1 1E1 dd (/) (d /) (d /) Q s CVVC 1 1 d1 d 1 1 CC 1 1 конденсаторы последовательно SS ЛЕКЦИЯ 14 слайд 8
9 Принцип эквивалентности металлических конструкций: размещение листа PEC на эквипотенциальной поверхности не меняет емкость распределения поля не изменяется, следует из теоремы единственности: значения потенциала на граничных поверхностях остаются прежними V 10 VV 6 VEV 0 V структура эффективно разделен на два конденсатора последовательно В 10 ЛЕКЦИЯ 14 В 6 ВВ 0 В 9
Емкость 10 В Пример: ферический конденсатор d Q 4r QD s E b E 1 Q 4 rar Q 1 1 Q (ba) E d L 4 ab 4 ab a Q ab C 4, FV (ba) EQQ arb ab Емкость одной сферы : Ca lim C lim 4 4 a, F bb (ba) ЛЕКЦИЯ 14 слайд 10
11 Емкость на единицу длины: линия с параллельными пластинами C A h wl h, F C w C, F / m l h h w l ЛЕКЦИЯ 14 слайд 11
12 Емкость на единицу длины: коаксиальный кабель примените закон Гаусса, чтобы найти поперечное сечение поля E 1 bl QE, В / мала, найдите напряжение из E b Q b V0 E d ln, V ala найдите емкость по напряжению Q l C, FV ln (b / a) 0 найти емкость PUL CC, Ф / мл ln (b / a) V 0 V 0 l ЛЕКЦИЯ 14 слайд 1 E
13 Емкость на единицу длины: двухжильный кабель 1 (опция) tep 1: Найдите уравнение эквипотенциальных линий двух линейных зарядов при x = s и x = s.
 l s l s в точке наблюдения P: V ln, V ln 1 l 1 V (P) V V ln y h h P r l s V s эквипотенциалы r x l ЛЕКЦИЯ 14 слайд 13
l s l s в точке наблюдения P: V ln, V ln 1 l 1 V (P) V V ln y h h P r l s V s эквипотенциалы r x l ЛЕКЦИЯ 14 слайд 1314 Емкость на единицу длины: двухжильный кабель (опция) на эквипотенциальной линии V = V c, мы имеем 1 Vc 1 Vc ln K exp ll K при P (x, y) K 1 (sx) y (sx) y возводя в квадрат и переставляя, получаем уравнение окружности 1 Ks K xs y K 1 K 1 x-координата центра hr радиуса ЛЕКЦИЯ 14 слайд 14
15 Емкость на единицу длины: двухжильный кабель 3 (опция) уравнение эквипотенциальной линии V = V c 1 Ks K xs y K 1 K 1 представляет собой круг радиуса Ks r K 1 hh K и центр на Ось x на расстоянии 1 rr от начала координат K 1 hsshr K 1 tep: Постройте эквивалентную задачу о проводах конечного радиуса r, разместив провода так, чтобы их поверхности совпадали с эквипотенциальными линиями идеальных линейных зарядов (расстояние h от происхождения).
 ЛЕКЦИЯ 14 слайд 15
ЛЕКЦИЯ 14 слайд 1516 Емкость на единицу длины: двухпроводной кабель 4 потенциал на положительном проводе l V1 ln K потенциал на отрицательном проводе l V ln K разность потенциалов между проводами l CV 1 hhlhh V1 V1 V ln 1 rr, Ф / м ln 1 rr KC, hhr ln r ЛЕКЦИЯ 14 слайд 16
17 Аналогия между емкостью и проводимостью QCVNE d PE ds L, FIGVNE d PE ds L, для данной геометрии выражения для емкости и проводимости идентичны, за исключением постоянной материала Примеры: 1) коаксиальный конденсатор / резистор ll ln (b / a ) C, FG,; R, ln (b / a) ln (b / a) l) домашнее задание: проводимость G резистора с параллельными пластинами ЛЕКЦИЯ 14 слайд 17
18 Проводимость на единицу длины 1 3) коаксиальный кабель с изолятором с потерями (рассеивающим) (σ d 0) d C, F / m G, / м ln (b / a) ln (b / a) обратите внимание, что кабель в целом претерпевает потери не только из-за проводящих проводов (обозначенных Rꞌ), но и из-за своего неидеального изолятора (ток течет через изолятор, описывается Gꞌ), потери в металлических выводах коаксиального кабеля Rꞌ были получены в лекции 10 : R, / mmacb скин-эффект не учитывается! I металл ПРИМЕЧАНИЕ: G 1 / R I металл I diel ЛЕКЦИЯ 14 слайд 18
19 Проводимость на единицу длины 4) двухжильный кабель с изолятором с потерями (σ d 0) C d, F / m G, / mhhhh ln 1 ln 1 rrrr Потери в металлических проводах двухжильного кабеля были получены в Лекция 10 1 R, / m A m G 1 / R 5) домашнее задание: вывести проводимость на единицу длины Gꞌ линии с параллельными пластинами ЛЕКЦИЯ 14 слайд 19
20 параметров на единицу длины в схемных моделях TL в 1 Rl Ll v N Gl Cl vn 1 l z ЛЕКЦИЯ 14 слайд 0
21 Вы узнали: что такое емкость и какая емкость на единицу длины, как рассчитать емкость по распределению поля, как емкость связана с накопленной электрической энергией, как рассчитать емкость на единицу длины и проводимость на единицу длины параллельного пластинчатая линия, коаксиальный кабель и двухжильный кабель ЛЕКЦИЯ 14 слайд 1
Конденсаторы
Конденсаторы
Далее: Уравнение Пуассона
Up: Электростатика
Пред . : Граничные условия на
: Граничные условия на
Конденсаторы
Можем хранить электрические
заряд на поверхности проводника.Однако,
электрические поля будут создаваться непосредственно над этой поверхностью.
Проводник может успешно хранить заряд только в том случае, если он электрически изолирован.
из его окрестностей. Воздух — очень хороший изолятор. К сожалению, воздух
перестает быть изолятором, когда напряженность электрического поля через него превышает некоторые
критическое значение, которое составляет около
вольт на метр. Этот
явление, которое называется обрывом , связано с образованием
искр. Самый известный пример поломки
воздух во время молнии
забастовка.Ясно, что хорошее устройство для хранения заряда — это устройство, вмещающее большое количество
заряда, но генерирует только небольшие электрические поля. Такое устройство называется
конденсатор .
Рассмотрим два тонких параллельных проводящих
пластины поперечного сечения, разделенные
малое расстояние (, т.е. ,). Предположим, что каждая пластина
несет равный и противоположный заряд. Мы ожидаем, что эта сумма будет
равномерно распределить по пластинам, чтобы обеспечить эффективную плотность заряда листана каждой тарелке.Предположим, что на верхней пластине находится
положительный заряд, а нижняя пластина несет отрицательный заряд. В соответствии с
Уравнения. (624) и (625) поле, создаваемое верхней пластиной, перпендикулярно пластине и
величины
Точно так же поле, создаваемое нижней пластиной, равно
Обратите внимание, что мы не учитываем любую « утечку » поля на краях пластин.
Это разумно, если пластины расположены близко друг к другу. Общее поле — это
сумма двух полей, создаваемых верхней и нижней пластинами.Таким образом, чистое поле
перпендикулярно пластинам и по величине
Поскольку электрическое поле однородно, разность потенциалов между
тарелки просто
(644)
Обычно емкость проводника или набора проводников измеряется
хранить заряд, но генерировать небольшие электрические поля с точки зрения параметра
называется емкость . Это
обычно обозначается.Емкость накопителя заряда
устройство — это просто отношение накопленного заряда к разности потенциалов
генерируется зарядом. Таким образом,
(645)
Очевидно, что хорошее устройство для накопления заряда имеет большую емкость. Кстати,
Емкость измеряется в кулонах на вольт или фарадах. Это довольно громоздкий
единица, поскольку
хорошие конденсаторы обычно имеют емкость, которая составляет всего около одной миллионной
фарада.Для конденсатора с параллельными пластинами ясно, что
(646)
Обратите внимание, что емкость зависит только от геометрических величин , таких как площадь
и расстояние между пластинами. Это следствие совместимости
электрические поля. Если удвоить заряд проводников, то удвоим
электрические поля, генерируемые вокруг них, и поэтому мы удваиваем потенциал
разница между проводниками.Таким образом, разность потенциалов между
проводники всегда прямо пропорциональны переносимому заряду:
постоянная
пропорциональности (обратной емкости) может зависеть только от геометрии.
Предположим, что заряд на каждой пластине постепенно накапливается за счет переноса
небольшие количества заряда от одной пластины к другой. Если
мгновенный заряд на пластинах, а бесконечно малое количество
положительный
заряд переносится с отрицательно заряженной пластины на положительно
зарядная пластина, то работа сделана
,
где мгновенное
разность напряжений между пластинами.Обратите внимание, что разница напряжений такая
что он противодействует любому увеличению заряда на любой из пластин.
Общая работа, проделанная при зарядке конденсатора
является
(647)
где использовалось уравнение. (645).
Энергия, запасенная в конденсаторе, такая же, как и работа, необходимая для
зарядите конденсатор. Таким образом,
(648)
Это общий результат, который справедлив для всех типов конденсаторов.Энергия
заряженная параллель
тарелка
Конденсатор фактически хранится в электрическом поле между пластинами. Это поле
имеет примерно постоянную величину и занимает
область объема. Таким образом, учитывая плотность энергии электрического
поле
, энергия, запасенная в
электрическое поле
(649)
где использовалось уравнение. (646).
Обратите внимание, что уравнения. (647) и (649) согласны.Все мы знаем, что если мы подключим конденсатор
через клеммы батареи, тогда переходный ток течет, поскольку конденсатор
заряжается.

 {-12}\;\frac Фм\).
{-12}\;\frac Фм\). Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле: ..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)
..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)



 Отметим, что смещение
Отметим, что смещение

 Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
 Рассчитать
Рассчитать
 12 м
12 м Виртуальный конденсатор между ними известен как паразитная или паразитная емкость.
Виртуальный конденсатор между ними известен как паразитная или паразитная емкость. (Источник: Википедия)
(Источник: Википедия)
 Приведенная выше формула показывает, что существует взаимосвязь между током, емкостью и потенциалом напряжения во времени. Электрический сигнал, который является постоянным во времени и не изменяется, называется постоянным током (DC), и поэтому dv / dt = 0, поскольку потенциал напряжения с течением времени не изменяется.Независимо от амплитуды постоянного напряжения постоянное напряжение не дает тока ( i = 0) из приведенной выше формулы, и, таким образом, конденсатор ведет себя как разомкнутая цепь. Батарея, управляющая контуром цепи, будет видеть конденсатор в этом контуре как разомкнутую цепь, как если бы провода были перерезаны. Но если у вас есть изменение потенциала напряжения (амплитуда напряжения меняется со временем), частота изменения амплитуды влияет на ток, и dv / dt сходится к значению. Глядя на приведенную выше формулу, если dv / dt отличное от нуля значение, то ток течет.[i]
Приведенная выше формула показывает, что существует взаимосвязь между током, емкостью и потенциалом напряжения во времени. Электрический сигнал, который является постоянным во времени и не изменяется, называется постоянным током (DC), и поэтому dv / dt = 0, поскольку потенциал напряжения с течением времени не изменяется.Независимо от амплитуды постоянного напряжения постоянное напряжение не дает тока ( i = 0) из приведенной выше формулы, и, таким образом, конденсатор ведет себя как разомкнутая цепь. Батарея, управляющая контуром цепи, будет видеть конденсатор в этом контуре как разомкнутую цепь, как если бы провода были перерезаны. Но если у вас есть изменение потенциала напряжения (амплитуда напряжения меняется со временем), частота изменения амплитуды влияет на ток, и dv / dt сходится к значению. Глядя на приведенную выше формулу, если dv / dt отличное от нуля значение, то ток течет.[i] На бесконечной частоте конденсатор действует как провод. Таким образом, паразитная емкость представляет собой реальную проблему на высоких частотах, поскольку ее эффекты не сильно влияют на вещи на более низких частотах. Однако паразитная емкость, возникающая на высоких частотах, неожиданно соединяет, помимо прочего, опорную плоскость печатной платы с шасси. Обратите внимание, что паразитная емкость будет формироваться между любым проводящим телом , несущим заряд, поэтому паразитная или паразитная емкость может образоваться между антенной и грязью / землей / землей (и тем более, если земля влажная и, следовательно, более проводящая).Паразитная емкость может образоваться между металлическим столом и печатной платой, расположенной на нем (но в меньшей степени, если стол сделан из изоляционного материала). Конструкция схемы для высоких частот означает, что необходимо уделить дополнительное внимание конструкции, особенно в отношении компоновки печатной платы или размещения любого проводящего тела по отношению к другому проводящему телу.
На бесконечной частоте конденсатор действует как провод. Таким образом, паразитная емкость представляет собой реальную проблему на высоких частотах, поскольку ее эффекты не сильно влияют на вещи на более низких частотах. Однако паразитная емкость, возникающая на высоких частотах, неожиданно соединяет, помимо прочего, опорную плоскость печатной платы с шасси. Обратите внимание, что паразитная емкость будет формироваться между любым проводящим телом , несущим заряд, поэтому паразитная или паразитная емкость может образоваться между антенной и грязью / землей / землей (и тем более, если земля влажная и, следовательно, более проводящая).Паразитная емкость может образоваться между металлическим столом и печатной платой, расположенной на нем (но в меньшей степени, если стол сделан из изоляционного материала). Конструкция схемы для высоких частот означает, что необходимо уделить дополнительное внимание конструкции, особенно в отношении компоновки печатной платы или размещения любого проводящего тела по отношению к другому проводящему телу.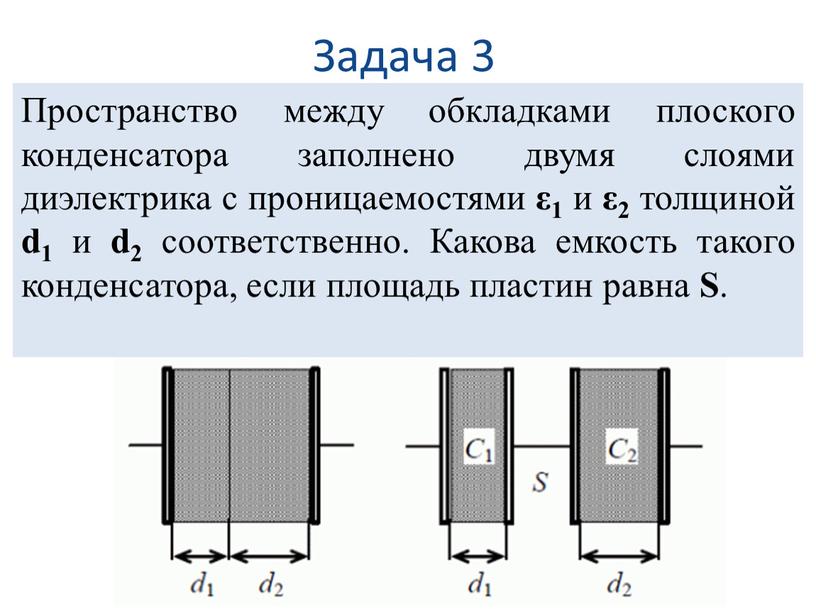
 Конденсатор, изолятор которого имеет относительную диэлектрическую проницаемость ε r1 = 1, имеет емкость C 1 = 1 мкФ. Какой будет его емкость, если заменить изолятор другим с ε r = 30? C. Если два конденсатора (C 1 и C) смещены напряжением V = 1 кВ, каковы будут их соответствующие заряды (Q 1 и Q)? Q1 Q 3. Каков характер зарядов Q 1 и Q? (а) свободный заряд, нанесенный на поверхность электрода (б) связанный заряд, нанесенный на поверхность изолятора у электрода (в) общий заряд на поверхности электрода-изолятора ЛЕКЦИЯ 14, слайд 4
Конденсатор, изолятор которого имеет относительную диэлектрическую проницаемость ε r1 = 1, имеет емкость C 1 = 1 мкФ. Какой будет его емкость, если заменить изолятор другим с ε r = 30? C. Если два конденсатора (C 1 и C) смещены напряжением V = 1 кВ, каковы будут их соответствующие заряды (Q 1 и Q)? Q1 Q 3. Каков характер зарядов Q 1 и Q? (а) свободный заряд, нанесенный на поверхность электрода (б) связанный заряд, нанесенный на поверхность изолятора у электрода (в) общий заряд на поверхности электрода-изолятора ЛЕКЦИЯ 14, слайд 4 l s l s в точке наблюдения P: V ln, V ln 1 l 1 V (P) V V ln y h h P r l s V s эквипотенциалы r x l ЛЕКЦИЯ 14 слайд 13
l s l s в точке наблюдения P: V ln, V ln 1 l 1 V (P) V V ln y h h P r l s V s эквипотенциалы r x l ЛЕКЦИЯ 14 слайд 13 ЛЕКЦИЯ 14 слайд 15
ЛЕКЦИЯ 14 слайд 15 : Граничные условия на
: Граничные условия на