Решение задач по теме Конденсаторы. Последовательное и парлалельное конденсаторов. Задачи на смешанное соединение конденсаторов с решением

Решение задач по теме Конденсаторы. Последовательное и парлалельное конденсаторов

Инфоурок › Физика › Презентации › Решение задач по теме Конденсаторы. Последовательное и парлалельное конденсаторов

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Решение задач по теме «Конденсаторы. Соединение конденсаторов.» Д\З Упр 17 1-4

2 слайд

Описание слайда:

Цель: познакомить с основными методами решения задач соединение конденсаторов№

3 слайд

Описание слайда:

Проверка домашнего задания запиши формулу Формула потенциала Формула напряженности Формула потенциала точечного заряда Формула напряженности электрического поля Электроемкость Формула электроёмкости плоского конденсатора Формула емкости при последовательном и параллельном соединении конденсаторов

4 слайд

Описание слайда:

Уровень А . Простые соединения Дано: C1=100 МкФ C2=200 МкФ C3=500 МкФ __________ С-? СИ: 1*10-4 Ф 2*10-4Ф 5*10-4Ф Решение: Это последовательное соединение

5 слайд

Описание слайда:

Уровень А . Простые соединения Дано: C1=100 МкФ C2=200 МкФ C3=500 МкФ __________ С-? СИ: 1*10-4 Ф 2*10-4Ф 5*10-4Ф Решение: Это параллельное соединение

6 слайд

Описание слайда:

Уровень Б . Составные соединения Дано: C1=100 МкФ C2=200 МкФ C3=500 МкФ __________ С-? СИ: 1*10-4 Ф 2*10-4Ф 5*10-4Ф Решение: Разобьём схему на два соединения а)параллельное соединение С2 иС3 б)последовательное соединение С23 и С1

7 слайд

Описание слайда:

Уровень Б . Составные соединения Дано: C1=100 МкФ C2=200 МкФ C3=500 МкФ __________ С-? СИ: 1*10-4 Ф 2*10-4Ф 5*10-4Ф Решение: Используя схему решения определите емкость цепи Нарисуйте оставшуюся аналогичную схему определите емкость цепи

8 слайд

Описание слайда:

Уровень Б . Составные соединения Дано: C1=100 МкФ C2=200 МкФ C3=500 МкФ __________ С-? СИ: 1*10-4 Ф 2*10-4Ф 5*10-4Ф Решение: Разобьём схему на два соединения а) последовательное соединение С2 и С1 б) параллельное соединение С12 и С3

9 слайд

Описание слайда:

10 слайд

Описание слайда:

Изобразите оставшиеся схемы и определите их общую ёмкость

11 слайд

Описание слайда:

Решение задач 1. Два заряженных металлических шара приводятся в соприкосновение. Чему будет равен заряд каждого шара после соприкосновения если С1=6мкФ, С2=3мкФ , а потенциалы равны 200 В, и 150 В 2. Два конденсатора емкости 2 и 1 мкФ соединены последовательно и присоединены к полюсам батареи с напряжением 120 В. Каково напряжение между обкладками первого и между обкладками второго конденсатора? 3. Какой заряд нужно сообщить батарее из двух лейденских банок емкости 0,0005 и 0,001 мкФ, соединенных параллельно, чтобы зарядить ее до напряжения 10 кВ? 4. Конденсатор, заряженный до напряжения 100 В, соединяется с конденсатором такой же емкости, но заряженным до 200 В, параллельно (т. е. положительная обкладка – с положительной, отрицательная – с отрицательной). Какое установится напряжение между обкладками? 5. Четыре одинаковых конденсатора соединены в одном случае параллельно, в другом – последовательно. В каком случае емкость этой группы конденсаторов больше и во сколько раз?

Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-427339

Пример решения задачи по теме «Соединение конденсаторов» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Примеры решения задач по электродинамике

Рис. 4.79. К задаче

Задача. Найти электроемкость системы конденсаторов, соединенных по схеме, показанной на рисунке 4.79. C1 = C2 = C4 = C5.

Решение.

Показанную на рис. 4.79 схему соединения конденсаторов можно изобразить иначе (рис. 4.80).

На схеме видно, что разность потенциалов между точками B и C равна нулю:

ΔφBC = 0.

Рис. 4.80. К задаче

Таким образом, ни один конденсатор, независимо от его электроемкости, присоединенный в точках B и C, не изменит электроемкости всей системы. Поэтому конденсатор C3 можно изъять из схемы и получить соединение по схеме рис. 4.81.

Общая электроемкость цепочки последовательно соединенных конденсаторов Q и C4 определится по формуле:

1 / C’ = 1 / C1 + 1 / C4,

или

C’ = C1C4 / (C1 + C4).

Рис. 4.81. К задаче

Такую же электроемкость будет иметь цепочка конденсаторов C2 и C5:

C’’ = C2C5 / (C2 + C5).

Вследствие параллельного соединения цепочек C1 — С4 и С2 — С5 их общая электроемкость Материал с сайта http://worldofschool.ru

C = С’ + C’’ = C1C4 / (C1 + C4) + C2C5 / (C2 + C5).

Если учесть, что C1 = C2 = C4 = C5, то получим

C = C12 / 2C1 + C12 / 2C1 = 2C12 / 2C1 = C1.

Ответ: общая электроемкость соединения конденсаторов равна C1.

На этой странице материал по темам:

Физика - задачи на комбинированное соединение конденсаторов
Задачи с смешаные соединения конденсатором
Соединения конденсаторов задачи
Конденсатор задачи с решениями
Примеры решения задач с двумя конденсаторами

worldofschool.ru

Задачи с конденсаторами: сборная солянка

В эту статью вошли задачи всех типов: здесь и определение эквивалентных емкостей, и напряжений между определенными точками схемы, и бесконечные цепочки, и даже исчезновение конденсаторов из схем (бесследное и без последствий).

Задача 1. Плоский конденсатор разрезают на равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторов соединяют последовательно. Чему равна емкость полученной батaреи конденсаторов, если емкость исходного конденсатора мкФ?

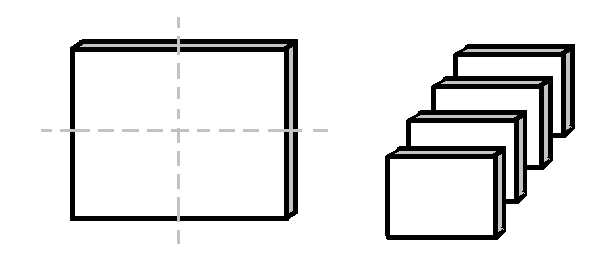
К задаче 1

Площадь исходного конденсатора:

Площадь нового конденсатора (одного) – в 4 раза меньше исходного (так как площадь меньше):

Теперь соединяем последовательно:

Ответ: 1 мкФ.

Задача 2. Два плоских конденсатора, емкостью каждый, соединили параллельно. В один из них вставили диэлектрическую пластину с проницаемостью , заполнившую весь объем конденсатора. Какой емкости и как необходимо подключить третий конденсатор, чтобы емкость системы стала равной ?

Так как первые два конденсатора соединены параллельно, то их емкости надо сложить, чтобы получить эквивалентную емкость:

После введения пластины емкость такого конденсатора стала равна , а эквивалентная емкость стала равна

Теперь к этой конструкции будем присоединять еще один конденсатор. Попробуем присоединить параллельно, тогда

Так как , то , .

Теперь присоединяем последовательно, тогда:

Решим неравенство:

Решение – – это решение не имеет смысла, .

Ответ: , при , параллельно.

, при , последовательно.

Задача 3. Разность потенциалов между точками А и В равна . Емкости конденсаторов известны. Определить заряды конденсаторов и разность потенциалов между точками А и D.

К задаче 3

Так как емкости и соединены параллельно, то напряжение на них одинаковое. Кроме того, заряды на емкостях и системе конденсаторов одинаковы, так как они соединены последовательно. Поэтому

Эквивалентная емкость , поэтому эквивалентная емкость всей схемы – произведение на сумму – .

Тогда заряд

Но вследствие (1)

Тогда

Находим :

Определим заряды и :

Ответ: , , , .Задача 4. Определить емкость батареи конденсаторов, показанной на рисунке, если мкФ, мкФ, мкФ.

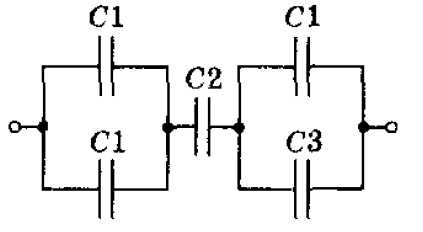
К задаче 4

Сначала два конденсатора подключены параллельно, при этом емкости складываются: . В конце параллельное соединение и : . Теперь имеем последовательное соединение емкостей , и . Тогда

Можно подставить числа и довести решение до конца:

Ответ: мкФ.

Задача 5. Найти емкость системы конденсаторов, изображенной на рисунке.

К задаче 5

На рисунке a) емкость оказывается незаряженной, так как схема совершенно симметрична и , поэтому .

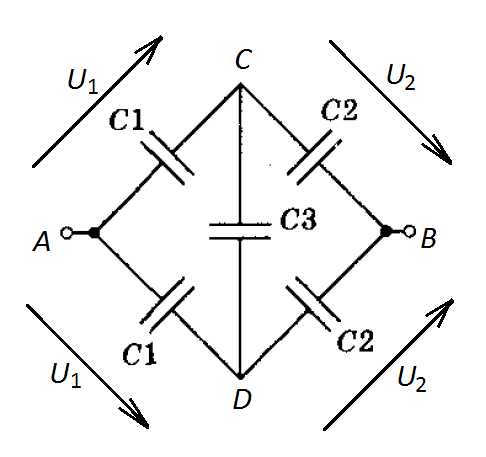
Рисунок 2 (задача 5)

Поэтому конденсатор не заряжен – разность потенциалов на его выводах нулевая. Следовательно, имеем две веточки, включенные в параллель: в каждой последовательное соединение и .

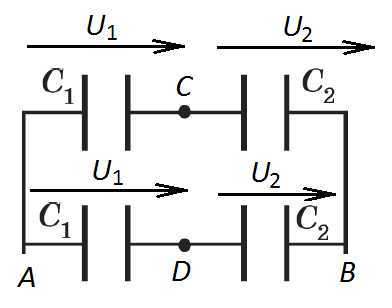
Рисунок 3 (к задаче 5)

Сопротивление одной ветки (емкость двух последовательно включенных конденсаторов – произведение, деленное на сумму):

А двух таких веток в параллель (емкости, включенные параллельно, складываются): .

На рисунке б) – если приглядеться, та же самая ситуация:

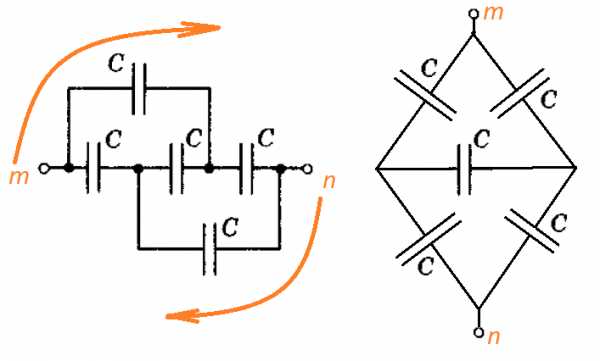
К задаче 5 – рисунок 4

Так что, аналогично первой схеме, сопротивление одной ветки с двумя последовательно включенными конденсаторами – , а две такие емкости в параллель дадут .

Ответ: а) ; б) .

Задача 6. Определить емкость Сх бесконечно длинной системы одинаковых конденсаторов, емкостью С каждый, соединенных друг с другом, как показано на рисунке.

К задаче 6, рисунок 1

Выделим в этой цепи повторяющийся элемент:

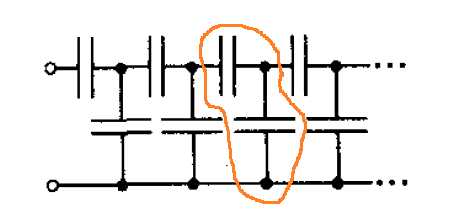
К задаче 6, рисунок 2

Эти элементы соединены параллельно. Так как емкость цепи бесконечна, то от нее не убудет, если мы один элемент удалим, или выделим. Тогда справа от выделенного элемента цепь с емкостью , и слева – тоже.

К задаче 6, рисунок 3

Можем записать для последовательно включенных емкостей:

Задача 7. Найти разность потенциалов между точками А и В в схеме, изображенной на рисунке. Емкость мкФ, мкФ, мкФ. Напряжение источника В.

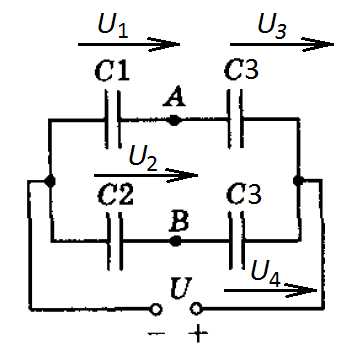
К задаче 7

Емкость верхней ветки:

Емкость нижней ветки:

Заряд верхней ветви (мкКл):

Заряд нижней ветви (мкКл):

Но соединен последовательно с , поэтому , и

Аналогично в нижней ветви:

В сумме .

Найдем разность потенциалов между точками и :

Ответ: B.

easy-physic.ru

Практическая работа по дисциплине Электротехника и электроника на тему "Расчет электрической цепи при смешанном соединении конденсаторов"

Практическая работа №1

Тема: Расчет электрической цепи при смешанном соединении конденсаторов.

Цель: Изучить методы соединения конденсаторов в электрических цепях постоянного тока. Рассчитать эквивалентную емкость, напряжение и заряд батареи конфденсаторов при смешанном соединении конденсаторов.

Ход работы:

Изучить свойства конденсаторов, способы соединения, формулы для определения основных величин.
Рассчитать эквивалентную емкость, напряжение и заряд батареи конденсаторов при смешанном соединении конденсаторов по заданному варианту.
Оформить отчет.

Теоретическая часть:

Сообщение электрического заряда проводнику называется электризацией. Чем больший заряд принял проводник, тем больше его электризация, или, иначе говоря, тем выше его электрический потенциал.

Между количеством электричества и потенциалом данного уединенного проводника существует линейная зависимость: отношение заряда проводника к его потенциалу есть величина постоянная:

Для какого-либо другого проводника отношение заряда к потенциалу есть также величина постоянная, но отличная от этого отношения для первого проводника.

Одной из причин, влияющих на эту разницу, являются размеры самого проводника. Один и тот же заряд, сообщенный различным проводникам, может создать различные потенциалы. Чтобы повысить потенциал какого-либо проводника на одну единицу потенциала, необходим определенный заряд.

Свойство проводящих тел накапливать и удерживать электрический заряд, измеряемое отношением заряда уединенного проводника к его потенциалу, называется электрической емкостью, или просто емкостью, и обозначается буквой С.

Приведенная формула позволяет установить единицу емкости.

Практически заряд измеряется в кулонах, потенциал в вольтах, а емкость в фарадах:

Емкостью в 1 фараду обладает проводник, которому сообщают заряд в 1 кулон и при этом потенциал проводника увеличивается на 1 вольт.

Единица емкости — фарада (обозначается ф или F) очень велика. Поэтому чаще пользуются более мелкими единицами — микрофарадой (мкф или ), составляющей миллионную часть фарады:

Устройство, предназначенное для накопления электрических зарядов, называется электрическим конденсатором. Конденсатор состоит из двух металлических пластин (обкладок), разделенных между собой слоем диэлектрика. Чтобы зарядить конденсатор, нужно его обкладки соединить с полюсами электрической машины. Разноименные заряды, скопившиеся на обкладках конденсатора, связаны между собой электрическим полем. Близко расположенные пластины конденсатора, влияя одна на другою, позволяют получить на обкладках большой электрический заряд при относительно невысокой разности потенциалов между обкладками. Емкость конденсатора есть отношение заряда конденсатора к разности потенциалов между его обкладками:

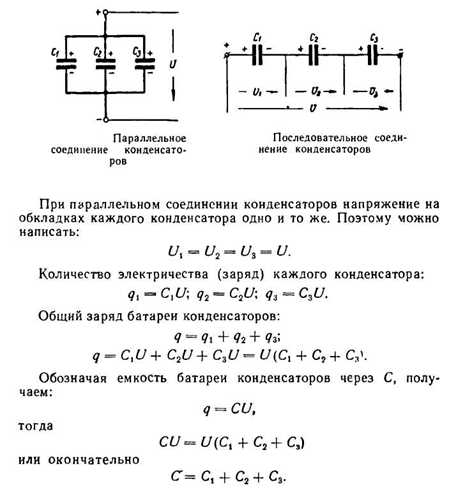
Следовательно, при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. При параллельном соединении каждый конденсатор окажется включенным на полное напряжение сети.Рассмотрим последовательное соединение конденсаторов:

Практическое задание:

Определить заряд, напряжение, энергию электрического поля каждого конденсатора, эквивалентную емкость цепи.

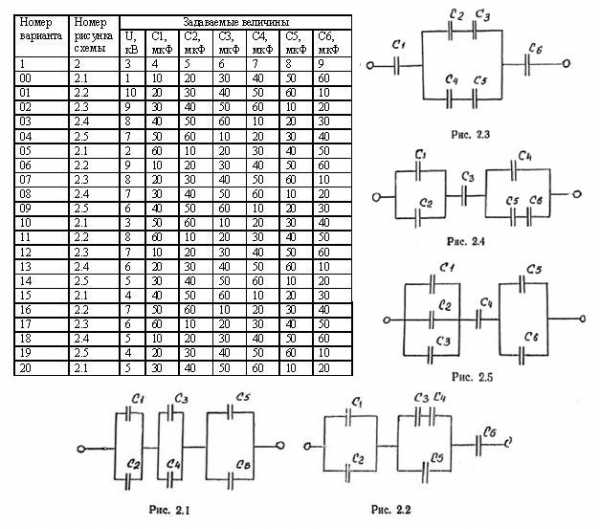
infourok.ru

Решение задач на смешанное соединение

Транскрипт

1 Решение задач на смешанное соединение Смешанным соединением называют такое соединение проводников, которое можно «разобрать» на участки последовательного и параллельного соединений Решим несколько задач из задачникa 7-9 класса: Генденштейн ЛЭ, Кирик ЛА, Гельфгат ИМ Задачи по физике для основной школы с примерами решений 7-9 классы Под ред ВА Орлова - М: Илекса, 0 Задача ( 9) Условие Найдите силу тока в каждом из резисторов (см рисунок) К цепи приложено напряжение 0 В, сопротивление каждого резистора 00 Ом Решение Несколько предварительных замечаний: В этой задаче резисторы пронумерованы Это удобно, так как все резисторы одинаковые, и объяснить применяемые формулы без нумерации было бы сложно Некоторые учащиеся из-за большого количества формул в решении любят записать закон Ома и законы соединений в ем виде, а затем показать только вычисления Это неправильно, формулы надо записывать для каждого конкретного случая, иначе невозможно доказать проверяющему, что знаешь законы, по которым рассчитываются электрические цепи Обозначать сопротивления резисторов будем в порядке нумерации, а вот ие сопротивления будем обозначать несколькими индексами Например, сопротивление резистора, а ее (эквивалентное) сопротивление резисторов,, 00Ом U = 0 В,,,,,? Начинать расчет схемы надо с того места цепи, где определенно просматривается последовательное или параллельное соединение Чаще всего самые простые участки лежат дальше всего от контактов схемы В данной схеме видно, что резисторы, и соединены последовательно Рассчитываем их сопротивление по законам последовательного соединения: = 00 Ом Теперь схему можно заменить «эквивалентной» схемой: заменяем резисторы, и резистором с вычисленным сопротивлением Из полученной схемы видно, что резисторы и соединены параллельно, а, значит, их сопротивление можно найти по формуле: Ом 00 Рисуем эквивалентную схему и видим, что оставшиеся резисторы соединены последовательно Находим ее сопротивление цепи: = 0 Ом Ну а теперь воспользуемся принципом, по которому, если две величины для элемента известны, можно найти третью по закону Ома Мы знаем ее сопротивление цепи и ее напряжение Можно найти «ую» силу тока, те силу тока, которая течет в неразветвленной цепи: U 0В 0, А Ом 0

2 Эта сила тока (обращаемся к последней эквивалентной схеме) протекает через резисторы, и группу резисторов :, Поскольку мы знаем силу тока, текущего через группу резисторов, можно найти напряжение U : U 0, 0 0В Возвращаемся еще на одну схему назад и видим, что это напряжение на резисторе и группе резисторов : U U U Находим силу тока на резисторе и на группе резисторов --: U 0 U 0 0, А, 0,0 А Можно проверить, что в сумме эти токи действительно дают ий ток 0, А Остается заметить, что, так как все эти три резистора включены последовательно Ответ: 0, А, 0, 0А, 0, А Послесловие После решения нескольких задач необходимость рисовать эквивалентные схемы в случае смешанного соединения проводников отпадает Но мы рассмотрим еще одну задачу с комментариями в виде эквивалентных схем Задача [ ] Условие Вычислите сопротивление цепи, представленной на рисунке, если = Ом Решение Пронумеруем резисторы, чтобы можно было записывать формулы Из рисунка сразу видно, что резисторы и соединены параллельно Все другие резисторы имеют контакты сразу с несколькими другими, так что «чистые» соединения невозможно распознать Заменим и эквивалентным сопротивлением: и нарисуем эквивалентную схему Следующее очевидное соединение это последовательное соединение резисторов и : Соответствующая эквивалентная схема - на рисунке Видно, что резисторы и соединены параллельно Находим ее сопротивление и рисуем эквивалентную схему: В последней схеме сразу ясно, что и соединены последовательно, а резистор параллельно им Получаем:,

3 Ответ: = Комментарии При определенном навыке такие задачи с резисторами одинаковых сопротивлений можно решать устно Действительно, для n резисторов сопротивлением, соединенных последовательно параллельно n справедливо: n Поэтому, если два резистора сопротивлением по соединены параллельно, сразу ясно, что их ее сопротивление равно Задачи для самостоятельного решения на нахождение его сопротивления цепи из того же задачника: 0,, 0,,, 7,, Задача [ в)] Условие Найдите силу тока в каждом из одинаковых резисторов К цепи приложено напряжение В, сопротивление резистора ком Решение В отличие от задачи здесь не надо находить ее сопротивление всей цепи, чтобы узнать ую силу тока Ведь эта сила тока складывается из трех, идущих по параллельным ветвям, и идет где-то за пределами рисунка В этой схеме важно увидеть, что ее напряжение является одновременно напряжением на каждой из трех параллельных ветвей: U U U Поэтому мы сразу можем найти токи, текущие через резисторы и : U U В U = ма, ма ком Мы также можем найти ток, протекающий через резисторы и, но для этого их надо представить в виде одного сопротивления, рассчитав эквивалентное сопротивление: U В ком, = ма ком Ответ: = = ма, = = ма Комментарии Часто в случае равных сопротивлений в схеме может возникнуть соблазн сказать: поскольку параллельно соединенные резисторы одинаковые, по ним течет одинаковый ток (например, токи и в предыдущей задаче) Действительно, при решении устных задач можно сказать: «в силу симметрии» токи будут одинаковы, но на письме (в контрольных работах и на экзамене) этот факт должен быть доказан n Последовательное соединение Параллельное соединение,, U U U, но U U U U, U U U, U но,

4 Задача [ ] Условие Найдите распределение токов и напряжений в цепи, изображенной на рисунке, если U ab = 00 В, = Ом, = Ом, = 7, Ом, = Ом, = Ом, = 0 Ом Решение Приведенная схема легко разделяется на три группы параллельных соединений Рассчитаем эффективную схему:, Ом, Ом Ом 0Ом 0Ом 0Ом Комментарии 0 Ом,Ом В расчетах, аналогичных последней строчке, встречается очень много ошибок: многие оставляют вместо сопротивления величину, обратную ему, забывая «перевернуть» дробь Или вовсе, переходят от величины, обратной сопротивлению, к самому сопротивлению с помощью знака равенства Это ошибки! Поэтому еще раз посмотрите на последнюю строчку: именно так надо переходить от одной формулы к другой Продолжим: найдем ее сопротивление цепи, 7,, 0Ом Uab Тогда ая сила тока будет равна 0А Именно такая сила тока будет в резисторе И такой же ток будет проходить через группы резисторов и Поэтому напряжения на этих группах резисторов и резисторе легко найти: U 0A, Ом В, U 0A7,Ом 7, В, U 0A,Ом, В Можно проверить себя: сумма всех трех напряжений должна быть равна ему напряжению U ab Каждое из напряжений U и U это напряжение на группе параллельно соединенных резисторов, а, значит и на каждом из этих резисторов: U = U = U и U = U = U = U Остается рассчитать силу тока в каждом из этих резисторов U U A, A, проверяем: U, U, U,,A,, A,, A 0 Проверяем: Ответ: = A, = A, = 0 A, =, A, =, A, =, A, U = B, U = B, U = 7, B, U =, B, U =, B, U =, B Послесловие Итак, если в задаче задано ее напряжение на схеме, чаще всего следует найти ее сопротивление цепи с тем, чтобы рассчитать ий ток Затем надо определить напряжения на отдельных участках и тд Но надо быть внимательным, если в схеме нет участка, по которому потечет ий ток, те представлено параллельное соединение как в задаче, на каждой ветви которого напряжение равно напряжению на всей цепи

5 Посмотрим, как рассчитать схему, если в задаче не дается ее напряжение, а задана одна из величин, напряжение или сила тока, для одного элемента цепи Задачи для самостоятельного решения на расчет сил токов и напряжений в цепи из этого же задачника: (а, б), 7,, 0,, 9, 0 Задача [ ] Условие Найдите распределение токов и напряжений в цепи, изображенной на рисунке, если вольтметр показывает В, а =, Ом, = Ом, = Ом, = Ом, = Ом, = Ом, 7 = 0 Ом Решение Будем использовать обычный принцип: если для резистора или группы резисторов известно две величины, можно найти третью Поскольку все сопротивления известны, достаточно даже одной известной величины: напряжения или силы тока Известно напряжение на первом резисторе найдем силу тока, текущего через него: U А = = Те мы отметили тот факт, что найденный ток течет также через другие группы резисторов Значит, можно найти напряжения на них, если будем знать эффективные сопротивления этих групп Ом, Ом, Ом Ом Ом Ом Ом Ом Ом A Ом В, U A, Ом В U Найдем силу тока в каждом из резисторов, учитывая, что в группах резисторы соединены параллельно, поэтому напряжения на группе равны напряжениям на отдельных резисторах: U U,7A,,A, проверяем: U U U A, A, A Проверяем: Резистор 7 параллелен всей группе резисторов, поэтому напряжение на нем должно быть равно напряжению на всей этой последовательной ветви групп резисторов: U7 U7 U U U В 7, 7А 7 0 Ответ: = A, =,7 A, =, A, =, A, =,7 A, = A, 7 =,7A, U = B, U = B, U = B, U = B, U = B, U = B, U 7 = B Задача для самостоятельного решения на расчет параметров резисторов цепи при заданном одном из того же задачника:

6 Так же для самостоятельного решения можно использовать следующие задачи = Ом = Ом = Ом = Ом Показания амперметра А = Ом = Ом = Ом = Ом Показания вольтметра В = Ом = Ом = Ом = Ом Показания амперметра А = Ом = Ом = Ом = Ом Показания вольтметра В = Ом = Ом = Ом = Ом Показания амперметра А

docplayer.ru

Лекция на тему: "Соединение конденсаторов"

ПЛАН УРОКА

Дисциплина: Электротехника

Тема: «Соединение конденсаторов»

Группа: А21

Тип урока: Комбинированный урок

Цель урока:

1. Познавательная:

- Формирование умения решать задачи при различных способах соединения конденсаторов

2. Развивающая: развитие умения формулировать проблему, предлагать способы ее решения

3. Воспитывающая: воспитание дисциплинированности в ходе проведения урока

Оборудование: раздаточный материал

Ход урока:

1.Организационный момент

Приветствие, запись даты и темы в журнале, отметить отсутствующих, объявление целей и хода урока

2.Постановка цели и задачи урока перед студентами:

Цель – освоить принципы нахождения параметров электрической цепи при различных способах соединения ее элементов

3.Проверка домашнего задания:

Проверка домашнего задания в виде проведения письменной работы 4 варианта по 2 задачи

Объяснение нового материала:

ПЛАН:

1.Последовательное соединение конденсаторов

2.Параллельное соединение конденсаторов

3.Смешанное соединение конденсаторов

4.Решение задач

ВОПРОС 1 Последовательное Соединение конденсаторов

Если соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 1).

Рисунок 1. Последовательное соединение конденсаторов.

В случае последовательно соединенных конденсаторов одинаковы заряды на всех конденсаторах Q1 = Q2 =…= Qn Действительно, если мы поместим, например, заряд на левую обкладку первого конденсатора, то вследствие индукции на правой его обкладке возникнет заряд , а на левой обкладке второго конденсатора – заряд . Наличие этого заряда на левой обкладке второго конденсатора опять-таки вследствие индукции создает на правой его обкладке заряд , а на левой обкладке третьего конденсатора – заряд и т. Д. Таким образом, заряд каждого из последовательно соединенных конденсаторов равен . Напряжение же на каждом из этих конденсаторов определяется емкостью соответствующего конденсатора:

, , …, ,

где – емкость одного конденсатора. Суммарное напряжение между крайними (свободными) обкладками всей группы конденсаторов

Следовательно, емкость всей системы конденсаторов

определяется выражением

Вопрос 2.

РИСУНОКМ 2

В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов , но заряды на них могут быть различными. Если емкости их равны , то соответствующие заряды будут

, , …, .

Общий заряд на всех конденсаторах

и, следовательно, емкость всей системы конденсаторов

. (35.1)

Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.

Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.

ВОПРОС 3

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 3 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 3. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 4.

Рисунок 4

Решение задачи

Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Рис. 6

Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно:

C12 = C1 + C2 = 200 мкФ,

эквивалентная емкость всей цепи равна:

C= C 12 ⋅ C 3 /C 12 + C 3 = 200⋅300/ 500 =120 мкФ.

Заряд на эквивалентной емкости:

Q = C·U = 120·10–6·240 = 288·10–4 Кл.

Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.

Напряжение на конденсаторах C1 и C2 равно

U1 = U2 = U – U3 = 240 – 96 = 144 В.

их заряды имеют следующие значения:

Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;

Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.

Первичная проверка понимания:

Определение емкости в общем виде

Закрепление материала

Рис. 6

Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.

Домашнее задание. Конспект

1. Четыре одинаковых конденсатора соединены в одном случае параллельно, в другом – последовательно. В каком случае емкость этой группы конденсаторов больше и во сколько раз?

2. Два конденсатора емкости 2 и 1 мкФ соединены последовательно и присоединены к полюсам батареи с напряжением 120 В. Каково напряжение между обкладками первого и между обкладками второго конденсатора?

Задачи для самостоятельного решения

1. Какой заряд нужно сообщить батарее из двух лейденских банок емкости 0,0005 и 0,001 мкФ, соединенных параллельно, чтобы зарядить ее до напряжения 10 кВ?

2. Конденсатор, заряженный до напряжения 100 В, соединяется с конденсатором такой же емкости, но заряженным до 200 В, параллельно (т. е. положительная обкладка – с положительной, отрицательная – с отрицательной). Какое установится напряжение между обкладками?

3. Два заряженных металлических шара одинакового диаметра приводятся в соприкосновение. Один из шаров – полый. Поровну ли распределятся заряды на обоих шарах?

Итог урока. Оценка знаний: Зафиксировать результат активной работы студентов на уроке

Просмотр содержимого документа «Лекция на тему: "Соединение конденсаторов" »

ПЛАН УРОКА

Дисциплина: Электротехника

Тема: «Соединение конденсаторов»

Группа: А21

Тип урока: Комбинированный урок

Цель урока:

Познавательная:

- Формирование умения решать задачи при различных способах соединения конденсаторов

Развивающая: развитие умения формулировать проблему, предлагать способы ее решения
Воспитывающая: воспитание дисциплинированности в ходе проведения урока

Оборудование: раздаточный материал

Ход урока:

1.Организационный момент

Приветствие, запись даты и темы в журнале, отметить отсутствующих, объявление целей и хода урока

2.Постановка цели и задачи урока перед студентами:

3.Проверка домашнего задания:

Проверка домашнего задания в виде проведения письменной работы 4 варианта по 2 задачи

Объяснение нового материала:

ПЛАН:

1.Последовательное соединение конденсаторов

2.Параллельное соединение конденсаторов

3.Смешанное соединение конденсаторов

4.Решение задач

ВОПРОС 1 Последовательное Соединение конденсаторов

Рисунок 1. Последовательное соединение конденсаторов.

, , …, ,

Следовательно, емкость всей системы конденсаторов

определяется выражением

Вопрос 2.

РИСУНОКМ 2

, , …, .

Общий заряд на всех конденсаторах

и, следовательно, емкость всей системы конденсаторов

. (35.1)

Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.

ВОПРОС 3

На рисунке 3 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 3. Последовательно-параллельное соединение конденсаторов.

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 4.

Рисунок 4

Решение задачи

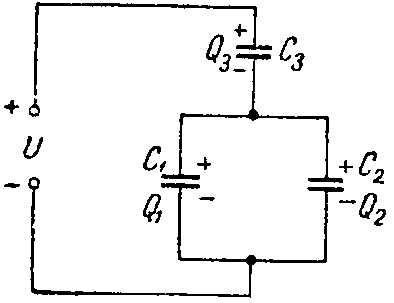
Рис. 6

Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно:

C12 = C1 + C2 = 200 мкФ,

эквивалентная емкость всей цепи равна:

C= C 12 ⋅ C 3 /C 12 + C 3 = 200⋅300/ 500 =120 мкФ.

Заряд на эквивалентной емкости:

Q = C·U = 120·10–6·240 = 288·10–4 Кл.

Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.

Напряжение на конденсаторах C1 и C2 равно

U1 = U2 = U – U3 = 240 – 96 = 144 В.

их заряды имеют следующие значения:

Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;

Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.

Первичная проверка понимания:

Определение емкости в общем виде

Закрепление материала

Рис. 6

Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.

Домашнее задание. Конспект

Задачи для самостоятельного решения

Итог урока. Оценка знаний: Зафиксировать результат активной работы студентов на уроке

kopilkaurokov.ru

Задачи по теме «Соединение конденсаторов» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Задачи по электродинамике

Четыре конденсатора имеют емкости 2пФ, 5пФ, 10пФ и 20пФ. Определить их общую емкость при параллельном и последовательном соединении.
Конденсатор переменной емкости состоит из 12 пластин, площадь каждой из которых составляет 10 см2. Воздушный зазор между соседними пластинами составляет 1 мм. Какую максимальную емкость имеет конденсатор?
Два конденсатора электроемкостью 2 мкФ и 4 мкФ соединены последовательно и заряжены так, что разность потенциалов между крайними точками соединения составляет 60 В. Найти заряд и разность потенциалов каждого конденсатора.
Два конденсатора, электроемкости которых 4 мкФ и 1 мкФ, соединены последовательно и заряжены от источника тока. Разность потенциалов на соединении составляет 220 В. Определить заряд и разность потенциалов на каждом конденсаторе.
Разность потенциалов на обкладках конденсатора электроемкостью 6 мкФ составляет 127 В. Его соединили параллельно с конденсатором, имеющим электроемкость 4 мкФ и разность потенциалов 220 В. Определить электроемкость батареи и разность потенциалов между ее выводами.

Ответы:

1. 37 пФ; 1,18 пФ. Материал с сайта http://worldofschool.ru

2. ≈ 102 пФ.

3. 8 • 10-5Кл; 40 В; 20 В.

4. 176 • 10-6 Кл; 44 В; 176 В.

5. 10 мкФ; 164 В.

На этой странице материал по темам:

Чотири конденсатори мають електроємності 2пф, 5пф, 10пф, 20пф
Смешанное соединение конденсаторов задачи с решением
Решение задачи на соединение конденсаторов в виде ромба
Чотири конденсатори мають ємность 2пф 5пф 10пф 20пф
Смешанное соединение конденсаторов решение задач

worldofschool.ru

Решение задач по теме Конденсаторы. Последовательное и парлалельное конденсаторов. Задачи на смешанное соединение конденсаторов с решением