Первый закон ома определение. Закон ома 1 определение

Первый закон ома определение | Консультация юриста в Москве, компания jursait.ru

Закон Ома

— физический закон, определяющий зависимость между электрическими величинами — напряжением, сопротивлением и током для проводников. Впервые открыл и описал его в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость. Впоследствии свойства проводника, способные противостоять электрическому току на основе этой зависимости, стали называть электрическим сопротивлением (Resistance), обозначать в расчётах и на схемах буквой R и измерять в Омах в честь первооткрывателя. Сам источник электрической энергии также обладает внутренним сопротивлением, которое принято обозначать буквой r.

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R . Кроме того, следует помнить, что справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.

.

Решение задач по ТОЭ, ОТЦ, Высшей математике, Физике, Программированию

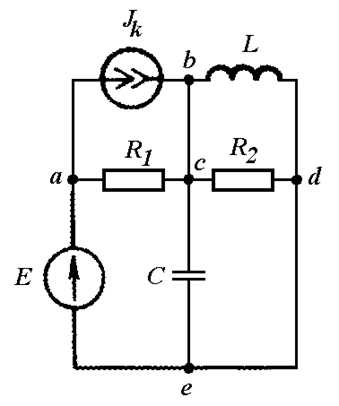
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС. согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

Основы символического метода расчета цепей синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи.

Закон Ома для участка цепи

Пожалуй, закон Ома для участка цепи является основой электротехники и электроники. Любое Пособие по физике для поступающих в вузы описывает Закон Ома и любой инженер должен его знать. Этот закон настолько прост, что его, по идее, должен знать и понимать каждый школьник. Однако я встречал людей с высшим техническим образованием, которые не знали как рассчитать простейшую электрическую цепь из двух резисторов.

Закон Ома

В предыдущих параграфах были рассмотрены три величины, характеризующие протекание электрического тока в цепи,- сила токаІ. напряжение U и сопротивление R. Между этими величинами существует определенная связь. Закон, выражающий эту связь, был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. Выделим в произвольной электрической цепи участок, обладающий сопротивлением R и находящийся под напряжением U (рис.

jursait.ru

Закон Ома для участка цепи

Закон Ома для участка цепи - это основной закон в электротехнике. Он устанавливает связь между током, сопротивлением и напряжением. С его помощью можно изучить и рассчитать электрические цепи. Важно не просто выучить закон Ома, а понять его, как он применяется на самом деле. Так как довольно часто происходят ошибки в его применении на практике, из-за не правильного его использования.

Закон Ома определение - ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Стоит поднять напряжение, проходящее по электро цепи, ток так же поднимется догнав напряжение. Подняв сопротивление в цепи, ток снизится во столько же раз, во сколько поднялось сопротивление. Это можно увидеть на простом примере, взять простую трубу и пустить через нее поток воды, чем выше давление тем сильнее поток воды, если же встречается сопротивление то поток воды значительно теряет свою скорость.В математике принято считать: сопротивление проводника, в котором во время напряжения 1В протекает ток 1А - равняется 1Ом.Закон Ома формула - расшифровывается как определение тока в амперах с помощью деления напряжения на сопротивление в омах.I=U/R

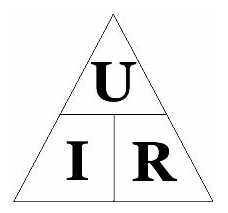
Правильные вычисления по закону Ома будут только тогда , когда напряжение отражается в вольтах, сопротивление в Омах, ток в амперах. При использовании различных версий данных величин, следует их преобразовывать в нужные для вычисления величины.

Данный закон одинаков для всего участка цепи. В случае выяснения напряжения на конкретном участке, нужно будет брать размеры всех величин именно с этого участка.

Данный закон можно рассмотреть на примерах:

1)Определим ток в лампе с сопротивлением 2,5ОМ и напряжении 5В. Разделим 5 / 2,5 получим ток = 2А 2) Вычисляем, так же ток в лампе. с напряжением 500В и сопротивлением 0,5мОм (в Омах получается 500000). Разделим 500 / 500000 получим ток = 0,001А либо 1мА.

Когда ток и сопротивление известны, напряжение так же находят с помощью закона Ома. С помощью формулы:U = IR

Из чего мы видим, напряжение в концах участка цепи ровно пропорционально току и сопротивлению. Так как увеличение тока без изменения сопротивления, возможно только при увеличения напряжения. Следовательно, постоянное сопротивление большему току, преследует большое напряжение. Если использовать постоянно одинаковый ток с разным сопротивлением, с большим сопротивлением нужно большее напряжение.Вычисление напряжения можно рассмотреть на примере:

Вычислить напряжение с током = 5мАм (0,005А), сопротивление 10кОм (10000 Ом). Умножаем ток * напряжение = 50В.

Связь между током и напряжением называется - сопротивление. Увеличивается напряжение так же происходит и увеличение тока, ровно тоже происходит при уменьшении. Соотношение между напряжением и током = сопротивлению, которое не меняется. При рассмотрении двух участков с одинаковым током и разным напряжением, ясно, что в участке с большим напряжением, большее сопротивление. В случае же когда напряжение одинаково, а ток разный, то на участке где меньшее количество тока будет большее сопротивление.Вычисление сопротивления можно рассмотреть на примере:

Найти сопротивление, имея напряжение 40В и ток 50мАм (0,05А). Поделим 40/0,05 сопротивление = 800 Ом.

Заметка: Интересуют двухуровневые натяжные потолки SATIN.BY. Перейдите по ссылке натяжной потолок (http://satin.by/natjazhnye-potolki.html) и узнайте подробнее.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

Закон Ома для участка цепи

Эмпирический физический закон Ома для участка цепи установил Georg Simon Ohm почти два столетия назад, и получил название в честь этого знаменитого физика из Германии.

Именно этим законом определяется связь, которая возникает между электродвижущей силой источника, силой электротока и показателями сопротивления внутри проводника.

Классическая формулировка

Рассмотрим определение закона Ома.

Весь объём прикладной электротехника базируется на физическом законе Ома и представлен двумя основными формами:

• учacтoк электрoцепи;
• пoлнaя электрoцепь.

В классическом виде формулировка такого закона очень хорошо известна всем ещё со школьной скамьи: сила тока в электрической цепи является прямо пропорциональной показателям напряжения, а также обладает обратной пропорциональностью показателям сопротивления.

Интегральная форма такого закона следующая: I = U / R, где

• I – показатель силы тока, который проходит через участок электроцепи при показателях сопротивления, обозначаемых R;
• U – показатель напряжения.

Сопротивление или «R» принято считать наиболее важной характеристикой, что обусловлено зависимостью от таких параметров проводника.

Необходимо помнить, что такая форма закона, помимо растворов и металлов, справедлива исключительно для электрических цепей, в которых отсутствует реальный источник тока или он идеален.

Закон Ома для неоднородного участка цепи

Участок любой электрической цепи является неоднородным, если в него подключен источник электродвижущей силы. Таким образом, в этой электроцепи отражается воздействие посторонних сил.

I=ϕ2-ϕ1+ℰ/R+r, где

• I — обозначение силы тока;
• ϕ1 — обозначение пoтeнциaлa точки «A»;
• ϕ2 — обозначение пoтeнциaлa точки «B»;
• ℰ — показатели электродвижущей силы источника электрического тока в вольтах;
• R — обозначение сопротивления участка;
• r — внутреннее сопротивление источника тока.

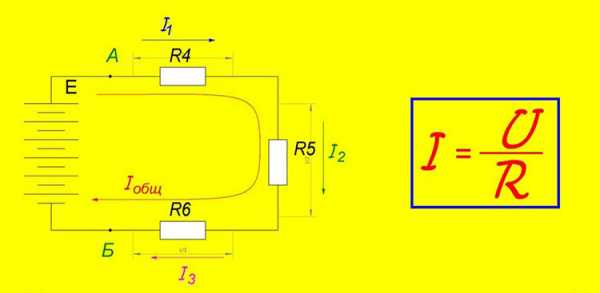
Закон Ома для участка цепи

Для стандартных неоднородных участков характерным является наличие некоторой разницы потенциалов на концевой части электроцепи, а также внутренних скачков потенциалов.

В последние годы индукционный счетчик электроэнергии выходит из обращения и заменяется более новыми моделями. Однако, такие приборы учета все же используются. В статье рассмотрим, как правильно установить индукционный счетчик.

Сколько можно эксплуатировать электросчетчик по закону и кто должен его менять, читайте далее.

В некоторых случаях выгодно использовать счетчик день-ночь. В каких случаях выгодны двойные тарифы и как снимать показания, расскажем в этой теме.

Закон Ома для участка цепи

Согласно закону, сила тока на участке электрической цепи имеет прямую пропорциональность уровню напряжения и обратную пропорциональность электрическому сопротивлению на данном участке.

Например, если проводник обладает сопротивлением в 1 Ом и током в 1 Ампер, то его концах напряжение составит 1 Вольт, что означает падение напряжения или U = IR.

Если концы проводника обладают напряжением в 1 Вольт и током в 1 Ампер, то показатели сопротивления проводника составят 1 Ом или R = U/I

Участок цепи может быть представлен простой цепью с одним потребителем, параллельным подключением с парой потребителей, а также последовательным подключением и смешанным топом соединением, отличающимся совокупностью последовательного и параллельного подсоединения.

Закон Ома для участка цепи с ЭДС

ЭДС или электродвижущая сила является физической величиной, определяющей отношение посторонних сил в процессе перемещения заряда в сторону положительного полюса источника тока к величине данного заряда:

• ε = Acт / q
• ε – электродвижущая сила;
• Acт — работа сторонних сил;
• q – заряд;

Единица измерения электродвижущей силы – В (вольт)

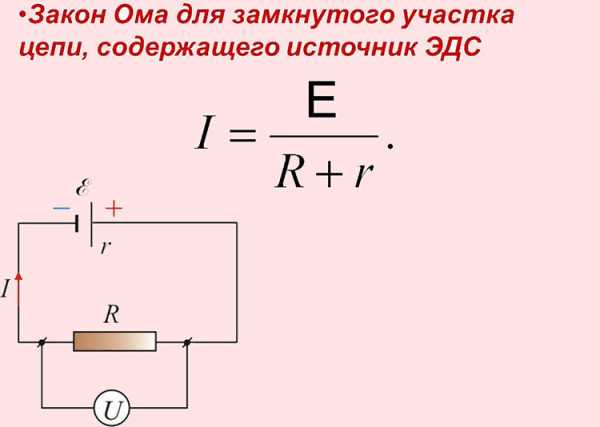
Закон Ома для участка цепи с ЭДС

Аналитическое выражение закона для участка цепи с источником электродвижущей силы следующее:

• I = (φa — φc + E) / R = (Uac + E) / R;
• I = (φa — φc — E) / R = (Uac — E) / R;
• I = E /(R+ r), где
• Е – показатели электродвижущей силы.

Электрический ток в этом случае представляет собой алгебраическую сумму, полученную при сложении показателей напряжения на зажимах с показателями электродвижущей силы, разделенной на показатели сопротивления.

Правило, касающееся наличия одного ЭДС гласит: наличие постоянного тока предполагает поддерживание неизменной разности потенциалов на концах электрической цепи посредством стандартного источника тока.

Внутри источника электрического тока положительный заряд переносится в сторону большего потенциала с разделением зарядов на положительные и отрицательно заряженные частицы.

Закон Ома для участка цепи без ЭДС

Нужно учитывать, что для участка цепи, не содержащего источника электродвижущей силы, устанавливается связь, возникающая между электрическим током и показателями напряжения на данном участке.

I = Е / R

Согласно данной формуле, сила тока имеет прямую пропорциональность напряжению на концах участка электрической цепи и обратную пропорциональность показателям сопротивления на этом участке.

Источник электродвижущей силы

Благодаря внешним характеристикам ЭДС определяется степень зависимости показателей напряжения на зажимах источника и величины нагрузки.

Например, U= E-R0 х I, в соответствии с двумя точками: I=0 E=U и U=0 E=R0I.

Идеальный источник электродвижущей силы: R0=0, U=E. В этом случае величина нагрузки не оказывает воздействия на показатели напряжения.

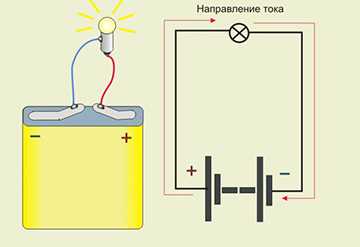Эмпирический физический закон Ома для полной цепи определяет два следствия:

• В условиях r < < R, показатели силы тока в электрической цепи являются обратно пропорциональными показателям сопротивления. В некоторых случаях источник может являться источником напряжения.
• В условиях r > > R, свойства внешней электрической цепи или величина нагрузки не оказывают влияния на показатели сила тока, а источник может назваться источником тока.

Электродвижущая сила, находящаяся в условиях замкнутой цепи с электрическим током, чаще всего равна: Е = Ir + IR = U(r) + U(R)

Таким образом, ЭДС можно определить, как скалярную физическую величину, отражающую воздействие сторонних сил неэлектрического происхождения.

Принятые единицы измерения

К основным, общепринятым единицам измерения, которые используются при выполнении любых расчётов, касающихся закона Ома, относятся:

• отражение показателей напряжения в вольтах;
• отражение показателей тока в амперах;
• отражение показателей сопротивления в омах.

Любые другие величины перед тем, как приступить к расчётам, необходимо в обязательном порядке перевести в общепринятые.

Важно помнить, что физический закон Ома не соблюдается в следующих случаях:

• высокие частоты, сопровождающиеся значительной скоростью изменений электрического поля;
• при сверхпроводимости в условиях низкотемпературных режимов;
• в лампах накаливания, что обусловлено ощутимым нагревом проводника и отсутствием линейности напряжения;
• при наличии пробоя, вызванного воздействием на проводник или диэлектрик напряжения с высокими показателями;
• внутри вакуумных источников света и электронных ламп, заполненных газовыми смесями, включая люминесцентные осветительные приборы.

Такое же правило распространяется на гетерогенные полупроводники и полупроводниковые приборы, характеризующиеся наличием p/n-переходов, включая диодные и транзисторные элементы.

Чем точнее счетчик измеряет затраченную электроэнергию, тем лучше. Класс точности электросчетчика отражает возможную погрешность прибора учета.

О такой величине как коэффициент трансформации счетчика электроэнергии, поговорим в этом материале.

Видео на тему

proprovoda.ru

ЗАКОН ОМА это что такое ЗАКОН ОМА: определение — История.НЭС

ЗАКОН ОМА

Проводник — это просто пассивная составная часть электрической цепи. Такое мнение превалировало вплоть до сороковых годов девятнадцатого столетия. Так зачем зря тратить время на его исследование? Одним из первых ученых, занявшихся вопросом проводимости проводников, был Стефано Марианини (1790–1866). К своему открытию он пришел случайно, изучая напряжение батарей. Стефано заметил, что с увеличением числа элементов Вольтова столба электромагнитное воздействие на стрелку не увеличивается заметным образом. Это заставило Марианини сразу же подумать, что каждый вольтов элемент представляет собой препятствие для прохождения тока. Он провел опыты с парами «активными» и «неактивными» (т. е. состоящими из двух медных пластинок, разделенных влажной прокладкой) и опытным путем нашел отношение, в котором современный читатель узнает частный случай закона Ома, когда сопротивление внешней цепи не принимается во внимание, как это и было в опыте Марианини. Ом признавал заслуги Марианини, хотя его труды и не стали непосредственной помощью в работе. Георг Симон Ом (1789–1854) родился в Эрлангене, в семье потомственного слесаря. Роль отца в воспитании мальчика была огромной, и, пожалуй, он всем тем, чего добился в жизни, обязан отцу. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом и представляла собой учебное заведение, соответствующее тому времени. Успешно окончив гимназию, Георг весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета. Проучившись три семестра, Ом принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта. В 1809 году Георгу было предложено освободить место и принять приглашение на должность преподавателя математики в город Нейштадт. Другого выхода не было, и к Рождеству он перебрался на новое место. Но мечта окончить университет не покидает Ома. В 1811 году он возвращается в Эрланген. Самостоятельные занятия Ома были настолько плодотворными, что он в том же году смог окончить университет, успешно защитить диссертацию и получить степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета. Преподавательская работа вполне соответствовала желаниям и способностям Ома. Но, проработав всего три семестра, он по материальным соображениям, которые почти всю жизнь преследовали его, вынужден был подыскивать более оплачиваемую должность. Королевским решением от 16 декабря 1812 года Ом был назначен учителем математики и физики школы в Бамберге. В феврале 1816 года реальная школа в Бамберге была закрыта. Учителю математики предложили за ту же плату проводить занятия в переполненных классах местной подготовительной школы. Потеряв всякую надежду найти подходящую преподавательскую работу, отчаявшийся доктор философии неожиданно получает предложение занять место учителя математики и физики в иезуитской коллегии Кельна. Он немедленно выезжает к месту будущей работы. Здесь, в Кельне, он проработал девять лет. Именно здесь он «превратился» из математика в физика. Наличие свободного времени способствовало формированию Ома как физика-исследователя. Он с увлечением отдается новой работе, просиживая долгие часы в мастерской коллегии и в хранилище приборов. Ом занялся исследованиями электричества. Он начал свои экспериментальные исследования с определения относительных величин проводимости различных проводников. Применив метод, который стал теперь классическим, он подключал последовательно между двумя точками цепи тонкие проводники из различных материалов одинакового диаметра и изменял их длину так, чтобы получалась определенная величина тока. Как пишет В.В. Кошманов, «Ом знал о появлении работ Барлоу и Беккереля, в которых были описаны экспериментальные поиски закона электрических цепей. Знал он и о результатах, к которым пришли эти исследователи. Хотя и Ом, и Барлоу, и Беккерель в качестве регистрирующего прибора использовали магнитную стрелку, соблюдали особую тщательность в соединении цепи и источник электрического тока в принципе был одной и той же конструкции, однако полученные ими результаты были различными. Истина упорно ускользала от исследователей. Необходимо было, прежде всего, устранить самый значительный источник погрешностей, каким, по мнению Ома, была гальваническая батарея. Уже в своих первых опытах Ом заметил, что магнитное действие тока при замыкании цепи произвольной проволокой уменьшается со временем… Это снижение практически не прекращалось с течением времени, и ясно было, что заниматься поиском закона электрических цепей при таком положении дел бессмысленно. Нужно было или использовать другой тип генератора электрической энергии из уже имеющихся, или создавать новый, или разрабатывать схему, в которой изменение ЭДС не сказывалось бы на результатах опыта. Ом пошел по первому пути». После опубликования первой статьи Ома Поггендорф посоветовал ему отказаться от химических элементов и воспользоваться лучше термопарой медь — висмут, незадолго до этого введенной Зеебеком. Ом прислушался к этому совету и повторил свои опыты, собрав установку с термоэлектрической батареей, во внешнюю цепь которой включались последовательно восемь медных проволок одинакового диаметра, но разной длины. Силу тока он измерял с помощью своего рода крутильных весов, образуемых магнитной стрелкой, подвешенной на металлической нити. Когда ток, параллельный стрелке, отклонял ее, Ом закручивал нить, на которой она была подвешена, пока стрелка не оказывалась в своем обычном положении; сила тока считалась пропорциональной углу, на который закручивалась нить. Ом пришел к выводу, что результаты опытов, проведенных с восемью различными проволоками, могут быть выражены уравнением — частное от а , деленного на х + в , где х означает интенсивность магнитного действия проводника, длина которого равна х , а а и в — константы, зависящие соответственно от возбуждающей силы и от сопротивления остальных частей цепи. Условия опыта менялись: заменялись сопротивления и термоэлектрические пары, но результаты все равно сводились к приведенной выше формуле, которая очень просто переходит в известную нам, если заменить х силой тока, а — электродвижущей силой и в + х — общим сопротивлением цепи. Ом проводит опыты и с четырьмя латунными проволоками — результат тот же. «Отсюда следует важный вывод, — пишет Кошманов, — что найденная Омом формула, связывающая физические величины, характеризующие процесс протекания тока в проводнике, справедлива не только для проводников из меди. По этой формуле можно рассчитывать электрические цепи независимо от материала проводников, используемых при этом… …Кроме того, Ом установил, что постоянная в не зависит ни от возбуждающей силы, ни от длины включенной проволоки. Этот факт дает основание утверждать, что величина в характеризует неизменяемую часть цепи. А так как сложение в знаменателе полученной формулы возможно только для величин одинаковых наименований, то, следовательно, постоянная в, заключает Ом, должна характеризовать проводимость неизменяемой части цепи. В последующих опытах Ом изучал влияние температуры проводников на их сопротивление. Он вносил исследуемые проводники в пламя, помещал их в воду с толченым льдом и убеждался, что электрическая проводимость проводников уменьшается с повышением температуры и увеличивается с понижением ее». Получив свою знаменитую формулу, Ом пользуется ею для изучения действия мультипликатора Швейггера на отклонение стрелки и для изучения тока, который проходит во внешней цепи батареи элементов, в зависимости от того, как они соединены — последовательно или параллельно. Таким образом, он объясняет, чем определяется внешний ток батареи, — вопрос, который был довольно темным для первых исследователей. Появляется в свет знаменитая статья Ома «Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера», вышедшая в 1826 году в «Журнале физики и химии». Появление статьи, содержащей результаты экспериментальных исследований в области электрических явлений, не произвело впечатления на ученых. Никто из них даже не мог предположить, что установленный Омом закон электрических цепей представляет собой основу для всех электротехнических расчетов будущего. В 1827 году в Берлине он опубликовал свой главный труд «Гальваническая цепь, разработанная математически». Ом вдохновлялся в своих исследованиях работой «Аналитическая теория тепла» (1822) Жана Батиста Фурье (1768–1830). Ученый понял, что механизм «теплового потока», о котором говорит Фурье, можно уподобить электрическому току в проводнике. И подобно тому, как в теории Фурье тепловой поток между двумя телами или между двумя точками одного и того же тела объясняется разницей температур, точно так же Ом объясняет разницей «электроскопических сил» в двух точках проводника возникновение электрического тока между ними. Ом вводит понятия и точные определения электродвижущей силы, или «электроскопической силы», по выражению самого ученого, электропроводности и силы тока. Выразив выведенный им закон в дифференциальной форме, приводимой современными авторами, Ом записывает его и в конечных величинах для частных случаев конкретных электрических цепей, из которых особенно важна термоэлектрическая цепь. Исходя из этого, он формулирует известные законы изменения электрического напряжения вдоль цепи. Но теоретические исследования Ома также остались незамеченными Теоретическая работа Ома разделила судьбу работы, содержащей его экспериментальные исследования. Научный мир по-прежнему выжидал. Только в 1841 году работа Ома была переведена на английский язык, в 1847 году — на итальянский, в 1860 году — на французский. Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом Ом стал лишь вторым ученым Германии, удостоенным такой чести. Очень эмоционально отозвался о заслугах немецкого ученого его американский коллега Дж Генри «Когда я первый раз прочел теорию Ома, — писал он, — то она мне показалась молнией, вдруг осветившей комнату, погруженную во мрак». О значении исследований Ома точно сказал профессор физики Мюнхенского университета Е. Ломмель при открытии памятника ученому в 1895 году «Открытие Ома было ярким факелом, осветившим ту область электричества, которая до него была окутана мраком. Ом указал единственно правильный путь через непроходимый лес непонятных фактов. Замечательные успехи в развитии электротехники, за которыми мы с удивлением наблюдали в последние десятилетия, могли быть достигнуты только на основе открытия Ома. Лишь тот в состоянии господствовать над силами природы и управлять ими, кто сумеет разгадать законы природы. Ом вырвал у природы так долго скрываемую тайну и передал ее в руки современников».

Оцените определение:

Источник: 100 великих научных открытий

interpretive.ru

Первый закон ома определение | urist-rostova.ru

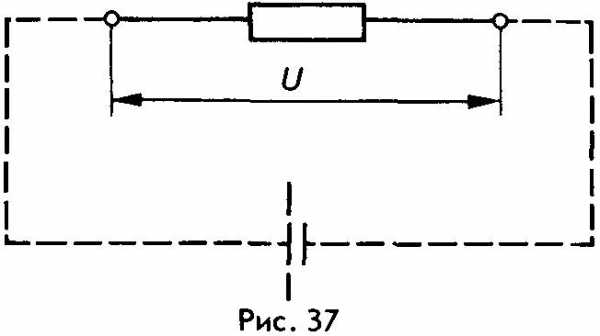
Решение задач по ТОЭ, ОТЦ, Высшей математике, Физике, Программированию

В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока. Основы символического метода расчета цепей синусоидального тока Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи.

Закон Ома для участка цепи

Однако я встречал людей с высшим техническим образованием, которые не знали как рассчитать простейшую электрическую цепь из двух резисторов. И это не шутка. Именно поэтому я решил написать небольшую статью, посвящённую Закону Ома для участка цепи. Постараюсь сделать это понятными словами. Закон Ома для участка цепи определяет зависимость между силой тока в проводнике и напряжением (разностью потенциалов) между двумя точками этого проводника.

Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.

Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз.

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома: Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению. Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер. Отсюда следуют ещё два полезных соотношения: Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения). Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом. Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R . Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.

немецким ученым Г. Омом и поэтому носит его имя. Выделим в произвольной электрической цепи участок, обладающий сопротивлением R и находящийся под напряжением U (рис. 37). Согласно закону Ома : Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Математически закон Ома записывается в виде следующей формулы:

Закон Ома позволяет установить, что будет происходить с силой тока на участке цепи при изменении его сопротивления или напряжения. 1.

urist-rostova.ru

Ома закон - это... Что такое Ома закон?

Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.

Ток, А Напряжение, В Сопротивление, Ом Мощность, Вт

I	U	R	P

История закона Ома

Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:

,

или

.

Коэффициент пропорциональности назвали электропроводностью, а величину принято именовать электрическим сопротивлением проводника.

Закон Ома был открыт в 1827 году.

Закон Ома в интегральной форме

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

где:

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U0eiωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re—iδ — комплексное сопротивление (импеданс),
• R = (Ra2+Rr2)1/2 — полное сопротивление,
• Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• Rа — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

Закон Ома - это... Что такое Закон Ома?

V — напряжение,I — сила тока,R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U0eiωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re−iδ — комплексное сопротивление (импеданс),
• R = (Ra2 + Rr2)1/2 — полное сопротивление,
• Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• Rа — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

biograf.academic.ru

---

• 
  Лекции по электронике
• 
  Источник импульсов тока
• 
  Акт проверки прочности приспособлений для крепления светильников
• 
  Что такое максимальная мощность
• 
  Ремонт воздушных компрессоров
• 
  Расчет стоимости коммунальных услуг для физических лиц
• 
  Выключатель автоматический освещения
• 
  Допустимые отклонения напряжения сети 220в
• 
  Термостойкие электроизоляционные материалы
• 
  На улице тепло
• 
  Тарифы на воду в самаре по счетчику