Закон Ома для переменного тока
После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.
При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
где
- I [А] – сила тока,
- U [В] – напряжение,
- Z [Ом] – полное сопротивление цепи.
Полное сопротивление цепи
В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:
Полное сопротивление цепи переменного тока можно вычислить по формуле:
где
- — индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
- — емкостное сопротивление, создается конденсатором.
Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.
Рис.1. Треугольник сопротивлений
Учитывая последние равенства, запишем формулу закона Ома для переменного тока:
– амплитудное значение силы тока.
Рис.2. Последовательная электрическая цепь из R, L, C элементов.
Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:
Решение задач:
Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?
На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?
Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
где, U-напряжение на элементе цепи,
I – ток через элемент цепи
R – активное сопротивление элемента
Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
|
| (2) |
где, Um-амплитудное значение напряжения на элементе цепи,
Im – амплитудное значение тока через элемент цепи
R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
Фаза тока отстает от фазы напряжения на 90 градусов.
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
|
| (3) |
|
| (4) |
где — UL-падение напряжение на чисто индуктивном сопротивлении ;
UС—падение напряжения на чисто емкостном сопротивлении;
I— значение тока в через реактивное сопротивление;
L— индуктивность реактивного элемента;
C— емкость реактивного элемента;
ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
|
| (5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Закон Ома для различных типовых цепей переменного тока
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
|
| (6) |
где —эффективное значение силы тока в А;
U—эффективное значение напряжения в В;
R—активное сопротивление в Ом;
ωL—индуктивное сопротивление в ом.
Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
|
| (7) |
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
|
| (8) |
где I-сила тока в А;
U-напряжение в В;
R-активное сопротивление в Ом;
ωL-индуктивное сопротивление в Ом;
1/ωС-емкостное сопротивление в Ом.
Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
формула взаимосвязи между электрическими величинами, порядок расчета
Фундаментальным положением, описывающим зависимость тока, сопротивления и напряжения друг от друга является закон Ома для цепи переменного тока. Основное его отличие от одноимённого положения для участка цепи заключается в учёте полного сопротивления. Эта величина зависит от активной и реактивной составляющей линии, то есть учитывает ёмкость и индуктивность. Поэтому и расчёт параметров для полной цепи по сравнению с участком выполнить будет сложнее.
Основное его отличие от одноимённого положения для участка цепи заключается в учёте полного сопротивления. Эта величина зависит от активной и реактивной составляющей линии, то есть учитывает ёмкость и индуктивность. Поэтому и расчёт параметров для полной цепи по сравнению с участком выполнить будет сложнее.
Основные понятия
Вся наука электротехника построена на оперировании такими понятиями, как заряд и потенциал. Кроме этого, важными явлениями в цепи являются электрические и магнитные поля. Для того чтобы разобраться в сущности закона Ома, необходимо понимать, что представляют собой эти величины, и от чего зависят те или иные электромагнитные процессы.
Электричеством называется явление, обусловленное взаимодействием зарядов между собой и их движением. Это слово было введено в обиход Уильямом Гилбертом в 1600 году после открытия им способности некоторых тел наэлектризовываться. Так как свои эксперименты он проводил с кусочками янтаря, то и свойство притягивать или отталкивать ими другие вещества им было названо «янтарностью», что в переводе с греческого звучит как электричество.
В дальнейшем различными ученными, такими как Эрстед, Ампер, Джоуль, Фарадей, Вольт, Ленц и Ом был открыт ряд явлений. Благодаря их исследованиям в обиходе появились понятия: электромагнитная индукция и поле, гальванический элемент, ток и потенциал. Ими была открыта связь между электричеством и магнетизмом, что привело к появлению науки, изучающей теорию электромагнитных явлений.
В 1880 году русский инженер Лачинов теоретически указал, какие условия необходимы для передачи электричества на расстояния. А через 8 лет Генрих Рудольф Герц во время экспериментов зарегистрировал электромагнитные волны.
Таким образом было установлено, что электрические заряды способны создавать вокруг себя электрическое излучение. Условно их разделили на частицы с положительным и отрицательным знаком заряда. Было установленно, что одноимённого знака заряды притягиваются, а разноимённого — отталкиваются. Для возникновения их движения к физическому телу необходимо приложить какую-либо энергию. При их перемещении возникает магнитное поле.
При их перемещении возникает магнитное поле.
Свойство материалов обеспечивать движение зарядов получило название проводимость, а величина, обратная ей, — сопротивление. Способность пропускать через себя заряды зависит от структуры кристаллической решётки вещества, её связей, дефектов и содержания примесей.
Определение напряжения
Учёными было установлено, что существует два вида перемещения зарядов — хаотичное и направленное. Первый тип не приводит ни к каким процессам, так как энергия находится в сбалансированном состоянии. Но если к телу приложить силу, заставляющую заряды следовать в одну сторону, то возникнет электрический ток. Существует два вида:
- Постоянный — сила и направление которого остаются постоянными во времени.
- Переменный — имеющий разную величину в определённой точке времени и изменяющий своё движение, при этом повторяющий через равные интервалы времени своё изменение (цикл).
 Эта переменчивость описывается по гармоническому закону синуса или косинуса.
Эта переменчивость описывается по гармоническому закону синуса или косинуса.
Заряд характеризуется таким понятием, как потенциал, то есть количеством энергии, которой он обладает. Необходимая сила для перемещения заряда из одной точки тела в другую называется напряжением.
Определяется она относительно изменения потенциала заряда. Сила тока определяется отношением количества заряда, прошедшего через тело за единицу времени, к величине этого периода. Математически она описывается выражением: Im = ΔQ/ Δt, измеряется в амперах (A).
Относительно переменного сигнала вводится дополнительная величина — частота f, которая определяет цикличность прохождения сигнала f = 1/T, где T — период. За её единицу измерения принят герц (Гц). Исходя из этого синусоидальный ток выражается формулой:
I = Im * sin (w*t+ Ψ), где:
- Im — это сила тока в определённый момент времени;
- Ψ — фаза, определяемая смещением волны тока по отношению к напряжению;
- w — круговая частота, эта величина зависит от периода и равна w = 2*p*f.

Напряжение же характеризуется работой, которую совершает электрическое поле для переноса заряда из одной точки в другую. Определяется она как разность потенциалов: Um = φ1 — φ2. Затрачиваемая работа же складывается из двух сил: электрических и сторонних, называется электродвижущей (ЭДС). Зависит она от магнитной индукции. Потенциал же равен отношению энергии взаимодействия заряда окружающего поля к значению его величины.
Поэтому для гармонического изменения сигнала значение напряжения выражается как:
U = Um * sin (w*t + Ψ).
Где Um — амплитудное значение напряжения. Измеряется переменное напряжение в вольтах (В).
Импеданс цепи
Каждое физическое тело имеет своё сопротивление. Обусловлено оно внутренним строением вещества. Характеризуется эта величина свойством проводника препятствовать прохождению тока и зависит от удельного электрического параметра. Определяется по формуле: R = ρ*L/S, где ρ — удельное сопротивление, являющееся скалярной величиной, Ом*м; L — длина проводника; м; S — площадь сечения, м2. Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.
Определяется по формуле: R = ρ*L/S, где ρ — удельное сопротивление, являющееся скалярной величиной, Ом*м; L — длина проводника; м; S — площадь сечения, м2. Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.
В то же время импеданс, полное сопротивление, находится как сумма пассивной и реактивной составляющей. Первая определяется только активным сопротивлением, состоящим из резистивной нагрузки источника питания и резисторов: R = R0 + r. Вторая находится как разность между ёмкостным и индуктивным сопротивлением: X = XL-Xc.
Если в электрическую цепь поместить идеальный конденсатор (без потерь), то после того, как на него поступит переменный сигнал, он зарядится. Ток начнёт поступать далее, в соответствии с периодами его заряда и разряда. Количество электричества, протекающее в цепи, равно: q = C * U, где С — ёмкость элемента, Ф; U — напряжение источника питания или на обкладках конденсатора, В.
Так как скорости изменения тока и напряжения прямо пропорциональны частоте w, то будет справедливым следующее выражение: I = 2* p * f * C * U. Отсюда получается, что ёмкостной импеданс вычисляется по формуле:
Отсюда получается, что ёмкостной импеданс вычисляется по формуле:
Xc = 1/ 2* p * f * C = 1/ w * C, Ом.
Индуктивное же сопротивление возникает вследствие появления в проводнике собственного поля, называемого ЭДС самоиндукции EL. Зависит она от индуктивности и скорости изменения тока. В свою очередь индуктивность зависит от форм и размеров проводника, магнитной проницаемости среды: L =Ф / I, измеряется в теслах (Тл). Поскольку напряжение, приложенное к индуктивности, по своей величине равно ЭДС самоиндукции, то справедливо EL = 2* p * f * L * I. При этом скорость изменения тока пропорциональна частоте w. Исходя из этого индуктивное сопротивление равно:
Xl = w * L, Ом.
Таким образом, импеданс цепи рассчитывается как: Z = (R 2 +(X c-X l) 2) ½, Ом.
То есть он зависит от частоты переменного сигнала, индуктивности и ёмкости цепи, а также активного сопротивления источника и электрической линии.
При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.
Закон для переменного тока
Классический закон был открыт физиком из Германии Симоном Омом в 1862 году. Проводя эксперименты, он обнаружил связь между током и напряжением. В результате ученый сформулировал утверждение, что сила тока пропорциональна разности потенциалов и обратно пропорциональна сопротивлению. Если в электрической цепи ток уменьшится в несколько раз, то и напряжение в ней станет меньше на столько же.
Математически закон Ома был описан как:
I = U / R, А.
Это выражение справедливо как для синусоидального, так и для постоянного тока. Но такая зависимость величин соответствует идеальной ситуации, в которой не учитываются паразитные составляющие и сопротивление источника тока. В случае же гармоничного сигнала на его прохождение влияет частота, из-за присутствия ёмкостной и индуктивной составляющей в электрической линии.
Поэтому закон Ома для переменного тока описывается формулой:
I = U / Z, где:
- I — сила переменного тока, А;
- U — разность потенциалов, В;
- Z — полное сопротивление цепи, Ом.
Полное сопротивление зависит от частоты гармоничного сигнала и вычисляется по следующей формуле:
Z = ((R+r)2 + (w*L — 1/w*C)2)½ = ((R+r)2+X2)½.
При прохождении тока переменной величины электромагнитное поле совершает работу, при этом из-за сопротивления, оказываемого в цепи, выделяется тепло. То есть электрическая энергия переходит в тепловую. Мощность же пропорциональна току и напряжению. Формула, описывающая мгновенное значение, выглядит как: P = I*U.
В то же время для переменного сигнала необходимо учитывать амплитудную и частотную составляющую. Поэтому:
P = I *U*cosw*t*cos (w*t+ Ψ), где I, U — амплитудные значения, а Ψ — фазовый сдвиг.
Для анализа процессов в электрических цепях переменного тока вводится понятие комплексного числа. Связанно это со смещением фаз, появляющихся между током, и разностью потенциалов. Обозначается это число латинской буквой j и состоит из мнимой Im и вещественной Re частей.
Так как на активном сопротивлении происходит трансформирование мощности в тепло, а на реактивном она преобразуется в энергию электромагнитного поля, возможны её переходы из любой формы в любую. Можно записать: Z = U / I = z * ej*Ψ.
Отсюда полное сопротивление цепи: Z = r + j * X, где r и x — соответственно активное и реактивное сопротивление. Если же сдвиг фаз принимается равный 900, то комплексное число можно не учитывать.
Использование формулы
Использование закона Ома позволяет построить временные характеристики различных элементов. С помощью него несложно рассчитать нагрузки для электрических схем, выбрать нужное сечение проводов, правильно подобрать защитные автоматы и предохранители. Понимание закона даёт возможность применить правильный источник питания.
Понимание закона даёт возможность применить правильный источник питания.
Использование Закона Ома можно применить на практике для решения задачи. Например, пускай есть электрическая линия, состоящая из последовательно соединённых элементов, таких как: ёмкость, индуктивность и резистор. При этом ёмкость C = 2*Ф, индуктивность L=10 мГн, а сопротивление R = 10 кОм. Требуется вычислить импеданс полной цепи и рассчитать силу тока. При этом блок питания работает на частоте равной f = 200 Гц и выдаёт сигнал с амплитудой U = 12 0 В. Внутреннее сопротивление источника питании составляет r = 1 кОм .
Вначале необходимо рассчитать реактивное сопротивление в цепи переменного тока. Так, ёмкостное сопротивление находится из выражения: Xc = 1/ (2 *p *F*C) и на частоте 200 Гц оно равно: Xc = 588 Ом.
Индуктивное сопротивление находится из выражения: XL = 2*p*F* L. На f = 200 Гц и оно оставляет: X*L = 1,25 Ом. Полное сопротивление RLC цепи будет: Z = ((10 *10 3 +1*10 3 ) 2 + (588−1,25) 2 ) ½ = 11 кОм.
Разность потенциалов, изменяющаяся по гармоническому закону синуса, будет определяться: U (t) = U * sin (2* p *f*t) = 120*sin (3,14*t). Ток будет равен: I (t) = 10* 10 −3 + sin (3,14*t+p/2).
По рассчитанным данным можно построить график тока, соответствующий частоте 100 Гц. Для этого в декартовой системе координат отображается зависимость тока от времени.
Следует отметить, закон Ома для переменного сигнала отличается от использующегося для классического расчёта лишь учётом полного сопротивления и частоты сигнала. А учитывать их важно, так как любой радиокомпонент обладает как активным, так и реактивным сопротивлением, что в итоге сказывается на работе всей схемы, особенно на высоких частотах. Поэтому при проектировании электронных конструкций, в частности импульсных устройств, для расчётов используется именно полный закон Ома.
Закон Ома.
Закон Ома.
Программа КИП и А
В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..
Для постоянного тока
Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
| I = U / R | где | I — сила тока, измеряемая в Амперах, (A) |
| U — напряжение, измеряемое в Вольтах, (V) | ||
| R — сопротивление, измеряется в Омах, (Ω) |
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома. .».
.».
Помимо закона Ома, важнейшим является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
| P = I × U | где | P — эл. мощность, измеряемая в Ваттах, (W) |
| I — сила тока, измеряемая в Амперах, (A) | ||
| U — напряжение, измеряемое в Вольтах, (V) |
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
| Сила тока, | I= | U/R | P/U | √(P/R) |
| Напряжение, | U= | I×R | P/I | √(P×R) |
| Сопротивление, | R= | U/I | P/I² | U²/P |
| Мощность, | P= | I×U | I²×R | U²/R |
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
Наиболее распространенные множительные приставки:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока. | |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I — сила переменного тока, измеряемая в Амперах, (A) |
| U — напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z — полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:
Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
Закон Ома для переменного тока: формула
Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.
Закон ома для участка цепи
Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.
В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.
Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.
Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.
Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.
Закон ома для полной цепи
Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.
Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.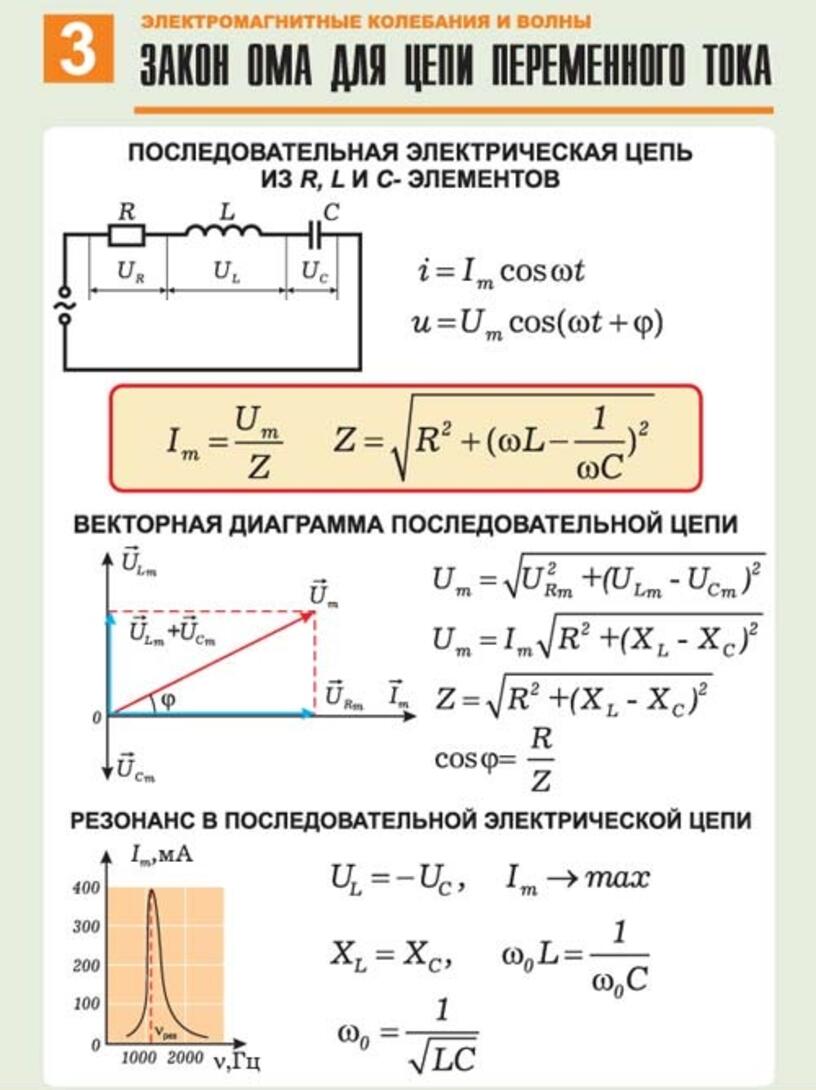
Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.
Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.
Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.
Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.
Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U < E.
ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.
Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.
Постепенно заряд батареи полностью исчезает без остатка.
Закон ома для цепи переменного тока
Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.
Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.
В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.
Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z.
Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.
Закон Ома для цепи переменного тока.
 Мощность
Мощность
RIR=UR; 1ωCIC=UC; ωLIL=UL.
Указанные выше формулы внешне могут напоминать закон Ома на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.
Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.
Определение 1
R – активное сопротивление резистора.
1ωС – емкостное сопротивление конденсатора.
ωL – индуктивное сопротивление катушки в цепи переменного тока.
Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.
Определение 2
Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.
Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:
P=Pcα=I0U0cos ωt cos ωt+φ.
В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю:
PR=IRURcos2ωt=IRUR2=IR2R2.
Действующие значения силы тока и напряжения
Определение 3
По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения:
IД=l02; UД=U02.
Мощность переменного тока на участке цепи
Определение 4
Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется:
PR=IДUД.
Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:
Отсюда, справедливо следующее выражение:
PC=ICUCcos ωt cosωt+π2=ICUCcos ωt-sin ωt=0.
Таким же способом можно проиллюстрировать, что PL=0.
Исходя из описанного выше получим следующие определение.
Определение 5
Мощность в цепи переменного тока выделяется только на активном сопротивлении, а среднее значение мощности переменного тока на конденсаторе и катушке индуктивности равняется нулю.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты ω. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) проявляется фазовый сдвиг на определенный угол φ.
Исходя из приведенных выше фактов, мы можем записать:
J(t)=I0cos ωt; e(t)=δ0cos ωt+φ.
Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. 2.3.2).
Рисунок 2.3.2. Гармонические колебания A cos (ωt+φ1), B cos (ωt+φ2) и их суммы C cos (ωt+φ) на векторной диаграмме.
Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:
P=I0δ0cos ωt cos ωt+φ=I0δ02cos φ=IДδД cos φ.
Исходя из данных векторной диаграммы можно заявить, что UR=δ0·cos φ, следовательно,
P=I0UR2, а вся мощность, которую развивает источник питания, теряется в виде джоулева тепла на резисторе.
В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока I0 и напряжений δ0 в условиях последовательной RLC-цепи:
I0=δ0R2+ωL-1ωC2
Определение 6
Z=R2+ωL-1ωC2– это величина, имеющая название полное сопротивление цепи переменного тока.
Определение 7
Связь между амплитудными значениями тока и напряжения в цепи имеет вид:
ZI0=δ0.
Данное выражение представляет собой закон Ома для цепи переменного тока.
Закон Ома в условиях параллельной RLC-цепи
В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. 2.4.1) RLC-контур:
Рисунок 2.4.1. Параллельный RLC-контур.
При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах R, C и L идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока. Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контур.
Исходя из вида диаграммы, следует:
I0=δ01R2+ωL-1ωC2.
Определение 8
Соответственно, полное сопротивление параллельного RLC-контура выражается в виде следующего соотношения:
Z=11R2+ωL-1ωC2.
Определение 9
При параллельном резонансе (ω2=1LC) полное сопротивление цепи принимает свое максимальное значение, которое эквивалентно активному сопротивлению резистора:
Z=Zmax=R.
А значение фазового сдвига φ между током и напряжением при параллельном резонансе равняется нулю.
Закон Ома для переменного тока
Приветствую всех на нашем сайте! В этот раз речь пойдёт про закон Ома для переменного тока.
Когда-то люди жили без электричества. Потом научились делать батарейки, и так появился постоянный электрический ток. Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи.
Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи.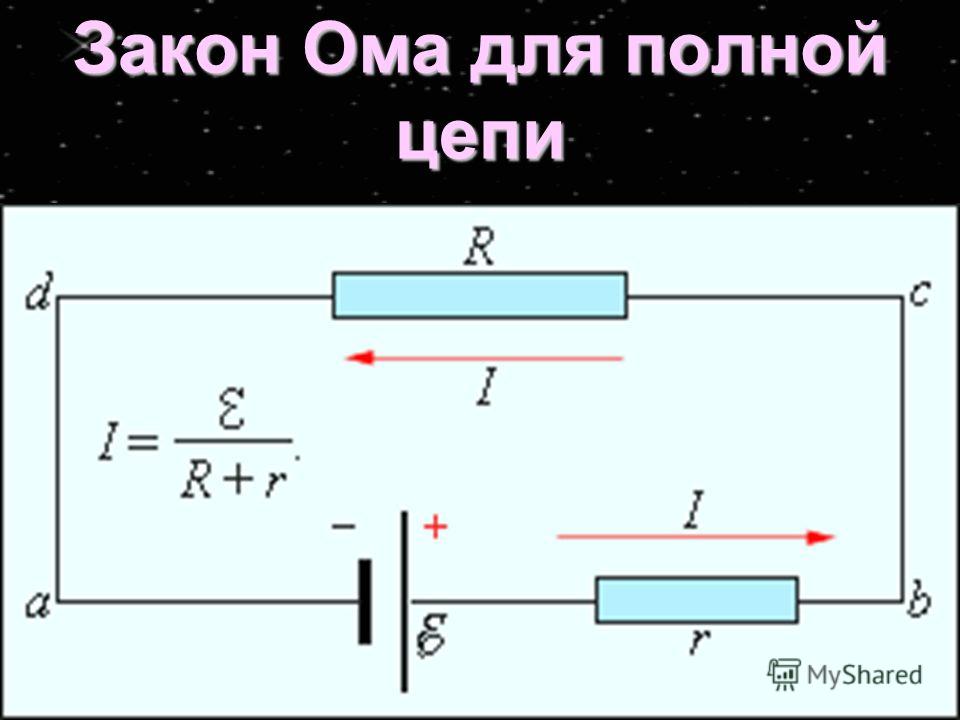 А мы двинемся дальше.
А мы двинемся дальше.
Сейчас вы поймете, почему так важен и что даёт закон Ома для цепи переменного тока. В современной жизни без этого закона никак не обойтись. Поскольку ток, это работа, а работа есть выделение тепла, то существенная задача электротехники в том, чтобы соблюдался термический режим, проще говоря, чтобы не произошло перегрева электроцепей. Итак, закон Ома гласит, что:
Измерить напряжение довольно просто, для этого понадобится вольтметр, в нашем случае для переменного напряжения. В цепях постоянного тока измерить сопротивление тоже не составляет сложности, для этого потребуется омметр. Почему же возникают сложности с переменным током? А проблема, именно, в его переменности, а точнее понятиях емкости и индукции, которые ведут себя при переменном токе несколько иначе, нежели при постоянном.
Формула Закона Ома для переменного тока:
Кому-то эта формула может показаться неожиданной, потому что все привыкли видеть другую формулу:
Теперь давайте разберёмся, что такое полное сопротивление цепи и всё сразу встанет на свои места. В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями. Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.
В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями. Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.
Ёмкостное сопротивление. При подаче напряжения на конденсатор сначала возникает сильный ток и потом поднимается напряжение, то есть в идеальных условиях ток опережает напряжение на угол 90. Другими словами, ток совершает работу из-за наличия сопротивления в цепи, которое можно посчитать по формуле:
Таким образом, чем выше частота переменного тока и чем выше емкость конденсатора, тем меньше ёмкостное сопротивление.
Индуктивное сопротивление. Здесь все происходит наоборот, сначала возникает напряжение, затем запускается индукционный процесс который препятствует возрастанию тока. Подробнее об этом читайте в статьях про индукцию.
Поэтому здесь мы видим уже обратную картину – чем выше частота и чем больше индуктивность катушки, тем больше индуктивное сопротивление переменному току.
Почему эти понятия не встречаются в цепях постоянного тока? Ответ можно узнать, посмотрев на формулы. Если ток постоянный, то f=0. То есть, емкостное сопротивление станет бесконечно большим, а это значит, что конденсатор в цепи постоянного тока становится похож на выключатель, который размыкает цепь и ток по ней не идёт, но при этом, конденсатор будет пропускать переменный ток. А индуктивное сопротивление станет равно нулю, значит, у нас останется просто провод, который имеет свое собственное сопротивление, которое еще называется активным, и его можно измерить обычным омметром. В отличие от конденсатора, у которого нет активного сопротивления, сопротивление катушки, если оно довольно большое, должно приниматься в расчёт. Как правило, активное сопротивление катушки очень маленькое по сравнению с индуктивным, поэтому его в расчёт не берут, но всё же правильно формула сопротивления катушки выглядит так:
По такому принципу в электронике изготавливают фильтры, которые должны отсечь переменный ток от постоянного, то есть пропускать только переменный ток или наоборот заглушить переменный ток, оставив только постоянный, или даже заглушить токи какой-то одной или нескольких частот.
А сейчас совсем вас запутаю… И катушка может иметь ёмкостные свойства и конденсатор – индуктивные, но как правило они слишком малы и носят паразитический характер.
Ну а сейчас мы рассмотрим закон Ома для электрической цепи переменного тока наглядно.
Допустим, у нас есть цепь из последовательно включенных резистора (активное сопротивление), конденсатора (реактивное ёмкостное сопротивление) и катушка (активно-реактивное индуктивное сопротивление). Теперь, чтобы узнать силу тока в цепи нам нужно правильно посчитать полное сопротивление цепи.
Осталось применить всё изложенное выше.
Реактивное сопротивление Х это разница между индуктивным сопротивлением XL и ёмкостным сопротивлением XC. Ну а дальше векторным сложением можем узнать полное реактивное сопротивление
следовательно:
дальнейший расчет:
или:
Что можно сказать в заключении. Как вы можете видеть, закон Ома для переменного тока точно такой же, как и для постоянного. Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное. И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях. Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.
Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное. И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях. Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.
Поделиться ссылкой:
Похожее
Понимание основ закона Ома — диаграммы переменного и постоянного тока …. в чем разница?AC = Z (импеданс) и DC = R (сопротивление) Формулы закона ОмаКолесо силы закона Ома переменного тока и колесо силы закона Ома постоянного тока(схемы, диаграмма, диаграмма, колесо, формулы, теория электроники) Если вам нужно иметь дело с формулами напряжения, тока, сопротивления или импеданса и мощности и вы хотите знать, в чем разница между тем, что мы называем формулами переменного и постоянного тока, вы можете найти эти колеса силы закона Ома. Два основных типа электричества — это переменный ток, известный как AC, и постоянный ток, известный как DC.Разница между системами переменного и постоянного тока заключается в том, как мощность передается по линиям. При переменном токе поток энергии меняет направление — фактически 60 раз в секунду, но при постоянном токе мощность будет двигаться только в одном направлении. Переменный ток переменного тока — Think Impedance Закон Ома и силовые формулы закона Джоуля.
ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ: Чтобы использовать диаграмму, в центральном круге выберите значение, которое необходимо найти; например, на диаграмме постоянного тока: I (амперы), R (Ом), E (вольты) или P (ватты). Эти колеса силы закона Ома выше показывают нашу цветовую таблицу резисторов, которая поможет вам определить цвета резисторов … это уникальная концепция, и вы найдете ее полностью объясненной на нашей странице технических примечаний слева.Мы включаем эти диаграммы на все наши часы, наклейки, брелки, диаграммы и часы с законом Ома, поэтому не забудьте заглянуть на страницу «Наши продукты», прежде чем покинуть наш сайт. Спасибо! Понятия (теория) напряжения, тока, сопротивления, импеданса и мощности необходимы для понимания основных электрических схем и спецификаций. Эти области должны быть полностью изучены, прежде чем можно будет понять внутренности даже самых простых электронных устройств, таких как дешевые мобильные телефоны. Как только эти концепции станут вам знакомы, вы обнаружите, что наладить правильное соединение между частями оборудования будет намного проще. Теория закона Ома может быть сформулирована как математический инструмент, который имеет наибольшее применение при определении неизвестного фактора тока, напряжения или сопротивления в электрической цепи, в которой известны два других фактора.Следовательно, его можно использовать вместо амперметра, вольтметра или омметра — когда вы пытаетесь определить значение цепи, в котором вам уже известны два других значения. Текущий ВСЕГДА выражается в АМПЕРАХ и обозначается буквой I Напряжение ВСЕГДА выражается в ВОЛЬТАХ и обозначается буквой E или V Сопротивление ВСЕГДА выражается в ОМ и обозначается буквой R Есть два типа тока: постоянный и переменный. Практически во всех электрических цепях существует некоторое сопротивление протеканию тока. Противодействие постоянному току называется сопротивлением, которое измеряется в единицах, называемых омами, и представлено в электрических уравнениях буквой R. Противодействие переменному току называется импедансом, который также измеряется в омах, но в электрических уравнениях он обозначается буквой Z. Для получения формул последовательной цепи и формул параллельной цепи для закона Ома постоянного тока и закона Ома переменного тока перейдите по этой ссылке: ohmslaw2.asp На КАРТОЧКАХ ФОРМУЛ также показаны следующие формулы:
Буква P означает мощность в ваттах. Напряжение, измеренное в вольтах, обозначается буквами E (или V) Электрический ток, измеряемый в амперах, обозначается буквой I Электрическое сопротивление, измеренное в Ом, обозначается буквой R Закон Ома: E = I R I = E / R R = E / I ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ: Джеймс Прескотт Джоуль, а не Георг Саймон Ом, первым открыл математическую связь между рассеиваемой мощностью и током через сопротивление.Это открытие, опубликованное в 1841 году, по праву известно как закон Джоуля. Однако эти уравнения мощности настолько часто связаны с уравнениями закона Ома, связывающими напряжение, ток и сопротивление (E = IR; I = E / R; и R = E / I), что они часто приписываются Ому. ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ: Законы Кирхгофа … n: (физика) два закона, управляющие электрическими сетями, в которых протекают установившиеся токи: сумма всех токов в точке равна нулю, а сумма приростов и падений напряжения в любой замкнутой цепи равно нулю. ЗАКОН ОМА ДЛЯ КОНДЕНСАТОРА: V C = I C X C где: В C = напряжение на конденсаторе ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ: Миллиампер X Килом = Вольт Микроампер X Мегаом = Вольт «Один ампер, протекающий на один ом, вызывает падение потенциала на один вольт.»Георг Симон Ом Пожалуйста, ознакомьтесь с нашими другими категориями, пока вы находитесь на нашем веб-сайте. Предлагаем товары в дополнение к контенту! Такие продукты, как часы закона Ома, часы, диаграммы, отличительные знаки и монеты закона Ома! Мы предлагаем другие подарки для электриков и инженеров, такие как наклейки на окна, забавные полноцветные наклейки, плакаты, кружки, украшения, поздравительные открытки и т. Д. Просто нажмите на любой из наших отделов подарков слева. Спасибо! |
Закон Ома в цепях переменного тока
Закон Ома в цепях переменного тока
Многие цепи переменного тока содержат только сопротивление.Правила для этих схем такие же
правила, применимые к цепям постоянного тока. Резисторы, лампы и нагревательные элементы являются примерами
резистивные элементы. Когда цепь переменного тока содержит только сопротивление, закон Ома, закон Кирхгофа
Закон, а также различные правила, применимые к напряжению, току и мощности в цепи постоянного тока.
применить к цепи переменного тока. Формулу закона Ома для цепи переменного тока можно записать как
Помните, если не указано иное, все значения переменного напряжения и тока даны как
эффективные значения.Формулу закона Ома можно также записать как
Важно помнить следующее: Не смешивайте значения переменного тока . Когда вы решаете
действующие значения, все значения, которые вы используете в формуле , должны быть действующими значениями .
Точно так же, когда вы решаете средние значения, все используемые вами значения должны быть средними значениями .
Этот момент станет более ясным после того, как вы решите следующую задачу: Последовательная цепь
состоит из двух резисторов (R1 = 5 Ом и R2 = 15 Ом) и источника переменного напряжения
120 вольт.Что такое avg ?
Предполагается, что переменное напряжение является действующим значением (поскольку оно не указано
быть иначе). Примените формулу закона Ома.
Проблема, однако, запрашивала среднее значение тока (I avg ). К
преобразовать действующее значение тока в среднее значение тока, вы должны сначала
определить пиковое или максимальное значение тока, I max .
Теперь вы можете найти I avg . Просто замените 8,484 ампера в I avg
формулу и решите относительно I avg .
Помните, что вы можете использовать формулы закона Ома для решения любого чисто резистивного переменного тока
проблема цепи. Используйте формулы так же, как при решении цепи постоянного тока
проблема.
Q.41 Последовательная цепь состоит из трех резисторов (R1 = 10
OHMSLAWFORAC
OHMSLAWFORAC ЗАКОН ОМА ДЛЯ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только в том случае, если
цепи содержат только сопротивление, как в случае с лампами и обогревом.
элементы.Чтобы использовать действующие значения напряжения и тока в переменном токе
цепи, влияние индуктивности и емкости с сопротивлением должно
быть на рассмотрении.
Комбинированный эффект сопротивления, индуктивного сопротивления и емкостной
реактивное сопротивление составляет полное противодействие протеканию тока в цепи переменного тока.
Это полное сопротивление называется импедансом и обозначается буквой
«Z.» Единицей измерения импеданса является ом.
Цепи переменного тока серии
| Если цепь переменного тока состоит только из сопротивления, значение импеданса совпадает с сопротивлением, а закон Ома для переменного тока Схема I = E / Z точно такая же, как и для цепи постоянного тока.На рисунке 8-188 последовательная цепь, содержащая лампу с сопротивлением 11 Ом, подключенную через источник иллюстрирован. Чтобы узнать, сколько тока будет протекать, если 110 вольт приложен постоянный ток и сколько тока будет протекать, если приложить переменный ток 110 вольт, решены следующие примеры: | |
| Когда цепи переменного тока содержат сопротивление и либо индуктивность или емкости, полное сопротивление Z не совпадает с сопротивлением R.Импеданс цепи — это полное сопротивление цепи потоку. тока. В цепи переменного тока это противостояние состоит из сопротивления и реактивное сопротивление, индуктивное или емкостное, либо их элементы. Сопротивление и реактивное сопротивление нельзя сложить напрямую, но их можно учитывать. | |
| Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формула для нахождения импеданса или полного противодействия току в цепи переменного тока можно найти, используя закон прямоугольных треугольников. Этот Теорема, называемая теоремой Пифагора, применима к любому прямоугольному треугольнику. В нем говорится, что квадрат гипотенузы равен сумме квадраты двух других сторон.Таким образом, ценность любой стороны права треугольник можно найти, если известны две другие стороны. Если цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 8-190, соотношение между сторонами можно записать как: Квадратный корень из обеих частей уравнения дает |
Эту формулу можно использовать для определения импеданса, когда значения
индуктивного реактивного сопротивления и сопротивления. Его можно изменить на
решить для импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление
заменив XC в формуле на XL.В схемах, содержащих
сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления
можно комбинировать, но поскольку их эффекты в схеме прямо противоположны,
они объединяются вычитанием: X = XL — XC или X = XC
— XL (меньшее число всегда вычитается из большего). В
рисунок 8-190, последовательная цепь, состоящая из сопротивления и индуктивности
последовательно подключен к источнику 110 вольт на 60 циклов
в секунду.Резистивным элементом является лампа с сопротивлением 6 Ом, а
индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какие
это значение импеданса и тока через лампу и
катушка?
Решение:
Сначала вычисляется индуктивное сопротивление катушки:
XL = 2 ш x ш x д
XL = 6,28 x 60 x 0,021
XL = индуктивное реактивное сопротивление 8 Ом.
Затем вычисляется полное сопротивление:
Z = квадратный корень из R2 + XL2
Z = квадратный корень из 62 + 82
Z = квадратный корень из 36 + 64
Z = квадратный корень из 100
Z = сопротивление 10 Ом.
Тогда текущий поток,
Падение напряжения на сопротивлении (ER) составляет
ER = I x R
ER = 11 x 6 = 66 вольт.
Падение напряжения на индуктивности (EXL) составляет
EXL = I x XL
EXL = 11 x 8 = 88 вольт.
Сумма двух напряжений больше приложенного напряжения. Этот
возникает из-за того, что два напряжения не совпадают по фазе и, как таковые,
представляют максимальное напряжение.Если напряжение в цепи измеряется
по вольтметру будет примерно 110 вольт, приложенное напряжение.
Это можно доказать уравнением
На рисунке 8-191 показана последовательная цепь, в которой конденсатор |
Решение:
Сначала емкость меняется с микрофарад на фарады.С 1
миллион микрофарад равен 1 фараду, тогда
Чтобы найти сопротивление,
Чтобы найти ток,
Падение напряжения на лампе (ER) составляет
ER = 6,7 x 10
ER = 67 вольт
Падение напряжения на конденсаторе (EXC) составляет
Сумма этих двух напряжений не равна приложенному напряжению, так как
ток опережает напряжение.Чтобы найти приложенное напряжение, формула
ET = используется квадратный корень из (ER) 2 + (EXC) 2.
Когда схема содержит сопротивление, индуктивность и емкость,
уравнение
Z = квадратный корень из R2 + (XL — XC) 2
используется для определения импеданса.
Пример:
Каково полное сопротивление последовательной цепи (рисунок 8-192), состоящей из
конденсатора с реактивным сопротивлением 7 Ом, катушки индуктивности с реактивным сопротивлением
10 Ом, а резистор сопротивлением 4 Ом?
Решение:
Предполагая, что реактивное сопротивление конденсатора составляет 10 Ом, а реактивное сопротивление
индуктивности 7 Ом, то XC больше XL.Таким образом,
Параллельные цепи переменного тока
| Методы, используемые при решении задач параллельных цепей переменного тока в основном такие же, как и те, которые используются для последовательных цепей переменного тока. Не в фазе напряжения и токи можно сложить, используя закон прямоугольных треугольников, но при решении схемных проблем токи через ветви добавлено, так как падение напряжения на разных ветвях одинаковое и равны приложенному напряжению.На рисунке 8-193 параллельная цепь переменного тока схематически показан содержащий индуктивность и сопротивление. Электрический ток протекающая через индуктивность IL составляет 0,0584 ампера, а протекающий ток через сопротивление составляет 0,11 ампер. Каков общий ток в схема? |
Решение:
Поскольку индуктивное реактивное сопротивление приводит к тому, что напряжение опережает ток, общее
ток, который содержит составляющую индуктивного тока, отстает от приложенного
Напряжение.Если на графике нанесены ток и напряжения, угол между
два, называемые фазовым углом, показывают, насколько ток отстает от
Напряжение.
На рисунке 8-194 генератор на 110 В подключен к нагрузке, состоящей из
емкости 2 и
параллельное сопротивление 10000 Ом. Какое значение импеданса
и общий ток?
Решение:
Сначала найдите емкостное сопротивление цепи:
Замена 2 на фарады и
ввод значений в приведенную формулу:
Чтобы найти импеданс, формула импеданса используется в последовательной цепи переменного тока.
должны быть изменены, чтобы соответствовать параллельной цепи:
Чтобы найти ток через емкость:
Чтобы найти ток, протекающий через сопротивление:
Чтобы найти ток, протекающий через сопротивление:
Чтобы найти полный ток в цепи:
Резонанс
Было показано, что оба индуктивных реактивного сопротивления (XL = 2
f L) и емкостное сопротивление
являются функциями частоты переменного тока.Уменьшение частоты
уменьшает омическое значение индуктивного сопротивления, но уменьшает
частота увеличивает емкостное реактивное сопротивление. На определенной частоте
известная как резонансная частота, реактивные эффекты конденсатора и
индуктор будет равен. Поскольку эти эффекты противоположны одному
другой, они отменит, оставив только омическое значение сопротивления
противодействовать протеканию тока в цепи. Если значение сопротивления невелико
или состоит только из сопротивления в проводниках, величина тока
расход может стать очень большим.
В цепи, где катушка индуктивности и конденсатор включены последовательно, а
частота — это резонансная частота или частота резонанса, контур
называется «резонансным» и называется последовательным резонансным контуром.
Обозначение резонансной частоты — Fn.
Если на частоте резонанса индуктивное сопротивление равно
к емкостному сопротивлению, то
Разделив обе стороны на 2 fL,
Извлечение квадратного корня из обеих частей дает
Где Fn — резонансная частота в циклах в секунду, C — емкость.
в фарадах, а L — индуктивность в генри.По этой формуле частота
при котором конденсатор и катушка индуктивности будут резонансными, можно определить.
Чтобы найти индуктивное сопротивление цепи, используйте
Формулу импеданса, используемую в последовательной цепи переменного тока, необходимо изменить на
поместите параллельную схему.
Для поиска параллельных цепей индуктивного и емкостного реакторов.
использовать
Найти параллельные сети с емкостным сопротивлением и индуктивностью.
использовать:
Поскольку на резонансной частоте XL отменяет XC, ток может стать равным
очень большой, в зависимости от величины сопротивления.В таких случаях напряжение
падение на катушке индуктивности или конденсаторе часто будет выше, чем применяемое
Напряжение.
| В параллельном резонансном контуре (рисунок 8-195) реактивные сопротивления равные и равные токи будут течь через катушку и конденсатор. Поскольку индуктивное реактивное сопротивление приводит к тому, что ток через катушку |
| Питание в цепях переменного тока В цепи постоянного тока мощность определяется по уравнению P = EI (ватт равен В цепи переменного тока вольтметр показывает действующее напряжение и |
Когда в цепи присутствует емкость или индуктивность, ток
и напряжение не точно совпадают по фазе, а истинная мощность меньше, чем
полная мощность. Истинная мощность определяется показаниями ваттметра. В
отношение истинной мощности к полной мощности называется коэффициентом мощности.
и обычно выражается в процентах.В форме уравнения соотношение
является:
Проблема:
Мотор переменного тока 220 вольт отнимает от линии 50 ампер, но ваттметр
в строке видно, что на двигатель потребляется всего 9350 Вт. Что такое
полная мощность и коэффициент мощности?
Решение:
Закон Ома | физика | Britannica
Закон Ома , описание взаимосвязи между током, напряжением и сопротивлением.Величина постоянного тока через большое количество материалов прямо пропорциональна разности потенциалов или напряжению на материалах. Таким образом, если напряжение В, (в единицах вольт) между двумя концами провода, сделанного из одного из этих материалов, утроится, ток I (амперы) также утроится; и отношение V / I остается постоянным. Частное В, / I для данного куска материала называется его сопротивлением, R, измеряется в единицах, называемых омами.Сопротивление материалов, для которых действует закон Ома, не изменяется в огромных диапазонах напряжения и тока. Математически закон Ома может быть выражен как V / I = R . То, что сопротивление или отношение напряжения к току для всей или части электрической цепи при фиксированной температуре, как правило, является постоянным, было установлено к 1827 году в результате исследований немецкого физика Георга Симона Ома.
Альтернативные утверждения закона Ома заключаются в том, что ток I в проводнике равен разности потенциалов V поперек проводника, деленной на сопротивление проводника, или просто I = V / R , и что разность потенциалов в проводнике равна произведению тока в проводнике и его сопротивления, В = IR .В цепи, в которой разность потенциалов или напряжение постоянна, ток можно уменьшить, добавив большее сопротивление, или увеличить, удалив некоторое сопротивление. Закон Ома также может быть выражен в терминах электродвижущей силы или напряжения E источника электроэнергии, такого как батарея. Например, I = E / R .
С изменениями закон Ома также применяется к цепям переменного тока, в которых соотношение между напряжением и током более сложное, чем для постоянного тока.Именно из-за того, что ток меняется, помимо сопротивления, возникают другие формы противодействия току, называемые реактивным сопротивлением. Комбинация сопротивления и реактивного сопротивления называется импедансом, Z. Когда полное сопротивление, эквивалентное отношению напряжения к току, в цепи переменного тока является постоянным, обычно применяется закон Ома. Например, V / I = Z .
С дальнейшими изменениями закон Ома был расширен до постоянного отношения магнитодвижущей силы к магнитному потоку в магнитной цепи.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
15.S: Цепи переменного тока (Резюме) — Physics LibreTexts
Ключевые термины
| переменный ток | ток, синусоидально колеблющийся во времени с фиксированной частотой |
| напряжение переменного тока | напряжение, которое синусоидально колеблется во времени с фиксированной частотой |
| переменный ток (ac) | Поток электрического заряда, который периодически меняет направление |
| средняя мощность | среднее время мгновенной мощности за один цикл |
| полоса пропускания | диапазон угловых частот, в которых средняя мощность больше половины максимального значения средней мощности |
| емкостное реактивное сопротивление | Противодействие конденсатора изменению тока |
| постоянный ток (dc) | поток электрического заряда только в одном направлении |
| сопротивление | переменный ток аналог сопротивления в цепи постоянного тока, который измеряет комбинированный эффект сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления |
| индуктивное сопротивление | Противодействие катушки индуктивности изменению тока |
| фазовый угол | величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи |
| Коэффициент мощности | величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе |
| добротность | безразмерная величина, описывающая резкость пика полосы пропускания; высокая добротность — острый или узкий резонансный пик |
| резонансная частота | частота, при которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения |
| действующее значение тока | среднеквадратичное значение текущего |
| действующее напряжение | среднеквадратичное значение напряжения |
| понижающий трансформатор | трансформатор, понижающий напряжение и увеличивающий ток |
| повышающий трансформатор | трансформатор, повышающий напряжение и понижающий ток |
| трансформатор | устройство, которое преобразует напряжения из одного значения в другое с помощью индукции |
| уравнение трансформатора | , показывающее, что отношение вторичного напряжения к первичному в трансформаторе равно отношению количества витков в их обмотках |
Ключевые уравнения
| Напряжение переменного тока | \ (\ Displaystyle v = V_0sinωt \) |
| Переменный ток | \ (\ Displaystyle я = I_0sinωt \) |
| емкостное реактивное сопротивление | \ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = \ гидроразрыва {1} {ωC} = X_C \) |
| действующее напряжение | \ (\ Displaystyle V_ {rms} = \ frac {V_0} {\ sqrt {2}} \) |
| действующий ток | \ (\ Displaystyle I_ {rms} = \ frac {I_0} {\ sqrt {2}} \) |
| индуктивное реактивное сопротивление | \ (\ Displaystyle \ гидроразрыва {V_0} {I_0} = ωL = X_L \) |
| Фазовый угол цепи последовательного RLC | \ (\ Displaystyle ϕ = загар ^ {- 1} \ гидроразрыва {X_L − X_C} {R} \) |
| Вариант закона Ома по переменному току | \ (\ Displaystyle I_0 = \ гидроразрыва {V_0} {Z} \) |
| Импеданс цепи серии RLC | \ (\ Displaystyle Z = \ sqrt {R ^ 2 + (X_L − X_C) ^ 2} \) |
| Средняя мощность, связанная с элементом схемы | \ (\ Displaystyle P_ {ave} = \ frac {1} {2} I_0V_0cosϕ \) |
| Средняя мощность, рассеиваемая резистором | \ (\ displaystyle P_ {ave} = \ frac {1} {2} I_0V_0 = I_ {rms} V_ {rms} = I ^ 2_ {rms} R \) |
| Резонансная угловая частота контура | \ (\ Displaystyle ω_0 = \ sqrt {\ frac {1} {LC}} \) |
| Добротность схемы | \ (\ Displaystyle Q = \ гидроразрыва {ω_0} {Δω} \) |
| Добротность цепи по параметрам цепи | \ (\ Displaystyle Q = \ гидроразрыва {ω_0L} {R} \) |
| Уравнение трансформатора с напряжением | \ (\ Displaystyle \ frac {V_S} {V_P} = \ frac {N_S} {N_P} \) |
| Уравнение трансформатора с током | \ (\ Displaystyle I_S = \ frac {N_P} {N_S} I_P \) |
Сводка
15.2 источника переменного тока
- Постоянный ток (dc) относится к системам, в которых напряжение источника постоянно.
- Переменный ток (ac) относится к системам, в которых напряжение источника периодически изменяется, особенно синусоидально.
- Источник напряжения системы переменного тока выдает напряжение, которое рассчитывается по времени, пиковому напряжению и угловой частоте.
- В простой схеме ток определяется делением напряжения на сопротивление.Переменный ток рассчитывается с использованием пикового тока (определяемого делением пикового напряжения на сопротивление), угловой частоты и времени.
15.3 Простые цепи переменного тока
- Для резисторов сквозной ток и напряжение совпадают по фазе.
- Что касается конденсаторов, мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла. Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току, называемую емкостным реактивным сопротивлением, которое измеряется в омах.
- Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, оно опережает ток на одну четверть цикла.
- Противодействие катушки индуктивности изменению тока выражается как тип реактивного сопротивления переменного тока. Это индуктивное реактивное сопротивление, измеряемое в омах, зависит от частоты источника переменного тока.
Цепи серии 15,4 RLC с переменным током
- Последовательная цепь RLC представляет собой последовательную комбинацию резистора, конденсатора и индуктора через источник переменного тока.
- Одинаковый ток течет через каждый элемент цепи последовательного соединения RLC во все моменты времени.
- Сопротивлением в цепи постоянного тока является импеданс, который измеряет совместное действие резисторов, конденсаторов и катушек индуктивности. Максимальный ток определяется версией закона Ома для переменного тока.
- Импеданс измеряется в омах и определяется как сопротивление, емкостное и индуктивное сопротивление.
15.5 Питание в цепи переменного тока
- Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения.
- Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на полное сопротивление.
- В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
- Коэффициент мощности варьируется от –1 до 1.
Закон
15,6 Резонанс в цепи переменного тока
- На резонансной частоте индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.
- График зависимости средней мощности от угловой частоты для цепи RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика называется полосой пропускания.
- Ширина полосы связана с безразмерной величиной, называемой коэффициентом качества.Высокое значение добротности — это острый или узкий пик.
15,7 Трансформаторы
- Электростанции передают высокое напряжение при малых токах для достижения более низких омических потерь на многокилометровых линиях передачи.
- Трансформаторы используют индукцию для преобразования напряжения из одного значения в другое.
- Для трансформатора напряжения на первичной и вторичной катушках или обмотках связаны уравнением трансформатора.
- Токи в первичной и вторичной обмотках связаны количеством первичных и вторичных петель или витков в обмотках трансформатора.
- Повышающий трансформатор увеличивает напряжение и снижает ток, тогда как понижающий трансформатор снижает напряжение и увеличивает ток.
Авторы и ссылки
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Закон Ома для простых электрических цепей, Рон Куртус
SfC Home> Физика> Электричество>
, автор: Рон Куртус (от 23 октября 2019 г.)
Закон Ома является наиболее фундаментальной формулой для простых электрических цепей .Он утверждает, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на проводнике. Впервые он был сформулирован в 1827 году немецким физиком Георгом Омом во время экспериментов по изучению того, насколько хорошо металлы проводят электричество.
Закон
Ома лучше всего демонстрируется в простой электрической цепи постоянного тока. Хотя это также относится к цепям переменного тока, необходимо учитывать другие возможные переменные.
Соотношение между током, напряжением и сопротивлением в цепи позволяет вычислить одну переменную, если вы используете значения двух других.
Вопросы, которые могут у вас возникнуть:
- Что означают параметры в уравнении?
- Какая конфигурация схемы?
- Как применить закон Ома?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц
Уравнение
Закон
Ома показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи. Самая простая форма уравнения:
В = ИК
где:
- V — напряжение в вольтах ( V )
- I — ток в амперах или амперах ( A )
- R — сопротивление в Ом ( Ом — греческая буква Омега)
Таким образом, если вы знаете ток и сопротивление, вы можете использовать формулу, чтобы найти напряжение.
С помощью алгебры вы можете переставить переменные в соответствии со своими потребностями. Например, если вы знаете напряжение и сопротивление и хотите найти ток, вы можете использовать:
I = V / R
Или, если вы знаете напряжение и ток и хотите найти сопротивление, вы можете использовать:
R = V / I
Конфигурация
Простая электрическая цепь состоит из металлических проводов, идущих к источнику питания и от него, а также источника сопротивления, такого как резисторы или электрическая лампочка, последовательно соединенных с источником.Типичным источником питания является батарея постоянного тока, хотя также может применяться генератор постоянного или переменного тока.
Примечание : Если цепь переменного тока включает в себя такие компоненты, как конденсаторы или катушки индуктивности, закон Ома не применяется.
Простая цепь постоянного тока
Используя уравнение
Важность закона Ома заключается в том, что, если вы знаете значение двух переменных в уравнении, вы можете определить третью. Вы можете измерить любой из параметров с помощью вольтметра.Большинство вольтметров или мультиметров измеряют напряжение, ток и сопротивление как переменного, так и постоянного тока.
Найти напряжение
Если вам известны ток и сопротивление, вы можете найти напряжение из В = I R . Например, если ток I = 0,2 А и сопротивление R = 1000 Ом , то
В = 0,2 А * 1000 Ом = 200 В
Найти текущий
Если вы знаете напряжение и сопротивление, вы можете использовать алгебру, чтобы изменить уравнение на I = V / R , чтобы найти ток.Например, если В = 110 В и R = 22000 Ом , то
I = 110 В / 22000 Ом = 0,005 А
Найти сопротивление
Если вы знаете напряжение и ток, вы можете использовать алгебру, чтобы изменить уравнение на R = V / I , чтобы найти сопротивление. Если В = 220 В и I = 5 А , то
R = 220 В / 5 A = 44 Ом
Сводка
Закон
Ома — это уравнение V = I R , которое показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи.Он может применяться как к цепям переменного, так и к постоянному току.
Будьте полны решимости сделать все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Немного истории об Ом — Краткая история
Закон Ома — Объяснение, включая калькулятор закона Ома
Основные электрические законы — Включает теорию цепей
Формулы электрических цепей — Уравнения высокого уровня для решения проблем
Электроэнергетические ресурсы постоянного и переменного тока
Физические ресурсы
Книги
Научитесь электричеству и электронике Стэна Гибилиско; Макгроу-Хилл; (2001) 34 доллара.95 — Руководство для профессионалов, любителей и технических специалистов, желающих изучить цепи переменного и постоянного тока
Вопросы и комментарии
У вас есть вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
electric_ohms_law.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Физические темы
Закон Ома для простых электрических цепей
Закон Ома
Закон Ома
Приборы и автоматика
Приложение для Windows ⁄ Android
В приложении Android Instrumentation & Automation в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока.Сначала немного теории ..
Постоянный ток
Закон Ома определяет соотношение между током (I), напряжением (U) и сопротивлением (R) в электрической цепи. Самая распространенная концепция:
Ток в цепи прямо пропорционален напряжению и обратно пропорционален электрическому сопротивлению цепи, т.е.
| I = U / R | где | I — сила тока, измеренная в амперах, (A) |
| U — напряжение, измеренное в вольтах, (V) | ||
| R — сопротивление, измеренное в омах, (Ω) |
Закон Ома является основным в электротехнике и электронике.Без его понимания работа специалиста в области КИПиА невозможна.
Помимо закона Ома, наиболее важным является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению тока (I) на напряжение (U), т.е.
| P = I × U | где | P — электрическая мощность, измеренная в ваттах, (Вт) |
| I — сила тока, измеренная в амперах, (A) | ||
| U — напряжение, измеренное в вольтах, (В) |
Объединение этих двух формул, мы выводим соотношение между силой тока, напряжением, сопротивлением и мощностью, и составляем следующую таблицу:
| Сила тока | I = | U / R | P / U | √ (P / R) |
| Напряжение | U = | I × R | P / I | √ (P × R) |
| Сопротивление | R = | U / I | P / I² | U² / P |
| Электропитание | P = | I × U | I² × R | U² / R |
Практический пример использования табличных формул: Покупка утюга в магазине мощностью 1 кВт (1 кВт = 1000 Вт ), рассчитайте минимальный ток, который должна выдержать розетка, на которую рассчитана эта покупка:
Несмотря на то, что в утюге используется переменный ток, мы пренебрегаем его реактивным сопротивлением (см. ниже) и используем упрощенную формулу для постоянного тока.Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В = 4,5 Ампера. Это минимальный ток, который должна выдержать розетка при подключении к ней нагрузки в 1 кВт.
Наиболее распространенные префиксы множителей:
- Сила тока, амперы (А): 1 килоампер (1 кА) = 1000 А. 1 миллиампер (1 мА) = 0,001 А. 1 микроампер (1 мкА) = 0,000001 А.
- Напряжение, вольт (В): 1 киловольт (1 кВ) = 1000 В. 1 милливольт (1 мВ) = 0,001 В. 1 микровольт (1 мкВ) = 0,000001 В.
- Сопротивление, Ом (Ом): 1 МОм (1 МОм) = 1000000 Ом.1 килограмм (1 кОм) = 1000 Ом.
- Электрическая мощность, ватт (Вт): 1 мегаватт (1 МВт) = 1000000 Вт. 1 киловатт (1 кВт) = 1000 Вт. 1 милливатт (1 мВт) = 0,001 Вт.
Переменный ток
В цепи переменного тока закон Ома может иметь некоторые из особенностей, описанных ниже.
Z — полное сопротивление
В цепи переменного тока сопротивление, за исключением активного (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса Z (полное или комплексное сопротивление для синусоидального сигнала).Упрощенные схемы комплексного сопротивления показаны на рисунках ниже, слева для последовательного соединения, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное соединение R, L, C
Параллельное соединение R, L, C
Кроме того, полное сопротивление Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс , Z | |
| R, L, C последовательно подключены | R, L, C подключены параллельно |
| Z = √ (R 2 + (ωL-1 / ωC) 2 ) | Z = 1 / √ (1 / R 2 + (1 / ωL-ωC) 2 ) |
| где, | |
| ω = 2πγ — циклическая угловая частота; γ — частота переменного тока | |
Коэффициент мощности Cos (φ)
Коэффициент мощности — это отношение активной мощности (P) потребителя электроэнергии к общей (S) потребляемой мощности, т.е.е.
Cos (φ) = P / S
Он также показывает, как переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения сдвигается по фазе.
Изменяется с 0 на 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), коэффициент мощности равен единице.
Чем ближе Cos (φ) к единице, тем меньше потери энергии в электрической цепи.
Основываясь на приведенных выше понятиях импеданса Z и коэффициента мощности Cos (φ), характерного для переменного тока, мы выводим формулу для закона Ома, коэффициента мощности и их производных для цепей переменного тока:
| I = U / Z | где | I — сила тока, измеренная в амперах, (A) |
| U — напряжение, измеренное в вольтах, (V) | ||
| Z — импеданс, измеренный в омах, (Ω) |
Производные формулы:
| Сила тока | I = | U / Z | P / (U × Cos (φ)) | √ (P / Z) |
| Напряжение | U = | I × Z | P / (I × Cos (φ)) | √ (P × Z) |
| Импеданс | Z = | U / I | P / I² | U² / P |
| Электрическая мощность | P = | I² × Z | I × U × Cos (φ) | U² / Z |
Приложение Android Instrumentation & Automation включает блок для вычисления закона Ома как для постоянного, так и для переменного тока, а также для вычисления сопротивление и коэффициент мощности Cos (φ).

 Эта переменчивость описывается по гармоническому закону синуса или косинуса.
Эта переменчивость описывается по гармоническому закону синуса или косинуса.
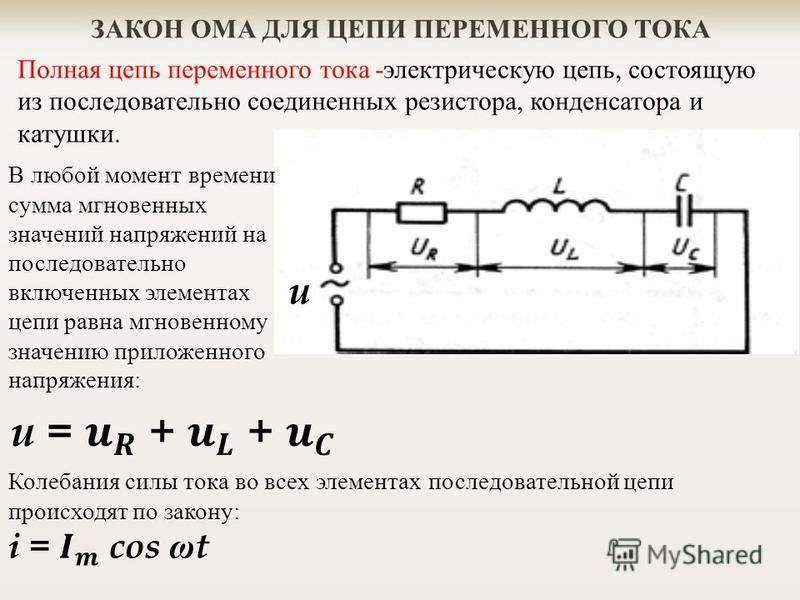 При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.
При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.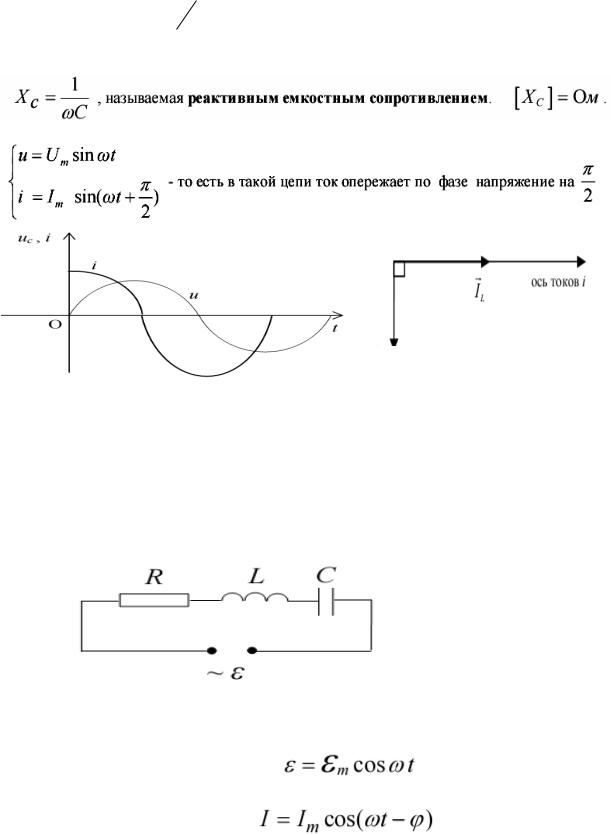 Форма с четырьмя квадрантами упрощает процесс поиска значений E, I, R или Z и P. Есть два колеса, одно для нашей диаграммы закона Ома постоянного тока (R — формулы сопротивления) и одна диаграмма закона Ома для нашего переменного тока ( Z — формулы импеданса). Если вам интересен цвет на колесе, мы используем его в качестве удобного справочника для определения цветов полос резистора … мы включаем их в наши часы и часы по закону Ома. Пожалуйста, прочтите дополнительную информацию о том, как читать эту диаграмму.
Форма с четырьмя квадрантами упрощает процесс поиска значений E, I, R или Z и P. Есть два колеса, одно для нашей диаграммы закона Ома постоянного тока (R — формулы сопротивления) и одна диаграмма закона Ома для нашего переменного тока ( Z — формулы импеданса). Если вам интересен цвет на колесе, мы используем его в качестве удобного справочника для определения цветов полос резистора … мы включаем их в наши часы и часы по закону Ома. Пожалуйста, прочтите дополнительную информацию о том, как читать эту диаграмму. Как правило, если вы МАСТЕР-электрик, специалист по устранению неполадок или инженер, вы можете предпочесть наши часы, часы, наклейки, диаграммы, брелки и т.продукты. Думайте расширенно — думайте об импедансе. Нужны формулы Z? Колесо питания переменного тока
Как правило, если вы МАСТЕР-электрик, специалист по устранению неполадок или инженер, вы можете предпочесть наши часы, часы, наклейки, диаграммы, брелки и т.продукты. Думайте расширенно — думайте об импедансе. Нужны формулы Z? Колесо питания переменного тока  Затем выберите формулу, содержащую значения, которые вы знаете из соответствующего квадранта диаграммы.
Затем выберите формулу, содержащую значения, которые вы знаете из соответствующего квадранта диаграммы. Вы также сможете лучше разбираться в спецификациях производителя, что поможет вам принимать более обоснованные решения о покупке. Законы Ома — один из фундаментальных законов физики. Ток в цепи увеличивается при увеличении напряжения и уменьшается при увеличении сопротивления ИЛИ ток, протекающий в цепи, прямо пропорционален напряжению, приложенному к цепи, и обратно пропорционален сопротивлению цепи.
Вы также сможете лучше разбираться в спецификациях производителя, что поможет вам принимать более обоснованные решения о покупке. Законы Ома — один из фундаментальных законов физики. Ток в цепи увеличивается при увеличении напряжения и уменьшается при увеличении сопротивления ИЛИ ток, протекающий в цепи, прямо пропорционален напряжению, приложенному к цепи, и обратно пропорционален сопротивлению цепи.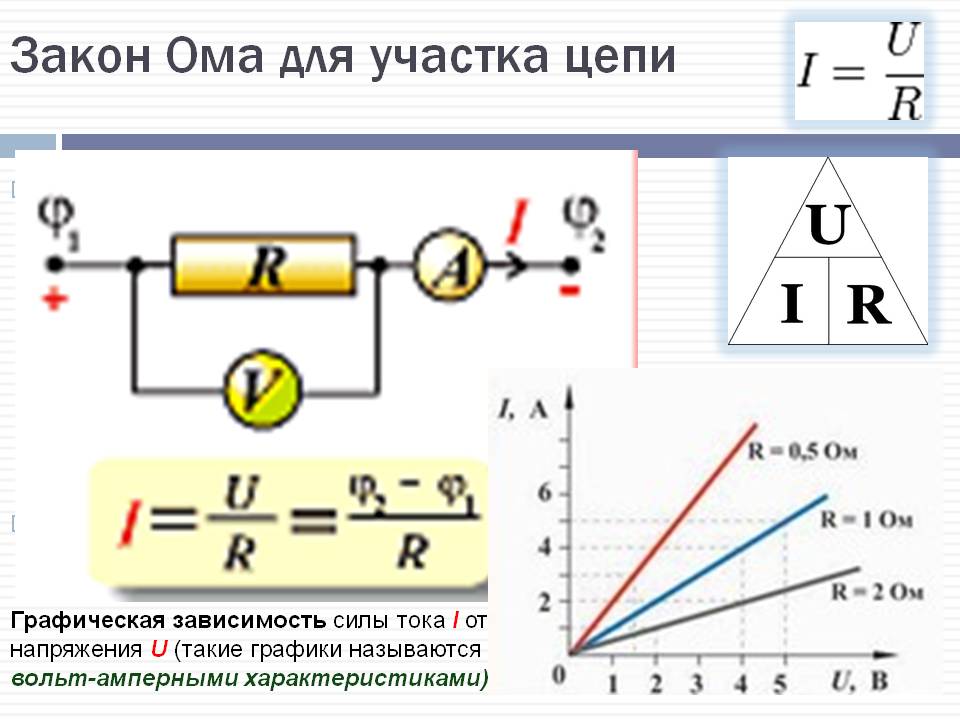 Постоянный ток (DC) равномерно течет в одном направлении через проводник; переменный ток (AC) изменяет направление в проводнике с различной частотой. Чтобы увидеть пример этого, перейдите на нашу страницу технических примечаний.
Постоянный ток (DC) равномерно течет в одном направлении через проводник; переменный ток (AC) изменяет направление в проводнике с различной частотой. Чтобы увидеть пример этого, перейдите на нашу страницу технических примечаний.