Энергия заряженного конденсатора. Применение конденсаторов
Энергия заряженного конденсатора. Применение конденсаторов
- Подробности
- Просмотров: 495
«Физика — 10 класс»
Как и любая система заряженных тел, конденсатор обладает энергией.
Вычислить энергию заряженного плоского конденсатора с однородным полем внутри него несложно.
Энергия заряженного конденсатора.
Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов.
Согласно закону сохранения энергии эта работа равна энергии конденсатора.
В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, содержащую лампу накаливания, рассчитанную на напряжение в несколько вольт (рис.14.37).
При разрядке конденсатора лампа вспыхивает.
Энергия конденсатора превращается в тепло и энергию света.
Выведем формулу для энергии плоского конденсатора.
Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины (рис.14.38).
Согласно формуле (14.14) для потенциальной энергии заряда в однородном поле энергия конденсатора равна:
где q — заряд конденсатора, а d — расстояние между пластинами.
Так как Ed=U, где U — разность потенциалов между обкладками конденсатора, то его энергия равна:
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную.
Если заряд на пластинах остаётся постоянным, при сближении пластин поле совершает положительную работу:
При этом энергия электрического поля уменьшается.
Заменив в формуле (14.25) разность потенциалов или заряд с помощью выражения (14.22) для электроемкости конденсатора, получим:
Можно доказать, что эти формулы справедливы для любого конденсатора, а не только для плоского.
Энергия электрического поля.
Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел.
Значит, энергия может быть выражена через основную характеристику поля — напряженность.
Так как напряженность электрического поля прямо пропорциональна разности потенциалов (U=Ed), то согласно формуле
энергия конденсатора прямопропорциональна квадрату напряженности электрического поля внутри него:
.
Применение конденсаторов.
Зависимость электроемкости конденсатора от расстояния между его пластинами используется при создании одного из типов клавиатур компьютера.
На тыльной стороне каждой клавиши располагается одна пластина конденсатора, а на плате, расположенной под клавишами, — другая.
Нажатие клавиши изменяет емкость конденсатора.
Электронная схема, подключенная к этому конденсатору, преобразует сигнал в соответствующий код, передаваемый в компьютер.
Энергия конденсатора обычно не очень велика — не более сотен джоулей.
К тому же она не сохраняется долго из-за неизбежной утечки заряда.
Поэтому заряженные конденсаторы не могут заменить, например, аккумуляторы в качестве источников электрической энергии.
Но это совсем не означает, что конденсаторы как накопители энергии не получили практического применения.
Они имеют одно важное свойство: конденсаторы могут накапливать энергию более или менее длительное время, а при разрядке через цепь с малым сопротивлением они отдают энергию почти мгновенно.
Именно это свойство широко используют на практике.
Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заряжаемого предварительно специальной батареей.
Возбуждение квантовых источников света — лазеров осуществляется с помощью газоразрядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроемкости.
Однако основное применение конденсаторы находят в радиотехнике.
Энергия конденсатора пропорциональна его электроемкости и квадрату напряжения между пластинами. Вся эта энергия сосредоточена в электрическом поле. Энергия поля пропорциональна квадрату напряженности поля.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Конденсатор. Энергия заряженного конденсатора
-
- Главная
- Политика конфиденциальности
- Q&A
- Новости и общество
- Знаменитости
-
Культура -
Экономика -
Окружающая среда -
Бесплатно -
Журналистика -
Природа -
Философия -
Политика -
Переработка -
Погода -
Женские вопросы
- Дом и семья
- Дети
- Пожилые люди
- Отцовство
- Генеалогия
- Праздники
- Воспитание
- Домашние животные
- Беременность
- Подростки
- Еда и напитки
- Шоколад
- Кофе
- Советы по приготовлению
- Рецепты
- Десерты
- Напитки
- Домашняя пивоварня
- Низкокаллорийные продукты
- Главный курс
- Блюда из макаронных иделий
- Рецепты
- Отзывы о ресторанах
- Салаты
- Супы
- Чай
- Вина и спиртные напитки
- Образование
-
Среднее образование и школы -
Колледжи и университеты -
Обучение на дому -
Международные исследования -
Языки -
Обучение инвалидов -
Интернет-образование -
Наука -
Репетиторство
-
- Путешествия
- Кемпинг
-
Круизы -
Направления -
Экзотические места -
Авиабилеты -
Отели -
Советы туристам -
Аренда
- Автомобили
- Легковые автомобили
-
Классика -
Мотоциклы -
Аренда -
РВС-технология -
Внедорожники -
Грузовые автомобили -
Фургоны
- Спорт
-
Аэробика -
Баскетбол -
Бодибилдинг -
Экстремальные виды спорта -
Рыбалка -
Фитнес -
Футбол -
Хоккей -
Боевые искусства -
Наращивание мышечной массы -
Пилатес -
Самооборона -
Теннис -
Легкая атлетика -
Водные виды спорта -
Снижение веса -
Йога
-
- Книги
- Новости и общество
- Знаменитости
-
Культура -
Экономика -
Окружающая среда -
Бесплатно -
Журналистика -
Природа -
Философия -
Политика -
Переработка -
Погода -
Женские вопросы
- Дом и семья
- Дети
- Пожилые люди
- Отцовство
- Генеалогия
- Праздники
- Воспитание
- Домашние животные
- Беременность
- Подростки
- Еда и напитки
- Шоколад
- Кофе
- Советы по приготовлению
- Рецепты
- Десерты
- Напитки
- Домашняя пивоварня
- Низкокаллорийные продукты
- Главный курс
- Блюда из макаронных иделий
- Рецепты
- Отзывы о ресторанах
- Салаты
- Супы
- Чай
- Вина и спиртные напитки
- Образование
-
СДВГ -
Среднее образование и школы -
Колледжи и университеты -
История -
Обучение на дому -
Международные исследования -
Языки -
Обучение инвалидов -
Интернет-образование -
Наука -
Репетиторство
-
- Путешествия
- Кемпинг
-
Круизы -
Направления -
Экзотические места -
Авиабилеты -
Отели -
Советы туристам -
Аренда
- Автомобили
- Легковые автомобили
-
Классика -
Мотоциклы -
Аренда -
РВС-технология -
Внедорожники -
Грузовые автомобили -
Фургоны
- Спорт
-
Аэробика -
Баскетбол -
Бодибилдинг -
Экстремальные виды спорта -
Рыбалка -
Фитнес -
Футбол -
Хоккей -
Боевые искусства -
Наращивание мышечной массы -
Пилатес -
Самооборона -
Теннис -
Легкая атлетика -
Водные виды спорта -
Снижение веса -
Йога
-
- Q&A
Энергия заряженного конденсатора
На прошлых уроках мы с вами вспоминали о том, что вещества, в
которых имеется значительное число свободных носителей зарядов, называются
проводниками.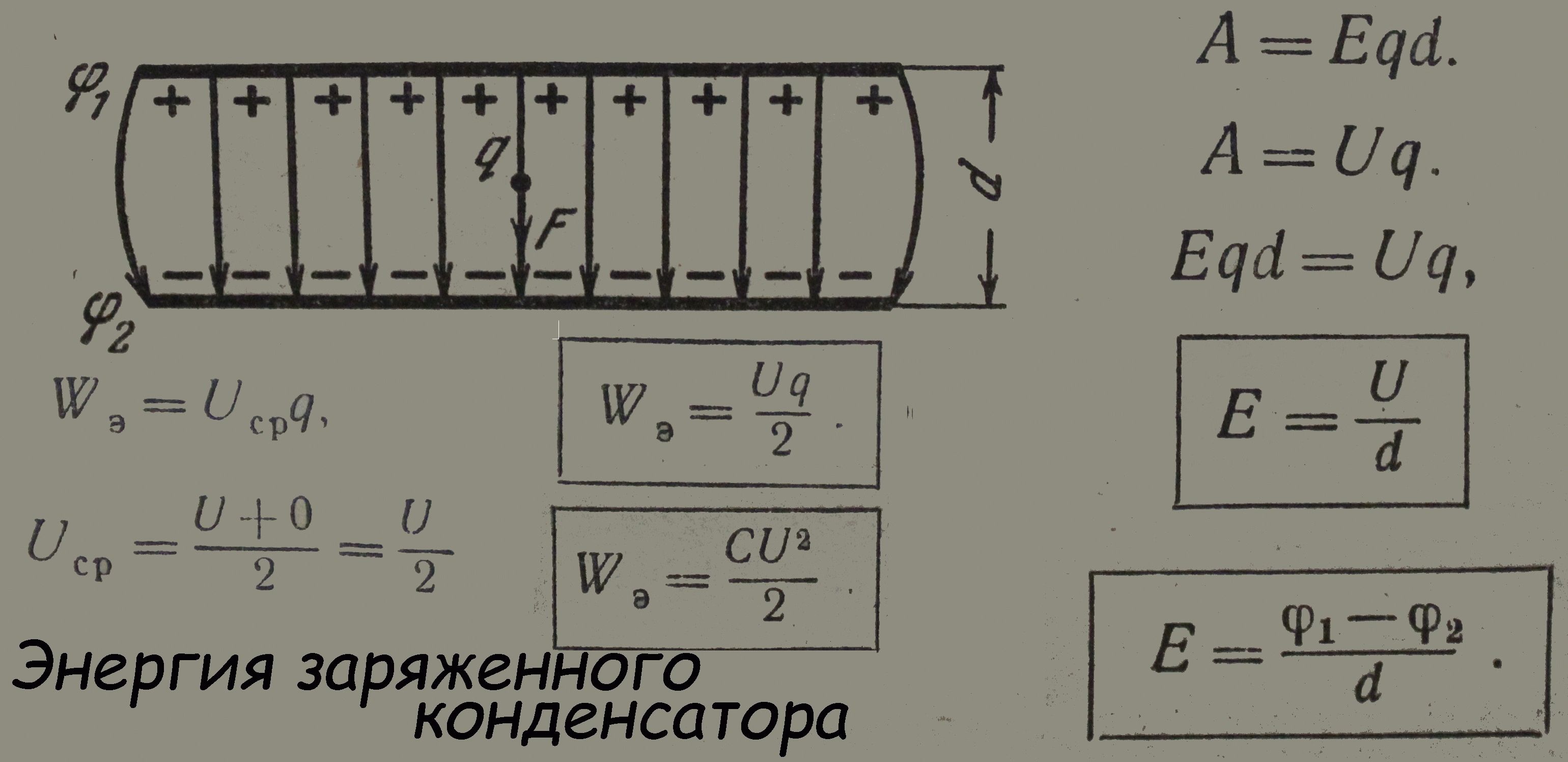 Проводники и системы, состоящие из нескольких проводников,
Проводники и системы, состоящие из нескольких проводников,
обладают одним очень важным свойством: они способны накапливать электрический
заряд, а, значит, и энергию, которая может быть использована в дальнейшем.
Ещё в девятом классе мы с вами говорили о том, что система,
состоящая из двух или более проводников и способная накапливать и отдавать
электрические заряды называется конденсатором.
А способность конденсатора накапливать электрические
заряды характеризуется скалярной физической величиной, называемой электрической
ёмкостью. Она равна отношению заряда конденсатора к разности потенциалов (или напряжению)
между его обкладками:
Простейший конденсатор представляет собой два проводника,
называемые обкладками, разделённые слоем диэлектрика, толщина которого мала по
сравнению с размерами проводников.
Если обкладки конденсатора подсоединить к полюсам источника
тока, то на его обкладках накопятся противоположные по знаку электрические
заряды, модули которых равны. При этом внешние силы совершат работу по переносу
При этом внешние силы совершат работу по переносу
заряда с одной обкладки конденсатора на другую. Эта работа равна энергии
электростатического поля заряженного конденсатора.
Убедиться в том, что заряженный конденсатор обладает энергией
достаточно просто. Достаточно соединить заряженный конденсатор с простой
лампочкой. При этом мы наблюдаем кратковременную вспышку света.
В данном случае во время разрядки конденсатора его энергия
превращается во внутреннюю энергию спирали лампы, часть этой энергии
расходуется на излучение света.
При прохождении электрического тока по цепи́ конденсатор
заряжался. При этом в окружающем конденсатор пространстве возникло
электростатическое поле.
Суммарный электрический заряд обеих обкладок конденсатора до
зарядки, во время зарядки и после разрядки равен нулю. Единственное изменение,
которое произошло при разрядке конденсатора, заключается в том, что исчезло электростатическое
поле. Следовательно, энергией обладало именно электростатическое поле,
Следовательно, энергией обладало именно электростатическое поле,
образованное зарядами на обкладках заряженного конденсатора.
Давайте рассчитаем энергию заряженного конденсатора, заряд
которого равен q, ёмкость — С, а
напряжение между обкладками — U.
Если форма и размеры обкладок конденсатора, а также
расстояние между ними и диэлектрические свойства среды, заполняющей
пространство между обкладками, остаются неизменными, то напряжение на
конденсаторе прямо пропорционально модулю заряда его обкладок:
Чтобы увеличить модуль заряда на обкладках внешней силе
необходимо совершить работу по перемещению бесконечно малой положительной
порции заряда с отрицательной обкладки на положительную. Этой работе на рисунке
соответствует площадь заштрихованного столбика.
Полная же работа по зарядке конденсатора равна сумме площадей
всех аналогичных столбиков, то есть площади фигуры под графиком зависимости напряжения
конденсатора от его заряда.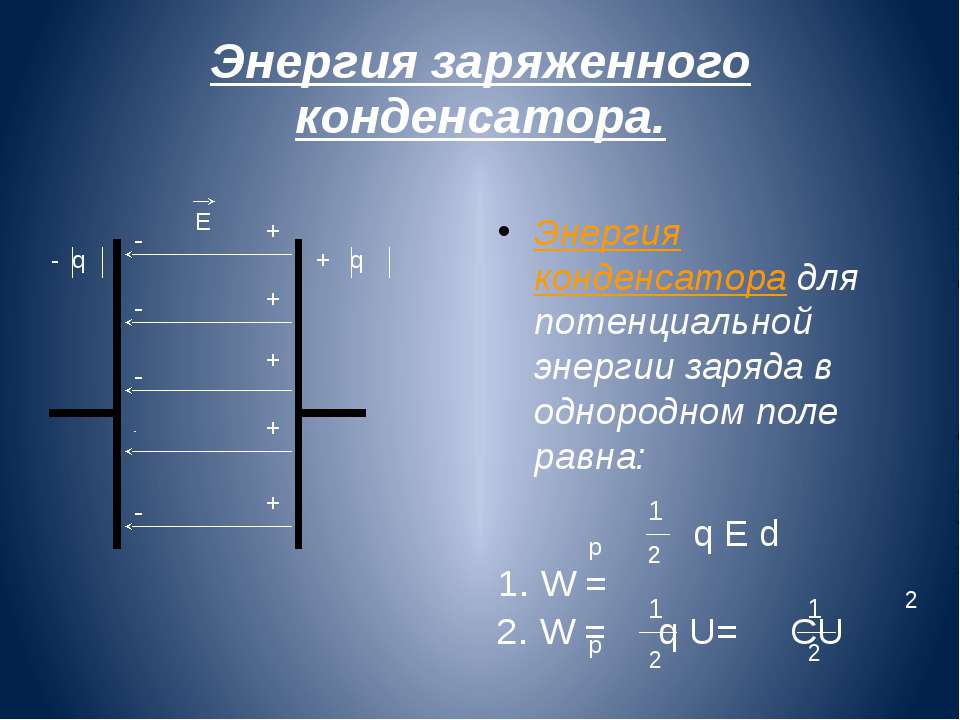 В данном случае — это площадь треугольника. А, как
В данном случае — это площадь треугольника. А, как
мы знаем из математики, площадь треугольника равна половине произведения его
основания на высоту:
Приращение же энергии электростатического поля заряженного
конденсатора равно работе, совершённой внешней силой при его зарядке:
Учитывая, что ,
получим ещё две формулы для определения энергии электростатического поля
заряженного конденсатора:
Когда мы с вами знакомились с теорией близкодействия, то
говорили о том, что вся энергия взаимодействия заряженных тел сосредоточена в их
электрическом поле. Следовательно, энергия может быть выражена через основную
характеристику поля — напряжённость. Как мы знаем, напряжённость электростатического
поля прямо пропорциональна разности потенциалов. Тогда энергия поля
конденсатора прямо пропорциональна квадрату напряжённости электростатического
поля внутри его:
И давайте ещё получим формулу для определения энергии электростатического
поля плоского конденсатора. Для этого вспомним, что ёмкость такого конденсатора
Для этого вспомним, что ёмкость такого конденсатора
зависит от площади пластин, расстояния между ними и свойств внесённого
диэлектрика:
Подставим это выражение в предыдущую формулу:
Обратите внимание вот на этот множитель — это есть не что
иное, как объём пространства между обкладками конденсатора. Тогда получается,
что энергия однородного электростатического поля плоского конденсатора пропорциональна
объёму, занимаемому полем:
Для закрепления материала, решим с вами такую задачу. Плоский
воздушный конденсатор, состоящий из двух обкладок площадью 150 см2
каждая, поместили в диэлектрик с диэлектрической проницаемостью 2,2 и
подключили к источнику тока, напряжение на полюсах которого равно 160 В.
Определите работу, которую необходимо совершить, чтобы после отключения
конденсатора от источника увеличить расстояние между его обкладками от 1,5 см
до 2,0 см.
В заключении урока отметим, что в настоящее время
конденсаторы находят широкое применение в электротехнике, радиотехнической и
телевизионной аппаратуре, радиолокационной технике и телефонии. Применяются конденсаторы
Применяются конденсаторы
и в электроэнергетике, например, для улучшения коэффициента мощности
промышленных установок, регулирования напряжения в распределительных сетях и
так далее. В металлопромышленности их используют для плавки и термической
обработки металлов. В добывающей промышленности — в электровзрывных устройствах.
В медицинской технике — в рентгеновской аппаратуре, приборах электротерапии. Используют
конденсаторы и в фототехнике для получения вспышки света при фотографировании.
Конденсаторы так же используют в схемах кодирования некоторых
клавиатур компьютера. Под каждой клавишей такой клавиатуры находится
конденсатор, электроёмкость которого изменяется при нажатии на клавишу.
Микросхема, подключённая к каждой клавише, при изменении электроёмкости выдаёт
кодированный сигнал, соответствующий данной букве.
В связи с этим наряду с миниатюрными конденсаторами, имеющими
массу менее грамма и размеры порядка нескольких миллиметров, существуют промышленные
конденсаторы с массой в несколько тонн.
Чему равна энергия заряженного конденсатора
Электроемкостью
(емкостью) C уединенного изолированного
проводника называется физическая
величина, равная отношению изменения
заряда проводника q к изменению
его потенциала f:
C = Dq/Df.
Электроемкость
уединенного проводника зависит только
от его формы и размеров, а также
от окружающей его диэлектрической
среды (e).
Единица
измерения емкости в системе
СИ называется Фарадой. Фарада (Ф) —
это емкость такого уединенного проводника,
потенциал которого повышается на 1 Вольт
при сообщении ему заряда в 1 Кулон.
1 Ф =
1 Кл/1 В.
Конденсатором
называют систему двух разноименно
заряженных проводников, разделенных
диэлектриком (например, воздухом).
Свойство
конденсаторов накапливать и сохранять
электрические заряды и связанное
с ними электрическое поле характеризуется
величиной, называемой электроемкостью
конденсатора. Электроемкость конденсатора
равна отношению заряда одной из пластин
Q к напряжению между ними U:
C =
Q/U.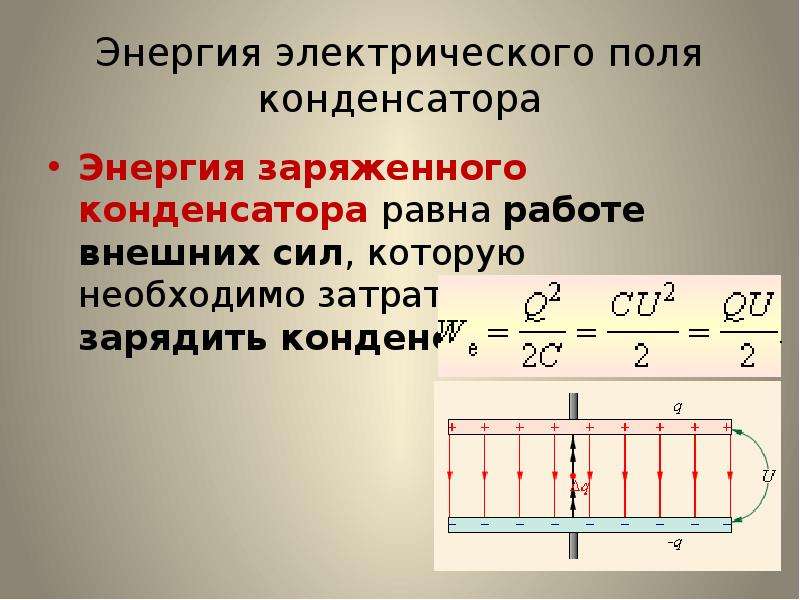
В
зависимости от формы обкладок,
конденсаторы бывают плоскими, сферическими
и цилиндрическими. Формулы для расчета
емкостей этих конденсаторов приведены
в таблице.
Соединение
конденсаторов в батареи.
На практике
конденсаторы часто соединяют в батареи —
последовательно или параллельно.
При
параллельном соединении напряжение
на всех обкладках одинаковое
U1 =
U2 = U3 = U = e, а емкость батареи
равняется сумме емкостей отдельных
конденсаторов C = C1 + C2 + C3.
При
последовательном соединении заряд
на обкладках всех конденсаторов
одинаков Q1 = Q2 = Q3, а напряжение
батареи равняется сумме напряжений
отдельных конденсаторов U = U1 + U2 +
U3.
Емкость
всей системы последовательно соединенных
конденсаторов рассчитывается
из соотношения:
1/C = U/Q = 1/C1 + 1/C2 +
1/C3.
Емкость
батареи последовательно соединенных
конденсаторов всегда меньше, чем емкость
каждого из этих конденсаторов
в отдельности.
Энергия электростатического
поля.
Энергия заряженного плоского
конденсатора Eк равна работе A, которая
была затрачена при его зарядке, или
совершается при его разрядке.
A =
CU2/2 = Q2/2С = QU/2 = Eк.
Поскольку
напряжение на конденсаторе может
быть рассчитано из соотношения:
U =
E*d,
где E — напряженность поля между
обкладками конденсатора,
d —
расстояние между пластинами
конденсатора,
то энергия заряженного
конденсатора равна:
Eк = CU2/2 =
ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2,
где V —
объем пространства между обкладками
конденсатора.
Энергия заряженного
конденсатора сосредоточена в его
электрическом поле.
Тип конденсатора | Формула для расчета | Примечания | Схематическое |
Плоский конденсатор | S — площадь пластины; | ||
Сферический конденсатор | C = 4pee0R1R2/(R2 — R1) | R2 и R1 — радиусы внешней | |
Цилиндрический | C = 2pee0h/ln(R2/R1) | h — высота цилиндров. |
Как
и любая система заряженных
тел, конденсатор
обладает
энергией. Вычислить энергию заряженного
плоского конденсатора с однородным
полем внутри него несложно.
Энергия
заряженного конденсатора.
Для
того чтобы зарядить конденсатор, нужно
совершить работу по разделению
положительных и отрицательных зарядов.
Согласно закону сохранения энергии эта
работа равна энергии конденсатора. В
том, что заряженный конденсатор обладает
энергией, можно убедиться, если разрядить
его через цепь, содержащую лампу
накаливания, рассчитанную на напряжение
в несколько вольт (рис.14.37
).
При разрядке конденсатора лампа
вспыхивает. Энергия конденсатора
превращается в тепло и энергию света.
Выведем
формулу для энергии плоского
конденсатора.
Напряженность поля, созданного зарядом
одной из пластин, равна Е/2
,
где Е
-напряженность
поля в конденсаторе. В однородном поле
одной пластины находится заряд q
,
распределенный по поверхности другой
пластины (рис. 2.
2.
Применение
конденсаторов
.
Зависимость электроемкости конденсатора
от расстояния между его пластинами
используется при создании одного из
типов клавиатур компьютера. На тыльной
стороне каждой клавиши располагается
одна пластина конденсатора, а на плате,
расположенной под клавишами, — другая.
Нажатие клавиши изменяет емкость
конденсатора. Электронная схема,
подключенная к этому конденсатору,
преобразует сигнал в соответствующий
код, передаваемый в компьютер.
Энергия конденсатора обычно не очень
велика — не более сотен джоулей. К тому
же она не сохраняется долго из-за
неизбежной утечки заряда. Поэтому
заряженные конденсаторы не могут
заменить, например, аккумуляторы в
качестве источников электрической
энергии.
Но это совсем не означает, что конденсаторы
как накопители энергии не получили
практического применения. Они имеют
одно важное свойство: конденсаторы
могут накапливать энергию более или
менее длительное время, а при разрядке
через цепь с малым сопротивлением они
отдают энергию почти мгновенно.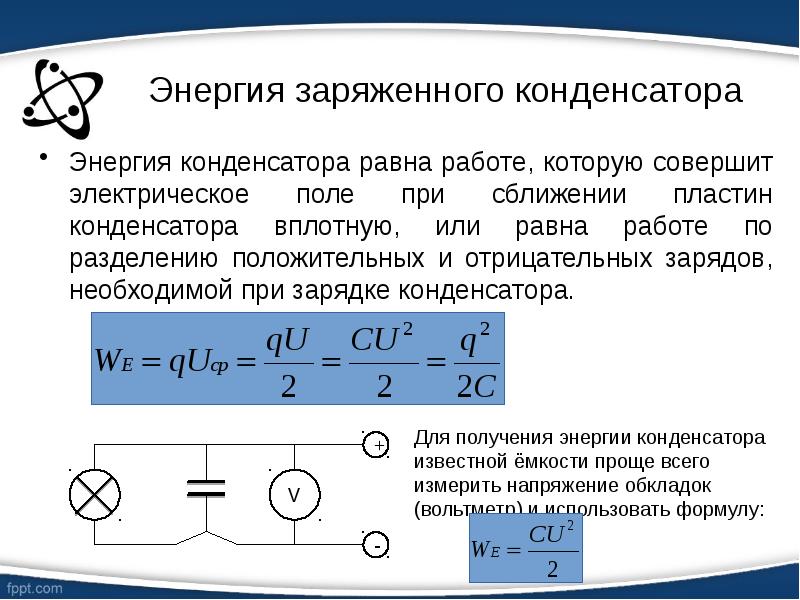 Именно
Именно
это свойство широко используют на
практике.
Лампа-вспышка, применяемая в фотографии
,
питается электрическим током разряда
конденсатора, заряжаемого предварительно
специальной батареей. Возбуждение
квантовых источников света — лазеров
осуществляется с помощью газоразрядной
трубки, вспышка которой происходит при
разрядке батареи конденсаторов большой
электроемкости.
Однако основное применение конденсаторы
находят в радиотехнике.
Энергия конденсатора пропорциональна
его электроемкости и квадрату напряжения
между пластинами. Вся эта энергия
сосредоточена в электрическом поле.
Энергия поля пропорциональна квадрату
напряженности поля.
В заряженном конденсаторе обкладки име-ют разноименные заряды и взаимодейст-вуют между собой благодаря электричес-кому полю, которое сосредоточено в прост-ранстве между обкладками. О телах, между которыми существует взаимодействие, гово-рят, что они имеют потенциальную энер-гию. Следовательно, можно говорить и об энергии заряженного конденсатора
.
Обкладки заряженного конден-сатора взаимодействуют между собой.
Наличие энергии
у заряженного конден-сатора можно подтвердить опытами.
Возьмем конденсатор достаточно боль-шой емкости, источник тока, лампочку на-кала и составим электрическую цепь, схема которой изображена на рис. 4.82. Переведем переключатель S
в положение 1 и зарядим конденсатор до определенной разности по-тенциалов от источника GB.
Если после этого перевести переключатель в положение 2, то можно наблюдать кратковременную вспышку света вследствие накала нити лам-почки. Наблюдаемое явление можно объяс-нить тем, что заряженный конденсатор имел энергию
, за счет которой была выполнена работа по накалу спирали лампочки.
В соответствии с законом сохранения энер-гии
работа, выполненная при разрядке кон-денсатора, равняется работе, выполненной при его зарядке. Расчет этой работы и, соответственно, потенциальной энергии кон-денсатора осложнен особенностями процес-са зарядки конденсатора. Пластины его за-ряжаются и разряжаются постепенно. Зави-симость заряда Q
Пластины его за-ряжаются и разряжаются постепенно. Зави-симость заряда Q
конденсатора от времени при зарядке показана на графике (рис. 4.83). Заряд не только увеличивается постепенно, но и скорость его изменения не остается постоянной. Итак, вести расчеты на осно-вании формулы A =
qEd
нельзя, поскольку напряженность электрического поля не остается постоянной. Разность потенциалов также изменяется от нуля до максимально-го значения. На рис. 4.84 показано, что разность потенциалов изменяется про-порционально заряду конденсатора. Такая зависимость характерна для силы упругос-ти, которая зависит от удлинения пружины (рис. 4.85).
Воспользовавшись таким подобием, мож-но сделать вывод, что энергия заряженного конденсатора
будет равна
W =
Q
Δφ / 2.
Материал с сайта
Эта энергия
равна работе по зарядке конденсатора, которая численно равна пло-щади заштрихованного треугольника на гра-фике рис. 4.84.
Учитывая, что Q =
C
Δφ
, получим
W =
C(Δφ)
2 / 2.
А если учесть связь разности потенциалов с зарядом Δφ =
Q /
C
, то потенциальная энер-гия конденсатора может быть вычислена по формуле
W = (Q / 2) . (Q /
C) =
Q 2 / 2
C.
На этой странице материал по темам:
Энергия заряженного конденсатора шпора
Энергия заряженного конденсатора
Какие физические величины определяют энергию конденсатора
Самостоятельная работа по теме электроемкость плоского конденсатора
Як визначити енергію конденсатора за допомогою графіка
Вопросы по этому материалу:
Пусть потенциал обкладки конденсатора, на которой находится заряд равен а потенциал обкладки, на которой находится заряд , равен Тогда каждый из элементарных зарядов на которые можно разделить заряд находится в точке с потенциалом а каждый из зарядов, на которые можно разделить заряд , в точке с потенциалом .
Согласно формуле (28. 1) энергия такой системы зарядов равна
1) энергия такой системы зарядов равна
Воспользовавшись соотношением (27.2), можно написать три выражения для энергии заряженного конденсатора:
Формулы (29.2) отличаются от формул (28.3) только заменой на
С помощью выражения для потенциальной энергии можно найти силу, с которой пластины плоского конденсатора притягивают друг друга. Допустим, что расстояние между пластинами может меняться. Свяжем начало оси х с левой пластиной (рис. 29.1). Тогда координата х второй пластины будет определять зазор d между обкладками. Согласно формулам (27.3) и (29.2)
Продифференцируем это выражение по х, полагая заряд на обкладках неизменным (конденсатор отключен от источника напряжения). В результате получим проекцию на ось х силы, действующей на правую пластину:
Модуль этого выражения дает величину силы, с которой обкладки притягивают друг друга:
Теперь попытаемся вычислить силу притяжения между обкладками плоского конденсатора как произведение напряженности поля, создаваемого одной из обкладок, на заряд, сосредоточенный на другой.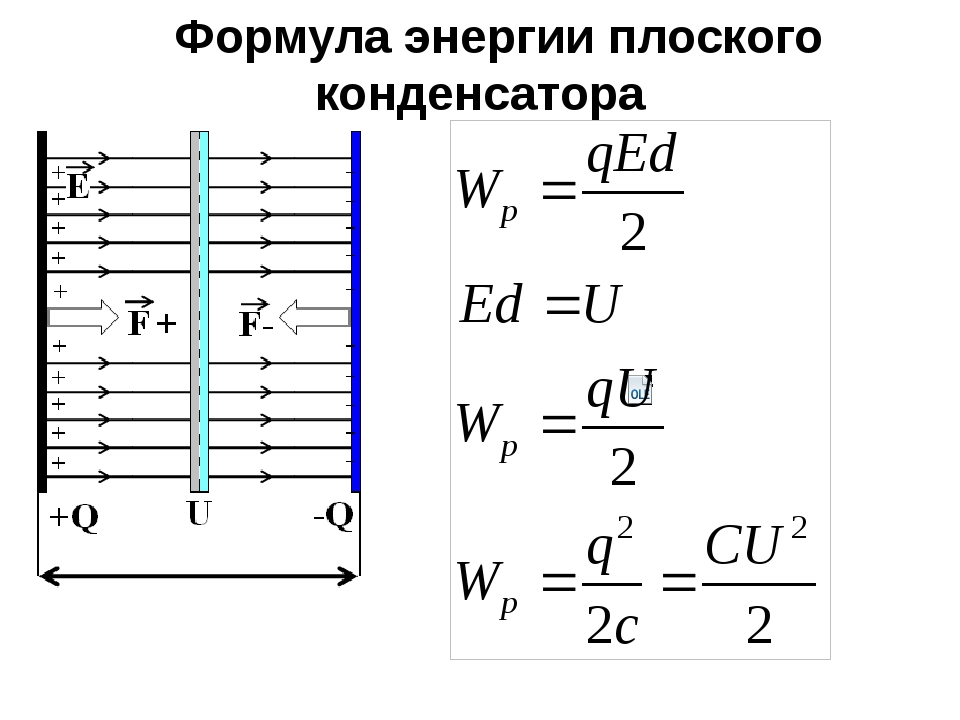 Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна
Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна
Диэлектрик ослабляет поле в зазоре в раз, но это имеет место только внутри диэлектрика (см. формулу (20.2) и связанный с нею текст). Заряды на обкладках располагаются вне диэлектрика и поэтому находятся под действием поля напряженности (29.4).
Умножив заряд обкладки q на эту напряженность, получим для силы выражение
Формулы (29.3) и (29.5) не совпадают. С опытом согласуется значение силы (29.3), получающееся из выражения для энергии. Это объясняется тем, что, кроме «электрической» силы (29.5), на обкладки действуют со стороны диэлектрика механические силы, стремящиеся их раздвинуть (см. § 22; отметим, что мы имеем в виду жидкий или газообразный диэлектрик). У края обкладок имеется рассеянное поле, убывающее по величине при удалении от краев (рис. 29.2). Молекулы диэлектрика, обладая дипольным моментом, испытывают дйствие силы, втягивающей их в область более сильного поля (см. формулу (9. 16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.
16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.
Если заряженный конденсатор с воздушным зазором частично погрузить в жидкий диэлектрик, наблюдается втягивание диэлектрика в пространство между пластинами (рис. 29.3). Это явление объясняется следующим образом. -Диэлектрическая проницаемость воздуха практически равна единице. Поэтому до погружения пластин в диэлектрик емкость конденсатора можно считать равной а энергию равной При частичном заполнении зазора диэлектриком конденсатор можно рассматривать как два параллельно включенных конденсатора, один из которых имеет площадь обкладки, равную — относительная часть зазора, заполненная жидкостью), и заполнен диэлектриком с второй с воздушным зазором имеет площадь обкладки, равную При параллельном включении конденсаторов емкости складываются:
Поскольку энергия будет меньше, чем (заряд q предполагается неизменным — перед погружением в жидкость конденсатор был отключен от источника напряжения). Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).
Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).
Втягивание диэлектрика в зазор между обкладками можно яснить также и с микроскопической точки зрения. У краев пластин конденсатора имеется неоднородное поле. Молекулы диэлектрика обладают собственным дипольным моментом либо приобретают его под действием поля; поэтому на них действуют силы, стремящиеся переместить их в область сильного поля, т. е. внутрь конденсатора. Под действием этих сил жидкость втягивается в зазор до тех пор, пока электрические силы, действующие на жидкость у края пластин, не будут уравновешены весом столба жидкости.
План конспект по физике на тему «Разность потенциалов электростатического поля. Электроемкость. Энергия заряженного конденсатора. Энергия электрического поля» (11 класс)
ГУ «Отдел оразования Аршалынского района »
«ЕЦ 166/5 мекмесiнi жанынагы №5 кешкi(аусымда) жалпы орта бiлiм беретiн мектебi» ММ басшысы
ГУ «Вечерняя(сменная) средняя общеобразовательная школа №5 при учреждении ЕЦ 166/5 »
УРОК
Разность потенциалов электростатического поля.
Электроемкость.
Энергия заряженного конденсатора.
Энергия электрического поля.
11 класс
Провела :
учитель физики Бережная Л.И.
2017 год
Урок № 4
Тема урока: Разность потенциалов электростатического поля. Электроемкость.
Электроемкость.
Энергия заряженного конденсатора. Энергия электрического поля.
Цели урока:
Образовательные:
-введение понятия потенциала электростатического поля, разность потенциалов;
-сформировать понятие электроёмкости, используя ПОХ рассказа о величине;
-ввести понятие конденсатора, как системы двух проводников, разделённых слоем диэлектрика;
— познакомить с понятием электроемкости
Развивающие:
—продолжить развитие экспериментальных умений, умения делать выводы;
-развивать познавательный интерес к физике и технике;
-развивать самооценку своей самостоятельной деятельности на уроке;
-закрепить полученные знания через самостоятельное решение задач.
Воспитательные:
—продолжить формировать научное мировоззрение, систему взглядов на мир и на технический прогресс; интерес к познанию законов природы и их применению;
Тип урока: урок усвоения новых знаний.
Вид урока: комбинированный
Учебник: Физика-10. Общественно-гуманитарное направление. Автор: Р.Башарулы, Г. Айжасарова, У. Токбергенова
План урока:
I.Организационный момент. Постановка цели урока.
II.Объяснение нового материала
III. Закрепление новой темы. Решение задач. IV. Подведение итогов урока. Рефлексия V. Домашнее задание
Организационный момент.
Приветствие учащихся, организация рабочего места.
Вступительное слово учителя: ребята, вы уже не первый год изучаете физику, из каждого урока узнаете все больше о законах и явлениях природы, пытаясь ответить на вопросы, что беспокоили человечество тысячелетиями. Сегодня на уроке мы познакомимся с понятием разности потенциалов электростатического поля, электроемкости плоского конденсатора, энергии электрического поля.
Науку всё глубже постигнуть стремись,
Познанием вечного жаждой томись.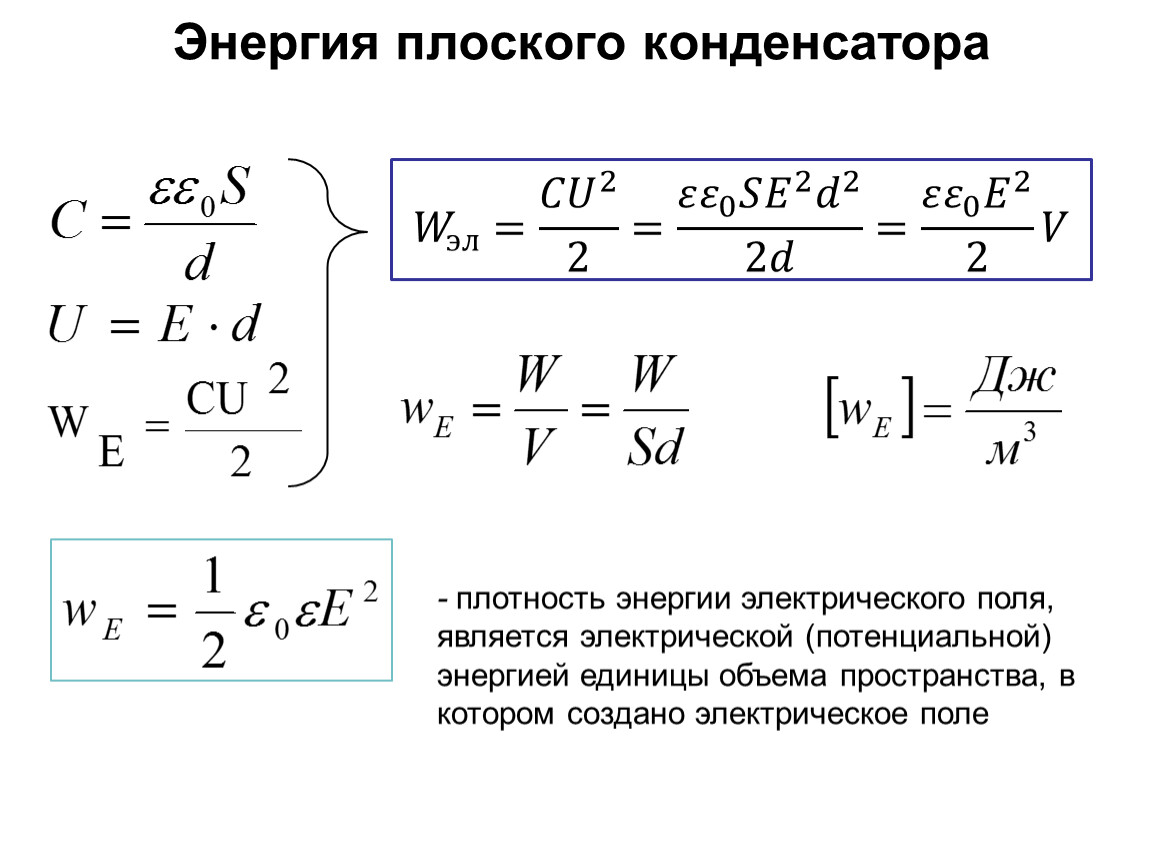
Лишь первых познаний блеснёт тебе свет,
Узнаешь: предела для знания нет.
Фирдоуси,
персидский и таджикский поэт
(940 – 1030 г.)
Объяснение нового материала (сопровождается презентацией).
1.Разность потенциалов электростатического поля
Работа любого электростатического поля А при перемещении в нем заряда q на расстояние d определяется: A+= F где d -расстояние между пластинами.
На замкнутой траектории работа электростатического поля всегда равна нулю.
Поля, обладающие таким свойством, называют потенциальными.
Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Отношение вида является еще одной характеристикой поля. Это отношение обозначается Т.е.
Разностью потенциалов называют физическую величину, равную отношению работы электрического поля при перемещении положительного заряда к величине этого заряда.
Разность потенциалов измеряется в вольтах (В) 1В=
Разность потенциалов является энергетической характеристикой электрического поля.
A= и А=q
q
=
модуль напряженности однородного электрического поля равен отношению разности потенциалов двух точек поля, лежащих на одной линии, к расстоянию межу этими точками
2. Электроемкость. Конденсаторы.
Вопрос. Приходилось ли вам сталкиваться с профессией мастера по ремонту телерадиоаппаратуры? Как вы думаете, чем он занимается?
Ответ. Выявляет причины неисправности, осуществляет замену вышедших из строя деталей.
Вопрос. Можете назвать эти детали?
Ответ. Диоды, триоды, транзисторы, конденсаторы…
Вопрос. Какие знания по физике нужны для работы телемастеру?
Ответ. Устройство, назначение, принцип действия, правила включения приборов.
Устройство, назначение, принцип действия, правила включения приборов.
С одной из радиодеталей познакомимся сегодня подробнее. Это конденсатор. Он может накапливать большой электрический заряд а, следовательно, тесно связан с материалом, который мы изучаем.
Конденсаторами называют систему проводников, заряженных разноименными и равными зарядами. Проводники, образующие конденсатор, называются обкладками.
Конденсатор в переводе на русский язык означает «сгуститель». Чтобы на емкость конденсатора не оказывали влияние окружающие тела, проводникам придают такую форму, чтобы поле было сосредоточено в узком зазоре между обкладками конденсатора. Такому условию удовлетворяют:
— Слайд №67 -6-две плоские пластины – плоский конденсатор;
два коаксиальных цилиндра – цилиндрические;
две концентрические сферы – сферические.
Слайд №67 –7-классификация конденсаторов
Слайд №67-8,9-формы конденсаторов
Слайд №67 -10- назначения конденсаторов
Результаты опытов показали, что разность потенциалов между обкладками конденсатора прямо пропорциональна его заряду. При этом отношение не зависит от знака заряда. Данное отношение принято называть электроемкостью конденсатора.
При этом отношение не зависит от знака заряда. Данное отношение принято называть электроемкостью конденсатора.
С= Ф=
На основе опытов было установлено, что емкость плоского конденсатора определяется формулой:
С=
где =8,85/Н- электрическая постоянная; d- расстояние между обкладками; S- площадь обкладки; — диэлектрическая проницаемость среды, в которой находится конденсатор.
3.Энергия заряженного конденсатора.
Заряженный конденсатор обладает энергией. Она зависит от его емкости и разности потенциалов между пластинами. Эта зависимость выражается формулой: W=
С= ⇒ тогда W=
Энергия заряженного конденсатора сосредоточена в его электрическом поле и прямо пропорциональна квадрату напряженности поля, т.е. W . Электрическое поле как и любой вещественный вид материи обладает энергией.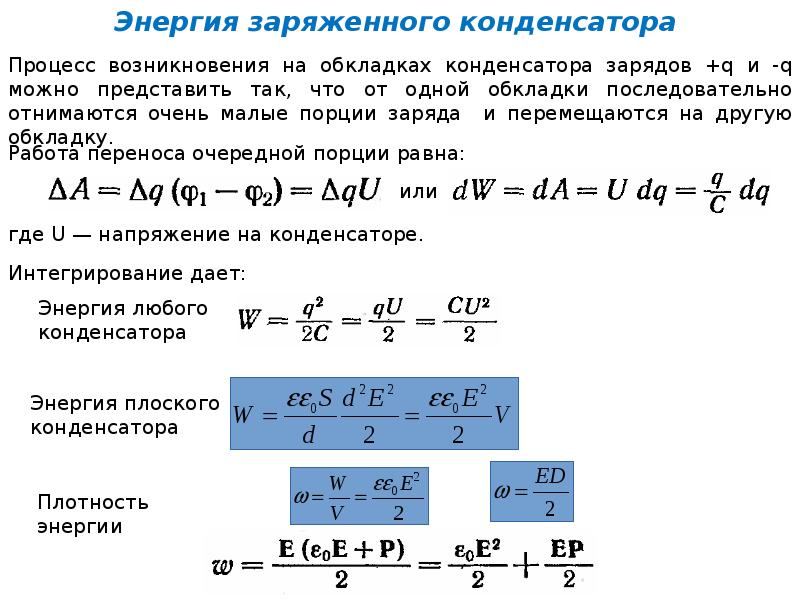 Наличие энергии- важнейшее свойство электрического поля.
Наличие энергии- важнейшее свойство электрического поля.
4.Применение конденсаторов
В современной технике конденсаторы находят себе исключительно широкое и разностороннее применение, прежде всего в областях электроники. Здесь можно отметить их применение для следующих основных целей:
1.В радиотехнической и телевизионной аппаратуре – для создания колебательных контуров, их настройки, блокировки, разделения цепей с различной частотой, в фильтрах выпрямителей и т.д.
2.В радиолакационной технике – для получения импульсов большей мощности, формирования импульсов и т.д.
3. В телефонии и телеграфии – для разделения цепей переменного и постоянного токов, разделения токов различной частоты, искрогашения в контактах, симметрирования кабельных линий и т.д.
4. В автоматике и телемеханике – для создания датчиков на емкостном принципе, разделения цепей постоянного и пульсирующего токов, искрогашения в контактах, в схемах тиратронных генераторов импульсов и т. д.
д.
5. В технике счетно-решающих устройств – в специальных запоминающих устройствах и т.д.
6. В электроизмерительной технике – для создания образцов емкости, получения переменной емкости (магазины емкости и лабораторные переменные конденсаторы), создания измерительных приборов на емкостном принципе и т. д.
7. В лазерной технике – для получения мощных импульсов.
Кроме электроники и электроэнергетики, конденсаторы применяют и в других неэлектротехнических областях техники и промышленности для следующих основных целей:
В металлопромышленности — в высокочастотных установках для плавки и термической обработки металлов, в электроэрозионных (электроискровых) установках, для магнитоимпульсной обработки металлов и т.д.
В добывающей промышленности (угольной, металлорудной и т.п.) – в рудничном транспорте на конденсаторных электровозах нормальной и повышенной частоты (бесконтактных), в электровзрывных устройствах с использованием электрогидравлического эффекта и т.
 д.
д.В автотракторной технике – в схемах зажигания для искрогашения в контактах и для подавления радиопомех.
В медицинской технике – в рентгеновской аппаратуре, в устройствах электротерапии и т.д.
В технике использования атомной энергии для мирных целей – для изготовления дозиметров, для кратковременного получения больших токов и т.д.
В фотографической технике – для аэрофотосъемки, получения вспышки света при обычном фотографировании и т.д.
Закрепление новой темы. Решение задач.
1.Какова напряженность однородного электрического поля между двумя пластинами, расположенными на расстоянии 5 см друг от друга в вакууме, если разность потенциалов между пластинами 50В? Какую работу совершают силы электрического поля при перемещении заряда 8
Дано: Решение:
d=5 см=0,05м Е=
=50В А=q
E==1000В/м
Е-? А-? А=
Ответ:Е=1000В/м; А=
2. Вычислить энергию конденсатора с электроемкость 20 мкФ, который имеет заряд 4 мкКл
Вычислить энергию конденсатора с электроемкость 20 мкФ, который имеет заряд 4 мкКл
Дано: Решение:
C= 20 = = 0,4мкДЖ
Q= 4 мкКл=410-6 Кл
Ответ:
3. Площадь пластин плоского конденсатора с слюдяной прокладкой
равно 15 см2, а расстояние между пластинами — 0,02см. Найдите электроемкость плоского конденсатора.
Решение:
S=15 см2 = 1510-4 м С =
d = 0,02см =210-4 м С =
ε = 7
ε0 = 8,8510-12 Ф/м
С- ? Ответ: С=46,4 пФ
IV.Подведение итогов урока. Рефлексия.
-какую физическую величину называют разностью потенциалов?
— в каких единицах измеряется разность потенциалов?
-что называют электрической емкостью?
-что представляет собой конденсатор?
-с какими видами конденсаторов вы познакомились?
-от каких величин зависит емкость плоского конденсатора?
— обладает ли электрическое поле энергией?
Домашнее задание: §5
Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве
Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.
Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.
Проводники и диэлектрики в электростатическом поле
Вещества в природе можно разделить на проводники и диэлектрики.
Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
Типичные проводники — металлы.
Диэлектрическая проницаемость вещества
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.
Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
Физическая величина, равная отношению модуля напряженности \(\vec{E}_0\) внешнего электрического поля в вакууме к модулю напряженности \(\vec{E}\) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества \(\varepsilon\).
\[\varepsilon=\dfrac{\vec{E}_0}{\vec{E}}\]
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда \(q\) одного из проводников к разности потенциалов \(\Delta \varphi\) между ними:
\[\fbox{$C=\dfrac{q}{\Delta \varphi}$}\]
Единицы измерения: \(\displaystyle [\text{Ф}]\) (фарад).
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.
Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электроемкость плоского конденсатора
Разность потенциалов \(\Delta \varphi\) между пластинами в однородном электрическом поле равна \(Ed\), где \(d\) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
\[C=\dfrac{q}{\Delta \varphi}=\dfrac{\sigma S}{Ed}=\dfrac{\varepsilon_0S}{d}\]
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в \(\varepsilon\) раз:
Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в \(\varepsilon\) раз:
\[\fbox{$C=\dfrac{\varepsilon_0\varepsilon S}{d}$}\]
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин.
 Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.Напряжение на данном участке цепи соотносятся следующим образом:
\[\fbox{$U=U_1+U_2$}\]
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
\[\dfrac{q}{C}=\dfrac{q}{C_1}+\dfrac{q}{C_2}\]
Сократив выражение на \(Q\), получим формулу:
\[\fbox{$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}$}\]
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
\[\fbox{$C=\dfrac{C_1C_2}{C_1+C_2}$}\]
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
\[\fbox{$q=q_1+q_2$}\]
Так как заряд конденсатора
\[q=CU\]
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
\[CU=C_1U+C_2U\]
\[\fbox{$C=C_1+C_2$}\]
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.
Вычислим эту энергию: начнём с плоского воздушного конденсатора.
Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора \(q\), площадь обкладок \(S\). Возьмём на второй обкладке настолько маленькую площадку, что заряд \(q_0\) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
\[F_0 = q_0E_1,\]
где \(E_1\) — напряжённость поля первой обкладки:
\[E_1=\dfrac{\sigma}{2\varepsilon_0}=\dfrac{q}{2\varepsilon_0S}\]
Значит
\[F_0=\dfrac{qq_0}{2\varepsilon_0S}\]
Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила \(F\) притяжения второй обкладки к первой складывается из всех этих сил \(F_0\), с которыми притягиваются к первой обкладке всевозможные маленькие заряды \(q_0\) второй обкладки. При этом суммировании постоянный множитель \(\displaystyle\dfrac{q}{2\varepsilon_0S}\) вынесется за скобку, а в скобке просуммируются все \(q_0\) и дадут \(q\). 2}{2}$}, (3)\]
2}{2}$}, (3)\]
Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Электростатика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Электрический заряд и его свойства
К оглавлению…
Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10–6 Кл), нанокулонами (1 нКл = 10–9 Кл) и пикокулонами (1 пКл = 10–12 Кл). Электрический заряд обладает следующими свойствами:
1. Электрический заряд является видом материи.
2. Электрический заряд не зависит от движения частицы и от ее скорости.
3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.
5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.
6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.
Электрический заряд любого тела всегда кратен элементарному заряду:
где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.
7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q1 и q2 (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.
Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов. Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.
Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.
Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:
1. Линейная плотность заряда. Используется для описания распределения заряда по нити:
где: L – длина нити. Измеряется в Кл/м.
2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:
где: S – площадь поверхности тела. Измеряется в Кл/м2.
3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:
где: V – объем тела. Измеряется в Кл/м3.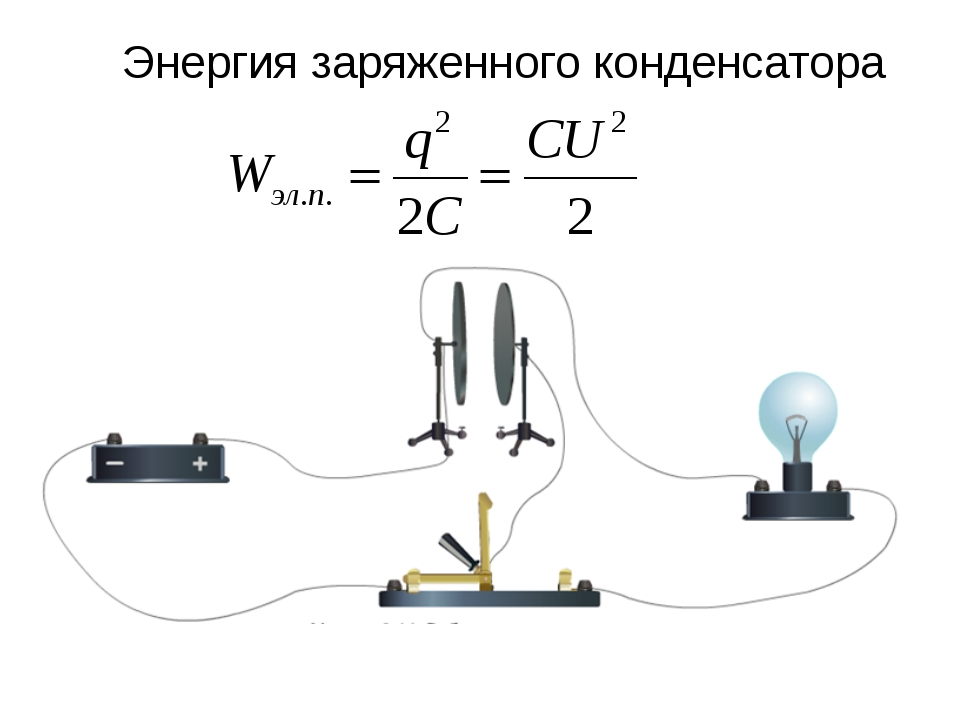
Обратите внимание на то, что масса электрона равна:
me = 9,11∙10–31 кг.
Закон Кулона
К оглавлению…
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:
k = 9∙109 м/Ф.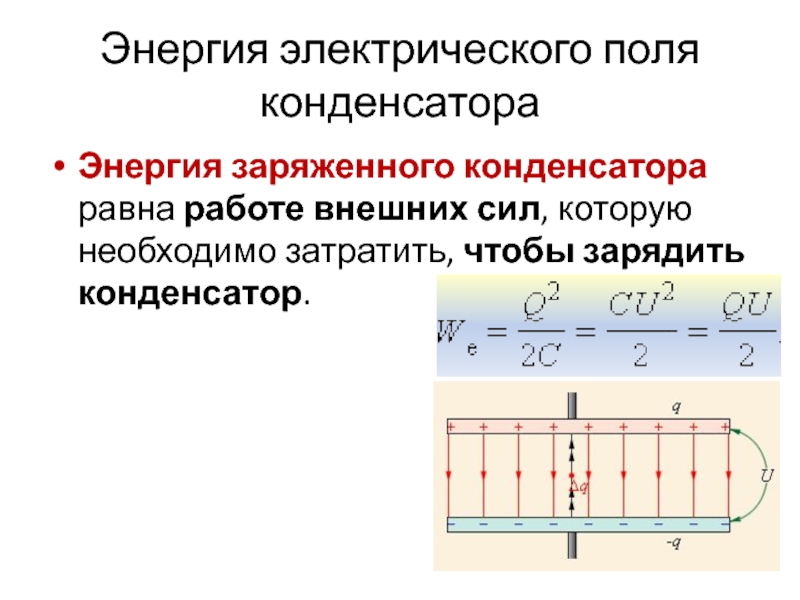
Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:
где: ε0 = 8,85∙10–12 Ф/м – электрическая постоянная.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Запомните также два важных определения:
Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.
Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.
Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):
Электрическое поле и его напряженность
К оглавлению…
По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.
Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.
Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика — напряженность электрического поля E.
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:
Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.
- Силовые линии электростатического поля никогда не пересекаются.
- Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
- При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
- Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.

- В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.
Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.
Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.
Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:
Принцип суперпозиции
К оглавлению. ..
..
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:
Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:
Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:
- Нарисовать рисунок.
- Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
- Вычислить каждую из напряжённостей по соответствующей формуле.
- Сложить вектора напряжённостей геометрически (т.е. векторно).
Потенциальная энергия взаимодействия зарядов
К оглавлению…
Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:
Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.
Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
Потенциал. Разность потенциалов. Напряжение
К оглавлению…
Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.
В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.
Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.
Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
В этих формулах:
- φ – потенциал электрического поля.

- ∆φ – разность потенциалов.
- W – потенциальная энергия заряда во внешнем электрическом поле.
- A – работа электрического поля по перемещению заряда (зарядов).
- q – заряд, который перемещают во внешнем электрическом поле.
- U – напряжение.
- E – напряженность электрического поля.
- d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.
Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.
Принцип суперпозиции потенциала
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):
Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Электрическая емкость. Плоский конденсатор
К оглавлению…
При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:
В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.
Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:
За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.
Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:
Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:
Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.
Энергия электрического поля
Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):
Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):
Соединения конденсаторов
К оглавлению…
Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:
При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Из закона сохранения заряда следует, что заряды на соседних обкладках равны:
Напряжение равно сумме напряжений на отдельных конденсаторах.
Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:
Для N одинаковых последовательно соединённых конденсаторов:
Проводящая сфера
К оглавлению…
Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.
Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.
На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.
Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Электрическая емкость шара радиуса R:
Если шар окружен диэлектриком, то:
Свойства проводника в электрическом поле
К оглавлению…
- Внутри проводника напряженность поля всегда равна нулю.
- Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
- Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
- Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности).
 Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся. - Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.
Замечания к решению сложных задач
К оглавлению…
1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:
- Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей.
 Одним словом, заземлить – означает обнулить потенциал объекта.
Одним словом, заземлить – означает обнулить потенциал объекта. - Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.
2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.
3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.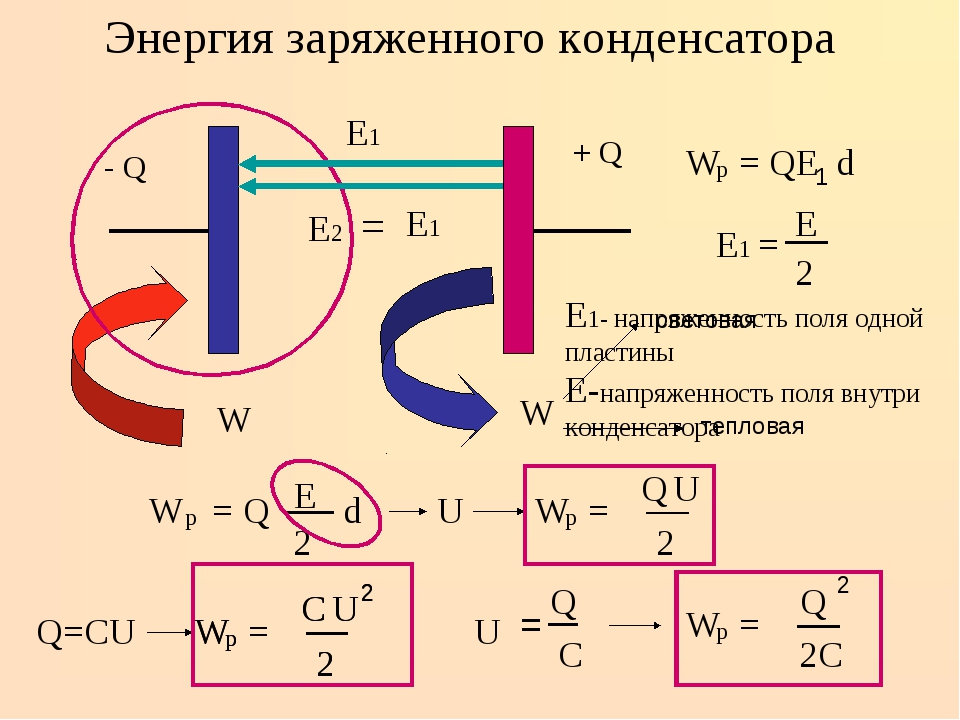
Лекция 4
gc6 tb16.11
К одному концу незаряженного металлического стержня подносят отрицательно заряженный стержень. Самый дальний от заряженного стержня конец металлического стержня будет заряжен
А. положительный
Б. отрицательный
С. нейтральный
D. ни один из этих
Ответ
Рыцарь2 29.CQ.10
Каковы соотношения полей и потенциалов в положениях, указанных на рисунке? Позволять
В = 0 В на отрицательной пластине.
Ответ
sj6 26,2
Проводники с зарядами +10 мкКл и -10 мкКл имеют разность потенциалов 10 В.
Какова емкость?
А. 1 пФ
Б. 10 пФ
С. 1 мкФ
D. 100 мкФ
Ответ
сж6 26.2б
Если заряды увеличить в десять раз, что произойдет с разностью потенциалов?
A. уменьшение в 100 раз
Б.уменьшение в 10 раз
C. остаться прежним
D. увеличить в 10 раз
Ответ
gc6 17,50
Конденсатор имеет фиксированный заряд на своих пластинах, так как расстояние между пластинами удваивается. Что происходит с запасенной энергией
Что происходит с запасенной энергией
в электрическом поле?
А. U 2 = 4 U 1
Б. 2 = 2 1
С. У 2 = 0.5 У 1
D. U 2 = 0,25 U 1
Ответ
сб5 26.47
Конденсатор с А = 25 см 2 и d = 1,5 см заряжен до 250 В. Чему равен заряд
на своих тарелках?
А. 151 нК
Б. 369 пС
С. 519 мкКл
D. 17.1 mC
Ответ
АПБ 1998.14
Две параллельные проводящие пластины подключены к источнику постоянного напряжения.Величина электрического поля
между пластинами составляет 2000 Н/Кл. Если напряжение увеличить вдвое, а расстояние между пластинами уменьшить до
1/5 исходного расстояния, величина нового электрического поля составляет
А. 800 Н/З
Б. 1600 Н/К
С. 2400 Н/С
Д. 5000 Н/К
E. 20 000 N/C
Ответ
Б. отрицательный
отрицательный
Положительные заряды в металлическом стержне будут притягиваться к отрицательно заряженному стержню, оставляя противоположный конец стержня отрицательным.
заряжен.Можно также сказать, что электроны в металлическом стержне отталкиваются от отрицательно заряженного стержня.
Поле постоянно между пластинами конденсатора, но
потенциал возрастает линейно.
С. 1 мкФ
D. увеличение в 10 раз
Емкость будет оставаться постоянной до тех пор, пока геометрия
конденсатор остается постоянным. Следовательно, поскольку C = Q/V , разность потенциалов будет увеличиваться линейно.
пропорционально сумме начисления.
B. U 2 = 2 U 1
Энергия, запасенная в конденсаторе, пропорциональна квадрату заряда
разделить на емкость, но емкость уменьшится вдвое, если расстояние между пластинами увеличится вдвое.
Следовательно, запасенная энергия удвоится. Это потому, что требуется работа, чтобы разорвать
Это потому, что требуется работа, чтобы разорвать
противоположно заряженные пластины притягиваются друг к другу.
Б. 369 ПК
Э.20 000 Н/З
Электрическое поле однородно и постоянно между пластинами и равно
Δ V / d (уравнение 20-4, см. также уравнение 20-11). Удвоение Δ V удвоит E ,
и уменьшение d в 5 раз увеличит E в 5 раз. Два изменения
вместе увеличит E в 10 раз.
Энергия, накопленная в конденсаторе
Проблема «энергии, запасенной в конденсаторе» является классической, поскольку в ней есть некоторые парадоксальные элементы.Разумеется, батарея выделяет энергию QV b в процессе зарядки конденсатора до равновесного напряжения батареи V b . Но половина этой энергии рассеивается в виде тепла на сопротивлении пути заряда, и только QV b /2 в конечном итоге накапливается на конденсаторе в состоянии равновесия. Нелогичная часть начинается, когда вы говорите: «Это слишком большие потери, чтобы их терпеть. Я просто уменьшу сопротивление пути зарядки, чтобы получить больше энергии на конденсаторе.Это не работает, потому что скорость потери энергии в сопротивлении I 2 R резко возрастает, даже если вы заряжаете конденсатор быстрее. В этом экспоненциальном процессе заряда совсем не интуитивно понятно, что вы все равно потеряете половину энергии в тепло, так что эта классическая задача становится прекрасным примером ценности исчисления и интеграла как инженерного инструмента.
Нелогичная часть начинается, когда вы говорите: «Это слишком большие потери, чтобы их терпеть. Я просто уменьшу сопротивление пути зарядки, чтобы получить больше энергии на конденсаторе.Это не работает, потому что скорость потери энергии в сопротивлении I 2 R резко возрастает, даже если вы заряжаете конденсатор быстрее. В этом экспоненциальном процессе заряда совсем не интуитивно понятно, что вы все равно потеряете половину энергии в тепло, так что эта классическая задача становится прекрасным примером ценности исчисления и интеграла как инженерного инструмента.
Часть интуитивной части, которая входит в настройку интеграла, заключается в том, что установка первого элемента заряда dq на пластины конденсатора требует гораздо меньше усилий, потому что большая часть напряжения батареи падает на сопротивлении R и только крошечная энергия dU = dqV сохраняется на конденсаторе.Интеграл, который принимает квадратичную форму по q, дает суммарную энергию на конденсаторе Q 2 /2C = CV b 2 /2 = QV b /2, где V b здесь это напряжение батареи. Таким образом, суть в том, что вам нужно выпустить 2 джоуля из батареи, чтобы поместить 1 джоуль на конденсатор, а другой джоуль безвозвратно уйдет на тепло — 2-й закон термодинамики снова вас кусает, независимо от вашей скорости зарядки. Неинтуитивный характер этой проблемы является причиной ценности интегрального подхода.
Таким образом, суть в том, что вам нужно выпустить 2 джоуля из батареи, чтобы поместить 1 джоуль на конденсатор, а другой джоуль безвозвратно уйдет на тепло — 2-й закон термодинамики снова вас кусает, независимо от вашей скорости зарядки. Неинтуитивный характер этой проблемы является причиной ценности интегрального подхода.
Хотя это не будет показано здесь, если вы продолжите решение этой проблемы, сделав зарядное сопротивление настолько малым, что начальный зарядный ток будет чрезвычайно высоким, значительная часть зарядной энергии фактически излучается в виде электромагнитной энергии. Это переступает порог теории антенн, потому что не все потери при зарядке были термодинамическими, но все же потери в процессе составляли половину энергии, выделяемой батареей при зарядке конденсатора.
Таким образом, энергия, выделяемая батареей, равна E = CV b 2 , но только половина этой энергии приходится на конденсатор — другая половина теряется на нагрев или, в случае чрезвычайно низкого зарядного сопротивления, на нагрев и электромагнитная энергия.
Электрическое поле | Основы | Руководство по конденсаторам
Что такое электрическое поле?
Электрическое поле – это особое состояние, существующее в пространстве, окружающем электрически заряженную частицу. Это особое состояние влияет на все заряженные частицы, помещенные в электрическое поле. Истинная природа электрических полей, как и истинная природа электрического заряда, до сих пор неизвестна ученым, но эффекты электрического поля можно измерить и предсказать с помощью известных уравнений.
Точно так же, как магнит создает вокруг себя невидимое магнитное поле, которое можно обнаружить, поместив второй магнит в его поле и измерив силу притяжения или отталкивания, действующую на магниты, электрические заряды создают электрическое поле, которое можно обнаружить с помощью тестовый заряд. Когда пробный заряд помещается в электрическое поле, на него действует сила притяжения или отталкивания. Эта сила называется силой Кулона. На самом деле магнитное и электрическое поля не являются совершенно отдельными явлениями. Магнитное поле, изменяющееся во времени, создает — или «индуцирует» электрическое поле, в то время как движущееся электрическое поле индуцирует магнитное поле как прямое следствие движения. Поскольку эти два поля так тесно связаны, магнитное и электрическое поля объединяются в одно единое электромагнитное поле.
Магнитное поле, изменяющееся во времени, создает — или «индуцирует» электрическое поле, в то время как движущееся электрическое поле индуцирует магнитное поле как прямое следствие движения. Поскольку эти два поля так тесно связаны, магнитное и электрическое поля объединяются в одно единое электромагнитное поле.
Определение электрического поля
Электрическое поле можно определить как векторное поле, которое описывает соотношение между зарядом пробной частицы, введенной в поле, и силой, действующей на эту заряженную пробную частицу.
Где E — электрическое поле, F — сила, действующая на пробную частицу, введенную в поле, а q — заряд пробной частицы. Единицей электрического поля является вольт на метр [В·м -1 ] или ньютон на кулон [N·C -1 ].
Применение электрического поля в конденсаторах
Электромагнетизм — это наука, изучающая статические и динамические заряды, электрические и магнитные поля и их различные эффекты. Конденсаторы — это устройства, которые накапливают электрическую потенциальную энергию с помощью электрического поля.Таким образом, конденсаторы подчиняются законам электромагнетизма. В этой статье будут определены и изложены некоторые термины, необходимые для понимания работы конденсаторов. В данной статье будет считаться, что электрическое поле однородно во всех точках пространства.
Конденсаторы — это устройства, которые накапливают электрическую потенциальную энергию с помощью электрического поля.Таким образом, конденсаторы подчиняются законам электромагнетизма. В этой статье будут определены и изложены некоторые термины, необходимые для понимания работы конденсаторов. В данной статье будет считаться, что электрическое поле однородно во всех точках пространства.
Электрическая потенциальная энергия
Электрическая потенциальная энергия – это потенциальная энергия заряженной частицы в электрическом поле, возникающая в результате действия кулоновской силы на частицу. Он определяется как отрицательная величина работы, необходимой для перемещения частицы из контрольной точки (часто бесконечно далекой) в точку в пространстве, где измеряется электрическая потенциальная энергия.Единицей потенциальной электрической энергии является джоуль [Дж], та же единица, которая используется для количества работы в физике.
Электрический потенциал
Электрический потенциал, также называемый потенциалом электрического поля, представляет собой количество потенциальной электрической энергии, которой обладает заряженная частица в определенной точке пространства. Напряжение, также называемое разностью потенциалов между двумя точками в пространстве, представляет собой разность электрических потенциалов этих двух точек. Единицей измерения электрического потенциала является вольт [В], названный в честь итальянского физика Алессандро Вольта.Та же единица используется для напряжения. Электрический потенциал между двумя точками в однородном поле равен отрицательному значению разности напряженности поля между этими двумя точками.
Напряжение, также называемое разностью потенциалов между двумя точками в пространстве, представляет собой разность электрических потенциалов этих двух точек. Единицей измерения электрического потенциала является вольт [В], названный в честь итальянского физика Алессандро Вольта.Та же единица используется для напряжения. Электрический потенциал между двумя точками в однородном поле равен отрицательному значению разности напряженности поля между этими двумя точками.
Напряженность электрического поля
В простом конденсаторе с плоскими пластинами напряжение, приложенное между двумя проводящими пластинами, создает однородное электрическое поле между этими пластинами. Напряженность электрического поля в конденсаторе прямо пропорциональна приложенному напряжению и обратно пропорциональна расстоянию между пластинами.Этот фактор ограничивает максимальное номинальное напряжение конденсатора, так как напряженность электрического поля не должна превышать напряженность поля пробоя используемого в конденсаторе диэлектрика. При превышении напряжения пробоя между пластинами возникает электрическая дуга. Эта электрическая дуга может мгновенно разрушить некоторые типы конденсаторов. Стандартной единицей измерения напряженности электрического поля является вольт на метр [В·м -1 ].
При превышении напряжения пробоя между пластинами возникает электрическая дуга. Эта электрическая дуга может мгновенно разрушить некоторые типы конденсаторов. Стандартной единицей измерения напряженности электрического поля является вольт на метр [В·м -1 ].
Емкость
Емкость представляет собой способность тела накапливать электрический заряд.Эта способность используется в конденсаторах для хранения электрической энергии за счет поддержания электрического поля. Когда на конденсатор подается напряжение, на одной пластине конденсатора накапливается определенное количество положительного электрического заряда (+q), а на другой пластине конденсатора накапливается такое же количество отрицательного электрического заряда (-q). Определяется как:
, где C — емкость, q — количество заряда, накопленного на пластинах, а V — напряжение на двух пластинах конденсатора.
Емкость зависит от геометрии конденсатора. Такие факторы, как площадь пластин, расстояние между пластинами и диэлектрическая проницаемость диэлектрика, используемого в конструкции конденсатора, влияют на результирующую емкость. В простой параллельной пластине электрическая емкость прямо пропорциональна площади пластин и диэлектрической проницаемости, а обратно пропорциональна расстоянию между пластинами. Единицей измерения емкости является фарад [F], названный в честь Майкла Фарадея, пионера исследований в области электричества и магнетизма.
В простой параллельной пластине электрическая емкость прямо пропорциональна площади пластин и диэлектрической проницаемости, а обратно пропорциональна расстоянию между пластинами. Единицей измерения емкости является фарад [F], названный в честь Майкла Фарадея, пионера исследований в области электричества и магнетизма.
Энергия, накопленная в конденсаторе
Конденсаторы — это устройства, которые используются для хранения электрической энергии в цепи. Энергия, подводимая к конденсатору, запасается в виде электрического поля, которое создается между пластинами конденсатора. При подаче напряжения на конденсатор на пластинах накапливается определенное количество заряда. Энергия, накопленная в конденсаторе:
, где W — запасенная энергия, C — емкость, а V — напряжение, приложенное к конденсатору.
Конденсаторы
Конденсаторы
Далее: Уравнение Пуассона
Вверх: Электростатика
Предыдущий: Граничные условия на
Конденсаторы
Мы можем хранить электрические
заряд на поверхности проводника. Тем не мение,
Тем не мение,
электрические поля будут генерироваться непосредственно над этой поверхностью.
Проводник может успешно накапливать заряд только в том случае, если он электрически изолирован.
из его окружения. Воздух очень хороший изолятор.К сожалению, воздух
перестает быть изолятором, когда напряженность электрического поля через него превышает некоторое
критическое значение, которое составляет около
вольт на метр. Этот
явление, которое называют пробой , связано с образованием
искр. Наиболее известный пример распада
воздух во время молнии
забастовка. Ясно, что хорошее устройство хранения заряда — это то, которое вмещает большое количество
заряда, но генерирует только небольшие электрические поля. Такое устройство называется
конденсатор .
Рассмотрим два тонких параллельных проводящих
пластины с площадью поперечного сечения, которые разделены
маленькое расстояние ( т.е. , ). Предположим, что каждая пластина
несет равный и противоположный заряд. Мы ожидаем, что этот заряд
Мы ожидаем, что этот заряд
равномерно распределить по пластинам, чтобы обеспечить эффективную плотность заряда листа
на каждой тарелке. Предположим, что верхняя пластина несет
положительный заряд, а нижняя пластина несет отрицательный заряд. В соответствии с
уравнения (624) и (625) поле, создаваемое верхней пластиной, перпендикулярно пластине и
величины
Точно так же поле, создаваемое нижней пластиной, равно
Заметим, что мы пренебрегаем «утечкой» поля на краях пластин.Это разумно, если пластины расположены близко друг к другу. Общее поле – это
сумма двух полей, создаваемых верхней и нижней пластинами. Таким образом, чистое поле
нормальна к пластинам и имеет величину
Поскольку электрическое поле однородно, разность потенциалов между
тарелки просто
| (644) |
Общепринято измерять емкость проводника или группы проводников,
хранить заряд, но генерировать небольшие электрические поля с точки зрения параметра
называется емкостью . Это
Это
обычно обозначают. Емкость накопителя заряда
устройство — это просто отношение накопленного заряда к разности потенциалов
генерируемый зарядом. Таким образом,
| (645) |
Ясно, что хорошее устройство накопления заряда имеет большую емкость. Кстати,
емкость измеряется в кулонах на вольт или фарадах. Это довольно громоздкий
единица, так как
хорошие конденсаторы обычно имеют емкость, которая составляет всего около одной миллионной
фарада.Для конденсатора с плоскими пластинами ясно, что
| (646) |
Обратите внимание, что емкость зависит только от геометрических величин, таких как площадь
и расстояние между пластинами. Это следствие суперпозитивности
электрические поля. Если мы удвоим заряд проводников, мы удвоим
Если мы удвоим заряд проводников, мы удвоим
электрические поля, генерируемые вокруг них, и мы, таким образом, удваиваем потенциал
разница между проводниками.Таким образом, разность потенциалов между
проводники всегда прямо пропорциональны переносимому заряду:
постоянная
пропорциональности (обратной емкости) может зависеть только от геометрии.
Предположим, что заряд на каждой пластине накапливается постепенно путем переноса
небольшие количества заряда от одной пластины к другой. Если
мгновенный заряд на пластинах равен , а бесконечно малое количество
положительный
заряд переносится с отрицательно заряженной пластины на положительно
пластина заряда, то работа
,
где мгновенный
разница напряжений между пластинами.Обратите внимание, что разница в напряжении такова
что он препятствует любому увеличению заряда на любой пластине.
Суммарная работа, совершенная при зарядке конденсатора
является
| (647) |
где использовалось уравнение (645).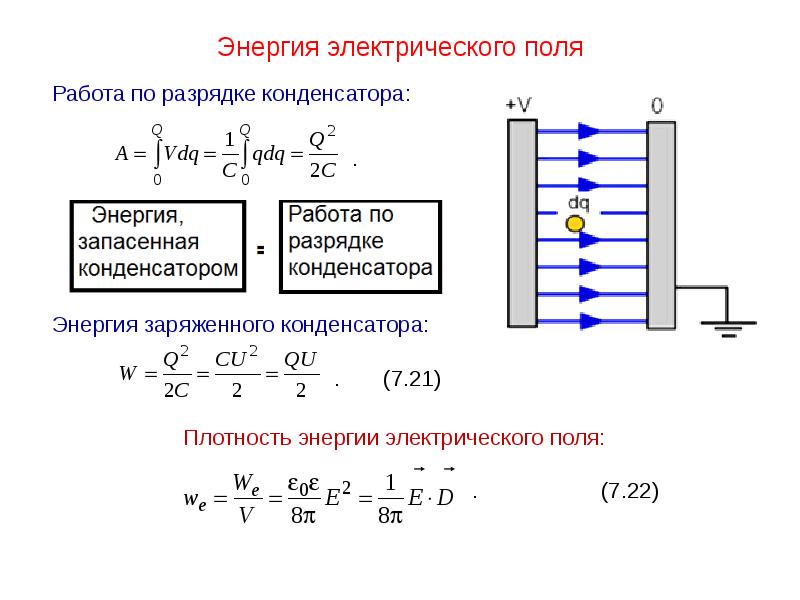
Энергия, запасенная в конденсаторе, равна работе, необходимой для
зарядить конденсатор. Таким образом,
| (648) |
Это общий результат, справедливый для всех типов конденсаторов.
Энергия
заряженная параллель
тарелка
конденсатор фактически сохраняется в электрическом поле между пластинами. Это поле
имеет примерно постоянную величину и занимает
область объема. Таким образом, учитывая плотность энергии электрического
поле,
, энергия, запасенная в
электрическое поле
| (649) |
где использовалось уравнение (646).
Обратите внимание, что уравнения. (647) и (649) совпадают.Все мы знаем, что если подключить конденсатор
через клеммы батареи, то переходный ток течет, поскольку конденсатор
заряжается. Затем конденсатор можно поместить в сторону, и через некоторое время
Затем конденсатор можно поместить в сторону, и через некоторое время
накопленный заряд можно использовать: например, для кратковременного зажигания лампочки в
электрическая цепь. Здесь интересно то, что энергия, запасенная в
конденсатор хранится в виде электрического поля, поэтому мы можем думать о конденсаторе как о
устройство, которое либо
накапливает энергию или извлекает энергию из электрического
поле.
Идея, которую мы обсуждали ранее, что электрическое поле оказывает отрицательное
давление
на проводниках сразу наводит на мысль, что
две пластины конденсатора с параллельными пластинами притягиваются друг к другу с
взаимная сила
| (650) |
Нет необходимости иметь два противоположно заряженных проводника
для изготовления конденсатора.
Рассмотрим изолированный
сфера радиуса которой
несет заряд. Радиальное электрическое поле, создаваемое вне сферы, равно
Радиальное электрическое поле, создаваемое вне сферы, равно
данный
| (651) |
Разность потенциалов между сферой и бесконечностью, или, более реалистично,
какой-то большой, относительно удаленный резервуар заряда, такой как Земля,
| (652) |
Таким образом, емкость шара
| (653) |
Энергия сферы, когда она несет заряд, снова определяется выражением
.Легко показать, что это действительно
энергия, содержащаяся в электрическом поле вокруг сферы.
Предположим, что у нас есть две сферы радиусов и , соответственно, которые
соединены электрическим проводом. Провод позволяет заряду перемещаться вперед и назад между
Провод позволяет заряду перемещаться вперед и назад между
сферы, пока они не достигнут того же потенциала (относительно бесконечности).
Пусть — заряд на первой сфере и заряд на
вторая сфера.
Конечно, общий заряд, переносимый двумя сферами, сохраняется.
количество.Это следует из уравнения (652) что
Обратите внимание, что если одна сфера намного меньше другой, , например. , , то
большая сфера захватывает большую часть заряда:
| (656) |
Отношение электрических полей, генерируемых непосредственно над поверхностями двух
сфер следует из уравнений (651) и (656):
| (657) |
Если , то поле над меньшей сферой
намного больше, чем над большей сферой.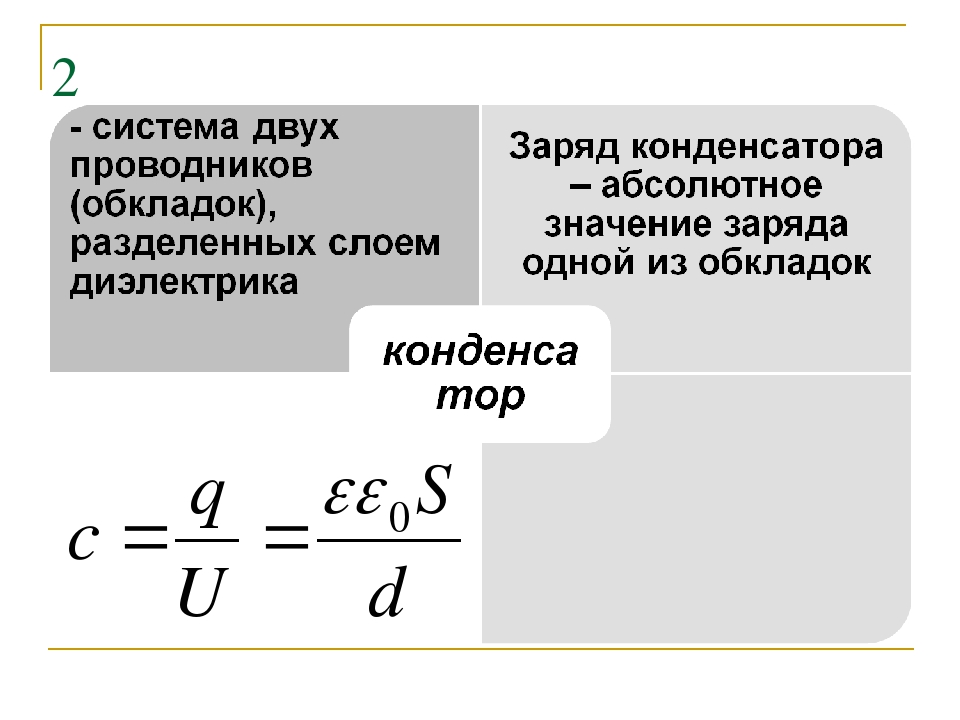 Уравнение (657) является простым примером гораздо более общего правила.
Уравнение (657) является простым примером гораздо более общего правила.
Электрическое поле над некоторой точкой
поверхность проводника обратно пропорциональна
локальный радиус кривизны поверхности.
Понятно, что если мы хотим накопить значительное количество заряда на проводнике
то поверхность проводника необходимо сделать как можно более гладкой. Любой острый
шипы на поверхности неизбежно
имеют сравнительно малый радиус кривизны. Сильные локальные электрические поля
генерируются в этих регионах.Они могут легко превысить критическое поле для пробоя воздуха,
что приводит к искрению и возможной потере заряда на проводнике.
Искрение также может быть очень разрушительным, поскольку связанное
электрические токи протекают через очень локализованные
области, вызывающие интенсивный омический нагрев.
В качестве последнего примера рассмотрим два коаксиальных
проводящие цилиндры радиусов и
, где . Предположим, что заряд на единицу длины, переносимый
наружный и внутренний цилиндры соответственно.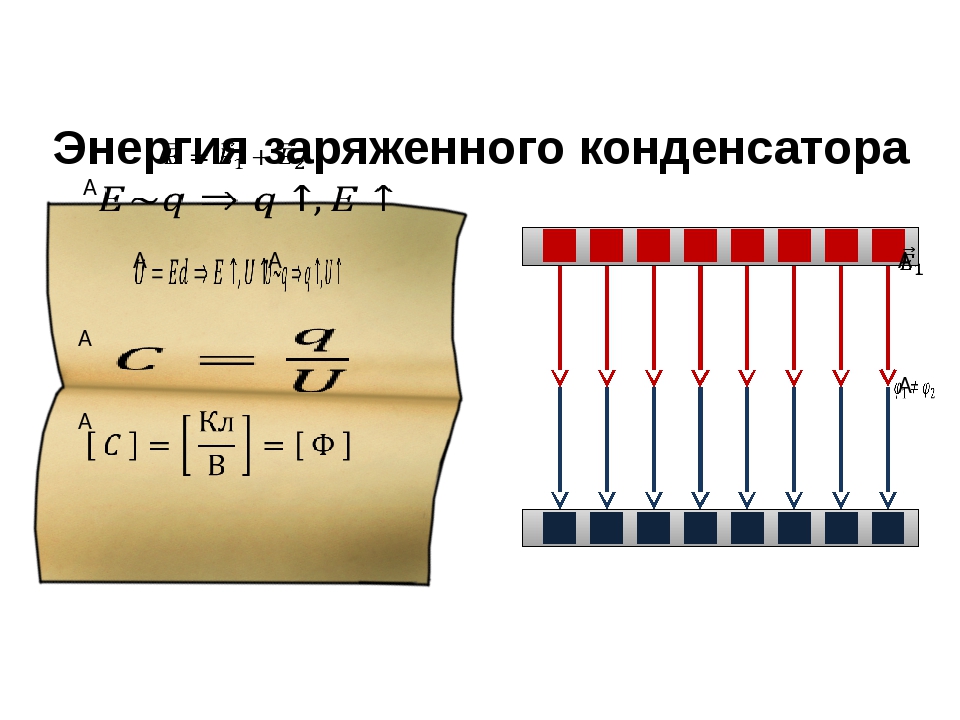 Мы можем безопасно
Мы можем безопасно
предположить, что
, по симметрии (принимая
стандартные цилиндрические полярные координаты). Давайте применим
Закон Гаусса к цилиндру радиуса , соосному с проводниками, и
длины. Для находим, что
| (658) |
так
| (659) |
за . Совершенно очевидно, что если не находится в диапазоне
к . Разность потенциалов между внутренним и внешним цилиндрами равна
так
| (661) |
Таким образом, емкость на единицу длины двух цилиндров равна
| (662) |
Далее: Уравнение Пуассона
Вверх: Электростатика
Предыдущий: Граничные условия на
2006-02-02
Энергия, хранящаяся в конденсаторе — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как энергия накапливается в конденсаторе
- Использование энергетических соотношений для определения энергии, запасенной в конденсаторной сети
Большинство из нас видели инсценировку медицинского персонала, использующего дефибриллятор для пропускания электрического тока через сердце пациента, чтобы заставить его нормально биться. Часто реалистичный в деталях, человек, применяющий разряд, приказывает другому человеку «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, сохраняется в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ – джоули. Менее драматично использование конденсаторов в микроэлектронике для подачи энергии при зарядке батарей ((Рисунок)). Конденсаторы также используются для питания ламп-вспышек на камерах.
Часто реалистичный в деталях, человек, применяющий разряд, приказывает другому человеку «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, сохраняется в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ – джоули. Менее драматично использование конденсаторов в микроэлектронике для подачи энергии при зарядке батарей ((Рисунок)). Конденсаторы также используются для питания ламп-вспышек на камерах.
Конденсаторы на печатной плате электронного устройства соответствуют соглашению по маркировке, согласно которому каждый из них идентифицируется кодом, начинающимся с буквы «C.(кредит: Уинделл Оскей)
Энергия, хранящаяся в конденсаторе, представляет собой электростатическую потенциальную энергию и, таким образом, связана с зарядом Q и напряжением В между пластинами конденсатора. Заряженный конденсатор запасает энергию в электрическом поле между своими пластинами. Когда конденсатор заряжается, электрическое поле нарастает. При отключении заряженного конденсатора от батареи его энергия остается в поле в пространстве между его пластинами.
Когда конденсатор заряжается, электрическое поле нарастает. При отключении заряженного конденсатора от батареи его энергия остается в поле в пространстве между его пластинами.
Чтобы понять, как эта энергия может быть выражена (в терминах Q и V ), рассмотрим заряженный пустой конденсатор с параллельными пластинами; то есть конденсатор без диэлектрика, но с вакуумом между его пластинами.Пространство между его пластинами имеет объем Ad и заполнено однородным электростатическим полем E . Вся энергия конденсатора заключена в этом пространстве. Плотность энергии в этом пространстве просто делится на объем Ad . Если мы знаем плотность энергии, то энергию можно найти как . В «Электромагнитных волнах» мы узнаем (после завершения изучения уравнений Максвелла), что плотность энергии в области свободного пространства, занятого электрическим полем E , зависит только от величины поля и составляет
Если мы умножим плотность энергии на объем между пластинами, мы получим количество энергии, запасенной между пластинами плоского конденсатора:.
В этом выводе мы использовали тот факт, что электрическое поле между пластинами однородно, так что и Поскольку , мы можем выразить этот результат в других эквивалентных формах:
Выражение (рисунок) для энергии, запасенной в конденсаторе с плоскими пластинами, в целом справедливо для всех типов конденсаторов. Чтобы убедиться в этом, рассмотрим любой незаряженный конденсатор (не обязательно пластинчатый). В какой-то момент мы подключаем его к батарее, задавая ему разность потенциалов между его пластинами.Первоначально заряд на обкладках равен По мере заряда конденсатора заряд на его обкладках постепенно накапливается и через некоторое время достигает значения Q . Чтобы переместить бесконечно малый заряд dq с отрицательной пластины на положительную (от более низкого потенциала к более высокому), количество работы dW , которое необходимо совершить на dq , равно .
Эта работа превращается в энергию, запасенную в электрическом поле конденсатора. Чтобы зарядить конденсатор до заряда ·, необходимо совершить общую работу
.
Поскольку геометрия конденсатора не указана, это уравнение верно для любого типа конденсатора.Полная работа Вт , необходимая для зарядки конденсатора, представляет собой запасенную в нем электрическую потенциальную энергию, или . Когда заряд выражается в кулонах, потенциал — в вольтах, а емкость — в фарадах, это соотношение дает энергию в джоулях.
Зная, что энергия, запасенная в конденсаторе, равна , теперь мы можем найти плотность энергии, хранящейся в вакууме между пластинами заряженного конденсатора с параллельными пластинами. Остается только разделить на объем Ad пространства между его пластинами и учесть, что для плоского конденсатора имеем и .Таким образом, мы получаем
Мы видим, что это выражение для плотности энергии, запасенной в плоском конденсаторе, соответствует общему соотношению, выраженному на (рис. ). Мы могли бы повторить этот расчет либо для сферического конденсатора, либо для цилиндрического конденсатора, либо для других конденсаторов, и во всех случаях мы пришли бы к общему соотношению, указанному на (рис.).
). Мы могли бы повторить этот расчет либо для сферического конденсатора, либо для цилиндрического конденсатора, либо для других конденсаторов, и во всех случаях мы пришли бы к общему соотношению, указанному на (рис.).
Проверьте свои знания Разность потенциалов на конденсаторе емкостью 5,0 пФ составляет 0,40 В.а) Какая энергия запасена в этом конденсаторе? б) Разность потенциалов увеличилась до 1,20 В. Во сколько раз увеличилась запасенная энергия?
а.; б. 9 раз
При неотложной сердечной деятельности портативное электронное устройство, известное как автоматический внешний дефибриллятор (AED), может спасти жизнь. Дефибриллятор ((Рисунок)) подает большой заряд коротким импульсом или разрядом в сердце человека, чтобы скорректировать аномальный сердечный ритм (аритмию). Сердечный приступ может возникнуть в результате быстрого, нерегулярного сокращения сердца, называемого сердечной или желудочковой фибрилляцией.Применение сильного разряда электрической энергии может остановить аритмию и позволить естественному водителю ритма вернуться к своему нормальному ритму. Сегодня машины скорой помощи обычно несут AED. AED также можно найти во многих общественных местах. Они предназначены для использования мирянами. Устройство автоматически диагностирует сердечный ритм пациента, а затем применяет разряд с соответствующей энергией и формой волны. СЛР (сердечно-легочная реанимация) рекомендуется во многих случаях перед использованием дефибриллятора.
Сегодня машины скорой помощи обычно несут AED. AED также можно найти во многих общественных местах. Они предназначены для использования мирянами. Устройство автоматически диагностирует сердечный ритм пациента, а затем применяет разряд с соответствующей энергией и формой волны. СЛР (сердечно-легочная реанимация) рекомендуется во многих случаях перед использованием дефибриллятора.
Автоматические наружные дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства дают словесные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (кредит: Оуайн Дэвис)
Емкость дефибриллятора сердца Дефибриллятор сердца вырабатывает энергию за счет первоначального разряда конденсатора. Какова его емкость?
Стратегия Нам даны и В, и нас просят найти емкость С и .Решаем (рисунок) для С и подставляем.
Решение Решая это выражение для C и вводя заданные значения, получаем
Резюме
- Конденсаторы используются для питания различных устройств, включая дефибрилляторы, микроэлектронику, такую как калькуляторы и импульсные лампы.
- Энергия, накопленная в конденсаторе, представляет собой работу, необходимую для зарядки конденсатора, начиная с незаряженных его пластин. Энергия запасается в электрическом поле в пространстве между пластинами конденсатора.Это зависит от количества электрического заряда на пластинах и от разности потенциалов между пластинами.
- Энергия, накопленная в сети конденсаторов, представляет собой сумму энергий, накопленных в отдельных конденсаторах сети. Его можно рассчитать как энергию, запасенную в эквивалентном конденсаторе сети.
Концептуальные вопросы
Если вы хотите хранить большое количество энергии в конденсаторной батарее, вы бы соединили конденсаторы последовательно или параллельно? Объяснять.
Глоссарий
- плотность энергии
- энергия, накопленная в конденсаторе, деленная на объем между пластинами
КОНДЕНСАТОРЫ И ДИЭЛЕКТРИКА
КОНДЕНСАТОРЫ И ДИЭЛЕКТРИКА
Конденсатор — это набор проводников, который используется для хранения электрического
обвинение. Очень простой конденсатор представляет собой изолированный металлический шар. потенциал
сферы радиусом R и зарядом Q равен
(27.1)
Уравнение (27.1) показывает, что потенциал шара пропорционален
заряд Q на проводнике. В общем случае это справедливо для любой конфигурации
проводники. Это отношение можно записать как
.
(27.2)
где C называется емкостью системы проводников.
Единицей емкости является фарад (F). Емкость
металлическая сфера равна
(27.3)
Другим примером конденсатора является система, состоящая из двух параллельных металлических
тарелки. В главе 26 было показано, что разность потенциалов между двумя
В главе 26 было показано, что разность потенциалов между двумя
пластин площадью A, расстоянием d и с зарядами +Q и -Q дается
по
(27.4)
Используя определение емкости (уравнение (27.2)), емкость этого
система может быть рассчитана:
(27.5)
Уравнение (27.2) показывает, что заряд конденсатора пропорционален
емкости C и к потенциалу V. Чтобы увеличить количество накопленного заряда
на конденсаторе при фиксированном потенциале (напряжении) емкость
конденсатор надо увеличить. Так как емкость параллельного
пластинчатый конденсатор пропорционален площади пластины A и обратно пропорционален
к расстоянию d между пластинами, этого можно добиться увеличением
площадь поверхности A и/или уменьшение разделительного расстояния d.Эти большие
конденсаторы обычно изготавливаются из двух параллельных листов алюминизированной фольги, несколько
дюймов в ширину и несколько метров в длину. Листы расположены очень близко
вместе, но защищены от соприкосновения тонким листом пластика, зажатым между
их. Весь бутерброд накрывается другим листом пластика и скручивается.
Весь бутерброд накрывается другим листом пластика и скручивается.
как рулон туалетной бумаги.
Пример: Задача 27.7
Трубка счетчика Гейгера состоит из тонкой прямой проволоки.
окружен коаксиальной проводящей оболочкой.Диаметр проволоки 0,0025
см, а у скорлупы 2,5 см. Длина трубки 10 см. Что
емкость счетчика Гейгера ?
Рисунок 27.1. Схема счетчика Гейгера.
Задача будет решаться в предположении, что электрическое поле
генерируется бесконечно длинная линия заряда. Схематический вид сбоку
трубы показано на рис. 27.1. Радиус провода r w ,
радиус цилиндра r c , длина счетчика L,
а заряд на проводе равен +Q.Электрическое поле в области между
проволоки и цилиндра можно рассчитать по закону Гаусса. Электрическое поле
в этой области будет иметь радиальное направление и его величина будет зависеть только
на радиальном расстоянии r. Рассмотрим цилиндр длиной L и радиусом r
показано на рис. 27.1. Электрический поток [Phi] через поверхность этого
цилиндр равен
(27. 6)
6)
Согласно закону Гаусса, поток [Phi] равен заключенному заряду, деленному на
по [эпсилон] 0 .Поэтому
(27.7)
Электрическое поле E(r) можно получить, используя уравнение (27.7):
(27.8)
Разность потенциалов между проводом и цилиндром может быть получена из
интегрирование электрического поля E(r):
(27.9)
Используя уравнение (27.2), можно рассчитать емкость трубки Гейгера:
(27.10)
Подставляя значения для r w , r c и L в уравнение.(27.10)
получаем
(27.11)
Символ конденсатора показан на рис. 27.2. Конденсаторы могут быть
соединены вместе; они могут быть соединены последовательно или параллельно. Фигура
27.3 показаны два конденсатора емкостью С 1 и С 2 ,
подключены параллельно. Разность потенциалов на обоих конденсаторах должна быть
равно и поэтому
(27. 12)
12)
Рисунок 27.2. Символ конденсатора.
Рисунок 27.3. Два конденсатора соединены параллельно.
Используя уравнение (27.12), можно рассчитать общий заряд обоих конденсаторов
(27.13)
Уравнение (27.13) показывает, что общий заряд системы конденсаторов, показанный на рис.
Рисунок 27.3 пропорционален разности потенциалов в системе. То
два конденсатора на рис. 27.3 можно рассматривать как один конденсатор с
емкость C, где C относится к C 1 и C 2 в
следующим образом
(27.14)
На рис. 27.4 показаны два конденсатора емкостью С 1 и
C 2 , соединены последовательно. Предположим, что разность потенциалов на
C 1 равно [Delta]V 1 , а разность потенциалов на
C 2 есть [Дельта]V 2 . Заряд Q на верхней пластине индуцирует
заряд -Q на нижней пластине C 1 . Так как электрический заряд
при сохранении заряд на верхней пластине C 2 должен быть равен Q. Таким образом, заряд нижней пластины C 2 равен -Q. То
Таким образом, заряд нижней пластины C 2 равен -Q. То
разность напряжений на C 1 определяется как
(27.15)
а разность напряжений на C 2 равна
(27.16)
Рисунок 27.4. Два конденсатора соединены последовательно. Задана общая разность напряжений на двух конденсаторах.
по
(27.17)
Уравнение (27.17) снова показывает, что напряжение на двух конденсаторах,
соединенных последовательно, пропорциональна заряду Q. Система действует как
один конденсатор C, емкость которого может быть получена из следующего
формула
(27.18)
Пример: Задача 27.10
Многопластинчатый конденсатор, используемый, например, в радиоприемниках, состоит из четырех
параллельные пластины, расположенные одна над другой, как показано на рис. 27.5. Площадь
каждой пластины равно A, а расстояние между соседними пластинами равно d.Что
емкость этой схемы?
Рисунок 27. 5. Многопластинчатый конденсатор.
5. Многопластинчатый конденсатор.
Многократный конденсатор, показанный на рис. 27.5, эквивалентен трем одинаковым
конденсаторы, соединенные параллельно (см. рис. 27.6). Емкость каждого из
три конденсатора равны и равны
(27.19)
Полную емкость многопластинчатого конденсатора можно рассчитать по формуле
уравнение (27.14):
(27.20)
Рисунок 27.6. Схема многопластинчатого конденсатора показана на рисунке.
27.5.
Три конденсатора емкостью C 1 = 2,0 мкФ, C 2
= 5,0 мкФ, а С 3 = 7,0 мкФ, первоначально заряжаются до 36 В от
подключив каждый на несколько мгновений к 36-вольтовой батарее. Батарея тогда
сняты, а заряженные конденсаторы соединены в замкнутую последовательную цепь,
с положительным и отрицательным выводами, соединенными, как показано на рисунке 27.7. Что
будет окончательный заряд на каждом конденсаторе? Какое будет напряжение на
точки PP’ ?
Рисунок 27. 7. Задача 27.13.
7. Задача 27.13.
Начальные заряды на каждом из трех конденсаторов, q 1 ,
q 2 и q 3 равны
(27.21)
После подключения трех конденсаторов заряд перераспределится.
Заряды трех конденсаторов после стабилизации системы равны
Q 1 , Q 2 и Q 3 .Так как заряд сохраняется
количество, существует соотношение между q 1 , q 2 и
q 3 и Q 1 , Q 2 и Q 3 :
(27.22)
Напряжение между P и P’ может быть выражено через C 3 и
Q 3 или в терминах C 1 , C 2 , Q 1 и
Q 2 :
(27.23)
и
(27.24)
Используя уравнение (27.22), следующие выражения для Q 1 и Q 2
можно получить:
(27.25)
(27.26)
Подставляя уравнение (27. 25) и уравнение (27.26) в уравнение (27.24), мы получаем
25) и уравнение (27.26) в уравнение (27.24), мы получаем
(27.27)
Комбинируя уравнение (27.27) и уравнение (27.23), Q 3 можно выразить через
известные переменные:
(27.28)
Подставив известные значения емкости и начальных зарядов, получим
получить
(27.29)
Напряжение на P и P’ можно найти, объединив уравнение (27.29) и
уравнение (27.23):
(27.30)
Заряды конденсатора 1 и конденсатора 2 равны
(27.31)
(27.32)
Если пространство между пластинами конденсатора заполнить изолятором,
емкость конденсатора будет случайной по сравнению с ситуацией, в которой
между пластинами вакуум.Изменение емкости вызвано
изменение электрического поля между пластинами. Электрическое поле между
пластины конденсатора будут индуцировать дипольные моменты в материале между
тарелки. Эти индуцированные дипольные моменты будут уменьшать электрическое поле в
области между пластинами. Материал, в котором индуцированный дипольный момент равен
Материал, в котором индуцированный дипольный момент равен
линейно пропорциональна приложенному электрическому полю, называется линейным
диэлектрик . В материалах этого типа полное электрическое поле между
пластины конденсатора E связаны с электрическим полем E , свободным , что
существовал бы, если бы не было диэлектрика:
(27.33)
где [каппа] называется диэлектрической проницаемостью. С момента окончательного электрического
поле E никогда не может превышать свободное электрическое поле E free ,
диэлектрическая постоянная [каппа] должна быть больше 1.
Разность потенциалов на конденсаторе пропорциональна электрическому
поле между пластинами. Поскольку наличие диэлектрика снижает
силы электрического поля, это также уменьшит разность потенциалов
между обкладками конденсатора (если общий заряд на обкладках сохраняется
константа):
(27.34)
Емкость C системы с диэлектриком обратно пропорциональна
разность потенциалов между пластинами и связана с емкостью
C свободный конденсатор без диэлектрика следующим образом
(27. 35)
35)
Поскольку [каппа] больше 1, емкость конденсатора может быть
значительно увеличивается за счет заполнения пространства между обкладками конденсатора
диэлектрик с большой каппа.
Электрическое поле между двумя пластинами конденсатора представляет собой векторную сумму
поля, создаваемые зарядами на конденсаторе, и поле, создаваемое
поверхностные заряды на поверхности диэлектрика. Генерируемое электрическое поле
зарядами на обкладках конденсатора (плотность заряда
[сигма] бесплатно ) дается
(27.36)
Полагая плотность заряда на поверхности диэлектрика равной
[сигма] связанный , поле, создаваемое этими связанными зарядами, равно
до
(27.37)
Электрическое поле между пластинами равно E свободное /каппа и
таким образом
(27.38)
Подстановка уравнения (27.36) и уравнения (27.37) в уравнение (27.38) дает
(27.39)
или
(27. 40)
40)
Пример: Задача 27.19
Конденсатор с параллельными пластинами с площадью пластин A и расстоянием d
содержит пластину диэлектрика толщиной d/2 (см. рис. 27.8) и диэлектрик
постоянная [каппа]. Разность потенциалов между пластинами равна [Delta]V.
а) Через заданные величины найти электрическое поле в пустом
область пространства между пластинами.
б) Найти электрическое поле внутри диэлектрика.
в) Найдите плотность связанных зарядов на поверхности диэлектрика.
Рисунок 27.8. Задача 27.19.
а) Предположим, что электрическое поле в конденсаторе без диэлектрика равно
к Е 0 .Электрическое поле в диэлектрике E d равно
относительно свободного электрического поля через диэлектрическую проницаемость [каппа]:
(27.41)
Разность потенциалов между пластинами можно получить, интегрируя
электрическое поле между пластинами:
(27.42)
Таким образом, электрическое поле в пустой области равно
.
(27.43)
б) Электрическое поле в диэлектрике можно найти, комбинируя уравнение(27.41)
и (27.43):
(27.44)
в) Плотность свободного заряда [сигма] свободный равна
(27.45)
Плотность связанного заряда связана с плотностью свободного заряда через
следующее отношение
(27.46)
Объединяя уравнение (27.45) и уравнение (27.46), мы получаем
(27.47)
Электрическое поле в «пустом» конденсаторе можно получить с помощью закона Гаусса.Рассмотрим идеальный конденсатор (без краевых полей) и интегрирование
объем, показанный на рис. 27.9. Площадь каждой пластины конденсатора равна A, а
заряды на пластинах +/-Q. Заряд, заключенный в объем интегрирования
показанный на рис. 27.9, равен +Q. Закон Гаусса гласит, что электрический поток
[Phi] через поверхность интегрированного объема относится к заключенному
плата:
(27.48)
Если между пластинами вставить диэлектрик, электрическое поле между пластинами
пластины изменятся (хотя заряд на пластинах остается постоянным). Очевидно, что закон Гаусса, сформулированный в уравнении (27.48), в данном случае не выполняется.
Очевидно, что закон Гаусса, сформулированный в уравнении (27.48), в данном случае не выполняется.
Электрическое поле E между пластинами конденсатора связано с
поле без диэлектрика E свободное :
(27.49)
где [каппа] — диэлектрическая проницаемость материала между пластинами.
Теперь закон Гаусса можно переписать как
.
(27.50)
Закон Гаусса в вакууме является частным случаем уравнения (27.50) с [каппа] = 1.
Рисунок 27.9. Идеальный конденсатор.
Пример: Задача 27.25
Металлический шар радиусом R окружен концентрическим диэлектриком.
оболочка с внутренним радиусом R и внешним радиусом 3R/2. Это окружено
концентрическая тонкая металлическая оболочка радиусом 2R (см. рис. 27.10). То
диэлектрическая проницаемость оболочки [каппа]. Какая емкость у этого
приспособление?
Предположим, что заряд внутренней сферы Q свободен .Электрический
поле внутри диэлектрика можно определить, применив закон Гаусса для
диэлектрика (уравнение (27. 50)) и используя в качестве интегрированного объема сферу радиуса
50)) и используя в качестве интегрированного объема сферу радиуса
r (где R < r < 3R/2)
(27.51)
Таким образом, электрическое поле в этой области определяется выражением
.
(27.52)
Рисунок 27.10. Задача 27.25. Электрическое поле в области между 3R/2 и 2R может быть
получено аналогичным образом и равно
(27.53)
Используя электрическое поле из уравнения (27.52) и уравнения (27.53), мы можем определить
разность потенциалов [Delta]V между внутренней и внешней сферой:
(27.54)
Емкость системы может быть получена из уравнения (27.54) с использованием
определение емкости через заряд Q и потенциал
разница [Дельта]V:
(27.55)
Электрическая потенциальная энергия конденсатора без диэлектрика и с
заряд +/-Q на его пластинах указан как
(27.56)
где V 1 и V 2 — потенциалы двух пластин.
Электрическая потенциальная энергия также может быть выражена через емкость
С конденсатора
(27. 57)
57)
Эта формула верна и для конденсатора с диэлектриком; свойства
диэлектрика входит в эту формулу через емкость C.
Пример: Задача 27.40
Десять одинаковых конденсаторов емкостью 5 мкФ подключены параллельно к сети 240 В.
батарея.Затем заряженные конденсаторы отсоединяют от батареи и
соединены последовательно, положительный вывод каждого конденсатора соединен
к минусовой клемме следующего. Какова разница потенциалов между
отрицательный вывод первого конденсатора и положительный вывод второго
последний конденсатор? Если эти терминалы подключены через внешнюю цепь, как
много заряда будет течь по этой цепи, когда последовательно разряжается
? Сколько энергии выделяется при разряде? Сравните этот заряд и этот
энергия с зарядом и энергией, хранящейся в исходном, параллельном расположении,
и объясните все несоответствия.
Заряд каждого конденсатора после подключения к батарее 240 В равен
равно
(27.58)
Разность потенциалов на каждом конденсаторе останется равной 240 В после
конденсаторы соединены последовательно. Полная разность потенциалов на
Полная разность потенциалов на
Таким образом, десять конденсаторов равны
.
(27.59)
Если два концевых вывода конденсаторной сети соединены, заряд
1.2 мКл потечет от положительной клеммы к отрицательной (см.
Рисунок 27.11).
Рисунок 27.11. Задача 27.40. Электроэнергия, запасенная в конденсаторной сети до
разряд равен
(27.60)
Энергия, запасенная в каждом конденсаторе после зарядки до 240 В, равна
до
(27.61)
Ясно, что в процессе замены конденсатора энергия не теряется.
Конфигурация с параллельного на последовательный.
Пример: Задача 27.39
Три конденсатора подключены, как показано на рис. 27.12. Их
емкости C 1 = 2,0 мкФ, C 2 = 6,0 мкФ и
С 3 = 8,0 мкФ. Если к двум свободным
выводы, какой будет заряд на каждом конденсаторе? Что будет
электрическая энергия каждого?
Рисунок 27.12. задача 27.39.
Предположим, что напряжение на конденсаторе C 1 равно V 1 , а
напряжение на конденсаторе (C 2 + C 3 ) равно V 2 .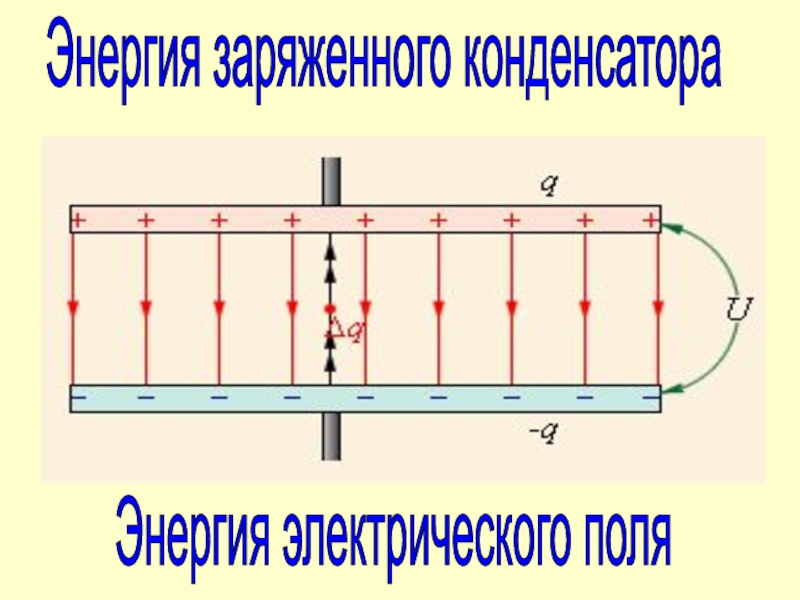 Если
Если
заряд конденсатора C 1 равен Q 1 , то
заряд параллельного конденсатора также равен Q 1 . потенциал
разница по этой системе равна
(27.62)
Таким образом, заряд конденсатора 1 определяется разностью потенциалов
[Дельта]В
(27.63)
Напряжение В 23 на конденсаторе (С 2 + С 3 )
относится к сбору Q 1
(27.64)
Заряд конденсатора С 2 равен
(27.65)
Заряд конденсатора С 3 равен
(27.66)
Электрическая потенциальная энергия, запасенная в каждом конденсаторе, равна
.
(27.67)
Для трех конденсаторов в этой задаче электрическая потенциальная энергия равна
до
(27.68)
(27.69)
(27.70)
Присылайте комментарии, вопросы и/или предложения по электронной почте wolfs@nsrl. rochester.edu и/или посетите домашнюю страницу Фрэнка Вольфса.
rochester.edu и/или посетите домашнюю страницу Фрэнка Вольфса.
Емкость — Элементы схемы — Содержание MCAT
Емкость — это мера способности объекта накапливать электрический заряд. Любое тело, способное каким-либо образом заряжаться, имеет значение емкости. Конденсаторы могут накапливать энергию при подключении батареи или источника напряжения.
Конденсатор с параллельными пластинами состоит из 2 проводящих пластин ( электродов ), разделенных изоляционным материалом ( диэлектрик ). Когда 2 электрода подключены к источнику питания, один к положительной и один к отрицательной клемме, на пластинах будет накапливаться заряд. Когда равновесие достигнуто, это означает, что конденсаторы полностью заряжены.
Для пластинчатых конденсаторов положительные заряды, накопленные от подключения к источнику напряжения , притягиваются к отрицательным зарядам, накопленным аналогичным образом, заряды сохраняются даже при снятии напряжения. Таким образом сохраняется энергия.
Таким образом сохраняется энергия.
Количество электрического заряда , накопленного в каждой из пластин, прямо пропорционально разности потенциалов между двумя пластинами (и источника напряжения):
Q = CV
- Q = количество заряда, накопленного в одном конденсаторе (+Q на одной пластине и -Q на другой пластине)
- В = разность потенциалов между двумя пластинами
- C = емкость конденсатора (зависит от формы конденсатора)
Емкость плоского конденсатора с диэлектриком между пластинами определяется приведенным ниже уравнением.Обратите внимание, что κ для вакуума точно равно 1. Диэлектрическая постоянная для воздуха очень близка к 1, поэтому конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом.
Энергия, запасенная в конденсаторе, равна электрической потенциальной энергии ΔPE = qΔV. Обратите внимание, что первый заряд, помещенный на конденсатор, испытывает изменение напряжения ΔV = 0, так как конденсатор имеет нулевое напряжение, когда он не заряжен.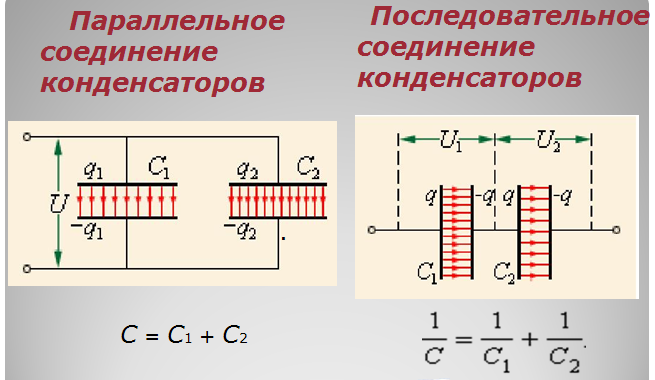 Окончательный заряд, размещенный на конденсаторе, испытывает ΔV = V, поскольку на конденсаторе теперь есть полное напряжение V.Среднее напряжение на конденсаторе в процессе заряда
Окончательный заряд, размещенный на конденсаторе, испытывает ΔV = V, поскольку на конденсаторе теперь есть полное напряжение V.Среднее напряжение на конденсаторе в процессе заряда
.
Конденсаторы, соединенные последовательно: общая емкость последовательно соединенных конденсаторов равна сумме инверсий каждого отдельного конденсатора.
Конденсаторы, включенные параллельно: Общая емкость конденсаторов, включенных параллельно, равна сумме емкостей каждого отдельного конденсатора.
Чтобы конденсатор сохранял заряд, должен быть разрыв цепи между двумя его сторонами.Это прерывание может происходить в форме вакуума (отсутствие какой-либо материи) или диэлектрика (изолятора).
При использовании диэлектрика материал между параллельными пластинами конденсатора поляризуется. Часть возле положительного конца конденсатора будет иметь избыток отрицательного заряда, а часть возле отрицательного конца конденсатора будет иметь избыток положительного заряда.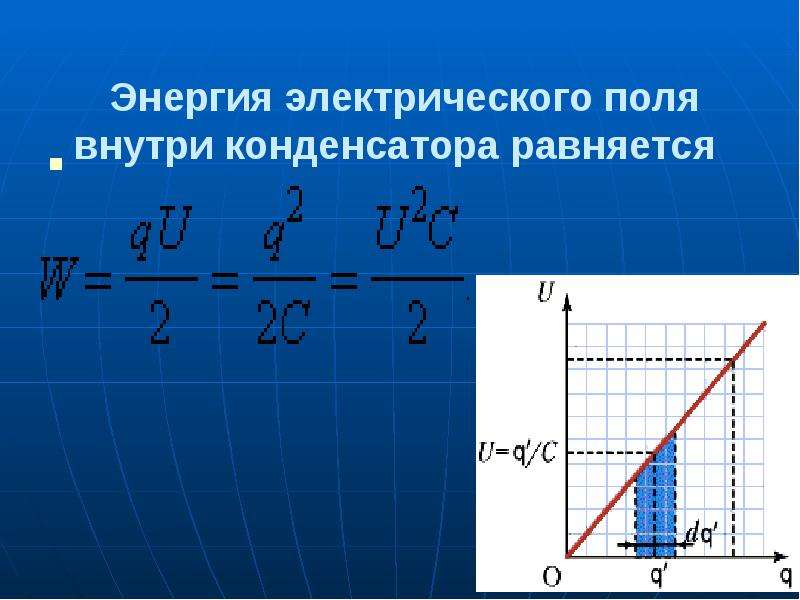 Таким образом, это перераспределение заряда в диэлектрике создаст электрическое поле, противоположное полю, создаваемому конденсатором.
Таким образом, это перераспределение заряда в диэлектрике создаст электрическое поле, противоположное полю, создаваемому конденсатором.
Таким образом, чистое поле, создаваемое конденсатором, будет частично уменьшено диэлектриком, как и разность потенциалов на нем. С другой стороны, диэлектрик предотвращает прямой контакт пластин конденсатора (что сделало бы конденсатор бесполезным). Если он имеет высокую диэлектрическую проницаемость, он также увеличивает емкость для любого заданного напряжения.
Любой изолятор может использоваться в качестве диэлектрика, но наиболее часто используемые материалы выбираются по их способности противостоять ионизации.Чем более устойчив материал к ионизации, тем более он устойчив к работе при более высоких напряжениях. В конце концов, у каждого материала есть «точка диэлектрического пробоя», при которой разность потенциалов становится слишком высокой для того, чтобы он мог изолировать, материал ионизируется и пропускает ток.
Практические вопросы
Академия Хана
Конденсаторы в электрокардиографических мониторах
Сердечная аритмия и дефибрилляторы
Лечение электрическим полем и электропорация
Официальный отчет MCAT Подготовка (AAMC)
Пакет вопросов по физике, отрывок 5, вопрос 30
Пакет вопросов по физике, отрывок 5, вопрос 33
Пакет вопросов по физике, отрывок 9, вопрос 53
Пакет вопросов по физике, отрывок 9, вопрос 55
Практический экзамен 3 C/P Section Pass 2 Question 5
Ключевые точки
• Конденсатор с параллельными пластинами состоит из 2 проводящих пластин (электродов), разделенных изоляционным материалом (диэлектриком).
• Конденсатор, подключенный к источнику напряжения, может накапливать энергию E = QV/2
• Общая емкость последовательно соединенных конденсаторов равна сумме инверсий каждого отдельного конденсатора.
• Общая емкость конденсаторов, включенных параллельно, равна сумме емкостей каждого отдельного конденсатора.
• Диэлектрик — это изолирующий материал между электродами. С константой k, характерной для каждого типа материала.
Основные термины
напряжение : Разность электрических потенциалов, выраженная в вольтах
электроды: проводник, по которому электричество входит или выходит из объекта, вещества или области.
диэлектрик : изоляционный материал или очень плохой проводник электрического тока
электрический заряд: физическое свойство материи, которое заставляет ее испытывать силу при помещении в электромагнитное поле
разность потенциалов: разность напряжения электрического потенциала между двумя точками
электрическая потенциальная энергия: — это потенциальная энергия, возникающая в результате действия консервативных кулоновских сил
.


 д.
д. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.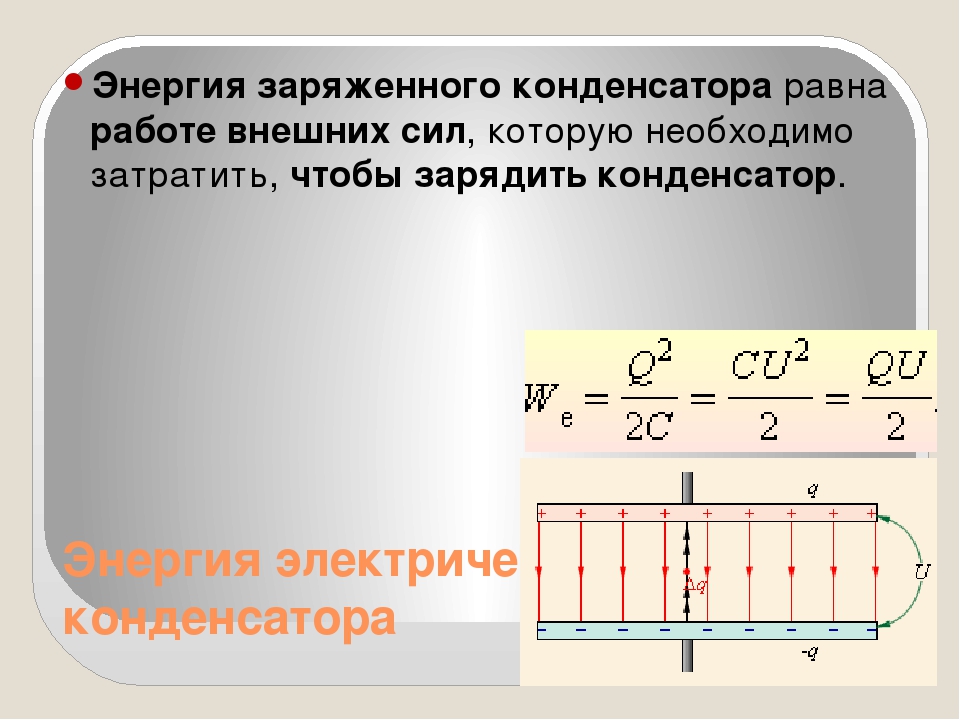


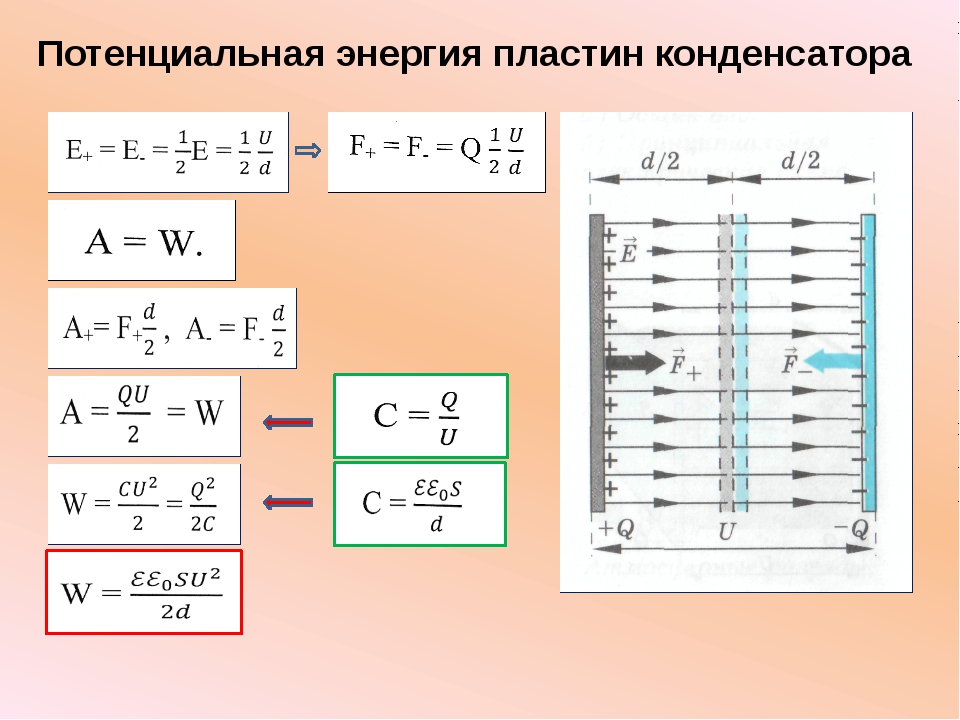 Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся. Одним словом, заземлить – означает обнулить потенциал объекта.
Одним словом, заземлить – означает обнулить потенциал объекта.