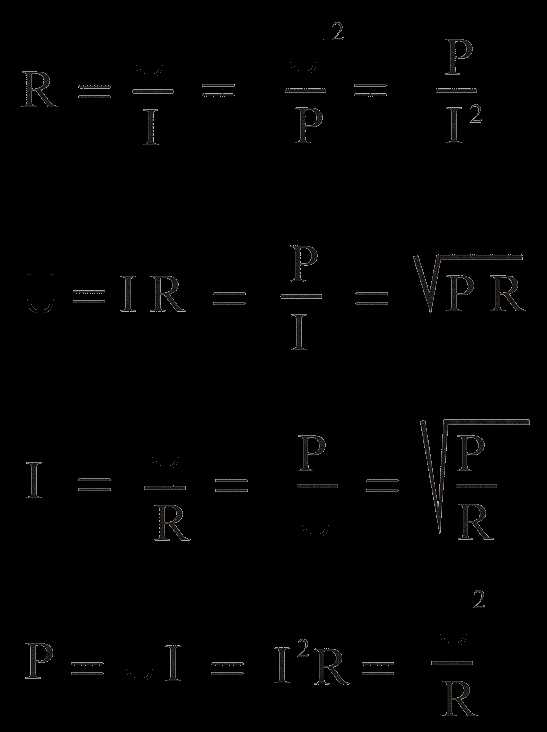Действующее и амплитудное значение напряжения. Амплитудное значение силы тока
Действующее и амплитудное значение напряжения
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.
Мгновенное значение
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u ( t ) , i ( t ) {\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.
Амплитудное значение
- Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):
Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.
Среднеквадратичное значение
Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.
U = 1 T ∫ 0 T u 2 ( t ) d t , I = 1 T ∫ 0 T i 2 ( t ) d t {\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) — постоянная составляющая напряжения или силы тока
U = 1 T ∫ 0 T u ( t ) d t , I = 1 T ∫ 0 T i ( t ) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.
Средневыпрямленное значение
Средневыпрямленное значение — среднее значение модуля сигнала
U = 1 T ∫ 0 T ∣ u ( t ) ∣ d t , I = 1 T ∫ 0 T ∣ i ( t ) ∣ d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}На практике используется редко, однако большинство измерительных приборов переменного тока - магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам: В 2-х т.; Под ред. Д. П. Линде — М.: Энергия, 1978
- Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
- ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения
Ссылки
- Электрические цепи постоянного тока
- Переменный ток. Изображение синусоидальных переменных
- Амплитудное, среднее, эффективное
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электропитания
ru.wikipedia.org>
Действующее значение переменного тока
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем
| , |
(1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
| , |
(2) |
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f= 50Гц.
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i - мгновенное значение тока
;u– мгновенное значение напряжения
;е- мгновенное значение ЭДС
;р- мгновенное значение мощности
.Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).
- амплитуда тока; - амплитуда напряжения; - амплитуда ЭДС.Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
| , |
(3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2соответствуют уравнения:
. Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и -начальной фазой ().
Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и -начальной фазой (). Величину
, характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2угол сдвига фаз:
.Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0),что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

|
Пусть, например, в точке разветвления цепи (рис. 5) общий ток
равен сумме токовидвух ветвей: .Каждый из этих токов синусоидален и может быть представлен уравнением
и.Результирующий ток также будет синусоидален:
.Определение амплитуды
и начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.Построение векторной диаграммы в масштабе позволяет определить значения
ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.StudFiles.ru>
Что такое амплитудное значение напряжения? какое амплитудное значение напряжение в сети 220в?
кто знает объясните пожалуйста что это такое! ! заранее спасибо!
White rabbit
Амплитудное значение - это МАКСИМАЛЬНОЕ мгновенное напряжение переменного тока. В то время как те 220 вольт - это ДЕЙСТВУЮЩЕЕ значение, то есть напряжение ПОСТОЯННОГО тока, такого, который греет проводник так же, как наш переменный (это - официальное ОПРЕДЕЛЕНИЕ :-) Для синусоидального тока действующее и амплитудное значение (как легко показать интегрированием) связано через Корень из 2. Для сети 220 амплитуное значение = 220*корень (2)=311 вольт
Принц уэльский
Синусоидальный ток (напряжение) характеризуется среднеквадратичным заначением.
Узнать амплитудное напряжение легко. Надо умножить среднеквадратичное на корень из двух (на 1,414, если коротко)
Таким образом для 220 вольт имеем 220*2^0.5 = 311 В
Алексей бараев
Амплитудное напряжение для однофазного тока больше эффетивоного в корень из двух (1.414) раз. Если эффективное = 220 вольт, то амплитудное будет чуть больше 311 вольт. Это необходимо учитывать при проектировании блоков питания - конденсаторы в сглаживающем фильтре выпрямителя должны быть расчитанаы на напряжение выше амплитудного напряжения выпрямляемого тока.
Инженер-констриктор
Амплитудное - это максимальное значение. 220 В - это действующее значение (синусоидальный ток выделяет на резисторе за время кратное периоду такую же мощность, что и постоянный с напряжением 220 В) . Амплитудное 311 В - в √2 раз больше действующего.
Николай фендеров
на корень из двух умножай. 220 В - это среддеквадратичное значение. Если сиснусоиду хитро проинтегрировать, то так корень из двух и получишь. Вроде так: Интеграл от 0 до 2π (синус квадрат x)
Напряжение электросети 220В - это амплитудное или действующее значение?
Foxius
220-действующее: Амплитуда переменного тока — наибольшее мгновенное значение тока на период (310 В) . При использовании электрической энергии переменного тока нас интересует не амплитудное и мгновенное его значения, а так называемое действующее значение, которое определяет тепловые величины переменного тока. Действующее значение переменного тока численно равно такому постоянному току, который в течение одинакового промежутка времени выделяет в некотором сопротивлении такое же количество тепла, как и данный переменный ток. Действующее значение переменного синусоидального тока в 1,41 раза меньше его амплитудного значения. Действующее значение переменного тока обозначается прописными буквами: I — действующее значение величины тока; U — действующее значение напряжения. Измерительные приборы обычно показывают действующие значения переменного тока.
Читайте также
zna4enie.ru
| Как рассчитать шунт для амперметра?Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.Как измерить, какую мощность выдаёт усилитель низкой частоты?Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности. Закон Ома.Основным законом, которым руководствуются радиолюбители - является Закон Ома..Георг Симон ОМGeorg Simon Ohm, 1787–1854Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.I = U/R, где R - электрическое сопротивление проводника.Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.Как Вы должны знать U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.
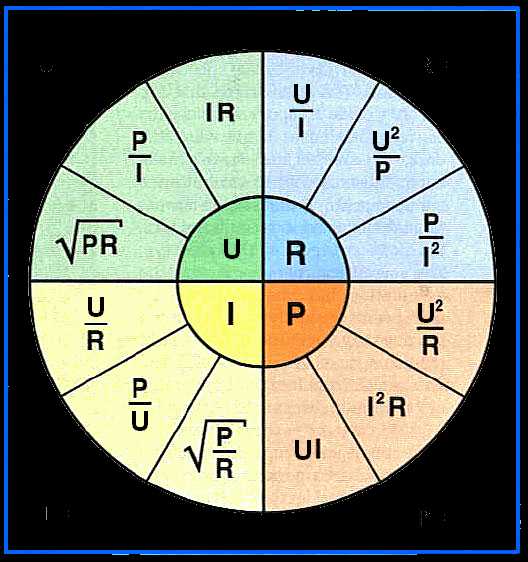
Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля - Ленца. Звучит так; Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка. Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.В центре искомые величины, а в секторах с соответствующими цветами - варианты решений в зависимости от известных величин.
Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье - треугольник Ома.Выглядит она следующим образом: В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.Закон Ома также применяется ко всей цепи, но в несколько изменённой форме: ,
Закон Ома для полной цепи звучит так - Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника. Электрические измерения.Нарисуем простейшую электрическую цепь, состоящую из батареи "В" и нагрузки "R", и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.
Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.Поэтому категорически нельзя измерять "ток приходящий на нагрузку" путём подключения амперметра параллельно нагрузке, или непосредственно у источника питания (без нагрузки) и таким образом попытаться замерить выходной ток выдаваемый источником питания или осветительной сетью.Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать - закоротить цепь.Если источник питания обладает хорошей мощностью - будет очень сильный Б А Х !!! Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током. Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра - сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения. На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь. Постоянный и переменный ток.Кратко напомню - постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.Переменный ток (AC) - это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению. На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.В течение одного периода своего изменения,ток дважды достигает максимального значения.Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока. Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие - "Действующее (или эффективное) значение" переменного тока. Что же такое действующее (или эффективное) и амплитудное значение переменного тока?Как Вам попроще объяснить, чтобы было понятно.Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии. То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) - то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока. Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения. Что такое "Амплитудное значение" переменного тока?Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.Амплитудное значение переменного тока можно измерить электронно - лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений. Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.Проще говоря - если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, - то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.Это справедливо только для переменного синусоидального тока (напряжения). Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения. Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41). Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя. Для действующего значения переменного синусоидального напряжения (тока) - справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений - приведённые выше в Законе Ома для постоянного тока. Ответим на вопросы в начале статьи; Как рассчитать шунт для амперметра?Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись "НШ - 75 мВ", или "Наружный шунт 75 мв", или что-то подобное.Нам стало известно две величины, а именно - необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление). Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного - надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) - амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт - до которых и заряжаются электролитические конденсаторы фильтра. Как правильно измерить мощность УНЧ?Давайте для начала вспомним теорию.Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля - Ленца) для первой магнитолы, которую она выдаст теоретически - будет 10,6 ватта, для второй - 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность. В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными "цешками" или бытовыми "цифровиками", так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт - это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь. |
vprl.ru
Амплитудное значение - сила - ток
Амплитудное значение - сила - ток
Cтраница 1
Амплитудное значение силы тока достигает при резонансе максимума, равного Uo / R, сдвиг фаз между напряжением и током отсутствует. Напряжения U L на индуктивности L и U c на емкости С равны по модулю и находятся в противофазе, так что полное напряжение на концах цепи U совпадает с напряжением U K на активном сопротивлении R. Напряжения на реактивных сопротивлениях могут по амплитуде значительно превышать приложенное напряжение. [1]
Определим амплитудное значение силы тока и положение якоря относительно сердечника при различных величинах относительных воздушных зазоров. [2]
Добычно амплитудным значением силы тока; если речь идет - г J3 о напряжении, то говорят об амплитудном значении напряжения. Во многих случаях эти величины являются очень важными. Так, например, при расчете изоляции какого-либо электрического аппарата приходится считаться именно с амплитудными значениями действующих в нем напряжений, так как в смысле пробоя наиболее опасными являются именно моменты максимума напряжения. Однако с точки зрения энергетических действий переменного тока, как - мы увидим ниже, оказывается более удобным характеризовать интенсивность тока иначе. [4]
Чему равны амплитудные значения силы тока и напряжения IB цепи, если амперметр показывает 2 А, а вольтметр 120 В. [6]
При этом в качестве расчетных необходимо прилимать амплитудные значения силы тока и напряжения. [7]
Как видно из выражения ( 56), амплитудные значения силы тока во вторичной обмотке отличаются друг от друга коэффициентами, зависящими только от относительных величин воздушных зазоров. [8]
На рис. 200 изображены графики / и 2 зависимости амплитудных значений силы тока /, в двух контурах от частоты ш вынужденных электромагнитных колебаний, происходящих в этих контурах. Резонанс в контуре с малым активным сопротивлением называют острым, а в контуре с большим активным сопротивлением - тупым. [9]
В колебательном контуре с индуктивностью 0 40 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 1 0 - Ю 1 А. Каким будет напряжение на конденсаторе в момент, когда энергия электрического и энергия магнитного полей будут равны. [10]
Из уравнений ( 1) следует, что основное внимание нужно сосредоточить на нахождении амплитудного значения силы тока / 0 и сдвига фазы ф, ибо неизвестные амплитудное значение напряжения С / 0 и круговая частота ( о легко находятся из данных условия задачи. [11]
Здесь вектор, изображающий напряжение, повернут относительно вектора тока на угол я / 2 в отрицательном направлении ( по часовой стрелке), / о и И с о - амплитудные значения силы тока и напряжения. [12]
В сеть переменного тока с действующим значением напряжения 120В последовательно включены проводник с активным сопротивлением 10 Ом и катушка индуктивностью 0 1 Гн. Определить частоту v тока, если амплитудное значение силы тока в цепи равно 5 А. [13]
УДАРНЫЙ ГЕНЕРАТОР - Синхронный генератор ( как правило, 3-фазного тока), предназнач. Применяется для испытаний элект-рич. Развиваемая мощность до неск. ГВ-А; амплитудное значение силы тока КЗ - неск. [14]
Представляет собой 3-фазную синхронную машину, работающую в режиме 2 - и 3-фазных КЗ и рассчитанную на неск. КЗ через определенные промежутки времени ( напр. MB А и более; амплитудное значение силы тока КЗ - неск. [15]
Страницы: 1 2
www.ngpedia.ru
Амплитудное значение - сила - ток
Амплитудное значение - сила - ток
Cтраница 1
Амплитудное значение силы тока достигает при резонансе максимума, равного Uo / R, сдвиг фаз между напряжением и током отсутствует. Напряжения U L на индуктивности L и U c на емкости С равны по модулю и находятся в противофазе, так что полное напряжение на концах цепи U совпадает с напряжением U K на активном сопротивлении R. Напряжения на реактивных сопротивлениях могут по амплитуде значительно превышать приложенное напряжение. [1]
Определим амплитудное значение силы тока и положение якоря относительно сердечника при различных величинах относительных воздушных зазоров. [2]
Добычно амплитудным значением силы тока; если речь идет - г J3 о напряжении, то говорят об амплитудном значении напряжения. Во многих случаях эти величины являются очень важными. Так, например, при расчете изоляции какого-либо электрического аппарата приходится считаться именно с амплитудными значениями действующих в нем напряжений, так как в смысле пробоя наиболее опасными являются именно моменты максимума напряжения. Однако с точки зрения энергетических действий переменного тока, как - мы увидим ниже, оказывается более удобным характеризовать интенсивность тока иначе. [4]
Чему равны амплитудные значения силы тока и напряжения IB цепи, если амперметр показывает 2 А, а вольтметр 120 В. [6]
При этом в качестве расчетных необходимо прилимать амплитудные значения силы тока и напряжения. [7]
Как видно из выражения ( 56), амплитудные значения силы тока во вторичной обмотке отличаются друг от друга коэффициентами, зависящими только от относительных величин воздушных зазоров. [8]
На рис. 200 изображены графики / и 2 зависимости амплитудных значений силы тока /, в двух контурах от частоты ш вынужденных электромагнитных колебаний, происходящих в этих контурах. Резонанс в контуре с малым активным сопротивлением называют острым, а в контуре с большим активным сопротивлением - тупым. [9]
В колебательном контуре с индуктивностью 0 40 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 1 0 - Ю 1 А. Каким будет напряжение на конденсаторе в момент, когда энергия электрического и энергия магнитного полей будут равны. [10]
Из уравнений ( 1) следует, что основное внимание нужно сосредоточить на нахождении амплитудного значения силы тока / 0 и сдвига фазы ф, ибо неизвестные амплитудное значение напряжения С / 0 и круговая частота ( о легко находятся из данных условия задачи. [11]
Здесь вектор, изображающий напряжение, повернут относительно вектора тока на угол я / 2 в отрицательном направлении ( по часовой стрелке), / о и И с о - амплитудные значения силы тока и напряжения. [12]
В сеть переменного тока с действующим значением напряжения 120В последовательно включены проводник с активным сопротивлением 10 Ом и катушка индуктивностью 0 1 Гн. Определить частоту v тока, если амплитудное значение силы тока в цепи равно 5 А. [13]
УДАРНЫЙ ГЕНЕРАТОР - Синхронный генератор ( как правило, 3-фазного тока), предназнач. Применяется для испытаний элект-рич. Развиваемая мощность до неск. ГВ-А; амплитудное значение силы тока КЗ - неск. [14]
Представляет собой 3-фазную синхронную машину, работающую в режиме 2 - и 3-фазных КЗ и рассчитанную на неск. КЗ через определенные промежутки времени ( напр. MB А и более; амплитудное значение силы тока КЗ - неск. [15]
Страницы: 1 2
www.ngpedia.ru
Эффективные значения силы тока и напряжения
Работа с переменным током, в случае вынужденных колебаний, достаточно сложна. Но есть возможность привести сложное электромагнитное колебание к виду достаточно простого постоянного тока.
Основная идея: представим переменный ток в виде постоянного при условии равенства мощности постоянного тока и мощности переменного тока за один период колебания.
Итак:
- для постоянного тока:
- где
- — мощность постоянного тока,
- — сила постоянного тока,
- — напряжение в цепи постоянного тока.
- для переменного тока
- где
- — мощность переменного тока в момент времени ,
- — амплитудное (максимальное) значение силы тока,
- — амплитудное (максимальное) значение напряжение,
- — циклическая частота колебания,
- — начальная фаза колебания,
- — момент времени.
Проанализируем фразу «средняя мощность за период». Усреднение (2) приводит к вопросу об усреднении синуса, из математики:
, тогда средняя мощность переменного тока за период можно записать как: (3)Воспользуемся необходимым условием равенства мощностей (1) и (3):
(4)- где
- — эффективное значение силы тока,
- — эффективное значение напряжения.
Дальнейшая логика достаточно проста: т.к. сила тока и напряжение равнозначны, то запишем (4) в виде:
(5)Таким образом:
(6)Вывод: для расчёта параметров цепей переменного тока достаточно заменить её цепью постоянного тока при условии равенства мощностей за период. Выполнение данного условия приводит к использованию в цепи постоянного тока эффективных значений тока и напряжения (6). Т.е. все закономерности, характеризующие постоянный ток, будут справедливы и для переменного только при использовании эффективных значений.
Словесные обозначения:
- амплитудное, максимальное — , ,
- эффективное, действующее — , .
Эффективные значения силы тока и напряжения обновлено: Сентябрь 7, 2017 автором: Иван Иванович
Поделиться ссылкой:
- Telegram
www.abitur.by
Переменный ток. ЭДС, напряжение, сила тока, заряд. Амплитудные значения. Формулы
Ранее мы познакомились с постоянным электрическим током — направленным движением зарядов, для которого сила тока постоянна. В случае, если значение силы тока непостоянно, тогда ток будем называть переменным.
Для школьной физики переменный ток рассматривается в двух, в общем-то, похожих случаях:
Рассмотрение свободных колебаний в случае переменного тока аналогично постоянному. Точно так же существует закон Ома для цепи переменного тока, рассчитываются мощности и энергии (работы) для такого случая.
Для школы характерно описание переменного тока через гармонические законы. Переменными параметрами в цепи могут быть ЭДС (
), напряжение на элементе (), сила тока (), заряд конденсатора (). Рассмотрим ЭДС источника гармонический колебаний: (1)Аналогичным образом можно ввести колебания напряжения
на элементе: (2)Таким же образом вводится и колебание силы тока:
(3)И, аналогично, заряд на конденсаторе:
(4)Важно: нужно помнить, что тригонометрически можно превратить синус в косинус:
(5)- где
- — новая начальная фаза колебания.
Вывод: таким образом, рассмотрение переменного тока в случае формульных задач, связанных с соотношениями (1) — (4), касается анализа сомножителей и слагаемых, входящих в само соотношение.
Поделиться ссылкой:
www.abitur.by
Закон Ома для действующих и амплитудных значений тока и напряжения.
⇐ ПредыдущаяСтр 7 из 10Следующая ⇒Пусть источник тока создает переменное гармоническое напряжение (рисунок)

U(t) = Uosinωt. (1)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
I(t) = U(t)/R = (Uo/R)sinωt = Iosinωt,
где Io = Uo/R ? амплитудное значение силы тока в цепи.Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.Величины Uo и Io = Uo/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность P(t) = U(t)I(t), которая, в отличие от цепей постоянного тока, изменяется с течением времени.С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
P(t) = U(t)I(t) = I2(t)R = Io2Rsin2ωt.
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.Перепишем формулу для мощности по-другому:
P = UI = UoIosin2ωt = (1/2)UoIo(1 ? cos2ωt) = UoIo/2 ? (UoIo/2)cos2ωt.
Первое слагаемое не зависит от времени. Второе слагаемое ? переменная составляющая ? функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рисунок).Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
Pcp = UoIo/2 = Io2/R.
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.Поскольку для постоянного тока
Pпост =I2R,
то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока
Iд = Io/?2.
Аналогично можно ввести действующее значение и для напряжения
Uд = Uo/?2.
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
P = UдIд = Iд2R = Uд2/R, Iд = Uд/R.
41.1. Треугольники напряжений и сопротивлений.

Амплитуды составляющих общего напряжения:
Действующие значения:
Вектор общего напряжения:
Для того, чтобы найти значение вектора U, построим векторную диаграмму (рис. а). За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительнымнаправлением оси, от которой отсчитываются фазовые углы.
Вектор по направлению совпадает с вектором тока I, а вектор направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор общего напряжения U опережает вектор тока I на угол >0, но < , а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения вактивном и индуктивном сопротивлениях и : =Ucos
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Ua =
Проекция вектора напряжения U на направление, перпендикулярное вектору тока называется реактивной составляющей вектора напряжения и обозначается Up. Up =
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. б), катетами которого являются активное и индуктивное сопротивления, а гипотенузой – величина .
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует:
41.2. Полное сопротивление.
Полное сопротивление (Z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.
- полное сопротивление цепи.
41.3. Угол сдвига фаз между напряжением и током.
Аргумент комплексного сопротивления j есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как j = arctg(X/R). Следовательно, сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи. Из выражения следует, что положительные значения j соответствуют отставанию тока по фазе, а отрицательные - опережению.
41.4. Закон Ома для действующих и амплитудных значений тока и напряжения.
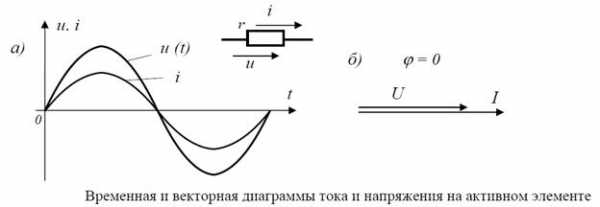
В активном элементе r происходит необратимое преобразование электрической
энергии в тепловую энергию. Мгновенные значения тока i и напряжения u связаны
законом Ома:
Если ток изменяется по синусоидальному закону тогда напряжение:
С другой стороны мгновенное значение напряжения:
Отсюда получен закон Ома для амплитудных значений: , и закон Ома для действующих значений:
42. Энергетический процесс. Мгновенная, активная, реактивная и полная мощности. Треугольник мощностей. Коэффициент мощности.
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепиПо определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:
Для единичного заряда на участке A-B:
Для всех зарядов:
Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:
Если участок цепи содержит резистор c электрическим сопротивлением R, то
Активная мощностьИзмеряется в W [Вт] Ватт.Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U иI — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
Реактивная мощность
Единица измерения — вольт-ампер реактивный (var, вар)
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Рсоотношением: .
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Единица полной электрической мощности — вольт-ампер (V·A, В·А)
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели,распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
ТРЕУГОЛЬНИК МОЩНОСТЕЙ - графическое изображение активной, реактивной и полной мощностей в цепи переменного тока. Треугольник мощностей получается из соотношения Р2 + Q2 = S2.
Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Численно коэффициент мощности равен косинусу этого фазового сдвига.
Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы:
1.
2.
3.
4.
Здесь — активная мощность, — полная мощность, — реактивная мощность.
43.1. Последовательное соединение активного, индуктивного и ёмкостного сопротивлений

При последовательном соединении активного r , индуктивного xL и ёмкостного xC
сопротивлений (рис.8 а) мгновенное значение напряжения источника согласно второму закону Кирхгофа определяется алгебраической суммой мгновенных значений напряжений на
отдельных элементах:
Если все эти напряжения представить в виде векторов на векторной диаграмме,
то действующее значение напряжения источника определяется, как векторная сумма
действующих значений напряжений на отдельных элементах и может быть рассчитано по
формуле:
Учитывая, что по закону Ома
Тогда , - закон Ома ,
где: - полное сопротивление цепи при последовательном соединении элементов.
Полное сопротивление цепи Z , активное r и реактивное образуют
треугольник сопротивлений , для которого справедливы следующие соотношения:
43.2. II закон Кирхгофа для мгновенных значений.
Второй закон Кирхгофа
Рассмотрим контур, выделенный из сложной цепи переменного тока

Запишем второй закон Кирхгофа для мгновенных значений:
.
Все мгновенные значения изобразим в виде комплексов, опустим знак мнимой части, сократим на и разделим на (по аналогии с законом Ома):
.
В контуре цепи синусоидального тока алгебраическая сумма комплексов ЭДС равна алгебраической сумме комплексов падений напряжений.
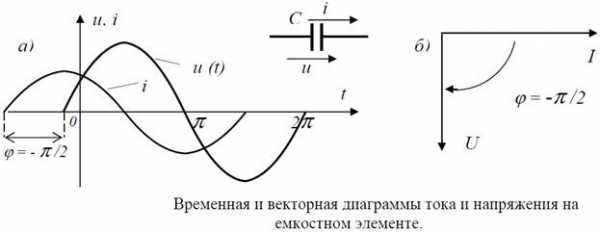
43.3.Временная и векторная диаграммы для различного характера цепи.
1) 
2)
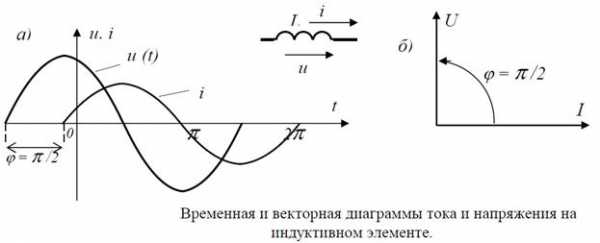
3) 
Читайте также:
lektsia.com
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.