Автор закон сохранения энергии: Как был открыт закон сохранения энергии

Как был открыт закон сохранения энергии

Закон сохранения энергии был открыт не физиком, а врачом.

В 1840 году на острове Ява судовой врач немец Роберт Майер вскрыл больному вену и… к своему ужасу обнаружил, что потекла не темная кровь, а алая! Неужели он вместо вены попал в артерию?! Испуг врача объяснялся тем, что алая кровь течет по артериям от сердца — это кровь, наполненная кислородом. А обратно, к сердцу кровь течет по венам. В венозной крови остается мало кислорода, поэтому цвет у нее темно-красный. Кровотечение же из артерии смертельно опасно.

Однако местные врачи успокоили Майера: они объяснили, что здесь, в тропиках, венозная кровь у людей такая же алая, как и артериальная.

«Почему же так происходит? — задумывается Майер. — Может, дело в том, что температура воздуха здесь почти равна температуре человеческого тела… Организму не нужно расходовать силу (в то время энергию еще называли силой!) на поддержание температуры тела, поэтому кислород остается в крови — ведь силу дает именно сгорание кислорода. Но это значит, что сила сохраняется: она только превращается из одного вида в другой, но никогда не исчезает и не появляется из ничего».

Развивая свою идею, Майер изучил все известные ему превращения энергии — кинетической в потенциальную и обратно, механической энергии во внутреннюю и внутренней энергии в механическую, рассмотрел электрическую и химическую энергии.

Независимо от Майера, но несколькими годами позже закон сохранения энергии был открыт английским физиком Джеймсом Джоулем и немецким естествоиспытателем Германом Гельмгольцем.

Все эти ученые были очень молоды, когда они совершили свое великое открытие: Майеру было 28 лет, Джоулю — 25, а Гельмгольцу — 26.

Задолго до открытий Майера, Джоуля и Гельмгольца очень близко к открытию закона сохранения энергии подошел выдающийся российский ученый Михаил Васильевич Ломоносов. Но, к сожалению, труды Ломоносова долгое время оставались неизвестными для европейских ученых.

Идея о взаимопревращении механической и внутренней энергии была высказана, также до открытий Майера, Джоуля и Гельмгольца, физиком и инженером Томпсоном, получившим известность как граф Румфорд.

История формулировки закона сохранения
энергии

История формулировки закона сохранения
энергии

ИСТОРИЯ НАУКИ

В.М.Дуков

Окончание. См. № 24/02

Начало установления
количественной связи между работой и теплотой
связано с именем молодого французского ученого
Сади Карно (1796–1832). Карно – инженер по роду
деятельности, физик по складу мышления –
племянник замечательного ученого и
государственного деятеля периода Великой
французской революции Лазара Карно (1753–1823).

В 1814 г. Сади Карно окончил Политехническую
школу в Париже, затем поступил в инженерные
войска. В 1827 г. он был произведен в капитаны и
вскоре вышел в отставку. О его научной
деятельности, которую он совмещал с военной
службой, известно очень мало. Зато вечную мировую
славу завоевала опубликованная в 1824 г. его
единственная небольшая книжка «Размышления о
движущей силе огня и о машинах, способных
развивать эту силу».

В течение 10 лет никто не обращал внимания на эту
брошюру, пока ее не «открыл» Клапейрон. Автора
уже не было в живых

Интересные записки опубликовал брат Карно
после его смерти. В них был, по существу,
сформулирован в частной форме закон сохранения
энергии. Карно писал в «Размышлениях»: «Тепло –
это не что иное, как движущая сила, или, вернее,
движение, изменившее свой вид. Это движение
частиц тела. Повсюду, где происходит уничтожение
движущей силы, возникает одновременно теплота в
количестве, точно пропорциональном количеству
исчезнувшей движущей силы. Обратно: при
исчезновении теплоты всегда возникает движущая
сила».

Таким образом, можно высказать общее
предположение: движущая сила существует в
природе в неизменном количестве; она, собственно,
никогда не создается, никогда не уничтожается; в
действительности она меняет форму, т.е. вызывает
то один род движений, то другой, но никогда не
исчезает.

Если «движущую силу» заменить словом
«энергия», то перед нами – четкая формулировка
закона сохранения энергии. В записках Карно
сказано следующее: «По некоторым представлениям,
которые у меня сложились относительно теории
тепла, создание единицы движущей силы требует
затраты 2,7 единицы тепла».

К сожалению, Карно не привел рассуждений,
которые привели его к такому результату. Если
единицей работы считать кг•м, а единицей теплоты
– калорию, то эта оценка близка к полученной
далее экспериментаторами.

Но для утверждения связи между работой и
теплотой необходим был количественный
эксперимент. Нужно было показать, что при затрате
единицы работы получается всегда одно и тоже
количество теплоты. Это продемонстрировал
английский физик Д.П.Джоуль (1818–1889) в своих
классических экспериментах, проведенных в 1850 г.

Джоуль родился в Сальфорде близ Манчестера. С
ранних лет он проявлял необычайную
любознательность и стремление раскрыть тайны
природы путем постановки искусного
эксперимента. Будучи владельцем большого
винного завода (в ученых кругах его называли
«пивоваром из Сальфорда»), он завел у себя хорошо
оборудованную домашнюю лабораторию, в которой в
течение многих лет проводил систематические
исследования, направленные на всестороннее
обоснование закона сохранения энергии. Его имя
увековечено в названии основной единицы энергии.

Схема установки Д.Джоуля

Идейную основу этих довольно сложных в
исполнении опытов легко усмотреть из схемы,
изображенной на риcунке. Падающие с определенной
высоты грузы приводили во вращение вертушку,
помещенную в калориметр. Конструкция последнего
была такова, что жидкость не могла вращаться всей
своей массой, вертушка испытывала сильное
сопротивление вращению, и жидкость нагревалась.
Зная массу и теплоемкость калориметра, можно по
повышению его температуры определить количество
выделившейся теплоты: Q = cmDt.
Совершенная при этом работа равна потенциальной
энергии падающих грузов: А = mgh. Результатом этих
опытов, которые затем многократно повторялись в
других вариантах, стало знаменитое равенство:

1 Дж = 0,24 кал.

Это так называемый термический эквивалент
работы.

Вместо термического эквивалента работы можно
говорить о механическом эквиваленте теплоты и
результат опытов Джоуля выражать равенством

1 кал = 4,18 Дж.

Заметим, что теплота – специфическая форма
движения материи, подчиненная статистическим
закономерностям. Энергия теплового движения
качественно отлична от механической энергии, что
проявляется при превращениях. Механическая
энергия целиком переходит в тепловую, равенство
1Дж=0,24кал – результат эксперимента. Но обратный
переход – необратимый процесс, – он протекает с
потерями, рассеянием энергии, поэтому источник,
который отдает количество теплоты, равное 1 кал,
производит работу, меньшую 4,18 Дж. Разница
переходит во внутреннюю энергию, так что
соблюдается закон сохранения энергии

Установление всеобщего закона сохранения
энергии и введение интернациональной системы
единиц СИ привело к исключению понятия
механического эквивалента теплоты. Измерение
количества теплоты можно производить в Дж, так
что в особой единице для тепловых измерений нет
нужды.

3. Осознание общности закона

Начало XIX в. замечательно открытием множества
явлений, демонстрировавших превращение сил
природы. Первую роль здесь сыграл электрический
ток с его химическими, тепловыми, магнитными и
электродинамическими действиями. Отсюда
умонастроение ученых, которое Фарадей выразил в
следующем откровении: «Я давно придерживался
мнения, ставшего почти убеждением, что различные
формы, в которых проявляются силы материи, имеют
общее происхождение или, иными словами, так
непосредственно связаны или взаимосвязаны, что
они могут превращаться друг в друга и обладают в
своих действиях эквивалентами сил».

Убеждение в единстве и взаимной превращаемости
сил природы играет роль компаса, ведущего
Фарадея в глубь неизведанного. По существу,
Фарадей владеет законом сохранения энергии и
использует его в качестве инструмента научного
исследования.

Вот еще один пример. В
«Экспериментальных исследованиях по
электричеству» он пишет: «Контактная теория
(речь идет о контактной теории гальванической
эдс. – В.Д.) принимает, что сила, способная
преодолеть мощные сопротивления, может
возникнуть из ничего. Это было бы сотворением
силы, что нигде не имеет места без
соответствующего исчерпания того, что питает ее.
Если бы контактная теория была верна, то
следовало бы отрицать равенство причины и
действия. Но тогда был бы возможен и perpetuum mobile».

Но наибольшего обобщения достиг немецкий врач
Юлиус Роберт Майер (1814–1878) – ученый с
необыкновенными интуицией и воображением.
Будучи судовым врачом, он провел физиологические
наблюдения изменений цвета крови у матросов,
перешедших из умеренного в тропический пояс.
Майер пришел к выводу, что «температурная
разница между собственным теплом организма и
теплом окружающей среды должна находиться в
количественном соотношении с разницей в цвете
обоих видов крови – артериальной и венозной. Эта
разница является выражением размера потребления
кислорода или силы процесса сгорания,
происходящего в организме» (подчеркнуто мною. –
В.Д.).

Из области медицинских наблюдений Майер
переходит к анализу физико-химических процессов
и опирается при этом на закон сохранения сил.
Свои размышления он оформил в виде статьи «О
количественном и качественном определении сил»
и послал в журнал. Редактор – известный физик
К.Поггендорф – бросил статью неизвестного врача
в корзину. Майер был вынужден печатать свои
работы в журнале «Анналы химии и фармации», так
что они стали известны физикам только после
смерти автора.

Майер утверждал, что «движение, теплота, и, как
мы намерены показать в дальнейшем, электричество
представляют собой явления, которые могут быть
сведены к единой силе, которые изменяются друг
другом и переходят друг в друга по определенным
законам». Он ставит принципиальной важности
задачи на закон сохранения энергии, например:
«Как высоко должен быть поднят определенный груз
над поверхностью земли, чтобы его сила падения
была эквивалентна нагреванию равного ему по весу
количеству воды от 0 до 1 °?»

Майер вычисляет из опытов над «сжатием
воздуха», что одна калория эквивалентна поднятию
одного килограмма на 0,365 м. При этом он использует
уравнение состояния идеальных газов и вычисляет
разность теплоемкостей при постоянном давлении
и постоянном объеме. Поэтому равенство с_p –
с_v = R, где R – универсальная газовая
постоянная, носит его имя.

vСвои выводы о сохранении сил
природы при превращениях Майер переносит на
органическую природу. В частности, он развивает
мысль о значении процесса ассимиляции в
растениях для поддержания жизнедеятельности
организмов. Внушительны его аргументы в
опровержение распространенной тогда в науке
теории о существовании особой жизненной силы.

В сочинении «Динамика неба» законы сохранения
переносятся на космические явления. Вот отрывок
из этой книги: «Часто и удачно Солнце сравнивают
с непрерывно звучащим колоколом. Но что же
поддерживает звучание этого небесного тела,
столь величественно и чудесно наполняющего
небесные пространства своими лучами, что
поддерживает его в вечно неослабевающей силе и
юности? Что предохраняет его от полного
истощения, от наступления равновесия, дабы ночь и
смертельный холод не заполнили пространства
нашей планетной системы? Всеобщий закон природы,
не допускающий никаких исключений, гласит, что
для образования тепла необходима известная
затрата. Эту затрату, как бы разнообразна она ни
была, всегда можно свести к двум главным
категориям, а именно, она сводится либо к
химическому материалу, либо к механической
работе».

Статья подготовлена при поддержке кредитного потребительского кооператива «ДаНаЯ». Если Вы решили получить кредит для своих нужд, то оптимальным решением станет обратиться в кооператив «ДаНаЯ». Перейдя по ссылке: «помощь в получении кредита», вы сможете, не отходя от экрана монитора, узнать более подробную информацию о получении кредита и действующих акциях. В кооперативе «ДаНаЯ» работают только высококвалифицированные специалисты с огромным опытом работы с клиентами в сфере кредитования населения.

Рядом с Майером стоит имя Джоуля. С такой же
целеустремленностью он шел к всестороннему
экспериментальному обоснованию общности закона
сохранения энергии. Выше говорилось о его
классическом опыте по определению термического
эквивалента работы. Но его первое исследование
было посвящено превращению электричества в
теплоту. В работе 1841 г. «О теплоте, выделяемой
металлическими проводниками электричества и
элементами батарей при электролизе» он приходит
к известному закону: Q=I²Rt.

Далее Джоуль перешел к другому виду
превращения энергии. В работе «Об электрическом
происхождении теплоты горения» он показал, что
количество теплоты, выделяемой током в цепи,
тождественно теплоте, которая может быть
получена непосредственным окислением
составляющих цепь металлов, включая водород.
Отсюда ученый заключил, что теплота,
выделяющаяся во внешней цепи гальванического
элемента, является результатом превращения
теплоты химических реакций.

Экспериментами, где электрический ток
одновременно выделяет теплоту и производит
механическую работу, Джоуль доказывает, что
энергия сохраняется и при сложных превращениях.

vВ серии работ 1843 г. «О
тепловом эффекте магнитоэлектричества и
механической величине тепла» Джоуль открывает,
что теплота, выделяющаяся в нагрузке
магнито-электрического генератора имеет своим
источником механическую работу. Он заставляет
вращаться катушку между полюсами сильного
магнита с помощью падающих грузов. Катушка была
помещена в стеклянную трубку с водой, последняя
выполняла роль калориметра. Возбуждаемый в
катушке индукционный ток приводил к выделению
теплоты и повышению температуры воды. Зная массу
грузов и высоту падения, можно было определить
затраченную энергию, а по величине массы воды и
повышению ее температуры – полученное
количество теплоты, отсюда получалось
соотношение между джоулем и калорией –
термический эквивалент работы: 1Дж=0,24 кал.

Далее Джоуль изучает непосредственное
превращение механической работы в теплоту.
Продавливая воду через узкие трубки, он
сравнивает произведенную работу и выделившееся
количество теплоты. Затем он сжимает воздух и
измеряет затраченную при этом работу и
полученное повышение его температуры. И во всех
случаях он обнаруживает пропорциональность
выделившегося количества теплоты произведенной
работе.

4. Первая точная формулировка закона. Переход к
понятию энергии

Хотя факт сохранения сил природы их
многообразных превращений был установлен целым
рядом независимых экспериментов, он не имел
точного выражения, поэтому оставался неким
утверждением философского толка, а физики
середины XIX в. скептически относились к таким
утверждениям, тем более что публиковались они не
профессионалами.

Необходимо было сформулировать закон в точных
понятиях и дать ему математическое выражение.
Это сделал Герман Гельмгольц (1821–1894).

Гельмгольц родился в Потсдаме, в семье учителя
гимназии. Мать его происходила из семьи
английских эмигрантов. Стесненный семейный
бюджет не позволил талантливому юноше поступить
в университет, пришлось выбрать карьеру врача. В
казармах Постдама Гельмгольц начал
физиологические исследования, одновременно
изучая труды классиков физики.

Он быстро вышел на путь самостоятельного
творчества и обобщений. Молодой военный врач
публикует в 1847 г. книгу «О сохранении силы»,
которая сразу сделала его известным физиком.
Однако это мало повлияло на его карьеру.

По рекомендации Гумбольта Гельмгольц получил
место ассистента в анатомо-физиологическом
музее Берлина, но его успехи в науке столь
впечатляющи, что его через год приглашает
Кеннингсбергский университет на должность
профессора анатомии и физиологии.

Постепенно растет удельный вес физической
тематики в его исследованиях, и Гельмгольц
становится главой немецкой физической школы. Он
поразительно разносторонен: наряду с работами по
обоснованию закона сохранения энергии,
исследования по термодинамике, по
электродинамике химических процессов, по
механике вихревых движений в жидкостях,
оптические, физические и физиологические
исследования, основополагающие труды по
физиологии слуха и зрения. Он первый измерил
теплообразование в мышцах, скорость
распространения нервных импульсов. Вместе с тем
Гельмгольц был блестящим популяризатором науки.

В поисках математической формулировки закона
сохранения сил природы Гельмгольц опирался на
последовательно механическую концепцию: материя
представляет собой совокупность материальных
точек, между которыми действуют центральные
силы. Целью физической науки, согласно
Гельмгольцу, является сведение явлений природы к
движению и взаимодействию материальных точек,
притягивающихся или отталкивающихся силами,
зависящими от расстояния между ними.

Если исходить из такой модели материи, то все
виды сил (энергии) можно свести к двум: живым
силам движущихся материальных точек (энергии
движения) и силам напряжения (энергии положения).
Тогда закон сохранения сил (энергии) можно
сформулировать так: «Когда тела природы
действуют друг на друга с силами притяжения или
отталкивания, не зависящими от времени и
скорости, то сумма их живых сил и сил напряжения
остается постоянной. Максимум работы, которую
можно получить, является, таким образом,
определенным, конечным».

М.Планк в своей книге «Принцип сохранения
энергии» следующим образом поясняет идею
Гельмгольца: «Преобразование принципа живой
силы, принятое Гельмгольцем для того, чтобы
превратить его в принцип сохранения силы,
заключается в том, что в уравнение, выражающее
соотношение живой силы L и работы А,
произведенной действующими силами L + А = const, он
вводит вместо понятия работы А понятие
количества сил напряжения U, равное и
противоположное по знаку величине работы А. Сила
напряжения, так же как и работа, зависит только от
мгновенного состояния системы, и вышеуказанное
уравнение можно сформулировать следующим
образом: сумма количества живой силы и силы
напряжения остается неизменной во времени: L + А =
const. Если мы эту сумму коротко обозначим как силу,
заключенную в системе, то тем самым мы получим
закон сохранения силы.

Как ни незначительным кажется, на первый
взгляд, это преобразование, перспектива, которую
он открывает во всех областях физики,
чрезвычайно велика, ибо возможность его
обобщения для любых явлений природы легко
бросается в глаза. Главное основание для такого
обобщения заключается в том, что принцип
сохранения силы выступает параллельно с давно
уже известным и, так сказать, перешедшим в
инстинкт, принципом сохранения материи. Так же,
как количество содержащейся в системе тел и
измеряемой их весом материи не может быть
никакими средствами уменьшено или увеличено,
какие бы различные физические и химические
превращения не происходили в системе, так и
количество содержащейся в системе силы
представляет собой самостоятельную, совершенно
неизменную величину. Сила, так же как и материя,
может быть представлена в многообразных формах,
но прежде всего она проявляется в двух основных
формах: как живая сила и как сила напряжения. Обе
эти формы могут выступать различнейшим образом:
живая сила – как видимое движение, как свет,
теплота; сила напряжения – как поднятие тяжести,
как упругое напряжение, как электрическое
напряжение».

Особый интерес в этом пояснении представляет
указание Планка на аналогию законов сохранения
материи и энергии.

Сформулировав закон, Гельмгольц далее
рассматривает его действенность во всех
разделах физики. Один из примеров применения
закона сохранения энергии, который он
рассматривает в своем мемуаре «О сохранении
силы», вошел в учебники физики: это вывод закона
электромагнитной индукции, опирающийся на закон
сохранения энергии.

Кроме Майера, Джоуля и Гельмгольца
обоснованием закона сохранения силы и
измерениями механического эквивалента теплоты
занимался целый ряд других исследователей. Тем
не менее вся эта гигантская волна
интеллектуальных усилий не привлекала внимания
маститых физиков. Резкий перелом произошел в
начале второй половины XIX в., и он совпал со
временем введения в лексикон физики понятия
энергии.

Интерес к закону прогрессивно возрастал,
естественно, стали задумываться над двойным
использованием фундаментального понятия силы.
Физики, конечно, не путали лейбницевскую «живую
силу» с ньютоновской, но неудобство такого
раздвоения понятия было очевидно. И тогда
вспомнили, что еще в 1807 г. в «Лекциях по
естественной философии» Т.Юнг вместо понятия
«живой силы» пользовался понятием энергии.
Последнее было единодушно принято ведущими
физиками мира. В 1852 г. в работе «Динамическая
теория тепла» В.Томсон дал первое определение
энергии: «Под энергией материальной системы в
определенном состоянии мы понимаем измеренную в
механических единицах работы сумму всех
действий, которые производятся вне системы,
когда она переходит из этого состояния любым
способом в произвольно выбранное нулевое
состояние».

Несколько позже Максвелл дал простое и точное
определение энергии как способности системы
совершать работу, подчеркнув неразрывность
связи понятий энергии и работы. Анализ этой связи
привел в итоге к современному пониманию работы
как процесса, приводящего к созданию источника
энергии.

В 1883 г. Гельмгольц ввел в физику понятия
свободной и связанной энергий. В своей
классической работе «Термодинамика химических
процессов» он писал: «Подобно тому, как теплота
может превращаться в работу частично, так же в
случае химических процессов должно быть принято
разделение между частью сил химического
сродства, способных к превращению в другие формы
и той частью, которая может превращаться только в
теплоту. Я позволю себе обозначить обе эти части
энергии, как свободную и связанную энергии».

Г.Гесс (1802–1850) на основании многочисленных
опытных исследований пришел к важному следствию
закона сохранения энергии: тепловой эффект
химических реакций не зависит от их
промежуточных стадий, а определяется только
начальным и конечным состояниями реагирующей
системы.

Независимость процессов преобразования
энергии от их промежуточных ступеней явилась
одним из выражений общей характерной
особенности закона сохранения, его
своеобразного удобства: при научных
исследованиях отпадала необходимость анализа
стадий превращений энергии, их механизмов,
качества материальных объектов, участвующих в
этих превращениях.

Так постепенно начало складываться
представление об энергии как общей
количественной мере движения и взаимодействия
всех видов материи. В изолированной системе
энергия может переходить из одной формы в другую,
но общее ее количество остается неизменным.

Мифы современной физики. Законы сохранения / Хабр

Продолжение. Начало тут и тут:

В этот раз мы замахнемся на святое: на законы сохранения, в том числе на закон сохранения энергии. Правда, вечного двигателя я вам не обещаю.

Закон сохранения энергии имеет такой ореол святости, что практически любой человек напрягается, услышав, что с ним не все хорошо. Между тем, энергия сохраняется в механике, в квантовой механике и даже в СТО – Специальной Теории Относительности. Но… не в ОТО – Общей Теории Относительности. Однако сказать, что энергия не сохраняется, тоже нельзя. Вначале разберемся,

Что же такое – сохраняться?

Вот мы положили в мешок два шара, синий и красный. Через какое-то время достали их. Ага, было два шара, и стало два шара, шары сохраняются в мешке! Так выглядит пространственно — временная картина этого эксперимента:

Однако с количеством шаров все просто – все наблюдатели, как бы они ни двигались, согласятся с тем, что шаров – два. А как быть с энергией? Вот, например, я стою около дома весом 1000 тонн. Кинетическая энергия его в моей системе отсчета равна нулю. Теперь я пойду от дома со скоростью 1 метр в секунду. В моей системе отсчета дом приобрел огромную энергию! Как я, слабый человек, мог дать дому такую энергию всего одним шагом?

Если вы внимательно следили за руками, то, несомненно, заметили, что я совершил грязный хак. Считал энергию вначале в одной системе отсчёта, а потом нагло перескочил в другую. Так делать нельзя. Для энергии состояние до и состояние после должно быть привязано к одной и той же системе отсчета.

Для нашей картинки с шарами это означает, что дно и крышка цилиндра (в общем случае любой фигуры) должны быть параллельны друг другу. А вот с этим в искривленном пространстве плохо: как вы помните, в искривленном пространстве могут быть много параллельных или не быть ни одной! Хуже того, пространство может быть таким кривым, что туда вообще не вписать такую фигуру!

Или время закольцовано – и понятия до и после не вполне определены. Таким образом, в ОТО не то, чтобы энергия не сохраняется, а само понятие “сохраняться” плохо определено.

Канонический пример несохранения энергии

Мы все знаем, что Вселенная расширяется. Когда ее линейный размер увеличивается в 10 раз, то ее объем увеличивается в 1000 раз, и плотность обычного вещества (ведь атомы – это шарики, и все наблюдатели согласны с тем, сколько их) падает тоже в 1000 раз

А вот плотность излучения, в частности реликтового излучения, падает в 10000 раз – помимо того, что фотоны рассеялись в большем объеме, каждый из них еще и покраснел. То есть плотность вещества падает как третья степень, а излучения – как четвертая.

У этого есть интересное следствие – если мы будем двигаться в прошлое, то плотность излучения будет расти быстрее, чем плотность материи, и мы можем дойти до периода, когда плотностью и давлением обычной материи можно будет вообще пренебречь. Гравитация в основном создавалась давлением фотонного газа.

Следует заметить, что космологическая точка зрения – “вся вселенная в такое-то время”, несмотря на ее интуитивную понятность и полезность, для каждого времени после Большого Взрыва образует в пространстве-времени кривую поверхность, то есть не является валидной системой отсчета.

Можно ли поднять себя за волосы?

Спойлер: ДА. Импульс, как вы догадались, тоже не сохраняется. Вы можете погуглить по словам Swimming in space. Вот видео, как это выглядит. Конечно, практической ценности в этом почти нет, но все равно интересно.

Закон сохранения энергии — Карта знаний

• Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда закономерность, его можно именовать не законом, а принципом сохранения энергии.

  С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающимся для разных систем.

  В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Возможен переход энергии из одного вида в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Однако, из-за условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.

  Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.

  С математической точки зрения, закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Источник: Википедия

Связанные понятия

Зако́ны сохране́ния — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени. Являются наиболее общими законами в любой физической теории. Имеют большое эвристическое значение.

Физи́ческий зако́н — эмпирически установленная и выраженная в строгой словесной и/или математической формулировке устойчивая, повторяющаяся во множестве опытов, связь между физическими величинами в повторяющихся явлениях, процессах и состояниях тел и других материальных объектов в окружающем мире.

Аксиоматика термодинамики имеет своей задачей выявление структуры термодинамических понятий и законов с целью логически непротиворечивого введения в научный оборот макроскопических физических величин, которым не даётся определения в других разделах физики, — внутренней энергии, энтропии и температуры: «в термодинамику вводятся две новые физические величины — энтропия и абсолютная температура; этот шаг подлежит обоснованию». Существует и другое представление о роли аксиоматики в термодинамике (Г…

Принципами механики называются исходные положения, отражающие столь общие закономерности механических явлений, что из них как следствия можно получить все уравнения, определяющие движение механической системы (или условия её равновесия). В ходе развития механики был установлен ряд таких принципов, каждый из которых может быть положен в основу механики, что объясняется многообразием свойств и закономерностей механических явлений. Эти принципы подразделяют на невариационные и вариационные.

Подробнее: Вариационные принципы

Термостатика — одно из названий классической термодинамики, акцентирующее внимание на том, что эта научная дисциплина представляет собой феноменологическую теорию стационарных состояний и квазистатических процессов в сплошных средах, и в явном виде отражающее современное деление термодинамики на статическую и нестатическую части — равновесную термодинамику и неравновесную термодинамику.

Упоминания в литературе

В 1918 г. Эмми Нетером было доказано, что если некоторая система инвариантна относительно некоторого глобального преобразования, то для нее существует определенная сохраняющая величина. Из этого следует, что закон сохранения энергии является следствием симметрии, существующих в реальном пространстве-времени.

16. Из закона сохранения энергии мы уже знаем, что всякая смена явлений есть только изменение в распределении или форме энергии, между тем как эта последняя сама остается неизменной. Закон же интенсивности показывает, что это изменение обусловлено: 1) различием (многообразием) того, что нам дано как пребывающее в пространстве и времени, именно, различием величины интенсивности и 2) тем, что дано направление, в котором происходит переход, изменение, именно, от большей к меньшей интенсивности. Этим изменение определяется как отношение содержаний пространства и времени как событие, т. е. определено место явления в порядке времени. В законе интенсивности выражено, следовательно, правило, что временная смена определена т. е. «что в том, что происходит, можно найти условие, определяющее во всякое время (т. е. необходимым образом) то, что происходит» (Кант, «Критика чистого разума»). Это условие возможности временного порядка есть не что иное, как «принцип временной смены, следующий закону причинности: все изменения происходят согласно закону связи причины и действия» (там же).

Так, закон сохранения энергии вытекает из однородности времени. Время симметрично относительно начала отсчета, все моменты времени равноправны.

Энергия – общая количественная мера разных форм движения материи. Закон сохранения энергии связывает воедино все явления природы. Согласно этому закону энергия не возникает из ничего и не исчезает, а переходит из одной формы в другую. Все материальные вещества состоят из множества частиц вещества. Собственно энергия вещества (материи) является совокупностью энергии частиц. Различают энергию покоя и энергию связи частиц вещества. Под энергией покоя частицы (вещества) понимают энергию частицы в системе отсчёта, в которой частица покоится. Количественно она определяется по формуле:

Связанные понятия (продолжение)

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) — закон, утверждающий, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю.

Пе́рвое нача́ло термодина́мики (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные и химические процессы. В форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потока и в неравновесной термодинамике. В равновесной термодинамике под первым законом термодинамики обычно подразумевают…

Симме́три́я в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого).

При́нцип наиме́ньшего де́йствия Га́мильтона (также просто принцип Гамильтона), точнее при́нцип стациона́рности де́йствия — способ получения уравнений движения физической системы при помощи поиска стационарного (часто — экстремального, обычно, в связи со сложившейся традицией определения знака действия, наименьшего) значения специального функционала — действия. Назван в честь Уильяма Гамильтона, использовавшего этот принцип для построения так называемого гамильтонова формализма в классической механике…

Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, его вызывающие), основанный на законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «ньютоновой механикой».

Второе начало термодинамики (второй закон термодинамики) устанавливает существование энтропии как функции состояния термодинамической системы и вводит понятие абсолютной термодинамической температуры, то есть «второе начало представляет собой закон об энтропии» и её свойствах. В изолированной системе энтропия остаётся либо неизменной, либо возрастает (в неравновесных процессах), достигая максимума при установлении термодинамического равновесия (закон возрастания энтропии). Встречающиеся в литературе…

Математи́ческая гипо́теза в физике — форма научной гипотезы, один из методов познания, широко используемый в теоретической физике, заключающийся в распространении на новую, неисследованную область известных математически выраженных законов из какой-либо из смежных областей в видоизменённой форме.

Вре́мя — форма протекания физических и психических процессов, условие возможности изменения. Одно из основных понятий философии и физики, мера длительности существования всех объектов, характеристика последовательной смены их состояний в процессах и самих процессов, изменения и развития, а также одна из координат единого пространства-времени, представления о котором развиваются в теории относительности.

Теоре́ма о кинети́ческой эне́ргии систе́мы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел.

Лоренц-ковариантность — свойство систем математических уравнений, описывающих физические законы, сохранять свой вид при применении преобразований Лоренца. Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено. Однако некоторые теории пока не удаётся построить так, чтобы выполнялась лоренц-ковариантность.

Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия.

Закон транзитивности термического равновесия (нулевой закон, нулевое начало термодинамики) вводит в физику представление об эмпирической температуре как физической величине, пригодной для характеристики состояния очень многих макроскопических объектов. Примером макроскопического объекта, не нуждающегося в использовании температуры и прочих термических величин для описания своего состояния, служит абсолютно твёрдое тело. Термические системы, то есть макроскопические системы, к которым применимо понятие…

Вну́тренняя эне́ргия — принятое в физике сплошных сред, термодинамике и статистической физике название для той части полной энергии термодинамической системы, которая не зависит от выбора системы отсчета и которая в рамках рассматриваемой проблемы может изменяться. То есть для равновесных процессов в системе отсчета, относительно которой центр масс рассматриваемого макроскопического объекта покоится, изменения полной и внутренней энергии всегда совпадают. Перечень составных частей полной энергии…

Термодина́мика (греч. θέρμη — «тепло», δύναμις — «сила») — раздел физики, изучающий наиболее общие свойства макроскопических систем и способы передачи и превращения энергии в таких системах. В термодинамике изучаются состояния и процессы, для описания которых можно ввести понятие температуры. Термодинамика — это феноменологическая наука, опирающаяся на обобщения опытных фактов. Процессы, происходящие в термодинамических системах, описываются макроскопическими величинами (температура, давление, концентрации…

При́нцип относи́тельности (принцип относительности Эйнштейна) — фундаментальный физический принцип, один из принципов симметрии, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Ось вре́мени — философский термин, используемый для краткого именования направленности и необратимости времени. Наглядно иллюстрируется как временна́я ось (именуемая также в контексте термодинамики стрелою времени) — концепция, описывающая время как прямую (то есть математически одномерный объект), протянутую из прошлого в будущее. Из любых двух несовпадающих точек оси времени одна всегда является будущим относительно другой. Выделяют три основные стрелы времени: термодинамическую, космологическую…

Эне́ргия (др.-греч. ἐνέργεια — действие, деятельность, сила, мощь) — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии.

Специа́льная тео́рия относи́тельности (СТО; также называемая ча́стная тео́рия относи́тельности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света (в рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей). Фактически СТО описывает геометрию четырёхмерного пространства-времени и базируется на плоском…

Энтропи́я (от др.-греч. ἐν «в» + τροπή «обращение; превращение») — широко используемый в естественных и точных науках термин. Впервые введён в рамках термодинамики как функция состояния термодинамической системы. Энтропия определяет меру необратимого рассеивания энергии или бесполезности энергии, ибо не всю энергию системы можно использовать для превращения в какую-нибудь полезную работу. Для понятия энтропии в данном разделе физики используют название термодинамическая энтропия. Термодинамическая…

Тео́рия относи́тельности — физическая теория пространства-времени, то есть теория, описывающая универсальные пространственно-временные свойства физических процессов.

Негэнтропи́я — философский и физический термин, образованный добавлением отрицательной приставки нег- (от лат. negativus — отрицательный) к понятию энтропия, и обозначающий его противоположность. В самом общем смысле противоположен по смыслу энтропии и означает меру упорядоченности и организованности системы или качество имеющейся в системе энергии. Термин иногда используется в физике и математике (теории информации, математической статистике) для обозначения величины, математически противоположной…

Начала термодинамики — совокупность лежащих в основе термодинамики независимых друг от друга постулатов, имеющих эмпирическое происхождение и до сих пор не опровергнутых практикой и научными экспериментами. Начала термодинамики развивают взятые из опытных фактов понятия с целью создания формального аппарата теории, однако с логической точки зрения приводимый ниже традиционный перечень законов термодинамики не представляет собой полноценной системы аксиом. Кроме того, термодинамика использует также…

О́бщая тео́рия относи́тельности (ОТО; нем. allgemeine Relativitätstheorie) — геометрическая теория тяготения, развивающая специальную теорию относительности (СТО), предложенная Альбертом Эйнштейном в 1915—1916 годах.

Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие её. К альтернативным теориям гравитации часто относят вообще любые теории, не совпадающие с общей теории относительности хотя бы в деталях или как-то обобщающие её. Тем не менее, нередко теории гравитации, особенно квантовые, совпадающие с общей теорией относительности в низкоэнергетическом пределе…

Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.

Метод ренормализационной группы (также часто называемый методом ренормгруппы, методом РГ) в квантовой теории поля — итеративный метод перенормировки, в котором переход от областей с меньшей энергией к областям с большей вызван изменением масштаба рассмотрения системы.

Подробнее: Ренормализационная группа

Многомирова́я интерпрета́ция (англ. many-worlds interpretation) или интерпретация Эверетта — интерпретация квантовой механики, которая предполагает существование, в некотором смысле, «параллельных вселенных», в каждой из которых действуют одни и те же законы природы и которым свойственны одни и те же мировые постоянные, но которые находятся в различных состояниях. Исходная формулировка принадлежит Хью Эверетту (1957 год).

Адиабатическая теорема — теорема квантовой механики. Впервые была сформулирована Максом Борном и Владимиром Фоком в 1928 году в таком виде…

В физике принцип локальности/близкодействия утверждает, что на объект влияет только его непосредственное окружение. Квантовая механика предсказывает посредством неравенств Белла прямое нарушение этого принципа. Эксперименты Белла показали, что квантово запутанные частицы нарушают этот принцип. Было показано, что они влияют друг на друга, будучи физически удаленными друг от друга на значительные расстояния, тем самым подтверждая, что принцип локальности/близкодействия неверен.

Тео́рия всего́ — гипотетическая объединённая физико-математическая теория, описывающая все известные фундаментальные взаимодействия. Первоначально данный термин использовался в ироническом ключе для обозначения разнообразных обобщённых теорий. Со временем термин закрепился в популяризациях квантовой физики для обозначения теории, которая объединила бы все четыре фундаментальных взаимодействий в природе. В современной научной литературе вместо термина «теория всего» как правило используется термин…

Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием…

Гамильто́нова меха́ника является одной из формулировок классической механики. Предложена в 1833 году Уильямом Гамильтоном. Она возникла из лагранжевой механики, другой формулировки классической механики, введённой Лагранжем в 1788 году. Гамильтонова механика может быть сформулирована без привлечения лагранжевой механики с использованием симплектических многообразий и пуассоновых многообразий.

Ква́нтовая меха́ника — раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Поскольку постоянная Планка является чрезвычайно малой величиной по сравнению с действием объектов при макроскопическом движении, квантовые эффекты в основном проявляются в микроскопических масштабах. Если физическое действие системы намного больше постоянной…

Копенга́генская интерпрета́ция — интерпретация (толкование) квантовой механики, которую сформулировали Нильс Бор и Вернер Гейзенберг во время совместной работы в Копенгагене около 1927 года. Бор и Гейзенберг усовершенствовали вероятностную интерпретацию волновой функции, данную М. Борном, и попытались ответить на ряд вопросов, возникающих вследствие свойственного квантовой механике корпускулярно-волнового дуализма, в частности на вопрос об измерении.

Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано…

Метод конечных объёмов (в русскоязычной литературе метод контрольных объёмов) — численный метод интегрирования систем дифференциальных уравнений в частных производных.

В физике, предел Бекенштейна — это верхний предел энтропии S, или количества информации I, которые могут содержаться в заданной ограниченной области пространства, имеющей конечное количество энергии; либо, с другой стороны, максимальное количество информации, необходимое для идеального описания заданной физической системы вплоть до квантового уровня. Это подразумевает, что информация о физической системе, или информация, необходимая для идеального описания системы, должна быть конечной, если система…

Причи́нная меха́ника (Теория времени) — не признанная научным сообществом и не имеющая достаточного экспериментального подтверждения гипотеза о физических свойствах времени и объективном отличии причин от следствий, предложенная советским астрофизиком Николаем Козыревым в 1958 году.

Суперве́нтность (англ. Supervenience) — отношение детерминированности состояния любой системы состоянием другой системы. Набор свойств одной системы супервентен относительно набора свойств другой системы в том случае, если существование различия между двумя фактами в свойствах первой системы невозможно без существования такого же различия между двумя фактами в свойствах второй системы. Понятие супервентности является центральным понятием современной аналитической философии и часто используется в…

Тео́рия ха́оса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос (динамический хаос, детерминированный хаос). Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной. Для акцентирования особого характера изучаемого в рамках этой теории явления обычно принято использовать название теория динамического хаоса.

Связь — философская категория, «выражающая взаимообусловленность существования явлений, разделённых в пространстве и (или) во времени», а также сами «отношения между объектами, проявляющиеся в том, что состояния или свойства любого из них меняются при изменении состояния и свойств других».

Эредитарность (от лат. hereditarity) — свойство системы или процесса сохранять память о своем прошлом.

Общее уравнение механики представляет собой математическую формулировку принципа Д’Аламбера — Лагранжа, дающего общий метод решения задач динамики и статики и являющегося одним из основных принципов теоретической механики.( Стр.142) Этот принцип объединяет принцип возможных перемещений и принцип Д’Аламбера…

Что такое Закон сохранения энергии и какие есть главные формулы энергии

Закон сохранения энергии — энергия не может появляться из ничего и пропадать никуда, она не может быть ни создана, ни уничтожена, но она может быть преобразована, таким образом энергия только принимает другой вид, и её количество при этом сохраняется во времени (если не существуют или не учитываются диссипативные силы, как например, силы внутреннего трения).

Ещё его называют законом сохранения и превращения энергии.

В замкнутой механической системе справедливо равенство:

Ek1 + Ep1 = Ek2 + Ep2

Где:

Ek1 – кинетическая энергия в определённый момент времени

Ep1 – потенциальная энергия в определённый момент времени

Ek2 – кинетическая энергия в последующий момент времени

Ep2 – потенциальная энергия в последующий момент времени

То же самое можно выразить этой формулой:

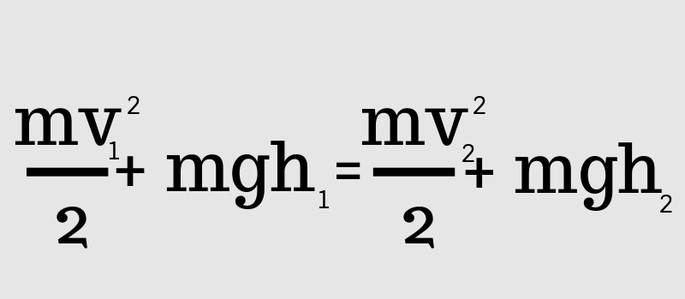
Где:

m – масса тела

g – ускорение свободного падения

h – высота

v – скорость движения тела

Обратите внимание, что полная энергия системы, представленная суммой энергии, связанной с движением (Eкин), и энергии, связанной с положением (Eпот), имеет одно и то же значение в разное время.

Преобразование энергии: рисунок потенциальной и кинетической энергии.
Пример закона сохранения энергии: бейсбольный мяч подбрасывается вверх, в верхней точке, когда мяч на секунду останавливается, вся кинетическая энергия превращается в потенциальную.

Формулы энергии

Потенциальная энергия (при гравитационном взаимодействии)

Eпот = mgh

Где:

m – масса тела

g – ускорение свободного падения

h – высота

Кинетическая энергия

Eкин = (mv²) / 2,

Где:

m – масса тела

v – скорость его движения

Из Ek1 + Ep1 = Ek2 + Ep2 и предыдущих двух формул следует:

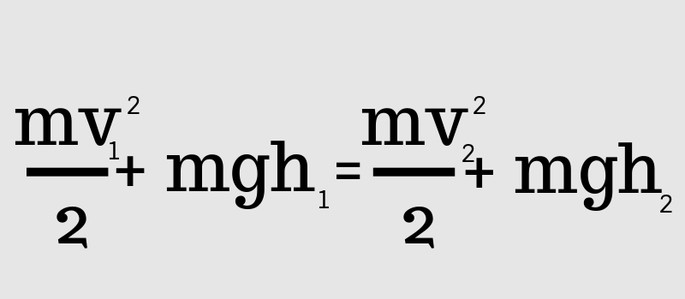
Полная механическая энергия

Это сумма кинетической и потенциальной энергии тела.

Полная механическая энергия: E = Eк + Ep

При минимальной высоте тела (h = 0): Eполная = (mv²) / 2

При средней высоте тела: Eполная = (mv²) / 2 + mgh

При максимальной высоте тела: Eполная = mgh

Эквивалентность массы и энергии

E = mc²,

Где:

Е – энергия,

m – масса

c – скорость света

Потенциальная энергия сжатой/растянутой пружины (Потенциальная энергия упругой деформации)

Ep = (kx²) / 2,

Где:

Ep — потенциальная энергия

k — коэффициент упругости/жёсткости

x — удлинение/сокращение пружины

Законы сохранения

Законы сохранения являются фундаментальными принципами физики. Они точны для изолированной физической системы.

Кроме закона сохранения энергии существуют и другие законы, в которых механические свойства системы не меняются (при отсутствии взаимодействия системы с окружением). Такие, как:

• закон сохранения момента импульса;
• закон сохранения массы;
• закон сохранения лептонного числа; и др.

Узнайте также, что такое Число Рейнольдса.

Закон сохранения энергии | Все Формулы

Закон сохранения энергии — один из наиболее важных законов, согласно которому физическая величина — энергия сохраняется в изолированной системе. Этому закону подчиняются все без исключения известные процессы в природе. В изолированной системе энергия может только превращаться из одной формы в другую, но ее количество остается постоянным.

Для того, чтоб понять что же представляет из себя закон и откуда это получается возьмем тело массой m, которое уроним на Землю. В точке 1 тело у нас находится на высоте h и покоится (скорость равна 0). В точке 2 тело тело имеет некоторую скорость v и находится на расстоянии h-h2. В точке 3 тело имеет максимальную скорость и оно почти лежит на нашей Земле, то есть h=0

Закон сохранения энергии

В точке 1 тело имеет только потенциальную энергию, так как скорость тела равно 0,так что полная механическая энергия равна.

После того как мы тело отпустили, оно стало падать. При падении потенциальная энергия тела уменьшается, так как уменьшается высота тела над Землей, а его кинетическая энергия увеличивается, так как увеличивается скорость тела. На участке 1-2 равном h2 потенциальная энергия будет равна

А кинетическая энергия будет равная в тот момент

— скорость тела в точке 2):

Чем ближе тело становится к Земле, тем меньше его потенциальная энергия, но в тот же момент увеличивается скорость тела, а из-за этого и кинетическая энергия. То есть в точке 2 работает закон сохранения энергии: потенциальная энергия уменьшается, кинетическая растет.

В точке 3 (на поверхности Земли) потенциальная энергия равна нулю (так как h = 0), а кинетическая максимальна

(где v3 — скорость тела в момент падения на Землю). Так как

, то кинетическая энергия в точке 3 будет равна Wk=mgh. Следовательно, в точке 3 полная энергия тела W3=mgh и равна потенциальной энергии на высоте h. Конечная формула закона сохранения механической энергии будет иметь вид:

Формула выражает закон сохранения энергии в замкнутой системе, в которой действуют только консервативные силы: полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию и обратно.

В Формуле мы использовали :

W — Полная энергия тела

— Потенциальная энергия тела

— Кинетическая энергия тела

m — Масса тела

g — Ускорение свободного падения

h — Высота на которой находится тело

\upsilon — Скорость тела

Закон сохранения энергии. | Объединение учителей Санкт-Петербурга

Сохранение энергии — Простая английская Википедия, бесплатная энциклопедия

Эта статья относится к закону сохранения энергии в физике. Об устойчивых энергетических ресурсах см .: Энергосбережение.

В физике закон сохранения энергии заключается в том, что энергия не может быть создана или уничтожена, она может быть изменена только из одной формы в другую, например, когда электрическая энергия превращается в тепловую. Формально это говорит о том, что общее количество энергии в изолированной системе остается постоянным, хотя она может менять форму, например.г. трение превращает кинетическую энергию в тепловую. В термодинамике первый закон термодинамики является заявлением о сохранении энергии для термодинамических систем.

С математической точки зрения закон сохранения энергии является следствием сдвиговой симметрии времени; Сохранение энергии является результатом эмпирического факта, что законы физики не меняются со временем. С философской точки зрения это можно сформулировать как «ничто не зависит от времени как такового (самого времени)».

Древние философы еще во времена Фалеса Милетского полагали, что существует некая основная субстанция, из которой состоит все. Но это не то же самое, что наша концепция «масса-энергия» сегодня (например, Фалес думал, что основным веществом была вода).
В 1638 году Галилей опубликовал свой анализ нескольких ситуаций. Сюда входил знаменитый «прерывистый маятник». Это можно описать (на современном языке) как консервативное преобразование потенциальной энергии в кинетическую и обратно.Однако Галилей не объяснил этот процесс современными терминами и не понял современной концепции. Немец Готфрид Вильгельм Лейбниц в течение 1676–1689 годов попытался математически сформулировать вид энергии, который связан с движением (кинетической энергией). Лейбниц заметил, что во многих механических системах (нескольких масс, м _и каждая со скоростью v _и ),

∑imivi2 {\ displaystyle \ sum _ {i} m_ {i} v_ {i} ^ {2}}

сохранялось до тех пор, пока массы не взаимодействовали.Он назвал это количество vis viva или живой силой системы. Принцип представляет собой точное утверждение о приблизительном сохранении кинетической энергии в ситуациях, когда нет трения.

Аппарат Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикрепленный к струне, заставляет весло в воде вращаться.

Между тем, в 1843 году Джеймс Прескотт Джоуль независимо открыл механический эквивалент в серии экспериментов.В самом известном, теперь называемом «аппаратом Джоуля», нисходящий груз, прикрепленный к струне, заставлял вращаться лопасть, погруженная в воду. Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, приблизительно равна тепловой энергии (теплу), полученной водой за счет трения о лопасть.

В период 1840-1843 годов подобная работа проводилась инженером Людвигом А. Колдингом, хотя за пределами его родной Дании она была малоизвестна.

Легко видеть, что

E = KE + PE {\ displaystyle E = KE + PE}

, который также

E = 12 мв2 + V {\ displaystyle E = {\ frac {1} {2}} мв ^ {2} + V}

E = 12mx′2 + V (x) {\ displaystyle E = {\ frac {1} {2}} mx ‘^ {2} + V (x)}

Если предположить, что x ′ (t) {\ displaystyle x ‘(t)} и x (t) {\ displaystyle x (t)}, то

dEdt = ∂E∂x′dx′dt + ∂E∂xdxdt {\ displaystyle {\ frac {dE} {dt}} = {\ frac {\ partial E} {\ partial x ‘}} {\ frac {dx ‘} {dt}} + {\ frac {\ partial E} {\ partial x}} {\ frac {dx} {dt}}}

dEdt = (mx ′) (x ″) — Fx ′ {\ displaystyle {\ frac {dE} {dt}} = (mx ‘) (x’ ‘) — Fx’}

(Поскольку V ′ (x) = — F {\ displaystyle V ‘(x) = — F})

dEdt = Fx′ − Fx ′ = 0 {\ displaystyle {\ frac {dE} {dt}} = Fx’-Fx ‘= 0}

Следовательно, энергия не меняется со временем.

Современные счета [изменение | изменить источник]

• Гольдштейн, Мартин и Инге Ф., 1993. Холодильник и Вселенная . Harvard Univ. Нажмите. Нежное введение.
• Kroemer, Herbert; Киттель, Чарльз (1980). Теплофизика (2-е изд.) . Компания W.H. Freeman. CS1 maint: несколько имен: список авторов (ссылка) ISBN 0-7167-1088-9
• Нолан, Питер Дж. (1996). Основы физики в колледже, 2-е изд. .Издательство Уильяма С. Брауна.

.

Что такое закон сохранения энергии? (с иллюстрациями)

Закон сохранения энергии — это физический принцип, который гласит, что в замкнутой системе энергия не может быть создана или разрушена. Это выражено в Первом законе термодинамики, который гласит, что энергия может быть преобразована во многие формы, такие как свет или тепло, но общая сумма энергий сохраняется или остается постоянной. Обычно этот закон иллюстрируется маятником. Высота, на которой мяч выпущен на одном конце маятника, будет равна высоте, которую мяч достигнет на другом конце.Фактически, в теоретически свободной от трения среде мяч будет продолжать раскачиваться вперед и назад бесконечно.

Энергия не может быть уничтожена, но может быть преобразована, например, когда солнечные панели преобразуют энергию света и излучения солнца в полезную электрическую энергию.

Как фундаментальная концепция в физике, закон сохранения энергии дает объяснение того, как энергия сохраняется и преобразуется в системе. Как правило, одна форма энергии может быть преобразована в другую форму энергии. Например, потенциальная энергия может быть преобразована в кинетическую энергию.

Пример потенциальной энергии — шар на вершине холма.

Кинетическая энергия конкретного объекта — это энергия, которой он обладает во время движения. В качестве выражения кинетическая энергия равна половине массы объекта, умноженной на квадрат скорости объекта, или KE = 1 / 2mv ² . Кинетическая энергия состоит из трех типов энергий. Колебательная кинетическая энергия — это энергия колебательного движения, а вращательная кинетическая энергия — это энергия вращательного движения.Поступательная кинетическая энергия — это энергия движения центра масс из одной точки в другую.

Как правило, потенциальная энергия объекта — это энергия, которая сохраняется в силовом поле в состоянии покоя. Гравитация — это сила, которая действует на объект и придает ему потенциальную энергию.Например, мяч на вершине холма имеет определенное количество энергии, накопленной за счет силы тяжести. Другие типы потенциальной энергии включают электрическую, магнитную и упругую. Примером упругой потенциальной энергии является растянутая пружина.

Закон сохранения энергии гласит, что потенциальная энергия мяча на холме обычно преобразуется в кинетическую энергию, когда мяч начинает катиться с холма под действием силы тяжести.Точно так же потенциальная энергия растянутой пружины становится кинетической энергией, когда пружина отпускается. В маятнике закон устанавливает, что, когда мяч находится в своей наивысшей точке, вся энергия является потенциальной, а кинетическая энергия равна нулю. В самой нижней точке мяча вся энергия в шаре кинетическая, а потенциальная энергия равна нулю. Полная энергия шара складывается из потенциальной энергии и кинетической энергии.

.

Что такое закон сохранения энергии?

• • БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
  • КОНКУРСНЫЕ ЭКЗАМЕНА
    • BNAT
    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 110003 CBSE
        • Книги NCERT
          • Книги NCERT для класса 5
          • Книги NCERT, класс 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • NCERT Книги для класса 11
          • NCERT Книги для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11

          9plar

          • RS Aggarwal
            • RS Aggarwal Решения класса 12
            • RS Aggarwal Class 11 Solutions
            • RS Aggarwal Решения класса 10
            • Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • RD Sharma
            • RD Sharma Class 6 Решения
            • RD Sharma Class 7 Решения
            • Решения RD Sharma Class 8
            • Решения RD Sharma Class 9
            • Решения RD Sharma Class 10
            • Решения RD Sharma Class 11
            • Решения RD Sharma Class 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика
            • Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Статистика
            • 9000 Pro Числа
            • Числа
            • 9000 Pro Числа Тр Игонометрические функции
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убытки
            • Полиномиальные уравнения
            • Деление фракций
          • Microology
            0003000
          • FORMULAS
            • Математические формулы
            • Алгебраные формулы
            • Тригонометрические формулы
            • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы

            0003000

            • 000 CALCULATORS
            • 000
            • 000 Калькуляторы по химии 900 Образцы документов для класса 6
            • Образцы документов CBSE для класса 7
            • Образцы документов CBSE для класса 8
            • Образцы документов CBSE для класса 9
            • Образцы документов CBSE для класса 10
            • Образцы документов CBSE для класса 1 1
            • Образцы документов CBSE для класса 12
          • Вопросники предыдущего года CBSE
            • Вопросники предыдущего года CBSE, класс 10
            • Вопросники предыдущего года CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Класс 11 Физика
            • HC Verma Solutions Класс 12 Физика
          • Решения Лакмира Сингха
            • Решения Лахмира Сингха класса 9
            • Решения Лахмира Сингха класса 10
            • Решения Лакмира Сингха класса 8

          9000 Класс

          9000BSE 9000 Примечания3 2 6 Примечания CBSE

        • Примечания CBSE класса 7

        Примечания

        • Примечания CBSE класса 8
        • Примечания CBSE класса 9
        • Примечания CBSE класса 10
        • Примечания CBSE класса 11
        • Примечания 12 CBSE
      • Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
      • CBSE Примечания к редакции класса 10
      • CBSE Примечания к редакции класса 11
      • Примечания к редакции класса 12 CBSE
    • Дополнительные вопросы CBSE
      • Дополнительные вопросы по математике класса 8 CBSE
      • Дополнительные вопросы по науке 8 класса CBSE
      • Дополнительные вопросы по математике класса 9 CBSE
      • Дополнительные вопросы по математике класса 9 CBSE Вопросы
      • CBSE Class 10 Дополнительные вопросы по математике
      • CBSE Class 10 Science Extra questions
    • CBSE Class
      • Class 3
      • Class 4
      • Class 5
      • Class 6
      • Class 7
      • Class 8 Класс 9
      • Класс 10
      • Класс 11
      • Класс 12
    • Учебные решения
  • Решения NCERT
    • Решения NCERT для класса 11
      • Решения NCERT для класса 11 по физике
      • Решения NCERT для класса 11 Химия
      • Решения NCERT для биологии класса 11
      • Решение NCERT s Для класса 11 по математике
      • NCERT Solutions Class 11 Accountancy
      • NCERT Solutions Class 11 Business Studies
      • NCERT Solutions Class 11 Economics
      • NCERT Solutions Class 11 Statistics
      • NCERT Solutions Class 11 Commerce
    • NCERT Solutions for Class 12
      • Решения NCERT для физики класса 12
      • Решения NCERT для химии класса 12
      • Решения NCERT для биологии класса 12
      • Решения NCERT для математики класса 12
      • Решения NCERT, класс 12, бухгалтерский учет
      • Решения NCERT, класс 12, бизнес-исследования
      • NCERT Solutions Class 12 Economics
      • NCERT Solutions Class 12 Accountancy Part 1
      • NCERT Solutions Class 12 Accountancy Part 2
      • NCERT Solutions Class 12 Micro-Economics
      • NCERT Solutions Class 12 Commerce
      • NCERT Solutions Class 12 Macro-Economics
    • NCERT Solut Ионы Для класса 4
      • Решения NCERT для математики класса 4
      • Решения NCERT для класса 4 EVS
    • Решения NCERT для класса 5
      • Решения NCERT для математики класса 5
      • Решения NCERT для класса 5 EVS
    • Решения NCERT для класса 6
      • Решения NCERT для математики класса 6
      • Решения NCERT для науки класса 6
      • Решения NCERT для класса 6 по социальным наукам
      • Решения NCERT для класса 6 Английский язык
    • Решения NCERT для класса 7
      • Решения NCERT для математики класса 7
      • Решения NCERT для науки класса 7
      • Решения NCERT для социальных наук класса 7
      • Решения NCERT для класса 7 Английский язык
    • Решения NCERT для класса 8
      • Решения NCERT для математики класса 8
      • Решения NCERT для науки 8 класса
      • Решения NCERT для социальных наук 8 класса ce
      • Решения NCERT для класса 8 Английский
    • Решения NCERT для класса 9
      • Решения NCERT для класса 9 по социальным наукам
    • Решения NCERT для математики класса 9
      • Решения NCERT для математики класса 9 Глава 1
      • Решения NCERT для математики класса 9, глава 2

      Решения NCERT

      • для математики класса 9, глава 3
      • Решения NCERT для математики класса 9, глава 4
      • Решения NCERT для математики класса 9, глава 5

      Решения NCERT

      • для математики класса 9, глава 6
      • Решения NCERT для математики класса 9, глава 7

      Решения NCERT

      • для математики класса 9, глава 8
      • Решения NCERT для математики класса 9, глава 9
      • Решения NCERT для математики класса 9, глава 10

      Решения NCERT

      • для математики класса 9, глава 11

      Решения

      • NCERT для математики класса 9 Глава 12

      Решения NCERT

      • для математики класса 9 Глава 13
      • NCER T Solutions

.

Закон о сохранении | физика | Britannica

Закон сохранения , также называемый законом сохранения , в физике, несколько принципов, которые заявляют, что определенные физические свойства (то есть измеримые величины) не изменяются с течением времени в изолированной физической системе. В классической физике законы этого типа регулируют энергию, импульс, угловой момент, массу и электрический заряд. В физике элементарных частиц другие законы сохранения применяются к свойствам субатомных частиц, которые инвариантны во время взаимодействий.Важная функция законов сохранения заключается в том, что они позволяют предсказать макроскопическое поведение системы без необходимости рассматривать микроскопические детали протекания физического процесса или химической реакции.

Британская викторина

Викторина «Все о физике»

В начале 18 века, к какому поразительному выводу пришел Джон Дальтон относительно «элементарных частиц» или атомов каждого из химических элементов?

Сохранение энергии подразумевает, что энергия не может быть ни создана, ни уничтожена, хотя ее можно изменить в одной форме (механической, кинетической, химической и т. Д.)) в другой. Таким образом, в изолированной системе сумма всех форм энергии остается постоянной. Например, падающее тело имеет постоянное количество энергии, но форма энергии меняется с потенциальной на кинетическую. Согласно теории относительности энергия и масса эквивалентны. Таким образом, массу покоя тела можно рассматривать как форму потенциальной энергии, часть которой может быть преобразована в другие формы энергии.

Сохранение количества движения выражает тот факт, что движущееся тело или система тел сохраняет свой общий импульс, произведение массы и векторной скорости, если к нему не приложена внешняя сила.В изолированной системе (такой как Вселенная) нет внешних сил, поэтому импульс всегда сохраняется. Поскольку импульс сохраняется, его компоненты в любом направлении также сохраняются. Применение закона сохранения количества движения важно при решении проблем столкновения. Работа ракет иллюстрирует сохранение количества движения: увеличенный поступательный импульс ракеты равен импульсу выбрасываемых выхлопных газов, но противоположен по знаку.

Сохранение момента количества движения во вращающихся телах аналогично сохранению количества движения.Угловой момент — это векторная величина, сохранение которой выражает закон, согласно которому тело или система, которые вращаются, продолжают вращаться с той же скоростью, если к ним не приложена скручивающая сила, называемая крутящим моментом. Момент количества движения каждого кусочка материи состоит из произведения его массы, расстояния от оси вращения и компонента скорости, перпендикулярного линии, идущей от оси.

Получите эксклюзивный доступ к контенту нашего 1768 First Edition с подпиской.
Подпишитесь сегодня

Сохранение массы подразумевает, что материя не может быть ни создана, ни уничтожена — i.е. процессы, которые изменяют физические или химические свойства веществ в изолированной системе (например, преобразование жидкости в газ), оставляют общую массу неизменной. Строго говоря, масса не сохраняется. Однако, за исключением ядерных реакций, преобразование массы покоя в другие формы массы-энергии настолько мало, что с высокой степенью точности можно считать, что масса покоя сохраняется.

Сохранение заряда означает, что общее количество электрического заряда в системе не меняется со временем.На субатомном уровне заряженные частицы могут быть созданы, но всегда парами с равным положительным и отрицательным зарядом, так что общее количество заряда всегда остается постоянным.

В физике элементарных частиц другие законы сохранения применяются к определенным свойствам ядерных частиц, таким как барионное число, лептонное число и странность. Такие законы применяются в дополнение к законам массы, энергии и импульса, встречающимся в повседневной жизни, и их можно рассматривать как аналог сохранения электрического заряда. См. Также симметрию .

Законы сохранения энергии, импульса и углового момента происходят из классической механики. Тем не менее, все остается верным в квантовой механике и релятивистской механике, которые заменили классическую механику как самый фундаментальный из всех законов. В самом глубоком смысле три закона сохранения выражают, соответственно, факты о том, что физика не меняется со временем, смещением в пространстве или вращением в пространстве.

.