Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
Кинематика
К оглавлению…
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
К оглавлению…
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
К оглавлению.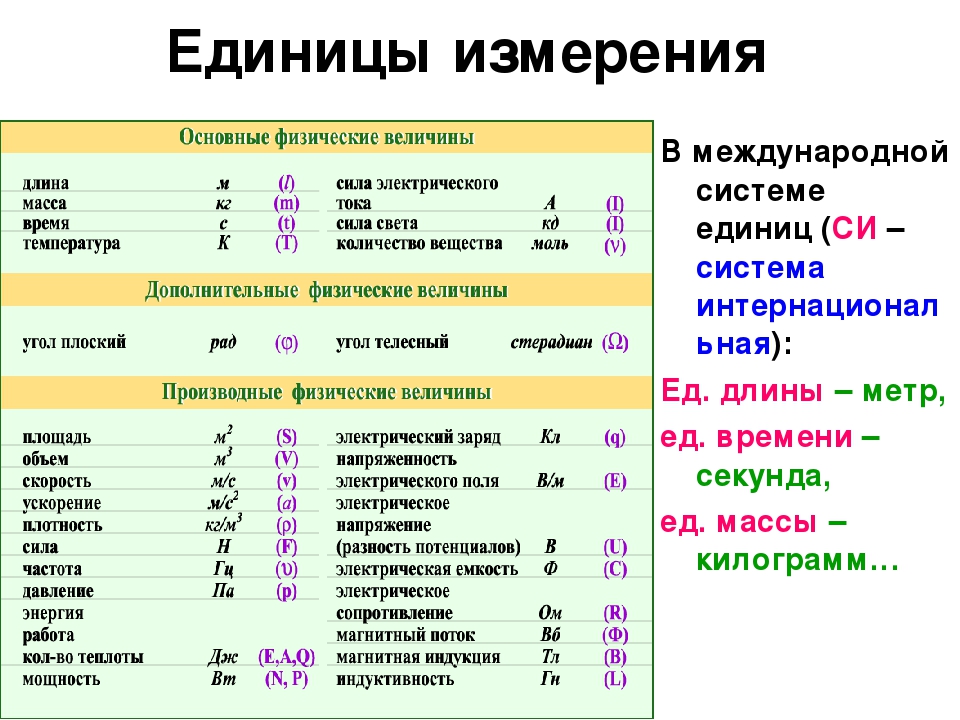 ..
..
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
К оглавлению…
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса.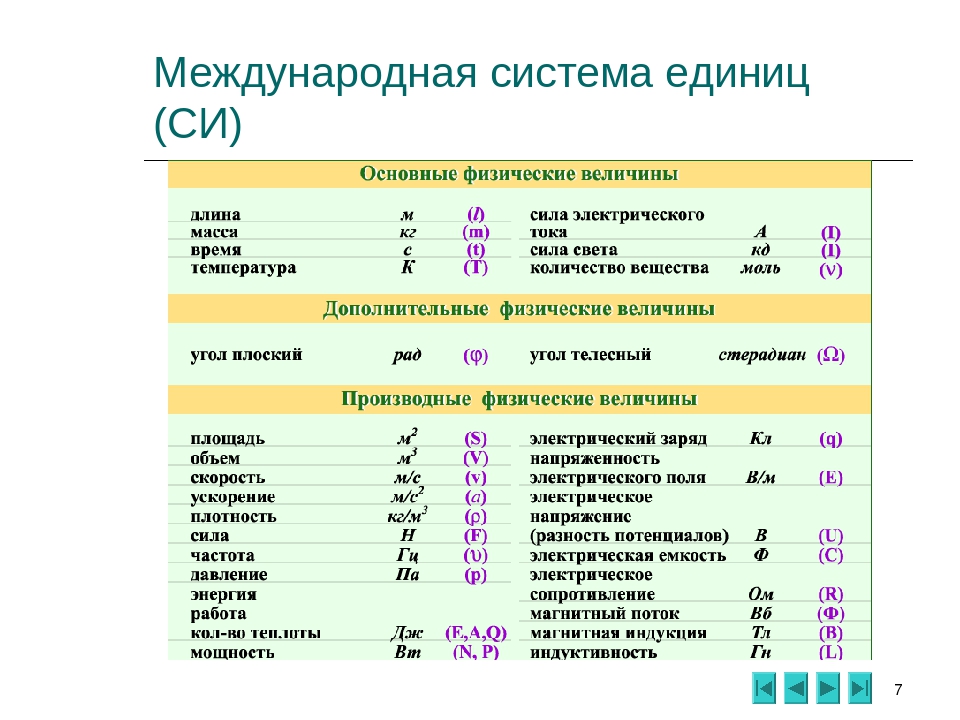 Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
К оглавлению…
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
К оглавлению…
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S:
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1.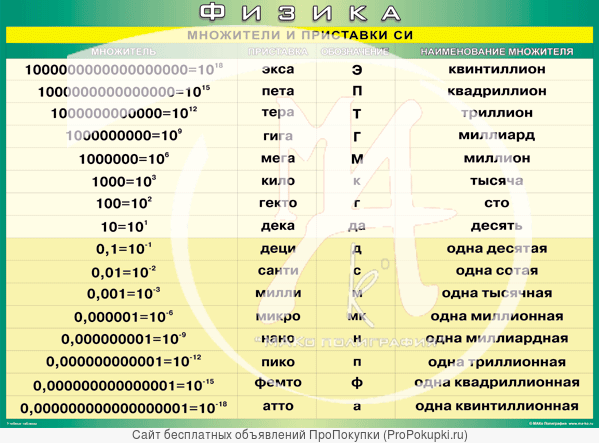 В этом случае высота столба жидкости в капилляре станет равной:
В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Электростатика
К оглавлению…
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
К оглавлению.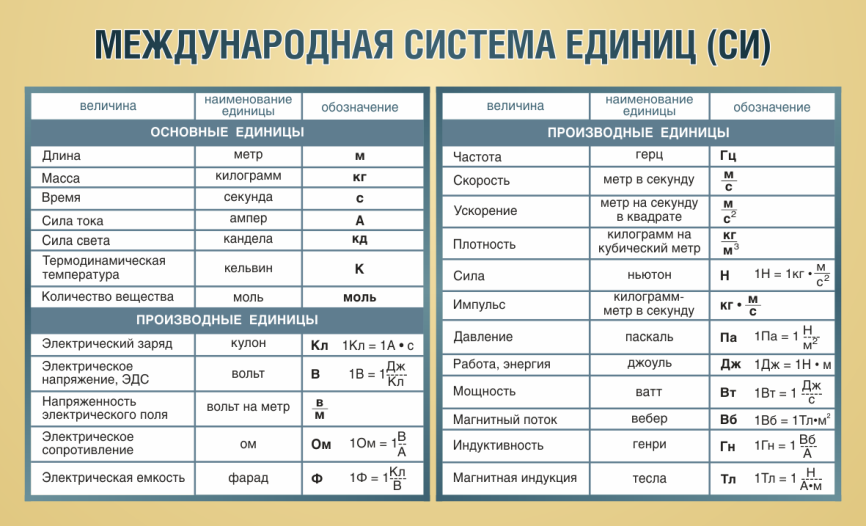 ..
..
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Он может быть рассчитан по формуле:
Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
К оглавлению…
Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R:
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
К оглавлению.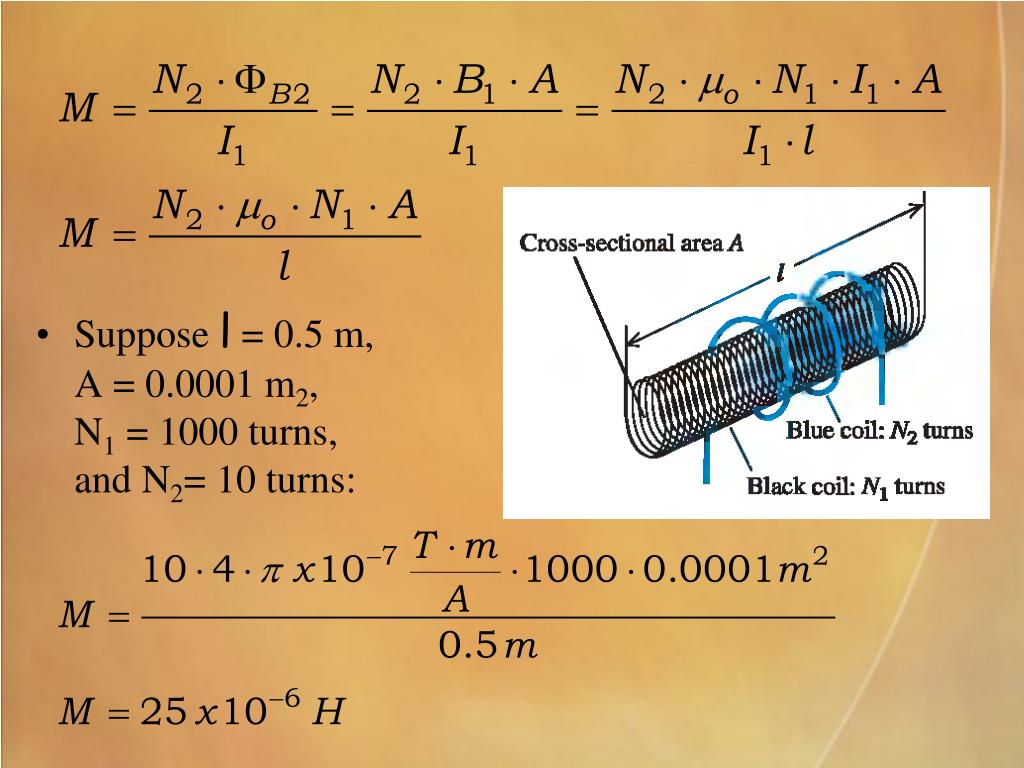 ..
..
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l:
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т. ч. света) в среде и в вакууме также связаны между собой формулой:
ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
К оглавлению…
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Формула дифракционной решетки:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом:
Формула тонкой линзы:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
К оглавлению. ..
..
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
К оглавлению. ..
..
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
К оглавлению…
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
К оглавлению. ..
..
физика элементарных частиц – Новости – Научно-образовательный портал IQ – Национальный исследовательский университет «Высшая школа экономики»
Всего лишь кинематика
Герцен Копылов
Эта книга, выпущенная в Москве издательством «Наука» в 1981 году, актуальна до сих пор. Её автор Герцен Исаевич Копылов – советский физик, специалист в области прикладной релятивистской кинематики, популяризатор науки. Своей целью он поставил объяснить физику частиц тем, кто знаком только со школьной математикой. Удачные примеры этой книги позволяют понять неподготовленному читателю основы теории относительности и физики частиц. Книгу можно смело рекомендовать даже школьникам.
Физика элементарных частиц
Лев Окунь
Сотрудник Института теоретической и экспериментальной физики (ИТЭФ), академик РАН, специалист в области теории элементарных частиц Лев Борисович Окунь в 1962 году ввёл понятие «адрон», которым теперь пользуются физики по всему миру. Его книга «Физика элементарных частиц» будет полезна всем, кто хочет детально разобраться в предмете и увидеть общую картину. Как и все книги Льва Борисовича, она написана простым и понятным языком.
Его книга «Физика элементарных частиц» будет полезна всем, кто хочет детально разобраться в предмете и увидеть общую картину. Как и все книги Льва Борисовича, она написана простым и понятным языком.
Введение в физику высоких энергий
Дональд Перкинс
Эта книга для тех, кто хочет почувствовать себя студентом Оксфорда. Её автор – Дональд Перкинс, британский физик и почетный профессор Оксфордского университета. Книга издаётся с 1972 года, но ее 14-е издание, вышедшее в 2014 году, охватывает все современные аспекты физики частиц. Книга будет полезна студентам и молодым исследователям, специализирующимся на ядерной физике, а также всем, у кого уже есть математическая подготовка. Первая глава рассказывает об осных вводных идеи и ее историческом развитии; вторая и третья главы посвящены экспериментальным методам, законам сохранения и принципам инвариантности. В книге дано подробное описание основных характеристик взаимодействий между адронами. На доступном уровне изложено обсуждение основ электромагнитных, слабых и сильных взаимодействий лептонов и кварков. В последних главах книги автор рассказывает о различных унифицированных взаимодействиях.
В последних главах книги автор рассказывает о различных унифицированных взаимодействиях.
Кварки и лептоны: Введение в физику частиц
Хелзен Ф. Мартин А.
Это уже классический учебник физики элементарных частиц, его авторы – физики-теоретики, профессора Висконсинского университета. Издание содержит большое количество сложных и не очень задач с решениями. Он будет полезен тем, кто хочет изучить методы современной физики элементарных частиц. Правда, знание основ нерелятивистской квантовой механики и специальной теории относительности будет не лишним. Тем, кто уверен в своём английском, рекомендуем читать в оригинале. Книга написана живым, непринужденным, разговорным языком, который, конечно, максимально старались сохранить при переводе, но оригинал обладает особым настроением.
Современная физика частиц
Марк Томсон
Этот учебник уникален, он охватывает все аспекты современной физики элементарных частиц, что обозначает четкую связь между теорией и недавними экспериментальными результатами, включая открытие бозона Хиггса в ЦЕРН. В конце каждой главы даны задания для закрепления результата. Книга основана на курсе лекций Кембриджского университета.
В конце каждой главы даны задания для закрепления результата. Книга основана на курсе лекций Кембриджского университета.
Statistical Analysis Techniques in Particle Physics: Fits, Density Estimation and Supervised Learning
Ilya Narsky, Frank C. Porter
Это одна из первых книг, в которой основное внимание уделяется методам статистического анализа данных и машинного обучения в физике высоких энергий. Описание начинается с основ построения алгоритмов регрессии и классификации. Затем внимание уделяется методу опорных векторов, деревьям решений, ансамблям алгоритмов и нейросетям. Авторы уделяют внимание одной из самых важных задач применения описанных методик в контексте большого адронного коллайдера – поиску распадов и частиц.
Data Analysis in High Energy Physics: A Practical Guide to Statistical Methods
Olaf Behnke, Kevin Kröninger, Grégory Schott, Thomas Schörner-Sadenius
Эта книга представляет собой сборник глав, охватывающих основные задачи анализа данных, встречающиеся в физике высоких энергий. Включает описания как теоретических подходов, так и практических методик анализа данных. Среди бонусов – в каждой главе можно найти огромное количество примеров и упражнений, а также список литературы и соответствующие ссылки.
Включает описания как теоретических подходов, так и практических методик анализа данных. Среди бонусов – в каждой главе можно найти огромное количество примеров и упражнений, а также список литературы и соответствующие ссылки.
IQ
29 июня, 2018 г.
Подпишись на IQ.HSE
Постоянные величины в физике. Физические постоянные, условные обозначения
Skip navigation
- ФизикаМатематикаАстрономия
- Элементы математики
- Физические величины
- Единицы измерения
- Постоянные величины в физике
- плотность вещества
- предел прочности, модуль Юнга
- скорость звука
- удельная теплота
- диэлектрическая проницаемость
- удельное сопротивление
- электрохимический эквивалент
- Формулы
- I.
 Механика
Механика - Кинематика
- Динамика
- Законы сохранения
- Статика
- Колебания и волны
- II. Молекулярная физика
- Молекулярная физика
- Термодинамика
- III. Основы электродинамики
- Электричество
- Электрический ток
- Магнетизм
- Электромагнетизм
- IV. Оптика
- Волновая оптика
- Геометрическая оптика
- V. Теория относительности
- Теория относительности
- VI. Квантовая физика
- Световые кванты
- Атомное ядро
- Современная физика*
Закрыть
- Меню
Логин
Пароль
Физика->Постоянные величины в физике->
Тестирование онлайн
Приставки единиц измерения
Основные физические постоянные
Периодическая система химических элементов Д.
 И. Менделеева
И. Менделеева
Условные обозначения на схемах
Астрономические постоянные
«Физика твердого тела»
Журнал «Физика Твердого Тела» основан в 1959 году А.Ф.Иоффе, который и был первым главным редактором журнала.
Журнал самого широкого тематического профиля публикует результаты экспериментальных и теоретических исследований во всех областях физики твердого тела, включая оптику, акустику, электронные и колебательные спектры, фазовые переходы, сегнетоэлектрики, магнетизм, сверхпроводимость, механические свойства. Предметом исследований публикуемых статей и заказных обзоров являются металлы, диэлектрики, полупроводники, твердотельные системы низкой размерности, тонкие пленки.
Периодичность выхода выпусков ФТТ в свет — ежемесячно.
ISSN: 0367-3294
Учредителями являются:
По соглашению с учредителями журнала издателем лицензионной переводной англоязычной версии является компания «Плеадес Паблишинг, Лтд». Распространение англоязычной версии журнала проводится компанией Springer. Выпуски журнала на русском и английском языках выходят в свет одновременно.
Распространение англоязычной версии журнала проводится компанией Springer. Выпуски журнала на русском и английском языках выходят в свет одновременно.
Издается ФТИ им. А.Ф.Иоффе.
Памяти Игоря Ивановича Пронина
Александр Александрович Каплянский, к 90-летию со дня рождения
Еугениюс Левович Ивченко, к 75-летию со дня рождения
Памяти Т.И. Максимовой
Уважаемые авторы!
С большим сожалением редколлегия журнала ”Физика твердого тела“ вынуждена констатировать, что начиная с третьего выпуска 2021 года компания ”Pleiades Publishing, Inc.“ прекратила выставлять на своем сайте и сайте компании — распространителя Springer журнал ”Physics of the Solid State“ с переводными версиями статей из нашего российского журнала. Это было сделано несмотря на то, что редколлегия журнала отправляла все подготовленные статьи на русском языке для перевода на английский язык своевременно, в полном соответствии с условиями Лицензионного соглашения. Такие действия представляют собой грубейшее нарушение Лицензионного соглашения между компанией ”Pleiades Publishing, Inc.“ и Соучредителями журнала в лице РАН и ФТИ им. А. Ф. Иоффе. Главный редактор журнала, а также ФТИ им. А. Ф. Иоффе как Издатель и Соучредитель журнала ”Физика твердого тела“ неоднократно письменно обращались к президенту компании «Pleiades Publishing, Inc.“ г-ну А. Е. Шусторовичу с законным требованием о выставлении всех отправленных ранее номеров журнала на сайте ”Physics of the Solid State“, но безрезультатно. Это вынудило редколлегию прервать дальнейшую отправку статей в компанию, начиная с одиннадцатого номера 2021 года. В настоящее время ФТИ им. А. Ф. Иоффе предпринимает практические шаги к самостоятельному изданию номеров журнала ”Physics of the Solid State“ 2022 года на английском языке с размещением их на журнальном портале института. Невыставленные компанией ”Pleiades Publishing, Inc.“ номера журнала ”Physics of the Solid State“ 2021 года будут также выставлены на журнальном портале института в течение первой половины следующего года.
Такие действия представляют собой грубейшее нарушение Лицензионного соглашения между компанией ”Pleiades Publishing, Inc.“ и Соучредителями журнала в лице РАН и ФТИ им. А. Ф. Иоффе. Главный редактор журнала, а также ФТИ им. А. Ф. Иоффе как Издатель и Соучредитель журнала ”Физика твердого тела“ неоднократно письменно обращались к президенту компании «Pleiades Publishing, Inc.“ г-ну А. Е. Шусторовичу с законным требованием о выставлении всех отправленных ранее номеров журнала на сайте ”Physics of the Solid State“, но безрезультатно. Это вынудило редколлегию прервать дальнейшую отправку статей в компанию, начиная с одиннадцатого номера 2021 года. В настоящее время ФТИ им. А. Ф. Иоффе предпринимает практические шаги к самостоятельному изданию номеров журнала ”Physics of the Solid State“ 2022 года на английском языке с размещением их на журнальном портале института. Невыставленные компанией ”Pleiades Publishing, Inc.“ номера журнала ”Physics of the Solid State“ 2021 года будут также выставлены на журнальном портале института в течение первой половины следующего года. Редколлегия журнала приносит искренние извинения за вынужденный сбой в издании английской версии нашего журнала.
Редколлегия журнала приносит искренние извинения за вынужденный сбой в издании английской версии нашего журнала.
Редколлегия
как сдать часть 2 ЕГЭ по физике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Илья Шолин,
старший преподаватель факультета фундаментальной физико-химической инженерии МГУ,
м.н.с. лаборатории физики высоких давлений ИФТТ РАН,
ведущий специалист направления образовательных технологий группы компаний InEnergy
Задание № 25
Что требуется
Решить задачу по механике или молекулярной физике.
Особенности
В этом задании проверяется умение решать стандартные, типовые задачи. Речь идет о применении одного или двух законов и соответствующих им формул. Такие задачи часто встречаются в наиболее распространенных задачниках, в них практически нет подводных камней, и для решения не требуется нестандартных подходов.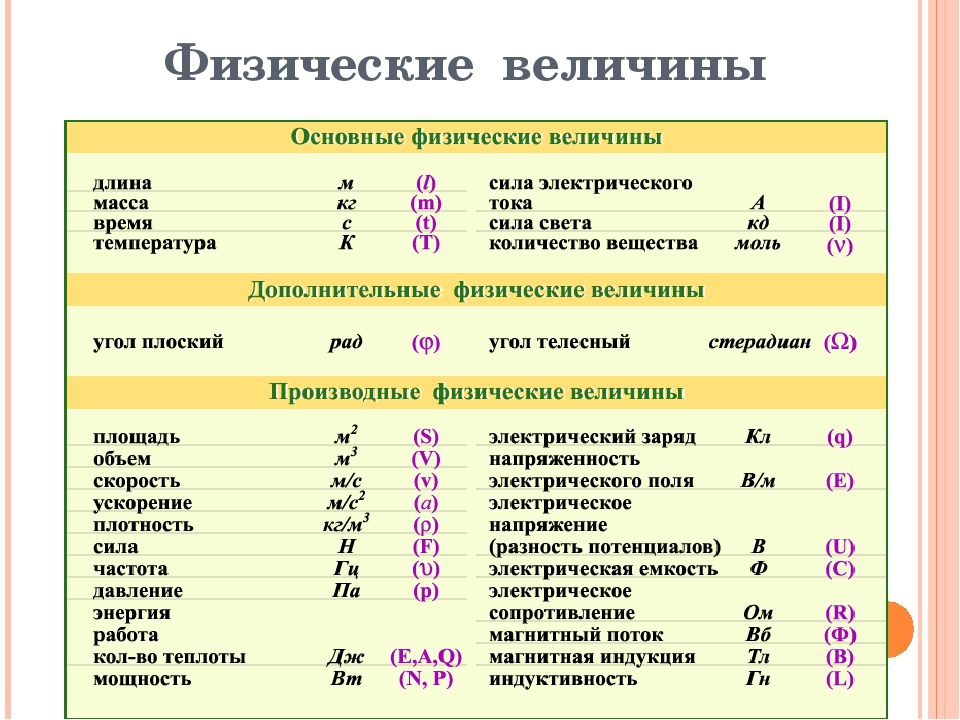
Советы
Чтобы успешно справиться с этим заданием, нужно брать стандартные школьные задачники и решать задачи по соответствующим разделам.
Задание № 26
Что требуется
Решить задачу по молекулярной физике или термодинамике.
Особенности
На ЕГЭ представлены пять разделов физики: механика, молекулярная физика и термодинамика, электродинамика, основы специальной теории относительности и квантовая физика. Основы специальной теории относительности являются достаточно специфическим разделом. Его освоению в школе уделяется совсем немного времени, но на ЕГЭ по физике он чаще всего встречается лишь в одном задании (№ 18). Из года в год статистика результатов экзамена показывает, что чем дальше по темам, тем хуже решаемость задач. Так, задачи по механике успешно решает значительный процент выпускников, по молекулярной физике — чуть меньше, по электродинамике — еще меньше, а по квантовой физике процент самый низкий. Разница в количестве абитуриентов, верно решивших задачи в рамках того или иного раздела, не столь велика (около 10—15%), но тенденция сохраняется из года в год.
Разница в количестве абитуриентов, верно решивших задачи в рамках того или иного раздела, не столь велика (около 10—15%), но тенденция сохраняется из года в год.
Распространенная ошибка, которая часто возникает в задаче № 26, связана с применением первого закона термодинамики к различным изопроцессам. Выпускники неправильно пишут знаки необходимых величин. Этот закон включает в себя теплоту, подводимую или отводимую из системы, изменение внутренней энергии и работу. В зависимости от того, расширяется газ или сжимается, нагревается или охлаждается, подводят теплоту в систему или, наоборот, отводят, у всех названных выше величин меняются знаки, и они входят в уравнение либо с плюсом, либо с минусом. Участники экзамена регулярно ошибаются при расстановке знаков. Здесь нужно вспомнить, что чему должно соответствовать, и подумать, с какими знаками величины подставить в уравнение, чтобы получить корректное решение и правильный ответ.
Успешнее всего ребята справляются с задачами на уравнение Менделеева — Клайперона и на формулу для внутренней энергии идеального газа. Если на ЕГЭ попадаются эти темы, большинство абитуриентов верно решает задачу.
Если на ЕГЭ попадаются эти темы, большинство абитуриентов верно решает задачу.
Советы
Статистика успешного выполнения задания № 26 может меняться в три-четыре раза в зависимости от темы. Поэтому советую внимательно повторить то, как правильно пользоваться первым законом термодинамики, а также темы, которые находятся в разделе молекулярной физики и термодинамики и вызывают у вас наибольшие трудности.
Задание № 27
Что требуется
Решить задачу по электродинамике или квантовой физике.
Особенности
В спецификации ФИПИ под этим номером идет задача по электродинамике или квантовой физике. При этом в методических рекомендациях по результатам ЕГЭ-2017 указано: «В следующем году последней расчетной задачей с кратким ответом на позиции 27 будут преимущественно задания по квантовой физике (на уравнение Эйнштейна для фотоэффекта или на формулу для энергии или импульса фотонов)». Эта информация сильно сужает список тем, которые стоит повторять при подготовке к этому заданию.
Советы
Обратите внимание на темы, о которых идет речь выше, и прорешайте соответствующие типичные задачи.
Задание № 28
Что требуется
Решить качественную задачу из любого раздела, который есть в кодификаторе.
Особенности
Качественная задача не имеет числового ответа. Ответ здесь может звучать как «больше», «меньше», «увеличится», «уменьшится», «вырастет», «упадет». В этих задачах, как правило, важен не столько результат, сколько сам ход решения. Например, в условии может быть схема электрической цепи, а затем в цепи происходит какое-то изменение (переключили ключ или заменили какой-нибудь элемент). В качестве решения надо указать, что изменится в системе или что произойдет с показаниями тех или иных измерительных приборов, которые содержатся в цепи.
Задание проверяет знание законов физики, умение их применить, а также логику переходов в построении решения. Насколько выпускник понимает то или иное явление? Нет ли логических ошибок в его рассуждениях? Могу сказать, что, по статистике, эта задача имеет один из самых низких процентов решаемости за всю историю ЕГЭ по физике.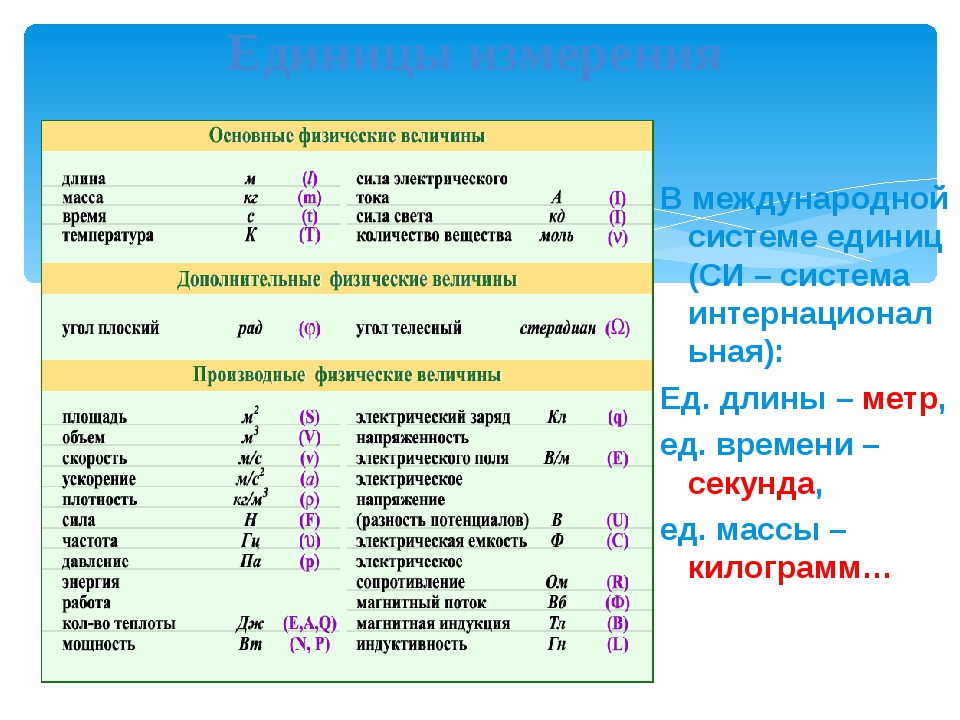
Советы
Если на экзамене вы претендуете на максимальный балл, вам стоит обратить особое внимание на это задание. Существуют отдельные сборники по качественным задачам (например, «Качественные задачи по физике в средней школе», М.Е. Тульчинский). Хочу отметить, в зависимости от года издания, список рассматриваемых в этих сборниках тем может оказаться шире, чем требуется на ЕГЭ. Например, в сборниках, изданных в советское время, часто встречаются задачи на тепловое расширение, а в ЕГЭ такой темы нет. Поэтому подберите соответствующие темы по кодификатору ЕГЭ и прорешайте задачи по ним из какого-нибудь сборника качественных задач.
В методических рекомендациях, на которые я уже ссылался выше, этому заданию уделяется особое внимание, методика его решения обсуждается на нескольких страницах (стр. 20—22). Там рассматривается несколько типичных ошибок участников ЕГЭ по физике 2018 года и подходы к решению такого рода заданий. Выпускникам будет полезно ознакомиться с этим документом. Его можно найти на сайте ФИПИ.
Его можно найти на сайте ФИПИ.
Задание № 29
Что требуется
Решить задачу по механике.
Особенности
Задачи № 25—28 относились к повышенному уровню сложности, а последние четыре, начиная с № 29, уже относятся к высокому. Здесь от участников экзамена требуется применить законы физики в необычных условиях, которые редко встречаются в типовых задачниках.
Есть еще и такой нюанс. В прошлом году в кодификатор ЕГЭ по физике были внесены изменения, расширился список рассматриваемых тем. Обратите внимание, что в раздел «Механика» добавилась вторая космическая скорость, которой раньше там не было. Теперь могут появиться задачи и по этой теме.
Советы
В первую очередь обратите внимание на такие разделы механики, как «Статика» и «Колебания и волны». Эти темы достаточно часто встречаются в этом задании и вызывают наибольшие затруднения у выпускников.
Задание № 30
Что требуется
Решить задачу по молекулярной физике или термодинамике.
Особенности
В спецификации ЕГЭ по физике есть противоречие. В одной части этого документа говорится, что под этим номером идет задача по молекулярной физике или термодинамике, а в другой части, где описываются уровни сложности заданий, указано, что успешное выполнение этого задания требует знаний из нескольких разделов физики. По своему опыту могу сказать, что правильным стоит считать второй вариант. Кстати, это замечание относится ко всем четырем последним заданиям (№ 29—32).
Если на экзамене вам досталась задача по молекулярной физике, то чаще всего для решения требуются знания из области механики. Например, здесь могут рассматриваться изопроцессы, происходящие с идеальным газом, и создаваемое газом давление приводит к движению поршня, которое тоже надо описать, используя соотношения, известные из механики.
Советы
Чаще всего эта задача посвящена изопроцессам, происходящим в газах, и применению к этим процессам первого начала термодинамики. Также под № 30 встречаются задачи на уравнение теплового баланса, которые обычно не вызывают серьезных затруднений.
Также под № 30 встречаются задачи на уравнение теплового баланса, которые обычно не вызывают серьезных затруднений.
Задание № 31
Что требуется
Решить задачу по электродинамике.
Особенности
Это задача по электродинамике, но здесь надо применить знания из разных разделов. Например, часто в условии возникающие электродинамические силы приводят к механическому движению. Таким образом всплывают элементы механики, в частности, в решении нередко приходится использовать закон сохранения энергии.
Советы
Обратите внимание на следующие темы: электромагнитная индукция, электромагнитные колебания и волны, элементы физической оптики (дифракция и интерференция света). Эти разделы достаточно сложные, и по ним необходимо отдельно готовиться.
Наименьшие же трудности у ребят вызывают задачи на геометрическую оптику и применение закона Ома.
Задание № 32
Что требуется
Решить задачу по электродинамике или квантовой физике.
Особенности
Чаще всего под № 32 на ЕГЭ дают задачу по электродинамике. Но попадаются и задачи из квантовой физики, в частности на уравнение Эйнштейна для фотоэффекта.
Советы
Повторите следующие темы: фотоэффект, геометрическая оптика, электромагнитные колебания.
Общие рекомендации по решению задач части 2
- Чтобы подготовиться к последним четырем заданиям, нужно решать задачи, которые рассматривают одно и то же явление с разных сторон. Допустим, у нас есть задача, в которой условие дано в форме обычного текста или рисунка со схемой. Что-то дано, что-то надо найти. Это первый подход. Второй вариант — это когда то же самое условие может быть в виде графика, который, например, описывает колебания той или иной величины (напряжение, сила тока, заряд на конденсаторе). Третий вариант — это условие в виде таблицы значений или функции. В итоге одно и то же явление можно описывать самыми разными способами. При подготовке я рекомендую найти и прорешать по несколько задач по каждой теме, в которых используются различные подходы.

- Не всегда полезно прорешивать задачи из открытого банка заданий и демоверсий ЕГЭ. Ведь они в большей степени предназначены для проверки знаний по определенным темам, а не для обучения. Если вам нужно разобрать конкретные темы, лучше использовать задачники по физике.
- Последние четыре задачи ЕГЭ рассчитаны на выпускников с очень высоким уровнем знаний по предмету. Другим школьникам они могут показаться нерешаемыми. Конечно, все основные законы физики большинство участников экзамена знает. Но здесь их нужно использовать в таких необычных условиях, что порой бывает сложно догадаться, о каком законе или явлении идет речь и какие соотношения эти явления описывают. Часто главная проблема заключается именно в этом — трудно понять, про что эта задача и какие законы в ней можно использовать.
Что означает формула E=mc2 и как с ее помощью раздобыть много энергии — T&P
Все знают формулу E=mc
2, и все слышали, что ее Эйнштейн придумал. Многие даже знают, что Е обозначает энергию, m — массу, а c — скорость света. Но что все это означает?
Многие даже знают, что Е обозначает энергию, m — массу, а c — скорость света. Но что все это означает?
Если взять обычную пальчиковую батарейку из пульта от телевизора, и превратить ее в энергию, то точно такую же энергию можно получить от 250 миллиардов таких же батареек, если использовать их по-старинке. Не очень хороший получается КПД.
А то и означает, что масса и энергия — это одно и то же. То есть масса — это частный случай энергии. Энергию, заключенную в массе чего угодно, можно посчитать по этой простой формуле.
Скорость света — это очень много. Это 299 792 458 метров в секунду или, если вам так удобнее, 1 079 252 848,8 километров в час. Из-за этой большой величины получается, что если превратить чайный пакетик целиком в энергию, то этого хватит, чтобы вскипятить 350 миллиардов чайников.
У меня есть пара грамм вещества, где мне получить мою энергию?
Перевести всю массу предмета в энергию можно, только если вы где-нибудь найдете столько же антиматерии. А ее получить в домашних условиях проблематично, этот вариант отпадает.
А ее получить в домашних условиях проблематично, этот вариант отпадает.
Термоядерный синтез
Существует очень много природных термоядерных реакторов, вы можете их наблюдать, просто взглянув на небо. Солнце и другие звезды — это и есть гигантские термоядерные реакторы.
Другой способ откусить от материи хоть сколько-то массы и превратить ее в энергию — это произвести термоядерный синтез. Берем два ядра водорода, сталкиваем их, получаем одно ядро гелия. Весь фокус в том, что масса двух ядер водорода немного больше, чем масса одного ядра гелия. Вот эта масса и превращается в энергию.
Но тут тоже не так все просто: ученые еще не научились поддерживать реакцию управляемого ядерного синтеза, промышленный термоядерный реактор фигурирует только в самых оптимистичных планах на середину этого столетия.
Ядерный распад
Ближе к реальности — реакция ядерного распада. Она вовсю используется в ядерных электростанциях. Это когда два больших ядра атома распадаются на два маленьких. При такой реакции масса осколков получается меньше массы ядра, пропавшая масса и уходит в энергию.
При такой реакции масса осколков получается меньше массы ядра, пропавшая масса и уходит в энергию.
Ядерный взрыв — это тоже ядерный распад, но неуправляемый, прекрасная иллюстрация этой формулы.
Горение
Превращение массы в энергию вы можете наблюдать прямо у вас в руках. Зажгите спичку — и вот она. При некоторых химических реакциях, например, горения, выделяется энергия от потери массы. Но она очень мала по сравнению с реакцией распада ядра, и вместо ядерного взрыва у вас в руках происходит просто горение спички.
Более того, когда вы поели, еда через сложные химические реакции благодаря мизерной потере массы отдает энергию, которую вы потом используете, чтобы сыграть в настольный теннис, ну или на диване перед телеком, чтобы поднять пульт и переключить канал.
Так что, когда вы едите бутерброд, часть его массы превратится в энергию по формуле E=mc2.
Урок 20. постулаты специальной теории относительности (сто) — Физика — 11 класс
Физика, 11 класс
Урок №20. Постулаты специальной теории относи-тельности (СТО)
Постулаты специальной теории относи-тельности (СТО)
Основные вопросы, рассматриваемые в теме: событие, постулат, собственная инерциальная система отсчёта, собственное время, собственная длина тела, масса покоя, инвариант; причины появления СТО; постулаты СТО: инвариантность модуля скорости света в вакууме, принцип относительности Эйнштейна.
Глоссарий:
Специальная теория относительности (СТО) – физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов.
Событие — физическое явление, которое происходит в определённый момент времени в данной точке пространства.
События могут происходить в одно и тоже время и их называют одновременными. Если координаты событий совпадают, то события называют одноместными.
Инерциальные системы отсчёта (ИСО) – это системы отсчёта, в которых выполняется первый закон Ньютона – закон инерции.
Два постулата теории:
1. Все физические явления протекают одинаково во всех инерциальных системах отсчёта.
Все физические явления протекают одинаково во всех инерциальных системах отсчёта.
2. Скорость света в вакууме одинакова во всех инерциальных системах отсчёта.
Постулат – это основное положение, которое не может быть логически доказано, а является результатом обобщения всех опытов.
Время, отсчитываемое покоящимися в ИСО часами, называется собственным временем.
Длину тела L0, относительно которого оно в ИСО находится в покое называют собственной длиной.
Массой покоя m0, называют массу тела в состоянии покоя относительно ИСО.
Скорость света c и собственное время Δτ инвариантны в любых ИСО.
Список основной и дополнительной литературы по теме:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 229 – 238.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 148
- Анциферов Л.
 И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 242-253.
И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 242-253. - Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.16-25
Теоретический материал для самостоятельного изучения
Человек, открывший новый взгляд на пространство и время мыслил образами. Альберт Эйнштейн всегда твёрдо верил, что именно воображение способно проникнуть в суть, в глубину, в основу сущего. Он никогда не заучивал теорию, он представлял её образами. В детстве Эйнштейну привили интерес к математике, естествознанию. Одной из любимых книг Альберта была книга Аарона Бернштейна «Популярные книги по естественной истории». От описаний научных историй у 12 летнего Эйнштейна захватывало дух. Мысленные эксперименты были самым занимательным в книгах Бернштейна.
В 1895 году Эйнштейну повезло, в 16-летнем возрасте, провалив экзамены в Цюрихский политехникум по французскому языку, литературе, политике и зоологии, но легко справившись с математикой и естествознанием, он поступил в сельскую школу Арау. Образование здесь строилось на методах, разработанных Иоганном Песталоцци, на проведении мысленных экспериментов, на более глубоком понимании явлений и ситуаций. Это были первые шаги на пути формирования специальной теории относительности (СТО).
Образование здесь строилось на методах, разработанных Иоганном Песталоцци, на проведении мысленных экспериментов, на более глубоком понимании явлений и ситуаций. Это были первые шаги на пути формирования специальной теории относительности (СТО).
Теория относительности – физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов.
В теории относительности часто будет использовано понятие «событие». Событием будем называть физическое явление, которое происходит в определённый момент времени в данной точке пространства.
В движущемся поезде, вывешенная в центре, вспыхивает лампочка в точке О – это одно событие. Свет от лампочки достигает точку А в одном конце помещения – это другое событие, а также достигает противоположного конца помещения в точке В – то третье событие.
События могут происходить в одно и тоже время и их называют одновременными. Если координаты событий совпадают, то события называют одноместными.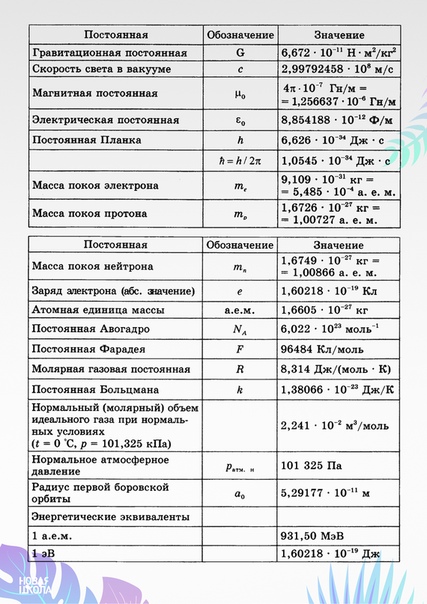 При этом учитываем, что реальные тела имеют размеры и события разворачиваются во времени.
При этом учитываем, что реальные тела имеют размеры и события разворачиваются во времени.
Одновременно ли достигнет свет две противолежащие точки А и В? Ведь корабль движется со скоростью в одном направлении и одна стенка приближается к летящему свету, а другая отдаляется.
Классический закон сложения скоростей не работает в описании распространения электромагнитного излучения от источника света.
Чтобы ответить на эти вопросы, необходимо выяснить, меняются ли основные законы электродинамики при переходе одной инерциальной системы отсчёта к другой, или же подобно принципам относительности Галилея и законам Ньютона, они остаются неизменными.
Принцип относительности Галилея.
Инерциальные системы отсчёта (ИСО) – это системы отсчёта, в которых выполняется первый закон Ньютона – закон инерции. Системы, которые ускоряются или вращаются называют неинерциальными. Система отсчёта, движущаяся равномерно и прямолинейна относительно ИСО, также инерциальная. Земля не совсем инерциальная система отсчёта, так как она вращается, но для большинства наших примеров, будем считать её инерциальной.
Земля не совсем инерциальная система отсчёта, так как она вращается, но для большинства наших примеров, будем считать её инерциальной.
К началу XX века в физике накопилось много наблюдений и опытов, которые не могли быть объяснены классическими теориями. В XVII – XIX веках большое место в теории отводилось гипотезе о существовании эфира. Эфир представляли себе, как занимающая всё пространство упругая среда, с помощью которой осуществляется взаимодействие между телами, благодаря которой распространяются волны звуковые, световые, электромагнитные. Считалось естественным связывать абсолютную систему отсчёта с мировым эфиром. Этой теории придерживался и основатель электронной теории Х. Лоренц и Г.Герц. Однако эксперименты, поставленные в 1881 году учёными А. Майкельсоном, Э.Морли и А.Физо об изотропности света, приводили к противоположным результатам. В опытах по изучению распространения света, А.Физо с помощью оптических приборов находил подтверждение, существования эфира. Опыты Майкельсона существование «эфирного ветра», то есть преимущественной системы отсчёта или «светового эфира» не подтверждали, за что подверглись критике со стороны прославленного учёного Х. Лоренца.
Лоренца.
Но противоречия в опытах классическими законами уже невозможно было объяснить. Эйнштейн, изменяя классические законы механики, а не законы электродинамики Максвелла, предложил наиболее революционный способ описания явлений в пространстве и времени. Из теории Максвелла следовало, что электромагнитные волны, в отличие от механических волн, могут распространяться в вакууме и подчиняются законам электромагнетизма, что свет – это электромагнитная волна и скорость света:
У Максвелла не было оговорок по поводу относительности скорости света.
И в 1905 году появилась работа А. Эйнштейна «К электродинамике движущихся сред», в которой излагались идеи новой теории – специальной теории относительности.
В основу теории были положены два постулата*:
- Все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.

- Скорость света в вакууме одинакова во всех инерциальных системах отсчёта. Она не зависит от ни от скорости источника света, ни от скорости светового приёмника сигнала.
Постулат – это основное положение, которое не может быть логически доказано, а является результатом обобщения всех опытов. В физической теории выполняет ту же роль, что и аксиома в математике.
Скорость света занимает особое положение в этой теории, распространение света в вакууме является максимально возможной скоростью передачи взаимодействий в природе.
С точки зрения классической физики первый и второй постулаты входят в противоречия друг с другом. По первому постулату законы механики (как частный случай законов физики) справедливы во всех ИСО. Следовательно, справедлив и закон сложения скоростей. Однако второй постулат противоречит классическому закону сложения скоростей. Значит, в СТО нельзя пользоваться преобразованиями Галилея. Заменив преобразования Галилея на преобразования Лоренца, Эйнштейн устранил кажущееся противоречие между постулатами, что позволило объяснить многие опыты по электродинамике и оптике.
Независимость скорости света от источника много раз проверялись на опытах. Советские учёные А.М. Бонч-Бруевич и В.А. Молчанов в 1955 году проводили опыты, измеряя скорости света от правого и левого краёв Солнца (один из которых из-за осевого вращения Солнца приближается к нам со скоростью 2,3 км/с, а другой с такой же скоростью удаляется). Учёные, проведя расчёты, пришли к выводу, что скорости распространения света с обоих концов одинаковы.
Преобразования Лоренца, которые использовал Эйнштейн, заменив преобразования Галилея, для описания распространения света в системе координат:
Если скорость намного меньше скорости света , то отношение квадратичной скорости движения системы к квадрату скорости света намного меньше 1 и величиной можно пренебречь. Тогда мы переходи к преобразованиям Галилея:
Новая теория раскрыла более глубокую физическую реальность и включает старую как предельный (частный) случай, который называют принципом соответствия.
Иначе это можно объяснить так: классическая механика (механика Ньютона) является частным случаем более общей механики, описывающих процессы в разных инерциальных системах отсчёта с учётом преобразований Лоренца.
Мы ещё неоднократно убедимся, что при малых скоростях, намного меньших, чем скорость света законы СТО переходят в законы классической механики.
Существование предельной конечной скорости изменяет наши привычные представления о пространстве и времени. Представление об абсолютном времени, которое течёт с навсегда заданным темпом, оказывается неверным.
Следствия постулатов относительности:
- Относительность одновременности
Рассмотрим простой метод синхронизации часов. Допустим, что космонавт хочет узнать, одинаково ли идут часы в разных концах корабля в точках А и В. С помощью источника света в центре корабля производят вспышку света, если часы идут синхронно, по показания на часах будут одинаковы при приёме света. Но так будет только в движущейся системе отсчёта К1, связанной с кораблём. И так же, как и в первом случае, вспышка для наблюдателя, находящегося в системе отсчёта К (неподвижная система), часы будут удалятся от вспышки света, и излучению нужно пройти большее расстояние, значит и время должно зафиксироваться отличное от часов в точке В. Вывод наблюдателя в системе отсчёта К: сигналы достигают часов не одновременно.
И так же, как и в первом случае, вспышка для наблюдателя, находящегося в системе отсчёта К (неподвижная система), часы будут удалятся от вспышки света, и излучению нужно пройти большее расстояние, значит и время должно зафиксироваться отличное от часов в точке В. Вывод наблюдателя в системе отсчёта К: сигналы достигают часов не одновременно.
Время, отсчитываемое покоящимися в ИСО часами, называется собственным временем и обозначают буквой τ (тау). Промежуток времени между событиями по часам наблюдателя, находящегося внутри объекта (ИСО К1). Промежуток времени между теми же событиями по часам наблюдателя относительно которой удаляется обозначим Δt. Между этими промежутками существует соотношение:
Это означает, что часы, движущиеся относительно ИСО идут медленнее, неподвижных часов и показывают меньший промежуток времени между событиями (замедление времени).
Преобразовав выражение Δt, получим:
А так как скорость света c постоянна и собственное время Δτ неизменно для данного события, то есть инвариантны, то получим:
Наряду с протонами и нейтронами в природе существуют мюоны – элементарные частицы. Мюоны могут образовываться в атмосфере Земли. Но мюоны не стабильны и довольно быстро распадаются, превращаясь в другие элементарные частицы. В лаборатории, где мюоны практически покоятся, среднее время их жизни Δτ =2·10-6с. Вычисляя скорость и другие параметры мюонов, физики обнаружили, что мюоны в атмосфере Земли (без распада) могут пройти расстояние 6 км за время Δt =2·10-5с. Это означает, что время жизни движущегося мюона в системе «Земля» в 10 раз больше собственного времени жизни Δτ.
Мюоны могут образовываться в атмосфере Земли. Но мюоны не стабильны и довольно быстро распадаются, превращаясь в другие элементарные частицы. В лаборатории, где мюоны практически покоятся, среднее время их жизни Δτ =2·10-6с. Вычисляя скорость и другие параметры мюонов, физики обнаружили, что мюоны в атмосфере Земли (без распада) могут пройти расстояние 6 км за время Δt =2·10-5с. Это означает, что время жизни движущегося мюона в системе «Земля» в 10 раз больше собственного времени жизни Δτ.
Рассмотрим ещё один парадокс: относительность расстояний или размеров тела. Допустим, что в космическом корабле измеряют длину стержня, расположенного вдоль направления скорости. Длину стержня внутри корабля, относительно которого он находится в покое обозначим L0 и назовём собственной длиной. При этом расчёты показывают, что линейный размер тела, движущегося относительно ИСО уменьшается в направлении движения.
Закон сложения скоростей в СТО записывается так:
𝟅 – скорость тела, относительно неподвижной системы отсчёта,
𝟅´ — скорость относительно подвижной системы отсчёта,
v – скорость подвижной системы отсчёта относительно неподвижной,
c – скорость света.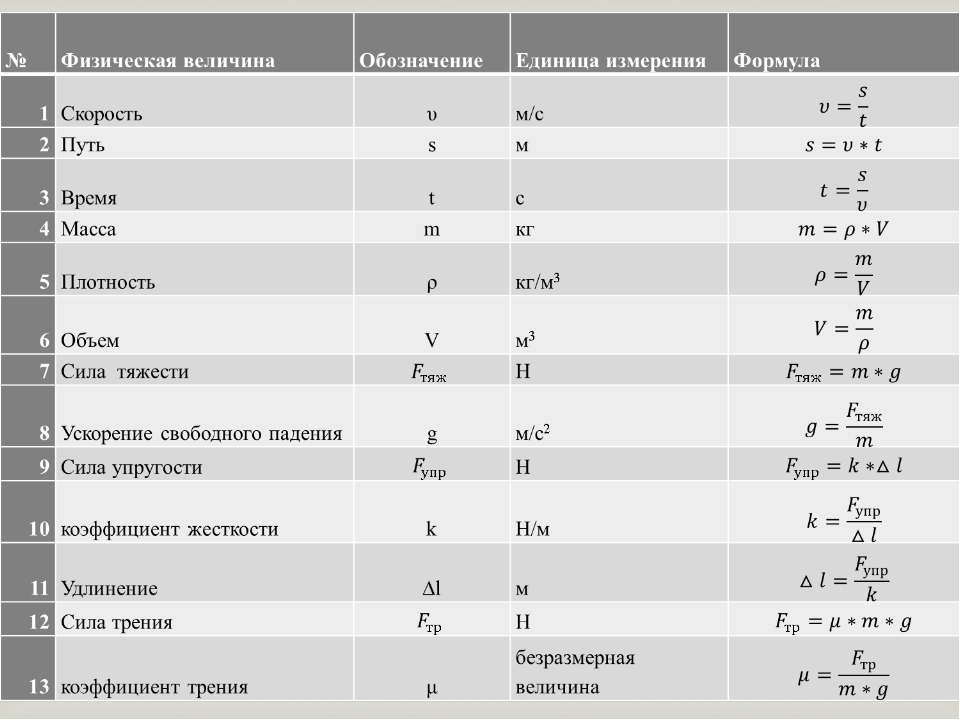
При скоростях движения намного меньших, чем скорость света закон сложения скоростей переходит в классический, а длина тела и интервал времени становятся одинаковыми в неподвижной и движущейся системах отсчёта.
Даже масса, такое непоколебимое в нашем представлении значение, меняет свои параметры в движущейся системе относительно неподвижной ИСО. Собственную массу тела, находящегося в состоянии покоя, относительно ИСО, называют m0 массой покоя.
Сам А. Эйнштейн говорил о том, что правильнее было бы называть его теорию относительности теорией абсолютности, так как в основе её заложена идея абсолютности во всех инерциальных системах отсчёта.
Примеры и разбор заданий
1. Две частицы удаляются друг от друга, имея скорость 0,6с каждая, относительно земного наблюдателя. Относительная скорость частиц составляет ______скорости света.
Решение:
Дано: 𝟅´ = 0,6 с, v = — 0,6 с.
Найти: 𝟅.
Решение:
Для решения задачи, необходимо перейти в ИСО, связанную с одной из частиц. Пусть частицы движутся вдоль одной прямой, в противоположные стороны. Используем закон сложения скоростей СТО:
𝟅 – скорость частицы, относительно неподвижной системы отсчёта,
𝟅´ — скорость частицы относительно подвижной системы отсчёта,
v – скорость подвижной системы отсчёта относительно неподвижной,
c – скорость света.
Примем скорость v = — 0,6с одной частицы за положительное значение, скорость 𝟅´ = 0,6с. Тогда формула примет вид:
Ответ значения скорости частицы будет корректен относительно скорости света, а не в м/с или км/с.
Ответ: 0,882 с.
1. Масса протона, летящего со скоростью 1,3·108 м/с, составляет_____ а.е.м. Массу покоя протона считать равной 1 а.е.м.
Решение:
Дано:
𝟅 = 1,3·108 м/с,
m0 = 1а. е.м.
е.м.
Найти: m.
Решение:
В атомной и ядерной физике для выражения массы пользуются специальной внесистемной единицей – атомной единицей массы (а.е.м.), равной 1/12 массы атома углерода.
1 а.е.м. = 1,66057·10-27кг.
Подставим числовые значения в формулу определения массы частицы, движущейся относительно неподвижной ИСО:
Ответ: 1,11 а.е.м.
| c | скорость света в вакууме | 299 792 458 м/с |
| Г | гравитационная постоянная | 6,67430 |
| ч | постоянная Планка | 6,62607015 4.1356676969 |
| з | 1,986445857 1239,841984 | |
| ч бар, приведенная постоянная Планка, постоянная Дирака | 1,054571817 6,582119570 | |
| f Cs | сверхтонкий переход 133 Cs | 9 192 631 770 |
| и | элементарный заряд | 1. 602176634 602176634 |
| ε 0 | электрическая постоянная, диэлектрическая проницаемость свободного пространства, диэлектрическая проницаемость вакуума | 8,8541878128 |
| мк 0 | магнитная постоянная, проницаемость свободного пространства, вакуумная проницаемость | 1.25663706212 |
| Н А | Постоянная Авогадро | 6.02214076 |
| к | Постоянная Больцмана | 1.380649 |
| Р = Н А к | газовая постоянная | 8.314462618 |
| Постоянная Стефана-Больцмана | 5. 670374419 670374419 | |
| б | Постоянная смещения Вина | 2.897771955 58,78925757 |
| м у | атомная постоянная массы | 1,66053 0 |
| м е | масса электрона | 9,1093837015 0,51099895000 МэВ/с 2 5.485795 |
| м р | масса протона | 1,67262192369 938,27208816 МэВ/c 2 1,007276466621 u |
| м н | масса нейтрона | 1,67492749804 939,56542052 МэВ/c 2 1,00866491595 u |
| К компакт-диск | световая отдача | 683 лм/Вт |
| Н 0 | постоянная Хаббла* | 69. 3 км/с/Мпк 3 км/с/Мпк 2,25 |
О значении константы «с» в современной физике
Borchers, HJ, & Hegerfeld, G.C. (1972). Über ein Problem der Relativitätstheorie: Wann sind Punktabbildungen des R n linear?. В Nachrichten der Akademie der Wissenschaften в Геттингене, II (стр. 205–229). Математико-физический класс, №10.
Карр, Б. (2007). Вселенная или мультивселенная? .Кембридж: Издательство Кембриджского университета.
Google Scholar
Ellis, G.F.R. et al. (2003). Мультивселенная и физическая космология. В arXiv: astro-ph/0305292v3.
Франк, Ф., и Роте, Х. (1911). Über die Transformation der Raum-Zeitkoordinaten von ruhenden auf bewegte Systeme. Аннален дер Физик,
34 , 825–855.
Артикул
Google Scholar
Гамов Г. (1946). Мистер Томпкинс в стране чудес . Нью-Йорк: Компания Macmillan.
(1946). Мистер Томпкинс в стране чудес . Нью-Йорк: Компания Macmillan.
Google Scholar
Хокинг С.В. и Эллис Г.Ф.Р. (1973). Крупномасштабная структура пространства-времени . Кембридж: Издательство Кембриджского университета.
Книга
Google Scholar
Игнатовский, В. В. (1910). Einige allgemeine Bemerkungen zum Relativitätsprinzip. Physikalische Zeitschrift,
11 , 972–976.
Google Scholar
Леви-Леблон, Дж. М. (1976). Еще один вывод преобразования Лоренца. Американский журнал физики,
44 , 271–277.
Артикул
Google Scholar
Линде, А. Д. (1990). Инфляция и квантовая космология .Сан-Диего, Лондон: Academic Press.
Google Scholar
Марцке, Р. Ф., и Уилер, Дж. А. (1964). Гравитация как геометрия. I: Геометрия пространства-времени и геометродинамический стандартный метр. В Х.-Ю. Chiu & WF Hoffman (Eds.), Гравитация и теория относительности (стр. 40–64). Нью-Йорк: В. А. Бенджамин.
Ф., и Уилер, Дж. А. (1964). Гравитация как геометрия. I: Геометрия пространства-времени и геометродинамический стандартный метр. В Х.-Ю. Chiu & WF Hoffman (Eds.), Гравитация и теория относительности (стр. 40–64). Нью-Йорк: В. А. Бенджамин.
Google Scholar
Мизнер, Ч. В., Торн, К.С., и Уилер, Дж.А. (1973). Гравитация . Сан-Франциско: WH Freeman.
Google Scholar
Миттельштадт, П. (1976, 1989). Der Zeitbegriff in der Physik (ред. 3 rd ). Мангейм: BI-Wissenschaftsverlag.
Миттельштадт, П. (1988). Über die Bedeutung und Begründung der Speziellen Relativitätstheorie. В J. Audretsch & K. Mainzer (Eds.), Philosophie der Physik und der Raum-Zeit .Мангейм: BI-Wissenschaftsverlag.
Google Scholar
Миттельштадт, П. (1995). Классическая механика (2-е изд. ). Мангейм: Библиографический институт.
). Мангейм: Библиографический институт.
Google Scholar
Миттельштадт, П. (2003). Hätte Newton die Relativitätstheorie finden können? В W. Buschlinger & C. Lütge (Eds.), Kaltblütig: Philosophie von Einem Rationalen Standpunkt (стр.221–240). Штутгарт: С. Хирцель Verlag.
Google Scholar
Миттельштадт, П. (2006). Интуитивность и истина в современной физике. В Э. Карсон и Р. Хубер (редакторы), Интуиция и аксиоматический метод (стр. 251–266). Дордрехт: Спрингер.
Глава
Google Scholar
Миттельштадт, П. (2008). Постоянная Планка в свете квантовой логики. Международный журнал теоретической физики,
47 , 104–113.
Артикул
Google Scholar
Пенроуз, Р. (1959). Видимая форма релятивистски движущейся сферы. Труды Кембриджского философского общества,
Труды Кембриджского философского общества,
55 , 137–139.
Артикул
Google Scholar
Сексл, Р.У. и Урбантке, Х.К. (1992). Relativät, Gruppen, Teilchen (3-е изд.). Вена, Нью-Йорк: Спрингер.
Google Scholar
Террелл, Дж. (1959). Невидимость лоренцевского сокращения. Физический обзор,
116 , 1041–1045.
Артикул
Google Scholar
Виленкин А. (1982). Создание вселенных из ничего. Письма по физике,
117Б , 25–28.
Google Scholar
Фоллмер, Г. (2007). Wie viel Metaphysik brauchen wir? В Д. Вестеркамп и А. фон дер Люэ (ред.), Metaphysik und Moderne . Вюрцбург: Кенигсхаузен и Нойманн.
Google Scholar
Дэвид С.
 Монтгомери | Факультет физики и астрономии
Монтгомери | Факультет физики и астрономии
Дэвид С.Монтгомери, «Загадка аэродинамического крыла: конкурирующие теории в аэродинамике, 1909–1930», Дэвид Блур [University of Chicago Press, Чикаго, Иллинойс, 2011] 547 стр. (обзор книги). Являюсь. Дж. Физ. 80, 649 (2012)
округ Колумбия Монтгомери и У.Х. Маттеус «Вихрь Озеена как максимальное энтропийное состояние двумерной жидкости» Physics of Fluids 23, 075104 (6 стр.), (2011)
Д. Дж. Роджерс, У. Х. Маттеус, Т. Б. Митчелл и Д. К. Монтгомери «Подобие распада энстрофии в электронной жидкости», Phys.Ред. PRL 105, 234501 (2010).
DC Монтгомери «Миры потока: история гидродинамики от Бернуллиса до Прандтля», Оливье Дарригол (рецензия на книгу), Am. Дж. Физ. 77, 767-768 (2009).
Д. Дж. Роджерс, 1 С. Сервидио, У. Х. Маттеус, 1 Д. К. Монтгомери, Т. Б. Митчелл и Т. Азиз, «Гидродинамическая релаксация электронной плазмы до состояния, близкого к максимальной энтропии», Phys. Ред. PRL 102, 244501 (2009).
Ред. PRL 102, 244501 (2009).
ИЗБРАННЫЕ ПУБЛИКАЦИИ (ТОЛЬКО С 1991 ГОДА)
С.Д. Мининни, Д.К. Монтгомери и Л. Тернер «Гидродинамические и магнитогидродинамические расчеты внутри вращающейся сферы» New J. Phys. 9, 303 (25 страниц), 2007.
Д. К. Монтгомери «Может ли ученый-физик внести значительный вклад в дело мира?» проц. Междунар. конф. по науке, технологиям и миру: преобразование и трансформация под ред. Питер Шмид и Пит Шрам, ISBN 978-90-810647-4-3 Эйндховенский технологический университет TU/e, Нидерланды, 2006.
Д.К. Монтгомери Пол М. Беллан (2006): Основы физики плазмы (обзор книги) Теор. вычисл. Динамик жидкости 21, 79-80 (2006).
П.Д. Мининни и Д.К. Монтгомери «Магнитогидродинамическая активность внутри сферы» Physics of Fluids 18, 116602 (13 страниц), (2006).
Дэвид С. Монтгомери «Некоторые замечания о затухающей двумерной турбулентности», глава «Математическая и физическая теория турбулентности», изд. Дж. Кэннон и Б. Шивамогги Бока-Ратон: Чепмен и Холл/CRC, 2006; стр.91-100.
Дж. Кэннон и Б. Шивамогги Бока-Ратон: Чепмен и Холл/CRC, 2006; стр.91-100.
П.Д. Мининни, А. Г. Пуке и Д. К. Монтгомери «Мелкомасштабные структуры в трехмерной магнитогидродинамической турбулентности» Physical Review Letters 97, 244503 (2006).
Пабло Д. Мининни и Дэвид К. Монтгомери «Динамо с малым магнитным числом Прандтля со спиральным воздействием» Physical Review E 72, 056320 (9 страниц) (2005).
Пабло Д. Мининни, Янник Понти, Дэвид С. Монтгомери, Жан-Франсуа Пинтон, Элен Политано и Анник Пуке «Динамо-режимы с невинтовым воздействием» Astrophysical Journal 626, 853-863 (2005).
Ю. Понти, П.Д. Мининни, Д.К. Монтгомери, Ж.-Ф. Пинтон, Х. Политано и А. Пуке, «Численное исследование действия динамо при низких магнитных числах Прандтля», Physical Review Letters 94, 164502 (2005) (4 страницы).
Пабло Д. Мининни, Дэвид С. Монтгомери и Анник Пуке «Численные решения трехмерной магнитогидродинамической альфа-модели» Physical Review E 71, 046304 (2005) (11 страниц).
Дэвид Монтгомери «Элегантный тур-де-форс» (рецензия на книгу) Nederlands Tijdschrift voor Natuurkunde 71, 186–187 (2005).
Пабло Д. Мининни, Дэвид С. Монтгомери и Анник Г. Пуке «Численное исследование альфа-модели двумерных магнитогидродинамических турбулентных течений» Physics of Fluids 17, 035112 (2005) (17 страниц)
Пабло Дмитрук и Дэвид К. Монтгомери Численное исследование распада энстрофии в двумерной жидкости Навье-Стокса в пределе очень малых вязкостей. Physics of Fluids 17, 035114 (2005) (5 страниц).
Леон П.Дж. Камп и Дэвид С. Монтгомери «Тороидальные устойчивые состояния в вязко-резистивной магнитогидродинамике» Journal of Plasma Physics 70, 113-142 (2004).
Дэвид К. Монтгомери «Магнитогидродинамическая турбулентность» (обзор книги) Eos 85, № 2, стр. 20 (2004).
Дэвид С. Монтгомери «Маркетинговая наука, маркетинг самих себя», Academe 89, № 5 (сентябрь-октябрь 2003 г. ) [онлайн: https://www.jstor.org/stable/40253386]
) [онлайн: https://www.jstor.org/stable/40253386]
З. Инь, Х.Дж. Х. Клеркс и Д. К. Монтгомери «Легко реализуемая параллельная схема на основе задач для псевдоспектрального решателя Фурье, применяемого к двумерной турбулентности Навье-Стокса» Computers and Fluids 33, 509-520 (2004).
З. Инь, Д.К. Монтгомери и Х.Дж.Х. Клеркс «Альтернативные статистико-механические описания затухающей двумерной турбулентности с точки зрения« участков »и« точек »» Physics of Fluids 15, 1937–1953 (2003).
Л.П. Камп и Д.К.Монтгомери, «Тороидальные течения в резистивных магнитогидродинамических стационарных состояниях», Physics of Plasmas 10, 157-167 (2003).
Антонио Понно, Луиджи Галгани и Дэвид С. Монтгомери, «Класс резистивных осесимметричных магнитогидродинамических равновесий в периодическом цилиндре», Journal of Plasma Physics 67, 251-269 (2002).
Дэвид С. Монтгомери и Анник Пуке, «Альтернативная интерпретация альфа-модели Холма», Physics of Fluids 14, 3365-3366 (2002).
округ Колумбия Монтгомери, В.Х. Маттеус, Л. Дж. Милано и П. Дмитрук «Очевидное подавление турбулентного магнитного динамо постоянным магнитным полем» Physics of Plasmas 9, 1221 (2002).
LJ Milano, WH Маттеус, П. Дмитрук и Д.К. Монтгомери «Локальная анизотропия в несжимаемой магнитогидродинамической турбулентности» Physics of Plasmas 8, 2673 (2001).
Томас С. Леви и Дэвид К. Монтгомери «Распределение поля скоростей из-за идеальных линейных вихрей» Physical Review E 63, 056311 1-8 (2001).
Дэвид С. Монтгомери «Комментарий к теме« Подавляет ли сдвиг потока турбулентность в неионизированных потоках? »» Physics of Plasmas 7, 4785-4786 (2000).
Брайан Т. Кресс и Дэвид С. Монтгомери «Определение давления несжимаемых жидкостей и магнитожидкостей» Journal of Plasma Physics 64, 371-377 (2000).
Б.Т. Кресс и Д.К. Монтгомери «Определение несжимаемого давления», Proc. 27-я конференция Европейского физического общества по управляемому синтезу и физике плазмы, Будапешт, Венгрия, 2000 г.(Документ P1.003).
27-я конференция Европейского физического общества по управляемому синтезу и физике плазмы, Будапешт, Венгрия, 2000 г.(Документ P1.003).
Дж.В. Бейтс и Д.К. Монтгомери «Неустойчивость Дьякова-Конторовича ударных волн в реальных газах», Phys. Преподобный Летт. 84, 1180 (2000), февраль. 7 выпуск.
Д.К. Монтгомери и Дж.В. Бейтс «Геометрия и симметрия магнитогидродинамической турбулентности: аномалии пространственной периодичности», Phys. Плазма 6, 2727 (1999).
Дж.В. Бейтс и Д.К. Монтгомери «Некоторые численные исследования поведения экзотических ударных волн» Phys.Жидкости 11, 462 (1999).
округ Колумбия Монтгомери, Дж.В. Бейтс и Л.П. Камп «Стационарные состояния МГД как модель ограниченной плазмы» Plasma Phys. & контр. Fusion 41, Доп. 3А, А507-А517 (1999).
Котельников А.Д., Монтгомери Д.К. «Турбулентность, вызванная ударами, в композиционных материалах при умеренных числах Рейнольдса» Phys. Жидкости 10, 2037 (1998).
Жидкости 10, 2037 (1998).
Дж.В. Бейтс и Д.К. Монтгомери «Тороидальные вязко-резистивные магнитогидродинамические устойчивые состояния содержат вихри» Phys.Плазма 5, 2649 (1998).
Л.П. Камп, Д.К. Монтгомери и Дж.В. Бейтс «Тороидальные течения в резистивных магнитогидродинамических стационарных состояниях» Phys. Жидкости 10, 1757 (1998).
Котельников А.Д., Монтгомери Д.К. «Численное исследование распространения ударной волны в неоднородном материале» Тр. Тематическая конференция APS «Ударное сжатие конденсированных сред — 1997» Амхерст, Массачусетс, 27-31 июля 1997 г.; изд. Автор: Schmidt/Dandekar/Forbes, стр. 183–186, Американский институт физики, 1998.
Д. Монтгомери и Дж.В. Бейтс «Полоидальные течения в резистивных МГД-равновесиях» Proc. 7-я Европейская конференция по теории термоядерного синтеза, Юлих, Германия, 8-10 октября 1997 г., изд. А. Рогистер; Forschungszentrum Juelich GmbH, Юлих, Германия, 1998, стр. 119-121.
119-121.
Котельников А.Д. и Монтгомери Д. «Кинетический метод расчета поведения неоднородной жидкости» Journal of Computational Physics 134, 364 (1997).
С.Ли, Д. Монтгомери и У.Б. Джонс «Двумерная турбулентность с жесткими круглыми стенками» Теоретическая вычислительная гидродинамика 9, 167 (1997).
Д. Монтгомери, Дж.В. Бейтс и С. Ли «Тороидальные вихри в резистивных магнитогидродинамических равновесиях» Physics of Fluids 9, 1188 (1997).
Д. Монтгомери, Дж.В. Бейтс и Х. Р. Льюис «Сопротивление магнитогидродинамическим равновесиям» Physics of Plasmas 4, 1080 (1997).
С.Ли, Д. Монтгомери и У.Б. Джонс «Обратные каскады углового момента» Journal of Plasma Physics 56, 615 (1996).
Д. Монтгомери «Энтропии для сплошных сред: жидкости и магнитожидкости», в МАКСИМАЛЬНОЙ ЭНТРОПИИ И БАЙЕСОВСКИХ МЕТОДАХ, изд. Дж. Скиллинг и С.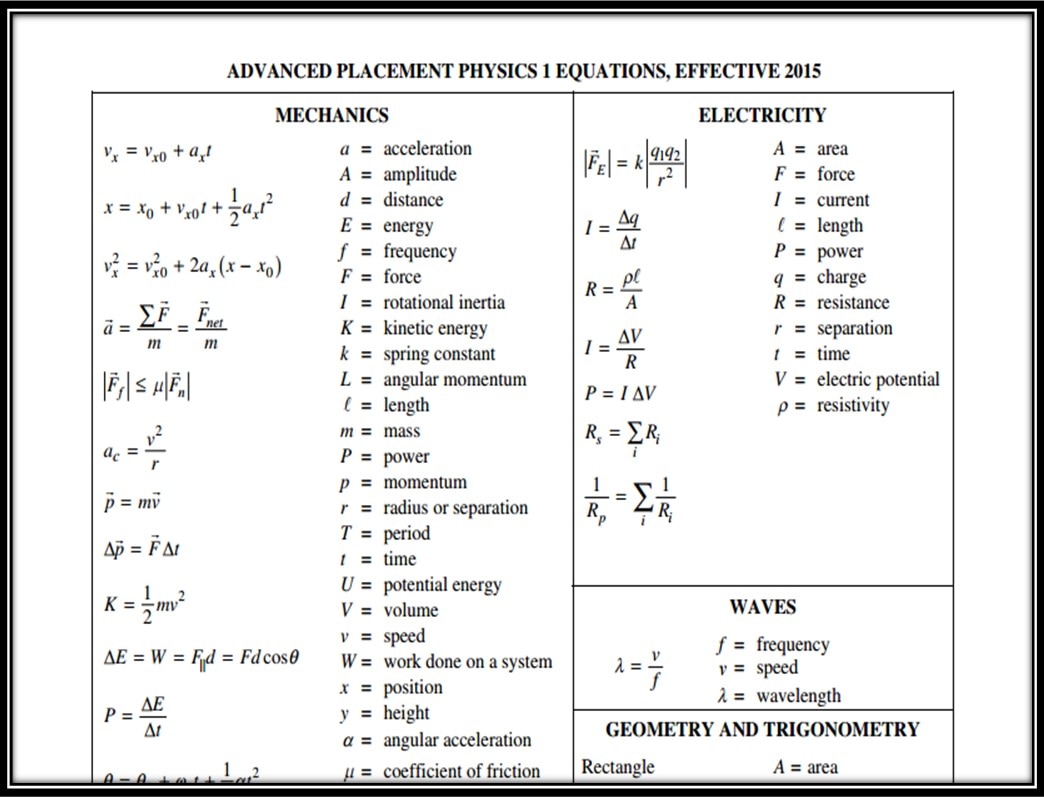 Сибизи (Дордрехт: Kluwer, 1996), стр. 303-314.
Сибизи (Дордрехт: Kluwer, 1996), стр. 303-314.
С. Ли, Д. Монтгомери «Затухающая двумерная турбулентность с жесткими стенками» Phys. лат. А 218, 281, 1996
Д.Монтгомери и К. Шан> «Магнитогидродинамическая турбулентность с чистыми течениями» в «Мелкомасштабных структурах в трехмерной гидродинамической и магнитогидродинамической турбулентности», под редакцией М. Менегуцци, А. Пуке и П.-Л. Сулем (Берлин, Springer-Verlag, 1995; стр. 241-254)
Д. Монтгомери и У.Х. Маттеус «Анизотропный модальный перенос энергии в межзвездной турбулентности» Astrophys. Журнал 447, 706 (1995)
X. Shan & D. Montgomery «Магнитогидродинамическая стабилизация посредством вращения» Phys.Преподобный Летт. 73, 1624 (1994)
Д. Монтгомери и X. Шан «Тороидальные резистивные МГД-равновесия» Комментарии о физике плазмы. & контр. Фьюжн 15, 315 (1994)
В.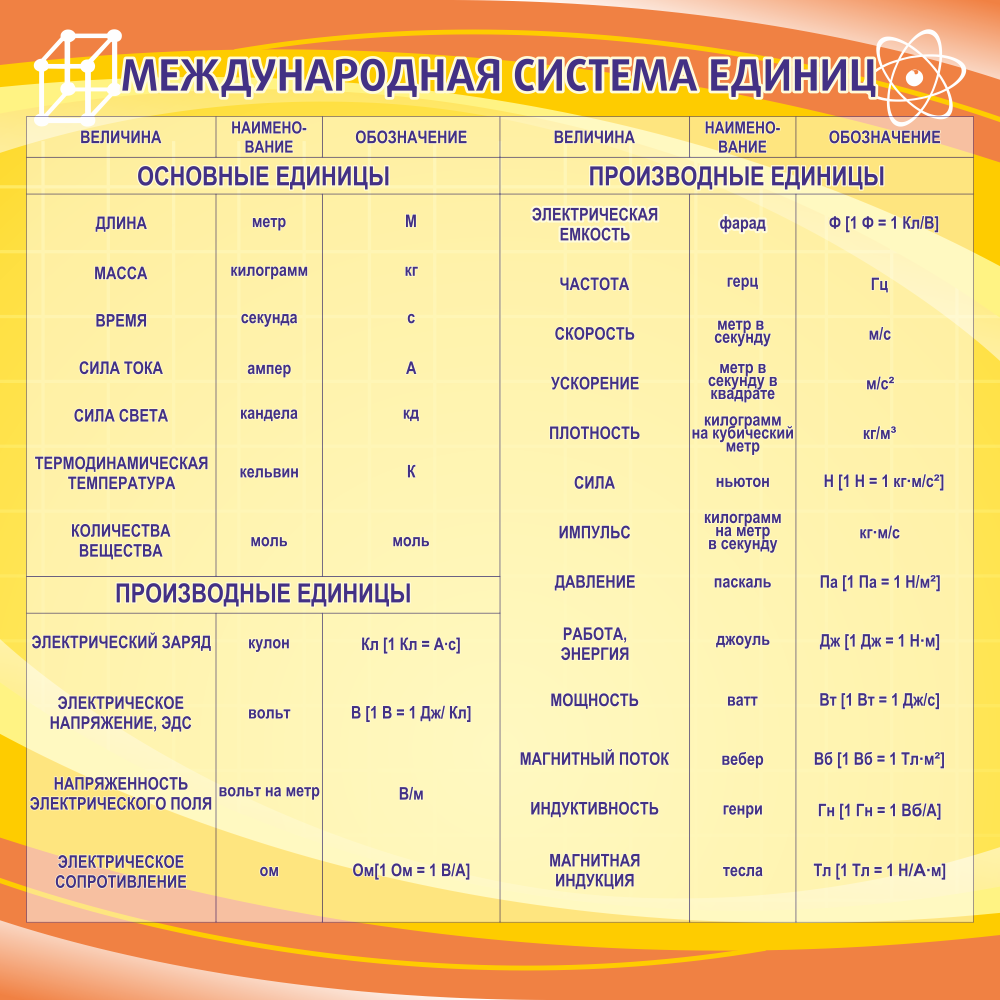 Б. Джонс и Д. Монтгомери «Установившиеся состояния конечной амплитуды двухмерного потока в канале с высоким числом Рейнольдса» Physica D 73, 227 (1994)
Б. Джонс и Д. Монтгомери «Установившиеся состояния конечной амплитуды двухмерного потока в канале с высоким числом Рейнольдса» Physica D 73, 227 (1994)
X. Шан и Д. Монтгомери О роли числа Гартмана в магнитогидродинамической активности «Физика плазмы.& контр. Fusion 35, 619 и 1019 (1993).
Х. Чен и Д. Монтгомери «Равновесные свойства вращающейся плазмы: различия между скоростью жидкости и скоростью дрейфа» J. Plasma Phys. 49, 341 (1993)
Д. Монтгомери, К. Шан и У.Х. Маттеус «Релаксация Навье-Стокса к состояниям Шинга-Пуассона при конечных числах Рейнольдса» Phys. Жидкости А 5, 2207 (1993).
Д. Монтгомери, У.Х. Маттеус, В.Т. Стриблинг, Д. Мартинес и С. Оутон «Релаксация в двух измерениях и уравнение Синха-Пуассона». Phys. Fluids A 4, 3 (1992)
Д. Монтгомери «Модификации магнитогидродинамики применительно к солнечному ветру» J. Geophys. Рез.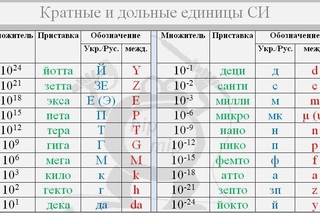 97, 4309 (1992)
97, 4309 (1992)
Д. Монтгомери «Пороги магнитогидродинамической устойчивости как функция числа Гартмана и коэффициента Пинча» Plasma Phys. & контр. Фьюжн 34, 1157 (1992)
Вт.Х. Маттеус, В. Т. Стриблинг, Д. Мартинес, С. Оутон и Д. Монтгомери «Затухающая двумерная турбулентность Навье-Стокса при очень длительных временах» Physica D 51, 531 (1991)
X. Шан, Д. Монтгомери и Х. Чен «Нелинейная магнитогидродинамика с помощью расчета методом Галеркина» Phys. Ред. А 44, 6800 (1991).
Physics4Kids.com: Свет и оптика: преломление
Когда ученые говорят о преломлении, они используют формулу.«n = c/v» «c» — скорость света в вакууме , «v» — скорость света в этом веществе, а «n» — показатель преломления . Согласно формуле, показатель преломления есть отношение скорости света в вакууме к скорости света в веществе. Но что такое преломление? Когда свет переходит из одного вещества в другое, он меняет скорость и направление . Это изменение направления называется преломлением. Некоторые показатели преломления алмазные (2.419), стекло (1,523) и вода (1,33).
Это изменение направления называется преломлением. Некоторые показатели преломления алмазные (2.419), стекло (1,523) и вода (1,33).
Давайте прыгнем сюда. Поскольку наша формула говорит, что n=c/v, и мы знаем, что значение c является константой, мы можем понять, что свет имеет разные скорости, когда он находится в разных веществах. Он движется на полной скорости в вакууме и медленнее везде. Используя наши примеры, мы можем обнаружить, что свет в воде движется быстрее, чем в алмазе. Свет движется с максимальной скоростью, когда находится в вакууме. Свет движется со скоростью около 124 000 000 метров в секунду (меньше половины скорости в вакууме) в алмазе по сравнению с 299 792 458 метрами в секунду в вакууме.
Свет преломляется только тогда, когда он падает на границу под углом, поэтому, если свет попадает прямо в вещество, он будет продолжать двигаться прямо вниз. Нужно понимать, что скорость света меняется в разных веществах. Если световой луч замедляется при попадании на вещество, он отклоняется в сторону нормали. Нормаль – это линия, которая перпендикулярна поверхности вещества. Если световой луч ускоряется при попадании на вещество, он отклоняется от нормали.
Нормаль – это линия, которая перпендикулярна поверхности вещества. Если световой луч ускоряется при попадании на вещество, он отклоняется от нормали.
Или поищите на сайтах по конкретной теме.
Оптика и алгебра (видео NASAConnect)
Encyclopedia.com:
http://www.encyclopedia.com/topic/refraction.aspx
Википедия:
http://en.wikipedia.org/wiki/Refraction
Британская энциклопедия:
http://www.britannica.com/EBchecked/topic/495648/refraction
Разделы Physics4Kids
Сеть научных и математических сайтов Rader
Расчет мощности цепи — AP Physics C Электричество
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится
на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.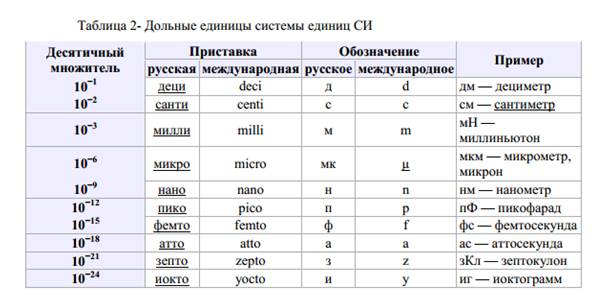 д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Филип С. Нельсон, биологическая физика, Пенсильванский университет
Пересмотрено, уточнено, обновлено в 2022 г. по сравнению с первым изданием (WH Freeman and Co, 2015).Доступно до 1 января 2022 года в виде электронной книги на Amazon. Чтобы получить печатную копию, перейдите по этой ссылке. Первое издание доступно в китайском переводе: 生命系统的物理建模 на этих сайтах.
по сравнению с первым изданием (WH Freeman and Co, 2015).Доступно до 1 января 2022 года в виде электронной книги на Amazon. Чтобы получить печатную копию, перейдите по этой ссылке. Первое издание доступно в китайском переводе: 生命系统的物理建模 на этих сайтах.
три ссылки.
Отзывы о новом выпуске:
«Что я нахожу особенным в этой книге, так это ее изящный переход от фундаментальной математики к приложениям в биологии и анализу реальных данных. Главы книги прекрасно сочетаются друг с другом, а наборы задач — редкое достояние». — проф.Амир Эрез, Еврейский университет
«Отличная книга, хорошо написанная и прекрасно иллюстрированная… Множество домашних заданий, сравнения с реальными данными и удачная комбинация слов, рисунков, уравнений и компьютерного кода… шедевр.» — Проф. Брэдли Рот, Univ. Окленда
«Замечательный учебник. Он позволяет студентам, изучающим биологические науки, не только увидеть, но и понять, как случайность в основе живых систем может привести к предсказуемым результатам.
Учащиеся моего класса, обучавшиеся с использованием PMLS, , сочли текст сложным для интеллектуального развития и, как следствие, интересным и запоминающимся», — проф. Дуглас Мартин, Университет Лоуренса
.
Рецензии на первое издание:
«Особенно привлекателен своей гладкой интеграцией биологических экспериментов, физических
модели и вычислительные упражнения. Читатели, закончившие текст, будут хорошо подготовлены
с вычислительными и математическими навыками, необходимыми для количественного понимания
ряд биологических систем…. Благодаря искусному письму Нельсона и отличному
сопровождающих интернет-ресурсы, эта книга понравится широкой аудитории и научит даже
новичок, как решать задачи численно.» — Ева-Мария Коллинз
по физике сегодня
«Филип Нельсон проделал потрясающую работу.
.. Есть множество черт, которые делают этот текст
уникальная среди очень многих книг по биологической физике…. Презентация материалов
разработан в новаторской манере…. Существует хороший баланс между концептуальным
примеры и задачи в конце главы….
Физические модели живых систем …. будет полезен студентам, а также
другие с явным интересом к геномике, протеомике, клеточной передаче сигналов, биоинженерии,
регенеративная медицина и синтетическая биология» — Ливиу Мовиляну в American Journal of
Физика 84 (6), июнь 2016
«Его превосходная книга понравится как студентам, так и профессиональным ученым в этой области.
количественной биологии…. [Э] книга кажется личной в выборе тем и
тренировочное путешествие, на которое он берет своих читателей.На наш взгляд, сочетание этого
уникальность с технической точностью делает книгу достойным внимания и ценным дополнением к
ресурсы для продвинутого образования в области биофизики … [Э] книга содержит богатую информацию,
четко структурирована и предоставляет исчерпывающие наборы данных… Нельсон показывает, как вычислительные
Программирование может быть эффективно использовано при моделировании биологических систем на клеточном и
молекулярные уровни.— Дитлинд Л. Герлофф
и Джонхун Кан. Образование в области клеточной биологии (2016), том. 15 (4) с. fe11-fe11.
Микаэль С. Рехтсман | Научный колледж Эберли
Избранные публикации
Топологическая защита мод фотонных дефектов средней запрещенной зоны, Джихо Но, Владимир А. Бенальказар, Шэн Хуан, Мэтью Дж. Коллинз, Кевин Чен, Тейлор Л. Хьюз и Микаэль С.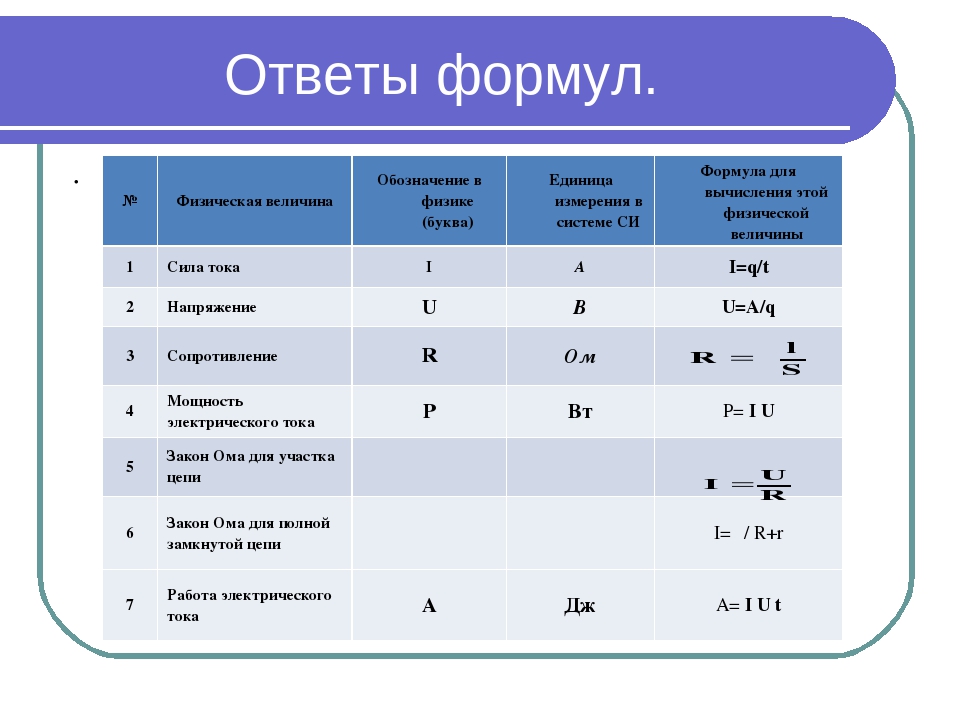 Рехтсман, , Nature Photonics , 12, 408–415 (2018 г.)
Рехтсман, , Nature Photonics , 12, 408–415 (2018 г.)
Фотонная топологическая граничная накачка как проба четырехмерной квантовой физики Холла, Одед Зильберберг, Шэн Хуанг, Джонатан Гульельмон, Мохан Ван, Кевин П.Чен, Яаков Краус, Микаэль К. Рехтсман, Nature , 553:59-62 (2018).
Экспериментальное наблюдение оптических точек Вейля и состояний поверхности, подобных ферми-дугам, Джихо Но, Шенг Хуан, Даниэль Лейкам, Ю. Д. Чонг, Кевин П. Чен и Микаэль С. Рехтсман, Nature Physics , 13(6):611–617 ( 2017).
Топологически защищенные связанные состояния в фотонных кристаллах с временной симметрией четности, С. Вейманн, М. Кремер, Ю. Плотник, Ю. Люмер, С. Нольте, К. Г. Макрис, М. Сегев, М. С. Рехтсман и А. Замейт, Nature Materials , 16:433438 (2017).
Топологические изоляторы флоке, вызванные беспорядком, Парадж Титум, Нетанел Х. Линднер, Микаэль С. Рехтсман и Гил Рафаэль, Physical Review Letters , 114(5):056801 (2015).
Наблюдение новых краевых состояний в фотонном графене, Ю. Плотник, М. С. Рехтсман, Д. Сонг, Дж. М. Цойнер, А. Самейт, М. Сегев, З. Чен, Nature Materials 13, 5762 (2014).
Самолокализованные состояния в фотонных топологических изоляторах, Ю. Люмер, Ю. Плотник, М. С. Рехтсман и М. Сегев, Phys.Преподобный Летт. 111, 243905 (2013 г.).
Photonic Floquet Topological Insulators, MC Rechtsman, JM Zeuner, Y Plotnik, Y Lumer, D Podolsky, S Nolte, F Dreisow, M Segev, A Szameit, Nature 496, 196–200 (2013).
Псевдомагнитное поле, индуцированное деформацией, и уровни Ландау в фотонных структурах, MC Rechtsman, JM Zeuner, M Heinrich, A Tunnermann, M Segev, A Szameit, Nature Photonics 7, 153-158 (2013).
— см. интервью Рэйчел Вон в Nature Photonics: «Может ли напряжение намагничивать свет?»
— см. статью «Новости и мнения» в журнале Nature Photonics, автор Томас Лепети,
.

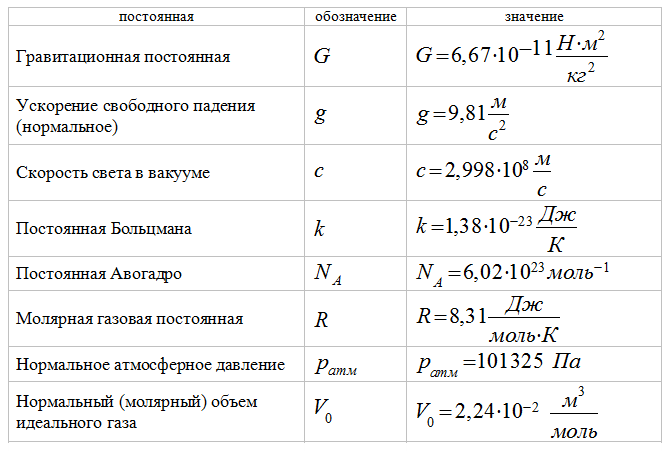 Механика
Механика
 И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 242-253.
И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 242-253.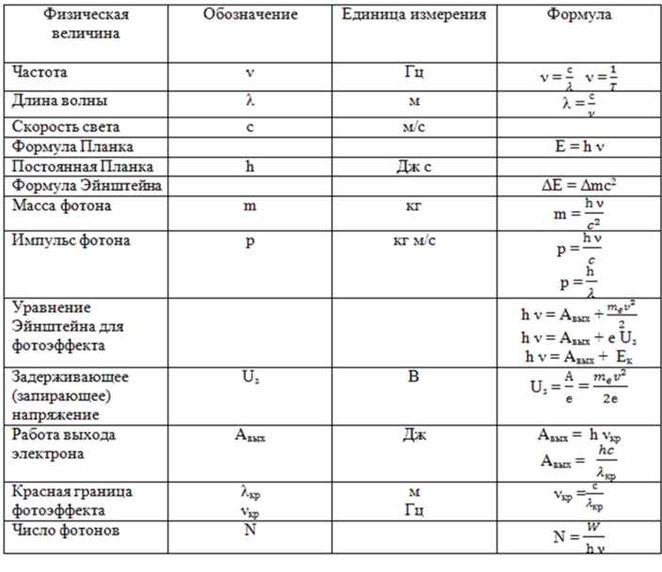
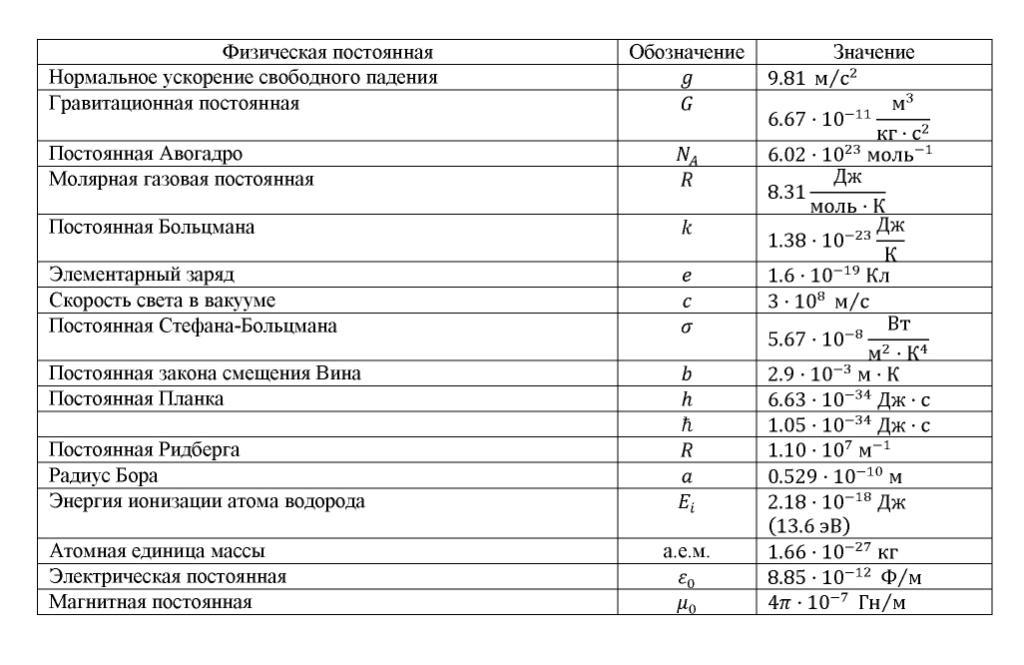 Учащиеся моего класса, обучавшиеся с использованием PMLS, , сочли текст сложным для интеллектуального развития и, как следствие, интересным и запоминающимся», — проф. Дуглас Мартин, Университет Лоуренса
Учащиеся моего класса, обучавшиеся с использованием PMLS, , сочли текст сложным для интеллектуального развития и, как следствие, интересным и запоминающимся», — проф. Дуглас Мартин, Университет Лоуренса .. Есть множество черт, которые делают этот текст
.. Есть множество черт, которые делают этот текст На наш взгляд, сочетание этого
На наш взгляд, сочетание этого