Симметричная и несимметричная нагрузка, что это такое
Симметричная и несимметричная нагрузка, что это такое
Трехфазный источник всегда представляет собой симметричную систему независимо от величины и характера нагрузки, так как внутреннее сопротивление источника ничтожно мало.
В нормально функционирующей трехфазной сети линейные напряжения (напряжения между каждой парой фазных проводников) равны друг другу по величине и различаются между собой по фазе на 120 градусов. Соответственно и фазные напряжения (напряжения между каждым фазным проводником и нейтральным проводником) равны между собой по величине и имеют аналогичные различия по фазе.
Как следует из вышесказанного, углы сдвига фаз между данными напряжениями равны между собой. Это и называется «симметричная трехфазная система напряжений».
Если к такой сети подключить симметричную нагрузку, то есть такую трехфазную нагрузку, при которой токи каждой из фаз будут равны по величине и по фазе, то такая нагрузка создаст симметричную систему токов (с одинаковыми углами сдвига фаз между ними).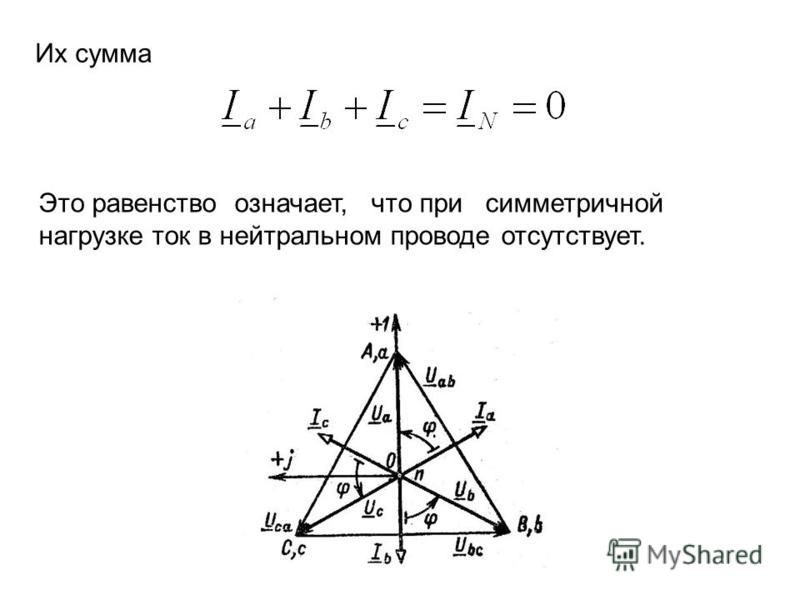 Это возможно при условии, когда во всех трех фазах нагрузки имеются одинаковые реактивные и активные сопротивления, то есть Za = Zb = Zc.
Это возможно при условии, когда во всех трех фазах нагрузки имеются одинаковые реактивные и активные сопротивления, то есть Za = Zb = Zc.
Поэтому и фазные токи оказываются в данных условиях равными по величине и по углу сдвига фаз между ними. Примеры симметричных нагрузок: трехфазный асинхронный двигатель, три одинаковые лампы накаливания — каждая на своей фазе, симметрично нагруженный трехфазный трансформатор и т.д.
Рассмотрим векторную диаграмму токов симметричной трехфазной нагрузки. Здесь легко увидеть, что геометрическая сумма векторов трех фазных токов обращается в ноль. Это значит, что при симметричной нагрузке ток нейтрального проводника будет равен нулю, и практически надобность в его использовании отпадает.
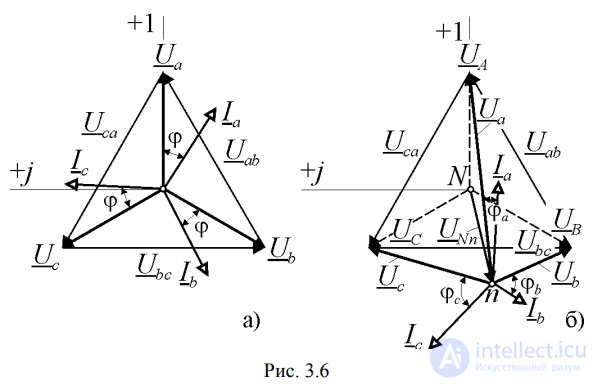
Если же к этой трехфазной сети с симметричной системой напряжений подключить несимметричную нагрузку, то есть такую нагрузку, при которой комплексные сопротивления нагрузки в каждой фазе различны (Za ≠ Zb ≠ Zc), то нагрузка создаст систему токов, которые будут различаться между собой по величине и по направлению (по сравнению с диаграммой токов, характерной для симметричной нагрузки). Значения этих фазных токов можно найти по закону Ома.
Значения этих фазных токов можно найти по закону Ома.
И тогда геометрическая сумма токов не обратится в ноль, а значит и в нейтральном проводнике будет иметь место переменный ток, поэтому нейтральный проводник в данном случае необходим. Примеры несимметричных нагрузок: лампы накаливания разной мощности в трех фазах, несимметрично нагруженный трехфазный трансформатор, нагрузки с разными коэффициентами мощности в трех фазах и т. д.
Нейтральный провод в данном случае обеспечит сохранение симметрии фазных напряжений несмотря на то, что нагрузка несимметрична. Вот почему четырехпроводная сеть допускает включение однофазных потребителей различной мощности и характера импеданса в разные фазы. Цепь каждой нагруженной фазы будет находится под фазным напряжением генератора независимо от разницы нагрузок между фазами.
Здесь изображена векторная диаграмма несимметричной нагрузки. На диаграмме легко видеть, что за счет наличия нулевого провода, ток в нем представляет собой геометрическую сумму векторов токов каждой из фаз, при этом фазные напряжения не испытывают перекоса, который непременно бы возник если бы нулевого провода при несимметричной нагрузке не было.
Если по какой-нибудь причине нейтральный провод оборвется во время питания несимметричной нагрузки, то возникнет резкий перекос напряжений и токов трехфазной сети, который может привести к аварии.
Перекос случится в этом случае потому, что три цепи нагрузки, питаемые трехфазным источником, вместе со внутренним сопротивлением источника, образуют три цепи разного импеданса, падение напряжения на каждой из которых будет разным и система напряжений трехфазной сети перестанет поэтому быть симметричной.
Ранее ЭлектроВести писали, что возложение спецобязательств по компенсации низких цен на электроэнергию для населения через включение в тариф ГП «НЭК« Укрэнерго» на передачу (вместо тарифа на диспетчеризацию) приведет к тому, что дополнительная финансовая нагрузка будет перераспределена между потребителями, а не производителями электроэнергии.
По материалам: electrik.info.
Контрольные вопросы и задачи — стр. 2
Контрольные
вопросы и задачи
Какой многофазный приемник является
симметричным?Какой
режим работы трехфазной цепи называется
симметричным?В
чем заключается специфика расчета
симметричных режимов работы трехфазных
цепей?С
помощью каких приемов трехфазная
симметричная схема сводится к расчетной
однофазной?Что
такое напряжение смещения нейтрали,
как оно определяется?Как
можно определить комплексы линейных
напряжений, если заданы их модули?Что
обеспечивает нейтральный провод с
нулевым сопротивлением?В
цепи на рис. 6,а
6,а
;
;
;
.
Линейное напряжение равно 380 В.
Определить ток
в нейтральном проводе.
Ответ:
.
В схеме предыдущей задачи
;
.
Остальные параметры те же.
Определить ток
в нейтральном проводе.
Ответ:
.
В задаче 8 нейтральный провод оборван.
Определить фазные
напряжения на нагрузке.
Ответ:
;
;
.
В задаче 9 нейтральный провод оборван.
Определить фазные
напряжения на нагрузке.
Ответ:
;
;
.
Лекция N 18
Применение векторных
диаграмм для анализа
несимметричных
режимов
Несимметричные
режимы в простейших характерных случаях
(короткое замыкание и холостой ход)
могут быть проанализированы на основе
построения векторных диаграмм.
Рассмотрим
режимы обрыва и короткого замыкания
фазы при соединении в звезду для трех-
и четырехпроводной систем. При этом
При этом
будем проводить сопоставление с
симметричным режимом работы цепи, фазные
напряжения и токи в которой будут
базовыми. Для этой цепи (см. рис.1,а)
векторная диаграмма токов и напряжений
приведена на рис. 1,б (принято, что нагрузка
носит
активно-индуктивный характер). Здесь
.
При
обрыве фазы А нагрузки приходим к
векторной диаграмме на рис. 2.
В
этом случае
.
При
коротком замыкании фазы А (трехпроводная
система) имеет место векторная диаграмма
на рис. 3. Из нее вытекает:
;
;
;
;
.
При
обрыве фазы А в четырехпроводной системе
(нейтральный провод на рис. 1,а показан
пунктиром, а вектор тока
—
пунктиром на рис. 1,б)
;
;
.
Симметричный
трехфазный приемник при соединении в
треугольник и соответствующая этому
случаю векторная диаграмма напряжений
и токов приведены на рис. 4.
Здесь
при том же способе соединения фаз
генератора
;
;
;
;
;
.
При
обрыве провода в фазе А-В нагрузки, как
это видно из схемы на рис. 5,
;
,
при этом сами токи
и
в
силу автономности режима работы фаз
при соединении нагрузки в треугольник
такие же, как и в цепи на рис. 4,а. Таким
образом,
;
;
.
Цепь
при обрыве линейного провода А-А’ и
соответствующая этому случаю векторная
диаграмма приведены на рис.6.
Здесь
;
;
.
Мощность
в трехфазных цепях
Мгновенная
мощность трехфазного источника энергии
равна сумме мгновенных мощностей его
фаз:
.
Активная
мощность генератора, определяемая как
среднее за период значение мгновенной
мощности, равна
.
Соответственно
активная мощность трехфазного приемника
с учетом потерь в сопротивлении
нейтрального провода
,
реактивная
и
полная
.
Суммарная
активная мощность симметричной трехфазной
системы
. | (1) |
Учитывая,
что в симметричном режиме для звезды
имеют место соотношения
и
для треугольника —
на
основании (1) для обоих способов соединения
фаз получаем
,
где
j — угол сдвига между фазными напряжением
и током.
Аналогично
Докажем
теперь указанное ранее свойство
уравновешенности двухфазной системы
Тесла и симметричной трехфазной системы.
1.
Двухфазная система Тесла
В
соответствии с рис. 7
| (2) |
. | (3) |
С
учетом (2) и (3)
.
Таким
образом, суммарная мгновенная мощность
фаз есть величина постоянная, равная
суммарной активной мощности источника.
2.
Симметричная трехфазная цепь
Тогда
Отсюда
,
т.е.
и для симметричной трехфазной цепи
свойство уравновешенности доказано.
Измерение
мощности в трехфазных цепях
Ниже
рассмотрены практические схемы включения
ваттметров для измерения мощности в
трехфазных цепях.
1.
Четырехпроводная система, несимметричный
режим.
Представленная
на рис. 8 схема называется схемой трех
ваттметров.
Суммарная
активная мощность цепи определяется
как сумма показаний трех ваттметров
.
2.
Четырехпроводная система, симметричный
режим.
Если
режим работы цепи симметричный, то для
определения суммарной активной мощности
достаточно ограничиться одним ваттметром
(любым), включаемым по схеме на рис. 8.
Тогда, например, при включении прибора
в фазу А,
. | (4) |
3.
Трехпроводная система, симметричный
режим.
При
отсутствии доступа к нейтральной точке
последняя создается искусственно с
помощью включения трех дополнительных
резисторов по схеме «звезда», как
показано на рис. 9 – схема ваттметра
с искусственной нейтральной точкой.
При этом необходимо выполнение условия
,
где
—
собственное сопротивление обмотки
ваттметра. Тогда суммарная активная
мощность трехфазной системы определяется
согласно (4).
4.
Трехпроводная система, симметричный
режим; измерение реактивной мощности.
С
помощью одного ваттметра при симметричном
режиме работы цепи можно измерить ее
реактивную мощность. В этом случае схема
включения ваттметра будет иметь вид по
рис. 10,а. Согласно векторной диаграмме
на рис. 10,б измеряемая прибором мощность
.
Таким
образом, суммарная реактивная мощность
.
5.
Трехпроводная система, несимметричный
режим.
Представленная
на рис. 11 схема называется схемой двух
ваттметров. В ней сумма показаний
В ней сумма показаний
приборов равна суммарной активной
мощности цепи.
Действительно,
показания приборов в данной схеме:
.
Тогда
В
заключение отметим, что если в схеме на
рис. 11 имеет место симметричный режим
работы, то на основании показаний
приборов можно определить суммарную
реактивную мощность цепи
. | (5) |
Литература
Основы теории цепей: Учеб. для вузов
/Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.:
Энергоатомиздат, 1989. -528с.Бессонов
Л.А. Теоретические основы электротехники:
Электрические цепи. Учеб. для студентов
электротехнических, энергетических и
приборостроительных специальностей
вузов. –7-е изд., перераб. и доп. –М.:
Высш. шк., 1978. –528с.
Контрольные
вопросы и задачи
В симметричной трехпроводной цепи
произошел обрыв фазы. Что покажет
Что покажет
вольтметр, включенный между найтральными
точками источника и приемника?
Ответ:
.
Во сколько раз мощность в цепи на рис.
6,а меньше мощности в цепи на рис. 4,а?
Ответ: в два раза.
В цепи на рис. 10,а симметричная нагрузка
составлена из резистивных элементов.
Что покажет ваттметр?
Ответ:
.
В цепи на рис. 10,а симметричная нагрузка
с фазным сопротивлением
соединена
в звезду. Линейное напряжение
.
Определить
показание ваттметра.
Ответ:
.
В цепи на рис. 11 нагрузкой служат два
одинаковых конденсатора с ХС=100 Ом,
включенные между линейными проводами
А и В, В и С соответственно. Линейное
напряжение
.
Определить
показания ваттметров.
Ответ:
.
На основе построения векторной диаграммы
токов и напряжений для симметричного
режима работы цепи на рис. 11 доказать
11 доказать
соотношение (5).
Лекция N 19
Метод симметричных
составляющих
Метод
симметричных составляющих относится
к специальным методам расчета трехфазных
цепей и широко применяется для анализа
несимметричных режимов их работы, в том
числе с нестатической нагрузкой. В
основе метода лежит представление
несимметричной трехфазной системы
переменных (ЭДС, токов, напряжений и
т.п.) в виде суммы трех симметричных
систем, которые называют симметричными
составляющими. Различают симметричные
составляющие прямой, обратной и
нулевой последовательностей, которые
различаются порядком чередования фаз.
Симметричную
систему прямой последовательности
образуют (см. рис. 1,а) три одинаковых по
модулю вектора
и
со
сдвигом друг по отношению к другу на
рад.,
причем
отстает
от
,
а
—
от
.
Введя,
оператор поворота
,
для симметричной системы прямой
последовательности можно записать
.
Симметричная
система обратной последовательности
образована равными по модулю векторами
и
с
относительным сдвигом по фазе на
рад.,
причем теперь
отстает
от
,
а
—
от
(см.
рис. 1,б). Для этой системы имеем
.
Система
нулевой последовательности состоит из
трех векторов, одинаковых по модулю и
фазе (см. рис. 1,в):
.
При
сложении трех указанных систем векторов
получается несимметричная система
векторов (см. рис. 2).
Любая
несимметричная система однозначно
раскладывается на симметричные
составляющие. Действительно,
; | (1) |
; | (2) |
. | (3) |
Таким
образом, получена система из трех
уравнений относительно трех неизвестных
,
которые, следовательно, определяются
однозначно. Для нахождения
Для нахождения
сложим
уравнения (1)…(3). Тогда, учитывая, что
,
получим
. | (4) |
Для
нахождения
умножим
(2) на
,
а (3) – на
,
после чего полученные выражения сложим
с (1). В результате приходим к соотношению
. | (5) |
Для
определения
с
соотношением (1) складываем уравнения
(2) и (3), предварительно умноженные
соответственно на
и
.
В результате имеем:
. | (6) |
Формулы
(1)…(6) справедливы для любой системы
векторов
,
в том числе и для симметричной. В последнем
случае
.
В
заключение раздела отметим, что помимо
вычисления симметричные составляющие
могут быть измерены с помощью специальных
фильтров симметричных составляющих,
используемых в устройствах релейной
защиты и автоматики.
Свойства
симметричных составляющих токов
и
напряжений различных последовательностей
Рассмотрим
четырехпроводную систему на рис. 3. Для
тока в нейтральном проводе имеем
.
Тогда
с учетом (4)
, | (7) |
т.е.
ток в нейтральном проводе равен утроенному
току нулевой последовательности.
Если
нейтрального провода нет, то
и
соответственно нет составляющих тока
нулевой последовательности.
Поскольку
сумма линейных напряжений равна нулю,
то в соответствии с (4) линейные напряжения
не содержат составляющих нулевой
последовательности.
Рассмотрим
трехпроводную несимметричную систему
на рис. 4.
Здесь
Тогда,
просуммировав эти соотношения, для
симметричных составляющих нулевой
последовательности фазных напряжений
можно записать
.
Если
система ЭДС генератора симметрична, то
из последнего получаем
. | (8) |
Из
(8) вытекает:
в фазных напряжениях симметричного
приемника отсутствуют симметричные
составляющие нулевой последовательности;симметричные
составляющие нулевой последовательности
фазных напряжений несимметричного
приемника определяются величиной
напряжения смещения нейтрали;фазные
напряжения несимметричных приемников,
соединенных звездой, при питании от
одного источника различаются только
за счет симметричных составляющих
нулевой последовательности; симметричные
составляющие прямой и обратной
последовательностей у них одинаковы,
поскольку однозначно связаны с
соответствующими симметричными
составляющими линейных напряжений.
При
соединении нагрузки в треугольник
фазные токи
и
могут
содержать симметричные составляющие
нулевой последовательности
.
При этом
(см.
рис. 5) циркулирует по контуру, образованному
фазами нагрузки.
Сопротивления
симметричной трехфазной цепи
для
токов различных последовательностей
Если
к симметричной цепи приложена симметричная
система фазных напряжений прямой
(обратной или нулевой) последовательностей,
то в ней возникает симметричная система
токов прямой (обратной или нулевой)
последовательности. При использовании
метода симметричных составляющих на
практике симметричные составляющие
напряжений связаны с симметричными
составляющими токов той же последовательности.
Отношение симметричных составляющих
фазных напряжений прямой (обратной или
нулевой) последовательности к
соответствующим симметричным составляющим
токов называется комплексным
сопротивлением прямой
,
обратной
и
нулевой
последовательностей.
Пусть
имеем участок цепи на рис. 6. Для фазы А
этого участка можно записать
. | (9) |
Тогда
для симметричных составляющих прямой
и обратной последовательностей с учетом,
того, что
,
на основании (9) имеем
.
Отсюда
комплексные сопротивления прямой и
обратной последовательностей одинаковы
и равны:
.
Для
симметричных составляющих нулевой
последовательности с учетом равенства
соотношение
(9) трансформируется в уравнение
,
откуда
комплексное сопротивление нулевой
последовательности
.
В
рассмотренном примере получено равенство
сопротивлений прямой и обратной
последовательностей. В общем случае
эти сопротивления могут отличаться
друг от друга. Наиболее типичный пример
– различие сопротивлений вращающейся
машины для токов прямой и обратной
последовательностей за счет многократной
разницы в скольжении ротора относительно
вращающегося магнитного поля для этих
последовательностей.
Применение
метода симметричных составляющих
для
симметричных цепей
Расчет
цепей методом симметричных составляющих
основывается на принципе наложения, в
виду чего метод применим только к
линейным цепям. Согласно данному методу
Согласно данному методу
расчет осуществляется в отдельности
для составляющих напряжений и токов
различных последовательностей, причем
в силу симметрии режимов работы цепи
для них он проводится для одной фазы
(фазы А). После этого в соответствии с
(1)…(3) определяются реальные искомые
величины. При расчете следует помнить,
что, поскольку в симметричном режиме
ток в нейтральном проводе равен нулю,
сопротивление нейтрального провода
никак ни влияет на симметричные
составляющие токов прямой и обратной
последовательностей. Наоборот, в схему
замещения для нулевой последовательности
на основании (7) вводится утроенное
значение сопротивления в нейтральном
проводе. С учетом вышесказанного исходной
схеме на рис. 7,а соответствуют расчетные
однофазные цепи для прямой и обратной
последовательностей (рис. 7,б) и нулевой
последовательности (рис. 7,в).
Существенно
сложнее обстоит дело при несимметрии
сопротивлений по фазам. Пусть в цепи на
рис. 3
.
Разложив токи на симметричные составляющие,
для данной цепи можно записать
| (10) |
В
свою очередь
(11) |
Подставив
в (11) значения соответствующих параметров
из (10) после группировки членов получим
(12) |
где
;
Из
полученных соотношений видно, что если
к несимметричной цепи приложена
несимметричная система напряжений, то
каждая из симметричных составляющих
токов зависит от симметричных составляющих
напряжений всех последовательностей.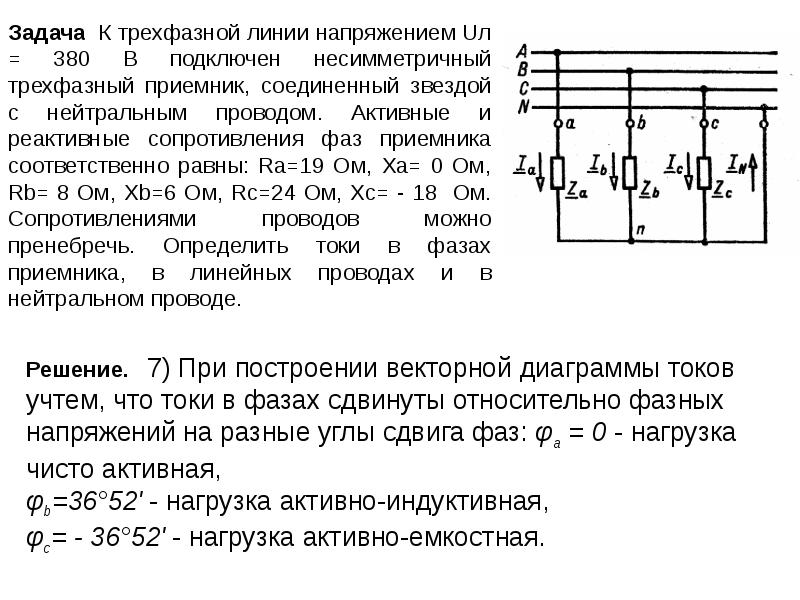
Поэтому, если бы трехфазная цепь на всех
участках была несимметрична, рассматриваемый
метод расчета не давал бы преимуществ.
На практике система в основном является
симметричной, а несимметрия обычно
носит локальный характер. Это
обстоятельство, как будет показано в
следующей лекции, значительно упрощает
анализ.
На
всех участках цепи, где сопротивления
по фазам одинаковы,
для
i¹k. Тогда из (12) получаем
.
Литература
Основы теории цепей: Учеб. для вузов
/Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.:
Энергоатомиздат, 1989. -528с.Бессонов
Л.А. Теоретические основы электротехники:
Электрические цепи. Учеб. для студентов
электротехнических, энергетических и
приборостроительных специальностей
вузов. –7-е изд., перераб. и доп. –М.:
Высш. шк., 1978. –528с.
Контрольные
вопросы и задачи
В каких случаях отсутствуют составляющие
нулевой последовательности в линейных
токах?Для
каких цепей сопротивления прямой и
обратной последовательностей одинаковы,
а для каких – различны?Для
анализа каких цепей возможно применение
метода симметричных составляющих?Как
при использовании метода симметричных
составляющих учитывается сопротивление
в нейтральном проводе?В
чем заключается упрощение расчета цепи
при использовании метода симметричных
составляющих?Определить
коэффициент несимметрии линейных
напряжений
,
если
,
.
Ответ:
.
До короткого замыкания в фазе А в цепи
на рис. 4 был симметричный режим, при
котором ток в фазе А был равен
.Разложить
токи на симметричные составляющие.
Ответ:
;
.
Линейные напряжения на зажимах двигателя
и
.
Определить действующие значения токов
в фазах двигателя, если его сопротивления
прямой и обратной последовательностей
соответственно равны:
;
.
Нейтральный провод отсутствует.
Ответ:
;
;
.
Лекция N 20
Теорема об активном
двухполюснике
для симметричных
составляющих
В
тех случаях, когда трехфазная цепь в
целом симметрична, а несимметрия носит
локальный характер (местное короткое
замыкание или обрыв фазы, подключение
несимметричной нагрузки), для расчета
удобно применять теорему об активном
двухполюснике.
При
мысленном устранении несимметрии
(несимметричного участка) для оставшейся
цепи имеет место симметричный режим
холостого хода. В соответствии с методом
В соответствии с методом
эквивалентного генератора теперь
необходимо определить эквивалентные
ЭДС и входные сопротивления симметричной
цепи. В общем случае – при несимметрии
в системе фазных напряжений источника
– помимо эквивалентной ЭДС прямой
последовательности
будут
также иметь место эквивалентные ЭДС
обратной
и
нулевой
последовательностей.
Однако обычно напряжения генераторов
симметричны – тогда
.
Величина
,
соответствующая напряжению холостого
хода
на
зажимах подключения локальной
несимметрии, определяется при отключении
локальной несимметричной нагрузки
любым известным методом расчета линейных
цепей, причем в силу симметрии цепи
расчет проводится для одной фазы.
В
отдельности рассчитываются входные
сопротивления симметричной цепи для
различных последовательностей, которая
предварительно преобразуется известными
методами в пассивную цепь. При этом при
расчете входного сопротивления нулевой
последовательности
необходимо
учитывать только те участки цепи, которые
соединены с нейтральным проводом или
заземленной нейтральной точкой, т. е.
е.
принимать во внимание только те ветви,
по которым могут протекать токи нулевой
последовательности. Схемы для расчета
входных сопротивлений прямой и обратной
последовательностей одинаковы, однако
в случае вращающихся машин величины
этих сопротивлений различны.
Поскольку
в отдельности для каждой симметричной
последовательности имеет место
симметричный режим, расчет указанным
методом ведется на одну фазу с
использованием расчетных схем для
прямой (рис. 1,а), обратной (рис. 1,б) и
нулевой (рис. 1,в) последовательностей.
Данным
схемам соответствуют соотношения
; | (1) |
; | (2) |
. | (3) |
Поскольку
соотношений три, а число входящих в них
неизвестных шесть
,
необходимо составление трех дополнительных
уравнений, учитывающих конкретный вид
несимметрии.
Рассмотрим
некоторые типовые примеры применения
метода.
Однополюсное
короткое замыкание на землю (рис. 2).
.
Поскольку
фаза А замкнута на землю, то дополнительные
уравнения имеют вид
| (4) |
;
.
Тогда
С
учетом последних соотношений уравнения
(1)…(3) можно записать в виде
; | (5) |
; | (6) |
. | (7) |
Принимая
во внимание (4), а также то, что источник
питания симметричный
,
просуммируем (5), (6) и (7):
,
откуда
получаем
Двухполюсное
короткое замыкание без земли
(рис.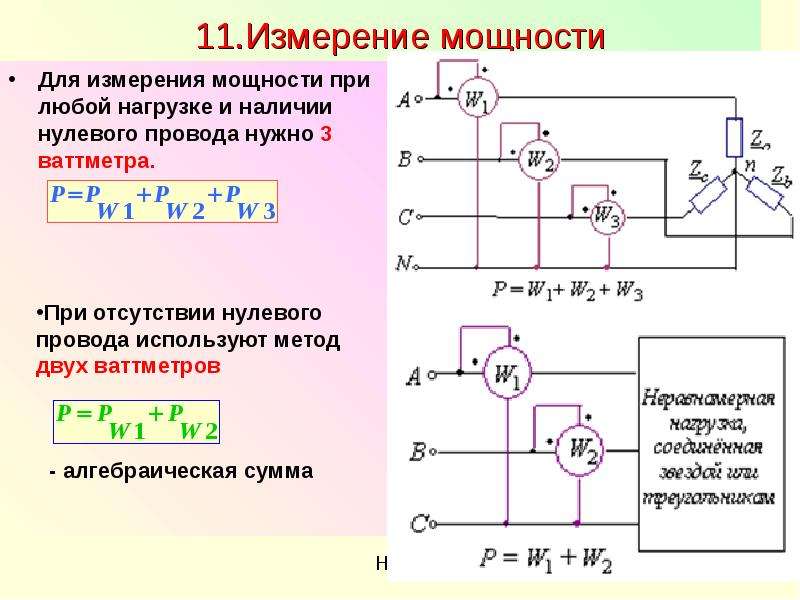 3).
3).
Для
рассматриваемого случая можно записать
Последнее
равенство объясняется отсутствием пути
для протекания токов нулевой
последовательности.
Из
двух последних соотношений вытекает,
что
.
При этом
,
так как
и
.
Подставив
полученные выражения для напряжений и
токов прямой и обратной последовательностей
в (1) и (2), запишем
; | (8) |
. | (9) |
Вычитая
из (8) соотношение (9) и учитывая, что в
силу симметрии источника
,
получим
,
откуда
.
Обрыв
линейного провода (рис. 4) – определить
напряжение в месте разрыва.
В
рассматриваемом случае дополнительные
уравнения имеют вид
; | (10) |
; | (11) |
. | (12) |
Из
соотношений (11) и (12) вытекает равенство:
. | (13) |
На
основании (1)…(3) с учетом (13) запишем
.
Принимая
во внимание симметричность источника
,
подставим последние выражения в (10):
,
—
откуда
.
Таким
образом, искомое напряжение
.
Подключение
несимметричной нагрузки
к
симметричной цепи (рис. 5).
Учитывая,
что
,
подставим в уравнения (1)…(3) определенные
в предыдущей лекции выражения
и
(см.
соотношение (12) в лекции №19):
Решая
данную систему уравнений, находим
и
.
Тогда
и
.
В
рассмотренных примерах предполагалось,
что необходимые для анализа цепи
параметры
и
предварительно
определены. Рассмотрим их расчет на
примере предыдущей задачи для некоторой
схемы на рис.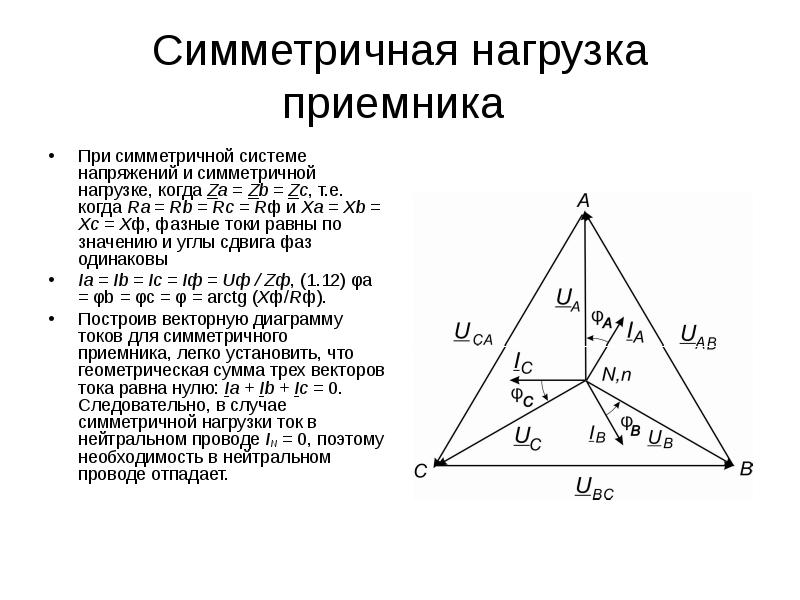 6.
6.
Поскольку
при отключении несимметричной нагрузки
оставшаяся
часть схемы будет работать в симметричном
режиме, для определения
получаем
расчетную однофазную схему на рис. 7.
Из
нее
.
Схема
для определения входных сопротивлений
прямой
и
обратной
последовательностей
одна и та же и соответствует цепи на
рис. 8,а. В соответствии с ней
.
Схема
для определения
,
полученная с учетом возможных путей
протекания токов нулевой последовательности,
приведена на рис. 8,б. Из нее
.
Выражение
мощности через симметричные составляющие
Комплекс
полной мощности в трехфазной цепи
. | (14) |
Для
фазных напряжений имеем
| (15) |
Учитывая,
что комплекс, сопряженный
,
равен
и
наоборот, для сопряженных комплексов
токов запишем:
| (16) |
Подставляя
(15) и (16) в (14), после соответствующих
преобразований получим
.
Отсюда
и
,
где
—
разности фаз соответствующих симметричных
составляющих напряжений и токов.
Литература
Основы теории цепей: Учеб. для вузов
/Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.:
Энергоатомиздат, 1989. -528с.Бессонов
Л.А. Теоретические основы электротехники:
Электрические цепи. Учеб. для студентов
электротехнических, энергетических и
приборостроительных специальностей
вузов. –7-е изд., перераб. и доп. –М.:
Высш. шк., 1978. –528с.
Контрольные
вопросы и задачи
В каких случаях целесообразно применение
теоремы об активном двухполюснике для
симмметричных составляющих?Как
рассчитываются эквивалентные
параметры симметричной цепи, к которой
подключается локальная несимметричная
нагрузка?В
чем заключаются особенности расчета
входного сопротивления нулевой
последовательности?Какова
последовательность анализа трехфазной
цепи с использованием теоремы об
активном двухполюснике для симметричных
составляющих?Определить
напряжения
и
в
цепи на рис. 3, если фазная ЭДС
3, если фазная ЭДС
,
а сопротивления прямой и обратной
последовательностей равны:
.
Ответ:
.
Фазы А и С симметричного трехфазного
источника замкнуты накоротко. Определить
ток короткого замыкания, если
,
а сопротивления прямой и обратной
последовательностей
.
Ответ:
.
Трехфазные цепи наиболее распространенные в современной электроэнергетике
Трехфазные цепи – наиболее распространенные в современной электроэнергетике. Это объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями: — экономичность производства и передачи энергии по сравнению с однофазными цепями; — возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя; — возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.
Трехфазная цепь состоит из трех основных элементов: трехфазного генератора, в котором механическая энергия преобразуется в электрическую с трехфазной системой ЭДС; линии передачи со всем необходимым оборудованием; приемников (потребителей), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания). Трехфазный генератор представляет собой синхронную машину двух типов: турбогенератор и гидрогенератор
Трехфазный генератор представляет собой синхронную машину двух типов: турбогенератор и гидрогенератор
Если ЭС одной фазы (например, фазы А) принять за исходную и считать её начальную фазу равной нулю, то выражения мгновенных значений ЭДС можно записать в виде (3. 1) e. A = Em sin ωt, e. B = Em sin (ωt — 120°), e. C = Em sin (ωt — 240°) = Em sin (ωt + 120°). e. A + e. B + e. C = 0
. Из векторных диаграмм рис 3. 4 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю: (3. 4) ĖA + ĖB + ĖC = 0.
Временная последовательность, в которой ЭДС достигает сначала максимума в фазе А, затем в фазе В и потом в фазе С, называется прямой последовательностью чередования фаз. Обратная последовательность может быть получена, если, например, вместо фазы В использовать фазу С и наоборот. От последовательности чередования фаз зависит, в частности, направление вращения ротора двигателя.
Способы соединения фаз трехфазного источника
Соединение фаз источника звездой При таком типе соединения (рис. 2) концы фаз X, Y, Z объединяют в одну общую точку Nи, которая называется нейтральной (индекс «и» обозначает принадлежность нейтральной точки источнику).
Напряжения на фазах источника U¢А, U¢В и U¢С, а также токи IА, IВ, IС в этих фазах принято называть фазными. Напряжения U¢АВ, U¢ВС и U¢СА между любыми двумя линейными проводами, а также токи в них принято называть линейными. Из рис. 2 видно, что при соединении звездой (l) линейные токи являются одновременно фазными. На этом же рисунке изображены принятые положительные направления ЭДС, токов и напряжений, а также векторная диаграмма линейных и фазных напряжений
на основании уравнений, составленных по П закону Кирхгофа для рассматриваемой цепи для контура I имеем: UАВ = U¢А — U¢В аналогично для других контуров: UВС = U¢В — U¢С UСА = U¢С — U¢А Из элементарных геометрических свойств равностороннего треугольника, образованного векторами линейных напряжений, которые тоже сдвинуты на 1200 относительно друга, видно, что при соединении фаз источника звездой (l) линейное напряжение вдля контура I имеем: раз больше фазного, т. е. UЛ =√ 3∙UФ. Таким образом, в четырехпроводной линии существуют две группы напряжений, отличающихся в √ 3∙ раз:
е. UЛ =√ 3∙UФ. Таким образом, в четырехпроводной линии существуют две группы напряжений, отличающихся в √ 3∙ раз:
Достоинством четырех проводной линии является то, что к ней возможно подключить однофазные потребителя, рассчитанные на различные напряжения (например, 380 В и 220
Соединение фаз источника треугольником (Δ). Такой способ соединения (рис. 3) реализуется, когда начало каждой фазы соединяют с концом предыдущей, соблюдая прямую последовательность чередования фаз А, В, С.
Из схемы (рис. 3) видно, что при соединении фаз источника треугольником (D) линейные напряжения тождественно равны фазным. При подключении к источнику трехфазного потребителя в линейных проводах возникнут линейные токи IА, IВ, IC, которые не будут равны фазным токам в обмотках источника IВА, I СВ и IАC (как в случае соединения звездой), а связаны с ними соотношениями, следующими из 1 закона Кирхгофа: IА = IВА – IАС IВ = IСВ – IВА IС = IАС – IСВ
Трехфазные потребители и способы их соединения
Соединение фаз генератора и приемника звездой
Провода A-a, B-b и C-c, соединяющие начала фаз генератора и приемника, называются линейными, провод N-n, соединяющий точку N генератора с точкой n приемника, – нейтральным. Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной. • Фазные (IФ) – это токи в фазах генератора и приемников. • Линейные (IЛ) – токи в линейных проводах. При соединении в звезду фазные и линейные токи равны (3. 5) IФ = IЛ. Ток, протекающий в нейтральном проводе, обозначают IN. По первому закону Кирхгофа для нейтральной точки n(N) имеем в комплексной форме (3. 6) İN = İA + İB + İC. В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа. (3. 7) ÚAB = ÚA — ÚB; ÚBC = ÚB — ÚC; ÚCA = ÚC — ÚA.
Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной. • Фазные (IФ) – это токи в фазах генератора и приемников. • Линейные (IЛ) – токи в линейных проводах. При соединении в звезду фазные и линейные токи равны (3. 5) IФ = IЛ. Ток, протекающий в нейтральном проводе, обозначают IN. По первому закону Кирхгофа для нейтральной точки n(N) имеем в комплексной форме (3. 6) İN = İA + İB + İC. В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа. (3. 7) ÚAB = ÚA — ÚB; ÚBC = ÚB — ÚC; ÚCA = ÚC — ÚA.
Согласно этим выражениям на рис. 3. 7 а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: UAB, UBC, UCA равны по величине и сдвинуты по фазе относительно друга на 120° (общее обозначение UЛ), и опережают, соответственно, векторы фазных напряжений UA, UB, UC, (UФ) на угол 30°.
Действующие значения линейных напряжений можно определить графически по векторной диаграмме или по формуле (3. 8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений: UЛ = 2 UФ cos 30° или UЛ = UФ. (3. 8) Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями: UЛ = 660 В; UФ = 380 В; UЛ = 380 В; UФ = 220 В; UЛ = 220 В; UФ = 127 В.
Классификация приемников в трехфазной цепи Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т. д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой : Za = Zb = Zc = Zejφ. Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
Соединение фаз генератора и приемника треугольником Соединение фаз источника в замкнутый треугольник возможно при симметричной системе ЭДС, так как (3. 17) ĖA + ĖB + ĖC = 0. Если соединение обмоток треугольником выполнено неправильно, т. е. в одну точку соединены концы или начала двух фаз, то суммарная ЭДС в контуре треугольника отличается от нуля и по обмоткам протекает большой ток. Это аварийный режим для источников питания, и поэтому недопустим.
Напряжение между концом и началом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению. UЛ = UФ , (3. 18) В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Токи в фазах приемника определяются по формулам İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca. Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c İA = İab — İca; İB = İbc — İab; İC = İca — İbc. (3. 19) Сложив левые и правые части системы уравнений, (3. 20), получим (3. 21) İA + İB + İC = 0, т. е. сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке.
Токи в фазах приемника определяются по формулам İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca. Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c İA = İab — İca; İB = İbc — İab; İC = İca — İbc. (3. 19) Сложив левые и правые части системы уравнений, (3. 20), получим (3. 21) İA + İB + İC = 0, т. е. сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке.
Четырехпроводная цепь Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Если полные комплексные сопротивления фаз приемника равны Za = Zb = Zc, то токи в каждой фазе можно определить по формулам (3. 10) İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc. В соответствии с первым законом Кирхгофа ток в нейтральном проводе (3. 11) İN = İa + İb + İc = İA + İB + İC.
Симметричная нагрузка приемника При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.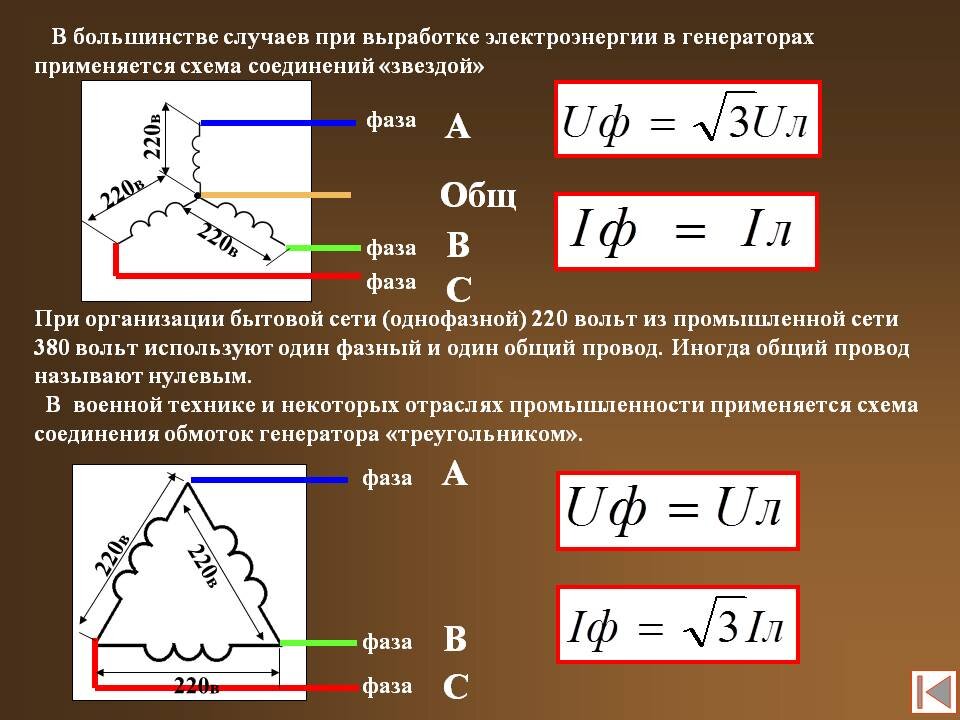 е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы (3. 12) Ia = Ib = Ic = Iф = Uф / Zф, (3. 13) φa = φb = φc = φ = arctg (Xф/Rф). Построив векторную диаграмму токов для симметричного приемника (рис. 3. 8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы (3. 12) Ia = Ib = Ic = Iф = Uф / Zф, (3. 13) φa = φb = φc = φ = arctg (Xф/Rф). Построив векторную диаграмму токов для симметричного приемника (рис. 3. 8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
Несимметричная нагрузка приемника При симметричной системе напряжений и несимметричной нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и определяются по закону Ома İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc. Ток в нейтральном проводе İN равен геометрической сумме фазных токов İN = İa + İb + İc. Напряжения будут Ua = UA; Ub = UB; Uc = UC, UФ = UЛ / , благодаря нейтральному проводу при ZN = 0. Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.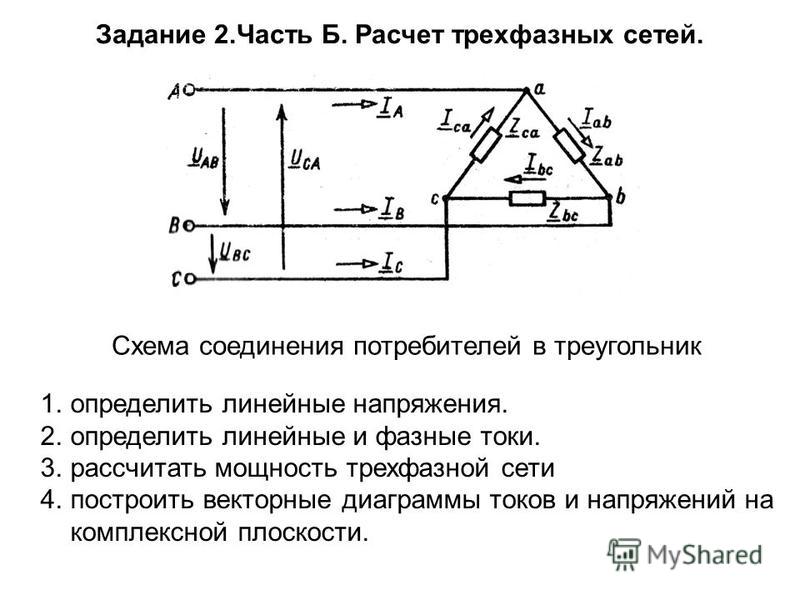
Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз. Векторная диаграмма при несимметричной нагрузке приведена на рис. 3. 9
Трехпроводная электрическая цепь Схема соединения источника и приемника звездой без нейтрального провода
При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, Un. N = 0. При несимметричной нагрузке Za ≠ Zb ≠ Zc между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали Un. N. Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3. 10 представляет собой схему с двумя узлами, (3.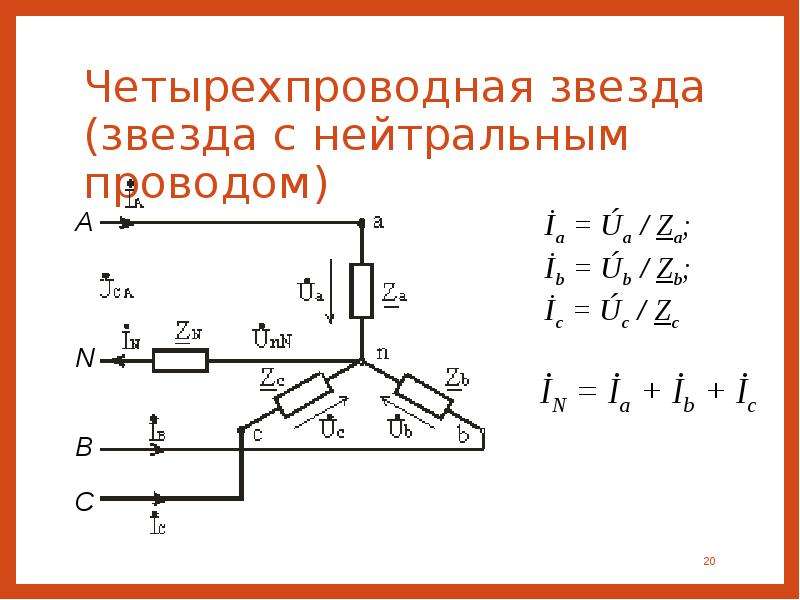 14) , где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки.
14) , где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки.
Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что (3. 15) Úa = ÚA — Ún. N; Úb = ÚB — Ún. N; Úc = ÚC — Ún. N. Зная фазные напряжения приемника, можно определить фазные токи: (3. 16) İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc. При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали Un. N может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно.
Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали). Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.
Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали). Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.
Поэтому нейтральный провод необходим для того, чтобы: • выравнивать фазные напряжения приемника при несимметричной нагрузке; • подключать к трехфазной цепи однофазные приемники с номинальным напряжением в раз меньше номинального линейного напряжения сети. Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.
Симметричная нагрузка в Zab = Zbc = Zca = Zejφ, İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca. Линейные токи İA = İab — İca; İB = İbc — İab; İC = İca — İbc; На векторной диаграмме (рис. 3. 14) фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т. е. φ > 0°). Здесь принято, что напряжение UAB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в UЛ = UФ; IЛ = IФ.
3. 14) фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т. е. φ > 0°). Здесь принято, что напряжение UAB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в UЛ = UФ; IЛ = IФ.
Несимметричная нагрузка приемника Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активноемкостная приведена на рис Построение векторов линейных токов произведено в соответствии с выражениями İA = İab — İca; İB = İbc — İab; İC = İca — İbc.
Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки.
Мощность трехфазной цепи, ее расчет и измерение Энергия, передаваемая при переменном синусоидальном напряжении от источника к потребителю, характеризуется активной мощностью Р. Активная мощность одной фазы: PФ=UФIФcosφФ, где cos φФ – коэффициент мощности фазы. Активная мощность трехфазного потребителя при симметричной и несимметричной нагрузке равна сумме мощностей всех фаз: PN = PА + PВ + PС. При симметричной нагрузке мощности всех фаз одинаковы. Суммарная активная мощность может быть выражена как P = PФ = 3 UФ IФ cos j. Ф.
Если фазы потребителя соединены звездой, то UФ = Up / √ 3, а IФ = Ip. Если фазы потребителя , соединены треугольником, то UФ = Up, а IФ = Ip / √ 3. Поэтому в обоих случаях выражение для мощности потребителя, определяемое по последней формуле и записанное через линейные токи и напряжения, будет иметь один и тот же вид P = √ 3 Up Ip cos j. Ф. Аналогично, реактивная мощность при симметричной нагрузке будет равна Q = √ 3 Up Ip sin j. Ф. Полная мощность цепи S для симметричной нагрузки S = 3 (P 2 + Q 2) = √ 3 Up Ip.
Ф. Полная мощность цепи S для симметричной нагрузки S = 3 (P 2 + Q 2) = √ 3 Up Ip.
Измерение активной мощности, потребляемой трехфазным приемником, осуществляют ваттметром, включенным по одной из схем (рис. 8) в зависимости от способа соединения фаз потребителя.
Если потребители симметричны, то для определения суммарной мощности показания ваттметра утраиваются. Если потребители несимметричны, ваттметры включают последовательно в каждую из фаз. Складывая их показания, вычисляют суммарную мощность несимметричного потребителя. P = 3 PФ = 3 UФ IФ cos φ. Q = 3 QФ = 3 UФ IФ cos φ. S = 3 SФ = 3 UФ IФ. P = P 1 + P 2 + P 3,
На практике наибольшее распространение получил метод измерения суммарной мощности с помощью двух ваттметров, включаемых по схеме, изображенной на рис. 9. Метод применим в трехпроводных линиях как при симметричной, так и при несимметричной нагрузке и любом способе соединения фаз потребителя. В этом случае суммарная мощность трехфазного потребителя определяется как сумма показаний этих двух ваттметров: P = W 1 + W 2 = UAC IA cos (UAC, IA) + UBC IB cos (UBC, IB).
В этом случае суммарная мощность трехфазного потребителя определяется как сумма показаний этих двух ваттметров: P = W 1 + W 2 = UAC IA cos (UAC, IA) + UBC IB cos (UBC, IB).
Трехфазная четырехпроводная система – обзор
Первый член суммы в скобках представляет показания ваттметра с i 1 в его цепи тока и v 1 − v
5
м по его вольтовой цепи, т.е. подключенной между клеммами 1 и М. Отсюда следует, что три ваттметра могут измерять мощность в трехфазной четырехпроводной системе, а два — в трехфазной трехпроводной системе. Некоторые из распространенных случаев перечислены ниже.
Трехфазный, четырехпроводный, несбалансированная нагрузка -Подключения показаны на Рисунок 3.23(a) . Ваттметры W 1 , W 2 и W 3 измеряют фазные мощности отдельно. Общая мощность складывается из показаний:
Рисунок 3. 23. Трехфазное измерение мощности
23. Трехфазное измерение мощности
P=P1+P2+P3
Трехфазное, четырехпроводное, сбалансированное по нагрузке — с соединениями, показанными на рис. 3.23(a) , все счетчики показывают одинаково. Два ваттметра можно не использовать, а показания остальных приборов умножить на 3.
Трехфазный, трехпроводный, с несимметричной нагрузкой — два ваттметра подключены своими цепями тока в любой пара линий, как в Рисунок 3.23(b) . Общая мощность представляет собой алгебраическую сумму показаний, независимо от формы сигнала. Двухэлементный ваттметр автоматически суммирует мощность; с отдельными инструментами при определенных условиях, указанных ниже, будет иметь тенденцию читаться наоборот.
Трехфазный, трехпроводной, сбалансированный по нагрузке — при синусоидальном напряжении и токе получают условия рис. 3.23(c) . WattMeters W 1 и W 2 Указывают мощности P 1 и P 2 , где
P1 = Vabiacos (30∘ + φ) = V1I1COS (30∘ + φ) P2 = VCBICCOS (30 ∘+ϕ)=V1I1cos(30∘−ϕ)
Суммарная активная мощность P = P 1 + P 2 равно
P=V1I1[cos(30)☉ (30∘−ϕ) ]=√3V1I1cosϕ
, где cos ϕ — коэффициент мощности фазы . Алгебраическая разница составляет P 1 — P 2 = I 1 I 1 I 1 Греля φ, откуда Реактивная мощность задается на
Алгебраическая разница составляет P 1 — P 2 = I 1 I 1 I 1 Греля φ, откуда Реактивная мощность задается на
q = √3v1i1sinφ = √3 ( P1−P2)
, а фазовый угол можно получить из ϕ = arctan ( Q/P ). При ϕ = 0 (единичный коэффициент мощности) показания обоих ваттметров одинаковы; для ϕ = 60° (коэффициент мощности 0,5 отставания) Вт 1 считывается как ноль; а для более низких отстающих коэффициентов мощности W 1 имеет тенденцию читаться в обратном порядке.
3-фазные значения мощности, напряжения и тока
Трехфазное соединение звездой: линия, фазный ток, напряжение и мощность в конфигурации Y
Что такое Star Connection (Y)?
Соединение звездой ( Y ) Система также известна как Трехфазная четырехпроводная система ( 3-фазная 4-проводная ) и является наиболее предпочтительной системой для распределения питания переменного тока, в то время как для передачи обычно используется соединение треугольником. использовал.
использовал.
В системе соединения Star (также обозначаемой Y ) начальные или конечные концы (аналогичные концы) трех катушек соединяются вместе, образуя нейтральную точку. Или
Соединение «звезда» получается путем соединения вместе одинаковых концов трех катушек, либо «Начальной», либо «Конечной». Другие концы присоединяются к линейным проводам. Общая точка называется нейтральной или звездной точкой , которая представлена N .(Как показано на рис. 1)
Star Connection также называется трехфазной 4-проводной системой (3-фазной, 4-проводной).
Читайте также:
Если балансная симметричная нагрузка подключена к трехфазной системе напряжения параллельно, то по нейтральному проводу потекут три тока, величины которых будут одинаковыми, но будут отличаться на 120° (в противофазе), следовательно, векторная сумма эти три тока = 0. т.е.
I R + I Y + I B = 0 ……………. Викторианский
Викторианский
Напряжение между любыми двумя клеммами или напряжение между линией и нейтралью (точка звезды) называется напряжением фазы или напряжением звезды, обозначаемым V Ph . А напряжение между двумя линиями называется линейным напряжением или линейным напряжением, обозначаемым V L .
Соединение звездой (Y) Трехфазная мощность, значения напряжения и силы тока
Значения напряжения, тока и мощности при соединении звездой (Y)
Теперь мы найдем значения линейного тока, линейного напряжения, фазного тока, фазных напряжений и мощности в трехфазной системе переменного тока звезды.
Линейные и фазные напряжения при соединении звездой
Мы знаем, что линейное напряжение между линией 1 и линией 2 (из рис. 3а) равно
.
В RY = В R – В Y …. (Разница векторов)
Таким образом, чтобы найти вектор V RY , увеличьте вектор V Y в обратном направлении, как показано пунктиром на рис. 2 ниже. Аналогично, на обоих концах вектора V R и вектора V Y , сделайте перпендикулярные пунктирные линии, которые выглядят как параллелограмм, как показано на рис. (2).Диагональная линия, которая делит параллелограмм на две части, показывает значение V RY . Угол между векторами V Y и V R равен 60°.
2 ниже. Аналогично, на обоих концах вектора V R и вектора V Y , сделайте перпендикулярные пунктирные линии, которые выглядят как параллелограмм, как показано на рис. (2).Диагональная линия, которая делит параллелограмм на две части, показывает значение V RY . Угол между векторами V Y и V R равен 60°.
Следовательно, если
В Р = В Y = В В = В РН
, затем
В RY = 2 x В PH x Cos (60°/2)
= 2 x V PH x Cos 30°
= 2 x V PH x (√3/2) …… Так как Cos 30° = √3/2
В RY = √3 В PH
Аналогично,
В YB = В Y – В В
В YB = √3 В РН
и
В БР = В Б – В Р
В BR = √3 В РН
Следовательно, доказано, что V RY = V YB = V BR – линейные напряжения (V L ) в соединении «звезда» , Следовательно, в соединении «звезда»;
В L = √3 В PH или В L = √3 E PH
Линейные и фазные напряжения при соединении звездой
Из рис.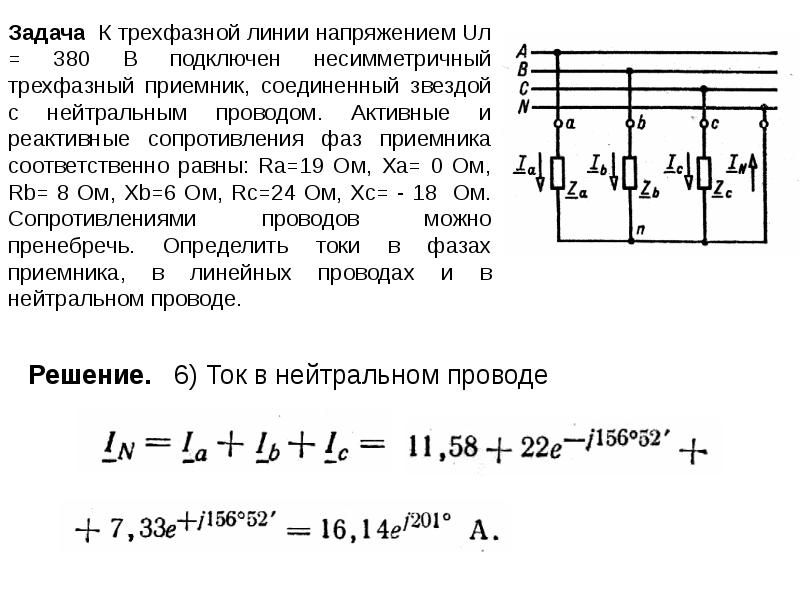 2 видно, что;
2 видно, что;
- Линейные напряжения отстоят друг от друга на 120°
- Линейные напряжения опережают на 30° соответствующие фазные напряжения
- Угол Ф между линейными токами и соответствующими линейными напряжениями составляет (30°+Ф), т.е.е. каждый линейный ток отстает (30°+Ф) от соответствующего линейного напряжения.
Связанная статья: Осветительные нагрузки, соединенные по схеме «звезда» и «треугольник»
Линейные и фазные токи при соединении звездой
Из рис. (3а) видно, что каждая линия соединена последовательно с отдельной фазной обмоткой, поэтому значение линейного тока такое же, как и в фазных обмотках, к которым подключена линия. то есть;
- Ток в линии 1 = I R
- Ток в линии 2 = I Y
- Ток в линии 3 = I B
Поскольку протекающие токи во всех трех линиях одинаковы, а индивидуальный ток в каждой линии равен току соответствующей фазы, следовательно;
I R = I Y = I B = I PH ….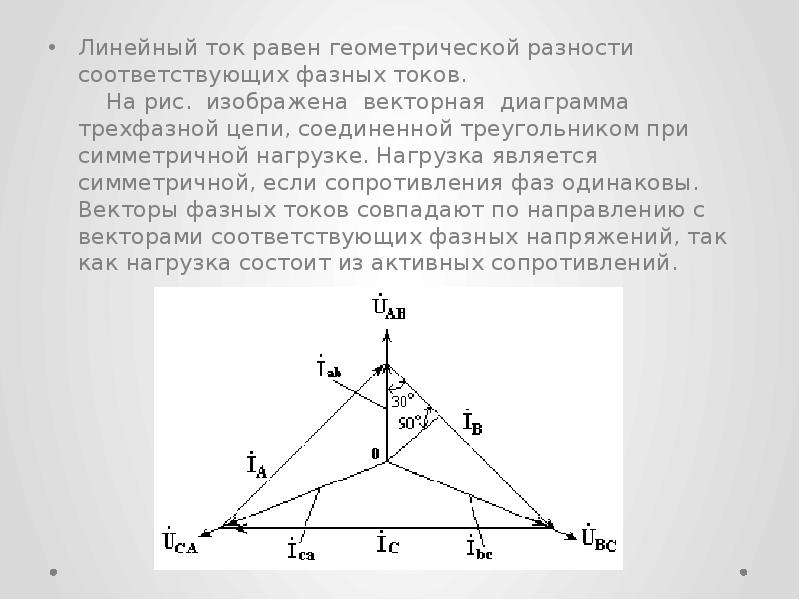 Фазный ток
Фазный ток
Линейный ток = фазный ток
I L = I РН
Проще говоря, значения линейных токов и фазных токов одинаковы в соединении звездой .
Соединение звездой (Y): значения линейных токов и напряжений и фазных токов и напряжений
Мощность в соединении звездой
В трехфазной цепи переменного тока общая истинная или активная мощность представляет собой сумму трехфазной мощности.Или сумма мощностей всех трех фаз является общей активной или истинной мощностью.
Следовательно, полная активная или действительная мощность в трехфазной системе переменного тока;
Суммарная истинная или активная мощность = 3-фазная мощность
или
P = 3 x V PH x I PH x CosФ ….. Уравнение … (1)
Мы знаем, что значения фазного тока и фазного напряжения при соединении звездой;
I L = I РН
В PH = В L /√3 ….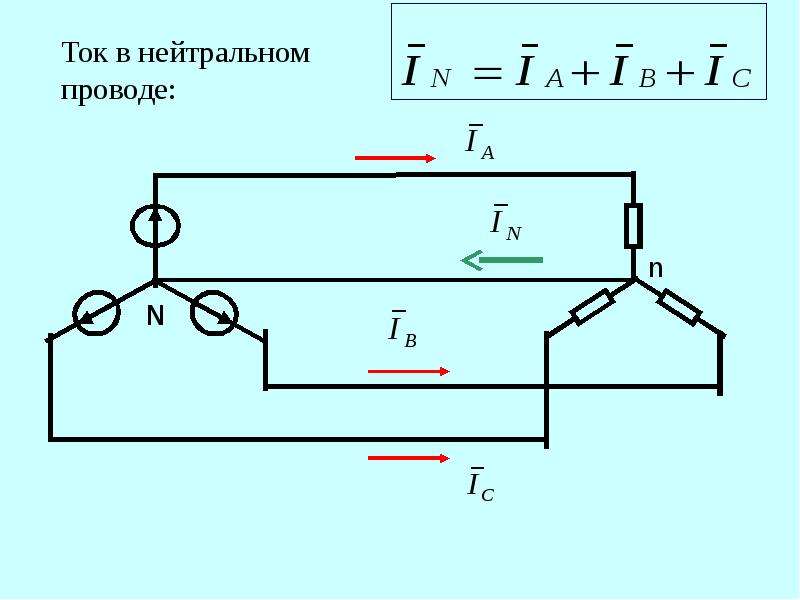 . (От В L = √3 В PH )
. (От В L = √3 В PH )
Ввод этих значений в экв. мощности……. (1)
P = 3 x (V L /√3) x I L x CosФ …….…. (V PH = V L /√3)
P = √3 x √3 x (V L /√3) x I L x CosФ ….… {3 = √3x√3}
P = √3 x V L x I L x CosФ
Отсюда доказано;
Мощность в звездообразном соединении ,
P = 3 x V PH x I PH x CosФ или
P = √3 x V L x I L x CosФ
То же самое объясняется в MCQ 3-Phase Circuit с поясняющим ответом (MCQ No.1)
Аналогично,
Суммарная реактивная мощность = Q = √3 x В L x I L x SinФ
Где Cos Φ = коэффициент мощности = фазовый угол между фазным напряжением и фазным током, а не между линейным током и линейным напряжением.
Полезно знать : Реактивная мощность катушки индуктивности принимается за положительную (+), а мощность конденсатора за отрицательную (-).
Также общая полная мощность трех фаз;
Полная полная мощность = S = √3 x V L x I L Или,
S = √ (P 2 + Q 2 )
Читайте также:
Несбалансированный фазный ток | Ток нулевой последовательности
Несбалансированный фазный ток:
Несимметричный фазный ток в 3-фазной системе может быть выражен через симметричные составляющие, как показано ниже:
Рис.18.6 показано векторное представление симметричных компонентов. Обычно в расчетах целесообразно выражать симметричные составляющие через несимметричный фазный ток. Выразим симметричные составляющие R-фазы через фазные токи I R , I Y и I B .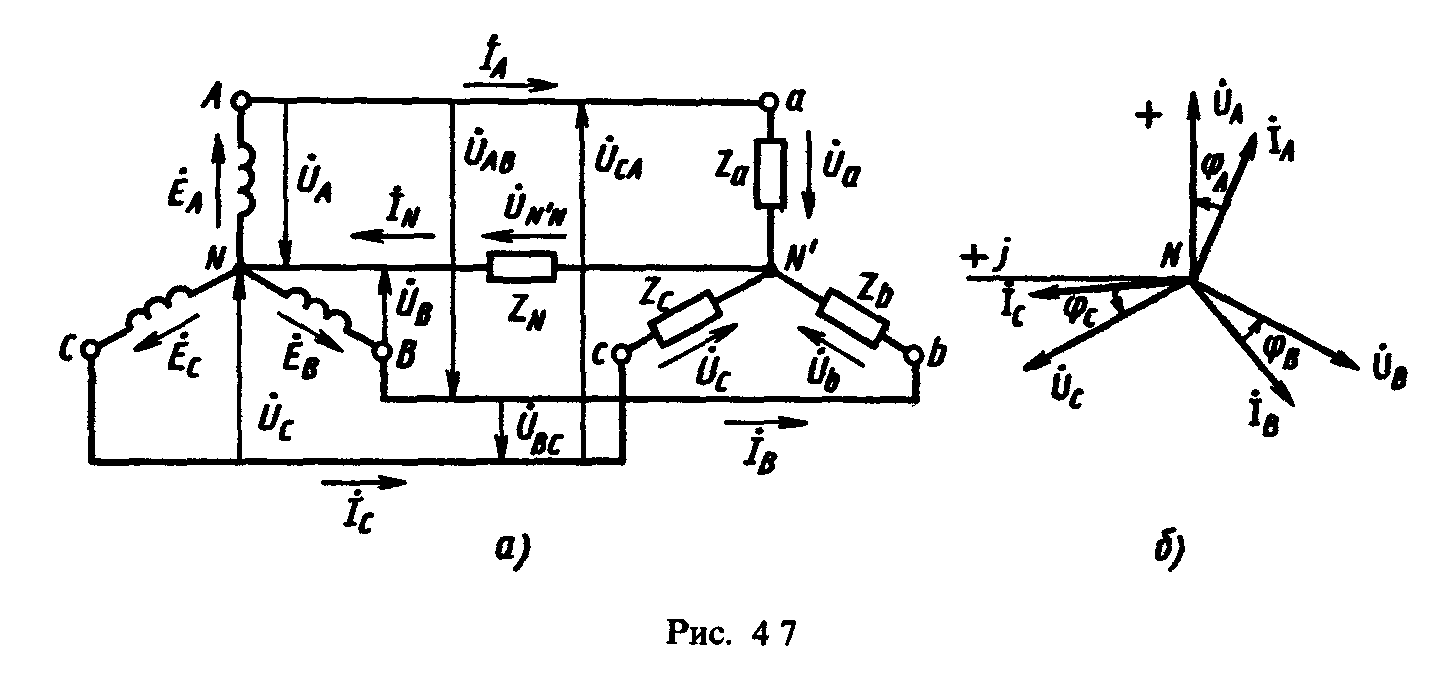 Для этого выразите все симметричные компоненты фаз Y и B через симметричные компоненты R-фазы с помощью оператора «а», как показано на рис. 18.6.
Для этого выразите все симметричные компоненты фаз Y и B через симметричные компоненты R-фазы с помощью оператора «а», как показано на рис. 18.6.
Обратите внимание, что набор прямой последовательности, показанный на рис.18.6 (i) можно выразить через I R1 с помощью оператора а. Таким образом, ток прямой последовательности I B1 в фазе B опережает I R1 на 120° и, следовательно, I B1 = a I R1 . Аналогично, ток прямой последовательности в фазе Y на 240° опережает I R1 так что I Y1 = a 2 I R1.
Точно таким же образом набор отрицательной последовательности может быть выражен через I R2 с помощью оператора «а», как показано на рис.18.6(ii). Из рис. 18.6 видно, что:
1. Ток нулевой последовательности: Путем добавления exps. (i), (ii) и (iii), мы получаем
Так как за эталонную фазу всегда принимается красная фаза, индекс R обычно опускается.
2. Ток прямой последовательности: Умножить exp.(ii) на «a» и exp. (iii) на ‘a 2, , а затем добавив эти exps. эксп. (i), получаем,
Опустив индекс R, мы имеем
3.Ток обратной последовательности: Умножить exp. (ii) на «a 2 » и exp. (iii) на «а», а затем добавить эти exps. к (i), получаем,
Следует обратить внимание на следующие моменты:
- Токи I 1 ,I 2 и I 0 являются симметричными составляющими R-фазы. Из-за симметрии каждого набора можно легко узнать симметричные компоненты желтой и синей фаз.
- Хотя обработка проводилась с учетом токов, метод в равной степени применим и к напряжениям.Таким образом, симметричные составляющие напряжения R-фазы относительно фазных напряжений должны быть:
Некоторые факты о токах последовательности:
Теперь желательно познакомить читателей со следующими фактами о токах прямой, обратной и нулевой последовательности:
- Сбалансированная трехфазная система состоит только из компонентов прямой последовательности; компоненты отрицательной и нулевой последовательности равны нулю.

- Наличие токов обратной или нулевой последовательности в трехфазной системе вносит асимметрию и указывает на ненормальное состояние цепи, в которой находятся эти компоненты
- Векторная сумма токов прямой и обратной последовательности трехфазной системы с несбалансированным током фаз равна нулю.Результирующая состоит только из трех токов нулевой последовательности e. Векторная сумма всех последовательных токов в трехфазной несимметричной системе
- В 3-фазной 4-проводной несимметричной системе величина компонентов нулевой последовательности составляет одну треть тока в нейтральном проводе, т. е.
При отсутствии пути через нейтраль трехфазной системы ток нейтрали равен нулю, а линейные токи не содержат компонентов нулевой последовательности.Нагрузка, соединенная треугольником, не имеет пути к нейтрали, а линейные токи, протекающие к нагрузке, соединенной треугольником, не могут содержать компоненты нулевой последовательности.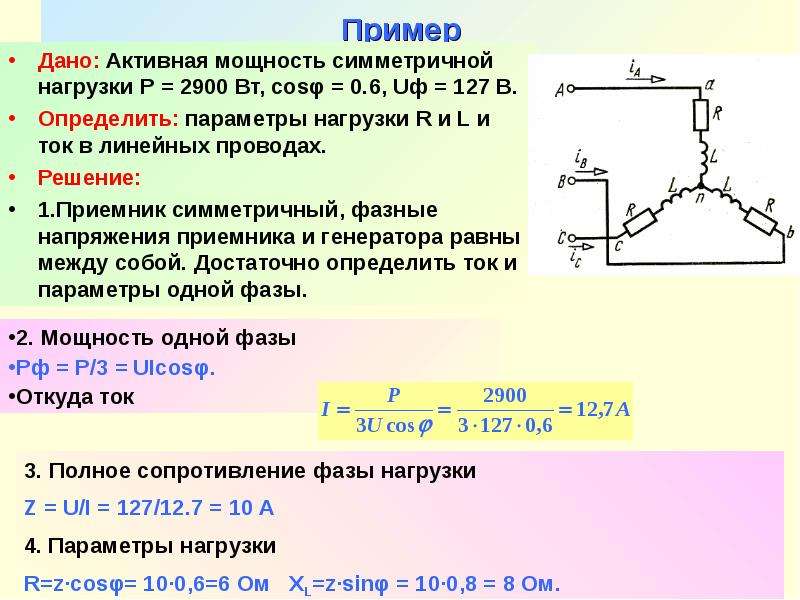
- В 3-фазной системе несимметричного фазного тока величина компонентов обратной последовательности не может превышать величину компонентов прямой последовательности. Если бы компоненты обратной последовательности были больше, последовательность фаз результирующей системы была бы обратной,
- Ток однофазной нагрузки, потребляемой от трехфазной системы, состоит из равных компонентов прямой, обратной и нулевой последовательности.
Симметричные компоненты энергосистемы
В этой статье мы обсудим: 1. Введение в симметричные компоненты 2. Фазовый оператор «а» 3. Оценка 4. Свойства 5. Трехфазная мощность 6. Физическое значение компонентов последовательности 7. Полное сопротивление последовательности и цепи последовательности
Введение в симметричные компоненты энергосистем:
Метод симметричных компонент является очень мощным подходом и упростил процедуру решения задач на несбалансированные многофазные системы. Метод симметричных составляющих был предложен К. Л. Фортеск в 1918 г. Хотя этот метод справедлив для любого числа фаз, наибольший интерес представляет трехфазная система.
Метод симметричных составляющих был предложен К. Л. Фортеск в 1918 г. Хотя этот метод справедлив для любого числа фаз, наибольший интерес представляет трехфазная система.
Согласно теореме Фортеск, любую неуравновешенную трехфазную систему токов, напряжений или других синусоидальных величин можно разложить на три уравновешенные системы векторов, которые называются симметричными компонентами исходной неуравновешенной системы.
Такие три сбалансированные системы составляют три сети последовательностей, которые решаются отдельно на основе одной фазы.Как только проблема решена с точки зрения симметричных компонентов, ее можно легко перенести обратно в фактическое состояние цепи путем наложения или векторного сложения этих величин (токов или напряжений).
Симметричные компоненты трехфазных систем :
Симметричные компоненты различаются последовательностью фаз, т. е. порядком, в котором фазовые величины достигают максимума. Может быть положительная последовательность фаз, обратная последовательность фаз и нулевая или однофазная последовательность. Таким образом, сбалансированные наборы компонентов могут быть представлены как компонент прямой последовательности, компонент обратной последовательности и компонент нулевой или однофазной последовательности.
Таким образом, сбалансированные наборы компонентов могут быть представлены как компонент прямой последовательности, компонент обратной последовательности и компонент нулевой или однофазной последовательности.
Система с прямой последовательностью фаз – это система, в которой фазные или линейные токи или напряжения достигают максимума в том же циклическом порядке, что и при нормальном питании, например, при обычном вращении против часовой стрелки, тогда векторы прямой последовательности фаз равны показанные на рис. 3.1 (а). Сбалансированная система, соответствующая нормальным условиям, содержит только положительную последовательность фаз.Это также условие для 3-фазного замыкания.
Компоненты прямой последовательности фаз отмечены нижним индексом 1. Три вектора системы прямой последовательности имеют одинаковую величину, разнесены на 120° и могут быть представлены в комплексной форме следующим образом:
Комплексное число e J2 /3 в приведенном выше выражении называется оператором трехфазной системы и обозначается буквой «а». Умножение вектора на a или e j2 /3 поворачивает вектор на 120° против часовой стрелки. Умножение вектора на 2 или e -j2 /3 поворачивает его на 240° против часовой стрелки, а положение вектора остается неизменным, если его умножить на 3 .
Умножение вектора на a или e j2 /3 поворачивает вектор на 120° против часовой стрелки. Умножение вектора на 2 или e -j2 /3 поворачивает его на 240° против часовой стрелки, а положение вектора остается неизменным, если его умножить на 3 .
Система с обратной последовательностью фаз — это система, в которой векторы все еще вращаются против часовой стрелки, но достигают максимума в обратном порядке i.е. A – C – B, как показано на рис. 3.1 (b). Эта последовательность возникает только в условиях дисбаланса, например, при возникновении несимметричной неисправности.
Такие замыкания включают в себя также систему прямой последовательности и, в случае замыканий на землю, нулевую последовательность, что объясняется следующим образом:
Компоненты отрицательной последовательности фаз отмечены нижним индексом 2. Три вектора отрицательной последовательности фаз, как и положительной последовательности фаз, имеют одинаковую величину и разнесены на 120°.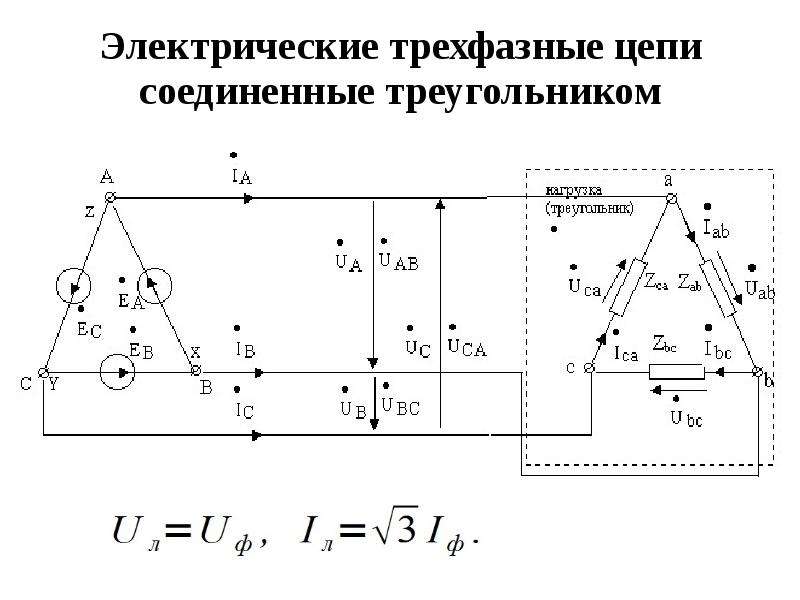
Они представлены в комплексной форме следующим образом:
Система с нулевой последовательностью фаз представляет собой однофазную векторную систему, объединяющую три равных фазовых вектора в фазе, как показано на рис. 3.1 (c), и представляет собой дифференциальный ток или напряжение, присутствующие в условиях неисправности в трехфазной системе с четвертым проводом. или присутствует возврат земли.
Очевидно, что нулевая последовательность фаз охватывает землю, следовательно, в дополнение к трем линейным проводам и представляет собой состояние неисправности на землю или на четвертый провод, если он есть.Его присутствие возникает только там, где токи замыкания на землю могут вернуться в систему через точку звезды этой системы или через искусственную нейтральную точку, предназначенную для заземления системы треугольника. При замыкании на землю также присутствуют положительная и отрицательная последовательности фаз.
Компоненты нулевой последовательности фаз отмечены нижним индексом 0. Три вектора системы нулевой или однофазной последовательности выражаются как –
А 0 = В 0 = С 0
Рис. 3.1 иллюстрирует векторную диаграмму для всех трех последовательностей фаз симметричных компонентов.
Фазовый оператор «а»:
Для удобства записи и обработки введен векторный оператор. В результате использования он стал известен как вектор а и определяется как /3 радиана) в положительном (против часовой стрелки) направлении от базовой оси.
Вектор, управляемый a, не изменяется по величине, а просто поворачивается на 120° в прямом направлении. Например, V’ = a V — это вектор, имеющий ту же длину, что и вектор V, но повернутый на 120° вперед относительно вектора V. Это соотношение показано на рис. 3.2. Квадрат вектора a — это другой единичный вектор, ориентированный на 120° в отрицательном направлении (по часовой стрелке) от базовой оси или на 240° вперед в положительном направлении.
Как показано на рис.3.2, результирующий a 2 , работающий с вектором V, представляет собой вектор V”, имеющий ту же длину, что и V, но расположенный под углом 120° по часовой стрелке от V.
Три вектора (1 + j 0), а 2 и а (взятые в этом порядке) образуют сбалансированный, симметричный набор векторов положительной фазовой последовательности, поскольку вектора имеют одинаковую длину и смещены на равные углы. на 120° друг от друга и пересекают опорную линию в порядке 1, 2 и а (следуя обычному соглашению о вращении против часовой стрелки для векторной диаграммы).
Векторы 1, a и 2 (взятые в этом порядке) образуют сбалансированный, симметричный набор векторов обратной последовательности фаз, поскольку векторы не пересекают опорную линию в указанном порядке, сохраняя то же соглашение вращения против часовой стрелки, но третье имя следует за первым и т. д.
Основные свойства векторов приведены ниже и показаны на векторе (рис.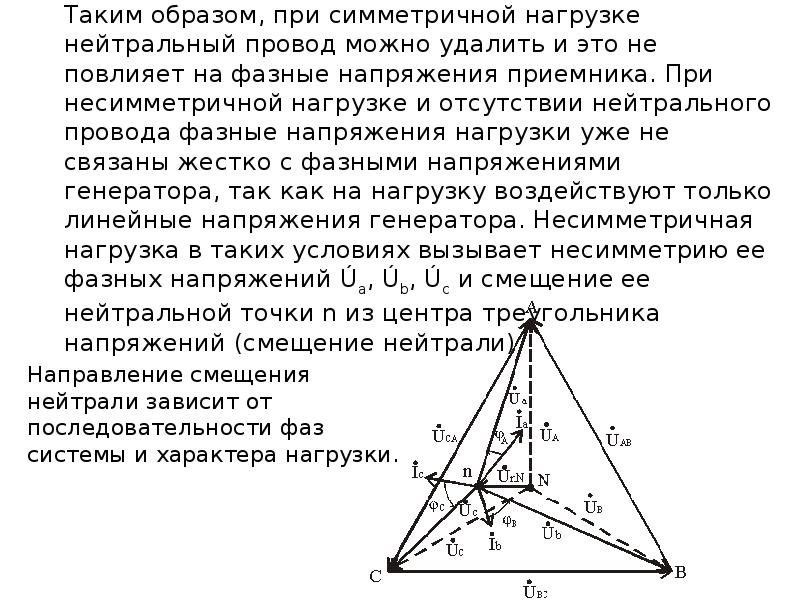 3.3):
3.3):
а = – 0,5 + j 0,866 = е j2 /3
а 2 = – 0.5 – j 0,866 = e -j2 /3
a 3 = 1 + j 0 = e j 0
4 = 4(j2 /3) =
a 5 = e 5(j2 /3) = a 2 и т. д.
Таким образом, a численно эквивалентно кубическому корню из единицы.
а + а 2 + 1 = (– 0,5 + j 0,866) + (– 0,5 – j 0,866) + 1 = 0
а + а 2 = – 1 + j 0 = е j
а 2 – а = ( – 0.5 – j 0,866) – ( – 0,5 + j 0,866
= 0 – j 1,732 = √3 e j 3 /2
а – а 2 = 0 j 1,732 = √3 e j /2
а – 1 = √3 e j 5 /6
1 – а = √3 e j 11 /6
a 2 – 1 = √3 e j7 /6
1 – a 2 = √3 e j /6
Оценка симметричных компонентов:
Выразим вектор неуравновешенной трехфазной системы через их симметричные составляющие –
A = A 1 + A 2 + A 0 …(i)
B = B 1 + B 2 + B 0 …(ii)
C = C 1 + C 2 + C 0 …(iii)
Выражая все векторы симметричной системы в приведенных выше уравнениях через A 1 , A 2 и A 0 , получаем –
A = A 1 + A 2 + A 0 …(iv)
B =
3 2 A 1 + AA 2 + A 0 + A 0 . .. (V) С B 1 = A 2 A 1 и B 2 = A A 2
.. (V) С B 1 = A 2 A 1 и B 2 = A A 2
и C = A 1 + A 2 A 2 + A 0 + A 0 … (VI) С C 1 = A A 1 и C 2 = A 2 A 2
Складывая уравнения (iv), (v) и (vi), получаем –
А + В + С = А 1 (1 + а 2 + а) + А 2 (1 + а + а 2 ) + 3 А 0
или A 0 = A + B + C/3 , поскольку 1 + a + a 2 = 0
Умножая уравнение (v) на a и уравнение (vi) на a 2 получаем –
(viii)
A 2 C =
3 3 A 3 A 1 + A 4 A 2 + A 2 A 0 … (IX)
Складывая уравнения (iv), (viii) и (ix), получаем –
А + а В + а 2 С = А 1 (1 + а 3 + а 3 ) + А 2 (1 + а 2 + а
4 ) 905 0 (1 + а + а 2 ) = 3 А 1 + А 2 (1 + а 2 + а) + А 0 (1 + а + а 2 ), так как а 4 = а и 3 = 1
(x)
Умножая уравнение (v) на a 2 и уравнение (vi) на a, получаем –
A 2 B = A 4 A
3 4 A 1 + A 3 A 2 + A 2 A 0 . .. (XI)
.. (XI)
(xii)
Складывая уравнения (iv), (xi) и (xii), получаем –
А + а 2 В + а С = А 1 (1 + а 4 + а 2 ) + А 2 (1 + а 3 + а 4 905 А 905 0 (1 + а 2 + а) = А 1 (1 + а + а 2 ) 3 А 2 + А 0 (1 + а + а 2 ) с 900 4 = а и 3 = 1
или A 2 = A + a 2 B + a C/3 …(xiii) поскольку 1 + a + a 2 = 0
В матричной форме мы можем выразить как –
Преобразование несбалансированной векторной системы в симметричную составляющую — это, по сути, математический метод, используемый для решения проблем трехфазной цепи в несимметричных условиях, которые могут быть вызваны несбалансированными нагрузками, неравными фазными напряжениями, одно- и двухфазными короткими замыканиями, обрывами линии и т. д. .
д. .
Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений:
В 3-фазной 4-проводной системе ток в нейтральном проводе равен сумме линейных токов и, следовательно, равен трехкратной составляющей токов нулевой последовательности.
Известно, что сумма линейных токов в 3-фазной 3-проводной системе, соединенной треугольником или звездой, равна нулю. Из уравнения (vii) следует, что линейные токи такой системы не несут никакой нуль-фазной составляющей.
Вышеизложенное в равной степени относится к любой трехфазной системе, в которой сумма линейных напряжений равна нулю. Это означает, что набор неуравновешенных трехфазных междуфазных напряжений может быть представлен положительной системой и отрицательной системой уравновешенных напряжений.
Степень неуравновешенности определяется коэффициентом несимметрии в терминах отношения составляющей обратной последовательности фаз к составляющей прямой последовательности фаз, т.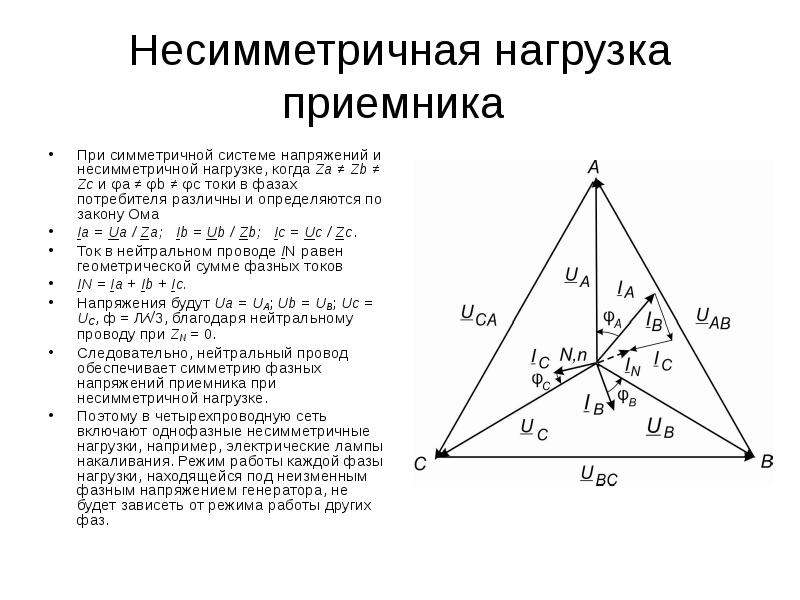 е. –
е. –
Система линейных напряжений считается уравновешенной, если этот коэффициент составляет менее 5%.
Отсутствие тока в одной или двух фазах при несимметричном состоянии означает, что сумма трех симметричных составляющих токов в этих фазах равна нулю.
Приведенное выше утверждение будет лучше понято при рассмотрении следующих примеров. Пусть в системе фазы В и С разомкнуты (рис. 3.4).
Затем,
I B = I c = 0
В соответствии с уравнениями (x), (xiii) и (vii) симметричными компонентами системы являются следующие:
(a) Составляющая тока прямой последовательности,
(b) Составляющая тока обратной последовательности,
(c) Составляющая тока нулевой последовательности,
Геометрическое сложение симметричных составляющих положительной, отрицательной и нулевой фазы дает –
Трехфазная мощность с точки зрения симметричных компонентов:
Мощность, потребляемая в трехфазной цепи, может быть определена непосредственно по симметричным компонентам при условии, что токи и напряжения заданы.
Полная комплексная мощность в 3-фазной цепи определяется как –
, где V a , V b и V c — напряжения относительно нейтрали, а l a , I b и I c — токи, протекающие в цепи по трем линиям, 3 -фазная цепь считается соединенной звездой. Верхний индекс T означает транспонирование.
Теперь скалярное произведение двух векторов не меняется, когда оба вектора поворачиваются на один и тот же угол.
Например, а 2 В а1 . a 2 I a1 = V a1 I a1 ; АВ а1 . aI a1 = V a1 I a1 ; а 2 В а1 . aI a2 = aV a1 . я а2 . и так далее.
Таким образом, выражение для S принимает вид –
.
или P = 3 [V A1 I A1 COS θ 1 + V A2 I A2 COS θ 2 + V A0 I A0 COS θ 0 ] . .. [ 3.4(а)]
.. [ 3.4(а)]
То же самое выражение мощности может быть очень легко получено с помощью матричных манипуляций.
Теперь из уравнения. (3.1) –
Теперь заменяем фазный ток соответствующими симметричными составляющими –
В приведенном выше выражении для мощности нет перекрестных членов (таких как V a1 , V a2 , V a1 V a0 и т. д.), потому что нет взаимной связи между тремя сетями последовательностей. Множитель 3 возникает из-за общего количества компонентов 9 (по 3 на каждую фазу). Видно, что трехфазная мощность равна сумме мощностей трех симметричных составляющих.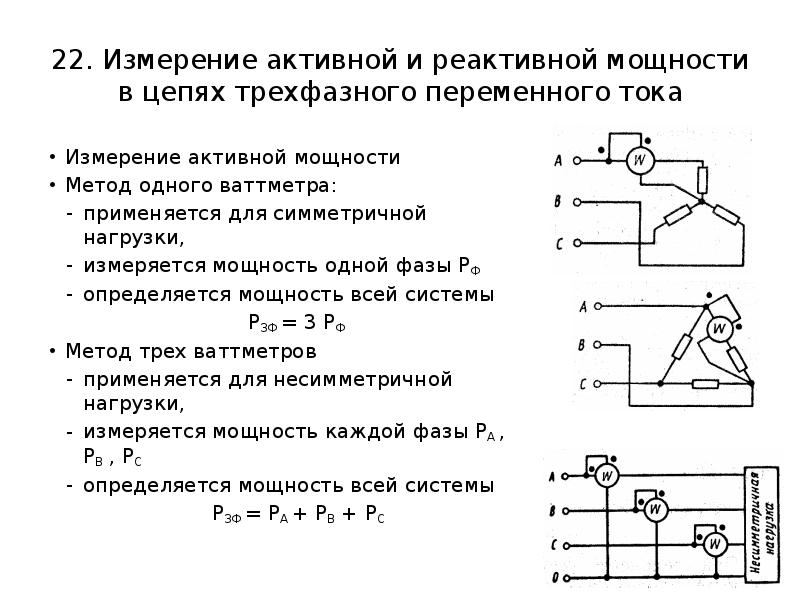
Физическое значение компонентов последовательности:
Физическое значение последовательных напряжений можно хорошо понять, рассмотрев поля, возникающие при приложении таких последовательных напряжений к статору трехфазной машины переменного тока (синхронной машины или асинхронной машины).Если к обмотке статора трехфазного асинхронного двигателя приложить набор напряжений прямой последовательности, возникнет магнитное поле, вращающееся в определенном направлении.
Теперь, если поменять местами два из трех фазных проводов питания к обмотке статора, направление вращения создаваемого поля будет противоположным. Видно, что для этого условия относительные положения фаз напряжений, приложенных к статору двигателя, такие же, как и для набора обратной последовательности.
Таким образом, поле, создаваемое набором напряжений обратной последовательности, будет вращаться в направлении, противоположном направлению поля, создаваемого набором напряжений прямой последовательности. Последовательность фаз не следует путать с вращением векторов.
Последовательность фаз не следует путать с вращением векторов.
Для обоих наборов напряжений прямой и обратной последовательности соблюдается стандартное соглашение о вращении против часовой стрелки. Напряжения нулевой последовательности являются однофазными напряжениями и поэтому вызывают в пространстве переменное поле.
Наборы прямой и обратной последовательности являются сбалансированными, т. е. если протекают только токи прямой и/или обратной последовательности, сумма векторов каждого из них будет равна нулю, и дифференциального тока не будет. Однако компоненты нулевой последовательности токов в трех фазах равны по величине и совпадают по фазе, и, следовательно, дифференциальный ток будет в три раза больше тока нулевой последовательности одной фазы. В случае замыкания на землю токи прямой и обратной последовательности уравновешиваются между собой, но токи нулевой последовательности протекают через заземляющий и заземляющий провода.
Импедансы последовательностей и сети последовательностей:
До сих пор мы обсуждали симметричные составляющие токов, напряжений и мощности. Теперь мы обсудим кое-что о импедансах последовательности энергосистемы. Импедансы последовательности сети или компонента энергосистемы представляют собой импедансы положительной, отрицательной и нулевой последовательности.
Теперь мы обсудим кое-что о импедансах последовательности энергосистемы. Импедансы последовательности сети или компонента энергосистемы представляют собой импедансы положительной, отрицательной и нулевой последовательности.
Они определяются следующим образом:
Полное сопротивление сети для протекания токов прямой последовательности называется полным сопротивлением прямой последовательности.Точно так же, если протекают только токи обратной последовательности, полное сопротивление сети, предназначенное для этих токов, называется полным сопротивлением обратной последовательности. Также полное сопротивление токов нулевой последовательности называется полным сопротивлением сети нулевой последовательности.
Если Z a , Z b и Z c представляют собой импедансы нагрузки между фазами a, b и c до нейтрали n, то импедансы последовательности задаются как –
Для трехфазной симметричной статической цепи без внутренних напряжений, такой как трансформаторы и линии электропередач, сопротивления токов любой последовательности одинаковы для трех фаз; также токи определенной последовательности вызовут падение напряжения той же последовательности, или напряжение определенной последовательности вызовет рост тока только той же последовательности, что означает отсутствие взаимной связи между сетями последовательности.
Поскольку в случае статического устройства последовательность не имеет значения, импедансы прямой и обратной последовательности равны; импеданс нулевой последовательности, включающий импеданс обратного пути через землю, обычно отличается от импедансов прямой и обратной последовательности. Импедансы, предлагаемые вращающейся машиной компонентам тока прямой последовательности, отличаются от импедансов, предлагаемых компонентам тока обратной последовательности.
Однофазная эквивалентная схема, составленная из сопротивлений току только одной последовательности, называется сетью последовательности для этой конкретной последовательности.Следовательно, соответствующие токам положительной, отрицательной и нулевой последовательности, мы имеем сети положительной, отрицательной и нулевой последовательности.
Таким образом, для каждой энергосистемы могут быть сформированы три сети последовательности, и эти сети последовательности, несущие токи l a1 , I a2 и I a0 , затем соединяются друг с другом различными способами для представления различных условий несбалансированного КЗ.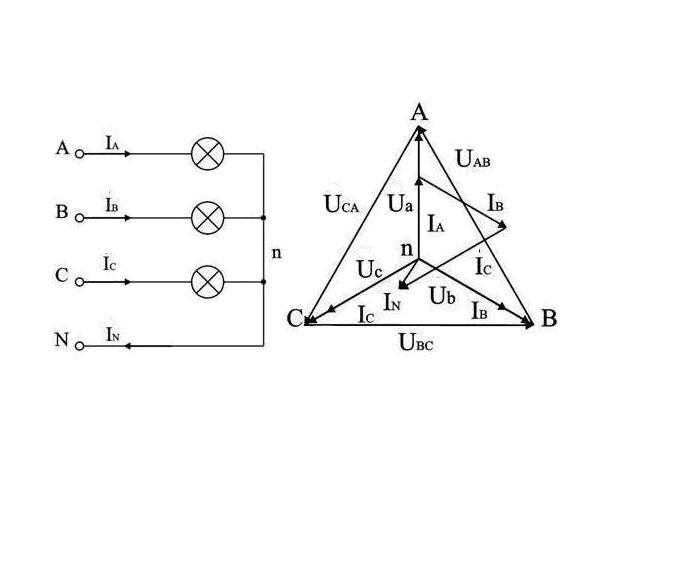 Затем рассчитываются последовательные токи и напряжения во время короткого замыкания, по которым можно определить фактические токи и напряжения короткого замыкания.
Затем рассчитываются последовательные токи и напряжения во время короткого замыкания, по которым можно определить фактические токи и напряжения короткого замыкания.
Сеть прямой последовательности учитывается при анализе симметричных неисправностей. Цепь прямой последовательности аналогична диаграмме импеданса или реактивного сопротивления.
Сеть отрицательной последовательности в целом очень похожа на сеть положительной последовательности, но отличается в следующих аспектах:
(i) Обычно нет источников ЭДС обратной последовательности.
(ii) Полное сопротивление обратной последовательности вращающихся машин обычно отличается от их полного сопротивления прямой последовательности.
Смещение фаз блоков трансформаторов обратной последовательности имеет противоположный знак по отношению к положительной последовательности.
Сеть нулевой последовательности также будет свободна от внутренних напряжений, поскольку протекание тока будет вызвано напряжением в точке повреждения. Импедансы токов нулевой последовательности очень часто отличаются от токов прямой или обратной последовательности.
Импедансы токов нулевой последовательности очень часто отличаются от токов прямой или обратной последовательности.
Реактивное сопротивление нулевой последовательности линий передачи выше, чем у прямой последовательности.Полное сопротивление трансформаторов и генераторов будет зависеть от типа соединения [треугольник или звезда (заземленный или изолированный)].
C:\files\courses\3414\ece3414notes1a.wpd
%PDF-1.6
%
106 0 объект
>
эндообъект
165 0 объект
>
эндообъект
104 0 объект
>поток
Acrobat Distiller 5.0.5 (Windows)2004-07-07T15:23:25Z2013-08-22T07:29:22-05:002013-08-22T07:29:22-05:00PScript5.dll Версия 5.2application/pdf
UUID: 3786948f-c39e-456b-ad4f-ee67c605ecc1uuid: b71a17ff-4d5e-4cd1-bca5-025288013c01
конечный поток
эндообъект
168 0 объект
>/Кодировка>>>>>
эндообъект
100 0 объект
>
эндообъект
99 0 объект
>
эндообъект
164 0 объект
>
эндообъект
101 0 объект
>
эндообъект
102 0 объект
>
эндообъект
58 0 объект
>
эндообъект
61 0 объект
>
эндообъект
64 0 объект
>
эндообъект
67 0 объект
>
эндообъект
70 0 объект
>
эндообъект
73 0 объект
>
эндообъект
76 0 объект
>
эндообъект
78 0 объект
>поток
Хл;;
+V7ssZ@BfJDq`
>_;qv/7_^;> _}?_/^ Z_{ K ||k~F’0r77Z銵x>-ĺd80w=!1Kvkup. PuexSWNlW27ErnmAFnaEr$rcV5gqp陾=+_}f9Uqx1r35fwYd3La6gph֍Zq.]0b(E(k
PuexSWNlW27ErnmAFnaEr$rcV5gqp陾=+_}f9Uqx1r35fwYd3La6gph֍Zq.]0b(E(k
l{_,x?lXF8Ų뙬./.’
mTMАЯ~d{o&̸’MF968gۻ$%f[;{SIW
aʖb45a39 x[7ǧK:bCn
3빍J*[8X9y4{n$_g1ƥVz8U~wpJA/v1CZ*,⥢UvR6lV
Курсы PDH онлайн. PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов HVAC; не только экологичность или энергосбережение
курсы.»
Рассел Бейли, ЧП
Нью-Йорк
«Это укрепило мои текущие знания и научило меня еще нескольким новым вещам
для раскрытия мне новых источников
информации.»
Стивен Дедак, ЧП
Нью-Джерси
«Материал был очень информативным и организованным. Я многому научился, и они были
очень быстро отвечают на вопросы.
Это было на высшем уровне. Буду использовать
еще раз.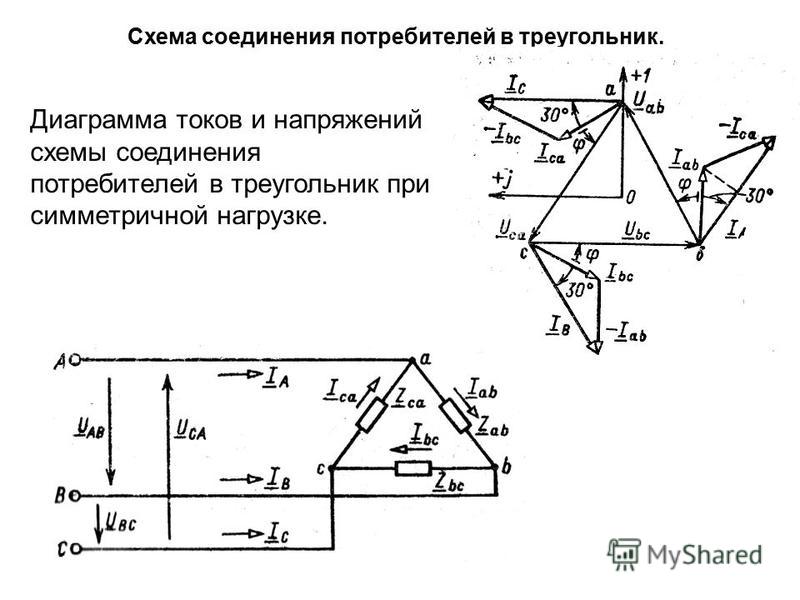 Спасибо.»
Спасибо.»
Блэр Хейворд, ЧП
Альберта, Канада
«Легкий в использовании веб-сайт.Хорошо организовано. Я действительно воспользуюсь вашими услугами снова.
Я передам вашу компанию
имя другим на работе.»
Рой Пфлейдерер, ЧП
Нью-Йорк
«Справочный материал был превосходным, и курс был очень информативным, тем более что я думал, что уже знаком
с реквизитами Канзас
Авария в городе Хаятт.»
Майкл Морган, ЧП
Техас
«Мне очень нравится ваша бизнес-модель. Мне нравится возможность просмотреть текст перед покупкой. Я нашел класс
информативный и полезный
на моей работе.»
Уильям Сенкевич, Ч.Е.
Флорида
«У вас отличный выбор курсов и очень информативные статьи. Вы
Вы
— лучшее, что я нашел.»
Рассел Смит, ЧП
Пенсильвания
«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, предоставляя время для просмотра
материал.»
Хесус Сьерра, ЧП
Калифорния
«Спасибо, что разрешили мне просмотреть неправильные ответы.На самом деле
человек узнает больше
от сбоев.»
Джон Скондрас, ЧП
Пенсильвания
«Курс был хорошо составлен, и использование тематических исследований является эффективным
способ обучения.»
Джек Лундберг, ЧП
Висконсин
«Я очень впечатлен тем, как вы представляете курсы; т.э., что позволяет
студент для ознакомления с курсом
материал до оплаты и
получение викторины.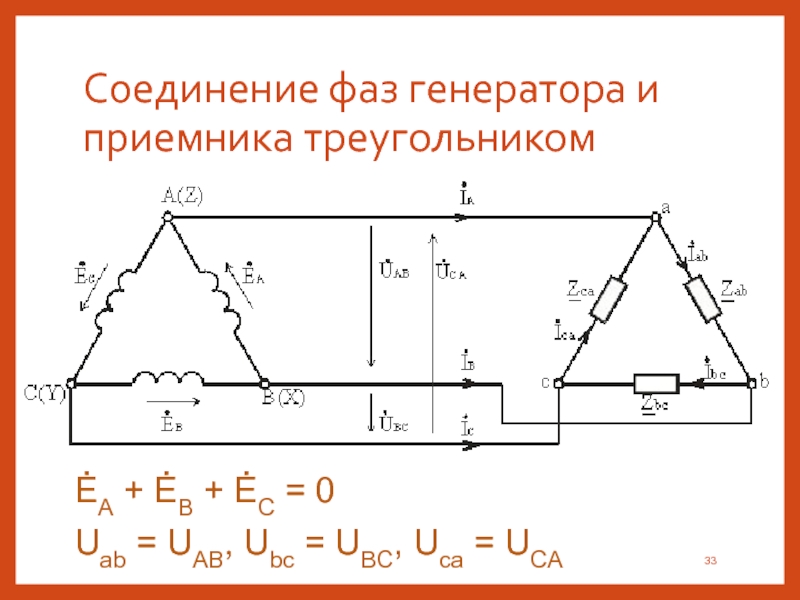 »
»
Арвин Свангер, ЧП
Вирджиния
«Спасибо, что предлагаете все эти замечательные курсы. Я, конечно, выучил и
очень понравилось.»
Мехди Рахими, ЧП
Нью-Йорк
«Я очень доволен предлагаемыми курсами, качеством материала и простотой поиска и
подключение к Интернету
курсы.»
Уильям Валериоти, ЧП
Техас
«Этот материал в значительной степени оправдал мои ожидания. Курс был легким для понимания. Фотографии в основном давали хорошее представление о
обсуждаемые темы.»
Майкл Райан, ЧП
Пенсильвания
«Именно то, что я искал. Нужен 1 балл по этике, и я нашел его здесь.»
Джеральд Нотт, ЧП
Нью-Джерси
«Это был мой первый онлайн-опыт получения необходимых кредитов PDH. Это был
Это был
.
информативно, выгодно и экономично.
Очень рекомендую
всем инженерам.»
Джеймс Шурелл, ЧП
Огайо
«Я ценю, что вопросы относятся к «реальному миру» и имеют отношение к моей практике, и
не основано на какой-то непонятной секции
законов, которые не применяются
до «обычная» практика.»
Марк Каноник, ЧП
Нью-Йорк
«Отличный опыт! Я многому научился, чтобы использовать его в своем медицинском устройстве
организация.»
Иван Харлан, ЧП
Теннесси
«Материал курса имеет хорошее содержание, не слишком математический, с хорошим акцентом на практическое применение технологии.»
Юджин Бойл, П.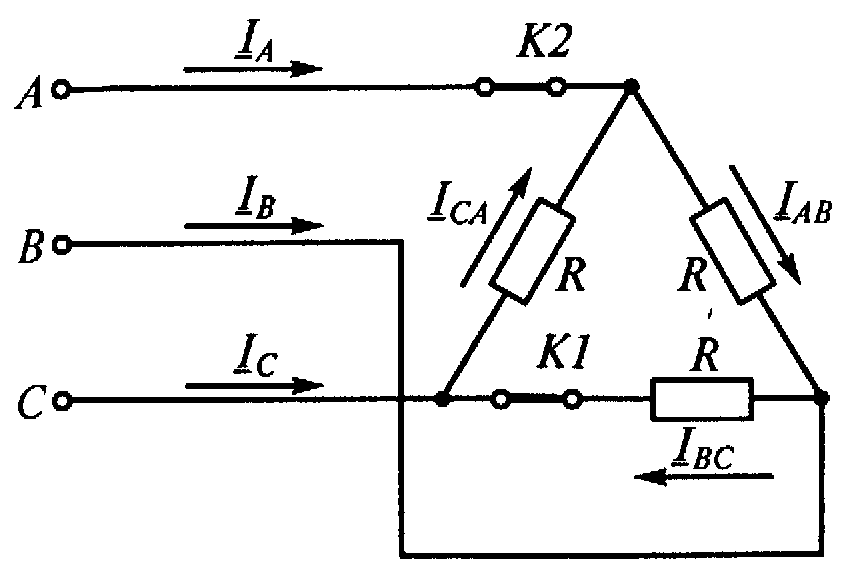 Е.
Е.
Калифорния
«Это был очень приятный опыт. Тема была интересной и хорошо представлена,
а онлайн формат был очень
доступный и простой
использование. Большое спасибо.»
Патрисия Адамс, ЧП
Канзас
«Отличный способ добиться соответствия непрерывному образованию PE в рамках временных ограничений лицензиата.»
Джозеф Фриссора, ЧП
Нью-Джерси
«Должен признаться, я действительно многому научился. Распечатанная викторина помогает во время
просмотр текстового материала. я
тоже оценил просмотр
фактические случаи предоставлены.»
Жаклин Брукс, ЧП
Флорида
«Документ Общие ошибки ADA в проектировании помещений очень полезен.
тест действительно требовал исследования в
документ но ответы были
легко доступны.»
Гарольд Катлер, ЧП
Массачусетс
«Это было эффективное использование моего времени. Спасибо за разнообразие выбора
в дорожной технике, который мне нужен
для выполнения требований
Сертификация PTOE.»
Джозеф Гилрой, ЧП
Иллинойс
«Очень удобный и доступный способ заработать CEU для выполнения моих требований к PG в Делавэре.»
Ричард Роудс, ЧП
Мэриленд
«Узнал много нового о защитном заземлении. До сих пор все курсы, которые я проходил, были отличными.
Надеюсь увидеть больше 40%
курсы со скидкой. »
»
Кристина Николас, ЧП
Нью-Йорк
«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду дополнительных
курсы. Процесс прост, и
намного эффективнее, чем
необходимость путешествовать.»
Деннис Мейер, ЧП
Айдахо
«Услуги, предоставляемые CEDengineering, очень полезны для профессионалов
Инженеры для приобретения блоков PDH
в любое время.Очень удобно.»
Пол Абелла, ЧП
Аризона
«Пока все было отлично! Поскольку я постоянно работаю матерью двоих детей, у меня не так много
пора искать куда
получить мои кредиты от.»
Кристен Фаррелл, ЧП
Висконсин
«Это было очень информативно и поучительно. Легко для понимания с иллюстрациями
Легко для понимания с иллюстрациями
и графики; определенно получается
проще впитать все
теории.»
Виктор Окампо, инженер.
Альберта, Канада
«Хороший обзор принципов полупроводников. Мне понравилось проходить курс по номеру
.
мой собственный темп во время моего утра
метро
на работу.»
Клиффорд Гринблатт, ЧП
Мэриленд
«Просто найти интересные курсы, скачать документы и получить
викторина. Я бы очень рекомендую
вам в любой PE нуждающийся
Единицы CE.»
Марк Хардкасл, ЧП
Миссури
«Очень хороший выбор тем во многих областях техники. »
»
Рэндалл Дрейлинг, ЧП
Миссури
«Я заново узнал то, что забыл. Я также рад принести пользу в финансовом отношении
от ваш рекламный адрес электронной почты который
сниженная цена
на 40%.»
Конрадо Касем, П.Е.
Теннесси
«Отличный курс по разумной цене. Буду пользоваться вашими услугами в будущем.»
Чарльз Флейшер, ЧП
Нью-Йорк
«Это был хороший тест, и я фактически проверил, что я прочитал профессиональную этику
Коды
и Нью-Мексико
правила.»
Брун Гильберт, П.Е.
Калифорния
«Мне очень понравились занятия. Они стоили времени и усилий.»
Они стоили времени и усилий.»
Дэвид Рейнольдс, ЧП
Канзас
«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng
при необходимости
Сертификация
.»
Томас Каппеллин, П.Е.
Иллинойс
«У меня истек срок действия курса, но вы все равно выполнили обязательство и дали
мне то, за что я заплатил — много
с благодарностью!»
Джефф Ханслик, ЧП
Оклахома
«CEDengineering предлагает удобные, экономичные и актуальные курсы
для инженера.»
Майк Зайдл, П.Е.
Небраска
«Курс был по разумной цене, а материал был кратким и
хорошо организовано. »
»
Глен Шварц, ЧП
Нью-Джерси
«Вопросы соответствовали урокам, а материал урока
хороший справочный материал
для дизайна под дерево.»
Брайан Адамс, П.Е.
Миннесота
«Отлично, я смог получить полезную информацию с помощью простого телефонного звонка.»
Роберт Велнер, ЧП
Нью-Йорк
«У меня был большой опыт прохождения курса «Строительство прибрежных зон — Проектирование»
Корпус Курс и
очень рекомендую.»
Денис Солано, ЧП
Флорида
«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики штата Нью-Джерси были очень
прекрасно приготовлено. »
»
Юджин Брекбилл, ЧП
Коннектикут
«Очень хороший опыт. Мне нравится возможность скачивать учебные материалы на
обзор где угодно и
когда угодно.»
Тим Чиддикс, ЧП
Колорадо
«Отлично! Поддерживайте широкий выбор тем на выбор.»
Уильям Бараттино, ЧП
Вирджиния
«Процесс прямой, никакой чепухи. Хороший опыт.»
Тайрон Бааш, П.Е.
Иллинойс
«Вопросы на экзамене были пробными и демонстрировали понимание
материала. Тщательный
и полный.»
Майкл Тобин, ЧП
Аризона
«Это мой второй курс, и мне понравилось то, что курс предложил мне, что
поможет в моей линии
работы. »
»
Рики Хефлин, ЧП
Оклахома
«Очень быстрая и простая навигация. Я определенно воспользуюсь этим сайтом снова.»
Анджела Уотсон, ЧП
Монтана
«Прост в исполнении. Нет путаницы при подходе к сдаче теста или записи сертификата.»
Кеннет Пейдж, П.Е.
Мэриленд
«Это был отличный источник информации о нагреве воды с помощью солнечной энергии. Информативный
и отличное освежение.»
Луан Мане, ЧП
Коннетикут
«Мне нравится подход к подписке и возможности читать материалы в автономном режиме, а затем
вернись, чтобы пройти тест.»
Алекс Млсна, П.Е.
Индиана
«Я оценил количество информации, предоставленной для класса. Я знаю
это вся информация, которую я могу
использование в реальных жизненных ситуациях.»
Натали Дерингер, ЧП
Южная Дакота
«Материалы обзора и образец теста были достаточно подробными, чтобы я мог
успешно завершено
курс.»
Ира Бродская, ЧП
Нью-Джерси
«Веб-сайт прост в использовании, вы можете скачать материал для изучения, а затем вернуться
и пройти тест. Очень
удобный а на моем
собственное расписание.»
Майкл Гладд, ЧП
Грузия
«Спасибо за хорошие курсы на протяжении многих лет.»
Деннис Фундзак, ЧП
Огайо
«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH
сертификат
. Спасибо за создание
Спасибо за создание
процесс простой.»
Фред Шайбе, ЧП
Висконсин
«Положительный опыт.Быстро нашел подходящий мне курс и закончил
PDH за один час в
один час.»
Стив Торкилдсон, ЧП
Южная Каролина
«Мне понравилась возможность загрузки документов для ознакомления с содержанием
и пригодность до
имея платить за
материал .»
Ричард Ваймеленберг, ЧП
Мэриленд
«Это хорошее пособие по ЭЭ для инженеров, не являющихся электриками.»
Дуглас Стаффорд, ЧП
Техас
«Всегда есть место для улучшения, но я ничего не могу придумать в вашем
процесс, которому требуется
улучшение. »
»
Томас Сталкап, ЧП
Арканзас
«Мне очень нравится удобство прохождения викторины онлайн и получения немедленного
Сертификат
.»
Марлен Делани, ЧП
Иллинойс
«Обучающие модули CEDengineering — очень удобный способ доступа к информации по
многие различные технические области внешние
по собственной специализации без
необходимость путешествовать.»
Гектор Герреро, ЧП
Грузия
Расчет тока короткого замыкания | Графические продукты
Ток неисправности — это непреднамеренное, неконтролируемое протекание сильного тока через электрическую систему. Токи повреждения вызваны короткими замыканиями с очень низким импедансом. Это могут быть короткие замыкания на землю или между фазами. В результате протекание сильного тока может привести к перегреву оборудования и проводников, чрезмерным усилиям, а иногда даже к серьезным дуговым разрядам, взрывам и взрывам.К причинам неисправностей относятся такие вещи, как удары молнии, животные, грязь и мусор, упавшие инструменты, коррозия и человеческий фактор.
Это могут быть короткие замыкания на землю или между фазами. В результате протекание сильного тока может привести к перегреву оборудования и проводников, чрезмерным усилиям, а иногда даже к серьезным дуговым разрядам, взрывам и взрывам.К причинам неисправностей относятся такие вещи, как удары молнии, животные, грязь и мусор, упавшие инструменты, коррозия и человеческий фактор.
Расчет тока короткого замыкания основан на законе Ома, согласно которому ток (I) равен напряжению (V), деленному на сопротивление (R). Формула I = V/R. Когда происходит короткое замыкание, сопротивление становится очень маленьким, а это означает, что ток становится очень большим.
Если бы сопротивление было равно нулю, то расчетный ток короткого замыкания стремился бы к бесконечности.Однако даже медный провод имеет некоторое сопротивление; это не идеальный проводник. Для определения тока короткого замыкания необходимо знать общее сопротивление от источника питания до места повреждения.
Требуется расчет тока неисправности
Знание доступного тока короткого замыкания важно при выборе защитных устройств, однако это также требуется по коду. В Национальном электрическом кодексе (NEC) 110.24 (A) указано:
В Национальном электрическом кодексе (NEC) 110.24 (A) указано:
.
«Сервисное оборудование в нежилых помещениях должно иметь четкую маркировку на месте с максимально допустимым током короткого замыкания.Полевая маркировка должна включать дату расчета тока короткого замыкания и должна быть достаточно прочной, чтобы выдерживать окружающую среду».
Это означает, что на электрическом оборудовании, например, на оборудовании служебного ввода, должны быть установлены этикетки, указывающие доступный ток короткого замыкания. Это позволяет легко сравнивать номинальный ток короткого замыкания (SCCR) оборудования с максимально допустимым током короткого замыкания.
Каждый раз при замене оборудования расчет тока короткого замыкания должен выполняться заново.Это указано в NEC 110.24(B):
.
«В случае модификаций электроустановки, влияющих на максимально доступный ток короткого замыкания в службе, максимально доступный ток короткого замыкания должен быть проверен или пересчитан по мере необходимости, чтобы гарантировать, что номинальные характеристики сервисного оборудования достаточны для максимального доступного тока короткого замыкания в линии. клеммы оборудования. Требуемая(ые) маркировка(и) поля в 110.24(A) должна быть скорректирована, чтобы отразить новый уровень максимально допустимого тока короткого замыкания.
Типы неисправностей
В электрической системе существует несколько типов возможных неисправностей:
- Короткое замыкание, в результате которого ток обходит нормальную нагрузку.
- «Замыкание на землю», при котором ток уходит в землю.
- В трехфазных системах может быть короткое замыкание между одной или несколькими фазами. Этот тип неисправности обычно создает самые высокие токи короткого замыкания.
Четвертый тип неисправности, обрыв цепи, не приводит к возникновению тока короткого замыкания. Открытая неисправность возникает в результате непреднамеренного прерывания тока.
Защитные системы должны предотвращать повреждение оборудования и защищать людей во всех вышеперечисленных ситуациях. Это означает, что должны быть выполнены расчеты токов короткого замыкания, чтобы можно было выбрать соответствующие защитные устройства.
Болтовые разломы и дуговые разломы
Электрическая неисправность может быть либо болтовой, либо дуговой.
В болтовом разломе имеется прочное соединение. Это позволяет току короткого замыкания течь по проводнику. Этот тип неисправности может произойти, когда установщик подключает источник питания к земле, а не к точке, где он должен быть подключен. При включении питания немедленно произойдет замыкание на болтах, которое приведет к срабатыванию защитного устройства. Поскольку текущий поток был ограничен, ущерб обычно ограничен. Однако замыкание на болтах создает самые высокие токи замыкания.
Дуговое замыкание возникает, когда нет надежного соединения, но проводники подходят достаточно близко, так что ток прыгает через зазор, создавая дугу.Начальная дуга ионизирует воздух, создавая плазму, которая позволяет потоку тока быстро увеличиваться и поддерживаться, что приводит к вспышке дуги или взрыву дуги. Когда возможна вспышка дуги, необходимо выполнить расчеты тока короткого замыкания, чтобы определить безопасные границы защиты и требуемые средства индивидуальной защиты, а также предоставить информацию, необходимую для этикеток вспышки дуги, которые должны быть установлены в дополнение к требуемым меткам тока короткого замыкания NEC 110.24.
Трехфазные неисправности
Стандарт
IEC 60909 «Токи короткого замыкания в трехфазных системах» дает принятый метод расчета трехфазных токов короткого замыкания.
Неисправность в трехфазной системе может быть как симметричной (сбалансированной), так и несимметричной (несбалансированной). При симметричном замыкании в равной степени страдают все три фазы. Однако такое случается редко. Большинство трехфазных замыканий несимметричны, что затрудняет расчет тока замыкания.
Источники контента
Прежде чем можно будет выполнить расчет тока короткого замыкания, необходимо определить все возможные источники тока. Сюда могут входить некоторые источники тока, которые, возможно, не были учтены.Существует четыре возможных источника тока короткого замыкания:
- Электрические генераторы на объекте: они расположены близко друг к другу, и ток короткого замыкания ограничен только импедансом самого генератора и электрической цепи.
- Синхронные двигатели: синхронный двигатель представляет собой двигатель переменного тока, в котором скорость двигателя пропорциональна частоте электроэнергии. При отключении питания, как это бывает при коротком замыкании, инерция механической нагрузки на двигатель будет продолжать вращать двигатель.В этом случае двигатель будет действовать как генератор, подающий ток, и это будет способствовать общему току, протекающему в месте повреждения.
- : этот тип двигателя также станет генератором, если где-то еще в системе произойдет короткое замыкание. Однако ток короткого замыкания, генерируемый асинхронным двигателем, сохраняется только в течение нескольких циклов. Ток будет примерно равен пусковому току двигателя с заторможенным ротором.
- Система электроснабжения: большая часть тока короткого замыкания обычно исходит от электросети.Уровень тока короткого замыкания будет зависеть от:
- номинальное вторичное напряжение трансформатора и импеданс
- Полное сопротивление генераторов
- Полное сопротивление цепи от трансформатора до КЗ.
Асинхронные двигатели
Для упрощения расчета тока короткого замыкания предполагается, что все электрические генераторы в системе находятся в фазе и работают при номинальном напряжении системы.
Болтовое трехфазное состояние
Для расчета тока короткого замыкания проводится исследование короткого замыкания.Обычно это включает в себя рассмотрение наихудшего сценария, который представляет собой трехфазное короткое замыкание с болтовым соединением. Основываясь на этой ситуации, можно аппроксимировать другие условия неисправности.
Вклад двигателей в системе в ток короткого замыкания важен. Во многих случаях двигатели могут в четыре-шесть раз превышать нормальный ток полной нагрузки. Даже если ток очень короткий, очень важно, чтобы он был включен в расчет тока короткого замыкания.
Когда проводится исследование вспышки дуги, расчет тока короткого замыкания должен по-прежнему производиться для самого высокого тока трехфазного короткого замыкания с болтовым соединением.
Маркировка тока неисправности
После расчета тока короткого замыкания на оборудование следует нанести этикетки с указанием доступного тока короткого замыкания. Если требуется этикетка дугового разряда, ее также следует распечатать и приклеить в соответствующем месте. Для каждой метки требуется пользовательская информация, полученная в результате расчета тока короткого замыкания.
Сделайте следующий шаг!
Теперь, когда у вас есть общее представление о переменных, используемых при расчете дугового разряда, загрузите наше бесплатное руководство по энергии дугового разряда, чтобы получить подробные рекомендации по внедрению системы безопасности на вашем предприятии.

 6,а
6,а
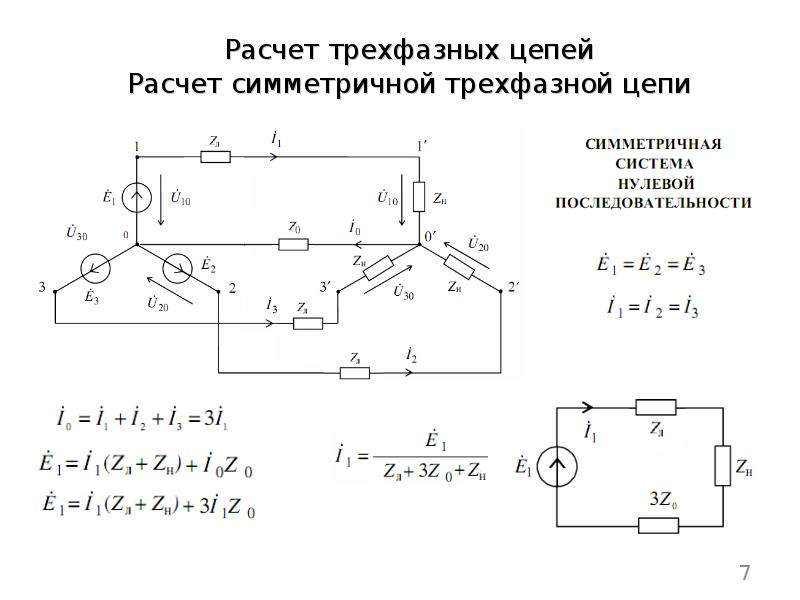 Что покажет
Что покажет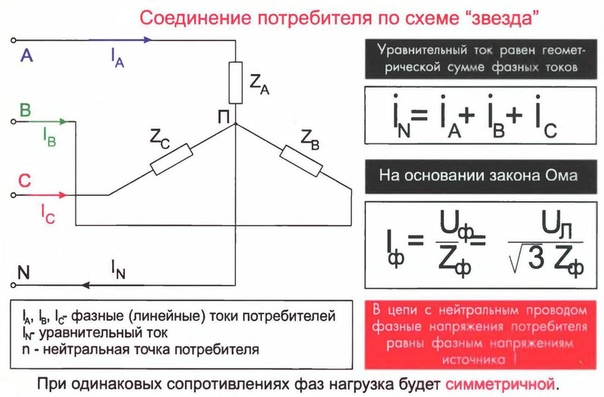 11 доказать
11 доказать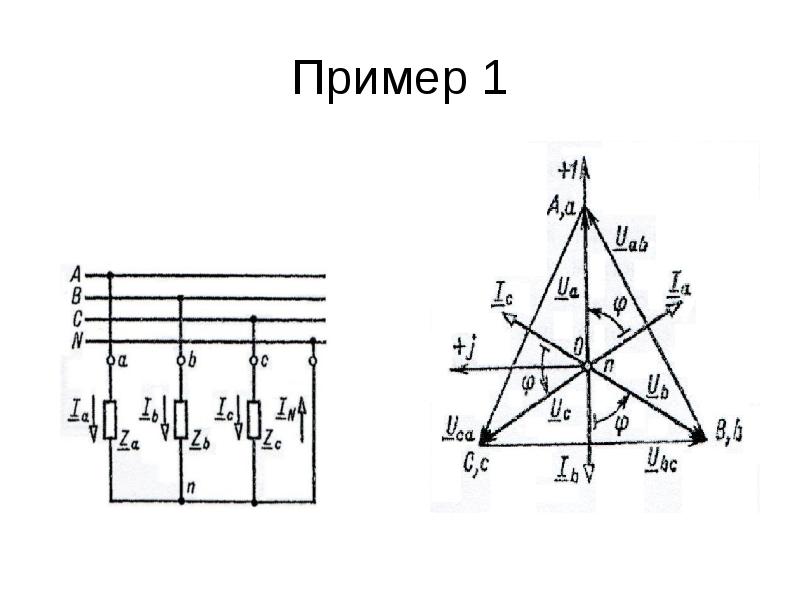


 3, если фазная ЭДС
3, если фазная ЭДС