Трехпроводная трехфазная система с соединением нагрузки по схеме «звезда» без нулевого (нейтрального) провода. Чему равен ток в нейтральном проводе при симметричной трехфазной нагрузке
Вопрос Ток в нейтральном проводе в трехфазных цепях.
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒Трехфазные цепи с нейтральным проводе называют четерехпроводными цепями.
Обычно сопротивлением проводов не учитывается /
Тогда фазные напр. приемника будут равны фазн. напряжением генератора. .
При том что комплексные сопротивления равны , то токи определяются
В соответствии с 1 зак. Киргофа ток в нейтр. проводе
При симмет. напр.
При несим. напр.
Нейтр провод выравнивает фазные напряжения.
Режимы работы трехфазного премника.
Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
Линейнымназывается провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной(на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным(на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной,с нейтральным проводом – четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных,к линии - линейных.Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А, В и С к нейтральной точке N; - фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
Отметим, что всегда - как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при осно. вании, равными 300), в этом случае
| (4) |
Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фазфазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; .
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
.
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| . | (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда - звезда» и «треугольник - треугольник» на практике также применяются схемы «звезда - треугольник» и «треугольник - звезда».
Читайте также:
lektsia.com
13. Элементы трехфазной электрической цепи. Фазные, линейные токи, напряжения.
Трехфазная цепь состоит из трех основных элементов: трехфазного генератора, линии передачи со всем необходимым оборудованием, приемников (потребителей). Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:
.
14. Симметричный и несимметричный приемники в трехфазных цепях, векторные диаграммы.
Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки.
Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки.
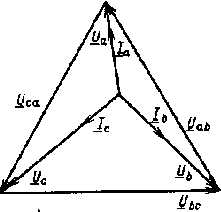
15. Ток в нейтральном проводе в трехфазных цепях. Нейтральный (нулевой рабочий) провод — провод, соединяющий между собой нейтрали электроустановок в трёхфазных электрических сетях. При соединении обмоток генератора и приёмника электроэнергии по схеме «звезда» фазное напряжение зависит от подключаемой к каждой фазе нагрузки. В случае подключения, например, трёхфазного двигателя, нагрузка будет симметричной, и напряжение между нейтральными точками генератора и двигателя будет равно нулю. Однако, в случае, если к каждой фазе подключается разная нагрузка, в системе возникнет так называемое напряжение смещения нейтрали, которое вызовет несимметрию напряжений нагрузки. На практике это может привести к тому, что часть потребителей будет иметь пониженное напряжение, а часть повышенное. Пониженное напряжение приводит к некорректной работе подключённых электроустановок, а повышенное может, кроме этого, привести к повреждению электрооборудования или возникновению пожара. Соединение нейтральных точек генератора и приёмника электроэнергии нейтральным проводом позволяет снизить напряжение смещения нейтрали практически до нуля и выровнять фазные напряжения на приёмнике электроэнергии. Небольшое напряжение будет обусловлено только сопротивлением нулевого провода.
15 Вопрос Ток в нейтральном проводе в трехфазных цепях.
Трехфазные цепи с нейтральным проводе называют четерехпроводными цепями.
Обычно сопротивлением проводов не учитывается /
Тогда фазные напр. приемника будут равны фазн. напряжением генератора. .
При том что комплексные сопротивления равны , то токи определяются
В соответствии с 1 зак. Киргофа ток в нейтр. проводе
При симмет. напр.
При несим. напр.
Нейтр провод выравнивает фазные напряжения.
16 Режимы работы трехфазного премника.
Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.

Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных, к линии - линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А, В и С к нейтральной точке N; - фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать

Отметим, что всегда - как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при осно. вании, равными 300), в этом случае
| (4) |
Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фаз фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; .
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
.
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями

Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| . | (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда - звезда» и «треугольник - треугольник» на практике также применяются схемы «звезда - треугольник» и «треугольник - звезда».
studfiles.net
Трехпроводная трехфазная система с соединением нагрузки по схеме «звезда» без нулевого (нейтрального) провода.
В четырехпроводной системе трехфазного тока, включенной по схеме звезда, при симметричной нагрузке ток в нейтральном проводе равен нулю. Следовательно, в этом случае от нейтрального провода можно отказаться, и четырехпроводная система при этом превращается в трехпроводную систему трехфазного тока (рис. 24.)
Проанализируем электрическое состояние трехпроводной трехфазной системы, соединенной по схеме «звезда», при активной нагрузке.
1) Симметричная активная нагрузка: ZA=ZB=ZC =RA=RB=RC=R
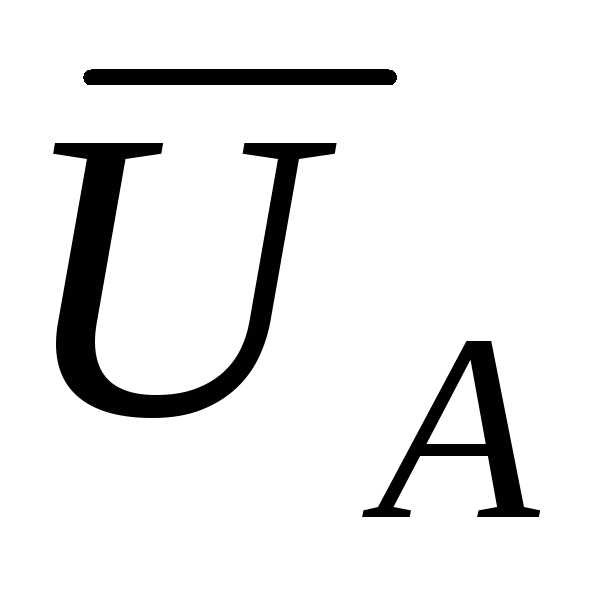 =
= 
 =
= 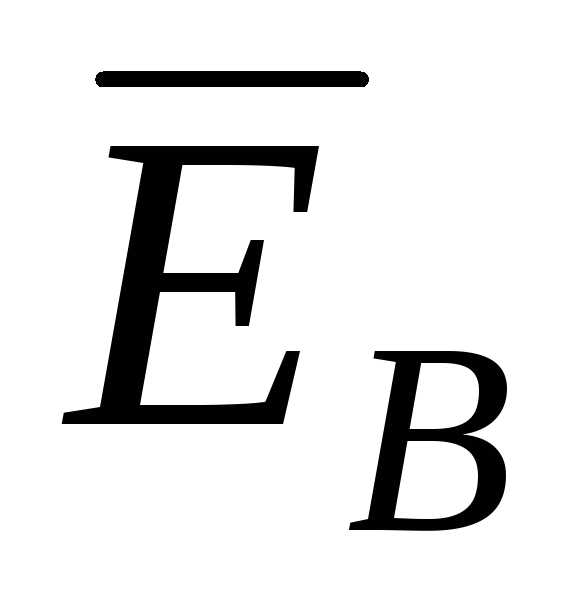
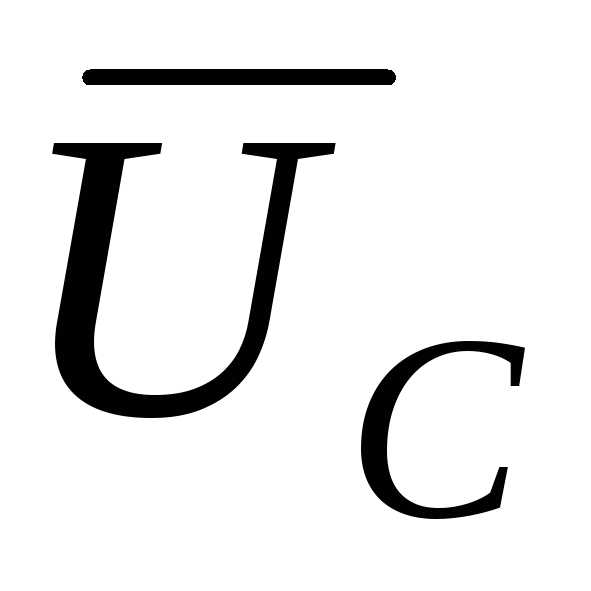 =
= 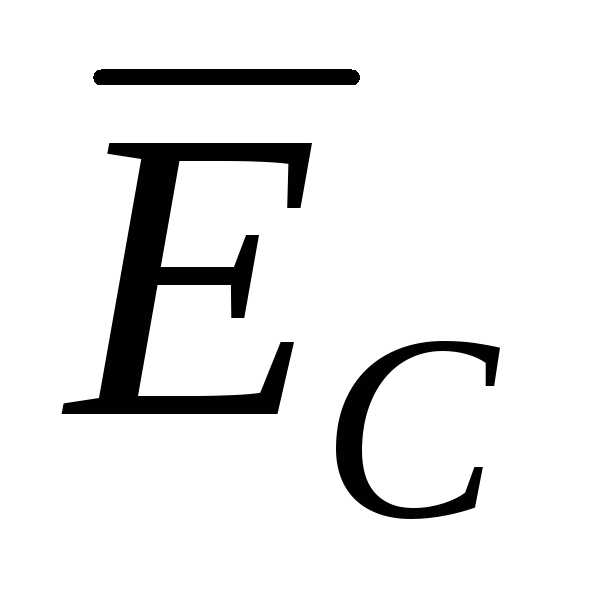
 nN = 0
nN = 0
 =
=  =
= 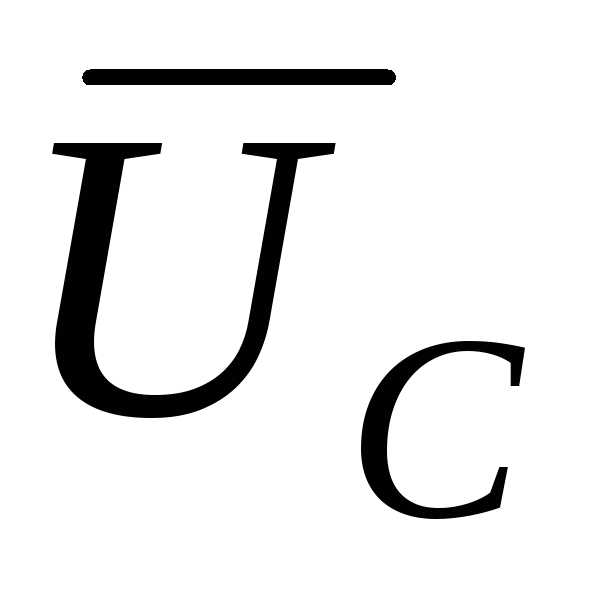 =
=
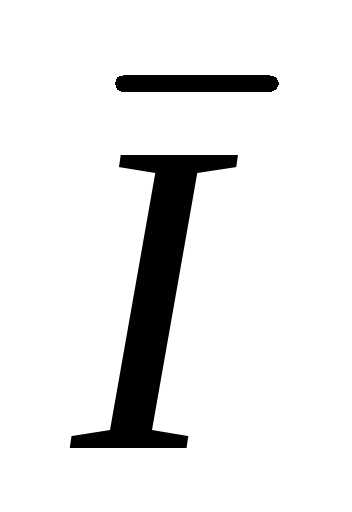 A +
A + 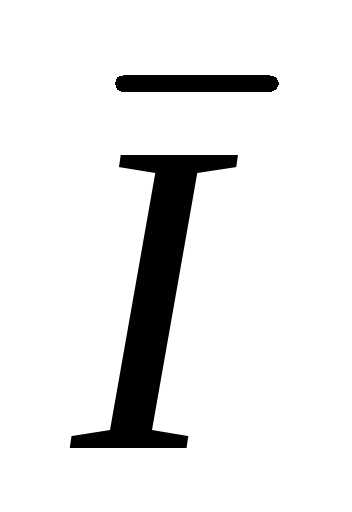 B +
B + 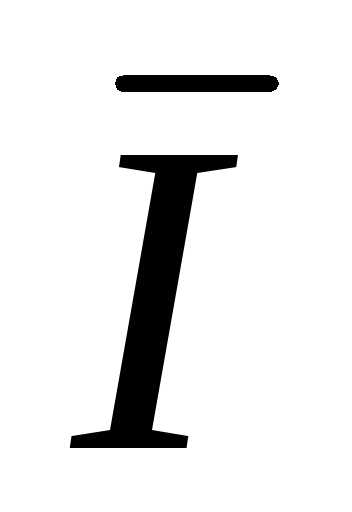 C =
C = 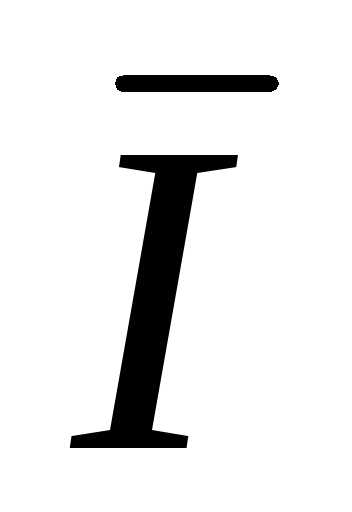 N = 0
N = 0
 A =
A = 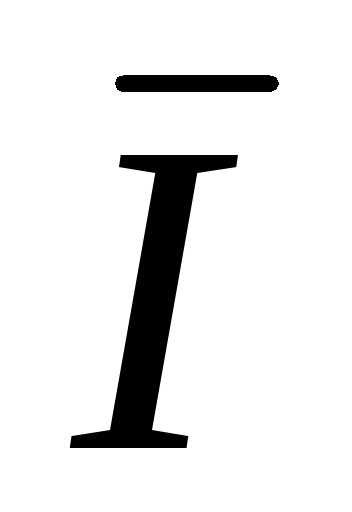 B =
B = 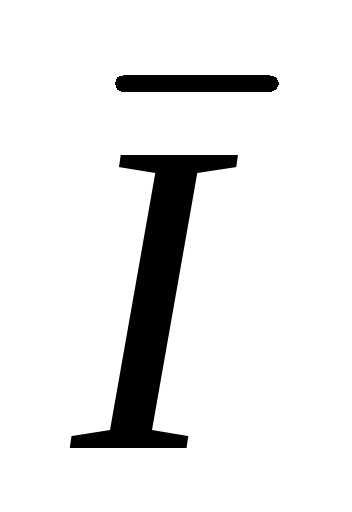 C =
C =  Ф=
Ф=

Рис.24. Трехпроводная система трехфазного переменного тока (соединение по схеме «звезда»).
Векторная диаграмма трехпроводной трехфазной системы «звезда» при симметричной активной нагрузке аналогична диаграмме, построенной для четырехпроводной системы с симметричной активной нагрузкой (рис.22).
2) Несимметричная активная нагрузка: ZA=RA ;ZB=RB ;ZC=RC ;RA≠RB≠RC ;IA≠IB≠IC
В трехпроводной системе, соединенной по схеме «звезда» при несимметричной нагрузке между нулевой точкой нагрузки и нулевой точкой генератора возникает напряжение UnN, которое в случае активной нагрузки можно выразить следующим образом
 nN=
nN= 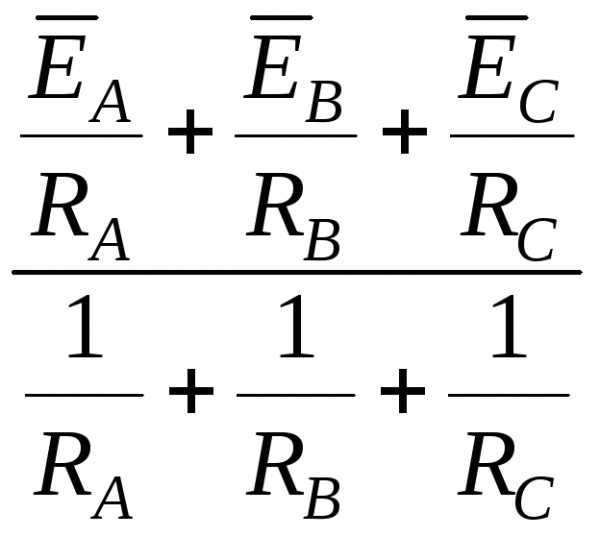 . (49)
. (49)
Составим уравнения по второму закону Кирхгофа
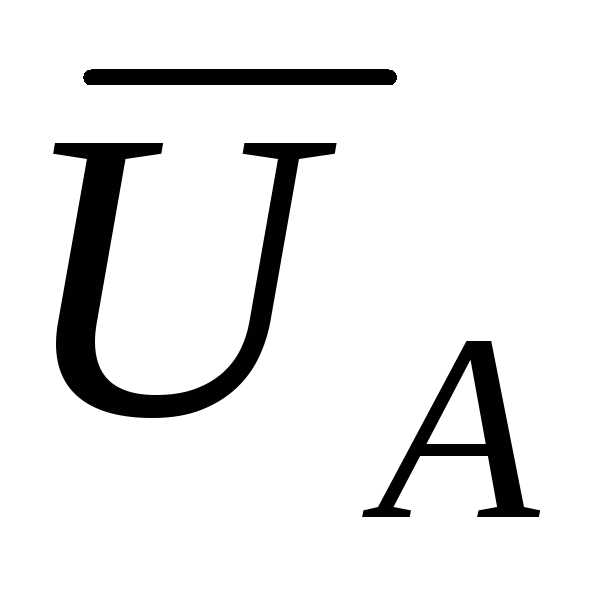 =
=  −
−  nN
nN
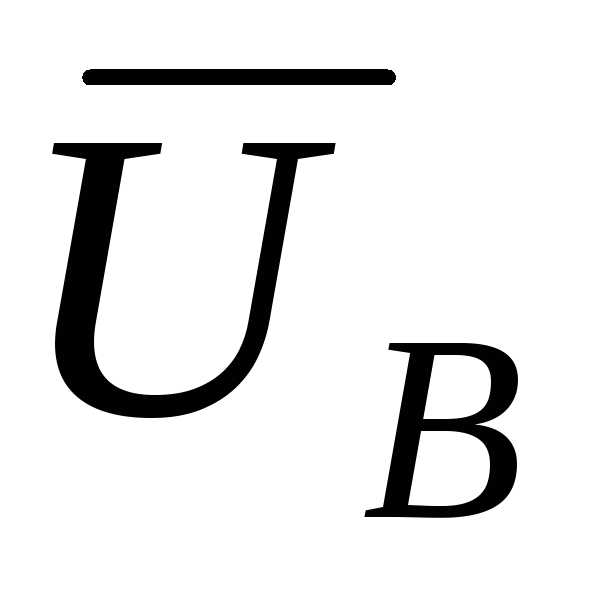 =
= 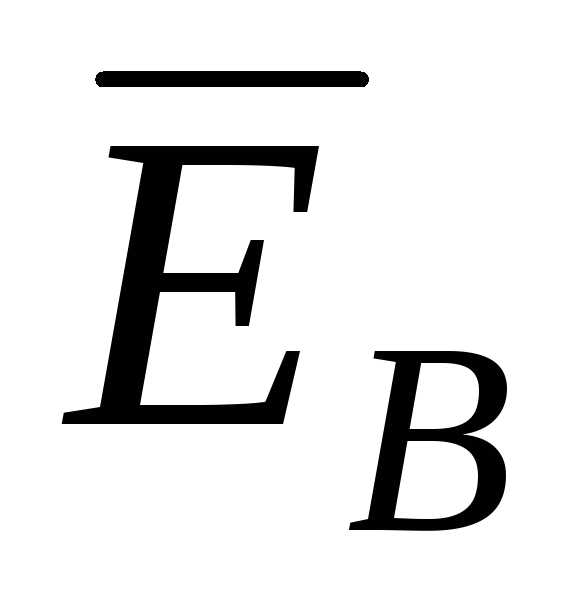 −
−  nN (50)
nN (50)
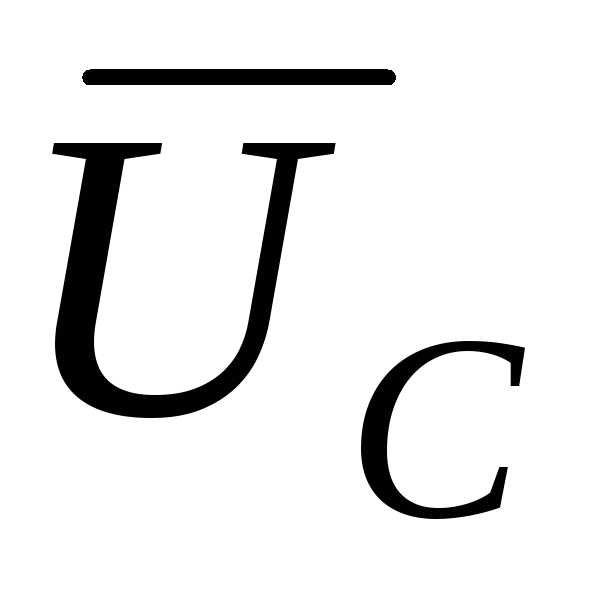 =
= 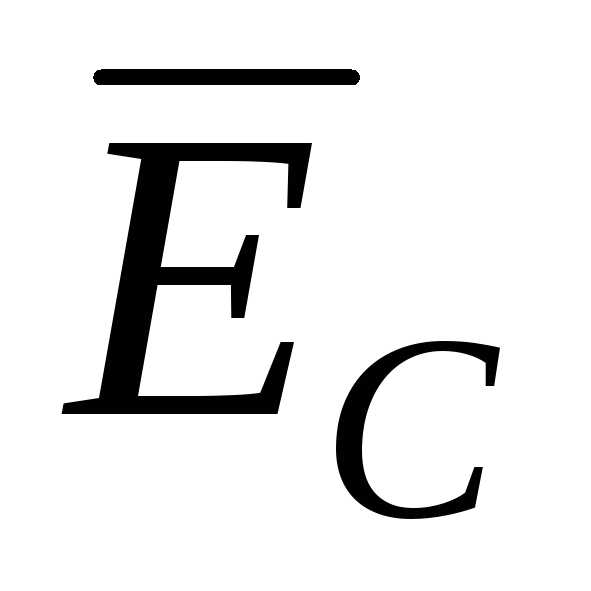 −
−  nN .
nN .
Токи в фазах нагрузки определяются
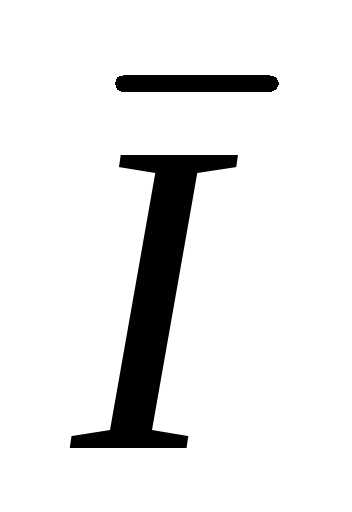 A =
A =  =
= 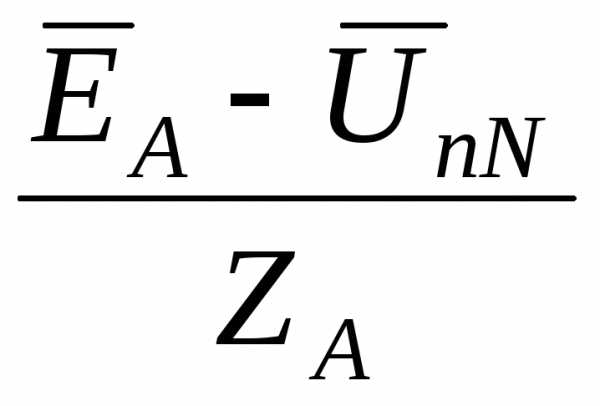
 B =
B = 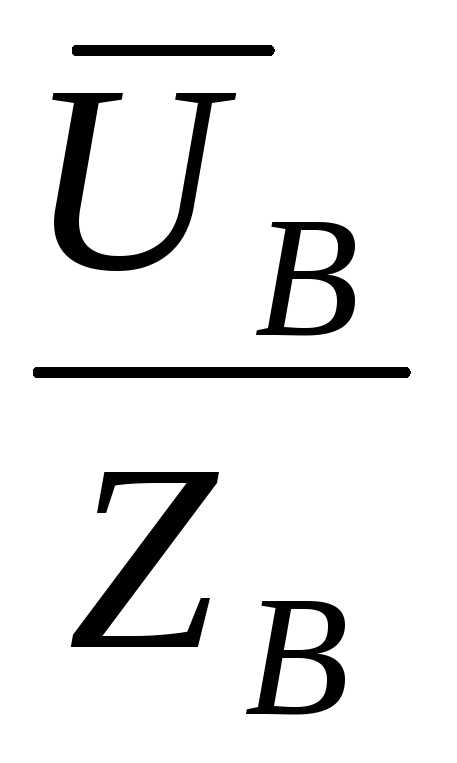 =
= 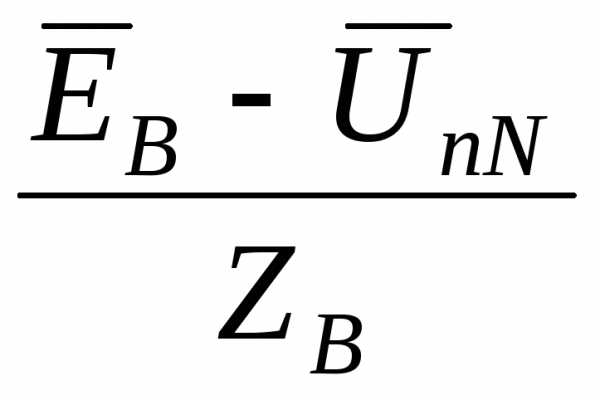 (51)
(51)
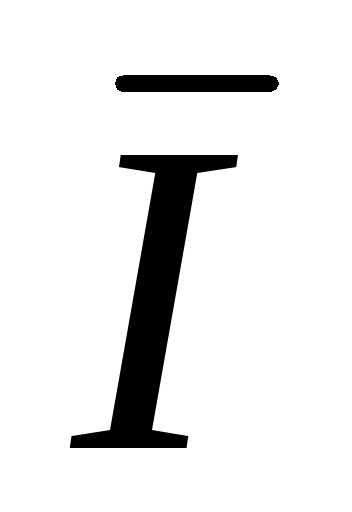 C =
C =  =
= 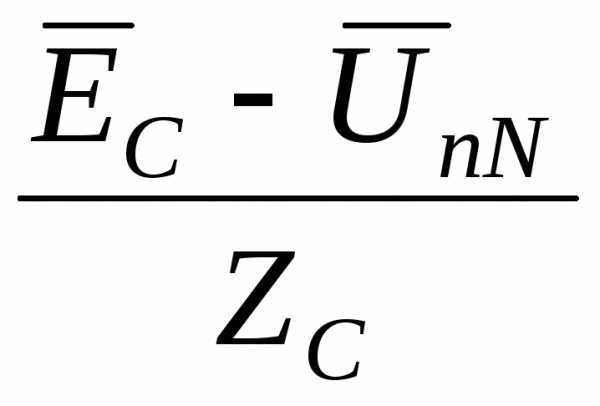
Векторная диаграмма трехпроводной системы при несимметричной нагрузке представлена на рис.25. Из нее следует, что фазные напряжения нагрузки не представляют собой симметричную систему векторов, т.к. действующие значения этих напряжений не будут равны между собой, а их фазовый сдвиг относительно друг друга будет отличаться от 120º.
Проведя геометрическое сложение векторов  ,
,  ,
, 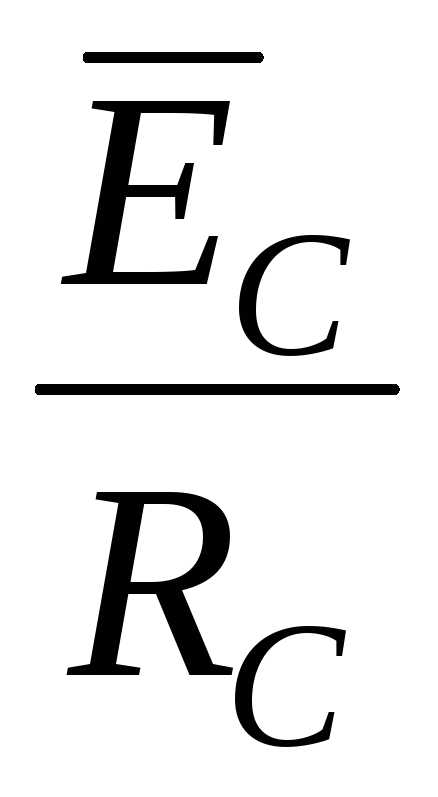 и разделив полученный результат на значение проводимостиY=
и разделив полученный результат на значение проводимостиY=  ,
,
в соответствии с выражением (49), получаем вектор  nN.
nN.
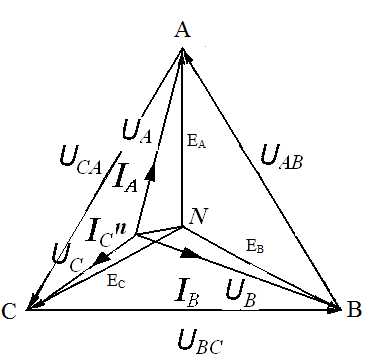
Рис.25. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке
Вычитая полученный результат из векторов  ,
,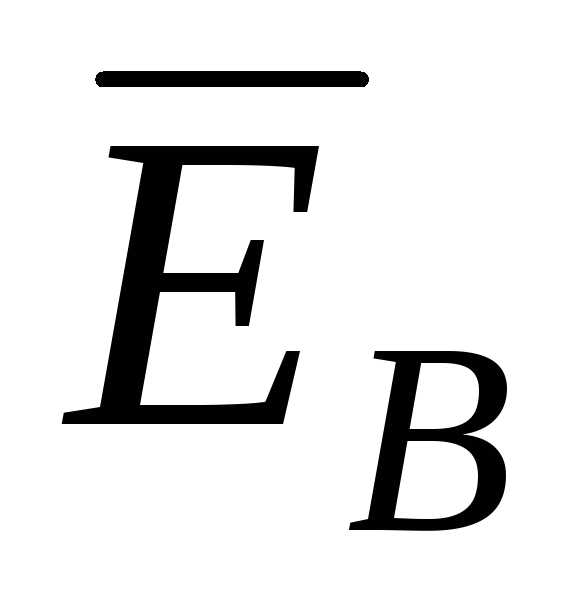 , и
, и , находим
, находим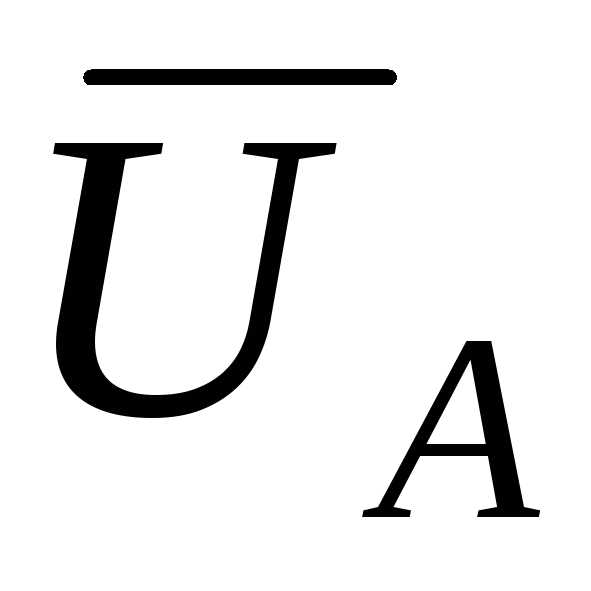 ,
,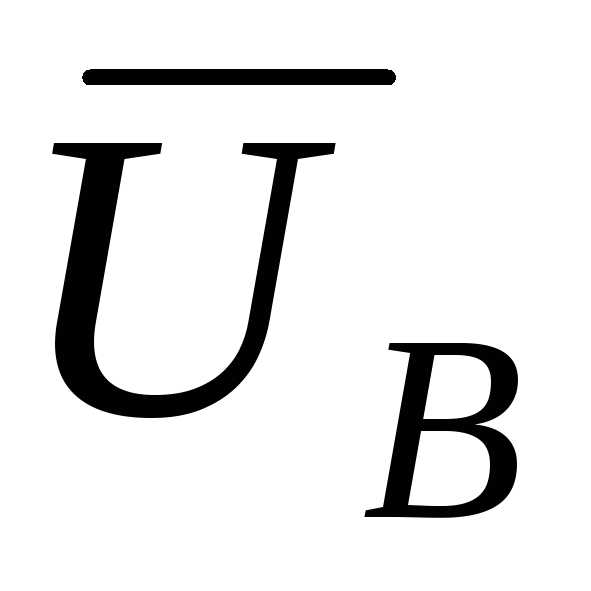 и
и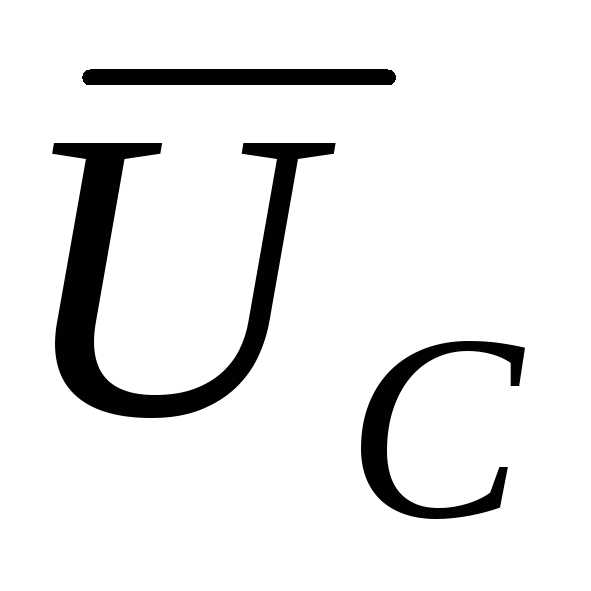 в соответствии с выражением (50).
в соответствии с выражением (50).
В результате получаем выражения для расчета действующих значений фазных напряжений UA,UВ,UСи токовIA,IВ,IС.
UА=UЛ∙ ;IA=
;IA= 
UВ=UЛ∙ ;IВ=
;IВ= 
UС=UЛ∙ ;IС=
;IС= 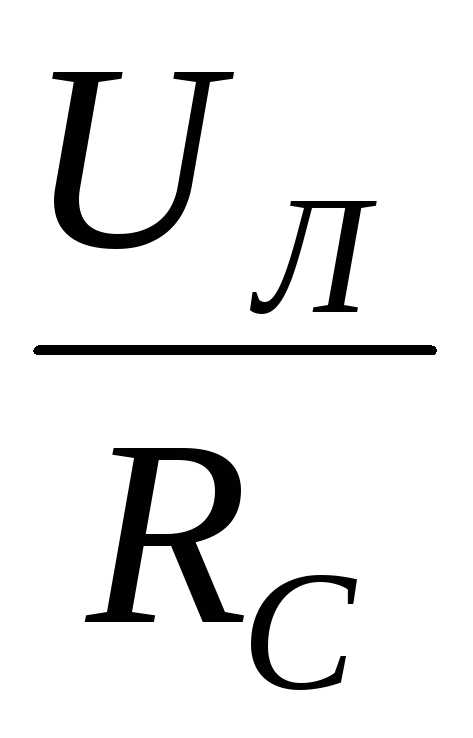 (52)
(52)
Для измерения мощности в работе используется метод двух ваттметров W1иW2(рис.26).
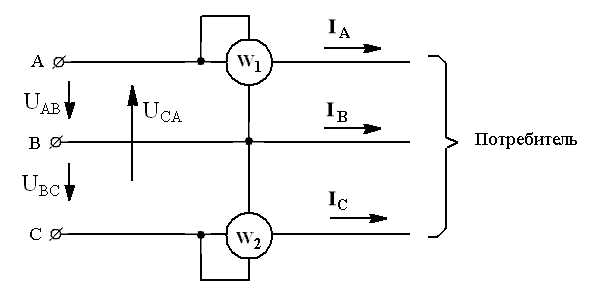
Рис.26. Схема измерения мощности методом двух ваттметров
Поясним принцип работы этого метода.
Приборы для измерения активной мощности (ваттметры), включенные в цепь однофазного переменного тока, измеряют величину
Р=U∙I∙cos(U^I) , (53)
где U- напряжение, приложенное к обмотке напряжения ваттметра;
I- ток, протекающий по токовой обмотке ваттметра;
U^I= φ - угол сдвига между напряжением и током.
Активная мощность трехфазной цепи при симметричной нагрузке фаз может быть выражена двумя равноценными формулами
Р= 3∙UФ ∙IФ∙cosφ или
Р= ∙UЛ ∙IФ∙cosφ . (54)
∙UЛ ∙IФ∙cosφ . (54)
Для измерения активной мощности в трехпроводных цепях трехфазного тока как при симметричной, так и при несимметричной нагрузке фаз (независимо от способа соединения нагрузки «звездой» или «треугольником»), широкое практическое применение получил метод двух ваттметров, включенных как показано на рис.27.
Показания ваттметров W1иW2можно записать следующим образом
Р1 =UАВ ∙IA∙cos(UAB^IA)
Р2 =UСВ ∙IC∙cos(UCB^IC) (55)
Обозначим через α и β соответственно углы (UAB^IA) и (UCB^IC) . Для определения α и β построим векторную диаграмму для случая симметричной активно-индуктивной нагрузки (рис.27). Согласно построению α = 30º + φ, β = 30º – φ.

Рис.27. Векторная диаграмма трехпроводной системы трехфазного переменного тока с симметричной активно-индуктивной нагрузкой
Учитывая, что при симметричной нагрузке UАВ =UСВ =UЛ иIА =IС =IЛ, показания ваттметров можно записать следующим образом:
Р=Р1 +Р2 =UЛ ∙IЛ∙ [cos(30º + φ) +cos(30º – φ)] = UЛ ∙IЛ∙cosφ.
UЛ ∙IЛ∙cosφ.
Полученное выражение совпадает с выражением (54). Таким образом, доказано, что сумма показаний двух ваттметров будет равна активной мощности трехфазной цепи.
Разность показаний двух ваттметров, умноженная на 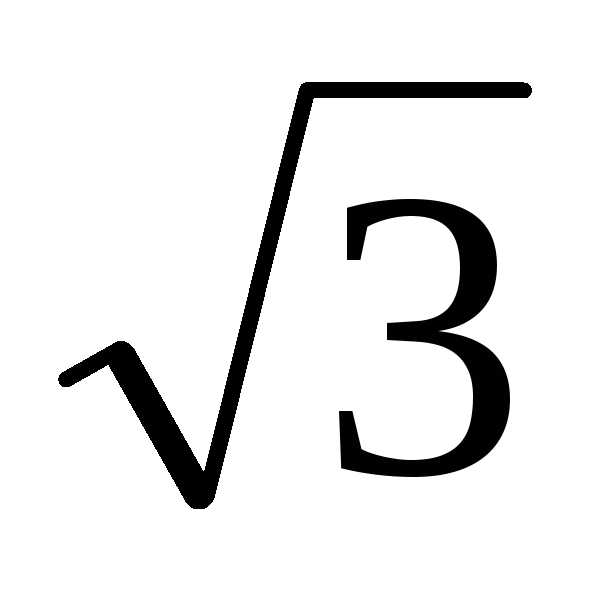 , будет равна реактивной мощности цепиQ.
, будет равна реактивной мощности цепиQ.
Q=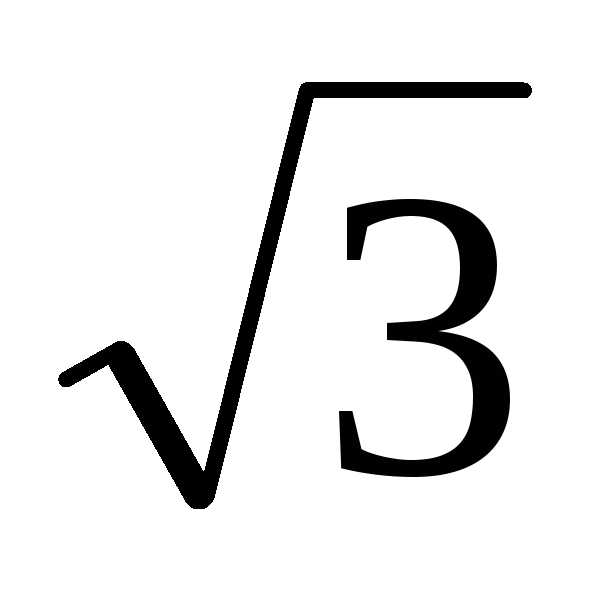 ( Р1 –Р2) =
( Р1 –Р2) =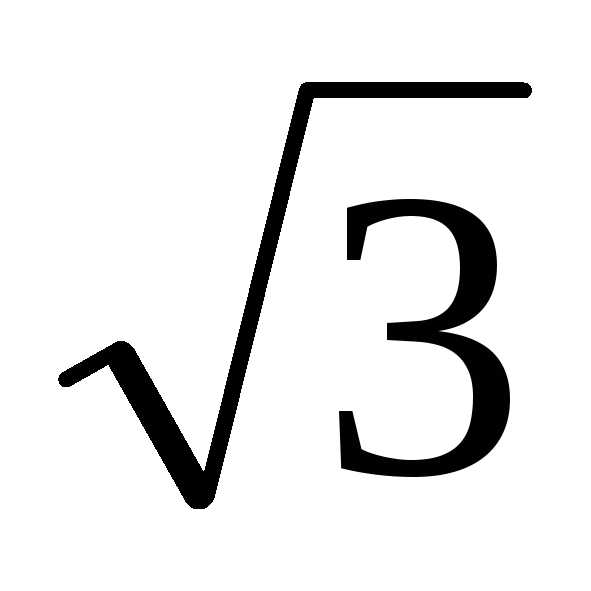 UЛ ∙IЛ∙ [cos(30º + φ) –cos(30º – φ)] =
UЛ ∙IЛ∙ [cos(30º + φ) –cos(30º – φ)] = UЛ ∙IЛ∙sinφ.
UЛ ∙IЛ∙sinφ.
Показания каждого из ваттметров в отдельности не имеют никакого физического смысла, за исключением случая симметричной и чисто активной нагрузки, при которой Р1 =Р2и составляет половину измеряемой мощности трехфазной цепи.
studfiles.net
3.3. Расчет трехфазных цепей при соединении звездой
Для расчета токов должна быть задана схема цепи, значение и тип сопротивлений, напряжение источника энергии. Расчеты обычно проводят для комплексных значений.
Симметричная нагрузка в схеме соединением «звезда – звезда» с нулевым проводом представлена на рис. 4.8.
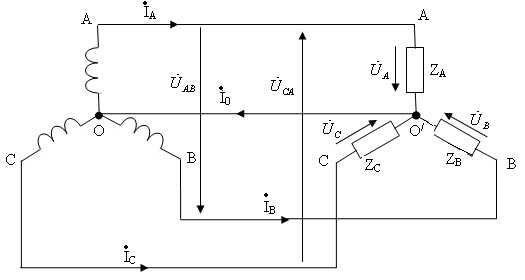
Рис. 4.8.
Если нулевой провод в схеме симметричного приемника () обладает весьма малым сопротивлением (Z0 = 0), то потенциал точки О/ практически равен потенциалу точки О, и точки сливаются в одну. В схеме образуются три обособленных контура, комплексные значения токов в каждом из которых определяются как в однофазной цепи 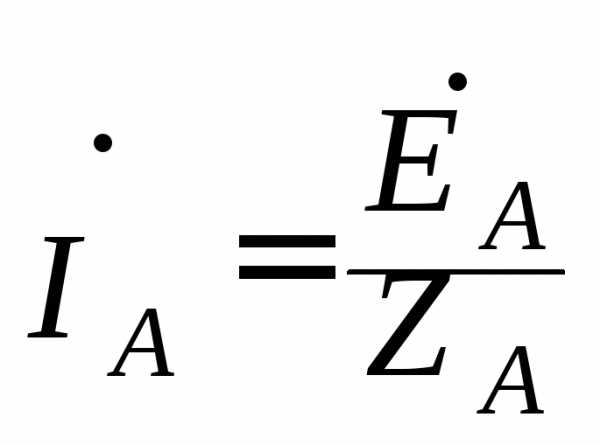 ;
; 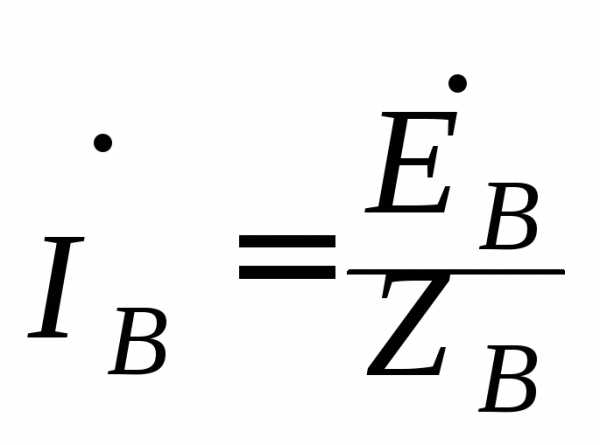 ;
; 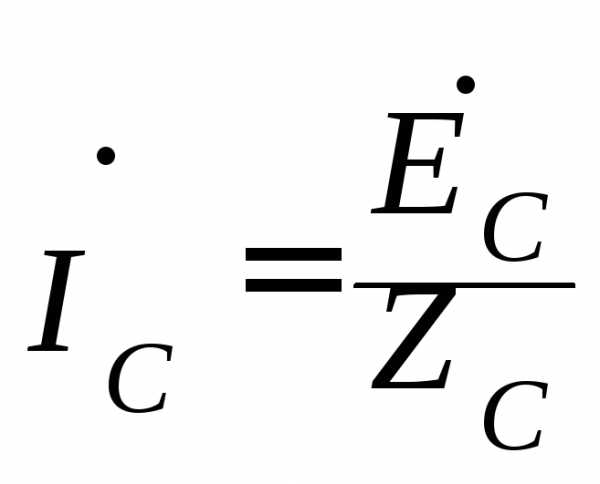
где ĖА, ĖВ, ĖС – фазные напряжения на зажимах генератора.
По первому закону Кирхгофа ток в нулевом проводе 4-х проводной системы равен геометрической сумме фазных токов 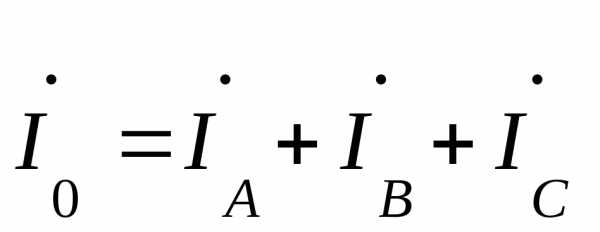 .
.
В общем случае комплексное напряжение между нулевыми точками 0 – 0` при наличии нейтрального провода 
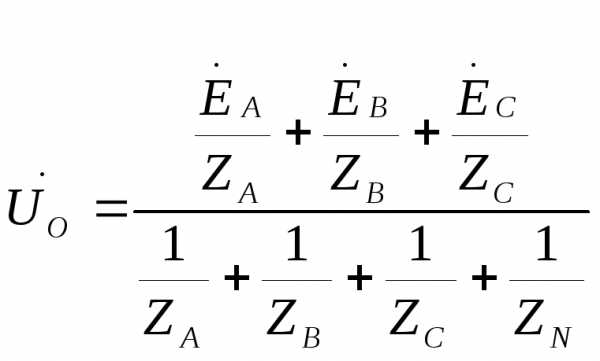 .
.
При равномерной симметричной нагрузке ток I0=0, и нулевой провод может быть изъят из схемы без изменения ее режима работы. Для 3-х проводной системы, т.е. не содержащей нейтральный провод (ZN = ∞) слагаемое 1/ ZNв знаменателе будет отсутствовать.
При определении напряжения фаз приемника если не учитывать сопротивления источника, то 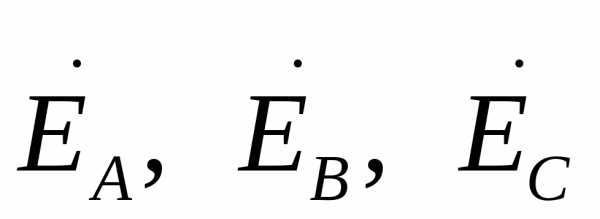 можно заменить на
можно заменить на 
Переходя к действующим значениям величин в случае, когда нагрузки во всех фазах равны и имеют активный характер ,
где 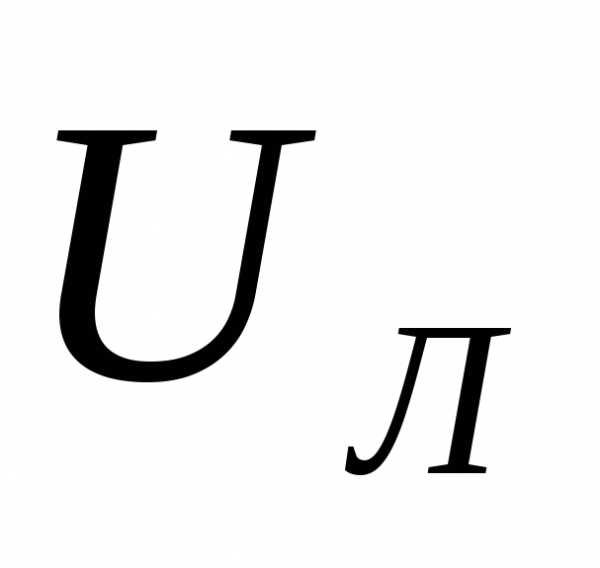 − значение линейного напряжения, токи соответственно принимают значения
− значение линейного напряжения, токи соответственно принимают значения ,
,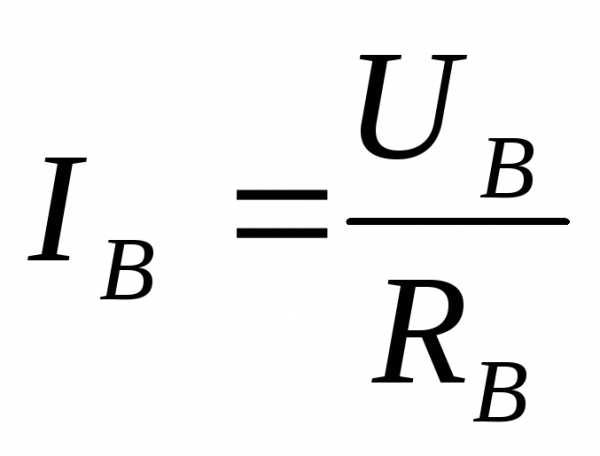 ,
,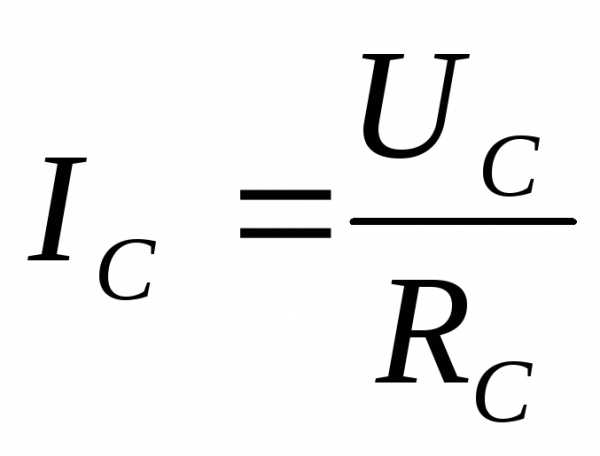 .
.
Общая мощность трехфазной цепи с активной нагрузкой равна
.
4.4. Несимметричная нагрузка при соединении звездой
При несимметричной нагрузке и отсутствии нулевого провода между нулевыми точками генератора О и приемника О/ появляется напряжение  , в результате чего фазные напряжения приемника оказываются различными. Расчетные соотношениемежду фазными и линейными напряжениями при этом нарушается. Для определения напряжения между нулевыми точками, а также фазных напряжений приемника предположим, что в электрической цепи имеется нейтральный (нулевой) провод, сопротивление которого
, в результате чего фазные напряжения приемника оказываются различными. Расчетные соотношениемежду фазными и линейными напряжениями при этом нарушается. Для определения напряжения между нулевыми точками, а также фазных напряжений приемника предположим, что в электрической цепи имеется нейтральный (нулевой) провод, сопротивление которого . Тогда напряжение между нулевыми точками источника и приемника
. Тогда напряжение между нулевыми точками источника и приемника
,
где g A, g B, g C, g N – проводимости фазных и нулевого проводов,
т
Рис. 3. 9. 3.10.
.е. для несимметричной системы при определении в знаменателе учитывается проводимость нейтрального провода gN..
в знаменателе учитывается проводимость нейтрального провода gN.. На рис. 4.9. приведена векторная диаграмма без нейтрального провода, на которой  ,
, ,
,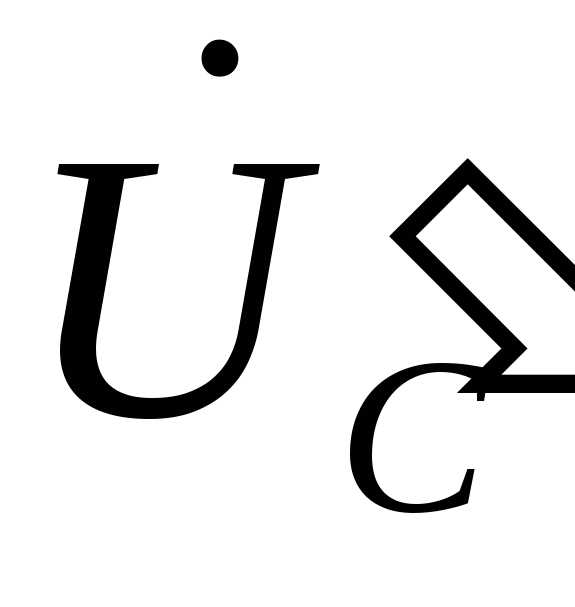 − векторы фазных напряжений источника, а
− векторы фазных напряжений источника, а ,
,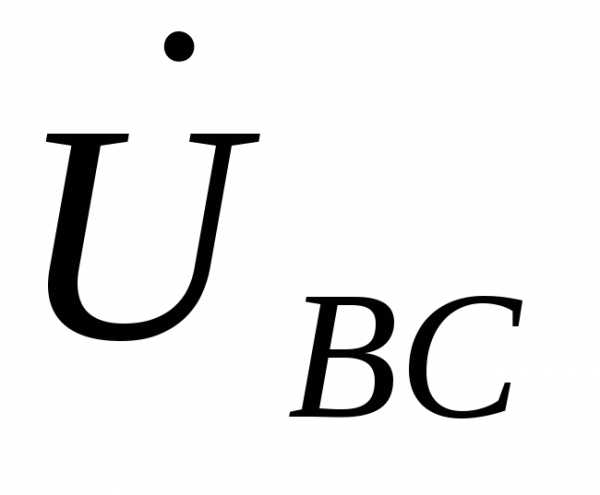 ,
, − векторы линейных напряжений источника, а также линейных напряжений приемника. Для построения вектора напряжения
− векторы линейных напряжений источника, а также линейных напряжений приемника. Для построения вектора напряжения 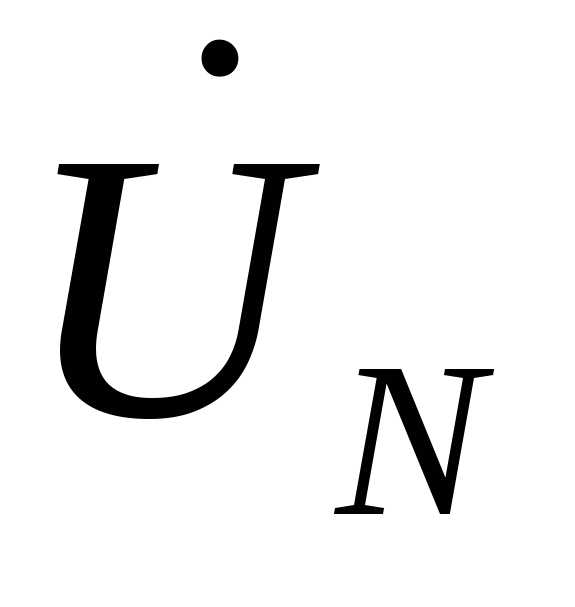 и векторов фазных напряжений приемника
и векторов фазных напряжений приемника 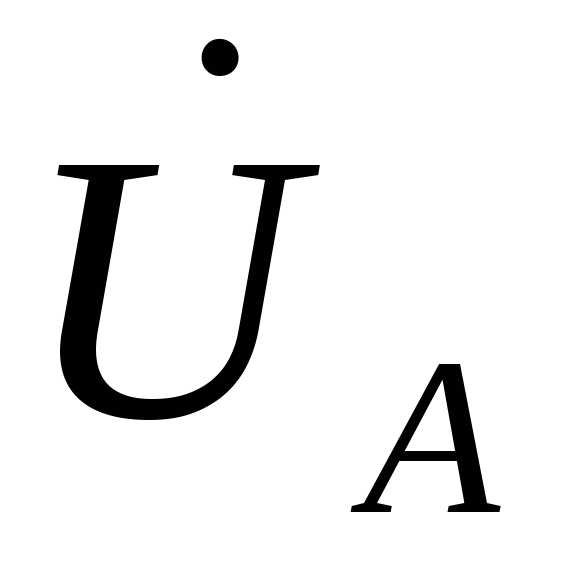 ,
,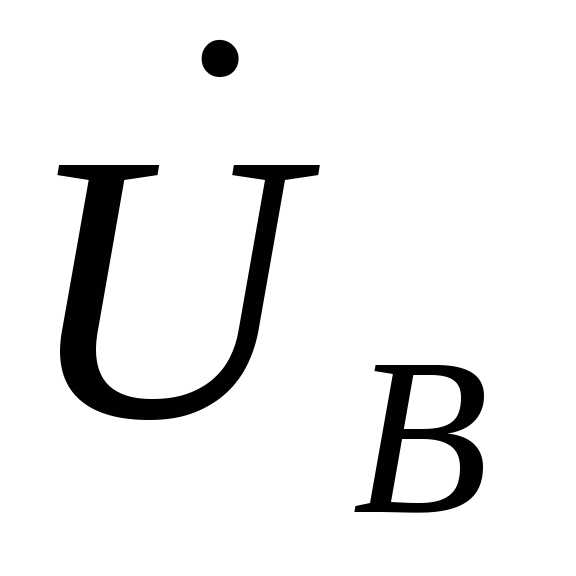 ,
,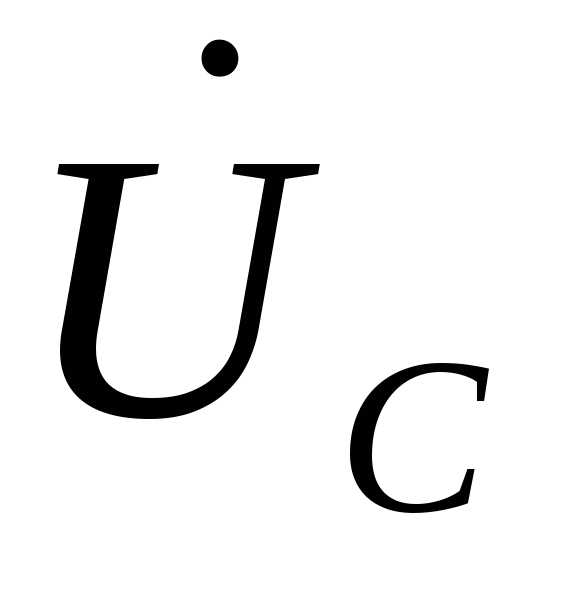 используем их значения, полученные выше.
используем их значения, полученные выше.
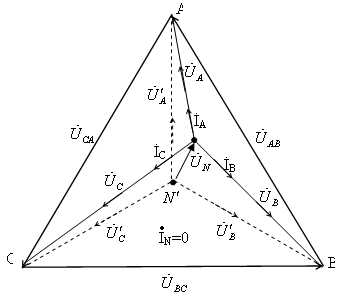
Рис. 4.9.
Связь между фазными и линейными векторами 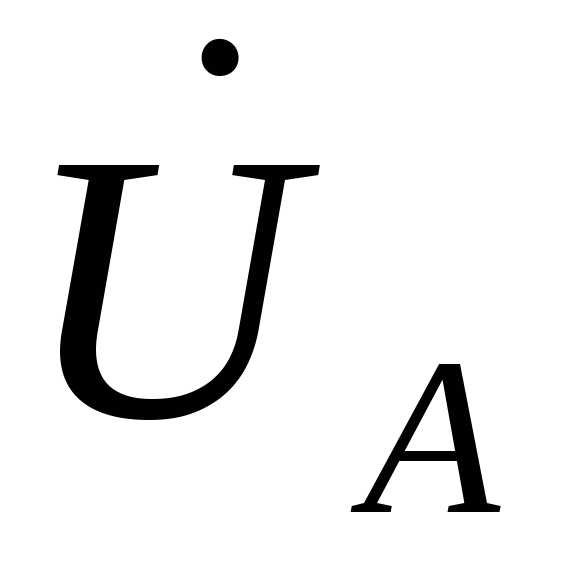 ,
,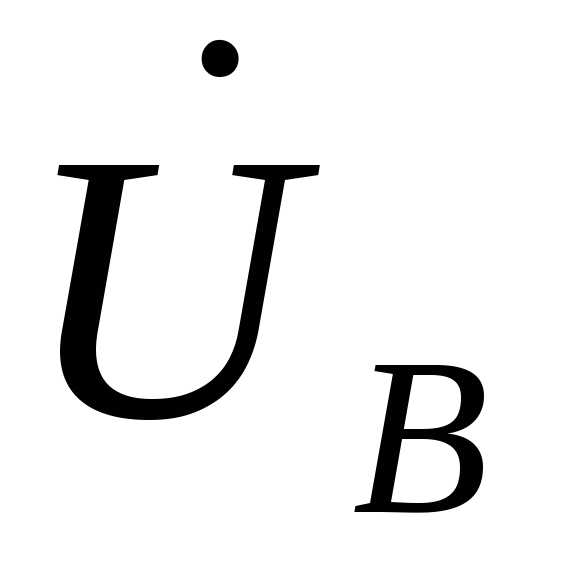 ,
,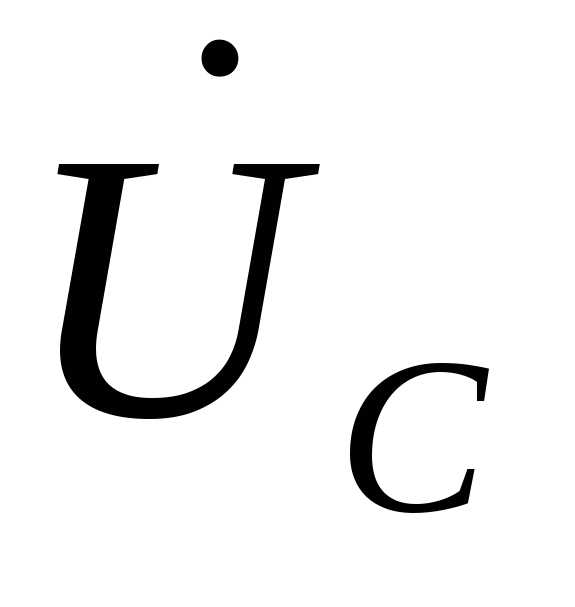 и
и ,
,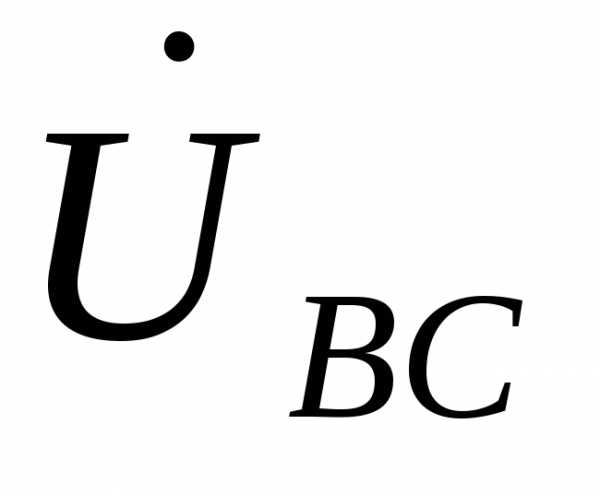 ,
, , определяем выражениями ,,.
, определяем выражениями ,,.
Векторная диаграмма построена для активной несимметричной нагрузки фаз ().
При изменении величины фазных активных сопротивлений напряжение  может изменяться в широких пределах. В соответствии с этим точкаN на диаграмме может занимать различные положения, а фазовые напряжения приемника могут отличаться друг от друга весьма существенно.
может изменяться в широких пределах. В соответствии с этим точкаN на диаграмме может занимать различные положения, а фазовые напряжения приемника могут отличаться друг от друга весьма существенно.
Рассмотрим, частный случай несимметричной нагрузки, когда  . Поскольку
. Поскольку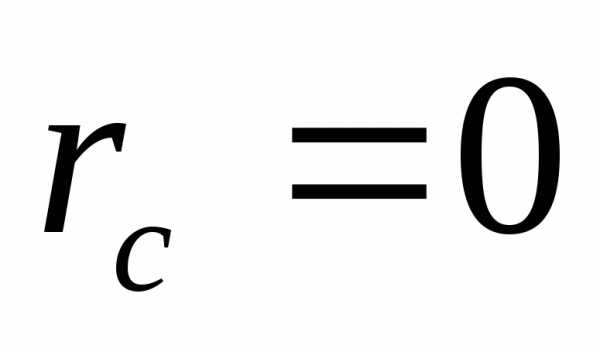 , то и, получим
, то и, получим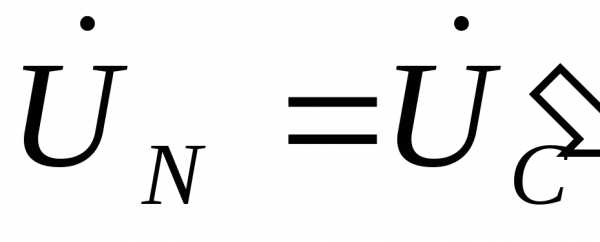 ,и
,и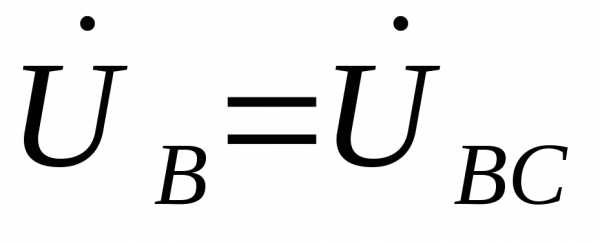 . ТочкаN на диаграмме переместится в точку С, напряжение
. ТочкаN на диаграмме переместится в точку С, напряжение  возрастет до фазного напряжения источника, а напряжения
возрастет до фазного напряжения источника, а напряжения  ,
, − до линейных напряжений.
− до линейных напряжений.

Рис. 4.10.
При изменении фазных напряжений происходит изменение фазных токов и мощностей − «перекос фаз».
Если при несимметричной нагрузке нулевые точки источника и приемника соединить нулевым проводом, то поскольку сопротивление нулевого провода мало, (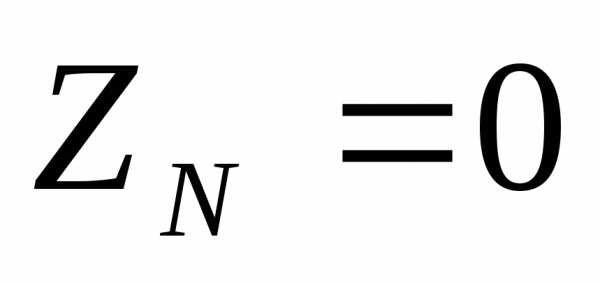 и), то фазные напряжения приемника получаются одинаковыми и сдвинутыми по фазе относительно друг друга на угол
и), то фазные напряжения приемника получаются одинаковыми и сдвинутыми по фазе относительно друг друга на угол . Включение нулевого провода приводит к соответствующим изменениям векторной диаграммы электрической цепи. Так, если электрической цепи без нулевого провода соответствует векторная диаграмма, изображенная на рис.3.9. сплошной линией, то той же цепи при включении нулевого провода соответствует диаграмма, изображенная на том же рисунке пунктиром.
. Включение нулевого провода приводит к соответствующим изменениям векторной диаграммы электрической цепи. Так, если электрической цепи без нулевого провода соответствует векторная диаграмма, изображенная на рис.3.9. сплошной линией, то той же цепи при включении нулевого провода соответствует диаграмма, изображенная на том же рисунке пунктиром.
Вектор 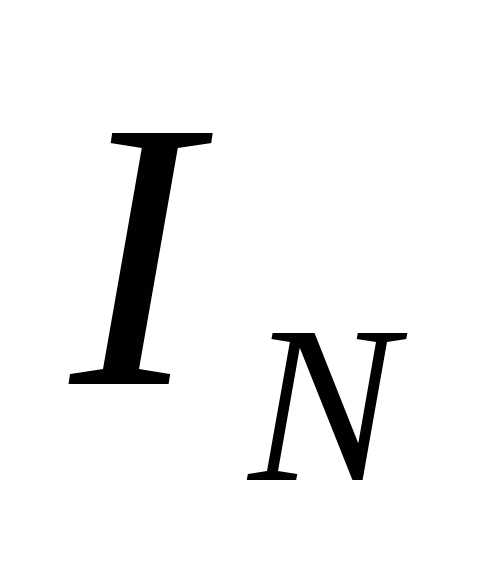 построен в соответствии с выражением. .
построен в соответствии с выражением. .
При наличии нулевого провода в схемах с несимметричной нагрузкой, так же как и в случае с симметричной нагрузкой остается в силе соотношение
.
На основании изложенного можно сделать вывод, что нулевой провод необходим для того, чтобы при несимметричной нагрузке выравнивать фазные напряжения приемника, т.е. получать во всех фазах приемника одинаковые напряжения, равные  .
.
Фазные токи, углы сдвига фаз между фазовыми напряжениями и токами, а также фазные мощности при несимметричной нагрузке в цепи с нулевым проводом будут в общем случае различными. Они могут быть определены по следующим формулам:  ,
,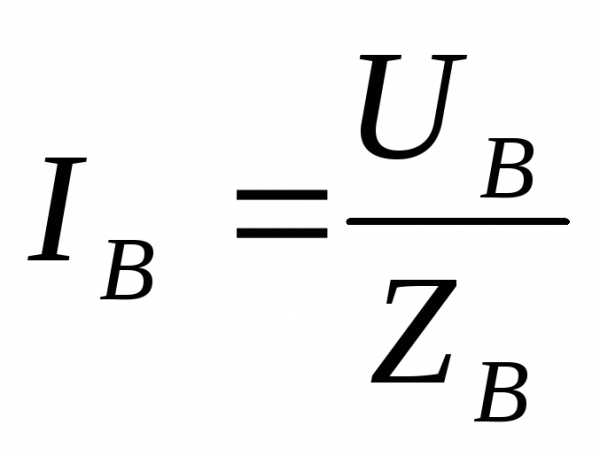 ,
, .
.
Углы сдвига фаз между фазными токами и напряжениями зависят от величины и характера сопротивлений фаз приемника и равны
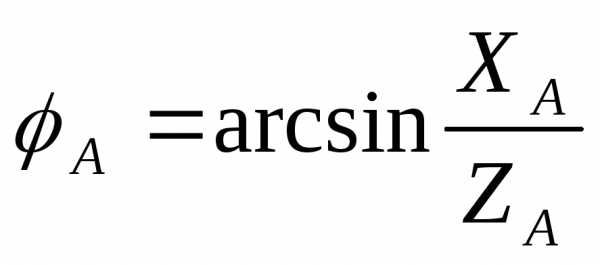 ,
, 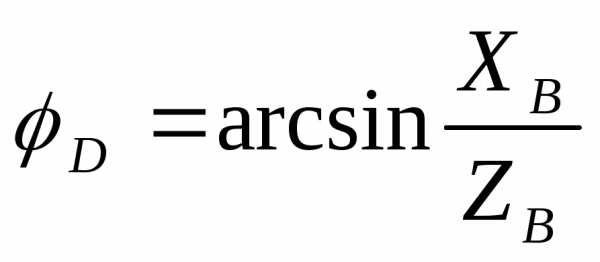 ,
,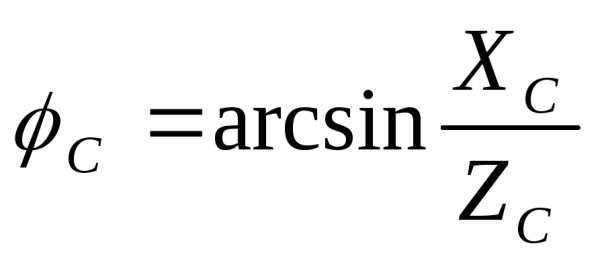 .
.
Мощности для фазы «А» равны
Активная и реактивная мощности трехфазного приемника при соединении звездой ,.
Если кроме фазных токов требуется найти ток в нулевом проводе, то задачу следует решать в комплексной форме. При этом необходимо прежде всего выразить в комплексной форме то  ,
,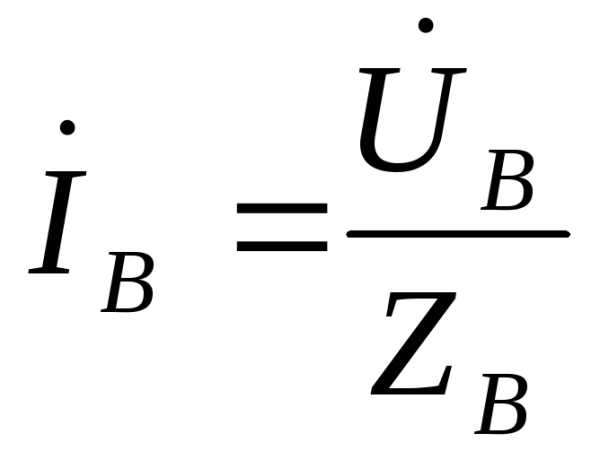 ,
,
Ток в нулевом проводе можно определить также по векторной диаграмме, не прибегая к решению задачи в комплексной форме.
studfiles.net
4.3. Трехфазные цепи при соединении приемников звездой
Соединение звездой при симметричной нагрузке. При соединении приемников звездой концы фаз приемника соединены в общий узел N'. При этом концы всех фаз генератора соединены в общий узел N, а начала фаз — с нагрузкой — звездой сопротивлений.
Если узлы N и N' соединить проводом, называемым нейтральным, с сопротивлением ZN, то получим четырехпроводную цепь (рис. 4.7, а). Сопротивления проводов, связывающих источник с нагрузкой, можно учесть в сопротивлениях нагрузки Za,Zb,Zc.

Так как при соединении звездой фазы генератора соединены последовательно с фазами нагрузки, линейные токи одновременно являются и фазными токами как в фазах генератора, так и в фазах нагрузки:
(4.8)
За условные положительные направления линейных токов IА, IВ, IС принимают направления от источника к нагрузке, а за положительное направление тока в нейтральном проводе - от нагрузки к источнику.
Согласно первому закону Кирхгофа, ток в нейтральном проводе
(4.9)
При симметричной нагрузке поэтому токи в фазах приемника равны по значению и сдвинуты по фазе на один и тот же угол относительно соответствующих напряжений, т. е. φA = φB = φC = φ. Векторная диаграмма напряжений и токов для симметричной нагрузки представлена на рис. 4.7, б. Из диаграммы видно, что ток в нейтральном проводе равен нулю (IN = 0), так как . Таким образом, если нагрузка равномерная, то необходимость в нейтральном проводе отпадает. Трехфазная цепь без нейтрального провода является трехпроводной.
Рассмотрим четырехпроводную цепь (рис. 4.7, а) более подробно. Найдем для этой цепи напряжение между нейтральными точками N и N', или смещение нейтрали, по методу двух узлов:
(4.10)
где - комплексы проводимостей фаз приемника;YN= 1/ZN -комплекс проводимости нейтрального провода. Так как при симметричной нагрузке Ya = Yb = Yc, то (4.10) можно переписать в виде
(4.11)
При симметричной системе напряжений имеем
а значит, согласно (4.11), UNN =0. Так как ток в нейтральном проводе то при симметричной нагрузкеIN = 0. Следовательно, еще раз можно подчеркнуть, что при симметричной нагрузке напряжение между нейтральными точками N и N' и ток в нейтральном проводе равны нулю.
Согласно второму закону Кирхгофа, для контуров (см. рис. 4.7, а) NAaN'N, NBbN'N, NCcN'N находим
(4.12) Так как при симметричной нагрузке UN’N =0, то из (4.12) следует, что
Итак, зная фазные напряжения и сопротивления нагрузки, находим токи в каждой фазе приемника:
(4-13)
Так как при симметричной нагрузке токи в фазах приемника равны, то достаточно определить ток только в одной из фаз трехфазной цепи.
Соединение звездой при несимметричной нагрузке. При несимметричной нагрузке сопротивления приемника не одинаковы, т. е. Za ≠ Zb ≠ Zc. Для несимметричных нагрузок применяют четырехпроводные цепи, так как между точками N и N' появляется напряжение UN’N и напряжения на фазах нагрузки различны. При этом нарушается соотношение между фазными и линейными напряжениями причем на одних фазах нагрузки напряжение становится большим, а на других — меньшим, чем
Наличие нейтрального провода в цепи с несимметричной нагрузкой позволяет выравнивать напряжение на фазах приемника и поддерживать их неизменными, равными фазным напряжениям источника Uл / , т. е. нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда ZN = 0, даже при несимметричной нагрузке фазные напряжения приемника равны друг другу и соблюдается соотношение между фазными и линейными напряжениями .
, т. е. нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда ZN = 0, даже при несимметричной нагрузке фазные напряжения приемника равны друг другу и соблюдается соотношение между фазными и линейными напряжениями .
Если нагрузка несимметрична (Za ≠ Zb ≠ Zc) и нейтральный провод имеет конечное сопротивление ZN, то напряжение UN’N между нейтральными точками N' и N определяется по формуле (4.10), а напряжения на фазах нагрузки — по формулам (4.12). Тогда токи в схеме рис. 4.7, а
Если напряжения источника UA, UB, UC образуют симметричную систему, то при отсутствии нейтрального провода и при UN'N ≠ 0 напряжения на фазе нагрузки Ua, Ub и Uc несимметричны, что видно из векторной топографической диаграммы, приведенной на рис. 4.8. Особенностью этой диаграммы является то, что каждой точке электрической цепи А, В, С, N и N' соответствует определенная точка на диаграмме.

При этом расположение этих точек на диаграмме должно быть таким, чтобы отрезок, соединяющий любые точки на диаграмме, по длине и фазе определял напряжение между соответствующими точками цепи.
Напряжения на фазах нагрузки тем больше отличаются друг от друга, чем больше напряжение UN'N. Из выражения (4.10) и из топографической диаграммы (рис. 4.8) следует, что напряжение между нейтральными точками UN'N будет изменяться при изменении нагрузки в любой фазе, при этом с изменением UN'N будет изменяться напряжение всех фаз приемника.
Чтобы напряжения на фазах нагрузки были одинаковыми, необходимо иметь UN'N= 0, что может быть получено двумя способами. Во-первых, выравниванием нагрузки в фазах приемника, когда YA = YB = YC = = Yф, а значит, согласно (4.10),
так как
В о-вторых, если имеется нейтральный провод с сопротивлением ZN’N = 0 (или YN’N = ∞ ), то напряжение UN'N, согласно (4.10), также принимает нулевое значение независимо от нагрузки фаз. Для этого случая построена векторная диаграмма (рис. 4.9). При обрыве нейтрального провода (ZN = ∞) и несимметричной нагрузке напряжение UN'N станет максимальным.
о-вторых, если имеется нейтральный провод с сопротивлением ZN’N = 0 (или YN’N = ∞ ), то напряжение UN'N, согласно (4.10), также принимает нулевое значение независимо от нагрузки фаз. Для этого случая построена векторная диаграмма (рис. 4.9). При обрыве нейтрального провода (ZN = ∞) и несимметричной нагрузке напряжение UN'N станет максимальным.
В фазах нагрузки могут возникнуть перенапряжения, поэтому в нейтральный провод плавкий предохранитель не ставят. Приемники электрической энергии можно подразделить на трехфазные и однофазные. К числу трехфазных относятся трехфазные электрические двигатели, имеющие симметричные обмотки и обеспечивающие равномерную нагрузку фаз. Такие электродвигатели включают в трехфазную цепь звездой без нейтрального провода Однофазные приемники, к которым относятся электрические лампы, нагревательные приборы и ряд других приемников, всегда подключают к четырехпроводной цепи. Эти приемники подключаются на фазное напряжение, которое в  раз меньше линейного напряжения сети.
раз меньше линейного напряжения сети.
Пример 4.1. К трехфазной линии напряжением Uл=380 В подключен несимметричный трехфазный приемник, соединенный звездой с нейтральным проводом (рис. а)). Активные и реактивные сопротивления фаз приемника соответственно равны: Ra = 19 Ом, Xa = 0 Ом, Rb= 8 Ом, Хb = 6 Ом, Rс = 24 Ом, Хc = 18 Ом. Сопротивлениями проводов можно пренебречь. Определить ток в фазах приемника, в линейных проводах и в нейтральном проводе.
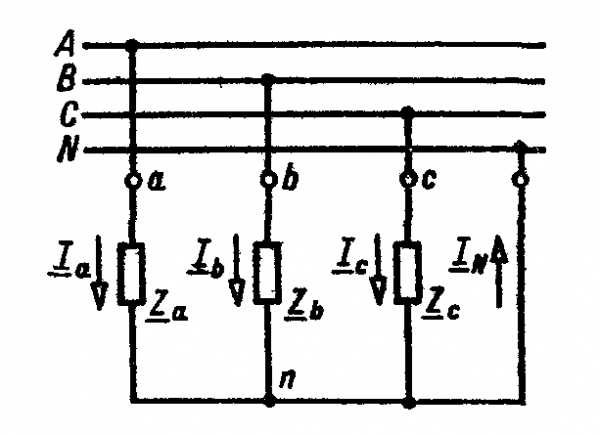
а)
Рисунок к примеру 4.1.
Решение. Токи в линейных проводах и фазах приемника одинаковы и рассчитываются по закону Ома:
-
Фазное напряжение
Комплексные фазные напряжения:
Комплексные сопротивления фаз:
Токи в фазах приемника и проводах линии:
Ток в нейтральном проводе
Для построения топографической диаграммы напряжений выберем масштаб напряжений. В выбранном масштабе строим топографическую диаграмму напряжений. При построении векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на разные углы сдвига фаз: φа =0 — нагрузка чисто активная (Х=0), φb = 36°52' — нагрузка активно-индуктивная, φc = - 36052'— нагрузка активно-емкостная.
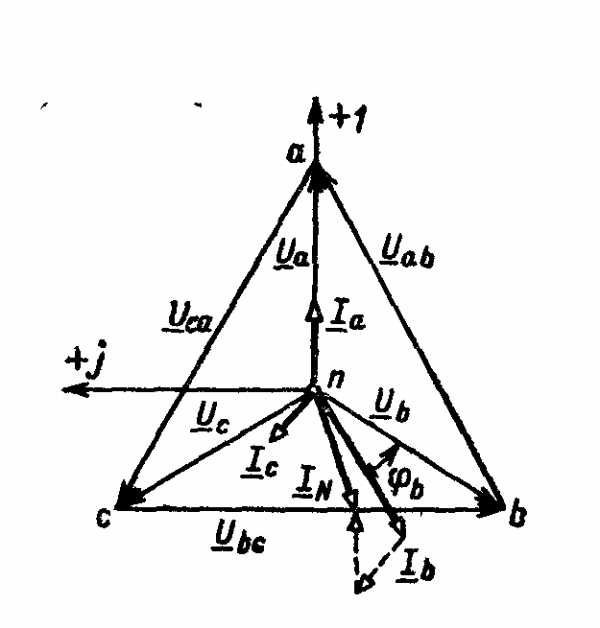 Действующее значение тока в нейтральном проводе равно 16,14 А, а его начальная фаза ψN= 2010. На диаграмме (рис. б) строим векторы токов
Действующее значение тока в нейтральном проводе равно 16,14 А, а его начальная фаза ψN= 2010. На диаграмме (рис. б) строим векторы токов
б)
Рисунок к примеру 4.1.
с учетом углов сдвига фаз. Вектор тока в нейтральном проводе можно построить двумя способами: или как сумму векторов или непосредственно отложить вектор IN в соответствии с расчетными данными.
 Пример 4.2. К трехпроводной трехфазной сети с линейным напряжением Uл=220 В подключен приемник, фазы которого соединены звездой, (рис.а)). Заданы сопротивления Rа = 10 Ом, Rb = 5 Ом, Хb = 9,66 Ом, Хс = 10 Ом. Определить токи в ветвях, построить совмещенную топографическую диаграмму напряжений и векторную диаграмму токов.
Пример 4.2. К трехпроводной трехфазной сети с линейным напряжением Uл=220 В подключен приемник, фазы которого соединены звездой, (рис.а)). Заданы сопротивления Rа = 10 Ом, Rb = 5 Ом, Хb = 9,66 Ом, Хс = 10 Ом. Определить токи в ветвях, построить совмещенную топографическую диаграмму напряжений и векторную диаграмму токов.
а)
Рисунок к примеру 4.2.
Решение. Фазные напряжения источника образуют симметричную систему
Комплексные сопротивления фаз приемника:
их комплексные подводимости
Смещение нейтрали

Рисунок к примеру 4.2.
Фазные напряжения приемника:
Фазные токи и токи в линии:
Для построения векторных диаграмм выбираем масштабы напряжения и тока. Строим симметричную топографическую диаграмму напряжений генератора ( рис. б)) и вектор смещения нейтрали UnN= 84e j205° В. Векторы, соединяющие точку n и точки а, b, с, соответственно будут векторами фазных напряжений приемника Ua, Ub, Uc. Из точки n строим векторы токов Ia, Ib, Iс учетом сдвига фаз относительно напряжений φa= 0°, φb= 60°, φc= — 90°.
Топографическая диаграмма напряжений показывает, что из-за смещения нейтрали симметрия фазных напряжений приемника нарушается: Ua= 206 В вместо Uф = 127 В; Uc = 145,6 В; Ub=75,5 В.
studfiles.net
Соединение фаз потребителей электроэнергии в звезду
Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:
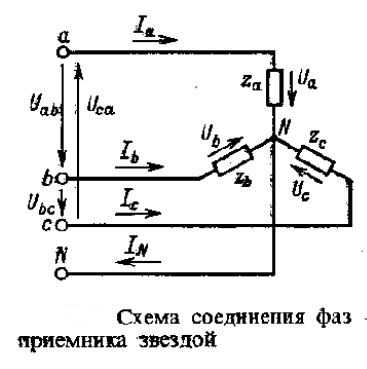
Из схемы видно, что фазные напряжения приемника Ua, Ub, Uc не равны линейным напряжениям Uab, Ubc, Uca. Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:
Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.
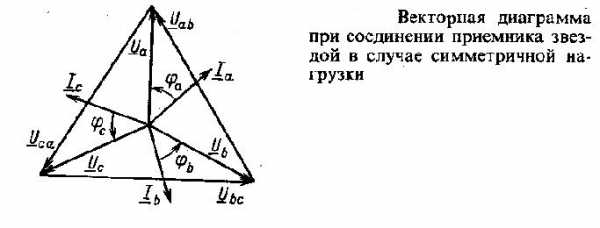
Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:
Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.
Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.
Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:
Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:
Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода IN. В случае отсутствия нейтрального провода справедливо будет выражение:
Симметричная нагрузка при соединении приемников звездой
Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:
Условие симметричности также может быть выражено через комплексные сопротивления Za = Zb = Zc.
Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.
В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:
Так как в четырехпроводной цепи Ua = Ub = Uc = Uл / , то при симметричной нагрузке:
Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше. Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен IN = Ia + Ib + Ic = 0.
Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.
Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.
Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:
Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:
Пример
К трехфазной электрической цепи с линейным напряжением Uл = Uab = Ubc = Uca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление rф = 10 Ом и индуктивное сопротивление хф = 10 Ом, которые соединены последовательно. Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.
Решение
Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.
Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:
Активная, реактивная и полная мощности приемника, а также любой фазы будут равны:
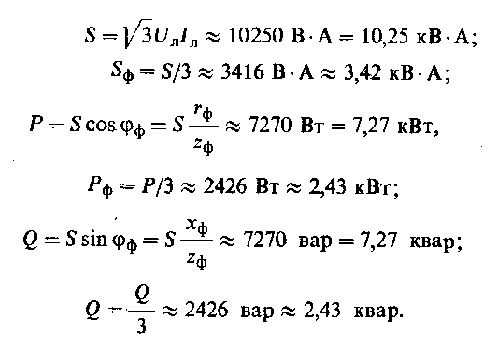
Векторная диаграмма для данной системы приводилась выше.
Несимметричная нагрузка при соединении приемников звездой
Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: ra = rb = rc, xa = xb ≠ xc. В общем случае считают, что несимметричная нагрузка возникает при отключении одной из фаз.
Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.
В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.
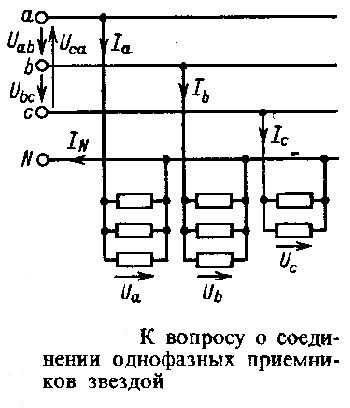
Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.
Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.
Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:
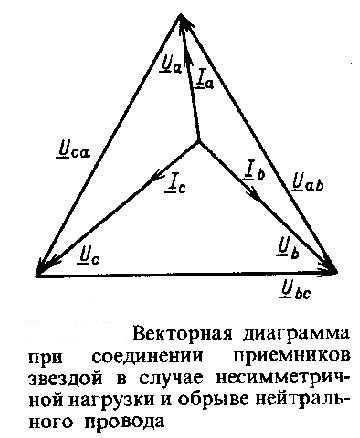
Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:
Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.
Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).
Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:
Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.
Пример
В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы Uном = 127 В, Рном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.
Решение
Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:
Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:
Для определения тока в нейтральном проводе IN решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:
Где комплексные значения фазных сопротивлений будут равны Za = 8,05 Ом, Zb = 16,1 Ом, Zс = 32,2 Ом.
Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:
elenergi.ru
Работа 5. Исследование цепи трехфазного тока при симметричной и несимметричной нагрузках фаз. Соединение звездой и треугольником.
Цель работы:
Экспериментальная проверка соотношений между линейными и фазными напряжениями и токами при соединении звездой и треугольником.
Изучение особенностей режимов работы трехфазных цепей при соединении приемников звездой и треугольником.
Изучение способов измерения мощности в трехфазных цепях.
Пояснения к работе.
Трехфазные цепи в современной электроэнергетике получили наибольшее распространение благодаря их преимуществам в отношении экономичного передачи электрической энергии, а также возможностей получения кругового вращающегося магнитного поля и двух эксплуатационных напряжений в одной установке – фазного и линейного.
Основными способами соединений фаз обмоток генераторов, трансформаторов, электродвигателей и других приемников являются соединения звездой и треугольником.
Соединение звездой.
При соединении фаз обмоток генераторов или приемников в звезду из конца (x, y, z) или начала (A, B, C) соединяют в одну большую точку, которая называется нейтральной точкой (рис.5.1). Провод, соединяющий нейтральные точки генератора О’ и приемника О называется нейтральным или нулевым: остальные провода – линейными. Напряжение между линейным проводом каждой фазы генератора или приемника и нулевым проводом, а также токи в фазах, называют фазными: Uф, Iф. Токи в линейных проводах и напряжения между ними называют, соответственно, линейными: Uл, Iл.
Нагрузка называется симметричной, если сопротивление всех фаз одинаковы по величине и характеру: za= zb= zc.
Е
IA
сли это условие не выполняется, то нагрузка будет несимметричной, при этом она может быть равномерной, если одинаковы величины (модули) сопротивления фаз, т.к.zA= zB= zC.
UBC
IC
Рис.5.1. Схема соединения звездой.
При соединении звездой по фазе течет тот же ток, что и в линейном проводе. Поэтому Iф=Iл. Линейные напряжения являются векторной разностью соответствующих фазных напряжений:
; ;. (5.1)
Векторная диаграмма для рассматриваемого соединения представлена на рис.5.2. За основу диаграммы взяты три вектора фазных напряжений , углы между которым равны120˚.
По отношению к каждому из этих направлений вектор соответствующего фазного тока сдвинут на угол φ, величина которого зависит от характера нагрузки и определяется по формуле: 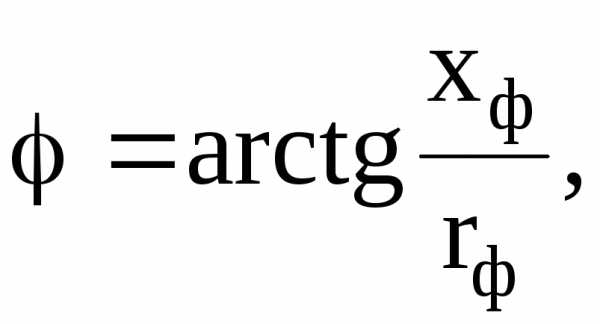 гдеrф и xф – соответственно активное и реактивное сопротивления фазы нагрузки.
гдеrф и xф – соответственно активное и реактивное сопротивления фазы нагрузки.
Векторы линейных напряжений строятся по уравнениям (5.1).
При симметричной нагрузке токи в фазах будут одинаковыми, а длина каждого из векторов линейного напряжения будет в 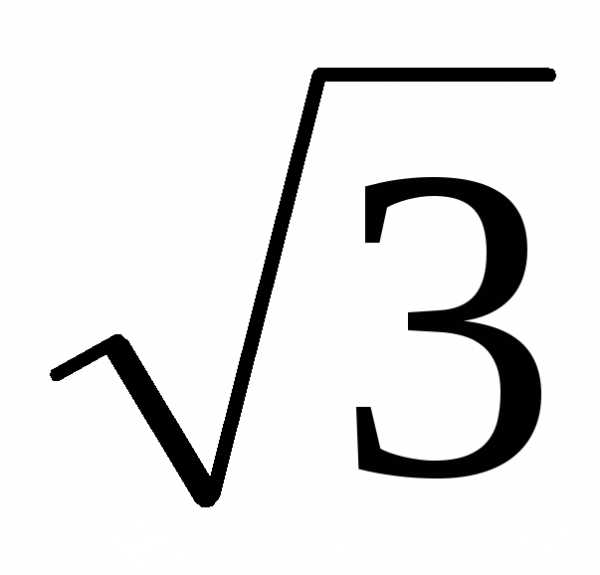 раз больше длины вектора фазного напряжения (см.рис.5.2).
раз больше длины вектора фазного напряжения (см.рис.5.2).
-UB
UAB
-UC
UC
-UA
UCA
Рис.5.2. Векторная диаграмма напряжений и токов
в соединении звездой.
При несимметричной нагрузке и наличии нейтрального провода напряжения на каждой фазе приемника Ua, Ub, Uc при изменениях нагрузки практически остаются неизменными и равными соответствующим фазным напряжениям генератора Ua, Ub, Uc. Это связано с тем, что сопротивление нейтрального провода обычно значительно меньше сопротивления фаз приемника. Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Поэтому режимы работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз. Расчет токов в фазах нагрузки и в нулевом проводе, если пренебречь падением напряжений в нейтральном и линейном проводах, осуществляется на основе следующих соотношений:
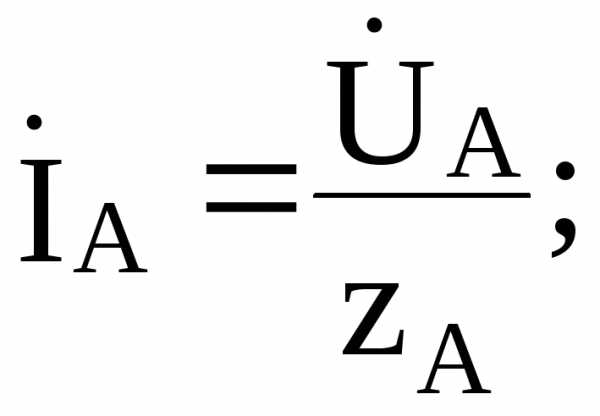

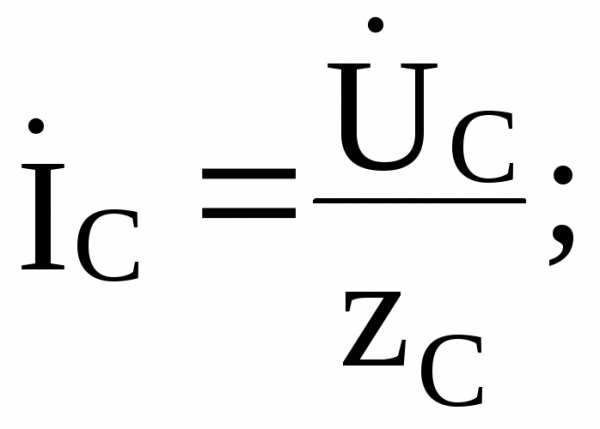 (5.2)
(5.2)
Если сопротивлением нейтрального провода не пренебрегать, то при Io= 0 напряжения на фазах нагрузки не будут равны соответствующим напряжениям генератора. В этом случае рассчитывается напряжение между нейтральными точками генератора и приемника:
(5.3)
где 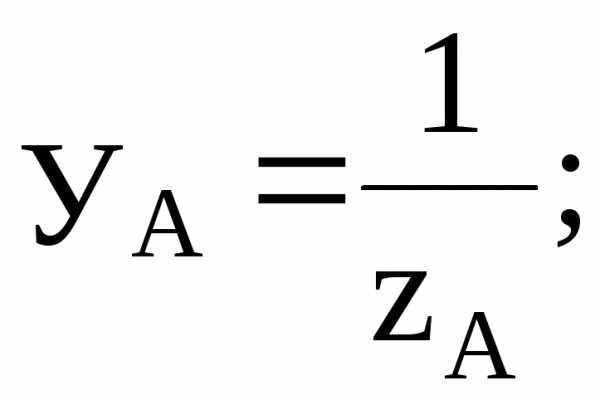
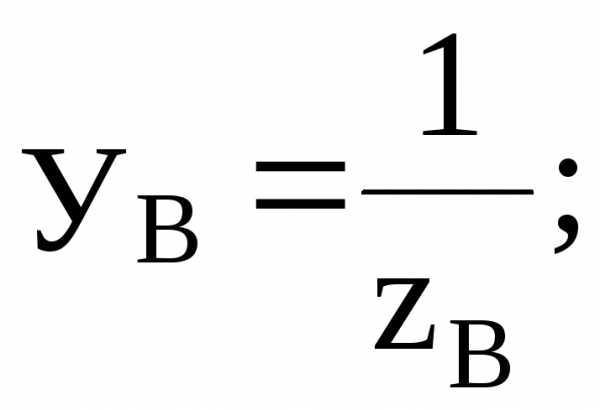
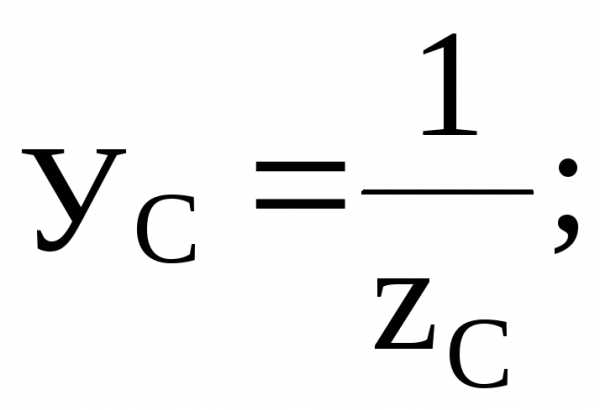
 – комплексные проводимости фаз нагрузки и нейтрального провода.
– комплексные проводимости фаз нагрузки и нейтрального провода.
Напряжения на фазах нагрузки определяется по следующим соотношениям:
При симметричной нагрузке ток в нейтральном проводе отсутствует:
и отпадает необходимость иметь этот провод.
Если приемники соединены звездой без нулевого провода, то изменение величины тока в одной из фаз оказывает существенное влияние на работу других фаз. При несимметричной нагрузке и отсутствии нейтрального провода расчет трехфазной цепи осуществляется аналогично. При этом в выражении (5.3) следует положить У0=0.
Соединение треугольником.
Фазные обмотки генератора или приемника соединяются в треугольники так (рис.5.3), чтобы конец первой фазной обмотки Х соединялся с началом B второй фазной обмотки, а конец У второй обмотки с началом третьей обмотки C и конец Z её с началом A первой обмотки.
Из схемы рис.5.3 видно, что независимо от характера нагрузки напряжение в каждой фазе приемника равно линейному Uф=Uл. Если напряжения и сопротивления фаз нагрузки заданы, то фазные токи определяются по формулам:
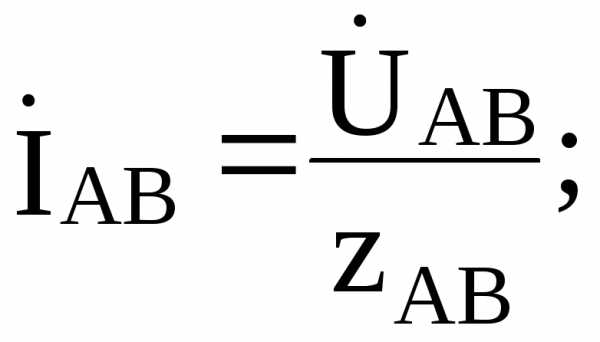
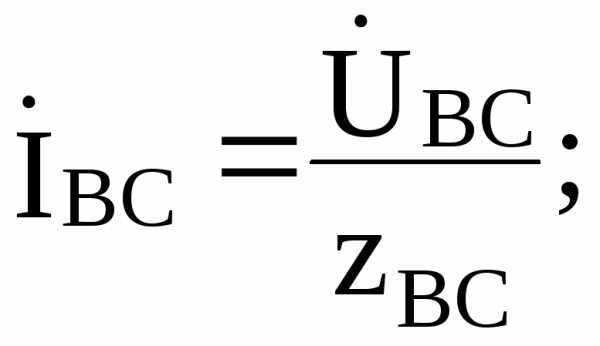
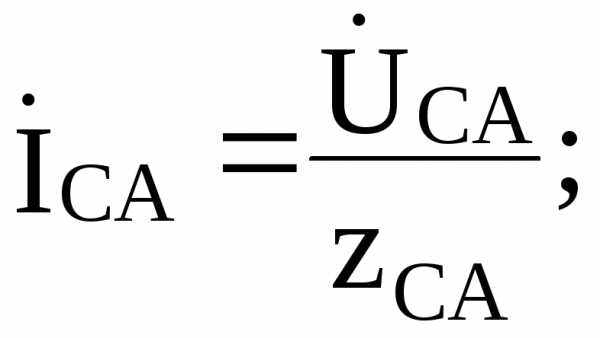
(z)
UCA
B
C
Р
UAB
ис.5.3.Схема соединения треугольником.
-IBC
-ICA
UCA
-IAB
Рис.5.4. Векторная диаграмма напряжений и токов
при соединении треугольником.
Линейные токи определяются по фазным токам из уравнений, составленным по первому закону Кирхгофа для узлов A, B, C:
(5.4)
Независимо от характера нагрузки .
Пример векторной диаграммы при соединении приемника треугольником дан на рис.5.4.
При построении векторной диаграммы в качестве исходных берутся три вектора линейных напряжений UAB, UBC, UCA, которые являются вместе с тем и фазными напряжениями. Углы между ними равны 120˚. Затем откладываются векторы фазных токов IAB, IBC, ICA. Векторы линейных токов IA, IB, IC, строятся по уравнениям (5.3). Если нагрузка симметрична, то соотношение между линейными и фазными токами аналогично соотношению между линейными и фазными напряжениями при соединении звездой: 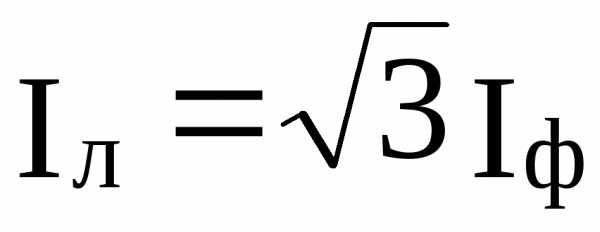 . Для рассматриваемого соединения при изменении сопротивления одной из фаз будут изменяться только ток данной фазы и линейные токи в проводах соединенных с этой фазой. Режим работы других фаз останется неизменным, так как линейные напряжения генератора постоянны. Поэтому схема соединения в треугольник широко используется для включения несимметричной нагрузки, в частности, в осветительных установках.
. Для рассматриваемого соединения при изменении сопротивления одной из фаз будут изменяться только ток данной фазы и линейные токи в проводах соединенных с этой фазой. Режим работы других фаз останется неизменным, так как линейные напряжения генератора постоянны. Поэтому схема соединения в треугольник широко используется для включения несимметричной нагрузки, в частности, в осветительных установках.
Измерение мощности в трехфазных цепях.
В симметричной трехфазной цепи, потребляемые каждой фазой мощности Pф, равны между собой, и в этом случае общая мощность P= 3 Pф, а для каждой из фаз справедливо общее выражение мощности в цепи переменного тока: Pф=UфIфcosφ, где φ угол сдвига между фазными напряжением и током.
При соединении звездой 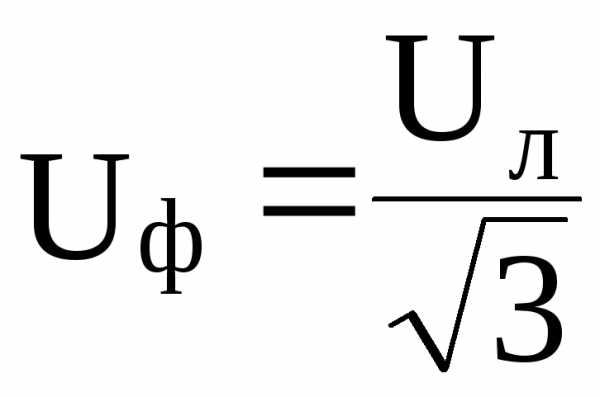 , Iф=Iл, а при соединении треугольником Uф= Uл;
, Iф=Iл, а при соединении треугольником Uф= Uл; 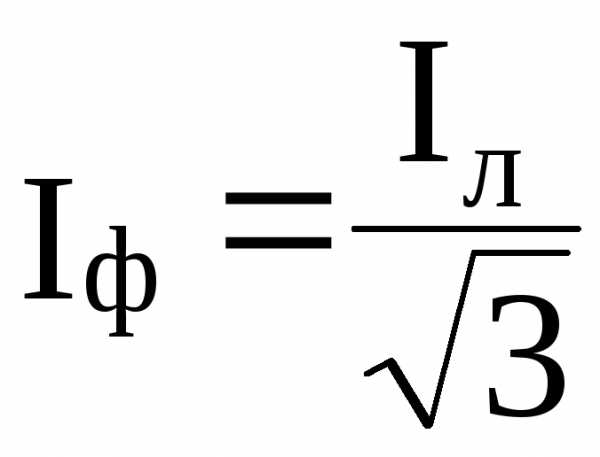 . В обоих случаях, заменяя фазные величины через линейные, мы получим одно и то же выражение для мощности симметричной трехфазной цепи:
. В обоих случаях, заменяя фазные величины через линейные, мы получим одно и то же выражение для мощности симметричной трехфазной цепи:
При симметричной нагрузке измеряют мощность Pф, P= 3Pф.При этом токовую обмотку ваттметра включают последовательно с одной из фаз нагрузки, обмотку напряжения – между началом и концом этой же фазы.
В случае несимметричной нагрузки измерение мощности в трехфазных трех проводных цепях (при соединении приемников треугольником или звездой без нулевого провода) в большинстве случаев производится по способу двух ваттметров (рис.5.5).
Рис.5.5. Схема для измерения мощности при несимметричной нагрузке в трех проводной цепи трехфазного тока.
Рис.5.6. Схема для измерения мощности в четырех проводной
цепи трехфазного тока.
Для измерения мощности в трехфазных четырех проводных системах простейшим является способ трех ваттметров (рис.5.6).
При таком соединении каждый из ваттметров измеряет мощности одной фазы. Мощность трехфазной системы равна суме показаний трех ваттметров.
Порядок выполнения работы.
Соединение звездой.
Собрать схему соединения звездой с нулевым проводом. В качестве нагрузок фаз используются ползунковые реостаты. Убедиться, что ток в нулевом проводе будет равен нулю. Произвести измерения токов, напряжений, мощности. Изменить сопротивления реостатов в фазах по отношению друг к другу. Произвести замеры токов, напряжений и мощности при неравномерной нагрузке фаз. Результаты измерений записать в табл.5.1.
Таблица 5.1.
| Характер нагрузки | Результаты измерений | Вычислено | |||||||||||||
| I0, А | IA, А | IB, А | IC, А | UА, В | UВ, В | UС, В | UAB, В | UBC, В | UCA, В | P1, Вт | P2, Вт | P3, Вт | Р, Вт | UЛ / UФ | |
| Равномер-ная | |||||||||||||||
| Неравномер-ная | |||||||||||||||
Отключить нулевой провод и произвести измерения токов, напряжения и мощности (по способу двух ваттметров) для случаев равномерной и неравномерной нагрузки фаз. Результаты измерений записать в табл.5.2.
Таблица 5.2.
| Характер нагрузки | Результаты измерений | Вычислено | ||||||||||||
| IA, А | IB, А | IC, А | UА, В | UВ, В | UС, В | UAB, В | UBC, В | UCA, В | P1, Вт | P2, Вт | P3, Вт | Р, Вт | UЛ / UФ | |
| Равномер-ная | ||||||||||||||
| Неравномер-ная | ||||||||||||||
По данным табл.5.1 и 5.2 вычислить отношение линейных и фазных напряжений и подсчитать общую мощность цепи; построить векторную диаграмму для случая неравномерной нагрузки фаз предварительно выбрав оптимальный масштаб диаграммы.
Сопоставить величины фазных напряжений для случаев неравномерной нагрузки с нулевым проводом и без нулевого провода.
Соединение треугольником.
Собрать схему соединения треугольником, использовав в качестве нагрузки те же реостаты, что и в схеме соединения звездой. Произвести измерения токов, напряжений и мощности для случаев равномерной и неравномерной нагрузки фаз. Результаты измерений записать в табл.5.3.
Таблица 5.3.
| Характер нагрузки | Результаты измерений | Вычислено | |||||||||||
| IA, А | IB, А | IC, А | IАB, В | IВC, В | IСA, В | UAB, В | UBC, В | UCA, В | P1, Вт | P2, Вт | Р, Вт | IЛ / IФ | |
| Равномер-ная | |||||||||||||
| Неравномер-ная | |||||||||||||
По данным табл.5.3 вычислить соотношение линейных и фазных токов, подсчитать общую мощность цепи; построить векторную диаграмму для случая неравномерной нагрузки фаз предварительно выбрав оптимальный масштаб диаграммы.
Для случаев равномерной нагрузки подсчитать мощность аналитически и сопоставить её с суммой показаний ваттметров.
Контрольные вопросы.
Почему наибольшее распространение в электроэнергетике получили трехфазные цепи?
Объясните способы соединения звездой и треугольником.
Какая нагрузка называется симметричной, равномерной и несимметричной?
Какие напряжения и соответственно токи называются линейными и фазными? Их соотношение при соединении звездой и треугольником.
В каком случае применяется соединение звездой с нулевым проводом и без него?
Приложение
| Наименование | Обозначение буквенное по ГОСТ 2.710.81 | Обозначение графическое | Стандарт |
| Линия электрической связи* | а) б) в) | ГОСТ 2.751-73 | |
| Резистор а – постоянный; б – переменный | а 10 )
б) | ГОСТ 2.728-74 | |
| Катушка индуктивности | L |
R 1,5…4 | ГОСТ 2.723-68 |
| Конденсатор постоянной емкости | С |
| ГОСТ 2.728-74 |
| Прибор электро-измерительный** | Р |
Ø10 | ГОСТ 2.729-68 |
* Линия электрической связи обозначается тонкой линией (а), её соединения с точкой (б), пересечения без точки (в). Толщина линий при выполнении схем выбирается 0,18 – 0,4 в зависимости от выбранного формата чертежа.
** Для указания назначения прибора в его графическое обозначение вписывают буквенное обозначение единиц измерения или измеряемых величин.
Например: РА – амперметр, РV– вольтметр.
studfiles.net
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
















