Емкость конденсатора: виды и применение; принципы работы и маркировка
 Конденсатором называется элемент электрической цепи, служащий в качестве накопителя заряда.
Конденсатором называется элемент электрической цепи, служащий в качестве накопителя заряда.
Областей применения этого устройства сейчас много, чем и обусловлен их большой ассортимент. Они различаются по материалам, из которых изготовлены, назначению, диапазону основного параметра. Но главной характеристикой конденсатора является его емкость.
Принцип работы конденсатора
Конструкция
На схемах конденсатор обозначается в виде двух параллельных линий, не связанных между собой:
Это соответствует его простейшей конструкции — двум пластинам (обкладкам), разделенным диэлектриком. Фактическое исполнение этого изделия чаще всего представляет собой завернутые в рулон обкладки с прослойкой диэлектрика или иные причудливые формы, но суть остается той же самой.
Емкость конденсатора
Электрическая ёмкость – способность проводника накапливать электрические заряды. Чем больше заряд вмещает проводник при данной разности потенциалов, тем больше ёмкость. Зависимость между зарядом Q и потенциалом φ выражается формулой:
C=Q/φ
где Q заряд в кулонах (Кл), φ потенциал в вольтах (В).
 Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Накопительная способность зависит от геометрических параметров проводника, диэлектрической проницаемости среды, где он находится. Так, для сферы из проводящего материала она будет выражаться формулой:
C=4πεε0R
где ε0—8,854·10^−12 Ф/м, электрическая постоянная, а ε диэлектрическая проницаемость среды (табличная величина для каждого вещества).
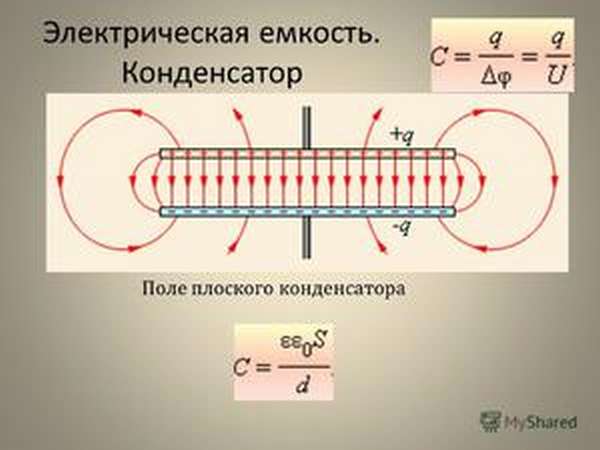
В реальной жизни нам чаще приходится иметь дело не с одним проводником, а с системами таковых. Так, в обычном плоском конденсаторе емкость будет прямо пропорциональна площади пластин и обратно — расстоянию между ними:
C=εε0S/d
ε здесь — диэлектрическая проницаемость прокладки между пластинами.
Емкость параллельных и последовательных систем
Параллельное соединение емкостей представляет собой один большой конденсатор с тем же слоем диэлектрика и суммарной площадью пластин, поэтому общая емкость системы представляет собой сумму таковых у каждого из элементов. Напряжение при параллельном соединении будет одним и тем же, а заряд распределится между элементами схемы.
C=C1+C2+C3
Последовательное соединение конденсаторов характеризуется общим зарядом и распределенным напряжением между элементами. Поэтому суммируется не емкость, а обратная ей величина:
1/C=1/С1+1/С2+1/С3
Из формулы емкости одиночного конденсатора можно вывести, что при одинаковых элементах, соединенных последовательно, их можно представить в виде одного большого с той же площадью обкладки, но с суммарной толщиной диэлектрика.
Свойства конденсатора
Реактивное сопротивление
Конденсатор не может проводить постоянный ток, что видно из его конструкции. В такой цепи он может только заряжаться. Зато в цепях переменного тока он прекрасно работает, постоянно перезаряжаясь. Если не ограничения, исходящие из свойств диэлектрика (его можно пробить при превышении предела напряжения), этот элемент заряжался бы бесконечно (т. н. идеальный конденсатор, что-то вроде абсолютно черного тела и идеального газа) в цепи постоянного тока, а ток через него проходить не будет. Проще говоря, сопротивление конденсатора в цепи постоянного тока бесконечно.
При переменном токе ситуация иная: чем выше частота в цепи, тем меньше сопротивление элемента. Такое сопротивление называется реактивным, и оно обратно пропорционально частоте и емкости:
Z=1/2πfC
где f частота в герцах.
Накопитель энергии
Энергия, запасенная заряженным конденсатором, может быть выражена формулой:
E=(CU^2)/2=(q^2)/2C
где U напряжение между обкладками, а q накопленный заряд.
Конденсатор в колебательном контуре
В замкнутом контуре, содержащем катушку и конденсатор, может быть сгенерирован переменный ток.
После зарядки конденсатора он начнет саморазряжаться, давая возрастающий по силе ток. Энергия разряженного конденсатора станет равной нулю, зато магнитная энергия катушки — максимальной. Изменение величины тока вызывает ЭДС самоиндукции катушки, и она по инерции пропустит ток в сторону второй обкладки, пока та полностью не зарядится. В идеальном случае такие колебания бесконечны, а в реальности они быстро затухают. Частота колебаний зависит от параметров как катушки, так и конденсатора:

где L индуктивность катушки.
Паразитная индуктивность
Конденсатор может обладать собственной индуктивностью, что можно наблюдать при повышении частоты тока в цепи. В идеальном случае эта величина незначительна, и ей можно пренебречь, но в реальности, когда обкладки представляют собой свернутые пластинки, не считаться с этим параметром нельзя, особенно если речь идет о высоких частотах. В таких случаях конденсатор совмещает в себе две функции, и представляет собой своеобразный колебательный контур с собственной резонансной частотой.
Чтобы добиться корректной работы схемы, рекомендуется применять конденсаторы, у которых резонансная f больше собственной частоты в цепи.
Эксплуатационные характеристики
Помимо указанных выше емкости, собственной индуктивности и энергоемкости, реальные конденсаторы (а не идеальные) обладают еще рядом свойств, которые нужно учитывать при выборе этого элемента для цепи. К ним относятся:
 номинальное напряжение,
номинальное напряжение,- полярность,
- ток утечки,
- сопротивление материала обкладок,
- диэлектрические потери,
- зависимость емкости от температуры.
Чтобы понять, откуда берутся потери, необходимо разъяснить, что представляют собой графики синусоидальных тока и напряжения в этом элементе. Когда конденсатор заряжен максимально, ток в его обкладках равен нулю. Соответственно, когда ток максимален, напряжение отсутствует. То есть напряжение и ток сдвинуты по фазе на угол 90 градусов. В идеале конденсатор обладает только реактивной мощностью:
Q=UIsin 90
В реальности же обкладки конденсатора обладают собственным сопротивлением, а часть энергии расходуется на нагрев диэлектрика, что обуславливает ее потери. Чаще всего они незначительны, но иногда ими пренебрегать нельзя. Основной характеристикой этого явления служит тангенс угла диэлектрических потерь, представляющий собой отношение активной мощности (даваемой малыми потерями в диэлектрике) и реактивной. Измерить эту величину можно теоретически, представив реальную емкость в виде эквивалентной схемы замещения — параллельной или последовательной.
Определение тангенса угла диэлектрических потерь

При параллельном соединении величина потерь определяется отношением токов:
tgδ = Ir/Ic = 1/(ωCR)
В случае последовательного соединения угол вычисляется соотношением напряжений:
tgδ = Ur/Uc = ωCR
В реальности для замеров tgδ пользуются прибором, собранным по мостовой схеме. Его применяют для диагностики потерь в изоляции у высоковольтного оборудования. С помощью измерительных мостов можно измерять и другие параметры сетей.
Номинальное напряжение
Этот параметр указывается на маркировке. Он показывает предельную величину напряжения, которое может быть подано на обкладки. Превышение номинала может привести к пробою конденсатора и выходу его из строя. Зависит этот параметр от свойств диэлектрика и его толщины.
Полярность
Некоторые конденсаторы имеют полярность, то есть в схему его необходимо подключать строго определенным образом. Связано это с тем, что в качестве одной из обкладок используется какой-либо электролит, а диэлектриком служит оксидная пленка на другом электроде. При изменении полярности электролит просто разрушает пленку и конденсатор перестает работать.
Температурный коэффициент емкости
Он выражается отношением ΔC/CΔT где ΔT изменение температуры окружающей среды. Чаще всего эта зависимость линейна и незначительна, но для конденсаторов, работающих в агрессивных условиях, ТКЕ указывается в виде графика.
Разрушение конденсатора
 Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Перегрев обусловлен как внешними причинами (нагреванием соседних элементов схемы), так и внутренними, в частности, последовательным эквивалентным сопротивлением обкладок. В электролитических конденсаторах он приводит к испарению электролита, а в оксиднополупроводниковых — к пробою и химической реакции между танталом и оксидом марганца.
Опасность разрушения в том, что часто оно происходит с вероятностью взрыва корпуса.
Техническое исполнение конденсаторов
Классифицировать конденсаторы можно по нескольким группам. Так, в зависимости от возможности регулировать емкость их разделяют на постоянные, переменные и подстроечные. По своей форме они могут быть цилиндрическими, сферическими и плоскими. Можно делить их по назначению. Но самой распространенной классификацией является таковая по типу диэлектрика.
Бумажные конденсаторы
В качестве диэлектрика используется бумага, очень часто промасленная. Как правило, такие конденсаторы отличает большой размер, но были варианты и в небольшом исполнении, без промасливания. Используются в качестве стабилизирующих и накопительных устройств, а из бытовой электроники постепенно вытесняются более современными пленочными моделями.
При отсутствии промасливания имеют существенный недостаток — реагируют на влажность воздуха даже при герметичной упаковке. Промокшая бумага увеличивает энергопотери.
Диэлектрик в виде органических пленок
Пленки могут быть выполнены из органических полимеров, таких как:
- полиэтилентерифталат,
- полиамид,
- поликарбонат,
- полисульфон,
- полипропилен,
- полистирол,
- фторопласт (политетрафторэтилен).
По сравнению с предыдущими, такие конденсаторы имеют более компактные размеры, не увеличивают диэлектрические потери при увеличении влажности, но многие из них подвергаются риску выхода из строя при перегреве, а те, что этого недостатка лишены, отличаются более высокой стоимостью.
Твердый неорганический диэлектрик
Это может быть слюда, стекло и керамика.
Преимуществом этих конденсаторов считается их стабильность и линейность зависимости емкости от температуры, приложенного напряжения, а у некоторых — даже от радиации. Но иногда сама такая зависимость становится проблемой, и чем она менее выражена, тем дороже изделие.
Оксидный диэлектрик
С ним выпускаются алюминиевые, твердотельные и танталовые конденсаторы. Они имеют полярность, поэтому выходят из строя при неправильном подключении и превышении номинала напряжения. Но при этом они обладают хорошей емкостью, компактны и стабильны в работе. При правильной эксплуатации могут работать около 50 тыс. часов.
Вакуум
Такие устройства представляют собой стеклянную или керамическую колбу с двумя электродами, откуда выкачан воздух. В них практически отсутствуют потери, но малая емкость и хрупкость ограничивают сферу их применения радиостанциями, где величина емкости не так важна, а вот устойчивость к нагреву имеет принципиальное значение.
Двойной электрический слой
Если посмотреть, для чего нужен конденсатор, то можно понять, что этот тип — не совсем он. Скорее, это дополнительный или резервный источник питания, в качестве чего они и используются. Одни категория таких устройств — ионисторы — содержат в себе активированный уголь и слой электролита, другие работают на ионах лития. Емкость этих приборов может составлять до сотен фарад. К их недостаткам можно отнести высокую стоимость и активное сопротивление с токами утечки.
Маркировка конденсаторов
 Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Помимо этого, на большинстве из них существует цифро-буквенное обозначение его характеристик. В соответствии с российскими стандартами конденсаторы маркируются четырьмя знаками.
Первая буква К означает «конденсатор», следующая цифра — вид диэлектрика, далее следует указатель назначения в виде буквы, последний значок может означать как тип конструкции, так и номер разработки, это уже зависит от завода-изготовителя. Третий пункт часто пропускается. Используется такая маркировка на достаточно крупных изделиях, где ее можно разместить. По ГОСТ расшифровка будет выглядеть так:
Первые буквы:
- К — конденсатор постоянной емкости.
- КТ — подстроечник.
- КП — конденсатор переменной емкости.
Вторая группа — тип диэлектрика:
 1, 61 вакуум,
1, 61 вакуум,- 2, 60 воздух,
- 3 газ,
- 4 твердый,
- 10, 15 керамика,
- 20 кварц,
- 21 стекло,
- 22 стеклокерамика,
- 23 стеклоэмаль,
- 31, 32 слюда,
- 40, 41, 42 бумага,
- 50 алюминиевый электролитический,
- 51 танталовый,
- 52 объемно-пористый,
- 53, 54 оксидные,
- 71 полистирол,
- 72 фторопласт,
- 73 ПЭТ,
- 75 комбинированный,
- 76 лак и пленка,
- 77 поликарбонат.
На маленьких конденсаторах всего этого не разместить, поэтому там применяется сокращенная маркировка, которая с непривычки может даже потребовать калькулятора, а иногда — лупу. В этой маркировке зашифрованы емкость, номинал напряжения и отклонения от основного параметра. Остальные параметры наносить нет смысла: это, как правило, керамические конденсаторы.
Маркировка керамических конденсаторов
 Иногда с ними все просто — емкость отмечена числом и единицами: pF — пикофарад, nF — нанофарад, μF микрофарад, mF — миллифарад. То есть, надпись 100nF можно читать прямо. Номинал, соответственно, числом и буквой V. Но иногда не умещается и это, потому применяют сокращения. Так, часто емкость умещается в трех цифрах (103, 109 и т. д.), где последняя означает число нулей, а первые две — емкость в пикофарадах. Если в конце стоит цифра 9, значит, нулей нет, а между первыми двумя ставят запятую. При цифре 8 на конце запятую переносят еще на один знак назад.
Иногда с ними все просто — емкость отмечена числом и единицами: pF — пикофарад, nF — нанофарад, μF микрофарад, mF — миллифарад. То есть, надпись 100nF можно читать прямо. Номинал, соответственно, числом и буквой V. Но иногда не умещается и это, потому применяют сокращения. Так, часто емкость умещается в трех цифрах (103, 109 и т. д.), где последняя означает число нулей, а первые две — емкость в пикофарадах. Если в конце стоит цифра 9, значит, нулей нет, а между первыми двумя ставят запятую. При цифре 8 на конце запятую переносят еще на один знак назад.
Например, обозначение 109 расшифровывается как 1 пикофарад, а 100–10 пикофарад, 681–680 пикофарад, или 0,68 нанофарад, а 104- 100 тыс. пФ или 100нФ
Часто можно встретить первую букву единицы измерения в качестве запятой: p50–0,5 пФ, 1n5–1,5 нФ, 15μ – 15 мкФ, 15m – 15 мФ. Иногда вместо p пишется R.
После трех цифр может стоять буква, означающая разброс параметра емкости:
 B +/-0,1 пФ.
B +/-0,1 пФ.- C +/-0,25 пФ.
- D- +/-0,5 пФ.
- F +/-1%.
- G +/-2%.
- J +/-5%.
- K +/-10%.
- M +/-20%.
- Z до 80% отклонение.
Если вы высчитываете характеристику цепи в единицах СИ, то для того, чтобы найти емкость в фарадах, необходимо помнить показатели степеней числа 10:
- -3 миллифарады,
- -6 микрофарады,
- -9 нанофарады,
- -12 пикофарады.
Таким образом, 01 пФ — это 0,1 *10^-12 Ф.
На устройствах SMD емкость в пикофарадах обозначает буква, а цифра после нее — степень 10, на которую надо умножить это значение.
| буква | C | буква | C | буква | C | буква | C |
| A | 1 | J | 2,2 | S | 4,7 | a | 2,5 |
| B | 1,1 | K | 2,4 | T | 5,1 | b | 3,5 |
| C | 1,2 | L | 2,7 | U | 5,6 | d | 4 |
| D | 1,3 | M | 3 | V | 6,2 | e | 4,5 |
| E | 1,5 | N | 3,3 | W | 6,8 | f | 5 |
| F | 1,6 | P | 3,6 | X | 7,5 | m | 6 |
| G | 1,8 | Q | 3,9 | Y | 8,2 | n | 7 |
| Y | 2 | R | 4,3 | Z | 9,1 | t | 8 |
Номинальное рабочее напряжение таким же образом может маркироваться буквой, если полностью его написать проблематично. В России принят следующий стандарт буквенного обозначения номинала:
| буква | V | буква | V |
| I | 1 | K | 63 |
| R | 1,6 | L | 80 |
| M | 2,5 | N | 100 |
| A | 3,2 | P | 125 |
| C | 4 | Q | 160 |
| B | 6,3 | Z | 200 |
| D | 10 | W | 250 |
| E | 16 | X | 315 |
| F | 20 | T | 350 |
| G | 25 | Y | 400 |
| H | 32 | U | 450 |
| S | 40 | V | 500 |
| J | 50 |
Несмотря на списки и таблицы, лучше все-таки изучить кодировку конкретного производителя — в разных странах они могут отличаться.
К некоторым конденсаторам прилагается более развернутое описание их характеристик.
Емкость конденсатора 




Урок 28. электрическая ёмкость. конденсатор — Физика — 10 класс
Физика, 10 класс
Урок 28. Электрическая ёмкость. Конденсатор
Перечень вопросов, рассматриваемых на уроке:
- Электрическая ёмкость
- Плоский конденсатор
- Энергия конденсатора
Глоссарий по теме:
Конденсатор – устройство для накопления электрического заряда.
Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Под зарядом конденсатора понимают модуль заряда одной из его обкладок.
Последовательное соединение – электрическая цепь не имеет разветвлений. Все элементы цепи включают поочередно друг за другом. При параллельном соединении концы каждого элемента присоединены к одной и той же паре точек.
Смешанное соединение — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Энергия конденсатора прямо пропорциональна квадрату напряжённости электрического поля внутри его: 
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения.
Основная и дополнительная литература по теме:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 97-100.
Теоретический материал для самостоятельного изучения
Конденсатор при переводе с латиницы означает, то что уплотняет, сгущает – устройство, предназначенное для накопления зарядов энергии электрического поля. Конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга. Главной характеристикой этого прибора, является его электроёмкость, которая зависит от площади его пластин, расстояния между ними и свойств диэлектрика.
Заряд конденсатора определяется – модулем заряда на любой одной из её обкладок. Заряд конденсатора прямо пропорционален напряжению между обкладками конденсатора. Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора.

Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Чем больше площадь проводников и чем меньше пространство заполняющего диэлектриком, тем больше увеличивается ёмкость обкладок конденсатора.

Измеряется электрическая ёмкость в Международной системе СИ в Фарадах. Эта единица имеет своё название в честь английского физика экспериментатора Майкла Фарадея который внёс большой вклад в развитие теории электромагнетизма. Один Фарад равен ёмкости такого конденсатора, между пластинами которого возникает напряжение, равное одному Вольту, при сообщении заряда в один Кулон.
Электрическая ёмкость конденсаторов определяется их конструкцией, самыми простыми из них являются плоские конденсаторы.
Чем больше площадь взаимного перекрытия обкладок и чем меньше расстояние между ними, тем значительнее будет увеличение ёмкости обкладок конденсатора. При заполнении в пространство между обкладками стеклянной пластины, электрическая ёмкость конденсатора значительно увеличивается, получается, что она зависит от свойств используемого диэлектрика.
Электрическая ёмкость плоского конденсатора зависит от площади его обкладок, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками и определяется по формуле:
 где
где  – электрическая постоянная.
– электрическая постоянная.
Для того чтобы получить необходимую определённую ёмкость, берут несколько конденсаторов и собирают их в батарею применяя при этом параллельное, последовательное или смешанное соединения.
Параллельное соединение:
q = q1 + q2 + q3
u = u1 = u2 = u3
с = с1+с2+с3
с = n∙с
Последовательное соединение:
q = q1 = q2 = q3
u = u1 + u2 + u3


Энергия конденсатора равна половине произведения заряда конденсатора напряжённости поля и расстояния между пластинами конденсатора: u = Еd

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин, это поле совершает положительную работу. При этом энергия электрического поля уменьшается:

Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения:

Примеры и разбор решения заданий:
1. Плоский конденсатор, расстояние между пластинами которого равно 3 мм, заряжен до напряжения 150 В и отключен от источника питания. Разность потенциалов между пластинами возросла до 300 В.
- Во сколько раз увеличилась разность потенциалов между пластинами?
- Какое расстояние между пластинами конденсатора стало после того, как пластины были раздвинуты?
- Во сколько раз изменилось расстояние между пластинами.
Решение:
Электрическая ёмкость конденсатора определяется по формуле:

1.По условию разность потенциалов увеличилось в два раза. U1 = 150В→ U2 = 300В.
2.По условию d = 3 мм, если разность потенциалов увеличилось в два раза, по формуле соответственно и расстояние между пластинами увеличилось в два раза, и d =2·3 мм = 6 мм.
3.Расстояние между пластинами увеличилось в два раза.
Ответ:
1. 2
2. 6мм
3. 2
2. Конденсатор электроёмкостью 20 мкФ имеет заряд 4 мкКл. Чему равна энергия заряженного конденсатора?
Дано: С = 20 мкФ = 20 · 10-6 Ф, q = 4 мкКл = 4·10-6 Кл.
Найти: W.
Решение:
Энергия заряженного конденсатора W через заряд q и электрическую ёмкость С определяется по формуле:


Ответ: W = 0,4 мкДж.
Электрическая ёмкость: определение, формулы, единицы измерения
Одним из важных параметров, учитываемых в электрических цепях, является электрическая емкость – способность проводников накапливать заряды. Понятие емкости применяется как для уединенного проводника, так и для системы, состоящей из двух и более проводников. В частности, емкостью обладают конденсаторы, состоящие из двух металлических пластин, разделенных диэлектриком или электролитом.
Для накопления зарядов широко применяютсяаккумуляторы, используемые в качестве источников постоянного тока для питания различных устройств. Количественной характеристикой, определяющей время работы аккумулятора, является его электроемкость.
Определение
Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.
Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.
Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.
На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.
Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.
На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.
 Рис. 1. Распределение зарядов
Рис. 1. Распределение зарядов
Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.
Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.
Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.
Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.
На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.
 Рис. 2. Схема простого конденсатора
Рис. 2. Схема простого конденсатора
Существуют конденсаторы других типов:
- переменные;
- электролитические;
- оксидные;
- бумажные;
- комбинированные и другие.
Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость.
Формулы
На рисунке 3 наглядно показано формулы для определения емкости, в т. ч. и для сферы.
 Рис. 3. Электроёмкость проводника
Рис. 3. Электроёмкость проводника
По отношению к конденсатору, для определения его емкости применяют формулу: C = q/U. То есть, эта величина прямо пропорциональна заряду одной из обкладок и обратно пропорциональна разнице потенциалов между обкладками (см. рис. 4).
 Ёмкость конденсатора
Ёмкость конденсатора
О других способах определения ёмкости конденсатора читайте в нашей статье: https://www.asutpp.ru/kak-opredelit-emkost-kondensatora.html
Единицы измерения
За единицу измерения величины электроемкости принято фараду: 1 Ф = 1 Кл/1В. Поскольку фарада величина огромная, то для измерения емкости на практике она мало пригодна. Поэтому используют приставки:
- мили (м) = 10-3;
- микро (мк) = 10-6;
- нано (н) = 10-9;
- пико (пк) = 10-12;
Например, электрическая емкость 1 мкф = 0,000001 Ф. Параметр зависит от геометрических размеров, конфигурации проводника и материала диэлектрика.
Уединенный проводник и его емкость
Уединенным называют проводник, влиянием на который других элементов цепей можно пренебречь. Предполагается, что все другие проводники бесконечно удалены от него, а как известно, потенциал точки, бесконечно удаленной в пространстве, равен 0.
Электрическую емкость C уединенного проводника, определяют как количество электричества q, которое требуется для повышения электрического потенциала на 1 В: С = q/ϕ. Параметр не зависит от материала, из которого изготовлен проводник.
Конденсаторы постоянной и переменной емкости
Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).
 Рис. 5. Конденсатор переменной емкости
Рис. 5. Конденсатор переменной емкости
Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.
Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.
Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.
Главные их преимущества электролитического конденсатора:
- высокие
показатели емкости при малом объеме; - применение в
цепях с постоянным током.
Недостатки:
- необходимо соблюдать полярность;
- ограниченный срок службы;
- чувствительность к повышенным напряжениям.
Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.
Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.
 Конденсаторы различных типов
Конденсаторы различных типов
Аккумуляторы и электроемкость
Накопители электричества большой емкости (аккумуляторы) состоят из положительных и негативных пластин, погруженных в электролит. Во время зарядки часть атомов электролита распадается на ионы, которые оседают на пластине. Образуется разность потенциалов между пластинами, что является причиной возникновения ЭДС при подключении нагрузки.
С целью увеличения напряжения аккумуляторы последовательно соединяют в батареи. Разница потенциалов одной секции около 2 В. Для получения аккумулятора на 6 В необходимо создать батарею из трех секций, а на 12 В – батарею из 6 секций.
Для характеристики аккумуляторов (батарей) используются параметры:
- емкости;
- номинального напряжения;
- максимального тока разряда.
Единицей емкости аккумулятора является ампер-час (А*ч) или кратные ей миллиампер-часы (мА*ч). Емкость аккумулятора зависит от площади пластин. Увеличить емкость можно путем параллельного подключения нескольких секций, но такой способ почти не применяется, так как проще и надежнее создать аккумулятор с большими пластинами.
конденсаторы, виды соединений, расчет емкости законом Гаусса
В статье мы расскажем про электроемкость, емкость конденсатора, про последовательное и параллельное соединение конденсаторов, а также как использовать закон Гаусса для расчета емкости конденсаторов с примерами и решениями.
Конденсатор (Электроемкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:


Величина ёмкости измеряется в фарадах (Ф).
1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.

 1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6.
1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6.
Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке.
Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома.
Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.
Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.

 Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.
Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.
Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве фильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xc или Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением:


Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.
Теперь представьте, что дифференцирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.

 То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.
То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.
Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе.
Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1.
Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.
Емкость конденсатора
Как мы уже видели, изолированный проводник может накапливать электрический заряд. Однако на практике мы используем устройства, называемые конденсаторами, для хранения нагрузки. Конденсатор представляет собой систему из двух произвольно изолированных проводников, зарядка конденсатора состоит не в отдельной зарядке каждого из проводников, а в переносе заряда (одинакового на обоих проводниках, но с противоположными знаками) от одного проводника к другому.


Мы определяем электрическую емкость C конденсатора точно так же, как емкость изолированного проводника.


Конденсаторы очень часто используются в технике. Они обычно строятся как система из двух поверхностей с разной изолированной поверхностью, которые обычно располагаются параллельно друг другу. Как будет видно далее, емкость такого конденсатора пропорциональна размеру поверхности пластин и обратно пропорциональна расстоянию между ними. Таким образом, конденсатор большой емкости имеет большие поверхностные панели, которые расположены как можно ближе друг к другу. Простейшим таким конденсатором является плоский конденсатор, схематически показанный на рисунке ниже.


Пример двух конденсаторов, соединенных вместе, как показано на рисунке ниже (параллельно), может служить иллюстрацией постоянства заряда на крышках конденсаторов, не подключенных к источнику напряжения. Первоначально система нагрузки , которая охватывает один конденсатор заряда Q1 и на крышке второго заряда Q2. Потенциал, на котором расположены верхние крышки, одинаков для обоих (крышки связаны с лампочкой). Когда мы начнем изменять расстояния между крышками одного из конденсаторов, то мы изменим его емкость — чем меньше зазор между крышками, тем больше емкость конденсатора. Поскольку общий заряд обоих конденсаторов неизменен, это изменение емкости вызовет перенос заряда между конденсаторами. Если конденсаторы заряжены достаточно большим зарядом, лампочка может светиться во время потока между крышками, образующими верхнюю пару. Энергия, необходимая для освещения лампы, исходит от работы, которую мы выполняем при перемещении крышки (верхняя и нижняя крышки заряжены противоположными знаками и поэтому притягиваются).


Схемы соединения конденсаторов
Существует множество различных схем соединения конденсаторов: последовательное подключение, параллельное, мостовое. И меняется абсолютно все показатели (Емкость, разность потенциалов, общая нагрузка) при различных видах подключения
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов, как показано на рисунке ниже, значения зарядов на всех крышках всех конденсаторов одинаковы.


Разность потенциала в последовательной цепи конденсаторов равно сумме разностей потенциалов на отдельных конденсаторах:


Следовательно, совокупная емкость С последовательной системы определяется по формуле


Параллельное соединение конденсаторов
В параллельном соединении конденсаторов


общая нагрузка Q, накопленная в системе, равна сумме зарядов на крышках всех конденсаторов.


Уменьшение потенциала одинаково на каждом из конденсаторов и, следовательно,


Следовательно, общая емкость C параллельной системы равна сумме емкостей всех конденсаторов.


Мостовое соединение конденсаторов
Последовательные и параллельные соединения не исчерпывают всех возможных конфигураций, которые могут быть получены при подключении конденсаторов. Мы сможем описать все возможные конфигурации только после завершения предыдущих соединений с мостовым соединением, схема которых показана на левом рисунке ниже.


Мы не можем напрямую заменить мостовые комбинации любой комбинацией последовательных и параллельных соединений. Чтобы рассчитать запасную емкость системы моста, используйте изменение треугольника конденсатора на эквивалентную звезду, как показано на среднем и правом рисунках выше.
Емкости между точками 1-2, 2-3 и 3-1, которые мы обозначаем как C 12, C23 и C31, должны быть одинаковыми в обеих конфигурациях. На основе значений емкости C1, C2 и C3 рассчитывают Cx, Cy и Cz. Условия равной емкости в обеих конфигурациях, для треугольника и для звезды, запишем как


Отсюда мы получаем искомые значения Cx, Cy и Cz:


После замены треугольника на звезду мостовое соединение исчезает, и на его месте мы получаем простую и удобную для вычисления комбинацию последовательных и параллельных конденсаторов.


Использование закона Гаусса для расчета емкости конденсаторов
Имея емкость конденсатора с заданной геометрией для расчета, мы используем следующую схему:
Мы исходим из определения емкости конденсатора. Вставьте разность потенциалов Vab в формулу, определяющую эту емкость. Нагрузка Q уменьшается.


но нам не хватает разности потенциалов Vab, которую мы находим из соотношения между полями E и V,


3. Однако сначала мы должны знать E, и для этого мы будем использовать универсальный инструмент, который является законом Гаусса:


Примеры закона Гаусса для расчета емкости конденсаторов
Закон Гаусса выполняется для каждой замкнутой поверхности А. Однако такую поверхность следует выбирать так, чтобы интегрирование было как можно более простым. В примерах, представленных ниже, форма предложенной поверхности Гаусса для обсуждаемых случаев обозначена контуром, нарисованным пунктирной кривой. Расчеты выполнены в соответствии с представленной схемой и не содержат дополнительных пояснений. ε0 — электрическая проницаемость вакуума.
Плоский конденсатор


Отсюда мы получаем емкость для плоского конденсатора


Цилиндрический конденсатор


Отсюда мы получаем емкость для цилиндрического конденсатора:


Сферический конденсатор


Отсюда мы получаем емкость для сферического конденсатора:


Цель представленных примеров — показать, как схема расчета работает на практике. Вы должны помнить только образец для емкости плоского конденсатора, который часто будет использоваться в дальнейшем вашем обучении.
Энергия заряженного конденсатора
Энергия заряженного конденсатора U равна той работе, которую мы будем выполнять при зарядке. Вся энергия U содержится в электрическом поле между крышками конденсатора.
При зарядке конденсатора разность потенциалов между его крышками V (q) зависит от заряда q, который в настоящее время находится на крышках. Работа по переносу между крышками дополнительной нагрузки составляет


Энергия поля в конденсаторе, полностью заряженном зарядом Q, становится


или


Плотность энергии электрического поля
Плотность энергии электрического поля u будет рассчитываться путем деления энергии U на объем, занимаемый полем. Используя простую геометрию плоского конденсатора с площадью крышки A и расстояние между крышками d, мы находим значение u, действительное для поля E любой геометрии:


Плоские конденсаторы, особенности, емкость и энергия плоских конденсаторов
Плоский конденсатор – это очень простое устройство для Емкость плоского конденсатора, зависит от его размеров, а именно от поверхности его обкладок. Также влияет диэлектрик. Основное удобство плоских моделей – их компактность. Они занимают меньше места на плате и схеме, тем сам экономя драгоценное пространство. Выглядит такая радиодеталь в виде двух пластинок, помещенных в тонкий плоский корпус. Электроны движутся с одной обкладки к плюсовому полюсу, то есть противоположный электрод. Преградой является диэлектрик.
В статье содержится вся полезная информация по определению плоского конденсатора, расчету его емкости и отличиям от конденсаторов, имеющие иную форму. В качестве бонуса читателю предложен файл с интересной лекцией, а также видеоролик на данную тему.

Плоский конденсатор.
Электрическая емкость плоского конденсатора
Электрическая емкость плоского конденсатора очень просто выражается через параметры его частей. Изменяя площадь пластин конденсатора и расстояние между ними легко убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластин (S) и обратно пропорциональна расстоянию между ними (d).

Емкость плоского конденсатора прямо пропорциональна площади его обкладок и диэлектрической проницаемости материала диэлектрика, разделяющего обкладки, и обратно пропорциональна расстоянию между ними:
C=εε0SdC=εε0Sd
Плоский конденсатор представляет из себя две плоские проводящие пластины, разделенные диэлектриком. Расстояние между пластинами много меньше характерного размера пластин. Поле вдали от краев пластин можно представить в виде суперпозиции полей бесконечно заряженных плоскостей.
Поле вдали от краев обкладок конденсатора
 Так как обкладки заряжены равными по величине разноименными зарядами, напряженность поля между обкладками складывается из напряженностей полей каждой из обкладок. Вне обкладок конденсатора их поля противоположно направлены и результирующее поле становится нулевым. Таким образом:
Так как обкладки заряжены равными по величине разноименными зарядами, напряженность поля между обкладками складывается из напряженностей полей каждой из обкладок. Вне обкладок конденсатора их поля противоположно направлены и результирующее поле становится нулевым. Таким образом:
Eрез=E++E−=2⋅σ2εε0Eрез=E++E-=2⋅σ2εε0
Используем связь между напряженностью и напряжением и напряженностью и определение поверхностной плотности заряда
E=UdE=Ud
σ=qSσ=qS
Получаем$
Ud=qεε0SUd=qεε0S
Откуда
C=qU=εε0Sd
Плоский конденсатор
 Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин. Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин. Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора.
Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит. Для определения величины этого поля рассмотрим еще одно изображение плоского конденсатора:

Плоские конденсаторы
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_
Здесь – это поверхностная плотность заряда: . А – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой. Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0.
Процессы зарядки и разрядки конденсаторов
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить? Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной.

В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов.
Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

Емкость и энергия конденсатора.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом.
Материал в тему: все о переменном конденсаторе.
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Емкость и энергия конденсатора
 Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками. Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).
Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками. Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом.

Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение – то есть величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные
заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками. В таблице ниже приведем основные параметры конденсаторов.

Стоит почитать: все об электолитических конденсаторах.
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин. Под зарядом конденсатора понимают заряд одной пластины.
Заключение
Более подробно о том, что такое плоский конденсатор и как рассчитать его электроемкость, можно узнать из статьи “Электроемкость“. Если у вас остались вопросы, можно задать их в комментариях на сайте. Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов.
Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vк.coм/еlеctroinfonеt. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.sverh-zadacha.ucoz.ru
www.ru.solverbook.com
www.xn--80ancbkzagjllo.xn--p1ai
www.microtechnics.ru
www.energetik.com.ru
www.easy-physic.ru
Предыдущая
КонденсаторыЧем отличается пусковой конденсатор от рабочего?
Следующая
КонденсаторыЧто такое полярность конденсатора и как ее определить?
Емкость
| Определение, формула, единицы измерения и факты
Емкость , свойство электрического проводника или набора проводников, которое измеряется количеством отделенного электрического заряда, который может храниться на нем на единицу изменения электрического потенциала. Емкость также подразумевает соответствующее накопление электрической энергии. Если электрический заряд передается между двумя первоначально незаряженными проводниками, оба становятся одинаково заряженными, один положительно, другой отрицательно, и между ними устанавливается разность потенциалов.Емкость C — это отношение количества заряда q на любом проводе к разности потенциалов V между проводниками, или просто C = q / В.
Британская викторина
Гаджеты и технологии: факт или вымысел?
В цифровых фотоаппаратах используется пленка.
Как в практических, так и в научных системах метр-килограмм-секунда единицей электрического заряда является кулон, а единицей разности потенциалов является вольт, так что единица емкости, называемая фарадом (обозначенная буквой F), равна единице. кулон на вольт. Один фарад — это чрезвычайно большая емкость. Обычно используются удобные деления на одну миллионную фарада, называемую микрофарад ( μ F), и одну миллионную микрофарада, называемую пикофарад (пФ; более старый термин, микромикрофарад, μμ F).В электростатической системе единиц емкость имеет размерность расстояния.
Емкость в электрических цепях намеренно вносится устройством, называемым конденсатором. Он был открыт прусским ученым Эвальдом Георгом фон Клейстом в 1745 году и независимо голландским физиком Питером ван Мушенбруком примерно в то же время, когда он исследовал электростатические явления. Они обнаружили, что электричество, полученное от электростатической машины, можно хранить в течение определенного периода времени, а затем высвобождать.Устройство, которое стало известно как лейденская банка, состояло из закрытого стеклянного флакона или сосуда, наполненного водой, с гвоздем, протыкающим пробку и погружающимся в воду. Держа банку в руке и прикоснувшись гвоздем к проводнику электростатической машины, они обнаружили, что удар можно получить от гвоздя после его отсоединения, прикоснувшись к нему свободной рукой. Эта реакция показала, что часть электричества от машины была сохранена.
Простой, но фундаментальный шаг в эволюции конденсатора был сделан английским астрономом Джоном Бевисом в 1747 году, когда он заменил воду металлической фольгой, образующей покрытие на внутренней поверхности стекла, и другим, покрывающим внешнюю поверхность.Эта форма конденсатора с проводником, выступающим из горловины сосуда и касающимся футеровки, в качестве основных физических характеристик имела два проводника протяженной площади, которые почти одинаково разделены изолирующим или диэлектрическим слоем, сделанным настолько тонким, насколько это возможно. Эти особенности сохранены во всех современных конденсаторах.
Получите эксклюзивный доступ к контенту из нашего первого издания 1768 с вашей подпиской.
Подпишитесь сегодня
Конденсатор, также называемый конденсатором, по сути, представляет собой сэндвич из двух пластин из проводящего материала, разделенных изоляционным материалом или диэлектриком.Его основная функция — хранить электрическую энергию. Конденсаторы различаются размером и геометрическим расположением пластин, а также типом используемого диэлектрического материала. Отсюда и такие названия, как слюдяные, бумажные, керамические, воздушные и электролитические конденсаторы. Их емкость может быть фиксированной или регулируемой в диапазоне значений для использования в схемах настройки.
Энергия, запасаемая конденсатором, соответствует работе, выполняемой (например, аккумулятором) по созданию противоположных зарядов на двух пластинах при приложенном напряжении.Количество заряда, которое может быть сохранено, зависит от площади пластин, расстояния между ними, диэлектрического материала в пространстве и приложенного напряжения.
Конденсатор, включенный в цепь переменного тока, попеременно заряжается и разряжается каждые полупериод. Таким образом, время, доступное для зарядки или разрядки, зависит от частоты тока, и если требуемое время превышает длину полупериода, поляризация (разделение заряда) не завершается.В таких условиях диэлектрическая проницаемость оказывается меньше, чем наблюдаемая в цепи постоянного тока, и изменяется с частотой, становясь ниже на более высоких частотах. Во время изменения полярности пластин заряды должны перемещаться через диэлектрик сначала в одном направлении, а затем в другом, и преодоление сопротивления, с которым они сталкиваются, приводит к выделению тепла, известному как диэлектрические потери, характеристика, которая должна быть учитывается при применении конденсаторов в электрических цепях, например, в радио- и телевизионных приемниках.Диэлектрические потери зависят от частоты и материала диэлектрика.
За исключением утечки (обычно небольшой) через диэлектрик, ток через конденсатор не протекает, когда на него действует постоянное напряжение. Однако переменный ток проходит легко и называется током смещения.
.Конденсаторы
— learn.sparkfun.com
Добавлено в избранное
Любимый
70
Теория конденсаторов
Примечание : Материал на этой странице не совсем критичен для понимания новичками в электронике … и к концу все становится немного сложнее. Мы рекомендуем прочитать раздел Как делается конденсатор , остальные, вероятно, можно пропустить, если они вызывают у вас головную боль.
Как делается конденсатор
Схема обозначения конденсатора на самом деле очень похожа на то, как он сделан.Конденсатор состоит из двух металлических пластин и изоляционного материала, называемого диэлектриком . Металлические пластины расположены очень близко друг к другу, параллельно, но диэлектрик находится между ними, чтобы они не соприкасались.
Ваш стандартный конденсаторный сэндвич: две металлические пластины, разделенные изолирующим диэлектриком.
Диэлектрик может быть изготовлен из любых изоляционных материалов: бумаги, стекла, резины, керамики, пластика или всего, что препятствует прохождению тока.
Пластины изготовлены из проводящего материала: алюминия, тантала, серебра или других металлов. Каждый из них подключен к клеммному проводу, который в конечном итоге подключается к остальной цепи.
Емкость конденсатора — сколько в нем фарад — зависит от его конструкции. Для большей емкости требуется конденсатор большего размера. Пластины с большей площадью перекрытия поверхности обеспечивают большую емкость, в то время как большее расстояние между пластинами означает меньшую емкость. Материал диэлектрика даже влияет на то, сколько фарад имеет колпачок.Полная емкость конденсатора может быть рассчитана по формуле:
Где ε r — относительная диэлектрическая проницаемость диэлектрика (постоянное значение, определяемое материалом диэлектрика), A — это площадь, на которой пластины перекрывают друг друга, а d — расстояние между пластинами.
Как работает конденсатор
Электрический ток — это поток электрического заряда, который электрические компоненты используют для зажигания, вращения или выполнения любых действий.Когда ток течет в конденсатор, заряды «застревают» на пластинах, потому что не могут пройти через изолирующий диэлектрик. Электроны — отрицательно заряженные частицы — засасываются в одну из пластин, и она становится в целом заряженной отрицательно. Большая масса отрицательных зарядов на одной пластине отталкивает, как заряды, на другой пластине, делая ее заряженной положительно.
Положительный и отрицательный заряды на каждой из этих пластин притягиваются друг к другу, потому что это то, что делают противоположные заряды.Но с диэлектриком, сидящим между ними, как бы они ни хотели соединиться, заряды навсегда останутся на пластине (до тех пор, пока им не будет куда-то идти). Стационарные заряды на этих пластинах создают электрическое поле, которое влияет на электрическую потенциальную энергию и напряжение. Когда заряды группируются на конденсаторе, как этот, конденсатор накапливает электрическую энергию так же, как батарея может накапливать химическую энергию.
Зарядка и разрядка
Когда положительный и отрицательный заряды объединяются на пластинах конденсатора, конденсатор становится на заряженным .Конденсатор может сохранять свое электрическое поле — удерживать свой заряд — потому что положительный и отрицательный заряды на каждой из пластин притягиваются друг к другу, но никогда не достигают друг друга.
В какой-то момент обкладки конденсатора будут настолько заряжены, что просто не смогут больше их принимать. На одной пластине достаточно отрицательных зарядов, чтобы они могли отразить любые другие, пытающиеся присоединиться. Здесь вступает в игру емкость (фарад) конденсатора, которая говорит вам о максимальном количестве заряда, которое может хранить конденсатор.
Если в цепи создается путь, который позволяет зарядам найти другой путь друг к другу, они выйдут из конденсатора, и он разрядит .
Например, в приведенной ниже схеме можно использовать батарею для создания электрического потенциала на конденсаторе. Это вызовет нарастание одинаковых, но противоположных зарядов на каждой из пластин, пока они не станут настолько полными, что оттолкнут ток. Светодиод, расположенный последовательно с крышкой, может обеспечивать путь для тока, а энергия, запасенная в конденсаторе, может использоваться для кратковременного освещения светодиода.
Расчет заряда, напряжения и тока
Емкость конденсатора — сколько в нем фарад — говорит вам, сколько заряда он может хранить. Сколько заряда хранит конденсатор в настоящее время, зависит от разности потенциалов (напряжения) между его пластинами. Эта взаимосвязь между зарядом, емкостью и напряжением может быть смоделирована следующим уравнением:
Заряд (Q), накопленный в конденсаторе, является произведением его емкости (C) и приложенного к нему напряжения (V).
Емкость конденсатора всегда должна быть постоянной известной величиной. Таким образом, мы можем регулировать напряжение, чтобы увеличить или уменьшить заряд крышки. Больше напряжения означает больше заряда, меньше напряжения … меньше заряда.
Это уравнение также дает нам хороший способ определить значение одного фарада. Один фарад (F) — это способность хранить одну единицу энергии (кулоны) на каждый вольт.
Расчет тока
Мы можем пойти дальше по уравнению заряда / напряжения / емкости, чтобы выяснить, как емкость и напряжение влияют на ток, потому что ток — это скорость потока заряда.Суть отношения конденсатора к напряжению и току такова: величина тока , проходящего через конденсатор , зависит как от емкости, так и от того, как быстро напряжение растет или падает . Если напряжение на конденсаторе быстро возрастает, через конденсатор будет индуцироваться большой положительный ток. Более медленный рост напряжения на конденсаторе означает меньший ток через него. Если напряжение на конденсаторе стабильное и неизменное, через него не будет проходить ток.
(Это некрасиво, и касается вычислений. Это не все, что необходимо, пока вы не перейдете к анализу во временной области, разработке фильтров и прочим грубым вещам, поэтому переходите к следующей странице, если вам не нравится это уравнение .) Уравнение для расчета тока через конденсатор:
Часть dV / dt этого уравнения является производной (причудливый способ сказать мгновенной скорости ) напряжения во времени, это эквивалентно тому, как «насколько быстро напряжение растет или падает в этот самый момент».Большой вывод из этого уравнения заключается в том, что если напряжение стабильно, , производная равна нулю, что означает, что ток также равен нулю . Вот почему ток не может течь через конденсатор, поддерживающий постоянное постоянное напряжение.
← Предыдущая страница
Условные обозначения и единицы
.
PPT — Урок 6 Конденсаторы и емкость PowerPoint Presentation, скачать бесплатно
Урок 6 Конденсаторы и емкость
Сегодня мы: • узнаем, что такое конденсатор. • узнать определение емкости. • найти электрическое поле и напряжение внутри конденсатора с параллельными пластинами. • найти емкость конденсатора. • узнать, что диэлектрик — это материал с полярными молекулами. • узнать, как диэлектрики увеличивают емкость.• найти энергию, запасенную в конденсаторе и в электрическом поле. Класс 16
Раздел 1 Емкость, заряд и напряжение
Что такое конденсатор? Проводники, способные удерживать заряд. Кабели, руки и т. Д. Имеют емкость. Для наших целей: два проводника, один с зарядом + Q и один с зарядом −Q.
Что такое конденсатор? Мы «заряжаем» конденсатор, подключая его к аккумулятору. +
Что такое конденсатор? • Когда отсоединяем аккумулятор, на проводниках остается заряд.Мы «заряжаем» конденсатор, подключая его к батарее.
Что такое конденсатор? • Когда отсоединяем аккумулятор, на проводниках остается заряд. Мы «заряжаем» конденсатор, подключая его к батарее. • Если мы соединим проводники, заряд будет перетекать от одного к другому.
Почему конденсаторы полезны? Конденсаторы могут создавать однородные электрические поля. Мы используем их для ускорения или отклонения заряженных лучей и т. Д. Мы можем сохранить заряд для дальнейшего использования.Мы можем заряжать множество конденсаторов, а затем разряжать их за один раз, создавая очень большие токи на короткое время. Конденсаторы важны в цепях переменного тока (переменный ток = синусоидальный), но мы рассмотрим это позже.
Зарядка конденсатора Когда мы присоединяем конденсатор к батарее: Заряд накапливается на проводниках. Заряд на + проводе равен заряду на отрицательном проводе и противоположен ему. Мы называем + Q «зарядом конденсатора». Напряжение на конденсаторе нарастает до тех пор, пока оно не станет равным напряжению батареи.В конденсаторе создается электрическое поле.
Зарядка конденсатора Q Мы обнаружили, что напряжение пропорционально заряду. В
Зарядка конденсатора Q Мы обнаружили, что напряжение пропорционально заряду. В
Q = CV Емкость Если емкость большая — — конденсатор удерживает большой заряд при небольшом напряжении.
Секция 2 Конденсаторы с параллельными пластинами
Конденсаторы с параллельными пластинами , состоящие из двух пластин, каждая из которых имеет площадь A (форма не имеет значения), пластины разделены расстоянием d.
Конденсаторы с параллельными пластинами Электрическое поле — это сумма электрических полей положительно заряженного неба…
Конденсаторы с параллельными пластинами … и отрицательно заряженной пластины.
Конденсаторы с параллельными пластинами … и отрицательно заряженная пластина.
Конденсаторы с параллельными пластинами Электрические поля вне пластин компенсируются.
Конденсаторы с параллельными пластинами Электрические поля вне пластин компенсируются.Сделайте так, чтобы внешние поля исчезли.
Конденсаторы с параллельными пластинами Электрические поля между пластинами складываются. Просто совместите стрелки…
Конденсаторы с параллельными пластинами Заряды перемещаются внутрь пластин. Переместите символы + и — к центру.
Конденсаторы с параллельными пластинами Электрическое поле внутри однородно. Электрическое поле снаружи небольшое.
Раздел 3 Электрическое поле, напряжение и емкость в конденсаторе с параллельными пластинами
Электрическое поле конденсатора Мы можем найти электрическое поле в конденсаторе из закона Кулона и наших знаний о силовых линиях!
Электрическое поле конденсатора Силовые линии внутри конденсатора:
Электрическое поле конденсатора Силовые линии внутри конденсатора:
Электрическое поле конденсатора с конденсатором заряд Q и площадь пластины Точечный заряд с зарядом Q.+ + + + + + + +
Электрическое поле конденсатора • Силовые линии начинаются с положительного заряда в обоих случаях. • Поскольку положительный заряд одинаковый, количество силовых линий такое же. + + + + + + + +
Электрическое поле конденсатора ← одинаковые линии N → N между пластинами! + + + + + + + +
Электрическое поле конденсатора + + + + + + + +
d Мы знаем, как напряжение соотносится с электрическим полем, потому что электрическое поле постоянно .Конденсаторы с параллельными пластинами Мы всегда игнорируем знак минус, поэтому V будет положительным:
d Теперь мы можем найти емкость: Конденсаторы с параллельными пластинами
d Теперь мы можем найти емкость: Параллельно -пластинчатые конденсаторы • Если площадь пластины большая, конденсатор • может удерживать больший заряд. • Если расстояние между пластинами невелико, заряды на двух пластинах • притягиваются друг к другу с большей силой, поэтому конденсатор может удерживать больший заряд.
Конденсатор с параллельными пластинами Уравнения
Раздел 4 Диэлектрики
Диэлектрики Диэлектрик — это изолятор с полярными молекулами, который помещен между пластинами конденсатора.
Диэлектрики Полярные молекулы вращаются в электрическом поле конденсатора.
Диэлектрики Чистый заряд внутри диэлектрика равен нулю.
Диэлектрики Но на поверхностях диэлектрика есть остатки заряда.
Диэлектрики Э пластин Этот заряд создает электрическое поле, которое противодействует электрическому полю пластин. E диэлектрика
Тип проблемы 1: Фиксированный заряд С диэлектриком: Без диэлектрика: Конденсатор заряжается вместе с батареей до заряда Q. Батарея удаляется, а диэлектрик вставляется.
Тип проблемы 1: Фиксированный заряд С диэлектриком: Конденсатор заряжается с батареей до заряда Q. Батарея извлекается и вставляется диэлектрик.
Тип проблемы 1: Постоянный заряд Электрическое поле диэлектрика снижает напряжение на конденсаторе, в результате чего емкость увеличивается. Конденсатор заряжается от батареи до заряда Q. Батарея удаляется и вставляется диэлектрик.
Тип проблемы 2: Фиксированное напряжение С диэлектриком: Без диэлектрика: Конденсатор подключен к батарее с напряжением V и остается подключенным, пока вставляется диэлектрик.
Тип проблемы 2: Фиксированное напряжение С диэлектриком: конденсатор подключен к батарее с напряжением V и остается подключенным, пока вставляется диэлектрик.
Тип проблемы 2: фиксированное напряжение Заряд на диэлектрике вытягивает дополнительный заряд от батареи к пластинам, вызывая повышение емкости. Конденсатор подключен к батарее с напряжением V и остается подключенным, пока вставляется диэлектрик.
Раздел 5 Энергия в конденсаторах и электрических полях
Энергия в конденсаторе Начните с двух параллельных пластин без заряда.Переместите один заряд с одной пластины на другую. Здесь нет электрического поля и силы, поэтому работы не требуется.
Энергия в конденсаторе После передачи заряда конденсатор имеет небольшой заряд и небольшое поле. Поле вызывает силу на следующий заряд, который мы перемещаем, заставляя нас выполнять работу.
Энергия в конденсаторе Когда заряд конденсатора равен q, напряжение равно q / C, а электрическое поле равно V / d = q / Cd. Сила на маленьком заряде dq составляет
Загрузить больше….

 номинальное напряжение,
номинальное напряжение, 1, 61 вакуум,
1, 61 вакуум, B +/-0,1 пФ.
B +/-0,1 пФ.