Формула силы Ампера
ОПРЕДЕЛЕНИЕ
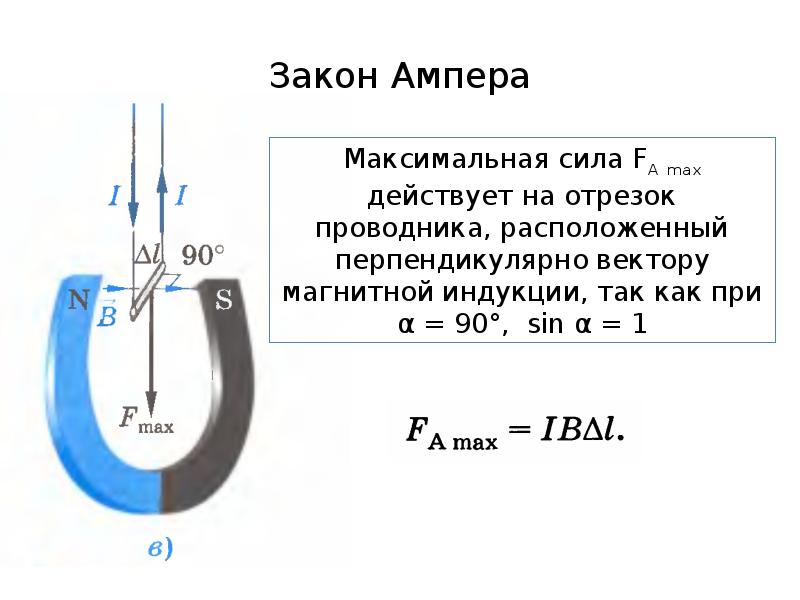
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Здесь – сила Ампера, – сила тока в проводнике, – модуль вектора индукции магнитного поля, – длина участка проводника, на который воздействует магнитное поле, – угол между вектором индукции магнитного поля и направления тока.
Единица измерения силы – Н (ньютон).
Сила Ампера — векторная величина. Сила Ампера принимает своё наибольшее значение когда векторы индукции и направления тока перпендикулярны ().
Направление силы ампера определяют по правилу левой руки:
Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Ампера.
Исторически электрическим током принято считать движение положительного заряда, то есть направление сила тока – от плюса к минусу.
Примеры решения задач по теме «Сила Ампера»
ПРИМЕР 1
| Задание | Найти силу Ампера, действующую на прямой проводник длиной 3 м, по которому проходит ток силой 7 А. Вектор магнитной индукции составляет угол с проводником, его абсолютное значение – 2 Тл. |
| Решение | Электрический ток течёт по проводнику, значит направлен он также, как расположен проводник. Следовательно, угол между вектором магнитной индукции и проводником равен углу между ним и вектором движения тока. Остаётся только подставить значения в формулу:
|
| Ответ | Сила ампера равна 21 ньютон. |
ПРИМЕР 2
| Задание | На рисунке изображены два параллельно расположенных проводника, указаны направления сил тока и вектора магнитной индукции. В ответе указать, каким образом будет действовать на них сила Ампера (сближать проводники, отталкивать или действовать как-то иначе). Как изменится ситуация, если направить вектор магнитной индукции параллельно проводникам? В ответе указать, каким образом будет действовать на них сила Ампера (сближать проводники, отталкивать или действовать как-то иначе). Как изменится ситуация, если направить вектор магнитной индукции параллельно проводникам?
|
| Решение | Определим направление силы Ампера по правилу левой руки. Очевидно, если расположить левую руку так, чтобы вектор входил в ладонь, а пальцы направить по линии движения тока в первом случае (вертикально вверх), то отогнутый большой палец будет направлен от наблюдателя. Также будет направлена и сила Ампера. Во втором проводнике ток направлен вертикально вниз, а сила Ампера – на наблюдателя. Оказалось, что под действием силы Ампера первый проводник отталкивается от наблюдателя, а второй притягивается к нему.
Пусть вектор сонаправлен движению тока в первом проводнике, тогда
и
При вычислении силы Ампера нас интересуют не сами углы, а их синусы:
и
Сила Ампера в обоих проводниках равна нулю.
|
| Ответ | Если вектор магнитной индукции направлен так, как показано на рисунке, то сила Ампера в первом проводнике будут направлена на наблюдателя, во втором – от него. Если вектор магнитной индукции направить параллельно проводникам, то сила Ампера возникать не будет. |
|
Понравился сайт? Расскажи друзьям! |
| ||
Электричество и магнетизм
Теперь мы готовы к обсуждению взаимодействия тока с магнитным полем.
Ампер установил наличие силового взаимодействия между двумя проводниками, по которым текут электрические токи. Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
Рис. 5.25. Опыт Ампера по исследованию взаимодействия параллельных токов:
1 — схема установки; 2 — отталкивание антипараллельных токов; 3 — притяжение параллельных токов
Если по ним пропускать токи, текущие в противоположных направлениях, то проводники будут отталкиваться друг от друга (см. рис. 5.25-2). Если же токи будут течь в одном направлении, то они будут притягиваться (см. рис. 5.25-3).
Видео 5.4. Взаимодействие параллельных токов.
Эксперименты, проведенные Ампером, показали, что на проводник с током, помещенный в магнитное поле, действует сила. Откуда же она берется? Обсуждая эффект Холла, мы видели, что сила электрического поля EХ уравновешивает силу Лоренца, действующую на электроны. Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl · S. В силу нейтральности проводника в целом таков же по абсолютной величине и полный заряд ионов кристаллической решетки. Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl · S. В силу нейтральности проводника в целом таков же по абсолютной величине и полный заряд ионов кристаллической решетки. Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
|
|
(5.30) |
где мы выразили плотность тока через его силу
Обращаем внимание, что в эту формулу не вошли характеристики конкретных носителей заряда, но лишь полный ток через проводник.
У нас внешнее магнитное поле было ортогонально току. В общем случае направление тока будем характеризовать вектором dl, имеющем длину dl и направленным вдоль течения тока. В холловскую напряженность электрического поля дает вклад только компонента магнитного поля, ортогональная вектору dl. Эта компонента равна по величине
где есть угол между векторами B и dl. Тогда для величины силы имеем
|
|
(5.31) |
Учитывая направление этой силы (правило винта), можем записать ее в векторной форме
|
|
(5. |
Выражение (5.32) носит название закона Ампера, а сила называется силой Ампера (рис. 5.26).
Сила Лоренца: формула, определение и направление
Наряду с силой Ампера, кулоновского взаимодействия, электромагнитными полями в физике часто встречается понятие сила Лоренца. Это явление является одним из основополагающих в электротехнике и электронике, на ряду с законом Кулона, электромагнитной индукцией Фарадея и прочими. Она воздействует на заряды, которые двигаются в магнитном поле. В этой статье мы кратко и понятно рассмотрим, что такое сила Лоренца и где она применяется.
Определение
Когда электроны движутся по проводнику – вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и двигать его – возникнет ЭДС электромагнитной индукции. Если через проводник, который находится в магнитном поле, протекает ток – на него действует сила Ампера.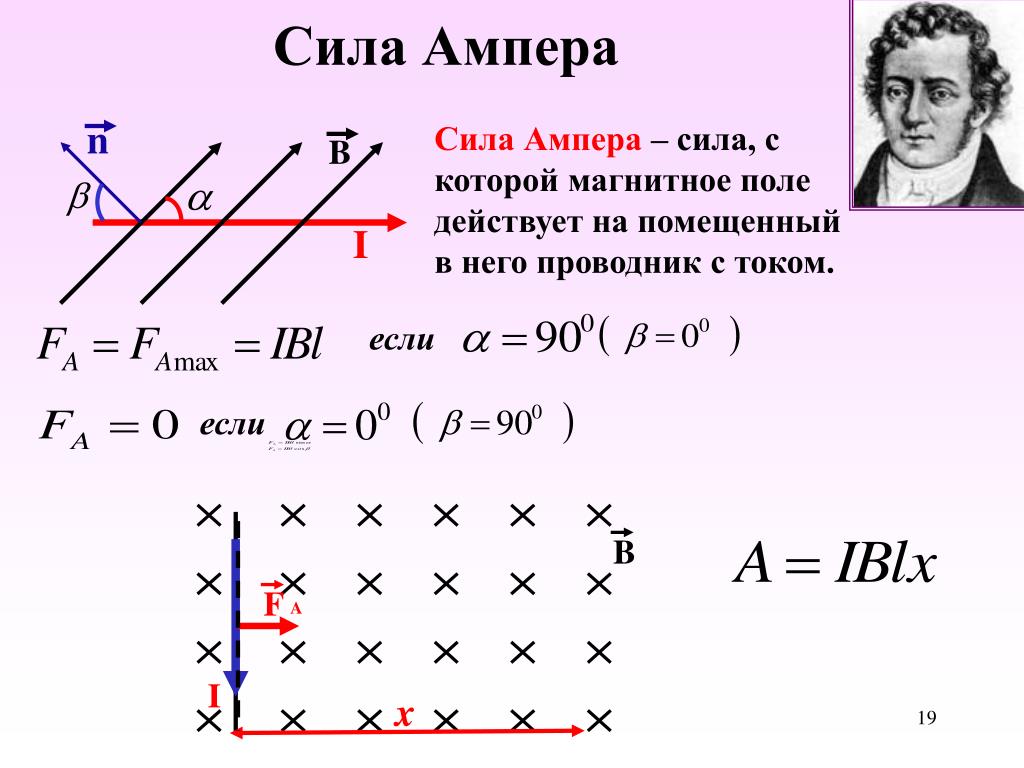
Её величина зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она вычисляются по формуле:
Рассматриваемая сила отчасти похожа на ту, что рассмотрена выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула имеет вид:
Важно! Сила Лоренца (Fл) действует на электрон, движущийся в магнитном поле, а на проводник – Ампера.
Из двух формул видно, что и в первом и во втором случае, чем ближе синус угла aльфа к 90 градусам, тем большее воздействие оказывает на проводник или заряд Fа или Fл соответственно.
Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое происходит воздействие со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Fл не совершает работы. Соответственно изменяется именно направление скорости движения заряженной частицы, а не её величина.
Что касается единицы измерения силы Лоренца, как и в случае с другими силами в физике используется такая величина как Ньютон. Её составляющие:
Как направлена сила Лоренца
Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости. Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.
Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции.
При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.
Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.
Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц. Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.
Применение
Из всех сфер, где используется сила Лоренца, одной из масштабнейших является движение частиц в магнитном поле земли. Если рассмотреть нашу планету как большой магнит, то частицы, которые находятся около северного магнитного полюсов, совершают ускоренное движение по спирали. В результате этого происходит их столкновение с атомами из верхних слоев атмосферы, и мы видим северное сияние.
Тем не менее, есть и другие случаи, где применяется это явление. Например:
- Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ мониторы.
- Электрические машины – генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства при работе которых наблюдается воздействие многих физических явлений.
- В ускорителях заряженных частиц для того, чтобы задавать им орбиты и направления.
Заключение
Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:
- Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
- Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.

- Не влияет на скорость частицы.
- Влияет на направление частицы.
Её роль достаточно велика в «электрических» сферах. Специалист не должен упускать из вида основные теоретические сведения об основополагающих физических законах. Эти знания пригодятся, как и тем, кто занимается научной работой, проектированием и просто для общего развития.
Напоследок рекомендуем просмотреть полезные видео для закрепления изученного материала:
Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если возникли вопросы, задавайте их в комментариях под статьей!
Материалы по теме:
Сила Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I = qnvS ( 2 )
Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
F = | I |B Δl sin α
Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:
F = | q | nvS Δl B sin α = v | q | NB sin α,
где N = nSΔl — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
где α — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Другие заметки по физике
Высшее образование БГПУ
Сила Ампера. Сила взаимодействия параллельных токов. Контур с то-ком в магнитном поле. Магнитный момент тока. Действие электриче-ского и магнитного полей на движущиеся заряды. Сила Лоренца. Опре-деление удельного заряда электрона. Эффект Холла и его применение. Принцип работы магнитогидродинамических генераторов.
Эффект Холла и его применение. Принцип работы магнитогидродинамических генераторов.
20.1. Сила Ампера. Взаимодействие параллельных токов
При исследовании действия магнитного поля на расположенный в нем прямолинейный проводник с током французский физик А.Ампер пришел к выводу, что модуль этой силы можно рассчитать по формуле
. (20.1)
Позднее эта сила была названа силой Ампера, а формула – законом Ампера. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы нормальная к проводнику составляющая B┴ вектора индукции магнитного поля B входила в ладонь, четыре вытянутых пальца были направлены по току, то отогнутый на 90° большой палец покажет направление силы Ампера, которая действует на проводник с током (рис.20.1).
Рис. 20.1
20.1
На основе закона Ампера можно объяснить взаимодействие параллельных проводников с током (рис.20.2).
Рис. 20.2
Ток I1 создает в месте расположения проводника с током I2 магнитное поле B1, которое действует на ток I2 с силой F12=B1I2l. Ток I2 в свою очередь также создает магнитное поле, индукция которого в месте расположения проводника с током I1 равна B2. Это поле действует на ток I1 с силой F21=B2I1l. Силы F12 и F21 находятся в одной плоскости с проводниками и являются силами притяжения, если токи направлены в одну сторону, и силами отталкивания, если токи направлены в противоположные стороны (рис.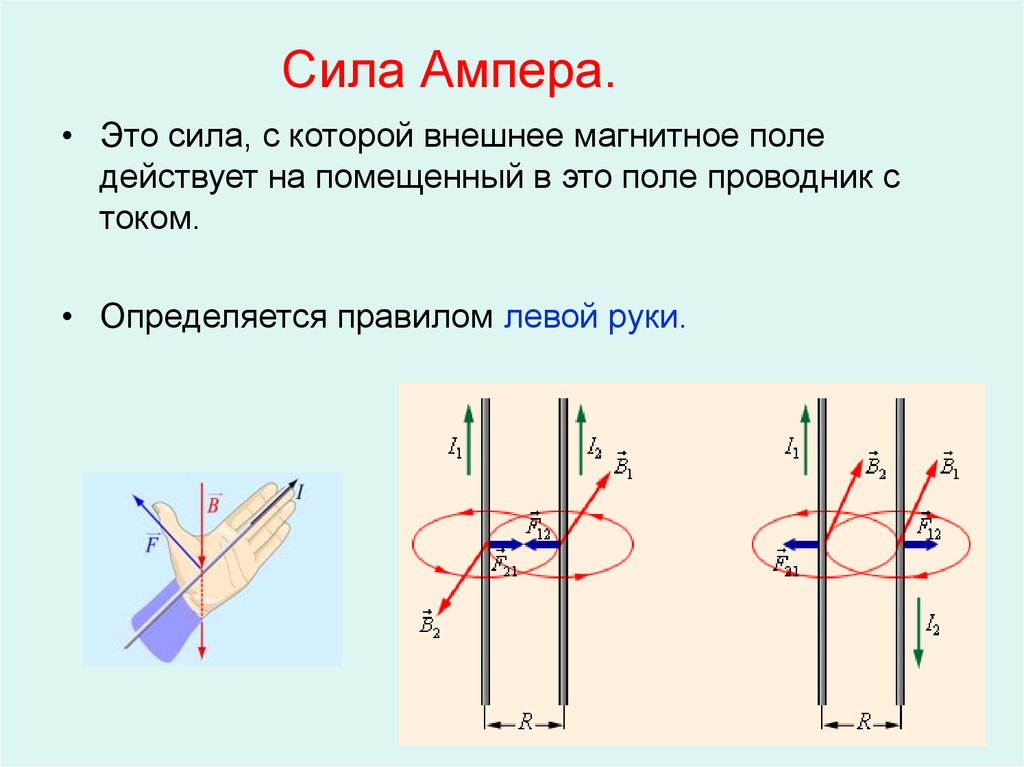 20.2).
20.2).
Если расстояние между проводниками равно d, то индукция магнитного поля, созданного током I1 в тех точках пространства, где находится второй проводник,
. (20.2)
Соответственно индукция магнитного поля, созданного током I2 в тех точках пространства, где расположен первый проводник,
. (20.3)
Таким образом, для проводников длиной l:
. (20.4)
Если проводники находятся в вакууме (μ=1) на расстоянии d=1 м м и токи в них одинаковые и равны единице, то сила взаимодействия между участками проводников длиной по 1 м F0=μ0/2π=2·10–7 Н. Эта формула используется для определения единицы силы тока – ампера – в СИ.
Эта формула используется для определения единицы силы тока – ампера – в СИ.
20.2. Контур с током в магнитном поле
Поместим замкнутый контур с током в однородное магнитное поле. Пусть плоскость контура перпендикулярна линиям индукции поля. Если разделить контур на элементы dl, то на каждый из них действует сила dF=IBdl, которая лежит в плоскости контура и направлена к его центру (рис.20.3).
Рис. 20.3
Если изменить направление тока на противоположное, то сила dF будет направлена в противоположную сторону (рис.20.4).
Рис. 20.4
Значит, силы, которые действуют на замкнутый контур с током в однородном перпендикулярном магнитном поле, могут только деформировать его (растянуть или сжать). Перемещение контура при этом не происходит.
Если расположить контур параллельно направлению линий магнитной индукции (рис.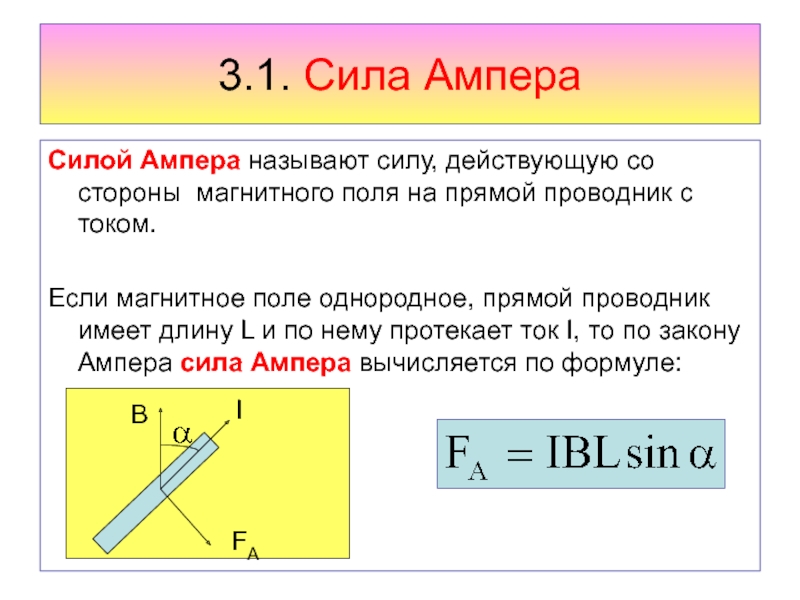 20.5), то на контур будет действовать вращательный момент сил M. Под действием этого момента контур поворачивается так, чтобы его плоскость стала перпендикулярной линиям магнитной индукции.
20.5), то на контур будет действовать вращательный момент сил M. Под действием этого момента контур поворачивается так, чтобы его плоскость стала перпендикулярной линиям магнитной индукции.
Рис. 20.5
Определим величину вращательного момента. Для этого разделим контур на малые элементы Δl. Выделим два элемента Δl1 и Δl2, заключенные между двумя параллельными линиями магнитной индукции, отстоящими друг от друга на расстоянии Δh. На эти элементы со стороны поля действуют силы ΔF1 и ΔF2, направленные соответственно перпендикулярно плоскости контура «от нас» и «к нам». Модули этих сил равны: ΔF1=IBΔl1sinα1 и ΔF2=IBΔl2sinα2. Если учесть, что Δl1sinα1=Δh, а Δl2sinα2=Δh, то очевидно, что эти силы равны по модулю и направлены в противоположные стороны. Они образуют пару сил, момент которой ΔM=ΔFx=IBΔhx=IBΔS, где x – среднее расстояние между элементами Δl1 и Δl2, ΔS=Δhx – площадь, ограниченная линиями магнитной индукции и элементами контура Δl1 и Δl2. Очевидно, что весь контур состоит из суммы всех пар элементов. Поэтому суммарный момент действующий на контур, равен
Если учесть, что Δl1sinα1=Δh, а Δl2sinα2=Δh, то очевидно, что эти силы равны по модулю и направлены в противоположные стороны. Они образуют пару сил, момент которой ΔM=ΔFx=IBΔhx=IBΔS, где x – среднее расстояние между элементами Δl1 и Δl2, ΔS=Δhx – площадь, ограниченная линиями магнитной индукции и элементами контура Δl1 и Δl2. Очевидно, что весь контур состоит из суммы всех пар элементов. Поэтому суммарный момент действующий на контур, равен
.
Если контур расположен в магнитном поле так, что угол между его нормалью n и вектором магнитной индукции B поля равен β, то под действием проекции вектора B на нормаль к контуру равную B┴=Bcosβ контур будет растягиваться (сжиматься), а под действием проекции B на плоскость контура Bsinβ – поворачиваться.
Поэтому в общем случае формула расчета вращательного момента имеет вид:
. (20.5)
Как уже отмечалось, величину pm=IS называют магнитным моментом контура с током. Это величина векторная, и она совпадает по направлению с единичным вектором нормали n: pm=ISn. Тогда формулу (20.5) можно записать в векторном виде:
. (20.6)
Если контур с током поместить в неоднородное магнитное поле, то кроме ориентирующего действия вращательного момента на контур будет действовать сила f в направлении возрастания магнитного поля (рис.20.6).
g
Рис. 20.6
Эта сила является равнодействующей всех сил dF┴ на каждый элемент тока со стороны составляющей поля B║. Расчет показывает, что модуль силы, которая действует на весь контур, равен:
Расчет показывает, что модуль силы, которая действует на весь контур, равен:
, (20.7)
где α – угол между векторами pm и B; – градиент индукции магнитного поля.
20.3. Сила Лоренца
Как уже отмечалось, на проводник с током, который находится в магнитном поле, действует сила Ампера FA=IBlsinα. Поскольку ток представляет упорядоченное движение свободных электрических зарядов, то это означает, что магнитное поле действует на каждый из этих зарядов. Сила, действующая на заряд, который движется в магнитном поле, называется силой Лоренца. Х.Лоренц (1853–1928), нидерландский физик, создатель классической электронной теории.
Если учесть, что сила тока в проводнике
,
где q – заряд носителей тока; n – концентрация носителей тока; υ – скорость их упорядоченного движения; S – площадь поперечного сечения проводника, то формула (20. 1) примет вид:
1) примет вид:
.
Силу Лоренца можно выразить, как
,
где N – общее количество носителей тока в проводнике (N=nV=nSl). С учетом того, что Sl=V (V – объем проводника):
, (20.8)
где α – угол между направлением вектора индукции магнитного поля и направлением вектора скорости движения положительного заряда. Направление силы Лоренца, как и силы Ампера, также определяется по правилу левой руки.
20.4. Определение удельного заряда электрона
Под действием силы Лоренца частицы, обладающие электрическим зарядом, движутся в магнитном поле по криволинейным траекториям. Причем если скорость частицы υ ┴ B, то траектория ее движения в магнитном поле представляет окружность (рис.20.7).
Рис. 20.7
20.7
Определив радиус этой окружности, скорость частицы и величину индукции магнитного поля, можно рассчитать удельный заряд этой частицы. Этот метод используется для определения удельного заряда электрона.
Так, ввиду малости величины силы тяжести, действующей на электрон, движущийся в перпендикулярном магнитном поле, можно записать в соответствии со вторым законом Ньютона:
или ,
откуда радиус окружности равен
,
а удельный заряд электрона:
. (20.9)
Для определения скорости необходимо знать ускоряющую разность потенциалов электрического поля. Известно, что на заряженную частицу со стороны электрического поля действует сила
,
где q – заряд частицы, E – напряженность электрического поля. Если скорость частицы υ<<c и электрическое поле является однородным, то она будет двигаться в поле с постоянным ускорением.
Если скорость частицы в момент включения электрического поля равна нулю, то изменение ее кинетической энергии происходит за счет работы сил поля, т.е.
,
где U – напряжение между точками входа и выхода частицы из электрического поля. Поэтому скорость частицы при выходе из электрического поля
. (20.10)
С учетом (20.10)выражение (20.9) примет вид:
. (20.11)
Опыты, проведенные таким образом, позволили рассчитать отношение
Если заряженная частица влетает в магнитное поле так, что направление ее скорости υ образует с вектором индукции магнитного поля B угол α (причем α≠0, α≠π), то траектория движения частицы представляет винтовую линию (рис.20.8).
Рис.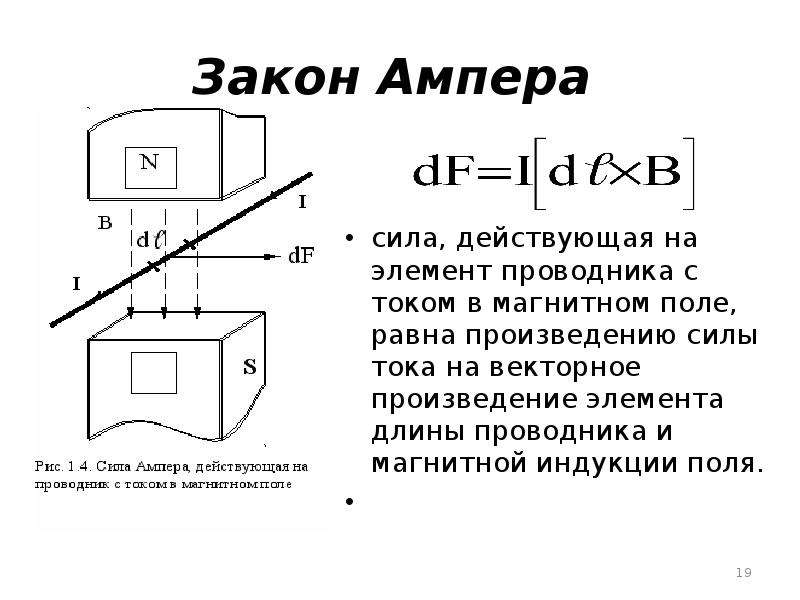 20.8
20.8
На частицу, которая движется вдоль линий индукции магнитного поля со скоростью υy, сила Лоренца не действует.
Перпендикулярная составляющая скорости υx обеспечивает движение частицы по окружности радиуса R. Таким образом, под действием двух составляющих скорости υy и υx частица движется по винтовой линии.
Радиус винтовой траектории согласно формуле (20.9) будет равен:
, (20.12)
а шаг винта
, (20.13)
где – период обращения по окружности радиуса R.
Как уже отмечалось ранее, электрическое и магнитное поля являются частями единого электромагнитного поля. Поэтому в произвольной системе отсчета полная сила, с которой электромагнитное поле действует на заряженную частицу, равна векторной сумме электрической Fэ и магнитной Fм составляющих, т. е.
е.
.
20.5. Эффект Холла
Если пластинку, вдоль которой течет постоянный ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлению тока и поля, возникает разность потенциалов. Это явление впервые исследовал американский физик Е.Холл (1811–1890) в 1879 г., и оно впоследствии было названо эффектом Холла (рис.20.9).
Рис. 20.9
Экспериментально определено, что разность потенциалов Холла определяется по формуле:
, (20.14)
где b – ширина пластинки, j – плотность тока, B – магнитная индукция поля, R – коэффициент пропорциональности, который называется постоянной Холла.
Эффект Холла можно объяснить согласно электронной теории. Если магнитное поле отсутствует, ток в пластинке обусловлен электрическим полем E0 (рис. 20.10).
20.10).
Рис. 20.10
Потенциал во всех точках поверхности одинаков, в том числе и в точках 1 и 2. Электроны как носители отрицательного заряда двигаются со скоростью υ против вектора плотности тока j. При включении магнитного поля на каждый электрон действует сила Лоренца, направленная вдоль стороны b и численно равная Fл=eυB. Поэтому электроны приобретают составляющую скорости, которая направлена к верхней грани пластинки. Значит, на этой грани накапливается отрицательный заряд, на нижней – положительный. Таким образом, возникает поперечное электрическое поле EB. Если сила FB=eEB уравновесит силу Лоренца Fл=eυB, то установится стационарное равновесие: eEB=eυB. Откуда EB=υB. Результирующее поле E равно векторной сумме полей E0 и EB. Так как эквипотенциальные линии перпендикулярны вектору напряженности поля E, то точки 1 и 2, которые ранее лежали на одной эквипотенциальной поверхности, уже имеют разный потенциал.
Откуда EB=υB. Результирующее поле E равно векторной сумме полей E0 и EB. Так как эквипотенциальные линии перпендикулярны вектору напряженности поля E, то точки 1 и 2, которые ранее лежали на одной эквипотенциальной поверхности, уже имеют разный потенциал.
Значит, разность потенциалов между этими точками равна:
. (20.15)
Сравнивая выражения (20.14) и (20.15), определим постоянную Холла:
. (20.16)
Из формулы (20.14) следует, что величина постоянной Холла, как и разности потенциалов Холла, зависит от концентрации носителей заряда в проводящей пластинке. Так как концентрация носителей тока в полупроводниках значительно меньше, чем в металлах, то и эффект Холла в полупроводниках наблюдать легче.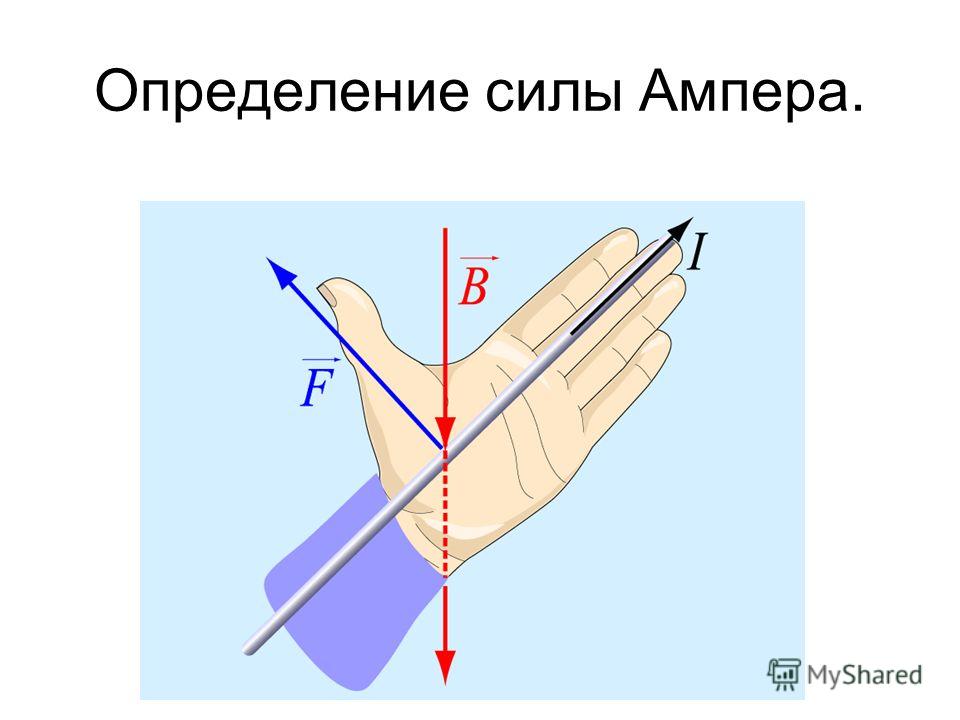
Эффект Холла используется в датчиках Холла, которые используют для измерения напряженности постоянных и переменных магнитных полей, силы и мощности электрического тока, превращения постоянного ток в переменный, модулирования и детектирования сигналов, анализа спектра частот, «чтения» магнитных записей и во многих элементах автоматики и вычислительной техники.
20.6. Принцип работымагнитогидродинамических генераторов
Магнитогидродинамический (МГД) генератор – энергетическая установка, в которой тепловая энергия рабочего тела (плазмы) превращается в электрическую. Принцип работы МГД-генератора основан на взаимодействии магнитного поля с заряженными частицами, которые движутся в нем (рис.20.11).
Рис. 20.11
Если создать поток плазмы в магнитном поле, линии индукции B которого перпендикулярны скорости зарядов υ, то под действием силы Лоренца произойдет их разделение. Это значит, положительные заряды магнитным полем будут отклоняться в одну сторону, а отрицательные – в другую. В результате один электрод заряжается положительно, а второй – отрицательно. Между ними возникает разность потенциалов. Если электроды соединить проводником, то в нем возникнет электрический ток.
В результате один электрод заряжается положительно, а второй – отрицательно. Между ними возникает разность потенциалов. Если электроды соединить проводником, то в нем возникнет электрический ток.
Использование МГД-генераторов является перспективным направлением развития тепловой энергетики, так как позволяет получать КПД 60 %, в то время как КПД тепловых станций достигает 40 %. Органическое топливо, которое используется в МГД-генераторах, вместе с нагретым воздухом поступает в камеру сгорания с температурой 3000°C. Там они превращаются в плазму. С целью увеличения электропроводности плазмы в нее могут добавлять специальные присадки – соли калия или цезия, уменьшающие выброс серы в атмосферу, тем самым решая часть экологических проблем.
КП.Сила Ампера.Сила Лоренца.10клdocx
Изучение
нового материала.
Действия учителя:Дать возможность самостоятельно определить
значение физических явлений в природе.Основная учебная проблема при
рассмотрении нового материала — изучение характеристик, которые можно
использовать для описания свойств магнитного поля.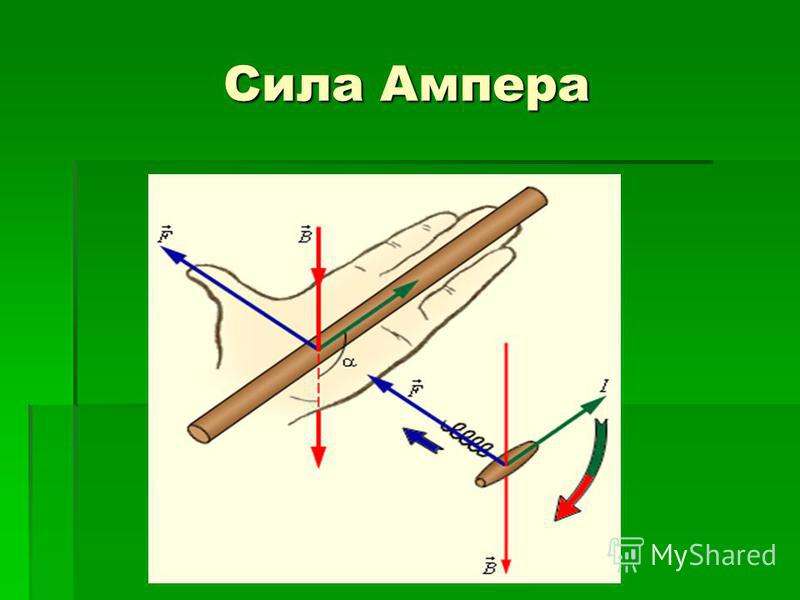 Необходимо повторить и
Необходимо повторить и
углубить представление о векторе магнитной индукции В.
1)
Чтохарактеризует величину В?( Это
векторная характеристика магнитного поля: она имеет направление и числовое
значение).
2)
Что называют линией магнитной
индукции?
3)
Для чего она вводится?
4) Есть ли линии магнитной индукции в природе?
Действия учащихся. Далее изучают магнитные поля по картине линий магнитной
индукции, отрабатывают правило буравчика. Примеры заданий (рисунки
выполнены на слайде).
1. Известно направление линий магнитной
индукции (рис. 3, 4). Укажите направление тока в проводнике.
Рис 1 Рис. 2 Рис. 3
2. 2. По расположению магнитных стрелок определите направление
тока в проводнике (рис.).
3. 3.Как установится магнитная стрелка, если по проводнику
пропустить постоянный электрический ток (рис.)?
4. 4.Определите полюсы источника питания, если магнитная
стрелка около проводника ориентирована так, как показано на рисинке.
Как определить направление вектора
магнитной индукции В — основная учебная проблема урока.
Демонстрация. Демонстрируется
действие магнитного поля подковообразного магнита на проводник с током
(элемент тока).
Вопросы для
организации беседы.
1)
Зависит ли отклонение провод-пика с
током (сила, действующая на проводник) от силы тока?
2)
Зависит ли отклонение проводника с
током от длины проводника?
3)
Зависит ли характеристика В магнитного
поля от силы тока, от длины проводника? (Ответ. Нет, не зависит.)
Записывают в тетради по учебнику: Вектор магнитной индукции можно
принять за характеристику магнитного поля, так как оно не зависит пи от
силы тока, ни от длины проводника.
Вопрос.В чем смысл
закона Ампера?
Нам известен экспериментальный факт:
магнитное поле действует на проводник с током. В 1826 г. французский физик А.
В 1826 г. французский физик А.
Ампер сформулировал закон,описывающий это действие магнитного поля. Закон
представленвыражением F = В \ I \ l sin а.
При этом направление силы определяется по правилу левой руки.
При объяснении материала важно сравнительно быстро ввести
закон, а усвоение отрабатывать при решении задач.
У любой физической величины есть единица.
Учитель. Дает определение единицы индукции В —
тесла.
Если левую руку расположитьтак, чтобы вектор
магнитной
индукции входил в ладонь, авытянутые пальцы
былинаправлены вдоль тока, тоотведенный большой палецукажет направление
действиясилы Ампера на проводник с током.
Вывод.
1.Сила Ампера – сила, действующая на проводник тока, находящийся в
магнитном поле и равная произведению силы тока в проводнике, модуля вектора
индукции магнитного поля, длины проводника и синуса угла между вектором
магнитного поля и направлением тока в проводнике.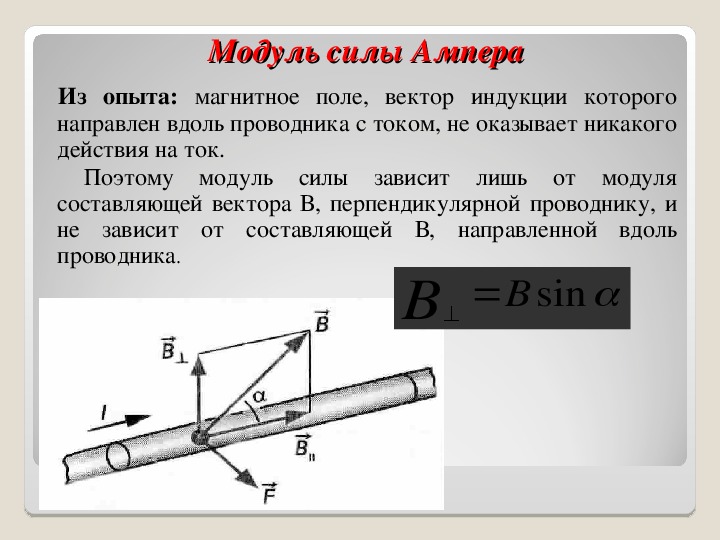
2.Сила Ампера принимает своё наибольшее
значение когда векторы индукции и направления тока перпендикулярны.
3.Если вектор
магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в
сторону направления вектора движения тока, тогда отогнутый в сторону большой
палец показывает направление силы Ампера.
Учитель.Т.к. магнитное поле действует на
ток – движущиеся
заряженные частицы, то оно действует и на каждую частицу в отдельности.
Действие магнитного поля на движущуюся заряженную частицу характеризует сила
Лоренца.
Самостоятельное изучение темы: построение новых
знаний на базе предыдущих.
Критерии оценивания.
·
Умение искать и выделять необходимую
информацию.
·
Умение оперировать гипотезами.
·
Умение аргументировать свою точку
зрения.
Ученик1.Хендрик Антон Лоренц (1853–1928) выдающийся голландский физик и математик , развил
электромагнитную теорию света и электронную теорию материи, а также
сформулировал теорию электричества, магнетизма и света, внёс большой вклад в
развитие теории относительности, лауреат Нобелевской премии 1902г.
, так как является её долей, значит, для определения её
направления можно применить то же мнемоническое правило, что и для
определения направления сил Ампера – правило левой руки, с оговоркой, что
заряд должен быть положительным, т.к. за направление тока мы принимаем направление
движения положительных зарядов. Если же заряд отрицательный, то направление
силы меняется на противоположное.Так как сила, действующая на заряд,
оказалась перпендикулярной скорости его движения, то модуль скорости
изменяться не будет, а будет меняться направление, т.о. частица будет
равномерно двигаться по окружности.
Учитель.
I.
Выведем формулу для расчёта
модуля силы Лоренца.Формулу
силы Лоренца можно найти с помощью силы Ампера.Так как Fл= F/N” где F- сила
Ампера, N – число заряженных частиц
I =
q n v S – сила тока; F= |I| ΔL В ; Подставим выражение для силы
тока и получим:
F=|q|
n v S ΔL Bsinα = v |q| N Вsinα; где N = n S ΔL- число
заряженных частиц в единице объема.
Значит
, на каждую движущуюся заряженную частицу магнитное поле действует с силой
Лоренца:
Fл= F/N = |q| v B , где α- угол между вектором скорости и вектором
II.
Направление силы Лоренца определяют
с помощью правила левой руки.
Ладонь левой руки располагают так, чтобы составляющая магнитной
индукции входила в ладонь, четыре, вытянутые пальца, показывали направление
движения положительного заряда
(против движения отрицательного), то тогда отогнутый на
90˚большой палец укажет направление действующей на заряд силы Лоренца
На заряженную частицу одновременно действуют
магнитное и электрическое поля, значит полная сила будет
равна: F̄= F̄ЭЛ+F̄Л
Под действием силы Лоренца не меняется модуль ее скорости, а меняется только
направление скорости частицы.
Демонстрация наблюдения
силы Лоренца с помощью осциллографа и постоянного магнита.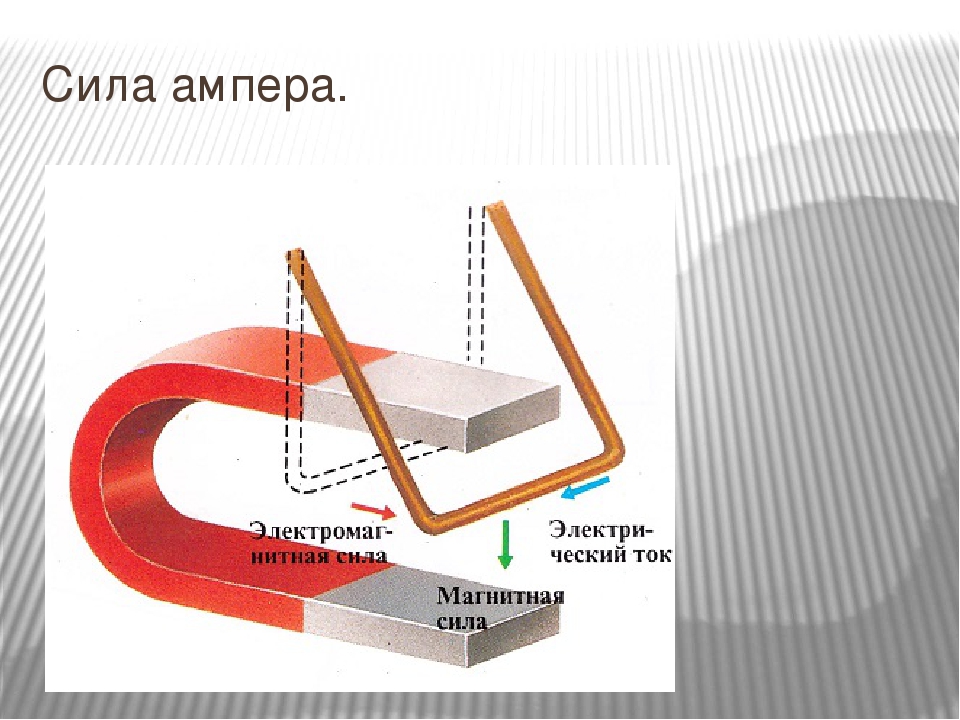
http://home-task.com/plan-konspekt-uroka-po-fizike-tema-dejstvie-magnitnogo-polya-na-dvizhushhijsya-zaryad-sila-lorenca/
Движение заряженной частицы под действием силы Лоренца, если α = 90°
Сила, перпендикулярная скорости, вызывает изменение
направления движения, т.е. центростремительное ускорение. Зная формулы
расчёта центростремительного ускорения и модуля силы Лоренца, которая его
вызывает, и, используя второй закон Ньютона, выведите формулу для расчёта
радиуса окружности, по которой будет двигаться частица.
Теперь не сложно узнать и период обращения частицы, т.к. , где r нами только что
найдено.
В.Сделайте
вывод: чем определяется период обращения частицы?(Предполагаемый ответ:
магнитной индукцией поля и удельным зарядом частицы, т.е. не зависит от
радиуса окружности, по которой частица движется.)
III.
Демонстрация наблюдения силы Лоренца с помощью
осциллографа и постоянного магнита.
IV.
Применение силы Лоренца.
Закрепление изученного
материала
№1.Определить,
используя рисунок направления В, FЛ, V; применяя правило левой руки.
№
2.Электрон под действием однородного магнитного поля обращается по окружности
радиуса R с периодом Т. Какими станут значения радиуса окружности и периода
обращения электрона при увеличении индукции магнитного поля в 2 раза?
http://home-task.com/plan-konspekt-uroka-po-fizike-tema-dejstvie-magnitnogo-polya-na-dvizhushhijsya-zaryad-sila-lorenca/
V.
Самостоятельная
работа.
(с
целью закрепления полученных знаний, в ходе которой они могут пользоваться
своими записями, текстом учебника, консультацией учителя.)
1.Проверка
основных формул (дописать пропущенные физические величины)
В=
F/I…; Fл= eB…sinα; A= …U; B= μ0μN…/ℓ;
T=2π…/υ; E=F/…; Fa=B……sinα; F=mац=m…/r.
2.Проверка
единиц измерения физических величин:
Тл=
Н/А*м; В= Дж/Кл; Гн= В*с/А; Н= кг* м/с2;
Кл=А*с; Дж=Н*м; Вб=Тл*м2
Εi
F I Ф
q L A B
3.
Проверка правила левой руки.
4.Самостоятельное
решение задач. Парная работа.
№ 1. Циклотрон
предназначен для ускорения протонов до энергии 5 МэВ. Определить наибольший
радиус орбиты, по которой движется протон, если индукция магнитного поля 1Тл.
№
2. В
направлении, перпендикулярном линиям магнитной индукции влетает электрон,
скорость которого 10 Мм/с. Электрон описал в магнитном поле окружность
радиусом 1 см. Чему равна индукция этого магнитного поля?
№
3.Электрон
движется в однородном магнитном поле с индукцией 4 мТл. Чему равен период
обращения электрона?
№
4.
Можно ли неизолированный провод намотав, на железный сердечник получить
самодельный электромагнит? ( Ответ: нет)
№
5.
Почему магнитное действие катушки, по которой идет ток, усиливается, если в
нее ввести железный сердечник?
№
6.
Почему корпус компаса делают из меди, алюминия, пластмассы и других
материалов, но никогда не делают его из железа?
№
7.
Если магнит дугообразный, то гвоздь одним концом притягивается к одному
полюсу, а другим – к другому. Почему?
http://home-task.com/reshenie-zadach-po-teme-sila-lorenca/
Сила лоренца. формула, определение
Пушка Гаусса
Математик Гаусс, когда познакомился с исследованиями Ампера, предложил создать оригинальную пушку (рис. 8), работающую на принципе действия магнитного поля на железный шарик – снаряд.
Рис. 8. Пушка Гаусса
Необходимо обратить внимание на то, в какую историческую эпоху были сделаны эти открытия. В первой половине XIX века Европа семимильными шагами шла по пути промышленной революции – это было благодатное время для научно-исследовательских открытий и быстрого внедрения их в практику
Ампер, несомненно, внес весомый вклад в этот процесс, дав цивилизации электромагниты, электродвигатели и телеграф, которые до сих пор находят широкое применение.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
FЛ=qvBsinα,
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям.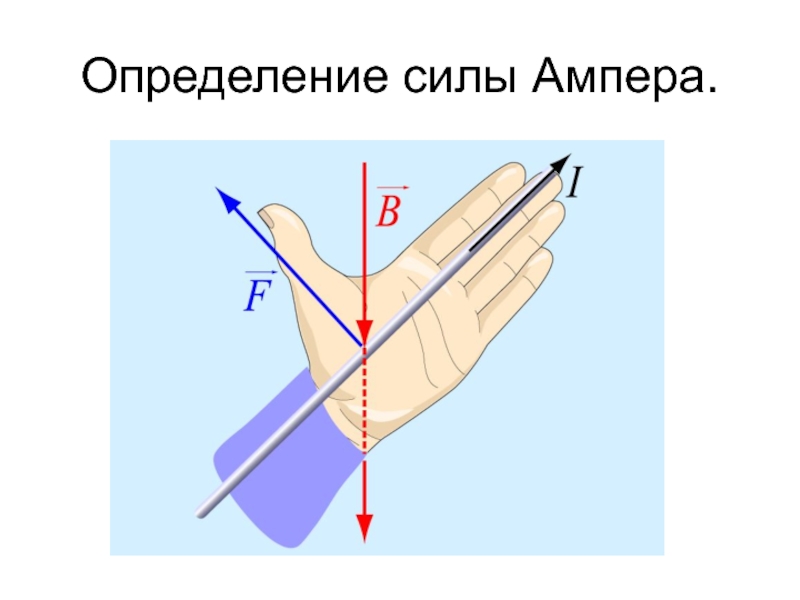 Чтобы найти радиус этой окружности, нужно знать массу частицы:
Чтобы найти радиус этой окружности, нужно знать массу частицы:
R=mvqB
Значение заряда не случайно взято как модуль
Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
R=mvsinαqB
h=2mvcosαqB
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы
Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля.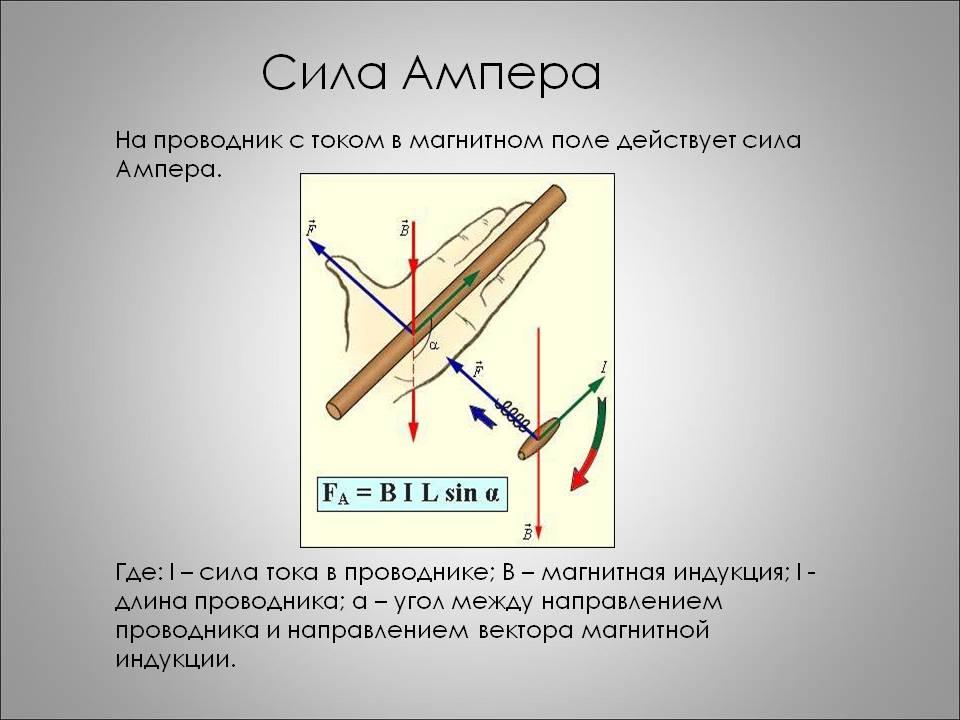 Свечение вызвано возбуждением атомов остаточного газа в баллоне
Свечение вызвано возбуждением атомов остаточного газа в баллоне
- Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД-генераторах.
- Сила Лоренца также используется в ускорителях заряженных частиц: она задаёт орбиту, по которой движутся эти частицы.
- Сила Лоренца используется в рельсотроне.
- Велосиметрия силой Лоренца заключается в бесконтактном измерении скорости движения проводящей жидкости.
Связь между силой Ампера и силой Лоренца
Действуя на проводник с током, магнитное поле воздействует на каждую заряженную частицу, создающую этот ток. А сила Ампера действует на весь проводник. Таким образом, сила Ампера равна сумме всех сил Лоренца, действующих на проводник с током.
FA= F·N
где F– сила Лоренца;
N— число частиц.
Отсюда F= FAN
I = nqvS
N = nSl
Подставив эти выражения в формулу, получим выражение для силы Лоренца в магнитном поле:
F = qvBˑsinα.
Это выражение позволяет вычислить силу Лоренца в магнитном поле. Но магнитное поле не существует отдельно. Изменяясь, вместе с электрическим полем они порождают друг друга, образуя электромагнитное поле. А оно в каждой точке своего пространства характеризуется напряжённостью электрического поля Еи индукцией магнитного поляВ. И если электрически заряженная частица движется в электромагнитном поле, то на неё одновременно действуют и электрическое, и магнитное поле. Значит, величина силы Лоренца, действующая со стороны электромагнитного поля на частицу с зарядом q, движущуюся со скоростью v, зависит от этих величин:
F = q(E + vxB).
F, E, vиB) – векторные величины.
vxB– векторное произведение скорости движения частицы и индукции магнитного поля.
Направление силы Лоренца, как и силы Ампера, определяют с помощью правила левой руки: «Если расположить ладонь левой руки таким образом, чтобы линии магнитного поля входили в неё перпендикулярно, а 4 пальца направить в сторону движения частицы с положительным зарядом, или против движения частицы с отрицательным зарядом, то отогнутый на 90 большой палец покажет направление силы Лоренца».
Если заряженная частица движется параллельно силовым линиям магнитного поля, то величина силы Лоренца равна нулю, так как в этом случае α = 0, следовательно, sinα = 0
F = qvBˑsinα= 0.
Если же направление движения частицы перпендикулярно силовым линиям, то частица будет двигаться по окружности радиусом r, а сила Лоренца направлена к её центру, то есть является центростремительной силой.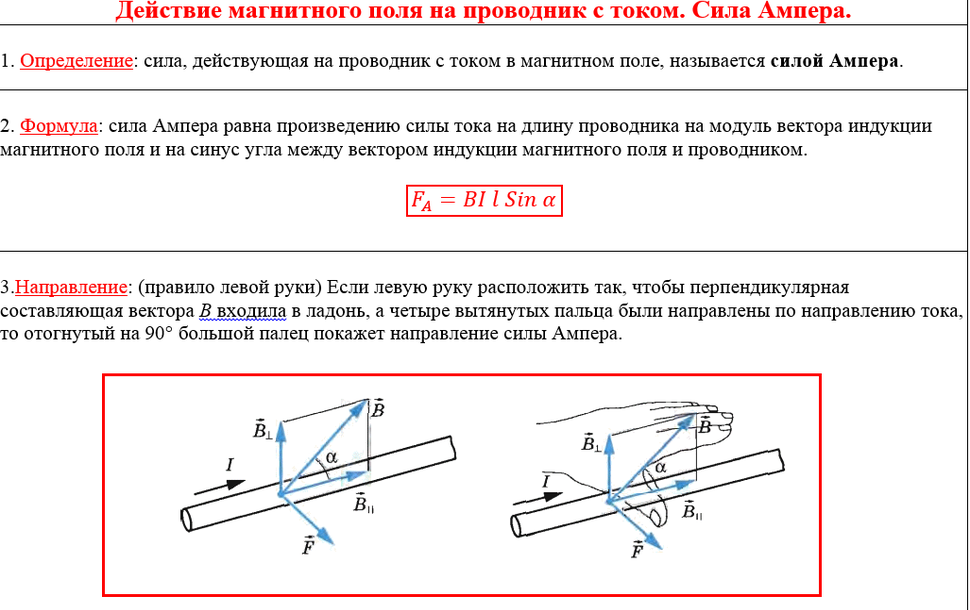
Согласно второму закону Ньютона сила Лоренца равна mv2r.
Отсюда
При движении частицы под углом к силовым линиям её траектория представляет собой винтовую (спиральную) линию, имеющую радиус r и шаг винта h.
Сила Лоренца не совершает работы, так как её направление всегда перпендикулярно направлению движения заряда.
Немного истории
Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.
В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.
И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».
Хендрик Лоренц.
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и электрическое), то сила, которая действует на нее, равна:
где – вектор напряженности электрического поля в точке, в которой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила , которая входит в формулу (4) так же называется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую и магнитную относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с такой же скоростью , как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Сила Ампера
Существование силы Ампера подтверждает простой опыт.
Если поместить между полюсами магнита проводник и пропустить по нему электрический ток, то можно увидеть, что проводник отклоняется от своего исходного положения. Это означает, что со стороны магнитного поля на него действует сила. Эта сила называется силой Ампера. Её величина определяется законом Ампера: «Со стороны магнитного поля на проводник с током действует сила, величина которой прямо пропорциональна силе тока, длине проводника в магнитном поле, модулю вектора магнитной индукции и синусу угла между вектором магнитной индукции и направление тока в проводнике». Математическое выражение этого закона выглядит так:
Это означает, что со стороны магнитного поля на него действует сила. Эта сила называется силой Ампера. Её величина определяется законом Ампера: «Со стороны магнитного поля на проводник с током действует сила, величина которой прямо пропорциональна силе тока, длине проводника в магнитном поле, модулю вектора магнитной индукции и синусу угла между вектором магнитной индукции и направление тока в проводнике». Математическое выражение этого закона выглядит так:
FA = I·l·В·sinα,
где I– величина тока в проводнике;
l– длина проводника с током в магнитном поле;
В – магнитная индукция;
α — угол между вектором магнитной индукции и направление тока в проводнике.
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
| Дано: q = 0,005 Кл B = 0,3 Тл v = 200 м/с α = 450 | Решение: В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле: FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н |
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
| Дано: q = 0,005 Кл B = 2 Тл FЛ = 32 Н α = 900 | Решение: Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца: FЛ=qvBsinαv=FЛqBsinα v=320,005×2×sin900=320,01×1=32000мс=32 км/с |
Задача 3
Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н.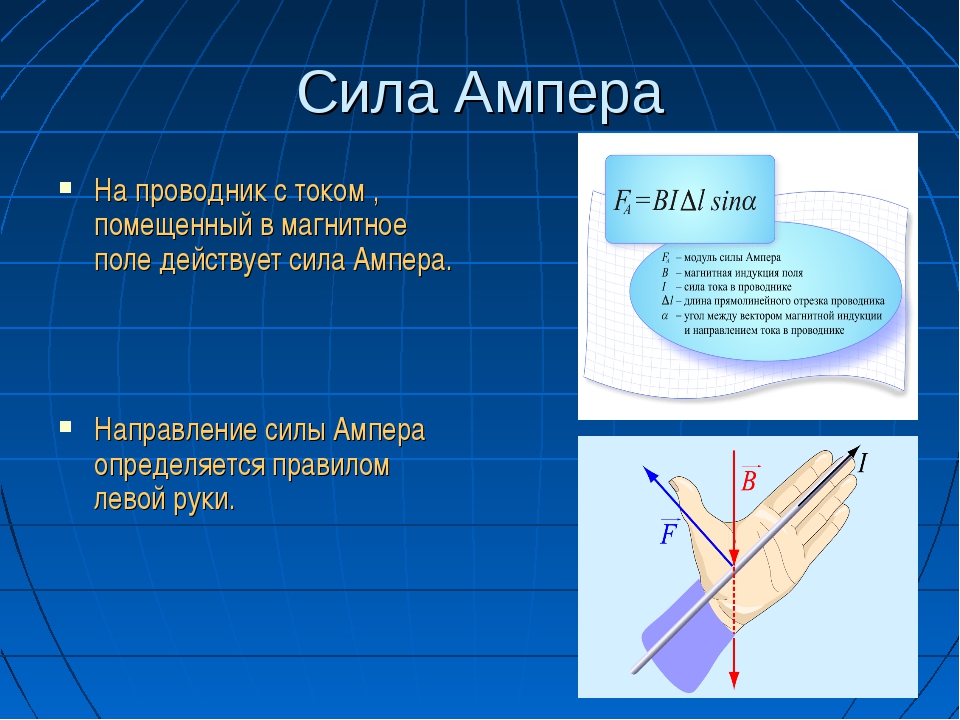 Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
| Дано: q = -1,6 × 10-19 Кл B = 0,05 Тл FЛ = 5 × 10-13 Н α = 900 | Решение: В этой задаче сила Лоренца ко всему прочему еще и заставляет двигаться электрон по окружности. Поэтому здесь под ускорением следует понимать центростремительное ускорение: aц=v2R На данный момент неизвестны ни скорость электрона, ни радиус окружности, по которой он движется. v=FЛqBsinα=5×10-13-1,6×10-19×0,05∙sin900=6×107мс R=mvqB=9×10-31×6×107-1,6×10-19×0,05=6,8×10-3мс |
aц=v2R=6×10726,8×10-3=5×1017мс2
Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.
Сила Лоренца. Движение заряженных частиц в магнитном поле» src=»https://www.youtube.com/embed/7IUpOAsKKvI?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Определение и формула
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Рис. 1. Выводы Лоренца
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º
Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.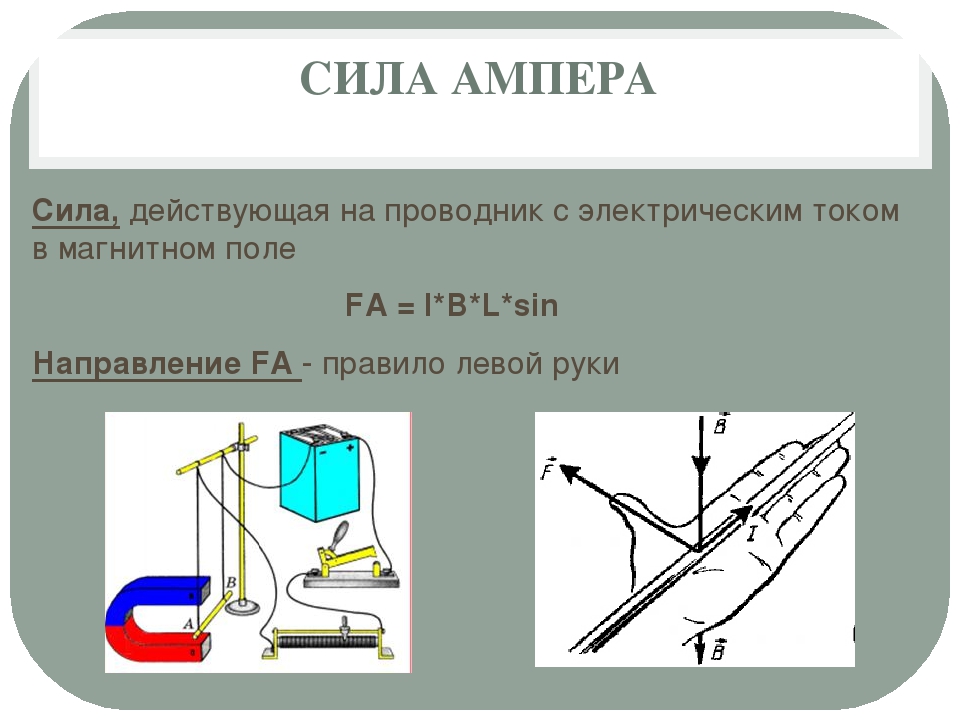
По закону Ампера:
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали.
 Направление вращения зависит от полярности заряда (рис. 3).
Направление вращения зависит от полярности заряда (рис. 3).
Рис. 2. Заряженная частица между полюсами магнитовРис. 3. Ориентация вектора в зависимости от полярности заряда
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Закон действия магнитного поля на проводник с током
Еще одно открытие Ампера – это закон действия магнитного поля на проводник с током. Он выражается прежде всего в действии магнитного поля на виток или рамку с током. Так, на виток с током в магнитном поле действует момент силы, которая стремится развернуть этот виток таким образом, чтобы его плоскость стала перпендикулярна линиям магнитного поля. Угол поворота витка прямо пропорционален величине тока в витке. Если внешнее магнитное поле в витке постоянно, то значение модуля магнитной индукции также величина постоянная. Площадь витка при не очень больших токах также можно считать постоянной, следовательно, справедливо то, что сила тока равна произведению момента сил, разворачивающих виток с током, на некоторую постоянную при неизменных условиях величину.
– сила тока,
– момент сил, разворачивающих виток с током.
Следовательно, появляется возможность измерять силу тока по величине угла поворота рамки, которая реализована в измерительном приборе – амперметре (рис. 2).
Рис. 2. Амперметр
22.2: Сила между двумя проводниками с током
Рассмотрим два бесконечных параллельных прямых провода, находящихся на расстоянии \(h\) друг от друга, по которым текут восходящие токи, \(I_{1}\) и \(I_{2}\), соответственно, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Два параллельных провода с током будут притягивать друг друга, если их токи имеют одинаковое направление.
Первый провод создаст магнитное поле \(\vec B_{1}\) в форме кругов, концентричных проводу.В месте расположения второго провода магнитное поле \(B_{1}\) находится внутри страницы и имеет величину:
\[\begin{align} B_{1}=\frac{\mu_{0}I_{1}}{2\pi h} \end{align}\]
Поскольку по второму проводу течет ток \(I_{2}\), направленный вверх, на него действует магнитная сила, \(\vec F_{2}\), со стороны магнитного поля, \(B_{1}\ ), то есть влево (как показано на рисунке \(\PageIndex{1}\) и определено по правилу правой руки). {◦}\).Мы ожидаем, согласно третьему закону Ньютона, что на первую проволоку должна действовать равная и противоположно направленная сила. Действительно, второй провод создаст магнитное поле \(\vec B_{2}\), которое находится за пределами страницы в месте расположения первого провода, с величиной:
{◦}\).Мы ожидаем, согласно третьему закону Ньютона, что на первую проволоку должна действовать равная и противоположно направленная сила. Действительно, второй провод создаст магнитное поле \(\vec B_{2}\), которое находится за пределами страницы в месте расположения первого провода, с величиной:
.
\[\begin{align} B_{2}=\frac{\mu_{0}I_{2}}{2\pi h} \end{align}\]
Это приводит к магнитной силе, \(\vec F_{1}\), действующей на первый провод, который указывает вправо (из правила правой руки). На участке длины \(l\) первого провода магнитная сила от магнитного поля \(\vec B_{2}\) имеет величину:
\[\begin{align} F_{1}=I_{1}||\vec l\times\vec B_{2}||=I_{1}lB_{2}\frac{\mu_{0}I_ {1}I_{2}}{2\pi h} \end{выровнено}\]
, которая действительно имеет ту же величину, что и сила, действующая на второй провод.Таким образом, когда по двум параллельным проводам течет ток в одном и том же направлении, они действуют друг на друга с равными и противоположными силами притяжения.
Упражнение \(\PageIndex{1}\)
Рисунок \(\PageIndex{2}\): два провода, по которым течет ток в противоположных направлениях.
По двум параллельным проводам течет ток в противоположных направлениях, как показано на рисунке \(\PageIndex{2}\). С какой силой они действуют друг на друга?
- Силы не будет, так как токи гаснут.
- Между проводами будет сила притяжения.
- Между проводами возникнет сила отталкивания.
- Ответить
Сила притяжения между двумя проводами раньше была основой для определения Ампера, базовой единицы измерения электрического тока в системе СИ. До 2019 года ампер определялся как «тот постоянный ток, который, если его поддерживать в двух прямолинейных параллельных проводниках бесконечной длины, незначительного круглого сечения и поместить в вакууме на расстоянии одного метра друг от друга, будет создавать между этими проводниками силу, равную \(2 × 10^{−17}\text{N}\) на метр длины». {−19}\text{C}\), а Ампер соответствует одному Кулону в секунду.
{−19}\text{C}\), а Ампер соответствует одному Кулону в секунду.
Сила между двумя проводами — это хорошая система для понимания того, как любая физическая величина не может зависеть от нашего выбора правой руки для определения перекрестных произведений. Как упоминалось в предыдущей главе, любая физическая величина, например направление силы, действующей на провод, всегда будет зависеть от двух последовательных движений правой рукой. В этой системе мы сначала использовали правило правой руки для осевых векторов, чтобы определить направление магнитного поля от одного из проводов.Затем мы использовали правило правой руки, чтобы определить направление векторного произведения, чтобы определить направление силы, действующей на другой провод. Вы можете убедиться, что получите тот же ответ, если вместо этого используете левую руку для определения направления магнитного поля (которое будет в противоположном направлении), а затем снова для перекрестного произведения. Это также подчеркивает, что магнитное поле (и электрическое поле) — всего лишь математический инструмент, который мы используем для описания движения зарядов или стрелки компаса.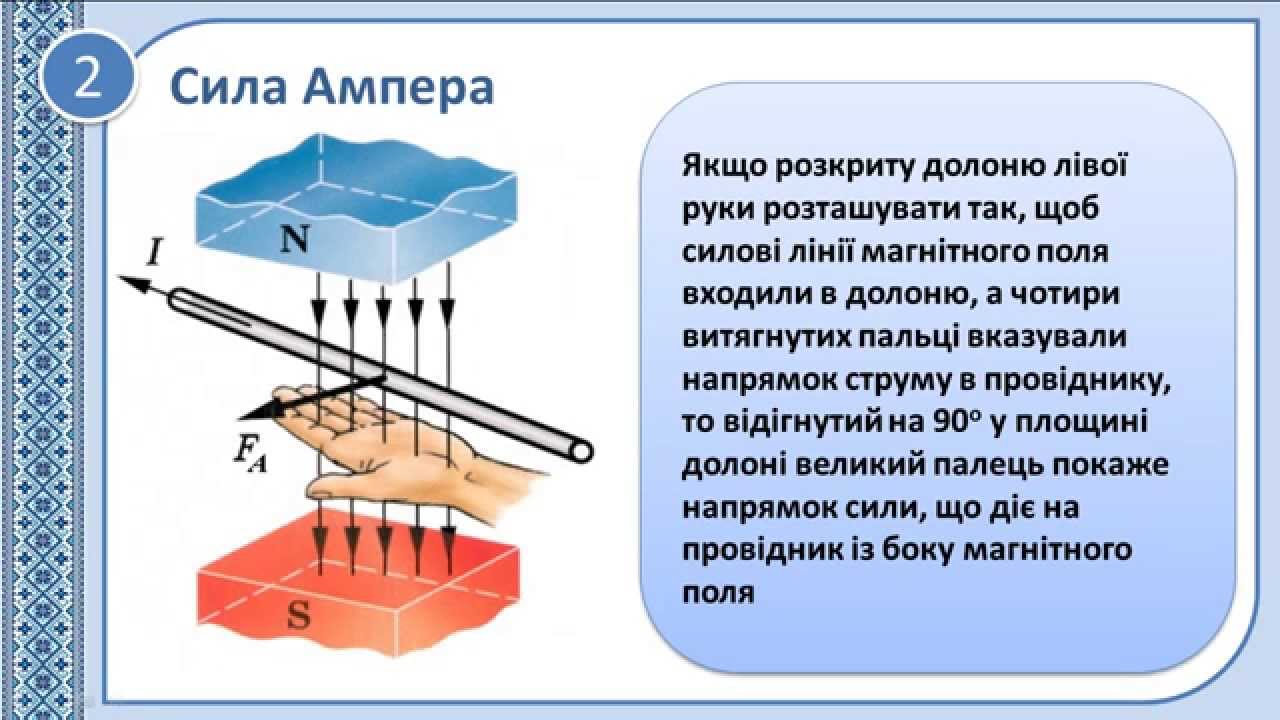
Упражнение \(\PageIndex{2}\)
Когда ток течет по прямому кабелю, как вы ожидаете, что заряды будут распределяться радиально по поперечному сечению кабеля?
- Равномерно по радиусу (плотность тока не зависит от \(r\)).
- На внешней стороне кабеля будет избыток положительных зарядов.
- На внешней стороне кабеля будет избыток отрицательных зарядов.
- Ответить
90 000 сил между параллельными проводниками — Узнайте — ScienceFlip
Силы между параллельными проводниками — узнайте
Когда по проводу протекает ток, вокруг провода возникает магнитное поле.Магнитное поле образует круговые петли вокруг провода, сила которых уменьшается по мере увеличения расстояния от провода. Направление магнитного поля определяется по правилу захвата правой рукой:
.
- обхватить пальцами токопроводящий проводник
- большой палец указывает направление течения тока
- пальцев указывают направление магнитного поля (часто описывается как по часовой стрелке или против часовой стрелки в зависимости от вида)
Два токонесущих проводника
Когда два провода, по которым течет ток, расположены параллельно друг другу, их магнитные поля будут взаимодействовать, в результате чего между проводами будет действовать сила.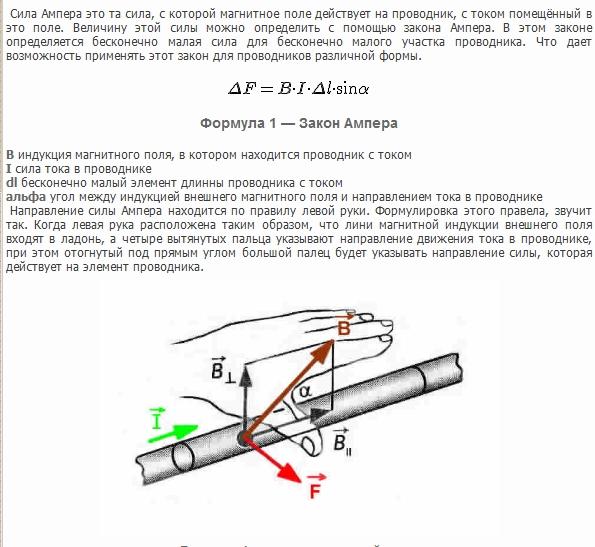 Величина силы, действующей на каждый провод, одинакова, но направления противоположны. Это справедливо даже в том случае, если по проводникам текут токи разной величины.
Величина силы, действующей на каждый провод, одинакова, но направления противоположны. Это справедливо даже в том случае, если по проводникам текут токи разной величины.
На приведенной ниже диаграмме показаны два примера, в которых направление магнитного поля вокруг каждого провода показано с помощью обозначения • ×. Диаграмма A показывает ток в проводах, идущих в одном направлении, а диаграмма B показывает ток, идущий в противоположных направлениях:
Определение направления силы
Направление силы определяется по направлению отдельных полей в области между проводниками:
- Диаграмма A: поля противоположны, что приводит к силе притяжения
- Диаграмма B: поля одинаковы, что приводит к силе отталкивания
Как правило; когда ток течет по проводникам в одном направлении, сила будет притягивающей, а когда токи противоположны по направлению, сила будет отталкивающей.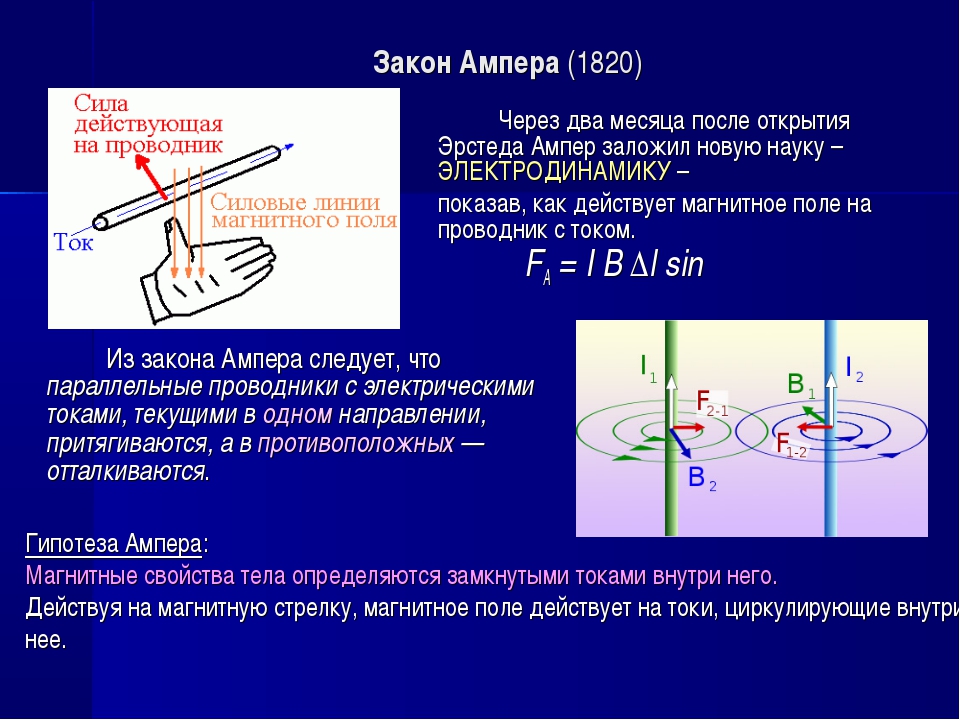
Определение величины силы между двумя параллельными проводниками
На величину силы, действующей между двумя параллельными проводниками с током, влияют несколько факторов:
- Ток в каждом проводнике
- Длина проводников
- Расстояние, разделяющее проводники
Величина силы, действующей между двумя параллельными проводниками с током, рассчитывается с использованием:
Где:
— сила на единицу длины между проводниками (в Нм −1 )
— магнитная проницаемость свободного пространства (4π × 10 −7 NA −2 )*
— ток в проводе 1 (в А)
ток в проводе 2 (в А)
— расстояние между проводниками (в м)
*примечание: и .
Уравнение можно записать:
где
Определение СИ для электрического тока; ампер и третий закон движения Ньютона
В Международной системе единиц (СИ) указано, что ампер является единицей измерения электрического тока. Формальное определение ампера таково: один ампер — это постоянный ток, который, если его поддерживать в двух прямолинейных параллельных проводниках бесконечной длины с ничтожно малым круглым поперечным сечением, расположенных на расстоянии одного метра друг от друга в вакууме, будет создавать между этими проводниками силу равно 2 × 10 −7 Н/м длины.
Формальное определение ампера таково: один ампер — это постоянный ток, который, если его поддерживать в двух прямолинейных параллельных проводниках бесконечной длины с ничтожно малым круглым поперечным сечением, расположенных на расстоянии одного метра друг от друга в вакууме, будет создавать между этими проводниками силу равно 2 × 10 −7 Н/м длины.
Это приложение третьего закона движения Ньютона, который гласит: в системе двух тел, если тело A действует на тело B, то тело B действует на тело A с силой, равной по величине, но противоположной по величине. направление.
Иногда утверждается третий закон движения Ньютона: на каждое действие есть равное и противоположное противодействие. Если один провод прикладывает силу ко второму проводу, второй провод приложит к первому проводу силу, равную по величине и противоположную по направлению.
Пример 1:
Два токопроводящих провода, А и В, по которым текут токи в разных направлениях и разделены расстоянием 4 см. Какова величина и направление силы на единицу длины, действующей между проводами, если в проводнике А протекает ток 2,5 А, а в проводнике В — 1,5 А?
Какова величина и направление силы на единицу длины, действующей между проводами, если в проводнике А протекает ток 2,5 А, а в проводнике В — 1,5 А?
Использование:
Где:
- I 1 = 2,5 А
- I 2 = 1.5 А
- г = 0,04 м
(сила отталкивания)
Магнитодвижущая сила – обзор
Приложение 4.B Связь вибраций асинхронного двигателя 2f, 4f, 6f и 8f с гармониками магнитного потока в воздушном зазоре
Плотность магнитного потока в воздушном зазоре двигателя получается путем произведения проницаемость магнитной цепи и магнитодвижущая сила (ммс), развиваемая токами в обмотках. Если не учитывать прорези на статоре и роторе, которые не влияют на магнитные силы 2f, 4f, 6f или 8f (f — частота питания), проводимость воздушного зазора можно считать постоянной, P 0 .
Первые несколько гармоник потока, обусловленные МДС обмотки статора, называемые пространственными гармониками или гармониками фазового пояса, составляют P0[F1−1cos(pθ−ω0t)+F5−1cos(5pθ+ω0t)+F7−1cos(7pθ−ω0t)+.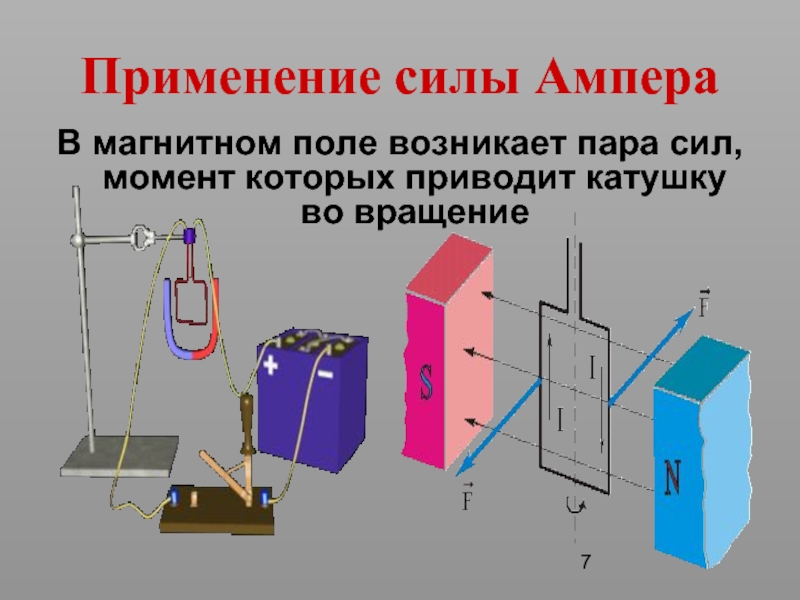 .
.
где
p = число пар полюсов двигателя
θ = смещение вдоль статора отверстие в радианах
Ω 0 = 2πF
F = Частота электропитания
9
F = Частота электропитания
T = Время в секундах
F AB = A- объемная гармоника обмотки статора m.м.ф. за счет b-й временной гармоники тока. (a=1 обозначает основную гармонику.)
В условиях насыщения к приведенному выше полю плотности потока должны быть добавлены следующие гармоники магнитного потока (Лившиц, 1942):
(4.B.3)B=B3cos(3pθ −3ω0t)+B5cos(5pθ−5ω0t)+B7cos(7pθ−7ω0t)+…
Эти гармоники насыщения проходят 3,5,7, … длины волны, когда основная гармоника проходит только одну длину волны. Гармоники насыщения движутся синхронно; они не меняют своего положения относительно основного или друг друга.
Суммарное магнитное поле в воздушном зазоре тогда: 7ω0t)+ B3cos(3pθ−3ω0t)+B5cos(5pθ−5ω0t)+B7cos(7pθ-7ω0t)+ члены более высокого порядка
Как показано в предыдущем разделе, распределение магнитной силы может быть аппроксимировано (2μ 0 ), где μ 0 — проницаемость пространства.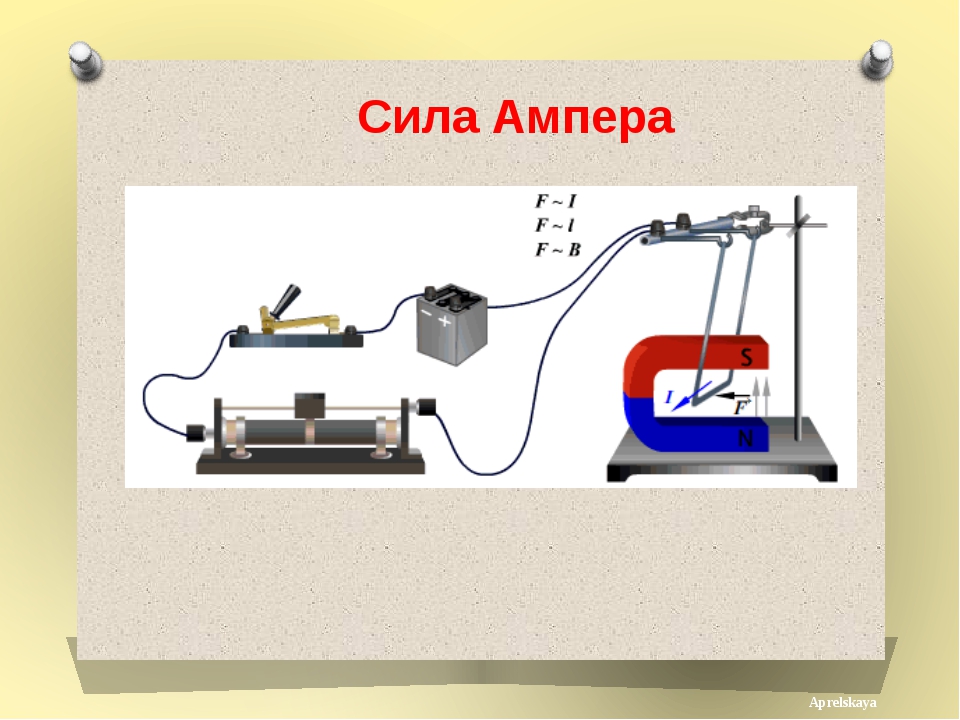
Процесс возведения в квадрат для получения силы дает квадрат каждого отдельного члена и перекрестное произведение каждой пары членов.Всего из уравнения (4.B.4) для B получается 42 члена, когда отношение
(4.B.5)cos(a)cos(b)=12[cos(a+b)+cos(ab )]
используется. Таблица 4.B.1 перечисляет каждую из результирующих 42 гармоник магнитной силы, их частоту (в кратных f, частоте сети) и их число силовых полюсов (в единицах p, число пар полюсов двигателя). В таблице также указано происхождение каждого из членов магнитной силы (т. Е. Комбинация членов потока создает каждый компонент силы).
Выделение наиболее важных составляющих сил:
(4.B.6)Force=+σ2fcos(2pθ+2ω0t)+σ4fcos(2pθ+4ω0t)+σ6fcos(2pθ+6ω0t)+σ8fcos(2pθ+8ω0t)+другие -terms
, где σ – амплитуда соответствующей составляющей магнитной силы.
Уравнение (4.B.6) показывает, что самые сильные частоты колебаний, включая гармоники насыщения, следующие: ;
4f (240 Гц.), с парами силовых полюсов 2p, 4p и 10p;
6f (360 Гц), с парами силовых полюсов 0, 6p и 12p;
8f (480 Гц), с парами силовых полюсов 2p, 8p и 14p;
для частоты питания 60 Гц.
В таблице 4.B.1 показано происхождение этих терминов, обозначенных звездочкой * . Таблица читается следующим образом: знак √ указывает на две составляющие плотности потока, которые в совокупности создают составляющую силы, описанную в двух левых столбцах.Две отметки √ в одном квадрате означают, что результирующая составляющая силы создается квадратом указанного члена плотности потока.
Если бы учитывались пазы ротора и статора, временные гармоники от источника питания, смещение ротора и ротора и/или влияние асимметрии статора, также появились бы дополнительные составляющие силы. Информация об анализе этих эффектов представлена в ссылках Alger (1954; 1970), Ellison and Yang (1971), Yang and Timar (1980) и Yang (1981; 1988).
Силовая волна 0-полюсной пары в точке 6f уникальна, поскольку она создается двумя волнами магнитного потока, распространяющимися в противоположных направлениях.В радиальном направлении эта силовая волна развивает «дышащий» или равномерный режим расширения/сжатия отклонения. Однако более важным следствием силовой волны с нулевым полюсом является производство крутильных колебаний из-за чередования полюсов противоположно бегущих волн от потоков насыщения и космических гармоник.
Однако более важным следствием силовой волны с нулевым полюсом является производство крутильных колебаний из-за чередования полюсов противоположно бегущих волн от потоков насыщения и космических гармоник.
Ampere Playground Основные моменты: Парки Нью-Йорка
Эта игровая площадка посвящена памяти Андре Ампера (1775-1836), выдающегося французского физика и математика, которого считают отцом электромагнитной теории.Ампер-авеню, расположенная недалеко от Радио-драйв и Ом-авеню в Бронксе, также названа в честь Андре Ампера. Улицы получили электрические названия после того, как Исаак Леопольд Райс, президент компании Electric Storage Battery Company, пожертвовал городу землю возле проспекта Ампер.
Родившийся в Лионе, Франция, 20 января 1775 года, Андре Ампер не получил формального образования. Вместо этого он учился у своего отца и запоминал отрывки из энциклопедии. К 13 годам Ампер представил в Лионскую академию статью о построении линии, равной заданной длине дуги вдоль окружности. Однако из-за своего изолированного образования Ампер не был осведомлен о текущих достижениях в математике, и его статьи были сочтены недостойными публикации.
Однако из-за своего изолированного образования Ампер не был осведомлен о текущих достижениях в математике, и его статьи были сочтены недостойными публикации.
Ампер понял, что если он собирается продолжать какую-либо серьезную работу, ему придется сначала изучить исчисление, а затем относительно новый раздел математики. Ампер начал свое первое серьезное изучение исчисления после прочтения « Macanique Analytique » Жозефа Луи Легранжа (1788). Однако исследования Ампера были остановлены после того, как его отец был убит во время Французской революции в 1792 году, и он не продолжал их до тех пор, пока не женился в 1799 году.
Заняв должность профессора математики и химии в Bourg Ecole Centrale , Ампер опубликовал работу о вероятности The Mathematical Theory of Games в 1803 году. в 1809 году, где он оставался до 1828 года. В Ecole Ампер сотрудничал с математиком Огюстеном Луи Коши в математической области анализа и механики, раздела физики. Он разработал систему классификации дифференциальных уравнений в частных производных, сложный тип математических уравнений, основанный на исчислении, и это достижение стало главным фактором победы Ампера над Коши на выборах в Национальный институт наук в 1814 году. Ампер был назначен на эту должность. на кафедру в Universite de France в 1826 году и сохранял эту должность до своей смерти.
Он разработал систему классификации дифференциальных уравнений в частных производных, сложный тип математических уравнений, основанный на исчислении, и это достижение стало главным фактором победы Ампера над Коши на выборах в Национальный институт наук в 1814 году. Ампер был назначен на эту должность. на кафедру в Universite de France в 1826 году и сохранял эту должность до своей смерти.
В дополнение к своей работе в области математики Ампер внес важный вклад в химию и физику.В 1811 году Ампер постулировал, что неизвестная кислота, обнаруженная двумя годами ранее, на самом деле была новым элементом, подобным водороду, который он назвал фтором. Ампер, однако, наиболее известен своей работой над комбинированной теорией электричества и магнетизма, основанной на более ранних экспериментах датского физика Ганса Христиана Орстеда, который обнаружил, что игла, помещенная в магнитное поле, подчиняется ранее установленным законам для электрической силы.
Через невероятный трехмесячный срок после публикации работы Орстеда Ампер опубликовал свою собственную теорию сил и симметрий, участвующих в электромагнетизме. В своих мемуарах 1926 года по математической теории электродинамических явлений Ампер представил математический вывод комбинированной электромагнитной силы. В документе было представлено то, что позже стало известно как закон Ампера, описывающий магнитное поле, создаваемое проводником, по которому течет ток. Амперу также приписывают изобретение соленоида, туго намотанного цилиндра из проволоки с особыми электромагнитными свойствами. Кроме того, Ампер еще больше объединил свою теорию комбинированной электромагнитной силы, открыв, что два провода, по которым течет ток в противоположных направлениях, отталкиваются, а те, по которым течет ток в том же направлении, притягиваются, подобно противоположным полюсам магнитов.В честь его работы единица электрического тока, равная одному кулону заряда в секунду, была названа Ампер в честь Андре Ампера.
В своих мемуарах 1926 года по математической теории электродинамических явлений Ампер представил математический вывод комбинированной электромагнитной силы. В документе было представлено то, что позже стало известно как закон Ампера, описывающий магнитное поле, создаваемое проводником, по которому течет ток. Амперу также приписывают изобретение соленоида, туго намотанного цилиндра из проволоки с особыми электромагнитными свойствами. Кроме того, Ампер еще больше объединил свою теорию комбинированной электромагнитной силы, открыв, что два провода, по которым течет ток в противоположных направлениях, отталкиваются, а те, по которым течет ток в том же направлении, притягиваются, подобно противоположным полюсам магнитов.В честь его работы единица электрического тока, равная одному кулону заряда в секунду, была названа Ампер в честь Андре Ампера.
Город приобрел это имущество 22 октября 1927 года по приговору суда, а 5 июня 1958 года на этом месте была открыта детская площадка. Название парка, первоначально П.С. Игровая площадка 64 была изменена в честь Ампера в 1985 году. В парке есть комфортная станция, скамейки, игровые столы, игровое оборудование и душевая лейка. Детская площадка была реконструирована в 2003 году с новым покрытием и игровым оборудованием.Парки поддерживают детскую площадку при значительной помощи местного сообщества, которое собирается на ежегодные дни волонтеров, организуемые Советом сообщества Квинса 9.
Название парка, первоначально П.С. Игровая площадка 64 была изменена в честь Ампера в 1985 году. В парке есть комфортная станция, скамейки, игровые столы, игровое оборудование и душевая лейка. Детская площадка была реконструирована в 2003 году с новым покрытием и игровым оборудованием.Парки поддерживают детскую площадку при значительной помощи местного сообщества, которое собирается на ежегодные дни волонтеров, организуемые Советом сообщества Квинса 9.
Ампер
Первоначальный килограмм заменен — новая международная система единиц (СИ) вступила в силу
21 мая 2019 г. — В дополнение к другим научным единицам килограмм теперь также определяется естественной константой. Это стало возможным благодаря монокристаллам, выращенным из высокообогащенного …
Могут ли магнитные поля мегатесла быть реализованы на Земле?
6 октября 2020 г. — Исследователи обнаружили новый механизм под названием «имплозия микротрубки», демонстрирующий генерацию магнитных полей порядка мегатесла, которые на три порядка выше, чем . ..
..
Зажги мой огонь: как каждый раз запускать устройства Fusion
10 октября 2019 г. — Исследователи создали основу для запуска и повышения температуры термоядерной плазмы до температуры, соперничающей с солнечной в сотни градусов…
Ускорение развития термоядерной энергетики для создания неограниченной энергии на Земле
19 марта 2019 г. — В новой статье подробно рассматриваются проблемы и компромиссы при разработке компактной термоядерной установки с высокотемпературной сверхпроводимостью …
Электромобили улучшают климат в 95% стран мира
23 марта 2020 г. — Согласно новому исследованию, опасения, что электромобили могут фактически увеличить выбросы углерода, необоснованны почти во всех частях мира…
Техника ударного анализа атомных колебаний в кристалле
14 июля 2020 г. — Колебания атомов в кристалле полупроводникового арсенида галлия (GaAs) импульсно сдвигаются на более высокую частоту с помощью оптически возбуждаемого электрического тока.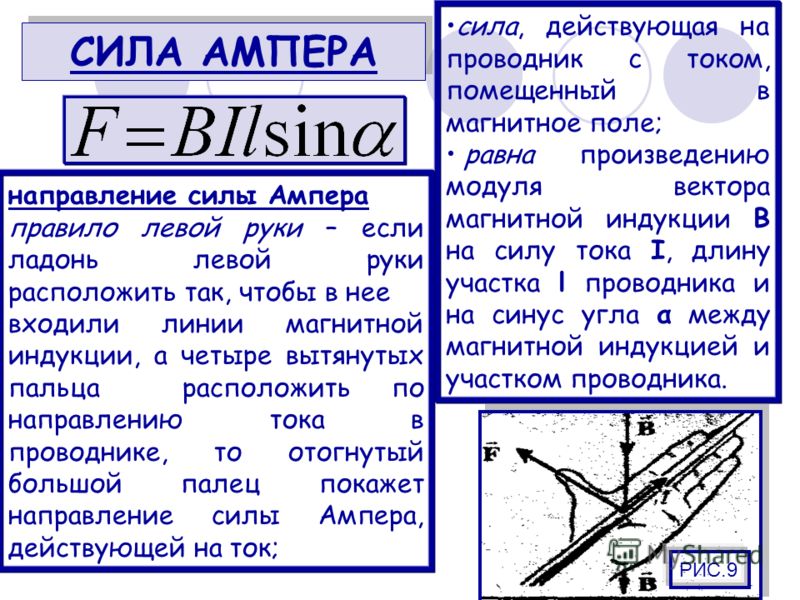 Связанное с этим изменение пространственного…
Связанное с этим изменение пространственного…
Движущиеся доменные стенки вызывают потери в гибридных системах сверхпроводник/ферромагнетик
6 января 2020 г. — Физики показали, что движение доменных стенок можно обнаружить, отслеживая напряжение, генерируемое в сверхпроводящих устройствах.Это открытие может облегчить магнитную память беговой дорожки …
Универсальный метод измерения мощности света
20 декабря 2019 г. — В постоянном поиске лучших способов измерения всевозможных вещей исследователи опубликовали подробное исследование, предлагающее «элегантное» улучшенное определение стандартной единицы света …
Зарядовая модель для расчета фотовозбужденных состояний одномерных изоляторов Мотта
Ян.17 февраля 2020 г. — Исследователи разработали зарядовую модель для описания фотовозбужденных состояний одномерных изоляторов Мотта. Им также удалось построить функцию Ванье многих тел как локализованную…
Исследование обнаружило неожиданное взаимодействие электронов в графене с «магическим углом»
18 марта 2021 г. — Новое исследование описывает метод, который ослабляет силу отталкивания между электронами в графеновых сверхпроводниках с «магическим углом», предоставляя физикам новые захватывающие подробности об этом…
— Новое исследование описывает метод, который ослабляет силу отталкивания между электронами в графеновых сверхпроводниках с «магическим углом», предоставляя физикам новые захватывающие подробности об этом…
Уравнения Максвелла: Закон Ампера
Четвертое уравнение Максвелла
На этой странице мы объясним значение последнего уравнения Максвелла,
Закон Ампера , который выражается уравнением [1]:
| [Уравнение 1] |
|---|
Ампер был ученым, экспериментировавшим с силами на проводах, по которым шел электрический ток.
Он проводил эти эксперименты еще в 1820-х годах, примерно в то же время, когда
Фардей работал над законом Фарадея.Ампер и Фардей не знали, что работу там объединит сам Максвелл,
примерно через 4 десятилетия.
Силы на проводах мне не особо интересны, так как никогда не
возможность использовать очень сложные уравнения в ходе моей работы
(который включает в себя докторскую степень, несколько работ в национальной лаборатории, а также
занятость в обороне
и отрасли бытовой электроники).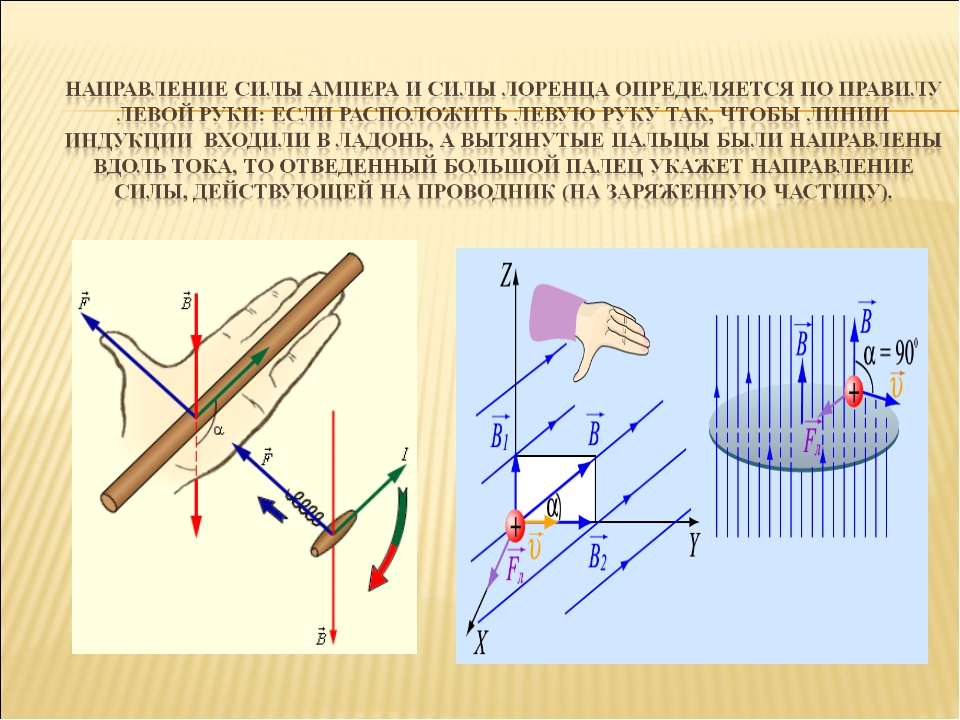 Итак, я начну с
Итак, я начну с
представляет закон Ампера, который связывает электрический ток, протекающий
и магнитное поле, огибающее его:
| [Уравнение 2] |
|---|
Уравнение [2] можно объяснить: предположим, у вас есть проводник (провод), несущий
тока, I .Затем этот ток создает
Магнитное поле
который окружает провод.
Левая часть уравнения [2] означает: если взять любое воображаемое
дорожка, опоясывающая провод,
и вы суммируете магнитное поле в каждой точке на этом пути, тогда оно
будет численно равно количеству тока, который окружает
этот путь (именно поэтому мы пишем
для окруженного или замкнутого тока).
Давайте сделаем пример для удовольствия. Предположим, у нас есть длинный провод, по которому
постоянный электрический ток, I [Ампер].Какое магнитное поле вокруг
провода, на любом расстоянии r [метров] от провода?
Посмотрим на схему на рисунке 1. Имеем длинный провод, по которому течет ток
Имеем длинный провод, по которому течет ток
I Ампер. Мы хотим знать, что представляет собой магнитное поле на расстоянии.
р из проволоки. Итак, мы рисуем воображаемый путь вокруг провода, т.е.
пунктирная синяя линия справа на рисунке 1:
Рис. 1. Расчет магнитного поля, обусловленного током, по закону Ампера.
Закон Ампера [уравнение 2] гласит, что если мы сложим (интегрируем) магнитное
Поле вдоль этой синей дорожки, то численно это должно быть равно
вложенный ток I .
Теперь в силу симметрии магнитное поле будет однородным (не меняющимся) при
расстояние r от провода. Длина пути синего пути
на рисунке 1 равна длине окружности радиусом r :
.
Если мы суммируем постоянное значение магнитного поля (назовем его
H ), то левая часть уравнения [2] становится простой:
| [Уравнение 3] |
|---|
Таким образом, мы выяснили, какова величина поля H . А так как r было произвольным, мы знаем, что такое H-поле везде.
А так как r было произвольным, мы знаем, что такое H-поле везде.
Уравнение [3] утверждает, что магнитное поле уменьшается по величине при движении
дальше от провода (из-за члена 1/r).
Итак, мы использовали закон Ампера (уравнение [2]), чтобы найти величину
Магнитное поле вокруг провода. Однако поле H является
Векторное поле,
что означает, что в каждом месте есть как величина, так и направление.
Направление H-поля везде касательно к воображаемым петлям,
как показано на рисунке 2.Правило правой руки определяет направление магнитного поля:
Рисунок 2. Величина и направление магнитного поля вокруг провода.
Манипуляции с математикой для закона Ампера
Мы собираемся проделать с теоремой Стокса тот же трюк, что и
при взгляде на
Закон Фарадея.
Мы можем переписать закон Ампера в уравнении [2]:
| [Уравнение 4] |
|---|
Для равенства правой части в уравнении [4] мы использовали теорему Стокса
преобразовать линейный интеграл вокруг замкнутого контура в
завиток
того же поля через поверхность, ограниченную петлей ( S ).
Мы также можем переписать общий ток () как
поверхностный интеграл
Плотность тока ( Дж ):
| [Уравнение 5] |
|---|
Итак, теперь у нас есть исходный закон Ампера (уравнение [2]), переписанный в терминах
поверхностные интегралы (уравнения [4] и [5]). Следовательно, мы можем заменить их
вместе и получим новую форму для закона Ампера:
| [Уравнение 6] |
|---|
Теперь у нас есть новая форма закона Ампера: ротор магнитного поля равен
к
Плотность электрического тока.Если вы проницательный ученик, вы можете заметить, что уравнение [6] не является
окончательная форма, которая записана в уравнении [1]. Существует проблема
с уравнением [6], но только в 1860-х годах Джеймс Клерк Максвелл
разобрался в проблеме и объединил электромагнетизм с уравнениями Максвелла.
Плотность тока смещения
Закон Ампера был записан в виде уравнения [6] вплоть до Максвелла. Итак, начнем
Итак, начнем
посмотри что с ним не так. Во-первых, я должен выбросить еще один
векторная идентичность —
расхождение
завиток
любого векторного поля всегда равно нулю:
| [Уравнение 7] |
|---|
Итак, давайте возьмем расхождение закона Ампера, записанное в уравнении [6]:
| [Уравнение 8] |
|---|
Итак, уравнение [8] следует из уравнений [6] и [7].Но это говорит, что
дивергенция плотности тока Дж всегда равна нулю. Это правда?
Если дивергенция J всегда равна нулю, это означает, что электрическая
ток, протекающий в любую область, всегда равен электрическому току, протекающему
вне региона (без расхождений). Это кажется несколько разумным, так как электрические
ток в цепях течет по петле. Но давайте посмотрим, что произойдет, если мы
поставить конденсатор в цепь:
Рис. 3. Напряжение, подаваемое на конденсатор.
3. Напряжение, подаваемое на конденсатор.
Из теории электрических цепей мы знаем, что если напряжение непостоянно
(например, любая периодическая волна, такая как напряжение 60 Гц, которое выходит из вашего
розетки), то через конденсатор будет протекать ток. То есть у нас есть
I не равно нулю на рисунке 3.
Однако конденсатор в основном представляет собой две параллельные проводящие пластины, разделенные
воздуха. Следовательно, нет проводящего пути для прохождения тока.
Это означает, что через воздух конденсатора не может протекать электрический ток.Это проблема, если мы подумаем об уравнении [8]. Чтобы показать это более четко,
возьмем объем, проходящий через конденсатор, и посмотрим,
дивергенция J равна нулю:
Рисунок 4. Дивергенция J не равна нулю.
На рисунке 4 мы нарисовали воображаемый объем красным цветом и хотим проверить
если дивергенция плотности тока равна нулю. Том, который мы выбрали,
Том, который мы выбрали,
имеет один конец (помеченный стороной 1), где ток входит в объем через черный провод.Другой конец нашего тома (помеченный стороной 2) разделяет конденсатор пополам.
Мы знаем, что в петле течет ток. Таким образом, ток поступает через сторону 1.
нашего красного тома. Однако на стороне 2 нет электрического тока.
В воздушной среде конденсатора ток не течет. Это означает, что текущий
входит в объем, но ничего не выходит из него — так что расходимость J равна
не ноль. Мы только что нарушили наше уравнение [8],
что означает, что теория не верна.Таково было положение вещей, пока
пришел наш друг Максвелл.
Максвелл знал, что электрическое поле (и
Плотность электрического потока ( D )
меняется внутри конденсатора. И он знал, что переменное во времени магнитное поле
породило соленоидальное электрическое поле (т.е. это закон Фардея —
завиток E равен производной по времени от B ). Итак, почему не то
изменяющееся во времени поле D привело бы к соленоидальному полю H
(я.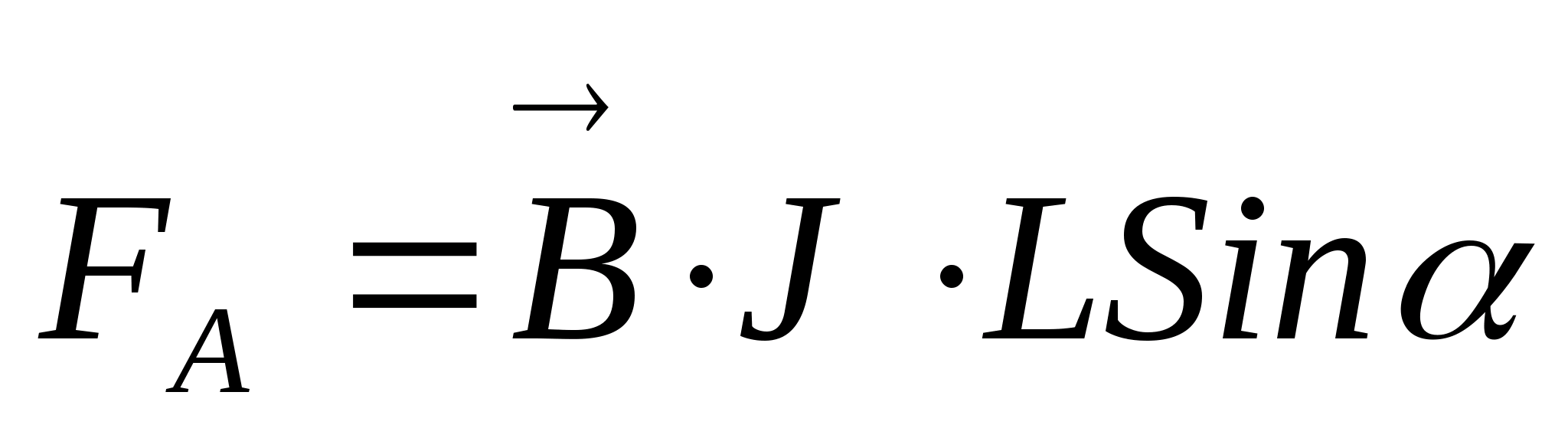 е. дает завиток H ).
е. дает завиток H ).
Вселенная любит симметрию, так почему бы не ввести этот термин? И так
Максвелл так и сделал, и он назвал этот термин плотностью тока смещения :
| [Уравнение 9] |
|---|
Этот термин «исправил бы» проблему со схемой, которую мы имеем на рис. 4, и сделал бы
Закон Фардея и закон Ампера более симметричны. Это был великий вклад Максвелла.
И вы можете подумать, что это слабый вклад.Но существование этого термина
объединили уравнения и привели к пониманию распространения электромагнитных
волны и доказательство того, что все волны распространяются с одинаковой скоростью (скоростью света)!
И именно это объединение уравнений, представленных Максвеллом, привело к
коллективный набор, известный как уравнения Максвелла. Итак, если мы добавим
тока смещения к закону Ампера, как написано в уравнении [6], тогда мы
иметь окончательную форму закона Ампера:
| [Уравнение 10] |
|---|
Так появился закон Ампера!
Интерпретация закона Ампера
Так что же означает уравнение [10]? Последствия этого закона следующие:
Закон Ампера с участием Максвелла заложил основу для
Электромагнетизм, как мы его понимаем. И поэтому мы знаем, что
И поэтому мы знаем, что
изменяющееся во времени D порождает поле H , но из поля Фардея
Закон мы знаем, что изменяющееся поле H порождает поле E …
и так далее и тому подобное и электромагнитные волны распространяются — и это круто.
Уравнения Максвелла
Эта страница о законе Ампера для цепей или о чем-то еще защищена авторским правом, в частности
как это относится к уравнениям Максвелла. Авторское право www.maxwells-equations.com,
2012.
Перевести единицы: килоампер-виток [кАт] в ампер [А] • Конвертер магнитодвижущей силы • Магнитостатика, магнетизм и электромагнетизм • Компактный калькулятор • Онлайн-конвертеры единиц измерения Конвертер измеренийПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь угловПреобразователь экономичности топлива, расхода топлива и экономии топливаКонвертер чиселКонвертер единиц информации и хранения данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиУгловая скорость и вращение Преобразователь частотыПреобразователь ускоренияПреобразователь углового ускоренияПреобразователь плотностиПреобразователь удельного объемаПреобразователь момента инерцииПреобразователь момента силыПреобразователь момента импульсаИмпульсПреобразователь крутящего моментаУдельная энергия, тепло Конвертер удельной энергии, теплоты сгорания (на единицу объема)Конвертер температурного интервала Конвертер коэффициента теплового расширения Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияКонвертер теплопроводностиКонвертер удельной теплоемкостиПлотность тепла, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаМасса Конвертер потока Конвертер молярной концентрацииКонвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер проницаемости, проницаемости, паропроницаемостиКонвертер коэффициента пропускания паров влагиКонвертер уровня звукаПреобразователь чувствительности микрофона Конвертер разрешения изображенияКонвертер частоты и длины волныОпт Конвертер оптической силы (диоптрий) в фокусное расстояниеКонвертер оптической силы (диоптрий) в увеличение (X)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаПреобразователь поверхностной плотности токаКонвертер напряженности электрического поляКонвертер электрического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивления ПреобразовательПреобразователь электропроводностиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь мощности американского проводаПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразование магнитодвижущей силыПреобразователь напряженности магнитного поляПреобразователь магнитного потокаПреобразователь плотности магнитного потокаПреобразователь мощности поглощенной дозы ионизирующего излученияПреобразователь мощности дозы ионизирующего излученияРадиоактивность.
 Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксов Конвертер передачи данных Конвертер типографских и цифровых изображений Конвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица характеризующая способность электрических токов создавать магнитный поток вокруг проводников с током.Он присутствует в ситуациях, когда электрический ток проходит через катушку для создания магнитодвижущей силы.
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксов Конвертер передачи данных Конвертер типографских и цифровых изображений Конвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица характеризующая способность электрических токов создавать магнитный поток вокруг проводников с током.Он присутствует в ситуациях, когда электрический ток проходит через катушку для создания магнитодвижущей силы.
Измеряется как количество электрического тока, протекающего через катушку катушки индуктивности или электромагнита, и пропорционально общему количеству витков, через которые проходит ток. Его также иногда называют магнитной разностью потенциалов.
Никелированные неодимовые магниты от жесткого диска
Многие считают его эквивалентом электродвижущей силы в электрических цепях.В системе СИ магнитодвижущая сила измеряется в амперах (А). Часто измеряется в ампер-витках (Ат). Альтернативной единицей измерения магнитодвижущей силы в СГС является гилберт (G).
Альтернативной единицей измерения магнитодвижущей силы в СГС является гилберт (G).
Постоянные магниты
Существует лишь несколько встречающихся в природе материалов, обладающих магнитными свойствами сами по себе, без применения к ним электричества для превращения их в электромагниты. Один из них — магнит. На самом деле он сделан из магнетита, но не каждый кусок магнетита является магнитом, потому что не весь магнетит является магнитным.Чтобы стать магнетитом, магнетит должен быть сначала намагничен. Мы не знаем наверняка, что намагничивает магнит в природе, но некоторые считают, что он намагничен молнией, потому что магнит находится ближе к поверхности Земли, а магнетит можно найти глубже. В наши дни постоянные магниты, которые мы используем, чаще всего изготавливаются из сплавов. Самые сильные магниты сделаны из редкоземельных металлов, таких как неодим (Nd 2 Fe 14 B).
Электромагниты
Электромагниты в шаговом двигателе
Для создания магнитного поля нам нужен провод, по которому течет электрический ток. Провода, которые не свернуты в катушки, обычно генерируют слабые магнитные поля, но если мы введем катушки, мы сможем усилить магнитное поле и увеличить магнитодвижущую силу. Как мы уже обсуждали, магнитодвижущая сила увеличивается с увеличением числа витков, поэтому чем больше витков — тем сильнее магнитное поле. Мы называем эти типы магнитов электромагнитами .
Провода, которые не свернуты в катушки, обычно генерируют слабые магнитные поля, но если мы введем катушки, мы сможем усилить магнитное поле и увеличить магнитодвижущую силу. Как мы уже обсуждали, магнитодвижущая сила увеличивается с увеличением числа витков, поэтому чем больше витков — тем сильнее магнитное поле. Мы называем эти типы магнитов электромагнитами .
Использование электромагнитов вместо постоянных магнитов имеет большое практическое преимущество, поскольку мы можем включать и выключать эти магниты по желанию.Это очень полезно, потому что дает нам контроль над тем, как и когда использовать магнит. Например, если мы используем очень мощный электромагнит для подъема и перемещения старых автомобилей на свалке, мы можем легко активировать магнит, когда поднимаем и перемещаем автомобиль, но затем отключаем его, когда хотим освободить автомобиль.
Эксперимент с двумя простыми электромагнитами, сделанными из двух гвоздей и отрезков проволоки длиной 25 и 90 см каждый. Один и тот же ток силой 1 А протекает через каждый из электромагнитов с 20 и 90 витками провода.Магнитодвижущая сила первого магнита составляет 25 витков × 1 А = 25 Ат (ампер-витков), а магнитодвижущая сила второго электромагнита составляет 90 Ат. Мы видим, что первый электромагнит может удерживать только одну гайку, а второй — 6 гаек. На правом рисунке показана визуализация магнитного поля этого электромагнита с использованием железных опилок
Один и тот же ток силой 1 А протекает через каждый из электромагнитов с 20 и 90 витками провода.Магнитодвижущая сила первого магнита составляет 25 витков × 1 А = 25 Ат (ампер-витков), а магнитодвижущая сила второго электромагнита составляет 90 Ат. Мы видим, что первый электромагнит может удерживать только одну гайку, а второй — 6 гаек. На правом рисунке показана визуализация магнитного поля этого электромагнита с использованием железных опилок
Примеры магнетизма и использования магнитодвижущей силы
Магнетизм широко используется в нашей повседневной жизни, и было бы невозможно иметь большинство наших современных удобств без Это.Рассмотрим несколько примеров его использования.
В навигации
Одно из первых применений магнитов было для навигации. У нас нет точной информации о том, когда был создан первый компас, но мы знаем, что естественный постоянный магнит, магнит, использовался для навигации еще в 12 веке, хотя многие историки считают, что он использовался намного раньше.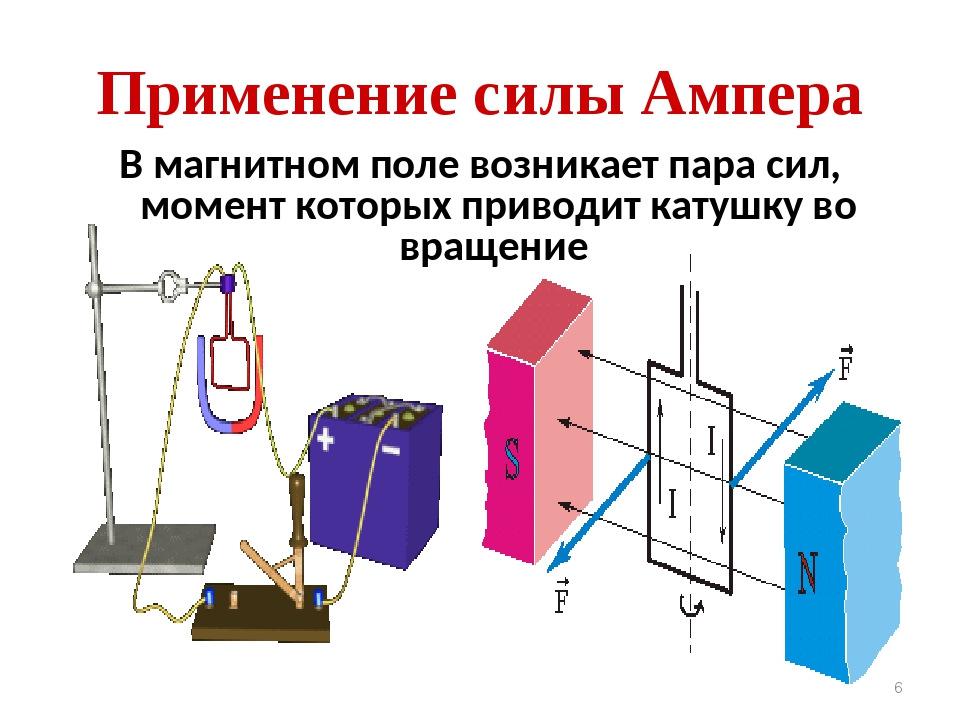 . Первоначально магнит подвешивали таким образом, чтобы он мог вращаться, но позже его стали использовать для намагничивания железной иглы.
. Первоначально магнит подвешивали таким образом, чтобы он мог вращаться, но позже его стали использовать для намагничивания железной иглы.
Магнитный компас (вверху справа) и гирокомпас (внизу слева) в кабине небольшого самолета Cessna
Конструкция компаса претерпела множество изменений, пока не стала компасом, который мы знаем сегодня. Одно из улучшений заключалось в том, чтобы стабилизировать стрелку в динамической среде движущегося корабля и предотвратить ее ненужное вращение, вызванное рысканием, качением и качке корабля. Это одна из причин, по которой жидкость иногда используется в компасе. В противном случае используется специальное крепление, известное как карданное крепление.Это позволяет внутренней части с самим компасом оставаться относительно стабильной, в то время как внешняя «оболочка» вращается вместе с окружающей средой. Обычная конструкция карданного подвеса имеет три шарнирных карданных шарнира, два внешних из которых вращаются, а внутренний кардан остается устойчивым относительно горизонта. Еще одно необходимое усовершенствование заключалось в том, чтобы металлическая конструкция корабля не мешала работе намагниченной стрелки.
Еще одно необходимое усовершенствование заключалось в том, чтобы металлическая конструкция корабля не мешала работе намагниченной стрелки.
Магнитный компас имеет два основных недостатка: он указывает направление магнитного полюса, а не истинный полюс Земли; он чрезвычайно чувствителен к внешним магнитным полям, например, к металлическим частям корабля (хотя есть улучшения, делающие его менее чувствительным, как мы обсуждали выше).Этих недостатков лишены «моторизованные компасы», то есть гирокомпасы. Гирокомпасы установлены на подвесе и содержат гироскоп, который приводится во вращение с помощью двигателя, который, в свою очередь, использует магнитодвижущую силу для обеспечения вращения своего ротора. Хотя гирокомпас не свободен от собственных недостатков.
В транспорте
Одним из интересных применений магнитодвижущей силы являются поезда на магнитной подвеске. Это имя не относится к имени изобретателя, хотя и звучит как таковое.На самом деле это аббревиатура от слов mag netic lev itation.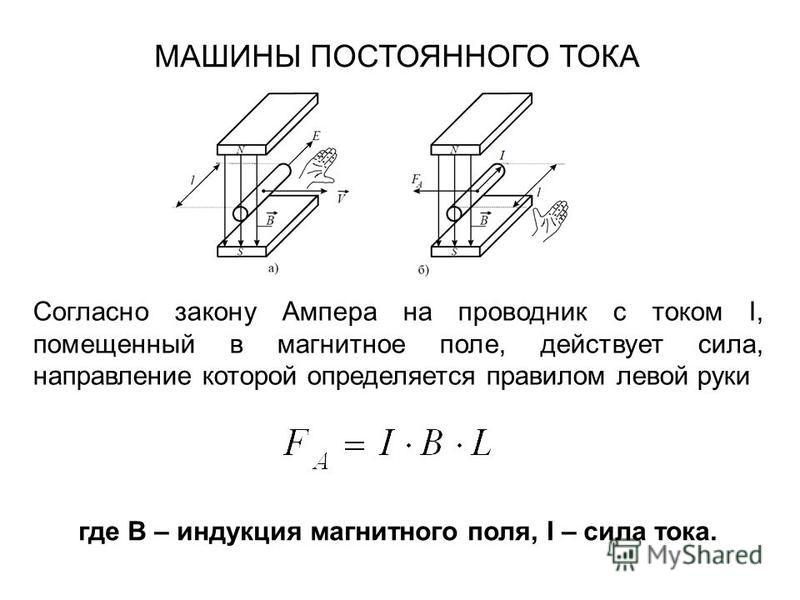 В некотором смысле мы можем думать о поездах на магнитной подвеске как о летающих поездах, потому что магнитные поля, создаваемые на пути и на корпусе поезда, заставляют поезд отталкиваться и/или притягиваться к пути, тем самым поднимая поезд над рельсом. . Магнитодвижущая сила также используется для движения поезда вперед. Эта конструкция привлекательна тем, что позволяет двигаться с высокой скоростью. Это также устраняет трение и предотвращает структурный износ и повреждения поезда и деталей пути, которые обычно вызываются трением.Хотя, несмотря на минимальные затраты на техническое обслуживание, эти поезда и пути в настоящее время обходятся дороже.
В некотором смысле мы можем думать о поездах на магнитной подвеске как о летающих поездах, потому что магнитные поля, создаваемые на пути и на корпусе поезда, заставляют поезд отталкиваться и/или притягиваться к пути, тем самым поднимая поезд над рельсом. . Магнитодвижущая сила также используется для движения поезда вперед. Эта конструкция привлекательна тем, что позволяет двигаться с высокой скоростью. Это также устраняет трение и предотвращает структурный износ и повреждения поезда и деталей пути, которые обычно вызываются трением.Хотя, несмотря на минимальные затраты на техническое обслуживание, эти поезда и пути в настоящее время обходятся дороже.
Существует несколько типов поездов на магнитной подвеске и рельсовых систем, которые различаются между монорельсом и двойным рельсом, а также механизмом работы. В настоящее время используются два типа систем электромагнитной подвески (EMS) и системы электродинамической подвески (EDS).
Электромагниты систем EMS ориентированы на рельсы. Обычно часть поезда с магнитами закручена вокруг путей, а магниты находятся в нижней части кривой, обращены вверх к пути.Эти системы менее динамически стабильны из-за своей конструкции и требуют наличия системы коррекции, чтобы расстояние между путями и левитирующим поездом оставалось постоянным. С другой стороны, их конструкция позволяет поездам на магнитной подвеске парить в воздухе даже на низких скоростях.
Обычно часть поезда с магнитами закручена вокруг путей, а магниты находятся в нижней части кривой, обращены вверх к пути.Эти системы менее динамически стабильны из-за своей конструкции и требуют наличия системы коррекции, чтобы расстояние между путями и левитирующим поездом оставалось постоянным. С другой стороны, их конструкция позволяет поездам на магнитной подвеске парить в воздухе даже на низких скоростях.
Пара редкоземельных магнитов в пробирке над большим кольцевым магнитом
Системы EDS могут иметь либо электромагниты, либо постоянные магниты, как на поезде, так и на направляющих. Магнитное поле используется для удержания поезда на нужном расстоянии относительно пути, а также для его продвижения вперед.Эти системы динамически устойчивы и не требуют постоянной коррекции на расстояние от пути. Недостатком систем EDS является то, что поезда на магнитной подвеске могут подниматься в воздух только после достижения определенной скорости (более 30 км/ч), и для работы на более низких скоростях им необходимы колеса или движущиеся пути. Как мы обсуждали ранее, это вызывает структурный износ и увеличивает затраты на техническое обслуживание.
Как мы обсуждали ранее, это вызывает структурный износ и увеличивает затраты на техническое обслуживание.
Поезда на маглеве требуют собственной инфраструктуры из-за их конструкции, а первоначальные затраты на строительство новых путей могут быть высокими, особенно в густонаселенных районах, из-за стоимости недвижимости в таких районах и потенциальной необходимости расчищать пространство для эта новая инфраструктура.Также необходимо иметь резервную систему колес на случай отключения электроэнергии, чтобы обеспечить безопасное перемещение пассажиров. Это особенно актуально, если дорожка приподнята. С другой стороны, по сравнению с обычными поездами, поезда на магнитной подвеске менее подвержены влиянию погоды, что делает их более надежными, если только погодные нарушения не вызывают отключения электроэнергии.
Основным источником энергозатрат является преодоление сопротивления воздуха. Поезда на маглеве, как правило, более энергоэффективны на более высоких скоростях, что делает более целесообразным использование этих систем для поездок на дальние расстояния.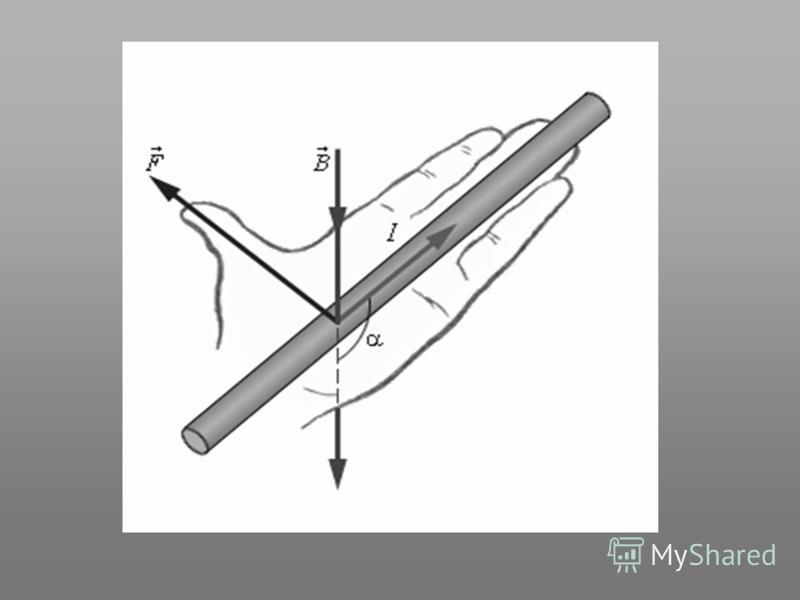 В настоящее время по всему миру используется несколько систем, в том числе в Шанхае, Китае, Японии и Южной Корее. Также есть несколько тестовых треков и несколько тестовых и эксплуатационных проектов, которые больше не используются, в том числе в Великобритании и Германии.
В настоящее время по всему миру используется несколько систем, в том числе в Шанхае, Китае, Японии и Южной Корее. Также есть несколько тестовых треков и несколько тестовых и эксплуатационных проектов, которые больше не используются, в том числе в Великобритании и Германии.
Интересные свойства магнитов
Земля как магнит
Земля сама по себе является гигантским магнитом. Он не очень мощный по сравнению со многими другими магнитами, но тем не менее важен. Он защищает Землю от солнечного ветра, который в противном случае повредил бы атмосферу Земли.
Благодаря этому магнетизму мы можем ориентироваться по компасу. Считается, что твердое внутреннее ядро Земли состоит из высокопроводящих сплавов железа. Жидкое внешнее ядро, которое окружает твердое ядро, также состоит из жидкостей с высокой проводимостью, которые движутся из-за теплового потока внутри ядра. Это движение превращает Землю в электромагнит.
Полярное сияние
Полярное сияние можно увидеть в высоких широтах, где магнитное поле Земли наиболее сильное.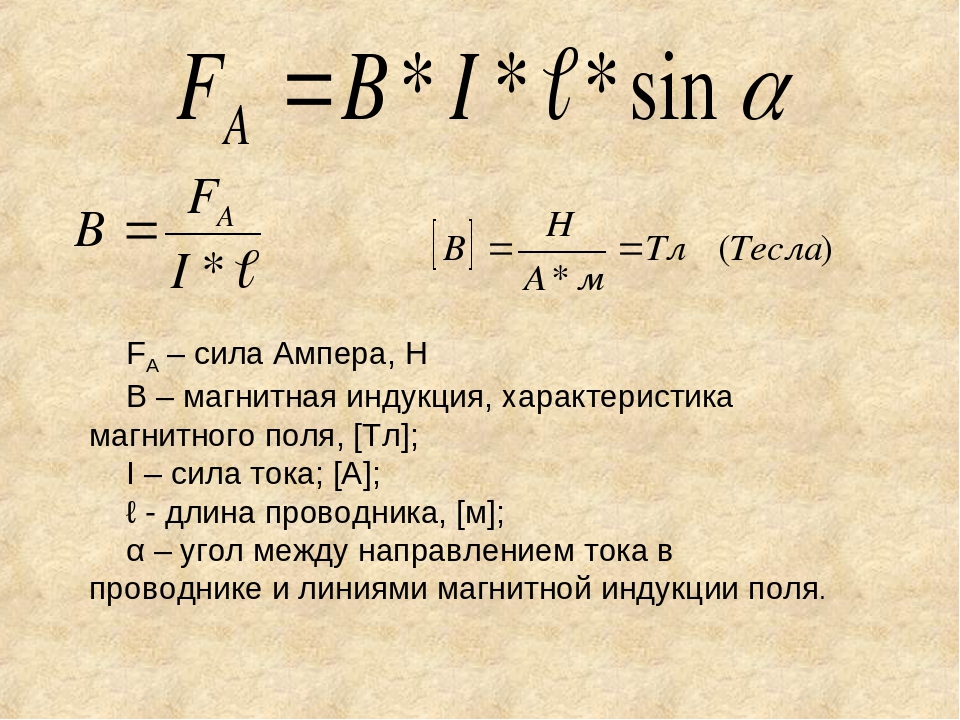 Североморск, Россия
Североморск, Россия
Полярное или северное сияние возможно благодаря магнитным полям Земли. Частицы солнечного ветра, в основном в виде протонов и электронов, взаимодействуют с молекулами и атомами газов в атмосфере Земли. В результате возбуждения и возврата в нормальное состояние они излучают свет. Эти частицы во время проявления полярных сияний концентрируются вдоль силовых линий магнитного поля, а поскольку эти линии более сближены вокруг северного и южного магнитных полюсов, сходясь на полюсах, полярное сияние более выражено вокруг полюсов.
Исследователи предполагают, что кошки и голуби могут найти дорогу домой с помощью магнитного поля Земли (при съемке этого снимка ни один голубь или кошка не пострадали)
Полярное сияние вокруг Северного полюса называется Южный полюс — это южное сияние. Следует помнить, что северный и южный магнитные полюса не пересекаются с реальными географическими Северным полюсом и Южным полюсом Земли, они смещены от географических полюсов и постоянно перемещаются. Из-за этого сдвига географические места, где можно увидеть северное сияние, не определяются широтой. На широтах ближе к экватору можно увидеть полярное сияние в некоторых районах на той же широте (например, в Торонто, Онтарио, Канаде на 44° северной широты), но невозможно увидеть его в других регионах на той же широте (Ялта). , Крым, Россия, 44° с.ш.). Вы можете визуализировать это явление, представив Землю с разноцветным головным убором полярного сияния, но вместо того, чтобы носить его прямо на макушке, как обычную шляпу, она носит его под наклоном, как берет.Только области под этим «беретом» имеют проявления северного сияния.
Из-за этого сдвига географические места, где можно увидеть северное сияние, не определяются широтой. На широтах ближе к экватору можно увидеть полярное сияние в некоторых районах на той же широте (например, в Торонто, Онтарио, Канаде на 44° северной широты), но невозможно увидеть его в других регионах на той же широте (Ялта). , Крым, Россия, 44° с.ш.). Вы можете визуализировать это явление, представив Землю с разноцветным головным убором полярного сияния, но вместо того, чтобы носить его прямо на макушке, как обычную шляпу, она носит его под наклоном, как берет.Только области под этим «беретом» имеют проявления северного сияния.
Магнитоцепция
Некоторые животные могут ощущать магнитное поле Земли и ориентироваться, используя это чувство. Это явление известно как магнитоцепция. Исследования в этой области находятся на предварительной стадии, но в настоящее время исследователи проводят эксперименты по определению механизма магнитоцепции у различных видов, таких как плодовые мушки, птицы, мыши, некоторые виды летучих мышей и даже более крупных млекопитающих, таких как лисы и олени.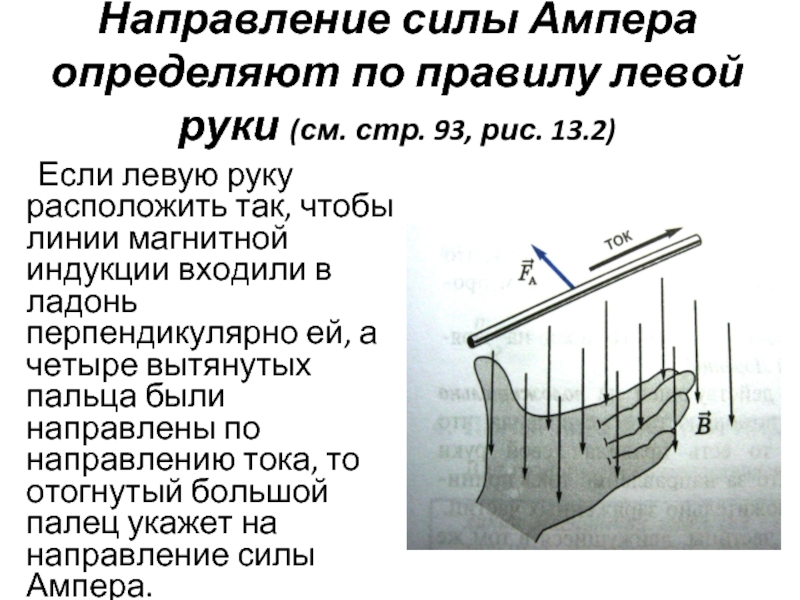 Некоторые из этих исследований предполагают, что животные могут ориентироваться и находить свой дом с помощью магнитоцепции, в то время как другие исследования предполагают, что некоторые животные демонстрируют поведение, соответствующее направлению магнитного поля Земли. Следует, однако, отметить, что большая часть этих исследований неубедительна, а некоторые из исследований, заявляющих о магнитоцепции у различных животных, еще не были воспроизведены.
Некоторые из этих исследований предполагают, что животные могут ориентироваться и находить свой дом с помощью магнитоцепции, в то время как другие исследования предполагают, что некоторые животные демонстрируют поведение, соответствующее направлению магнитного поля Земли. Следует, однако, отметить, что большая часть этих исследований неубедительна, а некоторые из исследований, заявляющих о магнитоцепции у различных животных, еще не были воспроизведены.
Магнитные дипольные системы
Акулы также могут ощущать магнитное поле Земли
Мы говорим о магнитах как о дипольных системах.Это означает, что у каждого магнита есть северный и южный полюса. Если мы разделим магнит пополам, у него все равно будут северный и южный полюса. Одинаковые полюса двух магнитов отталкиваются, а противоположные полюса притягиваются. Интересно, однако, что полюса Земли, которая сама по себе является гигантским магнитом, как мы обсуждали ранее, на самом деле помечены неправильно. Северный полюс магнита притягивается к Северному полюсу Земли, а это значит, что Северный полюс Земли на самом деле является южным полюсом магнита, которым является Земля.
Магнитный кислород
Кислород на самом деле является магнитным, когда находится в твердом состоянии. Это свойство очень интересно, хотя и имеет мало практического применения в быту. Это связано с тем, что для затвердевания кислорода нам нужно понизить его температуру как минимум до -218,79 °C. В качестве альтернативы мы можем добиться того же результата при комнатной температуре, но под давлением. В твердом состоянии кислород также меняет цвет, который в зависимости от его стадии может варьироваться от светло-голубого до оранжевого, до красного, до черного, до металлического.
Униполярный двигатель своими руками
Униполярный двигатель с подвесным ротором
Теперь давайте сделаем простой двигатель, который использует магнитодвижущую силу для своего вращения. Тип двигателя, который мы делаем, называется униполярным двигателем , и, хотя он не имеет большого практического применения, его очень легко сделать, и он является прекрасным примером магнитодвижущей силы в действии.
Для его изготовления нам понадобится батарейка, кусок проволоки, винт, круглый редкоземельный магнит и еще несколько небольших магнитов, которые в основном используются для утяжеления и устойчивости установки.Мы также можем использовать вертушку или какой-либо другой инструмент, который поможет нам легко увидеть, что двигатель движется. Здесь мы сделали два таких мотора, и тот, что вертушкой направлен вниз, очень прост.
Униполярный двигатель со стоячим ротором и дополнительным магнитом
Сначала прикрепляем к винту редкоземельный магнит. Затем мы добавляем еще несколько магнитов к нижней части редкоземельного магнита, чтобы сделать наш двигатель тяжелее и его легче стабилизировать. Затем прикрепляем вертушку к магнитам внизу.Теперь нам нужно создать магнитное поле с помощью проволоки. Присоединим один конец провода к отрицательному полюсу батареи. Для этого удобно использовать скотч. Затем давайте коснемся другого конца провода сбоку от редкоземельного магнита внизу. Виола, наш мотор завелся!
Виола, наш мотор завелся!
Вы можете легко сделать это дома. Редкоземельные магниты можно найти в хозяйственном магазине. Другие магниты можно найти в разделе ремесел долларового магазина, а остальные предметы вы также можете найти в долларовом магазине.Конечно, вы можете найти все на ebay.com. Вам не нужно использовать вертушку, если у вас ее нет, вы сможете увидеть, что винт вращается и без нее. Вы также можете сделать пропеллер или другую форму из проволоки и прикрепить его к нижним магнитам. Некоторые люди делают кукол и фигурки животных из проволоки. В Google Images и на YouTube есть много примеров, если вы ищете самодельные униполярные двигатели.
Второй двигатель, обращенный вверх, использует магнит над вертушкой для балансировки, чтобы удерживать ротор вверх.Нижний магнит также используется для поддержки двигателя. Как только вы поймете основную идею создания униполярного двигателя, вы сможете экспериментировать с различными конструкциями. Возможно, вы даже сможете найти этому мотору какое-нибудь полезное практическое применение!
Список литературы
Автор статьи: Екатерина Юрий
Конвертер единиц измерения, редактор и иллюстрации Анатолия Золоткова
У вас возникли трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и вы получите ответ от опытных технических переводчиков в считанные минуты.


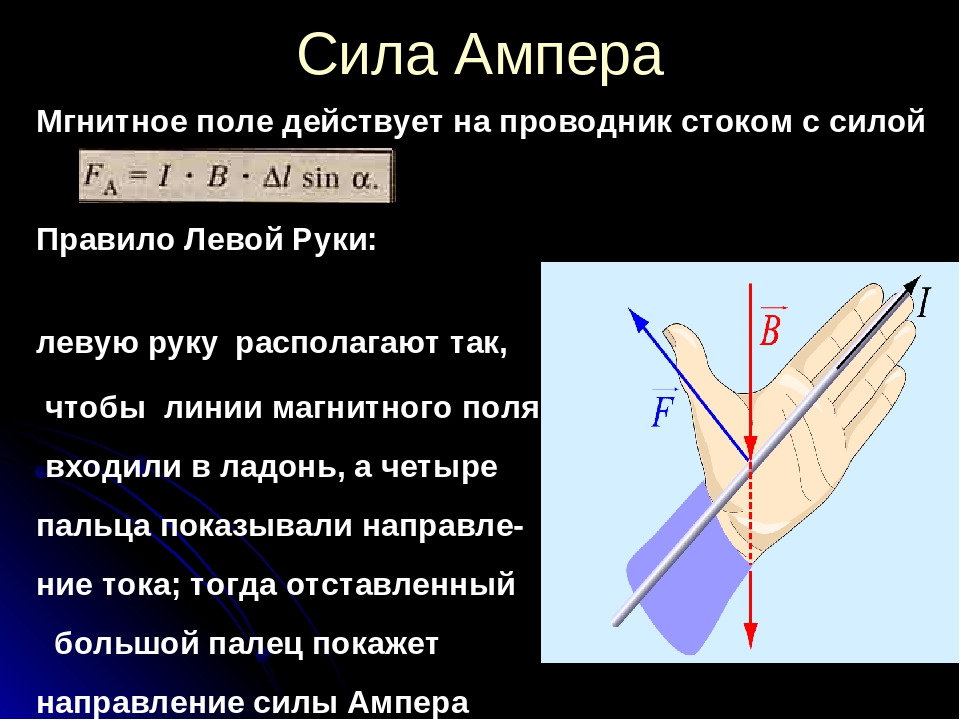 32)
32)
 Направление вращения зависит от полярности заряда (рис. 3).
Направление вращения зависит от полярности заряда (рис. 3).