Цепь переменного тока с активным сопротивлением
Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как u = Um sin ωt, то изменение тока i также идет по синусоиде:
Активное сопротивление
i = Im sin ωt
При этом
Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.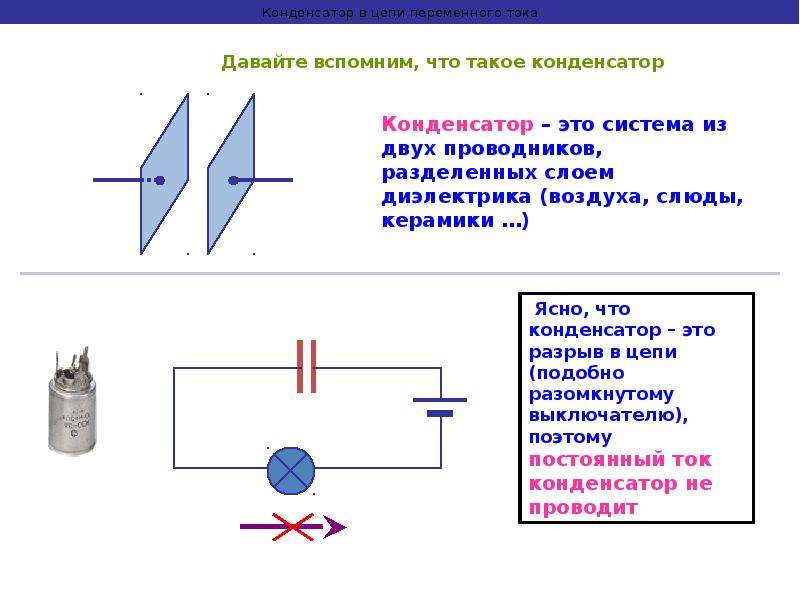
Мощность, ток, напряжение
Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается:
I = U/R.
Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного.
Электрическая мощность
Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения
Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt. Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.
В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.
Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
P = Pmax / 2 = UI
Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
P = I2R или P = U2/R.
Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.
Поверхностный эффект
Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.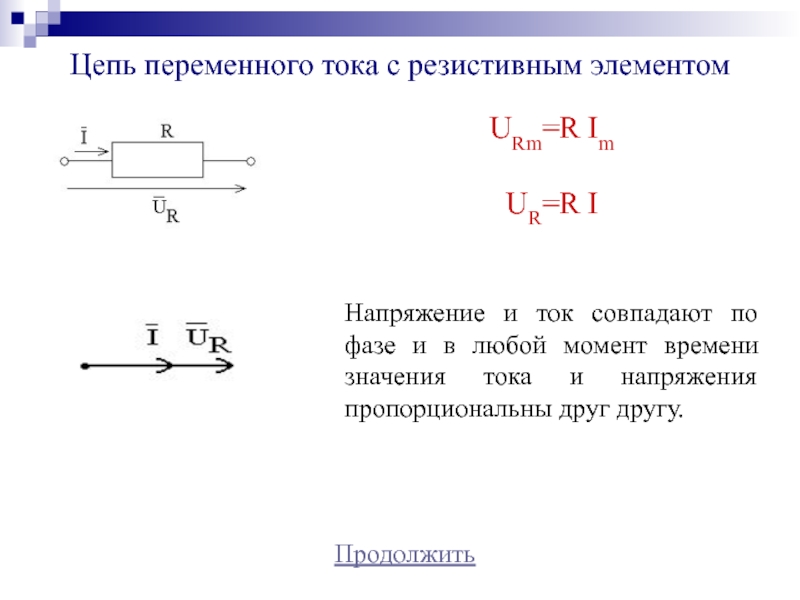
Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.
Основные понятия об электрических цепях переменного тока
ЭЛЕКТРИЧЕСКИЕ цепи переменного тока
Урок 5
Тема урока: Получение переменного тока. Основные понятия и определения, изображение переменного тока
Цель урока: формирование знаний по теме, воспитывать познавательный интерес; расширять кругозор учащихся; развивать мышление и память.
Теоретическая часть
Переменный ток, в отличие от тока постоянного, непрерывно изменяется как по величине, так и по направлению, причем изменения эти происходят периодически, т. е. точно повторяются через равные промежутки времени.
е. точно повторяются через равные промежутки времени.
Чтобы вызвать в цепи такой ток, используются источники переменного тока, создающие переменную ЭДС, периодически изменяющуюся по величине и направлению. Такие источники называются генераторами переменного тока.
На рисунке показана схема устройства (модель) простейшего генератора переменного тока.
Прямоугольная рамка, изготовленная из медной проволоки, укреплена на оси и при помощи ременной передачи вращается в поле магнита. Концы рамки припаяны к медным контактным кольцам, которые, вращаясь вместе с рамкой, скользят по контактным пластинам (щеткам).
Магнит создает между своими полюсами равномерное магнитное поле, в котором плотность магнитных силовых линий в любой части поля одинаковая. Вращаясь, рамка пересекает силовые линии магнитного поля, и в каждой из ее сторон а и б индуктируются ЭДС.
Стороны в и г рамки — нерабочие, так как при вращении рамки они не пересекают силовых линий магнитного поля и, следовательно, не участвуют в создании ЭДС.
В любой момент времени ЭДС, возникающая в стороне а, противоположна по направлению ЭДС, возникающей в стороне б, но в рамке обе ЭДС действуют согласно и в сумме составляют обшую ЭДС, т. е. индуктируемую всей рамкой. В этом можно убедиться, если использовать для определения направления ЭДС известное как правило правой руки.
Для этого надо ладонь правой руки расположить так, чтобы она была обращена в сторону северного полюса магнита, а большой отогнутый палец совпадал с направлением движения той стороны рамки, в которой мы хотим определить направление ЭДС. Тогда направление ЭДС в ней укажут вытянутые пальцы руки.
Для какого бы положения рамки мы ни определяли направление ЭДС в сторонах а и б, они всегда складываются и образуют общую ЭДС в рамке. При этом с каждым оборотом рамки направление общей ЭДС изменяется в ней на обратное, так как каждая из рабочих сторон рамки за один оборот проходит под разными полюсами магнита.
При этом с каждым оборотом рамки направление общей ЭДС изменяется в ней на обратное, так как каждая из рабочих сторон рамки за один оборот проходит под разными полюсами магнита.
Величина ЭДС также изменяется, так как изменяется скорость, с которой стороны рамки пересекают силовые линии магнитного поля. Действительно, в то время, когда рамка подходит к своему вертикальному положению и проходит его, скорость пересечения силовых линий сторонами рамки бывает наибольшей, и в рамке индуктируется наибольшая ЭДС. В те моменты времени, когда рамка проходит свое горизонтальное положение, ее стороны как бы скользят вдоль магнитных силовых линий, не пересекая их, и ЭДС не индуктируется.
Таким образом, при равномерном вращении рамки в ней будет индуктироваться ЭДС, периодически изменяющаяся как по величине, так и по направлению. ЭДС, возникающую в рамке, можно измерить прибором и использовать для создания тока во внешней цепи. Используя явление электромагнитной индукции, можно получить переменную ЭДС и, следовательно, переменный ток.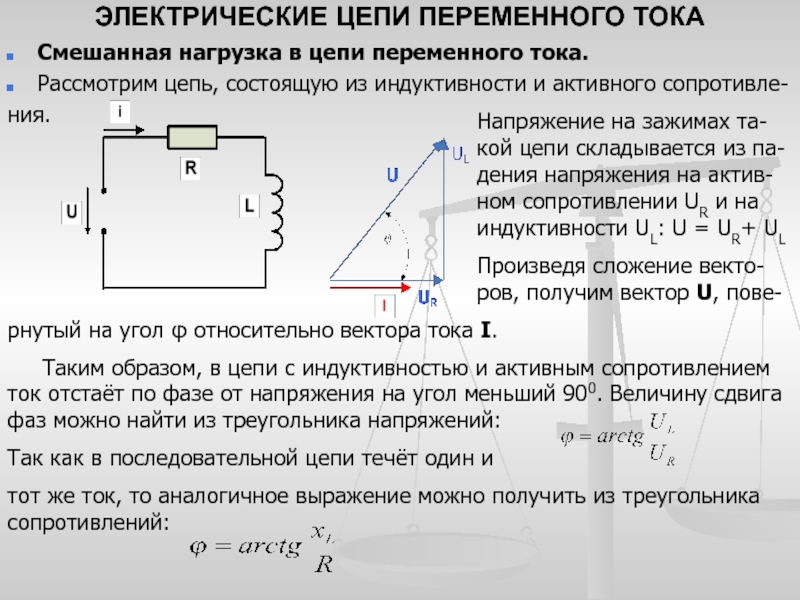
Переменный ток для промышленных целей и для освещения вырабатывается мощными генераторами, приводимыми во вращение паровыми или водяными турбинами и двигателями внутреннего сгорания.
Графическое изображение переменного тока
Построение графиков переменных величин, меняющихся с течением времени, начинают с построения двух взаимно перпендикулярных линий, называемых осями графика. Затем на горизонтальной оси в определенном масштабе откладывают отрезки времени (или угол поворота рамки), а на вертикальной, также в некотором масштабе, — значения той величины, график которой собираются построить (ЭДС, напряжения или тока).
Полученная волнообразная кривая называется синусоидой, а ток, ЭДС или напряжение, изменяющиеся по такому закону, называются синусоидальными.
Синусоидальный характер изменения тока — самый распространенный в электротехнике, поэтому, говоря о переменном токе, в большинстве случаев имеют в виду синусоидальный ток.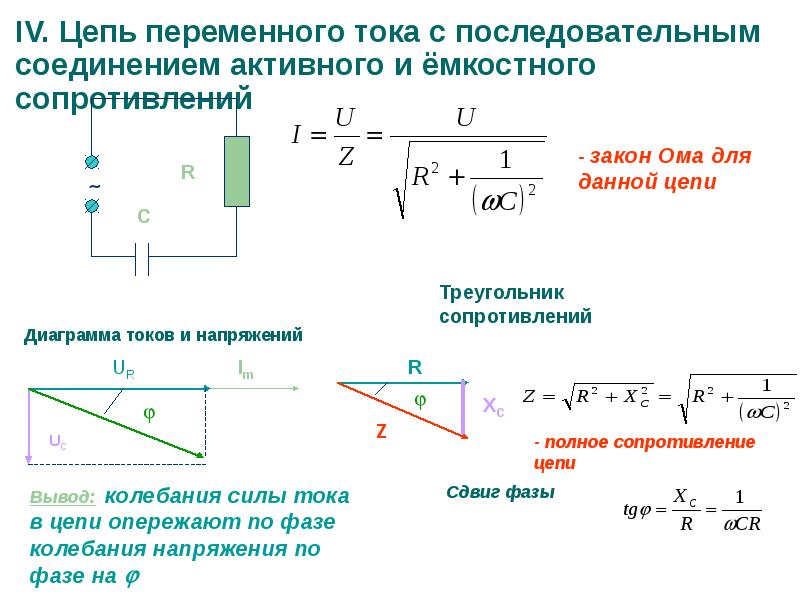
Для сравнения различных переменных токов (ЭДС и напряжений) существуют величины, характеризующие тот или иной ток. Они называются параметрами переменного тока.
Переменный ток характеризуется периодом, амплитудой и частотой.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока. Общепринятые обозначения амплитуд тока, ЭДС и напряжения — Im, Em и Um.
Значение переменного тока (ЭДС, напряжения), соответствующее любому выбранному моменту времени, называется его мгновенным значением (i, u, е соответственно).
Мгновенное значение тока, как и амплитудное его значение, легко определить с помощью графика. Для этого из любой точки на горизонтальной оси, соответствующей интересующему нас моменту времени, проведем вертикальную линию до точки пересечения с кривой тока; полученный отрезок вертикальной прямой определит значение тока в данный момент, т. е. мгновенное его значение.
Для этого из любой точки на горизонтальной оси, соответствующей интересующему нас моменту времени, проведем вертикальную линию до точки пересечения с кривой тока; полученный отрезок вертикальной прямой определит значение тока в данный момент, т. е. мгновенное его значение.
Число полных периодов, совершаемых током в 1 секунду, называется частотой переменного тока и обозначается латинской буквой f. Чтобы определить частоту переменного тока, т. е. узнать, сколько периодов своего изменения ток совершил в течение 1 секунды, необходимо 1 секунду разделить на время одного периода f = 1/T. Частота переменного тока измеряется единицей, называемой герцем.
При определении сопротивления различных цепей переменному току использовать еще одна вспомогательную величину, характеризующую переменный ток, так называемую угловую или круговую частоту.
Круговая частота обозначается буквой ω, измеряется в радианах и связана с частотой соотношением
ω = 2πf
В общем виде в момент времени t=0 мгновенное значение переменных величин можно записать в виде:
i = Im sin ωt ,
u = Um sin ωt,
е = Еmsin ωt.
При этом начальный период времени t=0 совпадает с нулевыми значениями функций. Но в общем случае на оси времени можно выбрать любой момент отсчета, тогда формулы мгновенных значений будут иметь вид:
i = Im sin(ωt + φi),
u = Um sin(ωt +φu),
е = Еm sin(ωt +φе),
где φi,φu,φе – начальный фазовый угол или начальная фаза.
Временно́й сдвиг между максимальными значениями в разных витках определяется разностью фаз:
Если для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если начальные фазы одинаковые и их разность равна 0, то это означает. Что они совпадают по фазе.
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений из-за емких расчетов.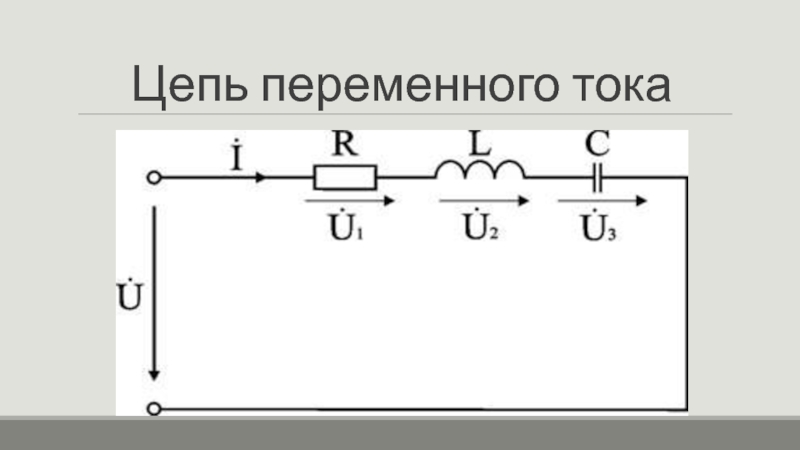 Для этих целей ввели понятие действующих значений тока, напряжения.
Для этих целей ввели понятие действующих значений тока, напряжения.
Действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электрические приборы показывают действующие значения переменных величин, которые обозначаются прописными буквами без индексов (I, U, Е).
; ;
Вопросы для самопроверки:
— Объясните понятие «переменный ток».
— Что такое амплитуда переменного тока?
— Что такое частота тока? Единицы измерения частоты?
— Что такое угловая частота? Единицы измерения угловой частоты?
— Что такое разность фаз?
— В чем разница между действующими и амплитудными значениями синусоидальных величин?
— Запишите и расшифруйте математическое выражение мгновенного синусоидального тока.
— Запишите и расшифруйте математическое выражение мгновенного синусоидального напряжения.
Практическая часть:
Пример 1. Определите угловую частоту, если частота сети равна 50Гц? 60Гц? 1кГц?
Пример 2. Амперметр показывает значение 10А. Определите амплитудное (максимальное) значение тока и запишите мгновенное значение тока (фазовый угол равен нулю).
Пример 3. Мгновенное значение напряжение равно u=282sin(ωt-47). Определить действующее значение и начальную фазу напряжения.
Урок 6
Тема урока: Элементы электрической цепи синусоидального тока.
Цель урока: расширение и обобщение знаний по теме, применение теоретических знаний на практике; развитие памяти и логики.
Теоретическая часть
На любом участке цепи переменного тока одновременно осуществляются необратимые процессы преобразования электрической энергии в другие виды и проявляется действие переменного электромагнитного поля.
При решении большинства электротехнических задач вводят допущения, которые позволяют раздельно учитывать каждое из явлений и упрощают задачу расчета электрических цепей переменного тока.
Цепь с идеальным резистивным элементом.
Рассмотрим, например, процессы, происходящие в обыкновенной лампе накаливания, включенной в сеть переменного тока. Между отдельными витками нити накаливания существует электрическая емкость, и нить обладает определенной индуктивностью, но они незначительны. Поэтому считают, что С=0 и L=0. В этом случае при анализе электрической цепи лампу называют идеальным резистивным элементом цепи с сопротивлением R.
Величина сопротивления переменному току больше, чем сопротивлению постоянному току, за счет неравномерного распределения тока в проводе (поверхностный эффект). Поэтому в отличие от сопротивления постоянному току сопротивление в цепи переменного тока называют активным сопротивлением.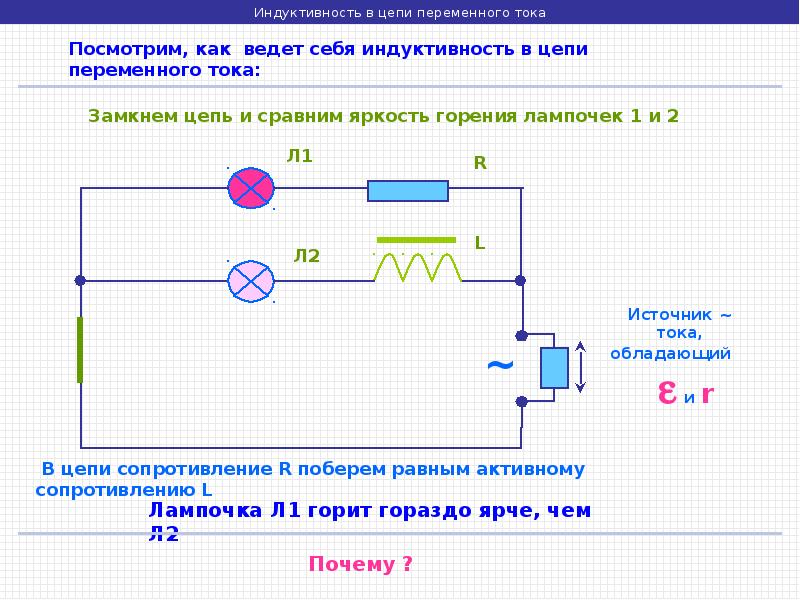 Активное сопротивление измеряется в омах.
Активное сопротивление измеряется в омах.
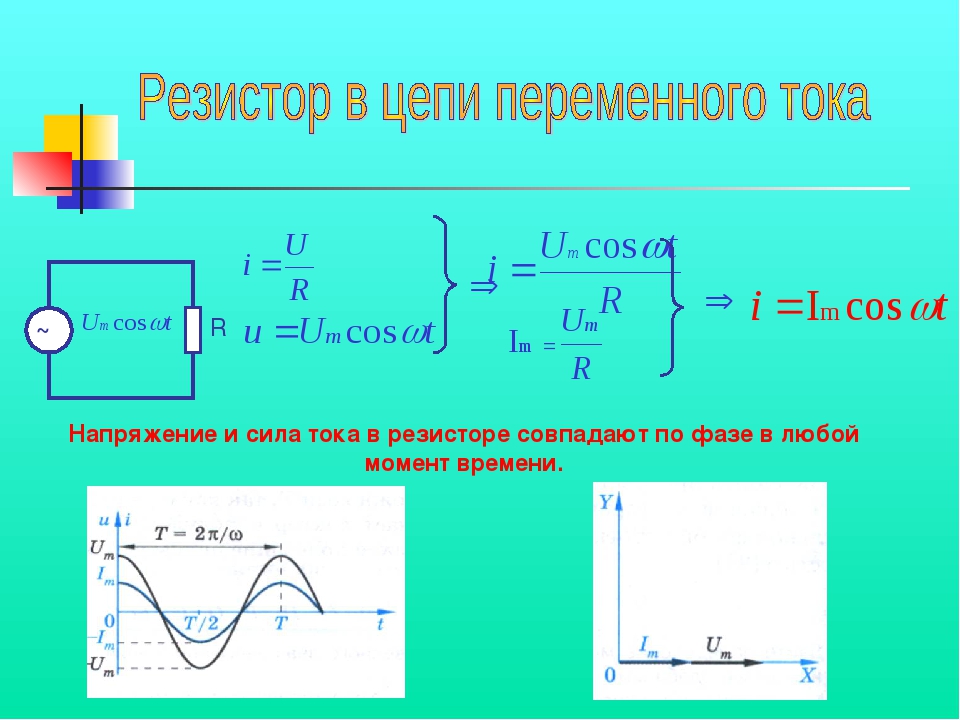
Если напряжение u = Umsinωt),подключить к сопротивлению R, то через него протекает ток
Это показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе: .
Напряжение, совпадающее по фазе с током, называют активным напряжением и обозначают Ua.
Цепь с идеальным индуктивным элементом.
Примером идеального индуктивного элемента может служить индуктивная катушка. Электрическая энергия, выделяемая в катушке за счет нагрева провода обмотки, как правило, невелика, как и межвитковая емкость, и во многих практических случаях ими можно пренебречь (R=0, C=0). При принятых допущениях индуктивную катушку называют идеальным индуктивным элементом цепи или L-элементом.
Параметром идеального индуктивного элемента является индуктивность L, а энергетические процессы в нем определяются только явлениями, происходящими в магнитном поле.
Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. На электрических схемах используют условные графические обозначения катушек индуктивностей, примеры которых приведены на рисунке.
Условные графические обозначения индуктивностей:
а – обозначение катушки индуктивности; б – с магнитодиэлектрическим сердечником;
в – с ферромагнитным сердечником
При прохождении электрического тока по катушке, ток создаст переменный магнитный поток Ф. Силовые линии этого потока, пересекая витки катушки, будут индуктировать в ней э.д.с. самоиндукции. По закону электромагнитной индукции
eL=
Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+eL=0, т. е. u = -eL Следовательно, напряжение источника всегда равно по величине и противо-положно по направлению э. д. с. самоиндукции.
е. u = -eL Следовательно, напряжение источника всегда равно по величине и противо-положно по направлению э. д. с. самоиндукции.
Если в формулу подставить значение тока и продифференцировать, то получим:
Обозначим величину ωL· равной амплитуде напряжения Um. Тогда по закону Ома
Величину называют индуктивным сопротивлением, измеряют в Омах и обозначают
Так как , то начальную фазу напряжения можно представить как φ u= φ i+ 90 и, следовательно,
Выведенное соотношение показывает, что если в катушке протекает синусоидальный ток, то напряжение также имеет синусоидальный характер, но при этом оно опережает ток на четверть периода (90).
Цепь с идеальным емкостным элементом
Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость (С). Этот параметр является коэффициентом пропорциональности между зарядом q (Кл) и прикладываемым напряжением u (В).
В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость (С). Этот параметр является коэффициентом пропорциональности между зарядом q (Кл) и прикладываемым напряжением u (В).
q = C·u,
При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток
Идеализированный конденсатор обладает только ёмкостью С (R=0, L=0).
Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом. Пусть напряжение источника изменяется по закону u = Um·sinωt, (φu = 0).
В цепи возникает ток
Из полученного выражения видно, что начальная фаза тока φi = . Угол сдвига фаз между напряжением и током составляет
Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол 90. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.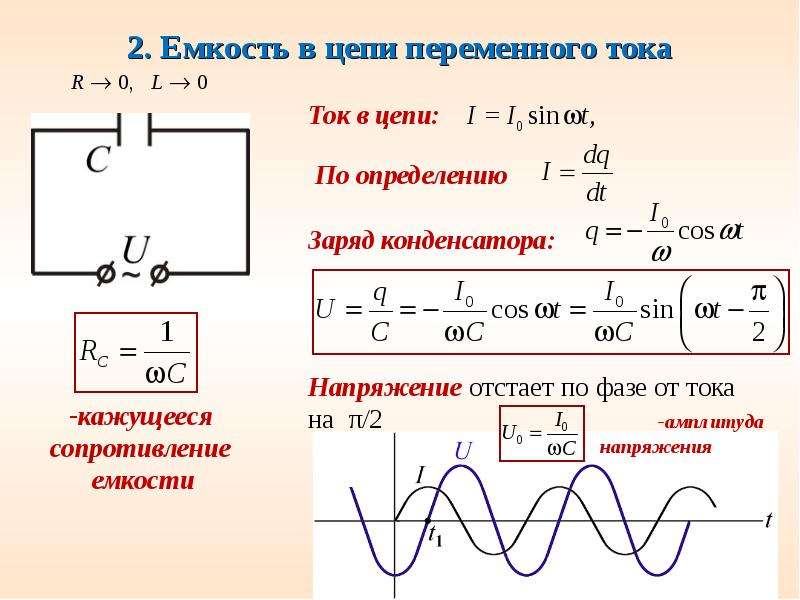
Амплитуда тока будет равна Im = ω·C·Um=.
Величину называют ёмкостным сопротивлением конденсатора и измеряют в Омах
Xc=1/ ω•C =1/2πfC.
Итак, в цепях переменного тока выделяют следующие виды сопротивлений:
— активное (активным называют сопротивление резистора). Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты сети.
— реактивное (индуктивное XL и емкостное ХС). Единицей измерения индуктивного и емкостного сопротивления также является Ом. Величина индуктивного сопротивления линейно зависит от частоты. А величина ёмкостного сопротивления обратнопропорциональна частоте сети. В цепях со смешанным соединением нагрузки (активной, индуктивной, ёмкостной) реактивным сопротивлением цепи называют величину
X = XL — XC.
Для того, чтобы найти общее сопротивление электрической цепи со смешанным соединением нагрузки используют понятие полного сопротивления цепи, которое определяется как
Вопросы для самопроверки:
— Объясните физический смысл активного сопротивления проводника переменному току по сравнению с сопротивлением проводника постоянному току?
— Что такое индуктивность катушки? От чего она зависит?
— Что понимается под действующим значением переменного синусоидального тока? Как его рассчитать через амплитудное значение тока?
— Опишите физические явления, наблюдаемые в резисторе в цепи переменного синусоидального тока?
— Запишите математическую связь между мгновенным напряжением, мгновенным током и активным сопротивлением?
— Запишите математические выражения мгновенного напряжения и тока на активном сопротивлении, приняв начальную фазу напряжения φ=45.
— Что понимается под углом сдвига фаз? Чему он равен на участке цепи с резистором? индуктивностью? ёмкостью?
— Как рассчитать индуктивное сопротивление идеальной катушки?
— Запишите математическое выражение мгновенного напряжения на индуктивном сопротивлении, приняв начальную фазу тока φ=45.
— Объясните физический смысл ёмкостного сопротивления. Как рассчитать ёмкостное сопротивление идеального конденсатора?
— Чему равен угол сдвига фаз в ёмкости?
— Что понимается под термином реактивное сопротивление? Как его определить?
— Как в сети переменного тока определяется полное сопротивление?
Практическая часть:
Пример 1. В цепи переменного тока к резистору подведено напряжение u=141sin(t-30)В. Сопротивление идеального резистора равно 100 Ом. Определить амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.
Пример 2. К идеальной катушке подведено напряжение u=141sin(t+73)В. Частота тока в сети равна 50Гц. Индуктивность катушки равна 12,7 мГн. Определить индуктивное сопротивление катушки, амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.
Пример 3. К идеальному конденсатору подведено напряжение u=282sin(t+30)В. Частота тока в сети равна 50Гц. Ёмкость конденсатора равна 159мкФ. Определить ёмкостное сопротивление конденсатора, амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.
Урок 7
Тема урока: Неразветвленные цепи переменного тока. Мощность цепи синусоидального тока. Коэффициент мощности.
Цель урока: получение практического навыка расчета элементов цепи переменного тока; расширение знаний о физических явлениях в реальной катушке и реальном конденсаторе.
Теоретическая часть
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и ёмкостное сопротивление.
1. Цепь с активно-индуктивным сопротивлением.
Фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока.
Полное сопротивление цепи с активным сопротивлением и индуктивностью
а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений
Произведем геометрическое сложение радиусов-векторов UL и UR. Результирующий вектор UAB будет являеться гипотенузой прямоугольного треугольника. Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление. Разделим обе части уравнение на
Извлекая квадратный корень из обеих частей этого равенства, получим,
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений
2. Цепь с активно-ёмкостным сопротивлением.
Цепь с активно-ёмкостным сопротивлением.
Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений.
Полное сопротивление цепи с активным сопротивлением и емкостью
а) — схема цепи; б) — треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его
В общем случае, когда цепь содержит все три вида сопротивлений, сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Полное сопротивление цепи содержащей R, L и C
а) — схема цепи; б) — треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности
Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений преобладает.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
3. Параллельное соединение активного и реактивного элемента
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно, нужно сначала вычислить проводимость каждой из параллельных ветвей.
Полное сопротивление цепи при параллельном соединении активного и реактивных элементов
а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т.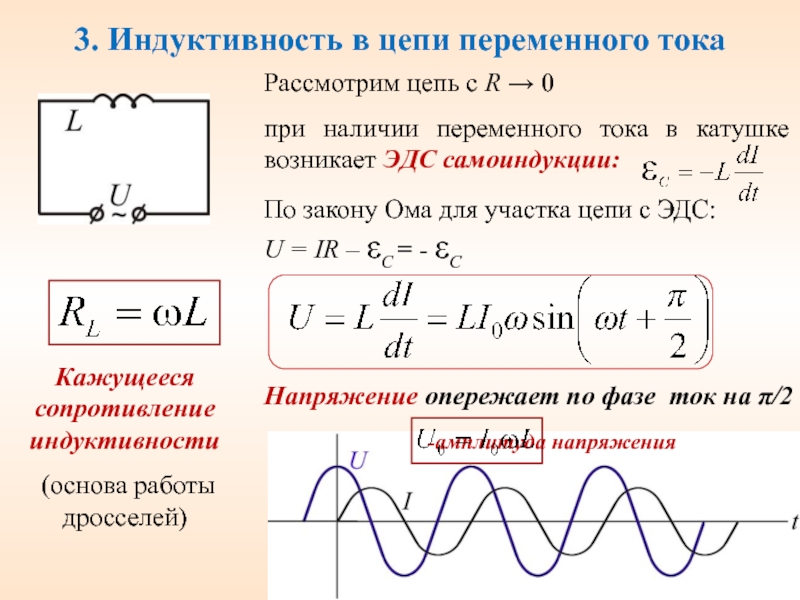 е.
е.
откуда:
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С :
Мощность цепи синусоидального тока
Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.
Пусть мгновенные напряжение и ток определяются по формулам:
Тогда
Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.
Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.
Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90. В реактивных элементах не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.
Реактивная мощность, измеряемая в вольтамперах реактивных (Вар), расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.
Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:
, ВА
В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер).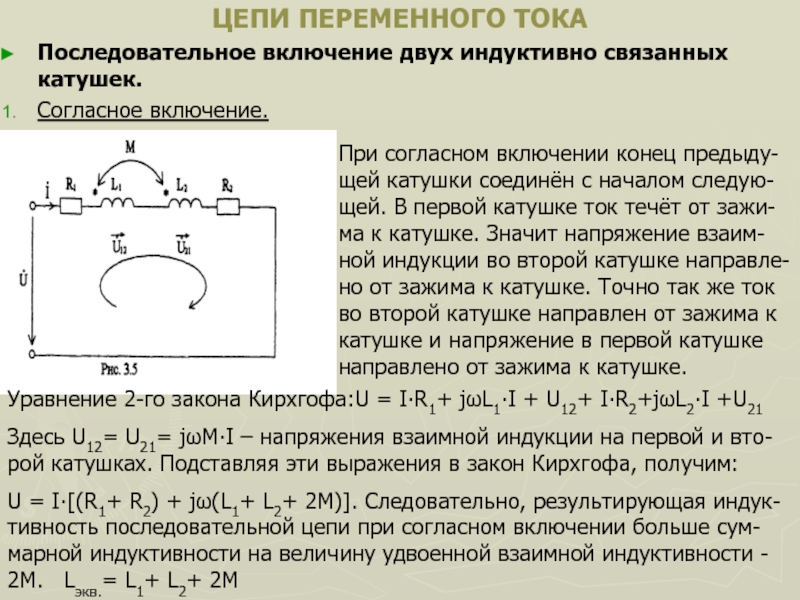 Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.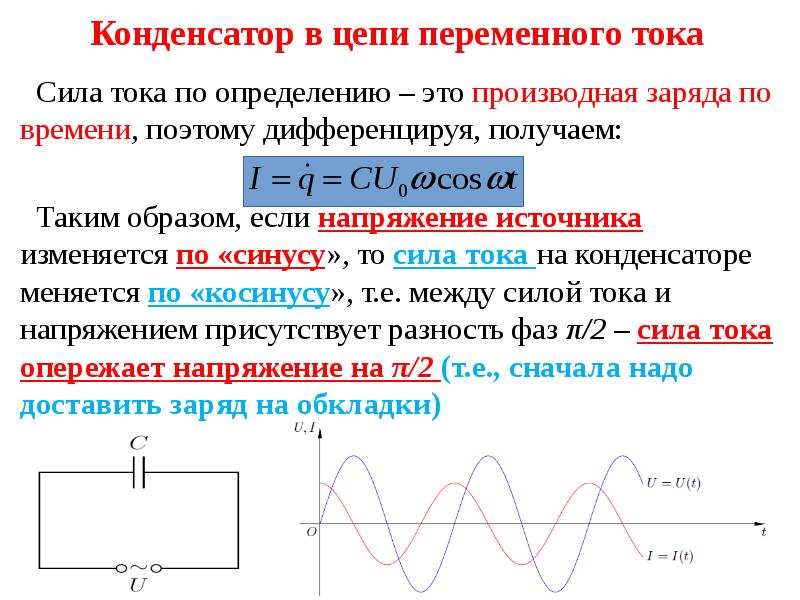
Измерительные преобразователи реактивной мощности, использующие формулу , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Коэффициент мощности и его экономическое значение
Коэффициент мощности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Численно коэффициент мощности равен косинусу этого фазового сдвига.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cosφ = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cosφ = 0,25-0,3).
Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cosφ = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cosφ = 0,25-0,3).
Коэффициент мощности учитывают при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Коэффициент мощности повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов.
Практическая часть
Задача. Катушка с активным сопротивлением R1=200 Ом и индуктивностью L=0,24 Гн соединена параллельно с конденсатором, активным сопротивлением R2=70 Ом и емкостью С=8*10-6Ф и подключена к источнику переменного тока с частотой f=200 Гц и амплитудным значением напряжения Um=300 В. Определить действующее значение токов в каждой ветке и общее значение тока в цепи, полное сопротивление цепи, полную, активную и реактивную мощности. Построить векторную диаграмму тока и напряжения.
Определить действующее значение токов в каждой ветке и общее значение тока в цепи, полное сопротивление цепи, полную, активную и реактивную мощности. Построить векторную диаграмму тока и напряжения.
Простейшие цепи переменного тока — Электротехника — Учебные материалы — Каталог статей
Список всех статей на технические темы
Простая электротехника все статьи
Сначала читаем статью «Переменный ток — краткие сведения»
Все электротехнические устройства состоят из сопротивлений индуктивностей и емкостей
Соотношение индуктивности емкости в цепи переменного тока принципиально определяют свойства цепи переменного тока.
Активное сопротивление R — это такой элемент электрической цепи, который оказывает сопротивление току с выделением тепла. Ведет себя одинаково в цепях постоянного и переменного тока, хотя величина сопротивления несколько отличается, это придется учитывать в точных расчетах.
Индуктивность L –это такой элемент электрической цепи, который состоит из витков провода и при протекании тока создает магнитное поле, это магнитное поле противодействует изменениям тока.
При протекании постоянного тока индуктивность ведет себя как проволока и не считается сопротивлением. Сопротивлением она является только для переменного тока, чем больше частота переменного тока, тем больше сопротивление индуктивности.
Емкость C – это такой элемент электрической цепи, который накапливает заряд, и проводит ток, только пока заряжается, или разряжается, поэтому в цепях постоянного тока, тока не проводит, а в цепях переменного тока все время заряжается – разряжается и, значит, проводит ток. Сопротивление емкости переменному току тем меньше, чем выше частота переменного тока.
Емкость и индуктивность взаимно противоположные по свойствам элементы, значит, они могут снижать взаимное влияние в цепях переменного тока или совсем отключать друг друга. Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.
Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.
Активное сопротивление R в цепи переменного тока
Что нам интересно знать про простейшую электрическую цепь содержащую R ?
Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.
Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток
Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.
Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.
Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,
Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.
Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.
P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2
Средняя мощность за период равна постоянной составляющей мощности
Uа Iа/2
Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P
Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P
Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.
Индуктивное сопротивление в цепи переменного тока
XL = ωL
Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку
Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.
Что же происходит в цепи с индуктивностью при протекании переменного тока.
Оказывается, ток и напряжение действуют не одновременно,
то есть, сдвинуты по фазе
На активном сопротивлении R, появление напряжения сразу – в тот же момент, вызывает появление тока, и они действуют в одной фазе.
На индуктивности так не получается.
Если напряжение от источника начинает нарастать, то ток за ним не успевает.
Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.
Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 900 то есть на π/2. Значит, фаза тока отрицательна и составляет — π/2
Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 900 то есть на π/2. Значит, фаза тока отрицательна и составляет — π/2
Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.
Более подробно об ЭДС самоиндукции смотри в статье Начальные представления об электромагнетизме
Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2
Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.
Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..
R — активное сопротивление — на нем выделяется тепло
X — реактивное сопротивление на нем не выделятся тепло
XL – сопротивление индуктивности
XL – сопротивление индуктивности L является реактивным, оно равно XL =ωL, то есть, оно прямо пропорционально частоте ω и индуктивности L, чем больше индуктивность, тем больше реактивное сопротивление и чем выше частота тем больше реактивное сопротивление.
Индуктивность тем сильнее ограничивает ток, чем выше частота тока.
Индуктивность пропускает переменный ток тем лучше, чем меньше индуктивность и чем меньше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток индуктивность пропускает без всякого сопротивления
Мощность на индуктивности
Мощность определяется как произведение тока на напряжение. Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.
Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.
Частота синусоиды мощности вдвое больше частоты тока и напряжения.
На индуктивности не получается выделение тепла, и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на индуктивности, называется реактивной и обозначается не Р, а другой буквой – QL
Емкость в цепи переменного тока
XC =1/ ωc
При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться.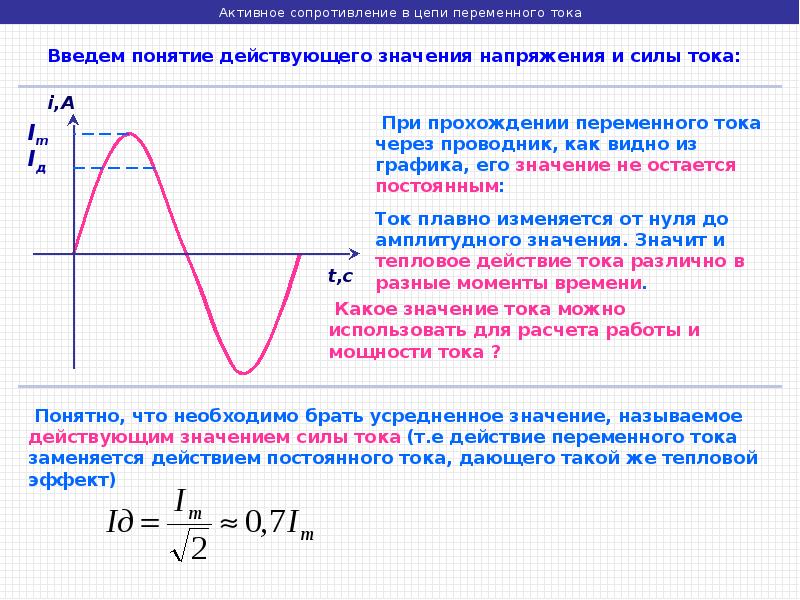 Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.
Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.
Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.
Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.
То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2
XC — сопротивление емкости
XC — сопротивление емкости является реактивным, оно равно XC =1/ ωc, то есть оно обратно пропорционально частоте и емкости, чем больше емкость, тем меньше реактивное сопротивление и чем выше частота тем меньше меньше реактивное сопротивление.
Емкость пропускает переменный ток тем лучше, чем больше емкость и чем выше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток емкость вообще не пропускает.
Конденсатор часто ставят в участки цепей, в которых не должен проходить постоянный ток
Мощность в цепи с емкостью
Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.
Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник. Частота синусоиды мощности вдвое больше частоты тока и напряжения.
Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.
Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.
Реактивные сопротивления
Индуктивность и емкость проявляют себя в электрических цепях как сопротивления.
XC – реактивное сопротивление емкости
XL — реактивное сопротивление индуктивности
Формулы сопротивлений позволяют их использовать для расчета задач по закону Ома для участка цепи.
Формула XC =1/ ωc показывает, что сопротивление емкости зависит от частоты ω. Это означает, что емкость по-разному пропускает ток низкой и высокой частоты.
Емкость пропускает переменный ток тем лучше, чем выше частота.
Емкость вообще не пропускает постоянный ток, и это ее важнейшее свойство. Одно из главных применений емкости (конденсатора) состоит в том, что его ставят в те ветви схем, где запрещено протекание постоянного тока.
Формула XL = ωL показывает, что сопротивление индуктивности зависит от частоты. Это означает, что индуктивность по-разному пропускает ток низкой и ток высокой частоты.
Индуктивность хуже пропускает переменный ток высокой частоты
Чем больше частота. Тем труднее проходит переменный ток. Катушка индуктивности используется для ограничения переменного тока.
Конденсатор и катушка являются противоположностями.
Конденсатор пропускает переменный ток и не пропускает постоянный
Катушка пропускает постоянный ток и не пропускает переменный
Такие цепи содержат сопротивление R, индуктивность L, и ёмкость C.
Реальное сопротивление цепи, содержащей одновременно R, L и C, зависит от величины каждого элемента цепи, и от частоты переменного тока, который протекает в этой цепи.
Расчет цепей переменного тока по аналогии с расчетом цепей постоянного тока невозможен, потому, что необходимо учитывать фазовый сдвиг между током и напряжением.
Можно упростить цепи, если какой-то элемент: R, L или C пренебрежительно мал.
Задачи на переменный ток решаются методом векторных диаграмм.
Ток и напряжение являются векторными величинами.Их изображают как вращающиеся радиус -векторы, в этом смысле они отличаются от векторов сил и скоростей в механике, но правила сложения и вычитания векторов аналогичны.
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
Выберем фазу общего тока равной 0, вектор тока откладывается как горизонтальный вектор слева на право. Далее строим векторную диаграмму напряжений. Сначала откладывается вектор напряжения на сопротивлении R. Этот вектор, пойдет горизонтально, так как его фаза совпадает с фазой тока. Затем строят вектор напряжения на индуктивности L.
 Его надо откладывать под углом 900 вверх, это потому, что напряжение на индуктивности впереди на 900.
Его надо откладывать под углом 900 вверх, это потому, что напряжение на индуктивности впереди на 900.
Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.
Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора к концу второго.
Получился прямоугольный треугольник. Любую сторону этого треугольника можно найти по теореме Пифагора.
Острый угол этого треугольника и есть реальный сдвиг фаз в этой цепи между током и общим напряжением. Он обязательно меньше 90 градусов, потому что только на идеально индуктивности он составляет 90 градусов. Активное сопротивление обязательно уменьшает сдвиг фаз.
Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление, обозначается Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и XL
Z2, = Rа2 + X2L
В цепи L R, в отличие от цепи только с L, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.
Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и QL
S2 = Р2 + Q2L
Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников.
Последовательное соединение RC
Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие «добротность» конденсатора, которая проявляет активную составляющую его сопротивления
При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.
Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.
К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.
Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.
Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.
Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и XС
Z 2 = Rа2 + X2С
В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.
Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и QС
S2 = Р2 + Q2С
Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников
Параллельное соединение RL
При параллельном соединении RL одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через катушку отстает по фазе от напряжения. на 900. Общий ток отстает от напряжения меньше чем на 900.
Для цепей с параллельным соединением элементов, гораздо удобнее использовать не сопротивления (активные и реактивные) а их обратные величины, которые называются проводимости. Вместо r используется g, вместо XL используется bL, вместо Xc используется bc
Вместо r используется g, вместо XL используется bL, вместо Xc используется bc
Параллельное соединение RC
При параллельном соединении RС одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через конденсатор опережает по фазе от напряжения. на 900. Общий ток опережает напряжение меньше чем на 900
Значение Cos φ
Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).
Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .
Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.
В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.
Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.
Цепи RLC
Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.
Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.
В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.
RLC последовательно
Как будет выглядеть векторная диаграмма в общем случае?
При последовательном соединении сопротивлений на каждом сопротивлении действует своя часть напряжения. На большем сопротивлении будет большая часть напряжения.
На первой векторной диаграмме видно, что напряжение на конденсаторе Uc больше, чем на катушке UL тогда суммарный вектор общего напряжения направлен вниз, и видно, xnj угол сдвига фаз отрицательный. На второй диаграмме видно, что напряжение на конденсаторе Uc, значительно меньше, чем UL , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.
На второй диаграмме видно, что напряжение на конденсаторе Uc, значительно меньше, чем UL , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.
В первом случае цепь имеет емкостный характер, во втором индуктивный.
На определенной частоте наступает равенство Uc = Ul, такое явление называется резонанс напряжений
Условие резонанса XL = XC
При резонансе напряжений Общее сопротивление цепи становится минимально, а ток становится максимальным, что может быть опасно для источника и требует надежной защиты.
RLC параллельно
Векторные диаграммы токов при параллельном соединении
При параллельно соединении элементов RLC напряжение на всех элементах действует одно и то же, а токи разные, чем меньше сопротивление ветви, тем больше ток.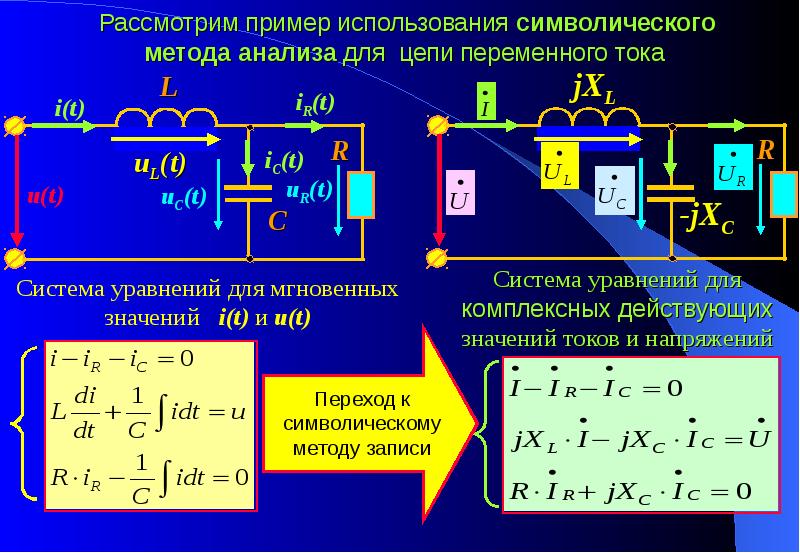 В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.
В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.
В первом случае цепь имеет индуктивный характер, во втором емкостный
На определенной частоте наступает равенство токов Ic = IL такое явление называется резонанс токов.
При резонансе токов сопротивление цепи становится максимальным и ток уменьшается до величины, которая определяется сопротивлением R, которое остается в цепи.
Условия резонанса
Резонанс широко применяется в радиотехнических и различных электронных схемах.
XL = XC
Устройства для переменного тока и устройства для постоянного тока
Устройства. Которые включаются в электрические цепи
Лампочки
Нагреватели
Электромоторы
Электроинструмент
Бытовые приборы
Электроника
И т. п.
п.
Лампочки и нагреватели работают одинаково в цепях переменного и постоянного тока. В некоторых случаях разница может быть заметной, так как активное сопротивление в цепи постоянного тока (омическое) может отличаться от сопротивления в цепи переменного тока.
Электромоторы и электроинструмент рассчитанный на переменный ток, при подключении в цепь постоянного тока скорее всего сгорят, так как, у них пропадает индуктивное сопротивление и ток сильно возрастает.
Если моторы, и инструмент рассчитанные на постоянный ток, включены на переменный ток, они сильно потеряют мощность, так как появившееся индуктивное сопротивление и сильно ограничит потребляемый ток.
Конденсатор в цепи переменного тока
Конденсатор в цепи переменного тока
- Подробности
- Просмотров: 568
«Физика — 11 класс»
Постоянный ток не может идти по цепи, содержащей конденсатор, так как обкладки конденсатора разделены диэлектриком.
Переменный же ток может идти по цепи, содержащей конденсатор.
Есть источники постоянного и переменного напряжений, в которых постоянное напряжение на зажимах источника равно действующему значению переменного напряжения.
Цепь состоит из конденсатора и лампы накаливания, соединенных последовательно.
При включении постоянного напряжения (переключатель влево) лампа не светится.
При включении переменного напряжения (переключатель вправо) лампа загорается, если емкость конденсатора достаточно велика.
Под действием переменного напряжения происходит периодическая зарядка и разрядка конденсатора.
Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.
Если сопротивлением проводов и обкладок конденсатора можно пренебречь,
то напряжение на конденсаторе равно напряжению на концах цепи.
Следовательно,
Заряд конденсатора меняется по гармоническому закону:
q = CUm cos ωt
Сила тока, представляющая собой производную заряда по времени, равна:
Колебания силы тока опережают по фазе колебания напряжения на конденсаторе на .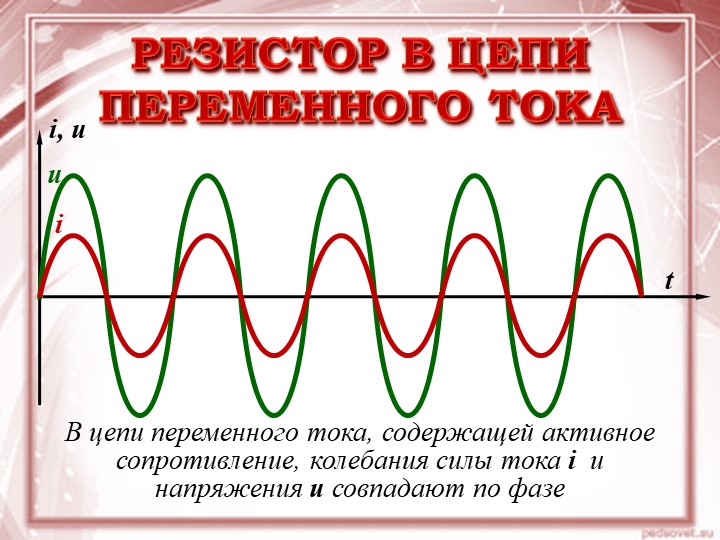
Амплитуда силы тока равна:
Im = UmCω
Если ввести обозначение
и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим
Величину Хс, обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением.
Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.
Это и позволяет рассматривать величину Хс как сопротивление конденсатора переменному току (емкостное сопротивление).
Чем больше емкость конденсатора, тем больше ток перезарядки.
Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.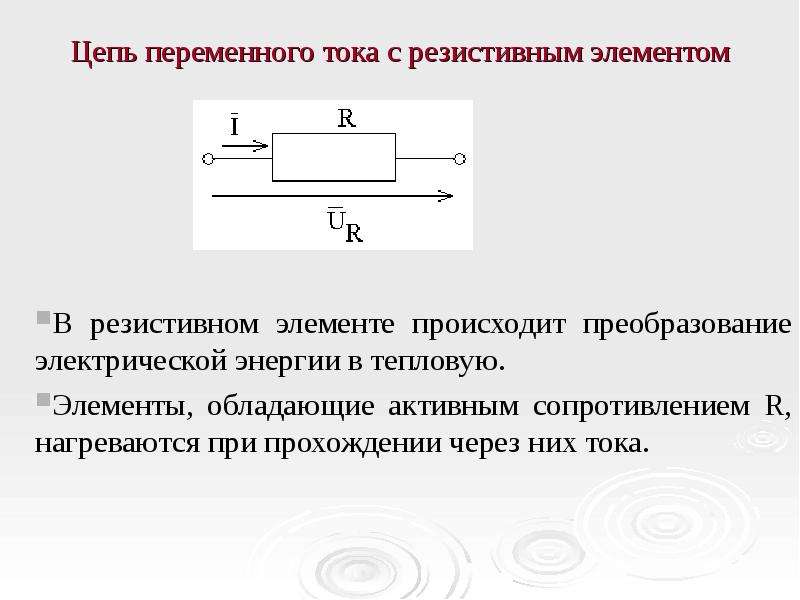
В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Хс.
С увеличением емкости оно уменьшается.
Уменьшается оно и с увеличением частоты ω.
На протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля.
В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.
Итак,
сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на .
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика
Свободные и вынужденные электромагнитные колебания.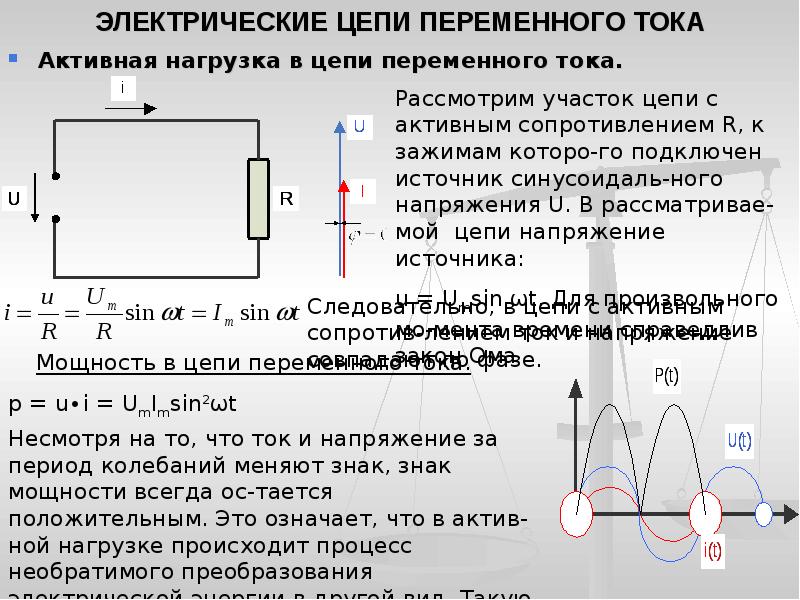 Колебательный контур. Превращение энергии при электромагнитных колебаниях —
Колебательный контур. Превращение энергии при электромагнитных колебаниях —
Аналогия между механическими и электромагнитными колебаниями —
Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний —
Переменный электрический ток —
Активное сопротивление. Действующие значения силы тока и напряжения —
Конденсатор в цепи переменного тока —
Катушка индуктивности в цепи переменного тока —
Резонанс в электрической цепи —
Генератор на транзисторе. Автоколебания —
Краткие итоги главы
Конденсатор в цепи переменного тока
Если конденсатор включить в цепь постоянного тока, то такая цепь будет разомкнутой, так как обкладки конденсатора разделяет диэлектрик, и ток в цепи идти не будет. Иначе происходит в цепи переменного тока. Переменный ток способен течь в цепи, если она содержит конденсатор. Это происходит не из-за того, что заряды вдруг получили возможность перемещаться между пластинами конденсатора. В цепи переменного тока происходит периодическая зарядка и разрядка конденсатора, который в нее включен благодаря действию переменного напряжения.
В цепи переменного тока происходит периодическая зарядка и разрядка конденсатора, который в нее включен благодаря действию переменного напряжения.
Рассмотрим цепь на рис.1, которая включает конденсатор. Будем считать, что сопротивление проводов и обкладок конденсатора не существенно, напряжение переменного тока изменяется по гармоническому закону:
По определению емкость на конденсаторе равна:
Следовательно, напряжение на конденсаторе:
Из выражения (3), очевидно, что заряд на конденсаторе будет изменяться по гармоническому закону:
Сила тока равна:
Сравнивая законы колебаний напряжения на конденсаторе и силы тока, видим, что колебания тока опережают напряжение на . Этот факт отражает то, что в момент начала зарядки конденсатора сила тока в цепи является максимальной при равенстве нулю напряжения. В момент времени, когда напряжение достигает максимума, сила тока падает до нуля.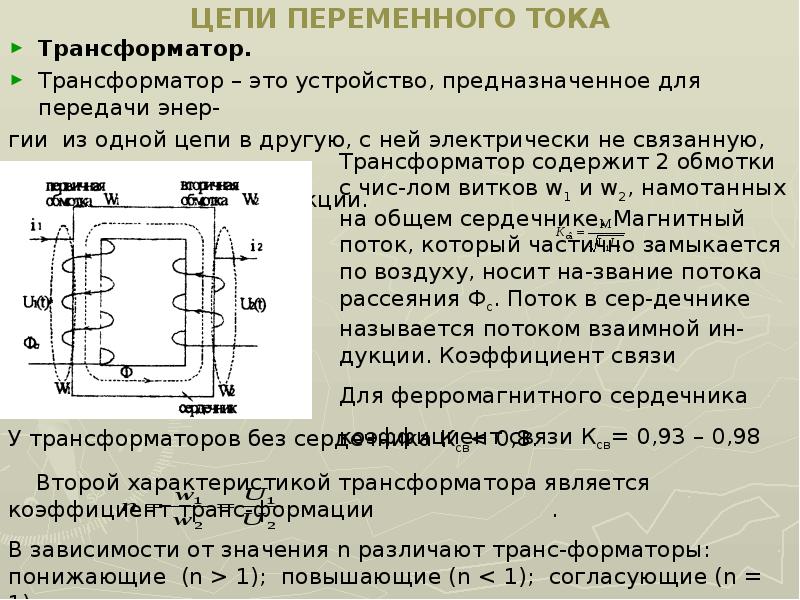
В течение периода, при зарядке конденсатора до максимального напряжения, энергия, поступающая в цепь, запасается на конденсаторе, в виде энергии электрического поля. За следующую четверть периода данная энергия возвращается обратно в цепь, когда конденсатор разряжается.
Амплитуда силы тока (), исходя из выражения (5), равна:
Емкостное сопротивление конденсатора
Физическую величину, равную обратному произведению циклической частоты на емкость конденсатора называют его емкостным сопротивлением ():
Роль емкостного сопротивления уподобляют роли активного сопротивления (R) в законе Ома:
где – амплитудное значение силы тока; – амплитуда напряжения. Для емкостного сопротивления действующая величина силы тока имеет связь с действующим значением напряжения аналогичную выражению (8) (как сила тока и напряжение для постоянного тока):
На основании (9) говорят, что сопротивление конденсатора переменному току.
При увеличении емкости конденсатора растет ток перезарядки. Тогда как сопротивление конденсатора постоянному току является бесконечно большим (в идеальном случае), ёмкостное сопротивление конечно. С увеличением емкости и (или) частоты уменьшается.
Примеры решения задач
цепь переменного тока содержащая емкость индуктивность и сопротивление
цепь переменного тока содержащая емкость индуктивность и сопротивление
38)
ЦЕПЬ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ
Если в цепь постоянного, тока включить конденсатор (идеальный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.
Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.
При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.
В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.
По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения Um, напряжение конденсатора также станет равным Um, заряд конденсатора прекращается и ток в цепи становится равным нулю. Ток в цепи конденсатора можно определить по формуле
где ∆q — количество электричества, протекающее по цепи за время ∆t.
Из электростатики известно:
где С — емкость конденсатора;
u — напряжение сети;
uc — напряжение конденсатора. Окончательно для тока имеем
Из последнего выражения видно, что, когда ∆u/∆t максимально (положения a, в, d), i также максимально.
Когда ∆u/∆t = 0 (положения б, г на рис. 143), то i также равно нулю.
Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.
В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.
Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.
Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.
Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению Uc, приложенному к конденсатору, угловой частоте w и величине емкости конденсатора C:
Обозначим
Величина Хс называется емкостным сопротивлением, или реактивным сопротивлением емкости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид
Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид
Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или реактивной слагающей напряжения) и обозначается Uc:
Емкостное сопротивление Хс, так же как индуктивное сопротивление xL, зависит от частоты переменного тока.
Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.
Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:
при частоте 400 гц:
На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.
Энергию, запасаемую конденсатором к моменту, когда напряжение на нем равно максимальному значению, можно определить по известной формуле CU2м/2.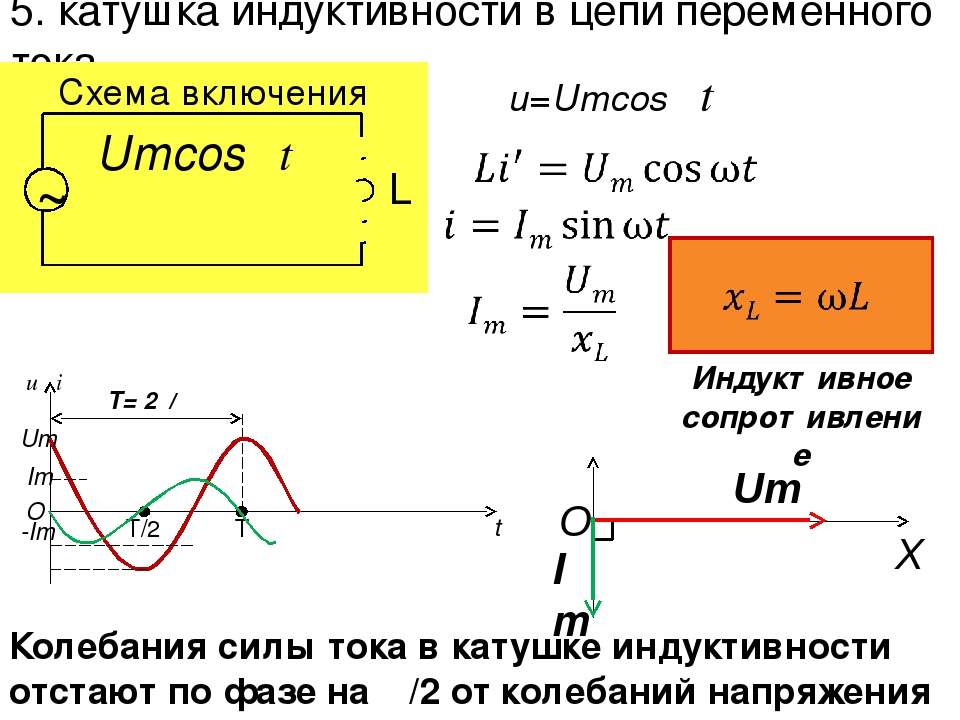
В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.
За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.
Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.
Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда wt = 45°, 135° и т. д.) достигает максимального значения, равного
Этой величиной принято характеризовать количественно процесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.
Учитывая,, что в рассматриваемой цепи U = IХc, получим следующее выражение для реактивной мощности:
Электрические цепи переменного тока — презентация онлайн
I. 2. Электрические
2. Электрические
цепи переменного
тока
Протирочная машина
Картофелечистка
Тестомесильная
машина
Хлеборезка
Электромясорубка
§1. Общие положения
Электрический ток величина и направление которого меняются
с течением времени называется ПЕРЕМЕННЫМ, т.е.
представляет
собой
вынужденные
электромагнитные
колебания.
1.1. Получение переменной ЭДС
Вращение рамки в магнитном
поле
Основано на явлении
ЭЛЕКТРОМАГНИТНОЙ
ИНДУКЦИИ.
Токопроводящую рамку
равномерно
вращают
(угловая скорость ω) в
однородном
магнитном
поле.
Значение угла α МЕЖДУ
нормалью к рамке и
вектором
магнитной
индукции:
t
Величина магнитного потока, пронизывающего
изменяется со временем по гармоническому закону:
Ф В S cos B S cos t
рамку,
Согласно ЗАКОНУ ФАРАДЕЯ для электромагнитной индукции,
при изменении потока магнитной индукции, пронизывающего
контур, в контуре возникает ЭДС индукции.
е Ф B S cos t B S sin t
/
t
m B S
/
t
— максимальное значение или амплитуда ЭДС.
Если рамка содержит N витков, амплитуда возрастает в N раз.
Подключив источник переменной ЭДС к концам проводника,
мы создадим на них переменное напряжение:
u U m sin t
Схема генератора
ИТАК! ПЕРЕМЕННЫЙ ТОК – это электрический ток, который
изменяется с течением времени по гармоническому
(синусоидальному) закону.
I = I0·sin(ωt+φ),
фаза колебаний
частота колебаний
амплитуда колебаний
По теореме Фурье любое колебание можно представить как
СУММУ
гармонических
колебаний.
Т. о., синусоидальные или гармонические колебания являются
одновременно:
и самым важным
типом колебаний
и самым простым
1.2. Общие соотношения между
напряжением и силой тока
Фаза колебаний силы
тока может не
совпадать с фазой
колебаний
напряжения.
Сдвиг фаз между колебаниями тока и напряжения.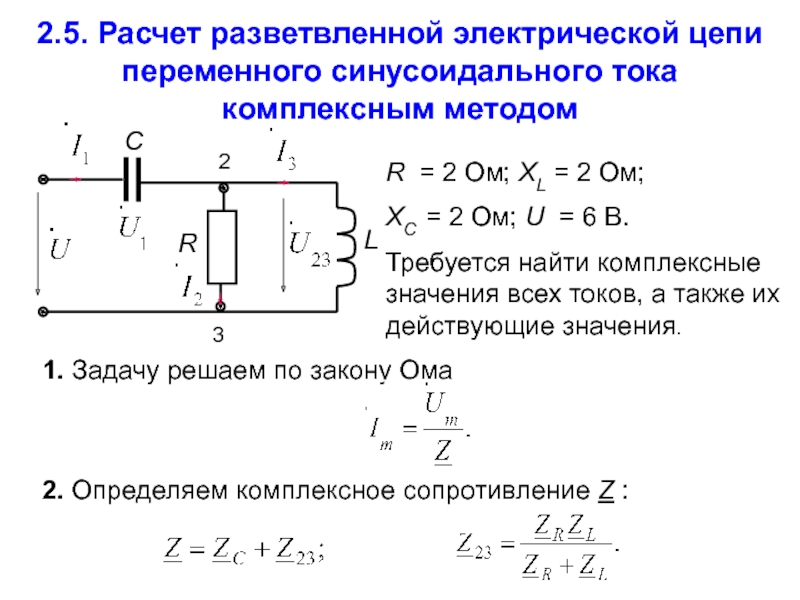
В общем случае мгновенное значение напряжения и силы тока
можно определить:
u U m sin t
u U m cos t
или
i I m sin t
i I m cos t
φ – сдвиг фаз между колебаниями тока и напряжения
Im – амплитуда тока, А.
1.3. Действующие значения напряжения и
силы тока
ФИЗИЧЕСКИЙ СМЫСЛ
Действующее
значение
силы переменного тока
РАВНО силе постоянного
тока,
выделяющего
в
проводнике
ТО
ЖЕ
количество
теплоты,
ЧТО и переменный ток за
то же время.
Im
I
2
Действующее значение
напряжения:
Um
U
2
Когда говорят, что напряжение в городской электрической сети
составляет 220 В, то речь идёт НЕ о мгновенном значении
напряжения и НЕ его амплитудном значении, а о
ДЕЙСТВУЮЩЕМ ЗНАЧЕНИИ.
Когда на электроприборах указывают силу тока, на которую
они рассчитаны, то также имеют в виду действующее значение
силы тока.
Переменный
ток
представляет
собой
вынужденные электромагнитные колебания, в
которых сила тока в цепи изменяется со
временем по гармоническому закону;
Получение переменной ЭДС в цепи основано
на явлении электромагнитной индукции;
ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ переменного
тока
и
напряжения
равны
значениям
постоянного тока и напряжения при которых в
цепи с тем же активным сопротивлением
выделялась бы та же энергия;
§2. Активные и реактивные
Активные и реактивные
элементы электрической цепи
Общие положения
Для учета процессов
преобразования электромагнитной энергии
в цепях вводятся ИДЕАЛИЗИРОВАННЫЕ ЭЛЕМЕНТЫ.
Элементы цепи рассматриваются как математические модели,
СВЯЗЫВАЮЩИЕ токи и напряжения.
Элементы цепи можно разделить на
Активные элементы
Пассивные элементы
АКТИВНЫЕ ЭЛЕМЕНТЫ –
источники электрической энергии,
в которых неэлектрические виды энергии
преобразуются в электрическую.
Различают два основных активных элемента:
источник напряжения (ЭДС)
источник тока
ПАССИВНЫЕ ЭЛЕМЕНТЫ –
приемники электромагнитной энергии.
Электрическая энергия в них:
ПРЕОБРАЗУЕТСЯ в неэлектрические виды
энергии – активное сопротивление
(проводимость), либо
НАКАПЛИВАЕТСЯ в виде энергии
электрического поля (емкость) или
магнитного поля (индуктивность).
ЕМКОСТЬ И ИНДУКТИВНОСТЬ являются
реактивными приемниками энергии
или
реактивными элементами.
2.1. Активные элементы
2.1.1. Источник тока
Условное графическое
обозначение
идеализированного
источника тока
ИДЕАЛИЗИРОВАННЫМ ИСТОЧНИКОМ ТОКА
называют элемент цепи, который создает заданный ток j(t)
независимо от напряжения на его полюсах.
Единица измерения – ампер (А).
Напряжение на элементе определяется величиной
сопротивления u = ir и принимает любое значение.
Ток в элементе НЕ зависит от величины сопротивления: i = j.
2.1.2. Источник напряжения (ЭДС)
Условное графическое
обозначение
идеализированного
источника напряжения
ИДЕАЛИЗИРОВАННЫМ ИСТОЧНИКОМ НАПРЯЖЕНИЯ
элемент цепи, который создает на своих зажимах напряжение
u(t) = e(t) НЕЗАВИСИМО от того, какой ток протекает в нем.
Единица измерения – вольт (В).
Напряжение на элементе НЕ зависит
от величины сопротивления: e = u.
Ток в элементе i = u/r и принимает любое значение.
Источник напряжения характеризует внесенную в цепь
энергию извне, поэтому он называется также
ИСТОЧНИКОМ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ.
2.2. Пассивные элементы
2.2.1. Сопротивление
Условное графическое
обозначение
активного сопротивления
Отношение, определяющее
сопротивление:
ur = irR или ir = ur /R.
Величина R называется
СОПРОТИВЛЕНИЕМ.
Единица измерения – ом (Ом).
Кратные единицы измерения
активного сопротивления:
килоом (кОм) 1кОм = 1000 Ом;
мегаом (МОм) 1мОм = 1000кОм.
Ток в сопротивлении
пропорционален
напряжению (Закон Ома)
Мощность, рассеиваемая
на активном
сопротивлении,
определяется по
формуле:
p U r ir Ri r2 u r2 R
2.2.2. Проводимость
Условное
графическое
обозначение
проводимости
ПРОВОДИМОСТЬЮ
называется величина,
обратная сопротивлению:
G = 1/R.
Единица измерения – СИМЕНС (См).
2.2.3. Емкость
Условное графическое
обозначение
проводимости
Отношение, определяющее емкость:
1
u C iC ( t )dt
C
или
du C ( t )
iC C
dt
Величина С называется ЕМКОСТЬЮ.
Единица измерения – ФАРАДА (Ф).
Кратные единицы измерения емкости, наиболее часто
встречающиеся в практике:
пикафарада (пФ), 1 пФ = 1 10-12 Ф;
нанофарада (нФ), 1 нФ = 1 10-9 Ф;
микрофарада (мкФ), 1 мкФ = 1 10-6 Ф.
Величина заряда на конденсаторе определяется по
формуле:
Q = CU, Кл.
Таким образом,
электрическая емкость –
это коэффициент пропорциональности, связывающий
накопленный заряд Q
с приложенным напряжением U.
Энергия, накапливающаяся в емкости,
определяется по формуле:
Wc = (CU2) / 2.
2.2.4. Индуктивность
Условное графическое
обозначение
проводимости
Отношение, определяющее индуктивность:
uL L
di L ( t )
dt
или
iL
1
u L ( t )dt
L
Величина L называется ИНДУКТИВНОСТЬЮ.
Единица измерения – ГЕНРИ (Гн).
Кратные единицы измерения индуктивности:
миллигенри (мГн), 1 мГн = 1 10-3 Гн.
ЭНЕРГИЯ, накапливающаяся в индуктивности:
WL = (LI2) / 2
2. 3. Основные характеристики
3. Основные характеристики
идеализированных элементов
электрических цепей
Основные характеристики идеализированных
элементов электрических цепей
2.4. В реальных электрических цепях:
1) Заданное сопротивление обычно обеспечивают включением
специального изделия, называемого РЕЗИСТОРОМ;
2) Заданную емкость – включением специального изделия,
называемого КОНДЕНСАТОРОМ;
3) Заданную индуктивность – включением катушек и просто
проводников.
В ОТЛИЧИЕ от идеализированных элементов
реальные элементы электрических цепей
характеризуются множеством параметров,
часть которых можно смоделировать
с помощью эквивалентных
электрических схем (схем замещения),
составленных из идеализированных элементов.
§3. Активное, индуктивное и
емкостное сопротивления в цепи
переменного тока
Х
Х
Конденсатор в цепи
постоянного тока (ток
в цепи не течет) –
РАЗРЫВ ЦЕПИ
Индуктивность в цепи
постоянного тока (ток
в цепи течет) – КУСОК
ПРОВОДА
i
В результате периодической зарядки и перезарядки
конденсатора в цепи постоянно протекает переменный ток.
В цепях переменного тока различают три вида сопротивлений:
АКТИВНОЕ
Сопротивление
переменному току
со стороны
материала
проводника
(нагревается, т.е.
потребляет
мощность).
ИНДУКТИВНОЕ
ЕМКОСТНОЕ
В цепи переменного тока в
катушке индуктивности
индуцируется э.д.с.
самоиндукции (т. к. магнитный
поток, пронизывающий витки
катушки, изменяется) =>
препятствует нарастанию тока
при его увеличении и
уменьшению тока при спаде.
Действие индуктивности при
переменном токе подобно
сопротивлению. С увеличением
индуктивности сопротивление
увеличивается.
В цепи течет ток заряда или
разряда конденсатора,
величина которого зависит от
емкости конденсатора: чем
больше емкость, тем больше
ток (заряда и разряда) =>
конденсатор можно
рассматривать как некоторое
сопротивление переменному
току
возникает вследствие того,
что при заряде конденсатора
между его обкладками
возникает напряжение (Uc),
направленное навстречу
напряжению, которое
приложено на зажимах.
2.1. Резистор в цепи переменного тока
Электрические устройства,
преобразующие электрическую
энергию во внутреннюю, называются
активными
сопротивлениями
Мгновенное значение силы тока прямо пропорционально
мгновенному значению напряжения — по закону Ома :
u U m cos t
i
I m cos t
R
R
Um
Im
R
При небольших значениях частоты переменного тока активное
сопротивление НЕ зависит от частоты и совпадает с
электрическим сопротивлением в цепи постоянного тока.
В
цепи
с
активным
сопротивлением сдвиг фаз между
колебаниями силы тока и
напряжения равен нулю,
т.е.
колебания
силы
тока
совпадают
по
фазе
с
колебаниями напряжения.
2.2. Векторная диаграмма при наличии в
цепи переменного тока только активного
сопротивления
Амплитуду колебаний напряжения в цепи переменного тока
можно выразить МЕТОДОМ ВЕКТОРНЫХ ДИАГРАММ.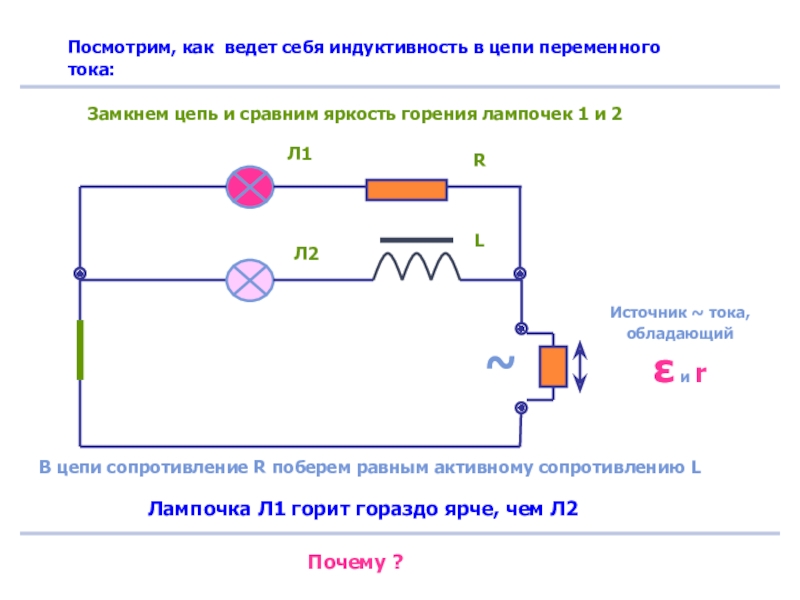
Выберем ось Х диаграммы таким образом, чтобы вектор,
изображающий колебания тока, был направлен вдоль этой оси.
В дальнейшем мы будем называть ее ОСЬЮ ТОКОВ.
Im
Так как угол φ между колебаниями напряжения и тока на
резисторе равен нулю, то вектор, изображающий колебания
напряжения на сопротивлении R, будет направлен вдоль оси
токов. Длина его равна Im·R.
2.3. Конденсатор в цепи переменного тока
Пусть на конденсатор
подано напряжение
НО! Так как I = dq/dt, то
a
+
U
δ
Тогда
φА-φВ = U = q/C,
q I dt
I
—
Поскольку ток
меняется по закону,
q I 0 sin t dt
I0
I = I0·sinωt
cos t q0 =0
Постоянная интегрирования q0 — заряд, не связанный с
колебаниями тока, поэтому можно считать q0 = 0.
ОТСЮДА
I0
I0
I0
U
cos t
sin( t )
sin( t )
C
C
2
C
2
UC
I
•Следовательно, колебания напряжения на
обкладках
конденсатора
в
цепи
переменного тока отстают по фазе от
колебаний силы тока на π/2 =>
•В момент, когда конденсатор начинает
заряжаться, сила тока максимальна, а
напряжение равно нулю.
•После того как напряжение достигает
максимума, сила тока становится равной
нулю и т.д.
Физический смысл: ЧТОБЫ возникло напряжение на
конденсаторе, должен натечь заряд за счет протекания тока в
цепи. ОТСЮДА — отставание напряжения.
Сдвиг по фазе в конденсаторе
Колебания силы тока на конденсаторе опережают
колебания напряжения по времени на четверть
периода, а по фазе на радиана.
0
π/2
I
U0=I0·1/ωC
Отношение амплитуды колебаний напряжения на конденсаторе
к амплитуде колебаний силы тока называют емкостным
сопротивлением конденсатора (обозначается XC):
1
а по закону Ома U = I·R
U 0 I0
C
Величина
1
XC
C
играет роль сопротивления
участка цепи
Она называется ЕМКОСТНЫМ СОПРОТИВЛЕНИЕМ
Векторная диаграмма при наличии в цепи переменного тока
только емкостного сопротивления
2.4. Индуктивность в цепи переменного
a
тока
Пусть напряжение подается на концы
катушки с индуктивностью L.
L
I
b
ИНДУКТИВНОСТЬ контура с током – это коэффициент
пропорциональности между протекающим по контуру током и
возникающем при этом магнитным потоком.
Индуктивность L зависит от формы и размеров контура, а
также свойств среды
Ф = L·I
При наличии переменного тока в катушке индуктивности
возникнет ЭДС самоиндукции
Ф
Закон Ома запишется
следующим образом:
–
U = I·R
=0
L I
ТОГДА:
dI
d
U L L [ I 0 sin t ] I 0 L cos t I 0 L sin( t )
dt
dt
2
Таким образом, колебания напряжения на индуктивности
ОПЕРЕЖАЮТ колебания тока на π/2.
UL
I
•Физический смысл: R=0, внешнее напряжение уравновешивает
ЭДС самоиндукции U = – .
•Но пропорциональна НЕ мгновенному значению тока, А
быстроте его изменения, которая будет макс. когда ток
проходит через ноль.
•Поэтому нулевые значения ТОКА СОВПАДАЮТ с макс. U
U 0 I 0 L I 0 RL
Отношение
амплитуды
колебаний
напряжения
на
индуктивности к амплитуде колебаний силы тока называют
ИНДУКТИВНЫМ
СОПРОТИВЛЕНИЕМ
катушки
индуктивности (обозначается XL=ωL )
Если индуктивность
измеряется в Генри, а
частота ω в с-1, то ХL
будет выражаться в Ом.
Колебания силы тока на катушке индуктивности
отстают от колебаний напряжения по времени на
четверть периода , а по фазе на
радиана.
ВЕКТОРНАЯ ДИАГРАММА при наличии в цепи
переменного тока только индуктивного сопротивления
Иными словами, когда напряжение в цепи переменного тока с
включенной катушкой индуктивности достигнет максимума,
ток не успеет достигнуть той величины, которой он достиг бы в
цепи без катушки индуктивности. Между напряжением U и
током I возникает сдвиг по фазе.
2.5. Закон Ома для переменного тока
Электрическая цепь состоит из последовательно соединенных
резистора, конденсатора и катушки.
К выводам цепи приложено напряжение, изменяющееся по
гармоническому закону с частотой ω и амплитудой Um.
В цепи возникнут вынужденные колебания силы тока с той
же частотой и некоторой амплитудой Im.
I= I ·sinωt
0
a
R
I
U
б
C
L
При
последовательном
соединении падения напряжения
на каждом из элементов цепи
СКЛАДЫВАЮТСЯ.
Напряжение
всей
цепи,
графическая
сумма
падения
напряжения на каждом элементе
цепи.
С учетом сдвига фаз между
UR,UC
и
UL
векторная
диаграмма будет иметь вид
При построении
векторной диаграммы
складываются
АМПЛИТУДНЫЕ
значения
напряжений!
ОТСЮДА
I0·ωL
U0р=I0·(ωL- 1/ωС)
φ
0
U0a=I0·R
I0/ωС
I
Таким образом,
полное напряжение
между концами
цепи а и б можно
рассматривать как
сумму двух
гармонических
колебаний:
напряжения U0а и
напряжения U0р,
U0а –активная составляющая напряжения
(совпадает с током по фазе)
U0р –реактивная составляющая напряжения
(отличается от силы тока по фазе на π/2)
Сумма Uа и Uр
U= U0·sin(ωt+φ).
Напряжения UR,UC и UL в сумме равны приложенному U. =>
Cложив векторы UR,UC и UL, получаем вектор, длиной U0
I0·ωL
U0p=I0·(ωL-1/ωC)
U0 φ
0
I0/ωС
U0a=I0·R
U0 I0
I
Амплитуду полного
напряжения можно найти
как модуль суммы
векторов:
1 2
R ( L
) I0 Z
C
2
Z — полное сопротивление цепи
или ИМПЕДАНС
Полный закон Ома
для переменного тока
Вектор U0 образует с осью токов угол φ, тангенс которого равен:
1
L
C
tg
R
Ua
X
R
I0
Up
1
Y
L
I0
C
– активное сопротивление цепи.
Активное сопротивление всегда
ПРИВОДИТ к выделению тепла
Джоуля-Ленца.
– реактивное сопротивление цепи.
Наличие реактивного сопротивления
НЕ СОПРОВОЖДАЕТСЯ выделением
тепла.
При наличии в цепи переменного тока
активного,
индуктивного
и
емкостного
сопротивлений
разность
фаз
между
колебаниями силы тока и напряжения равна ϕ
§4. Синусоидальные функции в
комплексной форме
Комплексное число м. б. в показательной или алгебраической
форме:
Где у комплексного числа:
с – модуль,
φ- аргумент;
a — вещественная часть,
b — мнимая часть,
j — мнимая единица, j = √-1.
Формула Эйлера — переход от
показательной к алгебраической.
От алгебраической
к показательной
КОМПЛЕКСНОЕ ЧИСЛО м. б.
представлено в виде вектора длина модуль C, под углом φ относительно
вещественной оси
Умножим комплексное число на множитель
Радиус – вектор повернется на угол β.
Если
, то вектор, умноженный на
превратится во вращающийся со скоростью ω радиус — вектор.
Синусоидальные функции времени могут быть представлены
векторами в комплексной плоскости, вращающимися против
часовой стрелки с постоянной угловой скоростью ω. Проекция
вектора на мнимую ось изменяется по синусоидальному закону.
3.1. Пример
§5. Мощность в цепи переменного
тока
Действующие значения напряжения и силы тока
фиксируются электроизмерительными приборами и позволяют
непосредственно вычислять мощность переменного тока .
Мощность в цепи ПЕРЕМЕННОГО ТОКА определяется
теми же соотношениями, что и мощность ПОСТОЯННОГО
ТОКА, в которые вместо силы постоянного тока и постоянного
напряжения — соответствующие ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ:
P U I
Когда между напряжением и силой тока СДВИГ ФАЗ, мощность
определяется по формуле:
P U I cos
1.Если в цепи переменного тока только АКТИВНОЕ
сопротивление, то выделяемая мощность максимальна.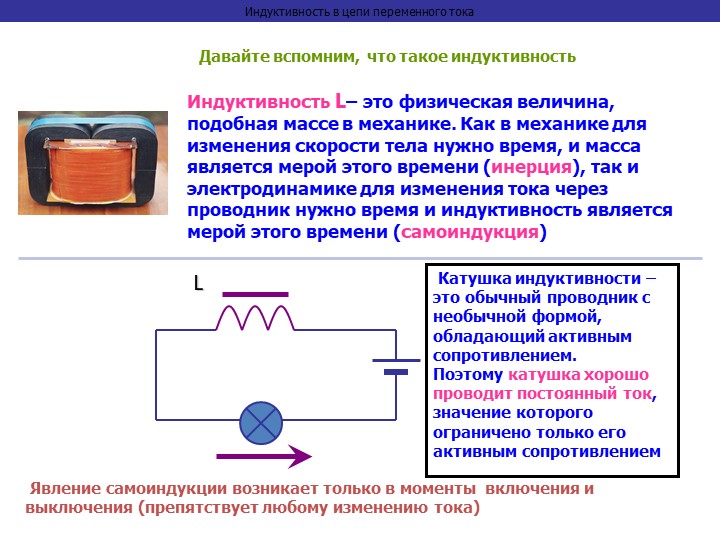
Активное сопротивление энергию из сети
полностью
превращает во внутреннюю, обратно в сеть не возвращается.
2.Если в цепи только
ЕМКОСТНОЕ сопротивление, то
конденсатор энергию, получаемую от сети, полностью
превращает в энергию электрического поля конденсатора,
затем эта энергия обратно полностью возвращается в сеть.
3.Если в цепи только ИНДУКТИВНОЕ сопротивление, катушка
индуктивности энергию, получаемую от
сети, полностью
превращает в энергию магнитного поля вокруг катушки, затем
эта энергия обратно полностью возвращается в сеть.
4.Если в цепи АКТИВНОЕ, ИНДУКТИВНОЕ, ЕМКОСТНОЕ
сопротивления — мощность (выделяемое тепло) максимальная.
Активное сопротивление часть энергии, получаемое от сети,
превращает во внутреннюю энергию, конденсатор и катушка
индуктивности энергию обратно возвращают в сеть.
МОЩНОСТЬ в цепи переменного тока
определяется теми же соотношениями,
что и мощность постоянного тока, в
которые ВМЕСТО силы постоянного
тока
и
постоянного
напряжения
подставляют
соответствующие
действующие значения.
§6. Резонанс
явление в электрической цепи,
содержащей индуктивные и емкостные элементы,
возникающее в случае, когда реактивное
сопротивление или реактивная проводимость этой
цепи равна нулю:
XL XC = 0
или
BC BL = 0
При резонансе цепь имеет место чисто активное сопротивление
или проводимость:
R j X X R
Z
L
C
Y G j BC BL G
Следовательно:
напряжение и ток в цепи совпадают по фазе,
реактивная мощность равна нулю.
Условие возникновения резонанса:
1
L
0
C
1
LC
0
То есть, резонанс возникает, когда частота внешнего
возмущения равна параметру цепи, называемому
РЕЗОНАНСНОЙ ЧАСТОТОЙ 0
Цепи, в которых используется эффект резонанса, называются
РЕЗОНАНСНЫМИ КОНТУРАМИ
Различают
ПОСЛЕДОВАТЕЛЬНЫЕ и ПАРАЛЛЕЛЬНЫЕ
резонансные контуры
6.1. В последовательном контуре
возникает резонанс НАПРЯЖЕНИЙ,
то есть, напряжение на емкости на резонансной частоте РАВНО
напряжению на индуктивности и противоположно по знаку:
1
0 LI
I I
0 C
1
L
0 L
0 C
C
где — ХАРАКТЕРИСТИЧЕСКОЕ СОПРОТИВЛЕНИЕ контура
Отношение величины электромагнитной энергии,
запасенной на реактивных элементах, к энергии,
рассеиваемой на активном сопротивлении контура,
называется
ДОБРОТНОСТЬЮ КОНТУРА
Для ПОСЛЕДОВАТЕЛЬНОГО контура
ДОБРОТНОСТЬ определяется:
Qпосл = /R
ЗАВИСИМОСТЬ модуля полного сопротивления от частоты
(последовательного контура):
6. 2. В параллельном контуре
2. В параллельном контуре
возникает резонанс токов, то есть, ток через емкость РАВЕН
току через индуктивность и противоположен по знаку (рис. б):
Параллельный резонансный контур (а) и векторная
диаграмма токов через его элементы (б)
Резонансная частота и характеристическое сопротивление
параллельного контура определяется также по формулам:
0
1
LC
0 L
1
L
0 C
C
Добротность параллельного контура:
Q пар R
Зависимость модуля
полного сопротивления
параллельного
резонансного контура от
частоты
Зависимость модуля полного сопротивления последовательного
и параллельного контуров от частоты:
Частотные характеристики
резонансных контуров
Цепь переменного тока: применение, типы и характеристики
Цепи переменного тока или цепи переменного тока — это просто цепи, питаемые от источника переменного тока либо тока, либо напряжения. Переменное напряжение или ток — это напряжение, в котором величина напряжения или тока изменяется примерно на определенное среднее значение и периодически меняет направление.
Большинство современных бытовых и промышленных систем и приборов питаются от переменного тока. Все устройства на основе перезаряжаемых аккумуляторов постоянного тока технически работают на основе переменного тока.Все устройства постоянного тока используют мощность постоянного тока, полученную от переменного тока, для зарядки своей системы питания и аккумуляторов.
Переменная цепь впервые была создана в 1980-х годах, когда Тесла стремился решить многочисленные проблемы с генераторами постоянного тока Томаса Эдисона. Он попытался представить способ передачи электричества при высоком напряжении. Затем, используя трансформаторы для повышения или понижения мощности при распределении, мы сможем свести к минимуму потери мощности на больших расстояниях, что в то время было главной проблемой Direct Current.
Постоянный ток и переменный ток (переменный и постоянный ток)
Переменный и постоянный ток во многом отличаются от передачи до генерации и распределения. Существенным отличием постоянного и переменного тока, которое также лежит в основе их разнообразных характеристик, является направление потока электричества. В системе постоянного тока электроны текут непрерывно в определенном направлении или вперед, но в системе переменного тока электроны меняют свое направление движения через периодические промежутки времени.Этот переменный ток также приводит к изменению значения напряжения, поскольку оно изменяется от отрицательного к положительному в соответствии с током.
Существенным отличием постоянного и переменного тока, которое также лежит в основе их разнообразных характеристик, является направление потока электричества. В системе постоянного тока электроны текут непрерывно в определенном направлении или вперед, но в системе переменного тока электроны меняют свое направление движения через периодические промежутки времени.Этот переменный ток также приводит к изменению значения напряжения, поскольку оно изменяется от отрицательного к положительному в соответствии с током.
Сравнение переменного и постоянного тока (Ссылка: Circuitdigest.com)
Что такое цепь переменного тока?
Электрические и электронные схемы включают множество различных соединительных компонентов, образующих замкнутую и законченную цепь. Основными пассивными компонентами, используемыми в любой схеме, являются конденсатор , резистор и индуктор .Все три названных пассивных компонента имеют одну общую черту; они ограничивают электрический ток в цепи, но совершенно по-разному.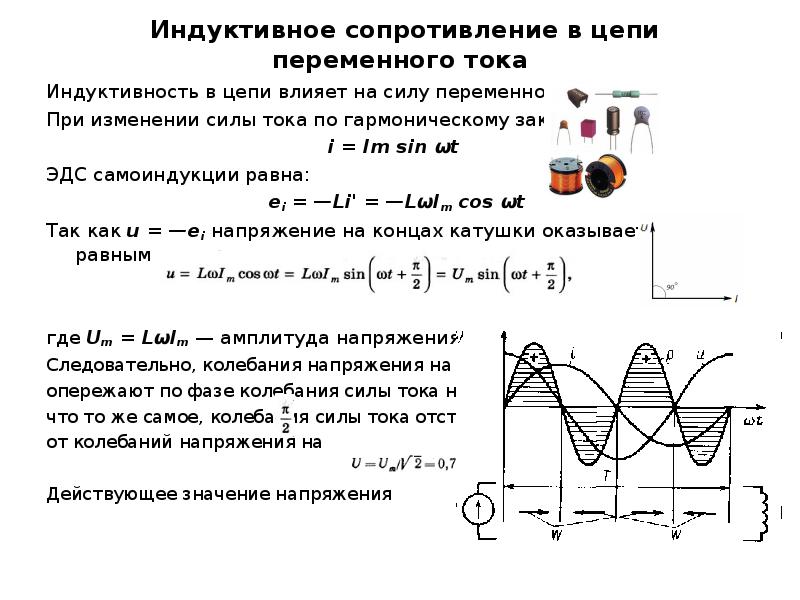
Электрический ток может проходить по цепи двумя путями. Если он проходит только в одном направлении, он называется постоянным током (DC). Если электрический ток чередуется в разных направлениях вперед и назад, он называется переменным током (AC). Поскольку они обеспечивают импеданс внутри цепи, пассивные компоненты в цепях переменного тока действуют совершенно иначе, чем в цепях постоянного тока.
Пассивные компоненты в цепи потребляют электроэнергию. Следовательно, они не могут усиливать или увеличивать мощность любых подаваемых на них электрических сигналов. Просто это все потому, что они пассивны и всегда будут иметь прирост меньше. Пассивные компоненты, помещенные в электрическую и электронную цепь, можно комбинировать в бесконечном количестве конструкций, как показано ниже, при этом характеристики этих цепей основаны на взаимодействии их различных электрических свойств.
Пример сложной цепи переменного тока (Ссылка: allaboutcircuits.com)
Что такое реагент и импеданс?
Типы цепей, в которых ток пропорционален напряжению, называются линейными цепями.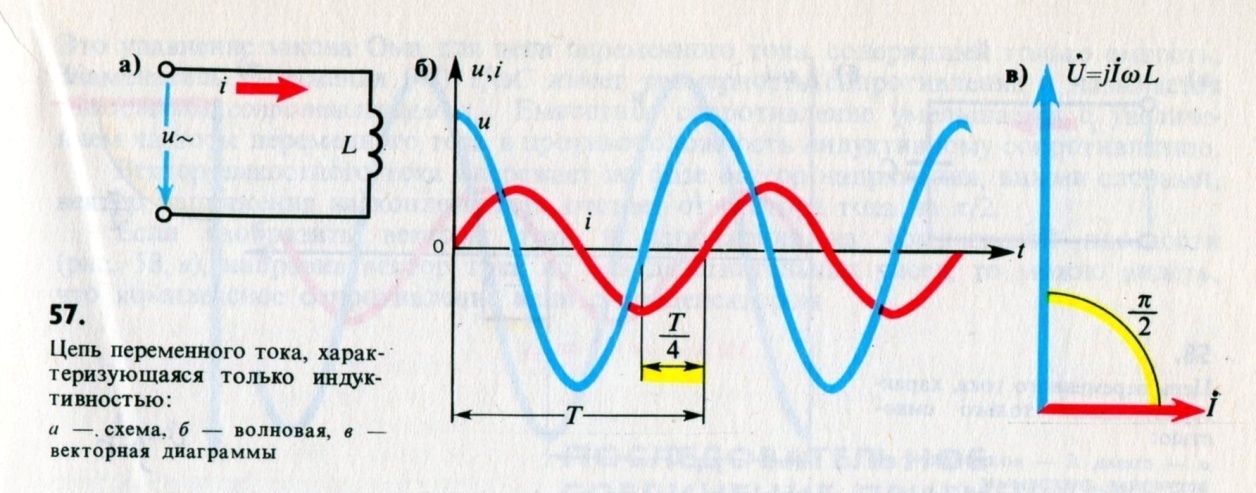 В резисторе отношение напряжения к току является его сопротивлением. Сопротивление не зависит от частоты и имеет две фазы. Тем не менее, схемы только с резисторами не очень интересны и применимы.
В резисторе отношение напряжения к току является его сопротивлением. Сопротивление не зависит от частоты и имеет две фазы. Тем не менее, схемы только с резисторами не очень интересны и применимы.
Как правило, частота не влияет на отношение напряжения к току, и имеется разность фаз.Таким образом, общее название отношения напряжения к току — импеданс. Символ импеданса Z. Сопротивление является частным случаем импеданса. Другой частный пример: ток и напряжение не совпадают по фазе на 90°; это важный случай, потому что при этом не происходит потери мощности в цепи. В этом случае, когда ток и напряжение не совпадают по фазе на 90°, мы называем реактивным сопротивлением отношение напряжения к току и обозначаем его буквой X.
Терминология
разница как напряжение.Мы будем рассматривать напряжения и токи как функцию, которая изменяется синусоидально во времени, и использовать строчные буквы i и v для тока и напряжения при явном анализе их изменения.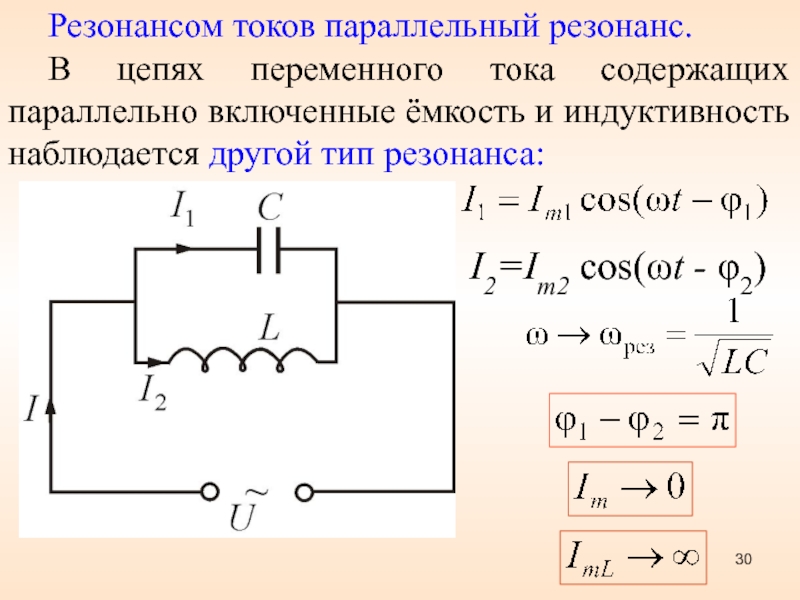 Мы будем представлять амплитуду или пиковое значение синусоидального изменения через Vm и I м , тогда как V = V м /√2 и I = I м /√2 без индексов относятся к их среднеквадратичные значения. Чтобы понять источник синусоидального изменения напряжения и то, как мы его используем, см. этот пост.
Мы будем представлять амплитуду или пиковое значение синусоидального изменения через Vm и I м , тогда как V = V м /√2 и I = I м /√2 без индексов относятся к их среднеквадратичные значения. Чтобы понять источник синусоидального изменения напряжения и то, как мы его используем, см. этот пост.
Напряжение и ток, которые мы используем в переменном токе, могут быть представлены в виде следующих уравнений: omega t +\varphi )
где:
\omega = 2πf = угловая частота
f = обыкновенная или циклическая частота = количество полных колебаний в секунду.
\varphi = разность фаз между напряжением и током. Синусоидальное напряжение и ток в цепи переменного тока (Справочник: учебники по электронике.ws)
Подробнее о Linquip
Пассивные компоненты в цепях переменного тока
Мы можем назвать R как сопротивление, C как 900,5 L как емкость и 900,50 как индуктивность. Независимо от того, используем ли мы резисторы в цепях постоянного или переменного тока, они всегда имеют одинаковое значение сопротивления в системе, независимо от частоты питания. Это все потому, что резисторы идентифицируются как чистые, имеющие паразитные характеристики, такие как нулевая индуктивность L = 0 и бесконечная емкость C = ∞.Кроме того, для полностью резистивной цепи у нас всегда есть синфазные напряжение и ток, поэтому мы можем найти потребляемую мощность в любой момент, умножив напряжение на ток.
Независимо от того, используем ли мы резисторы в цепях постоянного или переменного тока, они всегда имеют одинаковое значение сопротивления в системе, независимо от частоты питания. Это все потому, что резисторы идентифицируются как чистые, имеющие паразитные характеристики, такие как нулевая индуктивность L = 0 и бесконечная емкость C = ∞.Кроме того, для полностью резистивной цепи у нас всегда есть синфазные напряжение и ток, поэтому мы можем найти потребляемую мощность в любой момент, умножив напряжение на ток.
С другой стороны, конденсаторы и катушки индуктивности имеют особый тип сопротивления переменному току, известный как реактивное сопротивление , как упоминалось ранее (X L и X C ). Реактивное сопротивление также блокирует протекание тока, но значение реактивного сопротивления не является фиксированной величиной для одного конденсатора или катушки индуктивности по сравнению с резистором с фиксированным значением сопротивления.Величина реактивного сопротивления катушки индуктивности или конденсатора зависит от частоты питающего тока и значения постоянного тока самого элемента.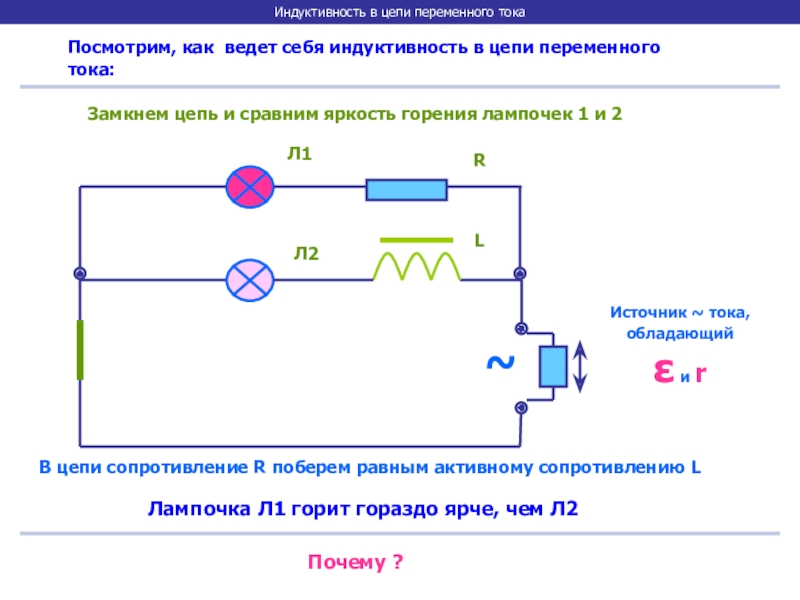
Кроме того, существует часто используемый список пассивных компонентов в цепях переменного тока и соответствующие им уравнения, которые можно применять для определения значения их импеданса и реактивного сопротивления тока цепи. Следует отметить, что здесь мы представили теоретически совершенную (чистую) катушку индуктивности или конденсатор, который не имеет никакого сопротивления. Но в реальном мире у нас всегда есть комбинация компонентов, упомянутых ранее, включая сопротивление.
Полностью резистивная цепь
Резисторы препятствуют, регулируют или задают протекание тока по определенному пути или вызывают отключение напряжения в электрической цепи на основе этого протекания тока. Резисторы имеют сопротивление, называемое , сопротивление (R). Резистивная величина резистора измеряется в Омах, Ом, и может быть найдена либо в фиксированном значении, либо в смещающемся значении (потенциометры).
Значение импеданса и тока можно найти с помощью следующих уравнений: \frac{V_S}{R}
Полностью емкостная цепь
Конденсатор — это компонент, обладающий емкостью и способный сохранять энергию в виде электрического заряда, как небольшая батарея. {\circ}=0-jX_C
{\circ}=0-jX_C
I_S= \frac{V_S}{X_S}
Полностью индуктивная цепь
к току, протекающему через катушку. Величина индуктивности катушки индуктивности измеряется в единицах Генри (Гн). В цепях постоянного тока катушка индуктивности является короткозамкнутой и имеет нулевое полное сопротивление. Напротив, на высоких частотах индуктор имеет бесконечный импеданс (разомкнутая цепь).{2}}
\следовательно, Z= X_C-X_L или X_L-X_C
Z=\угол (\phi _1+\phi _2)= 0 + jX_L-jX_C
f_r=\frac{1}{2\pi \sqrt{LC}}
I_S=I_L=I_C
Серийная LC-цепь (Ссылка: electronics-tutorials.ws)
Параллельные цепи переменного тока
Мы можем соединять пассивные компоненты вместе в последовательных комбинациях в цепях переменного тока для формирования Цепи RC, RL и LC, как описано ниже.
Параллельная RC-цепь
Принципиальная схема и уравнение для параллельной RC-цепи:
I_S=\sqrt{I_R^{2}+I_C^{2}}
\phi = tan^{-1}(\frac{I_C}{I_R})
Y= \frac{1}{ Z}=\sqrt{G^{2}+B_c^{2}}
V_S=V_C=V_R
Параллельная RC-цепочка (Ссылка: Electronics-tutorials. {2}}
{2}}
V_S=V_L=V_R
Параллельная цепь RL (Ссылка: electronics-tutorials.ws)
Параллельная цепь LC
Принципиальная схема и уравнение2 для параллельной цепи LC3 9000:
B_L=\frac{1}{X_L}, B_C=\frac{1}{X_C}
Y=\frac{1}{Z}=B_L+B_C
f_R=\frac{1} {2\pi \sqrt{LC}}
V_S=V_L=V_C
Параллельная LC-цепь (Ссылка: Electronics-tutorials.{2}}
f_R=\frac{1}{2\pi\sqrt{LC}}
V_S=V_C=V_R=V_L
Параллельная цепь RLC (Ссылка: electronics-tutorials.ws)
Имеет Как показано выше, в цепях переменного тока пассивные компоненты ведут себя совершенно иначе, чем при использовании в цепи постоянного тока из-за наличия частоты ( ƒ ). В полностью резистивной цепи ток и напряжение совпадают по фазе. В полностью емкостной цепи ток в конденсаторе составляет -90 o с напряжением, в то время как для полностью индуктивной цепи он составляет 90 o .
В последовательных цепях сумма векторов напряжений на компонентах цепи эквивалентна напряжению питания (V S ) . С другой стороны, в параллельной цепи сумма векторов протекающих токов в каждом элементе равна току питания (I S ).
Как для последовательного, так и для параллельного соединения цепей RLC резонанс возникает при XL = XC, когда ток источника «синфазен» с напряжением питания цепи. Последовательная резонансная цепь обозначается как приемная цепь , а параллельная резонансная цепь обозначается как отбрасывающая цепь .
Мощность в цепи переменного тока
В цепях постоянного тока мощность компонентов представляет собой произведение напряжения постоянного тока на ток в ваттах. Однако для цепи переменного тока с реактивными элементами приходится иначе оценивать потребляемую мощность.
Электрическая мощность — это энергия, потребляемая в цепи. Все электрические и электронные элементы и устройства имеют ограничение на количество электроэнергии, с которой они могут безопасно работать.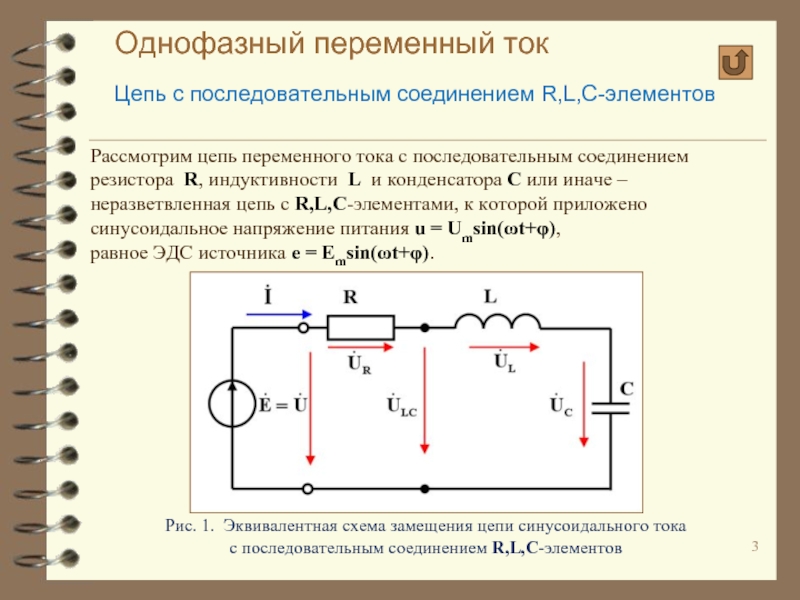 Например, у нас есть резистор на 1/4 Вт или усилитель на 20 Вт.
Например, у нас есть резистор на 1/4 Вт или усилитель на 20 Вт.
Количество энергии в цепях в любой момент называется мгновенной мощностью и известно известным соотношением мощности, равной амперам на вольты (P = VI). В результате один ватт будет равен результату вольт-ампер один вольт умноженный на один ампер (один ватт это скорость потребления энергии в один джоуль в секунду).
Таким образом, мощность, потребляемая или обеспечиваемая элементом схемы, представляет собой напряжение на элементе и ток, протекающий в нем. Предположим, у нас есть сопротивление «R» Ом в цепи постоянного тока.{2}}{R}
где:
В: напряжение постоянного тока
I: постоянный ток
R: значение сопротивления.
Электрическая мощность в цепи переменного тока
В цепях постоянного тока напряжения и токи постоянны и не изменяются со временем, поскольку нет функции синусоидальной формы сигнала, связанной с питанием. Напротив, мгновенные значения тока, напряжения и результирующей мощности в цепи переменного тока постоянно изменяются источником питания.Поэтому мы не можем рассчитать мощность в цепях переменного тока так же, как и предыдущим способом. Однако мы все еще можем предположить, что мощность равна амперам (i), умноженным на напряжение (v).
Напротив, мгновенные значения тока, напряжения и результирующей мощности в цепи переменного тока постоянно изменяются источником питания.Поэтому мы не можем рассчитать мощность в цепях переменного тока так же, как и предыдущим способом. Однако мы все еще можем предположить, что мощность равна амперам (i), умноженным на напряжение (v).
Еще одним важным моментом является то, что цепи переменного тока имеют реактивное сопротивление, поэтому компоненты создают магнитные и/или электрические поля. В отличие от чисто резистивного элемента, мощность выделяется, а затем возвращается обратно в цепь, когда синусоидальная форма волны проходит в одном полном периодическом цикле.
В результате средняя мощность, потребляемая цепью, представляет собой сумму запасенной и возвращенной энергии за один полный цикл.Средняя потребляемая мощность цепи — это средняя мгновенная мощность в течение одного полного цикла. Мгновенная мощность (p) может быть определена как произведение мгновенного напряжения (v) на мгновенный ток (i).
Предполагая синусоидальные формы напряжения и тока, мы имеем:
Синусоидальную форму волны напряжения (Ссылка: electronics-tutorials.ws)
P=v\times i
V=V_msin(\omega t+\phi _v)
i=I_msin(\omega t+\phi _i)
p= [V_msin(\omega t+\theta _v)\times I_msin(\omega t+\theta _i)]
\следовательно, V_mI_m(sin(\omega t+\ theta _i)\times sin(\omega t+\theta _v) )
Тригонометрическое произведение на сумму:
sin(A+B)=\frac{1}{2}[cos( AB)-cos(A+B)]
Где \theta =\theta _v-\theta _i , и, подставив в приведенное выше уравнение, мы получим:
p=\frac{V_mI_m}{2} )(cos(\theta)-cos(2\omega t+\theta))
\frac{V_mI_m}{2}=\frac{V_m}{\sqrt{2}}\times \frac{I_m}{\ sqrt{2}}=V_{RMS}\times I_{RMS}
, где V RMS и I RMS являются среднеквадратичными значениями t синусоидальные формы сигналов v и i , соответственно.Поэтому мы можем отобразить мгновенную мощность как:
P=VIcos\theta — cos(2\omega t+\theta ))
Это уравнение показывает нам, что мгновенная мощность переменного тока включает две разные части и представляет собой сумму из двух терминов. {2}Zcos\theta
{2}Zcos\theta
Купить оборудование или запросить услугу
поставщиков из разных отраслей и регионов.
Щелкните здесь, чтобы запросить коммерческое предложение от поставщиков и поставщиков услуг
Основные цепи переменного тока | Глава 2 — Анализ систем переменного тока
Мы начали эту главу с обсуждения мощности в цепях постоянного тока. Теперь мы подробно рассмотрим переменный ток, а также обсудим рассеивание мощности по отношению к переменному току, протекающему через чисто резистивную нагрузку.
Что такое переменный ток?
На первой странице этой главы мы видели, что «переменный ток» относится к току, который регулярно меняет направление, или к напряжению, которое регулярно меняет полярность.Напряжение и ток переменного тока обычно изменяются по синусоидальному закону:
Рис. 1. Синусоидальная волна, представляющая изменяющуюся амплитуду напряжения или тока переменного тока. При 0° и 180° значение синусоиды равно нулю. При углах 90° и 270° она достигает своего максимального абсолютного значения.
При 0° и 180° значение синусоиды равно нулю. При углах 90° и 270° она достигает своего максимального абсолютного значения.
Часть синусоидальной волны, в которой амплитуда начинается с заданного значения, меняет полярность и возвращается к исходному значению, называется одним циклом.Скорость, с которой синусоидальное напряжение или ток меняет полярность, может быть выражена в количестве циклов в секунду; это соответствует частоте и выражается в герцах (сокращенно Гц). В Соединенных Штатах электроэнергия распределяется в виде синусоидального напряжения, которое совершает 60 циклов в секунду, т. е. имеет частоту 60 Гц.
Радиан
Радиан — единица измерения углов в системе СИ. Допустим, у нас есть круг радиуса r и мы проводим дугу по окружности.Угол, соответствующий этой дуге, будет зависеть от длины дуги. Если мы нарисуем дугу, длина которой равна радиусу окружности, дуга образует (т. е. образует) угол в один радиан.
Рис.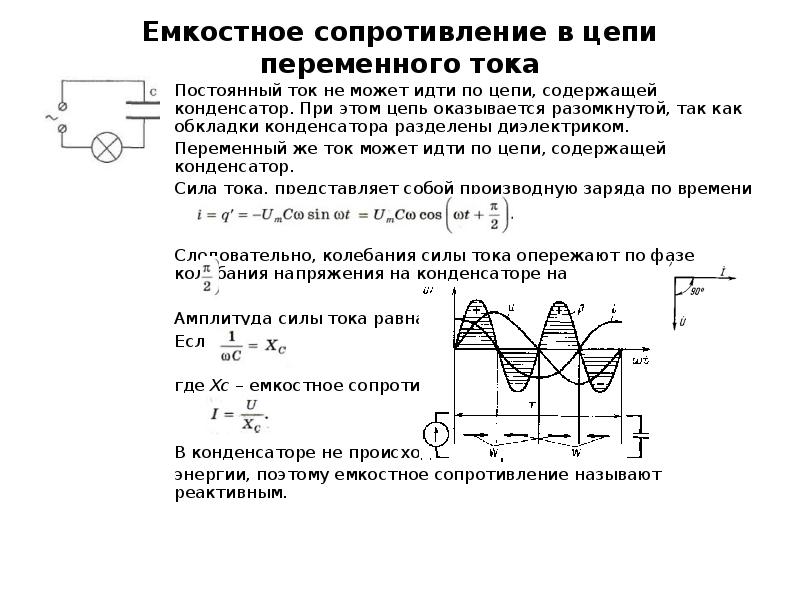 2. Радиан
2. Радиан
Чтобы понять преобразование радианов в градусы, обратите внимание на следующее: Длина окружности равна 2πr, а число градусов, соответствующее длине окружности, равно 360.Таким образом, если мы думаем в градусах, дуга длиной 2πr будет стягивать угол 360°, а дуга длиной r (которая равна 2πr/2π) будет стягивать угол 360°/2π. Таким образом, один радиан = 360°/2π ≈ 57,3°.
Когда мы работаем с углами в радианах, часто полезно использовать угловую частоту ; символ — ω, т. е. строчная омега (из греческого алфавита). Единицей нормальной частоты является число циклов в секунду. Один полный цикл равен 2π радианам, что означает, что частота одного цикла в секунду эквивалентна угловой частоте 2π радиан в секунду:
Мощность в цепях переменного тока
Если цепь переменного тока включает только резисторы (т.е., никаких катушек индуктивности или конденсаторов — о них подробнее позже), ток и напряжение всегда равны в фазе , а это означает, что их амплитуды изменяются идеально синхронно. Мы можем напрямую применить закон Ома к таким цепям, как эта: ток через резистор будет изменяться в соответствии с синусоидальной формой напряжения, но мгновенное значение тока всегда будет равно напряжению на резисторе, деленному на сопротивление.
Мы можем напрямую применить закон Ома к таким цепям, как эта: ток через резистор будет изменяться в соответствии с синусоидальной формой напряжения, но мгновенное значение тока всегда будет равно напряжению на резисторе, деленному на сопротивление.
Если мы прикладываем переменное напряжение к чисто резистивной нагрузке, напряжение и ток резистора по отношению ко времени можно выразить следующим образом:
На следующем графике показан синусоидальный ток и напряжение на резисторе.
Рис. 3. Синусоидальное напряжение и ток при резистивной нагрузке.
Выражение для мгновенной мощности, рассеиваемой резистором в цепи переменного тока, получается следующим образом:
Среднеквадратичное значение напряжения
Допустим, у вас есть цепь, состоящая из синусоидального источника питания 12 В и резистивной нагрузки. Когда мы говорим «двенадцать вольт» в этом контексте, мы имеем в виду максимальную амплитуду.Таким образом, если вы используете 12 В при расчете рассеиваемой мощности, результатом будет максимальная мгновенная рассеиваемая мощность.
Когда мы говорим «двенадцать вольт» в этом контексте, мы имеем в виду максимальную амплитуду.Таким образом, если вы используете 12 В при расчете рассеиваемой мощности, результатом будет максимальная мгновенная рассеиваемая мощность.
Если вы посмотрите на синусоиду на Рисунке 3, вы легко увидите, что большая часть формы волны имеет абсолютное значение, которое намного ниже максимума. Это означает, что средняя рассеиваемая мощность будет значительно ниже максимальной рассеиваемой мощности. Что нам нужно, так это способ сравнить напряжение переменного тока с эквивалентным напряжением постоянного тока — эквивалентным в том смысле, что средняя рассеиваемая мощность, создаваемая сигналом переменного тока, равна рассеиваемой мощности соответствующего значения постоянного тока.
Если вспомнить, что мощность пропорциональна квадрату напряжения, то неудивительно, что при расчетах средней мощности с использованием сигналов переменного тока используется среднеквадратичное значение (сокращенно RMS). Как следует из названия, эта величина получается путем нахождения квадратного корня из среднего квадрата значений данного сигнала.
Как следует из названия, эта величина получается путем нахождения квадратного корня из среднего квадрата значений данного сигнала.
Среднеквадратичное значение синусоидального сигнала переменного тока рассчитывается следующим образом:
Напряжение сети в Соединенных Штатах составляет примерно 115 VRMS, а это означает, что максимальное значение напряжения переменного тока в типичном домашнем хозяйстве составляет
.
Мощность в цепях переменного тока Обзор
Мы представили некоторые основные понятия, связанные с рассеиванием мощности в цепях с синусоидальными напряжениями и токами.
На следующей странице мы узнаем о двух основных компонентах, которые используются в бесчисленных электрических системах и электронных устройствах.
ЦЕПИ ПЕРЕМЕННОГО ТОКА
ЦЕПИ ПЕРЕМЕННОГО ТОКА
Ток от розетки 110 В является колебательной функцией времени. Этот тип
Этот тип
называется Переменный ток или Переменный ток . Источник
AC обозначается волнистой линией, заключенной в круг (см. рис. 34.1). То
временная зависимость переменного тока или ЭДС источника переменного тока имеет вид
(34.1)
где [эпсилон] max — максимальная амплитуда осциллирующей ЭДС
а [омега] – угловая частота.
Рисунок 34.1. Символ источника переменного тока.
На рис. 34.2 показана одноконтурная цепь с источником переменной ЭДС и
резистор. Ток через резистор будет функцией времени.То
величина этого тока может быть получена с помощью второго правила Кирхгофа, которое
подразумевает, что
(34.2)
Рисунок 32.2. Одноконтурная схема резистора переменного тока. Таким образом, ток I равен
.
(34.3)
Уравнение (34.3) показывает, что ток колеблется синфазно с ЭДС.
Мощность, рассеиваемая на резисторе, зависит от протекающего через него тока и
напряжение на резисторе и, следовательно, также является функцией времени:
(34. 4)
4)
Средняя мощность, рассеиваемая на резисторе за один цикл, равна
(34.5)
На последнем шаге вывода уравнения (34.5) мы использовали соотношение между
период Т и угловая частота омега (Т = 2пи/омега). Часто,
уравнение (34.5) записано через среднеквадратичное напряжение
[эпсилон] среднеквадратичное значение , которое определяется как
(34.6)
В терминах [эпсилон] среднеквадратичное значение мы можем переписать уравнение (34.5) как
(34.7)
Среднеквадратичное напряжение [эпсилон] действующее значение переменного тока
источник – это значение напряжения постоянного тока, которое рассеивает ту же мощность в
резистор как переменное напряжение с максимальным напряжением, равным
[эпсилон] макс . Бытовое напряжение 115 Вольт
среднеквадратичное напряжение; фактическое пиковое напряжение, выходящее из дома
розетка 163 В.
На рис. 34.3 показан конденсатор, подключенный к источнику переменной ЭДС. То
34.3 показан конденсатор, подключенный к источнику переменной ЭДС. То
Заряд на конденсаторе в любой момент можно получить, применив принцип Кирхгофа.
второе правило к схеме, показанной на рис. 34.3, и равно
(34.8)
Ток в цепи можно получить, продифференцировав уравнение (34.8) с
по времени
(34.9)
Рисунок 34.3. Цепь конденсатора переменного тока. Ток в цепи равен 90 град. не в фазе с ЭДС.
Поскольку максимумы тока возникают на четверть периода раньше максимумов тока
ЭДС, мы говорим, что ток опережает ЭДС.
Уравнение (34.9) принято переписывать как
(34.10)
где
(34.11)
называется емкостным реактивным сопротивлением . Обратите внимание, что уравнение (34.10) очень
аналогично уравнению(34.3) если сопротивление R заменить емкостным
реактивное сопротивление X C . Мощность, отдаваемая конденсатору, равна
(34.12)
Мощность колеблется между положительными и отрицательными крайними значениями и в среднем
равен нулю. Эти колебания соответствуют периодам, в течение которых ЭДС
Эти колебания соответствуют периодам, в течение которых ЭДС
источник обеспечивает питание аккумулятора (зарядку) и периоды, в течение которых
аккумулятор обеспечивает питание источника ЭДС (разрядка).
На рис. 34.4 показана цепь, состоящая из катушки индуктивности и источника
переменная эдс. ЭДС самоиндукции на катушке индуктивности равна LdI/dt.
Применяя второе правило Кирхгофа к схеме, показанной на рис. 34.4, получаем
следующее уравнение для dI/dt:
(34.13)
Рисунок 34.4. Цепь индуктивности переменного тока. Ток I можно получить из уравнения (34.13) путем интегрирования
по времени и требуя, чтобы величина постоянного тока
компонент равен нулю:
(34.14)
Ток снова 90 градусов. не в фазе с ЭДС, но на этот раз ЭДС
ведет ток. Уравнение (34.14) можно переписать как
(34.15)
где
(34.16)
называется индуктивным сопротивлением . Мощность, подаваемая на
индуктор равен
(34. 17)
17)
а средняя мощность, подводимая к индуктору, равна нулю.
Пример: Задача 34.10
Рассмотрим схему, показанную на рис. 34.5. ЭДС имеет вид
[эпсилон] 0 sin([omega]t). С точки зрения этой ЭДС и емкости
C и индуктивности L, найти мгновенные токи через конденсатор
и индуктор. Найдите мгновенный ток и мгновенную мощность
доставляется источником ЭДС.
Рисунок 34.5. Задача 34.10. Схема, показанная на рисунке 34.5 — простой многоконтурный
схема. Токи в этой цепи можно определить с помощью контура
техника. Рассмотрим две токовые петли I 1 и I 2 .
показано на рис. 34.5. Применяя второе правило Кирхгофа к петле номер 1, получаем
получить
(34.18)
Применяя второе правило Кирхгофа к петле номер 2, получаем
(34.19)
Уравнение (34.18) можно использовать для определения I 1 :
(34.20)
Уравнение (34.19) можно продифференцировать по времени, чтобы получить
я 2 :
(34. 21)
21)
Ток, отдаваемый источником ЭДС, равен сумме I 1 и
я 2
(34.22)
Мощность, отдаваемая источником ЭДС, равна
(34.23)
На рис. 34.6 показана одноконтурная цепь, состоящая из катушки индуктивности и
конденсатор.Предположим, что в момент времени t = 0 с конденсатор имеет заряд Q 0
а ток в цепи равен нулю. Ток в цепи
можно найти с помощью второго правила Кирхгофа, которое требует, чтобы
(34.24)
Рисунок 34.6. цепь ЛК. Текущий I(t) может быть получен из Q(t) путем дифференцирования Q
по времени:
(34.25)
Подставляя уравнение (34.25) в уравнение (34.24), получаем
(34.26)
или
(34.27)
Решение уравнения (34.27) равно
.
(34.28)
где [phi] — фазовая постоянная, которую необходимо отрегулировать, чтобы она соответствовала начальному
условия. Ток в цепи можно получить, подставив
Ток в цепи можно получить, подставив
уравнение (34.28) в уравнение (34.25):
(34.29)
Начальные условия для схемы, показанной на рис. 34.6, равны
.
(34.30)
(34.31)
Эти граничные условия выполняются, если [phi] = 0. В этом случае заряд
и ток в цепи LC
(34.32)
и
(34.33)
Энергия, накопленная в конденсаторе, является функцией времени, поскольку заряд на нем
является функцией времени. Запасенная энергия равна
(34.34)
Энергия, запасенная в катушке индуктивности, также зависит от времени, поскольку ток
через это является функцией времени. Запасенная энергия равна
(34.35)
Уравнение (34.34) и уравнение (34.35) показывают, что максимальная энергия запасается в
индуктивности, когда энергия, запасенная в конденсаторе, равна нулю, и наоборот. То
Полная энергия цепи может быть получена суммированием энергии, запасенной в
конденсатор и энергия, запасенная в катушке индуктивности:
(34. 36)
36)
Уравнение (34.36) показывает, что запасенная в цепи энергия сохраняется.
Этого можно ожидать, поскольку в контуре, в котором
ни один из элементов не имеет сопротивления.
На практике цепь, показанная на рис. 34.6, будет иметь некоторое сопротивление (даже
хорошие проводники будут иметь конечное сопротивление). Реалистичная схема LRC
показано на рис. 34.7. Применяя второе правило Кирхгофа к схеме, показанной на рис.
Рисунок 34.7 получаем
(34.37)
Поскольку ток I равен dQ/dt, мы можем переписать уравнение (34.37) как
(34.38)
Рисунок 34.7. Цепь ЛРК. Решение дифференциального уравнения, представленного в уравнении (34.38)
(34.39)
Константу [gamma] можно определить, подставив уравнение (34.39) в
уравнение (34.38):
(34.40)
Это уравнение должно выполняться всегда.Это будет только в том случае, если
члены в скобках равны нулю:
(34.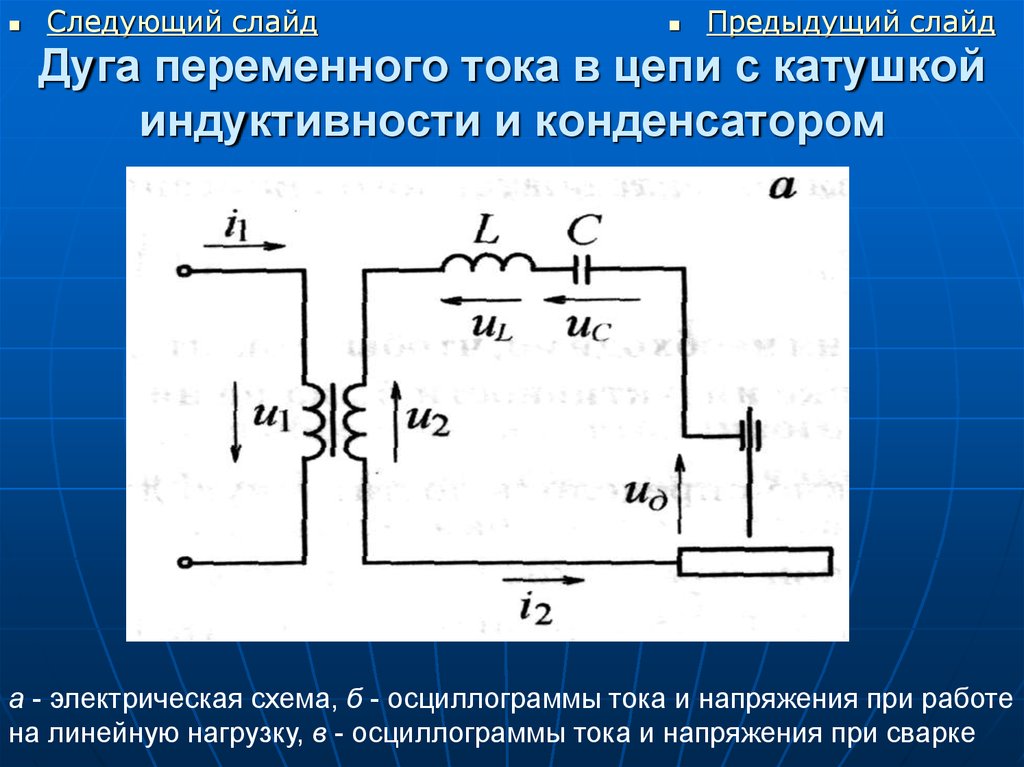 41)
41)
(34.42)
Константа [гамма] определяется уравнением (34.42)
(34.43)
Угловая частота [omega] может быть получена из уравнения (34.41) путем подстановки
уравнение (34.43) для [гамма]
(34.44)
Уравнение (34.39) показывает, что наличие резистора в цепи
производят затухающие гармонические движения.Постоянная затухания [gamma] пропорциональна
к сопротивлению R (см. формулу (34.43)). Изменение энергии системы
можно изучить, посмотрев на максимальный заряд конденсатора. В момент времени t =
0 с конденсатор полностью заряжен зарядом, равным Q 0 и
запасенная в конденсаторе энергия равна
(34.45)
После одного цикла (t = 2[pi]/[omega]) максимальный заряд конденсатора равен
уменьшилось. Это означает, что также энергия, запасенная в конденсаторе, имеет
уменьшилось
(34.46)
Поэтому относительное изменение электрической энергии системы равно
до
(34. 47)
47)
Потери электрической энергии в цепи LRC обычно выражают через
Q-значение качества»
(34.48)
Высокий коэффициент качества указывает на низкое сопротивление и, следовательно, небольшой
относительные потери энергии за цикл.
Рисунок 34.8. Управляемая схема LCR. В результате демпфирования в цепи LRC амплитуда
колебания будут постепенно уменьшаться.Для поддержания колебаний
в цепи LRC необходимо подавать энергию, например, путем подключения
колеблющийся источник ЭДС в цепи. Рассмотрим схему, показанную на рис.
34.8, состоящий из переменного источника ЭДС, резистора R, конденсатора С,
и индуктор L. Предположим, что ЭДС имеет угловую частоту [омега] и
максимальная амплитуда [эпсилон] макс :
(34.49)
Применение второго правила Кирхгофа к схеме, показанной на рисунке 34.8 производит
следующее отношение
(34.50)
В установившемся режиме ток в цепи будет колебаться с
той же угловой частоты [омега], что и источник ЭДС, но не обязательно в
фаза.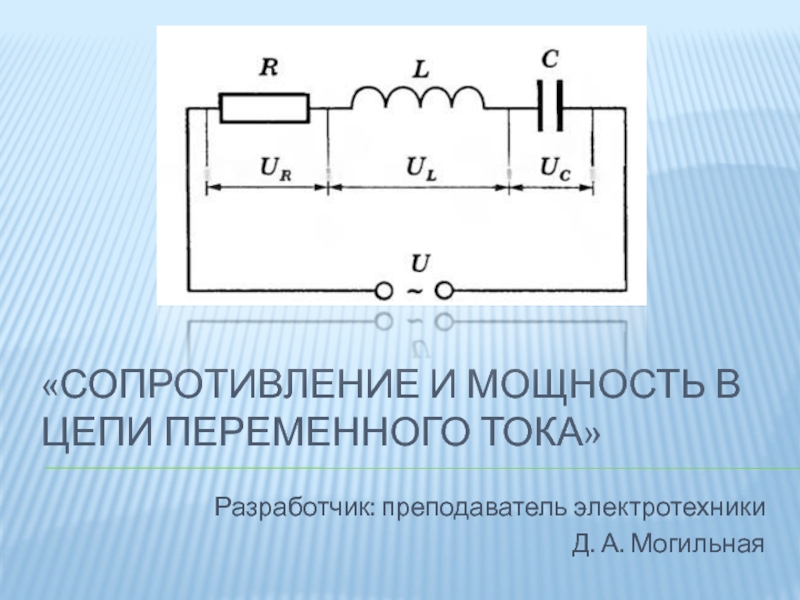 Таким образом, наиболее общее решение для тока
Таким образом, наиболее общее решение для тока
.
(34.51)
где [phi] называется фазовым углом между током и ЭДС. То
максимальный ток I max и фазовый угол [phi] можно определить по формуле
подставляя экв.(34.51) в уравнении (34.50):
(34.52)
Уравнение (34.52) можно переписать, используя тригонометрические тождества, как
(34.53)
Это уравнение может быть выполнено только в том случае, если выражения в скобках равны
равен нулю. Для этого необходимо, чтобы
(34.54)
и
(34.55)
Уравнение (34.55) можно использовать для определения фазового угла:
(34.56)
Уравнение (34.54) можно использовать для определения максимального тока:
(34.57)
Подставляя (34.56) в (34.57) получаем для максимального тока
(34.58)
Количество
(34.59)
называется импедансом цепи LCR.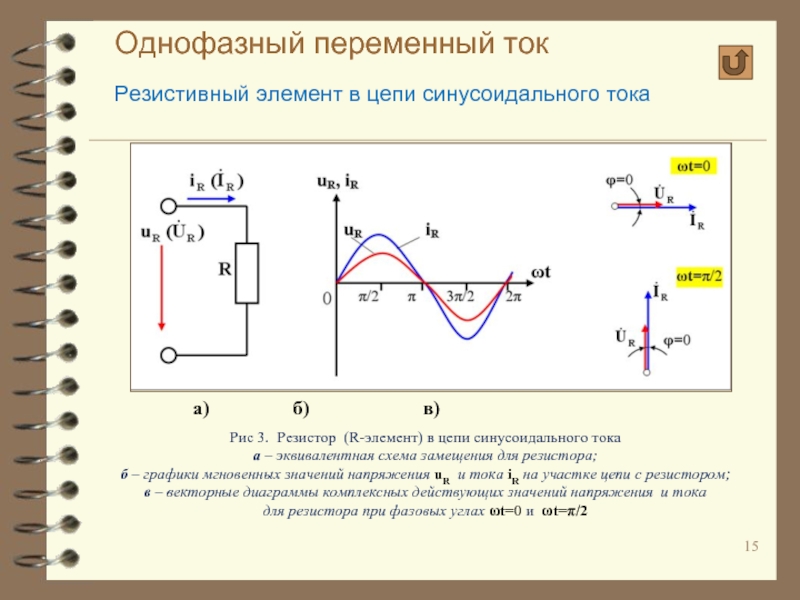
Уравнение (34.58) показывает, что максимальная амплитуда достигается, когда
(34.60)
Максимальная амплитуда тока
(34.61)
Система достигнет максимальной амплитуды, когда частота возбуждения [омега]
приложенной ЭДС равна
(34.62)
Эта частота является собственной частотой LC-контура, рассмотренного ранее.
Когда система приводится в движение с собственной частотой, говорят, что она находится в
резонанс.
Короткий путь, который можно использовать для определения амплитуды и фазы тока.
в цепи переменного тока есть векторная диаграмма.На векторной диаграмме амплитуда
Синусоидальная функция изображается отрезком, длина которого равна его
амплитуда. Фаза представлена углом между отрезком линии и
горизонтальная ось. Сумма падений напряжения на компонентах
тогда схема эквивалентна векторной сумме векторов. Чтобы проиллюстрировать
с помощью векторных диаграмм определяем амплитуду и фазу LCR-контура
только что обсудили. Приложенная ЭДС и индукционный ток определяются следующим образом:
Приложенная ЭДС и индукционный ток определяются следующим образом:
уравнения:
(34.63)
Напряжения на резисторе, конденсаторе и катушке индуктивности равны
(34.64)
Три вектора, соответствующие этим трем напряжениям, показаны на векторе
диаграмма на рис. 34.9. Падение напряжения на резисторе одинаково
фаза как ток. Также указана векторная сумма этих трех векторов
и должна быть равна приложенной ЭДС. Амплитуда векторной суммы
три вектора должны быть равны амплитуде приложенной ЭДС.Таким образом,
(34.65)
Фаза векторной суммы векторов на рис. 34.9 равна [omega]t,
и угол между током (и вектором, представляющим падение напряжения
через резистор), а векторная сумма векторов равна фазе
угол [фи]. Из рис. 34.9 видно, что
(34.66)
Рисунок 34.9. Схема вектора для схемы LCR.
Пример: Задача 34.26
Рассмотрим схему, показанную на рис. 34.10. Осциллирующий источник
ЭДС создает синусоидальную ЭДС с амплитудой 0,80 В и частотой 400 Гц.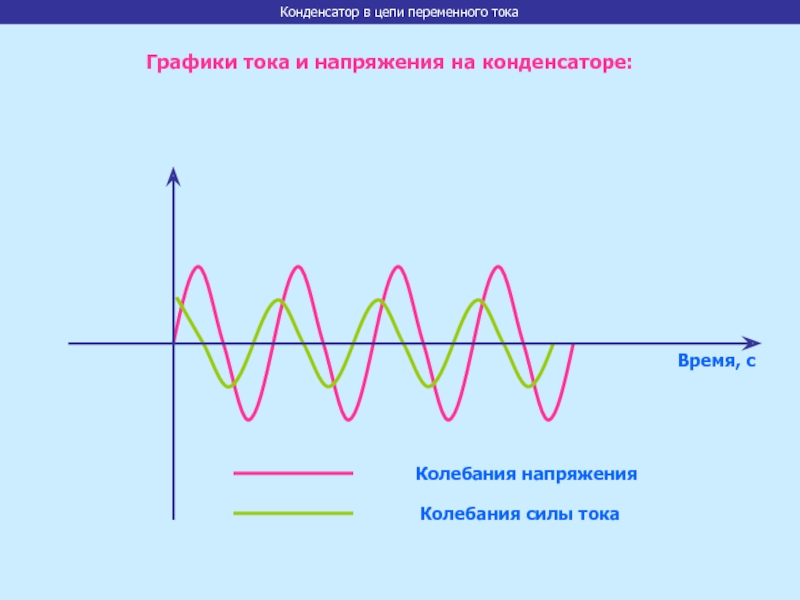 То
То
индуктивность 5,0 х 10 -2 Гн, а емкости 8,0 х
10 -7 F и 16,0 x 10 -7 F. Найдите максимальную мгновенную
ток в каждом конденсаторе.
Рассмотрим сначала два конденсатора. ЭДС на каждом конденсаторе должна
всегда быть одинаковым.Это означает, что
(34.67)
Рисунок 34.10. Задача 34.26. Переписав уравнение (34.67) через ток I 1
через конденсатор С 1 и ток I 2 через конденсатор
C 2 получаем
(34.68)
или
(34.69)
Уравнение (34.69) может быть верным всегда, только если подынтегральная функция равна
нуль.Для этого необходимо, чтобы
(34.70)
Для определения максимального тока в цепи используем вектор
только что обсуждалась техника. Рассмотрим векторную диаграмму, показанную на рис. 34.11.
Вектор, помеченный I, указывает ток в цепи. Напряжения на
катушка индуктивности и конденсатор сдвинуты по фазе на 90 градусов относительно тока и
обозначены на рис. 34.11 векторами, помеченными V L и
34.11 векторами, помеченными V L и
В С .Суммарное падение напряжения на элементах схемы (векторная сумма
V L и V C ) также на 90 градусов не совпадают по фазе с
ток. Так как общее падение напряжения на элементах цепи должно быть
равной приложенной ЭДС, заключаем, что фазовый угол между током
а ЭДС +/- 90 градусов. Знак зависит от значений индуктивности,
емкость и угловая частота ЭДС.
Рисунок 34.11. Векторная диаграмма для задачи 34.26. Величина векторной суммы напряжений на
катушка индуктивности и конденсатор должны быть равны по величине ЭДС. Таким образом,
(34.71)
Уравнение (34.71) можно использовать для определения максимального тока в цепи:
(34.72)
Емкость C, используемая в уравнении (34.72), представляет собой чистую емкость параллельного
сеть, состоящая из конденсатора C 1 и конденсатора C 2 (C =
С 1 + С 2 ). Сумма токов, протекающих через
Сумма токов, протекающих через
конденсаторов равен максимальному току в уравнении (34.73). Чтобы определить
ток через конденсатор C1 и конденсатор C2, мы можем объединить уравнение (34.72) и
уравнение (34,70). Таким образом, мы получаем
(34.73)
и
(34.74)
Пример: Задача 34.32
RC-цепь состоит из резистора с R = 0,80 [Омега] и
конденсатор с С=1.5 x 10 -4 F соединены последовательно с
колеблющийся источник ЭДС. Источник генерирует синусоидальную ЭДС с
e max = 0,40 В и угловая частота равна 9 x 10 3
рад/с. Найдите максимальную силу тока в цепи. Найдите фазовый угол
тока и нарисуйте векторную диаграмму с правильными длинами и углами для
фазоры. Найдите среднюю мощность рассеяния на резисторе.
Приложенная ЭДС и падение потенциала на элементах цепи в RC
цепи перечислены в ур.(34,75).
(34.75а)
(34.75б)
(34. 75с)
75с)
Векторы, представляющие падение напряжения на резисторе и на
конденсатора показаны на рис. 34.12. Векторная сумма этих векторов также
указано. Величина векторной суммы векторов должна быть равна
величина приложенной ЭДС. Таким образом,
(34.76)
Таким образом, максимальный ток равен
(34.77)
Рисунок 34.12. Векторная диаграмма для задачи 34.32. Фазовый угол [phi] можно легко рассчитать (см. рис.
34.12). Определяется
(34.78)
Трансформатор состоит из двух катушек, намотанных на железный сердечник (см.
34.13). Железный сердечник увеличивает силу магнитного поля в его
внутри на большую долю (до 5000) и, как следствие, силовые линии
должны концентрироваться в железе.Одна из катушек, первичная, подключена
к источнику переменной ЭДС.
ЭДС, индуцированная в первичной обмотке, связана со скоростью изменения
магнитный поток (закон индукции Фарадея):
(34. 79)
79)
Применяя второе правило Кирхгофа к первичной цепи, мы заключаем, что
ЭДС индукции в катушке должна быть равна приложенной ЭДС. Таким образом,
(34.80)
Рисунок 34.13. Трансформатор. Все силовые линии, проходящие через обмотку катушки 1, также будут
проходят через обмотку катушки 2. Поток через каждую обмотку первичной
Поэтому катушка равна потоку через каждую обмотку вторичной катушки.
Если первичная обмотка имеет витки N 1 , а вторичная обмотка имеет
N 2 обмотки , тогда общий поток через две катушки соотносится
(34.81)
или
(34.82)
Изменение вложенного потока первичной обмотки будет связано тем же
способ изменения потока во вторичной обмотке:
(34.83)
ЭДС, индуцированная во вторичной обмотке, может быть получена с помощью закона Фарадея.
и может быть выражено через ЭДС в первичной цепи:
(34.84)
Эта ЭДС доступна для различных нагрузок во вторичной цепи.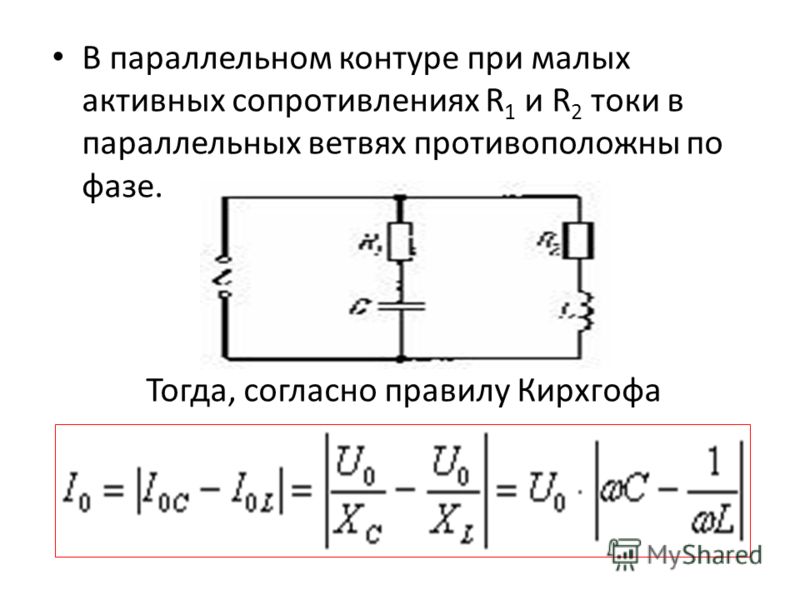
Если вторичная цепь разомкнута, то в ней не будет протекать ток, а первичная
цепь есть не что иное, как одноконтурная цепь с переменным источником
ЭДС и индуктор.Средняя мощность, рассеиваемая ЭДС в таком
цепь равна нулю, и, следовательно, трансформатор не потребляет электроэнергии.
власть.
Если вторичная цепь подключена к нагрузке, по ней будет течь ток. Этот
индукционный ток изменит магнитный поток в трансформаторе и вызовет
ток в первичной обмотке. Если это произойдет, первичный контур будет потреблять
власть. В идеальном конденсаторе мощность, отдаваемая источником ЭДС в
первичная цепь равна мощности, которую вторичная цепь отдает в свою
нагрузка.Таким образом,
(34.85)
Присылайте комментарии, вопросы и/или предложения по электронной почте [email protected] и/или посетите домашнюю страницу Фрэнка Вольфса.
Цепь переменного тока — обзор
II.E Емкость и индуктивность
Эти компоненты имеют значение только в цепях переменного тока. При постоянном токе емкость выглядит как разомкнутая цепь (за исключением небольшого тока утечки через сопротивление диэлектрика), а катушка индуктивности представляет собой небольшое сопротивление (сопротивление проводника катушки).Однако при подключении или отключении источника постоянного тока влияние емкости и индуктивности становится очевидным из-за изменения энергии, хранящейся в устройстве.
При постоянном токе емкость выглядит как разомкнутая цепь (за исключением небольшого тока утечки через сопротивление диэлектрика), а катушка индуктивности представляет собой небольшое сопротивление (сопротивление проводника катушки).Однако при подключении или отключении источника постоянного тока влияние емкости и индуктивности становится очевидным из-за изменения энергии, хранящейся в устройстве.
В цепях переменного тока на свойства катушек индуктивности и конденсаторов влияет частота, и хотя эти эффекты обычно не проявляются в конденсаторах до тех пор, пока не будут достигнуты частоты выше нескольких мегагерц, свойства индикаторов могут начать демонстрировать изменения при нескольких килогерцах. Поэтому при измерениях катушек индуктивности и конденсаторов уместно записывать частоту, на которой производилось измерение, и, если возможно, проводить измерения на предполагаемой рабочей частоте.Как и в случае измерения сопротивления, мостовые методы уже много лет широко используются для измерения как индуктивности, так и емкости.
При работе мостовой схемы необходимо учитывать как резистивную, так и реактивную составляющие неизвестного. Хотя небольшие конденсаторы, изготовленные с использованием современных диэлектрических материалов, представляют собой чистые реактивные сопротивления на низких и средних частотах, поскольку (параллельное) сопротивление утечки имеет очень высокое значение, 20 лет назад этого не было. Это также не относится к катушкам индуктивности или к конденсаторам большой емкости.Необходимость знать эти составные части привела к распространению мостовых схем на основе схемы Уитстона. Хорошо используемыми примерами мостов переменного тока являются мосты, приписываемые Максвеллу, Оуэну и Хевисайду для измерения индуктивности и Вейну, Де Соти и Шерингу для измерения емкости. Последний из них (рис. 37) все еще используется из-за его высоковольтных применений.
РИСУНОК 37. Схема моста Шеринга.
Альтернативой мостовым методам и подходящей для использования на частотах от 1 кГц до 300 МГц был измеритель Q , устройство, которое больше не фигурирует в каталогах производителей приборов, но, вероятно, все еще используется в некоторых местах, так как он способен измерять небольшие конденсаторы в широком диапазоне частот. Q компонента указывает на его качество и определяется как умноженное на 2π отношение накопленной энергии к энергии, потерянной за цикл. Численно это отношение реактивного сопротивления к сопротивлению на рассматриваемой частоте. Обратная величина Q (то есть 1/ Q ) представляет собой коэффициент рассеяния D , причем оба термина широко используются для обозначения качества катушек индуктивности и конденсаторов.
Q компонента указывает на его качество и определяется как умноженное на 2π отношение накопленной энергии к энергии, потерянной за цикл. Численно это отношение реактивного сопротивления к сопротивлению на рассматриваемой частоте. Обратная величина Q (то есть 1/ Q ) представляет собой коэффициент рассеяния D , причем оба термина широко используются для обозначения качества катушек индуктивности и конденсаторов.
Счетчик Q работает по принципу создания резонансного состояния между катушкой индуктивности и конденсатором.Фигура. 38 показана упрощенная схема Q метров, в которой резонанс может быть создан изменением частоты источника или регулировкой C q . В любом случае на резонанс указывает максимум напряжения E q на C q , когда
РИСУНОК 38. Q -метр, упрощенная схема.
EqEs=1ω0CR=ω0LR=QandQ=1D.
Навыки оператора, необходимые для выполнения надежных измерений с использованием мостовых схем и измерителя Q , были заметными, и современное стремление к цифровому отображению, доступность дешевой вычислительной мощности и повышение надежности электронных схем привели к замене этих приборы импедансом LCR или метров.В работе используется либо закон Ома, либо процесс отношения, последний по своей сути является более точным методом, но требует более сложного процесса переключения.
Базовая схема счетчика LCR показана на рис. 39, в котором ток известной частоты подается на неизвестное или «испытываемое устройство» (ИУ) при последовательном соединении с известным или эталонным сопротивлением . В пропорциональном режиме напряжение на эталоне ( В ref ), а затем на тестируемом устройстве ( В x ) по очереди подается на фазочувствительный детектор (PSD). ), так что можно определить синфазную и квадратурную составляющие обоих напряжений по отношению к опорному сигналу и подать их на аналого-цифровой преобразователь. Затем процессорное раздел содержит компоненты V Ref AS ( A + JB ) и те из V x AS ( C + JD ), из которого требуется параметры неизвестного могут быть оценены и отображены. Например, серия компонентов индуктора может быть отображена из Z x = Ref / V R x + jX ω L x или
Затем процессорное раздел содержит компоненты V Ref AS ( A + JB ) и те из V x AS ( C + JD ), из которого требуется параметры неизвестного могут быть оценены и отображены. Например, серия компонентов индуктора может быть отображена из Z x = Ref / V R x + jX ω L x или
РИСУНОК 39.Базовая схема счетчика LCR .
Rx=Rrefac+bda2+b2 и ωLx=ad-bca2+b2.
Должны ли необходимые параллельные компоненты конденсатора, то они могут быть получены от y x = V Ref / R Ref V x = G x — j ω C x , или
Rxp=Rrefc2+d2c+bdandωCx=ad
В дополнение к этим основным величинам счетчики LCR обычно способны отображать импеданс Z и его фазовый угол, активное и последовательное реактивное сопротивление, проводимость Y , проводимость, параллельную проводимость, Q и D .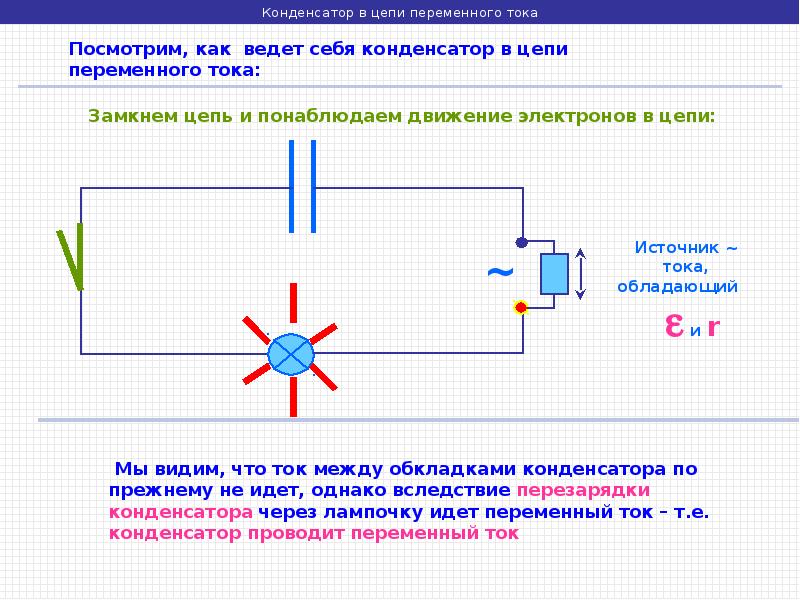
Цепь переменного тока — обзор
18.4 Краткий обзор решения проблем
Проблемы в цепи переменного тока самоидентифицируются. Наиболее распространенные цепи переменного тока управляются синусоидальной переменной ЭДС, Δ v = V sinω t , которую удобно представить вращающимся вектором длиной V , вращающимся с угловой скоростью ω.В таких цепях переменного тока компоненты R, L и C имеют мгновенные значения разности потенциалов Δ v R , Δ v L , и Δ v L , и Δ фаз V R , V L , и V C имеют разные фазовые отношения (фазовые углы) с соответствующими токами, I R , I L , и I C . В частности, δ V R V R и I R находятся в фазе, Δ V L LEDS I L на 90 °, а δ V C LAGS I C на 90°.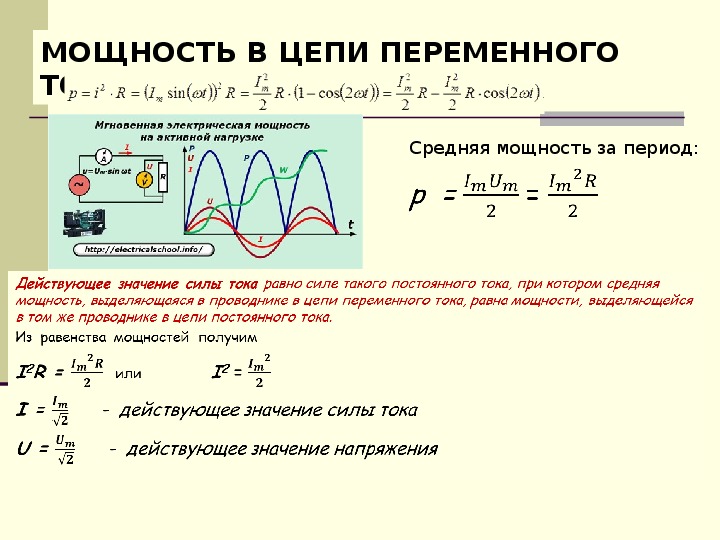
В цепи переменного тока реактивное сопротивление емкости C или индуктивности L является мерой способности этого компонента препятствовать прохождению заряда в этой цепи. Реактивное сопротивление зависит от частоты v переменного тока. Реактивное сопротивление X C емкости C равно 1/ω C = 1/2 (π vC ). Реактивное сопротивление X L индуктивности L равно ω L = 2π vL .Чистое реактивное сопротивление X цепи переменного тока определяется как X = X L – X C .
Мы начинаем анализ последовательной цепи переменного тока, комбинируя при необходимости аналогичные компоненты. Если эквивалентные компоненты находятся в цепи серии RLC , то в каждый компонент в любой момент времени поступает одинаковый ток. Поэтому удобно связать векторы компонентов схемы с текущим вектором I . В частности, вектор разности потенциалов В R = IR для сопротивления R находится в фазе с I , а вектор В R направлен в том же направлении, что и ток . вектор я .Разница потенциальных фазоров, V L = IX = IX L , для индуктивности L LEADS I на 90 ° и разница потенциал фазора, V C = IX C , для емкости отстает от I на 90°. Затем мы можем построить векторную диаграмму с I , нарисованную в произвольный момент времени t , так что I образует угол ω t с осью, соответствующей направлению I в t = 0.Затем, рисуя векторы V R , V L , и V C , в соответствующих направлениях, мы можем построить вектор разности потенциалов V 900.50 ЭДС.
В частности, вектор разности потенциалов В R = IR для сопротивления R находится в фазе с I , а вектор В R направлен в том же направлении, что и ток . вектор я .Разница потенциальных фазоров, V L = IX = IX L , для индуктивности L LEADS I на 90 ° и разница потенциал фазора, V C = IX C , для емкости отстает от I на 90°. Затем мы можем построить векторную диаграмму с I , нарисованную в произвольный момент времени t , так что I образует угол ω t с осью, соответствующей направлению I в t = 0.Затем, рисуя векторы V R , V L , и V C , в соответствующих направлениях, мы можем построить вектор разности потенциалов V 900.50 ЭДС.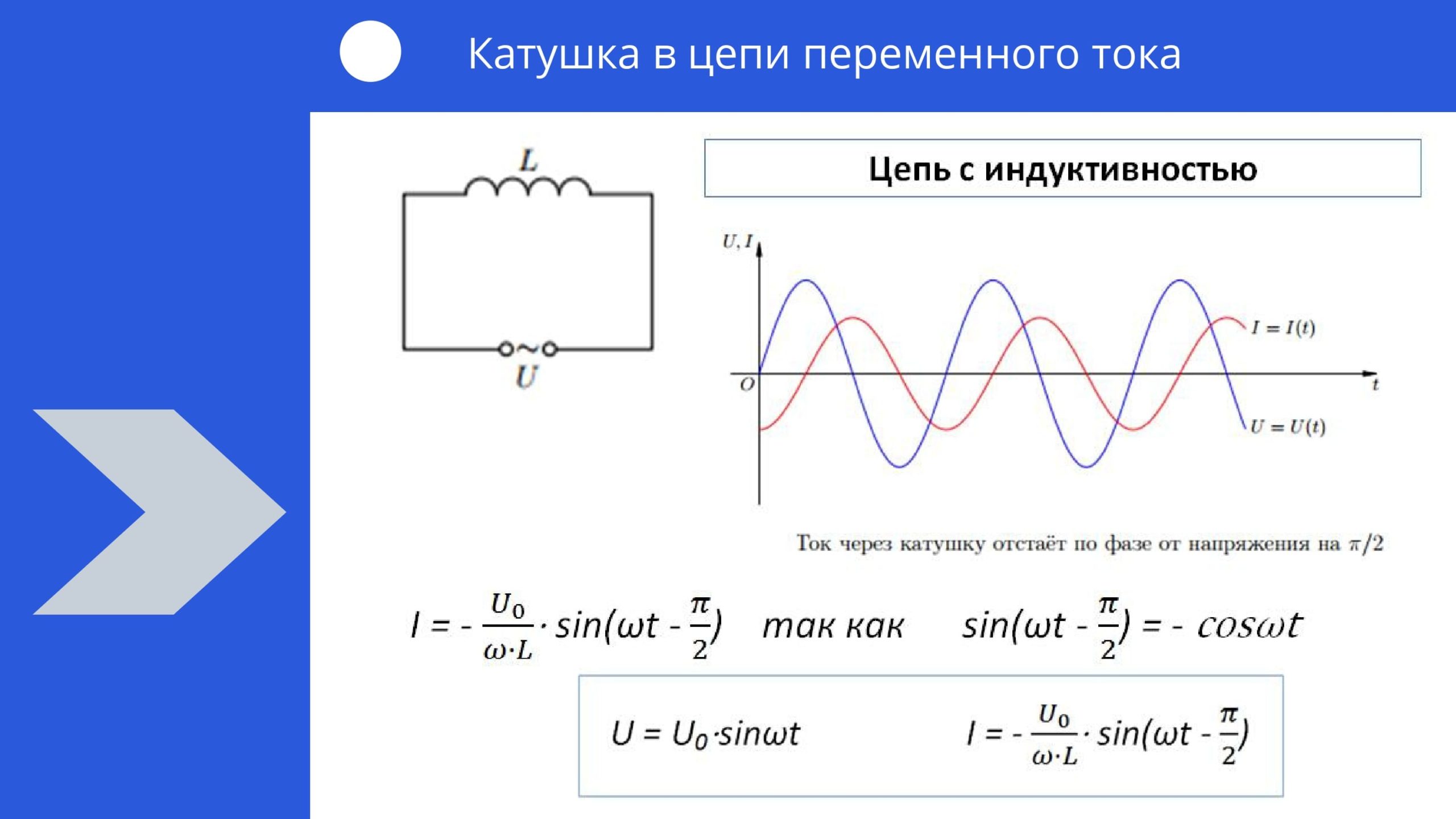 Величина и направление вектора V равны векторной сумме векторов V R , V L L , и 7
Величина и направление вектора V равны векторной сумме векторов V R , V L L , и 7
V
Фазовый угол ϕ между ЭДС и током в цепи представляет собой угол между векторами V и I , а величина ϕ определяется выражением ϕ = tan −1 ( X/R ).
Полное сопротивление Z = В/I цепи переменного тока играет ту же роль, что и сопротивление сети в цепи постоянного тока. Для данной последовательной цепи переменного тока импеданс Z=R2+(XL-XC)2 зависит от сопротивления и реактивного сопротивления цепи. Поскольку X L и X C зависят от частоты ЭДС, импеданс зависит от частоты. Частота, при которой импеданс минимален, называется резонансной частотой v o контура.Резонанс возникает, когда частота такова, что чистое реактивное сопротивление X L – X C , равно нулю, то есть когда X L = X C . Резонансная частота v o может быть выражена через индуктивность L и емкость C цепи как v o = 1/(2π√
Резонансная частота v o может быть выражена через индуктивность L и емкость C цепи как v o = 1/(2π√
0 LC ). На резонансной частоте ток в цепи переменного тока достигает наибольшей амплитуды.
Измерения мощности в цепях переменного тока удобно описывать в терминах среднеквадратичных (среднеквадратичных) значений ЭДС и тока. Используя V RMS RMS = V / √2 и I / √2 и I RMS = I / √2, мы можем выразить среднюю мощность P AV доставляется в цепь переменного тока на P av = В действующее значение I действующее значение cosϕ, где cosϕ называется коэффициентом мощности цепи. Снова ϕ является фазовым углом между вектором ЭДС В и текущим вектором I .Величина ϕ связана с чистым сопротивлением R и импедансом Z цепи переменного тока соотношением cosϕ = R/Z .
Электромагнитные (ЭМ) волны состоят из взаимно перпендикулярных электрических и магнитных полей, которые распространяются в свободном пространстве со скоростью света ( c = 3,0 × 10 8 м/с). Как электрическое поле E , так и магнитное поле B электромагнитной волны перпендикулярны направлению распространения волны.Направление распространения в каждой точке волны определяется как E × B . Вектор Пойнтинга S = (1/μ o ) E × B дает величину и направление энергии, переносимой электромагнитной волной через единицу площади в единицу времени. Таким образом, величина S представляет собой мощность, которую электромагнитная волна передает через единицу площади.
Длина волны электромагнитной волны λ — это расстояние между соседними максимумами электрического поля (или магнитного поля), измеренное вдоль направления распространения волны.Длина волны λ и частота v ЭМ волны в свободном пространстве связаны со скоростью распространения c соотношением c = v λ. Таким образом, указание длины волны электромагнитной волны, по сути, определяет ее частоту; точно так же, задав его частоту, мы получим его длину волны.
Таким образом, указание длины волны электромагнитной волны, по сути, определяет ее частоту; точно так же, задав его частоту, мы получим его длину волны.
Диапазон известных длин волн (или частот) электромагнитных волн называется электромагнитным спектром. Радио- и телевизионные волны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи и гамма-лучи составляют электромагнитный спектр.Хотя эти излучения производятся различными способами и очень по-разному взаимодействуют с веществом, существенное различие между этими электромагнитными излучениями заключается в их длине волны (или частоте).
Цепи переменного тока — Открытая библиотека учебников
Отзыв Дэвида Келли, доцента Университета Бакнелла, 06.03.19
Полнота
рейтинг:
2
видеть меньше
Книга, кажется, в основном представляет собой набор формул, иллюстрированных примерами, которые используют программное обеспечение для моделирования цепей Multisim. Важные уравнения и определения просто представлены как факты, которые необходимо принять, практически без каких-либо сопутствующих фундаментальных объяснений. Почти каждый пример представляет собой задачу «подключи и пыхни», подразумевая, что разработка — это просто поиск соответствующей формулы, а затем подстановка в нее значений для получения числового ответа. Нигде читателю не предлагается манипулировать переменными, чтобы получить символическое выражение или получить представление. Уровень аналитической сложности крайне низок.
Важные уравнения и определения просто представлены как факты, которые необходимо принять, практически без каких-либо сопутствующих фундаментальных объяснений. Почти каждый пример представляет собой задачу «подключи и пыхни», подразумевая, что разработка — это просто поиск соответствующей формулы, а затем подстановка в нее значений для получения числового ответа. Нигде читателю не предлагается манипулировать переменными, чтобы получить символическое выражение или получить представление. Уровень аналитической сложности крайне низок.
Практически нет доказательств или выводов каких-либо уравнений или определений, данных в книге.Это большой недостаток, так как студенты-инженеры должны практиковать этот навык, и в первую очередь они должны видеть его в своих учебниках.
Одним из примеров этого недостатка является обсуждение векторов в Модуле 2. Представлено много хороших примеров в отношении преобразования прямоугольной формы в полярную (и наоборот), сложения, вычитания, умножения, деления и приведения фазового угла к значение между -pi и +pi. Однако фундаментальная причина использования фазоров и их теоретическое обоснование вообще не представлены.Читателю просто безосновательно говорят, что вектора представляют собой синусоидальные функции. Таким образом, они остаются загадкой.
Однако фундаментальная причина использования фазоров и их теоретическое обоснование вообще не представлены.Читателю просто безосновательно говорят, что вектора представляют собой синусоидальные функции. Таким образом, они остаются загадкой.
В качестве другого примера, в гл. 3.4 (Расчет мощности переменного тока), понятие коэффициента мощности резко определяется как косинус фазового угла импеданса. Нет вводного обсуждения его значения или того, как его использование возникло исторически. При этом полностью игнорируется значение силового треугольника и его использование энергетиками. В конце разд.3.4, наконец, есть несколько предложений, которые объясняют, что энергетические компании пытаются приблизить значение коэффициента мощности к 1, но нет объяснения, почему.
Ярким примером отсутствия строгости является гл. 6.4 (Выпрямители). Формула, связывающая напряжение пульсаций со значением конденсатора фильтра, представлена полностью без вывода. Это упускает прекрасную возможность развить некоторую интуицию о том, как на самом деле работают конденсаторы фильтра.
Анализ переходных процессов не обсуждается; основное внимание уделяется синусоидальному анализу установившегося состояния.Индекса нет.
Точность содержания
рейтинг:
3
Книга в основном точна, но есть несколько пунктов, которые как минимум вводят в заблуждение, а в некоторых случаях и вовсе не соответствуют действительности. Большое их количество само по себе проблематично.
Утверждение (или его вариация) имеет несколько проявлений: «Хорошо думать о сигнале постоянного тока как о сигнале, который можно получить, заморозив время в сигнале переменного тока и взглянув на мгновенные значения напряжения или тока в этот момент. указанное время.Это заблуждение, а в некоторых случаях и неправильное. Это, конечно, неверно в случае катушки индуктивности или конденсатора.
На стр. 10 появляется фраза «плотность спектра мощности»; это должна быть «спектральная плотность мощности». Кроме того, PSD *не* является графиком зависимости частоты от времени.
В примере 3.9 (начиная со стр. 48) читателя ошибочно просят добавить компонент, чтобы «устранить кажущуюся мощность и получить коэффициент мощности, равный 1». Добавление конденсатора устраняет реактивную мощность, а не полную мощность.Будем надеяться, что это всего лишь ошибка по невнимательности, а не истинное непонимание кажущейся силы.
48) читателя ошибочно просят добавить компонент, чтобы «устранить кажущуюся мощность и получить коэффициент мощности, равный 1». Добавление конденсатора устраняет реактивную мощность, а не полную мощность.Будем надеяться, что это всего лишь ошибка по невнимательности, а не истинное непонимание кажущейся силы.
На стр. 52 утверждение о том, что «системы передачи и распределения электроэнергии являются [так в оригинале] наиболее важным применением цепей RLC», в лучшем случае сомнительно и, вероятно, явно ошибочно. В первом предложении Модуля 4 есть частичное исправление («фильтрация — это второе место» — но это, вероятно, № 1), но утверждение полностью игнорирует широкое использование цепей RLC в беспроводных устройствах и его фундаментальное использование в теории линии передачи.На стр. 53 подразумевается, что активные фильтры изготавливаются только с операционными усилителями. Их можно сделать и на дискретных транзисторах.
В Модуле 6 кремниевые диоды часто ошибочно называют «силиконовыми».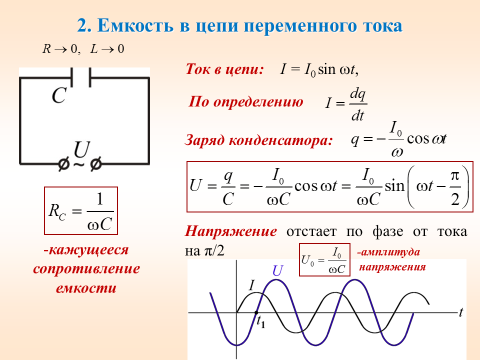 Уравнение диода вообще не представлено, и предполагается, что все диоды работают в модели постоянного напряжения. В положительном плане гл. 6.3 дает краткое описание защитных диодов, используемых с индуктивными нагрузками. Он не очень всеобъемлющий, но, по крайней мере, он присутствует; многие учебники не включают это важное приложение.
Уравнение диода вообще не представлено, и предполагается, что все диоды работают в модели постоянного напряжения. В положительном плане гл. 6.3 дает краткое описание защитных диодов, используемых с индуктивными нагрузками. Он не очень всеобъемлющий, но, по крайней мере, он присутствует; многие учебники не включают это важное приложение.
Актуальность/долговечность
рейтинг:
3
Книга охватывает материалы, которые останутся в основном неизменными, но, тем не менее, жизненно важны для инженеров-электриков и программистов, которые необходимо знать в ближайшие десятилетия. При этом в книге есть одно серьезное и одно незначительное отклонение от общепринятых стандартов.
Одним из самых серьезных недостатков книги является использование синусоидального соглашения ([например, v(t) = 170 sin(w*t + theta)] для выражения синусоидальных напряжений и токов вместо косинусного соглашения.Последнее соглашение является стандартом IEEE и используется почти во всех других современных учебниках по теории схем. Одна только эта проблема, вероятно, помешала бы мне использовать эту книгу на одном из моих курсов или рекомендовать ее другим.
Одна только эта проблема, вероятно, помешала бы мне использовать эту книгу на одном из моих курсов или рекомендовать ее другим.
Еще одним отклонением от стандартов является форма уравнений для индуктивного и емкостного реактивного сопротивления. В книге используются формулы L*w и -1/C*w (где «w» — частота в радианах) вместо стандартных w*L и -1/w*C соответственно. Это незначительная гнида, но это возможный источник путаницы для читателей, плохо знакомых с материалом, которые могут обращаться к другим ссылкам, в которых эти формулы представлены в стандартной форме.
Ясность
рейтинг:
4
Автор часто забывает, что читатель не знаком с материалом близко. В качестве примера можно привести два случая — ссылки на выборку на с. 10 и сбивающая с толку подпись к рис. 1.10 на с. 14. В подписи не сразу понятно, что фраза «сверху вниз» относится к меткам в правой части изображения экрана осциллографа. Хотя опытный читатель должен разобраться довольно быстро, я подозреваю, что новый студент будет в полной растерянности. На стр. 19 (и во многих других местах) автор признает, что пробная функция Multisim иногда выдает незначительные ошибки, но не объясняет, почему и, что более важно, ставит ли это под сомнение целесообразность использования Multisim в качестве основы для примеров. Такого рода необъяснимые ошибки могут только посеять путаницу у читателей, плохо знакомых с материалом.
На стр. 19 (и во многих других местах) автор признает, что пробная функция Multisim иногда выдает незначительные ошибки, но не объясняет, почему и, что более важно, ставит ли это под сомнение целесообразность использования Multisim в качестве основы для примеров. Такого рода необъяснимые ошибки могут только посеять путаницу у читателей, плохо знакомых с материалом.
При обсуждении рис. 3.3 (стр. 35) автор ссылается на функцию Multisim «фиксация тока». Опять же, токовый зажим не полностью объяснен.
Последовательность
рейтинг:
5
Текст в целом согласован, за исключением нескольких моментов, уже рассмотренных выше.
Модульность
рейтинг:
5
Книга четко разделена на семь модулей, и каждый модуль имеет четко обозначенные подразделы.
Организация/Структура/Поток
рейтинг:
3
Многочисленные ссылки на Multisim и его возможности предполагают знакомство с электронной книгой автора DC Circuits или хотя бы с Multisim. Хотя автор заявляет об этом в предисловии, тем не менее это ограничивает полезность книги для студентов, которые использовали другой учебник при изучении цепей постоянного тока и/или не использовали или не имеют доступа к Multisim. Уравнения часто не представлены в стандартном формате. Например, умножение обозначается точкой в центре. Общепринятая текущая практика заключается в простом написании переменных и функций рядом друг с другом для обозначения умножения. Центральную точку можно спутать с векторным скалярным произведением.
Уравнения часто не представлены в стандартном формате. Например, умножение обозначается точкой в центре. Общепринятая текущая практика заключается в простом написании переменных и функций рядом друг с другом для обозначения умножения. Центральную точку можно спутать с векторным скалярным произведением.
Не соблюдаются многие основные правила подготовки рисунков и подписей профессионального качества. Например, на рис. 1.6 (стр. 11) единицы измерения по оси частот не указаны, а подписи к рис.1.17 (стр. 20) и рис. 1.18 и 1.19 (стр. 21) неправильно используют заглавные буквы.
В окончательных ответах многих примеров отсутствуют единицы измерения.
Я обнаружил, что использование цветных шрифтов для выделения терминов, пошаговых инструкций и других элементов утомительно и немного снисходительно. Это дешевый способ оживить технический текст. Тем не менее, я полагаю, что некоторым читателям будет полезно найти важные элементы.
Интерфейс
рейтинг:
3
Обильное использование ссылок на разные части книги, как правило, полезно, но в некоторых случаях излишне, особенно для уравнений и рисунков, находящихся на той же странице, что и ссылка (или на следующей странице). Это несколько отвлекает, потому что ссылки выделены цветным шрифтом. Каждая страница испещрена ссылками, что приводит к перегруженности. По этой причине я нашел книгу утомительной для чтения.
Это несколько отвлекает, потому что ссылки выделены цветным шрифтом. Каждая страница испещрена ссылками, что приводит к перегруженности. По этой причине я нашел книгу утомительной для чтения.
Во многих случаях на рисунках и диаграммах текст слишком мал для чтения. Во многих случаях необходимо увеличение до 200%. Примерами этого являются рис. 1.2 (стр. 6) и снимок экрана, сопровождающий пример 1.5 (стр. 20). Есть также много страниц, на которых слишком много изображений, диаграмм, текста в рамках и/или цветного текста и других элементов, собранных в одном месте.Многие элементы настолько уменьшены в размерах, что их функции и текст невозможно прочитать без увеличения. Скученность часто бывает настолько сильной, что становится смешной. Я могу представить нового читателя, ошеломленного таким типом презентации. Примеры этой проблемы включают рис. 1.14 (стр. 18), все с. 42 и все с. 47. В последнем случае (с. 47) в подписи почти не объяснены столбцы цифр, занимающие доминирующее положение в левой половине страницы. Сомневаюсь, что большинство читателей, плохо знакомых с материалом, смогут его понять.На стр. 32 ссылка на Приложение ведет на гл. вместо 7.3.
Сомневаюсь, что большинство читателей, плохо знакомых с материалом, смогут его понять.На стр. 32 ссылка на Приложение ведет на гл. вместо 7.3.
Грамматические ошибки
рейтинг:
3
В книге присутствует большое количество грамматических ошибок, которые свидетельствуют о том, что либо практически не предпринимались усилия по корректировке, либо, возможно, автор просто не знал о них. Многие читатели могут не заметить их или быть обеспокоенными ими, но с растущим осознанием необходимости эффективного общения инженеров учебники должны служить хорошим примером.
Некоторые проблемы, которые появляются в нескольких местах, включают:
1.Слова необъяснимо написаны с заглавной буквы, когда они не должны быть.
2. Путаница в использовании слов «постоянно» и «постоянно».
3. Фраза «решить схему» (или аналогичная) встречается во многих местах. «Контуры» не разгадываются; уравнения и/или задачи.
4. Количество представлено цифрами, а не прописано (например, на стр. 5 «5» должно быть «пять»).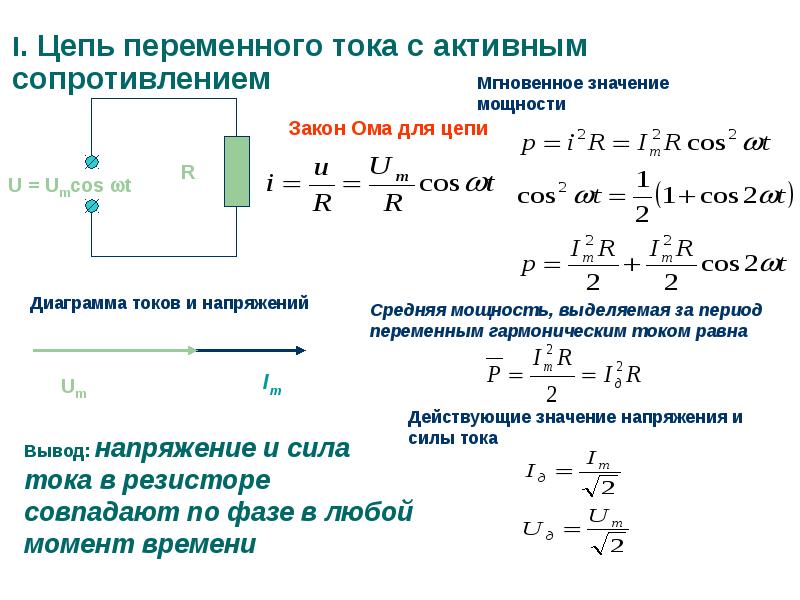
5. Неправильные времена глаголов.
Культурная значимость
рейтинг:
4
Культурных отсылок нет вообще.На самом деле это недостаток. Добавление обсуждений реальных приложений значительно улучшает любой учебник.
Комментарии
Приложение плохо организовано, поскольку в нем отсутствуют заголовки для примеров графика Боде. Также отсутствует вводный абзац, поясняющий структуру приложения. Книга страдает отсутствием каких-либо реальных примеров. Как и во многих других учебниках, во многих примерах используются нереально большие или маленькие значения компонентов.
15: Цепи переменного тока — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
Без заголовков
В этой главе мы используем законы Кирхгофа для анализа четырех простых цепей, в которых протекает переменный ток.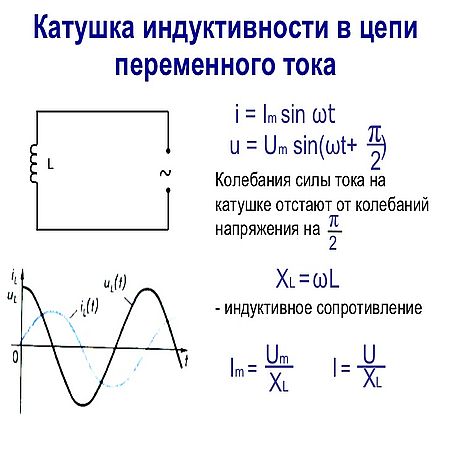 Мы обсудили использование резистора, конденсатора и катушки индуктивности в цепях с батареями. Эти компоненты также являются частью цепей переменного тока. Однако, поскольку требуется переменный ток, постоянный источник ЭДС, обеспечиваемый батареей, заменяется источником переменного напряжения, который создает колебательную ЭДС.
Мы обсудили использование резистора, конденсатора и катушки индуктивности в цепях с батареями. Эти компоненты также являются частью цепей переменного тока. Однако, поскольку требуется переменный ток, постоянный источник ЭДС, обеспечиваемый батареей, заменяется источником переменного напряжения, который создает колебательную ЭДС.
- 15.1: Прелюдия к цепям переменного тока
- Электроэнергия доставляется в наши дома переменным током (ac) по высоковольтным линиям электропередач.Как объяснялось в разделе «Трансформаторы», трансформаторы могут затем изменить амплитуду переменной разности потенциалов в более полезную форму. Это позволяет нам передавать электроэнергию при очень высоком напряжении, минимизируя тепловые потери в линиях, а затем поставлять эту электроэнергию в дома при более низком и более безопасном напряжении.
- 15.2: Источники переменного тока
- Большинство примеров, рассмотренных до сих пор в этой книге, особенно те, которые используют батареи, имеют источники постоянного напряжения.
 Таким образом, как только ток установлен, он является постоянным.Постоянный ток (dc) — это поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения.
Таким образом, как только ток установлен, он является постоянным.Постоянный ток (dc) — это поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения.
- 15.3: Простые цепи переменного тока
- В этом разделе мы изучаем простые модели источников переменного напряжения, подключенных к трем компонентам цепи: (1) резистору, (2) конденсатору и (3) катушке индуктивности.
- 15.4: Цепи серии RLC с переменным током
- Цепь серии RLC представляет собой последовательную комбинацию резистора, конденсатора и катушки индуктивности, подключенных к источнику переменного тока.
- 15.5: Мощность в цепи переменного тока
- Элемент цепи рассеивает или производит мощность в соответствии с P=IVP=IV , где I — ток через элемент, а V — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени.

- 15.6: Резонанс в цепи переменного тока
- В последовательной цепи RLC имеется резонансная частота, при которой индуктивное сопротивление равно емкостному сопротивлению.График зависимости средней мощности от угловой частоты для цепи RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика известна как ширина полосы. Полоса пропускания связана с безразмерной величиной, называемой добротностью. Высокое значение добротности – это острый или узкий пик.
- 15.7: Трансформаторы
- Устройство, преобразующее напряжение из одного значения в другое с помощью индукции, называется трансформатором. Трансформатор в основном состоит из двух отдельных катушек или обмоток, намотанных на сердечник из мягкого железа.
- 15.A: чередующиеся схемы (ответы)
- 15.

- 15.

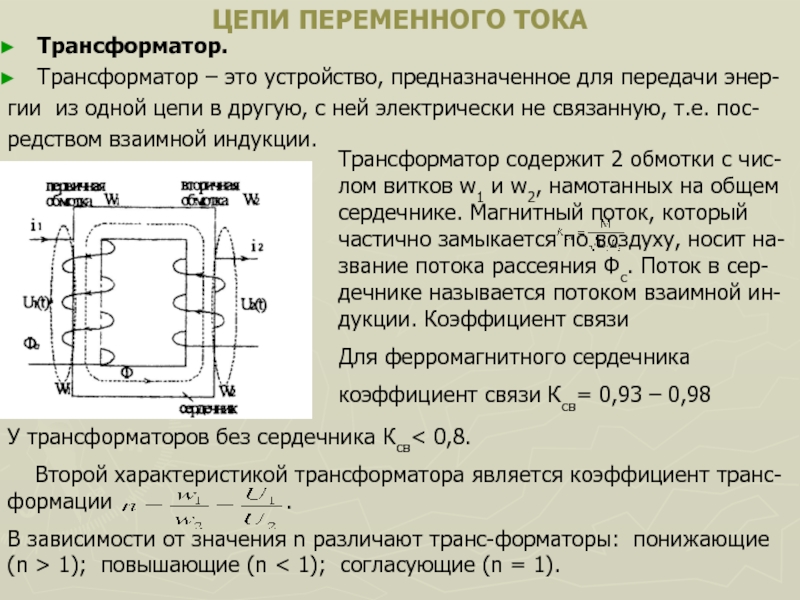 Таким образом, как только ток установлен, он является постоянным.Постоянный ток (dc) — это поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения.
Таким образом, как только ток установлен, он является постоянным.Постоянный ток (dc) — это поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения.
