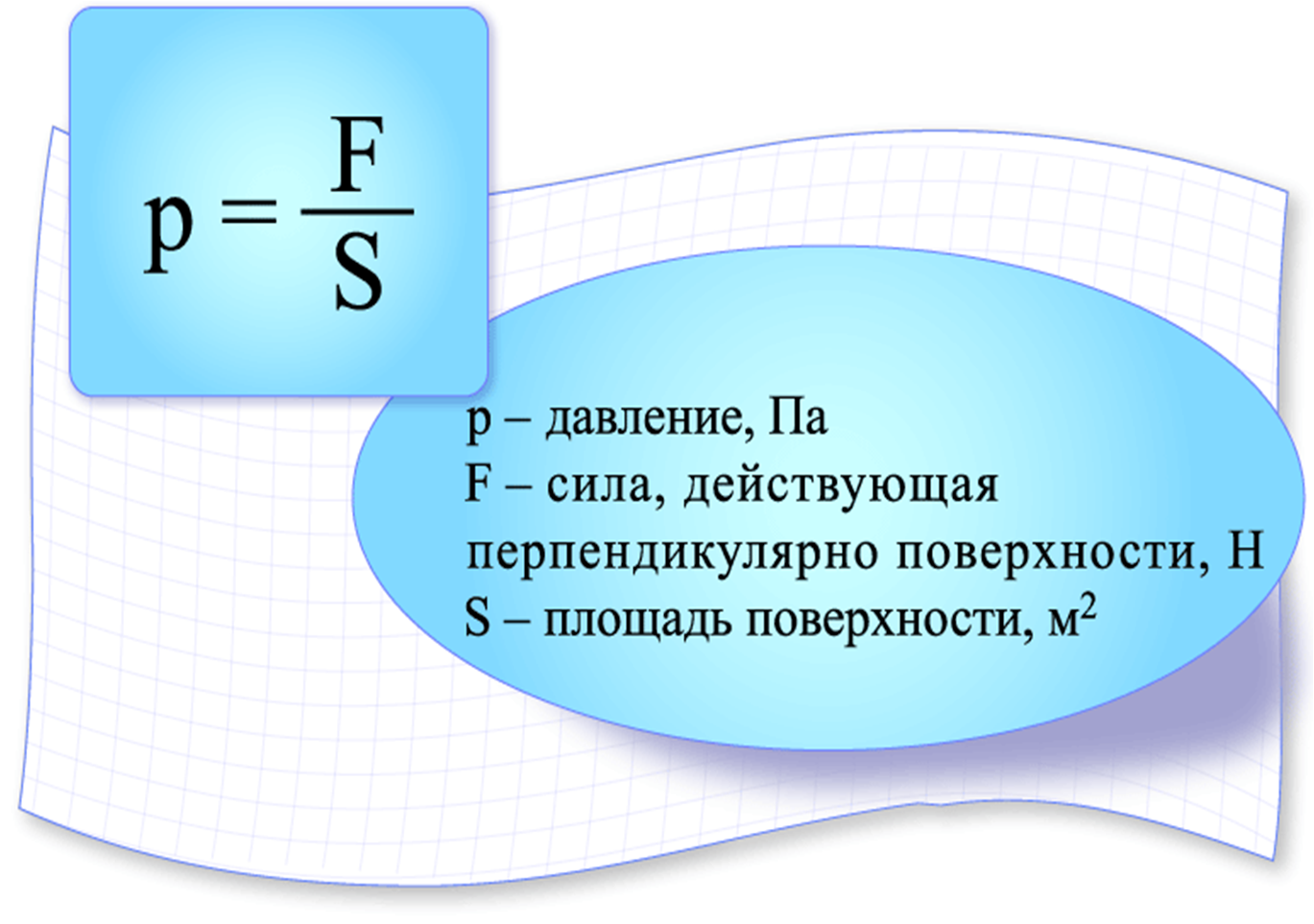
Формула давления
ОПРЕДЕЛЕНИЕ
Давление столба жидкости (гидростатическое давление) равно плотности этой жидкости, умноженной на высоту столба жидкости и ускорение свободного падения.
Здесь – давление, – плотность жидкости, – ускорение свободного падения ( м/с), – высота столба жидкости (глубина, на которой находится сдавливаемое тело).
Единица измерения давления – Па (паскаль).
Это векторная величина. В каждой точке жидкости давление одинаково во всех направлениях. Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Где – сила тяжести, действующая на жидкость (её вес), – площадь поверхности, на которую оказывается давление.
Примеры решения задач по теме «Давление»
ПРИМЕР 1
| Задание | Высота воды в аквариуме 1 м. Найти давление на дно аквариума. Найти давление на дно аквариума. |
| Решение | Напоминаем, плотность воды кг/м, а м/с. Таким образом:
(Па)
|
| Ответ | Давление воды составляет 9800 Паскаль. |
ПРИМЕР 2
| Задание | Закрытый сосуд устроен так, что его крышка подвижна (см. рисунок). Сосуд наполнен жидкостью, плотность которой известна. На крышку сосуда действует сила . Найти давление на дно сосуда, если известны площадь дна и крышки и объём жидкости в сосуде.
|
| Решение | Пусть:
– площадь крышки
– площадь дна
– объём жидкости
– плотность жидкости
Крышка подвижна, значит она давит на жидкость с той силой, с которой внешние силы давят на неё сверху.
Очевидно:
Попробуем найти давление жидкости:
Соберём всё вместе:
|
| Ответ |
Читайте также:
Все формулы по физике
Формула силы выталкивания
Формула напряжённости магнитного поля
Формула силы Ампера
Формула силы Лоренца
Формула ЭДС
Формула длины волны
Урок 15.
 основы гидромеханики — Физика — 10 класс
основы гидромеханики — Физика — 10 класс
Физика, 10 класс
Урок 15. Основы гидромеханики
Перечень вопросов, рассматриваемых на уроке:
1.Сила давления
2.Давление
3.Закон Паскаля
4.Гидростатическое давление
5.Атмосферное давление
6.Закон Архимеда
Глоссарий по теме
Гидростатика — раздел механики, в котором изучается равновесие покоящихся жидкостей и их давление на погруженные в них тела.
Давление – это величина равная отношению силы давления к площади поверхности, на которую эта сила действует.
Нормальное атмосферное давление – это величина давления, равная 760 мм рт. ст. или 101325 Па.
Сила Архимеда –выталкивающая сила, действующая на тело, погруженное в жидкость или газ
Основная и дополнительная литература по теме урока:
Грачев А.В., Погожев В.А., Салецкий А.М., Боков П.Ю. Физика.10 класс. М.: Вентана-Граф, 2017. — С. 222 – 229.
— С. 222 – 229.
Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006, С.36-50.
Основное содержание урока
Силой давления называется сила, действующая перпендикулярно некоторой поверхности.
Результатом действия силы давления является давление.
Отношение модуля силы давления F к площади поверхности S, на которую эта сила действует, называется давлением
Закон Паскаля.
Силы давления в данной точке покоящейся жидкости (газа) действуют во всех направлениях одинаково. При ведём простое доказательство закона.
Выделим в какой-нибудь точке покоящейся жидкости её малый объём в форме прямоугольного параллелепипеда или куба.
Если кубик покоится, значит сумма сил, действующих на его 6 граней равна нулю. Это означает, что силы, действующие попарно на противоположные грани куба, равны по модулю, а, следовательно, и давления будут равны по всем направлениям.
Ввиду произвольности ориентации выбранного нами малого объёма жидкости, очевидно, что давление по всем направлениям должно быть одинаково.
Гидростатическое давление. Атмосферное давление.
Это давление, оказываемое «столбом» жидкости на уровне плоскости своего нижнего основания.
Выделим в покоящейся жидкости «столб» — цилиндр высотой h и площадью основания S, верхнее основание которого совпадает со свободной поверхностью жидкости.
По первому закону Ньютона сумма проекций трех сил, действующих на столб жидкости: силы атмосферного давления, силы тяжести и силы давления жидкости- равна нулю
Fp– mg – Fатм = 0;
Но так как mg=ρ·V·g=ρ·S·h·g; Fp = p·S; Fатм = pатм ·S,
Получим p = pатм+ ρ·g·h;
где pатм — атмосферное давление; ρ – плотность жидкости; g – ускорение свободного падения; h – глубина.
Величина ρ·g·h называется гидростатическим давлением.
Атмосферное давление – это давление в какой-нибудь точке атмосферы.
Нормальное или среднее значение атмосферного давления равно 760 мм ртутного столба, что соответствует 101325 Па. Т.е. 1 мм рт. ст. = 133,322 Па.
Т.е. 1 мм рт. ст. = 133,322 Па.
Зависимость атмосферного давления от высоты имеет сложный вид из-за сжимаемости воздуха (в отличие от жидкостей).
Закон Архимеда. Сила Архимеда.
Выделим в жидкости объем прямоугольного параллелепипеда, ориентированного для удобства анализа так, чтобы нижняя и верхняя грани были параллельны поверхности жидкости
На тело в жидкости действуют сила тяжести и силы давления со стороны жидкости. Давление на боковые стенки равны. Сила давления снизу больше, чем сила давления сверху. Разность этих двух сил и есть выталкивающая сила – сила Архимеда.
FA=p2 S — p1 S =S( p2 — p1) = ρ g S(h2 – h1) = ρ gV
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.
где – плотность жидкости; g — ускорение свободного падения; Vm – объём погруженной в жидкость части тела
Разбор тренировочных заданий
1. Найдите силу нормального атмосферного давления на грань куба с ребром 1 м. Округлите до целых кПа.
Найдите силу нормального атмосферного давления на грань куба с ребром 1 м. Округлите до целых кПа.
Варианты ответов:
1) 100;
2) 125;
3) 101;
4) 110
Решение. По определению сила давления равна F = p x S;
Нормальное атмосферное давление p = 101325 Па; площадь грани куба (1м)2 = 1м2;
Получим значение силы давления F = (101325 Н/м2 ) х (1 м2) = 101325 Н =101,325 кН.
Ответ: 3) 101
2. В первой строке таблицы приведены значения атмосферного давления на разных высотах. Занесите во вторую строку соответствующие значения высот из перечня: h1, h2, h3, h4, если известно, что h3 > h4 > h1 > h2
P (мм рт. ст.) | 738 | 750 | 550 | 525 |
h(м) |
Решение.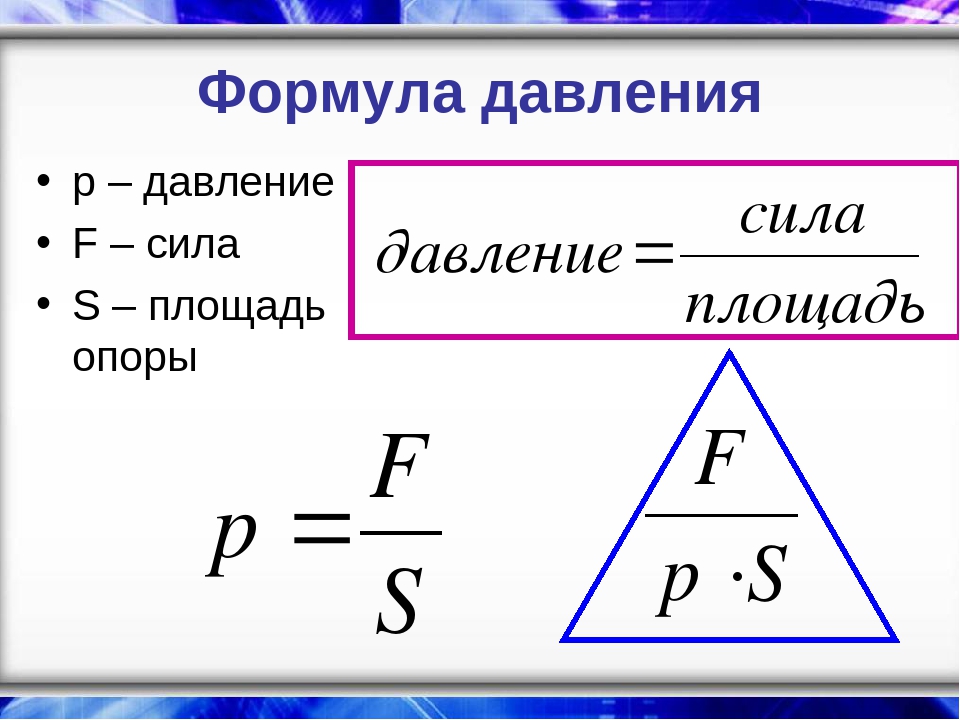 Как известно, давление атмосферы падает с высотой. Выпишем в порядке убывания давления: 750,738,550,525. Из приведённого неравенства имеем, что наименьшая высота h2, затем h1, h4 и h3. Наименьшей высоте соответствует наибольшее давление и т.д. Высота растёт, давление падает. Или наоборот. В таблицу теперь под каждым давлением впишем соответствующее значение высоты.
Как известно, давление атмосферы падает с высотой. Выпишем в порядке убывания давления: 750,738,550,525. Из приведённого неравенства имеем, что наименьшая высота h2, затем h1, h4 и h3. Наименьшей высоте соответствует наибольшее давление и т.д. Высота растёт, давление падает. Или наоборот. В таблицу теперь под каждым давлением впишем соответствующее значение высоты.
Ответ:
P (мм рт. ст.) | 738 | 750 | 550 | 525 |
h(м) | h1 | h2 | h4 | h3 |
Академия занимательных наук. Физика — Формула давления твёрдых тел. Видеоуроки физики
Формула давления твёрдых тел. Видеоуроки физики
Выпуск 16
В видеоуроке физики от Академии занимательных наук профессор Даниил Эдисонович познакомит юных телезрителей с новой физической величиной, которая служит для измерения давления — Паскалем. Посмотрев передачу вы узнаете, какое значение имеет площадь опоры твёрдого тела, как не провалиться под лёд или снег, а также познакомитесь с формулой давления твёрдых тел.
Посмотрев передачу вы узнаете, какое значение имеет площадь опоры твёрдого тела, как не провалиться под лёд или снег, а также познакомитесь с формулой давления твёрдых тел.
Формула давления твёрдых тел
Как вы наверное помните из прошлой передачи, вес — это сила, с которой тело давит на опору. Почему же один и тот же человек, идя по снегу в ботинках проваливается, а идя на лыжах — нет? Чтобы разобраться в этом вопросе профессор Даниил Эдисонович научит вас формуле давления твёрдых тел. Трактор весит гораздо больше автомобиля, а в рыхлой почве не вязнет. В то же время лёгкий автомобиль попав на такую почву скорее всего застрянет и его придётся вытаскивать трактором. Результат действия силы на поверхность зависит не только от величины этой силы, но и от площади, к которой приложена эта сила. Когда человек наступает в снег, вес его тела распределяется по площади его ступней. А если человек обут в лыжи, то вес распределяется по их площади, которая намного больше площади ступней. Поскольку площадь приложения стала больше, человек не провалится в снег. Давление – это скалярная физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности. Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь этой поверхности. Формула давления твёрдых тел записывается так: p=F/S, где р – это давление, F – сила давления, S – площадь опоры. За единицу давления принимается давление, которое производит сила в 1 ньютон, действующая на поверхность площадью 1м2 перпендикулярно этой поверхности. Измеряется давление в паскалях. Таким образом, по формуле давления твёрдых тел, 1 паскаль равен 1 ньютону на квадратный метр. Между силой давления и давлением существует прямо пропорциональная зависимость, то есть чем больше сила, тем больше давление и наоборот, чем меньше сила, тем меньше давление. Если говорить о зависимости давления от площади опоры, то здесь наблюдается обратно пропорциональная зависимость, то есть чем больше площадь опоры, тем меньше давление и наоборот, чем меньше площадь соприкосновения тел, тем давление больше.
Поскольку площадь приложения стала больше, человек не провалится в снег. Давление – это скалярная физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности. Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь этой поверхности. Формула давления твёрдых тел записывается так: p=F/S, где р – это давление, F – сила давления, S – площадь опоры. За единицу давления принимается давление, которое производит сила в 1 ньютон, действующая на поверхность площадью 1м2 перпендикулярно этой поверхности. Измеряется давление в паскалях. Таким образом, по формуле давления твёрдых тел, 1 паскаль равен 1 ньютону на квадратный метр. Между силой давления и давлением существует прямо пропорциональная зависимость, то есть чем больше сила, тем больше давление и наоборот, чем меньше сила, тем меньше давление. Если говорить о зависимости давления от площади опоры, то здесь наблюдается обратно пропорциональная зависимость, то есть чем больше площадь опоры, тем меньше давление и наоборот, чем меньше площадь соприкосновения тел, тем давление больше. Величина давления имеет большое значение не только в жизни человека, но и в жизни животных. Например, заяц, оказывающий давление в 1,2 кПа может сравнительно легко убежать от волка, который оказывает давление 12 кПа, по рыхлому снегу, но не спасется от него на твердой почве.
Величина давления имеет большое значение не только в жизни человека, но и в жизни животных. Например, заяц, оказывающий давление в 1,2 кПа может сравнительно легко убежать от волка, который оказывает давление 12 кПа, по рыхлому снегу, но не спасется от него на твердой почве.
Глава 13. Газовые законы
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
(13. |
где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
(13.2) |
Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
(13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа
(13.3) |
С учетом (13. 3) закон (13.2) можно переписать и в таком виде
3) закон (13.2) можно переписать и в таком виде
(13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
(13. |
где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
Второй график следует из соотношения
(13.6) |
где — постоянная при постоянном объеме.
Для изотермического процесса
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
(13.7) |
где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13. 1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
(13.8) |
где — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13. 1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
Отсюда , т. е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э.
Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э.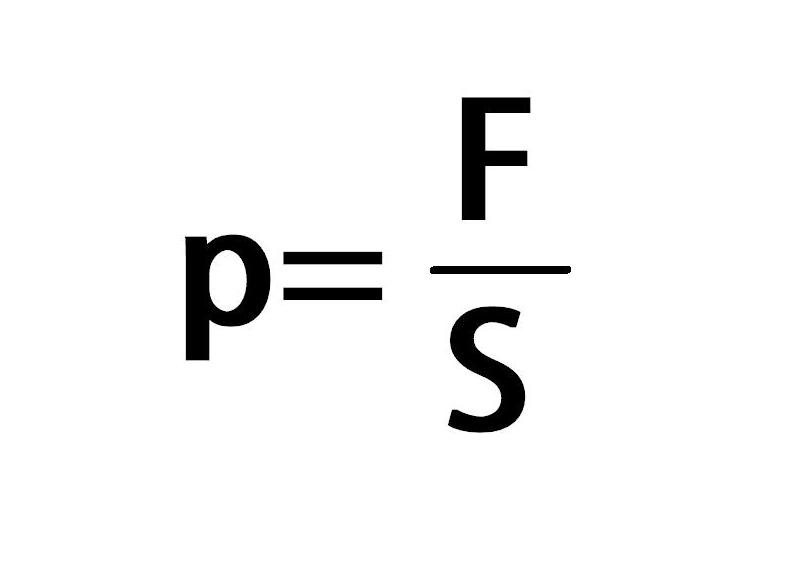 Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4). |
В изотермическом процессе давление зависит от объема как ; на диаграмме этот процесс изображается гиперболой. Поэтому изотермическими являются процессы 1 и 3 (задача 13.1.7), но в процессе 1 объем газа убывает. Следовательно, изотермическим расширением является процесс 3 (ответ 3). |
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. |
получим
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
(ответ 1).
Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13. 2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
(ответ 4).
Если бы точки, отвечающие состояниям 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13. 2.7 имеем (ответ 2).
2.7 имеем (ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т. е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
(ответ 4). Здесь — масса газа, — масса одной молекулы газа.
основные формулы, определение и примеры
Гидромеханика
Основные формулы
Формула давления
Здесь р — давление (Па), — сила давления (Н), S — площадь опоры .
Давление столба жидкости
Здесь р — давление (Па), — плотность жидкости , g — ускорение свободного падения , h — высота столба жидкости (м).
Выталкивающая (архимедова) сила
Здесь — выталкивающая сила (Н), — плотность жидкости , g — ускорение свободного падения , — объем тела, погруженного в жидкость .
Формула гидравлического пресса
Здесь — силы, действующие на поршни пресса (Н), — площади поршней .
Уравнение неразрывности струи (теорема Эйлера)
Здесь — скорость жидкости (м/с) в сечении площадью — скорость жидкости (м/с) в сечении площадью .
Уравнение Бернулли
Здесь — плотность жидкости , g — ускорение свободного падения — высоты элемента жидкости над землей (м), — скорости на этих высотах (м/с), и — давления в жидкости (Па).
В основе гидродинамики лежат законы Ньютона, следствием которых являются все основные законы гидродинамики. Особенность здесь состоит в том, что эти законы применяют не к твердым телам, сохраняющим в процессе перемещения свою форму, а к жидкостям, не сохраняющим формы в процессе движения. Кроме того, если давление силы, приложенной к твердому телу, передается только в направлении ее действия, то давление, производимое на жидкость или газ, передается по всем направлениям одинаково. В этом состоит закон Паскаля — один из основных законов гидродинамики. Поэтому и силы давления распространяются по всей поверхности жидкости.
В этом состоит закон Паскаля — один из основных законов гидродинамики. Поэтому и силы давления распространяются по всей поверхности жидкости.
Давлением р называется отношение силы давления к площади опоры тела S.
Силой давления называют силу, действующую на тело перпендикулярно его площади опоры. Следует знать, что, хоть сила давления — величина векторная, но давление р — величина скалярная, оно не имеет направления.
С увеличением глубины жидкости давление в ней возрастает, т.к. увеличивается высота столба жидкости над уровнем, на котором определяется давление. Если жидкость налита в сосуд, то с увеличением ее глубины давление растет линейно с высотой столба жидкости, поэтому среднее давление жидкости на стенку сосуда равно половине ее давления на дно:
Если сверху на данный уровень давит несколько жидкостей, то давление на данном уровне равно сумме давлений каждой жидкости в отдельности.
В поле сил тяжести и в условиях земной атмосферы давление жидкости р на глубине h складывается из давления атмосферы на поверхность жидкости и давления самой жидкости на глубине h:
Следствием закона Паскаля является закон сообщающихся сосудов: в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково.
Из закона сообщающихся сосудов вытекают два следствия.
Следствие 1: в неподвижных и открытых сообщающихся
сосудах высоты столбов жидкостей, отсчитываемые от уровня тп, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей (рис. 68):
Следствие 2: в неподвижных и открытых сообщающихся
сосудах однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов (рис. 69):
На законе Паскаля основано действие гидравлического пресса (рис. 70). — устройства, позволяющего получить выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего поршня. Формула гидравлического пресса:
Согласно золотому правилу механики выигрыша в работе гидравлический пресс не дает, так как во сколько раз мы выигрываем на большом поршне в силе, во столько раз он проходит меньшее расстояние по сравнению с малым поршнем.
Другим законом гидродинамики, определяющим действие жидкостей и газов на погруженные в них тела, является закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу жидкости или газа, вытесненных телом.
Выталкивающая сила прямо пропорциональна плотности жидкости и объему погруженного в нее тела.
Выталкивающая (архимедова) сила не всегда направлена вверх. Как и всякая сила давления жидкости, она всегда направлена перпендикулярно поверхности жидкости. Если сосуд с жидкостью движется с ускорением горизонтально, то ее поверхность располагается под углом к горизонту, тем большим, чем больше ускорение. Поэтому выталкивающая сила, которая всегда перпендикулярна поверхности жидкости, уже не будет направлена вертикально.
Благодаря действию выталкивающей силы тела плавают в жидкости или газе. Условие плавания тел: тело плавает в жидкости, когда выталкивающая сила равна весу тела.
Когда плотность тела значительно меньше плотности жидкости, то равновесия может не наступить, если вес тела при всплытии все время будет меньше выталкивающей силы. При этом тело будет находиться на поверхности жидкости, совсем не погружаясь в нее, как это делает надувной шарик, брошенный в воду. Если плотность тела равна плотности жидкости, в которую оно полностью погружено, то тело будет плавать в жидкости во взвешенном состоянии, т.е. не поднимаясь и не опускаясь, поскольку при этом вес тела будет равен выталкивающей силе.
Если вес тела окажется больше выталкивающей силы, то оно утонет.
Нашу Землю окружает атмосфера, простирающаяся на высоту в несколько тысяч километров. Вследствие земного тяготения на атмосферный воздух действует сила тяжести, в результате чего верхние слои атмосферы давят на нижние. Атмосферное давление на тело обусловлено весом воздушных слоев, расположенных над ним.
На уровне моря величина атмосферного давления в среднем составляет 760 мм рт.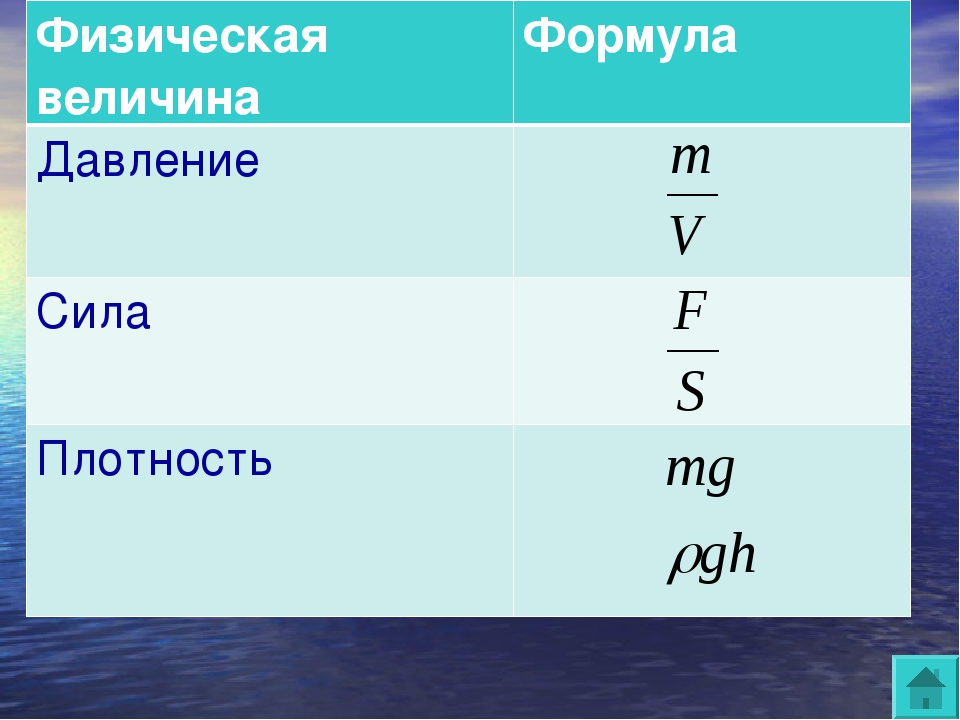 ст. или Па. С увеличением высоты над уровнем моря атмосферное давление убывает вместе с весом воздушных слоев из-за ослабления земного тяготения, уменьшаясь через каждые сто метров примерно на 10 мм рт. ст. = 1330 Па.
ст. или Па. С увеличением высоты над уровнем моря атмосферное давление убывает вместе с весом воздушных слоев из-за ослабления земного тяготения, уменьшаясь через каждые сто метров примерно на 10 мм рт. ст. = 1330 Па.
Одним из первых измерил атмосферное давление итальянский ученый Торричелли. Это случилось три столетия назад. Торричелли взял тонкую стеклянную трубку длиной около метра, запаянную с одного конца, и наполнил ее доверху ртутью. Затем, закрыв открытый конец трубки, перевернул ее и опустил этим концом в открытую чашу с ртутью, после чего открыл трубку. Сначала под действием силы тяжести ртуть стала выливаться из трубки в чашу, а затем перестала. Это случилось в тот момент, когда давление ртути в трубке на уровне открытой поверхности ртути в чаше стало равно атмосферному давлению на открытую поверхность ртути в чаше. Так был создан первый в мире ртутный барометр.
Над ртутью в трубке образовалось замкнутое пространство, заполненное парами ртути, давление которых мало по сравнению с атмосферным, поэтому им пренебрегают.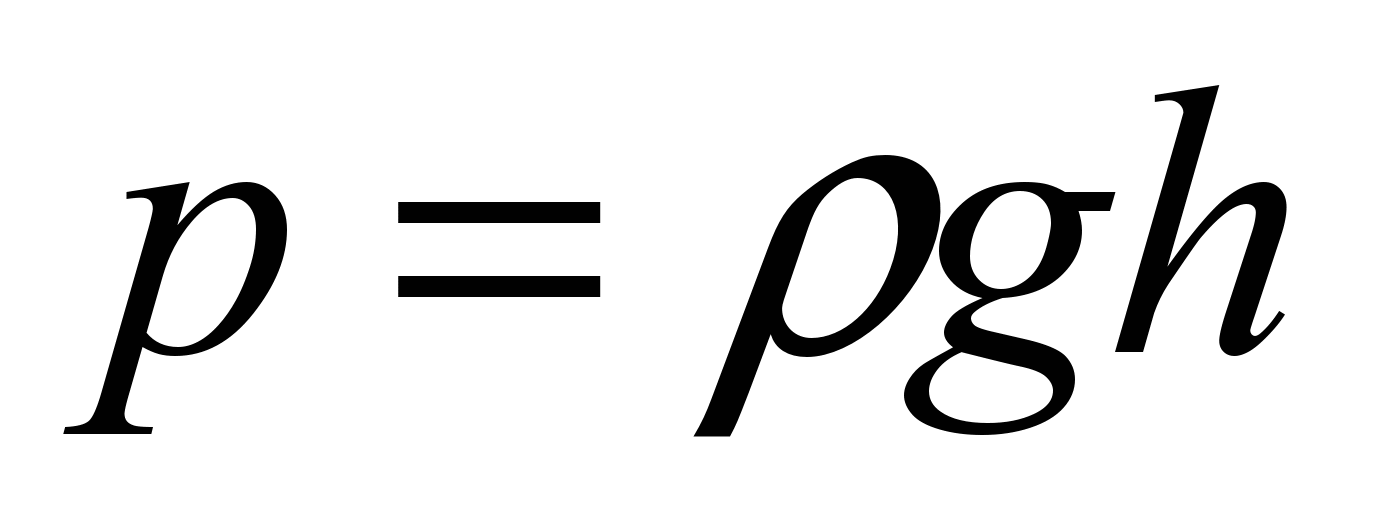 Это пространство было названо торричеллиевой пустотой.
Это пространство было названо торричеллиевой пустотой.
Когда атмосферное давление увеличивалось, т.е. атмосфера сильнее давила на открытую поверхность ртути в чаше, уровень ртути в трубке повышался, а когда оно уменьшалось, то понижался. Присоединив к трубке шкалу, проградуированную в единицах давления, стали измерять давление атмосферы с высокой степенью точности.
Нормальным атмосферным давлением называется давление атмосферы, численно равное давлению столбика ртути высотой 760 мм. Это давление называют также физической атмосферой, сокращенно атм.
Таким образом, нормальное атмосферное давление порядка Па.
Барометры — это приборы, применяемые для измерения атмосферного давления.
Первым ртутным барометром была трубка Торричелли. Ртутные барометры — очень точные приборы, поэтому их применяют там, где необходима высокая точность измерений, например, при научных экспериментах. Но у них есть ряд недостатков: они некомпактны, ртуть дорога, ее пары ядовиты, она может разлиться, стекло — разбиться и т. д. Поэтому в быту и технике широко применяют другие барометры — анероиды.
д. Поэтому в быту и технике широко применяют другие барометры — анероиды.
Большинство жидкостей, в том числе и вода, практически несжимаемы. Их плотность везде одинакова и с течением времени не меняется.
Теорема о неразрывности струи или теорема Эйлера: произведение скорости течения жидкости по трубе переменного сечения и площади поперечного сечения трубы в любом месте одинаково:
Теорема о неразрывности струи является выражением закона сохранения массы движущейся жидкости. Ее можно применять к реальным жидкостям, сжимаемостью которых можно пренебречь.
Другим важнейшим уравнением гидродинамики является уравнение Бернулли, представляющее собой закон сохранения механической энергии, примененный к течению жидкости:
Из этого уравнения следует, что если скорость в потоке жидкости возрастает, то давление в ней падает, и наоборот, там, где скорость меньше, давление больше. Например, если лодку, оставленную на ночь у берега, забыть привязать, то утром ее можно обнаружить уплывшей далеко по течению. Это произойдет вследствие того, что из-за большего давления воды, медленно текущей вблизи берега, лодку вытеснит на середину, туда, где течение имеет большую скорость и, следовательно, меньшее давление.
Это произойдет вследствие того, что из-за большего давления воды, медленно текущей вблизи берега, лодку вытеснит на середину, туда, где течение имеет большую скорость и, следовательно, меньшее давление.
Сформулированная выше зависимость давления от скорости течения среды справедлива и применительно к газам, когда их скорость невелика, так как при этом можно пренебречь сжимаемостью газов. Все должны знать, что вблизи мчащегося поезда стоять опасно, потому что воздух вблизи стенок вагонов увлекается поездом и движется с большей скоростью перед стоящим человеком, чем позади него. В результате, давление воздуха за спиной человека будет больше, чем между ним и поездом, и человека может толкнуть прямо под колеса.
Следствием уравнения Бернулли является возникновение подъемной силы крыла самолета. Подъемная сила крыла самолета обусловлена особым профилем крыла — профилем Жуковского, названным так в честь замечательного русского ученого-механика Н.Е. Жуковского, основоположника отечественной авиации.
Крыло самолета имеет особую несимметричную форму. Его профиль образует с линией горизонта угол атаки — угол между вектором скорости набегающего на крыло горизонтального потока воздуха и нижней плоскостью крыла (рис. 71). Благодаря несимметричности формы крыла и наличию угла атаки а воздушные массы за одно и то же время проходят над верхней поверхностью крыла больший путь, чем под нижней. В результате, давление , соответственно, меньше давления pt. Наличие разности давлений над и под крылом приводит к появлению подъемной силы, направленной снизу вверх, — оттуда, где давление больше, туда, где оно меньше. Величина подъемной силы в значительной степени зависит от угла атаки и при некотором критическом угле атаки достигает максимальной величины, после чего начинает убывать с дальнейшим ростом угла атаки. Расчет критического угла атаки является одной из важных задач самолетостроения.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Тест по теме «Давление» — физика, тесты
ТЕСТ по теме «Давление»
1.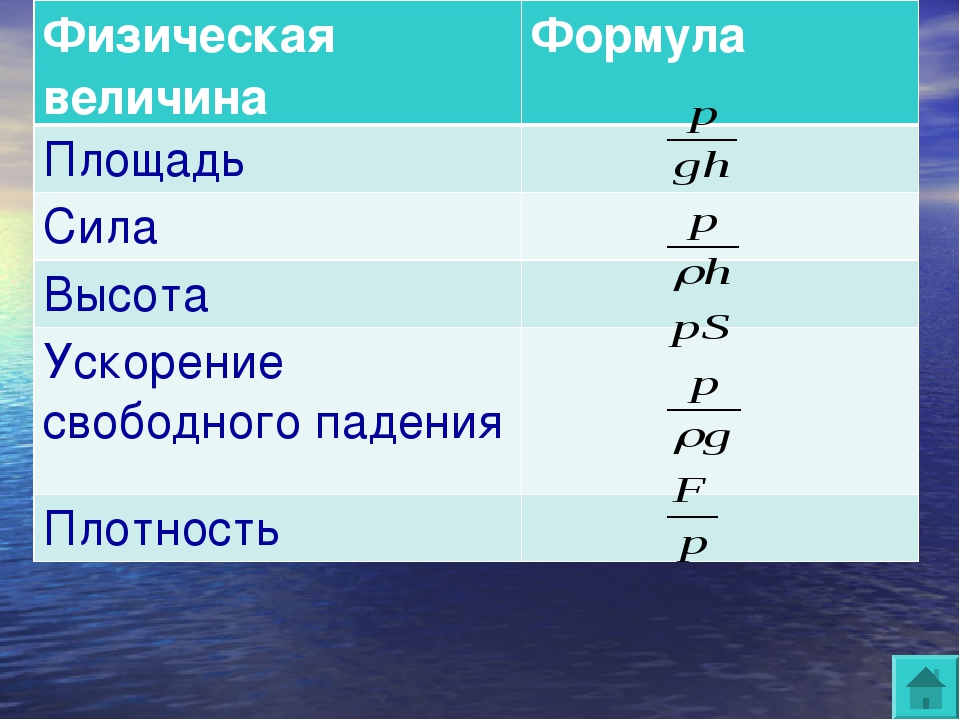 Давление вычисляется по формуле:
Давление вычисляется по формуле:
а) б) в) г)
2. Международная единица давления – 1 Паскаль – равен:
а) а) а) а)
3. Если произведенное на тело давление передается им по всем направлениям одинаково, то тело:
а) является жидкостью или газом;
б) является жидкостью;
в) является твердым;
г) может быть как газообразным, так и жидким, и твердым.
4. Чем … площадь опоры, тем … давление, производимое одной и той же силой на эту опору.
а) больше; меньше;
б) больше; больше;
в) меньше; меньше;
г) нет правильного варианта.
5. Давление, производимое жидкостью на дно сосуда, вычисляется по формуле:
а) б) в) г)
6. Давление, которое газ производит на стенки сосуда, возникает из-за:
а) хаотического движения его молекул;
б) действия земного притяжения;
в) того, что каждая молекула газа имеет вес;
г) непрерывных удавов молекул о стенки сосуда.
7. Вставьте подходящие по смыслу слова: «В положении 1 (см.рис.) сила давления бруска на стол … в положении 2; давление бруска в положении 2 … в положении 1»:
а) такая же, как, такое же, как;
б) такая же, как, больше, чем;
в) меньше, чем, такое же, как;
г) больше, чем, больше, чем.
8. Для того чтобы максимально увеличить давление, производимое на опору, необходимо увеличить:
а) силу давления;
б) площадь опоры;
в) и силу давления, и площадь опоры;
г) силу давления и уменьшить площадь опоры.
9. Из перечисленных ниже значений давления наибольшим является:
а) 0,5 * 104 Па б) 9 кПа в) 0,06 Мпа г) 0,5 мПа
10. При медленном сжатии газа а цилиндре его давление возрастает, т.к.:
а) при сближении молекул увеличиваются силы их взаимного отталкивания;
б) увеличиваются скорости молекул;
в) молекулы чаще сталкиваются друг с другом;
г) возрастает число ударов молекул на единицу площади стенки цилиндра.
11. Давление газа в закрытом сосуде тем больше, чем …температура газа, при условии, что масса и объём газа изменяются.
а) ниже;
б) выше.
12. При уменьшении объёма газа его давление …при условии, что масса и температура газа остаются неизменными.
а) увеличивается;
б) уменьшается;
в) не изменяется.
13. Давлением называют_____________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
14. Закон Паскаля гласит:____________________________________________________
Закон Паскаля гласит:____________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
Фамилия, Имя _________________________________ Класс ___________
Физика атмосферы Атмосферное давление Барометрическая формула Давление
Физика атмосферы Атмосферное давление. Барометрическая формула
Давление атмосферы давление (Fдавл. — сила давления, S – площадь) Атмосферное давление — давление атмосферы на все находящиеся в ней предметы и земную поверхность. Атмосферное давление создаётся гравитационным притяжением воздуха к Земле. Атмосферное давление измеряется барометром. Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °C, называется нормальным атмосферным давлением. Международная стандартная атмосфера — МСА, 101 325 Па. Паскаль – единица измерения давления, равная 1 Н/м 2. В системе СГС: 760 мм рт. ст. эквивалентно 1, 01325 бар (1013, 25 мбар) или 101 325 Па в Международной системе единиц (СИ). 1 мбар равен 1 гектопаскалю: 1 мбар =1 г. Па (102 Па) 1 атм= 105 Па= 760 мм рт. ст. = 1013, 25 мбар
Атмосферное давление создаётся гравитационным притяжением воздуха к Земле. Атмосферное давление измеряется барометром. Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °C, называется нормальным атмосферным давлением. Международная стандартная атмосфера — МСА, 101 325 Па. Паскаль – единица измерения давления, равная 1 Н/м 2. В системе СГС: 760 мм рт. ст. эквивалентно 1, 01325 бар (1013, 25 мбар) или 101 325 Па в Международной системе единиц (СИ). 1 мбар равен 1 гектопаскалю: 1 мбар =1 г. Па (102 Па) 1 атм= 105 Па= 760 мм рт. ст. = 1013, 25 мбар
Единицы измерения давления г. Па и мм. рт. ст. 1013, 25 г. Па = 760 мм. рт. ст Давление воздуха падает с высотой: 1 мм. рт. ст на 11 м Изменения давления При прохождении циклонов и атмосферных фронтов В лифте (на 12 этаж) ок. 0, 0007 мм. рт. ст. за 1 с 5 мм. рт. ст. за 1 с При перелете в Минводы (300 м) ? В салоне самолета при наборе 500 г. Па или снижении высоты ? мм. рт. ст.
История измерения давления Наличие атмосферного давления привело людей в замешательство в 1638 году, когда не удалась затея герцога Тосканского украсить сады Флоренции фонтанами — вода не поднималась выше 10, 3 метров. Поиски причин этого и опыты с более тяжёлым веществом — ртутью, предпринятые Эванджелистой Торричелли, привели к тому, что в 1643 году он доказал, что воздух имеет вес. Совместно с В. Вивиани, Торричелли провёл первый опыт по измерению атмосферного давления, изобретя трубку Торричелли (первый ртутный барометр) — стеклянную трубку, в которой нет воздуха. В такой трубке ртуть поднимается на высоту около 760 мм. Ртутный барометр
Поиски причин этого и опыты с более тяжёлым веществом — ртутью, предпринятые Эванджелистой Торричелли, привели к тому, что в 1643 году он доказал, что воздух имеет вес. Совместно с В. Вивиани, Торричелли провёл первый опыт по измерению атмосферного давления, изобретя трубку Торричелли (первый ртутный барометр) — стеклянную трубку, в которой нет воздуха. В такой трубке ртуть поднимается на высоту около 760 мм. Ртутный барометр
Магдебургские полушария названы так, поскольку опыт был проделан вблизи города Магдебурга Эксперимент XVII века, выполненный Отто фон Герике. Две металлические полусферы, между которыми откачали воздух, смогли разделить две восьмёрки лошадей, которые одновременно тянули их в разные стороны. При этом раздался звук, похожий на выстрел.
Ртутный барометр — давление столба газа (жидкости) с плотностью высотой h
Барометр — анероид
Барометр-анероид – прибор для измерения атмосферного давления (от греч. а — отрицательная частица, nerys — вода, т. е. действующий без помощи жидкости) Куда отклонится стрелка барометра при уменьшении давления вправо или влево? Приёмной частью анероида служит круглая металлическая коробка с гофрированными основаниями, где создано сильное разрежение. При увеличении атмосферного давления крышка коробочки прогибается вниз, а при уменьшении давления поднимается вверх Перемещение конца пружины (жёлтым цветом) передаётся стрелке, перемещающейся по шкале
а — отрицательная частица, nerys — вода, т. е. действующий без помощи жидкости) Куда отклонится стрелка барометра при уменьшении давления вправо или влево? Приёмной частью анероида служит круглая металлическая коробка с гофрированными основаниями, где создано сильное разрежение. При увеличении атмосферного давления крышка коробочки прогибается вниз, а при уменьшении давления поднимается вверх Перемещение конца пружины (жёлтым цветом) передаётся стрелке, перемещающейся по шкале
Барометрическая формула «-» в формуле означает, что атмосферное давление с высотой убывает
Барометрическая формула
Барометрическая формула
Барометрическая формула Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид: где P давление газа в слое, расположенном на высоте , P 0 давление на — — нулевом уровне h 0 — молярная масса газа, R универсальная газовая (), M — постоянная, T— абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону: где m масса молекулы газа, k постоянная Больцмана. — —
Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону: где m масса молекулы газа, k постоянная Больцмана. — —
Высота атмосферы Барический градиент
319 г, Уменьшение атмосферного давления с высотой тогда как на уровне моря — 1, 3 кг
Основная масса атмосферы сосредоточена в довольно тонком слое: до 5 -6 км – 50% массы, до 30 км – 99% массы атмосферы. Иначе говоря, плотность воздуха с высотой быстро уменьшается: 1 м 3 воздуха на уровне моря весит 1033 г, а на высоте 40 км — всего 4 г
Почему у Луны нет атмосферы?
Давление
Каждый человек в то или иное время находился под давлением или в определенных обстоятельствах действительно «чувствовал давление». Однако с научной точки зрения давление имеет очень конкретное определение, и его исследование приводит к некоторым очень важным приложениям.
В физике давление — это эффект силы, действующей на поверхность. Математически это скалярная величина, рассчитываемая как сила, приложенная на единицу площади, где приложенная сила всегда перпендикулярна поверхности.Единица давления в системе СИ, Паскаль (Па), эквивалентна Н / м 2 .
Все состояния вещества могут оказывать давление. Когда вы идете по покрытому льдом озеру, вы оказываете давление на лед, равное силе тяжести вашего тела (вашему весу), деленной на площадь, на которой вы соприкасаетесь со льдом. Вот почему важно распределять вес при движении по хрупким поверхностям. Ваши шансы прорваться сквозь лед чрезвычайно возрастают, если вы идете по льду на высоких каблуках, поскольку небольшая область, соприкасающаяся со льдом, приводит к высокому давлению.Это также причина того, что у снегоступов такая большая площадь. Они разработаны для уменьшения давления на верхнюю корку снега, чтобы вам было легче ходить, не проваливаясь в снежные заносы.
Жидкости также могут оказывать давление. Все жидкости оказывают внешнее давление во всех направлениях по бокам любого контейнера, содержащего жидкость. Даже атмосфера Земли оказывает давление, которое вы испытываете прямо сейчас. Однако давление внутри и снаружи вашего тела настолько хорошо сбалансировано, что вы редко замечаете 101 325 Паскалей из-за атмосферы (примерно 10 Н / см 2 ).Если вы летите в самолете и быстро меняете высоту (и, следовательно, давление), вы могли испытать ощущение «хлопка» в ушах — это происходит из-за давления внутри уха, уравновешивающего давление за пределами уха при переносе воздуха через маленькие трубки, соединяющие внутреннее ухо с горлом.
Вопрос: Давление воздуха составляет примерно 100 000 Па. Какая сила действует на эту книгу, когда она лежит на столе? Площадь обложки книги равна 0.035 м 2 .
Ответ:
Вопрос: Рыбак массой 75 кг засыпает на своем четвероногом стуле массой 5 кг.
Если каждая ножка стула имеет площадь поверхности 2,5 × 10 -4 м 2 в контакте с землей, каково среднее давление, оказываемое рыбаком и стулом на землю?
Ответ: Приложенная сила является силой тяжести, поэтому мы можем написать:
Вопрос: На поверхности планеты Физика помещена шкала, показывающая 0 в космическом вакууме.На поверхности планеты шкала показывает силу в 10 000 ньютонов. Вычислите площадь поверхности шкалы, учитывая, что атмосферное давление на поверхности Physica составляет 80 000 Паскалей.
Ответ:
Вопрос: Оцените следующее от максимального давления к самому низкому давлению на землю:
- Атмосфера на уровне моря
- Слон массой 7000 кг общей площадью 0.5 м 2 в контакте с землей
- Женщина весом 65 кг на высоких каблуках общей площадью 0,005 м 2 , соприкасающаяся с землей
- Автомобиль массой 1600 кг с общей площадью контакта шины 0,2 м 2
Ответ: От максимального давления к минимальному:
- Слон (137000 Па)
- Дама на высоких каблуках (127000 Па)
- Атмосфера (100000 Па)
- Автомобиль (78400 Па)
Давление, которое жидкость оказывает на объект, погруженный в эту жидкость, можно рассчитать почти так же просто.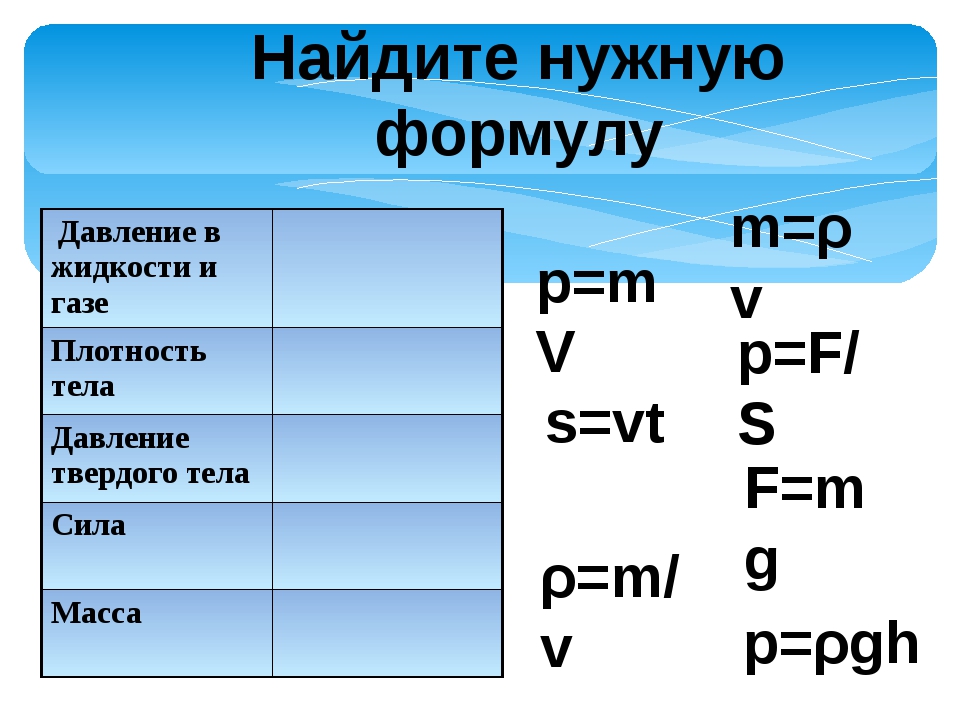 Если объект погружен на глубину (h), давление определяется путем умножения плотности жидкости на глубину погружения, умноженную на ускорение свободного падения.
Если объект погружен на глубину (h), давление определяется путем умножения плотности жидкости на глубину погружения, умноженную на ускорение свободного падения.
Это называется манометрическим давлением, потому что это значение, которое вы можете наблюдать на манометре. Если над жидкостью также есть атмосфера, как, например, здесь, на Земле, вы можете определить абсолютное давление или полное давление, добавив атмосферное давление (P 0 ), которое равно примерно 100000 Паскалей.
Вопрос: Саманта замечает закопанные сокровища во время подводного плавания на Карибских каникулах. Если ей придется спуститься на глубину 40 метров, чтобы проверить давление, какое манометрическое давление она увидит на своем акваланге? Плотность морской воды 1025 кг / м 3 .
Ответ:
Вопрос: Какое абсолютное давление оказывает на дайвера в предыдущей задаче вода и атмосфера?
Ответ:
Вопрос: Манометр дайвера показывает 250 000 Паскалей в пресной воде (ρ = 1000 кг / м 3 ).
Насколько глубоко ныряльщик?
Ответ:
11.4 Изменение давления в жидкости с глубиной — College Physics
Если у вас когда-либо ломались уши во время полета или болели во время глубокого погружения в бассейне, вы испытали влияние глубины на давление в жидкости. На поверхности Земли давление воздуха, оказываемое на вас, является результатом веса воздуха над вами. Это давление уменьшается по мере того, как вы поднимаетесь на высоту, и вес воздуха над вами уменьшается.Под водой оказываемое на вас давление увеличивается с увеличением глубины. В этом случае оказываемое на вас давление является результатом как веса воды над вами (), так и веса атмосферы над вами (). Вы можете заметить изменение давления воздуха во время поездки на лифте, который перенесет вас на много этажей, но вам нужно погрузиться всего на метр или около того ниже поверхности бассейна, чтобы почувствовать повышение давления. Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Рассмотрим контейнер на рисунке 11.9. Его дно выдерживает вес находящейся в нем жидкости. Вычислим давление, оказываемое на дно, на вес жидкости. Это давление представляет собой вес жидкости mgmg размером 12 {ital «mg»} {}, деленный на поддерживающую его площадь AA размером 12 {A} {} (площадь дна контейнера):
P = мгA.P = мгА. размер 12 {P = {{ital «mg»} больше {A}}} {}
11,12
Мы можем найти массу жидкости, исходя из ее объема и плотности:
m = ρV.m = ρV. размер 12 {m = ρV} {}
11.13
Объем VV жидкости размером 12 {V} {} зависит от размеров контейнера. Это
V = Ah, V = Ah, размер 12 {V = ital «Ah»} {}
11,14
где AA размер 12 {A} {} — это площадь поперечного сечения, а hh размер 12 {h} {} — это глубина. Объединение последних двух уравнений дает
m = ρAh.m = ρAh. размер 12 {m = ρ ital «Ah»} {}
11,15
Если ввести это в выражение для давления, мы получим
P = ρAhgA. P = ρAhgA. размер 12 {P = {{left (ρ ital «Ah» right) g} над {A}}} {}
P = ρAhgA. размер 12 {P = {{left (ρ ital «Ah» right) g} над {A}}} {}
11.16
Область отменяется, и перестановка переменных дает
P = hρg.P = hρg. размер 12 {P = hρg} {}
11,17
Это значение представляет собой давление , обусловленное весом жидкости . Уравнение имеет общую применимость за пределами особых условий, при которых оно получено здесь. Даже если бы емкости не было, окружающая жидкость все равно оказывала бы это давление, сохраняя статическое состояние жидкости. Таким образом, уравнение P = hρgP = hρg размер 12 {P = hρg} {} представляет давление из-за веса любой жидкости со средней плотностью ρρ размер 12 {ρ} {} на любой глубине hh размер 12 {h} { } под его поверхностью.Для жидкостей, которые почти несжимаемы, это уравнение справедливо до больших глубин. Для газов, которые достаточно сжимаемы, можно применять это уравнение до тех пор, пока изменения плотности на рассматриваемой глубине невелики. Пример 11.4 иллюстрирует эту ситуацию.
Пример 11.4 иллюстрирует эту ситуацию.
Рис. 11.9 Дно этого контейнера выдерживает весь вес находящейся в нем жидкости. Вертикальные стороны не могут оказывать на жидкость восходящую силу (так как она не может выдерживать силу сдвига), поэтому дно должно поддерживать все это.
Пример 11.3
Расчет среднего давления и прилагаемой силы: какую силу должна выдержать плотина?
В примере 11.1 мы вычислили массу воды в большом резервуаре. Теперь мы рассмотрим давление и силу, действующие на удерживающую воду плотину. (См. Рис. 11.10.) Ширина плотины составляет 500 м, а глубина воды у плотины — 80,0 м. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на плотину, и сравните ее с весом воды в плотине (ранее было установлено, что оно равно 1.96 × 1013N1.96 × 1013N).
Стратегия для (а)
Среднее давление P¯P¯
из-за веса воды давление на средней глубине h¯h¯
40,0 м, так как давление линейно растет с глубиной.
Решение для (а)
Среднее давление из-за веса жидкости
P¯ = h¯ρg.P¯ = h¯ρg. размер 12 {P = hρg} {}
11,18
Введите плотность воды из таблицы 11.1 и принимая h¯h¯ size 12 {h} {} за среднюю глубину 40.0 м получаем
P¯ = (40,0 м) 103 кгм39,80 мс2 = 3,92 × 105 Нм2 = 392 кПа. P¯ = (40,0 м) 103 кгм39,80 мс2 = 3,92 × 105 Нм2 = 392 кПа.
11,19
Стратегия для (b)
Сила, оказываемая водой на плотину, равна среднему давлению, умноженному на площадь контакта:
F = P¯A.F = P¯A. размер 12 {F = {overline {P}} A} {}
11.20
Решение для (b)
Мы уже нашли значение для P¯P¯ size 12 {{bar {P}}} {}. Площадь плотины A = 80,0 м × 500 м = 4,00 × 104 м2A = 80.0 м × 500 м = 4,00 × 104 м2 размер 12 {A = «80» «.» 0`m умножить на «500» `m = 4″. » «00» умножить на «10» rSup {размер 8 {4}} `m rSup {размер 8 {2}}} {}, так что
F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н . F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н. выравнивание {stack {
F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н. выравнивание {stack {
размер 12 {F = \ (3 «.» «92» умножить на «10» rSup {размер 8 {5}} `» N / m «rSup {size 8 {2}} \) \ (4». «» 00 «раз» 10 «rSup {размер 8 {4}}` m rSup {размер 8 {2}} \)} {} #
«» = 1 «.» «57» умножить на «10» rSup {size 8 {«10″}} `N». » {}
}} {}
11.21
Обсуждение
Хотя эта сила кажется большой, она мала по сравнению с 1.96 × 1013N1.96 × 1013N размер 12 {1 «.» «96» умножить на «10» rSup {size 8 {«13»}} `N} {} веса воды в резервуаре — фактически, это всего лишь
0,0800% 0,0800% вес. Обратите внимание, что давление, обнаруженное в части (а), полностью не зависит от ширины и длины озера — оно зависит только от его средней глубины у плотины. Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища. На диаграмме толщина дамбы увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличения давления. epth, чтобы уравновесить увеличивающуюся силу из-за увеличения давления.
epth, чтобы уравновесить увеличивающуюся силу из-за увеличения давления.
Рисунок 11.10 Плотина должна выдерживать силу, прилагаемую к ней удерживаемой водой. Эта сила мала по сравнению с весом воды за плотиной.
Атмосферное давление — еще один пример давления из-за веса жидкости, в данном случае из-за веса воздуха над заданной высотой. Атмосферное давление у поверхности Земли немного меняется из-за крупномасштабного потока атмосферы, вызванного вращением Земли (это создает погодные «максимумы» и «минимумы»).Однако среднее давление на уровне моря определяется стандартным атмосферным давлением PatmPatm размером 12 {P rSub {size 8 {«atm»}}} {}, измеренным как
1 атмосфера (атм) = Patm = 1,01 × 105 Н / м2 = 101 кПа. 1 атмосфера (атм) = Патм = 1,01 × 105 Н / м2 = 101 кПа. размер 12 {1` «атмосфера» `\ (» атм «\) = P rSub {размер 8 {» атм «}} = 1″. » «01» умножить на «10» rSup {размер 8 {5}} «Н / м» rSup {size 8 {2}} = «101» «« кПа »} {}
11,22
Это соотношение означает, что на в среднем, на уровне моря, столб воздуха выше 1. 00m21.00m2 поверхности Земли имеет вес 1.01 × 105N1.01 × 105N размер 12 {1 «.» «01» умножить на «10» rSup {size 8 {5}} `N} {}, что эквивалентно 1 атм1 атм. (См. Рисунок 11.11.)
00m21.00m2 поверхности Земли имеет вес 1.01 × 105N1.01 × 105N размер 12 {1 «.» «01» умножить на «10» rSup {size 8 {5}} `N} {}, что эквивалентно 1 атм1 атм. (См. Рисунок 11.11.)
Рисунок 11.11 Атмосферное давление на уровне моря в среднем составляет 1,01 × 105 Па1,01 × 105 Па размером 12 {1 «.» «01» умножить на «10» rSup {размер 8 {5}} «» Па «} {} (эквивалентно 1 атм.), Поскольку столб воздуха над этим 1м21м2 размером 12 {1`m rSup {размер 8 {2} }} {}, простираясь до верхних слоев атмосферы, весит 1,01 × 105 N1,01 × 105 N размером 12 {1 «.»» 01 «умножить на» 10 «rSup {size 8 {5}}» N «} {}.
Пример 11.4
Расчет средней плотности: насколько плотен воздух?
Рассчитайте среднюю плотность атмосферы, учитывая, что она простирается до высоты 120 км. Сравните эту плотность с плотностью воздуха, указанной в таблице 11.1.
Стратегия
Если мы решим для плотности P = hρgP = hρg size 12 {P = hρg} {}, мы увидим, что
ρ¯ = Phg. ρ¯ = Phg. размер 12 {{bar {ρ}} = {{P} over {ital «hg»}}} {}
ρ¯ = Phg. размер 12 {{bar {ρ}} = {{P} over {ital «hg»}}} {}
11.23
Затем мы принимаем размер PP 12 {P} {} за атмосферное давление, задан размер hh 12 {h} {} и известен размер gg 12 {g} {}, и мы можем использовать это для расчета ρ¯ρ¯ размер 12 {{bar {ρ}}} {}.
Раствор
Ввод известных значений в выражение для ρ¯ρ¯ размера 12 {{bar {ρ}}} {} дает
ρ¯ = 1,01 × 105 Н / м2 (120 × 103 м) (9,80 м / с2) = 8,59 × 10− 2 кг / м3. Ρ¯ = 1,01 × 105 Н / м2 (120 × 103 м) (9,80 м / с2) = 8,59 × 10–2 кг / м3. размер 12 {{bar {ρ}} = {{1 «.» «01» умножить на «10» rSup {размер 8 {5}} «» N / m «rSup {size 8 {2}}} больше {\ (» 120 «умножить на» 10 «rSup {размер 8 {3}}` м \) \ (9 «.»» 80 «` «м / с» rSup {размер 8 {2}} \)}} = 8 «.» «59» умножить на «10» rSup {размер 8 {- 2}} «» кг / м «rSup {размер 8 {3}}} {}
11,24
Обсуждение
Этот результат представляет собой среднюю плотность воздуха между поверхностью Земли и верхним слоем атмосферы Земли, которая по существу заканчивается на уровне 120 км. Плотность воздуха на уровне моря, указанная в таблице 11.1, составляет 1,29 кг / м 31,29 кг / м3 размер 12 {1 «». «29» «» кг / м «rSup {size 8 {3}}} {} — примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
Плотность воздуха на уровне моря, указанная в таблице 11.1, составляет 1,29 кг / м 31,29 кг / м3 размер 12 {1 «». «29» «» кг / м «rSup {size 8 {3}}} {} — примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
Пример 11.5
Расчет глубины под поверхностью воды: какая глубина воды создает такое же давление, как и вся атмосфера?
Вычислите глубину ниже поверхности воды, на которой давление, обусловленное весом воды, равно 1,00 атм.
Стратегия
Начнем с решения уравнения P = hρgP = hρg size 12 {P = hρg} {} для глубины hh size 12 {h} {}:
h = Pρg.h = Pρg. размер 12 {h = {{P} over {ρg}}} {}
11.25
Затем мы берем PP размер 12 {P} {} равным 1,00 атм и размер ρρ 12 {ρ} {} как плотность воды, которая создает давление.
Решение
Ввод известных значений в выражение для размера hh 12 {h} {} дает
h = 1,01 × 105 Н / м2 (1,00 × 103 кг / м3) (9,80 м / с2) = 10,3 м.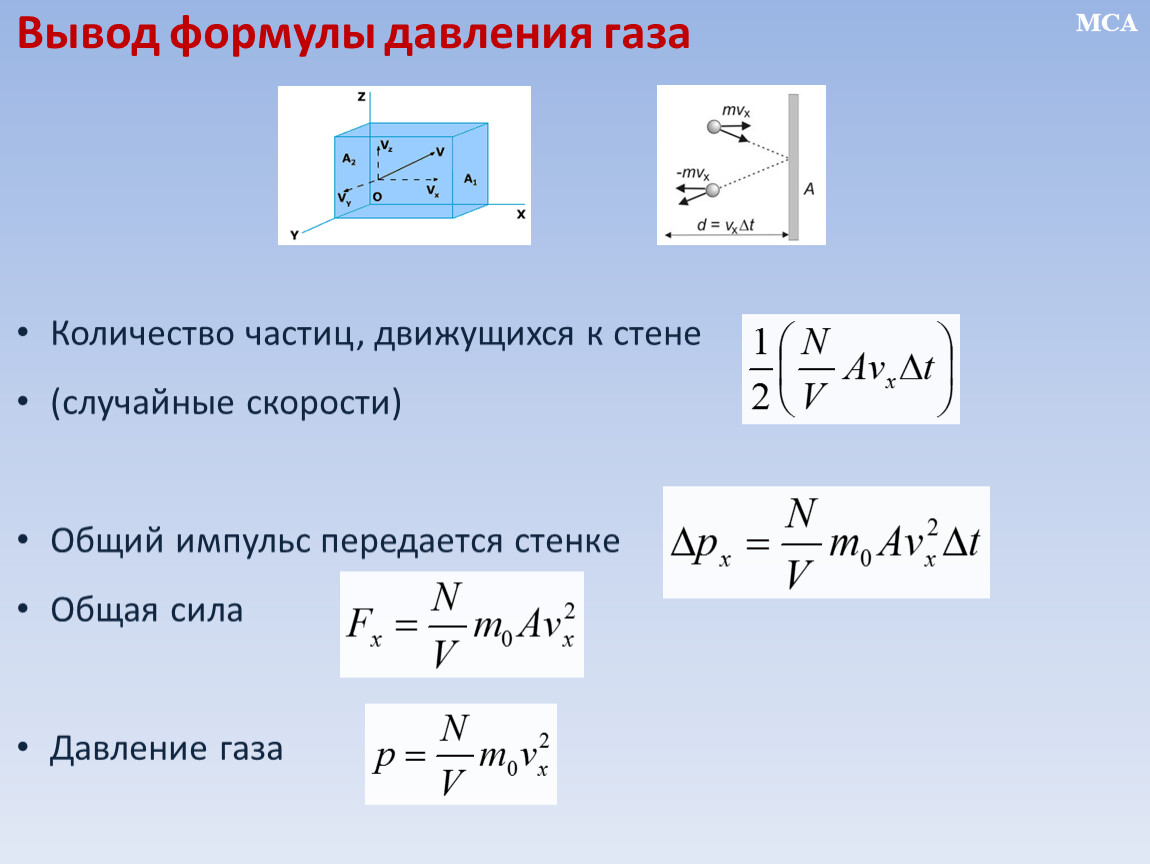 h = 1,01 × 105 Н / м2 (1,00 × 103 кг / м3) (9,80 м / с2) = 10,3 м. размер 12 {h = {{1 «.» «01» умножить на «10» rSup {размер 8 {5}} «» N / m «rSup {size 8 {2}}} больше {\ (1». «» 00 «умножить на» 10 «rSup {size 8 { 3}} `» кг / м «rSup {размер 8 {3}} \) \ (9″.»» 80 «` «m / s» rSup {size 8 {2}} \)}} = «10» «.» 3`m} {}
h = 1,01 × 105 Н / м2 (1,00 × 103 кг / м3) (9,80 м / с2) = 10,3 м. размер 12 {h = {{1 «.» «01» умножить на «10» rSup {размер 8 {5}} «» N / m «rSup {size 8 {2}}} больше {\ (1». «» 00 «умножить на» 10 «rSup {size 8 { 3}} `» кг / м «rSup {размер 8 {3}} \) \ (9″.»» 80 «` «m / s» rSup {size 8 {2}} \)}} = «10» «.» 3`m} {}
11,26
Обсуждение
Всего 10,3 м воды создают такое же давление, как 120 км воздуха. Поскольку вода почти несжимаема, мы можем пренебречь любым изменением ее плотности на этой глубине.
Как вы думаете, каково общее давление на глубине 10,3 м в бассейне? Влияет ли атмосферное давление на поверхность воды на давление под ней? Ответ положительный. Это кажется логичным, поскольку необходимо поддерживать вес воды и атмосферы.Таким образом, общее давление на глубине 10,3 м составляет 2 атм — половина от воды выше и половина от воздуха выше. Мы увидим в принципе Паскаля, что давление жидкости всегда увеличивается таким образом.
Гидростатическое давление: определение, уравнения и расчеты — стенограмма видео и урока
Давление в жидкости
Частицы газа не очень дружелюбны. Они расходятся, чтобы заполнить все пространство своего контейнера, наслаждаясь своим личным пространством и свободой.Но когда частицы газа летают, они иногда сталкиваются друг с другом, а также со стенками контейнера. Эти взаимодействия создают давление в контейнере, и в газе это давление одинаково для всей жидкости.
Но вы можете ясно видеть, что это не относится к жидкостям, потому что они не заполняют весь свой контейнер, как это делают газы. Это происходит из-за связей между молекулами жидкости, которые удерживают их вместе. Когда вы наливаете жидкость в емкость, она заполняет дно, потому что сила тяжести тянет ее вниз.Эта сила, вызванная гравитацией, такая же, как и на ваших весах — это вес жидкости, и именно она создает давление в этой жидкости.
Давление в жидкости также увеличивается с глубиной из-за силы тяжести. Жидкость внизу должна выдерживать вес всей жидкости над ней, а также всего воздуха над ней! Вы не замечаете веса воздуха вокруг вас, потому что ваше тело находится под таким же давлением, как и атмосфера, но любая жидкость под этой атмосферой определенно ощущает это.
Жидкость внизу должна выдерживать вес всей жидкости над ней, а также всего воздуха над ней! Вы не замечаете веса воздуха вокруг вас, потому что ваше тело находится под таким же давлением, как и атмосфера, но любая жидкость под этой атмосферой определенно ощущает это.
Вы можете почувствовать это изменение давления, когда плывете на дно бассейна. По мере того, как вы погружаетесь глубже под воду, вы чувствуете, как давление увеличивается, потому что на вас ложится все больше и больше веса. Но давление не просто на вас накапливается. Поскольку вы находитесь в жидкости, вы почувствуете, как увеличивается давление вокруг вас.
Расчет давления жидкости
Когда жидкость находится в состоянии покоя, что означает, что она не течет, мы можем определить ее давление на заданной глубине, известной как гидростатическое давление .Мы определяем это с помощью уравнения: P = rho * g * d , где P — давление, rho — плотность жидкости, g — сила тяжести и d — глубина.
Вы также можете увидеть уравнение гидростатики, записанное как P = rho * g * h , где h обозначает высоту. Это можно использовать, потому что иногда мы хотим рассчитать давление жидкости, когда она заполняет столбец (например, при измерении барометрического давления), поэтому нам нужно знать высоту жидкости.Это все равно, что взять глубину и перевернуть ее вверх дном. Если вы используете соответствующее измерение, можно использовать любую букву, но может помочь придерживаться той буквы, которая лучше всего представляет то, что вы измеряете — глубину или высоту.
Важно помнить, что плотность жидкости не меняется с глубиной так же, как плотность моноблока меняется, когда вы разбиваете его на отдельные части. Жидкости не сжимаются, это означает, что их молекулы уже расположены настолько близко друг к другу, насколько это возможно.Также самое время обратить внимание на г в уравнении. Он действует как постоянное напоминание о том, как сила тяжести играет решающую роль в давлении жидкости на любой заданной глубине.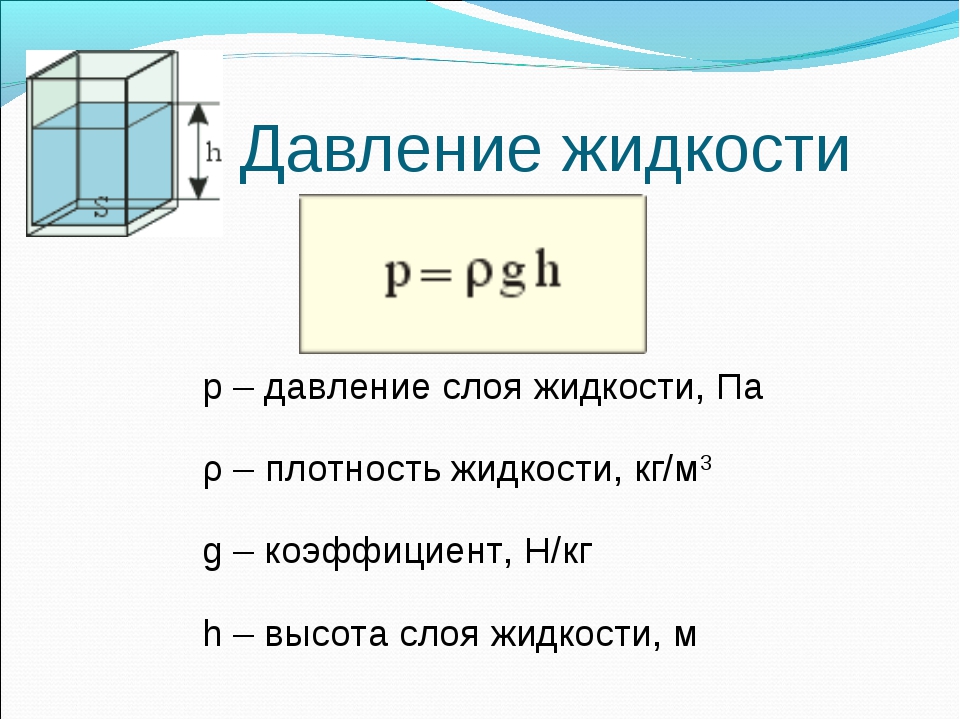 3.2, если вы знаете две другие переменные, вы можете легко вычислить третью. Все, что нужно, — это немного перестроить, а затем быстро произвести вычисления.
3.2, если вы знаете две другие переменные, вы можете легко вычислить третью. Все, что нужно, — это немного перестроить, а затем быстро произвести вычисления.
Краткое содержание урока
В жидкости давление воздействует не только на емкость, в которой находится жидкость, но и на все части самой жидкости. Давление в жидкости создается массой жидкости, которая является силой тяжести. По мере увеличения глубины увеличивается и давление, потому что сверху исходит больше веса (или силы).2), а d — глубина (или высота) жидкости.
Используя это уравнение, мы можем определить давление на любой заданной глубине в жидкости, если нам известна ее плотность. Мы также можем найти плотность или глубину жидкости, если мы знаем другие переменные и соответствующим образом изменим уравнение.
Результаты обучения
Когда вы дойдете до конца этого урока, вы сможете:
- Определить гидростатическое давление
- Понимать характеристики давления в жидкости
- Рассчитайте давление любой жидкости по уравнению гидростатики
Что такое давление — Физика | Определение и расчет
Паскаль определяется как сила в 1Н, действующая на единицу площади.
Однако это довольно маленькая единица для большинства инженерных задач, поэтому она удобна для работы с кратными паскалям: кПа , бар и МПа .
Обычно давление или сила, действующая на единицу площади на границах вещества, вызывается столкновениями молекул вещества с границами системы. Когда молекулы ударяются о стенки, они проявляют силы, которые пытаются вытолкнуть стенки наружу.Силы, возникающие в результате всех этих столкновений, вызывают давление , оказываемое системой на ее окружение. Давление как интенсивная переменная постоянно в замкнутой системе. Это актуально только для жидких или газообразных систем.
Шкалы давления — Единицы давления
Паскаль — Единицы давления
Как уже говорилось, единица измерения СИ для давления и напряжения — это паскаль .
- 1 паскаль 1 Н / м 2 = 1 кг / (м.
 s 2 )
s 2 )
Паскаль определяется как один Ньютон на квадратный метр. Однако это довольно маленький блок для большинства инженерных задач, поэтому он удобен для работы с кратными паскалям: кПа , бар и МПа .
- 1 МПа 10 6 Н / м 2
- 1 бар 10 5 Н / м 2
- 1 кПа 10 3 Н / м 2
Единица измерения, называемая стандартной атмосферой ( атм ), определяется как:
Стандартная атмосфера приблизительно соответствует среднему давлению на уровне моря на 45 ° северной широты.Обратите внимание, что существует разница между стандартной атмосферой (атм) и технической атмосферой (атм).
Техническая атмосфера — внесистемная единица измерения давления, равная одному килограмму-силе на квадратный сантиметр.
Фунтов на квадратный дюйм — psi
Стандартной единицей в английской системе является фунт-сила на квадратный дюйм (psi) . Это давление, возникающее в результате приложения силы в один фунт-сила к площади в один квадратный дюйм.
- 1 фунт / кв. Дюйм 1 фунт-сила / дюйм 2 = 4,45 Н / (0,0254 м) 2 ≈ 6895 кг / м 2
Таким образом, один фунт на квадратный дюйм составляет примерно 6895 Па.
Единица измерения, называемая стандартной атмосферой (атм), определяется как:
Стандартная атмосфера приблизительно соответствует среднему давлению на уровне моря на широте 45 ° северной широты. Обратите внимание, что существует разница между стандартной атмосферой (атм) и техническая атмосфера (ат).
Техническая атмосфера — внесистемная единица измерения давления, равная одному килограмму-силе на квадратный сантиметр.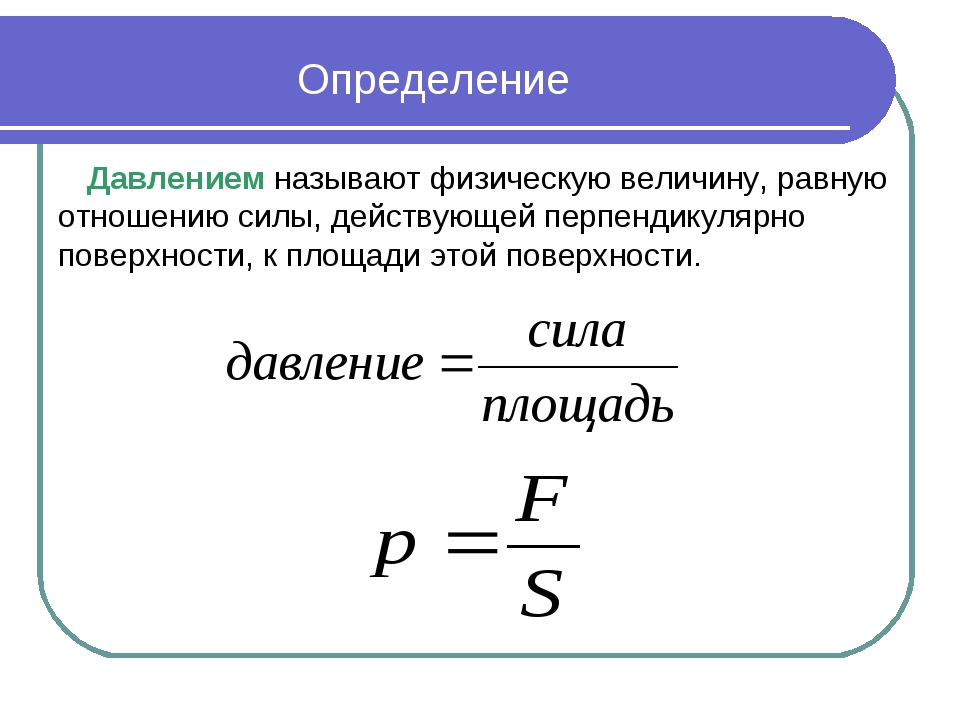
Бар — единица измерения давления
бар — метрическая единица измерения давления . Он не является частью Международной системы единиц (СИ). бар обычно используется в промышленности и метеорологии , а прибор, используемый в метеорологии для измерения атмосферного давления, называется барометром.
Один бар точно равен 100 000 Па и немного меньше среднего атмосферного давления на Земле на уровне моря ( 1 бар = 0,9869 атм). Атмосферное давление часто указывается в миллибарах, где стандартное давление на уровне моря определяется как 1013 мбар, 1,013 бар или 101,3 (кПа).
Иногда «бар (а)» и «бар» используются для обозначения абсолютного давления, а «бар (изб.)» И «бар» — для манометрического давления.
Абсолютное давление в сравнении с избыточным давлением
Давление, как обсуждалось выше, называется абсолютным давлением .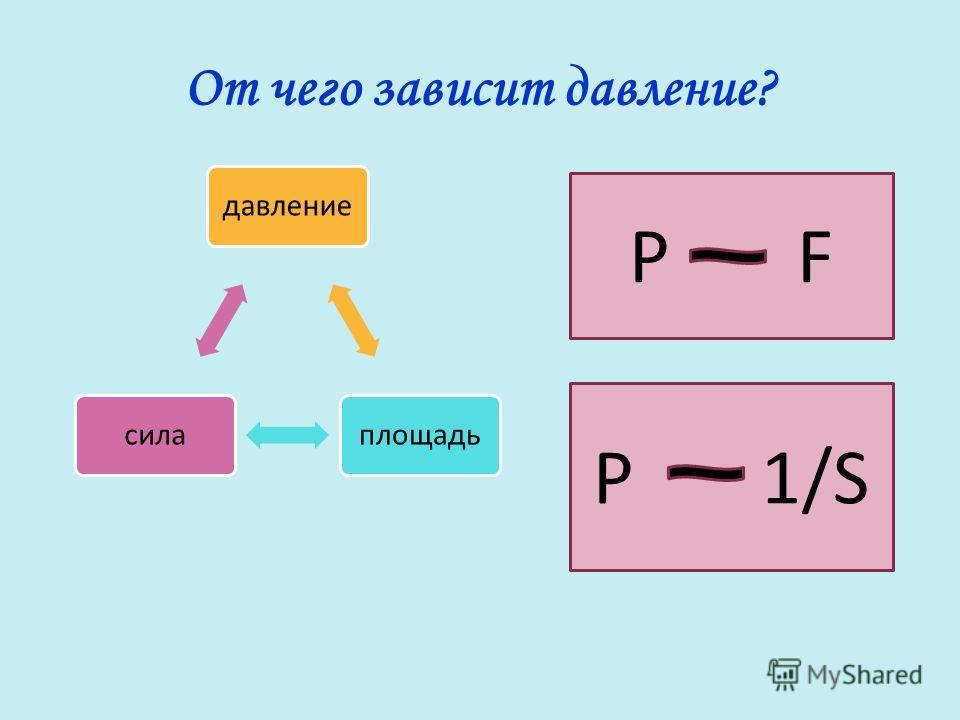 Часто бывает важно различать абсолютное давление и манометрическое давление . В этой статье термин «давление» относится к абсолютному давлению, если явно не указано иное. Но в технике мы часто имеем дело с давлением, которое составляет , измеренное некоторыми приборами . Хотя в термодинамических соотношениях необходимо использовать абсолютное давление, устройства для измерения давления часто показывают разницу между абсолютным давлением в системе и абсолютным давлением атмосферы, существующей вне измерительного устройства.Они измеряют манометрическое давление .
Часто бывает важно различать абсолютное давление и манометрическое давление . В этой статье термин «давление» относится к абсолютному давлению, если явно не указано иное. Но в технике мы часто имеем дело с давлением, которое составляет , измеренное некоторыми приборами . Хотя в термодинамических соотношениях необходимо использовать абсолютное давление, устройства для измерения давления часто показывают разницу между абсолютным давлением в системе и абсолютным давлением атмосферы, существующей вне измерительного устройства.Они измеряют манометрическое давление .
- Абсолютное давление. Когда давление измеряется относительно абсолютного вакуума, оно называется абсолютным давлением (psia). Абсолютные фунты на квадратный дюйм (psia) используются для пояснения того, что давление относится к вакууму, а не к окружающему атмосферному давлению. Поскольку атмосферное давление на уровне моря составляет около 101,3 кПа (14,7 фунта на квадратный дюйм), оно будет добавлено к любым показаниям давления, полученным в воздухе на уровне моря.

- Манометрическое давление. Когда давление измеряется относительно атмосферного давления (14,7 фунтов на квадратный дюйм), это называется манометрическим давлением (фунтов на квадратный дюйм). Термин «манометрическое давление» применяется, когда давление в системе превышает местное атмосферное давление, p атм . Последняя шкала давления была разработана, потому что почти все манометры регистрируют ноль, когда они открыты для атмосферы. Манометрическое давление положительное, если оно выше атмосферного, и отрицательное, если оно ниже атмосферного.
p калибр = p абсолютный — p абсолютный; атм
- Атмосферное давление. Атмосферное давление — это давление в окружающем воздухе на поверхности Земли или «близко» к ней. Атмосферное давление зависит от температуры и высоты над уровнем моря. Стандартное атмосферное давление приближается к среднему давлению на уровне моря на 45 ° северной широты.
 Стандартное атмосферное давление определяется на уровне моря 273 o K (0 o C) и составляет:
Стандартное атмосферное давление определяется на уровне моря 273 o K (0 o C) и составляет:- 101325 Па
- 1.01325 бар
- 14,696 psi
- 760 мм рт. Ст.
- 760 торр
- Отрицательное манометрическое давление — вакуумное давление. Когда местное атмосферное давление больше, чем давление в системе, используется термин давление вакуума . Идеальный вакуум соответствовал бы абсолютному нулевому давлению. Конечно, возможно отрицательное манометрическое давление, но невозможно отрицательное абсолютное давление.Например, абсолютное давление 80 кПа может быть описано как манометрическое давление -21 кПа (то есть на 21 кПа ниже атмосферного давления 101 кПа).
p вакуум = p абсолютный; атм — p абсолютное
Например, автомобильная шина, накачанная на 2,5 атм (36,75 фунта на кв.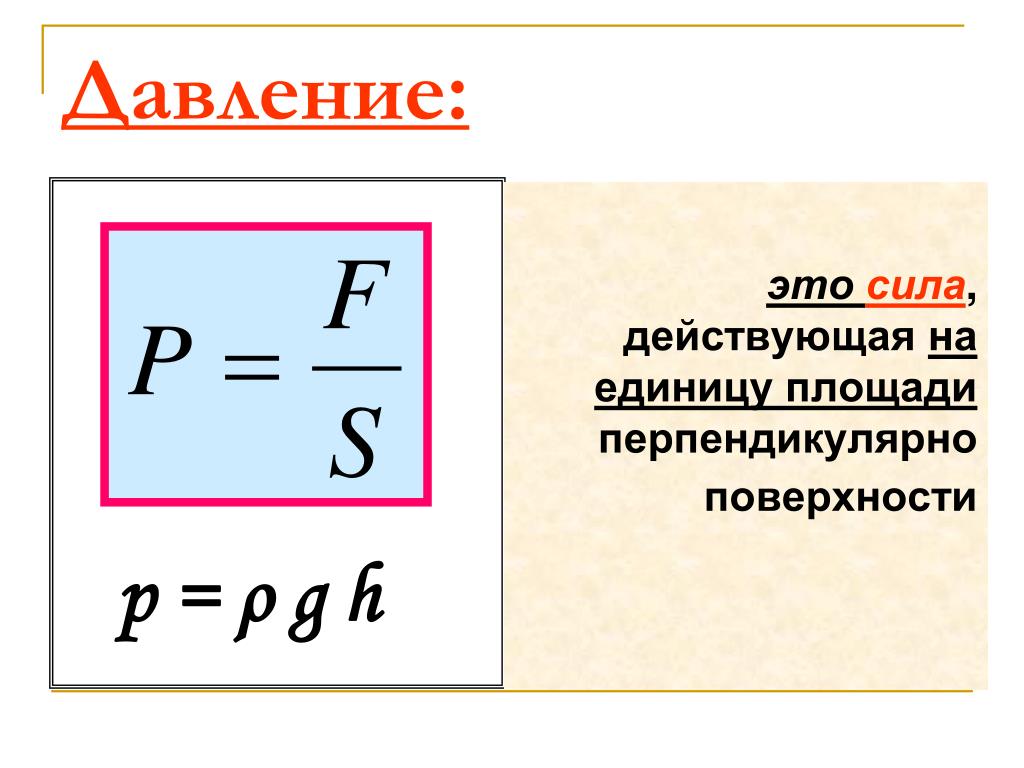 дюйм) выше местного атмосферного давления (скажем, на 1 атм или 14,7 фунта на кв. 2.5 + 1 = 3,5 атм (36,75 + 14,7 = 51,45 фунтов на кв. Дюйм или 36,75 фунтов на кв. Дюйм).
дюйм) выше местного атмосферного давления (скажем, на 1 атм или 14,7 фунта на кв. 2.5 + 1 = 3,5 атм (36,75 + 14,7 = 51,45 фунтов на кв. Дюйм или 36,75 фунтов на кв. Дюйм).
С другой стороны, конденсационные паровые турбины (на атомных электростанциях) отводят пар под давлением значительно ниже атмосферного (например, 0,08 бар, 8 кПа или 1,16 фунта на квадратный дюйм) и в частично конденсированном состоянии. В относительных единицах это отрицательное избыточное давление около — 0,92 бара, — 92 кПа или — 13,54 фунта на кв. Дюйм изб.
Закон идеального газа
Любое уравнение, которое связывает давление, температуру и удельный объем вещества, называется уравнением состояния .Самое простое и наиболее известное уравнение состояния для веществ в газовой фазе — это уравнение состояния идеального газа . Эмиль Клапейрон впервые сформулировал это в 1834 году как комбинацию эмпирического закона Бойля, закона Шарля и закона Авогадро. Это уравнение довольно точно предсказывает поведение p-v-T газа для разреженных газов или газов низкого давления. В идеальном газе молекулы не имеют объема и не взаимодействуют. Согласно закону идеального газа, давление изменяется линейно с температурой и количеством и обратно пропорционально с объемом .
Это уравнение довольно точно предсказывает поведение p-v-T газа для разреженных газов или газов низкого давления. В идеальном газе молекулы не имеют объема и не взаимодействуют. Согласно закону идеального газа, давление изменяется линейно с температурой и количеством и обратно пропорционально с объемом .
pV = nRT
где:
- p — абсолютное давление газа
- n — количество вещества
- T — абсолютная температура
- V — объем
- R — идеальная или универсальная газовая постоянная , равная произведению постоянной Больцмана и постоянной Авогадро ,
В этом уравнении символ R — это универсальная газовая постоянная , которая имеет одинаковое значение для всех газов, а именно R = 8. 31 Дж / моль К.
31 Дж / моль К.
Сила закона идеального газа заключается в его простоте . Когда любые , две термодинамические переменные , p, v и T, равны , при , , третья может быть легко найдена . Идеальный газ определяется как газ, в котором все столкновения между атомами или молекулами являются совершенно упругими и в котором отсутствуют межмолекулярные силы притяжения. Идеальный газ можно представить себе как набор идеально твердых сфер, которые сталкиваются, но в остальном не взаимодействуют.На самом деле никакие настоящие газы не похожи на идеальный газ, и поэтому никакие настоящие газы полностью не подчиняются закону или уравнению идеального газа. При температурах, близких к точке кипения газов, повышение давления вызовет конденсацию и резкое уменьшение объема. При очень высоких давлениях межмолекулярные силы газа значительны. Однако большинство газов примерно соответствуют друг другу при давлениях и температурах выше их точки кипения. Инженеры, работающие с газами, используют закон идеального газа, поскольку он прост и приближается к поведению реального газа.
Инженеры, работающие с газами, используют закон идеального газа, поскольку он прост и приближается к поведению реального газа.
Типичные значения давления в технике — Примеры
Паскаль (Па) как единица измерения давления широко используется во всем мире. Он в значительной степени заменил единицу фунтов на квадратный дюйм (psi), за исключением некоторых стран, которые все еще используют имперскую систему измерения, включая Соединенные Штаты. Для большинства инженерных задач паскаль (Па) — довольно малая единица, поэтому удобно работать с кратными паскалям: кПа, МПа или бар. В следующем списке приведены несколько примеров:
- Обычно на большинстве атомных электростанций работают многоступенчатые конденсационные паровые турбины .Эти турбины выпускают пар под давлением значительно ниже атмосферного (например, 0,08 бар, 8 кПа или 1,16 фунта на квадратный дюйм) и в частично конденсированном состоянии.
 В относительных единицах это отрицательное избыточное давление около — 0,92 бара, — 92 кПа или — 13,54 фунта на кв. Дюйм изб.
В относительных единицах это отрицательное избыточное давление около — 0,92 бара, — 92 кПа или — 13,54 фунта на кв. Дюйм изб. - Стандартное атмосферное давление приближается к среднему давлению на уровне моря на 45 ° северной широты. Стандартное атмосферное давление определяется на уровне моря 273 o K (0 o C) и составляет:
- 101325 Па
- 1.01325 бар
- 14,696 фунтов на кв. Дюйм
- 760 мм рт.
- Жаротрубный котел паровоза: 150–250 фунт / кв. , x = 1
- Реактор с кипящей водой охлаждается и замедляется водой, как PWR, но при более низком давлении (т.е.g., 7 МПа, 70 бар или 1015 фунт / кв.
- Реакторы с водой под давлением охлаждаются и замедляются жидкой водой под высоким давлением (например, 16 МПа, 160 бар или 2320 фунтов на кв.
 Дюйм). При таком давлении вода закипает при температуре около 350 ° C (662 ° F), что обеспечивает запас по переохлаждению около 25 ° C.
Дюйм). При таком давлении вода закипает при температуре около 350 ° C (662 ° F), что обеспечивает запас по переохлаждению около 25 ° C. - Реактор со сверхкритической водой (SCWR) работает при сверхкритическом давлении .Термин сверхкритический в данном контексте относится к термодинамической критической точке воды (T CR = 374 ° C; p CR = 22,1 МПа)
- Common Rail с прямым впрыском топлива: Он отличается высоким давлением (более 1000 бар или 100 МПа или 14500 фунтов на квадратный дюйм) топливная рампа на дизельных двигателях.
Давление в реакторе с водой под давлением
Компрессор является ключевым компонентом реакторов PWR.
В реакторах с водой под давлением используется корпус реактора под давлением (КР), в котором находятся ядерное топливо, замедлитель, регулирующие стержни и теплоноситель.Они охлаждаются и замедляются жидкой водой под высоким давлением (например, 16 МПа).
 При таком давлении вода закипает примерно при 350 ° C (662 ° F). Это высокое давление поддерживается компенсатором давления. Температура воды на входе составляет около 290 ° C (554 ° F). Вода (теплоноситель) нагревается в активной зоне реактора примерно до 325 ° C (617 ° F), когда вода протекает через активную зону. Как видно, реактор имеет переохлажденный теплоноситель примерно на 25 ° C (расстояние от насыщения).
При таком давлении вода закипает примерно при 350 ° C (662 ° F). Это высокое давление поддерживается компенсатором давления. Температура воды на входе составляет около 290 ° C (554 ° F). Вода (теплоноситель) нагревается в активной зоне реактора примерно до 325 ° C (617 ° F), когда вода протекает через активную зону. Как видно, реактор имеет переохлажденный теплоноситель примерно на 25 ° C (расстояние от насыщения).Компрессор давления является компонентом реактора с водой под давлением. Давление в первичном контуре PWR поддерживается компенсатором давления , отдельной емкостью, подключенной к первичному контуру (горячая ветвь) и частично заполненной водой, нагретой до температуры насыщения (точка кипения) для желаемого давления. погружными электронагревателями .
С другой стороны, имеются распылительных линий с по , которые снижают давление внутри компенсатора давления , что вызывает снижение давления в системе теплоносителя реактора.
 Эти распылительные линии распыляют охлаждающую жидкость реактора из холодного участка контура в паровое пространство и конденсируют часть пара. Закалочное действие снижает давление и ограничивает повышение давления.
Эти распылительные линии распыляют охлаждающую жидкость реактора из холодного участка контура в паровое пространство и конденсируют часть пара. Закалочное действие снижает давление и ограничивает повышение давления.Давления в конденсационных паровых турбинах
Цикл Ренкина — термодинамика как наука о преобразовании энергии
Обычно на большинстве атомных электростанций используются многоступенчатые паровые конденсационные турбины . В этих турбинах ступень высокого давления принимает пар (этот пар почти насыщенный пар — x = 0.995 — точка С на рисунке; 6 МПа ; 275,6 ° C) из парогенератора и отводит его в сепаратор-подогреватель влаги (точка D). Чтобы избежать повреждения лопаток паровой турбины некачественным паром, необходимо повторно нагреть пар. Подогреватель нагревает пар (точка D), а затем пар направляется в ступень низкого давления паровой турбины, где он расширяется (точка от E до F). Отработанный пар находится под давлением значительно ниже атмосферного (абсолютное давление 0,008 МПа, ) и находится в частично конденсированном состоянии (точка F), как правило, с качеством около 90%.

См. Также: Влажный пар
См. Также: Таблицы пара
«Давление
Коэффициент давления (или коэффициент плотности замедлителя) определяется как изменение реактивности на единицу изменения давления.
α P = dρ ⁄ dP
Выражается в единицах pcm / MPa. Величина и знак коэффициента давления (+ или -) в первую очередь зависят от отношения замедлитель / топливо . Значит, это в первую очередь зависит от конкретной конструкции реактора.
Хотя вода считается несжимаемой, на самом деле она слегка сжимаема (особенно при 325 ° C (617 ° F)). Влияние давления в первом контуре имеет последствия, аналогичные , как и температура замедлителя . По сравнению с эффектами изменений температуры замедлителя, изменения давления имеют влияние более низкого порядка на реактивность. Причины только в плотности замедлителя, а не в изменении микроскопических сечений.

Потеря давления — жидкости
Краткое описание: Потеря напора — потеря давления
Критическое давление воды
Фазовая диаграмма воды.
Источник: wikipedia.org CC BY-SAПри давлении, которое на выше критического, вода находится в особом состоянии, известном как сверхкритическое жидкое состояние . Сверхкритическая жидкость — это жидкость, которая находится под давлением, превышающим ее термодинамические критические значения. При критическом и сверхкритическом давлении жидкость считается однофазным веществом , , хотя все теплофизические свойства претерпевают значительные изменения в критической и псевдокритической областях.
Для воды критические параметры следующие:
- P cr = 22,09 МПа
- T cr = 374,14 ° C (или 647,3 K)
- v cr = 0,003155 м3 / кг
- u f = u g = 2014 кДж / кг
- h f = h g = 2084 кДж / кг
- s f = s g = 4,406 кДж / кг K
См.
 также: Критическая точка воды
также: Критическая точка водыСм. также: Сверхкритическая жидкость
Гидростатическое давление — Mini Physics
Жидкости и газы называются жидкостями, поскольку они могут легко изменять свою форму.Жидкость — это вещество, которое может течь. На рисунке выше мы замечаем, что вода из правого контейнера течет дальше, чем вода из левого контейнера. Единственная разница между двумя контейнерами — высота водяного столба. Следовательно, мы знаем, что величина давления внутри тела жидкости увеличивается с его глубиной (или высотой столба жидкости).
Давление в колонне жидкости
Давление, создаваемое столбом жидкости (p) = высота столба (h) X плотность жидкости ($ \ rho $) X напряженность гравитационного поля (g).(Вывод этой формулы можно найти внизу этого поста.)
$$ p = \ rho g h $$
В жидкости, если две точки разделены вертикальной высотой, их перепад давления составляет:
$$ \ Delta p = \ rho g \ Delta h $$
Из формулы $ p = \ rho g h $ видно, что давление зависит от глубины и плотности жидкости, а НЕ от площади поперечного сечения или объема жидкости.
 Следовательно, давление воды в нижней части контейнера на рисунке выше будет одинаковым во всем контейнере, так как уровень воды такой же! Форма емкости НЕ имеет значения при расчете давления воды!
Следовательно, давление воды в нижней части контейнера на рисунке выше будет одинаковым во всем контейнере, так как уровень воды такой же! Форма емкости НЕ имеет значения при расчете давления воды!Недвижимость (сводка)
- Давление передается по всей жидкости
- Давление действует во всех направлениях
- Все точки на одной и той же глубине в жидкости находятся под одинаковым давлением
- Давление увеличивается с глубиной
- Давление зависит не от формы контейнера, а по его глубине.
Давление на разной глубине
Объект, погруженный в однородную жидкость, будет испытывать давление, которое зависит только от высоты жидкости над объектом.
Рассмотрим картинку ниже.
$$ \ text {Давление в точке A} = P_ {0} + \ rho g h $$
, где $ P_ {0} $ — атмосферное давление
Простой вывод формулы для гидростатического давления ($ p = \ rho g h $):
Рассмотрим столб воды, занимающий общий объем V и площадь основания A.

Вес всей воды:
$$ W = мг $$
Напомним, что масса воды — это просто плотность воды X объема воды: $ m = \ rho V $. Следовательно,
$$ W = \ rho V g $$
Отметим, что объем является произведением площади поверхности и высоты: $ V = Ah $
.
$$ W = \ rho A h g $$
Напомним, что формула для давления: $ p = \ frac {F} {A} $. Sub. через W в F получить:
$$ \ begin {align} p & = \ frac {\ rho A h g} {A} \\ & = \ rho h g \ end {align} $$
Готово.
Введение в давление в механике жидкости
Введение в давление в механике жидкости
Введение в давление в механике жидкостей
- Давление всегда действует внутрь нормально к любому
поверхность (даже воображаемые поверхности, как в контрольном объеме). - Давление является нормальным напряжением и, следовательно, имеет размеры силы на
единица площади, или {ML -1 T -2 }.
В английской системе единиц давление выражается как «psi».
или фунт-сила / дюйм 2 .В метрической системе единиц давление выражается в паскалях.
или Н / м 2 . - Стандартное атмосферное давление составляет 101,3 кПа (0,1013 МПа) или 14,69 фунтов на квадратный дюйм.
Терминология по давлению
В литературе описаны три различных типа давления:
и важно знать терминологию:- Абсолютное давление измеряется относительно абсолютного нуля на
шкала давления, представляющая собой идеальный вакуум.(Абсолютное давление может
никогда не быть отрицательным.) Абсолютное давление обозначается буквой p,
и идентично известному термодинамическому давлению. - Манометрическое давление (иногда обозначаемое как «манометрическое давление») измеряется
относительно местного атмосферного давления. Таким образом, избыточное давление равно нулю.
когда давление такое же, как атмосферное. (Это возможно
иметь отрицательное избыточное давление. ) Избыточное давление обозначается значком
) Избыточное давление обозначается значком
p g , и относится к абсолютному давлению следующим образом:
p g = p — p a , где p a — локальный
атмосферное давление.- Пример: датчик автомобильных шин измеряет давление в шинах.
32,0 фунтов на квадратный дюйм. Местное атмосферное давление составляет 14,2 фунта на квадратный дюйм. Что
такое абсолютное давление воздуха в шине?
Решение: манометр измеряет избыточное давление относительно местного значения.
атмосферного давления. Таким образом, p = p g + p a
= 32,0 + 14,2 фунта / кв. Дюйм = 46,2 фунта / кв. Дюйм. Обратите внимание, что в английской системе
абсолютное давление в фунтах на квадратный дюйм часто обозначается как «psia», в то время как
манометрическое давление в фунтах на квадратный дюйм часто обозначается как «фунт / кв. дюйм».Там
В метрической системе такого различия нет. - Пример: Избыточное давление изменяется с повышением?
Решение: Нет. Поскольку манометрическое давление всегда относительно местного значения
Поскольку манометрическое давление всегда относительно местного значения
атмосферного давления, манометрическое давление атмосферы всегда равно нулю,
независимо от высоты.
Обратите внимание, что абсолютное давление уменьшается с увеличением высоты, как вода.
давление увеличивается с глубиной.
- Пример: датчик автомобильных шин измеряет давление в шинах.
- Давление вакуума также измеряется
относительно местного атмосферного давления, но используется, когда
избыточное давление отрицательное, т.е.е. когда абсолютное давление падает ниже
местное атмосферное давление. (Положительное вакуумное давление означает, что
избыточное давление отрицательное.)
Давление вакуума обозначается значком
p вакуум , и связан с абсолютным давлением следующим образом:
p вакуум = p a — p, где p a —
местное атмосферное давление.
Уравнения распределения давления в жидкости
- Рассмотрим небольшой жидкий элемент размеров dx, dy и dz как диаграмму свободного тела, на которой будут рассмотрены все силы, действующие на элемент.

- Существует три вида сил, важных для механики жидкости: гравитация (сила тела), силы давления и силы вязкости (из-за трения). Сила тяжести,
показана на эскизе. Обратите внимание на соглашение, согласно которому гравитация действует в направлении минус z.
- Представьте, что элемент жидкости сжимается до точки (dx, dy и
дз все идут в ноль). Тогда чистая сила, действующая на элемент, снизится.
к нулю. Таким образом, вместо силы более уместно рассмотреть
сила на единицу объема, которая будет обозначаться строчной буквой f.Итак, для гравитации
— сила тяжести
на единицу объема, действующего на элемент.
- Затем рассмотрим чистую силу давления. На каждой из шести граней жидкостного элемента среднее давление будет воздействовать на поверхность по нормали, и внутрь, . Поскольку p является полевой переменной, то есть p = p (x, y, z, t) в целом, среднее давление на одной стороне грани не обязательно будет идентично давлению на противоположной грани.
 Например, рассмотрим давления, действующие на две грани, которые лежат перпендикулярно оси x, т.е.е. силы давления в направлении x, как показано на эскизе
Например, рассмотрим давления, действующие на две грани, которые лежат перпендикулярно оси x, т.е.е. силы давления в направлении x, как показано на эскизеРяд Тейлора (усеченный до первого порядка) используется для учета изменения давления в направлении x на коротком расстоянии dx. Чистая составляющая силы давления на элемент в направлении x равна
, где, поскольку давление — это напряжение (сила на единицу площади), давление необходимо умножить на площадь поверхности (dydz), чтобы получить размеры силы. Два члена в приведенном выше выражении отменяют, и
- Аналогично, чистые силы давления в направлениях y и z
являютсяЗдесь представляет интерес чистый вектор силы давления на единицу
объем.Деление на объем элемента (dxdydz) и запись
эти три компонента как единый вектор приводит к, где правая часть — отрицательное значение градиента
давления. Таким образом, можно отметить, что это не само давление.
что вызывает чистую силу давления, а давление градиент . {- 3} \]
{- 3} \]g = сила тяжести в 9.{-2} \]
h = высота в м, а
P — давление воды в Па.
Формула для расчета давления воды
Выведем глубину формулы давления воды:
[Изображение будет загружено в ближайшее время]
На приведенной выше диаграмме мы видим, что высота контейнера равна «h», а площадь — «A.»
Мы видим, что дно контейнера выдерживает общий вес воды в нем. Однако вертикальные стороны не могут оказывать восходящее усилие на жидкость, потому что она недостаточно сильна, чтобы выдерживать силу сдвига, и поэтому нижняя часть поддерживает все это.
Как мы видим, дно контейнера выдерживает вес находящейся в нем жидкости, который определяется как;
w = mg
Также мы знаем, что давление — это вес жидкости mg, деленный на A, поддерживающий ее (здесь A — площадь дна емкости, которая определяется как:
P = mg /A….
 .(1)
.(1)Масса жидкости:
м = ρV….(2)
Формула для объема жидкости внутри контейнера:
V = Ah… .. (3)
Здесь
A = площадь поперечного сечения, а
h = глубина
Если ввести значения (2) и (3) в (1), мы получим вычислитель давления воды по высоте:
P = ρAhg / h
P = ρgh… .. (4)
Уравнение (4) — это требуемое давление по уравнению воды.Это уравнение помогает нам рассчитать давление воды в жидкости.
Уравнение давления воды
Уравнение давления воды имеет общую применимость далеко за пределами особых условий, при которых оно получено здесь. Предположим, что контейнера там не было, тогда окружающая жидкость все еще будет оказывать это давление, сохраняя статическое состояние жидкости.
Следовательно, уравнение P = hρg представляет давление из-за веса любой жидкости, имеющей среднюю плотность ρ на любой глубине h ниже ее поверхности.

Для жидкостей, которые почти несжимаемы, давление под водой сохраняется на больших глубинах.
Однако для газов, которые в некоторой степени сжимаемы, можно применять это уравнение до тех пор, пока изменения плотности не станут незначительными на рассматриваемой глубине.
Рассчитать давление воды
Рассмотрим пример калькулятора давления воды по высоте:
Предположим, что ширина емкости составляет 800 м, а глубина воды в емкости составляет 60 м.{13} \] N) = 0,00072
Итак, возраст в% будет 0,072%
Также мы видим, что давление полностью не зависит от ширины и длины контейнера или контейнера, оно зависит только от его среднего значения. глубина. Следовательно, сила зависит только от средней глубины воды и размеров контейнера, а не от горизонтальной протяженности контейнера
фунтов на квадратный дюйм в дюймах водяного столба Формула
PSI означает фунт на квадратный дюйм.

Итак, 1 фунт / кв. Дюйм = 27.7076 дюймов водяного столба.
Итак, Формула PSI to Inches of Water гласит, что для получения приблизительного результата мы должны умножить значение давления на 27,708.
Пример 1: Кроме того, один дюйм водяного столба равен давлению около 1/28 фунта на квадратный дюйм (psi). Другими словами, столб воды высотой 28 дюймов создает давление 1 фунт / кв. Дюйм.
Пример 2: Формула PSI в дюймы водяного столба:
Предположим, вы разделите 5 фунтов на квадратный дюйм на 27,708, какое значение вы получите, и укажите его единицу измерения.
Разделив 5 фунтов на квадратный дюйм на 27,708, вы получите около 138,54 дюйма водяного столба. Здесь дюймы WC обозначают дюймы водяного столба или просто WC. Это устройство предназначено для измерения определенных перепадов давления, например небольших перепадов давления в трубопроводе, валу или отверстии.
Пример 3: Атмосферное давление оказывает большую силу, т.


 1)
1) 5)
5)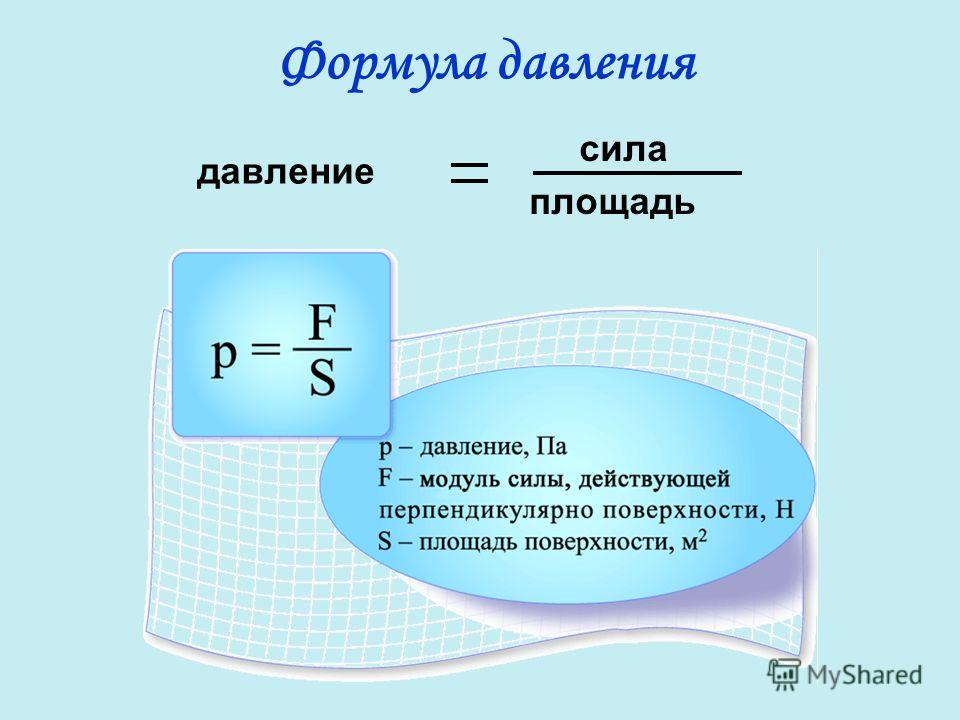 рисунок)
рисунок)
 Если каждая ножка стула имеет площадь поверхности 2,5 × 10 -4 м 2 в контакте с землей, каково среднее давление, оказываемое рыбаком и стулом на землю?
Если каждая ножка стула имеет площадь поверхности 2,5 × 10 -4 м 2 в контакте с землей, каково среднее давление, оказываемое рыбаком и стулом на землю?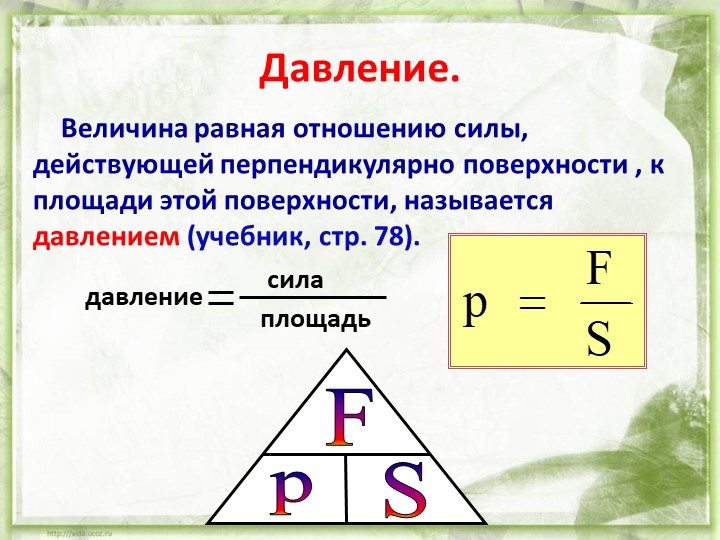 Насколько глубоко ныряльщик?
Насколько глубоко ныряльщик?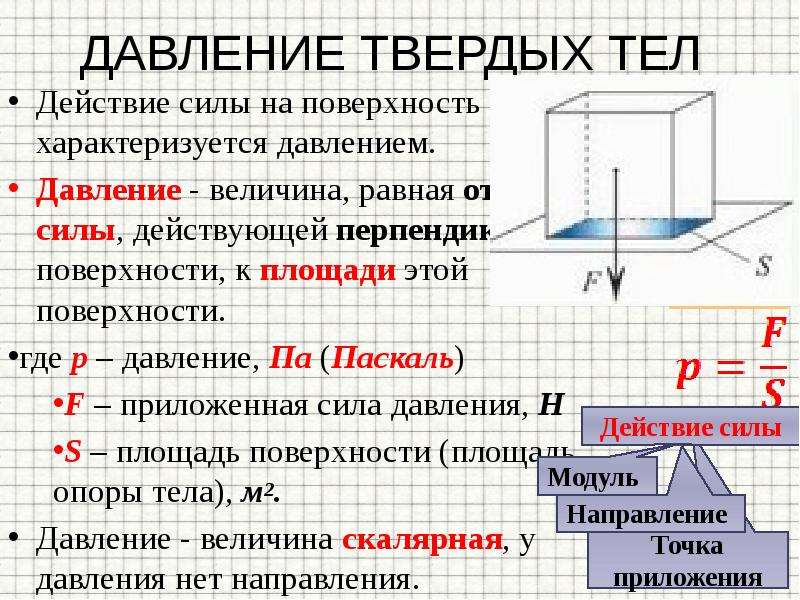 s 2 )
s 2 ) 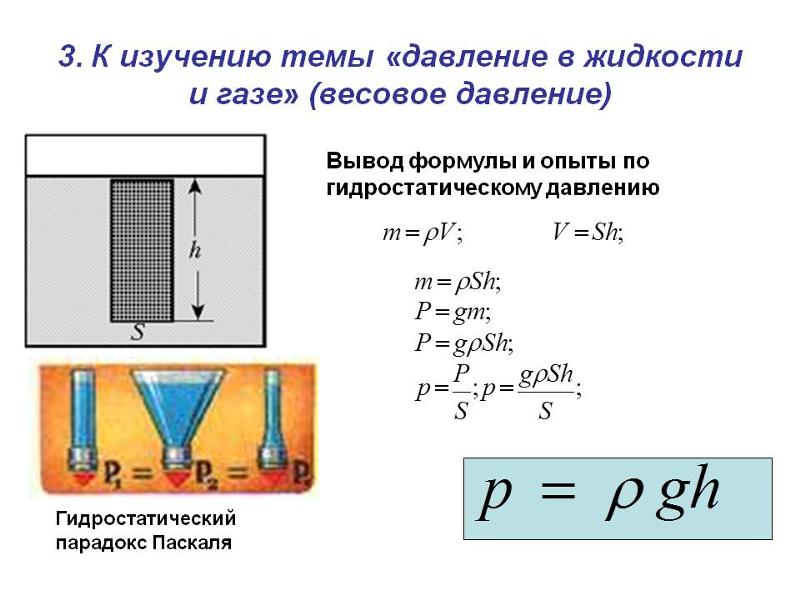
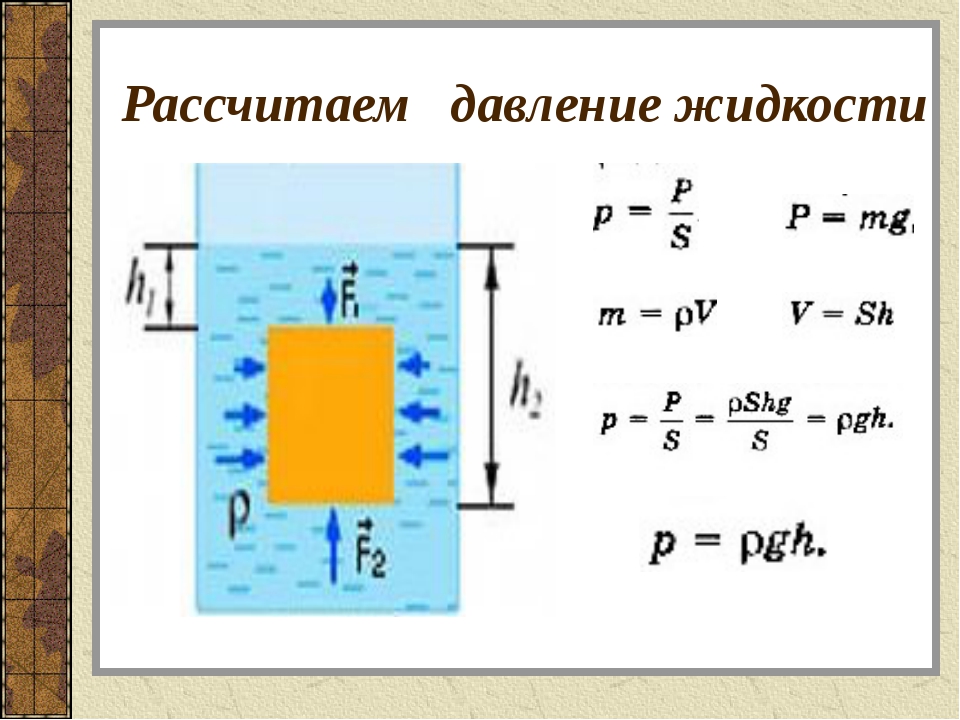 Стандартное атмосферное давление определяется на уровне моря 273 o K (0 o C) и составляет:
Стандартное атмосферное давление определяется на уровне моря 273 o K (0 o C) и составляет: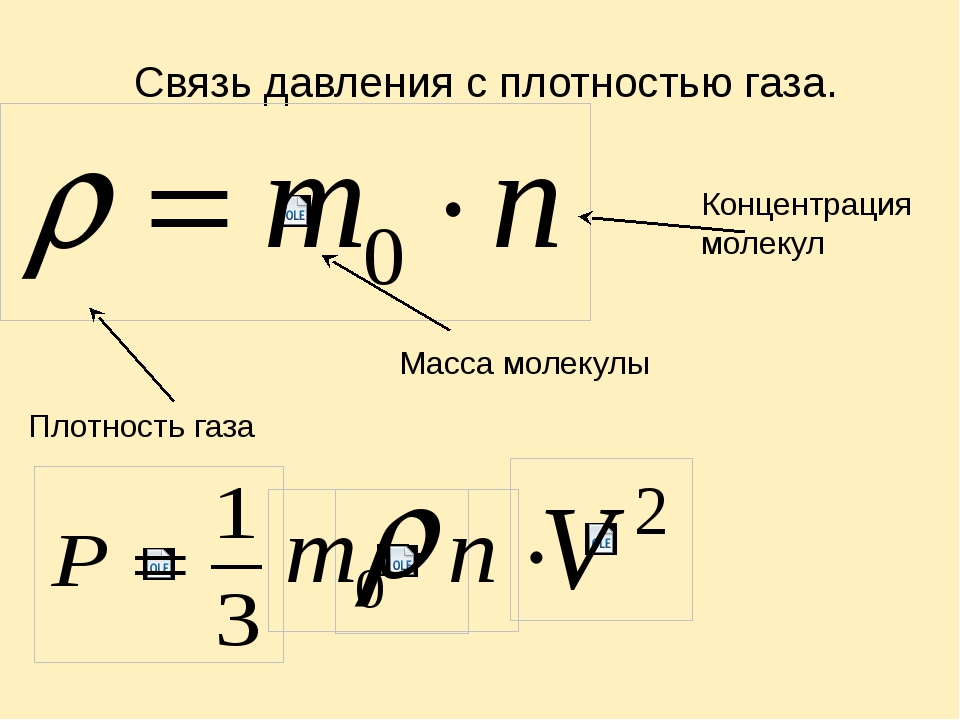 В относительных единицах это отрицательное избыточное давление около — 0,92 бара, — 92 кПа или — 13,54 фунта на кв. Дюйм изб.
В относительных единицах это отрицательное избыточное давление около — 0,92 бара, — 92 кПа или — 13,54 фунта на кв. Дюйм изб.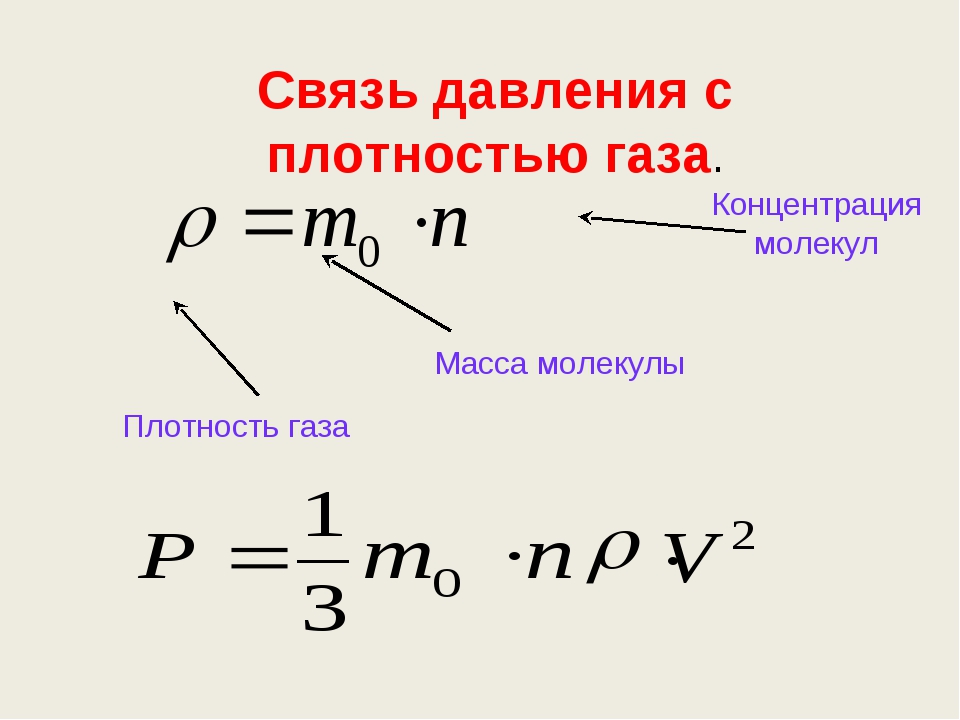 Дюйм). При таком давлении вода закипает при температуре около 350 ° C (662 ° F), что обеспечивает запас по переохлаждению около 25 ° C.
Дюйм). При таком давлении вода закипает при температуре около 350 ° C (662 ° F), что обеспечивает запас по переохлаждению около 25 ° C. При таком давлении вода закипает примерно при 350 ° C (662 ° F). Это высокое давление поддерживается компенсатором давления. Температура воды на входе составляет около 290 ° C (554 ° F). Вода (теплоноситель) нагревается в активной зоне реактора примерно до 325 ° C (617 ° F), когда вода протекает через активную зону. Как видно, реактор имеет переохлажденный теплоноситель примерно на 25 ° C (расстояние от насыщения).
При таком давлении вода закипает примерно при 350 ° C (662 ° F). Это высокое давление поддерживается компенсатором давления. Температура воды на входе составляет около 290 ° C (554 ° F). Вода (теплоноситель) нагревается в активной зоне реактора примерно до 325 ° C (617 ° F), когда вода протекает через активную зону. Как видно, реактор имеет переохлажденный теплоноситель примерно на 25 ° C (расстояние от насыщения). Эти распылительные линии распыляют охлаждающую жидкость реактора из холодного участка контура в паровое пространство и конденсируют часть пара. Закалочное действие снижает давление и ограничивает повышение давления.
Эти распылительные линии распыляют охлаждающую жидкость реактора из холодного участка контура в паровое пространство и конденсируют часть пара. Закалочное действие снижает давление и ограничивает повышение давления.

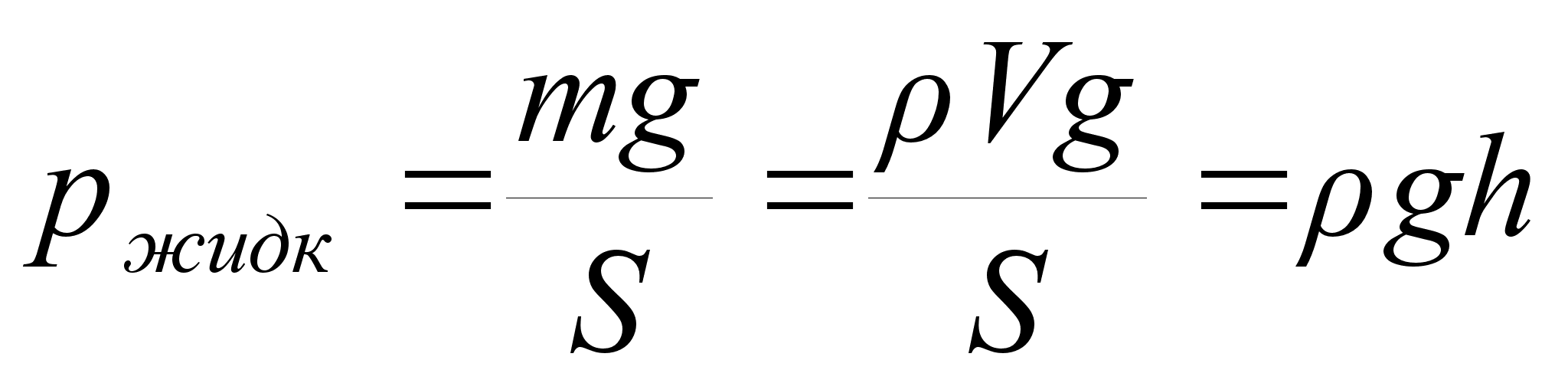 также: Критическая точка воды
также: Критическая точка воды Следовательно, давление воды в нижней части контейнера на рисунке выше будет одинаковым во всем контейнере, так как уровень воды такой же! Форма емкости НЕ имеет значения при расчете давления воды!
Следовательно, давление воды в нижней части контейнера на рисунке выше будет одинаковым во всем контейнере, так как уровень воды такой же! Форма емкости НЕ имеет значения при расчете давления воды!

 ) Избыточное давление обозначается значком
) Избыточное давление обозначается значком Поскольку манометрическое давление всегда относительно местного значения
Поскольку манометрическое давление всегда относительно местного значения 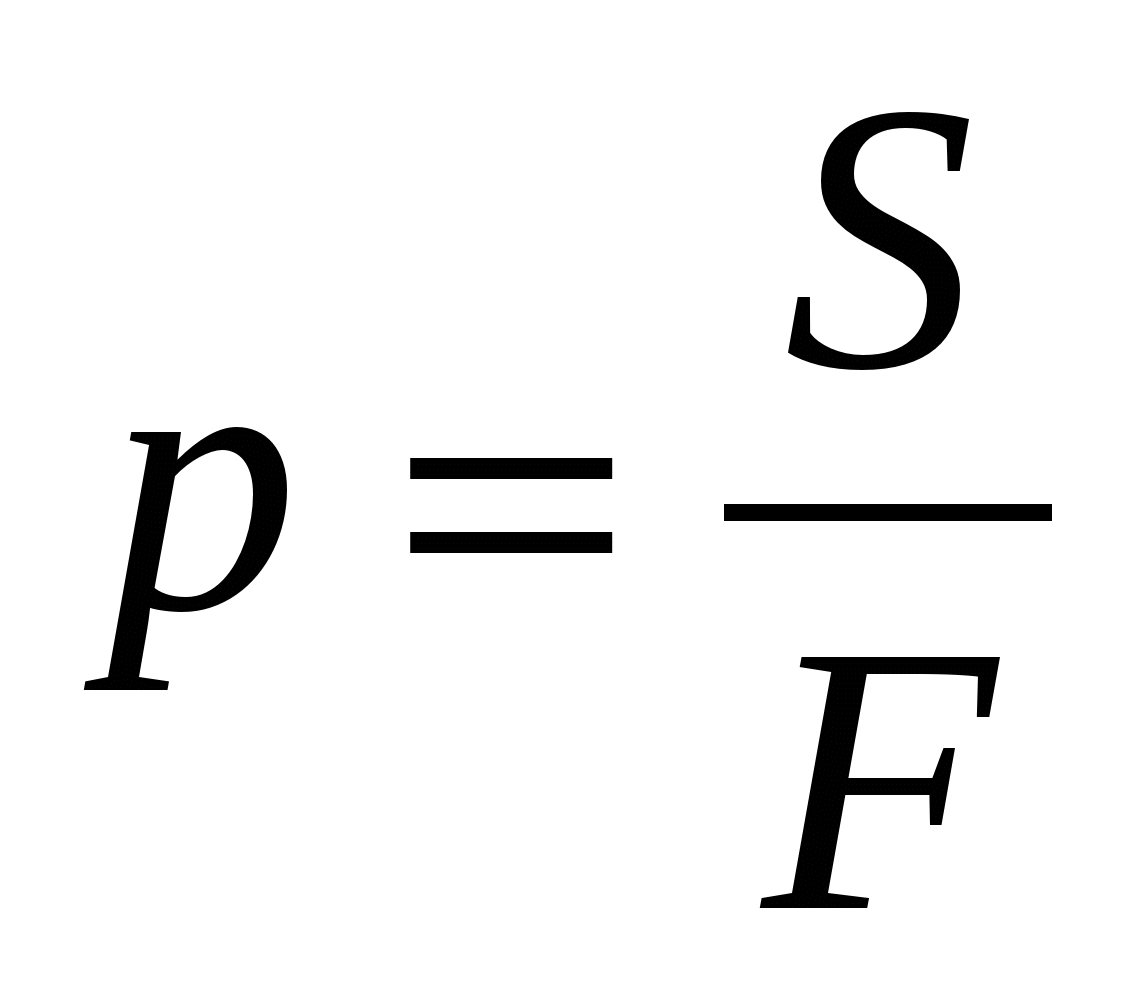
 Например, рассмотрим давления, действующие на две грани, которые лежат перпендикулярно оси x, т.е.е. силы давления в направлении x, как показано на эскизе
Например, рассмотрим давления, действующие на две грани, которые лежат перпендикулярно оси x, т.е.е. силы давления в направлении x, как показано на эскизе {- 3} \]
{- 3} \]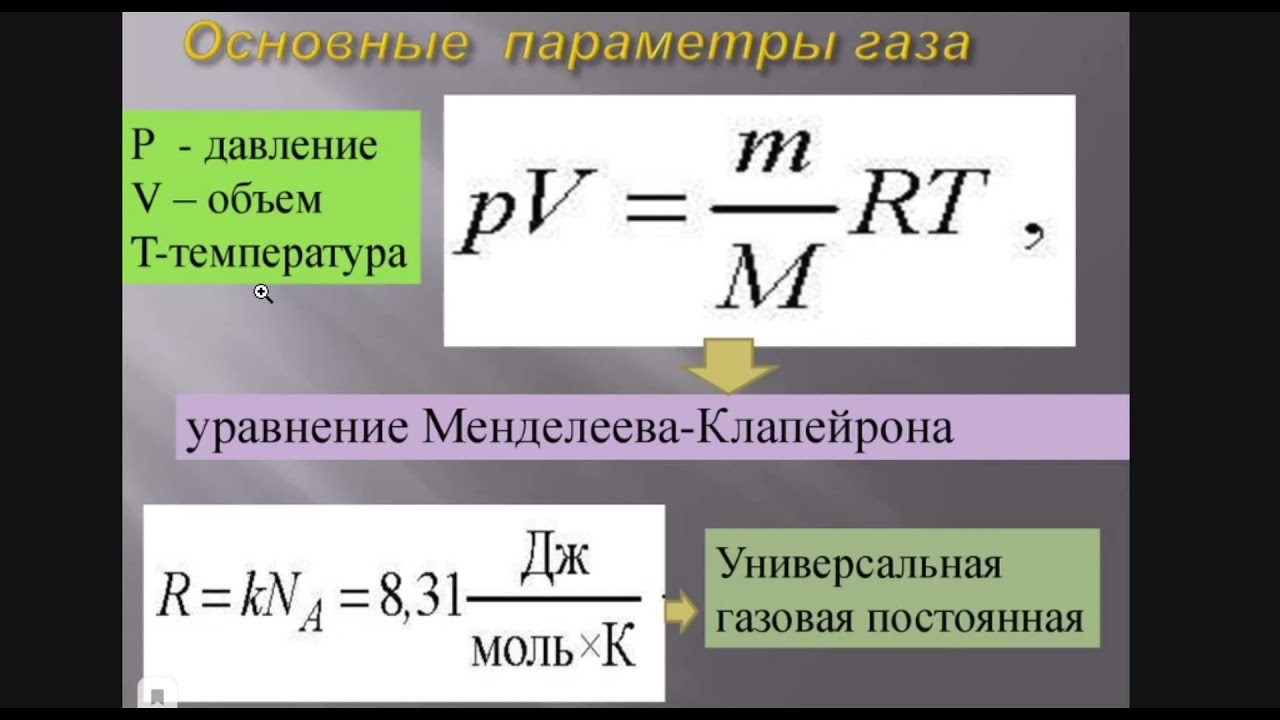 .(1)
.(1)

