Нормальные условия (НУ), число Авогадро. STP. NTP. SATP. Стандартная атмосфера и температура. Что это такое? Нормальные условия в физике, химии и технике. Стандартные температура и давление («атмосферное»). Стандартные условия на уровне моря.
1.1.1) Самые распространенные и уже устаревшие нормальные условия (НУ = STP = стандартная температура и давление) . Определены IUPAC — Международный союз чистой и прикладной химии. :
При этих НУ
1.1.2) Сейчас нормальные условия (НУ= STP = стандартная температура и давление). Определены IUPAC — Международный союз чистой и прикладной химии. :
1.1.3) Сейчас нормальные условия (НУ= STP или NTP = стандартная (нормальная) температура и давление). Определены NIST — National Institute for Standards and Technology :
1.2) В промышленности широко используются «стандартные окружающие температура и давление = SATP», которые могут называть также НУ:
2) ICAO — Международная организация гражданской авиации определяет некую «международную стандартную атмосферу на уровне моря», которую тоже, бывает, называют нормальными условиями:
3) Как минимум 50% ветеранов броуновского движения и сестер милосердия в РФ, из-за того, что газовики в России приводят, согласно ГОСТ 2939-63, объемы газов к «условиям для определения объема», считают, что НУ это:
Пользуйтесь этой информацией на здоровье, и помните, что не все так ясно, как кажется, но и сложного ничего при ближайшем рассмотрении нет.
|
ПРАВИЛЬНЫЙ ВЫБОР ШЛАНГОВ — Semperit Technische Produkte Gesellschaft m.
 b.H.
b.H.
Чтобы гарантировать оптимальную функцию шланга, его желательно выбирать в зависимости от специфических условий включения в работу. В этих целях основным является, если такое возможно, использование полной информации и полученных знаний о транспортируемом рабочем теле и требуемых присоединениях.
Следующие пункты должны Вам помочь найти в настоящем каталоге оптимальный шланг для Ваших нужд:
Рабочее тело:
Состав (напр. у масел, газов и горючего)
Концентрация (у химических реактивов)
Температура (максимальная, минимальная)
Давление:
Нагрузка давлением (максимальное рабочее давление)
Нагрузка при всасывании (максимальное давление ниже атмосферного)
Местное давление: вычисленное умножением рабочего давления на фактор безопасности, указанный в каталоге.
Наружные влияния:
Температура
Влияния атмосферных условий
Контакт с маслом, жиром, морской водой или агрессивными веществами
Сильная механическая абразия (например, скольжением шланга по абразивному полу, камням, кромкам и т. д.)
д.)
Радиус изгиба:
Указанный в каталоге минимальный радиус изгиба нельзя в течение включения в работу превысить, в противном случае может сократиться продолжительность службы шланга.
Внутренний диаметр: обозначает номинальный размер шланга.
Толщина стены: обозначает толщину стены шланга (состоящую из внутреннего слоя, прокладки и оболочки).
Длина: В данном столбце Вы найдете максимальную длину шланга, которую можно изготовить, или же стандартно поставляемую длину.
Стандарты и одобрения: За указанным пунктом в листах инструкции выписаны стандарты, которые соответствующий шланг или же его резиновые смеси удовлетворяют, и одобрения, которые Semperit для изделия или же для его конструктивных деталей получил.
Маркировка: Большинство шлангов Semperit на фабрике оснащается стандартной маркировкой. Кроме того, шланги можно описать трехзначным кодом, который, однако, служит только для внутреннего производственного контроля. По желанию и при соответствующем объеме отбора можно шланги Semperit заказать со специальной маркировкой.
По желанию и при соответствующем объеме отбора можно шланги Semperit заказать со специальной маркировкой.
Осмотическое давление.
Осмос-это самопроизвольный переход растворителя через полупроницаемую мембрану из разбавленного раствора или чистого растворителя в концентрированный раствор. Это явление можно продемонстрировать с помощью прибора, схематически изображенного на рис. 6.39. Широкий конец трубки, закрытый мембраной животного происхождения (например, бычьим пузырем), наполняют раствором сахара и погружают в стакан с водой. Через некоторое время вода переходит сквозь мембрану в раствор сахара.
Мембрана, пропускающая частицы растворителя, но не пропускающая частицы растворенного вещества, называется полупроницаемой мембраной. Полупроницаемая мембрана пропускает частицы растворителя в обоих направлениях. Однако, поскольку с той стороны мембраны, где концентрация раствора выше, концентрация растворителя, наоборот, ниже, происходит результирующий переход растворителя в концентрированный раствор. Это приводит к установлению разности давлений по обе стороны мембраны. Давление, которое необходимо приложить к концентрированному раствору, чтобы воспрепятствовать переносу растворителя через мембрану, называется осмотическим давлением. Его обозначают греческой буквой п.
Это приводит к установлению разности давлений по обе стороны мембраны. Давление, которое необходимо приложить к концентрированному раствору, чтобы воспрепятствовать переносу растворителя через мембрану, называется осмотическим давлением. Его обозначают греческой буквой п.
Осмотическое давление является коллигативным свойством, поскольку оно зависит только от концентрации растворенных частиц, а не от их химического состава.
Осмотическое давление играет важную роль в биологических процессах. Например, в организме животных некоторые типы клеток, например эритроциты, содержат солевой раствор. Эти клетки ограничены плазматической мембраной. В водной среде эритроциты подвергаются осмосу, набухают и лопаются. Однако, если они попадают в более концентрированный раствор соли, клетки сморщиваются.
Модули установки для получения сверхчистой воды на основе обратного осмоса. Такая вода необходима в полупроводниковой промышленности.
Амеба-одноклеточное существо. Вода непрерывно поступает в ее тело благодаря осмосу.
Растительные клетки содержат солевые растворы в особых полостях — вакуолях. Вакуоль окружена тонким слоем цитоплазмы, который обладает свойствами полупроницаемой мембраны и контролирует поглощение воды растительной клеткой.
Если давление, приложенное к концентрированному раствору, превышает осмотическое давление, растворитель переходит из концентрированного раствора через мембрану в разбавленный раствор. Этот процесс называется обратный осмос. Он находит промышленное применение с целью получения питьевой воды из морской воды.
Эксперименты, подобные описанному выше с сахарным раствором, показывают, что: 1) при постоянной температуре осмотическое давление прямо пропорционально разности концентраций в растворах, разделенных мембраной; 2) при фиксированной разности концентраций осмотическое давление прямо пропорционально абсолютной температуре.
Соотношение между осмотическим давлением и температурой аналогично уравнению состояния идеального газа (см. разд. 3.1). Оно называется уравнением Вант-Гоффа:
разд. 3.1). Оно называется уравнением Вант-Гоффа:
(11)
В этом уравнении тс — осмотическое давление, К-объем раствора, и-число молей растворенного вещества, T-абсолютная температура, Л-молярная газовая постоянная. Уравнение (11) может быть представлено в другой форме:
Уравнение Вант-Гоффа является приближенным и справедливо только для разбавленных растворов.
Определение относительной молекулярной массы растворенного вещества по осмотическому давлению раствора
Уравнение Вант-Гоффа может использоваться для определения относительной молекулярной массы растворенного вещества по создаваемому им осмотическому давлению, которое устанавливают экспериментальным путем. Этот метод особенно удобен для определения средней относительной молекулярной массы полимеров и других макро-молекулярных веществ.
Пример
Раствор сахара с концентрацией 2,5 г/дм3 создает осмотическое давление 8,3 х х 104 атм при 25 °С. Вычислим относительную молекулярную массу растворенного вещества.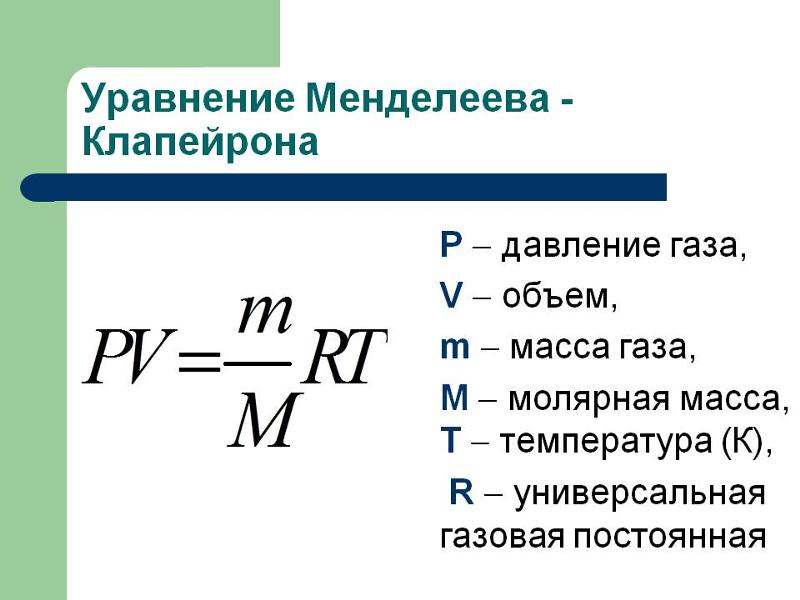
Решение
Искомое значение относительной молекулярной массы Мг растворенного вещества можно найти непосредственно с помощью уравнения Вант-Гоффа (11). Исходные данные задачи таковы:
Оглавление:
Мойка высокого давления Karcher K 2 Full Control (16734000)
8 930 руб руб
за 1 шт
Способы получения товара:
- Завтра
- Сегодня с 14:00
Способы оплаты
Минимойка Kercher K 2 Full Control со струйной трубкой Full Control Click Vario Power, обеспечивающей регулировку и индикацию давления, гарантирует пользователю полный контроль. 3 ступени давления и режим для нанесения чистящего средства обеспечивают оптимальную обработку любых поверхностей. Давление регулируется поворотом струйной трубки Vario Power в положение, соответствующее требуемому режиму. Ступени давления отображаются пиктограммами на струйной трубке. Струйная трубка Click Vario Power и грязевая фреза 3 ступени давления и режим для нанесения химии. Давление регулируется поворотом струйной трубки Vario Power. Ступень регулировки давления обозначается соответствующим символом на струйной трубке. Место для аксессуаров, пистолета и кабеля Струйные трубки всегда находятся под рукой, а после окончания работы их легко разместить на аппарате с экономией места. Кабель может храниться на крюке, который расположен непосредственно на мойке. Удобное применение чистящего средства Всасывающий шланг для использовани
3 ступени давления и режим для нанесения чистящего средства обеспечивают оптимальную обработку любых поверхностей. Давление регулируется поворотом струйной трубки Vario Power в положение, соответствующее требуемому режиму. Ступени давления отображаются пиктограммами на струйной трубке. Струйная трубка Click Vario Power и грязевая фреза 3 ступени давления и режим для нанесения химии. Давление регулируется поворотом струйной трубки Vario Power. Ступень регулировки давления обозначается соответствующим символом на струйной трубке. Место для аксессуаров, пистолета и кабеля Струйные трубки всегда находятся под рукой, а после окончания работы их легко разместить на аппарате с экономией места. Кабель может храниться на крюке, который расположен непосредственно на мойке. Удобное применение чистящего средства Всасывающий шланг для использовани
Внимание! Характеристики и комплектация товаров могут быть изменены фирмой-производителем без предварительного уведомления. Перед покупкой уточняйте важные для Вас технические характеристики и комплектацию у продавца. Если вы заметили ошибку, то пожалуйста, сообщите нам об этом.
Перед покупкой уточняйте важные для Вас технические характеристики и комплектацию у продавца. Если вы заметили ошибку, то пожалуйста, сообщите нам об этом.
Похожие товары
Персональные рекомендации
Давление — Введение в химию — 1-е канадское издание
- Определить давление .
- Изучите единицы давления и способы их преобразования
Кинетическая теория газов указывает на то, что частицы газа всегда находятся в движении и сталкиваются с другими частицами и удерживающими их стенками сосуда. Хотя столкновения со стенками контейнера упругие (т. е. при столкновении нет прироста или потери чистой энергии), частица газа оказывает силу на стенку во время столкновения.Совокупность всех этих сил, распределенных по площади стенок сосуда, вызывает то, что мы называем давлением. Давление ( P ) определяется как сила всех столкновений частиц газа со стенкой, деленная на площадь стенки:
Все газы оказывают давление; это одна из фундаментальных измеримых величин этой фазы материи. Давление оказывает даже наша атмосфера — в данном случае газ «удерживается» земным притяжением, а не газом, находящимся в контейнере.Атмосферное давление 101 325 Па.
Давление оказывает даже наша атмосфера — в данном случае газ «удерживается» земным притяжением, а не газом, находящимся в контейнере.Атмосферное давление 101 325 Па.
Давление имеет множество единиц измерения. Формальной единицей давления, утвержденной SI, является паскалей (Па), которая определяется как 1 Н/м 2 (один ньютон силы на площади в один квадратный метр). Однако, как правило, это слишком мало по величине, чтобы быть полезным. Общепринятой единицей давления является атмосфера (атм), которая изначально определялась как среднее атмосферное давление на уровне моря.
Однако «среднее атмосферное давление на уровне моря» трудно точно определить из-за колебаний атмосферного давления.Более надежной и распространенной единицей измерения является миллиметр ртутного столба (мм рт.ст.), который представляет собой величину давления, оказываемого столбиком ртути высотой ровно 1 мм. Эквивалентной единицей является торр, равный 1 мм рт. (Торр назван в честь Эванджелисты Торричелли, итальянского ученого семнадцатого века, который изобрел ртутный барометр. ) С этими определениями давления единица измерения атмосферы переопределена: 1 атм определяется точно как 760 мм рт.ст., или 760 торр. Таким образом, мы имеем следующие эквивалентности:
) С этими определениями давления единица измерения атмосферы переопределена: 1 атм определяется точно как 760 мм рт.ст., или 760 торр. Таким образом, мы имеем следующие эквивалентности:
1 атм = 760 мм рт. ст. = 760 торр
Мы можем использовать эти эквивалентности, как и любые эквивалентности — для выполнения преобразований из одних единиц в другие.Соотнося их с формальной единицей давления СИ, 1 атм = 101 325 Па.
Сколько атмосфер в 595 торр?
Решение
Используя эквиваленты давления, мы строим коэффициент преобразования между торр и атмосферами:
1 атм = 760 торр
Таким образом:
Поскольку числа в коэффициенте пересчета точны, количество значащих цифр в окончательном ответе определяется начальным значением давления.
Сколько атмосфер содержится в 1022 Торр?
Ответить
1,345 атм
Атмосфера на Марсе в основном состоит из CO 2 при давлении 6,01 мм рт. Чему равно это давление в атмосферах?
Чему равно это давление в атмосферах?
Решение
Используйте эквиваленты давления, чтобы построить правильный коэффициент преобразования между миллиметрами ртутного столба и атмосферами.
В конце мы выразили ответ в экспоненциальной записи.
Низкое атмосферное давление в эпицентре урагана.Во время урагана 1979 года в Тихом океане внутри глаза было зарегистрировано давление 0,859 атм. Каково это давление в торр?
Ответить
652 торр
- Давление — это сила, действующая на площадь.
- Давление имеет несколько общих единиц, которые можно преобразовать
- Определить давление . Что вызывает это?
- Дайте определение и свяжите три единицы давления.
- Если приложить силу 16,7 Н к площади 2.44 м 2 , какое давление в паскалях?
- Если к площади 0,0332 м 2 приложена сила 2,546 Н, чему равно давление в паскалях?
- Объясните, почему исходное определение атмосферы не работает.

- Какие единицы давления равны между собой?
- Сколько атмосфер в 889 мм рт.ст.?
- Сколько атмосфер в 223 Торр?
- Сколько торр в 2,443 атм?
- Сколько миллиметров ртутного столба в 0.334 атм?
- Сколько миллиметров ртутного столба в 334 Торр?
- Сколько торр в 0,777 мм рт.ст.?
- Сколько паскалей в 1 торр?
- Давление 0,887 атм равно скольким паскалям?
- Давление – это сила на единицу площади. Это вызвано ударами частиц газа о стенки их контейнера.
- 6,84 Па
- Поскольку атмосферное давление на уровне моря непостоянно, оно не является постоянной единицей измерения давления.
- 1,17 атм
- 1857 торр
- 334 мм рт.ст.
- 133 Па
9.12: Закон Дальтона о парциальных давлениях
Закон идеального газа можно также изменить, чтобы показать, что давление газа пропорционально количеству газа:
\[P=\frac{RT}{V}\,n\label{1}\]
Таким образом, коэффициент RT/V может использоваться для взаимного преобразования количества вещества и давления в контейнере определенного объема и температуры.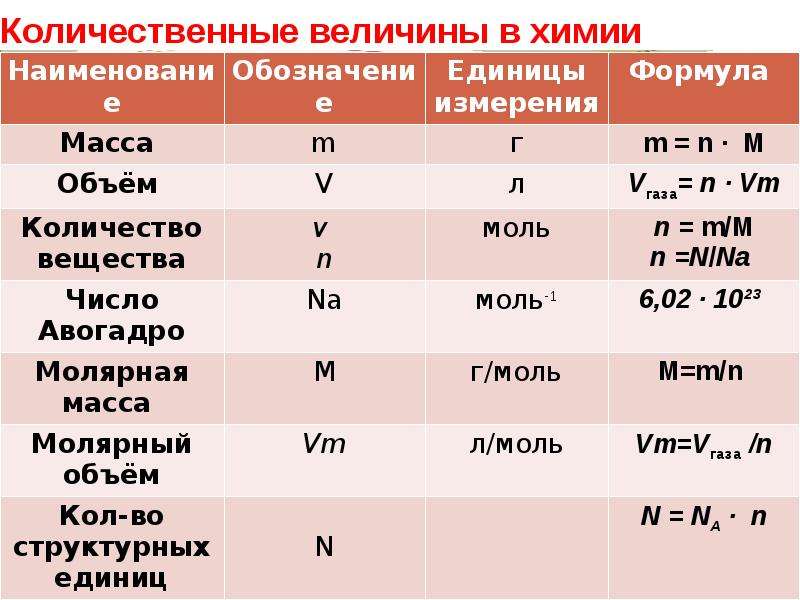 {-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 литров}}\,\times \text{ 0}\text{.006 моль}= \text{0}\text{0,60 атм}\]
{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 литров}}\,\times \text{ 0}\text{.006 моль}= \text{0}\text{0,60 атм}\]
Теперь предположим, что мы поместили 0,004 моль H 2 и 0,006 моль N 2 в одну и ту же колбу вместе. Какое будет давление? Поскольку закон идеального газа не зависит от того, какой -й газ у нас есть, а только от количества любого -го газа, давление (0,004 + 0,006) моля, или 0,010 моля, будет в точности таким, какое мы получили в нашем первом опыте. расчет.Но это всего лишь сумма давления, которое оказал бы H 2 , если бы он занимал контейнер один, плюс давление N 2 , если бы он был единственным присутствующим газом. То есть
\[P_{всего} = p_{\text{H}_{2}} + p_{\text{N}_{2}}\]
На приведенном ниже рисунке более конкретно представлена концепция парциального давления: показано давление каждого газа в отдельности в контейнере, а затем показано комбинированное давление газов после их смешивания.
Рисунок \(\PageIndex{1}\): На приведенном выше рисунке показано, как работает закон Дальтона для парциального давления.Один только водород имеет давление 0,4 атм, а азот — 0,6 атм. При помещении в один и тот же контейнер общее давление составляет 1 атм, при этом каждый газ вносит свое парциальное давление. Изображение предоставлено: OpenStax College
Мы только что разработали пример закона парциальных давлений Дальтона (названного в честь Джона Дальтона, его первооткрывателя). Этот закон гласит, что в смеси двух или более газов общее давление равно сумме парциальных давлений всех компонентов .Парциальное давление газа — это давление, которое оказал бы газ, если бы он сам занимал контейнер. Парциальное давление обозначается строчной буквой p .
Закон парциальных давлений Дальтона чаще всего встречается, когда газ собирается путем вытеснения воды, как показано на рисунке 2.
Рисунок \(\PageIndex{2}\): Общее давление влажного газа равно сумме парциального давления самого газа + давления паров воды при данной температуре. (При 20 °C давление паров воды составляет 17,3 мм рт. ст.)
(При 20 °C давление паров воды составляет 17,3 мм рт. ст.)
Поскольку газ барботируется через воду, он содержит некоторое количество молекул воды и называется «влажным». Полное давление этого влажного газа представляет собой сумму парциального давления самого газа и парциального давления содержащегося в нем водяного пара. Последнее парциальное давление называется давлением пара воды. Он зависит только от температуры эксперимента и может быть получен из справочника или из таблицы 1.
| Температура (°C) | Давление паров (мм рт.ст.) | Давление пара (кПа) |
|---|---|---|
| 0 | 4,6 | 0,61 |
| 5 | 6,5 | 0,87 |
| 10 | 9,2 | 1. 23 23 |
| 15 | 12,8 | 1,71 |
| 20 | 17,5 | 2,33 |
| 25 | 23,8 | 3,17 |
| 30 | 31,8 | 4,24 |
| 50 | 92,5 | 12.33 |
| 70 | 233,7 | 31,16 |
| 75 | 289,1 | 38,63 |
| 80 | 355,1 | 47,34 |
| 85 | 433,6 | 57,81 |
| 90 | 525,8 | 70. 10 10 |
| 95 | 633,9 | 84,51 |
| 100 | 760,0 | 101,32 |
Пример \(\PageIndex{1}\): Объем водорода
Предположим, что 0,321 г металлического цинка вступают в реакцию с избытком соляной кислоты (водный раствор газообразного HCl) в соответствии с уравнением
.
\[\text{Zn} (т) + 2 \text{HCL} (водн.) \rightarrow \text{Zn} \text{Cl}_{2} (водн.) + \text{H}_{2} (г)\]
Полученный газообразный водород собирают над водой при температуре 25°C и барометрическом давлении 745.4 мм рт.ст. Какой объем влажного водорода будет собран?
Раствор Из таблицы 1 находим, что при 25°С давление паров воды равно 23,8 мм рт. ст. Соответственно
ст. Соответственно
p H 2 = p всего – p H 2 O = 754 мм рт.ст.
Необходимо преобразовать в единицы, совместимые с R :
\[p_{\text{H}_{\text{2}}}=\text{721}\text{0,6 мм рт.ст.}\times \,\frac{\text{1 атм}}}{\text{ 760 мм рт.ст.}}=\текст{0}\текст{.949 атм}\]
Дорожная карта для этой проблемы
\[m _ {\ text {Zn}} \ xrightarrow {M _ {\ text {Zn}}} n _ {\ text {Zn}} \ xrightarrow {S \ left ( \ text {H} _ {\ text {2} }\text{/Zn} \right)}n_{\text{H}_{\text{2}}}\xrightarrow{RT/P}V_{\text{H}_{\text{2}}} \]
Так
\[\begin{align}V_{\text{H}_{\text{2}}} & =\text{0}\text{0,321 г Zn}\times \,\frac{\text{1 моль Zn}}{\text{65}\text{0,38 г Zn}}\,\times \,\frac{\text{1 моль H}_{\text{2}}}{\text{2 моль Zn}}\,\times \,\frac{\text{0}\text{.0820 литров атм}}{\text{1 К моль H}_{\text{2}}}\,\times \,\frac{\text{293}\text{0,15 K}}{\text{0} \text{0,987 атм}}\\ & =\text{0}\text{0,126 литра}\end{align}\]
Авторы и авторство
диковинка или практичное решение?
Все вы наверняка слышали, что «алмазы делаются под давлением» . Эта цитата принадлежит генералу Джорджу С. Паттону-младшему, который использовал ее как инструмент мотивации и вдохновения для своих войск. Для химика «алмазы делаются под давлением» имеет вполне буквальное значение, поскольку алмазы действительно могли образовываться в природе из различных углеродосодержащих источников под чрезвычайно высоким давлением около 50000 атм и при температурах, превышающих 1000 °C.Один из коммерческих методов изготовления синтетических алмазов использует такое давление и температуру около 1500 °C.
Эта цитата принадлежит генералу Джорджу С. Паттону-младшему, который использовал ее как инструмент мотивации и вдохновения для своих войск. Для химика «алмазы делаются под давлением» имеет вполне буквальное значение, поскольку алмазы действительно могли образовываться в природе из различных углеродосодержащих источников под чрезвычайно высоким давлением около 50000 атм и при температурах, превышающих 1000 °C.Один из коммерческих методов изготовления синтетических алмазов использует такое давление и температуру около 1500 °C.
Для химика-органика производство алмазов не является целью, не так ли? История изучения влияния высокого давления на химические реакции восходит к концу XIX века, когда В. К. Рентген обнаружил небольшое влияние высокого давления (тогда «высокое» означало 500 атм) на скорость инверсии сахаров под действием соляной кислоты. Исследования влияния высокого давления на скорость химических реакций были продолжены В.Ротмунда, но она действительно расширилась с развитием техники высоких давлений благодаря работам П. Бриджмена, американского физика, получившего в 1946 г. Нобелевскую премию по физике за работы по физике высоких давлений. Например, он и Дж. Б. Конант смогли определить в 1929 году, что давление до 12000 атмосфер вызывает полную полимеризацию изопрена в течение 50 часов, тогда как только следы полимера образуются через 68 часов, если реакция проводится при 3000 атм.
Бриджмена, американского физика, получившего в 1946 г. Нобелевскую премию по физике за работы по физике высоких давлений. Например, он и Дж. Б. Конант смогли определить в 1929 году, что давление до 12000 атмосфер вызывает полную полимеризацию изопрена в течение 50 часов, тогда как только следы полимера образуются через 68 часов, если реакция проводится при 3000 атм.
Чтобы понять влияние высокого давления на скорость реакции, необходимо ввести термин «объем активации», обычно обозначаемый как DV≠. Он определяется как разница молярных объемов между переходным состоянием и реагентами. Проще говоря, если переходное состояние более «компактно», чем реагенты (отрицательный член DV≠), «сжатие» реакционной смеси значительно облегчит реагентам формирование переходного состояния, и реакция ускорится.Существует достаточно много реакций, характеризующихся отрицательной DV≠, например, циклоприсоединения Дильса-Альдера, конъюгированные присоединения, различные конденсации, катализируемые палладием реакции сочетания, пептидные сочетания, реакция Виттига и многие-многие другие.
Основные преимущества использования химии высокого давления заключаются не только в ускорении реакций. Различия между реакциями, протекающими при высоком и нормальном давлении, могут быть впечатляющими. Во многих случаях можно синтезировать соединения, которые вообще не образуются при нормальном давлении или с очень низким выходом (пример 1).
Иногда более высокие температуры, необходимые для проведения реакции при нормальном давлении, неприемлемы, поскольку субстраты могут разлагаться. Ускорение реакции с помощью высокого давления позволяет поддерживать низкую температуру и предотвращает деградацию чувствительного субстрата (пример 2).
Высокое давление также может повлиять на предпочтительную стереохимию, если может образоваться несколько изомеров продукта. Кроме того, реакции циклизации, ведущие к макроциклам, могут быть облегчены высоким давлением, что позволяет избежать необходимости использования высоких разбавлений.И последнее, но не менее важное: реакции, проводимые под высоким давлением, могут давать очень стерически перегруженные структуры, такие как продукт присоединения Михаэля, показанный в примере 3.
Реакции можно проводить с использованием чистых реагентов или чаще в растворе. Поскольку точки замерзания растворителя зависят от давления, нужно быть осторожным при выборе растворителя. При очень высоких давлениях практически все обычные растворители затвердевают, и необходимо поддерживать достаточно высокую температуру, обычно комнатную и выше, чтобы растворитель оставался в жидком состоянии, а реагенты — в растворе.
Основным недостатком данной технологии является необходимость проведения реакций малыми партиями, объем которых определяется объемом реакционного сосуда (например, 10 – 100 мл). Это может объяснить, почему технология высокого давления (до 6000 атм) до сих пор не внедрена в промышленном масштабе. Однако свет в туннеле есть, и его осветили польские ученые.
Уже более 40 лет они находятся в авангарде химии высокого давления. Некоторые из наиболее важных вкладов в эту область были сделаны группой профессора Януша Юрчака из Института органической химии Польской академии наук. Их первая статья по стереохимии реакций Дильса-Альдера под высоким давлением была опубликована в 1978 году. Эта группа по-прежнему очень активна в этой области, хотя основное внимание было расширено от самой химии к тому, чтобы сделать ее более безопасной и масштабируемой. Например, высокое давление помогло им синтезировать и функционализировать незакрытые криптанды, которые могут служить потенциальными катализаторами межфазного переноса. Совсем недавно они решили проблему накипи, создав проточное оборудование для обработки под высоким давлением в непрерывном режиме.Стоит добавить, что Польша может стать единственным местом в мире, где химия может работать в проточном режиме под давлением 6000 атм.
Их первая статья по стереохимии реакций Дильса-Альдера под высоким давлением была опубликована в 1978 году. Эта группа по-прежнему очень активна в этой области, хотя основное внимание было расширено от самой химии к тому, чтобы сделать ее более безопасной и масштабируемой. Например, высокое давление помогло им синтезировать и функционализировать незакрытые криптанды, которые могут служить потенциальными катализаторами межфазного переноса. Совсем недавно они решили проблему накипи, создав проточное оборудование для обработки под высоким давлением в непрерывном режиме.Стоит добавить, что Польша может стать единственным местом в мире, где химия может работать в проточном режиме под давлением 6000 атм.
Selvita заинтересована в использовании такой технологии высокого давления. Мы думаем, что это поможет расширить ассортимент химикатов и продуктов, которые мы предлагаем нашим Клиентам. Мы собираемся внедрить технологию высокого давления в сотрудничестве с Институтом органической химии Польской академии наук. Будет ли он производить для нас драгоценные твердые алмазы? Возможно, нет, но некоторая прибыль в виде твердой валюты, вероятно, будет получена.
Будет ли он производить для нас драгоценные твердые алмазы? Возможно, нет, но некоторая прибыль в виде твердой валюты, вероятно, будет получена.
Названия и значения | ||||||||||||||||||||||||||||||||||||||||||||||||
| Это модуль прописан в «расширенной» части, несмотря на то, что хим. потенциал относится к базовой термодинамике. Причина в том, что люди с в основном физическим фоном (такие как я) могли часто узнавать интересные вещи. как конденсация Бозе-Эйнштейна и теорема Лиувилля в их курсах термодинамики, но не слишком много о химических потенциалах и химическом равновесии. | ||||||||||||||||||||||||||||||||||||||||||||||||
| Сначала мы несколько причудливо обратимся к некоторая проблема, связанная с названием «Химический потенциал» .  По мнению многих (в том числе профессоров и студентов), это несколько неудачное название. По мнению многих (в том числе профессоров и студентов), это несколько неудачное название.для количества ¶ G /¶ n я ; что означает частную производную свободной энтальпии по частица сортируется i , а все остальные переменные остаются постоянными (см. также чистый термодинамический сценарий). | ||||||||||||||||||||||||||||||||||||||||||||||||
| Другими словами, «химический потенциал м » является мерой того, насколько свободная энтальпия (или свободная энергия) системы меняет (на d G i ) если добавить или удалить число d n i частицы частицы видов i при сохранении числа остальных частиц (и температуры T и давление p ) постоянная: | ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
Подумайте о балансе луча, и вы получаете дрейф. | ||||||||||||||||||||||||||||||||||||||||||||||||
| Отсюда следует еще одно название: « Частица». сила » или « Сила изменения частиц «.Конечно, сейчас у нас будет сила измеряется с точки зрения энергии — тоже не очень приятно, но, может быть, что-то должно дать? | ||||||||||||||||||||||||||||||||||||||||||||||||
| К сожалению, есть еще один недостаток. Если мы посмотрим на токи (электрические или иные), т. е. на неравновесные условия, движущие силы для токов очень обычно можно отождествить с градиентами химических потенциалов (которые еще могут быть определена даже при глобальной неравновесности до тех пор, пока имеем локальных равновесий).Теперь у нас была бы сила производная силы — и это тоже не слишком ясно. В этом контексте потенциал было бы гораздо лучше имя. | ||||||||||||||||||||||||||||||||||||||||||||||||
Так что — забудь ! ¶ G /¶ n i называется и будет называться « химический потенциал частиц сорта i «. Но к настоящему времени вы Но к настоящему времени вызнаю, что это значит. Тем не менее, если вам не нравится название «Химический потенциал», в контексте рассмотрения нехимических вещей, например.грамм. поведение электронов, используйте свои собственное имя, думая об этом, помните, что оно означает, но обязательно запишите « химический потенциал ». | ||||||||||||||||||||||||||||||||||||||||||||||||
| Преимуществом химического потенциала является его простота — после того, как вы обычные термодинамические расчеты. Это особенно легко получить для (идеальных) газов. | ||||||||||||||||||||||||||||||||||||||||||||||||
| Идеальный газ — это система частиц любого вида , который подчиняется уравнению p·V = N· R ·T с N = Число молей в системе; или p·V = n· k ·T с n = Количество частиц в системе.  | ||||||||||||||||||||||||||||||||||||||||||||||||
| Давайте пройдемся это быстро (ха-ха), ведь нас газы особо не интересуют, а только хотят запомнить номенклатура и путь к ней. | ||||||||||||||||||||||||||||||||||||||||||||||||
| Из обычной термодинамики мы получаем множество соотношений между частными производными функций состояния и, следовательно, также для химического потенциала, например | ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
| в надлежащих количествах, поддерживаемых постоянными, и с осторожностью в отношении использования абсолютных или молярных значений | ||||||||||||||||||||||||||||||||||||||||||||||||
| Из этих уравнений получаем для химический потенциал чистого идеального газа, т. 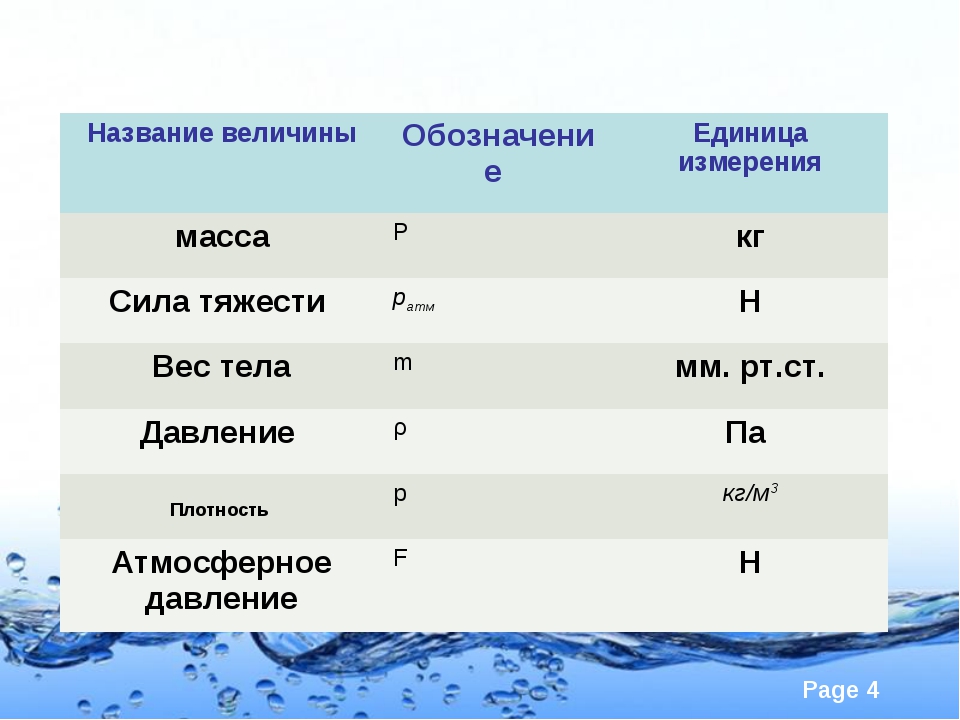 е.е. система, состоящая только из одного вида компонентов е.е. система, состоящая только из одного вида компонентов— связка O 2 молекул в контейнере, или связка Вакансий в кристалле : | ||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||
В случае вакансий у нас, кажется, два компонента
— вакансии и кристалл, не говоря уже о рассмотрении вакансий как идеального газа
кажется, немного растягивает концепцию.

есть вакуум, в котором движутся частицы. Пока «контейнер»
частицы идеального газа ничего не делают, мы можем игнорировать это (если мы этого не сделаем, математика сделает это за
нас, как только мы запишем уравнения типа массы
закон действия или другие, которые говорят нам, что происходит внутри «контейнера»).
идеальный газ для начала!
химический потенциал чистой фазы «.
 Давайте посмотрим, что это означает с точки зрения с двух точек зрения .
Давайте посмотрим, что это означает с точки зрения с двух точек зрения ., если мы останемся на вакансионном примере, т.е. рассмотрим идеальный газ вакансий,
давление определяется как pV = n · k T с n = число
вакансий в кристалле, или p = n · k T / V . Так же,
p 0 , давление в некотором исходном состоянии можно записать как p
0 = N k T / V 0 с N = количество вакансий
в эталонном состоянии и V 0 объем системы в эталоне
состояние.
дает (в 3 простых шага)
|
объем кристалла сильно не изменится в каком состоянии не посмотришь, имеем ( V
0 / В ) » 1 .
 Более того, в равновесии мы требуем м V = 0 .
Более того, в равновесии мы требуем м V = 0 .Это оставляет нас с
состояние будет N= количество атомов кристалла=количество мест для вакансий,
м В 0 должна быть энергия формирования одного
моль вакансий, а это просто энергия образования, измеренная в кДж/моль .если ты
как электрон-вольты, просто замените R на k .
стандартное ссылочное состояние очень важно, но также немного тривиально.
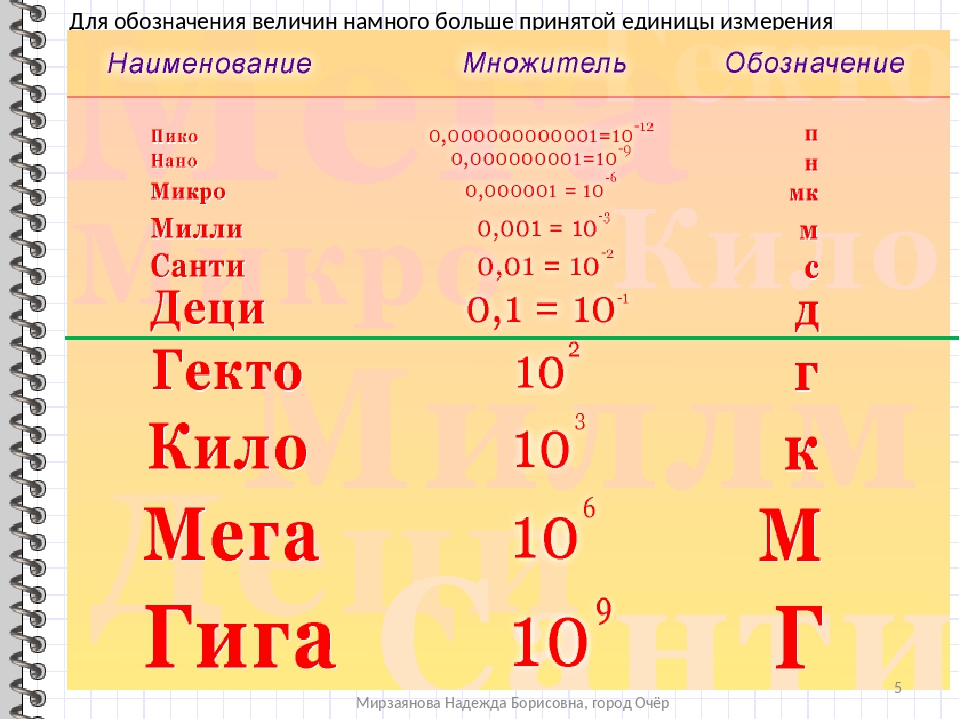 Вы можете выбрать любой
Вы можете выбрать любойкак угодно, но есть умных вариантов и
не очень разумный выбор . Лучше всего придерживаться условностей — обычно они разумны.
вариантов, и вы можете использовать числа, данные в книгах и таблицах, без преобразования в какие-либо другие
система.
химический потенциал представляет собой энергию (со многими свойствами, очень похожими на более известные
гравитационная или электростатическая потенциальная энергия), нет однозначного выбора его нулевой точки.
Все счетчики шляп равны изменений , то есть m i (состояние x) — m i
(состояние 0).
мы пишем м i 0 и называем его стандартным потенциалом.
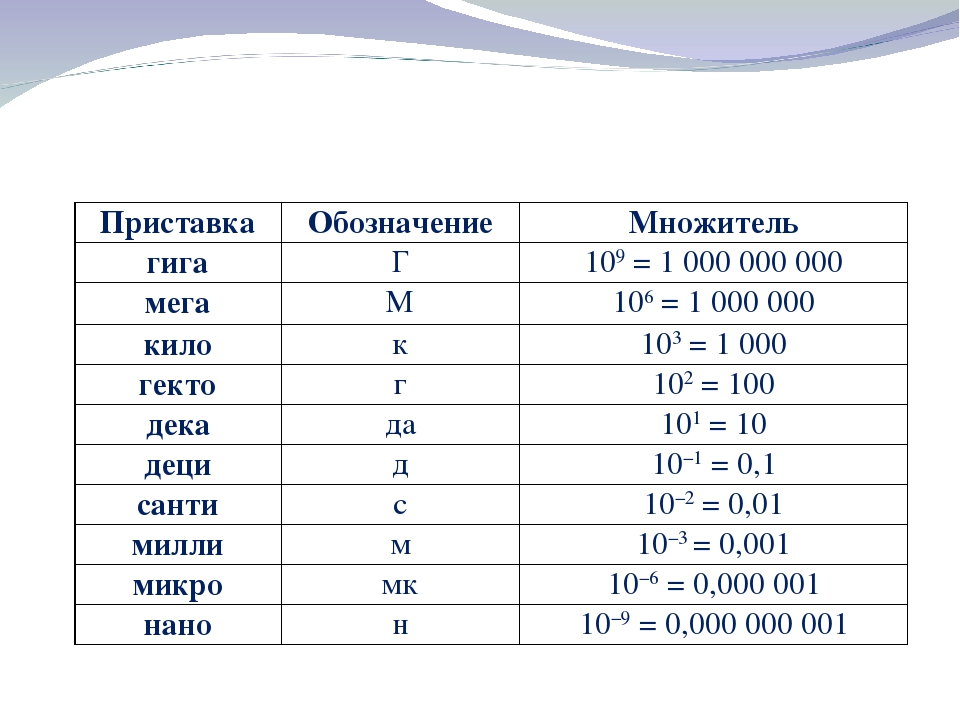
частицы) в смеси с другими частицами? Начать
легко, возьмем смесь идеальных газов — O 2 с N 2 ,
вакансии и междоузлия (оба незаряженные, поэтому взаимодействие незначительно).
( p , T ) компонента i в смеси идеальных газов в зависимости от
температура и (общее) давление.Сначала нам нужны количества » моль
дробь » и « парциальное давление »
для описания смеси.
разделить на сумму количеств всех фаз.

газа с номером i в смеси газов — это просто давление, которое должен дать газ с номером i .
есть, если убрать все остальные газы и позволить им занять доступный объем.Следует
что общее давление p =S i p i
и p i / p = x i (для идеальных газов).
что мы получаем для химического потенциала m i
Компонент I
3 I в смеси идеальных газов
|
i и p= фактическое давление=S p i
газа номер i в смеси газов при определенной температуре T
а давление p равно химическому потенциалу этого газа в чистой фазе
at p и T плюс R T ·
ln x i . Но учтите, что x i < 1
для всех случаев и, следовательно, R T · ln x i < 0 .

запутанный трюк:
( p , T ) теперь стандартное состояние и запись
это м я 0 что это одно и то же
как наши старые м я 0 пока р = р
0 , или, в примере с вакансией выше, N = N 0 = число Лошмидта (= число частиц в моле).
 Опять же, вы свободны в выборе стандартных состояний — используйте это с умом!
Опять же, вы свободны в выборе стандартных состояний — используйте это с умом!своего рода «основное уравнение » для химического
Потенциал компонента I в некоторой смеси идеальных газов:
|
| 1 | 1 | Член в просто содержит энтропию смешения; иначе, когда мы смешиваем два газа, мы складываем только энтальпию/энергию, содержащуюся в двух чистых газах.  компонентов перед смешиванием. | |||||
|---|---|---|---|---|---|---|---|
| Это один из способов записи химического потенциала для смеси газов . Еще раз отметим, что всякий раз, когда мы видим Газовая постоянная R вместо Больцмана константа к , вы знаете, что имеете дело с суммами, которые взяты на моль вещества, а не на частицу. | |||||||
| Опять же, что именно м i 0 сейчас? Ничего, кроме ссылки для шкалы энергий, но, тем не менее, величина первостепенной важности, называемая «стандартным потенциалом компонента i » (верхний индекс « 0 » всегда относится к «стандартной» системе отсчета; в случае газов в основном до атмосферного давления и комнатной температуры).Его также называют стандартная энтальпия реакции и дает изменение в полной свободной энтальпии при стандартных условиях если вы немного изменить концентрацию частицы i через | |||||||
| В другими словами: м i 0 =D G 0 /D n i или м i 0 = увеличение энтальпии (или, небрежно, энергии), если вы добавите единица рассматриваемых частиц к уже имеющимся частицам. 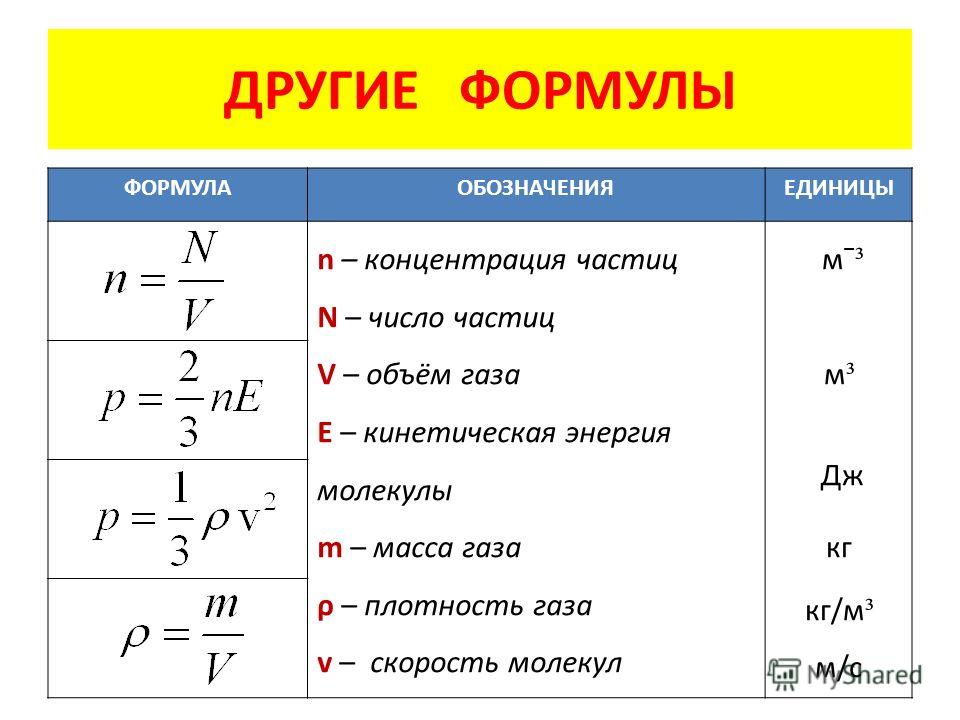 | |||||||
| Что имеют в виду уравнения? Если мы используем единицу «частица», м 0 — это в точности количество свободной энтальпии, необходимое для добавления (или вычитания) одной частицы; обычно указывается в [эВ/частица] , что равно [эВ] . Если мы используем единицу измерения « моль », это свободная энтальпия, необходимая для прибавления (или вычитания) одного моля, обычно выражаемая в [кДж/моль] . | |||||||
| До сих пор мы рассматривали довольно прямолинейная термодинамика; трудности возникают, если мы используем понятие химический потенциал для неидеальных газов , для жидкостей и твердых тел, для смесей газов, жидкостей и твердых тел или, как мы, для таких вещей, как вакансии, которые в любом случае обычно не описываются в этих терминах.  Первый шаг — рассмотреть неидеальные газы: Первый шаг — рассмотреть неидеальные газы: | |||||||
| Если газ неидеален, а это значит, что в нем есть какое-то взаимодействие между его частицами, оно будет подчиняться некоторому уравнению вириала (любому уравнению, заменяющему p·V = N ·R T ). Простейшее возможное вириальное уравнение V = R · T / P / P + B / B А для этого мы получаем | |||||||
| |||||||
соответствующую формулу для химического потенциала этого конкретного неидеального газа.
 Это
Этовсегда будет иметь некоторые дополнительные члены, содержащие давление.
даже в случае неидеальных газов на подставив реальное давление
p по количеству называемому летучесть f выбранный
таким образом, чтобы правильное значение для m non-id
Результаты.
всегда можно вычислить из уравнения вириала, применимого к ситуации. В нашем
например у нас есть
пока мы смотрим на газы, проблем нет.
 Летучесть — это четко определенное понятие, даже если
Летучесть — это четко определенное понятие, даже еслинужно привыкнуть. Следующий шаг, однако, немного более проблематичен.
обратимся к твердым телам (а одним махом включим сюда и жидкости). Хорошие новости
заключается в том, что уравнение для смеси идеальных газов в равной степени справедливо для смеси идеально конденсированных
фазы, то есть идеальные твердые тела . Плохая новость: идеальное твердое тело
по аналогии с газами, т.е.е. без взаимодействия между атомами
оксюморон (т.е. противоречие само по себе).
нам нужны взаимодействия между атомами или молекулами, мы должны иметь в виду нечто отличное от
газы.
 Под «идеальным» в данном случае понимается взаимодействие между
Под «идеальным» в данном случае понимается взаимодействие междусоставные части тела одинаковы независимо от их природы.
хорошее приближение для большинства твердых тел.Таким образом, мы используем тот же прием, что и в случае с газами, заменяем
мольная доля (концентрация) x i компонента i
по количеству, содержащему отклонение от идеальности; это количество называется « деятельность » a i .
компонента i по
теперь несущий бремя неидеальности.

i это а не все это легко вычисляется на самом деле
это почти совсем безнадежно. Возможно, вам придется прибегнуть к эксперименту и измерить его.
вместо концентрации или летучести (которые мы рассматриваем как частный случай активности), мы
являются полностью общими и получают для химических потенциалов любого компонента в любой смеси:
|
формула химического потенциала вакансии; он читал (если вы поставите различные уравнения
даны по ссылке вместе):
|
= n V равновесная концентрация вакансий, которую мы теперь также можем
звоните V , активность вакансий, если мы хотим быть полностью общими.

мы должны учитывать энергию на частицу, а не на моль, что мы и сделали. Поэтому мы
имеют не мольную долю, а долю числа частиц; но это идентично, в любом случае.
Все, что нам нужно сделать, это перетасовать ln :
|
газ или твердое тело, если мы идентифицируем энтальпию образования G F вакансии
со своим стандартным химическим потенциалом м 0 (вакансии)
— и мы уже сделали это тоже.

вакансий с активностью вакансий все в порядке — но к счастью для концентраций вакансий
в элементарных кристаллах нет разницы между концентрацией и активностью, потому что
концентрации вакансий всегда малы (ниже 10 –4 ) — вакансии
находятся далеко друг от друга и поэтому мало взаимодействуют — ведут себя
как идеальный газ !
в ионных кристаллах.
собственных точечных дефектов может зависеть от стехиометрии и от примесей : Если
есть напр.
 след Ca ++ в кристалле NaCl должен быть соответствующий
след Ca ++ в кристалле NaCl должен быть соответствующийконцентрация Na — вакансии для поддержания нейтральности заряда и эта концентрация
может быть не только намного больше, чем максимальная концентрация в тепловом равновесии для «идеального»
кристаллов, она также будет постоянной, т.е.е. независимо от температуры!
и действия в этом контексте описаны в серии модулей в разделе «Основа II» главы 2. Здесь мы рассмотрим только
приведите один пример — равновесие между фазами.
но с две возможные фазы .
лед или любое бинарное вещество заданного состава (например, Pb и Sn — припой)
в какой-то момент на его фазовой диаграмме, где две фазы сосуществуют (обратитесь к модулю «фазовые диаграммы»), если на то пошло.
будет содержаться в фазе 1 и сколько в фазе 2 ? Даны N частиц
всего мы будем иметь N 1 частиц в фазе 1 и N
2 = N – N 1 в фазе 2 .На сколько большой
N 1 ?
числа частиц.
 В общем случае имеем два уравнения:
В общем случае имеем два уравнения:
|
с постоянным давлением и температурой , мы имеем, что d T = 0 = d p .
| ||||||||||||||||
кв. э.д. э.д. | ||||||||||||||||
| Что произойдет, если м( N 1 ) > м( N 2 ) ; т. е. если мы имеем неравновесное условиях с м(N 1 ) , химический потенциал частиц в фазе 1 больше, чем в фазе 2 ? | ||||||||||||||||
| Теперь мы должны изменить числа частиц в фазах, пока не будет достигнуто равновесие. | ||||||||||||||||
| Так нам надо увеличивать N 1 (одновременно уменьшая N 2 ) или должно быть наоборот? | ||||||||||||||||
| Ну, что бы мы ни делали, это должно уменьшаться G , поэтому d G должно быть отрицательным, если мы изменим частицу числа правильно.  Для d G у нас было (несколько строк выше) Для d G у нас было (несколько строк выше) | ||||||||||||||||
| Для положительных d N 1 у нас будет d G > 0 с м( N 1 ) > м( N 2 ) .  Это обязательно приводит к общему заключению: Это обязательно приводит к общему заключению: | |||||||||||||||
| d N 1 должно быть < 0 , если система должна двигаться к равновесию. | ||||||||||||||||
| Прописью это означает: Фаза с большим химическим потенциалом должна сжиматься, а фаза с меньший химический потенциал будет расти до тех пор, пока не будет достигнуто равновесие и m( N 1 )=m( N 2 ) . | ||||||||||||||||
| Это очень общая истина . Электроны, например, переходят из фазы с более высоким химическим потенциалом (чем называется Ферми энергии) в фазу с нижней. | ||||||||||||||||
| Мы также можем повернуть это вспять: вакансии в пересыщении будут имеют тенденцию перемещаться в вакансионные агломераты и увеличивать их размеры.  Отсюда следует, что химический Отсюда следует, что химическийпотенциал пересыщенных одиночных вакансий должен быть больше, чем у вакансий в агломерате. | ||||||||||||||||
| Следование этой мысли ведет прямо к закону действующих масс, который будет рассмотрен в другом модуле. | ||||||||||||||||
Осмотическое давление: определение и формула – видео и стенограмма урока
Как рассчитывается осмотическое давление?
Осмотическое давление можно определить с помощью приведенного здесь уравнения.
Концентрация растворенного вещества и температура влияют на величину давления, создаваемого движением воды через мембрану. Более высокие концентрации и более высокие температуры увеличивают осмотическое давление.
Более высокие концентрации и более высокие температуры увеличивают осмотическое давление.
На осмос также влияет то, как растворенное вещество ведет себя в воде, и именно здесь вступает в действие фактор Вант-Гоффа. В основном, Коэффициент Вант-Гоффа растворенного вещества определяется тем, остается ли растворенное вещество вместе или распадается. отдельно в воде.Некоторые растворенные вещества распадаются и образуют в воде 90 183 ионов 90 184 или заряженных атомов. Как показано здесь, поваренная соль NaCl образует в воде ионы натрия (Na+) и хлора (Cl-). Фактор Вант-Гоффа NaCl равен двум, потому что он распадается на два иона.
При помещении в воду некоторые молекулы, такие как сахароза, остаются вместе и не образуют ионов. Поскольку сахароза не распадается на ионы, ее коэффициент Вант-Гоффа равен 1.
Примеры задач
Каково осмотическое давление для 0.5 М раствор сахарозы при 300 К (27°С), когда сахароза имеет фактор Вант-Гоффа 1?
Все, что вам нужно сделать, это подставить то, что вы знаете, в уравнение для определения осмотического давления, которое очень просто (пи).
- i будет 1, так как сахароза не образует ионов в воде
- М будет равно 0,5 моль/л или той концентрации сахарозы, которую вы используете.
- R – постоянная идеального газа 0,08206 л атм/моль K
- Т равно 300 К
- Поскольку все остальные единицы компенсируют друг друга, осмотическое давление измеряется в атм.
Попробуем еще. Какая концентрация NaCl необходима, чтобы иметь осмотическое давление 12,309 атм при 300К? Фактор Вант-Гоффа для NaCl равен 2.
Вы подставили бы то, что знаете, в уравнение, а затем нашли бы М или концентрацию.
- Пи = 12,309
- i будет 2, так как NaCl образует ионы Na и Cl в воде.
- М неизвестно
- R – постоянная идеального газа 0,08206 л атм/моль K
- Т равно 300 К
Потребуется только 0.25 М соли для достижения осмотического давления 12,309. Несмотря на то, что концентрация NaCl ниже при 0,25 М, общее количество частиц, растворенных в растворе, такое же, как и в 0,5 М растворе сахарозы. Скорость осмоса определяется общим количеством частиц, растворенных в воде.
Скорость осмоса определяется общим количеством частиц, растворенных в воде.
Краткий обзор урока
Осмотическое давление возникает, когда два раствора с разными концентрациями разделены мембраной. Осмотическое давление заставляет воду переходить в раствор с наибольшей концентрацией.Уравнение для осмотического давления: pi = i MRT. Чем выше концентрация (М) или температура (Т) раствора, тем выше осмотическое давление.
Осмотическое давление Словарь и определения
- Осмос : перемещение воды из области с низкой концентрацией растворенного вещества в область с более высокой концентрацией растворенного вещества
- Осмотическое давление : давление, создаваемое водой, проходящей через мембрану вследствие осмоса
- Фактор Вант-Гоффа : определяется тем, остается ли растворенное вещество вместе или распадается в воде
- Ионы : заряженные атомы
Результаты обучения
После завершения этого урока учащиеся должны уметь:
- Давать определение осмосу
- Опишите, что такое осмотическое давление
- Объясните, как определить осмотическое давление, используя соответствующую формулу
Осмос и осмотическое давление
Это упражнение предоставит дополнительные задачи, касающиеся осмотического давления, чтобы попрактиковаться в расчетах и понимании осмоса. Решения задач включены, чтобы помочь в расчетах, если это необходимо.
Решения задач включены, чтобы помочь в расчетах, если это необходимо.
Материалы
Ручка или карандаш
Бумага
Калькулятор
Вопросы
1. Определите осмотическое давление раствора, содержащего 5,0 г глюкозы в 10,0 л раствора при 24 градусах Цельсия.
2. Каково осмотическое давление 2,0 М раствора NaCl при 30°С?
3. Небольшое количество (0,005 г) неизвестного белкового соединения растворяется в 10.0 мл раствора. Осмотическое давление составляет 0,05 атм при 25 градусах Цельсия. Какова молярная масса неизвестного соединения?
Решения
1.
i = 1, так как глюкоза останется в 1 компоненте
молярная масса глюкозы = 180,18 г/моль
Молярность глюкозы = 5 разделить на 180,18 * 10,0 = 0,003 М
R = 0,0821 л атм / К моль
Т = 24 + 273 = 297 К
Пи = 0,003 * 0,0821 * 297 * 1
2.
i = 2, так как NaCl диссоциирует на 2 компонента
М = 2 М
Р = 0. 0821 л атм/К моль
0821 л атм/К моль
Тл = 30 + 273 = 303 К
Пи = 2 * 2 * 0,0821 * 303
Пи = 2 * 2 * 0,0821 * 303 = 99,5 атм.
3.
i = 1, так как белок не диссоциирует
R = 0,0821 л атм / К моль
Т = 25 + 273 = 298 К
Пи = 0,05 атм.
Масса соединения
= 0,005 г
Объем = 10/1000 = 0,010 л
молярная масса = (0,005 * 0,0821 * 298 * 1)/(0,05 * 0,010)
молярная масса = 244 г/моль
10.2: Давление — Химия LibreTexts
Цели обучения
- для описания и измерения давления газа.
На макроскопическом уровне полное физическое описание образца газа требует четырех величин:
- температура (выражается в кельвинах),
- объем (в литрах),
- количество (выражено в молях) и
- давление (в атмосферах).

Как мы показали ниже, эти переменные являются , а не независимыми (т. е. их нельзя варьировать произвольно). Если мы знаем значения любых трех этих величин, мы можем вычислить четвертую и тем самым получить полное физическое описание газа. Температура, объем и количество обсуждались в предыдущих главах. Теперь обсудим давление и его единицы измерения.
Единицы давления
Любой объект, будь то ваш компьютер, человек или образец газа, воздействует на любую поверхность, с которой соприкасается.Воздух в воздушном шаре, например, воздействует на внутреннюю поверхность воздушного шара, а жидкость, впрыскиваемая в форму, действует на внутреннюю поверхность формы, точно так же, как стул воздействует на пол из-за его масса и действие гравитации. Если воздух в воздушном шаре нагрет, увеличенная кинетическая энергия газа в конечном итоге приведет к тому, что воздушный шар лопнет из-за повышенного давления (\(P\)) газа, сила (\(F\)) на единицу площади (\(A\)) поверхности:
\[P=\dfrac{\rm Force}{\rm Area}=\dfrac{F}{A}\label{10. 2.1}\]
2.1}\]
Давление зависит от и приложенной силы, и размера области, к которой приложена сила. Из уравнения \(\ref{10.2.1}\) мы знаем, что приложение той же силы к меньшей площади создает более высокое давление. Например, когда мы используем шланг для мытья автомобиля, мы можем увеличить давление воды, уменьшив размер отверстия шланга большим пальцем.
Единицы давления получены из единиц, используемых для измерения силы и площади.2 \метка{10.2.2}\]
Пример \(\PageIndex{1}\)
Если предположить, что книга в мягкой обложке имеет массу 2,00 кг, длину 27,0 см, ширину 21,0 см и толщину 4,5 см, какое давление она оказывает на поверхность, если она
- лежит плашмя?
- стоит на краю книжного шкафа?
Дано: масса и размеры объекта
Запрашиваемый: давление
Стратегия:
- Рассчитайте силу, действующую на книгу, а затем рассчитайте площадь, соприкасающуюся с поверхностью.

- Подставьте эти два значения в уравнение \(\ref{10.2.1}\), чтобы найти давление, оказываемое на поверхность в каждой ориентации.
Решение:
Сила, действующая на книгу, , а не , зависит от ее ориентации. Напомним, что сила, действующая на объект, равна F = мА , где m — его масса, а a — его ускорение. В гравитационном поле Земли ускорение обусловлено силой тяжести (9.3 \;\rm Па \номер\]
Упражнение \(\PageIndex{1}\)
Какое давление оказывает на пол студент массой 60,0 кг
- при стоянии в лаборатории на плоской ступне в теннисных туфлях (площадь подошвы примерно 180 см 2 )?
- , когда она выходит на танцпол пяткой вперед в туфлях на высоком каблуке (площадь каблука = 1,0 см 2 )?
- Ответить на
3.27 × 10 4 Па
- Ответ б
5,9 × 10 6 Па
Барометрическое давление
Точно так же, как мы оказываем давление на поверхность из-за гравитации, то же самое делает и наша атмосфера. Мы живем на дне газового океана, который с увеличением высоты становится все менее плотным. Приблизительно 99 % массы атмосферы находится в пределах 30 км от поверхности Земли (рис. \(\PageIndex{1}\)).Каждая точка на поверхности Земли испытывает чистое давление, называемое барометрическим давлением . Давление, оказываемое атмосферой, велико: столб 1 м 2 , измеренный от уровня моря до верхней границы атмосферы, имеет массу около 10 000 кг, что дает давление около 101 кПа:
Мы живем на дне газового океана, который с увеличением высоты становится все менее плотным. Приблизительно 99 % массы атмосферы находится в пределах 30 км от поверхности Земли (рис. \(\PageIndex{1}\)).Каждая точка на поверхности Земли испытывает чистое давление, называемое барометрическим давлением . Давление, оказываемое атмосферой, велико: столб 1 м 2 , измеренный от уровня моря до верхней границы атмосферы, имеет массу около 10 000 кг, что дает давление около 101 кПа:
Рисунок \(\PageIndex{1}\): Атмосферное давление. Каждый квадратный метр земной поверхности поддерживает столб воздуха высотой более 200 км и весом около 10 000 кг у поверхности Земли.
Барометрическое давление можно измерить с помощью барометра, прибора, изобретенного в 1643 году одним из учеников Галилея, Эванджелистой Торричелли (1608–1647). Барометр может быть изготовлен из длинной стеклянной трубки, закрытой с одного конца. Его наполняют ртутью и помещают вверх дном в чашу с ртутью, не допуская попадания воздуха в трубку. Часть ртути вытечет из трубки, но внутри останется относительно высокий столбик (рис. \(\PageIndex{2}\)). Почему не кончается вся ртуть? Гравитация, безусловно, оказывает направленное вниз давление на ртуть в трубке, но ей противостоит давление атмосферы, давит на поверхность ртути в чашке, что в конечном итоге приводит к выталкиванию ртути вверх в трубку.Поскольку над ртутью внутри трубки в правильно заполненном барометре нет воздуха (в нем вакуум), давление на колонку не оказывается. Таким образом, ртуть вытекает из трубки до тех пор, пока давление самого ртутного столба точно не уравновесит давление атмосферы. Давление ртутного столба можно выразить как:
Часть ртути вытечет из трубки, но внутри останется относительно высокий столбик (рис. \(\PageIndex{2}\)). Почему не кончается вся ртуть? Гравитация, безусловно, оказывает направленное вниз давление на ртуть в трубке, но ей противостоит давление атмосферы, давит на поверхность ртути в чашке, что в конечном итоге приводит к выталкиванию ртути вверх в трубку.Поскольку над ртутью внутри трубки в правильно заполненном барометре нет воздуха (в нем вакуум), давление на колонку не оказывается. Таким образом, ртуть вытекает из трубки до тех пор, пока давление самого ртутного столба точно не уравновесит давление атмосферы. Давление ртутного столба можно выразить как:
\[\begin{align} P&=\dfrac{F}{A} \\[4pt] &= \dfrac{mg}{A} \\[4pt] &= \dfrac{\rho V\cdot g} {A} \\[4pt] &= \dfrac{ \rho \cdot Ah\cdot g}{A} \\[4pt] &= \rho gh \end{align}\]
с
- \(g\) ускорение свободного падения,
- \(m\) — масса,
- \(\rho\) — плотность,
- \(V\) — объем,
- \(A\) — нижняя область, а
- \(h\) — высота ртутного столба.

При нормальных погодных условиях на уровне моря две силы уравновешиваются, когда верхняя часть ртутного столба находится приблизительно на 760 мм выше уровня ртути в чашке, как показано на рисунке \(\PageIndex{2}\). Это значение зависит от метеорологических условий и высоты над уровнем моря. В Денвере, штат Колорадо, например, на высоте около 1 мили или 1609 м (5280 футов) высота ртутного столба составляет 630 мм, а не 760 мм.
Рисунок \(\PageIndex{2}\): Ртутный барометр.Давление, оказываемое атмосферой на поверхность ртутного бассейна, поддерживает столбик ртути в трубке высотой около 760 мм. Поскольку температура кипения ртути довольно высока (356,73 °С), паров ртути в пространстве над ртутным столбом очень мало.
Ртутные барометры использовались для измерения барометрического давления так долго, что у них есть собственная единица измерения давления: миллиметр ртутного столба (мм рт.ст.), часто называемый торром в честь Торричелли. Стандартное барометрическое давление — это барометрическое давление, необходимое для поддержания столба ртути высотой ровно 760 мм; это давление также называют 1 атмосферой (атм).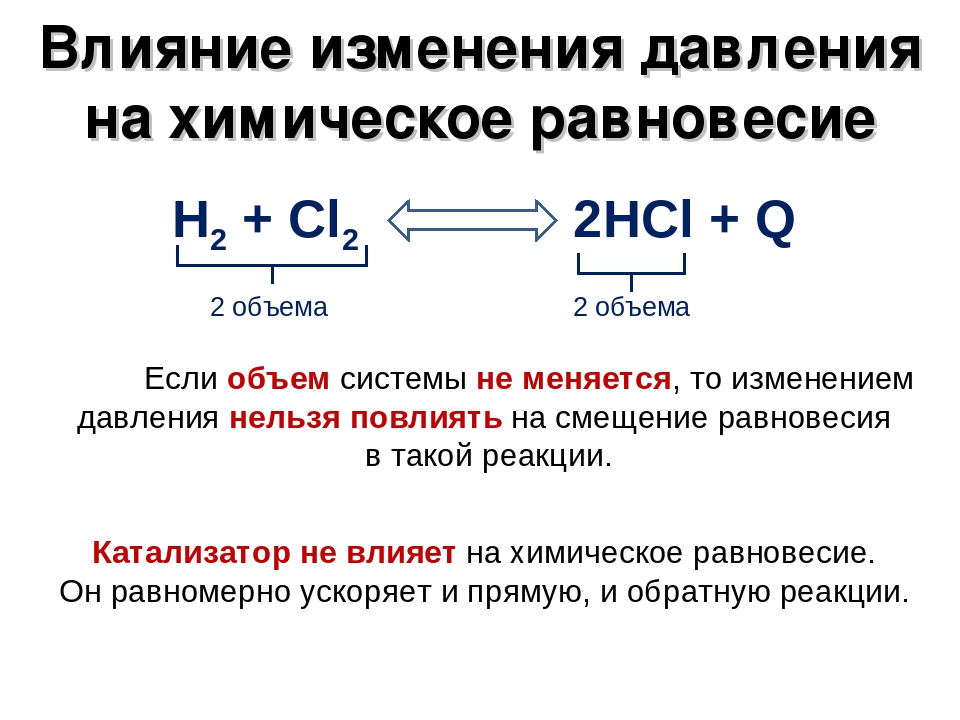 5 \; Па \\[4pt] &= 101,325 \; кПа\метка{10.2.3} \end{align}\]
5 \; Па \\[4pt] &= 101,325 \; кПа\метка{10.2.3} \end{align}\]
Таким образом, давление в 1 атм в точности равно 760 мм ртутного столба.
Мы так привыкли жить под этим давлением, что не замечаем его. Вместо этого мы замечаем изменения давления, например, когда наши уши щелкают в быстром лифте в небоскребе или в самолете при резком изменении высоты. Мы используем атмосферное давление разными способами. Мы можем использовать соломинку для питья, потому что всасывание через нее удаляет воздух и тем самым снижает давление внутри соломинки.Атмосферное давление давит на жидкость в стакане, а затем заставляет жидкость подниматься по соломинке.
Пример \(\PageIndex{2}\): атмосферное давление
Несколько лет назад один из авторов посетил национальный парк Роки-Маунтин. Вылетев из аэропорта на уровне моря на востоке Соединенных Штатов, он прибыл в Денвер (высота 5280 футов), арендовал машину и поехал к верхней части шоссе за пределами Эстес-парка (высота 14 000 футов). Он заметил, что на этой высоте, где барометрическое давление составляет всего 454 мм рт. ст., очень тяжело даже небольшое усилие.Преобразуйте это давление в
Он заметил, что на этой высоте, где барометрическое давление составляет всего 454 мм рт. ст., очень тяжело даже небольшое усилие.Преобразуйте это давление в
- атмосферы (атм).
- бар.
Дано: давление в миллиметрах ртутного столба
Запрашиваемый: давление в атмосфер и бар
Стратегия:
Используйте коэффициенты преобразования в уравнении \(\ref{10.2.3}\) для преобразования миллиметров ртутного столба в атмосферы и килопаскали.
Решение:
Из уравнения \(\ref{10.2.3}\) имеем 1 атм = 760 мм рт. ст. = 101.325 кПа. Таким образом, давление на высоте 14 000 футов в атм составляет
.
\[ \begin{align} P &=\rm 454 \;mmHg\times\dfrac{1\;atm}{760\;mmHg} \\[4pt] &= 0.597\;atm \nonumber \end{align } \номер\]
Давление в барах определяется как
\[ \begin{align} P&=\rm 0.597\;atm\times\dfrac{1.01325\;bar}{1\;atm}\\[4pt] &= 0. 605\;bar \nonumber \end{align} \номер\]
605\;bar \nonumber \end{align} \номер\]
Упражнение \(\PageIndex{2}\): Атмосферное давление
Гора Эверест, на высоте 29 028 футов над уровнем моря, является самой высокой горой в мире.Нормальное барометрическое давление на этой высоте составляет около 0,308 атм. Преобразуйте это давление в
- миллиметра ртутного столба.
- бар.
- Ответить на
234 мм рт.ст.;
- Ответ б
0,312 бар
Манометры
Барометры измеряют барометрическое давление, но манометры измеряют давление проб газов, содержащихся в аппарате.Ключевой особенностью манометра является U-образная трубка, содержащая ртуть (или иногда другую нелетучую жидкость). Манометр с закрытым концом схематично показан в части (а) на рисунке \(\PageIndex{3}\). Когда колба не содержит газа (т. е. когда внутри ее почти вакуум), высоты двух ртутных столбиков одинаковы, потому что пространство над ртутью слева представляет собой почти вакуум (оно содержит только следы паров ртути). ). Если газ выпустить в колбу справа, он будет оказывать давление на ртуть в правом столбике, и два столбика ртути больше не будут иметь одинаковую высоту.Разница между высотами двух столбцов равна давлению газа.
). Если газ выпустить в колбу справа, он будет оказывать давление на ртуть в правом столбике, и два столбика ртути больше не будут иметь одинаковую высоту.Разница между высотами двух столбцов равна давлению газа.
Рисунок \(\PageIndex{3}\): Два типа манометров. (а) В манометре с закрытым концом пространство над ртутным столбиком слева (эталонное плечо) представляет собой практически вакуум ( P ≈ 0), а разница в высоте двух столбиков дает давление газ, содержащийся непосредственно в колбе. (b) В манометре с открытым концом левое (эталонное) плечо открыто в атмосферу ( P ≈ 1 атм), а разница высот двух столбцов дает разность между барометрическим давлением и давление газа в баллоне.
Если трубка открыта в атмосферу, а не закрыта, как в манометре с открытым концом, показанном в части (b) на рисунке \(\PageIndex{3}\), то два ртутных столбика имеют одинаковую высоту, только если газ в колбе имеет давление, равное барометрическому давлению. Если давление газа в колбе на 90 004 больше, чем на 90 005, ртуть в открытой трубке будет вытесняться газом, давящим вниз на ртуть в другом плече U-образной трубки. Таким образом, давление газа в колбе представляет собой сумму барометрического давления (измеряемого барометром) и разницы высот двух столбцов.Если газ в колбе имеет давление на меньше, чем давление атмосферы на , то высота ртути будет больше в плече, прикрепленном к колбе. В этом случае давление газа в колбе равно барометрическому давлению за вычетом разницы высот двух столбцов.
Таким образом, давление газа в колбе представляет собой сумму барометрического давления (измеряемого барометром) и разницы высот двух столбцов.Если газ в колбе имеет давление на меньше, чем давление атмосферы на , то высота ртути будет больше в плече, прикрепленном к колбе. В этом случае давление газа в колбе равно барометрическому давлению за вычетом разницы высот двух столбцов.
Пример \(\PageIndex{3}\)
Предположим, вы хотите построить закрытый манометр для измерения давления газа в диапазоне 0,000–0,200 атм. Из-за токсичности ртути вы решили использовать воду, а не ртуть.Какой высоты столб воды вам нужен? (Плотность воды 1,00 г/см 3 ; плотность ртути 13,53 г/см 3 .)
Дано: диапазон давления и плотности воды и ртути
Запрашиваемый: высота столбца
Стратегия:
- Рассчитайте высоту столбика ртути, соответствующую 0,200 атм в миллиметрах ртутного столба.
 Это высота, необходимая для столба, заполненного ртутью.
Это высота, необходимая для столба, заполненного ртутью. - Из заданных плотностей используйте пропорцию, чтобы вычислить высоту, необходимую для столба, заполненного водой.
Решение:
A В миллиметрах ртутного столба давление газа 0,200 атм равно
\[P=\rm 0,200\;атм\раз\dfrac{760\;мм рт.ст.}{1\;атм}=152\;мм рт.ст\]
При использовании ртутного манометра вам потребуется ртутный столбик высотой не менее 152 мм.
B Поскольку плотность воды меньше плотности ртути, вам потребуется столб воды на выше, чем на , чтобы достичь того же давления, что и данный столб ртути. Высота, необходимая для заполненной водой колонны, соответствующая давлению 0.3}=2070\;мм\]
Ответ имеет смысл: для достижения того же давления требуется более высокий столб менее плотной жидкости.
Упражнение \(\PageIndex{3}\)
Предположим, вы хотите разработать барометр для измерения барометрического давления в среде, температура которой всегда превышает 30°C. Чтобы не использовать ртуть, вы решаете использовать галлий, который плавится при 29,76 °C; плотность жидкого галлия при 25°С составляет 6,114 г/см 3 . Какой высоты столбик галлия вам нужен, если P = 1.4\;мм \без номера \\[4pt] &= 10,3\;м \без номера \end{align} \без номера\]
Чтобы не использовать ртуть, вы решаете использовать галлий, который плавится при 29,76 °C; плотность жидкого галлия при 25°С составляет 6,114 г/см 3 . Какой высоты столбик галлия вам нужен, если P = 1.4\;мм \без номера \\[4pt] &= 10,3\;м \без номера \end{align} \без номера\]
Всасывающий насос — это просто более сложная версия соломинки: он создает вакуум над жидкостью и опирается на атмосферное давление, чтобы направить жидкость вверх по трубке. Если давление в 1 атм соответствует водяному столбу высотой 10,3 м (33,8 фута), то барометрическое давление физически не может поднять воду в колодце выше этого значения. До тех пор, пока не были изобретены электрические насосы для механического откачивания воды с больших глубин, этот фактор сильно ограничивал возможности проживания людей, поскольку добывать воду из колодцев глубиной более 33 футов было сложно.
Резюме
Давление определяется как сила, действующая на единицу площади; его можно измерить с помощью барометра или манометра. Для полного физического описания образца газа необходимо знать четыре величины: температура , объем , количество и давление . Давление — сила на единицу площади поверхности; единицей давления в системе СИ является паскалей (Па) , определяемая как 1 ньютон на квадратный метр (Н/м 2 ).Давление, оказываемое объектом, пропорционально силе, которую он оказывает, и обратно пропорционально площади, на которую действует сила. Давление, оказываемое атмосферой Земли, называемое барометрическим давлением , составляет около 101 кПа или 14,7 фунта/дюйм. 2 на уровне моря. барометрическое давление можно измерить барометром , закрытой перевернутой трубкой, наполненной ртутью. Высота ртутного столба пропорциональна барометрическому давлению, которое часто выражается в единицах миллиметров ртутного столба (мм рт.ст.) , также называемых торр .
Для полного физического описания образца газа необходимо знать четыре величины: температура , объем , количество и давление . Давление — сила на единицу площади поверхности; единицей давления в системе СИ является паскалей (Па) , определяемая как 1 ньютон на квадратный метр (Н/м 2 ).Давление, оказываемое объектом, пропорционально силе, которую он оказывает, и обратно пропорционально площади, на которую действует сила. Давление, оказываемое атмосферой Земли, называемое барометрическим давлением , составляет около 101 кПа или 14,7 фунта/дюйм. 2 на уровне моря. барометрическое давление можно измерить барометром , закрытой перевернутой трубкой, наполненной ртутью. Высота ртутного столба пропорциональна барометрическому давлению, которое часто выражается в единицах миллиметров ртутного столба (мм рт.ст.) , также называемых торр . Стандартное барометрическое давление , давление, необходимое для поддержания столба ртути высотой 760 мм, является еще одной единицей давления: 1 атмосферы (атм) . Манометр представляет собой прибор, используемый для измерения давления пробы газа.
Стандартное барометрическое давление , давление, необходимое для поддержания столба ртути высотой 760 мм, является еще одной единицей давления: 1 атмосферы (атм) . Манометр представляет собой прибор, используемый для измерения давления пробы газа.
2.2 Давление, температура и среднеквадратическая скорость – University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объяснить соотношение между микроскопическими и макроскопическими величинами в газе
- Решение задач на смеси газов
- Решение задач на расстояние и время между столкновениями молекул газа
Мы исследовали давление и температуру на основе их макроскопических определений.Давление — это сила, деленная на площадь, на которую действует сила, а температура измеряется термометром. Мы можем лучше понять давление и температуру из кинетической теории газов, теории, которая связывает макроскопические свойства газов с движением молекул, из которых они состоят. Во-первых, мы делаем два предположения о молекулах в идеальном газе.
Во-первых, мы делаем два предположения о молекулах в идеальном газе.
- Существует очень большое количество N молекул, все они идентичны и каждая имеет массу m .
- Молекулы подчиняются законам Ньютона и находятся в непрерывном движении, которое является случайным и изотропным, то есть одинаковым во всех направлениях.
Чтобы вывести закон идеального газа и связь между микроскопическими величинами, такими как энергия типичной молекулы, и макроскопическими величинами, такими как температура, мы анализируем образец идеального газа в жестком контейнере, относительно которого мы делаем два дополнительных предположения:
- Молекулы намного меньше среднего расстояния между ними, поэтому их общий объем намного меньше, чем объем их контейнера (объем которого V ).Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малым по сравнению с объемом моля газа в сосуде.

- Молекулы совершают совершенно упругие столкновения со стенками сосуда и друг с другом. Другие действующие на них силы, включая гравитацию и притяжение, представленное постоянной Ван-дер-Ваальса a , пренебрежимо малы (что необходимо для предположения об изотропии).
Столкновения между молекулами не учитываются при выводе закона идеального газа.Они также не мешают выводу, так как столкновения молекул, движущихся со случайными скоростями, дают новые случайные скорости. Кроме того, если скорости молекул газа в сосуде изначально не случайны и не изотропны, столкновения молекул делают их случайными и изотропными.
Сделаем еще предположения, упрощающие расчеты, но не влияющие на результат. Во-первых, пусть контейнер будет прямоугольной коробкой. Во-вторых, мы начнем с рассмотрения одноатомных газов, молекулы которых состоят из отдельных атомов, таких как гелий.Тогда мы можем предположить, что у атомов нет энергии, кроме их поступательной кинетической энергии; например, они не имеют ни вращательной, ни колебательной энергии. (Позже мы обсудим справедливость этого предположения для реальных одноатомных газов и обойдемся без него для рассмотрения двухатомных и многоатомных газов.)
(Позже мы обсудим справедливость этого предположения для реальных одноатомных газов и обойдемся без него для рассмотрения двухатомных и многоатомных газов.)
На рис. 2.9 показано столкновение молекулы газа со стенкой сосуда, так что она действует на стенку с силой (по третьему закону Ньютона). Эти столкновения являются источником давления в газе.По мере увеличения числа молекул увеличивается число столкновений и, следовательно, давление. Точно так же, если средняя скорость молекул выше, давление газа выше.
Фигура
2,9
Когда молекула сталкивается с твердой стенкой, составляющая ее импульса, перпендикулярная стенке, меняется на противоположную. Таким образом, на стену действует сила, создающая давление.
В образце газа в контейнере хаотичность движения молекул приводит к тому, что количество столкновений молекул с любой частью стенки в заданное время колеблется.Однако из-за того, что за короткое время со стенкой сталкивается огромное количество молекул, количество столкновений в масштабах времени и пространства, которые мы измеряем, колеблется лишь на крошечную, обычно ненаблюдаемую долю от среднего значения. Мы можем сравнить эту ситуацию с ситуацией в казино, где результаты ставок случайны, а доходы казино колеблются по минутам и часам. Тем не менее, в течение длительного времени, такого как год, доходы казино очень близки к средним значениям, ожидаемым от шансов. В баллоне с газом неимоверно больше молекул, чем игроков в казино за год, а за секунду молекулы совершают гораздо больше столкновений, чем ставок в казино.
Мы можем сравнить эту ситуацию с ситуацией в казино, где результаты ставок случайны, а доходы казино колеблются по минутам и часам. Тем не менее, в течение длительного времени, такого как год, доходы казино очень близки к средним значениям, ожидаемым от шансов. В баллоне с газом неимоверно больше молекул, чем игроков в казино за год, а за секунду молекулы совершают гораздо больше столкновений, чем ставок в казино.
Расчет средней силы, с которой молекулы действуют на стенки ящика, приводит нас к закону идеального газа и к связи между температурой и молекулярной кинетической энергией. (На самом деле мы возьмем два средних значения: одно по времени, чтобы получить среднюю силу, действующую на одну молекулу с заданной скоростью, а затем другое среднее значение по молекулам с разными скоростями.) Этот подход был разработан Даниэлем Бернулли (1700–1782). , который наиболее известен в физике своими работами по течению жидкости (гидродинамике).Примечательно, что Бернулли проделал эту работу до того, как Дальтон установил представление о материи, состоящей из атомов.
На рис. 2.10 показан контейнер, полный газа, и увеличенный вид упругого столкновения молекулы газа со стенкой контейнера, разбитого на составляющие. Мы предположили, что молекула мала по сравнению с расстоянием между молекулами в газе и что ее взаимодействием с другими молекулами можно пренебречь. В этих условиях закон идеального газа является экспериментально верным.Поскольку мы также предположили, что стена жесткая, а частицы — точки, столкновение является упругим (по закону сохранения энергии — кинетической энергии частицы некуда деваться). Следовательно, кинетическая энергия молекулы остается постоянной, а значит, ее скорость и величина импульса также остаются постоянными. Это предположение не всегда верно, но результаты в остальной части этого модуля также получены в моделях, которые позволяют молекулам обмениваться энергией и импульсом со стенкой.
Фигура
2.10
Газ в ящике оказывает внешнее давление на его стенки. Молекула, сталкивающаяся с твердой стенкой, имеет противоположную скорость и импульс в направлении x . Это направление перпендикулярно стене. Составляющие его импульса скорости в направлениях y — и z — не меняются, значит, сила, параллельная стенке, отсутствует.
Это направление перпендикулярно стене. Составляющие его импульса скорости в направлениях y — и z — не меняются, значит, сила, параллельная стенке, отсутствует.
Если скорость молекулы изменяется в направлении x , ее импульс изменяется от -mvx-mvx до +mvx.+мвх. Таким образом, его изменение импульса равно Δmv=+mvx−(−mvx)=2mvx.Δmv=+mvx−(−mvx)=2mvx. Согласно теореме об импульсе-импульсе, изложенной в главе о линейном количестве движения и столкновениях, сила, действующая на i -ю молекулу, где i обозначает молекулы от 1 до N , равна
Fi=ΔpiΔt=2mvixΔt.Fi=ΔpiΔt=2mvixΔt.
(Только в этом уравнении p представляет собой импульс, а не давление.) Между стенкой и молекулой нет никакой силы, за исключением момента, когда молекула касается стенки.В течение короткого времени столкновения сила между молекулой и стенкой относительно велика, но это не та сила, которую мы ищем.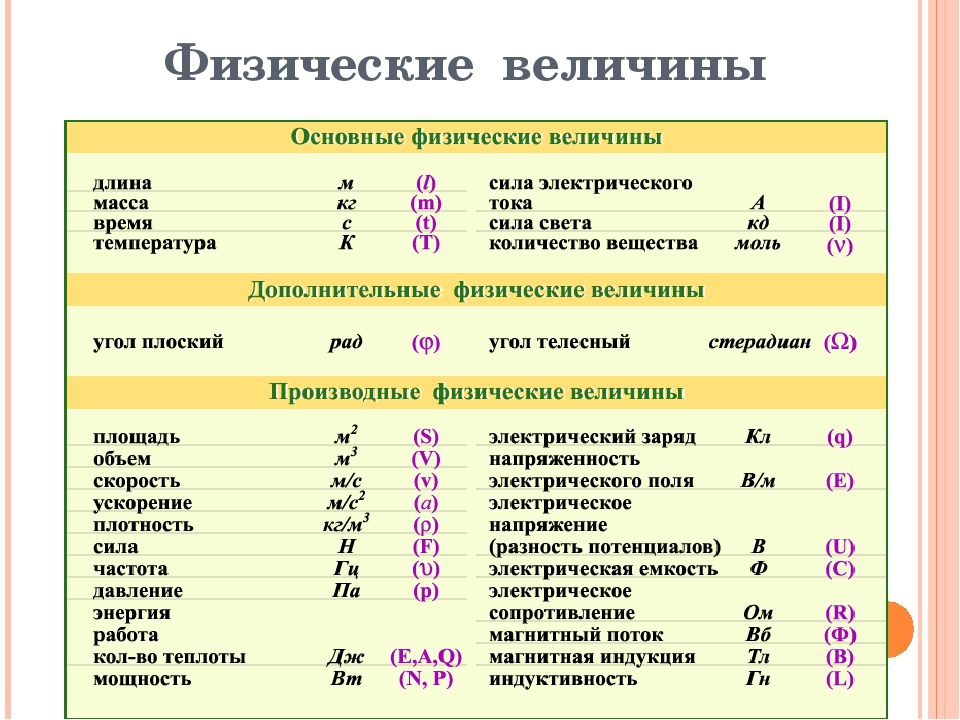 Мы ищем среднюю силу, поэтому мы принимаем ΔtΔt как среднее время между столкновениями данной молекулы с этой стенкой, то есть время, за которое мы ожидаем найти одно столкновение. Пусть l представляет собой длину коробки в направлении x . Тогда ΔtΔt — это время, за которое молекула пройдет через коробку и обратно на расстояние 2 l со скоростью vx.вх. Таким образом, Δt=2l/vx, Δt=2l/vx, и выражение для силы принимает вид
Мы ищем среднюю силу, поэтому мы принимаем ΔtΔt как среднее время между столкновениями данной молекулы с этой стенкой, то есть время, за которое мы ожидаем найти одно столкновение. Пусть l представляет собой длину коробки в направлении x . Тогда ΔtΔt — это время, за которое молекула пройдет через коробку и обратно на расстояние 2 l со скоростью vx.вх. Таким образом, Δt=2l/vx, Δt=2l/vx, и выражение для силы принимает вид
.
Fi=2mvix2l/vix=mvix2l.Fi=2mvix2l/vix=mvix2l.
Эта сила обусловлена одной молекулой . Чтобы найти общую силу, действующую на стенку, F , нам нужно сложить вклады всех N молекул:
F=∑i=1NFi=∑i=1Nmvix2l=ml∑i=1Nvix2.F=∑i=1NFi=∑i=1Nmvix2l=ml∑i=1Nvix2.
Теперь воспользуемся определением среднего, которое мы обозначили чертой, чтобы найти силу:
F=Nml(1N∑i=1Nvix2)=Nmvx2–l. F=Nml(1N∑i=1Nvix2)=Nmvx2–l.
F=Nml(1N∑i=1Nvix2)=Nmvx2–l.
Нам нужна сила в терминах скорости v , а не x -компонента скорости. Обратите внимание, что квадрат полной скорости представляет собой сумму квадратов ее составляющих, так что
v2–=vx2–+vy2–+vz2–.v2–=vx2–+vy2–+vz2–.
В предположении изотропии три средних значения в правой части равны, поэтому
v2–=3vix2–.v2–=3vix2–.
Подставляя это выражение для F , получаем
Давление равно F / A , значит получаем
p=FA=Nmv2–3Al=Nmv2–3V,p=FA=Nmv2–3Al=Nmv2–3V,
, где мы использовали V=AlV=Al для объема.Это дает важный результат
pV=13Nmv2–.pV=13Nmv2–.
2,5
Объединение этого уравнения с pV=NkBTpV=NkBT дает
13Nmv2–=NkBT.13Nmv2–=NkBT.
Мы можем получить среднюю кинетическую энергию молекулы, 12mv2–12mv2–, из левой части уравнения, разделив N и умножив на 3/2.
Средняя кинетическая энергия на молекулу
Средняя кинетическая энергия молекулы прямо пропорциональна ее абсолютной температуре:
К–=12мв2–=32кБТ.К–=12мв2–=32кБТ.
2,6
Уравнение K–=32kBTK–=32kBT представляет собой среднюю кинетическую энергию на молекулу. Обратите внимание, в частности, что ничто в этом уравнении не зависит от молекулярной массы (или любого другого свойства) газа, давления или чего-либо еще, кроме температуры. Если образцы газообразного гелия и ксенона с очень разными молекулярными массами находятся при одинаковой температуре, молекулы имеют одинаковую среднюю кинетическую энергию.
Внутренняя энергия термодинамической системы представляет собой сумму механических энергий всех молекул в ней.Теперь мы можем дать уравнение для внутренней энергии одноатомного идеального газа. В таком газе единственная энергия молекул — это их поступательная кинетическая энергия. Поэтому, обозначая внутреннюю энергию через Eint,Eint, имеем просто Eint=NK–,Eint=NK–, или
Eint=32NkBT. Eint=32NkBT.
Eint=32NkBT.
2,7
Часто мы хотели бы использовать это уравнение в молях:
Мы можем решить K–=12mv2–=32kBTK–=12mv2–=32kBT для типичной скорости молекулы в идеальном газе в терминах температуры, чтобы определить то, что известно как среднеквадратичное значение ( среднеквадратичное значение ) скорость молекулы.
Среднеквадратичная скорость молекулы
Среднеквадратическая (среднеквадратическая) скорость молекулы, или квадратный корень из среднего квадрата скорости v2–v2–, равна
.
vrms=v2–=3kBTm.vrms=v2–=3kBTm.
2,8
Среднеквадратичная скорость не является средней или наиболее вероятной скоростью молекул, как мы увидим в разделе «Распределение молекулярных скоростей», но она обеспечивает легко вычисляемую оценку скорости молекул, связанную с их кинетической энергией. Снова мы можем записать это уравнение через газовую постоянную R и молярную массу M в кг/моль:
Мы на мгновение отвлеклись, чтобы ответить на вопрос, который мог возникнуть у вас: когда мы применяем модель к атомам вместо теоретических точечных частиц, меняет ли кинетическая энергия вращения наши результаты? Чтобы ответить на этот вопрос, мы должны обратиться к квантовой механике. В квантовой механике кинетическая энергия вращения не может принимать любое значение; оно ограничено дискретным набором значений, а наименьшее значение обратно пропорционально инерции вращения. Вращательная инерция атома ничтожно мала, потому что почти вся его масса находится в ядре, которое обычно имеет радиус менее 10-14м10-14м. Таким образом, минимальная энергия вращения атома намного превышает 12kBT12kBT при любой достижимой температуре, а доступной энергии недостаточно, чтобы заставить атом вращаться.Мы вернемся к этому вопросу при обсуждении двухатомных и многоатомных газов в следующем разделе.
В квантовой механике кинетическая энергия вращения не может принимать любое значение; оно ограничено дискретным набором значений, а наименьшее значение обратно пропорционально инерции вращения. Вращательная инерция атома ничтожно мала, потому что почти вся его масса находится в ядре, которое обычно имеет радиус менее 10-14м10-14м. Таким образом, минимальная энергия вращения атома намного превышает 12kBT12kBT при любой достижимой температуре, а доступной энергии недостаточно, чтобы заставить атом вращаться.Мы вернемся к этому вопросу при обсуждении двухатомных и многоатомных газов в следующем разделе.
Пример
2,4
Расчет кинетической энергии и скорости молекулы газа
а) Какова средняя кинетическая энергия молекулы газа при температуре 20,0°C20,0°C (комнатная температура)? б) Найдите среднеквадратичную скорость молекулы азота (N2)(N2) при этой температуре.
Стратегия
а) Известная в уравнении для средней кинетической энергии температура:
K–=12mv2–=32kBT. K–=12mv2–=32kBT.
K–=12mv2–=32kBT.
Прежде чем подставлять значения в это уравнение, мы должны перевести заданную температуру в кельвины: T=(20.0+273)K=293K.T=(20.0+273)K=293K. Мы можем найти среднеквадратичную скорость молекулы азота, используя уравнение
.
vrms=v2–=3kBTm,vrms=v2–=3kBTm,
, но сначала надо найти массу молекулы азота. Получив молярную массу азота N2N2 из таблицы Менделеева, находим
m=MNA=2(14,0067)×10-3кг/моль)6,02×1023моль-1=4,65×10-26кг. m=MNA=2(14,0067)×10-3кг/моль)6,02×1023моль-1=4,65× 10-26кг.
Решение
- Одной температуры достаточно, чтобы найти среднюю поступательную кинетическую энергию. Подстановка температуры в уравнение поступательной кинетической энергии дает
K–=32kBT=32(1,38×10–23 Дж/К)(293K)=6,07×10–21 Дж. K–=32kBT=32(1,38×10–23 Дж/K)(293K)=6,07×10–21 Дж. - Подстановка этой массы и значения kBkB в уравнение для vrmsvrms дает
vrms=3kBTm=3(1,38×10-23 Дж/К)(293K)4,65×10-26кг=511м/с.vrms=3kBTm=3(1,38×10-23Дж/K)(293K)4,65×10-26кг= 511м/с.
Значение
Обратите внимание, что средняя кинетическая энергия молекулы не зависит от типа молекулы. Средняя поступательная кинетическая энергия зависит только от абсолютной температуры. Кинетическая энергия очень мала по сравнению с макроскопическими энергиями, поэтому мы не чувствуем, когда молекула воздуха попадает на нашу кожу. С другой стороны, это намного больше, чем типичная разница в гравитационной потенциальной энергии, когда молекула движется, скажем, от верха до низа комнаты, так что наше пренебрежение гравитацией оправдано в типичных реальных ситуациях.Среднеквадратичная скорость молекулы азота удивительно велика. Эти большие молекулярные скорости не дают макроскопического движения воздуха, так как молекулы движутся во всех направлениях с равной вероятностью. Средняя длина свободного пробега (расстояние, которое молекула проходит в среднем между столкновениями, обсуждаемое чуть позже в этом разделе) молекул в воздухе очень мала, поэтому молекулы движутся быстро, но не уходят очень далеко за секунду. Высокое значение среднеквадратичной скорости отражено в скорости звука, которая составляет около 340 м/с при комнатной температуре.Чем выше среднеквадратическая скорость молекул воздуха, тем быстрее звуковые колебания могут передаваться по воздуху. Скорость звука увеличивается с температурой и больше в газах с малой молекулярной массой, таких как гелий (см. рис. 2.11).
Высокое значение среднеквадратичной скорости отражено в скорости звука, которая составляет около 340 м/с при комнатной температуре.Чем выше среднеквадратическая скорость молекул воздуха, тем быстрее звуковые колебания могут передаваться по воздуху. Скорость звука увеличивается с температурой и больше в газах с малой молекулярной массой, таких как гелий (см. рис. 2.11).
Фигура
2.11
а) В обычном газе так много молекул движутся так быстро, что сталкиваются миллиарды раз каждую секунду. (б) Отдельные молекулы не перемещаются очень далеко за небольшой промежуток времени, но возмущения, подобные звуковым волнам, передаются со скоростями, связанными со скоростями молекул.
Пример
2,5
Расчет температуры: скорость убегания атомов гелия
Чтобы избежать гравитации Земли, объект в верхней части атмосферы (на высоте 100 км) должен удалиться от Земли со скоростью 11,1 км/с. Эта скорость называется скоростью убегания . При какой температуре атомы гелия будут иметь среднеквадратичную скорость, равную скорости убегания?
При какой температуре атомы гелия будут иметь среднеквадратичную скорость, равную скорости убегания?
Стратегия
Определите известные и неизвестные и определите, какие уравнения использовать для решения задачи.
Решение
- Определите известные значения: v — скорость убегания, 11,1 км/с.
- Определите неизвестные: Нам нужно найти температуру, T . Нам также нужно найти массу m атома гелия.
- Определите, какие уравнения необходимы.
- Чтобы получить массу m атома гелия, мы можем использовать информацию из периодической таблицы:
- Чтобы определить температуру T , мы можем переставить
12мв2–=32кБТ12мв2–=32кБТ
уступать
- Подставьте известные значения в уравнения и найдите неизвестные,
м=МНА=4. 0026×10-3 кг/моль6,02×1023моль=6,65×10-27кгм=MNA=4,0026×10-3кг/моль6,02×1023моль=6,65×10-27кг
0026×10-3 кг/моль6,02×1023моль=6,65×10-27кгм=MNA=4,0026×10-3кг/моль6,02×1023моль=6,65×10-27кг
а также
T=(6,65×10-27кг)(11,1×103м/с)23(1,38×10-23Дж/К)=1,98×104K.T=(6,65×10-27кг)(11,1×103м/с)23(1,38 ×10−23 Дж/К)=1,98×104 К.
Значение
Эта температура намного выше атмосферной температуры, которая составляет примерно 250 К (-25 ° C или -10 ° F) (-25 ° C или -10 ° F) на большой высоте. В атмосфере осталось очень мало атомов гелия, но многие из них присутствовали при формировании атмосферы, и все больше атомов гелия всегда создается в результате радиоактивного распада (см. главу о ядерной физике).Причина потери атомов гелия заключается в том, что небольшое количество атомов гелия имеет скорости выше, чем скорость убегания Земли даже при нормальных температурах. Скорость атома гелия изменяется от одного столкновения к другому, так что в любой момент существует небольшая, но ненулевая вероятность того, что скорость атома больше скорости убегания. Шанс достаточно высок, чтобы за время существования Земли почти все атомы гелия, побывавшие в атмосфере, достигли космической скорости на больших высотах и вырвались из-под земного притяжения. Более тяжелые молекулы, такие как кислород, азот и вода, имеют меньшую среднеквадратичную скорость, поэтому маловероятно, что какая-либо из них будет иметь скорость, превышающую скорость убегания. На самом деле вероятность настолько мала, что требуются миллиарды лет, чтобы потерять значительное количество более тяжелых молекул из атмосферы. На рис. 2.12 показано влияние отсутствия атмосферы на Луне. Поскольку гравитационное притяжение Луны намного слабее, она потеряла почти всю свою атмосферу. В упражнениях этой главы сравниваются атмосферы Земли и других тел.
Более тяжелые молекулы, такие как кислород, азот и вода, имеют меньшую среднеквадратичную скорость, поэтому маловероятно, что какая-либо из них будет иметь скорость, превышающую скорость убегания. На самом деле вероятность настолько мала, что требуются миллиарды лет, чтобы потерять значительное количество более тяжелых молекул из атмосферы. На рис. 2.12 показано влияние отсутствия атмосферы на Луне. Поскольку гравитационное притяжение Луны намного слабее, она потеряла почти всю свою атмосферу. В упражнениях этой главы сравниваются атмосферы Земли и других тел.
Фигура
2.12
Эта фотография командира «Аполлона-17» Юджина Сернана за рулем лунохода на Луне в 1972 году выглядит так, как будто она была сделана ночью с большим прожектором. На самом деле свет исходит от Солнца. Поскольку ускорение силы тяжести на Луне очень низкое (около 1/6 земного), скорость убегания Луны намного меньше. В результате молекулы газа очень легко покидают Луну, оставляя ее практически без атмосферы. Даже днем небо черное, потому что нет газа, рассеивающего солнечный свет.(кредит: Харрисон Х. Шмитт/НАСА)
Даже днем небо черное, потому что нет газа, рассеивающего солнечный свет.(кредит: Харрисон Х. Шмитт/НАСА)
Проверьте свое понимание
2,4
Проверьте свои знания Если рассмотреть очень маленький объект, например пыльцу, в газе, то количество молекул, ударяющихся о его поверхность, также будет относительно небольшим. Можно ли ожидать, что пыльцевое зерно испытывает какие-либо колебания давления из-за статистических колебаний числа молекул газа, сталкивающихся с ним за заданный промежуток времени?
Давление пара, парциальное давление и закон Дальтона
Давление, которое создал бы газ, если бы он занимал весь доступный объем, называется парциальным давлением газа.Если смешать два или более газа, они придут к тепловому равновесию в результате столкновений между молекулами; процесс аналогичен теплопроводности, описанной в главе о температуре и теплоте. Как мы видели из кинетической теории, когда газы имеют одинаковую температуру, их молекулы имеют одинаковую среднюю кинетическую энергию. Таким образом, каждый газ по отдельности подчиняется закону идеального газа и оказывает такое же давление на стенки сосуда, как если бы он был один. Таким образом, в смеси газов общее давление представляет собой сумму парциальных давлений газов-компонентов при идеальном газовом поведении и отсутствии химических реакций между компонентами.Этот закон известен как закон парциальных давлений Дальтона по имени английского ученого Джона Дальтона (1766–1844), который предложил его. Закон Дальтона согласуется с тем фактом, что давления складываются в соответствии с принципом Паскаля.
Таким образом, каждый газ по отдельности подчиняется закону идеального газа и оказывает такое же давление на стенки сосуда, как если бы он был один. Таким образом, в смеси газов общее давление представляет собой сумму парциальных давлений газов-компонентов при идеальном газовом поведении и отсутствии химических реакций между компонентами.Этот закон известен как закон парциальных давлений Дальтона по имени английского ученого Джона Дальтона (1766–1844), который предложил его. Закон Дальтона согласуется с тем фактом, что давления складываются в соответствии с принципом Паскаля.
В смеси идеальных газов, находящихся в тепловом равновесии, число молекул каждого газа пропорционально его парциальному давлению. Этот результат следует из применения к каждому закону идеального газа в виде p/n=RT/V.p/n=RT/V. Поскольку правая часть одинакова для любого газа при данной температуре в сосуде данного объема, то и левая часть одинакова.
- Парциальное давление — это давление, которое создал бы газ, если бы он существовал один.

- Закон Дальтона гласит, что общее давление равно сумме парциальных давлений всех присутствующих газов.
- Для любых двух газов (обозначенных цифрами 1 и 2), находящихся в равновесии в сосуде, p1n1=p2n2.p1n1=p2n2.
Важным применением парциального давления является то, что в химии оно действует как концентрация газа при определении скорости реакции. Здесь упомянем только, что парциальное давление кислорода в легких человека имеет решающее значение для жизни и здоровья.Вдыхание воздуха с парциальным давлением кислорода ниже 0,16 атм может ухудшить координацию и суждение, особенно у людей, не привыкших к большой высоте. Более низкие парциальные давления O2O2 имеют более серьезные последствия; парциальное давление ниже 0,06 атм может быстро привести к летальному исходу, и вероятны необратимые повреждения, даже если человека спасут. Однако ощущение необходимости дышать, как и при задержке дыхания, вызвано в большей степени высокой концентрацией углекислого газа в крови, чем низкой концентрацией кислорода. Так, если маленькое помещение или чулан наполнить воздухом с низкой концентрацией кислорода, возможно из-за того, что там хранится негерметичный баллон с каким-то сжатым газом, то человек не почувствует ощущения «удушья» и может впасть в судороги или потерять сознание. не замечая ничего плохого. Инженеры по технике безопасности уделяют этой опасности значительное внимание.
Так, если маленькое помещение или чулан наполнить воздухом с низкой концентрацией кислорода, возможно из-за того, что там хранится негерметичный баллон с каким-то сжатым газом, то человек не почувствует ощущения «удушья» и может впасть в судороги или потерять сознание. не замечая ничего плохого. Инженеры по технике безопасности уделяют этой опасности значительное внимание.
Другим важным применением парциального давления является давление пара, которое представляет собой парциальное давление пара, при котором он находится в равновесии с жидкой (или твердой, в случае сублимации) фазой того же вещества.При любой температуре парциальное давление воды в воздухе не может превышать давление пара над водой при этой температуре, потому что всякий раз, когда парциальное давление достигает давления пара, вода конденсируется из воздуха. Роса является примером такой конденсации. Температура, при которой происходит конденсация пробы воздуха, называется точкой росы . Его легко измерить, медленно охлаждая металлический шарик; точка росы – это температура, при которой на шаре впервые появляется конденсат.
Его легко измерить, медленно охлаждая металлический шарик; точка росы – это температура, при которой на шаре впервые появляется конденсат.
Давления паров воды при некоторых температурах, представляющих интерес для метеорологии, приведены в таблице 2.2.
| Т (°С)(°С) | Давление пара (Па) |
|---|---|
| 0 | 610,5 |
| 3 | 757,9 |
| 5 | 872,3 |
| 8 | 1073 |
| 10 | 1228 |
| 13 | 1497 |
| 15 | 1705 |
| 18 | 2063 |
| 20 | 2338 |
| 23 | 2809 |
| 25 | 3167 |
| 30 | 4243 |
| 35 | 5623 |
| 40 | 7376 |
Стол
2. 2
2
Давление паров воды при различных температурах
Относительная влажность (R.H.) при температуре T определяется
R.H.= парциальное давление водяного пара при Tдавление пара воды при T×100%. R.H.= парциальное давление водяного пара при TVдавление пара воды при T×100%.
Относительная влажность 100 %100 % означает, что парциальное давление воды равно давлению пара; другими словами, воздух насыщен водой.
Пример
2.6
Расчет относительной влажности
Какова относительная влажность воздуха при температуре воздуха 25ºC25ºC и точке росы 15ºC15ºC?
Стратегия
Мы просто смотрим давление пара при заданной температуре и точке росы и находим соотношение.
Решение
RH=Парциальное давление водяного пара при 15°CПарциальное давление водяного пара при 25°C×100%=1705Pa3167Pa×100%=53,8%.RH=Парциальное давление водяного пара при 15°CПарциальное давление водяного пара при 25°C×100%= 1705Па3167Па×100%=53. 8%.
8%.
Значение
RH важен для нашего комфорта. Значение 53,8%53,8% находится в диапазоне от 40% до 60% от 40% до 60%, рекомендованном для комфортного помещения.
Как отмечалось в главе о температуре и тепле, температура редко падает ниже точки росы, потому что, когда она достигает точки росы или точки замерзания, вода конденсируется и высвобождает относительно большое количество скрытой теплоты парообразования.
Средний свободный пробег и среднее время свободного хода
Теперь мы рассматриваем коллизии явно.Обычный первый шаг (это все, что мы предпримем) — вычислить длину свободного пробега, λ,λ, среднее расстояние, которое проходит молекула между столкновениями с другими молекулами, и среднее время свободного пробега ττ, среднее время между столкновениями с другими молекулами. столкновения молекулы. Если считать все молекулы сферами радиусом r , то одна молекула столкнется с другой, если их центры находятся на расстоянии 2 r друг от друга. Для данной частицы мы говорим, что площадь круга с этим радиусом, 4πr24πr2, является «поперечным сечением» для столкновений.При движении частица движется по цилиндру с такой площадью поперечного сечения. Средняя длина свободного пробега — это длина λλ, при которой ожидаемое число других молекул в цилиндре длины λλ и поперечного сечения 4πr24πr2 равно 1. Если мы временно проигнорируем движение молекул, отличных от той, которую мы рассматриваем, ожидаемое число — это числовая плотность молекул, N / V , умноженная на объем, а объем равен 4πr2λ4πr2λ, поэтому мы имеем (N/V)4πr2λ=1, (N/V)4πr2λ=1 или
Для данной частицы мы говорим, что площадь круга с этим радиусом, 4πr24πr2, является «поперечным сечением» для столкновений.При движении частица движется по цилиндру с такой площадью поперечного сечения. Средняя длина свободного пробега — это длина λλ, при которой ожидаемое число других молекул в цилиндре длины λλ и поперечного сечения 4πr24πr2 равно 1. Если мы временно проигнорируем движение молекул, отличных от той, которую мы рассматриваем, ожидаемое число — это числовая плотность молекул, N / V , умноженная на объем, а объем равен 4πr2λ4πr2λ, поэтому мы имеем (N/V)4πr2λ=1, (N/V)4πr2λ=1 или
.
Учет движения всех молекул значительно усложняет расчет, но единственное изменение — коэффициент 2.2. Результат
λ=V42πr2N.λ=V42πr2N.
2.10
В идеальном газе мы можем заменить V/N=kBT/pV/N=kBT/p, чтобы получить
λ=kBT42πr2p.λ=kBT42πr2p.
2.11
Среднее время свободного пробега ττ — это просто длина свободного пробега, деленная на типичную скорость, и обычно выбирают среднеквадратичную скорость. Затем
Затем
τ=kBT42πr2pvrms.τ=kBT42πr2pvrms.
2.12
Пример
2,7
Расчет среднего времени простоя
Найдите среднее время свободного пробега атомов аргона (М=39.9г/моль)(М=39,9г/моль) при температуре 0°С0°С и давлении 1,00 атм. Примем радиус атома аргона равным 1,70×10-10 м. 1,70×10-10 м.
Решение
- Определите известные значения и переведите их в единицы СИ. Мы знаем, что молярная масса 0,0399 кг/моль, температура 273 К, давление 1,01×105 Па, 1,01×105 Па и радиус 1,70×10-10 м. 1,70×10-10 м.
- Найдите среднеквадратичную скорость: vrms=3RTM=413msvrms=3RTM=413ms.
- Подставим в уравнение для среднего времени простоя:
τ=kBT42πr2pvrms=(1.38×10−23 Дж/К)(273K)42π(1,70×10−10 м)2(1,01×105 Па)(413 м/с)=1,76×10−10 с.τ=kBT42πr2pvrms=(1,38×10−23 Дж/К) (273K)42π(1,70×10-10м)2(1,01×105Па)(413м/с)=1,76×10-10с.
Значение
Мы вряд ли можем сравнить этот результат с нашими интуитивными представлениями о молекулах газа, но он дает нам картину столкновения молекул с чрезвычайно высокой частотой.


 ст.) — «стандартное атмосферное давление ИКАО»
ст.) — «стандартное атмосферное давление ИКАО»

 Как насчет
Как насчет Это так, потому что если вы определяете его относительно концентрации частиц
Это так, потому что если вы определяете его относительно концентрации частиц  Поскольку частные производные термодинамических потенциалов
Поскольку частные производные термодинамических потенциалов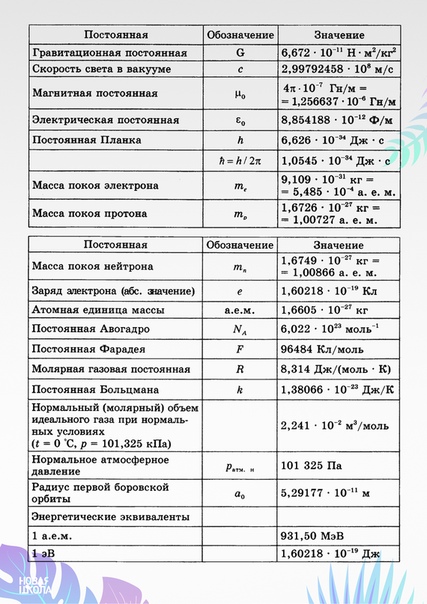




 Это высота, необходимая для столба, заполненного ртутью.
Это высота, необходимая для столба, заполненного ртутью.
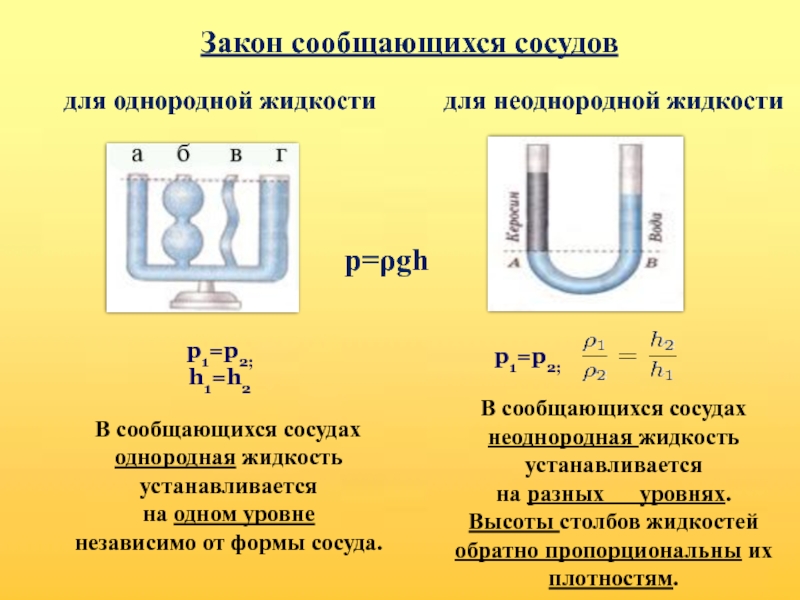
 0026×10-3 кг/моль6,02×1023моль=6,65×10-27кгм=MNA=4,0026×10-3кг/моль6,02×1023моль=6,65×10-27кг
0026×10-3 кг/моль6,02×1023моль=6,65×10-27кгм=MNA=4,0026×10-3кг/моль6,02×1023моль=6,65×10-27кг