Понятия о скорости, тангенциальном и нормальном ускорениях. Формулы — OneKu
Содержание статьи:
Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.
Понятие о скорости
Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:
 Вам будет интересно:Что такое туча? Определение
Вам будет интересно:Что такое туча? Определение
v¯ = dl¯/dt.
Здесь l¯ — является вектором перемещения. Иными словами, скорость — это производная по времени от пройденного пути.
Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.
Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.
Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.
Понятие об ускорении

В отличие от скорости, которая характеризует быстроту прохождения телом траектории, ускорение — это величина, описывающая быстроту изменения скорости, что математически записывается так:
a¯ = dv¯/dt.
Как и скорость, ускорение — это векторная характеристика. Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.
Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.

Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:
a = F/m.
Эта формула является прямым следствием из второго закона Ньютона.
Полное, нормальное и тангенциальное ускорения
Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:
v¯ = v*u¯.
Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.
Второе слагаемое — это нормальное ускорение. Оно количественно описывает изменение вектора скорости, не принимая во внимание изменение ее модуля.

Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:
a = √(at2 + an2).
Связь тангенциального ускорения и скорости
Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:
v = at*t;
v = v0 ± at*t.
В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.
Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:
at = dv/dt.
Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:
at = dv/dt = 9*t2 + 4.
Скорость и нормальное ускорение

Запишем в явном виде формулу для нормальной компоненты an, имеем:
an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯
Где re¯ — единичной длины вектор, который к центру кривизны траектории направлен. Это выражение устанавливает связь тангенциальной скорости и нормального ускорения. Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.
Источник
Полное ускорение и его компоненты. Ускорение тангенциальное и нормальное ускорение. Формулы и пример решения задачи :: SYL.ru
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике

Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
a¯ = dv¯/dt
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
a¯ = Δv¯/Δt
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с2).
Траектория движения и компоненты полного ускорения

Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
v¯ = v*ut¯
Здесь ut¯ — вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
a¯ = dv¯/dt = dv/dt*ut¯ + v*d(ut¯)/dt
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.

Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
at¯ = dv/dt*ut¯
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения — это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
an¯ = v*d(ut¯)/dt = v*d(ut¯)/dL*dL/dt
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
dL/dt = v;
d(ut¯)/dL = 1/r
Здесь dL — это пройденный телом путь за промежуток времени dt, r — радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
an¯ = v2/r
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное

Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
a = √(at2 + an2)
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
θ = arctg(at/an)
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
v = 2*t2 + 3*t
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.

Для тангенциального имеем:
at = dv/dt = 4*t + 3 = 19 м/с2
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
v = 2*42 + 3*4 = 44 м/с
Теперь можно воспользоваться формулой для an:
an = v2/r = 442/1 = 1936 м/с2
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
Тангенциальное ускорение — Мегаобучалка
Виды ускорений в СТО.
Итак, мы показали, что существует два вида измеримых скоростей. Кроме того, быстрота, измеряемая в тех же единицах, тоже очень интересна. При малых значениях все эти скорости равны.
А сколько же существует ускорений? Какое ускорение должно быть константой при равноускоренном движении релятивистской ракеты, чтобы космонавт всегда оказывал на пол ракеты одну и ту же силу, чтобы он не стал невесомым, или чтобы он не умер от перегрузок?
Введем определения разных видов ускорений.
Координатно-координатное ускорение dv/dt это изменение координатной скорости, измеренное по синхронизированным координатным часам, расставленным по ходу движения пробного тела:
dv/dt=d2r/dt2.
Забегая вперед, заметим , что dv/dt = 1·dv/dt = g0dv/dt.
Координатно-собственное ускорение dv/dt это изменение координатнойскорости, измеренное по собственным часам, связанным с движущимся телом:
dv/dt=d(dr/dt)/dt = gd2r/dt2.
dv/dt = g1dv/dt.
Собственно-координатное ускорение db/dt это изменение собственной скорости, измеренное по синхронизированным координатным часам, расставленным по ходу движения пробного тела:
db/dt = d(dr/dt)/dt = g3v(vdv/dt)/c2 + gdv/dt.
Если v|| dv/dt, тогда db/dt = g3dv/dt.
Если vперпендикулярно dv/dt, тогда db/dt = gdv/dt.
Собственно-собственное ускорениеdb/dt это изменение собственнойскорости, измеренное пособственным часам, связанным с движущимся телом:
db/dt = d(dr/dt)/dt = g4v(vdv/dt)/c2 + g2dv/dt.
Если v|| dv/dt, тогдаdb/dt = g4dv/dt.
Если vперпендикулярно dv/dt, тогда db/dt = g2dv/dt.
Сравнивая показатели при коэффициенте g в четырех типах ускорений, записанных выше, замечаем, что в этой группе отсутствует член с коэффициентом g2 при параллельных ускорениях. Но мы еще не взяли производные от быстроты. Это ведь тоже скорость. Возьмём производную по времени от быстроты, воспользовавшись формулой v/c = th(r/c):
dr/dt = (c·arth(v/c))’ = g2dv/dt.
А если взять dr/dt, получим:
dr/dt = g3dv/dt,
или dr/dt = db/dt.
Следовательно, мы имеем две измеримые скорости v и b, и ещё одну, неизмеримую, но наиболее симметричную, быстроту r. И шесть видов ускорений, два из которых dr/dt и db/dt совпадают. Какое же из этих ускорений является собственным, т.е. ощущаемым ускоряющимся телом?
К собственному ускорению мы вернемся ниже, а пока выясним, какое ускорение входит во второй закон Ньютона. Как известно, в релятивистской механике второй закон механики, записанный в видеf=ma, оказывается ошибочным. Вместо него силу и ускорение связывает уравнение
f = m (g3v(va)/c2 + ga),
которое является основой для инженерных расчетов релятивистских ускорителей. Если мы сравним это уравнение с только что полученным уравнением для ускорения db/dt:
db/dt = g3v(vdv/dt)/c2 + gdv/dt,
то заметим, что они отличаются лишь множителем m. То есть, можно записать:
f= m·db/dt.
Последнее уравнение возвращает массе статус меры инертности в релятивистской механике. Сила, действующая на тело, пропорциональна ускорению db/dt. Коэффициентом пропорциональности является инвариантная масса. Вектора силы fиускорение db/dt сонаправлены при любой ориентации векторов vиa, или b и db/dt.
Формула, записанная через ускорение dv/dt, не дает такой пропорциональности. Сила и координатно-координатное ускорение в общем случае не совпадают по направлению. Параллельными они будут лишь в двух случаях: если вектора vиdv/dtпараллельны друг другу, и если они перпендикулярны друг другу. Но в первом случае сила f=mg3dv/dt, а во втором — f=mgdv/dt.
Таким образом, в законе Ньютона мы должны использовать ускорение db/dt, то есть, изменениесобственной скоростиb, измеренное по синхронизированным часам.
Возможно с таким же успехом можно будет доказать, что f= mdr/dt, где dr/dt — вектор собственного убыстрения, но быстрота величина неизмеримая, хотя и легко вычисляема. Будет ли верно векторное равенство, сказать не берусь, но скалярное равенство справедливо в силу того, что dr/dt=db/dt и f=mdb/dt.
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ = — 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = — 0. Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости 2.
Если скорость тела по модулю уменьшается, то есть
v21
то направление вектора ускорения противоположно направлению вектора скорости 2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
= τ + n
Виды ускорений в СТО.
Итак, мы показали, что существует два вида измеримых
скоростей. Кроме того, быстрота, измеряемая
в тех же единицах, тоже очень интересна. При малых значениях все эти скорости
равны.
А сколько же существует ускорений? Какое ускорение должно быть константой
при равноускоренном движении релятивистской ракеты, чтобы космонавт всегда
оказывал на пол ракеты одну и ту же силу, чтобы он не стал невесомым, или
чтобы он не умер от перегрузок?
Введем определения разных видов ускорений.
Координатно-координатное ускорение dv/dt
это изменение координатной скорости, измеренное по синхронизированным
координатным часам, расставленным по ходу движения пробного
тела:
dv/dt=d2r/dt2.
Забегая вперед, заметим , что dv/dt = 1·dv/dt
= γ0dv/dt.
Координатно-собственное ускорение dv/dτ
это изменение координатной скорости, измеренное по
собственным часам, связанным с движущимся телом:
dv/dτ=d(dr/dt)/dτ
= γd2r/dt2.
dv/dτ =
γ1dv/dt.
Собственно-координатное ускорение db/dt
это изменение собственной скорости, измеренное по синхронизированным
координатным часам, расставленным по ходу движения пробного
тела:
db/dt = d(dr/dτ)/dt
= γ3v(vdv/dt)/c2
+ γdv/dt.
Если v || dv/dt, тогда db/dt
= γ3dv/dt.
Если v перпендикулярно dv/dt, тогда
db/dt = γdv/dt.
Собственно-собственное ускорение db/dτ
это изменение собственной скорости, измеренное по
собственным часам, связанным с движущимся телом:
db/dτ = d(dr/dτ)/dτ
= γ4v(vdv/dt)/c2
+ γ2dv/dt.
Если v || dv/dt, тогда
db/dτ =
γ4dv/dt.
Если v перпендикулярно dv/dt, тогда db/dτ
= γ2dv/dt.
Сравнивая показатели при коэффициенте γ в
четырех типах ускорений, записанных выше, замечаем, что в этой группе отсутствует
член с коэффициентом γ2 при параллельных
ускорениях. Но мы еще не взяли производные от быстроты. Это ведь тоже скорость.
Возьмём производную по времени от быстроты, воспользовавшись формулой v/c
= th(ρ/c):
dρ/dt = (c·arth(v/c))’ =
γ2dv/dt.
А если взять dρ/dτ,
получим:
dρ/dτ
= γ3dv/dt,
или dρ/dτ = db/dt.
Следовательно, мы имеем две измеримые скорости v и
b, и ещё одну, неизмеримую, но наиболее симметричную, быстроту
ρ. И шесть видов ускорений, два из которых dρ/dτ
и db/dt совпадают. Какое же из этих ускорений является собственным,
т.е. ощущаемым ускоряющимся телом?
К собственному ускорению мы вернемся ниже, а пока выясним, какое ускорение
входит во второй закон Ньютона. Как известно, в релятивистской механике
второй закон механики, записанный в виде f=ma,
оказывается ошибочным. Вместо него силу и ускорение связывает уравнение
f = m (γ3v(va)/c2
+ γa),
которое является основой для инженерных расчетов релятивистских ускорителей.
Если мы сравним это уравнение с только что полученным уравнением для ускорения
db/dt:
db/dt = γ3v(vdv/dt)/c2
+ γdv/dt,
то заметим, что они отличаются лишь множителем m. То есть, можно записать:
f = m·db/dt.
Последнее уравнение возвращает массе статус меры инертности в релятивистской
механике. Сила, действующая на тело, пропорциональна ускорению db/dt.
Коэффициентом пропорциональности является инвариантная масса. Вектора силы
f и ускорение db/dt сонаправлены
при любой ориентации векторов v и a, или
b и db/dt.
Формула, записанная через ускорение dv/dt, не дает такой
пропорциональности. Сила и координатно-координатное ускорение в общем случае
не совпадают по направлению. Параллельными они будут лишь в двух случаях:
если вектора v и dv/dt
параллельны друг другу, и если они перпендикулярны друг другу.
Но в первом случае сила f=mγ3dv/dt,
а во втором — f=mγdv/dt.
Таким образом, в законе Ньютона мы должны использовать ускорение db/dt,
то есть, изменение собственной скорости b,
измеренное по синхронизированным часам.
Возможно с таким же успехом можно будет доказать, что f=
mdρ/dτ,
где dρ/dτ
— вектор собственного убыстрения, но быстрота величина неизмеримая,
хотя и легко вычисляема. Будет ли верно векторное равенство, сказать не
берусь, но скалярное равенство справедливо в силу того, что dρ/dτ=db/dt
и f=mdb/dt.
Дальше: Четырех-ускорения.
Назад: Четырехмерные скорости.
К оглавлению раздела Некоторые вопросы СТО.
К другим разделам Космической Генетики.
Иван Горелик
Моё резюме
УСКОРЕНИЕ — Студопедия
Ускорение — это вектор, характеризующий изменение величины и направления скорости с течением времени. Среднее <a> и мгновенноеa ускорения определяются как:
<a> = Dv/Dt, a = lim(∆v/∆t) = dv/dt = d2s/dt2, при ∆t → 0. (3.9).
А модуль ускорения a = dv/dt = d2s/dt2. (3.10).
Модуль вектора мгновенного ускорения легко находится по теореме Пифагора. При двумерном движении a = √aх2 +.a2у . (3.11).
При криволинейном движении вектор полного ускорения целесообразно разложить по двум составляющим — тангенциальному ускорениюat ,направленному по касательной к траектории в сторону изменения скорости, и перпендикулярному нормальному (центростремительному) ускорениюan ,направленному по радиусу к центру траектории.
| Рис.12. Касательное и нормальное ускорения. |
Полное ускорение будет геометрической суммой тангенциальной и нормальной составляющих a = aτ + an. (3.12).
Тангенциальное ускорение отвечает за изменение модуля скорости, а нормальное ускорение — за изменение направления скорости. При ускоренном движении тангенциальная составляющая совпадает с вектором скорости, при замедленном — противоположна. Величина тангенциального ускорения равна производной от модуля вектора скорости по времени: aτ = dv/dt. (3.13).
Составляющая ускорения, характеризующая быстроту изменения скорости по направлению, называется нормальным ускорением. Она связана с приращением вектора скорости, направленным перпендикулярно касательной к траектории и равна an = v2/R, (3.14).
где R — радиус кривизны траектории. Нормальное ускорение всегда направлено к центру кривизны траектории. Вектор полного ускорения
(3.15).
Его модуль легко найти по теореме Пифагора: a = √aτ2 +.a2n (3.16).
Дело в том, что и аτ, и аn – каждый имеет свою «специализацию»: аτотвечает за изменение скорости по величине, а аn отвечает за изменение скорости по направлению. Если скорость тела меняется только по величине и, следовательно, сохраняет свое направление, то, в соответствии с определением скорости, мы имеем дело с прямолинейным движением, и его ускорение будет только тангенциальным: aτ = dv/dt. (3.17).
Если же скорость меняется лишь по направлению, а ее величина остается постоянной, то при таком криволинейном движении ускорение все равно будет, но оно полностью нормальноеan = v2/R, (3.18).
и в любой момент направлено к центру кривизны траектории:
Что это — ускорение в физике? Связь величины со скоростью и пройденным путем. Пример решения задачи
Движение тел в пространстве описывается набором характеристик, среди которых основными являются пройденный путь, скорость и ускорение. Последняя характеристика во многом определяет особенность и тип самого движения. В данной статье рассмотрим вопрос, что это — ускорение в физике, и приведем пример решения задачи с использованием данной величины.
Главное уравнение динамики
Перед тем как давать определение ускорению в физике, приведем главное уравнение динамики, которое носит название второго ньютоновского закона. Его часто записывают в следующем виде:
F¯ * dt = dp¯
То есть сила F¯, имеющая внешний характер, оказывала воздействие на некоторое тело в течение времени dt, что привело к изменению количества движения на величину dp¯. Левую часть равенства принято называть импульсом тела. Заметим, что величины F¯ и dp¯ носят векторный характер, и соответствующие им вектора направлены одинаково.
Каждому школьнику известна формула количества движения, она записывается так:
p¯ = m * v¯
Величина p¯ характеризует запасенную в теле кинетическую энергию (множитель скорости v¯), которая зависит от инерционных свойств тела (множитель массы m).
Если это выражение подставить в формулу 2-го закона Ньютона, то получим следующее равенство:
F¯ * dt = m * dv¯;
F¯ = m * dv¯ / dt;
F¯ = m * a¯, где a¯ = dv¯ / dt.
Введенную величину a¯ называют ускорением.
Что это — ускорение в физике?

Теперь поясним, что означает введенная в предыдущем пункте величина a¯. Запишем еще раз ее математическое определение:
a¯ = dv¯ / dt
Используя формулу, можно легко понять, что это — ускорение в физике. Физическая величина a¯ показывает, как быстро будет изменяться скорость со временем, то есть она является мерой скорости изменения самой скорости. Например, в соответствии с законом Ньютона, если на тело массой 1 килограмм действует сила 1 ньютон, то оно приобретет ускорение 1 м/с2, то есть за каждую секунду движения тело будет увеличивать свою скорость на 1 метр в секунду.
Ускорение и скорость

В физике это две разные величины, которые связаны между собой кинематическими уравнениями движения. Обе величины являются векторными, однако в общем случае они направлены по-разному. Ускорение всегда направлено вдоль направления действующей силы. Скорость же направлена вдоль траектории движения тела. Вектора ускорения и скорости будут совпадать друг с другом только тогда, когда внешняя сила по направлению действия совпадает с перемещением тела.
В отличие от скорости, ускорение может быть отрицательной величиной. Последний факт означает, что оно направлено против движения тела и стремится уменьшить его скорость, то есть происходит процесс торможения.
Общая формула, которая связывает модули скорости и ускорения, выглядит так:
v = v0 + a * t
Это одно из основных уравнений прямолинейного равноускоренного перемещения тел. Оно показывает, что с течением времени скорость возрастает линейно. Если движение будет равнозамедленным, то перед слагаемым a * t следует поставить минус. Величина v0 здесь является некоторой начальной скоростью.
При равноускоренном (равнозамедленном) движении справедлива также формула:
a¯ = Δv¯ / Δt
От аналогичного выражения в дифференциальной форме оно отличается тем, что здесь ускорение рассчитывается за конечный промежуток времени Δt. Это ускорение называют средним за отмеченный временной промежуток.
Путь и ускорение

Если тело движется равномерно и по прямой линии, то путь, проходимый им за время t, можно рассчитать так:
S = v * t
Если же v ≠ const, то при расчете пройденного расстояния телом следует учитывать ускорение. Соответствующая формула имеет вид:
S = v0 * t + a * t2 / 2
Это уравнение описывает равноускоренное движение (для равнозамедленного знак «+» нужно заменить на знак «-«).
Движение по окружности и ускорение

Выше было сказано, что ускорение в физике — это величина векторная, то есть ее изменение возможно как по направлению, так и по модулю. В случае рассмотренного прямолинейного ускоренного движения направление вектора a¯ и его модуль остаются неизменным. Если модуль станет изменяться, то такое движение уже не будет равноускоренным, но останется прямолинейным. Если же начнет меняться направление вектора a¯, то движение станет криволинейным. Одним из распространенных видов такого движения является перемещение материальной точки по окружности.
Для этого типа движения справедливы две формулы:
α¯ = dω¯ / dt;
ac = v2 / r
Первое выражение представляет собой угловое ускорение. Его физический смысл заключается в скорости изменения угловой скорости. Иными словами, α показывает, как быстро раскручивается или замедляет свое вращение тело. Величина α является тангенциальным ускорением, то есть направлена по касательной к окружности.
Второе выражение описывает центростремительное ускорение ac. Если линейная скорость вращения остается постоянной (v = const), то модуль ac не меняется, однако его направление всегда изменяется и стремится направить тело к центру окружности. Здесь r — радиус вращения тела.
Задача со свободным падением тела

Мы выяснили, что это — ускорение в физике. Теперь покажем, как пользоваться приведенными выше формулами для прямолинейного движения.
Одними из типовых являются задачи по физике с ускорением свободного падения. Это величина представляет собой ускорение, которое сила притяжения нашей планеты сообщает всем телам, имеющим конечную массу. В физике ускорение свободного падения вблизи поверхности Земли равно 9,81 м/с2.
Предположим, что некоторое тело находилось на высоте 20 метров. Затем его отпустили. Через какое время оно окажется на поверхности земли?
Так как начальная скорость v0 равна нулю, то для пройденного пути (высота h) можно записать уравнение:
h = g * t2 / 2
Откуда получаем время падения:
t = √(2 * h / g)
Подставляя данные из условия, находим, что тело на земле окажется через 2,02 секунды. В действительности это время будет немного большим из-за присутствия сопротивления воздуха.
Страничка эмбеддера » MOSFET и большая d(Vds)/dt
Про этот эффект я не знал, про него рассказал neon в ветке о UTC 4.0 (в которую всех и приглашаю). Ссори, что в этот раз не в видео формате, не хватает времени ![]()

На рисунке – эквивалентная схема MOSFET транзистора со всеми паразитными компонентами.
Суть эффекта сводится к тому, что когда изменяется напряжение сток-исток (оно-же drain-source, ds) на MOSFET-транзисторе, через конденсатор Cds начинает течь ток.
Этот ток создает напряжение на базе паразитного биполярного транзистора. И, если это напряжение превышает пороговую величину (тех-же 0.6В), то транзистор открывается и начинает сквозить покруче, чем сам полевой транзистор.
Конечно, как только паразитный транзистор приоткрывается, скорость изменения напряжения уменьшается. Но это не помогает – биполярный транзистор закрывается очень медленно и на нем выделяется много тепла.
В итоге, транзистор умирает из-за перегрева кристалла.
Этот эффект описан в конце этой и начале этой статьи от semikron.
Там упоминается Figure 1.3, но я нашел эту картинку под названием Figure 2.4.16 вот тут. Этак картинка – в заголовке статьи.
В даташитах предельную скорость нарастания напряжения называют dv/dt или “Peak Diode Recovery voltage slope”:

Защита от этого эффекта:
- не давать скорости нарастания превышать порог (затворными резисторами, снабберами, выбором транзисторов)
- (как по мне, очень сомнительный вариант) — не опускать напряжение на затворе ниже нуля. При этом эффект Миллера будет приоткрывать “полевую” часть транзистора и она будет уменьшать dv/dt до приемлемого уровня. Это лучше, чем открытие паразитного транзистора, но, все равно, сквозняк.
dV / dt Дроссели двигателя для длинных кабелей частотно-регулируемого привода
Спросите кого-нибудь в моторной мастерской, и они скажут вам, что частотно-регулируемые приводы плохо переносят моторы. Подшипники выходят из строя из-за подшипниковых токов, вызванных частотно-регулируемым приводом. Со временем изоляция выходит из строя из-за коронных разрядов. Один из сценариев, который представляет особую нагрузку для двигателей, — это когда двигатель и частотно-регулируемый привод устанавливаются на большом расстоянии друг от друга.
Длинные кабели могут привести к высокому повышению напряжения (или «dV / dt») на двигателе и могут способствовать преждевременному отказу двигателя.В этом посте описываются напряжения стоячей волны, связанные с частотно-регулируемым приводом, и способы защиты от них с помощью фильтров du / dt KEB.

Что такое скачки dV / dt?
В большинстве коммерческих частотно-регулируемых приводов переменного тока используется технология, называемая широтно-импульсной модуляцией (ШИМ), для имитации трехфазного синусоидального выходного напряжения переменного тока. ШИМ работает путем быстрого включения и выключения выходных биполярных транзисторов с изолированным затвором (IGBT) привода, модулируя тем самым напряжение шины постоянного тока привода. Когда IGBT замкнут, напряжение на выходных клеммах частотно-регулируемого привода повышается до напряжения на шине постоянного тока привода.
Видео по теме: Как работает широтно-импульсная модуляция в частотно-регулируемом преобразователе
 Рисунок 1 — Время нарастания / спада IGBT
Рисунок 1 — Время нарастания / спада IGBT
Изменение напряжения не мгновенно, а на самом деле возрастает до уровня шины постоянного тока в течение заданного времени (TRISE). Скорость увеличения напряжения называется временем нарастания dV / dt и является характеристикой конструкции транзистора.
Кабели двигателя и отраженная волна
Кабели между приводом и двигателем имеют характеристический импеданс, который зависит от длины кабеля и физических свойств материала кабеля.Кабель двигателя действует как линия передачи и передает выходное напряжение привода на двигатель. Если импеданс двигателя и кабеля не согласован, на нагрузке двигателя произойдет отражение волны — это приведет к выбросу напряжения
или «звену» на клеммах двигателя и отраженной волне обратно к приводу.
 Рисунок 2 — IGBT с перенапряжением (измеренным на клеммах двигателя)
Рисунок 2 — IGBT с перенапряжением (измеренным на клеммах двигателя)
В худшем случае отраженная волна может быть добавлена к основной форме волны, исходящей от привода, что приведет к значительно более высокому напряжению на клеммах двигателя.Более длинные выводы двигателя имеют большее сопротивление, что в конечном итоге увеличивает напряжение на выводах двигателя. По этой причине лучше всего устанавливать двигатель и привод как можно ближе друг к другу.
Что это означает на практике? Давайте посмотрим на типичную установку ЧРП с 25 футов. длина кабеля и отсутствие дросселя du / dt. На клеммах двигателя мы видим напряжение 988 В, хотя на шине постоянного тока частотно-регулируемого привода всего 675 В.
 Рисунок 3 — Без штуцера, 25 футов. Ведет. Пиковое напряжение двигателя = 988 В
Рисунок 3 — Без штуцера, 25 футов. Ведет. Пиковое напряжение двигателя = 988 В
С той же настройкой мы увеличим количество выводов двигателя с 25 футов.до 75 футов. в длину. Теперь мы видим максимальное напряжение на клеммах двигателя 1326 В — вдвое больше, чем на шине постоянного тока!
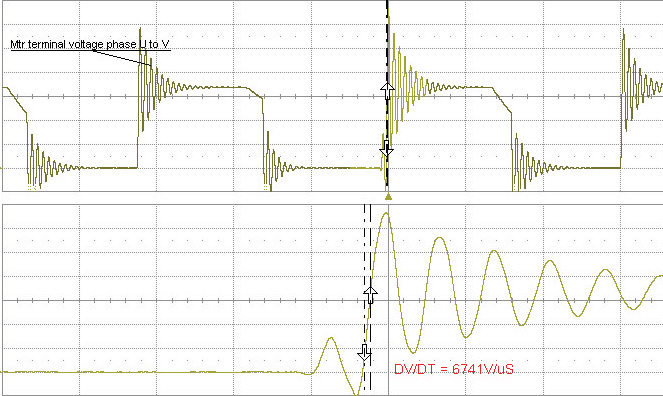 Рисунок 4 — Без штуцера, 75 футов. Ведет. Пиковое напряжение двигателя = 1,326 В
Рисунок 4 — Без штуцера, 75 футов. Ведет. Пиковое напряжение двигателя = 1,326 В
Влияние dV / dt на срок службы двигателя
Короче говоря, пики напряжения из-за высоких значений dV / dt нарушают изоляцию двигателя и сокращают срок его службы. Большинство производимых сегодня трехфазных электродвигателей переменного тока рассчитаны на инвертор, и в них используются провода и изоляция, которые выдерживают пиковое напряжение не менее 1600 В.Однако, даже если скачки dV / dt никогда не превышают номинальное значение изоляции 1600 В, повторяющееся воздействие скачков напряжения в течение срока службы двигателя вызовет нагрузку и ослабит изоляцию.
Со временем может выйти из строя система изоляции двигателя, что приведет к короткому замыканию между фазой или фазой на землю в обмотках и катастрофическому отказу двигателя.
Какие приложения VFD мне следует искать?
Длинные кабельные трассы
Любое приложение, в котором используются длинные кабели, которых нельзя избежать или сократить.Применения лифтов MRL, где двигатель установлен в шахте подъемника. Погружные насосы. Оборудование HVAC.
Как правило, KEB рекомендует использовать дроссель dV / dt для пробегов на расстояние более 40 футов.
Высокие частоты переключения
Приводы
KEB предлагают возможность выбора частоты коммутации. Более высокие частоты переключения дают некоторые преимущества применения. Во-первых, он снижает уровень шума, производимого частотно-регулируемым приводом, что важно в чувствительных установках, таких как лифт MRL возле пентхауса или театральный подъемник.Во-вторых, более высокие частоты переключения обеспечивают двигатель более качественной формой волны тока, что приводит к меньшим потерям двигателя и меньшему нагреву.
В связи с обсуждением dV / dt важно отметить, что более высокие частоты переключения требуют, чтобы транзисторы включались / выключались большее количество раз в течение заданного периода времени — тем самым подвергая двигатель воздействию повышенного количества пиков высокого напряжения. Работа на частоте 16 кГц подвергнет двигатель вдвое большему количеству скачков напряжения по сравнению с частотой 8 кГц.
Таким образом, приложения с приводами, использующие более высокие частоты коммутации, должны особенно беспокоиться о dV / dt.
480V Установки
Поскольку пиковое выходное напряжение привода напрямую связано с уровнем шины постоянного тока, скачки dV / dt, естественно, будут больше в установках на 480 В переменного тока по сравнению с установками на 230 В переменного тока.
Необходимо принять дополнительные меры для уменьшения скачков dV / dt в установках 400–480 В переменного тока.
Устранение dV / dt и фильтры
Если перечисленные выше факторы не могут быть устранены, следует рассмотреть возможность использования фильтра dV / dt KEB (или дросселя dV / dt), который уменьшит время нарастания IGBT и снизит пиковое напряжение на двигателе. Фильтр du / dt размещается непосредственно на выходе привода и ограничивает скорость изменения напряжения (dV / dt) до уровня, характерного для конструкции фильтра.
 Дроссель двигателя dV / dt KEB
Дроссель двигателя dV / dt KEB
Важно, чтобы фильтр располагался как можно ближе к выходу привода, чтобы пики напряжения не распространялись по кабелям двигателя.Если импедансы двигателя и кабелей не согласованы, отражение стоячей волны все еще может происходить, но отрицательные эффекты резко сводятся к минимуму за счет фильтрации пиков dV / dt.
Давайте вернемся к предыдущему примеру и установим на привод дроссель du / dt с 75-футовым. прокладка кабеля. Пиковое напряжение снижено с 1326 В до 951 В — снижение на 40%.
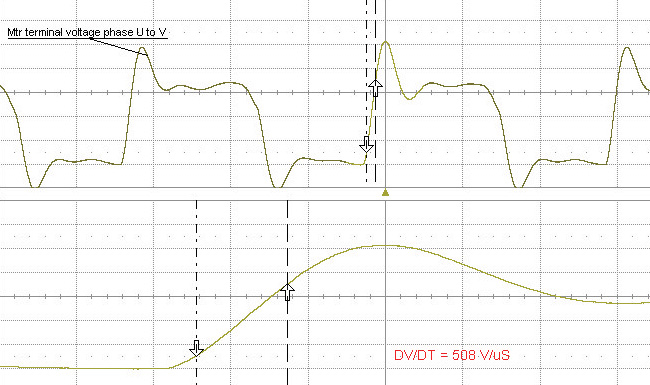 Рисунок 5 — С дросселем du / dt, 75 футов. Ведет. Пиковое напряжение двигателя = 951 В. Снижение пикового напряжения на 40%.
Рисунок 5 — С дросселем du / dt, 75 футов. Ведет. Пиковое напряжение двигателя = 951 В. Снижение пикового напряжения на 40%.
KEB Фильтры du / dt
Фильтры
KEB были разработаны специально для требовательных приложений с частотно-регулируемым приводом — они обладают высокой производительностью, но являются экономически выгодными.Некоторые конструктивные особенности фильтров du / dt KEB:
- Особенность: низкая индуктивность
- Преимущество: не искажает модель двигателя, как обычные реакторы нагрузки; может использоваться с двигателями с постоянными магнитами и асинхронными двигателями
- Функция: работает до 16 кГц
- Преимущество: хорошо подходит для высокочастотных преобразователей частоты
- Характеристика: минимальная вносимая потеря
- Преимущество: эффективная конструкция с минимальными потерями мощности
- Характеристика: Малая занимаемая площадь
- Преимущество: требуется меньше места на панели — Более низкая стоимость системы
- Характеристика: Пониженный EMI
- Преимущество: ограничение радиочастотного излучения (> 250 кГц)
Подходит ли звук дросселей KEB dVdt для вашего применения? Свяжитесь с нами сегодня, чтобы обсудить с инженером KEB.
.
Что означает DT?
| DT | Due To Медицина »Физиология | Оцените: | |||
| DT | Deutsch (немецкий) Кодексы (немецкий язык) ) | Оцените: | |||
| DT | Тип документа Правительственный »Правительство США |
000
000
47
9004 9000 DT
9004 9000 Опытный образец
Государственный »Военный
0004 Оценить:
| DT | Время задержки Государственное »Транспортное обеспечение | Оцените его: | |||||||||
| DT | Дата и время 4000 | Оцените: | |||||||||
| DT | Тип данных Вычисления »Общие вычисления | Оцените: | |||||||||
| DT | Цифровое телевидение 9005 9005 | Оцените: | |||||||||
| DT | Deutsche Telekom, A.G. Business »Символы NYSE | Оцените его: | |||||||||
| DT | Dream Team Sports | 9000 it5 | |||||||||
| DT | Дискретное время Академические и естественные науки »Математика | Оцените его: | |||||||||
| DT | Оцените: | ||||||||||
| DT | Не доверяйте Вычислительная техника »Cyber & Security — и многое другое… | Оцените это: | |||||||||
| DT | Delta T Академические и естественные науки »Математика | ||||||||||
| DT | Design Technology Business »General Business — и не только … | Оцените: | |||||||||
| DT | Dial Tone Computing »Телеком | Оцените: | |||||||||
| DT | Прямой перевод Правительственный» Юридический и юридический | ||||||||||
| DT | Delirium Tremens Медицина »Физиология 90 005 | Оцените: | |||||||||
| DT | The Daily Telegraph Сообщество »Новости и СМИ | 000 Оценить | DT | Don’t Touch Сообщество »Исполнительское искусство | Оцените: | ||||||
| DT | Devlet Tiyatrolari | 5 000 International» 48International | Оценить: | ||||||||
| DT | Ежедневный троян Сообщество »Новости и СМИ | Оценить: | |||||||||
| 9000 5 | Оцените это: | ||||||||||
| DT | Delta Time Академические и естественные науки »Математика | ||||||||||
Производная от T Академические науки и науки »Математика | Оцените: | ||||||||||
| DT | Динамический тест Академические науки и науки | 8 | Оцените: |
.
