Две электрические цепи содержат соответственно 3 и 4 элемента: Математическое Бюро. Страница 404

Содержание

Практическое занятие по математике по теме «Практическое применение задач по теории вероятности в электрических схемах»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АМУРСКОЙ ОБЛАСТИ

государственное профессиональное образовательное автономное учреждение

«Райчихинский индустриальный техникум»

Тема: Практическое применение задач по теории вероятности в электрических схемах

для специальности

Релейная защита и автоматизация электроэнергетических систем

Преподаватель: Ершова Е. В.

г. Райчихинск

2014г

Цели:

Учебные:

научить решать задачи на нахождение безотказной работы цепи через определение вероятности ее надежности;
расширить и обобщить представление студентов о надежности электрических цепей;
освоить новые приемы решения задач.

Воспитательные:

Развивающие:

Формируемые компетенции

ПК 1.3. Проводить испытания элементов и устройств релейной защиты, автоматики и средств измерений.

ПК 4.1. Планировать работу производственного подразделения.

Ход урока:

Составление опорного конспекта.
Решение задач на определение вероятности безотказной работы функциональной цепи.
Решение задач на определение вероятности безотказной работы элементов устройства.
Решение задач на определение вероятности безотказной работы сигнализаторов.
Практическая работа в парах.

Краткие теоретические сведения

На прошлых уроках вы изучили уроках теоремы сложения и умножения вероятностей, формулу полной вероятности, научились решать простейшие задачи с применением теорем.

Сегодня на уроке мы рассмотрим практическое применение задач по теории вероятностей в электрических схемах.

Надежность каждого элемента системы электроснабжения можно характеризовать вероятностью рабочего состояния p и вероятностью отказа q. Если не учитывать плановые простои (ремонты), то можно считать, что элементы в любой момент времени находятся в одном из этих состояний. Тогда сумма вероятностей этих состояний равна 1: .

Для группы из двух элементов возможны следующие сочетания:

оба элемента в рабочем состоянии;
первый элемент в вынужденном простое, второй в рабочем состоянии;
первый элемент в рабочем состоянии, второй в вынужденном простое;
оба элемента в вынужденном простое.

Вероятности этих состояний можно найти, воспользовавшись теоремой умножения вероятностей.

Надежность сложной электрической схемы определяется надежностью каждого элемента схемы и типом их соединения между собой.

(Перед вами на столах лежат бланки для опорных схем, по мере объяснения материала вам необходимо заполнить их: зарисовать схему, записать формулы и их словесное описание (Приложение 1)).

Вид заполненной схемы (Приложение 2).

Так при последовательном соединении двух элементов с надежностью каждого p₁ и p₂ надежность всей схемы определяется как

Рис.1

Другими словами схема работает, если работают оба элемента. При отказе одного (любого) из них схема работать не будет (ток через цепь не пойдет).

Рис. 2

Вероятность отказа для последовательного соединения

(для двух элементов).

, здесь (для n –элементов).

При параллельном соединении двух элементов с надежностью каждого р₁ и р₂ надежность всей схемы определяется как

Пользуясь формулой для вероятности появления хотя бы одного события, надежность схемы параллельного соединения записывают в виде

рис. 3

Другими словами схема работает, если работают оба элемента, но также она работает, если выйдет из строя и какой либо один из элементов.

Очевидно, что схема с п параллельно соединенными элементами будет иметь надежность , здесь .

Вероятность отказа для параллельного соединения

(для двух элементов).

, здесь (для n –элементов).

Решение задач совместно преподавателем

Решение задач на определение вероятности безотказной работы функциональной цепи

Задача 1: Цепь состоит из независимых блоков, соединенных в систему с одним входом и одним выходом.

рис. 4

Выход из строя за время Т различных элементов цепи — независимые события, имеющие следующие вероятности: Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Найти надежность системы.

Решение: Событие А – система надежна.

Событие A_i– i-й блок работает безотказно.

Элементы 1 и 2 соединены параллельно, и элементы 3 и 4 соединены параллельно, а между собой они соединены последовательно, тогда используя формулы, получим .

Задача 2:

рис.5

Элементы А₁ и А₂ электрической цепи соединены параллельно, а А₃ присоединен к ним последовательно. Вероятность выхода из строя за данный период времени элементов А₁, А₂и А₃равна соответственно , , .

, , .

Предполагается, что элементы выходят или не выходят из строя независимо друг от друга. Найти вероятность того, что за рассматриваемый период по цепи будет проходить ток.

Решение: Параллельное соединение элементов А₁ и А₂, работает, если работает хотя бы один из них. Событие А произойдет, если одновременно с этим работает элемент А_3.

Используя формулы, получим .

Задача 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность работы каждого элемента цепи равна p₁=0,8, p₂= p₃=0,7, p₄= p₅= p₆=0,9, p₇= p₈= p₉=0,8

Решение. _—надежность работы прибора, т. е. вероятность того, что ток пройдет через весь прибор.

Событие — сигнал пройдет через участок 1 -2 , если будет работать хотя бы один из элементов этого участка, т.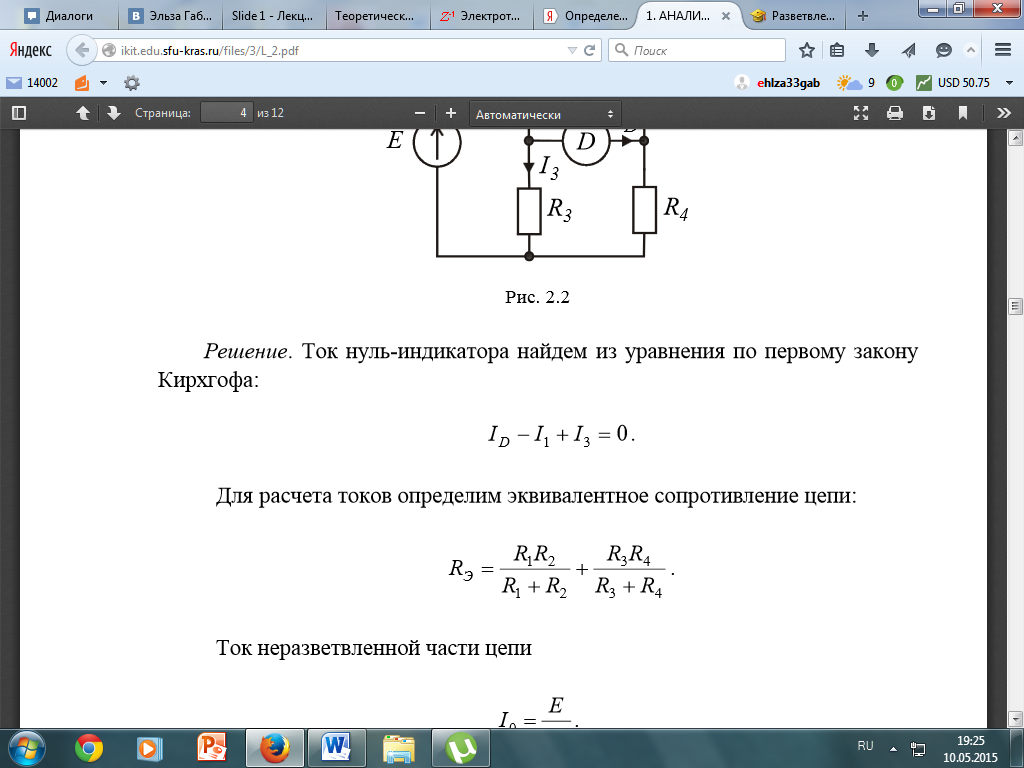 е. надежность этого участка

Событие — сигнал пройдет через участок 4 -5- 6 , если будет работать хотя бы один из элементов этого участка, т.е. надежность этого участка

Событие — сигнал пройдет через участок 7 — 8 , если будет работать хотя бы один из элементов этого участка, т.е. надежность этого участка

Событие А состоит в совмещении событий , , и безотказной работы 3-го и 9-го элементов, т.е. надежность всей системы:

Вывод по задаче: Обратите внимание, если элементы цепи соединены параллельно, то их надежность выше.

Решение задач на определение вероятности безотказной работы элементов устройства

Задача 4:

Прибор состоит из 3-х узлов, которые за время работы могут выходить из строя независимо друг от друга. Надежность (вероятность безотказной работы) i-го узла равна p_i, вероятность отказа q_i = 1 – p_i(i = 1, 2, 3).

p₁=0,95; p₂=0,98; p₃=0,9

Найти вероятности следующих событий: А — все узлы работают безотказно; В — первый узел отказал, остальные нет; С — один из узлов отказал, остальные нет; D — отказали два узла из 3-х; E — отказал хотя бы один узел.

Решение. Пусть А_i -работа i-го узла (i= 1,2,3), — отказ i-го узла.

1) Событие А произойдет, если одновременно произойдут события . Следовательно, оно является их произведением:

Применяя к этому равенству событий теорему умножения вероятностей для независимых событий, получим

2) Событие В произойдет, если одновременно произойдут события. Следовательно

Вероятность этого события будет равна

3) Событие С может осуществиться, если откажет первый узел, а остальные два работают или, если откажет второй узел, а работают первый и третий или, если откажет третий узел, а работают первый и второй. Следовательно, С — сложное событие, представляющее собой сумму произведений простых событий:

Применяя к этому равенству сначала теорему сложения вероятностей для несовместных событий, а затем к каждому слагаемому теорему умножения вероятностей для независимых событий, получим

4) D — событие, которое может осуществиться тремя различными способами:
.

Поэтому

5) Для вычисления вероятности события E применим теорему о вероятности появления хотя бы одного события. Тогда получим

Решение задач на определение вероятности безотказной работы сигнализаторов

Задача 5: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Решение: A – при аварии сработает только один сигнализатор.

Работа в парах

Карточка 1

Задача 1. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность работы каждого элемента цепи равна p=0,8.

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,6; 0,7; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает хотя бы один сигнализатор.

___________________________________________________________________

Карточка 2

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,9; 0,7; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3. Вероятность того что при аварии сигнализатор сработает, равна 0,8 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает хотя бы один сигнализатор.

Карточка 3

Задача 2: В электрическую цепь последовательно включены 5 элементов, работающих независимо друг от друга. Вероятность отказов первого, второго, третьего, четвертого, пятого элементов соответственно равны 0,1; 0,2; 0,3; 0,2; 0,1. Найти вероятность того, что тока в цепи не будет.

Задача 3: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равна 0,7, что сработает второй — равна 0,8. Найти вероятность того, что сработает только один сигнализатор.

___________________________________________________________________

Карточка 4

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,8; 0,75; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равна 0,7, что сработает второй — равна 0,8. Найти вероятность того, что не сработает ни один сигнализатор.

Карточка 5

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,9; 0,8; 0,85. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равна 0,85, что сработает второй — равна 0,8. Найти вероятность того, что сработает первый, но не сработает второй.

_________________________________________________________________

Карточка 6

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,95; 0,8; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равна 0,85, что сработает второй — равна 0,9. Найти вероятность того, что сработает хотя бы одни сигнализатор.

Карточка 7

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,85; 0,75; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равна 0,95, что сработает второй — равна 0,9. Найти вероятность того, что сработают оба сигнализатора.

______________________________________________________________________

Карточка 8

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,92; 0,6; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3: Для информирования про аварию установлены три независимых между собой сигнализатора. Вероятность того, что во время аварии сработает первый сигнализатор р₁=0,95, второй – р₂=0,9, третий – р₃=0,86. Найдите вероятность того, что во время аварии сработают все три сигнализатора.

Карточка 9

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,95; 0,75; 0,8. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Задача 3: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор равна 0,85, что сработает второй — равна 0,95. Найти вероятность того, что сработают оба сигнализатора.

_____________________________________________________________

Карточка 10

Задача 2. Устройство состоит из 3 элементов, работающих независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно равны: 0,8; 0,9; 0,95. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) два элемента; в) все три элемента.

Дополнительные карточки:

Питание потребителя осуществляется по одной цепи, состоящей из КЛ, трансформатора и выключателя. Вероятность безотказной работы за время t для этих элементов: . Отказ любого элемента приводит к перерыву питания, причем отказы взаимно независимы. Найти вероятность безотказной работы передачи.

Определить вероятность перерыва электроснабжения в схеме.

Известны вероятности отказов элементов схемы:

Пусть вероятность КЗ одной фазы ЛЭП; вероятность КЗ второй фазы при условии, что одна фаза повреждена, ; вероятность КЗ третьей фазы при повреждениях первых двух . Требуется определить вероятность полного выхода ЛЭП из строя.

Домашнее задание: Выучить формулы.

Выводы урока: Сегодня на уроке вы научились решать задачи на нахождение безотказной работы цепи через определение вероятности ее надежности, расширили и обобщили представление о надежности электрических цепей. Оценки за работу в парах на следующий урок.

Приложение 1

Соединение

Последовательное

Параллельное

Схема

2 элемента

n- элементов

2 элемента

n- элементов

Вероятность работы (формула)

Словесное описание

Вероятность отказа (формула)

Словесное описание

Приложение 2

Соединение

Последовательное

Параллельное

Схема

2 элемента

n- элементов

2 элемента

n- элементов

Вероятность работы (формула)

или

, где

где

Словесное описание

Схема работает, если работают оба элемента. При отказе одного (любого) из них схема работать не будет (ток через цепь не пойдет).

Схема работает, если работают оба элемента, но также она работает, если выйдет из строя и какой либо один из элементов.

Вероятность отказа (формула)

где

Словесное описание

Схема откажет, если откажет хотя бы один элемент.

Схема откажет, если откажут оба элемента.

Последовательное и параллельное соединения источников тока

Решение:
Внутреннее сопротивление элементов

Сопротивление параллельно включенных резисторов

Общая э. д. с. элементов e0=2e Согласно закону Ома для полной цепи

15 Сопротивления резисторов R₁ и R₂ и э. д. с. ε₁ и ε₂ источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. ε₃ третьего источника ток через резистор R₃ не течет?

Решение:
Выберем направления токов I₁, I₂ и I₃ через резисторы R₁, R₂ и R₃, указанные на рис. 363. Тогда I₃=I₁+I₂. Разность потенциалов между точками а и b будет равна

Если

Исключая I1 находим

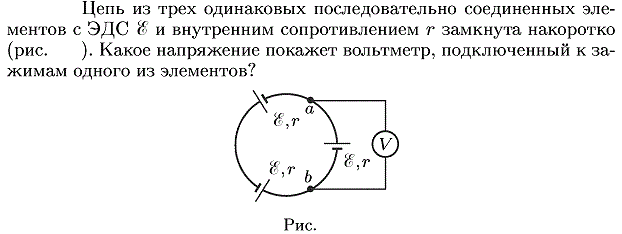
16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. ε и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?

Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим

Из закона Ома для участка цепи между точками а и b получим

Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.

17 Источник тока с э.д.с. ε₀ включен в схему, параметры которой даны на рис. 129. Найти э.д.с. ε источника тока и направление его подключения к выводам а и b, при которых ток через резистор с сопротивлением R₂ не идет.

Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I₀+I₂. При обходе контуров aefb и ecdf по часовой стрелке получим

Используя условие I2 = 0, находим

Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.

18 Два элемента с одинаковыми э.д.с. ε включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r₁ и r₂, если r₁=2r₂.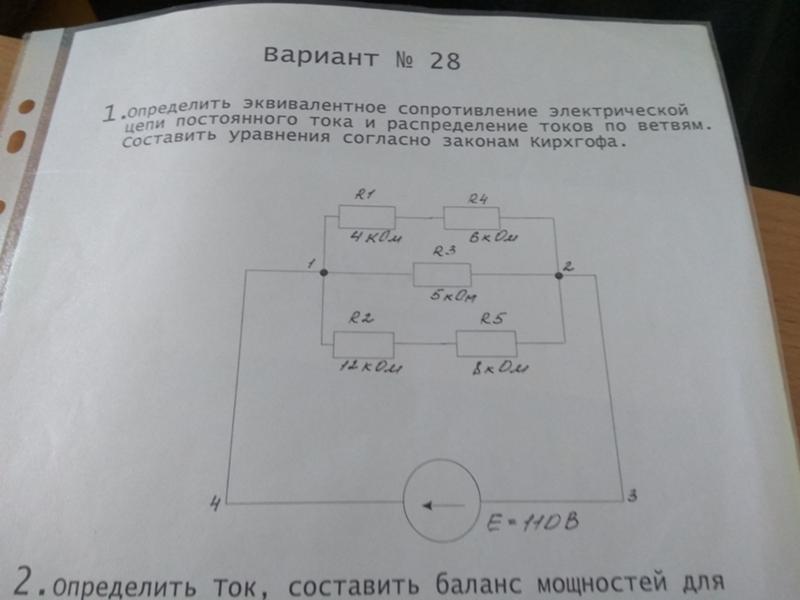

Решение:

19 Два одинаковых элемента с э.д.с. ε=1,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R₁=0,2 Oм, В другом — R₂ = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?

Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и ε при последовательном соединении они равны 2r и 2ε. Через резистор R при этом текут токи

Отсюда видно, что I₂>I₁, если R/2+r<R+r/2, т. е. если r₁=r; следовательно, токи при параллельном и последовательном соединениях одинаковы. Во втором случае R₂>r.Поэтому ток больше при последовательном соединении.

20 Два элемента с э.д.с. ε₁=4В и ε₂ = 2В и внутренними сопротивлениями r₁ = 0,25 Ом и r₂ = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R₁ = 1 Ом и R₂ = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.

Решение:

21 К батарее из двух параллельно включенных элементов с э.д.с. ε₁ и ε₂ и внутренними сопротивлениями r₁ и r₂ подключен резистор с сопротивлением R. Найти ток I, текущий через резистор R, и токи I₁ и I₂ в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?

Решение:
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I₁-I₂=0. При обходе контуров abef и bcde по часовой стрелке получим

Из этих уравнений находим

Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие

Ток I1=0 при

а ток I2 = 0 при

Токи I₁ и I₂ имеют направления, указанные на рис. 366, если

Они меняют свое направление при

22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом— параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?

Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R№r, задача не имеет решения (n=1).

23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r=2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R=10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.

Решение:

где V₁ — показание вольтметра при последовательном соединении элементов, V₂-при параллельном.

24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э. д.с. элемента ε = 2 В, его внутреннее сопротивление r = 0,2 Ом.

Решение:

25 Батарея составлена из N=600 одинаковых элементов так, что n групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента ε = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.

Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи

где r/m— внутреннее сопротивление группы из т параллельно соединенных элементов, а nr/m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов nr/m, т. е.

При этом через сопротивление R течет точек I=46 А.

26 Емкость аккумулятора Qo=80А⋅ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.

Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:

Заметим, однако, что энергия

отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э. д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.

27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Q₀=64 А⋅ч.

Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость

Три параллельно включенные группы дают общую емкость батареи

28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 1 Ом.

Решение:

29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока ε₁ = 6,5 В и ε₂ = 3,9 В. Сопротивления резисторов R₁=R₂=R₃=R₄=R₅=R₆=R=10 Ом.

Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I₁ + I₂ — I₃ = 0 для узла b;
I₃ — I₄ — I₅ =0 для узла h; I₅ — I₁ — I₆ = 0 для узла f: при этом

Для контура abfg (обход по часовой стрелке),

Для контура bcdh (обход против часовой стрелки) и

для контура hdef (обход по часовой стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим

Отрицательные значения токов I₂, I₄ и I₆ показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.

Электрическая схема

Главная
→
Теория электрических цепей
→
Электрическая схема

Электрическая схема, схема электрической цепи, схема замещения электрической цепи

1 Схема электрической цепи и элементы схемы [1, с. 16 – 17]

Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения.

Реальные элементы электрической цепи идеализируются для упрощения математического описания элемента электрической цепи. Однако идеализированные уравнения должны правильно отражать основные физические явления в том или ином реальном элементе электрической цепи.

Идеализированному элементу электрической цепи ставят в соответствие его математическую модель — схемный элемент. Уравнения, описывающие схемный элемент, идентичны идеализированным уравнениям реального элемента электрической цепи. Схемные элементы могут быть введены и как математические абстракции; при этом они необязательно должны соответствовать каким-либо реальным элементам электрической цепи. Однако любой реальный элемент электрической цепи с необходимой степенью точности можно представить с помощью одного или совокупности схемных элементов, соединенных определенным образом. Такую совокупность схемных элементов (в частном случае один схемный элемент) называют схемой замещения или эквивалентной схемой элемента электрической цепи при условии совпадения уравнений, описывающих эту схему и элемент электрической цепи.

Каждому схемному элементу соответствует условное геометрическое изображение. Тогда способ соединения элементов реальной цепи легко представить с помощью соответствующего соединения схемных элементов. Геометрическое изображение соединения схемных элементов, отображающее соединение реальных элементов электрической цепи и ее свойства, называют схемой электрической цепи (схемой цепи).

В схеме выделяют ветви — участки, которые характеризуются одним и тем же током в начале и конце в любой момент времени, и узлы — граничные (концевые) точки ветвей. Напряжение ветви тождественно разности потенциалов ее узлов.

Ветвям и узлам схемы электрической цепи, как правило, соответствуют ветви и узлы реальной электрической цепи. В схемах электрических цепей, содержащих многополюсные элементы, некоторые узлы и ветви могут не отображать узлы и ветви цепи. Кроме того, некоторые ветви схемы вводят для учета конструктивных и монтажных параметров цепи (например, паразитных емкостей между зажимами элемента, емкостей монтажа, индуктивностей выводов).

Применительно к электрической цепи ветвь часто определяют как участок цепи, в любом сечении которого ток имеет одно и то же значение в данный момент времени, а узел — как «место» соединения ветвей.

2 Схема электрической цепи[2, с. 131 – 136]

Электрическую цепь на чертежах изображают в виде схемы электрической цепи, под которой понимают графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающее соединения этих элементов. Например, на рис. 2.1 представлена электрическая схема цепи, в которую входят следующие устройства: генератор переменного тока 1, трансформаторы 2 и 5, линии электропередачи 3 и 4, преобразователь переменного тока в постоянный 6, нагрузка 7.

Рис. 2.1

Исследование процессов в электрической цепи требует знания связей между токами и напряжениями отдельных ее участков. Эти связи могут быть определены в виде математических соотношений, например, вида (u = r·i, u_L = L·di/dt и др.). Они могут быть заданы и в виде вольтамперных или иных характеристик.

Записанные в аналитической форме соотношения между токами, напряжениями, зарядами, потокосцеплениями элемента электрической цепи являются математической моделью этого элемента электрической цепи.

Так, например, u = r·i есть математическая модель резистора; u_L = L·di/dt – математическая модель идеальной индуктивной катушки; u = r·i + L·di/dt – приближенная математическая модель либо реальной катушки при условии пренебрежения токами смещения между витками катушки, либо цепи, содержащей резистор и идеальную индуктивную катушку, включенные последовательно.

Обратно, математическим соотношениям, приведенным выше, могут быть поставлены в соответствие электрические цепи, содержащие идеальные индуктивные катушки и резисторы.

Математическим соотношениям между, токами, напряжениями, потокосцеплениями, зарядами и другими величинами, следовательно, могут быть поставлены в соответствие электрические цепи, содержащие только идеализированные элементы г, L, С, M, E, J и др. Очевидно, схемы таких электрических цепей и сами электрические цепи тождественны, так как каждому элементу схемы электрической цепи соответствует единственный элемент идеализированной электрической цепи.

Таким образом, для расчета процессов в электрической цепи следует определить математические соотношения для отдельных участков исходной цепи, по этим соотношениям построить некую другую (идеализированную) электрическую цепь, анализ процессов в которой заменит анализ процессов в исходной реальной электрической цепи.

Схему этой другой (идеализированной) электрической цепи, отображающей при определенных условиях свойства реальной цепи, называют схемой замещения электрической цепи или кратко – схемой замещения.

Рассмотрим в качестве примера электрическую цепь, схема которой изображена на рис. 2.1. Можно составить некоторую схему замещения (рис. 2.2) этой цепи.

Рис. 2.2

Приведенная на рис. 2.2, а схема замещения электрической цепи, схема которой дана на рис. 2.1, является приближенной в пределах тех допущений, которые сделаны при представлении схем замещений отдельных устройств, входящих в состав цепи.

Для каждого элемента схемы рис. 2.2, а могут быть записаны в аналитическом или графическом виде соотношения между токами, напряжениями, зарядами и потокосцеплениями. Составление математических соотношений, а следовательно, и схем замещений является специфической для инженера задачей, решение которой требует глубокого понимания особенностей электромагнитных процессов, умения решать в общем случае задачи исследования распределения электромагнитного поля.

Обычно термин «электрическая цепь» применяется к цепи с идеализированными элементами, электрическая схема и схема замещения которой тождественны.

Электрическая цепь и соответственно схема цепи имеют в общем случае ветви и узлы.

Ветвью электрической цепи и соответственно ее схемы называют весь участок электрической цепи, в котором в любой момент бремени ток имеет одно и то оке значение вдоль всего участка.

Узлом электрической цепи и соответственно ее схемы называют место соединения ветвей. На схеме узел изображают точкой.

3. Модели и схема электрической цепи[3, с. 22 – 25]

Электрические цепи, используемые в современной радиоэлектронике, образуются, как правило, из связанных друг с другом соединительными проводами ее компонентов: резисторов, конденсаторов, катушек индуктивности и транзисторов, предназначенных для приближенной практической реализации соответственно резистивных сопротивлений, емкостей, индуктивностей и активных элементов электрических цепей.

При анализе колебаний в реальной электрической цепи она заменяется некоторой идеализированной цепью из того или иного числа элементов, колебания в которой пренебрежимо мало отличаются от колебаний в анализируемой электрической цепи. Идеализированную электрическую цепь, свойства которой аппроксимируют (представляют приближенно) свойства реальной электрической цепи, будем называть моделью электрической цепи. Каждой конкретной модели электрической цепи соответствует система уравнений, благодаря решению которой удается оценить те или иные свойства электрической цепи. Эта система уравнений получила название математической модели электрической цепи.

Графическое изображение модели электрической цепи называют схемой замещения цепи, или просто схемой цепи (иногда электрической схемой). Схема электрической цепи отражает как число и характер элементов электрической цепи, из которых состоит модель электрической цепи, так и порядок соединения их между собой.

Рис. 3.1

Различие между понятиями «электрическая цепь» и „модель электрической цепи“ иллюстрирует рис.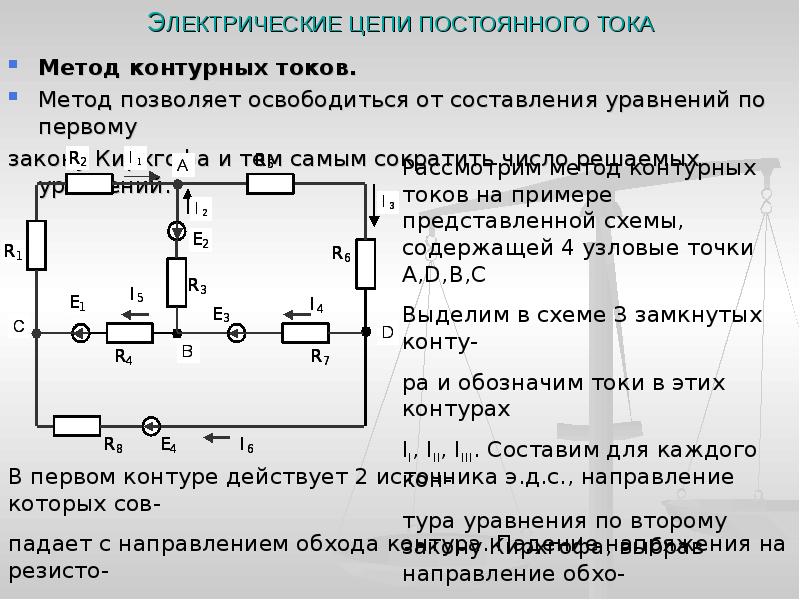 3.1. На нем приведены схематическое изображение цепи, составленной из дискретных резисторов, конденсаторов и катушек индуктивности (рис. 3.1, а), и схема модели этой цепи, составленная в предположении, что ее компоненты точно моделируются соответствующими пассивными элементами (рис. 3.1, б).

Понятия «электрическая цепь» и „схема электрической цепи“ часто отождествляются.

Чем полнее и точнее должна отражать модель электрической цепи свойства электрической цепи, тем сложнее она становится, т. е. тем большее число элементов она содержит. Ясно, что в каждом конкретном случае следует применять модель не сложнее той, которая позволяет решить задачу анализа с требуемой точностью.

Необходимо иметь в виду и принципиальную возможность физического осуществления электрической модели исходной электрической цепи, после чего эта модель становится, в свою очередь, электрической цепью. Вместе с тем следует помнить, что переход от реальной электрической цепи к схеме электрической связан с рядом допущений. Схема электрической цепи является схемой модели электрической цепи и может быть использована для изучения ее свойств лишь в границах, в которых модель с достаточной точностью воспроизводит свойства реальной электрической цепи.

Список литературы

1. Теоретические основы электротехники. Т. I. Основы теории линейных цепей. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, переработ. и доп. М., «Высш. школа», 1976. 544 с. с ил.

2. Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники: В 2-х т. Учебник вузов. Том 1. – 3-е изд., перераб. и доп. – Л.: Энергоиздат. Ленингр. отд-ние, 1981. – 536 с., ил.

3. Белецкий А. Ф. Теория линейных электрических цепей: Учебник для вузов. – Радио и связь, 1986. 544 с.: ил.

электрическая схема,
схема электрической цепи,
схема замещения электрической цепи

18.07.2011, 31614 просмотров.

Электрическая цепь и ее элементы

Электрической цепью называется совокупность электротехнических устройств, предназначенных для передачи, распределения и взаимного преобразования электрической и других видов энергии и информации.

Основными элементами электрической цепи являются источники электрической энергии и приемники электрической энергии.

В источниках механическая, химическая и другие виды энергии преобразуются в электрическую энергию. В приемниках электрическая энергия превращается в механическую, тепловую, световую и другие виды энергии.

В судовых электрических цепях в качестве источников могут использоваться дизель-генераторы, турбогенераторы, валогенераторы, аккумуляторные батареи (в режиме разрядки), гальванические элементы, статистические и машинные преобразователи. Основные приемники электрической энергии на судах – это электродвигатели, нагревательные элементы, светильники, устройства автоматики, аккумуляторные батареи (в режиме зарядки).

Электрические цепи содержат также вспомогательные элементы: соединительные провода (кабельные трассы, линии передачи), коммутационную аппаратуру (выключатели, переключатели), устройства измерения и контроля параметров.

Графическое изображение электрической цепи называется схемой. На рис. 1 приведен пример схемы электрической цепи постоянного тока, состоящей из источника, приемника и соединительных проводов.

Рис. 1. Схема простейшей электрической цепи постоянного тока

Процессы, происходящие в электрической цепи, описываются с помощью таких понятий как ток, напряжение, электродвижущая сила (ЭДС), мощность, энергия. В цепях постоянного тока ЭДС, напряжение, ток, мощность не зависят от времени. Символы этих величин для цепей, постоянного тока принято изображать прописными буквами E, U, I, P. В цепях переменного тока ЭДС, напряжение, ток, мощность являются функциями времени. Для обозначения мгновенных значений этих величин используются строчные буквы e, u, i, p.

Электрический ток (ток проводимости) как явление представляет собой упорядоченное движение носителей зарядов внутри проводника.

Количественно электрический ток (сила тока) определяется как скорость протекания зарядов q через любое поперечное сечение проводника:

Ток измеряется в амперах [А].

За истинное направление тока условно принято движение положительных зарядов. Поэтому во внешней по отношению к источнику цепи ток течет от точки схемы с большим потенциалом к точке схемы с меньшим потенциалом (от зажима «+» к зажиму «–» на рис. 1).

Напряжение на участке электрической цепи – это работа сил электрического поля по перемещению единичного положительного заряда между начальной и конечной точками этого участка. Напряжение равно разности электрических потенциалов начальной и конечной точек участка. Так, для участка ab на рис. 2

где φ_a, φ_b– потенциалы точек a и b соответственно.

Во внешней по отношению к источнику цепи направления напряжения и тока совпадают (см. рис. 1, 2).

Рис. 2. Участок электрической цепи

Перенос зарядов в электрических цепях в установившемся режиме работы осуществляется под воздействием ЭДС источников электрической энергии. ЭДС источника создается за счет затрат внешней по отношению к электрической цепи энергии: механической энергии приводного двигателя, вращающего генератор, электрохимической энергии аккумуляторной батареи или гальванического элемента, тепловой энергии в термопаре. ЭДС источника E численно равна разности потенциалов между положительным и отрицательным зажимами источника в режиме холостого хода (когда ток источника равен нулю).

Ток внутри источника ЭДС направлен от зажима «–» к зажиму «+», а стрелка внутри окружности, изображающей источник на схеме, направлена в сторону большего потенциала (см. рис. 1).

Напряжение и ЭДС измеряются в вольтах [В].

Электрическая энергия, выделяемая (потребляемая) на участке электрической цепи за время t, равна

Энергия измеряется в джоулях [Дж].

Электрическая мощность характеризует скорость изменения энергии

Мощность измеряется в ваттах [Вт].

Анализ работы электрической цепи значительно упрощается, если элементы считать идеальными. Поэтому на схемах реальные элементы цепи заменяются идеальными элементами схемы. Эти идеальные элементы схемы отражают какие-то определенные свойства реальных элементов цепи. Для отражения нескольких различных свойств реального элемента его схема может компоноваться из нескольких идеальных элементов с различными свойствами.

Для цепей постоянного тока используются понятия двух идеальных элементов: идеального источника и идеального приемника.

Идеальный приемник (см. рис. 1, 2) – это пассивный элемент цепи, в котором энергия электрического тока безвозвратно рассеивается в виде тепла. Свойствами идеального пассивного элемента практически обладает резистор, который характеризуется сопротивлением R или проводимостью g = 1/R. Единица измерения сопротивления называется ом [Ом], а проводимости – сименс [См], причем 1См = 1/Ом.

В соответствии с законом Джоуля-Ленца энергия, выделяющаяся в виде тепла в пассивном элементе, прямо пропорциональна сопротивлению, квадрату тока и времени. Этот закон выражается формулами:

Идеальный источник – это такой активный элемент цепи, который всю выработанную энергию отдает во внешнюю цепь. Коэффициент полезного действия (КПД) идеального источника h = 100 %. В природе такого источника не существует. По своим характеристикам к идеальному приближается источник, у которого потери энергии в виде тела внутри источника пренебрежимо малы по сравнению с энергией, отдаваемой приемнику.

Реальный источник в схеме электрической цепи можно представить, например, в виде совокупности двух идеальных элементов: идеального источника ЭДС Е и внутреннего сопротивления источника R_i (см. рис. 1). Введение в схему внутреннего сопротивления источника R_i позволяет учесть потери энергии в виде тепла внутри самого источника.

Элементы электрических цепей можно подразделить на линейные и нелинейные.

В пассивном линейном элементе отношение напряжения к току постоянно. В качестве пассивного линейного элемента можно рассматривать, например, резистор с постоянным сопротивлением R:

Графическую зависимость напряжения от тока (или тока от напряжения) для пассивных элементов принято называть вольт-амперной характеристикой. Вольт-амперная характеристика резистора приведена на рис. 3. Она представляет собой луч 1, выходящий из начала координат. У пассивного нелинейного элемента отношение напряжения к току непостоянно и вольт-амперная характеристика нелинейна (рис. 3, кривая 2).

Рис. 3. Вольт-амперные характеристики линейного 1

и нелинейного 2 пассивных элементов

Графическую зависимость напряжения от тока для источников электрической энергии принято называть внешней характеристикой. Внешняя характеристика реального линейного источника приведена на рис. 4. Она представляет собой отрезок прямой линии 1 между точкой холостого хода (U = E) и точкой короткого замыкания (U = 0). Пунктирной линией 2, параллельной оси абсцисс, на этом графике изображена внешняя характеристика идеального источника ЭДС. Внешняя характеристика реального нелинейного источника приведена на рис. 4, кривая 3. Цепь называется линейной, если все элементы цепи линейны. Если хотя бы один элемент цепи нелинеен, то цепь будет нелинейной. Практически все цепи нелинейные. Однако при рассмотрении изменений напряжений и токов в ограниченном диапазоне многие цепи можно считать линейными.

В настоящем учебном пособии рассматриваются линейные электрические цепи постоянного тока.

Рис. 4. Внешние характеристики линейного 1, идеального 2

и нелинейного 3 источников ЭДС

Узнать еще:

Теория сети — топология сети

Топология сети — это графическое представление электрических цепей. Это полезно для анализа сложных электрических цепей путем преобразования их в сетевые графы. Топология сети также называется теорией графов .

Основная терминология топологии сети

Теперь давайте поговорим об основной терминологии этой топологии сети.

график

Сетевой граф просто называется графом . Он состоит из набора узлов, соединенных ветвями. В графах узел является общей точкой двух или более ветвей. Иногда только одна ветвь может подключаться к узлу. Ветвь — это отрезок, соединяющий два узла.

Любую электрическую цепь или сеть можно преобразовать в ее эквивалентный график , заменив пассивные элементы и источники напряжения короткими замыканиями, а источники тока — разомкнутыми. Это означает, что линейные сегменты на графике представляют ветви, соответствующие либо пассивным элементам, либо источникам напряжения электрической цепи.

пример

Рассмотрим следующую электрическую цепь .

В вышеупомянутой схеме есть четыре главных узла, и те отмечены как 1, 2, 3 и 4. В вышеупомянутой схеме есть семь ветвей , среди которых одна ветвь содержит источник напряжения 20 В, другая ветвь содержит 4 А Источник тока и остальные пять ответвлений содержат резисторы с сопротивлениями 30 Ом, 5 Ом, 10 Ом, 10 Ом и 20 Ом соответственно.

Эквивалентный график, соответствующий вышеуказанной электрической цепи, показан на следующем рисунке.

На приведенном выше графике есть четыре узла, и они помечены 1, 2, 3 и 4 соответственно. Они такие же, как у основных узлов в электрической цепи. На приведенном выше графике есть шесть ветвей, которые помечены как a, b, c, d, e & f соответственно.

В этом случае на графике мы получили на одну ветвь меньше, потому что источник тока 4 А выполнен в виде разомкнутой цепи, при этом преобразовывая электрическую цепь в эквивалентный график.

Из этого примера мы можем сделать следующие выводы:

Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.
Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.

Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.

Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.

Типы графиков

Ниже приведены типы графиков —

Связанный график
Неподключенный график
Направленный граф
Ненаправленный граф

Теперь давайте обсудим эти графики один за другим.

Связанный график

Если существует хотя бы одна ветвь между любыми двумя узлами графа, то она называется связным графом . Это означает, что каждый узел в связанном графе будет иметь одну или несколько ветвей, которые связаны с ним. Таким образом, ни один узел не будет представлен как изолированный или разделенный.

График, показанный в предыдущем примере, является связным графом . Здесь все узлы связаны тремя ветвями.

Неподключенный график

Если в графе существует хотя бы один узел, который не связан даже одной ветвью, то он называется несвязанным графом . Таким образом, в несвязном графе будет один или несколько изолированных узлов.

Рассмотрим график, показанный на следующем рисунке.

На этом графике узлы 2, 3 и 4 соединены двумя ветвями каждый. Но ни одна ветвь не была подключена к узлу 1 . Таким образом, узел 1 становится изолированным узлом . Следовательно, приведенный выше граф является несвязным графом .

Направленный граф

Если все ветви графа представлены стрелками, то этот граф называется ориентированным графом . Эти стрелки указывают направление протекания тока в каждой ветви. Следовательно, этот граф также называется ориентированным графом .

Рассмотрим график, показанный на следующем рисунке.

На приведенном выше графике направление потока тока обозначено стрелкой в каждой ветви. Следовательно, это ориентированный граф .

Ненаправленный граф

Если ветви графа не представлены стрелками, то этот граф называется неориентированным графом . Поскольку нет направления потока тока, этот граф также называется неориентированным графом .

График, показанный в первом примере этой главы, является неориентированным графом , поскольку на ветвях этого графа нет стрелок.

Подграф и его виды

Часть графа называется подграфом . Мы получаем подграфы, удаляя некоторые узлы и / или ветви данного графа. Таким образом, количество ветвей и / или узлов подграфа будет меньше, чем у исходного графа. Отсюда можно сделать вывод, что подграф является подмножеством графа.

Ниже приведены два типа подграфов.

дерево

Дерево является связным подграфом данного графа, который содержит все узлы графа. Но в этом подграфе не должно быть петель. Ветви дерева называются ветками .

Рассмотрим следующий связанный подграф графа, который показан в Примере начала этой главы.

Этот связанный подграф содержит все четыре узла данного графа и петли нет. Следовательно, это Дерево .

Это дерево имеет только три ветви из шести ветвей данного графа. Потому что, если мы рассмотрим хотя бы одну ветвь из оставшихся ветвей графа, то в вышеуказанном подграфе будет цикл. Тогда результирующий связанный подграф не будет деревом.

Из вышеприведенного дерева мы можем сделать вывод, что количество ветвей , которые присутствуют в дереве, должно быть равно n — 1, где «n» — количество узлов данного графа.

Co-Tree

Co-Tree — это подграф, который состоит из ветвей, которые удаляются при формировании дерева. Следовательно, это называется дополнением дерева. Для каждого дерева будет соответствующее Co-Tree, и его ветви называются ссылками или аккордами. В общем, ссылки представлены пунктирными линиями.

Co-Tree, соответствующее вышеуказанному дереву, показано на следующем рисунке.

Это Co-Tree имеет только три узла вместо четырех узлов данного графа, потому что Узел 4 изолирован от вышеуказанного Co-Tree. Следовательно, Co-Tree не обязательно должен быть связанным подграфом. Это Co-Tree имеет три ветви, и они образуют петлю.

Количество ветвей , присутствующих в совместном дереве, будет равно разнице между количеством ветвей данного графа и количеством веток. Математически это можно записать как

l=b−(n−1)

l=b−n+1

Куда,

л количество ссылок.
b — количество ветвей, присутствующих в данном графике.
n — количество узлов, присутствующих в данном графе.

Если мы объединим дерево и соответствующее ему Co-дерево, мы получим исходный граф, как показано ниже.

Ветви дерева d, e & f представлены сплошными линиями. Ветви Co-Tree a, b & c представлены пунктирными линиями.

Полное сопротивление цепи переменного тока

В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока

На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения U_L (напряжение на индуктивном сопротивлении) и напряжения U_R (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.

Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов U_L и U_R. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор U_AB является гипотенузой прямоугольного треугольника.

Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.

Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z²) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

(1)

Извлекая квадратный корень из обеих частей этого равенства, получим,

(2)

Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.

Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.

В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.

Для данного случая:

(3)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

(4)

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (X_L или X_C преобладает).

После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

(5)

Или

(6)

Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.

Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

(7)

Приводя к общему знаменателю подкоренное выражение, получим:

(8)

откуда:

(9)

Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:

(10)

Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.

В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.

Формула полного сопротивления для этого случая будет:

(11)

Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

(12)

В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие

(13)

При соблюдении этого условия полное сопротивление колебательного контура будет равно:

(14)

где L—индуктивность катушки в Гн;

С—емкость конденсатора в Ф;

R—активное сопротивление катушки в Ом.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Работа № 2 – 1. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИ

ПАРАМЕТРОВ ЭЛЕМЕНТОВ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

Цель работы

Приобретение навыков определения параметров элементов в цепях переменного тока по результатам измерений, включения в цепь вольтметра и амперметра, измерения тока и напряжения, применения закона Ома в цепь переменного тока.

Перечень минимодулей

Наименование минимодулей	Количество
Дроссель
Конденсатор 22 мкФ
Резистор 2 Вт 68 Ом

Порядок выполнения работы

При расчете цепей переменного тока, в отличие от цепей постоянного тока, необходимо учитывать не один, а три простейших пассивных элемента: резистивный. индуктивный и емкостной, которые характеризуются соответственно параметрами: активным сопротивлением X. индуктивностью L (индуктивным сопротивлением X_L=wL) и емкостью С (емкостным сопротивлением X_C=I/wС).

где w — угловая частота.

В реальной цепи сопротивлением обладают не только резистор или реостат как устройства, предназначенные для использования их электрических сопротивлений, но и любой проводник, катушка, конденсатор, обмотка любого электромагнитного элемента и др. Общим свойством всех устройств, обладающих электрическим сопротивлением, является необратимое преобразование электрической энергии в тепловую энергию. При токе і в резисторе, обладающим сопротивлением за время t в соответствии с законом Джоуля — Ленца выделяется энергия dw=ri²dt.

Тепловая энергия, выделяемая в сопротивлении, полезно используется или рассеивается в пространстве. Но поскольку преобразование электрической энергии в тепловую энергию в пассивном элементе носит необратимый характер, то в схеме замещения во всех случаях, когда необходимо учесть необратимое преобразование энергии, включается сопротивление. В реальном устройстве, например, в электромагните, электрическая энергия может быть преобразована в механическую энергию (притяжение якоря), но в схеме замещения это устройство заменяется сопротивлением, в котором выделяется эквивалентное количество тепловой энергии. И при анализе схемы нам уже безразлично, что в действительности является потребителем энергии электромагнит или электроплитка.

В цепях переменного тока сопротивление называют активным, которое из — за явления поверхностного эффекта больше, чем электрическое сопротивление постоянному току. Однако при низких частотах этой разницей обычно пренебрегают.

Напряжение, подведенное к активному сопротивлению, по фазе совпадает е током, то есть напряжение и ток одновременно достигают максимальных значений и одновременно переходят через нуль. Если мгновенное значения тока имеет вид i(t)=I_м sin (2pft), то мгновенное значение напряжения будет u_R(t)=U_m sin (2pft).

Индуктивность L характеризует свойство участка пени или катушки накапливать энергию магнитного поля. В реальной цепи индуктивностью обладают не только индуктивные катушки как элементы цепи, предназначенные для использования их индуктивности, но и провода, и выводы конденсаторов, и реостаты. В целях упрощения обычно считают, что энергия магнитного поля сосредотачивается только в катушках.

При протекании переменного тока i(t) через катушку индуктивности, состоящей из из витков, возбуждается переменный магнитный поток Ф(t). который в соответствии с законом электромагнитной индукции наводит в пей же эдс самоиндукции e_l = — wdФ/dt = — Ldi/dt. Следовательно, индуктивность в цепи переменного тока влияет на величину протекающего тока как сопротивление. Соответствующая расчетная величина называется индуктивным сопротивлением и обозначается Л’,, и измеряется так же. как и активное сопротивление — в Омах.

Чем выше частота переменного тока, тем больше эдс самоиндукции и тем больше индуктивное сопротивление X_L=wL=2pf. Величина w=2pf называется угловой (циклической) частотой переменного тока.

В цепи постоянного тока в установившемся режиме индуктивность не влияет на режим работы цепи, так как эдс самоиндукции равна нулю.

Поскольку эдс самоиндукции возникает только при изменении тока, то и максимальные значения эдс наступают при максимальной скорости изменения тока в катушке, то есть при прохождении тока через пуль. Поэтому на участке цепи с индуктивностью эдс самоиндукции по времени отстает от тока на четверть периода или на p/2 электрических радиана. Напряжение на индуктивности, будучи противоположным эдс. наоборот, опережает ток на четверть периода или на /~2 электрических радиана. Если по катушке проходит ток. мгновенное значение которого i=(t)=I_М sin (2pft), то мгновенное значение напряжения на индуктивности U

u_L(t)=U_m sin (2pft+p/2)= X_L I_М sin (2pft+p/2).

Когда напряжение, изменяясь синусоидально, достигает максимума, ток в это мгновение равен нулю. Если напряжение на зажимах элемента цепи опережает ток на p/2 радиана, то говорят, что такой элемент представляет собой идеальную катушку индуктивности или чисто реактивное индуктивное сопротивление X_L. Это сопротивление учитывает реакцию электрической цепи на изменение магнитного поля в индуктивности и является линейной функцией частоты.

При включении в цепь переменного тока реальной катушки (рис. 1), обладающей кроме индуктивности L, и некоторых; значением активного сопротивления R, ток отстает по фазе от напряжения на некоторый угол j<p/2, который легко определяется из треугольника сопротивлений (рис. 3): tgj=X_L/R. Для такого участка электрической цепи уравнение на основании второго закона Кирхгофа имеет вид:

и =u_R – и_L= Ri + Ldi/dt.

В напряжении, подведенном к реальной катушке, условно можно выделить две составляющих: падение напряжения Ri на активном сопротивлении, обычно называемое активной составляющей приложенного напряжения, и напряжение на идеальной индуктивности u_L=Ldi/dt, называемое реактивной составляющей приложенного напряжения. Фазовые соотношения между этими составляющими, приложенным напряжением и протекаемым током обычно иллюстрируются векторной диаграммой для их действующих значений (рис. 2).

Рис. 1 Рис. 2 Рис. 3

Из векторной диаграммы видно, что

где – полное электрическое сопротивление реальной катушки. Из треугольника сопротивлений (рис. 3.3) следует, что

Закон Ома для цепи, по которой протекает переменный ток, записывается в виде I=U/R.

Из рассмотренного следует важный вывод: сопротивления в цепи переменного тока складывается в общем случае геометрически. Например, если катушки R=3 Ома и X_L=4 Ома, то Z=5 Ом.

Емкость, измеряемая в фарадах (Ф), характеризует способность элемента электрической цени или конденсатора накапливать энергию электрического поля. В реальной цепи емкость существует не только в конденсаторах, как элементах предназначенных специально для использования их емкости, ноли между проводниками, между витками катушек (межвитковая емкость), между проводом и землей или каркасом электротехнического устройства. Однако в схемах замещения принято, что емкостью обладают только конденсаторы.

В конденсаторе, точнее в диэлектрике, разделяющем пластины или проводники конденсатора, может существовать ток электрического смещения, в точности равный току проводимости в проводниках, присоединенных к обкладкам конденсатора, i=dq/dt, где – q заряд на обкладках конденсатора, измеряемый в кулонах и пропорциональный напряжению на конденсаторе U_c:

q=CU_c и при С=const dq=CdU_c.

Тогда ток, проходящий через конденсатор, i = C dU_c / dt, а энергия электрического поля, запасаемая в конденсаторе при возрастании напряжения, W = C U_C² /2.

Очевидно, что при постоянном напряжении dU_c/dt=0 и постоянный ток через конденсатор проходить не может.

При изменении напряжения на обкладках конденсатора через него протекает емкостной ток. Чем быстрее изменяется напряжение, тем больше емкостной ток.

Если приложить к конденсатору переменное синусоидальное напряжение, то через конденсатор потечет переменный синусоидальный ток, сдвинутый по фазе на p/2 по отношению к напряжению. Это происходит потому, что емкостной ток достигает максимального значения при максимальном изменении напряжения, т.е. при прохождении напряжения через нуль. Ток при этом опережает напряжение по фазе на p/2. Если мгновенное значение тока, протекаемого через конденсатор

i(t)=I_м sin (2pft), то мгновенное значение напряжения на нем

u_C(t)=U_m sin (2pft-p/2)= X_C I_М sin (2pft-p/2).

где Х_С — реактивное емкостное сопротивление. Векторная диаграмма для участка электрической цепи, содержащей конденсатор, изображена на рис. 4.

Рис. 4

Величина X_C = I/2pfC = I/wC = U_Cm / I_m = U_C /I называется реактивным емкостным сопротивлением. Это сопротивление учитывает реакцию электрической цепи на изменение электрического поля в конденсаторе и является обратно пропорциональной функцией частоты.

Закон Ома для участка электрической цени с конденсатором I =U_C /X_C, где I — действующее значение тока, протекаемого через конденсатор, U_C — действующее значение напряжения на конденсаторе.

Электрическая цепь переменного тока характеризуется реактивной и полной мощностью.

Активная мощность Р, измеряемая в ваттах (Вт), равна произведению действующего значения напряжения V на действующее значение ток U и на действующее значение ток I и на cosj, называемый коэффициентом мощности, или произведению квадрата действующего значения тока на активное сопротивление:

Р = UI cosj = I² R.

Реактивная мощность Q измеряемая в вольт-амперах реактивных (Вар), равна произведению действующего значения напряжения U на действующее значение тока I и на sinj произведению квадрата действующего значения тока на реактивное сопротивление:

Q=UIsinj=I²X.

Полная мощность S, измеряемая в вольт — амперах (ВА), равна произведению действующего значения тока U па действующее значение напряжения U:

Соотношения этих мощностей иллюстрируются треугольником мощностей (рис. 5).

Рис. 5

Порядок выполнения работы

3.1. Ознакомиться с лабораторной установкой (модуль ввода-вывода, модуль питания, набор минимодулей, наборное поле).

3.2. Собрать электрическую цепь для исследования цепи переменного тока, содержащей только активное сопротивление R (рис. 6). Дня измерения тока использовать вход 5 модуля ввода — вывода (гнезда Х25 и Х26). Для измерения напряжения U использовать вход 1 модуля ввода-вывода на пределе 30 В (гнезда Х9 и Х10). Представить схему для проверки преподавателю.

Рис. 6

3.3. Загрузить программу автоматического управления Delta Profi.

В левом верхнем углу в окне программы выбрать меню «Работы». Одинарный щелчок левой кнопкой мыши приводит к появлению контекстного меню, в котором надо выбрать раздел «Электрические цепи — мини». В появившемся списке работ выбрать «Работа №2 — 1. Простейшие цепи переменного тока». В появившемся списке выбрать «Цепь с активным сопротивлением»

На экране ПК отображается электрическая схема и набор виртуальных — измерительных приборов, необходимых в данном эксперименте.

Запустить программу в работу, нажатием кнопки «Пуск» или командой главного меню «Управление — Пуск» или горячей клавишей F5.

3.4. Включить электропитание стенда (автоматический выключатель QF. который выключается только в конце лабораторной работы) и модуля ввода — вывода.

На модуле питания включить источник переменного напряжения (SA1+SA2) и записать в табл. 1 показания виртуальных приборов.

Таблица 1

Включено	Измерено	Вычислено
U, В	I, А	Р, Вт	j, град	Z, Ом	R, Ом	Х, Ом
R
Z_k
С

Остановить программу, нажатием кнопки «Стоп» ▀. Выбрать закладку «Осциллограммы» и зарисовать осциллограммы напряжения и тока. На осциллограммах показать сдвиг по фазе между напряжением и током в данной цепи. Остановить программу, нажатием кнопки «Стоп» ▀ или командой главного меню «Управление — Стоп» или горячей клавишей F6.

3.5. Собрать электрическую цепь для исследования цепи переменного тока, содержащей только реальную индуктивность (рис. 7). Представить схему для проверки преподавателю.

3.6. В левом верхнем углу в окне программы выбрать меню «Работы». Одинарный щелчок левой кнопкой мыши приводит к появлению контекстного меню, в котором надо выбрать раздел «Электрические цепи — мини». В появившемся списке работ выбрать «Работа 2 — 1. Простейшие цепи переменного тока». В появившемся списке выбрать «Цепь с индуктивностью»

На экране ПК отображается электрическая схема и набор виртуальных измерительных приборов, необходимых в данном эксперименте.

Рис. 7

Запустить программа в работу, нажатием кнопки «Пуск» ► или командой главного меню «Управление — Пуск».

Остановить программу, нажатием кнопки «Стоп» ▀. Выбрать закладку «Осциллограммы» и зарисовать осциллограммы напряжения и тока. На осциллограммах показать сдвиг по фазе между напряжением и током в данной цепи. Остановить программу, нажатием кнопки «Стол» ▀ или командой главного меню «Управление — Стоп».

3.7. Собрать электрическую цепь для исследования цепи переменного тока, содержащей только конденсатор (рис. 8). Представить схему для проверки преподавателю.

Рис.8

3.8. В левом верхнем углу в окне программы выбрать меню «Работы». Одинарный щелчок левой кнопкой мыши приводит к появлению контекстного меню, в котором надо выбрать раздел «Электрические цепи — мини». В появившемся списке работ выбрать «Работа 2 — 1. Простейшие цепи переменного тока». В появившемся списке выбрать «Цепь с емкостью».

Запустить программу в работу, нажатием кнопки «Пуск» ► или командой главного меню «Управление — Пуск» или горячей клавишей F5.

Записать в табл. 1 показания виртуальных приборов.

Остановить программу, нажатием кнопки «Стоп» ▀.

Выбрать закладку «Осциллограммы» и зарисовать осциллограммы напряжения и тока. На осциллограммах показать сдвиг по фазе между напряжением и током в данной цепи. Остановить программу, нажатием кнопки Стоп» ▀ или командой главного меню «Управление — Стоп» или горячей клавишей F6.

Выключить источник переменного напряжения (55A1+SA2).

В конце лабораторной работы выключить питание стенда (автоматический выключатель QF модуля питания).

3.9. По результатам измерений рассчитать, используя закон Ома, полное сопротивление каждого потребителя, его активное и реактивное сопротивления. Результаты занести в табл. 1.

3.10. Считая, что частота переменного напряжения f = 50 Гц, определись величину индуктивности индуктивного потребителя L и емкости конденсатора.

Содержание отчета

Отчет по работе должен содержать:

а) наименование работы и цель работы;

б) электрические схемы опытов;

в) таблицы с результатами опытов и вычислений;

г) расчетные соотношения;

д) векторные диаграммы для резистора, реальной катушки и конденсатора;

е) выводы по работе.

5. Контрольные вопросы

1. В каких единицах измеряется ток, напряжение, сопротивление?

2. Что такое Ом, Ампер, Вольт?

3. Что такое «полное сопротивление»?

4. Что такое «активное сопротивление»?

5. Что такое «реактивное индуктивное сопротивление» и как оно определяется?

6. Что такое «реактивное емкостное сопротивление» и как оно определяется?

7. Какая связь между полным, активным и реактивным сопротивлениями цепи переменного тока?

8. Как формулируется закон Ома для цепи переменного тока?

9. Может ли через конденсатор протекать постоянный ток?

Работа № 2 – 2. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА С
ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ

Цель работы

Приобретение навыков сборки простых электрических цепей и измерения напряжений на отдельных участках цепи, изучение свойств цепей при последовательном соединении активных и реактивных элементов, знакомство с явлением резонанса напряжений, построение векторных диаграмм.

Перечень минимодулей

Наименование минимодулей	Количество
Дроссель
Батарея конденсаторов
Резистор 2 Вт 68 Ом

Пояснения к работе

Электрическая цепь синусоидального переменного тока с последовательным соединением резистора с активным сопротивлением R. реальной катушки индуктивности с полным сопротивлением Z_k(R_k,X_k) и конденсатора с емкостным сопротивлением X_c (рис. 1) описывается уравнением, записанным по второму закону Кирхгофа для мгновенных значений напряжений на этих элементах:

или в геометрической форме для векторов действующих значений этих напряжений

Последнее соотношение говорит о том, что вектор действующего значения напряжения, приложенного к такой цепи, равен геометрической сумме векторов напряжений на отдельных её участках (рис. 2).

Рис. 1 Рис. 2 Рис. 3

Из анализа векторной диаграммы для такой цепи следует, что величина входного напряжения U

где U_RK , U_LK – соответственно активная и реактивная составляющие напряжения на катушке, R_K, X_L – активное и реактивное индуктивное сопротивление катушки индуктивности (рис. 3)

Следовательно, действующее значение тока в этой цепи на основании закона Ома можно определит как где

– полное сопротивление цепи с последовательным соединением резистора, реальной катушки и индуктивности и конденсатора, которое легко определяется из многоугольника сопротивлений (рис. 3).

Угол сдвига фаз между входным синусоидальным напряжением U и потребляемым такой цепью током I определяется из треугольника сопротивлений

Если ωL > 1/ωC и угол φ > 0, вся цепь ведет себя как цепь с активным сопротивлением и идеальной индуктивностью. Говорят, что в этом случае цепь носит активно-индуктивный характер.

Если ωL < 1/ωC и угол φ < 0, вся цепь ведет себя как цепь с активным сопротивлением и емкостью. Говорят, что в этом случае цепь носит активно — емкостной характер.

Если в цепи реактивное сопротивления равны (ωL = 1/ωC), то угол φ = 0. При этом реактивная составляющая напряжения на индуктивности и напряжение на конденсаторе полностью себя компенсируют. Цепь ведет себя, как будто реактивные сопротивления в ней отсутствуют и ток достигает наибольшего значения, поскольку ток ограничивается только эквивалентным активным сопротивлением цепи

Это означает, что в цепи имеет место резонанс, называемый в данном случае резонансом напряжений.Резонанс напряжений можно получить изменением частоты источника питания, изменением параметров реактивных элементов, например, подбором значения величины емкости , где – резонансная частота цепи.

Порядок выполнения работы

3.1.Ознакомиться с лабораторной установкой (модуль ввода-вывода, набор минимодулей, наборное поле).

3.2.Собрать электрическую цепь с последовательным соединением элементов, установив минимодули резистора, батареи конденсаторов и дросселя L1 используемого в качестве индуктивного потребителя Z_k (рис.4) Подключить собранную цепь к источнику переменного напряжения (клеммы «А-N» источника питания). Для измерения тока использовать вход 5 модуля ввода-вывода (гнезда Х25 и Х26). Для измерения напряжений U_R U_K U_C и U использовать входы 1, 2, 3, 4 модуля ввода-вывода на пределе 30 В (гнезда Х9 и Х10, X11 и Х12, X13 и Х14, XI5 и Х16, соответственно). Представить схему для проверки преподавателю.

3.3.Загрузить программу автоматического управления Delta Profi.

В появившемся списке работ выбрать «Работа 2-2. Электрическая цепь переменного тока с последовательным соединением элементов». На экране ПК отображается электрическая схема и набор виртуальных измерительных приборов, необходимых в данном эксперименте.

Рис. 4

3.4.Подсоединить параллельно конденсатору дополнительный проводник (исключив этим конденсатор из цепи). Предъявить схему для проверки преподавателю.

3.5.Включить электропитание стенда (автоматический выключатель QF модуля питания, который выключается только в конце лабораторной работы) и модуля ввод-вывод.

На модуле питания включить источник переменного напряжения (SA1+SA3).

Произвести измерения указанных в таблице величин в цепи с последовательным соединением резистора R и катушки Z_K_.Результаты измерений занести в табл. 1.

Таблица 1

Схема	U, B	I, мA	U_R, В	U_K, В	U_C, В	P, Вт
R, Z_k					−−−−−
R, X_c				−−−−−
R, Z_k, X_c1
R, Z_k, X_c2
R, Z_k, X_c3

Выключить источник переменного напряжения (SA1+SA3), убрать дополнительный проводник, подключенный к конденсатору. Подсоединить параллельно индуктивному потребителю дополнительный проводник (исключив этим его из цепи). Установить заданное преподавателем значение емкости батареи конденсаторов. Предъявить схему для проверки преподавателю.

3.6. Произвести измерения указанных в таблице величин для цепи с последовательным соединением резистора R и конденсатора Хс. Результаты измерений занести в табл. 1. Выключить источник переменного напряжения (SA1+SA3), убрать дополнительный проводник.

3.7. Включить источник переменного напряжения (SA1+SA3). Изменяя величину емкости батареи конденсаторов, добиться наибольшего показания амперметра, т.е. обеспечить состояние цепи близкое к резонансу напряжений. Результаты измерений занести в табл. 1.

3.8.Уменьшая и увеличивая величину емкости батареи конденсаторов (от резонансного значения емкости) провести измерения указанных в таблице величин для двух состояний цепи. Результаты измерений занести в табл. 1. Выключить источник переменного напряжения (SA1+SA3).

3.9.Для цепи с последовательным соединением трех элементов ( R, Z_K, С) по результатам измерений рассчитать:

полную мощность цепи S, активные мощности отдельных участков P_R. Р_к и всей цепи Р. реактивную мощность цепи Q, коэффициент мощности цепи cosφ и угол сдвига фаз φ между напряжением на входе цепи и током, а также полное Z_э— активное R_э и реактивное Х_э сопротивления всей цепи, величину емкостного сопротивления Х_с. При определении активной мощности индуктивного потребителя учесть полученное в предшествующей лабораторной работе значение активного сопротивления индуктивного потребителя R_K. Результаты занести в табл.2.

Таблица 2

S=UI BA	P_R=U_RI Вт	P_R=R_KI² Вт	P=R_R+P_K Вт	Q= ВАр	cosφ= P/S	φ	Z_э Ом	R_э Ом	Х_э Ом	Х_с= U_с/I Ом

3.10.По результатам измерений построить для исследованных цепей в масштабе векторные диаграммы и сделать вывод о характере каждой исследованной цепи.

3.11.Построить зависимости потребляемого тока I, сопротивления цепи Z_э, реактивного сопротивления цепи Х_экоэффициента мощности цепи от величины емкостного сопротивления Х_с.

3.12.Сделать вывод о применении 2-го закона Кирхгофа в цепях переменного тока.

4. Содержание отчета

Отчет по работе должен содержать:

а) наименование работы и цель работы;

б) схему исследуемой цепи;

в) таблицы с результатами опытов и вычислений;

г) расчетные соотношения;

д) векторные диаграммы; с) выводы по работе.

5. Контрольные вопросы

1. Что такое активная, реактивная и полная мощности в цепи переменного

тока?

2. Какая взаимосвязь между полной, активной и реактивной мощностями?

3. Что такое «коэффициент мощности»?

4. Как вычислить полное сопротивление катушки, если известны её активное сопротивление, индуктивность и частота сети?

5. Как вычислить полное сопротивление цепи с последовательным соединением резистора, реальной катушки и конденсатора?

6. От чего зависит угол сдвига фаз между напряжением и током на участке электрической цепи переменного тока?

7. Что такое «треугольник сопротивлений»?

8. Чему равны реактивное сопротивление цепи и реактивная мощность цепи при резонансе?

9. В каком случае исследуемая цепь будет носить активно-индуктивный характер, и в каком — активно-емкостной характер?

Работа № 2-3. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ.

ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ

1. Цель работы

Ознакомиться с особенностями режимов работы цепи с параллельным соединения активных и реактивных элементов, явлением резонанса токов, повышением коэффициента мощности, применением 1-го закона Кирхгофа в цепях переменного тока.

Перечень минимодулей

Наименование минимодулей	Количество
Дроссель
Батарея конденсаторов
Резистор 2 Вт 100 Ом
Тумблер

Пояснения к работе

При параллельном соединении элементов получают разветвленную цепь (рис. 1). При параллельном соединении элементов токи r отдельных ветвях зависят от величины приложенного напряжения и полного сопротивления каждой ветви. При этом ток в ветви с резистором I_R совпадает по фазе с напряжением, ток в ветви с индуктивной катушкой I_K отстает по фазе от напряжения на угол φ, зависящий от активного и реактивного сопротивления реальной катушки индуктивности. Ток в ветви с конденсатором I_C опережает напряжение на 90⁰ (рис. 2). В соответствии с первым законом Кирхгофа общий ток I, потребляемый такой цепью от источника питания, определяется геометрической суммой токов отдельных ветвей:

Рис. 1

Геометрическое построение для определения величины и фазы общего тока представлено на рис. 2, где обозначено:

I_KA, I_A — активные составляющие тока в ветви с индуктивной катушкой и общего тока;

I_KP, I_P — реактивные составляющие тока в ветви с индуктивной катушкой и общего тока.

Рис. 2

Под активной составляющей тока понимают составляющую тока, совпадающую по фазе с приложенным напряжением. Под реактивной

составляющей тока — составляющую, расположенную под 90° к приложенному напряжению. Следует помнить, что активная и реактивная составляющие тока – это условие величины, не имеющие физического смысла в последовательной схеме замещения, но удобные для расчетов.

Из векторной диаграммы следует, что ,

Следовательно, величина общего тока I = ,

а угол сдвига фаз между общим током и приложенным напряжением

tgφ= / ( )/( ).

Данная векторная диаграмма построена в предположении, что емкостной ток меньше реактивной индуктивной составляющей тока в катушке . Поэтому общий ток отстает по фазе от напряжения. Такая цепь носит активно- индуктивный характер. Если бы емкостной ток был больше реактивной индуктивной составляющей тока в катушке , то ток, потребляемый цепью из сети опережал по фазе приложенное напряжение и цепь носила бы активно- емкостной характер.

При равенстве реактивной индуктивной составляющей тока в катушке и емкостного тока вектор общего тока совпадает по фазе с вектором приложенного напряжения, а его величина определяется только активными составляющими токов , При этом в цепи наступает явление резонанса токов, так как цепь, содержащая реактивные элементы, ведет себя как цепь с чисто активным сопротивлением. При резонансе токов токи в ветвях с реактивными элементами могут значительно превышать ток, потребляемый от источника питания.

3. Порядок выполнения работы

3.1. Ознакомиться с лабораторной установкой (модуль ввода-вывода, набор минимодулей ).

3.2. Собрать электрическую цепь с параллельным соединением резистора R, индуктивного потребителя Z_K и батареи конденсаторов С (рис. 3).

Рис. 3

Установить в заданную преподавателем позицию переключатель батареи конденсаторов С. В качестве индуктивного потребителя Z_K использовать дроссель L1. Для измерения тока использовать входы 5, 6, 7, 8 модуля ввода-вывода (гнезда Х25 и Х26. Х27 и Х28, Х29 и Х30, Х31 и Х32, соответственно). Для измерения напряжения U использовать вход I модуля ввода-вывода на пределе 30В (гнезда Х9 и Х10). Представить схему для проверки преподавателю.

3.3. Загрузить программу автоматического управления Delta Profi.

В появившемся списке работ выбрать «Работа № 2-3. Электрическая цепь переменного тока с параллельным соединением элементов». На экране ПК отображается электрическая схема и набор виртуальных измерительных приборов, необходимых в данном эксперименте.

3.4. Изучить работу электрической цепи при параллельном соединении потребителей.

Включить электропитание стенда (автоматический выключатель QF модуля питания, который выключается только в конце лабораторной работы) и модуля ввод-вывод.

На модуле питания включить источник переменного напряжения (SA1+SA2).

Поочередно подключая тумблерами соответствующие ветви, измерить напряжение и токи во включенных ветвях, а также ток, потребляемый от источника питания. Подключить с помощью тумблеров все ветви и измерить напряжение и токи в ветвях, а также ток, потребляемый от источника питания. Результаты измерений занести в табл. 1.

Таблица 1

Включены ветви	Измерено	Вычислено
U, В	I, мА	, мА	, мА	, мА	φ, град	cosφ
R				——	——
C			——		——
Z_K			——	——
R, С, Z_K
Z_K, С1			——
Z_K, С1			——
Z_K, С1			——

3.5. Исследовать влияние емкости С, включенной параллельно индуктивному потребителю Z_K, на коэффициент мощности цепи и величину тока I, потребляемого от источника питания. Для этого разомкнуть ветвь с резистором R и установить такое значение емкости батареи конденсаторов, при которой от источника потребляется минимальный ток (состояние, близ

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Закон Ома

| Электрические цепи

11,2 Закон Ома (ESBQ6)

Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:

Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.

Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.

Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .

Закон Ома

Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как

\ (I = \ frac {V} {R} \)

где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.

Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток — на ось y графика, мы получим прямую линию.

Наклон прямолинейного графика связан с сопротивлением проводника как
\ [\ frac {I} {V} = \ frac {1} {R}.\]

Это можно изменить с точки зрения постоянного сопротивления как:
\ [R = \ frac {V} {I}. \]

Закон Ома

Цель

Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.

Аппарат

4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода

Метод

Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.

Изменение напряжения:
1. Установите схему в соответствии со схемой 1), начиная с одной ячейки.
2. Нарисуйте следующую таблицу в своем лабораторном журнале.
  Количество ячеек
  Напряжение, В (\ (\ text {V} \))
  Ток, I (\ (\ text {A} \))
  \ (\ text {1} \)
  \ (\ text {2} \)
  \ (\ text {3} \)
  \ (\ text {4} \)
3. Попросите учителя проверить электрическую цепь перед включением питания.
4. Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
5. Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
6. Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
1. Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.
2. Нарисуйте следующую таблицу в своем лабораторном журнале.
  Напряжение, В (\ (\ text {V} \))
  Ток, I (\ (\ text {A} \))
3. Попросите учителя проверить вашу схему перед включением питания.
4. Измерьте ток и напряжение на единственном резисторе.
5. Теперь добавьте еще один резистор последовательно в схему и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.

Анализ и результаты

Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).

Выводы

Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Вопросы и обсуждение

Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?

Зарегистрируйтесь, чтобы получить стипендию и возможности карьерного роста.Используйте практику Сиявулы, чтобы получить наилучшие возможные оценки.

Зарегистрируйтесь, чтобы открыть свое будущее

Закон Ома

Упражнение 11.1

Постройте график напряжения (по оси X) и тока (по оси Y).

Какой тип графика вы получите (прямой, парабола, другая кривая)

прямая линия

Рассчитайте градиент графика.

Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:

\ begin {align *}
m & = \ frac {\ Delta I} {\ Delta V} \\
& = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\
& = \ текст {0,13}
\ end {выровнять *}

Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.

Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?

Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.

Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение на каждом из резисторов.

Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:

\ [V = IR \]

Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток одинаков во всей цепи, мы можем найти неизвестное сопротивление.

\ begin {align *}
V_ {0} & = IR_ {0} \\
I & = \ frac {V_ {0}} {R_ {0}} \\
V_ {U} & = IR_ {U} \\
I & = \ frac {V_ {U}} {R_ {U}} \\
\ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\
\ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}}
\ end {выровнять *}

Омические и неомические проводники (ESBQ7)

Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток, проходящий через них.Эти проводники называются омическими проводниками, проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторыми примерами омических проводников являются резисторы цепи и нихромовая проволока.

Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.

В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, возникающее в результате увеличение тока приведет к повышению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.

Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.

В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.

Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.

Омические и неомические проводники

Aim

Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома

Аппарат

4 ячейки, резистор, лампочка, провода соединительные, вольтметр, амперметр

Метод

Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:

Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
Измерьте ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.

Результаты

Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.

Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)

Анализ

Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.

Вопросы и обсуждение

Внимательно изучите свои графики и ответьте на следующие вопросы:

Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
Имеет ли лампочка омический или неомический провод?

Использование закона Ома (ESBQ8)

Теперь мы готовы увидеть, как закон Ома используется для анализа схем.

Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. При решении любой проблемы с электрическими схемами очень важно составить схему схемы перед тем, как производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:

Уравнение закона Ома:

\ [R = \ frac {V} {I} \]

, который можно преобразовать в:
\ [I = \ frac {V} {R} \]

Ток, протекающий через резистор:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\
& = \ текст {1} \ текст {А}
\ end {align *}

Рабочий пример 1: Закон Ома

Изучите принципиальную схему ниже:

Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?

Определите, как подойти к проблеме

Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя:
\ [R = \ frac {V} {I}. \]

Решить проблему

Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).

\ begin {align *}
R & = \ frac {V} {I} \\
R \ times I & = \ frac {V} {I} \ times I \\
V & = I \ раз R \\
& = \ текст {10} \ times \ text {4} \\
& = \ текст {40} \ текст {V}
\ end {align *}

Напишите окончательный ответ

Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).

Зарегистрируйтесь, чтобы получить стипендию и возможности карьерного роста. Используйте практику Сиявулы, чтобы получить наилучшие возможные оценки.

Зарегистрируйтесь, чтобы открыть свое будущее

Закон Ома

Упражнение 11.2

Вычислите сопротивление резистора, разность потенциалов которого равна \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {8} {2} \\
& = \ текст {4} \ текст {Ω}
\ end {выровнять *}

Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {18} {6} \\
& = \ текст {3} \ текст {А}
\ end {выровнять *}

Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {1,5}) (10) \\
& = \ текст {15} \ текст {V}
\ end {выровнять *}

Переплет резисторов последовательно и параллельно (ESBQ9)

В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.

Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .

Эквивалентное последовательное сопротивление

В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.

Эквивалентное сопротивление в последовательной цепи,

Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]

Применим это к следующей схеме.

Резисторы включены последовательно, следовательно:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\
& = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\
& = \ текст {18} \ текст {Ω}
\ end {align *}

Эквивалентное параллельное сопротивление

В цепи, в которой резисторы соединены параллельно, эквивалентное сопротивление определяется следующим определением.

Эквивалентное сопротивление в параллельной цепи

Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]

Применим эту формулу к следующей схеме.

Какое полное (эквивалентное) сопротивление в цепи?

\ begin {align *}
\ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \верно) \\
& = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\
& = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\
& = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\
R_ {p} & = \ text {0,625} \ text {Ω}
\ end {align *}

Последовательное и параллельное сопротивление

Упражнение 11.3

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} \\
& = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\
& = \ текст {20} \ текст {кОм}
\ end {выровнять *}

Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} \\
R_ {2} & = R_ {s} — R_ {1} \\
& = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\
& = \ текст {90} \ текст {Ω}
\ end {выровнять *}

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\
& = \ frac {1 + 10} {\ text {100}} \\
& = \ frac {11} {\ text {100}} \\
R_ {p} & = \ text {9,09} \ text {kΩ}
\ end {выровнять *}

Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
\ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\
& = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\
& = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\
& = \ frac {\ text {6,25}} {\ text {37,5}} \\
R_ {2} & = \ текст {6} \ текст {Ω}
\ end {выровнять *}

Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:

a) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\
& = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\
& = \ frac {\ text {5}} {\ text {6}} \\
R & = \ текст {1,2} \ текст {Ω}
\ end {выровнять *}

b) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]

Эквивалентное сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\
& = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\
& = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\
& = \ frac {\ text {25}} {\ text {12}} \\
R & = \ text {0,48} \ text {Ω}
\ end {выровнять *}

c) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} \\
& = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\
& = \ текст {5} \ текст {Ω}
\ end {выровнять *}

d) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]

Эквивалентное сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\
& = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\
& = \ текст {10} \ текст {Ω}
\ end {выровнять *}

Использование закона Ома в последовательных и параллельных цепях (ESBQB)

Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.

Последовательные цепи

Рассмотрим схему, состоящую из трех резисторов и
одиночная ячейка соединена последовательно.

Первый принцип, который необходимо понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.

Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:

\ [I = I_ {1} = I_ {2} = I_ {3}. \]

Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:

\ [V = V_ {1} + V_ {2} + V_ {3} \]

Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления последовательно соединенных резисторов, мы можем решить некоторые проблемы схемы.

Рабочий пример 2: Закон Ома, последовательная цепь

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найдите полное сопротивление в цепи

Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:

\ [R = R_ {1} + R_ {2} \]

Следовательно,

\ begin {align *}
R & = \ текст {2} + \ текст {4} \\
& = \ текст {6} \ текст {Ω}
\ end {align *}

Применить закон Ома

\ begin {align *}
R & = \ frac {V} {I} \\
R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\
I & = \ frac {V} {R} \\
& = \ frac {12} {6} \\
& = \ текст {2} \ текст {А}
\ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).

Рабочий пример 3: Закон Ома, последовательная цепь

Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).

Нарисуйте схему и введите все известные значения.

Определите, как подойти к проблеме.

Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:

\ [R = R_ {1} + R_ {2} \]

, потому что он находится в последовательной цепи.

Найдите полное сопротивление

\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {\ text {1,5}} {\ text {0,25}} \\
& = \ текст {6} \ текст {Ω}
\ end {align *}

Найдите неизвестное сопротивление

Мы знаем, что:

\ [R = \ text {6} \ text {Ω} \]

и что

\ [R_ {1} = \ text {1} \ text {Ω} \]

\ [R = R_ {1} + R_ {2} \]
\ [R_ {2} = R — R_ {1} \]

Следовательно,

\ [R_ {1} = \ text {5} \ text {Ω} \]

Рабочий пример 4: Закон Ома, последовательная цепь

Для следующей схемы рассчитайте:

падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)
сопротивление \ (R_3 \).

Определите, как подойти к проблеме

Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).

Рассчитать падение напряжения на \ (R_1 \)

Используя закон Ома:
\ begin {align *}
R_1 & = \ frac {V_1} {I} \\
I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\
V_1 & = {I} \ cdot {R_1} \\
& = 2 \ cdot 1 \\
V_1 & = \ текст {2} \ текст {V}
\ end {align *}

Рассчитать падение напряжения на \ (R_2 \)

Снова используя закон Ома:
\ begin {align *}
R_2 & = \ frac {V_2} {I} \\
I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\
V_2 & = {I} \ cdot {R_2} \\
& = 2 \ cdot 3 \\
V_2 & = \ текст {6} \ текст {V}
\ end {align *}

Рассчитать падение напряжения на \ (R_3 \)

Поскольку падение напряжения на всех резисторах вместе должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя:
\ begin {align *}
V & = V_1 + V_2 + V_3 \\
V_3 & = V — V_1 — V_2 \\
& = 18-2-6 \\
V_3 & = \ текст {10} \ текст {V}
\ end {align *}

Найдите сопротивление \ (R_3 \)

Мы знаем напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома для вычисления значения сопротивления:
\ begin {align *}
R_3 & = \ frac {V_3} {I} \\
& = \ frac {10} {2} \\
R_3 & = \ text {5} \ Omega
\ end {align *}

Напишите окончательный ответ

\ (V_1 = \ text {2} \ text {V} \)

\ (V_2 = \ text {6} \ text {V} \)

\ (V_3 = \ text {10} \ text {V} \)

\ (R_1 = \ text {5} \ Omega \)

Параллельные цепи

Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.

Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что
напряжение одинаково на всех компонентах в цепи. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Итак, для показанной схемы верно следующее:

\ [V = V_ {1} = V_ {2} = V_ {3}. \]

Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны в сумме равняться общему току в цепи:

\ [I = I_ {1} + I_ {2} + I_ {3}.\]

Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, мы теперь можем подойти к некоторым проблемам схемы, связанным с параллельными резисторами.

Рабочий пример 5: Закон Ома, параллельная схема

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найдите эквивалентное сопротивление в цепи

Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:

\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \]
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\
& = \ frac {1} {2} + \ frac {1} {4} \\
& = \ frac {2 + 1} {4} \\
& = \ frac {3} {4} \\
\ text {Следовательно,} R & = \ text {1,33} \ Omega
\ end {align *}

Применить закон Ома

\ begin {align *}
R & = \ frac {V} {I} \\
R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\
I & = \ frac {V} {R} \\
I & = V \ cdot \ frac {1} {R} \\
& = (12) \ left (\ frac {3} {4} \ right) \\
& = \ текст {9} \ текст {А}
\ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).

Рабочий пример 6: Закон Ома, параллельная схема

Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найдите сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ текст {9} \) \ (\ text {V} \).

Определите, что требуется

Нам нужно рассчитать сопротивление \ (R_2 \).

Определите, как подойти к проблеме

Поскольку резисторы омические и нам даны напряжение на элементе и ток через элемент, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи.\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {9} {\ text {4,8}} \\
& = \ text {1,875} \ \ Omega
\ end {align *}

Рассчитайте значение для \ (R_2 \)

Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для параллельных резисторов, чтобы найти сопротивление \ (R_2 \).
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2}
\ end {выровнять *}
Переставляем решение для \ (R_2 \):
\ begin {align *}
\ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\
& = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\
& = \ текст {0,2} \\
R_2 & = \ frac {1} {\ text {0,2}} \\
& = \ текст {5} \ \ Omega
\ end {align *}

Напишите окончательный ответ

Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)

Рабочий пример 7: Закон Ома, параллельная схема

Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.

Сначала нарисуйте схему перед выполнением любых расчетов

Определите, как подойти к проблеме

Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.

Рассчитать ток через ячейку

Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи.Резисторы включены параллельно и поэтому:
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\
& = \ frac {1} {4} + \ frac {1} {12} \\
& = \ frac {3 + 1} {12} \\
& = \ frac {4} {12} \\
R & = \ frac {12} {4} = \ text {3} \ \ Omega
\ end {выровнять *}
Теперь, используя закон Ома, чтобы найти ток через ячейку:
\ begin {align *}
R & = \ frac {V} {I} \\
I & = \ frac {V} {R} \\
& = \ frac {18} {3} \\
I & = \ text {6} \ text {A}
\ end {align *}

Теперь определите ток через один из параллельных резисторов

Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы:
\ begin {align *}
V & = V_1 = V_2 = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с расчета тока через \ (R_1 \) по закону Ома:
\ begin {align *}
R_1 & = \ frac {V_1} {I_1} \\
I_1 & = \ frac {V_1} {R_1} \\
& = \ frac {18} {4} \\
I_1 & = \ text {4,5} \ text {A}
\ end {align *}

Рассчитайте ток через другой параллельный резистор

Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \):
\ begin {align *}
R_2 & = \ frac {V_2} {I_2} \\
I_2 & = \ frac {V_2} {R_2} \\
& = \ frac {18} {12} \\
I_2 & = \ text {1,5} \ text {A}
\ end {выровнять *}

Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через ячейку:

\ begin {align *}
I & = I_1 + I_2 \\
I_2 & = I — I_1 \\
& = 6 — 4.5 \\
I_2 & = \ text {1,5} \ text {A}
\ end {align *}

Напишите окончательный ответ

Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).

Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).

Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).

Закон Ома в последовательной и параллельной цепях

Упражнение 11.4

Рассчитать номинал неизвестного резистора в цепи:

Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:

\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {9} {1} \\
& = \ текст {9} \ текст {Ω}
\ end {выровнять *}

Теперь мы можем найти неизвестное сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\
R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\
& = 9 — 3 — 3 — 1 \\
& = \ текст {2} \ текст {Ω}
\ end {выровнять *}

Рассчитайте значение тока в следующей цепи:

Сначала находим общее сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\
& = \ text {1} + \ text {2,5} + \ text {1,5} \\
& = \ текст {5} \ текст {Ω}
\ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {9} {5} \\
& = \ текст {1,8} \ текст {А}
\ end {выровнять *}

Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены последовательно с батареей \ (\ text {12} \) \ (\ text {V} \).Рассчитайте значение тока в цепи.

Рисуем принципиальную схему:

Теперь мы находим общее сопротивление:

\ begin {align *}
R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\
& = \ текст {1} + \ текст {5} + \ текст {10} \\
& = \ текст {16} \ текст {Ω}
\ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {12} {16} \\
& = \ текст {0,75} \ текст {A}
\ end {выровнять *}

Рассчитайте ток через ячейку, если оба резистора омические по своей природе.

Сначала находим общее сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\
& = \ frac {3 + 1} {\ text {3}} \\
& = \ frac {4} {\ text {3}} \\
& = \ текст {0,75} \ текст {Ω}
\ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {9} {\ text {0,75}} \\
& = \ текст {12} \ текст {А}
\ end {выровнять *}

Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:

Сначала находим общее сопротивление:

\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {24} {\ text {2}} \\
& = \ текст {12} \ текст {Ω}
\ end {выровнять *}

Теперь мы можем рассчитать неизвестное сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\
\ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ гидроразрыв {1} {R_ {3}} \\
& = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text { 60}} \\
& = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\
& = \ frac {4} {\ text {120}} \\
& = \ текст {30} \ текст {Ω}
\ end {выровнять *}

значение тока через аккумулятор

Рисуем принципиальную схему:

Чтобы вычислить значение тока через батарею, нам сначала нужно вычислить эквивалентное сопротивление:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\
& = \ frac {10 + 2 + 1} {\ text {10}} \\
& = \ frac {13} {\ text {10}} \\
& = \ текст {0,77} \ текст {Ω}
\ end {выровнять *}

Теперь можем посчитать ток через батарею:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {0,77}} \\
& = \ текст {26} \ текст {А}
\ end {выровнять *}

значение тока в каждом из трех резисторов.

Для параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из резисторов. Для этой схемы:

\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]

Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {1}} \\
& = \ текст {20} \ текст {А}
\ end {выровнять *}

Затем мы вычисляем ток через \ (R_ {2} \):

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {5}} \\
& = \ текст {4} \ текст {А}
\ end {выровнять *}

И наконец вычисляем ток через \ (R_ {3} \):

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {20} {\ text {10}} \\
& = \ текст {2} \ текст {А}
\ end {выровнять *}

Вы можете проверить, что они в сумме составляют общий ток.

Последовательные и параллельные сети резисторов (ESBQC)

Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы заняться цепями, которые объединяют эти две схемы, например, следующую схему:

Рисунок 11.1:
Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.

Проработать такие схемы относительно легко, потому что вы используете все, что вы уже узнали о последовательных и параллельных схемах.Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей, которые затем включены последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начинаете с вычисления общего сопротивления каждой из параллельных частей, а затем последовательно складываете эти сопротивления. Если бы все резисторы на рисунке 11.1 имели сопротивление \ (\ text {10} \) \ (\ text {Ω} \), мы можем вычислить эквивалентное сопротивление всей цепи.

Начнем с расчета общего сопротивления параллельной цепи 1 .{-1} \\
& = \ текст {5} \, \ Omega
\ end {align *}

Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:

Следовательно, эквивалентное сопротивление:
\ begin {align *}
R & = R_ {p1} + R_ {p2} \\
& = 5 + 5 \\
& = 10 \, \ Omega
\ end {align *}

Эквивалентное сопротивление цепи на рисунке 11.1 равно \ (\ text {10} \) \ (\ text {Ω} \).

Последовательные и параллельные сети

Упражнение 11.5

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {4} + \ frac {1} {2} \\
& = \ frac {3} {4} \\
R_ {p} & = \ text {1,33} \ text {Ω}
\ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *}
R_ {s} & = R_ {3} + R_ {p} \\
& = \ текст {2} + \ текст {1,33} \\
& = \ текст {3,33} \ текст {Ω}
\ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\
& = \ frac {1} {1} + \ frac {1} {2} \\
& = \ frac {3} {2} \\
R_ {p} & = \ text {0,67} \ text {Ω}
\ end {выровнять *}

Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *}
R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\
& = \ текст {4} + \ текст {6} + \ текст {0,67} \\
& = \ текст {10,67} \ текст {Ω}
\ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\
& = \ frac {23} {15} \\
R_ {p} & = \ text {0,652} \ text {Ω}
\ end {выровнять *}

\ begin {align *}
R_ {s} & = R_ {4} + R_ {p} \\
& = \ текст {2} + \ текст {0,652} \\
& = \ текст {2,652} \ текст {Ω}
\ end {выровнять *}

ток \ (I \) через ячейку.

Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *}
R_ {s} & = R_ {4} + R_ {p} \\
& = \ текст {2} + \ текст {0,652} \\
& = \ текст {2,652} \ текст {Ω}
\ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {12}} {\ text {2,652}} \\
& = \ текст {4,52} \ текст {А}
\ end {выровнять *}

ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).

Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ text {A} \). (Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):

\ begin {align *}
V & = I \ cdot R \\
& = (\ text {4,52}) (\ text {0,652}) \\
& = \ текст {2,95} \ текст {V}
\ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторе \ (\ text {5} \) \ (\ text {Ω} \).

Итак, теперь мы можем рассчитать ток через резистор:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {2,95}} {\ text {5}} \\
& = \ текст {0,59} \ текст {А}
\ end {выровнять *}

Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы омические, рассчитайте напряжение на ячейке и на каждом из резисторов, \ (R_1 \ ), \ (R_2 \) и \ (R_3 \) соответственно.

Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {2} + \ frac {1} {4} \\
& = \ frac {3} {4} \\
R_ {p} & = \ text {1,33} \ text {Ω}
\ end {выровнять *}

\ begin {align *}
R_ {s} & = R_ {1} + R_ {p} \\
& = \ text {4,66} + \ text {1,33} \\
& = \ текст {5,99} \ текст {Ω}
\ end {выровнять *}

Итак, напряжение на ячейке:

\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {2}) (\ текст {5,99}) \\
& = \ текст {12} \ текст {V}
\ end {выровнять *}

Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с нахождения напряжения на \ (R_ {1} \):

\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {2}) (\ текст {4,66}) \\
& = \ текст {9,32} \ текст {V}
\ end {выровнять *}

Теперь находим напряжение на параллельной комбинации:

\ begin {align *}
V & = I \ cdot R \\
& = (\ текст {2}) (\ текст {1,33}) \\
& = \ текст {2,66} \ текст {V}
\ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).

ток через ячейку

Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *}
\ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\
& = \ frac {1} {1} + \ frac {1} {1} \\
& = 2 \\
R_ {p} & = \ text {0,5} \ text {Ω}
\ end {выровнять *}

\ begin {align *}
R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\
& = \ text {2} + \ text {1,5} + \ text {0,5} \\
& = \ текст {4} \ текст {Ω}
\ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {10}} {\ text {4}} \\
& = \ текст {2,5} \ текст {А}
\ end {выровнять *}

падение напряжения на \ (R_4 \)

Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через \ (R_ {4} \):

\ begin {align *}
V & = I \ cdot R \\
& = (\ text {2,5}) (\ text {1,5}) \\
& = \ текст {3,75} \ текст {V}
\ end {выровнять *}

ток через \ (R_2 \)

Используя это, мы можем найти ток через \ (R_ {2} \).

Сначала нам нужно найти напряжение на параллельной комбинации:

\ begin {align *}
V & = I \ cdot R \\
& = (\ text {2,5}) (\ text {0,5}) \\
& = \ текст {1,25} \ текст {V}
\ end {выровнять *}

Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на всех резисторах в параллельной комбинации:

\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {1,25}} {\ text {1}} \\
& = \ текст {1,25} \ текст {А}
\ end {выровнять *}

электросчетчиков

Вольтметры

Вольтметры — это инструменты, используемые для измерения разности потенциалов между двумя точками в цепи.Вольтметр подключается параллельно измеряемому элементу, что означает создание пути переменного тока вокруг измеряемого элемента и через вольтметр. Вы правильно подключили вольтметр, если вы можете удалить вольтметр из цепи, не разрывая цепь. На схеме справа вольтметр подключен для правильного измерения разности потенциалов на лампе. Вольтметры имеют очень высокое сопротивление, чтобы минимизировать ток, протекающий через вольтметр, и влияние вольтметра на цепь.

Амперметры

Амперметры — это инструменты, используемые для измерения тока в цепи. Амперметр включен последовательно со схемой, так что измеряемый ток протекает непосредственно через амперметр. Чтобы правильно вставить амперметр, цепь должна быть разомкнута. Амперметры имеют очень низкое сопротивление, чтобы минимизировать падение потенциала через амперметр и воздействие амперметра на цепь, поэтому включение амперметра в цепь параллельно может привести к очень высоким токам и может вывести из строя амперметр.На схеме справа амперметр подключен правильно для измерения тока, протекающего по цепи.

Вопрос: На электрической схеме справа возможно
расположение амперметра и вольтметра
обозначены кружками 1, 2, 3 и 4. Где должен быть расположен амперметр, чтобы
правильно измерить полный ток и где
должен ли вольтметр быть правильно расположен
измерить общее напряжение?
Ответ: Для измерения полного тока амперметр должен быть помещен в положение 1, так как весь ток в цепи должен проходить через этот провод, а амперметры всегда подключаются последовательно.
Для измерения общего напряжения в цепи вольтметр может быть размещен либо в позиции 3, либо в позиции 4. Вольтметры всегда размещаются параллельно с анализируемым элементом цепи, а позиции 3 и 4 эквивалентны, потому что они соединены проводами ( и потенциал всегда одинаков в любом месте идеального провода).
Вопрос: На какой схеме ниже правильно показано соединение амперметра A и вольтметра V для измерения сквозного тока и разности потенциалов на резисторе R?
Ответ: (4) показывает амперметр, включенный последовательно, и вольтметр, подключенный параллельно резистору.
Вопрос: По сравнению с сопротивлением измеряемой цепи внутреннее сопротивление вольтметра спроектировано так, чтобы оно было очень высоким, поэтому счетчик не будет потреблять ток из цепи
мало тока из цепи
большая часть тока от цепи
весь ток из схемы
Ответ: (2) вольтметр должен потреблять как можно меньше тока из схемы, чтобы минимизировать его влияние на схему, но для работы требуется небольшое количество тока.

Схема

L-R-C — обзор

Решение

Мы действуем так же, как и в случае с дифференциальным уравнением, используя преобразование Лапласа для обеих сторон уравнения. Теорема свертки, уравнение (6.27), используется для определения преобразования Лапласа интеграла с

L {∫0tI (u) du} = L {1⁎I (t)} = L {1} L {I ( t)} = 1sL {I (t)}.

Следовательно, применение преобразования Лапласа дает

LsL {I (t)} — LI (0) + RL {I (t)} + 1C1sL {I (t)} = L {E (t)}.

Поскольку I (0) = 0, имеем LsL {I (t)} + RL {I (t)} + 1C1sL {I (t)} = L {E (t)}. Упрощение и решение для L {I (t)} приводит к L {I (t)} = CsL {E (t)} LCs2 + RCs + 1

Clear [i]

LaplaceTransform [li ′ [t] + ri [ t], t, s]

rLaplaceTransform [i [t], t, s] + l (−i [0] + sLaplaceTransform [i [t], t, s])

Решить [lslapi + rlapi + lapics == lape, lapi]

, так что I (t) = L − 1 {CsL {E (t)} LCs2 + RCs + 1}. В команде Solve мы используем lapi для обозначения L {I (t)} и lape для обозначения L {E (t)}.Для (b) заметим, что E (t) = {sin⁡t, 0⩽t <π / 20, t⩾π / 2 может быть записано как E (t) = sin⁡t (U (t) −U (t − π / 2)). Определим и построим вынуждающую функцию E (t) на интервале [0, π] на рис. 6.23 (a).

Рисунок 6.23. (a) График E (t) = sin⁡t (U (t) −U (t − π / 2)). (b) I ( т ). (Цвета Университета Миссури)

Мы используем строчные буквы, чтобы избежать возможной двусмысленности со встроенными функциями Mathematica, такими как E и I.

e [t _]: = Sin [t] (UnitStep [t] −UnitStep [t −π2])

p1 = График [e [t], {t, 0, π}, PlotStyle →

{{Толщина [.01], CMYKColor [0, .25, .9, .05]}}]

Затем мы вычисляем преобразование Лапласа L {E (t)} с помощью LaplaceTransform. Мы называем этот результат lcape.

lcape = LaplaceTransform [e [t], t, s]

11 + s2 − e − πs2s1 + s2

Используя общую формулу, полученную для преобразования Лапласа I (t), отметим, что знаменатель этого Выражение задается как s2 + s + 1, которое вводится как denom. Следовательно, преобразование Лапласа I (t), называемое lcapi, задается отношением s lcape / denom.

деном = s2 + s + 1;

lcapi = slcape / denom;

lcapi = Упростить [lcapi]

s − e − πs2s21 + s + 2s2 + s3 + s4

Мы определяем I (t) с помощью InverseLaplaceTransform.Обратите внимание, что HeavisideTheta [x] определяется как θ (x) = {0, если x <01, если x> 0.

i [t _] = InverseLaplaceTransform [lcapi, s, t]

Sin [t] −HeavisideTheta [−π2 + t] (- e14 (π − 2t) (3Cos [143 (π − 2t)] + Sin [ 143 (π − 2t)]) 3 + Sin [t]) — 2e − t / 2Sin [3t2] 3

Это решение отображается в p2 (черным цветом) и отображается с функцией принуждения (серым цветом) на рис. 6.23 (б). Обратите внимание на влияние функции принуждения на решение дифференциального уравнения.

p2 = График [i [t], {t, 0,10}, PlotStyle →

{{Толщина [.01], CMYKColor [0, 0,25, .9, .05]}}];

Показать [p1, p2, PlotRange → All]

Показать [GraphicsRow [{p1, p2}]]

В этом случае мы видим, что можем использовать DSolve для решения задачи начального значения

Q ″ + Q ′ + Q = E (t), Q (0) = 0, Q ′ (0) = 0

. Однако неупрощенный результат очень длинный, поэтому мы используем FullSimplify, чтобы попытаться максимально упростить результат.

Очистить [q]

sol = DSolve [{q ″ [t] + q ′ [t] + q [t] == e [t], q [0] == 0, q ′ [0] ==) 0} ,.

q [t], t] // FullSimplify

{{q [t] → {−Cos [t] + 13e − t / 2 (3Cos [3t2] + 3Sin [3t2]) t⩾0 && 2t⩽π13e− t / 2 (3Cos [3t2] +3 (−2eπ / 4Sin [143 (π − 2t)] + Sin [3t2])) 2t> π0True}}

Мы видим, что этот результат является вещественной функцией, используя ComplexExpand с последующим упрощением.

q [t _] = ComplexExpand [sol [[1,1,2]]] // Упростить

{−Cos [t] + 3Cos [3t2] + 3Sin [3t2] 3ett⩾0 && 2t⩽π3Cos [3t2] + 3 (−2eπ / 4Sin [143 (π − 2t)] + Sin [3t2]) 3et2t> π0True

Мы используем этот результат для построения графика Q (t) и I (t) = Q ′ (t) на рис. 6.24. .

Рисунок 6.24. Q ( t ) и I ( t ) = Q ^′ ( t ).

График [{q [t], q ′ [t]}, {t, 0,10},

PlotStyle → {{CMYKColor [0, .25, .9, .05]},

{CMYKColor [.6, .5, .4,1]}}] □

Патент США на электрическую цепь, имеющую средства сигнализации Патент (Патент № 8,379,362, выдан 19 февраля 2013 г.)

ССЫЛКА НА СООТВЕТСТВУЮЩИЕ ЗАЯВКИ

Это приложение является национальным этапом в соответствии с 35 U.S.C. 371 международной заявки РСТ № PCT / EP2009 / 052907, поданной 12 марта 2009 г., в которой испрашивается приоритет заявки Германии № 20 2008 005 085.5, поданной 11 апреля 2008 г. Она связана с заявкой изобретателя в США сер. №№ 12/934 937 и 12/935 001, оба поданы сен.27, 2010.

Уровень техники

1. Область изобретения

Устройство индикации предназначено для индикации рабочего состояния электрического компонента системы защиты от нагрузки, включая корпус, содержащий продольную камеру, индикаторный элемент. установленное с возможностью продольного смещения в камере корпуса, упругое устройство, обычно смещающее индикаторный элемент к первому концу корпуса, фиксирующее приспособление для удержания индикаторного элемента во втянутом положении рядом со вторым концом корпуса; и расцепляющее устройство, реагирующее на импульс напряжения неисправности, для приведения в действие защелкивающего устройства в разблокированное состояние, чтобы тем самым высвободить индикаторный элемент для смещения упругим устройством к позиции индикатора рядом с первым концом корпуса.

2. Описание предшествующего уровня техники

Электрические системы, например, электрические установки или электрические линии, защищены от аварийных ситуаций для обеспечения безотказной работы с помощью защитных устройств от нарушения их функции и / или от разрушения.

Эти электрические цепи со средствами сигнализации могут сигнализировать по крайней мере об одном функциональном состоянии, например, о функциональном состоянии или неисправности, для защитного устройства. Таким образом, можно упростить проверку и / или обслуживание защитных устройств, поскольку специалисту, которому поручено наблюдение, не нужно проводить никаких измерений на защитном устройстве, чтобы получить информацию о функциональном состоянии этого устройства.Функциональное состояние контролируемого защитного устройства может быть определено непосредственно с помощью сигнального воздействия, например, с помощью оптической сигнализации.

В контексте настоящего изобретения событие неисправности предназначено для обозначения события, возникновение которого воздействует на электрическую систему с помощью электрической энергии, в частности, таким образом, что упорядоченное функционирование электрической системы нарушается или нарушается. Примерами аварийных событий являются удары молнии или статические разряды, в результате которых импульсы перенапряжения и / или импульсы сверхтока вводятся, например, гальванически, индуктивно или емкостно в электрическую систему, тем самым нарушая или нарушая ее работу. система.Устройства защиты от импульсов перенапряжения имеют защитные элементы, в том числе, например, искровые разрядники, варисторы, диоды, подавляющие диоды, и хорошо знакомы специалисту. Такие защитные устройства также называются OVP (защита от перенапряжения).

Кроме того, в контексте этого изобретения под событием неисправности понимается скачок напряжения, при котором электрическая система, например, линия электропередачи, может быть перегружена и / или разрушена посредством короткого замыкания или короткого замыкания. К земле, приземляться.Защитные устройства, обеспечивающие защиту от токов перенапряжения, обычно называются плавкими предохранителями и знакомы специалисту по множеству различных моделей, например, в виде свинцовых плавких предохранителей или автоматических выключателей.

Также известны схемы со средствами сигнализации по меньшей мере одного функционального состояния. Обратимся теперь к фиг. 3 a и 3 b для объяснения такой известной схемы предшествующего уровня техники. Показан предохранитель, соединяющий две точки прямого электрического разрыва.Чтобы сигнализировать о функциональном состоянии предохранителя, параллельно к нему подключено последовательное соединение, состоящее из умножителя напряжения и встречная параллельная цепь, состоящая из двух светодиодов. Если предохранитель функционирует должным образом, тогда напряжение между двумя точками разрыва будет слишком маленьким для подачи на светодиоды напряжения, достаточного для их включения. Если, например, предохранитель разрушается из-за чрезмерно высокого тока и, следовательно, он прерывает прохождение тока, тогда напряжение между двумя точками прямого разрыва возрастает, и на светодиоды будет подаваться соответствующее напряжение, чтобы сигнализировать о неисправности. предохранителя в рабочем состоянии загорается таким образом.Очевидно, что в зависимости от типа напряжения, будь то постоянное или переменное напряжение, в каждом случае будут гореть только один или оба светодиода.

Недостатком известных схем является тот факт, что средства, используемые для сигнализации, например светодиоды, требуют электроэнергии для поддержания функции сигнализации и вызывают воздействие на защитное устройство, функция которого должна контролироваться и / или объект, поставляющий электроэнергию.

Настоящее изобретение было разработано для решения этих проблем с помощью усовершенствованной схемы электрической защиты, оснащенной средствами сигнализации для сигнализации о неисправных состояниях.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Соответственно, основной задачей настоящего изобретения является создание показывающего устройства для индикации рабочего состояния электрического компонента системы защиты от нагрузки, включая корпус, содержащий продольную камеру, установленный показывающий элемент. для продольного смещения в камере корпуса упругое устройство, обычно смещающее индикаторный элемент к первому концу корпуса, фиксирующее приспособление для удержания индикаторного элемента во втянутом положении рядом со вторым концом корпуса, а также спусковое устройство, реагирующее на импульс напряжения для приведения защелки в исходное состояние, чтобы высвободить показывающий элемент для смещения упругим устройством в направлении показывающего положения рядом с первым концом корпуса.

Согласно более конкретной цели изобретения, по меньшей мере, первый конец корпуса является прозрачным, чтобы обеспечивать визуальную индикацию, когда указывающий элемент находится в указательном положении. Указывающий элемент может иметь один или несколько отличительных цветов.

В соответствии с другой задачей могут быть предусмотрены переключающие контакты, которые работают между открытым и закрытым состояниями, когда указывающий элемент находится в показательном положении, тем самым обеспечивая электрическую индикацию положения показывающего элемента относительно корпуса.

Еще одна цель состоит в том, чтобы предоставить средство сигнализации, которое выполняется в импульсном и стабильном режиме, которое после активации импульса не имеет никаких последствий для схемы и которое предназначено для постоянной, энергонезависимой сигнализации.

В противном случае, предпочтительно для постоянной сигнализации функционального состояния, не требуется никакой электрической энергии, и можно предотвратить воздействие средств сигнализации.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Другие цели и преимущества изобретения станут очевидными из изучения следующего описания, если рассматривать его в свете сопроводительного чертежа, на котором:

ФИГ.1 a и 1 b — продольные виды в разрезе показывающего устройства согласно настоящему изобретению в условиях убранного и расширенного просмотра, соответственно;

РИС. 2 a и 2 b иллюстрируют модификацию устройства по фиг. 1 a и 1 b , включая электрические контакты, которые работают между первым и вторым состояниями, когда указывающий элемент находится в отведенном и выдвинутом положениях соответственно;

РИС.3 a и 3 b указывают состояние плавкого предохранителя, указывающее на расположение известного уровня техники, когда защитный плавкий предохранитель находится в проводящем и сгоревшем состояниях, соответственно, и фиг. 4 a и 4 b — соответствующие виды схемы защиты плавким предохранителем, снабженной показывающим устройством по настоящему изобретению; и

ФИГ. 5 a и 5 b — это принципиальные схемы полной системы защиты настоящего изобретения в неактивном и активном состояниях соответственно.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Сначала обратимся к фиг. 1 и 2, сигнальное устройство 1 настоящего изобретения включает в себя полый корпус 3 , который установлен в отверстии, содержащемся в опорной стенке 2 , причем указанный корпус содержит вертикальную продольную камеру C и включает верхнюю первую и нижние вторые концевые части 4 a и 4 b . Предпочтительно, по меньшей мере, верхняя концевая часть , 4, , , корпуса выполнена из прозрачного синтетического пластика.Для скользящего продольного смещения в камере С корпуса установлен индикаторный элемент 5 , имеющий в целом чашеобразную форму перевернутой формы. Спиральная пружина сжатия 7 смещает индикаторный элемент 5 вверх в камере C корпуса из втянутого положения на фиг. 1 a по направлению к верхнему положению индикации на фиг. 1 b рядом с прозрачным верхним концом корпуса 4 a . Показывающий элемент 5 обычно удерживается во втянутом положении, показанном на фиг.1 a с помощью средства захвата 8 , включая элемент захвата 8 c , поддерживаемый против вертикального смещения в камере C, этот элемент захвата снабжен выступом захвата 8 a , который проходит внутри противоположной защелки отверстие 8 b , содержащееся в кольцевой части стенки индикаторного элемента 5 .

Улавливающий элемент 8 c предпочтительно сформирован из ферромагнитного материала, который определяет якорь соленоидного средства 9 , включая соленоид 9 e , установленный против вертикального смещения в камере C.На соленоид 9 e подается импульс напряжения неисправности V _T от средств диагностики 16 через клеммы соленоида 9 c и 9 d и проводники 9 a и 9 b , соответственно, чтобы привлечь якорь 8 c , чтобы вывести выступ захвата 8 a из отверстия 8 b . Показывающий элемент 5 , таким образом, освобождается и смещается вверх пружиной 7 сжатия в направлении показывающего положения на фиг.1 b , после чего индикаторный элемент становится видимым через прозрачную торцевую стенку корпуса 4 a . Чтобы увеличить видимость указывающего элемента 5 , он может быть снабжен одним или несколькими отличительными цветами, включая флуоресцентные цвета.

Средство сброса предусмотрено для сброса показывающего элемента на его фиг. 1 во втянутом положении, указанное средство сброса включает в себя управляемый вручную стержень 30 , который с возможностью скольжения проходит вниз через отверстие, содержащееся в верхней концевой части корпуса 4 a .Следовательно, показывающий элемент 5 может быть сброшен из второго положения снова в первое положение, например, после ремонта защитного устройства, которое необходимо контролировать.

Согласно модификации изобретения, показанной на фиг. 2 a и 2 b , показывающее устройство 1 может быть снабжено нормально замкнутыми подвижными и стационарными переключающими контактами 10 c и 10 d соответственно.Подвижный контакт 10 c установлен на индикаторном элементе 5 для перекрытия зацепления с неподвижным контактом 10 d , когда индикаторный элемент 5 находится в отведенном положении, показанном на фиг. 2 а . Стационарный контакт имеет отдельные части, соединенные с выводами переключателя 10 a и 10 b , которые отходят от нижней второй концевой части корпуса 3 .Следовательно, когда импульс неисправности V _T подается на клеммы соленоида 9 c и 9 d , на соленоид 9 подается питание, чтобы притягивать якорь 8 c , тем самым отводя его. выступ защелки 8 a из отверстия 8 b . Индикаторный элемент освобождается для смещения вверх пружиной сжатия 7 , после чего контакты переключателя 10 c и 10 d разъединяются, чтобы разорвать внутреннее соединение между выводами переключателя 10 a и 10 б.

В устройстве предшествующего уровня техники на фиг. 3 a и 3 b было предложено предусмотреть средства индикации 12 в виде пары светодиодов противоположной полярности, соединенных параллельно для визуальной индикации рабочего состояния предохранителя 11 . Светодиодная система соединена последовательно с резистором Rv регулировки напряжения, чтобы определить ветвь индикации, которая подключена к предохранителю 11 .

В соответствии с настоящим изобретением, светодиодная система предшествующего уровня техники заменена средством сигнализации 1 настоящего изобретения, как показано на фиг. 4 a и 4 b . В этом случае, когда импульс неисправности отправляется в средство сигнализации 1 по фиг. 4 a , соленоидное средство 9 активируется для притяжения якоря для освобождения фиксатора 8 , после чего индикаторный элемент 5 смещается пружиной 7 в направлении состояния визуального отображения на ФИГ.4 b , а контакты средства переключения 10 разомкнуты. Таким образом, ток через электромагнит прерывается, электромагнит 9 не работает и, таким образом, не поглощает электрическую мощность. Сигнальный элемент 5 остается во втором положении, как показано на фиг. 4 b (см. Также фиг. 1 b и 2 b ) и постоянно сигнализирует о функциональном состоянии защитного устройства. При размыкании контактов 10 a , 10 b и 10 c , 10 d (см. РИС.2 a и 2 b ) гальваническое соединение между точками подключения 13 и 14 прерывается, так что сигнальный элемент 5 не оказывает никакого воздействия на цепь и на защитное устройство, которое подлежит контролю, в данном случае предохранитель 11 .

Теперь обратимся к фиг. 5 a и 5 b , средство индикации состояния неисправности 1 настоящего изобретения проиллюстрировано в связи с системой защиты от перенапряжения 15 , в которой электроэнергия от источника 32 подается на нагрузка 34 , например промышленная печатная плата, усилитель и т.п.Схема защиты включает три линии L 1 , L 2 , L 3 с входными клеммами E 1 , E 2 , E 3 , подключенными к источнику питания 32 , и три выхода клеммы A 1 , A 2 и A 3 , подключенные к нагрузке 34 соответственно. При возникновении серьезного аварийного события, такого как молния или серьезный скачок перенапряжения, устройство грубой защиты по напряжению FS служит для рассеивания большей части энергии электрической аварии.Как известно в данной области техники, устройство грубой защиты FS включает в себя полый корпус, содержащий средства, определяющие первый искровой промежуток между третьей и первой линиями L 3 и L 1 , а также средства, определяющие второй искровой промежуток между третьей и первой линиями. вторые линии L 3 и L 2 .

Средства точной защиты предназначены для защиты нагрузки от остаточной энергии, которая может оставаться в цепи. В связи с этим первая и вторая линии L 1 и L 2 содержат последовательно включенные резисторы R 1 и R 2 соответственно, а третья линия L 3 поддерживается при заданном потенциале PE. из источника 36 .Первый и второй подавляющие диоды SD 1 и SD 2 имеют первые электроды, подключенные к первой и второй линиям L 1 и L 2 , соответственно, а вторые электроды подключены к общему измерительному переходу M, который соединен с третьей линией L 3 через ответвление цепи, включающее пару диодов D 1 и D 2 противоположной полярности, соединенных параллельно.

Устройство искрового разрядника FS и подавляющие диоды SD 1 и SD 2 подлежат разрушению при возникновении серьезной неисправности.Чтобы указать состояние работы подавляющих диодов SD 1 и SD 2 , диагностическая схема 16 подключена между измерительным переходом M и третьей линией L 3 параллельно через параллельную ветвь, определяемую диоды D 1 и D 2 . Диагностическая схема 16 сравнивает напряжение на диодной ветви с опорным напряжением V _R, подаваемым источником 38 , и при обнаружении неисправности посылает сигнал неисправности V _T на соленоид 9 показывающего устройства 1 .Затем средство индикации 1 приводится в действие из начального втянутого состояния, показанного на фиг. 5 a к условию индикации на фиг. 5 b , так что показывающий элемент 5 находится в видимом положении относительно своего корпуса, а переключающий контакт 10 c приводится в разомкнутое состояние, тем самым отключая электрическое средство индикации 17 .

В любом случае защитное устройство 15 и электрическая система, которая должна быть защищена, установлены и подключены таким образом, что в случае возникновения неисправности на входе защитного устройства 15 будет подаваемая электрическая энергия.Импульс электрической неисправности V _T активирует сигнальное устройство 5 , так что будет постоянная и обесточенная сигнализация функционального состояния защитного устройства 15 . Кроме того, здесь снова любые последствия устраняются посредством схемы разводки, поясненной на основе фиг. 4 a и 4 b с сошником, образованным средствами 10 a , 10 b и 10 c , 10 d (см.2 a и 2 b ). В дополнение к уже описанному контакту средство сигнализации 5 может иметь другой контакт 17 a , например, дополнительную систему 17 для сообщения о функциональном состоянии и электрическую систему индикации или записи.

Хотя в соответствии с положениями Патентного устава были проиллюстрированы и описаны предпочтительные формы и варианты осуществления изобретения, для специалистов в данной области техники будет очевидно, что изменения могут быть внесены без отклонения от изобретения, описанного выше.

5. Применение ODE: Серия RL Circuit

Схема подключения

Цепь RL
на показанном выше резисторе и катушке индуктивности соединены последовательно. Постоянное напряжение В подается, когда переключатель находится в
закрыто.

(переменное) напряжение на резисторе определяется по формуле:

`V_R = iR`

(переменное) напряжение на катушке индуктивности определяется по формуле:

`V_L = L (di) / (dt)`

Закон Кирхгофа по напряжению гласит, что направленная сумма напряжений в цепи должна быть равна нулю.(- (R «/» L) t)) `

Проба

Начнем с:

`Ri + L (di) / (dt) = V`

Вычитая Ri с обеих сторон:

`L (di) / (dt) = V-Ri`

Разделите обе стороны на L :

` (di) / (dt) = (V-Ri) / L`

Умножьте обе стороны на dt и разделите обе на ( V — Ri ):

` (ди) / (V-Ri) = (dt) / L`

Интеграция (см. Интеграция: основная форма логарифма):

`int (di) / (V-Ri) = int (dt) / L`
`- (ln (V-Ri)) / R = 1 / Lt + K`

Теперь, поскольку `i = 0` при` t = 0`, мы имеем:

`К = — (ln \ V) / R`

Подставляя K обратно в наше выражение:

`- (ln (V-Ri)) / R = 1 / Lt- (ln V) / R`

Перестановка:

`(ln \ V) / R- (ln (V-Ri)) / R = 1 / Lt`

Умножение на — R :

`-ln \ V + ln (V-Ri) = — R / Lt`

Собираем части логарифма вместе:

`ln ((V-Ri) / V) = — R / Lt`

Принимая « e в обе стороны»:

`(V-Ri) / V = e ^ (- (R» / «L) t`
`1-R / Vi = e ^ (- (R» / «L) t`

Вычитая 1 с обеих сторон:

`-R / Vi = -1 + e ^ (- (R» / «L) t`

Умножение обеих сторон на `- (V / R)`:

`i = V / R (1-e ^ (- (R» / «L) t))`

[Мы сделали ту же проблему, но с определенными значениями в разделе 2.(-t «/» \ tau)) `

Давайте теперь рассмотрим несколько примеров цепей RL.

Пример 1

Цепь RL имеет ЭДС 5 В, сопротивление 50 Ом,
индуктивность 1 Гн, начальный ток отсутствует.

Найти ток в цепи в любой момент t .
Различают переходный и установившийся ток.

Ответ

Метод 1 — Решение DE

Формула: `Ri + L (di) / (dt) = V`

После замены: `50i + (di) / (dt) = 5`

Мы перестраиваем, чтобы получить:

` (di) / (dt) + 50i = 5`

Это линейное дифференциальное уравнение первого порядка.(-50т)) `.

В этом примере постоянная времени TC равна

`тау = L / R = 1/50 = 0,02`

Итак, мы видим, что ток достиг установившегося состояния к t = 0,02 \ times 5 = 0,1 \ «с».

Метод 3: Использование решения ODE

от Scientific Notebook’s Solve

Если у вас есть Scientific Notebook, действуйте следующим образом:

Этот DE имеет начальное условие i (0) = 0. (- 5t)) `.(-5t) `(серым цветом).

Постоянная времени TC для этого примера:

тау = L / R = 10/50 = 0,2`

ПРИМЕЧАНИЕ (просто для интереса и сравнения): Если бы мы не могли использовать формулу в (a) и не использовали разделение переменных, мы могли бы признать, что DE является линейным 1-го порядка, и поэтому мы могли бы решить его, используя интегрирующий фактор.

Используем формулу:

`Ri + L (di) / (dt) = V`

Требуемый DE:

`10 (ди) / (дт) + 50i = 100`

` (di) / (dt) + 5i = 10`

«» И.(-5т)) `

Работает 🙂

Цепи с двумя ячейками

Следующие два примера относятся к типам с двумя сетками, в которых дифференциальные уравнения становятся более сложными. Мы будем использовать Scientific Notebook для выполнения основной работы после того, как составим правильные уравнения.

Пример 3

В сети с двумя ячейками, показанной ниже, коммутатор замкнут в
t = 0, а источник напряжения равен В = 150
sin 1000 t В. Найти сеточные токи i ₁
и i ₂, как показано на схеме.

Ответ

Раньше мы не видели, как решать «2-ячеистые» сети. Мы рассматриваем полное напряжение внутреннего контура и полное напряжение внешнего контура. Затем мы решаем полученные два уравнения одновременно.

Используем основную формулу: `Ri + L (di) / (dt) = V`

С учетом внутреннего цикла:

`10 (i_1 + i_2) + 5i_1 + 0,01 (di_1) / (dt) =` 150 sin 1000t`

`15 \ i_1 + 10 \ i_2 + 0,01 (di_1) / (dt) =` 150 sin 1000t`

`3i_1 + 2i_2 + 0.002 (di_1) / (dt) = « 30 sin 1000t \ \ \ … (1) `

Теперь, учитывая внешний цикл:

`10 (i_1 + i_2) + 5i_2 = 150 sin 1000t`

`10i_1 + 15i_2 = 150 sin 1000t`

`2i_1 + 3i_2 = 30 sin 1000t \ \ \ … (2)`

Теперь мы решаем (1) и (2) одновременно:

(1) × 3 — (2) × 2 дает:

`5i_1 + 0,006 (di_1) / (dt) = 30 sin 1000t`

Решение этой проблемы с использованием SNB с граничным условием i ₁ (0) = 0 дает:

`i_1 (t) = — 2.(-833т) `

График i ₂:

График текущего `i_2` в момент` t`. Он также находится в устойчивом состоянии примерно на «t = 0,007».

Пример 4

Коммутатор замкнут при t = 0 в двухъячеистой сети
показано ниже. Источник напряжения равен В = 30 sin
100 t В. Найдите сеточные токи i ₁ и
i ₂, как показано на диаграмме.

Ответ

Решаем 2 способами:

1.Составление уравнений и получение помощи SNB для их решения.

2. Непосредственное использование SNB для одновременного решения 2 уравнений.

Решение 1

Используем основную формулу: `Ri + L (di) / (dt) = V`

Рассматривая левую петлю, ток через резистор 8 Ом противоположен для «i_1» и «i_2». Мы рассматриваем i_1 как имеющее положительное направление:

`0,2 (di_1) / (dt) +8 (i_1-i_2) =` `30 sin 100t \ \ \ … (1)`

Теперь мы рассматриваем правую петлю и считаем направление `i_2` положительным:

`8 (i_2-i_1) + 4i_2 = 0`

`12i_2-8i_1 = 0`

`i_2 = 2 / 3i_1 \ \ \.(-13,3 т) `

Это, конечно, тот же график, только это «2/3» амплитуды:

График текущего `i_2` в момент` t`. Он также находится в устойчивом состоянии примерно на t = 0,25.

Решение 2. Прямое использование SNB

Если мы попытаемся решить его с помощью Scientific Notebook, как показано ниже, не удастся , потому что он может решить только 2 дифференциальных уравнения одновременно (вторая строка не является дифференциальным уравнением):

`0,2 (di_1) / (dt) +8 (i_1-i_2) = 30 sin 100t`

`i_2 = 2 / 3i_1`

`i_1 (0) = 0`

`i_2 (0) = 0`

Но если мы дифференцируем вторую строку следующим образом (превращая ее в дифференциальное уравнение, чтобы у нас было 2 DE с 2 неизвестными), SNB с радостью решит его, используя Compute → Solve ODE.-9`.

Обрыв и короткое замыкание

Ultimate Electronics: практическое проектирование и анализ схем

Особое поведение при двух крайностях сопротивления: нуле и бесконечности.

Читать 4 мин

Обрыв цепи и короткое замыкание — два специальных термина, которые представляют противоположные крайние значения числовой линии сопротивления.

Мы можем посмотреть на схему, посмотрев на любую пару открытых клемм:

В контексте любых двух выводов цепи:

Короткое замыкание означает, что две клеммы соединены извне с сопротивлением R = 0
, так же, как идеальный провод.Это означает, что для любого значения тока существует нулевая разница напряжений. (Обратите внимание, что настоящие провода имеют ненулевое сопротивление!)

Разрыв цепи означает, что две клеммы являются точками, которые внешне отключены , что эквивалентно сопротивлению R = ∞
. Это означает, что между двумя выводами может течь нулевой ток, независимо от разницы напряжений. (Обратите внимание, что очень высокое напряжение может вызвать протекание дуги тока даже через большие воздушные или вакуумные зазоры!)

Концепция рассмотрения двух выводов цепи и изучения поведения этих двух крайностей является мощной.

Как в теории, так и на практике слово «внешне» не имеет особого значения. Это произвольная граница, отделяющая «исходное» поведение схемы от нового поведения, когда мы вносим определенные изменения в любую пару узлов. Эта искусственная граница рассматривает остальную часть схемы, внутренние части черного ящика, как немодифицированные. Сделав это предположение, мы можем сделать только одно небольшое изменение вне черного ящика и увидеть его влияние на черный ящик.

Идеальный вольтметр на обрыв.Обрыв цепи — это ограничивающее приближение для реального вольтметра, который будет иметь некоторое большое (но не бесконечное) сопротивление.

Идеальный амперметр — короткозамкнутый. Короткое замыкание — это ограничивающее приближение для реального амперметра, который будет иметь небольшое (но не нулевое) сопротивление.

Подробнее см. В разделе «Мультиметры и измерения».

Подобно тому, как вольтметр и амперметр измеряют, подключая два щупа к цепи, теоретический анализ часто выполняется, рассматривая только два узла цепи.

Обрыв и короткое замыкание обеспечивают две полезные точки на кривой V-I.

В частности:

Напряжение разомкнутой цепи — это разность напряжений, измеренная между двумя клеммами, когда ток не подается и не подается.
Ток короткого замыкания — это ток, который протекает, когда клеммы вынуждены иметь нулевую разность напряжений.

Мы будем использовать эти два значения в эквивалентных схемах Тевенина и Нортона.

На практике мы хотели бы, чтобы схемы, которые мы строим, выдерживали как нормальные условия, для которых они предназначены, так и некоторые необычные условия, которые случаются время от времени, но не должны приводить к необратимым повреждениям.

Обрыв цепи случается даже тогда, когда он нежелателен. Например, всякий раз, когда что-то отключается или отключается, у нас возникает состояние разомкнутой цепи.

Короткие замыкания случаются даже тогда, когда они нежелательны. Например, если разъем на мгновение закорачивает между двумя клеммами при установке или крошечная металлическая стружка оказывается в неправильном месте, мы имеем дело с коротким замыканием.

По возможности, мы должны спроектировать так, чтобы обрыв и короткое замыкание происходили в различных местах в цепи, особенно на любых открытых входах и выходах. Мы должны проектировать так, чтобы любые сбои были временными и / или устраняемыми, например, с автоматическим выключателем.

Преднамеренное R = 0 Ом
резисторы (короткое замыкание) иногда добавляются к печатной плате, потому что разработчик хочет гибкости для изменения значения без необходимости перепроектировать печатную плату позже, если они хотят добавить некоторое ненулевое последовательное сопротивление (или другой последовательный компонент) в будущем .

Точно так же иногда добавляются преднамеренные перемычки (разомкнутая цепь), потому что разработчик хочет гибкости для подключения секции позже, возможно, для добавления параллельного сопротивления.

Оба они позволяют гибко вносить изменения, разделяя при этом одни и те же производственные накладные расходы. Это снижает затраты на единицу и позволяет избежать дорогостоящих затрат времени на реконструкцию.

В следующем разделе, Эквивалентные схемы Thevenin и Norton Equivalent Circuits, мы увидим, как двухконтактную концепцию можно применить для упрощенного приближения того, что находится в «схеме черного ящика», помеченной выше.

Роббинс, Майкл Ф. Ultimate Electronics: Практическое проектирование и анализ схем. CircuitLab, Inc., 2021, ultimateelectronicsbook.com. Доступно. (Авторское право © CircuitLab, Inc., 2021)

Как использовать макетную плату

Убедитесь, что в вашем браузере включен JavaScript. Если вы оставите отключенным JavaScript, вы получите доступ только к части предоставляемого нами контента. Вот как.

Во многих проектах в области электроники используется так называемая макетная плата .Что такое макетная плата и как ее использовать? Это обучающее видео даст вам базовое введение в макетные платы и объяснит, как использовать их в проектах для начинающих электронщиков; вы также можете прочитать более подробную информацию и увидеть больше примеров в текстовых разделах.

Подробнее о макетных платах

Введение

Что такое макетная плата?

Макетная плата — это прямоугольная пластиковая плата с кучей крошечных отверстий.Эти отверстия позволяют легко вставлять электронные компоненты в прототип (что означает создание и тестирование ранней версии) электронной схемы, такой как эта, с батареей, переключателем, резистором и светодиодом (светоизлучающим диодом). Чтобы узнать больше об отдельных электронных компонентах, см. Наши
Электроника Праймер.

Соединения не являются постоянными, поэтому легко удалить компонент, если вы допустили ошибку, или просто начнете заново и выполните новый проект.Благодаря этому макетные платы отлично подходят для начинающих, которые плохо знакомы с электроникой. Вы можете использовать макеты для создания всевозможных забавных проектов в области электроники, от различных типов роботов или электронной барабанной установки до электронного датчика дождя, который помогает экономить воду в саду, и это лишь некоторые из них.

Откуда взялось название «макетная плата»?

Вам может быть интересно, какое отношение все это имеет к хлебу. Термин макетная плата пришла из первых дней развития электроники, когда люди буквально забивали гвозди или шурупы в деревянные доски, на которых они резали хлеб, чтобы соединить свои схемы.К счастью, поскольку вы, вероятно, не хотите портить все свои разделочные доски ради проекта электроники, сегодня есть варианты получше.

Существуют ли разные макеты?

Современные макеты изготавливаются из пластика и бывают разных форм, размеров и даже разных цветов. Хотя доступны большие и меньшие размеры, наиболее распространенными размерами, которые вы, вероятно, увидите, являются «полноразмерные», «половинные» и «мини» макеты. Большинство макетов также имеют выступы и выемки по бокам, которые позволяют соединять несколько плат вместе.Однако для многих проектов начального уровня достаточно одной макетной платы половинного размера.

Что такое макетная плата без пайки?

Технически эти макеты называются беспаечными макетами , потому что они не требуют пайки для соединения. Пайка (произносится как SAW-der-ing) — это метод, при котором электронные компоненты соединяются путем плавления металла особого типа, называемого припоем . Электронные компоненты могут быть спаяны друг с другом напрямую, но чаще они припаяны к печатным платам (PCB).Печатные платы — это то, что вы увидите, если снимете крышку со многих электронных устройств, таких как компьютер или мобильный телефон. Часто инженеры используют макетные платы без пайки для создания прототипа и тестирования схемы перед построением окончательной постоянной конструкции на печатной плате. На этом изображении показана одна и та же схема (батарея, переключатель, резистор и светодиод), построенная тремя разными способами: на макетной плате без пайки (слева), с компонентами, спаянными непосредственно вместе (в центре), и на печатной плате (справа):

Пайка — отличный способ изучить технику, если вы интересуетесь электроникой, но соединения намного более постоянны, и для начала требуется покупка некоторых инструментов.Остальная часть этого руководства будет посвящена беспаечным макетам, но вы можете прочитать наши
руководство по пайке
чтобы узнать больше о пайке.

Какие электронные компоненты совместимы с макетными платами?

Итак, как электронные компоненты помещаются в макетную плату? Многие электронные компоненты имеют длинные металлические ножки, называемые выводами (произносится как «светодиоды»). Иногда более короткие металлические ножки обозначаются как штифты . Почти все компоненты с выводами будут работать с макетной платой (чтобы узнать больше об этих компонентах и о том, какие типы работают с макетной платой, см.
Расширенный раздел).

Макетные платы

разработаны таким образом, что вы можете вставлять эти выводы в отверстия. Они будут удерживаться на месте достаточно плотно, чтобы они не выпали (даже если вы перевернули макетную плату), но достаточно легко, чтобы вы могли легко потянуть их, чтобы снять.

Нужны ли мне инструменты для работы с макетной платой?

Для использования макетной платы без пайки не требуется никаких специальных инструментов. Однако многие электронные компоненты очень крошечные, и вам может быть сложно с ними обращаться.С помощью миниатюрных плоскогубцев или пинцета легче извлекать мелкие детали.

Что внутри макета?

Выводы могут поместиться в макетную плату, потому что внутри макета состоит из рядов крошечных металлических зажимов. Так выглядят зажимы, снятые с макета.

Когда вы вставляете вывод компонента в отверстие в макете, один из этих зажимов захватывает его.

Некоторые макеты на самом деле сделаны из прозрачного пластика, поэтому вы можете видеть зажимы внутри.

Большинство макетных плат имеют защитный слой, предотвращающий выпадение металлических зажимов. Основа обычно представляет собой слой липкой двусторонней ленты, покрытой защитным слоем бумаги. Если вы хотите надолго «приклеить» макет к чему-то (например, к роботу), вам просто нужно снять слой бумаги, чтобы обнажить липкую ленту под ним.На этом изображении у макетной платы справа полностью удалена подложка (так что вы можете видеть все металлические зажимы). У макетной платы слева все еще есть липкая подложка, а один угол бумажного слоя оторван.

Макетные метки: строки, столбцы и шины

Что означают буквы и цифры на макете?

На большинстве макетов написано несколько цифр, букв, а также знаков «плюс» и «минус». Что все это значит? Хотя их внешний вид может отличаться от макета к макету, общее назначение всегда одно и то же.Эти метки помогут вам найти определенные отверстия на макетной плате, чтобы вы могли следовать указаниям при построении схемы. Если вы когда-либо использовали программу для работы с электронными таблицами, такую как Microsoft Excel® или Google Sheets ™, концепция в точности такая же. Номера строк и буквы столбцов помогают идентифицировать отдельные дыры в макете, как ячейки в электронной таблице. Например, все выделенные отверстия находятся в «столбце C».

Все выделенные отверстия находятся в «строке 12″.»

«Отверстие C12» — это место, где столбец C пересекает строку 12.

Что означают цветные линии и знаки плюс и минус?

А как насчет длинных полос на стороне макета, выделенных здесь желтым цветом?

Эти полосы обычно обозначаются красными и синими (или красными и черными) линиями со знаками плюс (+) и минус (-) соответственно. Они называются шинами , также называемыми рельсами , и обычно используются для подачи электроэнергии в вашу схему, когда вы подключаете их к аккумуляторной батарее или другому внешнему источнику питания.Вы можете услышать, что автобусы имеют разные названия; например, шина питания , положительная шина и шина напряжения все относятся к той, которая находится рядом с красной линией со знаком плюс (+). Точно так же отрицательная шина и заземляющая шина относятся к одной рядом с синей (или черной) линией со знаком минус (-). Это сбивает с толку? Используйте эту таблицу, чтобы запомнить — есть разные способы обозначения автобусов, но все они означают одно и то же. Не беспокойтесь, если вы увидите, что они упоминаются разными именами в разных местах (например, в разных проектах Science Buddies или в других местах в Интернете).Иногда вы можете услышать «силовые шины» (или рельсы), используемые для обозначения и автобусов (или рельсов) вместе, а не только положительного.

Положительный	Отрицательный
Питание	Земля
Знак плюс (+)	Знак минус (-)
Красный	Синий или черный

Обратите внимание, что между положительной и отрицательной шинами нет физической разницы, и их использование не является обязательным.Этикетки просто упрощают организацию вашей схемы, подобно цветовой кодировке проводов.

Как соединяются отверстия?

Помните, что внутренняя часть макета состоит из пяти металлических зажимов. Это означает, что каждый набор из пяти отверстий, образующих полустрочку (столбцы A – E или столбцы F – J), электрически соединены. Например, это означает, что отверстие A1 электрически соединено с отверстиями B1, C1, D1 и E1. Это , а не , подключенный к отверстию A2, потому что это отверстие находится в другом ряду с отдельным набором металлических зажимов.Это также , а не , подключенный к отверстиям F1, G1, h2, I1 или J1, потому что они находятся на другой «половине» макета — зажимы не соединены через зазор посередине (чтобы узнать о зазоре посередине макета см. раздел «Дополнительно»). В отличие от всех основных рядов макета, которые соединены в наборы из пяти отверстий, шины обычно проходят по всей длине макета (но есть некоторые исключения). На этом изображении показано, какие отверстия электрически соединены в типичной макетной плате половинного размера, выделенные желтыми линиями.

Автобусы на противоположных сторонах макета , а не соединены друг с другом. Обычно, чтобы питание и земля были доступны с обеих сторон макета, вы должны соединять шины с помощью перемычек, как это. Убедитесь, что вы подключили положительный полюс к положительному, а отрицательный — к отрицательному (см. Раздел, посвященный шинам, если вам нужно напоминание о том, какой цвет какой).

Все макеты имеют одинаковую маркировку?

Обратите внимание, что точные конфигурации могут отличаться от макета к макету.Например, на некоторых макетных платах этикетки напечатаны в «альбомной» ориентации вместо «портретной». На некоторых макетных платах шины разорваны пополам по длине макета (полезно, если вам нужно подать в схему два разных уровня напряжения). На большинстве «мини» макетов вообще нет шин или этикеток.

Могут быть небольшие различия в маркировке автобусов от макета к макету. На некоторых макетных платах есть только цветные линии и нет знаков плюса (+) или минуса (-).Некоторые макеты имеют положительные шины слева и отрицательные шины справа, а на других макетах это наоборот. Независимо от того, как они обозначены и их левое / правое положение, функции автобусов остаются прежними.

Использование макета

Что такое макетная схема?

Макетная плата — это компьютерный чертеж схемы на макетной плате. В отличие от принципиальной схемы или схемы (в которых используются символы для представления электронных компонентов; см. Раздел «Дополнительно», чтобы узнать больше), макетные схемы позволяют новичкам легко следовать инструкциям по созданию схемы, поскольку они разработаны так, чтобы выглядеть так: настоящая вещь.«Например, эта диаграмма (сделанная с помощью бесплатной программы под названием Fritzing) показывает базовую схему с батарейным блоком, светодиодом, резистором и кнопкой, которая очень похожа на физическую схему:

Иногда макетные схемы могут сопровождаться (или заменяться) письменными инструкциями, которые говорят вам, где разместить каждый компонент на макетной плате. Например, в инструкциях по этой цепи может быть сказано:

Подключите красный провод аккумуляторной батареи к шине питания.
Подключите черный провод аккумуляторной батареи к шине заземления.
Подключите резистор из отверстия B12 к шине заземления.
Вставьте четыре штифта кнопки в отверстия E10, F10, E12 и F12.
Вставьте длинный провод светодиода в шину питания, а короткий — в отверстие J10.

Эту информацию также можно отформатировать в виде таблицы:

Должна ли моя схема точно соответствовать макетной схеме?

Короткий ответ: «нет.«Однако, когда вы только начинаете использовать макетные платы, вероятно, лучше всего точно следовать макетным схемам.

Чтобы понять это, полезно понять, как электрически соединены отверстия макета. Существуют различные способы изменить физическую схему схемы на макетной плате без фактического изменения электрических соединений . Например, эти две схемы электрически идентичны; даже несмотря на то, что выводы светодиода переместились, все еще существует полный путь (называемый замкнутой цепью ) для прохождения электричества через светодиод (выделен желтыми стрелками).Таким образом, даже если в инструкциях указано «вставьте длинный вывод светодиода в отверстие F10», схема все равно будет работать, если вы вставите ее в отверстие h20 (но , а не , если вы вставите ее в отверстие F9 или F11, потому что разные строки Не подключен).

Однако вы также можете полностью переставить компоненты на макетной плате. Пока схема составляет в электрическом эквиваленте , она все равно будет работать. Несмотря на то, что эта схема «выглядит иначе», чем две предыдущие, потому что компоненты были переставлены, электричество по-прежнему проходит по эквивалентному пути через светодиод и резистор.

Что такое перемычки и какие типы я должен использовать?

Перемычки — это провода, которые используются для соединения на макетной плате. У них жесткие концы, которые легко вставить в отверстия в макете. При покупке перемычек доступно несколько различных вариантов.

Гибкие перемычки сделаны из гибкой проволоки с жесткими штырями, прикрепленными к обоим концам. Эти провода обычно поставляются в упаковках разного цвета. Это упрощает цветовое кодирование вашей схемы (см. Раздел о цветовом кодировании).Хотя эти провода просты в использовании для схем новичка, они могут сильно запутаться для более сложных схем; поскольку они такие длинные, вы получите запутанное гнездо проводов, которое трудно отследить (иногда его называют «крысиным гнездом» или «спагетти»).

Комплекты перемычек — это пакеты предварительно отрезанных отрезков провода, концы которых загнуты вниз под углом 90 градусов, чтобы их можно было вставить в макетную плату. Доступны наборы большего и меньшего размера.Эти комплекты очень удобны, потому что в них есть провода разной длины, предварительно отрезанные. Недостатком является то, что обычно бывает только одна длина каждого цвета. Это может затруднить цветовую кодировку вашей схемы (например, вам может понадобиться длинный черный провод, но в вашем комплекте могут быть только короткие черные провода). Ваша схема по-прежнему будет работать нормально, но цветовое кодирование может помочь вам оставаться более организованным (опять же, см. Раздел о цветовом кодировании для получения дополнительной информации). Обратите внимание на то, что эта схема выглядит менее запутанной, чем предыдущая, поскольку провода короче.

Наконец, вы также можете купить катушки со сплошным соединительным проводом и пару приспособлений для зачистки проводов и отрезать собственные перемычки. Это лучший долгосрочный вариант, если вы планируете заниматься множеством проектов в области электроники, потому что вы можете отрезать провода до нужной длины и выбрать нужный цвет. Это также намного более экономично в зависимости от длины провода. Для начала стоит купить набор из шести разных цветов. Важно покупать сплошную проволоку (которая сделана из цельного куска металла), а не многожильную проволоку (которая состоит из нескольких более мелких жил проволоки, например, каната).Многожильный провод намного более гибкий, поэтому его очень сложно вставить в отверстия макета. Вам также необходимо приобрести подходящий калибр для проволоки , который используется для измерения диаметра проволоки. 22 AWG (американский калибр проводов) является наиболее распространенным калибром, используемым для макетных плат. Чтобы узнать больше о калибрах и зачистке проводов, см. Учебное пособие по зачистке проводов от Science Buddies. Обратите внимание, как в этой схеме красный и черный используются для всех подключений к шинам (см. Раздел о цветовом кодировании, чтобы узнать больше).

Должен ли я кодировать мою схему цветом?

Укажите, какой цвет вы используете для своей схемы, во многом зависит от того, какой тип перемычки вы покупаете (см. Вопрос о перемычках). Цветовое кодирование — это вопрос удобства, поскольку оно может помочь вам оставаться более организованным, но использование разноцветных проводов не изменит принцип работы вашей схемы. Важно : Это утверждение применимо только к перемычкам . Некоторые компоненты схемы, такие как аккумуляторные блоки и определенные датчики, поставляются с уже подключенными к ним цветными проводами.Отслеживание этих цветов имеет значение (например, не перепутайте красный и черный провода на батарейном блоке). Однако все перемычки сделаны из металла внутри с цветной пластиковой изоляцией снаружи. Цвет пластика не влияет на прохождение электричества по проводу.

В электронике обычно используется красный провод для положительных (+) соединений и черный провод для отрицательных (-) соединений. Какие другие цвета вы используете, в значительной степени зависит от выбора и зависит от конкретной схемы, которую вы строите.Например, есть несколько разных способов соединить эту схему с красными, зелеными, синими и желтыми светодиодами, но все они будут работать одинаково:

Если вы приобрели комплект предварительно обрезанных перемычек, используйте провода подходящей длины любого доступного цвета (изображение слева).
Используйте красный и черный провода для положительной и отрицательной сторон каждого светодиода соответственно (центральное изображение).
Используйте только красный и черный провода для подключения к шине и используйте красный, зеленый, синий и желтый провода для соответствующих светодиодов (изображение справа).

Помните важную часть: цвет проводов не влияет на работу схемы! Все три схемы на этом изображении будут работать точно так же (светодиоды загорятся при включении аккумуляторной батареи), даже если у них есть провода разного цвета. Если на макетной схеме показан синий провод, а вместо него вы используете оранжевый, с вашей схемой все будет в порядке.

Как мне построить схему?

Для построения цепи:

Следуйте макетной схеме цепи, подключая по одному компоненту.
Всегда подключайте батареи или источник питания к вашей цепи последняя . Это даст вам возможность перепроверить все ваши подключения перед первым включением цепи.
Обращайте внимание на типичные ошибки, которые делают многие новички при использовании макета.

Как мне проверить мою схему?

То, как вы проверяете свою схему, будет зависеть от конкретной схемы, которую вы создаете. В общем, вы должны следовать этой процедуре:

Дважды проверьте свою схему и макетную схему, чтобы убедиться, что все компоненты находятся в нужном месте.
Проверьте, что ваша схема должна делать в соответствии с указаниями по проекту. Должен ли он мигать огнями, издавать шум, как-то реагировать на датчик (например, датчик движения или света) или заставлять робота двигаться? Многие проекты Science Buddies будут содержать письменное описание и / или видео того, как ваша схема должна работать.
Включите питание вашей цепи (например, сдвинув переключатель батарейного блока из положения OFF в положение ON). Если вы видите или чувствуете запах дыма, немедленно выключите или отсоедините источник питания .Это означает, что у вас короткое замыкание.
Следуйте указаниям проекта, чтобы использовать схему (например, направить фонарик на робота, отслеживающего свет, или помахать рукой перед датчиком движения).
Если ваша схема не работает, вам необходимо устранить неполадки (или отладить , что означает поиск проблем или «ошибок» в вашей схеме). См. Раздел «Типичные ошибки», чтобы узнать, что следует проверить.

Типичные ошибки

Неправильные номера строк

Можете ли вы заметить разницу между этими двумя схемами?

На первый взгляд они могут выглядеть точно так же.Однако, когда мы включаем аккумуляторы, загорается только светодиод слева. Что не так?

Давайте посмотрим на макетную схему цепи, чтобы увидеть, сможем ли мы определить проблему. Схема должна соответствовать этой схеме:

Теперь давайте подробнее рассмотрим две схемы. Тщательно сравните две картинки с макетной схемой. Вы можете заметить, что не так? Если вы по-прежнему не можете сказать, нажмите на изображение, чтобы выявить проблему.

Вы уже заметили проблему? В схеме слева красная перемычка идет от положительной шины к отверстию J10, что соответствует макетной схеме. В схеме справа он идет от плюсовой шины к отверстию J9 . Помните из раздела о том, как соединяются отверстия, что отверстия в разных рядах электрически не связаны друг с другом. Таким образом, с перемычкой в строке 9 и светодиодом в строке 10 нет возможности для подачи электричества на светодиод.

Может быть трудно обнаружить такую крошечную ошибку! Тем не менее, достаточно всего одного неправильно установленного провода или вывода компонента, чтобы цепь перестала работать полностью. Вот почему вы всегда должны тщательно проверять и перепроверять проводку перед тестированием цепи. Если ваша схема не работает, внимательно проверьте все свои соединения и обязательно подсчитайте номера строк.

Перемешивание питания и заземления

Подобно неправильному вводу номеров строк, перепутывание шин питания и заземления — еще одна распространенная ошибка.Можете ли вы заметить разницу между этими двумя схемами? Горит только светодиод слева.

Рассмотрим схемы подробнее. Вы можете заметить, что не так? Щелкните изображение, чтобы выявить проблему.

Вы уже заметили проблему? На фото слева красная перемычка идет к плюсовой (+) шине. На фото справа он идет на отрицательную (-) шину. Согласно макетной схеме из предыдущего раздела, он должен подключаться к положительной (+) шине.Помните, что «положительный» и «отрицательный» также могут называться «мощность» и «земля». См. Раздел об автобусах, если вам нужно напоминание.

Как насчет разницы между этими двумя схемами? Опять же, горит только светодиод слева.

Присмотритесь, можете ли вы определить проблему (щелкните изображение, чтобы раскрыть ее).

На этот раз провода аккумуляторной батареи перевернуты. Красный провод подключается к отрицательной (-) шине, а черный провод подключается к положительной (+) шине.Помните, что, в отличие от перемычек, цвета выводов аккумуляторной батареи имеют значение для . Красный используется для положительного, а черный — для отрицательного.

Наконец, помните, что на некоторых макетных платах положительная шина находится слева, а отрицательная — справа. На других макетах все наоборот. Будьте осторожны при переключении между макетными платами, так как левое-правое положение шин может измениться.

Не проталкивать провода до конца

Электронные компоненты и перемычки могут иметь выводы разной длины.Иногда учащиеся вставляют провода частично в отверстие в макете вместо того, чтобы полностью протолкнуть их вниз (до тех пор, пока они не смогут пройти дальше). Это может привести к ослаблению соединений, что приведет к странному поведению цепи, например, к миганию светодиода. Взгляните на эти два изображения рядом. На изображении слева показаны выводы, которые не полностью вставлены в макетную плату. На рисунке справа показаны выводы, которые правильно вставлены в макетную плату до упора.

Обратите внимание, что некоторые компоненты, например светодиоды, имеют очень длинные выводы, которые не полностью входят в макетную плату. У других компонентов, таких как предварительно нарезанные перемычки, обычно есть провода, обрезанные до нужной длины, поэтому они подходят вплотную к макетной плате.

Установка компонентов задним ходом

Для некоторых электронных компонентов имеет значение направление . Некоторые компоненты имеют полярность , что означает, что у них есть положительная и отрицательная стороны, которые должны быть подключены правильно.Другие компоненты имеют несколько контактов, которые выполняют разные функции. Включение этих компонентов в вашу схему обратной стороной или неправильной стороной может помешать правильной работе вашей схемы. Если ваша схема не работает и в ней задействованы какие-либо из этих компонентов, убедитесь, что они вставлены правильно.

Батареи имеют положительную и отрицательную клеммы. Есть много разных типов батарей, но положительный полюс почти всегда отмечен знаком «+».Обычно на держателях батарейки напечатаны символы «+» и «-»; Убедитесь, что символы «+» на батареях совпадают с символами «+» на держателе батареи.

Светодиоды имеют положительную сторону (называемую анодом , ) и отрицательную сторону (называемую катодом , ). Металлический вывод анода длиннее, чем вывод катода. Катодная сторона также обычно имеет плоский край на пластиковой части светодиода.

Диоды похожи на односторонние клапаны, которые пропускают электричество только в одном направлении.Обычно они представляют собой небольшие цилиндры с полосой или полосой на одном конце (это направление, в котором может течь электричество).

Конденсаторы — это компоненты, которые могут накапливать электрический заряд. Обычные «керамические дисковые» конденсаторы (маленькие оранжевые / желто-коричневые кружки) не поляризованы, но некоторые другие типы конденсаторов поляризованы и обычно имеют стрелки или минусовые знаки, указывающие на отрицательный вывод.

Транзисторы похожи на переключатели с электронным управлением, которые можно использовать для включения и выключения таких вещей, как двигатели и освещение.Транзисторы обычно имеют три контакта. Установка транзистора в макет обратной стороной изменит порядок контактов и помешает его работе. Транзисторы выпускаются в нескольких разных «корпусах», обычно это черный пластиковый корпус с небольшой надписью на одной стороне.

Интегральные схемы или IC для краткости (иногда также называемые «микросхемами») представляют собой черные прямоугольные элементы с двумя рядами контактов. У них обычно есть выемка или отверстие на одном конце, которые говорят вам, какой путь «вверх», поэтому вы не должны вставлять микросхему в макет вверх ногами.См. Расширенный раздел об интегральных схемах, чтобы узнать больше.

Указания на веб-сайте Science Buddies почти всегда указывают, в какую сторону должен быть обращен компонент; например, «убедитесь, что серая полоса на диоде обращена к положительной шине» или «убедитесь, что надпись на транзисторе обращена влево». Однако некоторые проекты продвинутой электроники могут предполагать, что вы знаете, как правильно подключать определенные компоненты.

Для некоторых электронных компонентов направление не имеет значения.Например, перемычки и резисторы работают одинаково в обоих направлениях. Посмотрите внимательно на эти два изображения. Несмотря на то, что на картинке справа перемычка и резистор были перевернуты (на одном конце перемычки есть черная метка, чтобы вы могли определить, какой конец какой, а на резисторе есть цветные полосы), светодиод все равно горит. . В электрическом плане в схеме ничего не изменилось.

Короткое замыкание

Короткие замыкания возникают, когда на макетной плате выполняются «случайные» соединения между двумя компонентами, которые не должны быть соединены.Это может произойти из-за того, что компоненты вставлены не в те ряды или шины, или из-за того, что открытые металлические части могут столкнуться друг с другом. Например, резисторы и светодиоды имеют длинные металлические выводы; если вы не будете осторожны, эти провода могут столкнуться друг с другом и вызвать короткое замыкание. Если в вашей схеме есть компоненты с длинными оголенными выводами, всегда следите за тем, чтобы выводы не касались друг друга.

В зависимости от схемы, иногда короткие замыкания безвредны.Они могут просто помешать правильной работе схемы, пока не будут обнаружены и отремонтированы. Однако иногда короткое замыкание может «сжечь» компоненты и вызвать необратимые повреждения. Особенно важно избегать коротких замыканий между шинами питания и заземления, поскольку они могут стать достаточно горячими, чтобы обжечь вас и даже расплавить пластик на макетной плате! На этом рисунке красный и черный провода от аккумуляторной батареи 4xAA были вставлены в шину заземления, а не один в шину заземления, а другой — в шину питания.Это приводит к тому, что макетная плата и изоляция проводов начинают плавиться.

Если вы когда-нибудь видите или чувствуете запах дыма при построении цепи, вероятно, у вас короткое замыкание. Вам следует немедленно отключить аккумуляторную батарею.

Продвинутый

Интегральные схемы (ИС)

Интегральные схемы , или для краткости ИС (иногда их называют просто «микросхемы»), представляют собой специализированные схемы, которые служат для самых разных целей, например, для управления двигателями роботов или обеспечения реакции светодиодов на музыку.Многие микросхемы поставляются в так называемом двойном линейном корпусе или DIP, что означает, что они имеют два параллельных ряда контактов. Зазор в середине макета (между столбцами E и F) — это именно та ширина, которая подходит для ИС, перекрывая зазор, с одним набором контактов в столбце E и одним набором контактов в столбце F. Проекты, которые Использование микросхем всегда говорит вам подключить их к макетной плате таким образом.

Схема

Схема

Схемы соединений или схемы — это способ представления схемы с использованием символов для каждого компонента.Принципиальные схемы, в отличие от макетов, используются профессиональными инженерами при проектировании схем, и они намного удобнее для более сложных схем. Вы можете познакомиться с основными принципиальными схемами на уроках физики в средней школе. Например, на этой принципиальной схеме показана базовая схема с батареей, переключателем, светодиодом и резистором.

Однако, в отличие от макетных схем, на принципиальных схемах показаны только электрические соединения между компонентами.Они не обязательно соответствуют физическому расположению компонентов на макетной плате. Например, хотя эта принципиальная схема выглядит иначе, она идентична предыдущей.

Если вам сложно это понять, попробуйте с помощью своей фигуры обвести «провод» (черная линия) в цепи, начиная с верхней части батареи. Обратите внимание, как ваш палец по-прежнему проходит через все компоненты в том же порядке, даже если они были физически переставлены.

Чтобы научиться читать и интерпретировать принципиальные схемы, требуется определенная практика. Большинство проектов в области электроники для начинающих, особенно на веб-сайте Science Buddies, предоставляют макетные схемы, по которым вы можете построить схему.

Детали для сквозного монтажа и поверхностного монтажа

Макетные платы предназначены для работы с электронными компонентами со сквозным отверстием. Эти компоненты имеют длинные металлические выводы, которые предназначены для вставки через отверстия в печатной плате (PCB), покрытые тонким медным покрытием, которое позволяет припаивать выводы компонентов к плате.

Макетные платы не работают с компонентами для поверхностного монтажа . Эти компоненты имеют короткие плоские штыри по бокам, которые предназначены для пайки к поверхности печатной платы, а не через сквозные отверстия.

Многие электронные компоненты доступны как для монтажа в сквозное отверстие, так и для поверхностного монтажа. Например, LM3914 — это интегральная схема, которая предназначена для управления 10 светодиодами в виде «гистограммы».Если вы выполните поиск Jameco Electronics по запросу «LM3914», появятся несколько разных результатов. Глядя на миниатюры, вы можете сказать, что эта часть является сквозным отверстием, а эта часть монтируется на поверхность. Хотя в большинстве проектов Science Buddies есть ссылки на то, какие именно детали вам нужно купить для проекта, будьте осторожны, если вы покупаете детали для своего собственного проекта. Если вы используете макетную плату, покупайте детали для сквозных отверстий, а не для поверхностного монтажа.

Ознакомьтесь с нашими научными видео

Почему не смешивается? Откройте для себя эффект бразильского ореха

Как собрать ArtBot

Как сделать винт Архимеда — STEM-упражнение

Практическое занятие по математике по теме «Практическое применение задач по теории вероятности в электрических схемах»

Последовательное и параллельное соединения источников тока

Электрическая схема

Электрическая цепь и ее элементы

Узнать еще:

Теория сети — топология сети

Основная терминология топологии сети

график

пример

Типы графиков

Связанный график

Неподключенный график

Направленный граф

Ненаправленный граф

Подграф и его виды

дерево

Co-Tree

Полное сопротивление цепи переменного тока

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Похожие материалы:

Добавить комментарий

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

| Электрические цепи

11,2 Закон Ома (ESBQ6)

Закон Ома

Цель

Аппарат

Метод

Анализ и результаты

Выводы

Вопросы и обсуждение

Закон Ома

Омические и неомические проводники (ESBQ7)

Омические и неомические проводники

Aim

Аппарат

Метод

Результаты

Анализ

Вопросы и обсуждение

Использование закона Ома (ESBQ8)

Рабочий пример 1: Закон Ома

Определите, как подойти к проблеме

Решить проблему

Напишите окончательный ответ

Закон Ома

Переплет резисторов последовательно и параллельно (ESBQ9)

Эквивалентное последовательное сопротивление

Эквивалентное параллельное сопротивление

Последовательное и параллельное сопротивление

Использование закона Ома в последовательных и параллельных цепях (ESBQB)

Последовательные цепи

Рабочий пример 2: Закон Ома, последовательная цепь

Определите, что требуется

Определите, как подойти к проблеме

Найдите полное сопротивление в цепи

Применить закон Ома

Напишите окончательный ответ

Рабочий пример 3: Закон Ома, последовательная цепь

Нарисуйте схему и введите все известные значения.

Определите, как подойти к проблеме.

Найдите полное сопротивление

Найдите неизвестное сопротивление

Рабочий пример 4: Закон Ома, последовательная цепь

Определите, как подойти к проблеме

Рассчитать падение напряжения на \ (R_1 \)

Рассчитать падение напряжения на \ (R_2 \)

Рассчитать падение напряжения на \ (R_3 \)

Найдите сопротивление \ (R_3 \)

Напишите окончательный ответ

Параллельные цепи

Рабочий пример 5: Закон Ома, параллельная схема

Определите, что требуется

Определите, как подойти к проблеме

Найдите эквивалентное сопротивление в цепи

Применить закон Ома

Напишите окончательный ответ

Рабочий пример 6: Закон Ома, параллельная схема

Определите, что требуется