4. Концентрация электронов и дырок в полупроводниках. Дырки и электроны в полупроводниках

2.10. Электроны и дырки

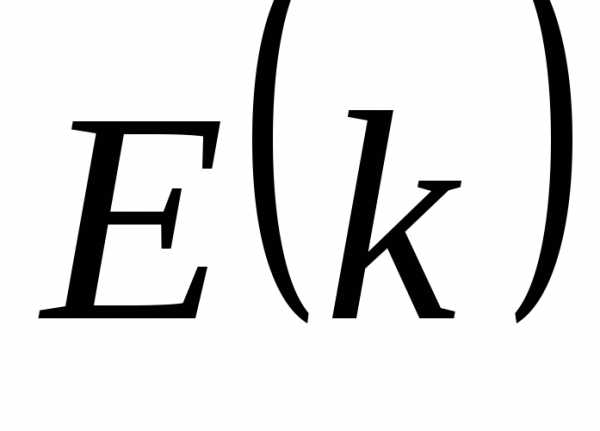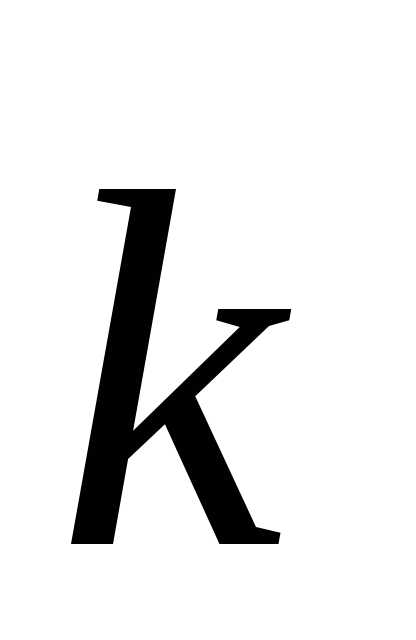Из (2.77) следует, что эффективная масса блоховских электронов в энергетической зоне определяется кривизной поверхности в-пространстве: чем больше эта кривизна, тем меньше эффективная масса.

Анализ дисперсионной зависимости (2.65) в модели сильной связи показывает, что для электронов, располагающихся у дна энергетической зоны

, (2.79)

т.е. эффективная масса m* положительна. Вблизи максимумов, т.е. у потолка зоны

, (2.80)

где вектор 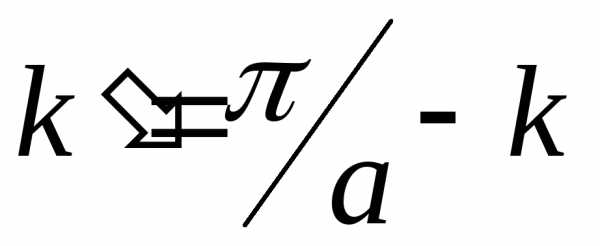, эффективная масса m* оказывается отрицательной. Поскольку масса не может быть отрицательной, то для состояний у верхнего края энергетической зоны вводится понятие дырки, рассматривая ее как квазичастицу с положительной эффективной массой, но и с положительным зарядом +е. Такая частица будет перемещаться по кристаллу по направлению действия внешней силы.

Главной особенностью дырки является то, что ее скорость совпадает со скоростью недостающего энергетического состояния в зоне; волновой пакет будет двигаться с той же скоростью, что и его соседи со всех сторон от дырки.

Поэтому, если считать, что ток переносится не электронами, а дырками, то электроны лучше всего рассматривать как отсутствие дырок; уровни, занятые дырками, есть уровни, не занятые дырками. Состояния, свободные от электронов, находятся в самой верхней части зоны, т.е. дырки располагаются у потолка зоны, где их энергия минимальна. Следовательно, энергия дырок отсчитывается в направлении, противоположном отсчету энергии для электрона.

Дырки простым способом описывают движение большого числа электронов в кристалле при почти заполненной зоне. Действительно, если из почти заполненной энергетической зоны удален один электрон, плотность тока в электрическом поле составит

, (2.81)

где 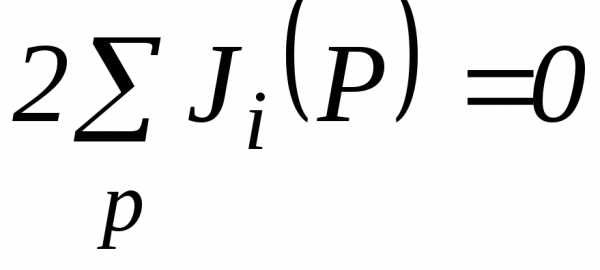- плотность тока в полностью заполненной зоне, поскольку каждому электрону с квазиимпульсом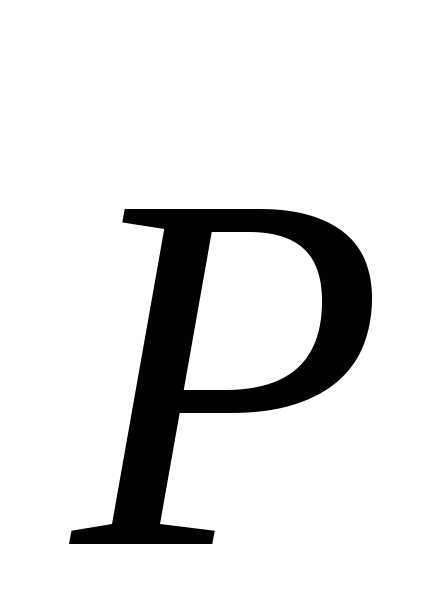в ней можно сопоставить электрон с квазиимпульсом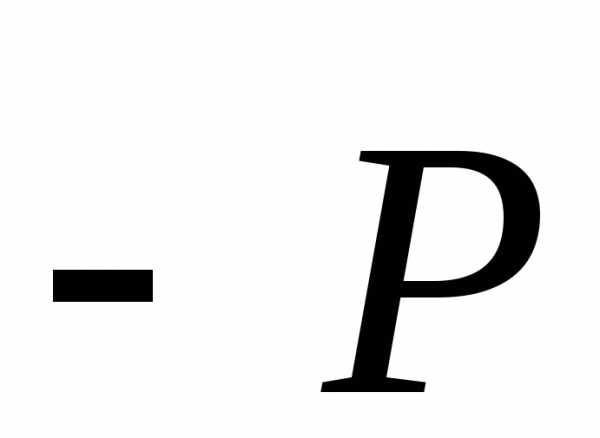и с то же энергией.

Следовательно, плотность тока, создаваемая электронами зоны с одним незаполненным состоянием, равна по величине и противоположна по направлению плотности тока, создаваемой недостающим электроном.

Плотность тока, связанная с одним электроном (n = 1), равна

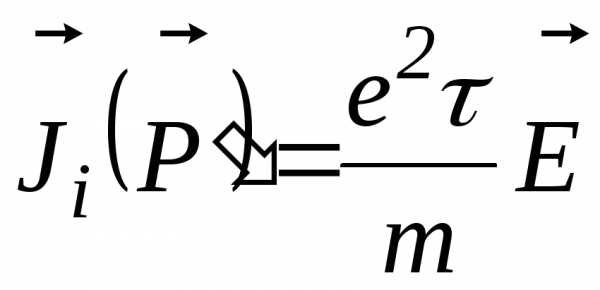. (2.82)

Так как 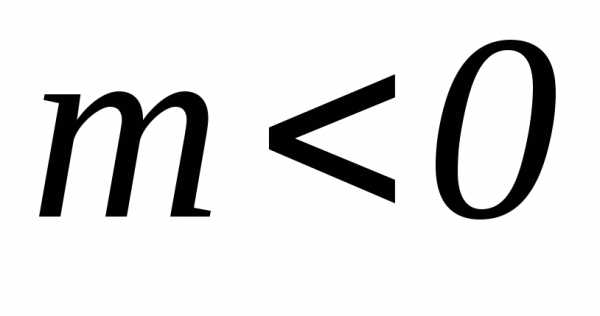, имеем

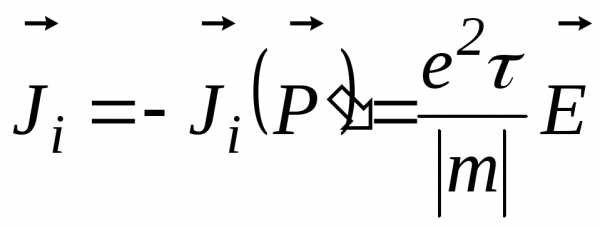. (2.83)

Это та плотность тока, которая создавалась бы частицей с массой 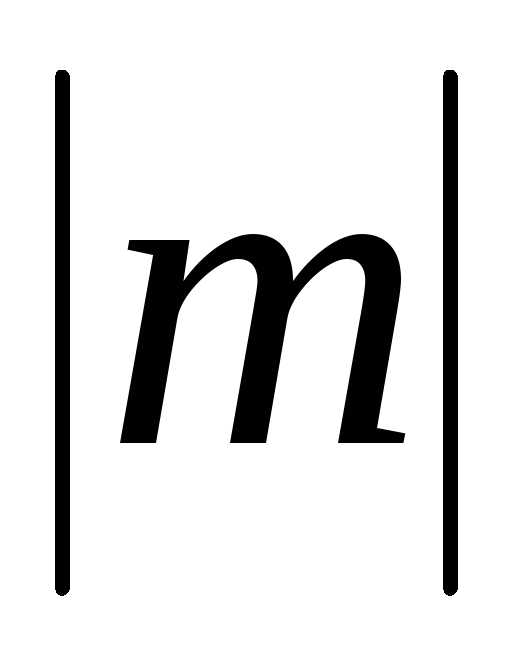и зарядомe. Фактически движутся, естественно, электроны. Однако электрон у потолка зоны движется против действия силы. По это причине удаление такого электрона приводит к увеличению плотности тока, такому, как если бы появилась частица с положительной массой и положительным зарядом.

Отметим еще раз: эффективная масса m* отражает способность электрона у дна зоны или дырки у ее потолка реагировать на внешнее поле, действующее совместно с межатомным периодическим потенциалом

2.11. Металлы, диэлектрики, полупроводники

в зонной теории

Рассмотрим теперь, как зонная теория твердого тела объяс­няет физические свойства реальных веществ и прежде всего раз­личие этих свойств для металлов, полупроводников и диэлек­триков.

Определим валентную зону как наивысшую энергетическую зону в твердом теле, которая целиком заполнена электронами в основном состоянии (при Т=0), зону проводимости - как самую нижнюю энергетическую зону в твердом теле, которая содержит свободные уровни в основном состоянии (незаполненную или содержащую некоторое число носителей при Т=0).

Рассмотрим случай, когда зона проводимости отделена от валентной зоны энергетической щелью Eg (рис.2.12). Пусть при Т=0 все состояния в зоне проводимости свободны, а в валентной зоне полностью заполнены электронами. В таком кристалле требуется конечная энергия возбуждения, больше ширины запрещенной зоны Eg, для перевода электронов вверх через энергетическую щель в зону проводимости. Если ширина запрещенной зоны Eg велика, так что ни температура, ни постоянное электрическое поле (и другие воздействия, которые не разрушают твердое тело) не могут сообщить электронам достаточную энергию для перехода в зону проводимости, то такое твердое тело не проводит электрический ток и я

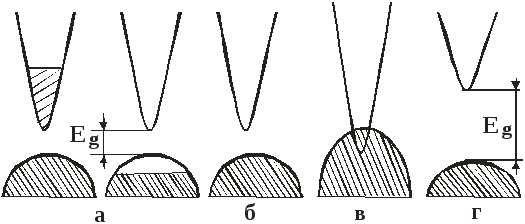
Рис. 2.12. Схема энергетических зон металла (а), полупроводника (б), полуметалла (в) и диэлектрика (г)

вляетсядиэлектриком.

Ана­логичный вывод мы получим, если рассмотрим полностью свобод­ную от носителей заряда разрешенную зону, так как при прило­жении электрического поля к такой зоне она не даст никакого вклада в электропроводность. Такой кристалл также будет диэлектриком.

Если ширина запрещенной щели невелика, то при конечной температуре T в результате тепловых флуктуаций некоторое число электронов, определяемое характерным больцмановским множителем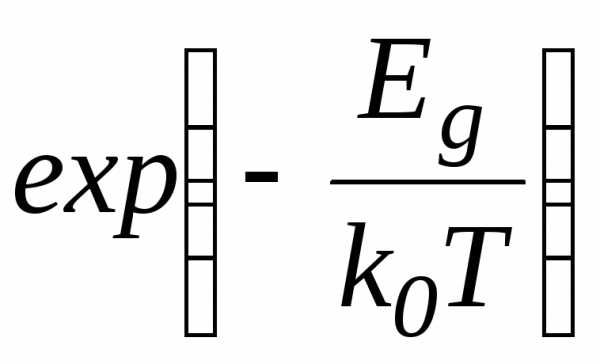, перейдет из валентной зоны в зону проводимости. Как электроны в зоне проводимости, так и дырки (свободные, незаполненные состояния), образовавшиеся в результате ухода электронов из валентной зоны, будут являться носителями тока и будут давать свой вклад в величину проводимости. Вещества с таким энергетическим спектром обладают конечной электропроводностью, быстро возрастающей с ростом температуры, называютсяполупроводниками.

Следовательно, в основном состоянии полупроводники не проводят тока, так как в основной разрешенной зоне все состояния заняты, и проводимость возникает только при сообще­нии электрону дополнительной энергии для перехода в незапол­ненную разрешенную зону. Значит, полупроводники и диэлек­трики относятся к одному типу веществ - между ними нет принципиальной разницы. Различие носит коли­чественный характер - по величине запрещенной зоны. Если 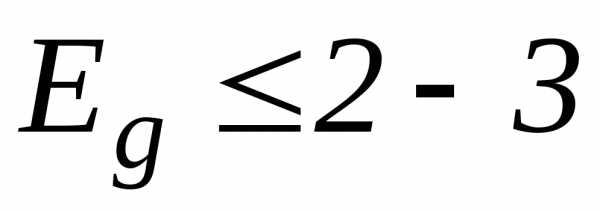эВ, то такие непроводники называют полупроводни­ками.

Удельное электросопротивление полупроводников при комнатной температуре лежит в интервале от 10-6 до 108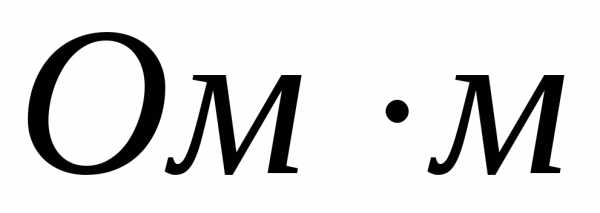. По величине сопротивления они находятся между хорошими проводниками (~ 10-8 – 10-6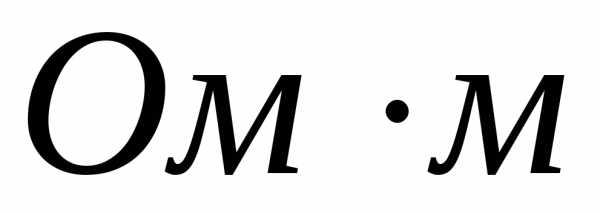) и изоляторами (>108).

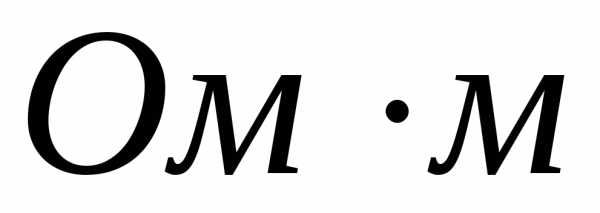Если зона проводимости заполнена не полностью и электронов достаточно много, то концентрация носителей тока не будет зависеть от температуры. Такие вещества являются металлами. Металли­ческая проводимость образуется и при перекрытии заполненной энергетической зоны с незаполненной зоной.

Зная, что число состояний в зоне Бриллюэна определяется как 2N, т. е. по два состояния на элементарную ячейку в зоне, можно, подсчи­тывая число электронов, приходящихся на элементарную ячейку, классифицировать вещество на металлы, полупроводники и диэлектрики.

• Вещества, в которых на элементарную ячейку приходится один свободный электрон, являются металлами, так как электроны заполняют половину зоны. К ним относятся одновалентные щелочные металлы Li, Na, K, Rb, Cs и благородные металлы Cu, Ag, Au.

• Вещества, в которых на элементарную ячейку приходится нечетное число электронов, также будут металлами, как и в предыдущем случае. К ним относятся металлы Al, Ga, In, Tl, в которых на один атом приходится три электрона. При этом валентная энергетическая зона заполнена полностью, а зона проводимости - наполовину.

• Вещества, в которых на элементарную ячейку приходится четное число электронов, не обязательно будет изоляторами, так как энергетические зоны, как мы уже видели, могут перекрываться.

Элементы As, Sb, Bi, в которых на элементарную ячейку приходится по два атома, а каждый атом имеет пять электронов, представляют собой полуметаллы. Зонную структуру их можно рассматривать, как для полупроводников, однако минимум зоны проводимости лежит немного ниже максимума валентной зоны, т. е. разрешенные энергетические зоны перекрываются, и понятие запрещенной зоны теряет, как и для металла, смысл. С этим об­стоятельством и связано название полуметалла.

Все двухвалентные вещества - металлы с хорошей проводимостью, за исключением Sr и Br, которые являются плохими проводниками из-за слабого перекрытия зон. Четырехвалентный углерод существует или в виде алмаза, со столь широкой запрещенной зоной, что его практически можно считать изолятором или в виде графита, являющегося полуметаллом. Кремний и германий - типичные полупроводники. Олово в одной фазе представляет собой металл, а в другой - полупроводник. Свинец - типичный металл.

studfiles.net

4. Концентрация электронов и дырок в полупроводниках

Для анализа поведения полупроводников обычно пользуются двухзонной моделью (рис.12). В литературе часто вместо закона дисперсии приводят

Рис.12 а б в

Рис.13

соответствующие ему энергетические диаграммы (рис.13) собственного полупроводника (а), примесного n-типа (б), примесногоp-типа (в), где ∆εА– энергия активизации примеси.

Заполненная зона от ε‘vдо εvназывается валентной. Зона от εсдо ε‘сназывается зоной проводимости. Обычно различают собственные и примесные полупроводники. Собственным полупроводником называют абсолютно чистый полупроводник, зонная структура которого показана на рис.12 и на энергетической диаграмме рис.13а. Наличие примесей приводит к появлению дополнительных уровней энергии для электронов. Полупроводники, у которых примесный уровень лежит в запрещенной зоне вблизи дна зоны проводимости (рис.13б), называют донорным. Те, у которых примесный уровень лежит вблизи потолка валентной зоны (рис.13в), называют акцепторными. Например, для четырехвалентного германия донорной примесью будут атомы пятивалентных элементов (мышьяк, фосфор), а акцепторной примесью – атомы трехвалентных элементов (индий, бор).

В силу того, что примесь в кристалле распределятся случайно, примесные состояния не образуют зону, т.е. электроны этих состояний не могут двигаться в кристалле, оставаясь связанными с примесными атомами. Однако если электроны донорных уровней перейдут в зону проводимости, например, при фотоэффекте или при термической возбуждении, они будут участвовать в переносе заряда так, как это описано в п. 2.

Переход электронов на акцепторный уровень из валентной зоны приводит к появлению в валентной зоне дырок, которые также могут участвовать в переносе заряда.

Для таких полупроводников, как германий и кремний, с достаточно хорошей точностью выполнятся условия: ∆ε >> kbТ, ε‘с-εс>>kbТ, εv-ε‘v>>kbТдля широкого интервала температур (заметим, чтоkbТ = 1эВ соответствуетТ11000К). Благодаря этому количество термически возбужденных электронов и дырок будет мало по сравнению с числом состояний в соответствующей зоне, т.е. электроны и дырки будут находиться вблизи экстремальных точек εvи εс(см. рис.12). Вблизи этих точек закон дисперсии можно представить квадратичными параболами ε = εс+- для зоны проводимости, ε = εс+- для валентной зоны, гдеmeиmp– эффективные массы электронов и дырок соответственно. Это обстоятельство позволяет считать электроны и дырки свободными частицами в соответствующих зонах и определить плотности состояний в зонах как для свободных частиц:

- плотность состояний электронов;

- плотность состояний дырок (для единичного объема полупроводника).

Среднее число электронов в квантовом состоянии описывается распределением Ферми-Дирака:

, (9)

где εF– химический потенциал, или энергия Ферми электронов. Очевидно, что среднее число дырок определится как

1-. (10)

Тогда концентрация электронов и дырок определяется следующими выражениями:

,, (11)

где цифра 2 учитывает краткость вырождения состояний за счет спина электрона. Заметим, что для электронов и дырок среднее число частиц в квантовом состоянии совпадает с вероятностью заполнения этих состояний.

При условии, что ε‘с-εс>>kbТ и εv-ε‘v>>kbТ, εс-εF>>kbТ и εF-εv>>kbТ в распределениях (9), (10) можно пренебречь единицей. Это означает, что электроны и дырки при этих условиях описываются квазиклассическим распределением. Подставляяи 1-в интегралы (11) и после введения новых переменныхиинтегралы (11) вычисляются довольно просто. В результате получаем

,. (12)

Для вычисления концентраций в последних выражениях не достает зависимости энергии Ферми от температуры.

Для собственных полупроводников n=p(условие электронейтральности) и тогда

εF=; (13)

n2=p2=npи тогдаn=p=. (14)

Как видно из последних формул, в собственных полупроводниках уровень Ферми лежит в середине запрещенной зоны при Т = 0и с ростом температуры движется в сторону зоны с меньшей эффективной массой. Например, еслиmе<mp, плотность состояний в зоне проводимости меньше, чем в валентной зоне, так какρ~.Для выполнения условияn = pнеобходимо увеличить вероятность заполнения уровней электронами в зоне проводимости и уменьшить вероятность заполнения состояний дырками в валентной зоне. Эта ситуация реализуется при смещении уровня Ферми в сторону зоны проводимости, т.е. в сторону меньшей эффективной массы.

Более сложная ситуация в примесных полупроводниках. Однако и в них положение уровня Ферми находится из условия электронейтральности: , где- концентрация ионизованной донорной примеси;;- концентрация акцепторной примеси.

Рассмотрим, например, донорный полупроводник (n- типа). Для негоNa=0. При абсолютном нуле уровень Ферми лежит между примесным уровнем и дном зоны проводимости. В этой области температурp<<nи. При дальнейшем росте температуры достигается такое состояние, когдаи увеличение концентрации электронов в зоне проводимости происходит за счет переходов электронов из валентной зоны. Естественно, что можно повысить температуру до такой величины, что будет выполняться условие, т.е. полупроводник станет собственным.

studfiles.net

4. Концентрация электронов и дырок в полупроводниках

Для анализа поведения полупроводников обычно пользуются двухзонной моделью (рис.12). В литературе часто вместо закона дисперсии приводят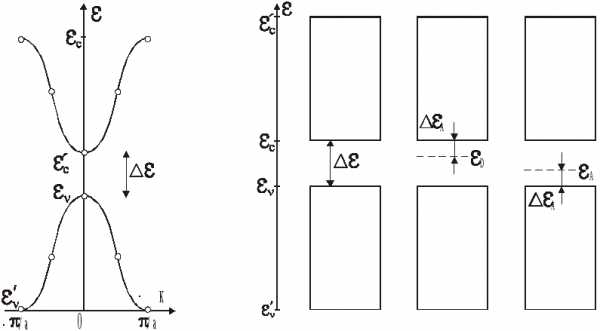

Рис.12 а б в

Рис.13

соответствующие ему энергетические диаграммы (рис.13) собственного полупроводника (а), примесного n-типа (б), примесногоp-типа (в), где ∆εА– энергия активизации примеси.

Заполненная зона от ε‘vдо εvназывается валентной. Зона от εсдо ε‘сназывается зоной проводимости. Обычно различают собственные и примесные полупроводники. Собственным полупроводником называют абсолютно чистый полупроводник, зонная структура которого показана на рис.12 и на энергетической диаграмме рис.13а. Наличие примесей приводит к появлению дополнительных уровней энергии для электронов. Полупроводники, у которых примесный уровень лежит в запрещенной зоне вблизи дна зоны проводимости (рис.13б), называют донорным. Те, у которых примесный уровень лежит вблизи потолка валентной зоны (рис.13в), называют акцепторными. Например, для четырехвалентного германия донорной примесью будут атомы пятивалентных элементов (мышьяк, фосфор), а акцепторной примесью – атомы трехвалентных элементов (индий, бор).

В силу того, что примесь в кристалле распределятся случайно, примесные состояния не образуют зону, т.е. электроны этих состояний не могут двигаться в кристалле, оставаясь связанными с примесными атомами. Однако если электроны донорных уровней перейдут в зону проводимости, например, при фотоэффекте или при термической возбуждении, они будут участвовать в переносе заряда так, как это описано в п. 2.

Переход электронов на акцепторный уровень из валентной зоны приводит к появлению в валентной зоне дырок, которые также могут участвовать в переносе заряда.

Для таких полупроводников, как германий и кремний, с достаточно хорошей точностью выполнятся условия: ∆ε >> kbТ, ε‘с-εс>>kbТ, εv-ε‘v>>kbТдля широкого интервала температур (заметим, чтоkbТ = 1эВ соответствуетТ11000К). Благодаря этому количество термически возбужденных электронов и дырок будет мало по сравнению с числом состояний в соответствующей зоне, т.е. электроны и дырки будут находиться вблизи экстремальных точек εvи εс(см. рис.12). 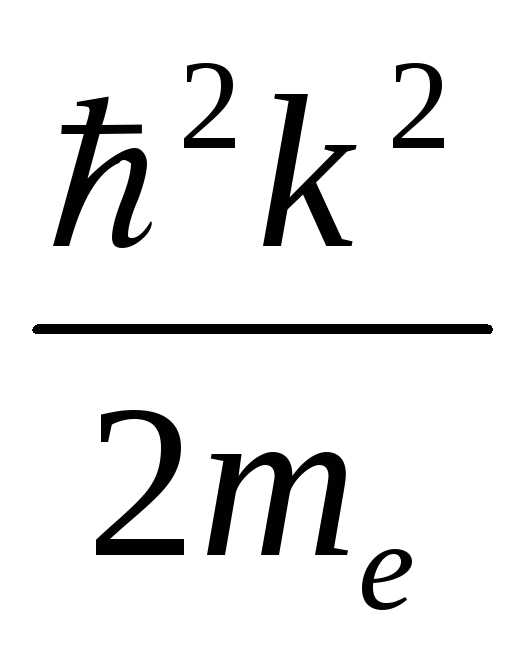Вблизи этих точек закон дисперсии можно представить квадратичными параболами ε = εс+- для зоны проводимости, ε = εс+- для валентной зоны, гдеmeиmp– эффективные массы электронов и дырок соответственно. Это обстоятельство позволяет считать электроны и дырки свободными частицами в соответствующих зонах и определить плотности состояний в зонах как для свободных частиц:

- плотность состояний электронов;

- плотность состояний дырок (для единичного объема полупроводника).

Среднее число электронов в квантовом состоянии описывается распределением Ферми-Дирака:

, (9)

где εF– химический потенциал, или энергия Ферми электронов. Очевидно, что среднее число дырок определится как

1-. (10)

Тогда концентрация электронов и дырок определяется следующими выражениями:

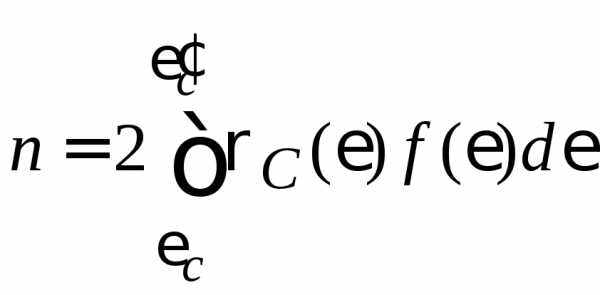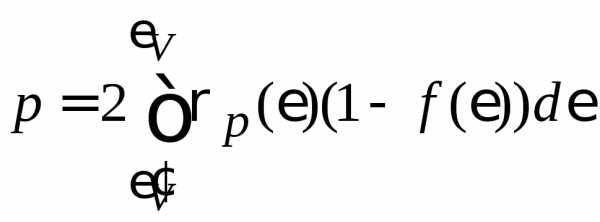,, (11)

где цифра 2 учитывает краткость вырождения состояний за счет спина электрона. Заметим, что для электронов и дырок среднее число частиц в квантовом состоянии совпадает с вероятностью заполнения этих состояний.

При условии, что ε‘с-εс>>kbТ и εv-ε‘v>>kbТ, εс-εF>>kbТ и εF-εv>>kbТ в распределениях (9), (10) можно пренебречь единицей. Это означает, что электроны и дырки при этих условиях описываются квазиклассическим распределением. Подставляя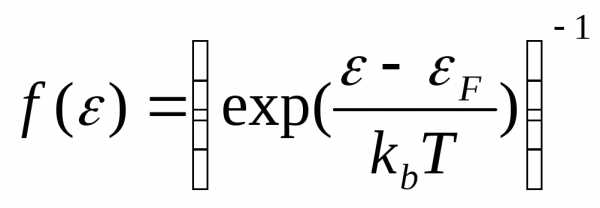и 1-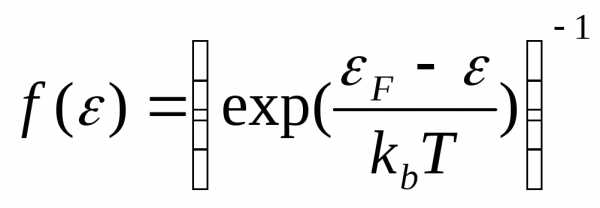в интегралы (11) и после введения новых переменных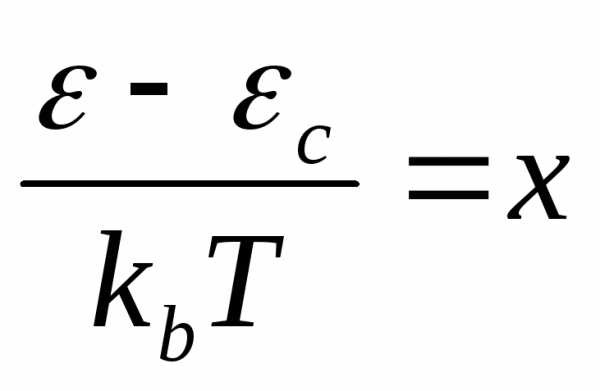и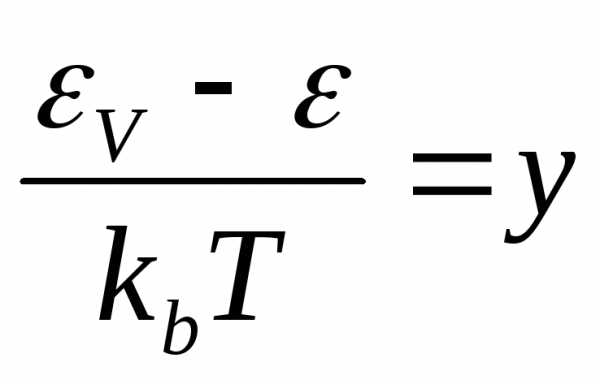интегралы (11) вычисляются довольно просто. В результате получаем

,. (12)

Для вычисления концентраций в последних выражениях не достает зависимости энергии Ферми от температуры.

Для собственных полупроводников n=p(условие электронейтральности) и тогда

εF=; (13)

n2=p2=npи тогдаn=p=. (14)

Как видно из последних формул, в собственных полупроводниках уровень Ферми лежит в середине запрещенной зоны при Т = 0и с ростом температуры движется в сторону зоны с меньшей эффективной массой. Например, еслиmе<mp, плотность состояний в зоне проводимости меньше, чем в валентной зоне, так какρ~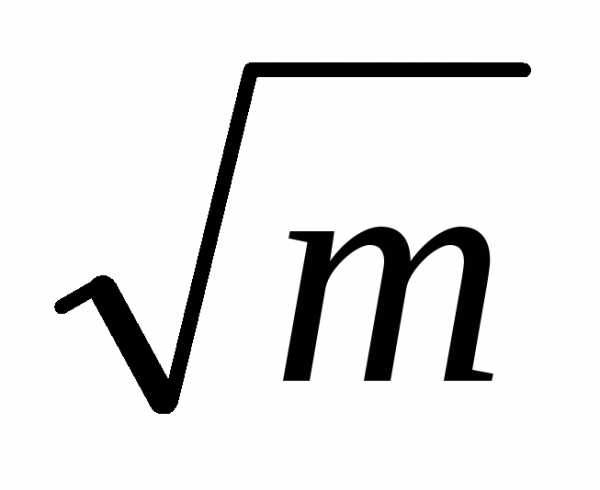.Для выполнения условияn = pнеобходимо увеличить вероятность заполнения уровней электронами в зоне проводимости и уменьшить вероятность заполнения состояний дырками в валентной зоне. Эта ситуация реализуется при смещении уровня Ферми в сторону зоны проводимости, т.е. в сторону меньшей эффективной массы.

Более сложная ситуация в примесных полупроводниках. Однако и в них положение уровня Ферми находится из условия электронейтральности: , где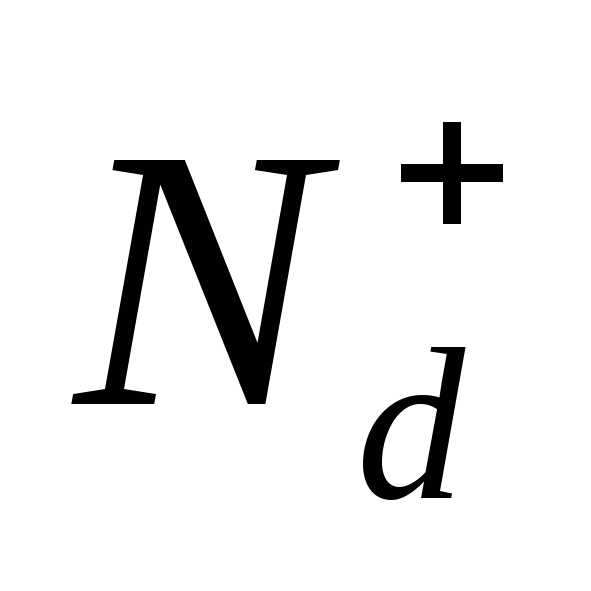- концентрация ионизованной донорной примеси;;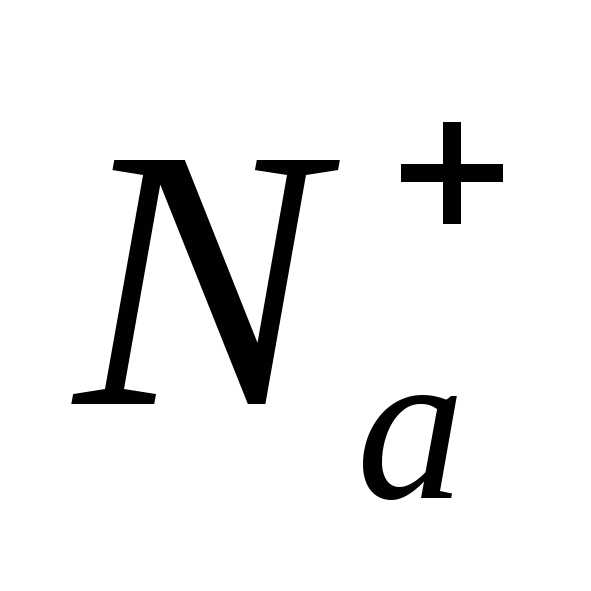- концентрация акцепторной примеси.

Рассмотрим, например, донорный полупроводник (n- типа). Для негоNa=0. При абсолютном нуле уровень Ферми лежит между примесным уровнем и дном зоны проводимости. В этой области температурp<<nи. При дальнейшем росте температуры достигается такое состояние, когда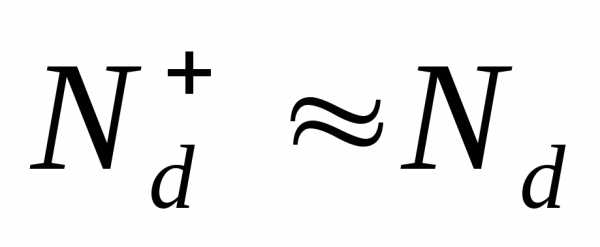и увеличение концентрации электронов в зоне проводимости происходит за счет переходов электронов из валентной зоны. Естественно, что можно повысить температуру до такой величины, что будет выполняться условие, т.е. полупроводник станет собственным.

studfiles.net

§ 67. Электроны и дырки в полупроводниках : Статическая физика 2 : Юридическая библиотека

Энергетический спектр чистых (или, как говорят, собствен­ных) полупроводниковых кристаллов отличается от спектра диэлектриков только в количественном отношении — меньшими значениями щели Д, в результате чего при обычных темерату- рах в полупроводнике имеется значительная (по сравнению с диэлектриком) плотность носителей тока. Ясно, что это раз­личие условно, и к тому -же зависит от интересующей нас об­ласти температур 2). В примесных (или легированных) полупро­водниках дополнительным источником электронов или дырок являются атомы примесей, для которых энергетическая щель

*) Интересно отметить, что вблизи верхнего края (максимума) зоны, где эффективные массы отрицательны, могут образовывать связанные состояния два электрона (или две дырки). Энергия таких состояний лежит в запрещенной области выше максимума суммарной энергии электронов.

2) Приведем значения энергетической щели Д для некоторых полупровод­ников: Si —1,17 зв, Ge —0,74 эв, InSb —0,24 эв, GaAs—1,52 эв, PbS—0,29 зв. Для типичного диэлектрика алмаза Д = 5,4 эв.

по отношению к отдаче электрона в решетку (донорная примесь) или его захвата из решетки (акцепторная примесь) оказывается меньше, чем энергетическая щель в основном спектре.

Рассмотрим .подробнее вопрос -о связи между величиной щели А и плотностью электронов проводимости и дырок в по­лупроводнике (или диэлектрике).

Попарное возникновение или исчезновение электрона (е) и дырки (К) можно рассматривать, с термодинамической точки зрения, как «химическую реакцию» e + h^O (основное состоя­ние кристалла играет роль «вакуума»). По общим правилам (см. V § 101) условие термодинамического равновесия этой реак­ции записывается в виде

Рг + Рй = 0,   (67,1)

где [ie и рй—химические потенциалы электронов и дырок. Ввиду сравнительно небольшой плотности электронов (пе) и дырок (nh) в полупроводнике (при Т А) распределение Ферми для них с большой точностью сводится к распределению Больцмана, так что электроны и дырки образуют классический газ1). Из усло­вия (67,1) следует тогда обычным образом (см. V § 101) закон действующих масс, согласно которому произведение равновес­ных плотностей

Пепл = К(Т),  (67,2)

где справа стоит функция температуры, зависящая только от свойств основной решетки, на атомах которой и происходит рождение и уничтожение электронов и дырок; эта функция не зависит от наличия или отсутствия примесей. Вычислим функ­цию К(Т), приняв для определенности, что энергии электронов и дырок являются квадратичными функциями квазиимпульса (66,1).

Распределение электронов (в единице объема) по квазиим­пульсам дается распределением Больцмана

/и.—ге (k)\ ~ d3k

exp (Cs-^J 2 w

(множитель 2 учитывает два направления спина). Переход к рас­пределению по энергиям осуществляется заменой

из и    Ylm'J2                       

где me= (/т^/тупз)1^, а ти /л2, т3—главные значения тензора эффективных масс mf£. Полное число электронов в единице

Плотности электронов и дырок в полупроводниках при обычных тем­пературах составляют 1013—1017 см-3, в то время как в металлах они со­ставляют 1022 —1023 см-з.

объема есть, следовательно,

ут>

пФ

д

(в виду быстрой сходимости интегрирование можно распрост­ранить до бесконечности). Вычислив интеграл, находим

Аналогичным образом, получим

Наконец, перемножив оба выражения и учтя (67,1), полу­чим искомый результат

ЯЛ-Ц'12 ТЧ-ит.        (б7)5)

2ic3A6

В собственном полупроводнике, где все электроны и дырки возникли парами:

vfS-l гз/2е"А/2Г- <67'6>

Приравняв же выражения (67,6) и (67,3), найдем химический потенциал электронов

Т + Т(67,7)

Что касается вклада электронов и дырок в термодинамиче­ские величины полупроводника, то при            он экспонен­циально мал. Учитывая, что на рождение одной пары электрон — дырка требуется энергия, близкая к А, имеем для электронно- дырочного вклада во внутреннюю энергию Eeh ж VneА с пе из (67,6). Этой величиной можно обычно пренебречь по сравнению с решеточным вкладом в энергию кристалла.

bookzie.com

Неравновесные электроны и дырки в полупроводниках

Рассмотрим опять контакт двух полупроводников р- и n-типа и предположим, что через него идет ток в проходном направлении (рис. 434). Дырки в р-области движутся к р-n-переходу и, проходя через него, вступают в n-область в качестве неосновных носителей заряда, где и рекомбинируют с электронами. То же относится и к электронам в n-области, которые, переходя границу раздела, попадают в р-область и рекомбинируют с дырками. Однако эта рекомбинация происходит не мгновенно, и поэтому в n-области окажется избыточная концентрация дырок nд, а в р-области — избыточная концентрация электронов nэ. При этом избыточные дырки в n-области будут притягивать к себе электроны, так что увеличится и концентрация электронов; объемный заряд, как и в отсутствии тока, не обра­зуется. То же будет происходить и в р-области, где увеличение концентрации электронов повлечет за собой увеличение концентрации дырок.

Таким образом, при наличии электрического тока через р-n-переход состояние электронов и дырок в полупроводнике становится неравновесным. Их концентрация делается больше ее равновесного значения, происходит как бы «впрыскивание» дырок в n-область и электронов в р-область. Описанное явление получило название инжекции электронов и дырок.

Отметим, что нарушение равновесного состояния электронов и дырок можно также получить под действием освещения полупроводника, даже если последний и однороден. В этом случае изменение концентрации электронов и дырок приводит к изменению электропроводности полупроводника под действием света (явление фотопроводимости).

По мере движения избыточные дырки и электроны будут рекомбинировать и их концентрация будет уменьшаться. Поэтому распределение концентраций избыточных электронов и дырок в кристалле существенно зависит от скорости их рекомбинации. Остановимся на этом вопросе подробнее.

Положим, что в полупроводнике каким-либо способом (инжекцией, освещением или другим) была создана концентрация избыточных электронов и дырок n0, одинаковая во всех местах кристалла, и что эти избыточные носители заряда исчезают вследствие рекомбинации. Уменьшение концентрации электронов или дырок —dп за время dt пропорционально избыточной их концентрации n и времени:

Здесь 1/τ коэффициент пропорциональности, определяющий вероятность рекомбинации, а величина τ получила название среднего времени жизни избыточных (или неравновесных) носителей заряда. Она зависит от рода и качества материала, от его состояния и от содержащихся в нем примесей. Интегрируя написанное уравнение, находим:

где n0 — начальная концентрация избыточных носителей. Отсюда видно, что τ есть такое время, через которое концентрация неравновесных носителей вследствие рекомбинации уменьшается в e = 2,71 раза.

Пользуясь понятием времени жизни, мы можем сейчас вернуться к распределению электронов и дырок в пространстве (рис. 434). Для этого рассмотрим в правой части кристалла (n-области) бесконечно тонкий слой, ограниченный плоскостями, параллельными р-n-переходу и удаленными от него на расстояния х и (х+dx).

 

Через каждую единицу поверхности плоскости х в единицу времени вследствие диффузии внутрь слоя будет входить число дырок где Dд — коэффициент диффузии дырок и n-области. Через плоскость (х+dх) будет выходить из слоя число дырок Поэтому полное приращение количества дырок за единицу времени вследствие диффузии, отнесенное к единице объема, равно + . Кроме этого внутри слоя будет происходить уменьшение числа дырок вследствие рекомбинации. Согласно сказанному выше число исчезающих дырок в единицу времени, также отнесенное к единице объема, есть В стационарном состоянии количество поступающих дырок вследствие диффузии должно быть равно числу дырок, исчезающих вследствие рекомбинации. Поэтому для определения пространственного распределения концентрации избыточных дырок (и равной ей концентрации избыточных электронов) в n-области мы получаем уравнение

где введено обозначение:

Граничные условия задачи имеют следующий вид. При х=0 пд=пд0, где пд0— концентрация избыточных дырок вблизи перехода. Кроме этого при х→∞ пд→0, так как на достаточно большом расстоянии от перехода все избыточные дырки успевают рекомбинировать с электронами.

Решение написанного уравнения, удовлетворяющее граничным условиям, имеет вид:

Оно показывает, что концентрация инжектированных дырок затухает с увеличением расстояния от перехода по экспоненциальному закону. Введенная нами характеристическая длина Lд, есть расстояние, на котором концентрация избыточных дырок уменьшается в е = 2,71 раза. Величина Lдносит название длины диффузионного смещения или, короче, длины диффузии дырок.

Совершенно аналогично концентрация инжектированных электронов в р-области будет тоже уменьшаться по экспоненциальному закону, но будет определяться длиной диффузии электронов где Dэ — коэффициент диффузии электронов, а τэ— время жизни электронов в p-области.

Укажем для примера, что в очень чистом германии при комнатных температурах τ может достигать нескольких миллисекунд, что соответствует L в несколько мм. При наличии примесей (или иных структурных дефектов) τи L могут уменьшаться на много порядков,

 

 



3-net.ru

---

• 
  Двунаправленный счетчик электроэнергии
• 
  Устройство лампы
• 
  Электросчетчики сами передающие показания
• 
  Филиал 7 оао моэк предприятие 7
• 
  Мощность переменного тока формула
• 
  Солнца мощность
• 
  Административно технический персонал по электробезопасности
• 
  Розетка на плиту электрическую
• 
  Измерения в физике
• 
  Авария на сшгэс 17 августа
• 
  Какое масло лить в бензиновый генератор