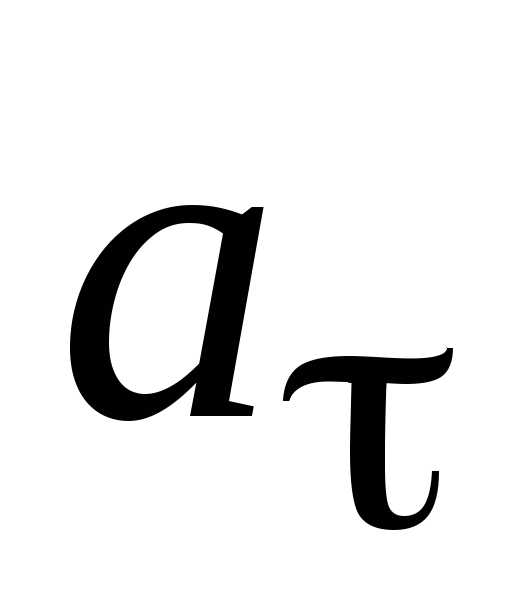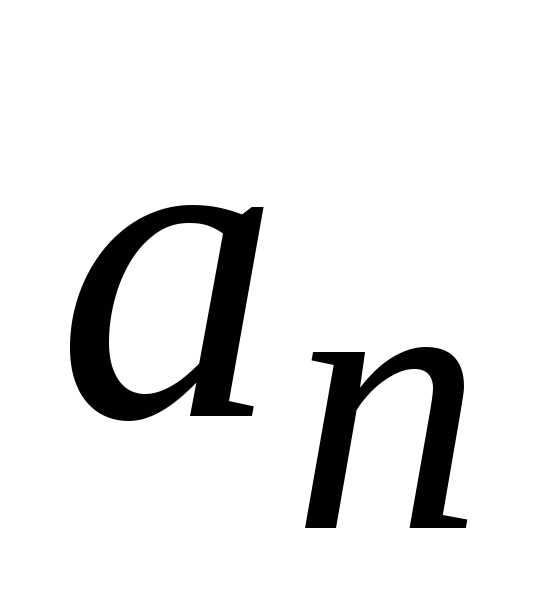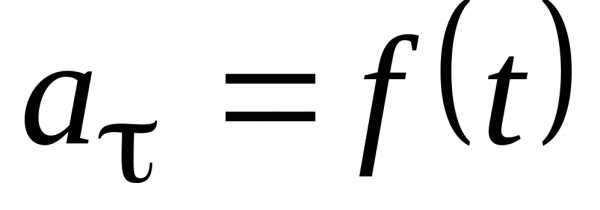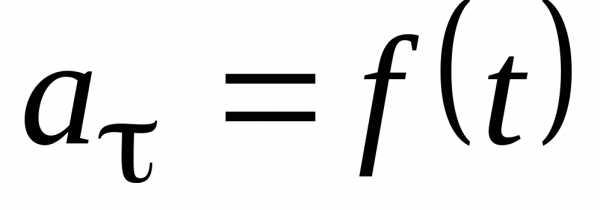1.3. Единицы измерения в физике. Измерения в физике

Единицы измерения в физике

Единицы измерения в физике:

В физике постоянно встречаются единицы измерения, которыми можно измерить тело или явление: метры, секунды, граммы, км/ч (километры в час),…

В природе таких единиц нет, как не бывает в природе цифр и букв. Все их придумали люди для удобства взаимопонимания.

В физике, химии, математике и других областях знаний есть много единиц измерений, однако все они предназначены только для пользы и удобства взаимопонимания между учеными разных стран.

Ведь все знают, что такое метр и вы даже можете представить сколько это. Можете представить, что такое секунда или, что такое килограмм.

И значительно проще сказать:

«Подожди 4 часа», чем «Подожди столько времени, сколько проходит между обедом и ужином». Ведь разные люди могут обедать и ужинать в разное время.

Чтобы ученые лучше понимали друг друга и измеряли все тела и явления, введена международная система единиц (СИ). Многие страны приняли эту систему. И в международном бюро мер и весов (во Франции) даже хранятся эталоны некоторых единиц измерений для сверки с ними. Эти меры позволяют избежать неприятных казусов, когда кто-то считает, например, время в часах, а кто-то в сутках или секундах; в некоторых странах измеряют расстояние футами, а в некоторых аршинами,...

И теперь, если мы хотим измерить массу, у нас есть общепринятая единица "килограмм", с которой мы сравниваем массу тела, чтобы, например, сказать: "Арбуз весит 8 килограмм". Что будет понятно практически в любой стране.

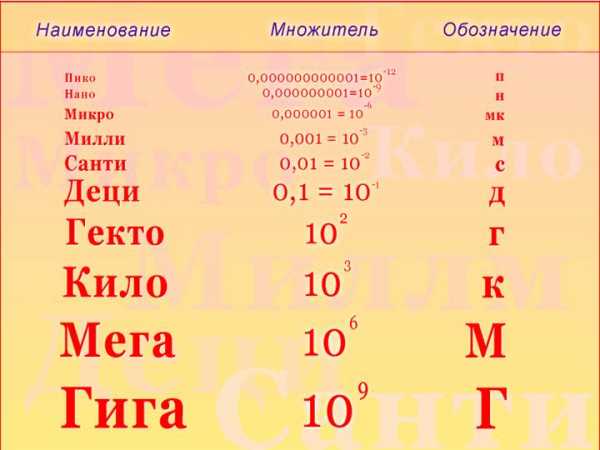
Чтобы считать было ещё удобнее, используют дополнительные приставки:

Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

Добавить новость и получить деньги

uchilegko.info

Измерение - это... Что такое Измерение?

Измерение — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

Принцип измерений — физическое явление или эффект, положенное в основу измерений.
Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути сравнивают её размер с единицей, хранимой линейкой, и, произведя отсчёт, получают значение величины (длины, высоты, толщины и других параметров детали).
С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчёт.

В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая, или не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам, например, Шкала Рихтера интенсивности землетрясений, Шкала Мооса — шкала твёрдости минералов.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

Классификация измерений

По видам измерений

Согласно РМГ 29-99 «Метрология. Основыне термины и определения» выделяют следующие виды измерений:

Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
Совместные измерения — проводимые одновременно измерения двух или нескольких неодноимённых величин для определения зависимости между ними.
Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
Равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
Неравноточные измерения — ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
Однократное измерение — измерение, выполненное один раз.
Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений
Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
Динамическое измерение — измерение изменяющейся по размеру физической величины.
Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительное измерение — измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Также стоит отметить, что в различных источниках дополнительно выделяют таки виды измерений: метрологически и технические, необходимые и избыточные и др.

По методам измерений

Метод непосредственной оценки — метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.
Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
- Нулевой метод измерений — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
- Метод измерений замещением — метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
- Метод измерений дополнением — метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
- Дифференциальный метод измерений — метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.

По условиям, определяющим точность результата

Метрологические измерения
- Измерения максимально возможной точности, достижимой при существующем уровне техники. В этот класс включены все высокоточные измерения и в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин. Сюда относятся также измерения физических констант, прежде всего универсальных, например измерение абсолютного значения ускорения свободного падения[1].
- Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения. В этот класс включены измерения, выполняемые лабораториями государственного контроля (надзора) за соблюдением требований технических регламентов, а также состоянием измерительной техники и заводскими измерительными лабораториями. Эти измерения гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения[1].
Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на промышленных предприятиях, в сфере услуг и др.[1]

По отношению к изменению измеряемой величины

Статические и динамические.

По результатам измерений

Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную.

Классификация рядов измерений

По точности

Равноточные измерения — однотипные результаты, получаемые при измерениях одним и тем же инструментом или им подобным по точности прибором, одним и тем же (или аналогичным) методом и в тех же условиях.
Неравноточные измерения — измерения, произведённые в случае, когда нарушаются эти условия.

По числу измерений

Однократное измерение — измерение выполненное один раз
Многократное измерение — Измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений

Классификация измеряемых величин

По точности

Детерминированные и случайные

По результатам измерений

Равнорассеянные и неравнорассеянные

История

Единицы и системы измерения

См. также

Примечания

↑ 1 2 3 Метрология и технические измерения. Колчков В. И. Ресурс «ТОЧНОСТЬ-КАЧЕСТВО»]

Литература и документация

Литература

Кушнир Ф. В. Радиотехнические измерения: Учебник для техникумов связи. — М.: Связь, 1980
Нефедов В. И., Хахин В. И., Битюков В. К. Метрология и радиоизмерения: Учебник для вузов. — 2006
Пронкин Н. С. Основы метрологии: Практикум по метрологии и измерениям. — М.: Логос, 2007

Нормативно-техническая документация

РМГ 29-99 ГСИ. Метрология. Основные термины и определения
ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения
МИ 2222-92 ГСИ. Виды измерений. Классификация

Ссылки

dic.academic.ru

1.3. Единицы измерения в физике

Физикам приходится иметь дело с измерением различных физических величин, таких как длина, объем, время, частота, температура, заряд и т.д. Измерение любой величины проводится по отношению к определенному стандарту (например, расстояние соизмеримо с метром), и эти единицы должны приводиться вместе с численным значением результата. Говорят, что данная физическая величина имеет такую-то размерность. Таким образом, в физике оперируют с величинами, которые представляют собой некоторое число и единицу измерения (например, скорость автомобиля 60 км/ч). Если единица измерения не указана, то величина теряет смысл. Единица измерения – неотъемлемая часть изучаемой величины.

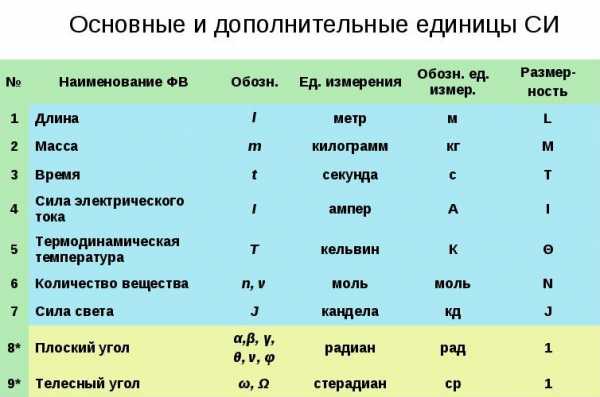
Все физические величины разделены на два класса: основные и производные. В физике существует семь независимых основных величин, через которые выражаются все остальные величины, встречающиеся в физике. В настоящее время общепринятой является международная система единиц СИ. Основные физические величины и их размерности в СИ следующие: сила тока  [ампер], температура – [кельвин], длина – [метр], время – [секунда], масса – [килограмм], количество вещества – [моль], сила света – [кандела]; дополнительные – радиан и стерадиан.

Большая часть физических величин является производными, т.е. определяются через основные величины. Так, например, скорость - есть длина, деленная на время, т.е. [м/с], объем – [] и т.д.

1.4. Физические основы классической механики

Простейшей формой движения материи является механическое движение. Механическим движением называется изменение взаимного расположения тел или частей одного и того же тела в пространстве с течением времени.

Механика – раздел физики, рассматривающий механическое движение и причины, вызывающие или изменяющие это движение. Основные законы механики были установлены итальянским физиком и астрономом Г. Галилеем (1564-1642 гг.) и окончательно сформулированы английским ученым И. Ньютоном (1643-1727 гг.). Механика Галилея-Ньютона называется классической. Она изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Механика делится на три раздела: 1) кинематику; 2) динамику; 3) статику.

Кинематика изучает движение тел, не рассматривая причины, которые это движение вызывают. Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Статика изучает условия равновесия тел.

1.5. Основные понятия кинематики поступательного движения материальной точки

1. Материальная точка. Для описания движения тел в физике пользуются абсолютными понятиями и моделями. Простейшей моделью является материальная точка. Материальная точка – тело, обладающее массой, размерами и формой которого можно пренебречь в данной задаче. Например, при изучении движения Земли вокруг Солнца размерами Земли можно пренебречь, т.к. ее диаметр много меньше расстояния между ними. При рассмотрении же суточного вращения Земли этого сделать нельзя.

2. Система отсчета. Механическое движение является относительным. О движение тел можно говорить лишь в том случае, когда указана система отсчета. Система отсчета включает в себя: тело отсчета – тело, которое условно принимается за неподвижное и относительно которого рассматривается движение других тел. С телом отсчета связывают систему координат (чаще всего используют декартову систему координат) и часы.

Рис.1.1

Таким образом, система отсчета – совокупность тела отсчета, связанная с ним система координат и часы.

3. Радиус-вектор. Положение материальной точки в пространстве определяется тремя координатами х, y, z или радиус-вектором 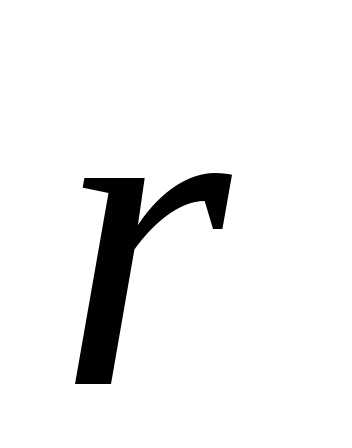(он проводится из начала отсчета координат в данную точку). При движении материальной точки ее координаты с течением времени изменяются.

Закон движения материальной точки в скалярной форме:

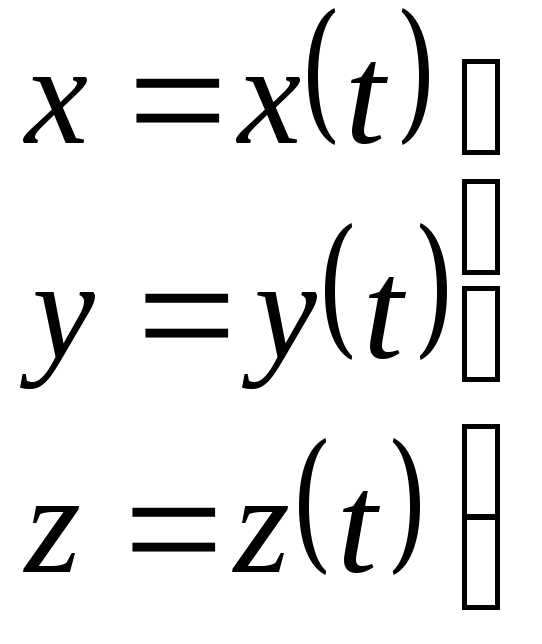кинематические уравнения движения материальной точки

Закон движения в векторной форме: .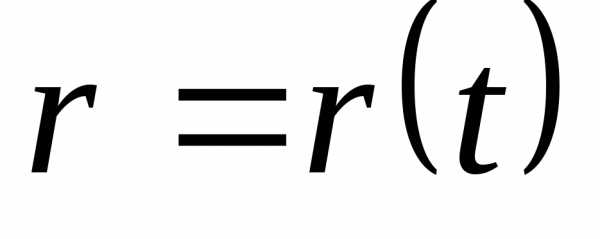

Радиус-вектор можно записать через его проекции на координатные оси:

где 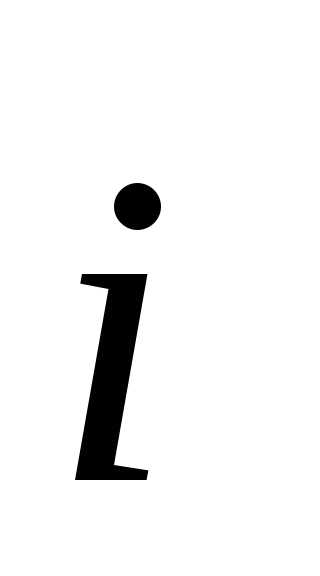,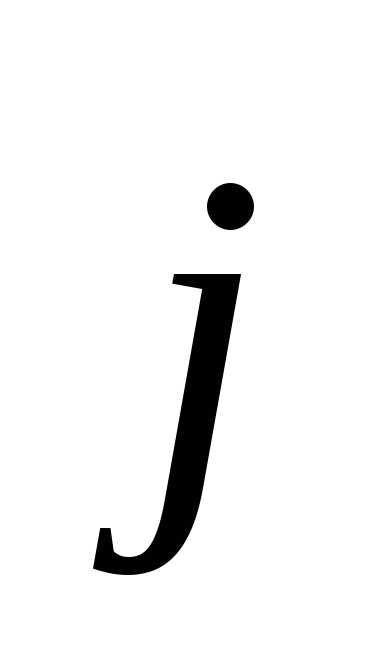и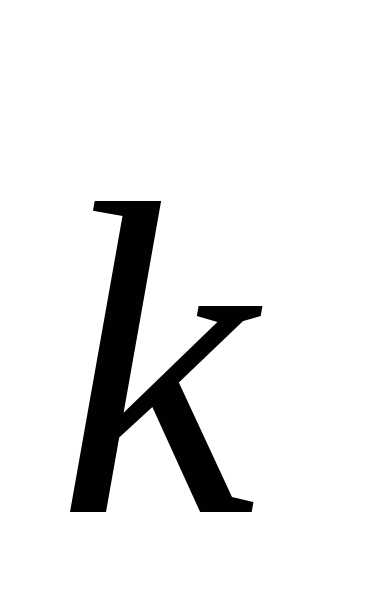 орты – единичные векторы, направленные вдоль координатных осей (рис.1.1).

4. Траектория движения. Линия, которую описывает материальная точка при движении относительно выбранной системы отсчета, называется траекторией. В зависимости от формы траектории различают прямолинейное движение, криволинейное движение и движение по окружности. Форма траектории зависит от выбора системы отсчета, т.е. форма траектории понятие относительное. Так, траектория концов пропеллера относительно системы отсчета, связанной с летящим самолетом, является окружностью, а в системе отсчета, связанной с землей – винтовой линией.

5. Перемещение. Путь. При описании движения тела надо уметь определять изменение его положения. С этой целью вводится понятие перемещения тела и пути, пройденного им. Перемещением называется вектор, проведенный из начального положения материальной точки в конечное:, где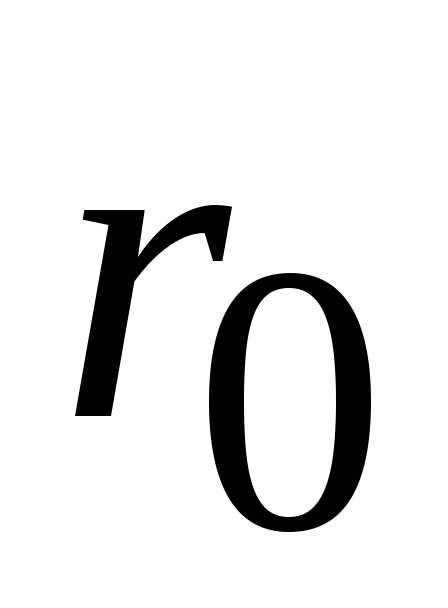и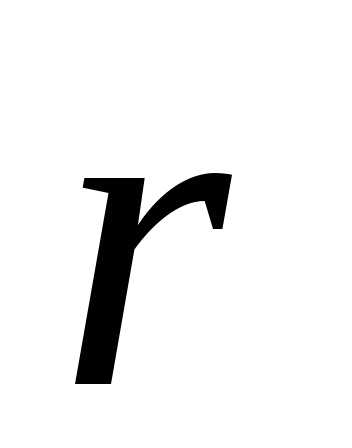 радиусы-векторы начального и конечного положения материальной точки, соответственно (рис.1.2)

Рис.1.2

Длину участка АВ траектории, пройденного данной материальной точкой за время t называют путем или длиной пути s.

Путь – скалярная величина, перемещение – вектор. Нельзя путать эти понятия. Различие между модулем перемещения и путемs исчезает лишь в двух случаях: когда движение происходит прямолинейно в одну сторону и если перемещение столь мало, что практически невозможно отличить дугу от стягивающей ее хорды. Обозначим такое перемещение и назовем егоэлементарным, а стягивающую дугу обозначим dl. Поскольку дуга dl неотличима от перемещения , а вектор, то и dl будем считать вектором, т.е. в этом случае .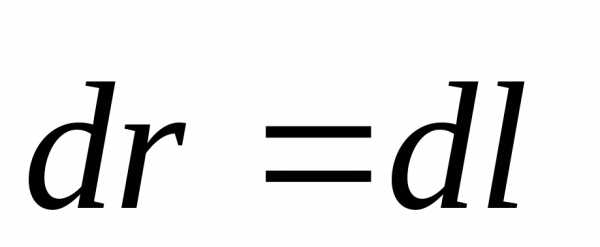

6. Скорость. За равные промежутки времени перемещения материальной точки могут быть различными. Скорость – векторная величина, которая определяет быстроту движения и его направление в данный момент времени.

Рис.1.3

Пусть материальная точка движется по криволинейной траектории и в начальный момент времени ее положение характеризуется радиус-вектором 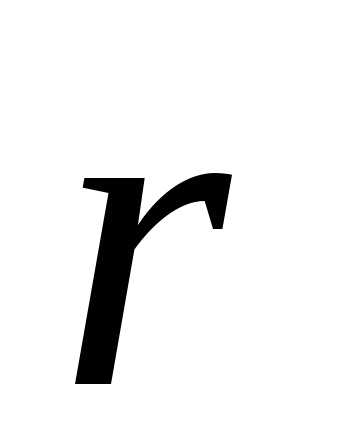. В течении малого промежутка времениточка пройдет путьи получит бесконечно малое перемещение(рис.1.3).

Вектором средней скорости 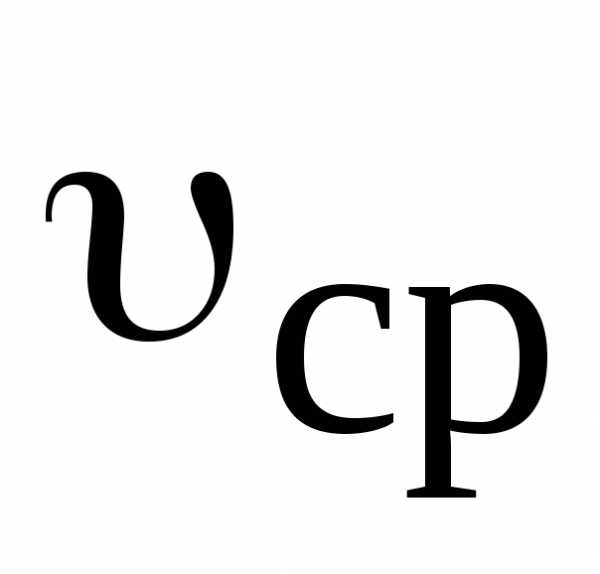называется отношение приращения радиус-вектора точки к интервалу времени, за которое произошло перемещение

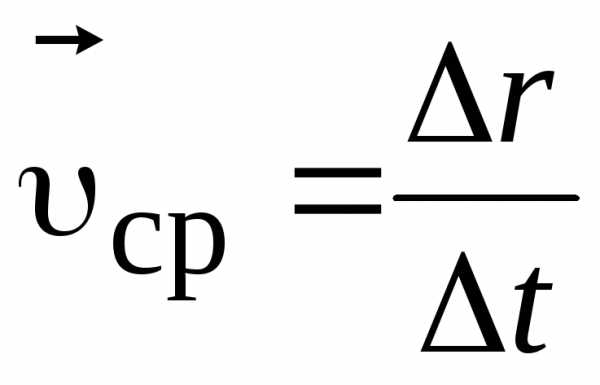. (1.1)

Направление вектора средней скорости совпадает с направлением . Если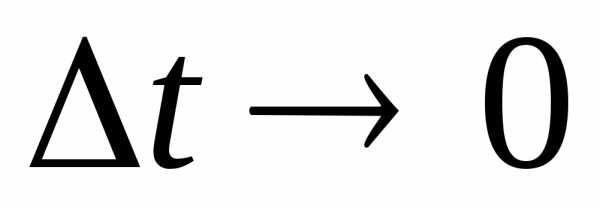, то средняя скорость стремится к предельному значению, которое называется мгновенной скоростью:

. (1.2)

Мгновенная скорость – векторная величина, определяемая первой производной радиус-вектора движущейся точки по времени. Это перемещение, отнесенное к единице времени. Так как секущая в пределе совпадает с касательной, то вектор скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости равен первой производной пути по времени:

. (1.3)

Единица скорости в СИ: 1 м/с – скорость прямолинейно и равномерно движущейся точки, при которой эта точка за время 1 с перемещается на расстояние 1 м.

Вектор скорости можно разложить на компоненты

где 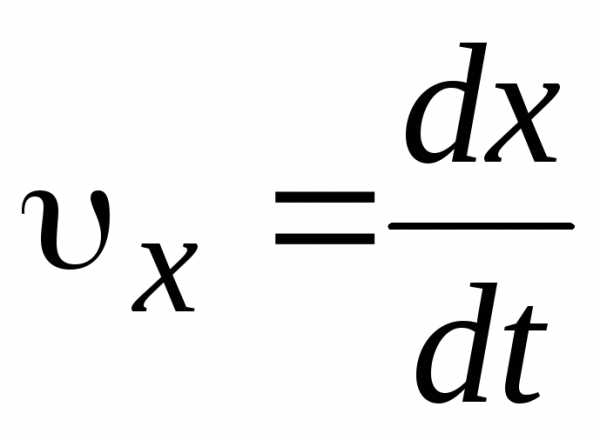;; проекции вектора скорости на оси координат. Тогда модуль скорости равен:

. (1.4)

Например, при движении материальной точки в плоскости ХY, ее cкорость и модуль скорости υ определяются выражениями:

где ; проекции вектора скорости на оси координат,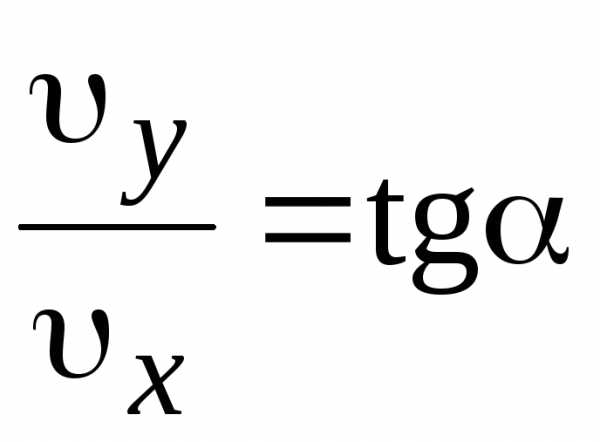(рис. 1.4).

Рис.1.4

7. Ускорение и его составляющие. Ускорение – характеристика неравномерного движения, определяющая быстроту изменения скорости по модулю (величине) и направлению. Рассмотрим плоское движение. Пусть вектор задает скорость точки в момент времениt. За время t точка перешла в положение В и приобрела скорость  изменение вектора скорости (рис.1.5).

Рис.1.5

Средним ускорением называется векторная величина, равная отношению изменения скорости 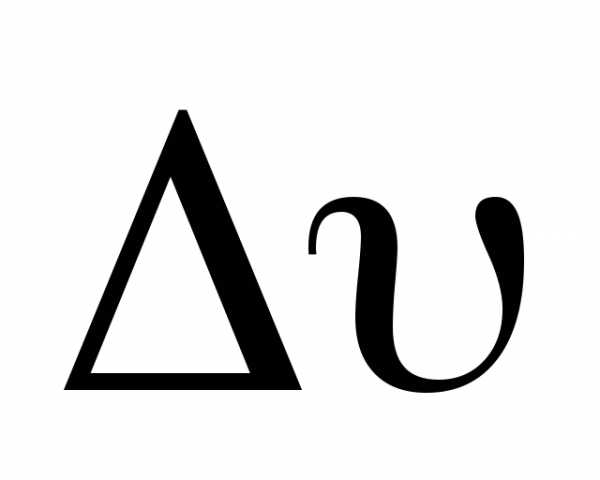к интервалу времениt, за которое это изменение произошло

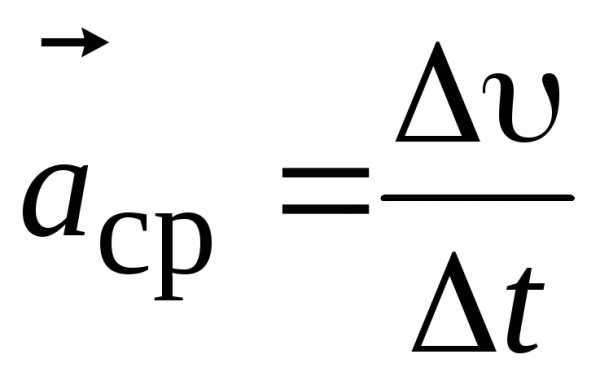. (1.5)

Мгновенное ускорение материальной точки в момент времениt – предел среднего ускорения – это векторная величина, определяемая первой производной скорости по времени

. (1.6)

Разложим вектор 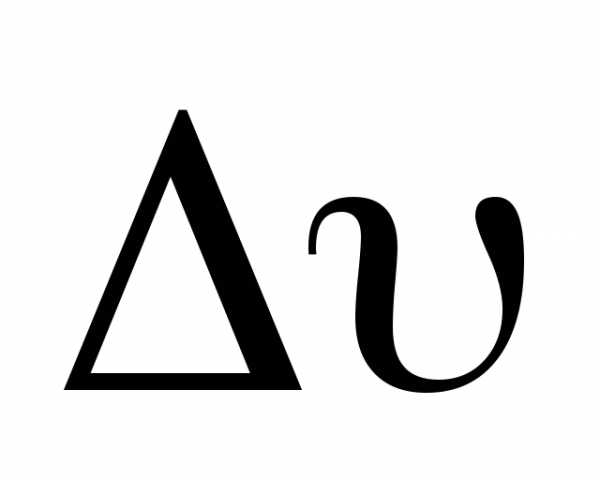на две составляющие. Из точкиА по направлению скорости отложим вектор. Вектор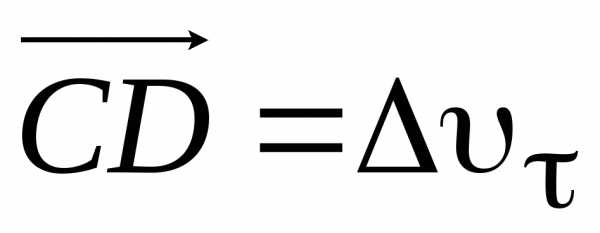определяет изменение скорости за времяпо модулю:. Вторая составляющаявектора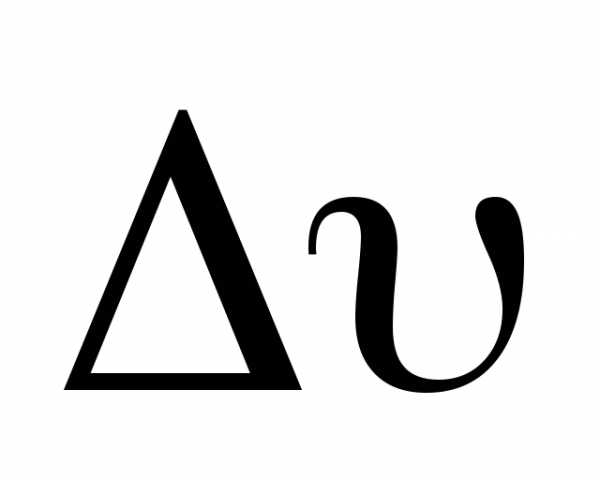характеризует изменение скорости за времяпо направлению.

Таким образом, составляющие ускорения – это

1)тангенциальная составляющая , которая характеризует быстроту изменения скорости,по модулю направлена по касательной к траектории и равна первой производной скорости по времени.

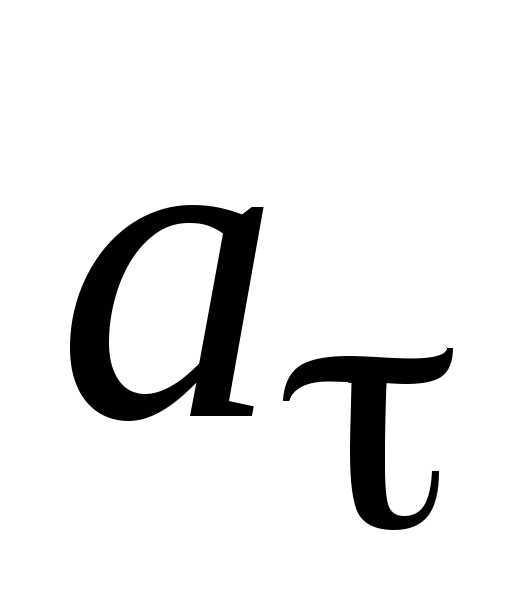2)нормальная составляющая  которая характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории). Составляющие и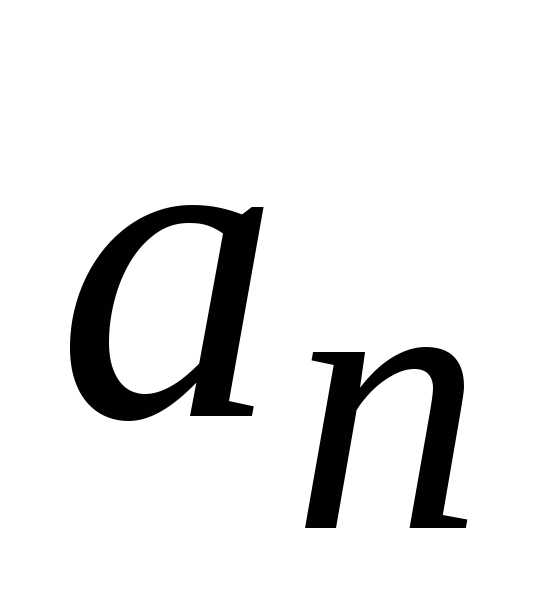перпендикулярны друг другу.

Полное ускорение при криволинейном движении – геометрическая сумма тангенциальной и нормальной составляющих ускорения.

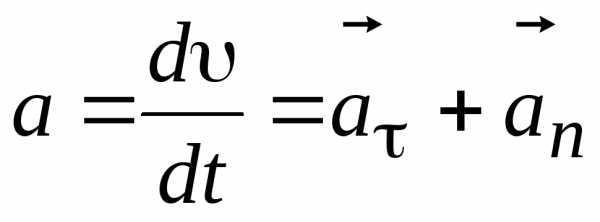. (1.7)

Модуль полного ускорения

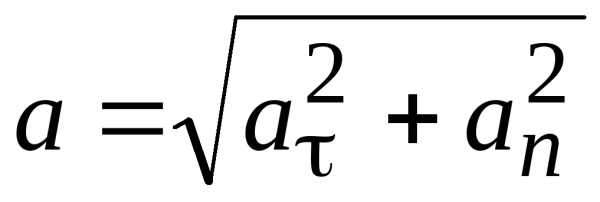; . (1.8)

Единица ускорения 1 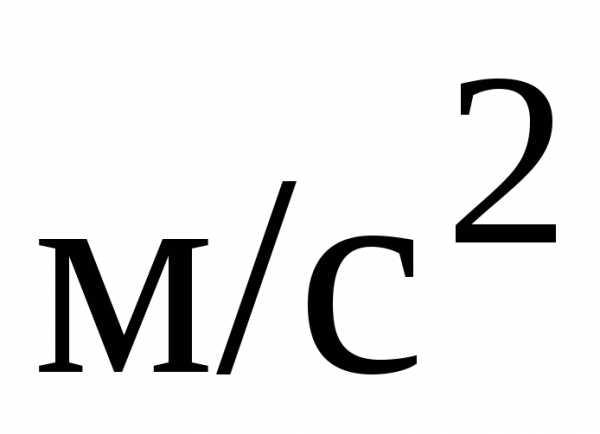– это ускорение прямолинейного ускоренного движения точки, при котором за 1 с скорость точки изменяется на 1 м/с.

В таблице 1.1 представлена классификация движения в зависимости от тангенциальной и нормальной составляющих ускорения.

Таблица 1.1

		Движение
0	0	равномерное прямолинейное
	0	прямолинейное равнопеременное
	0	прямолинейное с переменным ускорением
0	const	равномерное по окружности
0	 0	равномерное криволинейное
const	 0	криволинейное равнопеременное
	 0	криволинейное с переменным ускорением

При прямолинейном равнопеременном движении ,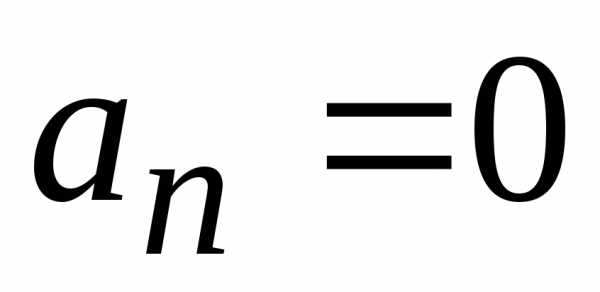; при таком виде движения. Если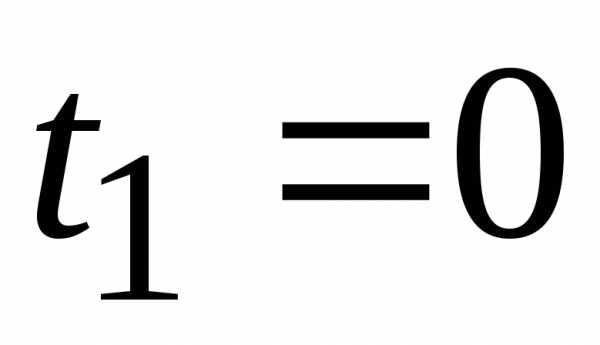, а начальная скорость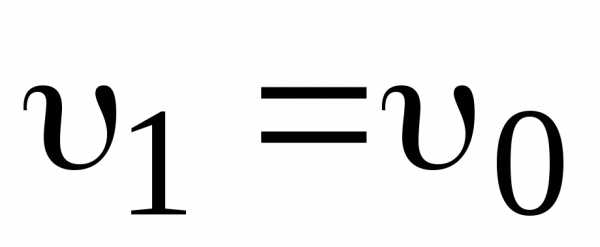, то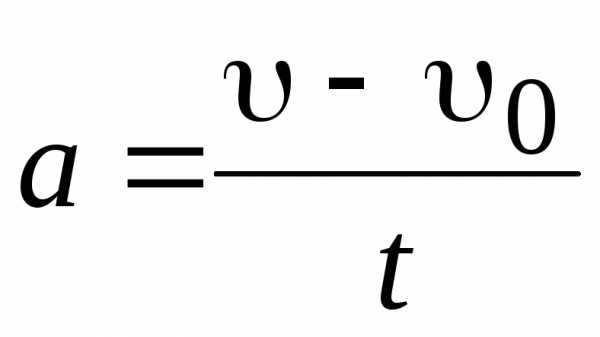, откуда

. (1.9)

Длина пути, пройденного точкой за промежуток времени определяется интегралом

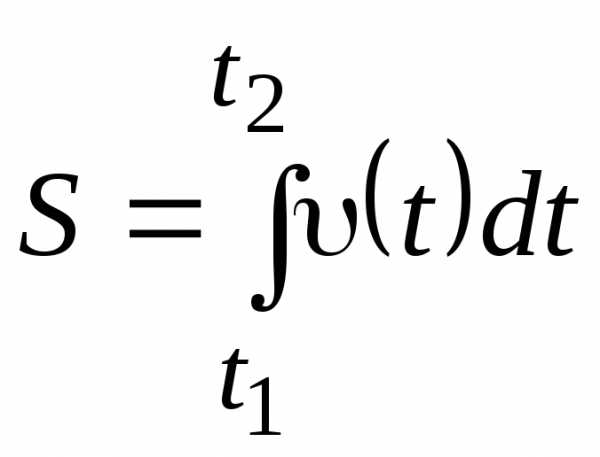. (1.10)

Проинтегрируем формулу (1.9) в пределах от t=0 до произвольного момента времени t и найдем, что длина пути, пройденного точкой равна

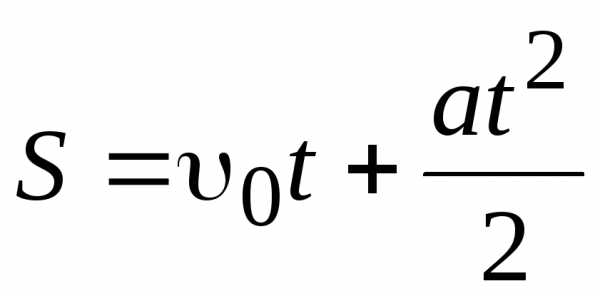. (1.11)

Для определения S надо знать функцию 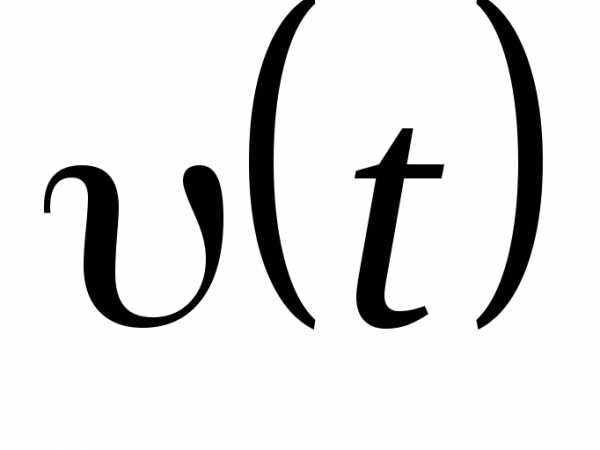. Тогда путь, пройденный за промежуток времени отдо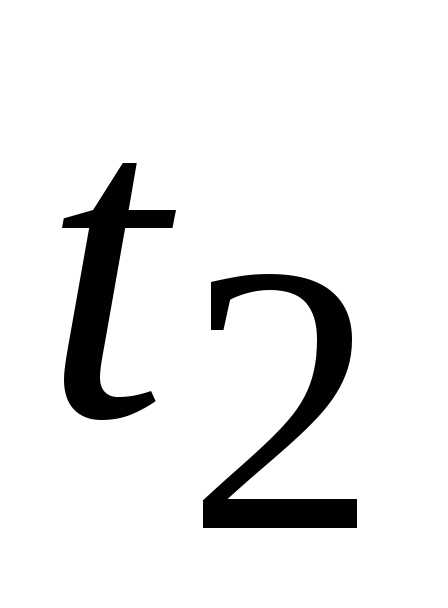определяется заштрихованной на рисунке площадью (рис.1.6).

Рис.1.6

studfiles.net

Измерение (физика) Википедия

Измерение — совокупность действий для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений).

Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

Принцип измерений — физическое явление или эффект, положенный в основу измерений.
Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути сравнивают её размер с единицей, хранимой линейкой, и, произведя отсчёт, получают значение величины (длины, высоты, толщины и других параметров детали).
С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчёт.

Частным случаем измерения является сравнение без указания количественных характеристик.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

Научная группа "Артефакт" предложила следующее определение термина: физические измерения - целенаправленные действия исследователей на получение достоверных, проверяемых, воспроизводимых данных о количестве (и качестве) эталонных физических событий в исследуемом процессе (или объекте) (или) за эталонную единицу времени, (или) на эталонную единицу пространства, (или) на эталонную единицу вещества.

Классификация измерений[ | код]

По видам измерений[ | код]

Согласно РМГ 29-99 «Метрология. Основные термины и определения» выделяют следующие виды измерений:

Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
Совместные измерения — проводимые одновременно измерения двух или нескольких не одноимённых величин для определения зависимости между ними.
Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
Равноточные измерения — ря

ru-wiki.ru

1 Измерения в физике

1.8. Измерения в физике

"Кто не имел опытов - мало знает"

(Сирах) Объект познается через свойства, которые мы наблюдаем. В быту свойства задаются качественно. Стоит задача перевода их в количественную форму. Возьмем в качестве объекта палку. Перечислим свойства палки: длинная, тонкая, прямая, твердая, холодная, серая, приятная, удобная... Эти свойства надо перевести в количественные. Возьмем и рассмотрим свойство "длинная". Введем количественную характеристику «длина», определив ее как расстояние между крайними граничными точками палки, обозначим ее L. Длина L есть расстояние между точками А и В:

Рис.134 Надо задать длине числовое значение, если мы хотим получить количественную характеристику. Надо это сделать так, чтобы она была объективной. Для этого возьмем другое тело: твердое, прямое, с резкими границами A'B' и назовем его эталоном. Примем длину этого тела l за единичную. Сравним длину АВ с длиной A'B', составив отношение = n. Тогда L = nl, то есть получим, что длина палки L равна n единицам длины эталона. Измеряя любое тело с помощью A'B', мы получим для каждого тела его длину Li выраженную в единицах l. Эта величина будет объективной и количественной. Количественной - поскольку имеется ее численное значение. Объективной - так как данное число есть отношение одинаковых свойств двух реальных объектов мира.

Субъективность проявляется в том, что волевым методом вводится единица меры - это не страшно; важно, чтобы длины всех объектов были измерены относительно одного эталона. Количественная характеристика объекта, полученная с помощью измерений, называется физической величиной.

Эталон должен обладать свойствами, обеспечивающими ему воспроизведение и хранение принятой единицы физической величины. Так, например, эталон метра (принятый в 1889 г.) представляет собой платиноиридиевый брусок, на который нанесены две параллельные метки. Расстояние между этими метками равно однодесятимиллионной доли расстояния от экватора до северного полюса вдоль меридиана, проходящего через Париж. Это и есть единица длины - метр. Эталон обеспечивает точность измерений длины до 10-7 По мере возникновения новых требований к точности измерений используются другие эталоны. Например, с 1983 г. метр определяется как длина пути, проходимого в вакууме светом за 1/299792458 секунды. Этот эталон обеспечивает точность измерений длины 10-10.

Итак, физическая величина задается способом измерений. Общий смысл ее - мера свойства. Смысл конкретной физической величины вытекает из интерпретации свойства, мерой которого является данная физическая величина. Интерпретация свойства должна строго соответствовать формальному определению этой величины. Измерения физических величин производят с помощью приборов. Измерительный прибор - искусственно созданный физический объект, имеющий шкалу, на которой в результате взаимодействия прибора с физическим объектом фиксируется число, являющееся результатом измерений. Это число и является значением физической величины, как свойства измеряемого объекта в конкретных условиях наблюдения.

Tехническиe приборы могут иметь разные фиксирующие устройства: ранее широко использовались шкалы, представляющие собой линейки, градуированные в единицах измеряемой длины. При этом указатель в виде стрелки или светового луча отмечал на шкале значение измеряемой величины. Современные приборы имеют цифровые индикаторы.

Итак, измерения проводят, чтобы получить численные значения физической величины. При прямых измерениях эти значения получают непосредственно, а при косвенных - вначале определяют одну или несколько исходных величин, а затем по их значениям вычисляют нужную величину.

В силу различных причин результат измерения всегда определяется приближенно. Всякое измерение устанавливает, что физическая величина имеет значение в интервале от - А до + А Значения , лежащие в середине интервала, называются измеренным значением , а величина интервала А - абсолютной погрешностью измерения или его ошибкой. Отношение абсолютной погрешности А к измеренному значению называется относительной погрешностью  значения физической величины или точностью значения. Напомним, что при измерении физической величины ее значение А сравнивают с единицей измерения [A]. Число, которое получается при измерениях, называют численным значением {A} физической величины, т.е. A = {A} [A] - любая физическая величина равна произведению численного значения и единицы измерения.

Физические величины связаны математическими зависимостями. Можно выделить несколько независимых величин, которые не сводятся одна к другой. Их называют основными физическими величинами и они могут быть выбраны произвольно.

Существуют международные соглашения, которые определяют основные физические величины. Все остальные величины называются производными. Они определяются математическими соотношениями, в которые входят основные физически величины или их комбинации.

Производные физически величины можно представить через произведение основных величин (обозначим основные величины через Вi)

A = B11 B22 B33 ... Bnn , где показатели степени n это положительные или отрицательные рациональные числа. В 1960 г. было заключено соглашение о выборе основных физических величин. Они составляют основу Международной системы единиц (СИ). Основными физическими величинами и единицами измерения являются:

Физическая величина	Обозначение	Единицы измерения	Обозначение
Длина	l	метр	м, L
Масса	m	килограмм	кг, M
Время	t	секунда	с, T
Сила электрического тока	I	ампер	А, I
Температура	T	Кельвин	К, 
Количество вещества	n	Моль	моль, N
Сила света	TV	канделла	кд, J

.В системе СИ размерность некоторой величины в общем виде выражается как

dim A = L1 M2 T3 I4 5 N6 J7.

В этом выражении все показатели степени  - целые числа. Так, размерность кинетической энергии Екин имеет вид

Екин= dim = ML2 T-2 кг м/сек2,

а коэффициент трения  имеет нулевую размерность. Физическая величина и ее размерность - это не одно и то же. Одинаковую размерность могут иметь разные по своей природе физически величины, например: работа и момент силы.. Однако она важна для проверки правильности соотношений между физическими величинами.

1.9. Физические модели

Для получения объективного количественного описания объекта надо его качественные характеристики перевести в количественные, т.е. в физические величины. Не для всех свойств можно найти способ измерений и потому число физических свойств объекта всегда меньше совокупности всех свойств, присущих данному объекту. Поэтому для объективного описания надо перевести объект в объект физический, т.е. оставить у него для рассмотрения только свойства физически и отбросить все остальные.

Заметим, что объективные эталоны (как объекты реального мира) имеются только для измерения физических свойств и потому физика является единственной фундаментальной основой других наук, которые, по сути, являются ее следствиями, работающими на более высоких этажах: химия, биология, психология, физиология...

Измерения физических величин объекта проводятся всегда в конкретных условиях наблюдения и в рамках определенных требований.

Например, требуется определить расстояние между двумя объектами. При этом требуется точность измерений  = 0,01. Пусть один объект лошадь, длина которой l = 2 м, а другой - дорожный столбик диаметром d = 5 см. Пусть лошадь находится от столбика на расстоянии более одного километра: L  1 км. Учитывая заданную точность мы получим, что погрешность измерений L = L мин = 10-2 103 м = 10 м. Лошадь имеет длину l= 2 м, столбик d = 5 см, т.е. d

Это значит, что длина лошади не играет роли и за точки измерения можно взять любые точки на объекте (лошади и столбика).

Если же лошадь находится от столбика на минимальном расстоянии L = 10 м, то в пределах заданной точности L = 10-2 10 = 10-1 м = 10 см, т.е. L L.

В этом случае условия наблюдения не позволяют определить L с заданной точностью. Надо вводить дополнительные требования: например, договариваться о конкретной точке на лошади или изменять .

Объективно в пределах заданной точности можно измерить расстояние между объектами, если выполняется условие l

Такое тело называется материальной точкой и является упрощением конкретного тела, т.е. физической моделью. Физические модели могут отличаться от объектов размерами, типом материала и другими характеристиками.

Физическая модель объекта - реальное тело (или система тел), в котором некоторые свойства берутся с упрощениями.

Использование физических моделей позволяет результаты измерений, полученные для данной модели, использовать для описания поведения любых объектов, описываемых этой моделью и делать обобщения, т.е. получать феноменологически законы: функциональную связь физических характеристик объекта (или процесса), имеющую место в жестко определенных условиях.

Вспомним задачу физики: объективное описание объектов материального мира. Как описывать свойства объектов материального мира мы рассмотрели: посредством измерения физических свойств объектов. Однако между физическими свойствами объекта и физическими свойствами различных объектов существуют устойчивые функциональные связи.

Описание материального мира требует и нахождения этих связей. Именно посредством этих связей и описывается совокупность закономерно связанных между собой изменений, происходящих с объектами с течением времени, т.е. описывается то, что мы называем физическим явлением (или процессом). Возникает вопрос - а почему существуют функциональные связи между свойствами объектов и объектами - опять же в силу исторического развития - так утверждает христианский принцип математического построения мира.

Для нахождения связей физических величин (т.е. для описания физического явления) измеряются физически величины, строятся графики зависимостей этих величин друг от друга и выявляется функциональная связь.

Например, будем кидать с башни камни, для которых выполнено условие представления их моделями материальных точек и для каждого камня будем измерять расстояние L, проходимое им за время t (при этом будем изменять и время). Получим набор расстояний Li и соответствующий набор времен ti Построим график L = f(t) - расстояния как функции времени. График описывается функциональной завсимостью L = kt2, где , a g = 9,8 м/сек для всех камней.

Рис.135

Это и есть феноменологический закон - связь физических величин явления, имеющая место в жестких определенных условиях. Среди этих условий: нет учета связи с окружающей средой, значение g считается одинаковым для всех точек земной поверхности и н зависит от высоты башни и т.д. Используя измерительные процессы, можно получить много феноменологических законов и использовать их для решения многих практических проблем.

1.10. Физические модели тел в механике.

1. Материальная точка - тело, размерами которого в условиях конкретной задачи можно пренебречь. Математической моделью материальной точки является геометрическая точка. Положение материальной точки в пространстве определяется положением отображающей ее геометрической точки.

2. Абсолютно твердое тело - твердое тело, изменением формы и размеров которого при его движении в условиях конкретной задачи можно пренебречь. Эту модель можно рассматривать как систему материальных точек, расстояние между которыми остаются неизменными.

3. Упругое твердое тело - твердое тело, движение которого или его взаимодействие с другими телами сопровождается такими изменениями формы, что при прекращении взаимодействия или возврате к исходному механическому состоянию его первоначальная форма сохраняется. Во многих случаях упругое твердое тело можно рассматривать как систему материальных точек, связанных пружинами.

Пружина - специальная модель деформируемого тела, обладающего пренебрежимой массой и двумя параметрами - длиной в недеформированном состоянии l и коэффициентом упругости k. Деформация пружины точно следует закону Гука.

Закон Гука выражается формулой F = k l , где l = l - l0 и l - длина в деформированном состоянии, F - величина силы.

4. Неупруго деформированное тело - тело, форма которого не восстанавливается после прекращения воздействия.

5. Математический маятник - система, состоящая из материальной точки, прикрепленной к концу невесомого стержня (подробнее в параграфе "Колебания").

1.11. ВОПРОСЫ ДЛЯ ОСВОЕНИЯ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА ПО КУРСУ "МЕХАНИКА"

Дайте определение физической величины.
Как задается физическая величина?
Как интерпретируется физическая величина?
Что называют смыслом физической величины?
Определить физический смысл механических величин - тех, которые вы знаете.
Что такое математический образ физической величины? Приведите примеры.
Что называют физическим измерением?
В чем состоит объективность физической величины?
Существуют ли в науке объективные нефизические величины? Если да - то приведите примеры, если нет - то объясните почему.
Что такое эталон?
Что такое мера?
Как определяется размерность физической величины?
Что называют системой единиц измерений?
Какие величины называют основными? Приведите основные величины системы СИ.
Что такое точность измерений?
Что называют физической моделью объекта? Что такое математическая модель объекта?
Как перевести объект в его физическую модель?
Как перевести физическую модель объекта в математическую модель?
В чем принципиальная разница физической и математической моделей?
Объективна ли математическая модель объекта? Если да - объяснить; если нет - объяснить.
Какой закон называют феноменологическим?
Какой закон называют фундаментальным?
Что называют общим принципом физики? Приведите примеры общих принципов.
Что является обоснованием принципа математического построения материального мира?
Что в науке понимают под термином "материя"?
Зачем в физике используются векторные величины?
Как разложить вектор на составляющие и на проекции?
Дать определение физической модели "материальная точка".
Дать определение математического движения точки.
Какие модели механики вы знаете? Перечислить и дать определение каждой.
Что такое система отсчета: состав и назначение.
Как используя систему отсчета, измерить расстояние до звезды?
Как ввести радиус-вектор и записать его выражение в заданной системе координат?
Зависит ли величина радиус-вектора от выбора системы отсчета; если зависит - то как связать радиусы-векторы одной точки относительно двух систем координат?
Что называют траекторией движения и как ее найти?
Что такое путь, пройденный точкой, и как его найти?
Что называют средней скоростью материальной точки?
Что называют мгновенной скоростью?
Что называют средним ускорением?
Что называют мгновенным ускорением?
Как определяется мгновенная скорость как физическая величина?
Как определяется мгновенная скорость как математическая модель?
Что называют абсолютной, относительной и переносной скоростями? Какая связь существует между ними?
Как, зная значение радиус-вектора как функции времени R = f(t) определить значение скорость и ускорения в те же моменты времени?
Как, зная значение ускорения как функции времени, определить значение скорости и положения точки в те же моменты времени?
Записать уравнение движения материальной точки при равномерном прямолинейном движении. Уравнение дать в векторной и скалярной формах.
Записать уравнение движения материальной точки при движении с постоянным ускорением. Уравнение дать в векторной и скалярной форме.
Записать уравнение движения материальной точки по окружности. Уравнение дать в векторной и скалярной форме.
Записать уравнение движения материальной точки, совершающей гармонически колебания. Записать связь между амплитудами ускорения, скорости и смещения.
Что называют фазой колебаний?
Что называют угловой скоростью?
Дать определение углового ускорения.
Записать связь между линейными и угловыми кинематическими величинами.
Что называют циклической частотой и круговой частотой?
Дать определение периода колебаний.
Записать полное ускорение при вращении тела по окружности.
Записать выражение для смещения при гармоническом колебании материальной точки с учетом начальных условий.
Дать определение физической величине "масса".
Что такое инертность?
Что такое инерция?
Дать определение гравитационной массе.
Можно ли логическими средствами доказать эквивалентность гравитационной и инертной массы?
Что называют инерциальной системой отсчета?
Почему в изначальной системе законов Ньютона ничего не говорится об инерциальной системе отсчета?
Дать формулировки законов Ньютона.
Почему постоянную G в законе всемирного тяготения называют универсальной?
Чем доказывается универсальность постоянной G?
Дать определение величине "импульс".
Дать определение величине "сила".
Какие виды и типы сил вам известны?
Дать определение силам упругости, трения, гравитации, тяжести, веса.
Объясните, что означает утверждение о полной аксиоматике механической системы Ньютона?
Для каких объектов аксиоматика Ньютона делается полной?
Какие постулаты являются доказательством правильности системы Ньютона в целом?
Как определяются (каким способом) границы области действий физической системы Ньютона?
Для каких объектов система законов механики Ньютона не применима?
Используя какие методы можно развивать механику Ньютона? Что конкретно можно развивать?
Дайте классификацию движений в механике и определение видом движения.
Определите величину: момент сил материальной точки.
Определите величину: момент инерции точки.
Определите величину : момент импульса материальной точки.
Что такое энергия материальной точки? Какая она бывает?
Определить величину "работа".
Зависит ли знак работы от направления координаты осей?
Что такое система материальных точек? Чем она отличается от совокупности материальных точек?
Назовите типы систем материальных точек, которые известны вам, и дайте им определение.
Дать определение следующим величинам, характеризующим систему материальных точек в целом: а) импульс системы; б) момент импульса системы; в) центр масс; г) момент инерции; д) полная механическая энергия системы точек.
Записать уравнение движения тел с переменной массой.
Что называют реактивной силой?
Дать определение потенциальной энергии.
Записать связь между приращением потенциальной энергии и работой консервативных сил.
Дать формулировку теоремы о кинетической энергии для системы материальных точек.
Записать потенциальную энергию упругих сил, сил тяжести, сил тяготения.
Записать полную механическую энергию системы материальных точек, если известны массы частиц, их скорости и расстояния между частицами.
Дать формулировки закона сохранения: импульса, момента импульса, механической энергии для системы материальных точек.
Дать определение физической модели "абсолютно твердое тело".
Записать общие формулы нахождения моментов инерции твердых тел.
Дать определение физического маятника.
Дать формулировку теоремы Штернера.
Сформулировать закон изменения момента импульса для твердого тела.
Дать определение гидростатического давления.
Нарисовать диаграмму растяжения и указать на ней характерные точки, определив их.
Записать основное уравнение движения идеальной жидкости.
Сформулировать законы Паскаля, Архимеда.
Сформулировать закон Бернулли.
Что такое полевое представление сплошной среды?
Что называют линией тока, трубкой тока?
Основные величины поля: поток вектора, циркуляция - дать определения.
Какое движение называют стационарным?
Что такое волна?
Какими параметрами характеризуются волны?
Записать уравнение плоской бегущей волны и его решение.
Энергия волны, бегущие и стоячие волны.

ВОПРОСЫ ПО ТЕМЕ.

ОБЩИЕ ПРОБЛЕМЫ РЕШЕНИЯ ЗАДАЧ

Какие задачи называют детерминированными?
Какие задачи называют задачи с риском? Приведите примеры.
Какие задачи называют закрытыми? Приведите примеры.
Какие задачи называют открытыми? Приведите примеры.
Как символически представить структуру задачи
Приведите общую структурную схему решения задач классической механики Ньютона.
Используя структурную схему решения, объясните процесс решения задачи в целом.
Как определить этапы процесса, заданного в условии задачи?
Как определяют возможные варианты решения задачи?
Почему необходим перевод изначальной ситуации в физический процесс?
Как переводится начальная ситуация в физический процесс?
Почему необходимо физический процесс перевести в его математический образ?
Как из физической модели ситуации перейти к математической модели ситуации?
Как решить задачу, оставаясь в рамках только физической модели ситуации?
Как возможно решение задачи в рамках математической модели процесса?
Какую систему уравнений называют полной?
Какие уравнения могут входить в полную систему уравнений при решении задач классической механики?
Что такое математическое решение задачи?
Как осуществляют перевод математического представления решения в физическое?
Как упорядочивают изначальную ситуацию, заданную в задачах?
Как производится выбор физической модели объекта?
Как перевести векторные уравнения в скалярные на математическом этапе решения задачи.
Как получить конечное значение физической величины?
Что означает проверка величины на размерность и реальность?
Зачем нужен поиск дополнительной информации и какие способы поиска вы знаете? (Перечислить.)
Как построить систему из первоначально заданных в условии задачи объектов?
Приведите примеры свойств моделей, которые дают дополнительную информацию в процессе решения задачи.
Приведите примеры условий, накладываемых на физически свойства объектов (или их систем), которые дают дополнительную информацию в процессе решения задачи.
Что такое уравнение кинематической связи, как и какую информацию находят при его использовании?

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ ДЛЯ ПОЛУЧЕНИЯ ЗАЧЕТА

Контрольная включает три вопроса:

1. Вопрос - из вопросов по освоению теоретического материала.

2. Вопрос - из вопросов по освоению проблемы решения задач.

3. Вопрос - на вычисление физической величины или использования физического закона.

Примеры вариантов

№ 1.

1. Записать уравнение движения материальной точки, совершающей колебательное движение, его решение с учетом заданных начальных условий.

2. Приведите общую структурную схему решения задач классической физики Ньютона.

3. Частица движется по закону х = -19 + 20t - t2 Найти путь, пройденный частицей за время t.

№ 2.

1. Записать уравнение движения тел с переменной массой. Дать определение реактивной силы.

2. Какие уравнения могут входить в полную систему уравнений при решении задач классической механики Ньютона?

3. Частица, положение которой задается радиус-вектором (-4, 2, -10), имеет импульс (2, 4, 6). Определить момент импульса частицы относительно оси Z - MZ

mognovse.ru

Измерение — WiKi

Принцип измерений — физическое явление или эффект, положенный в основу измерений.
Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути сравнивают её размер с единицей, хранимой линейкой, и, произведя отсчёт, получают значение величины (длины, высоты, толщины и других параметров детали).
С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчёт.

Частным случаем измерения является сравнение без указания количественных характеристик.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

Классификация измерений

По видам измерений

Согласно РМГ 29-99 «Метрология. Основные термины и определения» выделяют следующие виды измерений:

Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
Совместные измерения — проводимые одновременно измерения двух или нескольких не одноимённых величин для определения зависимости между ними.
Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
Равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
Неравноточные измерения — ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
Однократное измерение — измерение, выполненное один раз.
Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений
Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
Динамическое измерение — измерение изменяющейся по размеру физической величины.
Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную (см. ниже нулевой метод).

Также стоит отметить, что в различных источниках дополнительно выделяют такие виды измерений: метрологические и технические, необходимые и избыточные и др.

По методам измерений

Метод непосредственной оценки — метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.
Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
- Нулевой (компенсационный) метод измерений — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
- Метод измерений замещением — метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
- Метод измерений дополнением — метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчётом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
- Дифференциальный метод измерений — метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.

По условиям, определяющим точность результата

Метрологические измерения
- Измерения максимально возможной точности, достижимой при существующем уровне техники. В этот класс включены все высокоточные измерения и в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин. Сюда относятся также измерения физических констант, прежде всего универсальных, например измерение абсолютного значения ускорения свободного падения[1].
- Контрольно-поверочные измерения, погрешность которых с определённой вероятностью не должна превышать некоторого заданного значения. В этот класс включены измерения, выполняемые лабораториями государственного контроля (надзора) за соблюдением требований технических регламентов, а также состоянием измерительной техники и заводскими измерительными лабораториями. Эти измерения гарантируют погрешность результата с определённой вероятностью, не превышающей некоторого, заранее заданного значения[1].
Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на промышленных предприятиях, в сфере услуг и др.[1]

По отношению к изменению измеряемой величины

Динамическое и статическое.

По результатам измерений

Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную.

Классификация рядов измерений

По точности

Равноточные измерения — однотипные результаты, получаемые при измерениях одним и тем же инструментом или им подобным по точности прибором, одним и тем же (или аналогичным) методом и в тех же условиях.
Неравноточные измерения — измерения, произведённые в случае, когда нарушаются эти условия.

По числу измерений

Однократное измерение — измерение, выполненное один раз.
Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений.

Классификация измеряемых величин

По точности

Детерминированные и случайные.

По результатам измерений

Равнорассеянные и неравнорассеянные.

История

Стандартизация измерений

В начале 1840 г. во Франции была введена метрическая система мер.

В 1867 г. Д. И. Менделеев выступил с призывом содействовать подготовке метрической реформы в России. По его инициативе Петербургская академия наук предложила учредить международную организацию, которая обеспечивала бы единообразие средств измерений в международном масштабе. В 1875 г. была принята Метрическая конвенция. Принятие Конвенции ознаменовало начало международной стандартизации.

Единицы и системы измерения

В физике и технике единицы измерения (единицы физических величин, единицы величин[2]) используются для стандартизованного представления результатов измерений. Использование термина единица измерения противоречит нормативным документам[3] и рекомендациям метрологических изданий[4], однако он широко употребляется в научной литературе[5]. Численное значение физической величины представляется как отношение измеренного значения к некоторому стандартному значению, которое и является единицей измерения. Число с указанием единицы измерения называется именованным. Различают основные и производные единицы. Основные единицы в данной системе единиц устанавливаются для тех физических величин, которые выбраны в качестве основных в соответствующей системе физических величин. Так, Международная система единиц (СИ) основана на Международной системе величин (англ. International System of Quantities, ISQ), в которой основными являются семь величин: длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света. Соответственно, в СИ основными единицами являются единицы указанных величин. Размеры основных единиц устанавливаются по соглашению в рамках соответствующей системы единиц и фиксируются либо с помощью эталонов (прототипов), либо путём фиксации численных значений фундаментальных физических постоянных.

Международная система единиц

Основная статья: СИ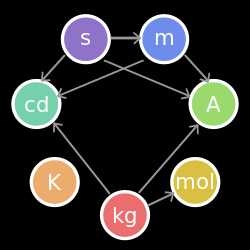

Семь базовых величин в СИ. Стрелки указывают зависимости между величинами.

Система единиц физических величин, современный вариант метрической системы. СИ является наиболее широко используемой системой единиц в мире, как в повседневной жизни, так и в науке и технике. В настоящее время СИ принята в качестве основной системы единиц большинством стран мира и почти всегда используется в области техники, даже в тех странах, в которых в повседневной жизни используются традиционные единицы. В этих немногих странах (например, в США) определения традиционных единиц были изменены таким образом, чтобы связать их фиксированными коэффициентами с соответствующими единицами СИ. Официальным международным документом по системе СИ является Брошюра СИ (фр. Brochure SI, англ. SI Brochure), издающаяся с 1970 года. С 1985 года выходит на французском и английском языках, переведена также на ряд других языков. В 2006 году вышло 8-е издание.

Метрическая система мер

Общее название международной десятичной системы единиц, основанной на использовании метра и килограмма. На протяжении двух последних веков существовали различные варианты метрической системы, различающиеся выбором основных единиц. В настоящее время международно признанной является система СИ. Основное отличие метрической системы от применявшихся ранее традиционных систем заключается в использовании упорядоченного набора единиц измерения. Для любой физической величины существует лишь одна главная единица и набор дольных и кратных единиц, образуемых стандартным образом с помощью десятичных приставок. Тем самым устраняется неудобство от использования большого количества разных единиц (таких, например, как дюймы, футы, фадены, мили и т. д.) со сложными правилами преобразования между ними. В метрической системе преобразование сводится к умножению или делению на степень числа 10, то есть к простой перестановке запятой в десятичной дроби.

Система СГС

Основная статья: СГС

Система единиц измерения, которая широко использовалась до принятия Международной системы единиц (СИ). Другое название — абсолютная[7] физическая система единиц. В рамках СГС существуют три независимые размерности (длина, масса и время), все остальные сводятся к ним путём умножения, деления и возведения в степень (возможно, дробную). Кроме трёх основных единиц измерения — сантиметра, грамма и секунды, в СГС существует ряд дополнительных единиц измерения, которые являются производными от основных. Некоторые физические константы получаются безразмерными. Есть несколько вариантов СГС, отличающихся выбором электрических и магнитных единиц измерения и величиной констант в различных законах электромагнетизма (СГСЭ, СГСМ, Гауссова система единиц). СГС отличается от СИ не только выбором конкретных единиц измерения. Из-за того, что в СИ были дополнительно введены основные единицы для электромагнитных физических величин, которых не было в СГС, некоторые единицы имеют другие размерности. Из-за этого некоторые физические законы в этих системах записываются по-разному (например, закон Кулона). Отличие заключается в коэффициентах, большинство из которых — размерные. Поэтому, если в формулы, записанные в СГС, просто подставить единицы измерения СИ, то будут получены неправильные результаты. Это же относится и к разным разновидностям СГС — в СГСЭ, СГСМ и Гауссовой системе единиц одни и те же формулы могут записываться по-разному.

Английская система мер

Используется в Великобритании, США и других странах. Отдельные из этих мер в ряде стран несколько различаются по своему размеру, поэтому ниже приводятся в основном округлённые метрические эквиваленты английских мер, удобные для практических расчётов.

Средство измерений

Техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени. Законом РФ «Об обеспечении единства измерений» средство измерений определено как техническое средство, предназначенное для измерений. Формальное решение об отнесении технического средства к средствам измерений принимает Федеральное агентство по техническому регулированию и метрологии. Классификация:

по техническому назначению
по степени автоматизации
по стандартизации средств измерений
по положению в поверочной схеме
по значимости измеряемой физической величины
по измерительным физико-химическим параметрам

Точность

Точность средства измерений — степень совпадения показаний измерительного прибора с истинным значением измеряемой величины. Чем меньше разница, тем больше точность прибора. Точность эталона или меры характеризуется погрешностью или степенью воспроизводимости. Точность измерительного прибора, откалиброванного по эталону, всегда хуже или равна точности эталона.
Точность результата измерений — одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения. Следует отметить, что о повышении качества измерений всегда говорят термином «увеличить точность» — притом, что величина, характеризующая точность, при этом должна уменьшиться.

Погрешность измерения

Оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99[8] термин ошибка измерения не рекомендуется применять как менее удачный). Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют действительное значение величины хд, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него[8]. Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. с некоторой оговорённой вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

См. также

Примечания

↑ 1 2 3 Метрология и технические измерения. Колчков В. И. Ресурс «ТОЧНОСТЬ-КАЧЕСТВО»]
↑ Официальное название по ГОСТ 8.417-2002 Государственная система обеспечения единства измерений. Единицы величин.
↑ Постановление Правительства РФ от 31 октября 2009 г. N 879 Об утверждении положения о единицах величин, допускаемых к применению в Российской Федерации
↑ «Не допускается применять термин единица измерения физической величины или единица измерения вместо стандартизированного термина единица физической величины или единица, поскольку понятие измерение определяют через понятие единица. Надо писать: ампер — единица силы тока, квадратный метр — единица площади и нельзя писать: ампер — единица измерения силы тока, квадратный метр — единица измерения площади» (Словарь-справочник автора / Сост. Л.А.Гильберг и Л.И.Фрид. — М.: Книга, 1979. — С. 98–99. — 304 с.).
↑ Аналогичная вариативность имеется и в иностранной терминологии. Так, в английском языке наряду с термином unit используется unit of measure(ment): Are, a metric unit of measurement, equal to 100 square metres (Concise Oxford English Dictionary, 11th edition, 2004).
↑ По историческим причинам, название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая в системе СИ сама является дольной: 1 г = 10−3 кг).
↑ Абсолютными называются системы, в которых в качестве основных единиц для механических величин приняты единицы длины, массы и времени.
↑ 1 2 РМГ 29-99 Рекомендации по межгосударственной сертификации. Основные термины и определения.

Литература и документация

Литература

Кушнир Ф. В. Радиотехнические измерения: Учебник для техникумов связи. — М.: Связь, 1980
Нефедов В. И., Хахин В. И., Битюков В. К. Метрология и радиоизмерения: Учебник для вузов. — 2006
Пронкин Н. С. Основы метрологии: Практикум по метрологии и измерениям. — М.: Логос, 2007
Воронцов Ю. И. Теория и методы макроскопических измерений. — М.: Наука, 1989. — 280 с. — ISBN 5-02-013852-5

Нормативно-техническая документация

Ссылки

ru-wiki.org

Что измеряет физическая величина

В природе существует большое количество самых разнообразных сил, влияющих на предметы и окружающую среду. Каждая из них имеет свою уникальную природу и оказывает определенное влияние на окружение. Для изучения и измерения такого воздействия и был введен термин "физическая величина". Сила давления, температура, трение и другие величины имеют собственное числовое и буквенное значение. Даже похожая физическая величина, например температура, может быть измерена в разных единицах, таких как шкалы Цельсия, Фаренгейта или Кельвина, а давление может измеряться в паскалях или барах.

Многие страны используют для обозначения веса или длины свои уникальные показатели. Единицы измерения физических величин различны. Например, в Великобритании расстояние оценивается ярдами и милями, а в России для этого используются уже метры и километры. Для унификации показаний была введена особая система СИ. Она позволила в учебниках, книгах, различных проектах использовать универсальные международные единицы измерения. В ней четко расписаны буквенные и числовые показатели, каждая физическая величина имеет свое обозначение и числовое значение.

Технический прогресс привел к росту химических и нефтеперерабатывающих предприятий. Слежение за технологическим процессом на современных производствах осуществляется системами автоматического управления производством. Для его правильного функционирования необходимо постоянно проводить измерение физических величин, которые задействованы в технологическом процессе. Это осуществляется при помощи контрольно-измерительных приборов, данные от которых поступают в центр АСУ, где после их обработки система выдает решение по изменению или продолжению работы. Центр автоматизации способен одновременно обрабатывать до нескольких тысяч данных и мгновенно реагировать на малейшее изменение давления или температуры во время производства. При помощи приборов КИПиА можно подсчитать расход продукта, ингредиентов, вычислить требуемые человеческие и энергетические ресурсы, а также большое количество других данных, благодаря которым будет обеспечиваться четкость и постоянство выполнения технологического процесса. Они позволяют максимально автоматизировать производство, повышая качество выпускаемой продукции.

Физическая величина изучается наукой метрологией. Специалисты в этой области определяют не только само значение и обозначение величины, а также устанавливают регламенты по допустимым погрешностям измерений для каждого из значений. Они проводят поверку и калибровку всех измерительных приборов, каждый из которых должен быть поставлен на учет, иметь паспорт и проверяться на соответствие своим техническим характеристикам.

Физическая величина – это единица измерения, позволяющая получить представление о силе воздействия. Она может иметь разное числовое значение, но буквенное обозначение должно соответствовать международным нормам и стандартам.

fb.ru

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

1.3. Единицы измерения в физике. Измерения в физике

Единицы измерения в физике

Измерение - это... Что такое Измерение?

Классификация измерений

По видам измерений

По методам измерений

По условиям, определяющим точность результата

По отношению к изменению измеряемой величины

По результатам измерений

Классификация рядов измерений

По точности

По числу измерений

Классификация измеряемых величин

По точности

По результатам измерений

История

Единицы и системы измерения

См. также

Примечания

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

1.3. Единицы измерения в физике

1.4. Физические основы классической механики

1.5. Основные понятия кинематики поступательного движения материальной точки

Измерение (физика) Википедия

Классификация измерений[ | код]

По видам измерений[ | код]

1 Измерения в физике

1.8. Измерения в физике

1.9. Физические модели

1.10. Физические модели тел в механике.

1.11. ВОПРОСЫ ДЛЯ ОСВОЕНИЯ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА ПО КУРСУ "МЕХАНИКА"

ВОПРОСЫ ПО ТЕМЕ.

ОБЩИЕ ПРОБЛЕМЫ РЕШЕНИЯ ЗАДАЧ

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ ДЛЯ ПОЛУЧЕНИЯ ЗАЧЕТА

Примеры вариантов

№ 1.

№ 2.

Измерение — WiKi

Классификация измерений

По видам измерений

По методам измерений

По условиям, определяющим точность результата

По отношению к изменению измеряемой величины

По результатам измерений

Классификация рядов измерений

По точности

По числу измерений

Классификация измеряемых величин

По точности

По результатам измерений

История

Стандартизация измерений

Единицы и системы измерения

Международная система единиц

Метрическая система мер

Система СГС

Английская система мер

Средство измерений

Точность

Погрешность измерения

См. также

Примечания

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

Что измеряет физическая величина

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ