Электрическое поле в диэлектрике
Если внести в электрическое поле диэлектрик, то электрическое поле изменится. Рассмотрим, как оно изменится и в чем причины его изменения.
Поляризация диэлектриков
Возьмем заряженный электрометр. Поднесем к нему пластинку из незаряженного диэлектрика. При этом показания электрометра уменьшатся. Удалим пластину, и показания электрометра восстановятся. При приближении к электрометру проводника будет наблюдаться подобное явление. Но мы знаем, что в электрическом поле на поверхности проводника появляются индукционные заряды, которые оказывают воздействие на внешнее поле. Из этого можно сделать вывод о том, что на диэлектрике в электрическом поле, тоже возникают заряды.
Возникновение зарядов на диэлектрическом теле приводит к появлению сил, которые действуют на диэлектрик, даже если он первоначально не был заряжен.
Повесим на тонкой нити палочку из парафина. Приблизим к ней заряженный шар (рис.1). Палочка будет поворачиваться и расположится так, что ее ось будет параллельна линии напряженности электрического поля, то есть так, что ее ось будет направлена к центру шара. Данный факт говорит о том, что на ближайшем к шару конце палочки возникают заряды по знаку противоположные заряду шара. На удаленной части палочки заряды будут одноименными с зарядами на шаре.
Данный факт говорит о том, что на ближайшем к шару конце палочки возникают заряды по знаку противоположные заряду шара. На удаленной части палочки заряды будут одноименными с зарядами на шаре.
Рисунок 1. Поляризация диэлектриков. Автор24 — интернет-биржа студенческих работ
Описанные эксперименты показывают, что на изначально не заряженных диэлектриках в электрическом поле появляются электрические заряды. На телах из диэлектрика возникают электрические полюсы, в этой связи само явление было названо поляризацией диэлектриков.
Замечание 1
Заряды, появляющиеся на диэлектриках, называют поляризационными зарядами.
Поляризация диэлектриков имеет сходство с индукцией в проводниках. Но между этими явлениями есть важное различие, так:
- При делении на части проводника, находящегося в электрическом поле, можно отделить друг от друга индукционный заряды. Если поле убрать, разъединенные части проводника останутся заряженными.

- Разделив в электрическом поле диэлектрик, убрав поле, мы получим части незаряженного диэлектрика. Отделить друг от друга поляризационные заряды не представляется возможным.
Данное отличие объясняет то, что в металлах имеются электроны проводимости, которые могут перемещаться на значительные расстояния, и они несут отрицательный заряд.
В диэлектриках заряды обоих знаков являются связанными между собой и могут смещаться на очень небольшие расстояния в пределах молекулы.
Неполяризованный диэлектрик можно представить в виде совокупности молекул, каждая имеет положительные и отрицательные заряды, распределенные равномерно по объему молекулы.
В состоянии поляризации диэлектрика заряды в каждой молекуле расходятся в противоположные стороны, при этом один конец молекулы приобретает положительный заряд, другой конец — отрицательный. Молекула становится электрическим диполем.
Расхождение зарядов в молекуле проявляется как появление зарядов на диэлектрике. Не поляризованный диэлектрик можно уподобить двум тождественным объемам, которые совпадают друг с другом. Эти объемы равномерно заполнены положительными и отрицательными зарядами. Поляризацию диэлектрика можно рассмотреть как смещение данных объемов на очень небольшое расстояние в противоположные стороны. Но внутри диэлектрика количество положительного и отрицательного заряда будет равно. На концах диэлектрика появляются тонкие слои некомпенсированных зарядов противоположных знаков.
Не поляризованный диэлектрик можно уподобить двум тождественным объемам, которые совпадают друг с другом. Эти объемы равномерно заполнены положительными и отрицательными зарядами. Поляризацию диэлектрика можно рассмотреть как смещение данных объемов на очень небольшое расстояние в противоположные стороны. Но внутри диэлектрика количество положительного и отрицательного заряда будет равно. На концах диэлектрика появляются тонкие слои некомпенсированных зарядов противоположных знаков.
Напряженность электрического поля в диэлектрике
Допустим, что пробный заряд мал в сравнении с расстоянием между молекулами диэлектрика и позволяет исследовать электрическое поле внутри него. С его помощью можно определить, что электрическое поле внутри диэлектрика от точки к точке отличается. Оно максимально около заряженных концов молекул – диполей. Данные изменения поля происходят только в микроскопических масштабах, их невозможно экспериментально наблюдать. Определенное данным образом поле называется микроскопическим ($ \vec E_m$).
В реальных условиях эксперименты проводят с телами, размеры которых много больше, чем расстояния между молекулами. В этом случае интерес представляет усредненная по объему величина микроскопического поля, то есть макроскопическое поле. Данная средняя величина напряженности электрического поля называется напряженностью электрического поля внутри диэлектрика.
Определение 1
Напряженность электрического поля внутри диэлектрика равна:
$\vec{E}=\frac{1}{V}\int\limits_V {\vec{E}_{m}dV\left( 1 \right),}$
где $V$ — объем, содержащий большое количество молекул.
Объем $V$ должен быть большим микроскопически, то есть содержать большое число молекул. Но он должен быть малым макроскопически, то есть значение поле в этом объеме должно быть неизменным.
Исследуем поле плоского конденсатора (рис.2), в котором пространство между пластинами полностью заполнено диэлектриком.
Рисунок 2. Поле плоского конденсатора. Автор24 — интернет-биржа студенческих работ
Напряженность поля ($\vec E$) будет равна сумме двух полей:
- поля ($\vec E_0$), которое создают заряды на обкладках конденсатора;
- поля, которое создано поляризованным диэлектриком ($\vec E’$)
Поле $E_0$ равно:
$E_{0}=\frac{\sigma }{\varepsilon_{0}}\left( 2 \right)$. {‘}}{\varepsilon_{0}}\left( 4 \right)$.
{‘}}{\varepsilon_{0}}\left( 4 \right)$.
Напряженность поля в диэлектрике совпадает с напряжённостью поля в вакууме, если поверхностная плотность заряда равна ($\sigma-\sigma’$). Разность заряда обкладок и поляризационного заряда называют свободным зарядом.
Напряженность поля внутри диэлектрика можно найти при помощи силы, которая будет действовать на пробный заряд. С этой целью представим узкую длинную щель, которую сделали внутри диэлектрика параллельно направлению смещения зарядов. Пробный заряд не будет касаться стенок полости. Поляризационные заряды возникнут только на торцах полости. При малом диаметре полости (в сравнении с ее длиной), поле, которое создают эти заряды, будет очень мало. В полости напряженность поля будем считать равной напряженности, создаваемой свободными зарядами $\sigma-\sigma’$ у внешней поверхности диэлектрика, а это напряженность поля внутри диэлектрика.
Напряженность поля в диэлектрике и напряжённость поля в нашей полости равны. Эта напряженность равна силе, которая действует на единичный положительный заряд внутри полости.
Для измерения напряженности поля внутри диэлектрика можно просто измерить напряжение между обкладками конденсатора. Тогда для плоского конденсатора напряженность найдем как:
$E=\frac{U}{d}\left( 5 \right)$,
где $U$ — разность потенциалов между обкладками; $d$ — расстояние между обкладками.
Электрическое поле в диэлектриках с неоднородной структурой
Поляризационные процессы в неоднородных диэлектриках
лежат в основе многих явлений, происходящих в изоляционной системе
высоковольтных трансформаторов и позволяющих оценивать их состояние и
срок службы. Вследствие применения электроизоляционных материалов с
различными диэлектрическим свойствами и наличия включений изоляция
высоковольтного оборудования имеет неоднородную структуру. У силовых
трансформаторов неоднородность образуется за счет чередующихся слоев
твердой (электротехнический картон) и жидкой (трансформаторное масло)
изоляции, газонаполненных сферических включений и др. [1, с. 17].
[1, с. 17].
Рассмотрим более подробно, как изменяется внешнее
электрическое поле в диэлектриках с неоднородной структурой.
1. Электрическое поле в двухслойном диэлектрике в случае
отсутствия токов проводимости.
Поместим двухслойный диэлектрик между обкладками плоского
конденсатора. Введем обозначения: толщина первого слоя диэлектрика
,
диэлектрическая проницаемость
,
второго слоя соответственно
и
.
Будем рассматривать идеальный случай, когда ток проводимости
отсутствует и проводимости слоев диэлектрика равны нулю
.
Зарядим конденсатор, подключив к его обкладкам источник постоянного
напряжения
.
На обкладках конденсатора появятся заряды противоположных знаков
(рис.1), которые создадут электрическое поле
,
где
– расстояние между обкладками конденсатора.
Диэлектрик, находясь в электрическом поле, созданном
обкладками конденсатора, поляризуется и на его границах появляются
связанные заряды. Эти заряды создают собственное электрическое поле,
Эти заряды создают собственное электрическое поле,
которое направлено противоположно внешнему полю и поэтому должно его
ослаблять. Вычислим электрические поля
и
в слоях диэлектрика.
Так как разность потенциалов на границах первого слоя диэлектрика
,
второго слоя диэлектрика
,
а разность потенциалов между обкладками конденсатора
,
то
|
. |
(1) |
Величина вектора электрического смещения
не зависит от среды, в которой создается электрическое поле, поэтому
,
следовательно:
|
. |
(2) |
Решая систему уравнений (1) и (2), получим выражения
для электрических полей в слоях диэлектрика:
|
,
|
(3) |
Таким образом, электрические поля в слоях
диэлектрика зависят от толщины слоев и их диэлектрических
проницаемостей.
Рассмотрим частный случай, когда
и уравнения (3) переходят в (4):
|
,
|
(4) |
Если между слоями электротехнического картона ()
находится тонкий слой трансформаторного масла ()
[1, с.18], то напряженность электрического поля в масле
,
то есть в тонкой прослойке масла электрическое поле увеличивается в
1,45 раза. Если же слои электротехнического картона разделены тонкой
воздушной прослойкой (),
то напряженность электрического поля в воздухе
,
то есть увеличивается в 4 раза.
2. Электрическое поле в двухслойном диэлектрике при наличии токов
проводимости.
Перейдем от идеального случая к реальному, когда слои диэлектрика
обладают удельными проводимостями
и
соответственно.
Плотность тока в диэлектрике
может быть определена как сумма плотности тока проводимости
и плотности тока смещения
.
Тогда для первого и второго диэлектриков получим соответственно:
и
.
Так как слои диэлектрика можно рассматривать как
соединенные последовательно, то
,
и, следовательно
|
. |
(5) |
Для нахождения электрических полей в слоях
диэлектрика решим систему уравнений (1) и (5), в результате получим:
.
Коэффициент
определим из начальных условий: при
.
Тогда
и для электрического поля внутри первого слоя диэлектрика получим
формулу:
|
. |
(6) |
Аналогичная формула получается для электрического
поля внутри второго слоя диэлектрика:
|
. |
(7) |
По прошествии большого промежутка времени
,
когда конденсатор полностью зарядится, для электрических полей в
слоях диэлектрика получим следующие формулы [2, с. 13]:
|
. |
(8) |
Рассмотрим частный случай, когда
и уравнения (8) переходят в уравнения (9):
|
,
|
(9) |
Если между слоями электротехнического картона ()
находится тонкий слой трансформаторного масла ()
[3, с. 169], то напряженность электрического поля в масле
169], то напряженность электрического поля в масле
.
Таким образом, в соответствии с теоретическим расчетом, электрическое
поле в масле может в 10 раз превышать внешнее электрическое поле.
3. Электрическое поле в трехслойном диэлектрике в
случае отсутствия токов проводимости.
Перейдем от конденсатора с двухслойным диэлектриком к более сложной
ситуации – конденсатору с трехслойным диэлектриком. Толщина
третьего слоя диэлектрика
,
диэлектрическая проницаемость
.
Сначала рассмотрим простой случай, когда проводимость слоев
диэлектрика
и ток проводимости отсутствует. Тогда уравнения (1) и (2)
преобразуются соответственно в уравнения (10) и (11):
|
, |
(10) |
|
. |
(11) |
Решая систему уравнений (10) и (11) получим систему
уравнений (12):
Аналогично ситуации с двухслойным диэлектриком
рассмотрим частный случай, когда
и
,
тогда уравнения (12) переходят в уравнения (13):
Пусть слой электротехнического картона ()
находится между тонкими слоями трансформаторного масла (),
тогда напряженность электрического поля в слоях масла будет равна
.
Полученный результат согласуется со значением электрического поля в
одиночном тонком слое масла, примыкающем к электротехническому
картону.
4. Электрическое поле в трехслойном диэлектрике при наличии
токов проводимости.
Перейдем от идеального случая к реальному, когда слои диэлектрика
обладают удельными проводимостями
,
и
соответственно. Тогда вместо уравнения (5) получим систему из двух
уравнений:
|
,
|
(14) |
Решая систему уравнений (10) и (14) можно получить
выражения для электрических полей в трехслойном диэлектрике. Однако
решение системы уравнений для трехслойного диэлектрика достаточно
сложно и громоздко, поэтому ограничимся рассмотрением частного
случая.
Пусть слой электротехнического картона,
предназначенный для трансформаторов с масляным наполнением, толщиной
[4], диэлектрической проницаемостью
и средней проводимостью
окружен с двух сторон тонкими слоями трансформаторного масла толщиной
,
диэлектрической проницаемостью,
удельной проводимостью
.
Решая систему дифференциальных уравнений (10), (14) численно для
данного частного случая получим, что напряженность электрического
поля в тонких слоях трансформаторного масла
,
то есть в 10 раз превышает напряженность внешнего электрического
поля.
5. Электрическое поле в газонаполненных сферических включениях.
Рассмотрим, как изменяется внешнее электрическое поле внутри
газонаполненных сферических включении, например воздушных пора в
масляном или бумажном слоях изоляции. На внешних границах поры,
вследствие поляризации и ориентации дипольных моментов молекул
диэлектрика по направлению внешнего поля, появляются связанные
заряды. Эти заряды создают электрическое поле, нормальная
составляющая напряженности которого внутри поры будет равна
и сонаправлена с внешним полем (рис. 2). Поэтому внутри полости будет
существовать электрическое поле
.
Так как газ, которым заполнена пора, является диэлектриком, то он
тоже будет поляризоваться и на внутренней границе полости появятся
связанные заряды (рис. 2). Эти связанные заряды создадут
2). Эти связанные заряды создадут
электрическое поле
,
нормальная составляющая которого направлена против поля
.
Таким образом, внутри газовой поры будет существовать электрическое
поле
.
Для нахождения напряженности электрического поля внутри
газонаполненного сферического включения воспользуемся формулой (15)
[5, с. 151]:
|
, |
(15) |
где
– диэлектрическая проницаемость газа, заполняющего пору,
– диэлектрическая проницаемость внешнего диэлектрика.
Пусть сферическая пора, заполненная воздухом с
,
находится в трансформаторном масле с
,
тогда напряженность электрического поля в поре составит
.
Если сферическая пора, заполненная воздухом (),
находится в бумажном слое изоляции (),
то напряженность электрического поля в воздухе
.
Таким образом, напряженность электрического поля внутри
газонаполненного сферического включения будет больше, чем
напряженность внешнего электрического поля.
Вывод. Вопреки распространенному
мнению, в соответствии с которым внешнее электрическое поле в
диэлектрике ослабляется, в диэлектриках с неоднородной структурой
внешнее электрическое поле может усиливаться. В тонких слоях
неоднородного диэлектрика, расположенных перпендикулярно к
направлению поля, а также в газонаполненных сферических включениях
электрическое поле может в несколько раз превышать внешнее. Данное
явление негативно сказывается на качестве электроизоляционной системы
высоковольтных трансформаторов и может приводить к возникновению
таких нежелательных дефектов, как частичные разряды и пробой
электроизоляционных промежутков. Образование воздушных пор в бумажной
составляющей изоляции может приводить к возникновению частичных
разрядов в воздушных промежутках, и, как следствие, разрушению
структуры целлюлозы и повреждению изоляции.
Литература:
Вдовико В.П. Частичные разряды в диагностировании высоковольтного
оборудования. – Новосибирск: Наука, 2007. – 155 с.
Сканави Г.И. Физика диэлектриков (область слабых полей) Т. 1.
–М.: Государственное изд-во Технико-технической литературы,
1949. – 500 с.
Колесов С.Н., Колесов И.С. Материаловедение и технология
конструкционных материалов. – М.: Высшая школа, 2004. –
519 с.
ГОСТ 4194-88. Картон электроизоляционный для трансформаторови аппаратов с масляным заполнением.
Технические условия.Матвеев А.Н. Электричество и магнетизм. –
М.: Высшая школа, 1983. – 463 с.
Электричество и магнетизм
Здесь — вектор дипольного момента одной молекулы, суммирование ведётся по всем молекулам, находящимся внутри физически бесконечно малого объема . Например, рассмотрим однородно поляризованный шар (рис. 3.17).
Например, рассмотрим однородно поляризованный шар (рис. 3.17).
Рис. 3.17. Поляризованность и электрическое поле однородно поляризованного шара
При поляризации неполярного диэлектрика электронная оболочка атома или молекулы деформируется — электроны смещаются против поляризующего поля, ядра смещаются по полю. Возникает некоторое расстояние между ранее (в отсутствие поляризующего поля) совпадавшими центрами положительных и отрицательных зарядов. В результате атом или молекула приобретают некоторый наведенный дипольный момент.
Более или менее очевидно, что наведенный дипольный момент будет пропорционален величине внешнего электрического поля. Понять это можно, рассматривая поведение потенциальной энергии П(x) взаимодействия двух частиц, где х — расстояние между ними. Пусть равновесному состоянию соответствует расстояние (частицы находятся в одной точке и дипольный момент отсутствует). При малых отклонениях от положения равновесия в разложении потенциальной энергии в ряд Тейлора можно ограничиться несколькими первыми членами
При малых отклонениях от положения равновесия в разложении потенциальной энергии в ряд Тейлора можно ограничиться несколькими первыми членами
Учитывая, что первая производная в точке равновесия равна нулю и что вторая производная в этой точке положительна , получаем, что вблизи точки устойчивого равновесия потенциальная энергия ведет себя как
Соответственно, при отклонении от этого положения возникает сила
,
подобная силе упругости при растяжении пружины. Если заряды в молекуле «соединены» такой «пружиной», то при наложении поля Е новое равновесное расстояние между частицами будет определяться соотношением
В результате находим величину возникшего под действием поля дипольного момента
Умножая наведенный дипольный момент на концентрацию поляризованных молекул N/V (N — их полное число в объеме V), получаем поляризованность диэлектрика
|
|
(3. |
Если записать поляризованность (3.16) в виде
где константа (для данного вещества) по определению есть диэлектрическая восприимчивость вещества, то для , то в рамках данной модели диэлектрическую восприимчивость можно вычислить по нижеследующей формуле
У молекул, называемых полярными, центры положительных и отрицательных зарядов сдвинуты друг относительно друга, поэтому такая молекула имеет собственный дипольный момент. При помещении такой молекулы в электрическое поле её электронная оболочка деформируется, расстояние между центрами зарядов увеличивается и к исходному собственному дипольному моменту добавляется некоторый наведенный дипольный момент. Однако, можно показать, что этот дополнительный наведенный дипольный момент много меньше собственного. Разумеется, это справедливо, если поляризующее поле много меньше поля, существующего внутри молекулы. По порядку величины внутримолекулярное поле равно атомной единице напряженности электрического поля: В/м. В написанном выражении для атомной единицы напряженности электрического поля масса электрона, его заряд, постоянная Планка. Учитывая, что, например, «пробойная» — приводящая к искровому разряду – напряженность поля для сухого воздуха составляет всего В/м, то есть на пять порядков меньше, можно утверждать, что в подавляющем большинстве экспериментов наведенным дипольным моментом, при наличии собственного, можно пренебречь. В дальнейшем, при рассмотрении поляризации дипольных диэлектриков, этот эффект (наведение дополнительного момента) учитываться не будет.
По порядку величины внутримолекулярное поле равно атомной единице напряженности электрического поля: В/м. В написанном выражении для атомной единицы напряженности электрического поля масса электрона, его заряд, постоянная Планка. Учитывая, что, например, «пробойная» — приводящая к искровому разряду – напряженность поля для сухого воздуха составляет всего В/м, то есть на пять порядков меньше, можно утверждать, что в подавляющем большинстве экспериментов наведенным дипольным моментом, при наличии собственного, можно пренебречь. В дальнейшем, при рассмотрении поляризации дипольных диэлектриков, этот эффект (наведение дополнительного момента) учитываться не будет.
Векторы собственных дипольных моментов отдельных молекул в обычном состоянии из-за теплового движения ориентированы хаотически. Поэтому при отсутствии внешнего электрического поля средний суммарный дипольный момент любого физически бесконечно малого объема диэлектрика равен нулю. Другими словами, диэлектрик не поляризован: его поляризованность равна нулю.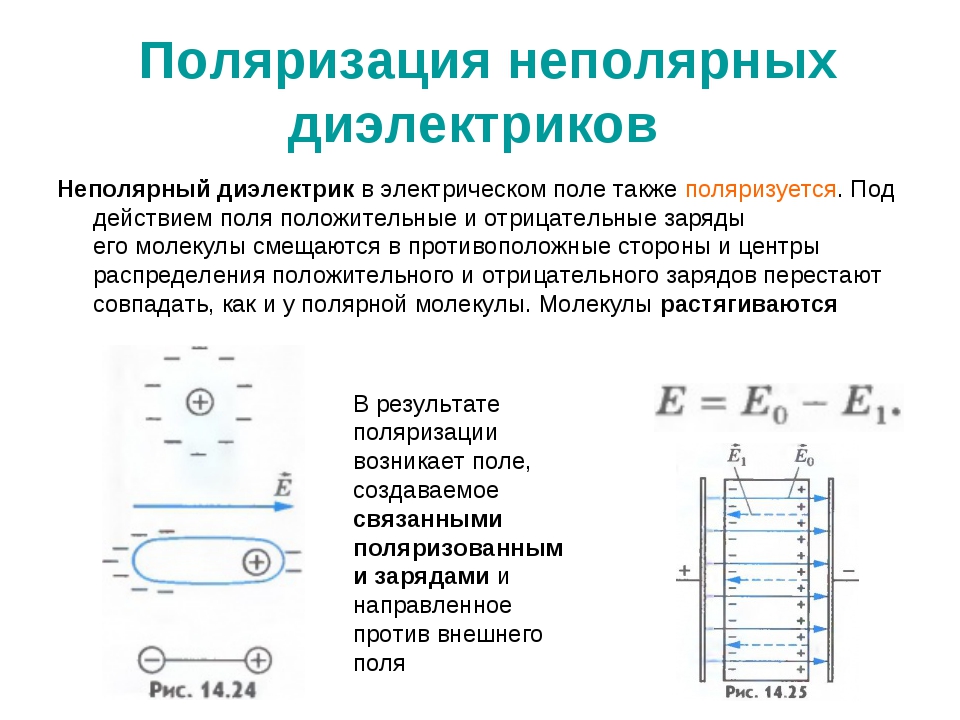
Внешнее электрическое поле стремится ориентировать дипольные моменты молекул параллельно вектору , а тепловое движение этому препятствует, диэлектрик поляризуется, при этом его поляризованность должна зависеть от температуры, а именно: с ростом температуры она должна убывать. Ниже эта зависимость вычисляется, также будет показано, что и в случае полярных диэлектриков их поляризованность пропорциональна напряженности поляризующего поля. Такая поляризация называется ориентационной (рис. 3.18).
Рис. 3.18. Ориентационная поляризация диэлектрика
2.3. Связанные заряды. Электрическое поле в диэлектриках
Связанные
заряды. В результате процесса поляризации в объеме (или на поверхности)
диэлектрика возникают нескомпенсированные заряды, которые называются
поляризационными, или связанными. Частицы, обладающие
этими зарядами, входят в состав молекул и под действием внешнего электрического
поля смещаются из своих положений равновесия, не покидая молекулы, в
состав которой они входят. Связанные заряды характеризуют поверхностной
Связанные заряды характеризуют поверхностной
плотностью .
Выделим в поляризованном диэлектрике наклонную призму с основанием S
и ребром L, параллельным вектору поляризации P (рис. 2.4).
В результате поляризации на одном из оснований призмы появятся отрицательные
заряды с поверхностной плотностью ,
а на другой положительные заряды с плотностью .
С макроскопической точки зрения, рассматриваемый объем эквивалентен
диполю, образованному зарядами
и ,
которые отстоят друг от друга на расстояние L, тогда электрический
момент призмы равен .
С другой стороны, электрический момент единицы объема равен ,
где
— угол, между направлением нормали к основанию призмы и вектором P.
Произведение
есть объем призмы.
Приравняв друг к другу оба выражения для электрического момента, получаем,
что поверхностная плотность связанных зарядов равна нормальной составляющей
вектора поляризации:
,
где n — единичный вектор нормали к поверхности диэлектрика.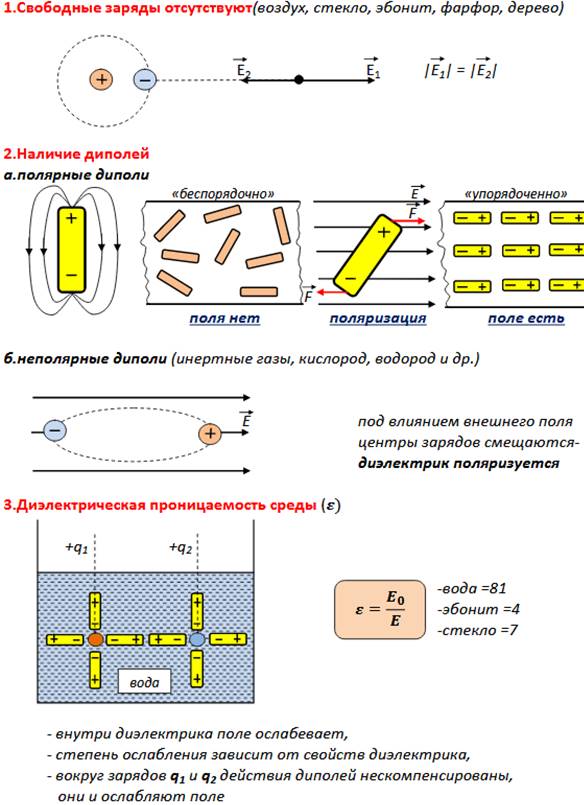
Если вектор поляризации P различен в разных точках объема диэлектрика,
то в диэлектрике возникают объемные поляризационные заряды, объемная
плотность которых .
Электрическое поле в диэлектрике. Рассмотрим плоский однородный
диэлектрический слой, расположенный между двумя разноименно заряженными
плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое
создается этими плоскостями в вакууме, равна ,
где
— поверхностная плотность зарядов на пластинах (эти заряды называют свободными).
Под действием поля диэлектрик поляризуется, и на его гранях появляются
поляризационные или связанные заряды. Эти заряды создают в диэлектрике
электрическое поле ,
которое направлено против внешнего поля .
,
где
— поверхностная плотность связанных зарядов. Результирующее поле внутри
Результирующее поле внутри
диэлектрика
.
Поверхностная плотность связанных зарядов
меньше плотности
свободных зарядов, и не все поле E0 компенсируется полем
диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая
часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика .
Следовательно, в результате поляризации поле внутри диэлектрика оказывается
слабее, чем внешнее .
Таким образом,
,
где
— диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая
проницаемость показывает, во сколько раз напряженность поля в вакууме
больше напряженности поля в диэлектрике. Для вакуума ,
для диэлектриков .
Вопросы
1) Почему заряды имеют различные названия: связанные, свободные заряды,
сторонние, поляризационные
2) Какой физический смысл имеет диэлектрическая проницаемость среды. Может
Может
ли величина диэлектрической проницаемости быть меньше 1
3) Чему равна: поверхностная и объемная плотность поляризационных зарядов
Напряженность электрического поля в диэлектрике
Рассмотрим диэлектрическую пластинку, заполняющую плоский конденсатор (рис.14.5) и находящуюся, следовательно, в практически однородном внешнем поле .
В результате поляризации на гранях диэлектрика, обращенных к пластинам конденсатора, концы молекулярных диполей окажутся нескомпенсированными соседними диполями. Поэтому на правой грани, обращенной к отрицательной пластине конденсатора, окажется избыток положительного заряда с некоторой поверхностной плотностью . На противоположной стороне диэлектрика . Эти так называемые поляризационные, или связанные заряды не могут быть переданы соприкосновением другому телу без разрушения молекул диэлектрика, т.к. они обусловлены самими поляризованными молекулами. Возникновение поляризованных зарядов приводит к возникновению дополнительного электрического поля , направленного против внешнего поля . Результирующее электрическое поле Е внутри диэлектрика равно
Результирующее электрическое поле Е внутри диэлектрика равно
Для определения применим формулу вычисления напряженности конденсатора
Свяжем с вектором поляризации Р. Для этого определим полный дипольный момент (во всем объеме) диэлектрика. Осуществим это двумя способами:
С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент
где S — площадь пластины конденсатора.
С другой стороны рассмотрим диэлектрик как большой диполь, у которого с одной стороны заряд , а с другой и расстояние d. Отсюда
Приравнивая (14.4) и (14.5), получим
Подставляя в (14.3), и затем результат в (14.2), получим
Подставим значение Р из выражения (14.1), тогда
Величина
называется диэлектрической проницаемостью или относительной диэлектрической проницаемостью. Диэлектрическая проницаемость показывает во сколько раз уменьшается напряженность в диэлектрике по сравнению с напряженностью в вакууме. и , т.е. с ростом температуры диэлектрические свойства
Диэлектрическая проницаемость показывает во сколько раз уменьшается напряженность в диэлектрике по сравнению с напряженностью в вакууме. и , т.е. с ростом температуры диэлектрические свойства
Проводники и диэлектрики в электрическом поле
Внесение некоторого вещества в электрическое поле может привести к существенному его изменению; это обусловлено тем, что вещество составляют заряженные частицы. Если внешнее поле отсутствует, распределение частиц вещества происходит таким образом, что электрическое поле, которое они создают, в среднем по объемам, включающим большое число атомов или молекул, равно нулю. Если внешнее поле присутствует, заряженные частицы перераспределяются, и в веществе возникает собственное электрическое поле. Полное электрическое поле E→ включает в себя (согласно принципу суперпозиции) внешнее поле E0→ и внутреннее поле E’→ которое создается заряженными частицами вещества.
Электрические свойства веществ обуславливают их многообразие. Самые широкие классы веществ – это проводники и диэлектрики.
Самые широкие классы веществ – это проводники и диэлектрики.
Проводники
Отличительная черта проводников заключается в наличии свободных зарядов (электронов), принимающих участие в тепловом движении и способных осуществлять перемещение по всему объему проводника. Типичным примером проводников служат металлы.
Определение 1
Если внешнее поле отсутствует, то в любом элементе объема проводника отрицательный свободный заряд будет компенсироваться положительным зарядом ионной решетки. В проводнике, который внесен в электрическое поле, произойдет перераспределение свободных зарядов, следствием чего будет возникновение на поверхности проводника нескомпенсированных положительных и отрицательных зарядов (рис. 1.5.1). Описанный процесс носит название электростатической индукции, а возникающие на поверхности проводника заряды называют индукционными зарядами.
Индукционными зарядами создается свое собственное поле E’→ и оно компенсирует внешнее поле E0→ во всем объеме проводника: E→=E0→+E’→=0 (внутри проводника).
Определение 2
Полное электростатическое поле внутри проводника есть нуль, а потенциалы во всех точках являются одинаковыми и равными потенциалу на поверхности проводника.
Рисунок 1.5.1. Электростатическая индукция.
Все внутренние области проводника, который внесен в электрическое поле, остаются электронейтральными. Удаление некоторого объема, выделенного внутри проводника, а соответственно образование пустой полости, приведет к тому, что электрическое поле внутри полости станет равным нулю. На этом основана электростатическая защита – приборы, имеющие чувствительность к электрическому полю в целях исключения влияния поля помещают в металлические ящики (рис. 1.5.2).
Рисунок 1.5.2. Схема электростатической защиты. Поле в металлической полости равно нулю.
Поскольку поверхность проводника эквипотенциальна, необходимо, чтобы силовые линии у поверхности являлись перпендикуляром к ней.
Диэлектрики
Диэлектрики (изоляторы) отличаются от проводников тем, что не имеют свободных электрических зарядов. Диэлектрики включают в себя нейтральные атомы или молекулы. Заряженные частицы в нейтральном атоме являются связанными друг с другом и не имеют способности к перемещению под действием электрического поля по всему объему диэлектрика.
Диэлектрики включают в себя нейтральные атомы или молекулы. Заряженные частицы в нейтральном атоме являются связанными друг с другом и не имеют способности к перемещению под действием электрического поля по всему объему диэлектрика.
Внесение диэлектрика во внешнее электрическое поле E0→ вызовет возникновение в нем некоторого перераспределения зарядов, которые входят в состав атомов или молекул. Следствием этого перераспределения является появление на поверхности диэлектрического образца избыточных нескомпенсированных связанных зарядов. Все заряженные частицы, которые образуют макроскопические связанные заряды, все так же входят в состав своих атомов.
Определение 3
Связанные заряды образуют электрическое поле E’→ направленное внутри диэлектрика противоположно вектору напряженности E0→ внешнего поля: данный процесс носит название поляризации диэлектрика.
Вследствие поляризации полное электрическое поле E→=E0→+E’→=0 внутри диэлектрика становится по модулю меньше внешнего поля E0→.
Определение 4
Диэлектрическая проницаемость вещества – это физическая величина, которая есть отношение модуля напряженности E0→ внешнего электрического поля, создаваемого в вакууме, к модулю напряженности E→ полного поля в однородном диэлектрике.
ε=E0E.
Известно несколько механизмов поляризации диэлектриков: основные — это ориентационная и электронная поляризации. Проявление этих механизмов происходит в основном при поляризации газообразных и жидких диэлектриков.
Ориентационная или дипольная поляризация появляется, когда полярные диэлектрики состоят из молекул, у которых имеет место несовпадение центов распределения положительных и отрицательных зарядов. Такие молекулы представляют собой микроскопические электрические диполи.
Определение 5
Микроскопические электрические диполи – это нейтральная совокупность двух зарядов, являющихся равными по модулю и противоположными по знаку, расположенных на расстоянии друг от друга.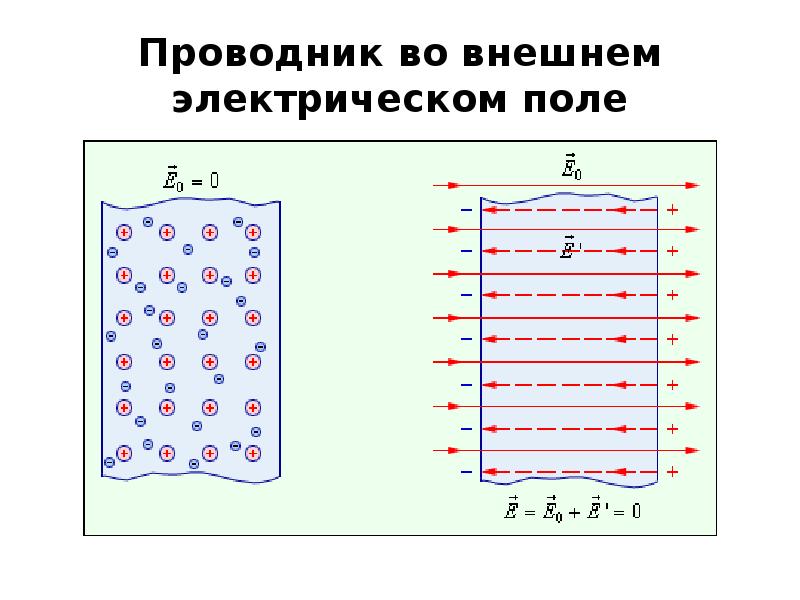
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание
К примеру, дипольный момент имеет молекула воды, а также молекулы некоторых прочих диэлектриков (h3S, NO2 и т. д.).
Когда внешнее электрическое поле отсутствует, оси молекулярных диполей по причине теплового движения имеют хаотичную ориентацию, в связи с чем на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем является равным нулю.
Если внести диэлектрик во внешнее поле E0→, возникнет частичная ориентация молекулярных диполей. Вследствие этого поверхность диэлектрика получит нескомпенсированные макроскопические связанные заряды, создающие поле E’→ направленное навстречу внешнему полю E0→ (рис. 1.5.3).
Рисунок 1.5.3. Ориентационный механизм поляризации полярного диэлектрика.
Поляризация полярных диэлектриков обладает сильной зависимостью от температуры, поскольку тепловое движение молекул выступает в качестве дезориентирующего фактора.
Электронный или упругий механизм возникает при поляризации неполярных диэлектриков, молекулы которых не имеют при отсутствии внешнего поля дипольного момента. Электрическое поле, воздействуя на молекулы неполярных диэлектриков, вызывает их деформацию – положительные заряды смещаются в направлении вектора E0→ а отрицательные – в противоположном направлении. В итоге каждая молекула становится электрическим диполем, ось которого имеет направление вдоль внешнего поля. Поверхность диэлектрика получает нескомпенсированные связанные заряды, которые создают свое поле E’→ имеющее направление навстречу внешнему полю E0→ Таким образом происходит поляризация неполярного диэлектрика (рис. 1.5.4).
Деформация неполярных молекул, испытывающих влияние внешнего электрического поля, не имеет зависимости от теплового движения, т.е. поляризация неполярного диэлектрика не зависит от температуры.
Пример 1
В качестве примера неполярной молекулы можно рассмотреть молекулу метана Ch5, в которой четырехкратно ионизированный ион углерода C4– расположен в центре правильной пирамиды; в вершинах этой пирамиды — ионы водорода H+.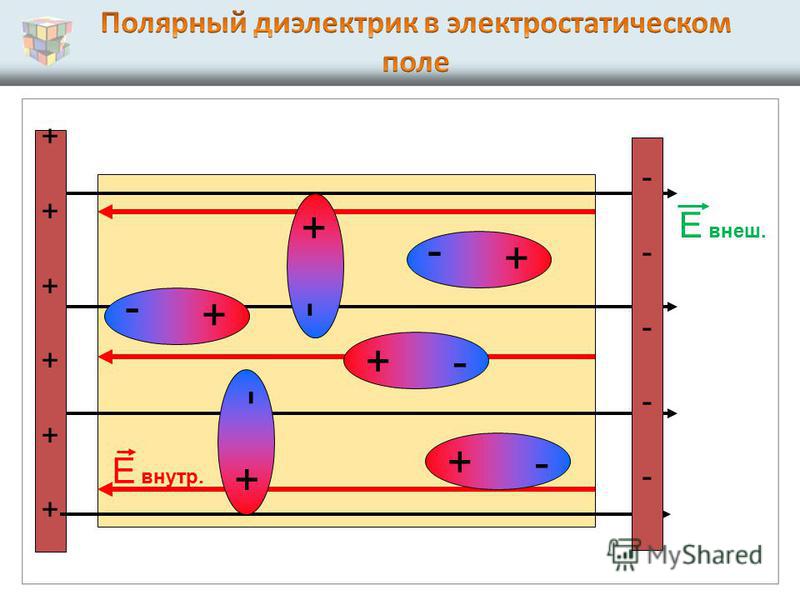 Наложение внешнего электрического поля вызовет смещение иона углерода из центра пирамиды: в этом случае у молекулы возникнет дипольный момент, пропорциональный внешнему полю.
Наложение внешнего электрического поля вызовет смещение иона углерода из центра пирамиды: в этом случае у молекулы возникнет дипольный момент, пропорциональный внешнему полю.
Рисунок 1.5.4. Поляризация неполярного диэлектрика.
В электрическом поле E’→ связанных зарядов, которое возникает при поляризации полярных и неполярных диэлектриков, происходит его изменение по модулю прямо пропорционально модулю внешнего поля E0→. В электрических полях значительной силы указанная закономерность может нарушаться: в таком случае получают проявление различные нелинейные эффекты. Для полярных диэлектриков в сильных полях возможно наблюдать эффект насыщения.
Определение 6
Эффект насыщения – это выстраивание всех молекулярных диполей вдоль силовых линий.
Когда диэлектрики неполярны, сильное внешнее поле, которое можно сравнить по модулю с внутриатомным полем, имеет возможность значимо деформировать атомы или молекулы вещества с изменением их электрических свойств. Но подобные явления почти никогда не наблюдаются, поскольку для этого необходимы поля, имеющие напряженность порядка 1010–1012 В/м. При этом гораздо раньше наступает электрический пробой диэлектрика.
Но подобные явления почти никогда не наблюдаются, поскольку для этого необходимы поля, имеющие напряженность порядка 1010–1012 В/м. При этом гораздо раньше наступает электрический пробой диэлектрика.
Определение 7
Электронная поляризация – это процесс поляризации, при котором непарные молекулы получают деформацию электронных оболочек.
Этот механизм универсален, так как деформация электронных оболочек под влиянием внешнего поля происходит в атомах, молекулах и ионах любого диэлектрика.
Определение 8
Ионная поляризация – это поляризация твердых кристаллических диэлектриков, следствием которой является смещение ионов различных знаков, составляющих кристаллическую решетку, в противоположных направлениях при воздействии внешнего поля. В результате смещения на гранях кристалла образуются связанные (нескомпенсированные) заряды.
Пример 2
В качестве примера описанного механизма, можно рассмотреть поляризацию кристалла NaCl, в котором ионы Na+ и Cl– составляют две подрешетки, вложенные друг в друга. При отсутствии внешнего поля каждая элементарная ячейка кристалла NaCl является электронейтральной и не обладающей дипольным моментом. Во внешнем электрическом поле обе подрешетки сместятся в противоположных направлениях, т. е. кристалл подвергнется процессу поляризации.
При отсутствии внешнего поля каждая элементарная ячейка кристалла NaCl является электронейтральной и не обладающей дипольным моментом. Во внешнем электрическом поле обе подрешетки сместятся в противоположных направлениях, т. е. кристалл подвергнется процессу поляризации.
Когда происходит процесс поляризации неоднородного диэлектрика, связанные заряды могут появиться не только на поверхности, но и в объеме диэлектрика. В таком случае электрическое поле E’→ связанных зарядов и полное поле E→ будут обладать сложной структурой, зависящей от геометрии диэлектрика. Утверждение о том, что электрическое поле _formula_ в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем E→ точно верно лишь, когда речь идет об однородном диэлектрике, который заполняет все пространство, где создано внешнее поле. В частности:
Определение 9
В случае, когда в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, напряженность электрического поля E→ этого точечного заряда и потенциал φ в ε раз меньше, чем в вакууме. Запишем данное утверждение в виде формул:
Запишем данное утверждение в виде формул:
E→=14πε0·Qεr3r→, φ=14πε0Qεr.
Проводники и диэлектрики в электрическом поле
1. Проводники в электрическом поле
Напомним, что заряженные частицы, которые могут перемещаться в веществе, называют свободными зарядами.
Если поместить проводник в электрическое поле, то находящиеся в нем свободные заряды придут в движение и в проводнике возникнет направленное движение зарядов, то есть электрический ток. Проводники потому так и называются, что они проводят электрический ток.
Лучшие проводники – металлы. Свободными зарядами в металлах являются свободные электроны. Поскольку электроны имеют отрицательный электрический заряд, действующая на них со стороны электрического поля сила направлена противоположно напряженности электрического поля.
За направление электрического тока принимают направление движения положительных зарядов. Поэтому в металлах направление электрического тока противоположно направлению движения свободных зарядов – электронов (рис. 52.1).
52.1).
Внесем, например, металлический шар в однородное электрическое поле (рис. 52.2).
? 1. В каком направлении будут двигаться при этом свободные электроны? Каким будет направление кратковременного электрического тока?
В результате на одной стороне шара появится избыток электронов, то есть возникнет отрицательный заряд, а на другой его стороне – недостаток электронов, то есть возникнет положительный заряд (рис. 52.3).
? 2. Объясните, почему поле, созданное этими зарядами внутри проводника, направлено противоположно внешнему полю.
Свободные электроны будут двигаться до тех пор, пока на них будет действовать сила со стороны электрического поля.
? 3. Объясните, почему равновесие зарядов в проводнике возможно только при условии, что напряженность электрического поля внутри проводника равна нулю (см. рис. 52.3).
Перераспределение зарядов в проводнике, в результате которого напряженность электрического поля внутри проводника обращается в нуль, называют электростатической индукцией.
При равновесии зарядов напряженность электрического поля внутри проводника равна нулю:
= 0.
Вследствие принципа суперпозиции полей перераспределение зарядов в проводнике изменяет и поле вне проводника. В результате линии напряженности поля вне проводника деформируются.
? 4. Объясните, почему вблизи поверхности проводника линии напряженности электрического поля перпендикулярны поверхности проводника (см. рис. 52.3).
Подсказка. Когда заряды в проводнике находятся в равновесии, на них не действует сила, направленная вдоль поверхности проводника (иначе заряды двигались бы вдоль поверхности проводника).
При равновесии электрических зарядов в проводнике они расположены всегда на поверхности проводника. Причем это справедливо как для незаряженного, так и для заряженного проводника.
Электростатическая защита
При равновесии зарядов напряженность электрического поля равна нулю не только в сплошном изолированном проводнике, но и внутри полого проводника. По этой причине, например, напряженность поля внутри однородно заряженной сферы равна нулю (если внутри сферы нет заряженных тел).
По этой причине, например, напряженность поля внутри однородно заряженной сферы равна нулю (если внутри сферы нет заряженных тел).
Это свойство проводников в электрическом поле используют для сования электростатической защиты: например, чувствительные к электрическому полю приборы заключат в металлические ящики. Причем я этого не обязательно даже, чтобы стенки ящиков были сплошными: достаточно использовать металлическую сетку, которую называют иногда «сеткой Фарадея» (рис. 52.4).
Электростатическую защиту используют также, чтобы защитить людей, работающих в сильном электрическом поле: в таком случае металлической сеткой окружают пространство, в котором работают люди.
2. Диэлектрики в электрическом поле
Как вы уже знаете, в диэлектриках нет свободных зарядов. Однако это не значит, что в них вообще нет заряженных частиц: ведь в атомах и молекулах диэлектриков, как и любых других веществ, есть положительно заряженные ядра и отрицательно заряженные электроны.
В диэлектриках все электроны сильно связаны со своими атомами, поэтому их называют «связанными электронами». Но под действием внешнего электрического поля молекулы диэлектриков поворачиваются или изменяют форму (деформируются).
Рассмотрим подробнее, как это происходит в диэлектриках разного вида.
Полярные диэлектрики. В молекулах некоторых веществ центры распределения положительных и отрицательных зарядов не совпадают.
Например, в молекуле воды, состоящей из одного атома кислорода и двух атомов водорода, электроны атомов водорода большую часть времени проводят вблизи атома кислорода, в результате чего возле атома кислорода образуется отрицательный полюс, а возле атомов водорода – положительный полюс.
Такие диэлектрики называют полярными, потому что у молекул этих диэлектриков есть два полюса зарядов – положительный и отрицательный (рис. 52.5, а).
Под действием электрического поля молекулы полярных диэлектриков поворачиваются (рис. 52.5, б) и ориентируются вдоль линий напряженности поля (рис. 52.5, в).
52.5, б) и ориентируются вдоль линий напряженности поля (рис. 52.5, в).
Неполярные диэлектрики. Диэлектрики, в молекулах которых центры распределения положительных и отрицательных зарядов совпадают, называют неполярными (рис. 52.6, а). К ним относятся, например, многие газы.
Под действием внешнего электрического поля положительные и отрицательные заряды в молекуле «растаскиваются» в противоположные стороны. В результате центры распределения положительных и отрицательных зарядов перестают совпадать (рис. 52.6, б).
Деформированная молекула с точи зрения распределения зарядов становится подобной полярной молекуле, ориентированной вдоль линий напряженности поля.
Поляризация диэлектриков
Итак, под действием внешнего электрического поля молекулы как полярных, так и неполярных диэлектриков выстраиваются по направлению напряженности внешнего электрического поля.
Это явление называют поляризацией диэлектрика.
В результате поляризации диэлектрика на его поверхности появляются заряды. Как мы уже говорили, эти заряды называют связанными, потому что они обусловлены смещением заряда только внутри молекул (а не во всем образце, как это происходит при движении свободных зарядов в проводнике).
Как мы уже говорили, эти заряды называют связанными, потому что они обусловлены смещением заряда только внутри молекул (а не во всем образце, как это происходит при движении свободных зарядов в проводнике).
На рисунке 52.7 схематически показано, как в результате поляризации диэлектрика на его поверхности появляются связанные заряды.
Мы видим, что положительные и отрицательные заряды, образовавшиеся вследствие поляризации, внутри диэлектрика компенсируют друг друга. А на поверхности диэлектрика такой компенсации нет: поэтому и возникают поверхностные заряды.
Рассмотрим теперь, как изменяется напряженность электрического поля при внесении в него диэлектрика вследствие появления связанных зарядов.
Заметим, что напряженность поля поляр, созданного связанными зарядами, направлена противоположно напряженности внеш внешнего электрического поля (см. рис. 52.7).
Поэтому согласно принципу суперпозиции поле, созданное связанными зарядами, уменьшает напряженность поля внутри диэлектрика (однако не до нуля, как в случае проводника).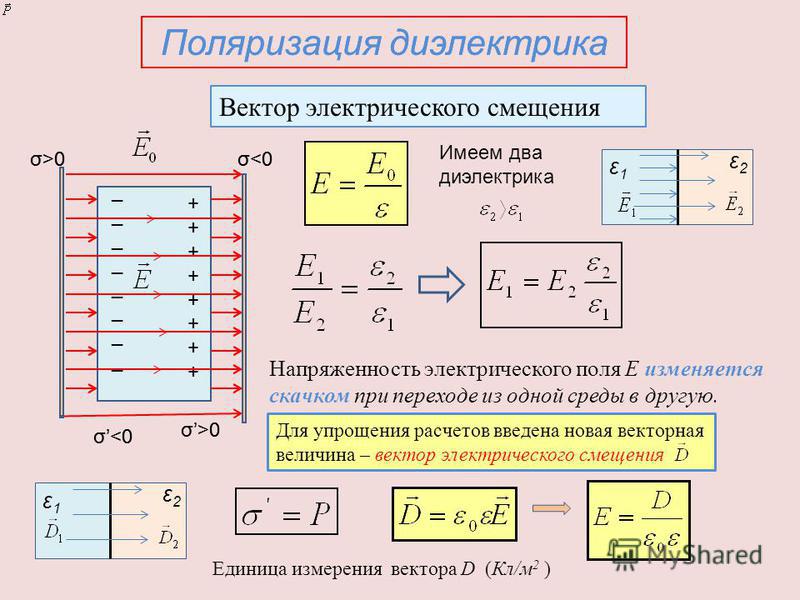
Таким образом,
вследствие поляризации диэлектрика напряженность электрического поля внутри диэлектрика уменьшается.
Благодаря поляризации незаряженные диэлектрики притягиваются к заряженному телу независимо от знака его заряда.
Дело в том, что электрическое поле вокруг заряженных тел неоднородно: чем ближе к заряженному телу, тем больше напряженность поля.
Когда незаряженный диэлектрик вносят в электрическое поле, на его поверхности появляются связанные заряды противоположных знаков. В результате на разные части диэлектрика со стороны поля действуют противоположно направленные силы (рис. 52.8). И в неоднородном поле «побеждает» та сила, которая действует на заряды, находящиеся в более сильном поле, то есть находящиеся ближе к заряженному телу. Поэтому незаряженное тело притягивается к заряженному.
Теперь становится понятным, почему электрическое отталкивание заметили только через две тысячи лет после того, как обнаружили электрическое притяжение.
Ведь чтобы тела притягивались, достаточно, чтобы заряжено было только одно из них, причем зарядом любого знака. А отталкиваются тела лишь тогда, когда они оба заряжены, причем обязательно одноименно.
? 5. В описанном в предыдущем параграфе опыте по визуализации линий напряженности было использовано то, что состоящие из диэлектрика продолговатые тела ориентируются в электрическом поле вдоль линий напряженности. Объясните, почему это происходит.
Диэлектрическая проницаемость
Величину, которая показывает, во сколько раз уменьшатся напряженность внешнего электрического поля внутри однородного диэлектрика, называют его диэлектрической проницаемостью и обозначают ε.
Значения диэлектрической проницаемости для разных веществ могут очень сильно различаться.
Например, для воздуха ε = 1,0006, то есть очень мало отличается от единицы. Очень близка к единице и диэлектрическая проницаемость других газов. Обусловлено это главным образом малой концентрацией молекул в газах.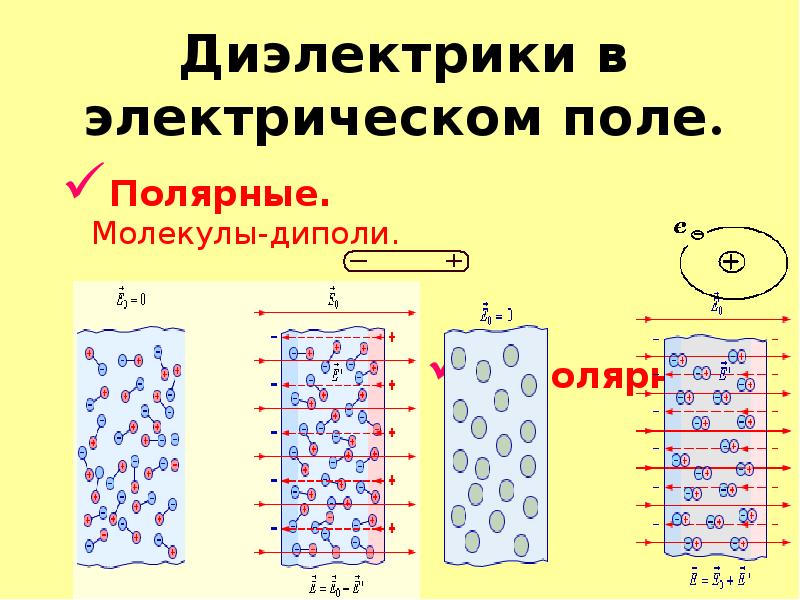
Значение диэлектрической проницаемости большинства жидкостей и твердых тел – от нескольких единиц до нескольких десятков. Сравнительно велика диэлектрическая проницаемость воды: ε = 81.
Но есть вещества (сегнетоэлектрики), у которых диэлектрическая проницаемость достигает десятков и сотен тысяч.
? 6. Металлическому шару радиусом 10 см сообщили положительный заряд 20 нКл и после этого поместили в большой сосуд с водой.
а) Сделайте в тетради схематический рисунок, на котором изобразите заряд шара и связанные заряды, возникшие вследствие поляризации воды.
б) Чему будет равна напряженность электрического поля на расстоянии от центра шара, равном 5 см? 15 см? 25 см?
Уменьшение силы взаимодействия заряженных тел, погруженных в диэлектрик. Поскольку взаимодействие заряженных тел осуществляется посредством электрического поля, а поле в диэлектрике уменьшается в ε раз, то в ε раз уменьшается и сила взаимодействия заряженных тел, полностью погруженных в однородный диэлектрик. Например, для очечных зарядов, находящихся в однородном диэлектрике с диэлектрической проницаемостью ε, закон Кулона принимает вид
Например, для очечных зарядов, находящихся в однородном диэлектрике с диэлектрической проницаемостью ε, закон Кулона принимает вид
? 7. Чему равна диэлектрическая проницаемость жидкости, если погруженные в нее небольшие шарики с зарядом 30 нКл каждый взаимодействуют с силой 7,8 мкН? Расстояние между шариками равно 20 см.
Увеличение силы взаимодействия заряженных тел, между которыми помещен диэлектрик. Если расположить диэлектрик между заряженными телами, то силы, действующие на каждое заряженное тело, увеличатся.
? 8. Объясните, почему это происходит.
Подсказка. Воспользуйтесь рисунком 52.9.
Дополнительные вопросы и задания
9. Два одинаковых заряженных шарика подвешены на нитях равной длины в одной точке, При этом нити отклонены от вертикали на некоторый угол. Когда всю эту систему погрузили в жидкий диэлектрик, угол отклонения нитей не изменился.
а) Изобразите на чертеже все силы, действующие на один из шариков до погружения в диэлектрик и после этого.
б) Во сколько раз плотность шариков больше плотности диэлектрика, если его диэлектрическая проницаемость равна 3?
10. Как изменится сила взаимодействия двух заряженных тел, если поместить между ними незаряженный проводник, который не касается этих тел?
Электрическое поле в диэлектрике
Если внести в электрическое поле диэлектрик, то электрическое поле изменится. Рассмотрим, как оно изменится и в чем причины его изменения.
Поляризация диэлектриков
Возьмем заряженный электрометр. Поднесем к нему пластинку из незаряженного диэлектрика. При этом показании электрометра уменьшатся. Удалим пластину, и показания электрометра восстановятся. При приближении к электрометру проводника будет наблюдаться подобное явление.Мы знаем, что в электрическом поле на поверхности проводника появляются индукционные заряды, которые оказывают воздействие на внешнее поле. Из этого можно сделать вывод о том, что на диэлектрике в электрическом поле, тоже заведите заряды.
Возникновение зарядов на диэлектрическим телескопом приводит к появлению сил, которые вызывают диэлектрик.
Повесим на тонкой нити палочку из парафина. Приблизим к ней заряженный шар (рис.1).Палочка будет направлена так, чтобы ее ось была направлена на линии напряженности электрического поля, что ее ось будет направлена к центру шара. Данный факт говорит о том, что нашем к шару конце палочки ближайшая заряды по знаку противоположные заряду шара. На удаленной части палочки заряды будут одноименными с зарядами на шаре.
Рисунок 1. Поляризация диэлектриков. Автор24 — интернет-биржа студенческих работ
Описанные эксперименты показывают, что на изначально не заряженных диэлектриках в электрическом поле появляются электрические заряды.На телах из диэлектрика установлены электрические полюсы, в этой связи само явление было названо поляризацией диэлектриков.
Замечание 1
Заряды, появляющиеся на диэлектриках, называют поляризационными зарядами.
Поляризация диэлектриков имеет сходство с индукцией в проводниках. Между этими явлениями есть важное различие, так:
- При делении на части проводника, находящегося в электрическом поле, можно отделить друг от друга индукционный заряды.Если поле убрать, разъединенные части проводника останутся заряженными.
- Разделив в электрическом поле диэлектрик, убрав поле, мы получим части незаряженного диэлектрика. Отделить друг от друга поляризационные заряды не возможным.
Специализированное объяснение того, что в металлах имеются электроны проводимости, которые перемещаются на значительные расстояния, и они несут отрицательный заряд.
В диэлектриках заряды обоих знаков являются связанными между собой и могут смещаться на очень небольшие расстояния в молекулы.
Неполяризованный диэлектрик можно представить в виде частиц, каждая имеет положительные и отрицательные заряды, распределенные равномерно по объему молекулы.
В состоянии поляризации диэлектрика заряды в каждой молекуле расходятся в противоположные стороны, при этом один конец молекулы приобретает положительный заряд, другой конец — отрицательный. Молекула становится электрическим диполем.
Молекула становится электрическим диполем.
Расхождение зарядов в молекуле появляется как появление зарядов на диэлектрике.Не поляризованный диэлектрик можно уподобить двум тождественным объемам, совпадающим друг с другом. Эти объемы равномерно заполнены положительными и отрицательными зарядами. Поляризацию диэлектрика можно рассмотреть как смещение данных на очень небольшое расстояние в противоположные стороны. Количество положительного и отрицательного заряда будет равно. На концах диэлектрика появляются тонкие слои некомпенсированных зарядов противоположных знаков.
Напряженность электрического поля в диэлектрике
Допустим, что пробный заряд мал в сравнении с расстоянием между молекулами диэлектрика и позволяет исследовать электрическое поле внутри него.С его помощью можно определить, что электрическое поле внутри диэлектрика от точки к точке отличается. Оно максимально около заряженных концов молекул — диполей. Данные изменения проходят только в микроскопических масштабах, их невозможно экспериментально наблюдать.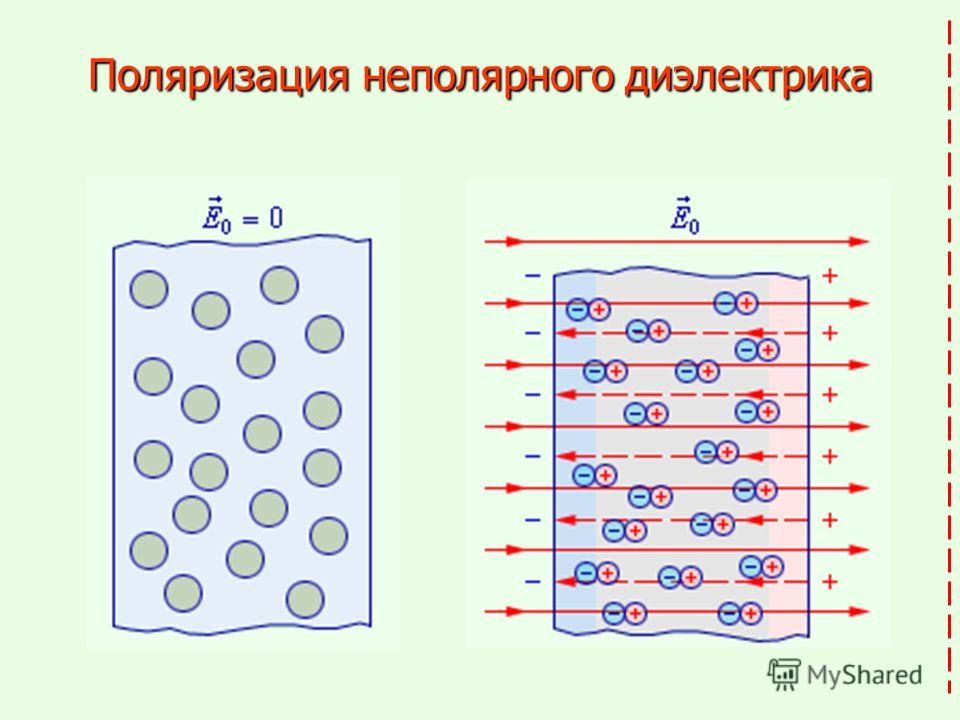 Определенное данным образом поле называется микроскопическим ($ \ vec E_m $).
Определенное данным образом поле называется микроскопическим ($ \ vec E_m $).
В реальных условиях эксперименты проводят с телами, размеры которых много больше, чем расстояние между молекулами. В этом случае интерес представляет усредненная по объему микроскопического поля, то есть макроскопическое поле.Данная средняя величина напряженности электрического поля называется напряженностью электрического поля внутри диэлектрика.
Определение 1
Напряженность электрического поля внутри диэлектрика равно:
$ \ vec {E} = \ frac {1} {V} \ int \ limits_V {\ vec {E} _ {m} dV \ left (1 \ right),}
долл. США
где $ V $ — объем, создав большое количество молекул.
Объем $ V $ должен быть большим микроскопически, то есть содержит большое число молекул. Но он должен быть малым макроскопически, то есть поле в этом объеме быть неизменным.
Исследуем поле плоского конденсатора (рис.2), в котором пространство между пластинами полностью заполнено диэлектриком.
Рисунок 2. Поле плоского конденсатора. Автор24 — интернет-биржа студенческих работ
Напряженность поля ($ \ vec E $) будет равна сумме двух полей:
- поля ($ \ vec E_0 $), которое дает заряды на обкладках конденсатора;
- поля, созданное поляризованным диэлектриком ($ \ vec E ’$)
Поле $ E_0 $ равно:
$ E_ {0} = \ frac {\ sigma} {\ varepsilon_ {0}} \ left (2 \ right) $.{‘}} {\ varepsilon_ {0}} \ left (4 \ right) $.
Напряженность поля в диэлектрике совпадает с напряжённостью поля в вакууме, если поверхностная плотность заряда равна ($ \ sigma- \ sigma ’$). Разность заряда обкладок и поляризационного заряда называют свободным зарядом.
Напряженность поля внутри диэлектрика можно найти при помощи силы, которая будет действовать на пробный заряд. С этой целью представим узкую длинную щель.Пробный заряд не будет касаться стенок полости. Поляризационные заряды возникнут только на торцах полости. При малом диаметре полости (в сравнении с ее длиной), поле, которое эти заряды, будет очень мало. В полости напряженности поля будем считать равной напряженности, создаваемой свободными зарядами $ \ sigma- \ sigma ’$ у внешней поверхности диэлектрика, а это напряженность поля внутри диэлектрика.
При малом диаметре полости (в сравнении с ее длиной), поле, которое эти заряды, будет очень мало. В полости напряженности поля будем считать равной напряженности, создаваемой свободными зарядами $ \ sigma- \ sigma ’$ у внешней поверхности диэлектрика, а это напряженность поля внутри диэлектрика.
Напряженность поля в диэлектрике и напряжённость поля в нашей полости. Эта напряженность равна силе, которая действует на единичный положительный заряд внутри полости.
Для измерения напряженности поля внутри диэлектрика можно просто измерить напряжение между обкладками конденсатора. Тогда для плоского конденсатора напряженность найдем как:
$ E = \ frac {U} {d} \ left (5 \ right) $,
где $ U $ — разность потенциалов между обкладками; $ d $ — расстояние между обкладками.
Электрическое поле в диэлектриках с неоднородной структурой
Поляризационные процессы в неоднородных диэлектриках
лежат в основе явлений, происходящих в изоляционной системе
высоковольтных трансформаторов и позволяющих оценивать их состояние и
срок службы. Вследствие применения электроизоляционных материалов с
Вследствие применения электроизоляционных материалов с
различные диэлектрические свойства и наличие включений изоляция
высоковольтного оборудования имеет неоднородную структуру. У силовых
трансформаторов неоднородность образует за счет чередующихся слоев
твердой (электротехнический картон) и жидкой (трансформаторное масло)
изоляции, газонаполненных сферических включений и др. [1, с. 17].
Рассмотрим более подробно, как изменяется внешнее
электрическое поле в диэлектриках с неоднородной структурой.
1. Электрическое поле в двухслойном диэлектрике в случае
отсутствие токов проводимости.
Поместим двухслойный диэлектрик между обкладками плоского
конденсатора. Введем обозначения: толщина первого слоя диэлектрика
,
диэлектрическая проницаемость
,
второго соответственно слоя
и
.
Будем рассматривать идеальный случай, когда ток проводимости
отсутствует и проводимости слоев диэлектрика равны нулю
.
Зарядим конденсатор, подключив к его обкладкам источник постоянного
напряжение
.
На обкладках конденсатора появятся заряды противоположных знаков
(рис.1), которые создадут электрическое поле
,
где
— расстояние между обкладками конденсатора.
Диэлектрик, находясь в электрическом поле, созданном
обкладками конденсатора, поляризуется и на его границах появляются
связанные заряды. Эти заряды представляют собственное электрическое поле,
которое направлено противоположно внешнему полю и поэтому его
ослаблять.Вычислим электрические поля
и
в слоях диэлектрика.
Так как разность потенциалов на границах первого слоя диэлектрика
,
второй слой диэлектрика
,
а разность потенциалов между обкладками конденсатора
,
то
. | (1) |
Величина вектора электрического смещения
не зависит от среды, в которой создается электрическое поле, поэтому
,
следовательно:
. | (2) |
Решая система уравнений (1) и (2), получим выражения
для электрических полей в слоях диэлектрика:
, г. | (3) |
Таким образом, электрические поля в слоях
диэлектрика зависит от толщины слоев и их диэлектрических
проницаемостей.
Рассмотрим частный случай, когда
и уравнения (3) переходят в (4):
, г. | (4) |
Если между слоями электротехнического картона ()
находится тонкий трансформаторного масла ()
[1, с.18], то напряженность электрического поля в масле
,
то есть в тонкой прослойке масла электрическое поле увеличивается в
1,45 раза. Если же слои электротехнического картона разделены тонкой
воздушной прослойкой (),
то напряженность электрического поля в воздухе
,
то есть увеличивается в 4 раза.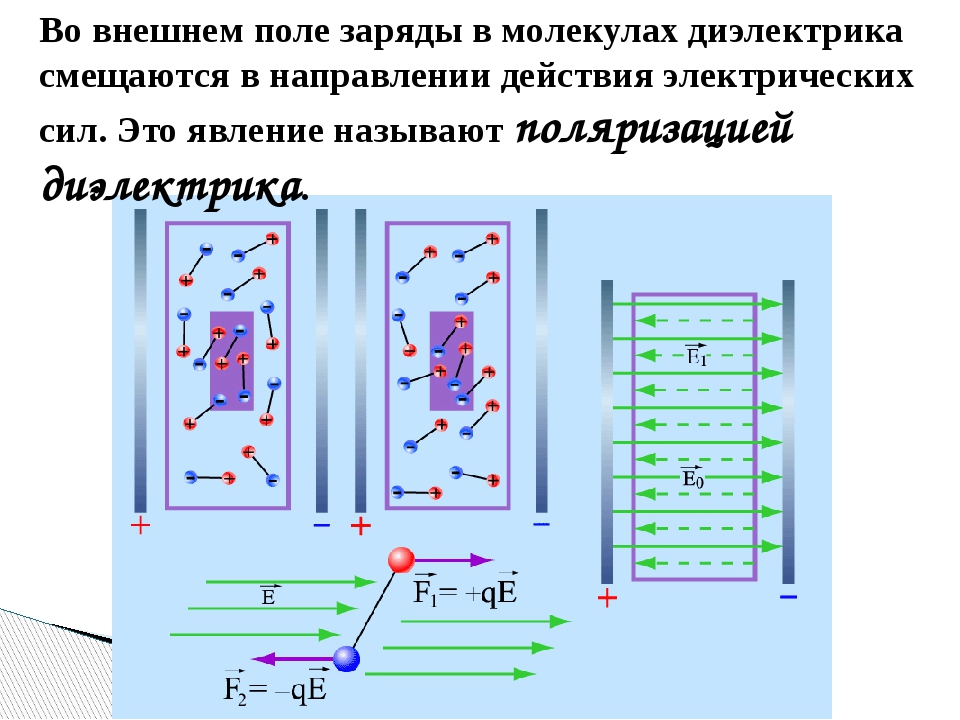
2. Электрическое поле в двухслойном диэлектрике при наличии токов
проводимости.
Перейдем от идеального случая к реальности, когда слои диэлектрика
обладают удельными проводимостями
и
соответственно.
Плотность тока в диэлектрике
может быть определена как сумма плотности тока проводимости
и плотности тока с ущерба
.
Тогда для первого и второго диэлектриков получим соответственно:
и
.
Так как слои диэлектрика можно рассматривать как рассматривать
соединенные последовательно, то
,
и, следовательно
. | (5) |
Для нахождения электрических полей в слоях
диэлектрика решим систему уравнений (1) и (5), в результате получим:
.
Коэффициент
определим из начальных условий: при
.Тогда
и для электрического поля внутри первого слоя диэлектрика получим
формулу:
. | (6) |
Аналогичная формула получается для электрического
поля внутри второго слоя диэлектрика:
. | (7) |
По прошествии большого промежутка времени
,
когда конденсатор полностью зарядится, для электрических полей в
слоях диэлектрика получим следующие формулы [2, с.13]:
. | (8) |
Рассмотрим частный случай, когда
и уравнения (8) переходят в уравнения (9):
, г. | (9) |
Если между слоями электротехнического картона ()
находится тонкий трансформаторного масла ()
[3, с.169], то напряженность электрического поля в масле
.
Таким образом, в соответствии с теоретическим расчетом, электрическое
поле в масле может в 10 раз внешнее электрическое поле.
3. Электрическое поле в трехслойном диэлектрике в
случае отсутствия токов проводимости.
Перейдем от конденсатора с двухслойным диэлектриком к более сложной
ситуации — конденсатору с трехслойным диэлектриком. Толщина
третьего слоя диэлектрика
,
диэлектрическая проницаемость
.Сначала проводим простой случай, когда проводимость рассмотрим слой
диэлектрика
и ток проводимости отсутствует. Тогда уравнения (1) и (2)
преобразуются соответственно в уравнения (10) и (11):
, | (10) |
. | (11) |
Решая система уравнений (10) и (11) получим систему
формулы (12):
Аналогично ситуации с двухслойным диэлектриком
рассмотрим частный случай, когда
и
,
тогда уравнения (12) переходят в уравнения (13):
Пусть слой электротехнического картона ()
находится между тонкими слоями трансформаторного масла (),
тогда напряженность электрического поля в слоях масла будет равна
. Полученный результат согласуется со значением электрического поля в
Полученный результат согласуется со значением электрического поля в
одиночный тонком слое масла, примыкающем к электротехническому
картону.
4. Электрическое поле в трехслойном диэлектрике при наличии
токов проводимости.
Перейдем от идеального случая к реальности, когда слои диэлектрика
обладают удельными проводимостями
,
и
соответственно. Тогда вместо уравнения (5) получим систему из двух
уравнения:
, | (14) |
Решая система уравнений (10) и (14) можно получить
выражения для электрических полей в трехслойном диэлектрике.Однако
решение системы для трехслойного диэлектрика достаточно
сложно и громоздко, поэтому ограничимся рассмотрением частным
случая.
Пусть слой электротехнического картона,
предназначенный для трансформаторов с масляным наполнением, толщиной
[4], диэлектрической проницаемостью
и средняя проводимостью
окружен с двух сторон тонкими слоями трансформаторного масла толщиной
,
диэлектрической проницаемостью,
удельной проводимостью
. Решая систему дифференциальных уравнений (10), (14) численно для
Решая систему дифференциальных уравнений (10), (14) численно для
данного частного случая получим, что напряженность электрического
поля в тонких слоях трансформаторного масла
,
то есть в 10 раз большой напряженность внешнего электрического
поля.
5. Электрическое поле в газонаполненных сферических включениях.
Рассмотрим, как изменяется внешнее электрическое поле внутри
газонаполненных сферических включении, например воздушных пора в
масляном или бумажном слоях изоляции.На внешних границах поры,
поляризации и ориентации дипольных моментов молекул
Связанные
заряды. Эти заряды электрическое поле, нормальная
составляющая напряженности которого внутри поры будет равна
и сонаправлена внешний полем (рис. 2). Поэтому внутри полости будет
существовать электрическое поле
.
Так как газ, которым заполнена пора, является диэлектриком, то он
тоже будет поляризоваться и на внутренней границе полости появятся
связанные заряды (рис.2). Эти связанные заряды создадут
Эти связанные заряды создадут
электрическое поле
,
нормальная составляющая которого направлена против поля
.
Таким образом, внутри газовой поры будет существовать электрическое
поле
.
Для нахождения напряженности электрического поля внутри
газонаполненного сферического включения воспользуемся формулой (15)
[5, с. 151]:
, | (15) |
где
— диэлектрическая проницаемость газа, заполняющего пору,
— диэлектрическая проницаемость внешней диэлектрика.
Пусть сферическая пора, заполненная воздухом с
,
находится в трансформаторном масле с
,
тогда напряженность электрического поля в поре составляет
.
Если сферическая пора, заполненная воздухом (),
находится в бумажном слое изоляции (),
то напряженность электрического поля в воздухе
.
Таким образом, напряженность электрического поля внутри
газонаполненного сферического включения будет больше, чем
напряженность внешнего электрического поля.
Вывод. Вопреки распространенному
оценка, в соответствии с которым внешнее электрическое поле в
диэлектрике ослабляется, в диэлектриках с неоднородной структурой
внешнее электрическое поле может усиливаться. В тонких слоях
неоднородного диэлектрика, суперпендикулярно к
направления поля, а также в газонаполненных сферических включениях
электрическое поле может в несколько раз внешнее. Чи
явление негативно сказывается на качестве электроизоляционной системы
высоковольтных трансформаторов и может приводить к возникновению
таких нежелательных дефектов, как частичные разряды и пробой
электроизоляционных промежутков.Образование воздушных пор в бумажной
составляющей изоляции приводить к возникновению частичных
разрядов в воздушных промежутках, и, как следствие, разрушению
структура целлюлозы и повреждению изоляции.
Литература:
Вдовико В.П. Частичные разряды в диагностировании высоковольтного
оборудования. — Новосибирск: Наука, 2007. — 155 с.
— 155 с.Сканави Г.И. Физика диэлектриков (область слабых полей) Т.1.
–М .: Государственное изд-во Технико-техническая литература,
1949. — 500 с.Колесов С.Н., Колесов И.С. Материаловедение и технология
конструкционных материалов. — М .: Высшая школа, 2004. —
519 с.ГОСТ 4194-88. Картон электроизоляционный для трансформаторов
и аппаратов с масляным заполнением.
Технические условия.Матвеев А.Н. Электричество и магнетизм. —
М .: Высшая школа, 1983. — 463 с.
Напряженность электрического поля в диэлектрике
Рассмотрим диэлектрическую пластинку, заполняющую плоский конденсатор (рис.14.5) и находящуюся, следовательно, в практически однородном внешнем поле.
В результате поляризации на гранях диэлектрика, обращенных к пластинам конденсатора, концы молекулярных диполей будут нескомпенсированными соседними диполями. Поэтому на правой грани, обращенной к отрицательной пластине конденсатора, превышток положительного заряда с некоторой поверхностной плотностью. На противоположной стороне диэлектрика. Эти так называемые поляризационные, или связанные заряды не могут быть переданы соприкосновением другому телу без разрушения молекулы диэлектрика, т.к. они обусловлены самими поляризованными молекулами. Возникновение поляризованных зарядов приводит к возникновению электрического поля, направленного против внешнего поля.Результирующее электрическое поле Е внутри диэлектрика равно
Поэтому на правой грани, обращенной к отрицательной пластине конденсатора, превышток положительного заряда с некоторой поверхностной плотностью. На противоположной стороне диэлектрика. Эти так называемые поляризационные, или связанные заряды не могут быть переданы соприкосновением другому телу без разрушения молекулы диэлектрика, т.к. они обусловлены самими поляризованными молекулами. Возникновение поляризованных зарядов приводит к возникновению электрического поля, направленного против внешнего поля.Результирующее электрическое поле Е внутри диэлектрика равно
Для применения формулу напряженности конденсатора
Свяжем с вектором поляризации Р. Для этого определим полный дипольный момент (во всем объеме) диэлектрика. Осуществим это двумя способами:
С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент
где S — площадь пластины конденсатора.
С другой стороны рассмотрим диэлектрик как большой диполь, у которого с одной стороны заряда, а с другой и расстояние d. Отсюда
Приравнивая (14.4) и (14.5), получим
Подставляя в (14.3), и затем результат в (14.2), получим
Подставим значение Р из выражения (14.1), тогда
Величина
называется диэлектрической проницаемостью или относительной диэлектрической проницаемостью.Диэлектрическая проницаемость показывает во сколько раз уменьшается напряженность в диэлектрике по сравнению с напряженностью в вакууме. и, т.е. с ростом температуры диэлектрические свойства
Проводники и диэлектрики в электрическом поле
Внесение некоторого вещества в электрическом поле может привести к существующему его изменению; это вызвано тем, что это заряженные частицы.Это электрическое поле, которое выглядит как среднее по объемам, включающее большое число атомов или молекул, равно нулю. Если внешнее поле присутствует, заряженные частицы перераспределяются, и в самом деле возникает собственное электрическое поле. Полное электрическое поле E → включает в себя (согласноу суперпозиции) внешнее поле E0 → и внутреннее поле E ‘→ создается заряженными частями вещества.
Если внешнее поле присутствует, заряженные частицы перераспределяются, и в самом деле возникает собственное электрическое поле. Полное электрическое поле E → включает в себя (согласноу суперпозиции) внешнее поле E0 → и внутреннее поле E ‘→ создается заряженными частями вещества.
Электрические свойства веществ обуславливают их многообразие. Самые широкие классы веществ — это проводники и диэлектрики.
Проводники
Отличная черта проводников заключается в наличии свободных зарядов (электронов), принимающих участие в тепловом движении и способных перемещаться по всему объему проводника. Типичным примером проводников сад металлы.
Определение 1
Если внешнее поле отсутствует, то в любом объеме проводника отрицательный свободный заряд будет компенсироваться положительным зарядом ионной решетки.В проводнике, который внесен в электрическое поле, произойдет перераспределение свободных зарядов, следствие чего будет возникновение на поверхности проводника нескомпенсированных положительных и отрицательных зарядов (рис. 1.5.1). Описанный процесс носит название электростатической индукции, а на поверхности проводника заряды вызывают индукционными зарядами.
1.5.1). Описанный процесс носит название электростатической индукции, а на поверхности проводника заряды вызывают индукционными зарядами.
Индукционными зарядами создается свое собственное поле E ‘→ и оно компенсирует внешнее поле E0 → во всем объеме проводника: E → = E0 → + E’ → = 0 (внутри проводника).
Определение 2
Полное электростатическое поле внутри проводника есть нуль, а потенциалы во всех точках имеют одинаковые и равные возможности на поверхности проводника.
Рисунок 1.5.1. Электростатическая индукция.
Все внутренние области проводника, который внесен в электрическое поле, остаются электронейтральными. Удаление некоторого размера, выделенного внутри полости, равного нулю.На этом полюсе электростатической защиты — приборы, имеющие чувствительность к электрическому полю воздействия поля помещают в металлические ящики (рис. 1.5.2).
Рисунок 1.5.2. Схема электростатической защиты. Поле в металлической полости равно нулю.
поверхность проводника эквипотенциальна, необходимо, чтобы силовые линии у поверхности перпендикуляром к ней.
Диэлектрики
Диэлектрики (изоляторы) отличаются от проводников тем, что не имеют свободных электрических зарядов.Диэлектрики включают в себя нейтральные атомы или молекулы. Заряженные частицы в нейтральном состоянии не имеют возможности перемещаться под действием электрического поля по всему объему диэлектрика.
Внесение диэлектрика во внешнее электрическое поле E0 → вызовет возникновение некоторого перераспределения зарядов, которые входят в состав атомов или молекул. Следствием этого перераспределения является появление на поверхности диэлектрического образца избыточных нескомпенсированных зарядов.Все заряженные частицы, образуют макроскопические связанные заряды, все так же входят в состав своих атомов.
Определение 3
Связанные заряды образуют электрическое поле E ‘→ направленное внутри диэлектрика противоположно вектору напряженности E0 → внешняя поля: данный процесс носит название поляризации диэлектрика.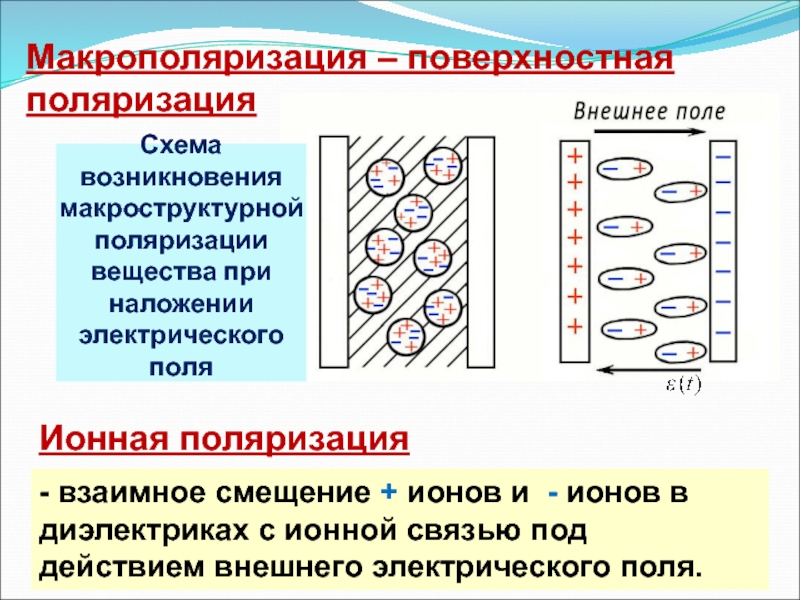
Вследствие поляризации полное электрическое поле E → = E0 → + E ‘→ = 0 внутри диэлектрика становится по модулю меньше внешнего поля E0 →.
Определение 4
Диэлектрическая проницаемость вещества — это физическая величина, которая есть отношение напряженности E0 → внешнее электрическое поле, создаваемое в вакууме, к модулю напряженности E → полного поля в однородном диэлектрике.
ε = E0E.
Известно несколько механизмов поляризации диэлектриков: основная — это ориентационная и электронная поляризации. Проявление этих механизмов происходит в основном при поляризации газообразных и жидких диэлектриков.
Ориентационная или дипольная поляризация появляется, когда полярные диэлектрики состоят из молекул, у которых есть несовпадение центов распределения положительных и отрицательных зарядов. Такие молекулы представляют собой микроскопические электрические диполи.
Определение 5
Микроскопические электрические диполи — это нейтральная совокупность двух зарядов, являющихся равными по модулю и противоположными по знаку, расположенным на расстоянии друг от друга.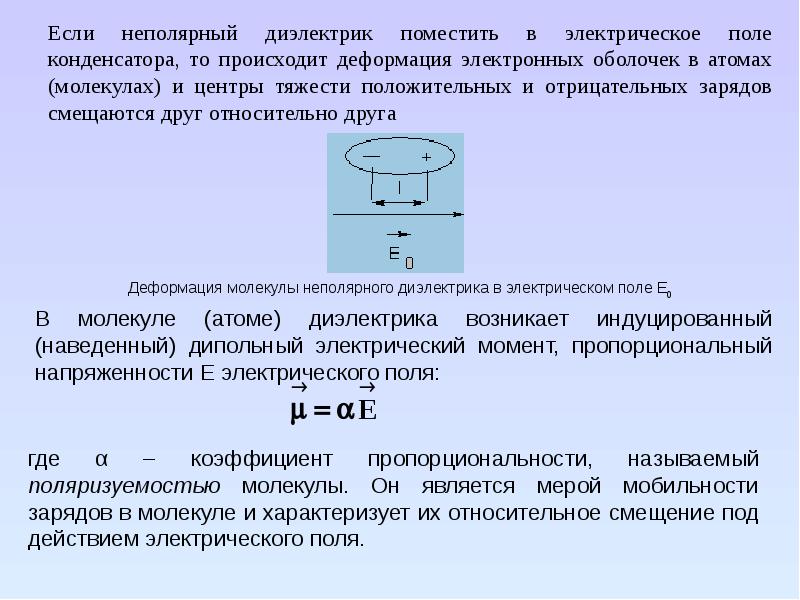
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание
К примеру, дипольный момент имеет молекула воды, а также молекулы некоторых других диэлектриков (h3S, NO2 и т.д.).
Когда внешнее электрическое поле отсутствует, оси молекулярных диполей по причине теплового движения имеют хаотическую ориентацию, в связи с чем на поверхности диэлектрика и в любом элементе электрического заряда в среднем равным нулю.
Если внести диэлектрик во внешнее поле E0 →, возникнет частичная ориентация молекулярных диполей. Вследствие этого внешнего вида диэлектрика получает нескомпенс макроскопические связанные заряды, создающие поле E ‘→ направленное навстречу внешнему полю E0 → (рис.1.5.3).
Рисунок 1.5.3. Ориентационный механизм поляризации полярного диэлектрика.
Поляризация полярных диэлектриков обладает сильной зависимостью от температуры, поскольку тепловое движение молекулы выступает в качестве дезориентирующего фактора.
Электронный или имеют упругий механизм при поляризации неполярных электронов, молекулы которых не возникают при отсутствии внешнего поля дипольного момента. Электрическое поле, воздействует на молекулы неполярных диэлектриков, вызывает их деформацию — положительные заряды смещаются в направлении E0 → отрицательные — в противоположном направлении.В конечном итоге становится электрическим диполем, ось которого имеет направление вдоль внешнего поля. Поверхность диэлектрика получает нескомпенсированные заряды, которые создают свое поле E ‘→ соответствующее направление навстречу внешнему полю E0 → Таким образом поляризация полярного диэлектрика (рис. 1.5.4).
Деформация неполярных молекул, испытывающих влияние внешнего электрического поля, не имеет зависимости от теплового движения, т.е. поляризация неполярного диэлектрика не зависит от температуры.
Пример 1
В качестве примера неполярной молекулы можно рассмотреть молекулу метана Ch5, в которой четырехкратно ионизированный ион C4 — расположен в центре правильной пирамиды; в вершинах этой пирамиды — ионы водорода H +. Наложение внешнего электрического поля вызовет смещение иона углерода из центра пирамиды: в этом случае молекулы возникнет дипольный момент, пропорциональный внешнему полю.
Наложение внешнего электрического поля вызовет смещение иона углерода из центра пирамиды: в этом случае молекулы возникнет дипольный момент, пропорциональный внешнему полю.
Рисунок 1.5.4. Поляризация неполярного диэлектрика.
В электрическом поле E ‘→ связано зарядов, возникающее при возникновении полярных и полярных диэлектриков, происходит его изменение по модулю прямо пропорционально модулю внешнего поля E0 →. В таких случаях происходит проявление нелинейных эффектов. Для полярных диэлектриков в сильных полях возможно наблюдать эффект насыщения.
Определение 6
Эффект насыщения — это выстраивание всех молекулярных диполей вдоль силовых линий.
Когда диэлектрики неполярны, сильное внешнее поле, которое можно сравнить по модулю с внутриатомным полем, имеет возможность значимо деформировать атомы или молекулы вещества с изменением их электрических свойств. Но явления почти не наблюдаются, поскольку для этого необходимы поля, имеющие свойство порядка 1010–1012 В / м. При этом гораздо раньше наступает электрический пробой диэлектрика.
При этом гораздо раньше наступает электрический пробой диэлектрика.
Определение 7
Электронная поляризация — это процесс поляризации, при котором непарные молекулы обеспечивают деформацию электронного оболочек.
Этот механизм универсален, как деформация электронных устройств в атомах, молекулах ионах любой диэлектрики.
Определение 8
Ионная поляризация — это поляризация твердых кристаллических диэлектриков, следствием которой является смещение различных знаков, составляющих кристаллическую решетку, в противоположных направлениях при воздействии внешней поля. В результате ущерба на гранях кристалла образуются связанные (нескомпенсированные) заряды.
Пример 2
В качестве примера описанного механизма, можно рассмотреть поляризацию кристалла NaCl, в котором ионы Na + и Cl– составляют две подрешетки, вложенные друг в друга. При внешней поляризации каждая элементарная ячейка кристалла NaCl является электронейтральной и не обладающей дипольным моментом. Во внешнем электрическом поле обе подрешетки сместятся в противоположных направлениях, т. е. подвергнется процессу поляризации.
Во внешнем электрическом поле обе подрешетки сместятся в противоположных направлениях, т. е. подвергнется процессу поляризации.
Когда процесс поляризации неоднородного диэлектрика, связанный заряд может появиться не только на поверхности, но и в объеме диэлектрика.В таком случае электрическое поле E ‘→ связанные зарядов и полное поле E → будут комплектоваться сложной сложной структурой, зависящей от геометрии диэлектрика. Утверждение о том, что электрическое поле _formula_ в диэлектрике в ε раз меньше модулю по сравнению с внешним полем E → точно лишь, когда речь идет об однородном диэлектрике, который заполняет все пространство, где создано внешнее поле. В частности:
Определение 9
В случае, когда в однородном диэлектрике с диэлектрической проницаемостью, находится точечный заряд Q , напряженность электрического поля E → этого точечного заряда и потенциал φ в ε раз меньше, чем в вакууме.Запишем утверждение в виде формул:
E → = 14πε0 · Qεr3r →, φ = 14πε0Qεr.
2.3. Связанные заряды. Электрическое поле в диэлектриках
Связанные
заряды. В результате процесса поляризации в объеме (или на поверхности)
диэлектрика возникают нескомпенсированные заряды, которые называются
поляризационными , или связанными . Частицы, обладающие
этими зарядами, входят в состав молекулы и под действием внешнего электрического
поля смещаются из своих положений равновесия, не покидая молекулы, в
состав, в который они входят.Связанные заряды характеризуют поверхностной
плотностью.
Выделим в поляризованном диэлектрике наклонную призму с основанием S
и ребром L , параллельному вектору поляризации P (рис. 2.4).
В результате поляризации на одном из оснований призмы появятся отрицательные
заряды с поверхностной плотностью,
а на другой положительные заряды с плотностью.
С макроскопической точки зрения, рассматриваемый объем эквивалентен
диполю, образованному заряддами
и,
которые отстоят друг от друга на расстояние L , тогда электрический
момент призмы равенство.
С другой стороны, электрический момент размера равенства,
где
— угол между направлением нормали к основанию призмы и вектором P .
Произведение
есть объем призмы.
Приравняв друг к другу оба выражения для электрического момента, получаем,
что поверхностная плотность связанной зарядов нормальной нормальной составляющей
вектор поляризации:
,
где n — единичный вектор нормали к поверхности диэлектрика.
Если вектор поляризации P различен в разных точках объема диэлектрика,
то в диэлектрике создайте объемные поляризационные заряды, объемная
плотность которых.
Электрическое поле в диэлектрике. Рассмотрим плоский однородный
диэлектрический слой, расположенный между двумя разноименно заряженными
плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое
создается этим уровнем в вакууме, равна,
где
— поверхностная плотность зарядов на пластинах (эти заряды называют свободными).Под действием поля диэлектрик поляризуется, и на его гранях появляются
поляризационные или связанные заряды. Эти заряды в диэлектрике
электрическое поле,
которое направлено против внешнего поля.
,
где
— поверхностная плотность связанных зарядов. Результирующее поле внутри
диэлектрика
.
Поверхностная плотность связанных зарядов
меньше плотности
свободных зарядов, и не все поле E 0 компенсируется полем
диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая
часть обрывается на зарядах (рис. 2.5). Вне диэлектрика.
2.5). Вне диэлектрика.
Следовательно, в результате поляризации поля внутри диэлектрика оказывается
слабее, чем внешнее.
Таким образом,
,
где
— диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая
проницаемость показывает, во сколько раз напряженность поля в вакууме
больше напряженности поля в диэлектрике. Для вакуума,
для диэлектриков.
Вопросы
1) Почему заряды имеют различные названия: связанные, свободные заряды,
сторонние, поляризационные
2) Какой физический смысл имеет диэлектрическая проницаемость среды.Может
ли величина диэлектрической проницаемости быть меньше 1
3) Чему равна: поверхностная и объемная плотность поляризационных зарядов
Лекция 6.6. Энергия электрического поля в диэлектриках — Энергия электростатического поля
Вот, давайте попробуем себе представить вот такую вещь. Значит, вот у нас есть такое выражение E² поделенное на 8п, да? Что это такое? Это объемная плотность энергии в пустом пространстве, где, в котором создано электрическое поле с напряженностью E.Да? Это энергия в единице объема. Но есть другая формула. Если бы всё это происходило в диэлектрике, то возникла бы вот такая формула εE² / 8п, ну вот такая формула. Да? Но ε — большее количество 1, значит, естественно, что второе выражение дает, ну, в общем, принимает значение. И мы говорим, что это энергия электрического поля. Тогда возникает вопрос: а почему же они отличаются? Если речь идет об энергии электрического поля, то почему при создании этого поля в диэлектрике получается другой результат, а не тот же самый, что и в вакууме? Какой ответ здесь… какой ответ на этот вопрос? Ответ на этот вопрос состоит вот в чём: эта энергия электрического поля определяется через работу, которую нужно затратить, чтобы это создать поле.Еще раз повторяю, электрическое поле определяется через работу внешних сил, которую нужно затратить, чтобы создать это поле.
Значит, вот у нас есть такое выражение E² поделенное на 8п, да? Что это такое? Это объемная плотность энергии в пустом пространстве, где, в котором создано электрическое поле с напряженностью E.Да? Это энергия в единице объема. Но есть другая формула. Если бы всё это происходило в диэлектрике, то возникла бы вот такая формула εE² / 8п, ну вот такая формула. Да? Но ε — большее количество 1, значит, естественно, что второе выражение дает, ну, в общем, принимает значение. И мы говорим, что это энергия электрического поля. Тогда возникает вопрос: а почему же они отличаются? Если речь идет об энергии электрического поля, то почему при создании этого поля в диэлектрике получается другой результат, а не тот же самый, что и в вакууме? Какой ответ здесь… какой ответ на этот вопрос? Ответ на этот вопрос состоит вот в чём: эта энергия электрического поля определяется через работу, которую нужно затратить, чтобы это создать поле.Еще раз повторяю, электрическое поле определяется через работу внешних сил, которую нужно затратить, чтобы создать это поле. Так вот, мы получим, если получается, что при создании электрического поля в диэлектрике, когда получается такая формула, вообще не вся работа идет на создание собственного электрического поля, а есть еще добавки. То есть вот, применяйте терминологию, то вот, первую формулу можно было бы назвать внутренней энергией электрического поля. Это собст… или как такой термин не всегда используется, но я хочу, чтобы вы поняли, это собственная энергия электрического поля.А вторая формула, которая отличает, дает и другой результат, это вся работа, которую нужно тратить, чтобы создать поле в диэлектрике. Из чего может состоять этот добавок? Почему вторая формула дает большее значение, чем первая? Вот, я хочу использовать это на одном простом примере. На примере диэлектрика с упругими диполями. Значит, мы представляем себе, что диэлектрик, вот, состоит из, ну, из диполей, которые меняют свой дипольный момент под внешнего поля, мы будем предполагать, что тут всё линейно, чтоб, что… мы будем предполагать, что всё линейно, и, так сказать, ну, для деформации этого диполя справедливо Гука, тогда мы напишем вот такую вещь: ну, что сила равняется капа на.
Так вот, мы получим, если получается, что при создании электрического поля в диэлектрике, когда получается такая формула, вообще не вся работа идет на создание собственного электрического поля, а есть еще добавки. То есть вот, применяйте терминологию, то вот, первую формулу можно было бы назвать внутренней энергией электрического поля. Это собст… или как такой термин не всегда используется, но я хочу, чтобы вы поняли, это собственная энергия электрического поля.А вторая формула, которая отличает, дает и другой результат, это вся работа, которую нужно тратить, чтобы создать поле в диэлектрике. Из чего может состоять этот добавок? Почему вторая формула дает большее значение, чем первая? Вот, я хочу использовать это на одном простом примере. На примере диэлектрика с упругими диполями. Значит, мы представляем себе, что диэлектрик, вот, состоит из, ну, из диполей, которые меняют свой дипольный момент под внешнего поля, мы будем предполагать, что тут всё линейно, чтоб, что… мы будем предполагать, что всё линейно, и, так сказать, ну, для деформации этого диполя справедливо Гука, тогда мы напишем вот такую вещь: ну, что сила равняется капа на. . на л. Капа — это некий коэффициент, который, ну, как бы жесткость соответствующей, так сказать, ну, ну, пружины что ли, если так моделировать диполь. Тогда можно такую формулу написать — представим себе, что такое диполь попал во внешнее электрическое поле, тогда его сила, которая действует от него, это есть Eq, это сила. Но, она должна равняться капа на l. Да? Теперь смотрите, пожалуйста, если я умножу здесь на l пополам, и здесь на l пополам, то видно, что капа l пополам, что это такое? Это упругая энергия, запасенная, ну, вот, упругая энергия деформации этого диполя.И, стало быть, это упругая энергия, она как раз равняется E… ну, а q на l — что такое? l — это расстояние, расстояние между плюсами, плюсом и минусом. Что такое q на l для диполя? Это дипольный момент. Да? Значит, получится, что Ep / 2 — это энергия диполя во внешнем поле. Ну, вот теперь мы запишем всю энергию, которая должна быть затрачена на то, чтобы создать электрическое поле в такой среде, и она будет равняться, вот эта энергия, она будет равняться E² / 8п.
. на л. Капа — это некий коэффициент, который, ну, как бы жесткость соответствующей, так сказать, ну, ну, пружины что ли, если так моделировать диполь. Тогда можно такую формулу написать — представим себе, что такое диполь попал во внешнее электрическое поле, тогда его сила, которая действует от него, это есть Eq, это сила. Но, она должна равняться капа на l. Да? Теперь смотрите, пожалуйста, если я умножу здесь на l пополам, и здесь на l пополам, то видно, что капа l пополам, что это такое? Это упругая энергия, запасенная, ну, вот, упругая энергия деформации этого диполя.И, стало быть, это упругая энергия, она как раз равняется E… ну, а q на l — что такое? l — это расстояние, расстояние между плюсами, плюсом и минусом. Что такое q на l для диполя? Это дипольный момент. Да? Значит, получится, что Ep / 2 — это энергия диполя во внешнем поле. Ну, вот теперь мы запишем всю энергию, которая должна быть затрачена на то, чтобы создать электрическое поле в такой среде, и она будет равняться, вот эта энергия, она будет равняться E² / 8п. Да? Это собственная энергия нашего электрического поля, и вот здесь вы напишем, энергия деформированных, ну, растянутых диполей.Каждый из них, вот, имеет вот такое вот, вот такую энергию, а стало быть полная энергия, будет Ep — это один диполь, да? Поделенное на 2. Что еще нужно сделать, чтобы перейти? Ведь эта энергия в единице объема. Что нужно сделать? Умножить нужно, вот, на N, добавить, да? Ну, а pN — что такое? p — дипольный элемент одного диполя, умноженный на концентрацию, это есть, ну, модуль поляризации. Да? Значит, это вот есть, вот это вот есть, ну, P, да? Ну, и получилось, что это равняется E² / 8п + E / 2.А что такое P? Это P, P = α, это коэффициент поляризации, на E, да? Значит, это, напишем E² * α. Вот так, последнее преобразуется. А что такое α? Ну, это 1 + 4пα = ε, да? Значит, отсюда α = ε — 1, поделенное на 4п, да? Ну, вот. Так, давайте подставим сюда это выражение, получится… я так эту формулу буду переписывать… будет E² / 8п, + E² / 8п а здесь будет (ε- 1). И какой будет результат? А результат будет такой: εE² / 8п, да? Кстати, это пример простейший, вот, для случая, таких квазиупругих молекул, он показывает, что та вся работа, которую мы затратим, только частично идет на соб.
Да? Это собственная энергия нашего электрического поля, и вот здесь вы напишем, энергия деформированных, ну, растянутых диполей.Каждый из них, вот, имеет вот такое вот, вот такую энергию, а стало быть полная энергия, будет Ep — это один диполь, да? Поделенное на 2. Что еще нужно сделать, чтобы перейти? Ведь эта энергия в единице объема. Что нужно сделать? Умножить нужно, вот, на N, добавить, да? Ну, а pN — что такое? p — дипольный элемент одного диполя, умноженный на концентрацию, это есть, ну, модуль поляризации. Да? Значит, это вот есть, вот это вот есть, ну, P, да? Ну, и получилось, что это равняется E² / 8п + E / 2.А что такое P? Это P, P = α, это коэффициент поляризации, на E, да? Значит, это, напишем E² * α. Вот так, последнее преобразуется. А что такое α? Ну, это 1 + 4пα = ε, да? Значит, отсюда α = ε — 1, поделенное на 4п, да? Ну, вот. Так, давайте подставим сюда это выражение, получится… я так эту формулу буду переписывать… будет E² / 8п, + E² / 8п а здесь будет (ε- 1). И какой будет результат? А результат будет такой: εE² / 8п, да? Кстати, это пример простейший, вот, для случая, таких квазиупругих молекул, он показывает, что та вся работа, которую мы затратим, только частично идет на соб.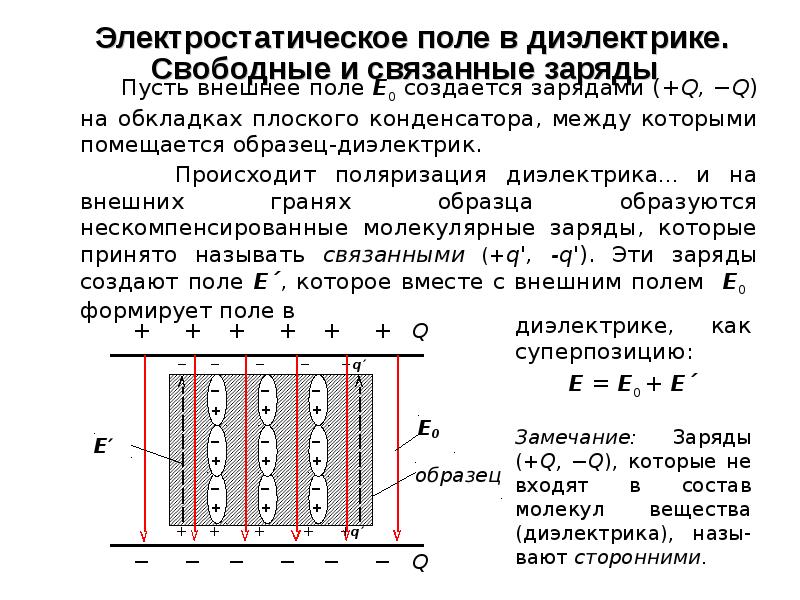 .. создание электрического поля. А её вторая часть идет на создание энергии вот этих квазиупругих диполей, и если всё сосчитать вместе, то получится правильный результат. Вот это очень важный момент. Хорошо. Теперь совсем коротко. А если речь идет о другом механизме поляризации, речь идет о механизме поляризации, где молекулы уже имеют, как говорят, врожденный дипольный момент, и все сводится к ориентации диполей во внешнем поле. Что там происходит в этом случае? В этом случае поляризация соединяется с тепловым движением, и в этом случае, как бы, от теплового движения ничего не зависит, каждая молекула ведет себя обособлено.А в случае, когда мы имеем дело с веществом, обладающим… у которого механизм поляризации, вот, по второму, когда молекулы имеют дипольный момент, то всякая ориентация этих молекул, их дипольных моментов, обязательно связана с взаимодействием с тепловым движением. Тепловое движение — это дезориентирующий фактор, оно стремится сбить правильную ориентацию этих дипольных моментов.
.. создание электрического поля. А её вторая часть идет на создание энергии вот этих квазиупругих диполей, и если всё сосчитать вместе, то получится правильный результат. Вот это очень важный момент. Хорошо. Теперь совсем коротко. А если речь идет о другом механизме поляризации, речь идет о механизме поляризации, где молекулы уже имеют, как говорят, врожденный дипольный момент, и все сводится к ориентации диполей во внешнем поле. Что там происходит в этом случае? В этом случае поляризация соединяется с тепловым движением, и в этом случае, как бы, от теплового движения ничего не зависит, каждая молекула ведет себя обособлено.А в случае, когда мы имеем дело с веществом, обладающим… у которого механизм поляризации, вот, по второму, когда молекулы имеют дипольный момент, то всякая ориентация этих молекул, их дипольных моментов, обязательно связана с взаимодействием с тепловым движением. Тепловое движение — это дезориентирующий фактор, оно стремится сбить правильную ориентацию этих дипольных моментов. И, короче говоря, при попытке поляризовать такое вещество, обязательно возникнет тепловой эффект.Появится тепло, которое нужно отдать, отдать термостату. Вот, если мы будем создавать электрическое поле в таком диэлектрике, то кроме E² / 8п нужно добавить сюда еще тепло, отданное термостату. Вот, дельта Q количество. И вот теперь, уже, так сказать, ну, понятно, еще раз повторяю, что вот это E² / 8п — это как бы собственная или внутренняя энергия электрического поля, а εE² / 8п — это полный эффект. Механизмы разные, так или иначе, когда мы создаем электрическое поле, то не вся энергия тратится на создание поля, часть, вот, в первом случае, идет на упругую энергию этих диполей, во втором случае возникает тепловой эффект, тепло должно быть убрано, термостат отбирает это тепло.Ну, теперь я просто, вот, скажу то умное слово, которое порекомендую вам, так, это сделав умное… попытка сделать умное выражение лица, вот, произносить это, если вас кто-нибудь об спросит. Да? Так вот, я напомню вам, что в термодинамике рассматривается, ну, разные функции состояния.
И, короче говоря, при попытке поляризовать такое вещество, обязательно возникнет тепловой эффект.Появится тепло, которое нужно отдать, отдать термостату. Вот, если мы будем создавать электрическое поле в таком диэлектрике, то кроме E² / 8п нужно добавить сюда еще тепло, отданное термостату. Вот, дельта Q количество. И вот теперь, уже, так сказать, ну, понятно, еще раз повторяю, что вот это E² / 8п — это как бы собственная или внутренняя энергия электрического поля, а εE² / 8п — это полный эффект. Механизмы разные, так или иначе, когда мы создаем электрическое поле, то не вся энергия тратится на создание поля, часть, вот, в первом случае, идет на упругую энергию этих диполей, во втором случае возникает тепловой эффект, тепло должно быть убрано, термостат отбирает это тепло.Ну, теперь я просто, вот, скажу то умное слово, которое порекомендую вам, так, это сделав умное… попытка сделать умное выражение лица, вот, произносить это, если вас кто-нибудь об спросит. Да? Так вот, я напомню вам, что в термодинамике рассматривается, ну, разные функции состояния.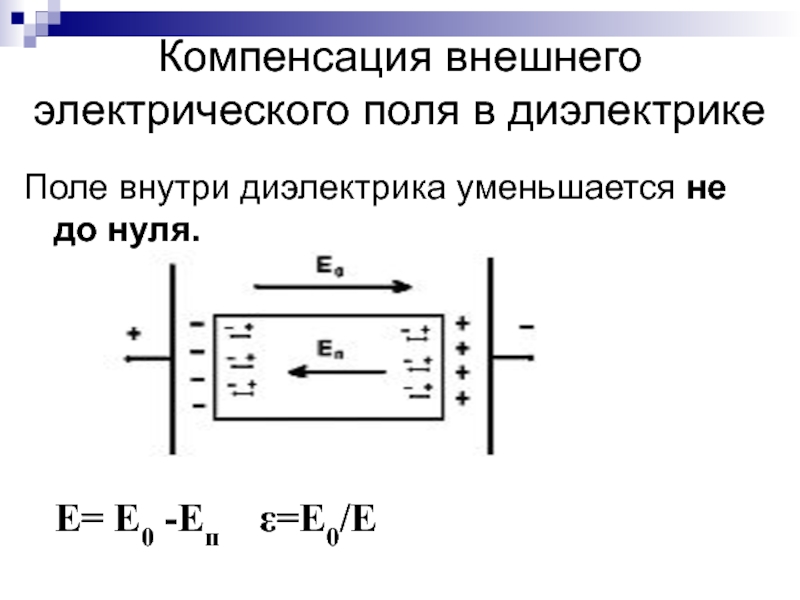 Да? Но такая, среди них, вот, есть, которая называется свободной энергией. Что такое свободная энергия? Я сейчас произнесу вот это определение. Это функция состояния, превращающая работу в обратимом процессе изотермического процесса совершаемой в этом процессе работы, работе внешних сил.Значит, функция состояния, превращение которого в изотермический обратимом процессе равно работе внешних сил. Так вот, то, что мы называем энергией электрического поля в диэлектриках, на самом деле, это есть свободная энергия электрического поля. Вот, термин «свободная энергия», напомню вам, эта функция, которая называется «свободная энергия», так: это есть U — TS, вот, T — это температура, S — это энтропия, U — внутренняя энергия. Так вот, роль внутренней энергии играет вот это выражение, ну, а, вот, пси — это и есть вот это, вот это выражение, ну, отнесенное к единице объема, конечно.Значит, εE² / 8п — это свободная энергия электрического поля, или, вернее, объемная плотность свободной энергии электрического поля вэлектрике.
Да? Но такая, среди них, вот, есть, которая называется свободной энергией. Что такое свободная энергия? Я сейчас произнесу вот это определение. Это функция состояния, превращающая работу в обратимом процессе изотермического процесса совершаемой в этом процессе работы, работе внешних сил.Значит, функция состояния, превращение которого в изотермический обратимом процессе равно работе внешних сил. Так вот, то, что мы называем энергией электрического поля в диэлектриках, на самом деле, это есть свободная энергия электрического поля. Вот, термин «свободная энергия», напомню вам, эта функция, которая называется «свободная энергия», так: это есть U — TS, вот, T — это температура, S — это энтропия, U — внутренняя энергия. Так вот, роль внутренней энергии играет вот это выражение, ну, а, вот, пси — это и есть вот это, вот это выражение, ну, отнесенное к единице объема, конечно.Значит, εE² / 8п — это свободная энергия электрического поля, или, вернее, объемная плотность свободной энергии электрического поля вэлектрике.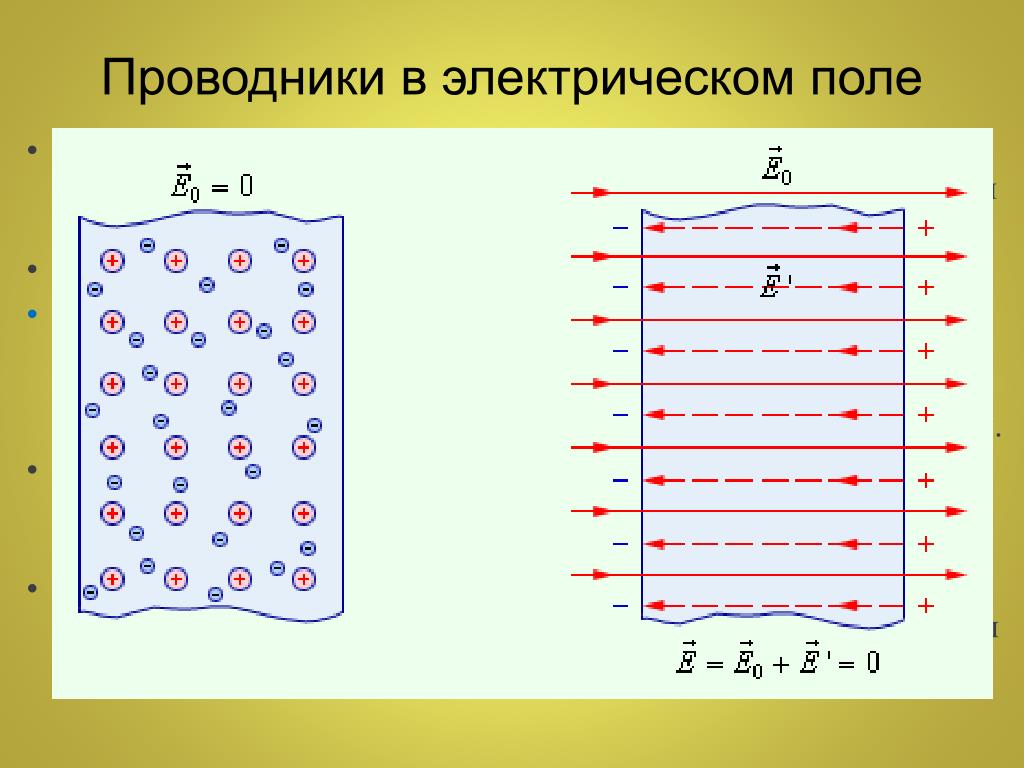
Диэлектрики в электрическом поле — презентация онлайн
1. Диэлектрики в электрическом поле
• Свободные и связанные заряды
Связанными заряддами называют заряды, входящие в состав атомов и
молекулы, а также заряды в кристаллических веществах с ионной
решеткой. Все остальные заряды называют свободными.Примерами
свободных зарядов могут служить электроны проводимости в металлах, ионы
в газах и электролитах.
Ионами называются атомы или молекулы, имеющие либо избыток, либо
недостаток электронов по сравнению с нормальным состоянием этих атомов
или молекулы.
Электроны, оторвавшиеся от атомов при их ионизации, не всегда
присоединяются к другим атомам; часто они остаются свободными.
Диапазоном называются вещества, в которых отсутствуют свободные
заряды (или их присутствие незначительно и этим присутствием можно
пренебречь в условиях рассматриваемой задачи).
В диэлектрике все заряды связаны.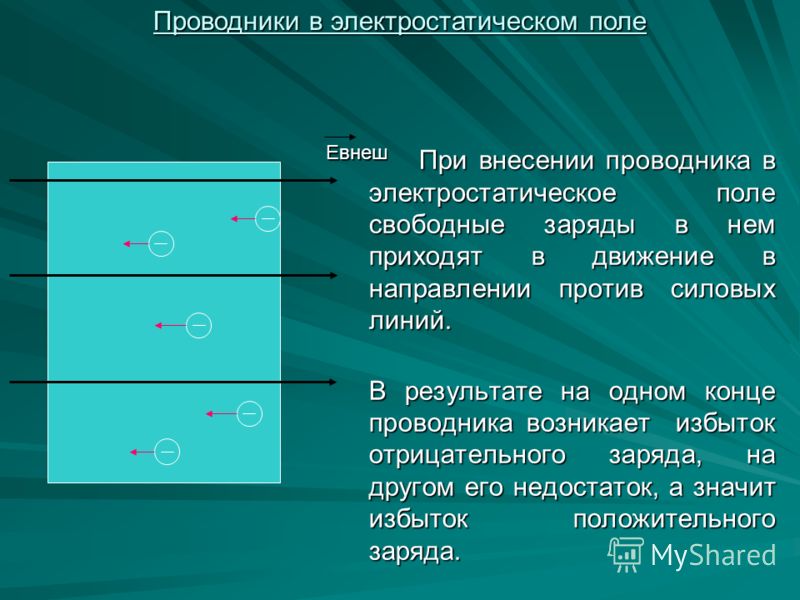
В диэлектриках свободные заряды отсутствуют. Когда на диэлектрик
переходит свободный электрон, он тут же присоединяется к какому-либо атому
или молекуле.
1
2. Диполь
Диполь — система связанных противоположных зарядов. Если говорить более
точно, система двух одинаковых по величине,
но противоположных по знаку
l r r — плечом диполя (расстояние
зарядов называется диполем, а
между зарядами).При этом заряды не обязательно являются точечными, и
если они не точечные,
и
— полез-электрические центры зарядов, образующих
диполь.
r
r
Точечный диполь. Пусть размеры заряженных тел, образующих диполь, и
расстояние между ними (плечо диполя) малы по сравнению с расстояниями от
точки наблюдения до центра диполя. (Другими словами, последнее
что в условиях рассматриваемой задачи два
противоположных зарядов можно считать слившимися в одну точку.) В этом
случае диполь называется точечным.
2
3. Дипольный момент или электрический момент диполя
pe ql
Дипольный
(1)
момент (электрический) определяет вектором
Здесь — l вектор, направленный вдоль оси диполя от отрицательного заряда к
положительному.
3
4. Поляризация диэлектриков
• Поляризация состоит в повороте осей жестких диполей вдоль E
диполь с моментом pe, помещенный во внешнее однородное
электрическое поле, действует пара сил с моментом
,
pe, E
.На
стремящаяся повернуть диполь в напряженности поля.
Потенциальная энергия жесткого диполя, помещенного во внешнее
электрическое поле, равна Wpot pe E
Знак минус показывает, что устойчивым положением диполя,
миниму потенциальной энергии, является
картина
расположение его
вдоль положительного направления
4
pe
E
.
5. Добавочное поле, созданное диполем поле, ослабляет внешнее.
Добавочное поле E add, созданное диполем, ослабляет внешнее поле.
Вектор поляризации
Молекула поляризованного диэлектрика может рассматриваться как диполь, то
есть как система противоположных зарядов.
P
(r
) или
Мерой поляризации диэлектрика является
вектор поляризации
поляризованность в точке среды M (r)
и определяется по формуле
—
П (г)
p
ei
dV
dV
Здесь суммирование на все молекулы-диполи,
находящиеся в физически бесконечноdV
малом объема
,
M
(r
)
содержащем
точка
.
я
пей
— дипольный момент
-й молекулы.
(2)
5
6. Потенциал поляризованного диэлектрика
V
r
Пусть молекулы-диполи распределены в объеме
.
Рассмотрим элемент объема dV, расположенный в точке с радиус-вектором
, как точечный диполь, электрический момент которого равен
pe P
(r) dV
Найдем потенциал, создаваемый этим диполем в точке наблюдения M (r).
Запишем приращение как для точечного заряда
т.з. (r r l) т.з. (r r) т.з. р р л о (л)
Если l 0, то
d (r) т. з. р р л
1
кк л кпэ
r r
Здесь использовали
Р р р,
1
1
кП (р) dV
r r
R
1
1
q
(), т.з. (r) к
R
r
R
1
— градиент по штрихованным координатам.
R
6
7. Следовательно,
получаем после интегрирования
Рассмотрим действие оператора
1
(r) к P (r) dV
R
V
П 1 1
П П
R
R R
1-П 1
• Выразим из этого равенства
П П
R
R R
П (г)
1
• В результате имеем
dV P (r) dV
(r) к
V
R
V R
П (р) DS
П (г)
k
dV
R
R
V
S
.
Воспользовались теоремой Остроградского-Гаусса
S — граница области V
В выражении (3) поверхностный интеграл эквивалентен потенциалу
некоторого поверхностного распределения зарядов; объемный интеграл —
потенциалу объемного распределения зарядов. Соответствующие плотности
Соответствующие плотности
зарядов равны:
P
P
P
n
P
(3)
(4)
7
8. Плотности зарядов
P
• При неоднородном распределении дипольных моментов представляет
собой плотность тех зарядов, которые нескомпенсированы из-за
неоднородности распределения, а
есть плотность зарядов,
P
обеспечивающих на поверхности отсутствия компенсирующих
соседей у тех диполей, концы которых лежат на этой поверхности
В общем случае потенциал поляризационных зарядов обоих
видов выражается с помощью:
П (р) DS
П (г)
(r) к
S
R
V
R
dV
(5)
Вывод.Дипольные моменты, порожденные поляризацией вещества,
Предложите собой разновидность средств поля.
Указанные дипольные моменты возникают в веществе под действием
электрическое поля, и поведение вещества можно описать с помощью
.
вектор поляризации.
8
9. Уравнение Пуассона
• Так как электрические поля разделены нами на два вида,
то уравнение Пуассона принимает следующий вид:
2
1
E P
0
(6)
Плотность P согласно (4) выражена через дивергенцию поляризации
P, то формула (6) преобразуется к виду: P
E
0 0
(7)
Введем вектор индукции D
, называемый также
электрическим смещением (термин, введенный еще Максвеллом):
D 0E P
(8)
Уравнение (6) можно записать теперь двумя способами:
всего P
D
всего 1
E
P
0
0
Ур-е Максвелла (9) удобно для расчетов, т.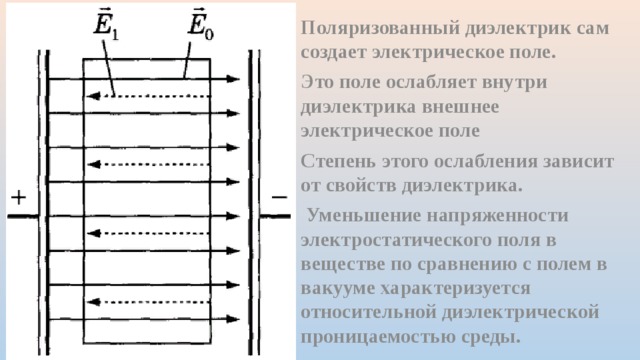 к. чаще всего известна
к. чаще всего известна
плотность свободных зарядов.
(9)
(10)
9
10. Теорема Гаусса для электрического смещения
С помощью теоремы Гаусса-Остроградского можно получить и
соответствующие интегральные соотношения:
D DS Q
S
Всего
E DS
(11,1) (11,2)
0
S
Q dV
Qtotal Q (P) dV
VS
VS
Здесь S произвольная замкнутая кусочно-гладкая поверхность
внутри диэлектрика V
— объем, ограниченная поверхность
S
(12)
S
D представляет собой лишь ту часть поля, которая создается свободными
зарядами.
Поле P создается только поляризационными зарядами.
Вектор E это поле, создаваемое как свободными,
так и связанными зарядами
10
11. Диэлектрическая проницаемость среды
Будем считать, что при не очень сильном
внешнем
поле в изотропном
диэлектрике вектор поляризации
P E
0
пропорционален напряженности поля.
10 9 Ф
0
36 м
называется электрической постоянной
D 0 1 E a E
(8)
(14)
диэлектрической восприимчивостью среды
0
для вакуума
1
1
(13)
относительная диэлектрическая проницаемость
(15)
для вакуума
а 0 (1)
а 0
абсолютная диэлектрическая проницаемость среды
(16)
11
12.Относительная диэлектрическая проницаемость
а
0
Абсолютная диэлектрическая проницаемость вакуума
(17)
а 0 0
Для применяемых в технике диэлектриков
относительная диэлектрическая проницаемость находится в пределах
2 8
Вектор электрической индукции или электрическое
смещение равенство
D 0 E
Замечание. Сказанное
относится
к изотропным диэлектрикам,
у которых пишут D, E, P
совпадают по направлению.
12
13. Классификация сред
Свойства среды по отношению к электрическому полюсу
параметром a
.
Различают следующие среды.
Линейные, в которых параметр
не зависит от электрического поля
нелинейные, в которых параметр a зависит от электрического поля
однородными называют диэлектрики,
параметр a которых не зависит от координат
Среды, у которых этот параметр является функцией координат,
называют неоднородными
Если свойства диэлектрика одинаковы по разным направлениям,
то его называют изотропным.
Соответственно среде, свойства которых различны по разным направлениям,
называют анизотропными.
В изотропных диэлектриках рекомендации
В изотропных диэлектриках
P, E
D, E
параллельны
— скалярные величины
В анизотропных этот параметр является тензором (линейным оператором).
D a E
13
14. Теорема Гаусса для различных сред
1
(
E
,
d
S
)
dV
S
V
0
1
(E, dS) dV
S
0 В
-для линейной изотропной
однородной среды
(18)
(19)
-для вакуума
Для линейной изотропной среды в общем случае (r)
теорема Гаусса в дифференциальной форме имеет вид
div (0 (r) E)
0div ((r) град)
(20)
(21)
Минус в (21) за счет появления проблемы
14
15. Кусочно-однородная среда
Кусочно-однородная среда
Рассмотрим случай кусочно-однородной среды. Пусть для
определенности имеется две различные среды, заполненные
однородными средами с различными
.
Условие сопряженности
Рассмотрим границу раздела двух диэлектриков
с относительными проницаемостями
1 и
Для элементарного контура
pqrs
2
,
расположенного по обе стороны границы раздела, запишем
закон электромагнитной индукции
Bn
(
E
,
d
л
)
S
т
pqrs
Bn нормальная составляющая индукции к площадке S
охваченной контуром интегрирования
(22)
,
15
16.Условие сопряженности
Распределение млрд в пределах малой площадки Принято
.
считать равномерным.
Такое же предположение примем и в отношении составляющих
напряженности на границах контура qr и ps
16
17. Условие сопряженности Сделанные предположения позволяют (22) записать в виде
Et1 l1 Et2 l2
Et1
Bn
(E, дл)
S
т
pq, RS
(23)
Et2 касательные составляющие напряженности электрического
и
поля на отрезках l1
и
l2
При предельном переходе, когда контур стягивается к границе раздела
.
л
, имеем l1 l
.
l2 l
Длины отрезков qr
и ps
стремятся к нулю, также стремится к нулю и
площадь
Из (23) получаем условие
Et1 = Et2
S
(24)
На границе раздела диэлектриков касательные составляющие вектора
напряженности электрического поля равны.
17
18. Вектор с границей раздела двух диэлектриков
Рассмотрим элементарный цилиндрический объем V, охватывающий границу
раздела двух диэлектриков S.Пусть внутри рассматриваемого объема имеются
не только объемно распределенные заряды, но и распределенный на границе
раздела заряд с поверхностной плотностью.
18
19. В этом случае из постулата Максвелла следует
(D, dS) S V
(25)
S
Пусть S поверхность цилиндра. Принимая условие постоянства
нормальных составляющих вектора D на малых торцевых
поверхностях цилиндра S, S2, перепишем (25) в виде
1
Дн1 С1
Дн2 С2
(D, dS) S V
(26)
S бок
При стягивании цилиндра к границе раздела
S
объем цилиндра будет стремиться к нулю:
V 0
Также S1 S, S2 S, Sбок 0 Из (26) получаем
2
Dn
1
Dn
(27)
Условия (24) и (27) являются граничными условиями
на границе раздела диэлектриков
19
.

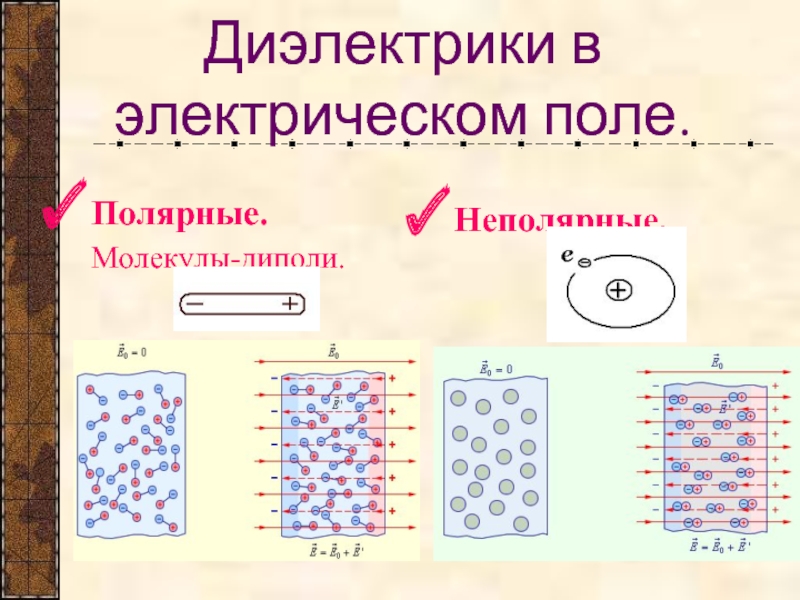

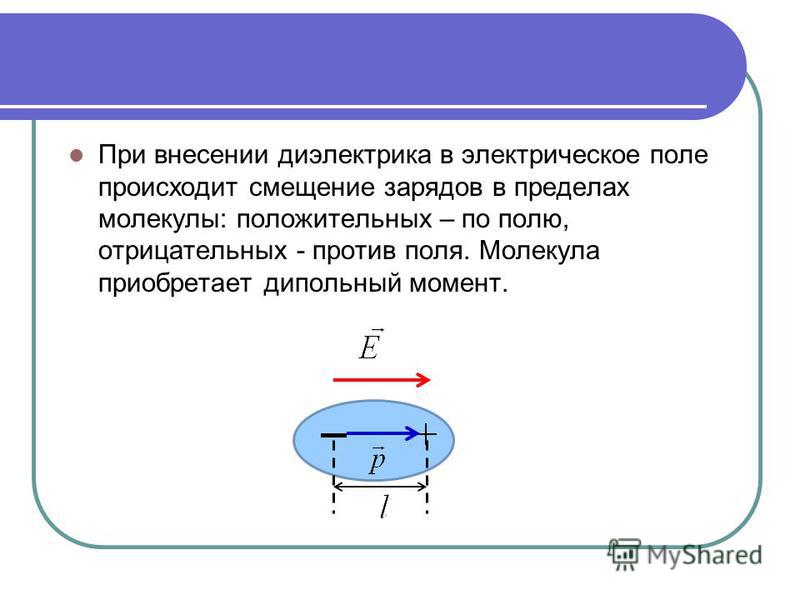
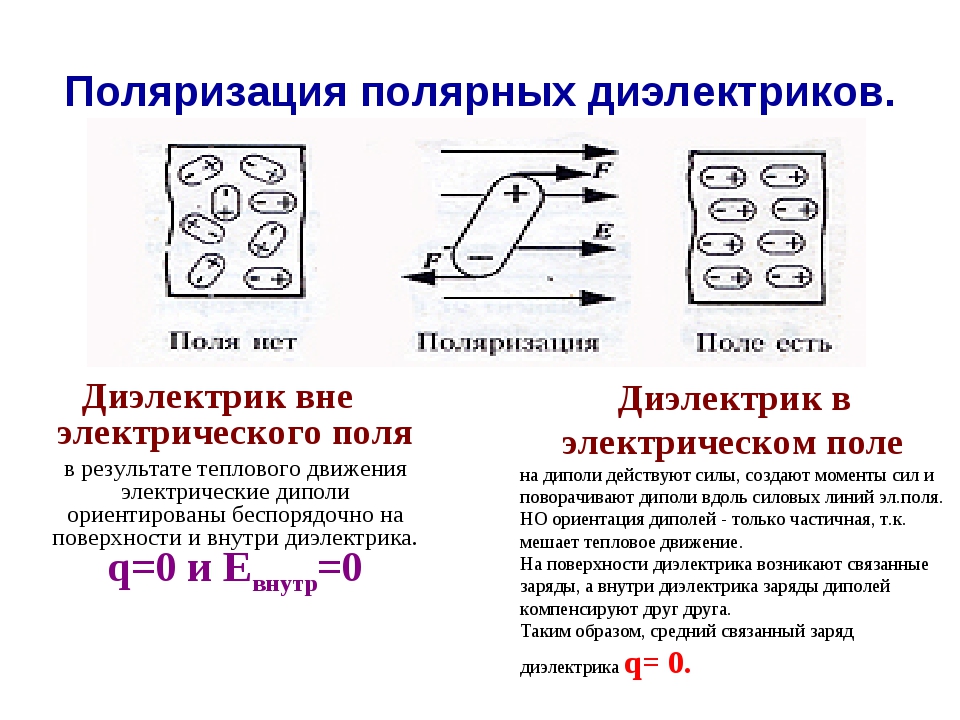 16)
16)

 — 155 с.
— 155 с. Кусочно-однородная среда
Кусочно-однородная среда