Электромагнитные силы, создаваемые магнитным полем. Электромагнитная сила

§ 25. Природа электромагнитной силы.

Объяснение механических действий магнитного поля тяжением магнитных линий предоставляет возможность дать весьма простое физическое толкование причин возникновения электромагнитной силы, т. е. силы механического взаимодействия проводника, несущего ток, с магнитным полем. Представим себе поле между двумя полюсами магнита и помешенный в это поле перпендикулярно к нему проводник, по которому течет ток. Мы знаем, что при прохождении по проводнику тока вокруг него возникает магнитное поле в виде кольцевых магнитных линий. Направление этого поля тока легко определяется по правилу штопора. Картина результирующего магнитного поля может быть получена аналитически или путем использования железных опилок и построения магнитного спектра. Не трудно будет убедиться, что по одну сторону проводника, как бы в силу наложения противоположных магнитных состояний среды, магнитное поле ослабится, в то время, как по другую сторону проводника, наоборот, магнитные линии располо-

107

жатся более густо. Поле тока, таким образом, исказит основное магнитное поле. В результате получится картина, данная на рисунке 59 (см. также рис. 26— 28).

Если достаточно освоиться с фарадеевским представлением о магнитном поле, как о системе реально существующих упругих нитей, стремящихся стянуться, то, не прибегая к правилу левой руки, по одному взгляду на рисунок 59 можно сказать, что проводник будет испытывать со стороны поля давление, стремящееся сдвинуть его влево.

Вообще, правильное представление о вероятном

механизме явлений, имеющих место в магнитном поле, делает запоминание разного рода мнемонических правил излишним.

Картину магнитного поля в каждом данном случае можно, как указано выше, получить аналитически путем расчета или же, что гораздо проще, при помощи магнитных спектров. Эти спектры известны еще со времени Гильберта (XVIвек), но только Фарадей научил нас (см. § 1) видеть в них определенный физический смысл, а именно схему какого то реально происходящего физического процесса. В этом—громадная заслуга Фарадея.

Совершенно аналогичным образом можно трактовать и механические процессы, происходящие в более сложных случаях. Рассмотрим, например, схему магнитного потока в двигателе постоянного тока (рис. 60).

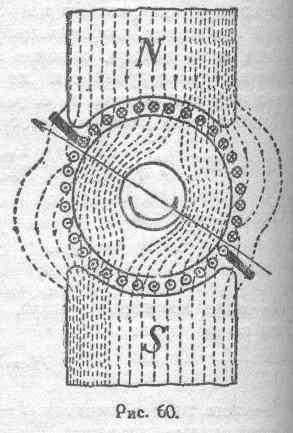
При прохождении тока по обмотке двигателя этой обмоткой, как таковой, создается поле, направление которого показано на рисунке прямой стрелкой. Взаимодействуя с основным

108

полем, поле якоря создает некоторое результирующее поле, скошенное под северным полюсом в одну сторону, под южным — в другую, как показано на рисунке 60. Деформированные таким образом магнитные линии, стягиваясь, естественно создадут пару сил, стремящуюся вращать якорь (против часовой стрелки в данном случае). Если бы не было коммутации, т. е. если бы направление тока в каждом данном проводнике не менялось при прохождении под щеткой, то якорь, повернувшись на такой угол, при котором несимметрия магнитного поля исчезает, остановился бы. Таким образом, коммутация необходима для того, чтобы искусственно поддерживать несимметрию магнитного поля.

Этот пример выясняет нам, каким путем происходит преобразование электрической энергии в механическую. Подводимая к двигателю электрическая энергия идет на деформирование магнитного поля. Это деформированное состояние поля и является непосредственной причиной возникновения вращающего момента (см. § 12). Обратное явление происходит в генераторе. Механическая энергия двигателя, вращающего генератор, расходуется на преодоление тяжения деформируемых проводниками якоря магнитных линий основного магнитного поля машины. Путем процесса, подробное рассмотрение которого будет дано в глазе V, „Природа электрического тока", и элементарной схемой которого является пример, приведенный нами на рисунках 26 — 28 (почкование магнитных линий), энергия деформированных магнитных линий распределяется по всей замкнутой цепи тока, состоящей из проводников арматуры и внешней части цепи. Таким образом, магнитный поток является физически необходимым посредником при преобразовании механической энергии в электрическую и обратно.

1) В том, что поле, создаваемое якорем, будет иметь именно такое направление, не трудно убедиться, рассмотрев распределение токов по проводникам обмотки. Ясно, что мы можем рассматривать якорь как электромагнит, отличающийся от обычного электромагнита лишь тем, что в якоре витки намагничивающей обмотки по краям его (у щеток) имеют меньшие размеры, чем посредине.

studfiles.net

Электромагнитные силы, создаваемые магнитным полем. — КиберПедия

Энергия, заключенная в магнитном поле, проявляет себя в виде электромагнитных сил, которые возникают при взаимодействии магнитного поля с движущимися электрическими зарядами. Электромагнитная сила, возникающая при движении электрического заряда в магнитном поле, действует на него в направлении, перпендикулярном движению и направлению силовых линий, и стремится вытолкнуть заряд за пределы поля (см. п.16, рис. 24).

Если поместить в магнитное поле проводник с током I, то между электронами, проходящими по проводнику, и магнитным полем возникнут электромагнитные силы, которые, складываясь, образуют результирующую силу F, стремящуюся вытолкнуть проводник из магнитного поля (рис. 34). Электромагнитная сила определяется законом Ампера. Он формулируется следующим образом. Электромагнитная сила, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поля В и длины проводника l:

F = IBl.

Направление действия силы F определяют по правилу левой руки: левую руку следует расположить так, чтобы магнитные линии входили в ладонь, а четыре вытянутых пальца совместить с направлением тока, тогда расположенный под прямым углом большой палец укажет направление действия cилы. Сила F возникает только в том случае, если проводник расположен перпендикулярно или под некоторым углом к магнитным силовым линиям поля. Если же проводник расположен вдоль силовых линий поля, то электромагнитная сила будет равна нулю.

Для того чтобы изменить направление электромагнитной силы, необходимо изменить направление тока в проводнике или же направление магнитного поля.

Возникновение электромагнитной силы F при взаимодействии проводника с током и магнитного поля можно наглядно представить как результат взаимодействия двух магнитных полей. Вокруг проводника с током возникает свое собственное круговое магнитное поле (рис. 35), которое будет складываться с внешним магнитным полем (например, постоянного магнита), в которое помещен проводник с током. При этом справа от проводника, где силовые линии поля проводника совпадают с линиями внешнего поля, происходит сгущение силовых линий; слева от проводника, где силовые линии поля проводника направлены навстречу линиям внешнего поля, происходит разрежение силовых линий. Магнитные силовые линии обладают свойством упругости, напоминающим свойство резиновых нитей, которые стремясь сократиться по длине, будут выталкивать проводник из области сгущения силовых линий в сторону их разрежения. В результате возникает электромагнитная сила F.

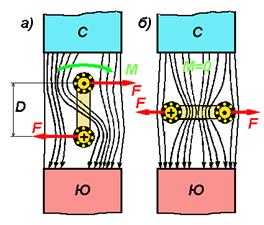Виток с током в магнитном поле. Если поместить в магнитное поле не проводник, а виток (или катушку) с током и расположить его вертикально (рис. 36,а), то, применяя правило левой руки к верхней и нижней сторонам витка, получим, что электромагнитные силы F, действующие на них, будут направлены в разные стороны. В результате действия этих двух сил возникает вращающий момент М, который вызовет поворот витка.

M = FD,

где: D — расстояние между сторонами витка.

Виток будет поворачиваться в магнитном поле до тех пор, пока он не займет положение, перпендикулярное магнитным силовым линиям поля (рис. 36,б). Для увеличения вращающего момента в электрических двигателях применяют не один виток, а несколько. Эти витки, соединенные соответствующим образом, образуют обмотку якоря электродвигателя.

Электромагнитная индукция.

При пересечении проводником силовых линий магнитного поля в нем возникает или, как говорят, индуцируется э. д. с. Это явление называется электромагнитной индукцией.

Возникновение э.д.с. объясняется действием сил магнитного поля на находящиеся в проводниках свободные электроны. Свободные электроны под влиянием этих сил начнут двигаться вдоль проводника (рис. 37). В результате этого движения на одном конце проводника накопятся свободные электроны и возникнет отрицательный электрический заряд, а на другом конце ввиду недостатка электронов появится положительный заряд.

Разность потенциалов на концах проводника численно равна индуцированной в проводнике э.д.с. Индуцирование э.д.с. в проводнике происходит независимо от того, включен ли он в какую-либо электрическую цепь или нет. Если присоединить концы этого проводника к какому-либо приемнику электрической энергии, то под влиянием разности потенциалов по замкнутой цепи потечет электрический ток.

Значение индуцированной э. д. с. определяется законом электромагнитной индукции Фарадея. Он формулируется следующим образом. Индуцированная э. д. с. е прямо пропорциональна индукции магнитного поля В, длине проводника l и скорости его перемещения v в направлении, перпендикулярном силовым линиям поля,

e = Blv.

Если проводник перемещается вдоль силовых линий поля, т. е. как бы скользит по ним, то э.д.с. в нем не возникает.

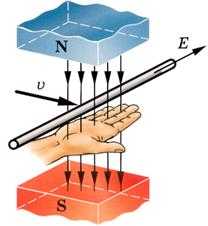Направление индуцированной э. д. с. определяют правилом правой руки. Правую руку следует расположить так, чтобы магнитные силовые линии входили в ладонь, а большой палец совместить с направлением движения проводника (т. е. направлением его скорости v), то вытянутые четыре пальца укажут направление индуцированной э.д.с. е (рис. 38). Пользуясь этим правилом, легко убедиться в том, что при изменении направления движения проводника будет изменяться и направление индуцированной э.д.с.

Индуцировать э.д.с. в неподвижном проводнике можно перемещением самого магнитного поля или изменением магнитного потока. При этом, чем быстрее изменяется магнитный поток, тем больше индуцированная э.д.с.

Способы индуцирования э. д. с. в электрических машинах. Явление электро-магнитной индукции широко используется в различных электрических машинах и устройствах. На этом принципе основано устройство электрических генераторов, 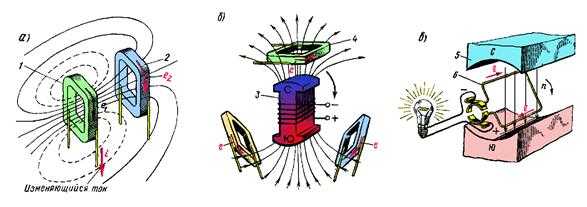двигателей и трансформаторов. Для индуцирования э. д. с. в них обычно применяются три способа:

-изменение тока в катушке 1 (рис. 39, а), в магнитном поле которой расположена вторая катушка 2. При этом непрерывно изменяется магнитный поток, охватываемый второй катушкой, и в ней, а также и в первой катушке, будут индуцироваться электродвижущие силы е1 и е2. Этот способ используют в трансформаторах;

-вращение магнитного поля, созданного постоянными магнитами или электромагнитами 3, относительно неподвижных катушек 4 (рис. 39, б). При этом непрерывно изменяется магнитный поток, пронизывающий каждую катушку, и в них индуцируются э. д. с. е. Такой способ используют в машинах переменного тока;

-вращение витков 6 или катушек в постоянном магнитном поле, созданном неподвижными постоянными магнитами 5 или электромагнитами (рис. 39, в). При этом непрерывно изменяется магнитный поток, охватываемый каждым витком или катушкой, вследствие чего в них индуцируется э. д. с. Этот способ используют в электрических машинах постоянного тока.

Вихревые токи.

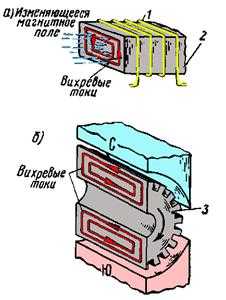Изменяющийся магнитный поток способен индуцировать э. д. с. не только в проводах или витках катушек, но и в массивных стальных сердечниках, кожухах и других металлических деталях электротехнических установок. Эти э. д. с. являются причиной появлений индуцированных токов, которые действуют в массивных металлических деталях, замыкаясь накоротко в их толще. Такие токи получили название вихревых.

Например, при изменении магнитного потока, созданного катушкой 1 (рис. 40, а), в ее стальном сердечнике 2 индуцируются вихревые токи, замыкающиеся в плоскости, перпендикулярной силовым линиям магнитного поля. Вихревые токи возникают также в сердечниках 3 якорей и роторов электрических машин при вращении их в магнитном поле (рис. 40, б). Природа вихревых токов такая же, как и токов, индуцированных в обычных проводах или катушках. Благодаря очень малому сопротивлению массивных проводников вихревые токи даже при небольшой индуцированной э. д. с. достигают очень больших значений, вызывая чрезмерное нагревание этих проводников.

Способы уменьшения вредного действия вихревых токов. В электрических машинах и аппаратах вихревые токи обычно нежелательны, так как они вызывают нагрев металлических сердечников, создают потери энергии (так называемые потери от вихревых токов), снижают к. п. д. электрических машин и аппаратов и оказывают согласно правилу Ленца размагничивающее действие. Для уменьшения вредного действия вихревых токов применяют два основных способа.

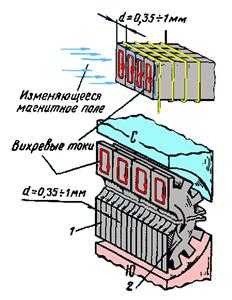
Сердечники электрических машин и аппаратов выполняют из отдельных стальных листов 1 (рис. 41) толщиной 0,35—1,0 мм, изолированных один от другого слоем изоляции 2 (лаковой пленкой, окалиной, образующейся при отжиге листов, и пр.). Благодаря этому преграждается путь распространению внхревых токов и уменьшается поперечное сечение каждого отдельного проводника, через которое протекают эти токи, что приводит к уменьшению силы тока.

Самоиндукция.

Э.д.с., индуцирования в проводнике или катушке в результате изменения магнитного потока, созданного током, проходящим по этому же проводнику или катушке, носит название э. д. с. самоиндукции. Эта э. д. с. возникает при всяком изменении тока: при замыкании и размыкании электрических цепей, а так же при изменении тока в цепи. Чем быстрее изменяется ток в проводнике или катушке, тем больше скорость изменения пронизывающего их магнитного потока и тем большая э. д. с. самоиндукции в них индуцируется. Направление э. д. с. самоиндукции определяется по правилу Ленца. Э.д.с. самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока. Следовательно, при возрастании тока в проводнике (катушке) индуцированная в них э. д. с. самоиндукции будет направлена против тока, т. е. будет препятствовать его возрастанию, и наоборот, при уменьшении тока в проводнике (катушке) возникает э. д. с. самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию. Если же ток в катушке не изменяется, то э.д.с. самоиндукции не возникает.

В электрической цепи (рис.42, а), состоящей из резистора с сопротивлением R и катушки К, ток i создается совместным действием напряжения U источника и э.д. с. самоиндукции eL индуцируемой в катушке.

При подключении рассматриваемой цепи к источнику э. д. с. самоиндукции eL (см. сплошную стрелку) сдерживает нарастание силы тока. Поэтому ток i достигает установившегося значения I=U/R (согласно закону Ома) не мгновенно, а в течение определенного промежутка времени (рис. 42, б). За это время в электрической цепи происходит переходный процесс, при котором изменяются eLи i. Точно так же при выключении электрической цепи ток i не уменьшается мгновенно до нуля, а из-за действия э. д. с. eL(см. штриховую стрелку) постепенно уменьшается.

Индуктивность. Способность различных проводников (катушек) индуцировать э.д.с. самоиндукции оценивается индуктивностью L. Она показывает, какая э. д. с. самоиндукции возникает в данном проводнике (катушке) при изменении тока на 1 А в течение 1 с. Индуктивность измеряется в генри (Гн).

Коммутационные перенапряжения. Особенно сильно проявляет себя э. д. с. самоиндукции при размыкании цепей, содержащих катушки с большим числом витков и со стальными сердечниками (обмотки генераторов, электродвигателей, трансформаторов и пр.), т. е. цепей, обладающих большой индуктивностью. В этом случае возникающая э. д. с. самоиндукции eLможет во много раз превысить напряжение U источника и, суммируясь с ним, послужить причиной возникновения перенапряжений в электрических цепях (рис. 43, а), называемых коммутационными (возникающими при коммутации — переключениях электрических цепей). Они являются опасными для обмоток электродвигателей, генераторов и трансформаторов, так как могут вызвать пробой их изоляции.

Большая э. д. с. самоиндукции способствует также возникновению электрической дуги в электрических аппаратах, осуществляющих коммутацию электрических цепей. Например, в момент размыкания контактов рубильника (рис. 43, б) образующаяся э.д.с. самоиндукции сильно увеличивает разность потенциалов между разомкнутыми контактами рубильника и пробивает воздушный промежуток. Возникающая при этом электрическая дуга поддерживается в течение некоторого времени э.д.с. самоиндукции, которая, таким образом, затягивает процесс отключения тока в цепи.

Взаимоиндукция.

Взаимоиндукцией называется явление индуцирования э. д. с. в проводнике или катушке при изменении магнитного потока, создаваемого другим проводником (катушкой). Индуцируемая таким образом э. д. с. ем носит название э. д. с. взаимоиндукции.

Контрольные вопросы:

1. Какие существуют способы усиления магнитных полей?

2. Что такое магнитная индукция, магнитный поток, напряженность магнитного поля?

3. Каковы основные характеристики ферромагнитных материалов?

4. В каких случаях магнитное поле создает механические силы и как они определяются?

5. Что такое индуцированная э.д.с. и как определяется ее значение и направление?

6. Что представляют собой вихревые токи и какие существуют способы уменьшения их вредного действия?

7. Что такое э. д. с. самоиндукции и взаимоиндукции?

cyberpedia.su

Электромагнитные силы - Большая Энциклопедия Нефти и Газа, статья, страница 1

Электромагнитные силы

Cтраница 1

Электромагнитные силы стремятся так изменить взаимное расположение контуров, чтобы увеличить поток взаимной индукции и тем самым при неизменных токах увеличить энергию системы. [1]

Электромагнитные силы ( ЭМС), действующие в индукционных печах, возбуждают движение расплава, интенсивность которого обычно на один или несколько порядков превышает интенсивность термогравитационной конвекции и может существеннейшим образом влиять на технологический процесс в печи. [2]

Электромагнитные силы чрезвычайно широко распространены в природе. Они действуют в атомном ядре, атоме, молекуле, между отдельными, молекулами в макроскопических телах. [3]

Электромагнитные силы возникают во всех алюминиевых электролизерах, их величина пропорциональна квадрату силы тока. При токе более 80 кА влияние этих сил становится значительным, а на ваннах большой мощности оно будет определяющим с точки зрения технико-экономических показателей. [4]

Электромагнитные силы в линейном двигателе могут быть определены так же, как и электромагнитный момент во вращающихся машинах, по изменению сконцентрированной в воздушном зазоре энергии магнитного поля при бесконечно малом перемещении подвижной части в направлении действия силы в условии постоянства либо токов возбуждающих контуров, либо потокосцеплений. [5]

Электромагнитные силы в конечном итоге определяют все свойства окружающих нас тел и все явления на Земле. [6]

Электромагнитные силы, производящие перемещение проводника, следует строго отличать от электродвижущих сил, стремящихся вызвать электрические токи. Допустим, что в металлической массе произвольной формы течет ток, причем плотность тока внутри металла определяется законами электропроводности. Другой постоянный ток течет через второй вблизи расположенный проводник. Если оба тока одинаково направлены, то оба проводника притягиваются и приближаются один к другому, если тому не препятствуют внешние силы. Несмотря на то, что вещество проводников и притягивается, токи, течение которых внутри металла может совершаться по любому направлению, не перемещаются внутри металла, наоборот, их распределение в металлической массе остается неизменным, и ни один из проводников не возбуждает в другом электродвижущих сил, которые изменяли бы в них распределение токов. [7]

Электромагнитные силы имеют определяющее влияние на движение заряженных частиц в областях, пространственные масштабы которых больше размеров ядра, но меньше астрономических размеров. В субатомных масштабах проявляются сильные ( ядерные) и слабые взаимодействия, а в астрономических - гравитационные. [8]

Электромагнитные силы могут возникать как при постоянных, так и переменных токах. [9]

Электромагнитные силы убывают обратно пропорционально квадрату расстояния между заряженными телами, а радиус действия их в принципе бесконечен. [10]

Электромагнитные силы ( электромагнитное взаимодействие) проявляются в природе весьма разнообразно. Ими объясняются, например, ранее изученные силы трения, силы упругости и силы взаимодействия молекул. Электромагнитные силы возникают между телами, которые имеют электрический заряд. Электрический заряд ( заряд) - это одно из свойств материи, которое проявляется в том, что между заряженными телами действуют силы отталкивания и притяжения. [11]

Электромагнитные силы и мощности для слоя жидкого металла и стенок канала при этом определяются так же, как и для плоской машины. [13]

Электромагнитные силы, действующие на индуктор и жидкий металл, равны по величине и об-ратны по знаку. Нас интересует электромагнитная сила РЭУ1, действующая на жидкий металл, однако проще вычислить силу, действующую на индуктор, и взять ее согласно сказанному с обратным знаком. [14]

Страницы: 1 2 3 4

www.ngpedia.ru

§ 107. Электромагнитная сила. Общие соображения.

При анализе связи между кинетической энергией, присущей электродинамической системе, и силами, возникающими в такой системе, было получено (см, § 96) общее выражение для так называемой электромагнитной силы, т. е. механической силы, возникающей

372

в системе вследствие происходящих в ней электромагнитных процессов.

Это общее выражение (72):

определяет электромагнитную силу как частную производную от электрокинетической энергии системы по геометрической координате.

В дальнейшей необходимо неукоснительно помнить, что при обследовании электродинамических систем при помощи второй формы лагранжевых уравнений мы принимаем в качестве независимых координат — количества электричества q и геометрические координаты g, определяющие размеры, форму и взаимное расположение всех частей системы. В связи с этим мы, следовательно, должны считать, с одной стороны количества электричества и их производные по времени, т. е. силы токов, независимыми от геометрических координат, и с другой стороны, геометрические координаты независимыми от каких бы то ни было обстоятельств, характеризующих систему с точки зрения электромагнитных процессов, в ней протекающих.

На основании изложенного, всякий раз, когда мы берем производную электрокинетической энергии по геометрической координате, необходимо принимать все точки в системе постоянными.

Для того, чтобы возможно лучше охватить содержание вышеприведенного выражения (72), удобно представить его в виде отношения частных дифференциалов:

Таким образом, электромагнитная сила, стремящаяся изменить некоторую геометрическую координату, численно равна приращению электрокинетической энергии, соответствующему приращению этой координаты на единицу, при условии, что токи поддерживаются постоянными.

Если, при условии постоянства токов в системе, электромагнитные силы совершают положительную механическую работу, то одновременно получается положительное приращение электрокинетической энергии. На это обстоятельство обратил в свое время внимание В. Томсон (Кельвин). Действительно, если под действием силы fe некоторая часть системы получила в направлении этой силы перемещение dg, то совершенная при этом работа dA будет положительна и равна произведению силы на перемещение:

dА=fеdg

или, так как

то

373

другими словами, положительной работе dA, совершаемой возникшей в системе электромагнитной силой, соответствует положительное же приращение электрокинетической энергии, по величине равное dA, при условии, что токи поддерживаются постоянными.

Отсюда непосредственно вытекает следующее весьма важное положение: во всякой электродинамической системе, силы токов в которой поддерживаются постоянными от каких-либо посторонних источников, возникают такие и только такие механические силы, которые приводят к увеличению электрокинетической энергии системы в результате вызываемых ими движений. Иногда этот закон формулируется короче: всякая электродинамическая система, в которой силы токов поддерживаются постоянными, стремится увеличить свою электрокинетическую энергию.

Основываясь на вышерассмотренных рассуждениях, приведших к соотношению (120), В. Томсон указал, что если в рассматриваемом случае система черпает энергию от постороннего источника, то последний должен доставить системе количество энергии dA', равное двойной величине произведенной в системе работы или удвоенному приращению электрокинетической энергии системы:

dA'=dA+dgTe=2dA=2dgTe.

Отсюда, между прочим, следует, что всякий электромагнитный механизм, питаемый постоянным током, без особых дополнительных приспособлений (напр., коммутаторов) может превратить в механическую работу не более половины получаемой им от внешнего источника электрической энергии, т. е не может иметь коэффициента полезного действия выше 50%. С рассматриваемой точки зрения необходимо признать, что коммутатор двигателя постоянного тока, сверх обычно учитываемых его функций, играет еще особо важную роль в энергетическом отношении. Именно, в процессе коммутации в течение того промежутка времени, когда некоторая секция коротко замкнута через щетку, за счет запаса электрокинетической энергии, соответствующей этой секции, совершается некоторая механическая работа до тех пор, пока сила тока в короткозамкнутой секции не сделается равной нулю. Эта механическая работа присоединяется к той работе, которая совершается за счет энергии постоянного тока, возбуждаемого в цепи двигателя непосредственно от генератора. Благодаря такому полезному превращению энергии, непрерывно накопляемой в отдельных секциях обмотки якоря, когда они находятся вне зоны коммутации, результирующий коэффициент полезного действия электродвигателя постоянного тока может возрастать и практически возрастает значительно выше 50%.

374

Сформулированный выше общий закон движений во всякой электродинамической системе, в которой сохраняются неизменными силы токов, а именно, положение о стремлении системы к увеличению ее электрокинетической энергии, в этом случае можно выразить еще иначе. Для этого обратимся к электрокинетической энергии в общем случае:

или, так как lk ik=Ф'k есть поток самоиндукции k-ого контура,

а поток взаимной индукции между контурами k и u, то можем написать:

Отсюда видно, что если силы токов в составляющих систему контурах поддерживаются постоянными при помощи внешних источников энергии, то приращение электрокинетической энергии может выразиться только суммой членов вида:

1/2idФs и idФm,

где Фs есть некоторый поток самоиндукции, а Фm — поток взаимной индукции. На основании соотношения (120) ясно, что этою же суммой выразится, вообще говоря, и работа каждой из электромагнитных сил, действующих в системе. При этом члены вида:

1/2idФs

обусловливаются изменениями коэффициентов самоиндукции и, соответственно, потоков самоиндукции, а члены вида:

idФm

обусловливаются изменениями коэффициентов взаимной индукции и, соответственно, потоков взаимной индукции, т. е. так называемых внешних потоков, сцепляющихся с каждым данным контуром.

Отсюда следует, что работа электромагнитной силы положительна, когда положительно приращение потока, что дает для закона движений в электродинамической системе такую формулировку: в электродинамической системе стремятся возникнуть такие движения, в результате которых поток, связанный с каждым из составляющих систему контуров, мог бы получить положительное приращение в случае постоянства всех токов.

В случае жестких, неизменяемых контуров, т. е. когда все коэффициенты самоиндукции сохраняют свое значение, каждая из электромагнитных сил fe, действующих в системе, может совершить работу dA только в связи с изменениями потоков взаимной индук-

375

ции Фm (внешних потоков) и потому имеет место следующее соотношение:

dA=fedg=idФm, (121)

справедливое в отношении каждого отдельного контура.

Отсюда вытекает простой способ для определения величины электромагнитной силы, действующей на тот или иной неизменяемый контур. Действительно, из соотношения (121) следует:

т. е. электромагнитная сила численно равна произведению силы тока в неизменяемом контуре на приращение сцепляющегося с ним внешнего магнитного потока, соответствующее приращению геометрической координаты на единицу, при условии, что ток поддерживается постоянным.

Если, следовательно, в данной системе некоторый постоянный ток протекает по неизменяемому (L=const) контуру, сцепляющемуся с внешним потоком, то этот контур стремится двигаться таким образом, чтобы охватить наибольший внешний поток.

Если этот внешний поток обусловливается током в определенном втором контуре, причем токи в рассматриваемых двух контурах одинаково направлены, то стремление к увеличению охватываемого внешнего потока выражается в стремлении к увеличению коэффициента взаимной индукции M.

Единичный контур, по которому течет постоянный ток и который находится в собственном магнитном поле, стремится увеличить потек самоиндукции, что ведет к увеличению коэффициента самоиндукции L. Но этот коэффициент является, как нам уже известно, функцией геометрических координат, т. е. размеров и конфигурации контура. В случае контура, кривизна которого во всех его частях одного знака, увеличение L сопровождается увеличением площади контура. Поэтому в этом частном случае можно говорить, что контур под действием электромагнитной силы стремится увеличить охватываемую им площадь. Подробнее об этом будем говорить ниже.

Уже из всего вышесказанного следует, что приведенные формулировки закона, которому подчиняется движение во всякой электродинамической системе, не независимы одна от другой, а являются различными выражениями некоторого основного, единого в своей сущности, физического свойства магнитного поля. Чтобы выяснить

376

эту основу возникающих в электродинамической системе сил и движений, уяснить взаимную связь приведенных выше формулировок и точнее установить, в каких случаях и как каждая из этих формулировок применима, обратимся к более детальному рассмотрению вопроса о физической природе электромагнитной силы с точки зрения фарадеевских представлений, касающихся магнитного поля, а также с точки зрения энергетических соотношений в системе.

studfiles.net

Электромагнитные силы, создаваемые магнитным полем

Количество просмотров публикации Электромагнитные силы, создаваемые магнитным полем - 317

Проводник с током в магнитном поле. Энергия, заключенная в магнитном поле, может проявлять себя в виде электромагнитных сил, которые возникают при взаимодействии магнитного поля с движущимися электрическими зарядами. Электромагнитная сила, возникающая при движении электрического заряда в магнитном поле, действует на него в направлении, перпендикулярном движению и направлению силовых линий, и стремится вытолкнуть заряд за пределы поля (см. рис. 34).

В случае если поместить в магнитное поле проводник с током I, то между электронами, проходящими по проводнику, и магнитным полем возникнут электромагнитные силы, которые, складываясь, образуют результирующую силу F, стремящуюся вытолкнуть проводник из магнитного поля (рис. 48). Электромагнитная сила определяется законом Ампера. Он формулируется следующим образом. Электромагнитная сила, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поля В и длины проводника l:

F = IBl (48)

В случае если проводник расположен под углом ? к силовым магнитным

F = BIlsin? (48′)

Чтобы получить F в ньютонах, нужно В брать в теслах, I — в амперax и l — в метрах.

Направление действия силы F обычно определяют по правилу левой руки: ладонь левой руки нужно расположить так, чтобы магнитные линии входили в нее и четыре вытянутых пальца совместить с направлением тока, тогда расположенный под прямым углом большой палец укажет направление действия электромагнитной силы. Сила F возникает только в том случае, в случае если проводник расположен перпендикулярно или под некоторым углом к магнитным силовым линиям поля. В случае если же проводник расположен вдоль силовых линий поля, то электромагнитная сила будет равна нулю.

Для того чтобы изменить направление электромагнитной силы, как следует из правила левой руки, крайне важно изменить направление тока в проводнике или же направление магнитного поля.

Возникновение электромагнитной силы F при взаимодействии проводника с током и магнитного поля можно наглядно представить как результат взаимодействия двух магнитных полей. Как известно, вокруг проводника с током возникает свое собственное круговое магнитное поле (рис. 49), ĸᴏᴛᴏᴩᴏᴇ будет складываться с внешним магнитным полем (к примеру, постоянного магнита), в ĸᴏᴛᴏᴩᴏᴇ помещен проводник с током. При этом справа от проводника, где силовые линии поля проводника совпадают с линиями внешнего поля, происходит сгущение силовых линий; слева от проводника, где силовые линии поля проводника направлены навстречу линиям внешнего поля, происходит разрежение силовых линий. Магнитные силовые линии обладают свойством упругости, напоминающим свойство резиновых нитей. Стремясь сократиться по длине, они будут выталкивать проводник из области сгущения силовых линий в сторону их разрежения, т. е. справа налево. В результате возникает электромагнитная сила F.

Рис. 48. Электромагнитная сила, действующая в магнитном поле на проводник с током

Рис. 49. Сгущение и разрежение магнитных силовых линий при наличии в магнитном поле проводника с током.

Рис. 50.Электромагнитные силы,действующие в магнитном поле на виток или катушку с током.

Виток с током в магнитном поле. В случае если поместить в магнитное поле не проводник, а виток (или катушку) с током и расположить его вертикально (рис. 50, а), то, применяя правило левой руки к верхней и нижней сторонам витка, получим, что электромагнитные силы F, действующие на них, будут направлены в разные стороны. В результате действия этих двух сил возникает электромагнитный вращающий момент М, который вызовет поворот витка, в данном случае по часовой стрелке. Этот момент

M = FD (49)

где D — расстояние между сторонами витка. Виток будет поворачиваться в магнитном поле до тех пор, пока он не займет положение, перпендикулярное магнитным силовым линиям поля (рис. 50, б). При таком положении через виток будет проходить наибольший магнитный поток. Следовательно, виток или катушка с током, внесенные во внешнее магнитное поле, всегда стремятся занять такое положение, чтобы через виток проходил возможно больший магнитный поток. Свойство витка и катушки с током поворачиваться в магнитном поле широко используется в электротехнике; электрические двигатели и ряд электроизмерительных приборов работают по этому принципу.

Для увеличения вращающего момента в электрических двигателях применяют не один виток, а несколько. Эти витки, соединенные соответствующим образом, образуют обмотку якоря электродвигателя.

referatwork.ru

Электромагнитные силы, создаваемые магнитным полем — Мегаобучалка

F = IBl.

M = FD,

где: D — расстояние между сторонами витка.

megaobuchalka.ru

Силы электромагнитного взаимодействия

УДК 537.63: 537.8 СИЛЫ ЭЛЕКТРОМАГНИТНОГО ВЗАИМОДЕЙСТВИЯ

О.Л. Сокол-Кутыловский На основе законов и представлений классической физики получены все фундаментальные силы электромагнитного взаимодействия. Показано, что из четырех видов электромагнитных сил три связаны с магнитным полем. При этом два вида магнитных сил, - сила электромагнитной инерции и силы, возникающие при повороте вращающихся зараженных частиц, в современной электродинамике до сих пор не известны. PACS 41.20-q

Ключевые слова: электромагнитное взаимодействие, электромагнитные силы, магнитные силы, электромагнетизм

Введение

В классической электродинамике считается, что электромагнитное воздействие на заряженные частицы осуществляется посредством электрического и магнитного полей, причем все фундаментальные силы электромагнитного взаимодействия представлены в уравнении Лоренца [1-3]

(1)

где q – электрический заряд частицы, E – напряженность электрического поля, v – скорость частицы и B – магнитная индукция.

Первая (электрическая) часть уравнения (1) – это запись закона Кулона для силы взаимодействия электрических зарядов, выраженная через напряженность электрического поля. Сила Кулона действует между любыми электрически зараженными частицами, которые покоятся или находятся в состоянии движения.

Вторая (магнитная) часть уравнения (1) представляет собственно силу Лоренца. Она применима только к электрически заряженным частицам, движущимся в магнитное поле, которое считается постоянным (Рис. 1).

Рис. 1. Направление силы Лоренца, действующей на электрон в проводнике с электрическим током; FL – сила Лоренца, В – магнитная индукция, v – скорость электрона.

Магнитная часть силы Лоренца в проводнике, по которому течет электрический ток, всегда направлена к ближайшей точке поверхности этого проводника.

Если электрически заряженная частица не движется, то согласно уравнению (1) силового воздействия на нее со стороны магнитного поля как бы нет. Однако, из опыта известно, что любое изменение магнитного поля:

движение источника магнитного поля по отношению к покоящейся заряженной частице;
поворот источника магнитного поля в пространстве;
изменение интенсивности магнитного поля при неподвижном его источнике;

- все эти изменения магнитного поля, взятые вместе или в отдельности, приводят к силовому воздействию как на движущуюся, так и на неподвижную электрически заряженную частицу, находящуюся в области изменения магнитного поля.

Классическая электродинамика в ее нынешнем виде полностью игнорирует инерцию свободных электрически заряженных частиц и инерцию электронов в металлическом проводнике. Инерция электронов не учитывается материальными уравнениями электродинамики, а сила инерции электронов, ее электромагнитный эквивалент, не входит в уравнение для электромагнитных сил. Поэтому сила (1) не может являться полной электромагнитной силой, действующей на заряженные частицы вещества. Как следует из [4], попытка выразить силу инерции электрона в электромагнитном виде предпринималась первооткрывателем электрона, Дж. Дж. Томсоном, однако, эта «сила самоиндукции»

где U – электрическая энергия электрона в состоянии покоя, c – скорость распространения света в вакууме и w – ускорение электрона, являлась смесью электрических и механических величин, не отражала реальные свойства электромагнитной инерции и не была введена ни в уравнение (1), ни в другие уравнения электродинамики. Аналогичные попытки предпринимал Г.А. Лоренц в своей «Теории электронов» (пункт 28 в работе [3]), в которой пытался обосновать существование целых трех видов массы электрона: материальной массы m0 и двух различных «электромагнитных масс», m’ и m’’, которые к тому же зависят от направления движения электрона. Для малых скоростей (vc) обе «электромагнитные массы» электрона по Лоренцу имеют одинаковое значение:

где re – радиус электрона.

Наделение массы свойствами пространственной анизотропии входит в противоречие с ее физическим смыслом. Такая виртуальная масса не объясняет инерционные свойства электронов и не была введена в основные уравнения классической электродинамики. 1. Электромагнитные силы, действующие на точечный электрический заряд

1.1. Воздействие электрического поля на электрический заряд хорошо известно и определяется законом Кулона, входящим в качестве первого слагаемого в формулу (1). При этом напряженность электрического поля является полноценным вектором в трехмерном пространстве. В отличие от вектора напряженности электрического поля вектор магнитной индукции является аксиальным вектором. Аксиальный вектор магнитной индукции недостаточен для определения всех возможных воздействий магнитного поля на электрически заряженную частицу, движущуюся в трехмерном пространстве. Физическая величина, в виде векторного произведения радиус-вектора, соединяющего ось симметрии источника магнитного поля с данной точкой пространства, на магнитную индукцию в этой же точке пространства, то есть «момент» магнитной индукции (rB), может характеризовать все возможные изменения магнитной индукции по величине и по направлению. Фактически, произведение электрического заряда на «момент» магнитной индукции, q·(rB), выполняет в электродинамике ту же функцию, что и импульс в механике вращательного движения, то есть является интегралом движения.

Электрическую часть электромагнитных сил оставим без изменений, а уравнение для магнитной части электромагнитной силы, действующей на заряженную частицу, должно быть распространено на все случаи изменения магнитного поля, как по величине, так и по направлению. Поэтому магнитную часть сил определим следующим образом. Так как сила со стороны магнитного поля возникает при любых изменениях магнитной индукции, то полная «магнитная» часть силы должна быть пропорциональна электрическому заряду электрона, e, умноженному на производную по времени от векторного произведения (rB), где r – радиальный вектор:

(2) 1.2. Из формулы (2) найдем все электромагнитные силы, действующие на точечный электрический заряд.

. (3)

Второе слагаемое в формуле (3) – это известная сила Лоренца, а третье слагаемое в современной электродинамике не применяется.

1.3. Третье слагаемое в формуле (3) представляет собой силу, ответственную как за инерцию отдельной электрически заряженной частицы, так и за явление самоиндукции в металлическом проводнике, вызванное инерцией электронов.

Сила электромагнитной инерции может быть представлена следующим образом [5, 6]:

, (4)

где q – электрический заряд, r – радиальный вектор, соединяющий ось симметрии источника магнитного поля B с электрически заряженной частицей и лежащий в плоскости, ортогональной оси симметрии (Рис. 2). Знак силы (4) определяется в соответствии с правилом Ленца: «минус», если dB/dt>0, и «плюс», если dB/dt

Рис. 2. Направление электромагнитной силы Fie, ответственной за самоиндукцию в проводнике с изменяющимся электрическим током при ∂B/∂t>0; r – радиальный вектор, соединяющий ось симметрии источника магнитного поля с электроном, движущимся со скоростью v. Сила электромагнитной инерции (4) может быть получена из уравнения (2) при его дифференцировании по времени, введена формально при интегрировании силы Лоренца и последующего нахождения полного дифференциала первообразной функции по времени, а также может быть получена из рассмотрения явления самоиндукции в прямолинейном металлическом проводнике [6].

1.4. Применительно к основной частице электродинамики – электрону полная электромагнитная сила, включающая силу электромагнитной инерции, но не учитывающая его внутреннего движения (собственные магнитный и механический моменты), может быть представлена в виде:

(5)

Электрический ток самоиндукции направлен в сторону первичного электрического тока или против него, поэтому направление электромагнитной силы инерции в прямолинейном проводнике или совпадает с направлением силы Кулона, или противоположно ей.

Из уравнения (3) и (5) видно, что сила Лоренца является лишь частным случаем полной электромагнитной силы, когда магнитное поле, характеризуемое аксиальным вектором магнитной индукции, не изменяется ни по величине, ни по направлению. 2. Электромагнитные силы, возникающие при повороте источника магнитного поля или при повороте вращающейся электрически заряженной частицы

Рассмотренная выше сумма электромагнитных сил (3) или (5) действует на электрически заряженную частицу, как целое, то есть на точечный электрон. Но электромагнитное поле может влиять и на внутреннее состояние электрона, в частности, на его магнитный и механический моменты. И наоборот, так как магнитный и механический моменты электрона связаны между собой, то изменение механического момента, возникающее при криволинейном движении электрона, может изменить магнитное поле вблизи него.

2.1. Ранее были рассмотрены все электромагнитные силы, действующие на движущиеся электрически заряженные частицы и приложенные к их центру масс. То есть частица рассматривалась, как точечный заряд, расположенный в центре масс. Возможный поворот вращающейся заряженной частицы вокруг ее собственной оси при этом во внимание не принимался. Поворот источника магнитного поля в пространстве и действие его на электрически заряженные частицы также не рассматривалось. Но в формуле для электромагнитных сил (2), действующих на электрически заряженную частицу со стороны магнитного поля, в принципе, заложены все возможные электромагнитные силы, в том числе и силы, возникающие при повороте источника магнитного поля. Чтобы увидеть это, распространим уравнение для электромагнитных сил (2) на движение, например, электрона по произвольной траектории, которая складывается из прямолинейного движения, вращательного движения и пространственного поворота оси вращения. При изменении вращательного движения относительно любой оси, проходящей через центр масс электрона, возникает изменение момента импульса, и, следовательно, появляется момент сил. При полном описании криволинейного движения электрона необходимо рассматривать и учитывать эти силы, возникающие при повороте оси вращения электрона. Ранее формула (2) была применена только к движению точечного электрона и, соответственно, в ней были использованы только те производные переменных величин, которые изменяются при движении точечной заряженной частицы. При повороте оси вращения электрона для получения действующих на него сил необходимо дифференцировать по времени переменные, зависящие от параметров вращательного движения электрона вокруг его собственной оси, которые, в свою очередь, зависят от времени. Такими параметрами могут быть угол поворота и угловая скорость.

Как следует из опыта, сила, действующая на прямолинейно движущийся электрон со стороны магнитного поля, возникает как при неизменном магнитном поле (сила Лоренца), так и при изменении величины магнитной индукции (сила электромагнитной инерции). Причем при изменении вектора магнитной индукции, как по величине, так и по направлению, на электрон со стороны магнитного поля действует сила, вне зависимости от того, движется этот электрон или покоится. Изменение вектора магнитной индукции по направлению аналогично повороту оси вращения заряженной вращающейся частицы, ранее не рассматривалось. Момент силы, получающийся при изменении вектора магнитной индукции по направлению, будет в обязательном порядке содержать угловую скорость вращения или угловую скорость поворота, из чего следует, что поворот или вращение источника магнитного поля в электродинамике осуществляется через вектор угловой скорости, который является одним из основных векторов механики вращательного движения.

Рассмотрим поворот вектора rB, как поворот единого вектора. Представим магнитную часть уравнения (2) в следующем виде:

, (6)

где rB– модуль вектора rB, а (rB)1 – единичный вектор, направленный по вектору rB. Производная величины вектора rB была рассмотрена ранее. При умножении ее на электрический заряд получаются сила Лоренца и сила электромагнитной инерции, а произведение модуля вектора rB на производную единичного вектора (rB)1 не рассматривалось. Так как векторы r и B всегда взаимно ортогональны, модуль вектора rB равен произведению модулей составляющих его векторов:

Производная по времени от единичного вектора (rB)1 при изменении его по направлению на угол  дает другой единичный вектор, h2, расположенный параллельно плоскости поворота (x, z) и ортогональный вектору rB (Рис. 3). В качестве сомножителя у него появляется коэффициент, численно равный производной по времени от угла поворота, =/t:

. (7)

Так как движение точек электрона является трехмерным, а поворот оси происходит только в плоскости (x, z), то модуль единичного вектора относительно плоскости поворота не постоянен, а изменяется при вращении в пределах от нуля до единицы. Поэтому при дифференцировании такого единичного вектора должна учитываться его величина относительно плоскости, в которой происходит поворот этого единичного вектора.

Длиной единичного вектора (rB)1 относительно плоскости поворота (x, z) является проекция этого единичного вектора на плоскость поворота.

Производная единичного вектора (rB)1 в плоскости поворота (x, z) может быть представлена в виде:

где  – угол между вектором rB и плоскостью поворота (x, z).

Таким образом, сила, действующая на любую i-тую точку поверхности электрически заряженного вращающегося тела, при повороте его оси вращения, приобретает следующий вид:

, (8)

где qi – дробная часть электрического заряда, приходящегося на область выбранной точки приложения силы, r – кратчайшее расстояние от данной точки поверхности, в которой определяется сила, до оси вращения, B – магнитная индукция,  – угловая скорость поворота оси вращения,  – угол между вектором rB и плоскостью поворота  (x, z), h2 – единичный вектор, направленный параллельно плоскости поворота и ортогональный вектору rB.

Если полагать, что весь заряд q сосредоточен на поверхности частицы, а  – поверхностная плотность заряда, и Si – площадка в окрестности каждой из n точек, на которые разбита поверхность заряженной частицы, малая по сравнению со всей площадью поверхности этой частицы, то: .

Рис. 3. Направление электромагнитной силы FB, возникающей при повороте оси вращения электрона в плоскости (x, z) при его вращении с угловой скоростью . Во всех точках, лежащих в плоскости (x, z), сила FB=0.

Сумма всех сил (8), действующих на электрически заряженную частицу при повороте ее оси вращения, имеет вид:

. (9)

2.2. Вследствие круговой симметрии относительно оси вращения в каждой точке, не находящейся на оси симметрии, действует сила (8), а в симметричной ей относительно оси вращения точке действует точно такая же, но противоположно направленная сила. Совместное действие симметричных пар сил (8) при повороте оси вращения электрически заряженной частицы создает момент сил, поворачивающий частицу в третьей плоскости (y, z) (Рис. 3), которая ортогональна плоскости поворота  (x, z) и всем параллельным плоскостям (x, y), в которых происходит вращение точек электрически заряженной частицы:

При этом в любой из точек тела, не совпадающей с центром симметрии (центром масс) выполняется следующее условие ортогональности:

где  – аксиальный вектор угловой скорости, возникающей в момент действия сил (9), B – аксиальный вектор магнитной индукции и  – аксиальный вектор угловой скорости поворота оси вращения электрически заряженной частицы.

3. Сумма всех электромагнитных сил, действующих на движущуюся и вращающуюся электрически заряженную частицу

3.1. Сумма всех электромагнитных сил, действующих на движущуюся и вращающуюся электрически заряженную частицу, ось вращения которой поворачивается в пространстве, имеет вид [6]:

(10)

где q – электрический заряд, E – вектор напряженности электрического поля, r – радиальный вектор, соединяющий ось источника магнитного поля (центр заряженной вращающейся частицы) с данной точкой, в которой определяется сила, B – вектор магнитной индукции,  – угловая скорость поворота оси вектора магнитной индукции (оси вращения электрически заряженной частицы), h2 – единичный вектор, лежащий в плоскости, параллельной плоскости поворота, и ортогональный вектору rB,  – угол между вектором rB и плоскостью поворота, qi – дробный электрический заряд, приходящийся на площадку в области приложения силы, n – количество элементарных площадок, на которые равномерно разбита поверхность электрически заряженной частицы и rq – радиус электрически заряженной частицы.

3.2. Применительно к электрону формула (10) приобретает вид:

(11)

где е – электрический заряд электрона, еi=e/n– электрический заряд каждой из nэлементарных площадок, на которые равномерно разбита поверхность электрона, и re – радиус электрона.

Заключение

Таким образом, в электромагнитном силовом взаимодействии имеются четыре вида первичных физических сил. Три из них действуют на точечную электрически заряженную частицу, а четвертый тип сил возникает при повороте оси вращения электрически заряженной частицы.

Формулы (10) и (11), включающие в себя все электромагнитные силы, содержат в себе систему основных уравнений микроскопической электродинамики.

Действие электромагнитных сил на электрический заряд лежит в основе теории излучения электромагнитных волн [6, 7].

Литература 1. Зисман Г.А., Тодес О.М. Курс общей физики., Т.2, М., «Наука», 1969.

2. Тамм И.Е. Основы теории электричества. М., «Наука», 1966.

3. Лорентц Г.А. Теория электронов и ее применение к явлениям света и теплового излучения. Государственное издательство технико-теоретической литературы. М., 1956.

4. Френкель Я.И. Собрание избранных трудов. Т.1., Электродинамика. М.-Л., 1956, С. 193.

5. Сокол-Кутыловский О.Л. Об электродинамике проводящих сред. // Практика приборостроения № 2, 2003, С. 85 – 90.

6. Сокол-Кутыловский О.Л. Русская физика, б/и, Екатеринбург, 2006, 174 с.

7. Сокол-Кутыловский О.Л. Об излучении радиоволн электрической антенной // Межвуз. науч. сб. «Элементы и устройства систем низких и сверхвысоких частот».- Саратов: Изд-во СГТУ, 2004, 58-66.

flatik.ru

Электромагнитные силы, создаваемые магнитным полем. Электромагнитная сила

§ 25. Природа электромагнитной силы.

Электромагнитные силы, создаваемые магнитным полем. — КиберПедия

Электромагнитные силы - Большая Энциклопедия Нефти и Газа, статья, страница 1

Электромагнитные силы

§ 107. Электромагнитная сила. Общие соображения.

Электромагнитные силы, создаваемые магнитным полем

Электромагнитные силы, создаваемые магнитным полем — Мегаобучалка

Силы электромагнитного взаимодействия

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30